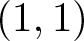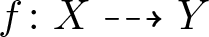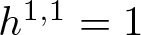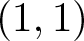1. Introduction
Let X be a compact complex manifold with a fixed positive Hermitian form ω. Let α be a closed ![]() $(1,1)$-form. We use
$(1,1)$-form. We use ![]() $[\alpha]$ to represent its class in the Bott–Chern
$[\alpha]$ to represent its class in the Bott–Chern  $H^{1,1}_{BC}(X)$. Recall the following positivity notions (independent of the choice of ω).
$H^{1,1}_{BC}(X)$. Recall the following positivity notions (independent of the choice of ω).
•
 $[\alpha]$ is Kähler if it contains a Kähler form, i.e., if there is a smooth function φ such that
$[\alpha]$ is Kähler if it contains a Kähler form, i.e., if there is a smooth function φ such that  $\alpha+\sqrt{-1}\partial \overline{\partial}\varphi \geq \epsilon \omega$ on X for some ϵ > 0.
$\alpha+\sqrt{-1}\partial \overline{\partial}\varphi \geq \epsilon \omega$ on X for some ϵ > 0.•
 $[\alpha]$ is nef if, for every ϵ > 0, there is a smooth function φϵ such that
$[\alpha]$ is nef if, for every ϵ > 0, there is a smooth function φϵ such that  $\alpha+\sqrt{-1}\partial \overline{\partial}\varphi_{\epsilon} \geq -\epsilon\omega$ on X.
$\alpha+\sqrt{-1}\partial \overline{\partial}\varphi_{\epsilon} \geq -\epsilon\omega$ on X.•
 $[\alpha]$ is big if it contains a Kähler current, i.e., if there exists a quasi-plurisubharmonic function (quasi-psh)
$[\alpha]$ is big if it contains a Kähler current, i.e., if there exists a quasi-plurisubharmonic function (quasi-psh)  $\varphi\colon X\longrightarrow \mathbb{R} \cup \{-\infty\}$ such that
$\varphi\colon X\longrightarrow \mathbb{R} \cup \{-\infty\}$ such that  $\alpha+\sqrt{-1}\partial \overline{\partial}\varphi \geq \epsilon\omega$ holds weakly as currents on X for some ϵ > 0.
$\alpha+\sqrt{-1}\partial \overline{\partial}\varphi \geq \epsilon\omega$ holds weakly as currents on X for some ϵ > 0.
We say X is in Fujiki’s class ![]() $\mathcal{C}$ (respectively Moishezon) if it is the meromorphic image of a compact Kähler manifold (respectively projective variety), or equivalently it is bimeromorphic to a compact Kähler manifold (respectively projective variety). It is also equivalent to X admitting a big
$\mathcal{C}$ (respectively Moishezon) if it is the meromorphic image of a compact Kähler manifold (respectively projective variety), or equivalently it is bimeromorphic to a compact Kähler manifold (respectively projective variety). It is also equivalent to X admitting a big ![]() $(1,1)$-class (respectively big Cartier divisor). We refer to [Reference Fujiki3, Definition 1.1 and Lemma 1.1], [Reference Varouchas22, Chapter IV, Theorem 5] and [Reference Demailly and Păun2, Theorem 0.7] for equivalent definitions and some properties of Fujiki’s class
$(1,1)$-class (respectively big Cartier divisor). We refer to [Reference Fujiki3, Definition 1.1 and Lemma 1.1], [Reference Varouchas22, Chapter IV, Theorem 5] and [Reference Demailly and Păun2, Theorem 0.7] for equivalent definitions and some properties of Fujiki’s class ![]() $\mathcal{C}$.
$\mathcal{C}$.
Throughout this article, we work in Fujiki’s class ![]() $\mathcal{C}$ where
$\mathcal{C}$ where ![]() $\partial \overline{\partial}$-lemma holds. So we are free to use the equivalent Bott–Chern and de Rham cohomologies.
$\partial \overline{\partial}$-lemma holds. So we are free to use the equivalent Bott–Chern and de Rham cohomologies.
We start with the following main theorem.
Theorem 1.1 Let ![]() $f\colon X\dashrightarrow Y$ be a bimeromorphic map of compact complex manifolds, which is isomorphic in codimension 1. Suppose X is Kähler with
$f\colon X\dashrightarrow Y$ be a bimeromorphic map of compact complex manifolds, which is isomorphic in codimension 1. Suppose X is Kähler with ![]() $h^{1,1}(X,\mathbb{R})=1$ and f is not biholomorphic. Then any nef
$h^{1,1}(X,\mathbb{R})=1$ and f is not biholomorphic. Then any nef ![]() $(1,1)$-class on Y is trivial. In particular, Y is a non-Kähler manifold in Fujiki’s class
$(1,1)$-class on Y is trivial. In particular, Y is a non-Kähler manifold in Fujiki’s class ![]() $\mathcal{C}$ with no nef and big
$\mathcal{C}$ with no nef and big ![]() $(1,1)$-classes.
$(1,1)$-classes.
One way to construct ![]() $f\colon X\dashrightarrow Y$ in Theorem 1.1 is by considering an elementary transformation or a (non-projective) flop.
$f\colon X\dashrightarrow Y$ in Theorem 1.1 is by considering an elementary transformation or a (non-projective) flop.
Example 1.2. Let ![]() $X\subset \mathbb{P}^4$ be a generic smooth quintic threefold. By a classical result of Clemens and Katz (cf. [Reference Clemens1, Reference Katz14]), X contains a smooth rational curve Cd of degree d with normal bundle
$X\subset \mathbb{P}^4$ be a generic smooth quintic threefold. By a classical result of Clemens and Katz (cf. [Reference Clemens1, Reference Katz14]), X contains a smooth rational curve Cd of degree d with normal bundle  $\mathcal{N}_{C_d/X}\cong \mathcal{O}_{C_d}(-1)^{\oplus 2}$. This result was later generalised to a complete intersection of degree
$\mathcal{N}_{C_d/X}\cong \mathcal{O}_{C_d}(-1)^{\oplus 2}$. This result was later generalised to a complete intersection of degree ![]() $(2,4)$ in
$(2,4)$ in ![]() $\mathbb{P}^5$ by Oguiso (cf. [Reference Oguiso19, Theorem 2]). Let
$\mathbb{P}^5$ by Oguiso (cf. [Reference Oguiso19, Theorem 2]). Let ![]() $p\colon Z_d\to X$ be the blow-up along Cd. Then the exceptional divisor
$p\colon Z_d\to X$ be the blow-up along Cd. Then the exceptional divisor ![]() $E\cong C_d\times C_d^\prime\cong \mathbb{P}^1\times \mathbb{P}^1$. By the contraction theorem of Nakano–Fujiki (cf. [Reference Fujiki and Nakano5]), there is a bimeromorphic morphism
$E\cong C_d\times C_d^\prime\cong \mathbb{P}^1\times \mathbb{P}^1$. By the contraction theorem of Nakano–Fujiki (cf. [Reference Fujiki and Nakano5]), there is a bimeromorphic morphism ![]() $q\colon Z_d\to Y_d$ to a smooth compact complex manifold Yd, which contracts E to
$q\colon Z_d\to Y_d$ to a smooth compact complex manifold Yd, which contracts E to ![]() $C_d^\prime$ along Cd. Then we can construct
$C_d^\prime$ along Cd. Then we can construct ![]() $f: = q\circ p^{-1}\colon X\dashrightarrow Y_d$, which is an isomorphism in codimension 1. By the Lefschetz hyperplane theorem, we see that
$f: = q\circ p^{-1}\colon X\dashrightarrow Y_d$, which is an isomorphism in codimension 1. By the Lefschetz hyperplane theorem, we see that ![]() $h^{2}(X,\mathbb{R})=1$ and hence
$h^{2}(X,\mathbb{R})=1$ and hence ![]() $h^{1,1}(X,\mathbb{R})=1$. Applying Theorem 1.1, we obtain infinitely many isomorphic classes of smooth Calabi–Yau Moishezon threefolds
$h^{1,1}(X,\mathbb{R})=1$. Applying Theorem 1.1, we obtain infinitely many isomorphic classes of smooth Calabi–Yau Moishezon threefolds ![]() $\{Y_d\}_{d \gt 0}$ satisfying the following theorem:
$\{Y_d\}_{d \gt 0}$ satisfying the following theorem:
Theorem 1.3 There exist infinitely many isomorphic classes of smooth compact Moishezon threefolds with no nef and big ![]() $(1,1)$-classes.
$(1,1)$-classes.
Nakamura (cf. [Reference Nakamura17, (3.3) Remark]) provides another example for the above theorem.
Example 1.4. There is a bimeromorphic map ![]() $f\colon \mathbb{P}^3\dashrightarrow X$ to a smooth Moishezon threefold X of
$f\colon \mathbb{P}^3\dashrightarrow X$ to a smooth Moishezon threefold X of ![]() $h^{1,1}(X,\mathbb{R})=1$ with no nef and big
$h^{1,1}(X,\mathbb{R})=1$ with no nef and big ![]() $(1,1)$-class. The map f is constructed by first blowing up a non-singular curve of bidegree
$(1,1)$-class. The map f is constructed by first blowing up a non-singular curve of bidegree ![]() $(3,k)$ with
$(3,k)$ with ![]() $k\geq 7$ in a smooth quadric surface
$k\geq 7$ in a smooth quadric surface ![]() $S\cong \mathbb{P}^1\times \mathbb{P}^1$ and then contracting the proper transform of S. Then
$S\cong \mathbb{P}^1\times \mathbb{P}^1$ and then contracting the proper transform of S. Then ![]() $H^{1,1}(X,\mathbb{R})$ is generated by a big divisor L with
$H^{1,1}(X,\mathbb{R})$ is generated by a big divisor L with ![]() $L^3 \lt 0$. So X admits no nef and big class. Note that, in this case, f is not isomorphic in codimension 1.
$L^3 \lt 0$. So X admits no nef and big class. Note that, in this case, f is not isomorphic in codimension 1.
The aim of the present note is to show a peculiarity of compact complex manifolds in Fujiki’s class ![]() $\mathcal{C}$, which also confutes a key theorem in the recent paper [Reference Kim15] as explained in the following remark:
$\mathcal{C}$, which also confutes a key theorem in the recent paper [Reference Kim15] as explained in the following remark:
Remark 1.5. In [Reference Kim15, Theorem 4.2(1)], the author asserts that a compact complex manifold X in Fujiki’s class ![]() $\mathcal{C}$ always admits a nef and big class. However, as we just discussed, Examples 1.2 and 1.4 or Theorem 1.3 confute this claim. Note that [Reference Kim15, Theorem 4.2(1)] plays a crucial role in the proof of [Reference Kim15, Corollary 4.3] that
$\mathcal{C}$ always admits a nef and big class. However, as we just discussed, Examples 1.2 and 1.4 or Theorem 1.3 confute this claim. Note that [Reference Kim15, Theorem 4.2(1)] plays a crucial role in the proof of [Reference Kim15, Corollary 4.3] that ![]() $\operatorname{Aut}_{\tau}(X)/\operatorname{Aut}_0(X)$ is finite where
$\operatorname{Aut}_{\tau}(X)/\operatorname{Aut}_0(X)$ is finite where ![]() $\operatorname{Aut}_{\tau}(X)$ is the group of automorphisms (pullback) acting trivially on
$\operatorname{Aut}_{\tau}(X)$ is the group of automorphisms (pullback) acting trivially on ![]() $H^2(X,\mathbb{R})$ and
$H^2(X,\mathbb{R})$ and ![]() $\operatorname{Aut}_0(X)$ is the neutral component. So the proof there does not work. Nevertheless, the statement [Reference Kim15, Corollary 4.3] still holds and was previously proved by showing the existence of equivariant Kähler model; see [Reference Jia and Meng13, Theorem 1.1, Corollary 1.3].
$\operatorname{Aut}_0(X)$ is the neutral component. So the proof there does not work. Nevertheless, the statement [Reference Kim15, Corollary 4.3] still holds and was previously proved by showing the existence of equivariant Kähler model; see [Reference Jia and Meng13, Theorem 1.1, Corollary 1.3].
It is known that a smooth compact surface in Fujiki’s class ![]() $\mathcal{C}$ is Kähler, and hence, a smooth Moishezon surface is projective. So Theorem 1.3 is optimal in terms of minimal dimension, and it is easy to construct examples, like those in Theorem 1.3, of arbitrary higher dimensions by further taking the product with a smooth projective variety of suitable dimensions. In the singular surface case, we summarize several examples constructed by Schröer (cf. [Reference Schröer21]) and Mondal (cf. [Reference Mondal16]) in the following remark:
$\mathcal{C}$ is Kähler, and hence, a smooth Moishezon surface is projective. So Theorem 1.3 is optimal in terms of minimal dimension, and it is easy to construct examples, like those in Theorem 1.3, of arbitrary higher dimensions by further taking the product with a smooth projective variety of suitable dimensions. In the singular surface case, we summarize several examples constructed by Schröer (cf. [Reference Schröer21]) and Mondal (cf. [Reference Mondal16]) in the following remark:
Remark 1.6. The examples in [Reference Schröer21] are constructed in a similar way by different elementary transformations of ![]() $\mathbb{P}^1\times C$, where the genus
$\mathbb{P}^1\times C$, where the genus ![]() $g(C) \gt 0$. However, they behave quite differently on Cartier divisors. The example in [Reference Mondal16, § 2] is a supplement to (1) on the rational case. It seems that we do not know any rational example for point (3).
$g(C) \gt 0$. However, they behave quite differently on Cartier divisors. The example in [Reference Mondal16, § 2] is a supplement to (1) on the rational case. It seems that we do not know any rational example for point (3).
(1) (cf. [Reference Schröer21, § 3]) There is a non-projective normal compact Moishezon surface S such that the Picard number of S is 0. In particular, S admits no non-trivial nef Cartier divisor.
(2) (cf. [Reference Mondal16, § 2]) There is a non-projective normal compact Moishezon rational surface S such that the Picard number of S is 0. The surface is
 $Y_2^\prime$ in [Reference Mondal16, § 2]. We give some explanation on the Picard number. Note that the Weil-Picard number of S is 1 (cf. [Reference Nakayama18, Definition 2.7 and Lemma 2.10]). Since S is not projective (cf. [Reference Mondal16, Theorem 4.1 and Example 3.19]), the Picard number of S has to be 0 (cf. [Reference Nakayama18, Definition 2.11–Remark 2.13, Remark on the top of page 303]).
$Y_2^\prime$ in [Reference Mondal16, § 2]. We give some explanation on the Picard number. Note that the Weil-Picard number of S is 1 (cf. [Reference Nakayama18, Definition 2.7 and Lemma 2.10]). Since S is not projective (cf. [Reference Mondal16, Theorem 4.1 and Example 3.19]), the Picard number of S has to be 0 (cf. [Reference Nakayama18, Definition 2.11–Remark 2.13, Remark on the top of page 303]).(3) (cf. [Reference Schröer21, § 4]) There is a non-projective normal compact Moishezon surface Z, which allows a non-projective birational morphism Z → S to a projective surface S. In particular, Z admits a nef and big Cartier divisor, which is the pullback of an ample Cartier divisor on S.
2. Proof of Theorem 1.1
We first reprove [Reference Golota6, Theorem 4.5] by the following Proposition 2.1. The first version of this proposition was formulated in [Reference Fujiki4, Corollary 3.3] where Fujiki works in the smooth setting and ![]() $f_*[\alpha]$ is assumed to be semi-positive. Later, it was generalized by Huybrechts (cf. [Reference Huybrechts12, Proposition 2.1]) to the situation when canonical bundles KX and KY are nef and
$f_*[\alpha]$ is assumed to be semi-positive. Later, it was generalized by Huybrechts (cf. [Reference Huybrechts12, Proposition 2.1]) to the situation when canonical bundles KX and KY are nef and ![]() $[\alpha]$ and
$[\alpha]$ and ![]() $f_*[\alpha]$ are only assumed to have positive intersections with all rational curves.
$f_*[\alpha]$ are only assumed to have positive intersections with all rational curves.
When dealing with the singular setting in Proposition 2.1, we refer to [Reference Höring and Peternell9] for the basic definitions involved. For example, a Kähler form ω on a Kähler space X is a positive closed real ![]() $(1,1)$-form such that for every singular point
$(1,1)$-form such that for every singular point ![]() $x\in X_{\mathrm{Sing}}$, there exists an open neighbourhood
$x\in X_{\mathrm{Sing}}$, there exists an open neighbourhood ![]() $x\in U\subset X$ and a closed embedding
$x\in U\subset X$ and a closed embedding ![]() $i_U\colon U\hookrightarrow V$ into an open set
$i_U\colon U\hookrightarrow V$ into an open set ![]() $V\subset \mathbb{C}^N$, as well as a strictly plurisubharmonic
$V\subset \mathbb{C}^N$, as well as a strictly plurisubharmonic ![]() $C^{\infty}$-function
$C^{\infty}$-function ![]() $f\colon V\to \mathbb{C}$ with
$f\colon V\to \mathbb{C}$ with ![]() $\omega|_{U\cap X_{\mathrm{sm}}} = (dd^c f)|_{U \cap X_{\mathrm{sm}}}$, where
$\omega|_{U\cap X_{\mathrm{sm}}} = (dd^c f)|_{U \cap X_{\mathrm{sm}}}$, where ![]() $X_{\mathrm{sm}}$ is the smooth locus of X. Note that for a normal compact complex space X with rational singularities,
$X_{\mathrm{sm}}$ is the smooth locus of X. Note that for a normal compact complex space X with rational singularities, ![]() $H^{1,1}(X,\mathbb{R})$ embeds into
$H^{1,1}(X,\mathbb{R})$ embeds into ![]() $H^2(X,\mathbb{R})$ naturally, and the intersection product on
$H^2(X,\mathbb{R})$ naturally, and the intersection product on ![]() $H^{1,1}(X,\mathbb{R})$ can be defined via the cup-product for
$H^{1,1}(X,\mathbb{R})$ can be defined via the cup-product for ![]() $H^2(X,\mathbb{R})$ (cf. [Reference Höring and Peternell9, Remark 3.7]). Of course, for the purpose of this note, one can focus on the smooth setting for simplicity.
$H^2(X,\mathbb{R})$ (cf. [Reference Höring and Peternell9, Remark 3.7]). Of course, for the purpose of this note, one can focus on the smooth setting for simplicity.
Proposition 2.1. (cf. Theorem 4.5 in [Reference Golota6] and Remark 2.3)
Let ![]() $f\colon X\dashrightarrow Y$ be a bimeromorphic map of normal compact complex spaces with rational singularities. Suppose f does not contract divisors, and there exists a Kähler class
$f\colon X\dashrightarrow Y$ be a bimeromorphic map of normal compact complex spaces with rational singularities. Suppose f does not contract divisors, and there exists a Kähler class ![]() $[\alpha]\in H^{1,1}(X,\mathbb{R})$ such that
$[\alpha]\in H^{1,1}(X,\mathbb{R})$ such that ![]() $f_*[\alpha]$ is nef. Then f −1 is holomorphic.
$f_*[\alpha]$ is nef. Then f −1 is holomorphic.
Proof. Consider the log resolution of the indeterminacy of f:

where ![]() $p\colon Z\to X$ and
$p\colon Z\to X$ and ![]() $q\colon Z\to Y$ are the two projections. By Chow’s lemma (cf. [Reference Hironaka11, Corollary 2 and Definition 4.1]), we may assume p is a projective morphism obtained by a finite sequence of blow-ups along smooth centres:
$q\colon Z\to Y$ are the two projections. By Chow’s lemma (cf. [Reference Hironaka11, Corollary 2 and Definition 4.1]), we may assume p is a projective morphism obtained by a finite sequence of blow-ups along smooth centres: ![]() $p=\pi_n\circ\dots\circ\pi_1$. Note that by [Reference Varouchas22, 1.3.1], Z is a Kähler manifold. Denote by
$p=\pi_n\circ\dots\circ\pi_1$. Note that by [Reference Varouchas22, 1.3.1], Z is a Kähler manifold. Denote by ![]() $\bigcup_{i=1}^n E_i$ the full union of exceptional prime divisors of p, and Fi the exceptional prime divisor of πi. The divisor
$\bigcup_{i=1}^n E_i$ the full union of exceptional prime divisors of p, and Fi the exceptional prime divisor of πi. The divisor ![]() $-F_i$ is πi-ample (cf. [Reference Hartshorne10, II, Proposition 7.13]), and hence
$-F_i$ is πi-ample (cf. [Reference Hartshorne10, II, Proposition 7.13]), and hence ![]() $\pi_2^*(-F_1)+\epsilon_1 (-F_2)$ is p-ample for some
$\pi_2^*(-F_1)+\epsilon_1 (-F_2)$ is p-ample for some ![]() $\epsilon_1 \gt 0$ (cf. [Reference Hartshorne10, II. Proposition 7.10]). For the same reason, one can find
$\epsilon_1 \gt 0$ (cf. [Reference Hartshorne10, II. Proposition 7.10]). For the same reason, one can find
 \begin{align*}
E= \sum_{i=1}^n \delta_i E_i
\end{align*}
\begin{align*}
E= \sum_{i=1}^n \delta_i E_i
\end{align*} with suitable ![]() $\delta_1,\ldots,\delta_n \gt 0$ such that −E is p-ample (cf. [Reference Demailly and Păun2, Proof of Lemma 3.5]). Here, if n = 0, then p is an isomorphism and
$\delta_1,\ldots,\delta_n \gt 0$ such that −E is p-ample (cf. [Reference Demailly and Păun2, Proof of Lemma 3.5]). Here, if n = 0, then p is an isomorphism and ![]() $-E=0$ is automatically p-ample.
$-E=0$ is automatically p-ample.
Note that ![]() $p^*[\alpha]$, being the pullback of a Kähler class, is represented by a smooth semi-positive form and q-exceptional divisors are also p-exceptional divisors since f does not contract divisors by the assumption. Applying [Reference Golota6, Lemma 4.4] (cf. [Reference Fujiki4, Lemma 2.4]) to
$p^*[\alpha]$, being the pullback of a Kähler class, is represented by a smooth semi-positive form and q-exceptional divisors are also p-exceptional divisors since f does not contract divisors by the assumption. Applying [Reference Golota6, Lemma 4.4] (cf. [Reference Fujiki4, Lemma 2.4]) to ![]() $p^*[\alpha]$, we have
$p^*[\alpha]$, we have
 \begin{align*}
q^*q_*p^*[\alpha]-p^*[\alpha]=\sum_{i=1}^n a_i [E_i]
\end{align*}
\begin{align*}
q^*q_*p^*[\alpha]-p^*[\alpha]=\sum_{i=1}^n a_i [E_i]
\end{align*} with ![]() $a_i\geq 0$.
$a_i\geq 0$.
Claim 2.2.
We claim that ![]() $q^*q_*p^*[\alpha]-p^*[\alpha]=0$.
$q^*q_*p^*[\alpha]-p^*[\alpha]=0$.
Proof. Suppose the contrary that ![]() $a_1 \gt 0$ without loss of generality. Note that
$a_1 \gt 0$ without loss of generality. Note that ![]() $q^*q_*p^*[\alpha]$ is nef and
$q^*q_*p^*[\alpha]$ is nef and ![]() $p^*[\alpha]$ is p-trivial. Then the divisor
$p^*[\alpha]$ is p-trivial. Then the divisor
 \begin{align*}
D & : = \sum_{i=1}^n a_i E_i-\epsilon E=\sum_{i=1}^n (a_i-\epsilon\delta_i) E_i \\
& = (q^*q_*p^*[\alpha]-p^*[\alpha]) + \epsilon(-E)
\end{align*}
\begin{align*}
D & : = \sum_{i=1}^n a_i E_i-\epsilon E=\sum_{i=1}^n (a_i-\epsilon\delta_i) E_i \\
& = (q^*q_*p^*[\alpha]-p^*[\alpha]) + \epsilon(-E)
\end{align*} is p-ample and −D is not effective whenever ![]() $0 \lt \epsilon \lt a_1/\delta_1$, noting that these Ei’s are distinct p-exceptional divisors. We can further find rational coefficients bi sufficiently closed to
$0 \lt \epsilon \lt a_1/\delta_1$, noting that these Ei’s are distinct p-exceptional divisors. We can further find rational coefficients bi sufficiently closed to ![]() $a_i-\epsilon\delta_i$ such that
$a_i-\epsilon\delta_i$ such that
 \begin{align*}
D^\prime: = \sum_{i=1}^n b_i E_i
\end{align*}
\begin{align*}
D^\prime: = \sum_{i=1}^n b_i E_i
\end{align*} is still p-ample and ![]() $-D^\prime$ is not effective. Note that mD ʹ is then a Cartier divisor for a suitable integer m and
$-D^\prime$ is not effective. Note that mD ʹ is then a Cartier divisor for a suitable integer m and ![]() $p_*(-mD^\prime)=0$. By the negativity lemma for Cartier divisors (cf. [Reference Wang23, Lemma 1.3]),
$p_*(-mD^\prime)=0$. By the negativity lemma for Cartier divisors (cf. [Reference Wang23, Lemma 1.3]), ![]() $-mD^\prime$ is effective, a contradiction. So the claim is proved.
$-mD^\prime$ is effective, a contradiction. So the claim is proved.
Applying Chow’s lemma again, there is a bimeromorphic morphism ![]() $\sigma\colon W\to Z$ such that
$\sigma\colon W\to Z$ such that ![]() $q\circ\sigma$ is a projective morphism. Note that
$q\circ\sigma$ is a projective morphism. Note that ![]() $(q\circ\sigma)_*(p\circ\sigma)^*[\alpha]=q_*p^*[\alpha]$. So we may replace Z by W and assume q is already projective (without requiring p to be projective). Let F be any fibre of q, which is projective. Let C be any curve in F. By the projection formula and Claim 2.2,
$(q\circ\sigma)_*(p\circ\sigma)^*[\alpha]=q_*p^*[\alpha]$. So we may replace Z by W and assume q is already projective (without requiring p to be projective). Let F be any fibre of q, which is projective. Let C be any curve in F. By the projection formula and Claim 2.2,
 \begin{align*}
\int \alpha\wedge \langle p_*C\rangle =\int p^*\alpha\wedge \langle C \rangle =\int q^*q_*p^*\alpha\wedge \langle C \rangle =\int q_*p^*\alpha\wedge \langle q_*C \rangle=0,
\end{align*}
\begin{align*}
\int \alpha\wedge \langle p_*C\rangle =\int p^*\alpha\wedge \langle C \rangle =\int q^*q_*p^*\alpha\wedge \langle C \rangle =\int q_*p^*\alpha\wedge \langle q_*C \rangle=0,
\end{align*} where ![]() $\langle-\rangle$ represents the integration current. Since
$\langle-\rangle$ represents the integration current. Since ![]() $[\alpha]$ is Kähler, p(C) is a point and hence p(F) is a point. By the rigidity lemma (cf. [Reference Golota6, Lemma 4.1]), which is essentially due to the Riemann extension theorem (cf. [Reference Grauert and Remmert8, Page 144]),
$[\alpha]$ is Kähler, p(C) is a point and hence p(F) is a point. By the rigidity lemma (cf. [Reference Golota6, Lemma 4.1]), which is essentially due to the Riemann extension theorem (cf. [Reference Grauert and Remmert8, Page 144]), ![]() $f^{-1}\colon Y\to X$ is a holomorphic map.
$f^{-1}\colon Y\to X$ is a holomorphic map.
Remark 2.3. Claim 2.2 was treated in the proof of [Reference Golota6, Theorem 4.5, Equation (4.4)]. However, the proof there seems incomplete after Εquation (4.2) where the author claims ‘the singular locus of the nef class is empty’. This is also mentioned after [Reference Golota6, Definition 4.3] where the author seems to have misinterpreted a result of Boucksom. Note that a nef class has an empty singular locus if and only if it is semi-positive. However, there are situations where non-semi-positive nef classes exist. Nevertheless, we can overcome this gap by applying the negativity lemma as in the proof of Claim 2.2.
Proof of Theorem 1.1
Note that ![]() $h^{1,1}(Y,\mathbb{R})=h^{1,1}(X,\mathbb{R})=1$ because f is isomorphic in codimension 1 (cf. [Reference Rao, Yang and Yang20, Corollary 1.5]). Let
$h^{1,1}(Y,\mathbb{R})=h^{1,1}(X,\mathbb{R})=1$ because f is isomorphic in codimension 1 (cf. [Reference Rao, Yang and Yang20, Corollary 1.5]). Let ![]() $[\alpha]$ be a Kähler class on X. Then
$[\alpha]$ be a Kähler class on X. Then ![]() $H^{1,1}(Y,\mathbb{R})$ is generated by the big class
$H^{1,1}(Y,\mathbb{R})$ is generated by the big class ![]() $f_*[\alpha]$, which is positive. Let
$f_*[\alpha]$, which is positive. Let ![]() $[\gamma]\in H^{1,1}(Y,\mathbb{R})$ be a nef class (and hence positive). Then
$[\gamma]\in H^{1,1}(Y,\mathbb{R})$ be a nef class (and hence positive). Then ![]() $[\gamma]=tf_*[\alpha]$ for some
$[\gamma]=tf_*[\alpha]$ for some ![]() $t\geq 0$ (cf. [Reference Fujiki4, Lemma 2.1]). So it suffices to show that
$t\geq 0$ (cf. [Reference Fujiki4, Lemma 2.1]). So it suffices to show that ![]() $f_*[\alpha]$ is not nef.
$f_*[\alpha]$ is not nef.
Suppose the contrary that ![]() $f_*[\alpha]\in H^{1,1}(Y,\mathbb{R})$ is nef. By Proposition 2.1, f −1 is holomorphic. By the purity (cf. [Reference Grauert and Remmert7, Satz 4]) and since f −1 is isomorphic in codimension 1, the exceptional locus of f −1 is empty. In particular, f is isomorphic, a contradiction.
$f_*[\alpha]\in H^{1,1}(Y,\mathbb{R})$ is nef. By Proposition 2.1, f −1 is holomorphic. By the purity (cf. [Reference Grauert and Remmert7, Satz 4]) and since f −1 is isomorphic in codimension 1, the exceptional locus of f −1 is empty. In particular, f is isomorphic, a contradiction.
Acknowledgements
The authors would like to thank Professor Boucksom, Professor Oguiso and Professor Zhang for the valuable discussion and suggestions. We would also like to thank the referee for the very careful reading and suggestions to improve the paper.
Funding statement
J. Jia. is partially supported by a President’s Graduate Scholarship from NUS and partially supported by the Shuimu Tsinghua Scholar Program and the China Postdoctoral Science Foundation (2023TQ0172). S. Meng. is supported by Fundamental Research Funds for the Central Universities, Science and Technology Commission of Shanghai Municipality (No. 22DZ2229014) and a National Natural Science Fund.