Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-16T16:59:28.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagonal quartic surfaces with a Brauer–Manin obstruction

Part of: Diophantine equations Multiplicative number theory

Published online by Cambridge University Press:  17 March 2023

Tim Santens
Tim Santens*
Affiliation:
Departement wiskunde, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we investigate the quantity of diagonal quartic surfaces 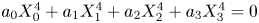$a_0 X_0^4 + a_1 X_1^4 + a_2 X_2^4 +a_3 X_3^4 = 0$ which have a Brauer–Manin obstruction to the Hasse principle. We are able to find an asymptotic formula for the quantity of such surfaces ordered by height. The proof uses a generalization of a method of Heath-Brown on sums over linked variables. We also show that there exists no uniform formula for a generic generator in this family.

Keywords

quartic surfacesrational pointsBrauer–Manin obstructionArtin L-series

MSC classification

Secondary: 11D25: Cubic and quartic equations 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 4 , April 2023 , pp. 659 - 710
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by FWO-Vlaanderen (Research Foundation–Flanders) with grant number 11I0621N.

References

Bright, M. J., Computations on diagonal quartic surfaces, PhD thesis, University of Cambridge (2002).Google Scholar
Bright, M. J., The Brauer–Manin obstruction on a general diagonal quartic surface, Acta Arith. 147 (2011), 291–302; MR 2773207.10.4064/aa147-3-8CrossRefGoogle Scholar
Bright, M. J., Bad reduction of the Brauer–Manin obstruction, J. Lond. Math. Soc. (2) 91 (2015), 643–666; MR 3355119.CrossRefGoogle Scholar
Bright, M., Obstructions to the Hasse principle in families, Manuscripta Math. 157 (2018), 529–550; MR 3858417.CrossRefGoogle Scholar
Bright, M. J., Browning, T. D. and Loughran, D., Failures of weak approximation in families, Compos. Math. 152 (2016), 1435–1475; MR 3530447.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Skorobogatov, A. N., The Brauer-Grothendieck group, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 71 (Springer, Cham, 2021); MR 4304038.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Xu, F., Brauer–Manin obstruction for integral points of homogeneous spaces and representation by integral quadratic forms, Compos. Math. 145 (2009), 309–363; MR 2501421.10.1112/S0010437X0800376XCrossRefGoogle Scholar
Deligne, P., La conjecture de Weil. II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252; MR 601520.10.1007/BF02684780CrossRefGoogle Scholar
Fogels, E., Über die Ausnahmenullstelle der Heckeschen $L$-Funktionen, Acta Arith. 8 (1962/63), 307–309; MR 156823.10.4064/aa-8-3-307-309CrossRefGoogle Scholar
Garibaldi, S., Merkurjev, A. and Serre, J.-P., Cohomological invariants in Galois cohomology, University Lecture Series, vol. 28 (American Mathematical Society, 2003); MR 1999383.Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology, Cambridge Studies in Advanced Mathematics, vol. 101 (Cambridge University Press, Cambridge, 2006); MR 2266528.10.1017/CBO9780511607219CrossRefGoogle Scholar
Grothendieck, A., Le groupe de Brauer: I, II, III, Dix exposés sur la cohomologie des schémas 3 (1968), 67–87.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Lecture Notes in Mathematics, vol. 224 (Springer, 1971).10.1007/BFb0058656CrossRefGoogle Scholar
Gvirtz, D., Loughran, D. and Nakahara, M., Quantitative arithmetic of diagonal degree $2$ K3 surfaces, Math. Ann. 384 (2022), 135–209; MR 4476231.CrossRefGoogle Scholar
Gvirtz, D. and Skorobogatov, A. N., Cohomology and the Brauer groups of diagonal surfaces, Duke Math. J. 171 (2022), 1299–1347; MR 4408122.CrossRefGoogle Scholar
Harpaz, Y., Second descent and rational points of Kummer varieties, Proc. Lond. Math. Soc. (3) 118 (2019), 606–648; MR 3932783.CrossRefGoogle Scholar
Harpaz, Y. and Skorobogatov, A. N., Hasse principle for Kummer varieties, Algebra Number Theory 10 (2016), 813–841; MR 3519097.CrossRefGoogle Scholar
Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, Invent. Math. 111 (1993), 171–195; MR 1193603.CrossRefGoogle Scholar
Ieronymou, E. and Skorobogatov, A. N., Odd order Brauer–Manin obstruction on diagonal quartic surfaces, Adv. Math. 270 (2015), 181–205; MR 3286534.CrossRefGoogle Scholar
Landau, E., Verallgemeinerung eines Pólyaschen satzes auf algebraische Zahlkörper, Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl. 1918 (1918), 478–488.Google Scholar
Lehmann, B. and Tanimoto, S., On the geometry of thin exceptional sets in Manin's conjecture, Duke Math. J. 166 (2017), 2815–2869; MR 3712166.CrossRefGoogle Scholar
Loughran, D., The number of varieties in a family which contain a rational point, J. Eur. Math. Soc. (JEMS) 20 (2018), 2539–2588; MR 3852186.CrossRefGoogle Scholar
Loughran, D. and Matthiesen, L., Frobenian multiplicative functions and rational points in fibrations. J. Eur. Math. Soc. (JEMS), to appear. Preprint (2019), arXiv:1904.12845.Google Scholar
Loughran, D., Rome, N. and Sofos, E., A new conjecture on rational points in families, Preprint (2022), arXiv:2210.13559.Google Scholar
Loughran, D. and Smeets, A., Fibrations with few rational points, Geom. Funct. Anal. 26 (2016), 1449–1482; MR 3568035.CrossRefGoogle Scholar
Loughran, D., Takloo-Bighash, R. and Tanimoto, S., Zero-loci of Brauer group elements on semi-simple algebraic groups, J. Inst. Math. Jussieu 19 (2020), 1467–1507; MR 4138949.CrossRefGoogle Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980); MR 559531.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory. I. Classical theory, Cambridge Studies in Advanced Mathematics, vol. 97 (Cambridge University Press, Cambridge, 2007); MR 2378655.Google Scholar
Pieropan, M. and Schindler, D., Hyperbola method on toric varieties, Preprint (2020), arXiv:2001.09815.Google Scholar
Pieropan, M., Smeets, A., Tanimoto, S. and Várilly-Alvarado, A., Campana points of bounded height on vector group compactifications, Proc. Lond. Math. Soc. (3) 123 (2021), 57–101; MR 4307130.CrossRefGoogle Scholar
Rome, N., The number of diagonal planar conics with a point (2022). Talk at ‘Rational points on higher-dimensional varieties’, International Centre for Mathematical Sciences, https://media.ed.ac.uk/playlist/dedicated/51612401/1_c3glvibl/1_wznl5zjb.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, New York–Heidelberg, 1977), translated from the second French edition by Leonard L. Scott; MR 0450380.CrossRefGoogle Scholar
Serre, J.-P., Lectures on $N_X (p)$, Chapman & Hall/CRC Research Notes in Mathematics, vol. 11 (CRC Press, Boca Raton, FL, 2012); MR 2920749.Google Scholar
Skorobogatov, A., Diagonal quartic surfaces, in Explicit methods in number theory, Oberwolfach Reports, vol. 6 (EMS Press, 2009), 1843–1920; MR 2664991.Google Scholar
Sofos, E. and Visse-Martindale, E., The density of fibres with a rational point for a fibration over hypersurfaces of low degree, Ann. Inst. Fourier (Grenoble) 71 (2021), 679–709; MR 4353917.CrossRefGoogle Scholar
Swinnerton-Dyer, P., Arithmetic of diagonal quartic surfaces. II, Proc. Lond. Math. Soc. (3) 80 (2000), 513–544; MR 1744774.CrossRefGoogle Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory, Cambridge Studies in Advanced Mathematics, vol. 46 (Cambridge University Press, Cambridge, 1995); translated from the second French edition (1995) by C. B. Thomas; MR 1342300.Google Scholar
Uematsu, T., On the Brauer group of diagonal cubic surfaces, Q. J. Math. 65 (2014), 677–701; MR 3230382.CrossRefGoogle Scholar
Uematsu, T., On the Brauer group of affine diagonal quadrics, J. Number Theory 163 (2016), 146–158; MR 3459565.10.1016/j.jnt.2015.11.015CrossRefGoogle Scholar