Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T18:58:02.881Z Has data issue: false hasContentIssue false
  • English
  • Français

The Maximum Term and the Rank of an Entire Function

Published online by Cambridge University Press:  20 November 2018

V. Sreenivasulu
V. Sreenivasulu*
Affiliation:
University of Poona, Poona, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. For an entire function 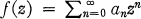, let M(r, f), μ(r, f), and v(r, f) denote the maximum modulus, the maximum term, and the rank for |z\ = r, respectively. Also, let

and λ(r) the lower proximate order relative to log M(r, f). For the properties of the lower proximate order, we refer the reader to the paper by Shah (1).

2. We prove the following theorems.

THEOREM 1. For an entire function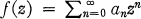

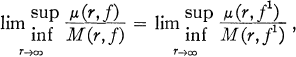
where μ(r, f1) and M(r, f1) correspond to fl(z), the derivative of f(z), provided (n + l)Rn > nRn+1, when L(f) > 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 257 - 261
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Shah, S. M., A note on lower proximate orders, J. Indian Math. Soc. (N.S.) 12 (1948), 31–32.Google Scholar
2. Valiron, G., Lectures on the general theory of integral functions, Translated by Collingwood, E. F. (Imprimerie et Librairie, Edouere Privât, Toulouse, 1923).Google Scholar