Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T15:48:28.365Z Has data issue: false hasContentIssue false
  • English
  • Français

On 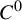$C^0$-genericity of distributional chaos

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  15 November 2021

NORIAKI KAWAGUCHI
NORIAKI KAWAGUCHI*
Affiliation:
Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa 223-8522, Japan
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be a compact smooth manifold without boundary. Based on results by Good and Meddaugh [Invent. Math. 220 (2020), 715–736], we prove that a strong distributional chaos is 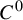$C^0$ -generic in the space of continuous self-maps (respectively, homeomorphisms) of M. The results contain answers to questions by Li, Li and Tu [Chaos 26 (2016), 093103] and Moothathu [Topology Appl. 158 (2011), 2232–2239] in the zero-dimensional case. A related counter-example on the chain components under shadowing is also given.

Keywords

distributional chaosgenericshadowingzero dimensionMycielski set

MSC classification

Primary: 37D45: Strange attractors, chaotic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 2 , February 2023 , pp. 615 - 645
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Glasner, E. and Weiss, B.. Generically there is but one self homeomorphism of the Cantor set. Trans. Amer. Math. Soc. 360 (2008), 3613–3630.CrossRefGoogle Scholar
Akin, E., Hurley, M. and Kennedy, J.. Dynamics of topologically generic homeomorphisms. Mem. Amer. Math. Soc. 164 (2003), 783.Google Scholar
Aoki, N. and Hiraide, K.. Topological Theory of Dynamical Systems: Recent Advances. (North-Holland Mathematical Library, 52). North-Holland, Amsterdam, 1994.Google Scholar
Balibrea, F. and Smítal, J.. Strong distributional chaos and minimal sets. Topology Appl. 156 (2009), 1673–1678.CrossRefGoogle Scholar
Bernardes, N. C. Jr. and Darji, U. B.. Graph theoretic structure of maps of the Cantor space. Adv. Math. 231 (2012), 1655–1680.CrossRefGoogle Scholar
Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li–Yorke pairs. J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385). Eds Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–37.CrossRefGoogle Scholar
Downarowicz, T.. Positive topological entropy implies chaos DC2. Proc. Amer. Math. Soc. 142 (2014), 137–149.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. The topological Rohlin property and topological entropy. Amer. J. Math. 123 (2001), 1055–1070.CrossRefGoogle Scholar
Good, C. and Meddaugh, J.. Shifts of finite type as fundamental objects in the theory of shadowing. Invent. Math. 220 (2020), 715–736.CrossRefGoogle Scholar
Guihéneuf, P. A. and Lefeuvre, T.. On the genericity of the shadowing property for conservative homeomorphisms. Proc. Amer. Math. Soc. 146 (2018), 4225–4237.CrossRefGoogle Scholar
Huang, W., Li, H. and Ye, X.. Family-independence for topological and measurable dynamics. Trans. Amer. Math. Soc. 364 (2012), 5209–5245.CrossRefGoogle Scholar
Huang, W., Li, J. and Ye, X.. Stable sets and mean Li–Yorke chaos in positive entropy systems. J. Funct. Anal. 266 (2014), 3377–3394.CrossRefGoogle Scholar
Kawaguchi, N.. Distributionally chaotic maps are ${C}^0$ -dense. Proc. Amer. Math. Soc. 147 (2019), 5339–5348.CrossRefGoogle Scholar
Kawaguchi, N.. A type of shadowing and distributional chaos. Dyn. Syst., to appear; doi:10.1080/14689367.2021.1957083.CrossRefGoogle Scholar
Kechris, A. S. and Rosendal, C.. Turbulence, amalgamation, and generic automorphisms of homogeneous structures. Proc. Lond. Math. Soc. (3) 94 (2007), 302–350.CrossRefGoogle Scholar
Kościelniak, P., Mazur, M., Oprocha, P. and Kubica, Ł.. Shadowing is generic on various one-dimensional continua with a special geometric structure. J. Geom. Anal. 30 (2020), 1836–1864.CrossRefGoogle Scholar
Krupski, P., Omiljanowski, K. and Ungeheuer, K.. Chain recurrent sets of generic mappings on compact spaces. Topology Appl. 202 (2016), 251–268.CrossRefGoogle Scholar
Kwietniak, D.. Topological entropy and distributional chaos in hereditary shifts with applications to spacing shifts and beta shifts. Discrete Contin. Dyn. Syst. 33 (2013), 2451–2467.CrossRefGoogle Scholar
Kwietniak, D., Łącka, M. and Oprocha, P.. A panorama of specification-like properties and their consequences. Dynamics and Numbers (Contemporary Mathematics, 669). Eds Kolyada, S., Möller, M., Moree, P. and Ward, T.. American Mathematical Society, Providence, RI, 2016, pp. 155–186.CrossRefGoogle Scholar
Li, J., Li, J. and Tu, S.. Devaney chaos plus shadowing implies distributional chaos. Chaos 26 (2016), 093103, 6 p.CrossRefGoogle ScholarPubMed
Li, J. and Oprocha, P.. On $n$ -scrambled tuples and distributional chaos in a sequence. J. Difference Equ. Appl. 19 (2013), 927–941.CrossRefGoogle Scholar
Li, T. Y. and Yorke, J. A.. Period three implies chaos. Amer. Math. Monthly 82 (1975), 985–992.CrossRefGoogle Scholar
Mazur, M. and Oprocha, P.. S-limit shadowing is ${C}^0$ -dense. J. Math. Anal. Appl. 408 (2013), 465–475.CrossRefGoogle Scholar
Mazur, M. and Oprocha, P.. Subshifts, rotations and the specification property. Topol. Methods Nonlinear Anal. 46 (2015), 799–812.Google Scholar
Moothathu, T. K. S.. Implications of pseudo-orbit tracing property for continuous maps on compacta. Topology Appl. 158 (2011), 2232–2239.CrossRefGoogle Scholar
Mycielski, J.. Independent sets in topological algebras. Fund. Math. 55 (1964), 139–147.CrossRefGoogle Scholar
Oprocha, P.. Specification properties and dense distributional chaos. Discrete Contin. Dyn. Syst. 17 (2007), 821–833.CrossRefGoogle Scholar
Oprocha, P.. Distributional chaos revisited. Trans. Amer. Math. Soc. 361 (2009), 4901–4925.CrossRefGoogle Scholar
Oprocha, P.. Families, filters and chaos. Bull. Lond. Math. Soc. 42 (2010), 713–725.CrossRefGoogle Scholar
Pikuła, R.. On some notions of chaos in dimension zero. Colloq. Math. 107 (2007), 167–177.CrossRefGoogle Scholar
Pilyugin, S. Y. and Plamenevskaya, O. B.. Shadowing is generic. Topology Appl. 97 (1999), 253–266.CrossRefGoogle Scholar
Richeson, D. and Wiseman, J.. Chain recurrence rates and topological entropy. Topology Appl. 156 (2008), 251–261.CrossRefGoogle Scholar
Ruette, S.. Chaos on the Interval (University Lecture Series, 67). American Mathematical Society, Providence, RI, 2017.CrossRefGoogle Scholar
Schweizer, B. and Smítal, J.. Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Amer. Math. Soc. 344 (1994), 737–754.CrossRefGoogle Scholar
Smítal, J.. Chaotic functions with zero topological entropy. Trans. Amer. Math. Soc. 297 (1986), 269–282.CrossRefGoogle Scholar
Tan, F. and Fu, H.. On distributional $n$ -chaos. Acta Math. Sci. 34 (2014), 1473–1480.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar
Xiong, J.. A chaotic map with topological entropy zero. Acta Math. Sci. 6 (1986), 439–443.CrossRefGoogle Scholar
Yano, K.. A remark on the topological entropy of homeomorphisms. Invent. Math. 59 (1980), 215–220.CrossRefGoogle Scholar