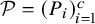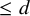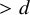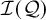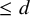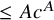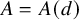1 Introduction
In [Reference Schmidt23], Schmidt introduced a notion of complexity, the Schmidt rank (also called the h-invariant)Footnote
1
for a collection of polynomials
![]() $\mathcal P=(P_i)_{i=1}^c$
, and used it to obtain conditions on the existence of integer solutions for a system of equations
$\mathcal P=(P_i)_{i=1}^c$
, and used it to obtain conditions on the existence of integer solutions for a system of equations
![]() $\{P_i(x)=0\}_{i=1}^c$
defined over the rational numbers. The most natural polynomials on which to define this quantity are homogeneous ones. If P is a polynomial of degree d, we denote by
$\{P_i(x)=0\}_{i=1}^c$
defined over the rational numbers. The most natural polynomials on which to define this quantity are homogeneous ones. If P is a polynomial of degree d, we denote by
![]() $\tilde {P}$
the degree d homogeneous component of
$\tilde {P}$
the degree d homogeneous component of
![]() $P.$
$P.$
Definition 1.1 (Schmidt rank).
The Schmidt rank of a homogeneous polynomial
![]() $P \in {\mathbb {F}}[x_1, \ldots , x_n]$
is the minimal length of a presentation
$P \in {\mathbb {F}}[x_1, \ldots , x_n]$
is the minimal length of a presentation
![]() $P=\sum _{i=1}^r Q_iR_i,$
where for all
$P=\sum _{i=1}^r Q_iR_i,$
where for all
![]() $i\in [r],\ Q_i, R_i$
are homogeneous polynomials of degree
$i\in [r],\ Q_i, R_i$
are homogeneous polynomials of degree
![]() $<\deg (P)$
, and is denoted by
$<\deg (P)$
, and is denoted by
![]() $rk(P).$
For a general polynomial P we set
$rk(P).$
For a general polynomial P we set
![]() ${rk(P) = rk(\tilde P).}$
The rank of a collection of homogeneous polynomials
${rk(P) = rk(\tilde P).}$
The rank of a collection of homogeneous polynomials
![]() $\mathcal P=(P_i)_{i=1}^c$
is
$\mathcal P=(P_i)_{i=1}^c$
is
If
![]() ${\mathcal P}$
is a general collection of polynomials, we set
${\mathcal P}$
is a general collection of polynomials, we set
![]() $rk(\mathcal P) = rk(\tilde {\mathcal {P}}),$
where
$rk(\mathcal P) = rk(\tilde {\mathcal {P}}),$
where
![]() $\tilde {\mathcal {P}} = (\tilde P_i)_{i=1}^c.$
$\tilde {\mathcal {P}} = (\tilde P_i)_{i=1}^c.$
Now assume
![]() ${\mathbb {F}} = {\mathbb {F}}_q$
is a finite field and fix a nontrivial character
${\mathbb {F}} = {\mathbb {F}}_q$
is a finite field and fix a nontrivial character
![]() $\chi :{\mathbb {F}}\to {\mathbb C}.$
We define the bias of a polynomial as follows.
$\chi :{\mathbb {F}}\to {\mathbb C}.$
We define the bias of a polynomial as follows.
Definition 1.2. For a function
![]() $P:{\mathbb {F}}^n\to {\mathbb {F}}$
, we define
$P:{\mathbb {F}}^n\to {\mathbb {F}}$
, we define
where
![]() ${\mathbb E}_{x\in E} := \frac {1}{|E|}\sum _{x\in E}$
for a finite set
${\mathbb E}_{x\in E} := \frac {1}{|E|}\sum _{x\in E}$
for a finite set
![]() $E,$
with the convention
$E,$
with the convention
![]() ${\mathbb E}_{x\in \emptyset } = 0.$
This quantity may of course depend on
${\mathbb E}_{x\in \emptyset } = 0.$
This quantity may of course depend on
![]() $\chi ,$
but we omit it from the notation.Footnote
2
$\chi ,$
but we omit it from the notation.Footnote
2
The relation between bias and rank can already be traced to the work of Schmidt; indeed, in his paper [Reference Schmidt23], Schmidt showed that over the complex field, the Schmidt rank of a polynomial is proportional to the codimension of the singular locus of the associated variety, and used this for estimating related exponential sums.
In [Reference Green and Tao10], Green and Tao observed that one can make the relation independent of the number of variables:Footnote 3
Theorem 1.3 (Bias implies low rank).
Let
![]() ${\mathbb {F}}={\mathbb {F}}_q$
be a finite field, let
${\mathbb {F}}={\mathbb {F}}_q$
be a finite field, let
![]() $0\le d < char({\mathbb {F}})$
, and let
$0\le d < char({\mathbb {F}})$
, and let
![]() $s>0$
. There exists a constant
$s>0$
. There exists a constant
![]() $C=C({\mathbb {F}},s,d)$
, such that the following holds: For any n,
$C=C({\mathbb {F}},s,d)$
, such that the following holds: For any n,
![]() $P\in {\mathbb {F}}[x_1,\ldots ,x_n]$
of degree
$P\in {\mathbb {F}}[x_1,\ldots ,x_n]$
of degree
![]() $\le d$
with
$\le d$
with
![]() $bias(P) \ge q^{-s}$
, we have
$bias(P) \ge q^{-s}$
, we have
![]() $rk(P) \le C$
.
$rk(P) \le C$
.
This result was subsequently extended to include the case
![]() $d \ge char({\mathbb {F}})$
by Kauffman and Lovett in [Reference Kaufman and Lovett13]. Bhowmick and Lovett [Reference Bhowmick and Lovett3] showed that the bound can be made independent of the field
$d \ge char({\mathbb {F}})$
by Kauffman and Lovett in [Reference Kaufman and Lovett13]. Bhowmick and Lovett [Reference Bhowmick and Lovett3] showed that the bound can be made independent of the field
![]() ${\mathbb {F}}$
in the sense that we can take
${\mathbb {F}}$
in the sense that we can take
![]() $C = C(s,d).$
Returning to the case
$C = C(s,d).$
Returning to the case
![]() $d < char({\mathbb {F}})$
, effective bounds for C were given by Milićević [Reference Milićević21] who proved
$d < char({\mathbb {F}})$
, effective bounds for C were given by Milićević [Reference Milićević21] who proved
Independently, Janzer [Reference Janzer12] proved a similar, slightly weaker result with
![]() $s \log q$
instead of s.
$s \log q$
instead of s.
Conjecture 1.4. For all finite fields
![]() ${\mathbb {F}}$
with
${\mathbb {F}}$
with
![]() $char({\mathbb {F}})>d$
, we have
$char({\mathbb {F}})>d$
, we have
![]() $C({\mathbb {F}},s,d) = A(d)(1+ s)$
.
$C({\mathbb {F}},s,d) = A(d)(1+ s)$
.
Conjecture 1.4 was recently proved in the case
![]() $d=3$
in [Reference Adiprasito, Kazhdan and Ziegler1], [Reference Cohen and Moshkovitz5] independently.
$d=3$
in [Reference Adiprasito, Kazhdan and Ziegler1], [Reference Cohen and Moshkovitz5] independently.
A key feature of high rank collections of polynomials, that can be easily derived from Theorem 1.3, is that all fibers of the map
![]() $\mathcal P:\mathbb {\mathbb {F}}^n \to \mathbb {\mathbb {F}}^c$
are essentially of the same size.
$\mathcal P:\mathbb {\mathbb {F}}^n \to \mathbb {\mathbb {F}}^c$
are essentially of the same size.
Theorem 1.5 (Size of fibers).
Let
![]() $d>0$
. Let
$d>0$
. Let
![]() ${\mathbb {F}}={\mathbb {F}}_q$
be a finite field of characteristic
${\mathbb {F}}={\mathbb {F}}_q$
be a finite field of characteristic
![]() $>d$
. There exists
$>d$
. There exists
![]() $A= A(d)$
, such that the following holds: For any n, any collection of polynomials
$A= A(d)$
, such that the following holds: For any n, any collection of polynomials
![]() $\mathcal P=(P_i)_{i=1}^c$
in
$\mathcal P=(P_i)_{i=1}^c$
in
![]() ${\mathbb {F}}[x_1,\ldots ,x_n]$
of degrees
${\mathbb {F}}[x_1,\ldots ,x_n]$
of degrees
![]() $\le d$
and rank
$\le d$
and rank
![]() $>Ac^A$
, any
$>Ac^A$
, any
![]() $a, b \in {\mathbb {F}}^c$
, we have
$a, b \in {\mathbb {F}}^c$
, we have
![]() $||\mathcal P^{-1}(a)| / |\mathcal P^{-1}(b)| - 1| <q^{-1}$
.
$||\mathcal P^{-1}(a)| / |\mathcal P^{-1}(b)| - 1| <q^{-1}$
.
Using model theoretic techniques, one can translate the data in Theorem 1.5 to an estimate of the dimension of the fibers of the map
![]() $\mathcal P:\mathbb {\mathbb A}^n \to {\mathbb A}^c$
for any algebraically closed field of characteristic zero or
$\mathcal P:\mathbb {\mathbb A}^n \to {\mathbb A}^c$
for any algebraically closed field of characteristic zero or
![]() $>\max \deg P_i$
(see, e.g. [Reference Kazhdan and Ziegler15, Reference Kazhdan and Ziegler16]).
$>\max \deg P_i$
(see, e.g. [Reference Kazhdan and Ziegler15, Reference Kazhdan and Ziegler16]).
In many proofs using the notion of Schmidt rank, a key procedure is regularization (e.g. [Reference Schmidt23], [Reference Bhowmick and Lovett3], [Reference Cook and Magyar6]): given a collection of polynomials, one applies procedure replacing the original collection of polynomials
![]() $\mathcal P$
with a new collection
$\mathcal P$
with a new collection
![]() ${\mathcal Q}$
that is of high Schmidt rank compared to its size, (so Theorem 1.5 holds) and such that the ideal generated by
${\mathcal Q}$
that is of high Schmidt rank compared to its size, (so Theorem 1.5 holds) and such that the ideal generated by
![]() $\mathcal P$
is contained in the ideal generated by
$\mathcal P$
is contained in the ideal generated by
![]() ${\mathcal Q}$
. The drawback in this regularization procedure is that the size of
${\mathcal Q}$
. The drawback in this regularization procedure is that the size of
![]() ${\mathcal Q}$
is far worse than even tower exponential in the size of
${\mathcal Q}$
is far worse than even tower exponential in the size of
![]() $\mathcal P$
(the bound that can be derived from Schmidt’s argument was worked out by Wooley in [Reference Wooley25]).
$\mathcal P$
(the bound that can be derived from Schmidt’s argument was worked out by Wooley in [Reference Wooley25]).
We introduce a new notion of rank, relative rank, associated with a filtered collection of polynomials, both in the algebraic and analytic contexts. We replace the ambient space
![]() ${\mathbb {F}}^n$
by certain affine varieties, and we replace Schmidt rank by an appropriate relative rank. The definition of relative rank is somewhat technical; we defer it to the next section (Definition 2.1). We remark that the new notion of relative rank coincides with the Schmidt rank and the analytic rank when the filtration consists of one set, but is different otherwise.
${\mathbb {F}}^n$
by certain affine varieties, and we replace Schmidt rank by an appropriate relative rank. The definition of relative rank is somewhat technical; we defer it to the next section (Definition 2.1). We remark that the new notion of relative rank coincides with the Schmidt rank and the analytic rank when the filtration consists of one set, but is different otherwise.
Our main result (Theorem 2.2), described in detail in the next section, is a relation between relative rank and relative bias, similar to the relation described above between rank and bias. The key advantage of our new notion of rank is that while it retains many of the properties of the ranks described above, for example, Theorem 1.5 remains valid, the regularization procedure with respect to this notion is polynomial in the size of the original collection. As such, we are able to give good quantitative bounds on a variety of problems in which a regularization procedure is used. We provide an example of an algebraic application in Theorem 2.6.
In the interest of exposition, we will start by presenting a special case of our main result. This special case is actually the result we initially set out to prove. First, we give our definitions of relative rank and relative bias.
Definition 1.6 (Relative rank).
The relative rank of a homogeneous polynomial P on a collection of homogeneous polynomials
![]() ${\mathcal Q} = (Q_1,\ldots ,Q_m)$
is
${\mathcal Q} = (Q_1,\ldots ,Q_m)$
is
 $$\begin{align*}rk_{\mathcal Q} (P) := \min \{rk(P+\sum_{i=1}^m R_i Q_i): \deg(R_i)+\deg(Q_i) \le \deg(P)\ \forall i\in[m] \}. \end{align*}$$
$$\begin{align*}rk_{\mathcal Q} (P) := \min \{rk(P+\sum_{i=1}^m R_i Q_i): \deg(R_i)+\deg(Q_i) \le \deg(P)\ \forall i\in[m] \}. \end{align*}$$
Note that whenever
![]() $\deg (Q_i)> \deg (P)$
, this implies
$\deg (Q_i)> \deg (P)$
, this implies
![]() $R_i = 0.$
For general polynomials, with
$R_i = 0.$
For general polynomials, with
![]() $ \tilde P,\tilde {\mathcal {Q}} $
the corresponding homogeneous polynomial and collection, set
$ \tilde P,\tilde {\mathcal {Q}} $
the corresponding homogeneous polynomial and collection, set
![]() $rk_{\mathcal Q} (P) := rk_{\tilde {\mathcal {Q}}} (\tilde P).$
$rk_{\mathcal Q} (P) := rk_{\tilde {\mathcal {Q}}} (\tilde P).$
Definition 1.7 (Relative bias).
The relative bias of a function
![]() $P:{\mathbb {F}}^n\to {\mathbb {F}}$
on a subset
$P:{\mathbb {F}}^n\to {\mathbb {F}}$
on a subset
![]() $X\subset {\mathbb {F}}^n$
is
$X\subset {\mathbb {F}}^n$
is
For a collection
![]() $ {\mathcal Q} = (Q_i)_{i\in [m]} $
of polynomials in
$ {\mathcal Q} = (Q_i)_{i\in [m]} $
of polynomials in
![]() $ {\mathbb {F}}[x_1,\ldots ,x_n] $
, denote the zero locus by
$ {\mathbb {F}}[x_1,\ldots ,x_n] $
, denote the zero locus by
A special case of our main result is then:
Theorem 1.8. Let
![]() $ {\mathbb {F}} $
be a finite field and
$ {\mathbb {F}} $
be a finite field and
![]() $0\le d < char({\mathbb {F}}).$
There exist constants
$0\le d < char({\mathbb {F}}).$
There exist constants
![]() $A(d), B(d)$
, such that if
$A(d), B(d)$
, such that if
![]() $ {\mathcal Q} = (Q_i)_{i=1}^m $
is a collection of polynomials with degrees
$ {\mathcal Q} = (Q_i)_{i=1}^m $
is a collection of polynomials with degrees
![]() $ \le d $
with
$ \le d $
with
![]() $ rk({\mathcal Q})> A(m+s)^B $
and P is a polynomial of degree
$ rk({\mathcal Q})> A(m+s)^B $
and P is a polynomial of degree
![]() $ \le d $
with
$ \le d $
with
![]() $ bias_{Z({\mathcal Q})}(P) \ge q^{-s} $
, then we have
$ bias_{Z({\mathcal Q})}(P) \ge q^{-s} $
, then we have
We briefly pause here and compare this to the result of Milićević (and Janzer). For
![]() $ {\mathcal Q} = \emptyset $
, this gives a new proof of their result. Moreover, when
$ {\mathcal Q} = \emptyset $
, this gives a new proof of their result. Moreover, when
![]() $ m \le s $
or when
$ m \le s $
or when
![]() $ {\mathcal Q} $
is composed of polynomials of degree
$ {\mathcal Q} $
is composed of polynomials of degree
![]() $ \ge \deg (P) $
, the above theorem, in fact, follows from their result. But it is new in the case that
$ \ge \deg (P) $
, the above theorem, in fact, follows from their result. But it is new in the case that
![]() $ {\mathcal Q} $
is composed of
$ {\mathcal Q} $
is composed of
![]() $\gg s$
polynomials of lower degree than P.
$\gg s$
polynomials of lower degree than P.
2 Main theorem
We now give our definitions in full and state our main theorem.
Definition 2.1.
-
1. The relative rank of a collection of homogeneous polynomials
 $\mathcal P = (P_i)_{i\in [m]}$
on another collection of polynomials
$\mathcal P = (P_i)_{i\in [m]}$
on another collection of polynomials
 ${\mathcal Q}$
is
${\mathcal Q}$
is  $$\begin{align*}rk_{\mathcal Q} (\mathcal P) = \min \left\lbrace rk_{\mathcal Q} \left( a\cdot \mathcal P \right) :\ 0\neq a\in{\mathbb{F}}^m \right\rbrace. \end{align*}$$
$$\begin{align*}rk_{\mathcal Q} (\mathcal P) = \min \left\lbrace rk_{\mathcal Q} \left( a\cdot \mathcal P \right) :\ 0\neq a\in{\mathbb{F}}^m \right\rbrace. \end{align*}$$
If
 ${\mathcal P}$
is a general collection of polynomials with corresponding homogeneous collection
${\mathcal P}$
is a general collection of polynomials with corresponding homogeneous collection
 $ \tilde {\mathcal {P}}, $
then
$ \tilde {\mathcal {P}}, $
then
 $ rk_{\mathcal Q} (\mathcal P) = rk_{\mathcal Q} (\tilde {\mathcal {P}}). $
$ rk_{\mathcal Q} (\mathcal P) = rk_{\mathcal Q} (\tilde {\mathcal {P}}). $
-
2. A tower
of height h is composed of h collections of polynomials $$\begin{align*}{\mathcal Q} = (Q_i)_{i\in [h]} \end{align*}$$
$$\begin{align*}{\mathcal Q} = (Q_i)_{i\in [h]} \end{align*}$$
 ${\mathcal Q}_i = (Q_{i,j}) _{j\in [m_i]}$
which we call layers, such that the polynomials in each layer all have the same degree
${\mathcal Q}_i = (Q_{i,j}) _{j\in [m_i]}$
which we call layers, such that the polynomials in each layer all have the same degree
 $d_i.$
The degree of the tower is
$d_i.$
The degree of the tower is
 $ \max \left (d_1,\ldots ,d_h \right ).$
The dimension of the tower is
$ \max \left (d_1,\ldots ,d_h \right ).$
The dimension of the tower is
 $ m_1+\ldots +m_h. $
We denote the truncated tower
$ m_1+\ldots +m_h. $
We denote the truncated tower
 ${\mathcal Q}_{<i} = ({\mathcal Q}_j)_{j\in [i-1]}.$
${\mathcal Q}_{<i} = ({\mathcal Q}_j)_{j\in [i-1]}.$
-
3. The tower
 $ {\mathcal Q} $
is
$ {\mathcal Q} $
is
 $(A,B,s)$
-regular if for every
$(A,B,s)$
-regular if for every
 $i\in [h]$
, we have
$i\in [h]$
, we have  $$\begin{align*}rk_{{\mathcal Q}_{<i}} ({\mathcal Q}_i)>A(m_i+m_{i+1}+\ldots+m_h+s)^B. \end{align*}$$
$$\begin{align*}rk_{{\mathcal Q}_{<i}} ({\mathcal Q}_i)>A(m_i+m_{i+1}+\ldots+m_h+s)^B. \end{align*}$$
The main theorem we prove is the following:
Theorem 2.2 (Relative bias implies relative low rank).
There exist constants
![]() $A(d,H), B(d,H)$
, such that if
$A(d,H), B(d,H)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular tower of degree
$(A,B,s)$
-regular tower of degree
![]() $\le d < char({\mathbb {F}})$
and height
$\le d < char({\mathbb {F}})$
and height
![]() $\le H,$
and P is a polynomial of degree
$\le H,$
and P is a polynomial of degree
![]() $\le d$
with
$\le d$
with
then
Theorem 2.2 implies that relatively regular collections of polynomials enjoy similar equidistribution properties to those of high rank collections of polynomials. In fact, all the results in [Reference Kazhdan and Ziegler15, Reference Kazhdan and Ziegler16, Reference Kazhdan and Ziegler17], [Reference Bhowmick and Lovett3], which were proved for collections of polynomials of high rank, are also valid for relatively regular collections of polynomials. Some examples of results that transfer seamlessly to the relatively regular setting are given in the Appendix.
The dependence of the constants
![]() $A,B$
on the parameters
$A,B$
on the parameters
![]() $d,H$
, which can be extracted from our proof, is quite weak and involves recursively defined functions. This is due to the rather involved inductive argument. It is natural to ask whether this result holds with a stronger dependence on
$d,H$
, which can be extracted from our proof, is quite weak and involves recursively defined functions. This is due to the rather involved inductive argument. It is natural to ask whether this result holds with a stronger dependence on
![]() $d,H.$
$d,H.$
Question: Can the constants
![]() $A,B$
in theorem 2.2 be taken to be “reasonable” functions of
$A,B$
in theorem 2.2 be taken to be “reasonable” functions of
![]() $d,H$
? Say, a tower of exponentials of bounded height as in Milićević’s result [Reference Milićević21]?
$d,H$
? Say, a tower of exponentials of bounded height as in Milićević’s result [Reference Milićević21]?
For a collection of polynomials
![]() $ {\mathcal Q}, $
we write
$ {\mathcal Q}, $
we write
![]() $ I({\mathcal Q}) $
for the ideal they generate. In many applications of the notion of rank (e.g [Reference Schmidt23], [Reference Cook and Magyar6]) one is given a collection of polynomials, to which one applies a regularization process, replacing the original collection
$ I({\mathcal Q}) $
for the ideal they generate. In many applications of the notion of rank (e.g [Reference Schmidt23], [Reference Cook and Magyar6]) one is given a collection of polynomials, to which one applies a regularization process, replacing the original collection
![]() ${\mathcal Q}$
with a new regular collection
${\mathcal Q}$
with a new regular collection
![]() ${\mathcal Q}'$
, such that any
${\mathcal Q}'$
, such that any
![]() ${\mathcal Q} \subset I({\mathcal Q}').$
The issue is that the regularization process is very costly (see [Reference Wooley25]). One of the advantages of relative rank is that it allows a very efficient process of regularization.
${\mathcal Q} \subset I({\mathcal Q}').$
The issue is that the regularization process is very costly (see [Reference Wooley25]). One of the advantages of relative rank is that it allows a very efficient process of regularization.
Theorem 2.3 (Polynomial regularity).
Let
![]() $A,B,d$
be given. There exist constants
$A,B,d$
be given. There exist constants
![]() $ C(A,B,d),D(A,B,d) $
, such that if
$ C(A,B,d),D(A,B,d) $
, such that if
![]() ${\mathcal Q}$
is a collection of m homogeneous polynomials of positive degrees
${\mathcal Q}$
is a collection of m homogeneous polynomials of positive degrees
![]() $\le d$
, then there exists a polynomial tower
$\le d$
, then there exists a polynomial tower
![]() ${\mathcal Q}'$
of dimension
${\mathcal Q}'$
of dimension
![]() $\le C(m+s)^D$
, degree
$\le C(m+s)^D$
, degree
![]() $ \le d $
, and height
$ \le d $
, and height
![]() $\le d$
, such that
$\le d$
, such that
![]() ${\mathcal Q}'$
is
${\mathcal Q}'$
is
![]() $(A,B,s)$
-regular, and
$(A,B,s)$
-regular, and
![]() ${\mathcal Q}\subset I({\mathcal Q}').$
${\mathcal Q}\subset I({\mathcal Q}').$
Definition 2.4. A collection of polynomials
![]() ${\mathcal Q} = (Q_i)_{i=1}^m \subset {\mathbb {F}}[x_1,\ldots ,x_n]$
is s-uniform if
${\mathcal Q} = (Q_i)_{i=1}^m \subset {\mathbb {F}}[x_1,\ldots ,x_n]$
is s-uniform if
 $$\begin{align*}\left| \frac{|Z({\mathcal Q})|}{q^{n-m}} -1 \right| \le q^{-s}.\end{align*}$$
$$\begin{align*}\left| \frac{|Z({\mathcal Q})|}{q^{n-m}} -1 \right| \le q^{-s}.\end{align*}$$
As a corollary of Theorem 2.2, we obtain:
Lemma 2.5 (Regular varieties are of the expected size).
There exist constants
![]() $A(d,H),B(d,H)$
, such that any
$A(d,H),B(d,H)$
, such that any
![]() $(A,B,s)$
-regular polynomial tower
$(A,B,s)$
-regular polynomial tower
![]() ${\mathcal Q}$
of degree
${\mathcal Q}$
of degree
![]() $\le d < char({\mathbb {F}})$
and height
$\le d < char({\mathbb {F}})$
and height
![]() $\le H$
is s-uniform.
$\le H$
is s-uniform.
In particular, we obtain the following algebraic consequence:
Theorem 2.6. Let
![]() $d>0$
. Let
$d>0$
. Let
![]() ${\mathbb {F}}$
be an algebraically closed field of characteristic zero or
${\mathbb {F}}$
be an algebraically closed field of characteristic zero or
![]() $>d$
. There exists a constant
$>d$
. There exists a constant
![]() $A=A(d)$
, such that if
$A=A(d)$
, such that if
![]() $\mathcal P$
is a collection of c homogeneous polynomials of positive degrees
$\mathcal P$
is a collection of c homogeneous polynomials of positive degrees
![]() $\le d,$
then there exists a collection
$\le d,$
then there exists a collection
![]() ${\mathcal Q}$
of
${\mathcal Q}$
of
![]() $ \le Ac^A$
homogeneous polynomials of degrees
$ \le Ac^A$
homogeneous polynomials of degrees
![]() $\le d$
, such that
$\le d$
, such that
![]() ${\mathcal Q}$
is a regular sequence, and
${\mathcal Q}$
is a regular sequence, and
![]() $P_i \in \mathcal I({\mathcal Q})$
.
$P_i \in \mathcal I({\mathcal Q})$
.
We prove Theorem 2.6 in the Appendix; it follows from Theorem 2.3 and an adaptation of the results in [Reference Kazhdan and Ziegler15] to the context of relative rank. We also obtain a robust Nullstellensatz result for regular collections.
Theorem 2.7 (Robust Nullstellensatz for regular collections).
There exist constants
![]() $A(d,H),B(d,H),s(d)$
, such that if
$A(d,H),B(d,H),s(d)$
, such that if
![]() ${\mathcal Q} = (Q_{i,j})_{i\in [h],j\in [m_i]} $
is an
${\mathcal Q} = (Q_{i,j})_{i\in [h],j\in [m_i]} $
is an
![]() $(A,B,s)$
-regular polynomial tower of deg
$(A,B,s)$
-regular polynomial tower of deg
![]() $\le d < char({\mathbb {F}})$
and height
$\le d < char({\mathbb {F}})$
and height
![]() $ \le H, $
and P is a polynomial of degree
$ \le H, $
and P is a polynomial of degree
![]() $ \le d $
which vanishes
$ \le d $
which vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}), $
then there exist polynomials
$ Z({\mathcal Q}), $
then there exist polynomials
![]() $ R_{i,j} $
satisfying
$ R_{i,j} $
satisfying
![]() $ \deg (R_{i,j}) + \deg (Q_{i,j}) \le \deg (P) $
and
$ \deg (R_{i,j}) + \deg (Q_{i,j}) \le \deg (P) $
and
In order to prove Theorem 2.2, as in [Reference Janzer12, Reference Milićević21], we first reduce it to an analogous statement for multilinear maps. However, the reduction of Theorem 2.2 to its multilinear version is not so straightforward in our case. This will be done by induction on the degree d and will require some intermediate results that appear during the proof of the theorem in the multilinear case. Therefore, we postpone it to Section 9. We now turn to the multilinear case.
2.1 Multilinear definitions and main theorem
Let
![]() $V_1,\ldots ,V_k$
be finite-dimensional vector spaces over the finite field
$V_1,\ldots ,V_k$
be finite-dimensional vector spaces over the finite field
![]() ${\mathbb {F}}.$
For
${\mathbb {F}}.$
For
![]() $I\subset [k],$
we denote
$I\subset [k],$
we denote
![]() $V^I=\prod _{i\in I} V_i.$
For
$V^I=\prod _{i\in I} V_i.$
For
![]() $ x\in V^{[k]}, $
we denote by
$ x\in V^{[k]}, $
we denote by
![]() $ x_I $
the projection of
$ x_I $
the projection of
![]() $ x $
to
$ x $
to
![]() $ V^I. $
$ V^I. $
In order to prove our main theorem for multilinear functions, we will need to work with a slightly larger class of functions which we call full multiaffine maps. Recall that a multiaffine map
![]() $ P:V^I\to {\mathbb {F}} $
has a unique presentation
$ P:V^I\to {\mathbb {F}} $
has a unique presentation
![]() $ P(x_I) = \sum _{J\subset I} P_J(x_J) $
, where
$ P(x_I) = \sum _{J\subset I} P_J(x_J) $
, where
![]() $ P_J:V^J\to {\mathbb {F}} $
is multilinear for all
$ P_J:V^J\to {\mathbb {F}} $
is multilinear for all
![]() $ J\subset I. $
By abuse of notation, we will also denote by P the function
$ J\subset I. $
By abuse of notation, we will also denote by P the function
![]() $V^{[k]}\to {\mathbb {F}} $
given by
$V^{[k]}\to {\mathbb {F}} $
given by
![]() $ x\mapsto P(x_I).$
$ x\mapsto P(x_I).$
Definition 2.8.
P is called full if
![]() $P_I \neq 0.$
We denote by
$P_I \neq 0.$
We denote by
![]() $\tilde P = P_I$
the multilinear part of
$\tilde P = P_I$
the multilinear part of
![]() $P.$
$P.$
In [Reference Naslund22], a notion of rank for multilinear functions is defined, called partition rank.
Definition 2.9. Let
![]() $ P:V^I\to {\mathbb {F}} $
be a multilinear function. The partition rank of P is the minimal length of a presentation
$ P:V^I\to {\mathbb {F}} $
be a multilinear function. The partition rank of P is the minimal length of a presentation
![]() $ P(x) = \sum _{i=1}^r Q_i(x_{I_i})R_i(x_{I\setminus I_i}), $
where
$ P(x) = \sum _{i=1}^r Q_i(x_{I_i})R_i(x_{I\setminus I_i}), $
where
![]() $ \emptyset \neq I_i \subsetneq I$
and
$ \emptyset \neq I_i \subsetneq I$
and
![]() $ Q_i:V^{I_i}\to {\mathbb {F}},\ R_i:V^{I\setminus I_i}\to {\mathbb {F}} $
are multilinear for all
$ Q_i:V^{I_i}\to {\mathbb {F}},\ R_i:V^{I\setminus I_i}\to {\mathbb {F}} $
are multilinear for all
![]() $ i\in [r]. $
We write
$ i\in [r]. $
We write
![]() $ r = prk(P). $
We extend this definition to full multiaffine maps via
$ r = prk(P). $
We extend this definition to full multiaffine maps via
![]() $ prk(Q) = prk(\tilde Q). $
$ prk(Q) = prk(\tilde Q). $
The bias of P on
![]() $ V^{[k]} $
is defined as before, but it has some interesting properties when
$ V^{[k]} $
is defined as before, but it has some interesting properties when
![]() $P:V^I\to {\mathbb {F}} $
is multilinear. Writing
$P:V^I\to {\mathbb {F}} $
is multilinear. Writing
![]() $P(x) = A(x_{I\setminus \{i_0\}})\cdot x_{i_0}$
, where
$P(x) = A(x_{I\setminus \{i_0\}})\cdot x_{i_0}$
, where
![]() $A:V^{I\setminus \{i_0\}}\to V_{i_0} $
is multilinear for some
$A:V^{I\setminus \{i_0\}}\to V_{i_0} $
is multilinear for some
![]() $ i_0\in [k],$
Fourier analysis yields
$ i_0\in [k],$
Fourier analysis yields
where
![]() $ \mathbb P_{x\in E} (T):= \frac {|T|}{|E|} $
for a subset
$ \mathbb P_{x\in E} (T):= \frac {|T|}{|E|} $
for a subset
![]() $ T\subset E. $
In particular, the character sum above is always positive and does not depend on our choice of character
$ T\subset E. $
In particular, the character sum above is always positive and does not depend on our choice of character
![]() $ \chi. $
It is not too difficult to show that multilinear maps with low partition rank exhibit significant bias (see [Reference Kazhdan and Ziegler14, Reference Lovett19]).
$ \chi. $
It is not too difficult to show that multilinear maps with low partition rank exhibit significant bias (see [Reference Kazhdan and Ziegler14, Reference Lovett19]).
Claim 2.10 (Low partition rank implies bias).
If
![]() $ P:V^I\to {\mathbb {F}} $
is multilinear with
$ P:V^I\to {\mathbb {F}} $
is multilinear with
![]() $ prk(P) =r $
, then
$ prk(P) =r $
, then
In [Reference Milićević21], the following (much more difficult) inequality was proved in the other direction:
Theorem 2.11 (Bias implies low partition rank).
Let
![]() $ {\mathbb {F}} $
be a finite field and
$ {\mathbb {F}} $
be a finite field and
![]() $0\le d < char({\mathbb {F}}).$
Suppose
$0\le d < char({\mathbb {F}}).$
Suppose
![]() $ P:V^I\to {\mathbb {F}}$
is multilinear with
$ P:V^I\to {\mathbb {F}}$
is multilinear with
![]() $ |I|\le d $
and
$ |I|\le d $
and
![]() $ bias(P) \ge q^{-s}.$
Then
$ bias(P) \ge q^{-s}.$
Then
where
![]() $ A=A(d),B=B(d) $
are constants.
$ A=A(d),B=B(d) $
are constants.
This result immediately extends to full multiaffine maps because a short calculation in [Reference Lovett26] (which we will follow in Lemma 4.2) shows that
and by definition, they have the same partition rank. We now make the corresponding relative definitions for full multiaffine maps.
Definition 2.12.
-
1. Let
 $ {\mathcal Q}=(Q_i:V^{I_i}\to {\mathbb {F}})_{i\in [m]} $
and
$ {\mathcal Q}=(Q_i:V^{I_i}\to {\mathbb {F}})_{i\in [m]} $
and
 $ P:V^I\to {\mathbb {F}} $
be multilinear maps. The partition rank of P relative to
$ P:V^I\to {\mathbb {F}} $
be multilinear maps. The partition rank of P relative to
 ${\mathcal Q}$
is If
${\mathcal Q}$
is If $$\begin{align*}prk_{\mathcal Q} (P) = \min \left\lbrace prk\left( P-\sum_{i\in[m],I_i\subset I} Q_i(x_{I_i})R_i(x_{I\setminus I_i}) \right) :\ R_i\ \text{are multilinear}\right\rbrace. \end{align*}$$
$$\begin{align*}prk_{\mathcal Q} (P) = \min \left\lbrace prk\left( P-\sum_{i\in[m],I_i\subset I} Q_i(x_{I_i})R_i(x_{I\setminus I_i}) \right) :\ R_i\ \text{are multilinear}\right\rbrace. \end{align*}$$
 $ P,{\mathcal Q} $
are full multiaffine, we define
$ P,{\mathcal Q} $
are full multiaffine, we define
 $ prk_{\mathcal Q} (P) = prk_{\tilde {\mathcal {Q}}} (\tilde P). $
$ prk_{\mathcal Q} (P) = prk_{\tilde {\mathcal {Q}}} (\tilde P). $
-
2. The partition rank of a collection of multilinear maps
 $ \mathcal P = (P_i:V^I\to {\mathbb {F}})_{i\in [c]} $
relative to
$ \mathcal P = (P_i:V^I\to {\mathbb {F}})_{i\in [c]} $
relative to
 $ {\mathcal Q} $
is If
$ {\mathcal Q} $
is If $$\begin{align*}prk_{\mathcal Q} (\mathcal P) = \min \left\lbrace prk_{\mathcal Q} \left( a\cdot\mathcal P \right):\ 0\neq\textbf{a}\in{\mathbb{F}}^c \right\rbrace. \end{align*}$$
$$\begin{align*}prk_{\mathcal Q} (\mathcal P) = \min \left\lbrace prk_{\mathcal Q} \left( a\cdot\mathcal P \right):\ 0\neq\textbf{a}\in{\mathbb{F}}^c \right\rbrace. \end{align*}$$
 $ \mathcal P,{\mathcal Q} $
are full multiaffine with all maps in
$ \mathcal P,{\mathcal Q} $
are full multiaffine with all maps in
 ${\mathcal P}$
defined on a fixed index set
${\mathcal P}$
defined on a fixed index set
 $ I, $
set
$ I, $
set
 $ prk_{\mathcal Q} (\mathcal P) = prk_{\tilde {\mathcal {Q}}} (\tilde {\mathcal {P}}). $
$ prk_{\mathcal Q} (\mathcal P) = prk_{\tilde {\mathcal {Q}}} (\tilde {\mathcal {P}}). $
-
3. A tower
is composed of h collections of full multiaffine functions $$\begin{align*}{\mathcal Q} = ({\mathcal Q}_i)_{i\in [h]} \end{align*}$$
$$\begin{align*}{\mathcal Q} = ({\mathcal Q}_i)_{i\in [h]} \end{align*}$$
 $ {\mathcal Q}_i = (Q_{i,j}:V^{I_i}\to {\mathbb {F}})_{j\in [m_i]}, $
which we call layers. The associated multilinear tower is
$ {\mathcal Q}_i = (Q_{i,j}:V^{I_i}\to {\mathbb {F}})_{j\in [m_i]}, $
which we call layers. The associated multilinear tower is
 $\tilde {\mathcal {Q}} = (\tilde {\mathcal {Q}}_i)_{i\in [h]}.$
We say the tower is multilinear if
$\tilde {\mathcal {Q}} = (\tilde {\mathcal {Q}}_i)_{i\in [h]}.$
We say the tower is multilinear if
 $\tilde {\mathcal {Q}} = {\mathcal Q}.$
The degree of the tower is
$\tilde {\mathcal {Q}} = {\mathcal Q}.$
The degree of the tower is
 $\max _i |I_i|,$
and the height of the tower is
$\max _i |I_i|,$
and the height of the tower is
 $h.$
The dimension of the tower is
$h.$
The dimension of the tower is
 $m = m_1+\ldots +m_h.$
For
$m = m_1+\ldots +m_h.$
For
 $i\in [h],$
we denote the truncated tower by
$i\in [h],$
we denote the truncated tower by
 $ {\mathcal Q}_{<i} = ({\mathcal Q}_j)_{j\in [i-1]}. $
$ {\mathcal Q}_{<i} = ({\mathcal Q}_j)_{j\in [i-1]}. $
-
4. Let
 $A,B,s>0.$
We say that
$A,B,s>0.$
We say that
 ${\mathcal Q}$
is
${\mathcal Q}$
is
 $(A,B,s)$
-regular if for each
$(A,B,s)$
-regular if for each
 $i\in [h]$
, we have
$i\in [h]$
, we have  $$\begin{align*}prk_{{\mathcal Q}_{<i}}({\mathcal Q}_i)>A\left(m_i+m_{i+1}+\ldots+m_h+s\right)^B. \end{align*}$$
$$\begin{align*}prk_{{\mathcal Q}_{<i}}({\mathcal Q}_i)>A\left(m_i+m_{i+1}+\ldots+m_h+s\right)^B. \end{align*}$$
Our main theorem for full multiaffine maps is
Theorem 2.13 (Relative bias implies low relative rank (d,H)).
There exist constants
![]() $A(d,H),B(d,H)$
, such that if
$A(d,H),B(d,H)$
, such that if
![]() $ P:V^I\to {\mathbb {F}}$
is a full multiaffine map with
$ P:V^I\to {\mathbb {F}}$
is a full multiaffine map with
![]() $|I|\le d$
,
$|I|\le d$
,
![]() ${\mathcal Q}$
is a tower on
${\mathcal Q}$
is a tower on
![]() $V^{[k]}$
of degree
$V^{[k]}$
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
, such that:
$\le H$
, such that:
-
1.
 $bias_{Z({\mathcal Q})} (P) \ge q^{-s}$
and
$bias_{Z({\mathcal Q})} (P) \ge q^{-s}$
and -
2.
 ${\mathcal Q}$
is
${\mathcal Q}$
is
 $(A,B,s)$
-regular,
$(A,B,s)$
-regular,
then
![]() $rk_{\mathcal Q} (P) \le A(1+s)^B.$
$rk_{\mathcal Q} (P) \le A(1+s)^B.$
We will also prove a relative version of Claim 2.10.
Claim 2.14 (Low relative rank implies relative bias).
There exist constants
![]() $A(d,H), B(d,H)$
, such that if
$A(d,H), B(d,H)$
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $(A,B,s)$
-regular multilinear tower on
$(A,B,s)$
-regular multilinear tower on
![]() $V^{[k]}$
of degree
$V^{[k]}$
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
and
$\le H$
and
![]() $P:V^I\to {\mathbb {F}}$
with
$P:V^I\to {\mathbb {F}}$
with
![]() $|I| \le d$
is multilinear with
$|I| \le d$
is multilinear with
![]() $rk_{\mathcal Q} (P) \le r,$
then
$rk_{\mathcal Q} (P) \le r,$
then
-
1.
 $Re[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))] \ge q^{-r}-q^{-s}$
and
$Re[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))] \ge q^{-r}-q^{-s}$
and -
2.
 $|Im[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))]| \le q^{-s}.$
$|Im[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))]| \le q^{-s}.$
Let us now give a high-level sketch of the proof of Theorem 2.13. This will proceed by induction on
![]() $d,$
where the base case
$d,$
where the base case
![]() $ d = 1 $
follows from basic Fourier analysis. Assuming the theorem holds at degree
$ d = 1 $
follows from basic Fourier analysis. Assuming the theorem holds at degree
![]() $ d, $
we present some useful consequences in Section 3 and make some reductions in Section 4. After these reductions, the task at hand is to prove the theorem for multilinear
$ d, $
we present some useful consequences in Section 3 and make some reductions in Section 4. After these reductions, the task at hand is to prove the theorem for multilinear
![]() $ P:V^{[d+1]}\to {\mathbb {F}} $
and a multilinear tower
$ P:V^{[d+1]}\to {\mathbb {F}} $
and a multilinear tower
![]() $ {\mathcal Q} $
on
$ {\mathcal Q} $
on
![]() $ V^{[d+1]} $
of degree
$ V^{[d+1]} $
of degree
![]() $ \le d. $
In Section 5, we show that there are many “derived” towers
$ \le d. $
In Section 5, we show that there are many “derived” towers
![]() $ {\mathcal Q}_t $
and multilinear functions
$ {\mathcal Q}_t $
and multilinear functions
![]() $ \phi _t:V^{[d]}\to {\mathbb {F}}^{100s} $
, such that P vanishes
$ \phi _t:V^{[d]}\to {\mathbb {F}}^{100s} $
, such that P vanishes
![]() $ q^{-s} $
-a.e. on the variety
$ q^{-s} $
-a.e. on the variety
![]() $ Z({\mathcal Q}_t)\cap \{\phi _t(x_{[d]}) = 0\}. $
This is similar in spirit to previous work on this subject, but the derived towers appearing here present a new challenge. In Section 6, we pause to describe the relative regularization process, which is the multilinear analogue of Theorem 2.3. In Section 7, the regularization process is applied to the collections
$ Z({\mathcal Q}_t)\cap \{\phi _t(x_{[d]}) = 0\}. $
This is similar in spirit to previous work on this subject, but the derived towers appearing here present a new challenge. In Section 6, we pause to describe the relative regularization process, which is the multilinear analogue of Theorem 2.3. In Section 7, the regularization process is applied to the collections
![]() $ {\mathcal Q}_t,\phi _t $
to obtain regular varieties on which P vanishes
$ {\mathcal Q}_t,\phi _t $
to obtain regular varieties on which P vanishes
![]() $ q^{-s} $
-a.e. In that section, we also show that this means that P vanishes identically on them, similarly to proposition 5.1 in [Reference Green and Tao10]. A key novel step in our proof consists in then showing that these varieties can be “summed” to obtain a single tower
$ q^{-s} $
-a.e. In that section, we also show that this means that P vanishes identically on them, similarly to proposition 5.1 in [Reference Green and Tao10]. A key novel step in our proof consists in then showing that these varieties can be “summed” to obtain a single tower
![]() $ \mathcal R $
of dimension
$ \mathcal R $
of dimension
![]() $ \le A(1+s)^B $
, such that
$ \le A(1+s)^B $
, such that
![]() $ P\restriction _{Z({\mathcal Q}\cup \mathcal R)} \equiv 0$
and
$ P\restriction _{Z({\mathcal Q}\cup \mathcal R)} \equiv 0$
and
![]() $ {\mathcal Q}\cup \mathcal R $
is regular. In Section 8, we prove a Nullstellensatz which allows us to conclude that
$ {\mathcal Q}\cup \mathcal R $
is regular. In Section 8, we prove a Nullstellensatz which allows us to conclude that
![]() $ rk_{{\mathcal Q}\cup \mathcal R} (P) = 0$
, so
$ rk_{{\mathcal Q}\cup \mathcal R} (P) = 0$
, so
![]() $ rk_{\mathcal Q} (P) \le \dim (\mathcal R) \le A(1+s)^B,$
which completes the inductive step.
$ rk_{\mathcal Q} (P) \le \dim (\mathcal R) \le A(1+s)^B,$
which completes the inductive step.
3 Some equidistribution lemmas
As mentioned before, the proof of Theorem 2.13 will proceed by induction on d, and the base case
![]() $ d=1 $
follows from Fourier analysis. For the purposes of the inductive argument, it will be useful to formulate a version of Theorem 2.13 with an auxiliary parameter, which we now do.
$ d=1 $
follows from Fourier analysis. For the purposes of the inductive argument, it will be useful to formulate a version of Theorem 2.13 with an auxiliary parameter, which we now do.
Theorem 3.1 (Relative bias implies low relative rank (d,H,l)).
There exist constants
![]() $A(d,H,l),B(d,H,l)$
, such that if
$A(d,H,l),B(d,H,l)$
, such that if
![]() $ P:V^I\to {\mathbb {F}}$
is a full multiaffine map with
$ P:V^I\to {\mathbb {F}}$
is a full multiaffine map with
![]() $|I|\le d$
,
$|I|\le d$
,
![]() ${\mathcal Q}$
is a tower on
${\mathcal Q}$
is a tower on
![]() $V^{[k]}$
of degree
$V^{[k]}$
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
, such that:
$\le H$
, such that:
-
1.
 $bias_{Z({\mathcal Q})} (P) \ge q^{-s},$
$bias_{Z({\mathcal Q})} (P) \ge q^{-s},$
-
2.
 ${\mathcal Q}$
is
${\mathcal Q}$
is
 $(A,B,s)$
-regular, and
$(A,B,s)$
-regular, and -
3.
 $ {\mathcal Q}_{\le H-l} $
is of degree
$ {\mathcal Q}_{\le H-l} $
is of degree
 $ <d,$
$ <d,$
then
![]() $rk_{\mathcal Q} (P) \le A(1+s)^B.$
$rk_{\mathcal Q} (P) \le A(1+s)^B.$
Theorem 2.13 corresponds, of course, to the case
![]() $ l=H. $
We call
$ l=H. $
We call
![]() $ {\mathcal Q} $
as above a tower of type (d,H,l) for short. In this section, we assume Theorem 3.1(d,H,l) holds and explore some of its useful consequences. We warm up with the following simple but important result.
$ {\mathcal Q} $
as above a tower of type (d,H,l) for short. In this section, we assume Theorem 3.1(d,H,l) holds and explore some of its useful consequences. We warm up with the following simple but important result.
Lemma 3.2 (Regular varieties are of the expected size (d,H+1,l+1)).
There exist constants
![]() $A(d,H,l),B(d,H,l)$
, such that for any
$A(d,H,l),B(d,H,l)$
, such that for any
![]() $s>0$
and for any
$s>0$
and for any
![]() $(A,B,s)$
-regular tower
$(A,B,s)$
-regular tower
![]() ${\mathcal Q}$
on
${\mathcal Q}$
on
![]() $V^{[k]}$
of type (d,h,l+1) and dimension
$V^{[k]}$
of type (d,h,l+1) and dimension
![]() $m,$
we have
$m,$
we have
 $$\begin{align*}\left|q^m \frac{|Z({\mathcal Q})|}{|V^{[k]}|}-1\right|\le q^{-s}. \end{align*}$$
$$\begin{align*}\left|q^m \frac{|Z({\mathcal Q})|}{|V^{[k]}|}-1\right|\le q^{-s}. \end{align*}$$
Proof. Let
![]() $A',B'$
be the constants from Theorem 3.1(d,H,l). If
$A',B'$
be the constants from Theorem 3.1(d,H,l). If
![]() $A, B$
are sufficiently large depending on
$A, B$
are sufficiently large depending on
![]() $ A',B' $
, then
$ A',B' $
, then
![]() ${\mathcal Q}$
is
${\mathcal Q}$
is
![]() $(A',B',s+H+2)$
- regular. So for any
$(A',B',s+H+2)$
- regular. So for any
![]() $i\in [H+1]$
the tower
$i\in [H+1]$
the tower
![]() ${\mathcal Q}_{<i}$
is
${\mathcal Q}_{<i}$
is
![]() $(A',B',s+H+m_i)$
-regular of type (d,H,l) and
$(A',B',s+H+m_i)$
-regular of type (d,H,l) and
By Theorem 3.1, it follows that for any
![]() $0\neq a\in {\mathbb {F}}^{m_i}$
, we have
$0\neq a\in {\mathbb {F}}^{m_i}$
, we have
Fourier analysis yields
 $$\begin{align*}q^{m_i}\frac{|Z({\mathcal Q}_{\le i})|}{|Z({\mathcal Q}_{<i})|} = \sum_{a\in {\mathbb{F}}^{m_i}}{\mathbb E}_{x\in Z({\mathcal Q}_{<i})} \chi( a\cdot {\mathcal Q}_i(x)) = 1+e_i, \end{align*}$$
$$\begin{align*}q^{m_i}\frac{|Z({\mathcal Q}_{\le i})|}{|Z({\mathcal Q}_{<i})|} = \sum_{a\in {\mathbb{F}}^{m_i}}{\mathbb E}_{x\in Z({\mathcal Q}_{<i})} \chi( a\cdot {\mathcal Q}_i(x)) = 1+e_i, \end{align*}$$
where
![]() $|e_i|\le q^{-(s+H+1)}.$
Then we multiply to get
$|e_i|\le q^{-(s+H+1)}.$
Then we multiply to get
 $$\begin{align*}\frac{|Z({\mathcal Q})|}{|V^{[k]}|} = \prod_{i\in[H+1]}\frac{|Z({\mathcal Q}_{\le i})|}{|Z({\mathcal Q}_{<i})|} = \prod_{i\in[H+1]} (1+e_i) q^{-m_i} = (1+e)q^{-m}, \end{align*}$$
$$\begin{align*}\frac{|Z({\mathcal Q})|}{|V^{[k]}|} = \prod_{i\in[H+1]}\frac{|Z({\mathcal Q}_{\le i})|}{|Z({\mathcal Q}_{<i})|} = \prod_{i\in[H+1]} (1+e_i) q^{-m_i} = (1+e)q^{-m}, \end{align*}$$
where
![]() $|e|\le q^{-s}.$
$|e|\le q^{-s}.$
We now introduce some notation. For a tower
![]() ${\mathcal Q}$
on
${\mathcal Q}$
on
![]() $V^{[k]}$
and a subset
$V^{[k]}$
and a subset
![]() $I\subset [k],$
we write
$I\subset [k],$
we write
![]() $ {{\mathcal Q}_I = ({\mathcal Q}_i)_{i\in [h],I_i\subset I} }$
for the restriction to a tower on
$ {{\mathcal Q}_I = ({\mathcal Q}_i)_{i\in [h],I_i\subset I} }$
for the restriction to a tower on
![]() $ V^I. $
Similarly, we define
$ V^I. $
Similarly, we define
![]() $ Z({\mathcal Q})_I = Z({\mathcal Q}_I) \subset V^I.$
For
$ Z({\mathcal Q})_I = Z({\mathcal Q}_I) \subset V^I.$
For
![]() $y\in V^I$
and a full multiaffine function
$y\in V^I$
and a full multiaffine function
![]() $ Q:V^J\to {\mathbb {F}}, $
the full multiaffine function
$ Q:V^J\to {\mathbb {F}}, $
the full multiaffine function
![]() $Q(y):V^{J\setminus I}\to {\mathbb {F}} $
is defined by
$Q(y):V^{J\setminus I}\to {\mathbb {F}} $
is defined by
![]() $ Q(y)(z)=Q(y_{I\cap J},z). $
Set
$ Q(y)(z)=Q(y_{I\cap J},z). $
Set
![]() $ {\mathcal Q}(y) = ({\mathcal Q}_i(y))_{i\in [h]} $
for the tower induced on
$ {\mathcal Q}(y) = ({\mathcal Q}_i(y))_{i\in [h]} $
for the tower induced on
![]() $ V^{[k]\setminus I}, $
where
$ V^{[k]\setminus I}, $
where
![]() $ {\mathcal Q}_i(y) = (Q_{i,j}(y):V^{I_i\setminus I}\to {\mathbb {F}})_{j\in [m_i]}. $
For the zero locus, we write
$ {\mathcal Q}_i(y) = (Q_{i,j}(y):V^{I_i\setminus I}\to {\mathbb {F}})_{j\in [m_i]}. $
For the zero locus, we write
![]() $ Z({\mathcal Q}) (y) = Z({\mathcal Q}(y))$
.
$ Z({\mathcal Q}) (y) = Z({\mathcal Q}(y))$
.
We now state several interrelated lemmas.
Lemma 3.3 (Derivatives(d,H+1,l+1)).
For any
![]() $C,D$
, there exist constants
$C,D$
, there exist constants
![]() $A(C,D,d,H,l)$
,
$A(C,D,d,H,l)$
,
![]() $B(C,D,d,H,l)$
, such that if
$B(C,D,d,H,l)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular tower on
$(A,B,s)$
-regular tower on
![]() $V^{[k]}$
of type (d,H+1,l+1) and
$V^{[k]}$
of type (d,H+1,l+1) and
![]() $I\subset [k],$
then for
$I\subset [k],$
then for
![]() $q^{-s}$
-a.e.
$q^{-s}$
-a.e.
![]() $y\in Z({\mathcal Q})_I$
, the tower
$y\in Z({\mathcal Q})_I$
, the tower
![]() ${\mathcal Q}(y)$
on
${\mathcal Q}(y)$
on
![]() $ V^{[k]\setminus I} $
is
$ V^{[k]\setminus I} $
is
![]() $(C,D,s)$
-regular.
$(C,D,s)$
-regular.
Lemma 3.4 (Fubini(d,H+1,l+1)).
There exist constants
![]() $A(d,H,l),B(d,H,l)$
, such that if
$A(d,H,l),B(d,H,l)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular tower on
$(A,B,s)$
-regular tower on
![]() $ V^{[k]} $
of type (d,H+1,l+1),
$ V^{[k]} $
of type (d,H+1,l+1),
![]() $ I\subset [k] $
and
$ I\subset [k] $
and
![]() $g:V^{[k]}\to {\mathbb C}$
satisfies
$g:V^{[k]}\to {\mathbb C}$
satisfies
![]() $ |g(x)|\le 1 $
for all
$ |g(x)|\le 1 $
for all
![]() $ x\in V^{[k]} $
, then
$ x\in V^{[k]} $
, then
Lemma 3.5 (Rank-bias(d,H+1,l+1)).
There exist constants
![]() $A(d,H,l), B(d,H,l)$
, such that if
$A(d,H,l), B(d,H,l)$
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $(A,B,s)$
-regular multilinear tower on
$(A,B,s)$
-regular multilinear tower on
![]() $V^{[k]}$
of type (d,H+1,l+1) and
$V^{[k]}$
of type (d,H+1,l+1) and
![]() $P:V^I\to {\mathbb {F}}$
is a multilinear map with
$P:V^I\to {\mathbb {F}}$
is a multilinear map with
![]() $|I| \le d+1$
, then
$|I| \le d+1$
, then
-
1.
 $|Im[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))]| \le q^{-s}$
and
$|Im[{\mathbb E}_{x\in Z({\mathcal Q})} \chi (P(x))]| \le q^{-s}$
and -
2. if
 $rk_{\mathcal Q} (P) = r,$
then
$rk_{\mathcal Q} (P) = r,$
then  $$\begin{align*}Re[{\mathbb E}_{x\in Z({\mathcal Q})} \chi(P(x))] \ge q^{-r}-q^{-s}. \end{align*}$$
$$\begin{align*}Re[{\mathbb E}_{x\in Z({\mathcal Q})} \chi(P(x))] \ge q^{-r}-q^{-s}. \end{align*}$$
The above lemmas will be proved together by induction on the height. The implications, assuming Theorem 3.1(d,H,l) throughout, are as follows
In the base case of height
![]() $0,$
where the tower is empty, Lemmas 3.3 and 3.4 are trivial and Lemma 3.5 is proved in [Reference Kazhdan and Ziegler14, Reference Lovett19]. We assume in the proofs that the tower is indeed of height
$0,$
where the tower is empty, Lemmas 3.3 and 3.4 are trivial and Lemma 3.5 is proved in [Reference Kazhdan and Ziegler14, Reference Lovett19]. We assume in the proofs that the tower is indeed of height
![]() $H+1,$
otherwise we are done by the inductive hypothesis.
$H+1,$
otherwise we are done by the inductive hypothesis.
Proof of Lemma 3.3 (Derivatives(d,H+1,l+1)).
We are interested in the regularity of
![]() ${\mathcal Q}(y),$
which is, by definition, the regularity of its associated multilinear tower. Which multilinear maps appear? For
${\mathcal Q}(y),$
which is, by definition, the regularity of its associated multilinear tower. Which multilinear maps appear? For
![]() $ Q_{i,j}\in {\mathcal Q}_i ,$
write
$ Q_{i,j}\in {\mathcal Q}_i ,$
write
![]() $Q_{i,j} = \sum _{J\subset I_i} Q_{i,j}^J$
as a sum of multilinear maps
$Q_{i,j} = \sum _{J\subset I_i} Q_{i,j}^J$
as a sum of multilinear maps
![]() $ Q_{i,j}^J:V^J\to {\mathbb {F}}, $
and set
$ Q_{i,j}^J:V^J\to {\mathbb {F}}, $
and set
![]() $Q^{\prime }_{i,j} = \sum _{I_i\setminus I\subset J\subset I_i} Q_{i,j}^J$
,
$Q^{\prime }_{i,j} = \sum _{I_i\setminus I\subset J\subset I_i} Q_{i,j}^J$
,
![]() ${\mathcal Q}^{\prime }_i = \{Q^{\prime }_{i,j}\}_{j\in m_i}.$
Note that the following properties hold:
${\mathcal Q}^{\prime }_i = \{Q^{\prime }_{i,j}\}_{j\in m_i}.$
Note that the following properties hold:
-
1.
 ${\mathcal Q},{\mathcal Q}'$
have the same associated multilinear variety (and hence the same regularity),
${\mathcal Q},{\mathcal Q}'$
have the same associated multilinear variety (and hence the same regularity), -
2.
 $Z({\mathcal Q}')_I = Z({\mathcal Q})_I$
, and
$Z({\mathcal Q}')_I = Z({\mathcal Q})_I$
, and -
3. for any
 $y\in Z({\mathcal Q})_I,$
the multilinear tower associated with
$y\in Z({\mathcal Q})_I,$
the multilinear tower associated with
 ${\mathcal Q}(y)$
is
${\mathcal Q}(y)$
is
 ${\mathcal Q}'(y).$
${\mathcal Q}'(y).$
So after replacing
![]() ${\mathcal Q}$
with
${\mathcal Q}$
with
![]() ${\mathcal Q}'$
, we can assume without loss of generality that
${\mathcal Q}'$
, we can assume without loss of generality that
![]() ${\mathcal Q}(y)$
is a multilinear tower for any
${\mathcal Q}(y)$
is a multilinear tower for any
![]() $y\in Z({\mathcal Q}_I).$
Write
$y\in Z({\mathcal Q}_I).$
Write
![]() $X=Z({\mathcal Q})$
for short. Let
$X=Z({\mathcal Q})$
for short. Let
![]() $ A',B' $
be the constants of Lemma 3.3 at height
$ A',B' $
be the constants of Lemma 3.3 at height
![]() $H.$
We deal separately with two cases.
$H.$
We deal separately with two cases.
The first case (and the easier one) is when
![]() $I_{H+1}\subset I.$
In this case, for any
$I_{H+1}\subset I.$
In this case, for any
![]() $y\in (X_I)_{<H+1}$
, we have
$y\in (X_I)_{<H+1}$
, we have
![]() ${\mathcal Q}(y) = {\mathcal Q}_{<H+1}(y).$
For
${\mathcal Q}(y) = {\mathcal Q}_{<H+1}(y).$
For
![]() $A = 2^{B'}A'$
,
$A = 2^{B'}A'$
,
![]() $B=B',$
we get that
$B=B',$
we get that
![]() ${\mathcal Q}_{<H+1}$
is
${\mathcal Q}_{<H+1}$
is
![]() $(A',B',s+m_{H+1}+1)$
-regular. Then by the inductive hypothesis, we have that for
$(A',B',s+m_{H+1}+1)$
-regular. Then by the inductive hypothesis, we have that for
![]() $q^{-(s+m_{H+1}+1)}$
a.e.
$q^{-(s+m_{H+1}+1)}$
a.e.
![]() $y\in (X_I)_{<H+1}$
, the tower
$y\in (X_I)_{<H+1}$
, the tower
![]() ${\mathcal Q}(y)={\mathcal Q}_{<H+1}(y)$
is
${\mathcal Q}(y)={\mathcal Q}_{<H+1}(y)$
is
![]() $(C,D,s)$
-regular. By Lemma 3.2, we know that if
$(C,D,s)$
-regular. By Lemma 3.2, we know that if
![]() $A,B$
are sufficiently large, then
$A,B$
are sufficiently large, then
![]() $\frac {|(X_I)_{<H+1}|}{|X_I|} \le q^{m_{H+1}+1}.$
Therefore,
$\frac {|(X_I)_{<H+1}|}{|X_I|} \le q^{m_{H+1}+1}.$
Therefore,
![]() ${\mathcal Q}(y)$
is regular for
${\mathcal Q}(y)$
is regular for
![]() $q^{-s}$
-a.e.
$q^{-s}$
-a.e.
![]() $y\in X_I,$
as desired.
$y\in X_I,$
as desired.
The second case is when
![]() $I_{H+1} \not \subset I.$
In this case, we have
$I_{H+1} \not \subset I.$
In this case, we have
![]() $X_I = (X_I)_{<H+1}.$
If
$X_I = (X_I)_{<H+1}.$
If
![]() $A,B$
are sufficiently large, then
$A,B$
are sufficiently large, then
![]() ${\mathcal Q}$
is
${\mathcal Q}$
is
![]() $(A',B',100C(m_{H+1}+s)^D)$
-regular. Let
$(A',B',100C(m_{H+1}+s)^D)$
-regular. Let
For the rest of this proof, we will assume, wherever needed, that
![]() $ A,B,A',B',C,D $
are sufficiently large with respect to
$ A,B,A',B',C,D $
are sufficiently large with respect to
![]() $ d,h,l.$
By the inductive hypothesis, we have that for
$ d,h,l.$
By the inductive hypothesis, we have that for
![]() $\varepsilon $
-a.e.
$\varepsilon $
-a.e.
![]() $y\in X_I$
, the tower
$y\in X_I$
, the tower
![]() ${\mathcal Q}_{<H+1}(y)$
is
${\mathcal Q}_{<H+1}(y)$
is
![]() $(C,D,s')$
-regular. By a union bound, it is enough to show that for
$(C,D,s')$
-regular. By a union bound, it is enough to show that for
![]() $ q^{-(s+1)} $
-a.e.
$ q^{-(s+1)} $
-a.e.
![]() $y\in X_I$
, we have
$y\in X_I$
, we have
Fix
![]() $0\neq a\in {\mathbb {F}}^{m_{H+1}}.$
Applying Theorem 3.1, we have
$0\neq a\in {\mathbb {F}}^{m_{H+1}}.$
Applying Theorem 3.1, we have
Lemma 3.4 at height H yields
![]() $ {\mathbb E}_{y\in X_I} Re \left [ {\mathbb E}_{z\in X_{<H+1}(y)}\chi (Q(y,z)) \right ] \le 2\varepsilon. $
For
$ {\mathbb E}_{y\in X_I} Re \left [ {\mathbb E}_{z\in X_{<H+1}(y)}\chi (Q(y,z)) \right ] \le 2\varepsilon. $
For
![]() $ \varepsilon $
-a.e.
$ \varepsilon $
-a.e.
![]() $ y\in X_I $
, we can apply Lemma 3.5 at height H to get
$ y\in X_I $
, we can apply Lemma 3.5 at height H to get
Therefore,
By Markov’s inequality, this means that for
![]() $2\sqrt {\varepsilon }$
-a.e.
$2\sqrt {\varepsilon }$
-a.e.
![]() $y\in X_I,$
we have
$y\in X_I,$
we have
Then, for
![]() $3\sqrt {\varepsilon }$
-a.e.
$3\sqrt {\varepsilon }$
-a.e.
![]() $y\in X_I$
, both the above inequality holds and the tower
$y\in X_I$
, both the above inequality holds and the tower
![]() ${\mathcal Q}^{<H+1}(y)$
is
${\mathcal Q}^{<H+1}(y)$
is
![]() $(C,D,s')$
-regular. Let
$(C,D,s')$
-regular. Let
![]() $r_a(y) = rk_{{\mathcal Q}^{<H+1}(y)} (a\cdot {\mathcal Q}_{H+1}(y)).$
Applying Lemma 3.5 at height H, we find that for these y, we have
$r_a(y) = rk_{{\mathcal Q}^{<H+1}(y)} (a\cdot {\mathcal Q}_{H+1}(y)).$
Applying Lemma 3.5 at height H, we find that for these y, we have
which implies
![]() $r_a(y)>C(m_{H+1}+s)^D.$
Running over all
$r_a(y)>C(m_{H+1}+s)^D.$
Running over all
![]() $0\neq a\in {\mathbb {F}}^{m_{H+1}},$
we get that for
$0\neq a\in {\mathbb {F}}^{m_{H+1}},$
we get that for
![]() $3\sqrt {\varepsilon }q^{m_{H+1}}\le q^{-(s+1)}$
-a.e.
$3\sqrt {\varepsilon }q^{m_{H+1}}\le q^{-(s+1)}$
-a.e.
![]() $y\in X_I$
, we have
$y\in X_I$
, we have
![]() $ r(y)> C(m_{H+1}+s)^D$
, where
$ r(y)> C(m_{H+1}+s)^D$
, where
![]() $ r(y) = \max _{0\neq a\in {\mathbb {F}}^{m_{H+1}}} r_a(y). $
This completes the proof.
$ r(y) = \max _{0\neq a\in {\mathbb {F}}^{m_{H+1}}} r_a(y). $
This completes the proof.
Proof of Lemma 3.4 Fubini(d,H+1,l+1).
By the triangle inequality,
 $$\begin{align*}\left| {\mathbb E}_{x\in X}g(x) - {\mathbb E}_{y\in X _I}{\mathbb E}_{z\in X(y)}g(y,z) \right| \le {\mathbb E}_{y\in X _I} \left| \frac{|X _I|\cdot |X(y)|}{|X|} - 1 \right|. \end{align*}$$
$$\begin{align*}\left| {\mathbb E}_{x\in X}g(x) - {\mathbb E}_{y\in X _I}{\mathbb E}_{z\in X(y)}g(y,z) \right| \le {\mathbb E}_{y\in X _I} \left| \frac{|X _I|\cdot |X(y)|}{|X|} - 1 \right|. \end{align*}$$
Denoting
![]() $ f(y) = \frac {|X _I|\cdot |X(y)|}{|X|},\ \varepsilon = q^{-(s+2)}, $
and assuming
$ f(y) = \frac {|X _I|\cdot |X(y)|}{|X|},\ \varepsilon = q^{-(s+2)}, $
and assuming
![]() $ A,B $
are sufficiently large, we note the following:
$ A,B $
are sufficiently large, we note the following:
-
1.
 $ f(y) \ge 0$
for all
$ f(y) \ge 0$
for all
 $y\in X _I, $
$y\in X _I, $
-
2.
 $ {\mathbb E}_{y\in X _I} f(y) = 1 $
, and
$ {\mathbb E}_{y\in X _I} f(y) = 1 $
, and -
3. by Lemmas 3.3(d,H+1,l+1) and 3.2(d,H+1,l+1), for
 $\varepsilon $
-a.e.
$\varepsilon $
-a.e.
 $ y\in X _I, $
we have
$ y\in X _I, $
we have
 $ 1-\varepsilon < f(y) < 1+\varepsilon .$
$ 1-\varepsilon < f(y) < 1+\varepsilon .$
Let
![]() $E\subset X_I$
be the set of y for which this last inequality holds, and let
$E\subset X_I$
be the set of y for which this last inequality holds, and let
![]() $ \rho = \frac {|E|}{|X _I|} $
(so
$ \rho = \frac {|E|}{|X _I|} $
(so
![]() $ 1-\varepsilon \le \rho \le 1 $
). Then
$ 1-\varepsilon \le \rho \le 1 $
). Then
The first term is
![]() $\le \varepsilon $
by the definition of
$\le \varepsilon $
by the definition of
![]() $ E. $
For the second term, we have
$ E. $
For the second term, we have
By the three properties listed above, we get that
![]() $ (1-\rho ) {\mathbb E}_{y\in E^c} f(y) \le 2\varepsilon. $
Plugging this into inequality (3.1) yields
$ (1-\rho ) {\mathbb E}_{y\in E^c} f(y) \le 2\varepsilon. $
Plugging this into inequality (3.1) yields
Proof of Lemma 3.5 rank-bias(d,H+1,l+1).
Let
![]() $X = Z({\mathcal Q}). $
First we apply Lemma 3.4(d,H+1,l+1) to get
$X = Z({\mathcal Q}). $
First we apply Lemma 3.4(d,H+1,l+1) to get
-
1.
 $Re[{\mathbb E}_{x\in X} \chi (P(x))] \ge Re[{\mathbb E}_{x\in X_I} \chi (P(x))]-q^{-2s} $
and
$Re[{\mathbb E}_{x\in X} \chi (P(x))] \ge Re[{\mathbb E}_{x\in X_I} \chi (P(x))]-q^{-2s} $
and -
2.
 $|Im[{\mathbb E}_{x\in X} \chi (P(x))]| \le |Im[{\mathbb E}_{x\in X_I} \chi (P(x))]|+ q^{-2s},$
$|Im[{\mathbb E}_{x\in X} \chi (P(x))]| \le |Im[{\mathbb E}_{x\in X_I} \chi (P(x))]|+ q^{-2s},$
so we can assume without loss of generality that
![]() $I=[k].$
We will prove the lemma by induction on
$I=[k].$
We will prove the lemma by induction on
![]() $|I|.$
For
$|I|.$
For
![]() $|I| = 1$
, the lemma follows from basic Fourier analysis. For the general case, we start by showing the second inequality holds. Apply Lemma 3.4 again to get
$|I| = 1$
, the lemma follows from basic Fourier analysis. For the general case, we start by showing the second inequality holds. Apply Lemma 3.4 again to get
Let
![]() $A',B'$
be the constants for Lemma 3.5 on an index set of size
$A',B'$
be the constants for Lemma 3.5 on an index set of size
![]() $ |I| -1. $
By Lemma 3.3(d,H+1,l+1), if
$ |I| -1. $
By Lemma 3.3(d,H+1,l+1), if
![]() $A,B$
are sufficiently large then for
$A,B$
are sufficiently large then for
![]() $q^{-10s}$
-a.e.
$q^{-10s}$
-a.e.
![]() $y\in X_1$
the multilinear tower
$y\in X_1$
the multilinear tower
![]() ${\mathcal Q}(y)$
is
${\mathcal Q}(y)$
is
![]() $(A',B',10s)$
-regular. The induction hypothesis implies that
$(A',B',10s)$
-regular. The induction hypothesis implies that
as desired.
Now for the first inequality, suppose modulo the maps in
![]() $ {\mathcal Q} $
, we have the low partition rank presentation
$ {\mathcal Q} $
, we have the low partition rank presentation
 $$\begin{align*}P(x_{[k]}) = \sum_{i=1}^m l_i(x_1)g_i(x_{[2,k]}) + \sum_{j=m+1}^r q_i(x_{I_j})r_i(x_{[k]\setminus I_j}), \end{align*}$$
$$\begin{align*}P(x_{[k]}) = \sum_{i=1}^m l_i(x_1)g_i(x_{[2,k]}) + \sum_{j=m+1}^r q_i(x_{I_j})r_i(x_{[k]\setminus I_j}), \end{align*}$$
where
![]() $I_j\neq \{1\},[2,k].$
Let
$I_j\neq \{1\},[2,k].$
Let
![]() $W = \{y\in X_1:l_i(y) = 0\ \forall i\in [m]\}.$
By Lemma 3.4,
$W = \{y\in X_1:l_i(y) = 0\ \forall i\in [m]\}.$
By Lemma 3.4,
 $$ \begin{align*} &Re[{\mathbb E}_{x\in X} \chi(P(x))] \ge {\mathbb E}_{y\in X_1}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))]-q^{-10s} \\ &\qquad = \frac{|W|}{|X_1|}{\mathbb E}_{y\in W}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))] + (1-\frac{|W|}{|X_1|}){\mathbb E}_{y\in X_1\setminus W}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))]-q^{-10s}. \end{align*} $$
$$ \begin{align*} &Re[{\mathbb E}_{x\in X} \chi(P(x))] \ge {\mathbb E}_{y\in X_1}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))]-q^{-10s} \\ &\qquad = \frac{|W|}{|X_1|}{\mathbb E}_{y\in W}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))] + (1-\frac{|W|}{|X_1|}){\mathbb E}_{y\in X_1\setminus W}Re[{\mathbb E}_{z\in X(y)} \chi(P(y,z))]-q^{-10s}. \end{align*} $$
Note that:
-
1. for any
 $y\in W$
, the rank of
$y\in W$
, the rank of
 $P(y,\cdot )$
on
$P(y,\cdot )$
on
 $X(y)$
is
$X(y)$
is
 $\le r-m,$
$\le r-m,$
-
2.
 $|W|/|X_1| \ge q^{-m}$
, and
$|W|/|X_1| \ge q^{-m}$
, and -
3. for
 $q^{-10s}$
-a.e.
$q^{-10s}$
-a.e.
 $y\in X_1$
, the multilinear tower
$y\in X_1$
, the multilinear tower
 ${\mathcal Q}(y)$
is
${\mathcal Q}(y)$
is
 $(A',B',10s)$
-regular.
$(A',B',10s)$
-regular.
By these properties and the induction hypothesis for
![]() $ P(y,\cdot ) $
on
$ P(y,\cdot ) $
on
![]() $X(y) $
, we can lower bound the first summand by
$X(y) $
, we can lower bound the first summand by
and the second summand by
4 Some reductions
In this section, we reduce the proof of Theorem 2.13 for degree
![]() $d+1$
to the
$d+1$
to the
![]() $ l=0 $
case of Theorem 3.1.
$ l=0 $
case of Theorem 3.1.
Lemma 4.1. Suppose Theorem 3.1(d+1,H,l) holds for
![]() $ l=0 $
and all
$ l=0 $
and all
![]() $ H $
. Then it holds for all
$ H $
. Then it holds for all
![]() $ l,H. $
$ l,H. $
Proof. By induction on l, suppose the theorem holds for (d+1,H,l). Let
![]() $ {\mathcal Q} $
be an
$ {\mathcal Q} $
be an
![]() $(A,B,s)$
-regular tower on
$(A,B,s)$
-regular tower on
![]() $ V^{[k]} $
of type (d+1,H,l+1) and
$ V^{[k]} $
of type (d+1,H,l+1) and
![]() $ P:V^I\to {\mathbb {F}} $
a full multiaffine map of degree
$ P:V^I\to {\mathbb {F}} $
a full multiaffine map of degree
![]() $ \le d+1, $
with
$ \le d+1, $
with
![]() $ bias_{Z({\mathcal Q})} (P) \ge q^{-s}. $
Again, we denote
$ bias_{Z({\mathcal Q})} (P) \ge q^{-s}. $
Again, we denote
![]() $X=Z({\mathcal Q}) $
for short. We saw in the last section that Theorem 3.1(d+1,H,l) implies Lemma 3.4 for (d+1,H+1,l+1), so
$X=Z({\mathcal Q}) $
for short. We saw in the last section that Theorem 3.1(d+1,H,l) implies Lemma 3.4 for (d+1,H+1,l+1), so
that is, we can assume without loss of generality that
![]() $ I=[k]. $
If
$ I=[k]. $
If
![]() $ {\mathcal Q} $
is of degree
$ {\mathcal Q} $
is of degree
![]() $ \le d $
, then we are done. Suppose not, then
$ \le d $
, then we are done. Suppose not, then
![]() $ k=d+1 $
, and there is some layer
$ k=d+1 $
, and there is some layer
![]() $ t\in [H] $
with
$ t\in [H] $
with
![]() $ {\mathcal Q}_t $
of degree
$ {\mathcal Q}_t $
of degree
![]() $ d+1 $
. Let
$ d+1 $
. Let
![]() $ {\mathcal Q}_{\neq t} = ({\mathcal Q}_i)_{i\in [H]\setminus \{t\}}$
and
$ {\mathcal Q}_{\neq t} = ({\mathcal Q}_i)_{i\in [H]\setminus \{t\}}$
and
![]() $X_{\neq t} = Z({\mathcal Q}_{\neq t}). $
By Fourier analysis, we have
$X_{\neq t} = Z({\mathcal Q}_{\neq t}). $
By Fourier analysis, we have
 $$ \begin{align} |{\mathbb E}_{x\in X} \chi(P(x))| \le \frac{|X_{\neq t}|}{|X|}q^{-m_t} \sum_{a\in{\mathbb{F}}^{m_t}} | {\mathbb E}_{x\in X_{\neq t}}\chi(P(x)+a\cdot {\mathcal Q}_t(x)) |. \end{align} $$
$$ \begin{align} |{\mathbb E}_{x\in X} \chi(P(x))| \le \frac{|X_{\neq t}|}{|X|}q^{-m_t} \sum_{a\in{\mathbb{F}}^{m_t}} | {\mathbb E}_{x\in X_{\neq t}}\chi(P(x)+a\cdot {\mathcal Q}_t(x)) |. \end{align} $$
By Lemma 3.2(d+1,H,l+1) (which follows from Theorem 3.1(d+1,H,l)),
![]() $ \frac {|X_{\neq t}|}{|X|}q^{-m_t} \le q$
. As for the second term, choose
$ \frac {|X_{\neq t}|}{|X|}q^{-m_t} \le q$
. As for the second term, choose
![]() $ b\in {\mathbb {F}}^{m_t} $
, such that
$ b\in {\mathbb {F}}^{m_t} $
, such that
![]() $ prk_{{\mathcal Q}_{\neq t}} ( P(x)+b\cdot {\mathcal Q}_t(x) ) $
is minimal. By subadditivity of relative partition rank, for any
$ prk_{{\mathcal Q}_{\neq t}} ( P(x)+b\cdot {\mathcal Q}_t(x) ) $
is minimal. By subadditivity of relative partition rank, for any
![]() $ b\neq a \in {\mathbb {F}}^{m_t}$
, we must have
$ b\neq a \in {\mathbb {F}}^{m_t}$
, we must have
By Theorem 3.1(d+1,H,l) (assuming
![]() $ A,B $
are sufficiently large), this means that for any
$ A,B $
are sufficiently large), this means that for any
![]() $ b\neq a \in {\mathbb {F}}^{m_t}, $
$ b\neq a \in {\mathbb {F}}^{m_t}, $
Plugging these estimates into inequality (4.1) yields
Now apply Theorem 3.1(d+1,h,l) to conclude that
Therefore, all we have to do is prove Theorem 3.1(d+1,H,0) in order to deduce Theorem 2.13 at degree
![]() $d+1$
. The following lemma allows us to reduce further to the case that
$d+1$
. The following lemma allows us to reduce further to the case that
![]() $ P,{\mathcal Q} $
are multilinear and defined on the same index set. From now on, we assume Theorem 2.13(d,H) holds for all
$ P,{\mathcal Q} $
are multilinear and defined on the same index set. From now on, we assume Theorem 2.13(d,H) holds for all
![]() $ H, $
and work toward proving Theorem 3.1(d+1,H,0) for all
$ H, $
and work toward proving Theorem 3.1(d+1,H,0) for all
![]() $ H.$
We may safely forget about the auxiliary parameter l of Theorem 3.1, it has served its purpose. The following lemma allows us to reduce further to the case where
$ H.$
We may safely forget about the auxiliary parameter l of Theorem 3.1, it has served its purpose. The following lemma allows us to reduce further to the case where
![]() $ P,{\mathcal Q} $
are multilinear and are defined on the same index set.
$ P,{\mathcal Q} $
are multilinear and are defined on the same index set.
Lemma 4.2. There exist
![]() $A(d,h),B(d,h)$
, such that if
$A(d,h),B(d,h)$
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $ (A,B,s) $
-regular tower of degree
$ (A,B,s) $
-regular tower of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le h $
on
$ \le h $
on
![]() $ V^{[k]}$
and
$ V^{[k]}$
and
![]() $P:V^I\to {\mathbb {F}}$
is a full multiaffine map of degree
$P:V^I\to {\mathbb {F}}$
is a full multiaffine map of degree
![]() $|I|\le d+1$
, then
$|I|\le d+1$
, then
where
![]() $X=Z({\mathcal Q}) $
and
$X=Z({\mathcal Q}) $
and
![]() $\tilde {P},\tilde {X}$
are the corresponding multilinear map and variety.
$\tilde {P},\tilde {X}$
are the corresponding multilinear map and variety.
Proof. By applying Lemma 3.4, we get
so we can assume without loss of generality that
![]() $ I=[k]. $
Now choose some
$ I=[k]. $
Now choose some
![]() $i\in [k]$
, and write
$i\in [k]$
, and write
![]() $ P(x) = A(x_{[k]\setminus \{i\}})\cdot x_i + b(x_{I\setminus \{i\}}),$
where
$ P(x) = A(x_{[k]\setminus \{i\}})\cdot x_i + b(x_{I\setminus \{i\}}),$
where
![]() $A,b$
are multiaffine maps. Again, using Lemma 3.4 twice, we have
$A,b$
are multiaffine maps. Again, using Lemma 3.4 twice, we have
 $$ \begin{align*} |{\mathbb E}_{x\in X} \chi(P(x))| &\le |{\mathbb E}_{x\in X_{I\setminus\{i\}}} \chi(b(x)) {\mathbb E}_{y\in X(x)} \chi(A(x)\cdot y)| + q^{-10ks} \\ &\qquad\qquad\quad\le {\mathbb E}_{x\in X_{I\setminus\{i\}}} |{\mathbb E}_{y\in X(x)} \chi(A(x)\cdot y)| + q^{-10ks} \\ &\qquad\qquad\quad={\mathbb E}_{x\in X_{I\setminus\{i\}}} {\mathbb E}_{y\in \widetilde{X(x)}} \chi(A(x)\cdot y) + q^{-10ks} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le |{\mathbb E}_{x\in X'} \chi(A(x_{[k]\setminus\{i\}})\cdot x_i)|+ q^{-5ks}, \end{align*} $$
$$ \begin{align*} |{\mathbb E}_{x\in X} \chi(P(x))| &\le |{\mathbb E}_{x\in X_{I\setminus\{i\}}} \chi(b(x)) {\mathbb E}_{y\in X(x)} \chi(A(x)\cdot y)| + q^{-10ks} \\ &\qquad\qquad\quad\le {\mathbb E}_{x\in X_{I\setminus\{i\}}} |{\mathbb E}_{y\in X(x)} \chi(A(x)\cdot y)| + q^{-10ks} \\ &\qquad\qquad\quad={\mathbb E}_{x\in X_{I\setminus\{i\}}} {\mathbb E}_{y\in \widetilde{X(x)}} \chi(A(x)\cdot y) + q^{-10ks} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le |{\mathbb E}_{x\in X'} \chi(A(x_{[k]\setminus\{i\}})\cdot x_i)|+ q^{-5ks}, \end{align*} $$
where
![]() $X'$
is the variety associated with X which is linear in the i-th coordinate and
$X'$
is the variety associated with X which is linear in the i-th coordinate and
![]() $ A(x_{[k]\setminus \{i\}})\cdot x_i $
is the multiaffine map associated with P which is linear in the i-th coordinate. Iterating this inequality over and over for all the other coordinates, we end up with
$ A(x_{[k]\setminus \{i\}})\cdot x_i $
is the multiaffine map associated with P which is linear in the i-th coordinate. Iterating this inequality over and over for all the other coordinates, we end up with
where the second inequality follows from Lemma 3.5.
5 Many low rank approximations
In the previous section, we showed that in order to prove Theorem 2.13 for degree
![]() $d+1,$
the only new case we have to deal with is when
$d+1,$
the only new case we have to deal with is when
![]() $P:V^{[d+1]}\to {\mathbb {F}}$
is multilinear and
$P:V^{[d+1]}\to {\mathbb {F}}$
is multilinear and
![]() $ {\mathcal Q} $
is a multilinear tower on
$ {\mathcal Q} $
is a multilinear tower on
![]() $V^{[d+1]}$
of degree
$V^{[d+1]}$
of degree
![]() $\le d.$
In this section, we will prove the existence of an abundance of relative low rank approximations, and in the next sections, we will “glue” them together to get a genuine relative low rank presentation. We start with a useful algebraic claim, which we will need here and in later sections.
$\le d.$
In this section, we will prove the existence of an abundance of relative low rank approximations, and in the next sections, we will “glue” them together to get a genuine relative low rank presentation. We start with a useful algebraic claim, which we will need here and in later sections.
Claim 5.1. Let
![]() ${\mathcal Q}$
be a tower on
${\mathcal Q}$
be a tower on
![]() $V^{[k]}$
and
$V^{[k]}$
and
![]() $\textbf {l}\in \mathbb N^k$
a vector. Define
$\textbf {l}\in \mathbb N^k$
a vector. Define
![]() $ {\mathcal Q}^{\otimes \textbf {l}} $
to be the tower on
$ {\mathcal Q}^{\otimes \textbf {l}} $
to be the tower on
![]() $ (V_1)^{l_1} \times \ldots \times (V_k)^{l_k}$
obtained by multiplying the first coordinate
$ (V_1)^{l_1} \times \ldots \times (V_k)^{l_k}$
obtained by multiplying the first coordinate
![]() $ l_1 $
times, the second
$ l_1 $
times, the second
![]() $ l_2 $
times and so on – that is, a tower of the same height as
$ l_2 $
times and so on – that is, a tower of the same height as
![]() $ {\mathcal Q} $
with
$ {\mathcal Q} $
with
 $$\begin{align*}\left( {\mathcal Q}^{\otimes \textbf{l}} \right)_i = \bigcup_{ \textbf{j}\in \prod_{t \in I_i} [l_t] } {\mathcal Q}_i( (x_{t,j_t})_{t \in I_i} ). \end{align*}$$
$$\begin{align*}\left( {\mathcal Q}^{\otimes \textbf{l}} \right)_i = \bigcup_{ \textbf{j}\in \prod_{t \in I_i} [l_t] } {\mathcal Q}_i( (x_{t,j_t})_{t \in I_i} ). \end{align*}$$
Define
![]() $ {\mathcal Q}^{\times \textbf {l}} $
to be the tower composed of the same equations, but on
$ {\mathcal Q}^{\times \textbf {l}} $
to be the tower composed of the same equations, but on
![]() $ V^{[kl_1\ldots l_k]}, $
so it has
$ V^{[kl_1\ldots l_k]}, $
so it has
![]() $ l_1\ldots l_k $
as many layers as
$ l_1\ldots l_k $
as many layers as
![]() $ {\mathcal Q} $
(we order the layers corresponding to
$ {\mathcal Q} $
(we order the layers corresponding to
![]() $ {\mathcal Q}_i $
arbitrarily within themselves, but keep the order otherwise). Then, if
$ {\mathcal Q}_i $
arbitrarily within themselves, but keep the order otherwise). Then, if
![]() ${\mathcal Q}$
is
${\mathcal Q}$
is
![]() $(A(l_1\ldots l_k)^B,B,s)$
-regular, then both
$(A(l_1\ldots l_k)^B,B,s)$
-regular, then both
![]() $ {\mathcal Q}^{\otimes \textbf {l}}$
and
$ {\mathcal Q}^{\otimes \textbf {l}}$
and
![]() $ {\mathcal Q}^{\times \textbf {l}}$
are
$ {\mathcal Q}^{\times \textbf {l}}$
are
![]() $ (A,B,s) $
-regular.
$ (A,B,s) $
-regular.
Proof. We may assume without loss of generality that
![]() $ {\mathcal Q} $
is multilinear. Because there are
$ {\mathcal Q} $
is multilinear. Because there are
![]() $ l_1\ldots l_k $
times as many maps, it is enough to show that the relative ranks are unchanged. Suppose we have a linear combination with
$ l_1\ldots l_k $
times as many maps, it is enough to show that the relative ranks are unchanged. Suppose we have a linear combination with
 $$\begin{align*}rk_{{\mathcal Q}^{\otimes \textbf{l}}_{<i}} \left( \sum_{\textbf{j} \in \prod_{t \in I_i} [l_t] } a_{\textbf{j}} \cdot {\mathcal Q}_i ( (x_{t,j_t})_{t \in I_i} ) \right) < rk_{{\mathcal Q}_{<i}} ({\mathcal Q}_i). \end{align*}$$
$$\begin{align*}rk_{{\mathcal Q}^{\otimes \textbf{l}}_{<i}} \left( \sum_{\textbf{j} \in \prod_{t \in I_i} [l_t] } a_{\textbf{j}} \cdot {\mathcal Q}_i ( (x_{t,j_t})_{t \in I_i} ) \right) < rk_{{\mathcal Q}_{<i}} ({\mathcal Q}_i). \end{align*}$$
For any
![]() $\textbf {j}\in \prod _{t \in I_i} [l_t],$
plugging in
$\textbf {j}\in \prod _{t \in I_i} [l_t],$
plugging in
![]() $x_{\alpha ,\beta } = 0$
for all
$x_{\alpha ,\beta } = 0$
for all
![]() $ \beta \neq j_\alpha , $
we get
$ \beta \neq j_\alpha , $
we get
which implies that
![]() $ a_{\textbf {j}} = 0.$
The proof for
$ a_{\textbf {j}} = 0.$
The proof for
![]() $ {\mathcal Q}^{\times \textbf {l}} $
is identical.
$ {\mathcal Q}^{\times \textbf {l}} $
is identical.
Now we are ready to prove that we can find an abundance of low rank approximations of P on
![]() $ Z({\mathcal Q}). $
The following is inspired by lemma 12 in [Reference Milićević21].
$ Z({\mathcal Q}). $
The following is inspired by lemma 12 in [Reference Milićević21].
Proposition 5.2 (Low rank approximations).
There exist constants
![]() $A(d,H),B(d,H)$
, such that the following holds: If
$A(d,H),B(d,H)$
, such that the following holds: If
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $(A,B,s)$
-regular multilinear tower on
$(A,B,s)$
-regular multilinear tower on
![]() $ V^{[d+1]}$
of degree
$ V^{[d+1]}$
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
,
$\le H$
,
![]() $X=Z({\mathcal Q}), $
and
$X=Z({\mathcal Q}), $
and
![]() $P:V^{[d+1]}\to {\mathbb {F}}$
is a multilinear map satisfying
$P:V^{[d+1]}\to {\mathbb {F}}$
is a multilinear map satisfying
![]() $bias_X (P) \ge q^{-s},$
then there exists a set
$bias_X (P) \ge q^{-s},$
then there exists a set
![]() $E\subset (X_{d+1})^{100s}$
of density
$E\subset (X_{d+1})^{100s}$
of density
![]() $\ge q^{-10s}$
, such that for all
$\ge q^{-10s}$
, such that for all
![]() $ t\in E $
, there is a multilinear function
$ t\in E $
, there is a multilinear function
![]() $\phi _t:V^{[d]}\to {\mathbb {F}}^{100s}$
with
$\phi _t:V^{[d]}\to {\mathbb {F}}^{100s}$
with
where
![]() $X_t = \{x\in X : x_{[d]}\in \bigcap _{i=1}^{100s} X(t_i)\}.$
$X_t = \{x\in X : x_{[d]}\in \bigcap _{i=1}^{100s} X(t_i)\}.$
Proof. Choosing a nondegenerate bilinear form on
![]() $V^{d+1},$
we can write
$V^{d+1},$
we can write
![]() $P(x) = A(x_{[d]})\cdot x_{d+1},$
where
$P(x) = A(x_{[d]})\cdot x_{d+1},$
where
![]() $A:V^{[d]}\to V^{d+1}$
is multilinear. Apply Lemma 3.4 to get
$A:V^{[d]}\to V^{d+1}$
is multilinear. Apply Lemma 3.4 to get
where
![]() $v\perp w$
means
$v\perp w$
means
![]() $v\cdot w =0.$
Now, fix
$v\cdot w =0.$
Now, fix
![]() $x_{[d]}\in X_{[d]}.$
To test for the event above, choose
$x_{[d]}\in X_{[d]}.$
To test for the event above, choose
![]() $ t\in (X(x_{[d]}))^l $
at random, where
$ t\in (X(x_{[d]}))^l $
at random, where
![]() $ l=100s $
and define
$ l=100s $
and define
If
![]() $ A(x_{[d]})\perp X(x_{[d]}), $
then
$ A(x_{[d]})\perp X(x_{[d]}), $
then
![]() $\phi _t(x) = 0$
for any
$\phi _t(x) = 0$
for any
![]() $t\in (X(x_{[d]}))^l$
, and if
$t\in (X(x_{[d]}))^l$
, and if
![]() $ A(x_{[d]})\not \perp X(x_{[d]}) $
, then
$ A(x_{[d]})\not \perp X(x_{[d]}) $
, then
Therefore,
If
![]() $ A,B $
are sufficiently large, then by Claim 5.1 and Lemma 3.4, we have
$ A,B $
are sufficiently large, then by Claim 5.1 and Lemma 3.4, we have
By Markov’s inequality, for
![]() $q^{-25s}$
-a.e.
$q^{-25s}$
-a.e.
![]() $t\in X_{d+1}^l,$
we have
$t\in X_{d+1}^l,$
we have
Also, by Lemma 3.4 together with inequality (5.1)
Markov’s inequality gives us
So for a collection of
![]() $t\in X_{d+1}^l$
of density
$t\in X_{d+1}^l$
of density
![]() $\ge q^{-10s}$
, we have both
$\ge q^{-10s}$
, we have both
and inequality (5.2). For these t, we have
 $$ \begin{align*} &{\mathbb P}_{x\in X_t\cap \{\phi_t(x_{[d]})=0\}} (P(x) = 0) \ge \mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}) | \phi_t(x)=0) \\ &\qquad\qquad\quad= \frac{\mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}))}{\mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}))+\mathbb P_{x\in X_t} (A(x_{[d]}) \not\perp X(x_{[d]}) ,\phi_t(x)=0)} \\ &\qquad\qquad\qquad\qquad \ \ge \frac{q^{-5s}}{q^{-5s}+\mathbb P_{x\in X_t} (A(x_{[d]})\not \perp X(x_{[d]}) ,\phi_t(x)=0)} \ge \frac{q^{-5s}}{q^{-5s}+q^{-25s}} \ge 1-q^{-s}. \end{align*} $$
$$ \begin{align*} &{\mathbb P}_{x\in X_t\cap \{\phi_t(x_{[d]})=0\}} (P(x) = 0) \ge \mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}) | \phi_t(x)=0) \\ &\qquad\qquad\quad= \frac{\mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}))}{\mathbb P_{x\in X_t} (A(x_{[d]}) \perp X(x_{[d]}))+\mathbb P_{x\in X_t} (A(x_{[d]}) \not\perp X(x_{[d]}) ,\phi_t(x)=0)} \\ &\qquad\qquad\qquad\qquad \ \ge \frac{q^{-5s}}{q^{-5s}+\mathbb P_{x\in X_t} (A(x_{[d]})\not \perp X(x_{[d]}) ,\phi_t(x)=0)} \ge \frac{q^{-5s}}{q^{-5s}+q^{-25s}} \ge 1-q^{-s}. \end{align*} $$
6 Regularization
In order to improve our approximation from the last section to a genuine low rank representation, we will have to take the
![]() $ 100s $
maps
$ 100s $
maps
![]() $ \phi _t:V^{[d]}\to {\mathbb {F}}^{100s} $
and replace them by a tower which is relatively regular together with the maps of
$ \phi _t:V^{[d]}\to {\mathbb {F}}^{100s} $
and replace them by a tower which is relatively regular together with the maps of
![]() $X_t. $
In this section, we describe an efficient algorithm for doing this. The following notion will come in handy:
$X_t. $
In this section, we describe an efficient algorithm for doing this. The following notion will come in handy:
Definition 6.1. Let
![]() $ \mathcal R=(\mathcal R_i)_{i\in [h]}, {\mathcal Q}=({\mathcal Q}_j)_{j\in [h]}$
be towers on
$ \mathcal R=(\mathcal R_i)_{i\in [h]}, {\mathcal Q}=({\mathcal Q}_j)_{j\in [h]}$
be towers on
![]() $ V^{[k]}$
and
$ V^{[k]}$
and
![]() $ m_i = |\mathcal R_i|.$
We say that
$ m_i = |\mathcal R_i|.$
We say that
![]() $ \mathcal R $
is
$ \mathcal R $
is
![]() $ (A,B,s) $
-regular relative to
$ (A,B,s) $
-regular relative to
![]() $ {\mathcal Q} $
if for all
$ {\mathcal Q} $
if for all
![]() $ i\in [h] $
, we have
$ i\in [h] $
, we have
Note that if
![]() ${\mathcal Q},\mathcal R$
are two towers, such that
${\mathcal Q},\mathcal R$
are two towers, such that
![]() $\mathcal R$
is
$\mathcal R$
is
![]() $(A,B,s)$
-regular relative to
$(A,B,s)$
-regular relative to
![]() $ {\mathcal Q} $
and
$ {\mathcal Q} $
and
![]() ${\mathcal Q}$
is
${\mathcal Q}$
is
![]() $(A,B,s+m)$
-regular (
$(A,B,s+m)$
-regular (
![]() $ m $
is the dimension of
$ m $
is the dimension of
![]() $ \mathcal R $
), then
$ \mathcal R $
), then
![]() ${\mathcal Q}\cup \mathcal R$
is
${\mathcal Q}\cup \mathcal R$
is
![]() $(A,B,s)$
-regular with the layers ordered by having
$(A,B,s)$
-regular with the layers ordered by having
![]() $ {\mathcal Q} $
on the bottom and
$ {\mathcal Q} $
on the bottom and
![]() $ \mathcal R $
on top.
$ \mathcal R $
on top.
Claim 6.2 (Regular decomposition).
For any
![]() $A,B$
, there exist constants
$A,B$
, there exist constants
![]() $C(A,B,d,k),D(A,B,d,k)$
, such that the following holds: If
$C(A,B,d,k),D(A,B,d,k)$
, such that the following holds: If
![]() ${\mathcal Q}$
is a tower on
${\mathcal Q}$
is a tower on
![]() $ V^{[k]} $
and
$ V^{[k]} $
and
![]() $\mathcal R$
is a collection of full multiaffine maps of degree
$\mathcal R$
is a collection of full multiaffine maps of degree
![]() $\le d$
, then there exist towers
$\le d$
, then there exist towers
![]() $\mathcal S_1,\ldots ,\mathcal S_l$
, such that:
$\mathcal S_1,\ldots ,\mathcal S_l$
, such that:
-
1.
 $\mathcal S_i$
is
$\mathcal S_i$
is
 $(A,B,s)$
-regular relative to
$(A,B,s)$
-regular relative to
 $ {\mathcal Q} $
,
$ {\mathcal Q} $
, -
2.
 $\mathcal S_i$
is of degree
$\mathcal S_i$
is of degree
 $\le d$
and height
$\le d$
and height
 $\le 2^k,$
$\le 2^k,$
-
3.
 $\dim (\mathcal S_i)\le C(s+\dim (\mathcal R))^D$
, and
$\dim (\mathcal S_i)\le C(s+\dim (\mathcal R))^D$
, and -
4. we have a decomposition
 $Z({\mathcal Q} \cup \mathcal R) = \bigsqcup _{i=1}^l Z({\mathcal Q} \cup \mathcal S_i). $
$Z({\mathcal Q} \cup \mathcal R) = \bigsqcup _{i=1}^l Z({\mathcal Q} \cup \mathcal S_i). $
In addition, if
![]() $ {\mathcal Q},\mathcal R $
are multilinear, then we can take
$ {\mathcal Q},\mathcal R $
are multilinear, then we can take
![]() $ \mathcal S_1 $
to be multilinear.
$ \mathcal S_1 $
to be multilinear.
Note that Theorem 2.3 is the above claim for homogeneous polynomials in the simplest case where
![]() ${\mathcal Q}$
is empty, and the proof we will now give of Claim 6.2 may be easily modified to prove Theorem 2.3.
${\mathcal Q}$
is empty, and the proof we will now give of Claim 6.2 may be easily modified to prove Theorem 2.3.
Proof. First, arrange
![]() $ \mathcal R $
in a tower
$ \mathcal R $
in a tower
![]() $ \mathcal R = (\mathcal R_i:V^{I_i}\to {\mathbb {F}})_{i\in [2^k]} $
, with the higher degree maps above the lower degree ones. As usual, denote
$ \mathcal R = (\mathcal R_i:V^{I_i}\to {\mathbb {F}})_{i\in [2^k]} $
, with the higher degree maps above the lower degree ones. As usual, denote
![]() $ m_i = |\mathcal R_i|. $
To the i-th layer we assign a number
$ m_i = |\mathcal R_i|. $
To the i-th layer we assign a number
![]() $n_i,$
according to a formula we will give later. We describe an algorithm for producing
$n_i,$
according to a formula we will give later. We describe an algorithm for producing
![]() $ \mathcal S_i $
and then show that it has the desired properties. If for every
$ \mathcal S_i $
and then show that it has the desired properties. If for every
![]() $ i $
$ i $
then we stop. Otherwise, there is some
![]() $0\neq a\in {\mathbb {F}}^{m_i} $
, such that
$0\neq a\in {\mathbb {F}}^{m_i} $
, such that
 $$\begin{align*}a\cdot \mathcal R_i = \sum_{j=1}^t q_j(x_{I_j}) r_j (x_{I_i\setminus I_j}) + \sum_{J \subsetneq I_i} u_J(x_J) + \sum_{f\in {\mathcal Q}\cup\mathcal R_{<i},\ I_f\subset I_i} f(x_{I_f})h_f(x_{I_i\setminus I_f}), \end{align*}$$
$$\begin{align*}a\cdot \mathcal R_i = \sum_{j=1}^t q_j(x_{I_j}) r_j (x_{I_i\setminus I_j}) + \sum_{J \subsetneq I_i} u_J(x_J) + \sum_{f\in {\mathcal Q}\cup\mathcal R_{<i},\ I_f\subset I_i} f(x_{I_f})h_f(x_{I_i\setminus I_f}), \end{align*}$$
where
![]() $t \le A(n_i+s)^B.$
Assume without loss of generality that
$t \le A(n_i+s)^B.$
Assume without loss of generality that
![]() $ a_{m_i} \neq 0. $
Let
$ a_{m_i} \neq 0. $
Let
![]() $ \mathcal R' $
be the tower obtained from
$ \mathcal R' $
be the tower obtained from
![]() $ \mathcal R $
by deleting
$ \mathcal R $
by deleting
![]() $ R_{i,m_i}. $
In
$ R_{i,m_i}. $
In
![]() $Z({\mathcal Q}\cup \mathcal R'),$
the value of
$Z({\mathcal Q}\cup \mathcal R'),$
the value of
![]() $R_{i,m_i}$
is determined by the
$R_{i,m_i}$
is determined by the
![]() $q_j,r_j,u_J.$
We add these maps to the lower layers of
$q_j,r_j,u_J.$
We add these maps to the lower layers of
![]() $\mathcal R'$
and call the new tower
$\mathcal R'$
and call the new tower
![]() $\mathcal R".$
We can then split
$\mathcal R".$
We can then split
 $$\begin{align*}Z({\mathcal Q}\cup\mathcal R) = \bigsqcup_{i=1}^c \left( Z({\mathcal Q}) \cap \{\mathcal R"=b_i\} \right) , \end{align*}$$
$$\begin{align*}Z({\mathcal Q}\cup\mathcal R) = \bigsqcup_{i=1}^c \left( Z({\mathcal Q}) \cap \{\mathcal R"=b_i\} \right) , \end{align*}$$
where
![]() $ b_1,\ldots ,b_c \in {\mathbb {F}}^{\mathcal R"}$
are the values causing the maps in
$ b_1,\ldots ,b_c \in {\mathbb {F}}^{\mathcal R"}$
are the values causing the maps in
![]() $ \mathcal R $
to vanish on
$ \mathcal R $
to vanish on
![]() $ Z({\mathcal Q}) \cap \{\mathcal R"=b_i\}. $
Now we do the same thing for each of the towers
$ Z({\mathcal Q}) \cap \{\mathcal R"=b_i\}. $
Now we do the same thing for each of the towers
![]() $ \mathcal R"-b_i $
(with the same
$ \mathcal R"-b_i $
(with the same
![]() $n_i$
we chose at the start) and so on. Because at each stage we replace a map by maps of lower degree (and when handling a linear map, we just delete it), this algorithm eventually terminates. We now give the definition of
$n_i$
we chose at the start) and so on. Because at each stage we replace a map by maps of lower degree (and when handling a linear map, we just delete it), this algorithm eventually terminates. We now give the definition of
![]() $n_i$
and check that the
$n_i$
and check that the
![]() $ \mathcal S_i $
we end up with satisfy requirements 1–4. Set
$ \mathcal S_i $
we end up with satisfy requirements 1–4. Set
We prove inductively that the total number of polynomials passing through layer i and above during this process is
![]() $\le n_i.$
For
$\le n_i.$
For
![]() $i = 2^k$
, this is clear, since during regularization we only add polynomials to lower layers. Now suppose this bound holds for
$i = 2^k$
, this is clear, since during regularization we only add polynomials to lower layers. Now suppose this bound holds for
![]() $i.$
Any polynomials added to layer
$i.$
Any polynomials added to layer
![]() $i-1$
come from regularizing the higher layers. Each polynomial upstairs can contribute at most
$i-1$
come from regularizing the higher layers. Each polynomial upstairs can contribute at most
![]() $2A(s+n_i)^B+2^d$
when regularizing, so the bound at layer
$2A(s+n_i)^B+2^d$
when regularizing, so the bound at layer
![]() $i-1$
is proved, assuming the bound at layer
$i-1$
is proved, assuming the bound at layer
![]() $i.$
Therefore, conditions 1 and 3 are satisfied. Conditions 2 and 4 clearly hold. If
$i.$
Therefore, conditions 1 and 3 are satisfied. Conditions 2 and 4 clearly hold. If
![]() $ {\mathcal Q},\mathcal R $
are multilinear, then we can take
$ {\mathcal Q},\mathcal R $
are multilinear, then we can take
![]() $ b_1 = 0 $
at every stage, leaving us with
$ b_1 = 0 $
at every stage, leaving us with
![]() $ \mathcal S_1 $
multilinear.
$ \mathcal S_1 $
multilinear.
7 Fixing the approximation
In this section, we will take the many approximations that we get from Proposition 5.2 and “glue” them together to get a single tower
![]() $ \mathcal R $
, such that P vanishes identically on
$ \mathcal R $
, such that P vanishes identically on
![]() $ Z ({\mathcal Q}\cup \mathcal R). $
A central tool will be the following proposition (cf. proposition 5.1 in [Reference Green and Tao10]):
$ Z ({\mathcal Q}\cup \mathcal R). $
A central tool will be the following proposition (cf. proposition 5.1 in [Reference Green and Tao10]):
Proposition 7.1 (Almost surely vanishing implies vanishing).
There exist constants
![]() $A(d,H),B(d,H),s(d)$
, such that if
$A(d,H),B(d,H),s(d)$
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $(A,B,s)$
-regular tower on
$(A,B,s)$
-regular tower on
![]() $ V^{[d+1]} $
of degree
$ V^{[d+1]} $
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
and
$\le H$
and
![]() $f:V^{[d+1]}\to {\mathbb {F}}$
is a polynomial map (not even necessarily multiaffine) of degree
$f:V^{[d+1]}\to {\mathbb {F}}$
is a polynomial map (not even necessarily multiaffine) of degree
![]() $ \le d+1 $
satisfying
$ \le d+1 $
satisfying
then
![]() $f(x) = 0$
for all
$f(x) = 0$
for all
![]() $x\in Z({\mathcal Q}).$
$x\in Z({\mathcal Q}).$
Let
![]() $ {\mathcal Q}=({\mathcal Q}_i)_{i\in [h]} $
, where
$ {\mathcal Q}=({\mathcal Q}_i)_{i\in [h]} $
, where
![]() $ \deg ({\mathcal Q}_i) = d_i $
, and write
$ \deg ({\mathcal Q}_i) = d_i $
, and write
![]() $X = Z({\mathcal Q}) $
for short. In order to prove this lemma, we will need to count parallelepipeds based at any point
$X = Z({\mathcal Q}) $
for short. In order to prove this lemma, we will need to count parallelepipeds based at any point
![]() $ x\in X. $
Given
$ x\in X. $
Given
![]() $x\in X$
and an integer
$x\in X$
and an integer
![]() $ l, $
for each layer
$ l, $
for each layer
![]() $ i\in [h] $
, we define a layer
$ i\in [h] $
, we define a layer
![]() $ ({\mathcal Q}_{x,l})_i $
of maps
$ ({\mathcal Q}_{x,l})_i $
of maps
![]() $ (V_1)^l\times \ldots \times (V_{d+1})^l\to {\mathbb {F}} $
by
$ (V_1)^l\times \ldots \times (V_{d+1})^l\to {\mathbb {F}} $
by
and
![]() $ {\mathcal Q}_{x,l} $
is the resulting tower. Writing
$ {\mathcal Q}_{x,l} $
is the resulting tower. Writing
![]() $X_{x,l} = Z({\mathcal Q}_{x,l}), $
note that
$X_{x,l} = Z({\mathcal Q}_{x,l}), $
note that
We will also need to count parallelepipeds containing an additional point of the form
![]() $ x+t_1. $
Given
$ x+t_1. $
Given
![]() $ t_1\in X-x $
and
$ t_1\in X-x $
and
![]() $ c\in [l], $
set
$ c\in [l], $
set
Lemma 7.2. If
![]() ${\mathcal Q}$
is
${\mathcal Q}$
is
![]() $(Cl^{(d+1)D},D,s)$
-regular, then
$(Cl^{(d+1)D},D,s)$
-regular, then
![]() ${\mathcal Q}_{x,l}$
is an
${\mathcal Q}_{x,l}$
is an
![]() $(C,D,s)$
-regular tower of the same degree and height. Also, if
$(C,D,s)$
-regular tower of the same degree and height. Also, if
![]() $ C,D $
are sufficiently large depending on
$ C,D $
are sufficiently large depending on
![]() $ A,B,d,H,l $
, then for
$ A,B,d,H,l $
, then for
![]() $ q^{-s} $
a.e.
$ q^{-s} $
a.e.
![]() $ t_1\in X-x $
, we have
$ t_1\in X-x $
, we have
![]() $X_{x,l,c}(t_1) = Z(\mathcal R) $
, where
$X_{x,l,c}(t_1) = Z(\mathcal R) $
, where
![]() $ \mathcal R $
is an
$ \mathcal R $
is an
![]() $ (A,B,s) $
-regular tower of the same degree as
$ (A,B,s) $
-regular tower of the same degree as
![]() $ {\mathcal Q} $
, height
$ {\mathcal Q} $
, height
![]() $ \le Hl^{d+1} $
and
$ \le Hl^{d+1} $
and
Proof. As usual, let
![]() $ \tilde {{\mathcal Q}} $
denote the multilinear tower corresponding to
$ \tilde {{\mathcal Q}} $
denote the multilinear tower corresponding to
![]() $ {\mathcal Q}. $
The multilinear tower corresponding to
$ {\mathcal Q}. $
The multilinear tower corresponding to
![]() $ {\mathcal Q}_{x,l} $
is then
$ {\mathcal Q}_{x,l} $
is then
![]() $ \tilde {{\mathcal Q}}_{0,l}, $
so we can assume without loss of generality that
$ \tilde {{\mathcal Q}}_{0,l}, $
so we can assume without loss of generality that
![]() $ {\mathcal Q} $
is multilinear and
$ {\mathcal Q} $
is multilinear and
![]() $ x=0. $
By Claim 5.1, the tower
$ x=0. $
By Claim 5.1, the tower
![]() $ {\mathcal Q}^{\otimes (l,\ldots ,l)} $
is
$ {\mathcal Q}^{\otimes (l,\ldots ,l)} $
is
![]() $(A,B,s)$
-regular. The maps in
$(A,B,s)$
-regular. The maps in
![]() $ {\mathcal Q}_{x,l} $
are linear combinations of the maps in
$ {\mathcal Q}_{x,l} $
are linear combinations of the maps in
![]() $ {\mathcal Q}^{\otimes (l,\ldots ,l)}, $
so we just need to verify that they are linearly independent. Let
$ {\mathcal Q}^{\otimes (l,\ldots ,l)}, $
so we just need to verify that they are linearly independent. Let
![]() $ Q\in {\mathcal Q} $
be a map of degree
$ Q\in {\mathcal Q} $
be a map of degree
![]() $ e $
, assume without loss of generality that
$ e $
, assume without loss of generality that
![]() $ Q:V^{[e]}\to {\mathbb {F}}, $
and suppose (to get a contradiction) that we have a nontrivial linear combination
$ Q:V^{[e]}\to {\mathbb {F}}, $
and suppose (to get a contradiction) that we have a nontrivial linear combination
 $$ \begin{align} \sum_{\omega\in\{0,1\}^l,0<|\omega|\le e} a_\omega Q(\omega\cdot t) = 0. \end{align} $$
$$ \begin{align} \sum_{\omega\in\{0,1\}^l,0<|\omega|\le e} a_\omega Q(\omega\cdot t) = 0. \end{align} $$
Let
![]() $ \omega _0 $
be the largest element with respect to the lexicographic ordering on
$ \omega _0 $
be the largest element with respect to the lexicographic ordering on
![]() $ \{0,1\}^l $
, such that
$ \{0,1\}^l $
, such that
![]() $ a_{\omega _0} \neq 0 $
, and choose
$ a_{\omega _0} \neq 0 $
, and choose
![]() $ i_1,\ldots ,i_e\in \omega _0 $
, such that for every other
$ i_1,\ldots ,i_e\in \omega _0 $
, such that for every other
![]() $ \omega $
with
$ \omega $
with
![]() $ a_\omega \neq 0 $
, we have
$ a_\omega \neq 0 $
, we have
![]() $ \{i_1,\ldots ,i_e\} \not \subset \omega. $
Then the coefficient of
$ \{i_1,\ldots ,i_e\} \not \subset \omega. $
Then the coefficient of
![]() $ Q(t_{i_1}(1),\ldots ,t_{i_e}(e)) $
in the left-hand side of equation (7.1) is
$ Q(t_{i_1}(1),\ldots ,t_{i_e}(e)) $
in the left-hand side of equation (7.1) is
![]() $ a_{\omega _0} \neq 0, $
contradiction. Now we turn to the second part of the lemma. Since invertible affine transformations do not affect regularity, the variety
$ a_{\omega _0} \neq 0, $
contradiction. Now we turn to the second part of the lemma. Since invertible affine transformations do not affect regularity, the variety
is the zero locus of a
![]() $ (C,D,s) $
-regular tower on
$ (C,D,s) $
-regular tower on
![]() $ (V_1)^l\times \ldots \times (V_{d+1})^l. $
This tower remains regular if we split up the layers into at most
$ (V_1)^l\times \ldots \times (V_{d+1})^l. $
This tower remains regular if we split up the layers into at most
![]() $l^{d+1}$
layers so that it is a tower on
$l^{d+1}$
layers so that it is a tower on
Then, by Lemma 3.3, we get that for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ t_1\in X-x $
the variety
$ t_1\in X-x $
the variety
is the zero locus of a tower
![]() $ \mathcal R $
which has the required properties.
$ \mathcal R $
which has the required properties.
We now use this to prove the proposition from the start of this section.
Proof of Proposition 7.1.
Let
![]() $G = \{x\in X : f(x) = 0\},$
and
$G = \{x\in X : f(x) = 0\},$
and
![]() $B = X\setminus G$
be the good and bad points of
$B = X\setminus G$
be the good and bad points of
![]() $X, $
respectively. Fix
$X, $
respectively. Fix
![]() $x\in X.$
Since
$x\in X.$
Since
![]() $ f $
is a polynomial of degree
$ f $
is a polynomial of degree
![]() $ \le d+1, $
for any
$ \le d+1, $
for any
![]() $ t_1,\ldots ,t_{d+2}\in V^{[d+1]} $
, we have
$ t_1,\ldots ,t_{d+2}\in V^{[d+1]} $
, we have
 $$\begin{align*}\sum_{\omega\in\{0,1\}^{d+2}} (-1)^{|\omega|}f(x+\omega\cdot t) = 0. \end{align*}$$
$$\begin{align*}\sum_{\omega\in\{0,1\}^{d+2}} (-1)^{|\omega|}f(x+\omega\cdot t) = 0. \end{align*}$$
This means that if we can find
![]() $ t\in X_{x,d+2}$
with
$ t\in X_{x,d+2}$
with
![]() $ x+\omega \cdot t\in G $
for all
$ x+\omega \cdot t\in G $
for all
![]() $ 0\neq \omega \in \{0,1\}^{d+2} $
, then
$ 0\neq \omega \in \{0,1\}^{d+2} $
, then
![]() $ x\in G $
as well. Since the previous claim (together with Lemma 3.2) implies, in particular, that
$ x\in G $
as well. Since the previous claim (together with Lemma 3.2) implies, in particular, that
![]() $X_{x,d+2} \neq \emptyset , $
it is enough to show the following bound for any fixed
$X_{x,d+2} \neq \emptyset , $
it is enough to show the following bound for any fixed
![]() $0\neq \omega \in \{0,1\}^{d+2}$
$0\neq \omega \in \{0,1\}^{d+2}$
By reordering the
![]() $ t_j $
, assume without loss of generality that
$ t_j $
, assume without loss of generality that
![]() $\omega = (1^c,0^{d+2-c}).$
By replacing
$\omega = (1^c,0^{d+2-c}).$
By replacing
![]() $ t_1 $
with
$ t_1 $
with
![]() $ t_1-t_2-\ldots -t_c, $
the left-hand side becomes
$ t_1-t_2-\ldots -t_c, $
the left-hand side becomes
By Lemma 7.2, the conclusion of Lemma 3.4 holds (the proof is the same), meaning
This proves the proposition for
![]() $ s \ge 3+d. $
$ s \ge 3+d. $
We now prove a claim which will allow us to glue the various approximations we get in Lemma 5.2 together.
Claim 7.3. There exist
![]() $A(d,H),B(d,H),s(d)$
, such that if
$A(d,H),B(d,H),s(d)$
, such that if
![]() $ f:V^{[d+1]}\to {\mathbb {F}} $
is multilinear,
$ f:V^{[d+1]}\to {\mathbb {F}} $
is multilinear,
![]() ${\mathcal Q},\mathcal G_1, \mathcal G_2$
are multilinear towers on
${\mathcal Q},\mathcal G_1, \mathcal G_2$
are multilinear towers on
![]() $V^{[d+1]}$
satisfying
$V^{[d+1]}$
satisfying
![]() $ f\restriction _{Z({\mathcal Q}\cup \mathcal G_j)} = 0 $
and
$ f\restriction _{Z({\mathcal Q}\cup \mathcal G_j)} = 0 $
and
![]() $ {\mathcal Q}\cup \mathcal G_1\cup \mathcal G_2 $
is
$ {\mathcal Q}\cup \mathcal G_1\cup \mathcal G_2 $
is
![]() $ (A,B,s) $
-regular of degree
$ (A,B,s) $
-regular of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le H, $
then for any
$ \le H, $
then for any
![]() $ i\in [d+1] $
, we have
$ i\in [d+1] $
, we have
Proof. Denote
![]() $ Z = Z({\mathcal Q})\ ,\ Z_j = Z(\mathcal G_j). $
For any
$ Z = Z({\mathcal Q})\ ,\ Z_j = Z(\mathcal G_j). $
For any
![]() $ x\in (Z\cap Z_1 \cap Z_2)_{[d+1]\setminus \{i\}} $
, we have
$ x\in (Z\cap Z_1 \cap Z_2)_{[d+1]\setminus \{i\}} $
, we have
![]() $ f(x,\cdot ) \restriction _{(Z\cap Z_j)(x)} = 0 $
for
$ f(x,\cdot ) \restriction _{(Z\cap Z_j)(x)} = 0 $
for
![]() $ j=1,2 $
so by multilinearity,
$ j=1,2 $
so by multilinearity,
By Lemma 3.3, for
![]() $ q^{-2s} $
-a.e. such
$ q^{-2s} $
-a.e. such
![]() $ x, $
the linear equations appearing in
$ x, $
the linear equations appearing in
![]() $ {\mathcal Q}(x)\cup \mathcal G_1(x)\cup \mathcal G_2(x) $
are linearly independent, in which case
$ {\mathcal Q}(x)\cup \mathcal G_1(x)\cup \mathcal G_2(x) $
are linearly independent, in which case
By Lemma 3.4,
Applying Proposition 7.1, we get that this holds for any
![]() $ x $
in the above variety.
$ x $
in the above variety.
Corollary 7.4. There exist
![]() $A(d,H),B(d,H),s(d)$
, such that when
$A(d,H),B(d,H),s(d)$
, such that when
![]() $ f:V^{[d+1]}\to {\mathbb {F}} $
is multilinear,
$ f:V^{[d+1]}\to {\mathbb {F}} $
is multilinear,
![]() ${\mathcal Q},\mathcal G_1,\ldots ,\mathcal G_{2^l}$
are multilinear towers on
${\mathcal Q},\mathcal G_1,\ldots ,\mathcal G_{2^l}$
are multilinear towers on
![]() $V^{[d+1]}$
, such that the
$V^{[d+1]}$
, such that the
![]() $ \mathcal G_j $
only depend on the first l coordinates,
$ \mathcal G_j $
only depend on the first l coordinates,
![]() $ {\mathcal Q}\cup \mathcal G_1\cup \ldots \cup \mathcal G_{2^l} $
is
$ {\mathcal Q}\cup \mathcal G_1\cup \ldots \cup \mathcal G_{2^l} $
is
![]() $ (A,B,s) $
-regular of degree
$ (A,B,s) $
-regular of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le H $
, and
$ \le H $
, and
then
![]() $ f\restriction _{Z({\mathcal Q})} \equiv 0.$
$ f\restriction _{Z({\mathcal Q})} \equiv 0.$
Proof. By induction on
![]() $l.$
For
$l.$
For
![]() $l = 0$
, this is clear. Suppose it holds up to some l and we are given
$l = 0$
, this is clear. Suppose it holds up to some l and we are given
![]() $ \mathcal G_1,\ldots ,\mathcal G_{2^{l+1}} $
depending on the first
$ \mathcal G_1,\ldots ,\mathcal G_{2^{l+1}} $
depending on the first
![]() $l+1$
coordinates. Applying Claim 7.3 to each pair
$l+1$
coordinates. Applying Claim 7.3 to each pair
![]() $\mathcal G_i,\mathcal G_{i+1} $
, we get that
$\mathcal G_i,\mathcal G_{i+1} $
, we get that
Then apply the inductive hypothesis to
We summarize our results thus far with the following proposition, which brings us very close to proving Theorem 2.13.
Proposition 7.5. There exist constants
![]() $C(A,B,d,H),D(A,B,d,H)$
, such that the following holds: If
$C(A,B,d,H),D(A,B,d,H)$
, such that the following holds: If
![]() $P:V^{[d+1]}\to {\mathbb {F}}$
is multilinear,
$P:V^{[d+1]}\to {\mathbb {F}}$
is multilinear,
![]() ${\mathcal Q}$
is a multilinear tower of degree
${\mathcal Q}$
is a multilinear tower of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
, such that
$\le H$
, such that
-
1.
 $bias_{Z({\mathcal Q})} (P) \ge q^{-s}$
and
$bias_{Z({\mathcal Q})} (P) \ge q^{-s}$
and -
2.
 ${\mathcal Q}$
is
${\mathcal Q}$
is
 $(C,D,s)$
-regular,
$(C,D,s)$
-regular,
then there exists a multilinear tower
![]() $ \mathcal R $
of degree
$ \mathcal R $
of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le 2^{d+1} $
satisfying
$ \le 2^{d+1} $
satisfying
-
1.
 $ \dim (\mathcal R) \le C(1+s)^D, $
$ \dim (\mathcal R) \le C(1+s)^D, $
-
2.
 $ \mathcal R\cup {\mathcal Q} $
is
$ \mathcal R\cup {\mathcal Q} $
is
 $ (A,B,s) $
-regular, and
$ (A,B,s) $
-regular, and -
3.
 $ P\restriction _{Z(\mathcal R\cup {\mathcal Q})} \equiv 0.$
$ P\restriction _{Z(\mathcal R\cup {\mathcal Q})} \equiv 0.$
Proof. Denote
![]() $X = Z({\mathcal Q}) $
, and let E be the set from Proposition 5.2. Given
$X = Z({\mathcal Q}) $
, and let E be the set from Proposition 5.2. Given
![]() $t\in E^{2^{d+1}},$
let
$t\in E^{2^{d+1}},$
let
![]() $Y_i = \{x\in V^{[d+1]}: \phi _{t_i}(x_{[d]}) = 0 \}$
– so P vanishes
$Y_i = \{x\in V^{[d+1]}: \phi _{t_i}(x_{[d]}) = 0 \}$
– so P vanishes
![]() $q^{-s}$
-a.e. on
$q^{-s}$
-a.e. on
![]() $X_{t_i}\cap Y_i.$
Applying Lemma 6.2, there are towers
$X_{t_i}\cap Y_i.$
Applying Lemma 6.2, there are towers
![]() $\mathcal R_{i,1},\ldots , \mathcal R_{i,l}$
which are
$\mathcal R_{i,1},\ldots , \mathcal R_{i,l}$
which are
![]() $(A,B,s)$
-regular relative to the tower defining
$(A,B,s)$
-regular relative to the tower defining
![]() $X_{t_i}, $
satisfy
$X_{t_i}, $
satisfy
![]() $\dim (\mathcal R_{i,j}) \le F(1+s)^G $
for some constants
$\dim (\mathcal R_{i,j}) \le F(1+s)^G $
for some constants
![]() $F(A,B,d),G(A,B,d)$
, and such that
$F(A,B,d),G(A,B,d)$
, and such that
 $$\begin{align*}X_{t_i}\cap Y_i = \bigsqcup_{j=1}^l (X_{t_i}\cap Y_{i,j}), \end{align*}$$
$$\begin{align*}X_{t_i}\cap Y_i = \bigsqcup_{j=1}^l (X_{t_i}\cap Y_{i,j}), \end{align*}$$
where
![]() $ Y_{i,j} = Z(\mathcal R_{i,j}). $
By averaging, there is some
$ Y_{i,j} = Z(\mathcal R_{i,j}). $
By averaging, there is some
![]() $ j\in [l] $
, such that P vanishes
$ j\in [l] $
, such that P vanishes
![]() $q^{-s}$
-a.e. on
$q^{-s}$
-a.e. on
![]() $X_{t_i}\cap Y_{i,j}$
– replace
$X_{t_i}\cap Y_{i,j}$
– replace
![]() $ Y_i $
by this
$ Y_i $
by this
![]() $ Y_{i,j}. $
Now suppose that
$ Y_{i,j}. $
Now suppose that
![]() $X_{t_i} $
is
$X_{t_i} $
is
![]() $ (A,B,s+F(1+s)^G) $
-regular (we will soon explain why we can choose
$ (A,B,s+F(1+s)^G) $
-regular (we will soon explain why we can choose
![]() $ t $
, such that this happens), and note that
$ t $
, such that this happens), and note that
![]() $X_{t_i}\cap Y_i $
is
$X_{t_i}\cap Y_i $
is
![]() $ (A,B,s) $
-regular. Applying Lemma 4.2, we can replace
$ (A,B,s) $
-regular. Applying Lemma 4.2, we can replace
![]() $ Y_i $
by
$ Y_i $
by
![]() $ \tilde {Y_i} $
and still have
$ \tilde {Y_i} $
and still have
![]() ${\mathbb P}_{x\in X_{t_i}\cap Y_i} \ge 1-q^{1-s}. $
By Lemma 7.1,
${\mathbb P}_{x\in X_{t_i}\cap Y_i} \ge 1-q^{1-s}. $
By Lemma 7.1,
![]() $P\restriction _{X_{t_i}\cap Y_i} \equiv 0.$
Setting
$P\restriction _{X_{t_i}\cap Y_i} \equiv 0.$
Setting
![]() $ Y= Y_1\cap \ldots \cap Y_{2^{d+1}}$
, we have
$ Y= Y_1\cap \ldots \cap Y_{2^{d+1}}$
, we have
![]() $ P\restriction _{X_{t_i}\cap Y} \equiv 0 $
for all
$ P\restriction _{X_{t_i}\cap Y} \equiv 0 $
for all
![]() $ i\in [2^{d+1}]. $
After applying Lemma 6.2 to
$ i\in [2^{d+1}]. $
After applying Lemma 6.2 to
![]() $ Y $
relative to
$ Y $
relative to
![]() $X_t := X_{t_1}\cap \ldots \cap X_{t_{2^{d+1}}} $
and assuming
$X_t := X_{t_1}\cap \ldots \cap X_{t_{2^{d+1}}} $
and assuming
![]() $X_t $
is
$X_t $
is
![]() $ (A,B,s+F(2^{d+1} F(1+s)^G)^G) $
-regular, we get that
$ (A,B,s+F(2^{d+1} F(1+s)^G)^G) $
-regular, we get that
![]() $X_t\cap Y $
is
$X_t\cap Y $
is
![]() $ (A,B,s) $
-regular. By Corollary 7.4, we conclude that
$ (A,B,s) $
-regular. By Corollary 7.4, we conclude that
![]() $ P\restriction _{X\cap Y} \equiv 0 $
as desired.
$ P\restriction _{X\cap Y} \equiv 0 $
as desired.
Now we need to justify our assumptions on the regularity of
![]() $X_t. $
Writing
$X_t. $
Writing
![]() $ n = 100s,$
Claims 3.3 and 5.1 imply that if
$ n = 100s,$
Claims 3.3 and 5.1 imply that if
![]() $ {\mathcal Q} $
is
$ {\mathcal Q} $
is
![]() $ (C,D,s) $
-regular for sufficiently large
$ (C,D,s) $
-regular for sufficiently large
![]() $ C(A,B,d,H),D(A,B,d,H), $
then for
$ C(A,B,d,H),D(A,B,d,H), $
then for
![]() $ q^{-2^{d+2} n} $
-a.e.
$ q^{-2^{d+2} n} $
-a.e.
![]() $ t\in \left ( X_{d+1}^n \right )^{2^{d+1}} $
, the variety
$ t\in \left ( X_{d+1}^n \right )^{2^{d+1}} $
, the variety
![]() $X_t $
is
$X_t $
is
![]() $ (A,B,s+F(2^{d+1} F(1+s)^G)^G) $
-regular as desired (in which case
$ (A,B,s+F(2^{d+1} F(1+s)^G)^G) $
-regular as desired (in which case
![]() $X_{t_i}, $
which is only defined by some of the equations, also must have the regularity we wanted). By Lemma 5.2,
$X_{t_i}, $
which is only defined by some of the equations, also must have the regularity we wanted). By Lemma 5.2,
![]() $ E $
has density at least
$ E $
has density at least
![]() $ q^{-n} $
in
$ q^{-n} $
in
![]() $X_{d+1} ^n, $
so
$X_{d+1} ^n, $
so
![]() $ E^{2^{d+1}} $
has density at least
$ E^{2^{d+1}} $
has density at least
![]() $ q^{-2^{d+1} n} $
in
$ q^{-2^{d+1} n} $
in
![]() $ \left ( X_{d+1}^n \right )^{2^{d+1}} $
, which means that there must be some
$ \left ( X_{d+1}^n \right )^{2^{d+1}} $
, which means that there must be some
![]() $ t\in E^{2^{d+1}} $
for which
$ t\in E^{2^{d+1}} $
for which
![]() $X_t $
has the desired regularity.
$X_t $
has the desired regularity.
8 Nullstellensatz
In this section, we finish the proof of Theorem 2.13 by proving a Nullstellensatz for regular towers. This is similar to section 3 of [Reference Milićević21], but by restricting our attention to regular towers, we can prove a stronger result for them. We start with the following definition.
Definition 8.1. We give
![]() $V^{[k]}$
a graph structure where two points
$V^{[k]}$
a graph structure where two points
![]() $ x,y \in V^{[k]} $
are connected by an edge if there exists some
$ x,y \in V^{[k]} $
are connected by an edge if there exists some
![]() $ i\in [k] $
, such that
$ i\in [k] $
, such that
![]() $ x_{[k]\setminus \{i\}} = y_{[k]\setminus \{i\}}, $
that is, they differ in at most one coordinate.
$ x_{[k]\setminus \{i\}} = y_{[k]\setminus \{i\}}, $
that is, they differ in at most one coordinate.
We will need the following technical lemma.
Lemma 8.2. There exist constants
![]() $A(d,H),B(d,H)$
, such that if
$A(d,H),B(d,H)$
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $(A,B,s)$
-regular tower on
$(A,B,s)$
-regular tower on
![]() $V^{[d+1]}$
of degree
$V^{[d+1]}$
of degree
![]() $\le d$
and height
$\le d$
and height
![]() $\le H$
,
$\le H$
,
![]() $X=Z({\mathcal Q}) $
and
$X=Z({\mathcal Q}) $
and
![]() $ I\subset [d+1] $
, then, for
$ I\subset [d+1] $
, then, for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ x\in X, $
for a.e.
$ x\in X, $
for a.e.
![]() $ y\in X\cap X(x_{\ge I}) $
(with
$ y\in X\cap X(x_{\ge I}) $
(with
![]() $X(x_{\ge I}) := \cap _{I\subset J} \left ( X(x_J)\times V^J \right ) ), $
the points
$X(x_{\ge I}) := \cap _{I\subset J} \left ( X(x_J)\times V^J \right ) ), $
the points
![]() $ x_I,y_I $
are connected by a path in
$ x_I,y_I $
are connected by a path in
![]() $X( y_{[d+1] \setminus I } ). $
$X( y_{[d+1] \setminus I } ). $
Proof. A sufficient condition for there to be a path in
![]() $X( y_{[d+1] \setminus I } ) $
between
$X( y_{[d+1] \setminus I } ) $
between
![]() $x_I,y_I$
is that there exists
$x_I,y_I$
is that there exists
![]() $z $
, such that for all
$z $
, such that for all
![]() $ K\subset I $
, we have
$ K\subset I $
, we have
Take the following variety
The equations defining it are partial to those of
![]() $ {\mathcal Q}^{\times 3}, $
so by Claim 5.1, we have
$ {\mathcal Q}^{\times 3}, $
so by Claim 5.1, we have
![]() $ Y=Z(\mathcal G) $
for a
$ Y=Z(\mathcal G) $
for a
![]() $ (C,D,s) $
-regular tower of degree
$ (C,D,s) $
-regular tower of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le 3^{d+1} H $
as long as
$ \le 3^{d+1} H $
as long as
![]() $ {\mathcal Q} $
is
$ {\mathcal Q} $
is
![]() $ (C(3^{d+1})^D,D,s) $
-regular. By Lemmas 3.3 and 3.4, for
$ (C(3^{d+1})^D,D,s) $
-regular. By Lemmas 3.3 and 3.4, for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ x\in X, $
for
$ x\in X, $
for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ y \in X\cap X(x_{\ge I}), $
the variety
$ y \in X\cap X(x_{\ge I}), $
the variety
![]() $ Y(x,y) $
(which is composed of the
$ Y(x,y) $
(which is composed of the
![]() $ z'$
s we want) is
$ z'$
s we want) is
![]() $ (C',D',s) $
-regular. In particular, by Lemma 3.2, it is nonempty.
$ (C',D',s) $
-regular. In particular, by Lemma 3.2, it is nonempty.
Now we are ready to prove:
Theorem 8.3 (Nullstellensatz).
There exist constants
![]() $A(d,H),B(d,H),s(d)$
, such that if
$A(d,H),B(d,H),s(d)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular multilinear tower on
$(A,B,s)$
-regular multilinear tower on
![]() $V^{[d+1]}$
of deg
$V^{[d+1]}$
of deg
![]() $\le d$
and height
$\le d$
and height
![]() $ \le H $
and
$ \le H $
and
![]() $P: V^{[d+1]}\to {\mathbb {F}}$
is a multilinear map which vanishes
$P: V^{[d+1]}\to {\mathbb {F}}$
is a multilinear map which vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}), $
then
$ Z({\mathcal Q}), $
then
![]() $ rk_{\mathcal Q} (P) = 0. $
$ rk_{\mathcal Q} (P) = 0. $
The proof of this theorem (like everything else in this paper) will be by induction. For the inductive step, we will use the following simple corollary many times.
Corollary 8.4. If
![]() $ R_1,R_2:V^I\to {\mathbb {F}} $
are multilinear maps,
$ R_1,R_2:V^I\to {\mathbb {F}} $
are multilinear maps,
![]() $ {\mathcal Q}_1\cup {\mathcal Q}_2 $
is a multilinear tower on
$ {\mathcal Q}_1\cup {\mathcal Q}_2 $
is a multilinear tower on
![]() $ V^{[d+1]} $
for which the conclusion of Theorem 8.3 holds, and
$ V^{[d+1]} $
for which the conclusion of Theorem 8.3 holds, and
then there exists a multilinear map
![]() $ R:V^I\to {\mathbb {F}} $
with
$ R:V^I\to {\mathbb {F}} $
with
![]() $ R\restriction _{Z({\mathcal Q}_1)} \equiv R_1\restriction _{Z({\mathcal Q}_1)} $
and
$ R\restriction _{Z({\mathcal Q}_1)} \equiv R_1\restriction _{Z({\mathcal Q}_1)} $
and
![]() $ R\restriction _{Z({\mathcal Q}_2)} \equiv R_2\restriction _{Z({\mathcal Q}_2)}. $
$ R\restriction _{Z({\mathcal Q}_2)} \equiv R_2\restriction _{Z({\mathcal Q}_2)}. $
Proof of corollary.
By Theorem 8.3,
![]() $ rk_{{\mathcal Q}_1\cup {\mathcal Q}_2} (R_1-R_2) = 0. $
Therefore, there exist multilinear maps
$ rk_{{\mathcal Q}_1\cup {\mathcal Q}_2} (R_1-R_2) = 0. $
Therefore, there exist multilinear maps
![]() $ f,g:V^I\to {\mathbb {F}} $
with
$ f,g:V^I\to {\mathbb {F}} $
with
![]() $ rk_{{\mathcal Q}_1} (f) = rk_{{\mathcal Q}_2} (g) = 0 $
and
$ rk_{{\mathcal Q}_1} (f) = rk_{{\mathcal Q}_2} (g) = 0 $
and
![]() $ R_1-R_2 = f+g. $
Setting
$ R_1-R_2 = f+g. $
Setting
![]() $ R = R_1-f = R_2+g$
does the job.
$ R = R_1-f = R_2+g$
does the job.
Proof of Theorem 8.3.
By Lemma 7.1, we have that
![]() $P\restriction _{Z({\mathcal Q})} = 0. $
The proof will proceed by induction on the degree of
$P\restriction _{Z({\mathcal Q})} = 0. $
The proof will proceed by induction on the degree of
![]() $ {\mathcal Q}, $
and then on the number of layers of maximal degree. For the base case
$ {\mathcal Q}, $
and then on the number of layers of maximal degree. For the base case
![]() $ {\mathcal Q} = \emptyset $
, this is trivial. For the inductive step, choose some
$ {\mathcal Q} = \emptyset $
, this is trivial. For the inductive step, choose some
![]() $ Q_0\in {\mathcal Q} $
with a maximal size index set
$ Q_0\in {\mathcal Q} $
with a maximal size index set
![]() $I,$
and write
$I,$
and write
![]() $ {\mathcal Q}' = {\mathcal Q}\setminus \{Q_0\}. $
Apply Lemma 8.2 to the variety
$ {\mathcal Q}' = {\mathcal Q}\setminus \{Q_0\}. $
Apply Lemma 8.2 to the variety
![]() $X = Z({\mathcal Q}')\cap \{Q_0 = 1\}. $
Choose
$X = Z({\mathcal Q}')\cap \{Q_0 = 1\}. $
Choose
![]() $ x^1,\ldots ,x^{2^{d+1}} \in X $
, such that for each j,
$ x^1,\ldots ,x^{2^{d+1}} \in X $
, such that for each j,
![]() $x^j $
satisfies the conclusion of Lemma 8.2 with
$x^j $
satisfies the conclusion of Lemma 8.2 with
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ y\in X\cap X(x^j_{\ge I}) $
and such that
$ y\in X\cap X(x^j_{\ge I}) $
and such that
![]() $ {\mathcal Q} \cup {\mathcal Q}(\textbf {x}_{\ge I})$
is
$ {\mathcal Q} \cup {\mathcal Q}(\textbf {x}_{\ge I})$
is
![]() $ (C,D,s) $
-regular, where
$ (C,D,s) $
-regular, where
![]() $ {\mathcal Q}(\textbf {x}_{\ge I}) := \bigcup _{j=1}^{2^{d+1}} {\mathcal Q}(x^j_{\ge I}). $
The reason we can choose such
$ {\mathcal Q}(\textbf {x}_{\ge I}) := \bigcup _{j=1}^{2^{d+1}} {\mathcal Q}(x^j_{\ge I}). $
The reason we can choose such
![]() $ x^j $
’s is that the first condition holds
$ x^j $
’s is that the first condition holds
![]() $ 2^{d+1}q^{-s} $
-a.s. by a union bound, and the second one holds (as long as
$ 2^{d+1}q^{-s} $
-a.s. by a union bound, and the second one holds (as long as
![]() $ A,B $
are sufficiently large)
$ A,B $
are sufficiently large)
![]() $ q^{-s} $
-a.s. by Claim 5.1 and Lemma 3.3. Let
$ q^{-s} $
-a.s. by Claim 5.1 and Lemma 3.3. Let
![]() $ {\mathcal Q}^j = {\mathcal Q}'\cup {\mathcal Q}(x^j_{\ge I}) $
, and define
$ {\mathcal Q}^j = {\mathcal Q}'\cup {\mathcal Q}(x^j_{\ge I}) $
, and define
![]() $ R^j(y_{[d+1]\setminus I}) = P(x^j_I,y_{[d+1]\setminus I}). $
We claim that
$ R^j(y_{[d+1]\setminus I}) = P(x^j_I,y_{[d+1]\setminus I}). $
We claim that
Note that
and both sides vanish on
![]() $ Z({\mathcal Q}) $
by assumption, so by scaling one of the coordinates, it is enough to prove that
$ Z({\mathcal Q}) $
by assumption, so by scaling one of the coordinates, it is enough to prove that
Recall that by our definitions,
![]() $ Z({\mathcal Q}^j) \cap \{Q_0 = 1\} = X\cap X(x^j_{\ge I}). $
Now, for any
$ Z({\mathcal Q}^j) \cap \{Q_0 = 1\} = X\cap X(x^j_{\ge I}). $
Now, for any
![]() $ y\in X\cap X(x^j_{\ge I}) $
, we have equality at the point
$ y\in X\cap X(x^j_{\ge I}) $
, we have equality at the point
![]() $ (x^j_I,y_{[d+1]\setminus I})\in Z({\mathcal Q}^j). $
Also, for
$ (x^j_I,y_{[d+1]\setminus I})\in Z({\mathcal Q}^j). $
Also, for
![]() $ q^{-s} $
-a.e. such
$ q^{-s} $
-a.e. such
![]() $ y, $
the points
$ y, $
the points
![]() $ x^j_I,y_I $
are connected in
$ x^j_I,y_I $
are connected in
![]() $X(y_{[d+1]\setminus I}). $
Each time two points in X differ by a single coordinate in
$X(y_{[d+1]\setminus I}). $
Each time two points in X differ by a single coordinate in
![]() $ I, $
the values of both sides do not change, because the difference of the two points is in
$ I, $
the values of both sides do not change, because the difference of the two points is in
![]() $Z({\mathcal Q}). $
This means that
$Z({\mathcal Q}). $
This means that
as desired, implying the same for
![]() $ Z({\mathcal Q}^j). $
$ Z({\mathcal Q}^j). $
By Lemma 7.1, we get that
![]() $ P(y) = R^j(y_{[d+1]\setminus I})Q(y_I) $
for all
$ P(y) = R^j(y_{[d+1]\setminus I})Q(y_I) $
for all
![]() $ y\in Z({\mathcal Q}^j). $
The following claim will complete the inductive step.
$ y\in Z({\mathcal Q}^j). $
The following claim will complete the inductive step.
Claim 8.5. There exist constants
![]() $ C(d,H),D(d,H) $
, such that if
$ C(d,H),D(d,H) $
, such that if
![]() $ \mathcal F,\mathcal G^j $
for
$ \mathcal F,\mathcal G^j $
for
![]() $ j\in [2^k] $
are towers on
$ j\in [2^k] $
are towers on
![]() $ V^{[d+1]}, $
of degree
$ V^{[d+1]}, $
of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le H, $
such that the
$ \le H, $
such that the
![]() $ \mathcal G^j $
depend only on the first
$ \mathcal G^j $
depend only on the first
![]() $ k $
coordinates, and
$ k $
coordinates, and
![]() $ Q:V^I\to {\mathbb {F}},R^j:V^{[d+1]\setminus I}\to {\mathbb {F}} $
are multilinear maps, where
$ Q:V^I\to {\mathbb {F}},R^j:V^{[d+1]\setminus I}\to {\mathbb {F}} $
are multilinear maps, where
-
1.
 $ P(y) = R^j(y_{[d+1]\setminus I})Q(y_I)\ \forall y\in Z(\mathcal F \cup \mathcal G^j),$
$ P(y) = R^j(y_{[d+1]\setminus I})Q(y_I)\ \forall y\in Z(\mathcal F \cup \mathcal G^j),$
-
2.
 $ \mathcal F \cup \{Q\} \cup \bigcup _{j\in [2^k]} \mathcal G^j $
is
$ \mathcal F \cup \{Q\} \cup \bigcup _{j\in [2^k]} \mathcal G^j $
is
 $ (C,D,s) $
-regular, and
$ (C,D,s) $
-regular, and -
3. the Nullstellensatz holds for
 $ \mathcal F \cup \bigcup _{j\in [2^k]} \mathcal G^j $
and towers contained in it,
$ \mathcal F \cup \bigcup _{j\in [2^k]} \mathcal G^j $
and towers contained in it,
then there exists a multilinear
![]() $ R:V^{[d+1]\setminus I}\to {\mathbb {F}} $
, such that
$ R:V^{[d+1]\setminus I}\to {\mathbb {F}} $
, such that
![]() $ P(y) = R(y_{[d+1]\setminus I})Q(y_I) $
for all
$ P(y) = R(y_{[d+1]\setminus I})Q(y_I) $
for all
![]() $ y\in Z(\mathcal F). $
$ y\in Z(\mathcal F). $
Proof of claim.
We prove this by induction on
![]() $ k. $
For
$ k. $
For
![]() $ k = 0 $
, there is nothing to prove. Now suppose we have proved it up to
$ k = 0 $
, there is nothing to prove. Now suppose we have proved it up to
![]() $ k $
and
$ k $
and
![]() $ \mathcal G^j $
are all defined on the first
$ \mathcal G^j $
are all defined on the first
![]() $ k+1 $
coordinates. By looking at
$ k+1 $
coordinates. By looking at
![]() $ Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1}) $
, we get
$ Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1}) $
, we get
![]() $ R^i(y_{[d+1]\setminus I})Q(y_I) = R^{i+1}(y_{[d+1]\setminus I})Q(y_I) $
on
$ R^i(y_{[d+1]\setminus I})Q(y_I) = R^{i+1}(y_{[d+1]\setminus I})Q(y_I) $
on
![]() $Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1}). $
By Lemma 3.3 (together with Lemma 3.2), for
$Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1}). $
By Lemma 3.3 (together with Lemma 3.2), for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $ y_{[d+1]\setminus I}\in Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1})_{[d+1]\setminus I}, $
there exists
$ y_{[d+1]\setminus I}\in Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1})_{[d+1]\setminus I}, $
there exists
![]() $ y_I $
, such that
$ y_I $
, such that
![]() $ {y\in Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1})\cap \{Q(y_I)=1\},} $
in which case,
$ {y\in Z(\mathcal F\cup \mathcal G^i\cup \mathcal G^{i+1})\cap \{Q(y_I)=1\},} $
in which case,
![]() $ R^i(y_{[d+1]\setminus I}) = R^{i+1}(y_{[d+1]\setminus I}). $
By Corollary 8.4, there exists
$ R^i(y_{[d+1]\setminus I}) = R^{i+1}(y_{[d+1]\setminus I}). $
By Corollary 8.4, there exists
![]() $ S^i $
, such that
$ S^i $
, such that
![]() $ P\restriction _{Z(\mathcal F \cup \mathcal G^j)} = S^i(x_{[d+1]\setminus I})Q(x_I) $
for
$ P\restriction _{Z(\mathcal F \cup \mathcal G^j)} = S^i(x_{[d+1]\setminus I})Q(x_I) $
for
![]() $ j=i,i+1. $
Applying Lemma 7.3, we get that
$ j=i,i+1. $
Applying Lemma 7.3, we get that
![]() $ P\restriction _{Z(\mathcal F \cup (\mathcal G^i \cup \mathcal G^{i+1})_{[k]})} = S^i(x_{[d+1]\setminus I})Q(x_I). $
Now apply the induction hypothesis to the collection
$ P\restriction _{Z(\mathcal F \cup (\mathcal G^i \cup \mathcal G^{i+1})_{[k]})} = S^i(x_{[d+1]\setminus I})Q(x_I). $
Now apply the induction hypothesis to the collection
![]() $ (\mathcal G^i \cup \mathcal G^{i+1})_{[k]} $
, and we are done.
$ (\mathcal G^i \cup \mathcal G^{i+1})_{[k]} $
, and we are done.
Applying the above claim with
![]() $ \mathcal F = {\mathcal Q}' $
and
$ \mathcal F = {\mathcal Q}' $
and
![]() $ \mathcal G^j = {\mathcal Q}(x^j_{\ge I}) $
(note that the equations coming from
$ \mathcal G^j = {\mathcal Q}(x^j_{\ge I}) $
(note that the equations coming from
![]() $ x^j_{\ge I} $
are of deg
$ x^j_{\ge I} $
are of deg
![]() $ < |I|, $
so the induction hypothesis applies to
$ < |I|, $
so the induction hypothesis applies to
![]() $ {\mathcal Q}'\cup \bigcup _{j\in [2^{d+1}]} Q^j $
and towers partial to it), we get that
$ {\mathcal Q}'\cup \bigcup _{j\in [2^{d+1}]} Q^j $
and towers partial to it), we get that
![]() $ P(y) = R(y_{[d+1]\setminus I})Q(y_I) $
on
$ P(y) = R(y_{[d+1]\setminus I})Q(y_I) $
on
![]() $ Z({\mathcal Q}'). $
By the inductive hypothesis,
$ Z({\mathcal Q}'). $
By the inductive hypothesis,
![]() $ rk_{{\mathcal Q}'} \left ( P(y) - R(y_{[d+1]\setminus I})Q(y_I) \right ) = 0 $
, and this completes the inductive step.
$ rk_{{\mathcal Q}'} \left ( P(y) - R(y_{[d+1]\setminus I})Q(y_I) \right ) = 0 $
, and this completes the inductive step.
9 Reduction to the multilinear case
In this section, we show that Theorems 2.2 and 2.7 follow from their multilinear analogues – Theorems 2.13 and 8.3. In order to do this, we will show that both relative bias and relative rank behave well when passing from polynomials to corresponding multilinear maps. We start by recalling the polarization identity, which associates a multilinear map to a polynomial. The following is well known.
Claim 9.1. Given a polynomial P on
![]() $ V $
of degree
$ V $
of degree
![]() $ d < char({\mathbb {F}}), $
the map
$ d < char({\mathbb {F}}), $
the map
![]() $ \bar P: V^d\to {\mathbb {F}} $
defined by
$ \bar P: V^d\to {\mathbb {F}} $
defined by
![]() $ \bar P(x_1,\ldots ,x_d) = \frac {1}{d!}\nabla _{x_1}\ldots \nabla _{x_d} P(0)$
is multilinear and satisfies
$ \bar P(x_1,\ldots ,x_d) = \frac {1}{d!}\nabla _{x_1}\ldots \nabla _{x_d} P(0)$
is multilinear and satisfies
![]() $ \bar P(x,\ldots ,x) = \tilde P(x) $
(the homogeneous part of P of highest degree).
$ \bar P(x,\ldots ,x) = \tilde P(x) $
(the homogeneous part of P of highest degree).
Definition 9.2. Given a polynomial tower
![]() $ {\mathcal Q} $
on
$ {\mathcal Q} $
on
![]() $ V, $
of degree
$ V, $
of degree
![]() $ \le d < char({\mathbb {F}}) $
and height
$ \le d < char({\mathbb {F}}) $
and height
![]() $ \le H, $
there exists a symmetric multilinear tower
$ \le H, $
there exists a symmetric multilinear tower
![]() $ {\mathcal Q}(k) $
of degree
$ {\mathcal Q}(k) $
of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le 2^k H $
on
$ \le 2^k H $
on
![]() $ V^k $
corresponding to it. For a layer
$ V^k $
corresponding to it. For a layer
![]() $ {\mathcal Q}_i $
of degree
$ {\mathcal Q}_i $
of degree
![]() $ e $
and a subset
$ e $
and a subset
![]() $ E\subset [k] $
of size
$ E\subset [k] $
of size
![]() $ e, $
we get
$ e, $
we get
![]() $ {\mathcal Q}(k)_{i,E}:V^E\to {\mathbb {F}} $
given by
$ {\mathcal Q}(k)_{i,E}:V^E\to {\mathbb {F}} $
given by
![]() $ \bar {{\mathcal Q}_i}. $
Conversely, given a multilinear tower
$ \bar {{\mathcal Q}_i}. $
Conversely, given a multilinear tower
![]() $ {\mathcal Q} $
on
$ {\mathcal Q} $
on
![]() $ V^k $
, it induces a polynomial tower
$ V^k $
, it induces a polynomial tower
![]() $ {\mathcal Q}\circ D $
on
$ {\mathcal Q}\circ D $
on
![]() $ V $
by precomposition with the diagonal map
$ V $
by precomposition with the diagonal map
![]() $ {\mathcal Q}\circ D = {\mathcal Q}(x,\ldots ,x). $
$ {\mathcal Q}\circ D = {\mathcal Q}(x,\ldots ,x). $
Claim 9.3. If
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $ (A2^{kB},B,s) $
-regular polynomial tower, then
$ (A2^{kB},B,s) $
-regular polynomial tower, then
![]() $ {\mathcal Q}(k) $
is
$ {\mathcal Q}(k) $
is
![]() $ (A,B,s) $
-regular. Conversely, if
$ (A,B,s) $
-regular. Conversely, if
![]() $ {\mathcal Q}(k) $
is
$ {\mathcal Q}(k) $
is
![]() $ (A2^{kB},B,s) $
-regular and
$ (A2^{kB},B,s) $
-regular and
![]() $ k \ge \deg ({\mathcal Q}) $
, then
$ k \ge \deg ({\mathcal Q}) $
, then
![]() $ {\mathcal Q} $
is
$ {\mathcal Q} $
is
![]() $ (A,B,s) $
-regular.
$ (A,B,s) $
-regular.
Proof. Assume without loss of generality that
![]() $ {\mathcal Q} $
is homogeneous. The polynomials of degree
$ {\mathcal Q} $
is homogeneous. The polynomials of degree
![]() $ d_i $
in
$ d_i $
in
![]() $ {\mathcal Q} $
give
$ {\mathcal Q} $
give
![]() $ \binom {k}{d_i} \le 2^k $
polynomials in
$ \binom {k}{d_i} \le 2^k $
polynomials in
![]() $ {\mathcal Q}(k), $
so we just need to check that
$ {\mathcal Q}(k), $
so we just need to check that
This follows by plugging in the diagonal for any relative low partition rank combination. For the converse, we need to check that
This follows from the polarization identity for any low relative polynomial rank combination.
We recall Theorem 2.2:
Theorem 9.4 (Relative bias implies relative low rank).
There exist constants
![]() $A(d,H), B(d,H)$
, such that if
$A(d,H), B(d,H)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular tower of degree
$(A,B,s)$
-regular tower of degree
![]() $\le d < char({\mathbb {F}})$
and height
$\le d < char({\mathbb {F}})$
and height
![]() $\le H$
and P is a polynomial of degree
$\le H$
and P is a polynomial of degree
![]() $\le d$
with
$\le d$
with
then
We call
![]() ${\mathcal Q}$
as above a tower of type
${\mathcal Q}$
as above a tower of type
![]() $(d,H)$
for short. The proof will be by induction on the degree
$(d,H)$
for short. The proof will be by induction on the degree
![]() $ d. $
For
$ d. $
For
![]() $ d = 1 $
, it follows from classical Fourier analysis. Now, we assume the theorem holds for degree d and explore some consequences.
$ d = 1 $
, it follows from classical Fourier analysis. Now, we assume the theorem holds for degree d and explore some consequences.
Lemma 9.5 (Regular varieties are of the expected size (d,H)).
There exist constants
![]() $A(d,H),B(d,H)$
, such that for any
$A(d,H),B(d,H)$
, such that for any
![]() $s>0$
and for any
$s>0$
and for any
![]() $(A,B,s)$
-regular polynomial tower
$(A,B,s)$
-regular polynomial tower
![]() ${\mathcal Q}$
of type
${\mathcal Q}$
of type
![]() $ (d,H) $
defined on
$ (d,H) $
defined on
![]() $ V $
of degree
$ V $
of degree
![]() $ \le d, $
height
$ \le d, $
height
![]() $ \le H $
and dimension
$ \le H $
and dimension
![]() $m,$
we have
$m,$
we have
 $$\begin{align*}\left|q^m \frac{|Z({\mathcal Q})|}{|V|}-1\right|\le q^{-s}. \end{align*}$$
$$\begin{align*}\left|q^m \frac{|Z({\mathcal Q})|}{|V|}-1\right|\le q^{-s}. \end{align*}$$
Proof. Identical to that of Lemma 3.2.
Now, we will prove a lemma analogous to Lemma 3.3. For a polynomial tower
![]() $ {\mathcal Q} $
and
$ {\mathcal Q} $
and
![]() $ t\in V $
, we denote
$ t\in V $
, we denote
Lemma 9.6 (Derivatives).
For any
![]() $C,D$
, there exist constants
$C,D$
, there exist constants
![]() $A(C,D,d,H)$
,
$A(C,D,d,H)$
,
![]() $B(C,D,d,H)$
, such that if
$B(C,D,d,H)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(Ak^B,B,s)$
-regular polynomial tower of type
$(Ak^B,B,s)$
-regular polynomial tower of type
![]() $ (d,H) $
, then for
$ (d,H) $
, then for
![]() $q^{-s}$
-a.e.
$q^{-s}$
-a.e.
![]() $t_1,\ldots ,t_k\in Z({\mathcal Q}(1))$
, the tower
$t_1,\ldots ,t_k\in Z({\mathcal Q}(1))$
, the tower
![]() ${\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k}$
is
${\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k}$
is
![]() $(C,D,s)$
-regular.
$(C,D,s)$
-regular.
Proof. By Claim 9.3, it is enough that
![]() $ ({\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k} )(d) $
is
$ ({\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k} )(d) $
is
![]() $ (C2^{dD},D,s) $
-regular. By the same claim,
$ (C2^{dD},D,s) $
-regular. By the same claim,
![]() $ {\mathcal Q}(d+1) $
is
$ {\mathcal Q}(d+1) $
is
![]() $ (Ek^F,F,s) $
-regular as long as
$ (Ek^F,F,s) $
-regular as long as
![]() $ A,B $
are large. By Claim 5.1 applied with multiplicity vector
$ A,B $
are large. By Claim 5.1 applied with multiplicity vector
![]() $ l = (1,\ldots ,1,k), $
the tower
$ l = (1,\ldots ,1,k), $
the tower
![]() $ {\mathcal Q}' = ({\mathcal Q}(d+1))^{\otimes l} $
is
$ {\mathcal Q}' = ({\mathcal Q}(d+1))^{\otimes l} $
is
![]() $ (E,F,s) $
-regular. Then by Lemma 3.3 for
$ (E,F,s) $
-regular. Then by Lemma 3.3 for
![]() $ E,F $
sufficiently large, it follows that for
$ E,F $
sufficiently large, it follows that for
![]() $ q^{-s} $
-a.e.
$ q^{-s} $
-a.e.
![]() $t_1,\ldots ,t_k\in Z({\mathcal Q}(1)),$
the tower
$t_1,\ldots ,t_k\in Z({\mathcal Q}(1)),$
the tower
![]() $ {\mathcal Q}'(t_1,\ldots ,t_k) $
is
$ {\mathcal Q}'(t_1,\ldots ,t_k) $
is
![]() $ (C,D,s) $
-regular.
$ (C,D,s) $
-regular.
![]() $ {\mathcal Q}'(t_1,\ldots ,t_k) = ({\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k} )(d), $
so we are done.
$ {\mathcal Q}'(t_1,\ldots ,t_k) = ({\mathcal Q}_{t_1}\cup \ldots \cup {\mathcal Q}_{t_k} )(d), $
so we are done.
Corollary 9.7 (Fubini).
There are constants
![]() $ A(d,H),B(d,H) $
, such that if
$ A(d,H),B(d,H) $
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $ (A,B,s) $
-regular polynomial tower of type
$ (A,B,s) $
-regular polynomial tower of type
![]() $ (d,H) $
and
$ (d,H) $
and
![]() $ f $
is a one-bounded function, then we have
$ f $
is a one-bounded function, then we have
Proof. Identical to the proof of Lemma 3.4.
For a function
![]() $f:V\to {\mathbb C}, $
and
$f:V\to {\mathbb C}, $
and
![]() $ t\in V, $
denote the (multiplicative) derivative by
$ t\in V, $
denote the (multiplicative) derivative by
![]() $ D_t f(x) = f(x+t)\bar f(x)$
. For
$ D_t f(x) = f(x+t)\bar f(x)$
. For
![]() $t = (t_1\ldots t_k)\in V^k, $
write
$t = (t_1\ldots t_k)\in V^k, $
write
![]() $ {\mathcal Q}_t = (\ldots ({\mathcal Q}_{t_1})_{t_2})\ldots )_{t_k}$
.
$ {\mathcal Q}_t = (\ldots ({\mathcal Q}_{t_1})_{t_2})\ldots )_{t_k}$
.
Lemma 9.8 (Cauchy-Schwarz).
There exist
![]() $ A(d,H,k),B(d,H,k) $
, such that if
$ A(d,H,k),B(d,H,k) $
, such that if
![]() $ {\mathcal Q} $
is an
$ {\mathcal Q} $
is an
![]() $ (A,B,s) $
-regular polynomial tower of degree
$ (A,B,s) $
-regular polynomial tower of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le H, $
and
$ \le H, $
and
![]() $ f:V\to {\mathbb C} $
is a one-bounded function, then
$ f:V\to {\mathbb C} $
is a one-bounded function, then
Proof. By induction on
![]() $ k. $
For
$ k. $
For
![]() $ k = 1 $
, this follows from Corollary 9.7. Suppose it holds up to
$ k = 1 $
, this follows from Corollary 9.7. Suppose it holds up to
![]() $ k-1. $
Then if
$ k-1. $
Then if
![]() $ A,B $
are sufficiently large, we can apply Corollary 9.7 to get
$ A,B $
are sufficiently large, we can apply Corollary 9.7 to get
 $$ \begin{align*} | {\mathbb E}_{x\in Z({\mathcal Q})} f(x) |^{2^k} = |{\mathbb E}_{x,y\in Z({\mathcal Q})} f(x) \bar f(y)|^{2^{k-1}} &\le | {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x) |^{2^{k-1}} + q^{-4s} \\ &\qquad\quad \ \le {\mathbb E}_{t\in Z({\mathcal Q}(1))} |{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x)|^{2^{k-1}} + q^{-4s}. \end{align*} $$
$$ \begin{align*} | {\mathbb E}_{x\in Z({\mathcal Q})} f(x) |^{2^k} = |{\mathbb E}_{x,y\in Z({\mathcal Q})} f(x) \bar f(y)|^{2^{k-1}} &\le | {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x) |^{2^{k-1}} + q^{-4s} \\ &\qquad\quad \ \le {\mathbb E}_{t\in Z({\mathcal Q}(1))} |{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x)|^{2^{k-1}} + q^{-4s}. \end{align*} $$
If
![]() $ A,B $
are sufficiently large, then by Lemma 9.6, the inductive hypothesis applies to
$ A,B $
are sufficiently large, then by Lemma 9.6, the inductive hypothesis applies to
![]() $ q^{-4s} $
-a.e.
$ q^{-4s} $
-a.e.
![]() $ {\mathcal Q}_t. $
Therefore,
$ {\mathcal Q}_t. $
Therefore,
 $$ \begin{align*} {\mathbb E}_{t\in Z({\mathcal Q}(1))} |{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x)|^{2^{k-1}} &\\ &\le Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{s\in Z({\mathcal Q}_t(k-1))} {\mathbb E}_{x\in Z(({\mathcal Q}_t)_s)} D_sD_t f(x) \right) +q^{-2s}. \end{align*} $$
$$ \begin{align*} {\mathbb E}_{t\in Z({\mathcal Q}(1))} |{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_t f(x)|^{2^{k-1}} &\\ &\le Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{s\in Z({\mathcal Q}_t(k-1))} {\mathbb E}_{x\in Z(({\mathcal Q}_t)_s)} D_sD_t f(x) \right) +q^{-2s}. \end{align*} $$
Finally, using the fact that
![]() $ {\mathcal Q}_t(k-1) = ({\mathcal Q}(k))(t) $
and applying Lemma 3.4 for
$ {\mathcal Q}_t(k-1) = ({\mathcal Q}(k))(t) $
and applying Lemma 3.4 for
![]() ${\mathcal Q}(k)$
, we get that
${\mathcal Q}(k)$
, we get that
 $$ \begin{align*} &Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{s\in Z({\mathcal Q}_t(k-1))} {\mathbb E}_{x\in Z({\mathcal Q}_{(t,s)})} D_sD_t f(x) \right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(k))}{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_{t_1}\ldots D_{t_k} f(x) \right) + q^{-2s}, \end{align*} $$
$$ \begin{align*} &Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(1))} {\mathbb E}_{s\in Z({\mathcal Q}_t(k-1))} {\mathbb E}_{x\in Z({\mathcal Q}_{(t,s)})} D_sD_t f(x) \right) \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le Re \left( {\mathbb E}_{t\in Z({\mathcal Q}(k))}{\mathbb E}_{x\in Z({\mathcal Q}_t)} D_{t_1}\ldots D_{t_k} f(x) \right) + q^{-2s}, \end{align*} $$
which completes the inductive step.
Corollary 9.9. Theorem 2.2 holds for polynomials of degree
![]() $ \le d+1 $
on towers of degree
$ \le d+1 $
on towers of degree
![]() $ \le d. $
$ \le d. $
Proof. When
![]() $ \deg (P) \le d $
, we are already assuming this holds, so we deal with the case
$ \deg (P) \le d $
, we are already assuming this holds, so we deal with the case
![]() $ \deg (P) =d+1. $
If
$ \deg (P) =d+1. $
If
![]() $ bias_{Z({\mathcal Q})} (P) \ge q^{-s} $
, then by Lemma 9.8, we get that
$ bias_{Z({\mathcal Q})} (P) \ge q^{-s} $
, then by Lemma 9.8, we get that
![]() $ bias_{Z({\mathcal Q}(d+1))} (\bar P) \ge q^{-2s}. $
By Claim 9.3, the tower
$ bias_{Z({\mathcal Q}(d+1))} (\bar P) \ge q^{-2s}. $
By Claim 9.3, the tower
![]() $ {\mathcal Q}(d+1) $
is regular, so we can apply Theorem 2.13 to deduce that
$ {\mathcal Q}(d+1) $
is regular, so we can apply Theorem 2.13 to deduce that
![]() $ prk_{{\mathcal Q}(d+1)} (\bar P) \le A(1+s)^B. $
Plugging in the diagonal, we get that
$ prk_{{\mathcal Q}(d+1)} (\bar P) \le A(1+s)^B. $
Plugging in the diagonal, we get that
![]() $ rk_{\mathcal Q} (P) \le A(1+s)^B. $
$ rk_{\mathcal Q} (P) \le A(1+s)^B. $
To deal with towers of degree
![]() $ d+1, $
we introduce an auxiliary parameter like we did in the proof of Theorem 2.13:
$ d+1, $
we introduce an auxiliary parameter like we did in the proof of Theorem 2.13:
Theorem 9.10 (Relative bias implies relative low rank).
There exist constants
![]() $A(d,H,l), B(d,H,l)$
, such that if
$A(d,H,l), B(d,H,l)$
, such that if
![]() ${\mathcal Q}$
is an
${\mathcal Q}$
is an
![]() $(A,B,s)$
-regular tower of degree
$(A,B,s)$
-regular tower of degree
![]() $\le d+1 < char({\mathbb {F}})$
and height
$\le d+1 < char({\mathbb {F}})$
and height
![]() $\le H$
, such that
$\le H$
, such that
![]() $ {\mathcal Q}_{\le H-l} $
is of degree
$ {\mathcal Q}_{\le H-l} $
is of degree
![]() $ \le d, $
and P is a polynomial of degree
$ \le d, $
and P is a polynomial of degree
![]() $\le d+1$
with
$\le d+1$
with
then
A tower
![]() ${\mathcal Q}$
as above is called a tower of type
${\mathcal Q}$
as above is called a tower of type
![]() $(d+1,H,l)$
for short. We have just seen this theorem holds for towers of type
$(d+1,H,l)$
for short. We have just seen this theorem holds for towers of type
![]() $(d+1,H,0).$
Theorem 2.2 is for towers of type
$(d+1,H,0).$
Theorem 2.2 is for towers of type
![]() $(d+1,H,H).$
$(d+1,H,H).$
Proof of Theorem 9.10.
By induction on
![]() $l.$
We have just seen the base case
$l.$
We have just seen the base case
![]() $l=0.$
Suppose the theorem holds for towers of type
$l=0.$
Suppose the theorem holds for towers of type
![]() $(d+1,H,l)$
and
$(d+1,H,l)$
and
![]() ${\mathcal Q}$
is now of type
${\mathcal Q}$
is now of type
![]() $(d+1,H,l+1).$
The inductive assumption implies Lemma 9.5 for
$(d+1,H,l+1).$
The inductive assumption implies Lemma 9.5 for
![]() ${\mathcal Q}$
and
${\mathcal Q}$
and
![]() ${\mathcal Q}_{<H}$
(as in the proof of Lemma 3.2), so we get
${\mathcal Q}_{<H}$
(as in the proof of Lemma 3.2), so we get
By subadditivity of relative rank, there is at most a single
![]() $ a_0\in {\mathbb {F}}^{m_H} $
with
$ a_0\in {\mathbb {F}}^{m_H} $
with
![]() $ rk_{{\mathcal Q}_{<H}} (P+a\cdot {\mathcal Q}_H) \le A/2(m_H+s)^B, $
and if
$ rk_{{\mathcal Q}_{<H}} (P+a\cdot {\mathcal Q}_H) \le A/2(m_H+s)^B, $
and if
![]() $ \deg (P) < \deg ({\mathcal Q}_H) $
, then
$ \deg (P) < \deg ({\mathcal Q}_H) $
, then
![]() $ a_0 = 0. $
By the theorem applied to
$ a_0 = 0. $
By the theorem applied to
![]() $ {\mathcal Q}_{<H} $
, we get that for all
$ {\mathcal Q}_{<H} $
, we get that for all
![]() $ a\neq a_0, $
$ a\neq a_0, $
so
![]() $ bias_{Z({\mathcal Q}_{<H})} (P+a_0\cdot {\mathcal Q}_H) \ge q^{-4s}. $
This gives
$ bias_{Z({\mathcal Q}_{<H})} (P+a_0\cdot {\mathcal Q}_H) \ge q^{-4s}. $
This gives
We are also ready to prove Theorem 2.7:
Theorem 9.11 (Robust Nullstellensatz for regular collections).
There exist constants
![]() $A(d,H),B(d,H),s(d)$
, such that if
$A(d,H),B(d,H),s(d)$
, such that if
![]() ${\mathcal Q} = (Q_{i,j})_{i\in [h],j\in [m_i]} $
is an
${\mathcal Q} = (Q_{i,j})_{i\in [h],j\in [m_i]} $
is an
![]() $(A,B,s)$
-regular polynomial tower of deg
$(A,B,s)$
-regular polynomial tower of deg
![]() $\le d < char({\mathbb {F}})$
and height
$\le d < char({\mathbb {F}})$
and height
![]() $ \le H, $
and P is a polynomial of degree
$ \le H, $
and P is a polynomial of degree
![]() $ \le d $
which vanishes
$ \le d $
which vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}), $
then there exist polynomials
$ Z({\mathcal Q}), $
then there exist polynomials
![]() $ R_{i,j} $
satisfying
$ R_{i,j} $
satisfying
![]() $ \deg (R_{i,j}) + \deg (Q_{i,j}) \le \deg (P) $
and
$ \deg (R_{i,j}) + \deg (Q_{i,j}) \le \deg (P) $
and
Proof. By induction on
![]() $ \deg (P). $
For constant P, there is nothing to prove, since we know by Lemma 9.5 that
$ \deg (P). $
For constant P, there is nothing to prove, since we know by Lemma 9.5 that
![]() $ Z({\mathcal Q}) \neq \emptyset. $
Suppose the theorem holds up to degree
$ Z({\mathcal Q}) \neq \emptyset. $
Suppose the theorem holds up to degree
![]() $ k-1 $
and
$ k-1 $
and
![]() $ \deg (P) = k. $
Suppose P vanishes
$ \deg (P) = k. $
Suppose P vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}). $
By Lemmas 3.4 and 9.8,
$ Z({\mathcal Q}). $
By Lemmas 3.4 and 9.8,
![]() $ \bar P $
vanishes
$ \bar P $
vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}(k)). $
By Theorem 8.3,
$ Z({\mathcal Q}(k)). $
By Theorem 8.3,
![]() $ rk_{{\mathcal Q}(k)} (\bar P) = 0. $
Plugging in the diagonal, this implies that
$ rk_{{\mathcal Q}(k)} (\bar P) = 0. $
Plugging in the diagonal, this implies that
![]() $ rk_{\tilde {\mathcal {Q}}} (\tilde P) = 0 $
so there exist
$ rk_{\tilde {\mathcal {Q}}} (\tilde P) = 0 $
so there exist
![]() $ R_{i,j} $
with
$ R_{i,j} $
with
![]() $ \tilde P = \sum R_{i,j} \tilde Q_{i,j}. $
The polynomial
$ \tilde P = \sum R_{i,j} \tilde Q_{i,j}. $
The polynomial
![]() $ P' = P-\sum R_{i,j} Q_{i,j} $
has
$ P' = P-\sum R_{i,j} Q_{i,j} $
has
![]() $ \deg (P') \le k-1 $
and also vanishes
$ \deg (P') \le k-1 $
and also vanishes
![]() $ q^{-s} $
-a.e. on
$ q^{-s} $
-a.e. on
![]() $ Z({\mathcal Q}). $
Applying the inductive hypothesis finishes the proof.
$ Z({\mathcal Q}). $
Applying the inductive hypothesis finishes the proof.
A Adaptations of results involving rank to relative rank
We formulate and prove the relevant parts of the Theorems in [Reference Kazhdan and Ziegler15, Reference Kazhdan and Ziegler17], replacing rank with relative rank. Let
![]() ${\mathbb {F}}$
be a field. For an algebraic
${\mathbb {F}}$
be a field. For an algebraic
![]() ${\mathbb {F}}$
-variety
${\mathbb {F}}$
-variety
![]() $\mathbb X$
, we write
$\mathbb X$
, we write
![]() $X({\mathbb {F}}):=\mathbb X ({\mathbb {F}})$
. To simplify notations, we often write X instead of
$X({\mathbb {F}}):=\mathbb X ({\mathbb {F}})$
. To simplify notations, we often write X instead of
![]() $X({\mathbb {F}})$
. In particular, we write
$X({\mathbb {F}})$
. In particular, we write
![]() $V:={\mathbb V} ({\mathbb {F}})$
when
$V:={\mathbb V} ({\mathbb {F}})$
when
![]() ${\mathbb V}$
is a vector space and write
${\mathbb V}$
is a vector space and write
![]() ${\mathbb {F}}^N$
for
${\mathbb {F}}^N$
for
![]() ${\mathbb A}^N({\mathbb {F}})$
.
${\mathbb A}^N({\mathbb {F}})$
.
For a
![]() ${\mathbb {F}}$
-vector space
${\mathbb {F}}$
-vector space
![]() ${\mathbb V}$
, we denote by
${\mathbb V}$
, we denote by
![]() $\mathcal P_{\bar d}({\mathbb V})$
the algebraic variety of tuples polynomials
$\mathcal P_{\bar d}({\mathbb V})$
the algebraic variety of tuples polynomials
![]() $\bar P= (P_1, \ldots , P_c)$
on
$\bar P= (P_1, \ldots , P_c)$
on
![]() ${\mathbb V}$
of degrees
${\mathbb V}$
of degrees
![]() $\le \bar d$
and by
$\le \bar d$
and by
![]() $\mathcal P_{\bar d}(V) $
the set of tuples of polynomials functions
$\mathcal P_{\bar d}(V) $
the set of tuples of polynomials functions
![]() $\bar P:V\to {\mathbb {F}}^c$
of degree
$\bar P:V\to {\mathbb {F}}^c$
of degree
![]() $\leq \bar d$
. We always assume that
$\leq \bar d$
. We always assume that
![]() $d < char({\mathbb {F}})$
, so the restriction map
$d < char({\mathbb {F}})$
, so the restriction map
![]() $\mathcal P_{\bar d}({\mathbb V})({\mathbb {F}})\to \mathcal P_{\bar d}(V)$
is a bijection.
$\mathcal P_{\bar d}({\mathbb V})({\mathbb {F}})\to \mathcal P_{\bar d}(V)$
is a bijection.
We recall some of the definitions in [Reference Kazhdan and Ziegler15].
Definition A.1.
-
1. For
 $m\geq 1$
and a
$m\geq 1$
and a
 ${\mathbb {F}}$
-vector space V, we denote by
${\mathbb {F}}$
-vector space V, we denote by
 $\text {Aff}_m({\mathbb V})$
the algebraic variety of affine maps
$\text {Aff}_m({\mathbb V})$
the algebraic variety of affine maps
 $\phi :{\mathbb A} ^m\to {\mathbb V}$
and write
$\phi :{\mathbb A} ^m\to {\mathbb V}$
and write
 $\text {Aff}_m(V) := \text {Aff}_m({\mathbb V}) ({\mathbb {F}})$
.
$\text {Aff}_m(V) := \text {Aff}_m({\mathbb V}) ({\mathbb {F}})$
. -
2. We define an algebraic morphism
 $\tilde \kappa _{\bar P}: \text {Aff}_m({\mathbb V}) \to \mathcal P_{\bar d}({\mathbb A} ^m)$
by
$\tilde \kappa _{\bar P}: \text {Aff}_m({\mathbb V}) \to \mathcal P_{\bar d}({\mathbb A} ^m)$
by
 $\tilde \kappa _{\bar P} (\phi ):= \bar P \circ \phi $
, and denote by
$\tilde \kappa _{\bar P} (\phi ):= \bar P \circ \phi $
, and denote by
 $\kappa _{\bar P}$
the corresponding map
$\kappa _{\bar P}$
the corresponding map
 $\text {Aff}_m(V) \to \mathcal P_{\bar d}({\mathbb {F}}^m) $
.
$\text {Aff}_m(V) \to \mathcal P_{\bar d}({\mathbb {F}}^m) $
.
Definition A.2. A map
![]() $\kappa :M\to N$
between finite sets is
$\kappa :M\to N$
between finite sets is
![]() $\varepsilon $
-uniform, where
$\varepsilon $
-uniform, where
![]() $\varepsilon>0$
, if for all
$\varepsilon>0$
, if for all
![]() $n\in N$
, we have
$n\in N$
, we have
Theorem A.3. There exist constants
![]() $ A(d,h),B(d,h) $
, such that for any
$ A(d,h),B(d,h) $
, such that for any
![]() $m, s\geq 1,$
any finite field
$m, s\geq 1,$
any finite field
![]() $ {\mathbb {F}}={\mathbb {F}}_q, $
and any
$ {\mathbb {F}}={\mathbb {F}}_q, $
and any
![]() $ (Am^B,B,s) $
-regular tower
$ (Am^B,B,s) $
-regular tower
![]() $ \bar {P} $
of degree
$ \bar {P} $
of degree
![]() $ \le d <char({\mathbb {F}}) $
and height
$ \le d <char({\mathbb {F}}) $
and height
![]() $ \le h, $
the map
$ \le h, $
the map
![]() $\kappa _{\bar P}:\text {Aff}_m({\mathbb V}) \to \mathcal P_{\bar d}({\mathbb A} ^m)$
is
$\kappa _{\bar P}:\text {Aff}_m({\mathbb V}) \to \mathcal P_{\bar d}({\mathbb A} ^m)$
is
![]() $q^{-s}$
uniform.
$q^{-s}$
uniform.
As a corollary, we obtain (as in [Reference Kazhdan and Ziegler15])
Theorem A.4. For any
![]() $m \geq 1$
, any algebraically closed field
$m \geq 1$
, any algebraically closed field
![]() ${\mathbb {F}}$
of characteristic zero or
${\mathbb {F}}$
of characteristic zero or
![]() $>d$
, any
$>d$
, any
![]() ${\mathbb {F}}$
-vector space V, and any
${\mathbb {F}}$
-vector space V, and any
![]() $ (Am^B,B,2) $
-regular tower
$ (Am^B,B,2) $
-regular tower
![]() $\bar P$
of degree
$\bar P$
of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le h, $
where
$ \le h, $
where
![]() $ A,B $
are the constants of Theorem A.3, we have
$ A,B $
are the constants of Theorem A.3, we have
-
1. The map
 $\kappa _{\bar P}$
is surjective,
$\kappa _{\bar P}$
is surjective, -
2. All fibers of the morphism
 $\tilde \kappa _{\bar P}$
are of the same dimension,
$\tilde \kappa _{\bar P}$
are of the same dimension, -
3. The morphism
 $\tilde \kappa _{\bar P}$
is flat, and
$\tilde \kappa _{\bar P}$
is flat, and -
4.
 $\bar P\subset {\mathbb {F}}[V^\vee ]$
is a regular sequence.
$\bar P\subset {\mathbb {F}}[V^\vee ]$
is a regular sequence.
Let
![]() $\epsilon>0$
, we say that a property holds for
$\epsilon>0$
, we say that a property holds for
![]() $\epsilon $
-a.e.
$\epsilon $
-a.e.
![]() $s \in S$
if it holds for all but
$s \in S$
if it holds for all but
![]() $(1-\epsilon )|S|$
of the elements in S.
$(1-\epsilon )|S|$
of the elements in S.
As in [Reference Kazhdan and Ziegler15], Theorem A.3 follows from the following result:
Theorem A.5. Let
![]() $d \ge 0$
. There exist
$d \ge 0$
. There exist
![]() $A(d,h),B(d,h)$
, such that for any
$A(d,h),B(d,h)$
, such that for any
![]() $s,m>0$
, the following holds: Let
$s,m>0$
, the following holds: Let
![]() ${\mathbb {F}}={\mathbb {F}}_q$
be a finite field of characteristic
${\mathbb {F}}={\mathbb {F}}_q$
be a finite field of characteristic
![]() $>d$
and let
$>d$
and let
![]() $\bar P$
be an
$\bar P$
be an
![]() $ (Am^B,B,s) $
-regular tower of degree
$ (Am^B,B,s) $
-regular tower of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le h $
composed of polynomials
$ \le h $
composed of polynomials
![]() $ (P_1,\ldots ,P_c) $
of degrees
$ (P_1,\ldots ,P_c) $
of degrees
![]() $ (d_1,\ldots ,d_c) $
on
$ (d_1,\ldots ,d_c) $
on
![]() $V={\mathbb {F}}^n.$
Then:
$V={\mathbb {F}}^n.$
Then:
-
1. For any collection of polynomials
 $\bar R=(R_i)_{ 1 \le i \le c}$
, with
$\bar R=(R_i)_{ 1 \le i \le c}$
, with
 $R_i:{\mathbb {F}}^m \to {\mathbb {F}}$
of degree
$R_i:{\mathbb {F}}^m \to {\mathbb {F}}$
of degree
 $d_i$
, there exists an affine map
$d_i$
, there exists an affine map
 $w:{\mathbb {F}}^m \to {\mathbb {F}}^n$
, such that
$w:{\mathbb {F}}^m \to {\mathbb {F}}^n$
, such that
 $\bar P(w(x))=\bar R(x)$
. Furthermore, if we denote by
$\bar P(w(x))=\bar R(x)$
. Furthermore, if we denote by
 $n_{\bar R}$
the number of such affine maps, then for any
$n_{\bar R}$
the number of such affine maps, then for any
 $\bar R_1, \bar R_2$
as above,
$\bar R_1, \bar R_2$
as above,
 $|1-n_{\bar R_1}/n_{\bar R_2}| <q^{-s}$
.
$|1-n_{\bar R_1}/n_{\bar R_2}| <q^{-s}$
. -
2. If
 $\bar P$
is homogeneous, then for any homogeneous collection
$\bar P$
is homogeneous, then for any homogeneous collection
 $\bar R=(R_i)_{ 1 \le i \le c}$
,
$\bar R=(R_i)_{ 1 \le i \le c}$
,
 $R_i:{\mathbb {F}}^m \to {\mathbb {F}}$
of degree
$R_i:{\mathbb {F}}^m \to {\mathbb {F}}$
of degree
 $d_i$
, there exists a linear map
$d_i$
, there exists a linear map
 $w:{\mathbb {F}}^m \to {\mathbb {F}}^n$
, such that
$w:{\mathbb {F}}^m \to {\mathbb {F}}^n$
, such that
 $\bar P(w(x))=\bar R(x)$
. Furthermore, if we denote by
$\bar P(w(x))=\bar R(x)$
. Furthermore, if we denote by
 $n_{\bar R}$
the number of such linear maps, then for any
$n_{\bar R}$
the number of such linear maps, then for any
 $\bar R_1, \bar R_2$
as above,
$\bar R_1, \bar R_2$
as above,
 $|1-n_{\bar R_1}/n_{\bar R_2}| <q^{-s}$
.
$|1-n_{\bar R_1}/n_{\bar R_2}| <q^{-s}$
.
Proof. We prove by induction on d. For
![]() $d=1$
, the statement is clear. Assume
$d=1$
, the statement is clear. Assume
![]() $d>1$
. We are given a filtered collection of polynomials
$d>1$
. We are given a filtered collection of polynomials
![]() $\mathcal P=\{P^{e,f}\}_{1\le e \le h, 0 \le f \le J_e}$
. We first make the following observation. Let P be of degree d.
$\mathcal P=\{P^{e,f}\}_{1\le e \le h, 0 \le f \le J_e}$
. We first make the following observation. Let P be of degree d.
![]() $P(t)=\sum _{I \in \mathcal I_k}a_{I}t_I$
, where
$P(t)=\sum _{I \in \mathcal I_k}a_{I}t_I$
, where
![]() $\mathcal I_{d}(n)$
is the set of ordered tuples
$\mathcal I_{d}(n)$
is the set of ordered tuples
![]() $I=(i_1, \ldots , i_{d})$
with
$I=(i_1, \ldots , i_{d})$
with
![]() $1 \le i_1 \le \ldots \le i_{d} \le n$
, and
$1 \le i_1 \le \ldots \le i_{d} \le n$
, and
![]() $t_I= t_{i_1} \ldots t_{i_{d}}$
. Note that for any polynomials
$t_I= t_{i_1} \ldots t_{i_{d}}$
. Note that for any polynomials
![]() $l(t)$
of degrees
$l(t)$
of degrees
![]() $<d$
, we have that
$<d$
, we have that
![]() $P(t)+l(t)$
is of the same rank as P. We can write
$P(t)+l(t)$
is of the same rank as P. We can write
 $$\begin{align*}P(w(x)) = \sum_{I \in \mathcal I_{d}(n)} a_{I}w^I(x) = \sum_{I \in \mathcal I_{d}(n)} a_{I}\sum_{l_1, \ldots, l_{d}=1}^m w^{i_1}_{l_1} \ldots w^{i_{d}}_{l_{d}}x_{l_1} \ldots x_{l_{d}}, \end{align*}$$
$$\begin{align*}P(w(x)) = \sum_{I \in \mathcal I_{d}(n)} a_{I}w^I(x) = \sum_{I \in \mathcal I_{d}(n)} a_{I}\sum_{l_1, \ldots, l_{d}=1}^m w^{i_1}_{l_1} \ldots w^{i_{d}}_{l_{d}}x_{l_1} \ldots x_{l_{d}}, \end{align*}$$
where
![]() $w^I = \prod _{i \in I} w^{i}$
. For
$w^I = \prod _{i \in I} w^{i}$
. For
![]() $( l_1, \ldots ,l_{d}) \in \mathcal I_{d}(m)$
, the term
$( l_1, \ldots ,l_{d}) \in \mathcal I_{d}(m)$
, the term
![]() $x_{l_1} \ldots x_{l_{d}}$
has as coefficient
$x_{l_1} \ldots x_{l_{d}}$
has as coefficient
Observe that restricted to the subspace
![]() $w_{l_1} = \ldots = w_{l_{d}}$
, we can write the above as
$w_{l_1} = \ldots = w_{l_{d}}$
, we can write the above as
where
![]() $w_j=(w_j^1, \ldots , w_j^n)$
, and
$w_j=(w_j^1, \ldots , w_j^n)$
, and
![]() $R(w)$
is of lower degree in
$R(w)$
is of lower degree in
![]() $w_{l_1}$
.
$w_{l_1}$
.
Now, consider the filtered system
![]() $\mathcal P$
. It gives rise to a filtered system
$\mathcal P$
. It gives rise to a filtered system
Given an element
![]() $Q^{e,f}_{( l_1, \ldots ,l_{d})}$
at level e of degree d, we restrict to a subspace as above and get
$Q^{e,f}_{( l_1, \ldots ,l_{d})}$
at level e of degree d, we restrict to a subspace as above and get
![]() $ Q^{e,f}(w)=d! P(w_{l_1}) + R^{e,f}(w)$
and
$ Q^{e,f}(w)=d! P(w_{l_1}) + R^{e,f}(w)$
and
![]() $R(w)$
is of lower degree in
$R(w)$
is of lower degree in
![]() $w_{l_1}$
. But the same holds for all lower degree polynomials as well – restricted to this subspace, they are of the form
$w_{l_1}$
. But the same holds for all lower degree polynomials as well – restricted to this subspace, they are of the form
![]() $j!P^{e,f}(w_{l_1}) + R^{e,f}(w)$
, where
$j!P^{e,f}(w_{l_1}) + R^{e,f}(w)$
, where
![]() $R^{e,f}$
of lower degree in
$R^{e,f}$
of lower degree in
![]() $w_{l_1}$
. Similarly, this holds for a linear combination of elements at lever h. This is sufficient since the relative rank can only decrease when restricting to a subspace. So we just need to make sure that the original relative rank beats the new number of polynomials at each level, which is
$w_{l_1}$
. Similarly, this holds for a linear combination of elements at lever h. This is sufficient since the relative rank can only decrease when restricting to a subspace. So we just need to make sure that the original relative rank beats the new number of polynomials at each level, which is
![]() $ \le m^{O(d)}$
.
$ \le m^{O(d)}$
.
We formulate a number of additional results that were proved in the context of high rank collections of polynomials and whose proofs can be easily adapted to the new notion of relative rank.
We recall the definition of weakly polynomial function from [Reference Kazhdan and Ziegler15].
Definition A.6.
-
1. Let V be a
 ${\mathbb {F}}$
-vector space and
${\mathbb {F}}$
-vector space and
 $X\subset V$
. We say that a function
$X\subset V$
. We say that a function
 $f:X \to {\mathbb {F}}$
is weakly polynomial of degree
$f:X \to {\mathbb {F}}$
is weakly polynomial of degree
 $\leq a$
if the restriction
$\leq a$
if the restriction
 $f_{|L}$
to any affine subspace
$f_{|L}$
to any affine subspace
 $L \subset X$
is a polynomial of degree
$L \subset X$
is a polynomial of degree
 $\leq a$
.
$\leq a$
. -
2. X satisfies
 $\star ^a$
if any weakly polynomial function of degree
$\star ^a$
if any weakly polynomial function of degree
 $\leq a$
on X is a restriction of a polynomial function of degree
$\leq a$
on X is a restriction of a polynomial function of degree
 $\leq a$
on V.
$\leq a$
on V.
Theorem A.7. For any
![]() $d, a\geq 1$
, there exist constants
$d, a\geq 1$
, there exist constants
![]() $A(d,h,a),B(d,h,a)$
, such that the following holds: for any field
$A(d,h,a),B(d,h,a)$
, such that the following holds: for any field
![]() ${\mathbb {F}}$
which is either finite with
${\mathbb {F}}$
which is either finite with
![]() $|{\mathbb {F}}|>ad$
or algebraically closed of characteristic zero or
$|{\mathbb {F}}|>ad$
or algebraically closed of characteristic zero or
![]() $>d$
, a
$>d$
, a
![]() ${\mathbb {F}}$
-vector space V, an
${\mathbb {F}}$
-vector space V, an
![]() $ (A,B,2) $
-regular tower
$ (A,B,2) $
-regular tower
![]() $\mathcal P$
of degree
$\mathcal P$
of degree
![]() $\le d$
, and height
$\le d$
, and height
![]() $ \le h,$
the subset
$ \le h,$
the subset
![]() $Z(\mathcal P)\subset V$
has the property
$Z(\mathcal P)\subset V$
has the property
![]() $\star _a$
.
$\star _a$
.
Combined with the polynomial cost regularization of Theorem 2.3, we obtain:
Theorem A.8. For any
![]() $d, a\geq 1$
, there exists
$d, a\geq 1$
, there exists
![]() $A=A(d,a)$
, such the following holds: for any field
$A=A(d,a)$
, such the following holds: for any field
![]() ${\mathbb {F}}$
which is either finite with
${\mathbb {F}}$
which is either finite with
![]() $|{\mathbb {F}}|>ad$
or algebraically closed of characteristic zero or
$|{\mathbb {F}}|>ad$
or algebraically closed of characteristic zero or
![]() $>d$
, a
$>d$
, a
![]() ${\mathbb {F}}$
-vector space V, a collection of polynomials
${\mathbb {F}}$
-vector space V, a collection of polynomials
![]() $\bar P=(P_i)_{ 1 \le i \le c}$
with
$\bar P=(P_i)_{ 1 \le i \le c}$
with
![]() $\deg P_i \le d$
, there exists a collection of polynomials
$\deg P_i \le d$
, there exists a collection of polynomials
![]() ${\mathcal Q}$
, such that
${\mathcal Q}$
, such that
![]() $\bar P \subset \mathcal I({\mathcal Q})$
, such that
$\bar P \subset \mathcal I({\mathcal Q})$
, such that
![]() $Z({\mathcal Q})\subset V$
has the property
$Z({\mathcal Q})\subset V$
has the property
![]() $\star _a$
, and
$\star _a$
, and
![]() $|{\mathcal Q}| \le Ac^A$
.
$|{\mathcal Q}| \le Ac^A$
.
Finally, we can also adapt the results from [Reference Kazhdan and Ziegler17] to the setting of relative rank: Let V be a vector space over a field
![]() ${\mathbb {F}}$
. An m-cube in a vector space V is a collection
${\mathbb {F}}$
. An m-cube in a vector space V is a collection
![]() $(u|\bar v),u\in V,\bar v\in V^m$
of
$(u|\bar v),u\in V,\bar v\in V^m$
of
![]() $2^m$
points
$2^m$
points
![]() $\{ u+\sum _{i=1}^m \omega _iv_i\}$
,
$\{ u+\sum _{i=1}^m \omega _iv_i\}$
,
![]() $\omega _i\in \{0 ,1\}$
.
$\omega _i\in \{0 ,1\}$
.
For any map
![]() $f:V\to H$
where H is an Abelian group, we denote by
$f:V\to H$
where H is an Abelian group, we denote by
![]() $f_m$
the map from the set
$f_m$
the map from the set
![]() $C_m(V)$
of m-cubes to H given by
$C_m(V)$
of m-cubes to H given by
 $$\begin{align*}f_m(u|\bar v)=\sum _{\bar \omega \in \{ 0 ,1\}^m}(-1)^{|w|}f(u+\sum _{i=1}^m\omega _iv_i),\end{align*}$$
$$\begin{align*}f_m(u|\bar v)=\sum _{\bar \omega \in \{ 0 ,1\}^m}(-1)^{|w|}f(u+\sum _{i=1}^m\omega _iv_i),\end{align*}$$
where
![]() $|\omega |=\sum _{i=1}^m\omega _i$
. For a subset
$|\omega |=\sum _{i=1}^m\omega _i$
. For a subset
![]() $X \subset V$
, we denote
$X \subset V$
, we denote
![]() $C_m(X)$
the set of m-cubes in V with all vertices in X. Note that in the case that
$C_m(X)$
the set of m-cubes in V with all vertices in X. Note that in the case that
![]() $H={\mathbb {F}}$
, where
$H={\mathbb {F}}$
, where
![]() ${\mathbb {F}}$
a prime field, functions
${\mathbb {F}}$
a prime field, functions
![]() $f:V \to {\mathbb {F}}$
, such that
$f:V \to {\mathbb {F}}$
, such that
![]() $f_m$
vanishes on
$f_m$
vanishes on
![]() $C_m(V)$
are precisely polynomials of degree
$C_m(V)$
are precisely polynomials of degree
![]() $<m$
.
$<m$
.
Theorem A.9. Let
![]() $m, d>0$
. There exists
$m, d>0$
. There exists
![]() $C=C(d,m,h)$
, such that the following holds: For any
$C=C(d,m,h)$
, such that the following holds: For any
![]() $0<\epsilon $
, a finite field
$0<\epsilon $
, a finite field
![]() ${\mathbb {F}}$
and an
${\mathbb {F}}$
and an
![]() ${\mathbb {F}}$
-vector space V, a
${\mathbb {F}}$
-vector space V, a
![]() $ (C,C,2) $
-regular tower
$ (C,C,2) $
-regular tower
![]() ${\mathcal P}$
of degree
${\mathcal P}$
of degree
![]() $ \le d $
and height
$ \le d $
and height
![]() $ \le h $
, and any
$ \le h $
, and any
![]() $f:X=Z(\mathcal P) \to H$
with
$f:X=Z(\mathcal P) \to H$
with
![]() $f_m(c)=0$
for
$f_m(c)=0$
for
![]() $\epsilon $
-a.e.
$\epsilon $
-a.e.
![]() $c \in C_m(X)$
, there exists a function
$c \in C_m(X)$
, there exists a function
![]() $h:X \to H$
, such that
$h:X \to H$
, such that
![]() $h_m\equiv 0$
, and
$h_m\equiv 0$
, and
![]() $h(x)=f(x)$
on
$h(x)=f(x)$
on
![]() $C \epsilon $
-a.e.
$C \epsilon $
-a.e.
![]() $x \in X$
.
$x \in X$
.
Acknowledgments
The first author would like to thank the second author for introducing him to this question and its various applications. He would also like to thank his wife, Noa, for her constant support and encouragement. The authors were supported by European Research Council grant ErgComNum 682150 and Israel Science Foundation grant 2112/20.
Competing interest
The authors have no competing interest to declare.