Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-17T15:00:48.562Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLIERS ON THE SECOND DUAL OF ABSTRACT SEGAL ALGEBRAS

Part of: Topological algebras, normed rings and algebras, Banach algebras Abstract harmonic analysis

Published online by Cambridge University Press:  06 October 2022

MEHDI NEMATI Open the ORCID record for MEHDI NEMATI [Opens in a new window]  and
ZHILA SOHAEI Open the ORCID record for ZHILA SOHAEI [Opens in a new window]
MEHDI NEMATI*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5746, Tehran, Iran
ZHILA SOHAEI
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterise the existence of certain (weakly) compact multipliers of the second dual of symmetric abstract Segal algebras in both the group algebra 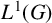$L^{1}(G)$ and the Fourier algebra 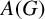$A(G)$ of a locally compact group G.

Keywords

abstract Segal algebratopologically invariant φ-meanmultiplier

MSC classification

Primary: 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 43A20: $L^1$-algebras on groups, semigroups, etc. 46H10: Ideals and subalgebras 46H20: Structure, classification of topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 133 - 141
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the first author was in part supported by a grant from IPM (No. 1401170411).

References

Alaghmandan, M., Nasr-Isfahani, R. and Nemati, M., ‘Character amenability and contractibility of abstract Segal algebras’, Bull. Aust. Math. Soc. 82 (2010), 274–281.CrossRefGoogle Scholar
Burnham, J. T., ‘Closed ideals in subalgebras of Banach algebras. I’, Proc. Amer. Math. Soc. 32 (1972), 551–555.CrossRefGoogle Scholar
Eymard, P., ‘L’algèbre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T.-M., ‘Multipliers and ideals in second conjugate algebras related to locally compact groups’, J. Funct. Anal. 132 (1995), 170–191.CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T.-M., ‘Multipliers and modulus on Banach algebras related to locally compact groups’, J. Funct. Anal. 150 (1997), 478–497.CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T.-M., ‘Approximate weak amenability, derivations and Arens regularity of Segal algebras’, Studia Math. 169 (2005), 189–205.CrossRefGoogle Scholar
Kaniuth, E., Lau, A. T.-M. and Pym, J., ‘On $\varphi$ -amenability of Banach algebras’, Math. Proc. Cambridge Philos. Soc. 144 (2008), 85–96.CrossRefGoogle Scholar
Kaniuth, E., Lau, A. T.-M. and Pym, J., ‘On character amenability of Banach algebras’, J. Math. Anal. Appl. 344 (2008), 942–955.CrossRefGoogle Scholar
Klawe, M., ‘On the dimension of left invariant means and left thick subsets’, Trans. Amer. Math. Soc. 231 (1977), 507–518.CrossRefGoogle Scholar
Lau, A. T.-M., ‘Uniformly continuous functionals on the Fourier algebra of any locally compact group’, Trans. Amer. Math. Soc. 251 (1979), 39–59.CrossRefGoogle Scholar
Lau, A. T.-M., ‘Analysis on a class of Banach algebras with application to harmonic analysis on locally compact groups and semigroups’, Fund. Math. 118 (1983), 161–175.Google Scholar
Lau, A. T.-M. and Paterson, A. L. T., ‘The exact cardinality of the set of topological left invariant means on an amenable locally compact group’, Proc. Amer. Math. Soc. 98 (1986), 75–80.CrossRefGoogle Scholar
Reiter, H., ${L}^1$ -algebras and Segal Algebras, Lecture Notes in Mathematics, 231 (Springer, Berlin, 1971).CrossRefGoogle Scholar
Sakai, S., ‘Weakly compact operators on operator algebras’, Pacific J. Math. 14 (1964), 659–664.CrossRefGoogle Scholar