Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-17T15:49:30.494Z Has data issue: false hasContentIssue false
  • English
  • Français

THE EMBEDDING PROPERTY FOR SORTED PROFINITE GROUPS

Part of: Other classes of algebra Model theory

Published online by Cambridge University Press:  20 March 2023

JUNGUK LEE Open the ORCID record for JUNGUK LEE [Opens in a new window]
JUNGUK LEE*
Affiliation:
DEPARTMENT OF MATHEMATICS CHANGWON NATIONAL UNIVERSITY CHANGWON 51140 SOUTH KOREA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the embedding property in the category of sorted profinite groups. We introduce a notion of the sorted embedding property (SEP), analogous to the embedding property for profinite groups. We show that any sorted profinite group has a universal SEP-cover. Our proof gives an alternative proof for the existence of a universal embedding cover of a profinite group. Also our proof works for any full subcategory of the sorted profinite groups, which is closed under taking finite quotients, fibre products, and inverse limits. We also show that any sorted profinite group having SEP has a sorted complete system whose theory is 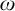$\omega $-categorical and 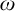$\omega $-stable under the assumption that the set of sorts is countable.

Keywords

sorted profinite groupssorted complete systemsorted embedding propertyco-sorted embedding propertysorted embedding cover

MSC classification

Primary: 03C60: Model-theoretic algebra
Secondary: 08C10: Axiomatic model classes
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 3 , September 2023 , pp. 1005 - 1037
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chatzidakis, Z., Model theory of profinite groups having the Iwasawa property . Illinois Journal of Mathematics , vol. 42 (1998), pp. 70–96.10.1215/ijm/1255985614CrossRefGoogle Scholar
Chatzidakis, Z., Amalgamation of types in pseudo-algebraically closed fields and applications . Journal of Mathematical Logic , vol. 19 (2019), Article no. 1950006, 28 pp.10.1142/S0219061319500065CrossRefGoogle Scholar
Cherlin, G., van den Dries, L., and Macintyre, A., The elementary theory of regularly closed fields. Available at http://sites.math.rutgers.edu/cherlin/Preprint/CDM2.pdf. Google Scholar
Dobrowolski, J., Hoffmann, D. M., and Lee, J., Elementary equivalence theorem for PAC structures, this Journal, vol. 85 (2020), 1467–1498.Google Scholar
Fried, M., Haran, D., and Jarden, M., Galois stratification over Frobenius fields . Advances in Mathematics , vol. 51 (1984), 1–34.CrossRefGoogle Scholar
Fried, M. and Jarden, M., Field Arithmetic , third ed., A Series of Modern Surveys in Mathematics, vol. 11, Springer, Cham, 2008.Google Scholar
Haran, D. and Lubotzky, A., Embedding covers and the theory of Frobenius fields . Israel Journal of Mathematics , vol. 41 (1982), pp. 181–202.CrossRefGoogle Scholar
Jarden, M. and Kiehne, U., The elementary theory of algebraic fields of finite corank . Inventiones Mathematicae , vol. 30 (1975), pp. 275–294.CrossRefGoogle Scholar
Hoffmann, D. M., On Galois groups and PAC structures . Fundamenta Mathematicae , vol. 250 (2020), pp. 151–177.CrossRefGoogle Scholar
Hoffmann, D. M. and Lee, J., Co-theory of sorted profinite groups for PAC structures . Journal of Mathematical Logic , https://doi.org/10.1142/S0219061322500301.Google Scholar
Iwasaw, K., On solvable extensions of algebraic number fields . Annals of Mathematics , vol. 58 (1953), pp. 548–572.CrossRefGoogle Scholar
Ramsey, N., Independence, amalgamation, and trees , Ph.D. thesis, University of California, Berkeley, 2018.Google Scholar
Ribes, P., Introduction of Profinite Groups and Galois Cohomology , Queen Papers in Pure and Applied Mathematics, vol. 24, Queen’s University, Kingston, 1970.Google Scholar
Waterhouse, W. C., Profinite groups are Galois groups . Proceedings of the American Mathematical Society , vol. 46 (1974), pp. 639–640.Google Scholar