Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T15:59:51.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of drops on inclined surfaces in the inertial regime

Published online by Cambridge University Press:  30 May 2013

Baburaj A. Puthenveettil ,
Vijaya K. Senthilkumar  and
E. J. Hopfinger
Baburaj A. Puthenveettil*
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai 600036, India
Vijaya K. Senthilkumar
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai 600036, India
E. J. Hopfinger
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental results on high-Reynolds-number motion of partially non-wetting liquid drops on inclined plane surfaces using: (i) water on fluoro-alkyl silane (FAS)-coated glass; and (ii) mercury on glass. The former is a high-hysteresis (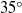$3{5}^{\circ } $) surface while the latter is a low-hysteresis one (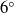${6}^{\circ } $). The water drop experiments have been conducted for capillary numbers 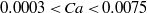$0. 0003\lt Ca\lt 0. 0075$ and for Reynolds numbers based on drop diameter 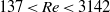$137\lt Re\lt 3142$. The ranges for mercury on glass experiments are 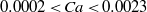$0. 0002\lt Ca\lt 0. 0023$ and 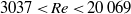$3037\lt Re\lt 20\hspace{0.167em} 069$. It is shown that when 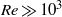$Re\gg 1{0}^{3} $ for water and 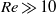$Re\gg 10$ for mercury, a boundary layer flow model accounts for the observed velocities. A general expression for the dimensionless velocity of the drop, covering the whole 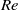$Re$ range, is derived, which scales with the modified Bond number (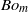$B{o}_{m} $). This expression shows that at low 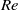$Re$, 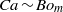$Ca\sim B{o}_{m} $ and at larg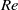e $Re$, 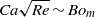$Ca \sqrt{Re} \sim B{o}_{m} $. The dynamic contact angle (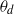${\theta }_{d} $) variation scales, at least to first-order, with 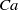$Ca$; the contact angle variation in water, corrected for the hysteresis, collapses onto the low-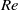$Re$ data of LeGrand, Daerr & Limat (J. Fluid Mech., vol. 541, 2005, pp. 293–315). The receding contact angle variation of mercury has a slope very different from that in water, but the variation is practically linear with 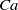$Ca$. We compare our dynamic contact angle data to several models available in the literature. Most models can describe the data of LeGrand et al. (2005) for high-viscosity silicon oil, but often need unexpected values of parameters to describe our water and mercury data. In particular, a purely hydrodynamic description requires unphysically small values of slip length, while the molecular-kinetic model shows asymmetry between the wetting and dewetting, which is quite strong for mercury. The model by Shikhmurzaev (Intl J. Multiphase Flow, vol. 19, 1993, pp. 589–610) is able to group the data for the three fluids around a single curve, thereby restoring a certain symmetry, by using two adjustable parameters that have reasonable values. At larger velocities, the mercury drops undergo a change at the rear from an oval to a corner shape when viewed from above; the corner transition occurs at a finite receding contact angle. Water drops do not show such a clear transition from oval to corner shape. Instead, a direct transition from an oval shape to a rivulet appears to occur.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 726 , 10 July 2013 , pp. 26 - 61
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1969 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bayer, I. S. & Megaridis, C. M. 2006 Contact angle dynamics in droplets impacting on flat surfaces with different wetting characteristics. J. Fluid Mech. 558, 415–449.Google Scholar
Ben Amar, M., Cummings, L. J. & Pomeau, Y. 2003 Transition of a moving contact line from smooth to angular. Phys. Fluids 15, 2949–2960.CrossRefGoogle Scholar
Bertozzi, A. L. & Brenner, M. P. 1997 Linear stability and transient growth in driven contact lines. Phys. Fluids 9, 530.Google Scholar
Bikerman, J. J. 1950 Sliding of drops from surfaces of different roughnesses. J.  Colloid Sci. 5, 349.Google Scholar
Blake, T. D., Bracke, M. & Shikhmurzaev, Y. 1999 Experimental evidence of non-local hydrodynamic influence on the dynamic contact angle. Phys. Fluids 11 (8), 1995–2007.CrossRefGoogle Scholar
Blake, T. D. & Haynes, J. M. 1969 Kinetics of liquid/liquid displacement. J. Colloid Interface Sci. 30, 421–423.CrossRefGoogle Scholar
Blake, T. D. & Ruschak, K. J. 1979 A maximal speed of wetting. Nature 489, 489–491.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.CrossRefGoogle Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. J. Fluid Mech. 168, 169–194.Google Scholar
Cox, R. G. 1998 Inertial and viscous effects on dynamic contact angles. J. Fluid Mech. 357, 249–278.Google Scholar
Durbin, P. A. 1988 Considerations on the moving contact-line singularity, with application to frictional drag on a slender drop. J. Fluid Mech. 197, 157–169.CrossRefGoogle Scholar
Dussan V., E. B. 1979 On the spreading of liquids on solid surfaces: static and dynamic contact lines. Annu. Rev. Fluid Mech. 11, 371–400.Google Scholar
Dussan V., E. B. 1985 On the ability of drops or bubbles to stick to non-horizontal surfaces of solids. Part 2. Small drops or bubbles having contact angles of arbitrary size. J. Fluid Mech. 151, 1–20.Google Scholar
Dussan V., E. B. & Chow, R. T. P. 1983 On the ability of drops or bubbles to stick to non-horizontal surfaces of solids. J. Fluid Mech. 137, 1–29.Google Scholar
Dussan V., E. B. & Davis, S. H. 1974 On the motion of a fluid–fluid interface along a solid surface. J. Fluid Mech. 65, 71–95.Google Scholar
Dussan V., E. B., Rame, E. & Garoff, S. 1991 On identifying the appropriate conditions at a moving contact line: an experimental investigation. J. Fluid Mech. 230, 97–116.Google Scholar
Eggers, J. 2004 Toward a description of contact line motion at higher capillary numbers. Phys. Fluids 16, 3491.CrossRefGoogle Scholar
Eggers, J. & Evans, R. 2004 Comment on ‘Dynamic wetting by liquids of different viscosity’ by T. D. Blake and Y. D. Shikhmurzaev. J. Colloid Interface Sci. 280, 537–538.CrossRefGoogle Scholar
Everest, F. 2001 The Master Handbook of Acoustics, 4th edn. McGraw Hill.Google Scholar
Furmidge, C. G. L. 1962 Studies at phase interfaces. i. The sliding of liquid drops on solid surfaces and a theory for spray retention. J. Colloid Sci. 17, 379.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.Google Scholar
de Gennes, P., Brochard-Wyart, F. & Quere, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Gupta, P. K., Inniss, D., Kurkjian, C. R. & Zhong, Q. 2000 Nanoscale roughness of oxide glass surfaces. J. Non-crystalline Solids 262 (1–3), 200–206.Google Scholar
Hayes, R. A. & Ralston, J. 1993 Forced liquid movement on low energy surfaces. J. Colloid Interface Sci. 159, 429–438.Google Scholar
Henderson, J. R. 2011 Discussion notes on ‘Some dry facts about dynamic wetting’, by Y. D. Shikhmurzaev. Eur. Phys. J. Special Topics 197, 61–62.Google Scholar
Holleman, A. F. & Wiberg, E. 2001 Inorganic Chemistry. Academic.Google Scholar
Hozumi, A., Ushiyama, K., Sugimura, H. & Takai, O. 1999 Fluoroalkylsilane monolayers formed by chemical vapor surface modification on hydroxylated oxide surfaces. Langmuir 15, 7600–7604.CrossRefGoogle Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.Google Scholar
Jerrett, J. M. & de Bruyn, J. R. 1992 Fingering instability of a gravitationally driven contact line. Phys. Fluids A 4, 234.CrossRefGoogle Scholar
Kim, H. Y., Lee, H. J. & Kang, B. H. 2002 Sliding of liquid drops down an inclined solid surface. J. Colloid Interface Sci. 247, 372–380.Google Scholar
Lamb, H. 1932 Hydrodynamics, chap. 5, p. 586. Cambridge University Press.Google Scholar
Le Grand, N., Daerr, A. & Limat, L. 2005 Shape and motion of drops sliding down an inclined plane. J. Fluid Mech. 541, 293–315.Google Scholar
Limat, L. & Stone, H. A. 2004 Three-dimensional lubrication model of a contact line corner singularity. Europhys. Lett. 65 (3), 365–371.CrossRefGoogle Scholar
Lopez, P. G., Bankoff, S. G. & Miksis, M. J. 1996 Non-isothermal spreading of a thin liquid film on an inclined plane. J. Fluid Mech. 324, 261–286.CrossRefGoogle Scholar
Lopez, P. G., Miksis, M. J. & Bankoff, S. G. 1997 Inertial effects on contact line instability in the coating of a dry inclined plate. Phys. Fluids 9, 2177.CrossRefGoogle Scholar
Mahadevan, L. & Pomeau, Y. 1999 Rolling droplets. Phys. Fluids 11, 2449–2452.CrossRefGoogle Scholar
Petrov, J. G., Ralston, J., Schneemilch, M. & Hayes, R. A. 2003 Dynamics of partial wetting and dewetting in well-defined systems. J. Phys. Chem. 107 (7), 1634–1645.Google Scholar
Petrov, P. G. & Petrov, J. G. 1992 A combined molecular-hydrodynamic approach to wetting kinetics. Langmuir 19, 1762–1767.CrossRefGoogle Scholar
Pismen, L. 2011 Discussion notes on ‘Some dry facts about dynamic wetting’, by Y. D. Shikhmurzaev. Eur. Phys. J. Special Topics 197, 63–65.Google Scholar
Podgorski, T., Flesselles, J. M. & Limat, L. 2001 Corners, cusps and pearls in running drops. Phys. Rev. Lett. 87, 036102.Google Scholar
Prabhala, B. R., Panchagnula, M. V. & Vedantam, S. 2013 Three-dimensional equilibrium shapes of drops on hysteretic surfaces. Colloid Polym. Sci. 291 (2), 279–289.CrossRefGoogle Scholar
Richard, D. & Quéré, D. 1999 Viscous drops rolling on a tilted non-wettable solid. Europhys. Lett. 3, 286–291.Google Scholar
Rio, E., Daerr, A., Andreotti, B. & Limat, L. 2005 Boundary conditions in the vicinity of a dynamic contact line: experimental investigation of viscous drops sliding down an inclined plane. Phys. Rev. Lett. 94 (2), 024503.Google Scholar
Rolley, E. & Guthmann, C. 2007 Dynamics and hysteresis of the contact line between liquid hydrogen and cesium substrates. Phys. Rev. Lett. 98, 166105.Google Scholar
Seveno, D., Vaillant, R. R., Adao, H., Conti, J. & DeConinck, J. 2009 Dynamics of wetting revisited. Langmuir 25 (22), 13034–13044.Google Scholar
Shikhmurzaev, Y. D. 1993 The moving contact line on a smooth solid surface. Intl J. Multiphase Flow 19 (4), 589–610.Google Scholar
Shikhmurzaev, Y. D. 2008 Capillary Flows with Forming Interfaces. Chapman and Hall/CRC.Google Scholar
Shikhmurzaev, Y. 2011a Discussion notes on ‘Disjoining pressure of planar adsorbed films’, by J. R. Henderson. Eur. Phys. J. Special Topics 197, 125–127.Google Scholar
Shikhmurzaev, Y. 2011b Discussion notes on ‘Some singular errors near the contact line singularity, and ways to resolve both’, by L. M. Pismen. Eur. Phys. J. Special Topics 197, 75–80.Google Scholar
Shikhmurzaev, Y. 2011c Some dry facts about dynamic wetting. Eur. Phys. J. Special Topics 197, 47–60.CrossRefGoogle Scholar
Shikhmurzaev, Y. D. & Blake, T. 2004 Response to the comment on [Jl. Colloid and Interface Science. 253, (2003), 196] by Eggers J and Evans R. J. Colloid Interface Sci. 280, 539–541.Google Scholar
Snoeijer, J. H., Le Grand, N., Limat, L., Stone, H. A. & Eggers, J. 2007 Cornered drops and rivulets. Phys. Fluids 19, 042104.Google Scholar
Snoeijer, J. H., Rio, E., Le Grand, N. & Limat, L. 2005 Self-similar flow and contact line geometry at the rear of cornered drops. Phys. Fluids 17, 072101.CrossRefGoogle Scholar
Thampi, S. P., Adhikari, R. & Govindarajan, R. 2013 Do liquid drops roll or slide on inclined surfaces? Langmuir 29, 3339–3346.Google Scholar
Thiele, U. 2011 Discussion notes: thoughts on mesoscopic continuum models. Eur. Phys. J. Special Topics 197, 67–71.CrossRefGoogle Scholar
Troian, S. M., Herbolzheimer, E., Safran, S. A. & Joanny, J. F. 1989 Fingering lnstabilities of driven spreading films. Europhys. Lett. 10, 25–30.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11, 714–721.CrossRefGoogle Scholar
Winkels, K. G., Peters, I. R., Evangelista, F., Riepen, M., Daerr, A., Limat, L. & Snoeijer, J. H. 2011 Receding contact lines: from sliding drops to immersion lithography. Eur. J. Phys. 192, 195–205.Google Scholar