We present experimental results on high-Reynolds-number motion of partially non-wetting liquid drops on inclined plane surfaces using: (i) water on fluoro-alkyl silane (FAS)-coated glass; and (ii) mercury on glass. The former is a high-hysteresis (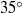 $3{5}^{\circ } $) surface while the latter is a low-hysteresis one (
$3{5}^{\circ } $) surface while the latter is a low-hysteresis one (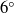 ${6}^{\circ } $). The water drop experiments have been conducted for capillary numbers
${6}^{\circ } $). The water drop experiments have been conducted for capillary numbers 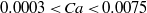 $0. 0003\lt Ca\lt 0. 0075$ and for Reynolds numbers based on drop diameter
$0. 0003\lt Ca\lt 0. 0075$ and for Reynolds numbers based on drop diameter 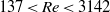 $137\lt Re\lt 3142$. The ranges for mercury on glass experiments are
$137\lt Re\lt 3142$. The ranges for mercury on glass experiments are 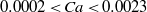 $0. 0002\lt Ca\lt 0. 0023$ and
$0. 0002\lt Ca\lt 0. 0023$ and 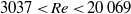 $3037\lt Re\lt 20\hspace{0.167em} 069$. It is shown that when
$3037\lt Re\lt 20\hspace{0.167em} 069$. It is shown that when 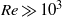 $Re\gg 1{0}^{3} $ for water and
$Re\gg 1{0}^{3} $ for water and 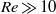 $Re\gg 10$ for mercury, a boundary layer flow model accounts for the observed velocities. A general expression for the dimensionless velocity of the drop, covering the whole
$Re\gg 10$ for mercury, a boundary layer flow model accounts for the observed velocities. A general expression for the dimensionless velocity of the drop, covering the whole 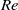 $Re$ range, is derived, which scales with the modified Bond number (
$Re$ range, is derived, which scales with the modified Bond number (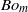 $B{o}_{m} $). This expression shows that at low
$B{o}_{m} $). This expression shows that at low 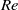 $Re$,
$Re$, 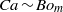 $Ca\sim B{o}_{m} $ and at large
$Ca\sim B{o}_{m} $ and at large 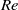 $Re$,
$Re$, 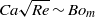 $Ca \sqrt{Re} \sim B{o}_{m} $. The dynamic contact angle (
$Ca \sqrt{Re} \sim B{o}_{m} $. The dynamic contact angle (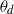 ${\theta }_{d} $) variation scales, at least to first-order, with
${\theta }_{d} $) variation scales, at least to first-order, with 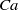 $Ca$; the contact angle variation in water, corrected for the hysteresis, collapses onto the low-
$Ca$; the contact angle variation in water, corrected for the hysteresis, collapses onto the low-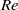 $Re$ data of LeGrand, Daerr & Limat (J. Fluid Mech., vol. 541, 2005, pp. 293–315). The receding contact angle variation of mercury has a slope very different from that in water, but the variation is practically linear with
$Re$ data of LeGrand, Daerr & Limat (J. Fluid Mech., vol. 541, 2005, pp. 293–315). The receding contact angle variation of mercury has a slope very different from that in water, but the variation is practically linear with 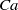 $Ca$. We compare our dynamic contact angle data to several models available in the literature. Most models can describe the data of LeGrand et al. (2005) for high-viscosity silicon oil, but often need unexpected values of parameters to describe our water and mercury data. In particular, a purely hydrodynamic description requires unphysically small values of slip length, while the molecular-kinetic model shows asymmetry between the wetting and dewetting, which is quite strong for mercury. The model by Shikhmurzaev (Intl J. Multiphase Flow, vol. 19, 1993, pp. 589–610) is able to group the data for the three fluids around a single curve, thereby restoring a certain symmetry, by using two adjustable parameters that have reasonable values. At larger velocities, the mercury drops undergo a change at the rear from an oval to a corner shape when viewed from above; the corner transition occurs at a finite receding contact angle. Water drops do not show such a clear transition from oval to corner shape. Instead, a direct transition from an oval shape to a rivulet appears to occur.
$Ca$. We compare our dynamic contact angle data to several models available in the literature. Most models can describe the data of LeGrand et al. (2005) for high-viscosity silicon oil, but often need unexpected values of parameters to describe our water and mercury data. In particular, a purely hydrodynamic description requires unphysically small values of slip length, while the molecular-kinetic model shows asymmetry between the wetting and dewetting, which is quite strong for mercury. The model by Shikhmurzaev (Intl J. Multiphase Flow, vol. 19, 1993, pp. 589–610) is able to group the data for the three fluids around a single curve, thereby restoring a certain symmetry, by using two adjustable parameters that have reasonable values. At larger velocities, the mercury drops undergo a change at the rear from an oval to a corner shape when viewed from above; the corner transition occurs at a finite receding contact angle. Water drops do not show such a clear transition from oval to corner shape. Instead, a direct transition from an oval shape to a rivulet appears to occur.