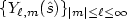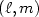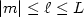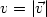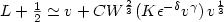Research Article
A new two-dimensional Shallow Water model including pressure effects and slow varying bottom topography
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 211-234
-
- Article
- Export citation
Energetics and switching of quasi-uniform statesin small ferromagnetic particles
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 235-248
-
- Article
- Export citation
Stick-slip transition capturing by using an adaptive finite element method
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 249-260
-
- Article
- Export citation
Galerkin time-stepping methods for nonlinear parabolic equations
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 261-289
-
- Article
- Export citation
Analysis of gradient flow of a regularized Mumford-Shahfunctional for image segmentation and image inpainting
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 291-320
-
- Article
- Export citation
A Maxwell-Bloch model with discrete symmetries for wave propagation in nonlinear crystals: an application to KDP
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 321-344
-
- Article
- Export citation
A note on (2K+1)-point conservative monotone schemes
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 345-357
-
- Article
- Export citation
Convergence of a high-order compact finite difference scheme for a nonlinear Black–Scholes equation
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 359-369
-
- Article
- Export citation
Error estimates in the fast multipole methodfor scattering problemsPart 1: Truncation of the Jacobi-Anger series
-
- Published online by Cambridge University Press:
- 15 March 2004, pp. 371-394
-
- Article
- Export citation