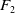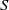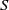1. Introduction
Grigorchuk exhibited continuously many quasi-isometry classes of residually finite three-generator groups by producing continuously many growth types [Reference Grigorchuk4, Thm 7.2]. Continuously many means having the cardinality of
![]() $\mathbb{R}$
. Here, we describe another family of such groups by building upon Bowditch’s method for distinguishing quasi-isometry classes [Reference Bowditch2] and use consequences of the theory of special cube complexes to obtain residual finiteness [Reference Agol1].
$\mathbb{R}$
. Here, we describe another family of such groups by building upon Bowditch’s method for distinguishing quasi-isometry classes [Reference Bowditch2] and use consequences of the theory of special cube complexes to obtain residual finiteness [Reference Agol1].
Consider the rank-2 free group
![]() $F_2=\langle a,b\rangle$
. Let
$F_2=\langle a,b\rangle$
. Let
![]() $w_n = [a,b^{2^{2^n}}][a^2,b^{2^{2^n}}]\cdots [a^{100},b^{2^{2^n}}]$
for
$w_n = [a,b^{2^{2^n}}][a^2,b^{2^{2^n}}]\cdots [a^{100},b^{2^{2^n}}]$
for
![]() $n\in{\mathbb{N}}$
.
$n\in{\mathbb{N}}$
.
Each subset
![]() $S\subseteq{\mathbb{N}}$
is associated to the following group:
$S\subseteq{\mathbb{N}}$
is associated to the following group:
In Section 3, we show that
![]() $G(S)$
is residually finite when
$G(S)$
is residually finite when
![]() $S\subseteq{\mathbb{N}}_{\gt 100}$
. We also observe that
$S\subseteq{\mathbb{N}}_{\gt 100}$
. We also observe that
![]() $G(S)$
and
$G(S)$
and
![]() $G(S')$
are not quasi-isometric when
$G(S')$
are not quasi-isometric when
![]() $S\Delta S'$
is infinite.
$S\Delta S'$
is infinite.
In fact, our proof of residual finiteness for
![]() $G(S)$
works in precisely the same way to prove the residual finiteness for the original examples of Bowditch having torsion. But it appears to fail for Bowditch’s torsion-free examples. We refer to Remark 3.3.
$G(S)$
works in precisely the same way to prove the residual finiteness for the original examples of Bowditch having torsion. But it appears to fail for Bowditch’s torsion-free examples. We refer to Remark 3.3.
We also produced an uncountable family of pairwise non-isomorphic residually finite groups in [Reference Chong and Wise3], and perhaps an appropriate subfamily also yields continuously many quasi-isometry classes.
Our simple approach arranges for certain infinitely presented small-cancellation groups to be residually finitely presented small-cancellation groups. This approach is likely to permit the construction of other interesting families of finitely generated groups.
2. Review of Bowditch’s result
We first recall some small-cancellation background. See [Reference Lyndon and Schupp5, Ch.V].
Definition 2.1.
For a presentation, a piece
![]() $p$
is a word appearing in more than one way among the relators. Note that for a relator
$p$
is a word appearing in more than one way among the relators. Note that for a relator
![]() $r=q^n$
, subwords that differ by a
$r=q^n$
, subwords that differ by a
![]() ${\mathbb{Z}}_n$
-action are regarded as appearing in the same way. A presentation is
${\mathbb{Z}}_n$
-action are regarded as appearing in the same way. A presentation is
![]() $C'\!\left(\dfrac{1}{6}\right)$
if
$C'\!\left(\dfrac{1}{6}\right)$
if
![]() $|p|\lt \dfrac{1}{6}|r|$
for any piece
$|p|\lt \dfrac{1}{6}|r|$
for any piece
![]() $p$
in a relator
$p$
in a relator
![]() $r$
.
$r$
.
A major subword
![]() $v$
of a relator
$v$
of a relator
![]() $r$
is a subword of a cyclic permutation of
$r$
is a subword of a cyclic permutation of
![]() $r^{\pm }$
with
$r^{\pm }$
with
![]() $|v| \gt \dfrac{|r|}{2}$
. A word
$|v| \gt \dfrac{|r|}{2}$
. A word
![]() $u$
is majority-reduced if
$u$
is majority-reduced if
![]() $u$
does not contain a major subword of a relator. We will use the following well-known property for
$u$
does not contain a major subword of a relator. We will use the following well-known property for
![]() $C'\!\left(\dfrac{1}{6}\right)$
groups [Reference Lyndon and Schupp5, Ch.V Thm 4.5].
$C'\!\left(\dfrac{1}{6}\right)$
groups [Reference Lyndon and Schupp5, Ch.V Thm 4.5].
Proposition 2.2.
Let
![]() $\langle x_1, x_2, \dots \mid r_1, r_2, \dots \rangle$
be a
$\langle x_1, x_2, \dots \mid r_1, r_2, \dots \rangle$
be a
![]() $C'\!\left(\dfrac{1}{6}\right)$
presentation. A non-empty cyclically reduced majority-reduced word in the generators must represent a nontrivial element in the group.
$C'\!\left(\dfrac{1}{6}\right)$
presentation. A non-empty cyclically reduced majority-reduced word in the generators must represent a nontrivial element in the group.
We now recall definitions leading to the main theorem of [Reference Bowditch2]. Let
![]() ${\mathbb{N}}^+ = \{n\in{\mathbb{Z}} \;:\; n\geq 1\}$
. Let
${\mathbb{N}}^+ = \{n\in{\mathbb{Z}} \;:\; n\geq 1\}$
. Let
![]() ${\mathbb{N}}_{\gt k}=\{n\in{\mathbb{N}} \;:\; n\gt k\}$
for some
${\mathbb{N}}_{\gt k}=\{n\in{\mathbb{N}} \;:\; n\gt k\}$
for some
![]() $k\in{\mathbb{N}}^+$
.
$k\in{\mathbb{N}}^+$
.
Definition 2.3.
Two subsets
![]() $L, L'\subseteq{\mathbb{N}}^+$
are related if for some
$L, L'\subseteq{\mathbb{N}}^+$
are related if for some
![]() $k\geq 1$
:
$k\geq 1$
:
-
1. for any
 $m\in L$
with
$m\in L$
with
 $m\gt k$
, there is
$m\gt k$
, there is
 $m'\in L'$
with
$m'\in L'$
with
 $m'\in \left[\dfrac{m}{k}, km\right]$
; and
$m'\in \left[\dfrac{m}{k}, km\right]$
; and
-
2. for any
 $m'\in L'$
with
$m'\in L'$
with
 $m'\gt k$
, there is
$m'\gt k$
, there is
 $m\in L$
with
$m\in L$
with
 $m\in \left[\dfrac{m'}{k}, km'\right]$
.
$m\in \left[\dfrac{m'}{k}, km'\right]$
.
We write
![]() $L\sim L'$
if
$L\sim L'$
if
![]() $L$
and
$L$
and
![]() $L'$
are related, and write
$L'$
are related, and write
![]() $L\not \sim L'$
otherwise.
$L\not \sim L'$
otherwise.
Remark 2.4.
This is a simplified but equivalent form of Bowditch’s definition [Reference Bowditch2, Def. before Lem 3] who used
![]() $m\gt (k+1)^2$
and
$m\gt (k+1)^2$
and
![]() $m'\gt (k+1)^2$
. The equivalence is easy by proving relatedness via
$m'\gt (k+1)^2$
. The equivalence is easy by proving relatedness via
![]() $(k+1)^2$
on one direction, and the other direction is clear since
$(k+1)^2$
on one direction, and the other direction is clear since
![]() $(k+1)^2\gt k$
.
$(k+1)^2\gt k$
.
Remark 2.5.
As pointed out by the referee, it is equivalent to say
![]() $L, L'\subseteq{\mathbb{N}}^+$
are related if there is
$L, L'\subseteq{\mathbb{N}}^+$
are related if there is
![]() $k\geq 1$
such that the sets
$k\geq 1$
such that the sets
![]() $M=L\cap{\mathbb{N}}_{\gt k}$
and
$M=L\cap{\mathbb{N}}_{\gt k}$
and
![]() $M'=L'\cap{\mathbb{N}}_{\gt k}$
satisfy that
$M'=L'\cap{\mathbb{N}}_{\gt k}$
satisfy that
![]() $|\log M, \log M'|\leq k$
. Here,
$|\log M, \log M'|\leq k$
. Here,
![]() $|Z, Z'| = \inf \{|z-z'| \;:\; z\in Z,z'\in Z'\}$
denotes the Hausdorff distance between sets
$|Z, Z'| = \inf \{|z-z'| \;:\; z\in Z,z'\in Z'\}$
denotes the Hausdorff distance between sets
![]() $Z$
and
$Z$
and
![]() $Z'$
. This observation could clarify the proofs below, especially Lemma 3.4, for some readers.
$Z'$
. This observation could clarify the proofs below, especially Lemma 3.4, for some readers.
Lemma 2.6.
The relation
![]() $\sim$
in Definition 2.3 is an equivalence relation on subsets of
$\sim$
in Definition 2.3 is an equivalence relation on subsets of
![]() ${\mathbb{N}}^+$
.
${\mathbb{N}}^+$
.
Proof. The relation
![]() $\sim$
is reflexive via
$\sim$
is reflexive via
![]() $k=1$
. The relation
$k=1$
. The relation
![]() $\sim$
is symmetric by definition. Hence, it suffices to show
$\sim$
is symmetric by definition. Hence, it suffices to show
![]() $\sim$
is transitive.
$\sim$
is transitive.
Let
![]() $S, S', S''\subseteq{\mathbb{N}}^+$
. Suppose
$S, S', S''\subseteq{\mathbb{N}}^+$
. Suppose
![]() $S\sim S'$
via
$S\sim S'$
via
![]() $k$
and
$k$
and
![]() $S'\sim S''$
via
$S'\sim S''$
via
![]() $k'$
. We claim that
$k'$
. We claim that
![]() $S\sim S''$
via
$S\sim S''$
via
![]() $kk'$
. Let
$kk'$
. Let
![]() $m\in S$
with
$m\in S$
with
![]() $m\gt kk'$
. There is
$m\gt kk'$
. There is
![]() $m'\in S'$
with
$m'\in S'$
with
![]() $m'\in\!\left[\dfrac{m}{k},km\right]$
by
$m'\in\!\left[\dfrac{m}{k},km\right]$
by
![]() $S\sim S'$
via
$S\sim S'$
via
![]() $k$
, hence
$k$
, hence
![]() $m'\gt k'$
. Then there is
$m'\gt k'$
. Then there is
![]() $m''\in S''$
with
$m''\in S''$
with
![]() $m''\in \!\left[\dfrac{m'}{k'},k'm'\right]$
by
$m''\in \!\left[\dfrac{m'}{k'},k'm'\right]$
by
![]() $S'\sim S''$
via
$S'\sim S''$
via
![]() $k'$
. Thus,
$k'$
. Thus,
![]() $m''\in \left [\dfrac{m}{kk'}, kk'm\right ]$
. Similarly, there is
$m''\in \left [\dfrac{m}{kk'}, kk'm\right ]$
. Similarly, there is
![]() $m\in \left [\dfrac{m''}{kk'}, kk'm''\right ]$
for any
$m\in \left [\dfrac{m''}{kk'}, kk'm''\right ]$
for any
![]() $m''\in S''$
with
$m''\in S''$
with
![]() $m''\gt kk'$
.
$m''\gt kk'$
.
Example 2.7.
All finite sets are related. All uniform nets are related.
![]() $\{2^n\}_{n\in{\mathbb{N}}}\sim \{3^n\}_{n\in{\mathbb{N}}}$
.
$\{2^n\}_{n\in{\mathbb{N}}}\sim \{3^n\}_{n\in{\mathbb{N}}}$
.
For sets
![]() $S,S'$
, their symmetric difference is
$S,S'$
, their symmetric difference is
![]() $S\Delta S' = (S - S')\cup (S' - S)$
.
$S\Delta S' = (S - S')\cup (S' - S)$
.
Example 2.8.
If
![]() $S,S'\subseteq{\mathbb{N}}^+$
with infinite
$S,S'\subseteq{\mathbb{N}}^+$
with infinite
![]() $S\Delta S'$
, then
$S\Delta S'$
, then
![]() $\{2^{2^n}\}_{n\in S} \not \sim \{2^{2^m}\}_{m\in S'}$
[Reference Bowditch2, Lem 4].
$\{2^{2^n}\}_{n\in S} \not \sim \{2^{2^m}\}_{m\in S'}$
[Reference Bowditch2, Lem 4].
With the notion of
![]() $\sim$
, the following is a simplified version of the main theorem in [Reference Bowditch2].
$\sim$
, the following is a simplified version of the main theorem in [Reference Bowditch2].
Theorem 2.9.
Let
![]() $G$
and
$G$
and
![]() $G'$
be the finitely generated
$G'$
be the finitely generated
![]() $C'\!\left(\dfrac{1}{6}\right)$
groups presented below. If
$C'\!\left(\dfrac{1}{6}\right)$
groups presented below. If
![]() $G$
is quasi-isometric to
$G$
is quasi-isometric to
![]() $G'$
, then
$G'$
, then
![]() $\{|w_i|\}_{i\in I} \sim \{|w'_{\!\!j}|\}_{j\in J}$
:
$\{|w_i|\}_{i\in I} \sim \{|w'_{\!\!j}|\}_{j\in J}$
:
3. Proving the family of groups have desired properties
3.1. Small cancellation
Proposition 3.1.
For any infinite subset
![]() $S\subseteq{\mathbb{N}}_{\gt 100}$
, the associated group
$S\subseteq{\mathbb{N}}_{\gt 100}$
, the associated group
![]() $G(S)$
is
$G(S)$
is
![]() $C'\!\left(\dfrac{1}{6}\right)$
. Furthermore,
$C'\!\left(\dfrac{1}{6}\right)$
. Furthermore,
![]() $G_k(S) = \left \langle a,b\ \middle|\ b^{2^{2^{k}}}, w_n \;:\; n\in S, n\lt k\right \rangle$
is
$G_k(S) = \left \langle a,b\ \middle|\ b^{2^{2^{k}}}, w_n \;:\; n\in S, n\lt k\right \rangle$
is
![]() $C'\!\left(\dfrac{1}{6}\right)$
for each
$C'\!\left(\dfrac{1}{6}\right)$
for each
![]() $k\in{\mathbb{N}}$
.
$k\in{\mathbb{N}}$
.
Proof. For the first statement, it suffices to show that
![]() $w_n$
and
$w_n$
and
![]() $w_m$
have small overlap for
$w_m$
have small overlap for
![]() $n\gt m\gt 100$
. The longest piece between
$n\gt m\gt 100$
. The longest piece between
![]() $w_n$
and
$w_n$
and
![]() $ w_m$
is
$ w_m$
is
![]() $b^{-2^{2^{m}}}a^{100}b^{2^{2^{m}}}$
. Thus,
$b^{-2^{2^{m}}}a^{100}b^{2^{2^{m}}}$
. Thus,
![]() $C'\!\left(\dfrac{1}{6}\right)$
holds since:
$C'\!\left(\dfrac{1}{6}\right)$
holds since:
For the second statement, we additionally show that
![]() $w_n$
and
$w_n$
and
![]() $b^{2^{2^k}}$
satisfy the
$b^{2^{2^k}}$
satisfy the
![]() $C'\!\left(\dfrac{1}{6}\right)$
condition for
$C'\!\left(\dfrac{1}{6}\right)$
condition for
![]() $100\lt n\lt k$
. Their longest piece is
$100\lt n\lt k$
. Their longest piece is
![]() $b^{2^{2^n}}$
, which is shorter than
$b^{2^{2^n}}$
, which is shorter than
![]() $\dfrac{1}{6}$
of the lengths of
$\dfrac{1}{6}$
of the lengths of
![]() $w_n$
and
$w_n$
and
![]() $b^{2^{2^k}}$
.
$b^{2^{2^k}}$
.
3.2. Residual finiteness
Observe that
![]() $G_k(S)=G(S)/\langle \!\langle b^{2^{2^k}}\rangle \!\rangle$
since
$G_k(S)=G(S)/\langle \!\langle b^{2^{2^k}}\rangle \!\rangle$
since
![]() $w_m\in \langle \!\langle b^{2^{2^k}}\rangle \!\rangle$
for
$w_m\in \langle \!\langle b^{2^{2^k}}\rangle \!\rangle$
for
![]() $m\geq k$
. Indeed,
$m\geq k$
. Indeed,
![]() $w_n = \left[a,b^{2^{2^n}}\right]\left[a^2,b^{2^{2^n}}\right]\cdots$
$w_n = \left[a,b^{2^{2^n}}\right]\left[a^2,b^{2^{2^n}}\right]\cdots$
![]() $\left[a^{100},b^{2^{2^n}}\right]$
is trivialised when
$\left[a^{100},b^{2^{2^n}}\right]$
is trivialised when
![]() $b^{2^{2^n}}$
becomes trivial.
$b^{2^{2^n}}$
becomes trivial.
Proposition 3.2.
For any infinite subset
![]() $S\subseteq{\mathbb{N}}_{\gt 100}$
, the associated group
$S\subseteq{\mathbb{N}}_{\gt 100}$
, the associated group
![]() $G(S)$
is residually finite.
$G(S)$
is residually finite.
Proof. Since
![]() $G_k(S)$
is a finitely presented
$G_k(S)$
is a finitely presented
![]() $C'\!\left(\dfrac{1}{6}\right)$
group, the hyperbolic group
$C'\!\left(\dfrac{1}{6}\right)$
group, the hyperbolic group
![]() $G_k(S)$
is cocompactly cubulated by [Reference Wise6]. Thus,
$G_k(S)$
is cocompactly cubulated by [Reference Wise6]. Thus,
![]() $G_k(S)$
is residually finite by [Reference Agol1].
$G_k(S)$
is residually finite by [Reference Agol1].
Each
![]() $g\in G(S)-\{1\}$
is represented by a cyclically reduced word
$g\in G(S)-\{1\}$
is represented by a cyclically reduced word
![]() $v$
with minimal length. Then
$v$
with minimal length. Then
![]() $v$
is majority-reduced since otherwise,
$v$
is majority-reduced since otherwise,
![]() $v$
contains a major subword of a relator, which can reduce the length of
$v$
contains a major subword of a relator, which can reduce the length of
![]() $v$
. Moreover,
$v$
. Moreover,
![]() $v$
does not contain a majority subword of
$v$
does not contain a majority subword of
![]() $b^{2^{2^{|v|}}}$
since
$b^{2^{2^{|v|}}}$
since
![]() $|v|\lt \dfrac{1}{2}\cdot 2^{2^{|v|}}=\dfrac{1}{2}\left |b^{2^{2^{|v|}}}\right |$
. Hence,
$|v|\lt \dfrac{1}{2}\cdot 2^{2^{|v|}}=\dfrac{1}{2}\left |b^{2^{2^{|v|}}}\right |$
. Hence,
![]() $v\neq 1_{G_{|v|}}$
by Proposition 2.2 since
$v\neq 1_{G_{|v|}}$
by Proposition 2.2 since
![]() $v$
is majority-reduced in
$v$
is majority-reduced in
![]() $G_{|v|}$
. Thus,
$G_{|v|}$
. Thus,
![]() $G(S)$
is residually residually finite and hence residually finite.
$G(S)$
is residually residually finite and hence residually finite.
Remark 3.3.
Bowditch’s original examples were
![]() $B(S) = \langle a, b \mid \big (a^{2^{2^n}}b^{2^{2^n}}\big )^7 \;:\; n\in S\subseteq{\mathbb{N}}\rangle$
. As in Proposition 3.2,
$B(S) = \langle a, b \mid \big (a^{2^{2^n}}b^{2^{2^n}}\big )^7 \;:\; n\in S\subseteq{\mathbb{N}}\rangle$
. As in Proposition 3.2,
![]() $B(S)$
is residually finite since it is residually finitely presented
$B(S)$
is residually finite since it is residually finitely presented
![]() $C'\!\left(\dfrac{1}{6}\right)$
using the quotients to
$C'\!\left(\dfrac{1}{6}\right)$
using the quotients to
![]() $B/\langle \!\langle a^{2^{2^n}}, b^{2^{2^n}}\rangle \!\rangle$
for
$B/\langle \!\langle a^{2^{2^n}}, b^{2^{2^n}}\rangle \!\rangle$
for
![]() $n\geq 3$
. However, the analogous argument fails for Bowditch’s torsion-free examples
$n\geq 3$
. However, the analogous argument fails for Bowditch’s torsion-free examples
![]() $B'(S) = \langle a, b \mid a\big (a^{2^{2^n}}b^{2^{2^n}}\big )^{12} \;:\; n\in S\subseteq{\mathbb{N}}\rangle$
.
$B'(S) = \langle a, b \mid a\big (a^{2^{2^n}}b^{2^{2^n}}\big )^{12} \;:\; n\in S\subseteq{\mathbb{N}}\rangle$
.
3.3. Pairwise non-quasi-isometric
We first prove a lemma about the relation
![]() $\sim$
.
$\sim$
.
Lemma 3.4.
![]() $S\sim nS\sim (S+n)$
for
$S\sim nS\sim (S+n)$
for
![]() $n\in{\mathbb{N}}^+$
and
$n\in{\mathbb{N}}^+$
and
![]() $S\subseteq{\mathbb{N}}^+$
.
$S\subseteq{\mathbb{N}}^+$
.
Proof. First,
![]() $S\sim nS$
via
$S\sim nS$
via
![]() $n$
. Indeed, for any
$n$
. Indeed, for any
![]() $s\in S$
,
$s\in S$
,
![]() $ns\in \left [\dfrac{s}{n},ns\right ]$
; for any
$ns\in \left [\dfrac{s}{n},ns\right ]$
; for any
![]() $ns\in nS$
,
$ns\in nS$
,
![]() $s\in \left [\dfrac{ns}{n},n\cdot ns\right ]$
.
$s\in \left [\dfrac{ns}{n},n\cdot ns\right ]$
.
Moreover,
![]() $S\sim (S+n)$
via
$S\sim (S+n)$
via
![]() $n+1$
. For any
$n+1$
. For any
![]() $s\in S$
,
$s\in S$
,
![]() $s+n\leq (n+1)s$
, so
$s+n\leq (n+1)s$
, so
![]() $s+n\in \left [\dfrac{s}{n+1},(n+1)s\right ]$
. On the other hand, for
$s+n\in \left [\dfrac{s}{n+1},(n+1)s\right ]$
. On the other hand, for
![]() $s+n\in S+n$
,
$s+n\in S+n$
,
![]() $(n+1)s\geq s+n$
implies
$(n+1)s\geq s+n$
implies
![]() $s\geq \dfrac{s+n}{n+1}$
. Hence,
$s\geq \dfrac{s+n}{n+1}$
. Hence,
![]() $s\in \left [\dfrac{s+n}{n+1}, (n+1)(s+n)\right ]$
.
$s\in \left [\dfrac{s+n}{n+1}, (n+1)(s+n)\right ]$
.
Proposition 3.5.
Let
![]() $S,S'\subseteq{\mathbb{N}}^+$
have infinite
$S,S'\subseteq{\mathbb{N}}^+$
have infinite
![]() $S\Delta S'$
, then
$S\Delta S'$
, then
![]() $\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
.
$\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
.
Proof.
![]() $\{|w_n| \;:\; n\in S\} = \{10100+200\cdot 2^{2^n} \;:\; n\in S\} = 10100+200\cdot \{2^{2^n} \;:\; n\in S\}$
. By Lemma 3.4,
$\{|w_n| \;:\; n\in S\} = \{10100+200\cdot 2^{2^n} \;:\; n\in S\} = 10100+200\cdot \{2^{2^n} \;:\; n\in S\}$
. By Lemma 3.4,
![]() $\{|w_n| \;:\; n\in S\}\sim \{2^{2^n} \;:\; n\in S\}$
. Similarly,
$\{|w_n| \;:\; n\in S\}\sim \{2^{2^n} \;:\; n\in S\}$
. Similarly,
![]() $\{|w_m| \;:\; m\in S'\}\sim \{2^{2^m} \;:\; m\in S'\}$
. By Example 2.8,
$\{|w_m| \;:\; m\in S'\}\sim \{2^{2^m} \;:\; m\in S'\}$
. By Example 2.8,
![]() $\{2^{2^n} \;:\; n\in S\}\not \sim \{2^{2^m} \;:\; m\in S'\}$
, so
$\{2^{2^n} \;:\; n\in S\}\not \sim \{2^{2^m} \;:\; m\in S'\}$
, so
![]() $\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
by Lemma 2.6.
$\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
by Lemma 2.6.
Corollary 3.6.
If
![]() $S,S'\subseteq{\mathbb{N}}_{\gt 100}$
have infinite
$S,S'\subseteq{\mathbb{N}}_{\gt 100}$
have infinite
![]() $S\Delta S'$
, then
$S\Delta S'$
, then
![]() $G(S)$
and
$G(S)$
and
![]() $G(S')$
are not quasi-isometric.
$G(S')$
are not quasi-isometric.
Proof.
![]() $\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
, hence
$\{|w_n|\}_{n\in S}\not \sim \{|w_m|\}_{m\in S'}$
, hence
![]() $G(S)$
and
$G(S)$
and
![]() $G(S')$
are not quasi-isometric by Theorem 2.9.
$G(S')$
are not quasi-isometric by Theorem 2.9.
For
![]() $A,B\subseteq N$
, declare
$A,B\subseteq N$
, declare
![]() $A\sim _{_\Delta }\!B$
if
$A\sim _{_\Delta }\!B$
if
![]() $\left |A\Delta B\right |\lt \infty$
. As noted by Bowditch, each
$\left |A\Delta B\right |\lt \infty$
. As noted by Bowditch, each
![]() $\sim _{_\Delta }\!$
equivalence class is countable. Hence, there are continuously many
$\sim _{_\Delta }\!$
equivalence class is countable. Hence, there are continuously many
![]() $\sim _{_\Delta }\!$
equivalence classes. Our construction thus produces continuously many pairwise non-quasi-isometric groups
$\sim _{_\Delta }\!$
equivalence classes. Our construction thus produces continuously many pairwise non-quasi-isometric groups
![]() $G(S)$
, which are
$G(S)$
, which are
![]() $C'\!\left(\dfrac{1}{6}\right)$
and residually finite.
$C'\!\left(\dfrac{1}{6}\right)$
and residually finite.
Acknowledgements
We are grateful to the referee for helpful comments. Research is supported by NSERC.