INTRODUCTION
Research in epidemiology may be concerned with assessing risk factors for complex health issues described by several variables. As an example in veterinary epidemiology, a disease can be jointly described by clinical signs observed in animals, post-mortem lesions on organs under study or diagnostic test results about viruses or bacterial pathogenicity. The key idea that several variables may describe a latent concept can be extended to the structure of explanatory variables. Veterinary epidemiological surveys usually consist of data gathered from animal characteristics, farm, transport conditions, slaughterhouse features, and laboratory results. As a consequence, explanatory variables may be organized into meaningful blocks related to the production stages. In a more formal way, epidemiological data are organized in (K+1) blocks of variables, consisting of a block of variables to be explained (Y) and a large number of explanatory variables organized in K meaningful blocks (X 1, …, X K). All these variables are measured in the same epidemiological units, e.g. animals or farms.
The statistical procedures usually performed pertain to generalized linear models (GLMs), especially complex models of logistic regression [Reference Dohoo, Martin and Stryhn1]. These models have appealing features that justify their wide use. However, in the case of a multivariate outcome such as a complex disease described by several variables (i.e. dependent variables), the epidemiologist needs to utilize successive GLMs using each dependent variable in turn, or, alternatively, a pooled variable which sums up the various dependent variables [Reference Rose2]. Moreover, all the potential explanatory variables can not be included in a single model because very often they are plagued by quasi-collinearity. It is well-known that under these circumstances, the relevance and the stability of the results obtained from GLMs are impaired [Reference Dohoo3]. For this reason, several authors have advocated that explanatory variables should be subjected to a selection procedure or alternatively summarized onto latent variables (or components) (see e.g. [Reference Berghaus4, Reference Boklund5]). Finally, the organization of the explanatory variables into meaningful blocks (e.g. environment, infectious agents, alimentary factors, management habits) is usually omitted in GLMs. This is a drawback because assessment of the importance of each block in the explanation of the dependent variables (Y) is of paramount interest to the epidemiologist.
Considering the aim and the specificity of such complex data, the research work focuses on methods related to the multiblock modelling framework. Within this framework, the well-known method is structural equation modelling (SEM), also known as LISREL [Reference Joreskog6]. It can be viewed as a joint point between path and factor analysis [Reference Musil, Jones and Warner7]. On the one hand, path models give direct relationships between explanatory variables and variables to be explained [Reference Woods8]. On the other hand, factor analysis summarizes the variable blocks, as expression of different concepts, with latent variables [Reference Manske, Hultgren and Bergsten9]. SEM is a confirmatory model to assess the relationships among several datasets through latent variables. It is based on a conceptual model which should be set up by the user beforehand. It is used extensively in economics, business and social science. As an alternative to SEM, partial least squares path modelling (PLS-PM) [Reference Wold, Jöreskog and Wold10] is a distribution-free data analysis approach and appears to be more adapted to biological data. It requires neither distributional nor sample size assumptions [Reference Rougoor11]. However, PLS-PM lacks a well-identified global optimization criterion and the iterative algorithm convergence is only proven in few particular cases [Reference Hanafi12]. For our purpose of exploring and modelling the relationships between a dataset Y and several datasets (X 1, …, X K), these problems can be circumvented by using multiblock (K+1) methods. Multiblock partial least squares (PLS) [Reference Wold and Wold13, Reference Wangen and Kowalski14] is a widely used multiblock modelling technique. It is designed as an extension of PLS regression [Reference Wold and Krishnaiah15], a popular method for linking two datasets X and Y. Multiblock PLS is mainly used in the field of process monitoring [Reference Kourti16], chemometrics [Reference Kohonen17] and sensometrics [Reference Tenenhaus18].
We propose yet another (K+1) multiblock method called multiblock redundancy analysis. This method of analysis is more focused towards the explanation of the Y variables than multiblock PLS [Reference Bougeard and Qannari19, Reference Bougeard20]. It can be viewed as an extension of redundancy analysis [Reference Rao21] which is designed to explore the relationships between two datasets. The underlying principle is that each dataset is summed up by latent variables which are linear combinations of the variables in the dataset under consideration. These latent variables are sought by maximizing a criterion which reflects the extent to which each latent variable from the explanatory blocks are linked to the latent variables from the Y block. The solution to this maximization problem is directly derived from a matrix eigenanalysis. Moreover, multiblock redundancy analysis gives valuable tools for the explanation and the investigation of the relationships among variables and datasets. The associated models explain each variable in Y with explanatory variables, through orthogonalized regression. As the method aims at describing datasets with a large numbers of variables, the epidemiologist needs to sum up the complex links between them and between the datasets. Overall indices and graphical displays associated with different interpretation levels are proposed.
The interest of multiblock redundancy analysis is illustrated using a dataset from an observational study devoted to the assessment of the overall risk factors for losses in broiler chicken flocks (Y) described by four variables, i.e. the first-week mortality rate, the mortality rate during the rest of the rearing, the mortality rate during the transport to the slaughterhouse and the condemnation rate at slaughterhouse. As a matter of fact, most studies reported in the literature focus on particular reasons for losses. For the epidemiologist interested in determining the most appropriate focus to contain losses in broiler chickens, integrating results from separate analysis into an overall approach is difficult and probably not relevant. Moreover, the investigation of risk factors in epidemiological surveys is consistently resulting from complex interactions between variables. Our objectives are to model the relationships between the losses as a composite block to be explained, with explanatory variables organized in thematic blocks related to the various production stages. In particular, we aim at assessing the impact of the different production stages on the whole losses and the specific risk factors for each element of losses. This pinpoints which production stages need to be improved and meets the specific expectations of the various factors in the poultry production chain confronted with health event complexity.
MATERIAL AND METHOD
Multiblock redundancy analysis
An original method, called multiblock redundancy analysis, is proposed in the multiblock modelling framework, adapted to the setting in which a block Y of several variables is to be explained by K explanatory variable blocks (X 1, …, X K). The main idea is that each dataset is summed up by a latent variable (or component) which is a linear combination of the variables derived from this dataset. Multiblock redundancy analysis can be considered as a component-based estimation technique where the latent variable estimation plays a central role. More precisely, the method derives a global component t (1), related to all the explanatory variables merged in the dataset X=[X 1|…|X K], closely related to a component u (1), linear combination of the variables in Y. Moreover, the component t (1) sums up the partial components (t 1(1), …, t K(1)), respectively, associated with the blocks (X 1, …, X K). A simplified example of a conceptual scheme, highlighting the relationships between the variable blocks and their associated components is proposed in Figure 1.
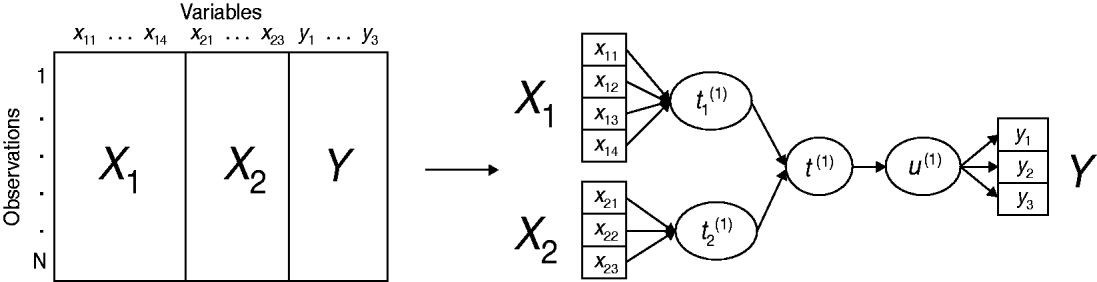
Fig. 1. Example of multiblock data structure and associated conceptual scheme of multiblock redundancy analysis, highlighting the relationships between the variable blocks (X 1, X 2, Y) and their associated components (t 1(1), t 2(1), u (1)) for the first dimension.
The global component t (1) sums up the partial components and is sought such as its squared covariance with u (1) is as large as possible. The solutions are derived from the eigenanalysis of a matrix which involves the datasets Y and (X 1, …, X K). Thereafter, the partial components t 1(1), …, t K(1) are given by the normalized projection of u (1) on each subspace spanned by variables in blocks X 1, X 2, …, XK . It follows that the global component t (1) is a synthesis of the partial components (t 1(1), …, t K(1)) and therefore, the relationships of a given block X k with Y is investigated through the relationships of t k(1) with t (1). (For a detailed account of multiblock redundancy analysis see [Reference Bougeard and Qannari19, Reference Bougeard20].)
In order to improve the prediction ability of the model, higher-order solutions are obtained by considering the residuals of the orthogonal projections of the datasets (X 1, …, X K) onto the subspace spanned by the first global component t (1). Thereafter, the second-order solution is performed by replacing the original datasets (X 1, …, XK
) by their residuals in the criterion to maximize. This leads to determination of a second component u (2) in the Y space, a second component t (2) in the space spanned by the X variables and the associated latent variables in the various blocks of variables. The rationale behind this step is to investigate other directions in the space spanned by the X variables in order to shed light on the Y variables from various perspectives thus improving their prediction. Subsequent components (t (2), …, t (H
)) can be found by reiterating this process. As a consequence, these components can be expressed as linear combinations of X, t (h
)=Xw *(h
), where w *(h
) is the vector of loadings associated with t (h
). They are mutually orthogonal with each other and ranked by order of importance in explaining the total variation of Y. This allows orthogonalized regression which takes into account all the explanatory variables, and Y is split up into ![]() for h=(1, …, H), Y (h
) being the matrix of residuals of the model based on h components. This leads to the model:
for h=(1, …, H), Y (h
) being the matrix of residuals of the model based on h components. This leads to the model: ![]() for h=(1, …, H). From a practical point of view, the final model may be obtained by selecting the optimal number of components to be retained with a validation technique such as twofold cross-validation [Reference Stone22]. This consists of splitting the whole dataset into two sets, namely a calibration set and a validation set. The calibration set is used to select the parameters of the model and the fitting ability of the model, and the validation set is used to compute the prediction ability. Among all the models corresponding to the various values of h, a model with a satisfactory fitting ability and good prediction ability is retained. Orthogonalized regression handles the multicollinearity problem by selecting a subset of orthogonal components and avoiding the latest components which can be deemed to reflect noise only.
for h=(1, …, H). From a practical point of view, the final model may be obtained by selecting the optimal number of components to be retained with a validation technique such as twofold cross-validation [Reference Stone22]. This consists of splitting the whole dataset into two sets, namely a calibration set and a validation set. The calibration set is used to select the parameters of the model and the fitting ability of the model, and the validation set is used to compute the prediction ability. Among all the models corresponding to the various values of h, a model with a satisfactory fitting ability and good prediction ability is retained. Orthogonalized regression handles the multicollinearity problem by selecting a subset of orthogonal components and avoiding the latest components which can be deemed to reflect noise only.
Interpretation tools
For the optimal dimension h, the exponential of the regression coefficients associated with each explanatory variable x p and each variable to be explained y q, ![]() , are interpreted as the incidence rate ratio (IRR) [Reference Dohoo, Martin and Stryhn1]. Bootstrapping simulations are performed to provide standard deviations and tolerance intervals (TIs), associated with the regression coefficient matrix [Reference Efron and Tibshirani23, Reference Rebafka, Clémençon and Feinberg24]. An explanatory variable is considered to be significantly associated with a variable in Y if the 95% TI associated with the IRR does not contain 1. IRRs are interesting indices to link explanatory variables with each of the variables in Y.
, are interpreted as the incidence rate ratio (IRR) [Reference Dohoo, Martin and Stryhn1]. Bootstrapping simulations are performed to provide standard deviations and tolerance intervals (TIs), associated with the regression coefficient matrix [Reference Efron and Tibshirani23, Reference Rebafka, Clémençon and Feinberg24]. An explanatory variable is considered to be significantly associated with a variable in Y if the 95% TI associated with the IRR does not contain 1. IRRs are interesting indices to link explanatory variables with each of the variables in Y.
However, if the number of variables in Y is large, the epidemiologist needs to sort the explanatory variables in a global order of priority. The variable importance for the projection (VIP) proposed in the PLS regression framework is a relevant tool [Reference Chong and Jun25, Reference Wold and Waterbeemd26]. The VIP values sum up the overall contribution of each explanatory variable to the explanation of the Y block for a model involving (t (1), …, t (h)) components. As the VIP indices verify, for a given dimension, the property ∑P p=1(VIP2 p)/P=1, where P is the total number of variables in X, they can be expressed as percentages. Associated standard deviations and tolerance intervals, computed using bootstrapped results, may additionally be computed. For the optimal dimension h, each explanatory variable is considered as significantly associated with the Y block if the 95% TI associated with the VIP does not contain the threshold value 0·8 [Reference Gosselin, Rodrigue and Duchesne27].
Finally, it interesting for the epidemiologist to assess the contributions of the explanatory blocks to the modelling task. Several indices are proposed in the literature and the block importance in the prediction (BIP) appears to be the most relevant [Reference Vivien, Verron and Sabatier28]. For an optimal dimension h, the BIP values are based on the weighted average values of the coefficients (a 1(h)2, …, a K(h)2) which reflect the importance of each block X k in the Y block explanation. Moreover, the BIP can also be computed to assess the importance of each block X k in explaining each variable in Y. As the BIP indices verify, for a given dimension the property ∑K k=1(BIP2 k)/K=1, where K is the number of explanatory blocks, can be expressed as percentages. Associated standard deviations and tolerance intervals, computed using bootstrapped results, may be given. It follows that for the optimal dimension h, each block X k is considered to be significantly associated with the overall block Y or with each variable in Y, if the 95% TI associated with the BIP does not contain the threshold value 0·8 [Reference Vivien, Verron and Sabatier28].
Software
Statistical procedures and associated interpretation tools were performed using code programs developed in Matlab®(The MathWorks Inc., USA) and also made available in R (http://www.r-project.org/). The code source is available upon request from the corresponding author.
Illustration dataset
Both in human and veterinary epidemiological surveys, it frequently occurs that the data at hand can be organized into blocks. The complex health issue (Y block), described by several variables, needs to be explained with a large number of explanatory variables organized into meaningful blocks (X 1, …, X K), related to feeding, environment, genetic heritage, among others.
An example is given in the field of veterinary epidemiology. The population consists of a cohort of slaughtered broiler chicken flocks from all the European Union licensed slaughterhouses in France [Reference Lupo29]. A large number (351) of broiler chicken flocks are randomly selected by two-stage sampling, stratified per slaughterhouse and based on random selection of the day of slaughter and of the flock sequence number in the slaughtering schedule of that day. On the one hand, the information collected on each flock is prospective at slaughterhouse, and consists of recording the transport conditions to the slaughterhouse, the number of dead animals on arrival, the slaughtering conditions, the condemnation rate and the official sanitary reasons for condemnation. On the other hand, retrospective information is collected and involves the conditions during the rearing period, health history, daily mortality, catching and loading conditions. The aim is to assess the overall risk factors for a composite outcome: losses in broiler chickens (Y), described by four variables, i.e. the first-week mortality rate, the mortality rate during the rest of the rearing, the mortality rate during the transport to the slaughterhouse, and the condemnation rate at the slaughterhouse.
The explanatory variables are first selected on the basis of the main factors reported in the literature and of an earlier univariate screening applied to each dependent variable. These 68 selected variables are organized in four thematic blocks related to farm structure and systematic husbandry management practices (X 1, 16 variables), flock characteristics and on-farm history of the chicks at placement (X 2, 14 variables), flock characteristics during the rearing period (X 3, 17 variables) and catching, transport and lairage conditions, slaughterhouse and inspection features (X 4, 21 variables). Indicator (dummy) variables are considered for the categorical variables. All the 68 putative explanatory variables are included in the multiblock analysis, fitted with a backwards-selection procedure.
As all the variables are expressed in different units, they are column centred and scaled to unit variance. As the explanatory variables have been standardized, the total variance in each block is equal to the number of variables in this block. This motivates the block scaling in order to put the blocks on the same footing [Reference Westerhuis and Coenegracht30]. For this purpose, each of the (K=4) explanatory block is accommodated with a scaling factor to set them at the same total variance 1/K.
RESULTS
Preliminary results
Among the 68 explanatory variables, 20 were significant risk factors for at least one variable relating to the losses and are retained for the final analysis. Among these 20 variables, five pertain to the farm structure and the systematic husbandry management practices (X 1), four are selected from the flock characteristics and the on-farm history of the chicks at placement (X 2), six relate to the flock characteristics during the rearing period (X 3), and five relate to the catching, transport and lairage conditions, slaughterhouse and inspection features (X 4). The twofold cross-validation results led us to a model with (h=4) components (m cv=500 cross-validated samples). This model explains 93% of the variation in Y, 15% in X 1, 30% in X 2, 30% in X 3 and 27% in X 4.
Risk factors for each element of the dependent block
A predictive model is set up by regressing the variables to be explained upon the first four global components. The regression coefficients, transformed into IRRs, the associated standard deviations and the tolerance intervals (m bt=500 bootstrapped samples) of the 20 explanatory variables are computed for each dependent variable. Table 1 gives the explanatory variables which are significantly associated with the four variables related to the losses.
Table 1. Contribution of the explanatory variables to the explanation of the four variables of losses Y=[y1, y2, y3, y4], by means of significant incidence rate ratio (IRR) associated with their 95% tolerance interval
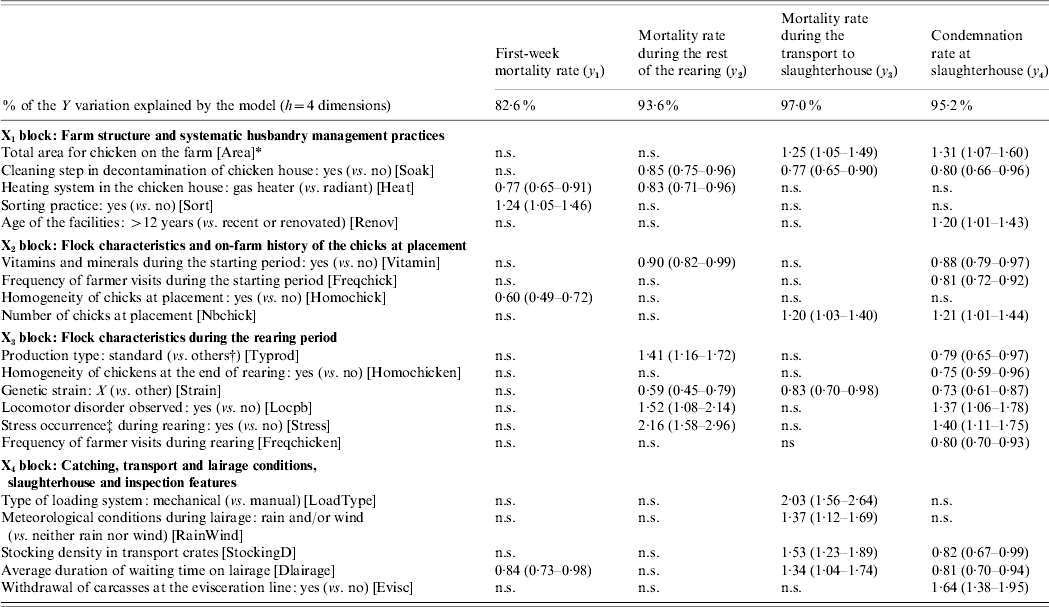
n.s., Non-significant.
* Abbreviation of the variable name given within square brackets.
† ‘Others’ includes light or heavy production types.
‡ Stress occurrence gathers feeding system defection, electrical defect, etc.
Each variable in Y is significantly related to a specific set of explanatory variables. First, the first-week mortality rate is related to four variables, two of which pertain to the farm structure. The mortality rate during the rest of the rearing is significantly linked with seven variables, four of which pertain to the flock characteristics during the rearing period. The mortality rate during the transport to the slaughterhouse is associated with eight variables, among which four pertain to the catching, transport and lairage conditions, slaughterhouse and inspection features. Finally, the condemnation rate at slaughterhouse is related to 15 variables, six of these variables refer to flock characteristics during the rearing period. Some explanatory variables are specifically related to one variable in Y, e.g. the chick homogeneity (from X 2), whereas others are linked with up to three (out of four) variables in Y, e.g. the genetic strain (from X 3).
Risk factors for the dependent block (Y)
In order to sort these explanatory variables by a global order of priority thus highlighting their overall contribution to the explanation of the Y block, the VIP are computed. Figure 2 depicts the VIP2 expressed as percentages, of the main explanatory variables.
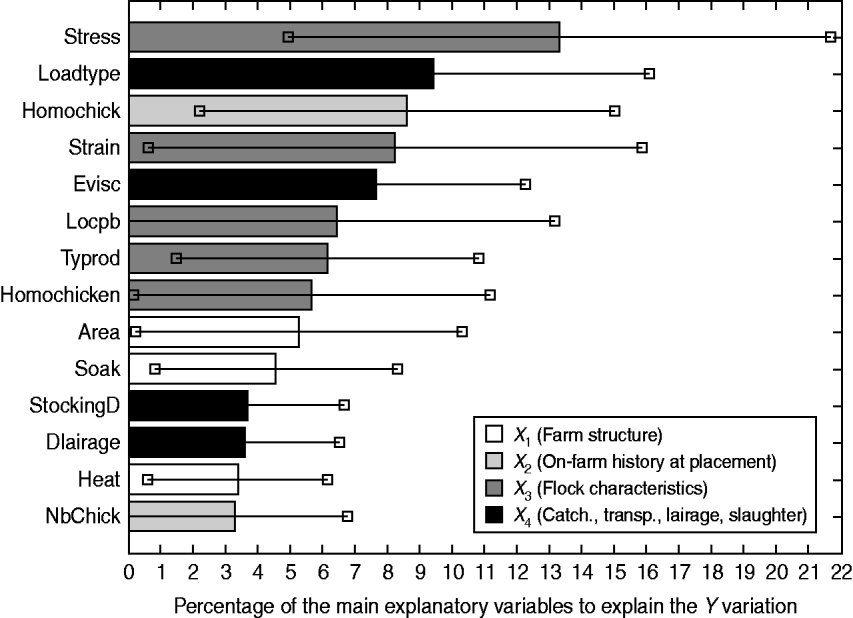
Fig. 2. Contribution of the main explanatory variables [variable importance for the projection (VIP)2 ⩾3%] to the explanation of the overall losses (Y), through VIP2 (expressed as percentages) associated with their 95% tolerance interval.
It turns out that four explanatory variables have a significant impact on the overall losses: the stress occurrence during rearing (VIP2 Stress=13·3%, 95% TI 4·9–21·7), the type of loading system (VIP2 LoadType=9·4%, 95% TI 2·8–16·1), chick homogeneity (VIP2 HomoChick=8·6%, 95% TI 2·2–15·0) and carcass withdrawal at the evisceration line (VIP2 Evisc=7·6%, 95% TI 3·0–12·3). Because of its high variability, the genetic strain has a relatively important although non-significant impact (VIP2 Strain=8·2%, 95% TI 0·6–15·9).
Explanatory block importance for the dependent block (Y) explanation
Figure 3 depicts the relative importance of the four production stages, i.e. the four explanatory blocks, in the overall losses explanation, highlighting the significant importance of two blocks.
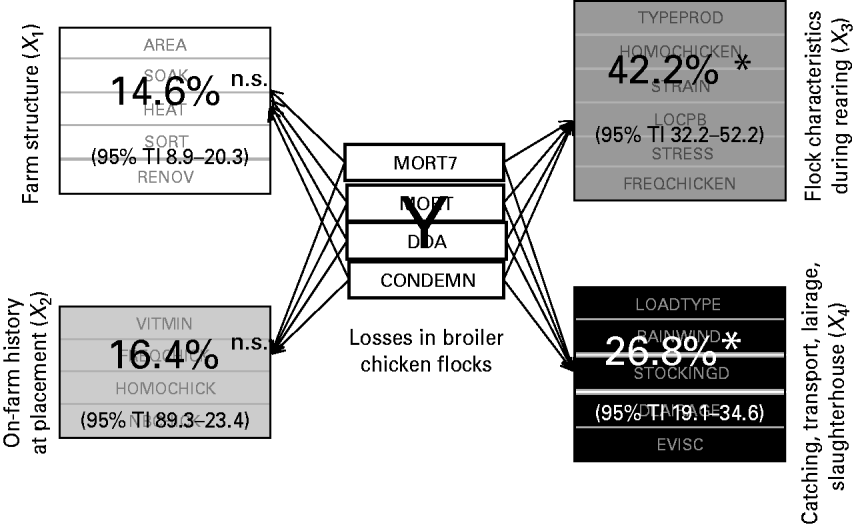
Fig. 3. Contribution of the four explanatory blocks (X 1, …, X 4) to the explanation of the overall losses (Y), through block importance in the prediction (BIP2; expressed as percentages) associated with their 95% tolerance interval (TI). * Significant association; n.s., non-significant.
More precisely, 42·2% (95% TI 32·2–52·2) of the overall losses variation are explained by the flock characteristics during the rearing period (X 3) and 26·8% (95% TI 19·1–34·6) by the catching, transport and lairage conditions, slaughterhouse and inspection features (X 4). In addition, the relative importance of the four production stages in the explanation of each element of the losses is given in Table 2.
Table 2. Contribution of the explanatory blocks (X1, …, X4) to the explanation of each variable of the losses Y=[y1, y2, y3, y4], by means of block importance in the prediction (BIP2 expressed as percentages) associated with their 95% tolerance interval
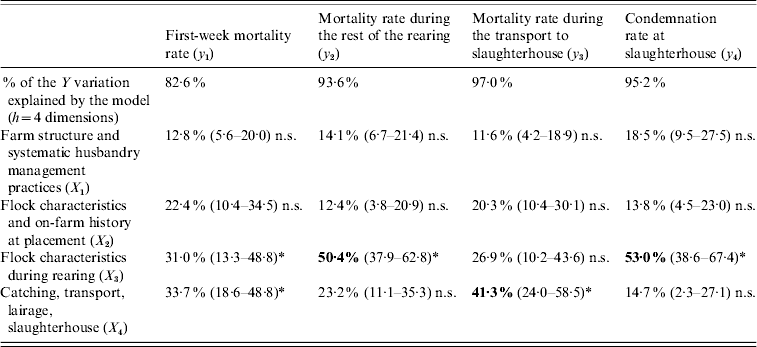
n.s., Non-significant.
* Significant association.
Neither the farm structure (X 1) nor the on-farm history at placement (X 2) have a significant impact on any variable of the losses. The most important findings are that the mortality rate during the rest of the rearing and the condemnation rate at slaughterhouse are mainly explained by the flock characteristics during rearing (X 3), and that the mortality rate during the transport to slaughterhouse is mainly related to the catching, transport and lairage conditions, slaughterhouse and inspection features (X 4).
DISCUSSION
Multiblock modelling for complex epidemiological data
On the whole, multiblock modelling results match up with those obtained from particular cases of GLMs, as both approaches lead to identification of specific risk factors related to each specific element of losses. (See e.g. [Reference Yassin31] for risk factors associated with the first-week mortality rate; see [Reference Heier, Hogasen and Jarp32] for risk factors for the mortality rate during the remainder of the rearing; see [Reference Chauvin33] for risk factors for the mortality rate during transport and see [Reference Lupo29] for risk factors for condemnation at slaughterhouse.) Although this classical risk factor analysis gives complete, accurate and sensible results, the epidemiologist needs to obtain overall results to pass them on to professionals. Multiblock redundancy analysis gives all the specific risk factors for each element of a composite outcome from a single analysis and gives additional information. It is well-adapted to complex health issues and integrates an overall epidemiological approach. The method gives operational conclusions to the multifactorial origin of complex outcome. The model under study explains 93% of the variation that occurred in overall losses. The main part of this variation, i.e. 13·3%, can be explained by the stress occurrence during rearing and 9·4% by the mechanical catching method, among others. If particular care is taken with respect to the four most important variables, i.e. stress during rearing, type of loading system, chick homogeneity at placement and genetic strain, the explained losses could be reduced by 39·6%. As a final remark, the variation in overall losses is explained by the flock characteristics during rearing (42·2% of explained variation) and the catching, transport and lairage conditions, slaughterhouse and inspection features (26·8% of explained variation). One of the main advantages of multiblock redundancy analysis is to assess measurable and relevant impacts of variable blocks in a single analysis. Moreover, these weights can be compared to each other and this provides valuable information for epidemiologists. These findings may be useful for global management decisions. The relevant process stages on which to focus can be determined, as a decision-support aid in health management. This meets the specific expectations of the various factors in the production chain confronted with health complexity.
Alternative multiblock methods
The structure of epidemiological data together with the specific aim of epidemiologists led us to develop a new multiblock method, called multiblock redundancy analysis. This method is adapted to the setting where a block of several variables is to be explained by several explanatory blocks. Some other methods that could also meet the epidemiologists' expectations, are proposed within the framework of canonical analysis [Reference Kissita34] or PLS regression [Reference Wold and Wold13]. Multiblock redundancy analysis was chosen considering its balanced behaviour with respect to robustness to multicollinearity and good fitting ability.
Multiblock modelling vs. successive GLMs
The overall approach of multiblock modelling can be compared to the standard approach which consists in setting up successive GLMs. GLMs boast some major advantages that justify their wide use in the epidemiological framework. First, the link between explanatory and dependent variables can be fitted (e.g. Poisson link function for the condemnation rate) whereas, in multiblock modelling, this link is the linear link function. Second, the explanatory variable status, i.e. quantitative or categorical, is taken into account in GLMs. By comparison, in the multiblock framework, dummy variables are considered for categorical variables and with this coding they are considered along with the quantitative variables. Third, in GLMs, explanatory variables can be selected in relation to the dependent variable under study. As an example, variables from the block relating to the catching, transport and lairage, and slaughterhouse are not selected to explain the first-week mortality. A limitation of multiblock modelling is the selection of all explanatory variables available in order to explain all the variables to be explained at the same time, even if some are not relevant. This may lead to the selection of irrelevant variables as risk factor (e.g. the average duration of waiting time on lairage as a significant risk factor for the first-week mortality). Finally, GLMs are well-known methods that are fully available on software.
Multiblock redundancy analysis is based on a single criterion that reflects the objectives to be addressed. The criterion is based on the determination of latent variables which highlight the relationships among the datasets. This method fits within the general framework of multivariate techniques and factor analysis. The appealing feature of these methods is that they provide visualization tools which can be helpful for researchers to unveil hidden patterns and relationships among variables. As this method is mainly exploratory, its results are expressed in relation to the explanatory variables. Using latent variables as a summary of manifest variables makes it possible to include a large number of variables in a single model. In comparison with GLMs, the multiblock approach does not necessitate recourse to the univariate step, whose aim is to select a subset of explanatory variables; as these variables are organized in blocks the method is less sensitive to multicollinearity. Moreover, multiblock redundancy analysis is likely to recover more variations in the Y dataset than GLMs because new dimensions can be added if necessary in order to explain additional variability in the data.
Multiblock modelling uses additional information available for grouping the variables into meaningful blocks and allows several variables to be explained at the same time. This avoids the necessity of setting up separate models or combining several dependent variables into one single variable. Multiblock redundancy analysis provides both standard epidemiological results, such as IRRs, and specific estimations, such as VIPs and BIPs. The structure of explanatory variables within thematic blocks can be used to estimate their respective weights (i.e. the BIP indices) in the dependent variable explanation. Multiblock redundancy analysis makes it possible to shed light on the significant explanatory variables affecting a composite dependent variable and to pinpoint the problems in the various explanatory blocks. Furthermore, multiblock redundancy analysis allows many possibilities for graphical displays and combines tools from factor analysis with tools pertaining to regression.
Research perspectives for multiblock modelling
Notwithstanding their high benefits, multiblock methods still present some limitations in comparison with GLMs and further investigations will be undertaken to handle more epidemiological data specificities. For instance, multiblock modelling does not efficiently handle the information from relevant external variables, such in hierarchical GLMs. At present, this information could be highlighted in graphical displays, but it is of paramount interest to include it in the criterion to be optimized. Furthermore, multiblock redundancy analysis could be adapted to more complex data, e.g. explanation of several blocks of health events, each being described by several variables, or the evolution of a complex health event at different periods of time. As in LISREL or PLS-PM framework, these kinds of methods can also be extended to situations where the explanatory blocks of variables are linked with each other, while integrating this information in the criterion. Further developments in multiblock analysis should lead to new breakthroughs in the statistical processing of epidemiological data. These developments together with the increase of the volume and complexity of data in biology will certainly contribute to making the use of multiblock modelling increasingly popular.
ACKNOWLEDGEMENTS
The authors thank the French Ministry of Agriculture and Fisheries and the Office de l'Elevage for funding this research project, the Official Veterinary Services and Jean Peraste for extensive data collection, and the farmers and slaughterhouses for their participation in the survey.
DECLARATION OF INTEREST
None.







