For the Keller–Segel model, it was conjectured by Childress and Percus (1984, Chemotactic collapse in two dimensions. In Lecture Notes in Biomath. Vol. 55, Springer, Berlin-Heidelberg-New York, 1984, pp. 61–66) that in a two-dimensional domain there exists a critical number C such that if the initial mass is strictly less than C, then the solution exists globally in time and if it is strictly larger than C blowup happens. For different versions of the Keller–Segel model, the conjecture has essentially been proved. The case of several chemotactic species introduces an additional question: What is the analogue for the critical mass obtained for the single species system? In this paper, we investigate for a two-species model for chemotaxis in 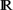 2 the conditions on the initial data, which determine blowup or global existence in time. Specifically, we find a curve in the plane of masses such that outside of it there is blowup and inside of it global existence in time is proved when the initial masses satisfy a threshold condition. Optimality of this condition is discussed through an analysis in the radial case. Finally, we show in the case of blowup for general data how it is possible to obtain a balance between entropies and prove what species should aggregates first.
2 the conditions on the initial data, which determine blowup or global existence in time. Specifically, we find a curve in the plane of masses such that outside of it there is blowup and inside of it global existence in time is proved when the initial masses satisfy a threshold condition. Optimality of this condition is discussed through an analysis in the radial case. Finally, we show in the case of blowup for general data how it is possible to obtain a balance between entropies and prove what species should aggregates first.
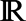 2
2