Sliding of till over bedrock: scratching, polishing, comminution and kinematic-wave theory

Abstract

The observed ratio of removal of material by (i) scratches gouged by large clasts and (ii) polishing by debris suggests that the latter is the dominant form of bedrock erosion. We examine this with a multi-stage breakdown model of glacial debris, which includes active erosion by fines. These models suggest that a mother clast can, through the action of its daughter debris, erode several times its own volume of bedrock.

Till-sliding over bedrock is likely to be a potent source of scouring. By proposing a till/bedrock sliding law, we investigate the kinematics of sliding till bodies. Ice flow naturally tends to thin and extend till cover, even in the absence of longitudinal gradients in the applied stress. Thicker till cover has an increased effective pressure at its base, a lower sliding velocity and, for larger thicknesses, a decrease in sediment flux with thickness. This implies backward-moving kinematic waves and shocks. It is suggested that this is related to the blunt upstream faces of drumlins, and that drumlinization can be a consequence of debris sliding over bedrock.

Introduction

A conservative assumption in understanding how ice sheets and glaciers erode must be that the debris which is carrying out abrasion and grinding is itself being comminuted and itself losing erosional efficacy. The resulting problem of how fresh debris is input to the glacier bed in order to continue erosion is usually resolved by assuming either (i) that debris is introduced supra- or englacially and descends to the base, (ii) that the glacier quarries rock, usually jointed and often further weakened by periglacial or other weathering, or (iii) that glaciers do not always erode significantly (Sugden and John, 1976).

The dominant expressions of ice-sheet basal activity in the shield areas of North America are intermittent cover by poorly sorted basal moraine and scratched and polished bedrock. In some areas the till cover comprises separate bodies or patches, while in other areas the cover becomes continuous, with intermittent exposure of bare rock. We shall concentrate on till patches in this paper, as single sliding bodies are more tractable to model than continuous cover. It is expected that many of the comments regarding separate patches will also apply to other areas where the till cover is more continuous.

These cratonic areas are old and flat, and so the origin of the till cover needs to be explained. Input of material to the glacier bed cannot be from supraglacial sources, which means either that the material in the till patches has been eroded directly by the ice sheet, or that, along with the large climatic fluctuations which permit the expansion and decay of large ice sheets, periglacial activity plays a crucial role in providing the debris which causes glacial erosion.

A common perception in those models which consider the action of large (≳ 1 cm) clasts is that these are the tools doing the erosional work, and that they are doing it by the action of indentors (e.g. Rabinowicz, 1965; Iverson, 1991), and so producing scratching. Empirical studies of wear (e.g. Riley, 1982) indicate that the erosional efficiency of large clasts with sharp edges is far greater than that of worn clasts and wear products, which implies that striations should be the dominant small-scale expression of glacial erosion.

Since there are, in general, relatively few striations per unit width on a typical glacial surface, it is natural to infer that it is polishing which removes the most material (Hindmarsh, 1985). One should question whether there is an essential difference between scratching and polishing, as the latter could be due to the action of many small scratches (e.g. Hambrey, 1994). While it is possible that polishing is being done by the blunted edges of clasts, it is not clear that these are smooth enough to polish bedrock. Polishing that results from grinding is typically carried out by very line silts (e.g.jeweller’s rouge). It does not appear to require very large contact stresses. In this paper we assume that large clasts erode by scratching, while polishing is carried out by debris.

Following Hindmarsh (1985), a very simple geometrical model of the erosion of a surface by scratching and polishing is presented in Figure 1. Material is removed from a surface either by a very fine-scale process which smooths the surface, or by scratching. In a time unit, a certain amount of material is removed by polishing and there are a certain number of scratching events. Examples are taken of one event per unit time and three events per unit time, and the resulting surfaces shown. Clearly, if more material is removed by scratching, the surface will be more scratched. There is also a prediction of observations of scratches of different depth, because the surface adjacent to the scratch at the time of its formation has been polished away.

Fig. 1. How the magnitude of removal by scratching and polishing affects the appearance of a glacially eroded surface.

Abrasional tools are themselves worn away by the act of eroding the bed (Röthlisberger, 1968), and the size distribution of abrading clasts and tills reflects this comminution process. Modelling studies of the abrasional process have tended to assume that only the large clasts are carrying out erosion. Those theories which assume that a tool has a limited life of efficacy (Lliboutry, 1994) suggest that the origin of the tools needed for glacial erosion presents a theoretical problem if renewal from englacial and supraglacial sources does not occur. More sophisticated models which include wear products in the abrasion process (Hindmarsh, 1985) suffer from the same problems. In the context of lithplogical variability (important in ice-sheet erosion if not in valley-glacier erosion), we should expect hard tools to be worn away less when eroding soft beds and vice versa (Sugden and John, 1976). Furthermore, large clasts which contain minerals of different hardness will break down into tools of different properties, and there is certainly a case for arguing that the very hardest constituents will survive for a long time as wear products, and effect substantial erosion.

The simple view of polishing as the result of wear by wear products would agree with the above observations. If much of the erosion of bedrock is being done by a very small size fraction which is itself a wear produci, there may be no need for substantial supplies of large mother clasts. Indeed if the action of abrasion is to increase relief, creating streamlined rock forms which can subsequently be plucked, then plucking of polished rocks may be a signal of intense abrasion which has created these streamlined forms. The advantages of having the small fraction carry a substantial part of the erosion are that it (i) considerably eases the debris production problem, as at the very least the debris is recycled once; (ii) makes multi-modal grain-size distributions rather easier to understand; and (iii) provides an intuitive explanation for the ubiquitous presence of polished surfaces. A potential problem is that wear by large clasts proceeds very much faster than wear by fine debris (Riley, 1982), and one must suppose that glacial action proceeds for long enough for erosion by fine products to be significant.

Gjessing (1965) suggested that till slurries slipping over bedrock were likely to be a potent scouring agent, with the implication that all sediment fractions were participating in the wear process. There is no particular need for till slurries to be present for fine-grained material to carry out the erosion, as clasts are frequently observed to ride on a carpet of wear products, but this paper will concentrate on till slurries.

One then needs a theory for the sliding of till patches. One such theory, presented in this paper, predicts backward-moving kinematic waves, as found in traffic (Whitham, 1974), with the implication that shocks form on the upstream side of till patches. It is suggested that this is related to the process of drumlinization of sediment bodies. This work is related to Boulton’s (1987), but concentrates on geomorphological features due to sliding of till over bedrock rather than the internal deformation of till, and emphasises the role of shock formation in drumlinization.

The aim of this paper is to bring together the observational facts of intense polishing, scratching, till patches and other shaped till features lying on bedrock and the sedimentology of tills, in particular drumlins. Many of these features seem to be explicable by a model of till-sliding over bedrock, and this deserves further investigation.

Polish and Polishing

Glacially abraded surfaces are typically described as “polished’, i.e., the reflected component of light is coherent, a situation described as specular reflection. Any surface which is rough will scatter light, leading to a diffuse component of reflection. The reflection of electromagnetic waves from rough surfaces has been considered by Berry (1973), who developed a theory applicable to small-bump height/span ratio, and found that coherent reflection requires bump elevations to be comparable with or less than the wavelength of visible light, or the bump span to be somewhat larger than the wavelength of light. Specular reflection is an asymptotic limit, and if these geometric conditions are not met, a coherent light beam of finite width will be reflected incoherently in many directions (scattered;) according to a probability distribution depending upon the statistics of the surface geometry. We shall not attempt to explain how sediment grains of size 100 nm can produce smooth surfaces of the order of the wavelength of light (1 nm).

The quality of polishes differs significantly from site to site. In Figure 2 some simple computer renditions of surfaces with different properties are given, using the Matlab visualisation routine, surfl (The Mathworks, 1992). Figure 2a and b show how the algorithm renders specular and Lambertian diffuse scattering of a flat surface, while Figure 2c shows a grooved, shiny surface, and Figure 2d a scratched surface, where the specular nature of the surface is being destroyed by the randomness of the surface in one direction. Very small or infrequent scratches yield the polished surface in Figure 2a. The perception of polishing in the field is partly subjective, but there is sufficient difference in observed surfaces (e.g. Huber, 1987, p. 41-49) to suggest that very detailed examination of polished surfaces could yield information about the material which has carried out the erosion.

Fig. 2. Illustrations of the effects of surface roughness on the specular properties of a surface, (a) is a smooth surface, (b) is a surface reflecting diffusely (Lambertian reflection), (c) is a grooved specular reflector, (d) is a rough specular surface which yields a somewhat diffuse refection.

Monolithological Breakdown Chains

Röthlisberger’s principle (Röthlisberger, 1968) states that all else being equal, we should expect equal erosion of tool and bed, with the implication that one mass unit of clast should produce two mass units of debris.

If the only effective abrading tool is a large clast, then this would predict beds to be heavily scratched. If, following our assumption that polishing is carried out by abrasional debris, we include debris as an active ingredient, then Röthlisberger’s principle can be used to predict scratch/polish ratios.

Consider a two-stage breakdown model. As above, we input one mass unit of large clasts, which comminutes and erodes the bed, producing two units of debris which is now supposed to be active. These two mass units also erode the bed by polishing, and produce four mass units of debris. One unit of the bed was scratched away by the large clasts, while two units were polished, yielding a scratch/polish ratio of one to two.

It is easy to see that under monolithological conditions, an N-stage breakdown model will yield 2 ^N as much debris as went in as large clasts, and a scratch/polish ratio of 2^1–N . Scratch/polish ratios are not systematically measured, but values of 1/4, indicating N = 3 are not unreasonable. This model has ignored comminution between clasts, which is likely to be most effective between large clasts, resulting in a reduced scratch/polish ratio.

If debris of a given size can erode bedrock such that debris is produced of the same size, it is possible that the gain of debris could exceed the loss by comminution, so that the concentration in this size range would grow until prevented by other limiting factors. For example, once the moraine cover becomes sufficiently thick, not all of the debris will be in contact with the bed, and its erosional efficacy will be diminished.

A steady distribution of grain-sizes can only occur if there is recharge of large clasts at a constant rate. This model neglects crushing within the till, which will create fines without scratching, and thus decrease the scratch/polish ratio from the theoretical prediction above. A recent discussion on crushing is by Hooke and Iverson (1995), who point out that when compared with simple crushing models, tills are over-represented in fines, which may indicate the role of scratching of bedrock in producing fines.

To summarise, we have discussed the way breakdown chains affect erosion, and suggested that where preglacial weathering has not provided a ready debris supply, the existence of breakdown chains with active debris products can significantly affect erosion, with three times the volume of plucked mother clasts being eroded from the bed by debris. The predicted scratch/polish ratio of one to two seems to be a little low. Of course, till from previous glaciations is also a debris source, but this begs the question of how an ice sheet maintains a ready supply of material to carry over to the next glacial cycle so as to be able to erode.

Kinematics of Sliding Till

We suppose that debris can move over bedrock as till patches separated by exposed bedrock. Here, we model the till patch on a deforming or failing soil with quasistatic stresses inside. The existence of such a soil guarantees positive effective pressures beneath it, and we shall discuss here those factors which affect the effective pressure.

Consider a till patch lying on a flat bedrock surface. This may be tens of centimetres to metres thick, and tens to hundreds of metres long; the dimensions are not crucial. The effective pressure is defined by p _e = p – p _w,where p = øp _s + (1 – ø)p _w is the bulk pressure of the soil, ø is the porosity of the soil, p _w is the water pressure, and p _s is the pressure in the sediment grains. Mixture theories for soils appropriate to subglacial conditions have been presented by Boulton and Hindmarsh (1987) and by Clarke (1987) who modelled deforming till as a non-linearly viscous material. We shall consider sliding of the till over bedrock.

We assume that the pressures are hydrostatic. This assumption is valid when viscous stresses are much less than gravitational stresses (in the soil) and when potential gradients are much less than hydrostatic gradients. Till seems to be inviscid enough for this assumption to be valid, and one requires quite high melt rates through impermeable clays for the potential gradient to become of the same order as the gravitational gradient.

The bulk stress p = p _i(s) + ρg(s – z) where ρ is the bulk density of the soil, g is the acceleration due to gravity, and s represents the upper surface of the till patch. The water pressure is given by p _w = p _i(s) – _e(s) +ρ _w g(s – z) where ρ_w is the density of water and p_e(s) is the effective pressure at the ice/till interface. The effective pressure is given by p _e = p _e(s) +(1 –ø)(ρ _s – ρ _w)g(s – z) and at the base of the patch by

. (1)

We let x be the horizontal coordinate, z the vertical coordinate and t the time unit. We consider plane flow, and denote the upstream and downstream ends by x = a,b. Away from the patch set, p _e = p _c, which is the clean-ice/bed interface effective pressure in hydraulic contact with the patch, not necessarily the thin-film effective pressure. For example, if the patch is in hydraulic contact with cavities it will represent the cavity pressure, or if the bed is permeable it will represent the pore-water pressure. If it is the thin-film pressure, then p _e = 0.

The horizontal pressure gradients along the upper surface of the till are

which, when combined with the definition of effective pressure, yields

and which integrates to

,

i.e., elevation causes an increase in the effective pressure. The effective pressure at the base of the till patch (i.e. at z = 0) is given by combining this expression with Equation (1) to obtain

where

. (2)

We shall assume that the till patch is sufficiently large that the viscous stresses established in the ice are small compared with the gravitational-stress (i.e. pressure) differences.

We suppose that the shear stress τ_b within the ice can be transmitted to the till patch. By analogy with postulated sediment-deformation laws (e.g. Boulton and Hindmarsh, 1987) we assume that the till slides over the bedrock with velocity u_s according to

. (3)

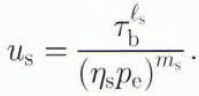
where η _s, l _s and m _s, are constants. We write it in this form to emphasise the affinity between these relationships and the Coulomb friction law, and justify the use of viscous rather than plastic models by pointing out that the individual constituents of the till patch will have different coefficients of friction, which when acting together as a bulk substance produce a viscous effect.

Our next step is to produce a kinematic-wave theory (e.g. Whitham, 1974), for which we need to know the sediment-discharge–thickness relationships. Substitution of the effective-pressure–depth relationship (Equation (2)) into the phenomenological relationship (Equation (3)) yields the following expressions for the sliding velocity and sediment discharge

Standard kinematic-wave theory (Whitham, 1974) yields the following expression for the kinematic wave velocity c:

.

The ratio γs/(γs + p_c) < 1 increases with s while the quantity m _s is expected to be greater than one―plasticity theory gives it as ∞. This expression permits kinematic waves that move both forwards and backwards, with velocities becoming more negative as the till becomes thicker. The implication of this is that shocks will form on the stoss side of the patches which will have blunt upstream ends, as do drumlins, for example. Figure 3 illustrates the dependence of sediment discharge, sliding velocity and kinematic-wave velocity on till thickness.

Fig. 3. Plots of till discharge, kinematic-wave velocity, sliding velocity and erosion potential against thickness. The applied shear stress τ, far-field effective pressure p_c, and vertical effective-pressure gradient γ are all one unit. The position of the maximum in the till flux is related to the far-field effective pressure.

The thickness-evolution equation is , where e is the rate of erosion of bedrock, and this can be written:

where (·) represents the other parameters which might have spatial dependence, for example τ_b and p _c. We require that the rate of erosion be proportional to the product of sliding velocity and normal stress:

where a is a phenomenological constant. This equation indicates an erosion rate decreasing with thickness for m _s > 1 (Fig. 3).

If we now explicitly consider the spatial variation of τ_b and p _e, we obtain

and the rate of change of thickness following the kinematic wave is given by

.

We shall present some solutions in dimensionless units. A scaling analysis not reported here shows that the depth scale is the depth over which the effective pressure increases by an amount comparable with the basal shear stress. The argument is essentially the same as that presented by Hart and others (1990), who suggested that the depth scale is around 10 m. The horizontal length scale is fixed by the rheological properties of the material and the applied shear stress through the sliding relationship. The aspect ratio of the model does not affect the (scaled) solutions. Thus, in interpreting the solutions, one should appreciate that one vertical unit represents around 10 m, while the horizontal unit is arbitrary, being fixed by the rheological assumptions, but is at least several tens of metres.

The ordinary differential equations are easily solved by numerical integration, although the presence of shocks creates some algorithmic complexity. We show solutions for three cases. In all of these the parameters τ _b, η _s, γ and p _c were set to unity, and m _s = −2.5. The first case has no erosion, and the basal shear stress and effective pressure fields are constant in space. It is initialised with two patches of parabolic form, with the downstream patch the larger of the two (Fig. 4). As they are moved by the glacier, the patches become wedges with the blunt face, a shock, on the upstream side. The smaller patch moves faster, catching up with the larger patch, and the two then coalesce into one patch. This patch moves as a wedge with the blunt face on the upstream side and gradually lengthens and thins.

Fig. 4. The coalescence of two (2D) patches; one horizontal axis is the time axis. Lines parallel to the space axis are isochrones; the dashed lines are characteristics, while heavier lines indicate shocks.

Where the effective pressure is increasing in the direction of flow, the patch lengthens more slowly, and indeed seems to reach a steady, migrating form. Figure 5 shows an example where . The thickness of this patch is less than the initial thickness. When one permits erosion to occur with an attrition constant a = 0.01, thickening, of course, takes place (Fig. 6) and the patch grows larger, with a convex upper surface (more realistic?) as compared with the flat or concave surfaces seen in the other cases.

Fig. 5. The motion of a till patch in the direction of increasing effective pressure.

Fig. 6. A moving till patch eroding its bed.

The success of the theory is the extent to which it predicts drumlinization, i.e. the generation of the blunt upstream faces of sediment bodies. Its major problem is in predicting the order 10 m or greater thickness of drumlins, since thickening can only be accomplished by erosion. Larger till bodies will move more slowly and entrain thinner, faster moving patches. The fact that the upstream edge is rather blunter than observed drumlins is not a problem, as one can invoke a large number of dynamical processes which will smooth this off. It is also worth noting that at small thicknesses the action of deformation within the till can be shown to produce shocks on the downstream face, which may explain why some drumlins are aligned in the opposite direction to normal.

Barkhan forms are qualitatively explained by this model. Consider a hemi-ellipsoid whose long axis is perpendicular to the flow. The lower flanks will move faster by the sliding relationship, creating a crescentic shape. More generally, any form parallel to the flow will find its thinner parts moved faster, leaving the higher parts behind. Clearly this work is closely related to Boulton’s (1987) theory of drumlin formation, but its focus is on till sliding over bedrock.

There is much to criticise in the simplifications used in the formulation of the model presented here, but the simple assumption that discharge can decrease with thickness creates most of the phenomenology and is likely to be robust to changes to the model that incorporate more realistic descriptions of the physics. Given that some solutions suggest stable forms migrating across the landscape, an intriguing possibility is that the first-order evolution could, through the inclusion of dispersive terms, become similar in form to the Korteweg–deVries equation (e.g. Drazin, 1983) and thus admit soliton solutions. In such a case, forms would persist, neither thickening nor thinning. Moreover, rather than coalescing, drumlins would pass through each other, which might be one explanation of the superimposed drumlins observed by Rose and Letzer (1977).

Summary and Conclusions

We have constructed the outlines of a model of ice-sheet erosion of hard beds. The main ideas are:

• (i) the existence of polish indicates that most erosion is carried out by a fine debris fraction―silts and maybe clays.

• (ii) This debris fraction is produced by subglacial action, and means that the production of debris to carry out erosion is not such an acute problem as has previously been suggested.

• (iii) Debris moves as sliding till which scours the bedrock.

• (iv) A simple but robust model of till-sliding produces qualitative predictions of the genesis, but not the survival, of blunter upstream faces and barkhan forms of till bodies. In particular, thick bodies produced by other sedimentary processes, e.g. outwash fans, become drumlinized by being slid over the bed.