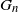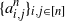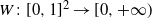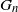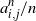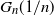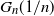The k-core in percolated dense graph sequences

Abstract

We determine the order of the k-core in a large class of dense graph sequences. Let $G_n$ be a sequence of undirected, n-vertex graphs with edge weights $\{a^n_{i,j}\}_{i,j \in [n]}$ that converges to a graphon $W\colon[0,1]^2 \to [0,+\infty)$ in the cut metric. Keeping an edge (i,j) of $G_n$ with probability ${a^n_{i,j}}/{n}$ independently, we obtain a sequence of random graphs $G_n({1}/{n})$. Using a branching process and the theory of dense graph limits, under mild assumptions we obtain the order of the k-core of random graphs $G_n({1}/{n})$. Our result can also be used to obtain the threshold of appearance of a k-core of order n.

1. Introduction

For an integer $k\geq 2$ , the k-core of a graph G is the largest induced subgraph of G with minimum degree at least k. It was first introduced in [5] to find large k-connected subgraphs, and since then several studies have been devoted to investigating the existence and the order of the k-core. Apart from theoretical interest, the k-core has been applied to the study of social networks [4, 19], graph visualizing [1, 13], and biology [32]. See also [24] for an extensive discussion on its applications. The seminal paper [30] determined the threshold for the appearance of a non-empty k-core in binomial random graphs and uniform random graphs. The order of the k-core has been studied in different random graph ensembles such as binomial random graphs [28], uniformly chosen random graphs and hypergraphs with specified degree sequence [17, 18, 21, 22, 29], the Poisson cloning model [23], and the pairing-allocation model [12]. While almost all the previous work focused on the k-core of homogeneous random graphs, [31] determined the asymptotic order of the k-core for a large class of inhomogeneous random graphs introduced in [7].

In this article we study the asymptotic order of the k-core in random subgraphs of convergent dense graph sequences. Let $G_n$ be a sequence of undirected weighted graphs on n vertices with edge weights $\{a^n_{i,j}\}$ that converges to a graphon W in the cut metric (see Section 2 for the definition of the cut metric). For some $c>0$ , we keep an edge (i,j) of $G_n$ with probability ${ca^n_{i,j}}/{n}$ independently, and denote the resulting random graph by $G_n({c}/{n})$ . For any graphon W, we can associate it with a branching process $X^W$ , i.e. the number of children of a particle with type x has a Poisson distribution with parameter $\int W(x,y)\,\mathrm{d} y$ (see Section 2 for a precise definition). As usual, if $A_n$ is a sequence of random variables, we write $A_n=o_\mathrm{p}(n)$ if $A_n/n \to 0$ in probability. Under some mild conditions, we show that

(1.1) \begin{align} \text{order of} \, \textit{k} \text{-core of } G_n({c}/{n}) = n\mathbb{P}_{X^{cW}}(\mathcal{A}) + o_\mathrm{p}(n),\end{align}

where $\mathcal{A}$ is the event that the initial particle has at least k children, each of which has at least $k-1$ children, each of which has at least $k-1$ children, and so on, and $ \mathbb{P}_{X^W}(\mathcal{A})$ represents the probability of the event $\mathcal{A}$ occurring for the branching process $X^{cW}$ .

Our contribution is two-fold. First, thanks to [27], every dense graph sequence has a convergent subsequence in the cut metric, and therefore our result applies to a large class of dense graph sequences. An important example is quasi-random graphs (see, e.g., [16]). Roughly, they are dense graph sequences that converge to a constant (non-zero) limit, such as Paley graphs (see Remark 2.3). It is worth pointing out that while the construction of various quasi-random graphs involves very different techniques (see [25]), this article first determines the order of the k-core in its random subgraphs up to the first-order term in a unified way. Actually, besides quasi-random graphs, there are plenty of examples of dense random graph models that converge to bounded graphons (see [2, 3, 14, 15]), where our result can be applied to get the size of the k-core. Second, as a by-product of our proof of the main result, for any sequence of kernels $W_n$ satisfying some mild assumptions that converges to W we have

\begin{align*}\mathbb{P}_{X^{W_n}}(\mathcal{A}) \rightarrow \mathbb{P}_{X^{W}}(\mathcal{A}),\end{align*}

a new continuity result concerning branching processes, which we believe is of independent interest. Even though the theory of graph limits has received enormous attention in the last two decades, the only similar result we can find is [8, Theorem 1.9], which concerns with the survival probability of a branching process.

Let us now point out the differences between [31] and the main ideas of our proof. First, while [31] obtains the size of the k-core of random graphs sampled from a kernel W, our result applies to the percolation of an arbitrary sequence $G_n$ that converges to W in the cut metric. Noticeably, our result, together with [8, Lemma 1.6], recovers the main result in [31] for bounded graphons, whereas the result in [31] is not applicable to quasi-random graphs. In other words, our result additionally shows that the size of the k-core in percolated random graphs is stable with respect to the underlying kernel W in the cut metric. Second, the proof of the upper bound in (1.1) is done by upper-bounding the order of the k-core in terms of the probability of the event $\mathcal{A}$ . In the case of random graphs generated by W [31] this probability can be directly expressed in terms of W. For us, the approximation of the probability of the event $\mathcal{A}$ is subtle: we first approximate the probability of $\mathcal{A}$ in terms of homomorphism densities of appropriate subgraphs, and then estimate this probability using the fact that homomorphism densities are continuous in the cut metric; see, e.g., [6, 27]. Third, the proof of the lower bound in (1.1) is more delicate. As a first step, we approximate W by a sequence of finitary kernels $F_m$ as in [7]. Then, we show that, for each fixed m, the branching process $X^{G_n}$ associated with $G_n$ contains $X^{(1-\varepsilon_m)F_m}$ as a subset for some $\varepsilon_m$ with $0<\varepsilon_m<{1}/{m}$ when n is large enough. To conclude the lower bound, we prove a continuity property which is non-trivial and relies on the properties of the cut metric, and then invoke a result (minor variant) from [31].

The rest of the paper is organized as follows. In Section 2, we present our main results with some discussions. In Sections 3 and 4, we prove the upper bound and lower bound respectively of the order of the k-core.

2. Main results and discussions

We now recall a few definitions in order to state our results. Denote [0,1] by I, and its Borel sigma-algebra by $\mathcal{B}(I)$ . For any symmetric measurable function $W\colon I \times I \to \mathbb{R}$ , we define its cut norm via

\begin{align*}\|W\|_\square \,:\!=\, \sup_{S,T \in \mathcal{B}(I)} \bigg|\int_{S \times T} W(u,v)\,\mathrm{d} u\,\mathrm{d} v\bigg|.\end{align*}

Such a symmetric measurable function W is said to be a graphon if it take values in $[0,\infty)$ , and the cut metric between two graphons $W_1$ and $W_2$ is defined by $d_\square(W_1,W_2) \,:\!=\, \|W_1-W_2\|_\square$ . An undirected finite graph $G_n$ with non-negative adjacency matrix $(a^n_{i,j})_{i,j=1}^n$ can be associated with a graphon in a natural way so that the cut metric gives rise to a proper distance between two finite graphs,

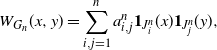(2.1) \begin{equation} W_{G_n}(x,y) = \sum_{i,j=1}^n a^n_{i,j} {\mathbf{1}}_{J_i^n}(x){\mathbf{1}}_{J_j^n}(y),\end{equation}

where $J_1^n = [0,{1}/{n}]$ and, for $i= 2,3,\ldots,n$ , $J_i^n = (({i-1})/{n},{i}/{n}]$ . We refer readers to [26, Chapter 8] for detailed discussions of the cut metric and (2.1).

Let $G_n$ be a sequence of simple graphs on n vertices with edge weights $\{a^n_{i,j}\}$ that converges to a graphon W with respect to the cut metric. For some $c>0$ , we keep an edge (i,j) of $G_n$ with probability $ {ca^n_{i,j}}/{n}$ independently, and denote the resulting random graph by $G_n({c}/{n})$ . Here and throughout the paper we assume that the edge weights $a^n_{i,j}$ are uniformly bounded above by $\bar{a}>0$ , and therefore for sufficiently large n we will have ${ca^n_{i,j}}/{n} \leq 1$ . Since retaining every edge independently is nothing but the bond-percolation on the graph, we call $G_n({c}/{n})$ a percolated graph sequence (bond-percolation on arbitrary dense graph sequences was first studied in [6]). Note that if we percolate on a dense graph sequence, where the number of edges is of order $n^2$ , the resulting graph becomes sparse, i.e. the number of edges is linear in n. Our aim is to study the order of the k-core of the random graph sequence $G_n({c}/{n})$ .

We will heavily use the branching process $X^W$ associated with the graphon W. The process starts with a single particle with type $x_0$ , which is chosen uniformly from [0,1]. Conditionally on generation t, each member in generation t has children in the next generation, independently of each other and everything else. The number of children with types in a set $A \subset [0,1]$ is Poisson with parameter $\int_{A} W(x,y) \,\mathrm{d} y$ , and these numbers are independent for disjoint sets.

Let $\mathcal{A}_d$ be the event in $X^W$ that the initial particle has at least k children, each of which has at least $k-1$ children, each of which has at least $k-1$ children, and so on until the dth generation. Define $\mathcal{A}= \cap_{d=1}^{\infty} \mathcal{A}_d$ . Let $C_k(G)$ denote the order of the k-core of a graph G. We are now ready to discuss our main result, which provides the asymptotic order of the k-core in percolated dense graph sequences. As usual, if $A_n$ is a sequence of random variables, we write $A_n=o_\mathrm{p}(f(n))$ if $A_n/f(n) \to 0$ in probability; if $A_n$ is a sequence of real numbers, we write $A_n=o(f(n))$ if $A_n/f(n) \to 0$ . First, we make the following assumption.

Assumption 2.1. The map $\lambda\to\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ is continuous from below at $\lambda = c$ .

Theorem 2.1. Let $G_n$ be a sequence of graphs with non-negative edge weights which are bounded above by a constant $\bar{a}>0$ . Suppose that $G_n$ converges to a graphon W as $n\rightarrow\infty$ , and that Assumption 2.1 holds. Then

(2.2) \begin{equation} C_k(G_n({c}/{n})) = n \mathbb{P}_{X^{cW}}(\mathcal{A}) + o_\mathrm{p}(n). \end{equation}

It suffices to prove the case $c=1$ in Theorem 2.1. To see this, let $G_n$ be a graph with edge weights $\{a^n_{i,j}\}$ and consider another graph $G^{\prime}_n$ with edge weights $\{ca^n_{i,j} \}$ . Therefore, the random subgraphs $G_n({c}/{n})$ and $G^{\prime}_n({1}/{n})$ are equal in distribution. Finally, by our assumption $G_n$ converges to W and thus $G^{\prime}_n$ converges to cW. The result (2.2) then follows from the result with $c=1$ .

Our proof of (2.2) is divided into two parts, which will be given in the next two sections. We should remark that for the proof of the upper bound, we only need the assumption that the edge weights of $G_n$ are uniformly bounded above by $\bar{a}$ and that $G_n \to W$ in the cut metric. The uniform boundedness of $G_n$ is used in Sections 3.1 and 3.2. Roughly speaking, the probability of event $\mathcal{A}$ can be written as an infinite sum of homomorphism densities. It is known that homomorphism densities are continuous in the cut metric. Thus, to show the inequality $\limsup \mathbb{P}_{X^{W_{G_n}}}(\mathcal{A}) \leq \mathbb{P}_{X^{W}}(\mathcal{A})$ , we need a dominating term provided by $\bar{a}$ . It is possible to avoid this assumption if we get the quantitative convergence rate of the homomorphism densities.

Assumption 2.1 is used only in the proof of the lower bound in Section 4, to approximate W by finitary graphons from below.

Remark 2.1. In Theorem 2.1, note that $\mathbb{P}_{X^{cW}}(\mathcal{A})$ could be zero, in which case we will only be able to say that there is no ‘giant’ k-core (as usual, by ‘giant’ we mean ‘of order linear in n’). From Theorem 2.1 we can also obtain the emergence threshold for the giant k-core from the function $c \rightarrow \mathbb{P}_{X^{cW}}(\mathcal{A})$ . More precisely, if there is a point $c_0>0$ such that for $0\leq c< c_0$ , $\mathbb{P}_{X^{cW}}(\mathcal{A})=0$ and for $c>c_0$ , $\mathbb{P}_{X^{cW}}(\mathcal{A})>0$ , then $c_0$ will be the threshold for the appearance of a giant k-core.

Remark 2.2. It is not difficult to show that the function $\lambda\to\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ is continuous from above (see [31, Section 3.2]), therefore under Assumption 2.1 we have continuity of $\lambda\to\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ at $\lambda=c$ . We now discuss why it is not possible to get rid of Assumption 2.1 in Theorem 2.1. First, let $c_k$ be the threshold of the appearance of a k-core in the binomial random graph on n vertices with edge probability ${c}/{n}$ . Then, from [22, Theorem 1.3(ii)], the assertion in Theorem 2.1 does not hold at the threshold (discontinuity point), which tells us that Assumption 2.1 is optimal. More precisely, at the threshold the k-core is empty with probability bounded away from 0 and 1 for large n.

Secondly, there could be more than one discontinuity point, and they could appear in different (non-trivial) ways. Let us now explain roughly how such discontinuities could appear; we refer the interested reader to the end of [31, Section 3.1] for the details. Consider the graphon

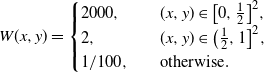\begin{equation*} W(x,y)= \begin{cases} 2000, & (x,y) \in \big[0,\frac12\big]^2, \\ 2, & (x,y) \in \big(\frac12,1\big]^2, \\ {1}/{100}, \quad & \text{otherwise}. \end{cases} \end{equation*}

It is not difficult to show that the 3-core first appears in the subgraph induced by the vertices that correspond to the bottom-left part, $\big[0,\frac12\big]^2$ , of the graphon, and this emerges near ${c_3}/{1000}$ , where $c=c_3$ is the threshold of appearance of the 3-core in the binomial random graph on n vertices with edge probability ${c}/{n}$ . It could also be shown that $\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ has another discontinuity near $\lambda=c_3$ , i.e. when the subgraph induced by the vertices that correspond to the top-right part, $\big(\frac12,1\big]^2$ , of the graphon will have a 3-core. There is another, more straightforward, way in which a discontinuity could appear in $\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ . Consider the graphon

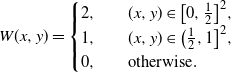\begin{equation*} W(x,y)= \begin{cases} 2, \quad & (x,y) \in \big[0,\frac12\big]^2, \\ 1, & (x,y) \in \big(\frac12,1\big]^2, \\ 0, & \text{otherwise}. \end{cases} \end{equation*}

It is easy to see that the emergence threshold of the k-core in the subgraph induced by the vertices that correspond to the bottom-left, $\big[0,\frac12\big]^2$ , part of the graphon and the subgraph induced by the vertices that correspond to the top-right part, $\big(\frac12,1\big]^2$ , of the graphon will be different.

Remark 2.3. (Paley graphs) Let us give a concrete example where Theorem 2.1 is applicable. Let q be a prime number of the form $4z+1$ with $z\in\mathbb{N}_+$ , $\mathrm{F}_q=\{0,\ldots,q-1\}$ be the finite field, and $\mathrm{F}_q^*=\mathrm{F}_q\setminus\{0\}$ . Consider the sequence of Paley graphs $G_q$ , where the vertex set is $V=\mathrm{F}_q$ and the edge set is given by $E=\{(a,b) \in V \times V\colon a-b \in\mathrm{F}_q^*\times\mathrm{F}_q^*\}$ . Due to [20, Example 10.10], $G_q$ converges to the constant graphon $\frac12$ in the cut metric as $q \to \infty$ . We can therefore apply Theorem 2.1 and conclude that the size of the k-core in $G_q(2c/q)$ is asymptotically the same as the size of the k-core in the binomial random graph with q vertices and parameter $c/q$ (for $c>0$ ), except for the threshold of appearance of the k-core. Let us emphasize that the Paley graph is an example of a quasi-random graph, and our result is applicable to any quasi-random graph.

As a by-product of the proof of Theorem 2.1, we also obtain a result regarding branching processes that might be of independent interest.

Proposition 2.1. Let $W_n$ be a sequence of graphons such that $d_\square(W_n,W) \rightarrow 0$ . Also, suppose $\lambda \to \mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ is continuous from below at $\lambda =1$ . Then $\mathbb{P}_{X^{W_n}}(\mathcal{A}) \rightarrow \mathbb{P}_{X^{W}}(\mathcal{A})$ as $n\rightarrow\infty$ .

Proof. This is proved in Propositions 3.5 and 4.1.

Note that Proposition 2.1 has the following important consequence. The function $\lambda \to \mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ is non-decreasing, and therefore it can have at most countably many discontinuity points. Hence, for almost every positive c, the next corollary provides a way to approximate the order of the k-core using only $G_n$ .

Corollary 2.1. Let $G_n$ be a sequence of graphs with non-negative edge weights which are bounded above by a constant $\bar{a}>0$ . Suppose that $G_n$ converges to a graphon W as $n\rightarrow\infty$ , where $\lambda\to\mathbb{P}_{X^{\lambda W}}(\mathcal{A})$ is continuous at $\lambda =c$ . Then

\begin{equation*} C_k(G_n({c}/{n})) = n \mathbb{P}_{X^{cW_{G_n}}}(\mathcal{A}) + o_\mathrm{p}(n). \end{equation*}

Proof of Corollary 2.1. The proof is immediate using Theorem 2.1 and Proposition 2.1.

3. Proof of the upper bound in Theorem 2.1

We will first prove the upper bound, i.e. $C_k(G_n({1}/{n})) \leq n \mathbb{P}_{X^W}(\mathcal{A}) + o_\mathrm{p}(n)$ . The idea is as follows: if a vertex v of a graph is in the k-core, then for any $d>0$ either v has property $\mathcal{A}_d$ or v is contained in a cycle of length smaller than 2d. Since the probability of occurrence of short cycles is small for large enough n, the probability that v is in the k-core is bounded above by the probability of having property $\mathcal{A}_d$ , ignoring an $o_\mathrm{p}(1)$ term. Therefore, to prove the upper bound, we explicitly calculate the probability of event $\mathcal{A}_d$ using homomorphism density, and a tightness argument. Finally, by letting $d \to \infty$ , we obtain $C_k(G_n({1}/{n})) \leq n \mathbb{P}_{X^W}(\mathcal{A}) + o_\mathrm{p}(n)$ . Note that we do not need the continuity assumption to show the upper bound.

Let us construct a branching process $^{*}X^{n}$ associated with the random graph $G_n({1}/{n})$ . $^*X^n$ has n-types of children, $1,2,\ldots,n$ . It starts with a single particle whose type is chosen uniformly from $1, 2,\ldots, n$ . Conditioning on generation t, each member of generation t has children in the next generation independently of each other, and of everything else. For any particle of type i, its number of children of type j is distributed as Bernoulli $(a^n_{i,j}/n)$ .

With some $\rho_n \geq {1}/{n}$ to be determined, we will also use another branching process where, for any particle of type i, its number of children of type j is distributed as Poisson $(a^n_{i,j}\rho_n)$ . This is actually the branching process associated with the graphon $n\rho_n W_{G_n}$ , and we denote it by $X^{n,\rho_n}$ . By taking $\rho_n={1}/({n-\bar{a}})$ , the Poisson branching process $X^{n, \rho_n}$ stochastically dominates, in the first order, $^* X^n$ for $n>3\bar{a}$ . To see this, it is sufficient to show the following inequality for any $i,j \in [n]$ :

\begin{align*}\mathbb{P}\big(\text{Poisson}\big(a_{i,j}^n\rho_n\big) > t\big) \geq\mathbb{P}\big(\text{Bernoulli}\big({a_{i,j}^n}/{n}\big) > t\big) \quad \text{for all $t \in \mathbb{Z}$.}\end{align*}

It is trivial for $t\geq 1$ and $t<0$ . We need to check only for $t=0$ . It can be easily verified that the above inequality is equivalent to

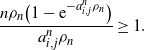\begin{align*}\frac{n\rho_n\big(1-\mathrm{e}^{-a_{i,j}^n\rho_n}\big)}{a_{i,j}^n\rho_n} \geq 1.\end{align*}

For $n > 3 \bar{a}$ , we have $a_{i,j}^n \rho_n = {a_{i,j}^n}/({n-\bar{a}}) < \frac12$ , and hence, according to the Taylor expansion of $\mathrm{e}^{-a_{i,j}^n \rho_n}$ ,

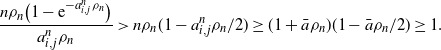\begin{equation*} \frac{n\rho_n\big(1-\mathrm{e}^{-a_{i,j}^n\rho_n}\big)}{a_{i,j}^n\rho_n} > n\rho_n(1-a_{i,j}^n\rho_n/2) \geq (1+\bar{a}\rho_n)(1-\bar{a}\rho_n/2) \geq 1.\end{equation*}

Note that we can write

\begin{align*}C_k(G_n({1}/{n})) = \sum_{v\in[n]}{\mathbf{1}}\{v\in\text{\textit{k}-core of }G_n({1}/{n})\}.\end{align*}

If a vertex v is in the k-core, then one of the following two things must be true:

1. (I) v is in a cycle within the d-neighborhood of v (this implies v is in a cycle of length at most 2d);

2. (II) starting from v there is a tree such that v has k neighbors, each of these k neighbors has at least $k-1$ neighbors, and this happens up to generation d. In this case we say vertex v has property $\mathcal{A}_d$ .

Therefore,

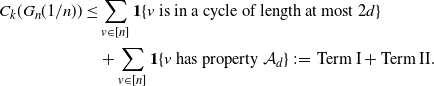(3.1) \begin{align} C_k(G_n({1}/{n})) & \leq \sum_{v\in[n]}{\mathbf{1}}\{v\text{ is in a cycle of length at most } 2d\} \notag \\ & \quad + \sum_{v\in[n]}{\mathbf{1}}\{v\text{ has property } \mathcal{A}_d\} \,:\!=\, \text{Term I}+\text{Term II}.\end{align}

Let $V_n$ be a uniformly random variable on $\{1,2,\ldots,n\}$ , independent of everything else. Then, according to the construction of $G_n({1}/{n})$ and the fact that $X^{n,\rho_n}$ stochastically dominates $^{*}X^n$ , we obtain

(3.2) \begin{align} \mathbb{E}(\text{Term II}) & \leq n\mathbb{P}(^{*}X^{n}\text{ with root }V_n\text{ has property }\mathcal{A}_d) \notag \\ & \leq n\mathbb{P}(X^{n,\rho_n}\text{ with root }V_n\text{ has property }\mathcal{A}_d).\end{align}

Before presenting our first proposition, we state an auxiliary result, the van den Berg–Kesten–Reimer (BKR) inequality (see, e.g., [11]). Consider a product space $\Omega$ of finite sets $\Omega_1, \dots, \Omega_k$ , $\Omega = \Omega_1 \times \cdots \times \Omega_k$ . Let $\mathcal{F}= 2^{\Omega}$ , and $\mu$ be a product of k probability measures $\mu_1, \dots, \mu_k$ . For any configuration $\omega=(\omega_1, \dots, \omega_k) \in \Omega$ , and any subset S of $[k]\,:\!=\,\{1,\dots,k\}$ , we define the cylinder $[\omega]_S$ by $[\omega]_S \,:\!=\, \{\hat{\omega}\colon\hat{\omega}_i = \omega_i$ for all $i \in S\}$ . For any two subsets $A, B \subset \Omega$ , define $A \circ B\,:\!=\, \{\omega\colon\text{there exists some } S=S(\omega) \subset [k]\text{ such that } [\omega]_S \subset A, \, [\omega]_{S^\mathrm{c}} \subset B\}$ .

Lemma 3.1. For any product space $\Omega$ of finite sets, product probability measure $\mu$ on $\Omega$ , and $A, B \subset \Omega$ , we have the inequality $\mu(A \circ B) \leq \mu(A) \mu(B)$ .

In this paper, to apply the BKR inequality we always take $\Omega^n_{i,j}=\{0,1\}$ , $i \not= j \in \{1, \dots, n\}$ , and $\Omega = \prod_{i \not= j \in [n]} \Omega^n_{i,j}$ . Then $\omega^n_{i,j}=1$ means that nodes i and j are linked in the random graph $G_n({1}/{n})$ . According to our construction, we also have $\mu_i(\{1\})= a^n_{i,j}/n$ .

Proposition 3.1. Let $G_n$ be a sequence of graphs with non-negative edge weights which are bounded above by a constant $\bar{a}>0$ . Then, for any fixed d,

\begin{align*}C_k(G_n({1}/{n})) \leq n\mathbb{P}(X^{n,\rho_n}\text{ with root }V_n\text{ has property } \mathcal{A}_d) + o_\mathrm{p}(n).\end{align*}

Proof. According to (3.1) and (3.2), it suffices to show that $\text{Term II} = \mathbb{E}(\text{Term II}) + o_\mathrm{p}(n)$ and $\text{Term I}=o_\mathrm{p}(n)$ . In the first two steps, we show the concentration of Term II and its variance, and in the last step we prove that Term I is small.

Step 1. For any two independently and uniformly chosen vertices U and V of $G_n({1}/{n})$ ,

\begin{align*} \mathbb{P}(d(U,V)\leq 2d) = \frac{1}{n^2}\sum_{u,v\in[n]}\mathbb{P}(d(u,v)\leq 2d) = o(1), \end{align*}

where $d(\cdot,\cdot)$ is the graph distance. To see this, note that $d(U,V)\leq 2d$ implies there is a path from U to V of length at most 2d. Thus,

\begin{align*} \mathbb{P}(d(U,V)\leq 2d) \leq \sum_{i=1}^{2d}\mathbb{P}(\#\{\text{paths of length }i\text{ from }U\text{ to } V\} \geq 1). \end{align*}

Using Markov’s inequality we get

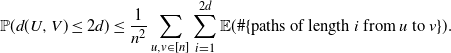\begin{align*} \mathbb{P}(d(U,V)\leq 2d) \leq \frac{1}{n^2}\sum_{u,v \in [n]}\sum_{i=1}^{2d} \mathbb{E}(\#\{\text{paths of length }i\text{ from }u\text{ to } v\}). \end{align*}

We can get a crude upper bound as

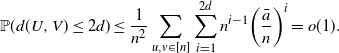\begin{align*} \mathbb{P}(d(U,V)\leq 2d) \leq \frac{1}{n^2}\sum_{u,v \in [n]}\sum_{i=1}^{2d} n^{i-1}\bigg(\frac{\bar{a}}{n}\bigg)^i = o(1). \end{align*}

Step 2. Let $G^d_n[v]$ be the subgraph of $G_n({1}/{n})$ induced by the vertices within distance d of $v\in[n]$ , and define $B_{v}=\{\text{root} \, \textit{v} \text{has property }\mathcal{A}_d \text{ in} G^d_n[v]\}$ . It can be easily verified that

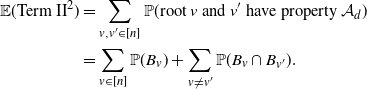(3.3) \begin{align} \mathbb{E}({\text{Term II}}^2) & = \sum_{v,v'\in[n]}\mathbb{P}(\text{root }v\text{ and }v'\text{ have property } \mathcal{A}_d) \notag \\ & = \sum_{ v \in [n]} \mathbb{P}(B_v) + \sum_{ v \not = v'} \mathbb{P}(B_v \cap B_{v^{\prime}}). \end{align}

For two different vertices v and v’, we break the probability into two parts:

\begin{equation*} \mathbb{P}(B_v \cap B_{v^{\prime}}) = \mathbb{P}(B_v \cap B_{v^{\prime}}, d(v,v') \leq 2d) + \mathbb{P}(B_v \cap B_{v^{\prime}}, d(v,v')> 2d ). \end{equation*}

For the second term, it can be easily seen that

\begin{align*}\{ d(v,v') > 2d\} \cap B_{v} \cap B_{v^{\prime}} \subset \{ d(v,v') > 2d\} \cap B_v \circ B_{v^{\prime}}.\end{align*}

Therefore,

\begin{align*} \mathbb{P}(B_v \cap B_{v^{\prime}}) & = \mathbb{P}( d(v,v')\leq 2d) + \mathbb{P}(B_{v} \circ B_{v^{\prime}} , d(v,v') > 2d) \\ & \leq \mathbb{P}(d(v,v') \leq 2d) + \mathbb{P}(B_{v} \circ B_{v^{\prime}}). \end{align*}

According to Lemma 3.1, we get $\mathbb{P}(B_{v} \cap B_{v^{\prime}}) \leq \mathbb{P}(d(v,v')\leq2d) + \mathbb{P}(B_{v})\mathbb{P}(B_{v^{\prime}})$ . Combining this with (3.3), we get

\begin{equation*} \mathbb{E}\big({\text{Term II}}^2\big) \leq n^2\mathbb{P}(d(U,V)\leq2d) + (\mathbb{E}(\text{Term II}))^2 + \sum_{v\in[n]}\big(\mathbb{P}(B_v)-\mathbb{P}(B_v)^2\big). \end{equation*}

Therefore, using Step 1, we get $\mathbb{V}({\text{Term II}}) = o(n^2)$ . Using Chebyshev’s inequality we conclude that $\text{Term II}= \mathbb{E}(\text{Term II})+o_\mathrm{p}(n)$ .

Step 3. We write $C_{v} \,:\!=\, \{v\text{ is in a cycle of length at most }2d\}$ . The first moment of Term I is given by

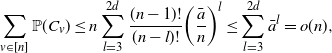(3.4) \begin{equation} \sum_{v\in[n]}\mathbb{P}(C_v) \leq n\sum_{l=3}^{2d}\frac{(n-1)!}{(n-l)!} \bigg(\frac{\bar{a}}{n}\bigg)^{l} \leq \sum_{l=3}^{2d} \bar{a}^{l} =o(n), \end{equation}

where ${(n-1)!}/{(n-l)!}$ is the number of all possible cycles of length l that contain v, and $({(n-1)!}/{(n-l)!})({\bar{a}}/{n})^{l}$ is an upper bound of the probability that v is in a cycle of length l. Therefore, by Markov’s inequality, $\text{Term I}=o_\mathrm{p}(n)$ .

3.1. Recursive formula

Let us first fix some notation. For any graphon W, we denote the initial particle of its associated branching process $X^W$ by $X^W_0$ , the type of $X^W_0$ by $T(W)_0$ , and the first generation by $X^W_{\{1\}},\dots,X^W_{\{N(W)_0\}}$ , where $N(W)_0$ is the number of children of $X^W_0$ . For $d\geq 2$ , we denote each element in the dth generation by $X^W_{\{i_1|i_2|\cdots|i_d\}}$ if it is the $i_d$ th child of $X^W_{\{i_1|i_2|\cdots|i_{d-1}\}}$ . Denote the number of children of $X^W_{\{i_1|i_2|\cdots|i_d\}}$ by $N(W)_{\{i_1|i_2|\cdots|i_d\}}$ , and the type of $X^W_{\{i_1|i_2|\cdots|i_d\}}$ by $T(W)_{\{i_1|i_2|\cdots|i_d\}}$ . Let ${\mathbf{N}}(W)^d$ denote the tree formed by the first d generations of $X^W$ .

Let ${\mathbf{K}}$ be a tree and $\mathrm{h}({\mathbf{K}})$ the height of the tree ${\mathbf{K}}$ . We define $g(x,{\mathbf{K}})\,:\!=\,\mathbb{P}({\mathbf{N}}(W)^{\mathrm{h}({\mathbf{K}})}={\mathbf{K}}\mid T(W)_0=x)$ . It is clear that $\mathbb{P}({\mathbf{N}}(W)^{\mathrm{h}({\mathbf{K}})}={\mathbf{K}})=\int g(x,{\mathbf{K}})\,\mathrm{d} x$ .

Proposition 3.2.

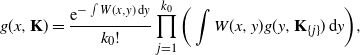(3.5) \begin{equation} g(x,{\mathbf{K}}) = \frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k_0!} \prod_{j=1}^{k_0}\bigg(\int W(x,y)g(y,{\mathbf{K}}_{\{j\}})\,\mathrm{d} y\bigg), \end{equation}

where $k_0$ is the number of the first generation in ${\mathbf{K}}$ , and ${\mathbf{K}}_{\{j\}}$ is the subtree of ${\mathbf{K}}$ whose root is the jth member of the elements of the first generation of ${\mathbf{K}}$ .

Proof. When $\mathrm{h}({\mathbf{K}})=1$ , it can be easily seen that

\begin{align*}g(x,{\mathbf{K}}) = \frac{1}{k_0!}\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^{k_0}.\end{align*}

For $\mathrm{h}({\mathbf{K}}) \geq 2$ , we get

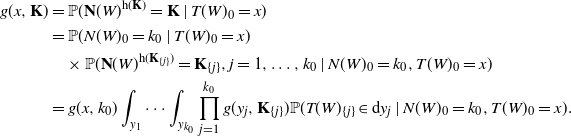\begin{align*} g(x,{\mathbf{K}}) & = \mathbb{P}({\mathbf{N}}(W)^{\mathrm{h}({\mathbf{K}})} = {\mathbf{K}} \mid T(W)_0=x) \\ & = \mathbb{P}(N(W)_0=k_0\mid T(W)_0=x) \\ & \quad \times \mathbb{P}({\mathbf{N}}(W)^{\mathrm{h}({\mathbf{K}}_{\{j\}})} = {\mathbf{K}}_{\{j\}}, j=1,\dots,k_0 \mid N(W)_0=k_0,T(W)_0=x) \\ & = g(x,k_0) \int_{y_1} \cdots \int_{y_{k_0}} \prod_{j=1}^{k_0} g(y_j,{\mathbf{K}}_{\{j\}})\mathbb{P}(T(W)_{\{j\}} \in \mathrm{d} y_j\mid N(W)_0=k_0, T(W)_0=x) . \end{align*}

Here we have used $\prod_{j=1}^{k_0} g(y_j, {\mathbf{K}}_{\{j\}}) \mathbb{P}(T(W)_{\{j\}} \in \mathrm{d} y_j\mid N(W)_0=k_0, T(W)_0=x)$ to denote the following density:

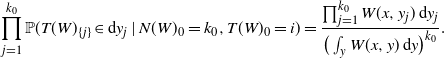\begin{equation*} \prod_{j=1}^{k_0} \mathbb{P}(T(W)_{\{j\}} \in \mathrm{d} y_j\mid N(W)_0 =k_0, T(W)_0=i) = \frac{\prod_{j=1}^{k_0} W(x, y_j) \, \mathrm{d} y_j }{ \big(\int_y W(x,y) \, \mathrm{d} y\big)^{k_0} }. \end{equation*}

Therefore, we obtain the recursive formula

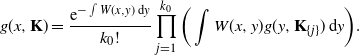\begin{equation*} g(x,{\mathbf{K}}) = \frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k_0!} \prod_{j=1}^{k_0}\bigg(\int W(x,y)g(y,{\mathbf{K}}_{\{j\}})\,\mathrm{d} y\bigg). \end{equation*}

3.2. Convergence

Let $W_n$ be a sequence of graphons such that $d_\square(W_n,W) \to 0$ and $\sup_{n,x,y} W_n(x,y) \leq \bar{a}$ for some positive constant $\bar{a}$ . Let $X^{W_n}$ be the associated branching process of $W_n$ , and $g_n(x,{\mathbf{K}})=\mathbb{P}( {\mathbf{N}}(W_n)^{\mathrm{h}({\mathbf{K}})}= {\mathbf{K}}\mid T(W_n)_0 =x)$ .

We want to show that, as $n \to \infty$ , $\int g_n(x,{\mathbf{K}}) \, \mathrm{d} x \to \int g(x,{\mathbf{K}}) \, \mathrm{d} x$ . To see this, for any graphon W, any finite tree T with root 0, and any $x \in [0,1]$ , we define the vertex-prescribed homomorphism density

\begin{equation*} t^x(T,W) = \int_{[0,1]^{|V(T)|-1}}\prod_{i\in E(T)}W(x,x_i) \prod_{ij\in E(T),i,j\geq1}W(x_i,x_j)\,\mathrm{d} x_1 \cdots \mathrm{d} x_{|V(T)|-1}\end{equation*}

and the homomorphism density $t(T,W)=\int_{[0,1]} t^x(T,W) \, \mathrm{d} x$ . It is well known that, for finite T, $t(T,W_n) \to t(T,W)$ as long as $d_\square(W_n,W) \to 0$ ; see, e.g., [9, 10, 27]. We will rewrite $\int g_n(x,{\mathbf{K}}) \, \mathrm{d} x $ and $\int g(x, {\mathbf{K}}) \,\mathrm{d} x$ as $\sum_{m \geq 0} \lambda_m t(T_m,W_n)$ and $\sum_{m \geq 0} \lambda_m t(T_m,W)$ respectively for a sequence of trees $T_m$ .

Proposition 3.3. For any $\bar{a} >0$ and any ${\mathbf{K}}$ with $\mathrm{h}({\mathbf{K}})=d<\infty$ , there exists a sequence of finite trees $(T_m)_{m \geq 0}$ and a sequence of real numbers $(\lambda_m)_{m \geq 0}$ such that, for any graphon W with $\sup_{x,y} W(x,y) \leq \bar{a}$ ,

1. (i) $\sum_{m \geq 0} |\lambda_m| \bar{a}^{|E(T_m)|}<+\infty$ ;

2. (ii) $g(x,{\mathbf{K}})=\sum_{m \geq 0} \lambda_m t^x(T_m,W)$ .

Proof. We proceed by induction. For $d=1$ ,

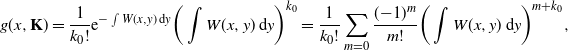\begin{equation*} g(x,{\mathbf{K}}) = \frac{1}{k_0!}\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^{k_0} = \frac{1}{k_0!}\sum_{m=0}\frac{({-}1)^m}{m!}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^{m+k_0}, \end{equation*}

where $k_0$ is the number of the first generation in ${\mathbf{K}}$ . For any $m\in\mathbb{N}$ , take $T_m$ to be an $(m+k_0)$ -star, i.e. a tree of height 1 with $(m+k_0)$ leaves. Define $\lambda_m\,:\!=\, {({-}1)^m}/({k_0!m!})$ . Then it can be easily seen that

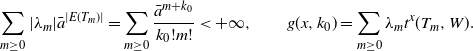\begin{align*} \sum_{m \geq 0}|\lambda_m|\bar{a}^{|E(T_m)|} = \sum_{m \geq 0}\frac{\bar{a}^{m+k_0}}{k_0!m!} < +\infty, \qquad g(x,k_0)=\sum_{ m \geq 0} \lambda_m t^x(T_m,W). \end{align*}

Now suppose that our claim is true for any configuration ${\mathbf{K}}^{d-1}$ . Using our recursive formula in (3.5), we expand the exponential term and obtain

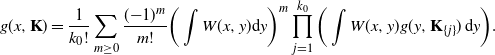\begin{equation*} g(x,{\mathbf{K}}) = \frac{1}{k_0!}\sum_{m\geq0}\frac{({-}1)^m}{m!}\bigg(\int W(x,y)\mathrm{d} y\bigg)^m \prod_{j=1}^{k_0}\bigg(\int W(x,y)g(y,{\mathbf{K}}_{\{j\}})\,\mathrm{d} y\bigg). \end{equation*}

For each ${\mathbf{K}}_{\{j\}}, j=1,\dots,k_0$ , we have sequences $\big(\lambda_m^j\big)_{m \geq 0}, \big(T^j_m\big)_{m \geq 0}$ such that our claim is satisfied. For each $m=(m_0, m_1, \dots, m_{k_0}) \in \mathbb{N}^{k_0+1}$ , we define

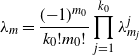\begin{align*}\lambda_m=\frac{({-}1)^{m_0}}{k_0!m_0!}\prod_{j=1}^{k_0}\lambda_{m_j}^{j}\end{align*}

and tree $T_m$ as in Figure 1. In $T_m$ , $m_0$ stands for the number of leaves attached to the root, and the additional trees $T^i_{m_i}$ , $i=1,\dots,k_0$ , are linked to the root. It is then clear that

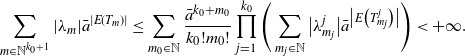\begin{equation*} \sum_{m\in\mathbb{N}^{k_0+1}}|\lambda_m|\bar{a}^{|E(T_m)|} \leq \sum_{m_0\in\mathbb{N}}\frac{\bar{a}^{k_0+m_0}}{k_0!m_0!} \prod_{j=1}^{k_0}\Bigg(\sum_{m_j\in\mathbb{N}}\big|\lambda_{m_j}^{j}\big|\bar{a}^{\big|E\big(T_{m_j}^j\big)\big|}\Bigg) < +\infty. \end{equation*}

According to our induction, we have $g(y,{\mathbf{K}}_{\{j\}}) = \sum_{m_j \geq 0} \lambda_{m_j}^{j}t^y\big(T^j_{m_j},W\big)$ . Therefore, we obtain

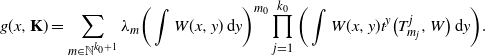\begin{equation*} g(x,{\mathbf{K}}) = \sum_{m\in\mathbb{N}^{k_0+1}}\lambda_m\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^{m_0} \prod_{j=1}^{k_0}\bigg(\int W(x,y)t^y\big(T_{m_j}^j,W\big)\,\mathrm{d} y\bigg). \end{equation*}

It can be easily verified that, for each $m \in \mathbb{N}^{k_0+1}$ ,

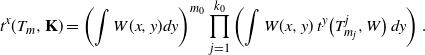\begin{equation*} t^x(T_m, {\mathbf{K}}) =\left(\int W(x,y) dy\right)^{m_0} \prod_{j=1}^{k_0} \left(\int W(x,y)\, t^y\big(T_{m_j}^j, W\big) \,dy \right). \end{equation*}

Thus, we conclude that $g(x,{\mathbf{K}}) = \sum_{m\in\mathbb{N}^{k_0+1}}\lambda_m t^x(T_m,W)$ .

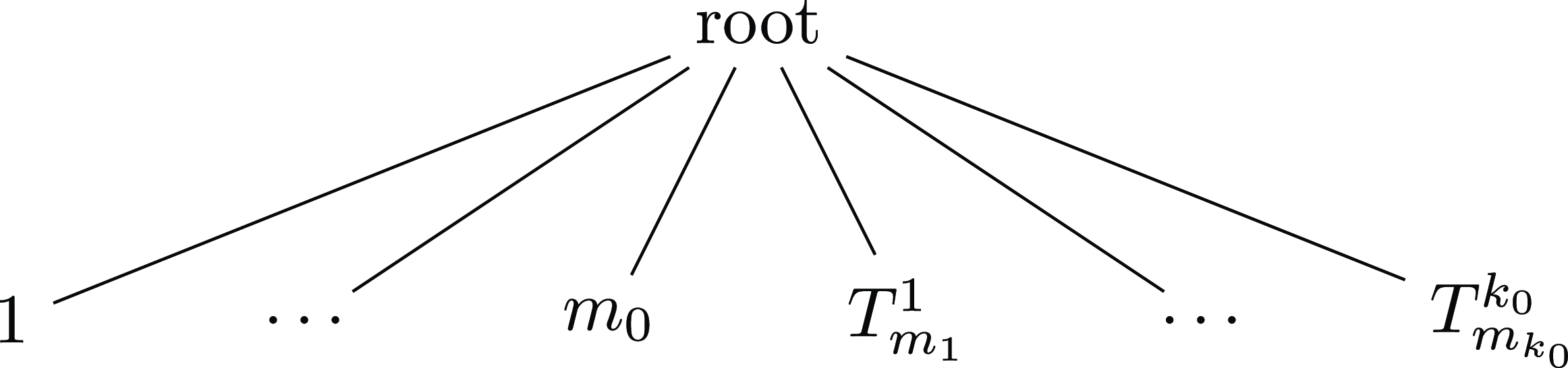
Figure 1. Tree $T_m$ .

Proposition 3.4. Suppose $W_n$ is a sequence of graphons such that $d_\square(W_n,W) \to 0$ satisfying $\sup_{n,x,y}W_n(x,y) \leq \bar{a}$ for some positive constant $\bar{a}$ . Let ${\mathbf{K}}^d$ be a tree of height d. Then $\lim_{n\to\infty}\mathbb{P}\big({\mathbf{N}}(W_n)^d = {\mathbf{K}}^d\big) = \mathbb{P}({\mathbf{N}}(W)^d = {\mathbf{K}}^d)$ .

Proof. According to Proposition 3.3, we get

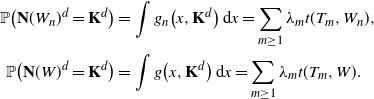\begin{align*} \mathbb{P}\big({\mathbf{N}}(W_n)^d = {\mathbf{K}}^d\big) & = \int g_n\big(x,{\mathbf{K}}^d\big)\,\mathrm{d} x = \sum_{m\geq1}\lambda_mt(T_m,W_n), \\ \mathbb{P}\big({\mathbf{N}}(W)^d = {\mathbf{K}}^d\big) & = \int g\big(x,{\mathbf{K}}^d\big)\,\mathrm{d} x = \sum_{m\geq1}\lambda_mt(T_m,W). \end{align*}

Since $W_n$ converges to W in that cut norm, $t(T_m,W_n) \to t(T_m, W)$ as $n \to \infty$ . Due to the uniform bound

\begin{align*}\sum_{m\geq1}\lambda_mt(T_m,W_n)\leq\sum_{m\geq1}\lambda_m\bar{a}^{|E(T_m)|} < +\infty,\end{align*}

we apply the dominated convergence theorem and conclude that $\mathbb{P}\big({\mathbf{N}}(W_n)^d={\mathbf{K}}^d\big)$ converges to $\mathbb{P}\big({\mathbf{N}}(W)^d={\mathbf{K}}^d\big) $ as $n \to \infty$ .

3.3. Tightness

Notice that $X^W \in \mathcal{A}_d$ is equivalent to ${\mathbf{N}}(W)^d \in \mathcal{A}_d$ . To make our computation clear, we will sometimes adopt the latter notation. Recall that we want to show that

\begin{equation*} \mathbb{P}\big({\mathbf{N}}(W)^d \in \mathcal{A}_d\big) = \lim\limits_{n \to \infty} \mathbb{P}\big({\mathbf{N}}(W_n)^d \in \mathcal{A}_d\big).\end{equation*}

To apply Proposition 3.4, we need a tightness result. For $K \in \mathbb{N}$ , we define ${\mathbf{N}}(W)^d \leq K$ if $N(W)_{\{i_1|i_2|\cdots|i_j\}} \leq K$ for any $X^W_{\{i_1|i_2|\cdots|i_j\}}$ in the first d generations.

Lemma 3.2. Suppose $\sup_{x,y}W(x,y) \leq \bar{a}$ for some positive constant $\bar{a}$ . Then, for any $\alpha>0$ , $d \in \mathbb{N}$ , there exists a large enough $K_0 \in \mathbb{N}$ uniformly for $x \in [0,1]$ such that $K \geq K_0$ implies $\mathbb{P}({\mathbf{N}}(W)^d \leq K \mid T(W)_0 = x) > 1 - (1/K)^{\alpha}$ . Here, the choice of $K_0$ only depends on $\alpha$ , d, and $\bar{a}$ .

Proof. We prove the result by induction. Recall that when $\mathrm{h}({\mathbf{K}})=1$ , we have

\begin{align*}g(x,{\mathbf{K}})=\frac{1}{k_0!}\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^{k_0},\end{align*}

where $k_0$ is the number of the first generation in ${\mathbf{K}}$ . For any $k\in\mathbb{N}$ , we define, for $c \in \mathbb{R}_+$ , $\psi_{k}(c) \,:\!=\, \sum_{l=k+1}^{\infty} ({1}/{l!}) \mathrm{e}^{-c} c^l$ . Thus we have

\begin{equation*} \mathbb{P}(N(W)_0 \leq k \mid T(W)_0=x) = 1 - \psi_k \bigg(\int W(x,y)\,\mathrm{d} y\bigg). \end{equation*}

It can be easily verified that $\psi^{\prime}_k(c)={\mathrm{e}^{-c}c^{k}}/{k!} \geq 0$ , and hence $\psi_k\big(\int W(x,y)\,\mathrm{d} y\big) \leq \psi_k(\bar{a})$ . Choosing K large enough that $\psi_K(\bar{a}) <K^{-\alpha}$ is indeed possible, it is clear that

\begin{equation*} \mathbb{P}(N(W)_0 \leq K \mid T(X^n)_0=x) = 1 - \psi_K\bigg(\int W(x,y)\,\mathrm{d} y\bigg) > 1 - (1/K)^{\alpha}. \end{equation*}

Assume our claim is true for $d-1$ . Then, for any $\beta >0$ , there exists a K such that

\begin{align*}\mathbb{P}({\mathbf{N}}(W)^d_{\{j\}} \leq K \mid T(W)^d_{\{j\}}=y) \geq 1 - (1/K)^{\beta}.\end{align*}

Note that

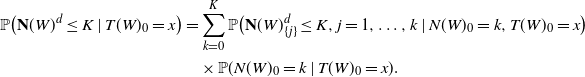\begin{align*} \mathbb{P}\big({\mathbf{N}}(W)^d \leq K \mid T(W)_0=x\big) & = \sum_{k=0}^{K}\mathbb{P}\big({\mathbf{N}}(W)^d_{\{j\}}\leq K,j=1,\dots,k\mid N(W)_0=k,T(W)_0=x\big) \\ & \quad \times \mathbb{P}(N(W)_0=k \mid T(W)_0=x). \end{align*}

As in the proof of Proposition 3.2, we have

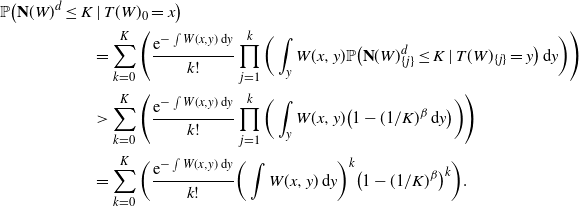\begin{align*} \mathbb{P}\big({\mathbf{N}}(W)^d \leq K & \mid T(W)_0=x\big) \\ & = \sum_{k=0}^{K}\Bigg(\frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k!}\prod_{j=1}^{k} \bigg(\int_y W(x,y)\mathbb{P}\big({\mathbf{N}}(W)^d_{\{j\}} \leq K \mid T(W)_{\{j\}}=y\big)\,\mathrm{d} y\bigg) \Bigg) \\ & > \sum_{k=0}^{K}\Bigg(\frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k!}\prod_{j=1}^{k} \bigg(\int_y W(x,y) \big(1-(1/K)^{\beta}\,\mathrm{d} y\big)\bigg)\Bigg) \\ & = \sum_{k=0}^{K}\bigg(\frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k!}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^k \big(1-(1/K)^{\beta}\big)^k\bigg). \end{align*}

Since $(1-(1/K)^{\beta})^K > 1- (1/K)^{\beta-2}$ for large K, we have

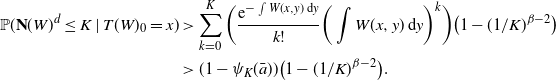\begin{align*} \mathbb{P}({\mathbf{N}}(W)^d \leq K \mid T(W)_0=x) & > \sum_{k=0}^{K}\bigg(\frac{\mathrm{e}^{-\int W(x,y)\,\mathrm{d} y}}{k!}\bigg(\int W(x,y)\,\mathrm{d} y\bigg)^k\bigg) \big(1- (1/K)^{\beta -2}\big) \\ & > (1-\psi_K(\bar{a}))\big(1- (1/K)^{\beta -2}\big). \end{align*}

Therefore, by taking $\beta =\alpha+3$ , and large K such that $\psi_K(\bar{a}) < (1/K)^{\alpha+1}$ , we conclude that $\mathbb{P} ({\mathbf{N}}(W)^d \leq K \mid T(W)_0 =x) > 1- (1/K)^{\alpha}$ .

Proposition 3.5. Suppose $W_n$ is a sequence of graphons such that $d_\square(W_n,W) \to 0$ and satisfying $\sup_{n,x,y} W_n(x,y) \leq \bar{a}$ for some positive constant $\bar{a}$ . Then, for any fixed d, we have $\lim_{n\to\infty}\mathbb{P}({\mathbf{N}}(W_n)^d\in\mathcal{A}_d) = \mathbb{P}({\mathbf{N}}(W)^d\in\mathcal{A}_d)$ , from which we conclude that $\limsup_{n\to\infty}\mathbb{P}_{X^{W_n}}(\mathcal{A})\leq\mathbb{P}_{X^W}(\mathcal{A})$ .

Proof. Due to Proposition 3.4, it can be seen that, for fixed d, K,

\begin{equation*} \lim_{n\to\infty}\mathbb{P}\big({\mathbf{N}}(W_n)^d\in\mathcal{A}_d,{\mathbf{N}}(W_n)^d \leq K\big) = \mathbb{P}\big({\mathbf{N}}(W)^d \in \mathcal{A}_d, {\mathbf{N}}(W)^d \leq K\big). \end{equation*}

Applying Lemma 3.2, we let $K \to \infty$ and obtain $\lim_{n\to\infty}\mathbb{P}\big({\mathbf{N}}(W_n)^d\in\mathcal{A}_d\big) = \mathbb{P}\big({\mathbf{N}}(W)^d \in \mathcal{A}_d\big)$ .

For any $\epsilon >0$ , there exists a d such that $\mathbb{P}\big({\mathbf{N}}(W)^d \in \mathcal{A}_d\big)=\mathbb{P}\big(X^W \in \mathcal{A}_d\big) \leq \mathbb{P}_{X^W}(\mathcal{A})+\epsilon$ . It can then be easily verified that

\begin{equation*} \limsup_{n\to\infty}\mathbb{P}_{X^{W_n}}(\mathcal{A}) \leq \limsup_{n\to\infty}\mathbb{P}\big({\mathbf{N}}({W_n})^d \in \mathcal{A}_d\big) = \mathbb{P}\big({\mathbf{N}}(W)^d \in \mathcal{A}_d\big) \leq \mathbb{P}_{X^W}(\mathcal{A})+\epsilon. \end{equation*}

Therefore, we obtain $\limsup_{n\to\infty}\mathbb{P}_{X^{W_n}}(\mathcal{A}) \leq \mathbb{P}_{X^W}(\mathcal{A})$ .

3.4. Completing the proof of the upper bound

Recalling Proposition 3.1, we have $C_k(G_n({1}/{n})\leq n\mathbb{P}(X^{n,\rho_n} \in \mathcal{A}_d) + o_\mathrm{p}(n)$ . Note that $X^{n,\rho_n}$ is the branching process associated with the graphon $n\rho_n W_{G_n}$ , $d_\square ( W_{G_n}, W) \to 0$ , and $n\rho_n \to 1$ . Applying Proposition 3.5 with $W_n = n\rho_n W_{G_n}$ , we obtain that $C_k(G_n({1}/{n})) \leq n \mathbb{P}_{X^W}(\mathcal{A}_d) + o_\mathrm{p}(n)$ . Letting $d \to \infty$ in the above inequality, we have our result.

4. The proof of the lower bound in Theorem 2.1

Before proceeding to our proof of the lower bound, we argue that it suffices to prove it for irreducible W. A graphon W is said to be irreducible if there is no measurable $A \subset [0,1]$ such that $\text{Leb}(A) \in (0,1)$ and $W=0$ almost everywhere on $A\times A^\mathrm{c}$ , where $\text{Leb}(A)$ stands for the Lebesgue measure of A.

According to [7, Lemma 5.17], for any graphon W, there exists a partition $[0,1]=\cup_{i=1}^N I_i$ with $0 \leq N \leq \infty$ such that $\text{Leb}(I_i) >0$ for each $i \geq 1$ , the restriction of W on $I_i \times I_i$ is irreducible for $i \geq 1$ , and $W=0$ almost everywhere on $([0,1] \times [0,1]) \setminus \cup_{i=1}^N(I_i \times I_i)$ . Let W be the graphon in Theorem 2.1, and let $I_1,\dots,I_N$ be the corresponding partition. Without loss of generality, we assume that, for each $i\geq 1$ , $I_i$ is an interval. Denote the restriction $W|_{I_i \times I_i}$ by $W_i$ . To properly define the branching process of $W_i$ , we identify it with a graphon $\widetilde{W}_i\colon I \times I \to [0,\infty)$ such that $\widetilde{W}_i(x,y)=W(x,y)$ for $x,y \in I_i$ and $\widetilde{W}_i(x,y)=0$ otherwise. It can then be easily verified that $\mathbb{P}_{X^{\lambda W}}(\mathcal{A})= \sum_{i=1}^N \mathbb{P}_{X^{\lambda \widetilde{W}_i}}(\mathcal{A})$ . Hence, under Assumption 2.1, $\lambda \mapsto \mathbb{P}_{X^{\lambda W_i}}(\mathcal{A})$ is continuous at $\lambda=1$ for each $i \geq 1$ . Fix $N_0 \leq N$ . There exists a partition $V^n_1,\dots, V^n_{N_0}, [n]\setminus(\cup_{i} V^n_i )$ , of [n] such that $G_n^i$ converges to $W|_{I_i \times I_i}$ in the cut norm, where $G_n^i$ is the subgraph of $G_n$ induced by $V^n_i$ . Assuming Theorem 2.1 holds for irreducible graphons, we obtain, after appropriate normalization of $G_n^i$ and $W_i$ , $C_k(G^i_n({1}/{n})) \geq n \mathbb{P}_{X^{W_i}}(\mathcal{A}) + o_\mathrm{p}(n)$ , and thus

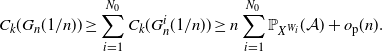\begin{align*} C_k(G_n({1}/{n})) \geq \sum_{i=1}^{N_0} C_k(G^i_n({1}/{n})) \geq n\sum_{i=1}^{N_0} \mathbb{P}_{X^{W_i}}(\mathcal{A}) + o_\mathrm{p}(n).\end{align*}

Letting $N_0 \to N$ , we can conclude the proof for the lower bound. From now on, let us assume that W is irreducible.

We say a graphon F is finitary if there exist finitely many disjoint intervals $I_{t_i}$ , $i=1, \dots, M$ , such that $\cup_{i=1}^M I_{t_i}=[0,1]$ and the restriction of F on $I_{t_i} \times I_{t_j}$ is a constant for any $1 \leq i, j \leq M$ . As we will see, the indexes $t_1,\dots,t_M$ will be used to label vertices of $G_n$ as well as particles of $X^n$ . According to [7, Lemma 7.3], the graphon W can be approximated pointwise from below by finitary graphons. More precisely, we have the following result.

Lemma 4.1. There exists a sequence of finitary graphons $(F_m)_{m\in\mathbb{N}}$ such that $F_m \leq W$ and $\lim_{m\to\infty}F_m(x,y)=W(x,y)$ almost surely.

Under Assumption 2.1, we prove in Section 4.1 that, for any $\varepsilon>0$ , $m \in \mathbb{N}$ ,

(4.1) \begin{equation} C_k(G_n({1}/{n})) \geq (1-2\varepsilon)n\mathbb{P}_{X^{(1-2\varepsilon)F_m}}(\mathcal{A}) + o_\mathrm{p}(n).\end{equation}

Then, in Section 4.2, we show the continuity property

(4.2) \begin{equation} \liminf_{\varepsilon\to0,m\to\infty}\mathbb{P}_{X^{(1-2\varepsilon)F_m}}(\mathcal{A}) \geq \mathbb{P}_{X^W}(\mathcal{A}).\end{equation}

It is clear that (4.1) and (4.2) together prove the lower bound part of Theorem 2.1, i.e. $C_k(G_n({1}/{n})) \geq n \mathbb{P}_{X^W}(\mathcal{A}) + o_\mathrm{p}(n)$ .

4.1. Proof of (4.1)

Fix $m \in \mathbb{N}$ and $\varepsilon \in (0,{1}/{m})$ such that $\lambda \to \mathbb{P}_{X^{\lambda (1-\varepsilon)F_m}}(\mathcal{A})$ is continuous at $\lambda =1$ . Since $F_m$ is finitary, there exists a partition $I_{t_j},j=1,\dots, M$ of [0,1] such that $F_m|_{I_{t_j} \times I_{t_k}}$ is a constant denoted by $F_m(t_j,t_k)$ . We will mark particles of the branching process $X^{G_n}$ by labels $t_h$ , $h=1,\dots,M$ .

Before proceeding to the rigorous proof, let us first give the main ideas of our argument. For each $G_n$ , we prove there exist M disjoint subsets $\mathbf{Good}_{n, t_1},\dots, \mathbf{Good}_{n, t_M}$ of vertices such that, for any vertex $i \in \mathbf{Good}_{n, t_h}$ and $k=1,\dots, M$ ,

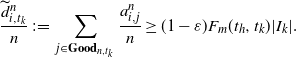\begin{equation*} \frac{\widetilde{d}^n_{i,t_k}}{n} \,:\!=\, \sum_{j\in\mathbf{Good}_{n,t_k}}\frac{a^n_{i,j}}{n} \geq (1-\varepsilon)F_m(t_h,t_k)|I_k|.\end{equation*}

Therefore, we can heuristically consider $G_n$ as a ‘finitary’ graph by labelling vertices in $\mathbf{Good}_{n,t_h}$ by $t_h$ , $h=1,\dots, M$ . Due to the above inequality, the branching process $X^{G_n}$ associated with $G_n$ stochastically dominates, in the first order, the branching process $X^{(1-\varepsilon)F_m}$ associated with $(1-\varepsilon)F_m$ . Take $F^{\varepsilon}_m({1}/{n})$ to be an n-vertex random graph sampled from $(1-\varepsilon)F_m$ , i.e. independently uniformly select vertices $v_i \in [0,1]$ and then connect $v_i,v_j$ independently with probability $(1-\varepsilon)F_m(v_i,v_j)/n$ . By the standard exploration argument (see, e.g., [7, Section 9]), locally the random graph $G_n({1}/{n})$ (respectively $F^{\varepsilon}_m({1}/{n})$ ) is almost the branching process $X^{G_n}$ (respectively $X^{(1-\varepsilon)F_m}$ ). Thus, heuristically the random graph $G_n({1}/{n})$ is more connected than the random graph $F^{\varepsilon}_m({1}/{n})$ , and thus has a k-core of larger order. Therefore, the inequality (4.1) follows from [31, Theorem 3.1], which says that

\begin{align*}C_k(F^{\varepsilon}_m({1}/{n})) = n \mathbb{P}_{X^{(1-\varepsilon)F_m}}(\mathcal{A})+o_\mathrm{p}(n).\end{align*}

The following simple lemma will be used to label vertices of $G_n$ . Therein, a vertex is defined to be ‘ $\mathbf{Bad}$ ’ if its degree is not bounded from below by that of $F_m$ , and ‘ $\mathbf{Good}$ ’ vertices are the complement of ‘ $\mathbf{Bad}$ ’ ones.

Lemma 4.2. Suppose $\varepsilon>0$ is a fixed constant, and $\|W_{G_n}-W\|_{\square} \to 0$ . Then there exists a collection of disjoint subsets $\widetilde{\mathbf{Bad}}_{n,t_j} \subset I_{t_j}$ , $j=1,\dots, M$ , such that [(i)]

1. (i) $|\widetilde{\mathbf{Bad}}_{n,t_j}| = o(1)$ , $j=1,\dots, M$ ;

2. (ii) for any $x \in I_{t_j} \setminus \widetilde{\mathbf{Bad}}_{n,t_j}$ ,

   (4.3) \begin{equation} \int_{I_{t_k}} W_{G_n}(x, y)\,\mathrm{d} y \geq (1-\varepsilon/2)F_m(t_j,t_k)|I_{t_k}|, \qquad k=1,\dots, M. \end{equation}

Proof. First, recall that we can also write

(4.4) \begin{equation} \|W\|_\square = \sup_{0\leq f,g \leq1 \text{ measurable}}\bigg|\int f(x)g(y)W(x,y)\,\mathrm{d} x\,\mathrm{d} y\bigg|. \end{equation}

For any $1 \leq j,k \leq M$ , define

\begin{equation*} \widetilde{\mathbf{Bad}}_{n,t_j,t_k} = \bigg\{x\in I_{t_j}\colon \int_{I_{t_k}}W_{G_n}(x,y)\,\mathrm{d} y < (1-\varepsilon/2) F_m(t_j,t_k) |I_{t_k}| \bigg\}. \end{equation*}

In the case that $F_m(t_j,t_k) =0$ , it is clear that $\widetilde{\mathbf{Bad}}_{n,t_j,t_k}= \emptyset$ . Let us assume that $F_m(t_j,t_k)>0$ .

Taking $f(x)=\mathbf{1}_{\{x\in\widetilde{\mathbf{Bad}}_{n,t_j,t_k}\}}$ and $g(y)=\mathbf{1}_{\{y\in I_{t_k}\}}$ in (4.4), we obtain

\begin{equation*} \int_{\widetilde{\mathbf{Bad}}_{n,t_j,t_k}}\mathrm{d} x\int_{I_{t_k}}(W_{G_n}(x,y)-W(x,y))\,\mathrm{d} y \geq -\|W_{G_n}-W\|_{\square} = -o(1), \end{equation*}

and, since $F_m \leq W$ ,

(4.5) \begin{equation} \int_{\widetilde{\mathbf{Bad}}_{n,t_j,t_k}}\mathrm{d} x\int_{I_{t_k}}(W_{G_n}(x,y)-F_m(x,y))\,\mathrm{d} y \geq -o(1). \end{equation}

Since, for any $x\in\widetilde{\mathbf{Bad}}_{n,t_j,t_k}$ ,

\begin{align*}\int_{I_{t_k}}(W_{G_n}(x,y)-F_m(x,y))\,\mathrm{d} y < -\varepsilon/2 F_m(t_j,t_k) |I_{t_k}|,\end{align*}

together with (4.5) it follows that $\varepsilon F_m(t_j,t_k)|I_{t_k}|\, |\widetilde{\mathbf{Bad}}_{n,t_j,t_k}| \leq o(1)$ . As a result of $F_m(t_j,t_k)>0$ , we obtain $|\widetilde{\mathbf{Bad}}_{n,t_j,t_k}| = o(1)$ .

If we take $\widetilde{\mathbf{Bad}}_{n,t_j}=\bigcup_{k=1}^M\widetilde{\mathbf{Bad}}_{n,t_j,t_k}$ , it is clear that $|\widetilde{\mathbf{Bad}}_{n, t_j}| = o(1)$ and satisfies (4.3).

Before proving the main result in this subsection, we would like to point out that our main contribution here is the observation that we can label vertices of $G_n$ so that heuristically it dominates the finitary graphon $(1-\varepsilon)F_m$ . The remaining part of the proof is just a modification of [31, Theorem 3.1]. We summarize it as the following lemma, and refer the reader to [31] for a detailed argument.

Lemma 4.3. Suppose $F_m$ is a finitary graphon with M labels $t_1,\dots,t_M$ , and $\lambda\to\mathbb{P}_{X^{\lambda F_m}}(\mathcal{A})$ is continuous at $\lambda=1$ . Let $G_n$ be a sequence of graphs such that $\sup_{i,j,n}\{a^n_{i,j}\} < +\infty$ . Denote by $X^{G_n}_i$ (respectively $X^{F_m}_{t_h}$ ) the branching process associated with $G_n$ (respectively $F_m$ ) that has the initial particle with type i (respectively label $t_h$ ). If, for each $G_n$ , there exist M disjoint subsets $\mathbf{G}_{n,t_h}$ , $h=1,\dots,M$ , of vertices such that, for some $\varepsilon \in (0,1)$ ,

1. (i) ${|\mathbf{G}_{n,t_h}|}/{n} \geq (1-\varepsilon)|I_{t_h}|$ , $h=1,\dots,M$ ;

2. (ii) for each vertex $i\in\mathbf{G}_{n,t_h}$ , the branching process $X^{G_n}_{i}$ stochastically dominates, in the first order, the branching process $X^{F_m}_{t_h}$ , then $C_k(G_n({1}/{n})) \geq (1-\varepsilon)n\mathbb{P}_{X^{(1-\varepsilon)F_m}}(\mathcal{A}) + o_\mathrm{p}(n)$ .

Completing the proof of (4.1). Since $\lambda\to\mathbb{P}_{X^{\lambda F_m}}(\mathcal{A})$ is non-decreasing with respect to $\lambda$ , it has only countably many discontinuity points. Therefore, we can choose an arbitrarily small $\varepsilon$ such that $\lambda\to\mathbb{P}_{X^{\lambda(1-\varepsilon)F_m}}(\mathcal{A})$ is continuous at $\lambda=1$ . We choose $0<\varepsilon<{1}/{m}$ , and take $\widetilde{\mathbf{Bad}}_{n,t_h}$ as in Lemma 4.2. For $h=1,\dots,M$ , define

\begin{equation*} \mathbf{Good}_{n,t_h} \,:\!=\, \{i\in[n]\colon(({i-1})/{n},{i}/{n}] \subset I_{t_h} \setminus \widetilde{\mathbf{Bad}}_{n,t_h}\}. \end{equation*}

Due to the construction of $W_{G_n}$ in (2.1), for any $(({i-1})/{n},{i}/{n}] \subset I_{t_h}$ , we have either $(({i-1})/{n},{i}/{n}] \subset \widetilde{\mathbf{Bad}}_{n,t_h}$ or $(({i-1})/{n},{i}/{n}] \cap \widetilde{\mathbf{Bad}}_{n,t_h}=\emptyset$ . Therefore, it can be easily verified that ${|\mathbf{Good}_{n,t_h}|}/{n} \geq |I_{t_h}| - o(1)$ . For any $i\in\mathbf{Good}_{n,t_h}$ , define $\widetilde{d}^n_{i,t_k}\,:\!=\,\sum_{j\in\mathbf{Good}_{n,t_k}}a^n_{i,j}$ , $k=1,\dots,M$ . As a result of (4.3), we obtain

\begin{equation*} \frac{\widetilde{d}^n_{i,t_k}}{n} \geq \int_{I_{t_k}}W_{G_n}(i/n,y)\,\mathrm{d} y - \bar{a}(|I_{t_k}|-{|\mathbf{Good}_{n,t_k}|}/{n}) \geq (1-\varepsilon/2)F_m(t_h,t_k)|I_{t_k}| - o(1)\bar{a}. \end{equation*}

We conclude that, for large enough n, there exists a collection of disjoint $\mathbf{Good}_{n,t_h} \subset [n]$ , $h=1,\dots,M$ , which satisfies the following:

1. (i) For all $h=1,\dots,M$ ,

   (4.6) \begin{equation} {|\mathbf{Good}_{n,t_h}|}/{n} \geq (1- \varepsilon)|I_{t_h}|. \end{equation}

2. (ii) For any $i\in\mathbf{Good}_{n,t_h}$ ,

   (4.7) \begin{equation} \frac{\widetilde{d}^n_{i,t_k}}{n} \geq (1-\varepsilon) F_m(t_h,t_k)|I_{t_k}|, \quad k=1,\dots, M. \end{equation}

For vertices in $\mathbf{Good}_{n,t_h}$ , $h=1,\dots,M$ , we label them with $t_h$ . Let us define $\mathbf{Good}_{n}\,:\!=\,\bigcup_{h=1}^M\mathbf{Good}_{n,t_h}$ , $\tilde{n}\,:\!=\,|\mathbf{Good}_{n}|$ . Let $\widetilde{G}_{\tilde{n}}$ be the graph with vertices $\mathbf{Good}_n$ such that $\widetilde{a}^n_{i,j}\,:\!=\,\tilde{n}a^n_{i,j}/n$ for all $i,j \in \mathbf{Good}_n$ . It is clear that $C_k(G_n({1}/{n})) \geq C_k(\widetilde{G}_{\tilde{n}}({1}/{\tilde{n}}))$ .

Take $\widetilde{X}^{\tilde{n}}$ to be a branching process sampled from $\widetilde{G}_{\tilde{n}}$ . For any $i \in \mathbf{Good}_{n,t_h}$ , take $\widetilde{X}^{\tilde{n}}_i$ to be a branching process sampled from graph $\widetilde{G}_{\tilde{n}}$ with root i. For any $t_h$ , take $X^{(1-\varepsilon)F_m}_{t_h}$ to be a branching process sampled from graphon $(1-\varepsilon)F_m$ with root of label $t_h$ . Suppose a particle in generation t of $\widetilde{X}_i^{\tilde{n}}$ is of type j with label $t_h$ . As a result of (4.7) the number of its $t_k$ -labelled children has Poisson distribution with parameter $\widetilde{d}^n_{j,t_k}/n$ , which is larger than $(1-\varepsilon) F_m(t_h,t_k)|I_{t_k}|$ . Therefore, for any $i \in \mathbf{Good}_{n,t_h}$ , we can consider $X^{(1-\varepsilon)F_m}_{t_h}$ as a subset of $\widetilde{X}_i^{\tilde{n}}$ . Thus, for any increasing event $\mathcal{I}$ , we have $\mathbb{P}_{\widetilde{X}_i^{\tilde{n}}}(\mathcal{I}) \geq \mathbb{P}_{X^{(1-\varepsilon)F_m}_{t_h}}(\mathcal{I})$ .

Now we apply Lemma 4.3 to $(1-\varepsilon)F_m$ and $\widetilde{G}_{\tilde{n}}$ to conclude that

\begin{align*} C_k(G_n({1}/{n})) & \geq C_k(\widetilde{G}_{\tilde{n}}({1}/{\tilde{n}})) \geq (1-\varepsilon)\tilde{n}\mathbb{P}_{X^{(1-2\varepsilon)F_m}}(\mathcal{A})+o_\mathrm{p}(n) \\ & \geq (1-2\varepsilon) n \mathbb{P}_{X^{(1-2\varepsilon)F_m}}(\mathcal{A})+o_\mathrm{p}(n), \end{align*}

where in the last inequality we used the fact that $\tilde{n}/n \geq 1- \varepsilon$ due to (4.6).

4.2. Proof of (4.2)

Note that if $F_m$ converges to W pointwise from below, by the dominated convergence theorem it can be easily seen that $\lim_{\varepsilon \to 0, m \to \infty} d_{\square}((1-2\varepsilon)F_m, W)=0$ . It is therefore sufficient to show that $\lim_{n\to\infty}\mathbb{P}_{X^{W_n}}(\mathcal{A}) \geq \mathbb{P}_{X^W}(\mathcal{A})$ if $\lim_{n\to\infty}d_{\square}(W_n,W)=0$ , which we prove in Proposition 4.1.

We say a branching process has property $\mathcal{B}_d$ if its root has at least $k-1$ children, each of these $k-1$ children has at least $k-1$ children, and this occurs up to generation d, and let $\mathcal{B}=\cap_{d=1}^{\infty} \mathcal{B}_d$ . Define the function $\mathbb{P}si_{k}(\lambda)\,:\!=\, \mathbb{P}( \text{Poi}(\lambda) \geq k)$ . For any graphon W, define

(4.8) \begin{equation}\beta_{W} (x,d)\,:\!=\, \mathbb{P}\big( X^W \in \mathcal{B}_d \mid X^W_0=x \big), \qquad\beta_W(x)\,:\!=\, \mathbb{P}\big(X^W \in \mathcal{B} \mid X^W_0=x\big),\end{equation}

where $X^W_0$ stands for the type of the root. For $W=W_n$ , we simply write $\beta_n(x,d)\,:\!=\,\beta_{W_n}(x,d)$ , $\beta_n(x)\,:\!=\,\beta_{W_n}(x)$ .

Lemma 4.4. Let $(W_n)_{n\in\mathbb{N}}$ be a sequence of graphons such that $\|W_n-W\|_\square \to 0$ . Suppose that W is irreducible, and $\alpha\colon[0,1]\rightarrow[0,1]$ is a strictly positive measurable function, i.e. $\mathrm{Leb}(\{x\colon\alpha(x)>0\})=1$ . Fix $\varepsilon>0$ and $\delta>0$ . Define a subset $\mathbf{Bad}_n \subset [0,1]$ via

\begin{equation*} \mathbf{Bad}_nv\,:\!=\, \bigg\{x\colon(1-\varepsilon/2)\int\alpha(y)W(x,y)\,\mathrm{d} y > \int\alpha(y)W_n(x,y)\,\mathrm{d} y\bigg\}. \end{equation*}

Then $\mathrm{Leb}(\mathbf{Bad}_n) \leq \delta$ for large enough n.

Proof. According to the definition of the cut norm (4.4),

\begin{equation*} \lVert W-W_n\rVert_{\square} \geq \int_{\mathbf{Bad}_n}\mathrm{d} x\int\alpha(y)(W(x,y)-W_n(x,y))\,\mathrm{d} y \geq \frac{\varepsilon}{2}\int_{\mathbf{Bad}_n}\,\mathrm{d} x\int\alpha(y)W(x,y)\,\mathrm{d} y. \end{equation*}

Note that $\widetilde{W}(x,y)=\alpha(x)\alpha(y)W(x,y)$ is still irreducible, and

\begin{equation*} \lVert W-W_n\rVert_{\square} \geq \frac{\varepsilon}{2}\int_{\mathbf{Bad}_n}\mathrm{d} x \int\alpha(y)W(x,y)\,\mathrm{d} y \geq \frac{\varepsilon}{2}\int_{\mathbf{Bad}_n}\mathrm{d} x\int\widetilde{W}(x,y)\,\mathrm{d} y. \end{equation*}

Applying [6, Lemma 7] to the irreducible $\widetilde{W}$ , we get that, given any $\delta \in \big(0,\frac12\big)$ , there exists a positive number $b(\widetilde{W},\delta)>0$ such that, for any $A \subset [0,1]$ with $\delta \leq \mathrm{Leb}(A) \leq 1-\delta$ , $\int_{A\times A^\mathrm{c}}\widetilde{W}(x,y)\,\mathrm{d} x\,\mathrm{d} y>b$ . Now, since

\begin{align*}\int_{\mathbf{Bad}_n\times\mathbf{Bad}_n^\mathrm{c}}\widetilde{W}(x,y)\,\mathrm{d} x\,\mathrm{d} y \leq \int_{\mathbf{Bad}_n}\mathrm{d} x\int\widetilde{W}(x,y)\,\mathrm{d} y \to 0,\end{align*}

we conclude that $\mathrm{Leb}(\mathbf{Bad}_n) \leq \delta$ for large enough n.

Lemma 4.5. Let $k \in \mathbb{N}$ , and W be an irreducible graphon such that

(4.9) \begin{align} \alpha(x) = \mathbb{P}si_k\bigg(\int W(x,y)\alpha(y)\,\mathrm{d} y\bigg) \end{align}

has a solution $\alpha(x)$ with $\mathrm{Leb}(\{x\colon\alpha(x)=0\})<1$ . Then $\alpha$ is strictly positive, i.e. $\mathrm{Leb}(\{x\colon\alpha(x)>0\})=1$ .

Proof. Suppose $\alpha$ is a non-zero solution of (4.9). Define $\mathcal{Z}\,:\!=\,\{x\colon\alpha(x)=0\}$ . For any $x \in \mathcal{Z}$ , $0 = \mathbb{P}si_k\big(\int W(x,y)\alpha(y)\,\mathrm{d} y\big)$ , which can only happen if $\int_{\mathcal{Z}^\mathrm{c}}W(x,y)\alpha(y)\,\mathrm{d} y = 0$ . Integrating this equation over $x \in \mathcal{Z}$ , we obtain

\begin{equation*} \int_{\mathcal{Z}}\mathrm{d} x\int_{\mathcal{Z}^\mathrm{c}}W(x,y)\alpha(y)\,\mathrm{d} y = 0. \end{equation*}

Since $\alpha>0$ over $\mathcal{Z}^\mathrm{c}$ , this violates the irreducibility of W.

Proposition 4.1. Let $(W_n)_{n\in\mathbb{N}}$ be a sequence of graphons such that $d_{\square}(W_n, W) \rightarrow 0$ with irreducible W. Then, for any $\varepsilon>0$ ,

(4.10) \begin{equation} \mathbb{P}_{X^{W_n}}(\mathcal{A}) \geq \mathbb{P}_{X^{(1-\epsilon)W}}(\mathcal{A})-\varepsilon^2 \end{equation}

for large enough n. Then, under Assumption 2.1, $\liminf_{n\to\infty}\mathbb{P}_{X^{W_n}}(\mathcal{A}) \geq \mathbb{P}_{X^W}(\mathcal{A})$ .

Proof. We will only prove (4.10), since the second statement follows directly from this. Assume there exists some $\varepsilon_0>0$ such that $\mathbb{P}_{X^{(1-\varepsilon_0) W}}(\mathcal{A})>0$ (otherwise, there is nothing to prove). Recalling the definition of $\beta_{(1-\varepsilon_0) W}(x) $ as in (4.8), we have the equality

\begin{align*} \mathbb{P}_{X^{(1-\varepsilon_0)W}}(\mathcal{A}) = \int\mathbb{P}si_{k}\bigg(\int(1-\varepsilon_0)W(x,y)\beta_{(1-\varepsilon_0)W}(y)\,\mathrm{d} y\bigg)\,\mathrm{d} x, \end{align*}

and hence $\mathrm{Leb}\{x\colon\beta_{(1-\varepsilon_0)W}(x)>0\}>0$ . Since $\beta_{(1-\varepsilon_0)W}(x)$ is a solution of

\begin{equation*} \alpha(x)=\mathbb{P}si_{k-1}\bigg(\int(1-\varepsilon_0)W(x,y)\alpha(y)\,\mathrm{d} y\bigg), \end{equation*}

$\beta_{(1-\varepsilon_0)W}(x)$ is strictly positive according to Lemma 4.5. Fix any $\varepsilon \in (0,\varepsilon_0)$ . We first prove the following statement by induction: for each $d \geq 1$ and $\delta >0$ , there exist subsets $\mathbf{Bad}_{n,d} \subset [0,1]$ for large enough n such that $\mathrm{Leb}(\mathbf{Bad}_{n,d})< \delta$ and $\beta_n(x,d)\geq\beta_{(1-\varepsilon)W}(x,d)$ , for any $x \in \mathbf{Bad}^\mathrm{c}_{n,d}$ , $d \geq 1$ .

Applying Lemma 4.4 with $\alpha(y)=1$ , for all $y \in [0,1]$ , we obtain some $\mathbf{Bad}_{n,1}$ with $\mathrm{Leb}(\mathbf{Bad}_{n,1}) \leq \delta$ such that $x\in\mathbf{Bad}_{n,1}^\mathrm{c}$ implies $\int W_n(x,y)\,\mathrm{d} y\geq(1-\varepsilon/2)\int W(x,y)\,\mathrm{d} y$ . It follows that

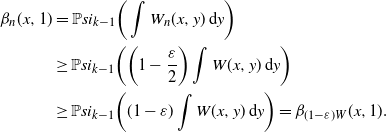\begin{align*} \beta_n(x,1) & = \mathbb{P}si_{k-1}\bigg(\int W_n(x,y)\,\mathrm{d} y\bigg) \\ & \geq \mathbb{P}si_{k-1}\bigg(\bigg(1-\frac{\varepsilon}{2}\bigg)\int W(x,y)\,\mathrm{d} y\bigg) \\ & \geq \mathbb{P}si_{k-1}\bigg((1-\varepsilon)\int W(x,y)\,\mathrm{d} y\bigg) = \beta_{(1-\varepsilon)W}(x,1). \end{align*}

Assume our assertion holds for $d-1$ and $\delta'>0$ , where $\delta'$ is to be chosen later. Let us now prove our claim for d and $\delta>0$ . Noting that

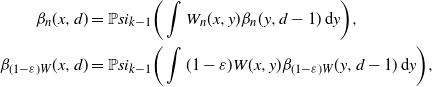\begin{align*} \beta_n(x,d) & = \mathbb{P}si_{k-1}\bigg(\int W_n(x,y)\beta_n(y,d-1)\,\mathrm{d} y\bigg), \\ \beta_{(1-\varepsilon)W}(x,d) & = \mathbb{P}si_{k-1}\bigg(\int(1-\varepsilon)W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y\bigg), \end{align*}

it is enough to show there exists $\mathbf{Bad}_{n,d}$ such that $x\in\mathbf{Bad}_{n,d}^\mathrm{c}$ implies

(4.11) \begin{equation} \int W_n(x,y)\beta_n(y,d-1)\,\mathrm{d} y \geq \int(1-\varepsilon)W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y. \end{equation}

Applying Lemma 4.4 with $\alpha(y)=\beta_{(1-\varepsilon)W}(y,d-1)>0$ , we obtain, for large enough n, a subset $\widetilde{\mathbf{Bad}}_{n,d}$ with $\mathrm{Leb}(\widetilde{\mathbf{Bad}}_{n,d}) \leq \delta/2$ such that $x\in\widetilde{\mathbf{Bad}}^\mathrm{c}_{n,d}$ implies

\begin{equation*} \int W_n(x,y)\beta_{(1-{\varepsilon})W}(y,d-1)\,\mathrm{d} y \geq \bigg(1-\frac{\varepsilon}{2}\bigg)\int W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y. \end{equation*}

Since $\beta_{(1-\varepsilon)W}(x)$ is strictly positive, $\lim_{\xi\searrow0}\mathrm{Leb}(\{x\colon\beta_{(1-\varepsilon)W}(x)\geq\xi\})=1$ . Therefore, there exists a subset $\mathbf{Bad} \subset [0,1]$ and a positive constant $\xi$ such that $\mathrm{Leb}(\mathbf{Bad}) \leq \delta/4$ and, for any $x \in \mathbf{Bad}^\mathrm{c}$ ,

\begin{equation*} \int W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y \geq \beta_{(1-\varepsilon)W}(x) \geq \xi. \end{equation*}

By induction, it follows that, for $x\in\mathbf{Bad}_{n,d}^\mathrm{c} \,:\!=\, \mathbf{Bad}_{n,d-1}^\mathrm{c} \cap \widetilde{\mathbf{Bad}}_{n,d}^\mathrm{c} \cap \mathbf{Bad}^\mathrm{c}$ ,

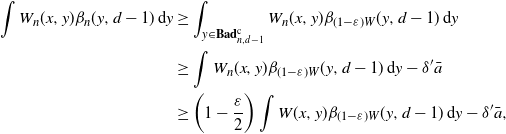\begin{align*} \int W_n(x,y)\beta_n(y,d-1)\,\mathrm{d} y & \geq \int_{y\in\mathbf{Bad}_{n,d-1}^\mathrm{c}}W_n(x,y)\beta_{(1-{\varepsilon})W}(y,d-1)\,\mathrm{d} y \\ & \geq \int W_n(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y - \delta'\bar{a} \\ & \geq \bigg(1-\frac{\varepsilon}{2}\bigg)\int W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y - \delta'\bar{a}, \end{align*}

where the first two inequalities are due to our induction hypothesis and the third inequality follows from our choice of $\widetilde{\mathbf{Bad}}_{n,d}$ . Choosing a small enough $\delta'\in(0,\delta/4)$ that $\delta'\bar{a} \leq {\varepsilon\xi}/{2}$ , it is clear that (4.11) holds for $x\in\mathbf{Bad}_{n,d}^\mathrm{c}$ with $\mathrm{Leb}(\mathbf{Bad}_{n,d}) \leq \delta$ .

Now we prove that $\mathbb{P}_{X^{W_n}}(\mathcal{A}) \geq \mathbb{P}_{X^{(1-\epsilon)W}}(\mathcal{A})-\varepsilon^2$ . Note that

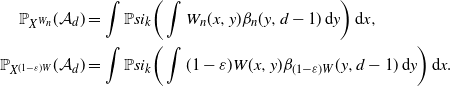\begin{align*} \mathbb{P}_{X^{W_n}}(\mathcal{A}_d) & = \int\mathbb{P}si_k\bigg(\int W_n(x,y)\beta_n(y,d-1)\,\mathrm{d} y\bigg)\,\mathrm{d} x, \\ \mathbb{P}_{X^{(1-\varepsilon)W}}(\mathcal{A}_d) & = \int\mathbb{P}si_k\bigg(\int(1-\varepsilon)W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y\bigg)\,\mathrm{d} x. \end{align*}

Choosing $\delta =\varepsilon^2$ , there exists, for large enough n, a subset $\mathbf{Bad}_{n,d}$ with $\mathrm{Leb}(\mathbf{Bad}_{n,d})\leq \delta$ such that $x \in \mathbf{Bad}_{n,d}^\mathrm{c}$ implies

\begin{equation*} \mathbb{P}si_k\bigg(\int W_n(x,y)\beta_n(y,d-1)\,\mathrm{d} y\bigg) \geq \mathbb{P}si_k\bigg(\int(1-\varepsilon)W(x,y)\beta_{(1-\varepsilon)W}(y,d-1)\,\mathrm{d} y\bigg). \end{equation*}

Since $\mathbb{P}si_k(x) \leq 1$ for all $x \geq 0$ , it can be easily verified that $\mathbb{P}_{X^{W_n}}(\mathcal{A}_d) \geq \mathbb{P}_{X^{(1-\varepsilon)W}}(\mathcal{A}_d)-\varepsilon^2$ . Letting $d \to \infty$ in this inequality, we conclude the result.