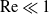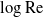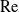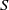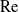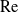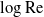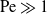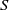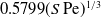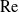Large Péclet number forced convection from a circular wire in a uniform stream: hybrid approximations at small Reynolds numbers

Abstract

We consider heat or mass transport from a circular cylinder under a uniform crossflow at small Reynolds numbers, $\mathrm{Re}\ll 1$. This problem has been thwarted in the past by limitations inherent in the classical analyses of the singular flow problem, which have used asymptotic expansions in inverse powers of $\log \mathrm{Re}$. We here make use of the hybrid approximation of Kropinski, Ward & Keller [(1995) SIAM J. Appl. Math. 55, 1484], based upon a robust asymptotic expansion in powers of $\mathrm{Re}$. In that approximation, the “inner” streamfunction is provided by the product of a pre-factor $S$, a slowly varying function of $\mathrm{Re}$, with a $\mathrm{Re}$-independent “canonical” solution of a simple mathematical form. The pre-factor, in turn, is determined as an implicit function of $\log \mathrm{Re}$ via asymptotic matching with a numerical solution of the nonlinear single-scaled “outer” problem, where the cylinder appears as a point singularity. We exploit the hybrid approximation to analyse the transport problem in the limit of large Péclet number, $\mathrm{Pe}\gg 1$. In that limit, transport is restricted to a narrow boundary layer about the cylinder surface – a province contained within the inner region of the flow problem. With $S$ appearing as a parameter, a similarity solution is readily constructed for the boundary-layer problem. It provides the Nusselt number as $0.5799(S\,\mathrm{Pe})^{1/3}$. This asymptotic prediction is in remarkably close agreement with that of the numerical solution of the exact problem [Dennis, Hudson & Smith (1968) Phys. Fluids 11, 933] even for moderate $\mathrm{Re}$-values.

1. Introduction

A canonical problem in modelling heat or mass transport from bodies under forced convection involves the specification of the excess value (relative to the equilibrium value in the fluid) of the transported quantity (e.g. temperature or solute concentration) at the boundary of the body. In the simplest description, the properties of the fluid are assumed uniform; the flow problem is then decoupled from the transport problem and may be solved independently. In a dimensionless form, it depends upon the Reynolds number $\mathrm{Re}$ . Due to advection, the transport is coupled to the flow; the relative role of advection is quantified by the Péclet number $\mathrm{Pe}$ . While both $\mathrm{Re}$ and $\mathrm{Pe}$ depend upon the imposed flow, the ratio $\sigma$ of $\mathrm{Pe}$ to $\mathrm{Re}$ is a material property of the fluid; in heat transport, $\sigma$ is known as the Prandtl number; in mass transport, it is the Schmidt number.

The quantity of interest is the net (heat or mass) flux from the body. Normalised by the flux corresponding to pure diffusion, it is known as the Nusselt number – a function of $\mathrm{Re}$ and $\mathrm{Pe}$ . It is desirable to derive correlations which describe the variations of the Nusselt number with $\mathrm{Re}$ and $\mathrm{Pe}$ ; while these are typically obtained empirically using experimental data [20], asymptotic approximations may be used to extract the limiting forms of these correlations from first principles [23]. The simplest problem involves uniform streaming at large distances; both the 3-D and 2-D geometries are of interest.

Unsurprisingly, original asymptotic analyses have been concerned with large Reynolds numbers [5, 26]. There is nonetheless a considerable interest in small $\mathrm{Re}$ . That limit is singular, with the neglect of inertia breaking down at large distances from the body. While initial confrontations with that obstacle made use of the ad hoc Oseen approximation, the proper way to address it was clarified in the 1950s by the connoisseurs of singular perturbations [16–30]. It requires the use of matched asymptotic expansions, with an “inner” region on the scale of the body, where inertia is subdominant, and an “outer” Oseen region at distances comparable with the ratio of body size to $\mathrm{Re}$ , where inertial and viscous forces (or, equivalently, advective and diffusive transport of momentum) are comparable.

In this asymptotic framework, there is a crucial difference between the 3-D and 2-D problems. In 3-D, one may simply set $\mathrm{Re}$ to zero. The resulting Stokes flow, which coincides with the leading-order inner solution, satisfies the far-field approach to a uniform stream. The non-uniformity of the small $\mathrm{Re}$ limit appears only at leading-order inner correction, which cannot satisfy far-field decay (the Whitehead paradox). In 2-D, on the other hand, setting $\mathrm{Re}$ to zero results in an ill-posed problem (the Stokes paradox). Matched asymptotic expansions must therefore be used even in leading-order calculations.

It is unsurprising then that key progress in the analysis of forced transport under a uniform stream was carried out in 3-D, with the prototypic configuration involving a spherical particle. The Stokes flow in that geometry is, of course, well known [12]. The calculation for large $\mathrm{Pe}$ is described by Levich [25]. In that limit, transport is effectively restricted to a narrow boundary layer, where diffusion is comparable to advection [24]. The other extreme, of small $\mathrm{Pe}$ , was analysed by Acrivos & Taylor [2]. In that limit, interest lies in the correction to the unity Nusselt number associated with pure diffusion. That limit is also singular, as the perturbation to the spherically symmetric reference state cannot satisfy far-field decay. Thus, it requires the use of matched asymptotic expansions in the spirit of Proudman & Pearson [30], now with an Oseen-like outer region at distances comparable with ratio of particle size to $\mathrm{Pe}$ .

While the 3-D configuration represents settling problems, the 2-D configuration constitutes a model for heat transfer from wires, a problem that has been studied experimentally since the 1940s [20, 29–27]. Here, the prototypic geometry entails an infinite circular cylinder in crossflow. For large Reynolds numbers, theoretical modelling goes back to the irrotational investigations of Boussinesq [4] and King [19]. For small Reynolds numbers, theoretical progress has been frustrated by the above-mentioned difficulties in the flow problem. Initial investigations, concerned with heat transport in air (where the Prandtl number $\sigma =0.73$ ), considered the situation where Péclet is small too [7, 32], using an Oseen approximation in the analysis of the energy equation. Systematic asymptotic expansions were carried out independently by Kassoy [18], who accounted for variations of the thermal conductivity with temperature, and by Hieber & Gebhart [13] who considered two cases: the first being moderate $\sigma$ , where the Reynolds and Péclet number are comparable; the second being moderately large $\sigma$ , where the Péclet number, while asymptotically larger than $\mathrm{Re}$ , remains small (that limit is realised by taking $\sigma$ proportional to $\mathrm{Re}^{-\alpha }$ , with $0\lt \alpha \lt 1$ ). The second case presumably provides a model for heat transport in water ( $\sigma =6.82$ ).

The discrepancies between the predictions of the above approximations and existing experimental data have motivated exact calculations using numerical solutions of the Full Navier–Stokes equations [9]. The Nusselt numbers calculated in that manner compared favourably with the experiments of Collis & Williams [8]. While these solutions supplement the empirical correlations in the field [20, 6], they still lack the convenience of an asymptotic approximation. Our goal is to derive such approximations for Nusselt numbers at small $\mathrm{Re}$ and large $\mathrm{Pe}$ , following the analysis of the comparable 3-D problem [23, 25]. Prior to providing a more precise plan, we need to address the shortcomings of the classical approximations in the singular limit $\mathrm{Re}\ll 1$ .

2. The hybrid method

To understand the deficiencies of classical small- $\mathrm{Re}$ approximations in 2-D, it is beneficial to discuss the difference between 3-D and 2-D in some detail. In the 3-D analysis of a sphere in a uniform stream, the asymptotic expansions are essentially carried out in powers of $\mathrm{Re}$ : while logarithmic terms appear, they may be grouped together with the associated powers, following Fraenkel’s warning [10]. This allows for a straightforward use of the Van Dyke matching rule [31]. Since the asymptotic error is algebraically small, the predictions are reasonably accurate for sufficiently small values of $\mathrm{Re}$ . In that scheme, moreover, the leading-order flow in the outer region is simply a uniform stream. This enables a convenient Oseen linearisation of the Navier–Stokes equations in that region.

In 2-D, the leading-order velocity field in the inner region diverges logarithmically with distance, in accordance with the Stokes paradox. As a consequence, a streaming flow would not constitute a solution to the leading-order outer problem when expanding in powers of $\mathrm{Re}$ . With the desire for a linearisation of the differential equation in the outer region, classical 2-D analyses resorted to an asymptotic expansion in inverse powers of $\log \mathrm{Re}$ (referred hereafter as “inverse-log expansion”). This procedure has serious shortcomings, which are all related. The first is that the asymptotic error is only logarithmically small; thus, unless $\mathrm{Re}$ is extremely small, the accuracy of the scheme is rather poor. The second is the mathematical complexity associated with the need to obtain more than one term in the inner region [17]. The third is that Van Dyke’s matching rule cannot be applied [10]. Asymptotic matching thus requires the more delicate apparatus of intermediate variables.

Ideally, one would want to “sum” the inverse-log expansion, thereby obtaining an algebraic accuracy. This goal was effectively accomplished in the (relatively) recent work Ward & coworkers [21, 14]. The key principle in this work is the adherence to expansion in powers of $\mathrm{Re}$ , disregarding its logarithms [10]. This allows for the use of Van Dyke’s matching rule and provides an algebraic accuracy. In the inner region, the streamfunction possesses a simple mathematical form and is derived up to an unknown pre-factor $S$ , a function of $\log \mathrm{Re}$ (representing the summation of an inverse-log expansion). The challenge in that methodology, of course, has to do with the leading-order problem in the outer region, which involves the nonlinear Navier–Stokes equation. Ward & coworkers adopted a hybrid approach, where the nonlinear equation is solved numerically, subject to matching with the inner solution, which appears as a point singularity. The key part in that nonlinear calculation involves the computation of the regular part of the singularity structure as a function of the strength of the singularity. This procedure, in turn, provides the missing pre-factor $S$ as an implicit function of $\log \mathrm{Re}$ . Since the outer region is single-scaled, the hybrid approach is superior to a direct solution of the full Navier–Stokes equation governing the exact problem, which would require the simultaneous resolution of two disparate length scales.

In the papers of Ward & coworkers, the quantity of interest is the hydrodynamic drag. Since that quantity is expressed in terms of the Newtonian stresses at the boundary, it may be calculated using the details of the inner solution. In particular, it is proportional to the pre-factor $S$ . Similarly, the present transport problem, focused at the limit of large $\mathrm{Pe}$ , is effectively restricted to a narrow layer about the boundary of the cylinder – a province contained in the inner region of the flow problem. From our perspective, then, the hybrid method transforms the entire complexity of the small- $\mathrm{Re}$ hydrodynamics to the calculation of the pre-factor, which has already been carried out by Ward & coworkers.

3. Problem formulation

A rigid circular cylinder (radius $a$ ) is held fixed within a viscous fluid (kinematic viscosity $\nu$ ) which is streaming perpendicular to the cylinder axis with velocity $\mathcal U$ . We are concerned with the associated forced convection of a scalar property which undergoes both passive advection and diffusion, say with a uniform diffusivity $D$ . We consider the common scenario where that property is uniformly prescribed on the cylinder boundary at a fixed value, say $\Delta$ , relative to the equilibrium value at large distances. For concreteness, we shall refer to heat transport, where said property is the temperature. The description is equally adequate to describe mass transport, where the transported property is the solute concentration.

It is convenient to employ a dimensionless notation, where length variables are normalised by $a$ and velocities by $\mathcal U$ . The dimensionless flow problem is governed by a single parameter, the Reynolds number $\mathrm{Re}=a\,\mathcal U/\nu$ . Similarly, the transport problem is governed by a single parameter, the Péclet number $\mathrm{Pe} = a\,\mathcal U/D$ . Their ratio,

(3.1) \begin{equation} \sigma = \mathrm{Pe}/\mathrm{Re}=\nu/D, \end{equation}

is the Prandtl number. Since the flow and transport problems are both two-dimensional, it is only the cylinder cross section that enters the geometry. Hereafter, it is referred to as “the circle.” The two-dimensional problem is schematically depicted in Figure 1.

Figure 1. Problem schematic, conceptually indicating the pertinent asymptotic regions in the double limit (3.15).

In describing the 2-D flow and transport problems we employ polar $(r,\theta )$ coordinates with the origin at the circle centre and the “leading edge” at $\theta =0$ , see Figure 1. We begin with formulating the flow problem, which is independent of the temperature. Writing the velocity field as $\textbf{u} = u\hat{\textbf{e}}_r + v\hat{\textbf{e}}_\theta$ , it is convenient to employ the streamfunction $\psi$ , defined by

(3.2) \begin{equation} u = \frac{1}{r}\frac{\partial \psi }{\partial \theta }, \quad v= - \frac{\partial \psi }{\partial r}, \end{equation}

so the continuity equation is trivially satisfied. In terms of $\psi$ , the Navier–Stokes equations read

(3.3) \begin{equation} \nabla ^4\psi = \frac{\mathrm{Re}}{r} \frac{\partial (\psi,\nabla ^2\psi )}{\partial (\theta,r)}, \end{equation}

wherein

(3.4) \begin{equation} \nabla ^2 = \frac{\partial ^2}{\partial r^2}+ \frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial ^2}{\partial \theta ^2} \end{equation}

is the Laplacian operator in polar coordinates. The streamfunction needs to satisfy the impermeability and no-slip conditions,

(3.5) \begin{equation} \psi = \frac{\partial \psi }{\partial r} = 0 \quad \text{at} \quad r=1, \end{equation}

where we exploit the freedom in the definition of $\psi$ , and the far-field approach to a uniform stream,

(3.6) \begin{equation} \psi \sim -r\sin \theta \quad \text{as} \quad r\to \infty. \end{equation}

It is evident from the problem symmetry that $\psi$ satisfies

(3.7) \begin{equation} \psi (r,-\theta ) = -\psi (r,\theta ). \end{equation}

Once $\textbf{u}$ is calculated from the above nonlinear problem, we can address the transport problem. The dependent variable is the excess temperature, relative to the far-field equilibrium value; normalised by $\Delta$ , it is denoted by $T$ . The transport problem is governed by the advection–diffusion equation,

(3.8) \begin{equation} \nabla ^2{T} = \mathrm{Pe} \,\textbf{u}\boldsymbol{\cdot }\boldsymbol{\nabla }{T} \end{equation}

(where the continuity equation has been used) together with the imposed temperature at the circle,

(3.9) \begin{equation}{T}=1 \quad \text{at} \quad r=1, \end{equation}

and the decay condition

(3.10) \begin{equation} \lim _{r\to \infty }{T}=0. \end{equation}

With $\textbf{u}$ regarded as known, the above problem is linear. It is evident from the problem symmetry that the temperature satisfies

(3.11) \begin{equation}{T}(r,-\theta ) ={T}(r,\theta ). \end{equation}

Our interest lies not in the detailed transport process but rather in the net flux from the cylinder. It is represented by the Nusselt number [33]

(3.12) \begin{equation} \mathrm{Nu} = -\frac{1}{2\pi }\int _{-\pi }^{\pi } \left .\frac{\partial{T}}{\partial r}\right |_{r=1}\, d \theta, \end{equation}

or, making use of the symmetry (3.11),

(3.13) \begin{equation} \mathrm{Nu} = -\frac{1}{\pi }\int _0^{\pi } \left .\frac{\partial{T}}{\partial r}\right |_{r=1}\, d \theta. \end{equation}

The Nusselt number is evidently a function of both $\mathrm{Re}$ and $\mathrm{Pe}$ :

(3.14) \begin{equation} \mathrm{Nu}=\mathrm{Nu}(\mathrm{Re},\mathrm{Pe}). \end{equation}

Our interest is in deriving an asymptotic approximation for $\mathrm{Nu}$ in the limit

(3.15) \begin{equation} \mathrm{Re}\to 0, \quad \mathrm{Pe}\to \infty, \end{equation}

which necessitates large Prandtl numbers [recall (3.1)]

(3.16) \begin{equation} \sigma \to \infty. \end{equation}

Given the expected boundary-layer structure, $\mathrm{Nu}$ is anticipated [23] to exhibit a $\mathrm{Pe}^{1/3}$ scaling at large $\mathrm{Pe}$ ,

(3.17) \begin{equation} \mathrm{Nu} \sim f(\mathrm{Re}) \mathrm{Pe}^{1/3} \quad \text{for} \quad \mathrm{Pe}\to \infty. \end{equation}

That scaling relation holds for all $\mathrm{Re}$ . As $\mathrm{Re}\to 0$ , $f(\mathrm{Re})$ does not attain a limit; rather, it becomes a slowly-varying function of $\mathrm{Re}$ . It is convenient to make that dependence explicit by writing

(3.18) \begin{equation} f(\mathrm{Re}) = F(\chi ), \end{equation}

wherein $F$ is a moderately-varying function. There is a freedom is defining $\chi$ , with some natural choices being $\log \mathrm{Re}$ , $\log (1/\mathrm{Re})$ and $1/\log (1/\mathrm{Re})$ . For compatibility with Hormozi & Ward [14], we here define

(3.19) \begin{equation} \chi = \left (\log \frac{1}{\mathrm{Re}}-\frac{1}{2}\right )^{-1}. \end{equation}

We conclude that

(3.20) \begin{equation} \mathrm{Nu} \sim F(\chi ) \mathrm{Pe}^{1/3} \quad \text{for} \quad \mathrm{Pe}\to \infty \quad \text{with} \quad \mathrm{Re}\to 0. \end{equation}

Our goal is accordingly the calculation of the rescaled Nusselt number $F(\chi )$ .

4. Flow problem at small $\mathrm{Re}$

We need an asymptotic approximation for $\textbf{u}$ in the limit $\mathrm{Re}\to 0$ . As explained in Sec. 2, this requires the use of matched asymptotic expansions. In what follows, we summarise briefly the approach of Ward and coworkers [21, 14]. It involves an asymptotic expansion in powers of the small parameter $\mathrm{Re}$ , grouping together terms that differ by $\log \mathrm{Re}$ . In the inner region, where $r=\text{ord}(1)$ , we pose the asymptotic expansion

(4.1) \begin{equation} \psi (r,\theta ;\;\mathrm{Re}) \sim \psi _0(r,\theta ;\;\chi ) + \text{alg} \end{equation}

wherein “alg” represents an asymptotic error which is algebraically small (i.e. smaller than some positive power of $\mathrm{Re}$ ). The leading term $\psi _0$ satisfies the biharmonic equation [cf. (3.3)],

(4.2) \begin{equation} \nabla ^4\psi _0 = 0, \end{equation}

and the boundary conditions [cf. (3.5)]

(4.3) \begin{equation} \psi _0 = \frac{\partial \psi _0}{\partial r} = 0 \quad \text{at} \quad r=1. \end{equation}

Since the far-field condition (3.6) does not apply in the inner region, the symmetry condition [cf. (3.7)]

(4.4) \begin{equation} \psi _0(r,-\theta ) = -\psi _0(r,\theta ) \end{equation}

must be explicitly enforced.

With $\psi _0$ governed by a homogeneous problem, it is determined up to a multiplicative constant. The solution of (4.2)–(4.4) that is least singular as $r\to \infty$ is of the form

(4.5) \begin{equation} \psi _0(r,\theta ;\;\chi )={S}(\chi )\psi _c(r,\theta ), \end{equation}

where the canonical solution,

(4.6) \begin{equation} \psi _c =\left (\frac{r}{2}-r\log r-\frac{1}{2r} \right )\sin \theta, \end{equation}

is $O(r\log r)$ at large $r$ ,

(4.7) \begin{equation} \psi _c \sim r\left (\frac{1}{2}-\log r\right )\sin \theta + \text{alg} \quad \text{as} \quad r \to \infty. \end{equation}

The pre-factor $S$ can only be determined via asymptotic matching. Consider now the outer region, at distances $r=\text{ord}(1/\mathrm{Re})$ , where inertial and viscous forces are comparable (see Figure 1). Using the stretched radial coordinate $\rho = \mathrm{Re} \,r$ , the outer streamfunction $\Psi = \mathrm{Re}^{-1}\psi$ is governed by the differential equation,

(4.8) \begin{equation} \nabla ^4_\rho \Psi = \frac{1}{\rho } \frac{\partial (\Psi,\nabla ^2_\rho \Psi )}{\partial (\theta,\rho )}, \end{equation}

wherein

(4.9) \begin{equation} \nabla ^2_\rho = \frac{\partial ^2}{\partial \rho ^2}+ \frac{1}{\rho }\frac{\partial }{\partial \rho }+\frac{1}{\rho ^2}\frac{\partial ^2}{\partial \theta ^2}. \end{equation}

is the Laplacian with respect to the stretched coordinates [cf. (3.4)]. In addition, it satisfies the approach to a uniform stream

(4.10) \begin{equation} \Psi \sim -\rho \sin \theta \quad \text{as} \quad \rho \to \infty \end{equation}

and the requirement of asymptotic matching with the inner solution.

Similarly to (4.1), we introduce the outer expansion,

(4.11) \begin{equation} \Psi (\rho,\theta ;\;\mathrm{Re}) \sim \Psi _0(\rho,\theta ;\;\chi ) + \text{alg}. \end{equation}

The leading-order field $\Psi _0$ satisfies the original equation (4.8),

(4.12) \begin{equation} \nabla ^4_\rho \Psi _0 = \frac{1}{\rho } \frac{\partial (\Psi _0,\nabla ^2_\rho \Psi _0)}{\partial (\theta,\rho )}, \end{equation}

and the remote condition (4.10),

(4.13) \begin{equation} \Psi _0 \sim -\rho \sin \theta \quad \text{as} \quad \rho \to \infty. \end{equation}

The separation by powers of $\mathrm{Re}$ allows for the use of Van-Dyke matching. Making use of (4.5) and (4.7) in conjunction with (3.19), it follows that

(4.14) \begin{equation} \Psi _0 \sim -{S}(\chi ) \rho \left (\log \rho +{1}/{\chi }\right )\sin \theta \quad \text{as} \quad \rho \to 0. \end{equation}

The nonlinear problem (4.12)–(4.14) was solved numerically in [14]. That solution provides $\Psi _0$ , and, more importantly, ${S}(\chi )$ . The function ${S}(\chi )$ is tabulated in Table 1, using values obtained in [14]. It is considered hereafter as known. Accordingly, so is $\psi _0$ .

Table 1. The function $S(\chi)$ , tabulated using the calculation of [14]. The range of $\chi$ -values is restricted to $\mathrm{Re}\lt 1/2$

5. The limit $\mathrm{Pe}\to \infty$

In analysing the transport problem (3.8)–(3.10) in the limit $\mathrm{Pe}\to \infty$ , we find from (3.8)

(5.1) \begin{equation} \textbf{u}\boldsymbol{\cdot }\boldsymbol{\nabla }{T}=0. \end{equation}

It follows that $T$ is constant along streamlines. Since the streamlines are open, originating at infinity, condition (3.10) gives

(5.2) \begin{equation}{T}\equiv 0. \end{equation}

In fact, with (5.2) being an exact solution of (3.8) and (3.10), the asymptotic correction to (5.2) is exponentially small.

Since the Dirichlet condition (3.9) is incompatible with (5.2), a boundary layer is formed about the boundary $r=1$ . In that layer, whose width $\delta (\ll 1)$ is yet undetermined, the diffusive and advective terms in (3.8) are comparable. To determine these terms, we need to approximate the velocity components in the layer, where $r-1\ll 1$ . We readily find from (4.5)–(4.6)

(5.3) \begin{equation} u_0 \sim -{S}(\chi )(r-1)^2\cos \theta, \quad v_0\sim 2{S}(\chi )(r-1)\sin \theta. \end{equation}

In what follows we denote the leading-order boundary-layer temperature by $\Theta$ . Defining the stretched radial coordinate,

(5.4) \begin{equation} Y = \frac{r-1}{\delta (\mathrm{Pe})}, \end{equation}

we find using (5.3) that the advective term (i.e. the right-hand side) of (3.8) is

(5.5) \begin{equation} \sim{S}(\chi ) \mathrm{Pe}\, \delta \left (2Y\frac{\partial \Theta }{\partial \theta }\sin \theta - Y^2\frac{\partial \Theta }{\partial Y}\cos \theta \right ) \end{equation}

within the boundary layer, while the diffusive term (i.e. the left-hand side) of (3.8) is $\sim \delta ^{-2} \partial ^2\Theta/\partial Y^2$ there, dominated by transverse variations. Balancing the terms provides the anticipated scaling

(5.6) \begin{equation} \delta = \mathrm{Pe}^{-1/3} \end{equation}

of the boundary-layer thickness, see Figure 1.

We conclude that, within the boundary layer, $\Theta$ is governed by the parabolic equation

(5.7) \begin{equation} \frac{\partial ^2\Theta }{\partial Y^2} ={S}(\chi ) \left (2Y\frac{\partial \Theta }{\partial \theta }\sin \theta - Y^2\frac{\partial \Theta }{\partial Y}\cos \theta \right ). \end{equation}

This equation is subject to the Dirichlet condition [cf. (3.9)],

(5.8) \begin{equation} \Theta =1 \quad \text{at} \quad Y=0, \end{equation}

and matching with (5.2),

(5.9) \begin{equation} \lim _{Y\to \infty }\Theta =0. \end{equation}

The associated approximation for the Nusselt number (3.13) is

(5.10) \begin{equation} \mathrm{Nu}\sim -\frac{\mathrm{Pe}^{1/3}}{\pi }\int _0^{\pi } \left .\frac{\partial \Theta }{\partial Y}\right |_{Y=0}\, d \theta. \end{equation}

6. Similarity solution

It is convenient to employ the independent variable $\eta =\cos \theta$ instead of $\theta$ . Thus, (5.7) becomes

(6.1) \begin{equation} \frac{\partial ^2\Theta }{\partial Y^2} = -{S}(\chi ) \left [2Y(1-\eta ^2)\frac{\partial \Theta }{\partial \eta } +Y^2\eta \frac{\partial \Theta }{\partial Y}\right ] \end{equation}

while (5.10) gives

(6.2) \begin{equation} \mathrm{Nu} \sim -\frac{\mathrm{Pe}^{1/3}}{\pi }\int _{-1}^1 \left .\frac{\partial \Theta }{\partial Y}\right |_{Y=0}\, \frac{d \eta }{(1-\eta ^2)^{1/2}}. \end{equation}

It is well known that problems governed by equations of the form (6.1) adopt a similarity solution [1]. We define the similarity variable,

(6.3) \begin{equation} \zeta = \frac{Y}{g(\eta )}, \end{equation}

where the function $g$ remains to be determined. The temperature becomes a function of the single variable $\zeta$ , say $\Omega (\zeta )$ . In terms of that function, (6.2) becomes

(6.4) \begin{equation} \mathrm{Nu}\sim -\frac{\mathrm{Pe}^{1/3}\Omega '(0)}{\pi }\int _{-1}^1 \frac{d \eta }{g(\eta )(1-\eta ^2)^{1/2}}, \end{equation}

where the prime denotes differentiation.

Substituting of (6.3) into conditions (5.8)–(5.9) gives

(6.5) \begin{equation} \Omega (0)=1, \quad \Omega (\infty )=0. \end{equation}

Also, substitution of (6.3) into (6.1) yields

(6.6) \begin{equation} \Omega ''(\zeta ) ={S}(\chi ) \zeta ^2 \Omega '(\zeta ) \left [\frac{2}{3}(1-\eta ^2)h'-\eta h\right ] \end{equation}

wherein

(6.7) \begin{equation} h=g^3. \end{equation}

For consistency with the similarity ansatz we require,

(6.8) \begin{equation} \frac{2}{3}(1-\eta ^2)h'-\eta h = \text{const}. \end{equation}

The constant cannot be zero, as the resulting equation $\Omega ''=0$ is incompatible with (6.5). For the same reason it cannot be positive. There is a freedom in choosing the negative constant: since any choice amounts to a rescaling of $g$ , it is merely equivalent to a redefinition of $\zeta$ . Here we find it convenient to set the constant to $-3$ , whereby (6.6) reduces to the ordinary differential equation,

(6.9) \begin{equation} \Omega ''(\zeta ) + 3{S}\zeta ^2\Omega '(\zeta ) = 0. \end{equation}

The solution of that equation subject to conditions (6.5) is

(6.10) \begin{equation} \Omega = 1-\frac{1}{ \Gamma (4/3)}\int _0^{{S}^{1/3}\zeta }e^{-t^3}\,d t, \end{equation}

wherein $\Gamma$ is the Gamma function. In particular, $\Omega '(0)= -{{S}^{1/3}}/{\Gamma (4/3)}$ . Substitution into (6.4) and comparing with (3.18) yields

(6.11) \begin{equation} F(\chi )= \frac{{S}^{1/3}(\chi )}{\pi \Gamma (4/3)}\int _{-1}^1 \frac{d \eta }{g(\eta )(1-\eta ^2)^{1/2}}. \end{equation}

All that remains is to determine the function $g$ , or, equivalently, $h$ . The latter is governed by the first-order differential equation (6.8), with the constant set to $-3$ . Integration gives

(6.12) \begin{equation} h = \frac{K}{(1-\eta ^2)^{3/4}} - \frac{9\eta }{2(1-\eta ^2)^{3/4}} F_2^1\left (\frac{1}{4},\frac{1}{2},\frac{3}{2},\eta ^2\right ), \end{equation}

wherein $F_2^1$ is the hypergeometric function. The integration constant $K$ is determined by the requirement that the solution does not blow up at the “leading edge” $\eta =1$ . Using

(6.13) \begin{equation} \lim _{\eta \to 1} F_2^1\left (\frac{1}{4},\frac{1}{2},\frac{3}{2},\eta ^2\right ) = \frac{\pi ^{3/2}}{2^{1/2} \Gamma (1/4) \Gamma (5/4)} \end{equation}

we obtain

(6.14) \begin{equation} K = \frac{9\pi ^{3/2}}{8^{1/2} \Gamma (1/4) \Gamma (5/4)}. \end{equation}

Note that $h$ still blows up at the “trailing edge” $\eta =-1$ . The associated divergence there of $g$ , like $(1-\eta ^2)^{-1/4}$ , is weaker than that found in the 3-D problem [23].

Substitution into (6.11) of (6.7), (6.12) and (6.14) yields the rescaled Nusselt number,

(6.15) \begin{equation} F(\chi )= \frac{1}{\Gamma (4/3)} \left [\frac{3{S}(\chi )}{2\Gamma ^2(1/4)\Gamma ^2(5/4)}\right ]^{1/3}. \end{equation}

Numerical evaluation of the Gamma function gives

(6.16) \begin{equation} F(\chi )= 0.5799 [{S}(\chi )]^{1/3}, \end{equation}

which corresponds to the expression quoted in the abstract. The error incurred by the use of (3.20) with (6.15) is algebraically small in both $\mathrm{Re}$ and $\mathrm{Pe}$ .

7. Comparison with numerical solution

It is illustrative to compare our approximation with the numerical calculations of Dennis et al. [9], who solved the full Navier–Stokes equations and the advection–diffusion equation governing the companion transport problem. (Note that their Reynolds and Nusselt numbers are based upon the circle diameter, rather than radius.) The only data in [9] relevant to the double limit (3.15) considered herein are presented in their table III, which provides $\mathrm{Nu}/\sigma ^{1/3}$ as a function of $\mathrm{Re}$ and $\sigma$ . The smallest Reynolds number in that table is (in the present notation) 0.25; at that $\mathrm{Re}$ , it gives (in the present notation) the value $0.256$ for $\mathrm{Nu}/\sigma ^{1/3}$ at the largest $\sigma$ -value employed there [corresponding to numerical convergence to the asymptotic limit (3.15)]. Comparing with (3.1) and (3.20), this corresponds to

(7.1) \begin{equation} F=0.4064. \end{equation}

Now, for $\mathrm{Re}=0.25$ , we find from (3.19) $\chi =1.1283$ . This value is close to $\chi =1.1469$ in the present Table 1, for which $S=0.332$ . Substituting that $S$ -value into (6.15) gives $F(\chi )=0.4016$ .

Since the Reynolds number is rather modest, the above agreement with (7.1) is quite remarkable. Given the singular nature of the small- $\mathrm{Re}$ limit, it is hardly surprising that [9] did not report numerical data for smaller values of $\mathrm{Re}$ : indeed, a numerical solution at small $\mathrm{Re}$ needs to resolve two disparate length scales, namely $1$ (cylinder scale) and $1/\mathrm{Re}$ (Oseen scale). The smaller is $\mathrm{Re}$ , the more difficult is the numerical challenge. On the other hand, the present approximation (6.16), where the asymptotic error is algebraically small, only improves as $\mathrm{Re}$ diminishes.

It is interesting to compare our asymptotic prediction with that provided by an inverse-log expansion [17, 30]. The leading-order approximation resulting from that expansion is equivalent to replacing $S$ by $a_1(\log \mathrm{Re})^{-1}$ with $a_1=-1$ . Substitution into (6.16) and (3.20) gives

(7.2) \begin{equation} \mathrm{Nu} \sim 0.5799 \left (\frac{-\mathrm{Pe}}{\log{\mathrm{Re}}}\right )^{1/3}. \end{equation}

This is a very simple approximation that does not require the use of the function $S(\chi )$ . It is, however, rather crude. For $\mathrm{Re}=0.25$ , it gives the value $0.5201$ for $\mathrm{Nu}/\mathrm{Pe}^{1/3}$ , about $25\%$ larger than the numerical prediction (7.1).

An attempt to improve the approximation by incorporating more terms only makes matters worse. (Hardly surprising, given the modest value of $\mathrm{Re}$ .) Thus, using a 2-term expansion amounts to replacing $S$ by

(7.3) \begin{equation}{a_1}({\log \mathrm{Re}})^{-1} +{a_2}({\log \mathrm{Re}})^{-2}, \end{equation}

where $a_2=\gamma _E-1/2-\log 4$ , $\gamma _{\text{E}}=0.57721\ldots$ being the Euler–Mascheroni constant. That “improved” approximation gives the value $0.1986$ for $\mathrm{Nu}/\mathrm{Pe}^{1/3}$ .

8. Concluding remarks

When adhering to the asymptotic principle of separation by powers, the inner flow field in the small- $\mathrm{Re}$ limit is given by the simple structure (4.5)–(4.6). The function $S(\chi )$ has already been calculated by the hybrid scheme of Hormozi & Ward [14]. This allows for analysing forced convection problem at low Reynolds number conditions. In this paper, we have focused upon the limit $\mathrm{Pe}\to \infty$ , where transport is effectively confined to a narrow boundary layer. The velocity in that layer is readily obtained via a Taylor approximation of the inner field of Hormozi & Ward [14]. With that closed-form approximation, it is straightforward to obtain a similarity solution of the boundary-layer transport, resembling the classical solution of Levich in 3-D [25]. In particular, that solution furnishes the Nusselt number (6.15), which is the quantity of interest. We found excellent agreement between our asymptotic prediction and the numerical results of Dennis et al. [9]; we reiterate that these results are in agreement with the experiments of Collis & Williams [8].

The present limit (3.15) of small $\mathrm{Re}$ and large $\mathrm{Pe}$ was briefly mentioned by Frankel & Acrivos [11], who present a formula of the form (7.2). Noting that their Péclet and Nusselt numbers are based upon the circle diameter, we find that the number pre-factor appearing in their formula (adapted to the present notation) is $0.5808$ . Frankel & Acrivos [11] cite Acrivos & Taylor [2] as the source of that approximation, but we could not find any relevant derivation in that earlier paper. In any event, it is evident at this stage that approximations based upon an inverse-log expansion are quite limited.

Otherwise, the present limit has been addressed by Kurdyumov & Dernández [22]. The streamfunction they employ [see their (8)], presumably valid at the inner region, is not the correct one, but that may be a mere typo. For some reason, Kurdyumov & Dernández [22] solve the resulting boundary-layer problem numerically, even though a similarity solution is known to exist [1]. Given the singular behaviour of the boundary-layer problem at the trailing edge, such numerical solutions are quite difficult to perform. Worse yet, they appear to offer little advantage over the exact solutions of Dennis et al. [9].

For the convenience of future users, we recapitulate our approximation in a dimensional form (say for the case of mass transfer, where $\Delta$ has the dimensions of solute concentration). Using (3.12) and (3.20), we find that the net flux from the cylinder, per unit length, is

(8.1) \begin{equation} J \left [ D^2 a\,\mathcal U{S}(\chi )\right ]^{1/3} \Delta \end{equation}

wherein [cf. (6.15)]

(8.2) \begin{equation} J = \frac{2\pi }{\Gamma (4/3)} \left [\frac{3}{2\Gamma ^2(1/4)\Gamma ^2(5/4)}\right ]^{1/3} = 3.6439\ldots. \end{equation}

The parameter $\chi$ appearing in (8.1) is given by (3.19), while the function $S$ is tabulated in Table 1.

As shown in [21], the hybrid scheme may be readily extended to non-circular cross sections. In the outer region, equations (4.12)–(4.13) are unaffected by the cross-sectional shape. The only difference would therefore enter through the matching condition (4.14), as the shape clearly affects the inner solution. In that region, $\psi _0$ is still governed by the biharmonic equation (4.2), with conditions (4.3) replaced by

(8.3) \begin{equation} \psi _0 = \frac{\partial \psi _0}{\partial n} = 0 \end{equation}

at the cylinder boundary. Generalising (4.6), the canonical solution $\psi _c$ is defined as the least singular solution of that homogeneous problem that is $\sim -r \log r \sin \theta$ for $r\to \infty$ . The pre-factor $S(\chi )$ is still defined by (4.5). It follows that the asymptotic behaviour (4.7) remains intact, provided the constant $1/2$ is replaced by a different constant, say $1/2-\log d$ :

(8.4) \begin{equation} \psi _c \sim r\left (\frac{1}{2}-\log d -\log r\right )\sin \theta + \text{alg} \quad \text{as} \quad r \to \infty. \end{equation}

The “effective radius” $d$ is determined by the inner solution, which provides the detailed expression for $\psi _c$ . It readily follows that (4.14) remains as is, provided $\mathrm{Re}$ in (3.19) is replaced by the product of $\mathrm{Re}$ with $d$ . Hormozi & Ward [14] showed how similar modifications may be applied to other generalisations (Navier slip, porosity) of the problem (for a circular cross section).

It is, therefore, plausible that the hybrid scheme may be applicable to numerous extensions of the fundamental problem considered in this contribution.