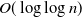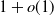Average distance in a general class of scale-free networks

Abstract

In Chung–Lu random graphs, a classic model for real-world networks, each vertex is equipped with a weight drawn from a power-law distribution, and two vertices form an edge independently with probability proportional to the product of their weights. Chung–Lu graphs have average distance $O(\log\log n)$ and thus reproduce the small-world phenomenon, a key property of real-world networks. Modern, more realistic variants of this model also equip each vertex with a random position in a specific underlying geometry. The edge probability of two vertices then depends, say, inversely polynomially on their distance.

In this paper we study a generic augmented version of Chung–Lu random graphs. We analyze a model where the edge probability of two vertices can depend arbitrarily on their positions, as long as the marginal probability of forming an edge (for two vertices with fixed weights, one fixed position, and one random position) is as in a Chung–Lu random graph. The resulting class contains Chung–Lu random graphs, hyperbolic random graphs, and geometric inhomogeneous random graphs as special cases.

Our main result is that every random graph model in this general class has the same average distance as a Chung–Lu random graph, up to a factor of $1+o(1)$. This shows in particular that specific choices, such as taking the underlying geometry to be Euclidean, do not significantly influence the average distance. The proof also shows that every random graph model in our class has a giant component and polylogarithmic diameter with high probability.

1. Introduction

Many large real-world networks, such as social networks or the internet infrastructure, are scale-free, i.e., their degree distribution follows a power law with parameter $2 \lt \beta \lt 3$ [22]. Such networks have been studied in detail since the 1960s. One of the key findings concerning them is the small-world phenomenon, which is the observation that two nodes in a network typically have very small graph-theoretic distance. In the nineties, this phenomenon was explained by theoretical models of random graphs. Since then, random graph models have been the basis for the statistical study of real-world networks, as they provide a macroscopic perspective and reproduce structural properties observed in real data. In this line of research, one studies the diameter of a graph, i.e., the largest distance between any pair of vertices in the largest component, and its average distance, i.e., the expected distance between two random nodes of the largest component. A random graph model is said to be small-world if its diameter is bounded by $(\!\log n)^{O(1)}$ or even $O(\!\log n)$ , and ultra-small-world if its average distance is only $O(\!\log \log n)$ .

Chung–Lu random graphs are a prominent model of scale-free networks [15, 16]. In this model, every vertex v is equipped with a weight ${\mathsf{w}_{v}}$ , and two vertices u,v are connected independently with probability $\min\{1, {\mathsf{w}_{u}} {\mathsf{w}_{v}} / {\mathsf{W}}\}$ , where ${\mathsf{W}}$ is the sum over all weights ${\mathsf{w}_{v}}$ . The weights are typically assumed to follow a power-law distribution with power-law exponent $\beta>2$ . Chung–Lu random graphs have the ultra-small-world property, since in the range $2 \lt \beta \lt 3$ the average distance is $(2 \pm o(1)) \frac{\log \log(n)}{|\log(\beta -2)|}$ [15, 16].

However, Chung–Lu random graphs fail to capture other important features of real-world networks, such as high clustering or navigability. This is why dozens of papers have proposed more realistic models which also possess some local structure, many of which combine Chung–Lu random graphs (or other classic models such as preferential attachment [3]) with an underlying geometry; see, e.g., hyperbolic random graphs [8, 28, 40], geometric inhomogeneous random graphs [12–14, 26, 30, 33], and many others [2, 9–11, 19, 20, 29, 42]. In these models, each vertex is additionally equipped with a random position in some underlying geometric space, and the edge probability of two vertices depends on their weights as well as the geometric distance between their positions. Typical choices for the geometric space are the unit square, circle, and torus, and typical choices for the dependence on the distance are inverse polynomial, exponential, and threshold functions. Such models can naturally yield a large clustering coefficient, since there are many edges among geometrically close vertices. For some of these models the average distance has been studied and shown to be the same as in Chung–Lu graphs, up to a factor $1+o(1)$ ; see, e.g., [1, 9, 19, 27].

It is unclear how much these results depend on the particular choice of the underlying geometry. In particular, it is not known whether any of the important properties of Chung–Lu random graphs transfer to versions with a non-metric underlying space. Such spaces are well motivated in the context of social networks, where two persons are likely to know each other if they share a feature (e.g., they are in the same sports club) regardless of their differences in other features (e.g., their profession), which gives rise to a non-metric distance (see Section 3).

Our contribution: As the main result of this paper, we prove that in the regime $2 \lt \beta \lt 3$ , all geometric variants of Chung–Lu random graphs have the same average distance $(2 \pm o(1)) \frac{\log \log(n)}{|\log(\beta -2)|}$ , showing universality of the ultra-small-world property.

We do this by analyzing a generic augmented and very general version of Chung–Lu random graphs. Here, each vertex is equipped with a power-law weight ${\mathsf{w}_{v}}$ and an independently random position ${\mathsf{x}_{v}}$ in some ground space $\mathcal{X}$ . Two vertices u,v form an edge independently with probability $p_{uv}$ that only depends on the positions ${\mathsf{x}_{u}}, {\mathsf{x}_{v}}$ (and u,v as well as model parameters like the weight sequence). The dependence on ${\mathsf{x}_{u}}, {\mathsf{x}_{v}}$ may be arbitrary, as long as the edge probability has the same marginal probabilities as in Chung–Lu random graphs. Specifically, for fixed ${\mathsf{x}_{u}}$ and random ${\mathsf{x}_{v}}$ we require that the marginal edge probability ${\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv} | {\mathsf{x}_{u}}]$ is within a constant factor of the Chung–Lu edge probability $\min\{1, {\mathsf{w}_{u}} {\mathsf{w}_{v}} / W\}$ . This is a natural property for any augmented version of Chung–Lu random graphs. Note that our model is stripped of any geometric specifics. In fact, the ground space is not even required to be metric. We retain only the most important features, namely power-law weights and the right marginal edge probabilities. Hence the main result also demonstrates that there exist random graph models with non-metric underlying geometry that still satisfy the ultra-small-world property.

Beyond the average distance, we establish that this general model is scale-free and has a giant component and polylogarithmic diameter. Thus all instantiations of augmented Chung–Lu random graphs share some basic properties that are considered important for models of real-world networks.

It it quite surprising that the average distance can be computed so precisely in this generality. For example, the clustering coefficient varies drastically between different instantiations of the model, as it encompasses the classic Chung–Lu random graphs, which have clustering coefficient $n^{-\Omega(1)}$ , as well as geometric variants that have constant clustering coefficient [14]. Therefore, our results hold on graphs with very different local structure. Note that by the scale-free property, all variants of the model contain $\Theta(n)$ edges. If an instance has high clustering, many edges are local edges inside well-connected subgraphs, and therefore useless for finding short paths between far vertices. Nevertheless, our main result implies that in such graphs the average distance is asymptotically the same as in Chung–Lu random graphs, where we have no clustering and every edge is potentially helpful when searching for short paths.

We also remark that our statements fail to hold for $\beta \gt 3$ . Indeed, graphs in this regime can look rather diverse depending on the model. For example, some instantiations in this regime do not even have a giant component; the largest component is of polynomial size $n^{1-\Omega(1)}$ [7]. On the other hand, it is also not hard to construct models for $\beta >3$ which do have a giant component, but still have polynomially large average distance; see Remark 1. This variety for $\beta >3$ makes it even more surprising that in the regime $2 \lt \beta \lt 3$ the average distance can be determined precisely for all instances at once. Moreover, models in which the marginal edge probability between u and v is not a function of the product ${\mathsf{w}_{u}} {\mathsf{w}_{v}}$ as in the Chung–Lu model also look rather diverse; see [27] for a systematic exploration.

A common property of all models in our general class is that for a set S of vertices whose weights sum to $W_S$ (often called volume in the literature), the expected number of half-edges going out from S is $\Theta(W_S)$ . For the classic Chung–Lu random graphs without geometry, the targets of these half-edges are independent of each other. Thus, the quantity $W_S$ is essentially sufficient to determine the size and the volume of the neighborhood $\Gamma(S)$ of S, and the analyses of Chung–Lu random graphs are based on this property. However, for non-trivial geometries the size of the neighborhood crucially depends on the geometric position of the vertices in S. For example, if the clustering coefficient is constant, then even if S consists of only two adjacent vertices there is already a non-negligible probability that they share some neighbors.

Note that this problem only affects the upper bound on the average distance, and indeed the lower bound carries over trivially from the analysis of Chung–Lu graphs: it is based on a first-moment method for counting the number of self-avoiding paths of length $(2-{{\varepsilon}})\frac{\log \log(n)}{|\log(\beta -2)|}$ with prescribed weight profile, and shows that the expected number of such paths between two random vertices is o(1) [21]. The expected number of such paths depends on the marginal probabilities ${\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv} | {\mathsf{x}_{u}}]$ , which we assume to be independent of ${\mathsf{x}_{u}}$ up to constant factors; see Section 7 for details. It is thus not surprising that the lower bound was already known.

However, the upper-bound proofs for classic Chung–Lu random graphs do not carry over to our general setting. Similarly, existing proofs for geometric scale-free networks [1, 19] cannot be transferred to our geometry-agnostic setting either, since they rely rather heavily on the specifics of the underlying geometry. Thus we need to develop new methods. Our key ingredient is the ‘bulk lemma’ (Lemma 9), which shows that it is unlikely that a vertex has a k-neighborhood of size at least k without having any vertex of high weight in this k-neighborhood. For Chung–Lu graphs, this statement is rather trivial, since each of the vertices in the k-neighborhood independently has a certain chance of connecting to a vertex of large weight. However, in geometric settings, these events are not independent: in an extreme case, all vertices in the k-neighborhood could occupy the same position $x\in \mathcal{X}$ , and a high-weight vertex might connect either to all of them or to none of them (cf. the threshold model in Example 3). So a priori it is not clear that increasing the size of the k-neighborhood will increase the chances that the k-neighborhood connects to a high-weight vertex. In previously studied geometric scale-free settings such as hyperbolic geometric graphs [1] or scale-free percolation [19], this problem can be avoided because vertices in these geometries do not cluster with arbitrary density. However, we do not have any such restrictions in our model. Instead, we prove Lemma 9 by a delicate and subtle analysis of the tail bounds of the degree distribution of vertices that would hold if the lemma were false; see the beginning of the proof of Lemma 9 for a more detailed proof sketch.

Once we have established the bulk lemma, the rest of the proof is more similar to previous proofs. By the bulk lemma, a vertex in the giant component can reach a vertex of polylogarithmic weight within k steps, with failure probability decaying in k. Then we use a ‘greedy path’ argument (Lemma 7), which constructs a path by always choosing the neighbor of highest weight. In this way, any vertex of polylogarithmic weight can be connected by an ultra-short path to the ‘heavy core’, which is well-connected and contains the vertices of highest weight. The length of this greedy path is so concentrated that it can be estimated by a worst-case estimate. For the initial part of the path, we bound its average length by applying the bulk lemma repeatedly for different values of k and carefully summing up the resulting terms.

Organization of the paper: In Section 2 we present the details and a precise definition of the model, and we formally state the results. In Section 2.3 we introduce some notation that we use throughout the paper. Then we discuss several special cases of the model in Section 3, including geometric inhomogeneous random graphs (GIRGs), the distance model with minimum component distance, and the threshold version of GIRGs, which includes threshold hyperbolic random graphs. We conclude this part of the paper with some remarks in Section 4.

The rest of the paper is dedicated to the proof of our main results. In Section 5 we prove a concentration inequality which will be used later in the proofs. After some basic and preliminary results in Section 6, we prove the connectivity properties and the main result in Section 7, and determine the degree distribution of our model in Section 8. Finally, we prove in Section 9 that the examples from Section 3 are indeed covered by our model.

2. Model and results

2.1. Definition of the model

In this paper we study the properties of a very general random graph model, where both the set of vertices V and the set of edges E are random. Each vertex v comes with a weight ${\mathsf{w}_{v}}$ , which will essentially be the expected degree of v, and with a random position ${\mathsf{x}_{v}}$ in a geometric space $\mathcal{X}$ . We now give the full definition, first for the weight sequence and then for the resulting random graph. In the discussion below and throughout the paper, we assume that the model parameters $\alpha,\beta, d, c_1, c_2, {\mathsf{w}_{\min}}$ are constants while $n\to \infty$ , and the hidden factors in Landau notation $O({\cdot}), \Omega({\cdot}), \ldots$ are universal for all vertices, edges, random variables, and non-constant parameters; see Section 2.3 for more detail.

Power-law weights: For every $n \in \mathbb{N}$ let ${\mathsf{w}_{}} = ({\mathsf{w}_{1}}, \ldots, {\mathsf{w}_{n}})$ be a non-increasing sequence of positive weights. We call ${\mathsf{W}} \,:\!=\, \sum_{v=1}^n {\mathsf{w}_{v}}$ the total weight. Throughout this paper we will assume that the weights follow a power law: the fraction of vertices with weight at least w is $\approx w^{1-\beta}$ for some $\beta > 2$ (the power-law exponent of ${\mathsf{w}_{}}$ ). More precisely, we assume that for some ${{\overline w}} = {{\overline w}}(n)$ with $n^{\omega(1/\log\log n)}\leq{{\overline w}} \leq n^{(1-\Omega(1))/(\beta-1)}$ , the sequence ${\mathsf{w}_{}}$ satisfies the following conditions:

(PL1) The minimum weight is bounded by constants, i.e.,

$${\mathsf{w}_{\min}} \,:\!=\, \min\{{\mathsf{w}_{v}} \mid 1 \le v \le n\} = \Theta(1).$$

(PL2) For all $\eta \gt 0$ there exist constants $c_1,c_2 \gt 0$ such that

$$c_1\frac{n}{w^{\beta-1+\eta}} \leq \#\{1 \le v \le n \mid {\mathsf{w}_{v}} \geq w\} \leq c_2\frac{n}{w^{\beta-1-\eta}},$$

where the first inequality holds for all ${\mathsf{w}_{\min}} \leq w \leq {{\overline w}}$ and the second for all $w \geq {\mathsf{w}_{\min}}$ .

We remark that these are standard assumptions for power-law graphs with average degree $\Theta(1)$ . Note that since ${{\overline w}} \leq {(1-\Omega(1))/(\beta-1)}$ , there are $n^{\Omega(1)}$ vertices with weight at least ${{\overline w}}$ . On the other hand, no vertex has weight larger than $(c_2n)^{1/(\beta-1-\eta)}$ .

Random graph model: Let $\mathcal{X}$ be a non-empty set, and assume we have a measure $\mu$ on $\mathcal{X}$ that allows us to sample elements from $\mathcal{X}$ . We call $\mathcal{X}$ the ground space of the model and the elements of $\mathcal{X}$ positions. The random graph $\mathcal{G}(n,\mathcal{X},{\mathsf{w}_{}},p)$ has vertex set $V=[n] = \{1,\ldots,n\}$ . For any vertex v we independently draw a position ${\mathsf{x}_{v}} \in \mathcal{X}$ according to the measure $\mu$ . Conditional on ${\mathsf{x}_{1}}, \ldots, {\mathsf{x}_{n}}$ , we connect any two vertices $u \ne v$ independently with probability

$$p_{uv} \,:\!=\, p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) \,:\!=\,p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}};\,n,\mathcal{X},{\mathsf{w}_{}}),$$

where $p = (p_{uv})_{u,v\in V, u\neq v}$ is a collection of measurable functions $\mathcal{X}\times \mathcal{X} \to [0,1]$ that is symmetric in in u,v (i.e. $p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) = p_{vu}({\mathsf{x}_{v}},{\mathsf{x}_{u}})$ ) and satisfies the following condition:

(EP1) For any u,v, if we fix position ${\mathsf{x}_{u}} \in \mathcal{X}$ and draw position ${\mathsf{x}_{v}}$ from $\mathcal{X}$ according to $\mu$ , then the marginal edge probability is

$$ {\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}}) \mid {\mathsf{x}_{u}}] = \Theta\Big(\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big\}\Big), $$

where the hidden constants are uniform over all u, v and ${\mathsf{x}_{u}}$ .

Note that the function $p_{uv}$ does not depends on ${\mathsf{x}_{v^{\prime}}}$ for $v^{\prime}\neq u,v$ .

For most of our results we also need an additional condition, to ensure the existence of a unique giant component:

(EP2) There exist $\eta > 0$ and a function $\rho = \rho(n) \ge \omega(1)$ such that for any u,v with ${\mathsf{w}_{u}},{\mathsf{w}_{v}} \geq {{\overline w}}$ , and any fixed positions ${\mathsf{x}_{u}},{\mathsf{x}_{v}} \in \mathcal{X}$ , we have

$$ p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}}) \geq \Big(\frac{n}{{{\overline w}}^{\beta-1+\eta}}\Big) ^{-1+\rho(n)/\log\log n}. $$

Discussion of the conditions (EP1) and (EP2): Let us first argue why (EP1) alone is not sufficient to yield a unique giant component. Suppose we have an instantiation of our model G on a space $\mathcal{X}$ . We will see in this paper that with high probability G has a giant component that contains all high-degree vertices. Now make a copy $\mathcal{X}^{\prime}$ of $\mathcal{X}$ , and consider a graph where all vertices draw geometric positions from $\mathcal{X} \cup \mathcal{X}^{\prime}$ . Vertices in $\mathcal{X}$ are never connected to vertices in $\mathcal{X}^{\prime}$ , but within $\mathcal{X}$ and $\mathcal{X}^{\prime}$ we use the same connection probabilities as for G. Then the resulting graph will satisfy all properties of our model except for (EP2), but it will have two giant components, one in $\mathcal{X}$ and one in $\mathcal{X}^{\prime}$ . Consequently, in general our result on average distances cannot hold without a condition like (EP2).

To see another property that can go wrong without the condition (EP2), let us slightly vary the above construction so that between any vertex in $\mathcal{X}$ and any vertex in $\mathcal{X}^{\prime}$ there is an edge with probability $1/n^2$ . (This probability is so small that it does not affect (EP1).) Then with probability $\Omega(1)$ we get no connecting edge and two giants components, while with probability $\Omega(1)$ we get a single edge connecting the two parts, and thus a single giant component. In the former case, the two giant components have internally the same average distances as a Chung–Lu random graph, up to a factor $1\pm o(1)$ . However, in the latter case the average distance in the unique giant component is larger by a factor of $1.5$ than that in Chung–Lu random graphs (twice as large for vertices in different copies, equally large for vertices in the same copy). Thus, without the condition (EP2), the average distance is not even concentrated around a single value in general.

As we will see, (EP2) ensures that the high-weight vertices form a single dense network, so that the graph indeed has a unique giant component. Now let us turn to the condition (EP1). Since its right-hand side is the edge probability of Chung–Lu graphs, (EP1) is a natural condition for any augmented version of Chung–Lu graphs. In particular, (EP1) ensures that the expected degree of a vertex v with weight ${\mathsf{w}_{v}}$ is indeed $\Theta({\mathsf{w}_{v}})$ . For reasons similar to those discussed for (EP2), we cannot further relax (EP1) to a condition on the marginal probability over random positions ${\mathsf{x}_{u}}$ and ${\mathsf{x}_{v}}$ , i.e, a condition like ${\mathbb{E}}_{{\mathsf{x}_{u}}, {\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}})] = \Theta\left(\min\left\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\right\}\right)$ . Indeed, consider the same setup as above, with G, $\mathcal{X}$ , and copy $\mathcal{X}^{\prime}$ . For two vertices of weight at most $\bar w$ , connect them only if they are in the same copy of $\mathcal{X}$ . For two vertices of weight larger than $\bar w$ , always treat them as if they came from the same copy (then the condition (EP2) is satisfied). For a vertex u of weight at most $\bar w$ and v of weight larger than $\bar w$ , connect them only if u is in $\mathcal{X}^{\prime}$ . Then the high-weight vertices form a unique component, but it is only connected to vertices in $\mathcal{X}^{\prime}$ , while the low-weight vertices in $\mathcal{X}$ may form a second giant component. Thus, in (EP1) it is necessary to allow any fixed ${\mathsf{x}_{u}}$ .

Sampling the weights: In the definition we assume that the weight sequence ${\mathsf{w}_{}}$ is fixed. However, if we sample the weights according to an appropriate distribution, then the sampled weights will follow a power law with probability $1 - n^{-\Omega(1)}$ , so that a model with sampled weights is almost surely included in our model. For the precise statement, see Lemma 5.

Examples: We regain the Chung–Lu model as a special case by setting $\mathcal{X} = \{x\}$ (the trivial ground space) and $p_{uv} = \min\left\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\right\}$ , since then (EP1) is trivially satisfied and (EP2) is satisfied for $2 \lt \beta \lt 3$ .

We discuss more examples in Sections 3. In particular, the model includes geometric inhomogeneous random graphs (GIRGs), which were introduced in [13, 14]. Consider the d-dimensional ground space $\mathcal{X}=[0,1]^d$ with the standard (Lebesgue) measure, where $d \ge 1$ is a (constant) parameter of the model. Let $\alpha \neq 1$ be a second parameter that determines how strongly the geometry influences edge probabilities. Finally, let $\|.\|$ be the Euclidean distance on $[0,1]^d$ , where we identify 0 and 1 in each coordinate (i.e., we take the distance on the torus). We show in Theorem 4 that every edge probability function p satisfying

(1) \begin{align} p_{uv} = \Theta\Big( \min\Big\{1, (\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|)^{-d\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\} \Big)\end{align}

follows (EP1) and (EP2), so it is a special case of our model. As was shown in [14], an instance of hyperbolic random graphs satisfies (1) asymptotically almost surely (over the choice of random weights ${\mathsf{w}_{}}$ ). Thus, hyperbolic random graphs, which have attracted considerable theoretical and experimental interest during the last few years (see, e.g., [6, 8, 28, 36]), are also a special case of our general model.

In Section 3 we will see that GIRGs can be varied as follows. As before, let $\mathcal{X}= [0,1]^d$ . For $x = (x_1,\ldots,x_d)$ and $y = (y_1,\ldots,y_d) \in \mathcal{X}$ , we define the minimum component distance $\|x-y\|_{\min}\,:\!=\, \min\{|x_i-y_i| \mid 1\leq i \leq d\}$ , where the differences $x_i-y_i \in [{-}1/2,1/2)$ are computed modulo 1, or, equivalently, on the circle. This distance reflects the property of social networks that two individuals may know each other because they are similar in only one feature (e.g., they share a hobby), regardless of their differences in other features. Note that the minimum component distance is not a metric, since there are $x,y,z\in \mathcal{X}$ such that x and y are close in one component, y and z are close in one (different) component, but x and z are not close in any component. Let V(r) be the volume of the ball $B_r(0) \,:\!=\, \{x \in \mathcal{X} \mid \|x\|_{\min} \leq r\}$ . Then any p satisfying

\begin{equation*} p_{uv} = \Theta\Big( \min\Big\{1, V(\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|)^{-\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\} \Big)\end{equation*}

satisfies the conditions (EP1) and (EP2), so it is a special case of our model.

These examples also show that our model is incomparable to the (also very general) model of inhomogeneous random graphs studied by Bollobás, Janson, and Riordan [9]. Their model requires sufficiently many long-range edges, so that setting $\alpha \gt 1$ in (1) yields an edge probability that is not supported by their model. Similarly, the example with the minimum component distance is also not supported by their model.

2.2. Results of this paper

Our results generalize and improve the understanding of Chung–Lu random graphs, hyperbolic random graphs, and other models, as they are special cases of our fairly general model. We study the following fundamental structural questions.

Scale-freeness: Since we plug in power-law weights ${\mathsf{w}_{}}$ , it is not surprising that our model is scale-free. More precisely, the degrees follow a power law with exponent $\beta$ . We say that an event holds with high probability (w.h.p.) if it holds with probability $1 - n^{-\omega(1)}$ .

Theorem 1. (Section 8.) Consider a random instance of our model that satisfies (EP1), but not necessarily (EP2). Then for all $\eta \gt 0$ , w.h.p., we have

\[\Omega\big(n d^{1-\beta-\eta}\big) \le \#\{v \in V \mid \deg(v) \geq d\} \le O \big(n d^{1-\beta+\eta}\big),\]

where the first inequality holds for all $1 \leq d \leq {{\overline w}}$ and the second inequality holds for all $d \ge 1$ . Moreover, w.h.p. the average degree is $\Theta(1)$ .

Giant component and diameter: The connectivity properties of the model for $\beta \gt 3$ are not very well behaved, in particular since in this case even threshold hyperbolic random graphs do not possess a giant component of linear size [7]. Hence, for connectivity properties we restrict our attention to the regime $2 \lt \beta \lt 3$ , which holds for most real-world networks [22].

Theorem 2. (Section 7.) Let $2 \lt \beta \lt 3$ . W.h.p. the largest component of our random graph model has linear size, while all other components have size at most $\log^{O(1)} n$ . Moreover, w.h.p. the diameter is at most $\log^{O(1)} n$ .

A better bound of $\Theta(\!\log n)$ holds for the diameter of Chung–Lu graphs [17] and for hyperbolic random graphs [25, 39]. It remains an open question whether the upper bound $O(\!\log n)$ holds in general for our model.

Average distance: As our main result, we determine the average distance between two randomly chosen nodes in the giant component to be the same as in Chung–Lu random graphs up to a factor $1+o(1)$ , showing that the underlying geometry is negligible for this graph parameter.

Theorem 3. (Section 7.) Let $2 \lt \beta \lt 3$ . Then the average distance of our random graph model is $(2 \pm o(1))\frac{\log \log n}{|\log(\beta-2)|}$ in expectation and with probability $1-o(1)$ .

2.3. Notation

In this section we collect the notation that we will use throughout the paper. For $w, w^{\prime}\in \mathbb{R}_{\geq 0}$ , $w\le w^{\prime}$ , we use the notation $ V_{\geq w} \,:\!=\, \{v\in V\; |\; {\mathsf{w}_{v}}\geq w\}$ and $V_{\leq w} \,:\!=\, \{v\in V\; |\; {\mathsf{w}_{v}}\leq w\}$ and $V_{[w,w^{\prime}]} \,:\!=\, V_{\geq w} \cap V_{\le w^{\prime}}$ . Similarly, we write $ {\mathsf{W}}_{\geq w}\,:\!=\,\sum_{v\in V_{\geq w}} {\mathsf{w}_{v}}$ , ${\mathsf{W}}_{\leq w}\,:\!=\,\sum_{v\in V_{\leq w}}{\mathsf{w}_{v}}$ , and ${\mathsf{W}}_{[w,w^{\prime}]} \,:\!=\, \sum_{v\in V_{[w,w^{\prime}]}}{\mathsf{w}_{v}}$ for sums of weights. Recall that ${\mathsf{w}_{\min}} = \min\{{\mathsf{w}_{v}} \mid 1 \le v \le n\}$ ; similarly we put ${\mathsf{w}_{\max}} \,:\!=\, \max\{{\mathsf{w}_{v}} \mid 1 \le v \le n\}$ for the maximum weight. For $u,v\in V$ we write $u\sim v$ if u and v are adjacent, and for $A,B\subseteq V$ we write $A\sim v$ if there exists $u\in A$ such that $u\sim v$ ; we write $A \sim B$ if there exists $v \in B$ such that $A\sim v$ . For a vertex $v\in V$ , we denote its neighborhood by $\Gamma(v)$ , i.e. $\Gamma(v)\,:\!=\,\{u \in V \mid u\sim v\}$ . For $A,B\subseteq V$ , we denote by $E(A,B) \,:\!=\, \{uv\in E \mid u\in A, v\in B\}$ the set of edges from A to B.

Throughout the paper we assume that $n\to\infty$ , while the model parameters $\alpha$ , $\beta$ , d, $c_1$ , $c_2$ , ${\mathsf{w}_{\min}}$ are constants. (The parameters $\alpha$ and d only appear in examples.) In particular, Landau notation $O({\cdot}),o({\cdot}),\Omega({\cdot}),\omega({\cdot}),\Theta({\cdot})$ may hide any factor that depends on these constants, but these factors must be universal for all vertices and edges of the graph, for all values of $({\mathsf{x}_{v}})_{v\in V}$ , and for all values of non-constant parameters in the statement (such as w or k, which will occur in some lemmas and theorems). For example, (EP1) can be rephrased as follows: there exist $C,C^{\prime} \gt 0$ and $n_0 \gt 0$ such that for all $n\ge n_0$ , all $u,v \in V = [n]$ , and all ${\mathsf{x}_{u}} \in \mathcal{X}$ ,

$$ C \cdot\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big\} \le {\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}}) \mid {\mathsf{x}_{u}}] \le C^{\prime}\cdot\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big\}. $$

As previously stated, we say that an event holds with high probability (w.h.p.) if it holds with probability $1 - n^{-\omega(1)}$ .

In the model, note that ${\mathsf{w}_{}}$ and $p_{uv}$ are parameters and thus fixed, while the probability space is over the positions ${\mathsf{x}_{u}}$ and the coin flips for the edges (with probability $p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}})$ for edge uv). Sometimes we make statements where we condition on part of the search space to be fixed. In such cases, we emphasize this restricted probability space by including the random components as subscripts on the symbols ${\mathbb{E}}$ and $\mathbb{P}$ . For example, we write ${\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}}) \mid {\mathsf{x}_{u}}]$ if ${\mathsf{x}_{u}}$ is fixed and ${\mathsf{x}_{v}}$ is random.

3. Example: GIRGs and generalizations

In this section, we further discuss the special cases of our model mentioned in Section 2.1. Mainly, we study a class which is still fairly general, the so-called distance model. We show that the GIRG model introduced in [14] is a special case, and we also discuss a non-metric example. In addition, with the threshold model we consider a variation which includes in particular threshold hyperbolic random graphs.

The distance model:

We consider the following situation, which will cover both GIRGs and the non-metric example. As our underlying geometry we specify the ground space $\mathcal{X}=[0,1]^d$ , where $d \ge 1$ is a (constant) parameter of the model. We sample uniformly from this set according to the standard (Lebesgue) measure. This is in the spirit of the classical random geometric graphs [41].

To describe the distance between two points $x,y \in \mathcal{X}$ , assume we have some measurable function $\|.\|: [{-}1/2,1/2)^d \to \mathbb{R}_{\geq 0}$ such that $\|0\| = 0$ and $\|-x\|=\|x\|$ for all $x\in [{-}1/2,1/2)^d$ . Note that $\|.\|$ does not need to be a norm or seminorm. We extend $\|.\|$ to $\mathbb{R}^d$ via $\|z\| \,:\!=\, \| z-u\|$ , where $u\in \mathbb{Z}^d$ is the unique lattice point such that $z-u \in [{-}1/2,1/2)^d$ . For $r\geq 0$ and $x \in \mathcal{X}$ , we define the r-ball around x to be $B_r(x)\,:\!=\,\{x \in \mathcal{X} \mid \|x-y\| \leq r\}$ , and we denote by V(r) the volume of the r-ball around 0. Intuitively, $B_r(x)$ is the ball around x in $[0,1]^d$ with the torus geometry, i.e., with 0 and 1 identified in each coordinate. Assume that $V\colon \mathbb{R}_{\geq 0} \to [0,1]$ is surjective, i.e., for each $V_0 \in [0,1]$ there exists r such that $V(r)=V_0$ .

Finally, let $\alpha \in \mathbb{R}_{>0}$ be a long-range parameter. Since the case $\alpha=1$ deviates slightly from the general case, we assume $\alpha \neq 1$ . Let p be any edge probability function that satisfies, for all u,v and ${\mathsf{x}_{u}},{\mathsf{x}_{v}} \in \mathcal{X} = [0,1]^d$ ,

(2) \begin{align} p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) = \Theta\Big( \min\Big\{1, V(\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|)^{-\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\} \Big).\end{align}

Then, as we will prove later in Theorem 4, p satisfies the conditions (EP1) and (EP2), so it is a special case of our model.

Example 1. If we choose $\|.\|$ to be the Euclidean distance $\|.\|_2$ (or any equivalent norm, such as $\|.\|_{\infty}$ ) then we obtain the GIRG model introduced in [14, 42], where the distance between two points x,y in $[0,1]^d$ is given by their geometric distance on the torus. In [14] it was shown that a graph from such a GIRG model w.h.p. has clustering coefficient $\Omega(1)$ , that it can be stored with O(n) bits in expectation, and that it can be sampled in expected time O(n). Moreover, it was shown that hyperbolic random graphs are contained in the one-dimensional GIRG model. These models have been intensively studied with respect to numerous properties, including component structure [32], clustering [14], diameter [25, 39], spectral gap [31], separators [5, 14, 38], clique number [6], and treewidth [5], as well as processes such as first-passage percolation [34, 35], bootstrap percolation [33], greedy routing [12], bidirectional search [4], and infection processes [26, 30]. With appropriate scaling, their infinite limits can also be defined [35, 45], and they are related to scale-free percolation [19]. In this latter model, the vertices are placed on an infinite grid, so it is not covered by our results. However, it behaves similarly to GIRGs in many respects [34, 35, 45], including average distances [19, 44].

The next distance measure, the minimum component distance, is particularly useful for modeling social networks, because it captures the following property: if two individuals share one feature (e.g., they are in the same sports club), but are very different in many other features (e.g., work, music), then they are still likely to know each other.

Example 2. Let the minimum component distance be defined by

$$\|x\|_{\min} \,:\!=\, \min\{x_i \mid 1\leq i \leq d\} \text{ for } x = (x_1,\ldots,x_d) \in[{-}1/2,1/2)^d.$$

Note that the minimum component distance is not a metric for $d\geq 2$ , since there are $x,y,z\in \mathcal{X}$ such that x and y are close in one component, y and z are close in one (different) component, but x and z are not close in any component. Thus the triangle inequality is not satisfied. However, it still satisfies the requirements specified above, so the results of this paper apply. In subsequent work, one of the authors has shown that the resulting graphs for $d \ge 2$ have a giant component which does not have any separators of sublinear size [38]. This is different from the case of the GIRG model, where it is possible to split the giant component into two halves by removing $n^{1-\Omega(1)}$ edges [14].

Theorem 4. In the distance model described above, let p be any function that satisfies Equation (2). Then the conditions (EP1) and (EP2) are satisfied, and we obtain an instance of the general model.

The threshold model:

Finally, we discuss a variation of Example 1 where we let $\alpha \to \infty$ and thus obtain a threshold function for p.

Example 3. Let $\|.\|$ be the Euclidean distance $\|.\|_2$ and let p again satisfy (2), but this time we assume that $\alpha=\infty$ . More precisely, we require

(3) \begin{align} p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) = \begin{cases} \Theta(1) & \text{if } \|{\mathsf{x}_{u}} - {\mathsf{x}_{v}}\| \le O\big(\big(\tfrac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{\mathsf{W}}\big)^{1/d}\big), \\[3pt] 0 & \text{if } \|{\mathsf{x}_{u}} - {\mathsf{x}_{v}}\| \ge \Omega\big(\big(\tfrac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{\mathsf{W}}\big)^{1/d}\big), \end{cases} \end{align}

where the constants hidden by O and $\Omega$ do not have to match, i.e., there can be an interval $[c_1 (\tfrac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{\mathsf{W}})^{1/d}, c_2 (\tfrac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{\mathsf{W}})^{1/d}]$ for $\|{\mathsf{x}_{u}} - {\mathsf{x}_{v}}\|$ where the behavior of $p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}})$ is arbitrary. This function p yields the case $\alpha = \infty$ of the GIRG model introduced in [14]. In [14] it was shown that threshold hyperbolic random graphs are contained in this class of models, and furthermore that the model w.h.p. has clustering coefficient $\Omega(1)$ , it can be stored with O(n) bits in expectation, and it can be sampled in expected time O(n).

Notice that the volume of a ball with radius $r_0=\Theta((\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}})^\frac{1}{d})$ around any fixed $x \in \mathcal{X}$ is $\Theta(\min\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\})$ . Thus, by (3), for fixed ${\mathsf{x}_{u}}$ it follows directly that

$${\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) \mid {\mathsf{x}_{u}}] = \Theta\big(\mathbb{P}_{{\mathsf{x}_{v}}}\big[\|{\mathsf{x}_{u}} - {\mathsf{x}_{v}}\| \le r \mid {\mathsf{x}_{u}}\big] \big) = \Theta\left(\min\left\{1,\tfrac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\right\}\right).$$

Since (EP1) is satisfied, Theorem 1 for the degree sequence already applies. In order to also fulfill (EP2), we additionally require that $2 \lt \beta \lt 3$ and ${{\overline w}}=\omega(n^{1/2})$ . Then for all ${\mathsf{w}_{u}}, {\mathsf{w}_{v}} \ge {{\overline w}}$ we have $\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}} = \omega(1)$ . For all positions ${\mathsf{x}_{u}},{\mathsf{x}_{v}} \in \mathcal{X}$ we thus obtain $p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}})=\Theta(1)$ by (3).

Remark 1. It follows from the definition that the low-weight vertices in a GIRG contain ordinary random geometric graphs as subgraphs, i.e., every pair of vertices connects with probability $\Omega(1)$ if the distance between the vertices is at most $cn^{-1/d}$ , where c is a constant that depends on the minimal weight ${\mathsf{w}_{\min}}$ . If ${\mathsf{w}_{\min}}$ is sufficiently large, then these subgraphs are supercritical, i.e., they have a giant component. On the other hand, in the threshold model for $\beta >3$ sufficiently large, all edges cover a polynomially small distance $n^{-\Omega(1)}$ . Thus, by combining these conditions we get a random graph model in the regime $\beta >3$ with giant components where the average distance is polynomially large.

4. Conclusion of first part

We have studied a class of random graphs that generically augment Chung–Lu random graphs by an underlying ground space, i.e., every vertex has a random position in the ground space and edge probabilities may depend arbitrarily on the vertex positions, as long as marginal edge probabilities are preserved. Since our model is very general, it contains numerous well-known models as special cases, including hyperbolic random graphs [8, 40] and geometric inhomogeneous random graphs [14]. Beyond these well-studied models, our model also includes graphs with non-metric ground spaces, which are motivated by social networks, where, for example, two persons are likely to know each other if they share one hobby, regardless of their other hobbies.

Despite its generality, we show that all instantiations of our model have similar connectivity properties, assuming that vertex weights follow a power law with exponent $2 \lt \beta \lt 3$ . In particular, there exists a unique giant component of linear size, and the diameter is polylogarithmic. Surprisingly, for all instantiations of our model the average distance is the same as in Chung–Lu random graphs, namely $(2 \pm o(1))\frac{\log \log n}{|\log(\beta-2)|}$ . In some sense, this shows universality of ultra-small worlds.

We leave it as an open problem to determine whether the diameter of our model is $O(\!\log n)$ for $2 \lt \beta \lt 3$ .

5. Concentration inequalities

The rest of the paper is dedicated to proofs. We will use the following concentration inequalities.

Theorem 5. (Chernoff–Hoeffding bound [24, Theorem 1.1].) Let $X\,:\!=\,\sum_{i\in [n]}X_i$ , where, for all $i \in [n]$ , the random variables $X_i$ are independently distributed in [0, 1]. Then the following hold:

1. (i) $\mathbb{P}[ X > (1+{{\varepsilon}}){\mathbb{E}}[X]] \leq \exp\left( -\frac{{{\varepsilon}}^2}{3}{\mathbb{E}}[X] \right)$ for all $0<{{\varepsilon}}<1$ ,

2. (ii) $\mathbb{P}[ X < (1-{{\varepsilon}}){\mathbb{E}}[X]] \leq \exp\left( -\frac{{{\varepsilon}}^2}{2}{\mathbb{E}}[X] \right)$ for all $0<{{\varepsilon}}<1$ , and

3. (iii) $\mathbb{P}[X>t]\leq 2^{-t}$ for all $t>2e{\mathbb{E}}[X]$ .

We will need a concentration inequality which bounds large deviations taking into account some bad event $\mathcal{B}$ . We start with the following variant of McDiarmid’s inequality as given in [37].

Theorem 6. (Theorem 3.6 in [37], slightly simplified.) Let $X_1,\ldots,X_m$ be independent random variables over $\Omega_1, \ldots, \Omega_m$ . Let $X = (X_1,\ldots,X_m)$ , $\Omega = \prod_{k=1}^m \Omega_k$ , and let $f\colon \Omega \to \mathbb{R}$ be measurable with $0 \le f(\omega) \le M$ for all $\omega \in \Omega$ . Let $\mathcal{B} \subseteq \Omega$ be such that, for some $c > 0$ and for all $\omega \in \overline{\mathcal{B}},\omega^{\prime} \in \Omega$ that differ in only one component, we have $|f(\omega)-f(\omega^{\prime})| \le c$ . Then for all $t \gt 0$ ,

(4) \begin{align}\mathbb{P}[\vert f(X)-{\mathbb{E}}[f(X)] \vert \ge t] \le 2e^{-\frac{t^2}{8mc^2}}+2\tfrac{mM}{c}\mathbb{P}[\mathcal{B}]. \\[-8pt] \nonumber \end{align}

Our improved version of this theorem is the following, where in the Lipschitz condition both $\omega$ and $\omega^{\prime}$ come from the good set $\overline{\mathcal B}$ , but we have to consider changes of two components at once. A similar inequality has recently been proven by Combes [18]; see also [46].

Theorem 7. Let $X_1,\ldots,X_m$ be independent random variables over $\Omega_1, \ldots, \Omega_m$ . Let $X=(X_1,\ldots,X_m)$ , $\Omega = \prod_{k=1}^m \Omega_k$ , and let $f\colon \Omega \to \mathbb{R}$ be measurable with $0 \le f(\omega) \le M$ for all $\omega \in \Omega$ . Let $\mathcal{B} \subseteq \Omega$ be such that, for some $c > 0$ and for all $\omega \in \overline{\mathcal{B}},\omega^{\prime} \in \overline{\mathcal{B}}$ that differ in at most two components, we have

(5) \begin{align}|f(\omega)-f(\omega^{\prime})| \le c.\end{align}

Then for all $t \ge 2 M \mathbb{P}[\mathcal B]$

$$\mathbb{P}\big[\vert f(X)-{\mathbb{E}}[f(X)] \vert \ge t \big] \le 2e^{-\frac{t^2}{32mc^2}}+(2\tfrac{mM}{c} + 1)\mathbb{P}[\mathcal{B}].$$

Proof. We say that $\omega, \omega^{\prime} \in \Omega$ are neighbors if they differ in exactly one component $\Omega_k$ . Given a function f as in the statement, we define a function f’ as follows. On $\overline{\mathcal B}$ the functions f and f’ coincide. Let $\omega \in \mathcal B$ . If $\omega$ has a neighbor $\omega^{\prime} \in \overline{\mathcal B}$ , then choose any such $\omega^{\prime}$ and set $f^{\prime}(\omega) \,:\!=\, f(\omega^{\prime})$ . Otherwise set $f^{\prime}(\omega) \,:\!=\, f(\omega)$ .

The constructed function f’ satisfies the precondition of Theorem 6. Indeed, let $\omega \in \overline{\mathcal B}$ and $\omega^{\prime} \in \Omega$ differ in only one position. If $\omega^{\prime} \in \overline{\mathcal B}$ , then since $f^{\prime}(\omega) = f(\omega)$ and $f^{\prime}(\omega^{\prime}) = f(\omega^{\prime})$ , and by the assumption on f, we obtain $|f^{\prime}(\omega) - f^{\prime}(\omega^{\prime})| \le c$ . Otherwise we have $\omega^{\prime} \in \mathcal B$ , and since $\omega^{\prime}$ has at least one neighbor in $\overline{\mathcal B}$ , namely $\omega$ , we have $f^{\prime}(\omega^{\prime}) = f(\omega^{\prime\prime})$ for some neighbor $\omega^{\prime\prime} \in \overline{\mathcal B}$ of $\omega^{\prime}$ . Note that both $\omega$ and $\omega^{\prime\prime}$ are in $\overline{\mathcal B}$ , and as they are both neighbors of $\omega^{\prime}$ they differ in at most two components. Thus, by the assumption on f we have $ |f^{\prime}(\omega) - f^{\prime}(\omega^{\prime})| = |f(\omega) - f(\omega^{\prime\prime})| \le c$ . Hence, we can use Theorem 6 on f’ and obtain concentration of f’(X). Specifically, since $\mathbb{P}[f(X) \ne f^{\prime}(X)] \le \mathbb{P}[\mathcal B]$ , and thus $|{\mathbb{E}}[f(X)] - {\mathbb{E}}[f^{\prime}(X)]| \le M \mathbb{P}[\mathcal B]$ , we obtain

\begin{align*} \mathbb{P}[|f(X) - {\mathbb{E}}[f(X)]| \ge t] &\le \mathbb{P}[\mathcal B] + \mathbb{P}[|f^{\prime}(X) - {\mathbb{E}}[f^{\prime}(X)]| \ge t - M \mathbb{P}[\mathcal B]] \\ &\le \mathbb{P}[\mathcal B] + \mathbb{P}[|f^{\prime}(X) - {\mathbb{E}}[f^{\prime}(X)]| \ge t/2], \end{align*}

since $t \ge 2 M \mathbb{P}[\mathcal B]$ , which together with Theorem 6 proves the claim.

6. Basic properties

In this section, we prove some basic properties of our random graph model which occur repeatedly in our proofs. In particular we calculate the expected degree of a vertex and the marginal probability that an edge between two vertices with given weights is present. Let us start by calculating the partial weight sums ${\mathsf{W}}_{\le w}$ and ${\mathsf{W}}_{\ge w}$ . The values of these sums will follow from the assumptions on power-law weights in Section 2.1.

Lemma 1. The total weight satisfies ${\mathsf{W}}=\Theta(n)$ . Moreover, for all sufficiently small $\eta > 0$ ,

1. (i) ${\mathsf{W}}_{\ge w} = O( n w^{2-\beta+\eta})$ for all $w \ge {\mathsf{w}_{\min}}$ ,

2. (ii) ${\mathsf{W}}_{\ge w} = \Omega( n w^{2-\beta-\eta})$ for all ${\mathsf{w}_{\min}} \le w \le {{\overline w}}$ ,

3. (iii) ${\mathsf{W}}_{\le w} = O(n)$ for all w, and

4. (iv) ${\mathsf{W}}_{\le w} = \Omega(n)$ for all $w=\omega(1)$ .

Proof. Let $w_1\ge w_0 \ge 0$ be two fixed weights. We start by summing up all vertex-weights between $w_0$ and $w_1$ . By Fubini’s theorem, we can rewrite this sum as

(6) \begin{align}\sum_{v \in V, w_0 \le {\mathsf{w}_{v}} \le w_1} {\mathsf{w}_{v}} & = \int_0^{\infty}|V_{\ge \max\{w_0,x\}} \setminus V_{> w_1}| dx \\& = w_0 \cdot |V_{\ge w_0}| + \int_{w_0}^{w_1} |V_{\ge x}| dx- w_1 \cdot |V_{ \gt w_1}| .\nonumber\end{align}

We start with (i) and apply (6) with $w_0=w$ and $w_1={\mathsf{w}_{\max}}$ . Then the set $V_{ \gt w_1}$ is empty, and we have ${\mathsf{W}}_{\ge w}=w \cdot |V_{\ge w}| + \int_{w}^{{\mathsf{w}_{\max}}} |V_{\ge x}|dx$ ; thus the assumption (PL2) implies that ${\mathsf{W}}_{\ge w}$ equals

\[|V_{\ge w}| \cdot w + \int_w^{\infty} |V_{\ge x}|dx = O\Big(nw^{2-\beta+\eta}+\int_w^{\infty} nx^{1-\beta+\eta}dx\Big)=O\Big(n w^{2-\beta+\eta}\Big).\]

For (ii) we similarly obtain

$${\mathsf{W}}_{\ge w} = \Omega\Big(nw^{2-\beta-\eta}+\int_w^{{\mathsf{w}_{\max}}}nx^{1-\beta-\eta}dx\Big)=\Omega\Big(n w^{2-\beta-\eta}\Big).$$

For (iii), we see that if $w \lt {\mathsf{w}_{\min}}$ , then clearly ${\mathsf{W}}_{\le w}=0$ . Otherwise, Equation (6) with $w_0={\mathsf{w}_{\min}}$ and $w_1=w$ implies

\begin{align*}{\mathsf{W}}_{\le w}&=|V_{\ge {\mathsf{w}_{\min}}}| \cdot {\mathsf{w}_{\min}} + \int_{{\mathsf{w}_{\min}}}^w |V_{\ge x}| dx - |V_{> w}| \cdot w \\& \le n{\mathsf{w}_{\min}} + O\Big(\int_{{\mathsf{w}_{\min}}}^w nx^{1-\beta+\eta} dx\Big)=O(n).\end{align*}

For (iv) we obtain

\begin{align*}{\mathsf{W}}_{\le w} & \ge \int_{{\mathsf{w}_{\min}}}^w |V_{\ge x}| dx- |V_{> w}| \cdot w = \Omega\Big(\int_{{\mathsf{w}_{\min}}}^w nx^{1-\beta-\eta} dx\Big)-O\Big(nw^{2-\beta+\eta}\Big) \\& =\Omega(n)-o(n)=\Omega(n).\end{align*}

In particular, with the choice $w={\mathsf{w}_{\max}}$ , the property ${\mathsf{W}}=\Theta(n)$ follows from (iii) and (iv).

Next we consider the marginal edge probability $\mathbb{P}[u \sim v]$ of two vertices u, v with weights ${\mathsf{w}_{u}}$ , ${\mathsf{w}_{v}}$ . For a fixed position ${\mathsf{x}_{u}} \in \mathcal{X}$ , we already know this probability by (EP1).

Lemma 2. Let $u \in [n]$ and let ${\mathsf{x}_{u}} \in \mathcal{X}$ be any fixed position. Then all edges $\{u,v\}$ , $u \ne v$ , are independently present, and we have

\begin{equation*}\mathbb{P}_{{\mathsf{x}_{u}},{\mathsf{x}_{v}}}[u \sim v] = \Theta\big(\mathbb{P}_{{\mathsf{x}_{v}}}[u \sim v \mid {\mathsf{x}_{u}}]\big) = \Theta\Big(\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}} \Big\}\Big).\end{equation*}

Proof. Let $u,v \in [n]$ . Then, from (EP1), it follows directly that

\begin{align*}\mathbb{P}[u \sim v] & = {\mathbb{E}}_{{\mathsf{x}_{u}}}\big[\mathbb{P}_{{\mathsf{x}_{v}}}[u \sim v \mid {\mathsf{x}_{u}}]\big]={\mathbb{E}}_{{\mathsf{x}_{u}}}\Big[\Theta\Big(\min\Big\{1,\frac{{\mathsf{w}_{u}}{\mathsf{w}_{v}}}{{\mathsf{W}}}\Big\}\Big)\Big] \\& =\Theta\Big(\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}} \Big\}\Big).\end{align*}

Furthermore, for every fixed ${\mathsf{x}_{u}} \in \mathcal{X}$ the edges incident to u are independently present with probability $\mathbb{P}_{{\mathsf{x}_{v}}}[u \sim v \mid {\mathsf{x}_{u}}]$ , as the event ‘ $u \sim v$ ’ only depends on ${\mathsf{x}_{v}}$ and an independent random choice for the edge uv (after fixing ${\mathsf{x}_{v}}$ ).

Remark 2. We will often use Lemma 2 in the following form. Let $S,T\subseteq [n]$ , $S\cap T = \emptyset$ , and let $\mathcal E$ be any event of non-zero probability that is determined (i.e., measurable) by $({\mathsf{x}_{v}})_{v\in S}$ . Moreover, let $v_0\in S$ . Then conditional on ${\mathsf{x}_{v_0}}$ , the events ‘ $u \sim v_0$ ’ for $u\in T$ are independent of each other, and have probability $ \Theta(\min\{1,{\mathsf{w}_{u}} {\mathsf{w}_{v_0}}/{\mathsf{W}}\})$ respectively. Since these bounds are independent of $x_{v_0}$ , they also hold conditional on $\mathcal E$ . In particular, using $1-x \le e^{-x}$ for all $x\in \mathbb{R}$ ,

(7) \begin{align} \mathbb{P}[\exists u\in T: u \sim v_0 \mid \mathcal E] & = 1- \prod_{u\in T} \left(1-\Theta\Big(\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}} \Big\}\Big)\right)\\[-32pt] \nonumber \end{align}

(8) \begin{align} \qquad\qquad\qquad\qquad \ge 1-\exp\left\{-\Theta\Big(\sum_{u\in T}\min\Big\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}} \Big\} \Big)\right\},\end{align}

where we can exchange the sum and $\Theta$ -notation in the last step because the hidden constants are uniform over all u. We express this by saying that the lower bounds $\Theta(\min\{1,{\mathsf{w}_{u}} {\mathsf{w}_{v_0}}/{\mathsf{W}}\})$ hold independently, even after conditioning on $\mathcal E$ .

The following lemma shows that the expected degree of a vertex is of the same order as the weight of the vertex; thus we can interpret a given weight sequence ${\mathsf{w}_{}}$ as a sequence of expected degrees.

Lemma 3. For any $v \in [n]$ and any ${\mathsf{x}_{v}} \in \mathcal{X}$ we have ${\mathbb{E}}[\deg(v) \mid {\mathsf{x}_{v}}] = \Theta({\mathbb{E}}[\deg(v)])=\Theta({\mathsf{w}_{v}})$ .

Proof. Let v be any vertex and ${\mathsf{x}_{v}} \in \mathcal{X}$ . We show first that ${\mathbb{E}}[\deg(v) \mid {\mathsf{x}_{v}}] =\Theta({\mathsf{w}_{v}})$ by estimating the expected degree both from below and from above. By Lemma 2, the expected degree of v is at most

\begin{align*}\sum_{u \neq v} \mathbb{P}[u \sim v \mid x_v ] & = \Theta\Big(\sum_{u \neq v} \min\Big\{1,\frac{{\mathsf{w}_{u}}{\mathsf{w}_{v}}}{{\mathsf{W}}}\Big\}\Big)=O\Big(\sum_{u \in V} \frac{{\mathsf{w}_{u}}{\mathsf{w}_{v}}}{{\mathsf{W}}}\Big) \\&= O\Big(\frac{{\mathsf{w}_{v}}}{{\mathsf{W}}}\sum_{u\in V} {\mathsf{w}_{u}}\Big) = O({\mathsf{w}_{v}}).\end{align*}

For the lower bound, $\mathbb{P}[u \sim v \mid x_v]=\Theta(\frac{{\mathsf{w}_{u}}{\mathsf{w}_{v}}}{{\mathsf{W}}})$ holds for all ${\mathsf{w}_{u}} \leq \frac{{\mathsf{W}}}{{\mathsf{w}_{v}}}$ . We set $w^{\prime} \,:\!=\, \frac{{\mathsf{W}}}{{\mathsf{w}_{v}}}$ and observe that $w^{\prime}=\omega(1)$ by (PL2). Using Lemma 1(iv), we obtain

$${\mathbb{E}}[\deg(v)] \ge \sum_{u \neq v, u \in V_{\le w^{\prime}}} \mathbb{P}[u \sim v] = \Omega\Big(\frac{{\mathsf{w}_{v}}}{{\mathsf{W}}} {\mathsf{W}}_{\leq w^{\prime}}\Big) = \Omega({\mathsf{w}_{v}}).$$

The formula ${\mathbb{E}}[\deg(v)] =\Theta({\mathsf{w}_{v}})$ follows from an analogous computation, or by observing that $\min_{x_v} {\mathbb{E}}[\deg(v) \mid {\mathsf{x}_{v}}] \le {\mathbb{E}}[\deg(v)] \le \max_{x_v} {\mathbb{E}}[\deg(v) \mid {\mathsf{x}_{v}}]$ .

As the expected degree of a vertex is roughly the same as its weight, it is no surprise that w.h.p. the degrees of all vertices with sufficiently large weight are concentrated around the expected value. The following lemma gives a precise statement.

Lemma 4. The following properties hold w.h.p.:

1. (i) $\deg(v) = O({\mathsf{w}_{v}} + \log^2 n)$ for all $v \in [n]$ ;

2. (ii) $\deg(v)= (1+o(1)){\mathbb{E}}[\deg(v)]= \Theta({\mathsf{w}_{v}})$ for all $v \in V_{\ge \omega(\log^2 n)}$ ;

3. (iii) $\sum_{v \in V_{\ge w}} \deg(v) = \Theta({\mathsf{W}}_{\ge w})$ for all $w=\omega(\log^2 n)$ .

Proof. Let $v \in V$ with fixed position ${\mathsf{x}_{v}} \in \mathcal{X}$ and let $\mu \,:\!=\, {\mathbb{E}}[\deg(v) \mid {\mathsf{x}_{v}}]=\Theta({\mathsf{w}_{v}})$ , where the last equation holds by Lemma 3. In particular, there exists a constant C such that $2e\mu \lt C \log^2 n$ holds for all vertices $v \in V_{\le \log^2 n}$ and all positions ${\mathsf{x}_{v}} \in \mathcal{X}$ . Moreover, by the definition of the model, conditioned on the position ${\mathsf{x}_{v}}$ , the degree of v is a sum of independent Bernoulli random variables. Thus, if $v \in V_{\le \log^2 n}$ , we may apply a Chernoff bound (Theorem 5(iii)) and obtain $\mathbb{P}[\deg(v) > C \log^2 n] \le 2^{-C \log^2 n}=n^{-\omega(1)}$ . If $v \in V_{\ge \log^2 n}$ , we similarly obtain $ \mathbb{P}[\deg(v) > 3\mu/2] \le e^{-\Theta(\mu)}=n^{-\omega(1)}$ and $\mu=\Theta({\mathsf{w}_{v}})$ by Lemma 3. Then (i) follows from applying a union bound over all vertices.

For (ii), let $v \in V$ such that ${\mathsf{w}_{v}}=\omega(\log^2 n)$ , let $\mu$ be as defined above and put ${{\varepsilon}}=\frac{\log n}{\sqrt{\mu}}=o(1)$ . Thus by the Chernoff bound,

\[ \mathbb{P}\big[|\deg(v)-\mu| > \varepsilon \cdot\mu\big] \le e^{-\Theta(\varepsilon^2 \cdot\mu)}=n^{-\omega(1)},\]

and we obtain (ii) by applying Lemma 3 and a union bound over all such vertices. Finally, from (ii) we infer $\sum_{v \in V_{\ge w}} \deg(v) = \sum_{v \in V_{\ge w}} \Theta({\mathsf{w}_{v}}) = \Theta({\mathsf{W}}_{\ge w})$ for all $w = \omega(\log^2 n)$ , which shows (iii).

We conclude this section by proving that if we sample the weights randomly from an appropriate distribution, then with probability $1-o(1)$ the resulting weights satisfy our conditions on power-law weights.

Lemma 5. Let ${\mathsf{w}_{\min}}, C_1, C_2 \gt 0$ be constants, let $F\,:\,\mathbb{R} \rightarrow [0,1]$ be non-decreasing such that $F(z)=0$ for all $z \le {\mathsf{w}_{\min}}$ , and assume $C_1 z^{1-\beta} \le 1- F(z) \le C_2 z^{1-\beta}$ for all $z \ge {\mathsf{w}_{\min}}$ . Suppose that for every vertex $v \in [n]$ we choose the weight ${\mathsf{w}_{v}}$ independently according to the cumulative probability distribution F. Then with ${{\overline w}} = (n/\log^2 n)^{1/(\beta-1)}$ , the resulting weight vector ${\mathsf{w}_{}}$ satisfies (PL1) deterministically, the lower bound of (PL2) w.h.p., and the upper bound of (PL2) with probability $1-n^{-\Omega(\eta)}$ for all $\eta=\eta(n)=\omega(\log \log n/\log n)$ .

In particular, this lemma proves that for all small constants $\eta \gt 0$ , with probability $1-n^{-\Omega(1)}$ , (PL1) and (PL2) are fulfilled for weights sampled according to $F({\cdot})$ . Moreover, it follows that any property which holds with probability $1-q$ for weights satisfying (PL1) and (PL2) also holds in a model of sampled weights with probability at least $1-q-n^{-\Omega(1)}$ .

Proof of Lemma 5. The condition (PL1) is fulfilled by definition of F, and we only need to prove (PL2). For all $z>{\mathsf{w}_{\min}}$ , denote by $Y_z$ the number of vertices with weight at least z and observe that

(9) \begin{align} {\mathbb{E}}[Y_z] = n (1-F(z))= \Theta(n z^{1-\beta}).\end{align}

Let us first consider the case $z \in [{\mathsf{w}_{\min}},{{\overline w}}]$ . For all z in this range we have ${\mathbb{E}}[Y_z] = \Omega(\log^2 n)$ , so for any $z \in [{\mathsf{w}_{\min}},{{\overline w}}]$ the Chernoff bound (Theorem 5(i)–(ii)) yields

$$ \mathbb{P}[|Y_z-{\mathbb{E}}[Y_z]| \ge 0.5 {\mathbb{E}}[Y_z]] \le \exp({-}\Omega({\mathbb{E}}[Y_z])) = n^{-\Omega(\!\log n)}. $$

We will argue in the following that we may use a union bound over a finite number of z to deduce that with probability $1-n^{-\Omega(\!\log n)}$ , the bound $|Y_z-{\mathbb{E}}[Y_z]| <0.5 {\mathbb{E}}[Y_z]$ holds for all $z\in [{\mathsf{w}_{\min}},{{\overline w}}]$ , even though there are infinitely many such z. Consider the sets

\begin{align*}S_1 &\,:\!=\, \big\{\inf\{z\in [{\mathsf{w}_{\min}},{{\overline w}}] : 0.5{\mathbb{E}}[Y_z] \ge i\} \mid i \in \{0,\ldots,n\}\big\}, \\S_2 &\,:\!=\, \big\{\sup\{z\in [{\mathsf{w}_{\min}},{{\overline w}}] : 1.5{\mathbb{E}}[Y_z] \le i\} \mid i \in \{0,\ldots,n\}\big\}, \\S &\,:\!=\, \{{\mathsf{w}_{\min}},{{\overline w}}\} \cup S_1 \cup S_2,\end{align*}

where we discard any infimum or supremum taken over the empty set. By construction, the set S has at most $2n+4 = O(n)$ elements. Thus, by a union bound, with probability $1-n^{-\Omega(\!\log n)}$ , the bound $|Y_z-{\mathbb{E}}[Y_z]| <0.5 {\mathbb{E}}[Y_z]$ holds for all $z\in S$ . Assume that this event occurs. We want to show that then deterministically the same bound also holds for all other $z\in [{\mathsf{w}_{\min}},{{\overline w}}]$ . To this end, let $z\in[{\mathsf{w}_{\min}},{{\overline w}}]\setminus S$ , and let $z^- \,:\!=\, \max\{z^{\prime}\in S \mid z^{\prime} < z\}$ and $z^+ \,:\!=\, \min\{z^{\prime}\in S \mid z^{\prime} > z\}$ be its closest lower and upper neighbors in S. Then $Y_{z^+} > 0.5{\mathbb{E}}[Y_{z^+}]$ since $z^+ \in S$ . Since $Y_{z^+}$ is an integer, we can strengthen this to $Y_{z^+} \ge i \,:\!=\, \min\{j\in\mathbb{N}\mid j > 0.5{\mathbb{E}}[Y_{z^+}]\}$ , and note that $0.5{\mathbb{E}}[Y_{z^+}] < i$ . By the definition of S, we have $0.5{\mathbb{E}}[Y_{z^{\prime}}] < i$ for all $z^{\prime}\in (z^-,z^+)$ , since otherwise S would need to contain another point in $(z^-,z^+)$ where $0.5{\mathbb{E}}[Y_{z^{\prime}}]$ crosses the integer i. Since $Y_z$ is non-increasing in z, we may conclude that $Y_z \ge Y_{z^+}\ge i > 0.5{\mathbb{E}}[Y_{z}]$ , which is half of the claim. The other inequality $Y_z \le 1.5{\mathbb{E}}[Y_{z}]$ follows analogously from considering $z^-$ .

Summarizing, we have shown that with probability $1-n^{-\omega(1)}$ , $Y_z=\Theta(nz^{1-\beta})$ holds for all $z \in [{\mathsf{w}_{\min}},{{\overline w}}]$ . In this case, all z in our range satisfy both the lower and the upper bound of (PL2) even for $\eta=0$ . In particular, this proves that with probability $1-n^{-\omega(1)}$ , the lower bound of (PL2) holds for all $\eta\ge 0$ .

It only remains to prove the upper bound of (PL2) for $z\ge {{\overline w}}$ . Let $z \ge {{\overline w}}$ and $\eta=\eta(n)=\omega(\log\log n/\log n)$ . By Markov’s inequality and (9),

(10) \begin{align} \mathbb{P}[Y_z \ge nz^{1-\beta+\eta}] \le \mathbb{P}[Y_z \ge\Omega(z^{\eta}){\mathbb{E}}[Y_z]] \le O(z^{-\eta}) \le n^{-\Omega(\eta)}.\end{align}

By the same argument as above, we can restrict z to ${{\overline w}}$ and values where the intended bound $\Omega(z^{\eta}){\mathbb{E}}[Y_z]$ is integral, which happens only for $O(\log^2 n)$ values of z above ${{\overline w}}$ . Hence we can use the union bound to obtain error probability

\[O(n^{-\Omega(\eta)} \log^2 n)=n^{-\Omega(\eta)},\]

since $\eta(n)=\omega(\log\log n/\log n)$ . In particular it also follows that with probability $1-n^{-\Omega(\eta)}$ , the maximum weight satisfies ${\mathsf{w}_{\max}} \le n^{1/(\beta-1-\eta)}$ .

7. Giant component, diameter, and average distance

Under the assumption $2<\beta <3$ , we prove that w.h.p. the general model has a giant component with diameter at most $(\!\log n)^{O(1)}$ , and that all other components are only of polylogarithmic size. We further show that the average distance between any two vertices in the giant component is $(2 + o(1))\log \log n/|\log(\beta -2)|$ in expectation and with probability $1-o(1)$ . The same formula has been shown to hold for various graph models, including Chung–Lu random graphs [17] and hyperbolic random graphs [1]. The lower bound follows from using the first-moment method on the number of paths of different types. Note that the probability that a fixed path $P=(v_1,\ldots,v_k)$ exists in our model is the same as in Chung–Lu random graphs, since the marginal probability of the event $v_i \sim v_{i+1}$ conditioned on the positions of $v_1,\ldots, v_i$ is $\Theta(\min\{1,{\mathsf{w}_{v_i}}{\mathsf{w}_{v_{i+1}}}/{\mathsf{W}}\})$ , as in the Chung–Lu model. In particular, the expected number of paths coincides for the two models (save the factors coming from the $\Theta({\cdot})$ -notation). Not surprisingly, the lower bound for the expected average distance follows from general statements on power-law graphs, bounding the expected number of too-short paths by o(1) [21, Theorem 2]; see also Section 6.2 in [43]. The main contribution of this section is to prove a matching upper bound for the average distance.

The proof strategy is as follows. We first prove that, w.h.p., for every vertex of weight at least $(\!\log n)^C$ there exists an ultra-short path to the ‘heavy core’, which has diameter $o(\log\log n)$ and contains the vertices of highest weight. Afterwards, we show that a random low-weight vertex has a large probability of connecting to a vertex of weight at least $(\!\log n)^C$ within a small number of steps. The statement is formalized below as the ‘bulk lemma’ (Lemma 9). This lemma is the crucial step of the main proof, and it is new relative to previous studies of Chung–Lu random graphs and similar models. It contains a delicate analysis of the k-hop neighborhood of a random vertex, restricted to small weights. Thus, the underlying geometry is used implicitly in order to make the argument applicable for the fairly general model that we study.

Throughout this section, let G be a graph sampled from our model. For the result on the heavy core and for the bulk lemma, we do not need the condition $\beta <3$ . This is only needed for the greedy paths. We start by considering the subgraph induced by the heavy vertices ${{\bar V}} \,:\!=\, V_{\geq {{\overline w}}}$ , where ${{\overline w}}$ is given by the definition of power-law weights; see the condition (PL2). In particular, recall that $n^{\omega(1/\log\log n)}\leq{{\overline w}} \leq n^{(1-\Omega(1))/(\beta-1)}$ . We call the induced subgraph ${{\bar G}} \,:\!=\, G[{{\bar V}}]$ the heavy core.

Lemma 6. (Heavy core) W.h.p. $\bar G$ is connected and has diameter $o(\log \log n)$ .

Proof. Let $\bar n$ be the number of vertices in the heavy core, and let $\eta \gt 0$ be small enough. Since ${{\overline w}} \leq n^{(1-\Omega(1))/(\beta-1)}$ , we may bound $\bar n = \Omega(n{{\overline w}}^{1-\beta -\eta}) = n^{\Omega(1)}$ . By (EP2), if $\eta$ is sufficiently small, the connection probability for any heavy vertices u,v, regardless of their position, is at least

\begin{equation*}p_{uv}({\mathsf{x}_{u}}, {\mathsf{x}_{v}}) \geq \Big(\frac{n}{{{\overline w}}^{\beta-1+\eta}}\Big) ^{-1+\omega(1/\log\log n)} \ge \bar n^{-1+\omega(1/\log\log n)}.\end{equation*}

Therefore, the diameter of the heavy core is at most the diameter of an Erdös–Rényi random graph $G(\bar n,p)$ , with $p= \bar n^{-1+\omega(1/\log\log n)}$ . However, with probability $1-\bar n^{-\omega(1)}$ this diameter is $\Theta(\log \bar n/\log(p\bar n))=o(\log \log n)$ [23], and in particular the graph is connected in this case. Since $\bar n = n^{\Omega(1)}$ , this proves the lemma.

Next we show that if we start at a vertex of weight w, going greedily to the neighbors of largest weight yields a short path to the heavy core with a probability that approaches 1 as w increases.

Lemma 7. (Greedy path) Let $2<\beta < 3$ .

1. (i) Let $0<{{\varepsilon}}<1$ be constant and let v be a vertex of weight $2 \le w < {{\overline w}}$ . Then with probability at least $1-O\left(\exp\left({-}w^{\Omega({{\varepsilon}})}\right)\right)$ there exists a weight-increasing path of length at most $(1+{{\varepsilon}})\frac{\log \log n}{|\log(\beta-2)|}$ from v to the heavy core.

2. (ii) For every constant ${{\varepsilon}} \gt 0$ there exists a constant $C=C({{\varepsilon}}) \gt 0$ such that w.h.p. for all $v \in V_{\geq (\!\log n)^{C}}$ there exists a weight-increasing path of length at most $(1+{{\varepsilon}})\frac{\log \log n}{|\log(\beta-2)|}$ from v to the heavy core.

Proof. Let $0<{{\varepsilon}}<1$ , let v be a vertex of weight $2 \le w \le {{\overline w}}$ , and let

\[\tau=\tau(\varepsilon) \,:\!=\, (\beta-2)^{-1/(1+{{\varepsilon}}/2)}.\]

Note that $1 < \tau < 1/(\beta-2)$ , and that $1/\log \tau = (1+{{\varepsilon}}/2)/|\log(\beta-2)|$ . Moreover, we define an increasing weight sequence $w_0, w_1, \ldots, w_{i_{\max}} \,:\!=\, {{\overline w}}$ such that for all $1 \le i \le i_{\max}$ it holds that $w_i \,:\!=\, w_{i-1}^{\tau}$ , and such that $w_0 \le {\mathsf{w}_{v}} < w_1$ . For all $i < i_{\max}$ we put $V_i \,:\!=\, V_{\ge w_i} \setminus V_{\ge w_{i+1}}$ . Furthermore, we put $V_{i_{\max}} \,:\!=\, {{\bar V}} = V_{\ge {{\overline w}}}$ and $v_0 \,:\!=\, v$ . We will show that with sufficiently high probability, for all $0 \le i < i_{\max}$ the vertex $v_{i}$ has at least one neighbor $v_{i+1} \in V_{i+1}$ . By picking such a $v_{i+1}$ , we iteratively define a weight-increasing path. Note that $i_{\max} = \lceil\log_\tau\left(\log {{\overline w}}/\log {\mathsf{w}_{v}}\right)\rceil$ , so this implies that there is a path from v to the heavy core of length at most

\[i_{\max} \leq (1+{{\varepsilon}}/2)\frac{\log \log n}{|\log(\beta-2)|} + 1 \le (1+{{\varepsilon}}) \frac{\log \log n }{|\log(\beta-2)|},\]

for sufficiently large n, and thus proves the statement (i).

Let $0\leq i< i_{\max}$ and assume that there exists a weight-increasing path from $v_0$ to some vertex $v_{i} \in V_i$ . Note that this event only depends on the random graph induced by the vertex set $V_{< w_{i+1}}$ . We want to verify that $v_{i}$ connects to at least one vertex $v_{i+1} \in V_{i+1}$ . First, observe that by the condition (PL2), each layer $V_i$ contains at least $\Omega(n w_i^{1-\beta-\eta})$ and at most $O(n w_i^{1-\beta+\eta})$ vertices. Next, by the condition (EP1), for any position ${\mathsf{x}_{v_i}}$ the edges from $v_{i}$ to vertices v with $v\in V_{i+1}$ , are independently present with probability $\Omega(\min\{{\mathsf{w}_{v}}w_{i}/{\mathsf{W}},1\})$ , respectively; see also Lemma 2. Note that this bound is independent of ${\mathsf{x}_{v_i}}$ and thus holds for any realization of $V_{< w_{i+1}}$ ; see also Remark 2. If $w_{i}w_{i+1} \geq {\mathsf{W}}$ , this probability is $\Omega(1)$ . However, then $w_{i} \ge n^{1/(1+\tau)}$ and we deduce $|V_{i+1}|=n^{\Omega(1)}$ . In this case, the probability that $v_{i}$ connects to at least one vertex of the next weight layer is $1-\exp({-}n^{\Omega(1)}) = 1-\exp({-}w_i^{\Omega({{\varepsilon}})})$ , where the second step is a trivial upper bound that holds since ${{\varepsilon}}$ is constant and $w_i \le {{\overline w}} \le n^{O(1)}$ . So assume $w_{i}w_{i+1} < {\mathsf{W}}$ , where we can lower-bound the edge probability by $\Omega(w_{i} w_{i+1} / {\mathsf{W}})$ . Thus, for any $\eta \gt 0$ the probability that $v_{i}$ does not connect to a vertex in $V_{i+1}$ is at most

\begin{align*}p_i \,:\!=\, \prod_{v \in V,\, {\mathsf{w}_{v}}\geq w_{i+1}} \Big(1-\Omega\Big(\frac{w_i w_{i+1}}{{\mathsf{W}}}\Big)\Big) & \leq \exp({-}\Omega\Big(\frac{w_i w_{i+1}}{\mathsf{W}} \cdot |V_{i+1}|\Big) \Big) \\& \leq \exp\Big({-}\Omega\big(w_i w_{i+1}^{2-\beta-\eta}\big) \Big),\end{align*}

where we used Lemma 1 in the last step. Since $w_{i+1} \le w_i^\tau$ , we obtain

\[p_i \le \exp\big({-}\Omega\big(w_i^{1-\tau(\beta-2+\eta)}\big) \big).\]

Note that as $\tau < 1/(\beta-2)$ , the exponent of $w_i$ in this expression is positive for sufficiently small $\eta \gt 0$ . More precisely, we have

\[1 - \tau(\beta-2) = 1 - (\beta-2)^{{{\varepsilon}}/(2+{{\varepsilon}})} = \Omega({{\varepsilon}}),\]

and thus for $\eta > 0$ sufficiently small compared to ${{\varepsilon}}$ ,

(11) \begin{align} p_i \le \exp\big({-}w_i^{\Omega({{\varepsilon}})} \big).\end{align}

By induction and a union bound, for $0\le j\le i_{\max}$ it follows that there is a weight-increasing path from $v_0$ to $V_{j}$ of length j with probability at least $1-\sum_{i=0}^{j-1}\exp({-} w_i^{\Omega({{\varepsilon}})} ) = 1-\exp({-}w^{\Omega({{\varepsilon}})} )$ . With $j=i_{\max}$ this proves the first claim. For the following step, let us denote the hidden constant in the last expression by C’, so that the probability is at least $1-\exp({-}w^{C^{\prime}{{\varepsilon}}} )$ .

For the second statement, let $C=C({{\varepsilon}}) \,:\!=\, 2/(C^{\prime}{{\varepsilon}}))$ . If a vertex v has weight at least $(\!\log n)^C$ , then the error probability estimated above is at least $1-e^{-(\!\log n)^2} = 1-n^{-\omega(1)}$ . The claim now follows from a union bound over all vertices of weight at least $(\!\log n)^C$ .

Lemma 7(i) implies that any vertex of sufficiently large constant weight has probability $\Omega(1)$ of being connected to the heavy core by a weight-increasing path. In particular, this means that the connected component of the heavy core has size $\Omega(n)$ in expectation. In the following lemma, we show that the same holds w.h.p., which is less obvious, and requires our improved variant of McDiarmid’s inequality in Theorem 7.

Lemma 8. (Giant component.) Let $2<\beta < 3$ . W.h.p. there are $\Omega(n)$ vertices in the same component as the heavy core.

Proof. Let ${{\varepsilon}} \gt 0$ be a sufficiently small constant, let $\eta \gt 0$ be a constant that is sufficiently small compared to ${{\varepsilon}}$ , and let $\tau \,:\!=\, (\beta-2)^{-1/(1+{{\varepsilon}}/2)}$ . We use a system of weight layers as in the proof of Lemma 7(i), starting with $w_0 \,:\!=\, 2$ , so let $w_i \,:\!=\, 2^{\tau^i}$ and $V_i \,:\!=\, V_{\ge w_i} \setminus V_{\ge w_{i+1}}$ for all $i\ge 0$ . We remark already here that we will only need to study indices i for which $w_i \le (\!\log n)^C$ , where $C = C({{\varepsilon}})$ is the constant from Lemma 7(ii), since we already know by Lemma 7(ii) that otherwise all vertices in $V_i$ are in the same component as the heavy core, w.h.p. Moreover, by (PL2), if we choose $i_0 =O(1)$ sufficiently large, then for all $i\ge i_0$ with $w_i\le (\!\log n)^C$ we have $|V_{\ge w_{i+1}}| \le |V_{\ge w_{i}}|/2$ , and hence $|V_i| \ge |V_{\ge w_{i}}|/2$ . In particular, again by (PL2) we have $|V_i| \ge n/(\!\log n)^{O(1)}$ for all $i \ge i_0$ with $w_i \le (\!\log n)^C$ , and we have $|V_{i_0}| = \Omega(n)$ since we assumed $i_0=O(1)$ . We will increase $i_0$ further in the proof, but maintain $i_0=O(1)$ .

As already mentioned, the tricky part of the lemma is that it should hold w.h.p. The general strategy will be to define recursively for each i two sets $B_i, B_i^{\prime}$ of ‘bad’ vertices, such that the following hold:

• • Deterministically, every vertex in $V_i\setminus (B_i \cup B_i^{\prime})$ has a weight-increasing path to a vertex of weight at least $(\!\log n)^C$ .

• • W.h.p., $B_i$ and $B_i^{\prime}$ are small. (This is made precise in Claim 1 and Equation (12) below.) In particular, if $i_0 = O(1)$ is sufficiently large then w.h.p. $|B_i \cup B_i^{\prime}| \le |V_i|/2$ .

It then follows that w.h.p., at least half of the vertices in $V_{i_0}$ are connected to the heavy core. Since $|V_{i_0}| = \Omega(n)$ , this proves the lemma.

So let $i \ge i_0$ be such that $w_i \le (\!\log n)^C$ . For every $v \in V_i$ , let $\Gamma_i(v) \,:\!=\, \{u \in V_{i+1} \mid v \sim u\}$ , and let $E_i(v) \,:\!=\, {\mathbb{E}}[|\Gamma_i(v)|]$ . Moreover, let $\gamma \,:\!=\, \tau(2-\beta-\eta)+1 \gt 0$ . Then for every $v \in V_i$ , by (EP1) and Lemma 2,

\[E_i(v) \geq \Omega\Big(n w_{i+1}^{1-\beta-\eta} \cdot \frac{w_i w_{i+1}}{{\mathsf{W}}}\Big) \geq \Omega(w_{i+1}^{2-\beta-\eta}w_i) \geq \Omega(w_i^{\tau(2-\beta-\eta)+1})\geq \Omega(w_i^{\gamma}).\]

As this lower bound is independent of v, we also have

\[E_i \,:\!=\, \min_{v\in V_i} E_i(v) = \Omega(w_i^{\gamma}).\]

Let $\lambda \,:\!=\, \min\{\gamma, \frac{1}{2C\tau}\}$ . Furthermore put $B_i \,:\!=\, \{v\in V_i \mid |\Gamma_i(v)| \leq E_i/2\}$ . This is the first set of ‘bad’ vertices.

Claim 1. There is a constant $c \gt 0$ such that w.h.p., for all $i \ge i_0$ with $w_i \le (\!\log n)^C$ , it holds that $|B_i| \leq 2\exp({-}cw_i^{\lambda})\cdot |V_i|$ .

We postpone the proof of Claim 1 (and Claim 2 below) until we have finished the main argument. We uncover the sets $V_i$ one by one, starting with the largest weights. Let $\delta \gt 0$ be so small that $\tau(\lambda -\delta) > \lambda$ . We will show by downwards induction in i that w.h.p., for all $i\ge i_0$ the fraction of vertices in $V_i$ with a weight-increasing path to the heavy core is at least $1-\exp({-}c w_i^{\lambda -\delta})$ . Recall that if $w_i \geq (\!\log n)^C$ then we already know that w.h.p. all vertices in $V_i$ are connected to the heavy core with weight-increasing paths, which gives the base case of the induction. For the remaining values $i \ge i_0$ ,

1. (a) denote by $V_{i}^{\prime}$ the set of vertices in $V_{i}$ for which there is no weight-increasing path to the heavy core that uses exactly one vertex per layer;

2. (b) let $\Lambda_i \subseteq V_i$ be the subset $V_i$ of size $\exp({-}c w_{i-1}^{\lambda -\delta})|V_{i}|$ consisting of the vertices in $V_i$ with the smallest number of neighbors in $V_{i+1} \setminus V_{i+1}^{\prime}$ (where we break ties according to some previously fixed order).

Recall that $E(V_i,\Lambda_i)$ denotes the set of edges from $V_i$ to $\Lambda_i$ . We then use the following claim (whose proof we also postpone).

Claim 2. There exists $D \gt 0$ such that w.h.p., for all $i \ge i_0$ with $w_i \le (\!\log n)^C$ , it holds that

\[|E(V_{i},\Lambda_{i+1})| \leq \exp({-}cw_{i+1}^{\lambda -\delta})\cdot |V_i| \cdot E_{i} \cdot w_{i}^{D}.\]

The induction now runs as follows. Consider some $i\ge i_0$ such that $w_i \le (\!\log n)^C$ , and assume by induction that for sufficiently many vertices of $V_{i+1}$ there is a weight-increasing path to the heavy core; that is, assume $|V_{i+1}^{\prime}| \leq \exp({-}cw_{i+1}^{\lambda -\delta})\cdot |V_{i+1}|$ . By the construction of $\Lambda_{i+1}$ , this implies $V_{i+1}^{\prime} \subseteq \Lambda_{i+1}$ . Now we consider $B_i^{\prime} \,:\!=\, \{v \in V_{i} \mid |E(\{v\}, V_{i+1}^{\prime})| \geq E_{i}/2\}$ . If the low-probability event of Claim 2 does not occur, using $w_{i+1}^{\lambda-\delta} = w_i^{\lambda+\Omega(1)}$ and increasing $i_0$ if necessary, we find that

(12) \begin{align}|B_i^{\prime}| & \leq \frac{2|E(V_{i},V_{i+1}^{\prime})|}{E_i}\leq 2\exp({-}cw_{i+1}^{\lambda -\delta})\cdot |V_i| \cdot w_{i}^{D} \leq 2\exp({-}cw_{i}^{\lambda})\cdot |V_i| ,\end{align}

provided that $i_0 = i_0(c,D)$ (and thus $w_{i_0}$ ) is a sufficiently large constant. Note that we may increase $i_0$ because Claims 1 and 2 become weaker as $i_0$ increases. It remains to observe that every vertex in $V_i \setminus (B_i \cup B_i^{\prime})$ has at least one edge into $V_{i+1} \setminus V_{i+1}^{\prime}$ . Since the latter vertices are all connected to the heavy core, we have at least $|V_i|-|B_i|-|B_{i}^{\prime}|$ vertices in $V_i$ that are connected to the heavy core. By Claim 1 and Equation (12), w.h.p. $B_i$ and $B_i^{\prime}$ both have size at most $2\exp({-}cw_{i}^{\lambda})|V_i|$ . So, together they have size at most $4\exp({-}cw_{i}^{\lambda})|V_i| \le \exp({-}cw_{i}^{\lambda-\delta})|V_i|$ , where the last step holds for all $i\ge i_0$ if $i_0$ (and thus $w_i \ge w_{i_0}$ ) is sufficiently large. This proves the induction hypothesis and thus concludes the induction modulo Claims 1 and 2. To conclude the proof, if $i_0=O(1)$ is sufficiently large then $\exp({-}cw_{i_0}^{\lambda-\delta}) \le 1/2$ . The existence of the giant component now follows since $|V_{i_0} \setminus (B_{i_0}\cup B_{i_0}^{\prime})|\ge (1-\exp({-}cw_{i_0}^{\lambda-\delta}))|V_{i_0}| \ge |V_{i_0}|/2$ . Hence, w.h.p. at least half of $V_{i_0}$ is connected to the heavy core, where $|V_{i_0}|=\Omega(n)$ .

Proof of Claim 1. Let $i\ge i_0$ be such that $w_i \le (\!\log n)^C$ , and recall that $|V_i| = n/(\!\log n)^{O(1)}$ . For a single $v \in V_i$ with given location, the events ‘ $v \sim u$ ’ are independent for all $u \in V_{i+1}$ by Lemma 2. So by the Chernoff bound (Theorem 5), there is a constant $c \gt 0$ such that $ \mathbb{P}[v \in B_i] \leq \exp({-}cw_i^{\gamma})$ and ${\mathbb{E}}[|B_i|] \leq \exp({-}cw_i^{\gamma})|V_i|$ . Let $G_i$ be the subgraph induced by $V_i$ and $V_{i+1}$ , and observe that the size of $B_i$ only depends on $G_i$ . In order to prove concentration of $|B_i|$ we will use Theorem 7. For this, we need to argue that we can write the distribution of $G_i$ as a product probability space, i.e., we need to describe it via independent random variables. Recall that two different random processes are applied to create the geometric graph. First, we choose the positions ${\mathsf{x}_{v}} \in \mathcal{X}$ independently at random. Afterwards, every edge $\{u,v\}$ is inserted with some probability $p_{uv}$ . So far, these random variables are not independent, so this description does not yield a product probability space.

Without loss of generality, let us assume that the vertices are sorted by weights in decreasing order. For every vertex $u \in V_i \cup V_{i+1}$ we first have the random variable ${\mathsf{x}_{u}}$ for its position. Now, for each $u \in V_i \cup V_{i+1}$ we introduce a second, independent random variable $Y_u \,:\!=\, (Y_u^1, \ldots, Y_u^{u-1})$ (which is the empty tuple for $u=1$ ), where each $Y_u^v$ is a real number chosen independently and uniformly at random from the interval [0, 1]. Then for $v<u$ , we include the edge $\{u,v\}$ in the graph if and only if

\[p_{uv} > Y_u^v.\]

We observe that indeed this implies $ \mathbb{P}[u \sim v \mid {\mathsf{x}_{u}},{\mathsf{x}_{v}}]=p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}})$ , as desired. Moreover, conditional on the vertex positions, the events $u \sim v$ and $u^{\prime} \sim v^{\prime}$ are independent as long as $\{u,v\} \neq \{u^{\prime},v^{\prime}\}$ . This matches exactly the definition of $G_i$ as (induced subgraph of) a GIRG. Thus, if we denote by $\Omega$ the product space of all random variables over all components in $({\mathsf{x}_{u}}, Y_u)_{u \in V_i \cup V_{i+1}}$ , then the distribution of $G_i$ is described by $\Omega$ : every $\omega \in \Omega$ defines a graph $G_i(\omega)$ , and the probability distribution of $G_i(\omega)$ equals the probability distribution of $G_i$ as subgraph of a GIRG. Note that in the definition of the product space $\Omega$ , the random variable $Y_u$ is counted as a single coordinate, and the outcomes of this coordinate are vectors in $[0,1]^{u-1}$ . Thus $\Omega$ has $2(|V_i|+|V_{i+1}|)$ coordinates. This convention is useful since then $\Omega$ is a product space of at most O(n) coordinates, rather than $O(n^2)$ .

Our aim is to apply Theorem 7 to the function $f(\omega) \,:\!=\, |B_i(\omega)|$ , which depends on $\omega$ since the graph $G_i$ depends on $\omega$ . In particular, $0 \le f(\omega) \le n \,=\!:\,M$ . We study the bad event $\mathcal{B}$ that there exists a vertex $v \in V_i \cup V_{i+1}$ with degree larger than $(\!\log n)^{2C\tau^2}$ in $G_{i}$ . By Lemma 4(i) we have $ \mathbb{P}[\mathcal{B}] = n^{-\omega(1)}$ , since $w_i \le (\!\log n)^C$ and therefore ${\mathsf{w}_{v}} \le (\!\log n)^{C\tau^2}$ for all $v \in V_i \cup V_{i+1}$ . Let $\omega,\omega^{\prime} \in \overline{\mathcal{B}}$ be elements that differ in at most two coordinates in our product probability space $\Omega$ . We observe that changing one coordinate ${\mathsf{x}_{u}}$ or $Y_u$ (the latter means changing a vector in $[0,1]^{u-1}$ ) can only influence the neighborhoods of u itself and of the vertices that are neighbors of u before or after the coordinate change. In formula, changing one coordinate ${\mathsf{x}_{u}}$ or $Y_u$ can add or remove at most

$$1+\deg_{G_i(\omega)}(u)+ \deg_{G_i(\omega^{\prime})}(u) \le 1+2(\!\log n)^{2C\tau^2}$$

vertices from $B_i$ , where the latter inequality follows from $\omega,\omega^{\prime} \in \overline{\mathcal{B}}$ . Therefore,

$$\left| |B_i(\omega)| - |B_i(\omega^{\prime})| \right|\le (\!\log n)^{O(1)}.$$

We pick $t = \exp({-}cw_i^{\lambda})\cdot (|V_i|+|V_{i+1}|)$ and observe that $w_i^{\lambda} \le (\!\log n)^{1/2}$ by our choice of $\lambda = \min\{\gamma, \frac{1}{2C\tau}\}$ . In particular, $t\ge 2M \mathbb{P}[\mathcal B]$ is satisfied for sufficiently large n, which allows us to apply Theorem 7 with $f(\omega) = |B_i(\omega)|$ , $c= (\!\log n)^{O(1)}$ , $m=2(|V_i|+|V_{i+1}|)$ , and $M = n$ and get

\begin{align*} \mathbb{P}[|B_i|-{\mathbb{E}}[|B_i|] \ge t] &\le 2\exp\Big({-}\frac{t^2}{64(|V_i|+|V_{i+1}|)(\!\log n)^{O(1)}}\Big)+n^{O(1)} \mathbb{P}[\mathcal{B}]\\ &\le 2\exp\Big({-}\frac{e^{-2cw_i^\lambda}(|V_i|+|V_{i+1}|}{64 (\!\log n)^{O(1)}}\Big)+n^{O(1)} \mathbb{P}[\mathcal{B}] = n^{-\omega(1)},\end{align*}

where the first summand is $2\exp({-}n^{1-o(1)}) \le n^{-\omega(1)}$ because $|V_i|+|V_{i+1}| \ge n/(\!\log n)^{O(1)}$ and $e^{-2cw_i^\lambda} \ge n^{-o(1)}$ .

Hence, w.h.p. we have $|B_i| \leq {\mathbb{E}}[|B_i|] + t \leq (\exp({-}cw_i^{\gamma})+\exp({-}cw_i^{\lambda}))\cdot |V_i|$ . For fixed $i\ge i_0$ , the statement now follows since $\lambda < \gamma$ and $w_i >1$ , and then the proof of the claim is finished by a union bound over all $O(\log\log n)$ choices of i.

Proof of Claim 2. Let $i\ge i_0$ be such that $w_i \le (\!\log n)^C$ . We assume that the subgraph induced by $V_{\ge w_{i+2}}$ is given, and now we uncover $V_i$ and $V_{i+1}$ to obtain the subgraph induced by $V_{\ge w_i}$ . Similarly as in the proof of Claim 1, we can assume that this probability space $\Omega$ is a product probability space with $2(|V_i|+|V_{i+1}|)$ coordinates. Recall that $G_i$ denotes the subgraph induced by $V_i \cup V_{i+1}$ . We consider the same bad event $\mathcal{B}$ as in the proof of Claim 1, i.e., $\mathcal{B}$ denotes the event that the maximum degree in $G_{i}$ is larger than $(\!\log n)^{2C\tau^2}$ . Note that $\mathcal{B}$ is independent of $V_{\ge w_{i+2}}$ , so indeed Lemma 4 can again be applied to deduce $ \mathbb{P}[\mathcal{B}]=n^{-\omega(1)}$ .

Let $Z_i \,:\!=\, |E(V_i, \Lambda_{i+1})|$ . We will apply Theorem 7 to the random variable $f(\omega) = Z_i(\omega)$ , so let $\omega, \omega^{\prime} \in \overline{\mathcal{B}}$ be such that they differ in at most two coordinates of $\Omega$ . If we change a coordinate of $\Omega$ that stems from a vertex $v \in V_i$ , under $\overline{\mathcal{B}}$ the influence on $Z_i$ is at most $(\!\log n)^{O(1)}$ . If a coordinate belonging to a vertex $v\in V_{i+1}$ is changed, this may result in a different set $\Lambda_{i+1}$ , because either v might enter the set $\Lambda_{i+1}$ and replace another vertex v’ in $\Lambda_{i+1}$ (namely the vertex with the largest number of neighbors in $V_{i+2}\setminus V_{i+2}^{\prime}$ ; see (b) on page 19 for the definition of $\Lambda_i$ ); or v might be removed from $\Lambda_{i+1}$ and be replaced by some other vertex v’. In either case, the symmetric difference between the old $\Lambda_{i+1}$ and the new $\Lambda_{i+1}$ is at most two, and $E(V_i,\Lambda_{i+1})$ can only change in edges incident to v or v’. Hence, under $\overline{\mathcal{B}}$ changing the coordinate of a vertex $v\in V_{i+1}$ can change $Z_i$ by at most $c = (\!\log n)^{O(1)}$ . Note that the same is also true if the set $\Lambda_{i+1}$ does not change. Since $\omega,\omega^{\prime}$ differ in at most two coordinates, we conclude that $|Z_i(\omega)-Z_i(\omega^{\prime})| \le (\!\log n)^{O(1)}$ .

Next, we want to upper-bound ${\mathbb{E}}[Z_i]$ . First, we uncover $V_{i+1}$ to obtain the subgraph induced by $V_{\ge w_{i+1}}$ . Then the set $\Lambda_{i+1}$ is determined. In a second step, we uncover $V_i$ . By (EP1) and linearity of expectation, we deduce that

\begin{align*}{\mathbb{E}}[Z_i] & \leq |\Lambda_{i+1}| \cdot |V_{i}| \cdot O\Big(\frac{w_{i+1}^{1+\eta} w_{i}^{1+\eta}}{{\mathsf{W}}}\Big)\\& = O\Big(\exp({-}cw_{i+1}^{\lambda-\delta})n w_{i+1}^{1-\beta+\eta}\cdot |V_i|\cdot \frac{w_{i+1}^{1+\eta} w_{i}^{1+\eta}}{{\mathsf{W}}}\Big) \\& \leq \exp({-}cw_{i+1}^{\lambda-\delta}) \cdot |V_i| \cdot O\big(w_{i+1}^{2-\beta+2\eta}w_{i}^{1+\eta}\big) \\& \leq \exp({-}cw_{i+1}^{\lambda-\delta})\cdot |V_i|\cdot O\big(w_{i}^{\tau(2-\beta)+1+\eta(2\tau+1)}\big) \\& \leq \exp({-}cw_{i+1}^{\lambda-\delta})\cdot |V_i|\cdot E_i \cdot O\big(w_{i}^{\eta(3\tau+1)}\big).\end{align*}

Since we assumed $w_i \geq 2$ , we may upper-bound the $O({\cdot})$ -term by $0.5w_i^{D}$ for a sufficiently large $D \gt 0$ .

Now we can apply Theorem 7 with $t = 0.5\exp({-}cw_{i+1}^{\lambda-\delta})\cdot |V_i| \cdot E_{i} \cdot w_{i}^{D}$ . It follows similarly as in the proof of Claim 1 that $ \mathbb{P}\big[|Z_i - {\mathbb{E}}[Z_i]| \ge t \big] = n^{-\omega(1)}$ , and we conclude that with probability $1-n^{-\omega(1)}$ it holds that

\[|Z_i| \le {\mathbb{E}}[|Z_i|]+ t \le \exp({-}cw_{i+1}^{\lambda-\delta})\cdot |V_i| \cdot E_{i} \cdot w_{i}^{D}.\]

Now the claim follows by a union bound over all $O(\log\log n)$ choices of i.

By Lemma 7(ii), w.h.p. every vertex of weight at least $(\!\log n)^C$ has small distance from the heavy core. It remains to show that every vertex in the giant component has a large probability of connecting to such a high-weight vertex in a small number of steps. The next lemma shows that the more vertices of small weight a vertex v is connected to, the more likely it is that v has small distance to a vertex of large weight.

Lemma 9. (Bulk lemma). Let ${{\varepsilon}} \gt 0$ . Let ${\mathsf{w}_{\min}} \leq w \leq {{\overline w}}$ be a weight such that there are $\Omega(n)$ nodes with weight less than w, and let $k \geq \max\{2, w^{\beta-1+{{\varepsilon}}}\}$ be an integer. For a vertex $v \in V_{ \lt w}$ , let $C_v \subseteq V_{ \lt w}$ be the connected component of v in the graph $G_{< w}$ . Then for a random vertex $v\in V_{ \lt w}$ ,

\[ \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \le k \text{ or } |C_v| < k\big] \geq 1 - O\big(e^{-w^{\Omega(1)}}\big).\]

Proof. For any node $v \in V_{ \lt w}$ , we define $N_v \subseteq V_{ \lt w}$ to be the set of all vertices within distance less than k from v in the graph $G_{< w}$ . Observe that $|C_v| < k$ holds if and only if $|N_v| < k$ : indeed, if $|C_v|<k$ , then $C_v$ contains no path of length k and thus all nodes in $C_v$ have distance less than k to v, i.e., $C_v=N_v$ and thus $|N_v| = |C_v| < k$ . If $|C_v| \ge k$ , then either $C_v = N_v$ and thus $|N_v| = |C_v| \ge k$ , or $C_v$ contains some node u at distance at least k from v, but then the first k nodes on a path from v to u are all contained in $N_v$ and thus $|N_v| \ge k$ .

It follows that proving the bulk lemma is equivalent to proving the following inequality:

(13) \begin{align} \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \gt k \text{ and } |N_v| \ge k\big] \leq O\big(e^{-w^{\Omega(1)}}\big).\end{align}

Before proving (13), let us sketch some of the ideas of the proof. We first uncover the graph $G_{ \lt w}$ induced by vertices of weight less than w. For a fixed realization of $G_{ \lt w}$ , we consider the probability $P_v$ that a random node in $V_{[w,\tilde w]}$ has a neighbor in $N_v$ , for an appropriately chosen $\tilde w > w$ . We consider two cases: that $P_v$ is large or that it is small.

If $P_v$ is large, then it is very likely that there is at least one edge between $N_v$ and $V_{[w,\tilde w]}$ , and thus it is very likely that $\text{dist}(v,V_{\ge w}) \le k$ , which proves (13). In a geometric setting, e.g. in hyperbolic random graphs or GIRGs (see Section 3), intuitively this case occurs if the nodes in $N_v$ are spread out in the geometric space. Note that this argument holds for every fixed realization of $G_{< w}$ for which $P_v$ is large.

The case of small $P_v$ intuitively occurs if the nodes in $N_v$ form a bulk, i.e., they are concentrated in a small geometric region. For this case, it suffices to bound the number of bad nodes, i.e., the size of the set $B = \{v \in V_{ \lt w} \mid |N_k| \ge k \text{ and } P_v \text{ is small} \}$ . Note that B is a random variable that is determined by $G_{ \lt w}$ . In the most technical part of our proof, we show that if $|B|$ is large, then a node in $V_{[w,\tilde w]}$ has a significantly increased probability of having large degree. Since node-degrees in our model are Chernoff-concentrated, this shows that $|B|$ is very unlikely to be large. So in contrast to the case of large $P_v$ , we argue (indirectly) about the distribution of $G_{ \lt w}$ , i.e., we show that $G_{ \lt w}$ is unlikely to have the property that $|B|$ is large. See Claims 4, 5, and 6 for the technical details of this argument. We deduce that a random node v is very unlikely to be bad, which proves the desired inequality (13).

For the formal proof, we let $0 < \eta \le {{\varepsilon}}/4$ be sufficiently small. Then by the power-law assumption (PL2) we may choose $\tilde w = O(w^{1+\eta})$ such that there are at least $\Omega(n/w^{\beta-1+\eta})$ vertices with weights between w and $\tilde w$ . We denote by $v^*$ a node chosen uniformly at random from $V_{[w,\tilde w]}$ .

We first uncover the graph $G_{ \lt w}$ induced by vertices of weight less than w, i.e., we uncover the positions of these vertices and the edges in the induced subgraph. Note that uncovering $G_{ \lt w}$ in particular yields the sets $N_v$ , $v \in V_{ \lt w}$ . Once $G_{< w}$ is fixed, consider the probability $P_v$ that a random node $v^* \in V_{[w,\tilde w]}$ is a neighbor of at least one node in $N_v$ :

\[P_v \,:\!=\, \mathbb{P}[\Gamma(v^*) \cap N_v \ne \emptyset \mid G_{ \lt w}].\]

Note that $P_v$ depends on the choice of the node v, and it is a random variable depending on the random choices in $G_{ \lt w}$ , i.e., $P_v$ is a number after uncovering the graph $G_{ \lt w}$ . The probability in the definition of $P_v$ runs over the random choice of $v^* \in V_{[w,\tilde w]}$ , the positions of the nodes in $V_{\ge w}$ , and the edges in G excluding the induced subgraph $G_{ \lt w}$ .

Now we choose a parameter $\tau \,:\!=\, w^{\beta - 1 + 2\eta} / n$ and split into two cases:

(14) \begin{align} \mathbb{P}_{G,v}\big[\text{dist}(v,&V_{\geq w}) \gt k \text{ and } |N_v| \ge k\big] \notag \\= \quad & \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \gt k \text{ and } |N_v| \ge k \text{ and } P_v \ge \tau \big] \\ \quad +\ & \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \gt k \text{ and } |N_v| \ge k \text{ and } P_v < \tau \big] \notag\end{align}

Case 1: Large $P_v$ . To bound the first summand, recall that the size of $V_{[w,\tilde w]}$ is at least $\Omega(n/w^{\beta-1+\eta})$ . Since the probability that a random node in $V_{[w,\tilde w]}$ has a neighbor in $N_v$ is equal to $P_v \ge \tau$ , we obtain

\begin{align*}{\mathbb{E}}_{G,v}\big[|\{ u \in V_{[w,\tilde w]} \mid \Gamma(u) \cap N_v \ne \emptyset\}| \mid P_v \ge \tau\big] &\geq \Omega\Big(\frac{n}{w^{\beta-1+\eta}} \cdot \tau \Big) \ge \Omega(w^{\eta}),\end{align*}

where we used $\tau = w^{\beta - 1 + 2\eta} / n$ . Since every $u \in V_{[w,\tilde w]}$ draws its position and its edges to $V_{< w}$ independently from the other nodes in $V_{[w,\tilde w]}$ , the Chernoff bound yields

(15) \begin{align} \mathbb{P}_{G,v}\big[\exists u \in V_{[w,\tilde w]} \colon \Gamma(u) \cap N_v \ne \emptyset \mid P_v \ge \tau \big] \geq 1-O\big(e^{-\Omega(w^{\eta})}\big) \geq 1-O\big(e^{-w^{\Omega(1)}}\big).\end{align}

Since every node in $N_v$ has distance less than k to v, if there exists a node $u \in V_{[w,\tilde w]}$ with $\Gamma(u) \cap N_v \ne \emptyset$ then the distance from v to $V_{\ge w} \supseteq V_{[w,\tilde w]}$ is at most k. Thus, (15) implies

\[ \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) > k \mid P_v \ge \tau \big] \leq O\big(e^{-w^{\Omega(1)}}\big).\]

This allows us to bound the first summand of Equation (14) by

\begin{align*}& \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \gt k \text{ and } |N_v| \ge k \text{ and } P_v \ge \tau \big] \\&\le \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) > k \text{ and } P_v \ge \tau \big] \le \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) > k \mid P_v \ge \tau \big]\leq O\big(e^{-w^{\Omega(1)}}\big).\end{align*}

Case 2: Small $P_v$ . For the second summand of Equation (14), we have the bound

\begin{align*}& \mathbb{P}_{G,v}\big[\text{dist}(v,V_{\geq w}) \gt k \text{ and } |N_v| \ge k \text{ and } P_v < \tau \big] \\&\le \mathbb{P}_{G,v}\big[|N_v| \ge k \text{ and } P_v < \tau \big]= \mathbb{P}_{G_{ \lt w},v}\big[|N_v| \ge k \text{ and } P_v < \tau \big],\end{align*}

since $N_v$ and $P_v$ depend only on the random choices in $G_{ \lt w}$ . Now we define the set of bad nodes B as

\[B \,:\!=\, \{ v \in V_{ \lt w} \mid |N_v| \ge k \text{ and } P_v < \tau \}.\]

Note that B is a random variable that depends only on the random choices in $G_{ \lt w}$ . Since v is a random node in $V_{ \lt w}$ , and $|V_{ \lt w}| = \Omega(n)$ by assumption on w, we obtain

\[ \mathbb{P}_{G_{ \lt w},v}\big[|N_v| \ge k \text{ and } P_v \lt \tau \big] = {\mathbb{E}}_{G_{ \lt w}}\big[|B|/|V_{ \lt w}|\big] = O\big( \tfrac 1n \big) \cdot {\mathbb{E}}_{G_{ \lt w}}\big[|B|\big].\]

It now remains to prove that ${\mathbb{E}}_{G_{ \lt w}}[|B|] \le O(n \cdot e^{-\Omega(w)})$ , which we will do in Claim 6 below. Taken together, these considerations yield a bound of $O(e^{-\Omega(w)})$ on the second summand of Equation (14).

We have thus shown, modulo Claim 6, that both summands of (14) are $O(e^{-w^{\Omega(1)}})$ . This yields (13), which as discussed above is equivalent to the lemma statement.

To finish the proof of the bulk lemma it remains to prove ${\mathbb{E}}_{G_{ \lt w}}[|B|] \le O(n \cdot e^{-\Omega(w)})$ ; see Claim 6 below. We prove this through a series of claims.

Claim 3. Fix $G_{ \lt w}$ (and thus the sets B and $N_v$ for $v \in V_{ \lt w}$ ). There exist a set $\tilde B \subseteq B$ and sets $\tilde N_v \subseteq N_v$ for all $v \in \tilde B$ such that the following hold:

1. (i) the sets $\tilde N_v$ for $v \in \tilde B$ are disjoint,

2. (ii) $\sum_{v \in \tilde B} |\tilde N_v| \ge |B|$ , and

3. (iii) $|\tilde N_v| \ge k/2$ for all $v \in \tilde B$ .

Proof. We greedily construct $\tilde B$ as follows. Initially let $L \,:\!=\, B$ . While L is non-empty, pick any $v \in L$ , add v to $\tilde B$ , and remove all nodes $u \in N_v$ from L.

After constructing $\tilde B$ , assign each node $u \in \bigcup_{v \in \tilde B} N_v$ to its closest node $v \in \tilde B$ , i.e., to the node $v \in \tilde B$ minimizing the distance from u to v in $G_{ \lt w}$ (breaking ties arbitrarily). For any $v \in \tilde B$ let $\tilde N_v$ be the set of all nodes u that were assigned to v.

This finishes the construction. We clearly have $\tilde B \subseteq B$ . Since each node $u \in \bigcup_{v \in \tilde B} N_v$ is contained in some set $N_v$ and thus is at distance less than k from some $v \in \tilde B$ , and since we assign u to its closest node in $\tilde B$ , each node u is assigned to a node within distance k. It follows that $\tilde N_v \subseteq N_v$ . It remains to show the properties (i)–(iii).

The property (i) holds since we assign each node $u \in \bigcup_{v \in \tilde B} N_v$ to a unique node $v \in \tilde B$ .

For (ii), observe that $B \subseteq \bigcup_{v \in \tilde B} N_v$ , since each $b \in B$ is initially in L, and b is removed from L only if we add b to $\tilde B$ or we add another node v to $\tilde B$ such that $b \in N_v$ ; in both cases b ends up in $\bigcup_{v \in \tilde B} N_v$ . Our assignment satisfies $\bigcup_{v \in \tilde B} N_v = \bigcup_{v \in \tilde B} \tilde N_v$ , and thus $B \subseteq \bigcup_{v \in \tilde B} \tilde N_v$ . Since the latter is a disjoint union by (i), we obtain $|B| \le \sum_{v \in \tilde B} |\tilde N_v|$ .

For (iii), fix a node $v \in \tilde B$ and recall that $N_v = N_v(k,w)$ is the set of all nodes with distance less than k to v in $G_{ \lt w}$ . We similarly define $N^{\prime}_v$ as the set of all nodes with distance less than $k/2$ to v in $G_{ \lt w}$ . Note that by construction any two nodes in $\tilde B$ have distance at least k. Since any node $u \in N^{\prime}_v$ is at distance less than $k/2$ from v, by the triangle inequality u has distance at least $k/2$ from any other node in $\tilde B$ , and thus u is assigned to v. This shows that $N^{\prime}_v \subseteq \tilde N_v$ .

Now if $N^{\prime}_v = N_v$ , then we have $|\tilde N_v| \ge |N^{\prime}_v| = |N_v| \ge k \ge k/2$ , where we used the fact that $v \in B$ and the definition of $B = \{ v \in V_{ \lt w} \mid |N_v| \ge k \text{ and } P_v < \tau \}$ . Otherwise there exists a node $u \in N_v \setminus N^{\prime}_v$ . Consider any path from v to u in $G_{ \lt w}$ . Since $u \not\in N^{\prime}_v$ this path has length at least $k/2$ , and the first $k/2$ of the nodes on the path are contained in $N^{\prime}_v$ , so we obtain $|\tilde N_v| \ge |N^{\prime}_v| \ge k/2$ . In both cases we arrive at $|\tilde N_v| \ge k/2$ .

In what follows, for any outcome of $G_{ \lt w}$ we fix sets $\tilde B$ and $\tilde N_v$ for all $v \in \tilde B$ , as guaranteed by the above claim. Let $c \gt 0$ be such that for every vertex v of weight at least w, every vertex $u \in V$ , and every fixed position ${\mathsf{x}_{u}} \in \mathcal{X}$ we have $ \mathbb{P}[v \sim u \mid {\mathsf{x}_{u}}] \geq cw/n$ , i.e., c is the hidden constant of the condition (EP1). Recall that $v^*$ is a random node in $V_{[w,\tilde w]}$ . We set

\[\lambda \,:\!=\, \frac c2 w^{2-\beta-2\eta}\]

and define the random variable

\[ S \,:\!=\, \sum_{v \in {\tilde B}} \lambda|\tilde N_{v}| \cdot \mathbb{1}\big\{ | \Gamma(v^{*}) \cap \tilde N_{v} | \ge \lambda | \tilde N_{v} | \big\},\]

where the indicator random variable $\mathbb{1}\{E\}$ is 1 if the event E is true and 0 otherwise. In the following we prove upper and lower bounds on ${\mathbb{E}}[S]$ and then we combine them to bound ${\mathbb{E}}[|B|]$ .

Claim 4. We have ${\mathbb{E}}_{G}[S] \le O(e^{-\Omega(w)})$ .

Proof. We will first argue that

\[{\mathbb{E}}_{G}[S] = \sum_{i \ge 1} i\lambda \cdot \mathbb{P}_{G}[S =i\lambda ] = \sum_{i \ge k/2} i\lambda \cdot \mathbb{P}_{G}[S = i\lambda] \le \sum_{i \ge k/2} i\lambda \cdot {\mathbb{P}}_{G}[\deg(v^*) \ge i\lambda].\]

Indeed, the first equation is true because S is an integer multiple of $\lambda$ . For the second equation, recall that by Claim 3(iii) we have $|\tilde N_v| \ge k/2$ for all $v \in \tilde B$ . It follows that $S \gt 0$ implies $S \ge \lambda k/2$ , so smaller summands are 0. For the last inequality, recall that by Claim 3(i) the sets $\tilde N_v$ are disjoint. Thus, S is a lower bound on the degree of $v^*$ .

Now consider any node $u \in V_{[w,\tilde w]}$ and the random variable $\deg(u)$ . Since u has weight at most $\tilde w$ , its expected degree is $O(\tilde w)$ . Moreover, even after conditioning on the position ${\mathsf{x}_{u}}$ , the expected degree of u is $O(\tilde w)$ , and it is the sum of independent random variables; see Lemmas 2 and 3. Therefore, by the Chernoff–Hoeffding bound (Theorem 5), there is a constant $C \gt 0$ (independent of ${\mathsf{w}_{u}}$ and ${\mathsf{x}_{u}}$ ) such that $ \mathbb{P}_G[\deg(u)\geq i\lambda] \leq e^{-\Omega(i\lambda)}$ for all $i \geq C \tilde w / \lambda$ . Since this holds for all $u \in V_{[w,\tilde w]}$ , for the random node $v^* \in V_{[w,\tilde w]}$ we also have $ \mathbb{P}_G[\deg(v^*)\geq i\lambda] \leq e^{-\Omega(i \lambda)}$ for all $i \geq C \tilde w / \lambda$ .

Recall that we assume $k \ge w^{\beta - 1 + {{\varepsilon}}} \ge w^{\beta - 1 + 4\eta}$ . Therefore, we have $\lambda k/2 = \Omega(w^{2-\beta-2\eta} \cdot w^{\beta - 1 + 4\eta}) = \Omega(w^{1+2\eta}) = \Omega(\tilde w \cdot w^\eta)$ , since $\tilde w = O(w^{1+\eta})$ . We first consider the case that w is at least a sufficiently large constant $c^{\prime} > 0$ . Then the $w^\eta$ factor is large enough to dominate any constant factor, so we can conclude $\lambda k/2 \ge C \tilde w$ . This yields

\[{\mathbb{E}}_{G}[S] \le \sum_{i \ge C \tilde w/\lambda} i\lambda \cdot \mathbb{P}_G[\deg(v^*) \ge i\lambda] \le \sum_{i \ge C \tilde w/\lambda} i\lambda \cdot e^{-\Omega(i\lambda)}.\]

To estimate this further, for $j\in \mathbb{N}$ consider the summands with $j/\lambda \le i < (j+1)/\lambda$ . There are $O(1 + 1/\lambda)$ such summands, each of them having value $i\lambda e^{-\Omega(i\lambda)} = O(j e^{-\Omega(j)})$ . Hence, we may continue as follows:

\[{\mathbb{E}}_{G}[S] \le \sum_{j \ge C \tilde w} O((1 + \tfrac1\lambda) \cdot j e^{-\Omega(j)}) \le O((1 + \tfrac1\lambda) \cdot e^{-\Omega(C \tilde w)}) \le O(e^{-\Omega(w)}), \]

where the last inequality uses $w \le \tilde w$ and $1/\lambda \le O(w^{O(1)})$ .

It remains to consider the case that $w < c^{\prime}$ , meaning w is bounded by a constant. In this case it suffices to show that ${\mathbb{E}}_{G}[S] = O(1)$ . This follows from the fact that ${\mathbb{E}}_{G}[S] \le {\mathbb{E}}_{G}[\deg(v^*)] \le O(\tilde w) \le O(w^{1+\eta}) \le O(1)$ , since w is bounded by a constant.

Claim 5. We have ${\mathbb{E}}_{G}[S] \ge \Omega\big(\frac 1{n w^{O(1)}}\big) \cdot {\mathbb{E}}_{G_{ \lt w}}[|B|]$ .

Proof. Let X be a random variable taking values in [0, M], and let $x \in [0,\,M]$ . Then

\[{\mathbb{E}}[X] \le \mathbb{P}[X \ge x] \cdot M + \mathbb{P}[0 < X < x] \cdot x\le \mathbb{P}[X \ge x] \cdot M + \mathbb{P}[X > 0] \cdot x.\]

Rearranging this yields

\[ \mathbb{P}[X \ge x] \ge \tfrac 1M \big({\mathbb{E}}[X] - x \cdot \mathbb{P}[X > 0] \big).\]

We first uncover $G_{ \lt w}$ , and then for any $v \in \tilde B$ we apply the above inequality on the random variable $X = |\Gamma(v^*) \cap \tilde N_v|$ given $G_{ \lt w}$ , which takes values in $[0,M] = [0,|\tilde N_v|]$ . Setting $x \,:\!=\, \lambda |\tilde N_v|$ , we obtain

\begin{align*} & \mathbb{P}\big[|\Gamma(v^*) \cap \tilde N_v| \ge \lambda |\tilde N_v| \mid G_{ \lt w} \big] \\&\ge \frac 1{|\tilde N_v|} \Big({\mathbb{E}}\big[|\Gamma(v^*) \cap \tilde N_v| \mid G_{ \lt w}\big] - \lambda |\tilde N_v| \cdot \mathbb{P}\big[\Gamma(v^*) \cap \tilde N_v \ne \emptyset \mid G_{ \lt w}\big] \Big).\end{align*}

Recall that we defined $\lambda = \frac c2 w^{2-\beta-2\eta}$ , where the constant $c \gt 0$ is such that for any node v of weight at least w, any node u, and every fixed position ${\mathsf{x}_{u}}$ we have $ \mathbb{P}[v \sim u \mid {\mathsf{x}_{u}}] \ge cw/n$ . It follows that even after fixing $G_{ \lt w}$ , any node $v^* \in V_{[w,\tilde w]}$ has probability at least $cw/n$ of connecting to any node in $V_{ \lt w}$ . This gives us the bound

\[{\mathbb{E}}\big[|\Gamma(v^*) \cap \tilde N_v| \mid G_{ \lt w}\big]\ge |\tilde N_v| \cdot \frac{cw}n.\]

Using the definition of $P_v$ and the property $P_v < \tau$ of any $v \in \tilde B \subseteq B$ , we have

\[ \mathbb{P}\big[\Gamma(v^*) \cap \tilde N_v \ne \emptyset \mid G_{ \lt w}\big]\le \mathbb{P}\big[\Gamma(v^*) \cap N_v \ne \emptyset \mid G_{ \lt w}\big]= P_v < \tau.\]

Combining the three inequalities above yields

\[ \mathbb{P}\big[|\Gamma(v^*) \cap \tilde N_v| \ge \lambda |\tilde N_v| \mid G_{ \lt w}\big] \ge \frac{cw}n - \lambda \tau.\]

Since we defined $\lambda = \frac c2 w^{2-\beta-2\eta}$ and $\tau = w^{\beta - 1 + 2\eta} / n$ , we have $\lambda \tau = \frac{cw}{2n}$ , and thus

\[ \mathbb{P}\big[|\Gamma(v^*) \cap \tilde N_v| \ge \lambda |\tilde N_v| \mid G_{ \lt w}\big] \ge \frac{cw}{2n} \ge \Omega\Big( \frac 1n \Big).\]

Now we have the bound

\[{\mathbb{E}}[S \mid G_{ \lt w}] = \sum_{v \in \tilde B} \lambda |\tilde N_v| \cdot \mathbb{P}\big[|\Gamma(v^*) \cap \tilde N_v| \ge \lambda |\tilde N_v| \mid G_{ \lt w}\big]\ge \Omega\Big(\frac \lambda n \Big) \cdot \sum_{v \in \tilde B} |\tilde N_v|.\]

By Claim 3(ii), the last sum is at least $|B|$ . Since we have $\lambda \ge \Omega(1/w^{O(1)})$ , we obtain

\[{\mathbb{E}}[S \mid G_{ \lt w}] \ge \Omega\Big(\frac 1{n w^{O(1)}}\Big) \cdot |B|.\]

So far we assumed that $G_{ \lt w}$ is fixed. Taking the expectation over $G_{ \lt w}$ finally yields

\[{\mathbb{E}}_{G}[S] = {\mathbb{E}}_{G_{ \lt w}}\big[ {\mathbb{E}}[S \mid G_{ \lt w}] \big] \ge \Omega\Big(\frac 1{n w^{O(1)}}\Big) \cdot {\mathbb{E}}_{G_{ \lt w}}[ |B| ].\]

We are now ready to prove the remaining claim needed in the proof of the bulk lemma.

Claim 6. We have ${\mathbb{E}}_{G_{ \lt w}}[|B|] \le O(n \cdot e^{-\Omega(w)})$ .

Proof. Combining Claims 4 and 5 and rearranging yields

\[{\mathbb{E}}_{G_{ \lt w}}[|B|] \le O\big(n w^{O(1)} e^{-\Omega(w)}\big) \le O\big(n e^{-\Omega(w)}\big),\]

as required.

The upper bounds on the diameter and the average distance now follow easily from the lemmas we have proved so far. We collect the results in the following theorem, which reformulates and specifies Theorem 2 and Theorem 3.

Theorem 8. (Components and distances). Let $2 \lt \beta \lt 3$ .

1. (i) W.h.p., there is a giant component, i.e., a connected component which contains $\Omega(n)$ vertices.

2. (ii) W.h.p., all other components have at most polylogarithmic size.

3. (iii) W.h.p., the giant component has polylogarithmic diameter.

4. (iv) In expectation and with probability $1-o(1)$ , the average distance (i.e., the expected distance between two uniformly random vertices in the largest component) is $\frac{2 + o(1)}{|\log \beta-2 |}\log \log n$ .

5. (v) With probability $1-o(1)$ , a $(1-o(1))$ -fraction of all pairs of vertices in the giant component have distance at most $\frac{2 + o(1)}{|\log(\beta-2)|} \log \log n$ .

Proof. (i). This was proved in Lemma 8 and is simply stated here for completeness.

(ii), (iii). We fix a sufficiently small constant ${{\varepsilon}} \gt 0$ and conclude from the same lemma that w.h.p. the giant component contains all vertices of weight at least $w\,:\!=\,(\!\log n)^C$ , for a suitable constant $C \gt 0$ , and that w.h.p. all such vertices have distance at most $\frac{1+{{\varepsilon}}}{|\log(\beta-2)|} \log \log n$ from the heavy core ${{\bar V}}$ . We apply Lemma 9 with $k=w^{\beta-1+{{\varepsilon}}}$ . Then a random vertex in $V_{< w}$ has probability at least $1- e^{-w^{\Omega(1)}}$ of either being at distance at most k of $V_{\geq w}$ , or being in a component of size less than k. Note that for sufficiently large C this probability is at least $1-n^{-\omega(1)}$ . By the union bound, w.h.p. one of the two possibilities happens for all vertices in $V_{< w}$ . This already shows that w.h.p. all non-giant components are of size less than $k=(\!\log n)^{O(1)}$ . For the diameter of the giant component, recall that w.h.p. the heavy core has diameter $o(\log \log n)$ by Lemma 6. Therefore, w.h.p. the diameter of the giant component is $O(k+\log \log n) = (\!\log n)^{O(1)}$ .

(iv). For the average distance, let ${{\varepsilon}} \gt 0$ , and let $v \in V$ be a vertex chosen uniformly at random. Fix $k\geq 3$ , $k = n^{o(1)}$ , and let $w \,:\!=\, w(k) = k^{1/\beta}$ so that Lemma 9 is applicable as $k= w^{\beta}$ . We sort the vertices by weight and uncover the graph vertex by vertex in increasing order, until either (1) we see for the first time a vertex $v^{\prime} \in V_{\ge w}$ such that in the subgraph induced by $V_{\le {\mathsf{w}_{v^{\prime}}}}$ there exists a path of length at most k from v to v’, or (2) we have uncovered the full graph and (1) never happened. If ${\mathsf{w}_{v}} \ge w$ , then (1) trivially occurs. Otherwise, by Lemma 9, with probability $1-O(\exp({-}w^{\Omega(1)}))$ either the event (1) happens or the connected component of v in G has size less than k. In the latter case, v is not connected to the core and there is nothing to show. Otherwise, we have uncovered only the vertices of weight at most ${\mathsf{w}_{v^{\prime}}}$ , which allows us to apply Lemma 7(i) since its statement only depends on vertices of higher weight. By Lemma 7(i), with probability $1-O(\exp({-}w^{\Omega({{\varepsilon}})}))$ there is a weight-increasing path from v’ to the heavy core of length at most $\lambda_{{\varepsilon}} \,:\!=\, (1+{{\varepsilon}}) \frac{\log \log n}{|\log(\beta-2)|}$ . Summarizing, we have shown that for a random vertex v and every $k\geq 3$ with $k = n^{o(1)}$ ,

(16) \begin{align} \mathbb{P}\big[\infty > \text{dist}(v,V_{\text{core}}) \geq k+ \lambda_{{\varepsilon}} \big] \leq e^{-\Omega(w(k)^{\Omega({{\varepsilon}})})} = O\big(e^{-k^{\Omega({{\varepsilon}})}}\big).\end{align}

Let us first consider the expectation of the average distance; i.e., if u,u’ denote random vertices in the largest component of a random graph G, then we consider ${\mathbb{E}}_{G}[ {\mathbb{E}}_{u,u^{\prime}} [\text{dist}(u,u^{\prime}) ] ]$ . Since $\text{dist}(u,u^{\prime}) \le n$ we can condition on any event happening with probability $1 - n^{-\omega(1)}$ ; in particular we can condition on the event $\mathcal E$ that G has a giant component containing $V_{\text{core}}$ , all other components have size $(\!\log n)^{O(1)}$ , G has diameter $(\!\log n)^{O(1)}$ , and finally the core has diameter $d_{\text{core}} = o(\log \log n)$ . Moreover, by the bound

\[\text{dist}(u,u^{\prime}) \le \text{dist}(u,V_{\text{core}}) + \text{dist}(u^{\prime},V_{\text{core}}) + d_{\text{core}},\]

it suffices to bound $2 \cdot {\mathbb{E}}_{G}[ {\mathbb{E}}_u[ \text{dist}(u,V_{\text{core}})] \mid \mathcal E] + d_{\text{core}}$ . Now we use the fact ${\mathbb{E}}[X] = \sum_{k> 0} \mathbb{P}[X\geq k]$ for a random variable X taking values in $\mathbb{N}_{\ge 0}$ to obtain the bound

\[ {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] \le \lambda_{{\varepsilon}} + \sum_{k = 1}^{(\!\log n)^{O(1)}} \mathbb{P}_u\big[ \text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{\varepsilon}} \big]. \]

Note that conditioned on $\mathcal E$ , since u is chosen uniformly at random from the giant component, $\text{dist}(u,V_{\text{core}}) < \infty$ . Taking the expectation over G, conditioned on $\mathcal E$ , we may use (16) to bound the probability that $\text{dist}(v,V_{\text{core}})$ is too large for a vertex chosen uniformly at random from V. Since the giant component has size $\Omega(n)$ , this probability increases at most by a constant factor if we instead choose v uniformly at random from the giant component. Hence, for every constant ${{\varepsilon}} \gt 0$ we obtain

(17) \begin{align}{\mathbb{E}}_{G}[ {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] \mid \mathcal E] \le \lambda_{{\varepsilon}} + \sum_{k = 1}^{(\!\log n)^{O(1)}} O(e^{-k^{\Omega({{\varepsilon}})}}) + n^{-\omega(1)}.\end{align}

We now use the inequality

\[ \sum_{k=1}^\infty e^{-k^\kappa} \le \int_{x=0}^\infty e^{-x^\kappa} d x = \Gamma(1+1/\kappa), \]

where $\Gamma$ is Euler’s gamma function. Since $\Gamma(x)$ is monotonically increasing on the real axis for $x \ge 2$ and $\Gamma(1+n) = n!$ , we have $\Gamma(1+1/\kappa) \le \lceil 1/\kappa \rceil ! \le (1/\kappa)^{O(1/\kappa)}$ for $\kappa \le 1$ . Plugging this into Equation (17) yields

\[{\mathbb{E}}_{G}\big[ {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] \mid \mathcal E\big] \le \lambda_{{\varepsilon}} + O(1/{{\varepsilon}})^{O(1/{{\varepsilon}})} + n^{-\omega(1)}. \]

Note that for sufficiently slowly falling ${{\varepsilon}} = {{\varepsilon}}(n) = o(1)$ we have

\[O(1/{{\varepsilon}})^{O(1/{{\varepsilon}})} = o(\log \log n).\]

This yields the desired bound on the expected average distance of

\[2\lambda_{o(1)} + o(\log \log n) = \frac{2+o(1)}{\log|\beta-2|}\log \log n.\]

For the concentration, we want to show $ \mathbb{P}_G[ {\mathbb{E}}_{u,u^{\prime}}[ \text{dist}(u,u^{\prime}) ] \ge 2\lambda_{{{\varepsilon}}}]=o(1)$ , where we choose the same ${{\varepsilon}}(n)=o(1)$ as before. Similarly as before, we may upper-bound $ \mathbb{P}_G[ {\mathbb{E}}_{u,u^{\prime}}[ \text{dist}(u,u^{\prime}) ] \ge 2\lambda_{{{\varepsilon}}}]$ by

\[ n^{-\omega(1)} + \mathbb{P}_G\big[ 2\cdot {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] + d_{\text{core}} \ge 2\lambda_{{{\varepsilon}}} \mid \mathcal E \big].\]

Let $\gamma > 0$ be a sufficiently small constant, and let

\[\rho =\rho(n) = \frac{{{\varepsilon}}}{3|\log(\beta-2)|} \cdot \log \log n = o(\log \log n).\]

We claim that for sufficiently large n, $2\cdot {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] + d_{\text{core}} \ge 2\lambda_{{{\varepsilon}}}$ can only happen if for some $k > \rho$ we have

(18) \begin{align} \mathbb{P}_u[\text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{{\varepsilon}}/3}] \ge e^{-2k^{\gamma \cdot {{\varepsilon}}}}.\end{align}

Indeed, otherwise we have (conditioned on $\mathcal E$ ), similarly as before,

\begin{align*}{\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] &\le \lambda_{{{\varepsilon}}/3} + \rho + \sum_{k = \rho}^{(\!\log n)^{O(1)}} \mathbb{P}_u\big[\text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{{\varepsilon}}/3}\big]\\ &\le \lambda_{2{{\varepsilon}}/3} + O(1/{{\varepsilon}})^{O(1/{{\varepsilon}})},\end{align*}

and thus, indeed ${\mathbb{E}}_{u,u^{\prime}}[\text{dist}(u,u^{\prime})]$ is at most

\[2 \cdot {\mathbb{E}}_u[\text{dist}(u,V_{\text{core}})] + d_{\text{core}} \le 2 \lambda_{2{{\varepsilon}}/3} + o(\log \log n) < 2 \lambda_{{{\varepsilon}}}=2\lambda_{o(1)},\]

if ${{\varepsilon}}={{\varepsilon}}(n) = o(1)$ decreases sufficiently slowly. However, using the union bound over all $\rho \le k \le (\!\log n)^{O(1)}$ , we see that the probability that G is such that (18) holds for some $k > \rho$ is bounded from above by

\[ \sum_{k = \rho}^{(\!\log n)^{O(1)}} \mathbb{P}_G\big[ \mathbb{P}_u[\text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{{\varepsilon}}/3}] \ge e^{-k^{\gamma \cdot {{\varepsilon}}}} \big| \mathcal E \big]. \]

By (16) it follows that

\[{\mathbb{E}}_{G}[ \mathbb{P}_u[\infty > \text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{{\varepsilon}}/3}]] \le O(\exp({-}2k^{\gamma\cdot{{\varepsilon}}})),\]

for $\gamma \gt 0$ sufficiently small. We apply Markov’s inequality and deduce that

\[ \mathbb{P}_G\big[ \mathbb{P}_u[\infty > \text{dist}(u,V_{\text{core}}) \ge k + \lambda_{{{\varepsilon}}/3}] > e^{-k^{\gamma \cdot {{\varepsilon}}}} \big] \le O(e^{-k^{\Omega({{\varepsilon}})}}).\]

Because the giant component has linear size, this probability increases at most by a constant factor if we instead draw v from the giant component (conditioned on $\mathcal E$ ). Thus, the desired probability is bounded by

(19) \begin{align}\sum_{k = \rho}^{(\!\log n)^{O(1)}} O(e^{-k^{\Omega({{\varepsilon}})}}),\end{align}

which is o(1), since $\rho = {{\varepsilon}} \cdot \log \log n$ grows sufficiently quickly compared to a sufficiently slowly falling ${{\varepsilon}} = o(1)$ . This shows the concentration of the average distance and proves the statement (iv).

(v). Regarding the last statement (v), (19) shows that with probability $1-o(1)$ G is such that (18) does not hold for any $k > \rho$ . However, in this case the fraction of pairs $\{u,u^{\prime}\}$ of vertices in the giant component that have distance at least $2k + 2\lambda_{{{\varepsilon}}/3}$ is at most $e^{-4k^{\gamma\cdot{{\varepsilon}}}}$ . Taking $k=2\rho$ and assuming that $\rho={{\varepsilon}}\log\log n$ grows sufficiently quickly compared to ${{\varepsilon}}=o(1)$ , we see that a $(1-o(1))$ -fraction of pairs $\{u,u^{\prime}\}$ have distance at most $2\lambda_{o(1)}$ , given that $\rho={{\varepsilon}} \cdot \log\log n$ grows sufficiently fast compared to ${{\varepsilon}}=o(1)$ . This finishes the proof of Theorem 8.

8. Degree sequence

By definition of the model, we are assuming that the weight sequence ${\mathsf{w}_{}}$ follows a power law. Since the expected degree of a vertex with weight ${\mathsf{w}_{v}}$ is $\Theta({\mathsf{w}_{v}})$ by Lemma 3, it is not surprising that the degree sequence of the random graph will also follow a power law. In this section, we give details and prove Theorem 1, using Theorem 7 to show concentration. Some of the ideas in our proof are based on [28]. We start with the maximum degree $\Delta(G)$ , which is a simple corollary of Lemma 4.

Corollary 1. W.h.p., $\Delta(G)=\Theta({\mathsf{w}_{\max}})$ , where ${\mathsf{w}_{\max}} = \max\{{\mathsf{w}_{v}} \mid v \in V\}$ . In particular, for all $\eta \gt 0$ , w.h.p., $\Delta(G)=\Omega({{\overline w}})$ and $\Delta(G)=O(n^{1/(\beta-1-\eta)})$ .

Proof. We deduce from the model definition that $\omega(\log^2 n) \le {{\overline w}} \le {\mathsf{w}_{\max}} =O(n^{1/(\beta-1-\eta)})$ . Then Lemma 4 directly implies the statement.

Next, we calculate the expected number of vertices that have degree at least d.

Lemma 10. Let $\eta \gt 0$ be sufficiently small. Then for all $d \ge 1$ , $d=d(n)=o({{\overline w}})$ , we have

$$\Omega\big(n d^{1-\beta-\eta}\big) \le {\mathbb{E}}[\#\{v \in V \mid \deg(v) \geq d\}] \le O \big(n d^{1-\beta+\eta}\big).$$

Proof. Let $\eta \gt 0$ be sufficiently small. Recall that by Lemma 3, it holds that ${\mathbb{E}}[\deg(v)]=\Theta({\mathsf{w}_{v}})$ for every vertex $v \in V$ . Let $1 \le d \ll {{\overline w}}$ and let v be any vertex with weight $w_v \ge \Omega(d)$ large enough so that ${\mathbb{E}}[\deg(v)] \ge 2d$ . Then by a Chernoff bound

$$ \mathbb{P}[\deg(v) < d] \le \mathbb{P}[\deg(v) < 0.5 {\mathbb{E}}[\deg(v)]] \le e^{-{\mathbb{E}}[\deg(v)]/8} \le e^{-d/4} \le e^{-1/4}.$$

By the power-law assumption (PL2), there are $\Omega(n d^{1-\beta-\eta})$ vertices with weight $\Omega(d)$ , and a single vertex in this set has degree at least d with probability at least $1-e^{-1/4}$ . By linearity of expectation, ${\mathbb{E}}[\#\{v \in V \mid \deg(v) \geq d\}]=\sum_{v \in [n]} \mathbb{P}[\deg(v)\geq d]=\Omega(n d^{1-\beta-\eta})$ .

Next let v be a vertex with weight ${\mathsf{w}_{v}} \le O(d)$ small enough so that $2e{\mathbb{E}}[\deg(v)] \le 3d/4$ . By a Chernoff bound (Theorem 5(iii)), we obtain

$$ \mathbb{P}[\deg(v) \ge d] \le \mathbb{P}[\deg(v) > 3d/4] \le 2^{-3d/4}.$$

Thus, for the upper bound it follows that

\begin{align*}{\mathbb{E}}[\#\{v \in V \mid \deg(v) \geq d\}]&=\sum_{v \in [n]} \mathbb{P}[\deg(v)\geq d] \\&\le \vert V_{\ge O(d)}\vert + \!\!\!\!\sum_{v \in V_{\le O(d)}}\!\! \mathbb{P}[\deg(v)\geq d]\\&\le O(n d^{1-\beta+\eta}) + n\cdot 2^{-3d/4}.\end{align*}

Note that $d^2 \le 3 \cdot 2^{3d/4}$ holds for all $d \ge 1$ . Hence $n\cdot 2^{-3d/4} \le 3nd^{-2} < 3nd^{1-\beta+\eta}$ and indeed it holds that ${\mathbb{E}}[\#\{v \in V \mid \deg(v) \geq d\}] =O( n d^{1-\beta+\eta})$ .

After these preparations we come to the main theorem of this section, which is a more precise formulation of Theorem 1 and states that the degree sequence follows a power law with the same exponent $\beta$ as the weight sequence.

Theorem 9. For all $\eta \gt 0$ , w.h.p. we have

$$\Omega\big(n d^{1-\beta-\eta}\big) \le \#\{v \in V \mid \deg(v) \geq d\} \le O \big(n d^{1-\beta+\eta}\big),$$

where the first inequality holds for all $1 \leq d \leq {{\overline w}}$ and the second inequality holds for all $d \ge 1$ .

Before we prove Theorem 9, we note that by combining it with the standard calculations from Lemma 1 we immediately obtain the average degree in the graph.

Corollary 2. W.h.p., $\frac{1}{n}\sum_{v \in V} \deg(v)= \Theta(1)$ and thus $|E|=\Theta(n)$ .

Proof of Theorem 9. We first consider the case where d is larger than $\log^3 n = o({{\overline w}})$ . From the condition (PL2) on the vertex weights and Lemma 3 it follows that

$$\#\{v \in V \mid {\mathbb{E}}[\deg(v)] \geq 1.5d\}=\Omega\big(nd^{1-\beta-\eta}\big)$$

holds for all $\log^3 n \le d \le {{\overline w}}$ . Then, by Lemma 4, w.h.p. every vertex v with ${\mathbb{E}}[\deg(v)] \geq 1.5d$ has degree at least $(1-o(1))1.5d \ge d$ for n large enough. Hence w.h.p. there exist at least $\Omega(nd^{1-\beta-\eta})$ vertices with degree at least d. Vice versa, by Lemma 3 we have

$$\#\{v \in V \mid {\mathbb{E}}[\deg(v)] \geq 0.5d\} =O\big(n d^{1-\beta+\eta}\big).$$

By the same arguments as above, w.h.p. every vertex v with ${\mathbb{E}}[\deg(v)] < 0.5d$ has degree at most $(1+o(1))0.5d \lt d$ . Thus in total there can be at most $O(n d^{1-\beta+\eta})$ vertices with degree at least d. This proves the theorem for $d \ge \log^3 n$ .

Let $1 \le d \le \log^3 n$ , let ${{\varepsilon}} \gt 0$ be sufficiently small, let $V^{\prime} \,:\!=\, V_{\le n^{{{\varepsilon}}}}$ be the set of small-weight vertices, and let $G^{\prime} \,:\!=\, G[V^{\prime}]$ . First, we introduce some notation: define the two random variables

$$g_d \,:\!=\, \#\{v\in V \mid \deg(v) \geq d\}\quad \text{and}\quad f_d \,:\!=\, \#\{v\in V^{\prime} \mid \deg_{G^{\prime}}(v) \geq d\}.$$

Note that by Lemma 10, we already have

\[\Omega\big(n d^{1-\beta-\eta}\big) \le {\mathbb{E}}[g_d] \le O\big(n d^{1-\beta+\eta}\big),\]

and it remains to prove concentration. Clearly,

(20) \begin{align} f_d \le g_d \le f_d + 2\sum_{v \in V\setminus V^{\prime}} \deg(v).\end{align}

Next we apply Lemma 4 together with Lemma 1 and see that w.h.p.,

$$\sum_{v \in V\setminus V^{\prime}} \deg(v) = \Theta\big({\mathsf{W}}_{\ge n^{{{\varepsilon}}}} \big) = O\big(n^{1+(2-\beta+\eta){{\varepsilon}}}\big)=n^{1-\Omega(1)}.$$

Recall that we assume $d \le \log^3 n$ , so in particular

\[{\mathbb{E}}[g_d] =\Omega( n / (\!\log n)^{3(\beta-1+\eta)}).\]

It follows that ${\mathbb{E}}\big[\sum_{v \in V\setminus V^{\prime}} \deg(v)\big] = o({\mathbb{E}}[g_d])$ . The inequality (20) thus implies ${\mathbb{E}}[f_d]=(1+o(1)){\mathbb{E}}[g_d]$ . Hence, it is sufficient to prove that the random variable $f_d$ is concentrated around its expectation, because this will transfer immediately to $g_d$ .

We aim to show this concentration result via Theorem 7. Similarly as in the proof of Claim 1, we can assume that the probability space $\Omega$ under consideration is a product space of independent random variables. More precisely, the n independent random variables ${\mathsf{x}_{1}}, \ldots, {\mathsf{x}_{n}}$ define the vertex set and the $n-1$ independent random variables $Y_2, \ldots, Y_n$ define the edge set, where each $Y_u$ has the form $(Y_u^1, \ldots, Y_u^{u-1})$ , each $Y_u^v$ is a real number chosen uniformly at random from [0, 1], and for $v < u$ , the edge $\{u,v\}$ is present in the graph if and only if $p_{uv} \gt Y_u^v$ . The $2n-1$ random variables then define the product probability space $\Omega$ , i.e., for every $\omega \in \Omega$ , we denote by $G(\omega)$ the resulting graph, and similarly we use $G^{\prime}=G^{\prime}(\omega)$ and $f_d = f_d(\omega)$ . We now consider the bad event:

(21) \begin{align} \mathcal{B} \,:\!=\, \{\omega \in \Omega: \text{ the maximum degree in }G^{\prime}(\omega) \text{ is at least }n^{2{{\varepsilon}}}\}.\end{align}

We observe that $ \mathbb{P}[\mathcal{B}]=n^{-\omega(1)}$ , since by Lemma 4 w.h.p. every vertex $v \in V^{\prime}$ has degree at most $O({\mathsf{w}_{v}} + \log^2 n) = o(n^{2{{\varepsilon}}})$ . Let $\omega,\omega^{\prime} \in \overline{\mathcal{B}}$ be such that they differ in at most two coordinates. We observe that changing one coordinate ${\mathsf{x}_{i}}$ or $Y_i$ can influence only the degrees of i itself and of the vertices which are neighbors of i either before or after the coordinate change. It follows that $|f_d(\omega)-f_d(\omega^{\prime})| \le 4 n^{2{{\varepsilon}}} \,=\!:\, c$ . Therefore, $f_d$ satisfies the Lipschitz condition of Theorem 7 with bad event $\mathcal{B}$ . Let $t = n^{1-{{\varepsilon}}}=o({\mathbb{E}}[f_d])$ . Then since $n \mathbb{P}[\mathcal B] = n^{-\omega(1)}$ , Theorem 7 implies

\begin{align*} \mathbb{P}\big[|f_d-{\mathbb{E}}[f_d]| \ge t \big] & \le 2e^{-\frac{t^2}{64c^2 n}} + (\tfrac{4n^2}{c}+1) \mathbb{P}[\mathcal{B}]\\ & = e^{-\Omega(n^{1-4{{\varepsilon}}})}+n^{-\omega(1)}=n^{-\omega(1)},\end{align*}

which proves concentration and concludes the proof.

9. Proof of Theorem 4

In this section we prove Theorem 4, which states that for any connection function p satisfying Equation 2, the corresponding distance model satisfies the conditions (EP1) and (EP2), and thus the results from Section 2.2 on degree sequences, component structure, and average distances apply.

Proof of Theorem 4. Fix u,v, and also the position ${\mathsf{x}_{u}}$ . Note that $V(r) = \mathbb{P}_{{\mathsf{x}_{v}}}(\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|\leq r)$ , so V(r) describes the cumulative probability distribution of the random variable $\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|$ . The marginal edge probability is given by the Riemann–Stieltjes integral over r,

\[E \,:\!=\, {\mathbb{E}}_{{\mathsf{x}_{v}}}[p_{uv}({\mathsf{x}_{u}},{\mathsf{x}_{v}}) \mid {\mathsf{x}_{u}}] = \Theta\Big( \int_0^\infty \Lambda_{u,v}(r) dV(r) \Big),\]

where

\[\Lambda_{u,v}(r) \,:\!=\, \min\Big\{1, V(r)^{-\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\}.\]

In particular, for every sequence of partitions $r^{(t)} = \{0=r_0^{(t)} < \ldots <r_{\ell(t)}^{(t)}\}$ with meshes tending to zero, the upper Darboux sum with respect to $r^{(t)}$ converges to the expectation,

\[E = \Theta\Big(\lim_{t\to \infty} \sum_{s=1}^{\ell(t)}\Big(\sup_{r_{s-1}^{(t)}\leq r\leq r_{s}^{(t)}} \Lambda_{u,v}(r)\Big) \big(V(r_{s}^{(t)})-V(r_{s-1}^{(t)})\big) \Big).\]

Since V is surjective, we may refine the meshes $r^{(t)}$ if necessary so that the meshes of the partitions $V^{(t)} = \{V(r_0^{(t)}), \ldots, V(r_{\ell(t)}^{(t)})\}\,=\!:\,\{V_0^{(t)}, \ldots, V_{\ell(t)}^{(t)}\}$ also tend to zero. Hence,

\begin{align*}E & = \Theta\Big(\lim_{t\to \infty} \sum_{s=1}^{\ell(t)}\min\Big\{1, (V_s^{(t)})^{-\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\} \Big(V_{s}^{(t)}-V_{s-1}^{(t)}\Big)\Big) \\& = \Theta\Big(\int_{0}^1 \min\Big\{1, V^{-\alpha} \cdot \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}} \Big\} dV\Big),\end{align*}

where the latter integral is an ordinary Riemann integral. If ${\mathsf{w}_{u}} {\mathsf{w}_{v}}/{\mathsf{W}} \geq 1$ , the integrand is 1 and we obtain $E = \Theta(1) = \Theta\left(\min\left\{1,\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\right\}\right)$ . On the other hand, if ${\mathsf{w}_{u}} {\mathsf{w}_{v}}/{\mathsf{W}} < 1$ , then let $r_0\,:\!=\, (\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}})^{\max\{\alpha,1\}/\alpha } < 1$ . Note that if $r_0 = \Theta(1)$ , then also $r_0 = \Theta({\mathsf{w}_{u}} {\mathsf{w}_{v}}/{\mathsf{W}})$ . Therefore,

\begin{align*}E & = \Theta\bigg(\int_0^{r_0} 1 dV+\Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}}\int_{r_0}^1 V^{-\alpha} dV\bigg) \\& = \begin{cases}\Theta\Big(r_0 + \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}(1-r_0^{1-\alpha})\Big) = \Theta \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)& \text{, if } \alpha < 1, \text{ and}\\\Theta\bigg(r_0 +\Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\alpha}(r_0^{1-\alpha}-1) \bigg) = \Theta \Big( \frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)& \text{, if } \alpha> 1,\end{cases}\end{align*}

as required.

It remains to show that p satisfies (EP2). Since $V(\|{\mathsf{x}_{u}}-{\mathsf{x}_{v}}\|) \leq 1$ , from Equation (2) we obtain the lower bound

\[p_{uv} \geq \Omega\Big( \min\Big\{1, \Big(\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}}\Big\}\Big).\]

If ${\mathsf{w}_{u}} {\mathsf{w}_{v}}/{\mathsf{W}} \geq 1$ then there is nothing to show (since the right-hand side of (EP2) is o(1) by the upper bound on ${{\overline w}}$ ). Otherwise, if ${\mathsf{w}_{u}} {\mathsf{w}_{v}}/{\mathsf{W}} < 1$ , then

\[p_{uv} \geq \Omega\Big( \Big(\frac{{\mathsf{w}_{u}} {\mathsf{w}_{v}}}{{\mathsf{W}}}\Big)^{\max\{\alpha,1\}}\Big) \geq \Omega\Big( \frac{{{\overline w}}^2}{n}\Big) \geq \Big(\frac{n}{{{\overline w}}^{\beta-1+\eta}}\Big) ^{-1+\omega(1/\log\log n)},\]

where the last step follows from the lower bound on ${{\overline w}}$ . This concludes the proof.