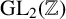1 Introduction
Associated with a finite simplicial graph
![]() $\Gamma $
whose vertex set and edge set are V and E, respectively, is the right-angled Artin group (RAAG)
$\Gamma $
whose vertex set and edge set are V and E, respectively, is the right-angled Artin group (RAAG)
![]() $A_\Gamma $
which is defined by the group presentation:
$A_\Gamma $
which is defined by the group presentation:
In these settings,
![]() $\Gamma $
is said to be the defining graph of
$\Gamma $
is said to be the defining graph of
![]() $A_\Gamma $
. As extreme examples, RAAGs can be free abelian groups
$A_\Gamma $
. As extreme examples, RAAGs can be free abelian groups
![]() $\mathbb {Z}^n$
, when the defining graphs are complete, or free groups
$\mathbb {Z}^n$
, when the defining graphs are complete, or free groups
![]() $\mathbb {F}_n$
, when the defining graphs have no edges. In contrast, generic RAAGs have interesting behaviours; for example, some of their subgroups may not be isomorphic to RAAGs. Subgroups of RAAGs, such as Bestvina–Brady groups [Reference Behrstock, Druu and Mosher3], are actually quite wild and have been used to construct examples of groups with peculiar properties. For a brief introduction to RAAGs, we refer to Charney’s note [Reference Charney5].
$\mathbb {F}_n$
, when the defining graphs have no edges. In contrast, generic RAAGs have interesting behaviours; for example, some of their subgroups may not be isomorphic to RAAGs. Subgroups of RAAGs, such as Bestvina–Brady groups [Reference Behrstock, Druu and Mosher3], are actually quite wild and have been used to construct examples of groups with peculiar properties. For a brief introduction to RAAGs, we refer to Charney’s note [Reference Charney5].
In this paper, we look at the automorphism and outer automorphism groups of
![]() $A_\Gamma $
denoted by
$A_\Gamma $
denoted by
![]() $\mathrm {Aut}(A_\Gamma )$
and
$\mathrm {Aut}(A_\Gamma )$
and
![]() $\mathrm {Out}(A_\Gamma )$
, respectively (the inner automorphism group is denoted by
$\mathrm {Out}(A_\Gamma )$
, respectively (the inner automorphism group is denoted by
![]() $\mathrm {Inn}(A_\Gamma )$
). Here,
$\mathrm {Inn}(A_\Gamma )$
). Here,
![]() $\mathrm {Out}(\mathbb {Z}^n)$
will usually be identified with
$\mathrm {Out}(\mathbb {Z}^n)$
will usually be identified with
![]() $\mathrm {GL}_n(\mathbb {Z})$
. Even though
$\mathrm {GL}_n(\mathbb {Z})$
. Even though
![]() $\mathbb {Z}^n$
and
$\mathbb {Z}^n$
and
![]() $\mathbb {F}_n$
have a lot of opposite properties in the algebraic sense,
$\mathbb {F}_n$
have a lot of opposite properties in the algebraic sense,
![]() $\mathrm {GL}_n(\mathbb {Z})$
and
$\mathrm {GL}_n(\mathbb {Z})$
and
![]() $\mathrm {Out}(\mathbb {F}_n)$
share many common properties: for example, both are virtually torsion-free, residually finite and have finite virtual cohomological dimension. Charney and Vogtmann extended these results to every
$\mathrm {Out}(\mathbb {F}_n)$
share many common properties: for example, both are virtually torsion-free, residually finite and have finite virtual cohomological dimension. Charney and Vogtmann extended these results to every
![]() $\mathrm {Out}(A_{\Gamma })$
in their papers [Reference Charney and Vogtmann6, Reference Charney and Vogtmann7].
$\mathrm {Out}(A_{\Gamma })$
in their papers [Reference Charney and Vogtmann6, Reference Charney and Vogtmann7].
Another interesting common feature of
![]() $\mathrm {GL}_n(\mathbb {Z})$
and
$\mathrm {GL}_n(\mathbb {Z})$
and
![]() $\mathrm {Out}(\mathbb {F}_n)$
is that they are not relatively hyperbolic, except when n is small enough, in which case they are actually hyperbolic. Anderson et al. [Reference Anderson, Aramayona and Shackleton1] established a simple criterion for showing nonrelative hyperbolicity of groups generated by infinite order elements. Using this criterion, they proved that, as long as
$\mathrm {Out}(\mathbb {F}_n)$
is that they are not relatively hyperbolic, except when n is small enough, in which case they are actually hyperbolic. Anderson et al. [Reference Anderson, Aramayona and Shackleton1] established a simple criterion for showing nonrelative hyperbolicity of groups generated by infinite order elements. Using this criterion, they proved that, as long as
![]() $n \geq 3$
,
$n \geq 3$
,
![]() $\mathrm {GL}_n(\mathbb {Z})$
and
$\mathrm {GL}_n(\mathbb {Z})$
and
![]() $\mathrm {Out}(\mathbb {F}_n)$
, and even
$\mathrm {Out}(\mathbb {F}_n)$
, and even
![]() $\mathrm {Aut}(\mathbb {F}_n)$
, are not relatively hyperbolic; see also Behrstock et al. [Reference Bestvina and Brady2]. It is then quite natural to ask whether
$\mathrm {Aut}(\mathbb {F}_n)$
, are not relatively hyperbolic; see also Behrstock et al. [Reference Bestvina and Brady2]. It is then quite natural to ask whether
![]() $\mathrm {Aut}(A_\Gamma )$
and
$\mathrm {Aut}(A_\Gamma )$
and
![]() $\mathrm {Out}(A_\Gamma )$
are always never hyperbolic. This turns out to be true, except for a few cases.
$\mathrm {Out}(A_\Gamma )$
are always never hyperbolic. This turns out to be true, except for a few cases.
Here are the two main theorems of this paper.
Theorem 3.1. If a finite simplicial graph
![]() $\Gamma $
contains at least three vertices, then the automorphism group of the right-angled Artin group of
$\Gamma $
contains at least three vertices, then the automorphism group of the right-angled Artin group of
![]() $\Gamma $
is not relatively hyperbolic.
$\Gamma $
is not relatively hyperbolic.
Theorem 4.1. If the outer automorphism group of a right-angled Artin group is infinite and relatively hyperbolic, then it is virtually cyclic or virtually isomorphic to
![]() $\mathrm {GL}_2(\mathbb {Z})$
.
$\mathrm {GL}_2(\mathbb {Z})$
.
We remark that even though
![]() $\mathrm {Aut}(A_{\Gamma })$
is almost never relatively hyperbolic, Genevois proved in [Reference Genevois9] that
$\mathrm {Aut}(A_{\Gamma })$
is almost never relatively hyperbolic, Genevois proved in [Reference Genevois9] that
![]() $\mathrm {Aut}(A_{\Gamma })$
is acylindrically hyperbolic if and only if
$\mathrm {Aut}(A_{\Gamma })$
is acylindrically hyperbolic if and only if
![]() $\Gamma $
is not a join and contains at least two vertices.
$\Gamma $
is not a join and contains at least two vertices.
The definition and study of relatively hyperbolic groups come from the following observation: even when a group G fails to be hyperbolic, it might still exhibit hyperbolic behaviours if we look only ‘outside’ some proper subgroups, called parabolic subgroups. With this observation in mind, one obstruction for being relatively hyperbolic is the existence of a specific collection
![]() $\mathcal {A}$
of proper subgroups which are far from being hyperbolic (for example, free abelian subgroups) and are well-networked. The term ‘well-networked’ means that (1) the union of all the subgroups in
$\mathcal {A}$
of proper subgroups which are far from being hyperbolic (for example, free abelian subgroups) and are well-networked. The term ‘well-networked’ means that (1) the union of all the subgroups in
![]() $\mathcal {A}$
generates a finite index subgroup of G and (2) for any
$\mathcal {A}$
generates a finite index subgroup of G and (2) for any
![]() $A,A'\in \mathcal {A}$
, there exists a sequence
$A,A'\in \mathcal {A}$
, there exists a sequence
![]() $A_1=A,\ldots ,A_n=A'$
such that
$A_1=A,\ldots ,A_n=A'$
such that
![]() $A_i\cap A_{i+1}$
is infinite. If we find such a collection of subgroups of G, then G is never relatively hyperbolic regardless of the choice of parabolic subgroups.
$A_i\cap A_{i+1}$
is infinite. If we find such a collection of subgroups of G, then G is never relatively hyperbolic regardless of the choice of parabolic subgroups.
Following the above idea, the notion of the commutativity graph of a group G is recalled in Section 2.2 as a tool to show that G is not relatively hyperbolic. One of the main assumptions to define the commutativity graph is the existence of a (possibly infinite) generating set of G which consists of infinite order elements. However, there are finite order elements in the usual generating sets of
![]() $\mathrm {Aut}(A_\Gamma )$
and
$\mathrm {Aut}(A_\Gamma )$
and
![]() $\mathrm {Out}(A_\Gamma )$
. To handle this problem, in Section 2.1, we find a finite index subgroup which is generated by a finite collection of infinite order elements. In Sections 3 and 4, we prove that
$\mathrm {Out}(A_\Gamma )$
. To handle this problem, in Section 2.1, we find a finite index subgroup which is generated by a finite collection of infinite order elements. In Sections 3 and 4, we prove that
![]() $\mathrm {Aut}(A_\Gamma )$
and
$\mathrm {Aut}(A_\Gamma )$
and
![]() $\mathrm {Out}(A_\Gamma )$
, respectively, are in general not relatively hyperbolic, by using those finite index subgroups and the fact that being (or not being) relatively hyperbolic is a quasi-isometry invariant.
$\mathrm {Out}(A_\Gamma )$
, respectively, are in general not relatively hyperbolic, by using those finite index subgroups and the fact that being (or not being) relatively hyperbolic is a quasi-isometry invariant.
2 Preliminaries
We always assume
![]() $\Gamma $
is a finite simplicial graph with vertex set V. For a vertex
$\Gamma $
is a finite simplicial graph with vertex set V. For a vertex
![]() $v \in V$
, the link of v, denoted by
$v \in V$
, the link of v, denoted by
![]() $\mathrm {lk}(v)$
, is the the full subgraph of
$\mathrm {lk}(v)$
, is the the full subgraph of
![]() $\Gamma $
spanned by vertices adjacent to v. Similarly, the star of v, denoted by
$\Gamma $
spanned by vertices adjacent to v. Similarly, the star of v, denoted by
![]() $\mathrm {st}(v)$
, is the full subgraph of
$\mathrm {st}(v)$
, is the full subgraph of
![]() $\Gamma $
spanned by vertices adjacent to v and v itself. We then say that
$\Gamma $
spanned by vertices adjacent to v and v itself. We then say that
![]() $v \leq w$
if
$v \leq w$
if
![]() $\mathrm {lk}(v) \subset \mathrm {st}(w)$
. This partial order induces an equivalence relation on V by setting
$\mathrm {lk}(v) \subset \mathrm {st}(w)$
. This partial order induces an equivalence relation on V by setting
![]() $v \sim w$
if
$v \sim w$
if
![]() $v\leq w$
and
$v\leq w$
and
![]() $w \leq v$
. The partial order then descends to a partial order on the collection of the equivalence classes of vertices by setting
$w \leq v$
. The partial order then descends to a partial order on the collection of the equivalence classes of vertices by setting
![]() $[v] \leq [w]$
if for some, and thus all, representatives
$[v] \leq [w]$
if for some, and thus all, representatives
![]() $v' \in [v]$
and
$v' \in [v]$
and
![]() $w' \in [w]$
, we have
$w' \in [w]$
, we have
![]() $v' \leq w'$
. A vertex
$v' \leq w'$
. A vertex
![]() $v \in V$
is maximal if any vertex w such that
$v \in V$
is maximal if any vertex w such that
![]() $v \leq w$
is actually equivalent to v.
$v \leq w$
is actually equivalent to v.
2.1 (Outer) automorphism groups of RAAGs
A theorem which was conjectured by Servatius [Reference Servatius12] and proved by Laurence [Reference Laurence10] says that
![]() $\mathrm {Aut}(A_{\Gamma })$
is generated by the following four finite classes of automorphisms.
$\mathrm {Aut}(A_{\Gamma })$
is generated by the following four finite classes of automorphisms.
-
(1) Graph automorphisms. An automorphism of
 $\Gamma $
induces an automorphism of
$\Gamma $
induces an automorphism of
 $A_{\Gamma }$
because it preserves the edges of
$A_{\Gamma }$
because it preserves the edges of
 $\Gamma $
and thus the relations of
$\Gamma $
and thus the relations of
 $A_{\Gamma }$
. The automorphism obtained this way is called a graph automorphism.
$A_{\Gamma }$
. The automorphism obtained this way is called a graph automorphism. -
(2) Inversions. An automorphism of
 $A_{\Gamma }$
sending one generator v to its inverse
$A_{\Gamma }$
sending one generator v to its inverse
 $v^{-1}$
is called an inversion.
$v^{-1}$
is called an inversion. -
(3) Transvections. Take two vertices v and w in
 $\Gamma $
such that
$\Gamma $
such that
 $v \leq w$
. Then the automorphism sending v to
$v \leq w$
. Then the automorphism sending v to
 $vw$
and fixing all the other vertices is called a right transvection and is denoted by
$vw$
and fixing all the other vertices is called a right transvection and is denoted by
 $R_ {vw}$
. We can similarly define a left transvection
$R_ {vw}$
. We can similarly define a left transvection
 $L_{vw}$
by sending v to
$L_{vw}$
by sending v to
 $wv$
and still fixing all the other vertices.
$wv$
and still fixing all the other vertices. -
(4) Partial conjugations. Let C be a connected component of
 $\Gamma - \mathrm {st}(v)$
, for a vertex
$\Gamma - \mathrm {st}(v)$
, for a vertex
 $v\in \Gamma $
. The automorphism defined by conjugating every vertex in C by v is called a partial conjugation and is denoted by
$v\in \Gamma $
. The automorphism defined by conjugating every vertex in C by v is called a partial conjugation and is denoted by
 $P_v^C$
. If a component C of
$P_v^C$
. If a component C of
 $\Gamma - \mathrm {st}(v)$
is composed of a single vertex w, we write
$\Gamma - \mathrm {st}(v)$
is composed of a single vertex w, we write
 $P_v^w$
instead of
$P_v^w$
instead of
 $P_v^{\{w\}}$
.
$P_v^{\{w\}}$
.
Transvections and partial conjugations have infinite order, in contrast to inversions and graph automorphisms which have finite order. The abelianisation map
![]() $A_\Gamma \rightarrow \mathbb {Z}^{n}$
for
$A_\Gamma \rightarrow \mathbb {Z}^{n}$
for
![]() $n=|V|$
induces a homomorphism
$n=|V|$
induces a homomorphism
![]() $\mathrm {Aut}(A_\Gamma )\rightarrow \mathrm {GL}_n(\mathbb {Z})$
, whose restriction on the subgroup generated by inversions and graph automorphisms is injective; in particular, this subgroup is finite because its image in
$\mathrm {Aut}(A_\Gamma )\rightarrow \mathrm {GL}_n(\mathbb {Z})$
, whose restriction on the subgroup generated by inversions and graph automorphisms is injective; in particular, this subgroup is finite because its image in
![]() $\mathrm {GL}_n(\mathbb {Z})$
is finite. Let
$\mathrm {GL}_n(\mathbb {Z})$
is finite. Let
![]() $\mathrm {Aut}^*(A_{\Gamma })$
be the subgroup of
$\mathrm {Aut}^*(A_{\Gamma })$
be the subgroup of
![]() $\mathrm {Aut}(A_{\Gamma })$
generated only by transvections and partial conjugations.
$\mathrm {Aut}(A_{\Gamma })$
generated only by transvections and partial conjugations.
Lemma 2.1.
![]() $\mathrm {Aut}^*(A_{\Gamma })$
is a finite index normal subgroup of
$\mathrm {Aut}^*(A_{\Gamma })$
is a finite index normal subgroup of
![]() $\mathrm {Aut}(A_{\Gamma })$
.
$\mathrm {Aut}(A_{\Gamma })$
.
Proof. The fact that
![]() $\mathrm {Aut}^*(A_{\Gamma })$
is a normal subgroup can be shown by checking that the conjugate of a transvection or a partial conjugation by an inversion or a graph automorphism is still a transvection or a partial conjugation. Because the image of the quotient map
$\mathrm {Aut}^*(A_{\Gamma })$
is a normal subgroup can be shown by checking that the conjugate of a transvection or a partial conjugation by an inversion or a graph automorphism is still a transvection or a partial conjugation. Because the image of the quotient map
![]() $\mathrm {Aut}(A_{\Gamma })\rightarrow \mathrm {Aut}(A_\Gamma )/\mathrm {Aut}^*(A_{\Gamma })$
is generated by the images of graph automorphisms and inversions, its cardinality is smaller than or equal to that of the subgroup generated by inversions and graph automorphisms, which is finite. We can thus deduce that
$\mathrm {Aut}(A_{\Gamma })\rightarrow \mathrm {Aut}(A_\Gamma )/\mathrm {Aut}^*(A_{\Gamma })$
is generated by the images of graph automorphisms and inversions, its cardinality is smaller than or equal to that of the subgroup generated by inversions and graph automorphisms, which is finite. We can thus deduce that
![]() $\mathrm {Aut}^*(A_{\Gamma })$
is of finite index.
$\mathrm {Aut}^*(A_{\Gamma })$
is of finite index.
Under the quotient map
![]() $\mathrm {Aut}(A_\Gamma )\rightarrow \mathrm {Out}(A_\Gamma ):=\mathrm {Aut}(A_\Gamma )/\mathrm {Inn}(A_\Gamma )$
,
$\mathrm {Aut}(A_\Gamma )\rightarrow \mathrm {Out}(A_\Gamma ):=\mathrm {Aut}(A_\Gamma )/\mathrm {Inn}(A_\Gamma )$
,
![]() $\mathrm {Out}(A_\Gamma )$
is generated by the images of graph automorphisms, inversions, transvections and partial conjugations. (Note that some images of partial conjugations may be trivial in
$\mathrm {Out}(A_\Gamma )$
is generated by the images of graph automorphisms, inversions, transvections and partial conjugations. (Note that some images of partial conjugations may be trivial in
![]() $\mathrm {Out}(A_\Gamma )$
.) Similarly,
$\mathrm {Out}(A_\Gamma )$
.) Similarly,
![]() $\mathrm {Out}^*(A_{\Gamma })$
is defined to be the subgroup generated by the images of transvections and partial conjugations in
$\mathrm {Out}^*(A_{\Gamma })$
is defined to be the subgroup generated by the images of transvections and partial conjugations in
![]() $\mathrm {Out}(A_\Gamma )$
; it can be considered as the image of
$\mathrm {Out}(A_\Gamma )$
; it can be considered as the image of
![]() $\mathrm {Aut}^*(A_{\Gamma })$
in
$\mathrm {Aut}^*(A_{\Gamma })$
in
![]() $\mathrm {Out}(A_{\Gamma })$
. By the above lemma,
$\mathrm {Out}(A_{\Gamma })$
. By the above lemma,
![]() $\mathrm {Out}^*(A_{\Gamma })$
is also a finite index normal subgroup of
$\mathrm {Out}^*(A_{\Gamma })$
is also a finite index normal subgroup of
![]() $\mathrm {Out}(A_{\Gamma })$
.
$\mathrm {Out}(A_{\Gamma })$
.
2.2 Nonrelative hyperbolicity
We first recall the definition of relative hyperbolicity by Bowditch [Reference Bowditch4]. Let G be a finitely generated group and
![]() $\mathcal {H}$
a finite collection of proper finitely generated subgroups of G. Choose a finite generating set S of G and consider the Cayley graph
$\mathcal {H}$
a finite collection of proper finitely generated subgroups of G. Choose a finite generating set S of G and consider the Cayley graph
![]() $\Lambda = \Lambda (G,S)$
. The coned-off Cayley graph
$\Lambda = \Lambda (G,S)$
. The coned-off Cayley graph
![]() $\hat {\Lambda }(G,\mathcal {H})$
is defined as follows: starting with the Cayley graph
$\hat {\Lambda }(G,\mathcal {H})$
is defined as follows: starting with the Cayley graph
![]() $\Lambda $
, for each coset
$\Lambda $
, for each coset
![]() $gH_i$
with
$gH_i$
with
![]() $g\in G$
,
$g\in G$
,
![]() $H_i\in \mathcal {H}$
, we add a vertex
$H_i\in \mathcal {H}$
, we add a vertex
![]() $v(gH_i)$
to
$v(gH_i)$
to
![]() $\Lambda $
and connect
$\Lambda $
and connect
![]() $v(gH_i)$
by an edge to each vertex in
$v(gH_i)$
by an edge to each vertex in
![]() $gH_i$
. We then say that G is relatively hyperbolic with respect to
$gH_i$
. We then say that G is relatively hyperbolic with respect to
![]() $\mathcal {H}$
if:
$\mathcal {H}$
if:
-
(1) the coned-off Cayley graph
 $\hat {\Lambda }(G,\mathcal {H})$
is
$\hat {\Lambda }(G,\mathcal {H})$
is
 $\delta $
-hyperbolic; and
$\delta $
-hyperbolic; and -
(2)
 $\hat {\Lambda }(G,\mathcal {H})$
is fine (this means that for each integer k, all edges e of
$\hat {\Lambda }(G,\mathcal {H})$
is fine (this means that for each integer k, all edges e of
 $\hat {\Lambda }(G,\mathcal {H})$
are contained in finitely many simple cycles of length k).
$\hat {\Lambda }(G,\mathcal {H})$
are contained in finitely many simple cycles of length k).
Whenever
![]() $\hat {\Lambda }(G,\mathcal {H})$
satisfies the first of the above conditions, an element in
$\hat {\Lambda }(G,\mathcal {H})$
satisfies the first of the above conditions, an element in
![]() $\mathcal {H}$
is said to be a parabolic subgroup of G and G is said to be weakly relatively hyperbolic (with respect to
$\mathcal {H}$
is said to be a parabolic subgroup of G and G is said to be weakly relatively hyperbolic (with respect to
![]() $\mathcal {H}$
). If G is not relatively hyperbolic with respect to any choice of a finite collection of proper finitely generated subgroups
$\mathcal {H}$
). If G is not relatively hyperbolic with respect to any choice of a finite collection of proper finitely generated subgroups
![]() $\mathcal {H}$
, then it is said to be not relatively hyperbolic.
$\mathcal {H}$
, then it is said to be not relatively hyperbolic.
There are two necessary conditions for parabolic subgroups of relatively hyperbolic groups. Let G be a finitely generated group which is relatively hyperbolic with respect to a finite collection
![]() $\mathcal {H}=\{H_i\}$
of parabolic subgroups. The first is about virtual malnormality of parabolic subgroups and the second slightly generalises [Reference Anderson, Aramayona and Shackleton1, Lemma 5].
$\mathcal {H}=\{H_i\}$
of parabolic subgroups. The first is about virtual malnormality of parabolic subgroups and the second slightly generalises [Reference Anderson, Aramayona and Shackleton1, Lemma 5].
Theorem 2.2 [Reference Osin11, Theorem 1.4]
For
![]() $H_i,H_j\in \mathcal {H}$
and
$H_i,H_j\in \mathcal {H}$
and
![]() $g_1,g_2\in G$
,
$g_1,g_2\in G$
,
![]() $g_1H_ig^{-1}_1\cap g_2H_jg^{-1}_2$
is finite if either
$g_1H_ig^{-1}_1\cap g_2H_jg^{-1}_2$
is finite if either
![]() $H_i$
and
$H_i$
and
![]() $H_j$
are distinct or
$H_j$
are distinct or
![]() $H_i=H_j$
and
$H_i=H_j$
and
![]() $g^{-1}_1g_2\notin H_i$
.
$g^{-1}_1g_2\notin H_i$
.
In particular, this implies that parabolic subgroups are almost malnormal.
Lemma 2.3. Suppose H is a subgroup of G isomorphic to a RAAG
![]() $A_\Gamma $
whose defining graph
$A_\Gamma $
whose defining graph
![]() $\Gamma $
is connected. Then H is contained in a conjugate of a parabolic subgroup
$\Gamma $
is connected. Then H is contained in a conjugate of a parabolic subgroup
![]() $H_i\in \mathcal {H}$
.
$H_i\in \mathcal {H}$
.
Proof. This is a direct consequence of Theorems 4.16 and 4.19 in [Reference Osin11], stating that a free abelian subgroup of rank 2 has to be contained in a conjugate of
![]() $H_i\in \mathcal {H}$
. Because the subgroup generated by the end points of each edge of
$H_i\in \mathcal {H}$
. Because the subgroup generated by the end points of each edge of
![]() $\Gamma $
is a free abelian subgroup of rank two, we can deduce that H is contained in a conjugate of a parabolic subgroup.
$\Gamma $
is a free abelian subgroup of rank two, we can deduce that H is contained in a conjugate of a parabolic subgroup.
From these necessary conditions for parabolic subgroups, a simple criterion for detecting nonrelative hyperbolicity is developed as in [Reference Anderson, Aramayona and Shackleton1]. Let G be a group and S be a (possibly infinite) generating set consisting only of infinite order elements. The commutativity graph
![]() $K(G,S)$
of G with respect to S is the simplicial graph with vertex set S in which two distinct vertices s and
$K(G,S)$
of G with respect to S is the simplicial graph with vertex set S in which two distinct vertices s and
![]() $s'$
are connected by an edge if there exist integers
$s'$
are connected by an edge if there exist integers
![]() $n_s$
and
$n_s$
and
![]() $n_{s'}$
such that
$n_{s'}$
such that
![]() $\langle s^{n_s},(s')^{n_{s'}}\rangle $
is abelian. The main theorem of [Reference Anderson, Aramayona and Shackleton1] is then the following result.
$\langle s^{n_s},(s')^{n_{s'}}\rangle $
is abelian. The main theorem of [Reference Anderson, Aramayona and Shackleton1] is then the following result.
Theorem 2.4 [Reference Anderson, Aramayona and Shackleton1]
Let G be a finitely generated group and S be a (possibly infinite) generating set of G which consists of infinite order elements and contains at least two elements. Suppose that
![]() $K(G,S)$
is connected and that there are at least two vertices s and
$K(G,S)$
is connected and that there are at least two vertices s and
![]() $s'$
in
$s'$
in
![]() $K(G,S)$
such that
$K(G,S)$
such that
![]() $\langle s^{n_s},(s')^{n_{s'}}\rangle $
is a rank two free abelian group for some integers
$\langle s^{n_s},(s')^{n_{s'}}\rangle $
is a rank two free abelian group for some integers
![]() $n_s$
and
$n_s$
and
![]() $n_{s'}$
. Then, G is not relatively hyperbolic.
$n_{s'}$
. Then, G is not relatively hyperbolic.
Finally, owing to the result of Druţu, to know whether a finitely generated group G is relatively hyperbolic or not, we may look at other groups quasi-isometric to G (for example, finite index subgroups).
Theorem 2.5 [Reference Druţu8]
In the class of finitely generated groups, being relatively hyperbolic is a quasi-isometry invariant.
3 Automorphism group
The goal of this section is to prove that
![]() $\mathrm {Aut}(A_{\Gamma })$
is in general not relatively hyperbolic. To use Theorem 2.4, we work with
$\mathrm {Aut}(A_{\Gamma })$
is in general not relatively hyperbolic. To use Theorem 2.4, we work with
![]() $\mathrm {Aut}^*(A_{\Gamma })$
instead of
$\mathrm {Aut}^*(A_{\Gamma })$
instead of
![]() $\mathrm {Aut}(A_{\Gamma })$
. Indeed,
$\mathrm {Aut}(A_{\Gamma })$
. Indeed,
![]() $\mathrm {Aut}^*(A_\Gamma )$
is generated by infinite order elements and is a finite index subgroup, by Lemma 2.1. By Theorem 2.5, it is then enough to show that
$\mathrm {Aut}^*(A_\Gamma )$
is generated by infinite order elements and is a finite index subgroup, by Lemma 2.1. By Theorem 2.5, it is then enough to show that
![]() $\mathrm {Aut}^*(A_{\Gamma })$
is not relatively hyperbolic.
$\mathrm {Aut}^*(A_{\Gamma })$
is not relatively hyperbolic.
Theorem 3.1. Let
![]() $\Gamma $
be a graph which has at least three vertices and S the set of all transvections and partial conjugations in
$\Gamma $
be a graph which has at least three vertices and S the set of all transvections and partial conjugations in
![]() $\mathrm {Aut}(A_\Gamma )$
. Then the commutativity graph
$\mathrm {Aut}(A_\Gamma )$
. Then the commutativity graph
![]() $K(\mathrm {Aut}^*(A_{\Gamma }), S)$
is connected. Hence,
$K(\mathrm {Aut}^*(A_{\Gamma }), S)$
is connected. Hence,
![]() $\mathrm {Aut}(A_{\Gamma })$
is not relatively hyperbolic.
$\mathrm {Aut}(A_{\Gamma })$
is not relatively hyperbolic.
Proof. The proof is divided into three steps. First, we show that, as long as they exist, any two transvections are joined by a path in
![]() $K=K(\mathrm {Aut}^*(A_{\Gamma }),S)$
. Then, we show that the same holds for any two partial conjugations. Finally, we show that any partial conjugation and transvection are joined by a path, as long as they exist.
$K=K(\mathrm {Aut}^*(A_{\Gamma }),S)$
. Then, we show that the same holds for any two partial conjugations. Finally, we show that any partial conjugation and transvection are joined by a path, as long as they exist.
Claim 1. If there are at least two distinct transvections, then any two transvections are joined by a path in K.
Let a and b be vertices in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $a \leq b$
. If a and b are adjacent, then
$a \leq b$
. If a and b are adjacent, then
![]() $R_{ab}=L_{ab}$
. Otherwise,
$R_{ab}=L_{ab}$
. Otherwise,
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ab}$
are distinct but
$L_{ab}$
are distinct but
![]() $[R_{ab},L_{ab}]=1$
, that is,
$[R_{ab},L_{ab}]=1$
, that is,
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ab}$
are joined by an edge in K. (In both cases,
$L_{ab}$
are joined by an edge in K. (In both cases,
![]() $[R_{ab},L_{ab}]=1$
.) Thus, to prove the claim, we only need to show that there is a path in K from
$[R_{ab},L_{ab}]=1$
.) Thus, to prove the claim, we only need to show that there is a path in K from
![]() $R_{ab}$
to either
$R_{ab}$
to either
![]() $R_{cd}$
or
$R_{cd}$
or
![]() $L_{cd}$
for any two vertices
$L_{cd}$
for any two vertices
![]() $c,d\in \Gamma $
with
$c,d\in \Gamma $
with
![]() $c\leq d$
. There are five cases to handle.
$c\leq d$
. There are five cases to handle.
Case 1. If
![]() $c = a$
, then
$c = a$
, then
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ad}$
are joined by an edge because
$L_{ad}$
are joined by an edge because
![]() $[R_{ab},L_{ad}]=1$
.
$[R_{ab},L_{ad}]=1$
.
Case 2. If
![]() $c \neq a,b$
and
$c \neq a,b$
and
![]() $d \neq a$
, then
$d \neq a$
, then
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{cd}$
are joined by an edge because
$R_{cd}$
are joined by an edge because
![]() $[R_{ab},R_{cd}]=1$
.
$[R_{ab},R_{cd}]=1$
.
Case 3. If
![]() $c \neq a,b$
and
$c \neq a,b$
and
![]() $d = a$
, then
$d = a$
, then
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ca}$
are joined by a path. Indeed,
$L_{ca}$
are joined by a path. Indeed,
![]() $c\leq d = a\leq b$
and thus,
$c\leq d = a\leq b$
and thus,
![]() $c\leq b$
. This means that there is a transvection
$c\leq b$
. This means that there is a transvection
![]() $R_{cb}$
. Then there is a path joining
$R_{cb}$
. Then there is a path joining
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ca}$
because
$L_{ca}$
because
![]() $[R_{ab},R_{cb}]=[R_{cb},L_{ca}]=1$
.
$[R_{ab},R_{cb}]=[R_{cb},L_{ca}]=1$
.
Case 4. If
![]() $c = b$
and
$c = b$
and
![]() $d \neq a,b$
, then
$d \neq a,b$
, then
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{bd}$
are joined by a path. Indeed,
$R_{bd}$
are joined by a path. Indeed,
![]() $a\leq b\leq d$
and thus,
$a\leq b\leq d$
and thus,
![]() $a\leq d$
so that there is a transvection
$a\leq d$
so that there is a transvection
![]() $L_{ad}$
. Then there is a path joining
$L_{ad}$
. Then there is a path joining
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{bd}$
because
$R_{bd}$
because
![]() $[R_{ab},L_{ad}]=[L_{ad},R_{bd}]=1$
.
$[R_{ab},L_{ad}]=[L_{ad},R_{bd}]=1$
.
Case 5. If
![]() $c =b$
and
$c =b$
and
![]() $d =a$
, then
$d =a$
, then
![]() $a\sim b$
. There are two subcases.
$a\sim b$
. There are two subcases.
Subcase 5-1: a and b are adjacent, that is,
![]() $\mathrm {st} (a)=\mathrm {st}(b)$
. In this case, we show that
$\mathrm {st} (a)=\mathrm {st}(b)$
. In this case, we show that
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{ba}$
are joined by a path. If
$R_{ba}$
are joined by a path. If
![]() $\mathrm {st}(a)$
does not cover the whole graph
$\mathrm {st}(a)$
does not cover the whole graph
![]() $\Gamma $
, choose
$\Gamma $
, choose
![]() $v\in \Gamma - \mathrm {st}(a)$
and let
$v\in \Gamma - \mathrm {st}(a)$
and let
![]() $\Gamma _0$
be the component of
$\Gamma _0$
be the component of
![]() $\Gamma - \mathrm {st}(a)$
containing v. Note that
$\Gamma - \mathrm {st}(a)$
containing v. Note that
![]() $\Gamma _0$
does not contain a and b. Then
$\Gamma _0$
does not contain a and b. Then
Otherwise,
![]() $\mathrm {st}(a)$
covers the whole graph so that
$\mathrm {st}(a)$
covers the whole graph so that
![]() $w\leq a\sim b$
for any vertex
$w\leq a\sim b$
for any vertex
![]() $w\neq a,b$
in
$w\neq a,b$
in
![]() $\Gamma $
. Then
$\Gamma $
. Then
Subcase 5-2: a and b are not adjacent, that is,
![]() $\mathrm {lk}(a)=\mathrm {lk}(b)$
. In this case, we show that
$\mathrm {lk}(a)=\mathrm {lk}(b)$
. In this case, we show that
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ba}$
are joined by a path. If the link
$L_{ba}$
are joined by a path. If the link
![]() $\mathrm {lk}(a)$
is empty, then
$\mathrm {lk}(a)$
is empty, then
![]() $a\sim b\leq w$
for any vertex
$a\sim b\leq w$
for any vertex
![]() $w\neq a,b$
in
$w\neq a,b$
in
![]() $\Gamma $
. Then
$\Gamma $
. Then
Otherwise, choose
![]() $w\in \mathrm {lk}(a)$
. If
$w\in \mathrm {lk}(a)$
. If
![]() $\mathrm {st}(w)$
does not cover the whole graph, then
$\mathrm {st}(w)$
does not cover the whole graph, then
where
![]() $\Gamma '$
is a component of
$\Gamma '$
is a component of
![]() $\Gamma - \mathrm {st}(w)$
. If
$\Gamma - \mathrm {st}(w)$
. If
![]() $\mathrm {st}(w)=\Gamma $
, then
$\mathrm {st}(w)=\Gamma $
, then
![]() $a\sim b\leq w$
, and so
$a\sim b\leq w$
, and so
By these five cases, any two transvections (if they exist) are joined by a path in K.
If
![]() $\Gamma $
is a complete graph, then there is no partial conjugation so that the theorem holds by the above claim. From now on, therefore, we assume that
$\Gamma $
is a complete graph, then there is no partial conjugation so that the theorem holds by the above claim. From now on, therefore, we assume that
![]() $\Gamma $
is not complete. In particular, there are at least two partial conjugations.
$\Gamma $
is not complete. In particular, there are at least two partial conjugations.
Claim 2. Any two partial conjugations
![]() $P_a^C$
and
$P_a^C$
and
![]() $P_b^D$
are joined by a path in K for any choices of
$P_b^D$
are joined by a path in K for any choices of
![]() $a,b,C,D$
.
$a,b,C,D$
.
Note that
![]() $[P_a^{C_1},P_a^{C_2}]=1$
whenever the partial conjugations are defined. Therefore, to see whether two partial conjugations
$[P_a^{C_1},P_a^{C_2}]=1$
whenever the partial conjugations are defined. Therefore, to see whether two partial conjugations
![]() $P_a^C$
and
$P_a^C$
and
![]() $P_b^D$
are joined by a path for any two distinct vertices a and b, it is enough to check only one particular choice of C and D.
$P_b^D$
are joined by a path for any two distinct vertices a and b, it is enough to check only one particular choice of C and D.
Suppose
![]() $\Gamma $
is connected. If there is no vertex in
$\Gamma $
is connected. If there is no vertex in
![]() $\Gamma $
whose star is the whole graph, then
$\Gamma $
whose star is the whole graph, then
![]() $\Gamma - \mathrm {st}(a)=\Gamma _1\sqcup \cdots \sqcup \Gamma _m$
and
$\Gamma - \mathrm {st}(a)=\Gamma _1\sqcup \cdots \sqcup \Gamma _m$
and
![]() $\Gamma - \mathrm {st}(b)=\Gamma _1'\sqcup \cdots \sqcup \Gamma _n'$
for any two vertices
$\Gamma - \mathrm {st}(b)=\Gamma _1'\sqcup \cdots \sqcup \Gamma _n'$
for any two vertices
![]() ${a,b\in \Gamma }$
, where each
${a,b\in \Gamma }$
, where each
![]() $\Gamma _i$
and
$\Gamma _i$
and
![]() $\Gamma _j'$
are components of
$\Gamma _j'$
are components of
![]() $\Gamma - \mathrm {st}(a)$
and
$\Gamma - \mathrm {st}(a)$
and
![]() $\Gamma - \mathrm {st}(b)$
, respectively. If
$\Gamma - \mathrm {st}(b)$
, respectively. If
![]() $[a,b]=1$
, this implies that
$[a,b]=1$
, this implies that
![]() $[P_a^{\Gamma _i},P_b^{\Gamma ^{\prime }_j}]=1$
for any i and j so that the claim holds by the connectivity of
$[P_a^{\Gamma _i},P_b^{\Gamma ^{\prime }_j}]=1$
for any i and j so that the claim holds by the connectivity of
![]() $\Gamma $
.
$\Gamma $
.
If
![]() $\Gamma =\mathrm {st}(b)$
for some vertex
$\Gamma =\mathrm {st}(b)$
for some vertex
![]() $b\in \Gamma $
, then one can easily see that
$b\in \Gamma $
, then one can easily see that
![]() $P_a^C$
and
$P_a^C$
and
![]() $R_{ab}$
commute for any
$R_{ab}$
commute for any
![]() $a\in \mathrm {lk}(b)$
the complement of whose star has a nonempty component C. By Claim 1, we can deduce that any two partial conjugations are joined by a path.
$a\in \mathrm {lk}(b)$
the complement of whose star has a nonempty component C. By Claim 1, we can deduce that any two partial conjugations are joined by a path.
Now, suppose
![]() $\Gamma $
has at least two components
$\Gamma $
has at least two components
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, and there are two conjugations
$\Gamma _2$
, and there are two conjugations
![]() $P_a^C$
and
$P_a^C$
and
![]() $P_b^D$
for
$P_b^D$
for
![]() $a\in \Gamma _1$
and
$a\in \Gamma _1$
and
![]() $b\in \Gamma _2$
. We only need to show that there are some components C and D of
$b\in \Gamma _2$
. We only need to show that there are some components C and D of
![]() $\Gamma -\mathrm {st}(a)$
and
$\Gamma -\mathrm {st}(a)$
and
![]() $\Gamma - \mathrm {st}(b)$
, respectively, such that
$\Gamma - \mathrm {st}(b)$
, respectively, such that
![]() $P_a^C$
and
$P_a^C$
and
![]() $P_b^D$
are joined by a path in K. There are two cases depending on the number of vertices in
$P_b^D$
are joined by a path in K. There are two cases depending on the number of vertices in
![]() $\Gamma _2$
.
$\Gamma _2$
.
Case 1. Suppose
![]() $\Gamma _2$
has at least two vertices. There are three subcases.
$\Gamma _2$
has at least two vertices. There are three subcases.
Subcase 1-1:
![]() $\mathrm {st}(b)\subsetneq \Gamma _2$
. Then
$\mathrm {st}(b)\subsetneq \Gamma _2$
. Then
![]() $[P_a^{\Gamma _2},P_b^D]=1$
, where D is a component of
$[P_a^{\Gamma _2},P_b^D]=1$
, where D is a component of
![]() $\Gamma _2 - \mathrm {st}(b)$
, because
$\Gamma _2 - \mathrm {st}(b)$
, because
and
for any vertex
![]() $s\in D$
.
$s\in D$
.
Subcase 1-2:
![]() $\mathrm {st}(b)=\Gamma _2$
but
$\mathrm {st}(b)=\Gamma _2$
but
![]() $\Gamma _2$
is not a complete graph. There is a vertex
$\Gamma _2$
is not a complete graph. There is a vertex
![]() $b_1\in \Gamma _2$
and a component
$b_1\in \Gamma _2$
and a component
![]() $D_1$
of
$D_1$
of
![]() $\Gamma _2 -\mathrm {st}(b_1)$
. Because b and
$\Gamma _2 -\mathrm {st}(b_1)$
. Because b and
![]() $b_1$
are adjacent,
$b_1$
are adjacent,
Subcase 1-3:
![]() $\Gamma _2$
is a complete graph. Then
$\Gamma _2$
is a complete graph. Then
for any vertex
![]() $b_1\neq b$
in
$b_1\neq b$
in
![]() $\Gamma _2$
because
$\Gamma _2$
because
![]() $b_1\leq b$
.
$b_1\leq b$
.
Case 2. Suppose
![]() $\Gamma _2$
has only one vertex b. There are two subcases.
$\Gamma _2$
has only one vertex b. There are two subcases.
Subcase 2-1:
![]() $\Gamma _1$
is not a complete graph. Let
$\Gamma _1$
is not a complete graph. Let
![]() $a_1$
be a vertex in
$a_1$
be a vertex in
![]() $\Gamma _1$
such that
$\Gamma _1$
such that
![]() $\mathrm {st}(a_1)\subsetneq \Gamma _1$
. If
$\mathrm {st}(a_1)\subsetneq \Gamma _1$
. If
![]() $a=a_1$
, then the claim holds because
$a=a_1$
, then the claim holds because
![]() $[P_{a}^{C},P_b^{\Gamma _1}]=1$
, where C is a component of
$[P_{a}^{C},P_b^{\Gamma _1}]=1$
, where C is a component of
![]() $\Gamma _1 - \mathrm {st}(a)$
. If
$\Gamma _1 - \mathrm {st}(a)$
. If
![]() $a\neq a_1$
but
$a\neq a_1$
but
![]() $\mathrm {st}(a)=\Gamma _1$
, then we additionally have
$\mathrm {st}(a)=\Gamma _1$
, then we additionally have
![]() $[P_{a_1}^{C},P_a^{\Gamma _2}]=1$
so the claim holds.
$[P_{a_1}^{C},P_a^{\Gamma _2}]=1$
so the claim holds.
Subcase 2-2:
![]() $\Gamma _1$
is a complete graph. We must divide into two cases again. If
$\Gamma _1$
is a complete graph. We must divide into two cases again. If
![]() $\Gamma _1$
has at least two vertices, then for any vertex
$\Gamma _1$
has at least two vertices, then for any vertex
![]() $a_1\neq a$
in
$a_1\neq a$
in
![]() $\Gamma _1$
,
$\Gamma _1$
,
![]() $a_1\leq a$
so that
$a_1\leq a$
so that
and
Thus,
If
![]() $\Gamma _1$
has only one vertex a, then
$\Gamma _1$
has only one vertex a, then
Because
![]() $\Gamma $
has at least 3 vertices, there is a vertex c such that
$\Gamma $
has at least 3 vertices, there is a vertex c such that
![]() $a\sim b\leq c$
. Since there is a path between
$a\sim b\leq c$
. Since there is a path between
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{ba}$
by Claim 1,
$R_{ba}$
by Claim 1,
![]() $P_a^{\Gamma _2}$
and
$P_a^{\Gamma _2}$
and
![]() $P_b^{\Gamma _1}$
are joined by a path in K.
$P_b^{\Gamma _1}$
are joined by a path in K.
Claim 3. Any transvection is adjacent to a partial conjugation in K.
Suppose a and b are vertices in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $a\leq b$
.
$a\leq b$
.
Case 1. If
![]() $\mathrm {st}(b)\subsetneq \Gamma $
, then
$\mathrm {st}(b)\subsetneq \Gamma $
, then
![]() $[R_{ab},P_{b}^C]=1$
for any component C of
$[R_{ab},P_{b}^C]=1$
for any component C of
![]() $\Gamma - \mathrm {st}(b)$
.
$\Gamma - \mathrm {st}(b)$
.
Case 2. Suppose
![]() $\mathrm {st}(b)=\Gamma $
. Because
$\mathrm {st}(b)=\Gamma $
. Because
![]() $\Gamma $
is not complete, there is a vertex c of
$\Gamma $
is not complete, there is a vertex c of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\mathrm {st}(c)\subsetneq \Gamma $
(c may be equal to a). For any component C of
$\mathrm {st}(c)\subsetneq \Gamma $
(c may be equal to a). For any component C of
![]() $\Gamma - \mathrm {st}(c)$
, we have
$\Gamma - \mathrm {st}(c)$
, we have
![]() ${[R_{ab},P_c^C]=1}$
. Therefore, there is an edge joining a transvection and a partial conjugation if they exist.
${[R_{ab},P_c^C]=1}$
. Therefore, there is an edge joining a transvection and a partial conjugation if they exist.
In summary, if
![]() $\Gamma $
is complete, by Claim 1, K is connected. Otherwise,
$\Gamma $
is complete, by Claim 1, K is connected. Otherwise,
![]() $\mathrm {Aut}^*(A_\Gamma )$
contains at least two partial conjugations. If it has no transvections, by Claim 2, K is connected. If it has a transvection, by combining the three claims, we can show that K is connected.
$\mathrm {Aut}^*(A_\Gamma )$
contains at least two partial conjugations. If it has no transvections, by Claim 2, K is connected. If it has a transvection, by combining the three claims, we can show that K is connected.
The only cases not covered by Theorem 3.1 are for RAAG’s whose defining graphs have one or two vertices. If
![]() $A_{\Gamma }$
is
$A_{\Gamma }$
is
![]() $\mathbb {Z}$
, then
$\mathbb {Z}$
, then
![]() $\mathrm {Aut}(A_\Gamma ) = \mathbb {Z}_2$
is finite. In the two remaining cases,
$\mathrm {Aut}(A_\Gamma ) = \mathbb {Z}_2$
is finite. In the two remaining cases,
![]() $A_{\Gamma }$
is either
$A_{\Gamma }$
is either
![]() $\mathbb {Z}^2$
or
$\mathbb {Z}^2$
or
![]() $\mathbb {F}_2$
so that
$\mathbb {F}_2$
so that
![]() $\mathrm {Aut}(A_\Gamma )$
is either
$\mathrm {Aut}(A_\Gamma )$
is either
![]() $\mathrm {GL}_2(\mathbb {Z})$
or
$\mathrm {GL}_2(\mathbb {Z})$
or
![]() $\mathrm {Aut}(\mathbb {F}_2)$
, respectively, and
$\mathrm {Aut}(\mathbb {F}_2)$
, respectively, and
![]() $\mathrm {GL}_2(\mathbb {Z})$
is hyperbolic because it is virtually free. For
$\mathrm {GL}_2(\mathbb {Z})$
is hyperbolic because it is virtually free. For
![]() $\mathrm{Aut}(\mathbb {F}_2)$
, consider the subgroup
$\mathrm{Aut}(\mathbb {F}_2)$
, consider the subgroup
![]() $\mathrm {Aut}^+(\mathbb {F}_2)$
which is the preimage of the special linear subgroup
$\mathrm {Aut}^+(\mathbb {F}_2)$
which is the preimage of the special linear subgroup
![]() $\mathrm {SL}_2(\mathbb {Z})\subset \mathrm {GL}_2(\mathbb {Z})$
under the homomorphism
$\mathrm {SL}_2(\mathbb {Z})\subset \mathrm {GL}_2(\mathbb {Z})$
under the homomorphism
![]() $\mathrm {Aut}(\mathbb {F}_2)\rightarrow \mathrm {GL}_2(\mathbb {Z})$
induced from the abelianisation map
$\mathrm {Aut}(\mathbb {F}_2)\rightarrow \mathrm {GL}_2(\mathbb {Z})$
induced from the abelianisation map
![]() $\mathbb {F}_2\rightarrow \mathbb {Z}^2$
. Then
$\mathbb {F}_2\rightarrow \mathbb {Z}^2$
. Then
![]() $\mathrm {Aut}^+(\mathbb {F}_2)$
is a finite index subgroup of
$\mathrm {Aut}^+(\mathbb {F}_2)$
is a finite index subgroup of
![]() $\mathrm {Aut}(\mathbb {F}_2)$
and can be shown to be isomorphic to the pure mapping class group of a twice punctured torus, which is not relatively hyperbolic by (the proof of) Theorem 8.1 in [Reference Bestvina and Brady2].
$\mathrm {Aut}(\mathbb {F}_2)$
and can be shown to be isomorphic to the pure mapping class group of a twice punctured torus, which is not relatively hyperbolic by (the proof of) Theorem 8.1 in [Reference Bestvina and Brady2].
We conclude this section with a remark that was pointed out to us by Anthony Genevois. If
![]() $\Gamma $
is connected, there is a shorter argument to prove that
$\Gamma $
is connected, there is a shorter argument to prove that
![]() $\mathrm {Aut}(A_\Gamma )$
is not relatively hyperbolic. Suppose that
$\mathrm {Aut}(A_\Gamma )$
is not relatively hyperbolic. Suppose that
![]() $\mathrm {Aut}(A_\Gamma )$
is relatively hyperbolic with respect to a finite collection
$\mathrm {Aut}(A_\Gamma )$
is relatively hyperbolic with respect to a finite collection
![]() $\mathcal {H}=\{H_i\}$
of parabolic subgroups. If there is a vertex
$\mathcal {H}=\{H_i\}$
of parabolic subgroups. If there is a vertex
![]() $v\in \Gamma $
which is adjacent to all other vertices, then the subgroup of
$v\in \Gamma $
which is adjacent to all other vertices, then the subgroup of
![]() $\mathrm {Aut}(A_\Gamma )$
generated by all transvections induced by this central vertex v is an infinite normal free abelian subgroup contained in some
$\mathrm {Aut}(A_\Gamma )$
generated by all transvections induced by this central vertex v is an infinite normal free abelian subgroup contained in some
![]() $H_i \in \mathcal {H}$
by Lemma 2.3. Otherwise,
$H_i \in \mathcal {H}$
by Lemma 2.3. Otherwise,
![]() $\mathrm {Inn}(A_\Gamma )$
is isomorphic to
$\mathrm {Inn}(A_\Gamma )$
is isomorphic to
![]() $A_\Gamma $
and it is thus an infinite normal subgroup, contained in some
$A_\Gamma $
and it is thus an infinite normal subgroup, contained in some
![]() $H_i \in \mathcal {H}$
by Lemma 2.3. In both cases, we find an infinite normal subgroup contained in an almost malnormal subgroup
$H_i \in \mathcal {H}$
by Lemma 2.3. In both cases, we find an infinite normal subgroup contained in an almost malnormal subgroup
![]() $H_i$
. By Theorem 2.2, this implies that
$H_i$
. By Theorem 2.2, this implies that
![]() $H_i = \mathrm {Aut}(A_\Gamma )$
, which is a contradiction.
$H_i = \mathrm {Aut}(A_\Gamma )$
, which is a contradiction.
4 Outer automorphism group
In this section, we look at the relative hyperbolicity of
![]() $\mathrm {Out}(A_\Gamma )$
. In the same spirit as the proof of relative hyperbolicity of
$\mathrm {Out}(A_\Gamma )$
. In the same spirit as the proof of relative hyperbolicity of
![]() $\mathrm {Aut}(A_\Gamma )$
, we work with the subgroup
$\mathrm {Aut}(A_\Gamma )$
, we work with the subgroup
![]() $\mathrm {Out}^*(A_{\Gamma })$
instead of the whole group
$\mathrm {Out}^*(A_{\Gamma })$
instead of the whole group
![]() $\mathrm {Out}(A_{\Gamma })$
. Let S be the set of all transvections and partial conjugations as before and
$\mathrm {Out}(A_{\Gamma })$
. Let S be the set of all transvections and partial conjugations as before and
![]() $S'$
the set of all the (nontrivial) images of elements of S in
$S'$
the set of all the (nontrivial) images of elements of S in
![]() $\mathrm {Out}(A_{\Gamma })$
. We want to investigate the connectivity of
$\mathrm {Out}(A_{\Gamma })$
. We want to investigate the connectivity of
![]() $K(\mathrm {Out}^*(A_{\Gamma }), S')$
. Unfortunately, the proof of the connectivity of
$K(\mathrm {Out}^*(A_{\Gamma }), S')$
. Unfortunately, the proof of the connectivity of
![]() $K(\mathrm {Aut}^*(A_{\Gamma }), S)$
does not directly imply that
$K(\mathrm {Aut}^*(A_{\Gamma }), S)$
does not directly imply that
![]() $K(\mathrm {Out}^*(A_{\Gamma }), S')$
is connected because some partial conjugations in
$K(\mathrm {Out}^*(A_{\Gamma }), S')$
is connected because some partial conjugations in
![]() $\mathrm {Aut}(A_{\Gamma })$
are sent to the identity element in
$\mathrm {Aut}(A_{\Gamma })$
are sent to the identity element in
![]() $\mathrm {Out}(A_{\Gamma })$
. For the rest of this section, when we refer to a transvection or a partial conjugation, we mean its image in
$\mathrm {Out}(A_{\Gamma })$
. For the rest of this section, when we refer to a transvection or a partial conjugation, we mean its image in
![]() $\mathrm {Out}(A_\Gamma )$
.
$\mathrm {Out}(A_\Gamma )$
.
Theorem 4.1. Suppose
![]() $\Gamma $
contains at least two vertices. If
$\Gamma $
contains at least two vertices. If
![]() $\mathrm {Out}(A_{\Gamma })$
is not finite, virtually
$\mathrm {Out}(A_{\Gamma })$
is not finite, virtually
![]() $\mathbb {Z}$
nor virtually
$\mathbb {Z}$
nor virtually
![]() $\mathrm {GL}_2(\mathbb {Z})$
, then
$\mathrm {GL}_2(\mathbb {Z})$
, then
![]() $\mathrm {Out}(A_{\Gamma })$
is not relatively hyperbolic.
$\mathrm {Out}(A_{\Gamma })$
is not relatively hyperbolic.
Proof. Clearly, if
![]() $\mathrm {Out}^*(A_\Gamma )$
is finite or isomorphic to
$\mathrm {Out}^*(A_\Gamma )$
is finite or isomorphic to
![]() $\mathbb {Z}$
, then
$\mathbb {Z}$
, then
![]() $\mathrm {Out}(A_\Gamma )$
is hyperbolic. In particular, it is relatively hyperbolic. Now we examine the commutativity graph
$\mathrm {Out}(A_\Gamma )$
is hyperbolic. In particular, it is relatively hyperbolic. Now we examine the commutativity graph
![]() $K = K(\mathrm {Out}^*(A_{\Gamma }), S')$
for the case that
$K = K(\mathrm {Out}^*(A_{\Gamma }), S')$
for the case that
![]() $S'$
has at least two distinct elements of
$S'$
has at least two distinct elements of
![]() $\mathrm {Out}^*(A_\Gamma )$
.
$\mathrm {Out}^*(A_\Gamma )$
.
Claim 1. If there are at least two nontrivial partial conjugations, then they are joined by a path in K.
Let
![]() $P_a^{C}$
and
$P_a^{C}$
and
![]() $P_b^{C'}$
be two such partial conjugations. If a and b commute (a may be equal to b), then so do
$P_b^{C'}$
be two such partial conjugations. If a and b commute (a may be equal to b), then so do
![]() $P_a^{C}$
and
$P_a^{C}$
and
![]() $P_b^{C'}$
, so we can assume that a and b do not commute. Because neither
$P_b^{C'}$
, so we can assume that a and b do not commute. Because neither
![]() $P_a^C$
nor
$P_a^C$
nor
![]() $P_b^{C'}$
is trivial, it means that
$P_b^{C'}$
is trivial, it means that
![]() $\Gamma - \mathrm {st}(a)$
and
$\Gamma - \mathrm {st}(a)$
and
![]() $\Gamma - \mathrm {st}(b)$
both consist of at least two components. Because a and b are not adjacent, there is a component D of
$\Gamma - \mathrm {st}(b)$
both consist of at least two components. Because a and b are not adjacent, there is a component D of
![]() $\Gamma - \mathrm {st}(a)$
and a component
$\Gamma - \mathrm {st}(a)$
and a component
![]() $D'$
of
$D'$
of
![]() $\Gamma - \mathrm {st}(b)$
which are disjoint. However, then
$\Gamma - \mathrm {st}(b)$
which are disjoint. However, then
![]() $[P_a^C, P_a^D] = [P_a^D, P_b^{D'}] = [P_b^{D'}, P_b^{C'}] = 1$
and this defines a path in K from
$[P_a^C, P_a^D] = [P_a^D, P_b^{D'}] = [P_b^{D'}, P_b^{C'}] = 1$
and this defines a path in K from
![]() $P_a^C$
to
$P_a^C$
to
![]() $P_b^{C'}$
.
$P_b^{C'}$
.
Claim 2. As long as they exist, any nontrivial partial conjugation and any transvection are joined by a path in K.
Let
![]() $R_{ab}$
be a transvection and suppose that there is a nontrivial partial conjugation
$R_{ab}$
be a transvection and suppose that there is a nontrivial partial conjugation
![]() $P_c^C$
. To show the existence of a path joining
$P_c^C$
. To show the existence of a path joining
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $P_c^C$
, we consider three cases according to the choice of the vertex c.
$P_c^C$
, we consider three cases according to the choice of the vertex c.
Case 1. If
![]() $c=b$
, then
$c=b$
, then
![]() $[R_{ab},P_{b}^C]=1$
for any component C.
$[R_{ab},P_{b}^C]=1$
for any component C.
Case 2. Suppose
![]() $c=a$
. If
$c=a$
. If
![]() $P_{b}^D$
represents a nontrivial element in
$P_{b}^D$
represents a nontrivial element in
![]() $\mathrm {Out}(A_{\Gamma })$
for some connected component D of
$\mathrm {Out}(A_{\Gamma })$
for some connected component D of
![]() $\Gamma - \mathrm {st}(b)$
, then by Claim 1, there is a path from
$\Gamma - \mathrm {st}(b)$
, then by Claim 1, there is a path from
![]() $P_a^C$
to
$P_a^C$
to
![]() $P_b^D$
and the claim follows from the fact that
$P_b^D$
and the claim follows from the fact that
![]() $P_b^D$
and
$P_b^D$
and
![]() $R_{ab}$
commute. If no such
$R_{ab}$
commute. If no such
![]() $P_b^D$
exists, then
$P_b^D$
exists, then
![]() $\Gamma - \mathrm {st}(b)$
has at most one connected component. Let
$\Gamma - \mathrm {st}(b)$
has at most one connected component. Let
![]() $\Gamma _1,\ldots ,\Gamma _n$
be the components of
$\Gamma _1,\ldots ,\Gamma _n$
be the components of
![]() $\Gamma - \mathrm {st}(a)$
. Note that
$\Gamma - \mathrm {st}(a)$
. Note that
![]() $n\geq 2$
. Because
$n\geq 2$
. Because
![]() $a \leq b$
, we have
$a \leq b$
, we have
![]() $\Gamma - \mathrm {st}(b)\subset \Gamma - \mathrm {lk}(a)$
. This means that
$\Gamma - \mathrm {st}(b)\subset \Gamma - \mathrm {lk}(a)$
. This means that
![]() $\Gamma - \mathrm {st}(b)$
is either empty or contains only a or is entirely contained in some
$\Gamma - \mathrm {st}(b)$
is either empty or contains only a or is entirely contained in some
![]() $\Gamma _i$
. In all cases, there is a j such that
$\Gamma _i$
. In all cases, there is a j such that
![]() $\Gamma _j \subset \mathrm {st}(b)$
. Let w be any vertex in
$\Gamma _j \subset \mathrm {st}(b)$
. Let w be any vertex in
![]() $\Gamma _j$
. Because
$\Gamma _j$
. Because
![]() $\mathrm {lk}(w)\subset \Gamma _j\cup \mathrm {lk}(a)$
, we have
$\mathrm {lk}(w)\subset \Gamma _j\cup \mathrm {lk}(a)$
, we have
![]() $\mathrm {lk}(w)\subset \mathrm {st}(b)$
and thus
$\mathrm {lk}(w)\subset \mathrm {st}(b)$
and thus
![]() $w\leq b$
. Choose
$w\leq b$
. Choose
![]() $w_0 \in \Gamma _j$
. Then
$w_0 \in \Gamma _j$
. Then
![]() $[R_{ab},R_{w_0 b}]=[R_{w_0 b},P_{a}^{\Gamma _k}]=1$
for any
$[R_{ab},R_{w_0 b}]=[R_{w_0 b},P_{a}^{\Gamma _k}]=1$
for any
![]() $k\neq j$
. Hence,
$k\neq j$
. Hence,
![]() $P_a^{\Gamma _k}$
and
$P_a^{\Gamma _k}$
and
![]() $R_{ab}$
are joined by a path.
$R_{ab}$
are joined by a path.
Case 3. Suppose that c is neither a nor b. If a or b is contained in
![]() $\mathrm {lk}(c)$
, then
$\mathrm {lk}(c)$
, then
![]() $P_c^C$
and
$P_c^C$
and
![]() $R_{ab}$
can be joined by a path. If a and b are in the same component C of
$R_{ab}$
can be joined by a path. If a and b are in the same component C of
![]() $\Gamma - \mathrm {st}(c)$
, then
$\Gamma - \mathrm {st}(c)$
, then
and
If instead a and b are contained in different components of
![]() $\Gamma - \mathrm {st}(c)$
, then
$\Gamma - \mathrm {st}(c)$
, then
![]() $a\leq c$
because
$a\leq c$
because
![]() $a\leq b$
. We have already checked that
$a\leq b$
. We have already checked that
![]() $P_c^C$
and
$P_c^C$
and
![]() $R_{ac}$
can be joined by a path for any component C of
$R_{ac}$
can be joined by a path for any component C of
![]() $\Gamma - \mathrm {st}(c)$
. Because
$\Gamma - \mathrm {st}(c)$
. Because
![]() $[R_{ab},L_{ac}]=[L_{ac},R_{ac}]=1$
,
$[R_{ab},L_{ac}]=[L_{ac},R_{ac}]=1$
,
![]() $P_c^C$
and
$P_c^C$
and
![]() $R_{ab}$
also can be joined by a path.
$R_{ab}$
also can be joined by a path.

Figure 1 Typical examples of
![]() $\Gamma $
with
$\Gamma $
with
![]() $\mathrm {Out}(A_{\Gamma })$
relatively hyperbolic.
$\mathrm {Out}(A_{\Gamma })$
relatively hyperbolic.
By these two claims, as long as
![]() $|S'|>1$
and there is at least one nontrivial partial conjugation, K is connected. The last remaining case is where
$|S'|>1$
and there is at least one nontrivial partial conjugation, K is connected. The last remaining case is where
![]() $S'$
only consists of transvections. By examining the paths between transvections in
$S'$
only consists of transvections. By examining the paths between transvections in
![]() $K(\mathrm {Aut}^*(A_\Gamma ),S)$
, there may exist a path in
$K(\mathrm {Aut}^*(A_\Gamma ),S)$
, there may exist a path in
![]() $K(\mathrm {Out}^*(A_\Gamma ),S')$
between two transvections, except possibly between
$K(\mathrm {Out}^*(A_\Gamma ),S')$
between two transvections, except possibly between
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $R_{ba}$
(the paths joining them in
$R_{ba}$
(the paths joining them in
![]() $K(\mathrm {Aut}^*(A_\Gamma ),S)$
may use partial conjugations which have trivial images in
$K(\mathrm {Aut}^*(A_\Gamma ),S)$
may use partial conjugations which have trivial images in
![]() $\mathrm {Out}(A_\Gamma )$
). So the only case still to be examined is the case with only four transvections
$\mathrm {Out}(A_\Gamma )$
). So the only case still to be examined is the case with only four transvections
![]() $R_{ab}$
,
$R_{ab}$
,
![]() $R_{ba}$
,
$R_{ba}$
,
![]() $L_{ab}$
and
$L_{ab}$
and
![]() $L_{ba}$
. In this case, we see that
$L_{ba}$
. In this case, we see that
![]() $R_{ab}$
and
$R_{ab}$
and
![]() $L_{ab}$
are equal in
$L_{ab}$
are equal in
![]() $\mathrm {Out}(A_\Gamma )$
and so are
$\mathrm {Out}(A_\Gamma )$
and so are
![]() $R_{ba}$
and
$R_{ba}$
and
![]() $L_{ba}$
. Therefore,
$L_{ba}$
. Therefore,
![]() $\mathrm {Out}^*(A_\Gamma )$
is isomorphic to
$\mathrm {Out}^*(A_\Gamma )$
is isomorphic to
![]() $\mathrm {Out}^*(\mathbb {F}_2)$
and
$\mathrm {Out}^*(\mathbb {F}_2)$
and
![]() $\mathrm {Out}(A_\Gamma )$
is virtually isomorphic to
$\mathrm {Out}(A_\Gamma )$
is virtually isomorphic to
![]() $\mathrm {GL}_2(\mathbb {Z})$
.
$\mathrm {GL}_2(\mathbb {Z})$
.
We finish by giving some examples of RAAGs whose outer automorphism groups are relatively hyperbolic. If the graph
![]() $\Gamma $
is a cycle with n vertices and n edges, then
$\Gamma $
is a cycle with n vertices and n edges, then
![]() $\mathrm {Out}(A_{\Gamma })$
is a finite group, as long as
$\mathrm {Out}(A_{\Gamma })$
is a finite group, as long as
![]() $n\geq 5$
. If
$n\geq 5$
. If
![]() $\Gamma $
is the graph on the left in Figure 1, then there are no transvections, and the central vertex induces the unique partial conjugation in
$\Gamma $
is the graph on the left in Figure 1, then there are no transvections, and the central vertex induces the unique partial conjugation in
![]() $\mathrm {Out}(A_{\Gamma })$
, which is thus virtually cyclic. If
$\mathrm {Out}(A_{\Gamma })$
, which is thus virtually cyclic. If
![]() $\Gamma $
is the graph on the right in Figure 1, then there is no partial conjugation in
$\Gamma $
is the graph on the right in Figure 1, then there is no partial conjugation in
![]() $\mathrm {Out}(A_{\Gamma })$
and the two equivalent vertices on the top and the bottom induce two transvections in
$\mathrm {Out}(A_{\Gamma })$
and the two equivalent vertices on the top and the bottom induce two transvections in
![]() $\mathrm {Out}(A_{\Gamma })$
. By the argument in the last paragraph of the proof of Theorem 4.1,
$\mathrm {Out}(A_{\Gamma })$
. By the argument in the last paragraph of the proof of Theorem 4.1,
![]() $\mathrm {Out}(A_{\Gamma })$
is virtually isomorphic to
$\mathrm {Out}(A_{\Gamma })$
is virtually isomorphic to
![]() $\mathrm {GL}_2(\mathbb {Z})$
.
$\mathrm {GL}_2(\mathbb {Z})$
.
Acknowledgements
We thank our advisor Hyungryul Baik for useful comments, Donggyun Seo for useful conversations and Anthony Genevois for giving us helpful feedback.