1. Introduction
Mean dimensions are quantities that measure the complexity of dynamical systems with infinite entropy. The concept of mean dimension was first introduced by Gromov in [Reference Gromov20], which is a topological invariant of dynamical systems to count the average number of parameters needed per iteration for describing a point. Later, Lindenstrauss and Weiss in [Reference Lindenstrauss and Weiss39] introduced the metric mean dimension and they related metric mean dimension to the problem that whether a dynamical system can be embedded in the shift system. The metric mean dimension of a dynamical system is not a topological invariant, as it depends on the specific metric chosen for the phase space X; however, there exists an intriguing invariant property for metrizable topological spaces. Specifically, the infimum of metric dimensions over all metrics on X that induce its topology is invariant under topological conjugacy. In general, the metric mean dimension of a system may not exceed its mean dimension. However, Lindenstrauss and Tsukamoto presented an exciting result in [Reference Lindenstrauss and Tsukamoto38]. They demonstrated that systems possessing the marker property can be endowed with a metric ρ compatible with the topology of the phase space. Remarkably, the metric mean dimension of ρ coincides with the mean dimension of the system. Besides, in [Reference Lindenstrauss and Tsukamoto37], Lindenstrauss and Tsukamoto delved into the concept of mean dimension alongside rate distortion theory, a field that investigates the lossy data compression of stochastic processes under distortion constraints. Within this study, they established a variational principle connecting rate distortion function to metric mean dimension. Later, Gutman and Śpiewak [Reference Gutman and Śpiewak19] demonstrated that in the Lindenstrauss–Tsukamoto variational principle, it suffices to consider the supremum over ergodic measures. In a more recent study, Shi [Reference Shi46] established variational principles linking metric mean dimension with Shapira’s entropy, Katok’s entropy and Brin-Katok’s entropy.
The fundamental theory of amenable group actions in the analysis of dynamical systems was established by Ornstein and Weiss in [Reference Ornstein and Weiss43], which provides an approach to generalize vast majority of entropic and ergodic theorems known for the actions of ![]() $\mathbb Z$ such as [Reference Danilenko1, Reference Lindenstrauss36, Reference Rudolph and Weiss45]. As the core techniques in the analysis of dynamical systems with amenable group actions, the ɛ-tiling and the ɛ-quasi-tiling were introduced in [Reference Ornstein and Weiss42, Reference Ornstein and Weiss43]. The ɛ-tiling has been further developed by Weiss in [Reference Weiss48], where he showed that countable amenable groups from a large class admit a precise tiling by only one monotile belonging to a selected Følner sequence. The ɛ-quasi-tiling has been developed by Downarowicz et al. [Reference Downarowicz, Huczek and Zhang17]. After Gromov–Lindenstrauss–Weiss’ fundamental works on mean dimension theory, there are sequences of studies on mean dimensions in the context of amenable group actions, for instance [Reference Chen, Dou and Zheng10, Reference Coornaert and Krieger12, Reference Dou13, Reference Krieger27, Reference Li and Liang30, Reference Tang, Wu and Li47].
$\mathbb Z$ such as [Reference Danilenko1, Reference Lindenstrauss36, Reference Rudolph and Weiss45]. As the core techniques in the analysis of dynamical systems with amenable group actions, the ɛ-tiling and the ɛ-quasi-tiling were introduced in [Reference Ornstein and Weiss42, Reference Ornstein and Weiss43]. The ɛ-tiling has been further developed by Weiss in [Reference Weiss48], where he showed that countable amenable groups from a large class admit a precise tiling by only one monotile belonging to a selected Følner sequence. The ɛ-quasi-tiling has been developed by Downarowicz et al. [Reference Downarowicz, Huczek and Zhang17]. After Gromov–Lindenstrauss–Weiss’ fundamental works on mean dimension theory, there are sequences of studies on mean dimensions in the context of amenable group actions, for instance [Reference Chen, Dou and Zheng10, Reference Coornaert and Krieger12, Reference Dou13, Reference Krieger27, Reference Li and Liang30, Reference Tang, Wu and Li47].
Scholars showed interest in the ergodic theory of random transformations since 1980s, which emerged from Kifer [Reference Kifer24], Crauel [Reference Crauel9], Ledrappier and Young [Reference Ledrappier and Young40], Bogenschutz [Reference Bogenschutz4, Reference Bogenschutz5], etc. For the classic ![]() $\mathbb Z_+$ or
$\mathbb Z_+$ or ![]() $\mathbb Z$-system, the random transformations can be regarded as skew-product transformations rather than iterations of just one map. The study within the framework of bundle random dynamical systems (RDSs) with amenable group actions was conducted by Dooley and Zhang in [Reference Dooley and Zhang16]. They introduced the notions of random local pressures as well as entropies and a concept of (factor) excellent or good covers as a crucial technique to establish the variational principle for random local pressures. We refer to the elegant literatures [Reference Arnold2, Reference Kifer and Liu26] for more information on the theory of RDSs and [Reference Huang and Lu21, Reference Liu29, Reference Li33–Reference Li and Zhu35, Reference Ma, Yang and Chen41, Reference Wang, Wu and Zhu51–Reference Wang, Wu and Zhu53] for the recent progresses on the entropy theory in RDSs.
$\mathbb Z$-system, the random transformations can be regarded as skew-product transformations rather than iterations of just one map. The study within the framework of bundle random dynamical systems (RDSs) with amenable group actions was conducted by Dooley and Zhang in [Reference Dooley and Zhang16]. They introduced the notions of random local pressures as well as entropies and a concept of (factor) excellent or good covers as a crucial technique to establish the variational principle for random local pressures. We refer to the elegant literatures [Reference Arnold2, Reference Kifer and Liu26] for more information on the theory of RDSs and [Reference Huang and Lu21, Reference Liu29, Reference Li33–Reference Li and Zhu35, Reference Ma, Yang and Chen41, Reference Wang, Wu and Zhu51–Reference Wang, Wu and Zhu53] for the recent progresses on the entropy theory in RDSs.
An approach rooted in convex analysis arises as a method to investigate the thermodynamic formalism of dynamical systems, along with the study of the metric mean dimension. In [Reference Cioletti, Silva and Stadlbauer8], Cioletti, Silva and Stadlbauer considered the pressure functional ![]() $P(\phi)$, which is convex for the bounded continuous potentials ϕ defined on the sequence space
$P(\phi)$, which is convex for the bounded continuous potentials ϕ defined on the sequence space ![]() $X= E^{\mathbb N}$, where E is a general standard Borel space. They obtained the existence of equilibrium states as finitely additive probability measures for any bounded continuous potential. Biś, Carvalho, Mendes and Varandas in [Reference Biś, Carvalho, Mendes and Varandas3] established an abstract variational principle for the so-called pressure functions acting on a Banach space of potentials of a compact metric space, for which equilibrium states always exist. This approach was later adapted by Yang, Chen and Zhou, as reported in [Reference Yang, Chen and Zhou54], where they successfully proved a variational principle for the upper metric mean dimension, incorporating the concept of potential. In [Reference Carvalho, Pessil and Varandas7], Carvalho, Pessil and Varandas introduced the concept of the upper metric mean dimension for a one-parameter family of scaled pressure functions. With the approach supported by convex analysis, they established a corresponding variational principle. Additionally, they examined the computability of this measure-theoretic map and presented several examples.
$X= E^{\mathbb N}$, where E is a general standard Borel space. They obtained the existence of equilibrium states as finitely additive probability measures for any bounded continuous potential. Biś, Carvalho, Mendes and Varandas in [Reference Biś, Carvalho, Mendes and Varandas3] established an abstract variational principle for the so-called pressure functions acting on a Banach space of potentials of a compact metric space, for which equilibrium states always exist. This approach was later adapted by Yang, Chen and Zhou, as reported in [Reference Yang, Chen and Zhou54], where they successfully proved a variational principle for the upper metric mean dimension, incorporating the concept of potential. In [Reference Carvalho, Pessil and Varandas7], Carvalho, Pessil and Varandas introduced the concept of the upper metric mean dimension for a one-parameter family of scaled pressure functions. With the approach supported by convex analysis, they established a corresponding variational principle. Additionally, they examined the computability of this measure-theoretic map and presented several examples.
The present work is dedicated to explore the notion of the random metric mean dimension with potentials in the context of amenable group actions, which is mainly inspired by the work on an abstract variational principle for upper semi-continuous affine entropy-like map [Reference Biś, Carvalho, Mendes and Varandas3] and the work on random metric mean dimension for skew product transformations [Reference Yang, Chen and Zhou55]. First, in §3.1, we introduce a notion of random upper metric mean dimension with potentials for amenable group actions and study its basic properties. Second, in §3.2, we introduce random upper measure-theoretic metric mean dimension and present its several characterizations. Third, in §4, we establish a variational principle between these two kinds of mean dimensions. Finally, in §5, we we introduce a notion of equilibrium state for amenable random upper metric mean dimension with potentials and discuss its properties.
2. Preliminaries and main result
In this section, we collect some basic notions and notations in literature and then state the main result. An action on a set X induced by a group G (or we say G acts on X) is a set of maps ![]() $f_G=\{f_g:X\to X|g\in G\}$ satisfying:
$f_G=\{f_g:X\to X|g\in G\}$ satisfying:
(1)
 $f_e=\mathrm{id}_X$, where e is the unit element of G,
$f_e=\mathrm{id}_X$, where e is the unit element of G,(2)
 $f_{g_2}\circ f_{g_1}=f_{g_2g_1}$ for every
$f_{g_2}\circ f_{g_1}=f_{g_2g_1}$ for every  $g_1,g_2\in G$.
$g_1,g_2\in G$.
Note that fg is a bijection for each ![]() $g\in G$. For simplicity, we identify the the group G with its action fG by writing
$g\in G$. For simplicity, we identify the the group G with its action fG by writing ![]() $gx:=f_g(x)$ for every
$gx:=f_g(x)$ for every ![]() $g\in G$ and
$g\in G$ and ![]() $x\in X$. A group action G of a measurable space
$x\in X$. A group action G of a measurable space ![]() $(X,\mathscr B,\mu)$ is said to be measure preserving (or we say µ is G-invariant), if
$(X,\mathscr B,\mu)$ is said to be measure preserving (or we say µ is G-invariant), if ![]() $\mu(gB)=\mu(B)$ for every
$\mu(gB)=\mu(B)$ for every ![]() $g\in G$ and
$g\in G$ and ![]() $B\in\mathscr B$. A probability measure µ on a measurable space
$B\in\mathscr B$. A probability measure µ on a measurable space ![]() $(X,\mathscr B)$ with a group action G is said to be G-ergodic, if for any given
$(X,\mathscr B)$ with a group action G is said to be G-ergodic, if for any given ![]() $B\in\mathscr B$, we have
$B\in\mathscr B$, we have ![]() $\mu(gB\Delta B)=0$ for every
$\mu(gB\Delta B)=0$ for every ![]() $g\in G$ if and only if
$g\in G$ if and only if ![]() $\mu(B)=1$ or
$\mu(B)=1$ or ![]() $\mu(B)=0$.
$\mu(B)=0$.
The setup of bundle RDS or RDS consists of a probability space ![]() $(\Omega,\mathscr F,\mathbb P)$ together with a group G acting on Ω measure preservingly, a compact metic space (X, d) with corresponding Borel σ-algebra
$(\Omega,\mathscr F,\mathbb P)$ together with a group G acting on Ω measure preservingly, a compact metic space (X, d) with corresponding Borel σ-algebra ![]() $\mathscr B$, and a bundle
$\mathscr B$, and a bundle ![]() $\mathcal E$ that is a measurable subset of
$\mathcal E$ that is a measurable subset of ![]() $\Omega\times X$ with respect to the product σ-algebra
$\Omega\times X$ with respect to the product σ-algebra ![]() $\mathscr F\times\mathscr B$ such that the fibres
$\mathscr F\times\mathscr B$ such that the fibres ![]() $\mathcal E_\omega=\{x\in X:(\omega,x)\in\mathcal E\}$ for all
$\mathcal E_\omega=\{x\in X:(\omega,x)\in\mathcal E\}$ for all ![]() $\omega\in\Omega$ are compact and non-empty. A bundle RDS associated to
$\omega\in\Omega$ are compact and non-empty. A bundle RDS associated to ![]() $(\Omega,\mathscr F,\mathbb P,G)$ is a set of maps
$(\Omega,\mathscr F,\mathbb P,G)$ is a set of maps ![]() $\mathbf F=\{\mathbf F_{g,\omega}:\mathcal E_\omega\to\mathcal E_{g\omega}|g\in G,\omega\in\Omega\}$ satisfying
$\mathbf F=\{\mathbf F_{g,\omega}:\mathcal E_\omega\to\mathcal E_{g\omega}|g\in G,\omega\in\Omega\}$ satisfying
(α)
 $\mathbf F_{e,\omega}=\mathrm{id}_{\mathcal E_\omega}$ for every
$\mathbf F_{e,\omega}=\mathrm{id}_{\mathcal E_\omega}$ for every  $\omega\in\Omega$, where e is the unit element of G;
$\omega\in\Omega$, where e is the unit element of G;(β) for any given
 $g\in G$, the map
$g\in G$, the map  $(\mathcal E,\mathscr F\times\mathscr B|_\mathcal E)\to(X,\mathscr B)$ given by
$(\mathcal E,\mathscr F\times\mathscr B|_\mathcal E)\to(X,\mathscr B)$ given by  $(\omega,x)\mapsto \mathbf F_{g,\omega}(x)$ is measurable, where
$(\omega,x)\mapsto \mathbf F_{g,\omega}(x)$ is measurable, where  $\mathscr F\times\mathscr B|_\mathcal E=\{A\cap\mathcal E:A\in\mathscr F\times\mathscr B\}$;
$\mathscr F\times\mathscr B|_\mathcal E=\{A\cap\mathcal E:A\in\mathscr F\times\mathscr B\}$;(γ)
 $\mathbf F_{g_2,g_1\omega}\circ \mathbf F_{g_1,\omega}=\mathbf F_{g_2g_1,\omega}$ for every
$\mathbf F_{g_2,g_1\omega}\circ \mathbf F_{g_1,\omega}=\mathbf F_{g_2g_1,\omega}$ for every  $g_1,g_2\in G$ and
$g_1,g_2\in G$ and  $\omega\in\Omega$.
$\omega\in\Omega$.
If for ![]() $\mathbb P\text{-a.e. }\omega\in\Omega$, and for every
$\mathbb P\text{-a.e. }\omega\in\Omega$, and for every ![]() $g\in G$, the random transformation
$g\in G$, the random transformation ![]() $\mathbf F_{g,\omega}$ is continuous (and is therefore a homeomorphism), then
$\mathbf F_{g,\omega}$ is continuous (and is therefore a homeomorphism), then ![]() $\mathbf F$ is called a continuous bundle RDS associated to
$\mathbf F$ is called a continuous bundle RDS associated to ![]() $(\Omega,\mathscr F,\mathbb P,G)$. The RDS
$(\Omega,\mathscr F,\mathbb P,G)$. The RDS ![]() $\mathbf F$ naturally induces an action
$\mathbf F$ naturally induces an action  $\tilde f_G=\{\tilde f_g:g\in G\}$ on
$\tilde f_G=\{\tilde f_g:g\in G\}$ on ![]() $\mathcal E$, given by
$\mathcal E$, given by  $\tilde f_g(\omega,x)=(g\omega,\mathbf F_{g,\omega}(x))$ for every
$\tilde f_g(\omega,x)=(g\omega,\mathbf F_{g,\omega}(x))$ for every ![]() $g\in G$ and
$g\in G$ and ![]() $(\omega,x)\in \mathcal E$; in the absence of ambiguity, we still identify
$(\omega,x)\in \mathcal E$; in the absence of ambiguity, we still identify ![]() $\tilde f_G$ with G by denoting
$\tilde f_G$ with G by denoting  $g(\omega,x):=\tilde f_g(\omega,x)$ for every
$g(\omega,x):=\tilde f_g(\omega,x)$ for every ![]() $g\in G$,
$g\in G$, ![]() $\omega\in\Omega$ and
$\omega\in\Omega$ and ![]() $x\in\mathcal E_\omega$. According to [Reference Castaing and Valadier11, Chapter III], the map
$x\in\mathcal E_\omega$. According to [Reference Castaing and Valadier11, Chapter III], the map ![]() $\omega\mapsto\mathcal E_\omega$ is measurable with respect to the Borel σ-algebra induced by the Hausdorff topology on the space
$\omega\mapsto\mathcal E_\omega$ is measurable with respect to the Borel σ-algebra induced by the Hausdorff topology on the space ![]() $\mathcal K(X)$ of compact subsets of X. This is equivalent to that for any given
$\mathcal K(X)$ of compact subsets of X. This is equivalent to that for any given ![]() $x\in X$ the distance function
$x\in X$ the distance function ![]() $\omega\mapsto d(x,\mathcal E_\omega)$ is measurable for
$\omega\mapsto d(x,\mathcal E_\omega)$ is measurable for ![]() $\mathscr F$. We denote
$\mathscr F$. We denote ![]() $\mathcal M_{\mathbb P}(\mathcal E)$ the set of all probability measures µ on
$\mathcal M_{\mathbb P}(\mathcal E)$ the set of all probability measures µ on ![]() $(\mathcal E,\mathscr F\times\mathscr B|_\mathcal E)$ admitting marginal measure
$(\mathcal E,\mathscr F\times\mathscr B|_\mathcal E)$ admitting marginal measure ![]() $\mathbb P$, denote
$\mathbb P$, denote ![]() $\mathcal M_{\mathbb P}^G(\mathcal E)=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\mu\circ g=\mu \text{ for every } g\in G\}$ the set of all the G-invariant measures in
$\mathcal M_{\mathbb P}^G(\mathcal E)=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\mu\circ g=\mu \text{ for every } g\in G\}$ the set of all the G-invariant measures in ![]() $\mathcal M_{\mathbb P}(\mathcal E)$. According to [Reference Kifer25, Lemma 2.1],
$\mathcal M_{\mathbb P}(\mathcal E)$. According to [Reference Kifer25, Lemma 2.1], ![]() $\mathcal M_{\mathbb P}^G(\mathcal E)$ is compact with respect to weak
$\mathcal M_{\mathbb P}^G(\mathcal E)$ is compact with respect to weak![]() $^*$-topology, that is, the topology induced by the convergency that a sequence
$^*$-topology, that is, the topology induced by the convergency that a sequence ![]() $(\sigma_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$ converges to
$(\sigma_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$ converges to ![]() $\sigma\in\mathcal M_{\mathbb P}(\mathcal E)$ if and only if
$\sigma\in\mathcal M_{\mathbb P}(\mathcal E)$ if and only if ![]() $\lim_{n\to\infty}\int f\,\mathrm{d}\sigma_n=\lim_{n\to\infty}\int f\,\mathrm{d}\sigma$ for every
$\lim_{n\to\infty}\int f\,\mathrm{d}\sigma_n=\lim_{n\to\infty}\int f\,\mathrm{d}\sigma$ for every ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ (see definition of
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ (see definition of ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$ in §3.1). To see more backgrounds and details about random dynamical systems, we refer to [Reference Arnold2, Reference Bogenschutz4, Reference Bogenschutz5, Reference Kifer24–Reference Kifer and Liu26].
$\mathbf L^1_\mathcal E(\Omega,C(X))$ in §3.1). To see more backgrounds and details about random dynamical systems, we refer to [Reference Arnold2, Reference Bogenschutz4, Reference Bogenschutz5, Reference Kifer24–Reference Kifer and Liu26].
We collect some examples of continuous bundle RDSs below.
Example 2.1. Among interesting examples of continuous bundle RDSs are random sub-shifts. In the case where ![]() $G = \mathbb Z$, these are treated in detail in [Reference Bogenschutz and Gundlach6, Reference Khanin and Kifer23, Reference Kifer25]. We present a brief recall of some of their properties. Let
$G = \mathbb Z$, these are treated in detail in [Reference Bogenschutz and Gundlach6, Reference Khanin and Kifer23, Reference Kifer25]. We present a brief recall of some of their properties. Let ![]() $(\Omega,\mathscr F,\mathbb P)$ be a Lebesgue space and
$(\Omega,\mathscr F,\mathbb P)$ be a Lebesgue space and ![]() $\vartheta :(\Omega,\mathscr F,\mathbb P)\to(\Omega,\mathscr F,\mathbb P)$ an invertible measure-preserving transformation. Set
$\vartheta :(\Omega,\mathscr F,\mathbb P)\to(\Omega,\mathscr F,\mathbb P)$ an invertible measure-preserving transformation. Set ![]() $X = \{(x_i : i\in\mathbb Z) : x_i\in\mathbb N \cup \{+\infty\}, i\in\mathbb Z\}$, a compact metric space equipped with the metric
$X = \{(x_i : i\in\mathbb Z) : x_i\in\mathbb N \cup \{+\infty\}, i\in\mathbb Z\}$, a compact metric space equipped with the metric
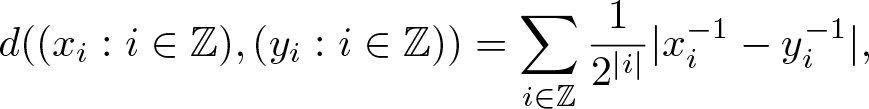 \begin{equation*}d((x_i :i\in\mathbb Z),(y_i :i\in\mathbb Z))=\sum_{i\in\mathbb Z}\frac{1}{2^{|i|}}|x_i^{-1}-y_i^{-1}|,\end{equation*}
\begin{equation*}d((x_i :i\in\mathbb Z),(y_i :i\in\mathbb Z))=\sum_{i\in\mathbb Z}\frac{1}{2^{|i|}}|x_i^{-1}-y_i^{-1}|,\end{equation*} and let ![]() $F:X\to X$ be the translation
$F:X\to X$ be the translation ![]() $(x_i : i \in\mathbb Z) \mapsto (x_{i+1} : i \in\mathbb Z)$. Then, the integer group
$(x_i : i \in\mathbb Z) \mapsto (x_{i+1} : i \in\mathbb Z)$. Then, the integer group ![]() $\mathbb Z$ acts on
$\mathbb Z$ acts on ![]() $( \Omega\times X, \mathscr F \times \mathscr B_X )$ measurably with
$( \Omega\times X, \mathscr F \times \mathscr B_X )$ measurably with ![]() $(\omega, x) \mapsto (\vartheta^i\omega, F^ix)$ for each
$(\omega, x) \mapsto (\vartheta^i\omega, F^ix)$ for each ![]() $i \in\mathbb Z$, where
$i \in\mathbb Z$, where ![]() $\mathscr B_X$ denotes the Borel σ-algebra of the space X. Now let
$\mathscr B_X$ denotes the Borel σ-algebra of the space X. Now let ![]() $\mathcal E \in\mathscr F \times \mathscr B_X$ be an invariant subset of
$\mathcal E \in\mathscr F \times \mathscr B_X$ be an invariant subset of ![]() $\Omega \times X$ (under the
$\Omega \times X$ (under the ![]() $\mathbb Z$-action) such that
$\mathbb Z$-action) such that ![]() $\emptyset\neq\mathcal E_\omega \subset X$ is compact for
$\emptyset\neq\mathcal E_\omega \subset X$ is compact for ![]() $\mathbb P\text{-a.e. }\omega\in\Omega$. This defines a continuous bundle RDS where, for
$\mathbb P\text{-a.e. }\omega\in\Omega$. This defines a continuous bundle RDS where, for ![]() $\mathbb P\text{-a.e. }\omega\in\Omega$,
$\mathbb P\text{-a.e. }\omega\in\Omega$, ![]() $F_{i,\omega}$ is just the restriction of Fi over
$F_{i,\omega}$ is just the restriction of Fi over ![]() $\mathcal E_\omega$ for every
$\mathcal E_\omega$ for every ![]() $i \in\mathbb Z$.
$i \in\mathbb Z$.
A very special case is when the subset ![]() $\mathcal E$ is given as follows. Let k be a random
$\mathcal E$ is given as follows. Let k be a random ![]() $\mathbb N$-valued random variable satisfying
$\mathbb N$-valued random variable satisfying
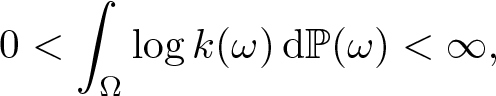 \begin{equation*}0 \lt \int_\Omega\log k(\omega)\,\mathrm d\mathbb P(\omega) \lt \infty,\end{equation*}
\begin{equation*}0 \lt \int_\Omega\log k(\omega)\,\mathrm d\mathbb P(\omega) \lt \infty,\end{equation*} and, for ![]() $\mathbb P\text{-a.e. }\omega\in\Omega$, let
$\mathbb P\text{-a.e. }\omega\in\Omega$, let ![]() $M(\omega)$ be a random matrix
$M(\omega)$ be a random matrix ![]() $(m_{i,j}(\omega) : i = 1,\ldots ,k(\omega), j= 1,\ldots, k(\vartheta\omega))$ with entries 0 and 1. Then, the random variable k and the random matrix M generate a random sub-shift of finite type, where
$(m_{i,j}(\omega) : i = 1,\ldots ,k(\omega), j= 1,\ldots, k(\vartheta\omega))$ with entries 0 and 1. Then, the random variable k and the random matrix M generate a random sub-shift of finite type, where
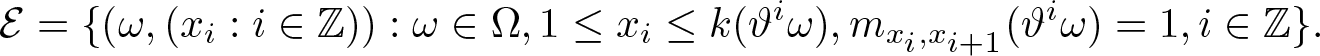 \begin{equation*}\mathcal E =\{(\omega,(x_i :i\in\mathbb Z)):\omega\in\Omega, 1\leq x_i \leq k(\vartheta^i\omega), m_{x_i,x_{i+1}}(\vartheta^i\omega)=1, i\in\mathbb Z\}.\end{equation*}
\begin{equation*}\mathcal E =\{(\omega,(x_i :i\in\mathbb Z)):\omega\in\Omega, 1\leq x_i \leq k(\vartheta^i\omega), m_{x_i,x_{i+1}}(\vartheta^i\omega)=1, i\in\mathbb Z\}.\end{equation*}It is not hard to see that this is a continuous bundle RDS. In [Reference Dooley and Zhang16], Dooley and Zhang studied the local variational principle of general group G action RDS.
Example 2.2. There are many other interesting examples of continuous bundle RDSs coming from smooth ergodic theory, see, for example [Reference Liu28, Reference Lian and Lu31], where one considers not only the action of ![]() $\mathbb Z$ or
$\mathbb Z$ or ![]() $\mathbb Z_+$ on a compact metric state space but also on Riemannian manifolds. Let M be a
$\mathbb Z_+$ on a compact metric state space but also on Riemannian manifolds. Let M be a ![]() $C^\infty$ compact connected Riemannian manifold without boundary and
$C^\infty$ compact connected Riemannian manifold without boundary and ![]() $C^r(M,M)$,
$C^r(M,M)$, ![]() $r\in\mathbb Z_+\cup\{+\infty\}$ the space of all Cr maps from M into itself endowed with the usual Cr topology and the Borel σ-algebra. Let
$r\in\mathbb Z_+\cup\{+\infty\}$ the space of all Cr maps from M into itself endowed with the usual Cr topology and the Borel σ-algebra. Let ![]() $(\Omega,\mathscr F,\mathbb P)$ be a Lebesgue space and
$(\Omega,\mathscr F,\mathbb P)$ be a Lebesgue space and ![]() $\{\phi_t:\Omega\to C^r(M,M)\}_{t\geq 0}$ be a stochastic flow of
$\{\phi_t:\Omega\to C^r(M,M)\}_{t\geq 0}$ be a stochastic flow of ![]() $C^r(M,M)$ diffeomorphisms. It is well known that every smooth stochastic differential equation (SDE) in a finite dimensional compact manifold has a stochastic flow of diffeomorphisms as its solution flow. When the SDE is non-degenerate, it has a unique stationary measure, which is ergodic and equivalent to Lebesgue measure. Hence, Pesin’s entropy formula holds true, which can be viewed as a sharp contradiction with the deterministic dynamical systems.
$C^r(M,M)$ diffeomorphisms. It is well known that every smooth stochastic differential equation (SDE) in a finite dimensional compact manifold has a stochastic flow of diffeomorphisms as its solution flow. When the SDE is non-degenerate, it has a unique stationary measure, which is ergodic and equivalent to Lebesgue measure. Hence, Pesin’s entropy formula holds true, which can be viewed as a sharp contradiction with the deterministic dynamical systems.
A measure space ![]() $(M,\mathcal B,m)$ is called Lebesgue space or standard probability space if there is an invertible map
$(M,\mathcal B,m)$ is called Lebesgue space or standard probability space if there is an invertible map ![]() $f:M\to\Delta$, where
$f:M\to\Delta$, where ![]() $\Delta\subset\mathbb R$ is composed of an interval
$\Delta\subset\mathbb R$ is composed of an interval ![]() $I\subset\mathbb R$ and at most countable set of points
$I\subset\mathbb R$ and at most countable set of points ![]() $\{x_j\in\mathbb R:j\in J\subset\mathbb N\}$, such that
$\{x_j\in\mathbb R:j\in J\subset\mathbb N\}$, such that ![]() $f,f^{-1}$ both are measurable and measure preserving, and m on I takes the usual Lebesgue measure and
$f,f^{-1}$ both are measurable and measure preserving, and m on I takes the usual Lebesgue measure and ![]() $m(x_j)=m_j$ such that
$m(x_j)=m_j$ such that  $m(\Delta)=m(I)+\sum_{j\in J}m_j=1$. Any Lebesgue space
$m(\Delta)=m(I)+\sum_{j\in J}m_j=1$. Any Lebesgue space ![]() $(M,\mathcal B,m)$ is complete and countably separated; the latter means that there is
$(M,\mathcal B,m)$ is complete and countably separated; the latter means that there is ![]() $(A_n)_{n\in\mathbb N}\subset\mathcal B$ such that
$(A_n)_{n\in\mathbb N}\subset\mathcal B$ such that ![]() $\{n\in\mathbb N:x\in A_n\}=\{n\in\mathbb N:y\in A_n\}$ implies x = y for every
$\{n\in\mathbb N:x\in A_n\}=\{n\in\mathbb N:y\in A_n\}$ implies x = y for every ![]() $x,y\in M$.
$x,y\in M$.
For G a group, we denote ![]() $\mathcal F_G$ the set of all non-empty finite subsets of G. For each
$\mathcal F_G$ the set of all non-empty finite subsets of G. For each ![]() $K\in\mathcal F_G$ and δ > 0, we say
$K\in\mathcal F_G$ and δ > 0, we say ![]() $F\in\mathcal F_G$ is (K,δ)-invariant, if
$F\in\mathcal F_G$ is (K,δ)-invariant, if  $\frac{|\partial_K F|}{|F|} \lt \delta$, where
$\frac{|\partial_K F|}{|F|} \lt \delta$, where ![]() $|\cdot|$ is the cardinality of a set and
$|\cdot|$ is the cardinality of a set and ![]() $\partial_K F=\{g\in G:Kg\cap F\not=\emptyset,Kg\cap F^c\not=\emptyset\}$ is the K-boundary of F. Moreover, a sequence
$\partial_K F=\{g\in G:Kg\cap F\not=\emptyset,Kg\cap F^c\not=\emptyset\}$ is the K-boundary of F. Moreover, a sequence ![]() $\{F_n\}_{n\in\mathbb N}\subset\mathcal F_G$ is called Følner sequence of G if
$\{F_n\}_{n\in\mathbb N}\subset\mathcal F_G$ is called Følner sequence of G if
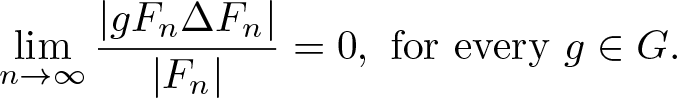 \begin{equation*}\lim_{n\to\infty}\frac{|gF_n\Delta F_n|}{|F_n|}=0, \text{ for every }g\in G.\end{equation*}
\begin{equation*}\lim_{n\to\infty}\frac{|gF_n\Delta F_n|}{|F_n|}=0, \text{ for every }g\in G.\end{equation*} A group G is said to be amenable if for any given ![]() $K\in\mathcal F_G$ and δ > 0, there is
$K\in\mathcal F_G$ and δ > 0, there is ![]() $F\in\mathcal F_G$ such that
$F\in\mathcal F_G$ such that  $\frac{|kF\Delta F|}{|F|}\leq\delta$ for every
$\frac{|kF\Delta F|}{|F|}\leq\delta$ for every ![]() $k\in K$. According to [Reference Ornstein and Weiss43, p. 11], if G is a countable group, then G is amenable if and only if G admits a Følner sequence. To see more details about amenable group action, we refer to [Reference Downarowicz, Huczek and Zhang17, Reference Kerr and Li22, Reference Ornstein and Weiss43, Reference Weiss49].
$k\in K$. According to [Reference Ornstein and Weiss43, p. 11], if G is a countable group, then G is amenable if and only if G admits a Følner sequence. To see more details about amenable group action, we refer to [Reference Downarowicz, Huczek and Zhang17, Reference Kerr and Li22, Reference Ornstein and Weiss43, Reference Weiss49].
Throughout the rest of this paper, let ![]() $(\Omega,\mathscr F,\mathbb P)$ always be a Lebesgue space together with G, a measure-preserving countable discrete amenable group action, and
$(\Omega,\mathscr F,\mathbb P)$ always be a Lebesgue space together with G, a measure-preserving countable discrete amenable group action, and ![]() $\mathfrak s=\{F_n\}_{n\in\mathbb N}$ be a Følner sequence of G. Moreover, let (X, d) always denote a compact metric space with corresponding Borel σ-algebra
$\mathfrak s=\{F_n\}_{n\in\mathbb N}$ be a Følner sequence of G. Moreover, let (X, d) always denote a compact metric space with corresponding Borel σ-algebra ![]() $\mathscr B$. Fix
$\mathscr B$. Fix ![]() $\mathcal E\in\mathscr F\times\mathscr B$ such that for each
$\mathcal E\in\mathscr F\times\mathscr B$ such that for each ![]() $\omega\in\Omega$ the fibre
$\omega\in\Omega$ the fibre ![]() $\mathcal E_\omega$ is non-empty and compact and
$\mathcal E_\omega$ is non-empty and compact and ![]() $\mathbf F=\{\mathbf F_{g,\omega}:\mathcal E_\omega\to\mathcal E_{g\omega}|g\in G,\omega\in\Omega\}$ a continuous bundle RDS associated with
$\mathbf F=\{\mathbf F_{g,\omega}:\mathcal E_\omega\to\mathcal E_{g\omega}|g\in G,\omega\in\Omega\}$ a continuous bundle RDS associated with ![]() $(\Omega,\mathscr F,\mathbb P,G)$. We emphasize under these settings
$(\Omega,\mathscr F,\mathbb P,G)$. We emphasize under these settings ![]() $\mathcal M_{\mathbb P}(\mathcal E)\not=\emptyset$ (see, for example [Reference Kifer25, Lemma 2.1 (i)]) and
$\mathcal M_{\mathbb P}(\mathcal E)\not=\emptyset$ (see, for example [Reference Kifer25, Lemma 2.1 (i)]) and ![]() $\mathcal M_{\mathbb P}^G(\mathcal E)\neq\emptyset$ (see [Reference Dooley and Zhang16, p. 30]).
$\mathcal M_{\mathbb P}^G(\mathcal E)\neq\emptyset$ (see [Reference Dooley and Zhang16, p. 30]).
The main results of this work are as follows:
Theorem 2.3. (Variational principle). Suppose Ω admits a compact metric, ![]() $\mathscr F$ is the corresponding Borel σ-algebra, and G acts ergodicly on
$\mathscr F$ is the corresponding Borel σ-algebra, and G acts ergodicly on ![]() $(\Omega,\mathscr F,\mathbb P)$. Let
$(\Omega,\mathscr F,\mathbb P)$. Let ![]() $\mathcal E=\Omega\times X$, if
$\mathcal E=\Omega\times X$, if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
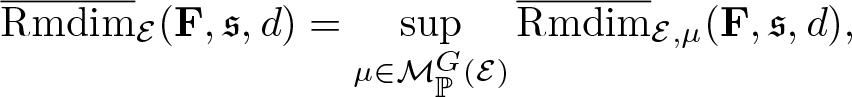 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d),\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d),\end{equation*} where ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ is the random upper metric mean dimension defined in Definition 3.3 and
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ is the random upper metric mean dimension defined in Definition 3.3 and ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$ is the random upper measure-theoretic mean dimension defined in Definition 3.16.
$\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$ is the random upper measure-theoretic mean dimension defined in Definition 3.16.
Let ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ denote the set of equilibrium states of a function
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ denote the set of equilibrium states of a function ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, as defined in Definition 5.1. Let
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, as defined in Definition 5.1. Let ![]() $\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ denote the set of tangent functionals at
$\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ denote the set of tangent functionals at ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, as defined in Definition 5.2. The second main result of our study establishes both the existence and uniqueness of the equilibrium states for
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, as defined in Definition 5.2. The second main result of our study establishes both the existence and uniqueness of the equilibrium states for ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Furthermore, it demonstrates that the set
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Furthermore, it demonstrates that the set ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ of equilibrium states for
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ of equilibrium states for ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ precisely coincides with the set
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ precisely coincides with the set ![]() $\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ of tangent functionals at
$\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ of tangent functionals at ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$.
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$.
Theorem 2.4. Suppose ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
(1)
 $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is non-empty, convex and compact for every
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is non-empty, convex and compact for every  $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$;
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$;(2) for every
 $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$,
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$,
 \begin{equation*}\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\geq1}\overline{M_n},\end{equation*}
\begin{equation*}\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\geq1}\overline{M_n},\end{equation*}where
 $M_n=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu \gt \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\frac{1}{n}\}$ for every
$M_n=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu \gt \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\frac{1}{n}\}$ for every  $n\in\mathbb N$;
$n\in\mathbb N$;(3) there exists a dense subset
 $\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ such that
$\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ such that  $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is a singleton for every
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is a singleton for every  $f\in\mathscr L$.
$f\in\mathscr L$.
3. Random metric mean dimension
3.1. Random upper metric mean dimension with potentials
In this subsection, we present the notion and several properties of random mean dimension with random potentials.
Let ![]() $L^1_\mathcal E(\Omega,C(X))$ be the set of all the measurable functions
$L^1_\mathcal E(\Omega,C(X))$ be the set of all the measurable functions ![]() $f:\mathcal E\to\mathbb R$ such that
$f:\mathcal E\to\mathbb R$ such that
(α) the function
 $f_\omega=f(\omega,\cdot):\mathcal E_\omega\to\mathbb R$ is continuous for
$f_\omega=f(\omega,\cdot):\mathcal E_\omega\to\mathbb R$ is continuous for  $\mathbb P$-a.e.
$\mathbb P$-a.e.  $\omega\in\Omega$,
$\omega\in\Omega$,(β)
 $||f||_{\mathbb P}:=\int||f_\omega||_\infty\,\mathrm d{\mathbb P} \lt \infty$,
$||f||_{\mathbb P}:=\int||f_\omega||_\infty\,\mathrm d{\mathbb P} \lt \infty$,
where ![]() $||f_\omega||_\infty=\sup_{x\in\mathcal E_\omega}|f_\omega(x)|$. Let
$||f_\omega||_\infty=\sup_{x\in\mathcal E_\omega}|f_\omega(x)|$. Let ![]() ${\mathbf L}^1_\mathcal E(\Omega,C(X))$ be the quotient set
${\mathbf L}^1_\mathcal E(\Omega,C(X))$ be the quotient set ![]() $L^1_{\mathcal E}(\Omega,C(X))$ mod
$L^1_{\mathcal E}(\Omega,C(X))$ mod ![]() $||\cdot||_{\mathbb P}$, that is, the set of all the equivalent classes of elements in
$||\cdot||_{\mathbb P}$, that is, the set of all the equivalent classes of elements in ![]() $L^1_{\mathcal E}(\Omega,C(X))$ in the sense that identify
$L^1_{\mathcal E}(\Omega,C(X))$ in the sense that identify ![]() $f,g\in L^1_\mathcal E(\Omega,C(X))$ if
$f,g\in L^1_\mathcal E(\Omega,C(X))$ if ![]() $||f-g||_{\mathbb P}=0$. Note that
$||f-g||_{\mathbb P}=0$. Note that ![]() $({\mathbf L}^1_\mathcal E(\Omega,C(X)),||\cdot||_{\mathbb P})$ is a Banach space.
$({\mathbf L}^1_\mathcal E(\Omega,C(X)),||\cdot||_{\mathbb P})$ is a Banach space.
Definition 3.1. A random potential on ![]() $\mathcal E$ is a map
$\mathcal E$ is a map ![]() $\phi:\mathcal F_G\to\mathbf L^1_\mathcal E(\Omega,C(X))$. The set of all random potentials on
$\phi:\mathcal F_G\to\mathbf L^1_\mathcal E(\Omega,C(X))$. The set of all random potentials on ![]() $\mathcal E$ is denoted by
$\mathcal E$ is denoted by ![]() $\mathfrak P(\mathcal E)$.
$\mathfrak P(\mathcal E)$.
For the sake of simplicity, for every ![]() $\phi,\psi\in\mathfrak P(\mathcal E)$,
$\phi,\psi\in\mathfrak P(\mathcal E)$,
1. let
 $\phi_F:=\phi(F)$ for every
$\phi_F:=\phi(F)$ for every  $F\in\mathcal F_G$;
$F\in\mathcal F_G$;2.
 $\phi_{F,\omega}$ denotes the function
$\phi_{F,\omega}$ denotes the function  $\phi_F(\omega,\cdot):\mathcal E_\omega\to\mathbb R$, for every
$\phi_F(\omega,\cdot):\mathcal E_\omega\to\mathbb R$, for every  $\omega\in\Omega$ and
$\omega\in\Omega$ and  $F\in\mathcal F_G$.
$F\in\mathcal F_G$.3.
 $\phi\leq\psi$ denotes that
$\phi\leq\psi$ denotes that  $\phi_F\leq\psi_F$ for every
$\phi_F\leq\psi_F$ for every  $F\in\mathcal F_G$;
$F\in\mathcal F_G$;4. ϕ = 0 denotes that
 $\phi_F(\omega,x)=0$ for every
$\phi_F(\omega,x)=0$ for every  $F\in\mathcal F_G$,
$F\in\mathcal F_G$,  $\omega\in\Omega$, and
$\omega\in\Omega$, and  $x\in\mathcal E_\omega$.
$x\in\mathcal E_\omega$.
For each ![]() $\omega\in\Omega$,
$\omega\in\Omega$, ![]() $\phi\in\mathfrak P(\mathcal E)$,
$\phi\in\mathfrak P(\mathcal E)$, ![]() $F\in\mathcal F_G$ and ɛ > 0, define
$F\in\mathcal F_G$ and ɛ > 0, define
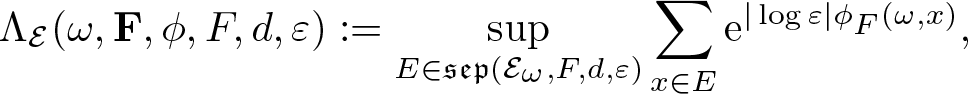 \begin{equation*}\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon):=\sup_{E\in \mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_F(\omega,x)},\end{equation*}
\begin{equation*}\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon):=\sup_{E\in \mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_F(\omega,x)},\end{equation*} where ![]() $\mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)$ is the set of all
$\mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)$ is the set of all ![]() $(F,\varepsilon)$-separated sets of
$(F,\varepsilon)$-separated sets of ![]() $\mathcal E_\omega$; i.e.
$\mathcal E_\omega$; i.e. ![]() $E\in \mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)$ if and only if
$E\in \mathfrak {sep}(\mathcal E_\omega,F,d,\varepsilon)$ if and only if ![]() $E\subset\mathcal E_\omega$ and
$E\subset\mathcal E_\omega$ and ![]() $d_F^\omega(x,y):=\max_{g\in F}d(\mathbf F_{g,\omega} x,\mathbf F_{g,\omega} y) \gt \varepsilon$ for every distinct
$d_F^\omega(x,y):=\max_{g\in F}d(\mathbf F_{g,\omega} x,\mathbf F_{g,\omega} y) \gt \varepsilon$ for every distinct ![]() $x,y\in E$.
$x,y\in E$.
With a slight modification to the proof of [Reference Kifer25, Lemma 1.2], it is easy to see that for any given ![]() $\phi\in\mathfrak P(\mathcal E)$,
$\phi\in\mathfrak P(\mathcal E)$, ![]() $F\in\mathcal F_G$, and ɛ > 0, the functions
$F\in\mathcal F_G$, and ɛ > 0, the functions ![]() $\omega\mapsto \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon)$ and
$\omega\mapsto \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon)$ and ![]() $\omega\mapsto s(\mathcal E_\omega,F,d,\varepsilon)$ are measurable with respect to
$\omega\mapsto s(\mathcal E_\omega,F,d,\varepsilon)$ are measurable with respect to ![]() $\mathscr F$, where
$\mathscr F$, where ![]() $s(\mathcal E_\omega,F_n,d,\varepsilon)=\max\{\mathrm{card\,} E:E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)\}$. Moreover, there is the following lemma:
$s(\mathcal E_\omega,F_n,d,\varepsilon)=\max\{\mathrm{card\,} E:E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)\}$. Moreover, there is the following lemma:
Lemma 3.2. Let ɛ > 0 and ![]() $\phi\in\mathfrak P(\mathcal E)$, then the function
$\phi\in\mathfrak P(\mathcal E)$, then the function ![]() $\omega\mapsto\log \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,{\varepsilon})$ belongs to
$\omega\mapsto\log \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,{\varepsilon})$ belongs to ![]() $L^1_{\mathbb P}(\Omega)$ for every
$L^1_{\mathbb P}(\Omega)$ for every ![]() $F\in\mathcal F_G$.
$F\in\mathcal F_G$.
Proof. The statement follows from that
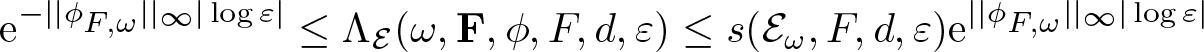 \begin{equation*}\mathrm{e}^{-||\phi_{F,\omega}||_\infty|\log\varepsilon|}\leq \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon)\leq s(\mathcal E_\omega,F,d,\varepsilon)\mathrm{e}^{||\phi_{F,\omega}||_\infty|\log\varepsilon|}\end{equation*}
\begin{equation*}\mathrm{e}^{-||\phi_{F,\omega}||_\infty|\log\varepsilon|}\leq \Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F,d,\varepsilon)\leq s(\mathcal E_\omega,F,d,\varepsilon)\mathrm{e}^{||\phi_{F,\omega}||_\infty|\log\varepsilon|}\end{equation*} for every ![]() $F\in\mathcal F_G$.
$F\in\mathcal F_G$.
This means that the following definition makes sense:
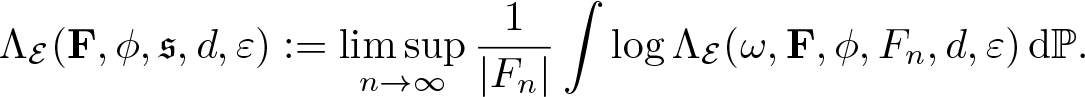 \begin{equation*}\Lambda_{\mathcal E}(\mathbf F,\phi,\mathfrak s,d,\varepsilon):=\limsup_{n\to\infty}\frac{1}{|F_n|}\int\log\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F_n,d,\varepsilon)\,\mathrm d\mathbb P.\end{equation*}
\begin{equation*}\Lambda_{\mathcal E}(\mathbf F,\phi,\mathfrak s,d,\varepsilon):=\limsup_{n\to\infty}\frac{1}{|F_n|}\int\log\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F_n,d,\varepsilon)\,\mathrm d\mathbb P.\end{equation*}Definition 3.3. Let ![]() $\phi\in\mathfrak P(\mathcal E)$, the quantity
$\phi\in\mathfrak P(\mathcal E)$, the quantity
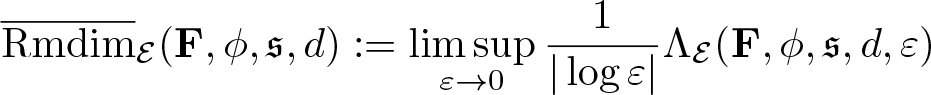 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d):=\limsup_{\varepsilon\to0}\frac{1}{|\log\varepsilon|}\Lambda_{\mathcal E}(\mathbf F,\phi,\mathfrak s,d,\varepsilon)\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d):=\limsup_{\varepsilon\to0}\frac{1}{|\log\varepsilon|}\Lambda_{\mathcal E}(\mathbf F,\phi,\mathfrak s,d,\varepsilon)\end{equation*} is called the random upper metric mean dimension of ![]() $\mathbf F$ with random potential ϕ on
$\mathbf F$ with random potential ϕ on ![]() $\mathcal E$ with respect to the Følner sequence
$\mathcal E$ with respect to the Følner sequence ![]() $\mathfrak s$. In addition, the quantity
$\mathfrak s$. In addition, the quantity
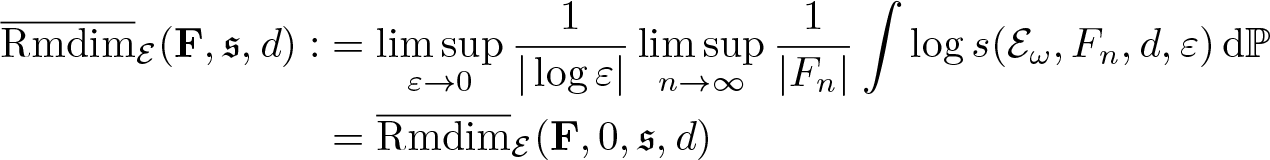 \begin{align*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d):&=\limsup_{\varepsilon\to0}\frac{1}{|\log\varepsilon|}\limsup_{n\to\infty}\frac{1}{|F_n|}\int\log s(\mathcal E_\omega,F_n,d,\varepsilon)\,\mathrm d\mathbb P\\
&={\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,0,\mathfrak s,d)}\end{align*}
\begin{align*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d):&=\limsup_{\varepsilon\to0}\frac{1}{|\log\varepsilon|}\limsup_{n\to\infty}\frac{1}{|F_n|}\int\log s(\mathcal E_\omega,F_n,d,\varepsilon)\,\mathrm d\mathbb P\\
&={\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,0,\mathfrak s,d)}\end{align*} is called the random upper metric mean dimension of ![]() $\mathbf F$ on
$\mathbf F$ on ![]() $\mathcal E$ with respect to the Følner sequence
$\mathcal E$ with respect to the Følner sequence ![]() $\mathfrak s$.
$\mathfrak s$.
Remark 3.4. By the definition of random upper metric mean dimensions, it is possible that the values of ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ and
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ and ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d)$ are influenced by the choice of the Følner sequence
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d)$ are influenced by the choice of the Følner sequence ![]() $\mathfrak{s}$. However, if (X, d) has tame growth of covering numbers, similar arguments as in [Reference Chen, Dou and Zheng10, Proposition 3.4] also give that
$\mathfrak{s}$. However, if (X, d) has tame growth of covering numbers, similar arguments as in [Reference Chen, Dou and Zheng10, Proposition 3.4] also give that ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ and
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ and ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d)$ are independent of the choice of the Følner sequence
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\phi,\mathfrak s,d)$ are independent of the choice of the Følner sequence ![]() $\mathfrak{s}$.
$\mathfrak{s}$.
We present several basic properties of random mean dimension with random potentials. We omit or only give a sketch of the proofs that can be directly deduced by the definition or are obvious.
Fact 3.5. (Monotonicity of mean dimension)
Let ![]() $\phi\leq\psi$ be random potentials, then
$\phi\leq\psi$ be random potentials, then
Fact 3.6.
If the function ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d):\mathfrak P(\mathcal E)\to\mathbb R\cup\{\infty\}$ takes finite value for every
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d):\mathfrak P(\mathcal E)\to\mathbb R\cup\{\infty\}$ takes finite value for every ![]() $\phi\in\mathfrak P(\mathcal E)$, then
$\phi\in\mathfrak P(\mathcal E)$, then ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d)$ is convex.
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d)$ is convex.
Proof. Let ![]() $\phi,\psi\in\mathfrak P(\mathcal E)$. For any
$\phi,\psi\in\mathfrak P(\mathcal E)$. For any ![]() $\omega\in\Omega$,
$\omega\in\Omega$, ![]() $t\in[0,1]$,
$t\in[0,1]$, ![]() $n\in\mathbb N$ and
$n\in\mathbb N$ and ![]() $\varepsilon\in(0,1)$, we have
$\varepsilon\in(0,1)$, we have
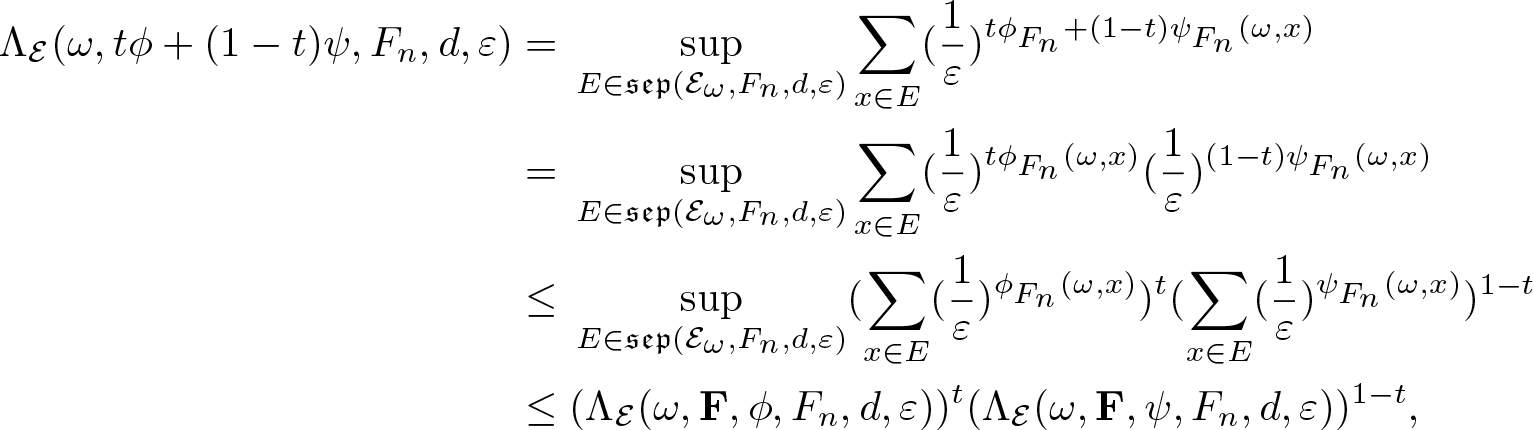 \begin{eqnarray*}
\Lambda_{\mathcal E}(\omega,t\phi+(1-t)\psi,F_n,d,\varepsilon)&=&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}\sum_{x\in E}(\frac{1}{\varepsilon})^{t\phi_{F_n}+(1-t)\psi_{F_n}(\omega,x)}\\
&=&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}\sum_{x\in E}(\frac{1}{\varepsilon})^{t\phi_{F_n}(\omega,x)}(\frac{1}{\varepsilon})^{(1-t)\psi_{F_n}(\omega,x)}\\
&\leq&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}(\sum_{x\in E}(\frac{1}{\varepsilon})^{\phi_{F_n}(\omega,x)})^t(\sum_{x\in E}(\frac{1}{\varepsilon})^{\psi_{F_n}(\omega,x)})^{1-t}\\
&\leq&(\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F_n,d,\varepsilon))^t(\Lambda_{\mathcal E}(\omega,\mathbf F,\psi,F_n,d,\varepsilon))^{1-t},
\end{eqnarray*}
\begin{eqnarray*}
\Lambda_{\mathcal E}(\omega,t\phi+(1-t)\psi,F_n,d,\varepsilon)&=&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}\sum_{x\in E}(\frac{1}{\varepsilon})^{t\phi_{F_n}+(1-t)\psi_{F_n}(\omega,x)}\\
&=&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}\sum_{x\in E}(\frac{1}{\varepsilon})^{t\phi_{F_n}(\omega,x)}(\frac{1}{\varepsilon})^{(1-t)\psi_{F_n}(\omega,x)}\\
&\leq&\sup_{E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)}(\sum_{x\in E}(\frac{1}{\varepsilon})^{\phi_{F_n}(\omega,x)})^t(\sum_{x\in E}(\frac{1}{\varepsilon})^{\psi_{F_n}(\omega,x)})^{1-t}\\
&\leq&(\Lambda_{\mathcal E}(\omega,\mathbf F,\phi,F_n,d,\varepsilon))^t(\Lambda_{\mathcal E}(\omega,\mathbf F,\psi,F_n,d,\varepsilon))^{1-t},
\end{eqnarray*} where the first inequality follows from the H![]() $\ddot{\mathrm o}$lder’s inequality. This shows the statement.
$\ddot{\mathrm o}$lder’s inequality. This shows the statement.
Fact 3.7. (Subadditivity of mean dimension)
For any ![]() $\phi,\psi\in\mathfrak P(\mathcal E)$, we have
$\phi,\psi\in\mathfrak P(\mathcal E)$, we have
Proof. The statement follows from that
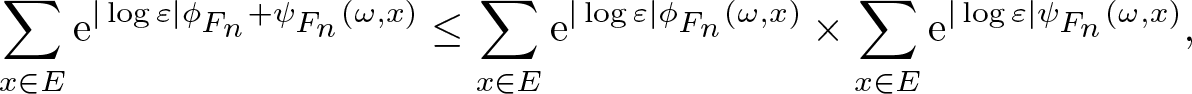 \begin{equation*}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_{F_n}+\psi_{F_n}(\omega,x)}\leq\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_{F_n}(\omega,x)}\times\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\psi_{F_n}(\omega,x)},\end{equation*}
\begin{equation*}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_{F_n}+\psi_{F_n}(\omega,x)}\leq\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\phi_{F_n}(\omega,x)}\times\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|\psi_{F_n}(\omega,x)},\end{equation*} for any ![]() $\omega\in\Omega$,
$\omega\in\Omega$, ![]() $n\in\mathbb N$, ɛ > 0 and
$n\in\mathbb N$, ɛ > 0 and ![]() $E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)$.
$E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)$.
Fact 3.8.
If ![]() $t\geq1$, then
$t\geq1$, then
if ![]() $0\leq t\leq1$, then
$0\leq t\leq1$, then
Proof. The statement follows from that the map ![]() $x\mapsto x^t$ on
$x\mapsto x^t$ on ![]() $\mathbb R_{\geq0}$ is convex when
$\mathbb R_{\geq0}$ is convex when ![]() $t\geq1$ and concave when
$t\geq1$ and concave when ![]() $t\leq1$.
$t\leq1$.
Fact 3.9.
Let ![]() $\phi\in\mathfrak P(\mathcal E)$, then
$\phi\in\mathfrak P(\mathcal E)$, then
Definition 3.10. Let ![]() $\phi\in\mathfrak P(\mathcal E)$, if there is
$\phi\in\mathfrak P(\mathcal E)$, if there is ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ such that
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ such that  $\phi_F=S_Ff:=\sum_{g\in F}f\circ g$ for every
$\phi_F=S_Ff:=\sum_{g\in F}f\circ g$ for every ![]() $F\in\mathcal F_G$, then for every
$F\in\mathcal F_G$, then for every ![]() $\omega\in\Omega$,
$\omega\in\Omega$, ![]() $F\in\mathcal F_G$, and ɛ > 0 denote
$F\in\mathcal F_G$, and ɛ > 0 denote
and
Fact 3.11.
Let ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and ![]() $c\in\mathbb R$, then
$c\in\mathbb R$, then
Fact 3.12.
Let ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, then
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, then
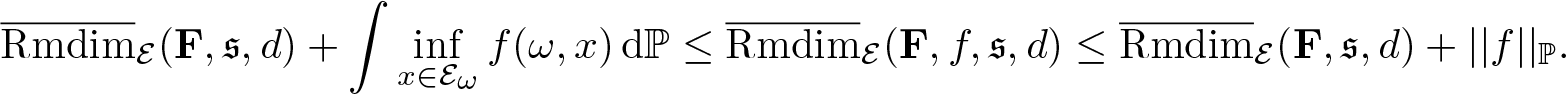 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\int\inf_{x\in\mathcal E_\omega}f(\omega,x)\,\mathrm d\mathbb P\leq\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,f,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+||f||_{\mathbb P}.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\int\inf_{x\in\mathcal E_\omega}f(\omega,x)\,\mathrm d\mathbb P\leq\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,f,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+||f||_{\mathbb P}.\end{equation*}In particular,
and
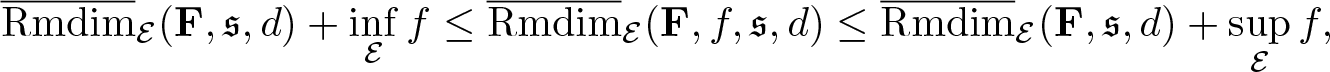 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\inf_\mathcal Ef\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\sup_\mathcal Ef,\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\inf_\mathcal Ef\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\sup_\mathcal Ef,\end{equation*} where ![]() $\inf_\mathcal Ef=\inf_{(\omega,x)\in\mathcal E}f(\omega,x)$ and
$\inf_\mathcal Ef=\inf_{(\omega,x)\in\mathcal E}f(\omega,x)$ and ![]() $\sup_\mathcal Ef=\sup_{(\omega,x)\in \mathcal E}f(\omega,x)$.
$\sup_\mathcal Ef=\sup_{(\omega,x)\in \mathcal E}f(\omega,x)$.
This immediately deduces the following as ![]() $||f||_{\mathbb P} \lt {\infty}$ for every
$||f||_{\mathbb P} \lt {\infty}$ for every ![]() $f\in\mathbf L^1_{\mathcal E}(\Omega,C(X))$.
$f\in\mathbf L^1_{\mathcal E}(\Omega,C(X))$.
Fact 3.13.
The function ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d):\mathbf L^1_\mathcal E(\Omega,C(X))\to\mathbb R\cup\{\infty\}$ either takes finite values at all
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\cdot,\mathfrak s,d):\mathbf L^1_\mathcal E(\Omega,C(X))\to\mathbb R\cup\{\infty\}$ either takes finite values at all ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ or constantly
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ or constantly ![]() $\infty$. Furthermore,
$\infty$. Furthermore, ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=\infty$ for all
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=\infty$ for all ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ if and only if
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ if and only if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
Fact 3.14.
Suppose ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$. For any
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$. For any ![]() $f,g\in\mathbf L^1_\mathcal E(\Omega,C(X))$, we have
$f,g\in\mathbf L^1_\mathcal E(\Omega,C(X))$, we have
In particular, the function
is continuous on ![]() $(\mathbf L^1_\mathcal E(\Omega,C(X)),{||\cdot||_{\mathbb P}})$.
$(\mathbf L^1_\mathcal E(\Omega,C(X)),{||\cdot||_{\mathbb P}})$.
Fact 3.15. (Invariance of mean dimension)
Let ![]() $f,f^*\in\mathbf L^1_\mathcal E(\Omega,C(X))$, then for any
$f,f^*\in\mathbf L^1_\mathcal E(\Omega,C(X))$, then for any ![]() $g\in G$ we have
$g\in G$ we have
In particular,
Proof. Let ![]() $g\in G$,
$g\in G$, ![]() $n\in\mathbb N$,
$n\in\mathbb N$, ![]() $(\omega,x)\in\mathcal E$,
$(\omega,x)\in\mathcal E$, ![]() $\varepsilon\in(0,1)$, and
$\varepsilon\in(0,1)$, and ![]() $E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)$, then
$E\in{\mathfrak {sep}}(\mathcal E_\omega,F_n,d,\varepsilon)$, then
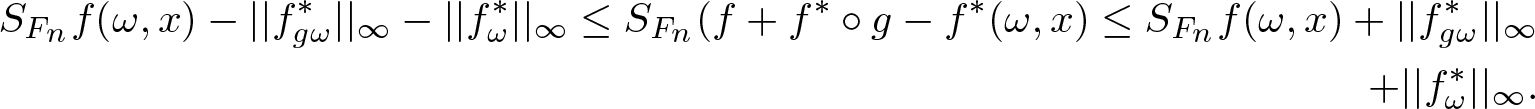 \begin{align*}
{S_{F_n}f(\omega,x)-||f^*_{g\omega}||_{\infty}-||f^*_{\omega}||_{\infty}}
\leq{S_{F_n}(f+f^*\circ g-f^*(\omega,x)}
\leq{S_{F_n}f(\omega,x)+||f^*_{g\omega}}||_{\infty}\\
+||f^*_{\omega}||_{\infty}.\end{align*}
\begin{align*}
{S_{F_n}f(\omega,x)-||f^*_{g\omega}||_{\infty}-||f^*_{\omega}||_{\infty}}
\leq{S_{F_n}(f+f^*\circ g-f^*(\omega,x)}
\leq{S_{F_n}f(\omega,x)+||f^*_{g\omega}}||_{\infty}\\
+||f^*_{\omega}||_{\infty}.\end{align*}This shows that
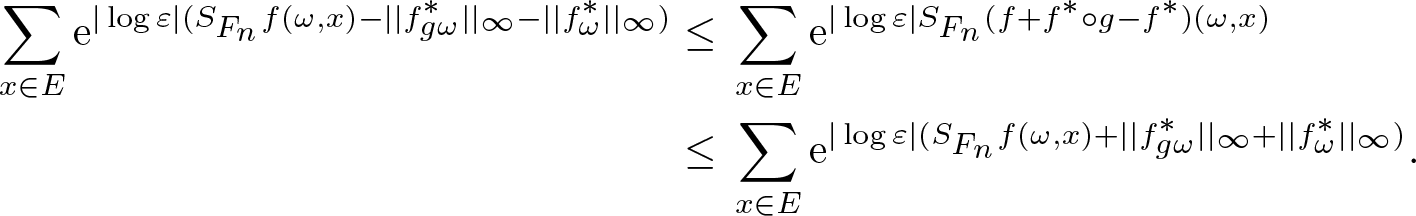 \begin{eqnarray*}
\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)-||f^*_{g\omega}||_{\infty}-||f^*_\omega||_\infty)}
&\leq&\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|S_{F_n}(f+f^*\circ g-f^*)(\omega,x)}\\
&\leq&\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)+||f^*_{g\omega}||_{\infty}+||f^*_\omega||_\infty)}.
\end{eqnarray*}
\begin{eqnarray*}
\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)-||f^*_{g\omega}||_{\infty}-||f^*_\omega||_\infty)}
&\leq&\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|S_{F_n}(f+f^*\circ g-f^*)(\omega,x)}\\
&\leq&\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)+||f^*_{g\omega}||_{\infty}+||f^*_\omega||_\infty)}.
\end{eqnarray*}Combining with the following equality
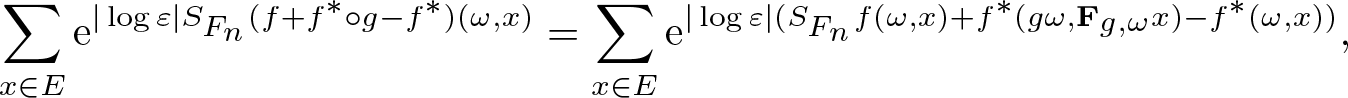 \begin{equation*}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|S_{F_n}(f+f^*\circ g-f^*)(\omega,x)}=\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)+f^*(g\omega,\mathbf F_{g,\omega} x)-f^*(\omega,x))},\end{equation*}
\begin{equation*}\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|S_{F_n}(f+f^*\circ g-f^*)(\omega,x)}=\sum_{x\in E}\mathrm{e}^{|\log\varepsilon|(S_{F_n}f(\omega,x)+f^*(g\omega,\mathbf F_{g,\omega} x)-f^*(\omega,x))},\end{equation*} then we derive the first part of the statement. The rest is immediately obtained if we replace ![]() $f^*$ with f.
$f^*$ with f.
3.2. Random measure-theoretical metric mean dimension
In this subsection, we present the notion and characteristics of random upper measure-theoretical mean dimension.
Define a set
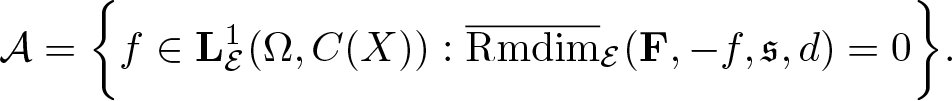 \begin{equation*}\mathcal A=\bigg\{f\in\mathbf L^1_\mathcal E(\Omega,C(X)):\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-f,\mathfrak s,d)=0\bigg\}.\end{equation*}
\begin{equation*}\mathcal A=\bigg\{f\in\mathbf L^1_\mathcal E(\Omega,C(X)):\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-f,\mathfrak s,d)=0\bigg\}.\end{equation*} Note that ![]() $\mathcal A=\emptyset$ if and only if
$\mathcal A=\emptyset$ if and only if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$. Indeed, if
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$. Indeed, if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$, then by fact 3.11, we have
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$, then by fact 3.11, we have ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-f\in\mathcal A$ for every
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-f\in\mathcal A$ for every ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$; conversely, according to fact 3.13,
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$; conversely, according to fact 3.13, ![]() $\mathcal A=\emptyset$ if
$\mathcal A=\emptyset$ if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
In this paper, we use the conventions: any infimum taking over the empty set equals ![]() $\infty$, and
$\infty$, and ![]() $\inf\infty:=\infty$.
$\inf\infty:=\infty$.
Definition 3.16. For each ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, the quantity
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, the quantity
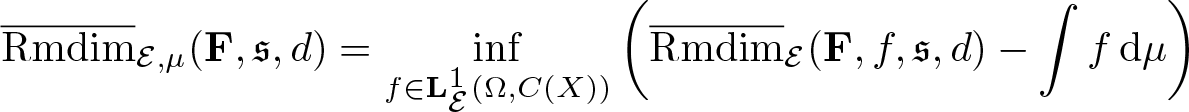 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu\bigg)\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu\bigg)\end{equation*}is called the random upper measure-theoretical metric mean dimension of µ.
It is obvious that ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\infty$ if and only if
$\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\infty$ if and only if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$.
Proposition 3.17. Let ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, then
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, then
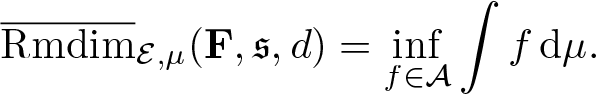 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A}\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A}\int f\,\mathrm{d}\mu.\end{equation*}Proof. Suppose ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$. Let
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$. Let ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and ![]() $\varphi=\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-f$, then by fact 3.11 we have
$\varphi=\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-f$, then by fact 3.11 we have ![]() $\varphi\in\mathcal A$. Thus,
$\varphi\in\mathcal A$. Thus,
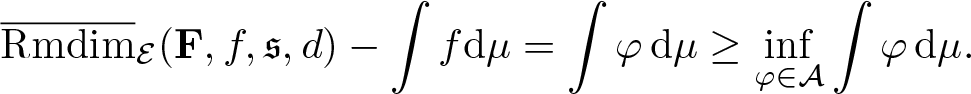 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\mathrm{d}\mu=\int\varphi\,\mathrm{d}\mu\geq\inf_{\varphi\in\mathcal A}\int \varphi\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\mathrm{d}\mu=\int\varphi\,\mathrm{d}\mu\geq\inf_{\varphi\in\mathcal A}\int \varphi\,\mathrm{d}\mu.\end{equation*} Letting f range over ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$ yields
$\mathbf L^1_\mathcal E(\Omega,C(X))$ yields
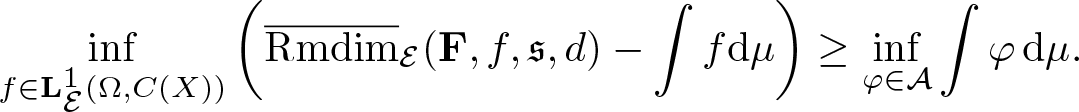 \begin{equation*}\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\mathrm{d}\mu\bigg)\geq\inf_{\varphi\in\mathcal A}\int \varphi\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\mathrm{d}\mu\bigg)\geq\inf_{\varphi\in\mathcal A}\int \varphi\,\mathrm{d}\mu.\end{equation*} To see the inequality in opposite direction, let ![]() $f\in\mathcal A$, then
$f\in\mathcal A$, then
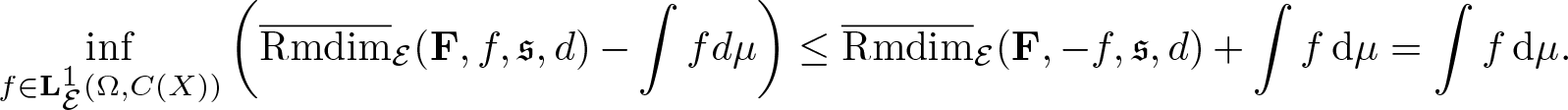 \begin{equation*}\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int fd\mu\bigg)\leq \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-f,\mathfrak s,d)+\int f\,\mathrm{d}\mu=\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int fd\mu\bigg)\leq \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-f,\mathfrak s,d)+\int f\,\mathrm{d}\mu=\int f\,\mathrm{d}\mu.\end{equation*}Therefore,
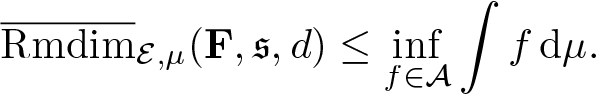 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq \inf_{f\in\mathcal A}\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq \inf_{f\in\mathcal A}\int f\,\mathrm{d}\mu.\end{equation*} When ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$, we have
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$, we have ![]() $\mathcal A=\emptyset$, so by the convention
$\mathcal A=\emptyset$, so by the convention ![]() $\inf_{f\in\emptyset}\int f\,\mathrm{d}\mu=\infty$, the statement holds.
$\inf_{f\in\emptyset}\int f\,\mathrm{d}\mu=\infty$, the statement holds.
For each ![]() $\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$, define
$\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$, define
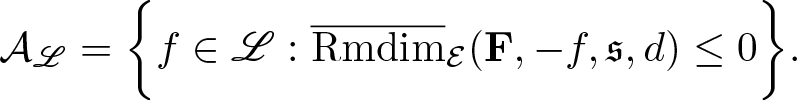 \begin{equation*}\mathcal A_\mathscr L=\bigg\{f\in\mathscr L:\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)\leq0\bigg\}.\end{equation*}
\begin{equation*}\mathcal A_\mathscr L=\bigg\{f\in\mathscr L:\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)\leq0\bigg\}.\end{equation*}Proposition 3.18. For any dense subset ![]() $\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ and
$\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ and ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, we have
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, we have
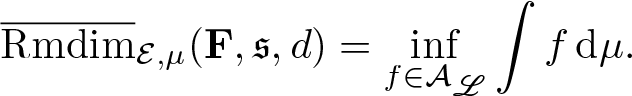 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu.\end{equation*}Proof. Fix ![]() $\mathscr L$ dense in
$\mathscr L$ dense in ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$ and
$\mathbf L^1_\mathcal E(\Omega,C(X))$ and ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. Set
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. Set
then by Proposition 3.17, we have the inequalities
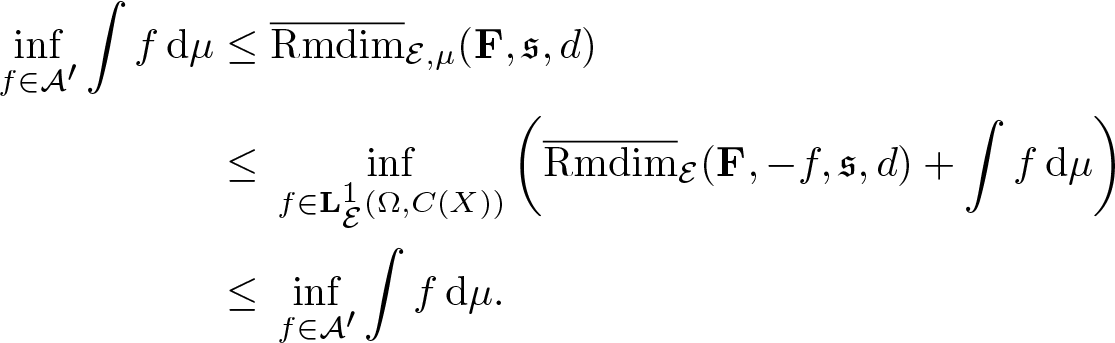 \begin{eqnarray*}
\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu&\leq&\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) \\
&\leq&\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)+\int f\,\mathrm{d}\mu\bigg)\\
&\leq&\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.
\end{eqnarray*}
\begin{eqnarray*}
\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu&\leq&\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) \\
&\leq&\inf_{f\in\mathbf L^1_\mathcal E(\Omega,C(X))}\bigg(\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)+\int f\,\mathrm{d}\mu\bigg)\\
&\leq&\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.
\end{eqnarray*} This shows  $\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu$, and what remains is to prove
$\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) =\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu$, and what remains is to prove
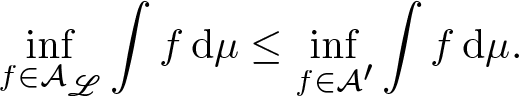 \begin{equation*}\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu\leq\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu\leq\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.\end{equation*} To this end, fix ![]() $f\in\mathcal A'$ and by fact 3.11 we can find an ɛ > 0 such that
$f\in\mathcal A'$ and by fact 3.11 we can find an ɛ > 0 such that
As for any ![]() $f_1,f_2\in\mathbf L^1_\mathcal E(\Omega,C(X))$, we have
$f_1,f_2\in\mathbf L^1_\mathcal E(\Omega,C(X))$, we have
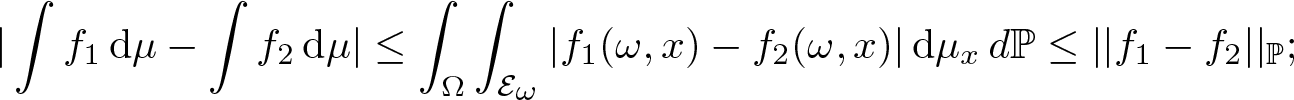 \begin{eqnarray*}
|\int f_1\,\mathrm{d}\mu-\int f_2\,\mathrm{d}\mu|\leq\int_\Omega\int_{\mathcal E_\omega}|f_1(\omega,x)-f_2(\omega,x)|\,\mathrm{d}\mu_x\, d{\mathbb P}\leq||f_1-f_2||_{\mathbb P};
\end{eqnarray*}
\begin{eqnarray*}
|\int f_1\,\mathrm{d}\mu-\int f_2\,\mathrm{d}\mu|\leq\int_\Omega\int_{\mathcal E_\omega}|f_1(\omega,x)-f_2(\omega,x)|\,\mathrm{d}\mu_x\, d{\mathbb P}\leq||f_1-f_2||_{\mathbb P};
\end{eqnarray*} hence, the map ![]() $f\mapsto\int f\,\mathrm{d}\mu$ is continuous on
$f\mapsto\int f\,\mathrm{d}\mu$ is continuous on ![]() $(\mathbf {L^1}_{\mathcal E}(\Omega,C(X)),||\cdot||_{\mathbb P})$. Pick a sequence
$(\mathbf {L^1}_{\mathcal E}(\Omega,C(X)),||\cdot||_{\mathbb P})$. Pick a sequence ![]() $(f_n)_{n\in\mathbb N}\subset\mathscr L$ such that
$(f_n)_{n\in\mathbb N}\subset\mathscr L$ such that ![]() $||f_n-(f+\varepsilon)||_{\mathbb P}\to0$ as
$||f_n-(f+\varepsilon)||_{\mathbb P}\to0$ as ![]() $n\to\infty$, then
$n\to\infty$, then
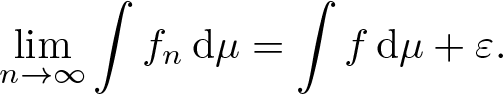 \begin{equation*}\lim_{n\to\infty}\int f_n\,\mathrm{d}\mu= \int f\,\mathrm{d}\mu+\varepsilon.\end{equation*}
\begin{equation*}\lim_{n\to\infty}\int f_n\,\mathrm{d}\mu= \int f\,\mathrm{d}\mu+\varepsilon.\end{equation*}Therefore, by fact 3.14,
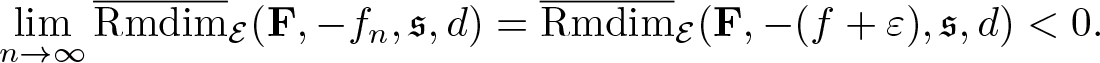 \begin{equation*}\lim_{n\to\infty}\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f_n,\mathfrak s,d)=\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-(f+\varepsilon),\mathfrak s,d) \lt 0.\end{equation*}
\begin{equation*}\lim_{n\to\infty}\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f_n,\mathfrak s,d)=\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-(f+\varepsilon),\mathfrak s,d) \lt 0.\end{equation*} Then, there is ![]() $N\in\mathbb N$ such that
$N\in\mathbb N$ such that ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f_N,\mathfrak s,d) \lt 0$ and
$\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f_N,\mathfrak s,d) \lt 0$ and
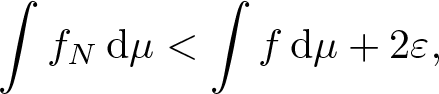 \begin{equation*}\int f_N\,\mathrm{d}\mu \lt \int f\,\mathrm{d}\mu+2\varepsilon,\end{equation*}
\begin{equation*}\int f_N\,\mathrm{d}\mu \lt \int f\,\mathrm{d}\mu+2\varepsilon,\end{equation*} which implies ![]() $f_N\in\mathcal A_\mathscr L$. Thus, letting ɛ → 0 we end at
$f_N\in\mathcal A_\mathscr L$. Thus, letting ɛ → 0 we end at
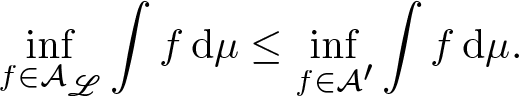 \begin{equation*}\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu\leq\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\inf_{f\in\mathcal A_\mathscr L}\int f\,\mathrm{d}\mu\leq\inf_{f\in\mathcal A'}\int f\,\mathrm{d}\mu.\end{equation*}Proposition 3.19. If ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$, then the function
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$, then the function ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d):\mathcal M_{\mathbb P}(\mathcal E)\to\mathbb R$ is
$\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d):\mathcal M_{\mathbb P}(\mathcal E)\to\mathbb R$ is
(1) concave;
(2) upper semi-continuous.
Proof. The concavity of ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)$ directly follows by the definition. Note that
$\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)$ directly follows by the definition. Note that ![]() $\mathcal M_{\mathbb P}(\mathcal E)$ is endowed with the weak
$\mathcal M_{\mathbb P}(\mathcal E)$ is endowed with the weak![]() $^*$-topology, then for every fixed
$^*$-topology, then for every fixed ![]() $f\in\mathcal A$ the function
$f\in\mathcal A$ the function ![]() $F_f(\mu)=\int f\,\mathrm{d}\mu$ is continuous on
$F_f(\mu)=\int f\,\mathrm{d}\mu$ is continuous on ![]() $\mathcal M_{\mathbb P}(\mathcal E)$. Hence
$\mathcal M_{\mathbb P}(\mathcal E)$. Hence ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)$ is upper semi-continuous since the infimum of a family of continuous functions is upper semi-continuous.
$\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)$ is upper semi-continuous since the infimum of a family of continuous functions is upper semi-continuous.
4. Variational principle
In this section, we present a variation principle between the random upper metric mean dimension and the measure-theoretic one as the first main result of this paper. To this end, we need the following notions and lemmas:
Suppose Y is a set and ![]() $\mathcal L$ is a family of real-valued functions on Y. We say that
$\mathcal L$ is a family of real-valued functions on Y. We say that ![]() $\mathcal L$ is a vector lattice if it is a linear space and
$\mathcal L$ is a vector lattice if it is a linear space and ![]() $f\vee g:=\max\{f,g\}\in\mathcal L$ for every
$f\vee g:=\max\{f,g\}\in\mathcal L$ for every ![]() $f,g\in\mathcal L$. If, in addition,
$f,g\in\mathcal L$. If, in addition, ![]() $f\wedge 1:=\min\{f,1\}\in\mathcal L$ for every
$f\wedge 1:=\min\{f,1\}\in\mathcal L$ for every ![]() $f\in\mathcal L$, then we call
$f\in\mathcal L$, then we call ![]() $\mathcal L$ a Stone vector space.
$\mathcal L$ a Stone vector space.
Let ![]() $\mathcal L$ be a vector lattice on Y. A function
$\mathcal L$ be a vector lattice on Y. A function ![]() $L:\mathcal L\to\mathbb R$ is called a pre-integral if L is linear, non-negative, and
$L:\mathcal L\to\mathbb R$ is called a pre-integral if L is linear, non-negative, and ![]() $L(f_n)$ decreases to 0 for every
$L(f_n)$ decreases to 0 for every ![]() $f_n\in\mathcal L$ with
$f_n\in\mathcal L$ with ![]() $f_n(x)$ decreasing to 0 for every
$f_n(x)$ decreasing to 0 for every ![]() $x\in Y$.
$x\in Y$.
Lemma 4.1. ([Reference Dudley18], Theorem 4.5.2)
Let Y be a set and L be a pre-integral on a Stone vector lattice ![]() $\mathcal L$. Then, there exists a measure µ on
$\mathcal L$. Then, there exists a measure µ on ![]() $(Y, \sigma(\mathcal L))$ such that for all
$(Y, \sigma(\mathcal L))$ such that for all ![]() $f \in\mathcal L$
$f \in\mathcal L$
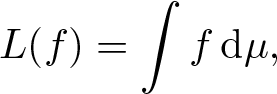 \begin{equation*}L(f)=\int f\,\mathrm{d}\mu,\end{equation*}
\begin{equation*}L(f)=\int f\,\mathrm{d}\mu,\end{equation*} where ![]() $\sigma(\mathcal L)$ is the smallest σ-algebra on Y such that all functions in
$\sigma(\mathcal L)$ is the smallest σ-algebra on Y such that all functions in ![]() $\mathcal L$ are measurable.
$\mathcal L$ are measurable.
Lemma 4.2. Let ![]() $(\nu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$, then the limit points in the weak
$(\nu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$, then the limit points in the weak![]() $^*$-topology of the sequence
$^*$-topology of the sequence
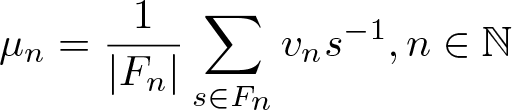 \begin{equation*}\mu_n=\frac{1}{|F_n|}\sum_{s\in F_n}v_ns^{-1}, n\in\mathbb N\end{equation*}
\begin{equation*}\mu_n=\frac{1}{|F_n|}\sum_{s\in F_n}v_ns^{-1}, n\in\mathbb N\end{equation*} is not empty and is contained in ![]() $\mathcal M_{\mathbb P}^G(\mathcal E)$.
$\mathcal M_{\mathbb P}^G(\mathcal E)$.
Proof. Note that ![]() $(\mu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$, then by the compactness of
$(\mu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E)$, then by the compactness of ![]() $\mathcal M_{\mathbb P}(\mathcal E)$ in the weak
$\mathcal M_{\mathbb P}(\mathcal E)$ in the weak![]() $^*$-topology there are
$^*$-topology there are ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ and a sequence
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ and a sequence ![]() $(n_j)_{j\geq1}$ such that,
$(n_j)_{j\geq1}$ such that,
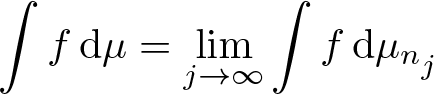 \begin{equation*}\int f\,\mathrm{d}\mu=\lim_{j\to\infty}\int f\,\mathrm{d}\mu_{n_j}\end{equation*}
\begin{equation*}\int f\,\mathrm{d}\mu=\lim_{j\to\infty}\int f\,\mathrm{d}\mu_{n_j}\end{equation*} for every ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Let ɛ > 0 and
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Let ɛ > 0 and ![]() $g\in G$, then there is
$g\in G$, then there is ![]() $k\in\mathbb N$ such that
$k\in\mathbb N$ such that
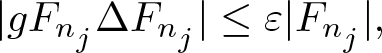 \begin{equation*}|gF_{n_j}\Delta F_{n_j}|\leq\varepsilon|F_{n_j}|,\end{equation*}
\begin{equation*}|gF_{n_j}\Delta F_{n_j}|\leq\varepsilon|F_{n_j}|,\end{equation*} for every ![]() $j\geq k$. Therefore, for any
$j\geq k$. Therefore, for any ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ and ![]() $(n_{j_l})_{l\in\mathbb N}$ such that
$(n_{j_l})_{l\in\mathbb N}$ such that ![]() $j_1\geq k$ we have
$j_1\geq k$ we have
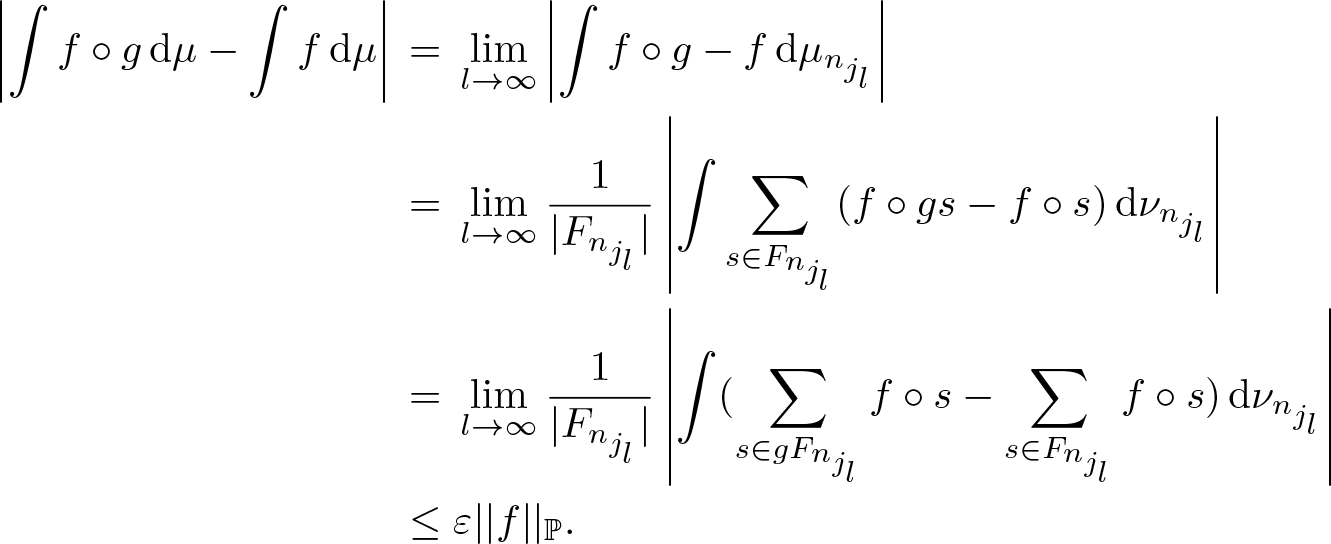 \begin{eqnarray*}
\left|\int f\circ g\,\mathrm{d}\mu-\int f\,\mathrm{d}\mu\right|
&=&\lim_{l\to\infty}\left|\int f\circ g - f\,\mathrm{d}\mu_{n_{j_l}}\right|\\
&=&\lim_{l\to\infty}\frac{1}{|F_{n_{j_l}}|}\left|\int\sum_{s\in F_{n_{j_l}}}(f\circ gs-f\circ s)\,\mathrm{d}\nu_{n_{j_l}}\right|\\
&=&\lim_{l\to\infty}\frac{1}{|F_{n_{j_l}}|}\left|\int(\sum_{s\in gF_{n_{j_l}}}f\circ s-\sum_{s\in F_{n_{j_l}}}f\circ s)\,\mathrm{d}\nu_{n_{j_l}}\right|\\
&\leq&\varepsilon||f||_{\mathbb P}.
\end{eqnarray*}
\begin{eqnarray*}
\left|\int f\circ g\,\mathrm{d}\mu-\int f\,\mathrm{d}\mu\right|
&=&\lim_{l\to\infty}\left|\int f\circ g - f\,\mathrm{d}\mu_{n_{j_l}}\right|\\
&=&\lim_{l\to\infty}\frac{1}{|F_{n_{j_l}}|}\left|\int\sum_{s\in F_{n_{j_l}}}(f\circ gs-f\circ s)\,\mathrm{d}\nu_{n_{j_l}}\right|\\
&=&\lim_{l\to\infty}\frac{1}{|F_{n_{j_l}}|}\left|\int(\sum_{s\in gF_{n_{j_l}}}f\circ s-\sum_{s\in F_{n_{j_l}}}f\circ s)\,\mathrm{d}\nu_{n_{j_l}}\right|\\
&\leq&\varepsilon||f||_{\mathbb P}.
\end{eqnarray*} As ɛ and g are arbitrarily chosen, we obtain ![]() $\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$, which shows the statement.
$\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$, which shows the statement.
Theorem 4.3. (Variational principle)
Suppose Ω admits a compact metric, ![]() $\mathscr F$ is the corresponding Borel σ-algebra, and G acts ergodicly on
$\mathscr F$ is the corresponding Borel σ-algebra, and G acts ergodicly on ![]() $(\Omega,\mathscr F,\mathbb P)$. Let
$(\Omega,\mathscr F,\mathbb P)$. Let ![]() $\mathcal E=\Omega\times X$, if
$\mathcal E=\Omega\times X$, if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
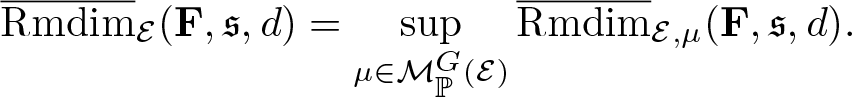 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) .\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) .\end{equation*}Proof. We firstly show
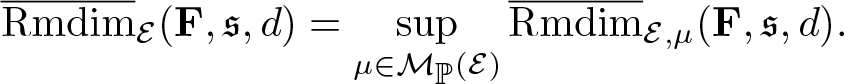 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) .\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) .\end{equation*} As the constant function ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ is an element of
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ is an element of ![]() $\mathcal A$, by Proposition 3.17,
$\mathcal A$, by Proposition 3.17, ![]() $\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) \leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ for every
$\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d) \leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)$ for every ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, which implies
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, which implies
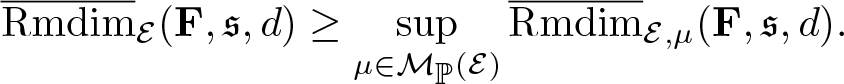 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\geq\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d).\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\geq\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d).\end{equation*}To see the opposite direction of the above inequality, let
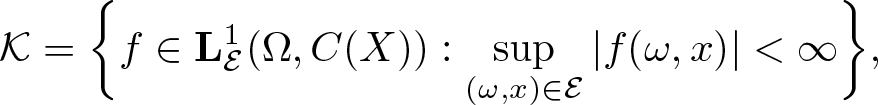 \begin{equation*}\mathcal K=\bigg\{f\in\mathbf L^1_\mathcal E(\Omega,C(X)):\sup_{(\omega,x)\in\mathcal E}|f(\omega,x)| \lt \infty\bigg\},\end{equation*}
\begin{equation*}\mathcal K=\bigg\{f\in\mathbf L^1_\mathcal E(\Omega,C(X)):\sup_{(\omega,x)\in\mathcal E}|f(\omega,x)| \lt \infty\bigg\},\end{equation*} then ![]() $\mathcal K$ is a normed subspace of
$\mathcal K$ is a normed subspace of ![]() $(\mathbf L^1_{\mathcal E}(\Omega,C(X)),||\cdot||_{\mathbb P})$. By the proof of [Reference Kifer25, Lemma 2.1 (i)], we know that
$(\mathbf L^1_{\mathcal E}(\Omega,C(X)),||\cdot||_{\mathbb P})$. By the proof of [Reference Kifer25, Lemma 2.1 (i)], we know that ![]() $C(\mathcal E)$ the set of all continuous functions on
$C(\mathcal E)$ the set of all continuous functions on ![]() $\mathcal E$ is dense in
$\mathcal E$ is dense in ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$. Then, the compactness of
$\mathbf L^1_\mathcal E(\Omega,C(X))$. Then, the compactness of ![]() $\mathcal E$ implies
$\mathcal E$ implies ![]() $\mathcal K$ is dense in
$\mathcal K$ is dense in ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$. Thus, by Proposition 3.18,
$\mathbf L^1_\mathcal E(\Omega,C(X))$. Thus, by Proposition 3.18,
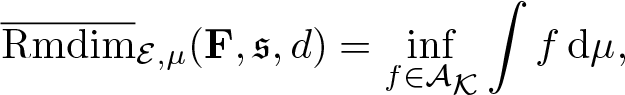 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)=\inf_{f\in\mathcal A_\mathcal K}\int f\,\mathrm{d}\mu,\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)=\inf_{f\in\mathcal A_\mathcal K}\int f\,\mathrm{d}\mu,\end{equation*} for every ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. By fact 3.14,
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. By fact 3.14, ![]() $\mathcal {A_K}$ is a closed convex subset of
$\mathcal {A_K}$ is a closed convex subset of ![]() $\mathcal K$. For simplicity, we write
$\mathcal K$. For simplicity, we write ![]() $\alpha:=\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d),\mathfrak s,d)$. Note that α = 0, so
$\alpha:=\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d),\mathfrak s,d)$. Note that α = 0, so ![]() $-(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\varepsilon)\not\in\mathcal{A_K}$, which means
$-(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+\varepsilon)\not\in\mathcal{A_K}$, which means ![]() $-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\not\in\mathcal{A_K}+\varepsilon$. Let
$-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\not\in\mathcal{A_K}+\varepsilon$. Let ![]() $K_1=\{\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\}$ and
$K_1=\{\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\}$ and ![]() $K_2=\mathcal{A_K}+\varepsilon$ be two disjoint closed subsets of
$K_2=\mathcal{A_K}+\varepsilon$ be two disjoint closed subsets of ![]() $\mathcal K$, then by Hahn–Banach separation theorem, there is a continuous linear functional
$\mathcal K$, then by Hahn–Banach separation theorem, there is a continuous linear functional ![]() $L:\mathcal K\to\mathbb R$ such that
$L:\mathcal K\to\mathbb R$ such that
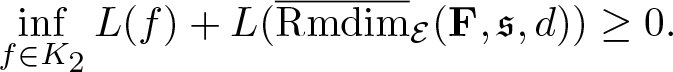 \begin{equation}
\inf_{f\in K_2}L(f)+L(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))\geq0.
\end{equation}
\begin{equation}
\inf_{f\in K_2}L(f)+L(\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))\geq0.
\end{equation} Fix ![]() $f_0\in\mathcal K$ with
$f_0\in\mathcal K$ with ![]() $f_0\geq0$. Then, by fact 3.11 and fact 3.5, for any c > 0,
$f_0\geq0$. Then, by fact 3.11 and fact 3.5, for any c > 0,
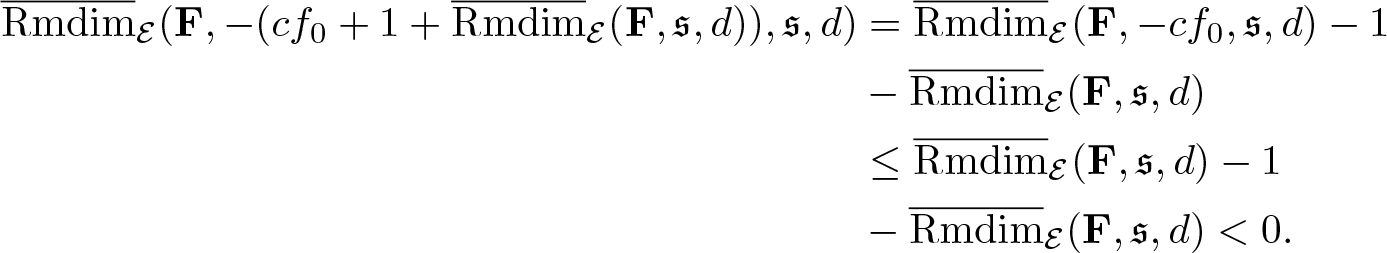 \begin{align*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-(cf_0+1+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)),\mathfrak s,d)
& =\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-cf_0,\mathfrak s,d)-1\\
& -\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\\
& \leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-1\\
& -\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt 0.
\end{align*}
\begin{align*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-(cf_0+1+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)),\mathfrak s,d)
& =\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,-cf_0,\mathfrak s,d)-1\\
& -\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\\
& \leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-1\\
& -\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt 0.
\end{align*} This means ![]() $cf_0+1+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\in\mathcal{A_K}$ and then
$cf_0+1+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\in\mathcal{A_K}$ and then
Hence, ![]() $L(f_0)\geq0$, otherwise letting
$L(f_0)\geq0$, otherwise letting ![]() $c\to\infty$ deduces
$c\to\infty$ deduces ![]() $L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))=-\infty$, which is conflict to (4.1). As f 0 is arbitrary, we have L is non-negative. Let
$L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))=-\infty$, which is conflict to (4.1). As f 0 is arbitrary, we have L is non-negative. Let ![]() $\{f_n\}\subset\mathcal K$ be a sequence pointwisely decreasing to 0, then
$\{f_n\}\subset\mathcal K$ be a sequence pointwisely decreasing to 0, then ![]() $\{f_n(\omega,\cdot)\}_{n\in\mathbb N}\subset C(\mathcal E_\omega)$ and
$\{f_n(\omega,\cdot)\}_{n\in\mathbb N}\subset C(\mathcal E_\omega)$ and ![]() $f_n(\omega,x)$ decreases to 0 as
$f_n(\omega,x)$ decreases to 0 as ![]() $n\to\infty$ for every
$n\to\infty$ for every ![]() $\omega\in\Omega$ and
$\omega\in\Omega$ and ![]() $x\in X$. Hence, for every
$x\in X$. Hence, for every ![]() $\omega\in\Omega$, by Dini’s theorem, the function
$\omega\in\Omega$, by Dini’s theorem, the function ![]() $f_n(\omega):=f_n(\omega,\cdot)$ uniformly convergences to 0 as
$f_n(\omega):=f_n(\omega,\cdot)$ uniformly convergences to 0 as ![]() $n\to\infty$; that is, for any ɛ > 0 and
$n\to\infty$; that is, for any ɛ > 0 and ![]() $\omega\in\Omega$, there is
$\omega\in\Omega$, there is ![]() $N(\omega,\varepsilon)$ such that
$N(\omega,\varepsilon)$ such that ![]() $||f_n(\omega)||_\infty \lt \varepsilon$ for every
$||f_n(\omega)||_\infty \lt \varepsilon$ for every ![]() $n\geq N(\omega,\varepsilon)$. This means
$n\geq N(\omega,\varepsilon)$. This means ![]() $||f_n(\omega)||_\infty$ decreases to 0 as
$||f_n(\omega)||_\infty$ decreases to 0 as ![]() $n\to\infty$ for every
$n\to\infty$ for every ![]() $\omega\in\Omega$. By monotone convergence theorem,
$\omega\in\Omega$. By monotone convergence theorem,
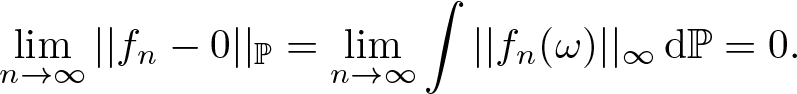 \begin{equation*}\lim_{n\to\infty}||f_n-0||_{\mathbb P}=\lim_{n\to\infty}\int||f_n(\omega)||_\infty \,{\mathrm d}\mathbb P=0.\end{equation*}
\begin{equation*}\lim_{n\to\infty}||f_n-0||_{\mathbb P}=\lim_{n\to\infty}\int||f_n(\omega)||_\infty \,{\mathrm d}\mathbb P=0.\end{equation*} This means that ![]() $L(f_n)$ decreases to 0 as
$L(f_n)$ decreases to 0 as ![]() $n\to\infty$, because L is non-negative, continuous and
$n\to\infty$, because L is non-negative, continuous and ![]() $L(0) = 0$. As L is not constantly zero and non-negative, we can find an
$L(0) = 0$. As L is not constantly zero and non-negative, we can find an ![]() $\varphi\in\mathcal K$ such that
$\varphi\in\mathcal K$ such that ![]() $\varphi\geq 0$ with
$\varphi\geq 0$ with ![]() $L(\varphi) \gt 0$. We set
$L(\varphi) \gt 0$. We set ![]() $0\leq h:= \frac{\varphi}{M} \leq1$, where
$0\leq h:= \frac{\varphi}{M} \leq1$, where ![]() $M:=\sup_{(\omega,x)\in\mathcal E}\varphi(\omega,x)$. Then,
$M:=\sup_{(\omega,x)\in\mathcal E}\varphi(\omega,x)$. Then, ![]() $0\leq1-h\leq1$ and hence,
$0\leq1-h\leq1$ and hence,  $L(1) = L(h)+L(1-h) = \frac{1}{M} L(\varphi)+L(1 - h) \gt 0$. This shows that
$L(1) = L(h)+L(1-h) = \frac{1}{M} L(\varphi)+L(1 - h) \gt 0$. This shows that  $\frac{L(\cdot)}{L(1)}$ is a pre-integral on
$\frac{L(\cdot)}{L(1)}$ is a pre-integral on ![]() $\mathcal K$. Note that
$\mathcal K$. Note that ![]() $\mathcal K$ is a Stone vector lattice, then by Lemma 4.1, there is a measure µ on
$\mathcal K$ is a Stone vector lattice, then by Lemma 4.1, there is a measure µ on ![]() $(\mathcal E,\sigma(\mathcal K))$ such that
$(\mathcal E,\sigma(\mathcal K))$ such that
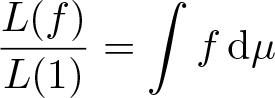 \begin{equation}
\frac{L(f)}{L(1)}=\int f\,\mathrm{d}\mu
\end{equation}
\begin{equation}
\frac{L(f)}{L(1)}=\int f\,\mathrm{d}\mu
\end{equation} for every ![]() $f \in\mathcal K$. Note that
$f \in\mathcal K$. Note that ![]() $\sigma(\mathcal K)$ is a sub-σ-algebra of
$\sigma(\mathcal K)$ is a sub-σ-algebra of ![]() $\mathscr F\times\mathscr B$. Let
$\mathscr F\times\mathscr B$. Let ![]() $A \in \mathscr F$ and B be a closed subset of X. For each
$A \in \mathscr F$ and B be a closed subset of X. For each ![]() $n\in\mathbb N$, let
$n\in\mathbb N$, let ![]() $\varphi_n(\omega,x) := 1_A(\omega) \cdot b_n(x) \in\mathcal K$, where
$\varphi_n(\omega,x) := 1_A(\omega) \cdot b_n(x) \in\mathcal K$, where ![]() $b_n(x) = 1 -\min\{nd(x, B), 1\}$. As
$b_n(x) = 1 -\min\{nd(x, B), 1\}$. As
 \begin{equation*}\limsup_{n\to\infty} \varphi_n(\omega, x) = 1_A(\omega)1_B(x),\end{equation*}
\begin{equation*}\limsup_{n\to\infty} \varphi_n(\omega, x) = 1_A(\omega)1_B(x),\end{equation*} for every ![]() $(\omega, x)\in\mathcal E$, we have
$(\omega, x)\in\mathcal E$, we have ![]() $A \times B \in \sigma(\mathcal K)$ for every
$A \times B \in \sigma(\mathcal K)$ for every ![]() $A \in \mathscr F$ and closed
$A \in \mathscr F$ and closed ![]() $B\subset X$. This means that
$B\subset X$. This means that ![]() $\sigma(\mathcal K)=\mathscr F\times\mathscr B$ and then µ is a probability measure on
$\sigma(\mathcal K)=\mathscr F\times\mathscr B$ and then µ is a probability measure on ![]() $\mathcal E$. For each
$\mathcal E$. For each ![]() $f \in\mathcal K$,
$f \in\mathcal K$, ![]() $n\in\mathbb N$ and
$n\in\mathbb N$ and ![]() $g\in F_n$, we have
$g\in F_n$, we have ![]() $f \circ g \in\mathcal K$, and then by (4.2),
$f \circ g \in\mathcal K$, and then by (4.2),
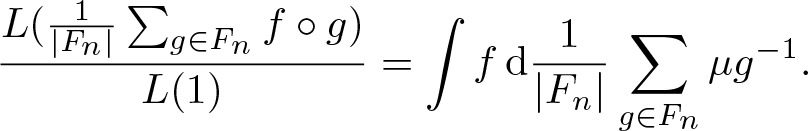 \begin{equation}
\frac{L(\frac{1}{|F_n|}\sum_{g\in F_n}f\circ g)}{L(1)}=\int f\,\mathrm{d}\frac{1}{|F_n|}\sum_{g\in F_n}\mu g^{-1}.
\end{equation}
\begin{equation}
\frac{L(\frac{1}{|F_n|}\sum_{g\in F_n}f\circ g)}{L(1)}=\int f\,\mathrm{d}\frac{1}{|F_n|}\sum_{g\in F_n}\mu g^{-1}.
\end{equation} As ![]() $\mathcal E$ is compact, by [Reference Walters50, Theorem 6.5], the set of all probability measures on
$\mathcal E$ is compact, by [Reference Walters50, Theorem 6.5], the set of all probability measures on ![]() $\mathcal E$ denoted by
$\mathcal E$ denoted by ![]() $\mathcal M(\mathcal E)$ is compact in the weak
$\mathcal M(\mathcal E)$ is compact in the weak![]() $^*$-topology which is the topology such that the map
$^*$-topology which is the topology such that the map ![]() $\mu\mapsto\int f\,\mathrm{d}\mu$ is continuous on
$\mu\mapsto\int f\,\mathrm{d}\mu$ is continuous on ![]() $\mathcal M(\mathcal E)$ for every
$\mathcal M(\mathcal E)$ for every ![]() $f\in C(\mathcal E)$. Without loss of generality, we may assume that
$f\in C(\mathcal E)$. Without loss of generality, we may assume that
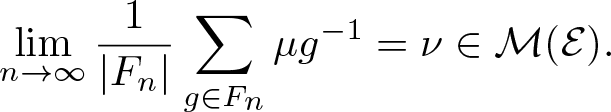 \begin{equation*}\lim_{n\to\infty}\frac{1}{|F_n|}\sum_{g\in F_n}\mu g^{-1}=\nu\in\mathcal M(\mathcal E).\end{equation*}
\begin{equation*}\lim_{n\to\infty}\frac{1}{|F_n|}\sum_{g\in F_n}\mu g^{-1}=\nu\in\mathcal M(\mathcal E).\end{equation*} Hence, by (4.3), for each compact subset ![]() $A\subset\Omega$, we have
$A\subset\Omega$, we have
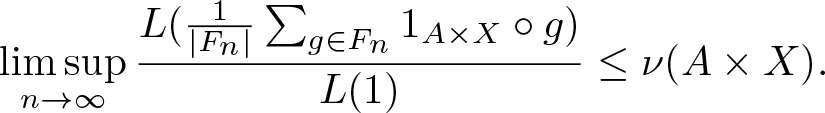 \begin{equation*}\limsup_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in F_n}1_{A\times X}\circ g)}{L(1)}\leq\nu(A\times X).\end{equation*}
\begin{equation*}\limsup_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in F_n}1_{A\times X}\circ g)}{L(1)}\leq\nu(A\times X).\end{equation*} For each ![]() $\mathbb P$-integrable function
$\mathbb P$-integrable function ![]() $h:\Omega\to\mathbb R$, we can regard h as a function
$h:\Omega\to\mathbb R$, we can regard h as a function ![]() $h^*(\cdot,\cdot) \in\mathbf L^1_\mathcal E(\Omega,C(X))$ by setting
$h^*(\cdot,\cdot) \in\mathbf L^1_\mathcal E(\Omega,C(X))$ by setting ![]() $h^*(\omega,x)=h(\omega)$ for every
$h^*(\omega,x)=h(\omega)$ for every ![]() $(\omega,x)\in\mathcal E$. Note that
$(\omega,x)\in\mathcal E$. Note that ![]() $1_K^*=1_{K\times X}$. As
$1_K^*=1_{K\times X}$. As ![]() $\mathbb P$ is G-ergodic, by mean ergodic theorem [Reference Kerr and Li22, Theorem 4.23],
$\mathbb P$ is G-ergodic, by mean ergodic theorem [Reference Kerr and Li22, Theorem 4.23],
 \begin{eqnarray*}
\lim_{n\to\infty}||(\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g)^*-\mathbb P(K)||_{\mathbb P}&=&\lim_{n\to\infty}\int|\frac{1}{|F_n|}\sum_{g\in Fn}1_K(g\omega)-\mathbb P(K)|\,\mathrm d{\mathbb P}\\
&=&\lim_{n\to\infty}||\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g-\mathbb P(K)||_{L^1}=0,
\end{eqnarray*}
\begin{eqnarray*}
\lim_{n\to\infty}||(\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g)^*-\mathbb P(K)||_{\mathbb P}&=&\lim_{n\to\infty}\int|\frac{1}{|F_n|}\sum_{g\in Fn}1_K(g\omega)-\mathbb P(K)|\,\mathrm d{\mathbb P}\\
&=&\lim_{n\to\infty}||\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g-\mathbb P(K)||_{L^1}=0,
\end{eqnarray*} where ![]() $||\cdot||_{L1}$ is the L 1-norm on the integrable function space
$||\cdot||_{L1}$ is the L 1-norm on the integrable function space ![]() $L^1(\Omega,\mathscr F,\mathbb P)$. As L is continuous, we obtain
$L^1(\Omega,\mathscr F,\mathbb P)$. As L is continuous, we obtain
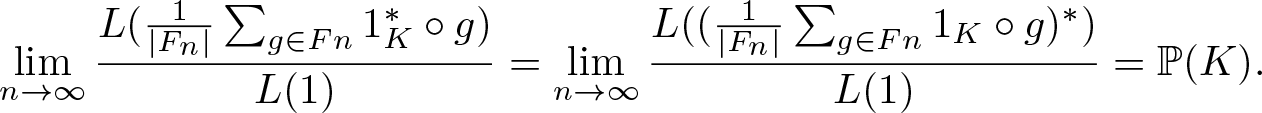 \begin{equation*}\lim_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in Fn}1_K^*\circ g)}{L(1)}=\lim_{n\to\infty}\frac{L((\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g)^*)}{L(1)}=\mathbb P(K).\end{equation*}
\begin{equation*}\lim_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in Fn}1_K^*\circ g)}{L(1)}=\lim_{n\to\infty}\frac{L((\frac{1}{|F_n|}\sum_{g\in Fn}1_K\circ g)^*)}{L(1)}=\mathbb P(K).\end{equation*} This means that ![]() $\mathbb P(K)\leq\nu(K\times X)$ for all compact subsets
$\mathbb P(K)\leq\nu(K\times X)$ for all compact subsets ![]() $K\subset\Omega$. Analogously, we can derive
$K\subset\Omega$. Analogously, we can derive ![]() $\mathbb P(O)\geq\nu(O\times X)$ for every open subset
$\mathbb P(O)\geq\nu(O\times X)$ for every open subset ![]() $O\subset\Omega$ with the similar argument. As the measures
$O\subset\Omega$ with the similar argument. As the measures ![]() $\mathbb P$ and ν are regular, we have
$\mathbb P$ and ν are regular, we have ![]() $\mathbb P(A)=\nu(A\times X)$ for every
$\mathbb P(A)=\nu(A\times X)$ for every ![]() $A\in\mathscr F$. Thus,
$A\in\mathscr F$. Thus,
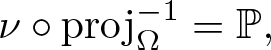 \begin{equation*}\nu\circ\mathrm{proj}_\Omega^{-1}=\mathbb P,\end{equation*}
\begin{equation*}\nu\circ\mathrm{proj}_\Omega^{-1}=\mathbb P,\end{equation*} where ![]() $\mathrm{proj}_\Omega:\Omega\times X\to\Omega$ is the natural projection. By (4.3), for any
$\mathrm{proj}_\Omega:\Omega\times X\to\Omega$ is the natural projection. By (4.3), for any ![]() $f\in C(\mathcal E)$, we have
$f\in C(\mathcal E)$, we have
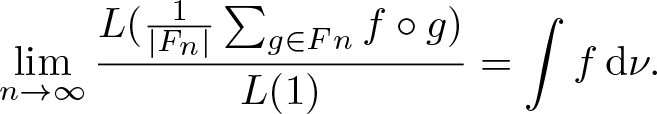 \begin{equation}
\lim_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in Fn}f\circ g)}{L(1)}=\int f\,\mathrm d\nu.
\end{equation}
\begin{equation}
\lim_{n\to\infty}\frac{L(\frac{1}{|F_n|}\sum_{g\in Fn}f\circ g)}{L(1)}=\int f\,\mathrm d\nu.
\end{equation}This shows
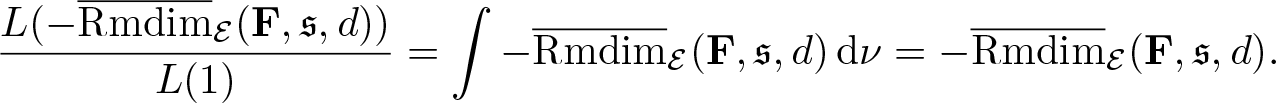 \begin{equation}
\frac{L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))}{L(1)}=\int-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\,\mathrm d\nu=-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d).
\end{equation}
\begin{equation}
\frac{L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))}{L(1)}=\int-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\,\mathrm d\nu=-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d).
\end{equation}By Proposition 3.18, there is the equality that
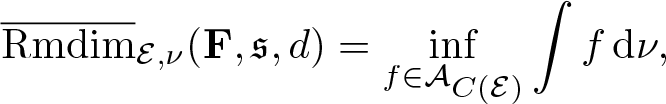 \begin{equation}
\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)=\inf_{f\in\mathcal A_{C(\mathcal E)}}\int f\,\mathrm d\nu,
\end{equation}
\begin{equation}
\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)=\inf_{f\in\mathcal A_{C(\mathcal E)}}\int f\,\mathrm d\nu,
\end{equation} where  $\mathcal A_{C(\mathcal E)}:=\{f\in C(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)\leq0\}$. By Fact 3.15, for each
$\mathcal A_{C(\mathcal E)}:=\{f\in C(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E}(\mathbf F,-f,\mathfrak s,d)\leq0\}$. By Fact 3.15, for each ![]() $f\in\mathcal A_{C(\mathcal E)}$ and
$f\in\mathcal A_{C(\mathcal E)}$ and ![]() $g\in G$, we have
$g\in G$, we have ![]() $f\circ g\in\mathcal{A_K}$, which yields by (4.4) and the linearity of L that
$f\circ g\in\mathcal{A_K}$, which yields by (4.4) and the linearity of L that
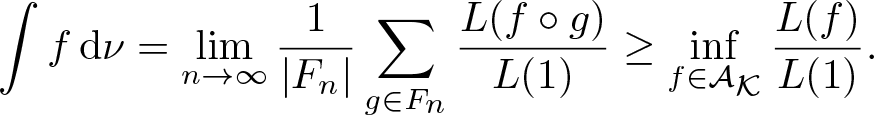 \begin{equation}
\int f\,\mathrm d\nu=\lim_{n\to\infty}\frac{1}{|F_n|}\sum_{g\in F_n}\frac{L(f\circ g)}{L(1)}\geq\inf_{f\in\mathcal{A_K}}\frac{L(f)}{L(1)}.
\end{equation}
\begin{equation}
\int f\,\mathrm d\nu=\lim_{n\to\infty}\frac{1}{|F_n|}\sum_{g\in F_n}\frac{L(f\circ g)}{L(1)}\geq\inf_{f\in\mathcal{A_K}}\frac{L(f)}{L(1)}.
\end{equation}Thus, by (4.1), (4.5), (4.6) and (4.7) and the linearity and non-negativity of L, we obtain
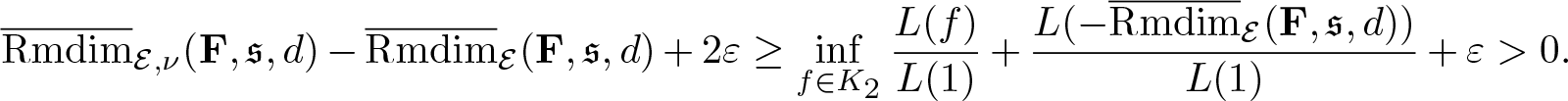 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+2\varepsilon
\geq\inf_{f\in K_2}\frac{L(f)}{L(1)}+\frac{L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))}{L(1)}+\varepsilon \gt 0.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)+2\varepsilon
\geq\inf_{f\in K_2}\frac{L(f)}{L(1)}+\frac{L(-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d))}{L(1)}+\varepsilon \gt 0.\end{equation*} Letting ɛ → 0 and µ range over ![]() $\mathcal M_{\mathbb P}(\mathcal E)$ yields
$\mathcal M_{\mathbb P}(\mathcal E)$ yields
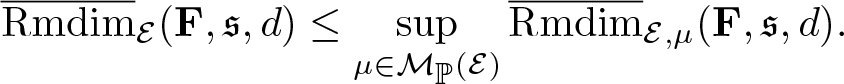 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d).\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\sup_{\mu\in\mathcal M_{\mathbb P}(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d).\end{equation*} To prove  $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$, it suffices to show that there exists
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\sup_{\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$, it suffices to show that there exists ![]() $\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$ such that
$\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$ such that ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$. By Fact 3.15, for every
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$. By Fact 3.15, for every ![]() $f\in\mathcal A$ and
$f\in\mathcal A$ and ![]() $g\in G$, we have
$g\in G$, we have ![]() $f\circ g\in\mathcal A$, and thus by Proposition 3.17, for each
$f\circ g\in\mathcal A$, and thus by Proposition 3.17, for each ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, there is the inequality that
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$, there is the inequality that
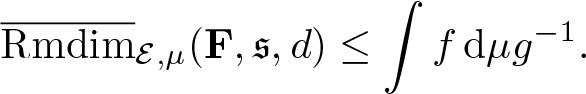 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq\int f\,\mathrm d\mu g^{-1}.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq\int f\,\mathrm d\mu g^{-1}.\end{equation*} This yields, by letting f range over ![]() $\mathcal A$,
$\mathcal A$,
 \begin{equation}
\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\mu g^{-1}}(\mathbf F,\mathfrak s,d),
\end{equation}
\begin{equation}
\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\mu g^{-1}}(\mathbf F,\mathfrak s,d),
\end{equation} for every ![]() $g\in G$. For each
$g\in G$. For each ![]() $n\in\mathbb N$, pick
$n\in\mathbb N$, pick ![]() $\nu_n\in\mathcal M_{\mathbb P}(\mathcal E)$ such that
$\nu_n\in\mathcal M_{\mathbb P}(\mathcal E)$ such that
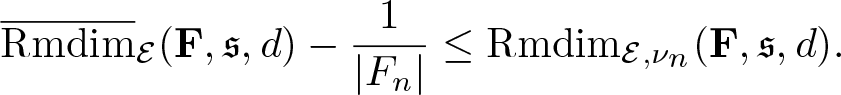 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|}\leq\mathrm{Rmdim}_{\mathcal E,\nu_n}(\mathbf F,\mathfrak s,d).\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|}\leq\mathrm{Rmdim}_{\mathcal E,\nu_n}(\mathbf F,\mathfrak s,d).\end{equation*} Let  $\mu_n=\frac{1}{|F_n|}\sum_{g\in F_n}\nu_ng^{-1}$. By Lemma 4.2, there is a limit point
$\mu_n=\frac{1}{|F_n|}\sum_{g\in F_n}\nu_ng^{-1}$. By Lemma 4.2, there is a limit point ![]() $\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$ of
$\mu\in\mathcal M_{\mathbb P}^G(\mathcal E)$ of ![]() $(\mu_n)_{n\in\mathbb N}$ in weak
$(\mu_n)_{n\in\mathbb N}$ in weak![]() $^*$-topology. Without loss of generality, we may assume
$^*$-topology. Without loss of generality, we may assume ![]() $\lim_{n\to\infty}\mu_n=\mu$. For every
$\lim_{n\to\infty}\mu_n=\mu$. For every ![]() $n\in\mathbb N$ and
$n\in\mathbb N$ and ![]() $g\in F_n$ by (4.8), we have
$g\in F_n$ by (4.8), we have
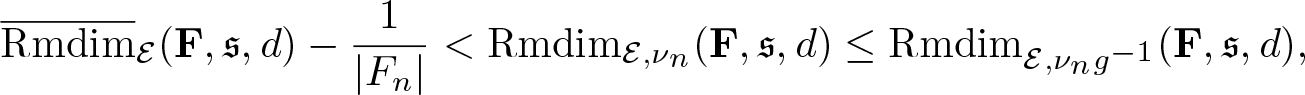 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|} \lt \mathrm{Rmdim}_{\mathcal E,\nu_n}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\nu_n g^{-1}}(\mathbf F,\mathfrak s,d),\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|} \lt \mathrm{Rmdim}_{\mathcal E,\nu_n}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\nu_n g^{-1}}(\mathbf F,\mathfrak s,d),\end{equation*} then summing ![]() $g\in F_n$ and dividing
$g\in F_n$ and dividing ![]() $|F_n|$ yields by (1) of Proposition 3.19 that
$|F_n|$ yields by (1) of Proposition 3.19 that
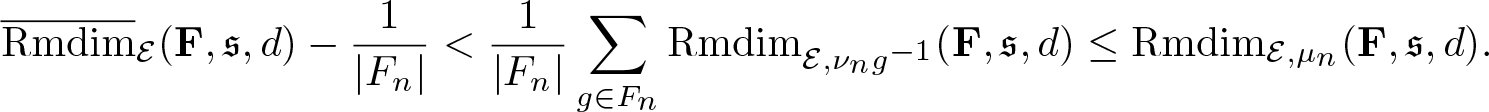 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|} \lt \frac{1}{|F_n|}\sum_{g\in F_n}\mathrm{Rmdim}_{\mathcal E,\nu_n g^{-1}}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\mu_n}(\mathbf F,\mathfrak s,d).\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)-\frac{1}{|F_n|} \lt \frac{1}{|F_n|}\sum_{g\in F_n}\mathrm{Rmdim}_{\mathcal E,\nu_n g^{-1}}(\mathbf F,\mathfrak s,d)\leq\mathrm{Rmdim}_{\mathcal E,\mu_n}(\mathbf F,\mathfrak s,d).\end{equation*} Letting ![]() $n\to\infty$ results in by (2) of Proposition 3.19 that
$n\to\infty$ results in by (2) of Proposition 3.19 that ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$, which shows the statement.
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)\leq\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)$, which shows the statement.
Remark 4.4. The first key technique in the proof of our variational principle is a convex analysis approach set up by Biś–Carvalho–Mendes–Varandas in [Reference Biś, Carvalho, Mendes and Varandas3] or Cioletti–Silva–Stadlbauer in [Reference Cioletti, Silva and Stadlbauer8], where they considered an upper semi-continuous affine entropy-like map, established an abstract variational principle for both countably and finitely additive probability measures and proved that equilibrium states always exist. As our mean dimensions can be regraded as is an entropy-like maps, we borrow part of their idea to establish our variational principle.
The second key technique is borrowed from [Reference Yang, Chen and Zhou55] by Yang et al. We use an approach of Stone vector lattice to overcome the problem: according to Biś’s method in [Reference Biś, Carvalho, Mendes and Varandas3], the Riesz’s representation is a critical tool to prove variational principle; however, the Riesz’s representation theorem holds only for all continuous functions. Unfortunately, ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ composing
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ composing ![]() $g\in G$ may be no longer continuous, which is an obstruction to construct a probability measure on
$g\in G$ may be no longer continuous, which is an obstruction to construct a probability measure on ![]() $\Omega\times X$ having marginal
$\Omega\times X$ having marginal ![]() $\mathbb P$. Moreover, although
$\mathbb P$. Moreover, although ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$ is also a Stone vector lattice, we still need construct the auxiliary set
$\mathbf L^1_\mathcal E(\Omega,C(X))$ is also a Stone vector lattice, we still need construct the auxiliary set ![]() $\mathcal K$, on which
$\mathcal K$, on which  $\frac{L(\cdot)}{L(1)}$ is a pre-integral, so that we can apply Lemma 4.1.
$\frac{L(\cdot)}{L(1)}$ is a pre-integral, so that we can apply Lemma 4.1.
5. Equilibrium states
In this section, we introduce a notion of equilibrium state for amenable random upper metric mean dimension with potentials and discuss its properties.
Definition 5.1. Let ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, if a measure
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, if a measure ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ satisfies
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ satisfies
 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm d\mu,\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm d\mu,\end{equation*} then µ is said to be an equilibrium state of f with respect to the Følner sequence ![]() $\mathfrak s$ and metric d. Denote
$\mathfrak s$ and metric d. Denote ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ the set of all equilibrium states of f with respect to
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ the set of all equilibrium states of f with respect to ![]() $\mathfrak s$ and d.
$\mathfrak s$ and d.
Note that if ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$ then by the convention that any infimum over empty set equals
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d)=\infty$ then by the convention that any infimum over empty set equals ![]() $\infty$ we have
$\infty$ we have ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal M_{\mathbb P}(\mathcal E)$.
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal M_{\mathbb P}(\mathcal E)$.
Definition 5.2. Let µ be a finite sign measure on ![]() $(\Omega\times X,\mathscr F\times\mathscr B)$ with marginal measure
$(\Omega\times X,\mathscr F\times\mathscr B)$ with marginal measure ![]() $\mathbb P$. We say µ is a tangent functional at
$\mathbb P$. We say µ is a tangent functional at ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ with respect to
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ with respect to ![]() $\mathfrak s$ and d if
$\mathfrak s$ and d if
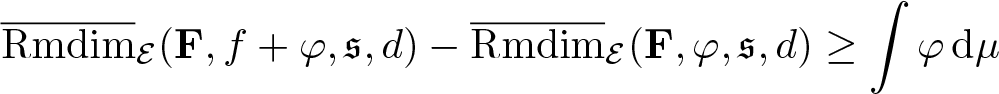 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\varphi,\mathfrak s,d)\geq\int\varphi\,\mathrm{d}\mu\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\varphi,\mathfrak s,d)\geq\int\varphi\,\mathrm{d}\mu\end{equation*} for every ![]() $\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Denote
$\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$. Denote ![]() $\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ the set of all tangent functional at f with respect to
$\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ the set of all tangent functional at f with respect to ![]() $\mathfrak s$ and d.
$\mathfrak s$ and d.
Theorem 5.3. Suppose ![]() $\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
$\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\mathfrak s,d) \lt \infty$ then
(1)
 $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is non-empty, convex and compact for every
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is non-empty, convex and compact for every  $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$;
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$;(2) For every
 $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$,
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$,
 \begin{equation*}\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\geq1}\overline{M_n},\end{equation*}
\begin{equation*}\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\geq1}\overline{M_n},\end{equation*}where
 $M_n=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu \gt \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\frac{1}{n}\}$ for every
$M_n=\{\mu\in\mathcal M_{\mathbb P}(\mathcal E):\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu \gt \overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\frac{1}{n}\}$ for every  $n\in\mathbb N$;
$n\in\mathbb N$;(3) there exists a dense subset
 $\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ such that
$\mathscr L\subset\mathbf L^1_\mathcal E(\Omega,C(X))$ such that  $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is a singleton for every
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is a singleton for every  $f\in\mathscr L$.
$f\in\mathscr L$.
Proof. (1) By Proposition 3.19, the function ![]() ${\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)}:\mathcal M_{\mathbb P}(\mathcal E)\to\mathbb R$ is upper semicontinuous, which implies
${\overline{\mathrm{Rmdim}}_{\mathcal E,\cdot}(\mathbf F,\mathfrak s,d)}:\mathcal M_{\mathbb P}(\mathcal E)\to\mathbb R$ is upper semicontinuous, which implies ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\not=\emptyset$.
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\not=\emptyset$.
Let ![]() $\mu,\nu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and
$\mu,\nu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and ![]() $t\in[0,1]$, then
$t\in[0,1]$, then
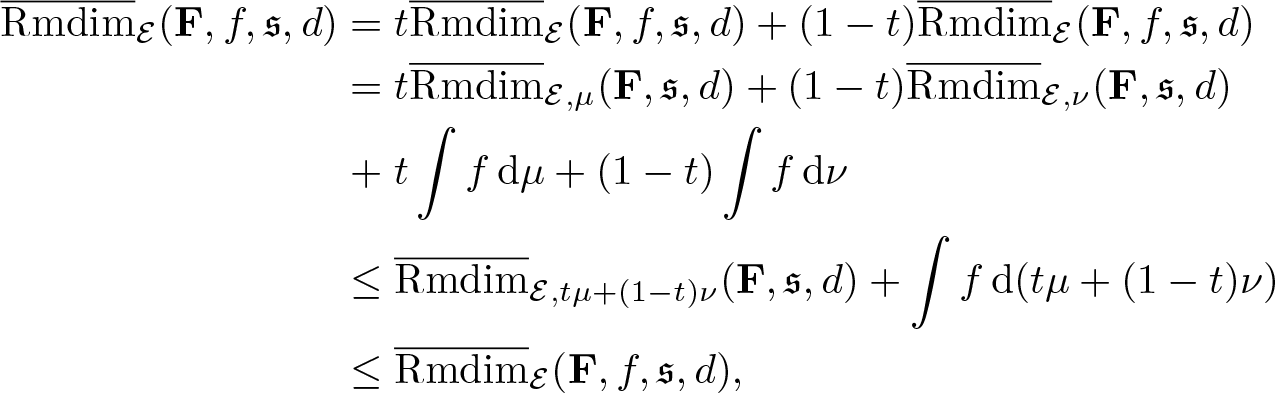 \begin{eqnarray*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)&=&t\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)+(1-t)\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&=&t\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+(1-t)\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)\\
\quad&+&t\int f\,\mathrm{d}\mu+(1-t)\int f\,\mathrm{d}\nu\\
&\leq&\overline{\mathrm{Rmdim}}_{\mathcal E,t\mu+(1-t)\nu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}(t\mu+(1-t)\nu)\\
&\leq&\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d),
\end{eqnarray*}
\begin{eqnarray*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)&=&t\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)+(1-t)\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&=&t\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+(1-t)\overline{\mathrm{Rmdim}}_{\mathcal E,\nu}(\mathbf F,\mathfrak s,d)\\
\quad&+&t\int f\,\mathrm{d}\mu+(1-t)\int f\,\mathrm{d}\nu\\
&\leq&\overline{\mathrm{Rmdim}}_{\mathcal E,t\mu+(1-t)\nu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}(t\mu+(1-t)\nu)\\
&\leq&\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d),
\end{eqnarray*} which shows ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is convex.
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is convex.
Let ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ and
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$ and ![]() $(\mu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ such that
$(\mu_n)_{n\in\mathbb N}\subset\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ such that ![]() $\lim_{n\to\infty}\mu_n=\mu$. By (2) of Proposition 3.19,
$\lim_{n\to\infty}\mu_n=\mu$. By (2) of Proposition 3.19,
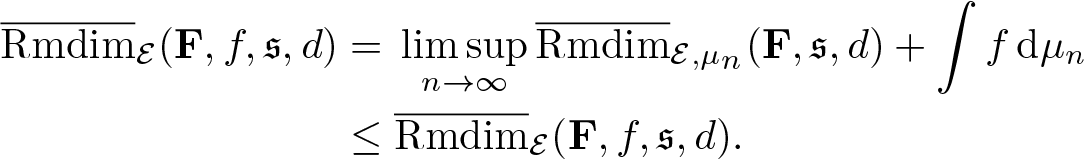 \begin{eqnarray*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)&=&\limsup_{n\to\infty}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu_n}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu_n\\
&\leq&\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d).
\end{eqnarray*}
\begin{eqnarray*}
\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)&=&\limsup_{n\to\infty}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu_n}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu_n\\
&\leq&\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d).
\end{eqnarray*} This yields ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is closed and compact.
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ is closed and compact.
(2) Note that ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\in\mathbb N} M_n$. Let
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)=\bigcap_{n\in\mathbb N} M_n$. Let ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, then
$\mu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, then
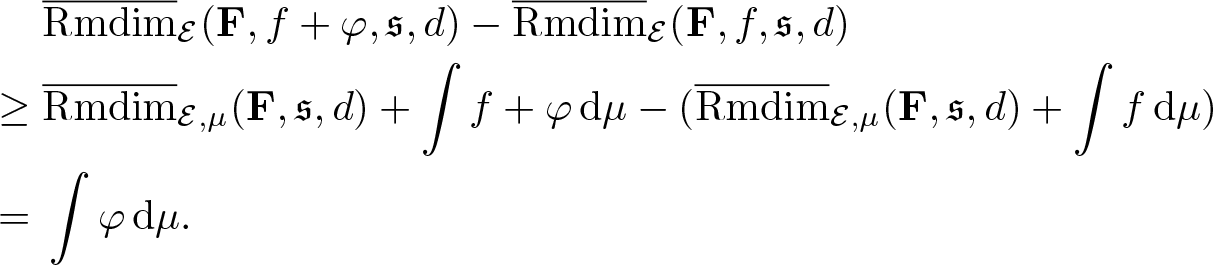 \begin{eqnarray*}
&\ &\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&\geq&\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f+\varphi\,\mathrm{d}\mu-(\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu)\\
&=&\int\varphi\,\mathrm{d}\mu.
\end{eqnarray*}
\begin{eqnarray*}
&\ &\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&\geq&\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f+\varphi\,\mathrm{d}\mu-(\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)+\int f\,\mathrm{d}\mu)\\
&=&\int\varphi\,\mathrm{d}\mu.
\end{eqnarray*} Thus, ![]() $\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and
$\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and ![]() $\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\subset\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$.
$\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\subset\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$.
Let ![]() $\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, then for any ɛ > 0 and
$\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, then for any ɛ > 0 and ![]() $\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$ with φ > 0,
$\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$ with φ > 0,
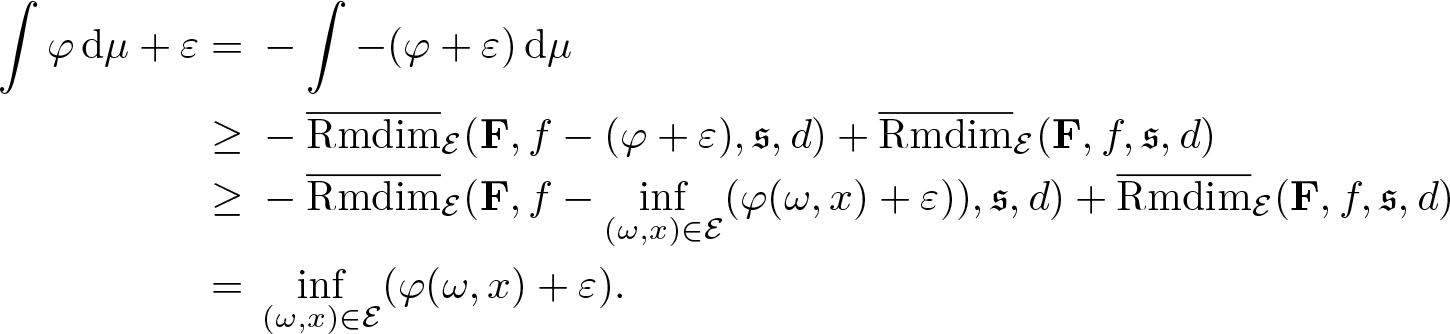 \begin{eqnarray*}
\int\varphi\,\mathrm{d}\mu+\varepsilon&=&-\int-(\varphi+\varepsilon)\,\mathrm{d}\mu\\
&\geq&-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f-(\varphi+\varepsilon),\mathfrak s,d)+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&\geq&-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f-\inf_{(\omega,x)\in\mathcal E}(\varphi(\omega,x)+\varepsilon)),\mathfrak s,d)+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&=&\inf_{(\omega,x)\in\mathcal E}(\varphi(\omega,x)+\varepsilon).
\end{eqnarray*}
\begin{eqnarray*}
\int\varphi\,\mathrm{d}\mu+\varepsilon&=&-\int-(\varphi+\varepsilon)\,\mathrm{d}\mu\\
&\geq&-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f-(\varphi+\varepsilon),\mathfrak s,d)+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&\geq&-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f-\inf_{(\omega,x)\in\mathcal E}(\varphi(\omega,x)+\varepsilon)),\mathfrak s,d)+\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)\\
&=&\inf_{(\omega,x)\in\mathcal E}(\varphi(\omega,x)+\varepsilon).
\end{eqnarray*} This means that µ is a non-negative measure on ![]() $\mathcal E$. By fact 3.11, if
$\mathcal E$. By fact 3.11, if ![]() $n\geq1$, then we have
$n\geq1$, then we have
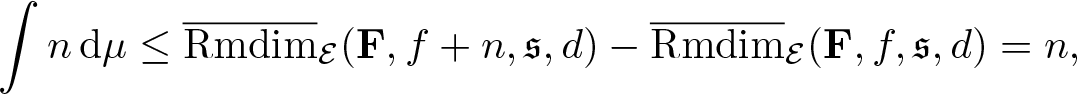 \begin{equation*}\int n\,\mathrm{d}\mu\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+n,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=n,\end{equation*}
\begin{equation*}\int n\,\mathrm{d}\mu\leq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+n,\mathfrak s,d)-\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)=n,\end{equation*} which shows ![]() $\mu(\mathcal E)\leq1$. Likewise, if
$\mu(\mathcal E)\leq1$. Likewise, if ![]() $n\leq-1$, then we can derive
$n\leq-1$, then we can derive ![]() $\mu(\mathcal E)\geq1$. Hence,
$\mu(\mathcal E)\geq1$. Hence, ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. Fix
$\mu\in\mathcal M_{\mathbb P}(\mathcal E)$. Fix ![]() $\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$. As
$\varphi\in\mathbf L^1_\mathcal E(\Omega,C(X))$. As ![]() $\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, we have
$\mu\in\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$, we have
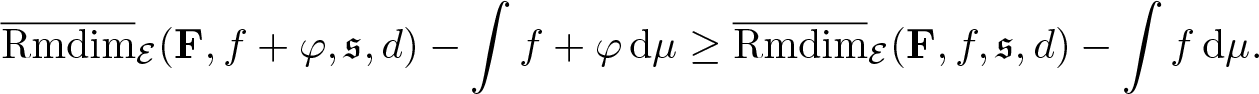 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\int f+\varphi\,\mathrm{d}\mu\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f+\varphi,\mathfrak s,d)-\int f+\varphi\,\mathrm{d}\mu\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu.\end{equation*} Then, by substituting φ with ![]() $\psi=\varphi-f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ in above inequality, we obtain
$\psi=\varphi-f\in\mathbf L^1_\mathcal E(\Omega,C(X))$ in above inequality, we obtain
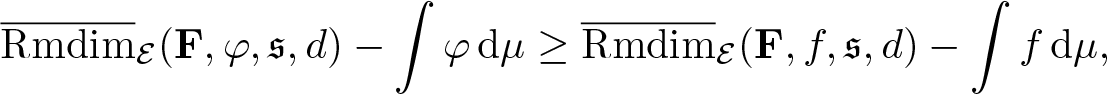 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\varphi,\mathfrak s,d)-\int\varphi\,\mathrm{d}\mu\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu,\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,\varphi,\mathfrak s,d)-\int\varphi\,\mathrm{d}\mu\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu,\end{equation*}which means
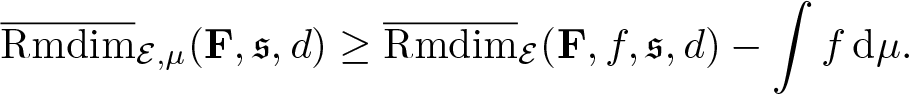 \begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)\geq\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,f,\mathfrak s,d)-\int f\,\mathrm{d}\mu.\end{equation*} Therefore, ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and then
$\mu\in\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$ and then ![]() $\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\subset\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$.
$\mathcal T_{\mathbb P}(\mathcal E,f,\mathfrak s,d)\subset\mathcal M_{\mathbb P}(\mathcal E,f,\mathfrak s,d)$.
(3) As ![]() $\mathbf L^1_\mathcal E(\Omega,C(X))$ is a Banach space, then by [Reference Dunford and Schwartz15, Theorem 8, V.9.8] and Fact 3.6, we derive the statement.
$\mathbf L^1_\mathcal E(\Omega,C(X))$ is a Banach space, then by [Reference Dunford and Schwartz15, Theorem 8, V.9.8] and Fact 3.6, we derive the statement.
Corollary 5.4. Let ![]() $f\in\mathbf L^1_\mathcal E(\Omega,C(X))$,
$f\in\mathbf L^1_\mathcal E(\Omega,C(X))$, ![]() $b\in\mathbb R$ and
$b\in\mathbb R$ and ![]() $\mu\in\mathcal M_{\mathbb P}(\mathcal E,bf,\mathfrak s,d)$ such that
$\mu\in\mathcal M_{\mathbb P}(\mathcal E,bf,\mathfrak s,d)$ such that ![]() $\int f\,\mathrm{d}\mu\not=0$, then
$\int f\,\mathrm{d}\mu\not=0$, then
 \begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,bf,\mathfrak s,d)=0\iff b=-\frac{\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)}{\int f\,\mathrm{d}\mu}.\end{equation*}
\begin{equation*}\overline{\mathrm{Rmdim}}_\mathcal E(\mathbf F,bf,\mathfrak s,d)=0\iff b=-\frac{\overline{\mathrm{Rmdim}}_{\mathcal E,\mu}(\mathbf F,\mathfrak s,d)}{\int f\,\mathrm{d}\mu}.\end{equation*}6. Open questions
There is still a problem untouched in this paper, i.e., what is the difference between a random action and the non-random action of a group with respect to its metric mean dimension? However, interesting examples of metric mean dimension for non-autonomous dynamical systems are considered in [Reference Rodrigues and Acevedo44, Examples 3.8, 5.7 and 5.8]. Their results suggest that there are important differences between of a non-autonomous dynamical system and an autonomous dynamical system with respect to its metric mean dimension. This motivates us that there could be many other differences between a random action and the non-random action of a group with respect to its metric mean dimension. We leave it as an open question and further work.
Acknowledgements
The authors are grateful to the referee for a careful reading of the paper and a multitude of corrections and helpful suggestions.
Funding Statement
This work is supported by the National Natural Science Foundation of China (NSFC) (No: 12201372).







