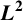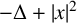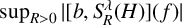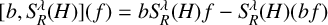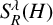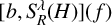1. Introduction
Let H denote the Hermite operator
 $$ \begin{align*} -\Delta + |x|^2 =-\sum_{i=1}^n {\partial^2\over \partial x_i^2} + |x|^2, \quad x=(x_1, \ldots, x_n), \quad n\geq 1. \end{align*} $$
$$ \begin{align*} -\Delta + |x|^2 =-\sum_{i=1}^n {\partial^2\over \partial x_i^2} + |x|^2, \quad x=(x_1, \ldots, x_n), \quad n\geq 1. \end{align*} $$
The operator H is nonnegative and self-adjoint with respect to the Lebesgue measure on
![]() $\mathbb {R}^n$
. The spectrum of the operator H is given by the set
$\mathbb {R}^n$
. The spectrum of the operator H is given by the set
![]() $ {2\mathbb N_0} + n$
. Here
$ {2\mathbb N_0} + n$
. Here
![]() ${\mathbb N_0}$
denotes the set of nonnegative integers. For each nonnegative integer k, the Hermite polynomials
${\mathbb N_0}$
denotes the set of nonnegative integers. For each nonnegative integer k, the Hermite polynomials
![]() $H_k(t) $
on
$H_k(t) $
on
![]() $\mathbb {R}$
are defined by
$\mathbb {R}$
are defined by
![]() $H_k(t)=(-1)^k e^{t^2} ({d^k}/{d t^k}) (e^{-t^2})$
, and the Hermite functions
$H_k(t)=(-1)^k e^{t^2} ({d^k}/{d t^k}) (e^{-t^2})$
, and the Hermite functions
![]() $h_k(t):=(2^k k ! \sqrt {\pi })^{-1/2} H_k(t) e^{-t^2/2}$
,
$h_k(t):=(2^k k ! \sqrt {\pi })^{-1/2} H_k(t) e^{-t^2/2}$
,
![]() $k=0, 1, 2, \ldots $
form an orthonormal basis of
$k=0, 1, 2, \ldots $
form an orthonormal basis of
![]() $L^2(\mathbb R)$
. For any multiindex
$L^2(\mathbb R)$
. For any multiindex
![]() $\mu \in {\mathbb N}^n_0$
, the n-dimensional Hermite functions are given by the tensor product of the one-dimensional Hermite functions:
$\mu \in {\mathbb N}^n_0$
, the n-dimensional Hermite functions are given by the tensor product of the one-dimensional Hermite functions:
 $$ \begin{align*} \Phi_{\mu}(x)=\prod_{i=1}^n h_{\mu_i}(x_i), \quad \mu=(\mu_1, \ldots, \mu_n). \end{align*} $$
$$ \begin{align*} \Phi_{\mu}(x)=\prod_{i=1}^n h_{\mu_i}(x_i), \quad \mu=(\mu_1, \ldots, \mu_n). \end{align*} $$
Then the functions
![]() $\Phi _{\mu }$
are eigenfunctions for the Hermite operator with eigenvalue
$\Phi _{\mu }$
are eigenfunctions for the Hermite operator with eigenvalue
![]() $(2|\mu |+n)$
and
$(2|\mu |+n)$
and
![]() $\{\Phi _{\mu }\}_{\mu \in \mathbb N_0^n}$
forms a complete orthonormal system in
$\{\Phi _{\mu }\}_{\mu \in \mathbb N_0^n}$
forms a complete orthonormal system in
![]() $L^2({\mathbb {R}^n})$
. Thus, for every
$L^2({\mathbb {R}^n})$
. Thus, for every
![]() $f\in L^2(\mathbb {R}^n)$
, we have the Hermite expansion
$f\in L^2(\mathbb {R}^n)$
, we have the Hermite expansion
 $$ \begin{align*} f(x)=\sum_{\mu\in \mathbb{N}_0^n}\langle f, \Phi_{\mu}\rangle \Phi_\mu(x)=\sum_{k=0}^{\infty}P_kf(x), \end{align*} $$
$$ \begin{align*} f(x)=\sum_{\mu\in \mathbb{N}_0^n}\langle f, \Phi_{\mu}\rangle \Phi_\mu(x)=\sum_{k=0}^{\infty}P_kf(x), \end{align*} $$
where
![]() $P_k$
denotes the Hermite projection operator given by
$P_k$
denotes the Hermite projection operator given by
 $$ \begin{align*} P_kf(x)=\sum_{2|\mu|+n=k}\langle f, \Phi_{\mu}\rangle\Phi_\mu(x). \end{align*} $$
$$ \begin{align*} P_kf(x)=\sum_{2|\mu|+n=k}\langle f, \Phi_{\mu}\rangle\Phi_\mu(x). \end{align*} $$
For
![]() $R>0$
, the Bochner–Riesz means for H of order
$R>0$
, the Bochner–Riesz means for H of order
![]() $\lambda \geq 0$
are defined by
$\lambda \geq 0$
are defined by
 $$ \begin{align*} S_R^{\lambda}(H)f(x) = \sum_{k=0}^{\infty} \bigg(1-{2k+n\over R^2}\bigg)_+^{\lambda} P_k f(x). \end{align*} $$
$$ \begin{align*} S_R^{\lambda}(H)f(x) = \sum_{k=0}^{\infty} \bigg(1-{2k+n\over R^2}\bigg)_+^{\lambda} P_k f(x). \end{align*} $$
The assumption
![]() $\lambda \geq 0$
is necessary for
$\lambda \geq 0$
is necessary for
![]() $S_R^{\lambda }(H)$
to be defined for all
$S_R^{\lambda }(H)$
to be defined for all
![]() $R>0$
. Note that
$R>0$
. Note that
![]() $S_R^{\lambda }(H)f$
cannot be defined with
$S_R^{\lambda }(H)f$
cannot be defined with
![]() $R^2=2k+n$
if
$R^2=2k+n$
if
![]() $\lambda <0$
.
$\lambda <0$
.
On the space
![]() $\mathbb {R}$
, Thangavelu [Reference Thangavelu28] showed that
$\mathbb {R}$
, Thangavelu [Reference Thangavelu28] showed that
![]() $S_R^\lambda (H)$
is uniformly bounded on
$S_R^\lambda (H)$
is uniformly bounded on
![]() $L^p(\mathbb {R})$
for
$L^p(\mathbb {R})$
for
![]() $1\leq p\leq \infty $
provided
$1\leq p\leq \infty $
provided
![]() $\lambda>1/6$
; if
$\lambda>1/6$
; if
![]() $0<\lambda <1/6$
, the uniform boundedness of
$0<\lambda <1/6$
, the uniform boundedness of
![]() $S_R^\lambda (H)$
holds if and only if
$S_R^\lambda (H)$
holds if and only if
![]() $4/(6\lambda +3) <p<4/(1-6\lambda )$
. On the space
$4/(6\lambda +3) <p<4/(1-6\lambda )$
. On the space
![]() $\mathbb {R}^n$
for dimension
$\mathbb {R}^n$
for dimension
![]() $n\geq 2$
, if
$n\geq 2$
, if
![]() $\lambda> (n-1)/2$
, Thangavelu [Reference Thangavelu29] showed that
$\lambda> (n-1)/2$
, Thangavelu [Reference Thangavelu29] showed that
![]() $S_R^\lambda (H)$
is uniformly bounded on
$S_R^\lambda (H)$
is uniformly bounded on
![]() $L^p(\mathbb {R}^n)$
for
$L^p(\mathbb {R}^n)$
for
![]() $1\leq p\leq \infty $
. Let
$1\leq p\leq \infty $
. Let
![]() $n\geq 2,\ 0\leq \lambda \leq (n-1)/2$
and
$n\geq 2,\ 0\leq \lambda \leq (n-1)/2$
and
![]() $p\in [1,\infty ]\backslash \, \{2\}$
. It was conjectured (see [Reference Thangavelu30, page 259]) that
$p\in [1,\infty ]\backslash \, \{2\}$
. It was conjectured (see [Reference Thangavelu30, page 259]) that
![]() $S_R^\lambda (H)$
is bounded on
$S_R^\lambda (H)$
is bounded on
![]() $L^p(\mathbb {R}^n)$
uniformly in R if and only if
$L^p(\mathbb {R}^n)$
uniformly in R if and only if
 $$ \begin{align*}\lambda>\lambda(p)=\max\bigg\{n\bigg|\frac1p-\frac12\bigg|-\frac12,0\bigg\}.\end{align*} $$
$$ \begin{align*}\lambda>\lambda(p)=\max\bigg\{n\bigg|\frac1p-\frac12\bigg|-\frac12,0\bigg\}.\end{align*} $$
Thangavelu showed that the
![]() $L^p$
boundedness of
$L^p$
boundedness of
![]() $S_R^\lambda (H)$
fails if
$S_R^\lambda (H)$
fails if
![]() $\lambda <\lambda (p)$
. Karadzhov [Reference Karadzhov19] showed the
$\lambda <\lambda (p)$
. Karadzhov [Reference Karadzhov19] showed the
![]() $L^p$
boundedness of
$L^p$
boundedness of
![]() $S_R^\lambda (H)$
by an optimal
$S_R^\lambda (H)$
by an optimal
![]() $L^2$
–
$L^2$
–
![]() $L^p$
spectral projection estimate when p is in the range of
$L^p$
spectral projection estimate when p is in the range of
![]() $[1,2n/(n+2)]\cup [2n/(n-2),\infty ]$
and
$[1,2n/(n+2)]\cup [2n/(n-2),\infty ]$
and
![]() ${\lambda>\lambda (p)}$
. Recently, Lee and Ryu [Reference Lee and Ryu22] invalidated the above conjecture by showing that
${\lambda>\lambda (p)}$
. Recently, Lee and Ryu [Reference Lee and Ryu22] invalidated the above conjecture by showing that
![]() $\sup _{R>0}\|S_R^\lambda (H)\|_{L^p\rightarrow L^p}\leq C$
only if
$\sup _{R>0}\|S_R^\lambda (H)\|_{L^p\rightarrow L^p}\leq C$
only if
![]() $\lambda \geq -1/(3p)+n/3(1/2-1/p)>\lambda (p)$
when
$\lambda \geq -1/(3p)+n/3(1/2-1/p)>\lambda (p)$
when
![]() ${p\in (2(n+1)/n,2(2n-1)/(2n-3))}$
for
${p\in (2(n+1)/n,2(2n-1)/(2n-3))}$
for
![]() $n\geq 2$
. Concerning the estimate of the maximal operator, it is known (see [Reference Chen, Lee, Sikora and Yan5]) that the maximal operator
$n\geq 2$
. Concerning the estimate of the maximal operator, it is known (see [Reference Chen, Lee, Sikora and Yan5]) that the maximal operator
![]() $\sup _{R>0}|S_R^\lambda (H)f|$
is bounded on
$\sup _{R>0}|S_R^\lambda (H)f|$
is bounded on
![]() $L^p(\mathbb {R}^n)$
for
$L^p(\mathbb {R}^n)$
for
![]() $n\geq 2$
whenever
$n\geq 2$
whenever
![]() $p\geq 2n/(n-2)$
and
$p\geq 2n/(n-2)$
and
![]() $\lambda>\lambda (p)$
. Further, Chen et al. [Reference Chen, Duong, He, Lee and Yan4] proved that
$\lambda>\lambda (p)$
. Further, Chen et al. [Reference Chen, Duong, He, Lee and Yan4] proved that
![]() $\sup _{R>0}|S_R^\lambda (H)f|$
is bounded on
$\sup _{R>0}|S_R^\lambda (H)f|$
is bounded on
![]() $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
if
$L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
if
![]() ${\lambda>\max \{(\alpha -1)/4,0\},}$
which implies the almost everywhere (a.e.) convergence of
${\lambda>\max \{(\alpha -1)/4,0\},}$
which implies the almost everywhere (a.e.) convergence of
![]() $S^\lambda _R(H)f$
for all
$S^\lambda _R(H)f$
for all
![]() $f\in L^p(\mathbb {R}^n)$
provided that
$f\in L^p(\mathbb {R}^n)$
provided that
![]() $\lambda>\lambda (p)/2$
with
$\lambda>\lambda (p)/2$
with
![]() $p\in [2,\infty )$
.
$p\in [2,\infty )$
.
Consider the commutator. Given an operator T and a local integral function b, the commutator of T and b is defined as follows:
It is well known that Coifman et al. [Reference Coifman, Rochberg and Weiss9] characterized the boundedness of the commutator
![]() $[b,T]$
with Riesz transforms and
$[b,T]$
with Riesz transforms and
![]() $b\in \mathrm {BMO}$
. Since then, many investigations have come out of this work: generalizations to spaces of homogeneous type by Uchiyama [Reference Uchiyama32]; multi-parameter extensions by Ferguson and Lacey [Reference Ferguson and Lacey12] and by Lacey et al. [Reference Lacey, Petermichl, Pipher and Wick20]; in the two-weight setting by Holmes et al. [Reference Holmes, Lacey and Wick14];
$b\in \mathrm {BMO}$
. Since then, many investigations have come out of this work: generalizations to spaces of homogeneous type by Uchiyama [Reference Uchiyama32]; multi-parameter extensions by Ferguson and Lacey [Reference Ferguson and Lacey12] and by Lacey et al. [Reference Lacey, Petermichl, Pipher and Wick20]; in the two-weight setting by Holmes et al. [Reference Holmes, Lacey and Wick14];
![]() $L^p$
to
$L^p$
to
![]() $L^q$
boundedness and applications with Jocobian operators by Hytönen [Reference Hytönen18]; div-curl lemmas by Coifman et al. [Reference Coifman, Lions, Meyer and Semmes8] and by Lacey et al. [Reference Lacey, Petermichl, Pipher and Wick21]; additional interpretations in operator theory by Uchiyama [Reference Uchiyama31] and by Nazarov et al. [Reference Nazarov, Pisier, Treil and Volberg23]; commutators with classical Bochner–Riesz operators by Álvarez et al. [Reference Álvarez, Bagby, Kurtz and Pérez1] and by Hu and Lu [Reference Hu and Lu15, Reference Hu and Lu17].
$L^q$
boundedness and applications with Jocobian operators by Hytönen [Reference Hytönen18]; div-curl lemmas by Coifman et al. [Reference Coifman, Lions, Meyer and Semmes8] and by Lacey et al. [Reference Lacey, Petermichl, Pipher and Wick21]; additional interpretations in operator theory by Uchiyama [Reference Uchiyama31] and by Nazarov et al. [Reference Nazarov, Pisier, Treil and Volberg23]; commutators with classical Bochner–Riesz operators by Álvarez et al. [Reference Álvarez, Bagby, Kurtz and Pérez1] and by Hu and Lu [Reference Hu and Lu15, Reference Hu and Lu17].
In [Reference Chen, Lin and Yan6], the authors of this article and Yan studied the
![]() $L^p$
-boundedness of the commutator
$L^p$
-boundedness of the commutator
![]() $[b, S_R^\lambda (H)](f)$
of a BMO function b and the Bochner–Riesz means
$[b, S_R^\lambda (H)](f)$
of a BMO function b and the Bochner–Riesz means
![]() $S_R^\lambda (H)$
, which are defined by
$S_R^\lambda (H)$
, which are defined by
They showed that if
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $1\leq p\leq 2n/(n+2)$
and
$1\leq p\leq 2n/(n+2)$
and
![]() $\lambda>\lambda (p)$
, then for all
$\lambda>\lambda (p)$
, then for all
![]() $b\in \mathrm {BMO(\mathbb {R}^n)}$
and all
$b\in \mathrm {BMO(\mathbb {R}^n)}$
and all
![]() $q\in (p,p')$
,
$q\in (p,p')$
,
The purpose of this paper is to follow this line to establish weighted
![]() $L^2$
estimates of the commutator of
$L^2$
estimates of the commutator of
![]() $S_R^\lambda (H)$
and a BMO function b. Our main result is the following theorem.
$S_R^\lambda (H)$
and a BMO function b. Our main result is the following theorem.
Theorem 1.1. Let
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
. For
$b\in \mathrm {BMO}(\mathbb {R}^n)$
. For
![]() $0\leq \alpha <n$
, if
$0\leq \alpha <n$
, if
![]() $\lambda>\max \{(\alpha -1)/4,0\}$
, then
$\lambda>\max \{(\alpha -1)/4,0\}$
, then
 $$ \begin{align*} \int_{\mathbb{R}^n} \sup_{R>0}| [b,S^{\lambda}_R(H)]f(x)|^2(1+|x|)^{-\alpha}\,dx\leq C(n,\alpha,\lambda)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n} \sup_{R>0}| [b,S^{\lambda}_R(H)]f(x)|^2(1+|x|)^{-\alpha}\,dx\leq C(n,\alpha,\lambda)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
As a consequence of Theorem 1.1, we have the following result.
Corollary 1.2. Let
![]() $2\leq p<\infty $
and
$2\leq p<\infty $
and
![]() $\lambda>\lambda (p)/2.$
Then for any
$\lambda>\lambda (p)/2.$
Then for any
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
and
$b\in \mathrm {BMO}(\mathbb {R}^n)$
and
![]() $f\in L^p(\mathbb {R}^n)$
,
$f\in L^p(\mathbb {R}^n)$
,
almost everywhere.
We would like to mention that the classical Bochner–Riesz means on
![]() $\mathbb {R}^n$
are defined by
$\mathbb {R}^n$
are defined by
 $$ \begin{align*} \widehat{S^{\lambda}_Rf}(\xi) =\bigg(1-{|\xi|^2\over R^2}\bigg)_+^{\lambda} \widehat{f}(\xi) \quad \text{for all }{\xi \in \mathbb{R}^n}. \end{align*} $$
$$ \begin{align*} \widehat{S^{\lambda}_Rf}(\xi) =\bigg(1-{|\xi|^2\over R^2}\bigg)_+^{\lambda} \widehat{f}(\xi) \quad \text{for all }{\xi \in \mathbb{R}^n}. \end{align*} $$
Hu and Lu [Reference Hu and Lu16] showed that for
![]() $\lambda>0$
, the maximal commutator operator
$\lambda>0$
, the maximal commutator operator
![]() $\sup _{R>0}|[b,S^\lambda _R]f|$
is bounded on
$\sup _{R>0}|[b,S^\lambda _R]f|$
is bounded on
![]() $L^2(\mathbb {R}^n)$
. Further, they proved a weighted estimate and showed that the maximal commutator operator
$L^2(\mathbb {R}^n)$
. Further, they proved a weighted estimate and showed that the maximal commutator operator
![]() $\sup _{R>0}|[b,S^\lambda _R]f|$
is bounded on
$\sup _{R>0}|[b,S^\lambda _R]f|$
is bounded on
![]() $L^2(\mathbb {R}^n,|x|^{-\alpha })$
whenever
$L^2(\mathbb {R}^n,|x|^{-\alpha })$
whenever
![]() $0<\alpha <n$
and
$0<\alpha <n$
and
![]() $\lambda>\max \{(\alpha -1)/2,0\}$
in [Reference Hu and Lu17].
$\lambda>\max \{(\alpha -1)/2,0\}$
in [Reference Hu and Lu17].
The proof of Theorem 1.1 relies on a weighted
![]() $L^2$
estimate for the square function
$L^2$
estimate for the square function
![]() $ G_{b,\delta }$
, which is defined by
$ G_{b,\delta }$
, which is defined by
 $$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg|\, \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$
$$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg|\, \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$
where
![]() $\phi \in C_c^\infty (\mathbb {R})$
with support
$\phi \in C_c^\infty (\mathbb {R})$
with support
![]() $\{x:1/8\leq |x| \leq 1/2\}$
and
$\{x:1/8\leq |x| \leq 1/2\}$
and
![]() $|\phi |\leq 1$
(see Proposition 3.1). Indeed, we show that for any
$|\phi |\leq 1$
(see Proposition 3.1). Indeed, we show that for any
![]() $0<\upsilon \leq 1/2$
, there exists a constant
$0<\upsilon \leq 1/2$
, there exists a constant
![]() $C_{\alpha ,\upsilon }>0$
independent of
$C_{\alpha ,\upsilon }>0$
independent of
![]() $\delta $
such that
$\delta $
such that
where
 $$ \begin{align} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mathrm{{if}}\ 0< \alpha< 1, n=1; \alpha=0, n\geq 1;\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mathrm{{if}}\ 1<\alpha <n, n\geq2. \end{cases} \end{align} $$
$$ \begin{align} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mathrm{{if}}\ 0< \alpha< 1, n=1; \alpha=0, n\geq 1;\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mathrm{{if}}\ 1<\alpha <n, n\geq2. \end{cases} \end{align} $$
To show Inequality (1-1), we use an extension of two nontrivial facts due to [Reference Chen, Duong, He, Lee and Yan4]. The first is that for any
![]() $\alpha \geq 0$
,
$\alpha \geq 0$
,
holds for any
![]() $f\in {\mathscr S} (\mathbb {R}^n)$
. The second fact is a type of trace lemma for the Hermite operator, that is, for
$f\in {\mathscr S} (\mathbb {R}^n)$
. The second fact is a type of trace lemma for the Hermite operator, that is, for
![]() $\alpha>1$
, there exists a constant
$\alpha>1$
, there exists a constant
![]() $C>0$
such that
$C>0$
such that
We would like to mention that when
![]() $0<\alpha <1$
, Inequality (1-3) is not applicable. To show the square function estimate in Inequality (1-1) for
$0<\alpha <1$
, Inequality (1-3) is not applicable. To show the square function estimate in Inequality (1-1) for
![]() $0<\alpha <1$
, we make use of a weighted Plancherel-type estimate (see Inequality (2-2) and refer to [Reference Chen, Duong, He, Lee and Yan4, Lemma 2.6] for the proof).
$0<\alpha <1$
, we make use of a weighted Plancherel-type estimate (see Inequality (2-2) and refer to [Reference Chen, Duong, He, Lee and Yan4, Lemma 2.6] for the proof).
This paper is organized as follows. In Section
![]() $2$
, we give some preliminary results about the Hermite operator, and some estimates of the commutator of spectral multipliers and BMO functions, which provide the basic estimates required for the proof of Theorem 1.1. We establish the weighted estimate in Inequality (1-1) of the square function
$2$
, we give some preliminary results about the Hermite operator, and some estimates of the commutator of spectral multipliers and BMO functions, which provide the basic estimates required for the proof of Theorem 1.1. We establish the weighted estimate in Inequality (1-1) of the square function
![]() $G_{b,\delta }$
in Section
$G_{b,\delta }$
in Section
![]() $3$
. The proof of Theorem 1.1 is given in Section
$3$
. The proof of Theorem 1.1 is given in Section
![]() $4$
by using the estimate in Inequality (1-1) of the square function
$4$
by using the estimate in Inequality (1-1) of the square function
![]() $G_{b,\delta }$
. As a consequence of Theorem 1.1, we obtain the proof of Corollary 1.2 at the end of Section
$G_{b,\delta }$
. As a consequence of Theorem 1.1, we obtain the proof of Corollary 1.2 at the end of Section
![]() $4$
.
$4$
.
2. Preliminary results
We start by recalling some properties of the Hermite operator H. The Hermite operator H satisfies the finite speed propagation property, that is,
See for example, [Reference Sikora25, Theorem 2]. By Fourier inversion, for any even function F,
 $$ \begin{align*}F(\!\sqrt{H})=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\widehat{F}(t)\cos(t\sqrt{H})\,dt.\end{align*} $$
$$ \begin{align*}F(\!\sqrt{H})=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\widehat{F}(t)\cos(t\sqrt{H})\,dt.\end{align*} $$
From [Reference Chen, Ouhabaz, Sikora and Yan7, Lemma I.1], if supp
![]() $\, \widehat {F}\subseteq [-t,t]$
, then
$\, \widehat {F}\subseteq [-t,t]$
, then
which is used in the following.
For any function F with support in
![]() $[-1,1]$
and
$[-1,1]$
and
![]() $2\leq p<\infty $
, we define
$2\leq p<\infty $
, we define
 $$ \begin{align*} \|F\|_{N, _p}:=\bigg(\frac{1}{N}\sum_{i=-N+1}^{N}\sup_{\lambda\in[({i-1})/{N},{i}/{N})}|F(\lambda)|^p\bigg)^{{1}/{p}},\quad N\in \mathbb{N}^+. \end{align*} $$
$$ \begin{align*} \|F\|_{N, _p}:=\bigg(\frac{1}{N}\sum_{i=-N+1}^{N}\sup_{\lambda\in[({i-1})/{N},{i}/{N})}|F(\lambda)|^p\bigg)^{{1}/{p}},\quad N\in \mathbb{N}^+. \end{align*} $$
The following is the trace lemma for the Hermite operator.
Lemma 2.1. For
![]() $\alpha>1$
, there exists a constant
$\alpha>1$
, there exists a constant
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $k\in \mathbb {N}^+$
,
$k\in \mathbb {N}^+$
,
As a consequence, for any function F supported in
![]() $[N/4,N]$
,
$[N/4,N]$
,
![]() $N\in \mathbb {N^+}$
and any
$N\in \mathbb {N^+}$
and any
![]() $\varepsilon>0$
, there exist constants C and
$\varepsilon>0$
, there exist constants C and
![]() $C_\varepsilon $
such that
$C_\varepsilon $
such that
 $$ \begin{align} \int_{\mathbb{R}^n}|F(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\leq \begin{cases} CN\|F(N\cdot)\|_{N^2, _2}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } \alpha>1; \\[4pt] C_{\varepsilon}N^{{\alpha}/({1+\varepsilon})}\|F(N\cdot)\|_{N^2,_{2(1+\varepsilon)/\alpha}}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } 0<\alpha\leq1. \end{cases} \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n}|F(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\leq \begin{cases} CN\|F(N\cdot)\|_{N^2, _2}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } \alpha>1; \\[4pt] C_{\varepsilon}N^{{\alpha}/({1+\varepsilon})}\|F(N\cdot)\|_{N^2,_{2(1+\varepsilon)/\alpha}}^2\|f\|_{L^2(\mathbb{R}^n)}^2 & \mbox{{if} } 0<\alpha\leq1. \end{cases} \end{align} $$
Proof. For the proof of Inequalities (2-1) and (2-2), we refer the reader to [Reference Chen, Duong, He, Lee and Yan4, Lemmas 1.5, 2.4 and 2.6]. We would like to mention that the estimate in Inequality (2-2) for
![]() $\alpha>1$
is equivalent to the estimate in Inequality (2-1). Inequality (2-2) for
$\alpha>1$
is equivalent to the estimate in Inequality (2-1). Inequality (2-2) for
![]() $0<\alpha \leq 1$
is a consequence of a bilinear interpolation of the estimate in Inequality (2-2) for
$0<\alpha \leq 1$
is a consequence of a bilinear interpolation of the estimate in Inequality (2-2) for
![]() $\alpha>1$
and the trivial fact
$\alpha>1$
and the trivial fact
![]() $\|F(\!\sqrt {H})f\|_{L^2(\mathbb {R}^n)}=\|F(N\cdot )\|_{L^{\infty }(\mathbb {R})} \|f\|_{L^2(\mathbb {R}^n)}$
.
$\|F(\!\sqrt {H})f\|_{L^2(\mathbb {R}^n)}=\|F(N\cdot )\|_{L^{\infty }(\mathbb {R})} \|f\|_{L^2(\mathbb {R}^n)}$
.
Lemma 2.2. Let
![]() $\alpha \geq 0$
. Then the estimate
$\alpha \geq 0$
. Then the estimate
holds for all
![]() $f\in {\mathscr S}({\mathbb R^n})$
. Here,
$f\in {\mathscr S}({\mathbb R^n})$
. Here,
![]() ${\mathscr S}({\mathbb R^n})$
stands for the class of Schwartz functions in
${\mathscr S}({\mathbb R^n})$
stands for the class of Schwartz functions in
![]() ${\mathbb R^n}.$
${\mathbb R^n}.$
Proof. For the proof, we refer the reader to [Reference Chen, Duong, He, Lee and Yan4, Lemma 1.4].
Lemma 2.3. Let
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
. By
$b\in \mathrm {BMO}(\mathbb {R}^n)$
. By
![]() $M_b$
, we denote the commutator of the Hardy–Littlewood maximal operator defined by
$M_b$
, we denote the commutator of the Hardy–Littlewood maximal operator defined by
 $$ \begin{align*} M_b(f)(x):=\sup_{r>0}r^{-n}\int_{|x-y|<r}|(b(x)-b(y))f(y)|\, dy. \end{align*} $$
$$ \begin{align*} M_b(f)(x):=\sup_{r>0}r^{-n}\int_{|x-y|<r}|(b(x)-b(y))f(y)|\, dy. \end{align*} $$
If
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $w\in A_p$
, then
$w\in A_p$
, then
![]() $M_b$
is bounded on
$M_b$
is bounded on
![]() $L^p(\mathbb {R}^n,w)$
with bound
$L^p(\mathbb {R}^n,w)$
with bound
![]() $C(n,p)\|b\|_{\mathrm {BMO}}$
.
$C(n,p)\|b\|_{\mathrm {BMO}}$
.
Proof. For the proof, we refer the reader to [Reference Hu and Lu17, Lemma 1] and [Reference Garcia-Cuerva, Harboure, Segovia and Torre13].
Lemma 2.4. Let
![]() $M_b(f)$
be defined as above and
$M_b(f)$
be defined as above and
![]() $\varphi \in C_c^{\infty }({\mathbb {R}})$
. Then for any
$\varphi \in C_c^{\infty }({\mathbb {R}})$
. Then for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
In addition, for any
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $w\in A_p$
,
$w\in A_p$
,
Proof. Let
![]() $G(t^{-2}H)=\varphi (t^{-2}H)e^{t^{-2}H}$
, then by the Fourier transform,
$G(t^{-2}H)=\varphi (t^{-2}H)e^{t^{-2}H}$
, then by the Fourier transform,
with the kernel
where
![]() $p_{t}(x,y)$
is the heat kernel of the semigroup
$p_{t}(x,y)$
is the heat kernel of the semigroup
![]() $e^{-tH}$
. Then,
$e^{-tH}$
. Then,
 $$ \begin{align} |[b,\varphi(t^{-2}H)]f(x)|&=\bigg|\!\int_{\mathbb{R}^n}K_{\varphi(t^{-2}H)}(x,y)(b(x)-b(y))f(y)\,dy\bigg|\nonumber\\ &\leq \int_{\mathbb{R}}|\widehat{G}(\tau)|\int_{\mathbb{R}^n}|p_{t^{-2}(1-i\tau)}(x,y)(b(x)-b(y))f(y)|\,dy\,d\tau. \end{align} $$
$$ \begin{align} |[b,\varphi(t^{-2}H)]f(x)|&=\bigg|\!\int_{\mathbb{R}^n}K_{\varphi(t^{-2}H)}(x,y)(b(x)-b(y))f(y)\,dy\bigg|\nonumber\\ &\leq \int_{\mathbb{R}}|\widehat{G}(\tau)|\int_{\mathbb{R}^n}|p_{t^{-2}(1-i\tau)}(x,y)(b(x)-b(y))f(y)|\,dy\,d\tau. \end{align} $$
The kernel of
![]() $e^{-t^{-2}H}$
has the Gaussian upper bound. Let
$e^{-t^{-2}H}$
has the Gaussian upper bound. Let
![]() $z=t^{-2}(1-i\tau )$
. By the Phragmen–Lindelöf theorem, the kernel of
$z=t^{-2}(1-i\tau )$
. By the Phragmen–Lindelöf theorem, the kernel of
![]() $e^{-zH}$
satisfies the following estimate (see [Reference Ouhabaz24, Theorem 7.2]):
$e^{-zH}$
satisfies the following estimate (see [Reference Ouhabaz24, Theorem 7.2]):
 $$ \begin{align} |p_{z}(x,y)|\leq C|z|^{-n/2}(1+|\tau|^2)^{n/4}\exp\bigg(-c\frac{|x-y|^2}{|z|(1+|\tau|^2)^{1/2}}\bigg). \end{align} $$
$$ \begin{align} |p_{z}(x,y)|\leq C|z|^{-n/2}(1+|\tau|^2)^{n/4}\exp\bigg(-c\frac{|x-y|^2}{|z|(1+|\tau|^2)^{1/2}}\bigg). \end{align} $$
Let
![]() $r=t^{-1}(1+|\tau |^2)^{1/2}$
,
$r=t^{-1}(1+|\tau |^2)^{1/2}$
,
![]() $U_0(B)=B(x,r)$
,
$U_0(B)=B(x,r)$
,
![]() $U_k(B)=2^{k}B-2^{k-1}B$
for
$U_k(B)=2^{k}B-2^{k-1}B$
for
![]() $k\geq 1$
. By Inequality (2-4),
$k\geq 1$
. By Inequality (2-4),
 $$ \begin{align} \int_{\mathbb{R}^n}|p_{z}(x,y)(b(x)-b(y))f(y)|\,dy &\leq C\sum_{k\geq 0}\frac{\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}r^n}\int_{U_k(B)}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}|2^kB|}\int_{2^{k}B}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}} M_b(f)(x)\nonumber \\ &\leq C(1+|\tau|^2)^{n/2}M_b(f)(x). \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n}|p_{z}(x,y)(b(x)-b(y))f(y)|\,dy &\leq C\sum_{k\geq 0}\frac{\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}r^n}\int_{U_k(B)}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}|2^kB|}\int_{2^{k}B}|b(x)-b(y)||f(y)|\,dy\nonumber \\ &\leq C\sum_{k\geq 0}\frac{2^{kn}\exp(-c2^{2k})}{(1+|\tau|^2)^{-n/2}} M_b(f)(x)\nonumber \\ &\leq C(1+|\tau|^2)^{n/2}M_b(f)(x). \end{align} $$
Note that supp
![]() $\varphi \subseteq \mathbb {R}^{+}$
and
$\varphi \subseteq \mathbb {R}^{+}$
and
![]() $\|\varphi \|_{W^2_{n+1/2+\varepsilon }}\approx \|G\|_{W^2_{n+1/2+\varepsilon }} $
. This, in combination with Inequalities (2-3) and (2-5), implies that
$\|\varphi \|_{W^2_{n+1/2+\varepsilon }}\approx \|G\|_{W^2_{n+1/2+\varepsilon }} $
. This, in combination with Inequalities (2-3) and (2-5), implies that
Finally, the
![]() $L^p(\mathbb {R}^n,w)$
of
$L^p(\mathbb {R}^n,w)$
of
![]() $\sup _{t>0}|[b,\varphi (t^{-2}H)]f|$
follows by Inequality (2-6) and Lemma 2.3.
$\sup _{t>0}|[b,\varphi (t^{-2}H)]f|$
follows by Inequality (2-6) and Lemma 2.3.
Lemma 2.5. Let
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
,
$b\in \mathrm {BMO}(\mathbb {R}^n)$
,
![]() $s>n/2$
and let
$s>n/2$
and let
![]() $r_0=\max \{1,n/s\}$
. Then for all Borel functions F such that
$r_0=\max \{1,n/s\}$
. Then for all Borel functions F such that
![]() $\sup _{R>0}\|\eta F(R\cdot )\|_{W_s^{\infty }}<\infty $
where
$\sup _{R>0}\|\eta F(R\cdot )\|_{W_s^{\infty }}<\infty $
where
![]() $\eta \in C_c^{\infty }(0,\infty )$
is a fixed function and not identically zero, the commutator
$\eta \in C_c^{\infty }(0,\infty )$
is a fixed function and not identically zero, the commutator
![]() $[b,F(\!\sqrt {H})]$
is bounded on
$[b,F(\!\sqrt {H})]$
is bounded on
![]() $L^p(\mathbb {R}^n,w)$
for all
$L^p(\mathbb {R}^n,w)$
for all
![]() $r_0<p<\infty $
and
$r_0<p<\infty $
and
![]() $w\in A_{p/{r_0}}$
. In addition,
$w\in A_{p/{r_0}}$
. In addition,
Proof. The Hermite operator has a Gaussian upper bound, and thus it satisfies the condition of [Reference Bui3, Theorem 1.1], which gives this lemma. See also [Reference Duong, Sikora and Yan11, Theorem 3.2].
Lemma 2.6. Let
![]() $\varphi \in C_c^{\infty }(\mathbb {R})$
be a nonzero function with support
$\varphi \in C_c^{\infty }(\mathbb {R})$
be a nonzero function with support
![]() $\{u:1\leq |u|\leq 3\}$
. For
$\{u:1\leq |u|\leq 3\}$
. For
![]() $-n<\alpha <n$
,
$-n<\alpha <n$
,
 $$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|\varphi(2^{-k}\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|\varphi(2^{-k}\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align} $$
and for any
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
,
$b\in \mathrm {BMO}(\mathbb {R}^n)$
,
 $$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|[b,\varphi(2^{-k}\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^n} \sum_{k\in\mathbb{Z}}|[b,\varphi(2^{-k}\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha} \,dx\leq C \|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx. \end{align} $$
Proof. For the proof of Inequality (2-7), we refer to [Reference Chen, Duong, He, Lee and Yan4, Proposition 2.7]. We show the proof of the estimate in Inequality (2-8) for completeness, although the proof is rather standard. Indeed, let
![]() $r_k(t)$
be the Rademacher functions and
$r_k(t)$
be the Rademacher functions and
![]() $\varphi _k(\lambda )=\varphi (2^{-k}\lambda )$
. Define a function
$\varphi _k(\lambda )=\varphi (2^{-k}\lambda )$
. Define a function
By the properties of Rademacher functions,
 $$ \begin{align*} \sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2 &\leq C\int_{0}^{1}\bigg|\sum_{k\in\mathbb{Z}}r_k(t)[b,\varphi_k(\!\sqrt{H})]f(x)\bigg|^2\,dt\\ &=C \int_{0}^{1}|[b,F(t,\!\sqrt{H})]f(x)|^2\,dt. \end{align*} $$
$$ \begin{align*} \sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2 &\leq C\int_{0}^{1}\bigg|\sum_{k\in\mathbb{Z}}r_k(t)[b,\varphi_k(\!\sqrt{H})]f(x)\bigg|^2\,dt\\ &=C \int_{0}^{1}|[b,F(t,\!\sqrt{H})]f(x)|^2\,dt. \end{align*} $$
Integrating in x with weight
![]() $(1+|x|)^{-\alpha }$
,
$(1+|x|)^{-\alpha }$
,
 $$ \begin{align*} \int_{\mathbb{R}^n}\sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\leq C\int_{0}^{1}\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\,dt. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^n}\sum_{k\in\mathbb{Z}}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\leq C\int_{0}^{1}\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\,dt. \end{align*} $$
Let
![]() $\eta \in C_c^\infty (\mathbb {R^+})$
. It is easy to obtain that
$\eta \in C_c^\infty (\mathbb {R^+})$
. It is easy to obtain that
![]() $\sup _{R>0}\|\eta F(t,R\cdot )\|_{W^\infty _{s}(\mathbb {R})}<\infty $
for
$\sup _{R>0}\|\eta F(t,R\cdot )\|_{W^\infty _{s}(\mathbb {R})}<\infty $
for
![]() $s>n/2$
. It follows by Lemma 2.5 and
$s>n/2$
. It follows by Lemma 2.5 and
![]() $(1+|x|)^{-\alpha }\in A_2$
whenever
$(1+|x|)^{-\alpha }\in A_2$
whenever
![]() $-n<\alpha <n$
that
$-n<\alpha <n$
that
 $$ \begin{align*} &\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\sup_{R>0}\|\eta F(t,R\cdot)\|_{W^\infty_{s}(\mathbb{R})}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}^n}|[b,F(t,\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\sup_{R>0}\|\eta F(t,R\cdot)\|_{W^\infty_{s}(\mathbb{R})}^2\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx\\ &\quad\leq C\|b\|^2_{\mathrm{BMO}}\int_{\mathbb{R}^n} |f(x)|^2(1+|x|)^{-\alpha} \,dx, \end{align*} $$
with C uniformly in
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
3. A weighted estimate for the square function
In this section, we show the following weighted
![]() $L^2$
estimates for the square function
$L^2$
estimates for the square function
![]() $ G_{b,\delta }$
, which is defined by
$ G_{b,\delta }$
, which is defined by
 $$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg| \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$
$$ \begin{align*} G_{b,\delta}(f)(x):=\bigg(\int_{0}^{\infty}\bigg| \bigg[b,\phi\bigg(\delta^{-1}\bigg( 1- {H\over t^2}\bigg) \bigg) \bigg] f(x)\bigg |^2\frac{dt}{t}\bigg)^{1/2}, \end{align*} $$
where
![]() $\phi \in C_c^\infty (\mathbb {R})$
with support
$\phi \in C_c^\infty (\mathbb {R})$
with support
![]() $\{x:1/8\leq |x| \leq 1/2\}$
and
$\{x:1/8\leq |x| \leq 1/2\}$
and
![]() $|\phi |\leq 1.$
$|\phi |\leq 1.$
Proposition 3.1. Let
![]() $0\leq \alpha <n$
,
$0\leq \alpha <n$
,
![]() $0<\delta < 1/2$
. Assume
$0<\delta < 1/2$
. Assume
![]() $b\in \mathrm {BMO}(\mathbb {R}^n)$
. Then for any
$b\in \mathrm {BMO}(\mathbb {R}^n)$
. Then for any
![]() $0<\upsilon \leq 1/2$
, there exists a constant
$0<\upsilon \leq 1/2$
, there exists a constant
![]() $C_{\alpha ,\upsilon }>0$
independent of
$C_{\alpha ,\upsilon }>0$
independent of
![]() $\delta $
such that
$\delta $
such that
where
 $$ \begin{align*} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mbox{{if} } 0< \alpha< 1, n=1; \alpha=0,\ n\geq 1,\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mbox{{if} } 1<\alpha <n, n\geq2. \end{cases} \end{align*} $$
$$ \begin{align*} B^{\upsilon}_{\alpha,n}(\delta)= \begin{cases} \delta^{1-\upsilon} & \mbox{{if} } 0< \alpha< 1, n=1; \alpha=0,\ n\geq 1,\\[4pt] \delta^{({3-\alpha})/{2}-\upsilon} & \mbox{{if} } 1<\alpha <n, n\geq2. \end{cases} \end{align*} $$
We select an even function
![]() $\eta \in C_c^{\infty }(\mathbb {R})$
supported in
$\eta \in C_c^{\infty }(\mathbb {R})$
supported in
![]() $\{u:1/2\leq |u|\leq 2\}$
such that
$\{u:1/2\leq |u|\leq 2\}$
such that
![]() $\sum _{j\in \mathbb {Z}}\eta (2^{-j}u)=1\text { for all }\ u>0.$
Given
$\sum _{j\in \mathbb {Z}}\eta (2^{-j}u)=1\text { for all }\ u>0.$
Given
![]() $0<\delta <1/2$
, let
$0<\delta <1/2$
, let
![]() $j_0=[-\log _2\delta ]-1$
. Set
$j_0=[-\log _2\delta ]-1$
. Set
![]() $\eta _j(u)=\eta (2^{-j}u)$
for
$\eta _j(u)=\eta (2^{-j}u)$
for
![]() $j>j_0$
and
$j>j_0$
and
![]() $\eta _{j_0}(u)=1-\sum _{j\geq j_0+1}\eta (2^{-j}u)$
, then we have
$\eta _{j_0}(u)=1-\sum _{j\geq j_0+1}\eta (2^{-j}u)$
, then we have
![]() $\sum _{j\geq j_0}\eta _j (u)\equiv 1 \text {for all } u>0.$
Let us use
$\sum _{j\geq j_0}\eta _j (u)\equiv 1 \text {for all } u>0.$
Let us use
![]() $\phi _{\delta }(s)$
to denote
$\phi _{\delta }(s)$
to denote
![]() $\phi (\delta ^{-1}(1-s^2))$
. For
$\phi (\delta ^{-1}(1-s^2))$
. For
![]() $j\geq j_0$
, we define
$j\geq j_0$
, we define
Following from the dyadic decomposition,
 $$ \begin{align} \phi_{\delta}(t^{-1}s)=\sum_{j\geq j_0}\phi_{\delta,j}(t^{-1}s). \end{align} $$
$$ \begin{align} \phi_{\delta}(t^{-1}s)=\sum_{j\geq j_0}\phi_{\delta,j}(t^{-1}s). \end{align} $$
The following is a useful estimate throughout the paper. For any
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $j\geq j_0$
,
$j\geq j_0$
,
 $$ \begin{align} |\phi_{\delta,j}(s)|\leq \begin{cases} C_N2^{(j_0-j)N} & \mbox{if } |s|\in[1-2\delta,1+2\delta],\\ C_N 2^{j-j_0}(1+2^j|\,s-1|)^{-N} & \mbox{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} |\phi_{\delta,j}(s)|\leq \begin{cases} C_N2^{(j_0-j)N} & \mbox{if } |s|\in[1-2\delta,1+2\delta],\\ C_N 2^{j-j_0}(1+2^j|\,s-1|)^{-N} & \mbox{otherwise}. \end{cases} \end{align} $$
See [Reference Chen, Duong, He, Lee and Yan4, page 23, Equation (3.16)] for the proof.
To prove Proposition 3.1, we need the following lemmas.
Lemma 3.2. Let
![]() $0\leq \alpha <n$
,
$0\leq \alpha <n$
,
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $j\geq j_0$
. We define an operator associated with
$j\geq j_0$
. We define an operator associated with
![]() $\phi _{\delta ,j}$
by
$\phi _{\delta ,j}$
by
 $$ \begin{align*}T_{j,k}^{\delta}(f):=\bigg(\int_{2^{k-1}}^{2^{k+2}} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})f|^2\frac{dt}{t}\bigg)^{1/2}.\end{align*} $$
$$ \begin{align*}T_{j,k}^{\delta}(f):=\bigg(\int_{2^{k-1}}^{2^{k+2}} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})f|^2\frac{dt}{t}\bigg)^{1/2}.\end{align*} $$
Then for any
![]() $0<\varepsilon \leq 1/2$
and
$0<\varepsilon \leq 1/2$
and
![]() $N\in \mathbb {N}$
, there exists a constant
$N\in \mathbb {N}$
, there exists a constant
![]() $C_{\varepsilon ,N}$
such that
$C_{\varepsilon ,N}$
such that
where
 $$ \begin{align} A^{\varepsilon}_{n}(\delta,\alpha):= \begin{cases} \delta& \mbox{{if} } \alpha=0, n\geq 1,\\ \delta^{1-\varepsilon} & \mbox{{if} } 0<\alpha<1 , n=1,\\ \delta^{({3-\alpha})/{2}} & \mbox{{if} } 1< \alpha<n, n\geq2. \end{cases} \end{align} $$
$$ \begin{align} A^{\varepsilon}_{n}(\delta,\alpha):= \begin{cases} \delta& \mbox{{if} } \alpha=0, n\geq 1,\\ \delta^{1-\varepsilon} & \mbox{{if} } 0<\alpha<1 , n=1,\\ \delta^{({3-\alpha})/{2}} & \mbox{{if} } 1< \alpha<n, n\geq2. \end{cases} \end{align} $$
Lemma 3.3. Let
![]() $T_{j,k}^{\delta }$
be defined as in Lemma 3.2 and
$T_{j,k}^{\delta }$
be defined as in Lemma 3.2 and
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $0\leq \alpha < n$
,
$0\leq \alpha < n$
,
![]() $j\geq j_0$
. Then for any
$j\geq j_0$
. Then for any
![]() $0<\varepsilon \leq 1/2$
and
$0<\varepsilon \leq 1/2$
and
![]() $N\in \mathbb {N}$
, there exists a constant
$N\in \mathbb {N}$
, there exists a constant
![]() $C_{\varepsilon ,N}$
such that
$C_{\varepsilon ,N}$
such that
where
![]() $\theta =2/r$
,
$\theta =2/r$
,
![]() $2< r<\infty $
.
$2< r<\infty $
.
Now, we prove Proposition 3.1 using Lemmas 3.2 and 3.3, whose proofs are given later.
Proof of Proposition 3.1
The facts that the eigenvalue of the Hermite operator is bigger than
![]() $1$
and supp
$1$
and supp
![]() $\,\phi \subseteq \{x:1/8\leq |x|\leq 1/2\}$
imply that
$\,\phi \subseteq \{x:1/8\leq |x|\leq 1/2\}$
imply that
 $$ \begin{align*} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{{d}t}{t}\\ &\quad= \int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
$$ \begin{align*} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{{d}t}{t}\\ &\quad= \int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
Choose a function
![]() $\varphi $
with support
$\varphi $
with support
![]() $\{s:1\leq |s|\leq 3\}$
and
$\{s:1\leq |s|\leq 3\}$
and
![]() $\sum _{k\in \mathbb {Z}}\varphi (2^{-k}s)=1\text { for all } s\,{>}\,0$
. Let
$\sum _{k\in \mathbb {Z}}\varphi (2^{-k}s)=1\text { for all } s\,{>}\,0$
. Let
![]() $\varphi _k(s)=\varphi (2^{-k}s)$
. There is a uniform bound C for any
$\varphi _k(s)=\varphi (2^{-k}s)$
. There is a uniform bound C for any
![]() $t\in [1/2,\infty )$
such that
$t\in [1/2,\infty )$
such that
![]() $\#\{k\in \mathbb {Z}:\phi _{\delta }(t^{-1}s)\varphi _k(s)\neq 0,s>0\}\leq C$
, where
$\#\{k\in \mathbb {Z}:\phi _{\delta }(t^{-1}s)\varphi _k(s)\neq 0,s>0\}\leq C$
, where
![]() $\#$
is the counting measure. Hence,
$\#$
is the counting measure. Hence,
 $$ \begin{align*} &\int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C\sum_{k\in\mathbb{Z}}\int_{1/2}^{\infty}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=C\sum_{k\geq0}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$
$$ \begin{align*} &\int_{1/2}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C\sum_{k\in\mathbb{Z}}\int_{1/2}^{\infty}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=C\sum_{k\geq0}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$
where in the last equality, we use the support property of
![]() $\phi _{\delta }(t^{-1}s)$
and
$\phi _{\delta }(t^{-1}s)$
and
![]() $\varphi _k(s)$
.
$\varphi _k(s)$
.
Note that
It follows that
 $$ \begin{align} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C\bigg(\sum_{k\geq0}I_1(k)+\sum_{k\geq0}I_2(k)\bigg), \end{align} $$
$$ \begin{align} &\int_{0}^{+\infty}\int_{\mathbb{R}^n} |[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C\bigg(\sum_{k\geq0}I_1(k)+\sum_{k\geq0}I_2(k)\bigg), \end{align} $$
where
 $$ \begin{align*} I_1(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$
$$ \begin{align*} I_1(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}, \end{align*} $$
 $$ \begin{align*} I_2(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
$$ \begin{align*} I_2(k):=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
For the first term
![]() $I_1(k)$
, it follows by Inequality (3-1) and Minkowski’s inequality that
$I_1(k)$
, it follows by Inequality (3-1) and Minkowski’s inequality that
 $$ \begin{align*} I_1(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$
$$ \begin{align*} I_1(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\phi_{\delta,j}(t^{-1}\!\sqrt{H})[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$
By Lemma 3.2,
 $$ \begin{align*} I_1(k) & \leq C_{\varepsilon,N}\bigg(\sum_{j\geq j_0}2^{(j_0-j)N}\bigg)^2A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\\ &\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} I_1(k) & \leq C_{\varepsilon,N}\bigg(\sum_{j\geq j_0}2^{(j_0-j)N}\bigg)^2A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx\\ &\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|[b,\varphi_k(\!\sqrt{H})]f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
Then taking the sum over k and using Inequality (2-8) in Lemma 2.6 gives
 $$ \begin{align} \sum_{k\geq0}I_1(k)\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$
$$ \begin{align} \sum_{k\geq0}I_1(k)\leq C_{\varepsilon}A^{\varepsilon}_{n}(\delta,\alpha) \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$
For the second term
![]() $I_2(k)$
, it follows by Inequality (3-1) and Minkowski’s inequality that
$I_2(k)$
, it follows by Inequality (3-1) and Minkowski’s inequality that
 $$ \begin{align*} I_2(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$
$$ \begin{align*} I_2(k) &\leq \bigg(\sum_{j\geq j_0}\bigg( \int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \bigg)^{1/2} \bigg)^2. \end{align*} $$
We decompose
![]() $\mathbb {R}^n$
into disjoint cubes with side length
$\mathbb {R}^n$
into disjoint cubes with side length
![]() $2^{j-k+2}$
. For a given
$2^{j-k+2}$
. For a given
![]() ${\mathbf {m}=(\mathbf {m}_1,\ldots ,\mathbf {m}_n)\in \mathbb {Z}^n}$
, we define an associated cube by
${\mathbf {m}=(\mathbf {m}_1,\ldots ,\mathbf {m}_n)\in \mathbb {Z}^n}$
, we define an associated cube by
 $$ \begin{align*} Q_{\mathbf{m}}&=[2^{j-k+2}(\mathbf{m}_1-1/2),2^{j-k+2}(\mathbf{m}_1+1/2))\\ &\quad\times\cdots\times[2^{j-k+2}(\mathbf{m}_n-1/2),2^{j-k+2}(\mathbf{m}_n+1/2)). \end{align*} $$
$$ \begin{align*} Q_{\mathbf{m}}&=[2^{j-k+2}(\mathbf{m}_1-1/2),2^{j-k+2}(\mathbf{m}_1+1/2))\\ &\quad\times\cdots\times[2^{j-k+2}(\mathbf{m}_n-1/2),2^{j-k+2}(\mathbf{m}_n+1/2)). \end{align*} $$
Clearly,
![]() $Q_{\mathbf {m}}$
is a cube with centre
$Q_{\mathbf {m}}$
is a cube with centre
![]() $2^{j-k+2}(\mathbf {m}_1,\ldots ,\mathbf {m}_n)$
and side length
$2^{j-k+2}(\mathbf {m}_1,\ldots ,\mathbf {m}_n)$
and side length
![]() $2^{j-k+2}$
. Here,
$2^{j-k+2}$
. Here,
![]() $\{Q_{\mathbf {m}}\}$
are disjoint and
$\{Q_{\mathbf {m}}\}$
are disjoint and
![]() $\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}.$
For each
$\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}.$
For each
![]() $\mathbf {m}\in \mathbb {Z}^n$
, we define
$\mathbf {m}\in \mathbb {Z}^n$
, we define
![]() $\widetilde {Q}_{\mathbf {m}}$
by
$\widetilde {Q}_{\mathbf {m}}$
by
 $$ \begin{align*}\widetilde{Q}_{\mathbf{m}} :=\bigcup_{\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq\sqrt{n}2^{j-k+3}}Q_{\mathbf{m}'}.\end{align*} $$
$$ \begin{align*}\widetilde{Q}_{\mathbf{m}} :=\bigcup_{\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq\sqrt{n}2^{j-k+3}}Q_{\mathbf{m}'}.\end{align*} $$
If
![]() $t\in [2^{k-1},2^{k+2}]$
, supp
$t\in [2^{k-1},2^{k+2}]$
, supp
![]() $\widehat {\phi _{\delta ,j}(t^{-1}}\cdot )\subseteq [-2^{j-k+2},2^{j-k+2}]$
. By finite speed of propagation in Display (FS),
$\widehat {\phi _{\delta ,j}(t^{-1}}\cdot )\subseteq [-2^{j-k+2},2^{j-k+2}]$
. By finite speed of propagation in Display (FS),
![]() $K_{\phi _{\delta ,j}(t^{-1}\!\sqrt {H})}\subseteq \mathfrak {D}_{2^{j-k+2}}$
. It follows that for any
$K_{\phi _{\delta ,j}(t^{-1}\!\sqrt {H})}\subseteq \mathfrak {D}_{2^{j-k+2}}$
. It follows that for any
![]() $t\in [2^{k-1},2^{k+2}]$
,
$t\in [2^{k-1},2^{k+2}]$
,
 $$ \begin{align} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]g| &=\bigg|\sum_{\mathbf{m},\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq \sqrt{n}2^{j-k+3}} \chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{Q_{\mathbf{m'}}}g\bigg|\nonumber\\[4pt] &\leq \sum_{\mathbf{m}\in \mathbb{Z}^n} |\kern1.2pt\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{\widetilde{Q}_{\mathbf{m}}}g|, \end{align} $$
$$ \begin{align} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]g| &=\bigg|\sum_{\mathbf{m},\mathbf{m}'\in \mathbb{Z}^n:\mathrm{dist}(Q_{\mathbf{m}},Q_{\mathbf{m}'})\leq \sqrt{n}2^{j-k+3}} \chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{Q_{\mathbf{m'}}}g\bigg|\nonumber\\[4pt] &\leq \sum_{\mathbf{m}\in \mathbb{Z}^n} |\kern1.2pt\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\chi_{\widetilde{Q}_{\mathbf{m}}}g|, \end{align} $$
where as usual
![]() $\chi _{Q_{\mathbf {m}}}$
is the characteristic function of
$\chi _{Q_{\mathbf {m}}}$
is the characteristic function of
![]() $Q_{\mathbf {m}}$
.
$Q_{\mathbf {m}}$
.
Let
![]() $b_{\widetilde {Q}_{\mathbf {m}}}=|\widetilde {Q}_{\mathbf {m}}|^{-1}\int _{\widetilde {Q}_{\mathbf {m}}}b(y)\;dy$
. Obviously,
$b_{\widetilde {Q}_{\mathbf {m}}}=|\widetilde {Q}_{\mathbf {m}}|^{-1}\int _{\widetilde {Q}_{\mathbf {m}}}b(y)\;dy$
. Obviously,
It follows from Inequalities (3-6), (3-7) and the disjointness of
![]() ${Q}_{\mathbf {m}}$
that
${Q}_{\mathbf {m}}$
that
 $$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=\sum_{\mathbf{m}\in \mathbb{Z}^n}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})] \chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad\leq C\sum_{\mathbf{m}\in \mathbb{Z}^n}\Big(E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\Big), \end{align*} $$
$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})]\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad=\sum_{\mathbf{m}\in \mathbb{Z}^n}\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}[b,\phi_{\delta,j}(t^{-1}\!\sqrt{H})] \chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\ &\quad\leq C\sum_{\mathbf{m}\in \mathbb{Z}^n}\Big(E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\Big), \end{align*} $$
where
 $$ \begin{align*} E^{1}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}(b-b_{\widetilde{Q}_{\mathbf{m}}})\phi_{\delta,j}(t^{-1}\!\sqrt{H})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t},\\ E^{2}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}\phi_{\delta,j}(t^{-1}\!\sqrt{H})(b-b_{\widetilde{Q}_{\mathbf{m}}})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
$$ \begin{align*} E^{1}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}(b-b_{\widetilde{Q}_{\mathbf{m}}})\phi_{\delta,j}(t^{-1}\!\sqrt{H})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t},\\ E^{2}_{j,k,\mathbf{m}}&:=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n} |\chi_{Q_{\mathbf{m}}}\phi_{\delta,j}(t^{-1}\!\sqrt{H})(b-b_{\widetilde{Q}_{\mathbf{m}}})\chi_{\widetilde{Q}_{\mathbf{m}}} \varphi_k(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
We select r and q such that
![]() $1/2=1/q+1/r$
and
$1/2=1/q+1/r$
and
![]() $\alpha r/2<n$
so that we can use Lemma 3.3. By Hölder’s inequality,
$\alpha r/2<n$
so that we can use Lemma 3.3. By Hölder’s inequality,
 $$ \begin{align} E^{1}_{j,k,\mathbf{m}}&\leq \|b-b_{\widetilde{Q}_{\mathbf{m}}}\|_{L^{q}(\widetilde{Q}_{\mathbf{m}})}^2 \bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r}. \end{align} $$
$$ \begin{align} E^{1}_{j,k,\mathbf{m}}&\leq \|b-b_{\widetilde{Q}_{\mathbf{m}}}\|_{L^{q}(\widetilde{Q}_{\mathbf{m}})}^2 \bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r}. \end{align} $$
By Lemma 3.3 and Hölder’s inequality again,
 $$ \begin{align*} &\bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r} \nonumber\\ &\quad \leq {} C_{\varepsilon,N} 2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} \bigg(\!\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{r'}(1+|x|)^{-\alpha r'/2}\,dx\bigg)^{2/{r'}}\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} |\widetilde{Q}_{\mathbf{m}}|^{2/q} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} &\bigg(\!\int_{\mathbb{R}^n}|T_{j,k}^{\delta}(\chi_{\widetilde{Q}_{\mathbf{m}}}\varphi_k(\!\sqrt{H})f)(x)|^r(1+|x|)^{-\alpha r/2}\,dx\bigg)^{2/r} \nonumber\\ &\quad \leq {} C_{\varepsilon,N} 2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} \bigg(\!\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{r'}(1+|x|)^{-\alpha r'/2}\,dx\bigg)^{2/{r'}}\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N} A_n^\varepsilon(\delta,r\alpha/2)^{2/r}2^{2kn(1-2/r)} |\widetilde{Q}_{\mathbf{m}}|^{2/q} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
By John–Nirenberg’s inequality,
Recall that
![]() $\widetilde {Q}_{\mathbf {m}}$
is contained in a ball with diameter
$\widetilde {Q}_{\mathbf {m}}$
is contained in a ball with diameter
![]() $5\sqrt {n}\cdot 2^{j-k+2}$
and
$5\sqrt {n}\cdot 2^{j-k+2}$
and
![]() $2^{j_0}\approx \delta ^{-1}$
. In combination with the estimates in Inequalities (3-8)–(3-9) and
$2^{j_0}\approx \delta ^{-1}$
. In combination with the estimates in Inequalities (3-8)–(3-9) and
![]() $2/q=1-2/r$
,
$2/q=1-2/r$
,
 $$ \begin{align*} E^{1}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} E^{1}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
Similarly, by Hölder’s inequality, Lemma 3.3 and John–Nirenberg’s inequality,
 $$ \begin{align*} E^{2}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} E^{2}_{j,k,\mathbf{m}}\leq C_{\varepsilon,r,N}\|b\|_{\mathrm{BMO}}^22^{2(j_0-j)(N-n(1-2/r))} \delta^{-2n(1-2/r)}A_n^\varepsilon(\delta,r\alpha/2)^{2/r} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align*} $$
Case 1.
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1<\alpha <n$
.
$1<\alpha <n$
.
For any
![]() $0<\upsilon \leq 1/2$
and
$0<\upsilon \leq 1/2$
and
![]() $1<\alpha <n$
, we choose r such that
$1<\alpha <n$
, we choose r such that
See Inequality (3-3) for the definition of
![]() $A_n^\varepsilon (\delta ,r\alpha /2)$
. By calculation,
$A_n^\varepsilon (\delta ,r\alpha /2)$
. By calculation,
then there exists a constant
![]() $C_1=C_{\alpha ,\upsilon ,N}$
such that
$C_1=C_{\alpha ,\upsilon ,N}$
such that
 $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}&\leq C_1\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{({3-\alpha})/{2}-\upsilon}\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$
$$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}&\leq C_1\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{({3-\alpha})/{2}-\upsilon}\int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$
Case 2.
![]() $n=1$
and
$n=1$
and
![]() $0<\alpha <1$
.
$0<\alpha <1$
.
For any small
![]() $0<\varepsilon \leq 1/4$
and
$0<\varepsilon \leq 1/4$
and
![]() $0<\upsilon '\leq 1/4$
, we choose r such that
$0<\upsilon '\leq 1/4$
, we choose r such that
![]() $2<r<\min \{2/\alpha ,2(3-\varepsilon )/(3-\varepsilon -\upsilon ')\}.$
By calculation,
$2<r<\min \{2/\alpha ,2(3-\varepsilon )/(3-\varepsilon -\upsilon ')\}.$
By calculation,
where
![]() $0<\upsilon \leq 1/2$
. Then there exists a constant
$0<\upsilon \leq 1/2$
. Then there exists a constant
![]() $C_2=C_{\alpha ,\upsilon ,N}$
such that
$C_2=C_{\alpha ,\upsilon ,N}$
such that
 $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}} &\leq C_2\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$
$$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}} &\leq C_2\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx. \end{align} $$
Case 3.
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\alpha =0$
.
$\alpha =0$
.
For any small
![]() $0<\upsilon \leq 1/2$
, we just need to select the r such that
$0<\upsilon \leq 1/2$
, we just need to select the r such that
![]() $2<r<2 (2n+1)/ (2n+1-\upsilon )$
. Then there exists a constant
$2<r<2 (2n+1)/ (2n+1-\upsilon )$
. Then there exists a constant
![]() $C_3=C_{0,\upsilon ,N}$
such that
$C_3=C_{0,\upsilon ,N}$
such that
 $$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\leq C_{3}\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}\,dx. \end{align} $$
$$ \begin{align} E^{1}_{j,k,\mathbf{m}}+E^{2}_{j,k,\mathbf{m}}\leq C_{3}\|b\|_{\mathrm{BMO}}^2 2^{2(j_0-j)(N-n(1-2/r))} \delta^{1-\upsilon} \int_{\widetilde{Q}_{\mathbf{m}}}|\varphi_k(\!\sqrt{H})f(x)|^{2}\,dx. \end{align} $$
Next we sum up the terms
![]() $E^{1}_{j,k,\mathbf {m}}+E^{2}_{j,k,\mathbf {m}}$
over j and
$E^{1}_{j,k,\mathbf {m}}+E^{2}_{j,k,\mathbf {m}}$
over j and
![]() $\mathbf {m}$
. Combining the estimates in Inequalities (3-10), (3-11) and (3-12), choosing N such that
$\mathbf {m}$
. Combining the estimates in Inequalities (3-10), (3-11) and (3-12), choosing N such that
![]() $N>n(1-2/r)$
, and using the fact that
$N>n(1-2/r)$
, and using the fact that
![]() $\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}$
and
$\mathbb {R}^n=\bigcup _{\mathbf {m}\in \mathbb {Z}^n}Q_{\mathbf {m}}$
and
![]() $\{\widetilde {Q}_{\mathbf {m}}\}$
has finite overlaps, then we obtain that there exists a constant
$\{\widetilde {Q}_{\mathbf {m}}\}$
has finite overlaps, then we obtain that there exists a constant
![]() $C_{\alpha ,\upsilon }$
such that
$C_{\alpha ,\upsilon }$
such that
 $$ \begin{align} I_2(k) &\leq C_4 B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \bigg(\sum_{j\geq j_0}\bigg(\sum_{m\in \mathbb{Z}^n} \kern-1.2pt\int_{\widetilde{Q}_m}\!|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\kern-0.2pt\bigg)^{\kern-1pt 1/2}\kern-0.5pt 2^{(j_0-j)(N-n(1-2/r))} \bigg)^{\kern-1pt2} \nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$
$$ \begin{align} I_2(k) &\leq C_4 B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \bigg(\sum_{j\geq j_0}\bigg(\sum_{m\in \mathbb{Z}^n} \kern-1.2pt\int_{\widetilde{Q}_m}\!|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\kern-0.2pt\bigg)^{\kern-1pt 1/2}\kern-0.5pt 2^{(j_0-j)(N-n(1-2/r))} \bigg)^{\kern-1pt2} \nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$
where
![]() $B^{\upsilon }_{\alpha ,n}(\delta )$
is defined in Equation (1-2) and
$B^{\upsilon }_{\alpha ,n}(\delta )$
is defined in Equation (1-2) and
![]() $C_4=C_1+C_2+C_3$
.
$C_4=C_1+C_2+C_3$
.
Finally, summing up the terms
![]() $I_2(k)$
over k in the estimate in Inequality (3-13) and using the estimate in Inequality (2-7) in Lemma 2.6,
$I_2(k)$
over k in the estimate in Inequality (3-13) and using the estimate in Inequality (2-7) in Lemma 2.6,
 $$ \begin{align} \sum_{k\geq0}I_2(k) &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \sum_{k\geq0}\int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n}|f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$
$$ \begin{align} \sum_{k\geq0}I_2(k) &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2 \sum_{k\geq0}\int_{\mathbb{R}^n}|\varphi_k(\!\sqrt{H})f(x)|^{2}(1+|x|)^{-\alpha}\,dx\nonumber\\ &\leq C_{\alpha,\upsilon}B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\int_{\mathbb{R}^n}|f(x)|^{2}(1+|x|)^{-\alpha}\,dx, \end{align} $$
where
![]() $n=1,0\leq \alpha <1$
;
$n=1,0\leq \alpha <1$
;
![]() $n\geq 2, 1< \alpha <n$
or
$n\geq 2, 1< \alpha <n$
or
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $\alpha =0$
.
$\alpha =0$
.
Combining the estimates in Inequalities (3-4), (3-5) and (3-14) and noting
![]() $A^{\upsilon }_{n}(\delta ,\alpha )<B^{\upsilon }_{\alpha ,n}(\delta )$
, we obtain that for any
$A^{\upsilon }_{n}(\delta ,\alpha )<B^{\upsilon }_{\alpha ,n}(\delta )$
, we obtain that for any
![]() $0<\upsilon \leq 1/2$
,
$0<\upsilon \leq 1/2$
,
 $$ \begin{align*} \int_{0}^{\infty}\!\!\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \leq C_{\alpha,\upsilon} B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\!\! \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\!\!\int_{\mathbb{R}^n}|[b,\phi_{\delta}(t^{-1}\!\sqrt{H})]f|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t} \leq C_{\alpha,\upsilon} B^{\upsilon}_{\alpha,n}(\delta)\|b\|_{\mathrm{BMO}}^2\!\! \int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align*} $$
Hence, we obtain Proposition 3.1 provided Lemmas 3.2 and 3.3 are proved.
Finally, let us prove Lemmas 3.2 and 3.3.
Proof of Lemma 3.2
We discuss this lemma by distinguishing two cases:
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $0<\alpha <n$
.
$0<\alpha <n$
.
Case 1.
![]() $\alpha =0$
.
$\alpha =0$
.
Pick a function
![]() $\psi \kern1.3pt{\in}\kern1.3pt C_c^{\infty }(\mathbb {R})$
with support
$\psi \kern1.3pt{\in}\kern1.3pt C_c^{\infty }(\mathbb {R})$
with support
![]() $\{s:1\kern1.3pt{\leq}\kern1.3pt |s|\kern1.3pt{\leq}\kern1.3pt 4\}$
such that
$\{s:1\kern1.3pt{\leq}\kern1.3pt |s|\kern1.3pt{\leq}\kern1.3pt 4\}$
such that
![]() ${\sum _{\ell \in \mathbb {Z}} \psi (2^{-\ell }s)\kern1.3pt{=}\kern1.3pt1}$
for
${\sum _{\ell \in \mathbb {Z}} \psi (2^{-\ell }s)\kern1.3pt{=}\kern1.3pt1}$
for
![]() $ s>0.$
For any
$ s>0.$
For any
![]() $\delta>0$
, let
$\delta>0$
, let
![]() $\psi _{\delta ,\ell }(s)=\psi (2^{-\ell }\delta ^{-1}(1-s))$
for all
$\psi _{\delta ,\ell }(s)=\psi (2^{-\ell }\delta ^{-1}(1-s))$
for all
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $\psi _{\delta ,0}(s)=\psi _0(\delta ^{-1}(1-s))$
, where
$\psi _{\delta ,0}(s)=\psi _0(\delta ^{-1}(1-s))$
, where
![]() $\psi _0(s)=1-\sum _{\ell \geq 1}\psi (2^{-\ell }s)$
. Then for
$\psi _0(s)=1-\sum _{\ell \geq 1}\psi (2^{-\ell }s)$
. Then for
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $j\geq j_0$
,
$j\geq j_0$
,
 $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0}P_{k,j,\ell}(f) ^{1/2}\bigg)^2, \end{align} $$
$$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0}P_{k,j,\ell}(f) ^{1/2}\bigg)^2, \end{align} $$
where
 $$ \begin{align*}P_{k,j,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f(x)|^2 \,dx\frac{dt}{t}.\end{align*} $$
$$ \begin{align*}P_{k,j,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f(x)|^2 \,dx\frac{dt}{t}.\end{align*} $$
Let
![]() $i=0,1,\ldots ,i_0=[8\delta ^{-1}]+1$
.
$i=0,1,\ldots ,i_0=[8\delta ^{-1}]+1$
.
![]() $I_i$
is defined by
$I_i$
is defined by
We decompose
![]() $[2^{k-1},2^{k+2}]$
into some intervals
$[2^{k-1},2^{k+2}]$
into some intervals
![]() $\{I_i\}$
with
$\{I_i\}$
with
![]() $[2^{k-1},2^{k+2}]\subseteq \bigcup _{i=0}^{i_0}I_i$
. We see that the
$[2^{k-1},2^{k+2}]\subseteq \bigcup _{i=0}^{i_0}I_i$
. We see that the
![]() $\,dt/t$
measure of
$\,dt/t$
measure of
![]() $I_i$
is less than
$I_i$
is less than
![]() $\delta $
. We also define a function
$\delta $
. We also define a function
![]() $\zeta _i$
associated with
$\zeta _i$
associated with
![]() $I_i$
by
$I_i$
by
 $$ \begin{align*}\zeta_i(s)=\zeta\bigg(i+\frac{2^{k-1}-s}{2^{k-1}\delta}\bigg),\end{align*} $$
$$ \begin{align*}\zeta_i(s)=\zeta\bigg(i+\frac{2^{k-1}-s}{2^{k-1}\delta}\bigg),\end{align*} $$
where
![]() $\zeta \in C_c^{\infty }([-1,1])$
and
$\zeta \in C_c^{\infty }([-1,1])$
and
![]() $\sum _{i\in \mathbb {Z}}\zeta (\cdot -i)=1$
. Since
$\sum _{i\in \mathbb {Z}}\zeta (\cdot -i)=1$
. Since
![]() $\psi _{\delta ,\ell }(t^{-1}s)\zeta _{i'}(s)= 0$
for every
$\psi _{\delta ,\ell }(t^{-1}s)\zeta _{i'}(s)= 0$
for every
![]() $t\in I_i$
if
$t\in I_i$
if
![]() $i'\notin [i-2^{\ell +6}, i+2^{\ell +6}]$
, then for any
$i'\notin [i-2^{\ell +6}, i+2^{\ell +6}]$
, then for any
![]() $t\in I_i$
,
$t\in I_i$
,
 $$ \begin{align} |(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f|^2 &=\bigg|\!\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\bigg|^2\nonumber\\ &\leq C2^{\ell}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f|^2. \end{align} $$
$$ \begin{align} |(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})f|^2 &=\bigg|\!\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\bigg|^2\nonumber\\ &\leq C2^{\ell}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f|^2. \end{align} $$
Then,
 $$ \begin{align} P_{k,j,\ell}(f)\leq C2^\ell\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}. \end{align} $$
$$ \begin{align} P_{k,j,\ell}(f)\leq C2^\ell\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}. \end{align} $$
From the estimate in Inequality (3-2) and supp
![]() $\psi _{\delta ,\ell }\subseteq [1-2^{\ell +2}\delta ,1+2^{\ell +2}\delta ], \,\text { for all} \ell \in \mathbb {Z}$
, the function
$\psi _{\delta ,\ell }\subseteq [1-2^{\ell +2}\delta ,1+2^{\ell +2}\delta ], \,\text { for all} \ell \in \mathbb {Z}$
, the function
![]() $\phi _{\delta ,j}\psi _{\delta ,\ell }$
satisfies
$\phi _{\delta ,j}\psi _{\delta ,\ell }$
satisfies
which, together with the
![]() $L^2$
-boundedness of the spectral multiplier, implies that
$L^2$
-boundedness of the spectral multiplier, implies that
 $$ \begin{align} \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}&\leq \|\phi_{\delta,j}\psi_{\delta,\ell}\|_{L^{\infty}(\mathbb{R})}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\leq C_N2^{-\ell N}2^{(j_0-j)N}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}&\leq \|\phi_{\delta,j}\psi_{\delta,\ell}\|_{L^{\infty}(\mathbb{R})}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\leq C_N2^{-\ell N}2^{(j_0-j)N}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}. \end{align} $$
Combining Inequality (3-19) with Inequality (3-17) and using Minkowski’s inequality,
 $$ \begin{align} \!\!\!\!P_{k,j,\ell}(f) &\leq C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i=0}^{i_0} \sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}\int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &= C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}. \end{align} $$
$$ \begin{align} \!\!\!\!P_{k,j,\ell}(f) &\leq C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i=0}^{i_0} \sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}}\int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &= C_N2^{-(2N-1)\ell}2^{2(j_0-j)N}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}. \end{align} $$
The decomposition of
![]() $[2^{k-2},2^{k+1}]$
into
$[2^{k-2},2^{k+1}]$
into
![]() $\{I_i\}_{i=0}^{i_0}$
makes sure that the
$\{I_i\}_{i=0}^{i_0}$
makes sure that the
![]() $\,dt/t$
measure of the interval
$\,dt/t$
measure of the interval
![]() $I_i$
is uniformly less than
$I_i$
is uniformly less than
![]() $\delta $
. Indeed,
$\delta $
. Indeed,
 $$ \begin{align*} \int_{2^{k-1}(1+i\delta)}^{2^{k-1}(1+(i+1)\delta)}1\ \frac{dt}{t}=\ln\bigg(1+\frac{\delta}{1+i\delta}\bigg)\leq \ln(1+\delta) \leq \delta. \end{align*} $$
$$ \begin{align*} \int_{2^{k-1}(1+i\delta)}^{2^{k-1}(1+(i+1)\delta)}1\ \frac{dt}{t}=\ln\bigg(1+\frac{\delta}{1+i\delta}\bigg)\leq \ln(1+\delta) \leq \delta. \end{align*} $$
It follows that
 $$ \begin{align} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t} &\leq \delta\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C2^{\ell}\delta \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} \sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t} &\leq \delta\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C2^{\ell}\delta \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
Combining Inequalities (3-20), (3-21) and using the
![]() $L^2$
-estimate of the square function for a Hermite operator gives
$L^2$
-estimate of the square function for a Hermite operator gives
 $$ \begin{align} P_{k,j,\ell}(f) &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\sum_{i'\in\mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} P_{k,j,\ell}(f) &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\sum_{i'\in\mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-(2N-2)\ell}2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
Combining Inequalities (3-15) and (3-22) and summing up the terms
![]() $P_{k,j,\ell }(f)$
over
$P_{k,j,\ell }(f)$
over
![]() $\ell $
gives
$\ell $
gives
 $$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$
$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$
Case 2.
![]() $0<\alpha <n$
. We discuss the estimate for two cases:
$0<\alpha <n$
. We discuss the estimate for two cases:
![]() $2^{k}\geq 2\delta ^{-1/2}$
and
$2^{k}\geq 2\delta ^{-1/2}$
and
![]() $1\leq 2^{k}<2\delta ^{-1/2}$
.
$1\leq 2^{k}<2\delta ^{-1/2}$
.
If
![]() $k\geq -\log _2\delta ^{1/2}+1$
, we use [Reference Chen, Duong, He, Lee and Yan4, Equations (3.38) and (3.39)] with f in place of
$k\geq -\log _2\delta ^{1/2}+1$
, we use [Reference Chen, Duong, He, Lee and Yan4, Equations (3.38) and (3.39)] with f in place of
![]() $\varphi _k(\!\sqrt {H})f$
to obtain
$\varphi _k(\!\sqrt {H})f$
to obtain
 $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C_N2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$
$$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\ &\quad\leq C_N2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx. \end{align} $$
The procedure is still valid if
![]() $\varphi _k(\!\sqrt {H})f$
in [Reference Chen, Duong, He, Lee and Yan4, Equations (3.38) and (3.39)] is replaced by f. This procedure rests on the trace lemma, the weighted Plancherel-type estimate in Inequality (2-2) and the localization strategy that is based on finite speed of propagation. Indeed, Inequality (2-2) gives the bound of spectral multipliers from
$\varphi _k(\!\sqrt {H})f$
in [Reference Chen, Duong, He, Lee and Yan4, Equations (3.38) and (3.39)] is replaced by f. This procedure rests on the trace lemma, the weighted Plancherel-type estimate in Inequality (2-2) and the localization strategy that is based on finite speed of propagation. Indeed, Inequality (2-2) gives the bound of spectral multipliers from
![]() $L^2(\mathbb {R}^n)$
to
$L^2(\mathbb {R}^n)$
to
![]() $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
. To come back to
$L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
. To come back to
![]() $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
, when the physical space is near
$L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
, when the physical space is near
![]() $\{x\in \mathbb {R}^n:|x|\leq 2^{j-k+2}\}$
, the previous procedure adds the weight
$\{x\in \mathbb {R}^n:|x|\leq 2^{j-k+2}\}$
, the previous procedure adds the weight
![]() $(1+|x|)^{-\alpha }$
into the integral, which would bring a factor
$(1+|x|)^{-\alpha }$
into the integral, which would bring a factor
![]() $2^{(j-k+1)\alpha }$
for
$2^{(j-k+1)\alpha }$
for
![]() $j>k$
. This factor is advantageous when
$j>k$
. This factor is advantageous when
![]() $2^{k}\geq 2\delta ^{-1/2}$
; however, it is useless when
$2^{k}\geq 2\delta ^{-1/2}$
; however, it is useless when
![]() $1\leq 2^{k}<2\delta ^{-1/2}$
. To overcome this, based on Lemma 2.2, we instead consider the operator:
$1\leq 2^{k}<2\delta ^{-1/2}$
. To overcome this, based on Lemma 2.2, we instead consider the operator:
![]() $\int _{2^{k-1}}^{2^{k+2}} |\phi _{\delta ,j}(t^{-1}\!\sqrt {H})(I+H)^{\alpha /4} f(x)|^2\,dt/t$
and estimate its bound from
$\int _{2^{k-1}}^{2^{k+2}} |\phi _{\delta ,j}(t^{-1}\!\sqrt {H})(I+H)^{\alpha /4} f(x)|^2\,dt/t$
and estimate its bound from
![]() $L^2(\mathbb {R}^n)$
to
$L^2(\mathbb {R}^n)$
to
![]() $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
.
$L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
.
If
![]() $0\leq k<-\log _2\delta ^{1/2}+1$
, we claim that for any
$0\leq k<-\log _2\delta ^{1/2}+1$
, we claim that for any
![]() $0<\varepsilon \leq 1/2$
, there exists a constant
$0<\varepsilon \leq 1/2$
, there exists a constant
![]() $C_{\varepsilon ,N}$
such that
$C_{\varepsilon ,N}$
such that
 $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2\,dx. \end{align} $$
$$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\nonumber\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2\,dx. \end{align} $$
Using Inequality (3-24) and Lemma 2.2,
 $$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H}) f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|(I+H)^{-\alpha/4}f(x)|^2\,dx\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx, \end{align*} $$
$$ \begin{align*} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H}) f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}\\&\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|(I+H)^{-\alpha/4}f(x)|^2\,dx\\ &\quad\leq C_{\varepsilon,N}2^{2(j_0-j)N}A^{\varepsilon}_{n}(\delta,\alpha)\int_{\mathbb{R}^n}|f(x)|^2(1+|x|)^{-\alpha}\,dx, \end{align*} $$
which in combination with Inequality (3-23) proves Lemma 3.2.
We now turn to verify the claim. Similar to the discussion of Inequality (3-15),
 $$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0} Q_{j,k,\ell}(f)^{1/2} \bigg)^2, \end{align} $$
$$ \begin{align} &\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq \bigg(\sum_{\ell\geq0} Q_{j,k,\ell}(f)^{1/2} \bigg)^2, \end{align} $$
where
 $$ \begin{align*}Q_{j,k,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}.\end{align*} $$
$$ \begin{align*}Q_{j,k,\ell}(f)=\int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}.\end{align*} $$
Arguing as Inequalities (3-16) and (3-17),
 $$ \begin{align*} &Q_{j,k,\ell}(f)\\&\quad\leq C2^{\ell}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} \zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
$$ \begin{align*} &Q_{j,k,\ell}(f)\\&\quad\leq C2^{\ell}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4} \zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\frac{dt}{t}. \end{align*} $$
The function
![]() $\psi _{\delta ,\ell }(t^{-1}s)$
is supported in
$\psi _{\delta ,\ell }(t^{-1}s)$
is supported in
![]() $[t(1-2^{\ell +2}\delta ),t(1+2^{\ell +2}\delta )]$
. Let
$[t(1-2^{\ell +2}\delta ),t(1+2^{\ell +2}\delta )]$
. Let
![]() $R=1+ [t(1+2^{\ell +2}\delta )]$
. When
$R=1+ [t(1+2^{\ell +2}\delta )]$
. When
![]() $n\geq 2$
, using Inequality (2-2) where
$n\geq 2$
, using Inequality (2-2) where
![]() $1<\alpha <n$
, then
$1<\alpha <n$
, then
 $$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq R\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq R\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
We see that
 $$ \begin{align} &\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\nonumber\\ &\quad\leq \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{L^\infty(\mathbb{R})}^2 \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2. \end{align} $$
$$ \begin{align} &\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{R^2,_2}^2\nonumber\\ &\quad\leq \|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4}\|_{L^\infty(\mathbb{R})}^2 \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2. \end{align} $$
From the estimate in Inequality (3-18) and the support property of
![]() $\psi _{\delta ,\ell }$
, we know that
$\psi _{\delta ,\ell }$
, we know that
The length of the interval
![]() $[tR^{-1}(1-2^{\ell +2}\delta ),tR^{-1}(1+2^{\ell +2}\delta )]$
is
$[tR^{-1}(1-2^{\ell +2}\delta ),tR^{-1}(1+2^{\ell +2}\delta )]$
is
![]() $8tR^{-1}2^\ell \delta $
, and thus
$8tR^{-1}2^\ell \delta $
, and thus
which implies that
 $$ \begin{align} \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2 &=\frac{1}{R^2}\sum_{i=-R^2+1}^{R^2}\sup_{s\in[({i-1})/{R^2},{i}/{R^2})} |\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}(s)|^2\nonumber\\ &\leq R^{-2}\min\{R^2,(1+8Rt2^\ell\delta)\}. \end{align} $$
$$ \begin{align} \|\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}\|_{R^2,_2}^2 &=\frac{1}{R^2}\sum_{i=-R^2+1}^{R^2}\sup_{s\in[({i-1})/{R^2},{i}/{R^2})} |\chi_{[tR^{-1}(1-2^{\ell+2}\delta),tR^{-1}(1+2^{\ell+2}\delta)]}(s)|^2\nonumber\\ &\leq R^{-2}\min\{R^2,(1+8Rt2^\ell\delta)\}. \end{align} $$
Combining Inequalities (3-27)–(3-29) gives
If
![]() $2^\ell \delta \leq 1$
, note that
$2^\ell \delta \leq 1$
, note that
![]() $1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$
. It is easy to see that
$1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$
. It is easy to see that
![]() $R\approx t\approx 2^k\leq C\delta ^{-1/2}$
. Then
$R\approx t\approx 2^k\leq C\delta ^{-1/2}$
. Then
If
![]() $2^\ell \delta \geq 1$
, note that
$2^\ell \delta \geq 1$
, note that
![]() $1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$
. It is easy to see that
$1/2\leq t\approx 2^k\leq C\delta ^{-1/2}$
. It is easy to see that
![]() $R\leq Ct2^\ell \delta $
. Then
$R\leq Ct2^\ell \delta $
. Then
Therefore, if
![]() $2^k\leq C\delta ^{-1/2}$
,
$2^k\leq C\delta ^{-1/2}$
,
As a consequence, for any
![]() $N>(\alpha +3)/2$
$N>(\alpha +3)/2$
which, in combination with the
![]() $\,dt/t$
measure of
$\,dt/t$
measure of
![]() $I_i$
is uniformly less than
$I_i$
is uniformly less than
![]() $\delta $
, Fubini’s theorem and the
$\delta $
, Fubini’s theorem and the
![]() $L^2$
-estimate of square function for Hermite operators, yields
$L^2$
-estimate of square function for Hermite operators, yields
 $$ \begin{align} Q_{j,k,\ell}(f)&\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &=C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}}\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}2^{\ell}\delta\sum_{i'\in \mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-3)}2^{2(j_0-j)N} \delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} Q_{j,k,\ell}(f)&\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i=0}^{i_0}\sum_{i'=i-2^{\ell+6}}^{i+2^{\ell+6}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &=C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}\sum_{i'=-2^{\ell+6}}^{i_0+2^{\ell+6}}\sum_{\{i\in\mathbb{N}\cap[0, i_0]\ :\ |i-i'|\leq2^{\ell+6}\}} \int_{I_i}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\frac{dt}{t}\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-2)}2^{2(j_0-j)N} \delta^{(1-\alpha)/2}2^{\ell}\delta\sum_{i'\in \mathbb{Z}} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\leq C_N2^{-\ell(2N-\alpha-3)}2^{2(j_0-j)N} \delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
Putting the estimate in Inequality (3-31) into the estimate in Inequality (3-25) and taking the sum over
![]() $\ell $
yields
$\ell $
yields
 $$ \begin{align} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_N2^{2(j_0-j)N}\delta^{(3-\alpha)/2}\|f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
When
![]() $n=1$
, this situation can be shown in the same manner as before, the difference is that we use the case where
$n=1$
, this situation can be shown in the same manner as before, the difference is that we use the case where
![]() $0<\alpha <1$
in Inequality (2-2). Similar to the discussion of Inequality (3-29),
$0<\alpha <1$
in Inequality (2-2). Similar to the discussion of Inequality (3-29),
From the estimate in Inequality (2-2) for the case
![]() $n=1,\ 0<\alpha <1$
and the estimates in Inequalities (3-28) and (3-33), then for any
$n=1,\ 0<\alpha <1$
and the estimates in Inequalities (3-28) and (3-33), then for any
![]() $\varepsilon>0$
, there exist constants
$\varepsilon>0$
, there exist constants
![]() $C_{\varepsilon }$
and
$C_{\varepsilon }$
and
![]() $C_{\varepsilon ,N}$
such that
$C_{\varepsilon ,N}$
such that
 $$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq C_{\varepsilon} R^{{\alpha}/({1+\varepsilon})}\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4} \|_{R^2,_{{2(1+\varepsilon)}/{\alpha}}}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{-2\ell N}2^{2(j_0-j)N} (R^{\varepsilon}\min\{R^2,(1+Rt2^\ell\delta)\})^{{\alpha}/({1+\varepsilon})} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
$$ \begin{align} &\int_{\mathbb{R}^n}|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}\zeta_{i'}(\!\sqrt{H})f(x)|^2(1+|x|)^{-\alpha}\,dx\nonumber\\ &\quad\leq C_{\varepsilon} R^{{\alpha}/({1+\varepsilon})}\|(\phi_{\delta,j}\psi_{\delta,\ell})(t^{-1}Rs)(I+|Rs|^2)^{\alpha/4} \|_{R^2,_{{2(1+\varepsilon)}/{\alpha}}}^2\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\nonumber\\ &\quad\leq C_{\varepsilon,N}2^{-2\ell N}2^{2(j_0-j)N} (R^{\varepsilon}\min\{R^2,(1+Rt2^\ell\delta)\})^{{\alpha}/({1+\varepsilon})} \|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align} $$
Similarly to the discussion of Inequality (3-30), if
![]() $2^k\leq C\delta ^{-1/2}$
,
$2^k\leq C\delta ^{-1/2}$
,
Putting the estimate in Inequality (3-35) into the estimate in Inequality (3-34) yields
 $$ \begin{align*} \mathrm{{RHS} \ of \ (3\text{-}34)}&\leq C_{\varepsilon,N}2^{-\ell (2N-\alpha(({2+\varepsilon})/({1+\varepsilon})))}2^{2(j_0-j)N}\delta^{-{\alpha\varepsilon}/{2(1+\varepsilon)}}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\\ &\leq C_{\varepsilon,N}2^{-2\ell (N-\alpha)}2^{2(j_0-j)N}\delta^{-\varepsilon}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$
$$ \begin{align*} \mathrm{{RHS} \ of \ (3\text{-}34)}&\leq C_{\varepsilon,N}2^{-\ell (2N-\alpha(({2+\varepsilon})/({1+\varepsilon})))}2^{2(j_0-j)N}\delta^{-{\alpha\varepsilon}/{2(1+\varepsilon)}}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2\\ &\leq C_{\varepsilon,N}2^{-2\ell (N-\alpha)}2^{2(j_0-j)N}\delta^{-\varepsilon}\|\zeta_{i'}(\!\sqrt{H})f\|_{L^2(\mathbb{R}^n)}^2. \end{align*} $$
In the same manner as the estimates in Inequalities (3-31) and (3-32),
and
 $$ \begin{align*} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_{\varepsilon,N}2^{2(j_0-j)N}\delta^{1-\varepsilon }\|f\|_{L^2(\mathbb{R}^n)}^2, \end{align*} $$
$$ \begin{align*} \int_{2^{k-1}}^{2^{k+2}} \int_{\mathbb{R}^n}|\phi_{\delta,j}(t^{-1}\!\sqrt{H})(I+H)^{\alpha/4}f(x)|^2 (1+|x|)^{-\alpha}\,dx\frac{dt}{t}\leq C_{\varepsilon,N}2^{2(j_0-j)N}\delta^{1-\varepsilon }\|f\|_{L^2(\mathbb{R}^n)}^2, \end{align*} $$
which in combination with Inequality (3-32) yields Inequality (3-24), so the claim holds. The proof of Lemma 3.2 is complete.
Proof of Lemma 3.3
The proof of the lemma is inspired by [Reference Hu and Lu17]. For convenience, we use
![]() $\|T\|_{p\to q} $
for the operator norm of T if T is a bounded linear operator from
$\|T\|_{p\to q} $
for the operator norm of T if T is a bounded linear operator from
![]() $L^p(\mathbb {R}^n)$
to
$L^p(\mathbb {R}^n)$
to
![]() $L^q(\mathbb {R}^n)$
for given
$L^q(\mathbb {R}^n)$
for given
![]() $1\leq p,q\leq \infty $
. We first obtain that
$1\leq p,q\leq \infty $
. We first obtain that
![]() $T_{j,k}^{\delta }$
is bounded from
$T_{j,k}^{\delta }$
is bounded from
![]() $L^1(\mathbb {R}^n)$
to
$L^1(\mathbb {R}^n)$
to
![]() $L^{\infty }(\mathbb {R}^n)$
. To do so, we need to estimate
$L^{\infty }(\mathbb {R}^n)$
. To do so, we need to estimate
![]() $\|\phi _{\delta ,j}(t^{-1}\!\sqrt {H})\|_{1\rightarrow \infty }$
:
$\|\phi _{\delta ,j}(t^{-1}\!\sqrt {H})\|_{1\rightarrow \infty }$
:
 $$ \begin{align*} \|\phi_{\delta,j}(t^{-1}\!\sqrt{H})\|_{1\rightarrow\infty}&\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{1\rightarrow2}\|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\nonumber\\ &\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|^2_{2\rightarrow\infty}\leq\bigg(\sum_{\ell\geq0}\|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\bigg)^2. \end{align*} $$
$$ \begin{align*} \|\phi_{\delta,j}(t^{-1}\!\sqrt{H})\|_{1\rightarrow\infty}&\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{1\rightarrow2}\|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\nonumber\\ &\leq \|\phi_{\delta,j}^{1/2}(t^{-1}\!\sqrt{H})\|^2_{2\rightarrow\infty}\leq\bigg(\sum_{\ell\geq0}\|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}\bigg)^2. \end{align*} $$
By [Reference Duong, Ouhabaz and Sikora10, Lemma 2.2], supp
![]() $\psi _{\delta ,\ell }(t^{-1}s)\subseteq \{s\in \mathbb {R}:|s|\leq (1+2^{\ell +2}\delta )t\}$
and Inequality (3-18),
$\psi _{\delta ,\ell }(t^{-1}s)\subseteq \{s\in \mathbb {R}:|s|\leq (1+2^{\ell +2}\delta )t\}$
and Inequality (3-18),
 $$ \begin{align*} \|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}&\leq \bigg(\int_{\mathbb{R}^n}|K_{(\phi^{1/2}_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})}(x,y)|^2dy\bigg)^{1/2}\\ &\leq C_Nt^{n/2}2^{-\ell (N-n)/2}2^{(j_0-j)N/2}. \end{align*} $$
$$ \begin{align*} \|(\phi_{\delta,j}^{1/2}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})\|_{2\rightarrow\infty}&\leq \bigg(\int_{\mathbb{R}^n}|K_{(\phi^{1/2}_{\delta,j}\psi_{\delta,\ell})(t^{-1}\!\sqrt{H})}(x,y)|^2dy\bigg)^{1/2}\\ &\leq C_Nt^{n/2}2^{-\ell (N-n)/2}2^{(j_0-j)N/2}. \end{align*} $$
Summing the terms
![]() $\|(\phi _{\delta ,j}^{\frac 12}\psi _{\delta ,\ell })(t^{-1}\!\sqrt {H})\|_{2\rightarrow \infty }$
over
$\|(\phi _{\delta ,j}^{\frac 12}\psi _{\delta ,\ell })(t^{-1}\!\sqrt {H})\|_{2\rightarrow \infty }$
over
![]() $\ell $
gives that
$\ell $
gives that
Finally, for any
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $j\geq j_0$
,
$j\geq j_0$
,
 $$ \begin{align} \|T_{j,k}^{\delta}(f)\|_{L^\infty(\mathbb{R}^n)} & \leq \bigg(\int_{2^{k-1}}^{2^{k+2}} ||\phi_{\delta,j}(t^{-1}\!\sqrt{H})f\|_{L^\infty(\mathbb{R}^n)}^2\frac{dt}{t}\bigg)^{1/2} \leq C_N2^{kn}2^{(j_0-j)N}\|f\|_{L^1(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} \|T_{j,k}^{\delta}(f)\|_{L^\infty(\mathbb{R}^n)} & \leq \bigg(\int_{2^{k-1}}^{2^{k+2}} ||\phi_{\delta,j}(t^{-1}\!\sqrt{H})f\|_{L^\infty(\mathbb{R}^n)}^2\frac{dt}{t}\bigg)^{1/2} \leq C_N2^{kn}2^{(j_0-j)N}\|f\|_{L^1(\mathbb{R}^n)}. \end{align} $$
Here,
![]() $T_{j,k}^{\delta }$
is a sub-linear operator. Using interpolation (see [Reference Stein and Weiss26, Theorem 2.11] or [Reference Bergh and Löfström2, page 120]) with the estimate in Inequality (3-36) and Lemma 3.2,
$T_{j,k}^{\delta }$
is a sub-linear operator. Using interpolation (see [Reference Stein and Weiss26, Theorem 2.11] or [Reference Bergh and Löfström2, page 120]) with the estimate in Inequality (3-36) and Lemma 3.2,
where
![]() $n\kern1.8pt{=}\kern1.8pt 1,0\kern1.8pt{\leq}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8pt 1$
;
$n\kern1.8pt{=}\kern1.8pt 1,0\kern1.8pt{\leq}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8pt 1$
;
![]() $n\kern1.8pt{\geq}\kern1.8pt 2, 1\kern1.8pt{<}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8ptn$
or
$n\kern1.8pt{\geq}\kern1.8pt 2, 1\kern1.8pt{<}\kern1.8pt \alpha \kern1.8pt{<}\kern1.8ptn$
or
![]() $n\kern1.8pt{\geq}\kern1.8pt 2$
,
$n\kern1.8pt{\geq}\kern1.8pt 2$
,
![]() $\alpha \kern1.8pt{=}\kern1.8pt0$
;
$\alpha \kern1.8pt{=}\kern1.8pt0$
;
![]() $1/r\kern1.8pt{=}\kern1.8pt\theta /2$
and
$1/r\kern1.8pt{=}\kern1.8pt\theta /2$
and
![]() $2\kern1.8pt{<}\kern1.8pt r\kern1.8pt{<}\kern1.8pt \infty $
.
$2\kern1.8pt{<}\kern1.8pt r\kern1.8pt{<}\kern1.8pt \infty $
.
4. Proof of Theorem 1.1
We now begin to prove Theorem 1.1.
Proof. Observe that for any
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $\rho <\lambda $
,
$\rho <\lambda $
,
 $$ \begin{align*} \bigg(1-\frac{m^2}{R^2}\bigg)^{\lambda}_+ & =\widetilde{C}_{\lambda,\,\rho} R^{-2\lambda}\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1}\bigg(1-\frac{m^2}{t^2}\bigg)^\rho_+\,dt. \end{align*} $$
$$ \begin{align*} \bigg(1-\frac{m^2}{R^2}\bigg)^{\lambda}_+ & =\widetilde{C}_{\lambda,\,\rho} R^{-2\lambda}\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1}\bigg(1-\frac{m^2}{t^2}\bigg)^\rho_+\,dt. \end{align*} $$
For
![]() $\rho <\lambda -1/2$
and
$\rho <\lambda -1/2$
and
![]() $\rho>-1/2$
, we apply the Hölder inequality to obtain
$\rho>-1/2$
, we apply the Hölder inequality to obtain
 $$ \begin{align} |[b,S_R^{\lambda}(H)]f|&=\widetilde{C}_{\lambda,\,\rho}R^{-2\lambda}\bigg|\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1} [b,S_t^{\rho}(H)]f\,dt\bigg|\nonumber\\ &\leq C_{\lambda,\,\rho}\bigg(\frac1R\int_{0}^{R}|[b,S_t^{\rho}(H)]f|^2\,dt\bigg)^{1/2}. \end{align} $$
$$ \begin{align} |[b,S_R^{\lambda}(H)]f|&=\widetilde{C}_{\lambda,\,\rho}R^{-2\lambda}\bigg|\int_{0}^{R}(R^2-t^2)^{\lambda-\rho-1}t^{2\rho+1} [b,S_t^{\rho}(H)]f\,dt\bigg|\nonumber\\ &\leq C_{\lambda,\,\rho}\bigg(\frac1R\int_{0}^{R}|[b,S_t^{\rho}(H)]f|^2\,dt\bigg)^{1/2}. \end{align} $$
Note that
![]() $x_+^{\rho }=\sum _{k\in \mathbb {Z}}2^{-k\rho }\phi (2^kx)$
for some
$x_+^{\rho }=\sum _{k\in \mathbb {Z}}2^{-k\rho }\phi (2^kx)$
for some
![]() $\phi \in C_c^{\infty } ([1/8,1/2])$
. Let
$\phi \in C_c^{\infty } ([1/8,1/2])$
. Let
![]() $\phi _k(s)=\phi (2^k(1-s^2))$
,
$\phi _k(s)=\phi (2^k(1-s^2))$
,
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $\phi _0(s)=\sum _{k\leq 0}2^{-k\rho }\phi (2^k(1-s))$
for
$\phi _0(s)=\sum _{k\leq 0}2^{-k\rho }\phi (2^k(1-s))$
for
![]() $s>0$
. Then,
$s>0$
. Then,
It follows from Displays (4-1) and (4-2) that
 $$ \begin{align*} \sup_{R>0}|[b,S_R^{\lambda}(H)]f| \leq & C_{\lambda,\,\rho}\bigg( \sup_{t>0}|[b,\phi_0(t^{-2}H)]f| +\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2\frac{dt}{t}\bigg)^{1/2}\bigg). \end{align*} $$
$$ \begin{align*} \sup_{R>0}|[b,S_R^{\lambda}(H)]f| \leq & C_{\lambda,\,\rho}\bigg( \sup_{t>0}|[b,\phi_0(t^{-2}H)]f| +\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2\frac{dt}{t}\bigg)^{1/2}\bigg). \end{align*} $$
Note that
![]() $\phi _0\in C_c^{\infty }$
with support
$\phi _0\in C_c^{\infty }$
with support
![]() $\{s:0\leq |s|\leq 1\}$
. By Lemma 2.4, for any
$\{s:0\leq |s|\leq 1\}$
. By Lemma 2.4, for any
![]() $0\leq \alpha <n$
,
$0\leq \alpha <n$
,
Let
![]() $\rho =\lambda -1/2-\eta $
for some
$\rho =\lambda -1/2-\eta $
for some
![]() $\eta>0$
. If
$\eta>0$
. If
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $n\in \mathbb {N}^+$
, by Proposition 3.1, for any
$n\in \mathbb {N}^+$
, by Proposition 3.1, for any
![]() $0<\upsilon \leq 1/2$
, there exists a constant
$0<\upsilon \leq 1/2$
, there exists a constant
![]() $C_{0,\upsilon }>0$
such that
$C_{0,\upsilon }>0$
such that
 $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq \sum_{k\geq1}2^{-k\rho}\bigg\|\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq C_{0,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n)}. \end{align} $$
$$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq \sum_{k\geq1}2^{-k\rho}\bigg\|\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n)}\nonumber\\ &\quad\leq C_{0,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n)}. \end{align} $$
Then the
![]() $\mathrm {RHS}$
of Inequality (4-4) is bounded by
$\mathrm {RHS}$
of Inequality (4-4) is bounded by
![]() $C_{0,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$
provided
$C_{0,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$
provided
![]() $\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-4), we can conclude that
$\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-4), we can conclude that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
![]() $L^2(\mathbb {R}^n)$
for any
$L^2(\mathbb {R}^n)$
for any
![]() $n\in \mathbb {N}^+$
.
$n\in \mathbb {N}^+$
.
Similarly, if
![]() $n=1$
and
$n=1$
and
![]() $0<\alpha <1$
, by Proposition 3.1, for any
$0<\alpha <1$
, by Proposition 3.1, for any
![]() $0<\upsilon \leq 1/2$
, there exists a constant
$0<\upsilon \leq 1/2$
, there exists a constant
![]() $C_{\alpha ,\upsilon }>0$
such that
$C_{\alpha ,\upsilon }>0$
such that
 $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}. \end{align} $$
$$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R},(1+|x|)^{-\alpha})}. \end{align} $$
Then the
![]() $\mathrm {RHS}$
of Inequality (4-5) is bounded by
$\mathrm {RHS}$
of Inequality (4-5) is bounded by
![]() $C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$
provided
$C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R},(1+|x|)^{-\alpha })}$
provided
![]() $\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-5), we can conclude that
$\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-5), we can conclude that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
![]() $L^2(\mathbb {R},(1+|x|)^{-\alpha })$
for
$L^2(\mathbb {R},(1+|x|)^{-\alpha })$
for
![]() $0< \alpha <1$
.
$0< \alpha <1$
.
If
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1<\alpha <n$
, by Proposition 3.1, for any
$1<\alpha <n$
, by Proposition 3.1, for any
![]() $0<\upsilon \leq 1/2$
, there exists a constant
$0<\upsilon \leq 1/2$
, there exists a constant
![]() $C_{\alpha ,\upsilon }>0$
such that
$C_{\alpha ,\upsilon }>0$
such that
 $$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-{(\alpha-1)}/{4}-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align} $$
$$ \begin{align} &\bigg\|\sum_{k\geq1}2^{-k\rho}\bigg(\int_{0}^{\infty}|[b,\phi_k(t^{-1}\!\sqrt{H})]f|^2 \frac{dt}{t}\bigg)^{1/2}\bigg\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\nonumber\\ &\quad\leq C_{\alpha,\upsilon}\|b\|_{\mathrm{BMO}}\sum_{k\geq1}2^{-k(\lambda-{(\alpha-1)}/{4}-\eta-\upsilon)}\|f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align} $$
Then the
![]() $\mathrm {RHS}$
of Inequality (4-6) is bounded by
$\mathrm {RHS}$
of Inequality (4-6) is bounded by
![]() $C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
provided
$C_{\alpha ,\upsilon }\|b\|_{\mathrm {BMO}}\|f\|_{L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
provided
![]() $\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-6), we can conclude that
$\eta ,\upsilon $
are small enough. From the estimates in Inequalities (4-3) and (4-6), we can conclude that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
![]() ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
![]() $1< \alpha <n$
whenever
$1< \alpha <n$
whenever
![]() $\lambda>(\alpha -1)/4$
. Combining this with the fact that
$\lambda>(\alpha -1)/4$
. Combining this with the fact that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on
![]() $L^2(\mathbb {R}^n)$
, we now use the complex interpolation method to obtain that
$L^2(\mathbb {R}^n)$
, we now use the complex interpolation method to obtain that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on the weighted space
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
is bounded on the weighted space
![]() ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
![]() $0<\alpha \leq 1$
when
$0<\alpha \leq 1$
when
![]() $n\geq 2$
. First, we deal with
$n\geq 2$
. First, we deal with
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
by Kolmogorov–Seliverstov–Plessner linearization (see [Reference Stein and Weiss27, page 280]). In fact, we define
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
by Kolmogorov–Seliverstov–Plessner linearization (see [Reference Stein and Weiss27, page 280]). In fact, we define
![]() $\mathcal {K}$
as the nonnegative measurable functions on
$\mathcal {K}$
as the nonnegative measurable functions on
![]() $\mathbb {R}^n$
that only have a finite number of distinct values. Let
$\mathbb {R}^n$
that only have a finite number of distinct values. Let
![]() $\mathcal {R}(x)\in \mathcal {K}$
. It is claimed that
$\mathcal {R}(x)\in \mathcal {K}$
. It is claimed that
It is easy to see that
The converse inequality can be seen from the fact that we can always choose a series of functions
![]() $\mathcal {R}_j(x)\in \mathcal {K}$
such that
$\mathcal {R}_j(x)\in \mathcal {K}$
such that
By Lebesgue’s dominated convergence theorem,
 $$ \begin{align*} \|\sup_{R>0}|[b,S_R^{\lambda}(H)]f|\ \|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}&= \lim_{j\rightarrow+\infty}\|[b,S_{\mathcal{R}_j(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\\ &\leq \sup_{\mathcal{R}(x)\in\mathcal{K}}\|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align*} $$
$$ \begin{align*} \|\sup_{R>0}|[b,S_R^{\lambda}(H)]f|\ \|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}&= \lim_{j\rightarrow+\infty}\|[b,S_{\mathcal{R}_j(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}\\ &\leq \sup_{\mathcal{R}(x)\in\mathcal{K}}\|[b,S_{\mathcal{R}(x)}^{\lambda}(H)]f\|_{L^2(\mathbb{R}^n,(1+|x|)^{-\alpha})}. \end{align*} $$
Therefore, the boundeness of the sub-linear operator
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]f|$
on
![]() $L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
is equivalent to
$L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
is equivalent to
where the constant C is independent of
![]() $\mathcal {R}(x)$
. Then the weighted
$\mathcal {R}(x)$
. Then the weighted
![]() $L^2$
estimate of
$L^2$
estimate of
![]() $[b,S_{\mathcal {R}(x)}^{\lambda }(H)]$
for
$[b,S_{\mathcal {R}(x)}^{\lambda }(H)]$
for
![]() $0<\alpha \leq 1$
when
$0<\alpha \leq 1$
when
![]() $\lambda>0$
can be deduced from the complex interpolation theorem (see [Reference Stein and Weiss26, Theorem 2.11]). As a consequence, we obtain that
$\lambda>0$
can be deduced from the complex interpolation theorem (see [Reference Stein and Weiss26, Theorem 2.11]). As a consequence, we obtain that
![]() $\sup _{R>0}|[b,S_R^{\lambda }(H)]|$
is bounded on
$\sup _{R>0}|[b,S_R^{\lambda }(H)]|$
is bounded on
![]() ${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
${L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })}$
for
![]() $0<\alpha \leq 1$
if
$0<\alpha \leq 1$
if
![]() $\lambda>0$
. The proof of Theorem 1.1 is complete.
$\lambda>0$
. The proof of Theorem 1.1 is complete.
Finally, we give a proof of Corollary 1.2.
Proof. For any
![]() $f\in C_c^\infty (\mathbb {R}^n)$
and supp
$f\in C_c^\infty (\mathbb {R}^n)$
and supp
![]() $f\subseteq B$
for some ball
$f\subseteq B$
for some ball
![]() $B\subseteq \mathbb {R}^n$
, then
$B\subseteq \mathbb {R}^n$
, then
![]() $(b-b_B)f\in L^2(\mathbb {R}^n)$
and
$(b-b_B)f\in L^2(\mathbb {R}^n)$
and
![]() $[b,S^{\lambda }_R(H)]f$
are well defined for any
$[b,S^{\lambda }_R(H)]f$
are well defined for any
![]() $\lambda>0$
. By the a.e. convergence of the Bochner–Riesz operator
$\lambda>0$
. By the a.e. convergence of the Bochner–Riesz operator
![]() $S_R^\lambda (H)$
(see [Reference Chen, Duong, He, Lee and Yan4, Theorem 1.1]),
$S_R^\lambda (H)$
(see [Reference Chen, Duong, He, Lee and Yan4, Theorem 1.1]),
Let
![]() $0\leq \alpha <n$
. Theorem 1.1 implies the a.e. convergence of
$0\leq \alpha <n$
. Theorem 1.1 implies the a.e. convergence of
![]() $[b,S^{\lambda }_R(H)]f$
for any
$[b,S^{\lambda }_R(H)]f$
for any
![]() $f\in L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
if
$f\in L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
if
![]() $\lambda>\max \{(\alpha -1)/4,0\}$
.
$\lambda>\max \{(\alpha -1)/4,0\}$
.
For given
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $\lambda>\lambda (p)/2$
, we can choose
$\lambda>\lambda (p)/2$
, we can choose
![]() $\alpha $
such that
$\alpha $
such that
![]() ${n(1-2/p)<\alpha <4\lambda +1}$
and
${n(1-2/p)<\alpha <4\lambda +1}$
and
![]() $L^p(\mathbb {R}^n)\subseteq L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
. Hence, the a.e. convergence of
$L^p(\mathbb {R}^n)\subseteq L^2(\mathbb {R}^n,(1+|x|)^{-\alpha })$
. Hence, the a.e. convergence of
![]() $[b,S^{\lambda }_R(H)]f$
holds for all
$[b,S^{\lambda }_R(H)]f$
holds for all
![]() $f\in L^p(\mathbb {R}^n)$
.
$f\in L^p(\mathbb {R}^n)$
.
Acknowledgement
The authors would like to thank L. Yan for helpful comments and suggestions.