Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-17T16:17:52.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Springer correspondence for the split symmetric pair in type 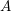$A$

Part of: Linear algebraic groups and related topics Algebraic groups

Published online by Cambridge University Press:  11 October 2018

Tsao-Hsien Chen ,
Kari Vilonen  and
Ting Xue
Tsao-Hsien Chen
Affiliation:
Department of Mathematics, University of Chicago, Chicago 60637, USA email [email protected]
Kari Vilonen
Affiliation:
School of Mathematics and Statistics, University of Melbourne, VIC 3010, Australia email [email protected] Department of Mathematics and Statistics, University of Helsinki, Helsinki 00014, Finland
Ting Xue
Affiliation:
School of Mathematics and Statistics, University of Melbourne, VIC 3010, Australia email [email protected] Department of Mathematics and Statistics, University of Helsinki, Helsinki 00014, Finland
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we establish Springer correspondence for the symmetric pair 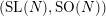$(\text{SL}(N),\text{SO}(N))$ using Fourier transform, parabolic induction functor, and a nearby cycle sheaf construction. As an application of our results we see that the cohomology of Hessenberg varieties can be expressed in terms of irreducible representations of Hecke algebras of symmetric groups at $q=-1$. Conversely, we see that the irreducible representations of Hecke algebras of symmetric groups at $q=-1$ arise in geometry.

Keywords

Springer correspondencenearby cycle sheavessymmetric pairsHecke algebrasHessenberg varietiesFourier transform

MSC classification

Primary: 20G99: None of the above, but in this section 14L99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 11 , November 2018 , pp. 2403 - 2425
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported in part by the AMS-Simons travel grant and the NSF grant DMS-1702337. The second author was supported in part by the ARC grants DP150103525 and DP180101445, the Academy of Finland, the Humboldt Foundation, the Simons Foundation, and the NSF grant DMS-1402928. The third author was supported in part by the ARC grants DE160100975, DP150103525 and the Academy of Finland.

References

A’Campo, N., Tresses, monodromie et le groupe symplectique , Comment. Math. Helv. 54 (1979), 318–327.Google Scholar
Brion, M. and Helminck, A. G., On orbit closures of symmetric subgroups in flag varieties , Canad. J. Math. 52 (2000), 265–292.Google Scholar
Chen, T. H., Vilonen, K. and Xue, T., Springer correspondence for symmetric spaces, Preprint (2015), arXiv:1510.05986 [math.RT].Google Scholar
Chen, T. H., Vilonen, K. and Xue, T., Hessenberg varieties, intersections of quadrics, and the Springer correspondence, Preprint (2015), arXiv:1511.00617 [math.AG].Google Scholar
Chen, T. H., Vilonen, K. and Xue, T., On the cohomology of Fano varieties and the Springer correspondence , Adv. Math. 318 (2017), 515–533.Google Scholar
Dipper, R. and James, G., Representations of Hecke algebras of general linear groups , Proc. Lond. Math. Soc. (3) 52 (1986), 20–52.Google Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Purity of equivalued affine Springer fibers , Represent. Theory 10 (2006), 130–146.Google Scholar
Grinberg, M., A generalization of Springer theory using nearby cycles , Represent. Theory 2 (1998), 410–431.Google Scholar
Grinberg, M., On the specialization to the asymptotic cone , J. Algebraic Geom. 10 (2001), 1–17.Google Scholar
Grinberg, M., Vilonen, K. and Xue, T., Nearby cycle sheaves for symmetric pairs, Preprint (2018), arXiv:1805.02794 [math.AG].Google Scholar
Grojnowski, I., Character sheaves on symmetric spaces, PhD thesis, Massachusetts Institute of Technology (1992).Google Scholar
Henderson, A., Fourier transform, parabolic induction, and nilpotent orbits , Transform. Groups 6 (2001), 353–370.Google Scholar
Kostant, B. and Rallis, S., Orbits and representations associated with symmetric spaces , Amer. J. Math. 93 (1971), 753–809.Google Scholar
Lusztig, G., Study of perverse sheaves arising from graded Lie algebras , Adv. Math. 112 (1995), 147–217.Google Scholar
Lusztig, G., From groups to symmetric spaces , in Representation theory and mathematical physics, Contemporary Mathematics, vol. 557 (American Mathematical Society, Providence, RI, 2011), 245–258.Google Scholar
Lusztig, G., Study of antiorbital complexes , in Representation theory and mathematical physics, Contemporary Mathematics, vol. 557 (American Mathematical Society, Providence, RI, 2011), 259–287.Google Scholar
Lusztig, G. and Spaltenstein, N., Induced unipotent classes , J. Lond. Math. Soc. (2) 19 (1979), 41–52.Google Scholar
Lusztig, G. and Yun, Z., Z/m-graded Lie algebras and perverse sheaves, I , Represent. Theory 21 (2017), 277–321.Google Scholar
Saito, M., Modules de Hodge polarisables , Publ. Res. Inst. Math. Sci. 24 (1988), 849–995.Google Scholar
Wilf, H. S., Three problems in combinatorial asymptotics , J. Combin. Theory Ser. A 35 (1983), 199–207.Google Scholar