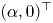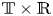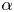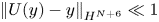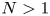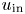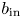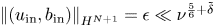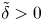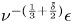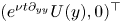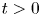1. Introduction
1.1 Problem statement and background
Consider the 2D incompressible MHD equations on $\mathbb {T}\times \mathbb {R}$![]() :
:

Here $\mathbb {T}$![]() is the periodized interval $[0,1]$
is the periodized interval $[0,1]$![]() , $\tilde u=\tilde u(t, x, y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}^2$
, $\tilde u=\tilde u(t, x, y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}^2$![]() denotes the velocity, $\tilde b=\tilde b(t,x,y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}^2$
denotes the velocity, $\tilde b=\tilde b(t,x,y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}^2$![]() denotes magnetic field, $\tilde p=\tilde p(t, x, y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}$
denotes magnetic field, $\tilde p=\tilde p(t, x, y): [0,\infty )\times \mathbb {T}\times \mathbb {R} \to \mathbb {R}$![]() denotes pressure, $\nu$
denotes pressure, $\nu$![]() denotes the inverse Reynolds number, and $\mu$
denotes the inverse Reynolds number, and $\mu$![]() denotes the inverse magnetic Reynolds number. For a derivation of (1.1) and a general overview of MHD equations we refer the reader to [Reference Davidson17, Reference Lifschitz30].
denotes the inverse magnetic Reynolds number. For a derivation of (1.1) and a general overview of MHD equations we refer the reader to [Reference Davidson17, Reference Lifschitz30].
Note that the shear profile $u_s=( e^{\nu t \partial _{yy}}U(y),0) ^\top$![]() is a solution of (1.1) in any uniform magnetic field $b_s=(\alpha,0 )^\top$
is a solution of (1.1) in any uniform magnetic field $b_s=(\alpha,0 )^\top$![]() , where $U(y)$
, where $U(y)$![]() is a given smooth function, and $\alpha$
is a given smooth function, and $\alpha$![]() is a constant in $\mathbb {R}$
is a constant in $\mathbb {R}$![]() . A natural question is to study the long time stability of the equilibrium state $(u_s, b_s)$
. A natural question is to study the long time stability of the equilibrium state $(u_s, b_s)$![]() . To this end, let us introduce the perturbations ${u}$
. To this end, let us introduce the perturbations ${u}$![]() and ${b}$
and ${b}$![]() by $\tilde {u}={u}+u_s$
by $\tilde {u}={u}+u_s$![]() and $\tilde {b}={b}+b_s$
and $\tilde {b}={b}+b_s$![]() . Then $({u},{b})$
. Then $({u},{b})$![]() solves
solves

where we have used the notations ${u}=( {u}_1,{u}_2)^\top,~{b}=( {b}_1,{b}_2)^\top$![]() and $\bar {U}=e^{\nu t \partial _{yy}}U(y)$
and $\bar {U}=e^{\nu t \partial _{yy}}U(y)$![]() . The corresponding perturbed vorticity and current density take the form of
. The corresponding perturbed vorticity and current density take the form of
Let $\psi$![]() and $\phi$
and $\phi$![]() be the steam functions such that
be the steam functions such that
Then we infer from (1.2) that the system of $( \omega,j)$![]() is of the following form
is of the following form

The mathematical theory of the stability of shear flows gained quite some attention in the last decade. The nonlinear stability of the 2D Couette flow on $\mathbb {T}\times \mathbb {R}$![]() in the Euler equation was first obtained by Bedrossian and Masmoudi in [Reference Bedrossian and Masmoudi6] when the initial perturbation is smoother than the Gevrey space of class 2. In particular, the inviscid damping, an important hydrodynamic phenomenon manifests itself as the algebraic decay of the velocity for the inviscid fluids, was rigorously justified at the nonlinear level in [Reference Bedrossian and Masmoudi6]. A generalization of the results in [Reference Bedrossian and Masmoudi6] to the finite channel $\mathbb {T}\times [0,1]$
in the Euler equation was first obtained by Bedrossian and Masmoudi in [Reference Bedrossian and Masmoudi6] when the initial perturbation is smoother than the Gevrey space of class 2. In particular, the inviscid damping, an important hydrodynamic phenomenon manifests itself as the algebraic decay of the velocity for the inviscid fluids, was rigorously justified at the nonlinear level in [Reference Bedrossian and Masmoudi6]. A generalization of the results in [Reference Bedrossian and Masmoudi6] to the finite channel $\mathbb {T}\times [0,1]$![]() for initial perturbation with compact support was given by Ionescu and Jia in [Reference Ionescu and Jia22]. The nonlinear inviscid damping for a class of monotone shear flows was proved in [Reference Ionescu and Jia23] and [Reference Masmoudi and Zhao33], independently. The stability results for the 2D Couette flow in inhomogeneous fluids can be found in [Reference Chen, Wei, Zhang and Zhang16, Reference Zhao51]. The instability result for the 2D Couette flow on $\mathbb {T}\times \mathbb {R}$
for initial perturbation with compact support was given by Ionescu and Jia in [Reference Ionescu and Jia22]. The nonlinear inviscid damping for a class of monotone shear flows was proved in [Reference Ionescu and Jia23] and [Reference Masmoudi and Zhao33], independently. The stability results for the 2D Couette flow in inhomogeneous fluids can be found in [Reference Chen, Wei, Zhang and Zhang16, Reference Zhao51]. The instability result for the 2D Couette flow on $\mathbb {T}\times \mathbb {R}$![]() was shown by Deng and Masmoudi in [Reference Deng and Masmoudi18] when the initial perturbation is less smooth than the Gevrey space of class 2. For more general shear flows, the stability/instability results are more difficult to achieve due to the presence of nonlocal term. We refer to [Reference Chen, Wei and Zhang15, Reference Jia25, Reference Jia26, Reference Wei, Zhang and Zhao45, Reference Zillinger52] for the linear inviscid damping results for general monotone shear flows, and to [Reference Ionescu, Iyer and Jia24, Reference Wei, Zhang and Zhao46, Reference Wei, Zhang and Zhao47] for the linear stability results for non-monotone shear flows.
was shown by Deng and Masmoudi in [Reference Deng and Masmoudi18] when the initial perturbation is less smooth than the Gevrey space of class 2. For more general shear flows, the stability/instability results are more difficult to achieve due to the presence of nonlocal term. We refer to [Reference Chen, Wei and Zhang15, Reference Jia25, Reference Jia26, Reference Wei, Zhang and Zhao45, Reference Zillinger52] for the linear inviscid damping results for general monotone shear flows, and to [Reference Ionescu, Iyer and Jia24, Reference Wei, Zhang and Zhao46, Reference Wei, Zhang and Zhao47] for the linear stability results for non-monotone shear flows.
If the viscosity is taken into consideration, consider the toy model
it is not difficult to show that the non-zero mode $g_{\neq }$![]() undergo enhanced dissipation, namely for some $c>0$
undergo enhanced dissipation, namely for some $c>0$![]() there holds
there holds
The inviscid damping mentioned above and the enhanced dissipation demonstrated in (1.4) are two main stability mechanisms which are closely related to the stability threshold problem. That is, how small should initial perturbations be in terms of the viscous coefficient to ensure nonlinear stability? Since the early experiments of Reynolds [Reference Reynolds36], the the linear stability or instability of shear flows at high Reynolds number has been a classical problem in applied fluid mechanics [Reference Case10, Reference Kelvin27, Reference Orr35, Reference Schmid and Henningson39, Reference Yaglom48]. Significant progress has been made by Bedrossian, Germain and Masmoudi in [Reference Bedrossian, Germain and Masmoudi3–Reference Bedrossian, Germain and Masmoudi5] for the nonlinear stability of the Couette flow on $\mathbb {T}\times \mathbb {R}\times \mathbb {T}$![]() by using the time dependent Fourier multiplier method. Then Wei and Zhang [Reference Wei and Zhang44] proved the nonlinear stability of the Couette flow on $\mathbb {T}\times \mathbb {R}\times \mathbb {T}$
by using the time dependent Fourier multiplier method. Then Wei and Zhang [Reference Wei and Zhang44] proved the nonlinear stability of the Couette flow on $\mathbb {T}\times \mathbb {R}\times \mathbb {T}$![]() as long as the initial perturbation satisfying $\|u_{\mathrm {in}}\|_{H^2}\ll \mathrm {Re}^{-1}$
as long as the initial perturbation satisfying $\|u_{\mathrm {in}}\|_{H^2}\ll \mathrm {Re}^{-1}$![]() with $\mathrm {Re}$
with $\mathrm {Re}$![]() the Reynolds number. For the 2D the domain $\mathbb {T}\times \mathbb {R}$
the Reynolds number. For the 2D the domain $\mathbb {T}\times \mathbb {R}$![]() , a series of results can be found in [Reference Bedrossian, Masmoudi and Vicol7, Reference Bedrossian, Vicol and Wang8, Reference Masmoudi and Zhao34]. Recently, Li, Masmoudi and the first author of this paper [Reference Li, Masmoudi and Zhao29] studied the relationship between the size and the regularity of the initial perturbation that ensures the nonlinear asymptotic stability. For the periodic finite channels, a delicate resolvent estimate method was developed in [Reference Chen, Li, Wei and Zhang12, Reference Chen, Wei and Zhang14]. In particular, Chen, Wei and Zhang showed that the size of the initial perturbation in [Reference Wei and Zhang44] still ensures the stability of the Couette flow in the presence of physical boundary in [Reference Chen, Wei and Zhang14].
, a series of results can be found in [Reference Bedrossian, Masmoudi and Vicol7, Reference Bedrossian, Vicol and Wang8, Reference Masmoudi and Zhao34]. Recently, Li, Masmoudi and the first author of this paper [Reference Li, Masmoudi and Zhao29] studied the relationship between the size and the regularity of the initial perturbation that ensures the nonlinear asymptotic stability. For the periodic finite channels, a delicate resolvent estimate method was developed in [Reference Chen, Li, Wei and Zhang12, Reference Chen, Wei and Zhang14]. In particular, Chen, Wei and Zhang showed that the size of the initial perturbation in [Reference Wei and Zhang44] still ensures the stability of the Couette flow in the presence of physical boundary in [Reference Chen, Wei and Zhang14].
In the presence of magnetic field, the behaviours of the shear flows become more complicated. On the one hand, it is classically known that a strong background magnetic field can have a stability effect on a conducting fluid, see [Reference Chandrasekhar11, Reference Shivamoggi and Debnath40, Reference Velikhov42], for instance. On the other hand, the magnetic field may destabilize the system [Reference Chen and Morrison13] even with shear flows (including Couette flow) that are asymptotically stable. Tataronis and Grossmam [Reference Tataronis and Grossmann41] predicted that the decaying of the vertical components of velocity and magnetic field due to the phase mixing. Ren and Zhao [Reference Ren and Zhao38] gave a rigorous mathematical proof under the assumption that the magnetic field is positive and strictly monotone. In [Reference Hirota, Tatsuno and Yoshida20], Hirota, Tatsuno and Yoshida investigated the linearized behaviour of the ideal MHD equation around Couette flow $(k_fy, 0)$![]() and linear magnetic field $(k_my,0)$
and linear magnetic field $(k_my,0)$![]() . They predicted that if $|k_f|<|k_m|$
. They predicted that if $|k_f|<|k_m|$![]() , then the magnetic island appears in the final state, namely the linear asymptotic stability fails, and if $|k_m|<|k_f|$
, then the magnetic island appears in the final state, namely the linear asymptotic stability fails, and if $|k_m|<|k_f|$![]() , then linear damping holds and the magnetic island will be destructed. Recently, the generation of magnetic island was rigorously proved by Zhai, Zhang and Zhao in [Reference Zhai, Zhang and Zhao49], and the rigorously mathematical proof for the destruction of magnetic fields was given by Ren, Wei and Zhang in [Reference Ren, Wei and Zhang37]. We refer to [Reference Knobel and Zillinger28, Reference Liu, Masmoudi, Zhai and Zhao32] for more recent results for the linear stability results on shear flows in magnetic field. For the nonlinear stability result on this direction, Liss [Reference Liss31] proved that for strong and suitably oriented background fields $\alpha (\sigma,0,1)^\top$
, then linear damping holds and the magnetic island will be destructed. Recently, the generation of magnetic island was rigorously proved by Zhai, Zhang and Zhao in [Reference Zhai, Zhang and Zhao49], and the rigorously mathematical proof for the destruction of magnetic fields was given by Ren, Wei and Zhang in [Reference Ren, Wei and Zhang37]. We refer to [Reference Knobel and Zillinger28, Reference Liu, Masmoudi, Zhai and Zhao32] for more recent results for the linear stability results on shear flows in magnetic field. For the nonlinear stability result on this direction, Liss [Reference Liss31] proved that for strong and suitably oriented background fields $\alpha (\sigma,0,1)^\top$![]() , the Couette flow $(y, 0,0)^\top$
, the Couette flow $(y, 0,0)^\top$![]() is asymptotically stable provided the initial perturbations $u_{\mathrm {in}}$
is asymptotically stable provided the initial perturbations $u_{\mathrm {in}}$![]() and $b_{\mathrm {in}}$
and $b_{\mathrm {in}}$![]() satisfy
satisfy
with $N$![]() sufficiently large.
sufficiently large.
In this paper, under the same condition $\nu =\mu$![]() in [Reference Liss31], we study the nonlinear stability of the time dependent shear flow $u_s=( \bar {U}(t,y),0)$
in [Reference Liss31], we study the nonlinear stability of the time dependent shear flow $u_s=( \bar {U}(t,y),0)$![]() in a uniform magnetic field $b_s=(\alpha,0)^\top$
in a uniform magnetic field $b_s=(\alpha,0)^\top$![]() on $\mathbb {T}\times \mathbb {R}$
on $\mathbb {T}\times \mathbb {R}$![]() . More precisely, for $0<\nu =\mu \ll 1$
. More precisely, for $0<\nu =\mu \ll 1$![]() , given an initial norm $X_i$
, given an initial norm $X_i$![]() and a final norm $X_f$
and a final norm $X_f$![]() , our goal in this paper is determine a constant $\gamma =\gamma (X_i, X_f)\ge 0$
, our goal in this paper is determine a constant $\gamma =\gamma (X_i, X_f)\ge 0$![]() as small as possible, such that if the initial perturbations $\bar {u}_{\mathrm {in}}$
as small as possible, such that if the initial perturbations $\bar {u}_{\mathrm {in}}$![]() and $\bar {b}_{\mathrm {in}}$
and $\bar {b}_{\mathrm {in}}$![]() satisfy
satisfy
for $c_0$![]() sufficiently small (independent of $\nu$
sufficiently small (independent of $\nu$![]() ), then the solution of (1.1) is global in time and converges back to $( u_s,b_s )$
), then the solution of (1.1) is global in time and converges back to $( u_s,b_s )$![]() as $t \to \infty$
as $t \to \infty$![]() in the sense that
in the sense that
1.2 The main result
Our main result is stated as follows.
Theorem 1.1 Let $N>1,$![]() $\mu =\nu \in (0,1]$
$\mu =\nu \in (0,1]$![]() . There exist two sufficiently large constants $\alpha _0>0$
. There exist two sufficiently large constants $\alpha _0>0$![]() and $C \ge 1$
and $C \ge 1$![]() independent of $\nu,$
independent of $\nu,$![]() such that for all $|\alpha |\ge \alpha _0,$
such that for all $|\alpha |\ge \alpha _0,$![]() if the shear flow $U=U(y)$
if the shear flow $U=U(y)$![]() satisfies
satisfies
with $\delta$![]() independent of $\nu$
independent of $\nu$![]() , and the initial perturbation obeys
, and the initial perturbation obeys
for any fixed $\tilde \delta >0$![]() , then the global in time solution $(\omega,j)$
, then the global in time solution $(\omega,j)$![]() to (1.3) obeys
to (1.3) obeys
and the enhanced dissipation estimate
Remark 1.2 The bounds (1.10) and (1.11) follow from (4.3), (4.5) in theorem 4.1 and lemma A.1 immediately. So the rest part of this paper aims to prove theorem 4.1.
Remark 1.3 It is not difficult to obtain the explicit enhanced dissipation decay $e^{-c\nu ^\frac {1}{3}t}$![]() for $(\omega _{\ne }, j_{\ne })$
for $(\omega _{\ne }, j_{\ne })$![]() like (1.4). In fact, we just need to change the multiplier $\tilde K$
like (1.4). In fact, we just need to change the multiplier $\tilde K$![]() (see (4.2)) slightly. Let ${\bf e}_{\ne }$
(see (4.2)) slightly. Let ${\bf e}_{\ne }$![]() be a multiplier defined by
be a multiplier defined by
Set
Replacing the multiplier $\tilde K$![]() in (4.10) by $\mathsf {M}$
in (4.10) by $\mathsf {M}$![]() , the proof of proposition 4.3 is still valid. In particular, one can use (3.21) to absorb the bad term $c\nu ^\frac {1}{3}\left \|\mathsf {M}Z^{\pm }_{\ne }\right \|_{L^2}^2$
, the proof of proposition 4.3 is still valid. In particular, one can use (3.21) to absorb the bad term $c\nu ^\frac {1}{3}\left \|\mathsf {M}Z^{\pm }_{\ne }\right \|_{L^2}^2$![]() arising from the time evolution of ${\bf e}_{\ne }$
arising from the time evolution of ${\bf e}_{\ne }$![]() for sufficiently small $c$
for sufficiently small $c$![]() (see § 2.3 for the definition of $Z^{\pm }$
(see § 2.3 for the definition of $Z^{\pm }$![]() ). We refer to [Reference Zhang and Zi50] for more details of the use of the multiplier ${\bf e}_{\ne }$
). We refer to [Reference Zhang and Zi50] for more details of the use of the multiplier ${\bf e}_{\ne }$![]() to get the explicit enhanced dissipation decay $e^{-c\nu ^\frac {1}{3}t}$
to get the explicit enhanced dissipation decay $e^{-c\nu ^\frac {1}{3}t}$![]() .
.
Remark 1.4 At first glance, it looks as if the loss $\nu ^{-\frac {1}{2}}$![]() on the right hand side of (1.11) might come from the diffusion $-\nu \Delta (\omega,j)$
on the right hand side of (1.11) might come from the diffusion $-\nu \Delta (\omega,j)$![]() . As a matter of fact, roughly speaking, due to the linear growth $\langle t \rangle$
. As a matter of fact, roughly speaking, due to the linear growth $\langle t \rangle$![]() caused by the stretch $2\bar {U}'\partial _{xy}\phi$
caused by the stretch $2\bar {U}'\partial _{xy}\phi$![]() (together with the oscillation stemming from the strong background magnetic field $(\alpha,0)^{\top }$
(together with the oscillation stemming from the strong background magnetic field $(\alpha,0)^{\top }$![]() ) and the enhanced dissipation $e^{-c\nu ^\frac {1}{3}t}$
) and the enhanced dissipation $e^{-c\nu ^\frac {1}{3}t}$![]() as mentioned in remark 1.3, $(\omega _{\ne }, j_{\ne })$
as mentioned in remark 1.3, $(\omega _{\ne }, j_{\ne })$![]() behaves like $\langle t\rangle e^{-c\nu ^\frac {1}{3}t}$
behaves like $\langle t\rangle e^{-c\nu ^\frac {1}{3}t}$![]() . Clearly, $\left \|\langle t\rangle e^{-c\nu ^\frac {1}{3}t}\right \|_{L^2_t}\approx \nu ^{-\frac {1}{2}}$
. Clearly, $\left \|\langle t\rangle e^{-c\nu ^\frac {1}{3}t}\right \|_{L^2_t}\approx \nu ^{-\frac {1}{2}}$![]() . This explains the loss $\nu ^{-\frac {1}{2}}$
. This explains the loss $\nu ^{-\frac {1}{2}}$![]() on the right hand side of (1.11).
on the right hand side of (1.11).
Remark 1.5 Compared with the Couette flow case $\bar {U}(t,y)=U(y)=y$![]() , the extra exponent $\tilde \delta$
, the extra exponent $\tilde \delta$![]() in (1.9) is derived from the linear stretch term $2\bar {U}'\partial _{xy}\phi$
in (1.9) is derived from the linear stretch term $2\bar {U}'\partial _{xy}\phi$![]() in (1.3), which is absent in the 2D Navier–Stokes equations around shear flows near Couette (see [Reference Bedrossian, Vicol and Wang8]). It is open whether one can remove the extra exponent $\tilde \delta$
in (1.3), which is absent in the 2D Navier–Stokes equations around shear flows near Couette (see [Reference Bedrossian, Vicol and Wang8]). It is open whether one can remove the extra exponent $\tilde \delta$![]() in (1.9).
in (1.9).
Remark 1.6 The constant $C$![]() in theorem 1.1 depends on $\frac {1}{|\alpha |}$
in theorem 1.1 depends on $\frac {1}{|\alpha |}$![]() . As a matter of fact, if $\alpha =0$
. As a matter of fact, if $\alpha =0$![]() , the oscillations $-\alpha \partial _xj$
, the oscillations $-\alpha \partial _xj$![]() and $-\alpha \partial _x\omega$
and $-\alpha \partial _x\omega$![]() disappear in (1.3). As a result, instead of the linear growth $\langle t\rangle$
disappear in (1.3). As a result, instead of the linear growth $\langle t\rangle$![]() in the case $|\alpha |\ge \alpha _0$
in the case $|\alpha |\ge \alpha _0$![]() , for $\alpha =0$
, for $\alpha =0$![]() the linear stretch term $2\bar {U}'\partial _{xy}\phi$
the linear stretch term $2\bar {U}'\partial _{xy}\phi$![]() in (1.3) will lead to $\langle t\rangle ^2$
in (1.3) will lead to $\langle t\rangle ^2$![]() growth even for $\bar {U}(t,y)=U(y)=y$
growth even for $\bar {U}(t,y)=U(y)=y$![]() , which costs more smallness of the initial perturbations in terms of some power of $\nu$
, which costs more smallness of the initial perturbations in terms of some power of $\nu$![]() to ensure the stability.
to ensure the stability.
1.3 Notations
(1) Throughout this paper, we use the standard notation
\[ \left\langle x\right\rangle =\sqrt{1+x^2} \]we write $\left \langle \nabla \right \rangle ^s$
 for the operator with symbol
\[ \left\langle \nabla\right\rangle^s=\left( 1+k^2+\eta^2\right) ^{\frac{s}{2}}. \]
for the operator with symbol
\[ \left\langle \nabla\right\rangle^s=\left( 1+k^2+\eta^2\right) ^{\frac{s}{2}}. \]
(2) We use the notation $f\lesssim g$
 to mean that there exist some constant $C>0$
to mean that there exist some constant $C>0$ such that $f\le Cg$
such that $f\le Cg$ . This constant $C$
. This constant $C$ may depend on $N$
may depend on $N$ and $\alpha$
and $\alpha$ , but not on $\nu$
, but not on $\nu$ .
.(3) For a function $f(x,y)$
 , We denote the projection of $f$
, We denote the projection of $f$ onto the zero frequencies in $x$
onto the zero frequencies in $x$ by
\[ f_0(y)=\int_{\mathbb{T}}f(x,y){\rm d}x. \]Then we write
by
\[ f_0(y)=\int_{\mathbb{T}}f(x,y){\rm d}x. \]Then we write \[ f_\ne(x,y)=f(x,y)-f_0(y) \]for the projection onto the nonzero frequencies in $x$
\[ f_\ne(x,y)=f(x,y)-f_0(y) \]for the projection onto the nonzero frequencies in $x$
 .
.(4) The Fourier transform of function $f$
 is denoted by
\[ \mathcal{F}(f)=\hat{f}(k,\eta)=\frac{1}{2\pi}\int_{\mathbb{T}\times \mathbb{R}}e^{{-}i(kx+\eta y)}f(x,y){\rm d}x{\rm d}y. \]The Fourier multiplier with symbol $m(t,k,\eta )$
is denoted by
\[ \mathcal{F}(f)=\hat{f}(k,\eta)=\frac{1}{2\pi}\int_{\mathbb{T}\times \mathbb{R}}e^{{-}i(kx+\eta y)}f(x,y){\rm d}x{\rm d}y. \]The Fourier multiplier with symbol $m(t,k,\eta )$
 is given by
\[ mf=\mathcal{F}^{{-}1}\left( m(t,k,\eta) \mathcal{F} f\right) . \]
is given by
\[ mf=\mathcal{F}^{{-}1}\left( m(t,k,\eta) \mathcal{F} f\right) . \]
(5) For any $a \in \mathbb {R}$
 , we use the shorthand notation
(1.12)\begin{equation} O_a^t=e^{a \partial_x t} \end{equation}to denote the multiplier with symbol $e^{iakt}$
, we use the shorthand notation
(1.12)\begin{equation} O_a^t=e^{a \partial_x t} \end{equation}to denote the multiplier with symbol $e^{iakt}$
 . We then write $\partial _t O_a^t$
. We then write $\partial _t O_a^t$ to denote the Fourier multiplier with symbol $iake^{iakt}$
to denote the Fourier multiplier with symbol $iake^{iakt}$ .
.(6) For $s\ge 0$
 , we define the Sobolev space $H^s$
, we define the Sobolev space $H^s$ by using the norm
\[ \left\| f\right\|_{H^s} := \left\| \left\langle \nabla\right\rangle^s f \right\|_{L^2}. \]The notation $L^pL^q=L^p_tL^q_{x,y}$
by using the norm
\[ \left\| f\right\|_{H^s} := \left\| \left\langle \nabla\right\rangle^s f \right\|_{L^2}. \]The notation $L^pL^q=L^p_tL^q_{x,y}$
 is used for the Banach space $L^p([0,T];L^q(\Omega ))$
is used for the Banach space $L^p([0,T];L^q(\Omega ))$ with norm
\[ \left\| f(t,x)\right\|_{L^pL^q}=\big\| \|f(t,\cdot)\|_{L^q} \big\|_{L^p}. \]
with norm
\[ \left\| f(t,x)\right\|_{L^pL^q}=\big\| \|f(t,\cdot)\|_{L^q} \big\|_{L^p}. \]
(7) For two real functions $f$
 and $g$
and $g$ , we write the associated inner product as
\[ \left\langle f,g \right\rangle=\int_{\mathbb{T}\times\mathbb{R}} f g {\rm d}x {\rm d}y, \]and denote
, we write the associated inner product as
\[ \left\langle f,g \right\rangle=\int_{\mathbb{T}\times\mathbb{R}} f g {\rm d}x {\rm d}y, \]and denote \[ \langle f,g \rangle _{H^s}= \left\langle \langle\nabla\rangle^sf, \langle\nabla\rangle^sg \right\rangle. \]
\[ \langle f,g \rangle _{H^s}= \left\langle \langle\nabla\rangle^sf, \langle\nabla\rangle^sg \right\rangle. \]
2. Reformulations and key ideas of the proof
2.1 Elsässer variables under the restriction $\mu =\nu$
Since we focus on the case $\nu =\mu$![]() in this paper, the symmetry of the system (1.3) enables us to reformulate it by using the Elsässer variables
in this paper, the symmetry of the system (1.3) enables us to reformulate it by using the Elsässer variables
Then $w^{\pm }$![]() solves
solves

Such kind of variables have played important roles in the study of large time behaviours of solutions to MHD equations in the absence of shear flows [Reference Bardos, Sulem and Sulem2, Reference Cai and Lei9, Reference He, Xu, Li and Yu19, Reference Wei and Zhang43], and the nonlinear stability result [Reference Liss31] where the three dimensional Couette flow $(y,0,0)^{\top }$![]() is taken into consideration as mentioned in § 1.
is taken into consideration as mentioned in § 1.
Similar to the 3D case, the background magnetic field $(\alpha, 0)^\top$![]() introduces oscillations (see the $-\alpha \partial _xw^\pm$
introduces oscillations (see the $-\alpha \partial _xw^\pm$![]() terms in (2.1)) that may stabilize the system. Following [Reference Liss31], we define the profiles
terms in (2.1)) that may stabilize the system. Following [Reference Liss31], we define the profiles
to hide the oscillations in the new unknowns $z^{\pm }$![]() , where $O^t_{\pm \alpha }$
, where $O^t_{\pm \alpha }$![]() is defined in (1.12). Then $z^{\pm }$
is defined in (1.12). Then $z^{\pm }$![]() solves
solves

2.2 Change of coordinates
In this paper we use the coordinate transform introduced by Bedrossian, Vicol and Wang in [Reference Bedrossian, Vicol and Wang8] to unwind the decaying background shear flow $\bar {U}(t,y)$![]() in (2.1):
in (2.1):
Denote the spatial derivatives of the shear flow in the new coordinates as follows

Note that by the chain rule, we have
For any function $\tilde {h}$![]() in the $(x,y)$
in the $(x,y)$![]() coordinates, the corresponding function $h$
coordinates, the corresponding function $h$![]() in the $(X,Y)$
in the $(X,Y)$![]() coordinates is given by
coordinates is given by
Then $\nabla \tilde h$![]() and $\Delta \tilde h$
and $\Delta \tilde h$![]() can be rewritten in the new coordinate system (2.2) in terms of $h$
can be rewritten in the new coordinate system (2.2) in terms of $h$![]() as follows (the notations $\nabla _t$
as follows (the notations $\nabla _t$![]() and $\Delta _t$
and $\Delta _t$![]() are introduced naturally):
are introduced naturally):
and

where we have used the notations
and the modified Laplace operator is given by
Finally, using the fact $\partial _t \bar {U} =\nu \partial _y^2\bar {U}$![]() and the definitions of $a$
and the definitions of $a$![]() and $b$
and $b$![]() , we have
, we have
In particular,
which, together with the fact $\partial _t\bar {U}=\nu \partial _y^2\bar {U}$![]() imply that
imply that
2.3 Definition of $\Delta _t^{-1}$ and system (2.1) under new coordinates
and system (2.1) under new coordinates
In this subsection, we first give the definition of the inverse of $\Delta _t$![]() in the spirit of Antonelli, Dolce, and Marcati [Reference Antonelli, Dolce and Marcati1]. For the sake of completeness, we sketch the definitions below.
in the spirit of Antonelli, Dolce, and Marcati [Reference Antonelli, Dolce and Marcati1]. For the sake of completeness, we sketch the definitions below.
To begin with, assume that $a^2-1=(a^2-1)(t, Y)$![]() and $b=b(t, Y)$
and $b=b(t, Y)$![]() are given functions in $L^\infty (\mathbb {R}^+; H^1(\mathbb {R}))$
are given functions in $L^\infty (\mathbb {R}^+; H^1(\mathbb {R}))$![]() , then the fact that $\Delta _L^{-1}$
, then the fact that $\Delta _L^{-1}$![]() is well defined for $k\ne 0$
is well defined for $k\ne 0$![]() enables us to define an operator on $L^2(\mathbb {T}\times \mathbb {R})$
enables us to define an operator on $L^2(\mathbb {T}\times \mathbb {R})$![]() :
:
with
for some constant $C_*\ge 1$![]() , see proposition 4.1 in [Reference Antonelli, Dolce and Marcati1] for more details.
, see proposition 4.1 in [Reference Antonelli, Dolce and Marcati1] for more details.
Definition 2.1 Assume that $(\|a^2-1\|_{L^\infty H^1}+\|b\|_{L^\infty H^1})\le \delta$![]() such that $C_*\delta <1$
such that $C_*\delta <1$![]() , then for $k\ne 0$
, then for $k\ne 0$![]() , let us define
, let us define
where

Remark 2.2 For the operator $\Lambda$![]() , we also have the following useful identity
, we also have the following useful identity
Now we are in a position to rewrite (2.1) under the coordinates defined by (2.2). To this end, let us denote

Note that
and
Then it follows from (2.1) that the equations of $Z^\pm$![]() take the form of
take the form of
or
where
with

and
Here ‘$\mathrm {NLT}$![]() ’, ‘$\mathrm {NLS}$
’, ‘$\mathrm {NLS}$![]() ’ and ‘$\mathrm {LP}$
’ and ‘$\mathrm {LP}$![]() ’ stand for ‘nonlinear transport’, ‘nonlinear stretch’ and ‘linear perturbation’, respectively.
’ stand for ‘nonlinear transport’, ‘nonlinear stretch’ and ‘linear perturbation’, respectively.
2.4 Toy model and key ideas
Compared with the Navier–Stokes equations around 2D shear flows near Couette [Reference Bedrossian, Vicol and Wang8], and the MHD equations around 3D Couette flows [Reference Liss31], we will encounter new difficulties for the MHD equations around 2D shear flows near Couette. In order to track the difficulties precisely, let us consider the toy model
or equivalently in Fourier variables
It is worth pointing out that if the shear flow is the Couette flow, i.e., $\bar {U}(t,y)=U(y)=y$![]() , the operator $\Lambda$
, the operator $\Lambda$![]() in (2.20) will not appear. This scenario is reminiscent of the toy model introduced by Bedrossian, Germain and Masmoudi in [Reference Bedrossian, Germain and Masmoudi3] for the 3D Navier–Stokes equations near Couette:
in (2.20) will not appear. This scenario is reminiscent of the toy model introduced by Bedrossian, Germain and Masmoudi in [Reference Bedrossian, Germain and Masmoudi3] for the 3D Navier–Stokes equations near Couette:

To balance the interaction between $\frac {2k(\eta -kt)}{k^2+(\eta -kt)^2+l^2}\hat {g}$![]() and $-\nu (k^2+(\eta -kt)^2+l^2)\hat {g}$
and $-\nu (k^2+(\eta -kt)^2+l^2)\hat {g}$![]() , the authors in [Reference Bedrossian, Germain and Masmoudi3] constructed a multiplier $m(t,k, \eta,l)$
, the authors in [Reference Bedrossian, Germain and Masmoudi3] constructed a multiplier $m(t,k, \eta,l)$![]() satisfying
satisfying
More precisely, the two dimensional analogue of the multiplier $m(t,k, \eta,l)$![]() is given as follows:
is given as follows:
(1) if $k = 0: m(t,0,\eta ) = 1$
 ;
;(2) if $k \ne 0, \frac {\eta }{k} < -1000\nu ^{-\frac {1}{3}}: m(t,k,\eta ) = 1$
 ;
;(3) if $k \ne 0, -1000\nu ^{-\frac {1}{3}} < \frac {\eta }{k} < 0$
 :
:
• $m(t,k,\eta ) = \frac {k^2+\eta ^2}{k^2+(\eta -kt)^2}$
 if $0 < t < \frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$
if $0 < t < \frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$ ,
,• $m(t,k,\eta ) = \frac {k^2+\eta ^2}{k^2+(1000k\nu ^{-\frac {1}{3}})^2}$
 if $t > \frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$
if $t > \frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$ ;
;
(4) if $k \ne 0, \frac {\eta }{k} > 0$
 :
:
• $m(t,k,\eta ) = 1$
 if $t < \frac {\eta }{k}$
if $t < \frac {\eta }{k}$ ,
,• $m(t,k,\eta ) = \frac {k^2}{k^2+(\eta -kt)^2}$
 if $\frac {\eta }{k} < t < \frac {\eta }{k} + 1000\nu ^{-\frac {1}{3}}$
if $\frac {\eta }{k} < t < \frac {\eta }{k} + 1000\nu ^{-\frac {1}{3}}$ ,
,• $m(t,k,\eta ) =\frac {k^2}{k^2+(1000k\nu ^{-\frac {1}{3}})^2}$
 if $t > \frac {\eta }{k} + 1000\nu ^{-\frac {1}{3}}$
if $t > \frac {\eta }{k} + 1000\nu ^{-\frac {1}{3}}$ .
.
Notice, in particular, that
and
In our case, for the Couette flow, it suffices to use $m^{\frac {1}{2}}(t,k,\eta )$![]() instead of $m(t,k,\eta )$
instead of $m(t,k,\eta )$![]() to suppress the potential growth caused by the linear stretch term $\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {f^{\pm }}$
to suppress the potential growth caused by the linear stretch term $\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {f^{\pm }}$![]() . Nevertheless, for general shear flows the presence of the operator $\Lambda$
. Nevertheless, for general shear flows the presence of the operator $\Lambda$![]() may amplify the linear stretch effect since the norm of $\Lambda$
may amplify the linear stretch effect since the norm of $\Lambda$![]() may be larger than 1 even though the shear flow $\bar {U}$
may be larger than 1 even though the shear flow $\bar {U}$![]() is close to Couette. Roughly speaking, one can regard the linear stretch term in (2.20) as $(1+O(\tilde \delta ))\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {f^{\pm }}$
is close to Couette. Roughly speaking, one can regard the linear stretch term in (2.20) as $(1+O(\tilde \delta ))\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {f^{\pm }}$![]() with $\tilde \delta >0$
with $\tilde \delta >0$![]() . Then it is natural to modify the multiplier $m^{\frac {1}{2}}(t,k,\eta )$
. Then it is natural to modify the multiplier $m^{\frac {1}{2}}(t,k,\eta )$![]() so as to suppress the extra growth resulting from the operator $\Lambda$
so as to suppress the extra growth resulting from the operator $\Lambda$![]() . To this end, our strategy is to replace $m^{\frac {1}{2}}(t,k,\eta )$
. To this end, our strategy is to replace $m^{\frac {1}{2}}(t,k,\eta )$![]() with $\tilde {m}^{\frac {1}{2}}(t,k,\eta )$
with $\tilde {m}^{\frac {1}{2}}(t,k,\eta )$![]() , where $\tilde m(t,k,\eta )$
, where $\tilde m(t,k,\eta )$![]() is defined by
is defined by
with arbitrary $\tilde \delta >0$![]() . Note that
. Note that
Then (2.21) and (2.22) reduce to
and

For $(t,k,\eta )\in [0,\infty )\times \mathbb {Z}\backslash \{0\}\times \mathbb {R}$![]() , let us define the following three disjoint sets
, let us define the following three disjoint sets

Then the effects of the linear stretch are summarized as follows:
(1) if $(t, k, \eta )\in D_{dam}$
 , then $k(\eta -kt)\ge 0$
, then $k(\eta -kt)\ge 0$ , and thus the linear stretch term behaves as a damping.
, and thus the linear stretch term behaves as a damping.(2) if $(t, k, \eta )\in D_{dis}$
 , we have
\[ \left|t-\frac{\eta}{k}\right|\ge1000\nu^{-\frac {1}{3}}, \]and thus
, we have
\[ \left|t-\frac{\eta}{k}\right|\ge1000\nu^{-\frac {1}{3}}, \]and thus (2.27)\begin{equation} \frac{|k(\eta-kt)|}{k^2+(\eta-kt)^2}\le \frac{1}{1000^3} \nu\left(k^2+(\eta-kt)^2\right), \end{equation}which means that the linear stretch is dominated by the dissipation.
(2.27)\begin{equation} \frac{|k(\eta-kt)|}{k^2+(\eta-kt)^2}\le \frac{1}{1000^3} \nu\left(k^2+(\eta-kt)^2\right), \end{equation}which means that the linear stretch is dominated by the dissipation.
(3) by the definition of $\tilde m$
 , there holds
(2.28)\begin{equation} \frac{|k(\eta-kt)|}{k^2+(\eta-kt)^2}{\bf 1}_{D_{mul}}(t, k,\eta)=\frac{1}{1+\frac 32\tilde\delta}\frac{-\partial_t(\tilde m^{1/2})(t, k,\eta)}{\tilde m^{1/2}(t, k, \eta)}, \end{equation}that is to say, the effect of the linear stretch is balanced by the evolution of ${\tilde m}^\frac {1}{2}$
, there holds
(2.28)\begin{equation} \frac{|k(\eta-kt)|}{k^2+(\eta-kt)^2}{\bf 1}_{D_{mul}}(t, k,\eta)=\frac{1}{1+\frac 32\tilde\delta}\frac{-\partial_t(\tilde m^{1/2})(t, k,\eta)}{\tilde m^{1/2}(t, k, \eta)}, \end{equation}that is to say, the effect of the linear stretch is balanced by the evolution of ${\tilde m}^\frac {1}{2}$
 on $D_{mul}$
on $D_{mul}$ .
.
Remark 2.3 Clearly, the following decomposition of unity holds
Then it follows from (2.27) and (2.28) that

The treatment of the general shear flow $(\bar {U},0)^\top$![]() is much more complicated than that of the Couette flow $(y,0)^\top$
is much more complicated than that of the Couette flow $(y,0)^\top$![]() . In fact, for the case $\bar {U}(t,y)=U(y)=y$
. In fact, for the case $\bar {U}(t,y)=U(y)=y$![]() , once the multiplier $m(t,k,\eta )$
, once the multiplier $m(t,k,\eta )$![]() is well defined as above, then it is straightforward to deal with the linear stretch term, see (3.24). In particular, the damping effect stemming from the linear stretch term when $(t,k,\eta )\in D_{dam}$
is well defined as above, then it is straightforward to deal with the linear stretch term, see (3.24). In particular, the damping effect stemming from the linear stretch term when $(t,k,\eta )\in D_{dam}$![]() can be ignored. However, for the case that $U(y)$
can be ignored. However, for the case that $U(y)$![]() is close to $y$
is close to $y$![]() , the appearance of the operator $\Lambda$
, the appearance of the operator $\Lambda$![]() makes the damping effect of the linear stretch $\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {\Lambda f^\pm }$
makes the damping effect of the linear stretch $\frac {k(\eta -kt)}{k^2+(\eta -kt)^2}\widehat {\Lambda f^\pm }$![]() unclear even though $(t,k,\eta )\in D_{dam}$
unclear even though $(t,k,\eta )\in D_{dam}$![]() . Our strategy is to isolate the damping effect by using (2.13):
. Our strategy is to isolate the damping effect by using (2.13):
The first term on the right hand side of (2.30) is the main part, and the second term is the perturbation. Some delicate commutator estimates will be performed to treat the perturbation. As a result, lots of errors appear. To close the estimates, the damping effect captured by the main part of the linear stretch in (2.30), together with the dissipation and other good terms, will be used to absorb the errors. See Step I of § 4.1 for more details.
In addition, the presence of the operator $\Lambda$![]() leads us to estimate the composition $B\circ \Lambda$
leads us to estimate the composition $B\circ \Lambda$![]() for some multiplier $B$
for some multiplier $B$![]() involved in this paper. The continuity of $B\circ \Lambda$
involved in this paper. The continuity of $B\circ \Lambda$![]() depends on the commutator estimates of $B$
depends on the commutator estimates of $B$![]() . That's why we give a collection of commutator estimates in Appendix B. In particular, some extra terms appear in the commutator estimate of $\sqrt {-\frac {\partial _t(\tilde m^\frac {1}{2})}{\tilde m^\frac {1}{2}}}\tilde K$
. That's why we give a collection of commutator estimates in Appendix B. In particular, some extra terms appear in the commutator estimate of $\sqrt {-\frac {\partial _t(\tilde m^\frac {1}{2})}{\tilde m^\frac {1}{2}}}\tilde K$![]() , see lemma B.4. This motivates us to establish a composition inequality for the multipliers whose commutator estimates have extra errors with better commutator estimates, see lemma C.1 for the details.
, see lemma B.4. This motivates us to establish a composition inequality for the multipliers whose commutator estimates have extra errors with better commutator estimates, see lemma C.1 for the details.
On the other hand, it is worth pointing out that the above toy model (2.19) ignored the oscillation terms $O^t_{\pm 2\alpha }S\Lambda f^{\mp }$![]() , which should be taken into consideration as well in the energy estimates. In order to take advantage of the oscillator $O^t_\alpha$
, which should be taken into consideration as well in the energy estimates. In order to take advantage of the oscillator $O^t_\alpha$![]() , noting that
, noting that
integrating by parts with respect to the time variable will be exploited as that in [Reference Liss31]. In this way, we will inevitably encounter the time derivative of the operator $\Lambda$![]() . To achieve this, using again (2.13), we obtain an important relation
. To achieve this, using again (2.13), we obtain an important relation
where $\partial _t\tilde \Lambda$![]() is derived from (2.10)
is derived from (2.10)
See the estimates of $\mathrm {OLS}_5$![]() in Step II of § 4.1 for more details.
in Step II of § 4.1 for more details.
Finally, we would like to remark that, unlike [Reference Antonelli, Dolce and Marcati1], the coefficients $a$![]() and $b$
and $b$![]() hidden in the definition of $\Delta _t^{-1}$
hidden in the definition of $\Delta _t^{-1}$![]() are time dependent (see (2.10) and (2.12)), and $\partial _ta$
are time dependent (see (2.10) and (2.12)), and $\partial _ta$![]() and $\partial _tb$
and $\partial _tb$![]() are involved when performing integrating by parts in time (see (2.33)). Accordingly, recalling (2.3) and (2.9), we find that some higher derivatives of $\bar {U}$
are involved when performing integrating by parts in time (see (2.33)). Accordingly, recalling (2.3) and (2.9), we find that some higher derivatives of $\bar {U}$![]() are actually involved. This partially explains the extra regularities required in (1.8).
are actually involved. This partially explains the extra regularities required in (1.8).
3. Stability of the Couette flow
For comparison, we discuss in this section the case that the shear flow is the Couette flow. In fact, under the condition $\bar {U}(t,y)=U(y)=y$![]() , the change of coordinates (2.2) reduces to
, the change of coordinates (2.2) reduces to
Without causing confusion, we continue to use the unknowns and notations introduced in § 2. Then it is easy to see that the system (2.15) now reads

The purpose of this section is to establish the following theorem.
Theorem 3.1 Let $\mu =\nu \in (0,1], N>1$![]() . There exist a universal constant $\alpha _0>0$
. There exist a universal constant $\alpha _0>0$![]() , and a positive constant $\delta$
, and a positive constant $\delta$![]() depending only on $N$
depending only on $N$![]() and $\alpha$
and $\alpha$![]() , such that if $|\alpha |\ge \alpha _0$
, such that if $|\alpha |\ge \alpha _0$![]() and
and
then the following estimates hold
and
Theorem 3.1 will be proved by using the Fourier multiplier method. In other words, the norms involved in the proof are defined based on special, time-dependent Fourier multipliers. Apart from the multiplier $m(t, k,\eta )$![]() defined in § 2, we also need two extra multipliers that are modified from the ones introduced in the study of the stability of the three dimensional Couette flow in [Reference Bedrossian, Germain and Masmoudi3]. More precisely, define
defined in § 2, we also need two extra multipliers that are modified from the ones introduced in the study of the stability of the three dimensional Couette flow in [Reference Bedrossian, Germain and Masmoudi3]. More precisely, define


The multiplier $M_1$![]() is used to capture the inviscid damping effect in terms of the $L^2$
is used to capture the inviscid damping effect in terms of the $L^2$![]() time integrability, and $M_2$
time integrability, and $M_2$![]() is designed to show the enhanced dissipation effect. Clearly, $M_1$
is designed to show the enhanced dissipation effect. Clearly, $M_1$![]() and $M_2$
and $M_2$![]() can be given explicitly, and then one deduces that
can be given explicitly, and then one deduces that
For more properties of multiplier $M_1$![]() and $M_2$
and $M_2$![]() , one can refer to lemma 4.1 of [Reference Bedrossian, Vicol and Wang8].
, one can refer to lemma 4.1 of [Reference Bedrossian, Vicol and Wang8].
Let us denote
Then from (2.21) and (3.9), we find that for any $f=f(X,Y)\in H^N$![]() ,
,
In addition, we need to estimate the interactions between the non-zero modes in the treatment of the nonlinear terms, so the following lemma is introduced.
Lemma 3.2 Let $N>1$![]() . Then for all $f\in L^2H^N$
. Then for all $f\in L^2H^N$![]() and $g$
and $g$![]() such that $\nabla _Lg\in L^2H^N$
such that $\nabla _Lg\in L^2H^N$![]() , there holds
, there holds

Proof. We first write
Thanks to (2.22), there hold
and
Combining these two estimates with (3.11) yields

To estimate $\partial _X\Delta _L^{-1}f_\neq \partial _Y^Lg_\neq$![]() , in view of (2.21), (2.22) and the definition of $M$
, in view of (2.21), (2.22) and the definition of $M$![]() , we arrive at
, we arrive at

and
Accordingly,

It follows from (3.15) and (3.18) that (3.12) holds. This completes the proof of lemma 3.2.
3.1 Proof of theorem 3.1
To prove theorem 3.1, it suffices to establish the following a priori estimates:

and
Indeed, (3.4) is a direct consequence of (3.11) and (3.19), and (3.5) is nothing but (3.20). To prove (3.6), by the definition of $M_2$![]() , we have
, we have

It follows that

Thus, (3.6) follows from (3.11), (3.19) and (3.22) immediately.
Next we will prove (3.19) and (3.20) by using the standard continuity method. First of all, the local well-posedness of the 2D MHD equations in $H^N$![]() ensures that there exists a $T_0>0$
ensures that there exists a $T_0>0$![]() , such that
, such that

and
Then define $T^* \le \infty$![]() to be the maximum of all time $T$
to be the maximum of all time $T$![]() such that (3.19) and (3.20) hold on $[0,T]$
such that (3.19) and (3.20) hold on $[0,T]$![]() . By the continuity, $T^* > T_0$
. By the continuity, $T^* > T_0$![]() .
.
We are left to prove that the constant 8 on the right of (3.19) and (3.20) can be replaced by 4, which implies that $T^* = \infty$![]() . In fact, we have the following propositon.
. In fact, we have the following propositon.
Proposition 3.3 Let $\mu =\nu \in (0,1], N>1$![]() . Assume that (3.19) and (3.20) hold on $[0, T^*]$
. Assume that (3.19) and (3.20) hold on $[0, T^*]$![]() . There exist a universal constant $\alpha _0>0$
. There exist a universal constant $\alpha _0>0$![]() and a positive constant $\delta$
and a positive constant $\delta$![]() depending only on $N$
depending only on $N$![]() and $\alpha$
and $\alpha$![]() , such that if $|\alpha |\ge \alpha _0$
, such that if $|\alpha |\ge \alpha _0$![]() and (3.3) holds, then the same estimates in (3.19) and (3.20) hold with the occurrences of 8 on the right-hand side replaced by 4.
and (3.3) holds, then the same estimates in (3.19) and (3.20) hold with the occurrences of 8 on the right-hand side replaced by 4.
The proof of proposition 3.3 will be achieved in the following two subsections.
3.2 Improvement of (3.19)
Recalling the definition of the multiplier $K$![]() in (3.10), from (3.2), we derive the following energy identity:
in (3.10), from (3.2), we derive the following energy identity:

By the definition of $m$![]() , we have
, we have

Thanks to the fact (2.31), one can estimate $\mathrm {OLS}$![]() by integrating by parts in time:
by integrating by parts in time:

where

Clearly,
To bound $\mathrm {OLS}_3$![]() , in Fourier variables, we find that
, in Fourier variables, we find that
On the support of $\dot {m}$![]() , there holds
, there holds
Thus,

Moreover,
It follows that

As for $\mathrm {OLS}_4$![]() , in view of (3.2), we have
, in view of (3.2), we have

with

Integrating by parts, and using the fact $|S|\le \frac {1}{2}$![]() , we have
, we have

Thanks to the fact $|S|\le \sqrt {-\frac {\dot {M}_1}{M_1}}$![]() , one deduces that
, one deduces that

Owing to the periodicity in $X$![]() variable, we find that
variable, we find that
To bound $\mathrm {OLS}_4^{(4)}$![]() , by (3.2), we get
, by (3.2), we get

with

By using lemma 3.2, we are led to

In view of (3.16), one deduces that

Recalling that $z^{\pm }=O^t_{\pm \alpha }w^{\pm }$![]() , we then have $z^\pm _0=w^\pm _0=\omega _0\mp j_0$
, we then have $z^\pm _0=w^\pm _0=\omega _0\mp j_0$![]() . Consequently,
. Consequently,
and hence
Using (3.13), we arrive at

$\mathcal {NLS}1$![]() and $\mathcal {NLS}2$
and $\mathcal {NLS}2$![]() can be treated in the same way, we only estimate $\mathcal {NLS}2$
can be treated in the same way, we only estimate $\mathcal {NLS}2$![]() now. To this end, we infer from (2.22) that
now. To this end, we infer from (2.22) that
This, together with (2.21) and the obvious fact $|\partial _{XX}\Delta _L^{-1}|\le 1$![]() , implies that
, implies that

Note that $\mathrm {OLS}_5$![]() can be treated in the same manner as $\mathrm {OLS}_4$
can be treated in the same manner as $\mathrm {OLS}_4$![]() , and $\mathcal {NL}$
, and $\mathcal {NL}$![]() in (3.23) can be treated in the same way as $\mathrm {OLS}_4^{(4)}$
in (3.23) can be treated in the same way as $\mathrm {OLS}_4^{(4)}$![]() . On the other hand, one can obtain an energy identity for $KZ^-$
. On the other hand, one can obtain an energy identity for $KZ^-$![]() similar to (3.23), and estimate the corresponding right hand side terms analogously. Putting the energy estimates for $KZ^+$
similar to (3.23), and estimate the corresponding right hand side terms analogously. Putting the energy estimates for $KZ^+$![]() and $KZ^-$
and $KZ^-$![]() together, we find that for sufficiently large $|\alpha |$
together, we find that for sufficiently large $|\alpha |$![]() , $\mathrm {LS}$
, $\mathrm {LS}$![]() , $\mathrm {OLS}_1$
, $\mathrm {OLS}_1$![]() , $\mathrm {OLS}_3$
, $\mathrm {OLS}_3$![]() , $\mathrm {OLS}_4^{(1)}$
, $\mathrm {OLS}_4^{(1)}$![]() , $\mathrm {OLS}_4^{(2)}$
, $\mathrm {OLS}_4^{(2)}$![]() can be obsorbed by the left hand. In conclusion, there exist a universal constant $\alpha _0>0$
can be obsorbed by the left hand. In conclusion, there exist a universal constant $\alpha _0>0$![]() , and a positive constant $C$
, and a positive constant $C$![]() depending only on $N$
depending only on $N$![]() and $\alpha$
and $\alpha$![]() , such that if $\left |\alpha \right | > \alpha _0$
, such that if $\left |\alpha \right | > \alpha _0$![]() , we have
, we have

which suffices to improve (3.19) as long as $\epsilon \ll \nu ^\frac 56$![]() .
.
3.3 Improvement of (3.20)
Since $u^2_0=b^2_0=0$![]() , we derive from (1.2) for $\bar {U}(t,y)=U(y)=y$
, we derive from (1.2) for $\bar {U}(t,y)=U(y)=y$![]() that $(u^1_0, b^1_0)$
that $(u^1_0, b^1_0)$![]() solves
solves

Accordingly, in the coordinate system (3.1), we have
Then

Thanks to the divergence free condition, we have

Note that
and
Then in view of (3.14) and (3.16), we find that

and
Substituting (3.44)–(3.46) into (3.43), noting that the coordinate system (3.1) is the same as the original system in $y$![]() variable, and using the hypotheses (3.19) and (3.20), we are led to
variable, and using the hypotheses (3.19) and (3.20), we are led to

which is sufficient to improve (3.20) provided $\epsilon \ll \nu ^{\frac {1}{2}}$![]() . Combining (3.41) with (3.47), we complete the proof of proposition 3.3 and hence of theorem 3.1.
. Combining (3.41) with (3.47), we complete the proof of proposition 3.3 and hence of theorem 3.1.
4. Stability of the shear flow close to Couette
In this section, we study the stability of the shear flow $(\bar {U}(t,y),0)^\top =(e^{\nu t \partial {yy}}U(y),0)^\top$![]() , with $U(y)$
, with $U(y)$![]() satisfying
satisfying
The multiplier that will be used in this section is given by
where $\tilde m$![]() and $M$
and $M$![]() are given in (2.23) and (3.10), respectively. To simplify the presentation, let us denote
are given in (2.23) and (3.10), respectively. To simplify the presentation, let us denote
The aim of this section is to establish the following theorem.
Theorem 4.1 Let $N>1$![]() . Assume that the shear flow $( U(y),0)$
. Assume that the shear flow $( U(y),0)$![]() satisfies (4.1), and $\|(\omega _{\mathrm {in}},j_{\mathrm {in}})\|_{H^N}+\|({u}_{\mathrm {in}}, {b}_{\mathrm {in}})\|_{H^N}=\epsilon \le \delta \nu ^{\frac 56+\tilde \delta }$
satisfies (4.1), and $\|(\omega _{\mathrm {in}},j_{\mathrm {in}})\|_{H^N}+\|({u}_{\mathrm {in}}, {b}_{\mathrm {in}})\|_{H^N}=\epsilon \le \delta \nu ^{\frac 56+\tilde \delta }$![]() . Then there exist two positive constants $\alpha _0$
. Then there exist two positive constants $\alpha _0$![]() and $\delta _0$
and $\delta _0$![]() independent of $\nu$
independent of $\nu$![]() , such that for all $|\alpha |\ge \alpha _0$
, such that for all $|\alpha |\ge \alpha _0$![]() and $\delta \le \delta _0$
and $\delta \le \delta _0$![]() , the solution to (1.2) and the profile $Z^\pm$
, the solution to (1.2) and the profile $Z^\pm$![]() satisfy the global in time estimates
satisfy the global in time estimates
and
Similar to lemma 3.2, we give the following lemma to treat the non-zero frequency interactions of the nonlinear term.
Lemma 4.2 Let $N>1$![]() . Assume that (4.1) holds with $\delta$
. Assume that (4.1) holds with $\delta$![]() sufficiently small. Then for all $f\in L^2H^N$
sufficiently small. Then for all $f\in L^2H^N$![]() and $g$
and $g$![]() such that $\nabla _Lg\in L^2H^N$
such that $\nabla _Lg\in L^2H^N$![]() , there holds
, there holds

Proof. In view of (2.25) and (2.26), there hold

and
Note that the condition (4.1) ensures that (A.3) holds. This, together with the commutator estimates (B.1), (B.9), enables us to use lemma C.1 and the fact
to obtain

Then (4.2) follows immediately.
4.1 Proof of theorem 4.1
The proof of theorem 4.1 is similar to that of theorem 3.1. By the definition of $M_2$![]() , (3.22) still holds with $K$
, (3.22) still holds with $K$![]() replaced by $\tilde K$
replaced by $\tilde K$![]() , it suffices to establish the following a priori estimates:
, it suffices to establish the following a priori estimates:

and
Let us define $T^*$![]() to be the end point of the largest interval $[0,T]$
to be the end point of the largest interval $[0,T]$![]() such that (4.10) and (4.11) hold for all $0\leq t\leq T$
such that (4.10) and (4.11) hold for all $0\leq t\leq T$![]() . We are left to establish the following proposition.
. We are left to establish the following proposition.
Proposition 4.3 Assume that the conditions in theorem 4.1 hold, and that (4.10) and (4.11) hold on $[0, T^*]$![]() . Then there exist two positive constants $\alpha _0$
. Then there exist two positive constants $\alpha _0$![]() and $\delta _0$
and $\delta _0$![]() independent of $\nu$
independent of $\nu$![]() , such that for all $|\alpha |\ge \alpha _0$
, such that for all $|\alpha |\ge \alpha _0$![]() and $\delta \le \delta _0$
and $\delta \le \delta _0$![]() , the same estimates in (4.10) and (4.11) hold with the occurrences of 8 on the right-hand side replaced by 4.
, the same estimates in (4.10) and (4.11) hold with the occurrences of 8 on the right-hand side replaced by 4.
Proof. We first improve (4.10). Similar to (3.23), from (2.16) and the definition of $\tilde K$![]() in (4.2), we have the following energy identity:
in (4.2), we have the following energy identity:

The improvement of (4.10) will be achieved by the following four steps.
Step I: estimates of $\mathrm {LS}$![]() . We first split $\mathrm {LS}$
. We first split $\mathrm {LS}$![]() into two parts:
into two parts:

Thanks to (2.13), one can split $\mathrm {LS}^{dam}$![]() into two parts
into two parts

By the definition of $\tilde \Lambda$![]() in (2.10), there holds
in (2.10), there holds

Combining this with (B.8), (B.11), and (A.3) yields

Using (B.8), (B.9), (B.11), lemma C.1 and (2.29), we find that

where $|S|$![]() denotes the multiplier with symbol $\frac {|k(\eta -kt)|}{k^2+(\eta -kt)^2}$
denotes the multiplier with symbol $\frac {|k(\eta -kt)|}{k^2+(\eta -kt)^2}$![]() . Substituting this into (4.14), and using (B.8), (B.9) and lemma C.1 again to bound the second term on the right hand side of (4.14), one deduces that
. Substituting this into (4.14), and using (B.8), (B.9) and lemma C.1 again to bound the second term on the right hand side of (4.14), one deduces that

Next we turn to bound $\mathrm {LS}^*$![]() . From (2.27) and (2.28), we infer that
. From (2.27) and (2.28), we infer that

By virtue of (B.8) and lemma C.1, we have
Now we are left to bound $\left \|\sqrt {-\frac {\partial _t(\tilde m^{1/2})}{\tilde m^{1/2}}}\tilde K\Lambda Z^+_{\neq }\right \|_{L^2L^2}$![]() . In fact, thanks to (B.8), (B.10), and lemma C.1, we are led to
. In fact, thanks to (B.8), (B.10), and lemma C.1, we are led to

where we have used (4.18) to bound $\|\nabla _L\tilde K\Lambda Z^+_{\neq }\|_{L^2L^2}$![]() , and used (B.8), (B.9) and lemma C.1 to bound $\left \|\sqrt {-\frac {\dot {M}_1}{M_1}}\tilde K\Lambda Z^+_{\neq }\right \|_{L^2L^2}$
, and used (B.8), (B.9) and lemma C.1 to bound $\left \|\sqrt {-\frac {\dot {M}_1}{M_1}}\tilde K\Lambda Z^+_{\neq }\right \|_{L^2L^2}$![]() , respectively. It follows from (4.15) and (4.19) that
, respectively. It follows from (4.15) and (4.19) that

Substituting (4.18) and (4.20) into (4.17), and using Cauchy–Schwarz inequality, we arrive at

where
which is increasing in $\delta \in (0, \frac {1}{3C}]$![]() , and $C_\delta \rightarrow 1$
, and $C_\delta \rightarrow 1$![]() as $\delta \rightarrow 0+$
as $\delta \rightarrow 0+$![]() .
.
Step II: estimates of $\mathrm {OLS}$![]() . Similar to (3.25), we write
. Similar to (3.25), we write

where

We postpone the treatment of the nonlinear terms in $\mathrm {OLS}_4$![]() and $\mathrm {OLS}_5$
and $\mathrm {OLS}_5$![]() to Step IV, and focus on the linear terms here. The estimates for $\mathrm {OLS}_1$
to Step IV, and focus on the linear terms here. The estimates for $\mathrm {OLS}_1$![]() and $\mathrm {OLS}_2$
and $\mathrm {OLS}_2$![]() are the same as (3.26), and thus omitted. To estimate $\mathrm {OLS}_3$
are the same as (3.26), and thus omitted. To estimate $\mathrm {OLS}_3$![]() , similar to (3.27)–(3.29), we have
, similar to (3.27)–(3.29), we have

and

Combining these calculations with (3.30), and using (B.8), (B.9) and lemma C.1, we are led to

To bound $\mathrm {OLS}_4$![]() , by (2.16), we have
, by (2.16), we have

where

Integrating by parts, using the fact $|S|\le \frac{1}{2}$![]() and (4.18), we have
and (4.18), we have

Thanks to the fact $|S|\le \sqrt {-\frac {\dot {M}_1}{M_1}}$![]() , one deduces that
, one deduces that

Owing to the periodicity in $X$![]() variable, we find that
variable, we find that
By (2.18), we deduce that

with

Using $|S|\le \sqrt {-\frac {\dot {M}_1}{M_1}}$![]() , (A.3) and lemma C.1, we have
, (A.3) and lemma C.1, we have

Noting that
and

then we have

Integrating by parts and using (2.4), we find that

where we have used (A.3), (A.8) to bound $\left \|\tilde K(b\partial _Y^L)\right \|_{L^2L^2}$![]() and $\left \|\tilde K((a^2-1)\partial _Y^L)\right \|_{L^2L^2}$
and $\left \|\tilde K((a^2-1)\partial _Y^L)\right \|_{L^2L^2}$![]() . The estimates of $\mathrm {OLS}_{4}^{(5)}$
. The estimates of $\mathrm {OLS}_{4}^{(5)}$![]() will be postponed in Step IV.
will be postponed in Step IV.
Now we rewrite $\mathrm {OLS}_5$![]() as follows:
as follows:

To estimate $\mathrm {OLS}_{5,1}$![]() , instead of using (2.16), up to the nonlinear terms and some linear errors, we write $\partial _tZ^{-}$
, instead of using (2.16), up to the nonlinear terms and some linear errors, we write $\partial _tZ^{-}$![]() in terms of $\nu \Delta _tZ^-$
in terms of $\nu \Delta _tZ^-$![]() by virtue of (2.6) and (2.15)
by virtue of (2.6) and (2.15)
Then thanks to the relation (2.12), we have

Thus,

where

Similar to (4.32), we obtain
Similar to (4.26) and (4.29), we arrive at

Clearly, $\mathrm {OLS}_{5,1}^{(4)}$![]() can be bounded in the same way as (4.31)
can be bounded in the same way as (4.31)

The estimates of $\mathrm {OLS}_{5,1}^{(5)}$![]() will be postponed in Step IV.
will be postponed in Step IV.
To estimate $\mathrm {OLS}_{5,2}$![]() , we split it into two parts according to (2.32) and (2.33):
, we split it into two parts according to (2.32) and (2.33):
where

From (A.8) and (3.29), we obtain

The rest part $\mathrm {OLS}_{5,2}^{(2)}$![]() can be bounded as follows. Using the definition of $\tilde \Lambda ^2_t$
can be bounded as follows. Using the definition of $\tilde \Lambda ^2_t$![]() in (2.33), lemmas A.2 and C.1, we are led to
in (2.33), lemmas A.2 and C.1, we are led to

Then it follows this and lemma C.1 that

Step III: estimates of $\mathcal {LP}$![]() . By (2.18), we rewrite $\mathcal {LP}$
. By (2.18), we rewrite $\mathcal {LP}$![]() as
as
where

To estimate $\mathcal {LP}_1$![]() , let us denote $Z_\ne :=Z^+_\ne -O^t_{2\alpha }Z^{-}_{\ne }$
, let us denote $Z_\ne :=Z^+_\ne -O^t_{2\alpha }Z^{-}_{\ne }$![]() , and rewrite $\mathcal {LP}_1$
, and rewrite $\mathcal {LP}_1$![]() as
as

Swapping the positions of $\eta$![]() and $\xi$
and $\xi$![]() in (A.11), then using the resulting inequality, (A.3), lemma C.1, and (4.15), we have
in (A.11), then using the resulting inequality, (A.3), lemma C.1, and (4.15), we have

Now we turn to estimate $\mathcal {LP}_2$![]() . Compared with (4.31), we need an extra commutator estimate of $\sqrt {\left |\partial _X\Delta _L^{-1}\right |}$
. Compared with (4.31), we need an extra commutator estimate of $\sqrt {\left |\partial _X\Delta _L^{-1}\right |}$![]() . Indeed, using (A.8), (A.9) and lemma C.1, one easily deduces that
. Indeed, using (A.8), (A.9) and lemma C.1, one easily deduces that

To bound $\mathcal {LP}_3$![]() , it is natural to divide it into two parts as follows
, it is natural to divide it into two parts as follows

Similar to (4.32), we obtain
For $\mathcal {LP}_{3,0}$![]() , integrating by parts and using (2.4) and (A.3) yields
, integrating by parts and using (2.4) and (A.3) yields

Step IV: nonlinear estimates. We first collect all the above nonlinear terms to be estimated:

Owing to lemma C.1 and the fact $|S|\le \frac{1}{2}$![]() , we observe that the bounds of the three quantities are essentially the same. To avoid unnecessary repetition, we only sketch the treatment of $\mathcal {NL}$
, we observe that the bounds of the three quantities are essentially the same. To avoid unnecessary repetition, we only sketch the treatment of $\mathcal {NL}$![]() by modifying the nonlinear estimates in the Couette case, see (3.35)–(3.40). In fact, recalling the definition of $\mathrm {NL}^\pm$
by modifying the nonlinear estimates in the Couette case, see (3.35)–(3.40). In fact, recalling the definition of $\mathrm {NL}^\pm$![]() (2.17), we write
(2.17), we write
here we use the shorthand notation $\mathrm {NLS}^\pm :=\mathrm {NLS}1^\pm +\mathrm {NLS}2^\pm$![]() . Noting that
. Noting that
by virtue of (4.6), (4.8), lemmas 4.2 and C.1, and the hypotheses (4.10) and (4.11), one deduces that

Similar to (3.40), using (2.21), (2.23), (3.39), (A.3), (A.1), and lemma C.1, we arrive at

Now collecting the above estimates in Step I–IV, we conclude that there exist positive constant $\alpha _0$![]() (sufficiently large) and $\delta _0$
(sufficiently large) and $\delta _0$![]() (sufficiently small) independent of $\nu$
(sufficiently small) independent of $\nu$![]() , such that if $|\alpha |\ge \alpha _0$
, such that if $|\alpha |\ge \alpha _0$![]() and $\delta \le \delta _0$
and $\delta \le \delta _0$![]() , there holds
, there holds

where the constant $C$![]() depends only on $N$
depends only on $N$![]() and $\alpha$
and $\alpha$![]() . It suffices to improve (4.10) as long as $\epsilon \ll \nu ^{\frac{5}{6}+\tilde \delta }$
. It suffices to improve (4.10) as long as $\epsilon \ll \nu ^{\frac{5}{6}+\tilde \delta }$![]() .
.
The improvement of (4.11) is similar to that of (3.20). Firstly, we write the equations of $U_0^1\mp B_0^1$![]() :
:

Then we have the energy identity

Using the divergence free condition $\nabla _t\cdot (U\pm B)=0$![]() , we find that
, we find that

Recalling (2.4), it is easy to rewrite $\partial _Ya$![]() as follows
as follows

Combining this with (A.3) yields $\nu ^{\frac{1}{2}}\|\partial _Ya\|_{L^2H^N}\lesssim \delta$![]() . On the other hand, similar to (3.45) and (3.46), we have
. On the other hand, similar to (3.45) and (3.46), we have

and
It follows that

Integrating by parts, and using (A.3), it is easy to see that
Substituting (4.48) and (4.49) into (4.47), and using the hypotheses (4.10) and (4.11), we have
for some constant $C$![]() independent of $\nu$
independent of $\nu$![]() . Combining (4.46) and (4.50), one deduces proposition 4.3 under the hypotheses $\epsilon \ll \nu ^{\frac{5}{6}+\tilde \delta }$
. Combining (4.46) and (4.50), one deduces proposition 4.3 under the hypotheses $\epsilon \ll \nu ^{\frac{5}{6}+\tilde \delta }$![]() and hence of theorem 4.1.
and hence of theorem 4.1.
Appendix A. Estimates for the coefficients $a$ and $b$
and $b$
To begin with, we give a lemma to discuss the relation between the new coordinate system (2.2) and the original $( x,y)$![]() . Please refer to [Reference Inci, Kappeler and Topalov21] and [Reference Bedrossian, Vicol and Wang8] for the proof.
. Please refer to [Reference Inci, Kappeler and Topalov21] and [Reference Bedrossian, Vicol and Wang8] for the proof.
Lemma A.1 Let $s'\ge 2,s'\geq s \geq 0, f\in H^s(\mathbb {R}),$![]() and $g \in H^{s'}(\mathbb {R})$
and $g \in H^{s'}(\mathbb {R})$![]() be such that $\left \| g\right \|_{H^{s'}} \leq \delta.$
be such that $\left \| g\right \|_{H^{s'}} \leq \delta.$![]() Then, there holds
Then, there holds
where the implicit constant obey $C_{s,s'}(\delta )\to 1$![]() as $\delta \to 0$
as $\delta \to 0$![]() .
.
From the properties of the heat equation and lemma A.1, we can deduce the energy estimates of the coefficients $a$![]() and $b$
and $b$![]() .
.
Lemma A.2 Let $s\ge 0$![]() . Assume that $U(y)$
. Assume that $U(y)$![]() satisfies
satisfies
then there holds
and
Proof. Note that $\partial _y^l\bar {U}, l\ge 0$![]() solves
solves
Therefore, integrating by parts, we have
and
Consequently,
and
Combining these two estimates with (2.3), (2.9) and lemma A.1, we find that

and

This completes the proof of lemma A.2.
Appendix B. Commutator estimates
To deal with the nonlinear terms, we need the following lemmas to exchange frequencies. The first one can be regarded as an analogue of Lemma A.1 in [Reference Bedrossian, Germain and Masmoudi3]. We give a proof below for the sake of completeness.
Lemma B.1 The multiplier $\tilde m$![]() satisfies
satisfies
Proof. We only consider the case $k \ne 0.$![]()
Case 1: $\frac {\eta }{k} < -1000\nu ^{-\frac {1}{3}}, \tilde m(t,k,\eta ) = 1$![]() . It suffices to estimate $\tilde m^{-1}(t,k,\xi )$
. It suffices to estimate $\tilde m^{-1}(t,k,\xi )$![]() .
.
Case 1.1: $-1000\nu ^{-\frac {1}{3}} < \frac {\xi }{k} < 0$![]() . Now we have
. Now we have

Case 1.2: if $\frac {\xi }{k}>0, \frac {\xi }{k}< t < \frac {\xi }{k}+1000\nu ^{-\frac {1}{3}}$![]() .
.

Case 1.3: if $\frac {\xi }{k}>0, t > \frac {\xi }{k}+1000\nu ^{-\frac {1}{3}}$![]() .
.

Case 2: $-1000\nu ^{-\frac {1}{3}} < \frac {\eta }{k} < 0$![]() .
.
Case 2.1: $0< t<\frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$![]() , and $\tilde m(t,k,\eta )=( \frac {k^2+\eta ^2}{k^2+(\eta -kt)^2}) ^{1+\frac{3}{2}\tilde \delta }$
, and $\tilde m(t,k,\eta )=( \frac {k^2+\eta ^2}{k^2+(\eta -kt)^2}) ^{1+\frac{3}{2}\tilde \delta }$![]() .
.
• Case 2.1.1: $-1000\nu ^{-\frac {1}{3}}<\frac {\xi }{k}<0$
 .
(B.2)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2+\xi^2}{k^2+(\xi-kt)^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \quad \forall ~t\ge0. \end{equation}Therefore,
.
(B.2)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2+\xi^2}{k^2+(\xi-kt)^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \quad \forall ~t\ge0. \end{equation}Therefore, \begin{align*} \frac{\tilde m(t, k,\eta)}{\tilde m(t, k, \xi)}& \le \left(\frac{1+\left(\frac{\eta}{k}\right)^2}{1+\left(\frac{\xi}{k}\right)^2}\cdot\frac{1+\left(\frac{\xi}{k}-t\right)^2}{1+\left(\frac{\eta}{k}-t\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}\\ & \le \begin{cases} \left(\frac{1+\left(\frac{\xi}{k}-t\right)^2}{1+\left(\frac{\eta}{k}-t\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}, \text{ if } \left|\frac{\eta}{k}\right|\le\left|\frac{\xi}{k}\right|\\ \left(\frac{1+\left(\frac{\eta}{k}\right)^2}{1+\left(\frac{\xi}{k}\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}, \, \text{ if } \left|\frac{\eta}{k}\right|>\left|\frac{\xi}{k}\right| \end{cases}\\ & \lesssim\langle \eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \end{align*}
\begin{align*} \frac{\tilde m(t, k,\eta)}{\tilde m(t, k, \xi)}& \le \left(\frac{1+\left(\frac{\eta}{k}\right)^2}{1+\left(\frac{\xi}{k}\right)^2}\cdot\frac{1+\left(\frac{\xi}{k}-t\right)^2}{1+\left(\frac{\eta}{k}-t\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}\\ & \le \begin{cases} \left(\frac{1+\left(\frac{\xi}{k}-t\right)^2}{1+\left(\frac{\eta}{k}-t\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}, \text{ if } \left|\frac{\eta}{k}\right|\le\left|\frac{\xi}{k}\right|\\ \left(\frac{1+\left(\frac{\eta}{k}\right)^2}{1+\left(\frac{\xi}{k}\right)^2}\right)^{1+\frac{3}{2}\tilde\delta}, \, \text{ if } \left|\frac{\eta}{k}\right|>\left|\frac{\xi}{k}\right| \end{cases}\\ & \lesssim\langle \eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \end{align*}
• Case 2.1.2: $\frac {\xi }{k}>0, t> \frac {\xi }{k}$
 . In this case,
(B.3)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2}{k^2+(\xi-kt)^2}\right)^{1+\frac{3}{2}\tilde{\delta}}. \end{equation}Therefore,
. In this case,
(B.3)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2}{k^2+(\xi-kt)^2}\right)^{1+\frac{3}{2}\tilde{\delta}}. \end{equation}Therefore, \begin{align*} \frac{\tilde m(t, k,\eta)}{\tilde m(t, k, \xi)}\le \left(\left( 1+\left(\frac{\eta}{k} \right)^2 \right) \cdot \frac{1+\left(\frac{\xi}{k}-t \right)^2 }{1+\left(\frac{\eta}{k}-t \right)^2}\right)^ {1+\frac{3}{2}\tilde\delta} & \le \left(1+\left( \frac{\eta}{k}-\frac{\xi}{k}\right)^2 \right) ^ {1+\frac{3}{2}\tilde\delta}\nonumber\\ & \lesssim \langle \eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \end{align*}where we have used $\frac {\eta }{k}<0<\frac {\xi }{k}< t$
\begin{align*} \frac{\tilde m(t, k,\eta)}{\tilde m(t, k, \xi)}\le \left(\left( 1+\left(\frac{\eta}{k} \right)^2 \right) \cdot \frac{1+\left(\frac{\xi}{k}-t \right)^2 }{1+\left(\frac{\eta}{k}-t \right)^2}\right)^ {1+\frac{3}{2}\tilde\delta} & \le \left(1+\left( \frac{\eta}{k}-\frac{\xi}{k}\right)^2 \right) ^ {1+\frac{3}{2}\tilde\delta}\nonumber\\ & \lesssim \langle \eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \end{align*}where we have used $\frac {\eta }{k}<0<\frac {\xi }{k}< t$
 .
.
Case 2.2: $t>\frac {\eta }{k}+1000\nu ^{-\frac{1}{3}}$![]() , and $\tilde m(t,k,\eta )=( \frac {k^2+\eta ^2}{k^2+(1000k\nu ^{-\frac{1}{3}})^2}) ^{1+\frac{3}{2}\tilde \delta }$
, and $\tilde m(t,k,\eta )=( \frac {k^2+\eta ^2}{k^2+(1000k\nu ^{-\frac{1}{3}})^2}) ^{1+\frac{3}{2}\tilde \delta }$![]() .
.
• Case 2.2.1: $-1000\nu ^{-\frac{1}{3}}<\frac {\xi }{k}<0$
 . In this case,
(B.4)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2+\xi^2}{k^2+(1000k\nu^{-\frac{1}{3}})^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \end{equation}Thus,
. In this case,
(B.4)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{k^2+\xi^2}{k^2+(1000k\nu^{-\frac{1}{3}})^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \end{equation}Thus, \[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left(\frac{k^2+\eta^2}{k^2+\xi^2}\right)^{1+\frac{3}{2}\tilde{\delta}}\lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left(\frac{k^2+\eta^2}{k^2+\xi^2}\right)^{1+\frac{3}{2}\tilde{\delta}}\lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
• Case 2.2.2: $\frac {\xi }{k}>0, t> \frac {\xi }{k}$
 . In this case,
(B.5)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{1}{1+(1000\nu^{-\frac{1}{3}})^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \end{equation}Thus,
. In this case,
(B.5)\begin{equation} \tilde m(t,k,\xi)\ge\left(\frac{1}{1+(1000\nu^{-\frac{1}{3}})^2}\right)^{1+\frac{3}{2}\tilde{\delta}}, \end{equation}Thus, \[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left(1+\left( \frac{\eta}{k}\right)^2\right)^{1+\frac{3}{2}\tilde{\delta}}\le \left(1+\left( \frac{\eta}{k}-\frac{\xi}{k}\right) ^2\right)^{1+\frac{3}{2}\tilde{\delta}}\lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left(1+\left( \frac{\eta}{k}\right)^2\right)^{1+\frac{3}{2}\tilde{\delta}}\le \left(1+\left( \frac{\eta}{k}-\frac{\xi}{k}\right) ^2\right)^{1+\frac{3}{2}\tilde{\delta}}\lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
Case 3: $\frac {\eta }{k}> 0$![]() .
.
Case 3.1: $\frac {\eta }{k}< t<\frac {\eta }{k}+1000\nu ^{-\frac {1}{3}}$![]() , and $\tilde m(t,k,\eta )=( \frac {k^2}{k^2+(\eta -kt)^2}) ^{1+\frac{3}{2}\tilde \delta }$
, and $\tilde m(t,k,\eta )=( \frac {k^2}{k^2+(\eta -kt)^2}) ^{1+\frac{3}{2}\tilde \delta }$![]() .
.
• Case 3.1.1: $-1000\nu ^{-\frac {1}{3}}<\frac {\xi }{k}<0.$
 In this case, (B.2) holds. Therefore,
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left( \frac{k^2}{k^2+\xi^2}\cdot \frac{k^2+(\xi-kt)^2}{k^2+(\eta-kt)^2}\right)^{1+\frac{3}{2}\tilde\delta} \lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
In this case, (B.2) holds. Therefore,
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left( \frac{k^2}{k^2+\xi^2}\cdot \frac{k^2+(\xi-kt)^2}{k^2+(\eta-kt)^2}\right)^{1+\frac{3}{2}\tilde\delta} \lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
• Case 3.1.2: $\frac {\xi }{k}>0$
 . Now (B.3) still holds. Thus,
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left( \frac{k^2+(\xi-kt)^2}{k^2+(\eta-kt)^2}\right)^{1+\frac{3}{2}\tilde\delta} \lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
. Now (B.3) still holds. Thus,
\[ \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le\left( \frac{k^2+(\xi-kt)^2}{k^2+(\eta-kt)^2}\right)^{1+\frac{3}{2}\tilde\delta} \lesssim\langle\eta-\xi\rangle^{2(1+\frac{3}{2}\tilde\delta)}. \]
Case 3.2: $t>\frac {\eta }{k}+1000\nu ^{-\frac{1}{3}},$![]() and $\tilde m(t,k,\eta )=( \frac {1}{1+(1000\nu ^{-\frac{1}{3}})^2}) ^{1+\frac{3}{2}\tilde \delta }$
and $\tilde m(t,k,\eta )=( \frac {1}{1+(1000\nu ^{-\frac{1}{3}})^2}) ^{1+\frac{3}{2}\tilde \delta }$![]() .
.
• Case 3.2.1:$-1000\nu ^{-\frac {1}{3}}<\frac {\xi }{k}<0$
 . Using (B.4), we have
(B.6)\begin{equation} \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le1. \end{equation}
. Using (B.4), we have
(B.6)\begin{equation} \frac{\tilde m(t, k,\eta)}{\tilde m(t,k,\xi)}\le1. \end{equation}
• Case 3.2.2: $\frac {\xi }{k}>0,$
 In this case, In this case, (B.5) holds. Consequently, (B.6) holds as well.
In this case, In this case, (B.5) holds. Consequently, (B.6) holds as well.
The proof of lemma B.1 is completed.
Recalling the definition of $\tilde K$![]() in (4.2), using (B.1) and the following fact
in (4.2), using (B.1) and the following fact
we get the following corollary immediately.
Corollary B.2 The multiplier $\tilde K$![]() satisfies
satisfies
In view of the definitions of $M_1$![]() and $M_2$
and $M_2$![]() in (3.7) and (3.8), respectively, using (B.7) again, one easily derives the commutator estimates for $\sqrt {-\frac {\dot {M}_i}{M_i}}, i=1, 2$
in (3.7) and (3.8), respectively, using (B.7) again, one easily derives the commutator estimates for $\sqrt {-\frac {\dot {M}_i}{M_i}}, i=1, 2$![]() .
.
Lemma B.3 For $k \ne 0$![]() there hold
there hold

Finally, the estimates of $\sqrt {-\frac {\partial _t(\tilde m^{1/2})}{\tilde m^{1/2}}}$![]() is given below.
is given below.
Lemma B.4 For $k \ne 0$![]() there holds
there holds

Proof. Using (B.7), it is not difficult to verify that

From the above inequality and (2.29) with $\eta$![]() replaced by $\xi$
replaced by $\xi$![]() , we are let to
, we are let to

Combining this with (2.28) yields

Then (B.10) is a consequence of (B.8) and (B.12). We complete the proof of lemma B.4.
Appendix C. Composition inequalities for the operator $\Lambda$ in $H^N$
in $H^N$
Since $\Lambda$![]() is involved in the definition of $\Delta _t^{-1}$
is involved in the definition of $\Delta _t^{-1}$![]() , recalling the relation (2.14), it is inevitable to deal with the composition $B_1\circ \Lambda$
, recalling the relation (2.14), it is inevitable to deal with the composition $B_1\circ \Lambda$![]() for some multiplier $B_1$
for some multiplier $B_1$![]() . Based on the commutator estimates of $B$
. Based on the commutator estimates of $B$![]() , we establish the following composition inequality.
, we establish the following composition inequality.
Lemma C.1 Let $l\in \mathbb {N}^+$![]() , and $B_i, 1\le i\le l$
, and $B_i, 1\le i\le l$![]() be Fourier multipliers, satisfying
be Fourier multipliers, satisfying

for some constants $C_i>0$![]() and $\beta _i\ge 0, 1\le i\le l$
and $\beta _i\ge 0, 1\le i\le l$![]() . If $\|{a^2-1}\|_{L^\infty H^{N+\beta +1}}+\|{b}\|_{L^\infty H^{N+\beta +1}}\le \frac {\delta }{2}$
. If $\|{a^2-1}\|_{L^\infty H^{N+\beta +1}}+\|{b}\|_{L^\infty H^{N+\beta +1}}\le \frac {\delta }{2}$![]() with $\beta =\max \left \{\beta _1,\cdots, \beta _l\right \}$
with $\beta =\max \left \{\beta _1,\cdots, \beta _l\right \}$![]() , then we have
, then we have

Proof. We first write $\Delta _L$![]() in terms of $\Delta _t$
in terms of $\Delta _t$![]()
Then
and thus

Thanks to (C.1), using Young's inequality for convolution, we find that

where we have used the fact $\Lambda =\Delta _L\Delta _t^{-1}$![]() in the last line above. Similarly, for $k\neq 0$
in the last line above. Similarly, for $k\neq 0$![]() , there holds
, there holds
Thus, we have

Substituting (C.5) and (C.6) into (C.4), and using the restriction on $a$![]() and $b$
and $b$![]() , we arrive at
, we arrive at

and hence (C.2) follows. This completes the proof of lemma C.1.
Corollary C.2 Let $B$![]() be Fourier multiplier satisfying
be Fourier multiplier satisfying
where $C$![]() and $\beta$
and $\beta$![]() are two positive constants. If $\|{a^2-1}\|_{H^{N+\beta +2}}+\|{b}\|_{H^{N+\beta +2}}\le \frac {\delta }{2}$
are two positive constants. If $\|{a^2-1}\|_{H^{N+\beta +2}}+\|{b}\|_{H^{N+\beta +2}}\le \frac {\delta }{2}$![]() , then we have
, then we have
and

where $\tilde \Lambda$![]() and $\tilde \Lambda _t^1$
and $\tilde \Lambda _t^1$![]() are given in (2.10) and (2.33), respectively.
are given in (2.10) and (2.33), respectively.
Proof. Recalling the definition of $\tilde \Lambda$![]() in (2.10), following the proof of (C.5) and (C.6) with $\Delta _t^{-1}$
in (2.10), following the proof of (C.5) and (C.6) with $\Delta _t^{-1}$![]() replaced by $(-\Delta _L)^{-1}$
replaced by $(-\Delta _L)^{-1}$![]() , we get (C.7) immediately. Now we turn to prove (C.8). In fact, using (2.33) and lemma C.1, we are led to
, we get (C.7) immediately. Now we turn to prove (C.8). In fact, using (2.33) and lemma C.1, we are led to

In view of (3.16) and (3.29), similar to (C.5) and (C.6), and using the commutator estimate (B.9) and lemma C.1, we arrive at

Moreover, it follows from (C.7), (3.29), and lemma C.1 that

Substituting the above two inequalities into (C.9) yields (C.8). The proof is completed.
Acknowledgements
R. Zi is partially supported by NSF of China under Grants 12222105.