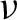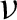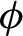1 Introduction
Let A and B be finite non-empty sets, let
![]() $X\subset A^{\mathbb Z}$
be an irreducible shift of finite type, and let
$X\subset A^{\mathbb Z}$
be an irreducible shift of finite type, and let
![]() $\pi :X\to B^{\mathbb Z}$
be a shift-commuting map so that
$\pi :X\to B^{\mathbb Z}$
be a shift-commuting map so that
![]() $Z=\pi (X)$
is a sofic factor of X. Given a shift-invariant measure
$Z=\pi (X)$
is a sofic factor of X. Given a shift-invariant measure
![]() $\nu $
on Z, we are interested in
$\nu $
on Z, we are interested in
![]() $\pi _*^{-1}\{\nu \}$
, the set of shift-invariant measures on X whose push-forward is
$\pi _*^{-1}\{\nu \}$
, the set of shift-invariant measures on X whose push-forward is
![]() $\nu $
. Relative thermodynamic formalism gives a means to identify distinguished elements of
$\nu $
. Relative thermodynamic formalism gives a means to identify distinguished elements of
![]() $\pi _*^{-1}\{\nu \}$
similar to standard thermodynamic formalism. In fact, standard thermodynamic formalism is the special case of relative thermodynamic formalism, where Z is the one-point space.
$\pi _*^{-1}\{\nu \}$
similar to standard thermodynamic formalism. In fact, standard thermodynamic formalism is the special case of relative thermodynamic formalism, where Z is the one-point space.
We make a standing assumption that the factor map has the property that
![]() $\pi (x)_0$
only depends on
$\pi (x)_0$
only depends on
![]() $x_0,x_1,\ldots $
(and in fact in this case, by the Curtis–Hedlund–Lyndon theorem,
$x_0,x_1,\ldots $
(and in fact in this case, by the Curtis–Hedlund–Lyndon theorem,
![]() $\pi (x)_0$
only depends on
$\pi (x)_0$
only depends on
![]() $x_0,\ldots ,x_{k-1}$
for some
$x_0,\ldots ,x_{k-1}$
for some
![]() $k\in \mathbb N_0$
). We call this a forward-looking factor map. The simplest case of such factor maps is the case where
$k\in \mathbb N_0$
). We call this a forward-looking factor map. The simplest case of such factor maps is the case where
![]() $\pi (x)_0$
depends only on
$\pi (x)_0$
depends only on
![]() $x_0$
, that is,
$x_0$
, that is,
![]() $\pi $
is a one-block factor map. It is well-known [Reference Lind and Marcus8, Proposition 1.5.12] that up to conjugacy, this is the general case. Let
$\pi $
is a one-block factor map. It is well-known [Reference Lind and Marcus8, Proposition 1.5.12] that up to conjugacy, this is the general case. Let
![]() $X^+\subset A^{\mathbb N_0}$
and
$X^+\subset A^{\mathbb N_0}$
and
![]() $Z^+\subset B^{\mathbb N_0}$
denote the one-sided versions of X and Z. By the assumption on the factor map,
$Z^+\subset B^{\mathbb N_0}$
denote the one-sided versions of X and Z. By the assumption on the factor map,
![]() $\pi $
induces a map from
$\pi $
induces a map from
![]() $X^+$
to
$X^+$
to
![]() $Z^+$
, which we also call
$Z^+$
, which we also call
![]() $\pi $
.
$\pi $
.
Given an invariant measure
![]() $\nu $
on Z, and a Hölder continuous function
$\nu $
on Z, and a Hölder continuous function
![]() $\phi $
on
$\phi $
on
![]() $X^+$
(which we call a potential and which we also view as a function on X), recall that a relative equilibrium state of
$X^+$
(which we call a potential and which we also view as a function on X), recall that a relative equilibrium state of
![]() $\phi $
over
$\phi $
over
![]() $\nu $
is an invariant measure
$\nu $
is an invariant measure
![]() $\mu $
on X such that
$\mu $
on X such that
![]() $\pi _*(\mu )=\nu $
and
$\pi _*(\mu )=\nu $
and
![]() $h_\mu +\int \phi \,d\mu =r_\pi (\nu )$
, where
$h_\mu +\int \phi \,d\mu =r_\pi (\nu )$
, where
![]() $r_\pi (\nu ):=\max _{\{\lambda \colon \pi _*(\lambda )=\nu \}}(h_\lambda +\int \phi \,d\lambda )$
. Since
$r_\pi (\nu ):=\max _{\{\lambda \colon \pi _*(\lambda )=\nu \}}(h_\lambda +\int \phi \,d\lambda )$
. Since
![]() $\phi $
is continuous, the existence of a relative equilibrium state follows from the compactness of the space of measures and upper semi-continuity of entropy. A number of papers [Reference Allahbakhshi, Antonioli and Yoo1, Reference Allahbakhshi and Quas3, Reference Petersen, Quas and Shin10] have given bounds on the number of ergodic relative equilibrium states and measures of relative maximal entropy (relative equilibrium states in the case where
$\phi $
is continuous, the existence of a relative equilibrium state follows from the compactness of the space of measures and upper semi-continuity of entropy. A number of papers [Reference Allahbakhshi, Antonioli and Yoo1, Reference Allahbakhshi and Quas3, Reference Petersen, Quas and Shin10] have given bounds on the number of ergodic relative equilibrium states and measures of relative maximal entropy (relative equilibrium states in the case where
![]() $\phi =0$
) in this setting.
$\phi =0$
) in this setting.
We are seeking to relate the number of relative equilibrium states of
![]() $\phi $
over
$\phi $
over
![]() $\nu $
to the Lyapunov exponents and Oseledets spaces of a cocycle of Perron–Frobenius operators that we describe below. For
$\nu $
to the Lyapunov exponents and Oseledets spaces of a cocycle of Perron–Frobenius operators that we describe below. For
![]() $0<\beta <1$
, we introduce a metric
$0<\beta <1$
, we introduce a metric
![]() $d_\beta $
on
$d_\beta $
on
![]() $X^+$
given by
$X^+$
given by
 $d_\beta (x,x')=\beta ^{\min \{n\colon x_n\ne x^{\prime }_n\}}$
and write
$d_\beta (x,x')=\beta ^{\min \{n\colon x_n\ne x^{\prime }_n\}}$
and write
![]() $C^\beta (X^+)$
for the Lipschitz functions with respect to this metric. For
$C^\beta (X^+)$
for the Lipschitz functions with respect to this metric. For
 $\beta \in [\tfrac 12,1)$
,
$\beta \in [\tfrac 12,1)$
,
![]() $C^\beta (X^+)$
is precisely the collection of
$C^\beta (X^+)$
is precisely the collection of
![]() $(-\log _2\beta )$
-Hölder continuous functions with respect to the standard metric
$(-\log _2\beta )$
-Hölder continuous functions with respect to the standard metric
![]() $d_{1/2}$
. More generally, as is common in symbolic dynamics, we refer to the spaces
$d_{1/2}$
. More generally, as is common in symbolic dynamics, we refer to the spaces
![]() $C^\beta (X^+)$
as the Hölder continuous functions on
$C^\beta (X^+)$
as the Hölder continuous functions on
![]() $X^+$
(even when
$X^+$
(even when
 $0<\beta <\tfrac 12$
). Once the potential
$0<\beta <\tfrac 12$
). Once the potential
![]() $\phi $
is fixed, we choose
$\phi $
is fixed, we choose
![]() $\beta $
so that
$\beta $
so that
![]() $\phi \in C^\beta (X^+)$
.
$\phi \in C^\beta (X^+)$
.
For
![]() $j\in B$
, define an operator
$j\in B$
, define an operator
![]() ${\mathcal L}_j$
on
${\mathcal L}_j$
on
![]() $C^\beta (X^+)$
by
$C^\beta (X^+)$
by
 $$ \begin{align*}{\mathcal L}_jf(x)=\sum_{\{i\colon ix\in X^+;(\pi(ix))_0=j\}} e^{\phi(ix)}f(ix), \end{align*} $$
$$ \begin{align*}{\mathcal L}_jf(x)=\sum_{\{i\colon ix\in X^+;(\pi(ix))_0=j\}} e^{\phi(ix)}f(ix), \end{align*} $$
where
![]() $ix$
denotes the point in
$ix$
denotes the point in
![]() $A^{\mathbb N_0}$
defined by
$A^{\mathbb N_0}$
defined by
![]() $(ix)_0=i$
,
$(ix)_0=i$
,
![]() $(ix)_n=x_{n-1}$
for
$(ix)_n=x_{n-1}$
for
![]() $n\ge 1$
. Similarly for a word
$n\ge 1$
. Similarly for a word
![]() $w=w_{0}\ldots w_{k-1}$
,
$w=w_{0}\ldots w_{k-1}$
,
![]() $(wx)_n=w_{n}$
if
$(wx)_n=w_{n}$
if
![]() $n<k$
and
$n<k$
and
![]() $(wx)_n=x_{n-k}$
if
$(wx)_n=x_{n-k}$
if
![]() $n\ge k$
. If x is an element of X or
$n\ge k$
. If x is an element of X or
![]() $X^+$
, we use the notation
$X^+$
, we use the notation
 $x_0^{n-1}$
to denote the word
$x_0^{n-1}$
to denote the word
![]() $x_0\ldots x_{n-1}$
. We shall study the cocycle over the dynamical system
$x_0\ldots x_{n-1}$
. We shall study the cocycle over the dynamical system
![]() $\sigma \colon Z\to Z$
where the map corresponding to z is
$\sigma \colon Z\to Z$
where the map corresponding to z is
![]() ${\mathcal L}_z\colon ={\mathcal L}_{z_0}$
. As usual, we define
${\mathcal L}_z\colon ={\mathcal L}_{z_0}$
. As usual, we define
 ${\mathcal L}_z^{(n)}={\mathcal L}_{\sigma ^{n-1}z}\circ \cdots \circ {\mathcal L}_z$
.
${\mathcal L}_z^{(n)}={\mathcal L}_{\sigma ^{n-1}z}\circ \cdots \circ {\mathcal L}_z$
.
An inductive calculation shows that
 $$ \begin{align*}{\mathcal L}_z^{(n)}f(x)=\sum_{\{w\colon (\pi(wx))_0^{n-1}=z_0^{n-1}, w_{0}\ldots w_{k-1}x\in X^+\}} e^{S_n\phi(wx)}f(wx), \end{align*} $$
$$ \begin{align*}{\mathcal L}_z^{(n)}f(x)=\sum_{\{w\colon (\pi(wx))_0^{n-1}=z_0^{n-1}, w_{0}\ldots w_{k-1}x\in X^+\}} e^{S_n\phi(wx)}f(wx), \end{align*} $$
where, as usual,
![]() $S_n\phi (wx)$
denotes the sum
$S_n\phi (wx)$
denotes the sum
![]() $\phi (wx)+\cdots +\phi (T^{n-1}(wx))$
.
$\phi (wx)+\cdots +\phi (T^{n-1}(wx))$
.
Our main theorem states that for an ergodic invariant measure
![]() $\nu $
on Z and a Hölder continuous potential, the number of ergodic relative equilibrium states on X is the multiplicity of the top Lyapunov exponent of the above cocycle. While we defer detailed definitions and statements which the theorem relies on, we mention Theorems 5 and 6 of Jisang Yoo which establish that a factor map
$\nu $
on Z and a Hölder continuous potential, the number of ergodic relative equilibrium states on X is the multiplicity of the top Lyapunov exponent of the above cocycle. While we defer detailed definitions and statements which the theorem relies on, we mention Theorems 5 and 6 of Jisang Yoo which establish that a factor map
![]() $\pi :X\to Z$
of the type that we consider may be expressed as a composition of factor maps
$\pi :X\to Z$
of the type that we consider may be expressed as a composition of factor maps
![]() $\pi _1\colon X\to Y$
and
$\pi _1\colon X\to Y$
and
![]() $\pi _2\colon Y\to Z$
with good properties defined in detail below:
$\pi _2\colon Y\to Z$
with good properties defined in detail below:
![]() $\pi _1$
is of class degree 1, and
$\pi _1$
is of class degree 1, and
![]() $\pi _2$
is finite-to-one of degree
$\pi _2$
is finite-to-one of degree
![]() $c_\pi $
, which is the class degree of the original map
$c_\pi $
, which is the class degree of the original map
![]() $\pi $
. Recall that for a finite-to-one factor map
$\pi $
. Recall that for a finite-to-one factor map
![]() $\pi _2\colon Y\to Z$
from one irreducible two-sided sofic system to another, the degree of
$\pi _2\colon Y\to Z$
from one irreducible two-sided sofic system to another, the degree of
![]() $\pi _2$
is the minimal cardinality of
$\pi _2$
is the minimal cardinality of
 $\pi _2^{-1}(z)$
as z runs over Z. The minimum is attained for all doubly transitive (that is, right and left transitive) points (see [Reference Lind and Marcus8, Theorem 9.1.11]).
$\pi _2^{-1}(z)$
as z runs over Z. The minimum is attained for all doubly transitive (that is, right and left transitive) points (see [Reference Lind and Marcus8, Theorem 9.1.11]).
If
![]() $\nu $
is a fully supported ergodic shift-invariant measure on Z, then since
$\nu $
is a fully supported ergodic shift-invariant measure on Z, then since
![]() ${\pi _2\colon Y\to Z}$
is of degree
${\pi _2\colon Y\to Z}$
is of degree
![]() $c_\pi $
,
$c_\pi $
,
![]() $\nu $
-almost every (a.e.)
$\nu $
-almost every (a.e.)
![]() $\omega \in Z$
has
$\omega \in Z$
has
![]() $c_\pi $
preimages. It may be shown that there are only finitely many ergodic invariant measures on Y that factor onto
$c_\pi $
preimages. It may be shown that there are only finitely many ergodic invariant measures on Y that factor onto
![]() $\nu $
,
$\nu $
,
![]() $\nu _1,\ldots ,\nu _k$
say. Yoo defines multiplicities
$\nu _1,\ldots ,\nu _k$
say. Yoo defines multiplicities
![]() $m_1,\ldots ,m_k$
of these measures with
$m_1,\ldots ,m_k$
of these measures with
![]() $m_1+\cdots +m_k=c_\pi $
and shows that for
$m_1+\cdots +m_k=c_\pi $
and shows that for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $z\in Z$
, of the
$z\in Z$
, of the
![]() $c_\pi $
elements of
$c_\pi $
elements of
 $\pi _2^{-1}(z)$
,
$\pi _2^{-1}(z)$
,
![]() $m_i$
are generic for
$m_i$
are generic for
![]() $\nu _i$
for each i.
$\nu _i$
for each i.
Since the multiplicative ergodic theory of infinite-dimensional operators is less well-known than in the finite-dimensional case, we include a quick summary. While there are multiple versions of operator-valued multiplicative ergodic theorems, we focus on the context in this article. Assume that there is a ‘base’ dynamical system
![]() $\sigma \colon Z\to Z$
which is a continuous homeomorphism from a compact metric space to itself. The space Z is assumed to be equipped with a
$\sigma \colon Z\to Z$
which is a continuous homeomorphism from a compact metric space to itself. The space Z is assumed to be equipped with a
![]() $\sigma $
-invariant ergodic Borel probability measure
$\sigma $
-invariant ergodic Borel probability measure
![]() $\nu $
. A function on Z is said to be
$\nu $
. A function on Z is said to be
![]() $\nu $
-continuous if for any
$\nu $
-continuous if for any
![]() $\epsilon>0$
, there exists a subset
$\epsilon>0$
, there exists a subset
![]() $Z'\subset Z$
of measure at least
$Z'\subset Z$
of measure at least
![]() $1-\epsilon $
on which the restriction of the function is continuous. Recall that by Lusin’s theorem, any Borel-measurable real-valued function on Z is
$1-\epsilon $
on which the restriction of the function is continuous. Recall that by Lusin’s theorem, any Borel-measurable real-valued function on Z is
![]() $\nu $
-continuous, but this is not necessarily true for functions with non-separable ranges. There is also a Banach space B and a collection
$\nu $
-continuous, but this is not necessarily true for functions with non-separable ranges. There is also a Banach space B and a collection
![]() $\{{\mathcal L}_z\colon z\in Z\}$
of linear maps from B to itself. One then studies the operators
$\{{\mathcal L}_z\colon z\in Z\}$
of linear maps from B to itself. One then studies the operators
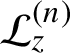 ${\mathcal L}_z^{(n)}$
, defined by
${\mathcal L}_z^{(n)}$
, defined by
 ${\mathcal L}_z^{(n)}={\mathcal L}_{\sigma ^{n-1}z}\circ \cdots \circ {\mathcal L}_z$
. Under conditions of quasi-compactness (which are satisfied in our context), there exists a leading Lyapunov exponent
${\mathcal L}_z^{(n)}={\mathcal L}_{\sigma ^{n-1}z}\circ \cdots \circ {\mathcal L}_z$
. Under conditions of quasi-compactness (which are satisfied in our context), there exists a leading Lyapunov exponent
![]() $\lambda _1$
, an exponent
$\lambda _1$
, an exponent
![]() $\lambda _2<\lambda _1$
, a multiplicity M, a
$\lambda _2<\lambda _1$
, a multiplicity M, a
![]() $\nu $
-continuous map E from Z into
$\nu $
-continuous map E from Z into
![]() $\mathcal G_{M}(B)$
, the collection of M-dimensional subspaces of B, and
$\mathcal G_{M}(B)$
, the collection of M-dimensional subspaces of B, and
![]() $\nu $
-continuous maps
$\nu $
-continuous maps
![]() $\eta _1,\ldots ,\eta _{M}$
from Z into
$\eta _1,\ldots ,\eta _{M}$
from Z into
![]() $B^*$
satisfying:
$B^*$
satisfying:
-
• (equivariance)
 ${\mathcal L}_z(E(z))=E(\sigma (z))$
,
${\mathcal L}_z(E(z))=E(\sigma (z))$
,
 $\nu $
-a.e.; and
$\nu $
-a.e.; and
 ${\mathcal L}_z(F(z))\subset F(\sigma (z))$
, where
${\mathcal L}_z(F(z))\subset F(\sigma (z))$
, where
 $F(z)=\bigcap _{i=1}^M\ker \eta _i(z)$
,
$F(z)=\bigcap _{i=1}^M\ker \eta _i(z)$
,
 $\nu $
-a.e.;
$\nu $
-a.e.; -
• (growth)
 $\lim _{n\to \infty }(1/n)\log \|{\mathcal L}_z^{(n)}f\|=\lambda _1$
for all
$\lim _{n\to \infty }(1/n)\log \|{\mathcal L}_z^{(n)}f\|=\lambda _1$
for all
 $f\in E(z)\setminus \{0\}$
; and
$f\in E(z)\setminus \{0\}$
; and
 $\lim _{n\to \infty }(1/n) \log \|{\mathcal L}_z^{(n)}|_{F(z)}\|=\lambda _2$
.
$\lim _{n\to \infty }(1/n) \log \|{\mathcal L}_z^{(n)}|_{F(z)}\|=\lambda _2$
.
A one sentence summary of this is that over a.e. z, B decomposes into two equivariant spaces of dimension M and co-dimension M on which the growth rates of the operator cocycle are
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
respectively.
$\lambda _2$
respectively.
Some of the terms appearing in the statement below of the main theorem will be defined in §3.
Theorem 1. Let
![]() $\pi $
be a forward-looking factor map from an irreducible (two-sided) shift of finite type X to a sofic shift Z and let
$\pi $
be a forward-looking factor map from an irreducible (two-sided) shift of finite type X to a sofic shift Z and let
![]() $\phi \in C^\beta (X^+)$
. Let
$\phi \in C^\beta (X^+)$
. Let
![]() $\pi =\pi _2\circ \pi _1$
be the factorization described above where
$\pi =\pi _2\circ \pi _1$
be the factorization described above where
![]() $\pi _1\colon X\to Y$
is of class degree one and map
$\pi _1\colon X\to Y$
is of class degree one and map
![]() $\pi _2:Y\to Z$
has degree equal to the class degree of
$\pi _2:Y\to Z$
has degree equal to the class degree of
![]() $\pi $
.
$\pi $
.
Let
![]() $\nu $
be a fully supported ergodic invariant measure on Z and let
$\nu $
be a fully supported ergodic invariant measure on Z and let
![]() $\nu _1,\ldots,\nu _k$
be the lifts of
$\nu _1,\ldots,\nu _k$
be the lifts of
![]() $\nu $
under
$\nu $
under
![]() $\pi _2$
with multiplicities
$\pi _2$
with multiplicities
![]() $m_1,\ldots ,m_k$
respectively. Let
$m_1,\ldots ,m_k$
respectively. Let
![]() $r_{\pi _1}(\nu _i)$
be the relative pressure of
$r_{\pi _1}(\nu _i)$
be the relative pressure of
![]() $\phi $
over
$\phi $
over
![]() $\nu _i$
and
$\nu _i$
and
![]() $r_\pi (\nu )$
be the relative pressure of
$r_\pi (\nu )$
be the relative pressure of
![]() $\phi $
over
$\phi $
over
![]() $\nu $
.
$\nu $
.
Let
 $({\mathcal L}_z^{(n)})$
be the cocycle of linear operators over Z acting on
$({\mathcal L}_z^{(n)})$
be the cocycle of linear operators over Z acting on
![]() $C^\beta (X^+)$
described above. Then the largest Lyapunov exponent of the cocycle is
$C^\beta (X^+)$
described above. Then the largest Lyapunov exponent of the cocycle is
![]() $r_\pi (\nu )$
and the multiplicity of this exponent is
$r_\pi (\nu )$
and the multiplicity of this exponent is
 $$ \begin{align*}\sum_{r_{\pi_1}(\nu_i)=r_\pi(\nu)}m_i. \end{align*} $$
$$ \begin{align*}\sum_{r_{\pi_1}(\nu_i)=r_\pi(\nu)}m_i. \end{align*} $$
In the case where
![]() $\phi $
is locally constant, we can give a more tangible description of this multiplicity as the multiplicity of the leading exponent of an explicit matrix cocycle.
$\phi $
is locally constant, we can give a more tangible description of this multiplicity as the multiplicity of the leading exponent of an explicit matrix cocycle.
Corollary 2. Let
![]() $\pi $
, X, Z and
$\pi $
, X, Z and
![]() $\nu $
be as in the statement of Theorem 1 and suppose additionally that
$\nu $
be as in the statement of Theorem 1 and suppose additionally that
![]() $\phi $
is locally constant. Then the action of
$\phi $
is locally constant. Then the action of
 ${\mathcal L}_z^{(n)}$
restricts to the space of locally constant functions (constant on cylinders of the same length). The multiplicity of the leading exponent of this cocycle is the same as that of the cocycle in Theorem 1.
${\mathcal L}_z^{(n)}$
restricts to the space of locally constant functions (constant on cylinders of the same length). The multiplicity of the leading exponent of this cocycle is the same as that of the cocycle in Theorem 1.
In the proof of this corollary, we assume (without loss of generality) that X is a 1-step shift of finite type and
![]() $\phi (x)$
depends only on
$\phi (x)$
depends only on
![]() $x_0$
. In this case, the locally constant functions in the proof also depend only on the zeroth coordinate. It is then straightforward to write down the matrix cocycle representing the action of
$x_0$
. In this case, the locally constant functions in the proof also depend only on the zeroth coordinate. It is then straightforward to write down the matrix cocycle representing the action of
 ${\mathcal L}_z^{(n)}$
on these functions.
${\mathcal L}_z^{(n)}$
on these functions.
2 An example
In this section, we give an example illustrating the objects appearing in the theorem and the corollary. The example is mostly self-contained, but we rely on one fact from the proof of the main theorem while presenting the example. In fact, where the corollary would give a cocycle of
![]() $3\times 3$
matrices, we are able to exploit some symmetries to build instead a cocycle of
$3\times 3$
matrices, we are able to exploit some symmetries to build instead a cocycle of
![]() $2\times 2$
matrices. Let
$2\times 2$
matrices. Let
![]() $X=\{0,1,2\}^{\mathbb Z}$
and
$X=\{0,1,2\}^{\mathbb Z}$
and
![]() $Z=\{F,N\}^{\mathbb Z}$
. The factor map is defined by
$Z=\{F,N\}^{\mathbb Z}$
. The factor map is defined by
![]() $\pi (x)_j=F$
(for flip) if
$\pi (x)_j=F$
(for flip) if
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
have opposite parities and
$x_{j+1}$
have opposite parities and
![]() $\pi (x)_j=N$
if
$\pi (x)_j=N$
if
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
have the same parity (modulo 2). We define the potential
$x_{j+1}$
have the same parity (modulo 2). We define the potential
![]() $\phi $
by
$\phi $
by
![]() $\phi (x)=x_0$
. For any
$\phi (x)=x_0$
. For any
![]() $z\in Z$
, the preimage set
$z\in Z$
, the preimage set
![]() $\pi ^{-1}\{z\}$
consists of two classes, one consisting of points where
$\pi ^{-1}\{z\}$
consists of two classes, one consisting of points where
![]() $x_0$
is 0 or 2 and the other consisting of points with
$x_0$
is 0 or 2 and the other consisting of points with
![]() $x_0=1$
. These two classes are mutually separated: at each
$x_0=1$
. These two classes are mutually separated: at each
![]() $j\in \mathbb Z$
, points in one class have even symbols while points in the other class have odd symbols, so that
$j\in \mathbb Z$
, points in one class have even symbols while points in the other class have odd symbols, so that
![]() $\pi $
has class degree 2. A suitable factorization of
$\pi $
has class degree 2. A suitable factorization of
![]() $\pi $
into the composition of a map of class degree 1 and a map of degree 2 is given by
$\pi $
into the composition of a map of class degree 1 and a map of degree 2 is given by
![]() $\pi =\pi _2\circ \pi _1$
, where
$\pi =\pi _2\circ \pi _1$
, where
![]() $Y=\{0,1\}^{\mathbb Z}$
,
$Y=\{0,1\}^{\mathbb Z}$
,
![]() $\pi _1(x)_i=x_i\mod 2$
and
$\pi _1(x)_i=x_i\mod 2$
and
![]() $\pi _2$
is
$\pi _2$
is
![]() $\pi |_Y$
. To see that
$\pi |_Y$
. To see that
![]() $\pi _1$
is of class degree 1, notice that if
$\pi _1$
is of class degree 1, notice that if
 $x,x'\in \pi _1^{-1}(y)$
, then the hybrid point
$x,x'\in \pi _1^{-1}(y)$
, then the hybrid point
![]() $\bar x$
agreeing with x on symbols up to the
$\bar x$
agreeing with x on symbols up to the
![]() $(k-1)$
st and agreeing with
$(k-1)$
st and agreeing with
![]() $x'$
thereafter belongs to X and is a preimage of y, so that x transitions to
$x'$
thereafter belongs to X and is a preimage of y, so that x transitions to
![]() $x'$
for any two elements of
$x'$
for any two elements of
 $\pi _1^{-1}(y)$
(as defined in §3). To see that
$\pi _1^{-1}(y)$
(as defined in §3). To see that
![]() $\pi _2$
has degree 2, notice that each
$\pi _2$
has degree 2, notice that each
![]() $z\in Z$
has exactly two preimages, one the image of the other under the map
$z\in Z$
has exactly two preimages, one the image of the other under the map
![]() $r\colon Y\to Y$
given by
$r\colon Y\to Y$
given by
![]() $r(y)_j=1-y_j$
.
$r(y)_j=1-y_j$
.
If
![]() $\mu _p$
is the Bernoulli measure on Y with 0’s with probability p and 1’s with probability
$\mu _p$
is the Bernoulli measure on Y with 0’s with probability p and 1’s with probability
![]() $1-p$
, then
$1-p$
, then
 $\mu _p\circ \pi _2^{-1}=\mu _{1-p}\circ \pi _2^{-1}$
(this follows from the facts that
$\mu _p\circ \pi _2^{-1}=\mu _{1-p}\circ \pi _2^{-1}$
(this follows from the facts that
![]() $\pi _2\circ r=\pi _2$
and
$\pi _2\circ r=\pi _2$
and
 $\mu _p\circ r^{-1}=\mu _{1-p}$
). We let
$\mu _p\circ r^{-1}=\mu _{1-p}$
). We let
 $\nu _p=\mu _p\circ \pi _2^{-1}$
. It is not hard to see that if
$\nu _p=\mu _p\circ \pi _2^{-1}$
. It is not hard to see that if
 $p=\tfrac 12$
, then
$p=\tfrac 12$
, then
![]() $\nu _p$
is the uniformly distributed Bernoulli measure on Z. However, for
$\nu _p$
is the uniformly distributed Bernoulli measure on Z. However, for
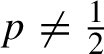 $p\ne \tfrac 12$
, the measure
$p\ne \tfrac 12$
, the measure
![]() $\nu _p$
is a Hidden Markov Measure where there is long range dependence between the entries (see for example [Reference Blackwell5]).
$\nu _p$
is a Hidden Markov Measure where there is long range dependence between the entries (see for example [Reference Blackwell5]).
We then look at the equilibrium states on X for
![]() $\phi $
relative to the factor
$\phi $
relative to the factor
![]() $\nu _p$
on Z. We find these by first understanding the lifts of
$\nu _p$
on Z. We find these by first understanding the lifts of
![]() $\nu _p$
to Y under
$\nu _p$
to Y under
![]() $\pi _2$
. The ergodic lifts of
$\pi _2$
. The ergodic lifts of
![]() $\nu _p$
to Y are
$\nu _p$
to Y are
![]() $\mu _p$
and
$\mu _p$
and
![]() $\mu _{1-p}$
, each with multiplicity 1 in the case
$\mu _{1-p}$
, each with multiplicity 1 in the case
 $p\ne \tfrac 12$
; and
$p\ne \tfrac 12$
; and
![]() $\mu _{1/2}$
with multiplicity 2 in the case
$\mu _{1/2}$
with multiplicity 2 in the case
 $p=\tfrac 12$
. To understand this, notice that a typical point of
$p=\tfrac 12$
. To understand this, notice that a typical point of
![]() $\nu _{1/2}$
has two preimages, both generic for the Bernoulli measure
$\nu _{1/2}$
has two preimages, both generic for the Bernoulli measure
![]() $\mu _{1/2}$
on Y where each is the image of the other under r.
$\mu _{1/2}$
on Y where each is the image of the other under r.
To find the relative equilibrium states for
![]() $\phi $
over
$\phi $
over
![]() $(Z,\nu _p)$
with the factor map
$(Z,\nu _p)$
with the factor map
![]() $\pi $
, we then look for the relative equilibrium states of
$\pi $
, we then look for the relative equilibrium states of
![]() $\phi $
over
$\phi $
over
![]() $(Y,\mu _p)$
and
$(Y,\mu _p)$
and
![]() $(Y,\mu _{1-p})$
with the factor map
$(Y,\mu _{1-p})$
with the factor map
![]() $\pi _1$
. By [Reference Allahbakhshi, Antonioli and Yoo1], since
$\pi _1$
. By [Reference Allahbakhshi, Antonioli and Yoo1], since
![]() $\pi _1$
has class degree 1, there is a unique relative equilibrium state of
$\pi _1$
has class degree 1, there is a unique relative equilibrium state of
![]() $\phi $
over
$\phi $
over
![]() $(Y,\mu _p)$
for each p. The relative pressures with the factor map
$(Y,\mu _p)$
for each p. The relative pressures with the factor map
![]() $\pi _1$
over
$\pi _1$
over
![]() $(Y,\mu _p)$
and
$(Y,\mu _p)$
and
![]() $(Y,\mu _{1-p})$
are
$(Y,\mu _{1-p})$
are
![]() $p\log (1+e^2)+(1-p)$
and
$p\log (1+e^2)+(1-p)$
and
![]() $(1-p)\log (1+e^2)+p$
. To see this, notice that to lift
$(1-p)\log (1+e^2)+p$
. To see this, notice that to lift
![]() $(Y,\mu _p)$
, the symbol
$(Y,\mu _p)$
, the symbol
![]() $0$
in Y with probability p is to be split into two states
$0$
in Y with probability p is to be split into two states
![]() $0$
and
$0$
and
![]() $2$
. Choosing
$2$
. Choosing
![]() $0$
with probability
$0$
with probability
![]() $p/(1+e^{2})$
and
$p/(1+e^{2})$
and
![]() $2$
with probability
$2$
with probability
![]() $pe^{2}/(1+e^{2})$
maximizes the relative pressure. For
$pe^{2}/(1+e^{2})$
maximizes the relative pressure. For
 $p=\tfrac 12$
, the relative equilibrium state is a lift of
$p=\tfrac 12$
, the relative equilibrium state is a lift of
![]() $\mu _{1/2}$
to X under
$\mu _{1/2}$
to X under
![]() $\pi _1$
. The relative equilibrium state is the Bernoulli measure with 0, 1 and 2 having weights
$\pi _1$
. The relative equilibrium state is the Bernoulli measure with 0, 1 and 2 having weights
 $\tfrac 12/(1+e^2)$
,
$\tfrac 12/(1+e^2)$
,
![]() $\tfrac 12$
and
$\tfrac 12$
and
 $\tfrac 12 e^2/(1+e^2)$
respectively. The relative pressure is
$\tfrac 12 e^2/(1+e^2)$
respectively. The relative pressure is
 $\tfrac 12(1+\log (1+e^2))$
.
$\tfrac 12(1+\log (1+e^2))$
.
Since it is not easy to directly compute exponents of Perron–Frobenius operator cocycles, we identify a finite-dimensional space V of piecewise constant functions, invariant under the cocycle, and do computations there. That this is possible is because the function
![]() $\phi $
is piecewise constant.
$\phi $
is piecewise constant.
We also need to see why the growth rates appearing in the subspace V are the maximal growth rates in the full Banach space. This follows since V intersects each of the cones
![]() $\mathcal C_a\cap S_P$
appearing in Lemma 12 for P satisfying the conditions appearing in Lemma 13.
$\mathcal C_a\cap S_P$
appearing in Lemma 12 for P satisfying the conditions appearing in Lemma 13.
Let the two-dimensional space V be the collection of functions on X, constant on cylinders of length 1, with the property that the value on the [0] and [2] cylinders are equal. We claim that both
![]() ${\mathcal L}_N$
and
${\mathcal L}_N$
and
![]() ${\mathcal L}_F$
map V onto itself. We represent an element f of V by a vector consisting of its values on the cylinder sets
${\mathcal L}_F$
map V onto itself. We represent an element f of V by a vector consisting of its values on the cylinder sets
![]() $[0]\cup [2]$
and
$[0]\cup [2]$
and
![]() $[1]$
respectively. We then compute the action of
$[1]$
respectively. We then compute the action of
![]() ${\mathcal L}_N$
and
${\mathcal L}_N$
and
![]() ${\mathcal L}_F$
on V as follows.
${\mathcal L}_F$
on V as follows.
We have
 $$ \begin{align*} {\mathcal L}_N f(x)&=\begin{cases} e^{\phi(1x)}f(1x)&\text{if}\ x_0=1,\\ e^{\phi(0x)}f(0x)+e^{\phi(2x)}f(2x)&\text{if}\ x_0\ \text{is 0 or 2;} \end{cases}\\ {\mathcal L}_F f(x)&=\begin{cases} e^{\phi(0x)}f(0x)+e^{\phi(2x)}f(2x)&\text{if}\ x_0=1,\\ e^{\phi(1x)}f(1x)&\text{if}\ x_0\ \text{is 0 or 2.} \end{cases} \end{align*} $$
$$ \begin{align*} {\mathcal L}_N f(x)&=\begin{cases} e^{\phi(1x)}f(1x)&\text{if}\ x_0=1,\\ e^{\phi(0x)}f(0x)+e^{\phi(2x)}f(2x)&\text{if}\ x_0\ \text{is 0 or 2;} \end{cases}\\ {\mathcal L}_F f(x)&=\begin{cases} e^{\phi(0x)}f(0x)+e^{\phi(2x)}f(2x)&\text{if}\ x_0=1,\\ e^{\phi(1x)}f(1x)&\text{if}\ x_0\ \text{is 0 or 2.} \end{cases} \end{align*} $$
Recalling that
![]() $\phi (x)=x_0$
and representing both f and its image by vectors in the order described above, we have
$\phi (x)=x_0$
and representing both f and its image by vectors in the order described above, we have
![]() ${\mathcal L}_N$
and
${\mathcal L}_N$
and
![]() ${\mathcal L}_F$
are represented on V by the matrices
${\mathcal L}_F$
are represented on V by the matrices
 $$ \begin{align*}A_N=\begin{pmatrix}1+e^2&0\\0&e\end{pmatrix} \quad\text{and}\quad A_F=\begin{pmatrix}0&e\\1+e^2&0\end{pmatrix}. \end{align*} $$
$$ \begin{align*}A_N=\begin{pmatrix}1+e^2&0\\0&e\end{pmatrix} \quad\text{and}\quad A_F=\begin{pmatrix}0&e\\1+e^2&0\end{pmatrix}. \end{align*} $$
Let
 $A_z^{(n)}$
denote the cocycle over z generated by these matrices. If y is a
$A_z^{(n)}$
denote the cocycle over z generated by these matrices. If y is a
![]() $\mu _p$
-generic point, then
$\mu _p$
-generic point, then
![]() $r(y)$
is
$r(y)$
is
![]() $\mu _{1-p}$
-generic and
$\mu _{1-p}$
-generic and
![]() $z=\pi _2(y)=\pi _2(r(y))$
is
$z=\pi _2(y)=\pi _2(r(y))$
is
![]() $\nu _p$
-generic. We can verify that if
$\nu _p$
-generic. We can verify that if
![]() $y_0\ldots y_n$
starts and ends with even symbols (which implies that
$y_0\ldots y_n$
starts and ends with even symbols (which implies that
![]() $z_0\ldots z_{n-1}$
has an even number of F’s), then
$z_0\ldots z_{n-1}$
has an even number of F’s), then
 $$ \begin{align*}A_z^{(n)}=\begin{pmatrix}(1+e^2)^Ee^O&0\\0&(1+e^2)^Oe^E\end{pmatrix}, \end{align*} $$
$$ \begin{align*}A_z^{(n)}=\begin{pmatrix}(1+e^2)^Ee^O&0\\0&(1+e^2)^Oe^E\end{pmatrix}, \end{align*} $$
where E denotes the number of even symbols in
![]() $y_0\ldots y_n$
and O is the number of odd symbols. Similarly, if
$y_0\ldots y_n$
and O is the number of odd symbols. Similarly, if
![]() $y_0\ldots y_{n}$
begins and ends with odd symbols,
$y_0\ldots y_{n}$
begins and ends with odd symbols,
 $$ \begin{align*}A_z^{(n)}=\begin{pmatrix}(1+e^2)^Oe^E&0\\0&(1+e^2)^Ee^O\end{pmatrix}. \end{align*} $$
$$ \begin{align*}A_z^{(n)}=\begin{pmatrix}(1+e^2)^Oe^E&0\\0&(1+e^2)^Ee^O\end{pmatrix}. \end{align*} $$
Finally, if
![]() $y_0\ldots y_n$
begins with an even symbol and ends with an odd symbol, or begins with an odd symbol and ends with an even symbol, then
$y_0\ldots y_n$
begins with an even symbol and ends with an odd symbol, or begins with an odd symbol and ends with an even symbol, then
 $A_z^{(n)}$
is respectively
$A_z^{(n)}$
is respectively
 $$ \begin{align*} \begin{pmatrix} 0&(1+e^2)^Ee^O\\ (1+e^2)^Oe^E&0 \end{pmatrix} \quad\text{or}\quad \begin{pmatrix} 0&(1+e^2)^Oe^E\\ (1+e^2)^Ee^O&0 \end{pmatrix}.\ \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0&(1+e^2)^Ee^O\\ (1+e^2)^Oe^E&0 \end{pmatrix} \quad\text{or}\quad \begin{pmatrix} 0&(1+e^2)^Oe^E\\ (1+e^2)^Ee^O&0 \end{pmatrix}.\ \end{align*} $$
In all of these cases, we see that the exponential growth rates of the matrix product along the orbit (and hence of the restriction of the Perron–Frobenius cocycle to V) are
![]() $\log ((1+e^2)^pe^{1-p})$
and
$\log ((1+e^2)^pe^{1-p})$
and
![]() $\log ((1+e^2)^{1-p}e^p)$
as computed above. In the case where
$\log ((1+e^2)^{1-p}e^p)$
as computed above. In the case where
 $p=\tfrac 12$
, the two exponents are both equal to
$p=\tfrac 12$
, the two exponents are both equal to
![]() $\log ((1+e^2)^{1/2}e^{1/2})$
as expected.
$\log ((1+e^2)^{1/2}e^{1/2})$
as expected.
3 Background
In this section, we collect a number of theorems and definitions that we will need for the proof, as well as setting out a number of related articles in the literature.
If
![]() $(Z,S)$
is a subshift,
$(Z,S)$
is a subshift,
![]() $\mathsf A(Z)$
is its alphabet (so that
$\mathsf A(Z)$
is its alphabet (so that
![]() $Z\subset \mathsf A(Z)^{\mathbb Z}$
) and
$Z\subset \mathsf A(Z)^{\mathbb Z}$
) and
![]() $\mathsf L(Z)$
denotes its language, that is, the set of all finite strings that appear in points of Z. A point
$\mathsf L(Z)$
denotes its language, that is, the set of all finite strings that appear in points of Z. A point
![]() $z\in Z$
is said to be right transitive if
$z\in Z$
is said to be right transitive if
![]() $\{S^n(z):n\ge 0\}$
is dense in Z.
$\{S^n(z):n\ge 0\}$
is dense in Z.
If
![]() $\pi \colon X\to Z$
is a factor map from a shift of finite type to a sofic shift and
$\pi \colon X\to Z$
is a factor map from a shift of finite type to a sofic shift and
![]() $\nu $
is an ergodic invariant measure on Z, Petersen, Quas and Shin [Reference Petersen, Quas and Shin10] established that the collection of ergodic invariant measures of relative maximal entropy is finite. These measures are the relative equilibrium states in the case where the potential function
$\nu $
is an ergodic invariant measure on Z, Petersen, Quas and Shin [Reference Petersen, Quas and Shin10] established that the collection of ergodic invariant measures of relative maximal entropy is finite. These measures are the relative equilibrium states in the case where the potential function
![]() $\phi $
is taken to be 0. In the case where the factor map
$\phi $
is taken to be 0. In the case where the factor map
![]() $\pi $
is a one-block map (that is
$\pi $
is a one-block map (that is
![]() $\pi (x)_0$
depends only on
$\pi (x)_0$
depends only on
![]() $x_0$
), they established that the number of ergodic measures of relative maximal entropy over any ergodic invariant measure
$x_0$
), they established that the number of ergodic measures of relative maximal entropy over any ergodic invariant measure
![]() $\nu $
on Z is bounded above by
$\nu $
on Z is bounded above by
 $\min _{j\in \mathsf A(Z)}|\rho ^{-1}(j)|$
, where
$\min _{j\in \mathsf A(Z)}|\rho ^{-1}(j)|$
, where
![]() $\rho $
is the symbol map giving rise to
$\rho $
is the symbol map giving rise to
![]() $\pi $
. This result shows that, in particular, the number of these measures is finite. The bound suffers from a failure to be invariant under conjugacies. This deficiency was remedied and the bound improved in the paper [Reference Allahbakhshi and Quas3] of Allahbakshi and Quas, some ideas from which will play an important role here.
$\pi $
. This result shows that, in particular, the number of these measures is finite. The bound suffers from a failure to be invariant under conjugacies. This deficiency was remedied and the bound improved in the paper [Reference Allahbakhshi and Quas3] of Allahbakshi and Quas, some ideas from which will play an important role here.
For
![]() $z\in Z$
, if
$z\in Z$
, if
![]() $x,x'\in \pi ^{-1}z$
, we say that x transitions to
$x,x'\in \pi ^{-1}z$
, we say that x transitions to
![]() $x'$
, and write
$x'$
, and write
![]() $x\to x'$
, if for all n, there exists
$x\to x'$
, if for all n, there exists
![]() $\bar x\in \pi ^{-1}z$
such that
$\bar x\in \pi ^{-1}z$
such that
![]() $\bar x_{-\infty }^n =x_{-\infty }^n$
and
$\bar x_{-\infty }^n =x_{-\infty }^n$
and
![]() $\bar x_m=x^{\prime }_m$
for all sufficiently large m. We then define an equivalence relation on
$\bar x_m=x^{\prime }_m$
for all sufficiently large m. We then define an equivalence relation on
![]() $\pi ^{-1}z$
by
$\pi ^{-1}z$
by
![]() $x\leftrightarrow x'$
if
$x\leftrightarrow x'$
if
![]() $x\to x'$
and
$x\to x'$
and
![]() $x'\to x$
. The equivalence classes are called transition classes (a pigeonhole argument using the finite type property shows there are finitely many transition classes). Let
$x'\to x$
. The equivalence classes are called transition classes (a pigeonhole argument using the finite type property shows there are finitely many transition classes). Let
![]() $\mathcal T(z)$
denote the collection of transition classes over z. The paper [Reference Allahbakhshi and Quas3] establishes that the number of transition classes over any right transitive point
$\mathcal T(z)$
denote the collection of transition classes over z. The paper [Reference Allahbakhshi and Quas3] establishes that the number of transition classes over any right transitive point
![]() $z\in Z$
is a constant
$z\in Z$
is a constant
![]() $c_\pi $
independent of z. This constant is called the class degree of
$c_\pi $
independent of z. This constant is called the class degree of
![]() $\pi $
.
$\pi $
.
Theorem 3. (Allahbakhshi and Quas [Reference Allahbakhshi and Quas3])
Let X be a shift of finite type and Z be a sofic shift. Let
![]() $\pi \colon X\to Z$
be a one-block factor map. There exists a word
$\pi \colon X\to Z$
be a one-block factor map. There exists a word
 $W=w_0^{n-1}$
in
$W=w_0^{n-1}$
in
![]() $\mathsf L(Z)$
, a position
$\mathsf L(Z)$
, a position
![]() $0\le l<n$
, and a subset
$0\le l<n$
, and a subset
![]() $B\subset \mathsf A(X)$
whose cardinality is the class degree
$B\subset \mathsf A(X)$
whose cardinality is the class degree
![]() $c_\pi $
, so that for each element
$c_\pi $
, so that for each element
 $u_0^{n-1}$
of
$u_0^{n-1}$
of
![]() $\pi ^{-1}(W)$
, there is a word
$\pi ^{-1}(W)$
, there is a word
 $v_0^{n-1}\in \pi ^{-1}(W)$
such that
$v_0^{n-1}\in \pi ^{-1}(W)$
such that
![]() $u_0=v_0$
,
$u_0=v_0$
,
![]() $u_{n-1}=v_{n-1}$
and
$u_{n-1}=v_{n-1}$
and
![]() $v_l\in B$
.
$v_l\in B$
.
The number of measures of relative maximal entropy over
![]() $\nu $
is bounded above by
$\nu $
is bounded above by
![]() $c_\pi $
.
$c_\pi $
.
The bound on the number of measures of relative maximal entropy was extended by Allahbakhshi, Antonioli and Yoo [Reference Allahbakhshi, Antonioli and Yoo1] to the number of relative equilibrium states of a Hölder continuous (or Bowen) potential function.
In the situation described in the above theorem, W is called a minimal transition block; B is a set of representatives and the word u is said to be routed through
![]() $v_l$
. (The minimality in the name refers to the fact that the set of representatives is as small as possible.) A pair of elements
$v_l$
. (The minimality in the name refers to the fact that the set of representatives is as small as possible.) A pair of elements
![]() $x,x'$
of X is said to be mutually separated if
$x,x'$
of X is said to be mutually separated if
![]() $x_n\ne x^{\prime }_n$
for each n. Two subsets
$x_n\ne x^{\prime }_n$
for each n. Two subsets
![]() $S_1$
and
$S_1$
and
![]() $S_2$
of X are mutually separated if for each
$S_2$
of X are mutually separated if for each
![]() $x\in S_1$
and
$x\in S_1$
and
![]() $x'\in S_2$
, x and
$x'\in S_2$
, x and
![]() $x'$
are mutually separated.
$x'$
are mutually separated.
Theorem 4. (Allahbakhshi, Hong and Jung [Reference Allahbakhshi, Hong and Jung2])
Let
![]() $\pi \colon X\to Z$
be a one-block factor map from an irreducible two-sided shift of finite type X to a two-sided sofic shift Z. If
$\pi \colon X\to Z$
be a one-block factor map from an irreducible two-sided shift of finite type X to a two-sided sofic shift Z. If
![]() $z\in Z$
is right transitive, then the elements of
$z\in Z$
is right transitive, then the elements of
![]() $\mathcal T(z)$
are mutually separated. In particular, for each copy of W in z, there exists a bijection between
$\mathcal T(z)$
are mutually separated. In particular, for each copy of W in z, there exists a bijection between
![]() $\mathcal T(z)$
and B so that for each
$\mathcal T(z)$
and B so that for each
![]() $C\in \mathcal T(z)$
, there exists a representative
$C\in \mathcal T(z)$
, there exists a representative
![]() $s\in B$
such that each
$s\in B$
such that each
![]() $x\in C$
may be routed through s over that copy of W and through no other element of B.
$x\in C$
may be routed through s over that copy of W and through no other element of B.
Theorem 5. (Yoo [Reference Yoo12])
Let X be an irreducible two-sided shift of finite type, Z a two-sided sofic shift, and
![]() $\pi \colon X\to Z$
be a continuous factor map. Then there is a sofic shift Y and factorization of
$\pi \colon X\to Z$
be a continuous factor map. Then there is a sofic shift Y and factorization of
![]() $\pi \colon X\to Z$
as a composition of factor maps,
$\pi \colon X\to Z$
as a composition of factor maps,
![]() $\pi _2\circ \pi _1$
where
$\pi _2\circ \pi _1$
where
![]() $\pi _1\colon X\to Y$
and
$\pi _1\colon X\to Y$
and
![]() $\pi _2\colon Y\to Z$
with the properties that
$\pi _2\colon Y\to Z$
with the properties that
![]() $\pi _2$
is finite-to-one of degree
$\pi _2$
is finite-to-one of degree
![]() $c_\pi $
, the class degree of
$c_\pi $
, the class degree of
![]() $\pi $
and
$\pi $
and
![]() $\pi _1$
is of class degree 1.
$\pi _1$
is of class degree 1.
Theorem 6. (Yoo [Reference Yoo13])
Let
![]() $\pi $
be a finite-to-one continuous factor map from a homeomorphism S of a compact metric space Y to a homeomorphism T of a compact metric space Z. Suppose that
$\pi $
be a finite-to-one continuous factor map from a homeomorphism S of a compact metric space Y to a homeomorphism T of a compact metric space Z. Suppose that
![]() $\nu $
is an ergodic T-invariant measure. Then:
$\nu $
is an ergodic T-invariant measure. Then:
-
(1) there exists
 $d\in \mathbb N$
such that for
$d\in \mathbb N$
such that for
 $\nu $
-a.e.
$\nu $
-a.e.
 $z\in Z$
,
$z\in Z$
,
 $|\pi ^{-1}z|=d$
;
$|\pi ^{-1}z|=d$
; -
(2) there are only finitely many ergodic measures
 $\mu _1,\ldots ,\mu _k$
on Y such that
$\mu _1,\ldots ,\mu _k$
on Y such that
 $\pi _*\mu _i=\nu $
and
$\pi _*\mu _i=\nu $
and
 $k\le d$
; if
$k\le d$
; if
 $\nu $
is fully supported, then so are the
$\nu $
is fully supported, then so are the
 $\mu _1,\ldots ,\mu _k$
;
$\mu _1,\ldots ,\mu _k$
; -
(3) there exist multiplicities
 $m_1,\ldots ,m_k$
whose sum is d.
$m_1,\ldots ,m_k$
whose sum is d.
In the case where Y is a shift space and
![]() $\pi $
is a one-block map, there exists a joining
$\pi $
is a one-block map, there exists a joining
![]() $\bar \mu $
on
$\bar \mu $
on
![]() $Y^d$
such that for
$Y^d$
such that for
![]() $\bar \mu $
-a.e.
$\bar \mu $
-a.e.
![]() $(y^1,\ldots ,y^d)$
,
$(y^1,\ldots ,y^d)$
,
![]() $\pi (y^1)=\cdots =\pi (y^d)$
; the
$\pi (y^1)=\cdots =\pi (y^d)$
; the
![]() $y^i$
are mutually separated; and
$y^i$
are mutually separated; and
![]() $y^{M_i+1},\ldots ,y^{M_i+m_i}$
are generic for
$y^{M_i+1},\ldots ,y^{M_i+m_i}$
are generic for
![]() $\mu _i$
, where
$\mu _i$
, where
![]() $M_i=m_1+\cdots +m_{i-1}$
.
$M_i=m_1+\cdots +m_{i-1}$
.
The joining
![]() $\bar \mu $
constructed in the above theorem is called an ergodic degree joining.
$\bar \mu $
constructed in the above theorem is called an ergodic degree joining.
The following theorem gives a criterion for simplicity of the top Lyapunov exponent of an operator cocycle based on contraction of cones and Birkhoff’s theorem on contraction of the Hilbert metric. Recall that a cone is a closed subset
![]() $\mathcal C$
of a real Banach space B that is closed under addition and scalar multiplication by a non-negative real number.
$\mathcal C$
of a real Banach space B that is closed under addition and scalar multiplication by a non-negative real number.
For
![]() $f,g\in \mathcal C$
, let
$f,g\in \mathcal C$
, let
![]() $m(f,g)=\sup \{t\ge 0\colon f-tg\in \mathcal C\}$
and let
$m(f,g)=\sup \{t\ge 0\colon f-tg\in \mathcal C\}$
and let
![]() $M(f,g)=\inf \{s\ge 0\colon sg-f\in \mathcal C\}$
. The projective distance between two points in the cone is defined as
$M(f,g)=\inf \{s\ge 0\colon sg-f\in \mathcal C\}$
. The projective distance between two points in the cone is defined as
![]() $\Theta _{\mathcal C}(f,g)=\log (M(f,g)/m(f,g))$
. (Note that this is not a metric as it may be infinite; also
$\Theta _{\mathcal C}(f,g)=\log (M(f,g)/m(f,g))$
. (Note that this is not a metric as it may be infinite; also
![]() $\Theta _{\mathcal C}(\beta f,\gamma g)= \Theta _{\mathcal C}(f,g)$
for all
$\Theta _{\mathcal C}(\beta f,\gamma g)= \Theta _{\mathcal C}(f,g)$
for all
![]() $\beta ,\gamma>0$
.) The diameter of a subset S of
$\beta ,\gamma>0$
.) The diameter of a subset S of
![]() $\mathcal C$
is
$\mathcal C$
is
![]() $\sup _{f,g\in S\setminus \{0\}}\Theta _{\mathcal C}(f,g)$
. A cone is said to be D-adapted if whenever
$\sup _{f,g\in S\setminus \{0\}}\Theta _{\mathcal C}(f,g)$
. A cone is said to be D-adapted if whenever
![]() $f\in B$
and
$f\in B$
and
![]() $g\in \mathcal C$
, then
$g\in \mathcal C$
, then
![]() $g\pm f\in \mathcal C$
implies
$g\pm f\in \mathcal C$
implies
![]() $\|f\|\le D\|g\|$
.
$\|f\|\le D\|g\|$
.
Theorem 7. (Horan [Reference Horan6, Theorem 2.14])
Let Y be a compact metric space and
![]() $S\colon Y\to Y$
be a continuous invertible transformation. Let
$S\colon Y\to Y$
be a continuous invertible transformation. Let
![]() $\nu $
be an ergodic S-invariant Borel probability measure on Y. Let B be a Banach space and let
$\nu $
be an ergodic S-invariant Borel probability measure on Y. Let B be a Banach space and let
![]() $\mathcal C$
be a D-adapted cone in B such that
$\mathcal C$
be a D-adapted cone in B such that
![]() $\mathcal C-\mathcal C=B$
,
$\mathcal C-\mathcal C=B$
,
![]() $\mathcal C\cap (-\mathcal C)=\{0\}$
.
$\mathcal C\cap (-\mathcal C)=\{0\}$
.
Suppose that for each
![]() $y\in Y$
,
$y\in Y$
,
![]() ${\mathcal L}_y$
is a linear operator from B to B such that
${\mathcal L}_y$
is a linear operator from B to B such that
![]() $y\mapsto {\mathcal L}_y$
is continuous (where the linear operators on B are equipped with the norm topology), that
$y\mapsto {\mathcal L}_y$
is continuous (where the linear operators on B are equipped with the norm topology), that
![]() ${\mathcal L}_y(\mathcal C)\subset \mathcal C$
for each y and that there is a measurable subset
${\mathcal L}_y(\mathcal C)\subset \mathcal C$
for each y and that there is a measurable subset
![]() $A\subset Y$
with
$A\subset Y$
with
![]() $\nu (A)>0$
and an
$\nu (A)>0$
and an
![]() $n>0$
such that
$n>0$
such that
 $\operatorname {\mathrm {diam}}(\mathcal L^{(n)}_y\mathcal C)<\infty $
for all
$\operatorname {\mathrm {diam}}(\mathcal L^{(n)}_y\mathcal C)<\infty $
for all
![]() $y\in A$
.
$y\in A$
.
Then the leading Lyapunov exponent of the cocycle
 $(\mathcal L^{(n)}_y)_{y\in Y}$
is simple. That is there exist
$(\mathcal L^{(n)}_y)_{y\in Y}$
is simple. That is there exist
![]() $\alpha>\beta $
, a measurable function
$\alpha>\beta $
, a measurable function
![]() $v\colon Y\to B$
and a measurable function
$v\colon Y\to B$
and a measurable function
![]() $\psi \colon Y\to B^*$
such that
$\psi \colon Y\to B^*$
such that
![]() ${\mathcal L}_y(v(y))$
is a multiple of
${\mathcal L}_y(v(y))$
is a multiple of
![]() $v(S(y))$
;
$v(S(y))$
;
 $(1/n)\log \|{\mathcal L}_y^{(n)}v(y)\|\to \alpha $
a.e.; and
$(1/n)\log \|{\mathcal L}_y^{(n)}v(y)\|\to \alpha $
a.e.; and
 $\limsup _{n\to \infty }(1/n)\log \| {\mathcal L}_y^{(n)}w\|\le \beta $
whenever
$\limsup _{n\to \infty }(1/n)\log \| {\mathcal L}_y^{(n)}w\|\le \beta $
whenever
![]() $w\in \ker \psi (y)$
.
$w\in \ker \psi (y)$
.
This theorem should be thought of as a skew product version of the Perron–Frobenius theorem.
We will use the relative variational principle of Ledrappier and Walters [Reference Ledrappier and Walters7]. Recall the Bowen definition of pressure:
 $$ \begin{align*}P(\phi)= \lim_{\epsilon\to 0}\limsup_{n\to\infty} \frac 1n\log\sup_E\sum_{x\in E}e^{S_n\phi(x)}, \end{align*} $$
$$ \begin{align*}P(\phi)= \lim_{\epsilon\to 0}\limsup_{n\to\infty} \frac 1n\log\sup_E\sum_{x\in E}e^{S_n\phi(x)}, \end{align*} $$
where the supremum is taken over
![]() $(n,\epsilon )$
-separated sets, that is, sets E such that for any distinct elements
$(n,\epsilon )$
-separated sets, that is, sets E such that for any distinct elements
![]() $x,x'$
of E, there is
$x,x'$
of E, there is
![]() $0\le j<n$
such that
$0\le j<n$
such that
![]() $d_\beta (T^jx,T^jx')\ge \epsilon $
. In the case of shift spaces, this may be simplified, fixing
$d_\beta (T^jx,T^jx')\ge \epsilon $
. In the case of shift spaces, this may be simplified, fixing
![]() $\epsilon $
to be 1 and taking E to be any set consisting of exactly one point in each cylinder set of length n (so that E has the same cardinality as
$\epsilon $
to be 1 and taking E to be any set consisting of exactly one point in each cylinder set of length n (so that E has the same cardinality as
![]() ${\mathcal L}_n(X)$
). For symbolic systems,
${\mathcal L}_n(X)$
). For symbolic systems,
 $$ \begin{align*}P(\phi)=\limsup_{n\to\infty}\frac 1n\log\sum_{x\in E}e^{S_n\phi(x)}, \end{align*} $$
$$ \begin{align*}P(\phi)=\limsup_{n\to\infty}\frac 1n\log\sum_{x\in E}e^{S_n\phi(x)}, \end{align*} $$
where E is any set with one representative of each cylinder set of length n. This definition is further refined by restricting the elements of E to lie in a fixed subset K:
 $$ \begin{align*}P(\phi,K)=\limsup_{n\to\infty}\frac 1n\log\sum_{\omega\in E\subset K}e^{S_n\phi(\omega)}, \end{align*} $$
$$ \begin{align*}P(\phi,K)=\limsup_{n\to\infty}\frac 1n\log\sum_{\omega\in E\subset K}e^{S_n\phi(\omega)}, \end{align*} $$
where E is any maximal
![]() $(n,1)$
-separated collection of points of K. We define
$(n,1)$
-separated collection of points of K. We define
 $p_n(\phi ,K)=\sup _{E\subset K;\ (n,1)\text {-separated}} \sum _{\omega \in E}e^{S_n\phi (\omega )}$
so that
$p_n(\phi ,K)=\sup _{E\subset K;\ (n,1)\text {-separated}} \sum _{\omega \in E}e^{S_n\phi (\omega )}$
so that
 $$ \begin{align*}P(\phi,K)=\limsup_{n\to\infty}\frac 1n\log p_n(\phi,K). \end{align*} $$
$$ \begin{align*}P(\phi,K)=\limsup_{n\to\infty}\frac 1n\log p_n(\phi,K). \end{align*} $$
Theorem 8. (Relative variational principle)
Let
![]() $T\colon X\to X$
and
$T\colon X\to X$
and
![]() $S\colon Y\to Y$
be continuous dynamical systems on compact spaces; let
$S\colon Y\to Y$
be continuous dynamical systems on compact spaces; let
![]() $\nu $
be an ergodic invariant measure for S and let
$\nu $
be an ergodic invariant measure for S and let
![]() $\pi \colon X\to Y$
be a continuous factor map from
$\pi \colon X\to Y$
be a continuous factor map from
![]() $(X,T)$
to
$(X,T)$
to
![]() $(Y,S)$
. Then for
$(Y,S)$
. Then for
![]() $\nu $
-a.e. y,
$\nu $
-a.e. y,
![]() $P(\phi ,\pi ^{-1}y)=r_{\pi }(\nu )$
.
$P(\phi ,\pi ^{-1}y)=r_{\pi }(\nu )$
.
4 Proofs
In this section, we start with some preliminary lemmas and then establish Theorem 14 (which is the special case of the main theorem in the case where
![]() $\pi $
has class degree 1), before using it to prove the main theorem.
$\pi $
has class degree 1), before using it to prove the main theorem.
The proof structure is as follows. We start with a factor map
![]() $\pi \colon X\to Z$
and an ergodic invariant measure
$\pi \colon X\to Z$
and an ergodic invariant measure
![]() $\nu $
on Z. Given a
$\nu $
on Z. Given a
![]() $\nu $
-typical point
$\nu $
-typical point
![]() $z\in Z$
, its preimages in X can be separated into a number of transition classes as described in the previous section. Those results show that one can associate pressure-maximizing measures on X to these classes, and that
$z\in Z$
, its preimages in X can be separated into a number of transition classes as described in the previous section. Those results show that one can associate pressure-maximizing measures on X to these classes, and that
![]() $\nu $
-a.e. z gives rise to the same collection of measures on X. Theorem 14 deals with the case where the class degree is 1 (so there is a single transition class). Some preparatory lemmas show that the cocycle of operators maps a family of cones inside itself, and from time to time maps a cone in the family into a finite diameter sub-cone of the cone in the family. This allows us to apply Theorem 7 showing that there is a simple leading Lyapunov exponent. A calculation shows that this exponent is the quantity appearing on the left side of the equality in the relative variational principle (while the conclusion of Theorem 14 is that the exponent is the right side of the equality). To deal with the case of class degree greater than 1, we express
$\nu $
-a.e. z gives rise to the same collection of measures on X. Theorem 14 deals with the case where the class degree is 1 (so there is a single transition class). Some preparatory lemmas show that the cocycle of operators maps a family of cones inside itself, and from time to time maps a cone in the family into a finite diameter sub-cone of the cone in the family. This allows us to apply Theorem 7 showing that there is a simple leading Lyapunov exponent. A calculation shows that this exponent is the quantity appearing on the left side of the equality in the relative variational principle (while the conclusion of Theorem 14 is that the exponent is the right side of the equality). To deal with the case of class degree greater than 1, we express
![]() $\pi $
as
$\pi $
as
![]() $\pi _2\circ \pi _1$
as in Theorem 5, and express the Perron–Frobenius cocycle as a sum of non-interacting cocycles, each of which satisfies the hypotheses of Theorem 14, with one summand per transition class.
$\pi _2\circ \pi _1$
as in Theorem 5, and express the Perron–Frobenius cocycle as a sum of non-interacting cocycles, each of which satisfies the hypotheses of Theorem 14, with one summand per transition class.
Finally, in the case where
![]() $\phi $
is locally constant, there is a corresponding family of locally constant functions that is mapped into itself by the Perron–Frobenius cocycle. We show that this family intersects each of the cones described above, so that the multiplicity of the top Lyapunov exponent is captured by the action on this finite-dimensional subspace.
$\phi $
is locally constant, there is a corresponding family of locally constant functions that is mapped into itself by the Perron–Frobenius cocycle. We show that this family intersects each of the cones described above, so that the multiplicity of the top Lyapunov exponent is captured by the action on this finite-dimensional subspace.
For this section, let
![]() $\phi $
be a fixed Hölder continuous function. Given
$\phi $
be a fixed Hölder continuous function. Given
![]() $\beta <1$
, we define a semi-norm on
$\beta <1$
, we define a semi-norm on
![]() $C^\beta (X^+)$
by
$C^\beta (X^+)$
by
 $|f|_\beta =\sup _{x\ne x'}|f(x)-f(x')|/d_\beta (x,x')$
(that is, the Lipschitz constant of f with respect to
$|f|_\beta =\sup _{x\ne x'}|f(x)-f(x')|/d_\beta (x,x')$
(that is, the Lipschitz constant of f with respect to
![]() $d_\beta $
) and a norm by
$d_\beta $
) and a norm by
![]() $\|f\|_\beta =\max (\|f\|_\infty ,|f|_\beta )$
. Let
$\|f\|_\beta =\max (\|f\|_\infty ,|f|_\beta )$
. Let
![]() $\beta $
be such that
$\beta $
be such that
![]() $\|\phi \|_\beta <\infty $
. This quantity will be fixed from here on. We also assume throughout this section that the factor map
$\|\phi \|_\beta <\infty $
. This quantity will be fixed from here on. We also assume throughout this section that the factor map
![]() $\pi $
is a one-block map as this is the context in the proof of the main theorem.
$\pi $
is a one-block map as this is the context in the proof of the main theorem.
We define a family of cones, one for each real
![]() $a>0$
, by
$a>0$
, by
 $$ \begin{align*}\mathcal C_a= \{f\in C^\beta(X^+)\colon f\ge 0; f(x')\le e^{ad_\beta(x,x')}f(x)\text{ whenever}\ x_0=x^{\prime}_0 \}. \end{align*} $$
$$ \begin{align*}\mathcal C_a= \{f\in C^\beta(X^+)\colon f\ge 0; f(x')\le e^{ad_\beta(x,x')}f(x)\text{ whenever}\ x_0=x^{\prime}_0 \}. \end{align*} $$
These cones are widely used in symbolic dynamics and appear, for instance, in the work of Parry and Pollicott [Reference Parry and Pollicott9], although our usage differs slightly as we do not impose any condition on
![]() $f(x)/f(x')$
when
$f(x)/f(x')$
when
![]() $x_0\ne x_0'$
. This is important for us, since some operators that we consider yield functions that are 0 on part of
$x_0\ne x_0'$
. This is important for us, since some operators that we consider yield functions that are 0 on part of
![]() $X^+$
.
$X^+$
.
Lemma 9. Let a be large enough that
![]() $b:=\beta (a+|\phi |_\beta )<a$
. Then
$b:=\beta (a+|\phi |_\beta )<a$
. Then
![]() ${\mathcal L}_j\mathcal C_a\subset \mathcal C_b$
for each
${\mathcal L}_j\mathcal C_a\subset \mathcal C_b$
for each
![]() $j\in \mathsf A(Y)$
.
$j\in \mathsf A(Y)$
.
Proof. Let
![]() $f\in \mathcal C_a$
. For each symbol
$f\in \mathcal C_a$
. For each symbol
![]() $i\in \mathsf A(X)$
, set
$i\in \mathsf A(X)$
, set
![]() $\tilde {\mathcal L}_if(x)=e^{\phi (ix)}f(ix)$
. Suppose x and
$\tilde {\mathcal L}_if(x)=e^{\phi (ix)}f(ix)$
. Suppose x and
![]() $x'$
agree for n symbols for some
$x'$
agree for n symbols for some
![]() $n\ge 1$
and suppose
$n\ge 1$
and suppose
![]() $f(ix')>0$
(so that
$f(ix')>0$
(so that
![]() $f(ix)>0$
also). Then
$f(ix)>0$
also). Then
 $$ \begin{align*} \frac{\tilde{\mathcal L}_i f(x')}{\tilde{\mathcal L}_if(x)}&=\frac{e^{\phi(ix')}f(ix')}{e^{\phi(ix)}f(ix)}\\[3pt] &\le e^{|\phi|_\beta\beta^{n+1}}e^{a\beta^{n+1}}\\[3pt] &\le e^{\beta(|\phi|_\beta+a)d_\beta(x,x')}=e^{bd_\beta(x,x')}. \end{align*} $$
$$ \begin{align*} \frac{\tilde{\mathcal L}_i f(x')}{\tilde{\mathcal L}_if(x)}&=\frac{e^{\phi(ix')}f(ix')}{e^{\phi(ix)}f(ix)}\\[3pt] &\le e^{|\phi|_\beta\beta^{n+1}}e^{a\beta^{n+1}}\\[3pt] &\le e^{\beta(|\phi|_\beta+a)d_\beta(x,x')}=e^{bd_\beta(x,x')}. \end{align*} $$
Since for
![]() $j\in \mathsf A(Y)$
,
$j\in \mathsf A(Y)$
,
 ${\mathcal L}_j=\sum _{i\in \pi ^{-1}j}\tilde {\mathcal L}_i$
(where
${\mathcal L}_j=\sum _{i\in \pi ^{-1}j}\tilde {\mathcal L}_i$
(where
![]() $\pi ^{-1}j$
denotes the symbols in
$\pi ^{-1}j$
denotes the symbols in
![]() $\mathsf A(X)$
that map to j under the alphabet map defining
$\mathsf A(X)$
that map to j under the alphabet map defining
![]() $\pi $
), the result follows.
$\pi $
), the result follows.
Lemma 10. For
![]() $f\in \mathcal C_a$
,
$f\in \mathcal C_a$
,
![]() $\|f\|_\beta \le \max (3,1+ae^a)\|f\|_\infty $
. It follows that
$\|f\|_\beta \le \max (3,1+ae^a)\|f\|_\infty $
. It follows that
![]() $\mathcal C_a$
is D-adapted with
$\mathcal C_a$
is D-adapted with
![]() $D=\max (6,2+2ae^a)$
.
$D=\max (6,2+2ae^a)$
.
Proof. Let
![]() $f\in C_a$
. If
$f\in C_a$
. If
![]() $x,x'\in X^+$
have different initial symbols, then
$x,x'\in X^+$
have different initial symbols, then
![]() $|f(x)-f(x')| \le ~2 \|f\|_\infty \le \max (2,ae^a)\|f\|_\infty d_\beta (x,x')$
. If they have the same initial symbol, then
$|f(x)-f(x')| \le ~2 \|f\|_\infty \le \max (2,ae^a)\|f\|_\infty d_\beta (x,x')$
. If they have the same initial symbol, then
 $|f(x)-f (x')|\le |f(x)|(e^{ad_\beta (x,x')}-1) \le \|f\|_\infty ae^ad_\beta (x,x')\le \max (2,ae^a)\|f\|_\infty d_\beta (x,x')$
, where we used the mean value theorem for the second inequality. Hence
$|f(x)-f (x')|\le |f(x)|(e^{ad_\beta (x,x')}-1) \le \|f\|_\infty ae^ad_\beta (x,x')\le \max (2,ae^a)\|f\|_\infty d_\beta (x,x')$
, where we used the mean value theorem for the second inequality. Hence
![]() $|f|_\beta \le \max (2,ae^a)\|f\|_\infty $
so that
$|f|_\beta \le \max (2,ae^a)\|f\|_\infty $
so that
![]() $\|f\|_\beta \le \max (3,1+ae^a)\|f\|_\infty $
.
$\|f\|_\beta \le \max (3,1+ae^a)\|f\|_\infty $
.
For the second statement in the lemma,
![]() $g\pm f\in \mathcal C_a$
implies
$g\pm f\in \mathcal C_a$
implies
![]() $\|f\|_\infty \le \|g\|_\infty $
, so that
$\|f\|_\infty \le \|g\|_\infty $
, so that
![]() $\|g\pm f\|_\infty \le 2\|g\|_\infty $
and
$\|g\pm f\|_\infty \le 2\|g\|_\infty $
and
![]() $\|g\pm f\|_\beta \le \max (6,2+2ae^a)\|g\|_\infty \le \max (6,2+2ae^a)\|g\|_\beta $
. Subtracting
$\|g\pm f\|_\beta \le \max (6,2+2ae^a)\|g\|_\infty \le \max (6,2+2ae^a)\|g\|_\beta $
. Subtracting
![]() $g-f$
from
$g-f$
from
![]() $g+f$
, we obtain the desired bound.
$g+f$
, we obtain the desired bound.
For these cones, we have the following lemma (which can be seen as a special case of a result of Andô [Reference Andô4]). Expressing arbitrary Hölder continuous functions as a difference of elements of the cone will allow us to prove the simplicity of the top Lyapunov exponent.
Lemma 11. For all
![]() $f\in C^\beta (X^+)$
, there exist
$f\in C^\beta (X^+)$
, there exist
![]() $g,h\in \mathcal C_a$
with
$g,h\in \mathcal C_a$
with
![]() $\|g\|_\beta ,\|h\|_\beta \le (2+1/a)\|f\|_\beta $
such that
$\|g\|_\beta ,\|h\|_\beta \le (2+1/a)\|f\|_\beta $
such that
![]() $f=g-h$
.
$f=g-h$
.
Proof. Let
![]() $f\in C^\beta (X^+)$
, let
$f\in C^\beta (X^+)$
, let
![]() $g=f+(1+1/a)\|f\|_\beta $
and
$g=f+(1+1/a)\|f\|_\beta $
and
![]() $h=(1+1/a)\|f\|_\beta $
. Clearly
$h=(1+1/a)\|f\|_\beta $
. Clearly
![]() $h\in \mathcal C_a$
. Notice that
$h\in \mathcal C_a$
. Notice that
![]() $\min g\ge (1/a)\|f\|_\beta $
, so that
$\min g\ge (1/a)\|f\|_\beta $
, so that
 $$ \begin{align*}\frac{g(x)}{g(x')}&=1+\frac{g(x)-g(x')}{g(x')}\le 1+\|f\|_\beta d_\beta(x,x')/(\|f\|_\beta/a)\\[3pt] &= 1+ad_\beta(x,x')\le e^{ad_\beta(x,x')}. \end{align*} $$
$$ \begin{align*}\frac{g(x)}{g(x')}&=1+\frac{g(x)-g(x')}{g(x')}\le 1+\|f\|_\beta d_\beta(x,x')/(\|f\|_\beta/a)\\[3pt] &= 1+ad_\beta(x,x')\le e^{ad_\beta(x,x')}. \end{align*} $$
In particular,
![]() $g\in \mathcal C_a$
and
$g\in \mathcal C_a$
and
![]() $\|g\|_\beta $
,
$\|g\|_\beta $
,
![]() $\|h\|_\beta $
are bounded above by
$\|h\|_\beta $
are bounded above by
![]() $(2+1/a)\|f\|_\beta $
.
$(2+1/a)\|f\|_\beta $
.
Lemma 12. Let
![]() $0<b<a$
and
$0<b<a$
and
![]() $A\ge 1$
. Let P be a non-empty subset of the alphabet of X. Write
$A\ge 1$
. Let P be a non-empty subset of the alphabet of X. Write
 $[P]=\bigcup _{j\in P}[j]$
and
$[P]=\bigcup _{j\in P}[j]$
and
Then there exists
![]() $K>0$
such that
$K>0$
such that
![]() $\Theta _{\mathcal C_a}(f,g)\le K$
for all
$\Theta _{\mathcal C_a}(f,g)\le K$
for all
![]() $f,g\in S_P\cap \mathcal C_b$
.
$f,g\in S_P\cap \mathcal C_b$
.
The conclusion here states that the diameter of the set is finite. This is a key hypothesis in Birkhoff’s cone contraction argument.
Proof. Let
![]() $t>0$
be chosen sufficiently small to ensure that
$t>0$
be chosen sufficiently small to ensure that
![]() ${2btA}/({1-tA})\le a-b$
. Let
${2btA}/({1-tA})\le a-b$
. Let
![]() $f,g\in S_P\cap \mathcal C_b$
. Using the scale-homogeneity of
$f,g\in S_P\cap \mathcal C_b$
. Using the scale-homogeneity of
![]() $\Theta _{\mathcal C_a}$
, we may scale f and g so that
$\Theta _{\mathcal C_a}$
, we may scale f and g so that
![]() $\min _{[P]} f=\min _{[P]} g=1$
, and hence
$\min _{[P]} f=\min _{[P]} g=1$
, and hence
![]() $\max f,\max g\le A$
.
$\max f,\max g\le A$
.
We claim that
![]() $f-tg\in \mathcal C_a$
. Let
$f-tg\in \mathcal C_a$
. Let
![]() $x,x'\in X^+$
have a common first symbol belonging to P (if
$x,x'\in X^+$
have a common first symbol belonging to P (if
![]() $x,x'$
have a common first symbol outside P, then
$x,x'$
have a common first symbol outside P, then
![]() $(f-tg)(x)$
is trivially bounded above by
$(f-tg)(x)$
is trivially bounded above by
![]() $e^{ad_\beta (x,x')}(f-tg)(x')$
since both of these quantities are zero). We have
$e^{ad_\beta (x,x')}(f-tg)(x')$
since both of these quantities are zero). We have
 $$ \begin{align*} \frac{f(x')-tg(x')}{f(x)-tg(x)}&\le \frac{e^{bd_\beta(x,x')}f(x)-te^{-bd_\beta(x,x')}g(x)}{f(x)-tg(x)}\\[3pt] &= e^{bd_\beta(x,x')}+\frac{t(e^{bd_\beta(x,x')}-e^{-bd_\beta(x,x')})g(x)}{f(x)-tg(x)}\\[3pt] &\le e^{bd_\beta(x,x')}\bigg(1+\frac{At}{1-At}(1-e^{-2bd_\beta(x,x')})\bigg)\\[3pt] &\le e^{bd_\beta(x,x')}\bigg(1+\frac{2Atb}{1-At}d_\beta(x,x')\bigg)\\[3pt] &\le e^{bd_\beta(x,x')}e^{(a-b)d_\beta(x,x')}=e^{ad_\beta(x,x')}, \end{align*} $$
$$ \begin{align*} \frac{f(x')-tg(x')}{f(x)-tg(x)}&\le \frac{e^{bd_\beta(x,x')}f(x)-te^{-bd_\beta(x,x')}g(x)}{f(x)-tg(x)}\\[3pt] &= e^{bd_\beta(x,x')}+\frac{t(e^{bd_\beta(x,x')}-e^{-bd_\beta(x,x')})g(x)}{f(x)-tg(x)}\\[3pt] &\le e^{bd_\beta(x,x')}\bigg(1+\frac{At}{1-At}(1-e^{-2bd_\beta(x,x')})\bigg)\\[3pt] &\le e^{bd_\beta(x,x')}\bigg(1+\frac{2Atb}{1-At}d_\beta(x,x')\bigg)\\[3pt] &\le e^{bd_\beta(x,x')}e^{(a-b)d_\beta(x,x')}=e^{ad_\beta(x,x')}, \end{align*} $$
so that
![]() $f-tg\in \mathcal C_a$
. By symmetry,
$f-tg\in \mathcal C_a$
. By symmetry,
![]() $g-tf\in \mathcal C_a$
, or equivalently
$g-tf\in \mathcal C_a$
, or equivalently
![]() $(1/t)g-f\in \mathcal C_a$
. Hence
$(1/t)g-f\in \mathcal C_a$
. Hence
![]() $\Theta _{\mathcal C_a}(f,g)\le \log (1/t^2)$
for all
$\Theta _{\mathcal C_a}(f,g)\le \log (1/t^2)$
for all
![]() $f,g\in S_P\cap \mathcal C_b$
.
$f,g\in S_P\cap \mathcal C_b$
.
Lemma 13. Let
![]() $\pi \colon X\to Y$
be a factor map of class degree 1. Let
$\pi \colon X\to Y$
be a factor map of class degree 1. Let
 $W=w_0^{n-1}$
be a minimal transition block in Y. Then there exists an
$W=w_0^{n-1}$
be a minimal transition block in Y. Then there exists an
![]() $A\ge 1$
such that for any
$A\ge 1$
such that for any
![]() $y\in [W]$
, and any
$y\in [W]$
, and any
![]() $f\in \mathcal C_a$
,
$f\in \mathcal C_a$
,
 $\mathcal L^{(n)}_y f\in S_P\cup \{0\}$
, where
$\mathcal L^{(n)}_y f\in S_P\cup \{0\}$
, where
![]() $S_P$
is the set in Lemma 12 (whose definition involves the constant A) and P is
$S_P$
is the set in Lemma 12 (whose definition involves the constant A) and P is
 $\{j\in \mathsf A(X)\colon \text { there exists } U\in \pi _b^{-1}(W) \colon Uj\in \mathsf L(X)\}$
.
$\{j\in \mathsf A(X)\colon \text { there exists } U\in \pi _b^{-1}(W) \colon Uj\in \mathsf L(X)\}$
.
Proof. Since
![]() $S_P\cup \{0\}$
is closed under addition and
$S_P\cup \{0\}$
is closed under addition and
 ${\mathcal L}_y^{(n)}$
is linear, it suffices to prove the statement for a function f supported on a single cylinder set. Suppose that f is supported on
${\mathcal L}_y^{(n)}$
is linear, it suffices to prove the statement for a function f supported on a single cylinder set. Suppose that f is supported on
![]() $[k]$
. If there is no preimage of W whose initial symbol is k, we see that
$[k]$
. If there is no preimage of W whose initial symbol is k, we see that
 ${\mathcal L}_y^{(n)}f=0$
since there are no positive summands. Suppose however that U is a preimage of W under
${\mathcal L}_y^{(n)}f=0$
since there are no positive summands. Suppose however that U is a preimage of W under
![]() $\pi $
starting with a k. Let
$\pi $
starting with a k. Let
![]() $j\in P$
and let V be a preimage of W under
$j\in P$
and let V be a preimage of W under
![]() $\pi $
such that
$\pi $
such that
![]() $Vj\in \mathsf L(X)$
. Since W is a minimal transition block with a single representative, there exists a preimage
$Vj\in \mathsf L(X)$
. Since W is a minimal transition block with a single representative, there exists a preimage
![]() $U'$
of W starting with the first symbol of U and ending with the last symbol of V. If
$U'$
of W starting with the first symbol of U and ending with the last symbol of V. If
![]() $x\in [j]$
, we now calculate
$x\in [j]$
, we now calculate
 $$ \begin{align*}\mathcal L^{(n)}_yf(x)\ge e^{S_n\phi(U'x)}f(U'x)\ge e^{n\min\phi}\|f\|_\infty/e^a. \end{align*} $$
$$ \begin{align*}\mathcal L^{(n)}_yf(x)\ge e^{S_n\phi(U'x)}f(U'x)\ge e^{n\min\phi}\|f\|_\infty/e^a. \end{align*} $$
However, it is clear that
 $\mathcal L^{(n)}_yf(x)\le |\mathsf A(X)|^ne^{n\max \phi }\|f\|_\infty $
for any
$\mathcal L^{(n)}_yf(x)\le |\mathsf A(X)|^ne^{n\max \phi }\|f\|_\infty $
for any
![]() $x\in X$
. Hence we have demonstrated the hypothesis of Lemma 12 is satisfied with
$x\in X$
. Hence we have demonstrated the hypothesis of Lemma 12 is satisfied with
![]() $A=e^{a+n(\max \phi -\min \phi )}| \mathsf A(X)|^n$
.
$A=e^{a+n(\max \phi -\min \phi )}| \mathsf A(X)|^n$
.
We point out that the idea of studying the Ruelle–Perron–Frobenius cocycle over a factor Y and expressing the operators corresponding to symbols in
![]() $\mathsf A(Y)$
as sums of operators indexed by symbols in
$\mathsf A(Y)$
as sums of operators indexed by symbols in
![]() $\mathsf A(X)$
, as well as some of the cones that we study here and the description of
$\mathsf A(X)$
, as well as some of the cones that we study here and the description of
![]() $S_P$
above, appear in the work of Piraino [Reference Piraino11].
$S_P$
above, appear in the work of Piraino [Reference Piraino11].
Theorem 14. (Main theorem, class degree 1 case)
Let X be an irreducible shift of finite type, let
![]() $\pi \colon X\to Y$
be a forward-looking factor map of class degree 1 and let
$\pi \colon X\to Y$
be a forward-looking factor map of class degree 1 and let
![]() $\phi $
be a Hölder continuous function on
$\phi $
be a Hölder continuous function on
![]() $X^+$
. Suppose
$X^+$
. Suppose
![]() $\nu $
is a fully supported invariant measure on Y. Then the cocycle
$\nu $
is a fully supported invariant measure on Y. Then the cocycle
 $({\mathcal L}_{y}^{(n)})$
has a simple top Lyapunov exponent, whose value is
$({\mathcal L}_{y}^{(n)})$
has a simple top Lyapunov exponent, whose value is
![]() $r_{\pi }(\nu )$
, the relative pressure of
$r_{\pi }(\nu )$
, the relative pressure of
![]() $\phi $
over
$\phi $
over
![]() $\nu $
.
$\nu $
.
Further, for
![]() $\nu $
-a.e. y,
$\nu $
-a.e. y,
 $$ \begin{align*}\lim_{n\to\infty}\frac 1n\log\|{\mathcal L}_y^{(n)}{\textbf 1}\|= \lim_{n\to\infty}\frac 1n\log\|{\mathcal L}_y^{(n)}{\textbf 1}_{\pi^{-1}[y_0]}\| =r_\pi(\nu). \end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\frac 1n\log\|{\mathcal L}_y^{(n)}{\textbf 1}\|= \lim_{n\to\infty}\frac 1n\log\|{\mathcal L}_y^{(n)}{\textbf 1}_{\pi^{-1}[y_0]}\| =r_\pi(\nu). \end{align*} $$
Proof. By conjugating X and Y if necessary, we may assume that
![]() $\pi $
is a one-block map. This does not affect any of the hypotheses or conclusions of the theorem (see [Reference Lind and Marcus8, Proposition 1.5.12] and [Reference Allahbakhshi and Quas3] for more details). Let
$\pi $
is a one-block map. This does not affect any of the hypotheses or conclusions of the theorem (see [Reference Lind and Marcus8, Proposition 1.5.12] and [Reference Allahbakhshi and Quas3] for more details). Let
![]() $\beta $
be such that
$\beta $
be such that
![]() $\|\phi \|_\beta <\infty $
and let a satisfy the hypothesis in Lemma 9. Let W be a minimal transition block for the factor map
$\|\phi \|_\beta <\infty $
and let a satisfy the hypothesis in Lemma 9. Let W be a minimal transition block for the factor map
![]() $\pi \colon X\to Y$
. By Lemma 11,
$\pi \colon X\to Y$
. By Lemma 11,
![]() $\mathcal C_a-\mathcal C_a=C^\beta (X^+)$
. By Lemmas 9, 12 and 13, we see that
$\mathcal C_a-\mathcal C_a=C^\beta (X^+)$
. By Lemmas 9, 12 and 13, we see that
 ${\mathcal L}_y^{(|W|)}\mathcal C_a$
is a finite diameter subset of
${\mathcal L}_y^{(|W|)}\mathcal C_a$
is a finite diameter subset of
![]() $\mathcal C_a$
for any
$\mathcal C_a$
for any
![]() $y\in [W]$
. Since the hypotheses of Theorem 7 are satisfied (the continuity of
$y\in [W]$
. Since the hypotheses of Theorem 7 are satisfied (the continuity of
![]() $y\mapsto {\mathcal L}_y$
is because the map is piecewise constant and the D-adaptedness condition on
$y\mapsto {\mathcal L}_y$
is because the map is piecewise constant and the D-adaptedness condition on
![]() $\mathcal C_a$
is satisfied by the second statement of Lemma 10), the top Lyapunov exponent of the cocycle
$\mathcal C_a$
is satisfied by the second statement of Lemma 10), the top Lyapunov exponent of the cocycle
 $({\mathcal L}_y^{(n)})$
acting on
$({\mathcal L}_y^{(n)})$
acting on
![]() $C^\beta (X^+)$
is simple.
$C^\beta (X^+)$
is simple.
Notice that for
![]() $y\in Y$
and
$y\in Y$
and
![]() $g\in \mathcal C_a$
,
$g\in \mathcal C_a$
,
 $$ \begin{align*}{\mathcal L}_y^{(n)}g(x)= \sum_{W\in\pi^{-1}(y_0^{n-1})\colon Wx_0\in\mathsf L(X)}e^{S_n\phi(Wx)}g(Wx), \end{align*} $$
$$ \begin{align*}{\mathcal L}_y^{(n)}g(x)= \sum_{W\in\pi^{-1}(y_0^{n-1})\colon Wx_0\in\mathsf L(X)}e^{S_n\phi(Wx)}g(Wx), \end{align*} $$
so that
 $\|{\mathcal L}_y^{(n)}g\|_\infty $
is bounded above by
$\|{\mathcal L}_y^{(n)}g\|_\infty $
is bounded above by
![]() $p_n(\phi ,\pi ^{-1}y)\|g\|_\infty $
. By Lemmas 9 and 10,
$p_n(\phi ,\pi ^{-1}y)\|g\|_\infty $
. By Lemmas 9 and 10,
 $\|{\mathcal L}_y^{(n)}g\|_\beta $
is bounded above by
$\|{\mathcal L}_y^{(n)}g\|_\beta $
is bounded above by
![]() $\max (3,1+e^a)p_n(\phi ,\pi ^{-1}y)\|g\|_\infty $
. If
$\max (3,1+e^a)p_n(\phi ,\pi ^{-1}y)\|g\|_\infty $
. If
![]() $f\in C^\beta (X^+)$
, using Lemma 11, we may write f as the difference
$f\in C^\beta (X^+)$
, using Lemma 11, we may write f as the difference
![]() $g-h$
with
$g-h$
with
![]() $g,h\in \mathcal C_a$
, each of
$g,h\in \mathcal C_a$
, each of
![]() $\|\cdot \|_\beta $
norm at most
$\|\cdot \|_\beta $
norm at most
![]() $(2+1/a)\|f\|_\beta $
. Hence
$(2+1/a)\|f\|_\beta $
. Hence
 $\|{\mathcal L}_y^{(n)}f\|_\beta \le 2(2+1/a)\max (3,1+e^a)p_n(\phi ,\pi ^{-1}y)\|f\|_\beta $
. As noted above, we have
$\|{\mathcal L}_y^{(n)}f\|_\beta \le 2(2+1/a)\max (3,1+e^a)p_n(\phi ,\pi ^{-1}y)\|f\|_\beta $
. As noted above, we have
![]() $\limsup _{n\to \infty }(1/n)\log p_n(\phi ,\pi ^{-1}y)=P(\phi ,\pi ^{-1}y)$
, which is
$\limsup _{n\to \infty }(1/n)\log p_n(\phi ,\pi ^{-1}y)=P(\phi ,\pi ^{-1}y)$
, which is
![]() $r_\pi (\nu )$
by Theorem 8, so that the top Lyapunov exponent is bounded above by
$r_\pi (\nu )$
by Theorem 8, so that the top Lyapunov exponent is bounded above by
![]() $r_\pi (\nu )$
.
$r_\pi (\nu )$
.
For the converse inequality, let
 $(x^i)_{i\in \mathsf A(X)}$
be a collection of points in
$(x^i)_{i\in \mathsf A(X)}$
be a collection of points in
![]() $X^+$
, where
$X^+$
, where
![]() $x^i$
starts with the symbol i. Now
$x^i$
starts with the symbol i. Now
 $$ \begin{align*}\sum_{i\in\mathsf A(X)}\mathcal L^{(n)}_y{\textbf 1}(x^i)\ge e^{-c}p_n(\phi,\pi^{-1}y), \end{align*} $$
$$ \begin{align*}\sum_{i\in\mathsf A(X)}\mathcal L^{(n)}_y{\textbf 1}(x^i)\ge e^{-c}p_n(\phi,\pi^{-1}y), \end{align*} $$
where c is a constant independent of n, where
![]() $|S_n\phi (x)-S_n\phi (x')|\le c$
whenever
$|S_n\phi (x)-S_n\phi (x')|\le c$
whenever
 $x_0^{n-1}={x'}\,_0^{n-1}$
(such a c exists since
$x_0^{n-1}={x'}\,_0^{n-1}$
(such a c exists since
![]() $\phi $
is Hölder). Then
$\phi $
is Hölder). Then
 $$ \begin{align*}\|\mathcal L^{(n)}_y{\textbf 1}\|_\beta\ge \|\mathcal L^{(n)}_y{\textbf 1}\|_\infty\ge \frac{e^{-c}}{|\mathsf A(X)|}p_n(\phi,1,\pi^{-1}y). \end{align*} $$
$$ \begin{align*}\|\mathcal L^{(n)}_y{\textbf 1}\|_\beta\ge \|\mathcal L^{(n)}_y{\textbf 1}\|_\infty\ge \frac{e^{-c}}{|\mathsf A(X)|}p_n(\phi,1,\pi^{-1}y). \end{align*} $$
In particular, for
![]() $\nu $
-a.e. y, the limit superior growth rate of
$\nu $
-a.e. y, the limit superior growth rate of
 $\|\mathcal L^{(n)}_y{\textbf 1}\|_\beta $
is at least
$\|\mathcal L^{(n)}_y{\textbf 1}\|_\beta $
is at least
![]() $r_\pi (\nu )$
, as required.
$r_\pi (\nu )$
, as required.
Proof of Theorem 1
We assume without loss of generality as above that
![]() $\pi $
is a one-block map. Using Theorem 5,
$\pi $
is a one-block map. Using Theorem 5,
![]() $\pi :X\to Z$
may be factorized as
$\pi :X\to Z$
may be factorized as
![]() $\pi _2\circ \pi _1$
, where
$\pi _2\circ \pi _1$
, where
![]() $\pi _1$
is of class degree 1 from X to a sofic shift Y; and
$\pi _1$
is of class degree 1 from X to a sofic shift Y; and
![]() $\pi _2$
is finite-to-one, and for
$\pi _2$
is finite-to-one, and for
![]() $\nu $
-a.e. point,
$\nu $
-a.e. point,
 $\pi _2^{-1}(z)$
consists of
$\pi _2^{-1}(z)$
consists of
![]() $c_\pi $
preimages.
$c_\pi $
preimages.
We need a more precise description of the construction of the sofic shift Y and the factor code
![]() $\pi _1$
, for which we will follow [Reference Yoo12]. The space Y is built from a minimal transition block W in
$\pi _1$
, for which we will follow [Reference Yoo12]. The space Y is built from a minimal transition block W in
![]() $\mathsf L(Z)$
. Recall the representatives of the transition block are a subset B of
$\mathsf L(Z)$
. Recall the representatives of the transition block are a subset B of
![]() $\mathsf A(X)$
of cardinality
$\mathsf A(X)$
of cardinality
![]() $c_\pi $
such that if
$c_\pi $
such that if
![]() $\pi (x)\in [W]$
, then x may be locally modified on the coordinates
$\pi (x)\in [W]$
, then x may be locally modified on the coordinates
![]() $(0,n-1)$
to give a point
$(0,n-1)$
to give a point
![]() $x'\in X$
with
$x'\in X$
with
![]() $x^{\prime }_l\in B$
.
$x^{\prime }_l\in B$
.
The alphabet of Y is then
![]() $\mathsf A(Z)\times (B\cup \{\star \})$
. The factor map
$\mathsf A(Z)\times (B\cup \{\star \})$
. The factor map
![]() $\pi _1$
is defined as follows:
$\pi _1$
is defined as follows:
 $$ \begin{align*}\pi_1(x)_m=\begin{cases} (\pi(x)_m,s),&\pi(x)_{m-l}^{m-l+n-1}=W, x_{m-l}^{m-l+n-1}\ \text{routable through}\ s\text{;}\\ (\pi(x)_m,\star),&\pi(x)_{m-l}^{m-l+n-1}\ne W. \end{cases} \end{align*} $$
$$ \begin{align*}\pi_1(x)_m=\begin{cases} (\pi(x)_m,s),&\pi(x)_{m-l}^{m-l+n-1}=W, x_{m-l}^{m-l+n-1}\ \text{routable through}\ s\text{;}\\ (\pi(x)_m,\star),&\pi(x)_{m-l}^{m-l+n-1}\ne W. \end{cases} \end{align*} $$
That is,
![]() $\pi _1(x)$
records the image in Z, together with the representatives in B through which the orbit of x may be routed each time that the orbit passes through a transition block. The factor map
$\pi _1(x)$
records the image in Z, together with the representatives in B through which the orbit of x may be routed each time that the orbit passes through a transition block. The factor map
![]() $\pi _2$
is the one-block factor map from Y to Z defined by the symbol map sending
$\pi _2$
is the one-block factor map from Y to Z defined by the symbol map sending
![]() $(a,b)$
to a for any
$(a,b)$
to a for any
![]() $(a,b)\in \mathsf A(Z)\times (B\cup \{\star \})$
.
$(a,b)\in \mathsf A(Z)\times (B\cup \{\star \})$
.
We then define an operator cocycle over Y. For each
![]() $s\in B$
, let
$s\in B$
, let
![]() $R_s\subset \mathsf A(X)$
be the collection of symbols in X that a preimage of W may pass through if it is routable through s. By Theorem 4, these sets are disjoint. Write
$R_s\subset \mathsf A(X)$
be the collection of symbols in X that a preimage of W may pass through if it is routable through s. By Theorem 4, these sets are disjoint. Write
![]() $[R_s]$
for
$[R_s]$
for
![]() $\bigcup _{i\in R_s}[i]$
and let q be the lth symbol of W.
$\bigcup _{i\in R_s}[i]$
and let q be the lth symbol of W.
The generator of the cocycle is then defined by
 $$ \begin{align*} \bar{\mathcal L}_{(j,\star)}f(x)&={\mathcal L}_jf(x)\quad\text{for}\ j\in\mathsf A(Z)\text{;}\\ \bar{\mathcal L}_{(q,s)}f(x)&={\mathcal L}_q({\textbf 1}_{[R_s]}f)(x)\quad\text{for}\ s\in B. \end{align*} $$
$$ \begin{align*} \bar{\mathcal L}_{(j,\star)}f(x)&={\mathcal L}_jf(x)\quad\text{for}\ j\in\mathsf A(Z)\text{;}\\ \bar{\mathcal L}_{(q,s)}f(x)&={\mathcal L}_q({\textbf 1}_{[R_s]}f)(x)\quad\text{for}\ s\in B. \end{align*} $$
That is, each time
![]() $\pi (x)$
passes through a transition block, the operator projects to the part of the function routable through the specified representative. Note that
$\pi (x)$
passes through a transition block, the operator projects to the part of the function routable through the specified representative. Note that
![]() $(q,\star )\in \mathsf A(Y)$
, and this appears in the image of points under
$(q,\star )\in \mathsf A(Y)$
, and this appears in the image of points under
![]() $\pi _1$
for points in X whose symbol maps to q, but where the word
$\pi _1$
for points in X whose symbol maps to q, but where the word
 $\pi (x)_{m-l}^{m-l+n-1}$
is not equal to W.
$\pi (x)_{m-l}^{m-l+n-1}$
is not equal to W.
By Theorem 6, there are finitely many ergodic invariant measures on Y projecting to
![]() $\nu $
, say
$\nu $
, say
![]() $\mu _1,\ldots ,\mu _k$
, each fully supported; as well as multiplicities
$\mu _1,\ldots ,\mu _k$
, each fully supported; as well as multiplicities
![]() $m_1,\ldots ,m_k$
summing to
$m_1,\ldots ,m_k$
summing to
![]() $c_\pi $
such that a
$c_\pi $
such that a
![]() $\nu $
-generic
$\nu $
-generic
![]() $z\in Z$
has
$z\in Z$
has
![]() $m_i\ \mu _i$
-generic preimages under
$m_i\ \mu _i$
-generic preimages under
![]() $\pi _2$
for each i, with the whole collection of
$\pi _2$
for each i, with the whole collection of
![]() $c_\pi $
preimages mutually separated. Further, there exists an ergodic measure
$c_\pi $
preimages mutually separated. Further, there exists an ergodic measure
![]() $\bar \mu $
on
$\bar \mu $
on
![]() $Y^{c_\pi }$
where
$Y^{c_\pi }$
where
![]() $\bar \mu $
-a.e. point is supported on the
$\bar \mu $
-a.e. point is supported on the
![]() $c_\pi $
preimages of some point
$c_\pi $
preimages of some point
![]() $z\in Z$
; the first
$z\in Z$
; the first
![]() $m_1$
being generic points for the ergodic measure
$m_1$
being generic points for the ergodic measure
![]() $\mu _1$
on Y; the next
$\mu _1$
on Y; the next
![]() $m_2$
being generic for the measure
$m_2$
being generic for the measure
![]() $\mu _2$
etc. We assume without loss of generality that
$\mu _2$
etc. We assume without loss of generality that
![]() $r_{\pi _1}(\mu _1)\ge r_{\pi _1}(\mu _2)\ge \cdots $
, where
$r_{\pi _1}(\mu _1)\ge r_{\pi _1}(\mu _2)\ge \cdots $
, where
![]() $r_{\pi _1}(\mu _i)$
is the
$r_{\pi _1}(\mu _i)$
is the
![]() $\pi _1$
-relative pressure of
$\pi _1$
-relative pressure of
![]() $\phi $
over
$\phi $
over
![]() $\mu _i$
; and that the maximal value of
$\mu _i$
; and that the maximal value of
![]() $r_{\pi _1}(\mu _i)$
is attained for
$r_{\pi _1}(\mu _i)$
is attained for
![]() $i=1,\ldots ,p$
(but not for
$i=1,\ldots ,p$
(but not for
![]() $i=p+1,\ldots ,k$
). Notice that
$i=p+1,\ldots ,k$
). Notice that
![]() $r_{\pi _1}(\mu _i)=r_\pi (\nu )$
for
$r_{\pi _1}(\mu _i)=r_\pi (\nu )$
for
![]() $i=1,\ldots ,p$
since any ergodic measure on X in
$i=1,\ldots ,p$
since any ergodic measure on X in
![]() $\pi _*^{-1}\{\nu \}$
lies in one of the
$\pi _*^{-1}\{\nu \}$
lies in one of the
![]() ${\pi _1}_*^{-1}\{\mu _i\}$
for some
${\pi _1}_*^{-1}\{\mu _i\}$
for some
![]() $\mu _i$
; and
$\mu _i$
; and
![]() $\pi _2$
is finite-to-one, so does not decrease entropy.
$\pi _2$
is finite-to-one, so does not decrease entropy.
Since
![]() $\pi _1\colon X\to Y$
and each
$\pi _1\colon X\to Y$
and each
![]() $\mu _i$
satisfies the conditions of Theorem 14, we see that there is a simple top exponent
$\mu _i$
satisfies the conditions of Theorem 14, we see that there is a simple top exponent
![]() $\lambda _i$
for the cocycle
$\lambda _i$
for the cocycle
 $(\bar {\mathcal L}_y^{(n)})_{y\in Y}$
for each of the measures
$(\bar {\mathcal L}_y^{(n)})_{y\in Y}$
for each of the measures
![]() $\mu _i$
. The set of
$\mu _i$
. The set of
![]() $y\in Y$
for which the exponent
$y\in Y$
for which the exponent
![]() $\lambda _i$
is achieved and for which the second Lyapunov exponent is strictly smaller is a collection of full
$\lambda _i$
is achieved and for which the second Lyapunov exponent is strictly smaller is a collection of full
![]() $\mu _i$
-measure.
$\mu _i$
-measure.
For
![]() $\bar \mu $
-a.e.
$\bar \mu $
-a.e.
![]() $(y^1,\ldots ,y^{c_\pi })\in Y^{c_\pi }$
, the simple top exponent of the cocycle
$(y^1,\ldots ,y^{c_\pi })\in Y^{c_\pi }$
, the simple top exponent of the cocycle
 $(\bar {\mathcal L}_{y})^{(n)}$
is
$(\bar {\mathcal L}_{y})^{(n)}$
is
![]() $\lambda _i$
for each
$\lambda _i$
for each
![]() $y=y^{M_i+k}$
with
$y=y^{M_i+k}$
with
![]() $k=1,\ldots ,m_i$
(where
$k=1,\ldots ,m_i$
(where
![]() $M_i=m_1+\cdots +m_{i-1}$
and
$M_i=m_1+\cdots +m_{i-1}$
and
![]() $M_1=0$
). In particular, the top exponent of the cocycle is almost surely simple with exponent
$M_1=0$
). In particular, the top exponent of the cocycle is almost surely simple with exponent
![]() $\lambda _1=r_{\pi _1}(\mu _1)$
over each of
$\lambda _1=r_{\pi _1}(\mu _1)$
over each of
![]() $y^1,\ldots ,y^{m_1+\cdots +m_p}$
and strictly smaller for the other y’s.
$y^1,\ldots ,y^{m_1+\cdots +m_p}$
and strictly smaller for the other y’s.
We now derive a relationship between the cocycle
 $(\mathcal L^{(n)}_z)$
over Z and the cocycle
$(\mathcal L^{(n)}_z)$
over Z and the cocycle
 $(\bar {\mathcal L}^{(n)}_y)$
over Y. Recall that for
$(\bar {\mathcal L}^{(n)}_y)$
over Y. Recall that for
![]() $\bar \mu $
-a.e.
$\bar \mu $
-a.e.
![]() $\bar y=(y^1,\ldots ,y^{c_\pi })$
, one has the equality
$\bar y=(y^1,\ldots ,y^{c_\pi })$
, one has the equality
![]() $\pi (y^1)=\cdots =\pi (y^{c_\pi })$
. Write
$\pi (y^1)=\cdots =\pi (y^{c_\pi })$
. Write
![]() $\bar \pi (\bar y)$
for this common value. Next, we claim that for
$\bar \pi (\bar y)$
for this common value. Next, we claim that for
![]() $\bar \mu $
-a.e.
$\bar \mu $
-a.e.
![]() $\bar y$
,
$\bar y$
,
 $$ \begin{align} {\mathcal L}_{\bar\pi(\bar y)}^{(n)}f(x)= \sum_{i=1}^{c_\pi}\bar{\mathcal L}^{(n)}_{y^i}f(x) \end{align} $$
$$ \begin{align} {\mathcal L}_{\bar\pi(\bar y)}^{(n)}f(x)= \sum_{i=1}^{c_\pi}\bar{\mathcal L}^{(n)}_{y^i}f(x) \end{align} $$
for all n such that
 $\bar \pi (\bar y)_0^{n-1}$
contains a copy of W, the minimal transition block used in the definition of
$\bar \pi (\bar y)_0^{n-1}$
contains a copy of W, the minimal transition block used in the definition of
![]() $\pi _1$
.
$\pi _1$
.
To see this, notice that if
![]() $q=w_l$
is the symbol in W over which the representatives lie, then the following identities hold:
$q=w_l$
is the symbol in W over which the representatives lie, then the following identities hold:
 $$ \begin{align*} {\mathcal L}_q&=\sum_{i\in S}\bar{\mathcal L}_{q,i};\\ {\mathcal L}_j&=\bar{\mathcal L}_{j,\star}\quad\text{for each}\ j\in\mathsf A(Z)\ \text{(including}\ q\text{)}. \end{align*} $$
$$ \begin{align*} {\mathcal L}_q&=\sum_{i\in S}\bar{\mathcal L}_{q,i};\\ {\mathcal L}_j&=\bar{\mathcal L}_{j,\star}\quad\text{for each}\ j\in\mathsf A(Z)\ \text{(including}\ q\text{)}. \end{align*} $$
So
 ${\mathcal L}_{z}^{(n)}$
is a composition in which a number of the terms (those occurring when z contains a copy of W) are replaced by a sum of
${\mathcal L}_{z}^{(n)}$
is a composition in which a number of the terms (those occurring when z contains a copy of W) are replaced by a sum of
 $\bar {\mathcal L}_{q,i}$
. Since the
$\bar {\mathcal L}_{q,i}$
. Since the
![]() $\bar {\mathcal L}$
are linear, we may distribute the composition over the sum. Since when z is right transitive, the transition classes are mutually separated (Theorem 4), almost all of the terms in the summation vanish; the only ones that survive are those in which the choices of representative are consistent: the representative over one instance of W together with the point z determines the representative over all of the other instances of W by virtue of the mutual separation of the classes in
$\bar {\mathcal L}$
are linear, we may distribute the composition over the sum. Since when z is right transitive, the transition classes are mutually separated (Theorem 4), almost all of the terms in the summation vanish; the only ones that survive are those in which the choices of representative are consistent: the representative over one instance of W together with the point z determines the representative over all of the other instances of W by virtue of the mutual separation of the classes in
![]() $\pi ^{-1}(z)$
.
$\pi ^{-1}(z)$
.
For
![]() $\bar \mu $
-a.e.
$\bar \mu $
-a.e.
![]() $\bar y=(y^1,\ldots ,y^{c_\pi })$
, each of the
$\bar y=(y^1,\ldots ,y^{c_\pi })$
, each of the
![]() $y^i$
terms is right transitive; and the map
$y^i$
terms is right transitive; and the map
![]() $\pi _1\colon X\to Y$
is of class degree 1. The preimages
$\pi _1\colon X\to Y$
is of class degree 1. The preimages
 $\pi _1^{-1}(y^i)$
for
$\pi _1^{-1}(y^i)$
for
![]() $i=1,\ldots ,c_\pi $
form the transition classes,
$i=1,\ldots ,c_\pi $
form the transition classes,
![]() $\mathcal T(\bar \pi (\bar y))$
in X over
$\mathcal T(\bar \pi (\bar y))$
in X over
![]() $\bar \pi (\bar y)\in Z$
. By Theorem 14, applied to
$\bar \pi (\bar y)\in Z$
. By Theorem 14, applied to
![]() $\pi _2\colon X\to Y$
, for
$\pi _2\colon X\to Y$
, for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $\bar \pi (\bar y)$
and each
$\bar \pi (\bar y)$
and each
![]() $y^i$
with
$y^i$
with
![]() $1\le i\le m_1+\cdots +m_p$
, the cocycle
$1\le i\le m_1+\cdots +m_p$
, the cocycle
 $(\bar {\mathcal L}_{y^i}^{(n)})$
has an equivariant one-dimensional space of functions growing at rate
$(\bar {\mathcal L}_{y^i}^{(n)})$
has an equivariant one-dimensional space of functions growing at rate
![]() $r_{\pi _1}(\mu _1)$
. In particular, the functions
$r_{\pi _1}(\mu _1)$
. In particular, the functions
 ${\textbf 1}_{\pi _1^{-1}[y^i_0]}$
for
${\textbf 1}_{\pi _1^{-1}[y^i_0]}$
for
![]() $i=1,\ldots ,M_p$
grow at rate
$i=1,\ldots ,M_p$
grow at rate
![]() $r_{\pi _1}(\mu _1)$
under the respective cocycles
$r_{\pi _1}(\mu _1)$
under the respective cocycles
 $\bar {\mathcal L}_{y^i}^{(n)}$
(and are eventually annihilated by the other cocycles). Since the
$\bar {\mathcal L}_{y^i}^{(n)}$
(and are eventually annihilated by the other cocycles). Since the
![]() $\mathcal T(\bar \pi (\bar y))$
are mutually separated, for each n, the
$\mathcal T(\bar \pi (\bar y))$
are mutually separated, for each n, the
 $\bar {\mathcal L}_{y^i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
are disjointly supported. By (1), the span of
$\bar {\mathcal L}_{y^i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
are disjointly supported. By (1), the span of
 $\{{\textbf 1}_{\pi _1^{-1}[y^i_0]}\colon 1\le i\le M_p\}$
is an
$\{{\textbf 1}_{\pi _1^{-1}[y^i_0]}\colon 1\le i\le M_p\}$
is an
![]() $M_p$
-dimensional space of functions, where the entire space grows under the cocycle
$M_p$
-dimensional space of functions, where the entire space grows under the cocycle
 ${\mathcal L}_{\bar y}^{(n)}$
at rate
${\mathcal L}_{\bar y}^{(n)}$
at rate
![]() $r_{\pi _1}(\mu _1)= r_{\pi }(\nu )$
.
$r_{\pi _1}(\mu _1)= r_{\pi }(\nu )$
.
Theorem 14 implies that in any two-dimensional space of functions supported on
 $\pi _1^{-1}(y^i)$
, there is a function whose growth rate is strictly smaller than
$\pi _1^{-1}(y^i)$
, there is a function whose growth rate is strictly smaller than
![]() $r_{\pi }(\nu )$
.
$r_{\pi }(\nu )$
.
However, by Theorem 14 for
![]() $i>M_p$
, the growth rate on
$i>M_p$
, the growth rate on
 $\pi _1^{-1}(y^i)$
is at most
$\pi _1^{-1}(y^i)$
is at most
![]() $r_{\pi _1}(\mu _{p+1})$
, which is strictly smaller. Combining these facts, it follows that the dimension of the fastest growing space is precisely
$r_{\pi _1}(\mu _{p+1})$
, which is strictly smaller. Combining these facts, it follows that the dimension of the fastest growing space is precisely
![]() $m_1+\cdots +m_p$
as required.
$m_1+\cdots +m_p$
as required.
Proof of Corollary 2
For this proof, we assume that
![]() $\pi $
is a one-block factor map, given by the map
$\pi $
is a one-block factor map, given by the map
![]() $\rho \colon \mathsf {A}(X)\to \mathsf {A}(Z)$
, (as in the previous theorem) and the locally constant function
$\rho \colon \mathsf {A}(X)\to \mathsf {A}(Z)$
, (as in the previous theorem) and the locally constant function
![]() $\phi (x)$
depends only on
$\phi (x)$
depends only on
![]() $x_0$
. The key observation in this case is that
$x_0$
. The key observation in this case is that
![]() ${\mathcal L}_z$
maps
${\mathcal L}_z$
maps
![]() $\mathsf {LC}$
, the finite-dimensional subspace of functions depending only on the zeroth coordinate, onto itself.
$\mathsf {LC}$
, the finite-dimensional subspace of functions depending only on the zeroth coordinate, onto itself.
Specifically, if f is the function taking the value
![]() $f_i$
on the cylinder
$f_i$
on the cylinder
![]() $[i]$
, then
$[i]$
, then
 $$ \begin{align*}{\mathcal L}_z f(x)=\sum_{i:ix_0\in\mathsf{L}(X), \rho(i)=z_0} e^{\phi_i}f_i, \end{align*} $$
$$ \begin{align*}{\mathcal L}_z f(x)=\sum_{i:ix_0\in\mathsf{L}(X), \rho(i)=z_0} e^{\phi_i}f_i, \end{align*} $$
another function whose value is determined by
![]() $x_0$
. That is,
$x_0$
. That is,
![]() ${\mathcal L}_z$
is represented by the matrix with entries
${\mathcal L}_z$
is represented by the matrix with entries
 $$ \begin{align*}(A_z)_{ij}={\textbf 1}_{ij\in\mathsf{L}(X)}{\textbf 1}_{\rho(i)=z_0} e^{\phi_i}. \end{align*} $$
$$ \begin{align*}(A_z)_{ij}={\textbf 1}_{ij\in\mathsf{L}(X)}{\textbf 1}_{\rho(i)=z_0} e^{\phi_i}. \end{align*} $$
Let
![]() $\pi =\pi _1\circ \pi _2$
as in the proof of Theorem 1, so that the symbol map
$\pi =\pi _1\circ \pi _2$
as in the proof of Theorem 1, so that the symbol map
![]() $\rho $
is the composition of maps
$\rho $
is the composition of maps
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
. We use the notation of the proof of Theorem 1. Let
$\rho _2$
. We use the notation of the proof of Theorem 1. Let
![]() $\bar y=(y^1,\ldots ,y^{c_\pi })$
be a generic element of the degree joining, where we assume that
$\bar y=(y^1,\ldots ,y^{c_\pi })$
be a generic element of the degree joining, where we assume that
![]() $y^1,\ldots ,y^{M_p}$
are generic for measures
$y^1,\ldots ,y^{M_p}$
are generic for measures
![]() $\mu _1,\ldots ,\mu _p$
with
$\mu _1,\ldots ,\mu _p$
with
![]() $r_{\pi _1}(\mu _i)=r_\pi (\nu )$
for
$r_{\pi _1}(\mu _i)=r_\pi (\nu )$
for
![]() $i=1,\ldots ,p$
. Then we showed above that
$i=1,\ldots ,p$
. Then we showed above that
 $\bar {\mathcal L}_{y_i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
grows at rate
$\bar {\mathcal L}_{y_i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
grows at rate
![]() $r_\pi (\nu )$
for
$r_\pi (\nu )$
for
![]() $i=1,\ldots ,M_p$
and for each n, these functions are disjointly supported. Further,
$i=1,\ldots ,M_p$
and for each n, these functions are disjointly supported. Further,
 $\bar {\mathcal L}_{y_i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]} ={\mathcal L}_{\bar \pi (\bar y)}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
.
$\bar {\mathcal L}_{y_i}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]} ={\mathcal L}_{\bar \pi (\bar y)}^{(n)}{\textbf 1}_{\pi _1^{-1}[y^i_0]}$
.
Since
 ${\textbf 1}_{\pi _1^{-1}[y^i_0]}\in \mathsf {LC}$
, we see that the multiplicity of the exponent
${\textbf 1}_{\pi _1^{-1}[y^i_0]}\in \mathsf {LC}$
, we see that the multiplicity of the exponent
![]() $r_\pi (\nu )$
for the matrix cocycle
$r_\pi (\nu )$
for the matrix cocycle
 $A_z^{(n)}$
is at least
$A_z^{(n)}$
is at least
![]() $M_p$
. However, multiplicity of the exponent
$M_p$
. However, multiplicity of the exponent
![]() $r_\pi (\nu )$
for the action of the cocycle on
$r_\pi (\nu )$
for the action of the cocycle on
![]() $C^\alpha (X^+)$
is an upper bound for the multiplicity on the subspace
$C^\alpha (X^+)$
is an upper bound for the multiplicity on the subspace
![]() $\mathsf {LC}$
. Hence the multiplicity of the leading exponent for the matrix cocycle is exactly
$\mathsf {LC}$
. Hence the multiplicity of the leading exponent for the matrix cocycle is exactly
![]() $M_p$
as required.
$M_p$
as required.
Acknowledgments
We would like to acknowledge a very helpful referee’s report that led to a substantial improvement in the presentation. For S.H., funding was provided by Hongik University, Korea. A.Q.’s research was partially supported by NSERC.