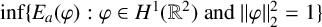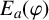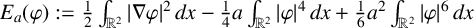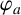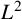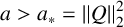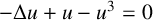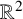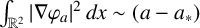1 Introduction and main results
We consider the two-dimensional (2D) cubic-quintic nonlinear Schrödinger equation
where the cubic nonlinearity is known as the Kerr nonlinearity [Reference Desyatnikov, Maimistov and Malomed4] and the quintic nonlinearity was introduced in [Reference Pushkarov, Pushkarov and Tomov15]. The incorporation of the defocusing quintic term is motivated by the stabilisation of two-dimensional vortex solitons [Reference Malomed13]. This kind of model can be used to describe nonlinear optics, field theory, the mean-field theory of superconductivity, the motion of Bose–Einstein condensates and Langmuir waves in plasma physics (see [Reference Desyatnikov, Maimistov and Malomed4] and the references therein).
The combination of a focusing cubic nonlinearity and defocusing quintic nonlinearity is very natural in many physical applications and leads to interesting mathematics. The nonlinear Schrödinger equations with the cubic-quintic nonlinearity (or general combined power-type nonlinearities) is very different from the purely cubic equation, since an effect of the quintic term is to prevent finite time blow-up (see [Reference Cazenave2]). Moreover, the arguments on the asymptotic behaviour of minimisers become much more complex and some new phenomena appear.
In particular, Soave [Reference Soave16, Reference Soave17] studied normalised ground states for the nonlinear Schrödinger equation with combined nonlinearities. The uniqueness and nondegeneracy of positive solutions for the time-independent cubic-quintic nonlinear Schrödinger equation was shown in [Reference Carles and Sparber1, Reference Lewin and Nodari11]. Tao et al. [Reference Tao, Visan and Zhang18] considered the Schrödinger equation with combined power-type nonlinearities including the cubic-quintic nonlinearity and studied local and global well-posedness, scattering, finite time blow-up and asymptotic behaviour. Killip et al. [Reference Killip, Oh, Pocovnicu and Visan9, Reference Killip, Rowan, Murphy and Visan10] studied solitons, scattering and the initial-value problem with nonvanishing boundary conditions for the cubic-quintic nonlinear Schrödinger equation on
![]() $\mathbb {R}^3$
.
$\mathbb {R}^3$
.
We focus on the normalised ground states of (1.1) and define the energy functional
A standing wave is a solution of (1.1) of the form
where
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $u(x)\in H^1(\mathbb {R}^2)$
is a time-independent function. Usually,
$u(x)\in H^1(\mathbb {R}^2)$
is a time-independent function. Usually,
![]() $u(x)$
is called a normalised ground state if it is a minimiser of the minimising problem under the prescribed
$u(x)$
is called a normalised ground state if it is a minimiser of the minimising problem under the prescribed
![]() $L^2$
mass:
$L^2$
mass:
Let
![]() $\varphi (x)=u(x)/\sqrt {a}$
. It is easy to check that u is a minimiser of
$\varphi (x)=u(x)/\sqrt {a}$
. It is easy to check that u is a minimiser of
![]() $I(a)$
if and only if
$I(a)$
if and only if
![]() $\varphi (x)$
is a minimiser of the minimisation problem for
$\varphi (x)$
is a minimiser of the minimisation problem for
![]() $e(a)$
, where
$e(a)$
, where
![]() $I(a)=a e(a)$
,
$I(a)=a e(a)$
,
and the energy functional is given by
 $$ \begin{align*} E_a(\varphi):=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx. \end{align*} $$
$$ \begin{align*} E_a(\varphi):=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx. \end{align*} $$
In what follows, we will consider this equivalent minimisation problem for
![]() $e(a)$
.
$e(a)$
.
Now let
where Q is the unique positive radial solution of the nonlinear scalar field equation
The following theorem follows by the same arguments as in [Reference Carles and Sparber1].
Theorem 1.1. Let Q be the unique positive radial solution of (1.3). Then:
-
(1) if
 $0< a\leq a_*={\lVert Q\rVert }^2_2$
, there is no minimiser for (1.2);
$0< a\leq a_*={\lVert Q\rVert }^2_2$
, there is no minimiser for (1.2); -
(2) if
 $a>a_*$
, there exists at least one minimiser for (1.2).
$a>a_*$
, there exists at least one minimiser for (1.2).
Moreover,
![]() $e(a)=0$
for
$e(a)=0$
for
![]() $0< a\leq a_*$
and
$0< a\leq a_*$
and
![]() $\lim _{a\searrow a_*}e(a)=e(a_*)=0$
for
$\lim _{a\searrow a_*}e(a)=e(a_*)=0$
for
![]() $a>a_*$
.
$a>a_*$
.
Remark 1.2. We can restrict the minimiser of (1.2) to nonnegative radially symmetric functions, since
![]() $E_a(\varphi )\geq E_a(|\varphi |)$
for any
$E_a(\varphi )\geq E_a(|\varphi |)$
for any
![]() $\varphi \in H^1(\mathbb {R}^2)$
(from the fact that
$\varphi \in H^1(\mathbb {R}^2)$
(from the fact that
![]() $|\nabla |\varphi ||\leq |\nabla \varphi |$
almost everywhere (a.e.) in
$|\nabla |\varphi ||\leq |\nabla \varphi |$
almost everywhere (a.e.) in
![]() $\mathbb {R}^2$
) and the symmetric decreasing rearrangement. Therefore, in what follows, we will assume that the ground state
$\mathbb {R}^2$
) and the symmetric decreasing rearrangement. Therefore, in what follows, we will assume that the ground state
![]() $\varphi _a(x)$
of (1.2) is nonnegative and radially symmetric decreasing.
$\varphi _a(x)$
of (1.2) is nonnegative and radially symmetric decreasing.
In view of Theorem 1.1, it is natural to ask what would happen for minimisers
![]() $\varphi _a$
of
$\varphi _a$
of
![]() $e(a)$
as
$e(a)$
as
![]() $a\searrow a_*$
. We obtain the following result.
$a\searrow a_*$
. We obtain the following result.
Theorem 1.3. Assume that
![]() $a>a_*$
and
$a>a_*$
and
![]() $\varphi _a$
is a nonnegative radially symmetric ground state of
$\varphi _a$
is a nonnegative radially symmetric ground state of
![]() $e(a)$
. Then,
$e(a)$
. Then,
Given a sequence
![]() $\{a_k\}$
with
$\{a_k\}$
with
![]() $a_k\searrow a_*$
as
$a_k\searrow a_*$
as
![]() $k\to \infty $
, there exists a subsequence (still denoted by
$k\to \infty $
, there exists a subsequence (still denoted by
![]() $\{a_k\}$
) such that
$\{a_k\}$
) such that
where
![]() $w_0$
satisfies
$w_0$
satisfies
Moreover,
 $$ \begin{align} \lim_{a\searrow a_*}(a-a_*)^{-{2}}e(a)=-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{align} $$
$$ \begin{align} \lim_{a\searrow a_*}(a-a_*)^{-{2}}e(a)=-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{align} $$
Remark 1.4. From (1.4), the vanishing phenomenon happens for the ground states as
![]() $a\searrow a_*$
. This is very different from the purely cubic equation or the cubic-quintic equation with an external potential (see [Reference Deng, Guo and Lu3, Reference Guo and Seiringer5–Reference Hmidi and Keraani8, Reference Merler and Tsutsumi14, Reference Wang and Feng19]). In particular, Guo and Seiringer [Reference Guo and Seiringer5] studied the mass concentration properties of normalised ground-state solutions for the purely cubic equation with an external potential as
$a\searrow a_*$
. This is very different from the purely cubic equation or the cubic-quintic equation with an external potential (see [Reference Deng, Guo and Lu3, Reference Guo and Seiringer5–Reference Hmidi and Keraani8, Reference Merler and Tsutsumi14, Reference Wang and Feng19]). In particular, Guo and Seiringer [Reference Guo and Seiringer5] studied the mass concentration properties of normalised ground-state solutions for the purely cubic equation with an external potential as
![]() $a\nearrow a_*$
(
$a\nearrow a_*$
(
![]() $a<a_*$
and a tends to
$a<a_*$
and a tends to
![]() $a_*$
). The second author and Feng [Reference Wang and Feng19] studied the blow-up properties of ground-state solutions of the 2D cubic-quintic nonlinear Schrödinger equation with a harmonic potential.
$a_*$
). The second author and Feng [Reference Wang and Feng19] studied the blow-up properties of ground-state solutions of the 2D cubic-quintic nonlinear Schrödinger equation with a harmonic potential.
The paper is organised as follows. In Section 2, we prove Theorem 1.1. In Section 3, we prove Theorem 1.3. Throughout this paper, we use standard notation. For simplicity, we write
![]() $\|\cdot \|_p$
to denote the
$\|\cdot \|_p$
to denote the
![]() $L^p(\mathbb {R}^2)$
norm for
$L^p(\mathbb {R}^2)$
norm for
![]() $p\geq 1$
;
$p\geq 1$
;
![]() $a\searrow a_*$
means that a tends to
$a\searrow a_*$
means that a tends to
![]() $a_*$
with
$a_*$
with
![]() $a>a_*$
;
$a>a_*$
;
![]() $X\sim Y$
means
$X\sim Y$
means
![]() $X\lesssim Y$
and
$X\lesssim Y$
and
![]() $Y\lesssim X$
, where
$Y\lesssim X$
, where
![]() $X\lesssim Y\ (X\gtrsim Y)$
means
$X\lesssim Y\ (X\gtrsim Y)$
means
![]() $X\leq CY\ (X\geq CY)$
for some appropriate positive constants C. The value of the positive constant C is allowed to change from line to line and also in the same formula.
$X\leq CY\ (X\geq CY)$
for some appropriate positive constants C. The value of the positive constant C is allowed to change from line to line and also in the same formula.
2 Proof of Theorem 1.1
We recall from [Reference Weinstein20] that
![]() $ a_*$
also corresponds to the best constant in the Gagliardo–Nirenberg inequality
$ a_*$
also corresponds to the best constant in the Gagliardo–Nirenberg inequality
which becomes an equality when
![]() $\varphi (x) = Q(|x|)$
, where Q is the unique positive radial solution of (1.3). It is easy to see that
$\varphi (x) = Q(|x|)$
, where Q is the unique positive radial solution of (1.3). It is easy to see that
(see also [Reference Cazenave2, Lemma 8.1.2]).
Lemma 2.1. For any
![]() $a>0$
, we have
$a>0$
, we have
![]() $e(a)\leq 0$
and
$e(a)\leq 0$
and
![]() $e(a)<0$
if and only if
$e(a)<0$
if and only if
![]() $a>a_*$
.
$a>a_*$
.
Proof. Let Q be the unique positive radial solution of (1.3). For
![]() $\gamma>0$
, define
$\gamma>0$
, define
so that
![]() $\|\varphi _\gamma (x)\|^2_{2}=1$
. Since
$\|\varphi _\gamma (x)\|^2_{2}=1$
. Since
![]() $\|\nabla Q\|^2_{2}=\tfrac 12\|Q\|^4_{4}=a_*$
(by (2.2)), then,
$\|\nabla Q\|^2_{2}=\tfrac 12\|Q\|^4_{4}=a_*$
(by (2.2)), then,
 $$ \begin{align} E_a(\varphi_\gamma)&=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi_\gamma|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi_\gamma|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi_\gamma|^6\,dx\nonumber\\ &=\frac{\gamma^2}{2}\bigg(1-\frac{a}{a_*} \bigg)+\frac{a^2\gamma^{4}}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx. \end{align} $$
$$ \begin{align} E_a(\varphi_\gamma)&=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi_\gamma|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi_\gamma|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi_\gamma|^6\,dx\nonumber\\ &=\frac{\gamma^2}{2}\bigg(1-\frac{a}{a_*} \bigg)+\frac{a^2\gamma^{4}}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx. \end{align} $$
By letting
![]() $\gamma \to 0^+$
, we deduce that
$\gamma \to 0^+$
, we deduce that
![]() $e(a)\leq 0$
.
$e(a)\leq 0$
.
To prove that
![]() $e(a)=0$
if and only if
$e(a)=0$
if and only if
![]() $0<a\leq a_*$
, we just need to show that for
$0<a\leq a_*$
, we just need to show that for
![]() ${0<a\leq a_*}$
, we have
${0<a\leq a_*}$
, we have
![]() $E_a(\varphi )\geq 0$
for any
$E_a(\varphi )\geq 0$
for any
![]() $\varphi \in H^1(\mathbb {R}^2)$
. We deduce from the Gagliardo– Nirenberg inequality (2.1) that
$\varphi \in H^1(\mathbb {R}^2)$
. We deduce from the Gagliardo– Nirenberg inequality (2.1) that
 $$ \begin{gather*} \begin{aligned} E_a(\varphi)=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla\varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx \geq\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\geq0. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} E_a(\varphi)=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla\varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx \geq\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\geq0. \end{aligned} \end{gather*} $$
Thus,
![]() $e(a)=0$
if and only if
$e(a)=0$
if and only if
![]() $0<a\leq a_*$
.
$0<a\leq a_*$
.
Next, we claim that for any
![]() $a>a_*$
, we have
$a>a_*$
, we have
![]() $e(a)<0$
. By (2.3),
$e(a)<0$
. By (2.3),
 $$ \begin{gather*} \begin{aligned} e(a)\leq\frac{\gamma^2}{2}\bigg(1-\frac{a}{a_*} \bigg)+\frac{a^2\gamma^{4}}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx =:-A(a-a_*)\gamma^2+B\gamma^{4}, \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} e(a)\leq\frac{\gamma^2}{2}\bigg(1-\frac{a}{a_*} \bigg)+\frac{a^2\gamma^{4}}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx =:-A(a-a_*)\gamma^2+B\gamma^{4}, \end{aligned} \end{gather*} $$
where
 $$ \begin{align*}A=\frac{1}{2a_*}>0\quad\text{and}\quad B=\frac{a^2}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx>0.\end{align*} $$
$$ \begin{align*}A=\frac{1}{2a_*}>0\quad\text{and}\quad B=\frac{a^2}{6a_*^3}\int_{\mathbb{R}^2}|Q|^6\,dx>0.\end{align*} $$
Now, let
![]() $\gamma =C_0(a-a_*)^{1/2}$
, taking
$\gamma =C_0(a-a_*)^{1/2}$
, taking
![]() $C_0$
small enough so that
$C_0$
small enough so that
![]() $AC_0^2-BC_0^4> 0$
. Then,
$AC_0^2-BC_0^4> 0$
. Then,
for any
![]() $a>a_*$
. This completes the proof of the Lemma 2.1.
$a>a_*$
. This completes the proof of the Lemma 2.1.
Proof of Theorem 1.1.
Part (2) of Theorem 1.1 comes from [Reference Carles and Sparber1], or it can be proved by the standard concentration-compactness principle [Reference Lions12].
Next, we prove that there is no minimiser for (1.2) with
![]() $0<a\leq a_*=\|Q\|_{2}^2$
. Suppose that there exists a minimiser
$0<a\leq a_*=\|Q\|_{2}^2$
. Suppose that there exists a minimiser
![]() $\varphi _a$
with
$\varphi _a$
with
![]() $0<a\leq a_*$
. As pointed out in Section 1, we can assume
$0<a\leq a_*$
. As pointed out in Section 1, we can assume
![]() $\varphi _a$
to be nonnegative. We deduce from the Gagliardo–Nirenberg inequality (2.1) and
$\varphi _a$
to be nonnegative. We deduce from the Gagliardo–Nirenberg inequality (2.1) and
![]() $e(a)=0$
that
$e(a)=0$
that
and
for
![]() $0<a\leq a_*$
. This implies
$0<a\leq a_*$
. This implies
![]() $\varphi _a=0$
a.e., which is a contradiction with
$\varphi _a=0$
a.e., which is a contradiction with
![]() $\| \varphi _a \|^2_2 =1$
. This completes the proof of the first part of Theorem 1.1.
$\| \varphi _a \|^2_2 =1$
. This completes the proof of the first part of Theorem 1.1.
To prove the stated properties of the energy
![]() $e(a)$
, note that Lemma 2.1 implies that
$e(a)$
, note that Lemma 2.1 implies that
![]() $e(a)=0$
for
$e(a)=0$
for
![]() $0<a\leq a_*=\|Q\|_{2}^2$
. We have already shown that
$0<a\leq a_*=\|Q\|_{2}^2$
. We have already shown that
![]() $e(a)\lesssim -(a-a_*)^{2}$
for
$e(a)\lesssim -(a-a_*)^{2}$
for
![]() ${a>a_*}$
in (2.4), hence it remains to show that
${a>a_*}$
in (2.4), hence it remains to show that
![]() $\lim _{a\searrow a_*}e(a)=e(a_*)=0$
for
$\lim _{a\searrow a_*}e(a)=e(a_*)=0$
for
![]() $a>a_*$
. This will complete the proof of Theorem 1.1.
$a>a_*$
. This will complete the proof of Theorem 1.1.
3 Asymptotic behaviour of ground states as
 $a\searrow a_*$
$a\searrow a_*$
Suppose that
![]() $\varphi _a(x)$
is a ground state of
$\varphi _a(x)$
is a ground state of
![]() $e(a)$
for
$e(a)$
for
![]() $a>a_*$
. Then
$a>a_*$
. Then
![]() $\varphi _a(x)$
satisfies the Euler–Lagrange equation
$\varphi _a(x)$
satisfies the Euler–Lagrange equation
for some suitable Lagrange multiplier
![]() $\lambda _a\in \mathbb {R}$
and the Pohozaev-type identity
$\lambda _a\in \mathbb {R}$
and the Pohozaev-type identity
![]() $\partial E_a(\tau \varphi _a(\tau x))|_{\tau =1}=0$
(see [Reference Cazenave2]), that is,
$\partial E_a(\tau \varphi _a(\tau x))|_{\tau =1}=0$
(see [Reference Cazenave2]), that is,
 $$ \begin{align} \int_{\mathbb{R}^2}|\nabla \varphi_a|^2\,dx-\frac{a}{2}\int_{\mathbb{R}^2}|\varphi_a|^4\,dx+\frac{2a^2}{3}\int_{\mathbb{R}^2}|\varphi_a|^6\,dx=0. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^2}|\nabla \varphi_a|^2\,dx-\frac{a}{2}\int_{\mathbb{R}^2}|\varphi_a|^4\,dx+\frac{2a^2}{3}\int_{\mathbb{R}^2}|\varphi_a|^6\,dx=0. \end{align} $$
Moreover,
![]() $\lambda _a$
in (3.1) can be given by
$\lambda _a$
in (3.1) can be given by
Lemma 3.1. For any
![]() $a>a_*$
, we have
$a>a_*$
, we have
![]() $e(a)\sim -(a-a_*)^2$
.
$e(a)\sim -(a-a_*)^2$
.
Proof. In view of (2.4), we just need to prove the lower bound. First, for any
![]() ${\varphi \in H^1(\mathbb {R}^2)}$
, by using the Hölder’s inequality and Young’s inequality with
${\varphi \in H^1(\mathbb {R}^2)}$
, by using the Hölder’s inequality and Young’s inequality with
![]() $\epsilon $
,
$\epsilon $
,
 $$ \begin{align} \int_{\mathbb{R}^2}|\varphi|^4\,dx&\leq\bigg(\int_{\mathbb{R}^2}|\varphi|^2\,dx \bigg)^{{1}/{2}} \bigg( \int_{\mathbb{R}^2}|\varphi|^6\,dx\bigg)^{{1}/{2}}\nonumber\\ &\leq \frac{3(a-a_*)}{8a^2}\int_{\mathbb{R}^2}|\varphi|^2\,dx+ \frac{2a^2(a-a_*)^{-1}}{3}\int_{\mathbb{R}^2}|\varphi|^6\,dx. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^2}|\varphi|^4\,dx&\leq\bigg(\int_{\mathbb{R}^2}|\varphi|^2\,dx \bigg)^{{1}/{2}} \bigg( \int_{\mathbb{R}^2}|\varphi|^6\,dx\bigg)^{{1}/{2}}\nonumber\\ &\leq \frac{3(a-a_*)}{8a^2}\int_{\mathbb{R}^2}|\varphi|^2\,dx+ \frac{2a^2(a-a_*)^{-1}}{3}\int_{\mathbb{R}^2}|\varphi|^6\,dx. \end{align} $$
Then, for any
![]() $\varphi (x)\in H^1(\mathbb {R}^2)$
with
$\varphi (x)\in H^1(\mathbb {R}^2)$
with
![]() $\|\varphi \|^2_{2}=1$
, by using the Gagliardo–Nirenberg inequality (2.1) and (3.4),
$\|\varphi \|^2_{2}=1$
, by using the Gagliardo–Nirenberg inequality (2.1) and (3.4),
 $$ \begin{gather*} \begin{aligned} E_a(\varphi) &=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\\ &\geq-\frac{a-a_*}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\\ &\gtrsim-(a-a_*)^{2}. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} E_a(\varphi) &=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla \varphi|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\\ &\geq-\frac{a-a_*}{4}\int_{\mathbb{R}^2}|\varphi|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi|^6\,dx\\ &\gtrsim-(a-a_*)^{2}. \end{aligned} \end{gather*} $$
This completes the proof of Lemma 3.1.
Lemma 3.2. Assume that
![]() $\varphi _a(x)$
is a ground state of
$\varphi _a(x)$
is a ground state of
![]() $e(a)$
. Then for any
$e(a)$
. Then for any
![]() $a>a_*$
,
$a>a_*$
,
Proof. From the Gagliardo–Nirenberg inequality (2.1),
However, by the definition of
![]() $e(a)$
and Lemma 3.1,
$e(a)$
and Lemma 3.1,
From the inequalities (3.6) and (3.7),
Moreover, by the Gagliardo–Nirenberg inequality (2.1) and (3.7),
From (3.1), (3.2) and Lemma 3.1,
 $$ \begin{align} \frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi_a|^6\,dx=-e(a)\sim(a-a_*)^2. \end{align} $$
$$ \begin{align} \frac{a^2}{6}\int_{\mathbb{R}^2}|\varphi_a|^6\,dx=-e(a)\sim(a-a_*)^2. \end{align} $$
By Hölder’s inequality together with (3.7) and (3.8),
 $$ \begin{gather*} \begin{aligned} \int_{\mathbb{R}^2}|\nabla \varphi_a(x)|^2\,dx\lesssim\int_{\mathbb{R}^2}|\varphi_a(x)|^4\,dx\lesssim\bigg( \int_{\mathbb{R}^2}|\varphi_a|^6\,dx\bigg)^{{1}/{2}} \lesssim(a-a_*). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \int_{\mathbb{R}^2}|\nabla \varphi_a(x)|^2\,dx\lesssim\int_{\mathbb{R}^2}|\varphi_a(x)|^4\,dx\lesssim\bigg( \int_{\mathbb{R}^2}|\varphi_a|^6\,dx\bigg)^{{1}/{2}} \lesssim(a-a_*). \end{aligned} \end{gather*} $$
This completes the proof of the lemma.
Let
![]() $\varphi _a$
be a nonnegative minimiser of (1.2) and define the
$\varphi _a$
be a nonnegative minimiser of (1.2) and define the
![]() $L^2$
-normalised function
$L^2$
-normalised function
where
![]() $\tau :=(a-a_*)^{-{1}/{2}}>0$
. From (3.5) and (3.8),
$\tau :=(a-a_*)^{-{1}/{2}}>0$
. From (3.5) and (3.8),
By the Euler–Lagrange equation (3.1) and Remark 1.2, the functions
![]() $w_\tau $
are nonnegative solutions and satisfy
$w_\tau $
are nonnegative solutions and satisfy
It follows from Lemma 3.2 and (3.3) that
![]() $\tau ^2\lambda _a$
is uniformly bounded as
$\tau ^2\lambda _a$
is uniformly bounded as
![]() $a\searrow a_*$
and strictly negative for a close to
$a\searrow a_*$
and strictly negative for a close to
![]() $a_*$
. By passing to a subsequence, if necessary, we can thus assume that
$a_*$
. By passing to a subsequence, if necessary, we can thus assume that
Proof of Theorem 1.3.
First, (1.4) in Theorem 1.3 comes from (3.5). Next, we prove (1.5). Note that
![]() $\{w_\tau \}$
is radially symmetric, since
$\{w_\tau \}$
is radially symmetric, since
![]() $\varphi _a$
is radially symmetric (see Remark 1.2). By (3.9),
$\varphi _a$
is radially symmetric (see Remark 1.2). By (3.9),
![]() $\{w_\tau \}$
is uniformly bounded in
$\{w_\tau \}$
is uniformly bounded in
![]() $H_{\mathrm {rad}}^1(\mathbb {R}^2)$
and there exists a subsequence
$H_{\mathrm {rad}}^1(\mathbb {R}^2)$
and there exists a subsequence
![]() $\{w_{\tau _k}\}$
such that
$\{w_{\tau _k}\}$
such that
![]() $w_{\tau _k}\rightharpoonup w_0$
weakly in
$w_{\tau _k}\rightharpoonup w_0$
weakly in
![]() $H_{{\mathrm { rad}}}^1(\mathbb {R}^2)$
, where
$H_{{\mathrm { rad}}}^1(\mathbb {R}^2)$
, where
![]() $H_{{\mathrm {rad}}}^1( \mathbb {R}^2)$
denotes the Sobolev space of radial
$H_{{\mathrm {rad}}}^1( \mathbb {R}^2)$
denotes the Sobolev space of radial
![]() $H^1( \mathbb {R}^2)$
functions. For
$H^1( \mathbb {R}^2)$
functions. For
![]() $2<p<+\infty $
, the embedding
$2<p<+\infty $
, the embedding
![]() $H_{{\mathrm {rad}}}^1(\mathbb {R}^2)\hookrightarrow L^p(\mathbb {R}^2)$
is compact, so
$H_{{\mathrm {rad}}}^1(\mathbb {R}^2)\hookrightarrow L^p(\mathbb {R}^2)$
is compact, so
![]() $w_{\tau _k}\to w_0$
strongly in
$w_{\tau _k}\to w_0$
strongly in
![]() $L^p(\mathbb {R}^2)$
. This implies that
$L^p(\mathbb {R}^2)$
. This implies that
By the Pohozaev identity (3.2),
![]() $w_{\tau _k}(x)$
satisfies
$w_{\tau _k}(x)$
satisfies
 $$ \begin{gather*} \begin{aligned} \int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx-\frac{a_k}{2}\int_{\mathbb{R}^2}|w_{\tau_k}|^4\,dx+\frac{2a_k^2}{3}\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx=0 \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx-\frac{a_k}{2}\int_{\mathbb{R}^2}|w_{\tau_k}|^4\,dx+\frac{2a_k^2}{3}\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx=0 \end{aligned} \end{gather*} $$
and it follows from (3.12) that
 $$ \begin{align} \lim_{k\to\infty}\int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx= \frac{a_*}{2}\int_{\mathbb{R}^2}|w_{0}|^4\,dx+\frac{2a_*^2}{3}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx= \frac{a_*}{2}\int_{\mathbb{R}^2}|w_{0}|^4\,dx+\frac{2a_*^2}{3}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{align} $$
By passing to the weak limit
![]() $\tau _k\to 0^+$
in (3.10), we see that
$\tau _k\to 0^+$
in (3.10), we see that
![]() $w_0(x)$
satisfies
$w_0(x)$
satisfies
We also have the Pohozaev identity (see [Reference Carles and Sparber1]),
 $$ \begin{align} \beta^2\int_{\mathbb{R}^2}|w_0 |^2\,dx-\frac{a_*}{2}\int_{\mathbb{R}^2}|w_0 |^4\,dx+\frac{a_*^2}{3}\int_{\mathbb{R}^2}|w_0|^6\,dx=0, \end{align} $$
$$ \begin{align} \beta^2\int_{\mathbb{R}^2}|w_0 |^2\,dx-\frac{a_*}{2}\int_{\mathbb{R}^2}|w_0 |^4\,dx+\frac{a_*^2}{3}\int_{\mathbb{R}^2}|w_0|^6\,dx=0, \end{align} $$
where
![]() $\beta ^2\in (0,3/16)$
since
$\beta ^2\in (0,3/16)$
since
![]() $w_0\not = 0$
(see [Reference Carles and Sparber1]). From (3.14) and (3.15),
$w_0\not = 0$
(see [Reference Carles and Sparber1]). From (3.14) and (3.15),
 $$ \begin{align} \int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx=\frac{a_*}{2}\int_{\mathbb{R}^2}|w_0|^4\,dx-\frac{2a_*^2}{3}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx=\frac{a_*}{2}\int_{\mathbb{R}^2}|w_0|^4\,dx-\frac{2a_*^2}{3}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{align} $$
It follows from (3.13) that
However, by (3.11) together with (3.12) and (3.17),
 $$ \begin{gather*} \begin{aligned} \lim_{k\to\infty} \int_{\mathbb{R}^2}|w_{\tau_k}|^2\,dx&=\lim_{k\to\infty}\frac{1}{\tau_k^2\lambda_{a_k}}\bigg( \int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx-a_k \int_{\mathbb{R}^2}|w_{\tau_k}|^4\,dx+ a_k^2\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx\bigg) \\ &=-\frac{1}{\beta^2}\bigg( \int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx-a_* \int_{\mathbb{R}^2}|w_{0}|^4\,dx+a_*^2 \int_{\mathbb{R}^2}|w_{0}|^6\,dx\bigg)\\ &=\int_{\mathbb{R}^2}|w_0|^2\,dx. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \lim_{k\to\infty} \int_{\mathbb{R}^2}|w_{\tau_k}|^2\,dx&=\lim_{k\to\infty}\frac{1}{\tau_k^2\lambda_{a_k}}\bigg( \int_{\mathbb{R}^2}|\nabla w_{\tau_k}|^2\,dx-a_k \int_{\mathbb{R}^2}|w_{\tau_k}|^4\,dx+ a_k^2\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx\bigg) \\ &=-\frac{1}{\beta^2}\bigg( \int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx-a_* \int_{\mathbb{R}^2}|w_{0}|^4\,dx+a_*^2 \int_{\mathbb{R}^2}|w_{0}|^6\,dx\bigg)\\ &=\int_{\mathbb{R}^2}|w_0|^2\,dx. \end{aligned} \end{gather*} $$
Combining this with (3.17) shows
![]() $w_{\tau _k}\to w_0$
strongly in
$w_{\tau _k}\to w_0$
strongly in
![]() $H^1(\mathbb {R}^2)$
and this yields (1.5).
$H^1(\mathbb {R}^2)$
and this yields (1.5).
 $$ \begin{align} \lim_{k\to\infty}\tau_k^4e(a_k)&=-\lim_{k\to\infty} \frac{\tau_k^4a_k^2}{6}\int_{\mathbb{R}^2}|\varphi_{a_k}|^6\,dx \nonumber\\ &=-\lim_{k\to\infty}\frac{a_k^2}{6}\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx =-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\tau_k^4e(a_k)&=-\lim_{k\to\infty} \frac{\tau_k^4a_k^2}{6}\int_{\mathbb{R}^2}|\varphi_{a_k}|^6\,dx \nonumber\\ &=-\lim_{k\to\infty}\frac{a_k^2}{6}\int_{\mathbb{R}^2}|w_{\tau_k}|^6\,dx =-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{align} $$
Finally, by applying the same argument as we used before to (3.18), we can take a subsequence
![]() $\{\tau _k\}$
with
$\{\tau _k\}$
with
![]() $\tau _k\to +\infty $
as
$\tau _k\to +\infty $
as
![]() $k\to +\infty $
, such that
$k\to +\infty $
, such that
 $$ \begin{align} \liminf_{a\searrow a_*}\tau^4e(a)=\lim_{k\to\infty}\tau_k^4e(a_k)=-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx, \end{align} $$
$$ \begin{align} \liminf_{a\searrow a_*}\tau^4e(a)=\lim_{k\to\infty}\tau_k^4e(a_k)=-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx, \end{align} $$
where
![]() $w_0(x)$
satisfies (3.15) with some
$w_0(x)$
satisfies (3.15) with some
![]() $\beta ^2\in (0,3/16)$
and
$\beta ^2\in (0,3/16)$
and
![]() $\int _{\mathbb {R}^2}|w_0(x)|^2\,dx=1$
. However, taking the test function
$\int _{\mathbb {R}^2}|w_0(x)|^2\,dx=1$
. However, taking the test function
![]() $\phi _\tau =\tau ^{-1}w_0(\tau ^{-1}x)$
in
$\phi _\tau =\tau ^{-1}w_0(\tau ^{-1}x)$
in
![]() $E_a(\cdot )$
, we deduce from (3.16) that
$E_a(\cdot )$
, we deduce from (3.16) that
 $$ \begin{gather*} \begin{aligned} \tau^4e(a)\leq \tau^4 E_a(\phi_\tau)&=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|w_0|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx\\ &=\frac{a_*-a}{4}\int_{\mathbb{R}^2}|w_0|^4\,dx+\frac{a^2-2a_*^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \tau^4e(a)\leq \tau^4 E_a(\phi_\tau)&=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla w_{0}|^2\,dx-\frac{a}{4}\int_{\mathbb{R}^2}|w_0|^4\,dx+\frac{a^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx\\ &=\frac{a_*-a}{4}\int_{\mathbb{R}^2}|w_0|^4\,dx+\frac{a^2-2a_*^2}{6}\int_{\mathbb{R}^2}|w_0|^6\,dx. \end{aligned} \end{gather*} $$
This means that
 $$ \begin{gather*} \begin{aligned} \limsup_{a\searrow a_*}\tau^4e(a)\leq-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \limsup_{a\searrow a_*}\tau^4e(a)\leq-\frac{a_*^2}{6}\int_{\mathbb{R}^2}|w_{0}|^6\,dx. \end{aligned} \end{gather*} $$
Combining this with (3.19) gives (1.6). This completes the proof of Theorem 1.3.