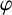A CLASS OF SYMBOLS THAT INDUCE BOUNDED COMPOSITION OPERATORS FOR DIRICHLET-TYPE SPACES ON THE DISC

Abstract

We study the problem of determining the holomorphic self maps of the unit disc that induce a bounded composition operator on Dirichlet-type spaces. We find a class of symbols $\varphi $ that induce a bounded composition operator on the Dirichlet-type spaces, by applying results of the multidimensional theory of composition operators for the weighted Bergman spaces of the bi-disc.

1. Introduction

The problem of finding necessary and sufficient conditions for a composition operator to be bounded and compact has attracted much attention. The resolution of the boundedness and compactness of composition operators on Hardy and Bergman spaces on the unit disc $\mathbb {D}$ is a classical result in holomorphic function theory, treated by Shapiro in [9]. Since then, many other seminal works have provided characterisations of the holomorphic self maps $\varphi :\mathbb {D}\to \mathbb {D}$ that induce a bounded composition operator. For instance, Pau and Perez [8, Theorem 3.1] gave necessary and sufficient conditions for both continuity and compactness of the composition operator on Dirichlet-type spaces. They used the Nevanlinna and generalised Nevanlinna counting functions to obtain these exceptional results. Their characterisation is obtained for specific exponents of the radial weight and not for all positive exponents.

Compared with [8], we will not make use of such tools and we will follow a completely different and somewhat novel approach that combines results from multidimensional cases, namely the bi-disc case. The work of Kosinski [6] and Bayart [2] dealt with the boundedness of composition operators in weighted Bergman spaces on the bi-disc and provided characterisations of symbols that induce bounded composition operators. We will provide only a sufficient condition, which works for all positive exponents of the radial weight of the Dirichlet space.

We exploit these multidimensional results to obtain bounded composition operators for the unit disc case. In particular, we give a sufficient condition for some symbols $\varphi $ to induce a bounded composition operator for the Dirichlet spaces $\mathcal {D}_p(\mathbb {D}), p>0,$ by applying one of the main results presented in [6], namely the rank sufficiency theorem for the weighted Bergman space on the bi-disc. Our approach can be described in a short manner as follows. Considering some holomorphic self map $\varphi $ of the unit disc, which is of class $\mathcal {C}^1$ on the boundary of the disc $\mathbb {T}$ , we induce a composition operator $C_{\Psi }$ which is continuous on the weighted Bergman space $A^p_{\beta }(\mathbb {D}^2)$ of the bi-disc, where $\Psi $ will be defined in terms of $\varphi .$ Then, by using the lift operator that we introduce in Section 2 and a recent double integral characterisation of the Dirichlet-type space $\mathcal {D}_p(\mathbb {D})$ that can be found in [1], we give a sufficient condition for the composition operator $C_{\varphi }$ to be bounded on $\mathcal {D}_p(\mathbb {D}).$

2. Notation and tools

Throughout this note, we will denote by $\mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$ the holomorphic self maps of the unit disc that are of class $\mathcal {C}^1$ on the boundary. In the same notation, by replacing $\mathbb {D}$ with $\mathbb {D}^2$ , we will talk about the holomorphic self maps of the bi-disc that are of class $\mathcal {C}^1$ at the (topological) boundary of the bi-disc, the bi-torus $\mathbb {T}^2$ . Whenever we refer to a holomorphic function on the disc, we will simply write $f\in H(\mathbb {D}).$ Whenever the notation $a\asymp b$ appears, it means that there exist two positive constants $C_1,C_2$ such that $C_1a\leq b\leq C_2 a$ and whenever we encounter the notation $a\lesssim b,$ it means that there is a positive constant $C>0$ such that $a\leq Cb.$ We recall that for $p>0$ , the Dirichlet type space of the unit disc, denoted by $\mathcal {D}_p(\mathbb {D}),$ consists of the holomorphic functions f on the unit disc $\mathbb {D},$ such that

$$ \begin{align*}\int_{\mathbb{D}}|f'(z)|^2(1-|z|^2)^p\,dA(z)<+\infty.\end{align*} $$

By $A_{\beta }^p(\mathbb {D}^2)$ , $\beta \ge -1,$ we denote the classical weighted Bergman space of the bi-disc $\mathbb {D}^2,$ comprising the holomorphic functions on the bi-disc such that

$$ \begin{align*}\int_{\mathbb{D}^2}|f(z,w)|^p\,dA_{\beta}(z)\,dA_{\beta}(w)<+\infty.\end{align*} $$

The measure $dA(z)={\pi }^{-1}\,dx\,dy$ is the normalised Lebesgue measure on the unit disc, while $dA_{\beta }(z)=c_{\beta }(1-|z|^2)^{\beta }\,dA(z)$ for $\beta \ge -1.$ The following recent result of Balooch and Wu [1] will be of critical importance in our note.

Theorem 2.1. Let $\sigma , \tau \ge -1 $ and $\beta \in \mathbb {R},$ with $\tfrac 12\max (\sigma ,\tau )-1<\beta \leq \tfrac 12 (\sigma +\tau ).$ Let $f\in H(\mathbb {D}).$ Then

$$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f(z)-f(w)|^2}{|1-\overline{w}z|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\tau}(w)\asymp ||f||^2_{\mathcal{D}_{\sigma+\tau-2\beta}(\mathbb{D})}.\end{align*} $$

We now define a lift-type operator, similarly to [7], but with an exponent of two positive parameters $p,\gamma>0$ .

Definition 2.2. Let $p,\gamma>0$ and $f\in H(\mathbb {D}).$ The lift-type operator is defined by

$$ \begin{align*}L^{p,\gamma}:H(\mathbb{D})\to H(\mathbb{D}^2), \quad L^{p,\gamma}(f):=\frac{f(z)-f(w)}{(1-\overline{w}z)^{p/ \gamma}},\quad z,w \in \mathbb{D}.\end{align*} $$

The first observation that one makes immediately is that the fraction that defines this operator appears in the characterisation of the Dirichlet-type spaces. The following proposition follows immediately.

Proposition 2.3. Let $f\in H(\mathbb {D})$ , $\sigma =\tau> -1$ and $\beta $ as in Theorem 2.1. The operator $L^{2,2(\beta +2)}(f)$ maps $\mathcal {D}_{2\sigma -2\beta }(\mathbb {D})$ into $A^2_{\sigma }(\mathbb {D}^2).$

Proof. The proof follows by a simple use of the asymptotic equality of Theorem 2.1 but we will write it down for convenience.

$$ \begin{align*} ||L^{2,2(\beta+2)}(f)||^2_{A^2_{\sigma}(\mathbb{D}^2)}&=\int_{\mathbb{D}}\int_{\mathbb{D}}|L^{2,2(\beta+2)}(f)(z,w)|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\bigg|\frac{f(z)-f(w)}{(1-\overline{w}z)^{{2(\beta+2)}/{2}}}\bigg|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &\lesssim ||f||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}.\\[-35pt] \end{align*} $$

The next theorem is a characterisation of the symbols $\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2})$ that induce a bounded composition operator on the weighted Bergman space $A_{\beta }^2(\mathbb {D}^2)$ , $\beta>-1$ .

Theorem 2.4 [6, Section 1, page 3]

Let $\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $ Then the composition operator $C_{\Psi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$ is bounded if and only if the derivative $d_{\zeta }\Psi $ is invertible for all $\zeta \in \mathbb {T}^2$ with $\Psi (\zeta )\in \mathbb {T}^2.$

Using this result, we can deduce the following lemma.

Lemma 2.5. Let $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}).$ Set $\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2 \in \mathbb {D}.$ Then $C_{\Phi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$ is bounded.

Proof. It is quite obvious that $\Phi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $ We only have to show that the derivative $d_{\zeta }\Phi $ is invertible for every $\zeta \in \mathbb {T}^2$ such that $\Phi (\zeta )\in \mathbb {T}^2$ . Let ${\zeta =(\zeta _1,\zeta _2)}$ be such that $\Phi (\zeta _1,\zeta _2)=(\varphi (\zeta _1),\varphi (\zeta _2))\in \mathbb {T}^2.$ Of course, this only occurs for the points $\zeta _1,\zeta _2\in \mathbb {T}$ such that $\varphi (\zeta _1),\varphi (\zeta _2)\in \mathbb {T},\zeta _1\neq \zeta _2.$ We calculate the Jacobian of the derivative $d_{\zeta }\Phi $ for such points $\zeta \in \mathbb {T}^2$ . It is an immediate observation that

$$ \begin{align*}\frac{\partial \varphi(z_1)}{\partial z_2}=\frac{\partial \varphi(z_2)}{\partial z_1}=0.\end{align*} $$

So the Jacobian is

$$ \begin{align*}|d_\zeta\Phi|=\varphi'(\zeta_1)\varphi'(\zeta_2)\neq 0.\end{align*} $$

By the fact that $\varphi $ is of class $\mathcal {C}^1$ , and hence continuous on the boundary, one can calculate the value of $\varphi '$ at the boundary points $\zeta _1,\zeta _2$ . By the Julia–Caratheodory theorem (see [3]), it follows that the value of the derivative of $\varphi $ is nonzero. Hence, by Theorem 2.4, $C_{\Phi }$ defines a bounded composition operator on the weighted Bergman space $A_{\beta }^2(\mathbb {D}^2)$ and the proof is complete.

3. Main result and proof

Here we state our main result and the proof of it. For what follows, we define

$$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}}, \quad z,w\in \mathbb{D},\end{align*} $$

for a function $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$ and denote by $||\cdot ||_{\infty }$ the supremum norm over the bi-disc $\mathbb {D}^2,$ that is, $||k||_{\infty }=\sup _{(z,w)\in \mathbb {D}^2}|k(z,w)|$ .

Theorem 3.1. Let $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$ such that $||k^{\varphi }(z,w)||_{\infty }<+\infty .$ Then the composition operator $C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D})$ is bounded for $p=2\sigma -2\beta ,$ where $\sigma>0$ and $\tfrac 12\sigma -1<\beta <\sigma $ .

Proof. Let $\sigma>0$ and $\beta \in \mathbb {R}$ satisfy the conditions that we gave in our statement. For convenience, set $q=2(\beta +2).$ Then

$$ \begin{align*} ||C_{\varphi}(f)||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}&\asymp \int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\frac{|1-\overline{\varphi(w)}\varphi(z)|^{q}}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &\leq \sup_{(z,w)\in \mathbb{D}^2}|k^{\varphi}(z,w)|^{q}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w). \end{align*} $$

At this point, we observe that the integral on the right-hand side can be expressed as the norm of a composition operator $C_{\Phi }$ on the weighted Bergman space $A_{\sigma }^2(\mathbb {D}^2),$ where $\Phi =\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2\in \mathbb {D}.$ To be precise,

$$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\sigma}(w)=||C_{\Phi}(L^{2,2(\beta+2)}(f))||^2_{A^2_{\sigma}(\mathbb{D}^2)}.\end{align*} $$

By Lemma 2.5, $C_\Phi :A^2_{\sigma }(\mathbb {D}^2)\to A^2_{\sigma }(\mathbb {D}^2)$ is bounded. Hence, by Proposition 2.3,

$$ \begin{align*}||C_{\Phi}(L^{2,2(\beta+2)}(f))||^2_{A^2_{\sigma}(\mathbb{D}^2)}\lesssim||L^{2,2(\beta+2)}(f)||^2_{A^2_{\sigma}(\mathbb{D}^2)}\lesssim ||f||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}.\end{align*} $$

Summarising,

$$ \begin{align*}||C_{\varphi}(f)||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}\lesssim ||k^{\varphi}(z,w)||_{\infty}^{2(\beta+2)}||f||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})},\end{align*} $$

which, by our assumption that the supremum is bounded, gives the desired result.

4. Concluding remark

The significance of the main result of this note lies mainly in the fact that we managed to apply results for the bi-disc to the case of the unit disc. Another interesting aspect of the result is the appearance of the De Branges–Rovnyak kernel $k^\varphi $ that is induced by the symbol $\varphi .$ Assuming that $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$ then it is known that $\varphi \in H^{\infty }(\mathbb {D})$ and also $||\varphi ||_{H^{\infty }(\mathbb {D})}\leq 1$ which means that the function

$$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}},\quad z,w\in \mathbb{D}\end{align*} $$

is the De Branges–Rovnyak reproducing kernel associated with $\varphi .$ We can reformulate the main result of the note in the following manner.

Corollary 4.1. Let $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$ and assume that $|k^{\varphi }|$ is a bounded function on the bi-disc. Then, the composition operator $C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D}), p>0, $ is bounded.

For more details about the De Branges–Rovnyak spaces and kernel, see [4]. Also, in the work of Jury (see [5]), one can study the connections of the De Branges–Rovnyak kernel associated to a holomorphic self map of the unit disc, and the corresponding composition operators in the Hardy and Bergman spaces of the unit disc and also of the unit ball of $\mathbb {C}^n.$