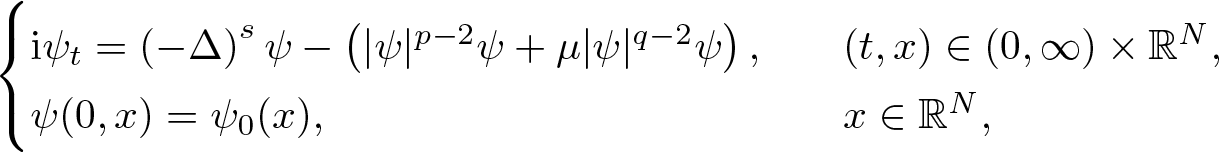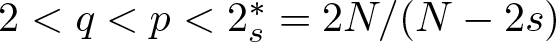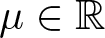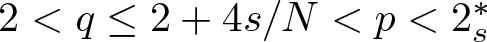1. Introduction and main results
We consider the following fractional nonlinear Schrödinger equation (NLS) with combined nonlinearities:
 \begin{equation}
\begin{cases}
\mathrm{i} \psi_{t}=\left(-\Delta\right)^s \psi-f(|\psi|)\psi, & \quad(t,x)\in(0,\infty)\times\mathbb{R}^N,\\
\psi(0,x)=\psi_0(x),&\quad x\in\mathbb{R}^N,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
\mathrm{i} \psi_{t}=\left(-\Delta\right)^s \psi-f(|\psi|)\psi, & \quad(t,x)\in(0,\infty)\times\mathbb{R}^N,\\
\psi(0,x)=\psi_0(x),&\quad x\in\mathbb{R}^N,
\end{cases}
\end{equation} where ![]() $N\geq2$,
$N\geq2$, ![]() $0 \lt s \lt 1$,
$0 \lt s \lt 1$, ![]() $2 \lt q \lt p \lt 2_s^*:=2N/(N-2s)$,
$2 \lt q \lt p \lt 2_s^*:=2N/(N-2s)$, ![]() $\mu\in\mathbb{R}$,
$\mu\in\mathbb{R}$, ![]() $f(t)=t^{p-2}+\mu t^{q-2}$, and
$f(t)=t^{p-2}+\mu t^{q-2}$, and ![]() $(-\Delta)^s$ is the fractional Laplacian operator defined by
$(-\Delta)^s$ is the fractional Laplacian operator defined by
 \begin{equation*}
(-\Delta)^su(x)=C(N,s)\lim_{\varepsilon\rightarrow0^+}\int_{\mathbb{R}^N\setminus B_\varepsilon(0)}\frac{u(x)-u(y)}{|x-y|^{N+2s}}dy,
\end{equation*}
\begin{equation*}
(-\Delta)^su(x)=C(N,s)\lim_{\varepsilon\rightarrow0^+}\int_{\mathbb{R}^N\setminus B_\varepsilon(0)}\frac{u(x)-u(y)}{|x-y|^{N+2s}}dy,
\end{equation*} where ![]() $C(N,s)$ is a dimensional constant (see [Reference Chen, Li and Li9, Reference Di Nezza, Palatucci and Valdinoci11]).
$C(N,s)$ is a dimensional constant (see [Reference Chen, Li and Li9, Reference Di Nezza, Palatucci and Valdinoci11]).
The fractional NLS was initially discovered by Laskin [Reference Laskin25]. Its inception traces back to the extension of the Feynman path integral from Brownian-like to Lévy-like quantum mechanical paths. It arises naturally in the continuum limit of discrete models featuring long-range interactions, as explored in [Reference Kirkpatrick, Lenzmann and Staffilani24]. Additionally, its presence is evident in the description of Boson stars and the dynamics of water waves. Beyond the realm of physics, the impact of the fractional NLS extends into interdisciplinary domains. Notably, it finds applications in biology, chemistry, and finance, as documented in [Reference Applebaum2].
The conservation of mass is a foundational principle for solutions to (1.1), ensuring that ![]() $|\psi(t,\cdot)|_{2}=|\psi(0,x)|_{2}$ for any t > 0. This motivates the exploration of solutions with a prescribed L 2 norm. We employ the standing wave ansatz
$|\psi(t,\cdot)|_{2}=|\psi(0,x)|_{2}$ for any t > 0. This motivates the exploration of solutions with a prescribed L 2 norm. We employ the standing wave ansatz ![]() $\psi(t,x)=e^{-\mathrm{i}\lambda t}u(x)$. Accordingly, u(x) solves
$\psi(t,x)=e^{-\mathrm{i}\lambda t}u(x)$. Accordingly, u(x) solves
Moreover, we impose the mass constraint
 \begin{equation}
\int_{\mathbb{R}^N}|u|^2=a^2,
\end{equation}
\begin{equation}
\int_{\mathbb{R}^N}|u|^2=a^2,
\end{equation}where a > 0 is a given constant.
For the classical Laplacian case, the existence and stability of normalized solutions to problems (1.2) and (1.3) has attracted considerable attention recently. In the case ![]() $f(u)= |u|^{p-2}u$ and
$f(u)= |u|^{p-2}u$ and ![]() $p \lt p^*:=2+4/N$ (L 2-subcritical), the energy functional is bounded below on the constrained manifold. Thus, the global minimizer is a good choice of the normalized solution. Lions [Reference Lions29, Reference Lions30] developed the concentration compactness principle to obtain the compactness of the minimizing sequences. Recalling the methods developed by Cazenave–Lions [Reference Cazenave and Lions7, Reference Lions30] and Shibata [Reference Shibata38], it is routine to prove the orbital stability. Besides, Hajaiej–Song [Reference Hajaiej and Song20], Hirata–Tanaka [Reference Hirata and Tanaka21], and Jeanjean–Lu [Reference Jeanjean and Lu23] discussed about multiplicity results. However, the constrained energy functional is unbounded from below in the L 2-supercritical case. Jeanjean [Reference Jeanjean22] exploited the mountain pass lemma and a smart compactness argument to prove the existence of normalized solutions. Berestycki–Cazenave [Reference Berestycki and Cazenave4] and Le Coz [Reference Le Coz26] showed that the associated standing wave is strongly unstable. If f(u) contains both L 2-subcritical term and L 2-supercritical term, Soave [Reference Soave39, Reference Soave40] proved the existence and stability results. Finally, one can find more general nonlinearities in the work of Bartsch–de Valeriola [Reference Bartsch and de Valeriola3], Jeanjean–Lu [Reference Jeanjean and Lu23], and Gou–Zhang [Reference Gou and Zhang18].
$p \lt p^*:=2+4/N$ (L 2-subcritical), the energy functional is bounded below on the constrained manifold. Thus, the global minimizer is a good choice of the normalized solution. Lions [Reference Lions29, Reference Lions30] developed the concentration compactness principle to obtain the compactness of the minimizing sequences. Recalling the methods developed by Cazenave–Lions [Reference Cazenave and Lions7, Reference Lions30] and Shibata [Reference Shibata38], it is routine to prove the orbital stability. Besides, Hajaiej–Song [Reference Hajaiej and Song20], Hirata–Tanaka [Reference Hirata and Tanaka21], and Jeanjean–Lu [Reference Jeanjean and Lu23] discussed about multiplicity results. However, the constrained energy functional is unbounded from below in the L 2-supercritical case. Jeanjean [Reference Jeanjean22] exploited the mountain pass lemma and a smart compactness argument to prove the existence of normalized solutions. Berestycki–Cazenave [Reference Berestycki and Cazenave4] and Le Coz [Reference Le Coz26] showed that the associated standing wave is strongly unstable. If f(u) contains both L 2-subcritical term and L 2-supercritical term, Soave [Reference Soave39, Reference Soave40] proved the existence and stability results. Finally, one can find more general nonlinearities in the work of Bartsch–de Valeriola [Reference Bartsch and de Valeriola3], Jeanjean–Lu [Reference Jeanjean and Lu23], and Gou–Zhang [Reference Gou and Zhang18].
For the fractional Laplacian case, it is well known that there exists an L 2-critical exponent
 \begin{equation*}\bar{p}:=2+\frac{4s}{N}.\end{equation*}
\begin{equation*}\bar{p}:=2+\frac{4s}{N}.\end{equation*} When ![]() $2 \lt q \lt p \lt 2_s^*$, the existence of normalized solutions has been widely studied by variational methods in the article [Reference Luo and Zhang33] of the last two authors. Recently, when
$2 \lt q \lt p \lt 2_s^*$, the existence of normalized solutions has been widely studied by variational methods in the article [Reference Luo and Zhang33] of the last two authors. Recently, when ![]() $p=2_s^*, 2 \lt q \lt 2_s^*$, Zhen–Zhang [Reference Zhen and Zhang43] proved several existence and nonexistence results for a perturbation term
$p=2_s^*, 2 \lt q \lt 2_s^*$, Zhen–Zhang [Reference Zhen and Zhang43] proved several existence and nonexistence results for a perturbation term ![]() $\mu|u|^{q-2}u$. In addition, Luo–Yang–Yang [Reference Luo, Yang and Yang35] studied the multiplicity and asymptotics of standing waves for the case
$\mu|u|^{q-2}u$. In addition, Luo–Yang–Yang [Reference Luo, Yang and Yang35] studied the multiplicity and asymptotics of standing waves for the case ![]() $s=1/2$ and
$s=1/2$ and ![]() $p=2_s^*, 2 \lt q \lt \bar{p}$. Colorado–Ortega [Reference Colorado and Ortega10] proved the existence of positive radial bound and ground state solutions for fractional systems. One can find more general nonlinearities and more results in [Reference Li, Zhang and Zhang28, Reference Liu, Luo and Zhang31, Reference Luo and Wu32, Reference Servadei and Valdinoci37, Reference Yan, Yang and Yu41].
$p=2_s^*, 2 \lt q \lt \bar{p}$. Colorado–Ortega [Reference Colorado and Ortega10] proved the existence of positive radial bound and ground state solutions for fractional systems. One can find more general nonlinearities and more results in [Reference Li, Zhang and Zhang28, Reference Liu, Luo and Zhang31, Reference Luo and Wu32, Reference Servadei and Valdinoci37, Reference Yan, Yang and Yu41].
Concerning the stability of standing waves, the existing literature is mainly related to the L 2-subcritical or L 2-critical case (see [Reference Guo and Huang19, Reference Peng and Shi36, Reference Zhu44]). For the L 2-supercritical case and µ = 0, Feng–Ren–Wang [Reference Feng, Ren and Wang15] considered the instability of standing waves to (1.1) when ![]() $\bar{p} \lt p \lt 2_s^*$, based on the homogeneity of the nonlinearity. A powerful tool for proving the strong instability of standing waves is the virial identity introduced by Bonheure–Casteras–Gou–Jeanjean [Reference Bonheure, Casteras, Gou and Jeanjean5] and Soave [Reference Soave39]. However, virial identity does not hold for non-local operators. Moreover, the instability result of standing waves is unknown for the L 2-supercritical nonlinearity with a perturbation term
$\bar{p} \lt p \lt 2_s^*$, based on the homogeneity of the nonlinearity. A powerful tool for proving the strong instability of standing waves is the virial identity introduced by Bonheure–Casteras–Gou–Jeanjean [Reference Bonheure, Casteras, Gou and Jeanjean5] and Soave [Reference Soave39]. However, virial identity does not hold for non-local operators. Moreover, the instability result of standing waves is unknown for the L 2-supercritical nonlinearity with a perturbation term ![]() $\mu|u|^{q-2}u$.
$\mu|u|^{q-2}u$.
This article deals with the instability of standing waves in this respect. The novelty of our article is as follows: First, for ![]() $2 \lt q \lt p \lt 2+4s/N$ and µ < 0, we find a threshold value to determine whether the least energy solution exists. If it exists, it is orbitally stable. Second, for
$2 \lt q \lt p \lt 2+4s/N$ and µ < 0, we find a threshold value to determine whether the least energy solution exists. If it exists, it is orbitally stable. Second, for ![]() $2+4s/N \lt q \lt p \lt 2_s^*$ and µ > 0, we give several new kinds of equivalent variational characterizations for ground states. Finally, we obtain the strong instability of the associated standing waves and give the blow-up criterion by constructing the equivalent variational characterization and the viral estimate.
$2+4s/N \lt q \lt p \lt 2_s^*$ and µ > 0, we give several new kinds of equivalent variational characterizations for ground states. Finally, we obtain the strong instability of the associated standing waves and give the blow-up criterion by constructing the equivalent variational characterization and the viral estimate.
Throughout the article, the ![]() $L^p(\mathbb{R}^N)$ (
$L^p(\mathbb{R}^N)$ (![]() $1\le p\le \infty$) norm is denoted by
$1\le p\le \infty$) norm is denoted by ![]() $|u|_p$. The Hilbert space
$|u|_p$. The Hilbert space ![]() $H^s(\mathbb{R}^N,\mathbb{C})$ is defined as
$H^s(\mathbb{R}^N,\mathbb{C})$ is defined as
 \begin{align*}H^s(\mathbb{R}^N,\mathbb{C})& \!=\!\!\Big\{u\in L^2(\mathbb{R}^N,\mathbb{C})\big|\!\int_{\mathbb{R}^N}|(-\Delta)^{\frac{s}{2}}u(x)|^2 \mathrm{d}x\\
& \quad :=\!\!\!\iint_{\mathbb{R}^{N}\!\times \mathbb{R}^N}\!\!\frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}\mathrm{d}x\mathrm{d}y \lt +\infty\Big\}.\end{align*}
\begin{align*}H^s(\mathbb{R}^N,\mathbb{C})& \!=\!\!\Big\{u\in L^2(\mathbb{R}^N,\mathbb{C})\big|\!\int_{\mathbb{R}^N}|(-\Delta)^{\frac{s}{2}}u(x)|^2 \mathrm{d}x\\
& \quad :=\!\!\!\iint_{\mathbb{R}^{N}\!\times \mathbb{R}^N}\!\!\frac{|u(x)-u(y)|^2}{|x-y|^{N+2s}}\mathrm{d}x\mathrm{d}y \lt +\infty\Big\}.\end{align*} For simplicity, we denote ![]() $H^s(\mathbb{R}^N)\!:=\! H^s(\mathbb{R}^N,\mathbb{C})$. The energy functional of (1.2) and (1.3) is defined by
$H^s(\mathbb{R}^N)\!:=\! H^s(\mathbb{R}^N,\mathbb{C})$. The energy functional of (1.2) and (1.3) is defined by
 \begin{equation*}
E_\mu: H^s(\mathbb{R}^N,\mathbb{C})\rightarrow\mathbb{R}, \ E_\mu(u):=\int_{\mathbb{R}^N}\Big(\frac{1}{2}|(-\Delta)^{\frac{s}{2}}u(x)|^2-\frac{1}{p}|u(x)|^p-\frac{\mu}{q}|u(x)|^q\Big)\mathrm{d}x.
\end{equation*}
\begin{equation*}
E_\mu: H^s(\mathbb{R}^N,\mathbb{C})\rightarrow\mathbb{R}, \ E_\mu(u):=\int_{\mathbb{R}^N}\Big(\frac{1}{2}|(-\Delta)^{\frac{s}{2}}u(x)|^2-\frac{1}{p}|u(x)|^p-\frac{\mu}{q}|u(x)|^q\Big)\mathrm{d}x.
\end{equation*}Then, the weak solution of (1.2) corresponds to a critical point of the energy functional Eµ on the manifold
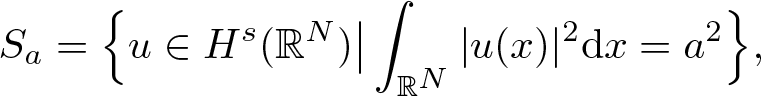 \begin{equation*}
S_a=\Big\{u\in H^s(\mathbb{R}^N)\big|\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x=a^2\Big\},
\end{equation*}
\begin{equation*}
S_a=\Big\{u\in H^s(\mathbb{R}^N)\big|\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x=a^2\Big\},
\end{equation*} with ![]() $\lambda\in \mathbb{R}$ is determined as the Lagrange multiplier (see, e.g., [Reference Zhang42]).
$\lambda\in \mathbb{R}$ is determined as the Lagrange multiplier (see, e.g., [Reference Zhang42]).
The following is the definition of ground state solutions:
Definition 1.1. The function ![]() $\hat{u}$ is called a ground state solution of (1.2) and (1.3) if
$\hat{u}$ is called a ground state solution of (1.2) and (1.3) if
Moreover,
Recall the notion of stability and instability as below.
Definition 1.2. (i) The set ![]() $\mathcal{G}_{a,\mu}$ is orbitally stable if, for every ɛ > 0, there exists δ > 0 such that whenever
$\mathcal{G}_{a,\mu}$ is orbitally stable if, for every ɛ > 0, there exists δ > 0 such that whenever ![]() $\psi_0\in H^s$ satisfies
$\psi_0\in H^s$ satisfies ![]() $\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_0-v\right\|_{H^s} \lt \delta$, then
$\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_0-v\right\|_{H^s} \lt \delta$, then
 \begin{equation*}
\sup_{t \gt 0} \inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi(t,\cdot)-v\right\|_{H^s} \lt \varepsilon,
\end{equation*}
\begin{equation*}
\sup_{t \gt 0} \inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi(t,\cdot)-v\right\|_{H^s} \lt \varepsilon,
\end{equation*} where ![]() $\psi(t,\cdot)$ is the solution to (1.1) with initial datum ψ 0.
$\psi(t,\cdot)$ is the solution to (1.1) with initial datum ψ 0.
(ii) A standing wave ![]() $e^{-\mathrm{i}\lambda t}u$ is strongly unstable if, for every ɛ > 0, there exists
$e^{-\mathrm{i}\lambda t}u$ is strongly unstable if, for every ɛ > 0, there exists ![]() $\psi_0\in H^s$ such that
$\psi_0\in H^s$ such that ![]() $\left\|\psi_0-u\right\|_{H^s} \lt \varepsilon$, but
$\left\|\psi_0-u\right\|_{H^s} \lt \varepsilon$, but ![]() $\psi(t,\cdot)$ blows up in finite time.
$\psi(t,\cdot)$ blows up in finite time.
Main results. First, we shall study the purely L 2-subcritical and defocusing case, i.e., ![]() $2 \lt q \lt p \lt \bar{p}=2+4s/N, \mu \lt 0$. Due to the Gagliardo–Nirenberg inequality, the energy functional Eµ is bounded from below on Sa, which leads to the following global minimization problem:
$2 \lt q \lt p \lt \bar{p}=2+4s/N, \mu \lt 0$. Due to the Gagliardo–Nirenberg inequality, the energy functional Eµ is bounded from below on Sa, which leads to the following global minimization problem:
 \begin{equation}
m_{a,\mu}:=\inf_{S_a}E_\mu.
\end{equation}
\begin{equation}
m_{a,\mu}:=\inf_{S_a}E_\mu.
\end{equation} We call ![]() $u\in S_a$ a least energy solution of (1.2) and (1.3) if
$u\in S_a$ a least energy solution of (1.2) and (1.3) if ![]() $E_\mu(u)=m_{a,\mu}$. Define
$E_\mu(u)=m_{a,\mu}$. Define
Indeed, the existence of least energy solutions depends on a 0. More precisely, our first result reads as follows.
Theorem 1.3. Let  $2 \lt q \lt p \lt 2+\frac{4s}{N}$ and µ < 0. Then, for
$2 \lt q \lt p \lt 2+\frac{4s}{N}$ and µ < 0. Then, for ![]() $m_{a,\mu}$, a 0 defined in (1.4) and (1.5), the following statements hold:
$m_{a,\mu}$, a 0 defined in (1.4) and (1.5), the following statements hold:
(i)
 $m_{a,\mu}=0$ for any
$m_{a,\mu}=0$ for any  $a\in(0, a_0]$, while
$a\in(0, a_0]$, while  $m_{a,\mu} \lt 0$ for any
$m_{a,\mu} \lt 0$ for any  $a \gt a_0$. Moreover, if
$a \gt a_0$. Moreover, if  $0 \lt a \lt a_0$, there exists no global minimizer for
$0 \lt a \lt a_0$, there exists no global minimizer for  $m_{a,\mu}$. In addition, there exists a global minimizer
$m_{a,\mu}$. In addition, there exists a global minimizer  $u\in S_a$ for
$u\in S_a$ for  $a\ge a_0$ and u is a ground state solution of (1.2) and (1.3).
$a\ge a_0$ and u is a ground state solution of (1.2) and (1.3).(ii)
 $a_0\geq\big(\frac{1}{2C_0C(s,N)}\big)^{\frac{N}{4s}}$, where
$a_0\geq\big(\frac{1}{2C_0C(s,N)}\big)^{\frac{N}{4s}}$, where  $C_0=C_0(p,q,s,|\mu|,N)$ is given by (2.2) and
$C_0=C_0(p,q,s,|\mu|,N)$ is given by (2.2) and  $C(s,N)$ is the best constant in the fractional Gagliardo–Nirenberg inequality for
$C(s,N)$ is the best constant in the fractional Gagliardo–Nirenberg inequality for  $\alpha=2+\frac{4s}{N}$ (see lemma A.1).
$\alpha=2+\frac{4s}{N}$ (see lemma A.1).(iii) The set
 $\mathcal{G}_{a,\mu}$ is orbitally stable for any
$\mathcal{G}_{a,\mu}$ is orbitally stable for any  $a \gt a_0$.
$a \gt a_0$.
Remark 1.4. Theorem 1.3 fills a gap in the previous work [Reference Luo and Zhang33, theorem 1.3 (ii)].
We remark that the global well-posedness of (1.1) can be obtained by Guo–Huang [Reference Guo and Huang19, theorem 2.6] similarly. In addition, Guo–Huang [Reference Guo and Huang19] proved that the set ![]() $\mathcal{G}_{a,\mu}$ is orbitally stable for
$\mathcal{G}_{a,\mu}$ is orbitally stable for  $2 \lt q \lt p \lt 2+\frac{4s}{N}$ and
$2 \lt q \lt p \lt 2+\frac{4s}{N}$ and ![]() $\mu\geq0$. Thus, our result is a complement to [Reference Guo and Huang19].
$\mu\geq0$. Thus, our result is a complement to [Reference Guo and Huang19].
Second, we focus on the case  $2+\frac{4s}{N} \lt q \lt p \lt \frac{2N}{N-2s}$ and µ > 0, i.e., the purely L 2-supercritical and focusing case. The energy functional Eµ is now unbounded from below on Sa. In this situation, we shall introduce the following minimizing problem on the constrained Pohozaev manifold:
$2+\frac{4s}{N} \lt q \lt p \lt \frac{2N}{N-2s}$ and µ > 0, i.e., the purely L 2-supercritical and focusing case. The energy functional Eµ is now unbounded from below on Sa. In this situation, we shall introduce the following minimizing problem on the constrained Pohozaev manifold:
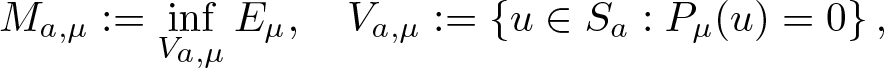 \begin{equation}
M_{a,\mu}:=\inf_{V_{a,\mu}}E_\mu, \quad V_{a,\mu}:=\left\{u\in S_a:P_\mu(u)=0\right\},
\end{equation}
\begin{equation}
M_{a,\mu}:=\inf_{V_{a,\mu}}E_\mu, \quad V_{a,\mu}:=\left\{u\in S_a:P_\mu(u)=0\right\},
\end{equation}with
 \begin{equation}
P_\mu(u)=\int_{\mathbb{R}^N}\big[|\left(-\Delta\right)^{\frac{s}{2}}u(x)|^2-\frac{N(p-2)}{2ps}|u(x)|^p-
\mu\frac{N(q-2)}{2qs}|u(x)|^q\big] \mathrm{d}x.
\end{equation}
\begin{equation}
P_\mu(u)=\int_{\mathbb{R}^N}\big[|\left(-\Delta\right)^{\frac{s}{2}}u(x)|^2-\frac{N(p-2)}{2ps}|u(x)|^p-
\mu\frac{N(q-2)}{2qs}|u(x)|^q\big] \mathrm{d}x.
\end{equation} It is well known that any critical point of ![]() $E_\mu|_{S_a}$ stays on
$E_\mu|_{S_a}$ stays on ![]() $V_{a,\mu}$ thanks to the Pohozaev identity (see [Reference Chang and Wang8, proposition 4.1]), so
$V_{a,\mu}$ thanks to the Pohozaev identity (see [Reference Chang and Wang8, proposition 4.1]), so ![]() $V_{a,\mu}$ is a natural constraint.
$V_{a,\mu}$ is a natural constraint.
In this case, we establish the existence and instability of standing waves as below.
Theorem 1.5 Assume  $2+\frac{4s}{N} \lt q \lt p \lt \frac{2N}{N-2s}$ and µ > 0. Then, the following statements hold for
$2+\frac{4s}{N} \lt q \lt p \lt \frac{2N}{N-2s}$ and µ > 0. Then, the following statements hold for ![]() $M_{a,\mu}$ defined in (1.6):
$M_{a,\mu}$ defined in (1.6):
(i)
 $M_{a,\mu}$ is achieved for any a > 0. Moreover, the minimizer u is a positive radial function, and u is a ground state solution of (1.2) and (1.3) with λ < 0.
$M_{a,\mu}$ is achieved for any a > 0. Moreover, the minimizer u is a positive radial function, and u is a ground state solution of (1.2) and (1.3) with λ < 0.(ii)
 $M_{a,\mu}$ is strictly decreasing with respect to a for µ > 0 given.
$M_{a,\mu}$ is strictly decreasing with respect to a for µ > 0 given.(iii) Suppose
 $N/(2N-1)\leq s \lt 1$ and
$N/(2N-1)\leq s \lt 1$ and  $p \lt 2+4s$ additionally. Let u be the ground state solution obtained in (i), then the standing wave
$p \lt 2+4s$ additionally. Let u be the ground state solution obtained in (i), then the standing wave  $e^{-i\lambda t}u$ of (1.1) is strongly unstable.
$e^{-i\lambda t}u$ of (1.1) is strongly unstable.
In this case, we stress that we [Reference Luo and Zhang33] obtained a solution with mountain pass geometry. Here, we give a different proof based on new variational characterizations of ground states. As one will see, these new variational characterizations also play a key role in proving the instability of the standing waves.
Remark 1.6. The restriction on s ensures the local well-posedness of (1.1) (see lemma A.3). In addition, it always holds that  $
\frac{2N}{N-2s} \lt 2+4s$ for
$
\frac{2N}{N-2s} \lt 2+4s$ for ![]() $N\geq3$.
$N\geq3$.
Finally, we deal with the combined nonlinearities and defocusing case, i.e., ![]() $2 \lt q\leq\bar{p} \lt p \lt 2_s^*,\mu \lt 0$.
$2 \lt q\leq\bar{p} \lt p \lt 2_s^*,\mu \lt 0$.
Similarly, define
 \begin{eqnarray*}
\hat{E}_\mu(u)\!:=\!E_{\mu}(u)\!-\!\!\frac{2s}{N(p-2)}P_{\mu}(u)\!=\!\Big(\frac{1}{2}\!-\!\frac{2s}{N(p-2)}\Big)|(-\Delta)^{\frac{s}{2}}u|_2^2
\!+\!\frac{\mu}{q}\Big(\frac{q-2}{p-2}\!-\!1\Big)|u|_p^p
\end{eqnarray*}
\begin{eqnarray*}
\hat{E}_\mu(u)\!:=\!E_{\mu}(u)\!-\!\!\frac{2s}{N(p-2)}P_{\mu}(u)\!=\!\Big(\frac{1}{2}\!-\!\frac{2s}{N(p-2)}\Big)|(-\Delta)^{\frac{s}{2}}u|_2^2
\!+\!\frac{\mu}{q}\Big(\frac{q-2}{p-2}\!-\!1\Big)|u|_p^p
\end{eqnarray*}and
 \begin{equation}
\hat{M}_{a,\mu}^r:=\inf_{\hat{V}_{a,\mu}}\hat{E}_\mu, \quad \hat{V}_{a,\mu}^r=\left\{u\in S_a:P_\mu(u)\leq0\right\},
\end{equation}
\begin{equation}
\hat{M}_{a,\mu}^r:=\inf_{\hat{V}_{a,\mu}}\hat{E}_\mu, \quad \hat{V}_{a,\mu}^r=\left\{u\in S_a:P_\mu(u)\leq0\right\},
\end{equation}and the existence and instability of the standing waves is established.
Theorem 1.7. Let  $2 \lt q\leq \bar{p}=2+\frac{4s}{N} \lt p \lt 2_s^*=\frac{2N}{N-2s}$ and µ < 0. We also suppose that
$2 \lt q\leq \bar{p}=2+\frac{4s}{N} \lt p \lt 2_s^*=\frac{2N}{N-2s}$ and µ < 0. We also suppose that
 \begin{equation*}
|\mu| a^{\beta(p,q)} \lt \Big(\frac{2ps}{NC(s,N,p)(p-2)}\Big)^{\frac{\bar{p}-q}{p-\bar{p}}}\Big(\frac{q(2_s^*-p)(N-2s)}{2NC(s,N,q)(p-q)}\Big),
\end{equation*}
\begin{equation*}
|\mu| a^{\beta(p,q)} \lt \Big(\frac{2ps}{NC(s,N,p)(p-2)}\Big)^{\frac{\bar{p}-q}{p-\bar{p}}}\Big(\frac{q(2_s^*-p)(N-2s)}{2NC(s,N,q)(p-q)}\Big),
\end{equation*}where
 \begin{equation*}
\beta(p,q)=\Big(p-\frac{N(p-2)}{2s}\Big)\frac{\bar{p}-q}{p-\bar{p}}+\Big(q-\frac{N(q-2)}{2s}\Big) \gt 0.
\end{equation*}
\begin{equation*}
\beta(p,q)=\Big(p-\frac{N(p-2)}{2s}\Big)\frac{\bar{p}-q}{p-\bar{p}}+\Big(q-\frac{N(q-2)}{2s}\Big) \gt 0.
\end{equation*}Then,
(i) Problems (1.2) and (1.3) admit a radial solution, denoted by
 $\hat{u}$. Moreover,
$\hat{u}$. Moreover,  $\hat{E}_\mu(\hat{u}) \gt 0$ and the Lagrange multiplier
$\hat{E}_\mu(\hat{u}) \gt 0$ and the Lagrange multiplier  $\hat{\lambda} \lt 0$.
$\hat{\lambda} \lt 0$.(ii) Suppose additionally
 $N/(2N-1)\leq s \lt 1$ and
$N/(2N-1)\leq s \lt 1$ and  $p \lt 2+4s$. Then, the standing wave
$p \lt 2+4s$. Then, the standing wave  $e^{-\mathrm{i}\hat{\lambda}t}\hat{u}$ is strongly unstable.
$e^{-\mathrm{i}\hat{\lambda}t}\hat{u}$ is strongly unstable.
In order to better explain our results, we give the following table 1 roughly.
Table 1. Existence and instability

This article is organized as follows: section 2 is devoted to the purely L 2-subcritical case. In this case, we discuss the existence and orbital stability of standing wave solutions to (1.1). Furthermore, theorem 1.3 will be established based on the concentration compactness principle. In section 3, we show theorem 1.5. In fact, we construct different variational characterizations to search for a solution to (1.2) and prove the strong instability of standing wave solutions. As a by-product, we give two invariant manifolds to determine global existence or blow-up behaviour. Section 4 considers the combined cases and proves theorem 1.7.
2. The purely L 2-subcritical and defocusing case:  $2 \lt q \lt p \lt \bar{p}=2+4s/N$ and µ < 0
$2 \lt q \lt p \lt \bar{p}=2+4s/N$ and µ < 0
By lemma A.6, it holds directly that
 \begin{equation}
C_0 t^{\bar{p}}-\frac{1}{p}t^p-\frac{\mu}{q} t^q\geq0,\quad \forall t\ge 0,
\end{equation}
\begin{equation}
C_0 t^{\bar{p}}-\frac{1}{p}t^p-\frac{\mu}{q} t^q\geq0,\quad \forall t\ge 0,
\end{equation}where
 \begin{equation}
C_0=
\frac{p-q}{p(\bar{p}-q)}\left[\frac{q(\bar{p}-p)}{p|\mu|(\bar{p}-q)}\right]^{\frac{\bar{p}-p}{p-q}}.
\end{equation}
\begin{equation}
C_0=
\frac{p-q}{p(\bar{p}-q)}\left[\frac{q(\bar{p}-p)}{p|\mu|(\bar{p}-q)}\right]^{\frac{\bar{p}-p}{p-q}}.
\end{equation}Lemma 2.1. Let ![]() $\{u_n\}_{n\in\mathbb{N}}$ be a bounded sequence in
$\{u_n\}_{n\in\mathbb{N}}$ be a bounded sequence in ![]() $H^s(\mathbb{R}^N)$ satisfying
$H^s(\mathbb{R}^N)$ satisfying ![]() $\lim_{n\rightarrow \infty}|u_n|_2^2=a^2 \gt 0$. Let
$\lim_{n\rightarrow \infty}|u_n|_2^2=a^2 \gt 0$. Let ![]() $\alpha_n=a/|u_n|_2$ and
$\alpha_n=a/|u_n|_2$ and ![]() $\tilde{u}_n=\alpha_n u_n$. Then, the following holds:
$\tilde{u}_n=\alpha_n u_n$. Then, the following holds:
 \begin{equation*}
\tilde{u}_n\in S_a,\quad \lim_{n\rightarrow \infty} \alpha_n=1,\quad \lim_{n\rightarrow \infty}| E_\mu(\tilde{u}_n)- E_\mu(u_n)|=0.
\end{equation*}
\begin{equation*}
\tilde{u}_n\in S_a,\quad \lim_{n\rightarrow \infty} \alpha_n=1,\quad \lim_{n\rightarrow \infty}| E_\mu(\tilde{u}_n)- E_\mu(u_n)|=0.
\end{equation*}Proof. The results could be derived by direct calculations, and we omit the details.
In what follows, we study the properties of ![]() $m_{a,\mu}$.
$m_{a,\mu}$.
(i)
 $m_{a,\mu}$ is bounded from below. Moreover,
$m_{a,\mu}$ is bounded from below. Moreover,  $m_{a,\mu}\leq0$ for any a > 0.
$m_{a,\mu}\leq0$ for any a > 0.(ii)
 $m_{\theta a,\mu}\leq \theta^2 m_{a,\mu}$ for any
$m_{\theta a,\mu}\leq \theta^2 m_{a,\mu}$ for any  $a \gt 0,\theta\geq1$.
$a \gt 0,\theta\geq1$.(iii) If
 $a^2=a_1^2+a_2^2$ with
$a^2=a_1^2+a_2^2$ with  $a_1,a_2 \gt 0$, then
$a_1,a_2 \gt 0$, then  $m_{a,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}$.
$m_{a,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}$.(iv)
 $a\mapsto m_{a,\mu}$ is non-increasing.
$a\mapsto m_{a,\mu}$ is non-increasing.(v) For sufficiently large a,
 $m_{a,\mu} \lt 0$ holds.
$m_{a,\mu} \lt 0$ holds.(vi)
 $a\mapsto m_{a,\mu}$ is continuous.
$a\mapsto m_{a,\mu}$ is continuous.
Proof. (i) On the one hand, by lemma A.1, we deduce that
 \begin{equation*}
E_\mu(u)\geq\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{C(s,N,p)}{p}a^{p-\frac{N(p-2)}{2s}}
\left(\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2\right)^{\frac{N(p-2)}{4s}}
\end{equation*}
\begin{equation*}
E_\mu(u)\geq\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{C(s,N,p)}{p}a^{p-\frac{N(p-2)}{2s}}
\left(\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2\right)^{\frac{N(p-2)}{4s}}
\end{equation*} for every ![]() $u\in S_a$. Since
$u\in S_a$. Since ![]() $2 \lt p \lt \bar{p}$, it holds that
$2 \lt p \lt \bar{p}$, it holds that  $0 \lt \frac{N(p-2)}{4s} \lt 1$. Hence, Eµ is coercive on Sa and
$0 \lt \frac{N(p-2)}{4s} \lt 1$. Hence, Eµ is coercive on Sa and ![]() $m_{a,\mu}$ is bounded from below. On the other hand, for
$m_{a,\mu}$ is bounded from below. On the other hand, for ![]() $u\in S_a$ and
$u\in S_a$ and ![]() $\tau\in\mathbb{R}$, set
$\tau\in\mathbb{R}$, set  $(\tau\star u)(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$, then
$(\tau\star u)(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$, then ![]() $\tau\star u \in S_a$ and
$\tau\star u \in S_a$ and
 \begin{equation}
E_\mu(\tau\star u)=\frac{e^{2s\tau}}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{e^{N\tau(\frac{p}{2}-1)}}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{e^{N\tau(\frac{q}{2}-1)}}{q}\int_{\mathbb{R}^N}|u|^q.
\end{equation}
\begin{equation}
E_\mu(\tau\star u)=\frac{e^{2s\tau}}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{e^{N\tau(\frac{p}{2}-1)}}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{e^{N\tau(\frac{q}{2}-1)}}{q}\int_{\mathbb{R}^N}|u|^q.
\end{equation} Since ![]() $2 \lt q \lt p$, we obtain
$2 \lt q \lt p$, we obtain ![]() $m_{a,\mu}\leq \lim_{\tau\rightarrow-\infty}E_\mu(\tau\star u)=0$.
$m_{a,\mu}\leq \lim_{\tau\rightarrow-\infty}E_\mu(\tau\star u)=0$.
(ii) Let ![]() $\theta\geq1$ and
$\theta\geq1$ and ![]() $u\in S_a$. Set
$u\in S_a$. Set ![]() $\tilde{u}(x)=u(\theta^{-2/N}x),x\in \mathbb{R}^N$, then
$\tilde{u}(x)=u(\theta^{-2/N}x),x\in \mathbb{R}^N$, then ![]() $\tilde{u}\in S_{\theta a}$ and
$\tilde{u}\in S_{\theta a}$ and
 \begin{align*}
E_\mu(\tilde{u})
&\leq \theta^2\Big(\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{1}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{1}{q}\int_{\mathbb{R}^N}|u|^q\Big).\nonumber
\end{align*}
\begin{align*}
E_\mu(\tilde{u})
&\leq \theta^2\Big(\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{1}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{1}{q}\int_{\mathbb{R}^N}|u|^q\Big).\nonumber
\end{align*} Since u could be chosen arbitrarily, we obtain ![]() $m_{\theta a,\mu}\leq \theta^2 m_{a,\mu}$.
$m_{\theta a,\mu}\leq \theta^2 m_{a,\mu}$.
(iii) Assume that ![]() $a_1\geq a_2$. As a consequence of (ii),
$a_1\geq a_2$. As a consequence of (ii),
 \begin{equation*}
m_{a,\mu}\leq\left(\frac{a}{a_1}\right)^2m_{a_1,\mu}=m_{a_1,\mu}+
\frac{a_2^2}{a_1^2}m_{\frac{a_1}{a_2}a_2,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}.
\end{equation*}
\begin{equation*}
m_{a,\mu}\leq\left(\frac{a}{a_1}\right)^2m_{a_1,\mu}=m_{a_1,\mu}+
\frac{a_2^2}{a_1^2}m_{\frac{a_1}{a_2}a_2,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}.
\end{equation*}(iv) This follows directly from (i) and (iii).
(v) For ![]() $u\in S_1$ given, we set
$u\in S_1$ given, we set ![]() $u_a(x)=au(x)$ for any a > 0, then it holds that
$u_a(x)=au(x)$ for any a > 0, then it holds that ![]() $u_a\in S_{a}$. Furthermore, we obtain
$u_a\in S_{a}$. Furthermore, we obtain
 \begin{equation*}
E_\mu(u_a)=\frac{a^2}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{a^p}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{a^q}{q}\int_{\mathbb{R}^N}|u|^q.
\end{equation*}
\begin{equation*}
E_\mu(u_a)=\frac{a^2}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2-\frac{a^p}{p}\int_{\mathbb{R}^N}|u|^p-
\mu\frac{a^q}{q}\int_{\mathbb{R}^N}|u|^q.
\end{equation*} Since ![]() $2 \lt q \lt p$, we know
$2 \lt q \lt p$, we know ![]() $E_\mu(u_a)\rightarrow-\infty$ as
$E_\mu(u_a)\rightarrow-\infty$ as ![]() $a\rightarrow\infty$. Thus, we get our conclusion.
$a\rightarrow\infty$. Thus, we get our conclusion.
(vi) The proof is similar to that of [Reference Luo and Zhang34, lemma 3.3 (v)] and standard.
(i) Assume that there exists a global minimizer
 $u\in S_a$ with respect to ma for some a > 0. Then,
$u\in S_a$ with respect to ma for some a > 0. Then,  $m_{\theta a,\mu} \lt \theta^2 m_{a,\mu}$ for any θ > 1.
$m_{\theta a,\mu} \lt \theta^2 m_{a,\mu}$ for any θ > 1.(ii) If there exists a global minimizer
 $u\in S_{a_1}$ with respect to
$u\in S_{a_1}$ with respect to  $m_{a_1}$ for some
$m_{a_1}$ for some  $a_1 \gt 0$, then for
$a_1 \gt 0$, then for  $a^2=a_1^2+a_2^2$ with
$a^2=a_1^2+a_2^2$ with  $a_2 \gt 0$, one has
$a_2 \gt 0$, one has  $m_{a,\mu} \lt m_{a_1,\mu}+m_{a_2,\mu}$.
$m_{a,\mu} \lt m_{a_1,\mu}+m_{a_2,\mu}$.
Proof. (i) If ![]() $u\in S_a$ satisfies
$u\in S_a$ satisfies ![]() $E_\mu(u)=m_{a,\mu}$, then
$E_\mu(u)=m_{a,\mu}$, then ![]() $u\not\equiv0$. Recalling the proof of lemma 2.2 (ii), one finds that
$u\not\equiv0$. Recalling the proof of lemma 2.2 (ii), one finds that
 \begin{equation*}
m_{\theta a,\mu}\leq E_\mu(\tilde{u}) \lt \theta^2 E_\mu(u)=\theta^2 m_{a,\mu}.
\end{equation*}
\begin{equation*}
m_{\theta a,\mu}\leq E_\mu(\tilde{u}) \lt \theta^2 E_\mu(u)=\theta^2 m_{a,\mu}.
\end{equation*} (ii) If ![]() $a_1\geq a_2 \gt 0$, by (i) and lemma 2.2 (iii), we have
$a_1\geq a_2 \gt 0$, by (i) and lemma 2.2 (iii), we have
 \begin{equation*}
m_{a,\mu} \lt \left(\frac{a}{a_1}\right)^2m_{a_1,\mu}=m_{a_1,\mu}+
\frac{a_2^2}{a_1^2}m_{a_1,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}.
\end{equation*}
\begin{equation*}
m_{a,\mu} \lt \left(\frac{a}{a_1}\right)^2m_{a_1,\mu}=m_{a_1,\mu}+
\frac{a_2^2}{a_1^2}m_{a_1,\mu}\leq m_{a_1,\mu}+m_{a_2,\mu}.
\end{equation*} If ![]() $a_2 \gt a_1 \gt 0$, by (i) and lemma 2.2 (iii) again, we get
$a_2 \gt a_1 \gt 0$, by (i) and lemma 2.2 (iii) again, we get
 \begin{equation*}
m_{a,\mu}\leq\left(\frac{a}{a_2}\right)^2m_{a_2,\mu}=m_{a_2,\mu}+
\frac{a_1^2}{a_2^2}m_{a_2,\mu} \lt m_{a_2,\mu}+m_{a_1,\mu}.
\end{equation*}
\begin{equation*}
m_{a,\mu}\leq\left(\frac{a}{a_2}\right)^2m_{a_2,\mu}=m_{a_2,\mu}+
\frac{a_1^2}{a_2^2}m_{a_2,\mu} \lt m_{a_2,\mu}+m_{a_1,\mu}.
\end{equation*}Proposition 2.4. There exists a constant ![]() $a_1 \gt 0$ such that
$a_1 \gt 0$ such that ![]() $m_{a,\mu}=0$ for any
$m_{a,\mu}=0$ for any ![]() $0 \lt a\leq a_1$. In particular, one has
$0 \lt a\leq a_1$. In particular, one has ![]() $a_0\geq a_1 \gt 0$, where a 0 is given in (1.5).
$a_0\geq a_1 \gt 0$, where a 0 is given in (1.5).
Proof. For any ![]() $u\in S_a$, by (2.1) and lemma A.1, we obtain
$u\in S_a$, by (2.1) and lemma A.1, we obtain
 \begin{align*}
E_\mu(u)
\ge\Big[\frac12-C_0C(s,N,\bar{p})a^{\frac{4s}{N}}\Big]\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2.
\end{align*}
\begin{align*}
E_\mu(u)
\ge\Big[\frac12-C_0C(s,N,\bar{p})a^{\frac{4s}{N}}\Big]\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u|^2.
\end{align*} Set  $a_1:=\big(\frac{1}{2C_0C(s,N,\bar{p})}\big)^{\frac{N}{4s}}$, then
$a_1:=\big(\frac{1}{2C_0C(s,N,\bar{p})}\big)^{\frac{N}{4s}}$, then ![]() $E_\mu(u)\geq0$ for any
$E_\mu(u)\geq0$ for any ![]() $a\in(0, a_1]$ and any
$a\in(0, a_1]$ and any ![]() $u\in S_a$. It follows by lemma 2.2 (i) that
$u\in S_a$. It follows by lemma 2.2 (i) that ![]() $m_{a,\mu}=0$ for any
$m_{a,\mu}=0$ for any ![]() $0 \lt a\leq a_1$ and
$0 \lt a\leq a_1$ and ![]() $a_0\ge a_1 \gt 0$.
$a_0\ge a_1 \gt 0$.
Proposition 2.5. Let ![]() $a \gt a_0$. Assume that
$a \gt a_0$. Assume that ![]() $\{u_n\}_{n\in\mathbb{N}}\subset S_a$ is a minimizing sequence for
$\{u_n\}_{n\in\mathbb{N}}\subset S_a$ is a minimizing sequence for ![]() $m_{a,\mu}$, i.e.,
$m_{a,\mu}$, i.e., ![]() $\lim_{n\rightarrow\infty}E_\mu(u_n)=m_{a,\mu}$. Then, up to a subsequence, there exist a family
$\lim_{n\rightarrow\infty}E_\mu(u_n)=m_{a,\mu}$. Then, up to a subsequence, there exist a family ![]() $\{y_n\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ and
$\{y_n\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ and ![]() $u\in S_a$ such that
$u\in S_a$ such that ![]() $\lim_{n\rightarrow\infty} u_n(\cdot-y_n)=u$ in
$\lim_{n\rightarrow\infty} u_n(\cdot-y_n)=u$ in ![]() $H^s(\mathbb{R}^N)$. Furthermore, u is a global minimizer for
$H^s(\mathbb{R}^N)$. Furthermore, u is a global minimizer for ![]() $m_{a,\mu}$.
$m_{a,\mu}$.
Proof. First, we claim that
 \begin{equation*}
\varlimsup_{n\rightarrow\infty}\sup_{z\in\mathbb{R}^N}\int_{B(z,1)}|u_n|^2dx \gt 0.
\end{equation*}
\begin{equation*}
\varlimsup_{n\rightarrow\infty}\sup_{z\in\mathbb{R}^N}\int_{B(z,1)}|u_n|^2dx \gt 0.
\end{equation*} Otherwise, in virtue of concentration compactness principle [Reference Felmer, Quaas and Tan14, lemma 2.2], we know ![]() $u_n\rightarrow0$ in
$u_n\rightarrow0$ in ![]() $L^p(\mathbb{R}^N)$ for any
$L^p(\mathbb{R}^N)$ for any ![]() $p\in(2,2_s^*)$. Then, it holds that
$p\in(2,2_s^*)$. Then, it holds that
 \begin{equation*}
m_{a,\mu}=\lim_{n\rightarrow\infty}E_\mu(u_n)\geq \liminf_{n\rightarrow\infty}\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u_n|^2\geq0,
\end{equation*}
\begin{equation*}
m_{a,\mu}=\lim_{n\rightarrow\infty}E_\mu(u_n)\geq \liminf_{n\rightarrow\infty}\frac{1}{2}\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u_n|^2\geq0,
\end{equation*} which contradicts with ![]() $m_{a,\mu} \lt 0$ for
$m_{a,\mu} \lt 0$ for ![]() $a \gt a_0$.
$a \gt a_0$.
From the claim above, there exists a sequence ![]() $\{y_n\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ such that, up to a subsequence,
$\{y_n\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ such that, up to a subsequence,
 \begin{equation}
0 \lt \lim_{n\rightarrow\infty}\int_{B(0,1)}|u_n(x-y_n)|^2dx \lt \infty.
\end{equation}
\begin{equation}
0 \lt \lim_{n\rightarrow\infty}\int_{B(0,1)}|u_n(x-y_n)|^2dx \lt \infty.
\end{equation} By lemma 2.2 (i), the minimizing sequence ![]() $\{u_n\}_{n\in\mathbb{N}}$ is uniformly bounded in
$\{u_n\}_{n\in\mathbb{N}}$ is uniformly bounded in ![]() $H^s(\mathbb{R}^N)$. Thus,
$H^s(\mathbb{R}^N)$. Thus, ![]() $\{u_n(\cdot-y_n)\}_{n\in\mathbb{N}}$ is also bounded in
$\{u_n(\cdot-y_n)\}_{n\in\mathbb{N}}$ is also bounded in ![]() $H^s(\mathbb{R}^N)$. As a consequence, there exists a
$H^s(\mathbb{R}^N)$. As a consequence, there exists a ![]() $u\in H^s(\mathbb{R}^N)$ such that, up to a subsequence,
$u\in H^s(\mathbb{R}^N)$ such that, up to a subsequence,
Via (2.4) and (2.5), we know ![]() $|u|_2 \gt 0$. Take
$|u|_2 \gt 0$. Take ![]() $v_n=u_n(\cdot-y_n)-u$, it holds that
$v_n=u_n(\cdot-y_n)-u$, it holds that ![]() $v_n\rightharpoonup 0$ weakly in
$v_n\rightharpoonup 0$ weakly in ![]() $H^s(\mathbb{R}^N)$. Therefore, by Brezis–Lieb lemma, as
$H^s(\mathbb{R}^N)$. Therefore, by Brezis–Lieb lemma, as ![]() $n\rightarrow\infty$,
$n\rightarrow\infty$,
 \begin{align*}
\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} u_n\right|^2dx
&=\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} u\right|^2dx+\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} v_n\right|^2dx+o(1).
\\
\int_{\mathbb{R}^N}\left|u_n\right|^rdx
&=\int_{\mathbb{R}^N}\left| u\right|^rdx+\int_{\mathbb{R}^N}\left| v_n\right|^rdx+o(1),\quad \forall r\in\big[2,\frac{2N}{N-2s}\big].
\end{align*}
\begin{align*}
\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} u_n\right|^2dx
&=\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} u\right|^2dx+\int_{\mathbb{R}^N}\left|\left(-\Delta\right)^{\frac{s}{2}} v_n\right|^2dx+o(1).
\\
\int_{\mathbb{R}^N}\left|u_n\right|^rdx
&=\int_{\mathbb{R}^N}\left| u\right|^rdx+\int_{\mathbb{R}^N}\left| v_n\right|^rdx+o(1),\quad \forall r\in\big[2,\frac{2N}{N-2s}\big].
\end{align*} Noting that ![]() $E_\mu(u_n)=E_\mu(u_n(\cdot-y_n))=E_\mu(u+v_n)$, it consequently follows that
$E_\mu(u_n)=E_\mu(u_n(\cdot-y_n))=E_\mu(u+v_n)$, it consequently follows that
 \begin{align}
E_\mu(u_n)=E_\mu(u)+E_\mu(v_n)+o(1),\quad
|u_n|_2^2=|u|_2^2+|v_n|_2^2+o(1).
\end{align}
\begin{align}
E_\mu(u_n)=E_\mu(u)+E_\mu(v_n)+o(1),\quad
|u_n|_2^2=|u|_2^2+|v_n|_2^2+o(1).
\end{align} We claim that ![]() $|v_n|_2^2\rightarrow0$ as
$|v_n|_2^2\rightarrow0$ as ![]() $n\rightarrow\infty$. Indeed, set
$n\rightarrow\infty$. Indeed, set ![]() $\zeta=|u|_2 \gt 0$, then
$\zeta=|u|_2 \gt 0$, then  $\lim\limits_{n\rightarrow\infty}|v_n|_2^2=a^2-\zeta^2$. If
$\lim\limits_{n\rightarrow\infty}|v_n|_2^2=a^2-\zeta^2$. If ![]() $\zeta=a$, then the claim holds directly. Suppose that
$\zeta=a$, then the claim holds directly. Suppose that ![]() $\zeta \lt a$ and set
$\zeta \lt a$ and set  $\tilde{v}_n=\frac{\sqrt{a^2-\zeta^2}}{|v_n|_2}v_n$. In virtue of lemma 2.1 and (2.6), we obtain
$\tilde{v}_n=\frac{\sqrt{a^2-\zeta^2}}{|v_n|_2}v_n$. In virtue of lemma 2.1 and (2.6), we obtain
 \begin{equation*}
E_\mu(u_n)=E_\mu(u)+E_\mu(v_n)+o(1)=E_\mu(u)+E_\mu(\tilde{v}_n)+o(1)\geq E_\mu(u)+m_{\sqrt{a^2-\zeta^2},\mu}+o(1).
\end{equation*}
\begin{equation*}
E_\mu(u_n)=E_\mu(u)+E_\mu(v_n)+o(1)=E_\mu(u)+E_\mu(\tilde{v}_n)+o(1)\geq E_\mu(u)+m_{\sqrt{a^2-\zeta^2},\mu}+o(1).
\end{equation*} Furthermore, letting ![]() $n\rightarrow\infty$ and by lemma 2.2 (iii), we deduce that
$n\rightarrow\infty$ and by lemma 2.2 (iii), we deduce that
 \begin{equation}
m_{a,\mu}\geq E_\mu(u)+m_{\sqrt{a^2-\zeta^2},\mu}\geq m_{\zeta,\mu}+m_{\sqrt{a^2-\zeta^2},\mu}\geq m_{a,\mu},
\end{equation}
\begin{equation}
m_{a,\mu}\geq E_\mu(u)+m_{\sqrt{a^2-\zeta^2},\mu}\geq m_{\zeta,\mu}+m_{\sqrt{a^2-\zeta^2},\mu}\geq m_{a,\mu},
\end{equation} which gives ![]() $E_\mu(u)=m_{\zeta,\mu}$. According to Corollary 2.3 (ii), it holds that
$E_\mu(u)=m_{\zeta,\mu}$. According to Corollary 2.3 (ii), it holds that
 \begin{equation*}
m_{a,\mu} \lt m_{\zeta,\mu}+m_{\sqrt{a^2-\zeta^2}},
\end{equation*}
\begin{equation*}
m_{a,\mu} \lt m_{\zeta,\mu}+m_{\sqrt{a^2-\zeta^2}},
\end{equation*} which contradicts with (2.7). Thus, the claim holds and ![]() $|u|_2^2=a^2$.
$|u|_2^2=a^2$.
Since ![]() $\lim_{n\rightarrow\infty}|v_n|_2^2=0$, recalling that
$\lim_{n\rightarrow\infty}|v_n|_2^2=0$, recalling that ![]() $\left\{v_n\right\}$ is bounded in
$\left\{v_n\right\}$ is bounded in ![]() $H^s(\mathbb{R}^N)$, it follows by Hölder inequality that
$H^s(\mathbb{R}^N)$, it follows by Hölder inequality that ![]() $\lim_{n\rightarrow\infty}|v_n|_p=0$ and
$\lim_{n\rightarrow\infty}|v_n|_p=0$ and ![]() $\lim_{n\rightarrow\infty}|v_n|_q=0$. Moreover,
$\lim_{n\rightarrow\infty}|v_n|_q=0$. Moreover,
 \begin{equation}
\liminf_{n\rightarrow\infty}E_\mu(v_n)=\liminf_{n\rightarrow\infty}\frac{1}{2}|(-\Delta)^{\frac{s}{2}}
v_n|_2^2\geq0.
\end{equation}
\begin{equation}
\liminf_{n\rightarrow\infty}E_\mu(v_n)=\liminf_{n\rightarrow\infty}\frac{1}{2}|(-\Delta)^{\frac{s}{2}}
v_n|_2^2\geq0.
\end{equation} In addition, by ![]() $|u|_2^2=a^2$ and (2.6),
$|u|_2^2=a^2$ and (2.6),
which implies
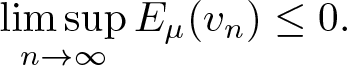 \begin{equation}
\limsup_{n\rightarrow\infty}E_\mu(v_n)\leq0.
\end{equation}
\begin{equation}
\limsup_{n\rightarrow\infty}E_\mu(v_n)\leq0.
\end{equation} It follows from (2.8) and (2.9) that  $\lim\limits_{n\rightarrow\infty}|(-\Delta)^{\frac{s}{2}}
v_n|_2^2\rightarrow0$. Hence,
$\lim\limits_{n\rightarrow\infty}|(-\Delta)^{\frac{s}{2}}
v_n|_2^2\rightarrow0$. Hence, ![]() $u_n(\cdot-y_n)\rightarrow u$ strongly in
$u_n(\cdot-y_n)\rightarrow u$ strongly in ![]() $H^s(\mathbb{R}^N)$.
$H^s(\mathbb{R}^N)$.
Remark 2.6. For the minimizing sequence with respect to ![]() $m_{a_0,\mu}$, either the vanishing case occurs or the compactness case holds.
$m_{a_0,\mu}$, either the vanishing case occurs or the compactness case holds.
Proof of theorem 1.3 (i) To begin with, we infer from proposition 2.4 that ![]() $a_0 \gt 0$. By lemma 2.2, we know
$a_0 \gt 0$. By lemma 2.2, we know ![]() $m_{a,\mu}$ is non-positive, non-increasing, and continuous in a. Thus, by the definition of a 0, we have
$m_{a,\mu}$ is non-positive, non-increasing, and continuous in a. Thus, by the definition of a 0, we have ![]() $m_{a,\mu}=0$ for any
$m_{a,\mu}=0$ for any ![]() $0 \lt a\leq a_0$ and
$0 \lt a\leq a_0$ and ![]() $m_{a,\mu} \lt 0$ for any
$m_{a,\mu} \lt 0$ for any ![]() $a \gt a_0$.
$a \gt a_0$.
Moreover, we claim that ![]() $m_{a,\mu}$ cannot be achieved for any
$m_{a,\mu}$ cannot be achieved for any ![]() $0 \lt a \lt a_0$. If not, assume
$0 \lt a \lt a_0$. If not, assume ![]() $m_{a,\mu}$ is achieved for some
$m_{a,\mu}$ is achieved for some ![]() $0 \lt a \lt a_0$, then it follows from corollary 2.3 (ii) that
$0 \lt a \lt a_0$, then it follows from corollary 2.3 (ii) that ![]() $m_{a_0,\mu} \lt m_{a,\mu}=0$, which contradicts with the definition of a 0.
$m_{a_0,\mu} \lt m_{a,\mu}=0$, which contradicts with the definition of a 0.
For ![]() $a \gt a_0$, the existence of a least energy solution to (1.2) and (1.3) follows directly from proposition 2.5. We know that the least energy solution is also a ground state solution.
$a \gt a_0$, the existence of a least energy solution to (1.2) and (1.3) follows directly from proposition 2.5. We know that the least energy solution is also a ground state solution.
Finally, we try to show that ![]() $m_{a,\mu}$ is achieved for
$m_{a,\mu}$ is achieved for ![]() $a=a_0$. Let un be a global minimizer for
$a=a_0$. Let un be a global minimizer for ![]() $m_{a_0+\frac{1}{n}, \mu}$ for any
$m_{a_0+\frac{1}{n}, \mu}$ for any ![]() $n\in\mathbb{N}$, then using the symmetric arrangement, we can assume that un is radially symmetric with respect to the origin and it is non-increasing. Since
$n\in\mathbb{N}$, then using the symmetric arrangement, we can assume that un is radially symmetric with respect to the origin and it is non-increasing. Since ![]() $E_{\mu}\left(u_n\right)$ and
$E_{\mu}\left(u_n\right)$ and ![]() $\left|u_n\right|_{2}$ are uniformly bounded,
$\left|u_n\right|_{2}$ are uniformly bounded, ![]() $\left\{u_n\right\}_{n\in\mathbb{N}}$ is a bounded sequence in
$\left\{u_n\right\}_{n\in\mathbb{N}}$ is a bounded sequence in ![]() $H^s\left(\mathbb{R}^N\right)$. What is more,
$H^s\left(\mathbb{R}^N\right)$. What is more,  $\lim\limits_{n\rightarrow \infty}\left|u_n\right|_{2}=a_0$. Set
$\lim\limits_{n\rightarrow \infty}\left|u_n\right|_{2}=a_0$. Set  $v_n=\frac{\sqrt{a_0}}{\left|u_n\right|_{2}}u_n,$ then we can deduce from lemma 2.1 that
$v_n=\frac{\sqrt{a_0}}{\left|u_n\right|_{2}}u_n,$ then we can deduce from lemma 2.1 that
 \begin{equation*}
v_n\in S_{a_0},\quad \lim\limits_{n\rightarrow \infty}E_{\mu}\left(v_n\right)=\lim\limits_{n\rightarrow \infty}E_{\mu}\left(u_n\right)=\lim\limits_{n\rightarrow \infty}m_{a_0+\frac{1}{n},\mu}=0,
\end{equation*}
\begin{equation*}
v_n\in S_{a_0},\quad \lim\limits_{n\rightarrow \infty}E_{\mu}\left(v_n\right)=\lim\limits_{n\rightarrow \infty}E_{\mu}\left(u_n\right)=\lim\limits_{n\rightarrow \infty}m_{a_0+\frac{1}{n},\mu}=0,
\end{equation*} where the last equality follows from the continuity of ![]() $m_{a,\mu}$ and
$m_{a,\mu}$ and ![]() $m_{a_0,\mu}=0$. Thus,
$m_{a_0,\mu}=0$. Thus, ![]() $\left\{v_n\right\}_{n\in\mathbb{N}}\subset S_{a_0}$ is a minimizing sequence for
$\left\{v_n\right\}_{n\in\mathbb{N}}\subset S_{a_0}$ is a minimizing sequence for ![]() $m_{a_0,\mu}.$
$m_{a_0,\mu}.$
Claim. Up to a subsequence, there exist ![]() $v\in S_{a_0}$ and
$v\in S_{a_0}$ and  $\left\{y_n\right\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ such that
$\left\{y_n\right\}_{n\in\mathbb{N}}\subset \mathbb{R}^N$ such that
 \begin{equation*}
v_n\left(\cdot -y_n\right)\rightarrow v\ \text{in}\ H^s\left(\mathbb{R}^N\right) \ \text{as}\ n\rightarrow \infty.
\end{equation*}
\begin{equation*}
v_n\left(\cdot -y_n\right)\rightarrow v\ \text{in}\ H^s\left(\mathbb{R}^N\right) \ \text{as}\ n\rightarrow \infty.
\end{equation*} In particular, v is a global minimizer of ![]() $m_{a_0,\mu}.$ If the claim fails, by the remark 2.6, since
$m_{a_0,\mu}.$ If the claim fails, by the remark 2.6, since  $v_n=\frac{\sqrt{a_0}}{\left|u_n\right|_{2}}u_n$, we obtain
$v_n=\frac{\sqrt{a_0}}{\left|u_n\right|_{2}}u_n$, we obtain
 \begin{equation}
\varlimsup_{n\rightarrow \infty} \sup\limits_{z\in\mathbb{R}^N}\int_{B\left(z,1\right)}\left|u_n\right|^2\mathrm{d}x=0.
\end{equation}
\begin{equation}
\varlimsup_{n\rightarrow \infty} \sup\limits_{z\in\mathbb{R}^N}\int_{B\left(z,1\right)}\left|u_n\right|^2\mathrm{d}x=0.
\end{equation} By a similar argument as the proof of Claim 2 in [Reference Li, Zhang and Zhang27, theorem 1.3], we can know ![]() $\left\{u_n\right\}_{n\in\mathbb{N}}$ is a uniformly bounded sequence in
$\left\{u_n\right\}_{n\in\mathbb{N}}$ is a uniformly bounded sequence in ![]() $C^{\gamma_0}\left(\mathbb{R}^N\right)$ for some small constant
$C^{\gamma_0}\left(\mathbb{R}^N\right)$ for some small constant ![]() $\gamma_0 \gt 0$. Together with
$\gamma_0 \gt 0$. Together with ![]() $\left(2.10\right)$, it follows that
$\left(2.10\right)$, it follows that ![]() $u_n\left(0\right)=\left\|u_n\right\|_{L^{\infty}}\rightarrow 0$ as
$u_n\left(0\right)=\left\|u_n\right\|_{L^{\infty}}\rightarrow 0$ as ![]() $n\rightarrow \infty.$
$n\rightarrow \infty.$
Define  $v_{\eta,n}:=\eta^{\frac{N}{2}}u_n(\eta x)$ for η > 1 large, then
$v_{\eta,n}:=\eta^{\frac{N}{2}}u_n(\eta x)$ for η > 1 large, then  $v_{\eta,n}\in S_{a_0+\frac{1}{n}}$. Note that
$v_{\eta,n}\in S_{a_0+\frac{1}{n}}$. Note that  $2 \lt q \lt p \lt 2+\frac{4s}{N}$, thus
$2 \lt q \lt p \lt 2+\frac{4s}{N}$, thus  $0 \lt \frac{N(q-2)}{2} \lt \frac{N(p-2)}{2} \lt 2s$ and
$0 \lt \frac{N(q-2)}{2} \lt \frac{N(p-2)}{2} \lt 2s$ and  $0 \lt \eta^{2s}-\eta^{\frac{N(p-2)}{2}} \lt \eta^{2s}-\eta^{\frac{N(q-2)}{2}}$. Consequently, for n large,
$0 \lt \eta^{2s}-\eta^{\frac{N(p-2)}{2}} \lt \eta^{2s}-\eta^{\frac{N(q-2)}{2}}$. Consequently, for n large, ![]() $\|u_n\|^{p-q}_{L^{\infty}} \lt |\mu|$, and
$\|u_n\|^{p-q}_{L^{\infty}} \lt |\mu|$, and
 \begin{equation*}
\begin{aligned}
E_{\mu}(v_{\eta,n})-\eta^{2s}E_{\mu}(u_n)
&=\int_{\mathbb{R}^N}|u_n|^q\left[\left(\eta^{2s}-\eta^{\frac{N(p-2)}{2}}\right)\frac{1}{p}|u_n|^{p-q}\right.\nonumber\\
& \quad \left. +\left(\eta^{2s}-\eta^{\frac{N(q-2)}{2}}\right)\frac{\mu}{q}\right]\mathrm{d}x \lt 0.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
E_{\mu}(v_{\eta,n})-\eta^{2s}E_{\mu}(u_n)
&=\int_{\mathbb{R}^N}|u_n|^q\left[\left(\eta^{2s}-\eta^{\frac{N(p-2)}{2}}\right)\frac{1}{p}|u_n|^{p-q}\right.\nonumber\\
& \quad \left. +\left(\eta^{2s}-\eta^{\frac{N(q-2)}{2}}\right)\frac{\mu}{q}\right]\mathrm{d}x \lt 0.
\end{aligned}
\end{equation*}We obtain
 \begin{equation*}
m_{a_0+\frac{1}{n},\mu}\le E_{\mu}\left(v_\eta,n\right) \lt \eta^{2s}E_{\mu}\left(u_n\right) \lt E_{\mu }\left(u_n\right)=m_{a_0+\frac{1}{n},\mu},
\end{equation*}
\begin{equation*}
m_{a_0+\frac{1}{n},\mu}\le E_{\mu}\left(v_\eta,n\right) \lt \eta^{2s}E_{\mu}\left(u_n\right) \lt E_{\mu }\left(u_n\right)=m_{a_0+\frac{1}{n},\mu},
\end{equation*} which is a contradiction; thus, there exists a global minimizer for ![]() $m_{a_0,\mu}.$
$m_{a_0,\mu}.$
(ii) The lower bound of a 0 is given by proposition 2.4.
(iii) We prove by contradiction. Suppose there exists ![]() $\varepsilon_0 \gt 0$, a sequence of solutions
$\varepsilon_0 \gt 0$, a sequence of solutions ![]() $\{\psi_n\}_{n\in\mathbb{N}}$ of (1.1), and a sequence
$\{\psi_n\}_{n\in\mathbb{N}}$ of (1.1), and a sequence ![]() $\{t_n\}_{n\in\mathbb{N}}$ such that
$\{t_n\}_{n\in\mathbb{N}}$ such that
 \begin{equation*}\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(0,\cdot)-v\right\|_{H^s} \lt 1/n,\end{equation*}
\begin{equation*}\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(0,\cdot)-v\right\|_{H^s} \lt 1/n,\end{equation*}but
 \begin{equation*}
\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(t_n,\cdot)-v\right\|_{H^s}\geq\varepsilon_0.
\end{equation*}
\begin{equation*}
\inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(t_n,\cdot)-v\right\|_{H^s}\geq\varepsilon_0.
\end{equation*}By the conservation of mass and energy, it holds that
 \begin{equation*}
|\psi_n(t_n,\cdot)|_2^2=|\psi_n(0,\cdot)|_2^2\rightarrow a^2,\quad E_\mu(\psi_n(t_n,\cdot))=E_\mu(\psi_n(0,\cdot))\rightarrow m_{a,\mu}.
\end{equation*}
\begin{equation*}
|\psi_n(t_n,\cdot)|_2^2=|\psi_n(0,\cdot)|_2^2\rightarrow a^2,\quad E_\mu(\psi_n(t_n,\cdot))=E_\mu(\psi_n(0,\cdot))\rightarrow m_{a,\mu}.
\end{equation*} Let ![]() $\alpha_n=a/|\psi_n(t_n,\cdot)|_2$ and
$\alpha_n=a/|\psi_n(t_n,\cdot)|_2$ and ![]() $\tilde{\psi}_n(x)=\alpha_n \psi_n(t_n,x)$. Then, by lemma 2.1, the following holds:
$\tilde{\psi}_n(x)=\alpha_n \psi_n(t_n,x)$. Then, by lemma 2.1, the following holds:
 \begin{equation*}
\tilde{\psi}_n\in S_a,\quad \lim_{n\rightarrow \infty} \alpha_n=1,\quad \lim_{n\rightarrow \infty}E_\mu(\tilde{\psi}_n)= m_{a,\mu}.
\end{equation*}
\begin{equation*}
\tilde{\psi}_n\in S_a,\quad \lim_{n\rightarrow \infty} \alpha_n=1,\quad \lim_{n\rightarrow \infty}E_\mu(\tilde{\psi}_n)= m_{a,\mu}.
\end{equation*} By proposition 2.5, there exist a family ![]() $\{y_n\}\subset \mathbb{R}^N$ and
$\{y_n\}\subset \mathbb{R}^N$ and ![]() $u\in\mathcal{G}_{a,\mu}$ such that
$u\in\mathcal{G}_{a,\mu}$ such that ![]() $\lim_{n\rightarrow\infty} \tilde{\psi}_n(\cdot-y_n)=u$ in
$\lim_{n\rightarrow\infty} \tilde{\psi}_n(\cdot-y_n)=u$ in ![]() $H^s(\mathbb{R}^N)$. Thus,
$H^s(\mathbb{R}^N)$. Thus,  $\lim\limits_{n\rightarrow\infty} \left\|\psi_n(t_n,\cdot-y_n)-u\right\|_{H^s}=0$. A contradiction follows from the following inequalities:
$\lim\limits_{n\rightarrow\infty} \left\|\psi_n(t_n,\cdot-y_n)-u\right\|_{H^s}=0$. A contradiction follows from the following inequalities:
 \begin{align*}
\varepsilon_0 & \le \inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(t_n,\cdot)-v\right\|_{H^s}\leq \left\|\psi_n(t_n,\cdot)-u(\cdot-y_n)\right\|_{H^s} \\
& =
\left\|\psi_n(t_n,\cdot-y_n)-u\right\|_{H^s}=o(1)
\end{align*}
\begin{align*}
\varepsilon_0 & \le \inf_{v\in\mathcal{G}_{a,\mu}}\left\|\psi_n(t_n,\cdot)-v\right\|_{H^s}\leq \left\|\psi_n(t_n,\cdot)-u(\cdot-y_n)\right\|_{H^s} \\
& =
\left\|\psi_n(t_n,\cdot-y_n)-u\right\|_{H^s}=o(1)
\end{align*} as ![]() $n\rightarrow\infty$.
$n\rightarrow\infty$.
3. The purely L 2-supercritical and focusing case:  $\bar{p}=2+4s/N \lt q \lt p \lt 2_s^*$ and µ > 0
$\bar{p}=2+4s/N \lt q \lt p \lt 2_s^*$ and µ > 0
Recall the minimizing problem:
 \begin{equation}
{M}_{a,\mu}=\inf_{{V}_{a,\mu}}E_\mu,\quad {V}_{a,\mu}=\Big\{u\in H^s(\mathbb{R}^N):\int_{\mathbb{R}^N}|u|^2= a^2,P_\mu(u)=0\Big\},
\end{equation}
\begin{equation}
{M}_{a,\mu}=\inf_{{V}_{a,\mu}}E_\mu,\quad {V}_{a,\mu}=\Big\{u\in H^s(\mathbb{R}^N):\int_{\mathbb{R}^N}|u|^2= a^2,P_\mu(u)=0\Big\},
\end{equation} where ![]() $P_{\mu}(u)$ is defined in (1.7). Next, we briefly explain our strategy for proving theorem 1.5(i) and (ii). Actually, to prove
$P_{\mu}(u)$ is defined in (1.7). Next, we briefly explain our strategy for proving theorem 1.5(i) and (ii). Actually, to prove ![]() ${M}_{a,\mu}$ is achieved, we consider another minimizing problem:
${M}_{a,\mu}$ is achieved, we consider another minimizing problem:
 \begin{equation*}
\overline{M}_{a,\mu}:=\inf_{\overline{V}_{a,\mu}}E_\mu,\quad \overline{V}_{a,\mu}:=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}\!:\!\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x\leq a^2,P_\mu(u)=0\Big\}.
\end{equation*}
\begin{equation*}
\overline{M}_{a,\mu}:=\inf_{\overline{V}_{a,\mu}}E_\mu,\quad \overline{V}_{a,\mu}:=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}\!:\!\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x\leq a^2,P_\mu(u)=0\Big\}.
\end{equation*} It is clear that ![]() $ {M}_{a,\mu}\ge \overline{M}_{a,\mu}$ since
$ {M}_{a,\mu}\ge \overline{M}_{a,\mu}$ since ![]() ${V}_{a,\mu}\subset \overline{V}_{a,\mu}$. For one thing, we will show that
${V}_{a,\mu}\subset \overline{V}_{a,\mu}$. For one thing, we will show that ![]() $\overline{M}_{a,\mu}$ is achieved based on the profile decomposition of bounded sequences in
$\overline{M}_{a,\mu}$ is achieved based on the profile decomposition of bounded sequences in ![]() $H^s(\mathbb{R}^N)$ (see lemma A.2). For another thing, we intend to prove the minimizer u actually stays in
$H^s(\mathbb{R}^N)$ (see lemma A.2). For another thing, we intend to prove the minimizer u actually stays in ![]() $V_{a,\mu}$ by showing
$V_{a,\mu}$ by showing
 \begin{align*}
& M_{a,\mu} \lt E_\mu(u) \quad \text{for\ every}\ u\in \mathring{V}_{a,\mu}\\
& \quad :=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}:\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x \lt a^2,P_\mu(u)=0\Big\}.
\end{align*}
\begin{align*}
& M_{a,\mu} \lt E_\mu(u) \quad \text{for\ every}\ u\in \mathring{V}_{a,\mu}\\
& \quad :=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}:\int_{\mathbb{R}^N}|u(x)|^2\mathrm{d}x \lt a^2,P_\mu(u)=0\Big\}.
\end{align*} It turns out that ![]() $M_{a,\mu}$ is achieved. In addition, we deduce the monotonicity of
$M_{a,\mu}$ is achieved. In addition, we deduce the monotonicity of ![]() $M_{a,\mu}$.
$M_{a,\mu}$.
First, we analyse the property of ![]() $ \overline{V}_{a,\mu}$ and
$ \overline{V}_{a,\mu}$ and ![]() $ \overline{M}_{a,\mu}$.
$ \overline{M}_{a,\mu}$.
Lemma 3.1. There exists a constant ![]() $\delta_0 \gt 0$ such that
$\delta_0 \gt 0$ such that
 \begin{equation*}
\inf_{u\in\overline{V}_{a,\mu}} |\left(-\Delta\right)^{\frac{s}{2}}u|_2^2\geq\delta_0.
\end{equation*}
\begin{equation*}
\inf_{u\in\overline{V}_{a,\mu}} |\left(-\Delta\right)^{\frac{s}{2}}u|_2^2\geq\delta_0.
\end{equation*} Moreover, Eµ is coercive on ![]() $\overline{V}_{a,\mu}$, and there exists a constant
$\overline{V}_{a,\mu}$, and there exists a constant ![]() $\delta_1 \gt 0$ such that
$\delta_1 \gt 0$ such that
Proof. First, by ![]() $P_{\mu}(u)=0$ and lemma A.1, one has, for every
$P_{\mu}(u)=0$ and lemma A.1, one has, for every ![]() $u\in\overline{V}_{a,\mu}$,
$u\in\overline{V}_{a,\mu}$,
 \begin{align*}
|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2
&\leq\frac{N(p-2)}{2ps}C(s,N,p)a^{p-\frac{N(p-2)}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(p-2)}{2s}}\\
& \quad +\mu\frac{N(q-2)}{2qs}C(s,N,q)a^{p-\frac{N(q-2)}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(q-2)}{2s}},
\end{align*}
\begin{align*}
|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2
&\leq\frac{N(p-2)}{2ps}C(s,N,p)a^{p-\frac{N(p-2)}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(p-2)}{2s}}\\
& \quad +\mu\frac{N(q-2)}{2qs}C(s,N,q)a^{p-\frac{N(q-2)}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(q-2)}{2s}},
\end{align*}which implies
 \begin{align*}
1\leq C_1(s,N,p,a)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(p-2)}{2s}-2}+C_2(s,N,p,a,\mu)
|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(q-2)}{2s}-2}.
\end{align*}
\begin{align*}
1\leq C_1(s,N,p,a)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(p-2)}{2s}-2}+C_2(s,N,p,a,\mu)
|\left(-\Delta\right)^{\frac{s}{2}}u|_2^{\frac{N(q-2)}{2s}-2}.
\end{align*} Noting that ![]() $p \gt q \gt 2+4s/N$, we have
$p \gt q \gt 2+4s/N$, we have  $\frac{N(p-2)}{2s}-2 \gt \frac{N(q-2)}{2s}-2 \gt 0$. Thus, there exists a constant
$\frac{N(p-2)}{2s}-2 \gt \frac{N(q-2)}{2s}-2 \gt 0$. Thus, there exists a constant ![]() $\delta_0 \gt 0$ such that
$\delta_0 \gt 0$ such that
 \begin{equation}
\inf_{u\in\overline{V}_{a,\mu}} |\left(-\Delta\right)^{\frac{s}{2}}u|_2^2\geq\delta_0.
\end{equation}
\begin{equation}
\inf_{u\in\overline{V}_{a,\mu}} |\left(-\Delta\right)^{\frac{s}{2}}u|_2^2\geq\delta_0.
\end{equation}Moreover, we note that
 \begin{align*}
\overline{M}_{a,\mu} & =\inf_{u\in\overline{V}_{a,\mu}}\Big[\Big(\frac{1}{2}-\frac{2s}{N(q-2)}\Big)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2
+\frac{1}{p}\Big(\frac{p-2}{q-2}-1\Big)|u|_p^p\Big]\\
& \geq \inf_{u\in\overline{V}_{a,\mu}}\Big(\frac{1}{2}-\frac{2s}{N(q-2)}\Big)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2.
\end{align*}
\begin{align*}
\overline{M}_{a,\mu} & =\inf_{u\in\overline{V}_{a,\mu}}\Big[\Big(\frac{1}{2}-\frac{2s}{N(q-2)}\Big)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2
+\frac{1}{p}\Big(\frac{p-2}{q-2}-1\Big)|u|_p^p\Big]\\
& \geq \inf_{u\in\overline{V}_{a,\mu}}\Big(\frac{1}{2}-\frac{2s}{N(q-2)}\Big)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2.
\end{align*} Therefore,  $E_{\mu}|_{\overline{V}_{a,\mu}}$ is coercive, and by (3.2), we obtain
$E_{\mu}|_{\overline{V}_{a,\mu}}$ is coercive, and by (3.2), we obtain  $ \overline{M}_{a,\mu}\geq \delta_1:=\big(\frac{1}{2}-\frac{2s}{N(q-2)}\big)\delta_0$.
$ \overline{M}_{a,\mu}\geq \delta_1:=\big(\frac{1}{2}-\frac{2s}{N(q-2)}\big)\delta_0$.
Proposition 3.2. ![]() $\overline{M}_{a,\mu}$ is achieved at some
$\overline{M}_{a,\mu}$ is achieved at some ![]() $u\in\overline{V}_{a,\mu}$. Moreover, the minimizer u is non-negative and radially symmetric.
$u\in\overline{V}_{a,\mu}$. Moreover, the minimizer u is non-negative and radially symmetric.
Proof. Let ![]() $\{v_n\}_{n\in\mathbb{N}}$ be a minimizing sequence of
$\{v_n\}_{n\in\mathbb{N}}$ be a minimizing sequence of ![]() $\overline{M}_{a,\mu}$, then we have
$\overline{M}_{a,\mu}$, then we have
By lemma 3.1, ![]() $\{v_n\}_{n\in\mathbb{N}}$ is bounded in
$\{v_n\}_{n\in\mathbb{N}}$ is bounded in ![]() $H^s(\mathbb{R}^N)$ and
$H^s(\mathbb{R}^N)$ and
 \begin{equation*}
\liminf_{n\rightarrow\infty} |\left(-\Delta\right)^{\frac{s}{2}}v_n|_2^2\geq\delta_0.
\end{equation*}
\begin{equation*}
\liminf_{n\rightarrow\infty} |\left(-\Delta\right)^{\frac{s}{2}}v_n|_2^2\geq\delta_0.
\end{equation*} Applying lemma A.2, we find a profile decomposition of ![]() $\{v_n\}_{n\in\mathbb{N}}$ satisfying
$\{v_n\}_{n\in\mathbb{N}}$ satisfying
 \begin{equation}
\limsup_{n\rightarrow +\infty}|v_n|_\gamma^\gamma=\sum_{j=1}^\infty |V^j|_\gamma^\gamma \quad \mbox{for every~}\gamma\in\Big(2,\frac{2N}{(N-2s)^+}\Big).
\end{equation}
\begin{equation}
\limsup_{n\rightarrow +\infty}|v_n|_\gamma^\gamma=\sum_{j=1}^\infty |V^j|_\gamma^\gamma \quad \mbox{for every~}\gamma\in\Big(2,\frac{2N}{(N-2s)^+}\Big).
\end{equation}Let
then ![]() $J\neq\emptyset$. Otherwise, we can deduce from (3.3) that
$J\neq\emptyset$. Otherwise, we can deduce from (3.3) that
 \begin{equation*}
\limsup_{n\rightarrow +\infty}|v_n|_p^p=\limsup_{n\rightarrow +\infty}|v_n|_q^q=0.
\end{equation*}
\begin{equation*}
\limsup_{n\rightarrow +\infty}|v_n|_p^p=\limsup_{n\rightarrow +\infty}|v_n|_q^q=0.
\end{equation*} Noting that ![]() $P_\mu(v_n)=0$, we get
$P_\mu(v_n)=0$, we get
 \begin{equation*}
\delta_0\le \limsup_{n\rightarrow +\infty}|\left(-\Delta\right)^{\frac{s}{2}}v_n|_2^2=0,
\end{equation*}
\begin{equation*}
\delta_0\le \limsup_{n\rightarrow +\infty}|\left(-\Delta\right)^{\frac{s}{2}}v_n|_2^2=0,
\end{equation*}which is a contradiction.
We claim that there exists some ![]() $j_0\in J$ such that
$j_0\in J$ such that
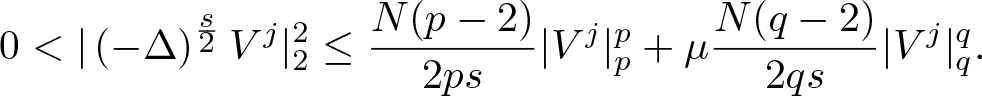 \begin{equation}
0 \lt |\left(-\Delta\right)^{\frac{s}{2}}V^j|_2^2\leq \frac{N(p-2)}{2ps}|V^j|_p^p+
\mu\frac{N(q-2)}{2qs}|V^j|_q^q.
\end{equation}
\begin{equation}
0 \lt |\left(-\Delta\right)^{\frac{s}{2}}V^j|_2^2\leq \frac{N(p-2)}{2ps}|V^j|_p^p+
\mu\frac{N(q-2)}{2qs}|V^j|_q^q.
\end{equation} Otherwise, we suppose that for all ![]() $j\in J$,
$j\in J$,
 \begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}V^j|_2^2 \gt \frac{N(p-2)}{2ps}|V^j|_p^p+
\mu\frac{N(q-2)}{2qs}|V^j|_q^q.
\end{equation*}
\begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}V^j|_2^2 \gt \frac{N(p-2)}{2ps}|V^j|_p^p+
\mu\frac{N(q-2)}{2qs}|V^j|_q^q.
\end{equation*} Then, by lemma A.2 and ![]() $P_\mu(v_n)=0$, we obtain
$P_\mu(v_n)=0$, we obtain
 \begin{align*}
& \limsup_{n\rightarrow +\infty}\Big(\frac{N(p-2)}{2ps}|v_n|_p^p+\mu\frac{N(q-2)}{2qs}|v_n|_q^q\Big)\\
& \quad \geq \sum_{j\in J}|\left(-\Delta\right)^{\frac{s}{2}}V^j|_{2}^2 \gt \sum_{j\in J}\Big(\frac{N(p-2)}{2ps}|V^j|_p^p+\mu\frac{N(q-2)}{2qs}|V^j|_q^q\Big)\\
& \quad =\limsup_{n\rightarrow +\infty}\Big(\frac{N(p-2)}{2ps}|v_n|_p^p+\mu\frac{N(q-2)}{2qs}|v_n|_q^q\Big),
\end{align*}
\begin{align*}
& \limsup_{n\rightarrow +\infty}\Big(\frac{N(p-2)}{2ps}|v_n|_p^p+\mu\frac{N(q-2)}{2qs}|v_n|_q^q\Big)\\
& \quad \geq \sum_{j\in J}|\left(-\Delta\right)^{\frac{s}{2}}V^j|_{2}^2 \gt \sum_{j\in J}\Big(\frac{N(p-2)}{2ps}|V^j|_p^p+\mu\frac{N(q-2)}{2qs}|V^j|_q^q\Big)\\
& \quad =\limsup_{n\rightarrow +\infty}\Big(\frac{N(p-2)}{2ps}|v_n|_p^p+\mu\frac{N(q-2)}{2qs}|v_n|_q^q\Big),
\end{align*}which is a contradiction. Thus the claim holds.
Let us define
 \begin{equation}
r_u:=\Big(\frac{\frac{N(p-2)}{2ps}|u|_p^p+\mu\frac{N(q-2)}{2qs}|u|_q^q}{|(-\Delta)^{\frac{s}{2}}u|_2^2}\Big)^{\frac{1}{2s}},
\end{equation}
\begin{equation}
r_u:=\Big(\frac{\frac{N(p-2)}{2ps}|u|_p^p+\mu\frac{N(q-2)}{2qs}|u|_q^q}{|(-\Delta)^{\frac{s}{2}}u|_2^2}\Big)^{\frac{1}{2s}},
\end{equation} then we know ![]() $P_\mu(u(r_u\cdot))=0$. Thus, by (3.4), there exists some
$P_\mu(u(r_u\cdot))=0$. Thus, by (3.4), there exists some ![]() $j_0\in J$ such that
$j_0\in J$ such that ![]() $r_{V^{j_0}}\geq1$ and
$r_{V^{j_0}}\geq1$ and  $P_\mu(V^{j_0}(r_{V^{j_0}}\cdot))=0$. Moreover,
$P_\mu(V^{j_0}(r_{V^{j_0}}\cdot))=0$. Moreover,
 \begin{equation*}
|V^{j_0}(r_{V^{j_0}}\cdot)|_2^2=r_{V^{j_0}}^{-N}|V^{j_0}|_2^2\leq r_{V^{j_0}}^{-N}a^2\leq a^2,
\end{equation*}
\begin{equation*}
|V^{j_0}(r_{V^{j_0}}\cdot)|_2^2=r_{V^{j_0}}^{-N}|V^{j_0}|_2^2\leq r_{V^{j_0}}^{-N}a^2\leq a^2,
\end{equation*} which implies  $V^{j_0}(r_{V^{j_0}}\cdot)\in \overline{V}_{a,\mu}$. In addition, we also note that
$V^{j_0}(r_{V^{j_0}}\cdot)\in \overline{V}_{a,\mu}$. In addition, we also note that
 \begin{align*}
\overline{M}_{a,\mu} & =\inf_{\overline{V}_{a,\mu}}E_\mu =\inf_{u\in\overline{V}_{a,\mu}}\left(E_\mu(u)-\frac{1}{2}P_\mu(u)\right)\\
& =\inf_{u\in\overline{V}_{a,\mu}}\left[\frac{1}{p}\left(\frac{N(p-2)}{4s}-1\right)|u|_p^p
+\frac{\mu}{q}\left(\frac{N(q-2)}{4s}-1\right)|u|_q^q\right].
\end{align*}
\begin{align*}
\overline{M}_{a,\mu} & =\inf_{\overline{V}_{a,\mu}}E_\mu =\inf_{u\in\overline{V}_{a,\mu}}\left(E_\mu(u)-\frac{1}{2}P_\mu(u)\right)\\
& =\inf_{u\in\overline{V}_{a,\mu}}\left[\frac{1}{p}\left(\frac{N(p-2)}{4s}-1\right)|u|_p^p
+\frac{\mu}{q}\left(\frac{N(q-2)}{4s}-1\right)|u|_q^q\right].
\end{align*}Thus, it holds that
 \begin{align*}
0 \lt \overline{M}_{a,\mu}\leq E_\mu\left(V^{j_0}(r_{V^{j_0}}\cdot)\right)
& \leq\frac{1}{p}\Big(\frac{N(p-2)}{4s}-1\Big)|V^{j_0}|_p^p
+\frac{\mu}{q}\Big(\frac{N(q-2)}{4s}-1\Big)|V^{j_0}|_q^q\\
& \le\limsup_{n\rightarrow +\infty}E_\mu(v_n)=\overline{M}_{a,\mu},
\end{align*}
\begin{align*}
0 \lt \overline{M}_{a,\mu}\leq E_\mu\left(V^{j_0}(r_{V^{j_0}}\cdot)\right)
& \leq\frac{1}{p}\Big(\frac{N(p-2)}{4s}-1\Big)|V^{j_0}|_p^p
+\frac{\mu}{q}\Big(\frac{N(q-2)}{4s}-1\Big)|V^{j_0}|_q^q\\
& \le\limsup_{n\rightarrow +\infty}E_\mu(v_n)=\overline{M}_{a,\mu},
\end{align*} which implies ![]() $r_{V^{j_0}}=1$,
$r_{V^{j_0}}=1$, ![]() $V^{j_0}\in\overline{V}_{a,\mu}$, and
$V^{j_0}\in\overline{V}_{a,\mu}$, and ![]() $E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu}$.
$E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu}$.
Finally, let ![]() $u:=|V^{j_0}|^*$ be the Schwartz symmetrization of
$u:=|V^{j_0}|^*$ be the Schwartz symmetrization of ![]() $|V^{j_0}|$, then by [Reference Almgren and Lieb1, theorem 9.2], one has
$|V^{j_0}|$, then by [Reference Almgren and Lieb1, theorem 9.2], one has
 \begin{equation*}
|u|_2^2=|V^{j_0}|_2^2, \ |u|_p^p=|V^{j_0}|_p^p, \ |u|_q^q=|V^{j_0}|_q^q,\quad\mbox{and}\ |\left(-\Delta\right)^{\frac{s}{2}}u|_{2}^2\leq |\left(-\Delta\right)^{\frac{s}{2}}V^{j_0}|_{2}^2.
\end{equation*}
\begin{equation*}
|u|_2^2=|V^{j_0}|_2^2, \ |u|_p^p=|V^{j_0}|_p^p, \ |u|_q^q=|V^{j_0}|_q^q,\quad\mbox{and}\ |\left(-\Delta\right)^{\frac{s}{2}}u|_{2}^2\leq |\left(-\Delta\right)^{\frac{s}{2}}V^{j_0}|_{2}^2.
\end{equation*} By (3.5) and ![]() $r_{V^{j_0}}=1$, one has
$r_{V^{j_0}}=1$, one has ![]() $r_u\geq1$ and
$r_u\geq1$ and ![]() $u(r_u\cdot)\in\overline{V}_{a,\mu}$. Suppose
$u(r_u\cdot)\in\overline{V}_{a,\mu}$. Suppose ![]() $r_u \gt 1$, then
$r_u \gt 1$, then
 \begin{align*}
\overline{M}_{a,\mu} & \leq E_\mu\left(u(r_u\cdot)\right) \lt \frac{1}{p}\Big(\frac{N(p-2)}{4s}-1\Big)|u|_p^p
+\frac{\mu}{q}\Big(\frac{N(q-2)}{4s}-1\Big)|u|_q^q\\
& =E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu},
\end{align*}
\begin{align*}
\overline{M}_{a,\mu} & \leq E_\mu\left(u(r_u\cdot)\right) \lt \frac{1}{p}\Big(\frac{N(p-2)}{4s}-1\Big)|u|_p^p
+\frac{\mu}{q}\Big(\frac{N(q-2)}{4s}-1\Big)|u|_q^q\\
& =E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu},
\end{align*} which is a contradiction. Therefore, we get ![]() $r_u=1$ and
$r_u=1$ and ![]() $E_\mu(u)=E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu}$.
$E_\mu(u)=E_\mu\left(V^{j_0}\right)=\overline{M}_{a,\mu}$.
Recall
 \begin{equation*}
\mathring{V}_{a,\mu}=\overline{V}_{a,\mu}\setminus{V}_{a,\mu}=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}:\int_{\mathbb{R}^N}|u|^2 \lt a^2,P_\mu(u)=0\Big\}.
\end{equation*}
\begin{equation*}
\mathring{V}_{a,\mu}=\overline{V}_{a,\mu}\setminus{V}_{a,\mu}=\Big\{u\in H^s(\mathbb{R}^N)\setminus\{0\}:\int_{\mathbb{R}^N}|u|^2 \lt a^2,P_\mu(u)=0\Big\}.
\end{equation*} If ![]() $ \overline{M}_{a,\mu}$ is achieved at some
$ \overline{M}_{a,\mu}$ is achieved at some ![]() $u\in {V}_{a,\mu}$, then
$u\in {V}_{a,\mu}$, then ![]() ${M}_{a,\mu}=\overline{M}_{a,\mu}$ and
${M}_{a,\mu}=\overline{M}_{a,\mu}$ and ![]() ${M}_{a,\mu}$ is achieved. To rule out the case that
${M}_{a,\mu}$ is achieved. To rule out the case that ![]() $ \overline{M}_{a,\mu}$ is achieved at some
$ \overline{M}_{a,\mu}$ is achieved at some  $u\in \mathring{V}_{a,\mu}$, we need the following lemma:
$u\in \mathring{V}_{a,\mu}$, we need the following lemma:
Lemma 3.3. For every  $u\in \mathring{V}_{a,\mu}$, it holds that
$u\in \mathring{V}_{a,\mu}$, it holds that
Proof. Suppose by contradiction that ![]() $\overline{M}_{a,\mu}=E_\mu(\tilde{u})\leq M_{a,\mu}$ for some
$\overline{M}_{a,\mu}=E_\mu(\tilde{u})\leq M_{a,\mu}$ for some  $\tilde{u}\in\mathring{V}_{a,\mu}.$ Hence,
$\tilde{u}\in\mathring{V}_{a,\mu}.$ Hence, ![]() $\tilde{u}$ is a local minimizer for Eµ on
$\tilde{u}$ is a local minimizer for Eµ on  $\mathring{V}_{a,\mu}$, and there exists a Lagrange multiplier
$\mathring{V}_{a,\mu}$, and there exists a Lagrange multiplier ![]() $\lambda\in\mathbb{R}$ such that
$\lambda\in\mathbb{R}$ such that
 \begin{equation*}
E_\mu'(\tilde{u})-\lambda P_\mu'(\tilde{u})=0,
\end{equation*}
\begin{equation*}
E_\mu'(\tilde{u})-\lambda P_\mu'(\tilde{u})=0,
\end{equation*} i.e., ![]() $\tilde{u}$ is a weak solution to
$\tilde{u}$ is a weak solution to
 \begin{equation}
\left(1-2\lambda\right)\left(-\Delta\right)^s\tilde{u}=\left[1-\lambda\frac{N(p-2)}{2s}\right]|\tilde{u}|^{p-2}\tilde{u}
+\mu\left[1-\lambda\frac{N(q-2)}{2s}\right]|\tilde{u}|^{q-2}\tilde{u}.
\end{equation}
\begin{equation}
\left(1-2\lambda\right)\left(-\Delta\right)^s\tilde{u}=\left[1-\lambda\frac{N(p-2)}{2s}\right]|\tilde{u}|^{p-2}\tilde{u}
+\mu\left[1-\lambda\frac{N(q-2)}{2s}\right]|\tilde{u}|^{q-2}\tilde{u}.
\end{equation} Moreover, ![]() $\tilde{u}$ satisfies the Pohozaev identity of equation (3.6), i.e.,
$\tilde{u}$ satisfies the Pohozaev identity of equation (3.6), i.e.,
 \begin{equation}
\frac{N-2s}{2} \left(1-2\lambda\right)|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=\frac{N}{p}\left[1-\lambda\frac{N(p-2)}{2s}\right]|\tilde{u}|_p^p+
\frac{\mu N}{q}\left[1-\lambda\frac{N(q-2)}{2s}\right]|\tilde{u}|_q^q.
\end{equation}
\begin{equation}
\frac{N-2s}{2} \left(1-2\lambda\right)|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=\frac{N}{p}\left[1-\lambda\frac{N(p-2)}{2s}\right]|\tilde{u}|_p^p+
\frac{\mu N}{q}\left[1-\lambda\frac{N(q-2)}{2s}\right]|\tilde{u}|_q^q.
\end{equation} In addition, ![]() $\tilde{u}$ satisfies the following Nehari-type identity:
$\tilde{u}$ satisfies the following Nehari-type identity:
 \begin{equation}
\left(1-2\lambda\right)|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=\Big[1-\lambda\frac{N(p-2)}{2s}\Big]|\tilde{u}|_p^p+
\mu\Big[1-\lambda\frac{N(q-2)}{2s}\Big]|\tilde{u}|_q^q.
\end{equation}
\begin{equation}
\left(1-2\lambda\right)|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=\Big[1-\lambda\frac{N(p-2)}{2s}\Big]|\tilde{u}|_p^p+
\mu\Big[1-\lambda\frac{N(q-2)}{2s}\Big]|\tilde{u}|_q^q.
\end{equation} Besides, since ![]() $P_\mu(\tilde{u})=0$, we obtain
$P_\mu(\tilde{u})=0$, we obtain
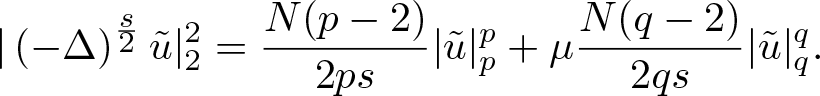 \begin{equation}
|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_2^2=\frac{N(p-2)}{2ps}|\tilde{u}|_p^p+
\mu\frac{N(q-2)}{2qs}|\tilde{u}|_q^q.
\end{equation}
\begin{equation}
|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_2^2=\frac{N(p-2)}{2ps}|\tilde{u}|_p^p+
\mu\frac{N(q-2)}{2qs}|\tilde{u}|_q^q.
\end{equation}After balancing the coefficients of (3.7), (3.8), and (3.9), we deduce that
 \begin{equation*}
\lambda \frac{N(p-2)}{p}\Big(1-\frac{N(p-2)}{4s}\Big)|\tilde{u}|_p^p+\lambda \mu \frac{N(q-2)}{q}\Big(1-\frac{N(q-2)}{4s}\Big)|\tilde{u}|_q^q=0.
\end{equation*}
\begin{equation*}
\lambda \frac{N(p-2)}{p}\Big(1-\frac{N(p-2)}{4s}\Big)|\tilde{u}|_p^p+\lambda \mu \frac{N(q-2)}{q}\Big(1-\frac{N(q-2)}{4s}\Big)|\tilde{u}|_q^q=0.
\end{equation*} Since ![]() $p \gt q \gt 2+4s/N$,
$p \gt q \gt 2+4s/N$, ![]() $\tilde{u}\neq0$, and µ > 0, it must hold that λ = 0. Thus,
$\tilde{u}\neq0$, and µ > 0, it must hold that λ = 0. Thus, ![]() $\tilde{u}$ is a weak solution to
$\tilde{u}$ is a weak solution to
In particular, ![]() $\tilde{u}$ satisfies the following Nehari-type identity:
$\tilde{u}$ satisfies the following Nehari-type identity:
 \begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=|\tilde{u}|_p^p+
\mu|\tilde{u}|_q^q.
\end{equation*}
\begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}\tilde{u}|_{2}^2=|\tilde{u}|_p^p+
\mu|\tilde{u}|_q^q.
\end{equation*}We combine the above identity with (3.9) to obtain
 \begin{equation*}
\frac{2N-p(N-2s)}{2ps}|\tilde{u}|_p^p+\mu\frac{2N-q(N-2s)}{2qs}|\tilde{u}|_q^q=0,
\end{equation*}
\begin{equation*}
\frac{2N-p(N-2s)}{2ps}|\tilde{u}|_p^p+\mu\frac{2N-q(N-2s)}{2qs}|\tilde{u}|_q^q=0,
\end{equation*} which is a contradiction since ![]() $q \lt p \lt 2^*_s$, µ > 0, and
$q \lt p \lt 2^*_s$, µ > 0, and ![]() $\tilde{u}\neq0$. Thus we conclude the proof.
$\tilde{u}\neq0$. Thus we conclude the proof.
With the preparation above at hand, we are now able to prove theorem 1.5(i) and (ii).
Proof of theorem 1.5 (i) and (ii) (i) From proposition 3.2 and lemma 3.3, we immediately have
Moreover, ![]() $M_{a,\mu}$ is attained by a non-negative and radially symmetric function u in
$M_{a,\mu}$ is attained by a non-negative and radially symmetric function u in ![]() $V_{a,\mu}$. Since it is well known that a critical point for
$V_{a,\mu}$. Since it is well known that a critical point for ![]() $E_\mu|_{V_{a,\mu}}$ is also a critical point for
$E_\mu|_{V_{a,\mu}}$ is also a critical point for ![]() $E_\mu|_{S_a}$, we apply Lagrange multiplier rules to deduce that there exists
$E_\mu|_{S_a}$, we apply Lagrange multiplier rules to deduce that there exists ![]() $\lambda\in\mathbb{R}$ such that
$\lambda\in\mathbb{R}$ such that
Thus,
 \begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}{u}|_{2}^2=|{u}|_p^p+
\mu|{u}|_q^q+\lambda|u|_2^2.
\end{equation*}
\begin{equation*}
|\left(-\Delta\right)^{\frac{s}{2}}{u}|_{2}^2=|{u}|_p^p+
\mu|{u}|_q^q+\lambda|u|_2^2.
\end{equation*} Combining with the identity ![]() $P_{\mu}(u)=0$, we get
$P_{\mu}(u)=0$, we get
 \begin{equation*}
\lambda a^2=\lambda|u|_2^2=-\left[\frac{2N-p(N-2s)}{2sp}|u|_p^p+\mu\frac{2N-q(N-2s)}{2sq}|u|_q^q\right].
\end{equation*}
\begin{equation*}
\lambda a^2=\lambda|u|_2^2=-\left[\frac{2N-p(N-2s)}{2sp}|u|_p^p+\mu\frac{2N-q(N-2s)}{2sq}|u|_q^q\right].
\end{equation*} Since µ > 0 and ![]() $q \lt p \lt 2_s^*$, we know λ < 0. Moreover, due to
$q \lt p \lt 2_s^*$, we know λ < 0. Moreover, due to ![]() $u\geq0$ and
$u\geq0$ and ![]() $u\not\equiv0$, by the maximum principle, it holds that u > 0 in
$u\not\equiv0$, by the maximum principle, it holds that u > 0 in ![]() $\mathbb{R}^N$.
$\mathbb{R}^N$.
(ii) Let ![]() $0 \lt a_1 \lt a_2$. There exist two functions u 1 and u 2 such that
$0 \lt a_1 \lt a_2$. There exist two functions u 1 and u 2 such that
 \begin{equation*}
M_{a_1,\mu}=E_\mu(u_1),\quad |u_1|_2^2=a_1^2,
\end{equation*}
\begin{equation*}
M_{a_1,\mu}=E_\mu(u_1),\quad |u_1|_2^2=a_1^2,
\end{equation*}and
 \begin{equation*}
M_{a_2,\mu}=E_\mu(u_2),\quad |u_2|_2^2=a_2^2.
\end{equation*}
\begin{equation*}
M_{a_2,\mu}=E_\mu(u_2),\quad |u_2|_2^2=a_2^2.
\end{equation*}Then, we use lemma 3.3 to get
which implies that ![]() $M_{a,\mu}$ is strictly decreasing with respect to a.
$M_{a,\mu}$ is strictly decreasing with respect to a.
In the following, we study the strong instability of standing wave solution ![]() $e^{-\mathrm{i}\lambda t}u$ to (1.1), where u is a radial minimizer for
$e^{-\mathrm{i}\lambda t}u$ to (1.1), where u is a radial minimizer for ![]() $M_{a,\mu}$ obtained in theorem 1.5. Our ideas are as follows. First, we find the third kind of variational characterization for
$M_{a,\mu}$ obtained in theorem 1.5. Our ideas are as follows. First, we find the third kind of variational characterization for ![]() $M_{a,\mu}$. Define
$M_{a,\mu}$. Define
 \begin{eqnarray*}
\widetilde{E}_\mu(u)\!:=\! E_\mu(u)\!-\!\!\frac{2s}{N(q-2)}P_\mu(u)\!=\!\Big(\frac{1}{2}\!-\!\frac{2s}{N(q-2)}\Big)|(-\Delta)^{\frac{s}{2}}u|_2^2
\!+\!\frac{1}{p}\Big(\frac{p-2}{q-2}\!-\!1\Big)|u|_p^p,
\end{eqnarray*}
\begin{eqnarray*}
\widetilde{E}_\mu(u)\!:=\! E_\mu(u)\!-\!\!\frac{2s}{N(q-2)}P_\mu(u)\!=\!\Big(\frac{1}{2}\!-\!\frac{2s}{N(q-2)}\Big)|(-\Delta)^{\frac{s}{2}}u|_2^2
\!+\!\frac{1}{p}\Big(\frac{p-2}{q-2}\!-\!1\Big)|u|_p^p,
\end{eqnarray*}and
 \begin{equation}
\widetilde{M}_{a,\mu}:=\inf_{\widetilde{V}_{a,\mu}}\widetilde{E}_\mu, \quad \widetilde{V}_{a,\mu}:=\left\{u\in S_a:P_\mu(u)\leq0\right\}.
\end{equation}
\begin{equation}
\widetilde{M}_{a,\mu}:=\inf_{\widetilde{V}_{a,\mu}}\widetilde{E}_\mu, \quad \widetilde{V}_{a,\mu}:=\left\{u\in S_a:P_\mu(u)\leq0\right\}.
\end{equation} We will show  $\widetilde{M}_{a,\mu}=M_{a,\mu}$. Second, we give the blow-up criterion (see proposition 3.7) by introducing two invariant manifolds, for which the proof is based on the localized virial action
$\widetilde{M}_{a,\mu}=M_{a,\mu}$. Second, we give the blow-up criterion (see proposition 3.7) by introducing two invariant manifolds, for which the proof is based on the localized virial action ![]() $M_{\varphi}\left(\psi(t,\cdot)\right)$ and the virial estimate for
$M_{\varphi}\left(\psi(t,\cdot)\right)$ and the virial estimate for ![]() $M_{\varphi}\left(\psi(t,\cdot)\right)$ (see lemma 3.6). Third, if u is a radial minimizer for
$M_{\varphi}\left(\psi(t,\cdot)\right)$ (see lemma 3.6). Third, if u is a radial minimizer for ![]() $M_{a,\mu}$, letting
$M_{a,\mu}$, letting  $\psi_0^\tau(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$ with τ > 0, we derive the strong instability of normalized ground states to (1.1) by the blow-up criterion. Hence, we conclude the proof of theorem 1.5(iii).
$\psi_0^\tau(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$ with τ > 0, we derive the strong instability of normalized ground states to (1.1) by the blow-up criterion. Hence, we conclude the proof of theorem 1.5(iii).
First, we prove the third kind of variational characterization of ![]() $M_{a,\mu}$. To this aim, we give some notations. For
$M_{a,\mu}$. To this aim, we give some notations. For ![]() $u\in S_a$ and
$u\in S_a$ and ![]() $\tau\in\mathbb{R}$, we define
$\tau\in\mathbb{R}$, we define
 \begin{equation*}
(\tau\star u)(x):=e^{\frac{N}{2}\tau}u(e^\tau x),\quad \mbox{for a.e.~}x\in\mathbb{R}^N,
\end{equation*}
\begin{equation*}
(\tau\star u)(x):=e^{\frac{N}{2}\tau}u(e^\tau x),\quad \mbox{for a.e.~}x\in\mathbb{R}^N,
\end{equation*} then ![]() $\tau\star u\in S_a$. Moreover, we introduce the fibre map
$\tau\star u\in S_a$. Moreover, we introduce the fibre map
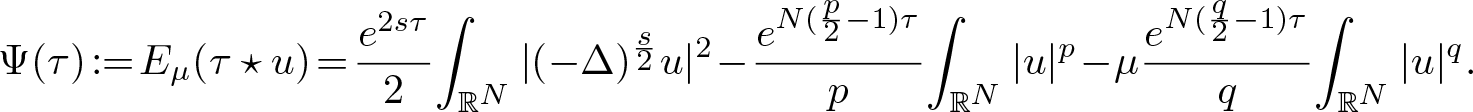 \begin{equation}
\Psi(\tau)\!:=\!E_\mu(\tau\star u)\!=\!\frac{e^{2s\tau}}{2}\!\int_{\mathbb{R}^N}|(-\Delta)^{\frac{s}{2}}u|^2\!-\!\frac{e^{N(\frac{p}{2}-1)\tau}}{p}\!\int_{\mathbb{R}^N}|u|^p\!-\!
\mu\frac{e^{N(\frac{q}{2}-1)\tau}}{q}\!\int_{\mathbb{R}^N}|u|^q.
\end{equation}
\begin{equation}
\Psi(\tau)\!:=\!E_\mu(\tau\star u)\!=\!\frac{e^{2s\tau}}{2}\!\int_{\mathbb{R}^N}|(-\Delta)^{\frac{s}{2}}u|^2\!-\!\frac{e^{N(\frac{p}{2}-1)\tau}}{p}\!\int_{\mathbb{R}^N}|u|^p\!-\!
\mu\frac{e^{N(\frac{q}{2}-1)\tau}}{q}\!\int_{\mathbb{R}^N}|u|^q.
\end{equation}Lemma 3.4. For any ![]() $u\in S_a$, there exists a unique constant
$u\in S_a$, there exists a unique constant ![]() $\tau_0\in\mathbb{R}$ such that
$\tau_0\in\mathbb{R}$ such that
 \begin{equation*}
E_\mu(\tau_0\star u)=\max_{\tau\in\mathbb{R}}E_\mu(\tau\star u).
\end{equation*}
\begin{equation*}
E_\mu(\tau_0\star u)=\max_{\tau\in\mathbb{R}}E_\mu(\tau\star u).
\end{equation*}Moreover,
(i) It holds that
 $P_\mu(\tau_0\star u)=0$. Furthermore, if
$P_\mu(\tau_0\star u)=0$. Furthermore, if  $\tau \lt \tau_0$ (respectively
$\tau \lt \tau_0$ (respectively  $\tau \gt \tau_0$), then
$\tau \gt \tau_0$), then  $P_\mu(\tau\star u) \gt 0$ (respectively
$P_\mu(\tau\star u) \gt 0$ (respectively  $P_\mu(\tau\star u) \lt 0$).
$P_\mu(\tau\star u) \lt 0$).(ii)
 $P_\mu(u)=0$ (respectively
$P_\mu(u)=0$ (respectively  $P_\mu(u) \lt 0$) if and only if
$P_\mu(u) \lt 0$) if and only if  $\tau_0=0$ (respectively
$\tau_0=0$ (respectively  $\tau_0 \lt 0$).
$\tau_0 \lt 0$).
Proof. By straightforward calculation, one has ![]() $\Psi'(\tau)
=sP_\mu(\tau\star u).$ In addition, we also see that
$\Psi'(\tau)
=sP_\mu(\tau\star u).$ In addition, we also see that
 \begin{align*}
\Psi'(\tau) & = e^{2s\tau}\Big(s|(-\Delta)^{\frac{s}{2}}u|_2^2-
\frac{N(p-2)}{2p}e^{\left(N(\frac{p}{2}-1)-2s\right)\tau}|u|_p^p\\
& \quad - \mu\frac{N(q-2)}{2q}e^{\left(N(\frac{q}{2}-1)-2s\right)\tau}|u|_q^q\Big).
\end{align*}
\begin{align*}
\Psi'(\tau) & = e^{2s\tau}\Big(s|(-\Delta)^{\frac{s}{2}}u|_2^2-
\frac{N(p-2)}{2p}e^{\left(N(\frac{p}{2}-1)-2s\right)\tau}|u|_p^p\\
& \quad - \mu\frac{N(q-2)}{2q}e^{\left(N(\frac{q}{2}-1)-2s\right)\tau}|u|_q^q\Big).
\end{align*} Since ![]() $2+4s/N \lt q \lt p$ and µ > 0,
$2+4s/N \lt q \lt p$ and µ > 0, ![]() $\Psi'(\tau)$ is strictly decreasing with respect to τ. Consequently, there exists a unique
$\Psi'(\tau)$ is strictly decreasing with respect to τ. Consequently, there exists a unique ![]() $\tau_0\in\mathbb{R}$ such that
$\tau_0\in\mathbb{R}$ such that ![]() $\Psi'(\tau_0)=0$. Other desired results follow directly.
$\Psi'(\tau_0)=0$. Other desired results follow directly.
Lemma 3.5. Let ![]() $M_{a,\mu}$ and
$M_{a,\mu}$ and  $\widetilde{M}_{a,\mu}$ be defined by (3.1) and (3.11), respectively, then
$\widetilde{M}_{a,\mu}$ be defined by (3.1) and (3.11), respectively, then
 \begin{equation*}
\widetilde{M}_{a,\mu}=M_{a,\mu}.
\end{equation*}
\begin{equation*}
\widetilde{M}_{a,\mu}=M_{a,\mu}.
\end{equation*}Proof. For any ![]() $u\in S_a$ with
$u\in S_a$ with ![]() $P_\mu(u) \lt 0$, by lemma 3.4, there exists a
$P_\mu(u) \lt 0$, by lemma 3.4, there exists a ![]() $\tau_0 \lt 0$ such that
$\tau_0 \lt 0$ such that ![]() $P_\mu(\tau_0\star u)=0$, i.e.,
$P_\mu(\tau_0\star u)=0$, i.e., ![]() $\tau_0\star u \in V_{a,\mu}$ defined in (3.1). Furthermore, it holds that
$\tau_0\star u \in V_{a,\mu}$ defined in (3.1). Furthermore, it holds that
 \begin{align*}
\widetilde{E}_\mu(\tau_0\star u)&=\left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}(\tau_0\star u)|_2^2
+\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|\tau_0\star u|_p^p\\
&=\left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)e^{2s\tau_0}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2+
\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)e^{N\tau_0(\frac{p}{2}-1)}|u|_p^p\\
& \lt \left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2+
\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|u|_p^p\\
&=\widetilde{E}_\mu(u).
\end{align*}
\begin{align*}
\widetilde{E}_\mu(\tau_0\star u)&=\left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}(\tau_0\star u)|_2^2
+\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|\tau_0\star u|_p^p\\
&=\left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)e^{2s\tau_0}|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2+
\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)e^{N\tau_0(\frac{p}{2}-1)}|u|_p^p\\
& \lt \left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}u|_2^2+
\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|u|_p^p\\
&=\widetilde{E}_\mu(u).
\end{align*} Hence,  $\widetilde{M}_{a,\mu}=\inf_{\widetilde{V}_{a,\mu}}\widetilde{E}_\mu=\inf_{V_{a,\mu}}\widetilde{E}_\mu=M_{a,\mu}$.
$\widetilde{M}_{a,\mu}=\inf_{\widetilde{V}_{a,\mu}}\widetilde{E}_\mu=\inf_{V_{a,\mu}}\widetilde{E}_\mu=M_{a,\mu}$.
Let ![]() $1/2\leq s \lt 1$ and
$1/2\leq s \lt 1$ and ![]() $\varphi:\mathbb{R}^N\rightarrow\mathbb{R}$ be such that
$\varphi:\mathbb{R}^N\rightarrow\mathbb{R}$ be such that ![]() $\nabla\varphi\in W^{3,\infty}(\mathbb{R}^N)$. Assume
$\nabla\varphi\in W^{3,\infty}(\mathbb{R}^N)$. Assume ![]() $\psi\in C\left([0,T),H^s\right)$ is a solution to (1.1). The localized virial action of ψ is defined by
$\psi\in C\left([0,T),H^s\right)$ is a solution to (1.1). The localized virial action of ψ is defined by
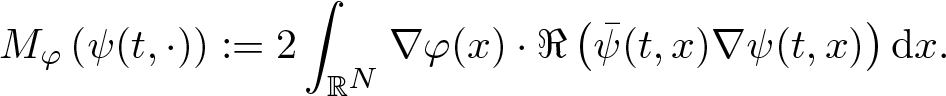 \begin{equation}
M_{\varphi}\left(\psi(t,\cdot)\right):=2\int_{\mathbb{R}^N}\nabla\varphi(x)\cdot\Re\left(\bar{\psi}(t,x)\nabla\psi(t,x)\right)\mathrm{d}x.
\end{equation}
\begin{equation}
M_{\varphi}\left(\psi(t,\cdot)\right):=2\int_{\mathbb{R}^N}\nabla\varphi(x)\cdot\Re\left(\bar{\psi}(t,x)\nabla\psi(t,x)\right)\mathrm{d}x.
\end{equation} It follows from lemma A.5 that ![]() $M_{\varphi}\left(\psi(t,\cdot)\right)$ is well-defined. Indeed, by lemma A.5,
$M_{\varphi}\left(\psi(t,\cdot)\right)$ is well-defined. Indeed, by lemma A.5,
 \begin{equation*}
|M_{\varphi}\left(\psi(t,\cdot)\right)|\leq C(N, |\nabla\varphi|_{W^{1,\infty}})
\left\|\psi(t,\cdot)\right\|^2_{H^{1/2}}\leq C(N, |\nabla\varphi|_{W^{1,\infty}})
\left\|\psi(t,\cdot)\right\|^2_{H^{s}} \lt \infty.
\end{equation*}
\begin{equation*}
|M_{\varphi}\left(\psi(t,\cdot)\right)|\leq C(N, |\nabla\varphi|_{W^{1,\infty}})
\left\|\psi(t,\cdot)\right\|^2_{H^{1/2}}\leq C(N, |\nabla\varphi|_{W^{1,\infty}})
\left\|\psi(t,\cdot)\right\|^2_{H^{s}} \lt \infty.
\end{equation*} Now let ![]() $\varphi\colon\mathbb{R}^N\rightarrow\mathbb{R}$ be as above. We assume in addition that φ is radially symmetric and satisfies
$\varphi\colon\mathbb{R}^N\rightarrow\mathbb{R}$ be as above. We assume in addition that φ is radially symmetric and satisfies
 \begin{equation*}
\varphi(r):=\begin{cases}
r^2,& \text{if}\ r\le 1,\\
const,& \text{if}\ r\ge 10.
\end{cases}
\quad \mbox{and~}\varphi''(r)\leq2 \mbox{~for~}r\geq0.
\end{equation*}
\begin{equation*}
\varphi(r):=\begin{cases}
r^2,& \text{if}\ r\le 1,\\
const,& \text{if}\ r\ge 10.
\end{cases}
\quad \mbox{and~}\varphi''(r)\leq2 \mbox{~for~}r\geq0.
\end{equation*} Here the precise value of the constant is not important. For R > 0 given, we define the rescaled function ![]() $\varphi_R:\mathbb{R}^N\rightarrow\mathbb{R}$ by
$\varphi_R:\mathbb{R}^N\rightarrow\mathbb{R}$ by
Then, we have the following virial estimate:
Lemma 3.6 ([Reference Dinh and Feng13, lemma 4.3], Hs radial virial estimate)
Let  $N\geq2,\frac{N}{2N-1}\leq s \lt 1$ and
$N\geq2,\frac{N}{2N-1}\leq s \lt 1$ and ![]() $2 \lt q \lt p \lt 2_s^*$, φR be as above, and
$2 \lt q \lt p \lt 2_s^*$, φR be as above, and ![]() $\psi\in C\left([0,T),H^s\right)$ be a radial solution to (1.1). Then, for any
$\psi\in C\left([0,T),H^s\right)$ be a radial solution to (1.1). Then, for any ![]() $t\in[0,T)$,
$t\in[0,T)$,
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
&\leq8s\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad+O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{q-2}{2s}+
\varepsilon_1}\\
&\quad+R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{p-2}{2s}+
\varepsilon_2}\Big)\\
&=4N(p-2)E_\mu\left(\psi(t,\cdot)\right)+\left(8s-2N(p-2)\right)\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^2\\
&\quad+\frac{4N(p-q)\mu}{q}|\psi(t,\cdot)|_q^q\\
&\quad+O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{q-2}{2s}+
\varepsilon_1}\\
&\quad+R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{p-2}{2s}+
\varepsilon_2}\Big),
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
&\leq8s\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad+O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{q-2}{2s}+
\varepsilon_1}\\
&\quad+R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{p-2}{2s}+
\varepsilon_2}\Big)\\
&=4N(p-2)E_\mu\left(\psi(t,\cdot)\right)+\left(8s-2N(p-2)\right)\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^2\\
&\quad+\frac{4N(p-q)\mu}{q}|\psi(t,\cdot)|_q^q\\
&\quad+O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{q-2}{2s}+
\varepsilon_1}\\
&\quad+R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}^{\frac{p-2}{2s}+
\varepsilon_2}\Big),
\end{align*} for any ![]() $0 \lt \varepsilon_1 \lt (2N-1)(q-2)/2s, 0 \lt \varepsilon_2 \lt (2N-1)(p-2)/2s$, and where
$0 \lt \varepsilon_1 \lt (2N-1)(q-2)/2s, 0 \lt \varepsilon_2 \lt (2N-1)(p-2)/2s$, and where  $\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}\!:=\!|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2$. Here the implicit constant depends only on
$\left\|\psi(t,\cdot)\right\|_{\dot{H}^s}\!:=\!|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2$. Here the implicit constant depends only on ![]() $|\psi_0|_2$, N, ɛ 1, ɛ 2, s, q, and p.
$|\psi_0|_2$, N, ɛ 1, ɛ 2, s, q, and p.
With the preparation above, we introduce the following two invariant manifolds:
 \begin{eqnarray*}
&\mathcal{A}_{a,\mu}:=\left\{u\in S_{a,r}: P_\mu(u) \gt 0, E_\mu(u) \lt M_{a,\mu}\right\},\\
&\mathcal{B}_{a,\mu}:=\left\{u\in S_{a,r}: P_\mu(u) \lt 0, E_\mu(u) \lt M_{a,\mu}\right\},
\end{eqnarray*}
\begin{eqnarray*}
&\mathcal{A}_{a,\mu}:=\left\{u\in S_{a,r}: P_\mu(u) \gt 0, E_\mu(u) \lt M_{a,\mu}\right\},\\
&\mathcal{B}_{a,\mu}:=\left\{u\in S_{a,r}: P_\mu(u) \lt 0, E_\mu(u) \lt M_{a,\mu}\right\},
\end{eqnarray*} where ![]() $S_{a,r}=\{u\in S_a: u(x)=u(|x|)\}$.
$S_{a,r}=\{u\in S_a: u(x)=u(|x|)\}$.
The following proposition tells us the global existence (respectively blow-up behaviour) of the solution to (1.1) if the initial data belong to ![]() $\mathcal{A}_{a,\mu}$ (respectively
$\mathcal{A}_{a,\mu}$ (respectively ![]() $\mathcal{B}_{a,\mu}$):
$\mathcal{B}_{a,\mu}$):
Proposition 3.7. Under the assumptions of theorem 1.5(iii). Then ![]() $\mathcal{A}_{a,\mu}$ and
$\mathcal{A}_{a,\mu}$ and ![]() $\mathcal{B}_{a,\mu}$ are two invariant manifolds of (1.1). More precisely,
$\mathcal{B}_{a,\mu}$ are two invariant manifolds of (1.1). More precisely,
(i) if the initial value
 $\psi_0\in \mathcal{A}_{a,\mu}$, then the solution
$\psi_0\in \mathcal{A}_{a,\mu}$, then the solution  $\psi(t,\cdot)$ to (1.1) always stays in
$\psi(t,\cdot)$ to (1.1) always stays in  $\mathcal{A}_{a,\mu}$ and exists globally over time.
$\mathcal{A}_{a,\mu}$ and exists globally over time.(ii) if the initial value
 $\psi_0\in \mathcal{B}_{a,\mu}$, then the solution
$\psi_0\in \mathcal{B}_{a,\mu}$, then the solution  $\psi(t,\cdot)$ of (1.1) always stays in
$\psi(t,\cdot)$ of (1.1) always stays in  $\mathcal{B}_{a,\mu}$ but blows up in finite time.
$\mathcal{B}_{a,\mu}$ but blows up in finite time.
Proof. First, we claim that ![]() $\mathcal{A}_{a,\mu}\neq\emptyset$ and
$\mathcal{A}_{a,\mu}\neq\emptyset$ and ![]() $\mathcal{B}_{a,\mu}\neq\emptyset$. As a matter of fact, for
$\mathcal{B}_{a,\mu}\neq\emptyset$. As a matter of fact, for ![]() $u\in S_{a,r}$, recall
$u\in S_{a,r}$, recall  $(\tau\star u)(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$. On the one hand, the following statements hold: (i)
$(\tau\star u)(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$. On the one hand, the following statements hold: (i) ![]() $\tau\star u\in S_{a,r}$ for every
$\tau\star u\in S_{a,r}$ for every ![]() $\tau\in \mathbb{R}$; (ii)
$\tau\in \mathbb{R}$; (ii) ![]() $E_\mu(\tau\star u)\rightarrow0$ as
$E_\mu(\tau\star u)\rightarrow0$ as ![]() $\tau\rightarrow-\infty$ by (2.3); and (iii)
$\tau\rightarrow-\infty$ by (2.3); and (iii) ![]() $P_\mu(\tau\star u) \gt 0$ for τ sufficiently negative by lemma 3.4. On the other hand, by lemma 3.1 and (3.10), we know
$P_\mu(\tau\star u) \gt 0$ for τ sufficiently negative by lemma 3.4. On the other hand, by lemma 3.1 and (3.10), we know ![]() $M_{a,\mu}\geq\delta_1 \gt 0$. Therefore,
$M_{a,\mu}\geq\delta_1 \gt 0$. Therefore, ![]() $\mathcal{A}_{a,\mu}\neq\emptyset$. Similarly, one has
$\mathcal{A}_{a,\mu}\neq\emptyset$. Similarly, one has ![]() $E_\mu(\tau\star u)\rightarrow-\infty$ and
$E_\mu(\tau\star u)\rightarrow-\infty$ and ![]() $P_\mu(\tau\star u)\rightarrow-\infty$ as
$P_\mu(\tau\star u)\rightarrow-\infty$ as ![]() $\tau\rightarrow+\infty$. Thus,
$\tau\rightarrow+\infty$. Thus, ![]() $\mathcal{B}_{a,\mu}\neq\emptyset$.
$\mathcal{B}_{a,\mu}\neq\emptyset$.
Second, we prove that ![]() $\mathcal{A}_{a,\mu}$ and
$\mathcal{A}_{a,\mu}$ and ![]() $\mathcal{B}_{a,\mu}$ are two invariant manifolds of (1.1). Let
$\mathcal{B}_{a,\mu}$ are two invariant manifolds of (1.1). Let ![]() $\psi_0\in \mathcal{A}_{a,\mu}$, and by lemma A.3, there exists a unique solution
$\psi_0\in \mathcal{A}_{a,\mu}$, and by lemma A.3, there exists a unique solution ![]() $\psi\in C\left([0,T^*),H^s\right)$ to (1.1) with initial data ψ 0. Moreover, we have
$\psi\in C\left([0,T^*),H^s\right)$ to (1.1) with initial data ψ 0. Moreover, we have
 \begin{equation*}
|\psi(t,\cdot)|_{2}^2=|\psi_0|_{2}^2=a^2,\quad E_\mu(\psi(t,\cdot))=E_\mu(\psi_0) \lt M_{a,\mu}
\end{equation*}
\begin{equation*}
|\psi(t,\cdot)|_{2}^2=|\psi_0|_{2}^2=a^2,\quad E_\mu(\psi(t,\cdot))=E_\mu(\psi_0) \lt M_{a,\mu}
\end{equation*} for any ![]() $t\in(0,T^*)$. If there exists some
$t\in(0,T^*)$. If there exists some ![]() $t_0\in [0,T^*)$ such that
$t_0\in [0,T^*)$ such that ![]() $P_\mu(\psi(t_0,\cdot))=0$, then
$P_\mu(\psi(t_0,\cdot))=0$, then ![]() $E_\mu(\psi(t_0,\cdot))\geq M_{a,\mu}$, which is a contradiction. Therefore, we deduce from the continuity with respect to t of
$E_\mu(\psi(t_0,\cdot))\geq M_{a,\mu}$, which is a contradiction. Therefore, we deduce from the continuity with respect to t of ![]() $\psi(t,\cdot)$ that
$\psi(t,\cdot)$ that ![]() $P_\mu(\psi(t,\cdot)) \gt 0$ for any
$P_\mu(\psi(t,\cdot)) \gt 0$ for any ![]() $t\in [0,T^*)$. As a result,
$t\in [0,T^*)$. As a result, ![]() $\psi(t,\cdot)$ stays in
$\psi(t,\cdot)$ stays in ![]() $A_{a,\mu}$ for any
$A_{a,\mu}$ for any ![]() $t\in [0,T^*)$. Similarly,
$t\in [0,T^*)$. Similarly, ![]() $\mathcal{B}_{a,\mu}$ is invariant under the flow of (1.1).
$\mathcal{B}_{a,\mu}$ is invariant under the flow of (1.1).
(i) Due to ![]() $\psi(t,\cdot)\in \mathcal{A}_{a,\mu}$ for any
$\psi(t,\cdot)\in \mathcal{A}_{a,\mu}$ for any ![]() $t\in [0,T^*)$, we deduce from the conservation of energy that
$t\in [0,T^*)$, we deduce from the conservation of energy that
 \begin{align*}
E_\mu(\psi_0)& \gt \left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2
+\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|\psi(t,\cdot)|_p^p,
\end{align*}
\begin{align*}
E_\mu(\psi_0)& \gt \left(\frac{1}{2}-\frac{2s}{N(q-2)}\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2
+\frac{1}{p}\left(\frac{p-2}{q-2}-1\right)|\psi(t,\cdot)|_p^p,
\end{align*} which together with lemma A.3 implies that the solution ![]() $\psi(t,\cdot)$ of (1.1) exists globally.
$\psi(t,\cdot)$ of (1.1) exists globally.
(ii) If ![]() $\psi_0\in\mathcal{B}_{a,\mu}$, then
$\psi_0\in\mathcal{B}_{a,\mu}$, then ![]() $P_\mu(\psi(t,\cdot)) \lt 0$ for any
$P_\mu(\psi(t,\cdot)) \lt 0$ for any ![]() $t\in [0,T^*)$. By lemma 3.5, we know
$t\in [0,T^*)$. By lemma 3.5, we know
 \begin{align*}
M_{a,\mu} & =\widetilde{M}_{a,\mu}\leq \widetilde{E}_\mu(\psi(t,\cdot))\\
&=E_\mu(\psi(t,\cdot))-\frac{2s}{N(q-2)}P_\mu(\psi(t,\cdot))
=E_\mu(\psi_0)-\frac{2s}{N(q-2)}P_\mu(\psi(t,\cdot)),
\end{align*}
\begin{align*}
M_{a,\mu} & =\widetilde{M}_{a,\mu}\leq \widetilde{E}_\mu(\psi(t,\cdot))\\
&=E_\mu(\psi(t,\cdot))-\frac{2s}{N(q-2)}P_\mu(\psi(t,\cdot))
=E_\mu(\psi_0)-\frac{2s}{N(q-2)}P_\mu(\psi(t,\cdot)),
\end{align*}which implies
 \begin{equation}
P_\mu(\psi(t,\cdot))\leq\frac{N(q-2)}{2s}\left(E_\mu(\psi_0)-M_{a,\mu}\right) \lt 0, \quad \forall t\in [0,T^*).
\end{equation}
\begin{equation}
P_\mu(\psi(t,\cdot))\leq\frac{N(q-2)}{2s}\left(E_\mu(\psi_0)-M_{a,\mu}\right) \lt 0, \quad \forall t\in [0,T^*).
\end{equation}The proof of blow-up behaviour will be divided into three steps as follows:
Step 1: We prove that there exists ![]() $C_1 \gt 0$ such that
$C_1 \gt 0$ such that
 \begin{equation}
|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2\geq C_1
\end{equation}
\begin{equation}
|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2\geq C_1
\end{equation} for every ![]() $t\in[0,T^*)$. Indeed, if not, then there exists
$t\in[0,T^*)$. Indeed, if not, then there exists ![]() $\{t_k\}\subseteq [0,T^*)$ such that
$\{t_k\}\subseteq [0,T^*)$ such that  $|\left(-\Delta\right)^{\frac{s}{2}}\psi(t_k, \cdot)|_2\rightarrow0$. However, we deduce from mass conservation and the sharp Gagliardo-Nirenberg inequality that
$|\left(-\Delta\right)^{\frac{s}{2}}\psi(t_k, \cdot)|_2\rightarrow0$. However, we deduce from mass conservation and the sharp Gagliardo-Nirenberg inequality that ![]() $|\psi(t_k,\cdot)|_\alpha^\alpha=o(1)$ as
$|\psi(t_k,\cdot)|_\alpha^\alpha=o(1)$ as ![]() $k\rightarrow\infty$, where
$k\rightarrow\infty$, where ![]() $\alpha=p\mbox{~or~}q$. Therefore, we have
$\alpha=p\mbox{~or~}q$. Therefore, we have
 \begin{equation*}
P_\mu(\psi(t_k,\cdot))=|\left(-\Delta\right)^{\frac{s}{2}}\psi(t_k,\cdot)|_2^2-\frac{N(p-2)}{2ps}|\psi(t_k,\cdot)|_p^p-
\mu\frac{N(q-2)}{2qs}|\psi(t_k,\cdot)|_q^q\rightarrow0
\end{equation*}
\begin{equation*}
P_\mu(\psi(t_k,\cdot))=|\left(-\Delta\right)^{\frac{s}{2}}\psi(t_k,\cdot)|_2^2-\frac{N(p-2)}{2ps}|\psi(t_k,\cdot)|_p^p-
\mu\frac{N(q-2)}{2qs}|\psi(t_k,\cdot)|_q^q\rightarrow0
\end{equation*} as ![]() $k\rightarrow\infty$, which contradicts to (3.14).
$k\rightarrow\infty$, which contradicts to (3.14).
Step 2: We claim that there exists ![]() $C_2 \gt 0$ such that
$C_2 \gt 0$ such that
 \begin{equation}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -C_2|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2,
\end{equation}
\begin{equation}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -C_2|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2,
\end{equation} where ![]() $M_{\varphi_R}(\psi(t,\cdot))$ is defined by (3.13).
$M_{\varphi_R}(\psi(t,\cdot))$ is defined by (3.13).
Observe that ![]() $\psi(t,\cdot)$ is radial for any
$\psi(t,\cdot)$ is radial for any ![]() $t\in[0,T^*)$, since the initial datum ψ 0 is radial. Therefore, we apply lemma 3.6 to have
$t\in[0,T^*)$, since the initial datum ψ 0 is radial. Therefore, we apply lemma 3.6 to have
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))&\leq8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad +O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{q-2}{2s}+
\varepsilon_1}\Big)\\
&\quad+O\left(R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{p-2}{2s}+
\varepsilon_2}\right)
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))&\leq8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad +O\Big(R^{-2s}+R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{q-2}{2s}+
\varepsilon_1}\Big)\\
&\quad+O\left(R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{p-2}{2s}+
\varepsilon_2}\right)
\end{align*} for all ![]() $t\in[0,T^*)$ and R > 1. Thanks to the assumption
$t\in[0,T^*)$ and R > 1. Thanks to the assumption ![]() $q \lt p \lt 2+4s$, we can apply Young’s inequality to obtain for any η > 0,
$q \lt p \lt 2+4s$, we can apply Young’s inequality to obtain for any η > 0,
 \begin{align*}
&R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{q-2}{2s}+
\varepsilon_1}\\
& \quad \leq \eta |(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\!+\!\eta^{-\frac{q-2+2\varepsilon_1s}{2+4s-q-2\varepsilon_1s}}
R^{-\frac{2s\left[(q-2)(N-1)-2\varepsilon_1s\right]}{2+4s-q-2\varepsilon_1s}},\\
&R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{p-2}{2s}+
\varepsilon_2}\\
& \quad \leq \eta |(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\!+\!\eta^{-\frac{p-2+2\varepsilon_2s}{2+4s-p-2\varepsilon_2s}}
R^{-\frac{2s\left[(p-2)(N-1)-2\varepsilon_2s\right]}{2+4s-p-2\varepsilon_2s}}.
\end{align*}
\begin{align*}
&R^{-\frac{(q-2)(N-1)}{2}+\varepsilon_1s}|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{q-2}{2s}+
\varepsilon_1}\\
& \quad \leq \eta |(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\!+\!\eta^{-\frac{q-2+2\varepsilon_1s}{2+4s-q-2\varepsilon_1s}}
R^{-\frac{2s\left[(q-2)(N-1)-2\varepsilon_1s\right]}{2+4s-q-2\varepsilon_1s}},\\
&R^{-\frac{(p-2)(N-1)}{2}+\varepsilon_2s}|(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^{\frac{p-2}{2s}+
\varepsilon_2}\\
& \quad \leq \eta |(-\Delta)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\!+\!\eta^{-\frac{p-2+2\varepsilon_2s}{2+4s-p-2\varepsilon_2s}}
R^{-\frac{2s\left[(p-2)(N-1)-2\varepsilon_2s\right]}{2+4s-p-2\varepsilon_2s}}.
\end{align*}Thus, there exists a constant C > 0 such that
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))&\leq8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad+C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+ I(\eta,R)
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))&\leq8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p\\
&\quad+C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+ I(\eta,R)
\end{align*} for all ![]() $t\in[0,T^*)$, any η > 0, and any R > 1, where
$t\in[0,T^*)$, any η > 0, and any R > 1, where
 \begin{align*}
I(\eta,R)&:=O\Big(R^{-2s}
+\eta^{-\frac{q-2+2\varepsilon_1s}{2+4s-q-2\varepsilon_1s}}
R^{-\frac{2s\left[(q-2)(N-1)-2\varepsilon_1s\right]}{2+4s-q-2\varepsilon_1s}}\\
& \quad +\eta^{-\frac{p-2+2\varepsilon_2s}{2+4s-p-2\varepsilon_2s}}
R^{-\frac{2s\left[(p-2)(N-1)-2\varepsilon_2s\right]}{2+4s-p-2\varepsilon_2s}}\Big).
\end{align*}
\begin{align*}
I(\eta,R)&:=O\Big(R^{-2s}
+\eta^{-\frac{q-2+2\varepsilon_1s}{2+4s-q-2\varepsilon_1s}}
R^{-\frac{2s\left[(q-2)(N-1)-2\varepsilon_1s\right]}{2+4s-q-2\varepsilon_1s}}\\
& \quad +\eta^{-\frac{p-2+2\varepsilon_2s}{2+4s-p-2\varepsilon_2s}}
R^{-\frac{2s\left[(p-2)(N-1)-2\varepsilon_2s\right]}{2+4s-p-2\varepsilon_2s}}\Big).
\end{align*} Since ![]() $2+4s/N \lt q \lt p \lt 2N/(N-2s)$ and
$2+4s/N \lt q \lt p \lt 2N/(N-2s)$ and ![]() $p \lt 2+4s$, we can choose
$p \lt 2+4s$, we can choose ![]() $\varepsilon_1 \gt 0,\varepsilon_2 \gt 0$ sufficiently small such that
$\varepsilon_1 \gt 0,\varepsilon_2 \gt 0$ sufficiently small such that
 \begin{align*}
&q-2+2\varepsilon_1s \gt 0,\quad 2+4s-q-2\varepsilon_1s \gt 0,\quad (q-2)(N-1)-2\varepsilon_1s \gt 0,\\
&p-2+2\varepsilon_2s \gt 0,\quad 2+4s-p-2\varepsilon_2s \gt 0,\quad (p-2)(N-1)-2\varepsilon_2s \gt 0.
\end{align*}
\begin{align*}
&q-2+2\varepsilon_1s \gt 0,\quad 2+4s-q-2\varepsilon_1s \gt 0,\quad (q-2)(N-1)-2\varepsilon_1s \gt 0,\\
&p-2+2\varepsilon_2s \gt 0,\quad 2+4s-p-2\varepsilon_2s \gt 0,\quad (p-2)(N-1)-2\varepsilon_2s \gt 0.
\end{align*} In addition, we fix ![]() $t\in[0,T^*)$ and denote
$t\in[0,T^*)$ and denote
 \begin{equation*}
\kappa:=\frac{4N(p-2)|E_\mu(\psi_0)|+1}{N(p-2)-4s}.
\end{equation*}
\begin{equation*}
\kappa:=\frac{4N(p-2)|E_\mu(\psi_0)|+1}{N(p-2)-4s}.
\end{equation*} Since ![]() $p \gt 2+4s/N$, we know κ > 0. We consider two cases.
$p \gt 2+4s/N$, we know κ > 0. We consider two cases.
Case 1:  $|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\leq\kappa$. Noting that
$|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\leq\kappa$. Noting that
 \begin{equation*}
8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p=8s P_\mu(\psi(t,\cdot)),
\end{equation*}
\begin{equation*}
8s|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2-\frac{4N\mu(q-2)}{q}|\psi(t,\cdot)|_q^q-
\frac{4N(p-2)}{p}|\psi(t,\cdot)|_p^p=8s P_\mu(\psi(t,\cdot)),
\end{equation*}and (3.14), we have
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq4N(q-2)
\left(E_\mu(\psi_0)-M_{a,\mu}\right)
+C\eta \kappa
+I(\eta,R).
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq4N(q-2)
\left(E_\mu(\psi_0)-M_{a,\mu}\right)
+C\eta \kappa
+I(\eta,R).
\end{align*}By choosing η > 0 small enough and R > 1 large enough depending on η, we can get
Thus, we obtain
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
\leq\frac{2N(q-2)\left(E_\mu(\psi_0)-M_{a,\mu}\right)}{\kappa}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2.
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
\leq\frac{2N(q-2)\left(E_\mu(\psi_0)-M_{a,\mu}\right)}{\kappa}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2.
\end{align*} Case 2:  $|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2 \gt \kappa$. By lemma 3.6, we obtain
$|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2 \gt \kappa$. By lemma 3.6, we obtain
 \begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
&\leq4N(p-2)|E_\mu\left(\psi_0\right)|+2\left(4s-N(p-2)\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\\
& \quad +C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+I(\eta,R)\\
&\leq-1+\left(4s-N(p-2)\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\\
& \quad +C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+I(\eta,R).
\end{align*}
\begin{align*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))
&\leq4N(p-2)|E_\mu\left(\psi_0\right)|+2\left(4s-N(p-2)\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\\
& \quad +C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+I(\eta,R)\\
&\leq-1+\left(4s-N(p-2)\right)|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2\\
& \quad +C\eta |\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2+I(\eta,R).
\end{align*} Since ![]() $p \gt 2+4s/N$, we choose η > 0 small enough so that
$p \gt 2+4s/N$, we choose η > 0 small enough so that
 \begin{equation*}
N(p-2)-4s-C\eta\geq\frac{N(p-2)-4s}{2}.
\end{equation*}
\begin{equation*}
N(p-2)-4s-C\eta\geq\frac{N(p-2)-4s}{2}.
\end{equation*}We next choose R > 1 large enough depending on η so that
We thus obtain
 \begin{equation*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -\frac{N(p-2)-4s}{2}
|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2.
\end{equation*}
\begin{equation*}
\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -\frac{N(p-2)-4s}{2}
|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2^2.
\end{equation*}Combined with the two cases above, we prove our claim (3.16).
Step 3: We are now able to show that the solution ![]() $\psi(t,\cdot)$ blows up in a finite time. Assume by contradiction that
$\psi(t,\cdot)$ blows up in a finite time. Assume by contradiction that ![]() $T^*=\infty$. It follows from (3.15) and (3.16) that
$T^*=\infty$. It follows from (3.15) and (3.16) that  $\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -C$ with some constant C > 0. As a consequence,
$\frac{d}{dt}M_{\varphi_R}(\psi(t,\cdot))\leq -C$ with some constant C > 0. As a consequence, ![]() $M_{\varphi_R}(\psi(t,\cdot)) \lt 0$ for all
$M_{\varphi_R}(\psi(t,\cdot)) \lt 0$ for all ![]() $t\geq t_1$ with some sufficiently large t 1. After integrating (3.16) on
$t\geq t_1$ with some sufficiently large t 1. After integrating (3.16) on ![]() $[t_1, t]$, we obtain
$[t_1, t]$, we obtain
 \begin{equation}
M_{\varphi_R}(\psi(t,\cdot))\!\leq\! -C_2\!\int_{t_1}^t
|(-\Delta)^{\frac{s}{2}}\psi(\tau,\cdot)|_2^2d\tau+
M_{\varphi_R}(\psi(t_1))
\!\leq\! -C_2\!\int_{t_1}^t
|(-\Delta)^{\frac{s}{2}}\psi(\tau,\cdot)|_2^2d\tau
\end{equation}
\begin{equation}
M_{\varphi_R}(\psi(t,\cdot))\!\leq\! -C_2\!\int_{t_1}^t
|(-\Delta)^{\frac{s}{2}}\psi(\tau,\cdot)|_2^2d\tau+
M_{\varphi_R}(\psi(t_1))
\!\leq\! -C_2\!\int_{t_1}^t
|(-\Delta)^{\frac{s}{2}}\psi(\tau,\cdot)|_2^2d\tau
\end{equation} for all ![]() $t\geq t_1$. On the other hand, we use lemma A.5 and L 2-mass conservation to find that
$t\geq t_1$. On the other hand, we use lemma A.5 and L 2-mass conservation to find that
 \begin{equation}
\left|M_{\varphi_R}(\psi(t,\cdot))\right|\leq C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})\left(|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{s}}+|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{2s}}\right),
\end{equation}
\begin{equation}
\left|M_{\varphi_R}(\psi(t,\cdot))\right|\leq C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})\left(|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{s}}+|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{2s}}\right),
\end{equation}where we used the interpolation estimate
 \begin{equation*}
\left||\nabla|^{1/2}\psi(t,\cdot)\right|_2\leq |\psi(t,\cdot)|_2^{1-\frac{1}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{2s}}
\end{equation*}
\begin{equation*}
\left||\nabla|^{1/2}\psi(t,\cdot)\right|_2\leq |\psi(t,\cdot)|_2^{1-\frac{1}{2s}}|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{2s}}
\end{equation*} for ![]() $s \gt 1/2$. So, we deduce from (3.15) and (3.18) that
$s \gt 1/2$. So, we deduce from (3.15) and (3.18) that
 \begin{equation*}
\left|M_{\varphi_R}(\psi(t,\cdot))\right|\leq C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{s}}.
\end{equation*}
\begin{equation*}
\left|M_{\varphi_R}(\psi(t,\cdot))\right|\leq C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_2
^{\frac{1}{s}}.
\end{equation*}This, together with (3.17), implies that
 \begin{equation}
M_{\varphi_R}(\psi(t,\cdot))\leq -C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})\int_{t_1}^t
\left|M_{\varphi_R}(\psi(\tau,\cdot))\right|^{2s}d\tau \quad \mbox{for ~}t\geq t_1.
\end{equation}
\begin{equation}
M_{\varphi_R}(\psi(t,\cdot))\leq -C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})\int_{t_1}^t
\left|M_{\varphi_R}(\psi(\tau,\cdot))\right|^{2s}d\tau \quad \mbox{for ~}t\geq t_1.
\end{equation} Let  $z(t):=\int_{t_1}^t\left|M_{\varphi_R}(\psi(\tau,\cdot))\right|^{2s}d\tau$, noting that
$z(t):=\int_{t_1}^t\left|M_{\varphi_R}(\psi(\tau,\cdot))\right|^{2s}d\tau$, noting that ![]() $M_{\varphi_R}(\psi(t,\cdot)) \lt 0$ for
$M_{\varphi_R}(\psi(t,\cdot)) \lt 0$ for ![]() $t \gt t_1$, hence z(t) is strictly increasing for
$t \gt t_1$, hence z(t) is strictly increasing for ![]() $t \gt t_1$ and we can find a
$t \gt t_1$ and we can find a ![]() $t_2 \gt t_1$ such that
$t_2 \gt t_1$ such that ![]() $z(t_2) \gt 0$. Furthermore, by (3.19), we obtain
$z(t_2) \gt 0$. Furthermore, by (3.19), we obtain
 \begin{equation*}
z'(t)\geq [C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}z^{2s}.
\end{equation*}
\begin{equation*}
z'(t)\geq [C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}z^{2s}.
\end{equation*} Therefore, for ![]() $t \gt t_2$, it holds that
$t \gt t_2$, it holds that ![]() $z'(t)z^{-2s}\ge [C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}$. Since
$z'(t)z^{-2s}\ge [C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}$. Since  $s \gt \frac{1}{2}$, we obtain
$s \gt \frac{1}{2}$, we obtain ![]() $(1-2s)z'(t)z^{-2s}\le (1-2s)[C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}$. After integration on
$(1-2s)z'(t)z^{-2s}\le (1-2s)[C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}$. After integration on ![]() $[t_2,t]$, one has
$[t_2,t]$, one has
 \begin{equation}
0 \lt z^{1-2s}(t)\le z^{1-2s}(t_2)-(2s-1)[C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}(t-t_2).
\end{equation}
\begin{equation}
0 \lt z^{1-2s}(t)\le z^{1-2s}(t_2)-(2s-1)[C(N, s, a, \|\nabla\varphi_R\|_{W^{1,\infty}})]^{2s}(t-t_2).
\end{equation} Note that the right-hand side of (3.20) goes to ![]() $-\infty$ as
$-\infty$ as ![]() $t\rightarrow+\infty$, while the left-hand side is positive. Hence, it must hold that
$t\rightarrow+\infty$, while the left-hand side is positive. Hence, it must hold that ![]() $T^* \lt +\infty$.
$T^* \lt +\infty$.
Proof of theorem 1.5(iii) Let u be a radial minimizer for ![]() $M_{a,\mu}$. Then, we know
$M_{a,\mu}$. Then, we know ![]() $P_\mu(u)=0$. Setting
$P_\mu(u)=0$. Setting  $\psi_0^\tau(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$ with τ > 0, by lemma 3.4, we obtain
$\psi_0^\tau(x)=e^{\frac{N}{2}\tau}u(e^\tau x)$ with τ > 0, by lemma 3.4, we obtain
for any τ > 0. Thus, ![]() $\psi_0^\tau\in \mathcal{B}_{a,\mu}$ for τ > 0. In addition, let
$\psi_0^\tau\in \mathcal{B}_{a,\mu}$ for τ > 0. In addition, let ![]() $\tau\rightarrow 0^+$, we have
$\tau\rightarrow 0^+$, we have ![]() $\|\psi_0^\tau-u\|_{H^s}\rightarrow0$. Therefore, we apply proposition 3.7 to get the strong instability of
$\|\psi_0^\tau-u\|_{H^s}\rightarrow0$. Therefore, we apply proposition 3.7 to get the strong instability of ![]() $e^{-\mathrm{i}\lambda t}u$.
$e^{-\mathrm{i}\lambda t}u$.
Remark 3.8. After completing this article, we learned that Feng and Zhu [Reference Feng and Zhu16] considered the instability of ground state solutions for the fixed frequency λ. The relationship between the two types of ground state solutions is still a delicate but important open problem.
4. The combined nonlinearities and defocusing case:  $2 \lt q\leq\bar{p} \lt p \lt 2_s^*$ and µ < 0
$2 \lt q\leq\bar{p} \lt p \lt 2_s^*$ and µ < 0
Via lemmas 6.14 and 6.15 and theorem 6.17 in [Reference Luo and Zhang33], there exists ![]() $\hat{u}$ such that the following variational characterization holds:
$\hat{u}$ such that the following variational characterization holds:
 \begin{equation*}
E_\mu(\hat{u})=M_{a,\mu}^r:=\inf_{u\in V_{a,\mu}^r}E_\mu(u),\quad V_{a,\mu}^r:=\left\{u\in S_a:u(x)=u(|x|), P_\mu(u)=0\right\}.
\end{equation*}
\begin{equation*}
E_\mu(\hat{u})=M_{a,\mu}^r:=\inf_{u\in V_{a,\mu}^r}E_\mu(u),\quad V_{a,\mu}^r:=\left\{u\in S_a:u(x)=u(|x|), P_\mu(u)=0\right\}.
\end{equation*} Once we obtain  $\hat{M}_{a,\mu}^r=M_{a,\mu}^r$ (see lemma 4.1), similar to the proof of theorem 1.5(iii), we deduce the strong instability of the standing wave
$\hat{M}_{a,\mu}^r=M_{a,\mu}^r$ (see lemma 4.1), similar to the proof of theorem 1.5(iii), we deduce the strong instability of the standing wave ![]() $e^{-\mathrm{i}\hat{\lambda}t}\hat{u}$. First, we recall (3.12), and note that lemma 3.4 still holds in this case.
$e^{-\mathrm{i}\hat{\lambda}t}\hat{u}$. First, we recall (3.12), and note that lemma 3.4 still holds in this case.
Lemma 4.1. Let  $\hat{M}_{a,\mu}^r$ be defined by (1.8), then
$\hat{M}_{a,\mu}^r$ be defined by (1.8), then
 \begin{equation*}
\hat{M}_{a,\mu}^r=\inf_{V_{a,\mu}^r}\hat{E}_\mu=M_{a,\mu}^r.
\end{equation*}
\begin{equation*}
\hat{M}_{a,\mu}^r=\inf_{V_{a,\mu}^r}\hat{E}_\mu=M_{a,\mu}^r.
\end{equation*}Proof. The proof is similar to the argument of lemma 3.5, so we omit it.
Similarly, we define the two manifolds by
 \begin{eqnarray*}
&\hat{\mathcal{A}}_{a,\mu}=\left\{u\in S_{a,r}: P_\mu(u) \gt 0, E_\mu(u) \lt M_{a,\mu}^r\right\},\\
&\hat{\mathcal{B}}_{a,\mu}=\left\{u\in S_{a,r}: P_\mu(u) \lt 0, E_\mu(u) \lt M_{a,\mu}^r\right\}.
\end{eqnarray*}
\begin{eqnarray*}
&\hat{\mathcal{A}}_{a,\mu}=\left\{u\in S_{a,r}: P_\mu(u) \gt 0, E_\mu(u) \lt M_{a,\mu}^r\right\},\\
&\hat{\mathcal{B}}_{a,\mu}=\left\{u\in S_{a,r}: P_\mu(u) \lt 0, E_\mu(u) \lt M_{a,\mu}^r\right\}.
\end{eqnarray*}Then, we have the following result:
Proposition 4.2. Under the assumptions of theorem 1.7(ii). Then  $\hat{\mathcal{A}}_{a,\mu}$ and
$\hat{\mathcal{A}}_{a,\mu}$ and  $\hat{\mathcal{B}}_{a,\mu}$ are two invariant manifolds of (1.1). More precisely,
$\hat{\mathcal{B}}_{a,\mu}$ are two invariant manifolds of (1.1). More precisely,
(i) if the initial value
 $\psi_0\in \hat{\mathcal{A}}_{a,\mu}$, then the solution
$\psi_0\in \hat{\mathcal{A}}_{a,\mu}$, then the solution  $\psi(t,\cdot)$ of (1.1) always stays in
$\psi(t,\cdot)$ of (1.1) always stays in  $\hat{\mathcal{A}}_{a,\mu}$ and exists globally over time.
$\hat{\mathcal{A}}_{a,\mu}$ and exists globally over time.(ii) if the initial value
 $\psi_0\in \hat{\mathcal{B}}_{a,\mu}$, then the solution
$\psi_0\in \hat{\mathcal{B}}_{a,\mu}$, then the solution  $\psi(t,\cdot)$ of (1.1) always stays in
$\psi(t,\cdot)$ of (1.1) always stays in  $\hat{\mathcal{B}}_{a,\mu}$ but will blow up in finite time.
$\hat{\mathcal{B}}_{a,\mu}$ but will blow up in finite time.
Proof. The proof is similar to that of proposition 3.7.
Proof of theorem 1.7 The conclusion (i) is established by [Reference Luo and Zhang33, theorems 1.9, 1.11]. The proof of item (ii) is similar to the argument of theorem 1.5(iii).
Acknowledgements
We thank the anonymous referee for their helpful comments. No conflict of interest exists in the submission of this manuscript, and all authors approve the manuscript for publication. Z. Li is funded by the Natural Science Foundation of Hebei Province (No. A2022205007), and by the Science and Technology Project of Hebei Education Department (No. QN2022047), and by Hebei Province Yanzhao Golden Stage Talent Gathering Program Key Talent Project (Study Abroad Returning Platform) (No. B2024018). H. Luo is supported by the National Natural Science Foundation of China (Nos. 12471105, 12171143 and 12171144). Z. Zhang is supported by the National Key R&D Program of China (No. 2022YFA1005601) and the National Natural Science Foundation of China (No. 12031015).
Appendix A.
Lemma A.1. [17] Let ![]() $2\le \alpha \lt 2_s^*$, then there exists a constant
$2\le \alpha \lt 2_s^*$, then there exists a constant ![]() $C(s,N,\alpha)$ such that for any
$C(s,N,\alpha)$ such that for any ![]() $u\in H^s(\mathbb{R}^N)$, the following inequality holds:
$u\in H^s(\mathbb{R}^N)$, the following inequality holds:
 \begin{align*}
\int_{\mathbb{R}^N}|u(x)|^\alpha\mathrm{d}x & \leq C(s,N,\alpha)\Big(\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u(x)|^2\mathrm{d}x\Big)^{\frac{N(\alpha-2)}{4s}}\\
& \quad \times \Big(\int_{\mathbb{R}^N} |u(x)|^2\mathrm{d}x\Big)^{\frac{\alpha}{2}-\frac{N(\alpha-2)}{4s}}.
\end{align*}
\begin{align*}
\int_{\mathbb{R}^N}|u(x)|^\alpha\mathrm{d}x & \leq C(s,N,\alpha)\Big(\int_{\mathbb{R}^N}|\left(-\Delta\right)^{\frac{s}{2}}u(x)|^2\mathrm{d}x\Big)^{\frac{N(\alpha-2)}{4s}}\\
& \quad \times \Big(\int_{\mathbb{R}^N} |u(x)|^2\mathrm{d}x\Big)^{\frac{\alpha}{2}-\frac{N(\alpha-2)}{4s}}.
\end{align*}Lemma A.2. [12, lemma 2.2] Let ![]() $N\geq1$ and
$N\geq1$ and ![]() $0 \lt s \lt 1$. Let
$0 \lt s \lt 1$. Let ![]() $\{v_n\}_{n\ge 1}$ be a bounded sequence in
$\{v_n\}_{n\ge 1}$ be a bounded sequence in ![]() $H^s(\mathbb{R}^N)$. Then, there exist a subsequence of
$H^s(\mathbb{R}^N)$. Then, there exist a subsequence of ![]() $\{v_n\}_{n\in\mathbb{N}}$, a family
$\{v_n\}_{n\in\mathbb{N}}$, a family ![]() $\{x_n^j\}_{n\in\mathbb{N}}$ of sequences in
$\{x_n^j\}_{n\in\mathbb{N}}$ of sequences in ![]() $\mathbb{R}^N$ and a sequence
$\mathbb{R}^N$ and a sequence ![]() $\{V^j\}_{j\in\mathbb{N}}$ of
$\{V^j\}_{j\in\mathbb{N}}$ of ![]() $H^s(\mathbb{R}^N)$ functions such that for every k ≠ j,
$H^s(\mathbb{R}^N)$ functions such that for every k ≠ j, ![]() $|x_n^k-x_n^j|\rightarrow +\infty$ as
$|x_n^k-x_n^j|\rightarrow +\infty$ as ![]() $n\rightarrow +\infty.$ Furthermore, for every
$n\rightarrow +\infty.$ Furthermore, for every ![]() $l\geq1$ and every
$l\geq1$ and every ![]() $x\in \mathbb{R}^N$,
$x\in \mathbb{R}^N$, ![]() $v_n(x)$ can be decomposed into
$v_n(x)$ can be decomposed into
 \begin{equation*}
v_n(x)=\sum_{j=1}^l V^j(x-x_n^j)+v_n^l(x),
\end{equation*}
\begin{equation*}
v_n(x)=\sum_{j=1}^l V^j(x-x_n^j)+v_n^l(x),
\end{equation*} with ![]() $\varlimsup_{n\rightarrow +\infty}|v_n^l|_\gamma\rightarrow0$ as
$\varlimsup_{n\rightarrow +\infty}|v_n^l|_\gamma\rightarrow0$ as ![]() $l\rightarrow\infty$ for every
$l\rightarrow\infty$ for every  $\gamma\in\big(2,\frac{2N}{(N-2s)^+}\big)$. In addition, for every
$\gamma\in\big(2,\frac{2N}{(N-2s)^+}\big)$. In addition, for every ![]() $l\geq1$, the following expansions hold true as
$l\geq1$, the following expansions hold true as ![]() $n\rightarrow+\infty$:
$n\rightarrow+\infty$:
 \begin{equation*}
\begin{aligned}
& |v_n|_2^2=\sum_{j=1}^l |V^j|_2^2+|v_n^l|_2^2+o_n(1),\qquad |v_n|_\gamma^\gamma=\sum_{j=1}^l |V^j|_\gamma^\gamma+|v_n^l|_\gamma^\gamma+o_n(1),\\
& |\left(-\Delta\right)^{\frac{s}{2}}v_n|_{2}^2=\sum_{j=1}^l|\left(-\Delta\right)^{\frac{s}{2}}V^j|_{2}^2
+|\left(-\Delta\right)^{\frac{s}{2}}v_n^l|_{2}^2+o_n(1).
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
& |v_n|_2^2=\sum_{j=1}^l |V^j|_2^2+|v_n^l|_2^2+o_n(1),\qquad |v_n|_\gamma^\gamma=\sum_{j=1}^l |V^j|_\gamma^\gamma+|v_n^l|_\gamma^\gamma+o_n(1),\\
& |\left(-\Delta\right)^{\frac{s}{2}}v_n|_{2}^2=\sum_{j=1}^l|\left(-\Delta\right)^{\frac{s}{2}}V^j|_{2}^2
+|\left(-\Delta\right)^{\frac{s}{2}}v_n^l|_{2}^2+o_n(1).
\end{aligned}
\end{equation*}Lemma A.3. [13, proposition 3.3] Radial Hs local well-posedness Assume  $N\geq2, \frac{N}{2N-1}\leq s \lt 1$, and
$N\geq2, \frac{N}{2N-1}\leq s \lt 1$, and  $2 \lt q \lt p \lt \frac{2N}{N-2s}$. Let
$2 \lt q \lt p \lt \frac{2N}{N-2s}$. Let
 \begin{eqnarray*}
& q_1=\frac{4sq}{(q-2)(N-2s)},\quad q_2=\frac{Nq}{N+(q-2)s},\quad
p_1=\frac{4sp}{(p-2)(N-2s)},\\
& p_2=\frac{Np}{N+(p-2)s}.
\end{eqnarray*}
\begin{eqnarray*}
& q_1=\frac{4sq}{(q-2)(N-2s)},\quad q_2=\frac{Nq}{N+(q-2)s},\quad
p_1=\frac{4sp}{(p-2)(N-2s)},\\
& p_2=\frac{Np}{N+(p-2)s}.
\end{eqnarray*} Then, for any ![]() $\psi_0\in H^s$ radial, there exist
$\psi_0\in H^s$ radial, there exist ![]() $T\in (0,+\infty]$ and a unique solution to (1.1) satisfying
$T\in (0,+\infty]$ and a unique solution to (1.1) satisfying
Moreover, the following properties hold:
(i)
 $\psi\in L^{a}_{\text{loc}}\left([0,T),W^{s,b}\right)$ for any fractional admissible pair (a, b).
$\psi\in L^{a}_{\text{loc}}\left([0,T),W^{s,b}\right)$ for any fractional admissible pair (a, b).(ii) If
 $T \lt +\infty$, then
$T \lt +\infty$, then  $|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_{2}^2\rightarrow\infty$ as
$|\left(-\Delta\right)^{\frac{s}{2}}\psi(t,\cdot)|_{2}^2\rightarrow\infty$ as  $t\uparrow T$.
$t\uparrow T$.(iii) The laws of conservation of mass and energy hold, i.e.,
 $|\psi(t,\cdot)|_{2}^2=|\psi_0|_{2}^2$ and
$|\psi(t,\cdot)|_{2}^2=|\psi_0|_{2}^2$ and  $E_\mu(\psi(t,\cdot))=E_\mu(\psi_0)$ for all
$E_\mu(\psi(t,\cdot))=E_\mu(\psi_0)$ for all  $t\in[0,T)$.
$t\in[0,T)$.
Remark A.4. In fact, the ![]() $\psi(t,\cdot)$ is also radial for every
$\psi(t,\cdot)$ is also radial for every ![]() $t\in [0,T)$.
$t\in [0,T)$.
Lemma A.5. [6, lemma A.1] Let ![]() $N\geq1$ and
$N\geq1$ and ![]() $\varphi\colon\mathbb{R}^N\rightarrow\mathbb{R}$ be such that
$\varphi\colon\mathbb{R}^N\rightarrow\mathbb{R}$ be such that ![]() $\nabla\varphi\in W^{1,\infty}(\mathbb{R}^N)$. Then, for all
$\nabla\varphi\in W^{1,\infty}(\mathbb{R}^N)$. Then, for all ![]() $u\in H^{1/2}(\mathbb{R}^N)$, it holds that
$u\in H^{1/2}(\mathbb{R}^N)$, it holds that
 \begin{equation*}
\Big|\int_{\mathbb{R}^N}\bar{u}(x)\nabla\varphi(x)\cdot\nabla u(x)\Big|\leq C\Big(\left||\nabla|^{1/2}u\right|_2^2+|u|_2
\left||\nabla|^{1/2}u\right|_2\Big),
\end{equation*}
\begin{equation*}
\Big|\int_{\mathbb{R}^N}\bar{u}(x)\nabla\varphi(x)\cdot\nabla u(x)\Big|\leq C\Big(\left||\nabla|^{1/2}u\right|_2^2+|u|_2
\left||\nabla|^{1/2}u\right|_2\Big),
\end{equation*} for some C > 0 depending only on ![]() $\left\|\nabla\varphi\right\|_{W^{1,\infty}}$ and N.
$\left\|\nabla\varphi\right\|_{W^{1,\infty}}$ and N.
Lemma A.6. Let ![]() $0 \lt \gamma \lt \beta$,
$0 \lt \gamma \lt \beta$, ![]() $A,B \gt 0$ and
$A,B \gt 0$ and
Then ![]() $g(t)\geq0$ for any
$g(t)\geq0$ for any ![]() $t\in[0,\infty)$ if and only if
$t\in[0,\infty)$ if and only if  $A\geq
\frac{\gamma}{\beta}\big(\frac{\beta-\gamma}{\beta B}\big)^{\frac{\beta-\gamma}{\gamma}}.$
$A\geq
\frac{\gamma}{\beta}\big(\frac{\beta-\gamma}{\beta B}\big)^{\frac{\beta-\gamma}{\gamma}}.$
Proof. Since ![]() $g'(t)=t^{\gamma-1}\left(\beta At^{\beta-\gamma}-\gamma\right)$, the minimum of g(t) is attained at
$g'(t)=t^{\gamma-1}\left(\beta At^{\beta-\gamma}-\gamma\right)$, the minimum of g(t) is attained at  $t_0=\big(\frac{\gamma}{A\beta}\big)^{\frac{1}{\beta-\gamma}}$. Therefore, it is equivalent to
$t_0=\big(\frac{\gamma}{A\beta}\big)^{\frac{1}{\beta-\gamma}}$. Therefore, it is equivalent to ![]() $g(t_0)\geq0$, namely,
$g(t_0)\geq0$, namely,  $A\geq \frac{\gamma}{\beta}\big(\frac{\beta-\gamma}{\beta B}\big)^{\frac{\beta-\gamma}{\gamma}}.$
$A\geq \frac{\gamma}{\beta}\big(\frac{\beta-\gamma}{\beta B}\big)^{\frac{\beta-\gamma}{\gamma}}.$