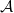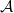1. Introduction
The classification of various types of subcategories is a fundamental problem in many different contexts. It will help us to better understand the structure of categories. Let
![]() $R$
be a commutative Noetherian ring, and Spec
$R$
be a commutative Noetherian ring, and Spec
![]() $R$
be the set of prime ideals
$R$
be the set of prime ideals
![]() $\textsf{p}$
in
$\textsf{p}$
in
![]() $R$
. For
$R$
. For
![]() $\textsf{p}\in \text{Spec}R$
, set
$\textsf{p}\in \text{Spec}R$
, set
![]() $S=R\backslash \textsf{p}$
and denote by
$S=R\backslash \textsf{p}$
and denote by
![]() $R_{\textsf{p}}=R[S^{-1}]$
the localization. The support of a
$R_{\textsf{p}}=R[S^{-1}]$
the localization. The support of a
![]() $R$
-module
$R$
-module
![]() $X$
is the set of points
$X$
is the set of points
![]() $ \textsf{p}$
in
$ \textsf{p}$
in
![]() $ \text{Spec}R$
such that
$ \text{Spec}R$
such that
![]() $X_{\textsf{p}}\;:\!=\;X\otimes R_{\textsf{p}}\neq 0$
. Using this support, Gabriel [Reference Gabriel4] showed that there exist one-to-one correspondences between the set of localizing subcategories of
$X_{\textsf{p}}\;:\!=\;X\otimes R_{\textsf{p}}\neq 0$
. Using this support, Gabriel [Reference Gabriel4] showed that there exist one-to-one correspondences between the set of localizing subcategories of
![]() ${{\mathrm{Mod}}}R$
, Serre subcategories of
${{\mathrm{Mod}}}R$
, Serre subcategories of
![]() ${{\mathrm{mod}}}R$
, and the specialization-closed subsets of the prime spectrum Spec
${{\mathrm{mod}}}R$
, and the specialization-closed subsets of the prime spectrum Spec
![]() $A$
. For complexes of modules, Foxby [Reference Foxby3] introduced useful notions of support, which are defined as follows: Let
$A$
. For complexes of modules, Foxby [Reference Foxby3] introduced useful notions of support, which are defined as follows: Let
![]() $k(\textsf{p})$
be the residue field
$k(\textsf{p})$
be the residue field
![]() $R_{\textsf{p}}/\textsf{p}R_{\textsf{p}}$
of the local ring
$R_{\textsf{p}}/\textsf{p}R_{\textsf{p}}$
of the local ring
![]() $R_{\textsf{p}}$
. The
$R_{\textsf{p}}$
. The
![]() $support$
of a complex
$support$
of a complex
![]() $X$
of
$X$
of
![]() $R$
-modules is the subset
$R$
-modules is the subset
Using this support of the complex, Hopkins [Reference Hopkins6] and Neeman [Reference Neeman13] classified all localizing subcategories of the unbounded derived category
![]() $D(R)$
. Kanda [Reference Kanda9] classified the Serre subcategories in an abelian category using the atom spectrum consisting of equivalence classes of monoform objects. Many authors have classified various types of subcategories, see [Reference Arentz-Hansen1, Reference Balmer2, Reference Herzog5, Reference Hovey7, Reference Iyama and Kimura8, Reference Krause10, Reference Neeman14–Reference Takahashi17] and so on.
$D(R)$
. Kanda [Reference Kanda9] classified the Serre subcategories in an abelian category using the atom spectrum consisting of equivalence classes of monoform objects. Many authors have classified various types of subcategories, see [Reference Arentz-Hansen1, Reference Balmer2, Reference Herzog5, Reference Hovey7, Reference Iyama and Kimura8, Reference Krause10, Reference Neeman14–Reference Takahashi17] and so on.
Let
![]() $R$
be a commutative Noetherian ring, and
$R$
be a commutative Noetherian ring, and
![]() $M$
be a
$M$
be a
![]() $R$
-module. Consider
$R$
-module. Consider
![]() $M$
to be a stalk complex. Following Foxby [Reference Foxby3], the
$M$
to be a stalk complex. Following Foxby [Reference Foxby3], the
![]() $support$
of
$support$
of
![]() $M$
is
$M$
is
Using this support, Krause [Reference Krause11] classified all full subcategories of
![]() $R$
-modules which are thick (i.e. closed under taking kernels, cokernels, and extensions) and closed under taking arbitrary direct sums. In this paper, we want to generalize Krause’s result from commutative noetherian rings to locally noetherian Grothendieck categories. So we need to find a new support in abelian category. Foxby [Reference Foxby3, 2.8,2.9] proved that a point
$R$
-modules which are thick (i.e. closed under taking kernels, cokernels, and extensions) and closed under taking arbitrary direct sums. In this paper, we want to generalize Krause’s result from commutative noetherian rings to locally noetherian Grothendieck categories. So we need to find a new support in abelian category. Foxby [Reference Foxby3, 2.8,2.9] proved that a point
![]() $\textsf{p}$
is in the support of a complex
$\textsf{p}$
is in the support of a complex
![]() $X$
with
$X$
with
![]() ${{\mathrm{H}}}^{n}(X)=0$
for
${{\mathrm{H}}}^{n}(X)=0$
for
![]() $n\ll 0$
if and only if the injective envelope of
$n\ll 0$
if and only if the injective envelope of
![]() $R/\textsf{p}$
appears in the minimal semi-injective resolution of
$R/\textsf{p}$
appears in the minimal semi-injective resolution of
![]() $X$
. When
$X$
. When
![]() $X$
is a
$X$
is a
![]() $R$
-module, the minimal semi-injective resolution of
$R$
-module, the minimal semi-injective resolution of
![]() $X$
is just the minimal injective resolution of
$X$
is just the minimal injective resolution of
![]() $X$
. So we get the equivalent characterization of
$X$
. So we get the equivalent characterization of
![]() ${{\mathrm{Supp}}}_{R}X$
:
${{\mathrm{Supp}}}_{R}X$
:
![]() $\textsf{p}\in{{\mathrm{Supp}}}_{R}X$
if and only if the injective envelope of
$\textsf{p}\in{{\mathrm{Supp}}}_{R}X$
if and only if the injective envelope of
![]() $R/\textsf{p}$
appears in the minimal injective resolution of
$R/\textsf{p}$
appears in the minimal injective resolution of
![]() $X$
. Let
$X$
. Let
![]() ${{\mathrm{Sp(Mod}}}A)$
denote the representative set of the isomorphism classes of indecomposable injective objects in
${{\mathrm{Sp(Mod}}}A)$
denote the representative set of the isomorphism classes of indecomposable injective objects in
![]() ${{\mathrm{Mod}}}A$
. Then, there is a bijection between
${{\mathrm{Mod}}}A$
. Then, there is a bijection between
![]() $\text{Spec}R$
and
$\text{Spec}R$
and
![]() ${{\mathrm{Sp(Mod}}}A)$
[Reference Krause12, Corollary 2.4.15]. We use the equivalent characterization to define the support of objects in locally noetherian Grothendieck category and get the following main result.
${{\mathrm{Sp(Mod}}}A)$
[Reference Krause12, Corollary 2.4.15]. We use the equivalent characterization to define the support of objects in locally noetherian Grothendieck category and get the following main result.
Theorem 1.1.
Let
![]() $ \mathcal{A}$
be a locally noetherian Grothendieck category. Then, the assignment
$ \mathcal{A}$
be a locally noetherian Grothendieck category. Then, the assignment
![]() $\mathcal{X}\mapsto{{\mathrm{Supp}}}\mathcal{X}$
induces an inclusion-preserving bijection between the set of thick subcategories of
$\mathcal{X}\mapsto{{\mathrm{Supp}}}\mathcal{X}$
induces an inclusion-preserving bijection between the set of thick subcategories of
![]() $ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
$ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
, with inverse
${{\mathrm{Sp}}}(\mathcal{A})$
, with inverse
![]() ${{\mathrm{Supp}}}^{-1}$
.
${{\mathrm{Supp}}}^{-1}$
.
The paper is organized as follows. In Section 2, we give some definitions and notations. In Section 3, we prove the main result.
2. Preliminaries
In this section, we introduce some basic properties and definitions which we will use later.
A category
![]() $\mathcal{A}$
is a
$\mathcal{A}$
is a
![]() $ Grothendieck$
$ Grothendieck$
![]() $category$
if
$category$
if
-
(Gr1) the category
 $\mathcal{A}$
is abelian,
$\mathcal{A}$
is abelian, -
(Gr2) for every set of objects
 $(X_{i})_{i\in I}$
there is a coproduct
$(X_{i})_{i\in I}$
there is a coproduct
 $\coprod _{i\in I}X_{i}$
in
$\coprod _{i\in I}X_{i}$
in
 $\mathcal{A}$
,
$\mathcal{A}$
, -
(Gr3) there is a
 $generator$
$generator$
 $G$
, that is, for every object
$G$
, that is, for every object
 $X$
the canonical morphism
$X$
the canonical morphism
 $\coprod _{\phi \in{{\mathrm{Hom}}}_{\mathcal{A}}(G,X)}G\to X$
is an epimorphism, and
$\coprod _{\phi \in{{\mathrm{Hom}}}_{\mathcal{A}}(G,X)}G\to X$
is an epimorphism, and -
(Gr4) every filtered colimit of exact sequences is exact.
A monomorphism
![]() $\phi \;:\;X\to Y$
is
$\phi \;:\;X\to Y$
is
![]() $essential$
if any morphism
$essential$
if any morphism
![]() $\alpha \;:\; Y\to Y^{\prime}$
is a monomorphism provided that the composite
$\alpha \;:\; Y\to Y^{\prime}$
is a monomorphism provided that the composite
![]() $\alpha \phi$
is a monomorphism. This condition can be rephrased as follows: if
$\alpha \phi$
is a monomorphism. This condition can be rephrased as follows: if
![]() $U\subseteq Y$
is a subobject with
$U\subseteq Y$
is a subobject with
![]() $U\bigcap{{\mathrm{Im}}} \phi$
= 0, then
$U\bigcap{{\mathrm{Im}}} \phi$
= 0, then
![]() $U$
= 0. A monomorphism
$U$
= 0. A monomorphism
![]() $\phi \;:\;X\to I$
is an
$\phi \;:\;X\to I$
is an
![]() $injective$
$injective$
![]() $ envelope$
of
$ envelope$
of
![]() $X$
if
$X$
if
![]() $I$
is injective and
$I$
is injective and
![]() $\phi$
is essential. For
$\phi$
is essential. For
![]() $X\in \mathcal{A}$
, an
$X\in \mathcal{A}$
, an
![]() $injective$
$injective$
![]() $resolution$
of
$resolution$
of
![]() $X$
is an exact sequence
$X$
is an exact sequence
![]() $0 \to X\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
with all
$0 \to X\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
with all
![]() $ I^{i}$
are injective. In addition, the above injective resolution is called
$ I^{i}$
are injective. In addition, the above injective resolution is called
![]() $minimal$
if
$minimal$
if
![]() $I^{n}$
is the injective envelope of
$I^{n}$
is the injective envelope of
![]() ${{\mathrm{Ker}}}i_{n+1}$
, for
${{\mathrm{Ker}}}i_{n+1}$
, for
![]() $n\in \mathbb{N}$
. Every object in a Grothendieck category admits an injective envelope [Reference Krause12, Corollary 2.5.4].
$n\in \mathbb{N}$
. Every object in a Grothendieck category admits an injective envelope [Reference Krause12, Corollary 2.5.4].
Let
![]() $\mathcal{A}$
be a Grothendieck category.
$\mathcal{A}$
be a Grothendieck category.
![]() $\mathcal{A}$
is called
$\mathcal{A}$
is called
![]() $locally$
$locally$
![]() $noetherian$
if
$noetherian$
if
![]() $\mathcal{A}$
has a generating set of noetherian objects. If
$\mathcal{A}$
has a generating set of noetherian objects. If
![]() $\mathcal{A}$
is locally noetherian, then the full subcategory of injective objects is closed under coproducts [Reference Krause12, Theorem 11.2.12].
$\mathcal{A}$
is locally noetherian, then the full subcategory of injective objects is closed under coproducts [Reference Krause12, Theorem 11.2.12].
Let
![]() $\mathcal{A}$
be a locally noetherian Grothendieck category. A full subcategory
$\mathcal{A}$
be a locally noetherian Grothendieck category. A full subcategory
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $\mathcal{A}$
is called
$\mathcal{A}$
is called
![]() $thick$
if for each exact sequence
$thick$
if for each exact sequence
![]() $M_{1}\to M_{2} \to M_{3} \to M_{4} \to M_{5}$
with
$M_{1}\to M_{2} \to M_{3} \to M_{4} \to M_{5}$
with
![]() $M_{i}$
in
$M_{i}$
in
![]() $\mathcal{C}$
for
$\mathcal{C}$
for
![]() $i = 1, 2, 4, 5$
, the module
$i = 1, 2, 4, 5$
, the module
![]() $M_{3}$
belongs to
$M_{3}$
belongs to
![]() $\mathcal{C}$
. It is clear that
$\mathcal{C}$
. It is clear that
![]() $\mathcal{C}$
is thick if and only if
$\mathcal{C}$
is thick if and only if
![]() $\mathcal{C}$
is closed under taking kernels, cokernels, and extensions. A thick subcategory is an abelian category, and the inclusion functor is exact. A full subcategory
$\mathcal{C}$
is closed under taking kernels, cokernels, and extensions. A thick subcategory is an abelian category, and the inclusion functor is exact. A full subcategory
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $\mathcal{A}$
is called
$\mathcal{A}$
is called
![]() $closed$
$closed$
![]() $under$
$under$
![]() $taking$
$taking$
![]() $injective$
$injective$
![]() $envelopes$
if for each
$envelopes$
if for each
![]() $X\in \mathcal{C}$
, the injective envelope
$X\in \mathcal{C}$
, the injective envelope
![]() $I(X)$
of
$I(X)$
of
![]() $X$
is also in
$X$
is also in
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
3. Main result
In this section,
![]() $\mathcal{A}$
is always a locally noetherian Grothendieck category and Sp
$\mathcal{A}$
is always a locally noetherian Grothendieck category and Sp
![]() $\mathcal{A}$
is a representative set of the isomorphism classes of indecomposable injective objects in
$\mathcal{A}$
is a representative set of the isomorphism classes of indecomposable injective objects in
![]() $\mathcal{A}$
(the spectrum of
$\mathcal{A}$
(the spectrum of
![]() $\mathcal{A}$
), unless otherwise specified.
$\mathcal{A}$
), unless otherwise specified.
We wish to classify all thick subcategories of
![]() $\mathcal{A}$
which are closed under taking arbitrary direct sums and taking injective envelopes. Firstly, we list some definitions which will be used later.
$\mathcal{A}$
which are closed under taking arbitrary direct sums and taking injective envelopes. Firstly, we list some definitions which will be used later.
Definition 3.1.
Let
![]() $M\in \mathcal{A}$
and
$M\in \mathcal{A}$
and
![]() $0 \to M\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
be the minimal injective resolution of
$0 \to M\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
be the minimal injective resolution of
![]() $M$
. The support of
$M$
. The support of
![]() $M$
is defined by
$M$
is defined by
For
![]() $\mathcal{X}\subseteq \mathcal{A}$
,
$\mathcal{X}\subseteq \mathcal{A}$
,
Denote
![]() ${{\mathrm{Ind}}}X$
be the set of the indecomposable direct summand of object
${{\mathrm{Ind}}}X$
be the set of the indecomposable direct summand of object
![]() $X$
.
$X$
.
Definition 3.2.
Let
![]() $\Phi$
be a subset of
$\Phi$
be a subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
. We call
${{\mathrm{Sp}}}(\mathcal{A})$
. We call
![]() $\Phi$
coherent if each morphism
$\Phi$
coherent if each morphism
![]() $I^0 \to I^1$
with
$I^0 \to I^1$
with
![]() ${{\mathrm{Ind}}}(I^0\oplus I^1) \in \Phi$
can be completed to an exact sequence
${{\mathrm{Ind}}}(I^0\oplus I^1) \in \Phi$
can be completed to an exact sequence
![]() $I^0 \to I^1 \to I^2$
with
$I^0 \to I^1 \to I^2$
with
![]() ${{\mathrm{Ind}}}I^2$
in
${{\mathrm{Ind}}}I^2$
in
![]() $\Phi$
.
$\Phi$
.
Let
![]() $\Phi$
be a subset of
$\Phi$
be a subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
. Denote
${{\mathrm{Sp}}}(\mathcal{A})$
. Denote
![]() ${{\mathrm{Supp}}}^{-1}\Phi \;:\!=\;\{M \in \mathcal{A} |{{\mathrm{Supp}}} M \subseteq \Phi \}.$
The following lemma is obvious.
${{\mathrm{Supp}}}^{-1}\Phi \;:\!=\;\{M \in \mathcal{A} |{{\mathrm{Supp}}} M \subseteq \Phi \}.$
The following lemma is obvious.
Lemma 3.3.
Let
![]() $\Phi$
be a coherent subset of
$\Phi$
be a coherent subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
, and
${{\mathrm{Sp}}}(\mathcal{A})$
, and
![]() $0 \to M\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
be the minimal injective resolution of
$0 \to M\to I^{0}\stackrel{i_{1}}\to I^{1} \stackrel{i_{2}}\to I^{2} \stackrel{i_{3}}\to \ldots$
be the minimal injective resolution of
![]() $M$
. Then,
$M$
. Then,
![]() $M\in{{\mathrm{Supp}}}^{-1}\Phi$
if and only if
$M\in{{\mathrm{Supp}}}^{-1}\Phi$
if and only if
![]() ${{\mathrm{Ind}}}( I^{0}\oplus I^{1})\subseteq \Phi$
.
${{\mathrm{Ind}}}( I^{0}\oplus I^{1})\subseteq \Phi$
.
Lemma 3.4.
Let
![]() $\Phi$
be a coherent subset of
$\Phi$
be a coherent subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
. Then,
${{\mathrm{Sp}}}(\mathcal{A})$
. Then,
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is a thick subcategory of
${{\mathrm{Supp}}}^{-1}\Phi$
is a thick subcategory of
![]() $ \mathcal{A}$
.
$ \mathcal{A}$
.
Proof. Taking
![]() $M$
,
$M$
,
![]() $N\in{{\mathrm{Supp}}}^{-1}\Phi$
, we have
$N\in{{\mathrm{Supp}}}^{-1}\Phi$
, we have
![]() ${{\mathrm{Supp}}} M,{{\mathrm{Supp}}} N\subseteq \Phi$
. Thus,
${{\mathrm{Supp}}} M,{{\mathrm{Supp}}} N\subseteq \Phi$
. Thus,
![]() ${{\mathrm{Supp}}} (M\oplus N)\subseteq \Phi$
. Hence,
${{\mathrm{Supp}}} (M\oplus N)\subseteq \Phi$
. Hence,
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is an additive category. In the following, we prove that
${{\mathrm{Supp}}}^{-1}\Phi$
is an additive category. In the following, we prove that
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels, cokernels, and extensions.
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels, cokernels, and extensions.
(a)
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels. For any
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels. For any
![]() $M\stackrel{f}\to N$
with
$M\stackrel{f}\to N$
with
![]() $M, N \in{{\mathrm{Supp}}}^{-1}\Phi$
, suppose
$M, N \in{{\mathrm{Supp}}}^{-1}\Phi$
, suppose
![]() $g:K\to M$
is the kernel of
$g:K\to M$
is the kernel of
![]() $f:M\to N$
. Take the minimal injective resolutions of
$f:M\to N$
. Take the minimal injective resolutions of
![]() $K$
,
$K$
,
![]() $M$
,
$M$
,
![]() $N$
as follows:
$N$
as follows:
Since
![]() $M,$
$M,$
![]() $N\in{{\mathrm{Supp}}}^{-1}\Phi$
,
$N\in{{\mathrm{Supp}}}^{-1}\Phi$
,
![]() ${{\mathrm{Ind}}}(\oplus _{i\in \textbf{N}}(I_{M}^{i}\oplus I_{N}^{i}))\subseteq \Phi$
. To prove that
${{\mathrm{Ind}}}(\oplus _{i\in \textbf{N}}(I_{M}^{i}\oplus I_{N}^{i}))\subseteq \Phi$
. To prove that
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels, it is enough to prove that
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels, it is enough to prove that
![]() ${{\mathrm{Ind}}}(I_{K}^{0}\oplus I_{K}^{1})\subseteq \Phi$
by
${{\mathrm{Ind}}}(I_{K}^{0}\oplus I_{K}^{1})\subseteq \Phi$
by
![]() $\Phi$
coherent. Since
$\Phi$
coherent. Since
![]() $I_{M}^{0}$
is injective, there is a morphism
$I_{M}^{0}$
is injective, there is a morphism
![]() $g^{0}\;:\;I_{K}^{0}\to I_{M}^{0}$
such that the following diagram is commutative:
$g^{0}\;:\;I_{K}^{0}\to I_{M}^{0}$
such that the following diagram is commutative:

Since
![]() $g^{0} i_{K}^{0}$
is monic and
$g^{0} i_{K}^{0}$
is monic and
![]() $i_{K}^{0}$
is essential, we have
$i_{K}^{0}$
is essential, we have
![]() $g^{0}$
is monic. Thus,
$g^{0}$
is monic. Thus,
![]() $ I_{K}^{0}$
is a direct summand of
$ I_{K}^{0}$
is a direct summand of
![]() $I_{M}^{0}$
. Hence,
$I_{M}^{0}$
. Hence,
![]() ${{\mathrm{Ind}}}I_{K}^{0}\subseteq \Phi$
.
${{\mathrm{Ind}}}I_{K}^{0}\subseteq \Phi$
.
Take the minimal injective resolution of
![]() ${{\mathrm{Im}}}f$
:
${{\mathrm{Im}}}f$
:
Similarly to the proof of
![]() $g_{0}$
, we can get the following commutative diagram
$g_{0}$
, we can get the following commutative diagram

where
![]() $k^{0}$
is monic. Hence,
$k^{0}$
is monic. Hence,
![]() ${{\mathrm{Ind}}}I_{f}^{0}\subseteq \Phi$
. Consider the exact sequence
${{\mathrm{Ind}}}I_{f}^{0}\subseteq \Phi$
. Consider the exact sequence
![]() $0\to K\to M\to{{\mathrm{Im}}}f \to 0$
. By the Horseshoe Lemma, we have the following commutative diagram with exact rows and columns
$0\to K\to M\to{{\mathrm{Im}}}f \to 0$
. By the Horseshoe Lemma, we have the following commutative diagram with exact rows and columns

Since
![]() $I_{M}^{0}$
is an injective envelope of
$I_{M}^{0}$
is an injective envelope of
![]() $M$
, we can construct an isomorphism
$M$
, we can construct an isomorphism
![]() $\phi \;:\;I_{M}^{0}\oplus E \stackrel{\sim }\to I_{K}^{0}\oplus I_{f}^{0}$
such that the following diagram commutative
$\phi \;:\;I_{M}^{0}\oplus E \stackrel{\sim }\to I_{K}^{0}\oplus I_{f}^{0}$
such that the following diagram commutative

Hence,
![]() ${{\mathrm{Ind}}}E\subseteq \Phi$
and
${{\mathrm{Ind}}}E\subseteq \Phi$
and
![]() $\psi ^{-1}\omega \;:\;\text{Coker} i_{K}^{0}\to \text{Coker} i_{M}^{0}\oplus E$
is monic. Consider the following commutative diagram
$\psi ^{-1}\omega \;:\;\text{Coker} i_{K}^{0}\to \text{Coker} i_{M}^{0}\oplus E$
is monic. Consider the following commutative diagram

Similarly to the proof of
![]() ${{\mathrm{Ind}}}I_{K}^{0}\subseteq \Phi$
, we can get
${{\mathrm{Ind}}}I_{K}^{0}\subseteq \Phi$
, we can get
![]() ${{\mathrm{Ind}}}I_{K}^{1}\subseteq \Phi$
. Therefore,
${{\mathrm{Ind}}}I_{K}^{1}\subseteq \Phi$
. Therefore,
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels.
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking kernels.
(b)
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking extensions. This follows from the Horseshoe Lemma.
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking extensions. This follows from the Horseshoe Lemma.
(c)
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking cokernels. For any
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking cokernels. For any
![]() $M\stackrel{f}\to N$
with
$M\stackrel{f}\to N$
with
![]() $M,N\in{{\mathrm{Supp}}}^{-1}\Phi$
, suppose
$M,N\in{{\mathrm{Supp}}}^{-1}\Phi$
, suppose
![]() $g:N\to C$
is the cokernel of
$g:N\to C$
is the cokernel of
![]() $f\;:\;M\to N$
. Take the minimal injective resolutions of
$f\;:\;M\to N$
. Take the minimal injective resolutions of
![]() $M$
,
$M$
,
![]() $N$
, then we can get the following commutative diagram with exact rows:
$N$
, then we can get the following commutative diagram with exact rows:

Consider the following push-out square

Taking the injective envelope
![]() $ I$
of
$ I$
of
![]() $D$
, then we have the following exact sequence
$D$
, then we have the following exact sequence

where
![]() $g^{0}=kb$
. Since
$g^{0}=kb$
. Since
![]() $M,$
$M,$
![]() $ N\in{{\mathrm{Supp}}}^{-1}\Phi$
and
$ N\in{{\mathrm{Supp}}}^{-1}\Phi$
and
![]() $\Phi$
is coherent, we have
$\Phi$
is coherent, we have
![]() ${{\mathrm{Ind}}}I\subseteq \Phi$
.
${{\mathrm{Ind}}}I\subseteq \Phi$
.
Claim that there is a monomorphism
![]() $i^{0}\;:\;C\to I$
such that
$i^{0}\;:\;C\to I$
such that
![]() $i^{0}g=g^{0}i_{N}^{0}.$
In fact, by the properties of the push-out square, we have the following exact commutative diagram:
$i^{0}g=g^{0}i_{N}^{0}.$
In fact, by the properties of the push-out square, we have the following exact commutative diagram:

where
![]() $\tilde{f^{0}}$
is epic. Then, we have the following exact commutative diagram:
$\tilde{f^{0}}$
is epic. Then, we have the following exact commutative diagram:

Since
![]() $\tilde{f^{0}}$
is epic and
$\tilde{f^{0}}$
is epic and
![]() $i_{N}^{0}$
is monic,
$i_{N}^{0}$
is monic,
![]() $h$
is monic. Taking
$h$
is monic. Taking
![]() $i^{0}\;:\!=\;k\circ h$
, obviously
$i^{0}\;:\!=\;k\circ h$
, obviously
![]() $i^{0}\;:\;C \to I$
is monic and
$i^{0}\;:\;C \to I$
is monic and
![]() $i^{0}g=g^{0}i_{N}^{0}.$
$i^{0}g=g^{0}i_{N}^{0}.$
Consider the following push-out square

Taking the injective envelope
![]() $ I^{\prime}$
of
$ I^{\prime}$
of
![]() $D^{\prime}$
, then we have the following exact sequence
$D^{\prime}$
, then we have the following exact sequence

where
![]() $g^{1}=k^{\prime}a^{\prime}$
,
$g^{1}=k^{\prime}a^{\prime}$
,
![]() $i^{1}=k^{\prime}b^{\prime}$
. Since
$i^{1}=k^{\prime}b^{\prime}$
. Since
![]() ${{\mathrm{Ind}}}(I_{N}^{0}\oplus I_{N}^{1} \oplus I )\subseteq \Phi$
and
${{\mathrm{Ind}}}(I_{N}^{0}\oplus I_{N}^{1} \oplus I )\subseteq \Phi$
and
![]() $\Phi$
is coherent, we have
$\Phi$
is coherent, we have
![]() ${{\mathrm{Ind}}}I^{\prime}\subseteq \Phi$
. Based on the above discussion, we get the following commutative diagram
${{\mathrm{Ind}}}I^{\prime}\subseteq \Phi$
. Based on the above discussion, we get the following commutative diagram

Next, we prove that the second row in the above commutative diagram is exact. Since both
![]() $i^{0}$
and
$i^{0}$
and
![]() $k^{\prime}$
are monic, it is enough to prove that
$k^{\prime}$
are monic, it is enough to prove that
![]() $C\simeq \text{ker}b^{\prime}$
. By the properties of push-out, we can get the following exact commutative diagram such that
$C\simeq \text{ker}b^{\prime}$
. By the properties of push-out, we can get the following exact commutative diagram such that
![]() $\tilde{g^{0}}\;:\;N\to \text{ker}b^{\prime}$
is epic.
$\tilde{g^{0}}\;:\;N\to \text{ker}b^{\prime}$
is epic.

Since
![]() $b^{\prime}i^{0}$
=0 and
$b^{\prime}i^{0}$
=0 and
![]() $i^{0}$
is monic, there is a monomorphism
$i^{0}$
is monic, there is a monomorphism
![]() $j\;:\;C\to \text{ker}b^{\prime}$
such that
$j\;:\;C\to \text{ker}b^{\prime}$
such that
![]() $i^{0}=i^{\prime}j$
. It’s easy to get that
$i^{0}=i^{\prime}j$
. It’s easy to get that
![]() $j$
is also epic by the following commutative diagram.
$j$
is also epic by the following commutative diagram.

Hence,
![]() $C\simeq \text{ker}b^{\prime}\simeq \text{ker}i^{1}$
. Since
$C\simeq \text{ker}b^{\prime}\simeq \text{ker}i^{1}$
. Since
![]() $\Phi$
is coherent,
$\Phi$
is coherent,
![]() $C\in{{\mathrm{Supp}}}^{-1}\Phi$
.
$C\in{{\mathrm{Supp}}}^{-1}\Phi$
.
Lemma 3.5.
Let
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
![]() $\mathcal{Y}$
be two thick subcategories closed under taking direct sums and injective envelopes. Then,
$\mathcal{Y}$
be two thick subcategories closed under taking direct sums and injective envelopes. Then,
![]() $\mathcal{X}\subseteq \mathcal{Y}$
if and only if
$\mathcal{X}\subseteq \mathcal{Y}$
if and only if
![]() ${{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}$
.
${{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}$
.
Proof. The “only if” part. It is clear that
![]() ${{\mathrm{Supp}}}\mathcal{X}\subseteq \mathcal{X} \subseteq \mathcal{Y}$
. So
${{\mathrm{Supp}}}\mathcal{X}\subseteq \mathcal{X} \subseteq \mathcal{Y}$
. So
![]() ${{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}$
.
${{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}$
.
The “if” part. For any
![]() $X\in \mathcal{X}$
. Taking the minimal injective resolution of
$X\in \mathcal{X}$
. Taking the minimal injective resolution of
![]() $X$
,
$X$
,
we have
![]() ${{\mathrm{Ind}}}I^{i}\subseteq{{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}\subseteq \mathcal{Y}$
. Since
${{\mathrm{Ind}}}I^{i}\subseteq{{\mathrm{Supp}}}\mathcal{X}\subseteq{{\mathrm{Supp}}}\mathcal{Y}\subseteq \mathcal{Y}$
. Since
![]() $\mathcal{Y}$
is closed under taking kernel and direct sums,
$\mathcal{Y}$
is closed under taking kernel and direct sums,
![]() $X\in \mathcal{Y}$
.
$X\in \mathcal{Y}$
.
Theorem 3.6.
Let
![]() $ \mathcal{A}$
be a locally noetherian Grothendieck category. Then, the assignment
$ \mathcal{A}$
be a locally noetherian Grothendieck category. Then, the assignment
![]() $\mathcal{X}\mapsto{{\mathrm{Supp}}}\mathcal{X}$
induces an inclusion-preserving bijection between the set of thick subcategories of
$\mathcal{X}\mapsto{{\mathrm{Supp}}}\mathcal{X}$
induces an inclusion-preserving bijection between the set of thick subcategories of
![]() $ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
$ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
, with inverse
${{\mathrm{Sp}}}(\mathcal{A})$
, with inverse
![]() ${{\mathrm{Supp}}}^{-1}$
.
${{\mathrm{Supp}}}^{-1}$
.
Proof. For any coherent subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
,
${{\mathrm{Sp}}}(\mathcal{A})$
,
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is a thick subcategory of
${{\mathrm{Supp}}}^{-1}\Phi$
is a thick subcategory of
![]() $ \mathcal{A}$
by Lemma 3.4. Since
$ \mathcal{A}$
by Lemma 3.4. Since
![]() $ \mathcal{A}$
is locally noetherian, it is clear that
$ \mathcal{A}$
is locally noetherian, it is clear that
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking arbitrary direct sums. Obviously,
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking arbitrary direct sums. Obviously,
![]() ${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking injective envelopes. Claim that
${{\mathrm{Supp}}}^{-1}\Phi$
is closed under taking injective envelopes. Claim that
![]() ${{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )=\Phi$
. In fact, for any
${{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )=\Phi$
. In fact, for any
![]() $I\in{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
, there is an object
$I\in{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
, there is an object
![]() $X\in{{\mathrm{Supp}}}^{-1}\Phi$
, that is
$X\in{{\mathrm{Supp}}}^{-1}\Phi$
, that is
![]() ${{\mathrm{Supp}}}X\subseteq \Phi$
, such that
${{\mathrm{Supp}}}X\subseteq \Phi$
, such that
![]() $I\in{{\mathrm{Supp}}}X$
. So
$I\in{{\mathrm{Supp}}}X$
. So
![]() ${{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )\subseteq \Phi$
. Conversely, for any
${{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )\subseteq \Phi$
. Conversely, for any
![]() $I^{\prime}\in \Phi$
,
$I^{\prime}\in \Phi$
,
![]() ${{\mathrm{Supp}}}I^{\prime}=\{I^{\prime}\}\subseteq \Phi$
. Hence,
${{\mathrm{Supp}}}I^{\prime}=\{I^{\prime}\}\subseteq \Phi$
. Hence,
![]() $I^{\prime}\in{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
. Therefore,
$I^{\prime}\in{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
. Therefore,
![]() $\Phi \subseteq{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
.
$\Phi \subseteq{{\mathrm{Supp}}}({{\mathrm{Supp}}}^{-1}\Phi )$
.
Now let
![]() $\mathcal{X}$
be a thick subcategory of
$\mathcal{X}$
be a thick subcategory of
![]() $ \mathcal{A}$
, which is closed under taking arbitrary direct sums and injective envelopes. Let
$ \mathcal{A}$
, which is closed under taking arbitrary direct sums and injective envelopes. Let
![]() $\Phi ={{\mathrm{Supp}}}\mathcal{X}$
. Firstly,
$\Phi ={{\mathrm{Supp}}}\mathcal{X}$
. Firstly,
![]() $\Phi \subseteq \mathcal{X}$
since
$\Phi \subseteq \mathcal{X}$
since
![]() $\mathcal{X}$
is closed under taking injective envelopes. We claim that
$\mathcal{X}$
is closed under taking injective envelopes. We claim that
![]() $\Phi$
is coherent. In fact, each morphisms
$\Phi$
is coherent. In fact, each morphisms
![]() $I^{0}\stackrel{f}\to I^{1}$
with
$I^{0}\stackrel{f}\to I^{1}$
with
![]() ${{\mathrm{Ind}}}(I^{0}\oplus I^{1})\subseteq \Phi$
can be completed to an exact sequence
${{\mathrm{Ind}}}(I^{0}\oplus I^{1})\subseteq \Phi$
can be completed to an exact sequence
where
![]() $I^{2}$
is the injective envelope of
$I^{2}$
is the injective envelope of
![]() ${{\mathrm{Coker}}}f$
. Since
${{\mathrm{Coker}}}f$
. Since
![]() $\mathcal{X}$
is closed under taking cokernels and injective envelopes, we have
$\mathcal{X}$
is closed under taking cokernels and injective envelopes, we have
![]() $I^{2}\in \mathcal{X}$
. Hence,
$I^{2}\in \mathcal{X}$
. Hence,
![]() ${{\mathrm{Ind}}}I^{2}={{\mathrm{Supp}}}I^{2}\subseteq \Phi$
. So
${{\mathrm{Ind}}}I^{2}={{\mathrm{Supp}}}I^{2}\subseteq \Phi$
. So
![]() $\Phi$
is coherent. Next, we prove that
$\Phi$
is coherent. Next, we prove that
![]() ${{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})=\mathcal{X}$
. For any
${{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})=\mathcal{X}$
. For any
![]() $X\in{{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})$
, we have
$X\in{{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})$
, we have
![]() ${{\mathrm{Supp}}}X\subseteq{{\mathrm{Supp}}}\mathcal{X}$
. Take the minimal injective resolution of
${{\mathrm{Supp}}}X\subseteq{{\mathrm{Supp}}}\mathcal{X}$
. Take the minimal injective resolution of
![]() $X$
$X$
we have
![]() ${{\mathrm{Ind}}}I^{i}\subseteq{{\mathrm{Supp}}}\mathcal{X}\subseteq \mathcal{X}$
. Since
${{\mathrm{Ind}}}I^{i}\subseteq{{\mathrm{Supp}}}\mathcal{X}\subseteq \mathcal{X}$
. Since
![]() $\mathcal{X}$
is closed under taking direct sums and kernels,
$\mathcal{X}$
is closed under taking direct sums and kernels,
![]() $X\in \mathcal{X}$
. Conversely, for any
$X\in \mathcal{X}$
. Conversely, for any
![]() $X^{\prime}\in \mathcal{X}$
, we have
$X^{\prime}\in \mathcal{X}$
, we have
![]() ${{\mathrm{Supp}}}X^{\prime}\subseteq{{\mathrm{Supp}}}\mathcal{X}$
, that is,
${{\mathrm{Supp}}}X^{\prime}\subseteq{{\mathrm{Supp}}}\mathcal{X}$
, that is,
![]() $X^{\prime}\in{{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})$
.
$X^{\prime}\in{{\mathrm{Supp}}}^{-1}({{\mathrm{Supp}}}\mathcal{X})$
.
In conclusion, the map sending a subcategory
![]() $\mathcal{X}$
to
$\mathcal{X}$
to
![]() ${{\mathrm{Supp}}}\mathcal{X}$
induces a bijection between the set of thick subcategories of
${{\mathrm{Supp}}}\mathcal{X}$
induces a bijection between the set of thick subcategories of
![]() $ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
$ \mathcal{A}$
, which are closed under taking arbitrary direct sums and injective envelopes, and the set of coherent subsets of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
. By Lemma 3.5, this bijection is inclusion-preserving.
${{\mathrm{Sp}}}(\mathcal{A})$
. By Lemma 3.5, this bijection is inclusion-preserving.
Let
![]() $A$
be a commutative noetherian ring. Then,
$A$
be a commutative noetherian ring. Then,
![]() ${{\mathrm{Mod}}}A$
is a locally noetherian Grothendieck category. Let
${{\mathrm{Mod}}}A$
is a locally noetherian Grothendieck category. Let
![]() $\mathcal{X}$
be a thick subcategory of
$\mathcal{X}$
be a thick subcategory of
![]() ${{\mathrm{Mod}}}A$
, which is closed under taking arbitrary direct sums. Then,
${{\mathrm{Mod}}}A$
, which is closed under taking arbitrary direct sums. Then,
![]() $\mathcal{X}$
is closed under taking injective envelopes (see [Reference Krause11, Lemma 3.5]). Take
$\mathcal{X}$
is closed under taking injective envelopes (see [Reference Krause11, Lemma 3.5]). Take
![]() $ \mathcal{A}={{\mathrm{Mod}}}A$
. Applying Theorem 3.6 to
$ \mathcal{A}={{\mathrm{Mod}}}A$
. Applying Theorem 3.6 to
![]() ${{\mathrm{Mod}}}A$
, we can get the following corollary.
${{\mathrm{Mod}}}A$
, we can get the following corollary.
Corollary 3.7.
Let
![]() $A$
be a commutative noetherian ring. Then, we have an inclusion-preserving bijection between the set of thick subcategories of
$A$
be a commutative noetherian ring. Then, we have an inclusion-preserving bijection between the set of thick subcategories of
![]() ${{\mathrm{Mod}}}A$
, which are closed under taking arbitrary direct sums and the set of coherent subsets of
${{\mathrm{Mod}}}A$
, which are closed under taking arbitrary direct sums and the set of coherent subsets of
![]() ${{\mathrm{Spec}}}(A)$
.
${{\mathrm{Spec}}}(A)$
.
Finally, we give an example where every subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
is coherent. Let
${{\mathrm{Sp}}}(\mathcal{A})$
is coherent. Let
![]() $\mathcal{A}$
be an abelian category. For a pair of objects
$\mathcal{A}$
be an abelian category. For a pair of objects
![]() $X$
,
$X$
,
![]() $Y$
and
$Y$
and
![]() $n\geqslant 1$
, let
$n\geqslant 1$
, let
![]() ${{\mathrm{Ext}}}^{n}_{\mathcal{A}}(X,Y)$
denote the abelian group of
${{\mathrm{Ext}}}^{n}_{\mathcal{A}}(X,Y)$
denote the abelian group of
![]() $n$
-
$n$
-
![]() $extensions$
in the sense of Yoneda, that is equivalence classes of exact sequences
$extensions$
in the sense of Yoneda, that is equivalence classes of exact sequences
![]() $\xi \;:\; 0\to Y\to E_{n}\to \cdots \to E_{1}\to X\to 0$
. The
$\xi \;:\; 0\to Y\to E_{n}\to \cdots \to E_{1}\to X\to 0$
. The
![]() $injective$
$injective$
![]() $dimension$
of
$dimension$
of
![]() $X$
is by definition
$X$
is by definition
Recall that an abelian category
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
![]() $hereditary$
provided that the functor
$hereditary$
provided that the functor
![]() ${{\mathrm{Ext}}}^{2}_{\mathcal{A}}(-,-)$
vanishes. If
${{\mathrm{Ext}}}^{2}_{\mathcal{A}}(-,-)$
vanishes. If
![]() $\mathcal{A}$
has enough injective objects, that is for every objects
$\mathcal{A}$
has enough injective objects, that is for every objects
![]() $X\in \mathcal{A}$
,
$X\in \mathcal{A}$
,
![]() $X$
has injective envelope,
$X$
has injective envelope,
![]() $\mathcal{A}$
is hereditary if and only if for any
$\mathcal{A}$
is hereditary if and only if for any
![]() $X\in \mathcal{A}$
,
$X\in \mathcal{A}$
,
![]() ${{\mathrm{inj.dim}}}X\leqslant 1$
, if and only if for any
${{\mathrm{inj.dim}}}X\leqslant 1$
, if and only if for any
![]() $X\in \mathcal{A}$
, there is an exact sequence
$X\in \mathcal{A}$
, there is an exact sequence
![]() $0\to X\to I_{0}\to I_{1}\to 0$
such that
$0\to X\to I_{0}\to I_{1}\to 0$
such that
![]() $I_{0},$
$I_{0},$
![]() $I_{1}$
are injective objects. Then we have the following result.
$I_{1}$
are injective objects. Then we have the following result.
Corollary 3.8.
Let
![]() $\mathcal{A}$
be a locally noetherian Grothendieck category. If
$\mathcal{A}$
be a locally noetherian Grothendieck category. If
![]() $\mathcal{A}$
is hereditary, then every subset of
$\mathcal{A}$
is hereditary, then every subset of
![]() ${{\mathrm{Sp}}}(\mathcal{A})$
is coherent.
${{\mathrm{Sp}}}(\mathcal{A})$
is coherent.
Acknowledgment
This work is supported by the China Scholarship Council under Grant No. 202006860027.