Study of crossed-beam energy transfer process with large crossing angle in three-dimension

Abstract

In this paper, a three-dimensional (3D) model as a new module of LAP3D code is presented to study the crossed-beam energy transfer (CBET) process. This model is not limited by the paraxial approximation and can be used to deal with a large crossing angle case. Besides, this model is also appropriate for the multi-ion species conditions and even multi-beams problems, which will be very helpful in relevant experiment analysis and the target design. In our 3D simulations, we take the overlapped beams with a 60° crossing angle as an example, and observe obvious energy transfer process, which indicates CBET process might occur between the incident laser beams with a large crossing angle when the matching condition is satisfied. This large crossing angle CBET process also can change the spatial shape of the beam spot, and may have some potential important influence on other laser–plasma interaction instabilities and the energy symmetry in hohlraum.

1. INTRODUCTION

Presently, because of the physical limit for an individual laser beam and the consideration of the radiation symmetry, multiple laser beams are used in the indirect-drive inertial confinement fusion (ICF) design (Lindl et al., 2004). These incident beams are overlapped each other at the laser entrance hole (LEH) when they enter a hohlraum. If the beat wave driven by a couple of two beams satisfies the dispersion relation of the ion-acoustic waves, energy transfers between the crossed beams through a three-wave coupling process (McKinstrie et al., 1996). This phenomenon, which is commonly named crossed-beam energy transfer (CBET), is a very important process because of its influence on the capsule implosion symmetry (Kruer et al., 1996) and other laser–plasma interaction (LPI) instabilities, such as stimulated Raman scattering (SRS) and simulated Brillouin scattering (SBS) (Karttunen & Salomaa, 1992; Kline & Montgomery, 2005; Sharma et al., 2009, 2012; Huller & Porzio, 2010; Hao et al., 2012; Vyas et al., 2014). During the latest decades, many experimental works about CBET have been carried out on the Nova and the Omega laser facilities (Wharton et al., 1998; Kirkwood et al., 2002). Subsequently, CBET has been used as an efficient method to control the implosion symmetry in the experiments performed on the National Ignition Facility and relevant optimized schemes are proposed based on those experiments (Michel et al., 2010; Moody et al., 2012). Recently, new kinetic saturated mechanism in multi-laser beams condition are put forward (Michel et al., 2013), which indicates that theoretical knowledge of CBET is not enough to explain the experiments totally, and further study of CBET is still necessary.

Presently, most of the previous works mainly focused on the small angle CBET process, which are corresponding to the crossed beams coming from the same incident side. And the existing three-dimensional (3D) code is based on the paraxial approximation, which limits the angle of each incident beam to be <10°. However, in the practical situation, CBET also has certain possibilities to happen in the hohlraum plasma between the crossed beams coming from the opposite incident sides with a large crossing angle, and this kind of CBET should be also important because of its potential impact on other instabilities and the radiation symmetry in hohlraum. Although large angle CBET process needs large wavelength shift Δλ to satisfy the matching condition between the ion-acoustic wave and the beat of crossed beams. On consideration of the complicated hohlraum plasma conditions, suitable plasma flow can induce the Doppler shift to the frequency of ion-acoustic wave and reduce the needed Δλ for the large angle CBET process. Furthermore, the bandwidth of incident beams can be broadened by some laser smoothing methods such as the smoothing by spectral dispersion (SSD) (Skupsky et al., 1989), which also increases the chance of the large angle CBET. Indeed, in recent work (Michel et al., 2013), they have considered the potential effect of large angle CBET and included it in their model, but each beam was simplified as a one-dimensional ray in their model. Besides, big angle CBET is also an important issue in the direct-drive ignition, because it transfers energy from the center-beam rays to the reflected edge-beam rays and reduces the energy delivered to the coronal plasma (Froula et al., 2013). So reasonable modeling of large angle CBET and multi-beams CBET in high dimension has wide and important application prospects in ICF.

In order to study the LPI instabilities, a 3D fluid code named LAP3D (Li et al., 2014) has been developed, which can simulate the coupling of SRS, SBS, and filamentation under certain laser beam smoothing methods such as continuous phase plate (Dixit et al., 1996) and SSD. Similar to PF3D code (Berger et al., 1998), the solver scale of LAP3D can reach up to mm³ volumes. In this paper, as a new module of LAP3D code (Li et al., 2014), a 3D model is introduced to study the CBET process. Because the paraxial approximation is not used in our physics model, our code can be used to solve the large crossing angle Δθ problem in 3D simulations. And it is actually appropriate for the multi-ion species and even multi-beams problems, which could be very helpful to estimate the influence of CBET process in the target design engineering project. Based on this code, the CBET process with Δθ = 60° is studied with relevant analysis of its growth rate under different parameters. Our simulated results show that CBET process occurs between two incident beams with a large crossing angle when the matching condition is fulfilled, and the spatial shape of the wave front is changed obviously after the beam pass through the crossed region. This phenomenon is similar with the results obtained in small crossing angle CBET process (Michel et al., 2009), which indicates that CBET not only transfers energy between two beams but also changes the spatial distribution of the energy within the beam spot. So under an applicable combination of wavelength shift Δλ and plasma flow velocity $\vec u$, large angle CBET also has potential effect on the radiation symmetry and influence on other kinds of LPI instabilities.

2. PHYSICAL MODEL

In this section, we briefly introduce the physical model of the CBET module of LAP3D code, which is presently focused on the case of uniform or weak non-uniform spatial distribution of electron density n _e, because the CBET process mainly happens at LEH, where the gradient scale length of n _e is very large. So in our model, we do not consider the influence of weak non-uniform density on the propagation of light waves, and only consider its effect on the coupling between overlapped beams. As usual, we denote parameters I, n _e, T _e, T _j, ω_pe, n _c, m _e, m _j, Z _j, c, e, λ_D, C _s, and ν_ej as the laser intensity, electron density, electron temperature, ion temperature, electron plasma frequency, critical density, electron mass, ion mass, ion charge state, speed of light, electron charge, Debye length, ion acoustic velocity, and electron–ion collision frequency, respectively. Here, subscript j is used to denote different ion species.

Considering two crossed beams transmit along $\hat z$-axis with angles θ_α, and projected angles on $\hat x - \hat y$-plane ϕ_α with subscript α = 0, 1 for two beams, respectively, we define ${\vec A_{\rm \alpha}} = (1/2)$$({A_{\rm \alpha}} \exp (i{\Psi _{\rm \alpha}} ) + {\rm c}{\rm. c}.)$ as the vector potential of the light field, where Ψ_α is the rapidly varying phase, ω_α = −∂_tΨ_α is the frequency, and A _α is the slowly varying complex amplitude. The wave vector ${\vec k_{\rm \alpha}} = \nabla {\Psi _{\rm \alpha}} = {k_{\rm \alpha}} \cos ({{\rm \theta} _{\rm \alpha}} )\hat z +{k_{\rm \alpha}} \sin ({{\rm \theta} _{\rm \alpha}} )$$\cos ({{\rm \phi} _{\rm \alpha}} )\hat x + {k_{\rm \alpha}} \sin ({{\rm \theta} _{\rm \alpha}} )\sin ({{\rm \phi} _{\rm \alpha}} )\hat y$, where ${k_{\rm \alpha}} = \sqrt {{\rm \omega} _{\rm \alpha} ^2 - {\rm \omega} _{{\rm pe}}^2} /c$, and ${\rm \omega} _{{\rm pe}}^2 = 4{\rm \pi} {e^2}{n_{\rm e}}/{m_{\rm e}}$. Then, the frequency and wave vector of their beat wave are Δω = ω₀ − ω₁, and $\vec \Delta k = {\vec k_0} - {\vec k_1}$. Customarily, the electron density perturbation of ion-acoustic wave excited by the beat wave can also be described in enveloped expression ${\rm \delta} {\tilde n_{\rm a}} = (1/2)({\rm \delta} {n_{\rm a}}\exp (i{\, \Psi _{\rm a}}) + c.c.)$, where Ψ_a = Ψ₀ − Ψ₁, and the slowly varying enveloped perturbation

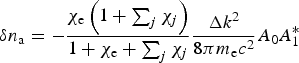(1)$${\rm \delta} {n_{\rm a}} = - \displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + \sum\nolimits_j {{\rm \chi} _j}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + \sum\nolimits_j {{\rm \chi} _j}}}\displaystyle{{\Delta {k^2}} \over {8{\rm \pi} {m_{\rm e}}{c^2}}}{A_0}A_1^{\ast} $$

can be derived from Poisson and linearized Vlasov equations (Drake et al., 1974). For CBET process, the electron susceptibility and the ion susceptibility of j component are

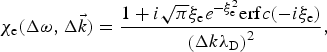(2)$${{\rm \chi} _{\rm e}}(\Delta {\rm \omega}, \Delta \vec k) = \displaystyle{{1 + i\sqrt {\rm \pi} {{\rm \xi} _{\rm e}}{e^{ - {\rm \xi} _{\rm e}^2}} {\rm erf}c( - i{{\rm \xi} _{\rm e}})} \over {{{\left( {\Delta k{{\rm \lambda} _{\rm D}}} \right)}^2}}},$$

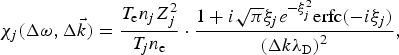(3)$${{\rm \chi} _j}(\Delta {\rm \omega}, \Delta \vec k) = \displaystyle{{{T_{\rm e}}{n_j}Z_j^2} \over {{T_j}{n_{\rm e}}}} \cdot \displaystyle{{1 + i\sqrt {\rm \pi} {{\rm \xi} _j}{e^{ - {\rm \xi} _j^2}} {\rm erfc}( - i{{\rm \xi} _j})} \over {{{\left( {\Delta k{{\rm \lambda} _{\rm D}}} \right)}^2}}},$$

in assumption of the Maxwellian distribution, where ${{\rm \xi} _{\rm e}} =$$(\Delta {\rm \omega} - \Delta k{u_{{\rm \Delta k}}})/\sqrt 2 \Delta k{v_{{\rm te}}}$, ${{\rm \xi} _j} = (\Delta {\rm \omega} - \Delta k{u_{{\rm \Delta k}}})/\sqrt 2 \Delta k{v_{{\rm t}j}}$, ${v_{{\rm te}}} =$$\sqrt {{T_{\rm e}}/{m_{\rm e}}} $, ${v_{{\rm t}j}} = \sqrt {{T_j}/{m_j}} $, and u _Δk is the projection of plasma flow velocity along the direction of $\Delta \vec k$. Based on this kinetic expression of electron perturbation, the steady-state equations of two crossed beams are derived from Maxwell equations under standard envelop approximations (Berger et al., 1998; Hao et al., 2013) in all three directions as

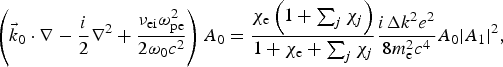(4)$$\left( {{{\vec k}_0} \cdot \nabla - \displaystyle{i \over 2}{\nabla ^2} + \displaystyle{{{{\rm \nu} _{{\rm ei}}}{\rm \omega} _{{\rm pe}}^2} \over {2{{\rm \omega} _0}{c^2}}}} \right){A_0} = \displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + \sum\nolimits_j {{\rm \chi} _j}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + \sum\nolimits_j {{\rm \chi} _j}}}\displaystyle{{i\Delta {k^2}{e^2}} \over {8m_{\rm e}^2 {c^4}}}{A_0}{\left \vert {{A_1}} \right \vert ^2},$$

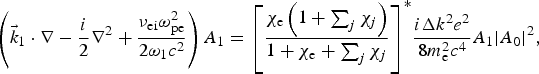(5)$$\left( {{{\vec k}_1} \cdot \nabla - \displaystyle{i \over 2}{\nabla ^2} + \displaystyle{{{{\rm \nu} _{{\rm ei}}}{\rm \omega} _{{\rm pe}}^2} \over {2{{\rm \omega} _1}{c^2}}}} \right){A_1} = {\left[ {\displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + \sum\nolimits_j {{\rm \chi} _j}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + \sum\nolimits_j {{\rm \chi} _j}}}} \right]^{\ast}}\displaystyle{{i\Delta {k^2}{e^2}} \over {8m_{\rm e}^2 {c^4}}}{A_1}{\left \vert {{A_0}} \right \vert ^2},$$

where the three terms on the left side represent the propagation, diffraction, inverse bremsstrahlung absorption, respectively, and the right side term describes the coupling between two beams through the excited ion-acoustic wave. We solve Eqs. (4) and (5) by adding a ∂/∂t term on the left side and simulate the time-dependent process of the propagating, damping, and coupling of crossed beams by the operator splitting technique until the solutions reach a steady state. We launch the incident light wave on the ${\hat x} - {\hat y}$-plane at z = 0, and use the open boundary at the other end of ${\hat z}$-axis. Periodic boundary conditions are used at two ends of ${\hat x}$-axis and ${\hat y}$-axis.

Our model can also be expanded to multi-beams cases. Supposing there are N overlapped beams propagating along different directions with frequency ω_α and wave vector ${{\vec k}_{\rm \alpha}} $, we can describe the CBET process among these light waves by N equations as follows,

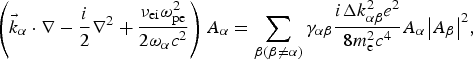(6)$$\left( {{{\vec k}_{\rm \alpha}} \cdot \nabla - \displaystyle{i \over 2}{\nabla ^2} + \displaystyle{{{{\rm \nu} _{{\rm ei}}}{\rm \omega} _{{\rm pe}}^2} \over {2{{\rm \omega} _{\rm \alpha}} {c^2}}}} \right){A_{\rm \alpha}} = \sum\limits_{{\rm \beta} ({\rm \beta} \ne {\rm \alpha} )} {{\rm \gamma} _{{\rm \alpha} {\rm \beta}}} \displaystyle{{i\Delta k_{{\rm \alpha} {\rm \beta}} ^2 {e^2}} \over {8m_{\rm e}^2 {c^4}}}{A_{\rm \alpha}} {\left \vert {{A_{\rm \beta}}} \right \vert ^2},$$

where subscripts α, β = 0, 1, …, N − 1(α ≠ β), and Δω_αβ = ω_α − ω_β, and $\Delta {\vec k_{{\rm \alpha} {\rm \beta}}} = {\vec k_{\rm \alpha}} - {\vec k_{\rm \beta}} $. The coupling coefficient

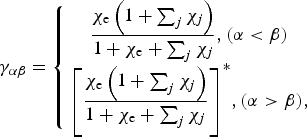(7)$${{\rm \gamma} _{{\rm \alpha} {\rm \beta}}} = \left\{ {\matrix{ {\displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + \sum\nolimits_j {{\rm \chi} _j}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + \sum\nolimits_j {{\rm \chi} _j}}},({\rm \alpha} \lt {\rm \beta} )} \cr {{{\left[ {\displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + \sum\nolimits_j {{\rm \chi} _j}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + \sum\nolimits_j {{\rm \chi} _j}}}} \right]}^{\ast}},({\rm \alpha} \gt {\rm \beta} ),} \cr}} \right.$$

where the susceptibilities χ _e and χ _j are functions of Δω_αβ and $\Delta {\vec k_{{\rm \alpha} {\rm \beta}}} $ with the same formulas as Eqs. (2) and (3) introduced above.

Our model is based on the envelop approximations both in time and space, which is beneficial for large-scale simulations. Since we mainly focus on the uniform or weak non-uniform density condition, and ignore the influence of weak non-uniform density on light waves, we do spatial envelop approximations in all directions of the three axes, which is not limited by paraxial approximation and feasible to simulate the propagation for the diagonal incident beams with a large angle is feasible. So our model is different from the existing models (Eliseev et al., 1996). Besides, the kinetic model of density perturbation (Strozzi et al., 2008) provides convenience to deal with the multi-ion species problem and the non-uniform conditions of temperature and flow velocity. Overall, our model could be useful for the comprehension and estimation of the CBET process during the target design.

3. SIMULATION RESULT OF CBET WITH LARGE CROSSING ANGLE

In this section, we present 3D simulations of CBET process between two overlapped Gaussian beams with Δθ = 60° and typical LEH plasma parameters, where n _e = 0.03 n _c, T _e = 2.8 keV, and T _i = 0.8 keV (Michel et al., 2013). Two Gaussian beams incident symmetrically about $\hat y$-axis from z = 0 plane with angles (θ₀ = 30°, ϕ₀ = 0°) for beam 0 and (θ₁ = 30°, ϕ₁ = 180°) for beam 1. The maximum intensity of beams are chosen to be I _M0 = I _M1 = 4 × 10¹⁵ W/cm². Wavelength of beam 0 is fixed to be λ₀ = 0.351 μm, and wavelength shift is defined as Δλ = λ₁ − λ₀. Although our model is feasible to multi-ion species case, we just choose the plasma component as fully ionized helium (Z _He = 2) for simplicity. In order to find the best matching condition, we present the spatial growth rate of CBET K as a function of Δλ with different u _Δk in Figure 1, when Δθ = 60°, n _e = 0.03 n _c, T _e = 2.8 keV, and T _i = 0.8 keV. Customarily, K is defined as

(8)$$K = \displaystyle{{\Delta {k^2}} \over {4{k_1}}} \displaystyle{{I{{\rm \lambda} _0}{{[{\rm \mu} m]}^2}} \over {{P_{\rm m}}\sqrt {1 - {n_{\rm e}}/{n_{\rm c}}} }} {\rm Im} \left[ {\displaystyle{{{{\rm \chi} _{\rm e}}\left( {1 + {{\rm \chi} _{\rm i}}} \right)} \over {1 + {{\rm \chi} _{\rm e}} + {{\rm \chi} _{\rm i}}}}} \right], $$

where P _m = 1.368 × 10¹⁸W · cm⁻² · μm² (Williams et al., 2004), which is very important because it indicates the local energy transfer efficiency and determines the fraction of transferred energy when the cross region is given. Obviously, K reaches its peak value when the ion-acoustic wave dispersion relation Δω = ±ΔkC _s + Δku _Δk is satisfied. The plasma flow results in a Doppler shift in frequency, which has no effect on the peak value but changes the matching relation effectively. Although the best matching condition for Δθ = 60° needs a large wavelength shift, which Δλ = 5.02 Å, when u _Δk = 0. The matching condition becomes easy to be fulfilled when there is a flow velocity, which decreases the needed wavelength shift such as the red dash-dot line shown in Figure 1. So, CBET process between the beams with large crossing angle has certain chance to occur under the complicated hohlraum plasma conditions.

Fig. 1. K vs. Δλ with different u _Δk, when Δθ = 60°, n _e = 0.03 n _c, T _e = 2.8 keV, and T _i = 0.8 keV.

Our 3D simulation results are shown in Figure 2, where the wavelength shift is chosen to be Δλ = λ₁ − λ₀ = 5.02 Å and u _Δk = 0, which corresponds to the peak value of blue solid curve in Figure 1. We also simulated the process with Δλ = 2.51 Å and u _Δk = −0.5 C _s corresponding to the peak value of red dash–dot curve in Figure 1, and obtained the same results as in the former case. The waists of two beams are 40 λ₀, and the simulation box size is 256 × 256 × 256 with the length unit λ₀. Intensities labeled by color are normalized by I _M0 in all of the sub figures. Figure 2a shows the 3D CBET process. In order to display the simulation result evidently, we give the slice of ${\hat x} - {\hat z}$-plane at the center of ${\hat y}$-axis in Figure 2b. The intensity of beam 1 (propagating from right to left) increases rapidly after it passes through the cross region along with the depletion of beam 0 (propagating from left to right), which is consistent with the theoretical expectations. Spatial distribution of laser intensity on the slice of ${\hat x} - {\hat y}$-plane at z = 0 are shown in Figure 2c. Spots of beam 1 and beam 0 on the slice of ${\hat x} - {\hat y}$-plane at z = 230 are shown in Figures 2d and e, respectively. Initially, two beams have the same Gaussian shape intensity profiles on the incident plane according to our boundary conditions. After they pass through the cross region, the spatial distribution of intensity within the beam spot is changed seriously, especially for the depleted beam 0. This phenomenon is caused by the 3D effect of CBET process. In fact, the distribution of energy transfer efficiency is commonly non-uniform in space, and asymmetric to the incident beams. In our simulations, the energy transfer efficiency should be larger at the center of the Gaussian beams. So, more energy has been transferred from the center of beam 0 than from its boundary. Our simulation indicates that both the energy distribution between two beams with large crossing angle and the energy distribution within the beam spots can be changed by CBET process. Even if the intensity distribution of beam spots is initially flat, the energy distribution within the beam spots should also be inevitably changed by CBET, because the depletion of the pump wave and the increase of the seed wave are different along their cross sections. This phenomenon might be more serious and important in the ignition hohlraum, where the smoothed laser spots and the cross region are much larger than our simulated case. Because the non-uniform laser spots may stimulate severe instabilities such as SRS, SBS, and filamentation, and further may induce the spatio-temporal drive asymmetries in hohlraum (Hinkel et al., 2011).

Fig. 2. Simulation result of CBET with Δλ = 5.02Å and I _M0 = I _M1 = 4 × 10¹⁵ W/cm², when n _e = 0.03 n _c, T _e = 2.8 keV, T _i = 0.8 keV, and u _Δk = 0. (a) 3D image of two beams. (b) 2D slice of $\hat x - \hat z$-plane at y = 128. (c) 2D slice of ${\hat x} - {\hat y}$-plane at z = 0 labeled as black dashed line in (b). (d) 2D slice of ${\hat x} - {\hat y}$-plane for beam 1 at z = 230 labeled as red dashed line in (b). (e) 2D slice of ${\hat x} - {\hat y}$-plane for beam 0 at z = 230 labeled as blue dashed line in (b).

4. CONCLUSIONS

In summary, a new module of LAP3D code has been developed to study the CBET process, which can directly calculate the amount of transferred energy between two crossed beams with large crossing angle under uniform or weak non-uniform density conditions. Based on our code, we presented our 3D simulations of CBET process between two overlapped beams with 60°. Evident energy transfer effect is obtained when the theoretical matching condition is fulfilled, and the spatial distribution of the energy within the beam spot is also changed. Our simulation indicate that CBET process with large crossing angle has certain chance to occur under the complicated hohlraum plasma conditions, and might be very important because of its potential to induce other LPI instabilities and destroy the spatio-temporal symmetry. Besides, our model can also be expanded to multi-beams cases, and our simulation method establishes a basic for analysis of future multi-beams experiments on the Shenguang series facilities (Li et al., 2012; Hao et al., 2014; Huo et al., 2014) and provides valuable references for the intending ignition target design.