Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T11:43:41.058Z Has data issue: false hasContentIssue false
  • English
  • Français

The classical hydraulic jump in a model of shear shallow-water flows

Published online by Cambridge University Press:  16 May 2013

G. L. Richard  and
S. L. Gavrilyuk
G. L. Richard
Affiliation:
Aix-Marseille Université, UMR CNRS 7343, IUSTI, 5 rue E. Fermi, 13453 Marseille CEDEX 13, France
S. L. Gavrilyuk*
Affiliation:
Aix-Marseille Université, UMR CNRS 7343, IUSTI, 5 rue E. Fermi, 13453 Marseille CEDEX 13, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A conservative hyperbolic two-parameter model of shear shallow-water flows is used to study the classical turbulent hydraulic jump. The parameters of the model, which are the wall enstrophy and the roller dissipation coefficient, are determined from measurements of the roller length and the deviation from the Bélanger equation of the sequent depth ratio (experimental data by Hager & Bremen, J. Hydraul. Res., vol. 27, 1989, pp. 565–585; and Hager, Bremen & Kawagoshi, J. Hydraul. Res., vol. 28, 1990, pp. 591–608). Stationary solutions to the model describe with a good accuracy the free-surface profile of the hydraulic jump. The model is also capable of predicting the oscillations of the jump toe. 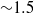We show that if the upstream Froude number is larger than ${\sim }1. 5$, the jump toe oscillates with a particular frequency, while for the Froude number smaller than 1.5 the solution becomes stationary. In particular, we show that for a given flow discharge, the oscillation frequency is a decreasing function of the Froude number.

JFM classification

Geophysical and Geological Flows: Shallow water flows Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 492 - 521
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ali, A. & Kalisch, H. 2010 Energy balance for undular bores. C. R. Mécanique 338, 67–70.Google Scholar
Binnie, A. M. & Orkney, J. C. 1955 Experiments on the flow of water from a reservoir through an open horizontal channel. II. The formation of hydraulic jumps. Proc. R. Soc. Lond. Ser. A 230, 237–246.Google Scholar
Brock, R. R. 1967 Development of roll waves in open channels. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Brock, R. R. 1969 Development of roll wave trains in open channels. J. Hydraul. Div. 95, 1401–1427.CrossRefGoogle Scholar
Brock, R. R. 1970 Periodic permanent roll waves. J. Hydraul. Div. 96, 2565–2580.CrossRefGoogle Scholar
Chachereau, Y. & Chanson, H. 2011 Free-surface fluctuations and turbulence in hydraulic jumps. Exp. Therm. Fluid Sci. 35, 896–909.Google Scholar
Chanson, H. 2010 Convective transport of air bubbles in strong hydraulic jumps. Intl J. Multiphase Flow 36, 798–814.Google Scholar
Chanson, H. 2011 Hydraulic jumps: turbulence and air bubble entrainment. La Houille Blanche 3, 5–16.Google Scholar
Chow, V. T. 1959 Open Channel Hydraulics. McGraw Hill.Google Scholar
Courant, R. & Friedrichs, K. O. 1999 Supersonic Flow and Shock Waves, 5th edn. Springer.Google Scholar
El, G. A., Grimshaw, R. H. J. & Kamchatnov, A. M. 2005 Analytic model for a weakly dissipative shallow water undular bore. Chaos 15, 037102.Google Scholar
El, G. A., Grimshaw, R. H. J. & Smyth, N. F. 2006 Unsteady undular bores in fully non-linear shallow-water theory. Phys. Fluids 18, 027104.Google Scholar
Hager, W. H. & Bremen, R. 1989 Classical hydraulic jump: sequent depths. J. Hydraul. Res. 27 (5), 565–585.Google Scholar
Hager, W. H., Bremen, R. & Kawagoshi, N. 1990 Classical hydraulic jump: length of roller. J. Hydraul. Res. 28 (5), 591–608.Google Scholar
Henderson, F. M. 1966 Open Channel Flow. MacMillan.Google Scholar
Hornung, H. G., Willert, C. & Turner, S. 1995 The flow field downstream of a hydraulic jump. J. Fluid Mech. 287, 299–316.Google Scholar
Le Metayer, O., Gavrilyuk, S. & Hank, S. 2010 A numerical scheme for the Green–Naghdi model. J. Comput. Phys. 229, 2034–2045.Google Scholar
Leutheusser, H. J. & Kartha, V. C. 1972 Effects of inflow condition on hydraulic jump. J. Hydraul. Div. 98 (8), 1367–1383.Google Scholar
Long, D., Rajaratnam, M., Steffler, P. M. & Smy, P. R. 1991 Structure of flow in hydraulic jumps. J. Hydraul. Res. 29, 207–218.Google Scholar
Mok, K. M. 2004 Relation of surface roller eddy formation and surface fluctuation in hydraulic jumps. J. Hydraul. Res. 42, 207–212.CrossRefGoogle Scholar
Murzyn, F. & Chanson, H. 2009 Free-surface fluctuations in hydraulic jumps: experimental observations. Exp. Therm. Fluid Sci. 33, 1055–1064.Google Scholar
Resch, F. J. & Leutheusser, H. J. 1971 Mesures de turbulence dans le ressaut hydraulique. La Houille Blanche 1, 17–31.CrossRefGoogle Scholar
Richard, G. L. & Gavrilyuk, S. L. 2012 A new model of roll waves: comparison with Brock’s experiments. J. Fluid Mech. 698, 374–405.CrossRefGoogle Scholar
Svendsen, I. A., Veeramony, J., Bakunin, J. & Kirby, J. T. 2000 The flow in weak turbulent hydraulic jumps. J. Fluid Mech. 418, 25–57.Google Scholar
Teshukov, V. M. 2007 Gas-dynamics analogy for vortex free-boundary flows. J. Appl. Mech. Tech. Phys. 48 (N 3), 303–309.Google Scholar
Toro, E. F. 2009 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 3rd edn. Springer.Google Scholar
Valiani, A. 1997 Linear and angular momentum conservation in hydraulic jump. J. Hydraul. Res. 35, 323–354.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar