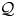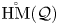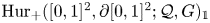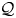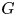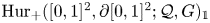1. Introduction
In [Reference BianchiBia21, Section 2] we introduced the algebraic notion of partially multiplicative quandle (PMQ) and the related notion of PMQ–group pair: roughly speaking, a PMQ is a set endowed with two binary operations, called conjugation and product (the second being partially defined), subject to axioms capturing the usual interrelations between conjugation and product in a group; and a PMQ–group pair is a pair of a PMQ ![]() ${\mathcal {Q}}$ and a group
${\mathcal {Q}}$ and a group ![]() $G$, together with a map of PMQs
$G$, together with a map of PMQs ![]() ${\mathcal {Q}}\to G$ and an action of
${\mathcal {Q}}\to G$ and an action of ![]() $G$ on
$G$ on ![]() ${\mathcal {Q}}$, satisfying axioms resembling the case in which
${\mathcal {Q}}$, satisfying axioms resembling the case in which ![]() ${\mathcal {Q}}$ is a conjugation-invariant subset of
${\mathcal {Q}}$ is a conjugation-invariant subset of ![]() $G$. In [Reference BianchiBia23a, Section 3] we defined a Hurwitz–Ran space
$G$. In [Reference BianchiBia23a, Section 3] we defined a Hurwitz–Ran space ![]() $\mathrm {Hur}({\mathcal {X}},{\mathcal {Y}};{\mathcal {Q}},G)$ associated with a nice couple
$\mathrm {Hur}({\mathcal {X}},{\mathcal {Y}};{\mathcal {Q}},G)$ associated with a nice couple ![]() $({\mathcal {X}},{\mathcal {Y}})$ of subspaces
$({\mathcal {X}},{\mathcal {Y}})$ of subspaces ![]() ${\mathcal {Y}}\subseteq {\mathcal {X}}\subseteq \mathbb {H}$ of the closed upper half-plane in
${\mathcal {Y}}\subseteq {\mathcal {X}}\subseteq \mathbb {H}$ of the closed upper half-plane in ![]() $\mathbb {C}$ and with a PMQ–group pair
$\mathbb {C}$ and with a PMQ–group pair ![]() $({\mathcal {Q}},G)$. In the case
$({\mathcal {Q}},G)$. In the case ![]() ${\mathcal {Y}}=\emptyset$ the group
${\mathcal {Y}}=\emptyset$ the group ![]() $G$ plays no essential role and we can write
$G$ plays no essential role and we can write ![]() $\mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ for the Hurwitz space: the reader may think of this as the absolute situation, whereas the general case corresponds to the relative situation.
$\mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ for the Hurwitz space: the reader may think of this as the absolute situation, whereas the general case corresponds to the relative situation.
In this article, for a PMQ ![]() ${\mathcal {Q}}$, we introduce a topological monoid
${\mathcal {Q}}$, we introduce a topological monoid ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ arising from Hurwitz spaces: an element of
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ arising from Hurwitz spaces: an element of ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ is a finite configuration
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ is a finite configuration ![]() $P$ of points in a rectangle
$P$ of points in a rectangle ![]() $(0,t)\times (0,1)$ of variable width
$(0,t)\times (0,1)$ of variable width ![]() $t\ge 0$, together with a
$t\ge 0$, together with a ![]() $Q$-valued monodromy, defined on certain loops of
$Q$-valued monodromy, defined on certain loops of ![]() $\mathbb {C}\setminus P$. The monoid product is defined according to a well-established principle, relying on the fact that a rectangle of width
$\mathbb {C}\setminus P$. The monoid product is defined according to a well-established principle, relying on the fact that a rectangle of width ![]() $t+t'$ can be regarded as the union of two rectangles of widths
$t+t'$ can be regarded as the union of two rectangles of widths ![]() $t$ and
$t$ and ![]() $t'$ joined along a vertical side. If
$t'$ joined along a vertical side. If ![]() ${\mathcal {Q}}$ is a PMQ with trivial product, then
${\mathcal {Q}}$ is a PMQ with trivial product, then ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ recovers the monoid of Hurwitz spaces appearing in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 2.6] and [Reference Randal-WilliamsRW19, Subsection 4.2].
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ recovers the monoid of Hurwitz spaces appearing in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 2.6] and [Reference Randal-WilliamsRW19, Subsection 4.2].
1.1 Statement of results
Throughout the article we fix a PMQ–group pair ![]() $({\mathcal {Q}},G)=({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$ (see [Reference BianchiBia21, Definition 2.15]) and assume that
$({\mathcal {Q}},G)=({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$ (see [Reference BianchiBia21, Definition 2.15]) and assume that ![]() $G$ is generated by the image of the map of PMQs
$G$ is generated by the image of the map of PMQs ![]() $\mathfrak {e}\colon {\mathcal {Q}}\to G$.
$\mathfrak {e}\colon {\mathcal {Q}}\to G$.
In addition to the aforementioned topological monoid ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$, we will introduce in this article an auxiliary topological monoid
$\mathring {\mathrm {HM}}({\mathcal {Q}})$, we will introduce in this article an auxiliary topological monoid ![]() $\breve {\mathrm {HM}}({\mathcal {Q}},G)$. The two main theorems of the article, that we briefly describe in this subsection, show together that a component of the group completion of
$\breve {\mathrm {HM}}({\mathcal {Q}},G)$. The two main theorems of the article, that we briefly describe in this subsection, show together that a component of the group completion of ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ is equivalent to a component of the double loop space of a certain relative Hurwitz space
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ is equivalent to a component of the double loop space of a certain relative Hurwitz space ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$.
For present and future convenience of the reader, we recall that the index ‘![]() $+$’ selects the subspace of configurations with non-empty support in a Hurwitz space; the index ‘
$+$’ selects the subspace of configurations with non-empty support in a Hurwitz space; the index ‘![]() $\mathbb {1}$’ selects the subspace of configurations with trivial total monodromy
$\mathbb {1}$’ selects the subspace of configurations with trivial total monodromy ![]() $\mathbb {1}\in G$; an index given by a finite subset of
$\mathbb {1}\in G$; an index given by a finite subset of ![]() $\mathbb {C}$, such as ‘
$\mathbb {C}$, such as ‘![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$’, selects configurations whose support contains the given finite subset; and the index ‘
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$’, selects configurations whose support contains the given finite subset; and the index ‘![]() $G,G^{\rm op}$’ refers to a quotient of another Hurwitz space by a certain free action of the group
$G,G^{\rm op}$’ refers to a quotient of another Hurwitz space by a certain free action of the group ![]() $G\times G^{\rm op}$. This notation is introduced in detail in [Reference BianchiBia23a].
$G\times G^{\rm op}$. This notation is introduced in detail in [Reference BianchiBia23a].
In favourable cases, the rational cohomology ring of ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ can be computed explicitly solely in terms of the PMQ
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ can be computed explicitly solely in terms of the PMQ ![]() ${\mathcal {Q}}$ and one can then use standard rational homotopy theory to access
${\mathcal {Q}}$ and one can then use standard rational homotopy theory to access ![]() $H^*(\Omega ^2_0\,\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}};\mathbb {Q})$, which by the group completion theorem is the ring of stable rational cohomology classes of components of
$H^*(\Omega ^2_0\,\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}};\mathbb {Q})$, which by the group completion theorem is the ring of stable rational cohomology classes of components of ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$.
$\mathring {\mathrm {HM}}({\mathcal {Q}})$.
The first, main result of the article is the following theorem, describing the weak homotopy type of the bar constructions ![]() $B\mathring {\mathrm {HM}}({\mathcal {Q}})$ and
$B\mathring {\mathrm {HM}}({\mathcal {Q}})$ and ![]() $B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ in terms of certain relative Hurwitz spaces. The nice couples
$B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ in terms of certain relative Hurwitz spaces. The nice couples ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }\breve {\diamond }^{\mathrm {lr}})$ and
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }\breve {\diamond }^{\mathrm {lr}})$ and ![]() $(\diamond,\partial \diamond )$ are explicitly given in Definition 2.23; for instance,
$(\diamond,\partial \diamond )$ are explicitly given in Definition 2.23; for instance, ![]() $\diamond$ is the closed rhombus with vertices
$\diamond$ is the closed rhombus with vertices ![]() $1/2$,
$1/2$, ![]() $\sqrt {-1}/2$,
$\sqrt {-1}/2$, ![]() $1/2+\sqrt {-1}$ and
$1/2+\sqrt {-1}$ and ![]() $1+\sqrt {-1}/2$.
$1+\sqrt {-1}/2$.
Theorem 1 (Theorem 4.1)
There are weak homotopy equivalences
Now the space ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial };{\mathcal {Q}},G)_{G,G^{\rm op}}$ admits the space
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial };{\mathcal {Q}},G)_{G,G^{\rm op}}$ admits the space ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial };{\mathcal {Q}},G)_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ as a finite covering space and the latter space is weakly equivalent to
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial };{\mathcal {Q}},G)_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ as a finite covering space and the latter space is weakly equivalent to ![]() $\breve {\mathrm {HM}}_+({\mathcal {Q}},G)_{\mathbb {1}}$. Similarly, the space
$\breve {\mathrm {HM}}_+({\mathcal {Q}},G)_{\mathbb {1}}$. Similarly, the space ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ is weakly equivalent to a covering space of
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ is weakly equivalent to a covering space of ![]() $\mathrm {Hur}(\diamond,\partial ;{\mathcal {Q}},G)_{G,G^{\rm op}}$: see § 4.4 for more details. Passing to loop spaces and double loop spaces, we obtain a weak homotopy equivalence
$\mathrm {Hur}(\diamond,\partial ;{\mathcal {Q}},G)_{G,G^{\rm op}}$: see § 4.4 for more details. Passing to loop spaces and double loop spaces, we obtain a weak homotopy equivalence
where ![]() ${\mathcal {G}}({\mathcal {Q}})$ is the (discrete) enveloping group of
${\mathcal {G}}({\mathcal {Q}})$ is the (discrete) enveloping group of ![]() ${\mathcal {Q}}$.
${\mathcal {Q}}$.
Under the additional assumption that ![]() $G$ is a finite group and
$G$ is a finite group and ![]() ${\mathcal {Q}}$ is finite and rationally Poincaré, the second, main result of the article computes the rational cohomology ring of
${\mathcal {Q}}$ is finite and rationally Poincaré, the second, main result of the article computes the rational cohomology ring of ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ in terms of a certain algebra
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ in terms of a certain algebra ![]() ${\mathcal {A}}({\mathcal {Q}})$, that we briefly recall after the statement.
${\mathcal {A}}({\mathcal {Q}})$, that we briefly recall after the statement.
Theorem 2 (Theorem 6.1)
Let ![]() $({\mathcal {Q}},G)$ be a PMQ–group pair with
$({\mathcal {Q}},G)$ be a PMQ–group pair with ![]() ${\mathcal {Q}}$ finite and rationally Poincaré and with
${\mathcal {Q}}$ finite and rationally Poincaré and with ![]() $G$ finite. Then there is an isomorphism of rings
$G$ finite. Then there is an isomorphism of rings
We recall that a PMQ is rationally Poincaré (or ![]() $\mathbb {Q}$-Poincaré) if it is locally finite and each component of
$\mathbb {Q}$-Poincaré) if it is locally finite and each component of ![]() $\mathrm {Hur}_+((0,1)^2;{\mathcal {Q}})$ is a rational homology manifold [Reference BianchiBia23a, Definition 9.4]. The graded commutative
$\mathrm {Hur}_+((0,1)^2;{\mathcal {Q}})$ is a rational homology manifold [Reference BianchiBia23a, Definition 9.4]. The graded commutative ![]() $\mathbb {Q}$-algebra
$\mathbb {Q}$-algebra ![]() ${\mathcal {A}}({\mathcal {Q}})$ is defined as the sub-algebra of conjugation-invariant elements of
${\mathcal {A}}({\mathcal {Q}})$ is defined as the sub-algebra of conjugation-invariant elements of ![]() $\mathbb {Q}[{\mathcal {Q}}]$, the rational PMQ-algebra associated with the PMQ
$\mathbb {Q}[{\mathcal {Q}}]$, the rational PMQ-algebra associated with the PMQ ![]() ${\mathcal {Q}}$ (see [Reference BianchiBia21, Definition 4.26]). When
${\mathcal {Q}}$ (see [Reference BianchiBia21, Definition 4.26]). When ![]() ${\mathcal {Q}}$ is Poincaré we can consider
${\mathcal {Q}}$ is Poincaré we can consider ![]() $\mathbb {Q}[{\mathcal {Q}}]$ as a graded
$\mathbb {Q}[{\mathcal {Q}}]$ as a graded ![]() $\mathbb {Q}$-algebra, by putting the generator
$\mathbb {Q}$-algebra, by putting the generator ![]() $[\! [a]\! ]\in \mathbb {Q}[{\mathcal {Q}}]$ in degree equal to the dimension of
$[\! [a]\! ]\in \mathbb {Q}[{\mathcal {Q}}]$ in degree equal to the dimension of ![]() $\mathrm {Hur}_+((0,1)^2;{\mathcal {Q}})_a$, for
$\mathrm {Hur}_+((0,1)^2;{\mathcal {Q}})_a$, for ![]() $a\in {\mathcal {Q}}$. The degree of
$a\in {\mathcal {Q}}$. The degree of ![]() $[\! [a]\! ]$ agrees, in fact, with
$[\! [a]\! ]$ agrees, in fact, with ![]() $2h(a)$, where
$2h(a)$, where ![]() $h\colon {\mathcal {Q}}\to \mathbb {N}$ is the intrinsic norm of
$h\colon {\mathcal {Q}}\to \mathbb {N}$ is the intrinsic norm of ![]() ${\mathcal {Q}}$ (see [Reference BianchiBia23a, Proposition 9.7]). This makes also
${\mathcal {Q}}$ (see [Reference BianchiBia23a, Proposition 9.7]). This makes also ![]() ${\mathcal {A}}({\mathcal {Q}})$ into a graded
${\mathcal {A}}({\mathcal {Q}})$ into a graded ![]() $\mathbb {Q}$-algebra and then Theorem B gives an isomorphism of graded
$\mathbb {Q}$-algebra and then Theorem B gives an isomorphism of graded ![]() $\mathbb {Q}$-algebras.
$\mathbb {Q}$-algebras.
The rational cohomology ring of ![]() $\Omega _0 B\mathring {\mathrm {HM}}({\mathcal {Q}})$, i.e. the stable rational cohomology ring of the components of
$\Omega _0 B\mathring {\mathrm {HM}}({\mathcal {Q}})$, i.e. the stable rational cohomology ring of the components of ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$, can then in principle be computed by ‘looping twice’ the rational cohomology of the space
$\mathring {\mathrm {HM}}({\mathcal {Q}})$, can then in principle be computed by ‘looping twice’ the rational cohomology of the space ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$, using that the latter space is simply connected. More precisely, this requires the computation of a minimal Sullivan model for the space
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$, using that the latter space is simply connected. More precisely, this requires the computation of a minimal Sullivan model for the space ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$. We conclude the article with an explicit computation, dealing with the case in which
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$. We conclude the article with an explicit computation, dealing with the case in which ![]() ${\mathcal {Q}}$ is a finite PMQ with trivial product; this recovers, in particular, [Reference Randal-WilliamsRW19, Corollary 5.4].
${\mathcal {Q}}$ is a finite PMQ with trivial product; this recovers, in particular, [Reference Randal-WilliamsRW19, Corollary 5.4].
1.2 Outline of the article
In § 2 we introduce the topological monoids ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ and
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ and ![]() $\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and compute the associated discrete monoids of path components
$\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and compute the associated discrete monoids of path components ![]() $\pi _0(\mathring {\mathrm {HM}}({\mathcal {Q}}))$ and
$\pi _0(\mathring {\mathrm {HM}}({\mathcal {Q}}))$ and ![]() $\pi _0(\breve {\mathrm {HM}}({\mathcal {Q}},G))$, see Theorems 2.15 and 2.19.
$\pi _0(\breve {\mathrm {HM}}({\mathcal {Q}},G))$, see Theorems 2.15 and 2.19.
In § 3 we recall the simplicial space ![]() $B_\bullet M$ associated with a unital, topological monoid
$B_\bullet M$ associated with a unital, topological monoid ![]() $M$ and we distinguish between ‘bar construction’
$M$ and we distinguish between ‘bar construction’ ![]() $BM$ and ‘thin bar construction’
$BM$ and ‘thin bar construction’ ![]() $\bar {B} M$, i.e. the geometric realisations of
$\bar {B} M$, i.e. the geometric realisations of ![]() $B_\bullet M$ as a semisimplicial space and, respectively, a simplicial space. We prove in Theorem 3.4 a homotopy equivalence
$B_\bullet M$ as a semisimplicial space and, respectively, a simplicial space. We prove in Theorem 3.4 a homotopy equivalence ![]() $\breve {\mathrm {HM}}_+({\mathcal {Q}},G)\simeq \Omega B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and check that the group completion theorem [Reference McDuff and SegalMS76, Reference Friedlander and MazurFM94] applies to the topological monoid
$\breve {\mathrm {HM}}_+({\mathcal {Q}},G)\simeq \Omega B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and check that the group completion theorem [Reference McDuff and SegalMS76, Reference Friedlander and MazurFM94] applies to the topological monoid ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$.
$\mathring {\mathrm {HM}}({\mathcal {Q}})$.
The main result of § 4 is Theorem 4.1, whose direct consequence is that the bar constructions ![]() $B\mathring {\mathrm {HM}}({\mathcal {Q}})$ and
$B\mathring {\mathrm {HM}}({\mathcal {Q}})$ and ![]() $B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ admit covering spaces that are homotopy equivalent to the Hurwitz spaces
$B\breve {\mathrm {HM}}({\mathcal {Q}},G)$ admit covering spaces that are homotopy equivalent to the Hurwitz spaces ![]() $\breve {\mathrm {HM}}_+({\mathcal {Q}},G)_{\mathbb {1}}$ and
$\breve {\mathrm {HM}}_+({\mathcal {Q}},G)_{\mathbb {1}}$ and ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$, respectively. The main application is Theorem 4.22, computing the homology of the group completion of
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$, respectively. The main application is Theorem 4.22, computing the homology of the group completion of ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ as the tensor product of the group ring
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ as the tensor product of the group ring ![]() $\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})]$ and the homology of a component of the double loop space
$\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})]$ and the homology of a component of the double loop space ![]() $\Omega ^2\,\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here
$\Omega ^2\,\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$; here ![]() ${\mathcal {G}}({\mathcal {Q}})$ is the enveloping group of
${\mathcal {G}}({\mathcal {Q}})$ is the enveloping group of ![]() ${\mathcal {Q}}$.
${\mathcal {Q}}$.
In § 5 we replace ![]() $\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ by a smaller, homotopy equivalent subspace
$\mathrm {Hur}_+([0,1]^2,\partial [0,1]^2;{\mathcal {Q}},G)_{\mathbb {1}}$ by a smaller, homotopy equivalent subspace ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$, assuming that
$\mathbb {B}({\mathcal {Q}}_+,G)$, assuming that ![]() ${\mathcal {Q}}$ is augmented. Assuming further that
${\mathcal {Q}}$ is augmented. Assuming further that ![]() ${\mathcal {Q}}$ is a normed PMQ, we prove that
${\mathcal {Q}}$ is a normed PMQ, we prove that ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ admits a norm filtration, whose strata are fibre bundles over the space
$\mathbb {B}({\mathcal {Q}}_+,G)$ admits a norm filtration, whose strata are fibre bundles over the space ![]() ${\mathcal {B}} G:=\mathrm {Hur}(\partial [0,1]^2;G)_{0;1 }$; the space
${\mathcal {B}} G:=\mathrm {Hur}(\partial [0,1]^2;G)_{0;1 }$; the space ![]() ${\mathcal {B}} G$ is, in turn, shown to be an Eilenberg–MacLane space of type
${\mathcal {B}} G$ is, in turn, shown to be an Eilenberg–MacLane space of type ![]() $K(G,1)$.
$K(G,1)$.
In § 6 we assume that ![]() ${\mathcal {Q}}$ is a finite and
${\mathcal {Q}}$ is a finite and ![]() $\mathbb {Q}$-Poincaré PMQ and
$\mathbb {Q}$-Poincaré PMQ and ![]() $G$ is a finite group and compute the rational cohomology ring of
$G$ is a finite group and compute the rational cohomology ring of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$, using the Leray spectral sequence associated with the filtration on
$\mathbb {B}({\mathcal {Q}}_+,G)$, using the Leray spectral sequence associated with the filtration on ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$: Theorem 6.1 identifies
$\mathbb {B}({\mathcal {Q}}_+,G)$: Theorem 6.1 identifies ![]() $H^*(\mathbb {B}({\mathcal {Q}}_+,G);\mathbb {Q})$ with the ring
$H^*(\mathbb {B}({\mathcal {Q}}_+,G);\mathbb {Q})$ with the ring ![]() ${\mathcal {A}}({\mathcal {Q}})\subset \mathbb {Q}[{\mathcal {Q}}]$ of conjugation
${\mathcal {A}}({\mathcal {Q}})\subset \mathbb {Q}[{\mathcal {Q}}]$ of conjugation ![]() ${\mathcal {G}}({\mathcal {Q}})$-invariants of the PMQ-ring
${\mathcal {G}}({\mathcal {Q}})$-invariants of the PMQ-ring ![]() $\mathbb {Q}[{\mathcal {Q}}]$. As an application, we compute the stable rational cohomology of classical Hurwitz spaces, recovering, in particular, [Reference Randal-WilliamsRW19, Corollary 5.4].
$\mathbb {Q}[{\mathcal {Q}}]$. As an application, we compute the stable rational cohomology of classical Hurwitz spaces, recovering, in particular, [Reference Randal-WilliamsRW19, Corollary 5.4].
Throughout the article we make heavy use of the results of [Reference BianchiBia21, Sections 2–6] and [Reference BianchiBia23a, Sections 2–6]: we cite every time which specific fact we are needing, so that the reader does not need to be familiar with all details of [Reference BianchiBia21] and [Reference BianchiBia23a].
1.3 Motivation
This is the third article in a series about Hurwitz spaces. Our main motivation to study generalised Hurwitz spaces comes from the relation between Hurwitz spaces and moduli spaces of Riemann surfaces given by considering the family of PMQs ![]() $\mathfrak {S}_d^{\mathrm {geo}}$, for
$\mathfrak {S}_d^{\mathrm {geo}}$, for ![]() $d\ge 2$: Theorems A and B are applied in [Reference BianchiBia23b] to give an alternative proof of the Mumford conjecture on the stable rational cohomology of moduli spaces of Riemann surfaces, originally proved by Madsen and Weiss [Reference Madsen and WeissMW07].
$d\ge 2$: Theorems A and B are applied in [Reference BianchiBia23b] to give an alternative proof of the Mumford conjecture on the stable rational cohomology of moduli spaces of Riemann surfaces, originally proved by Madsen and Weiss [Reference Madsen and WeissMW07].
Moreover, this article shows how generalised Hurwitz spaces can be useful also in the study of classical Hurwitz spaces as topological monoids: the (double) delooping of the classical monoid of Hurwitz spaces is described by Theorem A as a relative Hurwitz space.
2. Hurwitz spaces as topological monoids
We start by fixing some conventions to simplify the notation. We fix a PMQ–group pair ![]() $({\mathcal {Q}},G)=({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$ throughout the article; recall that
$({\mathcal {Q}},G)=({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$ throughout the article; recall that ![]() $\mathfrak {e}\colon {\mathcal {Q}}\to G$ is a map of PMQs and
$\mathfrak {e}\colon {\mathcal {Q}}\to G$ is a map of PMQs and ![]() $\mathfrak {r}\colon G\to \operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$ is a map of groups, giving a right action of
$\mathfrak {r}\colon G\to \operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$ is a map of groups, giving a right action of ![]() $G$ on
$G$ on ![]() ${\mathcal {Q}}$, see [Reference BianchiBia21, Definition 2.15]. We assume in the entire article that the image of
${\mathcal {Q}}$, see [Reference BianchiBia21, Definition 2.15]. We assume in the entire article that the image of ![]() $\mathfrak {e}$ generates
$\mathfrak {e}$ generates ![]() $G$ as a group. Two examples that the reader may keep in mind are as follows:
$G$ as a group. Two examples that the reader may keep in mind are as follows:
•
 $G$ is a group,
$G$ is a group,  ${\mathcal {Q}}_+\subset G$ is a conjugation-invariant subset and
${\mathcal {Q}}_+\subset G$ is a conjugation-invariant subset and  ${\mathcal {Q}}={\mathcal {Q}}_+\sqcup \{1 _{{\mathcal {Q}}}\}$ with the adjoined element
${\mathcal {Q}}={\mathcal {Q}}_+\sqcup \{1 _{{\mathcal {Q}}}\}$ with the adjoined element  $\mathbb {1}_{{\mathcal {Q}}}$ being the unit of
$\mathbb {1}_{{\mathcal {Q}}}$ being the unit of  ${\mathcal {Q}}$; we put the trivial product on
${\mathcal {Q}}$; we put the trivial product on  ${\mathcal {Q}}$, we define
${\mathcal {Q}}$, we define  $\mathfrak {e}$ by
$\mathfrak {e}$ by  $\mathbb {1}_{{\mathcal {Q}}}\mapsto \mathbb {1}_G$ and
$\mathbb {1}_{{\mathcal {Q}}}\mapsto \mathbb {1}_G$ and  ${\mathcal {Q}}_+\hookrightarrow G$; we let the action of
${\mathcal {Q}}_+\hookrightarrow G$; we let the action of  $G$ fix
$G$ fix  $\mathbb {1}_{{\mathcal {Q}}}$ and conjugate elements of
$\mathbb {1}_{{\mathcal {Q}}}$ and conjugate elements of  ${\mathcal {Q}}_+$;
${\mathcal {Q}}_+$;•
 $G=\mathfrak {S}_d$ is the
$G=\mathfrak {S}_d$ is the  $d$th symmetric group for some
$d$th symmetric group for some  $d\ge 2$,
$d\ge 2$,  ${\mathcal {Q}}=\mathfrak {S}_d^{\mathrm {geo}}$ is the geodesic PMQ from [Reference BianchiBia21, Subsection 7.1], obtained from
${\mathcal {Q}}=\mathfrak {S}_d^{\mathrm {geo}}$ is the geodesic PMQ from [Reference BianchiBia21, Subsection 7.1], obtained from  $\mathfrak {S}_d$ by restricting the product,
$\mathfrak {S}_d$ by restricting the product,  $\mathfrak {e}$ is the identity of the common underlying set and
$\mathfrak {e}$ is the identity of the common underlying set and  $\mathfrak {S}_d$ acts on
$\mathfrak {S}_d$ acts on  $\mathfrak {S}_d^{\mathrm {geo}}$ by usual conjugation of permutations.
$\mathfrak {S}_d^{\mathrm {geo}}$ by usual conjugation of permutations.
We usually denote by ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ a nice couple, i.e. a couple of semialgebraic subspaces of the closed upper half-plane
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ a nice couple, i.e. a couple of semialgebraic subspaces of the closed upper half-plane ![]() $\mathbb {H}\subset \mathbb {C}$, with
$\mathbb {H}\subset \mathbb {C}$, with ![]() ${\mathcal {Y}}$ closed in
${\mathcal {Y}}$ closed in ![]() ${\mathcal {X}}$: see [Reference BianchiBia23a, Definition 2.3]. In the entire article, we abbreviate the Hurwitz space
${\mathcal {X}}$: see [Reference BianchiBia23a, Definition 2.3]. In the entire article, we abbreviate the Hurwitz space ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$, defined in [Reference BianchiBia23a, Section 3], as
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$, defined in [Reference BianchiBia23a, Section 3], as ![]() $\mathrm {Hur}(\mathfrak {C})$; in particular, if
$\mathrm {Hur}(\mathfrak {C})$; in particular, if ![]() ${\mathcal {Y}}=\emptyset$, we abbreviate
${\mathcal {Y}}=\emptyset$, we abbreviate ![]() $\mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ as
$\mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ as ![]() $\mathrm {Hur}({\mathcal {X}})$.
$\mathrm {Hur}({\mathcal {X}})$.
Recall from [Reference BianchiBia23a, Definition 2.9] that if ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ is a nice couple and if
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ is a nice couple and if ![]() $P\subset {\mathcal {X}}$ is a finite subset, we can define a PMQ
$P\subset {\mathcal {X}}$ is a finite subset, we can define a PMQ ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)$ as the subset of
$\mathfrak {Q}_{\mathfrak {C}}(P)$ as the subset of ![]() $\mathfrak {G}(P):=\pi _1(\mathbb {C}\setminus P,*)$ of conjugacy classes of small simple loops spinning clockwise around exactly one point of
$\mathfrak {G}(P):=\pi _1(\mathbb {C}\setminus P,*)$ of conjugacy classes of small simple loops spinning clockwise around exactly one point of ![]() $P$ among those lying in
$P$ among those lying in ![]() ${\mathcal {X}}\setminus {\mathcal {Y}}$ (together with the neutral element
${\mathcal {X}}\setminus {\mathcal {Y}}$ (together with the neutral element ![]() $\mathbb {1}_{\mathfrak {G}(P)}$; the inclusion
$\mathbb {1}_{\mathfrak {G}(P)}$; the inclusion ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)\subseteq \mathfrak {G}(P)$ and the conjugation action of
$\mathfrak {Q}_{\mathfrak {C}}(P)\subseteq \mathfrak {G}(P)$ and the conjugation action of ![]() $\mathfrak {G}(P)$ on
$\mathfrak {G}(P)$ on ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)$ make
$\mathfrak {Q}_{\mathfrak {C}}(P)$ make ![]() $(\mathfrak {Q}_{\mathfrak {C}}(P),\mathfrak {G}(P))$ into a PMQ–group pair.
$(\mathfrak {Q}_{\mathfrak {C}}(P),\mathfrak {G}(P))$ into a PMQ–group pair.
Notation 2.1 Let ![]() $\mathbb {Y}\subset \mathbb {H}$ be closed semialgebraic subspace. Then for every semialgebraic subspace
$\mathbb {Y}\subset \mathbb {H}$ be closed semialgebraic subspace. Then for every semialgebraic subspace ![]() ${\mathcal {X}}\subset \mathbb {H}$ we obtain a nice couple
${\mathcal {X}}\subset \mathbb {H}$ we obtain a nice couple ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ by setting
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ by setting ![]() ${\mathcal {Y}}=\mathbb {Y}\cap {\mathcal {X}}$; for all finite subsets
${\mathcal {Y}}=\mathbb {Y}\cap {\mathcal {X}}$; for all finite subsets ![]() $P\subset {\mathcal {X}}$ we then have that
$P\subset {\mathcal {X}}$ we then have that ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)$ and
$\mathfrak {Q}_{\mathfrak {C}}(P)$ and ![]() $\mathfrak {Q}_{(\mathbb {H},\mathbb {Y})}(P)$ are the same subset of
$\mathfrak {Q}_{(\mathbb {H},\mathbb {Y})}(P)$ are the same subset of ![]() $\mathfrak {G}(P)$.
$\mathfrak {G}(P)$.
We will abuse notation and abbreviate ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)$ as
$\mathfrak {Q}_{\mathfrak {C}}(P)$ as ![]() $\mathfrak {Q}(P)$ also in certain situations in which there may be some ambiguity on the nice couple
$\mathfrak {Q}(P)$ also in certain situations in which there may be some ambiguity on the nice couple ![]() $\mathfrak {C}$ we are considering; we leverage on the fact that all nice couples
$\mathfrak {C}$ we are considering; we leverage on the fact that all nice couples ![]() $\mathfrak {C}$ that might reasonably be involved in the argument are obtained as above, for a fixed and evident subspace
$\mathfrak {C}$ that might reasonably be involved in the argument are obtained as above, for a fixed and evident subspace ![]() $\mathbb {Y}\subset \mathbb {H}$, so that the fundamental PMQ
$\mathbb {Y}\subset \mathbb {H}$, so that the fundamental PMQ ![]() $\mathfrak {Q}_{\mathfrak {C}}(P)$ is unambiguously identified as a subset of
$\mathfrak {Q}_{\mathfrak {C}}(P)$ is unambiguously identified as a subset of ![]() $\mathfrak {G}(P)$.
$\mathfrak {G}(P)$.
Notation 2.2 We usually denote by ![]() $P=\{z_1,\ldots,z_k\}$ a finite collection of distinct points in
$P=\{z_1,\ldots,z_k\}$ a finite collection of distinct points in ![]() $\mathbb {H}$, for some
$\mathbb {H}$, for some ![]() $k\geq 0$. If a nice couple
$k\geq 0$. If a nice couple ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ is under consideration, we will usually assume
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ is under consideration, we will usually assume ![]() $P\subset {\mathcal {X}}$ and that there is
$P\subset {\mathcal {X}}$ and that there is ![]() $0\leq l\leq k$ such that
$0\leq l\leq k$ such that ![]() $z_1,\ldots,z_l$ are precisely the points of
$z_1,\ldots,z_l$ are precisely the points of ![]() $P$ lying in
$P$ lying in ![]() ${\mathcal {X}}\setminus {\mathcal {Y}}$. We let
${\mathcal {X}}\setminus {\mathcal {Y}}$. We let ![]() $*=-\sqrt {-1}\in \mathbb {C}$ be our preferred choice of basepoint. If
$*=-\sqrt {-1}\in \mathbb {C}$ be our preferred choice of basepoint. If ![]() $f_1,\ldots,f_k$ is an admissible generating set of
$f_1,\ldots,f_k$ is an admissible generating set of ![]() $\mathfrak {G}(P)=\pi _1(\mathbb {C}\setminus P,*)$ (see [Reference BianchiBia23a, Definition 2.8]), then we usually assume that
$\mathfrak {G}(P)=\pi _1(\mathbb {C}\setminus P,*)$ (see [Reference BianchiBia23a, Definition 2.8]), then we usually assume that ![]() $f_i$ is represented by a small simple loop spinning clockwise around
$f_i$ is represented by a small simple loop spinning clockwise around ![]() $z_i$.
$z_i$.
A configuration ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ is usually presented as
$\mathfrak {c}\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ is usually presented as ![]() $(P,\psi,\varphi )$, with
$(P,\psi,\varphi )$, with ![]() $P$ as above and
$P$ as above and ![]() $(\psi,\varphi )\colon (\mathfrak {Q}(P),\mathfrak {G}(P))\to ({\mathcal {Q}},G)$ a map of PMQ–group pairs. Similarly, a configuration
$(\psi,\varphi )\colon (\mathfrak {Q}(P),\mathfrak {G}(P))\to ({\mathcal {Q}},G)$ a map of PMQ–group pairs. Similarly, a configuration ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ is usually presented as
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {X}};{\mathcal {Q}})$ is usually presented as ![]() $(P,\psi )$, with
$(P,\psi )$, with ![]() $P$ as above and
$P$ as above and ![]() $\psi \colon \mathfrak {Q}(P)\to {\mathcal {Q}}$ a map of PMQs.
$\psi \colon \mathfrak {Q}(P)\to {\mathcal {Q}}$ a map of PMQs.
2.1 Definition of the Hurwitz–Moore spaces
We first introduce notation for rectangles and horizontal strips in the plane.
Notation 2.3 For ![]() $t\geq 0$ we denote by
$t\geq 0$ we denote by ![]() ${\mathcal {R}}_t\subset \mathbb {H}$ the standard closed rectangle
${\mathcal {R}}_t\subset \mathbb {H}$ the standard closed rectangle ![]() $[0,t]\times [0,1]$ of width
$[0,t]\times [0,1]$ of width ![]() $t$ and height 1; we also denote
$t$ and height 1; we also denote ![]() ${\mathcal {R}}_{\infty }=[0,\infty )\times [0,1]$ the half-infinite, closed strip and by
${\mathcal {R}}_{\infty }=[0,\infty )\times [0,1]$ the half-infinite, closed strip and by ![]() ${\mathcal {R}}_{\mathbb {R}}=(-\infty,+\infty )\times [0,1]$ the infinite, closed strip.
${\mathcal {R}}_{\mathbb {R}}=(-\infty,+\infty )\times [0,1]$ the infinite, closed strip.
For ![]() $0\leq t\leq +\infty$ we denote by
$0\leq t\leq +\infty$ we denote by ![]() $\mathring {{\mathcal {R}}}_t=(0,t)\times (0,1)$ the standard open rectangle (or half-infinite strip) of width
$\mathring {{\mathcal {R}}}_t=(0,t)\times (0,1)$ the standard open rectangle (or half-infinite strip) of width ![]() $t$ and height 1 and by
$t$ and height 1 and by ![]() $\mathring {{\mathcal {R}}}_{\mathbb {R}}=(-\infty,+\infty )\times (0,1)$ the infinite open strip. Also let
$\mathring {{\mathcal {R}}}_{\mathbb {R}}=(-\infty,+\infty )\times (0,1)$ the infinite open strip. Also let ![]() $\partial {\mathcal {R}}_t={\mathcal {R}}_t\setminus \mathring {{\mathcal {R}}}_t$ for all
$\partial {\mathcal {R}}_t={\mathcal {R}}_t\setminus \mathring {{\mathcal {R}}}_t$ for all ![]() $0\leq t\leq \infty$ and
$0\leq t\leq \infty$ and ![]() $\partial {\mathcal {R}}_{\mathbb {R}}={\mathcal {R}}_{\mathbb {R}}\setminus \mathring {{\mathcal {R}}}_{\mathbb {R}}$, denote the boundary of
$\partial {\mathcal {R}}_{\mathbb {R}}={\mathcal {R}}_{\mathbb {R}}\setminus \mathring {{\mathcal {R}}}_{\mathbb {R}}$, denote the boundary of ![]() ${\mathcal {R}}_t$ and
${\mathcal {R}}_t$ and ![]() ${\mathcal {R}}_{\mathbb {R}}$, respectively. We use the abbreviations
${\mathcal {R}}_{\mathbb {R}}$, respectively. We use the abbreviations ![]() $({\mathcal {R}}_t,\partial )$ and
$({\mathcal {R}}_t,\partial )$ and ![]() $({\mathcal {R}}_{\mathbb {R}},\partial )$ for the nice couples
$({\mathcal {R}}_{\mathbb {R}},\partial )$ for the nice couples ![]() $({\mathcal {R}}_t,\partial {\mathcal {R}}_t)$ and
$({\mathcal {R}}_t,\partial {\mathcal {R}}_t)$ and ![]() $({\mathcal {R}}_{\mathbb {R}},\partial {\mathcal {R}}_{\mathbb {R}})$, respectively.
$({\mathcal {R}}_{\mathbb {R}},\partial {\mathcal {R}}_{\mathbb {R}})$, respectively.
For ![]() $0\leq t\leq +\infty$ we denote by
$0\leq t\leq +\infty$ we denote by ![]() $\breve {{\mathcal {R}}}_t=(0,t)\times [0,1]$ the standard, vertically closed rectangle (or vertically closed half-infinite strip) of width
$\breve {{\mathcal {R}}}_t=(0,t)\times [0,1]$ the standard, vertically closed rectangle (or vertically closed half-infinite strip) of width ![]() $t$ and height 1 and by
$t$ and height 1 and by ![]() $\breve {\partial }\breve {{\mathcal {R}}}_t=(0,t)\times \{0,1\}\subset \breve {{\mathcal {R}}}_t$ the horizontal boundary of
$\breve {\partial }\breve {{\mathcal {R}}}_t=(0,t)\times \{0,1\}\subset \breve {{\mathcal {R}}}_t$ the horizontal boundary of ![]() $\breve {{\mathcal {R}}}$. Similarly, we denote
$\breve {{\mathcal {R}}}$. Similarly, we denote ![]() $\breve {{\mathcal {R}}}_{\mathbb {R}}={\mathcal {R}}_{\mathbb {R}}$ and
$\breve {{\mathcal {R}}}_{\mathbb {R}}={\mathcal {R}}_{\mathbb {R}}$ and ![]() $\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}}=\partial \breve {{\mathcal {R}}}_{\mathbb {R}}=(-\infty,+\infty )\times \{0,1\}$. We use the abbreviations
$\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}}=\partial \breve {{\mathcal {R}}}_{\mathbb {R}}=(-\infty,+\infty )\times \{0,1\}$. We use the abbreviations ![]() $(\breve {{\mathcal {R}}}_t,\breve {\partial })$ and
$(\breve {{\mathcal {R}}}_t,\breve {\partial })$ and ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ for the nice couples
$(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ for the nice couples ![]() $(\breve {{\mathcal {R}}}_t,\breve {\partial }\breve {{\mathcal {R}}}_t)$ and
$(\breve {{\mathcal {R}}}_t,\breve {\partial }\breve {{\mathcal {R}}}_t)$ and ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}};\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}})$, respectively.
$(\breve {{\mathcal {R}}}_{\mathbb {R}};\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}})$, respectively.
Whenever ![]() $t=1$ we drop it from the notation, so we abbreviate
$t=1$ we drop it from the notation, so we abbreviate ![]() ${\mathcal {R}}_1$ as
${\mathcal {R}}_1$ as ![]() ${\mathcal {R}}$,
${\mathcal {R}}$, ![]() $\mathring {{\mathcal {R}}}_1$ as
$\mathring {{\mathcal {R}}}_1$ as ![]() $\mathring {{\mathcal {R}}}$ and
$\mathring {{\mathcal {R}}}$ and ![]() $\breve {{\mathcal {R}}}_1$ as
$\breve {{\mathcal {R}}}_1$ as ![]() $\breve {{\mathcal {R}}}$. See Figure 1.
$\breve {{\mathcal {R}}}$. See Figure 1.

Figure 1. Left: the rectangle ![]() $\mathring {{\mathcal {R}}}_{1/2}$. Right: the nice couple
$\mathring {{\mathcal {R}}}_{1/2}$. Right: the nice couple ![]() $(\breve {{\mathcal {R}}}_{3/4},\breve {\partial }\breve {{\mathcal {R}}}_{3/4})$.
$(\breve {{\mathcal {R}}}_{3/4},\breve {\partial }\breve {{\mathcal {R}}}_{3/4})$.
Note that ![]() $\breve {{\mathcal {R}}}_0=\mathring {{\mathcal {R}}}_0=\emptyset$. For
$\breve {{\mathcal {R}}}_0=\mathring {{\mathcal {R}}}_0=\emptyset$. For ![]() $t\leq t'$ the identity of
$t\leq t'$ the identity of ![]() $\mathbb {C}$ restricts to an inclusion
$\mathbb {C}$ restricts to an inclusion ![]() $\mathring {{\mathcal {R}}}_t\subset \mathring {{\mathcal {R}}}_{t'}$ and induces an inclusion of Hurwitz spaces
$\mathring {{\mathcal {R}}}_t\subset \mathring {{\mathcal {R}}}_{t'}$ and induces an inclusion of Hurwitz spaces ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)\subseteq \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})$.
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)\subseteq \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})$.
Definition 2.4 The open Hurwitz–Moore space associated with the PMQ ![]() ${\mathcal {Q}}$, denoted by
${\mathcal {Q}}$, denoted by ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ and abbreviated as
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ and abbreviated as ![]() $\mathring {\mathrm {HM}}$ in the entire article, is the subspace of
$\mathring {\mathrm {HM}}$ in the entire article, is the subspace of ![]() $[0,\infty )\times \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ containing couples
$[0,\infty )\times \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ containing couples ![]() $(t,\mathfrak {c})$ such that
$(t,\mathfrak {c})$ such that ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ is a configuration supported on
$\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ is a configuration supported on ![]() $\mathring {{\mathcal {R}}}_t$, i.e.
$\mathring {{\mathcal {R}}}_t$, i.e. ![]() $\mathfrak {c}$ takes the form
$\mathfrak {c}$ takes the form ![]() $(P,\psi )$ with
$(P,\psi )$ with ![]() $P\subset \mathring {{\mathcal {R}}}_t$.
$P\subset \mathring {{\mathcal {R}}}_t$.
Similarly, the vertically closed Hurwitz–Moore space associated with ![]() $({\mathcal {Q}},G)$, denoted by
$({\mathcal {Q}},G)$, denoted by ![]() $\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and abbreviated as
$\breve {\mathrm {HM}}({\mathcal {Q}},G)$ and abbreviated as ![]() $\breve {\mathrm {HM}}$ in the entire article, is the subspace of
$\breve {\mathrm {HM}}$ in the entire article, is the subspace of ![]() $[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ containing couples
$[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ containing couples ![]() $(t,\mathfrak {c})$ such that
$(t,\mathfrak {c})$ such that ![]() $\mathfrak {c}$ is supported on
$\mathfrak {c}$ is supported on ![]() $\breve {{\mathcal {R}}}_t$, i.e.
$\breve {{\mathcal {R}}}_t$, i.e. ![]() $\mathfrak {c}=(P,\psi,\varphi )$ with
$\mathfrak {c}=(P,\psi,\varphi )$ with ![]() $P\subset \breve {{\mathcal {R}}}_t$.
$P\subset \breve {{\mathcal {R}}}_t$.
Note that, for fixed ![]() $t\geq 0$, the slice of
$t\geq 0$, the slice of ![]() $\mathring {\mathrm {HM}}$ containing couples of the form
$\mathring {\mathrm {HM}}$ containing couples of the form ![]() $(t,\mathfrak {c})$ is homeomorphic to
$(t,\mathfrak {c})$ is homeomorphic to ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$: thus,
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$: thus, ![]() $\mathring {\mathrm {HM}}$, as a set, is the disjoint union
$\mathring {\mathrm {HM}}$, as a set, is the disjoint union ![]() $\bigsqcup _{t\geq 0}\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$. Similarly,
$\bigsqcup _{t\geq 0}\mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$. Similarly, ![]() $\breve {\mathrm {HM}}$ is in natural bijection with the set
$\breve {\mathrm {HM}}$ is in natural bijection with the set ![]() $\bigsqcup _{t\geq 0}\mathrm {Hur}(\breve {{\mathcal {R}}}_t,\breve {\partial })$.
$\bigsqcup _{t\geq 0}\mathrm {Hur}(\breve {{\mathcal {R}}}_t,\breve {\partial })$.
Notation 2.5 For a nice couple ![]() $\mathfrak {C}$ we denote by
$\mathfrak {C}$ we denote by ![]() $(\emptyset,\mathbb {1},\mathbb {1})\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ the unique configuration supported on the empty set, i.e. of the form
$(\emptyset,\mathbb {1},\mathbb {1})\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ the unique configuration supported on the empty set, i.e. of the form ![]() $(P,\psi,\varphi )$ with
$(P,\psi,\varphi )$ with ![]() $P=\emptyset$. The complement of
$P=\emptyset$. The complement of ![]() $\{(\emptyset,\mathbb {1},\mathbb {1})\}$ is denoted by
$\{(\emptyset,\mathbb {1},\mathbb {1})\}$ is denoted by ![]() $\mathrm {Hur}_+(\mathfrak {C};{\mathcal {Q}},G)$.
$\mathrm {Hur}_+(\mathfrak {C};{\mathcal {Q}},G)$.
Note that ![]() $(\emptyset,\mathbb {1},\mathbb {1})$ is the only point in the spaces
$(\emptyset,\mathbb {1},\mathbb {1})$ is the only point in the spaces ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_0)$ and
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_0)$ and ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_0,\breve {\partial })$, since
$\mathrm {Hur}(\breve {{\mathcal {R}}}_0,\breve {\partial })$, since ![]() ${\mathring {{\mathcal {R}}}_0=\breve {{\mathcal {R}}}_0=\emptyset}$. In other words, we have
${\mathring {{\mathcal {R}}}_0=\breve {{\mathcal {R}}}_0=\emptyset}$. In other words, we have ![]() $\mathrm {Hur}_+(\mathring {{\mathcal {R}}}_0)=\mathrm {Hur}_+(\breve {{\mathcal {R}}}_0,\breve {\partial })=\emptyset$.
$\mathrm {Hur}_+(\mathring {{\mathcal {R}}}_0)=\mathrm {Hur}_+(\breve {{\mathcal {R}}}_0,\breve {\partial })=\emptyset$.
Notation 2.6 We write ![]() $\breve {\mathrm {HM}}$ as the disjoint union
$\breve {\mathrm {HM}}$ as the disjoint union ![]() $[0,\infty )\times \{(\emptyset,\mathbb {1},\mathbb {1})\}\sqcup \breve {\mathrm {HM}}_+$, where we set
$[0,\infty )\times \{(\emptyset,\mathbb {1},\mathbb {1})\}\sqcup \breve {\mathrm {HM}}_+$, where we set
By the previous discussion, every couple ![]() $(t,\mathfrak {c})\in \breve {\mathrm {HM}}_+$ satisfies
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}_+$ satisfies ![]() $t>0$.
$t>0$.
Lemma 2.7 The inclusions ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})\subset \mathring {\mathrm {HM}}$ and
$\mathrm {Hur}(\mathring {{\mathcal {R}}})\subset \mathring {\mathrm {HM}}$ and ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })\subset \breve {\mathrm {HM}}$ are homotopy equivalences.
$\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })\subset \breve {\mathrm {HM}}$ are homotopy equivalences.
Proof. The proof is almost identical in the two cases, so we will focus on the second case, which is slightly more difficult.
For ![]() $s>0$ the map
$s>0$ the map ![]() $\Lambda _s\colon \mathbb {C}\to \mathbb {C}$ given by
$\Lambda _s\colon \mathbb {C}\to \mathbb {C}$ given by ![]() $\Lambda _s(z)=(s\Re (z),\Im (z))$ is a morphism of nice couples
$\Lambda _s(z)=(s\Re (z),\Im (z))$ is a morphism of nice couples ![]() $\Lambda _s\colon (\breve {{\mathcal {R}}}_\infty,\breve {\partial })\to (\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$. Putting all values of
$\Lambda _s\colon (\breve {{\mathcal {R}}}_\infty,\breve {\partial })\to (\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$. Putting all values of ![]() $s\geq 0$ together we obtain a continuous map
$s\geq 0$ together we obtain a continuous map ![]() $\Lambda \colon \mathbb {C}\times (0,\infty )\to \mathbb {C}$; by [Reference BianchiBia23a, Proposition 4.4] we obtain a continuous map
$\Lambda \colon \mathbb {C}\times (0,\infty )\to \mathbb {C}$; by [Reference BianchiBia23a, Proposition 4.4] we obtain a continuous map
Define ![]() $\tilde \Lambda \colon (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })\times (0,\infty )\to (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ by the formula
$\tilde \Lambda \colon (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })\times (0,\infty )\to (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ by the formula ![]() $\tilde \Lambda (t,\mathfrak {c};s)=(ts,\Lambda _*(\mathfrak {c},s))$. We are now able to define a homotopy
$\tilde \Lambda (t,\mathfrak {c};s)=(ts,\Lambda _*(\mathfrak {c},s))$. We are now able to define a homotopy ![]() ${\mathcal {H}}^{\Lambda }\colon \breve {\mathrm {HM}}\times [0,1]\to \breve {\mathrm {HM}}$ by setting
${\mathcal {H}}^{\Lambda }\colon \breve {\mathrm {HM}}\times [0,1]\to \breve {\mathrm {HM}}$ by setting
 \[
{\mathcal{H}}^{\Lambda}(t,\mathfrak{c};s)=\left\{\begin{array}{@{}ll}
(ts+1-s,\tilde\Lambda(\mathfrak{c},(ts+1-s)/t)) & \text{for
all }t>0\text{ and }\mathfrak{c}\in\breve{\mathrm{HM}}_+;\\
(ts+1-s,(\emptyset,\mathbb {1},\mathbb {1})) & \text{for
}\mathfrak{c}=(\emptyset,\mathbb {1},\mathbb {1}) \text{
and all }t\geq 0. \end{array}\right. \]
\[
{\mathcal{H}}^{\Lambda}(t,\mathfrak{c};s)=\left\{\begin{array}{@{}ll}
(ts+1-s,\tilde\Lambda(\mathfrak{c},(ts+1-s)/t)) & \text{for
all }t>0\text{ and }\mathfrak{c}\in\breve{\mathrm{HM}}_+;\\
(ts+1-s,(\emptyset,\mathbb {1},\mathbb {1})) & \text{for
}\mathfrak{c}=(\emptyset,\mathbb {1},\mathbb {1}) \text{
and all }t\geq 0. \end{array}\right. \]
Note that ![]() ${\mathcal {H}}^{\Lambda }((1,\mathfrak {c}),s)=(1,\mathfrak {c})$ for all
${\mathcal {H}}^{\Lambda }((1,\mathfrak {c}),s)=(1,\mathfrak {c})$ for all ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$, including
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$, including ![]() $(\emptyset,\mathbb {1},\mathbb {1})$ and all
$(\emptyset,\mathbb {1},\mathbb {1})$ and all ![]() $0\leq s\leq 1$; moreover, the map
$0\leq s\leq 1$; moreover, the map ![]() ${\mathcal {H}}(-;1)$ is the identity of
${\mathcal {H}}(-;1)$ is the identity of ![]() $\breve {\mathrm {HM}}$, whereas the map
$\breve {\mathrm {HM}}$, whereas the map ![]() ${\mathcal {H}}^{\Lambda }(-;0)$ has image inside
${\mathcal {H}}^{\Lambda }(-;0)$ has image inside ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$.
$\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$.
The reason for the name Moore in Definition 2.4 is that, as we will see in § 2.2, there is a natural structure of topological monoid on both ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$. In contrast,
$\breve {\mathrm {HM}}$. In contrast, ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})$ and
$\mathrm {Hur}(\mathring {{\mathcal {R}}})$ and ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}})$ are only endowed with the structure of
$\mathrm {Hur}(\breve {{\mathcal {R}}})$ are only endowed with the structure of ![]() $E_1$-algebras in a natural way. The spaces
$E_1$-algebras in a natural way. The spaces ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$ play the role of the strictification of the
$\breve {\mathrm {HM}}$ play the role of the strictification of the ![]() $E_1$-algebras
$E_1$-algebras ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})$ and
$\mathrm {Hur}(\mathring {{\mathcal {R}}})$ and ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}})$ to actual topological monoids, just as the Moore loop space
$\mathrm {Hur}(\breve {{\mathcal {R}}})$ to actual topological monoids, just as the Moore loop space ![]() $\Omega ^{\mathrm {Moore}}X$ of a pointed topological space
$\Omega ^{\mathrm {Moore}}X$ of a pointed topological space ![]() $X$ is a strictly associative and strictly unital replacement of the
$X$ is a strictly associative and strictly unital replacement of the ![]() $E_1$-algebra given by the usual loop space
$E_1$-algebra given by the usual loop space ![]() $\Omega X$.
$\Omega X$.
2.2 Topological monoid structure
In this subsection we define a topological monoid structure on ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$. For
$\breve {\mathrm {HM}}$. For ![]() $\mathring {\mathrm {HM}}$ the basic idea is to juxtapose two configurations
$\mathring {\mathrm {HM}}$ the basic idea is to juxtapose two configurations ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$ and
$\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_t)$ and ![]() $\mathfrak {c}'\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})$ to obtain a larger configuration supported on the rectangle
$\mathfrak {c}'\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})$ to obtain a larger configuration supported on the rectangle ![]() $\mathring {{\mathcal {R}}}_{t+t'}$; for
$\mathring {{\mathcal {R}}}_{t+t'}$; for ![]() $\breve {\mathrm {HM}}$ the idea is similar, but using vertically closed rectangles and juxtaposing also their horizontal boundaries.
$\breve {\mathrm {HM}}$ the idea is similar, but using vertically closed rectangles and juxtaposing also their horizontal boundaries.
In the entire subsection we focus on ![]() $\mathring {\mathrm {HM}}$ and write in parentheses the changes needed in the analogous discussion about
$\mathring {\mathrm {HM}}$ and write in parentheses the changes needed in the analogous discussion about ![]() $\breve {\mathrm {HM}}$. Whenever we write
$\breve {\mathrm {HM}}$. Whenever we write ![]() $\mathfrak {Q}(P)$ for a subset
$\mathfrak {Q}(P)$ for a subset ![]() $P\subset \mathbb {H}$, we use Notation 2.1 with
$P\subset \mathbb {H}$, we use Notation 2.1 with ![]() $\mathbb {Y}=\emptyset$ (respectively,
$\mathbb {Y}=\emptyset$ (respectively, ![]() $\mathbb {Y}=\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}}$, see Notation 2.3).
$\mathbb {Y}=\breve {\partial }\breve {{\mathcal {R}}}_{\mathbb {R}}$, see Notation 2.3).
Notation 2.8 For ![]() $t,t'\geq 0$ we denote by
$t,t'\geq 0$ we denote by ![]() $\mathring {{\mathcal {R}}}_{t'}+t$ the space
$\mathring {{\mathcal {R}}}_{t'}+t$ the space ![]() $(t,t+t')\times (0,1)$. Similarly, we denote by
$(t,t+t')\times (0,1)$. Similarly, we denote by ![]() $(\breve {{\mathcal {R}}}_{t'},\breve {\partial })+t$ the nice couple
$(\breve {{\mathcal {R}}}_{t'},\breve {\partial })+t$ the nice couple ![]() $((t,t+t')\times [0,1],(t,t+t')\times \{0,1\})$, compare with Notation 2.3.
$((t,t+t')\times [0,1],(t,t+t')\times \{0,1\})$, compare with Notation 2.3.
For a finite subset ![]() $P\subset \mathbb {H}$ as in Notation 2.2 and for
$P\subset \mathbb {H}$ as in Notation 2.2 and for ![]() $t\geq 0$ we denote by
$t\geq 0$ we denote by ![]() $P+t$ the subset
$P+t$ the subset ![]() $\{z_1+t,\ldots,z_k+t\}\subset \mathbb {H}$.
$\{z_1+t,\ldots,z_k+t\}\subset \mathbb {H}$.
Note that for ![]() $P,t,t'$ as in Notation 2.8, if
$P,t,t'$ as in Notation 2.8, if ![]() $P\subset \mathring {{\mathcal {R}}}_{t'}$ (respectively
$P\subset \mathring {{\mathcal {R}}}_{t'}$ (respectively ![]() $P\subset \breve {{\mathcal {R}}}_{t'})$, then
$P\subset \breve {{\mathcal {R}}}_{t'})$, then ![]() $P+t\subset \mathring {{\mathcal {R}}}_{t'}+t\subset \mathring {{\mathcal {R}}}_{t+t'}$ (respectively,
$P+t\subset \mathring {{\mathcal {R}}}_{t'}+t\subset \mathring {{\mathcal {R}}}_{t+t'}$ (respectively, ![]() $P+t\subset \breve {{\mathcal {R}}}_{t'}+t\subset \breve {{\mathcal {R}}}_{t+t'}$).
$P+t\subset \breve {{\mathcal {R}}}_{t'}+t\subset \breve {{\mathcal {R}}}_{t+t'}$).
Definition 2.9 (Definition 6.7 in [Reference BianchiBia23a])
For ![]() $t\in \mathbb {R}$ we define a homeomorphism
$t\in \mathbb {R}$ we define a homeomorphism ![]() $\tau _t\colon (\mathbb {C},*)\to (\mathbb {C},*)$ by
$\tau _t\colon (\mathbb {C},*)\to (\mathbb {C},*)$ by
 \[ \tau_t(z)=\left\{\begin{array}{@{}ll} z
& \text{if }\Im(z)\leq -1,\\ z+t & \text{if }
\Im(z)\geq 0,\\ z+(\Im(z)+1)t & \text{if }{-}1\leq
\Im(z)\leq 0. \end{array}\right. \]
\[ \tau_t(z)=\left\{\begin{array}{@{}ll} z
& \text{if }\Im(z)\leq -1,\\ z+t & \text{if }
\Im(z)\geq 0,\\ z+(\Im(z)+1)t & \text{if }{-}1\leq
\Im(z)\leq 0. \end{array}\right. \]
Note that for ![]() $t,t'\geq 0$ we have
$t,t'\geq 0$ we have ![]() $\tau _t(\mathring {{\mathcal {R}}}_{t'})=\mathring {{\mathcal {R}}}_{t'}+t$ (respectively,
$\tau _t(\mathring {{\mathcal {R}}}_{t'})=\mathring {{\mathcal {R}}}_{t'}+t$ (respectively, ![]() $\tau _t(\breve {{\mathcal {R}}}_{t'},\breve {\partial })=(\breve {{\mathcal {R}}}_{t'},\breve {\partial })+t$).
$\tau _t(\breve {{\mathcal {R}}}_{t'},\breve {\partial })=(\breve {{\mathcal {R}}}_{t'},\breve {\partial })+t$).
Notation 2.10 (Notation 6.8 in [Reference BianchiBia23a])
For ![]() $t\in \mathbb {R}$ we denote by
$t\in \mathbb {R}$ we denote by ![]() $\mathbb {C}_{\Re \geq t}\subset \mathbb {C}$ the subspace containing all
$\mathbb {C}_{\Re \geq t}\subset \mathbb {C}$ the subspace containing all ![]() $z\in \mathbb {C}$ with
$z\in \mathbb {C}$ with ![]() $\Re (z)\geq t$. Similarly, we define
$\Re (z)\geq t$. Similarly, we define ![]() $\mathbb {C}_{\Re >t}$,
$\mathbb {C}_{\Re >t}$, ![]() $\mathbb {C}_{\Re \leq t}$,
$\mathbb {C}_{\Re \leq t}$, ![]() $\mathbb {C}_{\Re < t}$ and
$\mathbb {C}_{\Re < t}$ and ![]() $\mathbb {C}_{\Re =t}$, the latter being a vertical line. For all
$\mathbb {C}_{\Re =t}$, the latter being a vertical line. For all ![]() $-\infty \leq t\leq t'\leq +\infty$ we define a subspace
$-\infty \leq t\leq t'\leq +\infty$ we define a subspace ![]() $\mathbb {S}_{t,t'}\subset \mathbb {C}$ by
$\mathbb {S}_{t,t'}\subset \mathbb {C}$ by
where we use the conventions ![]() $\tau _{-\infty }(\mathbb {C}_{\Re \geq 0})=\tau _{+\infty }(\mathbb {C}_{\Re \leq 0})=\mathbb {C}$ and
$\tau _{-\infty }(\mathbb {C}_{\Re \geq 0})=\tau _{+\infty }(\mathbb {C}_{\Re \leq 0})=\mathbb {C}$ and ![]() $\tau _{-\infty }(\mathbb {C}_{\Re \leq 0})=\tau _{+\infty }(\mathbb {C}_{\Re \geq 0})=\emptyset$.
$\tau _{-\infty }(\mathbb {C}_{\Re \leq 0})=\tau _{+\infty }(\mathbb {C}_{\Re \geq 0})=\emptyset$.
For all ![]() $t,t'\geq 0$, we have that
$t,t'\geq 0$, we have that ![]() $\mathbb {S}_{0,t+t'}$ is contractible and can be written as the union of the contractible spaces
$\mathbb {S}_{0,t+t'}$ is contractible and can be written as the union of the contractible spaces ![]() $\mathbb {S}_{0,t}$ and
$\mathbb {S}_{0,t}$ and ![]() $\mathbb {S}_{t,t+t'}$ along the contractible space
$\mathbb {S}_{t,t+t'}$ along the contractible space ![]() $\mathbb {S}_{t,t}$. Moreover,
$\mathbb {S}_{t,t}$. Moreover, ![]() $\mathring {{\mathcal {R}}}_t\subset \mathring {\mathbb {S}}_{0,t}$ (respectively,
$\mathring {{\mathcal {R}}}_t\subset \mathring {\mathbb {S}}_{0,t}$ (respectively, ![]() $\breve {{\mathcal {R}}}_t\subset \mathring {\mathbb {S}}_{0,t}$), whereas
$\breve {{\mathcal {R}}}_t\subset \mathring {\mathbb {S}}_{0,t}$), whereas ![]() $\mathring {{\mathcal {R}}}_{t'}+t\subset \mathring {\mathbb {S}}_{t,t+t'}$ (respectively,
$\mathring {{\mathcal {R}}}_{t'}+t\subset \mathring {\mathbb {S}}_{t,t+t'}$ (respectively, ![]() $\breve {{\mathcal {R}}}_{t'}+t\subset \mathring {\mathbb {S}}_{t,t+t'}$). Note also that
$\breve {{\mathcal {R}}}_{t'}+t\subset \mathring {\mathbb {S}}_{t,t+t'}$). Note also that ![]() $\tau _t$ restricts to a homeomorphism
$\tau _t$ restricts to a homeomorphism ![]() $\mathbb {S}_{0,t'}\to \mathbb {S}_{t,t+t'}$.
$\mathbb {S}_{0,t'}\to \mathbb {S}_{t,t+t'}$.
Recall [Reference BianchiBia23a, Definitions 3.15 and 3.16]: if ![]() $\mathbb {T}\subseteq \mathbb {C}$ is a contractible subspace containing
$\mathbb {T}\subseteq \mathbb {C}$ is a contractible subspace containing ![]() $*=-\sqrt {-1}$, then for any nice couple of subspaces
$*=-\sqrt {-1}$, then for any nice couple of subspaces ![]() ${\mathcal {Y}}\subseteq {\mathcal {X}}\subseteq \mathring {\mathbb {T}}$ we can give an alternative definition of
${\mathcal {Y}}\subseteq {\mathcal {X}}\subseteq \mathring {\mathbb {T}}$ we can give an alternative definition of ![]() $\mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})$, denoted by
$\mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})$, denoted by ![]() $\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})$, using
$\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})$, using ![]() $\mathbb {T}$ instead of the entire
$\mathbb {T}$ instead of the entire ![]() $\mathbb {C}$ as ‘ambient space’: indeed, for any finite set
$\mathbb {C}$ as ‘ambient space’: indeed, for any finite set ![]() $P\subseteq {\mathcal {X}}$, the fundamental group
$P\subseteq {\mathcal {X}}$, the fundamental group ![]() $\pi _1(\mathbb {T}\setminus P,*)$ is canonically identified with
$\pi _1(\mathbb {T}\setminus P,*)$ is canonically identified with ![]() $\mathfrak {G}(P)=\pi _1(\mathbb {C}\setminus P,*)$ and similarly for fundamental PMQs. We thus get an identification
$\mathfrak {G}(P)=\pi _1(\mathbb {C}\setminus P,*)$ and similarly for fundamental PMQs. We thus get an identification ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}\colon \mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})\overset {\cong }{\to }\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})$.
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}\colon \mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})\overset {\cong }{\to }\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})$.
If, moreover, ![]() $\xi \colon (\mathbb {C},*)\to (\mathbb {C},*)$ is a semialgebraic and orientation-preserving homeomorphism of the plane preserving the upper half-plane
$\xi \colon (\mathbb {C},*)\to (\mathbb {C},*)$ is a semialgebraic and orientation-preserving homeomorphism of the plane preserving the upper half-plane ![]() $\mathbb {H}$ and if
$\mathbb {H}$ and if ![]() $\mathbb {T}',{\mathcal {X}}',{\mathcal {Y}}'$ are three other subspaces of
$\mathbb {T}',{\mathcal {X}}',{\mathcal {Y}}'$ are three other subspaces of ![]() $\mathbb {C}$ as above such that
$\mathbb {C}$ as above such that ![]() $\xi$ maps
$\xi$ maps ![]() $\mathbb {T}\to \mathbb {T}'$,
$\mathbb {T}\to \mathbb {T}'$, ![]() ${\mathcal {X}}\to {\mathcal {X}}'$ and
${\mathcal {X}}\to {\mathcal {X}}'$ and ![]() ${\mathcal {Y}}\to {\mathcal {Y}}'$, then
${\mathcal {Y}}\to {\mathcal {Y}}'$, then ![]() $\xi$ induces a map
$\xi$ induces a map ![]() $\xi _*\colon \mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})\to \mathrm {Hur}^{\mathbb {T}'}({\mathcal {X}},{\mathcal {Y}})$.
$\xi _*\colon \mathrm {Hur}^{\mathbb {T}}({\mathcal {X}},{\mathcal {Y}})\to \mathrm {Hur}^{\mathbb {T}'}({\mathcal {X}},{\mathcal {Y}})$.
There is finally a ‘disjoint union’ map ![]() $-\sqcup -\colon \mathrm {Hur}^{\mathbb {T}_1}({\mathcal {X}}_1,{\mathcal {Y}}_1)\times \mathrm {Hur}^{\mathbb {T}_2}({\mathcal {X}}_2,{\mathcal {Y}}_2)\to \mathrm {Hur}^{\mathbb {T}_1\cup \mathbb {T}_2}({\mathcal {X}}_1\sqcup {\mathcal {X}}_2,{\mathcal {Y}}_1\sqcup {\mathcal {Y}}_2)$, defined when
$-\sqcup -\colon \mathrm {Hur}^{\mathbb {T}_1}({\mathcal {X}}_1,{\mathcal {Y}}_1)\times \mathrm {Hur}^{\mathbb {T}_2}({\mathcal {X}}_2,{\mathcal {Y}}_2)\to \mathrm {Hur}^{\mathbb {T}_1\cup \mathbb {T}_2}({\mathcal {X}}_1\sqcup {\mathcal {X}}_2,{\mathcal {Y}}_1\sqcup {\mathcal {Y}}_2)$, defined when ![]() $\mathbb {T}_1\cap \mathbb {T}_2$ is contractible and disjoint from both
$\mathbb {T}_1\cap \mathbb {T}_2$ is contractible and disjoint from both ![]() ${\mathcal {X}}_1,{\mathcal {X}}_2$ (in particular, this implies that
${\mathcal {X}}_1,{\mathcal {X}}_2$ (in particular, this implies that ![]() ${\mathcal {X}}_1$ and
${\mathcal {X}}_1$ and ![]() ${\mathcal {X}}_2$ are disjoint).
${\mathcal {X}}_2$ are disjoint).
Definition 2.11 For ![]() $t,t'\geq 0$ we define the maps
$t,t'\geq 0$ we define the maps ![]() $\mu _{t,t'}\colon \mathrm {Hur}(\mathring {{\mathcal {R}}}_t)\times \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t+t'})$ and
$\mu _{t,t'}\colon \mathrm {Hur}(\mathring {{\mathcal {R}}}_t)\times \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t'})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t+t'})$ and ![]() $\mu _{t,t'}\colon \mathrm {Hur}(\breve {{\mathcal {R}}}_t,\breve {\partial })\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{t'},\breve {\partial })\to \mathrm {Hur}(\breve {{\mathcal {R}}}_{t+t'},\breve {\partial })$ as the following compositions:
$\mu _{t,t'}\colon \mathrm {Hur}(\breve {{\mathcal {R}}}_t,\breve {\partial })\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{t'},\breve {\partial })\to \mathrm {Hur}(\breve {{\mathcal {R}}}_{t+t'},\breve {\partial })$ as the following compositions:


Definition 2.12 Recall Definition 2.11. We define a map of sets
by the formula ![]() $\mu (\,(t,\mathfrak {c}),\,(t',\mathfrak {c}')\,)=(t+t',\,\mu _{t,t'}(\mathfrak {c},\mathfrak {c}'))$. See Figure 2.
$\mu (\,(t,\mathfrak {c}),\,(t',\mathfrak {c}')\,)=(t+t',\,\mu _{t,t'}(\mathfrak {c},\mathfrak {c}'))$. See Figure 2.

Figure 2. Left: two configurations in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,1/2}}(\breve {{\mathcal {R}}}_{1/2},\breve {\partial })\cong \mathrm {Hur}(\breve {{\mathcal {R}}}_{1/2},\breve {\partial })\subset \breve {\mathrm {HM}}$. Right: their product in
$\mathrm {Hur}^{\mathbb {S}_{0,1/2}}(\breve {{\mathcal {R}}}_{1/2},\breve {\partial })\cong \mathrm {Hur}(\breve {{\mathcal {R}}}_{1/2},\breve {\partial })\subset \breve {\mathrm {HM}}$. Right: their product in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,1}}(\breve {{\mathcal {R}}},\breve {\partial })\cong \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })\subset \breve {\mathrm {HM}}$.
$\mathrm {Hur}^{\mathbb {S}_{0,1}}(\breve {{\mathcal {R}}},\breve {\partial })\cong \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })\subset \breve {\mathrm {HM}}$.
Proposition 2.13 The map ![]() $\mu \colon \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}\to \mathring {\mathrm {HM}}$ (respectively,
$\mu \colon \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}\to \mathring {\mathrm {HM}}$ (respectively, ![]() $\mu \colon \breve {\mathrm {HM}}\times \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$) is continuous and makes
$\mu \colon \breve {\mathrm {HM}}\times \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$) is continuous and makes ![]() $\mathring {\mathrm {HM}}$ (respectively,
$\mathring {\mathrm {HM}}$ (respectively, ![]() $\breve {\mathrm {HM}}$) into a topological monoid, with unit
$\breve {\mathrm {HM}}$) into a topological monoid, with unit ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$.
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$.
The proof of Proposition 2.13 is in Appendix A.1.
Recall the notion of total monodromy from [Reference BianchiBia23a, Definitions 6.1 and 6.3]: for a generic nice couple ![]() $({\mathcal {X}},{\mathcal {Y}})$ we have a map
$({\mathcal {X}},{\mathcal {Y}})$ we have a map ![]() $\omega \colon \mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})\to G$ sending a configuration
$\omega \colon \mathrm {Hur}({\mathcal {X}},{\mathcal {Y}})\to G$ sending a configuration ![]() $(P,\psi,\varphi )$ to the value of the monodromy
$(P,\psi,\varphi )$ to the value of the monodromy ![]() $\psi$ at the ‘large loop’, i.e. the element of
$\psi$ at the ‘large loop’, i.e. the element of ![]() $\mathfrak {G}(P)$ represented by a simple loop spinning clockwise around all points of
$\mathfrak {G}(P)$ represented by a simple loop spinning clockwise around all points of ![]() $P$.
$P$.
If ![]() ${\mathcal {Y}}=\emptyset$, one can lift this to a total monodromy
${\mathcal {Y}}=\emptyset$, one can lift this to a total monodromy ![]() $\hat \omega \colon \mathrm {Hur}({\mathcal {X}})\to \hat {{\mathcal {Q}}}$, where
$\hat \omega \colon \mathrm {Hur}({\mathcal {X}})\to \hat {{\mathcal {Q}}}$, where ![]() $\hat {{\mathcal {Q}}}$ is the completion of the PMQ
$\hat {{\mathcal {Q}}}$ is the completion of the PMQ ![]() ${\mathcal {Q}}$, as in [Reference BianchiBia21, Definition 2.19]. Concretely,
${\mathcal {Q}}$, as in [Reference BianchiBia21, Definition 2.19]. Concretely, ![]() $\hat {{\mathcal {Q}}}$ can be defined as the free, non-unital monoid generated by elements
$\hat {{\mathcal {Q}}}$ can be defined as the free, non-unital monoid generated by elements ![]() $\hat a$ for
$\hat a$ for ![]() $a\in {\mathcal {Q}}$, satisfying
$a\in {\mathcal {Q}}$, satisfying ![]() $\hat a\hat b=\hat b\widehat {a^b}$ for all
$\hat a\hat b=\hat b\widehat {a^b}$ for all ![]() $a,b\in {\mathcal {Q}}$ and satisfying
$a,b\in {\mathcal {Q}}$ and satisfying ![]() $\hat a\hat b=\widehat {ab}$ for all
$\hat a\hat b=\widehat {ab}$ for all ![]() $a,b\in {\mathcal {Q}}$ such that the product
$a,b\in {\mathcal {Q}}$ such that the product ![]() $ab$ is already defined in
$ab$ is already defined in ![]() ${\mathcal {Q}}$. The non-unital monoid
${\mathcal {Q}}$. The non-unital monoid ![]() $\hat {{\mathcal {Q}}}$ happens to have a unit, namely
$\hat {{\mathcal {Q}}}$ happens to have a unit, namely ![]() $\hat {\mathbb {1}}$ and a natural binary operation of conjugation can be defined on it, so that it becomes a PMQ with complete product; there is a natural inclusion of PMQs
$\hat {\mathbb {1}}$ and a natural binary operation of conjugation can be defined on it, so that it becomes a PMQ with complete product; there is a natural inclusion of PMQs ![]() ${\mathcal {Q}}\hookrightarrow \hat {{\mathcal {Q}}}$, which is the universal map from
${\mathcal {Q}}\hookrightarrow \hat {{\mathcal {Q}}}$, which is the universal map from ![]() ${\mathcal {Q}}$ to a complete PMQ. In the lift
${\mathcal {Q}}$ to a complete PMQ. In the lift ![]() $\hat \omega$ of
$\hat \omega$ of ![]() $\omega$ we need
$\omega$ we need ![]() $\hat {{\mathcal {Q}}}$ rather than
$\hat {{\mathcal {Q}}}$ rather than ![]() ${\mathcal {Q}}$ as target because the large loop in
${\mathcal {Q}}$ as target because the large loop in ![]() ${\mathcal {G}}(P)$ is not, in general, an element of the fundamental PMQ
${\mathcal {G}}(P)$ is not, in general, an element of the fundamental PMQ ![]() $\mathfrak {Q}(P)$ (unless
$\mathfrak {Q}(P)$ (unless ![]() $P$ is a singleton), so we cannot directly evaluate
$P$ is a singleton), so we cannot directly evaluate ![]() $\psi$ on it; but we can factor the large loop as a product of elements in
$\psi$ on it; but we can factor the large loop as a product of elements in ![]() $\mathfrak {Q}(P)$, evaluate
$\mathfrak {Q}(P)$, evaluate ![]() $\psi$ on the factors and compute in
$\psi$ on the factors and compute in ![]() $\hat {{\mathcal {Q}}}$ the corresponding product of elements of
$\hat {{\mathcal {Q}}}$ the corresponding product of elements of ![]() ${\mathcal {Q}}$.
${\mathcal {Q}}$.
Notation 2.14 For ![]() $(t,\mathfrak {c})$ and
$(t,\mathfrak {c})$ and ![]() $(t',\mathfrak {c}')$ in
$(t',\mathfrak {c}')$ in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$) we denote by
$\breve {\mathrm {HM}}$) we denote by ![]() $(t,\mathfrak {c})\cdot (t',\mathfrak {c}')$ the configuration
$(t,\mathfrak {c})\cdot (t',\mathfrak {c}')$ the configuration ![]() $\mu ((t,\mathfrak {c}),(t',\mathfrak {c}'))$.
$\mu ((t,\mathfrak {c}),(t',\mathfrak {c}'))$.
We denote by ![]() $\hat \omega \colon \mathring {\mathrm {HM}}\to \hat {{\mathcal {Q}}}$ (respectively,
$\hat \omega \colon \mathring {\mathrm {HM}}\to \hat {{\mathcal {Q}}}$ (respectively, ![]() $\omega \colon \breve {\mathrm {HM}}\to G$) the composition
$\omega \colon \breve {\mathrm {HM}}\to G$) the composition


where the first map is the projection on the second component and ![]() $\hat {{\mathcal {Q}}}$ denotes the completion of the PMQ
$\hat {{\mathcal {Q}}}$ denotes the completion of the PMQ ![]() ${\mathcal {Q}}$.
${\mathcal {Q}}$.
2.3 Computation of  $\pi _0(\mathring {\mathrm {HM}})$
$\pi _0(\mathring {\mathrm {HM}})$
In this subsection we study the discrete monoid of path components of ![]() $\mathring {\mathrm {HM}}$. We will prove the following theorem, which is similar to [Reference BianchiBia23a, Proposition 6.4].
$\mathring {\mathrm {HM}}$. We will prove the following theorem, which is similar to [Reference BianchiBia23a, Proposition 6.4].
Theorem 2.15 Recall Notations 2.6 and 2.14. The map ![]() $\hat \omega \colon \pi _0(\mathring {\mathrm {HM}})\to \hat {{\mathcal {Q}}}$ is a map of unital monoids and it restricts to a bijection
$\hat \omega \colon \pi _0(\mathring {\mathrm {HM}})\to \hat {{\mathcal {Q}}}$ is a map of unital monoids and it restricts to a bijection ![]() $\pi _0(\mathring {\mathrm {HM}}_+)\cong \hat {{\mathcal {Q}}}$.
$\pi _0(\mathring {\mathrm {HM}}_+)\cong \hat {{\mathcal {Q}}}$.
Notation 2.16 We denote by ![]() $z_{\mathrm {c}}=\frac 12+\frac {\sqrt {-1}}{2}\in \mathbb {C}$ the centre of
$z_{\mathrm {c}}=\frac 12+\frac {\sqrt {-1}}{2}\in \mathbb {C}$ the centre of ![]() $\mathring {{\mathcal {R}}}$.
$\mathring {{\mathcal {R}}}$.
Definition 2.17 For all ![]() $a\in {\mathcal {Q}}$ we define a configuration
$a\in {\mathcal {Q}}$ we define a configuration ![]() $\mathfrak {c}_a=(\{z_{\mathrm {c}}\},\psi _a)\in \mathrm {Hur}(\mathring {{\mathcal {R}}})$, where
$\mathfrak {c}_a=(\{z_{\mathrm {c}}\},\psi _a)\in \mathrm {Hur}(\mathring {{\mathcal {R}}})$, where ![]() $\psi _a$ sends the (unique) element
$\psi _a$ sends the (unique) element ![]() $f_{\mathrm {c}}$ in
$f_{\mathrm {c}}$ in ![]() $\mathfrak {Q}(\{z_{\mathrm {c}}\})\setminus \{\mathbb {1}\}$ to
$\mathfrak {Q}(\{z_{\mathrm {c}}\})\setminus \{\mathbb {1}\}$ to ![]() $a$.
$a$.
For a space ![]() $X$ we denote by
$X$ we denote by ![]() $\pi _0\colon X\to \pi _0(X)$ the map assigning to each point of
$\pi _0\colon X\to \pi _0(X)$ the map assigning to each point of ![]() $X$ its path component. We denote by
$X$ its path component. We denote by ![]() $\cdot$ the product of the discrete monoid
$\cdot$ the product of the discrete monoid ![]() $\pi _0(\mathring {\mathrm {HM}})$.
$\pi _0(\mathring {\mathrm {HM}})$.
Lemma 2.18 The monoid ![]() $\pi _0(\mathring {\mathrm {HM}})$ is generated by
$\pi _0(\mathring {\mathrm {HM}})$ is generated by ![]() $\pi _0(0,(\emptyset,\mathbb {1},\mathbb {1}))$, which is the unit and by the elements of the form
$\pi _0(0,(\emptyset,\mathbb {1},\mathbb {1}))$, which is the unit and by the elements of the form ![]() $\pi _0(1,\mathfrak {c}_a)$, for
$\pi _0(1,\mathfrak {c}_a)$, for ![]() $a\in {\mathcal {Q}}$. Moreover, the following equalities hold in
$a\in {\mathcal {Q}}$. Moreover, the following equalities hold in ![]() $\pi _0(\mathring {\mathrm {HM}})$:
$\pi _0(\mathring {\mathrm {HM}})$:
• if
 $a,b\in {\mathcal {Q}}$, then
$a,b\in {\mathcal {Q}}$, then  $\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{b})\cdot \pi _0(1,\mathfrak {c}_{a^b})$;
$\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{b})\cdot \pi _0(1,\mathfrak {c}_{a^b})$;• if
 $a,b\in {\mathcal {Q}}$ and the product
$a,b\in {\mathcal {Q}}$ and the product  $ab$ is defined in
$ab$ is defined in  ${\mathcal {Q}}$, then
${\mathcal {Q}}$, then  $\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{ab})$.
$\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{ab})$.
The proof of Lemma 2.18 is in Appendix A.2.
Proof of Theorem 2.15 First we prove that ![]() $\hat \omega \colon \mathring {\mathrm {HM}}\to \hat {{\mathcal {Q}}}$ is a map of monoids. Let
$\hat \omega \colon \mathring {\mathrm {HM}}\to \hat {{\mathcal {Q}}}$ is a map of monoids. Let ![]() $(t,\mathfrak {c}),(t',\mathfrak {c}')\in \mathring {\mathrm {HM}}$ and use Notation 2.2: we can choose simple loops
$(t,\mathfrak {c}),(t',\mathfrak {c}')\in \mathring {\mathrm {HM}}$ and use Notation 2.2: we can choose simple loops ![]() $\gamma \subset \mathbb {S}_{-\infty,t}$ and
$\gamma \subset \mathbb {S}_{-\infty,t}$ and ![]() $\gamma '\subset \mathbb {S}_{t,+\infty }$, spinning clockwise around
$\gamma '\subset \mathbb {S}_{t,+\infty }$, spinning clockwise around ![]() $P$ and
$P$ and ![]() $P'+t$, respectively; the product
$P'+t$, respectively; the product ![]() $[\gamma ]\cdot [\gamma ']\in \mathfrak {G}(P\cup (P'+t))$ is represented by a simple loop spinning clockwise around
$[\gamma ]\cdot [\gamma ']\in \mathfrak {G}(P\cup (P'+t))$ is represented by a simple loop spinning clockwise around ![]() $P\cup (P'+t)$. Denoting
$P\cup (P'+t)$. Denoting ![]() $(t,\mathfrak {c})\cdot (t',\mathfrak {c}')=(t+t',(P'',\psi ''))$, by definition of
$(t,\mathfrak {c})\cdot (t',\mathfrak {c}')=(t+t',(P'',\psi ''))$, by definition of ![]() $\psi ''$ we have
$\psi ''$ we have
Note that ![]() $\hat \omega ((0,(\emptyset,\mathbb {1},\mathbb {1})))=\mathbb {1}$, so
$\hat \omega ((0,(\emptyset,\mathbb {1},\mathbb {1})))=\mathbb {1}$, so ![]() $\hat \omega$ is a map of unital monoids; moreover,
$\hat \omega$ is a map of unital monoids; moreover, ![]() $\hat \omega (1,\mathfrak {c}_a)=\hat a\in \hat {{\mathcal {Q}}}$ for all
$\hat \omega (1,\mathfrak {c}_a)=\hat a\in \hat {{\mathcal {Q}}}$ for all ![]() $a\in {\mathcal {Q}}$, so that
$a\in {\mathcal {Q}}$, so that ![]() $\hat \omega \colon \pi _0(\mathring {\mathrm {HM}})\to \hat {{\mathcal {Q}}}$ hits the generators of
$\hat \omega \colon \pi _0(\mathring {\mathrm {HM}})\to \hat {{\mathcal {Q}}}$ hits the generators of ![]() $\hat {{\mathcal {Q}}}$ and is thus surjective.
$\hat {{\mathcal {Q}}}$ and is thus surjective.
By Lemma 2.18, the corresponding relations among the elements ![]() $\pi _0(1,\mathfrak {c}_a)\in \pi _0(\mathring {\mathrm {HM}})$ hold, so that the assignment
$\pi _0(1,\mathfrak {c}_a)\in \pi _0(\mathring {\mathrm {HM}})$ hold, so that the assignment ![]() $\hat a\mapsto \pi _0(1,\mathfrak {c}_a)$ defines a map of non-unital monoids
$\hat a\mapsto \pi _0(1,\mathfrak {c}_a)$ defines a map of non-unital monoids ![]() $\Omega \colon \hat {{\mathcal {Q}}}\to \pi _0(\mathring {\mathrm {HM}})$; note that, though both the source and the target of
$\Omega \colon \hat {{\mathcal {Q}}}\to \pi _0(\mathring {\mathrm {HM}})$; note that, though both the source and the target of ![]() $\Omega$ are indeed unital monoids,
$\Omega$ are indeed unital monoids, ![]() $\pi _0(1,\mathfrak {c}_\mathbb {1})=\Omega (\mathbb {1})$ is not the unit of
$\pi _0(1,\mathfrak {c}_\mathbb {1})=\Omega (\mathbb {1})$ is not the unit of ![]() $\pi _0(\mathring {\mathrm {HM}})$, so that
$\pi _0(\mathring {\mathrm {HM}})$, so that ![]() $\Omega$ is not a map of unital monoids.
$\Omega$ is not a map of unital monoids.
In fact ![]() $\Omega$, as a map of sets, is a right inverse of
$\Omega$, as a map of sets, is a right inverse of ![]() $\hat \omega$, i.e.
$\hat \omega$, i.e. ![]() $\hat \omega \circ \Omega$ is the identity of
$\hat \omega \circ \Omega$ is the identity of ![]() $\hat {{\mathcal {Q}}}$. Moreover,
$\hat {{\mathcal {Q}}}$. Moreover, ![]() $\Omega$ hits all elements of
$\Omega$ hits all elements of ![]() $\pi _0(\mathring {\mathrm {HM}})$ of the form
$\pi _0(\mathring {\mathrm {HM}})$ of the form ![]() $\pi _0(1,\mathfrak {c}_a)$ and by Lemma 2.18 every element of
$\pi _0(1,\mathfrak {c}_a)$ and by Lemma 2.18 every element of ![]() $\pi _0(\mathring {\mathrm {HM}}_+)$ can be written as a product of one or more elements of the form
$\pi _0(\mathring {\mathrm {HM}}_+)$ can be written as a product of one or more elements of the form ![]() $\pi _0(1,\mathfrak {c}_a)$. It follows that
$\pi _0(1,\mathfrak {c}_a)$. It follows that ![]() $\Omega$ is a bijection between
$\Omega$ is a bijection between ![]() $\hat {{\mathcal {Q}}}$ and
$\hat {{\mathcal {Q}}}$ and ![]() $\pi _0(\mathring {\mathrm {HM}}_+)$ and this concludes the proof.
$\pi _0(\mathring {\mathrm {HM}}_+)$ and this concludes the proof.
2.4 Computation  $\pi _0(\breve {\mathrm {HM}})$
$\pi _0(\breve {\mathrm {HM}})$
We conclude the section by computing ![]() $\pi _0(\breve {\mathrm {HM}})$. Recalling Notations 2.5 and 2.6, it suffices to compute
$\pi _0(\breve {\mathrm {HM}})$. Recalling Notations 2.5 and 2.6, it suffices to compute ![]() $\pi _0(\breve {\mathrm {HM}}_+)$. The canonical structure we have on this last set is that of non-unital monoid, since the multiplication
$\pi _0(\breve {\mathrm {HM}}_+)$. The canonical structure we have on this last set is that of non-unital monoid, since the multiplication ![]() $\mu$ of
$\mu$ of ![]() $\breve {\mathrm {HM}}$ restricts to a map
$\breve {\mathrm {HM}}$ restricts to a map ![]() $\breve {\mathrm {HM}}_+\times \breve {\mathrm {HM}}_+\to \breve {\mathrm {HM}}_+$. The total monodromy gives again a morphism of non-unital monoids
$\breve {\mathrm {HM}}_+\times \breve {\mathrm {HM}}_+\to \breve {\mathrm {HM}}_+$. The total monodromy gives again a morphism of non-unital monoids
Theorem 2.19 Recall the map of PMQs ![]() $\mathfrak {e}\colon {\mathcal {Q}}\to G$, which is part of the PMQ–group pair structure on
$\mathfrak {e}\colon {\mathcal {Q}}\to G$, which is part of the PMQ–group pair structure on ![]() $({\mathcal {Q}},G)$. Suppose that the image
$({\mathcal {Q}},G)$. Suppose that the image ![]() $\mathfrak {e}({\mathcal {Q}})\subset G$ generates
$\mathfrak {e}({\mathcal {Q}})\subset G$ generates ![]() $G$ as a group. Then the map
$G$ as a group. Then the map ![]() $\omega \colon \pi _0(\breve {\mathrm {HM}}_+)\to G$ is bijective.
$\omega \colon \pi _0(\breve {\mathrm {HM}}_+)\to G$ is bijective.
In other words, the unital monoid ![]() $\pi _0(\breve {\mathrm {HM}})$ is isomorphic to
$\pi _0(\breve {\mathrm {HM}})$ is isomorphic to ![]() $G\sqcup \{\mathbb {1}\}$, where the extra element
$G\sqcup \{\mathbb {1}\}$, where the extra element ![]() $\mathbb {1}$ plays the role of the monoid unit and the old unit
$\mathbb {1}$ plays the role of the monoid unit and the old unit ![]() $\mathbb {1}_G\in G$ still satisfies
$\mathbb {1}_G\in G$ still satisfies ![]() $\mathbb {1}_G\cdot g=g\cdot \mathbb {1}_G=g$ for all
$\mathbb {1}_G\cdot g=g\cdot \mathbb {1}_G=g$ for all ![]() $g\in G$, but
$g\in G$, but ![]() $\mathbb {1}\cdot \mathbb {1}_G=\mathbb {1}_G\cdot \mathbb {1}=\mathbb {1}_G$.
$\mathbb {1}\cdot \mathbb {1}_G=\mathbb {1}_G\cdot \mathbb {1}=\mathbb {1}_G$.
We observe that the hypothesis that ![]() $G$ is generated by
$G$ is generated by ![]() $\mathfrak {e}({\mathcal {Q}})$ is necessary in Theorem 2.19: if, for instance,
$\mathfrak {e}({\mathcal {Q}})$ is necessary in Theorem 2.19: if, for instance, ![]() ${\mathcal {Q}}=\{\mathbb {1}\}$ and
${\mathcal {Q}}=\{\mathbb {1}\}$ and ![]() $G$ is any non-trivial group, then
$G$ is any non-trivial group, then ![]() $\pi _0(\breve {\mathrm {HM}}_+)$ can rather be identified (as a set) with
$\pi _0(\breve {\mathrm {HM}}_+)$ can rather be identified (as a set) with ![]() $G\times G$ and
$G\times G$ and ![]() $\omega$ with the product map
$\omega$ with the product map ![]() $G\times G\to G$.
$G\times G\to G$.
The rough idea of the proof of Theorem 2.19 is the following: given a configuration ![]() $(t,\mathfrak {c})$, we can shrink or stretch it until we have
$(t,\mathfrak {c})$, we can shrink or stretch it until we have ![]() $t=1$; we can move points of
$t=1$; we can move points of ![]() $\mathfrak {c}$ to either horizontal side of
$\mathfrak {c}$ to either horizontal side of ![]() $\breve {{\mathcal {R}}}$, reducing to a configuration
$\breve {{\mathcal {R}}}$, reducing to a configuration ![]() $\mathfrak {c}$ supported on
$\mathfrak {c}$ supported on ![]() $\breve {\partial }$; we can let all points on either component of
$\breve {\partial }$; we can let all points on either component of ![]() $\breve {\partial }$ collide with each other, reducing to a configuration
$\breve {\partial }$ collide with each other, reducing to a configuration ![]() $\mathfrak {c}$ supported on at most two points lying on
$\mathfrak {c}$ supported on at most two points lying on ![]() $\breve {\partial }$; finally, we can use that
$\breve {\partial }$; finally, we can use that ![]() $\mathfrak {e}(Q)$ generates
$\mathfrak {e}(Q)$ generates ![]() $G$ to ‘trade’ factors of the total monodromy from one component of
$G$ to ‘trade’ factors of the total monodromy from one component of ![]() $\breve {\partial }$ to the other, reaching a configuration
$\breve {\partial }$ to the other, reaching a configuration ![]() $\mathfrak {c}$ supported on a single point.
$\mathfrak {c}$ supported on a single point.
The rest of the subsection is devoted to the proof of Theorem 2.19. We replace ![]() $\breve {\mathrm {HM}}$ by the homotopy equivalent space
$\breve {\mathrm {HM}}$ by the homotopy equivalent space ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$, see Lemma 2.7.
$\mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$, see Lemma 2.7.
Notation 2.20 We denote by ![]() $\breve {{\mathcal {R}}}^{\mathrm {lr}}$ the horizontally closed square
$\breve {{\mathcal {R}}}^{\mathrm {lr}}$ the horizontally closed square ![]() $[0,1]\times (0,1)\subset \mathbb {H}$ and by
$[0,1]\times (0,1)\subset \mathbb {H}$ and by ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}=\{0,1\}\times (0,1)$ the union of the vertical sides of
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}=\{0,1\}\times (0,1)$ the union of the vertical sides of ![]() $\breve {{\mathcal {R}}}^{\mathrm {lr}}$. We abbreviate the nice couple
$\breve {{\mathcal {R}}}^{\mathrm {lr}}$. We abbreviate the nice couple ![]() $(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}})$ as
$(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}})$ as ![]() $(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$. See Figure 3.
$(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$. See Figure 3.

Figure 3. The nice couples ![]() $(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and
$(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$.
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$.
We fix once and for all a semialgebraic homeomorphism ![]() $\xi ^{\mathrm {rot}}\colon \mathbb {C}\to \mathbb {C}$ which fixes the basepoint
$\xi ^{\mathrm {rot}}\colon \mathbb {C}\to \mathbb {C}$ which fixes the basepoint ![]() $*=-\sqrt {-1}$ and restricts to the homeomorphism
$*=-\sqrt {-1}$ and restricts to the homeomorphism ![]() $\breve {{\mathcal {R}}}^{\mathrm {lr}}\to \breve {{\mathcal {R}}}$ given by the
$\breve {{\mathcal {R}}}^{\mathrm {lr}}\to \breve {{\mathcal {R}}}$ given by the ![]() $90^\circ$ clockwise rotation around
$90^\circ$ clockwise rotation around ![]() $z_{\mathrm {c}}$ (see Notation 2.16).
$z_{\mathrm {c}}$ (see Notation 2.16).
By functoriality we have a homeomorphism ![]() $\xi ^{\mathrm {rot}}_*\colon \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$. We will prove Theorem 2.19 by classifying connected components of
$\xi ^{\mathrm {rot}}_*\colon \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$. We will prove Theorem 2.19 by classifying connected components of ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$; from now on we will focus on the latter space.
$\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$; from now on we will focus on the latter space.
Lemma 2.21 Let ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$; then
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$; then ![]() $\mathfrak {c}$ is connected to a configuration
$\mathfrak {c}$ is connected to a configuration ![]() $\mathfrak {c}'$ supported in
$\mathfrak {c}'$ supported in ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$.
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$.
To prove Lemma 2.21 we will use the following family of homotopies of ![]() $\mathbb {C}$.
$\mathbb {C}$.
Definition 2.22 For all ![]() $0< t<1$ we define homotopies
$0< t<1$ we define homotopies ![]() ${\mathcal {H}}^{\mathrm {l}}_t,{\mathcal {H}}^{\mathrm {r}}_t\colon \colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formulas:
${\mathcal {H}}^{\mathrm {l}}_t,{\mathcal {H}}^{\mathrm {r}}_t\colon \colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formulas:
 \begin{gather*}
{\mathcal{H}}^{\mathrm{l}}_t(z,s)=\left\{\begin{array}{@{}ll}
z & \text{if } \Re(z)\leq0 \text{ or }\Re(z)\geq
1, \\ z-s\Re(z) & \text{if } 0\leq \Re(z)\leq
t, \\ z - \Big(\dfrac1{1-st} -1\Big)(1-\Re(z)) &
\text{if } t\leq \Re(z)\leq 1; \end{array}\right.\\
{\mathcal{H}}^{\mathrm{r}}_t(z,s)=\left\{\begin{array}{@{}ll}
z & \text{if } \Re(z)\leq0 \text{ or }\Re(z)\geq
1, \\ z + \Big(\dfrac1{1-s+st} -1\Big)\Re(z) &
\text{if } 0\leq \Re(z)\leq t, \\ z+s(1-\Re(z)) &
\text{if } t\leq \Re(z)\leq 1. \end{array}\right.
\end{gather*}
\begin{gather*}
{\mathcal{H}}^{\mathrm{l}}_t(z,s)=\left\{\begin{array}{@{}ll}
z & \text{if } \Re(z)\leq0 \text{ or }\Re(z)\geq
1, \\ z-s\Re(z) & \text{if } 0\leq \Re(z)\leq
t, \\ z - \Big(\dfrac1{1-st} -1\Big)(1-\Re(z)) &
\text{if } t\leq \Re(z)\leq 1; \end{array}\right.\\
{\mathcal{H}}^{\mathrm{r}}_t(z,s)=\left\{\begin{array}{@{}ll}
z & \text{if } \Re(z)\leq0 \text{ or }\Re(z)\geq
1, \\ z + \Big(\dfrac1{1-s+st} -1\Big)\Re(z) &
\text{if } 0\leq \Re(z)\leq t, \\ z+s(1-\Re(z)) &
\text{if } t\leq \Re(z)\leq 1. \end{array}\right.
\end{gather*}
Roughly speaking, ![]() ${\mathcal {H}}^{\mathrm {l}}_t$ collapses the vertical strip
${\mathcal {H}}^{\mathrm {l}}_t$ collapses the vertical strip ![]() $[0,t]\times \mathbb {R}$ to the vertical line
$[0,t]\times \mathbb {R}$ to the vertical line ![]() $\mathbb {C}_{\Re =0}$ and expands the vertical strip
$\mathbb {C}_{\Re =0}$ and expands the vertical strip ![]() $[t,1]\times \mathbb {R}$ to the vertical strip
$[t,1]\times \mathbb {R}$ to the vertical strip ![]() $[0,1]\times \mathbb {R}$; similarly
$[0,1]\times \mathbb {R}$; similarly ![]() ${\mathcal {H}}^{\mathrm {r}}_t$ collapses
${\mathcal {H}}^{\mathrm {r}}_t$ collapses ![]() $[t,1]\times \mathbb {R}$ to
$[t,1]\times \mathbb {R}$ to ![]() $\mathbb {C}_{\Re =1}$ and expands
$\mathbb {C}_{\Re =1}$ and expands ![]() $[0,t]\times \mathbb {R}$ to
$[0,t]\times \mathbb {R}$ to ![]() $[0,1]\times \mathbb {R}$. Both homotopies restrict at each time
$[0,1]\times \mathbb {R}$. Both homotopies restrict at each time ![]() $s$ to an endomorphism of the nice couple
$s$ to an endomorphism of the nice couple ![]() $(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$, so they induce homotopies
$(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$, so they induce homotopies
Proof of Lemma 2.21 Let ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and use Notation 2.2. Let
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and use Notation 2.2. Let ![]() $0< t<1$ be close enough to 1 so that for all
$0< t<1$ be close enough to 1 so that for all ![]() $z\in P$ we have
$z\in P$ we have ![]() $\Re (z)=1$ or
$\Re (z)=1$ or ![]() $\Re (z)\leq t$. Then
$\Re (z)\leq t$. Then ![]() ${\mathcal {H}}^{\mathrm {l}}_t(-;1)$ sends
${\mathcal {H}}^{\mathrm {l}}_t(-;1)$ sends ![]() $P$ inside
$P$ inside ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ and, therefore,
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ and, therefore, ![]() $({\mathcal {H}}^{\mathrm {l}}_t)_*$ induces a path in
$({\mathcal {H}}^{\mathrm {l}}_t)_*$ induces a path in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ from
$\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ from ![]() $\mathfrak {c}$ to a configuration
$\mathfrak {c}$ to a configuration ![]() $\mathfrak {c}':=({\mathcal {H}}^{\mathrm {l}}_t)_*(\mathfrak {c},1)$ which is supported in
$\mathfrak {c}':=({\mathcal {H}}^{\mathrm {l}}_t)_*(\mathfrak {c},1)$ which is supported in ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$.
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$.
The following rhombus will help us to define a homotopy of ![]() $\mathbb {C}$ that squeezes the two segments in
$\mathbb {C}$ that squeezes the two segments in ![]() $\breve {\partial }$ to the two central points.
$\breve {\partial }$ to the two central points.
Definition 2.23 We define ![]() $\diamond$ as the closed subspace of
$\diamond$ as the closed subspace of ![]() $\mathbb {H}$ given by
$\mathbb {H}$ given by
Geometrically, ![]() $\diamond$ is a closed rhombus centred at the point
$\diamond$ is a closed rhombus centred at the point ![]() $z_{\mathrm {c}}$ (see Notation 2.16). The boundary
$z_{\mathrm {c}}$ (see Notation 2.16). The boundary ![]() $\partial \diamond$ contains points
$\partial \diamond$ contains points ![]() $z$ for which equality holds in the formula above. The corners of
$z$ for which equality holds in the formula above. The corners of ![]() $\diamond$ are denoted by
$\diamond$ are denoted by ![]() $z_{\diamond }^{\mathrm {l}}=\frac {\sqrt {-1}}2$,
$z_{\diamond }^{\mathrm {l}}=\frac {\sqrt {-1}}2$, ![]() $z_{\diamond }^{\mathrm {r}}=1+\frac {\sqrt {-1}}2$,
$z_{\diamond }^{\mathrm {r}}=1+\frac {\sqrt {-1}}2$, ![]() $z_{\diamond }^{\mathrm {u}}=\frac 12+ \sqrt {-1}$ and
$z_{\diamond }^{\mathrm {u}}=\frac 12+ \sqrt {-1}$ and ![]() $z_{\diamond }^{\mathrm {d}}=\frac 12$. We denote by
$z_{\diamond }^{\mathrm {d}}=\frac 12$. We denote by ![]() $\breve {\diamond }^{\mathrm {lr}}$ the subspace of
$\breve {\diamond }^{\mathrm {lr}}$ the subspace of ![]() $\diamond$ given by
$\diamond$ given by
we use the notation ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}=\breve {\diamond }^{\mathrm {lr}}\cap \breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ and we abbreviate the nice couple
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}=\breve {\diamond }^{\mathrm {lr}}\cap \breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ and we abbreviate the nice couple ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }\breve {\diamond }^{\mathrm {lr}})$ as
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }\breve {\diamond }^{\mathrm {lr}})$ as ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$; compare with Notation 2.3 and see Figure 3.
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$; compare with Notation 2.3 and see Figure 3.
We have an inclusion of nice couples ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset (\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$, inducing an inclusion
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset (\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$, inducing an inclusion ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$.
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$.
Lemma 2.24 The inclusion ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is a homotopy equivalence.
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is a homotopy equivalence.
Before proving Lemma 2.24 we define a suitable homotopy of ![]() $\mathbb {C}$.
$\mathbb {C}$.
Definition 2.25 For ![]() $z\in \mathbb {C}$ let
$z\in \mathbb {C}$ let ![]() $\mathfrak {d}^{\diamond }(z)=\min \{|\Re (z)-\frac 12| ;\frac 12\}$. We define a homotopy
$\mathfrak {d}^{\diamond }(z)=\min \{|\Re (z)-\frac 12| ;\frac 12\}$. We define a homotopy ![]() ${\mathcal {H}}^{\diamond }\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formula:
${\mathcal {H}}^{\diamond }\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formula:
 \[
{\mathcal{H}}^{\diamond}(z,s)=\left\{\begin{array}{@{}ll} z-s
\mathfrak{d}^{\diamond}(z)\sqrt{-1} & \text{if } \Im(z)\geq
1,\\ z-
2s\mathfrak{d}^{\diamond}(z)\left(\Im(z)-\dfrac
12\right)\sqrt{-1} & \text{if } 0 \leq \Im(z)\leq
1,\\ z+s\Big(\dfrac{\Im(z)}2
+\mathfrak{d}^\diamond(z)\Big)\sqrt{-1} & \text{if }
\Im(z)\leq 0. \end{array}\right. \]
\[
{\mathcal{H}}^{\diamond}(z,s)=\left\{\begin{array}{@{}ll} z-s
\mathfrak{d}^{\diamond}(z)\sqrt{-1} & \text{if } \Im(z)\geq
1,\\ z-
2s\mathfrak{d}^{\diamond}(z)\left(\Im(z)-\dfrac
12\right)\sqrt{-1} & \text{if } 0 \leq \Im(z)\leq
1,\\ z+s\Big(\dfrac{\Im(z)}2
+\mathfrak{d}^\diamond(z)\Big)\sqrt{-1} & \text{if }
\Im(z)\leq 0. \end{array}\right. \]
The homotopy ![]() ${\mathcal {H}}^{\diamond }$ satisfies the following properties:
${\mathcal {H}}^{\diamond }$ satisfies the following properties:
• for all
 $0\leq s\leq 1$, the map
$0\leq s\leq 1$, the map  ${\mathcal {H}}^{\diamond }(-;s)\colon \mathbb {C}\to \mathbb {C}$ induces an endomorphism of the nice couple
${\mathcal {H}}^{\diamond }(-;s)\colon \mathbb {C}\to \mathbb {C}$ induces an endomorphism of the nice couple  $(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and an endomorphism of the nice couple
$(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ and an endomorphism of the nice couple  $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$;
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$;•
 ${\mathcal {H}}^{\diamond }(-;0)$ is the identity of
${\mathcal {H}}^{\diamond }(-;0)$ is the identity of  $\mathbb {C}$;
$\mathbb {C}$;•
 ${\mathcal {H}}^{\diamond }(-;1)$ sends
${\mathcal {H}}^{\diamond }(-;1)$ sends  $\breve {{\mathcal {R}}}^{\mathrm {lr}}$ onto
$\breve {{\mathcal {R}}}^{\mathrm {lr}}$ onto  $\breve {\diamond }^{\mathrm {lr}}$ and
$\breve {\diamond }^{\mathrm {lr}}$ and  $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ onto
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$ onto  $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$.
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$.
Proof of Lemma 2.24 By [Reference BianchiBia23a, Proposition 4.4] the homotopy ![]() ${\mathcal {H}}^{\diamond }$ induces a homotopy
${\mathcal {H}}^{\diamond }$ induces a homotopy ![]() ${\mathcal {H}}^{\diamond }_*\colon \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\times [0,1]\to \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ starting from the identity and ending with a map
${\mathcal {H}}^{\diamond }_*\colon \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\times [0,1]\to \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ starting from the identity and ending with a map ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$. The homotopy
$\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$. The homotopy ![]() ${\mathcal {H}}^{\diamond }_*$ preserves the subspace
${\mathcal {H}}^{\diamond }_*$ preserves the subspace ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ at all times and, thus, witnesses that the inclusion of
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ at all times and, thus, witnesses that the inclusion of ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ in
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is a homotopy equivalence.
$\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is a homotopy equivalence.
Note also that if ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is supported in
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ is supported in ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$, then the entire path
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$, then the entire path ![]() ${\mathcal {H}}^{\diamond }_*(\mathfrak {c},-)$ consists of configurations supported in
${\mathcal {H}}^{\diamond }_*(\mathfrak {c},-)$ consists of configurations supported in ![]() $\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$. Using Lemmas 2.21 and 2.24 together, we can therefore connect any
$\breve {\partial }\breve {{\mathcal {R}}}^{\mathrm {lr}}$. Using Lemmas 2.21 and 2.24 together, we can therefore connect any ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ to a configuration
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ to a configuration ![]() $\mathfrak {c}'\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ supported in
$\mathfrak {c}'\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ supported in ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$.
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$.
We next define auxiliary configurations, supported on the three points ![]() $z_{\mathrm {c}},z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$: by moving
$z_{\mathrm {c}},z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$: by moving ![]() $z_{\mathrm {c}}$ towards
$z_{\mathrm {c}}$ towards ![]() $z_{\diamond }^{\mathrm {l}}$ or towards
$z_{\diamond }^{\mathrm {l}}$ or towards ![]() $z_{\diamond }^{\mathrm {r}}$, we can construct paths between configurations supported on
$z_{\diamond }^{\mathrm {r}}$, we can construct paths between configurations supported on ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$.
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$.
Definition 2.26 Recall Definition 2.17. For all ![]() $g,h\in G$ and
$g,h\in G$ and ![]() $a\in {\mathcal {Q}}$ we define a configuration
$a\in {\mathcal {Q}}$ we define a configuration ![]() $\mathfrak {c}_{g,a,h}=(P,\psi,\varphi )\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ as follows:
$\mathfrak {c}_{g,a,h}=(P,\psi,\varphi )\in \mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ as follows:
•
 $P=\{z_{\mathrm {c}},z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$; let
$P=\{z_{\mathrm {c}},z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$; let  $f_{\mathrm {c}},f_{\diamond }^{\mathrm {l}},f_{\diamond }^{\mathrm {r}}$ be an admissible generating set for
$f_{\mathrm {c}},f_{\diamond }^{\mathrm {l}},f_{\diamond }^{\mathrm {r}}$ be an admissible generating set for  $\mathfrak {G}(P)$, where
$\mathfrak {G}(P)$, where  $f_{\mathrm {c}}$ is represented by a loop in
$f_{\mathrm {c}}$ is represented by a loop in  $\mathbb {S}_{0,1}\setminus P$,
$\mathbb {S}_{0,1}\setminus P$,  $f_{\diamond }^{\mathrm {l}}$ by a loop in
$f_{\diamond }^{\mathrm {l}}$ by a loop in  $\mathbb {S}_{-\infty,1/2}\setminus P$ and
$\mathbb {S}_{-\infty,1/2}\setminus P$ and  $f_{\diamond }^{\mathrm {r}}$ by a loop in
$f_{\diamond }^{\mathrm {r}}$ by a loop in  $\mathbb {S}_{1/2,\infty }\setminus P$;
$\mathbb {S}_{1/2,\infty }\setminus P$;•
 $\psi$ maps
$\psi$ maps  $f_{\mathrm {c}}\mapsto a$;
$f_{\mathrm {c}}\mapsto a$;•
 $\varphi$ maps
$\varphi$ maps  $f_{\mathrm {c}}\mapsto \mathfrak {e}(a)$,
$f_{\mathrm {c}}\mapsto \mathfrak {e}(a)$,  $f_{\diamond }^{\mathrm {l}}\mapsto g$ and
$f_{\diamond }^{\mathrm {l}}\mapsto g$ and  $f_{\diamond }^{\mathrm {r}}\mapsto h$.
$f_{\diamond }^{\mathrm {r}}\mapsto h$.
We also define configurations ![]() $\mathfrak {c}_{\emptyset,a,h}$,
$\mathfrak {c}_{\emptyset,a,h}$, ![]() $\mathfrak {c}_{g,\emptyset,h}$,
$\mathfrak {c}_{g,\emptyset,h}$, ![]() $\mathfrak {c}_{g,a,\emptyset }$,
$\mathfrak {c}_{g,a,\emptyset }$, ![]() $\mathfrak {c}_{g,\emptyset,\emptyset }$,
$\mathfrak {c}_{g,\emptyset,\emptyset }$, ![]() $\mathfrak {c}_{\emptyset,a,\emptyset }$ and
$\mathfrak {c}_{\emptyset,a,\emptyset }$ and ![]() $\mathfrak {c}_{\emptyset,\emptyset, h}$ in a similar way: for every occurrence of ‘
$\mathfrak {c}_{\emptyset,\emptyset, h}$ in a similar way: for every occurrence of ‘![]() $\emptyset$’ we remove the corresponding point from
$\emptyset$’ we remove the corresponding point from ![]() $P$ and we define
$P$ and we define ![]() $\psi$ and
$\psi$ and ![]() $\psi$ on the relevant elements of the admissible generating set by the same formulas.
$\psi$ on the relevant elements of the admissible generating set by the same formulas.
Proof of Theorem 2.19 Note first that ![]() $\omega (\mathfrak {c}_{\mathbb {1}_G,\emptyset, h})=h\in G$: this shows surjectivity of
$\omega (\mathfrak {c}_{\mathbb {1}_G,\emptyset, h})=h\in G$: this shows surjectivity of ![]() $\omega \colon \pi _0(\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial }))\to G$.
$\omega \colon \pi _0(\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial }))\to G$.
Lemma 2.21 and the proof of Lemma 2.24 imply that every configuration ![]() $\mathfrak {c}\in \mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration supported on
$\mathfrak {c}\in \mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration supported on ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$, i.e. of the form
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$, i.e. of the form ![]() $\mathfrak {c}_{g,\emptyset,h}$,
$\mathfrak {c}_{g,\emptyset,h}$, ![]() $\mathfrak {c}_{g,\emptyset,\emptyset }$ or
$\mathfrak {c}_{g,\emptyset,\emptyset }$ or ![]() $\mathfrak {c}_{\emptyset,\emptyset, h}$.
$\mathfrak {c}_{\emptyset,\emptyset, h}$.
For all ![]() $g,h\in G$ the homotopies
$g,h\in G$ the homotopies ![]() ${\mathcal {H}}^{\mathrm {l}}_{1/2}$ and
${\mathcal {H}}^{\mathrm {l}}_{1/2}$ and ![]() ${\mathcal {H}}^{\mathrm {r}}_{1/2}$ give paths joining the configuration
${\mathcal {H}}^{\mathrm {r}}_{1/2}$ give paths joining the configuration ![]() $\mathfrak {c}_{\emptyset,\mathbb {1},h}$ to
$\mathfrak {c}_{\emptyset,\mathbb {1},h}$ to ![]() $\mathfrak {c}_{\mathbb {1}_G,\emptyset,h}$ and
$\mathfrak {c}_{\mathbb {1}_G,\emptyset,h}$ and ![]() $\mathfrak {c}_{\emptyset,\emptyset,h}$, respectively; the same homotopies give paths joining the configuration
$\mathfrak {c}_{\emptyset,\emptyset,h}$, respectively; the same homotopies give paths joining the configuration ![]() $\mathfrak {c}_{g,\mathbb {1},\emptyset }$ to
$\mathfrak {c}_{g,\mathbb {1},\emptyset }$ to ![]() $\mathfrak {c}_{g,\emptyset,\emptyset }$ and
$\mathfrak {c}_{g,\emptyset,\emptyset }$ and ![]() $\mathfrak {c}_{g,\emptyset,\mathbb {1}_G}$, respectively. Thus,
$\mathfrak {c}_{g,\emptyset,\mathbb {1}_G}$, respectively. Thus, ![]() $\mathfrak {c}_{\emptyset,\emptyset,h}$ is connected to
$\mathfrak {c}_{\emptyset,\emptyset,h}$ is connected to ![]() $\mathfrak {c}_{\mathbb {1}_G,\emptyset,h}$ and
$\mathfrak {c}_{\mathbb {1}_G,\emptyset,h}$ and ![]() $\mathfrak {c}_{g,\emptyset,\emptyset }$ is connected to
$\mathfrak {c}_{g,\emptyset,\emptyset }$ is connected to ![]() $\mathfrak {c}_{g,\emptyset,\mathbb {1}_G}$: we conclude that every configuration in
$\mathfrak {c}_{g,\emptyset,\mathbb {1}_G}$: we conclude that every configuration in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration of the form
$\mathrm {Hur}(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration of the form ![]() $\mathfrak {c}_{g,\emptyset,h}$.
$\mathfrak {c}_{g,\emptyset,h}$.
Similarly, for all ![]() $g,h\in G$ and
$g,h\in G$ and ![]() $a\in {\mathcal {Q}}$ the homotopies
$a\in {\mathcal {Q}}$ the homotopies ![]() ${\mathcal {H}}^{\mathrm {l}}_{1/2}$ and
${\mathcal {H}}^{\mathrm {l}}_{1/2}$ and ![]() ${\mathcal {H}}^{\mathrm {r}}_{1/2}$ give paths joining the configuration
${\mathcal {H}}^{\mathrm {r}}_{1/2}$ give paths joining the configuration ![]() $\mathfrak {c}_{g,a,h}$ to
$\mathfrak {c}_{g,a,h}$ to ![]() $\mathfrak {c}_{g\mathfrak {e}(a),\emptyset,h}$ and
$\mathfrak {c}_{g\mathfrak {e}(a),\emptyset,h}$ and ![]() $\mathfrak {c}_{g,\emptyset,\mathfrak {e}(a)h}$, respectively. Thus,
$\mathfrak {c}_{g,\emptyset,\mathfrak {e}(a)h}$, respectively. Thus, ![]() $\mathfrak {c}_{g\mathfrak {e}(a),\emptyset,h}$ is connected to
$\mathfrak {c}_{g\mathfrak {e}(a),\emptyset,h}$ is connected to ![]() $\mathfrak {c}_{g,\emptyset,\mathfrak {e}(a)h}$.
$\mathfrak {c}_{g,\emptyset,\mathfrak {e}(a)h}$.
Since we assumed that ![]() $\mathfrak {e}({\mathcal {Q}})$ generates
$\mathfrak {e}({\mathcal {Q}})$ generates ![]() $G$, we can write
$G$, we can write ![]() $g=\mathfrak {e}(a_1)^{\pm 1}\cdot \cdots \cdot \mathfrak {e}(a_r)^{\pm 1}$. Using
$g=\mathfrak {e}(a_1)^{\pm 1}\cdot \cdots \cdot \mathfrak {e}(a_r)^{\pm 1}$. Using ![]() $r$ instances of the paths described above, or their inverses, we can connect any configuration of the form
$r$ instances of the paths described above, or their inverses, we can connect any configuration of the form ![]() $\mathfrak {c}_{g,\emptyset,h}$ to the corresponding configuration
$\mathfrak {c}_{g,\emptyset,h}$ to the corresponding configuration ![]() $\mathfrak {c}_{\mathbb {1}_G,\emptyset,gh}$. We have thus proved that every configuration in
$\mathfrak {c}_{\mathbb {1}_G,\emptyset,gh}$. We have thus proved that every configuration in ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration of the form
$\mathrm {Hur}_+(\breve {{\mathcal {R}}}^{\mathrm {lr}},\breve {\partial })$ can be connected to a configuration of the form ![]() $\mathfrak {c}_{\mathbb {1}_G,\emptyset, h}$ and these are sent bijectively to
$\mathfrak {c}_{\mathbb {1}_G,\emptyset, h}$ and these are sent bijectively to ![]() $G$ along
$G$ along ![]() $\omega$.
$\omega$.
3. Bar constructions of Hurwitz spaces
In this section we study the bar constructions of the topological monoids ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$. Many arguments of this and the next section are adapted from [Reference HatcherHat14], so familiarity with this paper may be valuable.
$\breve {\mathrm {HM}}$. Many arguments of this and the next section are adapted from [Reference HatcherHat14], so familiarity with this paper may be valuable.
Recall that a topological monoid ![]() $M$ is group-like if the monoid
$M$ is group-like if the monoid ![]() $\pi _0(M)$ is a group; a standard argument ensures, in this case, that for every
$\pi _0(M)$ is a group; a standard argument ensures, in this case, that for every ![]() $m\in M$ the maps given by left multiplication
$m\in M$ the maps given by left multiplication ![]() $\mu (m,-)\colon M\to M$ and right multiplication
$\mu (m,-)\colon M\to M$ and right multiplication ![]() $\mu (-,m)$ are self-homotopy equivalences of
$\mu (-,m)$ are self-homotopy equivalences of ![]() $M$. For left multiplication, for instance, one chooses an element
$M$. For left multiplication, for instance, one chooses an element ![]() $m'\in M$ with
$m'\in M$ with ![]() $\mu (m',m)$ and
$\mu (m',m)$ and ![]() $\mu (m,m')$ contained in the same component of the neutral element
$\mu (m,m')$ contained in the same component of the neutral element ![]() $e$; then a homotopy inverse of
$e$; then a homotopy inverse of ![]() $\mu (m,-)$ is given by
$\mu (m,-)$ is given by ![]() $\mu (m',-)$. Note that this argument strongly relies on
$\mu (m',-)$. Note that this argument strongly relies on ![]() $M$ having a strict neutral element
$M$ having a strict neutral element ![]() $e$.
$e$.
Unfortunately ![]() $\breve {\mathrm {HM}}$ is a unital, but not group-like topological monoid; on the other hand its subspace
$\breve {\mathrm {HM}}$ is a unital, but not group-like topological monoid; on the other hand its subspace ![]() $\breve {\mathrm {HM}}_+$ (see Notation 2.6) is a non-unital, but group-like topological monoid: see Theorem 2.19. We will consider the space
$\breve {\mathrm {HM}}_+$ (see Notation 2.6) is a non-unital, but group-like topological monoid: see Theorem 2.19. We will consider the space ![]() $\breve {\mathrm {HM}}_+$ as a left module over
$\breve {\mathrm {HM}}_+$ as a left module over ![]() $\breve {\mathrm {HM}}$ in order to exploit the good properties of both spaces.
$\breve {\mathrm {HM}}$ in order to exploit the good properties of both spaces.
3.1 Bar constructions
We recall the classical definition of bar construction with respect to a topological monoid ![]() $M$ and a left
$M$ and a left ![]() $M$-module
$M$-module ![]() $X$.
$X$.
Definition 3.1 Let ![]() $M$ be a topological monoid, let
$M$ be a topological monoid, let ![]() $X$ be a left
$X$ be a left ![]() $M$-module and denote by
$M$-module and denote by ![]() $\mu$ both multiplication maps
$\mu$ both multiplication maps ![]() $M\times M\to M$ and
$M\times M\to M$ and ![]() $M\times X\to X$. We define a semisimplicial space
$M\times X\to X$. We define a semisimplicial space ![]() $B_{\bullet }(M,X)$. For
$B_{\bullet }(M,X)$. For ![]() $p\geq 0$, the space
$p\geq 0$, the space ![]() $B_p(M,X)$ of
$B_p(M,X)$ of ![]() $p$-simplices is
$p$-simplices is ![]() $M^p\times X$. The face maps
$M^p\times X$. The face maps ![]() $d_i\colon B_p(M,X)\to B_{p-1}(M,X)$ are defined as follows:
$d_i\colon B_p(M,X)\to B_{p-1}(M,X)$ are defined as follows:
•
 $d_0\colon (m_1,\ldots,m_p,x)\mapsto (m_2,\ldots,m_p,x)$;
$d_0\colon (m_1,\ldots,m_p,x)\mapsto (m_2,\ldots,m_p,x)$;•
 $d_i\colon (m_1,\ldots,m_p)\mapsto (m_1,\ldots,\mu (m_i,m_{i+1}),\ldots,m_p,x)$, for
$d_i\colon (m_1,\ldots,m_p)\mapsto (m_1,\ldots,\mu (m_i,m_{i+1}),\ldots,m_p,x)$, for  $1\leq i\leq p-1$;
$1\leq i\leq p-1$;•
 $d_p\colon (m_1,\ldots,m_p)\mapsto (m_1,\ldots, m_{p-1},\mu (m_p,x))$.
$d_p\colon (m_1,\ldots,m_p)\mapsto (m_1,\ldots, m_{p-1},\mu (m_p,x))$.
The space ![]() $B(M,X)$ is the thick geometric realisation of the semisimplicial space
$B(M,X)$ is the thick geometric realisation of the semisimplicial space ![]() $B_{\bullet }(M,X)$, i.e. it is the quotient of
$B_{\bullet }(M,X)$, i.e. it is the quotient of ![]() $\coprod _{p\geq 0}\Delta ^p\times M^p\times X$ by the equivalence relation
$\coprod _{p\geq 0}\Delta ^p\times M^p\times X$ by the equivalence relation ![]() $\sim$ generated by
$\sim$ generated by ![]() $(d^i(\underline {w}),\underline {m},x)\sim (\underline {w},d_i(\underline {m},x))$, for all choices of the following data:
$(d^i(\underline {w}),\underline {m},x)\sim (\underline {w},d_i(\underline {m},x))$, for all choices of the following data:
•
 $p\geq 0$ and
$p\geq 0$ and  $0\leq i\leq p$;
$0\leq i\leq p$;• a point
 $\underline {w}=(w_0,\ldots,w_{p-1})$ in
$\underline {w}=(w_0,\ldots,w_{p-1})$ in  $\Delta ^{p-1}$, represented by its barycentric coordinates
$\Delta ^{p-1}$, represented by its barycentric coordinates  $w_0,\ldots,w_{p-1}\ge 0$ with
$w_0,\ldots,w_{p-1}\ge 0$ with  $w_0+\cdots +w_{p-1}=1$;
$w_0+\cdots +w_{p-1}=1$;• a point
 $(\underline {m},x)=(m_1,\ldots,m_p,x)\in M^p\times X$.
$(\underline {m},x)=(m_1,\ldots,m_p,x)\in M^p\times X$.
Here ![]() $d^i\colon \Delta ^{p-1}\to \Delta ^p$ denotes the standard
$d^i\colon \Delta ^{p-1}\to \Delta ^p$ denotes the standard ![]() $i$th face inclusion.
$i$th face inclusion.
When ![]() $X=*$ is a point, we also write
$X=*$ is a point, we also write ![]() $BM$ for
$BM$ for ![]() $B(M,*)$; when
$B(M,*)$; when ![]() $X=M$ with left multiplication coming from the monoid structure, we also write
$X=M$ with left multiplication coming from the monoid structure, we also write ![]() $EM$ for
$EM$ for ![]() $B(M,M)$.
$B(M,M)$.
In fact Definition 3.1 only uses that ![]() $M$ is an associative non-unital monoid; in § 3.3 we will recall the thin bar construction, which is a simplicial space whose degeneracy maps are defined using the unit
$M$ is an associative non-unital monoid; in § 3.3 we will recall the thin bar construction, which is a simplicial space whose degeneracy maps are defined using the unit ![]() $e\in M$.
$e\in M$.
It is a standard fact that if ![]() $M$ is a topological monoid,
$M$ is a topological monoid, ![]() $X$ is a left
$X$ is a left ![]() $M$-module and for all
$M$-module and for all ![]() $m\in M$ the map
$m\in M$ the map ![]() $\mu (m;-)\colon X\to X$ is a self-homotopy equivalence of
$\mu (m;-)\colon X\to X$ is a self-homotopy equivalence of ![]() $X$, then the natural projection map
$X$, then the natural projection map ![]() $p_X\colon B(M,X)\to BM=B(M,*)$ induced by the constant,
$p_X\colon B(M,X)\to BM=B(M,*)$ induced by the constant, ![]() $M$-equivariant map
$M$-equivariant map ![]() $X\to *$ is a quasi-fibration with fibres homeomorphic to
$X\to *$ is a quasi-fibration with fibres homeomorphic to ![]() $X$. See, for instance, [Reference HatcherHat14, Lemma D.1].
$X$. See, for instance, [Reference HatcherHat14, Lemma D.1].
Lemma 3.2 Recall Definitions 2.4 and 2.12 and let ![]() $(t,\mathfrak {c})\in \breve {\mathrm {HM}}$; then the left multiplication
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}$; then the left multiplication ![]() $\mu ((t,\mathfrak {c}),-)$ restricts to a self-homotopy equivalence of
$\mu ((t,\mathfrak {c}),-)$ restricts to a self-homotopy equivalence of ![]() $\breve {\mathrm {HM}}_+$; moreover, if
$\breve {\mathrm {HM}}_+$; moreover, if ![]() $\omega (\mathfrak {c})=\mathbb {1}\in G$, then
$\omega (\mathfrak {c})=\mathbb {1}\in G$, then ![]() $\mu ((t,\mathfrak {c}),-)|_{\breve {\mathrm {HM}}_+}$ is homotopic to the identity of
$\mu ((t,\mathfrak {c}),-)|_{\breve {\mathrm {HM}}_+}$ is homotopic to the identity of ![]() $\breve {\mathrm {HM}}_+$. It follows that
$\breve {\mathrm {HM}}_+$. It follows that
is a quasifibration with fibre ![]() $\breve {\mathrm {HM}}_+$.
$\breve {\mathrm {HM}}_+$.
Proof. It suffices to prove the statement for one configuration ![]() $(t,\mathfrak {c})$ in each connected component of
$(t,\mathfrak {c})$ in each connected component of ![]() $\breve {\mathrm {HM}}$: the statement is obvious for
$\breve {\mathrm {HM}}$: the statement is obvious for ![]() $(t,\mathfrak {c})=(0,(\emptyset, \mathbb {1},\mathbb {1}))\in \breve {\mathrm {HM}}$, which is the neutral element of
$(t,\mathfrak {c})=(0,(\emptyset, \mathbb {1},\mathbb {1}))\in \breve {\mathrm {HM}}$, which is the neutral element of ![]() $\breve {\mathrm {HM}}$. Using Theorem 2.19 we can then assume that
$\breve {\mathrm {HM}}$. Using Theorem 2.19 we can then assume that ![]() $t=1$ and
$t=1$ and ![]() $\mathfrak {c}$ has the form
$\mathfrak {c}$ has the form ![]() $\mathfrak {c}^{\mathrm {d}}_g:=(P,\psi,\varphi )$ for some
$\mathfrak {c}^{\mathrm {d}}_g:=(P,\psi,\varphi )$ for some ![]() $g\in G$, where:
$g\in G$, where:
•
 $P=\{z_{\diamond }^{\mathrm {d}}\}$ consists of the only point
$P=\{z_{\diamond }^{\mathrm {d}}\}$ consists of the only point  $z_{\diamond }^{\mathrm {d}}$ (see Definition 2.23);
$z_{\diamond }^{\mathrm {d}}$ (see Definition 2.23);•
 $\psi \colon \mathfrak {Q}(P)=\{\mathbb {1}\}\to {\mathcal {Q}}$ is the trivial map of PMQs;
$\psi \colon \mathfrak {Q}(P)=\{\mathbb {1}\}\to {\mathcal {Q}}$ is the trivial map of PMQs;•
 $\varphi \colon \mathfrak {G}(P)\to G$ sends the unique standard generator of
$\varphi \colon \mathfrak {G}(P)\to G$ sends the unique standard generator of  $\mathfrak {G}(P)$ to
$\mathfrak {G}(P)$ to  $g$.
$g$.
We start with the case ![]() $g=\mathbb {1}$. We claim that
$g=\mathbb {1}$. We claim that ![]() $\mu ((1,\mathfrak {c}^{\mathrm {d}}_{\mathbb {1}}),-)|_{\breve {\mathrm {HM}}_+}$ is homotopic to the identity of
$\mu ((1,\mathfrak {c}^{\mathrm {d}}_{\mathbb {1}}),-)|_{\breve {\mathrm {HM}}_+}$ is homotopic to the identity of ![]() $\breve {\mathrm {HM}}_+$; by Lemma 2.7 it suffices to prove that the restriction
$\breve {\mathrm {HM}}_+$; by Lemma 2.7 it suffices to prove that the restriction
is homotopic to the natural inclusion ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\hookrightarrow \breve {\mathrm {HM}}_+$.
$\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\hookrightarrow \breve {\mathrm {HM}}_+$.
First we prove that the maps ![]() $\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$ and
$\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$ and ![]() $\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic maps
$\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic maps ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$. We use an argument similar to the proof [Reference BianchiBia23a, Proposition 7.10]. Recall from [Reference BianchiBia23a, Definition 3.1] that the Ran space
$\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$. We use an argument similar to the proof [Reference BianchiBia23a, Proposition 7.10]. Recall from [Reference BianchiBia23a, Definition 3.1] that the Ran space ![]() $\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ is the space of non-empty finite subsets of
$\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ is the space of non-empty finite subsets of ![]() $\breve {{\mathcal {R}}}_2$; it is weakly contractible [Reference LurieLur17, Theorem 5.5.1.6] and using the notion of standard explosion from [Reference BianchiBia23a, Subsection 7.2], one can find a homotopy
$\breve {{\mathcal {R}}}_2$; it is weakly contractible [Reference LurieLur17, Theorem 5.5.1.6] and using the notion of standard explosion from [Reference BianchiBia23a, Subsection 7.2], one can find a homotopy ![]() $\mathscr {E}^{z_{\diamond }^{\mathrm {d}}}\colon \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)\times [0,1]\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ contracting
$\mathscr {E}^{z_{\diamond }^{\mathrm {d}}}\colon \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)\times [0,1]\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ contracting ![]() $\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ onto the configuration
$\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ onto the configuration ![]() $\{z_{\diamond }^{\mathrm {d}}\}$. Recall also that there is an external product
$\{z_{\diamond }^{\mathrm {d}}\}$. Recall also that there is an external product ![]() $-\times -\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\times \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2) \to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$, which essentially superposes to a configuration in
$-\times -\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\times \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2) \to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$, which essentially superposes to a configuration in ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ another configuration with trivial monodromies (i.e. a configuration in
$\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ another configuration with trivial monodromies (i.e. a configuration in ![]() $\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$); see [Reference BianchiBia23a, Definition 5.7 and Notation 5.9].
$\mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$); see [Reference BianchiBia23a, Definition 5.7 and Notation 5.9].
We consider the following homotopy ![]() ${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\times [0,1]\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$
${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\times [0,1]\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$

where ![]() $\varepsilon \colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ is the canonical map
$\varepsilon \colon \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_2)$ is the canonical map ![]() $(P,\psi,\varphi )\mapsto P$. Roughly speaking, each point in the support of a configuration in
$(P,\psi,\varphi )\mapsto P$. Roughly speaking, each point in the support of a configuration in ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is split at time 0 into two points: the first keeps the original local monodromy and does not move; the second carries a trivial local monodromy and moves straightly to
$\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is split at time 0 into two points: the first keeps the original local monodromy and does not move; the second carries a trivial local monodromy and moves straightly to ![]() $z_{\diamond }^{\mathrm {d}}$; at time 1 all the second points have merged at
$z_{\diamond }^{\mathrm {d}}$; at time 1 all the second points have merged at ![]() $z_{\diamond }^{\mathrm {d}}$. We observe the following:
$z_{\diamond }^{\mathrm {d}}$. We observe the following:
• the composition
 ${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,0)\circ \mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is equal to
${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,0)\circ \mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is equal to  $\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$, since
$\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$, since  ${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,0)$ is the identity of
${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,0)$ is the identity of  $\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$;
$\mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$;• the composition
 ${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,1)\circ \mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is equal to
${\mathcal {H}}^{z_{\diamond }^{\mathrm {d}}}(-,1)\circ \mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)\colon \mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })$ is equal to  $\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$.
$\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$.
We thus obtain that ![]() $\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$ and
$\mu ((1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}),-)$ and ![]() $\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic as maps
$\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic as maps ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\subset \breve {\mathrm {HM}}_+$.
$\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \mathrm {Hur}_+(\breve {{\mathcal {R}}}_2,\breve {\partial })\subset \breve {\mathrm {HM}}_+$.
We then note that ![]() $(1,(\emptyset,\mathbb {1},\mathbb {1}))$ is connected by a path to
$(1,(\emptyset,\mathbb {1},\mathbb {1}))$ is connected by a path to ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$ in
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$ in ![]() $\breve {\mathrm {HM}}$; as a consequence
$\breve {\mathrm {HM}}$; as a consequence ![]() $\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ and
$\mu ((1,(\emptyset,\mathbb {1},\mathbb {1})),-)$ and ![]() $\mu ((0,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic as maps
$\mu ((0,(\emptyset,\mathbb {1},\mathbb {1})),-)$ are homotopic as maps ![]() $\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \breve {\mathrm {HM}}_+$ and the second map is the natural inclusion. This concludes the case
$\mathrm {Hur}_+(\breve {{\mathcal {R}}},\breve {\partial })\to \breve {\mathrm {HM}}_+$ and the second map is the natural inclusion. This concludes the case ![]() $g=\mathbb {1}$.
$g=\mathbb {1}$.
Now let ![]() $g\neq \mathbb {1}$; by Theorem 2.19 the three configurations
$g\neq \mathbb {1}$; by Theorem 2.19 the three configurations ![]() $\mu ((1,\mathfrak {c}_g^{\mathrm {d}}),(1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}))$,
$\mu ((1,\mathfrak {c}_g^{\mathrm {d}}),(1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}))$, ![]() $\mu ((1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}), (1,\mathfrak {c}_g^{\mathrm {d}}))$ and
$\mu ((1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}), (1,\mathfrak {c}_g^{\mathrm {d}}))$ and ![]() $(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}})$ are in the same connected component of
$(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}})$ are in the same connected component of ![]() $\breve {\mathrm {HM}}_+$: hence,
$\breve {\mathrm {HM}}_+$: hence, ![]() $\mu ((1,\mathfrak {c}_g^{\mathrm {d}}),-)$ and
$\mu ((1,\mathfrak {c}_g^{\mathrm {d}}),-)$ and ![]() $\mu ((1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}),-)$ are homotopy inverses as maps
$\mu ((1,\mathfrak {c}_{g^{-1}}^{\mathrm {d}}),-)$ are homotopy inverses as maps ![]() $\breve {\mathrm {HM}}_+\to \breve {\mathrm {HM}}_+$.
$\breve {\mathrm {HM}}_+\to \breve {\mathrm {HM}}_+$.
It is a classical fact that if ![]() $M$ is a unital, topological monoid, then
$M$ is a unital, topological monoid, then ![]() $EM$ is contractible. In the following proposition we prove an analogous statement for
$EM$ is contractible. In the following proposition we prove an analogous statement for ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$.
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$.
Proposition 3.3 The space ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ is weakly contractible.
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ is weakly contractible.
The proof of Proposition 3.3 is in Appendix A.3. As a consequence of Lemma 3.2 and Proposition 3.3 we obtain the following theorem.
Theorem 3.4 There is a weak equivalence ![]() $\breve {\mathrm {HM}}_+\simeq \Omega B\breve {\mathrm {HM}}$.
$\breve {\mathrm {HM}}_+\simeq \Omega B\breve {\mathrm {HM}}$.
3.2 Pontryagin ring and group completion
If ![]() $M$ is a unital topological monoid,
$M$ is a unital topological monoid, ![]() $H_*(M)$ is an associative, graded ring with unit, called a Pontryagin ring. We usually denote by
$H_*(M)$ is an associative, graded ring with unit, called a Pontryagin ring. We usually denote by ![]() $x\cdot y\in H_*(M)$ the Pontryagin product of two homology classes
$x\cdot y\in H_*(M)$ the Pontryagin product of two homology classes ![]() $x,y\in H_*(M)$. The unit
$x,y\in H_*(M)$. The unit ![]() $1\in H_0(M)$ is the homology class corresponding to the connected component of
$1\in H_0(M)$ is the homology class corresponding to the connected component of ![]() $e$ in
$e$ in ![]() $\pi _0(M)$. The subset
$\pi _0(M)$. The subset ![]() $\pi _0(M)\subset H_0(M)\subset H_*(M)$ is closed under multiplication.
$\pi _0(M)\subset H_0(M)\subset H_*(M)$ is closed under multiplication.
Definition 3.5 A topological monoid ![]() $M$ is weakly braided if there is a homeomorphism
$M$ is weakly braided if there is a homeomorphism ![]() $\mathfrak {br}\colon M\times M\to M\times M$ such that:
$\mathfrak {br}\colon M\times M\to M\times M$ such that:
• if
 $p_1,p_2\colon M\times M\to M$ are the two natural projections, then
$p_1,p_2\colon M\times M\to M$ are the two natural projections, then  $p_1\circ \mathfrak {br}=p_2$ as maps
$p_1\circ \mathfrak {br}=p_2$ as maps  $M\times M\to M$;
$M\times M\to M$;•
 $\mu$ and
$\mu$ and  $\mu \circ \mathfrak {br}$ are homotopic as maps
$\mu \circ \mathfrak {br}$ are homotopic as maps  $M\times M\to M$.
$M\times M\to M$.
Note that if ![]() $M$ is weakly braided, then the ring localisation
$M$ is weakly braided, then the ring localisation ![]() $H_*(M)[\pi _0(M)^{-1}]$ can be constructed by right fractions: for all
$H_*(M)[\pi _0(M)^{-1}]$ can be constructed by right fractions: for all ![]() $x\in H_*(M)$ and
$x\in H_*(M)$ and ![]() $a\in \pi _0(M)$ there exist
$a\in \pi _0(M)$ there exist ![]() $y\in H_*(M)$ and
$y\in H_*(M)$ and ![]() $b\in \pi _0(M)$ with
$b\in \pi _0(M)$ with ![]() $x\cdot b=a\cdot y$. This follows from setting
$x\cdot b=a\cdot y$. This follows from setting ![]() $b=a$ and
$b=a$ and ![]() $y=(p_2)_*\circ \mathfrak {br}_*(x\times a)$, where
$y=(p_2)_*\circ \mathfrak {br}_*(x\times a)$, where ![]() $\times$ denotes the homology cross-product and
$\times$ denotes the homology cross-product and ![]() $p_2\colon M\times M\to M$ is as in Definition 3.5.
$p_2\colon M\times M\to M$ is as in Definition 3.5.
Lemma 3.6 The topological monoid ![]() $\mathring {\mathrm {HM}}$ is weakly braided.
$\mathring {\mathrm {HM}}$ is weakly braided.
Proof. We define ![]() $\mathfrak {br}\colon \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}\to \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}$ by the formula
$\mathfrak {br}\colon \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}\to \mathring {\mathrm {HM}}\times \mathring {\mathrm {HM}}$ by the formula
where ![]() $\hat \omega$ is the
$\hat \omega$ is the ![]() $\hat {{\mathcal {Q}}}$-valued total monodromy (see Notation 2.14) and we use the action by global conjugation [Reference BianchiBia23a, Definition 6.6]. It is clear that
$\hat {{\mathcal {Q}}}$-valued total monodromy (see Notation 2.14) and we use the action by global conjugation [Reference BianchiBia23a, Definition 6.6]. It is clear that ![]() $\mathfrak {br}$ is a homeomorphism and that the first property in Definition 3.5 holds. To check the second property, note that
$\mathfrak {br}$ is a homeomorphism and that the first property in Definition 3.5 holds. To check the second property, note that ![]() $\mathfrak {br}$ restricts to a map
$\mathfrak {br}$ restricts to a map
By Lemma 2.7 it suffices to prove that ![]() $\mu$ and
$\mu$ and ![]() $\mu \circ \mathfrak {br}$ are homotopic when considered as maps
$\mu \circ \mathfrak {br}$ are homotopic when considered as maps ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})\times \mathrm {Hur}(\mathring {{\mathcal {R}}})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$. Let
$\mathrm {Hur}(\mathring {{\mathcal {R}}})\times \mathrm {Hur}(\mathring {{\mathcal {R}}})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$. Let ![]() $\mathring {{\mathcal {R}}}^{1/2}\subset \mathring {{\mathcal {R}}}$ be the open unit square
$\mathring {{\mathcal {R}}}^{1/2}\subset \mathring {{\mathcal {R}}}$ be the open unit square ![]() $(1/4,3/4)\times (1/4,3/4)$ of side length
$(1/4,3/4)\times (1/4,3/4)$ of side length ![]() $1/2$ centred at
$1/2$ centred at ![]() $z_{\mathrm {c}}\in \mathring {{\mathcal {R}}}$; we can regard
$z_{\mathrm {c}}\in \mathring {{\mathcal {R}}}$; we can regard ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})$ as an open subspace of
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})$ as an open subspace of ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})$, containing all configurations supported in
$\mathrm {Hur}(\mathring {{\mathcal {R}}})$, containing all configurations supported in ![]() $\mathring {{\mathcal {R}}}^{1/2}$. Note that
$\mathring {{\mathcal {R}}}^{1/2}$. Note that ![]() $\mathfrak {br}$ restricts to a map
$\mathfrak {br}$ restricts to a map
Let ![]() ${\mathcal {H}}^{1/2}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ be a semialgebraic isotopy of
${\mathcal {H}}^{1/2}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ be a semialgebraic isotopy of ![]() $\mathbb {C}$ fixing
$\mathbb {C}$ fixing ![]() $*$ at all times, such that
$*$ at all times, such that ![]() ${\mathcal {H}}^{1/2}(-,0)=\operatorname {Id}_{\mathbb {C}}$ and
${\mathcal {H}}^{1/2}(-,0)=\operatorname {Id}_{\mathbb {C}}$ and ![]() ${\mathcal {H}}^{1/2}(-,1)$ restricts to a homeomorphism
${\mathcal {H}}^{1/2}(-,1)$ restricts to a homeomorphism ![]() $\mathring {{\mathcal {R}}}\to \mathring {{\mathcal {R}}}^{1/2}$. Then by functoriality there is a deformation of
$\mathring {{\mathcal {R}}}\to \mathring {{\mathcal {R}}}^{1/2}$. Then by functoriality there is a deformation of ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}})$ into the subspace
$\mathrm {Hur}(\mathring {{\mathcal {R}}})$ into the subspace ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})$. Thus, it suffices to prove that the following restricted maps are homotopic:
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})$. Thus, it suffices to prove that the following restricted maps are homotopic:
Let ![]() ${\mathcal {H}}^{\mathfrak {br}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ be a semialgebraic isotopy of
${\mathcal {H}}^{\mathfrak {br}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ be a semialgebraic isotopy of ![]() $\mathbb {C}$ fixing pointwise
$\mathbb {C}$ fixing pointwise ![]() $\mathbb {C}\setminus \mathring {{\mathcal {R}}}_2$ at all times, such that
$\mathbb {C}\setminus \mathring {{\mathcal {R}}}_2$ at all times, such that ![]() ${\mathcal {H}}^{\mathfrak {br}}(-,0)=\operatorname {Id}_{\mathbb {C}}$ and
${\mathcal {H}}^{\mathfrak {br}}(-,0)=\operatorname {Id}_{\mathbb {C}}$ and ![]() ${\mathcal {H}}^{\mathfrak {br}}(-,1)\colon \mathbb {C}\to \mathbb {C}$ has the following properties:
${\mathcal {H}}^{\mathfrak {br}}(-,1)\colon \mathbb {C}\to \mathbb {C}$ has the following properties:
•
 ${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to
${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to  $\tau _1\colon \mathring {{\mathcal {R}}}^{1/2}\to \tau _1(\mathring {{\mathcal {R}}}^{1/2})$ (see Definition 2.9);
$\tau _1\colon \mathring {{\mathcal {R}}}^{1/2}\to \tau _1(\mathring {{\mathcal {R}}}^{1/2})$ (see Definition 2.9);•
 ${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to
${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to  $\tau _{-1}\colon \tau _1(\mathring {{\mathcal {R}}}^{1/2})\to \mathring {{\mathcal {R}}}^{1/2}$;
$\tau _{-1}\colon \tau _1(\mathring {{\mathcal {R}}}^{1/2})\to \mathring {{\mathcal {R}}}^{1/2}$;•
 ${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to a self-homeomorphism of
${\mathcal {H}}^{\mathfrak {br}}(-,1)$ restricts to a self-homeomorphism of  $\mathbb {C}\setminus (\mathring {{\mathcal {R}}}^{1/2}\cup \tau _1(\mathring {{\mathcal {R}}}^{1/2}))$ representing a clockwise half Dehn twist, for instance we may assume that there is a simple loop
$\mathbb {C}\setminus (\mathring {{\mathcal {R}}}^{1/2}\cup \tau _1(\mathring {{\mathcal {R}}}^{1/2}))$ representing a clockwise half Dehn twist, for instance we may assume that there is a simple loop  $\gamma \subset \mathbb {S}_{1,2}\setminus \tau _1(\mathring {{\mathcal {R}}}^{1/2})$ spinning clockwise around
$\gamma \subset \mathbb {S}_{1,2}\setminus \tau _1(\mathring {{\mathcal {R}}}^{1/2})$ spinning clockwise around  $\tau _1(\mathring {{\mathcal {R}}}^{1/2})$, such that
$\tau _1(\mathring {{\mathcal {R}}}^{1/2})$, such that  ${\mathcal {H}}^{\mathfrak {br}}(-,1)\circ \gamma$ is a simple loop contained in
${\mathcal {H}}^{\mathfrak {br}}(-,1)\circ \gamma$ is a simple loop contained in  $\mathbb {S}_{0,1}\setminus \mathring {{\mathcal {R}}}^{1/2}$ and spinning clockwise around
$\mathbb {S}_{0,1}\setminus \mathring {{\mathcal {R}}}^{1/2}$ and spinning clockwise around  $\mathring {{\mathcal {R}}}^{1/2}$.
$\mathring {{\mathcal {R}}}^{1/2}$.
Then the composition of ![]() $\mu$ with
$\mu$ with ![]() ${\mathcal {H}}^{\mathfrak {br}}_*$ gives a homotopy from
${\mathcal {H}}^{\mathfrak {br}}_*$ gives a homotopy from ![]() $\mu$ to
$\mu$ to ![]() $\mu \circ \mathfrak {br}$ as maps
$\mu \circ \mathfrak {br}$ as maps ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})\times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$.
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})\times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{1/2})\to \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$.
Recall that for any topological monoid ![]() $M$ there is a canonical map
$M$ there is a canonical map ![]() $M\to \Omega BM$: the induced map in homology
$M\to \Omega BM$: the induced map in homology ![]() $H_*(M)\to H_*(\Omega BM)$ sends the multiplicative subset
$H_*(M)\to H_*(\Omega BM)$ sends the multiplicative subset ![]() $\pi _0(M)\subset H_*(M)$ to the set of invertible elements of the Pontryagin ring
$\pi _0(M)\subset H_*(M)$ to the set of invertible elements of the Pontryagin ring ![]() $H_*(\Omega BM)$. Therefore, there is an induced map of rings
$H_*(\Omega BM)$. Therefore, there is an induced map of rings
We recall the group completion theorem (see [Reference McDuff and SegalMS76] and [Reference Friedlander and MazurFM94, Theorem Q.4]).
Theorem 3.7 (Group completion theorem)
Let ![]() $M$ be a topological monoid and suppose that the localisation
$M$ be a topological monoid and suppose that the localisation ![]() $H_*(M)[\pi _0(M)^{-1}]$ can be constructed by right fractions. Then the canonical map
$H_*(M)[\pi _0(M)^{-1}]$ can be constructed by right fractions. Then the canonical map
is an isomorphism of rings.
Using Theorem 3.7 together with Lemma 3.6 we obtain an isomorphism of rings
3.3 Thin bar construction
Recall Definition 3.1: the semisimplicial space ![]() $B_{\bullet } (M,X)$ can be enhanced to a simplicial space by defining the degeneracy map
$B_{\bullet } (M,X)$ can be enhanced to a simplicial space by defining the degeneracy map ![]() $s_i\colon B_k(M,X)\to B_{k+1}(M,X)$, for
$s_i\colon B_k(M,X)\to B_{k+1}(M,X)$, for ![]() $0\leq i\leq k$, by the following formula, where
$0\leq i\leq k$, by the following formula, where ![]() $e$ denotes the neutral element of
$e$ denotes the neutral element of ![]() $M$,
$M$,
Definition 3.8 The simplicial space defined above is denoted by ![]() $\bar {B}_{\bullet }(M,X)$; its geometric realisation as a simplicial space is denoted by
$\bar {B}_{\bullet }(M,X)$; its geometric realisation as a simplicial space is denoted by ![]() $\bar {B} (M,X)$ and called the thin bar construction. It is the quotient of
$\bar {B} (M,X)$ and called the thin bar construction. It is the quotient of ![]() $BM$ by the equivalence relation
$BM$ by the equivalence relation ![]() $\bar \sim$ generated by
$\bar \sim$ generated by ![]() $[s^i(\underline {w}),\underline {m},x]\bar \sim [\underline {w},s_i(\underline {m},x)]$ for all choices of the following data:
$[s^i(\underline {w}),\underline {m},x]\bar \sim [\underline {w},s_i(\underline {m},x)]$ for all choices of the following data:
•
 $p\geq 0$ and
$p\geq 0$ and  $0\leq i\leq p$;
$0\leq i\leq p$;• a point
 $\underline {w}=(w_0,\ldots,w_{p+1})$ in
$\underline {w}=(w_0,\ldots,w_{p+1})$ in  $\Delta ^{p+1}$, represented by its barycentric coordinates;
$\Delta ^{p+1}$, represented by its barycentric coordinates;• a point
 $(\underline {m},x)=(m_1,\ldots,m_p,x)\in M^p\times X$.
$(\underline {m},x)=(m_1,\ldots,m_p,x)\in M^p\times X$.
Here ![]() $s^i\colon \Delta ^{p+1}\to \Delta ^p$ denotes the
$s^i\colon \Delta ^{p+1}\to \Delta ^p$ denotes the ![]() $i$th degeneracy. The natural projection map is denoted by
$i$th degeneracy. The natural projection map is denoted by ![]() $p_{\bar {B}}\colon B(M,X)\to \bar {B} (M,X)$. In the case
$p_{\bar {B}}\colon B(M,X)\to \bar {B} (M,X)$. In the case ![]() $X=*$ we also write
$X=*$ we also write ![]() $\bar {B} M$ for
$\bar {B} M$ for ![]() $\bar {B}(M,*)$.
$\bar {B}(M,*)$.
It is a classical fact that if ![]() $M$ is well-pointed, then
$M$ is well-pointed, then ![]() $p_{\bar {B}}\colon BM\to \bar {B} M$ is a weak homotopy equivalence, as
$p_{\bar {B}}\colon BM\to \bar {B} M$ is a weak homotopy equivalence, as ![]() $\bar {B}_{\bullet }(M)$ is a good simplicial space in the sense of [Reference SegalSeg73, Appendix 2]. The monoids
$\bar {B}_{\bullet }(M)$ is a good simplicial space in the sense of [Reference SegalSeg73, Appendix 2]. The monoids ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$ are well-pointed, as the connected component of the unit
$\breve {\mathrm {HM}}$ are well-pointed, as the connected component of the unit ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is contractible in both cases.
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is contractible in both cases.
4. Deloopings of Hurwitz spaces
In this section we describe the weak homotopy types of ![]() $B\mathring {\mathrm {HM}}$ and
$B\mathring {\mathrm {HM}}$ and ![]() $B\breve {\mathrm {HM}}$ using suitable, relative Hurwitz spaces. Recall from [Reference BianchiBia23a, Definition 6.9] that a left–right-based (lr-based) nice couple
$B\breve {\mathrm {HM}}$ using suitable, relative Hurwitz spaces. Recall from [Reference BianchiBia23a, Definition 6.9] that a left–right-based (lr-based) nice couple ![]() $(z^{\mathrm {l}},\mathfrak {C},z^{\mathrm {r}})$ is a nice couple
$(z^{\mathrm {l}},\mathfrak {C},z^{\mathrm {r}})$ is a nice couple ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$, together with a choice of two points
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$, together with a choice of two points ![]() $z^{\mathrm {l}},z^{\mathrm {r}}\in {\mathcal {Y}}$ satisfying
$z^{\mathrm {l}},z^{\mathrm {r}}\in {\mathcal {Y}}$ satisfying
We denote by ![]() $\mathrm {Hur}(\mathfrak {C})_{z^{\mathrm {l}},z^{\mathrm {r}}}=\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)_{z^{\mathrm {l}},z^{\mathrm {r}}}$ the subspace of
$\mathrm {Hur}(\mathfrak {C})_{z^{\mathrm {l}},z^{\mathrm {r}}}=\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)_{z^{\mathrm {l}},z^{\mathrm {r}}}$ the subspace of ![]() $\mathrm {Hur}(\mathfrak {C})$ of configurations whose support contains
$\mathrm {Hur}(\mathfrak {C})$ of configurations whose support contains ![]() $\{z^{\mathrm {l}},z^{\mathrm {r}}\}$; recall from [Reference BianchiBia23a, Definition 6.12] that there is an action of
$\{z^{\mathrm {l}},z^{\mathrm {r}}\}$; recall from [Reference BianchiBia23a, Definition 6.12] that there is an action of ![]() $G\times G^{\rm op}$ on the Hurwitz space
$G\times G^{\rm op}$ on the Hurwitz space ![]() $\mathrm {Hur}(\mathfrak {C})_{z^{\mathrm {l}},z^{\mathrm {r}}}$, i.e. there are compatible actions of
$\mathrm {Hur}(\mathfrak {C})_{z^{\mathrm {l}},z^{\mathrm {r}}}$, i.e. there are compatible actions of ![]() $G$ on left and on right on this space; by [Reference BianchiBia23a, Lemma 6.16] the quotient map
$G$ on left and on right on this space; by [Reference BianchiBia23a, Lemma 6.16] the quotient map
is a covering map, with ![]() $G\times G^{\rm op}$ as the group of deck transformations.
$G\times G^{\rm op}$ as the group of deck transformations.
Theorem 4.1 Recall Definitions 2.4, 2.23 and 3.1. Let ![]() $({\mathcal {Q}},G)$ be a PMQ–group pair and assume that
$({\mathcal {Q}},G)$ be a PMQ–group pair and assume that ![]() $\mathfrak {e}({\mathcal {Q}})$ generates
$\mathfrak {e}({\mathcal {Q}})$ generates ![]() $G$ as a group; then there are weak homotopy equivalences
$G$ as a group; then there are weak homotopy equivalences
Here we consider the lr-based nice couples ![]() $(z_{\diamond }^{\mathrm {l}},(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }),z_{\diamond }^{\mathrm {r}})$ and
$(z_{\diamond }^{\mathrm {l}},(\breve {\diamond }^{\mathrm {lr}},\breve {\partial }),z_{\diamond }^{\mathrm {r}})$ and ![]() $(z_{\diamond }^{\mathrm {l}},(\diamond,\partial ),z_{\diamond }^{\mathrm {r}})$.
$(z_{\diamond }^{\mathrm {l}},(\diamond,\partial ),z_{\diamond }^{\mathrm {r}})$.
We will use a classical approach, going back to Segal [Reference SegalSeg73], which allows us to model the classifying space of a monoid ![]() $M$, arising from configuration spaces, with another, relative configuration space. We will follow tightly the strategy of the proof of [Reference HatcherHat14, Proposition 3.1] and to some extent we will use the same notation: we do this for convenience of the reader. We focus on the case of
$M$, arising from configuration spaces, with another, relative configuration space. We will follow tightly the strategy of the proof of [Reference HatcherHat14, Proposition 3.1] and to some extent we will use the same notation: we do this for convenience of the reader. We focus on the case of ![]() $\mathring {\mathrm {HM}}$ and write in parentheses the necessary changes for
$\mathring {\mathrm {HM}}$ and write in parentheses the necessary changes for ![]() $\breve {\mathrm {HM}}$.
$\breve {\mathrm {HM}}$.
We will first define the comparison map ![]() $\sigma$ in the two cases and then show that it induces isomorphisms on all homotopy groups.
$\sigma$ in the two cases and then show that it induces isomorphisms on all homotopy groups.
4.1 Definition of the comparison map
By Definition 3.1 the space ![]() $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}$) arises as a quotient of the disjoint union
$B\breve {\mathrm {HM}}$) arises as a quotient of the disjoint union ![]() $\coprod _{p\geq 0}\Delta ^p\times \mathring {\mathrm {HM}}^p$ (respectively,
$\coprod _{p\geq 0}\Delta ^p\times \mathring {\mathrm {HM}}^p$ (respectively, ![]() $\coprod _{p\geq 0}\Delta ^p\times \breve {\mathrm {HM}}^p$). We will first define
$\coprod _{p\geq 0}\Delta ^p\times \breve {\mathrm {HM}}^p$). We will first define ![]() $\sigma$ on this disjoint union and then prove that the given assignment induces a map on the quotient.
$\sigma$ on this disjoint union and then prove that the given assignment induces a map on the quotient.
Notation 4.2 We usually denote by ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ a point in
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ a point in ![]() $\coprod _{p\geq 0}\Delta ^p\times \mathring {\mathrm {HM}}^p$ (respectively,
$\coprod _{p\geq 0}\Delta ^p\times \mathring {\mathrm {HM}}^p$ (respectively, ![]() $\coprod _{p\geq 0}\Delta ^p\times \breve {\mathrm {HM}}^p$), where:
$\coprod _{p\geq 0}\Delta ^p\times \breve {\mathrm {HM}}^p$), where:
•
 $\underline {w}=(w_0,\ldots,w_p)$ is a system of barycentric coordinates in
$\underline {w}=(w_0,\ldots,w_p)$ is a system of barycentric coordinates in  $\Delta ^p$, i.e.
$\Delta ^p$, i.e.  $w_0,\ldots,w_p\geq 0$ and
$w_0,\ldots,w_p\geq 0$ and  $w_0+\cdots +w_p=1$;
$w_0+\cdots +w_p=1$;•
 $\underline {t}=(t_1,\ldots,t_p)$ and
$\underline {t}=(t_1,\ldots,t_p)$ and  $\underline {\mathfrak {c}}=(\mathfrak {c}_1,\ldots \mathfrak {c}_p)$, such that
$\underline {\mathfrak {c}}=(\mathfrak {c}_1,\ldots \mathfrak {c}_p)$, such that  $(t_i,\mathfrak {c}_i)$ is an element in
$(t_i,\mathfrak {c}_i)$ is an element in  $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in  $\breve {\mathrm {HM}}$) for all
$\breve {\mathrm {HM}}$) for all  $1\leq i\leq p$.
$1\leq i\leq p$.
We usually present ![]() $\mathfrak {c}_i$ as
$\mathfrak {c}_i$ as ![]() $(P_i,\psi _i)$ (respectively, as
$(P_i,\psi _i)$ (respectively, as ![]() $(P_i,\psi _i,\varphi _i)$).
$(P_i,\psi _i,\varphi _i)$).
Given ![]() $(\underline {w},\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, note that the product
$(\underline {w},\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, note that the product ![]() $(t_1,\mathfrak {c}_1)\cdots (t_p,\mathfrak {c}_p)$ has the form
$(t_1,\mathfrak {c}_1)\cdots (t_p,\mathfrak {c}_p)$ has the form ![]() $(t_1+\cdots +t_p,\mathfrak {c})$, with
$(t_1+\cdots +t_p,\mathfrak {c})$, with ![]() $\mathfrak {c}$ supported on the set
$\mathfrak {c}$ supported on the set
By Definition 2.4 we have ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ (respectively,
$\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{\infty })$ (respectively, ![]() $\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$), but in the following we will consider
$\mathfrak {c}\in \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$), but in the following we will consider ![]() $\mathfrak {c}$ as a configuration in
$\mathfrak {c}$ as a configuration in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$, see Notation 2.3).
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$, see Notation 2.3).
Definition 4.3 The above assignment ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})\mapsto \mathfrak {c}$ gives a continuous map
$(\underline {w};\underline {t},\underline {\mathfrak {c}})\mapsto \mathfrak {c}$ gives a continuous map
 \[ \hat{\mu}\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\mathring{{\mathcal{R}}}_{\mathbb{R}}) \quad \bigg( \text{respectively, } \hat{\mu}\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{{\mathcal{R}}}_{\mathbb{R}},\breve{\partial}) \bigg). \]
\[ \hat{\mu}\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\mathring{{\mathcal{R}}}_{\mathbb{R}}) \quad \bigg( \text{respectively, } \hat{\mu}\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{{\mathcal{R}}}_{\mathbb{R}},\breve{\partial}) \bigg). \]
Note that ![]() $\hat {\mu }$ factors, on each subspace
$\hat {\mu }$ factors, on each subspace ![]() $\Delta ^p\times (\mathring {\mathrm {HM}})^p$ (respectively,
$\Delta ^p\times (\mathring {\mathrm {HM}})^p$ (respectively, ![]() $\Delta ^p\times (\breve {\mathrm {HM}})^p$), through the projection on the factor
$\Delta ^p\times (\breve {\mathrm {HM}})^p$), through the projection on the factor ![]() $(\mathring {\mathrm {HM}})^p$ (respectively,
$(\mathring {\mathrm {HM}})^p$ (respectively, ![]() $(\breve {\mathrm {HM}})^p$). The first subspace
$(\breve {\mathrm {HM}})^p$). The first subspace ![]() $\Delta ^0$ is sent to the empty product in
$\Delta ^0$ is sent to the empty product in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$), i.e. to the neutral element
$\breve {\mathrm {HM}}$), i.e. to the neutral element ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$.
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$.
Definition 4.4 For ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, define
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, define ![]() $a_0=0$ and
$a_0=0$ and ![]() $a_i=\sum _{j=1}^i t_j$ for all
$a_i=\sum _{j=1}^i t_j$ for all ![]() $1\leq i\leq p$. Define the barycentre of
$1\leq i\leq p$. Define the barycentre of ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as ![]() $b=\sum _{i=0}^pw_ia_i$. Set
$b=\sum _{i=0}^pw_ia_i$. Set ![]() $a_i^+=\max \{a_i,b\}$ and
$a_i^+=\max \{a_i,b\}$ and ![]() $a_i^-=\min \{a_i,b\}$ for all
$a_i^-=\min \{a_i,b\}$ for all ![]() $0\leq i\leq p$ and define the upper barycentre and the lower barycentre as
$0\leq i\leq p$ and define the upper barycentre and the lower barycentre as ![]() $b^+=\sum _{i=0}^pw_ia_i^+$ and
$b^+=\sum _{i=0}^pw_ia_i^+$ and ![]() $b^-=\sum _{i=0}^pw_ia_i^-$.
$b^-=\sum _{i=0}^pw_ia_i^-$.
See Figure 5(left). Note that the barycentres ![]() $b,b^+,b^-$ vary continuously on
$b,b^+,b^-$ vary continuously on ![]() $\coprod _{p\geq 0} \Delta ^p\times (\mathring {\mathrm {HM}})^p$ (on
$\coprod _{p\geq 0} \Delta ^p\times (\mathring {\mathrm {HM}})^p$ (on ![]() $\coprod _{p\geq 0} \Delta ^p\times (\breve {\mathrm {HM}})^p$), but do not factor to continuous functions on
$\coprod _{p\geq 0} \Delta ^p\times (\breve {\mathrm {HM}})^p$), but do not factor to continuous functions on ![]() $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}$): indeed, if
$B\breve {\mathrm {HM}}$): indeed, if ![]() $w_0=0$, the triple
$w_0=0$, the triple ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equivalent to the triple
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equivalent to the triple ![]() $(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ obtained by removing
$(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ obtained by removing ![]() $w_0$,
$w_0$, ![]() $t_1$ and
$t_1$ and ![]() $\underline {\mathfrak {c}}_1$; all barycentres
$\underline {\mathfrak {c}}_1$; all barycentres ![]() $b,b^+,b^-$ drop by
$b,b^+,b^-$ drop by ![]() $t_1$ when passing from the first to the second triple. Nevertheless, the differences
$t_1$ when passing from the first to the second triple. Nevertheless, the differences ![]() $b^+-b$ and
$b^+-b$ and ![]() $b-b^-$ factor to continuous functions defined on
$b-b^-$ factor to continuous functions defined on ![]() $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}$).
$B\breve {\mathrm {HM}}$).
Note also that for all ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ we have
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ we have ![]() $a_0\leq b^-\leq b\leq b^+\leq a_p$. More precisely, let
$a_0\leq b^-\leq b\leq b^+\leq a_p$. More precisely, let ![]() $i_{\rm min}\ge 0$ be minimal with
$i_{\rm min}\ge 0$ be minimal with ![]() $w_{i_{\rm min}}>0$ and let
$w_{i_{\rm min}}>0$ and let ![]() $i_{\rm max}\le p$ be maximal with
$i_{\rm max}\le p$ be maximal with ![]() $w_{i_{\rm max}}>0$; then
$w_{i_{\rm max}}>0$; then ![]() $a_{i_{\rm min}}\leq b^-\leq b\leq b^+\leq a_{i_{\rm max}}$, with all these inequalities strict unless they are all equalities: in this case all
$a_{i_{\rm min}}\leq b^-\leq b\leq b^+\leq a_{i_{\rm max}}$, with all these inequalities strict unless they are all equalities: in this case all ![]() $t_i$ with
$t_i$ with ![]() $i_{\rm min}< i\le i_{\rm max}$ are equal to
$i_{\rm min}< i\le i_{\rm max}$ are equal to ![]() $0$ and all corresponding
$0$ and all corresponding ![]() $\mathfrak {c}_i$ are equal to
$\mathfrak {c}_i$ are equal to ![]() $(\emptyset,\mathbb {1},\mathbb {1})$, so that
$(\emptyset,\mathbb {1},\mathbb {1})$, so that ![]() $\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is equal to the product
$\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is equal to the product ![]() $(t_1,\mathfrak {c}_1)\cdots (t_{i_{\rm min}},\mathfrak {c}_{i_{\rm min}})\cdot (t_{i_{\rm max}+1},\mathfrak {c}_{i_{\rm max}+1})\cdots (t_p,\mathfrak {c}_p)$. In particular, if
$(t_1,\mathfrak {c}_1)\cdots (t_{i_{\rm min}},\mathfrak {c}_{i_{\rm min}})\cdot (t_{i_{\rm max}+1},\mathfrak {c}_{i_{\rm max}+1})\cdots (t_p,\mathfrak {c}_p)$. In particular, if ![]() $b^-=b=b^+$, then we have that
$b^-=b=b^+$, then we have that ![]() $\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is supported away from
$\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is supported away from ![]() $\mathbb {S}_{b,b}$, in fact it is supported away from
$\mathbb {S}_{b,b}$, in fact it is supported away from ![]() $\mathbb {S}_{b-\varepsilon,b+\varepsilon }$ for
$\mathbb {S}_{b-\varepsilon,b+\varepsilon }$ for ![]() $\varepsilon >0$ small enough.
$\varepsilon >0$ small enough.
Definition 4.5 We define a continuous function ![]() $\varepsilon \colon \coprod _{p\geq 0} \Delta ^p\times (\mathring {\mathrm {HM}})^p\to [0,1]$ (respectively,
$\varepsilon \colon \coprod _{p\geq 0} \Delta ^p\times (\mathring {\mathrm {HM}})^p\to [0,1]$ (respectively, ![]() $\varepsilon \colon \coprod _{p\geq 0} \Delta ^p\times (\breve {\mathrm {HM}})^p\to [0,1]$): for
$\varepsilon \colon \coprod _{p\geq 0} \Delta ^p\times (\breve {\mathrm {HM}})^p\to [0,1]$): for ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, we denote by
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ as in Notation 4.2, we denote by ![]() $P\subset \mathbb {R}\times [0,1]$ the support of
$P\subset \mathbb {R}\times [0,1]$ the support of ![]() $\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and set
$\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and set
where upper and lower barycentres are computed with respect to ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$. We denote
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$. We denote ![]() $b^-_\varepsilon =b^--\varepsilon$ and
$b^-_\varepsilon =b^--\varepsilon$ and ![]() $b^+_\varepsilon =b^++\varepsilon$.
$b^+_\varepsilon =b^++\varepsilon$.
We observe that ![]() $\varepsilon$ satisfies the following properties:
$\varepsilon$ satisfies the following properties:
• for all
 $(\underline {w},\underline {t},\underline {\mathfrak {c}})$ satisfying
$(\underline {w},\underline {t},\underline {\mathfrak {c}})$ satisfying  $b^-=b^+$, we have
$b^-=b^+$, we have  $\varepsilon (\underline {w},\underline {t},\underline {\mathfrak {c}})>0$;
$\varepsilon (\underline {w},\underline {t},\underline {\mathfrak {c}})>0$;• for all
 $(\underline {w},\underline {t},\underline {\mathfrak {c}})$ with
$(\underline {w},\underline {t},\underline {\mathfrak {c}})$ with  $\varepsilon (\underline {w},\underline {t},\underline {\mathfrak {c}})>0$, the configuration
$\varepsilon (\underline {w},\underline {t},\underline {\mathfrak {c}})>0$, the configuration  $\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is supported away from
$\hat {\mu }(\underline {w},\underline {t},\underline {\mathfrak {c}})$ is supported away from  $\mathbb {S}_{b^--\varepsilon,b^++\varepsilon }$.
$\mathbb {S}_{b^--\varepsilon,b^++\varepsilon }$.
The advantage of replacing ![]() $b^-$ and
$b^-$ and ![]() $b^+$ by
$b^+$ by ![]() $b^-_\varepsilon$ and
$b^-_\varepsilon$ and ![]() $b^+_\varepsilon$ is that we now have strict inequalities
$b^+_\varepsilon$ is that we now have strict inequalities ![]() $b^-_\varepsilon < b< b^+_\varepsilon$ for all
$b^-_\varepsilon < b< b^+_\varepsilon$ for all ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$. As we will see, the disadvantage that
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$. As we will see, the disadvantage that ![]() $b^+_\varepsilon -b^-_\varepsilon$ does not factor through a function defined on
$b^+_\varepsilon -b^-_\varepsilon$ does not factor through a function defined on ![]() $B\mathring {\mathrm {HM}}$ (respectively, on
$B\mathring {\mathrm {HM}}$ (respectively, on ![]() $B\breve {\mathrm {HM}}$) will be inessential.
$B\breve {\mathrm {HM}}$) will be inessential.
Recall the proof of Lemma 2.7: for ![]() $s>0$ the map
$s>0$ the map ![]() $\Lambda _s\colon \mathbb {C}\to \mathbb {C}$ is an endomorphism of the nice couple
$\Lambda _s\colon \mathbb {C}\to \mathbb {C}$ is an endomorphism of the nice couple ![]() $(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )$ (respectively,
$(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )$ (respectively, ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$), depending continuously on
$(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$), depending continuously on ![]() $s$. We obtain a continuous map
$s$. We obtain a continuous map
Similarly, recall Definition 2.9: for all ![]() $t\in \mathbb {R}$ the map
$t\in \mathbb {R}$ the map ![]() $\tau _t$ is an endomorphism of the nice couple
$\tau _t$ is an endomorphism of the nice couple ![]() $(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )$ (respectively,
$(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )$ (respectively, ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$), depending continuously on
$(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$), depending continuously on ![]() $t$. We obtain a continuous map
$t$. We obtain a continuous map
Definition 4.6 We define a map
 \[ \hat{\mu}^b\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\mathring{{\mathcal{R}}}_{\mathbb{R}})\quad \bigg(\text{respectively, } \hat{\mu}^b\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{{\mathcal{R}}}_{\mathbb{R}})\bigg) \]
\[ \hat{\mu}^b\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\mathring{{\mathcal{R}}}_{\mathbb{R}})\quad \bigg(\text{respectively, } \hat{\mu}^b\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{{\mathcal{R}}}_{\mathbb{R}})\bigg) \]
by the following assignment:
Roughly speaking, the map ![]() $\hat {\mu }^b$ has the effect of a horizontal translation and a dilation of the configuration
$\hat {\mu }^b$ has the effect of a horizontal translation and a dilation of the configuration ![]() $\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$: the effect of the translation and dilation is to map the rectangle
$\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$: the effect of the translation and dilation is to map the rectangle ![]() $[b^-_\varepsilon,b^+_\varepsilon ]\times [0,1]$ homeomorphically onto the unit square
$[b^-_\varepsilon,b^+_\varepsilon ]\times [0,1]$ homeomorphically onto the unit square ![]() ${\mathcal {R}}$.
${\mathcal {R}}$.
Definition 4.7 Let ![]() $\mathring {\diamond }$ denote the interior of
$\mathring {\diamond }$ denote the interior of ![]() $\diamond$ (see Definition 2.23) and denote
$\diamond$ (see Definition 2.23) and denote ![]() $\mathbb {R}+ {\sqrt {-1}}/{2}=\{t+ {\sqrt {-1}}/{2}\,|\,t\in \mathbb {R}\}\subset \mathbb {H}$. We introduce several nice couples:
$\mathbb {R}+ {\sqrt {-1}}/{2}=\{t+ {\sqrt {-1}}/{2}\,|\,t\in \mathbb {R}\}\subset \mathbb {H}$. We introduce several nice couples:
 \[ \begin{array}{ll} \bullet\
\breve{\mathfrak{C}}^{\Box}=(\mathring{{\mathcal{R}}}_{\mathbb{R}},\mathring{{\mathcal{R}}}_{\mathbb{R}}\setminus\mathring{{\mathcal{R}}});
& \bullet\
\breve{\mathfrak{C}}^{\diamond}=\bigg(\breve{\diamond}^{\mathrm{lr}}\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right),\left(\breve{\diamond}^{\mathrm{lr}}\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right)\right)
\setminus\mathring{\diamond}\bigg);\\ \bullet\
{\mathfrak{C}}^{\Box}=(\breve{{\mathcal{R}}}_{\mathbb{R}},\breve{{\mathcal{R}}}_{\mathbb{R}}\setminus\mathring{{\mathcal{R}}});
& \bullet\ {\mathfrak{C}}^{\diamond}= \bigg(\diamond\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right),\left(\diamond\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right)\right)
\setminus\mathring{\diamond}\bigg). \end{array}
\]
\[ \begin{array}{ll} \bullet\
\breve{\mathfrak{C}}^{\Box}=(\mathring{{\mathcal{R}}}_{\mathbb{R}},\mathring{{\mathcal{R}}}_{\mathbb{R}}\setminus\mathring{{\mathcal{R}}});
& \bullet\
\breve{\mathfrak{C}}^{\diamond}=\bigg(\breve{\diamond}^{\mathrm{lr}}\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right),\left(\breve{\diamond}^{\mathrm{lr}}\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right)\right)
\setminus\mathring{\diamond}\bigg);\\ \bullet\
{\mathfrak{C}}^{\Box}=(\breve{{\mathcal{R}}}_{\mathbb{R}},\breve{{\mathcal{R}}}_{\mathbb{R}}\setminus\mathring{{\mathcal{R}}});
& \bullet\ {\mathfrak{C}}^{\diamond}= \bigg(\diamond\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right),\left(\diamond\cup
\left(\mathbb{R}+\dfrac{\sqrt{-1}}{2}\right)\right)
\setminus\mathring{\diamond}\bigg). \end{array}
\]
Since ![]() $\operatorname {Id}_\mathbb {C}$ is a map of nice couples
$\operatorname {Id}_\mathbb {C}$ is a map of nice couples ![]() $(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )\to \breve {\mathfrak {C}}^{\Box }$ (respectively,
$(\mathring {{\mathcal {R}}}_{\mathbb {R}},\emptyset )\to \breve {\mathfrak {C}}^{\Box }$ (respectively, ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })\to {\mathfrak {C}}^{\Box }$), it induces a map
$(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })\to {\mathfrak {C}}^{\Box }$), it induces a map ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})\to \mathrm {Hur}(\breve {\mathfrak {C}}^{\Box })$ (respectively,
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})\to \mathrm {Hur}(\breve {\mathfrak {C}}^{\Box })$ (respectively, ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })\to \mathrm {Hur}({\mathfrak {C}}^{\Box })$). See Figure 4.
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })\to \mathrm {Hur}({\mathfrak {C}}^{\Box })$). See Figure 4.
Notation 4.8 By abuse of notation we will also denote by ![]() $\hat {\mu }^b$ the composition
$\hat {\mu }^b$ the composition



Figure 4. Top: nice couples ![]() $\breve {\mathfrak {C}}^{\Box }$ and
$\breve {\mathfrak {C}}^{\Box }$ and ![]() $\breve {\mathfrak {C}}^{\diamond }$. Bottom: nice couples
$\breve {\mathfrak {C}}^{\diamond }$. Bottom: nice couples ![]() ${\mathfrak {C}}^{\Box }$ and
${\mathfrak {C}}^{\Box }$ and ![]() ${\mathfrak {C}}^{\diamond }$.
${\mathfrak {C}}^{\diamond }$.
Definition 4.9 We define maps ![]() $\kappa ^-$ and
$\kappa ^-$ and ![]() $\kappa ^+ \colon \mathbb {C}\times [0,\infty )\to \mathbb {C}$ by the formulas
$\kappa ^+ \colon \mathbb {C}\times [0,\infty )\to \mathbb {C}$ by the formulas
 \begin{gather*}
\kappa^-(z,s)= \begin{cases} z & \text{if } \Re(z)\geq
0,\\ z-\Re(z) & \text{if } -s\leq \Re(z)\leq
0,\\ z+s & \text{if }\Re(z)\leq -s ;
\end{cases}\\ \kappa^+(z,s)=\begin{cases}
z & \text{if } \Re(z)\leq 1,\\ z- \Re(z)+1 &
\text{if } 1\leq \Re(z)\leq 1+s,\\ z-s & \text{if
}\Re(z)\geq 1+s . \end{cases}\end{gather*}
\begin{gather*}
\kappa^-(z,s)= \begin{cases} z & \text{if } \Re(z)\geq
0,\\ z-\Re(z) & \text{if } -s\leq \Re(z)\leq
0,\\ z+s & \text{if }\Re(z)\leq -s ;
\end{cases}\\ \kappa^+(z,s)=\begin{cases}
z & \text{if } \Re(z)\leq 1,\\ z- \Re(z)+1 &
\text{if } 1\leq \Re(z)\leq 1+s,\\ z-s & \text{if
}\Re(z)\geq 1+s . \end{cases}\end{gather*}
Roughly speaking, both ![]() $\kappa ^-$ and
$\kappa ^-$ and ![]() $\kappa ^+$ fix the vertical strip
$\kappa ^+$ fix the vertical strip ![]() $[0,1]\times \mathbb {R}$ for all
$[0,1]\times \mathbb {R}$ for all ![]() $s\geq 0$; the map
$s\geq 0$; the map ![]() $\kappa ^-(-,s)$ collapses the strip
$\kappa ^-(-,s)$ collapses the strip ![]() $[-s,0]\times \mathbb {R}$ to the vertical line
$[-s,0]\times \mathbb {R}$ to the vertical line ![]() $\mathbb {C}_{\Re =0}$ and translates
$\mathbb {C}_{\Re =0}$ and translates ![]() $(-\infty,s]\times \mathbb {R}$ to the right; instead
$(-\infty,s]\times \mathbb {R}$ to the right; instead ![]() $\kappa ^+(-,s)$ collapses the strip
$\kappa ^+(-,s)$ collapses the strip ![]() $[1,1+s]\times \mathbb {R}$ to the vertical line
$[1,1+s]\times \mathbb {R}$ to the vertical line ![]() $\mathbb {C}_{\Re =1}$ and translates
$\mathbb {C}_{\Re =1}$ and translates ![]() $[1+s,\infty )\times \mathbb {R}$ to the left.
$[1+s,\infty )\times \mathbb {R}$ to the left.
Both ![]() $\kappa ^-(-,s)$ and
$\kappa ^-(-,s)$ and ![]() $\kappa ^+(-,s)$ are morphisms of nice couples
$\kappa ^+(-,s)$ are morphisms of nice couples ![]() $\breve {\mathfrak {C}}^{\Box }\to \breve {\mathfrak {C}}^{\Box }$ (respectively,
$\breve {\mathfrak {C}}^{\Box }\to \breve {\mathfrak {C}}^{\Box }$ (respectively, ![]() ${\mathfrak {C}}^{\Box }\to {\mathfrak {C}}^{\Box }$) for all
${\mathfrak {C}}^{\Box }\to {\mathfrak {C}}^{\Box }$) for all ![]() $s\geq 0$. We obtain continuous maps
$s\geq 0$. We obtain continuous maps
 \begin{gather*} \kappa^-_*,\,\kappa^+_*\,\colon\mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\times[0,\infty)\to \mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\\ (\text{respectively, }\kappa^-_*,\,\kappa^+_*\,\colon\mathrm{Hur}({\mathfrak{C}}^{\Box})\times[0,\infty)\to \mathrm{Hur}({\mathfrak{C}}^{\Box})). \end{gather*}
\begin{gather*} \kappa^-_*,\,\kappa^+_*\,\colon\mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\times[0,\infty)\to \mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\\ (\text{respectively, }\kappa^-_*,\,\kappa^+_*\,\colon\mathrm{Hur}({\mathfrak{C}}^{\Box})\times[0,\infty)\to \mathrm{Hur}({\mathfrak{C}}^{\Box})). \end{gather*}
Notation 4.10 Recall Definition 2.25; we use the notation ![]() ${\mathcal {H}}^{\diamond }_1:={\mathcal {H}}^{\diamond }(-;1)\colon \mathbb {C}\to \mathbb {C}$.
${\mathcal {H}}^{\diamond }_1:={\mathcal {H}}^{\diamond }(-;1)\colon \mathbb {C}\to \mathbb {C}$.
Note that ![]() ${\mathcal {H}}^{\diamond }_1$ is a morphism of nice couples
${\mathcal {H}}^{\diamond }_1$ is a morphism of nice couples ![]() $\breve {\mathfrak {C}}^{\Box }\to \breve {\mathfrak {C}}^{\diamond }$ (respectively,
$\breve {\mathfrak {C}}^{\Box }\to \breve {\mathfrak {C}}^{\diamond }$ (respectively, ![]() ${\mathfrak {C}}^{\Box }\to {\mathfrak {C}}^{\diamond }$).
${\mathfrak {C}}^{\Box }\to {\mathfrak {C}}^{\diamond }$).
Definition 4.11 We define a map
 \[ \hat{\mu}^\Box\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\quad \bigg(\text{respectively, }\hat{\mu}^\Box\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}({\mathfrak{C}}^{\Box})\bigg) \]
\[ \hat{\mu}^\Box\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{\mathfrak{C}}^{\Box})\quad \bigg(\text{respectively, }\hat{\mu}^\Box\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}({\mathfrak{C}}^{\Box})\bigg) \]
by the following assignment, where ![]() $p$,
$p$, ![]() $a_p$,
$a_p$, ![]() $b^-_\varepsilon$ and
$b^-_\varepsilon$ and ![]() $b^+_\varepsilon$ depend on
$b^+_\varepsilon$ depend on ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$:
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$:
We further define
 \[ \hat{\mu}^\diamond\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{\mathfrak{C}}^{\diamond})\quad \bigg(\text{respectively, }\hat{\mu}^\diamond\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}({\mathfrak{C}}^{\diamond})\bigg) \]
\[ \hat{\mu}^\diamond\colon \coprod_{p\geq 0} \Delta^p\times(\mathring{\mathrm{HM}})^p \to \mathrm{Hur}(\breve{\mathfrak{C}}^{\diamond})\quad \bigg(\text{respectively, }\hat{\mu}^\diamond\colon \coprod_{p\geq 0} \Delta^p\times(\breve{\mathrm{HM}})^p \to \mathrm{Hur}({\mathfrak{C}}^{\diamond})\bigg) \]
as the composition ![]() $({\mathcal {H}}^{\diamond }_1)_*\circ \hat {\mu }^\Box$.
$({\mathcal {H}}^{\diamond }_1)_*\circ \hat {\mu }^\Box$.
Roughly speaking, ![]() $\hat {\mu }^\Box$ improves the effect of
$\hat {\mu }^\Box$ improves the effect of ![]() $\hat {\mu }^b$ as follows:
$\hat {\mu }^b$ as follows: ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is a configuration supported in the rectangle
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is a configuration supported in the rectangle ![]() $[ ({b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-})]\times [0,1]$ and the further application of
$[ ({b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-})]\times [0,1]$ and the further application of ![]() $\kappa ^-_*$ and
$\kappa ^-_*$ and ![]() $\kappa ^+_*$ collapse
$\kappa ^+_*$ collapse ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ to a configuration supported in
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ to a configuration supported in ![]() ${\mathcal {R}}$. The further composition
${\mathcal {R}}$. The further composition ![]() $\hat {\mu }^\diamond$ changes the configuration
$\hat {\mu }^\diamond$ changes the configuration ![]() $\hat {\mu }^\Box (\underline {w};\underline {t},\underline {\mathfrak {c}})$ to a configuration
$\hat {\mu }^\Box (\underline {w};\underline {t},\underline {\mathfrak {c}})$ to a configuration ![]() $\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$ supported in
$\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$ supported in ![]() $\diamond$.
$\diamond$.
Note that there is a natural inclusion of spaces ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {\mathfrak {C}}^{\diamond })$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\subset \mathrm {Hur}(\breve {\mathfrak {C}}^{\diamond })$ (respectively, ![]() $\mathrm {Hur}(\diamond,\partial )\subset \mathrm {Hur}({\mathfrak {C}}^{\diamond })$). The following lemma summarises the previous discussion.
$\mathrm {Hur}(\diamond,\partial )\subset \mathrm {Hur}({\mathfrak {C}}^{\diamond })$). The following lemma summarises the previous discussion.
Lemma 4.12 The map ![]() $\hat {\mu }^\diamond$ has values inside
$\hat {\mu }^\diamond$ has values inside ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (inside
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (inside ![]() $\mathrm {Hur}(\diamond,\partial )$).
$\mathrm {Hur}(\diamond,\partial )$).
Proof. Let ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2. Then
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2. Then ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is supported in the rectangle
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is supported in the rectangle ![]() $( ({-b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-}))\times (0,1)$ (in the rectangle
$( ({-b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-}))\times (0,1)$ (in the rectangle ![]() $( ({-b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-}))\times [0,1]$). This rectangle is mapped to
$( ({-b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}),1+ ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-}))\times [0,1]$). This rectangle is mapped to ![]() $\breve {{\mathcal {R}}}^{\mathrm {lr}}$ (to
$\breve {{\mathcal {R}}}^{\mathrm {lr}}$ (to ![]() ${\mathcal {R}}$) by the composition
${\mathcal {R}}$) by the composition ![]() $\kappa ^-_*(\kappa ^+_*(-; ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-})) ; ({b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}))$ and the map
$\kappa ^-_*(\kappa ^+_*(-; ({a_p-b_\varepsilon ^+})/({b_\varepsilon ^+-b_\varepsilon ^-})) ; ({b_\varepsilon ^--a_0})/({b_\varepsilon ^+-b_\varepsilon ^-}))$ and the map ![]() ${\mathcal {H}}^{\diamond }_1$ sends
${\mathcal {H}}^{\diamond }_1$ sends ![]() $\breve {{\mathcal {R}}}^{\mathrm {lr}}$ to
$\breve {{\mathcal {R}}}^{\mathrm {lr}}$ to ![]() $\breve {\diamond }^{\mathrm {lr}}$ (respectively,
$\breve {\diamond }^{\mathrm {lr}}$ (respectively, ![]() ${\mathcal {R}}$ to
${\mathcal {R}}$ to ![]() $\diamond$).
$\diamond$).
We consider now the external product
 \begin{gather*} -\times-\colon \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\times\mathrm{Ran}(\breve{\diamond}^{\mathrm{lr}})\to \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\\ (\text{respectively, }-\times-\colon \mathrm{Hur}(\diamond,\partial)\times\mathrm{Ran}(\diamond)\to \mathrm{Hur}(\diamond,\partial)) \end{gather*}
\begin{gather*} -\times-\colon \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\times\mathrm{Ran}(\breve{\diamond}^{\mathrm{lr}})\to \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\\ (\text{respectively, }-\times-\colon \mathrm{Hur}(\diamond,\partial)\times\mathrm{Ran}(\diamond)\to \mathrm{Hur}(\diamond,\partial)) \end{gather*}
from [Reference BianchiBia23a, Definition 5.7 and Notation 5.9] and evaluate the second component at ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$, thus obtaining a map
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}=\{z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}\}$, thus obtaining a map ![]() $-\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}}\colon \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (respectively,
$-\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}}\colon \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (respectively, ![]() $-\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}}\colon \mathrm {Hur}(\diamond,\partial )\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$).
$-\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}}\colon \mathrm {Hur}(\diamond,\partial )\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$).
Definition 4.13 We denote by ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ the composition
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ the composition


We denote by ![]() $\check \sigma$ the composition of
$\check \sigma$ the composition of ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ with the covering projection
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ with the covering projection
 \begin{gather*} p_{G,G^{\rm op}}\colon \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{\breve{\partial}\breve{\diamond}^{\mathrm{lr}}}\to \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\\ (\text{respectively, }p_{G,G^{\rm op}}\colon \mathrm{Hur}(\diamond,\partial)_{\breve{\partial}\breve{\diamond}^{\mathrm{lr}}}\to \mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}). \end{gather*}
\begin{gather*} p_{G,G^{\rm op}}\colon \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{\breve{\partial}\breve{\diamond}^{\mathrm{lr}}}\to \mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\\ (\text{respectively, }p_{G,G^{\rm op}}\colon \mathrm{Hur}(\diamond,\partial)_{\breve{\partial}\breve{\diamond}^{\mathrm{lr}}}\to \mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}). \end{gather*}
Here we regard ![]() $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (respectively,
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (respectively, ![]() $(\diamond,\partial )$) as an lr-based nice couple, using the two points
$(\diamond,\partial )$) as an lr-based nice couple, using the two points ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ of
$z_{\diamond }^{\mathrm {r}}$ of ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$. See Figure 5.
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$. See Figure 5.

Figure 5. Left: the product ![]() $(t_1,\mathfrak {c}_1)(t_2,\mathfrak {c}_2)(t_3,\mathfrak {c}_3)$ of three configurations in
$(t_1,\mathfrak {c}_1)(t_2,\mathfrak {c}_2)(t_3,\mathfrak {c}_3)$ of three configurations in ![]() $\breve {\mathrm {HM}}$; for a given
$\breve {\mathrm {HM}}$; for a given ![]() $\underline {w}\in \mathring {\Delta }^3$ the barycentres
$\underline {w}\in \mathring {\Delta }^3$ the barycentres ![]() $b,b_\varepsilon ^+,b_\varepsilon ^-$ are shown as dotted, vertical lines. We use the letter ‘
$b,b_\varepsilon ^+,b_\varepsilon ^-$ are shown as dotted, vertical lines. We use the letter ‘![]() $q$’ to represent the
$q$’ to represent the ![]() ${\mathcal {Q}}$-valued monodromies around points in
${\mathcal {Q}}$-valued monodromies around points in ![]() $\mathring {{\mathcal {R}}}_{\mathbb {R}}$. Right: the image of
$\mathring {{\mathcal {R}}}_{\mathbb {R}}$. Right: the image of ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ along
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ along ![]() $\check \sigma$; the question marks suggest that, because of the quotient by the
$\check \sigma$; the question marks suggest that, because of the quotient by the ![]() $G\times G^{\rm op}$-action, the monodromies of the loops spinning around
$G\times G^{\rm op}$-action, the monodromies of the loops spinning around ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ are just not defined.
$z_{\diamond }^{\mathrm {r}}$ are just not defined.
Roughly speaking, ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ improves the effect of
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ improves the effect of ![]() $\hat {\mu }^\diamond$ by forcing the presence of
$\hat {\mu }^\diamond$ by forcing the presence of ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ in support of the configuration
$z_{\diamond }^{\mathrm {r}}$ in support of the configuration ![]() $\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$, which is already supported in
$\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$, which is already supported in ![]() $\breve {\diamond }^{\mathrm {lr}}$ (in
$\breve {\diamond }^{\mathrm {lr}}$ (in ![]() $\diamond$); if either point
$\diamond$); if either point ![]() $z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$ is already in support of
$z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$ is already in support of ![]() $\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$, then its local monodromy does not change when passing to
$\hat {\mu }^\diamond (\underline {w};\underline {t},\underline {\mathfrak {c}})$, then its local monodromy does not change when passing to ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(\underline {w};\underline {t},\underline {\mathfrak {c}})$. The further composition
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(\underline {w};\underline {t},\underline {\mathfrak {c}})$. The further composition ![]() $\check \sigma$ forgets the monodromy information around the two points
$\check \sigma$ forgets the monodromy information around the two points ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ of the support of
$z_{\diamond }^{\mathrm {r}}$ of the support of ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(\underline {w};\underline {t},\underline {\mathfrak {c}})$.
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(\underline {w};\underline {t},\underline {\mathfrak {c}})$.
Notation 4.14 We endow ![]() $B\mathring {\mathrm {HM}}$ and
$B\mathring {\mathrm {HM}}$ and ![]() $\bar {B}\mathring {\mathrm {HM}}$ (respectively,
$\bar {B}\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}$ and
$B\breve {\mathrm {HM}}$ and ![]() $\bar {B}\breve {\mathrm {HM}}$) with the basepoint corresponding to the (unique)
$\bar {B}\breve {\mathrm {HM}}$) with the basepoint corresponding to the (unique) ![]() $0$-simplex in
$0$-simplex in ![]() $B_{\bullet }(\mathring {\mathrm {HM}},*)$ (in
$B_{\bullet }(\mathring {\mathrm {HM}},*)$ (in ![]() $B_{\bullet }(\breve {\mathrm {HM}},*)$). Similarly
$B_{\bullet }(\breve {\mathrm {HM}},*)$). Similarly ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) is endowed with the basepoint given by
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) is endowed with the basepoint given by ![]() $p_{G,G^{\rm op}}((\emptyset,\mathbb {1},\mathbb {1})\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}})$. We denote this basepoint by
$p_{G,G^{\rm op}}((\emptyset,\mathbb {1},\mathbb {1})\times \breve {\partial }\breve {\diamond }^{\mathrm {lr}})$. We denote this basepoint by ![]() $\mathfrak {c}^{\mathrm {lr}}\in \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\mathfrak {c}^{\mathrm {lr}}\in \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\mathfrak {c}^{\mathrm {lr}}\in \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$).
$\mathfrak {c}^{\mathrm {lr}}\in \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$).
Proposition 4.15 The map ![]() $\check \sigma$ from Definition 4.13 sends every sequence
$\check \sigma$ from Definition 4.13 sends every sequence ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ satisfying
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ satisfying ![]() $\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})>0$ to the basepoint
$\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})>0$ to the basepoint ![]() $\mathfrak {c}^{\mathrm {lr}}$. Moreover,
$\mathfrak {c}^{\mathrm {lr}}$. Moreover, ![]() $\check \sigma$ descends to a pointed map
$\check \sigma$ descends to a pointed map ![]() $\sigma \colon B\mathring {\mathrm {HM}}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\sigma \colon B\mathring {\mathrm {HM}}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\sigma \colon B\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$); the map
$\sigma \colon B\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$); the map ![]() $\sigma$ descends further to a pointed map
$\sigma$ descends further to a pointed map ![]() $\bar \sigma \colon \bar {B}\mathring {\mathrm {HM}}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\bar \sigma \colon \bar {B}\mathring {\mathrm {HM}}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\bar \sigma \colon \bar {B}\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$).
$\bar \sigma \colon \bar {B}\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$).
The proof of Proposition 4.15 is in Appendix A.4. Since the quotient map ![]() $B\mathring {\mathrm {HM}}\to \bar {B}\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}\to \bar {B}\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}\to \bar {B}\breve {\mathrm {HM}}$) is a weak equivalence, Theorem 4.1 reduces to proving that the map
$B\breve {\mathrm {HM}}\to \bar {B}\breve {\mathrm {HM}}$) is a weak equivalence, Theorem 4.1 reduces to proving that the map ![]() $\bar \sigma$ is a weak equivalence. In fact, we will prove surjectivity of
$\bar \sigma$ is a weak equivalence. In fact, we will prove surjectivity of ![]() $\sigma _*$ and injectivity of
$\sigma _*$ and injectivity of ![]() $\bar \sigma _*$ on homotopy groups.
$\bar \sigma _*$ on homotopy groups.
4.2 Surjectivity on homotopy groups
We fix ![]() $q\geq 0$ and want to show that
$q\geq 0$ and want to show that ![]() $\sigma _*\colon \pi _q( B\mathring {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively,
$\sigma _*\colon \pi _q( B\mathring {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively, ![]() $\sigma _*\colon \pi _q(B\breve {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is surjective. For
$\sigma _*\colon \pi _q(B\breve {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is surjective. For ![]() $q=0$ this will imply, in particular, that
$q=0$ this will imply, in particular, that ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) is connected.
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) is connected.
Notation 4.16 We denote by ![]() $\mathring {\mathrm {HM}}_\emptyset \subset \mathring {\mathrm {HM}}$ (respectively,
$\mathring {\mathrm {HM}}_\emptyset \subset \mathring {\mathrm {HM}}$ (respectively, ![]() $\breve {\mathrm {HM}}_\emptyset \subset \breve {\mathrm {HM}}$) the component of the neutral element: it contains all couples
$\breve {\mathrm {HM}}_\emptyset \subset \breve {\mathrm {HM}}$) the component of the neutral element: it contains all couples ![]() $(t,(\emptyset,\mathbb {1},\mathbb {1}))$ for
$(t,(\emptyset,\mathbb {1},\mathbb {1}))$ for ![]() $t\ge 0$.
$t\ge 0$.
Note that ![]() $\mathring {\mathrm {HM}}_\emptyset$ (respectively,
$\mathring {\mathrm {HM}}_\emptyset$ (respectively, ![]() $\breve {\mathrm {HM}}_\emptyset$) is a contractible topological monoid, hence the subspace
$\breve {\mathrm {HM}}_\emptyset$) is a contractible topological monoid, hence the subspace ![]() $B\mathring {\mathrm {HM}}_\emptyset \subset B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}_\emptyset \subset B\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}_\emptyset \subset B\breve {\mathrm {HM}}$) is also contractible. Moreover, the map
$B\breve {\mathrm {HM}}_\emptyset \subset B\breve {\mathrm {HM}}$) is also contractible. Moreover, the map ![]() $\sigma$ sends
$\sigma$ sends ![]() $B\mathring {\mathrm {HM}}_\emptyset$ (respectively,
$B\mathring {\mathrm {HM}}_\emptyset$ (respectively, ![]() $B\breve {\mathrm {HM}}_\emptyset$) constantly to the basepoint
$B\breve {\mathrm {HM}}_\emptyset$) constantly to the basepoint ![]() $\mathfrak {c}^{\mathrm {lr}}$.
$\mathfrak {c}^{\mathrm {lr}}$.
In order to prove that ![]() $\sigma$ induces an isomorphism on
$\sigma$ induces an isomorphism on ![]() $q$-homotopy groups, it suffices to prove that the map
$q$-homotopy groups, it suffices to prove that the map ![]() $\sigma _*\colon \pi _q(B\mathring {\mathrm {HM}},B\mathring {\mathrm {HM}}_\emptyset )\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively,
$\sigma _*\colon \pi _q(B\mathring {\mathrm {HM}},B\mathring {\mathrm {HM}}_\emptyset )\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively, ![]() $\sigma _*\colon \pi _q(B\breve {\mathrm {HM}},B\breve {\mathrm {HM}}_\emptyset )\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is an isomorphism, i.e. we can consider relative homotopy groups.
$\sigma _*\colon \pi _q(B\breve {\mathrm {HM}},B\breve {\mathrm {HM}}_\emptyset )\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is an isomorphism, i.e. we can consider relative homotopy groups.
To show that ![]() $\sigma _*$ is surjective, represent an element of
$\sigma _*$ is surjective, represent an element of ![]() $\pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (of
$\pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (of ![]() $\pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) by a map
$\pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) by a map
sending ![]() $\partial D^q$ to the basepoint
$\partial D^q$ to the basepoint ![]() $\mathfrak {c}^{\mathrm {lr}}$. Thus, for all
$\mathfrak {c}^{\mathrm {lr}}$. Thus, for all ![]() $v\in D^q$ we have an orbit
$v\in D^q$ we have an orbit ![]() $f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$ of the action of
$f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$ of the action of ![]() $G\times G^{\rm op}$ on
$G\times G^{\rm op}$ on ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (on
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (on ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$). We choose for all
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$). We choose for all ![]() $v\in D^q$ a representative
$v\in D^q$ a representative ![]() $\mathfrak {c}_v=(P_v,\psi _v,\varphi _v)$ of
$\mathfrak {c}_v=(P_v,\psi _v,\varphi _v)$ of ![]() $f(v)$; note that the sets
$f(v)$; note that the sets ![]() $P_v\subset \breve {\diamond }^{\mathrm {lr}}$ (respectively,
$P_v\subset \breve {\diamond }^{\mathrm {lr}}$ (respectively, ![]() $P_v\subset \diamond$) do not depend on this choice; similarly the evaluation of
$P_v\subset \diamond$) do not depend on this choice; similarly the evaluation of ![]() $\psi _v$ and
$\psi _v$ and ![]() $\varphi _v$ is independent of the choice of
$\varphi _v$ is independent of the choice of ![]() $\mathfrak {c}_v$ on those elements of
$\mathfrak {c}_v$ on those elements of ![]() $\mathfrak {Q}(P_v)$ and
$\mathfrak {Q}(P_v)$ and ![]() $\mathfrak {G}(P_v)$ that can be represented by a loop contained in
$\mathfrak {G}(P_v)$ that can be represented by a loop contained in ![]() $[0,1]\times \mathbb {R}\,\setminus P_v$.
$[0,1]\times \mathbb {R}\,\setminus P_v$.
For all ![]() $v\in D^q$ we can find an open interval
$v\in D^q$ we can find an open interval ![]() $J_v\subset (0,1)$ and a neighbourhood
$J_v\subset (0,1)$ and a neighbourhood ![]() $v\in V_v\subseteq D^q$ such that for all
$v\in V_v\subseteq D^q$ such that for all ![]() $v'\in V_v$ the finite set
$v'\in V_v$ the finite set ![]() $\Re (P_{v'})$ is disjoint from
$\Re (P_{v'})$ is disjoint from ![]() $J_v$. Using the compactness of
$J_v$. Using the compactness of ![]() $D^q$, we can then choose a cover of
$D^q$, we can then choose a cover of ![]() $D^q$ by finitely many open sets
$D^q$ by finitely many open sets ![]() $V_i$ with corresponding open intervals
$V_i$ with corresponding open intervals ![]() $J_i\subset (0,1)$, satisfying
$J_i\subset (0,1)$, satisfying ![]() $\Re (P_v)\cap J_i=\emptyset$ for all
$\Re (P_v)\cap J_i=\emptyset$ for all ![]() $v\in V_i$. After shrinking the intervals
$v\in V_i$. After shrinking the intervals ![]() $J_i$ appropriately, we can assume they are disjoint. To fix notation, we assume that we have
$J_i$ appropriately, we can assume they are disjoint. To fix notation, we assume that we have ![]() $r$ open sets
$r$ open sets ![]() $V_1,\ldots, V_r$, such that the corresponding intervals
$V_1,\ldots, V_r$, such that the corresponding intervals ![]() $J_1,\ldots,J_r$ appear in this order, from left to right, on
$J_1,\ldots,J_r$ appear in this order, from left to right, on ![]() $(0,1)$.
$(0,1)$.
We choose numbers ![]() $A_i\in J_i$: note that
$A_i\in J_i$: note that ![]() $\mathbb {S}_{A_i,A_i}$ is disjoint from
$\mathbb {S}_{A_i,A_i}$ is disjoint from ![]() $P_v$ for all
$P_v$ for all ![]() $v\in V_i$ and that the numbers
$v\in V_i$ and that the numbers ![]() $A_1,\ldots,A_r$ are all distinct. We fix weights
$A_1,\ldots,A_r$ are all distinct. We fix weights ![]() $W_i\colon D^q\to [0,1]$ giving a partition of unity on
$W_i\colon D^q\to [0,1]$ giving a partition of unity on ![]() $D^q$ subordinate to the covering
$D^q$ subordinate to the covering ![]() $\{V_1,\ldots,V_r\}$. We also assume that for each
$\{V_1,\ldots,V_r\}$. We also assume that for each ![]() $v\in D^q$ there are at least two distinct indices
$v\in D^q$ there are at least two distinct indices ![]() $1\le i\le r$ such that
$1\le i\le r$ such that ![]() $W_i(v)>0$.
$W_i(v)>0$.
Notation 4.17 Let ![]() $0< t< t'< 1$. We denote by
$0< t< t'< 1$. We denote by ![]() $\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (respectively,
$\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (respectively, ![]() $(\diamond _{t,t'},\partial )$) the space
$(\diamond _{t,t'},\partial )$) the space ![]() $\breve {\diamond }^{\mathrm {lr}}\cap (t,t')\times \mathbb {R}$ (the nice couple
$\breve {\diamond }^{\mathrm {lr}}\cap (t,t')\times \mathbb {R}$ (the nice couple ![]() $(\diamond \cap (t,t')\times \mathbb {R},\partial \diamond \cap (t,t')\times \mathbb {R})$).
$(\diamond \cap (t,t')\times \mathbb {R},\partial \diamond \cap (t,t')\times \mathbb {R})$).
Recall Notation 2.3: we denote by ![]() $\mathring {{\mathcal {R}}}_{t,t'}$ (by
$\mathring {{\mathcal {R}}}_{t,t'}$ (by ![]() $(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })$) the space
$(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })$) the space ![]() $(t,t')\times (0,1)$ (the nice couple
$(t,t')\times (0,1)$ (the nice couple ![]() $((t,t')\times [0,1],(t,t')\times \{0,1\})$).
$((t,t')\times [0,1],(t,t')\times \{0,1\})$).
Lemma 4.18 For all ![]() $0< t< t'<1$ the map
$0< t< t'<1$ the map ![]() ${\mathcal {H}}^{\diamond }_1$ induces a homeomorphism
${\mathcal {H}}^{\diamond }_1$ induces a homeomorphism ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{t,t'})\cong \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{t,t'})$ (respectively,
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{t,t'})\cong \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{t,t'})$ (respectively, ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })\cong \mathrm {Hur}(\diamond _{t,t'},\partial )$).
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })\cong \mathrm {Hur}(\diamond _{t,t'},\partial )$).
Proof. Note that ![]() ${\mathcal {H}}^{\diamond }_1$ restricts to a semialgebraic homeomorphism of the subspace
${\mathcal {H}}^{\diamond }_1$ restricts to a semialgebraic homeomorphism of the subspace
The space ![]() $\mathbb {T}$ is contractible and the interior
$\mathbb {T}$ is contractible and the interior ![]() $\mathring {\mathbb {T}}$ contains the spaces
$\mathring {\mathbb {T}}$ contains the spaces ![]() $\mathring {{\mathcal {R}}}_{t,t'}$ and
$\mathring {{\mathcal {R}}}_{t,t'}$ and ![]() $\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (the spaces
$\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (the spaces ![]() $\breve {{\mathcal {R}}}_{t,t'}$ and
$\breve {{\mathcal {R}}}_{t,t'}$ and ![]() $\diamond _{t,t'}$). Moreover, the space
$\diamond _{t,t'}$). Moreover, the space ![]() $\mathring {{\mathcal {R}}}_{t,t'}$ (the nice couple
$\mathring {{\mathcal {R}}}_{t,t'}$ (the nice couple ![]() $(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })$) is mapped along
$(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })$) is mapped along ![]() ${\mathcal {H}}^{\diamond }_1$ homeomorphically to the space
${\mathcal {H}}^{\diamond }_1$ homeomorphically to the space ![]() $\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (to the nice couple
$\breve {\diamond }^{\mathrm {lr}}_{t,t'}$ (to the nice couple ![]() $(\diamond _{t,t'},\partial )$). It follows that
$(\diamond _{t,t'},\partial )$). It follows that ![]() ${\mathcal {H}}^{\diamond }_1$ induces a homeomorphism
${\mathcal {H}}^{\diamond }_1$ induces a homeomorphism ![]() $\mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}}_{t,t'})\cong \mathrm {Hur}^{\mathbb {T}}(\breve {\diamond }^{\mathrm {lr}}_{t,t'})$ (respectively,
$\mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}}_{t,t'})\cong \mathrm {Hur}^{\mathbb {T}}(\breve {\diamond }^{\mathrm {lr}}_{t,t'})$ (respectively, ![]() $\mathrm {Hur}^{\mathbb {T}}(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })\cong \mathrm {Hur}^{\mathbb {T}}(\diamond _{t,t'},\partial )$) and the statement is a consequence of the natural homeomorphism
$\mathrm {Hur}^{\mathbb {T}}(\breve {{\mathcal {R}}}_{t,t'},\breve {\partial })\cong \mathrm {Hur}^{\mathbb {T}}(\diamond _{t,t'},\partial )$) and the statement is a consequence of the natural homeomorphism ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}\colon \mathrm {Hur}(\mathfrak {C})\cong \mathrm {Hur}^{\mathbb {T}}(\mathfrak {C})$ holding for all nice couples
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}\colon \mathrm {Hur}(\mathfrak {C})\cong \mathrm {Hur}^{\mathbb {T}}(\mathfrak {C})$ holding for all nice couples ![]() $\mathfrak {C}$ contained in the interior of
$\mathfrak {C}$ contained in the interior of ![]() $\mathbb {T}$.
$\mathbb {T}$.
Notation 4.19 For all ![]() $v\in D^q$ we list the indices
$v\in D^q$ we list the indices ![]() $1\leq i_0<\cdots < i_{p_v}\leq r$ satisfying
$1\leq i_0<\cdots < i_{p_v}\leq r$ satisfying ![]() $W_{i_j}(v)>0$, for some
$W_{i_j}(v)>0$, for some ![]() $p_v\ge 1$ depending on
$p_v\ge 1$ depending on ![]() $v$: here, recall our assumption that for each
$v$: here, recall our assumption that for each ![]() $v\in D^q$ there are at least two indices
$v\in D^q$ there are at least two indices ![]() $i$ with
$i$ with ![]() $W_i(v)>0$. We denote by
$W_i(v)>0$. We denote by ![]() $A_0^v,\ldots, A_{p_v}^v$ the list
$A_0^v,\ldots, A_{p_v}^v$ the list ![]() $A_{i_0},\ldots,A_{i_{p_v}}$. We set
$A_{i_0},\ldots,A_{i_{p_v}}$. We set ![]() $B^v=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^v$. For all
$B^v=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^v$. For all ![]() $0\le j\le p_v$ we set
$0\le j\le p_v$ we set ![]() $A_i^{v,+}=\max \{A_i^v,B^v\}$ and
$A_i^{v,+}=\max \{A_i^v,B^v\}$ and ![]() $A_i^{v,-}=\min \{A_i^v,B^v\}$. We set
$A_i^{v,-}=\min \{A_i^v,B^v\}$. We set ![]() $B^{v,+}=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^{v,+}$ and
$B^{v,+}=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^{v,+}$ and ![]() $B^{v,-}=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^{v,-}$.
$B^{v,-}=\sum _{j=0}^{p_v} W_{i_j}(v)A_{i_j}^{v,-}$.
Note that the numbers ![]() $B^v$,
$B^v$, ![]() $B^{v,+}$ and
$B^{v,+}$ and ![]() $B^{v,-}$ vary continuously in
$B^{v,-}$ vary continuously in ![]() $v\in D^q$ and attain values in
$v\in D^q$ and attain values in ![]() $(0,1)$. Note also that we have a sequence of strict inequalities
$(0,1)$. Note also that we have a sequence of strict inequalities ![]() $0< A_0^v< B^{v,-}< B^v< B^{v,+}< A_{p_v}^v<1$. In the following, for all
$0< A_0^v< B^{v,-}< B^v< B^{v,+}< A_{p_v}^v<1$. In the following, for all ![]() $1\leq j\leq p_v$ we construct a configuration
$1\leq j\leq p_v$ we construct a configuration ![]() $\mathfrak {c}_{v,j}=(P_{v,j},\psi _{v,j},\varphi _{v,j})$ in
$\mathfrak {c}_{v,j}=(P_{v,j},\psi _{v,j},\varphi _{v,j})$ in ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A_{j-1}^v,A_j^v},\breve {\partial })$ (in
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A_{j-1}^v,A_j^v},\breve {\partial })$ (in ![]() $\mathrm {Hur}(\diamond _{A_{j-1}^v,A_j^v},\partial )$): roughly speaking,
$\mathrm {Hur}(\diamond _{A_{j-1}^v,A_j^v},\partial )$): roughly speaking, ![]() $\mathfrak {c}_{v,j}$ will be the part of
$\mathfrak {c}_{v,j}$ will be the part of ![]() $\mathfrak {c}_v$ contained in the vertical strip
$\mathfrak {c}_v$ contained in the vertical strip ![]() $(A_{j-1}^v,A_j^v)\times \mathbb {R}$. See Figure 6.
$(A_{j-1}^v,A_j^v)\times \mathbb {R}$. See Figure 6.

Figure 6. Left: a configuration ![]() $\mathfrak {c}_v\in \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$, in the case
$\mathfrak {c}_v\in \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$, in the case ![]() $p_v=1$. Right: the clipped configuration
$p_v=1$. Right: the clipped configuration ![]() $\mathfrak {c}_{v,1}\in \mathrm {Hur}(\diamond _{A_0^v,A_1^v},\partial )$.
$\mathfrak {c}_{v,1}\in \mathrm {Hur}(\diamond _{A_0^v,A_1^v},\partial )$.
To define ![]() $\mathfrak {c}_{v,j}$, note that
$\mathfrak {c}_{v,j}$, note that ![]() $P_v$ is disjoint from the vertical lines
$P_v$ is disjoint from the vertical lines ![]() $\{A_{j-1}^v,A_j^v\}\times \mathbb {R}$; as a consequence
$\{A_{j-1}^v,A_j^v\}\times \mathbb {R}$; as a consequence ![]() $P_v$ is contained in the disjoint union
$P_v$ is contained in the disjoint union ![]() $\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j} \sqcup (\breve {\diamond }^{\mathrm {lr}}\setminus \mathbb {S}_{A^v_{j-1},A^v_j})$ (respectively,
$\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j} \sqcup (\breve {\diamond }^{\mathrm {lr}}\setminus \mathbb {S}_{A^v_{j-1},A^v_j})$ (respectively, ![]() $\diamond _{A^v_{j-1},A^v_j} \sqcup (\diamond \setminus \mathbb {S}_{A^v_{j-1},A^v_j})$); note that the first space
$\diamond _{A^v_{j-1},A^v_j} \sqcup (\diamond \setminus \mathbb {S}_{A^v_{j-1},A^v_j})$); note that the first space ![]() $\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j}$ (respectively,
$\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j}$ (respectively, ![]() $\diamond _{A^v_{j-1},A^v_j}$) is contained in the interior of
$\diamond _{A^v_{j-1},A^v_j}$) is contained in the interior of ![]() $\mathbb {S}_{A^v_{j-1},A^v_j}$, whereas the second space
$\mathbb {S}_{A^v_{j-1},A^v_j}$, whereas the second space ![]() $\breve {\diamond }^{\mathrm {lr}}\setminus \mathbb {S}_{A^v_{j-1},A^v_j}$ (respectively,
$\breve {\diamond }^{\mathrm {lr}}\setminus \mathbb {S}_{A^v_{j-1},A^v_j}$ (respectively, ![]() $\diamond \setminus \mathbb {S}_{A^v_{j-1},A^v_j}$) is contained in the interior of
$\diamond \setminus \mathbb {S}_{A^v_{j-1},A^v_j}$) is contained in the interior of ![]() $\mathbb {C}\setminus \mathbb {S}_{A^v_{j-1},A^v_j}$. We use the restriction map
$\mathbb {C}\setminus \mathbb {S}_{A^v_{j-1},A^v_j}$. We use the restriction map
 \begin{gather*} \mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}}\colon \mathrm{Hur}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j} \sqcup \big(\breve{\diamond}^{\mathrm{lr}}\setminus\mathbb{S}_{A^v_{j-1},A^v_j}\big),\breve{\partial}\breve{\diamond}^{\mathrm{lr}}\Big) \to \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\\ \Big(\text{respectively, }\mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}}\colon\!\mathrm{Hur}\!\Big(\diamond_{A^v_{j-1},A^v_j} \sqcup \big(\diamond\setminus\mathbb{S}_{A^v_{j-1},A^v_j}\big),\partial\!\Big) \to \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\Big) \end{gather*}
\begin{gather*} \mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}}\colon \mathrm{Hur}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j} \sqcup \big(\breve{\diamond}^{\mathrm{lr}}\setminus\mathbb{S}_{A^v_{j-1},A^v_j}\big),\breve{\partial}\breve{\diamond}^{\mathrm{lr}}\Big) \to \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\\ \Big(\text{respectively, }\mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}}\colon\!\mathrm{Hur}\!\Big(\diamond_{A^v_{j-1},A^v_j} \sqcup \big(\diamond\setminus\mathbb{S}_{A^v_{j-1},A^v_j}\big),\partial\!\Big) \to \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\Big) \end{gather*}
from [Reference BianchiBia23a, Definition 3.15] and define ![]() $\mathfrak {c}_{v,j}$ as the image of
$\mathfrak {c}_{v,j}$ as the image of ![]() $\mathfrak {c}_v$ along this map. We can then use the canonical identification
$\mathfrak {c}_v$ along this map. We can then use the canonical identification
 \begin{gather*} \mathfrak{i}^{\mathbb{C}}_{\mathbb{S}_{A^v_{j-1},A^v_j}}\colon \mathrm{Hur}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\cong \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\\ \Big(\text{respectively, }\mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}} \colon \mathrm{Hur}\big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\to\mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}} \big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\Big) \end{gather*}
\begin{gather*} \mathfrak{i}^{\mathbb{C}}_{\mathbb{S}_{A^v_{j-1},A^v_j}}\colon \mathrm{Hur}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\cong \mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}}\Big(\breve{\diamond}^{\mathrm{lr}}_{A^v_{j-1},A^v_j}\Big)\\ \Big(\text{respectively, }\mathfrak{i}_{\mathbb{S}_{A^v_{j-1},A^v_j}}^{\mathbb{C}} \colon \mathrm{Hur}\big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\to\mathrm{Hur}^{\mathbb{S}_{A^v_{j-1},A^v_j}} \big(\diamond_{A^v_{j-1},A^v_j},\partial\big)\Big) \end{gather*}
to regard ![]() $\mathfrak {c}_{v,j}$ as a configuration in
$\mathfrak {c}_{v,j}$ as a configuration in ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j})$ (in
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j})$ (in ![]() $\mathrm {Hur}(\diamond _{A^v_{j-1},A^v_j},\partial )$).
$\mathrm {Hur}(\diamond _{A^v_{j-1},A^v_j},\partial )$).
Note that ![]() $\mathfrak {c}_{v,j}$ does not depend on the choice of a representative
$\mathfrak {c}_{v,j}$ does not depend on the choice of a representative ![]() $\mathfrak {c}_v$ of
$\mathfrak {c}_v$ of ![]() $f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$. Let
$f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$. Let ![]() $\mathbb {T}$ be as in the proof of Lemma 4.18; then we can regard
$\mathbb {T}$ be as in the proof of Lemma 4.18; then we can regard ![]() $\mathfrak {c}_{v,j}$ as a configuration in
$\mathfrak {c}_{v,j}$ as a configuration in ![]() $\mathrm {Hur}^{\mathbb {T}}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j})$ (in
$\mathrm {Hur}^{\mathbb {T}}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_j})$ (in ![]() $\mathrm {Hur}^{\mathbb {T}}(\diamond _{A^v_{j-1},A^v_j},\partial )$) using the canonical identification
$\mathrm {Hur}^{\mathbb {T}}(\diamond _{A^v_{j-1},A^v_j},\partial )$) using the canonical identification ![]() $\mathfrak {i}^{\mathbb {T}}_{\mathbb {S}_{A^v_{j-1},A^v_j}}$.
$\mathfrak {i}^{\mathbb {T}}_{\mathbb {S}_{A^v_{j-1},A^v_j}}$.
By Lemma 4.18 we can consider for all ![]() $1\le j\le p_v$ the configuration
$1\le j\le p_v$ the configuration ![]() $({\mathcal {H}}^{\diamond }_1)_*^{-1}(\mathfrak {c}_{v,j})$ lying in the space
$({\mathcal {H}}^{\diamond }_1)_*^{-1}(\mathfrak {c}_{v,j})$ lying in the space ![]() $\mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}}_{A_{j-1}^v,A_j^v})$ (in
$\mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}}_{A_{j-1}^v,A_j^v})$ (in ![]() $\mathrm {Hur}^{\mathbb {T}}(\breve {{\mathcal {R}}}_{A_{j-1}^v,A_j^v},\breve {\partial })$); using the identification
$\mathrm {Hur}^{\mathbb {T}}(\breve {{\mathcal {R}}}_{A_{j-1}^v,A_j^v},\breve {\partial })$); using the identification ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ we can regard
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ we can regard ![]() $({\mathcal {H}}^{\diamond }_1)_*^{-1}(\mathfrak {c}_{v,j})$ as lying in
$({\mathcal {H}}^{\diamond }_1)_*^{-1}(\mathfrak {c}_{v,j})$ as lying in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_{j-1}^v,A_j^v})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_{j-1}^v,A_j^v})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{A_{j-1}^v,A_j^v},\breve {\partial })$). Composing further with the map
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{A_{j-1}^v,A_j^v},\breve {\partial })$). Composing further with the map ![]() $\tau _{-A_{j-1}^v}$ we obtain configurations
$\tau _{-A_{j-1}^v}$ we obtain configurations
lying in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_j^v-A_{j-1}^v})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_j^v-A_{j-1}^v})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{A_j^v-A_{j-1}^v},\breve {\partial })$), for
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{A_j^v-A_{j-1}^v},\breve {\partial })$), for ![]() $1\leq j\leq p_v$.
$1\leq j\leq p_v$.
In other words, we obtain couples ![]() $(A_1^v-A_0^v,\mathfrak {c}'_{v,1}),\ldots,(A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ in
$(A_1^v-A_0^v,\mathfrak {c}'_{v,1}),\ldots,(A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$); the product
$\breve {\mathrm {HM}}$); the product ![]() $(A_1^v-A_0^v,\mathfrak {c}'_{v,1})\cdots (A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ of these configurations has the form
$(A_1^v-A_0^v,\mathfrak {c}'_{v,1})\cdots (A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ of these configurations has the form ![]() $(A_{p_v}^v-A_0^v,\mathfrak {c}')$, for some
$(A_{p_v}^v-A_0^v,\mathfrak {c}')$, for some ![]() $\mathfrak {c}'\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_{p_v}^v-A_0^v})$ (respectively,
$\mathfrak {c}'\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{A_{p_v}^v-A_0^v})$ (respectively, ![]() $\mathfrak {c}'\in \mathrm {Hur}(\breve {{\mathcal {R}}}_{A_{p_v}^v-A_0^v},\breve {\partial })$): we then have, roughly speaking, that
$\mathfrak {c}'\in \mathrm {Hur}(\breve {{\mathcal {R}}}_{A_{p_v}^v-A_0^v},\breve {\partial })$): we then have, roughly speaking, that ![]() ${\mathcal {H}}^{\diamond }_1(\tau _{A_0^v}(\mathfrak {c}'))$ recovers the part of
${\mathcal {H}}^{\diamond }_1(\tau _{A_0^v}(\mathfrak {c}'))$ recovers the part of ![]() $\mathfrak {c}_v$ in the vertical strip
$\mathfrak {c}_v$ in the vertical strip ![]() $(A_0^v,A_{p_v}^v)\times \mathbb {R}$.
$(A_0^v,A_{p_v}^v)\times \mathbb {R}$.
We can define a map ![]() $g\colon D^q\to B\mathring {\mathrm {HM}}$ (respectively,
$g\colon D^q\to B\mathring {\mathrm {HM}}$ (respectively, ![]() $g\colon D^q\to B\breve {\mathrm {HM}}$) by the formula
$g\colon D^q\to B\breve {\mathrm {HM}}$) by the formula
To see that ![]() $g$ is continuous, note that if a weight
$g$ is continuous, note that if a weight ![]() $W_{i_j}(v)$ goes to 0, then the number
$W_{i_j}(v)$ goes to 0, then the number ![]() $A^v_j$ is dropped from the list
$A^v_j$ is dropped from the list ![]() $A_0^v,\ldots,A_{p_v}^v$ and the following happens:
$A_0^v,\ldots,A_{p_v}^v$ and the following happens:
• if
 $1\leq j\leq p_v-1$, then the configurations
$1\leq j\leq p_v-1$, then the configurations  $(A_j^v-A_{j-1}^v,\mathfrak {c}'_{v,j})$ and
$(A_j^v-A_{j-1}^v,\mathfrak {c}'_{v,j})$ and  $(A_{j+1}^v-A_j^v,\mathfrak {c}'_{v,j+1})$ are replaced in the formula above by their product in
$(A_{j+1}^v-A_j^v,\mathfrak {c}'_{v,j+1})$ are replaced in the formula above by their product in  $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in  $\breve {\mathrm {HM}}$), according to the identifications defining
$\breve {\mathrm {HM}}$), according to the identifications defining  $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively,  $B\breve {\mathrm {HM}}$); this is compatible with the fact that the configurations
$B\breve {\mathrm {HM}}$); this is compatible with the fact that the configurations  $\mathfrak {c}_{v,j}$ and
$\mathfrak {c}_{v,j}$ and  $\mathfrak {c}_{v,j+1}$ are ‘adjacent’ in
$\mathfrak {c}_{v,j+1}$ are ‘adjacent’ in  $\breve {\diamond }^{\mathrm {lr}}$ (in
$\breve {\diamond }^{\mathrm {lr}}$ (in  $\diamond$) and if
$\diamond$) and if  $A^v_j$ is dropped these two configurations are replaced in the construction by their ‘concatenation’ in
$A^v_j$ is dropped these two configurations are replaced in the construction by their ‘concatenation’ in  $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_{j+1}})$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}}_{A^v_{j-1},A^v_{j+1}})$ (respectively,  $\mathrm {Hur}(\diamond {A^v_{j-1},A^v_{j+1}},\partial )$), which is up to canonical identifications the configuration
$\mathrm {Hur}(\diamond {A^v_{j-1},A^v_{j+1}},\partial )$), which is up to canonical identifications the configuration  $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{A^v_{j-1},A^v_{j+1}}}(\mathfrak {c}_v)$;
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{A^v_{j-1},A^v_{j+1}}}(\mathfrak {c}_v)$;• if
 $j=0$ or
$j=0$ or  $j=p_v$, then the configuration
$j=p_v$, then the configuration  $(A_1^v-A_0^v,\mathfrak {c}'_{v,1})$ or
$(A_1^v-A_0^v,\mathfrak {c}'_{v,1})$ or  $(A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ is dropped in the formula above, according to the identifications defining of
$(A_{p_v}^v-A_{p_v-1}^v,\mathfrak {c}'_{v,p_v})$ is dropped in the formula above, according to the identifications defining of  $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively,  $B\breve {\mathrm {HM}}$); this is compatible with the fact that the configuration
$B\breve {\mathrm {HM}}$); this is compatible with the fact that the configuration  $\mathfrak {c}_{v,0}$ or
$\mathfrak {c}_{v,0}$ or  $\mathfrak {c}_{v,p_v}$ is also dropped in the construction, as soon as
$\mathfrak {c}_{v,p_v}$ is also dropped in the construction, as soon as  $A^v_0$ or
$A^v_0$ or  $A^v_{p_v}$ is dropped.
$A^v_{p_v}$ is dropped.
Note also that ![]() $g$ sends
$g$ sends ![]() $\partial D^q$ inside
$\partial D^q$ inside ![]() $B\mathring {\mathrm {HM}}_\emptyset$ (inside
$B\mathring {\mathrm {HM}}_\emptyset$ (inside ![]() $B\breve {\mathrm {HM}}_\emptyset$): in fact, if
$B\breve {\mathrm {HM}}_\emptyset$): in fact, if ![]() $f(v)=\mathfrak {c}^{\mathrm {lr}}$, then all configurations
$f(v)=\mathfrak {c}^{\mathrm {lr}}$, then all configurations ![]() $\mathfrak {c}'_{v,j}$ are supported on the empty set. For
$\mathfrak {c}'_{v,j}$ are supported on the empty set. For ![]() $v\in D^q$ we remark, moreover, the equalities
$v\in D^q$ we remark, moreover, the equalities ![]() $B^{v,-}-A_0^v=b^-(g(v))$ and
$B^{v,-}-A_0^v=b^-(g(v))$ and ![]() $B^{v,+}-A_0^v=b^+(g(v))$, by virtue of which the lower and upper barycentres of
$B^{v,+}-A_0^v=b^+(g(v))$, by virtue of which the lower and upper barycentres of ![]() $g(v)$ can be recovered from the numbers
$g(v)$ can be recovered from the numbers ![]() $B^{v,-}$ and
$B^{v,-}$ and ![]() $B^{v,+}$ and vice versa, once the ‘translation parameter’
$B^{v,+}$ and vice versa, once the ‘translation parameter’ ![]() $A_0^v$ is known; in particular,
$A_0^v$ is known; in particular, ![]() $B^{v,+}-B^{v,-}=b^+(g(v))-b^-(g(v))$.
$B^{v,+}-B^{v,-}=b^+(g(v))-b^-(g(v))$.
We are left to prove that ![]() $\sigma g$ is homotopic to
$\sigma g$ is homotopic to ![]() $f$, relative to
$f$, relative to ![]() $\partial D^q$, i.e. they represent the same element in
$\partial D^q$, i.e. they represent the same element in ![]() $\pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (in
$\pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (in ![]() $\pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$).
$\pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$).
Definition 4.20 Recall Definitions 2.22 and 2.25. For all ![]() $0< t<1$ we define homotopies
$0< t<1$ we define homotopies ![]() ${\mathcal {H}}^{\diamond,\mathrm {l}}_t,{\mathcal {H}}^{\diamond,\mathrm {r}}_t\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formula:
${\mathcal {H}}^{\diamond,\mathrm {l}}_t,{\mathcal {H}}^{\diamond,\mathrm {r}}_t\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ by the following formula:
 \[
{\mathcal{H}}^{\diamond,\bullet}_t(z,s)=\left\{\begin{array}{@{}ll}
{\mathcal{H}}^{\bullet}_t(z,s)+(\mathfrak{d}^{\diamond}(z)-\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s)))\sqrt{-1}
& \text{if } z\notin\mathring{\diamond},\ \Im(z)\geq \dfrac
12\\
{\mathcal{H}}^{\bullet}_t(z,s)-(\mathfrak{d}^{\diamond}(z)-\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s)))\sqrt{-1}
& \text{if } z\notin\mathring{\diamond},\ \Im(z)\leq \dfrac
12\\
{\mathcal{H}}^{\bullet}_t(z,s)-\left(\Im(z)-\dfrac12\right)\dfrac{\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s))-\mathfrak{d}^{\diamond}(z)}{\dfrac
12-\mathfrak{d}^{\diamond}(z)}\sqrt{-1} & \text{if }
z\in\diamond,\ z\neq
z_{\diamond}^{\mathrm{l}},z_{\diamond}^{\mathrm{r}}.
\end{array}\right. \]
\[
{\mathcal{H}}^{\diamond,\bullet}_t(z,s)=\left\{\begin{array}{@{}ll}
{\mathcal{H}}^{\bullet}_t(z,s)+(\mathfrak{d}^{\diamond}(z)-\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s)))\sqrt{-1}
& \text{if } z\notin\mathring{\diamond},\ \Im(z)\geq \dfrac
12\\
{\mathcal{H}}^{\bullet}_t(z,s)-(\mathfrak{d}^{\diamond}(z)-\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s)))\sqrt{-1}
& \text{if } z\notin\mathring{\diamond},\ \Im(z)\leq \dfrac
12\\
{\mathcal{H}}^{\bullet}_t(z,s)-\left(\Im(z)-\dfrac12\right)\dfrac{\mathfrak{d}^{\diamond}({\mathcal{H}}^{\bullet}_t(z,s))-\mathfrak{d}^{\diamond}(z)}{\dfrac
12-\mathfrak{d}^{\diamond}(z)}\sqrt{-1} & \text{if }
z\in\diamond,\ z\neq
z_{\diamond}^{\mathrm{l}},z_{\diamond}^{\mathrm{r}}.
\end{array}\right. \]
Here ![]() $\bullet$ is either
$\bullet$ is either ![]() $\mathrm {l}$ or
$\mathrm {l}$ or ![]() $\mathrm {r}$.
$\mathrm {r}$.
Roughly speaking, ![]() ${\mathcal {H}}^{\diamond,\mathrm {l}}_t$ collapses the part of
${\mathcal {H}}^{\diamond,\mathrm {l}}_t$ collapses the part of ![]() $\diamond$ contained in
$\diamond$ contained in ![]() $[0,t]\times \mathbb {R}$ to
$[0,t]\times \mathbb {R}$ to ![]() $z_{\diamond }^{\mathrm {l}}$ and expands the other part
$z_{\diamond }^{\mathrm {l}}$ and expands the other part ![]() $\diamond \setminus [0,t]\times \mathbb {R}$ inside
$\diamond \setminus [0,t]\times \mathbb {R}$ inside ![]() $\diamond$; similar remarks hold for
$\diamond$; similar remarks hold for ![]() ${\mathcal {H}}^{\diamond,\mathrm {r}}_t$.
${\mathcal {H}}^{\diamond,\mathrm {r}}_t$.
Note that for ![]() $z\in \diamond$ close to
$z\in \diamond$ close to ![]() $z_{\diamond }^{\mathrm {l}}$ we have the equalities
$z_{\diamond }^{\mathrm {l}}$ we have the equalities
Similarly, for ![]() $z\in \diamond$ close to
$z\in \diamond$ close to ![]() $z_{\diamond }^{\mathrm {r}}$ we have
$z_{\diamond }^{\mathrm {r}}$ we have
In particular, the homotopies ![]() ${\mathcal {H}}^{\diamond,\mathrm {l}}_t,{\mathcal {H}}^{\diamond,\mathrm {r}}_t$ are continuous; note also that they depend continuously on
${\mathcal {H}}^{\diamond,\mathrm {l}}_t,{\mathcal {H}}^{\diamond,\mathrm {r}}_t$ are continuous; note also that they depend continuously on ![]() $t\in (0,1)$, so that we can define continuous maps
$t\in (0,1)$, so that we can define continuous maps
by ![]() ${\mathcal {H}}^{\diamond,\mathrm {l}}(z,s,t)={\mathcal {H}}^{\diamond,\mathrm {l}}_t(z,s)$ and
${\mathcal {H}}^{\diamond,\mathrm {l}}(z,s,t)={\mathcal {H}}^{\diamond,\mathrm {l}}_t(z,s)$ and ![]() ${\mathcal {H}}^{\diamond,\mathrm {r}}(z,s,t)={\mathcal {H}}^{\diamond,\mathrm {r}}_t(z,s)$. Note also that, for
${\mathcal {H}}^{\diamond,\mathrm {r}}(z,s,t)={\mathcal {H}}^{\diamond,\mathrm {r}}_t(z,s)$. Note also that, for ![]() $\bullet =\mathrm {l},\mathrm {r}$, the following properties hold:
$\bullet =\mathrm {l},\mathrm {r}$, the following properties hold:
(1)
 ${\mathcal {H}}^{\diamond,\bullet }_t(-,s)$ is an endomorphism of the nice couple
${\mathcal {H}}^{\diamond,\bullet }_t(-,s)$ is an endomorphism of the nice couple  $(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (respectively,
$(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })$ (respectively,  $(\diamond,\partial )$) for all
$(\diamond,\partial )$) for all  $(s,t)\in [0,1]\times (0,1)$;
$(s,t)\in [0,1]\times (0,1)$;(2)
 ${\mathcal {H}}^{\diamond,\bullet }_t(-,s)$ fixes pointwise the subspaces
${\mathcal {H}}^{\diamond,\bullet }_t(-,s)$ fixes pointwise the subspaces  $\mathbb {C}_{\Re \leq 0}$ and
$\mathbb {C}_{\Re \leq 0}$ and  $\mathbb {C}_{\Re \geq 1}$ and preserves the subspaces
$\mathbb {C}_{\Re \geq 1}$ and preserves the subspaces  $\diamond$,
$\diamond$,  $[0,1]\times \big (-\infty,\frac 12\big ]\setminus \mathring {\diamond }$ and
$[0,1]\times \big (-\infty,\frac 12\big ]\setminus \mathring {\diamond }$ and  $[0,1]\times \big [\frac 12, \infty \big )\setminus \mathring {\diamond }$; in particular, it fixes the points
$[0,1]\times \big [\frac 12, \infty \big )\setminus \mathring {\diamond }$; in particular, it fixes the points  $z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$;
$z_{\diamond }^{\mathrm {l}},z_{\diamond }^{\mathrm {r}}$;(3)
 ${\mathcal {H}}^{\diamond,\bullet }_t(-,0)=\operatorname {Id}_\mathbb {C}$ for all
${\mathcal {H}}^{\diamond,\bullet }_t(-,0)=\operatorname {Id}_\mathbb {C}$ for all  $t\in (0,1)$.
$t\in (0,1)$.
It follows from property (1) and [Reference BianchiBia23a, Proposition 4.4] that for ![]() $\bullet =\mathrm {l},\mathrm {r}$ there is an induced map
$\bullet =\mathrm {l},\mathrm {r}$ there is an induced map
 \begin{gather*} {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\times[0,1]\times(0,1)\to\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\\ (\text{respectively,}\ {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\diamond,\partial)\times[0,1]\times(0,1)\to\mathrm{Hur}(\diamond,\partial)). \end{gather*}
\begin{gather*} {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\times[0,1]\times(0,1)\to\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})\\ (\text{respectively,}\ {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\diamond,\partial)\times[0,1]\times(0,1)\to\mathrm{Hur}(\diamond,\partial)). \end{gather*}
Property (2) ensures that for all ![]() $(s,t)\in [0,1]\times (0,1)$ the map
$(s,t)\in [0,1]\times (0,1)$ the map ![]() ${\mathcal {H}}^{\diamond,\bullet }_*(-,s,t)$ restricts to a self-map of the subspace
${\mathcal {H}}^{\diamond,\bullet }_*(-,s,t)$ restricts to a self-map of the subspace ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (respectively, ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$) and is equivariant with respect to the
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$) and is equivariant with respect to the ![]() $G\times G^{\rm op}$ action on this subspace. In particular, there is an induced map
$G\times G^{\rm op}$ action on this subspace. In particular, there is an induced map
 \begin{gather*} {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\times[0,1]\times(0,1)\to\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\\ (\text{respectively, }{\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}\times[0,1]\times(0,1)\to\mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}). \end{gather*}
\begin{gather*} {\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\times[0,1]\times(0,1)\to\mathrm{Hur}(\breve{\diamond}^{\mathrm{lr}},\breve{\partial})_{G,G^{\rm op}}\\ (\text{respectively, }{\mathcal{H}}^{\diamond,\bullet}_*\colon\mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}\times[0,1]\times(0,1)\to\mathrm{Hur}(\diamond,\partial)_{G,G^{\rm op}}). \end{gather*}
Property (3) ensures that ![]() ${\mathcal {H}}^{\diamond,\bullet }_*(-,0,t)$ is the identity of
${\mathcal {H}}^{\diamond,\bullet }_*(-,0,t)$ is the identity of ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (of
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) for all
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) for all ![]() $t\in (0,1)$. We can now define a map
$t\in (0,1)$. We can now define a map ![]() $H\colon D^q \times [0,1] \to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$H\colon D^q \times [0,1] \to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $H\colon D^q \times [0,1] \to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) by setting
$H\colon D^q \times [0,1] \to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) by setting
where we recall that ![]() $0< B^{v,-}< B^{v,+}<1$. By the construction of
$0< B^{v,-}< B^{v,+}<1$. By the construction of ![]() $g$ we have
$g$ we have ![]() $H(-,1)=\sigma g$. This concludes the proof that
$H(-,1)=\sigma g$. This concludes the proof that ![]() $\sigma _*$ is surjective on
$\sigma _*$ is surjective on ![]() $\pi _q$.
$\pi _q$.
In the particular case ![]() $q=0$ we obtain that, since
$q=0$ we obtain that, since ![]() $B\mathring {\mathrm {HM}}$ and
$B\mathring {\mathrm {HM}}$ and ![]() $B\breve {\mathrm {HM}}$ are connected, then
$B\breve {\mathrm {HM}}$ are connected, then ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ and
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ and ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ are also connected. The fact that
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ are also connected. The fact that ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ is connected can also be proved by combining [Reference BianchiBia23a, Lemma 6.16 and Proposition 7.10], Theorem 2.19 and Lemma 2.24: the space
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ is connected can also be proved by combining [Reference BianchiBia23a, Lemma 6.16 and Proposition 7.10], Theorem 2.19 and Lemma 2.24: the space ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ is the quotient of the space
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ is the quotient of the space ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ by the action of
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ by the action of ![]() $G\times G^{\rm op}$ and on
$G\times G^{\rm op}$ and on ![]() $\pi _0(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}})\cong G$ this action can be identified with the action by left and right multiplication, which is transitive. The fact that
$\pi _0(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}})\cong G$ this action can be identified with the action by left and right multiplication, which is transitive. The fact that ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ is connected is instead new in our discussion, although it could have been proved directly using simpler arguments.
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ is connected is instead new in our discussion, although it could have been proved directly using simpler arguments.
4.3 Injectivity on homotopy groups
For ![]() $q\geq 0$ we want now to prove that
$q\geq 0$ we want now to prove that ![]() $\sigma _*\colon \pi _q(B\mathring {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively,
$\sigma _*\colon \pi _q(B\mathring {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}})$ (respectively, ![]() $\sigma _*\colon \pi _q(B\breve {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is injective. We fix a basepoint
$\sigma _*\colon \pi _q(B\breve {\mathrm {HM}})\to \pi _q(\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}})$) is injective. We fix a basepoint ![]() $*\in S^q\subset D^{q+1}$ and start with a pointed map
$*\in S^q\subset D^{q+1}$ and start with a pointed map ![]() $\tilde f\colon S^q\to B\mathring {\mathrm {HM}}$ (respectively,
$\tilde f\colon S^q\to B\mathring {\mathrm {HM}}$ (respectively, ![]() $\tilde f\colon S^q\to B\breve {\mathrm {HM}}$) and a map
$\tilde f\colon S^q\to B\breve {\mathrm {HM}}$) and a map ![]() $f\colon D^{q+1}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$f\colon D^{q+1}\to \mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $f\colon D^{q+1}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$), such that the restriction of
$f\colon D^{q+1}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$), such that the restriction of ![]() $f$ on
$f$ on ![]() $S^q=\partial D^{q+1}$ is equal to
$S^q=\partial D^{q+1}$ is equal to ![]() $\sigma \tilde f$.
$\sigma \tilde f$.
We can construct a map ![]() $g\colon D^{q+1}\to B\mathring {\mathrm {HM}}$ (respectively,
$g\colon D^{q+1}\to B\mathring {\mathrm {HM}}$ (respectively, ![]() $g\colon D^{q+1}\to B\breve {\mathrm {HM}}$) in the same way as we constructed
$g\colon D^{q+1}\to B\breve {\mathrm {HM}}$) in the same way as we constructed ![]() $g\colon D^q\to B\mathring {\mathrm {HM}}$ (respectively,
$g\colon D^q\to B\mathring {\mathrm {HM}}$ (respectively, ![]() $g\colon D^q\to B\breve {\mathrm {HM}}$) in the previous subsection: using compactness of
$g\colon D^q\to B\breve {\mathrm {HM}}$) in the previous subsection: using compactness of ![]() $D^{q+1}$, we can find a suitable cover
$D^{q+1}$, we can find a suitable cover ![]() $V_1,\ldots,V_r$ of
$V_1,\ldots,V_r$ of ![]() $D^{q+1}$ and disjoint intervals
$D^{q+1}$ and disjoint intervals ![]() $J_1,\ldots,J_r\subset (0,1)$, ordered from left to right, such that for all
$J_1,\ldots,J_r\subset (0,1)$, ordered from left to right, such that for all ![]() $v\in V_i$, if
$v\in V_i$, if ![]() $\mathfrak {c}_v$ is a representative of
$\mathfrak {c}_v$ is a representative of ![]() $f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$, then
$f(v)=[\mathfrak {c}_v]_{G,G^{\rm op}}$, then ![]() $\mathfrak {c}_v$ is supported on a set
$\mathfrak {c}_v$ is supported on a set ![]() $P_v$ with
$P_v$ with ![]() $\Re (P_v)\cap J_i=\emptyset$. We also fix
$\Re (P_v)\cap J_i=\emptyset$. We also fix ![]() $A_i\in J_i$ for all
$A_i\in J_i$ for all ![]() $1\leq i\leq r$ and a partition of unity
$1\leq i\leq r$ and a partition of unity ![]() $W_1,\ldots W_r$ subordinate to the covering
$W_1,\ldots W_r$ subordinate to the covering ![]() $V_i$; again we assume that for all
$V_i$; again we assume that for all ![]() $v\in D^{q+1}$ there are at least two indices
$v\in D^{q+1}$ there are at least two indices ![]() $1\le i\le r$ such that
$1\le i\le r$ such that ![]() $W_i(v)>0$. The rest of the construction is the same as in the previous subsection; note that, in general,
$W_i(v)>0$. The rest of the construction is the same as in the previous subsection; note that, in general, ![]() $g(*)$ is a point in the contractible subspace
$g(*)$ is a point in the contractible subspace ![]() $B\mathring {\mathrm {HM}}_\emptyset$ (respectively,
$B\mathring {\mathrm {HM}}_\emptyset$ (respectively, ![]() $B\breve {\mathrm {HM}}_\emptyset$), but
$B\breve {\mathrm {HM}}_\emptyset$), but ![]() $g(*)$ is not necessarily the basepoint of
$g(*)$ is not necessarily the basepoint of ![]() $B\mathring {\mathrm {HM}}$ (of
$B\mathring {\mathrm {HM}}$ (of ![]() $B\breve {\mathrm {HM}}$). For our scopes it suffices to prove that
$B\breve {\mathrm {HM}}$). For our scopes it suffices to prove that ![]() $g|_{S^q}$ is homotopic to
$g|_{S^q}$ is homotopic to ![]() $\tilde f$ as maps
$\tilde f$ as maps ![]() $S^q\to B\mathring {\mathrm {HM}}$ (as maps
$S^q\to B\mathring {\mathrm {HM}}$ (as maps ![]() $S^q\to B\breve {\mathrm {HM}}$), through a homotopy sending
$S^q\to B\breve {\mathrm {HM}}$), through a homotopy sending ![]() $*\in S^q$ inside
$*\in S^q$ inside ![]() $B\mathring {\mathrm {HM}}_\emptyset$ (respectively,
$B\mathring {\mathrm {HM}}_\emptyset$ (respectively, ![]() $B\breve {\mathrm {HM}}_\emptyset$) at all times. We are thus replacing
$B\breve {\mathrm {HM}}_\emptyset$) at all times. We are thus replacing ![]() $\pi _q(B\mathring {\mathrm {HM}})$ (respectively,
$\pi _q(B\mathring {\mathrm {HM}})$ (respectively, ![]() $\pi _q(B\breve {\mathrm {HM}})$) with the set of homotopy classes of maps of pairs from
$\pi _q(B\breve {\mathrm {HM}})$) with the set of homotopy classes of maps of pairs from ![]() $(S^q,*)$ to
$(S^q,*)$ to ![]() $(B\mathring {\mathrm {HM}},B\mathring {\mathrm {HM}}_\emptyset )$ (respectively, to
$(B\mathring {\mathrm {HM}},B\mathring {\mathrm {HM}}_\emptyset )$ (respectively, to ![]() $(B\breve {\mathrm {HM}},B\breve {\mathrm {HM}}_\emptyset$).
$(B\breve {\mathrm {HM}},B\breve {\mathrm {HM}}_\emptyset$).
At this point of the discussion it becomes convenient to switch our focus to the thin bar construction. Recall Definition 3.8: the projection ![]() $p_{\bar {B}}\colon B\mathring {\mathrm {HM}}\to \bar {B}\mathring {\mathrm {HM}}$ (respectively,
$p_{\bar {B}}\colon B\mathring {\mathrm {HM}}\to \bar {B}\mathring {\mathrm {HM}}$ (respectively, ![]() $p_{\bar {B}}\colon B\breve {\mathrm {HM}}\to \bar {B}\breve {\mathrm {HM}}$) is a weak homotopy equivalence; similarly, note that the subspace
$p_{\bar {B}}\colon B\breve {\mathrm {HM}}\to \bar {B}\breve {\mathrm {HM}}$) is a weak homotopy equivalence; similarly, note that the subspace ![]() $\bar {B}\mathring {\mathrm {HM}}_\emptyset \subset \bar {B}\mathring {\mathrm {HM}}$ (respectively,
$\bar {B}\mathring {\mathrm {HM}}_\emptyset \subset \bar {B}\mathring {\mathrm {HM}}$ (respectively, ![]() $\bar {B}\breve {\mathrm {HM}}_\emptyset \subset \bar {B}\breve {\mathrm {HM}}$) is contractible. Therefore, it suffices to prove that
$\bar {B}\breve {\mathrm {HM}}_\emptyset \subset \bar {B}\breve {\mathrm {HM}}$) is contractible. Therefore, it suffices to prove that ![]() $p_{\bar {B}}\circ g|_{S^q}$ and
$p_{\bar {B}}\circ g|_{S^q}$ and ![]() $p_{\bar {B}}\circ \tilde f$ are homotopic as maps
$p_{\bar {B}}\circ \tilde f$ are homotopic as maps ![]() $S^q\to \bar {B}\mathring {\mathrm {HM}}$ (as maps
$S^q\to \bar {B}\mathring {\mathrm {HM}}$ (as maps ![]() $S^q\to \bar {B}\breve {\mathrm {HM}}$), by a homotopy sending
$S^q\to \bar {B}\breve {\mathrm {HM}}$), by a homotopy sending ![]() $*\in S^q$ inside
$*\in S^q$ inside ![]() $\bar {B}\mathring {\mathrm {HM}}_\emptyset$ (inside
$\bar {B}\mathring {\mathrm {HM}}_\emptyset$ (inside ![]() $\bar {B}\breve {\mathrm {HM}}_\emptyset$) at all times. Exhibiting such homotopy will be much easier than comparing
$\bar {B}\breve {\mathrm {HM}}_\emptyset$) at all times. Exhibiting such homotopy will be much easier than comparing ![]() $g|_{S^q}$ and
$g|_{S^q}$ and ![]() $\tilde f$ directly.
$\tilde f$ directly.
One of the advantages of the thin bar construction occurs already in the construction of the map ![]() $g\colon D^{q+1}\to B\mathring {\mathrm {HM}}$ (respectively,
$g\colon D^{q+1}\to B\mathring {\mathrm {HM}}$ (respectively, ![]() $g\colon D^{q+1}\to B\breve {\mathrm {HM}}$). Recall that we had to shrink the intervals
$g\colon D^{q+1}\to B\breve {\mathrm {HM}}$). Recall that we had to shrink the intervals ![]() $J_1,\ldots,J_r$ to make them disjoint, in order to ensure that the numbers
$J_1,\ldots,J_r$ to make them disjoint, in order to ensure that the numbers ![]() $A_1,\ldots,A_r$ are all distinct. This was crucial when defining
$A_1,\ldots,A_r$ are all distinct. This was crucial when defining ![]() $g(v)$ for
$g(v)$ for ![]() $v\in D^{q+1}$ (or, in the previous subsection, for
$v\in D^{q+1}$ (or, in the previous subsection, for ![]() $v\in D^q$): we started from the list of indices
$v\in D^q$): we started from the list of indices ![]() $1< i_0<\cdots < i_{p_v}< l$ satisfying
$1< i_0<\cdots < i_{p_v}< l$ satisfying ![]() $W_{i_j}(v)>0$; we denoted by
$W_{i_j}(v)>0$; we denoted by ![]() $A_0^v,\ldots,\ldots A_{p_v}^v$ the list
$A_0^v,\ldots,\ldots A_{p_v}^v$ the list ![]() $A_{i_0},\ldots,A_{i_{p_v}}$ and used the portions of
$A_{i_0},\ldots,A_{i_{p_v}}$ and used the portions of ![]() $f(v)$ contained in the slices
$f(v)$ contained in the slices ![]() $\breve {\diamond }^{\mathrm {lr}}_{A_{j-1}^v,A_j^v}$ (in
$\breve {\diamond }^{\mathrm {lr}}_{A_{j-1}^v,A_j^v}$ (in ![]() $(\diamond _{A_{j-1}^v,A_j^v},\partial )$) to define the configurations
$(\diamond _{A_{j-1}^v,A_j^v},\partial )$) to define the configurations ![]() $\mathfrak {c}'_{v,1},\ldots,\mathfrak {c}'_{v,{p_v}}$. The fact that the numbers
$\mathfrak {c}'_{v,1},\ldots,\mathfrak {c}'_{v,{p_v}}$. The fact that the numbers ![]() $A_1,\ldots,A_r$ are all distinct was crucial in ensuring that all slices have strictly positive width and, most important, the numbers
$A_1,\ldots,A_r$ are all distinct was crucial in ensuring that all slices have strictly positive width and, most important, the numbers ![]() $W_{i_0}(v),\ldots,W_{i_{p_v}}(v)$ naturally form an ordered list of
$W_{i_0}(v),\ldots,W_{i_{p_v}}(v)$ naturally form an ordered list of ![]() $p+1$ numbers: this is crucial, as we want to use these numbers to define the barycentric coordinates of a point in
$p+1$ numbers: this is crucial, as we want to use these numbers to define the barycentric coordinates of a point in ![]() $\Delta ^p$.
$\Delta ^p$.
Suppose instead that we repeat the above construction of ![]() $g$, but using directly the thin bar construction; in other words, consider the composition of
$g$, but using directly the thin bar construction; in other words, consider the composition of ![]() $g$ with the projection
$g$ with the projection ![]() $p_{\bar {B}}$: then the fact that
$p_{\bar {B}}$: then the fact that ![]() $A_1,\ldots,A_r$ are all distinct ceases to be important. Indeed, suppose that for some
$A_1,\ldots,A_r$ are all distinct ceases to be important. Indeed, suppose that for some ![]() $v\in D^{q+1}$ we write a list
$v\in D^{q+1}$ we write a list ![]() $A_0^v,\ldots,\ldots A_{p_v}^v$ as above and suppose that for some
$A_0^v,\ldots,\ldots A_{p_v}^v$ as above and suppose that for some ![]() $1\leq j\leq p_v$ we have
$1\leq j\leq p_v$ we have ![]() $A^v_{j-1}=A^v_j$: this means, in particular, that
$A^v_{j-1}=A^v_j$: this means, in particular, that ![]() $\mathfrak {c}'_{v,j}=(\emptyset,\mathbb {1},\mathbb {1})$. On the one hand, we cannot unequivocally determine which of the barycentric coordinates
$\mathfrak {c}'_{v,j}=(\emptyset,\mathbb {1},\mathbb {1})$. On the one hand, we cannot unequivocally determine which of the barycentric coordinates ![]() $W_{i_{j-1}}(v)$ and
$W_{i_{j-1}}(v)$ and ![]() $W_{i_j}(v)$ should come first in the list of barycentric coordinates for
$W_{i_j}(v)$ should come first in the list of barycentric coordinates for ![]() $g(v)$; on the other hand, the two possibilities give rise to the same configuration in
$g(v)$; on the other hand, the two possibilities give rise to the same configuration in ![]() $\bar {B}\mathring {\mathrm {HM}}$ (in
$\bar {B}\mathring {\mathrm {HM}}$ (in ![]() $\bar {B}\breve {\mathrm {HM}}$). For simplicity, in the following we keep assuming that the numbers
$\bar {B}\breve {\mathrm {HM}}$). For simplicity, in the following we keep assuming that the numbers ![]() $0< A_1<\cdots < A_r<1$ are distinct and we keep considering
$0< A_1<\cdots < A_r<1$ are distinct and we keep considering ![]() $g$ and
$g$ and ![]() $\tilde f$ as maps with values in
$\tilde f$ as maps with values in ![]() $B\mathring {\mathrm {HM}}$ (in
$B\mathring {\mathrm {HM}}$ (in ![]() $B\breve {\mathrm {HM}}$).
$B\breve {\mathrm {HM}}$).
Fix ![]() $v\in S^q$ and let
$v\in S^q$ and let ![]() $\tilde f(v)\in B\mathring {\mathrm {HM}}$ (respectively,
$\tilde f(v)\in B\mathring {\mathrm {HM}}$ (respectively, ![]() $\tilde f(v)\in B\breve {\mathrm {HM}}$) be represented, for some
$\tilde f(v)\in B\breve {\mathrm {HM}}$) be represented, for some ![]() $\tilde {p}_v\geq 0$, by the
$\tilde {p}_v\geq 0$, by the ![]() $\tilde {p}_v$-tuple
$\tilde {p}_v$-tuple ![]() $(t^v_1,\mathfrak {c}^v_1),\ldots,(t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ of configurations in
$(t^v_1,\mathfrak {c}^v_1),\ldots,(t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ of configurations in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$), with barycentric coordinates
$\breve {\mathrm {HM}}$), with barycentric coordinates ![]() $w^v_0,\ldots,w^v_{\tilde {p}_v}$. Let the numbers
$w^v_0,\ldots,w^v_{\tilde {p}_v}$. Let the numbers ![]() $a^v_0,\ldots,a^v_{\tilde {p}_v}$ and the barycentres
$a^v_0,\ldots,a^v_{\tilde {p}_v}$ and the barycentres ![]() $b_v$,
$b_v$, ![]() $b_{\varepsilon,v}^-$ and
$b_{\varepsilon,v}^-$ and ![]() $b_{\varepsilon,v}^+$ be computed as in Definitions 4.4 and 4.5 with respect to
$b_{\varepsilon,v}^+$ be computed as in Definitions 4.4 and 4.5 with respect to ![]() $(t^v_1,\mathfrak {c}^v_1),\ldots,(t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ and
$(t^v_1,\mathfrak {c}^v_1),\ldots,(t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ and ![]() $w^v_0,\ldots,w^v_{\tilde {p}_v}$.
$w^v_0,\ldots,w^v_{\tilde {p}_v}$.
Using the notation from § 4.2, for ![]() $v\in S^q$ let
$v\in S^q$ let ![]() $1\leq i_0<\cdots < i_{p_v}\leq r$ be the list of all indices
$1\leq i_0<\cdots < i_{p_v}\leq r$ be the list of all indices ![]() $i_j$ satisfying
$i_j$ satisfying ![]() $W_{i_j}(v)>0$; again let
$W_{i_j}(v)>0$; again let ![]() $A_0^v,\ldots,\ldots A_{p_v}^v$ denote the corresponding list of numbers
$A_0^v,\ldots,\ldots A_{p_v}^v$ denote the corresponding list of numbers ![]() $0< A_{i_0}<\cdots < A_{i_{p_v}}<1$. Recall that
$0< A_{i_0}<\cdots < A_{i_{p_v}}<1$. Recall that ![]() $g(v)\in B\mathring {\mathrm {HM}}$ (respectively,
$g(v)\in B\mathring {\mathrm {HM}}$ (respectively, ![]() $g(v)\in B\breve {\mathrm {HM}}$) is constructed using the numbers
$g(v)\in B\breve {\mathrm {HM}}$) is constructed using the numbers ![]() $W_{i_0}(v),\ldots,W_{i_{p'}}(v)$ as barycentric coordinates and using the portions of
$W_{i_0}(v),\ldots,W_{i_{p'}}(v)$ as barycentric coordinates and using the portions of ![]() $\mathfrak {c}_v$ contained in the slices
$\mathfrak {c}_v$ contained in the slices ![]() $[A_{i_0},A_{i_1}]\times \mathbb {R},\ldots,[A_{i_{p'-1}},A_{i_{p'}}]\times \mathbb {R}$ to obtain configurations
$[A_{i_0},A_{i_1}]\times \mathbb {R},\ldots,[A_{i_{p'-1}},A_{i_{p'}}]\times \mathbb {R}$ to obtain configurations ![]() $(A_{i_j}-A_{i_{j-1}},\mathfrak {c}'_{v,j})$ in
$(A_{i_j}-A_{i_{j-1}},\mathfrak {c}'_{v,j})$ in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$).
$\breve {\mathrm {HM}}$).
For ![]() $0\leq j\leq p_v$ define
$0\leq j\leq p_v$ define ![]() $\alpha ^v_j=b^-_{\varepsilon,v}+(b^+_{\varepsilon,v}-b^-_{\varepsilon,v})A^v_j$. Then
$\alpha ^v_j=b^-_{\varepsilon,v}+(b^+_{\varepsilon,v}-b^-_{\varepsilon,v})A^v_j$. Then ![]() $b^-_{\varepsilon,v}\leq \alpha ^v_0\leq \cdots \leq \alpha ^v_{p'}\leq b^+_{\varepsilon,v}$ and the inequality
$b^-_{\varepsilon,v}\leq \alpha ^v_0\leq \cdots \leq \alpha ^v_{p'}\leq b^+_{\varepsilon,v}$ and the inequality ![]() $b^-_{\varepsilon,v}< b^+_{\varepsilon,v}$ is strict. To fix notation, let
$b^-_{\varepsilon,v}< b^+_{\varepsilon,v}$ is strict. To fix notation, let
be the union of the lists of numbers ![]() $a^v_0,\ldots,a^v_{\tilde {p}_v}$ and
$a^v_0,\ldots,a^v_{\tilde {p}_v}$ and ![]() $\alpha ^v_0,\ldots,\alpha ^v_{p_v}$: all numbers
$\alpha ^v_0,\ldots,\alpha ^v_{p_v}$: all numbers ![]() $\beta ^v_j$, as well as the numbers
$\beta ^v_j$, as well as the numbers ![]() $b_v$,
$b_v$, ![]() $b^-_{\varepsilon,v}$ and
$b^-_{\varepsilon,v}$ and ![]() $b^+_{\varepsilon,v}$, belong to the interval
$b^+_{\varepsilon,v}$, belong to the interval ![]() $[a^v_0-\varepsilon,a^v_{\tilde {p}_v}+\varepsilon ]=[-\varepsilon,a^v_{\tilde {p}_v}+\varepsilon ]$.
$[a^v_0-\varepsilon,a^v_{\tilde {p}_v}+\varepsilon ]=[-\varepsilon,a^v_{\tilde {p}_v}+\varepsilon ]$.
In writing the list ![]() $\beta ^v_0\leq \cdots \leq \beta ^v_{\tilde {p}_v+p_v+1}$ we choose a shuffle of the sets
$\beta ^v_0\leq \cdots \leq \beta ^v_{\tilde {p}_v+p_v+1}$ we choose a shuffle of the sets ![]() $\{0,\ldots,\tilde {p}_v\}$ and
$\{0,\ldots,\tilde {p}_v\}$ and ![]() $\{0,\ldots,p_v\}$ into
$\{0,\ldots,p_v\}$ into ![]() $\{0,\ldots,\tilde {p}_v+p_v+1\}$, i.e. a pair of strictly increasing and commonly surjective maps
$\{0,\ldots,\tilde {p}_v+p_v+1\}$, i.e. a pair of strictly increasing and commonly surjective maps
In the generic case, the numbers ![]() $a^v_0,\ldots,a^v_{\tilde {p}_v},\alpha ^v_0,\ldots,\alpha ^v_{p_v}$ are all distinct and the choice of the shuffle is unique, but nothing prevents that, for some
$a^v_0,\ldots,a^v_{\tilde {p}_v},\alpha ^v_0,\ldots,\alpha ^v_{p_v}$ are all distinct and the choice of the shuffle is unique, but nothing prevents that, for some ![]() $v\in S^q$, some of these numbers become equal.
$v\in S^q$, some of these numbers become equal.
Let ![]() $\hat {w}^v_0,\ldots,\hat {w}^v_{\tilde {p}_v+p_v+1}$ denote the corresponding shuffle of the lists of barycentric coordinates, i.e.
$\hat {w}^v_0,\ldots,\hat {w}^v_{\tilde {p}_v+p_v+1}$ denote the corresponding shuffle of the lists of barycentric coordinates, i.e. ![]() $\hat {w}^v_{\tilde \eta (j)}=w^v_j$ and
$\hat {w}^v_{\tilde \eta (j)}=w^v_j$ and ![]() $\hat {w}^v_{\eta (j)}=W_{i_j}(v)$. Define also
$\hat {w}^v_{\eta (j)}=W_{i_j}(v)$. Define also
Let ![]() $(a^v_{\tilde {p}_v},\mathfrak {c})$ be the product
$(a^v_{\tilde {p}_v},\mathfrak {c})$ be the product ![]() $(t^v_1,\mathfrak {c}^v_1)\cdots (t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ in
$(t^v_1,\mathfrak {c}^v_1)\cdots (t^v_{\tilde {p}_v},\mathfrak {c}^v_{\tilde {p}_v})$ in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$) and use Notation 2.2. Then for all
$\breve {\mathrm {HM}}$) and use Notation 2.2. Then for all ![]() $0\leq j\leq \tilde {p}_v+p_v+1$ the vertical line
$0\leq j\leq \tilde {p}_v+p_v+1$ the vertical line ![]() $\mathbb {C}_{\Re =\beta _j}$ is disjoint from
$\mathbb {C}_{\Re =\beta _j}$ is disjoint from ![]() $P$. We can then cut the rectangle
$P$. We can then cut the rectangle ![]() $\mathring {{\mathcal {R}}}_{a^v_{\tilde {p}_v}}$ (respectively,
$\mathring {{\mathcal {R}}}_{a^v_{\tilde {p}_v}}$ (respectively, ![]() $\breve {{\mathcal {R}}}_{a^v_{\tilde {p}_v}}$) along these vertical lines and define configurations
$\breve {{\mathcal {R}}}_{a^v_{\tilde {p}_v}}$) along these vertical lines and define configurations ![]() $\bar {\mathfrak {c}}^v_j$ in
$\bar {\mathfrak {c}}^v_j$ in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\beta _{j-1},\beta _j})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\beta _{j-1},\beta _j})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{\beta _{j-1},\beta _j},\breve {\partial })$) as the parts of
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{\beta _{j-1},\beta _j},\breve {\partial })$) as the parts of ![]() $\mathfrak {c}$ lying in the regions
$\mathfrak {c}$ lying in the regions ![]() $\mathbb {S}_{\beta _{j-1},\beta _j}$, for all
$\mathbb {S}_{\beta _{j-1},\beta _j}$, for all ![]() $1\leq j\leq \tilde {p}_v+p_v+1$: formally, we evaluate the restriction maps
$1\leq j\leq \tilde {p}_v+p_v+1$: formally, we evaluate the restriction maps ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{\beta _{j-1},\beta _j}}$ on
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{\beta _{j-1},\beta _j}}$ on ![]() $\mathfrak {c}$. Let
$\mathfrak {c}$. Let ![]() $\hat {\mathfrak {c}}^v_j$ be the configuration in
$\hat {\mathfrak {c}}^v_j$ be the configuration in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\beta _j-\beta _{j-1}})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\beta _j-\beta _{j-1}})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{\beta _j-\beta _{j-1}},\breve {\partial })$) given by
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{\beta _j-\beta _{j-1}},\breve {\partial })$) given by ![]() $(\tau _{-\beta _{j-1}})_*(\bar {\mathfrak {c}}^{v}_j)$, for all
$(\tau _{-\beta _{j-1}})_*(\bar {\mathfrak {c}}^{v}_j)$, for all ![]() $1\leq j\leq \tilde {p}_v+p_v+1$.
$1\leq j\leq \tilde {p}_v+p_v+1$.
We define a homotopy ![]() $H\colon S^q\times [0,1]\to \bar {B}\mathring {\mathrm {HM}}$ (respectively,
$H\colon S^q\times [0,1]\to \bar {B}\mathring {\mathrm {HM}}$ (respectively, ![]() $H\colon S^q\times [0,1]\to \bar {B}\breve {\mathrm {HM}}$) by the formula
$H\colon S^q\times [0,1]\to \bar {B}\breve {\mathrm {HM}}$) by the formula
 \begin{align*} H(v,s)&=
\big(\mathbf{e}(0,s)\hat{w}^v_0,\ldots,\mathbf{e}(\tilde{p}_v+p_v+1,s)\hat{w}^v_{\tilde{p}_v+p_v+1};\\
&\quad\,\, (\beta_1-\beta_0,\hat{\mathfrak{c}}^v_1),\ldots,\big(\beta_{\tilde{p}_v+p_v+1}-\beta_{\tilde{p}_v+p_v},
\hat{\mathfrak{c}}^v_{\tilde{p}_v+p_v+1}\big)\big).
\end{align*}
\begin{align*} H(v,s)&=
\big(\mathbf{e}(0,s)\hat{w}^v_0,\ldots,\mathbf{e}(\tilde{p}_v+p_v+1,s)\hat{w}^v_{\tilde{p}_v+p_v+1};\\
&\quad\,\, (\beta_1-\beta_0,\hat{\mathfrak{c}}^v_1),\ldots,\big(\beta_{\tilde{p}_v+p_v+1}-\beta_{\tilde{p}_v+p_v},
\hat{\mathfrak{c}}^v_{\tilde{p}_v+p_v+1}\big)\big).
\end{align*}
The continuity of the formula relies on the fact that we are using the thin bar construction: if varying ![]() $v\in S^q$ two consecutive values
$v\in S^q$ two consecutive values ![]() $\beta _{j-1}$ and
$\beta _{j-1}$ and ![]() $\beta _j$ become equal, then the corresponding configuration
$\beta _j$ become equal, then the corresponding configuration ![]() $(\beta _j-\beta _{j-1},\hat {\mathfrak {c}}^v_{j-1})$ becomes equal to
$(\beta _j-\beta _{j-1},\hat {\mathfrak {c}}^v_{j-1})$ becomes equal to ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$ and can, thus, be dropped from the list: the weights
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$ and can, thus, be dropped from the list: the weights ![]() $\mathbf {e}(j-1,s)\hat {w}^v_{j-1}$ and
$\mathbf {e}(j-1,s)\hat {w}^v_{j-1}$ and ![]() $\mathbf {e}(j,s)\hat {w}^v_j$ are replaced by their sum
$\mathbf {e}(j,s)\hat {w}^v_j$ are replaced by their sum ![]() $\mathbf {e}(j-1,s)\hat {w}^v_{j-1}+\mathbf {e}(j,s)\hat {w}^v_j$ and we obtain a description of the same configuration in
$\mathbf {e}(j-1,s)\hat {w}^v_{j-1}+\mathbf {e}(j,s)\hat {w}^v_j$ and we obtain a description of the same configuration in ![]() $\bar {B}\mathring {\mathrm {HM}}$ (in
$\bar {B}\mathring {\mathrm {HM}}$ (in ![]() $\bar {B}\breve {\mathrm {HM}}$) which is formally symmetric in the indices
$\bar {B}\breve {\mathrm {HM}}$) which is formally symmetric in the indices ![]() $j-1$ and
$j-1$ and ![]() $j$.
$j$.
For ![]() $s=1$ the list of weights
$s=1$ the list of weights ![]() $\mathbf {e}(0,s)\hat {w}^v_0,\ldots,\mathbf {e}(p+p'+1,s)\hat {w}^v_{\tilde {p}_v+p_v+1}$ reduces to the list of weights
$\mathbf {e}(0,s)\hat {w}^v_0,\ldots,\mathbf {e}(p+p'+1,s)\hat {w}^v_{\tilde {p}_v+p_v+1}$ reduces to the list of weights ![]() $w^v_0,\ldots,w^v_{\tilde {p}_v}$, shuffled with
$w^v_0,\ldots,w^v_{\tilde {p}_v}$, shuffled with ![]() $p_v+1$ occurrences of
$p_v+1$ occurrences of ![]() $0$; if we drop the zeros and perform the corresponding products of consecutive elements in the list
$0$; if we drop the zeros and perform the corresponding products of consecutive elements in the list ![]() $(\beta _1-\beta _0,\hat {\mathfrak {c}}^v_1),\ldots,(\beta _{\tilde {p}_v+p_v+1}-\beta _{\tilde {p}_v+p_v},\hat {\mathfrak {c}}^v_{\tilde {p}_v+p_v+1})$, we recover
$(\beta _1-\beta _0,\hat {\mathfrak {c}}^v_1),\ldots,(\beta _{\tilde {p}_v+p_v+1}-\beta _{\tilde {p}_v+p_v},\hat {\mathfrak {c}}^v_{\tilde {p}_v+p_v+1})$, we recover ![]() $\tilde f(v)$.
$\tilde f(v)$.
Similarly, for ![]() $s=0$ we obtain the weights
$s=0$ we obtain the weights ![]() $W_{i_1}(v),\ldots,W_{i_{p_v}}(v)$ shuffled with
$W_{i_1}(v),\ldots,W_{i_{p_v}}(v)$ shuffled with ![]() $\tilde {p}_v+1$ occurrences of
$\tilde {p}_v+1$ occurrences of ![]() $0$; in particular, since
$0$; in particular, since ![]() $\beta _0=a_0=0$ and
$\beta _0=a_0=0$ and ![]() $\beta _{\tilde {p}_v+p_v+1}=a_p$, at least one zero at the beginning and at least one zero at the end of the list of all weights are dropped. If we perform the corresponding products of consecutive elements in the list
$\beta _{\tilde {p}_v+p_v+1}=a_p$, at least one zero at the beginning and at least one zero at the end of the list of all weights are dropped. If we perform the corresponding products of consecutive elements in the list ![]() $(\beta _1-\beta _0,\hat {\mathfrak {c}}^v_1),\ldots,(\beta _{\tilde {p}_v+p_v+1}-\beta _{\tilde {p}_v+p_v},\hat {\mathfrak {c}}^v_{\tilde {p}_v+p_v+1})$ and if we drop the corresponding elements at the two ends of the list, we recover
$(\beta _1-\beta _0,\hat {\mathfrak {c}}^v_1),\ldots,(\beta _{\tilde {p}_v+p_v+1}-\beta _{\tilde {p}_v+p_v},\hat {\mathfrak {c}}^v_{\tilde {p}_v+p_v+1})$ and if we drop the corresponding elements at the two ends of the list, we recover ![]() $g(v)$.
$g(v)$.
Finally, note that for ![]() $v=*\in S^q$ we have that all configurations
$v=*\in S^q$ we have that all configurations ![]() $\hat {\mathfrak {c}}^v_j$ are supported on the empty set, so that
$\hat {\mathfrak {c}}^v_j$ are supported on the empty set, so that ![]() $H(v,-)$ is a path in
$H(v,-)$ is a path in ![]() $\bar {B}\mathring {\mathrm {HM}}_\emptyset$ (in
$\bar {B}\mathring {\mathrm {HM}}_\emptyset$ (in ![]() $\bar {B}\breve {\mathrm {HM}}_\emptyset$). This concludes the proof that
$\bar {B}\breve {\mathrm {HM}}_\emptyset$). This concludes the proof that ![]() $\sigma _*$ is injective on homotopy groups.
$\sigma _*$ is injective on homotopy groups.
4.4 Homology of the group completion of  $\mathring {\mathrm {HM}}$
$\mathring {\mathrm {HM}}$
The second part of Theorem 4.1 implies, together with Theorem 3.4, that there is a weak equivalence
If we select one connected component on each side, using Theorem 2.19 for the left-hand side, we obtain a weak equivalence
By [Reference BianchiBia23a, Lemma 6.16] we have that ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ is a (disconnected) covering of
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ is a (disconnected) covering of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$: more precisely, there is a free and properly discontinuous action of
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$: more precisely, there is a free and properly discontinuous action of ![]() $G\times G^{\rm op}$ on the former space and the latter is the quotient by this action. Hence, also the connected component
$G\times G^{\rm op}$ on the former space and the latter is the quotient by this action. Hence, also the connected component ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\subseteq \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ is a covering of
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\subseteq \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ is a covering of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$, with deck transformation group given by the stabiliser in
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$, with deck transformation group given by the stabiliser in ![]() $G\times G^{\rm op}$ of this component, which is the ‘diagonal’ copy of
$G\times G^{\rm op}$ of this component, which is the ‘diagonal’ copy of ![]() $G$, consisting of pairs
$G$, consisting of pairs ![]() $(g,g^{-1,op})$ for varying
$(g,g^{-1,op})$ for varying ![]() $g\in G$. We obtain a weak equivalence
$g\in G$. We obtain a weak equivalence
and Lemmas 2.7 and 2.24 and [Reference BianchiBia23a, Proposition 7.10] yield a weak equivalence
Now we use the first part of Theorem 4.1, together with the fact that ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is a covering of
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is a covering of ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$, again by [Reference BianchiBia23a, Lemma 6.16]; taking one component of loop spaces we obtain a weak equivalence
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$, again by [Reference BianchiBia23a, Lemma 6.16]; taking one component of loop spaces we obtain a weak equivalence
Putting the above weak equivalences together, we obtain
Finally, Theorem 3.7 (which is applicable thanks to Lemma 3.6) and Theorem 2.15, imply the following homology isomorphism,
Here ![]() ${\mathcal {G}}({\mathcal {Q}})$ denotes the enveloping group of the PMQ
${\mathcal {G}}({\mathcal {Q}})$ denotes the enveloping group of the PMQ ![]() ${\mathcal {Q}}$, as in [Reference BianchiBia21, Definition 2.9]: concretely, this is the group generated by elements
${\mathcal {Q}}$, as in [Reference BianchiBia21, Definition 2.9]: concretely, this is the group generated by elements ![]() $[a]$ for
$[a]$ for ![]() $a$ ranging in
$a$ ranging in ![]() ${\mathcal {Q}}$, under the relations
${\mathcal {Q}}$, under the relations ![]() $[a][b]=[b][a^b]$ for all
$[a][b]=[b][a^b]$ for all ![]() $a,b\in {\mathcal {Q}}$ and
$a,b\in {\mathcal {Q}}$ and ![]() $[a]\hat b=\widehat {ab}$ for all
$[a]\hat b=\widehat {ab}$ for all ![]() $a,b\in {\mathcal {Q}}$ such that the product
$a,b\in {\mathcal {Q}}$ such that the product ![]() $ab$ is already defined in
$ab$ is already defined in ![]() ${\mathcal {Q}}$. In fact,
${\mathcal {Q}}$. In fact, ![]() ${\mathcal {G}}({\mathcal {Q}})$ is the universal group receiving a map of PMQs from
${\mathcal {G}}({\mathcal {Q}})$ is the universal group receiving a map of PMQs from ![]() ${\mathcal {Q}}$; moreover,
${\mathcal {Q}}$; moreover, ![]() ${\mathcal {G}}({\mathcal {Q}})$ coincides with the enveloping group of both the monoid
${\mathcal {G}}({\mathcal {Q}})$ coincides with the enveloping group of both the monoid ![]() $\hat {{\mathcal {Q}}}$ and its free unitalisation
$\hat {{\mathcal {Q}}}$ and its free unitalisation ![]() $\hat {{\mathcal {Q}}}\sqcup \{\mathbb {1}\}\cong \pi _0(\mathring {\mathrm {HM}})$.
$\hat {{\mathcal {Q}}}\sqcup \{\mathbb {1}\}\cong \pi _0(\mathring {\mathrm {HM}})$.
In fact, the combination of Theorems 2.19, 3.4 and 4.1 implies the following isomorphisms of discrete monoids (which happen to be groups):
On the other hand, [Reference BianchiBia23a, Lemma 6.16] implies that ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is a covering of
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is a covering of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ with group of deck transformations
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ with group of deck transformations ![]() $G$ and
$G$ and ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is connected by Theorem 2.19. In the next lemma we prove that
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is connected by Theorem 2.19. In the next lemma we prove that ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is, in fact, the universal cover of
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is, in fact, the universal cover of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$.
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$.
Lemma 4.21 The space ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is simply connected.
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$ is simply connected.
Proof. Recall the weak equivalence ![]() $\sigma \colon B\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$. For
$\sigma \colon B\breve {\mathrm {HM}}\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}},\mathbb {1}}$. For ![]() $g\in G$ let
$g\in G$ let ![]() $(1,\mathfrak {c}_g)\in \breve {\mathrm {HM}}_+$ be the pair with
$(1,\mathfrak {c}_g)\in \breve {\mathrm {HM}}_+$ be the pair with ![]() $\mathfrak {c}_g$ being a configuration supported on the unique point
$\mathfrak {c}_g$ being a configuration supported on the unique point ![]() $\frac 12$, carrying local monodromy
$\frac 12$, carrying local monodromy ![]() $g\in G$. Consider the loop
$g\in G$. Consider the loop ![]() $\gamma _g\colon [0,1]\to B\breve {\mathrm {HM}}$ sending
$\gamma _g\colon [0,1]\to B\breve {\mathrm {HM}}$ sending ![]() $t\in [0,1]$ to the class of
$t\in [0,1]$ to the class of ![]() $(t,1-t;(1,\mathfrak {c}_g))\in \Delta ^1\times \breve {\mathrm {HM}}\subset \coprod _{p\ge 0}\Delta ^p\times \breve {\mathrm {HM}}^p$ in the quotient. Observe that the class of
$(t,1-t;(1,\mathfrak {c}_g))\in \Delta ^1\times \breve {\mathrm {HM}}\subset \coprod _{p\ge 0}\Delta ^p\times \breve {\mathrm {HM}}^p$ in the quotient. Observe that the class of ![]() $\gamma _g$ in
$\gamma _g$ in ![]() $\pi _1(B\breve {\mathrm {HM}})$ corresponds to the class of
$\pi _1(B\breve {\mathrm {HM}})$ corresponds to the class of ![]() $(1,\mathfrak {c}_g)\in \pi _0(\breve {\mathrm {HM}}_+)$, which along the total monodromy corresponds to the element
$(1,\mathfrak {c}_g)\in \pi _0(\breve {\mathrm {HM}}_+)$, which along the total monodromy corresponds to the element ![]() $g\in G$; in particular, every element of
$g\in G$; in particular, every element of ![]() $\pi _1(B\breve {\mathrm {HM}})$ is represented by a loop
$\pi _1(B\breve {\mathrm {HM}})$ is represented by a loop ![]() $\gamma _g$.
$\gamma _g$.
Recall now Definition 2.22 and the proof of Theorem 2.19 and let ![]() $\hat {\mathfrak {c}}_{g^{-1},g,\mathbb {1}_G}\in \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}$ be the configuration supported on the set
$\hat {\mathfrak {c}}_{g^{-1},g,\mathbb {1}_G}\in \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}$ be the configuration supported on the set ![]() $\{0,\frac 12,1\}$, such that the
$\{0,\frac 12,1\}$, such that the ![]() $G$-valued total monodromy sends small loops spinning clockwise around
$G$-valued total monodromy sends small loops spinning clockwise around ![]() $0,\frac 12,1$ to
$0,\frac 12,1$ to ![]() $g^{-1},g,\mathbb {1}$, respectively. Let
$g^{-1},g,\mathbb {1}$, respectively. Let ![]() $\hat \gamma _g\colon [0,1]\to \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}$ be the path defined by
$\hat \gamma _g\colon [0,1]\to \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}$ be the path defined by
 \[
\hat\gamma_g(t)=\left\{\begin{array}{@{}ll}
{\mathcal{H}}^{\mathrm{l}}_{1/2}(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1)
& \text{if }0\le t\le 1-\dfrac{1}{\sqrt{2}};\\
{\mathcal{H}}^{\mathrm{l}}_{1/2}\Big(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1-\dfrac{1-2(1-t)^2}{2t(1-t)}\Big)
& \text{if }1-\dfrac{1}{\sqrt{2}}\le t\le \dfrac 12;\\
{\mathcal{H}}^{\mathrm{r}}_{1/2}\Big(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},\dfrac{1-2(1-t)^2}{2t(1-t)}-1\Big)
& \text{if }\dfrac12\le t\le \dfrac{1}{\sqrt{2}};\\
{\mathcal{H}}^{\mathrm{r}}_{1/2}(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1) & \text{if }\dfrac{1}{\sqrt{2}}\le t\le 1.
\end{array}\right. \]
\[
\hat\gamma_g(t)=\left\{\begin{array}{@{}ll}
{\mathcal{H}}^{\mathrm{l}}_{1/2}(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1)
& \text{if }0\le t\le 1-\dfrac{1}{\sqrt{2}};\\
{\mathcal{H}}^{\mathrm{l}}_{1/2}\Big(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1-\dfrac{1-2(1-t)^2}{2t(1-t)}\Big)
& \text{if }1-\dfrac{1}{\sqrt{2}}\le t\le \dfrac 12;\\
{\mathcal{H}}^{\mathrm{r}}_{1/2}\Big(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},\dfrac{1-2(1-t)^2}{2t(1-t)}-1\Big)
& \text{if }\dfrac12\le t\le \dfrac{1}{\sqrt{2}};\\
{\mathcal{H}}^{\mathrm{r}}_{1/2}(\hat{\mathfrak{c}}_{g^{-1},g,\mathbb {1}_G},1) & \text{if }\dfrac{1}{\sqrt{2}}\le t\le 1.
\end{array}\right. \]
Consider also the map ![]() $({\mathcal {H}}^{\diamond }_1)_*\colon \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ induced by
$({\mathcal {H}}^{\diamond }_1)_*\colon \mathrm {Hur}({\mathcal {R}},\partial )_{0,1;\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ induced by ![]() ${\mathcal {H}}^{\diamond }_1$; then
${\mathcal {H}}^{\diamond }_1$; then ![]() $\tilde \gamma _g:=({\mathcal {H}}^{\diamond }_1)_*\circ \hat \gamma _g\colon [0,1]\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ is a path lifting the loop
$\tilde \gamma _g:=({\mathcal {H}}^{\diamond }_1)_*\circ \hat \gamma _g\colon [0,1]\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ is a path lifting the loop ![]() $\sigma \circ \gamma _g\colon [0,1]\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ along the covering
$\sigma \circ \gamma _g\colon [0,1]\to \mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ along the covering ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$.
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$.
Both configurations ![]() $\tilde \gamma _g(0)$ and
$\tilde \gamma _g(0)$ and ![]() $\tilde \gamma _g(1)$ are supported on
$\tilde \gamma _g(1)$ are supported on ![]() $\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$; the local monodromies around
$\breve {\partial }\breve {\diamond }^{\mathrm {lr}}$; the local monodromies around ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ are
$z_{\diamond }^{\mathrm {r}}$ are ![]() $\mathbb {1}_G$ and
$\mathbb {1}_G$ and ![]() $\mathbb {1}_G$, respectively, for the first configuration and are
$\mathbb {1}_G$, respectively, for the first configuration and are ![]() $g^{-1}$ and
$g^{-1}$ and ![]() $g$, respectively, for the second. It follows that the path
$g$, respectively, for the second. It follows that the path ![]() $\tilde \gamma _g$ is a loop if and only if
$\tilde \gamma _g$ is a loop if and only if ![]() $g=\mathbb {1}_G$. This shows that
$g=\mathbb {1}_G$. This shows that ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ is a universal covering and, in particular,
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}\to \mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$ is a universal covering and, in particular, ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ is simply connected.
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}};\mathbb {1}}$ is simply connected.
From now on it is convenient to replace the nice couple ![]() $(\diamond,\partial )$ with the nice couple
$(\diamond,\partial )$ with the nice couple ![]() $({\mathcal {R}},\partial )$. For this, fix an orientation-preserving, semialgebraic homeomorphism
$({\mathcal {R}},\partial )$. For this, fix an orientation-preserving, semialgebraic homeomorphism ![]() $\xi \colon \mathbb {C}\to \mathbb {C}$ fixing
$\xi \colon \mathbb {C}\to \mathbb {C}$ fixing ![]() $*$ and restricting to a homeomorphism of couples
$*$ and restricting to a homeomorphism of couples ![]() $(\diamond,\partial )\cong ({\mathcal {R}},\partial )$; then
$(\diamond,\partial )\cong ({\mathcal {R}},\partial )$; then ![]() $\xi$ induces a homeomorphism
$\xi$ induces a homeomorphism ![]() $\xi _*\colon \mathrm {Hur}(\diamond,\partial )\cong \mathrm {Hur}({\mathcal {R}},\partial )$, restricting to a homeomorphism
$\xi _*\colon \mathrm {Hur}(\diamond,\partial )\cong \mathrm {Hur}({\mathcal {R}},\partial )$, restricting to a homeomorphism ![]() $\mathrm {Hur}_+(\diamond,\partial )_{\mathbb {1}}\cong \mathrm {Hur}_+({\mathcal {R}},\partial )_{\mathbb {1}}$. Using again [Reference BianchiBia23a, Proposition 7.10] we can then replace
$\mathrm {Hur}_+(\diamond,\partial )_{\mathbb {1}}\cong \mathrm {Hur}_+({\mathcal {R}},\partial )_{\mathbb {1}}$. Using again [Reference BianchiBia23a, Proposition 7.10] we can then replace ![]() $\mathrm {Hur}_+({\mathcal {R}},\partial )_{\mathbb {1}}$ by the weakly equivalent space
$\mathrm {Hur}_+({\mathcal {R}},\partial )_{\mathbb {1}}$ by the weakly equivalent space ![]() $\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}}$, where
$\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}}$, where ![]() $0\in \partial {\mathcal {R}}$ is the lower left vertex.
$0\in \partial {\mathcal {R}}$ is the lower left vertex.
We rephrase the last homology isomorphism, together with the discussion about simply connectedness, as the following theorem.
Theorem 4.22 In the hypotheses of Theorem 4.1 there is an isomorphism of graded abelian groups
Moreover, the space ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is simply connected.
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is simply connected.
We immediately observe that the left-hand side of the isomorphism in Theorem 4.22 only depends on the PMQ ![]() ${\mathcal {Q}}$ and not on the PMQ–group pair
${\mathcal {Q}}$ and not on the PMQ–group pair ![]() $({\mathcal {Q}},G)$ (in particular, not on the group
$({\mathcal {Q}},G)$ (in particular, not on the group ![]() $G$). In fact, the isomorphism of Theorem 4.22 is an isomorphism of rings, if we consider on
$G$). In fact, the isomorphism of Theorem 4.22 is an isomorphism of rings, if we consider on ![]() $\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})] \otimes H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ the correct structure of twisted tensor product of rings, which we briefly describe in the following.
$\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})] \otimes H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ the correct structure of twisted tensor product of rings, which we briefly describe in the following.
The group ![]() ${\mathcal {G}}({\mathcal {Q}})$ acts on the right on
${\mathcal {G}}({\mathcal {Q}})$ acts on the right on ![]() $\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}}=\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ by global conjugation: in fact,
$\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}}=\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ by global conjugation: in fact, ![]() $G$ acts on the right on this space by global conjugation and we consider the map of groups
$G$ acts on the right on this space by global conjugation and we consider the map of groups ![]() ${\mathcal {G}}(\mathfrak {e})\colon {\mathcal {G}}({\mathcal {Q}})\to G$. Consequently,
${\mathcal {G}}(\mathfrak {e})\colon {\mathcal {G}}({\mathcal {Q}})\to G$. Consequently, ![]() ${\mathcal {G}}({\mathcal {Q}})$ acts on the right on
${\mathcal {G}}({\mathcal {Q}})$ acts on the right on ![]() $H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ by automorphisms of rings.
$H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ by automorphisms of rings.
For ![]() $g_1,g_2\in {\mathcal {G}}({\mathcal {Q}})$ and
$g_1,g_2\in {\mathcal {G}}({\mathcal {Q}})$ and ![]() $x_1,x_2\in H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ we define the twisted product
$x_1,x_2\in H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ we define the twisted product ![]() $(g_1\otimes x_1)\cdot (g_2\otimes x_2):=(g_1g_2\otimes (x_1^{g_2}\cdot x_2)$. This assignment extends to an associative product on
$(g_1\otimes x_1)\cdot (g_2\otimes x_2):=(g_1g_2\otimes (x_1^{g_2}\cdot x_2)$. This assignment extends to an associative product on ![]() $\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})] \otimes H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ and with this ring structure the isomorphism of Theorem 4.22 is an isomorphism of rings.
$\mathbb {Z}[{\mathcal {G}}({\mathcal {Q}})] \otimes H_*(\Omega ^2_0 \,\mathrm {Hur}({\mathcal {R}},\partial )_{0;\mathbb {1}})$ and with this ring structure the isomorphism of Theorem 4.22 is an isomorphism of rings.
The isomorphism of Theorem 4.22 is a bit surprising at first glance, because ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$ is not, in general, weakly equivalent to an
$\mathring {\mathrm {HM}}({\mathcal {Q}})$ is not, in general, weakly equivalent to an ![]() $E_2$-algebra.
$E_2$-algebra.
5. The space  $\mathbb {B}({\mathcal {Q}}_+,G)$
$\mathbb {B}({\mathcal {Q}}_+,G)$
For concrete homology computations the space ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is too large. In this section, we introduce a homotopy equivalent subspace
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is too large. In this section, we introduce a homotopy equivalent subspace
under the assumption that ![]() ${\mathcal {Q}}$ is augmented. If, in addition, we assume that
${\mathcal {Q}}$ is augmented. If, in addition, we assume that ![]() ${\mathcal {Q}}$ is normed, then
${\mathcal {Q}}$ is normed, then ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ admits a natural filtration by closed subspaces. In the next section, assuming further that
$\mathbb {B}({\mathcal {Q}}_+,G)$ admits a natural filtration by closed subspaces. In the next section, assuming further that ![]() ${\mathcal {Q}}$ is finite and rationally Poincaré, we will exploit this filtration to compute explicitly the rational cohomology ring of
${\mathcal {Q}}$ is finite and rationally Poincaré, we will exploit this filtration to compute explicitly the rational cohomology ring of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$.
$\mathbb {B}({\mathcal {Q}}_+,G)$.
Recall from [Reference BianchiBia21, Definitions 4.1 and 4.9] that a PMQ is augmented if the set ![]() ${\mathcal {Q}}_+:={\mathcal {Q}}\setminus \{\mathbb {1}\}$ is an ideal for the partial product, i.e. if for all
${\mathcal {Q}}_+:={\mathcal {Q}}\setminus \{\mathbb {1}\}$ is an ideal for the partial product, i.e. if for all ![]() $a,b\in {\mathcal {Q}}$ such that
$a,b\in {\mathcal {Q}}$ such that ![]() $ab=\mathbb {1}$ we have
$ab=\mathbb {1}$ we have ![]() $a,b=\mathbb {1}$. A normed PMQ is a PMQ
$a,b=\mathbb {1}$. A normed PMQ is a PMQ ![]() ${\mathcal {Q}}$ together with a morphism of PMQs
${\mathcal {Q}}$ together with a morphism of PMQs ![]() $N\colon {\mathcal {Q}}\to \mathbb {N}$ such that
$N\colon {\mathcal {Q}}\to \mathbb {N}$ such that ![]() $N^{-1}(0)=\{\mathbb {1}\}$. Every normed PMQ is also augmented.
$N^{-1}(0)=\{\mathbb {1}\}$. Every normed PMQ is also augmented.
Definition 5.1 Let ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ and use Notation 2.2, so that the support
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ and use Notation 2.2, so that the support ![]() $P$ of
$P$ of ![]() $\mathfrak {c}$ splits as
$\mathfrak {c}$ splits as ![]() $\{z_1,\ldots,z_l\}\subset \mathring {{\mathcal {R}}}$ and
$\{z_1,\ldots,z_l\}\subset \mathring {{\mathcal {R}}}$ and ![]() $\{z_{l+1},\ldots,z_k\}\subset \partial {\mathcal {R}}$. Let
$\{z_{l+1},\ldots,z_k\}\subset \partial {\mathcal {R}}$. Let ![]() $\beta \subset \mathring {{\mathcal {R}}}$ be a clockwise oriented simple closed curve in
$\beta \subset \mathring {{\mathcal {R}}}$ be a clockwise oriented simple closed curve in ![]() $\mathring {{\mathcal {R}}}\setminus P$ such that the disc bounded by
$\mathring {{\mathcal {R}}}\setminus P$ such that the disc bounded by ![]() $\beta$ contains all points
$\beta$ contains all points ![]() $z_1,\ldots,z_l$.
$z_1,\ldots,z_l$.
The configuration ![]() $\mathfrak {c}$ lies in the subspace
$\mathfrak {c}$ lies in the subspace ![]() $\mathbb {B}({\mathcal {Q}},G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ if the conjugacy class of
$\mathbb {B}({\mathcal {Q}},G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ if the conjugacy class of ![]() $\mathfrak {G}(P)$ corresponding to
$\mathfrak {G}(P)$ corresponding to ![]() $\beta$ is contained in the PMQ
$\beta$ is contained in the PMQ ![]() $\mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }\subset \mathfrak {G}(P)$ (see [Reference BianchiBia23a, Definition 2.13]).
$\mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }\subset \mathfrak {G}(P)$ (see [Reference BianchiBia23a, Definition 2.13]).
If ![]() ${\mathcal {Q}}$ is augmented, we define
${\mathcal {Q}}$ is augmented, we define ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ as the intersection
$\mathbb {B}({\mathcal {Q}}_+,G)$ as the intersection
Roughly speaking, a configuration ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ lies in
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ lies in ![]() $\mathbb {B}({\mathcal {Q}},G)$ if, using Notation 2.2, the
$\mathbb {B}({\mathcal {Q}},G)$ if, using Notation 2.2, the ![]() $l$ values of the monodromy
$l$ values of the monodromy ![]() $\psi$ around the
$\psi$ around the ![]() $l$ points of
$l$ points of ![]() $P\cap \mathring {{\mathcal {R}}}$ can be multiplied in
$P\cap \mathring {{\mathcal {R}}}$ can be multiplied in ![]() ${\mathcal {Q}}$. See Figure 7.
${\mathcal {Q}}$. See Figure 7.
Definition 5.2 Let ![]() $\mathfrak {C}$ be a nice couple and let
$\mathfrak {C}$ be a nice couple and let ![]() $({\mathcal {Q}},G)$ be a PMQ–group pair with
$({\mathcal {Q}},G)$ be a PMQ–group pair with ![]() ${\mathcal {Q}}$ augmented. Let
${\mathcal {Q}}$ augmented. Let ![]() $\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$; a point
$\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$; a point ![]() $z\in P$ is inert for
$z\in P$ is inert for ![]() $\mathfrak {c}$ if
$\mathfrak {c}$ if ![]() $z\in {\mathcal {X}}\setminus {\mathcal {Y}}$ and
$z\in {\mathcal {X}}\setminus {\mathcal {Y}}$ and ![]() $\psi$ sends to
$\psi$ sends to ![]() $\mathbb {1}_{{\mathcal {Q}}}$ each element of
$\mathbb {1}_{{\mathcal {Q}}}$ each element of ![]() $\mathfrak {Q}(P)$ represented by a small loop spinning clockwise around
$\mathfrak {Q}(P)$ represented by a small loop spinning clockwise around ![]() $z$.
$z$.

Figure 7. The configuration ![]() $\mathfrak {c}$ lies in the space
$\mathfrak {c}$ lies in the space ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ if
$\mathbb {B}({\mathcal {Q}}_+,G)$ if ![]() $g_6\mathfrak {e}(a_1)g_4\mathfrak {e}(a_2)g_5\mathfrak {e}(a_3)=\mathbb {1}\in G$, none of
$g_6\mathfrak {e}(a_1)g_4\mathfrak {e}(a_2)g_5\mathfrak {e}(a_3)=\mathbb {1}\in G$, none of ![]() $a_1,a_2,a_3$ is equal to
$a_1,a_2,a_3$ is equal to ![]() $\mathbb {1}\in {\mathcal {Q}}$ and the product
$\mathbb {1}\in {\mathcal {Q}}$ and the product ![]() $a_1a_2(a_3^{g_5^{-1}})$ is defined in
$a_1a_2(a_3^{g_5^{-1}})$ is defined in ![]() ${\mathcal {Q}}$.
${\mathcal {Q}}$.
If ![]() ${\mathcal {Q}}$ is augmented, a configuration
${\mathcal {Q}}$ is augmented, a configuration ![]() $\mathfrak {c}$ lies in
$\mathfrak {c}$ lies in ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ if it lies in
$\mathbb {B}({\mathcal {Q}}_+,G)$ if it lies in ![]() $\mathbb {B}({\mathcal {Q}},G)$ and, moreover, no point of the support of
$\mathbb {B}({\mathcal {Q}},G)$ and, moreover, no point of the support of ![]() $\mathfrak {c}$ is inert: in other words,
$\mathfrak {c}$ is inert: in other words, ![]() $\psi$ attains values different from
$\psi$ attains values different from ![]() $\mathbb {1}$ around all
$\mathbb {1}$ around all ![]() $l$ points of
$l$ points of ![]() $P\cap \mathring {{\mathcal {R}}}$.
$P\cap \mathring {{\mathcal {R}}}$.
Example 5.3 Suppose that ![]() ${\mathcal {Q}}$ is finite and normed and let
${\mathcal {Q}}$ is finite and normed and let ![]() $N_{\mathrm {max}}\in \mathbb {N}$ be the maximal norm of an element of
$N_{\mathrm {max}}\in \mathbb {N}$ be the maximal norm of an element of ![]() ${\mathcal {Q}}$. Let
${\mathcal {Q}}$. Let ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}},G)$ and use Notation 2.2. Then at most
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}},G)$ and use Notation 2.2. Then at most ![]() $N_{\mathrm {max}}$ of the
$N_{\mathrm {max}}$ of the ![]() $l$ points in
$l$ points in ![]() $P\cap \mathring {{\mathcal {R}}}_1$ can be non-inert; in particular, if
$P\cap \mathring {{\mathcal {R}}}_1$ can be non-inert; in particular, if ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, then
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, then ![]() $l\leq N_{\mathrm {max}}$. There is also another evident restriction on the behaviour of
$l\leq N_{\mathrm {max}}$. There is also another evident restriction on the behaviour of ![]() $\psi$: if
$\psi$: if ![]() $f_1,\ldots,f_k$ is an admissible generating set for
$f_1,\ldots,f_k$ is an admissible generating set for ![]() $\mathfrak {G}(P)$, then
$\mathfrak {G}(P)$, then ![]() $\sum _{i=1}^l N(\psi (f_i))\leq N_{\mathrm {max}}$.
$\sum _{i=1}^l N(\psi (f_i))\leq N_{\mathrm {max}}$.
Example 5.4 Let ![]() ${\mathcal {Q}}$ be the abelian PMQ
${\mathcal {Q}}$ be the abelian PMQ ![]() $\{\mathbb {1},\bullet \}$ with trivial partial multiplication and let
$\{\mathbb {1},\bullet \}$ with trivial partial multiplication and let ![]() $G=\{\mathbb {1}\}$ be the trivial group. Let
$G=\{\mathbb {1}\}$ be the trivial group. Let ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$ and use Notation 2.2. Then
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$ and use Notation 2.2. Then ![]() $P\cap \mathring {{\mathcal {R}}}$ is either empty or it contains exactly one point. We can define a map
$P\cap \mathring {{\mathcal {R}}}$ is either empty or it contains exactly one point. We can define a map ![]() $\mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {R}}/\partial {\mathcal {R}}\cong S^2$ by looking at the position of the unique point of
$\mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {R}}/\partial {\mathcal {R}}\cong S^2$ by looking at the position of the unique point of ![]() $P$ in
$P$ in ![]() $\mathring {{\mathcal {R}}}$ and taking the quotient point
$\mathring {{\mathcal {R}}}$ and taking the quotient point ![]() $[\partial {\mathcal {R}}]\in {\mathcal {R}}/\partial {\mathcal {R}}$ if
$[\partial {\mathcal {R}}]\in {\mathcal {R}}/\partial {\mathcal {R}}$ if ![]() $P\cap \mathring {{\mathcal {R}}}=\emptyset$. In fact, the map
$P\cap \mathring {{\mathcal {R}}}=\emptyset$. In fact, the map ![]() $\mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {R}}/\partial {\mathcal {R}}$ is a quasifibration with fibre the Ran space
$\mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {R}}/\partial {\mathcal {R}}$ is a quasifibration with fibre the Ran space ![]() $\mathrm {Ran}(\partial {\mathcal {R}})$, so it is a weak homotopy equivalence.
$\mathrm {Ran}(\partial {\mathcal {R}})$, so it is a weak homotopy equivalence.
We will see in Proposition 5.5 that the inclusion ![]() $\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathrm {Hur}({\mathcal {R}},\partial {\mathcal {R}};{\mathcal {Q}},G)_{0;\mathbb {1}}$ is also a homotopy equivalence; hence, in this case, Theorem 4.22 reduces to a classical result of Segal [Reference SegalSeg73] stating that the group completion of the topological monoid
$\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathrm {Hur}({\mathcal {R}},\partial {\mathcal {R}};{\mathcal {Q}},G)_{0;\mathbb {1}}$ is also a homotopy equivalence; hence, in this case, Theorem 4.22 reduces to a classical result of Segal [Reference SegalSeg73] stating that the group completion of the topological monoid ![]() $\coprod _{n\geq 0}\mathrm {Conf}_n(\mathbb {R}^2)$ is
$\coprod _{n\geq 0}\mathrm {Conf}_n(\mathbb {R}^2)$ is ![]() $\Omega ^2S^2$. Passing from
$\Omega ^2S^2$. Passing from ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ to its subspace
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ to its subspace ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ should thus be regarded as the analogue of passing from the relative configuration space
$\mathbb {B}({\mathcal {Q}}_+,G)$ should thus be regarded as the analogue of passing from the relative configuration space ![]() $\mathrm {Conf}({\mathcal {R}},\partial )$ to the sphere
$\mathrm {Conf}({\mathcal {R}},\partial )$ to the sphere ![]() $\mathring {{\mathcal {R}}}/\partial \mathring {{\mathcal {R}}}$ by a scanning argument.
$\mathring {{\mathcal {R}}}/\partial \mathring {{\mathcal {R}}}$ by a scanning argument.
5.1 Deformation retraction onto  $\mathbb {B}({\mathcal {Q}},G)$
$\mathbb {B}({\mathcal {Q}},G)$
In this subsection we will prove that ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ admits a deformation retraction onto its subspace
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ admits a deformation retraction onto its subspace ![]() $\mathbb {B}({\mathcal {Q}},G)$; if
$\mathbb {B}({\mathcal {Q}},G)$; if ![]() ${\mathcal {Q}}$ is augmented, the same argument will give by restriction a deformation retraction of
${\mathcal {Q}}$ is augmented, the same argument will give by restriction a deformation retraction of ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ onto its subspace
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ onto its subspace ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$. Using [Reference BianchiBia23a, Proposition 7.4], we will therefore obtain the following proposition.
$\mathbb {B}({\mathcal {Q}}_+,G)$. Using [Reference BianchiBia23a, Proposition 7.4], we will therefore obtain the following proposition.
Proposition 5.5 For any PMQ–group pair ![]() $({\mathcal {Q}},G)$ the inclusion of
$({\mathcal {Q}},G)$ the inclusion of ![]() $\mathbb {B}({\mathcal {Q}},G)$ into
$\mathbb {B}({\mathcal {Q}},G)$ into ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is a homotopy equivalence. If
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ is a homotopy equivalence. If ![]() ${\mathcal {Q}}$ is augmented, the following is a square of inclusions which are homotopy equivalences:
${\mathcal {Q}}$ is augmented, the following is a square of inclusions which are homotopy equivalences:

The rough idea of the proof of Proposition 5.5 is that each configuration ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ can be gradually magnified around the centre
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ can be gradually magnified around the centre ![]() $z_{\mathrm {c}}\in {\mathcal {R}}$, letting gradually more and more points collide with
$z_{\mathrm {c}}\in {\mathcal {R}}$, letting gradually more and more points collide with ![]() $\partial {\mathcal {R}}$: such points are downgraded to points in the support of
$\partial {\mathcal {R}}$: such points are downgraded to points in the support of ![]() $\mathfrak {c}$ around which only the
$\mathfrak {c}$ around which only the ![]() $G$-valued monodromy is defined and they remain fixed during further magnification. At some finite time we obtain a configuration satisfying the properties of Definition 5.1 and we stop the magnification.
$G$-valued monodromy is defined and they remain fixed during further magnification. At some finite time we obtain a configuration satisfying the properties of Definition 5.1 and we stop the magnification.
Definition 5.6 Let ![]() $z_0\in \mathring {{\mathcal {R}}}$. For
$z_0\in \mathring {{\mathcal {R}}}$. For ![]() $z\in \mathbb {C}$ let
$z\in \mathbb {C}$ let ![]() $\mathfrak {d}^{\mathbb {B}}_{z_0}(z)\in [1,\infty ]$ be the infimum of all
$\mathfrak {d}^{\mathbb {B}}_{z_0}(z)\in [1,\infty ]$ be the infimum of all ![]() $s\ge 1$ such that
$s\ge 1$ such that ![]() $z_0+s(z-z_0)\notin {\mathcal {R}}$; note that
$z_0+s(z-z_0)\notin {\mathcal {R}}$; note that ![]() $\mathfrak {d}^{\mathbb {B}}_{z_0}(z)=\infty$ if and only if
$\mathfrak {d}^{\mathbb {B}}_{z_0}(z)=\infty$ if and only if ![]() $z=z_0$. We define a map
$z=z_0$. We define a map ![]() ${\mathcal {H}}^{\mathbb {B}}_{z_0}\colon \mathbb {C}\times [1,\infty )\to \mathbb {C}$ by the formula
${\mathcal {H}}^{\mathbb {B}}_{z_0}\colon \mathbb {C}\times [1,\infty )\to \mathbb {C}$ by the formula
 \[
{\mathcal{H}}^{\mathbb{B}}_{z_0}(z,s)=\begin{cases}
z & \text{if } z\notin \mathring{{\mathcal{R}}},\\
z_0+s(z-z_0) & \text{if }z\in{\mathcal{R}} \text{ and }
z_0+s(z-z_0)\in{\mathcal{R}},\\
z_0+\mathfrak{d}^{\mathbb{B}}_{z_0}(z)\cdot(z-z_0) &
\text{if }z\in{\mathcal{R}} \text{ and }
z_0+s(z-z_0)\notin{\mathcal{R}}. \end{cases}
\]
\[
{\mathcal{H}}^{\mathbb{B}}_{z_0}(z,s)=\begin{cases}
z & \text{if } z\notin \mathring{{\mathcal{R}}},\\
z_0+s(z-z_0) & \text{if }z\in{\mathcal{R}} \text{ and }
z_0+s(z-z_0)\in{\mathcal{R}},\\
z_0+\mathfrak{d}^{\mathbb{B}}_{z_0}(z)\cdot(z-z_0) &
\text{if }z\in{\mathcal{R}} \text{ and }
z_0+s(z-z_0)\notin{\mathcal{R}}. \end{cases}
\]
Roughly speaking, the map ![]() ${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,s)$ expands the square
${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,s)$ expands the square ![]() $ ({s-1})/s z_0+ (1/s) \mathring {{\mathcal {R}}}$, which has side length
$ ({s-1})/s z_0+ (1/s) \mathring {{\mathcal {R}}}$, which has side length ![]() $1/s$, to the entire
$1/s$, to the entire ![]() ${\mathcal {R}}$, by a homothety centred at
${\mathcal {R}}$, by a homothety centred at ![]() $z_0$ of rescaling factor
$z_0$ of rescaling factor ![]() $s$ and collapses
$s$ and collapses
onto ![]() $\partial {\mathcal {R}}$. Note that for all
$\partial {\mathcal {R}}$. Note that for all ![]() $s\geq 1$ the map
$s\geq 1$ the map ![]() ${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,s)$ is an endomorphism of the nice couples
${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,s)$ is an endomorphism of the nice couples ![]() $({\mathcal {R}},\partial )$; note also that
$({\mathcal {R}},\partial )$; note also that ![]() ${\mathcal {H}}^{\mathbb {B}}_{z_0}(0,s)=0$ for all
${\mathcal {H}}^{\mathbb {B}}_{z_0}(0,s)=0$ for all ![]() $s\ge 1$ and that
$s\ge 1$ and that ![]() ${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,1)$ is the identity of
${\mathcal {H}}^{\mathbb {B}}_{z_0}(-,1)$ is the identity of ![]() $\mathbb {C}$. Thus, we obtain a continuous map
$\mathbb {C}$. Thus, we obtain a continuous map
such that ![]() $({\mathcal {H}}^{\mathbb {B}}_{z_0})_*(-,1)$ is the identity of
$({\mathcal {H}}^{\mathbb {B}}_{z_0})_*(-,1)$ is the identity of ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$.
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$.
Definition 5.7 Let ![]() $z_0\in \mathring {{\mathcal {R}}}$. For each
$z_0\in \mathring {{\mathcal {R}}}$. For each ![]() $0<\varepsilon <1$ denote by
$0<\varepsilon <1$ denote by ![]() $\beta _{z_0,\varepsilon }\subset \mathring {{\mathcal {R}}}$ the simple closed curve whose support is the square
$\beta _{z_0,\varepsilon }\subset \mathring {{\mathcal {R}}}$ the simple closed curve whose support is the square ![]() $(1-\varepsilon )z_0+\varepsilon (\partial {\mathcal {R}})$, i.e. the boundary of the square of side length
$(1-\varepsilon )z_0+\varepsilon (\partial {\mathcal {R}})$, i.e. the boundary of the square of side length ![]() $\varepsilon$ obtained from
$\varepsilon$ obtained from ![]() $\partial {\mathcal {R}}$ by a homothety centred at
$\partial {\mathcal {R}}$ by a homothety centred at ![]() $z_0$ of rescaling factor
$z_0$ of rescaling factor ![]() $\varepsilon$; we orient
$\varepsilon$; we orient ![]() $\beta _{z_0,\varepsilon }$ clockwise. Let
$\beta _{z_0,\varepsilon }$ clockwise. Let ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial )_{\mathbb {1}}$ and use Notation 2.2. We denote by
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial )_{\mathbb {1}}$ and use Notation 2.2. We denote by ![]() $\mathfrak {W}_{z_0}(\mathfrak {c})\in [0,1]$ the supremum of all
$\mathfrak {W}_{z_0}(\mathfrak {c})\in [0,1]$ the supremum of all ![]() $0<\varepsilon <1$ satisfying the following properties:
$0<\varepsilon <1$ satisfying the following properties:
•
 $P\cap \beta _{z_0,\varepsilon }=\emptyset$;
$P\cap \beta _{z_0,\varepsilon }=\emptyset$;• every element
 $\mathfrak {g}\in \mathfrak {G}(P)$ in the conjugacy class corresponding to
$\mathfrak {g}\in \mathfrak {G}(P)$ in the conjugacy class corresponding to  $\beta _{z_0,\varepsilon }$ belongs to
$\beta _{z_0,\varepsilon }$ belongs to  $\mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }\subseteq \mathfrak {G}(P)$.
$\mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }\subseteq \mathfrak {G}(P)$.
Note that ![]() $\mathfrak {W}_{z_0}(\mathfrak {c})\leq 1$ for all
$\mathfrak {W}_{z_0}(\mathfrak {c})\leq 1$ for all ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{\mathbb {1}}$; moreover,
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{\mathbb {1}}$; moreover, ![]() $\mathfrak {W}_{z_0}(\mathfrak {c})= 1$ if and only if
$\mathfrak {W}_{z_0}(\mathfrak {c})= 1$ if and only if ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}},G)$. Note, on the other hand, that
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}},G)$. Note, on the other hand, that ![]() $\mathfrak {W}_{z_0}(\mathfrak {c})>0$, as for a generic and very small
$\mathfrak {W}_{z_0}(\mathfrak {c})>0$, as for a generic and very small ![]() $\varepsilon >0$ the curve
$\varepsilon >0$ the curve ![]() $\beta _{z_0,\varepsilon }$ is disjoint from
$\beta _{z_0,\varepsilon }$ is disjoint from ![]() $P$ and encloses at most one point of
$P$ and encloses at most one point of ![]() $P$, so it corresponds to a conjugacy class of
$P$, so it corresponds to a conjugacy class of ![]() $\mathfrak {G}(P)$ which is contained in
$\mathfrak {G}(P)$ which is contained in ![]() $\mathfrak {Q}(P)\subset \mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }$. Note also that the assignment
$\mathfrak {Q}(P)\subset \mathfrak {Q}^{\mathrm {ext}}(P)_{\psi }$. Note also that the assignment ![]() $\mathfrak {c}\mapsto \mathfrak {W}_{z_0}(\mathfrak {c})$ is continuous in
$\mathfrak {c}\mapsto \mathfrak {W}_{z_0}(\mathfrak {c})$ is continuous in ![]() $\mathfrak {c}$.
$\mathfrak {c}$.
Notation 5.8 Recall Notation 2.16. We simplify the notation and write ![]() ${\mathcal {H}}^{\mathbb {B}}={\mathcal {H}}^{\mathbb {B}}_{z_{\mathrm {c}}}$ and
${\mathcal {H}}^{\mathbb {B}}={\mathcal {H}}^{\mathbb {B}}_{z_{\mathrm {c}}}$ and ![]() $\mathfrak {W}=\mathfrak {W}_{z_{\mathrm {c}}}$.
$\mathfrak {W}=\mathfrak {W}_{z_{\mathrm {c}}}$.
Proof of Proposition 5.5 We define a homotopy
 \begin{gather*} H^{\mathbb{B}}\colon \mathrm{Hur}({\mathcal{R}},\partial;{\mathcal{Q}},G)_{0;\mathbb {1}}\times[0,1]\to\mathrm{Hur}({\mathcal{R}},\partial;{\mathcal{Q}},G)_{0;\mathbb {1}},\\ H^{\mathbb{B}}(\mathfrak{c},s)={\mathcal{H}}^{\mathbb{B}}_*\bigg(\mathfrak{c},\,1-s+s\frac 1{\mathfrak{W}(\mathfrak{c})}\bigg). \end{gather*}
\begin{gather*} H^{\mathbb{B}}\colon \mathrm{Hur}({\mathcal{R}},\partial;{\mathcal{Q}},G)_{0;\mathbb {1}}\times[0,1]\to\mathrm{Hur}({\mathcal{R}},\partial;{\mathcal{Q}},G)_{0;\mathbb {1}},\\ H^{\mathbb{B}}(\mathfrak{c},s)={\mathcal{H}}^{\mathbb{B}}_*\bigg(\mathfrak{c},\,1-s+s\frac 1{\mathfrak{W}(\mathfrak{c})}\bigg). \end{gather*}
Note that ![]() $H^{\mathbb {B}}(-,0)$ is the identity of
$H^{\mathbb {B}}(-,0)$ is the identity of ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$, that
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$, that ![]() $H^{\mathbb {B}}(-,1)$ takes values in
$H^{\mathbb {B}}(-,1)$ takes values in ![]() $\mathbb {B}({\mathcal {Q}},G)$ and that
$\mathbb {B}({\mathcal {Q}},G)$ and that ![]() $H^{\mathbb {B}}(-,s)$ restricts to the identity of
$H^{\mathbb {B}}(-,s)$ restricts to the identity of ![]() $\mathbb {B}({\mathcal {Q}},G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)$ for all
$\mathbb {B}({\mathcal {Q}},G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)$ for all ![]() $0\leq s\leq 1$.
$0\leq s\leq 1$.
This proves the first homotopy equivalence in the statement. The second homotopy equivalence is completely analogous: we have constructed the deformation retraction of ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ onto its subspace
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)_{0;\mathbb {1}}$ onto its subspace ![]() $\mathbb {B}({\mathcal {Q}},G)$ using enriched functoriality with respect to maps of nice couples; this implies that
$\mathbb {B}({\mathcal {Q}},G)$ using enriched functoriality with respect to maps of nice couples; this implies that ![]() $H^{\mathbb {B}}(-,s)$ restricts at all times to a self-map of
$H^{\mathbb {B}}(-,s)$ restricts at all times to a self-map of ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ and, in particular, the restriction of
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ and, in particular, the restriction of ![]() $H^{\mathbb {B}}(-,1)$ on
$H^{\mathbb {B}}(-,1)$ on ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ takes values in
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}$ takes values in ![]() $\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}\cap \mathbb {B}({\mathcal {Q}},G)=\mathbb {B}({\mathcal {Q}}_+,G)$.
$\mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}}_+,G)_{0;\mathbb {1}}\cap \mathbb {B}({\mathcal {Q}},G)=\mathbb {B}({\mathcal {Q}}_+,G)$.
5.2 Norm filtration
In the rest of the section we assume that ![]() ${\mathcal {Q}}$ is endowed with a norm
${\mathcal {Q}}$ is endowed with a norm ![]() $N\colon {\mathcal {Q}}\to \mathbb {N}$. Our aim is to introduce a filtration
$N\colon {\mathcal {Q}}\to \mathbb {N}$. Our aim is to introduce a filtration ![]() $F_{\bullet }$ on
$F_{\bullet }$ on ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$. It will be convenient to define a norm filtration
$\mathbb {B}({\mathcal {Q}}_+,G)$. It will be convenient to define a norm filtration ![]() $F_{\bullet }$ more generally on the Hurwitz space
$F_{\bullet }$ more generally on the Hurwitz space ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ associated with any nice couple
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ associated with any nice couple ![]() $\mathfrak {C}$.
$\mathfrak {C}$.
Definition 5.9 Let ![]() $\mathfrak {C}$ be a nice couple, let
$\mathfrak {C}$ be a nice couple, let ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and use Notation 2.2. Let
$\mathfrak {c}\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and use Notation 2.2. Let ![]() $f_1,\ldots,f_k$ be an admissible generating set for
$f_1,\ldots,f_k$ be an admissible generating set for ![]() $\mathfrak {G}(P)$. We define a function of sets
$\mathfrak {G}(P)$. We define a function of sets ![]() $N\colon \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\to \mathbb {N}$ by
$N\colon \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\to \mathbb {N}$ by
and call ![]() $N(\mathfrak {c})$ the norm of the configuration
$N(\mathfrak {c})$ the norm of the configuration ![]() $\mathfrak {c}$.
$\mathfrak {c}$.
For ![]() $\nu \geq 0$ we define the
$\nu \geq 0$ we define the ![]() $\nu$th filtration layer
$\nu$th filtration layer ![]() $F_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ as the subspace of configurations
$F_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ as the subspace of configurations ![]() $\mathfrak {c}$ with
$\mathfrak {c}$ with ![]() $N(\mathfrak {c})\leq \nu$. We also set
$N(\mathfrak {c})\leq \nu$. We also set ![]() $F_{-1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)=\emptyset$.
$F_{-1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)=\emptyset$.
For ![]() $\nu \geq 0$ we denote by
$\nu \geq 0$ we denote by ![]() $\mathfrak {F}_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ the
$\mathfrak {F}_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ the ![]() $\nu$th filtration stratum
$\nu$th filtration stratum
Recall from [Reference BianchiBia23a, Definition 2.5] that given a nice couple ![]() $\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ and a finite subset
$\mathfrak {C}=({\mathcal {X}},{\mathcal {Y}})$ and a finite subset ![]() $P\subset {\mathcal {X}}$, an adapted covering of
$P\subset {\mathcal {X}}$, an adapted covering of ![]() $P$ is a collection
$P$ is a collection ![]() $\underline {U}$ of disjoint, semialgebraic open discs in
$\underline {U}$ of disjoint, semialgebraic open discs in ![]() $\mathbb {C}$ containing each a single point of
$\mathbb {C}$ containing each a single point of ![]() $P$ and such that each point in
$P$ and such that each point in ![]() $P\setminus {\mathcal {Y}}$ is surrounded by a disc disjoint from
$P\setminus {\mathcal {Y}}$ is surrounded by a disc disjoint from ![]() ${\mathcal {Y}}$. The topology on
${\mathcal {Y}}$. The topology on ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ has a basis given by the open neighbourhoods
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ has a basis given by the open neighbourhoods ![]() $\mathfrak {U}(\mathfrak {c};\underline {U})$, for varying
$\mathfrak {U}(\mathfrak {c};\underline {U})$, for varying ![]() $\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and varying
$\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and varying ![]() $\underline {U}$ among adapted covers of
$\underline {U}$ among adapted covers of ![]() $P$.
$P$.
Lemma 5.10 For all ![]() $\nu \geq 0$ we have that
$\nu \geq 0$ we have that ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ is open in
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ is open in ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
Proof. Let ![]() $\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and assume that
$\mathfrak {c}=(P,\psi,\varphi )\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and assume that ![]() $N(\mathfrak {c})\geq \nu$. Let
$N(\mathfrak {c})\geq \nu$. Let ![]() $\underline {U}$ be an adapted covering of
$\underline {U}$ be an adapted covering of ![]() $P$. We claim that the open neighbourhood
$P$. We claim that the open neighbourhood ![]() $\mathfrak {U}(\mathfrak {c},\underline {U})$ is contained in
$\mathfrak {U}(\mathfrak {c},\underline {U})$ is contained in ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
Let ![]() $\mathfrak {c}'\in \mathfrak {U}(\mathfrak {c},\underline {U})$ and use Notation 2.2. For all
$\mathfrak {c}'\in \mathfrak {U}(\mathfrak {c},\underline {U})$ and use Notation 2.2. For all ![]() $1\leq i\leq l$ let
$1\leq i\leq l$ let ![]() $P'_i=P'\cap U_i$ and let
$P'_i=P'\cap U_i$ and let ![]() $P'_i=\{z'_{i,1},\ldots,z'_{i,k'_i}\}$. Choose an admissible generating set
$P'_i=\{z'_{i,1},\ldots,z'_{i,k'_i}\}$. Choose an admissible generating set ![]() $f_1,\ldots,f_k$ of
$f_1,\ldots,f_k$ of ![]() $\mathfrak {G}(P)\cong \mathfrak {G}(\underline {U})$. We can regard
$\mathfrak {G}(P)\cong \mathfrak {G}(\underline {U})$. We can regard ![]() $\mathfrak {G}(\underline {U})$ as a subgroup of
$\mathfrak {G}(\underline {U})$ as a subgroup of ![]() $\mathfrak {G}(P')$. We can choose an admissible generating set
$\mathfrak {G}(P')$. We can choose an admissible generating set ![]() $f'_1,\ldots,f'_{k'}$ of
$f'_1,\ldots,f'_{k'}$ of ![]() $\mathfrak {G}(P')$ with the following property: for all
$\mathfrak {G}(P')$ with the following property: for all ![]() $1\leq i\leq l$, if
$1\leq i\leq l$, if ![]() $f'_{i,1},\ldots,f'_{i,k'_i}$ are the elements represented by loops spinning around the points
$f'_{i,1},\ldots,f'_{i,k'_i}$ are the elements represented by loops spinning around the points ![]() $z'_{i,1},\ldots,z'_{i,k'_i}$, respectively, then the product
$z'_{i,1},\ldots,z'_{i,k'_i}$, respectively, then the product ![]() $f'_{i,1}\cdots f'_{i,k'_i}$ is equal to
$f'_{i,1}\cdots f'_{i,k'_i}$ is equal to ![]() $f_i$ in
$f_i$ in ![]() $\mathfrak {G}(P')$. The hypothesis
$\mathfrak {G}(P')$. The hypothesis ![]() $\mathfrak {c}'\in \mathfrak {U}(\mathfrak {c},\underline {U})$ implies the following equality in
$\mathfrak {c}'\in \mathfrak {U}(\mathfrak {c},\underline {U})$ implies the following equality in ![]() ${\mathcal {Q}}$, for all
${\mathcal {Q}}$, for all ![]() $1\leq i\leq l$:
$1\leq i\leq l$:
whence, using the norm on ![]() ${\mathcal {Q}}$, we obtain
${\mathcal {Q}}$, we obtain
Summing over ![]() $1\leq i\leq l$ and recalling that
$1\leq i\leq l$ and recalling that ![]() $P'_1\cup \cdots \cup P'_l$ might be a proper subset of
$P'_1\cup \cdots \cup P'_l$ might be a proper subset of ![]() $P'\setminus {\mathcal {Y}}=\{z'_1,\ldots,z'_{l'}\}$, we obtain
$P'\setminus {\mathcal {Y}}=\{z'_1,\ldots,z'_{l'}\}$, we obtain
 \[ \nu\leq N(\mathfrak{c})=\sum_{i=1}^lN(\psi(f_i))=\sum_{i=1}^l \sum_{j=1}^{k'_i}N(\psi'(f'_{i,j}))\leq\sum_{i=1}^{l'}N(\psi'(f'_i))=N(\mathfrak{c}'), \]
\[ \nu\leq N(\mathfrak{c})=\sum_{i=1}^lN(\psi(f_i))=\sum_{i=1}^l \sum_{j=1}^{k'_i}N(\psi'(f'_{i,j}))\leq\sum_{i=1}^{l'}N(\psi'(f'_i))=N(\mathfrak{c}'), \]
which shows that ![]() $\mathfrak {U}(\mathfrak {c},\underline {U})$ is contained in
$\mathfrak {U}(\mathfrak {c},\underline {U})$ is contained in ![]() $\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
$\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\setminus F_{\nu -1}\,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$.
Notation 5.11 For every subspace ![]() $X\subset \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and for
$X\subset \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ and for ![]() $\nu \ge -1$, we use the notation
$\nu \ge -1$, we use the notation ![]() $F_\nu X=F_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\cap X$. For
$F_\nu X=F_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\cap X$. For ![]() $\nu \ge 0$, we use the notation
$\nu \ge 0$, we use the notation ![]() $\mathfrak {F}_\nu X=\mathfrak {F}_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\cap X$.
$\mathfrak {F}_\nu X=\mathfrak {F}_\nu \,\mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)\cap X$.
We will use Notation 5.11 mainly in the case ![]() $X=\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)$.
$X=\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathrm {Hur}({\mathcal {R}},\partial ;{\mathcal {Q}},G)$.
5.3 A model for  $BG$
$BG$
Our next goal is to analyse the strata ![]() $\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$. We start with
$\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$. We start with ![]() $\mathfrak {F}_0\mathbb {B}({\mathcal {Q}}_+,G)$, which can be identified with
$\mathfrak {F}_0\mathbb {B}({\mathcal {Q}}_+,G)$, which can be identified with ![]() $\mathrm {Hur}(\partial {\mathcal {R}},\partial {\mathcal {R}};{\mathcal {Q}},G)_{0;\mathbb {1}}$. By [Reference BianchiBia23a, Lemmas 5.4 and 5.5] we can equivalently consider the space
$\mathrm {Hur}(\partial {\mathcal {R}},\partial {\mathcal {R}};{\mathcal {Q}},G)_{0;\mathbb {1}}$. By [Reference BianchiBia23a, Lemmas 5.4 and 5.5] we can equivalently consider the space ![]() $\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, where the group
$\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, where the group ![]() $G$ is considered as a (complete) PMQ. In this subsection we prove the following proposition.
$G$ is considered as a (complete) PMQ. In this subsection we prove the following proposition.
Proposition 5.12 The space ![]() $\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is an Eilenberg–Maclane space of type
$\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is an Eilenberg–Maclane space of type ![]() $K(G,1)$.
$K(G,1)$.
Definition 5.13 We denote by ![]() $\sqcap \subset \partial {\mathcal {R}}$ the union of the three closed sides of
$\sqcap \subset \partial {\mathcal {R}}$ the union of the three closed sides of ![]() ${\mathcal {R}}$
${\mathcal {R}}$
Lemma 5.14 The spaces ![]() $\mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ and
$\mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ and ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ are contractible.
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ are contractible.
Proof. Note that ![]() $\sqcap$ is contractible; more precisely, we can fix a semialgebraic homotopy
$\sqcap$ is contractible; more precisely, we can fix a semialgebraic homotopy ![]() ${\mathcal {H}}^{\sqcap }\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ with the following properties:
${\mathcal {H}}^{\sqcap }\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ with the following properties:
•
 ${\mathcal {H}}^{\sqcap }(-,s)$ is a lax endomorphism of the nice couple
${\mathcal {H}}^{\sqcap }(-,s)$ is a lax endomorphism of the nice couple  $(\sqcap,\emptyset )$, for all
$(\sqcap,\emptyset )$, for all  $0\le s\le 1$ (see [Reference BianchiBia23a, Definition 4.2]);
$0\le s\le 1$ (see [Reference BianchiBia23a, Definition 4.2]);•
 ${\mathcal {H}}^{\sqcap }(0,s)=0\in \mathbb {C}$ for all
${\mathcal {H}}^{\sqcap }(0,s)=0\in \mathbb {C}$ for all  $0\leq s\leq 1$;
$0\leq s\leq 1$;•
 ${\mathcal {H}}^{\sqcap }(-,0)=\operatorname {Id}_{\mathbb {C}}$;
${\mathcal {H}}^{\sqcap }(-,0)=\operatorname {Id}_{\mathbb {C}}$;•
 ${\mathcal {H}}^{\sqcap }(-,1)$ maps
${\mathcal {H}}^{\sqcap }(-,1)$ maps  $\sqcap$ constantly to
$\sqcap$ constantly to  $0$.
$0$.
By functoriality, using that ![]() $G$ is a complete PMQ, we obtain a homotopy
$G$ is a complete PMQ, we obtain a homotopy
Note that the map ![]() ${\mathcal {H}}^{\sqcap }_*(-,1)$ takes values in
${\mathcal {H}}^{\sqcap }_*(-,1)$ takes values in ![]() $\mathrm {Hur}(\{0\},G)_{0;\mathbb {1}}$, which is just a point. Thus, the homotopy
$\mathrm {Hur}(\{0\},G)_{0;\mathbb {1}}$, which is just a point. Thus, the homotopy ![]() ${\mathcal {H}}^{\sqcap }_*$ exhibits
${\mathcal {H}}^{\sqcap }_*$ exhibits ![]() $\mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ as a contractible space.
$\mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ as a contractible space.
By [Reference BianchiBia23a, Proposition 7.10], the inclusion ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\subset \mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ is a homotopy equivalence, hence
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\subset \mathrm {Hur}(\sqcap ;G)_{0;\mathbb {1}}$ is a homotopy equivalence, hence ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ is also contractible.
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ is also contractible.
Now let ![]() $\xi ^{\sqcap }\colon \mathbb {C}\to \mathbb {C}$ be a semialgebraic map with the following properties:
$\xi ^{\sqcap }\colon \mathbb {C}\to \mathbb {C}$ be a semialgebraic map with the following properties:
(1)
 $\xi ^{\sqcap }$ is a lax endomorphism of the nice couple
$\xi ^{\sqcap }$ is a lax endomorphism of the nice couple  $(\partial {\mathcal {R}},\emptyset )$, in particular it restricts to a map
$(\partial {\mathcal {R}},\emptyset )$, in particular it restricts to a map  $\partial {\mathcal {R}}\to \partial {\mathcal {R}}$;
$\partial {\mathcal {R}}\to \partial {\mathcal {R}}$;(2)
 $\xi ^{\sqcap }$ fixes
$\xi ^{\sqcap }$ fixes  $\mathbb {C}_{\Re \le 0}$ pointwise;
$\mathbb {C}_{\Re \le 0}$ pointwise;(3)
 $\xi ^{\sqcap }$ maps the horizontal segment
$\xi ^{\sqcap }$ maps the horizontal segment  $[0,1]\times \{0\}$ constantly to
$[0,1]\times \{0\}$ constantly to  $0$;
$0$;(4)
 $\xi ^{\sqcap }$ restricts to a homeomorphism
$\xi ^{\sqcap }$ restricts to a homeomorphism  $\mathbb {C}\setminus ([0,1]\times \{0\})\to \mathbb {C}\setminus \{0\}$.
$\mathbb {C}\setminus ([0,1]\times \{0\})\to \mathbb {C}\setminus \{0\}$.
Note that ![]() $\xi ^{\sqcap }$ is a lax morphism of nice couples
$\xi ^{\sqcap }$ is a lax morphism of nice couples ![]() $(\sqcap,\emptyset )\to (\partial {\mathcal {R}},\emptyset )$; we obtain by functoriality a map
$(\sqcap,\emptyset )\to (\partial {\mathcal {R}},\emptyset )$; we obtain by functoriality a map ![]() $\xi ^{\sqcap }_*\colon \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, see Figure 8.
$\xi ^{\sqcap }_*\colon \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, see Figure 8.

Figure 8. Left: a configuration ![]() $\mathfrak {c}\in \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$. Right: a configuration
$\mathfrak {c}\in \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$. Right: a configuration ![]() $\mathfrak {c}'$ in the fibre
$\mathfrak {c}'$ in the fibre ![]() $(\xi ^{\sqcap }_*)^{-1}(\mathfrak {c})\subset \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$.
$(\xi ^{\sqcap }_*)^{-1}(\mathfrak {c})\subset \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$.
We will prove that ![]() $\xi ^{\sqcap }_*$ is a covering map.
$\xi ^{\sqcap }_*$ is a covering map.
Lemma 5.15 For ![]() $\mathfrak {c}\in \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, the fibre of
$\mathfrak {c}\in \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$, the fibre of ![]() $\xi ^{\sqcap }_*$ over
$\xi ^{\sqcap }_*$ over ![]() $\mathfrak {c}$ is a non-empty and discrete subspace of
$\mathfrak {c}$ is a non-empty and discrete subspace of ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$.
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$.
Proof. Write ![]() $\mathfrak {c}=(P,\psi )$, where
$\mathfrak {c}=(P,\psi )$, where ![]() $P=\{z_1,\ldots,z_k\}$ and
$P=\{z_1,\ldots,z_k\}$ and ![]() $\psi \colon \mathfrak {Q}_{(\partial {\mathcal {R}},\emptyset )}(P)\to G$ is a map of PMQs; without loss of generality suppose
$\psi \colon \mathfrak {Q}_{(\partial {\mathcal {R}},\emptyset )}(P)\to G$ is a map of PMQs; without loss of generality suppose ![]() $z_k=0$. Assume that we are given
$z_k=0$. Assume that we are given ![]() $\mathfrak {c}'=(P',\psi ')\in (\xi ^{\sqcap }_*)^{-1}(\mathfrak {c})$. Note that if
$\mathfrak {c}'=(P',\psi ')\in (\xi ^{\sqcap }_*)^{-1}(\mathfrak {c})$. Note that if ![]() $\xi ^{\sqcap }_*(\mathfrak {c}')=\mathfrak {c}$, then, in particular,
$\xi ^{\sqcap }_*(\mathfrak {c}')=\mathfrak {c}$, then, in particular, ![]() $\xi ^{\sqcap }(P')=P$ and by properties (3) and (4) of
$\xi ^{\sqcap }(P')=P$ and by properties (3) and (4) of ![]() $\xi ^{\sqcap }$ we must have
$\xi ^{\sqcap }$ we must have ![]() $P'=(\xi ^{\sqcap })^{-1}(P)\cap \sqcap \subset \mathbb {C}$. To fix notation, let
$P'=(\xi ^{\sqcap })^{-1}(P)\cap \sqcap \subset \mathbb {C}$. To fix notation, let ![]() $z'_i=(\xi ^{\sqcap })^{-1}(z_i)\in P'$ for
$z'_i=(\xi ^{\sqcap })^{-1}(z_i)\in P'$ for ![]() $1\leq i\leq k-1$ and let
$1\leq i\leq k-1$ and let ![]() $z'_k=0\in P'$ and
$z'_k=0\in P'$ and ![]() $z'_{k+1}=1\in P'$.
$z'_{k+1}=1\in P'$.
Fix an admissible generating set ![]() $f_1,\ldots,f_k$ for
$f_1,\ldots,f_k$ for ![]() $\mathfrak {G}(P)$ and assume that
$\mathfrak {G}(P)$ and assume that ![]() $f_k$ is represented by a loop supported in a small neighbourhood of the vertical segment
$f_k$ is represented by a loop supported in a small neighbourhood of the vertical segment ![]() $\{0\}\times [-1,0]\subset \mathbb {C}$ joining
$\{0\}\times [-1,0]\subset \mathbb {C}$ joining ![]() $*$ to 0. Then we can consider
$*$ to 0. Then we can consider ![]() $(\xi ^{\sqcap })^{-1}$ as a map
$(\xi ^{\sqcap })^{-1}$ as a map ![]() $\mathbb {C}\setminus P\to \mathbb {C}\setminus ([0,1]\times \{0\}\cup P')\subset \mathbb {C}\setminus P'$ and map the generators
$\mathbb {C}\setminus P\to \mathbb {C}\setminus ([0,1]\times \{0\}\cup P')\subset \mathbb {C}\setminus P'$ and map the generators ![]() $f_1,\ldots,f_k$ to elements of
$f_1,\ldots,f_k$ to elements of ![]() $\mathfrak {G}(P')$. Note that
$\mathfrak {G}(P')$. Note that ![]() $f_1,\ldots,f_{k-1}$ are mapped to simple loops spinning clockwise around the points
$f_1,\ldots,f_{k-1}$ are mapped to simple loops spinning clockwise around the points ![]() $z'_1,\ldots,z'_{k-1}$, whereas
$z'_1,\ldots,z'_{k-1}$, whereas ![]() $f_k$ is mapped to a simple loop spinning clockwise around the segment
$f_k$ is mapped to a simple loop spinning clockwise around the segment ![]() $[0,1]\subset \mathbb {C}$. We decompose
$[0,1]\subset \mathbb {C}$. We decompose ![]() $(\xi ^{\sqcap })^{-1}_*(f_k)$ as a product of two elements
$(\xi ^{\sqcap })^{-1}_*(f_k)$ as a product of two elements ![]() $f'_k,f'_{k+1}$, represented by simple loops in
$f'_k,f'_{k+1}$, represented by simple loops in ![]() $\mathbb {C}\setminus P'$ spinning clockwise around
$\mathbb {C}\setminus P'$ spinning clockwise around ![]() $z'_k$ and
$z'_k$ and ![]() $z'_{k+1}$, respectively, and define
$z'_{k+1}$, respectively, and define ![]() $f'_i=(\xi ^{\sqcap })^{-1}_*(f_i)$ for
$f'_i=(\xi ^{\sqcap })^{-1}_*(f_i)$ for ![]() $1\leq i\leq k-1$: thus, we obtain an admissible generating set
$1\leq i\leq k-1$: thus, we obtain an admissible generating set ![]() $f'_1,\ldots,f'_{k+1}$ for
$f'_1,\ldots,f'_{k+1}$ for ![]() $\mathfrak {G}(P')$. Note that for
$\mathfrak {G}(P')$. Note that for ![]() $1\le i\le k-1$ the generator
$1\le i\le k-1$ the generator ![]() $f'_i$ can be represented by a simple loop in
$f'_i$ can be represented by a simple loop in ![]() $\mathbb {C}\setminus P'$ supported in
$\mathbb {C}\setminus P'$ supported in ![]() $\mathbb {C}\setminus (P'\cup [0,1]\times \{0\})$; similarly
$\mathbb {C}\setminus (P'\cup [0,1]\times \{0\})$; similarly ![]() $f'_k$ and
$f'_k$ and ![]() $f'_{k+1}$ can be represented by loops supported on small neighbourhoods of the straight segments in
$f'_{k+1}$ can be represented by loops supported on small neighbourhoods of the straight segments in ![]() $\mathbb {C}$ joining
$\mathbb {C}$ joining ![]() $*$ with
$*$ with ![]() $0$ and
$0$ and ![]() $1$, respectively.
$1$, respectively.
Since ![]() $\xi ^{\sqcap }_*(\mathfrak {c}')=\mathfrak {c}$, we have in
$\xi ^{\sqcap }_*(\mathfrak {c}')=\mathfrak {c}$, we have in ![]() $G$ the equalities
$G$ the equalities ![]() $\psi '(f'_i)=\psi (f_i)$ for
$\psi '(f'_i)=\psi (f_i)$ for ![]() $1\leq i\leq k-1$ and
$1\leq i\leq k-1$ and ![]() $\psi (f_k)=\psi '(f'_k)\psi '(f'_{k+1})$.
$\psi (f_k)=\psi '(f'_k)\psi '(f'_{k+1})$.
Vice versa, for any factorisation of ![]() $\psi (f_k)\in G$ as the product
$\psi (f_k)\in G$ as the product ![]() $gh$ of two elements in
$gh$ of two elements in ![]() $G$, we can define a configuration
$G$, we can define a configuration ![]() $\mathfrak {c}'=(P',\psi ')$ by setting
$\mathfrak {c}'=(P',\psi ')$ by setting ![]() $P'=(\xi ^{\sqcap })^{-1}(P)\cap \sqcap$ and by defining
$P'=(\xi ^{\sqcap })^{-1}(P)\cap \sqcap$ and by defining ![]() $\varphi '$ by sending
$\varphi '$ by sending ![]() $f'_i\mapsto \psi (f_i)$ for
$f'_i\mapsto \psi (f_i)$ for ![]() $1\leq i\leq k-1$,
$1\leq i\leq k-1$, ![]() $f'_k\mapsto g$ and
$f'_k\mapsto g$ and ![]() $f'_{k+1}\mapsto h$. This shows that
$f'_{k+1}\mapsto h$. This shows that ![]() $(\xi ^{\sqcap })^{-1}(\mathfrak {c})$ is non-empty.
$(\xi ^{\sqcap })^{-1}(\mathfrak {c})$ is non-empty.
Now note that, for ![]() $\mathfrak {c}'$ as above and for any adapted covering
$\mathfrak {c}'$ as above and for any adapted covering ![]() $\underline {U}'$ of
$\underline {U}'$ of ![]() $P'$, we have that
$P'$, we have that ![]() $\mathfrak {c}'$ is the unique configuration in
$\mathfrak {c}'$ is the unique configuration in ![]() $\mathfrak {U}(P';\underline {U}')\subset \mathrm {Hur}(\sqcap )_{0,1;\mathbb {1}}$ supported on the set
$\mathfrak {U}(P';\underline {U}')\subset \mathrm {Hur}(\sqcap )_{0,1;\mathbb {1}}$ supported on the set ![]() $P'$. In fact, the normal neighbourhoods
$P'$. In fact, the normal neighbourhoods ![]() $\mathfrak {U}(\bar {\mathfrak {c}};\underline {U}')$, for fixed
$\mathfrak {U}(\bar {\mathfrak {c}};\underline {U}')$, for fixed ![]() $\underline {U}'$ and varying
$\underline {U}'$ and varying ![]() $\bar {\mathfrak {c}}$ in
$\bar {\mathfrak {c}}$ in ![]() $(\xi ^{\sqcap })^{-1}(\mathfrak {c})$, are disjoint: compare with the proof of [Reference BianchiBia23a, Proposition 3.8]. This proves that
$(\xi ^{\sqcap })^{-1}(\mathfrak {c})$, are disjoint: compare with the proof of [Reference BianchiBia23a, Proposition 3.8]. This proves that ![]() $(\xi ^{\sqcap })^{-1}(\mathfrak {c})$ is a discrete topological space.
$(\xi ^{\sqcap })^{-1}(\mathfrak {c})$ is a discrete topological space.
Lemma 5.16 There is a free action of ![]() $G$ on
$G$ on ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ whose orbits are precisely the fibres of
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ whose orbits are precisely the fibres of ![]() $\xi ^{\sqcap }_*$.
$\xi ^{\sqcap }_*$.
Proof. Let ![]() $\mathfrak {c}'\in \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ and write
$\mathfrak {c}'\in \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ and write ![]() $\mathfrak {c}'=(P',\psi ')$ with
$\mathfrak {c}'=(P',\psi ')$ with ![]() $P'=\{z'_1,\ldots,z'_{k+1}\}$, where we assume
$P'=\{z'_1,\ldots,z'_{k+1}\}$, where we assume ![]() $z'_k=0$,
$z'_k=0$, ![]() $z'_{k+1}=1$. For
$z'_{k+1}=1$. For ![]() $g\in G$ we can define a new configuration
$g\in G$ we can define a new configuration ![]() $g*\mathfrak {c}'=(P',g*\psi ')\in \mathrm {Hur}(\sqcap )_{0,1;\mathbb {1}}$ by setting
$g*\mathfrak {c}'=(P',g*\psi ')\in \mathrm {Hur}(\sqcap )_{0,1;\mathbb {1}}$ by setting ![]() $g*\psi '(f'_i)=\psi '(f_i)$ for all
$g*\psi '(f'_i)=\psi '(f_i)$ for all ![]() $1\leq i\leq k-1$,
$1\leq i\leq k-1$, ![]() $g*\psi '(f'_k)=\psi '(f'_k) g^{-1}$ and
$g*\psi '(f'_k)=\psi '(f'_k) g^{-1}$ and ![]() $g*\psi '(f'_{k+1})=g \psi '(f'_k)$, where
$g*\psi '(f'_{k+1})=g \psi '(f'_k)$, where ![]() $f'_1,\ldots,f'_{k+1}$ is an admissible generating set of
$f'_1,\ldots,f'_{k+1}$ is an admissible generating set of ![]() $\mathfrak {G}(P')$ as in the proof of Lemma 5.15.
$\mathfrak {G}(P')$ as in the proof of Lemma 5.15.
This defines a left action of ![]() $G$ on the set
$G$ on the set ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$. This action can also be obtained by identifying
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$. This action can also be obtained by identifying ![]() $\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ with
$\mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}$ with ![]() $\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ via [Reference BianchiBia23a, Lemma 5.4] and by considering
$\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ via [Reference BianchiBia23a, Lemma 5.4] and by considering ![]() $(0,(\sqcap,\sqcap ),1)$ as a left–right-based nice couple [Reference BianchiBia23a, Definition 6.9] and by restricting the action of
$(0,(\sqcap,\sqcap ),1)$ as a left–right-based nice couple [Reference BianchiBia23a, Definition 6.9] and by restricting the action of ![]() $G\times G^{\rm op}$ on
$G\times G^{\rm op}$ on ![]() $\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ to the diagonal subgroup
$\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ to the diagonal subgroup ![]() $G\subset G\times G^{\rm op}$, which leaves the subspace
$G\subset G\times G^{\rm op}$, which leaves the subspace ![]() $\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ invariant. This proves, in particular, that the action is continuous.
$\mathrm {Hur}(\sqcap,\sqcap ;G,G)_{0,1;\mathbb {1}}$ invariant. This proves, in particular, that the action is continuous.
For ![]() $\mathfrak {c}'$ as above, we use the notation
$\mathfrak {c}'$ as above, we use the notation ![]() $\mathfrak {c}=(P,\psi ):=\xi ^{\sqcap }_*(\mathfrak {c}')$, with
$\mathfrak {c}=(P,\psi ):=\xi ^{\sqcap }_*(\mathfrak {c}')$, with ![]() $P=\{z_1,\ldots,z_k\}$ and assume
$P=\{z_1,\ldots,z_k\}$ and assume ![]() $z_k=0$ and
$z_k=0$ and ![]() $z_i=\xi ^{\sqcap }(z'_i)$ for all
$z_i=\xi ^{\sqcap }(z'_i)$ for all ![]() $1\le i\le k-1$. Choose an admissible generating set
$1\le i\le k-1$. Choose an admissible generating set ![]() $f_1,\ldots,f_k$ of
$f_1,\ldots,f_k$ of ![]() $\mathfrak {G}(P)$ as in Lemma 5.15. Then
$\mathfrak {G}(P)$ as in Lemma 5.15. Then ![]() $\psi (f_i)=\psi '(f'_i)=g*\psi '(f'_i)$ for all
$\psi (f_i)=\psi '(f'_i)=g*\psi '(f'_i)$ for all ![]() $1\le i\le k-1$ and
$1\le i\le k-1$ and
It follows that ![]() $\xi ^{\sqcap }_*(\mathfrak {c}')=\xi ^{\sqcap }_*(g*\mathfrak {c}')$.
$\xi ^{\sqcap }_*(\mathfrak {c}')=\xi ^{\sqcap }_*(g*\mathfrak {c}')$.
Lemma 5.17 The map ![]() $\xi ^{\sqcap }_*$ is open.
$\xi ^{\sqcap }_*$ is open.
Proof. Let ![]() $\mathfrak {c}$ and
$\mathfrak {c}$ and ![]() $\mathfrak {c}'$ be as in the proof of Lemma 5.15, i.e.
$\mathfrak {c}'$ be as in the proof of Lemma 5.15, i.e. ![]() $\xi ^{\sqcap }_*\colon \mathfrak {c}'\mapsto \mathfrak {c}$ and let
$\xi ^{\sqcap }_*\colon \mathfrak {c}'\mapsto \mathfrak {c}$ and let ![]() $\underline {U}'$ be an adapted covering of
$\underline {U}'$ be an adapted covering of ![]() $P'$. We want to find an adapted covering
$P'$. We want to find an adapted covering ![]() $\underline {U}$ of
$\underline {U}$ of ![]() $P$ such that
$P$ such that ![]() $\xi ^{\sqcap }_*(\mathfrak {U}(P';\underline {U}'))$ contains
$\xi ^{\sqcap }_*(\mathfrak {U}(P';\underline {U}'))$ contains ![]() $\mathfrak {U}(P,\underline {U})$. We choose
$\mathfrak {U}(P,\underline {U})$. We choose ![]() $\underline {U}$ with the following properties:
$\underline {U}$ with the following properties:
• for all
 $1\leq i\leq k$ the intersection
$1\leq i\leq k$ the intersection  $U_i\cap \partial$ is contractible;
$U_i\cap \partial$ is contractible;• for all
 $1\leq i\leq k-1$ the intersection
$1\leq i\leq k-1$ the intersection  $(\xi ^{\sqcap })^{-1}(U_i)\cap \sqcap$ is contained in
$(\xi ^{\sqcap })^{-1}(U_i)\cap \sqcap$ is contained in  $U'_i$;
$U'_i$;• the intersection
 $(\xi ^{\sqcap })^{-1}(U_k)\cap \sqcap$ is contained in
$(\xi ^{\sqcap })^{-1}(U_k)\cap \sqcap$ is contained in  $U'_k\cup U'_{k+1}$.
$U'_k\cup U'_{k+1}$.
Let ![]() $\tilde {\mathfrak {c}}=(\tilde {P},\tilde {\psi })\in \mathfrak {U}(\mathfrak {c},\underline {U})$: we want to find a configuration
$\tilde {\mathfrak {c}}=(\tilde {P},\tilde {\psi })\in \mathfrak {U}(\mathfrak {c},\underline {U})$: we want to find a configuration ![]() $\tilde {\mathfrak {c}}'\in \mathfrak {U}(\mathfrak {c}',\underline {U}')$ with
$\tilde {\mathfrak {c}}'\in \mathfrak {U}(\mathfrak {c}',\underline {U}')$ with ![]() $\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$. Write
$\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$. Write ![]() $\tilde {P}=\{\tilde {z}_1,\ldots,\tilde {z}_{\tilde k}\}$, with
$\tilde {P}=\{\tilde {z}_1,\ldots,\tilde {z}_{\tilde k}\}$, with ![]() $\tilde {z}_{\tilde k}=0$. Then the finite set
$\tilde {z}_{\tilde k}=0$. Then the finite set ![]() $\tilde {P}':=(\xi ^{\sqcap })^{-1}(\tilde {P})\cap \sqcap$ is contained in
$\tilde {P}':=(\xi ^{\sqcap })^{-1}(\tilde {P})\cap \sqcap$ is contained in ![]() $\underline {U}'$ and it intersects non-trivially every component of
$\underline {U}'$ and it intersects non-trivially every component of ![]() $\underline {U}'$. We write
$\underline {U}'$. We write ![]() $\tilde {P}'=\{\tilde {z}'_1,\ldots,\tilde {z}'_{\tilde k+1}\}$ and assume
$\tilde {P}'=\{\tilde {z}'_1,\ldots,\tilde {z}'_{\tilde k+1}\}$ and assume ![]() $\tilde {z}'_{\tilde k}=0$ and
$\tilde {z}'_{\tilde k}=0$ and ![]() $\tilde {z}'_{\tilde k+1}=1$.
$\tilde {z}'_{\tilde k+1}=1$.
Let ![]() $\tilde {f}'_1,\ldots,\tilde {f}'_{\tilde k+1}$ be an admissible generating set for
$\tilde {f}'_1,\ldots,\tilde {f}'_{\tilde k+1}$ be an admissible generating set for ![]() $\mathfrak {G}(\tilde {P}')$ as in the proof of Lemma 5.15. Note that we can regard
$\mathfrak {G}(\tilde {P}')$ as in the proof of Lemma 5.15. Note that we can regard ![]() $f'_k$ and
$f'_k$ and ![]() $f'_{k+1}$ as elements of
$f'_{k+1}$ as elements of ![]() $\mathfrak {G}(\tilde {P}')$ by the composition
$\mathfrak {G}(\tilde {P}')$ by the composition ![]() $\mathfrak {G}(P')\cong \mathfrak {G}(\underline {U}')\subset \mathfrak {G}(\tilde {P}')$; moreover, the sequence of elements
$\mathfrak {G}(P')\cong \mathfrak {G}(\underline {U}')\subset \mathfrak {G}(\tilde {P}')$; moreover, the sequence of elements ![]() $\tilde {f}'_1,\ldots,\tilde {f}'_{\tilde k-1},f'_k,f'_{k+1}$ is also a free generating set for
$\tilde {f}'_1,\ldots,\tilde {f}'_{\tilde k-1},f'_k,f'_{k+1}$ is also a free generating set for ![]() $\mathfrak {G}(\tilde {P}')$, although in general it is not an admissible generating set: in fact,
$\mathfrak {G}(\tilde {P}')$, although in general it is not an admissible generating set: in fact, ![]() $f'_k$ can be decomposed as a product of distinct elements
$f'_k$ can be decomposed as a product of distinct elements ![]() $\tilde {f}'_i$, with one element equal to
$\tilde {f}'_i$, with one element equal to ![]() $\tilde {f}'_{\tilde k}$ and similarly
$\tilde {f}'_{\tilde k}$ and similarly ![]() $f'_{k+1}$ can be decomposed as a product with one factor equal to
$f'_{k+1}$ can be decomposed as a product with one factor equal to ![]() $\tilde {f}'_{\tilde k +1}$. Nevertheless we can define a morphism of groups
$\tilde {f}'_{\tilde k +1}$. Nevertheless we can define a morphism of groups ![]() $\tilde {\varphi }'\colon \mathfrak {G}(\tilde {P}')\to G$ by setting
$\tilde {\varphi }'\colon \mathfrak {G}(\tilde {P}')\to G$ by setting ![]() $\tilde {\varphi }'\colon \tilde {f}'_i\mapsto \tilde {\varphi }(\tilde {f}_i)$ for
$\tilde {\varphi }'\colon \tilde {f}'_i\mapsto \tilde {\varphi }(\tilde {f}_i)$ for ![]() $1\leq i\leq \tilde k-1$ and
$1\leq i\leq \tilde k-1$ and ![]() $\tilde {\varphi }'\colon f'_i\mapsto \varphi '(f'_i)$ for
$\tilde {\varphi }'\colon f'_i\mapsto \varphi '(f'_i)$ for ![]() $i=k,k+1$. We can restrict
$i=k,k+1$. We can restrict ![]() $\tilde {\varphi }'$ to
$\tilde {\varphi }'$ to ![]() $\mathfrak {Q}_{(\sqcap,\emptyset )}(P')$ and obtain a morphism of PMQs
$\mathfrak {Q}_{(\sqcap,\emptyset )}(P')$ and obtain a morphism of PMQs ![]() $\tilde {\psi }'\colon \mathfrak {G}_{(\sqcap,\emptyset )}(P')\to G$.
$\tilde {\psi }'\colon \mathfrak {G}_{(\sqcap,\emptyset )}(P')\to G$.
We can use the previous to define a configuration ![]() $\tilde {\mathfrak {c}}'=(\tilde {P}',\tilde {\psi }')\in \mathfrak {U}(\mathfrak {c}';\underline {U}')$, satisfying
$\tilde {\mathfrak {c}}'=(\tilde {P}',\tilde {\psi }')\in \mathfrak {U}(\mathfrak {c}';\underline {U}')$, satisfying ![]() $\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$.
$\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$.
In the last step of the proof, note that ![]() $\tilde {\mathfrak {c}}'$ is, in fact, the unique configuration in
$\tilde {\mathfrak {c}}'$ is, in fact, the unique configuration in ![]() $\mathfrak {U}(\mathfrak {c}';\underline {U})$ with
$\mathfrak {U}(\mathfrak {c}';\underline {U})$ with ![]() $\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$. This shows, in particular, that for
$\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}')=\tilde {\mathfrak {c}}$. This shows, in particular, that for ![]() $\mathfrak {c}$,
$\mathfrak {c}$, ![]() $\mathfrak {c}'$,
$\mathfrak {c}'$, ![]() $\underline {U}'$ and
$\underline {U}'$ and ![]() $\underline {U}$ as in the proof of Lemma 5.17, there is a unique map of sets
$\underline {U}$ as in the proof of Lemma 5.17, there is a unique map of sets ![]() $\mathfrak {s}\colon \mathfrak {U}(\mathfrak {c};\underline {U})\to \mathfrak {U}(\mathfrak {c}';\underline {U}')$ which is a section of
$\mathfrak {s}\colon \mathfrak {U}(\mathfrak {c};\underline {U})\to \mathfrak {U}(\mathfrak {c}';\underline {U}')$ which is a section of ![]() $\xi ^{\sqcap }_*$, i.e. such that
$\xi ^{\sqcap }_*$, i.e. such that ![]() $\xi ^{\sqcap }_*\circ \mathfrak {s}$ is equal to the inclusion of
$\xi ^{\sqcap }_*\circ \mathfrak {s}$ is equal to the inclusion of ![]() $\mathfrak {U}(\mathfrak {c};\underline {U})$ in
$\mathfrak {U}(\mathfrak {c};\underline {U})$ in ![]() $\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$.
$\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$.
Lemma 5.18 Let ![]() $\mathfrak {c}$,
$\mathfrak {c}$, ![]() $\mathfrak {c}$,
$\mathfrak {c}$, ![]() $\underline {U}'$ and
$\underline {U}'$ and ![]() $\underline {U}$ be as in the proof of Lemma 5.17 and let
$\underline {U}$ be as in the proof of Lemma 5.17 and let ![]() $\mathfrak {s}\colon \mathfrak {U}(\mathfrak {c};\underline {U})\to \mathfrak {U}(\mathfrak {c}';\underline {U}')$ be the section defined above. Then
$\mathfrak {s}\colon \mathfrak {U}(\mathfrak {c};\underline {U})\to \mathfrak {U}(\mathfrak {c}';\underline {U}')$ be the section defined above. Then ![]() $\mathfrak {s}$ is continuous.
$\mathfrak {s}$ is continuous.
Proof. Let ![]() $\tilde {\mathfrak {c}}\in \mathfrak {U}(\mathfrak {c};\underline {U})$, denote
$\tilde {\mathfrak {c}}\in \mathfrak {U}(\mathfrak {c};\underline {U})$, denote ![]() $\tilde {\mathfrak {c}}'=\mathfrak {s}(\tilde {\mathfrak {c}})\in \mathfrak {U}(\mathfrak {c}';\underline {U}')$ and use the notation from the proof of Lemma 5.17. By continuity of
$\tilde {\mathfrak {c}}'=\mathfrak {s}(\tilde {\mathfrak {c}})\in \mathfrak {U}(\mathfrak {c}';\underline {U}')$ and use the notation from the proof of Lemma 5.17. By continuity of ![]() $\xi ^{\sqcap }_*$ there is an adapted covering
$\xi ^{\sqcap }_*$ there is an adapted covering ![]() $\tilde {\underline {U}}'$ of
$\tilde {\underline {U}}'$ of ![]() $\tilde {P}'$ with
$\tilde {P}'$ with ![]() $\tilde {\underline {U}}'\subset \underline {U}'$ and such that
$\tilde {\underline {U}}'\subset \underline {U}'$ and such that ![]() $\xi ^{\sqcap }_*$ maps
$\xi ^{\sqcap }_*$ maps ![]() $\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}})$ inside
$\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}})$ inside ![]() $\mathfrak {U}(\mathfrak {c};\underline {U})$.
$\mathfrak {U}(\mathfrak {c};\underline {U})$.
First, note that ![]() $\xi ^{\sqcap }_*$ is injective on
$\xi ^{\sqcap }_*$ is injective on ![]() $\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')$: for a configuration
$\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')$: for a configuration ![]() $\tilde {\mathfrak {c}}''\in \mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')$ we have, in fact,
$\tilde {\mathfrak {c}}''\in \mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')$ we have, in fact, ![]() $\mathfrak {s}(\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}''))=\tilde {\mathfrak {c}}''$.
$\mathfrak {s}(\xi ^{\sqcap }_*(\tilde {\mathfrak {c}}''))=\tilde {\mathfrak {c}}''$.
By Lemma 5.17 we know that ![]() $\xi ^{\sqcap }_*$ is open; it follows that the map
$\xi ^{\sqcap }_*$ is open; it follows that the map ![]() $\xi ^{\sqcap }_*\colon \mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is a homeomorphism onto its image and, hence,
$\xi ^{\sqcap }_*\colon \mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}')\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is a homeomorphism onto its image and, hence, ![]() $\mathfrak {s}$ is continuous on the open set
$\mathfrak {s}$ is continuous on the open set ![]() $\xi ^{\sqcap }_*(\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}'))$, which contains
$\xi ^{\sqcap }_*(\mathfrak {U}(\tilde {\mathfrak {c}}';\tilde {\underline {U}}'))$, which contains ![]() $\tilde {\mathfrak {c}}$.
$\tilde {\mathfrak {c}}$.
Proof of Proposition 5.12 The combination of Lemmas 5.15, 5.17 and 5.18 shows that the map ![]() $\xi ^{\sqcap }_*\colon \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is a covering. Lemma 5.14 shows that the total space is contractible, in particular connected and Lemma 5.16 exhibits
$\xi ^{\sqcap }_*\colon \mathrm {Hur}(\sqcap ;G)_{0,1;\mathbb {1}}\to \mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ is a covering. Lemma 5.14 shows that the total space is contractible, in particular connected and Lemma 5.16 exhibits ![]() $G$ as the group of deck transformations of
$G$ as the group of deck transformations of ![]() $\xi ^{\sqcap }_*$.
$\xi ^{\sqcap }_*$.
Notation 5.19 We denote by ![]() ${\mathcal {B}} G$ the space
${\mathcal {B}} G$ the space
5.4 Bundles over  ${\mathcal {B}} G$
${\mathcal {B}} G$
In this subsection we define for all ![]() $\nu \geq 0$ a bundle map
$\nu \geq 0$ a bundle map ![]() $\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$; the fibre of
$\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$; the fibre of ![]() $\mathfrak {p}_\nu$ can be identified with
$\mathfrak {p}_\nu$ can be identified with
where ![]() ${\mathcal {Q}}_\nu \subset {\mathcal {Q}}$ is the subset of elements of norm
${\mathcal {Q}}_\nu \subset {\mathcal {Q}}$ is the subset of elements of norm ![]() $\nu$. In the case
$\nu$. In the case ![]() $\nu =0$, the map
$\nu =0$, the map ![]() $\mathfrak {p}_0$ is just the identity of
$\mathfrak {p}_0$ is just the identity of ![]() ${\mathcal {B}} G=\mathfrak {F}_0\mathbb {B}({\mathcal {Q}}_+,G)$ and the fibre is a point, i.e. the space
${\mathcal {B}} G=\mathfrak {F}_0\mathbb {B}({\mathcal {Q}}_+,G)$ and the fibre is a point, i.e. the space ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}}$.
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}}$.
In the next section we will investigate the rational cohomology of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ using the Leray spectral sequence associated with the filtration
$\mathbb {B}({\mathcal {Q}}_+,G)$ using the Leray spectral sequence associated with the filtration ![]() $F_{\bullet }=F_{\bullet }\mathbb {B}({\mathcal {Q}}_+,G)$: the first page of this spectral sequence contains the relative cohomology groups
$F_{\bullet }=F_{\bullet }\mathbb {B}({\mathcal {Q}}_+,G)$: the first page of this spectral sequence contains the relative cohomology groups ![]() $H^*(F_\nu,F_{\nu -1})$, rather than the cohomology groups of the strata
$H^*(F_\nu,F_{\nu -1})$, rather than the cohomology groups of the strata ![]() $\mathfrak {F}_\nu$. To acquire information about these relative cohomology groups, we introduce in this subsection certain subspaces
$\mathfrak {F}_\nu$. To acquire information about these relative cohomology groups, we introduce in this subsection certain subspaces ![]() $F^{\mathrm {fat}}_{\nu -1}=F^{\mathrm {fat}}_{\nu -1}\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathbb {B}({\mathcal {Q}}_+,G)$, for
$F^{\mathrm {fat}}_{\nu -1}=F^{\mathrm {fat}}_{\nu -1}\mathbb {B}({\mathcal {Q}}_+,G)\subset \mathbb {B}({\mathcal {Q}}_+,G)$, for ![]() $\nu \geq 0$. We will prove, between this subsection and the next section, that
$\nu \geq 0$. We will prove, between this subsection and the next section, that ![]() $F^{\mathrm {fat}}_{\nu -1}\subset F_{\nu }$, that
$F^{\mathrm {fat}}_{\nu -1}\subset F_{\nu }$, that ![]() $F_{\nu -1}$ is contained in the interior of
$F_{\nu -1}$ is contained in the interior of ![]() $F^{\mathrm {fat}}_{\nu -1}$ when the latter is regarded as a subspace of
$F^{\mathrm {fat}}_{\nu -1}$ when the latter is regarded as a subspace of ![]() $F_{\nu }$ and that the inclusion
$F_{\nu }$ and that the inclusion ![]() $F_{\nu -1}\subset F^{\mathrm {fat}}_{\nu -1}$ is a homotopy equivalence. In particular, after setting
$F_{\nu -1}\subset F^{\mathrm {fat}}_{\nu -1}$ is a homotopy equivalence. In particular, after setting ![]() $\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }:=\mathfrak {F}_{\nu }\cap F^{\mathrm {fat}}_{\nu -1}$, we will obtain in Lemma 6.2 an isomorphism
$\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }:=\mathfrak {F}_{\nu }\cap F^{\mathrm {fat}}_{\nu -1}$, we will obtain in Lemma 6.2 an isomorphism
In this subsection we will prove that ![]() $\mathfrak {p}_\nu$ exhibits
$\mathfrak {p}_\nu$ exhibits ![]() $(\mathfrak {F}_{\nu },\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )$ as a couple of bundles over
$(\mathfrak {F}_{\nu },\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )$ as a couple of bundles over ![]() ${\mathcal {B}} G$, with fibre a suitable couple of spaces
${\mathcal {B}} G$, with fibre a suitable couple of spaces
 \[ (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_\nu,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_\nu)= \bigg(\coprod_{a\in{\mathcal{Q}}_\nu}\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a, \coprod_{a\in{\mathcal{Q}}_\nu}\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a\bigg); \]
\[ (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_\nu,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_\nu)= \bigg(\coprod_{a\in{\mathcal{Q}}_\nu}\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a, \coprod_{a\in{\mathcal{Q}}_\nu}\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a\bigg); \]
the computation of the rational cohomology ![]() $H^*(\mathfrak {F}_{\nu },\partial ^{\mathrm {fat}}\mathfrak {F}_\nu ;\mathbb {Q})$ will then be possible using the Serre spectral sequence associated with
$H^*(\mathfrak {F}_{\nu },\partial ^{\mathrm {fat}}\mathfrak {F}_\nu ;\mathbb {Q})$ will then be possible using the Serre spectral sequence associated with ![]() $\mathfrak {p}_\nu$.
$\mathfrak {p}_\nu$.
Definition 5.20 Recall Definition 5.9. Denote by ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}$ the closed neighbourhood of
$\partial ^{\mathrm {fat}}{\mathcal {R}}$ the closed neighbourhood of ![]() $\partial {\mathcal {R}}$ in
$\partial {\mathcal {R}}$ in ![]() ${\mathcal {R}}=[0,1]^2$ given by
${\mathcal {R}}=[0,1]^2$ given by ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}={\mathcal {R}}\setminus ( {z_{\mathrm {c}}}2+ (1/2)\mathring {{\mathcal {R}}})$, where
$\partial ^{\mathrm {fat}}{\mathcal {R}}={\mathcal {R}}\setminus ( {z_{\mathrm {c}}}2+ (1/2)\mathring {{\mathcal {R}}})$, where ![]() ${z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}}$ is the image of
${z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}}$ is the image of ![]() $\mathring {{\mathcal {R}}}$ along the homothety centred at
$\mathring {{\mathcal {R}}}$ along the homothety centred at ![]() $z_{\mathrm {c}}$ of rescaling factor
$z_{\mathrm {c}}$ of rescaling factor ![]() $\frac 12$; in other words,
$\frac 12$; in other words, ![]() $ {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}}$ is the open square of side length
$ {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}}$ is the open square of side length ![]() $\frac 12$ centred at
$\frac 12$ centred at ![]() $z_{\mathrm {c}}$.
$z_{\mathrm {c}}$.
The identity of ![]() $\mathbb {C}$ induces a map
$\mathbb {C}$ induces a map
Recall that ![]() $\mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ has a filtration by subspaces
$\mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ has a filtration by subspaces ![]() $F_\nu \,\mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ for
$F_\nu \,\mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ for ![]() $\nu \ge -1$; we define
$\nu \ge -1$; we define ![]() $F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ as the intersection
$F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ as the intersection
In particular, we have ![]() $F^{\mathrm {fat}}_{-1}\mathbb {B}({\mathcal {Q}}_+,G)=\emptyset$. Roughly speaking, for
$F^{\mathrm {fat}}_{-1}\mathbb {B}({\mathcal {Q}}_+,G)=\emptyset$. Roughly speaking, for ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, we can use Notation 2.2 and suppose without loss of generality that
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, we can use Notation 2.2 and suppose without loss of generality that ![]() $\{z_1,\ldots,z_{l'}\}=P\cap (1/4,3/4)^2$ for some
$\{z_1,\ldots,z_{l'}\}=P\cap (1/4,3/4)^2$ for some ![]() $0\le l'\le l$; if
$0\le l'\le l$; if ![]() $f_1,\ldots,f_k$ is an admissible generating set for
$f_1,\ldots,f_k$ is an admissible generating set for ![]() $\mathfrak {G}(P)$, then
$\mathfrak {G}(P)$, then ![]() $\mathfrak {c}$ belongs to
$\mathfrak {c}$ belongs to ![]() $F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ if the following hold:
$F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ if the following hold:
•
 $\sum _{i=1}^l N(\psi (f_i))\le \nu +1$, that is,
$\sum _{i=1}^l N(\psi (f_i))\le \nu +1$, that is,  $\mathfrak {c} \in F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)$;
$\mathfrak {c} \in F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)$;•
 $\sum _{i=1}^{l'} N(\psi (f_i))\le \nu$.
$\sum _{i=1}^{l'} N(\psi (f_i))\le \nu$.
Another characterisation is the following: ![]() $F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ is the preimage of the space
$F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ is the preimage of the space ![]() $F_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ along the restricted map
$F_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ along the restricted map ![]() ${\mathcal {H}}^{\mathbb {B}}(-,2)\colon F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)\to \mathbb {B}({\mathcal {Q}}_+,G)$, see Definition 5.6. Note that, in fact,
${\mathcal {H}}^{\mathbb {B}}(-,2)\colon F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)\to \mathbb {B}({\mathcal {Q}}_+,G)$, see Definition 5.6. Note that, in fact, ![]() ${\mathcal {H}}^{\mathbb {B}}(-,2)$ restricts to a self-map of
${\mathcal {H}}^{\mathbb {B}}(-,2)$ restricts to a self-map of ![]() $F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)$. By construction, we have inclusions
$F_{\nu +1}\mathbb {B}({\mathcal {Q}}_+,G)$. By construction, we have inclusions
Notation 5.21 For a subspace ![]() $X\subseteq \mathbb {B}({\mathcal {Q}}_+,G)$ and
$X\subseteq \mathbb {B}({\mathcal {Q}}_+,G)$ and ![]() $\nu \ge -1$ we denote by
$\nu \ge -1$ we denote by ![]() $F^{\mathrm {fat}}_\nu X$ the intersection
$F^{\mathrm {fat}}_\nu X$ the intersection ![]() $X\cap F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$. For
$X\cap F^{\mathrm {fat}}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$. For ![]() $\nu \ge 0$ we denote by
$\nu \ge 0$ we denote by ![]() $\partial ^{\mathrm {fat}}\mathfrak {F}_\nu X$ the intersection
$\partial ^{\mathrm {fat}}\mathfrak {F}_\nu X$ the intersection ![]() $\mathfrak {F}_\nu X\cap F^{\mathrm {fat}}_{\nu -1}X$.
$\mathfrak {F}_\nu X\cap F^{\mathrm {fat}}_{\nu -1}X$.
Example 5.22 Let ![]() $a\in {\mathcal {Q}}$ and let
$a\in {\mathcal {Q}}$ and let ![]() $X=\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$; the inclusion of nice couples
$X=\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$; the inclusion of nice couples ![]() $(\mathring {{\mathcal {R}}},\emptyset )\subset ({\mathcal {R}},\partial )$ induces an inclusion of spaces
$(\mathring {{\mathcal {R}}},\emptyset )\subset ({\mathcal {R}},\partial )$ induces an inclusion of spaces ![]() $X\subset \mathbb {B}({\mathcal {Q}}_+,G)$; let
$X\subset \mathbb {B}({\mathcal {Q}}_+,G)$; let ![]() $\nu = N(a)\ge 0$ and note that
$\nu = N(a)\ge 0$ and note that ![]() $F_{\nu -1}X=\emptyset$ and, hence,
$F_{\nu -1}X=\emptyset$ and, hence, ![]() $X=F_\nu X=\mathfrak {F}_\nu X$. The space
$X=F_\nu X=\mathfrak {F}_\nu X$. The space ![]() $F^{\mathrm {fat}}_{\nu -1} X$ contains all configurations
$F^{\mathrm {fat}}_{\nu -1} X$ contains all configurations ![]() $\mathfrak {c}\in X$ such that, using Notation 2.2,
$\mathfrak {c}\in X$ such that, using Notation 2.2, ![]() $P$ intersects non-trivially
$P$ intersects non-trivially ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}$: in fact, the condition
$\partial ^{\mathrm {fat}}{\mathcal {R}}$: in fact, the condition ![]() $\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$ implies that the monodromy
$\mathfrak {c}\in \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$ implies that the monodromy ![]() $\psi$ attains values of norm
$\psi$ attains values of norm ![]() $\ge 1$ (i.e. different from
$\ge 1$ (i.e. different from ![]() $\mathbb {1}\in {\mathcal {Q}}$) around all points of
$\mathbb {1}\in {\mathcal {Q}}$) around all points of ![]() $P$. The space
$P$. The space ![]() $\partial ^{\mathrm {fat}}\mathfrak {F}_\nu X$ coincides with
$\partial ^{\mathrm {fat}}\mathfrak {F}_\nu X$ coincides with ![]() $F^{\mathrm {fat}}_{\nu -1} X$ in this case and by abuse of notation we will also write
$F^{\mathrm {fat}}_{\nu -1} X$ in this case and by abuse of notation we will also write
Example 5.23 Let ![]() $X=\mathbb {B}({\mathcal {Q}}_+,G)$; then
$X=\mathbb {B}({\mathcal {Q}}_+,G)$; then ![]() $F^{\mathrm {fat}}_{-1} X=\partial ^{\mathrm {fat}}\mathfrak {F}_0 X=\emptyset$ and
$F^{\mathrm {fat}}_{-1} X=\partial ^{\mathrm {fat}}\mathfrak {F}_0 X=\emptyset$ and ![]() $\mathfrak {F}_0 X={\mathcal {B}} G$; hence, the identity of
$\mathfrak {F}_0 X={\mathcal {B}} G$; hence, the identity of ![]() ${\mathcal {B}} G$ can be regarded as a pair of bundles
${\mathcal {B}} G$ can be regarded as a pair of bundles
with fibre the couple ![]() $(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}}, \partial ^{\mathrm {fat}}\, \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}})=(\{(\emptyset,\mathbb {1},\mathbb {1})\},\emptyset )$. In the rest of the subsection we generalise this example to the other strata of
$(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}}, \partial ^{\mathrm {fat}}\, \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\mathbb {1}})=(\{(\emptyset,\mathbb {1},\mathbb {1})\},\emptyset )$. In the rest of the subsection we generalise this example to the other strata of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$.
$\mathbb {B}({\mathcal {Q}}_+,G)$.
Fix in the following ![]() $\nu \ge 1$, let
$\nu \ge 1$, let ![]() $\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and use Notation 2.2. Let
$\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and use Notation 2.2. Let ![]() $\zeta _1,\ldots,\zeta _k$ be embedded arcs in
$\zeta _1,\ldots,\zeta _k$ be embedded arcs in ![]() $\mathbb {C}$ joining
$\mathbb {C}$ joining ![]() $*$ with the points
$*$ with the points ![]() $z_1,\ldots,z_k$ of
$z_1,\ldots,z_k$ of ![]() $P$, intersecting pairwise only at the endpoint
$P$, intersecting pairwise only at the endpoint ![]() $*$ and such that
$*$ and such that ![]() $\zeta _i\subset \mathbb {C}\setminus \mathring {{\mathcal {R}}}$ for
$\zeta _i\subset \mathbb {C}\setminus \mathring {{\mathcal {R}}}$ for ![]() $l+1\le i\le k$. Recall that, since
$l+1\le i\le k$. Recall that, since ![]() $\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, the point
$\mathfrak {c}\in \mathbb {B}({\mathcal {Q}}_+,G)$, the point ![]() $0$ belongs to
$0$ belongs to ![]() $P$; we use the convention that
$P$; we use the convention that ![]() $z_k=0$. Let
$z_k=0$. Let ![]() $f_1,\ldots,f_k$ be the admissible generating set of
$f_1,\ldots,f_k$ be the admissible generating set of ![]() $\mathfrak {G}(P)$ obtained by replacing each
$\mathfrak {G}(P)$ obtained by replacing each ![]() $\zeta _i$ by a loop contained in a small neighbourhood of
$\zeta _i$ by a loop contained in a small neighbourhood of ![]() $\zeta _i$ and spinning clockwise only around
$\zeta _i$ and spinning clockwise only around ![]() $z_i$.
$z_i$.
We define a new configuration ![]() $\mathfrak {c}'=(P',\psi ')\in {\mathcal {B}} G=\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ as follows:
$\mathfrak {c}'=(P',\psi ')\in {\mathcal {B}} G=\mathrm {Hur}(\partial {\mathcal {R}};G)_{0;\mathbb {1}}$ as follows:
•
 $P'$ is the intersection
$P'$ is the intersection  $P\cap \partial {\mathcal {R}}$;
$P\cap \partial {\mathcal {R}}$;•
 $\psi '$ sends, for
$\psi '$ sends, for  $l+1\le i\le k-1$, the generator
$l+1\le i\le k-1$, the generator  $f_i$ to
$f_i$ to  $\varphi (f_i)\in G$ and it sends
$\varphi (f_i)\in G$ and it sends  $f_k$ to the unique element
$f_k$ to the unique element  $\psi '(f_k)\in G$ such that the resulting configuration
$\psi '(f_k)\in G$ such that the resulting configuration  $\mathfrak {c}'=(P',\psi ')$ satisfies
$\mathfrak {c}'=(P',\psi ')$ satisfies  $\omega (\mathfrak {c}')=\mathbb {1}\in G$.
$\omega (\mathfrak {c}')=\mathbb {1}\in G$.
Note that ![]() $G$ is treated as a complete PMQ when defining
$G$ is treated as a complete PMQ when defining ![]() $\mathfrak {c}'$. See Figure 9.
$\mathfrak {c}'$. See Figure 9.
Definition 5.24 The previous assignment ![]() $\mathfrak {c}\mapsto \mathfrak {c}'$ defines a map of sets
$\mathfrak {c}\mapsto \mathfrak {c}'$ defines a map of sets

Figure 9. The configuration ![]() $\mathfrak {c}$ from Figure 7 belongs to
$\mathfrak {c}$ from Figure 7 belongs to ![]() $\partial ^{\mathrm {fat}}\mathfrak {F}_\nu$, where
$\partial ^{\mathrm {fat}}\mathfrak {F}_\nu$, where ![]() $\nu =N(a_1)+N(a_2)+N(a_3)$, because the two points
$\nu =N(a_1)+N(a_2)+N(a_3)$, because the two points ![]() $z_1$ and
$z_1$ and ![]() $z_3$ lie in
$z_3$ lie in ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}$. On the right, the image of
$\partial ^{\mathrm {fat}}{\mathcal {R}}$. On the right, the image of ![]() $\mathfrak {c}$ along
$\mathfrak {c}$ along ![]() $\mathfrak {p}_\nu$; note that the loop with label
$\mathfrak {p}_\nu$; note that the loop with label ![]() $g_4$ on the left is not constructed using an arc contained in
$g_4$ on the left is not constructed using an arc contained in ![]() $\mathbb {C}\setminus \mathring {{\mathcal {R}}}$; as a consequence the monodromy on right around the ‘same’ loop is changed by conjugation: we have, in fact,
$\mathbb {C}\setminus \mathring {{\mathcal {R}}}$; as a consequence the monodromy on right around the ‘same’ loop is changed by conjugation: we have, in fact, ![]() $g'_1=g_4^{\mathfrak {e}(a_2)(\mathfrak {e}(a_3)^{g_5^{-1}})}$,
$g'_1=g_4^{\mathfrak {e}(a_2)(\mathfrak {e}(a_3)^{g_5^{-1}})}$, ![]() $g'_2=g_5$ and
$g'_2=g_5$ and ![]() $g'_3=g_6\mathfrak {e}(a_1)\mathfrak {e}(a_2)g_5(\mathfrak {e}(a_3)^{g_5^{-1}})$.
$g'_3=g_6\mathfrak {e}(a_1)\mathfrak {e}(a_2)g_5(\mathfrak {e}(a_3)^{g_5^{-1}})$.
To check that the previous is a good definition, we need to verify that the choice of the arcs ![]() $\zeta _1,\ldots,\zeta _k$ is not relevant in computing
$\zeta _1,\ldots,\zeta _k$ is not relevant in computing ![]() $\mathfrak {p}_\nu (\mathfrak {c})$. The generator
$\mathfrak {p}_\nu (\mathfrak {c})$. The generator ![]() $f_i$ is uniquely defined up to conjugation by a power of the element
$f_i$ is uniquely defined up to conjugation by a power of the element ![]() $[\gamma ]\in \mathfrak {G}(P)$ represented by a loop
$[\gamma ]\in \mathfrak {G}(P)$ represented by a loop ![]() $\gamma$ spinning clockwise around
$\gamma$ spinning clockwise around ![]() ${\mathcal {R}}$. It follows that
${\mathcal {R}}$. It follows that ![]() $\psi (f_i)$ is well-defined, as an element of
$\psi (f_i)$ is well-defined, as an element of ![]() $G$, up to conjugation by a power of
$G$, up to conjugation by a power of ![]() $\psi ([\gamma ])$, i.e. up to conjugation by a power of
$\psi ([\gamma ])$, i.e. up to conjugation by a power of ![]() $\omega (\mathfrak {c})=\mathbb {1}\in G$: here we use that the total monodromy attains constantly the value
$\omega (\mathfrak {c})=\mathbb {1}\in G$: here we use that the total monodromy attains constantly the value ![]() $\mathbb {1}\in G$ on configurations of
$\mathbb {1}\in G$ on configurations of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$; this shows that
$\mathbb {B}({\mathcal {Q}}_+,G)$; this shows that ![]() $\psi (f_i)\in G$ is well-defined for
$\psi (f_i)\in G$ is well-defined for ![]() $1\le i\le k-1$ and
$1\le i\le k-1$ and ![]() $\psi (f_k)$ is also uniquely determined by the values
$\psi (f_k)$ is also uniquely determined by the values ![]() $\psi (f_i)$ for
$\psi (f_i)$ for ![]() $1\le i\le k-1$ and by its characterising property. Therefore,
$1\le i\le k-1$ and by its characterising property. Therefore, ![]() $\mathfrak {p}_\nu (\mathfrak {c})$ is well-defined.
$\mathfrak {p}_\nu (\mathfrak {c})$ is well-defined.
We next check that ![]() $\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is continuous. Roughly speaking,
$\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is continuous. Roughly speaking, ![]() $\mathfrak {p}_\nu$ splits a configuration in
$\mathfrak {p}_\nu$ splits a configuration in ![]() $\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ in two parts, the part supported on
$\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ in two parts, the part supported on ![]() $\partial {\mathcal {R}}$ and the part supported on
$\partial {\mathcal {R}}$ and the part supported on ![]() $\mathring {{\mathcal {R}}}$ and it pushes all points in the second part to
$\mathring {{\mathcal {R}}}$ and it pushes all points in the second part to ![]() $0$, thus giving rise to a new configuration supported only on
$0$, thus giving rise to a new configuration supported only on ![]() $\partial {\mathcal {R}}$. Continuity of
$\partial {\mathcal {R}}$. Continuity of ![]() $\mathfrak {p}_\nu$ depends on the fact that if we perturb a configuration staying inside the stratum
$\mathfrak {p}_\nu$ depends on the fact that if we perturb a configuration staying inside the stratum ![]() $\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, then no point in
$\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, then no point in ![]() $\mathring {{\mathcal {R}}}$ can collide with
$\mathring {{\mathcal {R}}}$ can collide with ![]() $\partial {\mathcal {R}}$ and vice versa no point in
$\partial {\mathcal {R}}$ and vice versa no point in ![]() $\partial {\mathcal {R}}$ can move in the interior, as this would let the internal total norm jump (down and up, respectively). Here it is important that, working with
$\partial {\mathcal {R}}$ can move in the interior, as this would let the internal total norm jump (down and up, respectively). Here it is important that, working with ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$, the local monodromy of a point lying in
$\mathbb {B}({\mathcal {Q}}_+,G)$, the local monodromy of a point lying in ![]() $\mathring {{\mathcal {R}}}$ is required to have positive norm.
$\mathring {{\mathcal {R}}}$ is required to have positive norm.
Formally, let ![]() $\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and let
$\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and let ![]() $\underline {U}$ be an adapted covering of
$\underline {U}$ be an adapted covering of ![]() $P$: in particular, we have
$P$: in particular, we have ![]() $z_i\in U_i\subset \mathring {{\mathcal {R}}}$ for all
$z_i\in U_i\subset \mathring {{\mathcal {R}}}$ for all ![]() $1\le i\le l$. Denote by
$1\le i\le l$. Denote by ![]() $\mathfrak {c}'=\mathfrak {p}_\nu (\mathfrak {c})\in {\mathcal {B}} G$ and let
$\mathfrak {c}'=\mathfrak {p}_\nu (\mathfrak {c})\in {\mathcal {B}} G$ and let ![]() $\underline {U}'$ be the restricted, adapted covering of
$\underline {U}'$ be the restricted, adapted covering of ![]() $P'$, i.e.
$P'$, i.e. ![]() $\underline {U}'=(U_{l+1},\ldots, U_k)$. Then
$\underline {U}'=(U_{l+1},\ldots, U_k)$. Then ![]() $\mathfrak {p}_\nu$ sends the intersection
$\mathfrak {p}_\nu$ sends the intersection ![]() $\mathfrak {U}(\mathfrak {c};\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ inside
$\mathfrak {U}(\mathfrak {c};\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ inside ![]() $\mathfrak {U}(\mathfrak {c}';\underline {U}')\subset {\mathcal {B}} G$: this essentially follows from the observation that, for
$\mathfrak {U}(\mathfrak {c}';\underline {U}')\subset {\mathcal {B}} G$: this essentially follows from the observation that, for ![]() $\tilde {\mathfrak {c}}=(\tilde {P},\tilde {\psi },\tilde {\varphi })\in \mathfrak {U}(\mathfrak {c};\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, we have
$\tilde {\mathfrak {c}}=(\tilde {P},\tilde {\psi },\tilde {\varphi })\in \mathfrak {U}(\mathfrak {c};\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, we have ![]() $\tilde {P}\subset U_1\cup \cdots \cup U_l\cup (\underline {U}'\cap \partial {\mathcal {R}})$.
$\tilde {P}\subset U_1\cup \cdots \cup U_l\cup (\underline {U}'\cap \partial {\mathcal {R}})$.
Notation 5.25 Let ![]() $\nu \ge 0$, let
$\nu \ge 0$, let ![]() $\mathbb {T}\subset \mathbb {C}$ be a contractible subspace containing
$\mathbb {T}\subset \mathbb {C}$ be a contractible subspace containing ![]() $*$, let
$*$, let ![]() ${\mathcal {X}}\subset \mathring {\mathbb {T}}$ be a semialgebraic subspace and let
${\mathcal {X}}\subset \mathring {\mathbb {T}}$ be a semialgebraic subspace and let ![]() $X$ be a subspace of
$X$ be a subspace of ![]() $\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}};{\mathcal {Q}})$. We denote
$\mathrm {Hur}^{\mathbb {T}}({\mathcal {X}};{\mathcal {Q}})$. We denote ![]() $X_\nu =\coprod _{a\in {\mathcal {Q}}_\nu } (X\cap \mathrm {Hur}^{\mathbb {T}}({\mathcal {X}};{\mathcal {Q}})_a)$.
$X_\nu =\coprod _{a\in {\mathcal {Q}}_\nu } (X\cap \mathrm {Hur}^{\mathbb {T}}({\mathcal {X}};{\mathcal {Q}})_a)$.
Proposition 5.26 The map ![]() $\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is a bundle map with fibre
$\mathfrak {p}_\nu \colon \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is a bundle map with fibre ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$. The restricted map
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$. The restricted map ![]() $\mathfrak {p}_\nu \colon \partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is also a bundle map with fibre
$\mathfrak {p}_\nu \colon \partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\to {\mathcal {B}} G$ is also a bundle map with fibre ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$. The two bundles admit compatible local trivialisations, i.e. they form a couple of bundles.
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$. The two bundles admit compatible local trivialisations, i.e. they form a couple of bundles.
Proof. Choose a small closed interval ![]() $J\subset (0,1)\times \{0\}\subset \partial {\mathcal {R}}$ and choose an arc
$J\subset (0,1)\times \{0\}\subset \partial {\mathcal {R}}$ and choose an arc ![]() $\zeta _J$ joining
$\zeta _J$ joining ![]() $*$ with the midpoint of
$*$ with the midpoint of ![]() $J$. Let
$J$. Let ![]() $\mathbb {T}$ be the union
$\mathbb {T}$ be the union ![]() $\mathbb {T}=\mathring {{\mathcal {R}}}\cup J\cup \zeta _J\subset \mathbb {C}$ and note that
$\mathbb {T}=\mathring {{\mathcal {R}}}\cup J\cup \zeta _J\subset \mathbb {C}$ and note that ![]() $\mathbb {T}$ is contractible and contains
$\mathbb {T}$ is contractible and contains ![]() $\mathring {{\mathcal {R}}}$ in its interior. We can define a map of sets
$\mathring {{\mathcal {R}}}$ in its interior. We can define a map of sets
in the spirit of [Reference BianchiBia23a, Definition 3.15]. To define this map, let
Using Notation 2.2, this means that ![]() $\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and the support
$\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ and the support ![]() $P$ of
$P$ of ![]() $\mathfrak {c}$ does not intersect
$\mathfrak {c}$ does not intersect ![]() $J$. The inclusion
$J$. The inclusion ![]() $\mathbb {T}\setminus P\subset \mathbb {C}\setminus P$ gives rise to an inclusion of groups
$\mathbb {T}\setminus P\subset \mathbb {C}\setminus P$ gives rise to an inclusion of groups ![]() $\mathfrak {G}^{\mathbb {T}}(P\cap \mathring {{\mathcal {R}}})\subset \mathfrak {G}(P)$ and, by restriction, an inclusion of PMQs
$\mathfrak {G}^{\mathbb {T}}(P\cap \mathring {{\mathcal {R}}})\subset \mathfrak {G}(P)$ and, by restriction, an inclusion of PMQs ![]() $\mathfrak {Q}^{\mathbb {T}}_{(\mathring {{\mathcal {R}}},\emptyset )}(P\cap \mathring {{\mathcal {R}}})\subset \mathfrak {Q}_{({\mathcal {R}},\partial )}(P)$. We define
$\mathfrak {Q}^{\mathbb {T}}_{(\mathring {{\mathcal {R}}},\emptyset )}(P\cap \mathring {{\mathcal {R}}})\subset \mathfrak {Q}_{({\mathcal {R}},\partial )}(P)$. We define ![]() $\mathfrak {i}_{\mathbb {T}}^{\mathbb {C}}(\mathfrak {c})$ to be the configuration
$\mathfrak {i}_{\mathbb {T}}^{\mathbb {C}}(\mathfrak {c})$ to be the configuration ![]() $\mathfrak {c}'=(P',\psi ')$, where
$\mathfrak {c}'=(P',\psi ')$, where ![]() $P'=P\cap \mathring {{\mathcal {R}}}$ and
$P'=P\cap \mathring {{\mathcal {R}}}$ and ![]() $\psi '\colon \mathfrak {Q}^{\mathbb {T}}_{(\mathring {{\mathcal {R}}},\emptyset )}(P')\to {\mathcal {Q}}$ is the composition of the above inclusion with
$\psi '\colon \mathfrak {Q}^{\mathbb {T}}_{(\mathring {{\mathcal {R}}},\emptyset )}(P')\to {\mathcal {Q}}$ is the composition of the above inclusion with ![]() $\psi \colon \mathfrak {Q}_{({\mathcal {R}},\partial )}(P)\to {\mathcal {Q}}$.
$\psi \colon \mathfrak {Q}_{({\mathcal {R}},\partial )}(P)\to {\mathcal {Q}}$.
To show that ![]() $\mathfrak {i}_{\mathbb {T}}^{\mathbb {C}}$ is continuous at
$\mathfrak {i}_{\mathbb {T}}^{\mathbb {C}}$ is continuous at ![]() $\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\cap \mathrm {Hur}({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J;{\mathcal {Q}},G)$, let
$\mathfrak {c}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\cap \mathrm {Hur}({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J;{\mathcal {Q}},G)$, let ![]() $\underline {U}$ be an adapted covering of
$\underline {U}$ be an adapted covering of ![]() $P$ with
$P$ with ![]() $\underline {U}\subset \mathbb {C}\setminus J$, let
$\underline {U}\subset \mathbb {C}\setminus J$, let ![]() $\mathfrak {c}'=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})$ as above and let
$\mathfrak {c}'=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})$ as above and let ![]() $\underline {U}'$ be the restriction of
$\underline {U}'$ be the restriction of ![]() $\underline {U}$ to
$\underline {U}$ to ![]() $P'\subset P$, i.e.
$P'\subset P$, i.e. ![]() $\underline {U}'$ consists of those components of
$\underline {U}'$ consists of those components of ![]() $\underline {U}$ that intersect non-trivially
$\underline {U}$ that intersect non-trivially ![]() $P'$; equivalently,
$P'$; equivalently, ![]() $\underline {U}'$ consists of those components of
$\underline {U}'$ consists of those components of ![]() $\underline {U}$ that are contained in
$\underline {U}$ that are contained in ![]() $\mathring {{\mathcal {R}}}$.
$\mathring {{\mathcal {R}}}$.
We claim that ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ sends
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ sends ![]() $\mathfrak {U}(\mathfrak {c},\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ inside
$\mathfrak {U}(\mathfrak {c},\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$ inside ![]() $\mathfrak {U}(\mathfrak {c}',\underline {U}')\subset \mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$; since every small enough adapted covering
$\mathfrak {U}(\mathfrak {c}',\underline {U}')\subset \mathrm {Hur}^{\mathbb {T}}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$; since every small enough adapted covering ![]() $\underline {U}'$ of
$\underline {U}'$ of ![]() $P'$ with respect to
$P'$ with respect to ![]() $(\mathring {{\mathcal {R}}},\emptyset )$ can be extended to an adapted covering
$(\mathring {{\mathcal {R}}},\emptyset )$ can be extended to an adapted covering ![]() $\underline {U}$ of
$\underline {U}$ of ![]() $P$ with respect to
$P$ with respect to ![]() $({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J)$, the claim suffices to prove continuity of
$({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J)$, the claim suffices to prove continuity of ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$.
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$.
For the claim, let ![]() $\hat {\mathfrak {c}}=(\hat P,\hat \psi,\hat \varphi )\in \mathfrak {U}(\mathfrak {c},\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$; fix an admissible generating set
$\hat {\mathfrak {c}}=(\hat P,\hat \psi,\hat \varphi )\in \mathfrak {U}(\mathfrak {c},\underline {U})\cap \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$; fix an admissible generating set ![]() $f_1,\ldots,f_k$ of
$f_1,\ldots,f_k$ of ![]() $\mathfrak {G}(P)$ extending an admissible generating set
$\mathfrak {G}(P)$ extending an admissible generating set ![]() $f_1,\ldots,f_l$ of
$f_1,\ldots,f_l$ of ![]() $\mathfrak {G}^{\mathbb {T}}(P')$ and regard
$\mathfrak {G}^{\mathbb {T}}(P')$ and regard ![]() $f_1,\ldots,f_k$ as elements of
$f_1,\ldots,f_k$ as elements of ![]() $\mathfrak {G}(\hat P)$ by the inclusion
$\mathfrak {G}(\hat P)$ by the inclusion ![]() $\mathfrak {G}(P)\cong \mathfrak {G}(\underline {U})\subset \mathfrak {G}(\hat P)$. Let
$\mathfrak {G}(P)\cong \mathfrak {G}(\underline {U})\subset \mathfrak {G}(\hat P)$. Let ![]() $\hat P_i=\hat P\cap U_i$ for all
$\hat P_i=\hat P\cap U_i$ for all ![]() $1\le i\le k$ and write
$1\le i\le k$ and write ![]() $\hat P_i=\{z_{i,1},\ldots,z_{i,k_i}\}$. Choose an admissible generating set
$\hat P_i=\{z_{i,1},\ldots,z_{i,k_i}\}$. Choose an admissible generating set ![]() $(\hat {f}_{i,j})_{1\le i\le k,1\le j\le k_i}$ of
$(\hat {f}_{i,j})_{1\le i\le k,1\le j\le k_i}$ of ![]() $\mathfrak {G}(\hat P)$, such that the equality
$\mathfrak {G}(\hat P)$, such that the equality ![]() $f_i=\hat {f}_{i,1}\cdot \cdots \cdot \hat {f}_{i,k_i}$ holds in
$f_i=\hat {f}_{i,1}\cdot \cdots \cdot \hat {f}_{i,k_i}$ holds in ![]() $\mathfrak {G}(\hat P)$ for all
$\mathfrak {G}(\hat P)$ for all ![]() $1\le i\le k$. The hypothesis on
$1\le i\le k$. The hypothesis on ![]() $\hat {\mathfrak {c}}$ implies that for all
$\hat {\mathfrak {c}}$ implies that for all ![]() $1\le i\le l$ the product
$1\le i\le l$ the product ![]() $\hat \psi (\hat {f}_{i,1})\cdots \hat \psi (\hat {f}_{i,k_i})$ is defined in
$\hat \psi (\hat {f}_{i,1})\cdots \hat \psi (\hat {f}_{i,k_i})$ is defined in ![]() ${\mathcal {Q}}$ and is equal to
${\mathcal {Q}}$ and is equal to ![]() $\psi (f_i)$, in particular
$\psi (f_i)$, in particular ![]() $\sum _{j=1}^{k_i}N(\hat \psi (\hat {f}_{i,j}))=N(\psi (f_i))$. Summing over
$\sum _{j=1}^{k_i}N(\hat \psi (\hat {f}_{i,j}))=N(\psi (f_i))$. Summing over ![]() $1\le i\le l$ and recalling that
$1\le i\le l$ and recalling that ![]() $\hat {\mathfrak {c}}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, we obtain the equality
$\hat {\mathfrak {c}}\in \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, we obtain the equality ![]() $\sum _{i=1}^l\sum _{j=1}^{k_i}N(\hat \psi (\hat {f}_{i,j}))=\nu$. This implies that
$\sum _{i=1}^l\sum _{j=1}^{k_i}N(\hat \psi (\hat {f}_{i,j}))=\nu$. This implies that ![]() $\hat P$ can only intersect the open sets
$\hat P$ can only intersect the open sets ![]() $U_{l+1},\ldots,U_k$ in points of
$U_{l+1},\ldots,U_k$ in points of ![]() $\partial {\mathcal {R}}$ or in inert points for
$\partial {\mathcal {R}}$ or in inert points for ![]() $\hat {\mathfrak {c}}$; since
$\hat {\mathfrak {c}}$; since ![]() $\hat {\mathfrak {c}}$ has no inert point, we have that
$\hat {\mathfrak {c}}$ has no inert point, we have that ![]() $\hat P$ is contained in the union
$\hat P$ is contained in the union ![]() $\partial {\mathcal {R}}\cup \underline {U}'$. It follows that
$\partial {\mathcal {R}}\cup \underline {U}'$. It follows that ![]() $\hat {\mathfrak {c}}'=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\hat {\mathfrak {c}})$ is supported on
$\hat {\mathfrak {c}}'=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\hat {\mathfrak {c}})$ is supported on ![]() $\underline {U}'$; the fact that
$\underline {U}'$; the fact that ![]() $\hat {\mathfrak {c}}'$ is contained in
$\hat {\mathfrak {c}}'$ is contained in ![]() $\mathfrak {U}(\mathfrak {c}',\underline {U}')$ follows now directly from the definition of
$\mathfrak {U}(\mathfrak {c}',\underline {U}')$ follows now directly from the definition of ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ and from the already mentioned equalities
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ and from the already mentioned equalities ![]() $\hat \psi (\hat {f}_{i,1})\cdot \cdots \cdot \hat \psi (\hat {f}_{i,k_i})=\psi (f_i)$ for
$\hat \psi (\hat {f}_{i,1})\cdot \cdots \cdot \hat \psi (\hat {f}_{i,k_i})=\psi (f_i)$ for ![]() $1\le i\le l$.
$1\le i\le l$.
Now note that the intersection ![]() $\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\cap \mathrm {Hur}({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J;{\mathcal {Q}},G)$ is precisely the preimage along
$\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\cap \mathrm {Hur}({\mathcal {R}}\setminus J,\partial {\mathcal {R}}\setminus J;{\mathcal {Q}},G)$ is precisely the preimage along ![]() $\mathfrak {p}_\nu$ of the open subspace
$\mathfrak {p}_\nu$ of the open subspace ![]() $\mathrm {Hur}(\partial {\mathcal {R}}\setminus J;G)_{0;\mathbb {1}}\subset {\mathcal {B}} G$. The product map
$\mathrm {Hur}(\partial {\mathcal {R}}\setminus J;G)_{0;\mathbb {1}}\subset {\mathcal {B}} G$. The product map ![]() $\mathfrak {p}_\nu \times \mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ gives a homeomorphism
$\mathfrak {p}_\nu \times \mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ gives a homeomorphism
Since the open sets ![]() $\mathrm {Hur}(\partial {\mathcal {R}}\setminus J;G)_{0;\mathbb {1}}$ form an open covering of
$\mathrm {Hur}(\partial {\mathcal {R}}\setminus J;G)_{0;\mathbb {1}}$ form an open covering of ![]() ${\mathcal {B}} G$, for varying
${\mathcal {B}} G$, for varying ![]() $J$, we obtain that
$J$, we obtain that ![]() $\mathfrak {p}_\nu$ is a bundle map, i.e. it admits local trivialisations. The fibre of the bundle is homeomorphic to the space
$\mathfrak {p}_\nu$ is a bundle map, i.e. it admits local trivialisations. The fibre of the bundle is homeomorphic to the space ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$.
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$.
The local trivialisation ![]() $\mathfrak {p}_\nu \times \mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ restricts to a local trivialisation of the restriction of
$\mathfrak {p}_\nu \times \mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}$ restricts to a local trivialisation of the restriction of ![]() $\mathfrak {p}_\nu$ to
$\mathfrak {p}_\nu$ to ![]() $\partial ^{\mathrm {fat}}\,\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\subset \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, with restricted fibre
$\partial ^{\mathrm {fat}}\,\mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)\subset \mathfrak {F}_\nu \mathbb {B}({\mathcal {Q}}_+,G)$, with restricted fibre ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$.
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_\nu$.
6. Rational cohomology
In this section we assume that ![]() ${\mathcal {Q}}$ is a finite,
${\mathcal {Q}}$ is a finite, ![]() $\mathbb {Q}$-Poincaré PMQ and
$\mathbb {Q}$-Poincaré PMQ and ![]() $G$ is a finite group and compute the rational cohomology of
$G$ is a finite group and compute the rational cohomology of ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$. Recall from [Reference BianchiBia23a, Definition] that a PMQ
$\mathbb {B}({\mathcal {Q}}_+,G)$. Recall from [Reference BianchiBia23a, Definition] that a PMQ ![]() ${\mathcal {Q}}$ is
${\mathcal {Q}}$ is ![]() $\mathbb {Q}$-Poincaré if
$\mathbb {Q}$-Poincaré if ![]() ${\mathcal {Q}}$ is locally finite and for all
${\mathcal {Q}}$ is locally finite and for all ![]() $a\in {\mathcal {Q}}$ the space
$a\in {\mathcal {Q}}$ the space ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$ is a
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$ is a ![]() $\mathbb {Q}$-homology manifold of some dimension: in this case
$\mathbb {Q}$-homology manifold of some dimension: in this case ![]() ${\mathcal {Q}}$ admits an intrinsic norm
${\mathcal {Q}}$ admits an intrinsic norm ![]() $h\colon {\mathcal {Q}}\to \mathbb {N}$ and
$h\colon {\mathcal {Q}}\to \mathbb {N}$ and ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$ is an orientable
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$ is an orientable ![]() $\mathbb {Q}$-homology manifold of dimension
$\mathbb {Q}$-homology manifold of dimension ![]() $2h(a)$ for all
$2h(a)$ for all ![]() $a\in {\mathcal {Q}}$. See [Reference BianchiBia23a, Proposition 9.7].
$a\in {\mathcal {Q}}$. See [Reference BianchiBia23a, Proposition 9.7].
Our interest for the space ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ and its cohomology comes from Theorem 4.22 and Proposition 5.5, relating
$\mathbb {B}({\mathcal {Q}}_+,G)$ and its cohomology comes from Theorem 4.22 and Proposition 5.5, relating ![]() $\mathbb {B}({\mathcal {Q}}_+,G)$ to the topological monoid
$\mathbb {B}({\mathcal {Q}}_+,G)$ to the topological monoid ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})$. Note that, for a fixed PMQ
$\mathring {\mathrm {HM}}({\mathcal {Q}})$. Note that, for a fixed PMQ ![]() ${\mathcal {Q}}$, we are free to choose a group
${\mathcal {Q}}$, we are free to choose a group ![]() $G$ completing
$G$ completing ![]() ${\mathcal {Q}}$ to a PMQ–group pair
${\mathcal {Q}}$ to a PMQ–group pair ![]() $({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$. If
$({\mathcal {Q}},G,\mathfrak {e},\mathfrak {r})$. If ![]() ${\mathcal {Q}}$ is finite we can, for instance, take
${\mathcal {Q}}$ is finite we can, for instance, take ![]() $G={\mathcal {G}}({\mathcal {Q}})/{\mathcal {K}}({\mathcal {Q}})$, which is a finite group; here
$G={\mathcal {G}}({\mathcal {Q}})/{\mathcal {K}}({\mathcal {Q}})$, which is a finite group; here ![]() ${\mathcal {K}}({\mathcal {Q}})$ denotes the kernel of the map
${\mathcal {K}}({\mathcal {Q}})$ denotes the kernel of the map ![]() $\rho \colon {\mathcal {G}}({\mathcal {Q}})\to \operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$, giving the right action of
$\rho \colon {\mathcal {G}}({\mathcal {Q}})\to \operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$, giving the right action of ![]() ${\mathcal {G}}({\mathcal {Q}})$ on
${\mathcal {G}}({\mathcal {Q}})$ on ![]() ${\mathcal {Q}}$ by conjugation: if
${\mathcal {Q}}$ by conjugation: if ![]() ${\mathcal {Q}}$ is finite, then
${\mathcal {Q}}$ is finite, then ![]() $\operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$ is also finite and contains a subgroup isomorphic to
$\operatorname {Aut}_{\mathbf {PMQ}}({\mathcal {Q}})^{\rm op}$ is also finite and contains a subgroup isomorphic to ![]() ${\mathcal {G}}({\mathcal {Q}})/{\mathcal {K}}({\mathcal {Q}})$. See also [Reference BianchiBia21, Lemma 2.13]. Thus, if we are given a finite,
${\mathcal {G}}({\mathcal {Q}})/{\mathcal {K}}({\mathcal {Q}})$. See also [Reference BianchiBia21, Lemma 2.13]. Thus, if we are given a finite, ![]() $\mathbb {Q}$-Poincaré PMQ
$\mathbb {Q}$-Poincaré PMQ ![]() ${\mathcal {Q}}$, we can complete
${\mathcal {Q}}$, we can complete ![]() ${\mathcal {Q}}$ to a PMQ–group pair by adjoining a suitable finite group
${\mathcal {Q}}$ to a PMQ–group pair by adjoining a suitable finite group ![]() $G$.
$G$.
Recall from [Reference BianchiBia21, Definition 4.29] that ![]() ${\mathcal {A}}({\mathcal {Q}})\subset \mathbb {Q}[{\mathcal {Q}}]$ is defined as the subring of the PMQ–group ring
${\mathcal {A}}({\mathcal {Q}})\subset \mathbb {Q}[{\mathcal {Q}}]$ is defined as the subring of the PMQ–group ring ![]() $\mathbb {Q}[{\mathcal {Q}}]$ consisting of the invariants under conjugation by
$\mathbb {Q}[{\mathcal {Q}}]$ consisting of the invariants under conjugation by ![]() $G$:
$G$:
As a ![]() $\mathbb {Q}$-vector space,
$\mathbb {Q}$-vector space, ![]() ${\mathcal {A}}({\mathcal {Q}})$ is spanned by elements
${\mathcal {A}}({\mathcal {Q}})$ is spanned by elements ![]() $[\! [S]\! ]=\sum _{a\in S}[\! [a]\! ]$, for each conjugacy class
$[\! [S]\! ]=\sum _{a\in S}[\! [a]\! ]$, for each conjugacy class ![]() $S\subset {\mathcal {Q}}$. In this section we consider
$S\subset {\mathcal {Q}}$. In this section we consider ![]() $\mathbb {Q}[{\mathcal {Q}}]^G$ as a graded, associative ring, by putting the generator
$\mathbb {Q}[{\mathcal {Q}}]^G$ as a graded, associative ring, by putting the generator ![]() $[\! [a]\! ]$ in degree
$[\! [a]\! ]$ in degree ![]() $2h(a)$, for all
$2h(a)$, for all ![]() $a\in {\mathcal {Q}}$; similarly
$a\in {\mathcal {Q}}$; similarly ![]() ${\mathcal {A}}({\mathcal {Q}})$ is a graded ring with
${\mathcal {A}}({\mathcal {Q}})$ is a graded ring with ![]() $[\! [S]\! ]$ in degree
$[\! [S]\! ]$ in degree ![]() $2h(a)$, for any
$2h(a)$, for any ![]() $a\in S$. By [Reference BianchiBia21, Lemma 4.31] the ring
$a\in S$. By [Reference BianchiBia21, Lemma 4.31] the ring ![]() ${\mathcal {A}}({\mathcal {Q}})$ is a commutative ring, hence by our choice of degrees it is a graded-commutative ring, supported in even degrees. We will prove the following theorem.
${\mathcal {A}}({\mathcal {Q}})$ is a commutative ring, hence by our choice of degrees it is a graded-commutative ring, supported in even degrees. We will prove the following theorem.
Theorem 6.1 Let ![]() $({\mathcal {Q}},G)$ be a PMQ–group pair with
$({\mathcal {Q}},G)$ be a PMQ–group pair with ![]() ${\mathcal {Q}}$ finite and
${\mathcal {Q}}$ finite and ![]() $\mathbb {Q}$-Poincaré and with
$\mathbb {Q}$-Poincaré and with ![]() $G$ finite. Then there is an isomorphism of rings
$G$ finite. Then there is an isomorphism of rings
In this entire section we use the abbreviation ![]() $\mathbb {B}=\mathbb {B}({\mathcal {Q}}_+,G)$.
$\mathbb {B}=\mathbb {B}({\mathcal {Q}}_+,G)$.
6.1 Two spectral sequence arguments
Since the space ![]() $\mathbb {B}$ is equipped with a filtration by subspaces
$\mathbb {B}$ is equipped with a filtration by subspaces ![]() $F_\nu \mathbb {B}$, we can compute
$F_\nu \mathbb {B}$, we can compute ![]() $H^*(\mathbb {B};\mathbb {Q})$ by the associated Leray spectral sequence, whose first page reads
$H^*(\mathbb {B};\mathbb {Q})$ by the associated Leray spectral sequence, whose first page reads ![]() $E_1^{p,\nu }=H^{p+\nu }(F_\nu \mathbb {B},F_{\nu -1}\mathbb {B})$.
$E_1^{p,\nu }=H^{p+\nu }(F_\nu \mathbb {B},F_{\nu -1}\mathbb {B})$.
Lemma 6.2 For ![]() $\nu \ge 0$ the inclusion
$\nu \ge 0$ the inclusion ![]() $F_{\nu -1}\mathbb {B}\subset F^{\mathrm {fat}}_{\nu -1}\mathbb {B}$ is a homotopy equivalence. Moreover, we have cohomology isomorphisms
$F_{\nu -1}\mathbb {B}\subset F^{\mathrm {fat}}_{\nu -1}\mathbb {B}$ is a homotopy equivalence. Moreover, we have cohomology isomorphisms
Proof. Recall Definitions 5.6 and 5.7. For ![]() $\mathfrak {c} \in F_\nu \mathbb {B}$ let
$\mathfrak {c} \in F_\nu \mathbb {B}$ let ![]() $\mathfrak {W}_\nu (\mathfrak {c})$ be the supremum in
$\mathfrak {W}_\nu (\mathfrak {c})$ be the supremum in ![]() $[1/2,1]$ of all
$[1/2,1]$ of all ![]() $1/2<\varepsilon <1$ for which
$1/2<\varepsilon <1$ for which ![]() ${\mathcal {H}}^{\mathbb {B}}_*(\mathfrak {c},1/\varepsilon ) \in F_{\nu -1}\mathbb {B}$. We define a homotopy
${\mathcal {H}}^{\mathbb {B}}_*(\mathfrak {c},1/\varepsilon ) \in F_{\nu -1}\mathbb {B}$. We define a homotopy
The homotopy ![]() $H^{\mathbb {B}}_\nu$ restricts to a deformation retraction of
$H^{\mathbb {B}}_\nu$ restricts to a deformation retraction of ![]() $F^{\mathrm {fat}}_{\nu -1}\mathbb {B}$ onto
$F^{\mathrm {fat}}_{\nu -1}\mathbb {B}$ onto ![]() $F_{\nu -1}\mathbb {B}$, whence the first cohomology isomorphism follows. The second cohomology isomorphism follows from excision: in fact,
$F_{\nu -1}\mathbb {B}$, whence the first cohomology isomorphism follows. The second cohomology isomorphism follows from excision: in fact, ![]() $F_{\nu -1}\mathbb {B}=(\mathfrak {W}_\nu )^{-1}(1)$ and the open set
$F_{\nu -1}\mathbb {B}=(\mathfrak {W}_\nu )^{-1}(1)$ and the open set ![]() $(\mathfrak {W}_\nu )^{-1}((1/2,1])$ is contained in
$(\mathfrak {W}_\nu )^{-1}((1/2,1])$ is contained in ![]() $F^{\mathrm {fat}}_{\nu -1}(\mathbb {B})$, so we can apply excision.
$F^{\mathrm {fat}}_{\nu -1}(\mathbb {B})$, so we can apply excision.
We can now focus on the relative cohomology groups ![]() $H^*(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B};\mathbb {Q})$.
$H^*(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B};\mathbb {Q})$.
Proposition 6.3 For ![]() $\nu \ge 0$, the cohomology groups
$\nu \ge 0$, the cohomology groups ![]() $H^*(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B};\mathbb {Q})$ are concentrated in degree
$H^*(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B};\mathbb {Q})$ are concentrated in degree ![]() $*=2\nu$; the group
$*=2\nu$; the group ![]() $H^{2\nu }(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B};\mathbb {Q})$ is isomorphic to
$H^{2\nu }(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B};\mathbb {Q})$ is isomorphic to ![]() ${\mathcal {A}}({\mathcal {Q}})_{2\nu }$, i.e. the degree-
${\mathcal {A}}({\mathcal {Q}})_{2\nu }$, i.e. the degree-![]() $2\nu$ part of
$2\nu$ part of ![]() ${\mathcal {A}}({\mathcal {Q}})$.
${\mathcal {A}}({\mathcal {Q}})$.
Proof. We use the Serre spectral sequence ![]() ${\mathcal {E}}(\nu )$ associated with the couple of bundles
${\mathcal {E}}(\nu )$ associated with the couple of bundles ![]() $\mathfrak {p}_\nu \colon (\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B})\to {\mathcal {B}} G$: its second page reads
$\mathfrak {p}_\nu \colon (\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu }\mathbb {B})\to {\mathcal {B}} G$: its second page reads
The first step is to compute ![]() $H^*(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a;\mathbb {Q})$ for
$H^*(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a;\mathbb {Q})$ for ![]() $a\in {\mathcal {Q}}_\nu$ and the argument for this will be similar to the proof of Lemma 6.2. Consider the closed unit square
$a\in {\mathcal {Q}}_\nu$ and the argument for this will be similar to the proof of Lemma 6.2. Consider the closed unit square ![]() ${\mathcal {R}}$ and define
${\mathcal {R}}$ and define ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}(( {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}});{\mathcal {Q}}_+)_a$ and
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}(( {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}});{\mathcal {Q}}_+)_a$ and ![]() $\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$. The subspace
$\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$. The subspace ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\subset \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ contains configurations whose support intersects
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\subset \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ contains configurations whose support intersects ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}$ (see Definition 5.20), whereas
$\partial ^{\mathrm {fat}}{\mathcal {R}}$ (see Definition 5.20), whereas ![]() $\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\subset \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ contains configurations whose support intersects
$\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a\subset \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ contains configurations whose support intersects ![]() $\partial {\mathcal {R}}$.
$\partial {\mathcal {R}}$.
Recall Definition 5.6: for all ![]() $s\ge 1$ the map
$s\ge 1$ the map ![]() ${\mathcal {H}}^{\mathbb {B}}(-,s)\colon \mathbb {C}\to \mathbb {C}$ is a lax endomorphism of the nice couple
${\mathcal {H}}^{\mathbb {B}}(-,s)\colon \mathbb {C}\to \mathbb {C}$ is a lax endomorphism of the nice couple ![]() $({\mathcal {R}},\emptyset )$; if we consider
$({\mathcal {R}},\emptyset )$; if we consider ![]() $\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ as a connected component of
$\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ as a connected component of ![]() $\mathrm {Hur}({\mathcal {R}};\hat {{\mathcal {Q}}}_+)$, under the inclusion
$\mathrm {Hur}({\mathcal {R}};\hat {{\mathcal {Q}}}_+)$, under the inclusion ![]() ${\mathcal {Q}}\subset \hat {{\mathcal {Q}}}$, we obtain by functoriality a homotopy
${\mathcal {Q}}\subset \hat {{\mathcal {Q}}}$, we obtain by functoriality a homotopy
For ![]() $\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ denote by
$\mathfrak {c}\in \mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ denote by ![]() $\mathfrak {W}_a(\mathfrak {c})$ the supremum in
$\mathfrak {W}_a(\mathfrak {c})$ the supremum in ![]() $[1/2,1]$ of all
$[1/2,1]$ of all ![]() $1/2<\varepsilon <1$ for which
$1/2<\varepsilon <1$ for which ![]() ${\mathcal {H}}^{\mathbb {B}}_*(\mathfrak {c},1/\varepsilon )\in \partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$. We define a homotopy
${\mathcal {H}}^{\mathbb {B}}_*(\mathfrak {c},1/\varepsilon )\in \partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$. We define a homotopy
The homotopy ![]() $H^{\mathbb {B}}_a$ restricts to a deformation retraction of
$H^{\mathbb {B}}_a$ restricts to a deformation retraction of ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ onto
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ onto ![]() $\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$; moreover, the subspace
$\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$; moreover, the subspace ![]() $\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ of
$\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ of ![]() $\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ is contained in the interior of
$\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ is contained in the interior of ![]() $\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ and
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a$ and
We thus obtain cohomology isomorphisms
 \begin{align*} H^*(\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a;\mathbb{Q}) &\cong H^*(\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a;\mathbb{Q})\\ &\cong H^*(\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a,\partial\,\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a;\mathbb{Q}). \end{align*}
\begin{align*} H^*(\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a;\mathbb{Q}) &\cong H^*(\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a;\mathbb{Q})\\ &\cong H^*(\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a,\partial\,\mathrm{Hur}({\mathcal{R}};{\mathcal{Q}}_+)_a;\mathbb{Q}). \end{align*}
Since ![]() ${\mathcal {Q}}$ is
${\mathcal {Q}}$ is ![]() $\mathbb {Q}$-Poincaré, as a consequence of [Reference BianchiBia23a, Lemma 9.5 and Proposition 9.7] the cohomology
$\mathbb {Q}$-Poincaré, as a consequence of [Reference BianchiBia23a, Lemma 9.5 and Proposition 9.7] the cohomology ![]() $H^*(\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a,\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a;\mathbb {Q})$ vanishes in degrees
$H^*(\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a,\partial \,\mathrm {Hur}({\mathcal {R}};{\mathcal {Q}}_+)_a;\mathbb {Q})$ vanishes in degrees ![]() $*\neq 2\nu =2h(a)$ and it is equal to
$*\neq 2\nu =2h(a)$ and it is equal to ![]() $\mathbb {Q}$ in degree
$\mathbb {Q}$ in degree ![]() $*=2\nu$. Going back to the Serre spectral sequence, the group
$*=2\nu$. Going back to the Serre spectral sequence, the group ![]() ${\mathcal {E}}(\nu )_2^{p,q}$ vanishes for
${\mathcal {E}}(\nu )_2^{p,q}$ vanishes for ![]() $q\neq 2\nu$ and
$q\neq 2\nu$ and ![]() ${\mathcal {E}}(\nu )_2^{p,2\nu }$ is equal to the twisted cohomology group
${\mathcal {E}}(\nu )_2^{p,2\nu }$ is equal to the twisted cohomology group ![]() $H^p({\mathcal {B}} G;\oplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q})$; this already shows that the spectral sequence collapses on its second page. Moreover, since
$H^p({\mathcal {B}} G;\oplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q})$; this already shows that the spectral sequence collapses on its second page. Moreover, since ![]() $G$ is a finite group and we are considering twisted cohomology with coefficients in a
$G$ is a finite group and we are considering twisted cohomology with coefficients in a ![]() $G$-representation over
$G$-representation over ![]() $\mathbb {Q}$, all cohomology groups except possibly
$\mathbb {Q}$, all cohomology groups except possibly ![]() $H^0$ vanish, i.e. the entire page
$H^0$ vanish, i.e. the entire page ![]() ${\mathcal {E}}(\nu )_2$ vanishes except possibly
${\mathcal {E}}(\nu )_2$ vanishes except possibly ![]() ${\mathcal {E}}(\nu )_2^{0,2\nu }=H^0({\mathcal {B}} G;\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q})$.
${\mathcal {E}}(\nu )_2^{0,2\nu }=H^0({\mathcal {B}} G;\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q})$.
The action of ![]() $G$ on
$G$ on ![]() $\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q}$ is the
$\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q}$ is the ![]() $\mathbb {Q}$-linearisation of the action of
$\mathbb {Q}$-linearisation of the action of ![]() $G$ on the set
$G$ on the set ![]() ${\mathcal {Q}}_\nu$ by conjugation; the invariants of the action of
${\mathcal {Q}}_\nu$ by conjugation; the invariants of the action of ![]() $G$ on
$G$ on ![]() $\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q}$ are therefore the
$\bigoplus _{a\in {\mathcal {Q}}_\nu }\mathbb {Q}$ are therefore the ![]() $\mathbb {Q}$-vector space spanned by conjugacy classes of
$\mathbb {Q}$-vector space spanned by conjugacy classes of ![]() ${\mathcal {Q}}$ of norm
${\mathcal {Q}}$ of norm ![]() $\nu$: this vector space is isomorphic to the degree-
$\nu$: this vector space is isomorphic to the degree-![]() $2\nu$ part of
$2\nu$ part of ![]() ${\mathcal {A}}({\mathcal {Q}})$.
${\mathcal {A}}({\mathcal {Q}})$.
Proposition 6.3 implies that the ![]() $E_1$-page of the Leray spectral sequence associated with the filtered space
$E_1$-page of the Leray spectral sequence associated with the filtered space ![]() $\mathbb {B}$ is supported on the main diagonal, i.e.
$\mathbb {B}$ is supported on the main diagonal, i.e. ![]() $E_1^{p,\nu }=0$ whenever
$E_1^{p,\nu }=0$ whenever ![]() $p\neq \nu$. This implies that the spectral sequence collapses on its first page and, thus, we obtain an isomorphism of graded
$p\neq \nu$. This implies that the spectral sequence collapses on its first page and, thus, we obtain an isomorphism of graded ![]() $\mathbb {Q}$-vector spaces
$\mathbb {Q}$-vector spaces
It will be convenient to specify a particular isomorphism of graded ![]() $\mathbb {Q}$-vector spaces. Recall that, since
$\mathbb {Q}$-vector spaces. Recall that, since ![]() ${\mathcal {Q}}$ is
${\mathcal {Q}}$ is ![]() $\mathbb {Q}$-Poincaré, it is locally finite and coconnected; in particular, for all
$\mathbb {Q}$-Poincaré, it is locally finite and coconnected; in particular, for all ![]() $\nu \ge 0$ and for all
$\nu \ge 0$ and for all ![]() $b\in {\mathcal {Q}}_\nu$ there is a canonical fundamental class
$b\in {\mathcal {Q}}_\nu$ there is a canonical fundamental class
see [Reference BianchiBia21, Definition 6.25]. Recall also the map of pairs
by [Reference BianchiBia23a, Lemma 8.23] ![]() $\upsilon$ is a continuous bijection and the hypothesis that
$\upsilon$ is a continuous bijection and the hypothesis that ![]() ${\mathcal {Q}}$ is locally finite implies that
${\mathcal {Q}}$ is locally finite implies that ![]() $|\mathrm {Arr}({\mathcal {Q}})_b|$ is compact, hence
$|\mathrm {Arr}({\mathcal {Q}})_b|$ is compact, hence ![]() $\upsilon _b$ is a homeomorphism. We thus obtain a fundamental class
$\upsilon _b$ is a homeomorphism. We thus obtain a fundamental class
Using the homotopy equivalences of pairs
and excision we obtain a fundamental class
Notation 6.4 Let ![]() $[\! [S]\! ]\in {\mathcal {A}}({\mathcal {Q}})_{2\nu }$ be the generator corresponding to the conjugacy class
$[\! [S]\! ]\in {\mathcal {A}}({\mathcal {Q}})_{2\nu }$ be the generator corresponding to the conjugacy class ![]() $S\subset {\mathcal {Q}}_\nu$. We regard
$S\subset {\mathcal {Q}}_\nu$. We regard ![]() $[\! [S]\! ]$ as the (unique) cohomology class
$[\! [S]\! ]$ as the (unique) cohomology class
satisfying the following property: for all ![]() $b\in {\mathcal {Q}}_\nu$, the Kronecker pairing of
$b\in {\mathcal {Q}}_\nu$, the Kronecker pairing of ![]() $[\! [S]\! ]$ with the fundamental homology class
$[\! [S]\! ]$ with the fundamental homology class ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b]$ is
$[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b]$ is ![]() $1$ if
$1$ if ![]() $b\in S$ and is
$b\in S$ and is ![]() $0$ if
$0$ if ![]() $b\notin S$.
$b\notin S$.
Note that ![]() $[\! [S]\! ]$ is invariant under the action of
$[\! [S]\! ]$ is invariant under the action of ![]() $G$ by conjugation, hence
$G$ by conjugation, hence ![]() $[\! [S]\! ]$ corresponds to a cohomology class in
$[\! [S]\! ]$ corresponds to a cohomology class in ![]() $H^{2\nu }(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B};\mathbb {Q})$, which we also denote
$H^{2\nu }(\mathfrak {F}_\nu \mathbb {B},\partial ^{\mathrm {fat}}\mathfrak {F}_\nu \mathbb {B};\mathbb {Q})$, which we also denote ![]() $[\! [S]\! ]$. Finally, we use the canonical isomorphisms
$[\! [S]\! ]$. Finally, we use the canonical isomorphisms
to regard ![]() $[\! [S]\! ]$ as a cohomology class in
$[\! [S]\! ]$ as a cohomology class in ![]() $H^{2\nu }(\mathbb {B}({\mathcal {Q}}_+,G);\mathbb {Q})$.
$H^{2\nu }(\mathbb {B}({\mathcal {Q}}_+,G);\mathbb {Q})$.
6.2 A strategy to compute the cup product
We fix ![]() $\nu,\nu '\ge 0$ throughout the rest of the section; our aim is to compute the cup product
$\nu,\nu '\ge 0$ throughout the rest of the section; our aim is to compute the cup product ![]() $H^{2\nu }(\mathbb {B};\mathbb {Q})\otimes H^{2\nu '}(\mathbb {B};\mathbb {Q})\to H^{2\nu +2\nu '}(\mathbb {B};\mathbb {Q})$. We fix
$H^{2\nu }(\mathbb {B};\mathbb {Q})\otimes H^{2\nu '}(\mathbb {B};\mathbb {Q})\to H^{2\nu +2\nu '}(\mathbb {B};\mathbb {Q})$. We fix ![]() $[\! [S]\! ]\in H^{2\nu }(\mathbb {B};\mathbb {Q})$ and
$[\! [S]\! ]\in H^{2\nu }(\mathbb {B};\mathbb {Q})$ and ![]() $[\! [S']\! ]\in H^{2\nu '}(\mathbb {B};\mathbb {Q})$: our aim is to express the cup product
$[\! [S']\! ]\in H^{2\nu '}(\mathbb {B};\mathbb {Q})$: our aim is to express the cup product ![]() $[\! [S]\! ]\smile [\! [S']\! ]\in H^{2\nu +2\nu '}(\mathbb {B};\mathbb {Q})$ as a linear combination of generators
$[\! [S]\! ]\smile [\! [S']\! ]\in H^{2\nu +2\nu '}(\mathbb {B};\mathbb {Q})$ as a linear combination of generators ![]() $[\! [T]\! ]$, for
$[\! [T]\! ]$, for ![]() $T$ varying among conjugacy classes of
$T$ varying among conjugacy classes of ![]() ${\mathcal {Q}}$ contained in
${\mathcal {Q}}$ contained in ![]() ${\mathcal {Q}}_{\nu +\nu '}$.
${\mathcal {Q}}_{\nu +\nu '}$.
The restriction map ![]() $H^*(\mathbb {B};\mathbb {Q})\to H^*(F_{\nu +\nu '}\mathbb {B};\mathbb {Q})$ is an isomorphism in degrees
$H^*(\mathbb {B};\mathbb {Q})\to H^*(F_{\nu +\nu '}\mathbb {B};\mathbb {Q})$ is an isomorphism in degrees ![]() $*\leq 2\nu +2\nu '$: therefore, it suffices to compute the cup product
$*\leq 2\nu +2\nu '$: therefore, it suffices to compute the cup product ![]() $H^{2\nu }\otimes H^{2\nu '}\to H^{2\nu +2\nu '}$ for the space
$H^{2\nu }\otimes H^{2\nu '}\to H^{2\nu +2\nu '}$ for the space ![]() $F_{\nu +\nu '}\mathbb {B}$. In the rest of the subsection we use the abbreviation
$F_{\nu +\nu '}\mathbb {B}$. In the rest of the subsection we use the abbreviation ![]() $F_\bullet =F_\bullet \mathbb {B}$.
$F_\bullet =F_\bullet \mathbb {B}$.
The argument to compute the cup product on ![]() $F_{\nu +\nu '}$ is based on certain subspaces
$F_{\nu +\nu '}$ is based on certain subspaces ![]() $F_{\mathrm {lr}}$,
$F_{\mathrm {lr}}$, ![]() $F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\mathrm {r}}^{\mathrm {fat}}$ of
$F_{\mathrm {r}}^{\mathrm {fat}}$ of ![]() $F_{\nu +\nu '}$; there are inclusions
$F_{\nu +\nu '}$; there are inclusions ![]() $F_{\nu +\nu '-1}\subset F_{\mathrm {lr}}$ as well as
$F_{\nu +\nu '-1}\subset F_{\mathrm {lr}}$ as well as ![]() $F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$ and we will prove that the last two inclusions are, in fact, homotopy equivalences. Postponing the actual definition of
$F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$ and we will prove that the last two inclusions are, in fact, homotopy equivalences. Postponing the actual definition of ![]() $F_{\mathrm {lr}}$,
$F_{\mathrm {lr}}$, ![]() $F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\mathrm {r}}^{\mathrm {fat}}$, we introduce some notation.
$F_{\mathrm {r}}^{\mathrm {fat}}$, we introduce some notation.
Notation 6.5 We introduce several subspaces of ![]() $F_{\nu +\nu '}$:
$F_{\nu +\nu '}$:
 \begin{gather*} F_{\mathrm{lr}}^{\mathrm{fat}}=F_{\mathrm{l}}^{\mathrm{fat}}\cup F_{\mathrm{r}}^{\mathrm{fat}};\quad \mathfrak{F}_{\nu,\nu'}=F_{\nu+\nu'}\setminus F_{\mathrm{lr}};\\ \partial_{\mathrm{l}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{l}}^{\mathrm{fat}}; \quad \partial_{\mathrm{r}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{r}}^{\mathrm{fat}};\quad \partial_{\mathrm{lr}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{lr}}^{\mathrm{fat}};\\ \partial_{\mathrm{l}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{l}}^{\mathrm{fat}};\quad \partial_{\mathrm{r}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{r}}^{\mathrm{fat}};\quad \partial_{\mathrm{lr}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{lr}}^{\mathrm{fat}}. \end{gather*}
\begin{gather*} F_{\mathrm{lr}}^{\mathrm{fat}}=F_{\mathrm{l}}^{\mathrm{fat}}\cup F_{\mathrm{r}}^{\mathrm{fat}};\quad \mathfrak{F}_{\nu,\nu'}=F_{\nu+\nu'}\setminus F_{\mathrm{lr}};\\ \partial_{\mathrm{l}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{l}}^{\mathrm{fat}}; \quad \partial_{\mathrm{r}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{r}}^{\mathrm{fat}};\quad \partial_{\mathrm{lr}}^{\mathrm{fat}}\mathfrak{F}_{\nu+\nu'}=\mathfrak{F}_{\nu+\nu'}\cap F_{\mathrm{lr}}^{\mathrm{fat}};\\ \partial_{\mathrm{l}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{l}}^{\mathrm{fat}};\quad \partial_{\mathrm{r}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{r}}^{\mathrm{fat}};\quad \partial_{\mathrm{lr}}^{\mathrm{fat}}\mathfrak{F}_{\nu,\nu'}=\mathfrak{F}_{\nu,\nu'}\cap F_{\mathrm{lr}}^{\mathrm{fat}}. \end{gather*}
There is the following square of inclusions of subspaces, where both horizontal arrows are inclusions of a closed subspace of ![]() $F_{\nu +\nu '}$ in the interior of a larger subspace of
$F_{\nu +\nu '}$ in the interior of a larger subspace of ![]() $F_{\nu +\nu '}$:
$F_{\nu +\nu '}$:

This implies that the inclusions of couples ![]() $(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})\subset (F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ and
$(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})\subset (F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ and ![]() $(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})\subset (F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ satisfy excision. Finally, the bundle projection
$(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})\subset (F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ satisfy excision. Finally, the bundle projection ![]() $\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu +\nu '}\to {\mathcal {B}} G$ exhibits also the subspaces
$\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu +\nu '}\to {\mathcal {B}} G$ exhibits also the subspaces ![]() $\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$,
$\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$, ![]() $\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$,
$\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$, ![]() $\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$,
$\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}$, ![]() $\mathfrak {F}_{\nu,\nu '}$,
$\mathfrak {F}_{\nu,\nu '}$, ![]() $\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$,
$\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$, ![]() $\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$ and
$\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$ and ![]() $\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$ as bundles over
$\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}$ as bundles over ![]() ${\mathcal {B}} G$, with suitable fibres: local trivialisations for these bundles can be obtained by restricting the local trivialisations of
${\mathcal {B}} G$, with suitable fibres: local trivialisations for these bundles can be obtained by restricting the local trivialisations of ![]() $\mathfrak {p}_{\nu +\nu '}$ given in the proof of Proposition 5.26.
$\mathfrak {p}_{\nu +\nu '}$ given in the proof of Proposition 5.26.
The previous technical results will allow us to write two commutative diagrams of cohomology groups, where we understand ![]() $\mathbb {Q}$-coefficients for cohomology. We state the two diagrams as propositions for future reference.
$\mathbb {Q}$-coefficients for cohomology. We state the two diagrams as propositions for future reference.
Proposition 6.6 There is a commutative diagram of cohomology groups as follows.

We will consider ![]() $[\! [S]\! ]\otimes [\! [S']\! ]$ as an element in
$[\! [S]\! ]\otimes [\! [S']\! ]$ as an element in ![]() $H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})\otimes H^{2\nu '}(F_{\nu +\nu '},F_{\mathrm {r}}^{\mathrm {fat}})$ in the previous diagram and compute explicitly the image of the cup product
$H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})\otimes H^{2\nu '}(F_{\nu +\nu '},F_{\mathrm {r}}^{\mathrm {fat}})$ in the previous diagram and compute explicitly the image of the cup product ![]() $[\! [S]\! ]\smile [\! [S']\! ]$ in
$[\! [S]\! ]\smile [\! [S']\! ]$ in ![]() $H^{2\nu +2\nu '}(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}) \cong H^{2\nu +2\nu '}(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$.
$H^{2\nu +2\nu '}(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '}) \cong H^{2\nu +2\nu '}(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$.
Proposition 6.7 There is a commutative diagram of cohomology groups as follows.

We will compute the image along the natural map ![]() $\theta$ of
$\theta$ of ![]() $[\! [S]\! ]\smile [\! [S']\! ]$ and identify it with the class
$[\! [S]\! ]\smile [\! [S']\! ]$ and identify it with the class ![]() $[\! [S]\! ]\cdot [\! [S']\! ]\in {\mathcal {A}}({\mathcal {Q}})_{2\nu +2\nu '}$.
$[\! [S]\! ]\cdot [\! [S']\! ]\in {\mathcal {A}}({\mathcal {Q}})_{2\nu +2\nu '}$.
6.3 Proof of Propositions 6.6 and 6.7
Definition 6.8 Recall Definition 5.20. We let ![]() $z_{\mathrm {c,l}}= 2/7+ {\sqrt {-1}}/2$ and
$z_{\mathrm {c,l}}= 2/7+ {\sqrt {-1}}/2$ and ![]() $z_{\mathrm {c,r}}= 5/7+ {\sqrt {-1}}/2$; note that the homothety centred at
$z_{\mathrm {c,r}}= 5/7+ {\sqrt {-1}}/2$; note that the homothety centred at ![]() $z_{\mathrm {c,l}}$ with rescaling factor
$z_{\mathrm {c,l}}$ with rescaling factor ![]() $1/4$ maps
$1/4$ maps ![]() $\mathring {{\mathcal {R}}}$ to the open square
$\mathring {{\mathcal {R}}}$ to the open square ![]() $(1/4,3/8)\times (7/16,9/16)$, i.e.
$(1/4,3/8)\times (7/16,9/16)$, i.e. ![]() $(1/4,3/8)\times (7/16,9/16)= {7z_{\mathrm {c,l}}}/8 + (1/8)\mathring {{\mathcal {R}}}$; similarly
$(1/4,3/8)\times (7/16,9/16)= {7z_{\mathrm {c,l}}}/8 + (1/8)\mathring {{\mathcal {R}}}$; similarly ![]() $(5/8,3/4)\times (7/16,9/16)= {7z_{\mathrm {c,r}}}/8 + (1/8)\mathring {{\mathcal {R}}}$. See Figure 10.
$(5/8,3/4)\times (7/16,9/16)= {7z_{\mathrm {c,r}}}/8 + (1/8)\mathring {{\mathcal {R}}}$. See Figure 10.

Figure 10. The complement of the left (respectively, right) white square is ![]() $\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}}$ (respectively,
$\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}}$ (respectively, ![]() $\partial _{\mathrm {r}}^{\mathrm {fat}}{\mathcal {R}}$), whereas the total grey area is
$\partial _{\mathrm {r}}^{\mathrm {fat}}{\mathcal {R}}$), whereas the total grey area is ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}$; the dotted vertical line splits the total grey area into
$\partial ^{\mathrm {fat}}{\mathcal {R}}$; the dotted vertical line splits the total grey area into ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}^{\mathrm {l}}$ and
$\partial ^{\mathrm {fat}}{\mathcal {R}}^{\mathrm {l}}$ and ![]() $\partial ^{\mathrm {fat}}{\mathcal {R}}^{\mathrm {r}}$.
$\partial ^{\mathrm {fat}}{\mathcal {R}}^{\mathrm {r}}$.
For ![]() $\bullet =\mathrm {l},\mathrm {r}$, we define a subspace
$\bullet =\mathrm {l},\mathrm {r}$, we define a subspace ![]() $\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}}$ of
$\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}}$ of ![]() ${\mathcal {R}}$ by
${\mathcal {R}}$ by ![]() $\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}}:={\mathcal {R}}\setminus ( {7z_{\mathrm {c},\bullet }}/8 + (1/8)\mathring {{\mathcal {R}}})$. The identity of
$\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}}:={\mathcal {R}}\setminus ( {7z_{\mathrm {c},\bullet }}/8 + (1/8)\mathring {{\mathcal {R}}})$. The identity of ![]() $\mathbb {C}$ is a map of nice couples
$\mathbb {C}$ is a map of nice couples ![]() $({\mathcal {R}},\partial {\mathcal {R}})\to ({\mathcal {R}},\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}})$, giving rise to a map
$({\mathcal {R}},\partial {\mathcal {R}})\to ({\mathcal {R}},\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}})$, giving rise to a map ![]() $(\operatorname {Id}_\mathbb {C})_*\colon F_{\nu +\nu '}=F_{\nu +\nu '}\mathbb {B}\to \mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}};{\mathcal {Q}},G)$. Recall Definition 5.9: we define
$(\operatorname {Id}_\mathbb {C})_*\colon F_{\nu +\nu '}=F_{\nu +\nu '}\mathbb {B}\to \mathrm {Hur}({\mathcal {R}},\partial ^{\mathrm {fat}}_{\bullet }{\mathcal {R}};{\mathcal {Q}},G)$. Recall Definition 5.9: we define ![]() $F_{\mathrm {l}}^{\mathrm {fat}}\subset F_{\nu +\nu '}$ as the preimage along
$F_{\mathrm {l}}^{\mathrm {fat}}\subset F_{\nu +\nu '}$ as the preimage along ![]() $(\operatorname {Id}_\mathbb {C})_*$ of
$(\operatorname {Id}_\mathbb {C})_*$ of ![]() $F_{\nu -1}\,\mathrm {Hur}({\mathcal {R}},\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ and, respectively,
$F_{\nu -1}\,\mathrm {Hur}({\mathcal {R}},\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$ and, respectively, ![]() $F_{\mathrm {r}}^{\mathrm {fat}}\subset F_{\nu +\nu '}$ as the preimage along
$F_{\mathrm {r}}^{\mathrm {fat}}\subset F_{\nu +\nu '}$ as the preimage along ![]() $(\operatorname {Id}_\mathbb {C})_*$ of
$(\operatorname {Id}_\mathbb {C})_*$ of ![]() $F_{\nu '-1}\,\mathrm {Hur}({\mathcal {R}},\partial _{\mathrm {r}}^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$.
$F_{\nu '-1}\,\mathrm {Hur}({\mathcal {R}},\partial _{\mathrm {r}}^{\mathrm {fat}}{\mathcal {R}};{\mathcal {Q}},G)$.
Roughly speaking, a configuration ![]() $\mathfrak {c}=(P,\psi,\varphi ) \in F_{\nu +\nu '}$ lies in
$\mathfrak {c}=(P,\psi,\varphi ) \in F_{\nu +\nu '}$ lies in ![]() $F_{\mathrm {l}}^{\mathrm {fat}}$ if the sum of the norms of the values of the monodromy
$F_{\mathrm {l}}^{\mathrm {fat}}$ if the sum of the norms of the values of the monodromy ![]() $\psi$ around points of
$\psi$ around points of ![]() $P$ lying in the open square
$P$ lying in the open square ![]() $(1/4,3/8)\times (7/16,9/16)$ does not exceed
$(1/4,3/8)\times (7/16,9/16)$ does not exceed ![]() $\nu -1$; similarly for
$\nu -1$; similarly for ![]() $F_{\mathrm {r}}^{\mathrm {fat}}$, referring to the open square
$F_{\mathrm {r}}^{\mathrm {fat}}$, referring to the open square ![]() $(5/8,3/4)\times (7/16,9/16)$ and replacing the threshold
$(5/8,3/4)\times (7/16,9/16)$ and replacing the threshold ![]() $\nu -1$ with
$\nu -1$ with ![]() $\nu '-1$. To keep the notation simple, we avoid adding the indices
$\nu '-1$. To keep the notation simple, we avoid adding the indices ![]() $\nu$ and
$\nu$ and ![]() $\nu '$ to
$\nu '$ to ![]() $F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\mathrm {r}}^{\mathrm {fat}}$. Note that
$F_{\mathrm {r}}^{\mathrm {fat}}$. Note that ![]() $F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$.
$F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$.
Lemma 6.9 The inclusions ![]() $F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and
$F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$ and ![]() $F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$ are homotopy equivalences.
$F_{\nu '-1}\subset F_{\mathrm {r}}^{\mathrm {fat}}$ are homotopy equivalences.
Proof. We focus on the inclusion ![]() $F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$, the other one being analogous. Recall Definition 5.6 and the proof of Lemma 6.2. For
$F_{\nu -1}\subset F_{\mathrm {l}}^{\mathrm {fat}}$, the other one being analogous. Recall Definition 5.6 and the proof of Lemma 6.2. For ![]() $\mathfrak {c} \in F_{\nu +\nu '}$ we denote by
$\mathfrak {c} \in F_{\nu +\nu '}$ we denote by ![]() $\mathfrak {W}_{\mathrm {l},\nu }(\mathfrak {c})$ the supremum in
$\mathfrak {W}_{\mathrm {l},\nu }(\mathfrak {c})$ the supremum in ![]() $[1/8,1]$ of all
$[1/8,1]$ of all ![]() $1/8<\varepsilon <1$ for which
$1/8<\varepsilon <1$ for which ![]() $({\mathcal {H}}^{\mathbb {B}}_{z_{\mathrm {c,l}}})_*(\mathfrak {c},1/\varepsilon )\in F_{\nu -1}\mathbb {B}$. We define a homotopy
$({\mathcal {H}}^{\mathbb {B}}_{z_{\mathrm {c,l}}})_*(\mathfrak {c},1/\varepsilon )\in F_{\nu -1}\mathbb {B}$. We define a homotopy
The homotopy ![]() $H^{\mathbb {B}}_{\mathrm {l},\nu }$ restricts to a deformation retraction of
$H^{\mathbb {B}}_{\mathrm {l},\nu }$ restricts to a deformation retraction of ![]() $F_{\mathrm {l}}^{\mathrm {fat}}$ onto
$F_{\mathrm {l}}^{\mathrm {fat}}$ onto ![]() $F_{\nu -1}$.
$F_{\nu -1}$.
Lemma 6.9 implies the top left isomorphism in Proposition 6.6.
Lemma 6.10 The space ![]() $F^{\mathrm {fat}}_{\nu +\nu '-1}$ is contained in the union
$F^{\mathrm {fat}}_{\nu +\nu '-1}$ is contained in the union ![]() $F_{\mathrm {l}}^{\mathrm {fat}}\cup F_{\mathrm {r}}^{\mathrm {fat}}$.
$F_{\mathrm {l}}^{\mathrm {fat}}\cup F_{\mathrm {r}}^{\mathrm {fat}}$.
Proof. Let ![]() $\mathfrak {c}\in F^{\mathrm {fat}}_{\nu +\nu '-1}$, use Notation 2.2 and for
$\mathfrak {c}\in F^{\mathrm {fat}}_{\nu +\nu '-1}$, use Notation 2.2 and for ![]() $\bullet =\mathrm {l,r}$ denote by
$\bullet =\mathrm {l,r}$ denote by ![]() $P_\bullet \subset P$ the intersection of
$P_\bullet \subset P$ the intersection of ![]() $P$ with the open square
$P$ with the open square ![]() $( {7z_{\mathrm {c},\bullet }}/8+ (1/8)\mathring {{\mathcal {R}}})$. Without loss of generality, we may assume that there are indices
$( {7z_{\mathrm {c},\bullet }}/8+ (1/8)\mathring {{\mathcal {R}}})$. Without loss of generality, we may assume that there are indices ![]() $0\le l'\le l''\le l$ such that
$0\le l'\le l''\le l$ such that ![]() $P_\mathrm {l}=\{z_1,\ldots,z_{l'}\}$ and
$P_\mathrm {l}=\{z_1,\ldots,z_{l'}\}$ and ![]() $P_{\mathrm {r}}=\{z_{l'+1},\ldots,z_{l''}\}$. Let
$P_{\mathrm {r}}=\{z_{l'+1},\ldots,z_{l''}\}$. Let ![]() $f_1,\ldots,f_k$ be an admissible generating set. Then the hypothesis
$f_1,\ldots,f_k$ be an admissible generating set. Then the hypothesis ![]() $\mathfrak {c}\in F^{\mathrm {fat}}_{\nu +\nu '-1}$, together with the fact that
$\mathfrak {c}\in F^{\mathrm {fat}}_{\nu +\nu '-1}$, together with the fact that ![]() $( {7z_{\mathrm {c,l}}}/8+ (1/8)\mathring {{\mathcal {R}}})$ and
$( {7z_{\mathrm {c,l}}}/8+ (1/8)\mathring {{\mathcal {R}}})$ and ![]() $( {7z_{\mathrm {c,r}}}/8+ (1/8)\mathring {{\mathcal {R}}})$ are disjoint and contained in
$( {7z_{\mathrm {c,r}}}/8+ (1/8)\mathring {{\mathcal {R}}})$ are disjoint and contained in ![]() $( {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}})$, implies the inequality
$( {z_{\mathrm {c}}}/2+ (1/2)\mathring {{\mathcal {R}}})$, implies the inequality
 \begin{align*} \sum_{i=1}^{l'}N(\psi(f_i))+\sum_{i=l'+1}^{l''} N(\psi(f_i))\le \nu+\nu'-1. \end{align*}
\begin{align*} \sum_{i=1}^{l'}N(\psi(f_i))+\sum_{i=l'+1}^{l''} N(\psi(f_i))\le \nu+\nu'-1. \end{align*}
It follows that at least one of the following two inequalities holds:
 \[ \sum_{i=1}^{l'}N(\psi(f_i))\le \nu-1,\quad\sum_{i=l'+1}^{l''} N(\psi(f_i))\le \nu'-1; \]
\[ \sum_{i=1}^{l'}N(\psi(f_i))\le \nu-1,\quad\sum_{i=l'+1}^{l''} N(\psi(f_i))\le \nu'-1; \]
the first inequality implies ![]() $\mathfrak {c}\in F_{\mathrm {l}}^{\mathrm {fat}}$, the second implies
$\mathfrak {c}\in F_{\mathrm {l}}^{\mathrm {fat}}$, the second implies ![]() $\mathfrak {c}\in F_{\mathrm {r}}^{\mathrm {fat}}$.
$\mathfrak {c}\in F_{\mathrm {r}}^{\mathrm {fat}}$.
Notation 6.11 We introduce several subspaces of ![]() ${\mathcal {R}}$, see Figure 10:
${\mathcal {R}}$, see Figure 10:
 \begin{gather*}
{\mathcal{R}}^{\mathrm{l}}=[0,1/2]\times[0,1],\quad
{\mathcal{R}}^{\mathrm{r}}=[1/2,1]\times[0,1],\\
\mathring{{\mathcal{R}}}^{\mathrm{l}}=(0,1/2)\times(0,1),\quad
{\mathcal{R}}^{\mathrm{r}}=(1/2,1)\times(0,1),\\
\partial{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\setminus\mathring{{\mathcal{R}}}^{\mathrm{l}},\quad
\partial{\mathcal{R}}^{\mathrm{r}}={\mathcal{R}}^{\mathrm{r}}\setminus\mathring{{\mathcal{R}}}^{\mathrm{r}},\\
\partial^{\mathrm{fat}}{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\quad
\partial^{\mathrm{fat}}{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\\
\partial^{\mathrm{fat}}\mathring{{\mathcal{R}}}^{\mathrm{l}}=\mathring{{\mathcal{R}}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\quad
\partial^{\mathrm{fat}}\mathring{{\mathcal{R}}}^{\mathrm{l}}=\mathring{{\mathcal{R}}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg).
\end{gather*}
\begin{gather*}
{\mathcal{R}}^{\mathrm{l}}=[0,1/2]\times[0,1],\quad
{\mathcal{R}}^{\mathrm{r}}=[1/2,1]\times[0,1],\\
\mathring{{\mathcal{R}}}^{\mathrm{l}}=(0,1/2)\times(0,1),\quad
{\mathcal{R}}^{\mathrm{r}}=(1/2,1)\times(0,1),\\
\partial{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\setminus\mathring{{\mathcal{R}}}^{\mathrm{l}},\quad
\partial{\mathcal{R}}^{\mathrm{r}}={\mathcal{R}}^{\mathrm{r}}\setminus\mathring{{\mathcal{R}}}^{\mathrm{r}},\\
\partial^{\mathrm{fat}}{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\quad
\partial^{\mathrm{fat}}{\mathcal{R}}^{\mathrm{l}}={\mathcal{R}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\\
\partial^{\mathrm{fat}}\mathring{{\mathcal{R}}}^{\mathrm{l}}=\mathring{{\mathcal{R}}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg),\quad
\partial^{\mathrm{fat}}\mathring{{\mathcal{R}}}^{\mathrm{l}}=\mathring{{\mathcal{R}}}^{\mathrm{l}}\biggl\backslash
\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac
18\mathring{{\mathcal{R}}}\bigg).
\end{gather*}
Definition 6.12 Recall Definition 5.9. The identity of ![]() $\mathbb {C}$ induces maps of nice couples
$\mathbb {C}$ induces maps of nice couples ![]() $({\mathcal {R}};\partial )\to ({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {l}})$ and
$({\mathcal {R}};\partial )\to ({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {l}})$ and ![]() $({\mathcal {R}};\partial )\to ({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {r}})$. We define
$({\mathcal {R}};\partial )\to ({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {r}})$. We define ![]() $F_{\mathrm {lr}}\subset F_{\nu +\nu '}$ as the subspace of configurations
$F_{\mathrm {lr}}\subset F_{\nu +\nu '}$ as the subspace of configurations ![]() $\mathfrak {c}$ such that at least one of the following conditions holds:
$\mathfrak {c}$ such that at least one of the following conditions holds:
•
 $(\operatorname {Id}_\mathbb {C})_*(\mathfrak {c})\in \mathrm {Hur}({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+,G)$ has norm
$(\operatorname {Id}_\mathbb {C})_*(\mathfrak {c})\in \mathrm {Hur}({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+,G)$ has norm  $\leq \nu -1$;
$\leq \nu -1$;•
 $(\operatorname {Id}_\mathbb {C})_*(\mathfrak {c})\in \mathrm {Hur}({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+,G)$ has norm
$(\operatorname {Id}_\mathbb {C})_*(\mathfrak {c})\in \mathrm {Hur}({\mathcal {R}},{\mathcal {R}}\setminus \mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+,G)$ has norm  $\leq \nu '-1$.
$\leq \nu '-1$.
Roughly speaking, the complement ![]() $\mathfrak {F}_{\nu,\nu '}$ of
$\mathfrak {F}_{\nu,\nu '}$ of ![]() $F_{\mathrm {lr}}$ in
$F_{\mathrm {lr}}$ in ![]() $F_{\nu +\nu '}$ contains those configurations
$F_{\nu +\nu '}$ contains those configurations ![]() $\mathfrak {c}=(P,\psi,\varphi )$ such that
$\mathfrak {c}=(P,\psi,\varphi )$ such that ![]() $P\subset \mathring {{\mathcal {R}}}\setminus \{1/2\}\times (0,1)$, the sum of the norms of the values of
$P\subset \mathring {{\mathcal {R}}}\setminus \{1/2\}\times (0,1)$, the sum of the norms of the values of ![]() $\psi$ around points of
$\psi$ around points of ![]() $P\cap \mathring {{\mathcal {R}}}^{\mathrm {l}}$ is equal to
$P\cap \mathring {{\mathcal {R}}}^{\mathrm {l}}$ is equal to ![]() $\nu$ and the sum of the norms of the values of
$\nu$ and the sum of the norms of the values of ![]() $\psi$ around points of
$\psi$ around points of ![]() $P\cap \mathring {{\mathcal {R}}}^{\mathrm {r}}$ is equal to
$P\cap \mathring {{\mathcal {R}}}^{\mathrm {r}}$ is equal to ![]() $\nu '$.
$\nu '$.
Lemma 6.13 The space ![]() $F_{\mathrm {lr}}$ is contained in the interior of
$F_{\mathrm {lr}}$ is contained in the interior of ![]() $F_{\mathrm {lr}}^{\mathrm {fat}}$, considered as subspace of
$F_{\mathrm {lr}}^{\mathrm {fat}}$, considered as subspace of ![]() $F_{\nu +\nu '}$.
$F_{\nu +\nu '}$.
Proof. Given ![]() $\mathfrak {c}=(P,\psi,\varphi )\in F_{\mathrm {lr}}$, it suffices to note that for any adapted covering
$\mathfrak {c}=(P,\psi,\varphi )\in F_{\mathrm {lr}}$, it suffices to note that for any adapted covering ![]() $\underline {U}$ of
$\underline {U}$ of ![]() $P$ with the sets
$P$ with the sets ![]() $U_i$ of diameter at most
$U_i$ of diameter at most ![]() $1/8$, the restricted normal neighbourhood
$1/8$, the restricted normal neighbourhood ![]() $\mathfrak {U}(\mathfrak {c};\underline {U})\cap F_{\nu +\nu '}$ is contained in
$\mathfrak {U}(\mathfrak {c};\underline {U})\cap F_{\nu +\nu '}$ is contained in ![]() $F_{\mathrm {lr}}^{\mathrm {fat}}$.
$F_{\mathrm {lr}}^{\mathrm {fat}}$.
Lemma 6.13 implies, together with the inclusion ![]() $F_{\nu +\nu '-1}\subset F_{\mathrm {lr}}$, that the couple
$F_{\nu +\nu '-1}\subset F_{\mathrm {lr}}$, that the couple ![]() $(F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ satisfies excision with respect to the subspaces
$(F_{\nu +\nu '},F_{\mathrm {lr}}^{\mathrm {fat}})$ satisfies excision with respect to the subspaces ![]() $F_{\nu +\nu '-1}$ and
$F_{\nu +\nu '-1}$ and ![]() $F_{\mathrm {lr}}$, i.e. the two bottom right vertical isomorphisms in Proposition 6.6 hold. This concludes the proof of Proposition 6.6.
$F_{\mathrm {lr}}$, i.e. the two bottom right vertical isomorphisms in Proposition 6.6 hold. This concludes the proof of Proposition 6.6.
In the same way, the two bottom vertical isomorphisms of Proposition 6.7 follow from excision of the subspace ![]() $F_{\nu +\nu '-1}$, whereas the top diagonal isomorphism follows from the computation of
$F_{\nu +\nu '-1}$, whereas the top diagonal isomorphism follows from the computation of ![]() $H^*(\mathbb {B};\mathbb {Q})$ using the Leray spectral sequence. This concludes also the proof of Proposition 6.7.
$H^*(\mathbb {B};\mathbb {Q})$ using the Leray spectral sequence. This concludes also the proof of Proposition 6.7.
6.4 Conclusion of the proof of Theorem 6.1
As remarked already, ![]() $\mathfrak {p}_{\nu +\nu '}$ exhibits all subspaces of
$\mathfrak {p}_{\nu +\nu '}$ exhibits all subspaces of ![]() $\mathfrak {F}_{\nu +\nu '}$ occurring in the bottom rows of Propositions 6.6 and 6.7 as bundles over
$\mathfrak {F}_{\nu +\nu '}$ occurring in the bottom rows of Propositions 6.6 and 6.7 as bundles over ![]() ${\mathcal {B}} G$: the proof of Proposition 5.26 provides local trivialisations also for these bundles. Our next aim is to compute the cohomology groups of these bundles and of the couples of bundles they form.
${\mathcal {B}} G$: the proof of Proposition 5.26 provides local trivialisations also for these bundles. Our next aim is to compute the cohomology groups of these bundles and of the couples of bundles they form.
Definition 6.14 For ![]() $\nu,\nu '\ge 0$ we denote by
$\nu,\nu '\ge 0$ we denote by ![]() ${\mathcal {Q}}_{\nu,\nu '}\subset {\mathcal {Q}}_{\nu }\times {\mathcal {Q}}_{\nu '}$ the subset of couples
${\mathcal {Q}}_{\nu,\nu '}\subset {\mathcal {Q}}_{\nu }\times {\mathcal {Q}}_{\nu '}$ the subset of couples ![]() $(a,b)$ for which the product
$(a,b)$ for which the product ![]() $ab$ is defined in
$ab$ is defined in ![]() ${\mathcal {Q}}$. We set
${\mathcal {Q}}$. We set
We regard ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ as a subspace of
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ as a subspace of ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ by regarding each product
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ by regarding each product ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a\times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b$ as a subspace of
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a\times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b$ as a subspace of ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{ab}$ under the inclusion given by
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{ab}$ under the inclusion given by

The generic fibre of the bundle ![]() $\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is homeomorphic to the space
$\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is homeomorphic to the space ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$. To see this, note that the same argument of the proof of Proposition 5.26 identifies the fibre of
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$. To see this, note that the same argument of the proof of Proposition 5.26 identifies the fibre of ![]() $\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ with the subspace of
$\mathfrak {p}_{\nu +\nu '}\colon \mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ with the subspace of ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}}\cup \mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu +\nu '}$ containing configurations
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}}\cup \mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu +\nu '}$ containing configurations ![]() $\mathfrak {c}$ with the following properties:
$\mathfrak {c}$ with the following properties:
•
 $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}$ sends
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}$ sends  $\mathfrak {c}$ to a configuration in
$\mathfrak {c}$ to a configuration in  $\mathrm {Hur}^{\mathbb {S}_{0,1/2}}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)$ with total monodromy in
$\mathrm {Hur}^{\mathbb {S}_{0,1/2}}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)$ with total monodromy in  ${\mathcal {Q}}_\nu$;
${\mathcal {Q}}_\nu$;•
 $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}$ sends
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}$ sends  $\mathfrak {c}$ to a configuration in
$\mathfrak {c}$ to a configuration in  $\mathrm {Hur}^{\mathbb {S}_{1/2,1}}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)$ with total monodromy in
$\mathrm {Hur}^{\mathbb {S}_{1/2,1}}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)$ with total monodromy in  ${\mathcal {Q}}_{\nu '}$;
${\mathcal {Q}}_{\nu '}$;• the product of the elements
 $\omega (\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}(\mathfrak {c}))$ and
$\omega (\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}(\mathfrak {c}))$ and  $\omega (\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}(\mathfrak {c}))$ is defined in
$\omega (\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}(\mathfrak {c}))$ is defined in  ${\mathcal {Q}}$.
${\mathcal {Q}}$.
We can further identify the fibres of the following restrictions of ![]() $\mathfrak {p}_{\nu +\nu '}$:
$\mathfrak {p}_{\nu +\nu '}$:
• the fibre of
 $\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with
$\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with  $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$, as already mentioned;
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$, as already mentioned;• the fibre of
 $\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the intersection of
$\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the intersection of  $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ with the product
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ with the product  $\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_\nu \times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu '}$, i.e. with the space
where
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_\nu \times \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu '}$, i.e. with the space
where \[ \partial_{\mathrm{l}}^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_{\nu,\nu'}:=\coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}} \partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a\times\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b, \]
\[ \partial_{\mathrm{l}}^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_{\nu,\nu'}:=\coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}} \partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a\times\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b, \]
 $\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}( {7z_{\mathrm {c,l}}}/8+ (1/8)\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$;
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a:=\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a\setminus \mathrm {Hur}( {7z_{\mathrm {c,l}}}/8+ (1/8)\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a$;• the fibre of
 $\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the intersection of
$\partial _{\mathrm {r}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the intersection of  $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ with the product
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$ with the product  $\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_\nu \times \partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu '}$, i.e. with the space
where
$\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_\nu \times \partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_{\nu '}$, i.e. with the space
where \[ \partial_{\mathrm{r}}^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_{\nu,\nu'}:=\coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a\times\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b, \]
\[ \partial_{\mathrm{r}}^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_{\nu,\nu'}:=\coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a\times\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b, \]
 $\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b:=\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b\setminus \mathrm {Hur}( {7z_{\mathrm {c,r}}}/8+ (1/8)\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b$;
$\partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b:=\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b\setminus \mathrm {Hur}( {7z_{\mathrm {c,r}}}/8+ (1/8)\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_b$;• the fibre of
 $\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the union
$\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '}\to {\mathcal {B}} G$ is identified with the union  $\partial _{\mathrm {lr}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}:=\partial _{\mathrm {l}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}; {\mathcal {Q}}_+)_{\nu,\nu '}\cup \partial _{\mathrm {r}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$.
$\partial _{\mathrm {lr}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}:=\partial _{\mathrm {l}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}}; {\mathcal {Q}}_+)_{\nu,\nu '}\cup \partial _{\mathrm {r}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu,\nu '}$.
By using functoriality with respect to suitable semialgebraic homeomorphisms of ![]() $\mathbb {C}$, we can identify the couples of spaces
$\mathbb {C}$, we can identify the couples of spaces
 \begin{gather*} (\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a) \cong (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a);\\ (\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b) \cong (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b). \end{gather*}
\begin{gather*} (\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{l}};{\mathcal{Q}}_+)_a) \cong (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_a);\\ (\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}}^{\mathrm{r}};{\mathcal{Q}}_+)_b) \cong (\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b,\partial^{\mathrm{fat}}\,\mathrm{Hur}(\mathring{{\mathcal{R}}};{\mathcal{Q}}_+)_b). \end{gather*}
Notation 6.15 For ![]() $d\ge 0$ we denote by
$d\ge 0$ we denote by ![]() $\mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d]$ the graded
$\mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d]$ the graded ![]() $\mathbb {Q}$-vector space concentrated in degree
$\mathbb {Q}$-vector space concentrated in degree ![]() $d$, with basis the set
$d$, with basis the set ![]() ${\mathcal {Q}}_{\nu,\nu '}$.
${\mathcal {Q}}_{\nu,\nu '}$.
For ![]() $d,d'\ge 0$ we denote by
$d,d'\ge 0$ we denote by ![]() $\mu _{\nu,\nu '}\colon \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d]\otimes \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d']\to \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d+d']$ the pairing given by
$\mu _{\nu,\nu '}\colon \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d]\otimes \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d']\to \mathbb {Q}\langle {\mathcal {Q}}_{\nu,\nu '}\rangle [d+d']$ the pairing given by ![]() $(a,b)\otimes (a,b)\mapsto (a,b)$ for
$(a,b)\otimes (a,b)\mapsto (a,b)$ for ![]() $(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$ and
$(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$ and ![]() $(a,b)\otimes (a',b')\mapsto 0$ for
$(a,b)\otimes (a',b')\mapsto 0$ for ![]() $(a,b)\neq (a',b')\in {\mathcal {Q}}_{\nu,\nu '}$.
$(a,b)\neq (a',b')\in {\mathcal {Q}}_{\nu,\nu '}$.
Consider the bottom row of Proposition 6.6: all groups involved are cohomology groups of couples of bundles over ![]() ${\mathcal {B}} G$. The cup product on fibres reads as follows, where we simplify the notation by writing
${\mathcal {B}} G$. The cup product on fibres reads as follows, where we simplify the notation by writing ![]() $\mathrm {Hur}$ for
$\mathrm {Hur}$ for ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$:
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$:

Notation 6.16 For ![]() $a\in {\mathcal {Q}}_\nu$ we denote by
$a\in {\mathcal {Q}}_\nu$ we denote by ![]() $\mathfrak {c}_{\mathrm {l},a}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a$ the unique configuration supported on
$\mathfrak {c}_{\mathrm {l},a}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a$ the unique configuration supported on ![]() $\{z_{\mathrm {c,l}}\}$; similarly, for
$\{z_{\mathrm {c,l}}\}$; similarly, for ![]() $b\in {\mathcal {Q}}_{\nu '}$ we denote by
$b\in {\mathcal {Q}}_{\nu '}$ we denote by ![]() $\mathfrak {c}_{\mathrm {r},b}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b$ the unique configuration supported on
$\mathfrak {c}_{\mathrm {r},b}\in \mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b$ the unique configuration supported on ![]() $\{z_{\mathrm {c,r}}\}$.
$\{z_{\mathrm {c,r}}\}$.
The three cohomology groups in the top row of the previous diagram have bases in bijection with the set ![]() ${\mathcal {Q}}_{\nu,\nu '}$. For instance,
${\mathcal {Q}}_{\nu,\nu '}$. For instance, ![]() $H^{2\nu }(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}))$ has a basis given by the cohomology duals of the homology classes
$H^{2\nu }(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}))$ has a basis given by the cohomology duals of the homology classes ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}]$. Here
$[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}]$. Here ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\in H_{2\nu }(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}};\mathbb {Q})$ is the fundamental homology class and
$[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\in H_{2\nu }(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}};\mathbb {Q})$ is the fundamental homology class and ![]() $[\mathfrak {c}_{\mathrm {r},b}]\in H_0(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b;\mathbb {Q})$ denotes the ‘ground’ homology class.
$[\mathfrak {c}_{\mathrm {r},b}]\in H_0(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b;\mathbb {Q})$ denotes the ‘ground’ homology class.
A similar description gives a basis for ![]() $H^{2\nu '}(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {r}}^{\mathrm {fat}})$ in bijection with
$H^{2\nu '}(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {r}}^{\mathrm {fat}})$ in bijection with ![]() ${\mathcal {Q}}_{\nu,\nu '}$, whereas for
${\mathcal {Q}}_{\nu,\nu '}$, whereas for ![]() $H^{2\nu +2\nu '}(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}})$ we consider the cohomology duals of the homology classes
$H^{2\nu +2\nu '}(\mathrm {Hur}_{\nu,\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}})$ we consider the cohomology duals of the homology classes ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}]$. Taking
$[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}]$. Taking ![]() $G$-invariants, we obtain an explicit computation of the bottom row of Proposition 6.6 as follows:
$G$-invariants, we obtain an explicit computation of the bottom row of Proposition 6.6 as follows:

Lemma 6.17 Let ![]() $S\subset {\mathcal {Q}}_\nu$ be a conjugacy class of
$S\subset {\mathcal {Q}}_\nu$ be a conjugacy class of ![]() ${\mathcal {Q}}$ and consider
${\mathcal {Q}}$ and consider ![]() $[\! [S]\! ]$ as a cohomology class in the group
$[\! [S]\! ]$ as a cohomology class in the group ![]() $\in H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})\cong H^{2\nu }(F_{\nu +\nu '},F_{\nu -1})\cong H^{2\nu }(F_{\nu +\nu '})$; the restriction of
$\in H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})\cong H^{2\nu }(F_{\nu +\nu '},F_{\nu -1})\cong H^{2\nu }(F_{\nu +\nu '})$; the restriction of ![]() $[\! [S]\! ]$ to
$[\! [S]\! ]$ to ![]() $H^{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$ is the element
$H^{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$ is the element
Similarly, for a conjugacy class ![]() $S'\subset {\mathcal {Q}}_{\nu '}$, the class
$S'\subset {\mathcal {Q}}_{\nu '}$, the class ![]() $[\! [S']\! ]\in H^{2\nu '}(F_{\nu +\nu '},F_{\mathrm {r}}^{\mathrm {fat}})$ restricts to
$[\! [S']\! ]\in H^{2\nu '}(F_{\nu +\nu '},F_{\mathrm {r}}^{\mathrm {fat}})$ restricts to
Proof. We focus on the first part of the statement, the second being analogous. Fix ![]() $(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$; the couple of spaces
$(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$; the couple of spaces ![]() $(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})\times \mathfrak {c}_{\mathrm {r},b}$ can be embedded into the couple of bundles
$(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})\times \mathfrak {c}_{\mathrm {r},b}$ can be embedded into the couple of bundles ![]() $(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$ as part of the fibre over the basepoint of
$(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '})$ as part of the fibre over the basepoint of ![]() ${\mathcal {B}} G$. We consider the homology class
${\mathcal {B}} G$. We consider the homology class
such classes generate the group ![]() $H_{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '};\mathbb {Q})$, so in order to identify the restriction of
$H_{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '};\mathbb {Q})$, so in order to identify the restriction of ![]() $[\! [S]\! ]\in H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}};\mathbb {Q})$ to
$[\! [S]\! ]\in H^{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}};\mathbb {Q})$ to ![]() $H^{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '};\mathbb {Q})$, it suffices to compute the Kronecker pairing of the restricted
$H^{2\nu }(\mathfrak {F}_{\nu,\nu '},\partial _{\mathrm {l}}^{\mathrm {fat}}\mathfrak {F}_{\nu,\nu '};\mathbb {Q})$, it suffices to compute the Kronecker pairing of the restricted ![]() $[\! [S]\! ]$ with all homology classes of the form
$[\! [S]\! ]$ with all homology classes of the form ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}]$. Let
$[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}]$. Let ![]() $\mathfrak {j}$ be the composite
$\mathfrak {j}$ be the composite
then we can also consider the homology class ![]() $\mathfrak {j}_*([\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}])$ in
$\mathfrak {j}_*([\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}])$ in ![]() $H_{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}};\mathbb {Q})$ and compute its Kronecker pairing with
$H_{2\nu }(F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}};\mathbb {Q})$ and compute its Kronecker pairing with ![]() $[\! [S]\! ]$.
$[\! [S]\! ]$.
Fix a homotopy ![]() ${\mathcal {H}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ with the following properties:
${\mathcal {H}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ with the following properties:
• for all
 $0\le s\le 1$,
$0\le s\le 1$,  ${\mathcal {H}}(-,s)$ is a semialgebraic self-map of
${\mathcal {H}}(-,s)$ is a semialgebraic self-map of  $\mathbb {C}$ fixing
$\mathbb {C}$ fixing  $\mathbb {C}\setminus \mathring {{\mathcal {R}}}$ pointwise and sending
$\mathbb {C}\setminus \mathring {{\mathcal {R}}}$ pointwise and sending  $\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}}$ into itself;
$\partial _{\mathrm {l}}^{\mathrm {fat}}{\mathcal {R}}$ into itself;•
 ${\mathcal {H}}(-,0)$ is the identity of
${\mathcal {H}}(-,0)$ is the identity of  $\mathbb {C}$;
$\mathbb {C}$;•
 ${\mathcal {H}}(-,1)$ restricts to a homeomorphism of couples
${\mathcal {H}}(-,1)$ restricts to a homeomorphism of couples  $(\mathring {{\mathcal {R}}}^{\mathrm {l}},\partial ^{\mathrm {fat}}\mathring {{\mathcal {R}}}^{\mathrm {l}})\overset {\cong }{\to }(\mathring {{\mathcal {R}}},\partial ^{\mathrm {fat}}\mathring {{\mathcal {R}}})$ and it sends
$(\mathring {{\mathcal {R}}}^{\mathrm {l}},\partial ^{\mathrm {fat}}\mathring {{\mathcal {R}}}^{\mathrm {l}})\overset {\cong }{\to }(\mathring {{\mathcal {R}}},\partial ^{\mathrm {fat}}\mathring {{\mathcal {R}}})$ and it sends  $z_{\mathrm {c,r}}\mapsto z_{\diamond }^{\mathrm {r}}$.
$z_{\mathrm {c,r}}\mapsto z_{\diamond }^{\mathrm {r}}$.
Then ![]() ${\mathcal {H}}$ induces a homotopy of maps of couples
${\mathcal {H}}$ induces a homotopy of maps of couples
and composing this homotopy with ![]() $\mathfrak {j}$ we obtain a homotopy of maps of couples
$\mathfrak {j}$ we obtain a homotopy of maps of couples
Since ![]() $H(-,0)=\mathfrak {j}$, we have
$H(-,0)=\mathfrak {j}$, we have
so we can focus on the Kronecker pairing of the latter homology class with ![]() $[\! [S]\! ]$.
$[\! [S]\! ]$.
Now note that, by construction, ![]() $H(-,1)$ can be considered as a map of couples
$H(-,1)$ can be considered as a map of couples
more precisely ![]() $H(-,1)$ restricts to a homeomorphism of
$H(-,1)$ restricts to a homeomorphism of ![]() $(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})\times \{\mathfrak {c}_{\mathrm {r},b}\}$ onto
$(\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})\times \{\mathfrak {c}_{\mathrm {r},b}\}$ onto ![]() $(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})$, where the latter couple is considered as part of the fibre of
$(\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}})$, where the latter couple is considered as part of the fibre of ![]() $\mathfrak {p}_\nu \colon (\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )\to {\mathcal {B}} G$ over the unique configuration
$\mathfrak {p}_\nu \colon (\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )\to {\mathcal {B}} G$ over the unique configuration ![]() $\mathfrak {c}_{\mathrm {r},\mathfrak {e}(b)}=(P,\psi )$ satisfying the following properties:
$\mathfrak {c}_{\mathrm {r},\mathfrak {e}(b)}=(P,\psi )$ satisfying the following properties:
•
 $\mathfrak {c}_{\mathrm {r},\mathfrak {e}(b)}$ is supported on the set
$\mathfrak {c}_{\mathrm {r},\mathfrak {e}(b)}$ is supported on the set  $P=\{0,z_{\diamond }^{\mathrm {r}}\}$;
$P=\{0,z_{\diamond }^{\mathrm {r}}\}$;• if
 $\gamma$ is a simple loop in
$\gamma$ is a simple loop in  $\mathbb {S}_{0,\infty }$ spinning clockwise around
$\mathbb {S}_{0,\infty }$ spinning clockwise around  $z_{\diamond }^{\mathrm {r}}$, then
$z_{\diamond }^{\mathrm {r}}$, then  $\psi ([\gamma ])=\mathfrak {e}(b)\in G$.
$\psi ([\gamma ])=\mathfrak {e}(b)\in G$.
It follows that ![]() $H(-,1)_*([\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}])$ is the image of the homology class
$H(-,1)_*([\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathfrak {c}_{\mathrm {r},b}])$ is the image of the homology class ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\in H_{2\nu }(\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )$ under the inclusion
$[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\in H_{2\nu }(\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )$ under the inclusion ![]() $(\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )\subset (F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})$; the Kronecker pairing of the latter class with
$(\mathfrak {F}_\nu,\partial ^{\mathrm {fat}}\mathfrak {F}_\nu )\subset (F_{\nu +\nu '},F_{\mathrm {l}}^{\mathrm {fat}})$; the Kronecker pairing of the latter class with ![]() $[\! [S]\! ]$ is 1 if and only if
$[\! [S]\! ]$ is 1 if and only if ![]() $a$ belongs to
$a$ belongs to ![]() $S$.
$S$.
Lemma 6.17 implies that for ![]() $S\subset {\mathcal {Q}}_\nu$ and
$S\subset {\mathcal {Q}}_\nu$ and ![]() $S'\subset {\mathcal {Q}}_{\nu '}$, the restriction of the cup product
$S'\subset {\mathcal {Q}}_{\nu '}$, the restriction of the cup product ![]() $[\! [S]\! ]\smile [\! [S']\! ]$ to the cohomology group in the bottom right corner of Proposition 6.6, can be identified with the
$[\! [S]\! ]\smile [\! [S']\! ]$ to the cohomology group in the bottom right corner of Proposition 6.6, can be identified with the ![]() $G$-invariant element
$G$-invariant element
The following lemma concludes the proof of Theorem 6.1.
Lemma 6.18 There is a commutative diagram

Here the vertical maps are the canonical isomorphisms, given by the bases of the top homology groups of elements of the form ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}]$, for
$[\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {l}};{\mathcal {Q}}_+)_a,\partial ^{\mathrm {fat}}]\otimes [\mathrm {Hur}(\mathring {{\mathcal {R}}}^{\mathrm {r}};{\mathcal {Q}}_+)_b,\partial ^{\mathrm {fat}}]$, for ![]() $(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$ and, respectively, of the form
$(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$ and, respectively, of the form ![]() $[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_c,\partial ^{\mathrm {fat}}]$, for
$[\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_c,\partial ^{\mathrm {fat}}]$, for ![]() $c\in {\mathcal {Q}}_{\nu +\nu '}$. Moreover,
$c\in {\mathcal {Q}}_{\nu +\nu '}$. Moreover, ![]() $[\! [-]\! ]\cdot [\! [-]\! ]$ denotes the map
$[\! [-]\! ]\cdot [\! [-]\! ]$ denotes the map ![]() $(a,b)\mapsto [\! [a]\! ]\cdot [\! [b]\! ]$. Passing to
$(a,b)\mapsto [\! [a]\! ]\cdot [\! [b]\! ]$. Passing to ![]() $G$-invariants, we obtain the following commutative diagram:
$G$-invariants, we obtain the following commutative diagram:

Proof. We first argue that commutativity of the first diagram implies commutativity of the second. The Serre spectral sequences computing the cohomology of the couples of bundles ![]() $(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})$ and
$(\mathfrak {F}_{\nu +\nu '},\partial _{\mathrm {lr}}^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})$ and ![]() $(\mathfrak {F}_{\nu +\nu '},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})$ have both a second page concentrated in the single entry in position
$(\mathfrak {F}_{\nu +\nu '},\partial ^{\mathrm {fat}}\mathfrak {F}_{\nu +\nu '})$ have both a second page concentrated in the single entry in position ![]() $(0,2\nu +\nu ')$, with value, respectively, the
$(0,2\nu +\nu ')$, with value, respectively, the ![]() $G$-invariants
$G$-invariants
This implies that the spectral sequences collapse and that the top row of the second diagram is obtained from the top row of the first diagram by taking ![]() $G$-invariants. This, together with the fact that all arrows in the first diagram are
$G$-invariants. This, together with the fact that all arrows in the first diagram are ![]() $G$-equivariant, shows that the second diagram is obtained from the first by taking
$G$-equivariant, shows that the second diagram is obtained from the first by taking ![]() $G$-invariants.
$G$-invariants.
It suffices therefore to prove commutativity of the first diagram. Recall that ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ is an orientable
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ is an orientable ![]() $\mathbb {Q}$-homology manifold; moreover, both differences
$\mathbb {Q}$-homology manifold; moreover, both differences ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ and
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ and ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ are relatively compact inside
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}}\,\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$ are relatively compact inside ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$. We can therefore apply Poincaré–Lefschetz duality and reduce to proving commutativity of the following diagram, where we use the abbreviation
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)_{\nu +\nu '}$. We can therefore apply Poincaré–Lefschetz duality and reduce to proving commutativity of the following diagram, where we use the abbreviation ![]() $\mathrm {Hur}$ for
$\mathrm {Hur}$ for ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$:
$\mathrm {Hur}(\mathring {{\mathcal {R}}};{\mathcal {Q}}_+)$:

Here the bottom right group is abstractly isomorphic to ![]() $\mathbb {Q}[{\mathcal {Q}}]_{2\nu +2\nu '}$, but lives naturally in degree 0. The vertical isomorphisms are given as follows:
$\mathbb {Q}[{\mathcal {Q}}]_{2\nu +2\nu '}$, but lives naturally in degree 0. The vertical isomorphisms are given as follows:
• the left vertical map comes from the identification of
 $\mathrm {Hur}_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ with
induced by the maps
$\mathrm {Hur}_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ with
induced by the maps \[ \coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}}\, \mathrm{Hur}\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac 18\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_a\times \mathrm{Hur}\bigg(\frac{7z_{\mathrm{c,r}}}8+\frac 18\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_b \]
\[ \coprod_{(a,b)\in{\mathcal{Q}}_{\nu,\nu'}}\, \mathrm{Hur}\bigg(\frac{7z_{\mathrm{c,l}}}8+\frac 18\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_a\times \mathrm{Hur}\bigg(\frac{7z_{\mathrm{c,r}}}8+\frac 18\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_b \]
 $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}$ and
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,1/2}}$ and  $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}$; the second space has connected components in bijection with
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{1/2,1}}$; the second space has connected components in bijection with  ${\mathcal {Q}}_{\nu,\nu '}$, by taking the total monodromies of the two factors;
${\mathcal {Q}}_{\nu,\nu '}$, by taking the total monodromies of the two factors;• the right vertical map comes from the identification of
 $\mathrm {Hur}_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ with
the second space has connected components in bijection with
$\mathrm {Hur}_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ with
the second space has connected components in bijection with \[ \mathrm{Hur}\bigg(\frac{z_{\mathrm{c}}}2+\frac 12\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_{\nu+\nu'}; \]
\[ \mathrm{Hur}\bigg(\frac{z_{\mathrm{c}}}2+\frac 12\mathring{{\mathcal{R}}};{\mathcal{Q}}_+\bigg)_{\nu+\nu'}; \]
 ${\mathcal {Q}}_{\nu +\nu '}$ by taking the total monodromy.
${\mathcal {Q}}_{\nu +\nu '}$ by taking the total monodromy.
Commutativity of the last diagram follows from the observation that for all ![]() $(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$, if we set
$(a,b)\in {\mathcal {Q}}_{\nu,\nu '}$, if we set ![]() $c=ab\in {\mathcal {Q}}$, then the inclusion of
$c=ab\in {\mathcal {Q}}$, then the inclusion of ![]() $\mathrm {Hur}_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ into
$\mathrm {Hur}_{\nu +\nu '}\setminus \partial _{\mathrm {lr}}^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ into ![]() $\mathrm {Hur}_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ restricts to an inclusion
$\mathrm {Hur}_{\nu +\nu '}\setminus \partial ^{\mathrm {fat}} \,\mathrm {Hur}_{\nu +\nu '}$ restricts to an inclusion
6.5 Stable rational cohomology of classical Hurwitz spaces
We apply Theorem 6.1 in the case of a finite PMQ ![]() ${\mathcal {Q}}$ with trivial multiplication: recall from [Reference BianchiBia21, Example 6.20] that every PMQ with trivial product is Poincaré, in particular it is
${\mathcal {Q}}$ with trivial multiplication: recall from [Reference BianchiBia21, Example 6.20] that every PMQ with trivial product is Poincaré, in particular it is ![]() $\mathbb {Q}$-Poincaré. The algebra
$\mathbb {Q}$-Poincaré. The algebra ![]() ${\mathcal {A}}({\mathcal {Q}})$ is isomorphic in this case to
${\mathcal {A}}({\mathcal {Q}})$ is isomorphic in this case to ![]() $\mathbb {Q}[x_S\,|\, S\in \mathrm {conj}({\mathcal {Q}}_+)]/(x_S^2)$, i.e. the quotient of the polynomial ring over
$\mathbb {Q}[x_S\,|\, S\in \mathrm {conj}({\mathcal {Q}}_+)]/(x_S^2)$, i.e. the quotient of the polynomial ring over ![]() $\mathbb {Q}$ with one variable
$\mathbb {Q}$ with one variable ![]() $x_S$ in degree two for each conjugacy class
$x_S$ in degree two for each conjugacy class ![]() $S\subset {\mathcal {Q}}_+$, modulo the ideal generated by the squares
$S\subset {\mathcal {Q}}_+$, modulo the ideal generated by the squares ![]() $x_S^2$. A minimal Sullivan model for
$x_S^2$. A minimal Sullivan model for ![]() ${\mathcal {A}}({\mathcal {Q}})$ is given by the commutative differential graded algebra
${\mathcal {A}}({\mathcal {Q}})$ is given by the commutative differential graded algebra ![]() $(\mathbb {A}({\mathcal {Q}}),d)$, where
$(\mathbb {A}({\mathcal {Q}}),d)$, where
with ![]() $x_S$ in degree two and
$x_S$ in degree two and ![]() $y_S$ in degree three and where the unique non-trivial differentials are
$y_S$ in degree three and where the unique non-trivial differentials are ![]() $d(y_S)=x_S^2$ for all
$d(y_S)=x_S^2$ for all ![]() $S\in \mathrm {conj}({\mathcal {Q}}_+)$. Looping twice the minimal Sullivan model (i.e. decreasing all degrees of the
$S\in \mathrm {conj}({\mathcal {Q}}_+)$. Looping twice the minimal Sullivan model (i.e. decreasing all degrees of the ![]() $x_S$ and
$x_S$ and ![]() $y_S$ by 2) and restricting to one connected component, we obtain that the rational cohomology of
$y_S$ by 2) and restricting to one connected component, we obtain that the rational cohomology of ![]() $\Omega _0B\mathring {\mathrm {HM}}({\mathcal {Q}})$ is isomorphic to
$\Omega _0B\mathring {\mathrm {HM}}({\mathcal {Q}})$ is isomorphic to ![]() $\Lambda _{\mathbb {Q}}[y'_S\,|\, S\in \mathrm {conj}({\mathcal {Q}}_+)]$, i.e. it is the free exterior algebra over
$\Lambda _{\mathbb {Q}}[y'_S\,|\, S\in \mathrm {conj}({\mathcal {Q}}_+)]$, i.e. it is the free exterior algebra over ![]() $\mathbb {Q}$ generated by classes
$\mathbb {Q}$ generated by classes ![]() $y'_S$ in degree one, one for each
$y'_S$ in degree one, one for each ![]() $S\in \mathrm {conj}({\mathcal {Q}}_+)$: the class
$S\in \mathrm {conj}({\mathcal {Q}}_+)$: the class ![]() $y'_S$ is obtained by looping twice
$y'_S$ is obtained by looping twice ![]() $y_S\in \mathbb {A}({\mathcal {Q}})$.
$y_S\in \mathbb {A}({\mathcal {Q}})$.
There is a special case of interest, namely when ![]() ${\mathcal {Q}}$ has the form
${\mathcal {Q}}$ has the form ![]() $c\sqcup \{\mathbb {1}_{{\mathcal {Q}}}\}$, for
$c\sqcup \{\mathbb {1}_{{\mathcal {Q}}}\}$, for ![]() $c\subset G$ a finite, conjugacy invariant subset of a group
$c\subset G$ a finite, conjugacy invariant subset of a group ![]() $G$: then by [Reference BianchiBia23a, Proposition 7.3] the space
$G$: then by [Reference BianchiBia23a, Proposition 7.3] the space ![]() $\mathring {\mathrm {HM}}_+({\mathcal {Q}})$ is homotopy equivalent to the topological monoid
$\mathring {\mathrm {HM}}_+({\mathcal {Q}})$ is homotopy equivalent to the topological monoid ![]() $\mathrm {Hur}^c_G:=\coprod _{n\ge 0}\mathrm {Hur}^c_{G,n}$ of classical Hurwitz spaces with monodromies in
$\mathrm {Hur}^c_G:=\coprod _{n\ge 0}\mathrm {Hur}^c_{G,n}$ of classical Hurwitz spaces with monodromies in ![]() $c$, see [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 2.6] and [Reference Randal-WilliamsRW19, Subsection 4.2]. Adding a disjoint unit, we obtain a homotopy equivalence of topological monoids
$c$, see [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 2.6] and [Reference Randal-WilliamsRW19, Subsection 4.2]. Adding a disjoint unit, we obtain a homotopy equivalence of topological monoids ![]() $\mathring {\mathrm {HM}}({\mathcal {Q}})\simeq \{\mathbb {1}\}\sqcup \mathrm {Hur}^c_G$; we can now recall that the weak homotopy type of the group completion of a topological monoid does not change up to homotopy if we add a disjoint unit to the monoid and, thus, we obtain weak equivalences
$\mathring {\mathrm {HM}}({\mathcal {Q}})\simeq \{\mathbb {1}\}\sqcup \mathrm {Hur}^c_G$; we can now recall that the weak homotopy type of the group completion of a topological monoid does not change up to homotopy if we add a disjoint unit to the monoid and, thus, we obtain weak equivalences
Thus, we obtain a computation of the rational cohomology of ![]() $\Omega B\,\mathrm {Hur}^c_G$, which is computed already in [Reference Randal-WilliamsRW19, Corollary 5.4]; a claim of the result already appears in the withdrawn preprint [Reference Ellenberg, Venkatesh and WesterlandEVW12], as a combination of the statement of [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 2.8.1] for
$\Omega B\,\mathrm {Hur}^c_G$, which is computed already in [Reference Randal-WilliamsRW19, Corollary 5.4]; a claim of the result already appears in the withdrawn preprint [Reference Ellenberg, Venkatesh and WesterlandEVW12], as a combination of the statement of [Reference Ellenberg, Venkatesh and WesterlandEVW12, Theorem 2.8.1] for ![]() $n=2$ and
$n=2$ and ![]() $X=BG$ and the discussion in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Subsection 5.6]. See also the conjecture in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 1.5], which predicts the previous computation for
$X=BG$ and the discussion in [Reference Ellenberg, Venkatesh and WesterlandEVW12, Subsection 5.6]. See also the conjecture in [Reference Ellenberg, Venkatesh and WesterlandEVW16, Subsection 1.5], which predicts the previous computation for ![]() $c$ being the conjugacy class of transpositions in a symmetric group on at least three letters.
$c$ being the conjugacy class of transpositions in a symmetric group on at least three letters.
Acknowledgements
This series of articles is a generalisation and a further development of my PhD thesis [Reference BianchiBia20]. I am grateful to my PhD supervisor Carl-Friedrich Bödigheimer, Bastiaan Cnossen, Florian Kranhold, Jeremy Miller, Martin Palmer, Dan Petersen, Oscar Randal-Williams, Ulrike Tillmann and Nathalie Wahl for helpful comments and mathematical explanations related to this article. I am also thankful to the anonymous referee for a deep and meticulous analysis of a previous version of the article and for several suggestions on how to improve the exposition.
Conflicts of interest
None.
Financial support
This work was partially supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy (EXC-2047/1, 390685813), by the European Research Council under the European Union's Seventh Framework Programme (ERC StG 716424 - CASe, PI Karim Adiprasito), and by the Danish National Research Foundation through the Copenhagen Centre for Geometry and Topology (DNRF151).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.
Appendix A. Deferred proofs
A.1 Proof of Proposition 2.13
The two cases ![]() $\mathring {\mathrm {HM}}$ and
$\mathring {\mathrm {HM}}$ and ![]() $\breve {\mathrm {HM}}$ are analogous, so we will focus on the case of
$\breve {\mathrm {HM}}$ are analogous, so we will focus on the case of ![]() $\breve {\mathrm {HM}}$, which is slightly more difficult.
$\breve {\mathrm {HM}}$, which is slightly more difficult.
Recall Definition 2.4. We define in a symmetric way ![]() $\breve {\mathrm {HM}}^-$ as the subspace of
$\breve {\mathrm {HM}}^-$ as the subspace of ![]() $[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ containing couples
$[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ containing couples ![]() $(t,\mathfrak {c})$ with
$(t,\mathfrak {c})$ with ![]() $\mathfrak {c}$ supported in
$\mathfrak {c}$ supported in ![]() $\mathring {\mathbb {S}}_{-t,0}$.
$\mathring {\mathbb {S}}_{-t,0}$.
Note that ![]() $\breve {\mathrm {HM}}^-$ is contained in the subspace
$\breve {\mathrm {HM}}^-$ is contained in the subspace ![]() $[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}^-},\breve {\partial })$, where we define
$[0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}^-},\breve {\partial })$, where we define ![]() $(\breve {{\mathcal {R}}}_{\mathbb {R}^-},\breve {\partial })$ as the nice couple
$(\breve {{\mathcal {R}}}_{\mathbb {R}^-},\breve {\partial })$ as the nice couple ![]() $((-\infty,0)\times [0,1],(-\infty,0)\times \{0,1\})$.
$((-\infty,0)\times [0,1],(-\infty,0)\times \{0,1\})$.
By [Reference BianchiBia23a, Proposition 4.4] the assignment ![]() $(t,\mathfrak {c})\mapsto (t,(\tau _{-t})_*(\mathfrak {c}))$ gives a continuous map
$(t,\mathfrak {c})\mapsto (t,(\tau _{-t})_*(\mathfrak {c}))$ gives a continuous map ![]() $\tau ^-\colon \breve {\mathrm {HM}}\to [0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$; note that
$\tau ^-\colon \breve {\mathrm {HM}}\to [0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$; note that ![]() $\tau ^-$ has values in the subspace
$\tau ^-$ has values in the subspace ![]() $\breve {\mathrm {HM}}^-$; in fact,
$\breve {\mathrm {HM}}^-$; in fact, ![]() $\tau ^-$ is a homeomorphism
$\tau ^-$ is a homeomorphism ![]() $\breve {\mathrm {HM}}\cong \breve {\mathrm {HM}}^-$.
$\breve {\mathrm {HM}}\cong \breve {\mathrm {HM}}^-$.
Recall [Reference BianchiBia23a, Definition 3.16]. The following composition of continuous maps takes values in ![]() $\breve {\mathrm {HM}}\subset [0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ and it coincides with
$\breve {\mathrm {HM}}\subset [0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$ and it coincides with ![]() $\mu \colon \breve {\mathrm {HM}}\times \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$ as a map of sets:
$\mu \colon \breve {\mathrm {HM}}\times \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$ as a map of sets:

Here, by abuse of notation, we denote by ![]() $-\sqcup -$ the map
$-\sqcup -$ the map ![]() $(t,\mathfrak {c},t',\mathfrak {c}')\mapsto (t,t',\mathfrak {c}\sqcup \mathfrak {c}')$; the map
$(t,\mathfrak {c},t',\mathfrak {c}')\mapsto (t,t',\mathfrak {c}\sqcup \mathfrak {c}')$; the map ![]() $\hat \tau$ is defined by
$\hat \tau$ is defined by ![]() $(t,t',\mathfrak {c})\mapsto (t+t',(\tau _t)_*(\mathfrak {c}))$. This shows continuity of the product
$(t,t',\mathfrak {c})\mapsto (t+t',(\tau _t)_*(\mathfrak {c}))$. This shows continuity of the product ![]() $\mu$.
$\mu$.
To prove associativity of ![]() $\mu$, let
$\mu$, let ![]() $\mathfrak {c}_i=(P_i,\psi _i,\varphi _i)$ be a configuration in
$\mathfrak {c}_i=(P_i,\psi _i,\varphi _i)$ be a configuration in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$ for
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$ for ![]() $i=1,2,3$. Under the identification
$i=1,2,3$. Under the identification ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,t_i}}$ we can regard
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{0,t_i}}$ we can regard ![]() $\mathfrak {c}_i$ as a configuration in
$\mathfrak {c}_i$ as a configuration in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$. Then
$\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$. Then ![]() $(\tau _{t_1})_*(\mathfrak {c}_2)$ is a configuration in
$(\tau _{t_1})_*(\mathfrak {c}_2)$ is a configuration in ![]() $\mathrm {Hur}^{\mathbb {S}_{t_1,t_1+t_2}}(\breve {{\mathcal {R}}}_{t_2}+t_1,\breve {\partial })$ and
$\mathrm {Hur}^{\mathbb {S}_{t_1,t_1+t_2}}(\breve {{\mathcal {R}}}_{t_2}+t_1,\breve {\partial })$ and ![]() $(\tau _{t_1+t_2})_*(\mathfrak {c}_3)$ is a configuration in
$(\tau _{t_1+t_2})_*(\mathfrak {c}_3)$ is a configuration in ![]() $\mathrm {Hur}^{\mathbb {S}_{t_1+t_2,t_1+t_2+t_3}}(\breve {{\mathcal {R}}}_{t_3}+t_1+t_2,\breve {\partial })$). The compositions
$\mathrm {Hur}^{\mathbb {S}_{t_1+t_2,t_1+t_2+t_3}}(\breve {{\mathcal {R}}}_{t_3}+t_1+t_2,\breve {\partial })$). The compositions ![]() $\mathfrak {c}_1\sqcup ((\tau _{t_1})_*(\mathfrak {c}_2)\sqcup (\tau _{t_1+t_2})_*(\mathfrak {c}_3))$ and
$\mathfrak {c}_1\sqcup ((\tau _{t_1})_*(\mathfrak {c}_2)\sqcup (\tau _{t_1+t_2})_*(\mathfrak {c}_3))$ and ![]() $\big (\mathfrak {c}_1\sqcup (\tau _{t_1})_*(\mathfrak {c}_2)\big )\sqcup (\tau _{t_1+t_2})_*(\mathfrak {c}_3)$ represent the same configuration in
$\big (\mathfrak {c}_1\sqcup (\tau _{t_1})_*(\mathfrak {c}_2)\big )\sqcup (\tau _{t_1+t_2})_*(\mathfrak {c}_3)$ represent the same configuration in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,t_1+t_2+t_3}}(\breve {{\mathcal {R}}}_{t_1}\cup \breve {{\mathcal {R}}}_{t_2}+t_1\cup \breve {{\mathcal {R}}}_{t_3}+t_1+t_2,\breve {\partial })$ and by inclusion and change of ambient to
$\mathrm {Hur}^{\mathbb {S}_{0,t_1+t_2+t_3}}(\breve {{\mathcal {R}}}_{t_1}\cup \breve {{\mathcal {R}}}_{t_2}+t_1\cup \breve {{\mathcal {R}}}_{t_3}+t_1+t_2,\breve {\partial })$ and by inclusion and change of ambient to ![]() $\mathbb {C}$, the same configuration in
$\mathbb {C}$, the same configuration in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{t_1+t_2+t_3},\breve {\partial })$. This proves associativity of
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{t_1+t_2+t_3},\breve {\partial })$. This proves associativity of ![]() $\mu$.
$\mu$.
The fact that ![]() $(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is a two-sided unit for
$(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is a two-sided unit for ![]() $\mu$ follows directly from Definition 2.11, together with the fact that
$\mu$ follows directly from Definition 2.11, together with the fact that ![]() $\tau _0$ is the identity of
$\tau _0$ is the identity of ![]() $\mathbb {C}$.
$\mathbb {C}$.
A.2 Proof of Lemma 2.18
We start by proving that the elements ![]() $\pi _0(1,\mathfrak {c}_a)$ generate
$\pi _0(1,\mathfrak {c}_a)$ generate ![]() $\pi _0(\mathring {\mathrm {HM}})$ as a monoid. Let
$\pi _0(\mathring {\mathrm {HM}})$ as a monoid. Let ![]() $(t,\mathfrak {c})\in \mathring {\mathrm {HM}}$ and use Notation 2.2. If
$(t,\mathfrak {c})\in \mathring {\mathrm {HM}}$ and use Notation 2.2. If ![]() $P=\emptyset$, then we can continuously reduce
$P=\emptyset$, then we can continuously reduce ![]() $t$ to 0, so that
$t$ to 0, so that ![]() $\pi _0(t,\mathfrak {c})=\pi _0(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is the neutral element of
$\pi _0(t,\mathfrak {c})=\pi _0(0,(\emptyset,\mathbb {1},\mathbb {1}))$ is the neutral element of ![]() $\pi _0(\mathring {\mathrm {HM}})$. Suppose from now on that
$\pi _0(\mathring {\mathrm {HM}})$. Suppose from now on that ![]() $P\neq \emptyset$.
$P\neq \emptyset$.
Suppose first that ![]() $P=\{z\}$ consists of a single point. By Lemma 2.7 we can connect
$P=\{z\}$ consists of a single point. By Lemma 2.7 we can connect ![]() $(t,\mathfrak {c})$ with a configuration of the form
$(t,\mathfrak {c})$ with a configuration of the form ![]() $(1,\mathfrak {c}')$; we can then connect
$(1,\mathfrak {c}')$; we can then connect ![]() $(1,\mathfrak {c}')$ with a configuration of the form
$(1,\mathfrak {c}')$ with a configuration of the form ![]() $\mathfrak {c}_a$: for this we can use any homotopy of
$\mathfrak {c}_a$: for this we can use any homotopy of ![]() $\mathbb {C}$ through semialgebraic homeomorphisms which is at all times supported on
$\mathbb {C}$ through semialgebraic homeomorphisms which is at all times supported on ![]() $\mathring {{\mathcal {R}}}$ (i.e.
$\mathring {{\mathcal {R}}}$ (i.e. ![]() $\mathbb {C}\setminus \mathring {{\mathcal {R}}}$ is fixed pointwise at all times) and pushes the unique point
$\mathbb {C}\setminus \mathring {{\mathcal {R}}}$ is fixed pointwise at all times) and pushes the unique point ![]() $z'\in P'$ to
$z'\in P'$ to ![]() $z_{\mathrm {c}}$. It follows that
$z_{\mathrm {c}}$. It follows that ![]() $(t,\mathfrak {c})$ and
$(t,\mathfrak {c})$ and ![]() $(1,\mathfrak {c}_a)$ are connected in
$(1,\mathfrak {c}_a)$ are connected in ![]() $\mathring {\mathrm {HM}}$.
$\mathring {\mathrm {HM}}$.
Suppose now that ![]() $|P|\geq 2$. We can perturb the positions of the points
$|P|\geq 2$. We can perturb the positions of the points ![]() $z_i\in P$ inside
$z_i\in P$ inside ![]() $\mathring {{\mathcal {R}}}_t$ and assume that their real parts
$\mathring {{\mathcal {R}}}_t$ and assume that their real parts ![]() $\Re (z_i)$ are all different: again, we use a semialgebraic isotopy of
$\Re (z_i)$ are all different: again, we use a semialgebraic isotopy of ![]() $\mathbb {C}$ supported on
$\mathbb {C}$ supported on ![]() $\mathring {{\mathcal {R}}}_t$, starting from the identity of
$\mathring {{\mathcal {R}}}_t$, starting from the identity of ![]() $\mathbb {C}$ and ending with a semialgebraic homeomorphism of
$\mathbb {C}$ and ending with a semialgebraic homeomorphism of ![]() $\mathbb {C}$ mapping
$\mathbb {C}$ mapping ![]() $P$ to a set of points with distinct real parts.
$P$ to a set of points with distinct real parts.
Without loss of generality we assume that ![]() $P$ already has this property and we also assume
$P$ already has this property and we also assume ![]() $\Re (z_1)<\cdots <\Re (z_k)$; choose positive real numbers
$\Re (z_1)<\cdots <\Re (z_k)$; choose positive real numbers ![]() $0=t_0< t_1<\cdots < t_k=t$ such that
$0=t_0< t_1<\cdots < t_k=t$ such that ![]() $t_{i-1}<\Re (z_i)< t_i$ for all
$t_{i-1}<\Re (z_i)< t_i$ for all ![]() $1\leq i\leq k$. In particular, we can regard
$1\leq i\leq k$. In particular, we can regard ![]() $\mathfrak {c}$ as a configuration in
$\mathfrak {c}$ as a configuration in
Recall [Reference BianchiBia23a, Definition 3.15] and for all ![]() $1\leq i\leq k$ let
$1\leq i\leq k$ let ![]() $\mathfrak {c}_i\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t_i-t_{i-1}})$ be the image of
$\mathfrak {c}_i\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_{t_i-t_{i-1}})$ be the image of ![]() $\mathfrak {c}$ along the following composition:
$\mathfrak {c}$ along the following composition:

Then ![]() $(t,\mathfrak {c})$ is equal to the product
$(t,\mathfrak {c})$ is equal to the product ![]() $(t_1-t_0,\mathfrak {c}_1)\cdot \cdots \cdot (t_k-t_{k-1},\mathfrak {c}_k)$ in
$(t_1-t_0,\mathfrak {c}_1)\cdot \cdots \cdot (t_k-t_{k-1},\mathfrak {c}_k)$ in ![]() $\mathring {\mathrm {HM}}$ and each
$\mathring {\mathrm {HM}}$ and each ![]() $\mathfrak {c}_i$ is supported on the single point
$\mathfrak {c}_i$ is supported on the single point ![]() $\tau _{-t_{i-1}}(z_i)$. It follows that the elements
$\tau _{-t_{i-1}}(z_i)$. It follows that the elements ![]() $\pi _0(1,\mathfrak {c}_a)$ generate
$\pi _0(1,\mathfrak {c}_a)$ generate ![]() $\pi _0(\mathring {\mathrm {HM}})$ as a monoid.
$\pi _0(\mathring {\mathrm {HM}})$ as a monoid.
Now let ![]() $a,b\in {\mathcal {Q}}$ and note that
$a,b\in {\mathcal {Q}}$ and note that ![]() $(1,\mathfrak {c}_a)\cdot (1,\mathfrak {c}_b)$ has the form
$(1,\mathfrak {c}_a)\cdot (1,\mathfrak {c}_b)$ has the form ![]() $(2,\mathfrak {c})$, for some
$(2,\mathfrak {c})$, for some ![]() $\mathfrak {c}=(P,\psi )\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$ with
$\mathfrak {c}=(P,\psi )\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$ with ![]() $P=\{z_1=z_{\mathrm {c}},z_2=z_{\mathrm {c}}+1\}$. Let
$P=\{z_1=z_{\mathrm {c}},z_2=z_{\mathrm {c}}+1\}$. Let ![]() $f_1,f_2$ be the admissible generating set for
$f_1,f_2$ be the admissible generating set for ![]() $\mathfrak {G}(P)$ with
$\mathfrak {G}(P)$ with ![]() $f_1$ represented by a loop supported on
$f_1$ represented by a loop supported on ![]() $\mathbb {S}_{-\infty,1}$ and
$\mathbb {S}_{-\infty,1}$ and ![]() $f_2$ represented by a loop supported on
$f_2$ represented by a loop supported on ![]() $\mathbb {S}_{1,+\infty }$.
$\mathbb {S}_{1,+\infty }$.
We can fix a semialgebraic isotopy ![]() ${\mathcal {H}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ supported on
${\mathcal {H}}\colon \mathbb {C}\times [0,1]\to \mathbb {C}$ supported on ![]() $\mathring {{\mathcal {R}}}_2$, starting from the identity of
$\mathring {{\mathcal {R}}}_2$, starting from the identity of ![]() $\mathbb {C}$ and swapping at time 1 the two points of
$\mathbb {C}$ and swapping at time 1 the two points of ![]() $P$ according to a clockwise half Dehn twist. We use the notation
$P$ according to a clockwise half Dehn twist. We use the notation ![]() $\mathfrak {c}'=(P,\psi '):={\mathcal {H}}_*(\mathfrak {c};1)\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$.
$\mathfrak {c}'=(P,\psi '):={\mathcal {H}}_*(\mathfrak {c};1)\in \mathrm {Hur}(\mathring {{\mathcal {R}}}_2)$.
The homeomorphism ![]() ${\mathcal {H}}(-,1)\colon \mathbb {C}\setminus P\to \mathbb {C}\setminus P$ induces an automorphism of the fundamental group
${\mathcal {H}}(-,1)\colon \mathbb {C}\setminus P\to \mathbb {C}\setminus P$ induces an automorphism of the fundamental group ![]() ${\mathcal {H}}(-,1)_*\colon \mathfrak {G}(P)\to \mathfrak {G}(P)$ which restricts to an automorphism of the fundamental PMQ
${\mathcal {H}}(-,1)_*\colon \mathfrak {G}(P)\to \mathfrak {G}(P)$ which restricts to an automorphism of the fundamental PMQ ![]() ${\mathcal {H}}(-,1)_*\colon \mathfrak {Q}_{\mathring {{\mathcal {R}}}_2}(P)\to \mathfrak {Q}_{\mathring {{\mathcal {R}}}_2}(P)$.
${\mathcal {H}}(-,1)_*\colon \mathfrak {Q}_{\mathring {{\mathcal {R}}}_2}(P)\to \mathfrak {Q}_{\mathring {{\mathcal {R}}}_2}(P)$.
Note that ![]() ${\mathcal {H}}(-,1)_*$ sends
${\mathcal {H}}(-,1)_*$ sends ![]() $f_2\mapsto f_1$ and
$f_2\mapsto f_1$ and ![]() $f_1^{f_2}\mapsto f_2$. By definition, we have
$f_1^{f_2}\mapsto f_2$. By definition, we have ![]() $\psi '=\psi \circ {\mathcal {H}}(-,1)_*^{-1}$, hence
$\psi '=\psi \circ {\mathcal {H}}(-,1)_*^{-1}$, hence ![]() $\psi '(f_1)=\psi (f_2)=b$ and
$\psi '(f_1)=\psi (f_2)=b$ and ![]() $\psi '(f_2)=\psi (f_1^{f_2})=a^b$. It follows that
$\psi '(f_2)=\psi (f_1^{f_2})=a^b$. It follows that ![]() $(P,\psi ')=(1,\mathfrak {c}_b)\cdot (1,\mathfrak {c}_{a^b})$, hence
$(P,\psi ')=(1,\mathfrak {c}_b)\cdot (1,\mathfrak {c}_{a^b})$, hence ![]() $\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{b})\cdot \pi _0(1,\mathfrak {c}_{a^b})$.
$\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}_{b})\cdot \pi _0(1,\mathfrak {c}_{a^b})$.
Suppose now that the product ![]() $ab$ is defined in
$ab$ is defined in ![]() ${\mathcal {Q}}$. Again by Lemma 2.7 we can connect
${\mathcal {Q}}$. Again by Lemma 2.7 we can connect ![]() $(2,\mathfrak {c}):=(1,\mathfrak {c}_a)\cdot (1,\mathfrak {c}_b)$ to a configuration of the form
$(2,\mathfrak {c}):=(1,\mathfrak {c}_a)\cdot (1,\mathfrak {c}_b)$ to a configuration of the form ![]() $(1,\mathfrak {c}'')$, with
$(1,\mathfrak {c}'')$, with ![]() $\mathfrak {c}''\in \mathrm {Hur}(\mathring {{\mathcal {R}}})$; for instance we can take
$\mathfrak {c}''\in \mathrm {Hur}(\mathring {{\mathcal {R}}})$; for instance we can take ![]() $\mathfrak {c}''=\Lambda _*(\mathfrak {c},1/2)$, where the semialgebraic isotopy
$\mathfrak {c}''=\Lambda _*(\mathfrak {c},1/2)$, where the semialgebraic isotopy ![]() $\Lambda \colon \mathbb {C}\times (0,\infty )\to \mathbb {C}$ was introduced in the proof of Lemma 2.7. In fact, we have
$\Lambda \colon \mathbb {C}\times (0,\infty )\to \mathbb {C}$ was introduced in the proof of Lemma 2.7. In fact, we have ![]() $\mathfrak {c}''\in \mathrm {Hur}_+(\mathring {{\mathcal {R}}})_{ab}$; by [Reference BianchiBia23a, Corollary 6.5] the space
$\mathfrak {c}''\in \mathrm {Hur}_+(\mathring {{\mathcal {R}}})_{ab}$; by [Reference BianchiBia23a, Corollary 6.5] the space ![]() $\mathrm {Hur}_+(\mathring {{\mathcal {R}}})_{ab}$ is contractible, in particular it is connected; hence,
$\mathrm {Hur}_+(\mathring {{\mathcal {R}}})_{ab}$ is contractible, in particular it is connected; hence, ![]() $\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}'')=\pi _0(1,\mathfrak {c}_{ab})$.
$\pi _0(1,\mathfrak {c}_a)\cdot \pi _0(1,\mathfrak {c}_b)=\pi _0(1,\mathfrak {c}'')=\pi _0(1,\mathfrak {c}_{ab})$.
A.3 Proof of Proposition 3.3
Definition A.1 We introduce a subspace ![]() $\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$. A couple
$\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$. A couple ![]() $(t,\mathfrak {c})\in \breve {\mathrm {HM}}_+$ belongs to
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}_+$ belongs to ![]() $\breve {\mathrm {HM}}^{\flat }_+$ if
$\breve {\mathrm {HM}}^{\flat }_+$ if ![]() $t\geq 1$ and the point
$t\geq 1$ and the point ![]() $z^{\flat }_t:=t-\frac 12$ belongs to the support of
$z^{\flat }_t:=t-\frac 12$ belongs to the support of ![]() $\mathfrak {c}$.
$\mathfrak {c}$.
Note that ![]() $\breve {\mathrm {HM}}^{\flat }_+$ is invariant under the action of
$\breve {\mathrm {HM}}^{\flat }_+$ is invariant under the action of ![]() $\breve {\mathrm {HM}}$ by left multiplication.
$\breve {\mathrm {HM}}$ by left multiplication.
Definition A.2 Let ![]() $\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}\in \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$ be as in the proof of Lemma 3.2 and note that
$\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}\in \mathrm {Hur}(\breve {{\mathcal {R}}},\breve {\partial })$ be as in the proof of Lemma 3.2 and note that ![]() $(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}})\in \breve {\mathrm {HM}}^{\flat }_+$; in fact, the right multiplication map
$(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}})\in \breve {\mathrm {HM}}^{\flat }_+$; in fact, the right multiplication map ![]() $\mu (-;(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}))\colon \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$ has image inside
$\mu (-;(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}))\colon \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}$ has image inside ![]() $\breve {\mathrm {HM}}^{\flat }_+$. We define
$\breve {\mathrm {HM}}^{\flat }_+$. We define ![]() $\breve {\mathrm {HM}}^{\sharp }_+\subset \breve {\mathrm {HM}}^{\flat }_+$ as the image of
$\breve {\mathrm {HM}}^{\sharp }_+\subset \breve {\mathrm {HM}}^{\flat }_+$ as the image of ![]() $\mu (-;(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}))$.
$\mu (-;(1,\mathfrak {c}_{\mathbb {1}}^{\mathrm {d}}))$.
See Figure A.1. Note that also the subspace ![]() $\breve {\mathrm {HM}}^{\sharp }_+$ is invariant under the action of
$\breve {\mathrm {HM}}^{\sharp }_+$ is invariant under the action of ![]() $\breve {\mathrm {HM}}$ by left multiplication. Moreover,
$\breve {\mathrm {HM}}$ by left multiplication. Moreover, ![]() $\mu (-,(1,\mathfrak {c}_{\mathbb {1}}))\colon \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}^{\sharp }_+$ is a homeomorphism of
$\mu (-,(1,\mathfrak {c}_{\mathbb {1}}))\colon \breve {\mathrm {HM}}\to \breve {\mathrm {HM}}^{\sharp }_+$ is a homeomorphism of ![]() $\breve {\mathrm {HM}}$-left modules and
$\breve {\mathrm {HM}}$-left modules and ![]() $\breve {\mathrm {HM}}^{\sharp }_+\subset \breve {\mathrm {HM}}^{\flat }_+$ contains precisely all couples
$\breve {\mathrm {HM}}^{\sharp }_+\subset \breve {\mathrm {HM}}^{\flat }_+$ contains precisely all couples ![]() $(t,\mathfrak {c})$ such that, using Notation 2.2, the following hold:
$(t,\mathfrak {c})$ such that, using Notation 2.2, the following hold:
•
 $\{z^{\flat }_t\}\subseteq P\subset \{z^{\flat }_t\}\cup \breve {{\mathcal {R}}}_{t-1}$;
$\{z^{\flat }_t\}\subseteq P\subset \{z^{\flat }_t\}\cup \breve {{\mathcal {R}}}_{t-1}$;•
 $\psi \colon \mathfrak {Q}(P)\to {\mathcal {Q}}$ factors through
$\psi \colon \mathfrak {Q}(P)\to {\mathcal {Q}}$ factors through  $\mathfrak {Q}(P\setminus \{z^{\flat }_t\})$ along the point-forgetting map
$\mathfrak {Q}(P\setminus \{z^{\flat }_t\})$ along the point-forgetting map  $\mathfrak {i}^P_{P\setminus \{z^{\flat }_t\}}\colon \mathfrak {Q}(P)\to \mathfrak {Q}(P\setminus \{z^{\flat }_t\})$, see [Reference BianchiBia23a, Notation 2.17];
$\mathfrak {i}^P_{P\setminus \{z^{\flat }_t\}}\colon \mathfrak {Q}(P)\to \mathfrak {Q}(P\setminus \{z^{\flat }_t\})$, see [Reference BianchiBia23a, Notation 2.17];• similarly,
 $\varphi \colon \mathfrak {G}(P)\to G$ factors through
$\varphi \colon \mathfrak {G}(P)\to G$ factors through  $\mathfrak {G}(P\setminus \{z^{\flat }_t\})$ along
$\mathfrak {G}(P\setminus \{z^{\flat }_t\})$ along  $\mathfrak {i}^P_{P\setminus \{z^{\flat }_t\}}\colon \mathfrak {G}(P)\to \mathfrak {G}(P\setminus \{z^{\flat }_t\})$.
$\mathfrak {i}^P_{P\setminus \{z^{\flat }_t\}}\colon \mathfrak {G}(P)\to \mathfrak {G}(P\setminus \{z^{\flat }_t\})$.
Passing to bar constructions, we obtain inclusions of spaces
The first space ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\sharp }_+)$ is homeomorphic to
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\sharp }_+)$ is homeomorphic to ![]() $E\breve {\mathrm {HM}}$ and, hence, is contractible, as
$E\breve {\mathrm {HM}}$ and, hence, is contractible, as ![]() $\breve {\mathrm {HM}}$ is a unital monoid. We will prove that the inclusions
$\breve {\mathrm {HM}}$ is a unital monoid. We will prove that the inclusions ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)\hookrightarrow B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ and
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)\hookrightarrow B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ and ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\sharp }_+)\hookrightarrow B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)$ are weak homotopy equivalences: this will conclude the proof of Proposition 3.3.
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\sharp }_+)\hookrightarrow B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)$ are weak homotopy equivalences: this will conclude the proof of Proposition 3.3.
Lemma A.3 The inclusion ![]() $\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$ is a homotopy equivalence.
$\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$ is a homotopy equivalence.

Figure A.1. Two configurations in ![]() $\breve {\mathrm {HM}}^{\flat }_+$; note that only the right one belongs to
$\breve {\mathrm {HM}}^{\flat }_+$; note that only the right one belongs to ![]() $\breve {\mathrm {HM}}^{\sharp }_+$.
$\breve {\mathrm {HM}}^{\sharp }_+$.
Proof. The argument is similar to that of the proof of Lemma 3.2, but a bit more care is needed.
We define a continuous map ![]() $\mathscr {E}^{\flat }\colon (0,\infty )\times \mathrm {Ran}_+(\breve {{\mathcal {R}}}_\infty )\times [0,1]\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_\infty )$ by the formula
$\mathscr {E}^{\flat }\colon (0,\infty )\times \mathrm {Ran}_+(\breve {{\mathcal {R}}}_\infty )\times [0,1]\to \mathrm {Ran}_+(\breve {{\mathcal {R}}}_\infty )$ by the formula
We also let ![]() $\mathfrak {j}\colon (0,\infty )\to (0,\infty )$ be given by the formula
$\mathfrak {j}\colon (0,\infty )\to (0,\infty )$ be given by the formula
 \[
\mathfrak{j}(t)=\left\{\begin{array}{@{}ll} t-\dfrac 12 &
\text{for }t\ge 1,\\ \dfrac t2 & \text{for }t\le
1. \end{array}\right. \]
\[
\mathfrak{j}(t)=\left\{\begin{array}{@{}ll} t-\dfrac 12 &
\text{for }t\ge 1,\\ \dfrac t2 & \text{for }t\le
1. \end{array}\right. \]
We consider then the homotopy ![]() ${\mathcal {H}}^{\flat }\colon \breve {\mathrm {HM}}_+\times [0,1]\to (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ given by the formula
${\mathcal {H}}^{\flat }\colon \breve {\mathrm {HM}}_+\times [0,1]\to (0,\infty )\times \mathrm {Hur}(\breve {{\mathcal {R}}}_{\infty },\breve {\partial })$ given by the formula
Let ![]() $\breve {\mathrm {HM}}_{+,t\geq 1}$ denote the subspace of
$\breve {\mathrm {HM}}_{+,t\geq 1}$ denote the subspace of ![]() $\breve {\mathrm {HM}}_+$ containing all couples
$\breve {\mathrm {HM}}_+$ containing all couples ![]() $(t,\mathfrak {c})$ with
$(t,\mathfrak {c})$ with ![]() $t\geq 1$. Then the homotopy
$t\geq 1$. Then the homotopy ![]() ${\mathcal {H}}^{\flat }$ has the following properties:
${\mathcal {H}}^{\flat }$ has the following properties:
•
 ${\mathcal {H}}^{\flat }(-,s)$ sends
${\mathcal {H}}^{\flat }(-,s)$ sends  $\breve {\mathrm {HM}}_+$ inside
$\breve {\mathrm {HM}}_+$ inside  $\breve {\mathrm {HM}}_+$ for all
$\breve {\mathrm {HM}}_+$ for all  $0\le s \le 1$;
$0\le s \le 1$;•
 ${\mathcal {H}}^{\flat }(-,0)$ is the identity of
${\mathcal {H}}^{\flat }(-,0)$ is the identity of  $\breve {\mathrm {HM}}_+$;
$\breve {\mathrm {HM}}_+$;•
 ${\mathcal {H}}^{\flat }(-,s)$ preserves the subspaces
${\mathcal {H}}^{\flat }(-,s)$ preserves the subspaces  $\breve {\mathrm {HM}}^{\flat }_+$ and
$\breve {\mathrm {HM}}^{\flat }_+$ and  $\breve {\mathrm {HM}}_{+,t\geq 1}$ at all times;
$\breve {\mathrm {HM}}_{+,t\geq 1}$ at all times;•
 ${\mathcal {H}}^{\flat }(-,1)$ sends
${\mathcal {H}}^{\flat }(-,1)$ sends  $\breve {\mathrm {HM}}_{+,t\geq 1}$ inside
$\breve {\mathrm {HM}}_{+,t\geq 1}$ inside  $\breve {\mathrm {HM}}^{\flat }_+$.
$\breve {\mathrm {HM}}^{\flat }_+$.
This shows that the inclusion ![]() $\breve {\mathrm {HM}}^{\flat }_+\hookrightarrow \breve {\mathrm {HM}}_{+,t\geq 1}$ is a homotopy equivalence. Moreover, there is a deformation retraction of
$\breve {\mathrm {HM}}^{\flat }_+\hookrightarrow \breve {\mathrm {HM}}_{+,t\geq 1}$ is a homotopy equivalence. Moreover, there is a deformation retraction of ![]() $\breve {\mathrm {HM}}_+$ onto
$\breve {\mathrm {HM}}_+$ onto ![]() $\breve {\mathrm {HM}}_{+,t\geq 1}$ given by the formula
$\breve {\mathrm {HM}}_{+,t\geq 1}$ given by the formula
It follows that the inclusion ![]() $\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$ is a homotopy equivalence.
$\breve {\mathrm {HM}}^{\flat }_+\subset \breve {\mathrm {HM}}_+$ is a homotopy equivalence.
By Lemma A.3 the inclusion of semisimplicial spaces
is levelwise a homotopy equivalence; after (thick) geometric realisation we obtain the following corollary.
Corollary A.4 The inclusion ![]() $B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)\subset B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ is a weak homotopy equivalence.
$B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}^{\flat }_+)\subset B(\breve {\mathrm {HM}},\breve {\mathrm {HM}}_+)$ is a weak homotopy equivalence.
For the second step of the proof of Proposition 3.3 we define a homotopy
by setting ![]() ${\mathcal {H}}^{\sharp }\colon ((t,\mathfrak {c});s)\mapsto (t+s, \mathfrak {c}\times \{z^{\flat }_{t+s}\})$ for
${\mathcal {H}}^{\sharp }\colon ((t,\mathfrak {c});s)\mapsto (t+s, \mathfrak {c}\times \{z^{\flat }_{t+s}\})$ for ![]() $0\leq s\leq 1$ and
$0\leq s\leq 1$ and ![]() $(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$; here
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$; here ![]() $\mathfrak {c}\times \{z^{\flat }_{t+s}\}$ is the evaluation at
$\mathfrak {c}\times \{z^{\flat }_{t+s}\}$ is the evaluation at ![]() $(\mathfrak {c},\{z^{\flat }_{t+s}\})$ of the external product
$(\mathfrak {c},\{z^{\flat }_{t+s}\})$ of the external product
Roughly speaking, the homotopy ![]() ${\mathcal {H}}^{\sharp }$ has the following effects on configurations
${\mathcal {H}}^{\sharp }$ has the following effects on configurations ![]() $(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$:
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$:
• it increases by 1 the first component
 $t$ of a couple
$t$ of a couple  $(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$;
$(t,\mathfrak {c})\in \breve {\mathrm {HM}}^{\flat }_+$;• it splits
 $z^{\flat }_t$, which already belongs to the support of
$z^{\flat }_t$, which already belongs to the support of  $\mathfrak {c}$, into two points; one point remains at the position
$\mathfrak {c}$, into two points; one point remains at the position  $z^{\flat }_t$ and ‘keeps the local monodromy’ (which is only defined as an element of
$z^{\flat }_t$ and ‘keeps the local monodromy’ (which is only defined as an element of  $G$, because
$G$, because  $z^{\flat }_t\in \breve {\partial }\breve {{\mathcal {R}}}_{\infty }$); the other point moves gradually to a distance 1 to right and has trivial local monodromy
$z^{\flat }_t\in \breve {\partial }\breve {{\mathcal {R}}}_{\infty }$); the other point moves gradually to a distance 1 to right and has trivial local monodromy  $\mathbb {1}$ (also only defined as element of
$\mathbb {1}$ (also only defined as element of  $G$).
$G$).
Note that ![]() ${\mathcal {H}}^{\sharp }$ has the following properties:
${\mathcal {H}}^{\sharp }$ has the following properties:
•
 ${\mathcal {H}}^{\sharp }(-;0)$ is the identity of
${\mathcal {H}}^{\sharp }(-;0)$ is the identity of  $\breve {\mathrm {HM}}^{\flat }_+$;
$\breve {\mathrm {HM}}^{\flat }_+$;•
 ${\mathcal {H}}^{\sharp }(-;1)$ has values inside
${\mathcal {H}}^{\sharp }(-;1)$ has values inside  $\breve {\mathrm {HM}}^{\sharp }_+$;
$\breve {\mathrm {HM}}^{\sharp }_+$;• for all
 $0\leq s\leq 1$ the map
$0\leq s\leq 1$ the map  ${\mathcal {H}}^{\sharp }(-;s)$ is equivariant with respect to the action of
${\mathcal {H}}^{\sharp }(-;s)$ is equivariant with respect to the action of  $\breve {\mathrm {HM}}$ on
$\breve {\mathrm {HM}}$ on  $\breve {\mathrm {HM}}^{\flat }_+$ by left multiplication.
$\breve {\mathrm {HM}}^{\flat }_+$ by left multiplication.
As a consequence, ![]() ${\mathcal {H}}^{\sharp }$ induces a homotopy of
${\mathcal {H}}^{\sharp }$ induces a homotopy of ![]() $B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ starting from the identity and ending with a map
$B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ starting from the identity and ending with a map ![]() $B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)\to B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\sharp }_+)$. We obtain the following lemma, which is the last step needed to prove Proposition 3.3.
$B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)\to B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\sharp }_+)$. We obtain the following lemma, which is the last step needed to prove Proposition 3.3.
Lemma A.5 The space ![]() $B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ admits a deformation into its contractible subspace
$B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ admits a deformation into its contractible subspace ![]() $B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\sharp }_+)$. As a consequence
$B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\sharp }_+)$. As a consequence ![]() $B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ is weakly contractible.
$B(\breve {\mathrm {HM}}_+,\breve {\mathrm {HM}}^{\flat }_+)$ is weakly contractible.
A.4 Proof of Proposition 4.15
We first give a rough idea of the proof: the value of ![]() $\check \sigma$ at a given sequence
$\check \sigma$ at a given sequence ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ in
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ in ![]() $\Delta ^p\times (\mathring {\mathrm {HM}})^p$ (respectively, in
$\Delta ^p\times (\mathring {\mathrm {HM}})^p$ (respectively, in ![]() $\Delta ^p\times (\breve {\mathrm {HM}})^p$) is obtained by combining several steps: the first step is computing the product
$\Delta ^p\times (\breve {\mathrm {HM}})^p$) is obtained by combining several steps: the first step is computing the product ![]() $\hat \mu (\underline {w};\underline {t},\underline {\mathfrak {c}})=(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ in
$\hat \mu (\underline {w};\underline {t},\underline {\mathfrak {c}})=(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ in ![]() $\mathring {\mathrm {HM}}$ (in
$\mathring {\mathrm {HM}}$ (in ![]() $\breve {\mathrm {HM}}$). The product map
$\breve {\mathrm {HM}}$). The product map ![]() $\hat \mu$, however, does not factor through
$\hat \mu$, however, does not factor through ![]() $B\mathring {\mathrm {HM}}$ (respectively,
$B\mathring {\mathrm {HM}}$ (respectively, ![]() $B\breve {\mathrm {HM}}$): one of the reasons is that if
$B\breve {\mathrm {HM}}$): one of the reasons is that if ![]() $w_0=0$, the sequence
$w_0=0$, the sequence ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equivalent in
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equivalent in ![]() $B\mathring {\mathrm {HM}}$ (respectively, in
$B\mathring {\mathrm {HM}}$ (respectively, in ![]() $B\breve {\mathrm {HM}}$) to the sequence obtained by forgetting
$B\breve {\mathrm {HM}}$) to the sequence obtained by forgetting ![]() $w_0$ and
$w_0$ and ![]() $(t_1,\mathfrak {c}_1)$; yet the product
$(t_1,\mathfrak {c}_1)$; yet the product ![]() $(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ is, in general, different from the product
$(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ is, in general, different from the product ![]() $(t_2,\mathfrak {c}_2)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$. In fact, letting
$(t_2,\mathfrak {c}_2)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$. In fact, letting ![]() $0\le i_{\rm min}\le i_{\rm max}\le p$ be as in the discussion before Definition 4.5, we might reduce
$0\le i_{\rm min}\le i_{\rm max}\le p$ be as in the discussion before Definition 4.5, we might reduce ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ to an equivalent sequence
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ to an equivalent sequence ![]() $(w_{i_{\rm min}},\ldots,w_{i_{\rm max}};t_{i_{\rm min}+1},\ldots,t_{i_{\rm max}};\mathfrak {c}_{i_{\rm min}+1},\ldots,\mathfrak {c}_{i_{\rm max}})$, yet the product
$(w_{i_{\rm min}},\ldots,w_{i_{\rm max}};t_{i_{\rm min}+1},\ldots,t_{i_{\rm max}};\mathfrak {c}_{i_{\rm min}+1},\ldots,\mathfrak {c}_{i_{\rm max}})$, yet the product ![]() $(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ is, in general, different from the subproduct
$(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ is, in general, different from the subproduct ![]() $(t_{i_{\rm min}+1},\mathfrak {c}_{i_{\rm min}+1})\cdot \cdots \cdot (t_{i_{\rm max}},\mathfrak {c}_{i_{\rm max}})$.
$(t_{i_{\rm min}+1},\mathfrak {c}_{i_{\rm min}+1})\cdot \cdots \cdot (t_{i_{\rm max}},\mathfrak {c}_{i_{\rm max}})$.
We solve this problem by using the barycentres ![]() $b^-_\varepsilon < b^+_\varepsilon$ and by considering only the part of the configuration
$b^-_\varepsilon < b^+_\varepsilon$ and by considering only the part of the configuration ![]() $(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ lying in the strip
$(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ lying in the strip ![]() $\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$: more precisely, using a suitable expansion and translation (implemented via the homotopies
$\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$: more precisely, using a suitable expansion and translation (implemented via the homotopies ![]() $\tau _*$ and
$\tau _*$ and ![]() $\Lambda _*$), we map the strip
$\Lambda _*$), we map the strip ![]() $\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ to the strip
$\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ to the strip ![]() $\mathbb {S}_{0,1}$ and then we collapse the two parts of the obtained configuration lying outside the strip
$\mathbb {S}_{0,1}$ and then we collapse the two parts of the obtained configuration lying outside the strip ![]() $\mathbb {S}_{0,1}$: we first collapse all points lying on left (respectively, on right) of
$\mathbb {S}_{0,1}$: we first collapse all points lying on left (respectively, on right) of ![]() $\mathbb {S}_{0,1}$ to the segment
$\mathbb {S}_{0,1}$ to the segment ![]() $0\times [0,1]$ (respectively,
$0\times [0,1]$ (respectively, ![]() $1\times [0,1]$) via the homotopies
$1\times [0,1]$) via the homotopies ![]() $\kappa ^+_*$ and
$\kappa ^+_*$ and ![]() $\kappa ^-_*$, we further collapse these vertical segments to the two points
$\kappa ^-_*$, we further collapse these vertical segments to the two points ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ via
$z_{\diamond }^{\mathrm {r}}$ via ![]() $({\mathcal {H}}^{\diamond }_1)_*$ and finally we get rid of the residual information of the
$({\mathcal {H}}^{\diamond }_1)_*$ and finally we get rid of the residual information of the ![]() $G$-valued local monodromy at
$G$-valued local monodromy at ![]() $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and ![]() $z_{\diamond }^{\mathrm {r}}$ by quotienting by the action of
$z_{\diamond }^{\mathrm {r}}$ by quotienting by the action of ![]() $G\times G^{\rm op}$. The key observation is that the part of
$G\times G^{\rm op}$. The key observation is that the part of ![]() $(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ lying in the strip
$(t_1,\mathfrak {c}_1)\cdot \cdots \cdot (t_p,\mathfrak {c}_p)$ lying in the strip ![]() $\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ only depends on the subproduct
$\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ only depends on the subproduct ![]() $(t_{i_{\rm min}+1},\mathfrak {c}_{i_{\rm min}+1})\cdot \cdots \cdot (t_{i_{\rm max}},\mathfrak {c}_{i_{\rm max}})$. The conditions on
$(t_{i_{\rm min}+1},\mathfrak {c}_{i_{\rm min}+1})\cdot \cdots \cdot (t_{i_{\rm max}},\mathfrak {c}_{i_{\rm max}})$. The conditions on ![]() $\varepsilon$, moreover, ensure that either
$\varepsilon$, moreover, ensure that either ![]() $\varepsilon =0$, i.e.
$\varepsilon =0$, i.e. ![]() $b_\varepsilon ^-=b^-$ and
$b_\varepsilon ^-=b^-$ and ![]() $b_\varepsilon ^+=b^+$, or the part of
$b_\varepsilon ^+=b^+$, or the part of ![]() $\hat \mu (\underline {w};\underline {t},\underline {\mathfrak {c}})$ lying inside
$\hat \mu (\underline {w};\underline {t},\underline {\mathfrak {c}})$ lying inside ![]() $\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ is ‘empty’ and, in particular, independent of the positive value of
$\mathbb {S}_{b^-_\varepsilon,b_\varepsilon ^+}$ is ‘empty’ and, in particular, independent of the positive value of ![]() $\varepsilon$; this is the rough reason why
$\varepsilon$; this is the rough reason why ![]() $\check \sigma$ and, hence,
$\check \sigma$ and, hence, ![]() $\sigma$ and
$\sigma$ and ![]() $\bar \sigma$, do not depend on
$\bar \sigma$, do not depend on ![]() $\varepsilon$.
$\varepsilon$.
Before starting the proof of Proposition 4.15, we give a definition.
Definition A.6 Let ![]() $\mathfrak {C}$ be a nice couple, let
$\mathfrak {C}$ be a nice couple, let ![]() $\mathfrak {c},\mathfrak {c}'\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ be two configurations and let
$\mathfrak {c},\mathfrak {c}'\in \mathrm {Hur}(\mathfrak {C};{\mathcal {Q}},G)$ be two configurations and let ![]() $*\in \mathbb {T}\subset \mathbb {C}$ be a contractible subspace. We say that
$*\in \mathbb {T}\subset \mathbb {C}$ be a contractible subspace. We say that ![]() $\mathfrak {c}$ and
$\mathfrak {c}$ and ![]() $\mathfrak {c}'$ agree on
$\mathfrak {c}'$ agree on ![]() $\mathbb {T}$ if the following hold, using Notation 2.2:
$\mathbb {T}$ if the following hold, using Notation 2.2:
•
 $P\cap \mathbb {T}=P'\cap \mathbb {T}$;
$P\cap \mathbb {T}=P'\cap \mathbb {T}$;• for every loop
 $\gamma \subset \mathbb {T}\setminus P$ representing an element
$\gamma \subset \mathbb {T}\setminus P$ representing an element  $[\gamma ]$ in
$[\gamma ]$ in  $\mathfrak {Q}_{\mathfrak {C}}(P)$ we have
$\mathfrak {Q}_{\mathfrak {C}}(P)$ we have  $\psi (\gamma )=\psi '(\gamma )$;
$\psi (\gamma )=\psi '(\gamma )$;• for every loop
 $\gamma \subset \mathbb {T}\setminus P$ representing an element
$\gamma \subset \mathbb {T}\setminus P$ representing an element  $[\gamma ]$ in
$[\gamma ]$ in  $\mathfrak {G}(P)$ we have
$\mathfrak {G}(P)$ we have  $\varphi (\gamma )=\varphi '(\gamma )$).
$\varphi (\gamma )=\varphi '(\gamma )$).
Consider the particular case in which ![]() $\mathfrak {C}$ splits as a disjoint union of nice couples
$\mathfrak {C}$ splits as a disjoint union of nice couples ![]() $\mathfrak {C}_1,\mathfrak {C}_2$ with
$\mathfrak {C}_1,\mathfrak {C}_2$ with ![]() $\mathfrak {C}_1\subset \mathring {\mathbb {T}}$ and
$\mathfrak {C}_1\subset \mathring {\mathbb {T}}$ and ![]() $\mathfrak {C}_2$ contained in the interior of
$\mathfrak {C}_2$ contained in the interior of ![]() $\mathbb {C}\setminus \mathbb {T}$: then [Reference BianchiBia23a, Definition 3.15] gives configurations
$\mathbb {C}\setminus \mathbb {T}$: then [Reference BianchiBia23a, Definition 3.15] gives configurations ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})$ and
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})$ and ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c}')$ in
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c}')$ in ![]() $\mathrm {Hur}^{\mathbb {T}}(\mathfrak {C}_1;{\mathcal {Q}},G)$ and the condition that
$\mathrm {Hur}^{\mathbb {T}}(\mathfrak {C}_1;{\mathcal {Q}},G)$ and the condition that ![]() $\mathfrak {c}$ and
$\mathfrak {c}$ and ![]() $\mathfrak {c}'$ agree on
$\mathfrak {c}'$ agree on ![]() $\mathbb {T}$ is equivalent to the equality
$\mathbb {T}$ is equivalent to the equality ![]() $\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c}')$.
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c})=\mathfrak {i}^{\mathbb {C}}_{\mathbb {T}}(\mathfrak {c}')$.
Now let ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2 and assume
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2 and assume ![]() $w_j=0$ for a fixed
$w_j=0$ for a fixed ![]() $0\leq j\leq p$; let
$0\leq j\leq p$; let ![]() $(\underline {t}',\underline {\mathfrak {c}}')=d_j(\underline {t},\underline {\mathfrak {c}})$ (see Definition 3.1), let
$(\underline {t}',\underline {\mathfrak {c}}')=d_j(\underline {t},\underline {\mathfrak {c}})$ (see Definition 3.1), let ![]() $\underline {w}'$ be obtained from
$\underline {w}'$ be obtained from ![]() $\underline {w}$ by removing the (vanishing)
$\underline {w}$ by removing the (vanishing) ![]() $j$th coordinate and present
$j$th coordinate and present ![]() $\underline {w}'$ as
$\underline {w}'$ as ![]() $(w'_0,\ldots,w'_{p-1})$,
$(w'_0,\ldots,w'_{p-1})$, ![]() $\underline {t}'$ as
$\underline {t}'$ as ![]() $(t'_1,\ldots,t'_{p-1})$ and
$(t'_1,\ldots,t'_{p-1})$ and ![]() $\underline {\mathfrak {c}}'$ as
$\underline {\mathfrak {c}}'$ as ![]() $(\mathfrak {c}'_1,\ldots,\mathfrak {c}'_{p-1})$. We want to prove that
$(\mathfrak {c}'_1,\ldots,\mathfrak {c}'_{p-1})$. We want to prove that ![]() $\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$: this implies that
$\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$: this implies that ![]() $\check \sigma$ descends to a map
$\check \sigma$ descends to a map ![]() $\sigma$ defined on
$\sigma$ defined on ![]() $B\mathring {\mathrm {HM}}$ (on
$B\mathring {\mathrm {HM}}$ (on ![]() $B\breve {\mathrm {HM}}$).
$B\breve {\mathrm {HM}}$).
Let ![]() $a_0,\ldots,a_p,b,b^+,b^-$ be computed as in Definition 4.4 with respect to
$a_0,\ldots,a_p,b,b^+,b^-$ be computed as in Definition 4.4 with respect to ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and, similarly, let
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and, similarly, let ![]() $a'_0,\ldots,a'_{p-1},b',(b^+)',(b^-)'$ be computed with respect to
$a'_0,\ldots,a'_{p-1},b',(b^+)',(b^-)'$ be computed with respect to ![]() $(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. We observe that
$(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. We observe that ![]() $\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})=0$ if and only if the support
$\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})=0$ if and only if the support ![]() $P$ of
$P$ of ![]() $\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$ intersects non-trivially the strip
$\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})$ intersects non-trivially the strip ![]() $\mathbb {S}_{b^-,b^+}$. Similarly,
$\mathbb {S}_{b^-,b^+}$. Similarly, ![]() $\varepsilon (\underline {w}';\underline {t},\underline {\mathfrak {c}})=0$ if and only if the support
$\varepsilon (\underline {w}';\underline {t},\underline {\mathfrak {c}})=0$ if and only if the support ![]() $P'$ of
$P'$ of ![]() $\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ intersects non-trivially
$\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ intersects non-trivially ![]() $\mathbb {S}_{(b^-)',(b^+)'}$. We now observe that for
$\mathbb {S}_{(b^-)',(b^+)'}$. We now observe that for ![]() $j>0$ we have
$j>0$ we have ![]() $P\cap \mathbb {S}_{b^-,b^+}=P'\cap \mathbb {S}_{(b^-)',(b^+)'}$, whereas for
$P\cap \mathbb {S}_{b^-,b^+}=P'\cap \mathbb {S}_{(b^-)',(b^+)'}$, whereas for ![]() $j=0$ we have
$j=0$ we have ![]() $\tau (P\cap \mathbb {S}_{b^-,b^+},-t_1)=P'\cap \mathbb {S}_{(b^-)',(b^+)'}$. In particular, either intersection is empty if and only if the other is or, in other words,
$\tau (P\cap \mathbb {S}_{b^-,b^+},-t_1)=P'\cap \mathbb {S}_{(b^-)',(b^+)'}$. In particular, either intersection is empty if and only if the other is or, in other words, ![]() $\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})>0$ if and only if
$\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})>0$ if and only if ![]() $\varepsilon (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')>0$. In this case, however, we have that both
$\varepsilon (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')>0$. In this case, however, we have that both ![]() $\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})$ and
$\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})$ and ![]() $\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ coincide with the basepoint
$\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ coincide with the basepoint ![]() $\mathfrak {c}^{\mathrm {lr}}$ of
$\mathfrak {c}^{\mathrm {lr}}$ of ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, of
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, of ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) and, in particular, they are equal. This proves also the first statement of Proposition 4.15.
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$) and, in particular, they are equal. This proves also the first statement of Proposition 4.15.
From now on we assume ![]() $\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})=\varepsilon (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')=0$, allowing us to use the lower and upper barycentres instead of their
$\varepsilon (\underline {w};\underline {t},\underline {\mathfrak {c}})=\varepsilon (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')=0$, allowing us to use the lower and upper barycentres instead of their ![]() $\varepsilon$-variations in the computations of the rest of the argument. Note that
$\varepsilon$-variations in the computations of the rest of the argument. Note that ![]() $b-b^-=b'-(b^-)'$ and
$b-b^-=b'-(b^-)'$ and ![]() $b^+-b=(b^+)'-b'$. In particular, in the following we assume
$b^+-b=(b^+)'-b'$. In particular, in the following we assume ![]() $b^+-b^-=(b^+)'-(b^-)'>0$.
$b^+-b^-=(b^+)'-(b^-)'>0$.
First, we give an alternative description of the configuration ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$. We regard
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$. We regard ![]() $\mathfrak {c}_i$, for
$\mathfrak {c}_i$, for ![]() $1\leq i\leq p$, as a configuration in
$1\leq i\leq p$, as a configuration in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\mathring {{\mathcal {R}}}_{t_i})$ (in
$\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\mathring {{\mathcal {R}}}_{t_i})$ (in ![]() $\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$) and consider the configuration
$\mathrm {Hur}^{\mathbb {S}_{0,t_i}}(\breve {{\mathcal {R}}}_{t_i},\breve {\partial })$) and consider the configuration
 \begin{gather*} (\tau_{a_{i-1}-b^-})_*(\mathfrak{c}_i)\in\mathrm{Hur}^{\mathbb{S}_{a_{i-1}-b^-,a_i-b^-}}(\mathring{{\mathcal{R}}}_{t_i}+a_i-b^-)\\ \big(\text{respectively, }(\tau_{a_{i-1}-b^-})_*(\mathfrak{c}_i) \in \mathrm{Hur}^{\mathbb{S}_{a_{i-1}-b^-,a_i-b^-}}(\breve{{\mathcal{R}}}_{t_i}+a_i-b^-,\breve{\partial})\big). \end{gather*}
\begin{gather*} (\tau_{a_{i-1}-b^-})_*(\mathfrak{c}_i)\in\mathrm{Hur}^{\mathbb{S}_{a_{i-1}-b^-,a_i-b^-}}(\mathring{{\mathcal{R}}}_{t_i}+a_i-b^-)\\ \big(\text{respectively, }(\tau_{a_{i-1}-b^-})_*(\mathfrak{c}_i) \in \mathrm{Hur}^{\mathbb{S}_{a_{i-1}-b^-,a_i-b^-}}(\breve{{\mathcal{R}}}_{t_i}+a_i-b^-,\breve{\partial})\big). \end{gather*}
Using the disjoint union map ![]() $-\sqcup -$ from [Reference BianchiBia23a, Definition 3.16] we obtain a configuration
$-\sqcup -$ from [Reference BianchiBia23a, Definition 3.16] we obtain a configuration
which a priori belongs to
 \begin{gather*} \mathrm{Hur}^{\mathbb{S}_{a_0-b^-,a_p-b^-}}\big(\mathring{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\cdots\sqcup\mathring{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-\big)\\ \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{a_0-b^-,a_p-b^-}}\big(\breve{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\cdots\sqcup\breve{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-,\breve{\partial}\big)\big), \end{gather*}
\begin{gather*} \mathrm{Hur}^{\mathbb{S}_{a_0-b^-,a_p-b^-}}\big(\mathring{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\cdots\sqcup\mathring{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-\big)\\ \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{a_0-b^-,a_p-b^-}}\big(\breve{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\cdots\sqcup\breve{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-,\breve{\partial}\big)\big), \end{gather*}
but can be naturally considered as a configuration in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})$ (respectively,
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_{\mathbb {R}})$ (respectively, ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$). The equality
$\mathrm {Hur}(\breve {{\mathcal {R}}}_{\mathbb {R}},\breve {\partial })$). The equality ![]() $(\tau _{-b^-})_*(\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}}))=\mathfrak {c}$ follows directly from Definitions 2.11 and 4.6. It follows then from Definition 4.6 that
$(\tau _{-b^-})_*(\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}}))=\mathfrak {c}$ follows directly from Definitions 2.11 and 4.6. It follows then from Definition 4.6 that ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equal to
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ is equal to ![]() $\Lambda _*(\mathfrak {c}; {1}/({b^+-b^-}))$. In a similar way, we obtain a configuration
$\Lambda _*(\mathfrak {c}; {1}/({b^+-b^-}))$. In a similar way, we obtain a configuration
which we consider as a configuration in ![]() $\mathrm {Hur}(\mathring {{\mathcal {R}}}_\mathbb {R})$ (in
$\mathrm {Hur}(\mathring {{\mathcal {R}}}_\mathbb {R})$ (in ![]() $\mathrm {Hur}(\breve {{\mathcal {R}}}_\mathbb {R},\breve {\partial })$) and identifications
$\mathrm {Hur}(\breve {{\mathcal {R}}}_\mathbb {R},\breve {\partial })$) and identifications ![]() $\mathfrak {c}'=(\tau _{-(b^-)'})_*(\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}'))$ and
$\mathfrak {c}'=(\tau _{-(b^-)'})_*(\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}'))$ and ![]() $\hat {\mu }^b(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')=\Lambda _*(\mathfrak {c}'; {1}/({(b^+)'-(b^-)'}))$.
$\hat {\mu }^b(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')=\Lambda _*(\mathfrak {c}'; {1}/({(b^+)'-(b^-)'}))$.
Lemma A.7 The configurations ![]() $\mathfrak {c}$ and
$\mathfrak {c}$ and ![]() $\mathfrak {c}'$ agree on the vertical strip
$\mathfrak {c}'$ agree on the vertical strip ![]() $[0,b^+-b^-]\times \mathbb {R}$.
$[0,b^+-b^-]\times \mathbb {R}$.
Proof. We use Notation 2.2 and argue the statement differently, depending on the value of ![]() $j$.
$j$.
• If
 $1\leq j\leq p-1$, then
$1\leq j\leq p-1$, then  $\mathfrak {c}=\mathfrak {c}'$.
$\mathfrak {c}=\mathfrak {c}'$.• If
 $j=0$, note that
$j=0$, note that  $a_1-b^-=a'_0-(b^-)'\ge 0$ and
$a_1-b^-=a'_0-(b^-)'\ge 0$ and  $a_p-b^-=a'_{p-1}-(b^-)'\ge b^+-b^-$; then both
$a_p-b^-=a'_{p-1}-(b^-)'\ge b^+-b^-$; then both  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ can be regarded as configurations in
and the restriction map
$\mathfrak {c}'$ can be regarded as configurations in
and the restriction map \begin{gather*} \mathrm{Hur}(\mathring{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-),\\ \big(\text{respectively, }\mathrm{Hur}(\breve{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\breve{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-,\breve{\partial})\big), \end{gather*}
\begin{gather*} \mathrm{Hur}(\mathring{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-),\\ \big(\text{respectively, }\mathrm{Hur}(\breve{{\mathcal{R}}}_{t_1}+a_0-b^-\sqcup\breve{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-,\breve{\partial})\big), \end{gather*}
 $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{a_1-b^-,a_p-b^-}}$ from [Reference BianchiBia23a, Definition 3.15] sends
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{a_1-b^-,a_p-b^-}}$ from [Reference BianchiBia23a, Definition 3.15] sends  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ to the same configuration in the space
this common image is essentially the configuration
$\mathfrak {c}'$ to the same configuration in the space
this common image is essentially the configuration \[ \mathrm{Hur}^{\mathbb{S}_{a_1-b^-,a_p-b^-}}(\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-)\quad \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{a_1-b^-,\infty}}(\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-)\big); \]
\[ \mathrm{Hur}^{\mathbb{S}_{a_1-b^-,a_p-b^-}}(\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-)\quad \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{a_1-b^-,\infty}}(\mathring{{\mathcal{R}}}_{a_p-a_1}+a_1-b^-)\big); \]
 $\mathfrak {c}'$. Now we use that
$\mathfrak {c}'$. Now we use that  $\mathbb {S}_{0,b^+-b^-}\subset \mathbb {S}_{a_1-b^-,a_p-b^-}$ to conclude that
$\mathbb {S}_{0,b^+-b^-}\subset \mathbb {S}_{a_1-b^-,a_p-b^-}$ to conclude that  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ also agree on
$\mathfrak {c}'$ also agree on  $\mathbb {S}_{0,b^+-b^-}$ and, finally, we note that agreeing on
$\mathbb {S}_{0,b^+-b^-}$ and, finally, we note that agreeing on  $\mathbb {S}_{0,b^+-b^-}$ is equivalent to agreeing on
$\mathbb {S}_{0,b^+-b^-}$ is equivalent to agreeing on  $[0,b^+-b^-]\times \mathbb {R}$, as all configurations are supported in
$[0,b^+-b^-]\times \mathbb {R}$, as all configurations are supported in  $\mathbb {H}$.
$\mathbb {H}$.• If
 $j=p$, note that
$j=p$, note that  $a_0=a'_0$,
$a_0=a'_0$,  $b^-=(b^-)'$ and
$b^-=(b^-)'$ and  $b^+=(b^+)'\le a_{p-1}=a'_{p-1}$; then both
$b^+=(b^+)'\le a_{p-1}=a'_{p-1}$; then both  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ can be regarded as configurations in
and
$\mathfrak {c}'$ can be regarded as configurations in
and \begin{gather*} \mathrm{Hur}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-\sqcup\mathring{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-),\\ \big(\text{respectively, }\mathrm{Hur}(\breve{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-\sqcup\breve{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-,\breve{\partial})\big), \end{gather*}
\begin{gather*} \mathrm{Hur}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-\sqcup\mathring{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-),\\ \big(\text{respectively, }\mathrm{Hur}(\breve{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-\sqcup\breve{{\mathcal{R}}}_{t_p}+a_{p-1}-b^-,\breve{\partial})\big), \end{gather*}
 $\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{a_0-b^-,a_{p-1}-b^-}}$ sends
$\mathfrak {i}^{\mathbb {C}}_{\mathbb {S}_{a_0-b^-,a_{p-1}-b^-}}$ sends  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ to the same configuration in the space
this common image is essentially the configuration
$\mathfrak {c}'$ to the same configuration in the space
this common image is essentially the configuration \begin{gather*} \mathrm{Hur}^{\mathbb{S}_{-\infty,a_{p-1}-b^-}}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-)\\ \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{-\infty,a_{p-1}-b^-}}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-)\big)\!; \end{gather*}
\begin{gather*} \mathrm{Hur}^{\mathbb{S}_{-\infty,a_{p-1}-b^-}}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-)\\ \big(\text{respectively, }\mathrm{Hur}^{\mathbb{S}_{-\infty,a_{p-1}-b^-}}(\mathring{{\mathcal{R}}}_{a_{p-1}}+a_0-b^-)\big)\!; \end{gather*}
 $\mathfrak {c}'$. Now we use that
$\mathfrak {c}'$. Now we use that  $\mathbb {S}_{0,b^+-b^-}\subset \mathbb {S}_{a_0-b^-,a_{p-1}-b^-}$ to conclude that
$\mathbb {S}_{0,b^+-b^-}\subset \mathbb {S}_{a_0-b^-,a_{p-1}-b^-}$ to conclude that  $\mathfrak {c}$ and
$\mathfrak {c}$ and  $\mathfrak {c}'$ also agree on
$\mathfrak {c}'$ also agree on  $\mathbb {S}_{0,b^+-b^-}$ and again we note that agreeing on
$\mathbb {S}_{0,b^+-b^-}$ and again we note that agreeing on  $\mathbb {S}_{0,b^+-b^-}$ is equivalent to agreeing on
$\mathbb {S}_{0,b^+-b^-}$ is equivalent to agreeing on  $[0,b^+-b^-]\times \mathbb {R}$.
$[0,b^+-b^-]\times \mathbb {R}$.
By applying ![]() $\Lambda _*(-; {1}/({b^+-b^-}))=\Lambda _*(-; {1}/({(b^+)'-(b^-)'}))$ we obtain that, in a similar way,
$\Lambda _*(-; {1}/({b^+-b^-}))=\Lambda _*(-; {1}/({(b^+)'-(b^-)'}))$ we obtain that, in a similar way, ![]() $\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and
$\hat {\mu }^b(\underline {w};\underline {t},\underline {\mathfrak {c}})$ and ![]() $\hat {\mu }^b(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ agree on the vertical strip
$\hat {\mu }^b(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ agree on the vertical strip ![]() $[0,1]\times \mathbb {R}$.
$[0,1]\times \mathbb {R}$.
Note that the vertical strip ![]() $[0,1]\times \mathbb {R}$ is preserved by the homotopies
$[0,1]\times \mathbb {R}$ is preserved by the homotopies ![]() $\kappa ^-,\kappa ^+$ and
$\kappa ^-,\kappa ^+$ and ![]() ${\mathcal {H}}^{\diamond }$ at all times and the homotopies
${\mathcal {H}}^{\diamond }$ at all times and the homotopies ![]() $\kappa ^-,\kappa ^+$ restrict even to the identity on
$\kappa ^-,\kappa ^+$ restrict even to the identity on ![]() $[0,1]\times \mathbb {R}$. This, together with Lemma 4.12, implies that
$[0,1]\times \mathbb {R}$. This, together with Lemma 4.12, implies that ![]() $\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}\mathfrak {c}:=\tilde \sigma (w_i;t_i,\mathfrak {c}_i)$ and
$\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}\mathfrak {c}:=\tilde \sigma (w_i;t_i,\mathfrak {c}_i)$ and ![]() $\tilde {\mathfrak {c}}':=\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(w'_i;t'_i,\mathfrak {c}'_i)$ are both supported on the set
$\tilde {\mathfrak {c}}':=\hat {\mu }^{\diamond }_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}(w'_i;t'_i,\mathfrak {c}'_i)$ are both supported on the set ![]() $\tilde P:={\mathcal {H}}^{\diamond }_1(P)\cup \breve {\partial }\breve {\diamond }^{\mathrm {lr}}$. Let
$\tilde P:={\mathcal {H}}^{\diamond }_1(P)\cup \breve {\partial }\breve {\diamond }^{\mathrm {lr}}$. Let ![]() $\tilde k=|\tilde P|$ and
$\tilde k=|\tilde P|$ and ![]() $\tilde l=|P\setminus \partial \diamond |$.
$\tilde l=|P\setminus \partial \diamond |$.
Recall that ![]() $\tilde {\mathfrak {c}}=(\tilde P,\tilde \psi,\tilde \varphi )$ and
$\tilde {\mathfrak {c}}=(\tilde P,\tilde \psi,\tilde \varphi )$ and ![]() $\tilde {\mathfrak {c}}'=(\tilde P,\tilde \psi ',\tilde \varphi ')$ are configurations in
$\tilde {\mathfrak {c}}'=(\tilde P,\tilde \psi ',\tilde \varphi ')$ are configurations in ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (in
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$ (in ![]() $\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$). We can choose an lr-based admissible generating set
$\mathrm {Hur}(\diamond,\partial )_{\breve {\partial }\breve {\diamond }^{\mathrm {lr}}}$). We can choose an lr-based admissible generating set ![]() $\tilde {f}_1,\ldots,\tilde {f}_{\tilde k}$ of
$\tilde {f}_1,\ldots,\tilde {f}_{\tilde k}$ of ![]() $\mathfrak {G}(\tilde P)$ (see [Reference BianchiBia23a, Definition 6.10]) with the following properties:
$\mathfrak {G}(\tilde P)$ (see [Reference BianchiBia23a, Definition 6.10]) with the following properties:
• two generators, denoted
 $\tilde {f}^{\mathrm {l}}$ and
$\tilde {f}^{\mathrm {l}}$ and  $\tilde {f}^{\mathrm {r}}$, are represented by loops spinning clockwise around
$\tilde {f}^{\mathrm {r}}$, are represented by loops spinning clockwise around  $z_{\diamond }^{\mathrm {l}}$ and
$z_{\diamond }^{\mathrm {l}}$ and  $z_{\diamond }^{\mathrm {r}}$, respectively;
$z_{\diamond }^{\mathrm {r}}$, respectively;• the other generators are represented by loops contained in the strip
 $[0,1]\times \mathbb {R}$; in particular, we assume that
$[0,1]\times \mathbb {R}$; in particular, we assume that  $\tilde {f}_1,\ldots,\tilde {f}_{\tilde l}$ correspond to points in
$\tilde {f}_1,\ldots,\tilde {f}_{\tilde l}$ correspond to points in  $P\setminus \partial \diamond$.
$P\setminus \partial \diamond$.
Since ![]() $\tilde {\mathfrak {c}}$ and
$\tilde {\mathfrak {c}}$ and ![]() $\tilde {\mathfrak {c}}'$ agree on
$\tilde {\mathfrak {c}}'$ agree on ![]() $[0,1]\times \mathbb {R}$, we have that
$[0,1]\times \mathbb {R}$, we have that ![]() $\tilde \psi$ and
$\tilde \psi$ and ![]() $\tilde \psi '$ agree on the admissible generators
$\tilde \psi '$ agree on the admissible generators ![]() $\tilde {f}_1,\ldots,\tilde {f}_{\tilde l}$, whereas
$\tilde {f}_1,\ldots,\tilde {f}_{\tilde l}$, whereas ![]() $\tilde \varphi$ and
$\tilde \varphi$ and ![]() $\tilde \varphi '$ agree on all admissible generators
$\tilde \varphi '$ agree on all admissible generators ![]() $\tilde {f}_1,\ldots,\tilde {f}_{\tilde k}$ except, possibly, the two generators
$\tilde {f}_1,\ldots,\tilde {f}_{\tilde k}$ except, possibly, the two generators ![]() $\tilde {f}^{\mathrm {l}}$ and
$\tilde {f}^{\mathrm {l}}$ and ![]() $\tilde {f}^{\mathrm {r}}$. It follows that
$\tilde {f}^{\mathrm {r}}$. It follows that ![]() $\tilde {\mathfrak {c}}$ and
$\tilde {\mathfrak {c}}$ and ![]() $\tilde {\mathfrak {c}}'$ have the same image in the quotient
$\tilde {\mathfrak {c}}'$ have the same image in the quotient ![]() $\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively,
$\mathrm {Hur}(\breve {\diamond }^{\mathrm {lr}},\breve {\partial })_{G,G^{\rm op}}$ (respectively, ![]() $\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$), i.e.
$\mathrm {Hur}(\diamond,\partial )_{G,G^{\rm op}}$), i.e. ![]() $\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. This concludes the proof that
$\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. This concludes the proof that ![]() $\check \sigma$ descends to a map
$\check \sigma$ descends to a map ![]() $\sigma$ defined on
$\sigma$ defined on ![]() $B\mathring {\mathrm {HM}}$ (on
$B\mathring {\mathrm {HM}}$ (on ![]() $B\breve {\mathrm {HM}}$).
$B\breve {\mathrm {HM}}$).
For the second statement of the proposition, let ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2 and assume
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ be as in Notation 4.2 and assume ![]() $(t_j,\mathfrak {c}_j)=(0,(\emptyset,\mathbb {1},\mathbb {1}))$ for a fixed
$(t_j,\mathfrak {c}_j)=(0,(\emptyset,\mathbb {1},\mathbb {1}))$ for a fixed ![]() $0\leq j\leq p$; let
$0\leq j\leq p$; let ![]() $(\underline {t}',\underline {\mathfrak {c}}')=d_j(\underline {t},\underline {\mathfrak {c}})$, so that vice versa
$(\underline {t}',\underline {\mathfrak {c}}')=d_j(\underline {t},\underline {\mathfrak {c}})$, so that vice versa ![]() $(\underline {t},\underline {\mathfrak {c}})=s_j(\underline {t}',\underline {\mathfrak {c}}')$ and let
$(\underline {t},\underline {\mathfrak {c}})=s_j(\underline {t}',\underline {\mathfrak {c}}')$ and let ![]() $\underline {w}'$ be obtained from
$\underline {w}'$ be obtained from ![]() $\underline {w}$ by replacing the consecutive entries
$\underline {w}$ by replacing the consecutive entries ![]() $w_j$ and
$w_j$ and ![]() $w_{j+1}$ with their sum
$w_{j+1}$ with their sum ![]() $w_j+w_{j+1}$; present
$w_j+w_{j+1}$; present ![]() $\underline {w}'$ as
$\underline {w}'$ as ![]() $(w'_0,\ldots,w'_{p-1})$,
$(w'_0,\ldots,w'_{p-1})$, ![]() $\underline {t}'$ as
$\underline {t}'$ as ![]() $(t'_1,\ldots,t'_{p-1})$ and
$(t'_1,\ldots,t'_{p-1})$ and ![]() $\underline {\mathfrak {c}}'$ as
$\underline {\mathfrak {c}}'$ as ![]() $(\mathfrak {c}'_1,\ldots,\mathfrak {c}'_{p-1})$. We want to prove that
$(\mathfrak {c}'_1,\ldots,\mathfrak {c}'_{p-1})$. We want to prove that ![]() $\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$: this implies that
$\check \sigma (\underline {w};\underline {t},\underline {\mathfrak {c}})=\check \sigma (\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$: this implies that ![]() $\check \sigma$ descends to a map
$\check \sigma$ descends to a map ![]() $\sigma$ defined on
$\sigma$ defined on ![]() $B\mathring {\mathrm {HM}}$ (on
$B\mathring {\mathrm {HM}}$ (on ![]() $B\breve {\mathrm {HM}}$).
$B\breve {\mathrm {HM}}$).
For this it suffices to note that ![]() $\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})=\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ and also the barycentres
$\hat {\mu }(\underline {w};\underline {t},\underline {\mathfrak {c}})=\hat {\mu }(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$ and also the barycentres ![]() $b,b^-,b^+$ are equal when computed with respect to
$b,b^-,b^+$ are equal when computed with respect to ![]() $(\underline {w};\underline {t},\underline {\mathfrak {c}})$ or
$(\underline {w};\underline {t},\underline {\mathfrak {c}})$ or ![]() $(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. The formula for
$(\underline {w}';\underline {t}',\underline {\mathfrak {c}}')$. The formula for ![]() $\check \sigma$ only depends on these parameters.
$\check \sigma$ only depends on these parameters.