1. CORRECTIONS TO SECTION 4
The version of this manuscript originally published contained a sign error that appears at the re-transformation of the equations into laboratory frame in Section 4. The correctly re-transformed Eq. (8) reads:
and subsequently Eq. (9) is:
 $$k = \pm \displaystyle{{\rm \omega} \over c}\sqrt {1 - \displaystyle{{1 + u_{\rm e}^1 /c} \over {1 - u_{\rm e}^1 /c}}\displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \omega} ^2}}}.$$
$$k = \pm \displaystyle{{\rm \omega} \over c}\sqrt {1 - \displaystyle{{1 + u_{\rm e}^1 /c} \over {1 - u_{\rm e}^1 /c}}\displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \omega} ^2}}}.$$The sign error in the original letter also led to a misinterpretation: The Doppler-shifting does not limit the maximum velocity, achieved by the RPA, but it has impact on the admissible lower target thickness. Re-arranging the corrected Eq. (11) for d 0 yields:
 $$\eqalign{d_0{\rm \gg} & \displaystyle{{c{\rm \varkappa} _{\rm e}} \over {\rm \omega}} \left( {\displaystyle{{1 + u_{\rm e}^1 /c} \over {1 - u_{\rm e}^1 /c}}\displaystyle{{{\rm \varkappa} _{\rm e}{\rm \omega} _{{\rm pe},0}^2} \over {{\rm \omega} ^2}} - 1} \right)^{ - 1/2} \cr \approx & \displaystyle{{c\sqrt {{\rm \varkappa} _{\rm e}}} \over {{\rm \omega} _{{\rm pe},0}}}\sqrt {\displaystyle{{1 - u_{\rm e}^1 /c} \over {1 + u_{\rm e}^1 /c}}},}$$
$$\eqalign{d_0{\rm \gg} & \displaystyle{{c{\rm \varkappa} _{\rm e}} \over {\rm \omega}} \left( {\displaystyle{{1 + u_{\rm e}^1 /c} \over {1 - u_{\rm e}^1 /c}}\displaystyle{{{\rm \varkappa} _{\rm e}{\rm \omega} _{{\rm pe},0}^2} \over {{\rm \omega} ^2}} - 1} \right)^{ - 1/2} \cr \approx & \displaystyle{{c\sqrt {{\rm \varkappa} _{\rm e}}} \over {{\rm \omega} _{{\rm pe},0}}}\sqrt {\displaystyle{{1 - u_{\rm e}^1 /c} \over {1 + u_{\rm e}^1 /c}}},}$$ where the last term holds true for
ωpe,0 ≫ ω. Therefore, Eqs (12) and
(13) in the original manuscript are obsolete, such as Figure 3. The correct
interpretation is given in Figures 1 and
2: Figure 1 shows the lower limit for the initial target width as a
function of the compression achieved at the RPA: The target thickness scales with ![]() $d \propto {\rm \varkappa} _{\rm e}^{ - 1} $, whereas the penetration depth scales with
$d \propto {\rm \varkappa} _{\rm e}^{ - 1} $, whereas the penetration depth scales with ![]() ${\rm \delta} \propto {\rm \varkappa} _{\rm e}^{ - 1/2} $ and it is:
${\rm \delta} \propto {\rm \varkappa} _{\rm e}^{ - 1/2} $ and it is: ![]() $d/{\rm \delta} \propto {\rm \varkappa} _{\rm e}^{ - 1/2} $.
$d/{\rm \delta} \propto {\rm \varkappa} _{\rm e}^{ - 1/2} $.
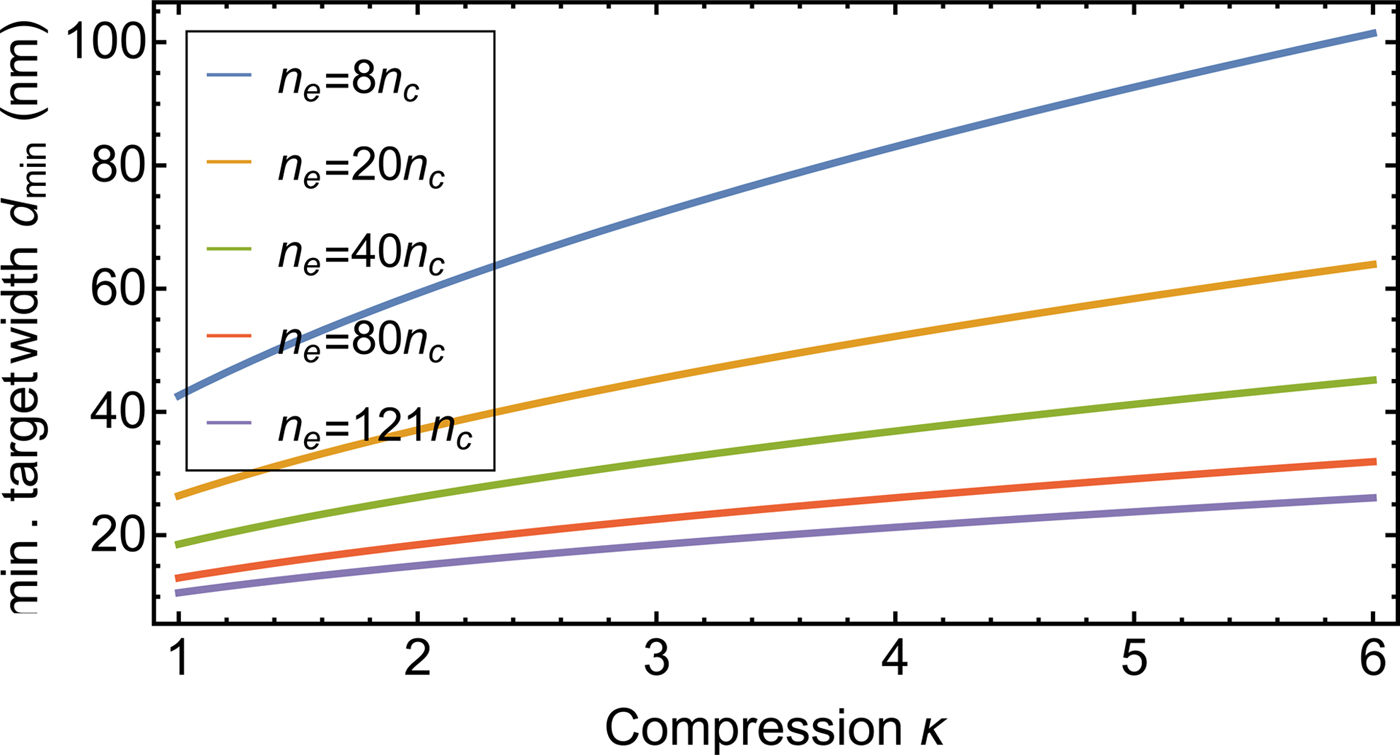
Fig. 1. Minimum admissible target width from Eq. (3) as a function of the compression ϰe, for different initial densities with β = 0.3.
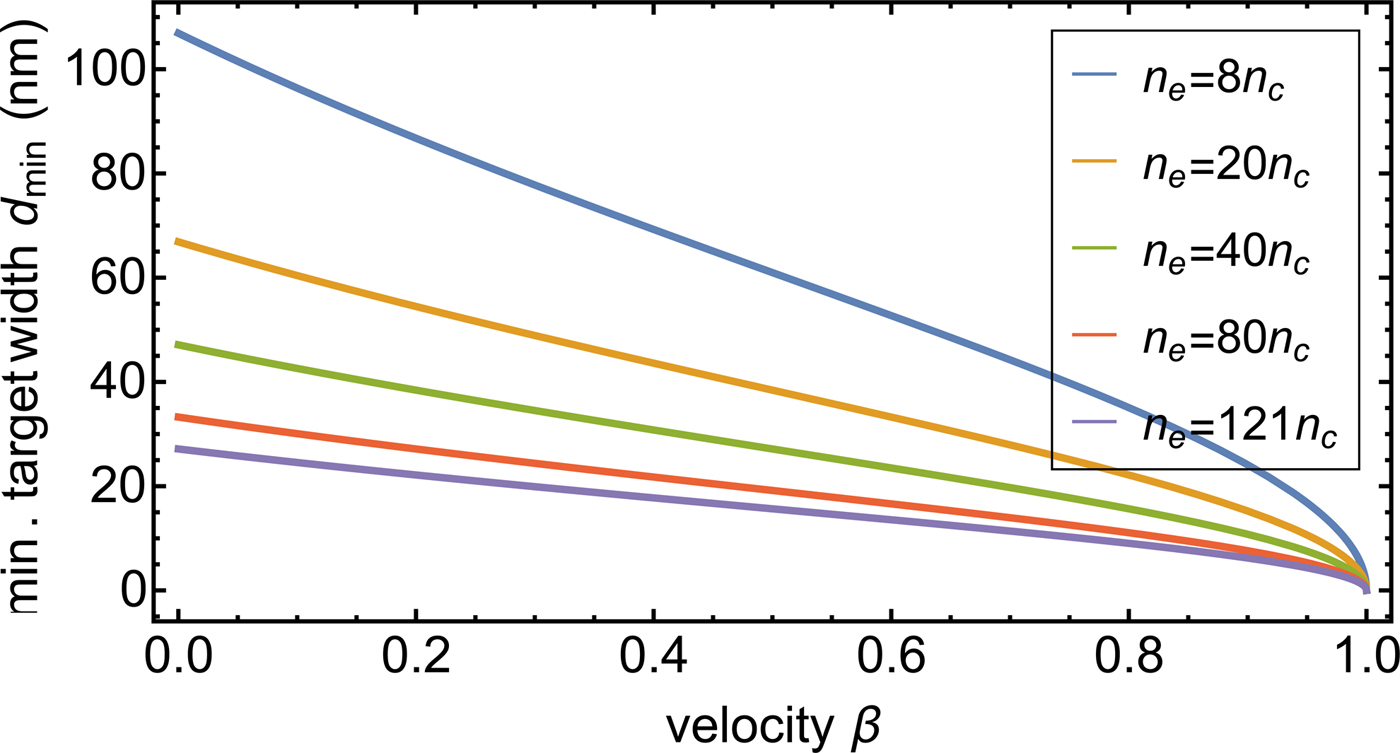
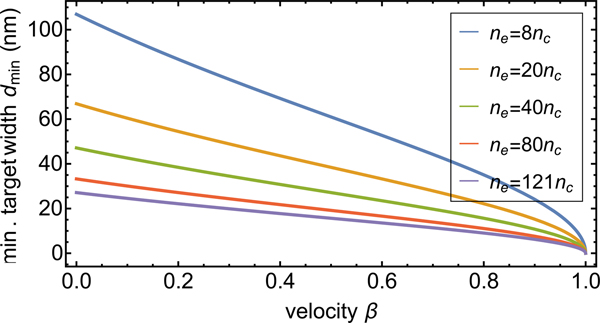
Fig. 2. Minimum admissible target width from Eq. (3) as a function of the
longitudinal velocity ![]() ${\rm \beta} = u_{\rm e}^1 /c$, for different initial densities
with ϰe = 3.5.
${\rm \beta} = u_{\rm e}^1 /c$, for different initial densities
with ϰe = 3.5.
This effect is countered by the Doppler-shifting, as depicted in Figure 2: With increasing velocity, the laser frequency
decreases due to the Doppler-shifting and the limit for the target width decreases.
At the RPA, both effects compete and for β ≪ 1, the
lower target width is ![]() $d_0 \approx (1 + {\rm \beta} ){\rm \varkappa} _{\rm e}^{ - 1/2} $.
$d_0 \approx (1 + {\rm \beta} ){\rm \varkappa} _{\rm e}^{ - 1/2} $.
Here, the average longitudinal velocity ![]() ${\rm \beta} = u_{\rm e}^1 /c$ can be calculated from the prevalent model of a
flying mirror (see, e.g. Macchi et al., 2009), whereas the
evaluation of the compression ϰe requires a more extensive model
(see, e.g. Schmidt & Boine-Frankenheim, 2016).
${\rm \beta} = u_{\rm e}^1 /c$ can be calculated from the prevalent model of a
flying mirror (see, e.g. Macchi et al., 2009), whereas the
evaluation of the compression ϰe requires a more extensive model
(see, e.g. Schmidt & Boine-Frankenheim, 2016).