MAXIMAL TOWERS AND ULTRAFILTER BASES IN COMPUTABILITY THEORY

Abstract

The tower number 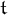${\mathfrak t}$ and the ultrafilter number 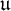$\mathfrak {u}$ are cardinal characteristics from set theory. They are based on combinatorial properties of classes of subsets of 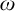$\omega $ and the almost inclusion relation 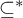$\subseteq ^*$ between such subsets. We consider analogs of these cardinal characteristics in computability theory.

We say that a sequence 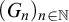$(G_n)_{n \in {\mathbb N}}$ of computable sets is a tower if 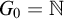$G_0 = {\mathbb N}$, 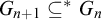$G_{n+1} \subseteq ^* G_n$, and 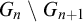$G_n\smallsetminus G_{n+1}$ is infinite for each n. A tower is maximal if there is no infinite computable set contained in all 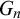$G_n$. A tower 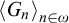${\left \langle {G_n}\right \rangle }_{n\in \omega }$ is an ultrafilter base if for each computable R, there is n such that 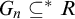$G_n \subseteq ^* R$ or 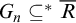$G_n \subseteq ^* \overline R$; this property implies maximality of the tower. A sequence 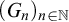$(G_n)_{n \in {\mathbb N}}$ of sets can be encoded as the “columns” of a set 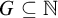$G\subseteq \mathbb N$. Our analogs of 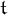${\mathfrak t}$ and 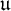${\mathfrak u}$ are the mass problems of sets encoding maximal towers, and of sets encoding towers that are ultrafilter bases, respectively. The relative position of a cardinal characteristic broadly corresponds to the relative computational complexity of the mass problem. We use Medvedev reducibility to formalize relative computational complexity, and thus to compare such mass problems to known ones.

We show that the mass problem of ultrafilter bases is equivalent to the mass problem of computing a function that dominates all computable functions, and hence, by Martin’s characterization, it captures highness. On the other hand, the mass problem for maximal towers is below the mass problem of computing a non-low set. We also show that some, but not all, noncomputable low sets compute maximal towers: Every noncomputable (low) c.e. set computes a maximal tower but no 1-generic 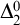$\Delta ^0_2$-set does so.

We finally consider the mass problems of maximal almost disjoint, and of maximal independent families. We show that they are Medvedev equivalent to maximal towers, and to ultrafilter bases, respectively.

1 Introduction

Cardinal characteristics measure how far the set-theoretic universe deviates from satisfying the continuum hypothesis. They are natural cardinals greater than $\aleph _0$ and at most $2^{\aleph _0}$ . For instance, the bounding number $\mathfrak {b}$ is the least size of a collection of functions $f\colon \omega \to \omega $ such that no single function dominates the entire collection. ¹ Related is the dominating number $\mathfrak {d}$ , the least size of a collection of functions $f\colon \omega \to \omega $ such that every function is dominated by some function in the collection. Here, for functions $f, g \colon \omega \to \omega $ , we say that g dominates f if $g(n) \ge f(n)$ for sufficiently large n. An important program in set theory is to prove less than or equal-relations between characteristics in ZFC, and to separate them in suitable forcing extensions.

Analogs of cardinal characteristics in computability theory were first studied by Rupprecht [15, 16] and further investigated by Brendle, Brooke-Taylor, Ng, and Nies [2]. An article by Greenberg, Kuyper, and Turetsky [6], in part based on Rupprecht’s work, provides a systematic approach to the two connected settings of set theory and computability, at least for certain types of cardinal characteristics. The relevant characteristics are given by binary relations, such as the domination relation $\le ^*$ between functions; their computability-theoretic analogs are ordered by reducibilities that measure relative computability. A well-understood example of this is how the relation $\le ^*$ gives rise to the bounding number $\mathfrak {b}(\le ^*)$ and the dominating number $\mathfrak {d}(\le ^*)$ , and their analogs in computability, which are highness and having hyperimmune degree. A general reference in set theory is the survey paper by Blass [1]. The brief survey by Soukup [19] contains a diagram displaying the ZFC inequalities between the most important characteristics in this setting, along with $\mathfrak {b}(\le ^*)$ and $\mathfrak {d}(\le ^*)$ .

In this paper, we consider cardinal characteristics that do not fit into the framework of Rupprecht, and Greenberg, Kuyper, and Turetsky [6]. In particular, we initiate the study of the computability-theoretic analogs of the ultrafilter, tower, and independence numbers. These characteristics are defined in the setting of subsets of $\omega $ up to almost inclusion $\subseteq ^*$ ; we give definitions below.

The ultrafilter number $\mathfrak {u}$ is the least size of a subset of $[\omega ]^{\omega }$ with upward closure a nonprincipal ultrafilter on $\omega $ . We note that one cannot in general require here that the subset is linearly ordered by $\subseteq ^*$ : Recall that an ultrafilter F on $\omega $ is a P-point if for each partition ${\left \langle {C_n}\right \rangle }$ of $\omega $ such that $C_n \not \in F$ for each n, there is $A \in F$ such that $C_n \cap A$ is finite for each n. An ultrafilter with a linear base is a P-point. Shelah (see Wimmers [20]) has shown that it is consistent with ZFC that there are no P-points. So it is consistent with ZFC that the version of $\mathfrak {u}$ relying on linear bases would be undefined.

The tower number ${\mathfrak t}$ is the minimum size of a subset of $[\omega ]^{\omega }$ that is linearly ordered by $\subseteq ^*$ and cannot be extended by adding a new element below all given elements. To define the pseudointersection number ${\mathfrak p}$ , the requirement in the definition of towers that the sets in the class be linearly ordered under $\subseteq ^*$ is weakened to requiring that every finite subset of the class has an infinite intersection. So, trivially, ${\mathfrak p} \le {\mathfrak t}$ . In celebrated work, Malliaris and Shelah [12] showed (in ZFC) that ${\mathfrak p} = {\mathfrak t}$ (see also [19]). It is not hard to see that ZFC proves ${\mathfrak t} \le \mathfrak {u} $ . It is consistent that ${\mathfrak t} < \mathfrak {u} $ (see [1] for both statements).

A class $\mathcal {C}$ of subsets of $\omega $ is independent if any intersection of finitely many sets in $\mathcal {C}$ or their complements is infinite. The independence number ${\mathfrak i}$ is the least cardinal of a maximal independent family. There has been much work recently on ${\mathfrak i}$ in set theory, in particular, the descriptive complexity of maximal independent families, such as in Brendle, Fischer, and Khomskii [3].

1.1 Comparing the complexity of the analogs in computability

The main setting for our analogy is given by the Boolean algebra of computable sets modulo finite differences. We consider maximal towers, the closely related maximal almost disjoint sets, and thereafter ultrafilter bases and maximal independent sets. As already demonstrated in the above-mentioned papers [2, 6, 15, 16], the relative position of a cardinal characteristic tends to correspond to the relative computational complexity of the associated class of objects.

The usual formal definitions of computation relative to an oracle only directly apply to functions $f \colon \omega \to \omega $ , and hence to subsets of $\omega $ (simply called sets from now on), which can be identified with their characteristic functions. The complexity of other objects is studied indirectly, via names that are functions on $\omega $ giving discrete representations of the object in question. A particular choice of names has to be made. For instance, real numbers can be named by rapidly converging Cauchy sequences of rational numbers.

The witnesses for cardinal characteristics are always uncountable. In contrast, in our setting, the analogous objects are countable. They will be considered as sequences of sets rather than unordered collections. For, a single set X can be used as a name for such a sequence of sets: Let $X^{[n]}$ denote the “column” $ \{ u \colon \langle u, n \rangle \in X \}$ . ² To every set X, we can associate a sequence ${\left \langle {X_n}\right \rangle }_{n\in \omega }$ in a canonical way by setting $X_n = X^{[n]}$ . (When introducing terminology, we will sometimes ignore the difference between ${\left \langle {X_n}\right \rangle }_{n\in \omega }$ and X.) An alternate viewpoint is that a set X is a name for the unordered collection of sets in its coded sequence. Although such a name includes more information than is in the unordered family, this information is suppressed when we quantify over all names; our results can be read in this context.

With this naming system, one can now use sequences as oracles in computations. We view the combinatorial classes of sequences as mass problems. To measure their relative complexity, we compare them via Medvedev reducibility $\le _s$ : Let $\mathcal {C}$ and $\mathcal {D}$ be sets of functions on $\omega $ , also known as mass problems. One says that $\mathcal {C}$ is Medvedev reducible to $\mathcal {D}$ and writes $\mathcal {C}\le _s \mathcal {D}$ if there is a Turing functional $\Theta $ such that $\Theta ^g \in \mathcal {C}$ for each $g \in \mathcal {D}$ . Less formally, one says that functions in $\mathcal {D}$ uniformly compute functions in $\mathcal {C}$ . We will also refer to the weaker Muchnik reducibility: $\mathcal {C}\le _w \mathcal {D}$ if each function in $\mathcal {D}$ computes a function in $\mathcal {C}$ .

With subsequent research in mind, we will set up our framework to apply to general countable Boolean algebras rather than merely the Boolean algebra of the computable sets. Throughout, we fix a countable Boolean algebra ${\mathbb B}$ of subsets of $\omega $ closed under finite differences. Our basic objects will be sequences of sets in ${{\mathbb B}}$ . We will obtain meaningful results already when we fix a countable Turing ideal $\mathcal {I}$ and let ${{\mathbb B}}$ be the sets with degree in $\mathcal {I}$ . While we mainly study the case when ${{\mathbb B}}$ consists of the computable sets, in Section 6, we briefly consider two other cases: the K-trivial sets and the primitive recursive sets.

1.2 The mass problem $\mathcal {T}_{{\mathbb B}}$ of maximal towers

Definition 1.1. We say that a sequence ${\left \langle {G_n}\right \rangle }_{n\in \omega }$ of sets in ${{\mathbb B}}$ is a $\mathbb B$ -tower if $G_0= \omega $ , $G_{n+1} \subseteq ^* G_n$ , and $G_n\smallsetminus G_{n+1}$ is infinite for each n. If ${{\mathbb B}}$ consists of the computable sets, we use the term tower of computable sets.

Definition 1.2. We say that a function p is associated with a tower G if p is strictly increasing and $p(n ) \in \bigcap _{i\le n} G_i$ for each n.

The following fact is elementary.

Fact 1.3. A tower G uniformly computes a function p associated with it.

Proof Let $\Phi $ be the Turing functional such that $\Phi ^G(0) = \min (G_0)$ , and ${\Phi ^G(n+1)}$ is the least number in $\bigcap _{i\le n+1} G_i$ greater than $\Phi ^G(n)$ . This $\Phi $ establishes the required uniform reduction.

Definition 1.4. Given a countable Boolean algebra ${{\mathbb B}}$ of sets, the mass problem $\mathcal {T}_{{\mathbb B}}$ is the class of sets G such that ${\left \langle {G_n}\right \rangle }_{n\in \omega }$ is a ${{\mathbb B}}$ -tower that is maximal, i.e., such that for each infinite set $R \in {{\mathbb B}}$ , there is n such that $R\smallsetminus G_n $ is infinite.

Clearly, being maximal implies that no associated function is computable. In particular, a maximal tower is never computable. (Note that our notion of maximality only requires that the tower cannot be extended from below, in keeping with our set-theoretic analogy.)

1.3 The mass problem $\mathcal {U}_{{\mathbb B}}$ of ultrafilter bases

We now define the mass problem $\mathcal {U}_{{\mathbb B}}$ corresponding to the ultrafilter number. Since all filters of our Boolean algebras are countable, any base will compute a linearly ordered base by taking finite intersection. So for measuring the relative complexity via Medvedev reducibility, we can restrict ourselves to linearly ordered bases. Importantly, we require that each ultrafilter base is a tower; in particular, the difference between a set and its successor is infinite. (Asking that an ultrafilter base is linearly ordered is not always possible in the setting of set theory, as discussed in the introduction.)

Definition 1.5. Given a countable Boolean algebra ${{\mathbb B}}$ of sets, let $\mathcal {U}_{{\mathbb B}}$ be the class of sets $F $ such that F is a ${{\mathbb B}}$ -tower as in Definition 1.1 and for each set $R\in {{\mathbb B}}$ , there is n such that $F_n \subseteq ^* \overline R$ or $F_n \subseteq ^* R$ . We will call a set F in $\mathcal {U}_{{\mathbb B}}$ a ${{\mathbb B}}$ -ultrafilter base.

Each ultrafilter base is a maximal tower. In the cardinal setting, one has ${\mathfrak t} \le {\mathfrak u}$ . Correspondingly, since $\mathcal {U}_{{\mathbb B}} \subseteq \mathcal {T}_{{\mathbb B}}$ , we trivially have $\mathcal {T}_{{\mathbb B}} \le _s \mathcal {U}_{{{\mathbb B}}}$ via the identity reduction. The following indicates that for many natural Boolean algebras, ultrafilter bases necessarily have computational strength.

Proposition 1.6. Given a Turing ideal $\mathcal {K}$ , let ${{\mathbb B}}$ be the Boolean algebra of sets with degree in $\mathcal {K}$ . Then for each ${{\mathbb B}}$ -ultrafilter base F and associated function p in the sense of Definition 1.2, the function p is not dominated by a function with Turing degree in $\mathcal {K}$ .

Proof Assume that there is a function $f \ge p$ in $\mathcal {K}$ . The conditions $n_0=0$ and $n_{k+1} = f(n_k)+1$ define a sequence that is computable from some oracle in $\mathcal {K}$ , and for every k we have that $[n_k, n_{k+1})$ contains an element of $\bigcap _{i\leq k} F_i$ . So the set

$$\begin{align*}E= \bigcup_{i\in\omega}\; [n_{2i}, n_{2i+1}) \end{align*}$$

is in $\mathcal {K}$ , and clearly $F_n \not \subseteq ^* E$ and $F_n \not \subseteq ^* \overline E$ for each n. Therefore, F is not a ${{\mathbb B}}$ -ultrafilter base.

1.4 The Boolean algebra of computable sets

We finish the introduction by summarizing our results in the case that ${{\mathbb B}}$ is the Boolean algebra of all computable sets. By Theorem 3.1, every non-low set computes a set in $\mathcal {T}_{{\mathbb B}}$ , and this is uniform. This is not a characterization, however, because by Corollary 5.3, every noncomputable c.e. set computes a maximal tower. On the other hand, we know that there are noncomputable (necessarily low) sets that do not compute maximal towers; in particular, no 1-generic $\Delta ^0_2$ -set does so. This is because 1-generic $\Delta ^0_2$ -sets are index guessable by Theorem 3.4, and by Proposition 2.4, no index guessable set can compute a maximal tower. Here, an oracle G is index guessable if $\emptyset '$ can find a computable index for $\varphi _e^G$ uniformly in e, provided that $\varphi _e^G$ is computable. We do not know whether index guessability characterizes the oracles that are unable to compute a maximal tower. It seems unlikely; index guessability appears to be stronger than necessary.

As already mentioned, in the setting of cardinal characteristics, ${\mathfrak t} < {\mathfrak u}$ is consistent with ZFC. Since non-low oracles can be computably dominated, it follows from Proposition 1.6 that there is a member of $\mathcal {T}_{{\mathbb B}}$ that does not compute any member of $\mathcal {U}_{{\mathbb B}}$ . In other words, $\mathcal {U}_{{\mathbb B}} \not \le _w \mathcal {T}_{{\mathbb B}}$ in the case that ${{\mathbb B}}$ consists of the computable sets.

The separation above only uses the fact that members of $\mathcal {U}_{{\mathbb B}}$ are not computably dominated; in fact, they are high. As we show in Theorems 3.6 and 3.8, $\mathcal {U}_{{\mathbb B}}$ is Medvedev equivalent to the mass problem of dominating functions. In Section 4, we prove that the mass problem $\mathcal {I}_{{\mathbb B}}$ of maximal independent families is also Medvedev equivalent to the mass problem of dominating functions. Thus, in the case that ${{\mathbb B}}$ is the Boolean algebra of computable sets, we have $\mathcal {U}_{{\mathbb B}}\equiv _s\mathcal {I}_{{\mathbb B}}$ . Interestingly, we do not have a direct proof. Contrast this with the equivalence of $\mathcal {T}_{{\mathbb B}}$ and $\mathcal {A}_{{\mathbb B}}$ , the mass problem of maximal almost disjoint families; this equivalence is direct and holds for an arbitrary Boolean algebra, as we will see presently.

2 Basics of the mass problems $\mathcal {T}_{{\mathbb B}}$

2.1 The equivalent mass problems $\mathcal {T}_{{\mathbb B}}$ and $\mathcal {A}_{{\mathbb B}}$

Recall that in set theory, the almost disjointness number $\mathfrak a$ is the least possible size of a maximal almost disjoint (MAD) family of subsets of $\omega $ . In our analogous setting, we call a sequence ${\left \langle {F_n}\right \rangle }_{n\in \omega }$ of sets in ${{\mathbb B}}$ almost disjoint (AD) if each $F_n$ is infinite and $F_n \cap F_k $ is finite for distinct n and k.

Definition 2.1. In the context of a Boolean algebra ${{\mathbb B}}$ of sets, the mass problem $\mathcal {A}_{{\mathbb B}}$ is the class of sets F such that ${\left \langle {F_n}\right \rangle }_{n\in \omega }$ is a maximal almost disjoint (MAD) family in ${{\mathbb B}}$ . Namely, the sequence is AD, and for each infinite set $R \in {{\mathbb B}}$ , there is n such that $R\cap F_n $ is infinite.

Fact 2.2. $\mathcal {A}_{{\mathbb B}} \le _s \mathcal {T}_{{\mathbb B}} \le _s \mathcal {A}_{{\mathbb B}}$ .

Proof We suppress the subscript ${{\mathbb B}}$ . To check that $\mathcal {A} \le _s \mathcal {T}$ , given a set G, let $\mathrm {Diff}(G) $ be the set F such that $F_n = G_n\smallsetminus G_{n+1}$ for each n. Clearly, the operator $\mathrm {Diff} $ can be seen as a Turing functional. If G is a maximal ${{\mathbb B}}$ -tower, then $F=\mathrm {Diff}(G) $ is MAD. For, if $R\in {{\mathbb B}}$ is infinite, then $R\smallsetminus G_n$ is infinite for some n, and hence $R\cap F_i$ is infinite for some $i<n$ .

For $\mathcal {T} \le _s \mathcal {A}$ , given a set F, let $G =\mathrm {Cp}(F) $ be the set such that

$$\begin{align*}x \in G_n \leftrightarrow \forall i < n \, [ x \not \in F_n]. \end{align*}$$

Again, $\mathrm {Cp}$ is a Turing functional. If F is an almost disjoint family of sets from ${{\mathbb B}}$ , then G is a ${{\mathbb B}}$ -tower, and if F is MAD, then G is a maximal tower.

Recall that a maximal tower is not computable. Hence no MAD family is computable. (This corresponds to the cardinal characteristics being uncountable.)

2.2 Descriptive complexity and index complexity for maximal towers

For the rest of this section, as well as the subsequent three sections, we will mainly be interested in the case that ${{\mathbb B}}$ is the Boolean algebra of all computable sets. We will omit the parameter ${{\mathbb B}}$ when we name the mass problems. In the final section, we will consider other Boolean algebras.

Besides looking at the relative complexity of mass problems such as $\mathcal {T}$ and $\mathcal {U}$ , one can also look at the individual complexity of their members (as sets encoding sequences). Recall that a characteristic index for a set M is a number e such that $\chi _M= \varphi _e$ . The following two questions arise:

1. (1) How low in the arithmetical hierarchy can the set be located?

2. (2) How hard is it to find characteristic indices for the sequence members?

2.2.1 Arithmetical complexity

Fact 2.3. No maximal tower G is c.e., and no MAD set is co-c.e.

Proof For the first statement, note that otherwise, there is a computable function p associated with G in the sense of Definition 1.2. The range of p extends the tower G, contrary to its maximality.

For the second statement, note that the reduction $\mathrm {Cp}$ introduced in the proof of Fact 2.2 to show that $\mathcal {T} \le _s \mathcal {A}$ turns a co-c.e. set F into a c.e. set G.

We will return to Question (1) in Section 5, where we show that c.e. MAD sets exist in every nonzero c.e. Turing degree, and that some ultrafilter base is co-c.e.

2.2.2 Complexity of finding characteristic indices for the sequence members

In several constructions of towers ${\left \langle {G_n}\right \rangle }_{n\in \omega }$ below, such as in Corollary 5.3 and Theorem 5.4, the oracle $\emptyset "$ is able to compute, given n, a characteristic index for $G_n$ . The oracle $\emptyset '$ does not suffice by the following result.

Proposition 2.4. Suppose that $G $ is a maximal tower. There is no computation procedure with oracle ${\emptyset '} $ that computes, from input n, a characteristic index for $G_n$ .

Proof Assume the contrary. Then there is a computable function f such that $\varphi _{\lim _s f(n,s)}$ is the characteristic function of $G_n$ . Let $\widehat G$ be defined as follows. Given n and x, compute the least $s> x$ such that $\varphi _{f(n,s),s}(x) \downarrow $ . If the output is not $0$ , put x into $\widehat G_n$ . Clearly $\widehat G$ is computable. Since $G_n = ^* \widehat G_n$ for each n, $\widehat G$ is a maximal tower, contrary to Fact 2.3, or to the earlier observation that maximal towers cannot be computable.

3 Complexity of $\mathcal {T}$ and of $\mathcal {U}$

In this section, we compare our two principal mass problems, maximal towers and ultrafilter bases, to well-known benchmark mass problems: non-lowness and highness. We also define index guessability. No index guessable oracle computes a maximal tower. We show that every 1-generic $\Delta ^0_2$ -set is index guessable.

As we said above, we restrict ourselves to the case that ${{\mathbb B}}$ is the Boolean algebra of computable sets, and usually drop the subscripts ${{\mathbb B}}$ .

3.1 Maximal towers, non-lowness, and index guessability

We now show that each non-low oracle computes a set in $\mathcal {T}$ . The result is uniform in the sense of mass problems. Let NonLow denote the class of oracles Z such that $Z' \not \le _T \emptyset '$ .

Theorem 3.1. $\mathcal {T} \le _s \mathrm {NonLow}$ .

Proof In the following, x, y, and z denote binary strings; we identify such a string x with the number whose binary expansion is $1x$ . For example, the string $000$ is identified with 8, the number with binary representation $1000$ . Define a Turing functional $\Theta $ for the Medvedev reduction as follows: Set $\Theta ^Z = G$ , where for each n,

$$\begin{align*}G_n= \{x \colon \, n \le s:= |x| \land Z^{\prime}_s \operatorname{\mathrm{\upharpoonright}} n= x \operatorname{\mathrm{\upharpoonright}} n\}. \end{align*}$$

Here $Z'$ denotes the jump of Z, which is computably enumerated relative to Z in a standard way. Note that, for each n, for sufficiently large s, the string $Z^{\prime }_s \operatorname {\mathrm {\upharpoonright }} n$ settles. So it is clear that for each n, we have $G_{n+1} \subseteq ^* G_n$ and $G_n\smallsetminus G_{n+1}$ is infinite. Also $G_n$ is computable.

Suppose now that R is an infinite set such that $R \subseteq ^* G_n$ for each n. Then for each k,

$$\begin{align*}Z'(k)= \lim_{x \in G_k,|x|> k } x(k) = \lim_{x \in R,|x| > k } x(k), \end{align*}$$

and hence $Z'\le _T R'$ . So if $Z \in \mathrm {NonLow}$ , then R cannot be computable, and hence $\Theta ^Z \in \mathcal {T}$ .

Remark 3.2. The proof above yields a more general result. Suppose that $\mathcal K$ is a countable Turing ideal and ${{\mathbb B}}$ is the Boolean algebra of sets with degree in $\mathcal K$ . Then $\mathcal T_{{\mathbb B}} \le _s \mathrm {NonLow}_{\mathcal K}$ , where $\mathrm {NonLow}_{\mathcal K} : = \{ Z \colon \forall R \in \mathcal K \, [Z' \not \le _T R']\}$ .

We next introduce a property of oracles that we call index guessability; it implies that an oracle does not compute a maximal tower. As usual, let ${\left \langle {\Phi _e}\right \rangle }_{e\in \omega }$ be an effective list of the Turing functionals with one input, and write $\varphi _e $ for $\Phi _e^{\emptyset }$ . Note that if L is a $\Delta ^0_2$ -oracle, then $\emptyset "$ can compute from e a characteristic index for $\Phi _e^L$ in case that the function $\Phi _e^L$ is computable. To be index guessable means that ${\emptyset '} $ suffices.

Definition 3.3. We call an oracle L index guessable if ${\emptyset '}$ can compute from e an index for $\Phi _e^L $ whenever $\Phi _e^L$ is a computable function. In other words, there is a functional $\Gamma $ such that

$$ \begin{align*} \Phi_e^L \text{ is computable } \Rightarrow \Phi_e^L = \varphi_{\Gamma({\emptyset'};e)}. \end{align*} $$

No assumption is made on the convergence of $\Gamma ({\emptyset '};e)$ in case $\Phi _e^L$ is not a computable function.

Clearly, being index guessable is closed downward under $\le _T$ . A total function is computable if and only if its graph is computable, in a uniform way. So for index guessability of L, it suffices that there is a Turing functional $\Gamma $ such that $\Gamma ({\emptyset '};e)$ provides an index for $\Phi _e^L$ in case it is a computable $\{0,1\}$ -valued function.

Every index guessable oracle D is low. To see this, for $i \in \omega $ , let $B_i= \{t\colon i\in D^{\prime }_t\}$ . If $i \in D'$ then $B_i$ is cofinite, otherwise $B_i= \emptyset $ . There is a computable function g such that $\Phi _{g(i)}^D $ is the characteristic function of ${B_i}$ . To show that $D '\le _T {\emptyset '}$ , on input i, let $\emptyset '$ compute a computable index $r(i)$ for $B_i$ . Now use $\emptyset ' $ again to determine $\lim _k \varphi _{r(i)}(k)$ , which equals $D'(i)$ .

By Proposition 2.4, an index guessable oracle D does not compute a maximal tower. The following provides examples of such oracles.

Theorem 3.4. If L is $\Delta ^0_2$ and $1$ -generic, then L is index guessable.

Proof Suppose that $F = \Phi _e^L$ and F is a computable set. Let $S_e$ be the c.e. set of strings $\sigma $ above which there is a $\Phi _e$ -splitting in the sense that

$$\begin{align*}S_e = \{\sigma \colon (\exists p)(\exists \tau_1\succ\sigma) (\exists \tau_2\succ\sigma) \, \Phi_e^{\tau_1}(p)\neq \Phi_e^{\tau_2}(p)\}. \end{align*}$$

Suppose that $S_e$ is dense along L. Then we claim that the set

$$\begin{align*}C_e = \{\tau \colon (\exists p) \, \Phi_e^{\tau}(p)\neq F(p)\} \end{align*}$$

is also dense along L, i.e., for every k, there is some $\tau \succeq L\operatorname {\mathrm {\upharpoonright }} k$ such that $\tau \in C_e$ . Indeed, let $\sigma \succeq L\operatorname {\mathrm {\upharpoonright }} k$ be a member of $S_e$ and let p, $\tau _1$ , and $\tau _2$ witness this. Let $\tau _i$ for $i = 1$ or $2$ be such that $ \Phi _e^{\tau _i}(p)\neq F(p)$ . Then $\tau _i\succeq L\operatorname {\mathrm {\upharpoonright }} k$ is in $C_e$ . The set $C_e$ is c.e. and hence L meets $C_e$ , contradicting our assumption that $F = \Phi _e^L$ .

It follows that $S_e$ is not dense along L. In other words, there is some least $k_e$ such that there is no splitting of $\Phi _e$ above $L\operatorname {\mathrm {\upharpoonright }} k_e$ . On input e, the oracle $\emptyset '$ can compute $k_e$ and $L\operatorname {\mathrm {\upharpoonright }} k_e$ . This allows $\emptyset '$ to find an index for F, given by the following procedure: To compute $F(p)$ , find the least $\tau \succeq L\operatorname {\mathrm {\upharpoonright }} k_e$ such that $\Phi _e^{\tau }(p)\downarrow $ (in $|\tau |$ many steps). Such a $\tau $ exists because $\Phi _e^L(p)\downarrow $ . By our choice of $k_e$ , it follows that $\Phi _e^{\tau }(p) = \Phi _e^L(p) = F(p)$ .

We summarize the known implications:

$$ \begin{align*} \text{1-generic } \Delta^0_2 \ \Rightarrow \text{ index guessable } \Rightarrow \text{ computes no maximal tower } \Rightarrow \text{ low.} \end{align*} $$

The last implication cannot be reversed by Theorem 5.1; the others might. In particular, we ask whether any oracle that computes no maximal tower is index guessable. This would strengthen Theorem 3.1. Note that the following apparent weakening of index guessability of L still implies that the oracle L computes no maximal tower: For each $S \le _T L$ such that each $S^{[n]}$ is computable, there is a functional $\Gamma $ such that $ \varphi _{\Gamma ({\emptyset '};n)}$ is the characteristic function of $S^{[n]}$ . To see this, assume S is a maximal tower G. Such an S contradicts Proposition 2.4.

Aside. We pause briefly to mention a potential connection of our topic to computational learning theory. One says that a class S of computable functions is EX-learnable if there is a total Turing machine M such that $\lim _s M(f\operatorname {\mathrm {\upharpoonright }} s)$ exists for each $f\in S$ and is an index for f. For an oracle A, one says that S is EX $[A]$ -learnable if there is an oracle machine M that is total for each oracle and such that $\lim _s M^A(f\operatorname {\mathrm {\upharpoonright }} s)$ exists for each $f\in S$ and is an index for f. One calls an oracle A EX-trivial if EX = EX $[A]$ . Slaman and Solovay [17] showed that A is EX-trivial if and only if A is $\Delta ^0_2$ and has 1-generic degree. This used an earlier result of Haught [7] that the Turing degrees of the 1-generic $\Delta ^0_2$ -sets are closed downward.

3.2 Ultrafilter bases and highness

Let $\text {Tot} =\{e \colon \varphi _e\text { is total}\}$ . Let $\mathrm {DomFcn}$ denote the mass problem of functions h that dominate every computable function and also satisfy $h(s) \ge s$ for all s. Note that a set F is high if and only if $\text {Tot} \le _T F'$ . To represent highness by a mass problem in the Medvedev degrees, one can equivalently choose the set of functions dominating each computable function, or the set of approximations to $\text {Tot}$ , i.e., the $\{0,1\}$ -valued binary functions f such that $\lim _s f(e,s) = \text {Tot}(e)$ . This follows from the next fact; we omit the standard proof.

Fact 3.5. $\mathrm {DomFcn}$ is Medvedev equivalent to the mass problem of approximations to $\text {Tot}= \{e \colon \varphi _e\text { is total}\}$ .

We show that exactly the high oracles compute ultrafilter bases, and that the reductions are uniform. By Fact 3.5, it suffices to show that $\mathcal {U} \equiv _s \mathrm {DomFcn}$ . We will obtain the two Medvedev reductions through separate theorems, with proofs that are unrelated.

Theorem 3.6. Every ultrafilter base uniformly computes a dominating function. In other words, $\mathcal {U} \ge _s \mathrm {DomFcn}$ .

Our proof is directly inspired by a proof of Jockusch [8, Theorem 1, (iv) $\Rightarrow$ (i)], who showed that any family of sets containing exactly the computable sets must have high degree.

Lemma 3.7. There is a uniformly computable sequence $P_0, P_1,\dots $ of nonempty $\Pi ^0_1$ -classes such that for every e:

• • if $\varphi _e$ is total, then $P_e$ contains a single element, and

• • if $\varphi _e$ is not total, then $P_e$ contains only bi-immune elements.

Proof Note that each Martin-Löf (or even Kurtz) random set is bi-immune: For an infinite computable set R, the class of sets containing R is a $\Pi ^0_{1}$ -null class and hence determines a Kurtz test. A similar fact holds for the class of sets disjoint from R.

For each s, let $n_s$ be the largest number such that $\varphi _{e,s}$ converges on $[0,n_s)$ . We build the $\Pi ^0_1$ -class $P_e$ in stages, where $P_{e,s}$ is the nonempty clopen set we have before stage s of the construction. Let $P_{e,0}=2^{\omega }$ .

Stage $0$ . Start constructing $P_e$ as a nonempty $\Pi ^0_1$ -class containing only Martin-Löf random elements.

Stage s. If $n_s = n_{s-1}$ , continue the construction that is currently underway, which will produce a nonempty $\Pi ^0_1$ -class of random elements.

On the other hand, if $n_s> n_{s-1}$ , fix a string $\sigma $ such that $[\sigma ]\subseteq P_{e,s}$ and $|\sigma |>s$ . Let $P_{e,s+1} = [\sigma ]$ . End the construction that we have been following and start a new construction for $P_e$ , starting at stage $s+1$ , as a nonempty $\Pi ^0_1$ -subclass of $[\sigma ]$ containing only Martin-Löf random elements.

It is clear that if $\varphi _e$ is total, then $P_e$ will be a singleton. Otherwise, there will be a final construction of a nonempty $\Pi ^0_1$ -class of randoms which will run without further interruption.

Of course, when $P_e$ is a singleton, its lone element must be computable.

Proof of Theorem 3.6

For any set C, let $S_C = \{X\in 2^{\omega } \colon C\subseteq X\}$ . Note that if C is computable (or even merely c.e.), then $S_C$ is a $\Pi ^0_1$ -class. Let $Q_e = \{X \colon \overline {X}\in P_e\}$ be the $\Pi ^0_1$ -class of complements of elements of $P_e$ .

Now let F be an ultrafilter base. We have that

$$ \begin{align*} \varphi_e\text{ is total} \iff& (\exists i)(\exists n)\; [F_i\smallsetminus [0,n] \text{ is a subset of some } \\ & \qquad\qquad X\in P_e\text{ or its complement}] \\ \iff& (\exists i)(\exists n)\; [P_e\cap S_{F_i\smallsetminus [0,n]} \neq\emptyset \text{ or }Q_e\cap S_{F_i \smallsetminus [0,n]}\neq\emptyset]. \end{align*} $$

Even though $S_{F_i \smallsetminus [0,n]}$ is a $\Pi ^0_{1}$ -class, we cannot hope to compute an index using F. However, $S_{F_i \smallsetminus [0,n]}$ is a $\Pi ^0_{1}[F]$ -class uniformly in $i,n$ . Using the fact that the nonemptiness of a $\Pi ^0_1[F]$ -class is a $\Pi ^0_1[F]$ -property, we see that $\text {Tot} =\{e \colon \varphi _e\text { is total}\}$ is $\Sigma ^0_2[F]$ . Note that the $\Sigma ^0_2$ -index does not depend on F. Since Tot is also $\Pi ^0_2$ , it is $\Delta ^0_2[F]$ via a fixed pair of indices, and hence Turing reducible to $F'$ via a fixed reduction. One direction of the usual proof of the (relativized) Limit Lemma now shows that we can uniformly compute an approximation to $\text {Tot}$ from F. Hence, from F we can uniformly compute a dominating function by Fact 3.5.

Theorem 3.8. Every dominating function uniformly computes an ultrafilter base. In other words, $\mathcal {U} \le _s \mathrm {DomFcn}$ .

Proof Let ${\left \langle {\psi _e}\right \rangle }_{e\in \omega }$ be an effective listing of the $\{0,1\}$ -valued partial computable functions defined on an initial segment of $\omega $ . Let $V_{e,k} =\{x\colon \psi _e(x)=k\}$ so that ${\left \langle {(V_{e,0}, V_{e,1})}\right \rangle }$ is an effective listing that contains all pairs of computable sets and their complements.

Let $T=\{0,1,2\}^{< \omega }$ . Uniformly in $\alpha \in T$ , we will define a set $S_{\alpha }$ . We first explain the basic idea and then modify it to make it work. The basic idea is to start with $S_{\emptyset } = \omega $ and build $S_{\alpha \widehat {\ } k} = S_{\alpha } \cap V_{e,k}$ for $k= 0,1$ and $e = |\alpha |$ , that is, we split $S_{\alpha }$ according to the listing above. We then consider the leftmost path g such that $S_{g\operatorname {\mathrm {\upharpoonright }} e}$ is infinite for each e. A dominating function h can eventually discover each initial segment of this path, and use this to compute a set F such that $F_e = ^*S_{g\operatorname {\mathrm {\upharpoonright }} e}$ for each e.

The problem is that both $S_{\alpha } \cap V_{e,0}$ and $S_{\alpha } \cap V_{e,1}$ could be finite (because e is not a proper index of a computable set). In this case we still need to make sure that $F_e \smallsetminus F_{e+1}$ is infinite. So the rightmost option at level n is a set $S_{\alpha \widehat {\ } 2 }= \widetilde S_{\alpha }$ that simply removes every other element from $S_{\alpha }$ (so as to obtain an infinite coinfinite subset). The sets $S_{\alpha \widehat {\ } k}$ for $k \le 1$ will be subsets of $\widetilde S_{\alpha }$ .

We now provide the details. The set $S_{\alpha }$ is enumerated in increasing fashion, and possibly finite. So each $S_{\alpha }$ is computable, though not uniformly in $\alpha $ . All the sets and functions defined below can be interpreted at stages.

Let $S_{\emptyset ,s}= [0,s)$ . If we have defined (at stage s) the set $S_{\alpha } = \{r_0< \cdots <r_k\}$ , let $\widetilde S_{\alpha }$ contain the numbers of the form $r_{2i}$ . Let $S_{\alpha \widehat {\ } 2 } = \widetilde S_{\alpha }$ . Let $S_{\alpha \widehat {\ } k} = \widetilde S_{\alpha } \cap V_{e,k}$ for $k= 0,1$ , $e = |\alpha |$ . We define a uniform list of Turing functionals $\Gamma _e$ so that the sequence ${\left \langle {\Gamma ^h_e(t)}\right \rangle }_{t\in \omega }$ is nondecreasing and unbounded, for each e and each oracle function h such that $h(s) \ge s$ for each s. We will let $F_e = \{\Gamma ^h_e(t)\colon t \in \omega \}$ .

Definition of $\Gamma _e$ . Given an oracle function h, we will write $a_s$ for $\Gamma ^h_e(s)$ . Let $a_0=0$ . Suppose $s>0$ and $a_{s-1}$ has been defined. Check if there is $\alpha \in T$ of length e such that $|S_{\alpha , h(s)}|\ge s$ . If there is no such $\alpha $ , let $a_s=a_{s-1}$ . Otherwise, let $\alpha $ be leftmost such. If $\max S_{\alpha , h(s)}> a_{s-1}$ , let $a_s= \max S_{\alpha , h(s)} $ . Otherwise, again let $a_s=a_{s-1}$ .

Note that the sequence $\{a_s\}_{s<\omega }$ is unbounded because for the rightmost string $\alpha \in T$ of length e (i.e., the string consisting only of $2$ ’s), the set $S_{\alpha ,t}$ consists of the numbers in $[0,t)$ divisible by $2^{e}$ . We may combine the functionals $\Gamma _e$ to obtain a functional $\Psi $ such that $(\Psi ^h)_e = F_e$ for each h with $h(s) \ge s$ for each s.

Claim 3.9. If $h\in \mathrm {DomFcn}$ , then $F=\Psi ^h \in \mathcal {U}$ .

To verify this, let $g \in 2^{\omega }$ denote the leftmost path in $\{0,1,2\}^{\omega }$ such that the set $S_{g \operatorname {\mathrm {\upharpoonright }} e}$ is infinite for every e. Note that g is an infinite path, because for every $\alpha $ , if the set $S_{\alpha }$ is infinite then so is $S_{\alpha \widehat {\ } 2}$ .

Fix e and let $\alpha = g\operatorname {\mathrm {\upharpoonright }} e$ . Let $p(s)$ be the least stage t such that $S_{\alpha ,t}$ has at least s elements. Since h dominates the computable function p, we will eventually always pick $\alpha $ in the definition of $a_s= \Gamma ^h_e(s)$ . Hence $F_e=^* S_{\alpha }$ . This implies that $F_e$ is computable and $F_{e+1}\subseteq ^*F_e$ . Clearly, if $S_{\alpha }$ is infinite, then $S_{\alpha } \smallsetminus S_{\beta }$ is infinite for every $\beta \succ \alpha $ . Thus $F_{e} \smallsetminus F_{e+1}$ is infinite.

Now let R be a computable set. Pick e such that $R= V_{e, 0}$ and $\overline R= V_{e,1}$ . If $g(e)=0$ , then $S_{g\, \operatorname {\mathrm {\upharpoonright }} {e+1}} \subseteq V_{e,0}$ and hence $F_{e+1} \subseteq ^* R$ . Otherwise, $S_{g\, \operatorname {\mathrm {\upharpoonright }} {e+1}} \subseteq V_{e,1}$ and hence $F_{e+1} \subseteq ^* \overline R$ .

4 Maximal independent families in computability

In this short section, we determine the complexity of the computability-theoretic analog of the independence number ${\mathfrak i}$ for the Boolean algebra of computable sets. It turns out that in the context of the computable sets, maximal independent families behave in a way similar to ultrafilter bases.

Given a sequence ${\left \langle {F_n}\right \rangle }_{n\in \omega }$ , let $F_{\emptyset } = \omega $ ; for each nonempty binary string $\sigma $ we write

(1) $$ \begin{align} F_{\sigma} = \bigcap_{\sigma(i)= 1} F_i \cap \bigcap_{\sigma(i)=0} \overline{F}_i. \end{align} $$

We call (a set F encoding) such a sequence independent if each set $F_{\sigma }$ is infinite.

Definition 4.1. Given a Boolean algebra of sets ${{\mathbb B}}$ , the mass problem $\mathcal {I}_{{\mathbb B}}$ is the class of sets F such that ${\left \langle {F_n}\right \rangle }_{n\in \omega }$ is a family that is maximal independent, namely, it is independent, and for each set $R \in {{\mathbb B}}$ , there is $\sigma $ such that $F_{\sigma } \subseteq ^* R $ or $F_{\sigma }\subseteq ^* \overline R$ .

In the following, we let ${{\mathbb B}}$ be the Boolean algebra of computable sets, and we drop the parameter ${{\mathbb B}}$ as usual. An easy modification of the proof of Theorem 3.6 yields the following.

Theorem 4.2. Every maximal independent family F uniformly computes a dominating function. In other words, $\mathcal {I} \ge _s \mathrm {DomFcn}$ .

Proof Define the $\Pi ^0_{1}$ -classes $P_e$ as in Lemma 3.7. As before let $Q_e = \{X \colon \overline {X}\in P_e\}$ be the $\Pi ^0_1$ -class of complements of elements of $P_e$ . Recall that for any set C, we let $S_C = \{X\in 2^{\omega } \colon C\subseteq X\}$ . Now we have that

$$ \begin{align*} \varphi_e\text{ is total} \iff& (\exists \sigma)(\exists n)\; [F_{\sigma}\smallsetminus [0,n] \text{ is a subset of some } \\ & \qquad\qquad X\in P_e \text{ or its complement}] \\ \iff& (\exists \sigma )(\exists n)\; [P_e\cap S_{F_{\sigma}\smallsetminus [0,n]}\neq\emptyset \text{ or }Q_e\cap S_{F_{\sigma}\smallsetminus [0,n]} \neq\emptyset]. \end{align*} $$

As before, this shows that from F one can uniformly compute a dominating function.

Theorem 4.3. Every dominating function h uniformly computes a maximal independent family. In other words, $\mathcal {I} \le _s \mathrm {DomFcn}$ .

In fact, we will prove that a dominating function h uniformly computes a set F such that the $=^*$ -equivalence classes of the sets $F_e$ freely generate the Boolean algebra of computable sets modulo finite sets. This clearly implies that F is maximal independent: If R is an infinite computable set, then for some e and nonempty set S of strings of length e, one has $R=^* \bigcup _{\sigma \in S} F_{\sigma }$ , and hence $F_{\sigma }\subseteq ^* R$ for some $\sigma $ .

Proof As in the proof of Theorem 3.8, let ${\left \langle {\psi _e}\right \rangle }_{e\in \omega }$ be an effective listing of the $\{0,1\}$ -valued partial computable functions defined on an initial segment of $\omega $ , and let $V_{e,k} =\{x\colon \psi _e(x)=k\}$ for $k = 0,1$ .

In Phase e of the construction, we will define a computable set $F_e$ such that $F_e= \Theta _e^h$ for a Turing functional $\Theta _e$ determined uniformly in e. Suppose we have defined $\Theta _i$ for $i< e$ , and thereby have defined the sets $F_{\sigma }$ given by (1) for each string $\sigma $ of length e.

The idea for building $F_e$ is to attempt to follow $V_{e,0}$ while maintaining independence from the previous sets. We apply this strategy separately on each $F_{\sigma }$ . Using h as an oracle we compute recursively an increasing sequence $ {\left \langle {r^e_n}\right \rangle }_{n\in \omega }$ . We carry out the attempts on intervals $[r^e_n, r^e_{n+1})$ . If $V_{e,0}$ appears to split $F_{\sigma }$ on the current interval, then we follow it; otherwise, we merely make sure that $F_e$ remains independent from $F_{\sigma }$ on the interval by putting one number in and leaving another one out. To decide which case holds, we consult the dominating function h as an oracle.

We now provide the details for Phase e. Let $r^e_0=0$ . If $r^e_n$ has been defined, let $r^e_{n+1}> r^e_n$ be the least number r such that for each $\sigma $ of length e, the following two conditions hold:

• (a) $_{\sigma }$ $|[r^e_n, r) \cap F_{\sigma } | \ge 2$ ;

• (b) $_{\sigma }$ if there are $u, w \in \mathrm {dom} (\psi _{e, h(r^e_n)})\cap F_{\sigma }$ with $r^e_n \le u< w$ such that $\psi _e(u)= 1 $ and $\psi _e(w) =0$ , then $r>w$ for the least such w.

We define $F_e(x) = \Theta _e^h(x)$ for $x\in [r^e_n, r^e_{n+1})$ as follows. Let $\sigma $ be the string of length e such that $x \in F_{\sigma }$ .

• • If the hypothesis of condition (b) $_{\sigma }$ holds and $\psi _e$ is defined on $[r^e_n, r^e_{n+1})$ , then let $F_e(x)= \psi _e(x)$ ;

• • otherwise, if $x=\min ([r^e_n, r^e_{n+1}) \cap F_{\sigma })$ , let $F_e(x) = 1$ , else let $F_e(x)=0$ .

Verification. By induction on e, one verifies that for each function h, the set $F_{\sigma }$ is infinite for each $\sigma $ with $|\sigma | = e$ , and that the sequence ${\left \langle {r^e_n}\right \rangle }_{n\in \omega }$ defined in Phase e of the construction is infinite. Thus $\Theta ^h_e$ is total. So $F \le _T h$ where $F_e=\Theta ^h_e$ , and F is an independent family.

Claim 4.4. Each set $F_e$ is computable.

We verify this by induction on e. Suppose it holds for each $i<e$ . So $F_{\sigma }$ is computable for $|\sigma | =e$ .

First assume that $\mathrm {dom} (\psi _e)$ is finite. Then for sufficiently large n, condition (b) $_{\sigma }$ does not apply to any string $\sigma $ of length e, and so the sequence ${\left \langle {r^e_n}\right \rangle }_{n\in \omega }$ is computable. Hence $F_e$ is computable.

Now assume that $\psi _e$ is total. Let

$$\begin{align*}D_e = \{\sigma \colon \, |\sigma| = e \land |F_{\sigma} \cap V_{e,0} | = |F_{\sigma} \cap V_{e,1}| = \infty\}. \end{align*}$$

Define a function p by letting $p(m)$ be the least stage s such that for each $\sigma \not \in D_e$ , condition (a) $_{\sigma }$ holds with $r^e_n= m$ and $r=s$ , and for each $\sigma \in D_e$ , there are $u,w \in \mathrm {dom} ({\psi _{e,s}})$ such that $m \le u<w $ as in the hypothesis of condition (b) $_{\sigma }$ . (Let $p(m) = 0$ if m is not of the form $r^e_n$ .) Since $F_{\sigma }$ is computable for each $\sigma $ of length e, the function p is computable. Since h dominates p, for sufficiently large n, we will define $r^e_{n+1}$ by checking the convergence of computations $\psi _e(z)$ at a stage $h(r^e_n) \ge p(r^e_n)$ ; since in Phase e of the construction, we chose the witnesses minimal, $r^e_{n+1}$ is determined by stage $p(r^e_n)$ . So we might as well check the convergence of computations $\psi _e(z)$ at stage $p(r^e_n)$ . Hence again, the sequence ${\left \langle {r^e_n}\right \rangle }_{n\in \omega }$ is computable.

Claim 4.5. Suppose that $\psi _e$ is total. Then for each string $\tau = \sigma \widehat {\ } a$ of length $e+1$ , $F_{\tau } \subseteq ^* V_{e,0} $ or $F_{\tau } \cap V_{e,0} =^* \emptyset $ (so that $V_{e,0}=^*\bigcup _{\tau } \{ F_{\tau } \colon F_{\tau } \subseteq ^* V_{e,0}\}$ ) .

Let $D_e$ be as above. If $\sigma \not \in D_e$ , then this is immediate since $F_{\sigma } \subseteq ^* V_{e,i}$ for some i. Otherwise, Phase e of the construction ensures that $F_{\sigma \widehat {\ } 0} =^* F_{\sigma } \cap V_{e,0}$ .

By the last claim, the $=^*$ -equivalence classes of the $F_e$ freely generate the Boolean algebra of the computable sets modulo finite sets. In particular, F is a maximal independent family.

As mentioned in the introduction, we do not know at present whether there is a “natural” Medvedev equivalence between the two mass problems $\mathcal {U}$ and $\mathcal {I}$ as is the case for $\mathcal {A}$ and $\mathcal {T}$ . This would require direct proofs avoiding the detour via the mass problem of dominating functions. For what it is worth, the cardinal characteristics $\mathfrak {u}$ and $\mathfrak {i}$ are incomparable (i.e., ZFC cannot determine their order).

5 The case of computably enumerable complements

Recall from Fact 2.3 that no maximal tower, and in particular no ultrafilter base, can be computably enumerable. In contrast, in this section we will see that even ultrafilter bases can have computably enumerable complement. As in the previous sections, we are restricting our attention to the Boolean algebra of all computable sets.

Recall that a coinfinite c.e. set A is called simple if it meets every infinite c.e. (or, equivalently, every computable) set; A is called r-maximal if $\overline A \subseteq ^* \overline R$ or $\overline A \subseteq ^* R$ for each computable set R. Each r-maximal set is simple. For more background, see Soare [18].

5.1 Computably enumerable MAD sets, and co-c.e. towers

We will show that if A is a noncomputable c.e. set, then there is a co-c.e. maximal tower $G\leq _T A$ . Given that it is more standard to build c.e. rather than co-c.e. sets, it will be convenient to first build a c.e. MAD set $F\le _T A$ and then use the Medvedev reduction in Fact 2.2 to obtain a co-c.e. maximal tower. We employ a priority construction with requirements that act only finitely often.

Theorem 5.1. For each noncomputable c.e. set A, there is a MAD c.e. set $F \le _T A$ .

Proof The construction is akin to Post’s construction of a simple set. In particular, it is compatible with permitting.

Let ${\left \langle {M_e}\right \rangle } _{e\in \omega }$ be a uniformly c.e. sequence of sets such that $M_{2e} = W_e$ and $M_{2e+1} = \omega $ for each e. We will build an auxiliary c.e. set $H \le _T A$ and let the c.e. set $F\le _T A $ be defined by $F^{[e]} = H^{[2e]} \cup H^{[2e+1]}$ . The purpose of the sets $M_{2e+1}$ is to make the sets $H^{[2e+1]}$ , and hence the sets $F^{[e]}$ , infinite. The construction also ensures that H, and hence F, is AD, and that $\bigcup _n H^{[n]}$ is coinfinite.

As usual, we will write $H_e$ for $H^{[e]}$ . We provide a stage-by-stage construction to meet the requirements

$$\begin{align*}P_n \colon M_e\smallsetminus \bigcup_{i<n} H_i \text { infinite } \Rightarrow |H_e \cap M_e | \ge k \text{, where } n= \langle e, k \rangle. \end{align*}$$

(Note that the union is over all i such that $i<n$ , not $i<e$ .) At stage s, we say that $P_n$ is permanently satisfied if $|H_{e,s} \cap M_{e,s}| \ge k$ .

Construction.

Stage $s>0$ . See if there is $n< s$ such that $P_n$ is not permanently satisfied, and, where $ n= \langle e, k \rangle $ , there is $x \in M_{e,s}\smallsetminus \bigcup _{i<n} H_{i,s}$ such that

$$ \begin{align*} x> \max (H_{e,s-1}), x \ge 2n, \text{ and } A_s \operatorname{\mathrm{\upharpoonright}} x \neq A_{s-1} \operatorname{\mathrm{\upharpoonright}} x. \end{align*} $$

If so, choose n least, and put $\langle x, e \rangle $ into H (i.e., put x into $H_e$ ).

Verification. Each $H_e$ is enumerated in increasing fashion and hence computable.

Each $P_n$ is active at most once. This ensures that $\bigcup _e H_e$ is coinfinite: For each N, if $x< 2N$ enters this union, then this is due to the action of a requirement $P_n$ with $n < N$ , so there are at most N many such x.

To see that a requirement $P_n$ for $ n= \langle e, k \rangle $ is met, suppose that its hypothesis holds. Then there are potentially infinitely many candidates x that can go into $H_e$ . Since A is noncomputable, one of them will be permitted.

Now, by the choice of $M_{2e+1}$ and the fact that $\bigcup _e H_e$ is coinfinite, each $H_{2e+1}$ , and hence each $F_e$ , is infinite. We claim that for $e< m$ , we have $|H_e \cap H_m| \le m$ . For suppose that $x \in H_m$ enters $H_e$ at stage s. Then $x \in H_{m,s}$ since $r \ge \langle m,0\rangle> e$ for any requirement $P_r$ putting x into $H_m$ . Suppose $P_n$ puts x into $H_e$ at stage s, where $n= \langle e,k\rangle $ . Then $n \le m$ , so the claim follows as each requirement is active at most once. We conclude that the family described by H, and therefore also the one described by F, is almost disjoint.

To show that F is MAD, it suffices to verify that if $M_e$ is infinite then $H_p \cap M_e $ is infinite for some p. If all the $P_{\langle e,k\rangle }$ are satisfied during the construction, we let $p=e$ . Otherwise, we let k be least such that $P_{n}$ is never satisfied where $n= \langle e,k \rangle $ . Then its hypothesis fails, so $M_e \subseteq ^* \bigcup _{i<n} H_i $ . Hence $H_p \cap M_e $ is infinite for some $p < n$ by the pigeonhole principle.

Since an index guessable set computes no MAD set by Proposition 2.4, we obtain the following.

Corollary 5.2. If a c.e. set L is index guessable, then L is computable.

Downey and Nies have given a direct proof of this fact; see [14].

Corollary 5.3. For each noncomputable c.e. set A, there is a co-c.e. set $G \le _T A$ such that $G \in \mathcal {T}$ , i.e., ${\left \langle {G_n}\right \rangle }_{n\in \omega }$ is a maximal tower.

Proof Let F be the MAD set obtained above. Recall the Turing reduction $\mathrm {Cp}$ showing that $\mathcal {T} \le _s \mathcal {A}$ in Fact 2.2. The set $G =\mathrm {Cp}(F)$ , given by

$$\begin{align*}x \in G_n \leftrightarrow \forall i < n \, [ x \not \in F_n] \end{align*}$$

is as required.

5.2 Co-c.e. ultrafilter bases

We next construct a co-c.e. ultrafilter base F for the Boolean algebra of computable sets. That is, F is co-c.e., each $F_e$ is computable (but not uniformly so), and F is a tower satisfying the condition in Definition 1.5.

Theorem 5.4. There is a co-c.e. ultrafilter base F.

Proof We adapt the construction from the proof of the main result in [11], which states that there is an r-maximal set A such that the index set $\mathrm {Cof}_A= \{e \colon W_e \cup A =^* \omega \}$ is $\Sigma ^0_{3}$ -complete. Both the original and the adapted version make use of the fact that we are given a c.e. index for a computable set and also one for its complement (see the pairs $(V_{e,0},V_{e,1})$ below). Our proof can also be viewed as a variation on the proof of Theorem 3.8 in the setting of co-c.e. sets. We remark that by standard methods, one can extend the present construction to include permitting below a given high c.e. set.

We build a co-c.e. tower F by providing uniformly co-c.e. sets $F_e$ for $e \in \omega $ that form a descending sequence with $F_e \supseteq F_{e+1}$ . We achieve the latter condition by agreeing that whenever we remove x from $F_e$ at a stage s, we also remove it from all $F_i$ for $i>e$ . Furthermore, no element is ever removed from $F_0$ , so $F_0= \omega $ .

Let ${\left \langle {(V_{e,0}, V_{e,1})}\right \rangle }_{_{e\in \omega }}$ be an effective listing of all pairs of disjoint c.e. sets as defined in the proof of Theorem 3.8. The construction will ensure that the following requirements are met:

$$ \begin{align*} M_e &\colon F_e \smallsetminus F_{e+1}\text{ is infinite,}\\ P_e &\colon V_{e,0} \cup V_{e,1} = \omega \Rightarrow F_{e+1} \subseteq^* V_{e,0} \vee F_{e+1} \subseteq^* V_{e,1}. \end{align*} $$

This suffices to establish that F is an ultrafilter base.

The tree of strategies is $T=\{0,1,2\}^{< \omega }$ . Each string $\alpha \in T$ of length e is tied to $M_e$ and also to $P_e$ . We write $\alpha \colon M_e$ and $\alpha \colon P_e$ to indicate that we view $\alpha $ as a strategy of the respective type.

Streaming. For each string $\alpha \in T$ with $|\alpha | = e$ , at each stage of the construction, we have a computable set $S_{\alpha }$ , thought of as a stream of numbers used by $\alpha $ . The purpose of the sets $S_{\alpha }$ is twofold:

1. (a) to be able to provide candidates for $P_e$ by a procedure of reserving numbers from the stream, and processing them making use of its hypothesis, and

2. (b) to show that $F_e$ is computable.

For (b), in Claim 5.7 we will verify that $F_e=^* S_{\alpha }$ where $\alpha $ is the string of length e on the true path. Since the true path is merely computable in $\emptyset "$ , we cannot directly define the co-c.e. set F using the $S_{\alpha }$ . Rather, we need to spread the construction of the $F_e$ over the whole e-th level of the tree of strategies.

We provide some more detail on the dynamics of the streams. Each time $\alpha $ is initialized, $S_{\alpha }$ is removed from $F_{e+1}$ , and $S_{\alpha }$ is reset to be empty. Also, $S_{\alpha }$ is enlarged only at stages at which $\alpha $ appears to be on the true path.

We will verify the following conditions on the final versions of the $S_{\alpha }$ :

1. (1) $S_{\emptyset } = \omega $ ;

2. (2) if $\alpha $ is not the empty node, then $S_{\alpha }$ is a subset of $S_{\alpha ^-}$ (where $\alpha ^-$ is the immediate predecessor of $\alpha $ );

3. (3) at every stage, $S_{\gamma } \cap S_{\beta } = \emptyset $ for incomparable strings $\gamma $ and $\beta $ ;

4. (4) any number x is in $F_{e+1}$ at the time it first enters $S_{\alpha }$ ;

5. (5) if $\alpha $ is along the true path of the construction, then $S_{\alpha }$ is an infinite computable set.

Note that $S_{\alpha }$ is d.c.e. uniformly in $\alpha $ . The set $S_{\alpha }$ is finite if $\alpha $ is to the left of the true path of the construction; $S_{\alpha }$ is an infinite computable set if $\alpha $ is along the true path; and $S_{\alpha }$ is empty if $\alpha $ is to the right of the true path.

The intuitive strategy $\alpha \colon P_e$ is as follows. Only strategies associated with a string of length $\le e$ can remove numbers from $F_{e+1}$ . A strategy $\alpha \colon P_e$ removes elements from $S_{\alpha }$ , and at the same time from $F_{e+1}$ . It regards the set of remaining numbers as its own version of $F_{e+1}$ ; if $\alpha $ is on the true path then this version is the true $F_{e+1}$ up to $=^*$ , as mentioned above. The strategy has to make sure that no strategies $\beta $ to its right remove numbers from $F_{e+1}$ that it wants to keep. On the other hand, it can only process a number x once it knows whether x is in $V_{e,0}$ or $V_{e,1}$ . The solution to this conflict is that $\alpha $ reserves a number x from the stream $S_{\alpha }$ , which, by an initialization $\alpha $ carries out at this stage, withholds it from any action of such a $\beta $ . It then waits until all numbers $\le x$ are in $V_{e,0}\cup V_{e,1}$ . If that never happens for some reserved x, then $\alpha $ is satisfied finitarily with eventual outcome $2$ . Otherwise, it will eventually process x: If $x \in V_{e,0}$ , it continues its attempt to build $F_{e+1}$ inside $V_{e,0}$ ; else it continues to build $F_{e+1}$ inside $V_{e,1}$ . It takes outcome $0$ or $1$ , respectively, according to which case applies. Each time the apparent outcome is $0$ , then the current $S_{\alpha \widehat {\ } 1}$ (i.e., the content of its output stream based on the assumption that the true outcome is $1$ ) is removed from $F_{e+1}$ . So if $0$ is the true outcome, then indeed $F_{e+1}\subseteq ^* V_{e,0}$ ; and if $1$ is the true outcome, then indeed $F_{e+1}\subseteq ^* V_{e,1}$ .

The intuitive strategy $\alpha \colon M_e$ simply removes every other element of $S_{\alpha }$ from $F_{e+1}$ . Then $\alpha :P_e$ actually only works with the stream of remaining numbers. There is no further interaction between the two types of strategies. (Note here that making $F_{e+1}$ smaller is to the advantage of $P_e$ .) Recall that if $\alpha $ is initialized, $S_{\alpha }$ is removed from $F_{e+1}$ , and $S_{\alpha }$ is reset to be empty.

Construction.

Stage $0$ . Let $\delta _0$ be the empty string. Let $F_{e}= \omega $ for each e. Initialize all strategies.

Stage $s>0$ . Let $S_{\emptyset ,s}= [0,s)$ . Stage s consists of substages $e=0, \ldots ,s-1$ , during which we inductively define $\delta _s$ , a string of length s.

Substage e. We suppose that $\alpha = \delta _{s}\operatorname {\mathrm {\upharpoonright }} e$ and $S_{\alpha }$ have been defined.

The strategy $\alpha \colon M_e$ acts as follows. If at the current stage $S_{\alpha } = \{r_0< \cdots <r_k\}$ and $r_k$ is new in $S_{\alpha }$ , it puts $r_k$ into $\widetilde S_{\alpha }$ if and only if k is even; otherwise, $r_k$ is removed from $F_{e+1}$ .

The strategy $\alpha \colon P_e$ picks the first applicable case below.

Case 1: Each reserved number of $\alpha $ has been processed: If there is a number x from $\widetilde S_{\alpha }$ greater than $\alpha $ ’s last reserved number (if any) and greater than the last stage at which $\alpha $ was initialized, pick x least and reserve it. Note that $x<s$ since by definition $S_{\emptyset ,s}= [0,s)$ . Initialize all strategies $\gamma \succeq \alpha \widehat {\ } 2$ , and let $\alpha \widehat {\ } 2$ be eligible to act next.

If Case 1 does not apply then $\alpha $ has a unique reserved, but unprocessed number x.

Case 2: $[0,x] \subseteq V_{e,0} \cup V_{e,1}$ and $x \in V_{e,0}$ : Let t be the greatest stage $<s$ at which $\alpha $ was initialized. Add x to $S_{\alpha \widehat {\ } 0}$ and remove from $F_{e+1}$ all numbers in the interval $(t,x)$ that are not in $S_{\alpha \widehat {\ } 0}$ . Declare that $\alpha $ has processed x. Let ${\alpha \widehat {\ } 0}$ be eligible to act next.

Case 3: $[0,x] \subseteq V_{e,0} \cup V_{e,1}$ and $x \in V_{e,1}$ : Let t be the greatest stage $<s$ at which $\alpha $ was initialized or $\alpha \widehat {\ } 0$ was eligible to act. Add x to $S_{\alpha \widehat {\ } 1}$ and remove from $F_{e+1}$ all numbers in the interval $(t,x)$ that are not in $S_{\alpha \widehat {\ } 1}$ . Declare that $\alpha $ has processed x. Let ${\alpha \widehat {\ } 1}$ be eligible to act next.

Case 4: Otherwise, that is, $[0,x] \not \subseteq V_{e,0} \cup V_{e,1}$ : Let t be the greatest stage $<s$ at which $\alpha $ was initialized, or $\alpha \widehat {\ } 0$ or $\alpha \widehat {\ } 1$ was eligible to act. Let $S_{\alpha \widehat {\ } 2}= \widetilde S_{\alpha } \cap (t, s)$ . Let $\alpha \widehat {\ } 2$ be eligible to act.

We define $\delta _{s}(e)=i$ where $\alpha \widehat {\ } i$ , $0 \le i \le 2$ , has been declared eligible to act next. If $e+1< s$ , then carry out the next substage. Else initialize all the strategies $\beta $ such that $\delta _s <_L \beta $ and end stage s.

Verification. By construction and our convention above, $F_e$ is co-c.e., and $F_e \supseteq F_{e+1}$ for each e.

Let $g \in 3^{\omega }$ denote the true path, namely, the leftmost path in $\{0,1,2\}^{\omega }$ such that $\forall e\; \exists ^{\infty } s \, [ g\operatorname {\mathrm {\upharpoonright }} e \preceq \delta _s]$ . In the following, given e, let $\alpha = g \operatorname {\mathrm {\upharpoonright }} e$ . We verify a number of claims.

Claim 5.5. $\alpha $ is only initialized finitely often.

To see this, let $s_0>0$ be a stage such that $\alpha \le _L \delta _s$ for each $s \ge s_0$ . Suppose the strategy $\alpha $ is initialized at stage $s \ge s_0$ . Then $\alpha \succeq \beta \widehat {\ } 2$ for a strategy $\beta \colon P_i$ , where $i= |\beta |$ , and this initialization occurs at Case 1 of substage i of stage s, namely, when the strategy $\beta $ reserves a new number y. However, $\alpha $ can only be initialized once in that way for each such $\beta $ : If $\beta $ processes y at a later stage t, then this causes $\delta _t <_L \alpha $ , contrary to the choice of $s_0$ . This shows the claim.

Let $s_{\alpha }$ be the largest stage s such that $\alpha $ is initialized at stage s. Note that $\alpha \preceq \gamma $ implies $s_{\alpha } \le s_{\gamma }$ .

Claim 5.6. The conditions $(1)$ – $(5)$ related to streaming hold.

(1), (2), and (4) hold by construction. (3) Assume this fails for incomparable $\gamma $ and $\beta $ , so $x \in S_{\gamma } \cap S_{\beta }$ at stage s. By (2), we may as well assume that $\gamma = \alpha \widehat {\ } i$ and $\beta = \alpha \widehat {\ } k$ where $i<k$ . By construction, $k\le 1$ is not possible, so $k=2$ . Since $x \in S_{\alpha \widehat {\ } i}$ and $i \le 1$ , x was reserved by $\alpha $ at some stage $t\le s$ . So x can never enter $S_{\alpha \widehat {\ } 2}$ by the initialization of $\alpha \widehat {\ } 2$ when x was reserved by the strategy $\alpha \colon P_e$ in its Case 1.

(5) holds inductively, by the definition of the true path and because $S_{\alpha }$ is enumerated in increasing fashion at stages $\ge s_{\alpha }$ .

Claim 5.7. $F_e =^* S_{\alpha }$ (and hence, $F_e$ is computable).

The claim is verified by induction on e. We show that for all $x> s_{\alpha }$ , we have $x\in F_e$ if and only if $x\in S_{\alpha }$ . This holds for $e=0$ because $F_0= S_{\emptyset }= \omega $ . For the inductive step, let $\gamma = g \operatorname {\mathrm {\upharpoonright }}(e+1)$ .

First, we verify that $F_{e+1}\cap (s_{\gamma }, \infty )\subseteq S_{\gamma }$ . Suppose that $x>s_{\gamma }$ and $x \in F_{e+1}$ . Then $x \in F_e$ and $x>s_{\alpha }$ , so by the inductive hypothesis $x \in S_{\alpha }$ . By construction, any element x that does not enter $S_{\gamma }$ is also removed from $F_{e+1}$ unless x is the last element $\alpha $ reserves. However, in that case necessarily $\gamma = \alpha \widehat {\ } 2$ and $\gamma $ is initialized when x is reserved, so $x< s_{\gamma }$ contrary to our assumption.

Next, we verify that $ S_{\gamma }\cap (s_{\gamma }, \infty ) \subseteq F_{e+1} $ . Suppose that $x \in S_{\gamma }$ and $x>s_{\gamma }$ . Then $x \in S_{\alpha }$ , so by the inductive hypothesis $x \in F_e$ . At a stage $s \ge s_{\gamma }$ , an element x of $S_{\alpha }$ cannot be removed from $F_{e+1}$ by a strategy $\beta>_L \alpha $ because $S_{\beta }\cap S_{\alpha }= \emptyset $ by (3) as verified above and since $\beta $ can only remove elements from $S_{\beta }$ . So x can only be removed from $F_{e+1}$ by $\alpha \colon M_e$ or $\alpha \colon P_e$ .

If $\alpha \colon M_e$ removes x from $F_{e+1}$ , then $x \not \in \widetilde S_{\alpha }$ , which contradicts that $x \in S_{\gamma }$ . So, by construction, the only way x can be removed from $F_{e+1}$ is by the strategy $\alpha \colon P_e$ . Since $x>s_{\gamma }$ this would mean that x does not enter $S_{\gamma }$ either, contrary to our assumption.

Claim 5.8. Each requirement $ M_e$ is met, namely, $F_e \smallsetminus F_{e+1}$ is infinite.

To see this, recall that $\alpha = g \operatorname {\mathrm {\upharpoonright }} e$ . The action of $\alpha :M_e$ removes infinitely many elements of $S_{\alpha } $ from $F_{e+1}$ . This suffices by Claim 5.7.

Claim 5.9. Each requirement $ P_e$ is met.

Suppose the hypothesis of $P_e$ holds. Then every number that $\alpha $ reserves is eventually processed. So either $g(e)= 0$ , in which case $F_{e+1} \subseteq ^* V_{e,0}$ by Claim 5.7, or $g(e)= 1$ , in which case $F_{e+1} \subseteq ^* V_{e,1}$ , also by Claim 5.7.

6 Ultrafilter bases for other Boolean algebras

As mentioned, we have set up our framework to apply to general countable Boolean algebras, rather than merely the Boolean algebra of the computable sets, mainly with subsequent research in mind. In this last section of our paper, we provide two results in the setting of other Boolean algebras of sets.

Recall that $K(x)$ denotes the prefix-free complexity of a string x, and that a set $A\subseteq \omega $ is K-trivial if $\exists c\, \forall n \, K(A\operatorname {\mathrm {\upharpoonright }} n) \le K(0^n)+c$ . For more background on K-trivial sets, see [13, Chapter 5] or [4, Chapter 11]. Note that by combining results of various authors, the K-trivial degrees form a Turing ideal in the $\Delta ^0_2$ -degrees (see, e.g., [13, Sections 5.2 and 5.4]). Thus the K-trivial sets form a Boolean algebra.

Theorem 6.1. There is a $\Delta ^0_2$ ultrafilter base for the Boolean algebra of the K-trivial sets.

Proof Kučera and Slaman [10] noted that there is a function $h \le _{\mathrm {T}} {\emptyset '}$ that dominates all functions that are partial computable in some K-trivial set. We use h in a variation of the proof of Theorem 3.8.

Let ${\left \langle {V_{e,0}, V_{e,1}}\right \rangle }_{e\in \omega }$ be a uniform listing of the K-trivials and their complements given by wtt-reductions to ${\emptyset '}$ ; such a listing exists by Downey, Hirschfeldt, Nies, and Stephan [5] (see also [13, Theorem 5.3.28]).

Let $T=\{0,1\}^{< \omega }$ . For each $\alpha \in T$ , we define a (possibly finite) K-trivial set $S_{\alpha }$ . Let $S_{\emptyset }= \omega $ . Suppose we have defined the set $S_{\alpha } = \{r_0< r_1 < \cdots \}$ . Let $\widetilde S_{\alpha }$ contain the numbers of the form $r_{2i}$ . Let $S_{\alpha \widehat {\ } k} = \widetilde S_{\alpha } \cap V_{e,k}$ for $e = |\alpha |$ and $k= 0,1$ . Since $\widetilde S_{\alpha } \le _{\mathrm {T}} S_{\alpha }$ , one verifies inductively that all these sets are K-trivial.

Uniformly recursively in ${\emptyset '}$ , we build sets $F_e$ , given as the set of members of nondecreasing unbounded sequences $a^e_0 \le a^e_1\le \cdots $ . Suppose we have defined $a^e_{k-1}$ . Try to let $\alpha \in T$ be the leftmost string of length e such that $S_{\alpha }$ has at least $k+1$ elements less than $h(k)$ . If such $\alpha $ exists, let $a^e_k$ be the k-th element of $S_{\alpha }$ , unless this is less than $a^e_{k-1}$ , in which case we let $a^e_k= a^e_{k-1}$ .

Let $g \in 2^{\omega }$ denote the leftmost path in $\{0,1\}^{\omega }$ such that for every e, the set $S_{g \operatorname {\mathrm {\upharpoonright }} e}$ is infinite. Fix e and let $\alpha = g\operatorname {\mathrm {\upharpoonright }} e$ . Let $p(k)$ be the $(k+1)$ -st element of $S_{\alpha }$ . Since h dominates the function p, eventually in the definition of $F_e$ we will always pick $\alpha $ . Hence $F_e=^* S_{\alpha }$ . In particular, $F_e$ is K-trivial. To see that $F\le _{\mathrm {T}} {\emptyset '}$ , given input $n =\langle r, e\rangle $ , with ${\emptyset '}$ as an oracle, compute the least k such that $r\le a^e_k$ , using that the sequences ${\left \langle {a^e_k}\right \rangle }_{k\in \omega }$ are unbounded for each e. Then $n \in F$ iff $r= a^e_k$ .

Clearly, if $S_{\alpha }$ is infinite, then $S_{\alpha } \smallsetminus S_{\beta }$ is infinite for $\alpha \prec \beta $ . So $ F_e \smallsetminus F_{e+1}$ is infinite.

To verify that F is an ultrafilter base for the K-trivials, let R be a K-trivial set. Pick e such that $R= V_{e, 0}$ and $\overline R= V_{e,1}$ . If $g(e)=0$ then $S_{g\, \operatorname {\mathrm {\upharpoonright }} {e+1}} \subseteq V_{e,0}$ , and hence $F_{e+1} \subseteq ^* R$ . Otherwise, $S_{g\, \operatorname {\mathrm {\upharpoonright }} {e+1}} \subseteq V_{e,1}$ , and hence $F_{e+1} \subseteq ^* \overline R$ .

Remark 6.2. Any ultrafilter base for the K-trivials must have high degree. We can see this by modifying the proof of Theorem 3.6: Every Martin-Löf random set X is Martin-Löf random relative to every K-trivial (i.e., K-trivial sets are low for ML-randomness). Hence neither X nor $\overline X$ contains an infinite K-trivial subset.

Finally, we consider the Boolean algebra of the primitive recursive sets. One says that an oracle L is of PA degree if it computes a completion of Peano arithmetic. Recall that L is of PA degree if and only if it computes a separating set for each disjoint pair of c.e. sets.

Theorem 6.3. An oracle C computes an ultrafilter base for the primitive recursive sets if and only if $C'$ is of PA degree relative to ${\emptyset '}$ .

Proof We modify the proof of Jockusch and Stephan [9, Theorem 2.1]. They say that a set $S \subseteq \omega $ is p-cohesive if S is cohesive for the primitive recursive sets. Their theorem states that S is p-cohesive if and only if $S'$ is of PA degree relative to ${\emptyset '}$ .

$\Rightarrow :$ Suppose that C computes an ultrafilter base F for the primitive recursive sets. Let $g\le _{\mathrm {T}} F$ be a function associated with F as in Definition 1.2. Then the range S of g is p-cohesive. Hence $S'$ and therefore $C'$ is of PA degree relative to ${\emptyset '}$ by one implication of [9, Theorem 2.1].

$\Leftarrow :$ We modify the proof of the other implication of [9, Theorem 2.1]. Let ${\left \langle {A_i}\right \rangle }_{i\in \omega }$ be a uniformly recursive list of all the primitive recursive sets. We call i a primitive recursive index for $A_i$ (or index, for short). By our hypothesis on C, there is a function $g\le _{\mathrm {T}} C'$ such that

$$ \begin{align*} |A_i \cap A_n| < |A_i \cap \overline A_n| & \Rightarrow g(i,n) = 0, \\ |A_i \cap \overline A_n| < |A_i \cap A_n| & \Rightarrow g(i,n) = 1 \end{align*} $$

(because the conditions on the left are both $\Sigma ^0_{2}$ , and so $C'$ computes a separating set for them).

We inductively define a $C'$ -computable sequence of indices ${\left \langle {e_n}\right \rangle } _{n\in \omega }$ . Let $e_0$ be an index for $\omega $ . If $e_n$ has been defined and $A_{e_n} = \{r_0 < r_1< \cdots \}$ (possibly finite), let $e^{\prime }_n$ be an index, uniformly obtained from $e_n$ , such that $A_{e^{\prime }_n}= \{r_0, r_2, \ldots \}$ . Now let

$$ \begin{align*} A_{e_{n+1}}&= A_{e^{\prime}_n} \cap \overline A_n \text{ if } g(e^{\prime}_n, n )= 0, \text{ and} \\ A_{e_{n+1}}&= A_{e^{\prime}_n} \cap A_n \text{ if } g(e^{\prime}_n, n )= 1. \end{align*} $$

By induction on n, one verifies that $A_{e_n}$ is infinite and $A_{e_n} \smallsetminus A_{e_{n+1}}$ is infinite. Since $g\le _{\mathrm {T}} C'$ , the numbers $e_n$ have a uniformly C-computable approximation ${\left \langle {e_{n,x}}\right \rangle } _{x\in \omega }$ .

Let the ultrafilter base $F\le _{\mathrm {T}} C$ be given by $F_n(x)= A_{e_{n,x}}(x)$ . Then $F_n =^* A_{e_n}$ is primitive recursive. Since $F_{n+1} \subseteq ^* \overline A_n$ or $F_{n+1} \subseteq ^* A_n$ for each n, the set F is an ultrafilter base for the primitive recursive sets.