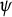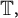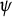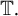Asymptotic first boundary value problem for elliptic operators

Abstract

In 1955, Lehto showed that, for every measurable function $\psi $ on the unit circle $\mathbb T,$ there is a function f holomorphic in the unit disc, having $\psi $ as radial limit a.e. on $\mathbb T.$ We consider an analogous problem for solutions f of homogenous elliptic equations $Pf=0$ and, in particular, for holomorphic functions on Riemann surfaces and harmonic functions on Riemannian manifolds.

1 Introduction

In 1955, Lehto [4] showed that given an arbitrary measurable function $\psi $ on the interval $[0,2\pi ),$ there exists a function f holomorphic in the unit disc $\mathbb D \subset \mathbb C $ such that

$$ \begin{align*}\lim_{\rho \to 1} f(\rho e^{i\theta}) = \psi(\theta), \quad \mbox{for} \quad a.e. \quad \theta\in[0,2\pi). \end{align*} $$

Lehto’s theorem shows that the radial boundary values of holomorphic functions in the unit disc can be prescribed almost everywhere on the boundary of the disc. On the other hand, any attempt to prescribe angular boundary values fails dramatically due to the Luzin–Privalov uniqueness theorem [6]. This result asserts that if a meromorphic function f in the unit disc $\mathbb D $ has angular limit $0$ at each point of a subset of the boundary having positive linear measure, then $f= 0.$

Having recalled this uniqueness result on angular limits, we recall the well-known existence result on angular limits. Namely, functions in Nevanlinna class, and in particular in Hardy spaces, have angular limits at almost all points of the unit circle.

For $p\in \mathbb C $ and $r>0,$ we denote by $B(p,r)$ the open disc of center p and radius r. We will denote the Lebesgue $2$ -measure by m. Our main result is the following.

Theorem 1.1 Given an arbitrary measurable function $\psi $ on the interval $[0,2\pi ),$ whose restriction to some closed subset $S\subset [0,2\pi )$ is continuous, there exists a function f holomorphic in $\mathbb D ,$ and for every $\theta \in S$ and a.e. $\theta \in [0,2\pi )$ , there is a set $E_\theta \subset \mathbb D ,$ such that

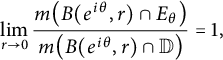$$ \begin{align*}\lim_{r\to 0}\frac{m\big(B(e^{i\theta},r)\cap E_\theta\big)}{m\big(B(e^{i\theta},r)\cap\mathbb D \big)}=1, \end{align*} $$

and

$$ \begin{align*}f(z)\to \psi(\theta) \quad \mbox{as} \quad z\to e^{i\theta}, \, z\in E_{\theta}. \end{align*} $$

Notice that points $e^{i\theta }$ satisfying the first limit are necessarily accumulation points of the corresponding sets $E_\theta .$

More generally, we shall present such a result for solutions of elliptic equations on manifolds. Our result applies, in particular, to harmonic functions on Riemannian manifolds and to holomorphic functions on Riemann surfaces.

Let M be an oriented real analytic manifold with countable base. We shall denote by $*$ the ideal point of the one-point compactification $M^*$ of $M.$ Fix a distance function d on M and a positive Borel measure $\mu $ for which open sets have positive measure and compact sets have finite measure. Then, $\mu $ is regular (see [7, Theorem 2.18]). On M, the Lebesgue measure of a measurable set is not well defined, but because M is smooth, Lebesgue measure zero is invariant under change of coordinates, so the notion of absolute continuity of the measure $\mu $ (with respect to Lebesgue measure) is well defined. We shall assume that our measure $\mu $ is absolutely continuous. Let U be an open subset of $M, p$ a boundary point of U, and F a closed subset of $U.$ For $\alpha \in [0,1]$ , we shall say that the set $F\subset U$ has $\mu $ -density $\alpha $ at p relative to $U,$ if

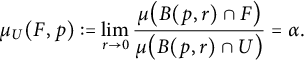$$ \begin{align*}\mu_{U}(F,p):=\lim_{r\to 0}\frac{\mu\big( B(p,r)\cap F\big)}{\mu\big(B(p,r)\cap U\big)}=\alpha. \end{align*} $$

Denote by $\vartheta $ the trivial vector bundle $\vartheta =M\times \mathbb R ^k.$ For a (Borel) measurable subset $S\subset M,$ denote by $\mathcal M(S,\vartheta ),$ the family of measurable sections of $\vartheta $ over $S.$ Thus, an element $u\in \mathcal M(S,\vartheta )$ can be identified with a k-tuple $u=(u_1,\ldots ,u_k)$ of measurable functions $u_j:S\to \mathbb R , \, j=1,\ldots ,k.$ For an open set $U\subset M,$ we denote by $C^\infty (U,\vartheta )$ the family of smooth sections on U endowed with the topology of uniform convergence on compact subsets of all derivatives. For $u\in C^\infty (U,\vartheta )$ and $x\in U,$ we denote $|u(x)|=\max \{|u_1(x)|,\ldots ,|u_k(x)|\}.$ Let $P:\vartheta \to \eta $ be an elliptic operator on M with analytic coefficients, where $\eta $ is a real analytic vector bundle on M of the same rank $k.$

If $M=\mathbb R ^n$ and

$$ \begin{align*}(Pu)(x) = \sum_{|\alpha|\le m}a_\alpha(x)D^\alpha u(x), \end{align*} $$

where the $a_\alpha $ are analytic maps into the space of $s\times r$ matrices, then P is a linear differential operator on $\mathbb R ^r.$ It maps an r-tuple $u=(u_1,\ldots ,u_r)$ of functions on $\mathbb R ^n$ to an s-tuple $Pu=v=(v_1,\ldots ,v_s)$ of functions on $\mathbb R ^n.$ The operator P is of order $m,$ if not all of the coefficients $a_\alpha , |\alpha |=m$ vanish. The symbol of P is the expression

$$ \begin{align*}\sigma_P(x,\xi) = \sum_{|\alpha|\le m}a_\alpha(x)\xi^\alpha, \quad (x,\xi)\in \mathbb R ^n\times (\mathbb R ^n\backslash\{0\}). \end{align*} $$

Because the $a_\alpha (x)$ are $s\times r$ matrices and the $\xi ^\alpha $ are scalars,

$$ \begin{align*}\sigma_P: \mathbb R ^n\times (\mathbb R ^n\backslash\{0\}) \longrightarrow Hom(\mathbb R ^r,\mathbb R ^s). \end{align*} $$

The operator P is elliptic, if for every $x\in \mathbb R ^n$ and every $\xi \in \mathbb R ^n\backslash \{0\}, \sigma _P(x,\xi )$ is injective as an element of $Hom(\mathbb R ^r,\mathbb R ^s),$ that is, if the matrix $\sigma _P(x,\xi )$ always has rank $r.$ If $a_0\equiv 0,$ then P annihilates constants. Such elliptic operators on $\mathbb R ^n$ with analytic coefficients and which annihilate constants are concrete examples of operators satisfying the hypotheses of the following theorem.

Theorem 1.2 Let $M, d, \mu , \vartheta , \eta , P$ be as above, and suppose that P annihilates constants. Let $U\subset M$ be an arbitrary open subset and $\varphi \in \mathcal M(\partial U,\vartheta )$ an arbitrary Borel measurable section on the boundary $\partial U,$ whose restriction to some closed subset $S\subset \partial U$ is continuous. Then, for an arbitrary regular $\sigma $ -finite Borel measure $\nu $ on $\partial U,$ there exists $ \widetilde \varphi \in C^\infty (U,\vartheta )$ with $P \widetilde \varphi =0,$ such that, for $\nu $ -almost every $p\in \partial U$ , and for every $p\in S, \widetilde \varphi (x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U.$

Consider the two extremal situations, where S is empty and S is the entire boundary $\partial U$ , respectively. If $S=\emptyset ,$ then Theorem 1.2 solves an asymptotic measurable first boundary value problem. If $S=\partial U,$ then Theorem 1.2 solves an asymptotic continuous first boundary value problem. The following two corollaries simply state that Theorem 1.2 applies, in particular, for harmonic functions of several variables and to holomorphic functions of a single complex variable.

Corollary 1.3 Let M be a Riemannian manifold, and let $\mu $ be the associated volume measure on $M.$ Let $U\subset M$ be an arbitrary open subset and $\varphi $ an arbitrary Borel measurable function $\varphi $ on the boundary $\partial U,$ whose restriction to some closed subset $S\subset \partial U$ is continuous. Then, for an arbitrary regular $\sigma $ -finite Borel measure $\nu $ on $\partial U,$ there exists a harmonic function $\widetilde \varphi $ on $U,$ such that, for $\nu $ -almost every $p\in \partial U$ and for every $p\in S, \widetilde \varphi (x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U.$

Corollary 1.4 Let M be an open Riemann surface, $\pi :M\rightarrow \mathbb C$ a holomorphic immersion, and $\mu $ the associated measure on $M.$ Let $U\subset M$ be an arbitrary open subset and $\varphi $ an arbitrary Borel measurable function $\varphi $ on the boundary $\partial U,$ whose restriction to some closed subset $S\subset \partial U$ is continuous. Then, for an arbitrary regular $\sigma $ -finite Borel measure $\nu $ on $\partial U,$ there exists a holomorphic function $\widetilde \varphi $ on $U,$ such that, for $\nu $ -almost every $p\in \partial U$ and for every $p\in S, \widetilde \varphi (x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U$ .

Proof Although the theorem is for real vector bundles and the $\overline \partial $ -operator on a Riemann surface is generally considered as an operator between complex vector bundles of rank 1, we may also consider it as an operator between real vector bundles of rank 2 (see [5, Remark 3.10.10 and Theorem 3.10.11]).▪

Remark Riemann surfaces are complex manifolds of dimension 1. Our proof does not allow us to prove an analogue of Corollary 1.4 for holomorphic functions on higher-dimensional complex manifolds, because the proof of Theorem 1.2 is based on the Malgrange–Lax theorem [5], which is for differential operators $P:\xi \to \eta $ between bundles of equal rank. On complex manifolds, the Cauchy–Riemann operator $\overline \partial $ maps forms of type $(p,q)$ to forms of type $(p,q+1).$ Thus, $\overline \partial :\mathcal E^{p,q}\to \mathcal E^{p,q+1}.$ For $\overline \partial :\mathcal E^{p,0}\to \mathcal E^{0,1},$ it is elliptic, and, in particular, it is elliptic for the case $\overline \partial :\mathcal E^{0,0}\to \mathcal E^{0,1},$ mapping functions to forms of type $(0,1).$ On a complex manifold of dimension $n,$ this is a map between bundles of respective (complex) ranks $1$ and n (see [5, Remark 3.10.10]). Thus, in order to have an operator between bundles of equal rank, we must restrict our attention to complex manifolds of dimension $1,$ that is, Riemann surfaces.

When $S=\partial U,$ Corollaries 1.3 and 1.4 were proved in [2] and [1], respectively. When $M=\mathbb C , \, U=\mathbb D $ , and $S=\emptyset ,$ Corollary 1.4 gives Theorem 1.1.

2 Runge–Carleman approximation

A closed subset E of M is said to satisfy the open $K-Q$ -condition if, for every compact $K\subset M$ , there is a compact $Q\subset M$ such that $K\subset Q^\circ $ and $E\cap Q$ is contained in $Q^\circ $ .

An exhaustion $(K_j)_{j=1}^\infty $ of M is said to be regular if, for each n, the sets $K_{n}$ are compact, $ K_{n}\subset K_{n+1}^\circ , M^*\backslash K_n$ is connected, and $M=\cup _{n=1}^{\infty } K_{n}^\circ $ . We say that an exhaustion $(K_j)_{j=1}^\infty $ of M is open compatible with a closed subset E of M if, for every $j=1,2,\ldots , E\cap K_j$ is contained in $K_j^\circ .$

Lemma 2.1 Let E be a closed subset of $M,$ satisfying the open $K-Q$ -condition, then there exists a regular exhaustion of M which is open compatible with $E.$

Proof Let $(K_j)_{j=1}^\infty $ be a regular exhaustion of M. We shall define recursively an exhaustion $(Q_{n})_{n=1}^{\infty }$ of M with certain properties. From the $K-Q$ condition, we choose a compact set $Q_1,$ such that $K_1\subset Q_1^\circ $ and $E\cap Q_1\subset Q_1^\circ .$ Now, we may choose a compact set $Q_2,$ such that $K_1\cup Q_1\subset Q_2^\circ $ and $E\cap Q_2\subset Q_2^\circ .$ Suppose we have selected compact sets $Q_1,\ldots ,Q_{n},$ such that $K_j\cup Q_j\subset Q_{j+1}^\circ $ and $E\cap Q_{j+1}\subset Q_{j+1}^\circ ,$ for $j=1,\ldots ,n-1.$ We may choose a compact set $Q_{n+1},$ such that $K_n\cup Q_n\subset Q_{n+1}^\circ $ and $E\cap Q_{n+1}\subset Q_{n+1}^\circ .$ Thus, we have inductively constructed an exhaustion $(Q_n)_{n=1}^\infty $ such that, for each $n, K_n\cup Q_n\subset Q_{n+1}^\circ $ and $E\cap Q_n\subset Q_n^\circ .$ We denote by $Q_{n,*}^c$ the connected component of $M^*\backslash Q_n$ that contains the point $*$ and put $ L_n=M\backslash Q_{n,*}^c$ . Then, $(L_{n})_{n=1}^{\infty }$ is a regular exhaustion of M (see [5, p. 224]). Furthermore, for each $n, E\cap \partial Q_n=\emptyset ,$ so $E\cap L_n\subset L_n^\circ $ . Thus, the exhaustion $(L_n)_{n=1}^\infty $ is open compatible with $E$ .▪

A closed set $E\subset M$ is said to be a set of Runge–Carleman approximation for an operator $P,$ if for every open neighborhood U of $E,$ every section $f\in C^\infty (U,\mathcal \vartheta ),$ with $Pf=0,$ and every positive continuous function $\varepsilon $ on $E,$ there is a global section $u\in C^\infty (M,\mathcal \vartheta ),$ with $Pu=0,$ such that $|u-f|<\varepsilon $ on $E.$

Theorem 2.2 Let P be an elliptic operator on M with analytic coefficients. Let E be a closed subset of M satisfying the open $K-Q$ condition, with $M^*\backslash E$ connected. Then, E is a set of Runge–Carleman approximation for the operator $P.$

Proof By Lemma 2.1, let $(L_{n})_{n=1}^{\infty }$ be a regular exhaustion of M which is open compatible with E and set $L_0=\emptyset $ . Fix an open neighborhood U of $E,$ and a section $f\in C^\infty (U,\mathcal \vartheta ),$ with $Pf=0$ . Consider $\varepsilon $ a continuous and positive function on $E,$ which we may assume is continuous and positive on all of M, and set

$$ \begin{align*}\varepsilon_{n}=\min\{\varepsilon(x):x\in L_n\}>0, \quad n=1,2,\ldots. \end{align*} $$

Now, we construct recursively a sequence $(u_n)_{n=0}^\infty $ of sections $u_{n}\in C^\infty (M,\vartheta )$ such that $|u_{n}-u_{n-1}|<\varepsilon _{n}/2^{n}$ on $ L_{n-1}$ and $|u_{n}-f|<\varepsilon _{n}/2^{n}$ on $E\cap (L_{n}\backslash L_{n-1})$ . Consider $u_0=0$ . For $n=1$ , we only need to check the second condition on $u_1$ , because the first condition is void. Note that $U_1=L_1^\circ \cap U$ is an open set containing $E\cap L_1$ such that $M\backslash U_1$ has no compact connected components and $Pf=0$ on $U_1$ . By the Malgrange–Lax theorem (see [5]), there exists a section $u_{1}\in C^\infty (M,\vartheta )$ with $Pu_{1}=0,$ such that $|u_1-f|<\varepsilon _{1}/2$ on $E\cap L_{1}.$

Assume now that we have fixed $(u_{n})_{n=1}^{N-1}$ satisfying the required conditions. Consider two open sets $V_N, W_N$ such that

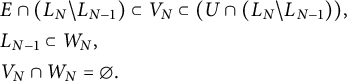$$ \begin{align*} &E\cap (L_N\backslash L_{N-1})\subset V_N\subset (U\cap (L_N\backslash L_{N-1})),&\\ &L_{N-1}\subset W_N,&\\ &V_N\cap W_N=\emptyset.& \end{align*} $$

Because $M^*\backslash E$ is connected and $(L_n)_{n=1}^\infty $ is a regular exhaustion, without loss of generality, we can assume that $M\backslash (V_N\cup W_N)$ has no compact connected components.

Define $g\in C^\infty (G,\vartheta ),$ by putting $g=u_{N-1}$ on $ W_{N}$ and $g=f$ on $V_{N}$ . Set

$$ \begin{align*}K=L_{N-1}\cup\left(E \cap (L_N\backslash L_{N-1})\right) \end{align*} $$

and $U_N=(V_N\cup W_n)\cap U$ . Then, $Pg=0$ on $U_N$ and $M\backslash U_N$ has no compact connected components. By the Malgrange–Lax theorem again, there exists a section $u_{N}\in C^\infty (M,\vartheta )$ with $Pu_{N}=0,$ such that

$$ \begin{align*}\max_{x\in K}|u_{N}(x)-g(x)|< \frac{\varepsilon_N}{2^{N}}. \end{align*} $$

The section $u_N$ has the required properties, which completes the inductive construction of the sequence $(u_n)_{n=0}^\infty .$

For every $x\in M,$ the sequence $\{u_n(x)\}_{n=0}^\infty $ is Cauchy, and hence u converges pointwise to a section $\vartheta .$ Let $u(x)=\lim _{n\to \infty }u_{n}(x)$ for every $x\in M$ . Because, for every natural number $j,$ the sequence $(u_{n})_{n=j}^{\infty }$ converges to u in $C^\infty (L_j^\circ ,\vartheta )$ and $Pu_{n}=0$ on $M,$ we have that $u\in C^\infty (L_j^\circ ,\vartheta )$ and also $Pu=0$ on $L_j^\circ .$ Because this holds for every $j=1,2,\ldots ,$ we have that $u\in C^\infty (M,\vartheta )$ and $Pu=0.$

To finish, we show that $|u(x)-f(x)|\le \varepsilon (x)$ on E. Fix $x\in E.$ Then, there exists a unique natural number $n=n(x),$ such that $x\in L_n\backslash L_{n-1}.$ We have

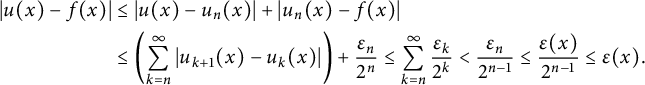$$ \begin{align*} |u(x)-f(x)|&\le |u(x)-u_n(x)|+|u_n(x)-f(x)|\\ &\le \left( \sum_{k=n}^\infty|u_{k+1}(x)-u_k(x)|\right)+\frac{\varepsilon_n}{2^n} \le \sum_{k=n}^\infty\frac{\varepsilon_k}{2^k} < \frac{\epsilon_n}{2^{n-1}} \le \frac{\varepsilon(x)}{2^{n-1}}\le \varepsilon(x). \end{align*} $$

▪

Corollary 2.3 Let E be a subset of M that is a union of a locally finite family of disjoint continua, and suppose that $M^*\backslash E$ is connected. Then, E is a set of Runge–Carleman approximation.

Proof Notice that E is closed, because it is the union of a locally finite family of closed sets. We only need to show that E satisfies the open $K-Q$ condition. For this, fix a compact set K in M. We denote the connected components of E by $E_j$ , and we may assume that they are ordered, so that $E_1, \ldots , E_m$ are the connected components that meet $K.$ Set $L = K\cup E_1\cup \cdots \cup E_m$ , and let Q be a compact neighborhood of L disjoint from the closed set $E_{m+1}\cup E_{m+2}\cup \cdots .$ Then, Q satisfies the required conditions.▪

3 Proof of Theorem 1.2

Lemma 3.1 Let U be a proper open subset of a manifold M and Q and K be disjoint compact subsets of $\partial U.$ Then, for each $\varepsilon>0,$ there exist $\delta>0$ and an open set $V_\delta $ that is a $\delta $ -neighborhood of K in M disjoint from Q such that

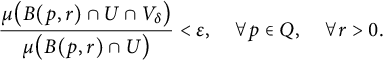$$ \begin{align*} \frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)} < \varepsilon, \quad \forall p\in Q, \quad \forall r>0. \end{align*} $$

Furthermore, $\delta $ can be chosen, so that $B(p,r)\cap V_\delta =\emptyset $ , for all $p\in Q$ and $r<\delta $ .

Proof Set $r_0=d(Q,K)/2>0$ . We claim that

(3.1) $$ \begin{align} \rho:=\min_{p\in Q}\mu\big(B(p,r_0)\cap U\big)>0. \end{align} $$

Assume that this was not the case and we have that $\rho =0$ . Then, by the compactness of Q, we could find a sequence of points $(p_n)_{n=1}^\infty \subset Q$ convergent to a point $p_0\in Q$ , so that $\mu \big (B(p_n,r_0)\cap U\big )<1/n$ and $d(p_n,p_0)<r_0/2$ . But then, we would have that $\mu \big (B(p_0,r_0/2)\cap U\big )\leq \mu \big (B(p_n,r_0)\cap U\big )<1/n$ for every natural number n. Hence, $\mu \big (B(p_0,r_0/2)\cap U\big )=0$ , contradicting the fact that $\mu $ has positive measure on open sets. Thus, equation (3.1) holds.

Consider $V_\delta $ a $\delta $ -neighborhood of K in M with $\delta <r_0$ and $\mu (U\cap V_\delta )<\varepsilon \rho $ . It is clear that, for such $\delta $ , we have that $V_\delta $ and Q are disjoint and $B(p,r)\cap V_\delta =\emptyset ,$ for all $p\in Q$ and all $r<r_0.$ Thus, the last statement of the lemma is obvious by choosing $\delta =r_0$ . Furthermore, for any $r\geq r_0$ , we have that

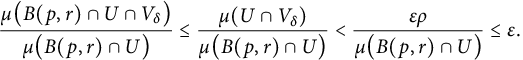$$ \begin{align*} \hspace{3.2pc}\frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)}\leq \frac{\mu(U\cap V_\delta)}{\mu\big(B(p,r)\cap U\big)} < \frac{\varepsilon\rho}{\mu\big(B(p,r)\cap U\big)}\leq \varepsilon.\hspace{3.2pc} \end{align*} $$

The following lemma was stated in [2, Lemma 4] for volume measure on a Riemannian manifold, but the same proof yields the following more general version.

Lemma 3.2 Let U be a proper open subset of a manifold M and C a connected compact subset of U with $\mu (C)=0.$ Then, for each $\epsilon>0$ , there is a connected open neighborhood R of C in U such that

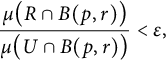$$ \begin{align*} \frac{\mu\big(R\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \epsilon, \end{align*} $$

for every $p\in \partial U$ and every $r>0.$

We recall that an open subset W of a real manifold M is an open parametric ball if there is a chart $\varphi :W\to \mathbb B ,$ where $\mathbb B $ is an open ball in the euclidean space and $\varphi (W)=\mathbb B $ . A subset $H\subset M$ is a closed parametric ball if there is a parametric ball $\varphi :W\to \mathbb B $ and a closed ball $\overline B\subset \mathbb B ,$ such that $H=\varphi ^{-1}(\overline B).$

Lemma 3.3 Under the hypotheses of Theorem 1.2, there exists a set $F,$ with $S\subset F\subset \partial U$ and $\nu (\partial U\backslash F)=0,$ and $u\in C(U,\xi )$ on $U,$ such that, for every $p\in F$ , $u(x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U.$

Proof In the following proof, we use the symbol $\dot \cup $ to denote the disjoint union. We start by showing that there exists a subset $F\subset \partial U$ containing S of the form

$$ \begin{align*}F=S\dot\cup\left(\dot\cup_{n=1}^\infty Q_n\right), \end{align*} $$

with $Q_n$ compact, so that the restriction of $\varphi $ is continuous on $Q_n$ and $\nu (\partial U\backslash F)=0$ .

First, we assume that $\nu (\partial U\backslash S)<+\infty $ . By Lusin’s theorem (see [3] and [8, Theorem 2]), there exists a compact set $Q_1$ in $\partial U\backslash S$ such that $\nu \left ((\partial U\backslash S)\backslash Q_1\right )<2^{-1}$ and the restriction of $\varphi $ to $Q_1$ is continuous. Now, again by Lusin’s theorem, we can find a compact set $Q_2$ in $(\partial U\backslash S)\backslash Q_1$ with $\nu (\big ((\partial U\backslash S)\backslash Q_1)\backslash Q_2\big )<2^{-2}$ , so that the restriction of $\varphi $ to $Q_1\dot \cup Q_2$ is continuous. By induction, we can construct a sequence of compact sets $(Q_n)_{n=1}^\infty $ , so that $Q_{n}\subset (\partial U\backslash S)\backslash \cup _{j=1}^{n-1} Q_j$ , $\nu ((\partial U\backslash S)\backslash \cup _{j=1}^{n} Q_j)<2^{-n}$ , and the restriction of $\varphi $ to $Q_1\dot \cup \cdots \dot \cup Q_n$ is continuous for $n=1,2,3,\ldots $ . We set

$$ \begin{align*} F=S\dot\cup\left(\dot\cup_{n=1}^\infty Q_n\right). \end{align*} $$

It is obvious that $(Q_n)_{n=1}^\infty $ is a family of pairwise disjoint compact sets and $\nu (\partial U\backslash F)=0$ .

If $\nu (\partial U\backslash S)$ is not finite, by the $\sigma $ -finiteness of the measure $\nu $ , there exists a pairwise disjoint sequence of measurable sets $(R_l)_{l=1}^\infty $ with $\nu (R_l)<+\infty $ and $\partial U\backslash S=\dot {\bigcup }_{l=1}^\infty R_l$ . By the previous argument applied to the section $\varphi $ restricted to the set $R_l$ , we can find a pairwise disjoint sequence of compact sets $(Q_{n,l})_{n=1}^\infty $ of $R_l,$ so that the restriction of $\varphi $ is continuous on $Q_{n,l}$ and $\nu (R_l\backslash \dot \cup _{n=1}^\infty Q_{n,l})=0.$ Then,

$$ \begin{align*} F=S\dot\cup\left(\dot\cup_{n=1}^\infty \dot\cup_{l=1}^\infty Q_{n,l}\right) \end{align*} $$

satisfies the desired result.

We now begin to extend the section $\varphi $ . For this, we shall construct inductively a sequence of increasing sets $(E_n)_{n=1}^\infty $ and a sequence of sections $(f_n)_{n=1}^\infty $ . We can write $S=\cup _{n=1}^\infty S_n$ and $F=S\dot \cup \left (\dot \cup _{n=1}^\infty Q_n\right )$ , with $S_n$ and $Q_n$ compact, $S_n$ increasing, and $Q_n$ pairwise disjoint, so that the restriction $\varphi _n$ of $\varphi $ to $F_n=S\cup Q_1\dot \cup \cdots \dot \cup Q_n$ is continuous. By Lemma 3.1, for $l=2,3,\ldots ,$ there is an open $\delta _{1,l}$ -neighborhood $V_{1,l}$ of $Q_l$ in M such that

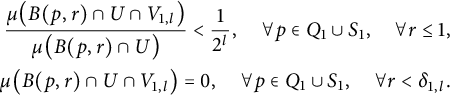(3.2) $$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in Q_{1}\cup S_1, \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{1,l}\big)=0, \quad \forall p\in Q_1 \cup S_1, \quad \forall r<\delta_{1,l}. \end{aligned} \end{align} $$

By the compactness of $Q_l$ , the sets $V_{1,l}$ can be chosen to be a finite union of open parametric balls in M. Let

$$ \begin{align*} E_1=U\backslash \cup_{l=2}^\infty V_{1,l}. \end{align*} $$

Because $S\cup Q_1$ is closed in $E_1\cup S\cup Q_1,$ by the Tietze extension theorem, we can extend the section $\varphi _1$ to a continuous section $f_1$ on $E_1\cup S\cup Q_1.$

Set $E_0=\emptyset $ , and assume that, for $j=1,\ldots ,n,$ we have fixed positive constants $\delta _{j,l}<1/j,$ for $l\ge j+1,$ sets $E_j=U\backslash \cup _{l=j+1}^\infty V_{j,l}$ with $V_{j,l}$ being an open $\delta _{j,l}$ -neighborhood of $Q_l$ in $M\backslash E_j$ that is a finite union of open parametric balls in M, and sections $f_j$ continuous on $E_j\cup F_j$ such that

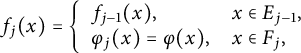$$ \begin{align*}f_j(x) = \left\{ \begin{array}{ll} f_{j-1}(x), & x\in E_{j-1},\\ \varphi_j(x)=\varphi(x), & x\in F_j, \end{array} \right. \end{align*} $$

and

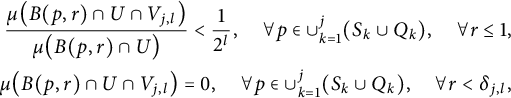(3.3) $$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{j,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{j,l}\big)=0, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r<\delta_{j,l}, \end{aligned} \end{align} $$

for $j=1,\ldots ,n$ and $l=j+1,j+2,\ldots $ . For the step $n+1$ , using Lemma 3.1 again, we have that, for every natural number $l>n+1$ , there is an open $\delta _{n+1,l}$ -neighborhood $V_{n+1,l}$ of $Q_l$ in $M\backslash E_n$ such that

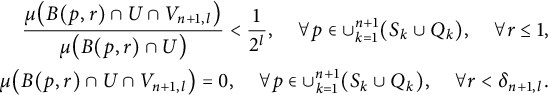$$ \begin{align*} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)=0, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r<\delta_{n+1,l}. \end{aligned} \end{align*} $$

Without loss of generality, we can assume that $\delta _{n+1,l}<1/(n+1)$ , and, by the compactness of $Q_l$ , the sets $V_{n+1,l}$ can be chosen to be a finite union of open parametric balls in M. Set

$$ \begin{align*} E_{n+1}=U\backslash \cup_{l=n+2}^\infty V_{n+1,l}. \end{align*} $$

Note that $E_n\cup F_{n+1}$ is relatively closed in $E_{n+1}\cup F_{n+1}$ . Furthermore, the section $f_{n+1}$ defined as $f_{n+1}=f_{n}$ on $E_n$ and $f_{n+1}=\varphi _{n+1}=\varphi $ on $F_{n+1}$ is continuous on the set $E_n\cup F_{n+1}$ , because $E_n\cap V_{n,n+1}=\emptyset $ . Therefore, by the Tietze extension theorem, we can extend the section $f_{n+1}$ to a continuous section on $E_{n+1}\cup F_{n+1}$ that we denote in the same way.

Note also that $\cup _{n=1}^\infty E_n=U$ . Indeed, if $x\in U$ , because U is open, there exists $r_x>0$ , so that $B(x,r_x)\subset U$ . Fix a natural number $l_0$ , so that $\frac {1}{l_0}<r_x$ . Then, for every $l>l_0$ , because $V_{n,l}$ is a $\frac {1}{l}$ -neighborhood of $Q_l\subset \partial U$ in M, we have that $x\notin V_{n,l}$ for every natural number n. Thus, for $n\geq l_0$ , we have that $x\in E_{n}=U\backslash \cup _{l=n+1}^\infty V_{n,l}$ . Then, the section $u,$ defined on U as $u(x)=f_n(x)$ if $x\in E_n,$ is continuous at $x.$ Because x is arbitrary, we have the u is continuous on U.

There only remains to show that, for every $p\in F$ , $u(x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U.$ For this, fix $p\in F.$ Then, we can find a natural number n, so that $p\in F_n$ . Note that $f_n$ is continuous on $E_n\cup F_n$ , and we have defined $u=f_n$ on $E_n$ and $f_n=\varphi _n=\varphi $ on $F_n.$ Therefore, for every $p\in F$ , $u(x)\to \varphi (p)$ , as $x\to p$ in $E_n.$ By construction, $U\backslash E_n$ has $\mu $ -density $0$ at p relative to $U$ .▪

Before we continue, we introduce some terminology. A compact subset $K\subset M$ is a parametric Mergelyan set if there is an open parametric ball $\varphi :W\to \mathbb B $ , with $K\subset W$ , and a compact set $Q\subset \mathbb B ,$ such that $\mathbb B \backslash Q$ is connected and $K=\varphi ^{-1}(Q).$ A subset E of a manifold M is a Mergelyan chaplet, which we simply call a chaplet, if it is the countable disjoint union of a (possibly infinite) locally finite family $E_{j}$ of pairwise disjoint parametric Mergelyan sets $E_j.$ We denote the chaplet by $E=(E_j)_j.$ By Corollary 2.3, a chaplet is a Runge–Carleman set.

Proof Proof of Theorem 1.2

By Lemma 3.3, there exists a set $F,$ with $S\subset F\subset \partial U$ and $\nu (\partial U\backslash F)=0,$ and $u\in C(U,\xi )$ on $U,$ such that, for every $p\in F$ , $u(x)\to \varphi (p)$ , as $x\to p$ outside a set of $\mu $ -density 0 at p relative to $U.$

Let $\mathcal S=\{S_l\}_{l=1}^{\infty }$ be a locally finite family of smoothly bounded compact parametric balls $S_l$ in U such that $U=\cup _lS_l^0$ and $|S_l|<dist(S_l,\partial U),$ where $|S_l|$ denotes the diameter of $S_l$ . Assume also that none of these balls contains another. We may also assume that the balls become smaller as we approach $\partial U$ , so that the oscillation $\omega _l=\omega _l(u)$ of u on $S_l$ is less than $1/l,$ for each $l.$ Let $s_l=\partial S_l$ for $l\in \mathbb N$ . Because $\mu $ is absolutely continuous, Lemma 3.2 tells us that there is an open neighborhood $R_{j}$ of $s_j$ in U such that

(3.4) $$ \begin{align} \frac{\mu\big(R_{j}\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \frac{1}{2^j}, \quad \forall \, p\in \partial U, \quad \forall \, r>0. \end{align} $$

Without loss of generality, we may assume that each $R_{j}$ is a smoothly bounded shell. That is, that in a local coordinate system, $R_{j}=\{x: 0<\rho _{j}<\|x\|<1\}$ . By the local finiteness of $\mathcal S$ , we may also assume that if $s_j\cap s_l=\emptyset $ , then $R_j\cap R_l=\emptyset $ .

Consider the closed set $A=U\backslash \bigcup _{k=1}^\infty R_{k}$ . Then, denoting by $H_j=S_j^0\cap A$ and $A_j=H_j\backslash \bigcup _{k=1}^{j-1}S_k^0$ , we have that

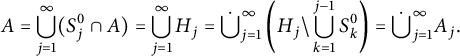$$ \begin{align*} A = \bigcup_{j=1}^\infty( S_j^0\cap A) = \bigcup_{j=1}^\infty H_j = \dot{\bigcup}_{j=1}^\infty\left( H_j\backslash\bigcup_{k=1}^{j-1}S_k^0\right) = \dot{\bigcup}_{j=1}^\infty A_j. \end{align*} $$

For each $j,$ the set $H_j$ is a parametric Mergelyan set in $S_j^0$ and the family $(H_j)_{j=1}^\infty $ is locally finite, but they may not be disjoint. However, the $(A_j)_{j=1}^\infty $ form a locally finite family of disjoint compacta, and hence $A=(A_j)_{j=1}^\infty $ is a Mergelyan chaplet.

Let us fix now a continuous function $\varepsilon :A\to (0,1]$ , so that $\varepsilon (x)\to 0,$ when $x\to \partial U$ . Because $(A_j)_{j=1}^\infty $ is a locally finite family of compacta, we may construct a family $(V_j)_{j=1}^\infty $ of disjoint open neighborhoods $A_j\subset V_j, \, j=1,2,\ldots .$ For each $A_j$ of A, we choose a point $x_{A_{j}}\in A_{j}$ and define a function g on $V=\cup _jV_j$ as $g(x)=\sum _{j}u(x_{A_{j}})\chi _{V_{j}}(x).$ Because the function g is constant in each connected component $V_j$ and P annihilates constants, we have that $Pg=0$ on V.

We claim that $U^*\backslash A=\cup _kR_k$ is connected. Choose some $R_j$ , and let $\mathcal R_j$ be the connected component of $\cup _kR_k$ containing $R_j.$ Then, $\mathcal R_j$ is the union of a subfamily of $(R_k)_{k=1}^\infty .$ Let us show that this subfamily connects $R_j$ with $*$ in $U^*$ . Suppose this is not the case. Consider the sets $V=\cup _{s_l\subset \mathcal R_j} S_l^{\circ }$ and $W=\cup _{s_l\not \subset \mathcal R_j} S_l^{\circ }$ . Both sets are open because they are the union of open sets. Note that if $s_k\cap s_l=\emptyset $ , then $R_k\cap R_l=\emptyset .$ Now, for every set $s_l$ , either $s_l$ intersects some $s_k\subset \mathcal R_j$ or it is disjoint from every $s_k\subset \mathcal R_j,$ in which case $R_\ell $ is disjoint from every $R_k\subset \mathcal R_j.$ In the second case, $R_\ell $ cannot be in the bounded complementary component of any $R_k$ with $R_k\subset \mathcal R_j$ , for then $S_\ell $ would be a subset of $S_k^0$ which is forbidden. Therefore, $R_\ell $ and consequently $S_\ell ^0$ lie in the unbounded complementary component of every $R_k$ with $R_k\subset \mathcal R_j$ . This means that $S_ \ell \cap S_k=\emptyset .$ We have shown that, if $s_\ell \not \subset \mathcal R_j,$ then $S_\ell \cap S_k=\emptyset ,$ for every $s_k\subset \mathcal R_j$ and consequently $V\cap W=\emptyset .$ If, as we supposed, $\mathcal R_j$ is bounded in $U,$ both V and W are nonempty and this contradicts the assumption that U is connected. Thus, every $\mathcal R_j$ is unbounded in $U.$ Because $U^*\backslash A=\cup _j(\mathcal R_j\cup \{*\})$ is the union of a family of connected sets having point $*$ in common, it follows that $U^*\backslash A$ is connected as claimed.

By Corollary 2.3, there exists a function $\widetilde \varphi \in C^\infty (U,\vartheta )$ with $P\widetilde \varphi =0,$ such that $|\widetilde \varphi -g|<\varepsilon $ on A. We show now that

(3.5) $$ \begin{align} |\widetilde\varphi(x)-u(x)|\to 0, \quad \mbox{as} \quad x\to p \in \partial U, \quad x\in A. \end{align} $$

If $(x_n)_{n=1}^\infty $ is a sequence of points in A tending to $p\in \partial U$ , then $(x_{A_{j_n}})_{n=1}^\infty $ is also a sequence of points in A tending to $p\in \partial U$ , where $x_{A_{j_n}}$ is the previously fixed point in the $A_{j_n}$ of A containing $x_n$ . Indeed, this follows automatically, because

$$ \begin{align*} d(x_{A_{j_n}},x_n)\leq \vert A_{j_n}\vert\leq d(A_{j_n},\partial U)\leq d(x_n,\partial U)\to 0, \end{align*} $$

when n goes to infinity.

Furthermore,

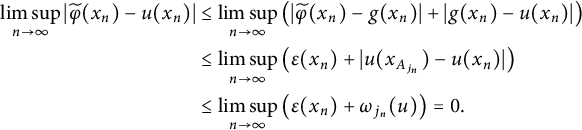$$ \begin{align*} \limsup_{n\to\infty}\vert \widetilde \varphi(x_{n})-u(x_n)\vert & \leq\limsup_{n\to\infty}\big(\vert \widetilde \varphi(x_{n}) -g(x_n)\vert+\vert g(x_{n})-u(x_n)\vert\big)\\ & \leq\limsup_{n\to\infty}\big(\varepsilon(x_{n})+\vert u(x_{A_{j_{n}}})-u(x_n)\vert\big)\\ & \leq \limsup_{n\to\infty}\big(\varepsilon(x_{n})+ \omega_{j_n}(u)\big) =0. \end{align*} $$

We now show that A satisfies that,

(3.6) $$ \begin{align} \mu_{U}(A,p)=\liminf_{r\rightarrow 0}\frac{\mu\big(B(p,r)\cap A\big)}{\mu\big(B(p,r)\cap U\big)}=1. \end{align} $$

For this, we shall show that

$$ \begin{align*}\limsup_{r\rightarrow 0}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)}=0. \end{align*} $$

For fixed $\varepsilon>0$ , consider $j_\varepsilon $ , so that

$$ \begin{align*}\sum_{j\ge j_\varepsilon} 2^{-j}<\varepsilon. \end{align*} $$

Consider $r_\varepsilon>0$ , so that $B(p,r_\varepsilon )$ is disjoint from the neighborhoods $R_{j}$ of the sets $s_j$ for $j\le j_\varepsilon $ . Then, for all $r<r_\varepsilon $ , because $U\backslash A = \cup _j R_{j}$ , we have that

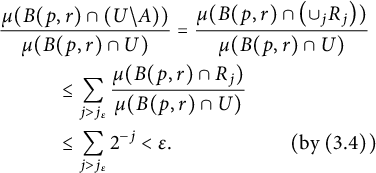$$ \begin{align*} \hspace{1cm}&\hspace{-1cm}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)} = \frac{\mu(B(p,r) \cap\left( \cup_j R_{j}\right))}{\mu(B(p,r)\cap U)}\\ &\le\sum_{j>j_\varepsilon}\frac{\mu(B(p,r)\cap R_{j})}{\mu(B(p,r)\cap U)}\\ &\le \sum_{j>j_\varepsilon}2^{-j} <\varepsilon.\hspace{2cm}(\text{by } (3.4)) \end{align*} $$

Thus, the $\mu $ -density of $U\backslash A$ relative to U at p is at most $\varepsilon .$ Because p and $\varepsilon $ are arbitrary, this proves (3.6).

Note that the function u has all the properties desired in the theorem, except that of satisfying the differential equation $Pu=0.$ The function $\widetilde \varphi $ does satisfy the equation $P\widetilde \varphi =0$ and also satisfies the desired properties, because of (3.5) and (3.6).▪