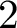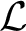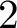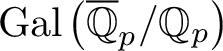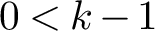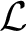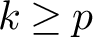1 Introduction
Let p be a prime number and
 $\overline {\mathbb Q}_p$
be an algebraic closure of the p-adic numbers
$\overline {\mathbb Q}_p$
be an algebraic closure of the p-adic numbers
![]() $\mathbb Q_p$
. The goal of this article is to determine the reductions of certain
$\mathbb Q_p$
. The goal of this article is to determine the reductions of certain
![]() $2$
-dimensional p-adic representations of
$2$
-dimensional p-adic representations of
 $G_{\mathbb Q_p} = \mathrm {Gal}\left (\overline {\mathbb Q}_p/\mathbb Q_p\right )$
that are semistable and not crystalline in the sense of Fontaine [Reference Fontaine15]. Examples of such representations arise from local p-adic representations associated with eigenforms with
$G_{\mathbb Q_p} = \mathrm {Gal}\left (\overline {\mathbb Q}_p/\mathbb Q_p\right )$
that are semistable and not crystalline in the sense of Fontaine [Reference Fontaine15]. Examples of such representations arise from local p-adic representations associated with eigenforms with
![]() $\Gamma _0(p)$
-level.
$\Gamma _0(p)$
-level.
1.1 Main result
Write
![]() $v_p$
for the p-adic valuation on
$v_p$
for the p-adic valuation on
 $\overline {\mathbb {Q}}_p$
, normalized so that
$\overline {\mathbb {Q}}_p$
, normalized so that
![]() $v_p(p) = 1$
. Choose
$v_p(p) = 1$
. Choose
 $\varpi \in \overline {\mathbb {Q}}_p$
such that
$\varpi \in \overline {\mathbb {Q}}_p$
such that
![]() $\varpi ^2 = p$
. Then for each integer
$\varpi ^2 = p$
. Then for each integer
![]() $k\geq 2$
and each
$k\geq 2$
and each
 $\mathcal L \in \overline {\mathbb {Q}}_p$
, there is a
$\mathcal L \in \overline {\mathbb {Q}}_p$
, there is a
![]() $2$
-dimensional filtered
$2$
-dimensional filtered
![]() $(\varphi ,N)$
-module
$(\varphi ,N)$
-module
 $D_{k,\mathcal L} = \overline {\mathbb {Q}}_pe_1 \oplus \overline {\mathbb {Q}}_pe_2$
where, in the basis
$D_{k,\mathcal L} = \overline {\mathbb {Q}}_pe_1 \oplus \overline {\mathbb {Q}}_pe_2$
where, in the basis
![]() $(e_1,e_2)$
, we have
$(e_1,e_2)$
, we have
 $$ \begin{align} \varphi &= \begin{pmatrix} \varpi^k & 0 \\ 0 & \varpi^{k-2} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{k,\mathcal L} &= \begin{cases} D_{k,\mathcal L} & \text{if }i \leq 0,\\ \overline{\mathbb{Q}}_p\cdot(e_1 + \mathcal Le_2) & \text{if }1 \leq i \leq k-1,\\ \{0\} & \text{if }k \leq i. \end{cases} \end{align} $$
$$ \begin{align} \varphi &= \begin{pmatrix} \varpi^k & 0 \\ 0 & \varpi^{k-2} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{k,\mathcal L} &= \begin{cases} D_{k,\mathcal L} & \text{if }i \leq 0,\\ \overline{\mathbb{Q}}_p\cdot(e_1 + \mathcal Le_2) & \text{if }1 \leq i \leq k-1,\\ \{0\} & \text{if }k \leq i. \end{cases} \end{align} $$
Each
![]() $D_{k,\mathcal L}$
is weakly admissible, so a theorem of Colmez and Fontaine implies there is a unique
$D_{k,\mathcal L}$
is weakly admissible, so a theorem of Colmez and Fontaine implies there is a unique
![]() $2$
-dimensional
$2$
-dimensional
 $\overline {\mathbb {Q}}_p$
-linear representation
$\overline {\mathbb {Q}}_p$
-linear representation
![]() $V_{k,\mathcal L}$
of
$V_{k,\mathcal L}$
of
![]() $G_{\mathbb {Q}_p}$
such that
$G_{\mathbb {Q}_p}$
such that
![]() $D_{k,\mathcal L} = D_{\operatorname {\mathrm {{st}}}}^{\ast }\left (V_{k,\mathcal L}\right )$
. Up to a twist by a crystalline character, the representations
$D_{k,\mathcal L} = D_{\operatorname {\mathrm {{st}}}}^{\ast }\left (V_{k,\mathcal L}\right )$
. Up to a twist by a crystalline character, the representations
![]() $V_{k,\mathcal L}$
enumerate all
$V_{k,\mathcal L}$
enumerate all
 $\overline {\mathbb {Q}}_p$
-linear
$\overline {\mathbb {Q}}_p$
-linear
![]() $2$
-dimensional semistable and non-crystalline representations of
$2$
-dimensional semistable and non-crystalline representations of
![]() $G_{\mathbb {Q}_p}$
. They are irreducible except if
$G_{\mathbb {Q}_p}$
. They are irreducible except if
![]() $k = 2$
.
$k = 2$
.
We aim to determine the semisimple mod p reductions
![]() $\overline V_{k,\mathcal L}$
of
$\overline V_{k,\mathcal L}$
of
![]() $V_{k,\mathcal L}$
. Twenty years ago, Breuil and Mézard determined
$V_{k,\mathcal L}$
. Twenty years ago, Breuil and Mézard determined
![]() $\overline V_{k,\mathcal L}$
for even
$\overline V_{k,\mathcal L}$
for even
![]() $k < p$
and any
$k < p$
and any
![]() $\mathcal L$
[Reference Breuil and Mézard7, Théorème 4.2.4.7]. Guerberoff and Park recently studied odd
$\mathcal L$
[Reference Breuil and Mézard7, Théorème 4.2.4.7]. Guerberoff and Park recently studied odd
![]() $k < p$
[Reference Guerberoff and Park17, Theorem 5.0.5]. The reader who takes a moment to examine the cited theorems should be left with an impression of the complicated dependence of
$k < p$
[Reference Guerberoff and Park17, Theorem 5.0.5]. The reader who takes a moment to examine the cited theorems should be left with an impression of the complicated dependence of
![]() $\overline V_{k,\mathcal L}$
on
$\overline V_{k,\mathcal L}$
on
![]() $\mathcal L$
, and that is just for
$\mathcal L$
, and that is just for
![]() $k < p$
.
$k < p$
.
Prior results are limited by their ambition to determine
![]() $\overline V_{k,\mathcal L}$
for all
$\overline V_{k,\mathcal L}$
for all
![]() $\mathcal L$
. Here, we focus on determining
$\mathcal L$
. Here, we focus on determining
![]() $\overline V_{k,\mathcal L}$
for any k while restricting to
$\overline V_{k,\mathcal L}$
for any k while restricting to
![]() $\mathcal L$
that place
$\mathcal L$
that place
![]() $V_{k,\mathcal L}$
in a p-adic neighborhood of a crystalline representation (see §1.2). Write
$V_{k,\mathcal L}$
in a p-adic neighborhood of a crystalline representation (see §1.2). Write
![]() $\mathbb Q_{p^2}$
for the unramified quadratic extension of
$\mathbb Q_{p^2}$
for the unramified quadratic extension of
![]() $\mathbb Q_p$
,
$\mathbb Q_p$
,
![]() $\chi $
for its quadratic character modulo p, and
$\chi $
for its quadratic character modulo p, and
![]() $\omega _2$
for a niveau
$\omega _2$
for a niveau
![]() $2$
fundamental character on
$2$
fundamental character on
 $G_{\mathbb Q_{p^2}}$
.
$G_{\mathbb Q_{p^2}}$
.
Theorem 1.1 Theorem 4.1
Assume
![]() $ k \geq 4$
and
$ k \geq 4$
and
![]() $p \neq 2$
. Then, if
$p \neq 2$
. Then, if
 $$ \begin{align*} v_p(\mathcal L) < 2 - \frac{k}{2} - v_p((k-2)!), \end{align*} $$
$$ \begin{align*} v_p(\mathcal L) < 2 - \frac{k}{2} - v_p((k-2)!), \end{align*} $$
we have
 $\overline V_{k,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
.
$\overline V_{k,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
.
To be accurate, our method proves Theorem 1.1 when
![]() $k \geq 5$
or
$k \geq 5$
or
![]() $p=3$
and
$p=3$
and
![]() $k=4$
. The theorem holds for
$k=4$
. The theorem holds for
![]() $k =4$
and
$k =4$
and
![]() $p \geq 5$
by the work of Breuil and Mézard, and it is consistent with their work and the work of Guerberoff and Park for
$p \geq 5$
by the work of Breuil and Mézard, and it is consistent with their work and the work of Guerberoff and Park for
![]() $5 \leq k < p$
. Our method also directly obtains a result for
$5 \leq k < p$
. Our method also directly obtains a result for
![]() $k = 3$
and
$k = 3$
and
![]() $k = 4$
with a weaker bound (see Remark 4.8 for a more detailed discussion). Our exclusion of
$k = 4$
with a weaker bound (see Remark 4.8 for a more detailed discussion). Our exclusion of
![]() $p=2$
is more fundamental (see Remark 1.4).
$p=2$
is more fundamental (see Remark 1.4).
Remark 1.2. When
![]() $k < p$
and k is even, the bound in Theorem 1.1 is optimal by the results of Breuil and Mézard. The same can be said if
$k < p$
and k is even, the bound in Theorem 1.1 is optimal by the results of Breuil and Mézard. The same can be said if
![]() $5 \leq k < p$
and k is odd, by the work of Guerberoff and Park. We do not know to what extent the bound is optimal for higher weights (see §1.3).
$5 \leq k < p$
and k is odd, by the work of Guerberoff and Park. We do not know to what extent the bound is optimal for higher weights (see §1.3).
Theorem 1.1 is a natural analogue of widely studied theorems that determine reductions of
![]() $2$
-dimensional, irreducible, crystalline representations of
$2$
-dimensional, irreducible, crystalline representations of
![]() $G_{\mathbb Q_p}$
. For instance, Buzzard and Gee [Reference Buzzard and Gee9] developed a strategy to determine reductions of certain crystalline representations, with unbounded Hodge–Tate weights, using the p-adic local Langlands correspondence. We do not know whether a direct analogue for semistable but non-crystalline representations has been tried, or even whether such an approach would be feasible.
$G_{\mathbb Q_p}$
. For instance, Buzzard and Gee [Reference Buzzard and Gee9] developed a strategy to determine reductions of certain crystalline representations, with unbounded Hodge–Tate weights, using the p-adic local Langlands correspondence. We do not know whether a direct analogue for semistable but non-crystalline representations has been tried, or even whether such an approach would be feasible.
Another approach in the crystalline case is via integral p-adic Hodge theory. Berger [Reference Berger4] and Berger, Li, and Zhu [Reference Berger, Li and Zhu5] proved local constancy results for reductions of crystalline representations using Wach modules. Recently, the first two authors of this article improved the Berger–Li–Zhu result using Kisin modules [Reference Bergdall and Levin3]. Those are what we will use here also. One incentive to write the previous article was as training to conduct the current research.
Finally, an indirect approach to calculating
![]() $\overline V_{k,\mathcal L}$
is explained in a recent preprint by Chitrao, Ghate, and Yasuda [Reference Chitrao, Ghate and Yasuda10], though their investigation heads in a interesting separate direction from ours.
$\overline V_{k,\mathcal L}$
is explained in a recent preprint by Chitrao, Ghate, and Yasuda [Reference Chitrao, Ghate and Yasuda10], though their investigation heads in a interesting separate direction from ours.
1.2 Overview of strategy
We now describe our strategy, first recontextualizing Theorem 1.1 through the lens of local constancy of reductions as in [Reference Bergdall and Levin3, Reference Berger4, Reference Berger, Li and Zhu5].
The parametrization of semistable and non-crystalline representations by
 $\mathcal L\in \overline {\mathbb Q}_p$
extends to a
$\mathcal L\in \overline {\mathbb Q}_p$
extends to a
 $\mathbb P^1\left (\overline {\mathbb Q}_p\right )$
-parametrization with a crystalline representation at
$\mathbb P^1\left (\overline {\mathbb Q}_p\right )$
-parametrization with a crystalline representation at
![]() $\infty $
. Namely, for
$\infty $
. Namely, for
![]() $\mathcal L \neq 0$
we consider
$\mathcal L \neq 0$
we consider
![]() $D_{k,\mathcal L}$
with basis
$D_{k,\mathcal L}$
with basis
![]() $\left (e_1',e_2'\right ) = (e_1,\mathcal L e_2)$
– in which case, rather than equation (1.1), we have
$\left (e_1',e_2'\right ) = (e_1,\mathcal L e_2)$
– in which case, rather than equation (1.1), we have
 $$ \begin{align} \varphi &= \begin{pmatrix} \varpi^k & 0 \\ 0 & \varpi^{k-2} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ \mathcal L^{-1} & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{k,\mathcal L} &= \begin{cases} D_{k,\mathcal L} & \text{if }i \leq 0,\\ \overline{\mathbb{Q}}_p\cdot\left(e_1' + e_2'\right) & \text{if }1 \leq i \leq k-1,\\ \{0\} & \text{if }k \leq i. \end{cases} \end{align} $$
$$ \begin{align} \varphi &= \begin{pmatrix} \varpi^k & 0 \\ 0 & \varpi^{k-2} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ \mathcal L^{-1} & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{k,\mathcal L} &= \begin{cases} D_{k,\mathcal L} & \text{if }i \leq 0,\\ \overline{\mathbb{Q}}_p\cdot\left(e_1' + e_2'\right) & \text{if }1 \leq i \leq k-1,\\ \{0\} & \text{if }k \leq i. \end{cases} \end{align} $$
Thus,
![]() $D_{k,\mathcal L} \rightarrow D_{k,\infty }$
as
$D_{k,\mathcal L} \rightarrow D_{k,\infty }$
as
![]() $\mathcal L^{-1} \rightarrow 0$
, where
$\mathcal L^{-1} \rightarrow 0$
, where
![]() $D_{k,\infty }$
is the filtered
$D_{k,\infty }$
is the filtered
![]() $(\varphi ,N)$
-module with the same
$(\varphi ,N)$
-module with the same
![]() $\varphi $
and filtration as equation (1.2) but with
$\varphi $
and filtration as equation (1.2) but with
![]() $N = 0$
. In fact,
$N = 0$
. In fact,
![]() $D_{k,\infty } \cong D_{\operatorname {crys}}^{\ast }\left (V_{k,\infty }\right )$
, where
$D_{k,\infty } \cong D_{\operatorname {crys}}^{\ast }\left (V_{k,\infty }\right )$
, where
![]() $V_{k,\infty }$
is a
$V_{k,\infty }$
is a
![]() $2$
-dimensional crystalline representation of
$2$
-dimensional crystalline representation of
![]() $G_{\mathbb Q_p}$
whose Frobenius trace is
$G_{\mathbb Q_p}$
whose Frobenius trace is
![]() $a_p = \varpi ^{k-2} + \varpi ^{k}$
. Replacing the filtered
$a_p = \varpi ^{k-2} + \varpi ^{k}$
. Replacing the filtered
![]() $(\varphi ,N)$
-modules with Galois representations, we have
$(\varphi ,N)$
-modules with Galois representations, we have
![]() $V_{k,\mathcal L} \rightarrow V_{k,\infty }$
as
$V_{k,\mathcal L} \rightarrow V_{k,\infty }$
as
![]() $\mathcal L^{-1} \rightarrow 0$
(see the description in [Reference Colmez12, §§4.5, 4.6] in terms of the space of trianguline representations, for instance). Thus,
$\mathcal L^{-1} \rightarrow 0$
(see the description in [Reference Colmez12, §§4.5, 4.6] in terms of the space of trianguline representations, for instance). Thus,
![]() $\overline V_{k,\mathcal L} \cong \overline V_{k,\infty }$
for
$\overline V_{k,\mathcal L} \cong \overline V_{k,\infty }$
for
![]() $\mathcal L^{-1} \rightarrow 0$
. Furthermore,
$\mathcal L^{-1} \rightarrow 0$
. Furthermore,
 $v_p\left (a_p\right ) = \frac {k-2}{2}$
and so
$v_p\left (a_p\right ) = \frac {k-2}{2}$
and so
 $\left \lfloor {\frac {k-1}{p}}\right \rfloor < v_p\left (a_p\right )$
, except if
$\left \lfloor {\frac {k-1}{p}}\right \rfloor < v_p\left (a_p\right )$
, except if
![]() $p = 2$
or k is small, and so
$p = 2$
or k is small, and so
 $\overline V_{k,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
by [Reference Bergdall and Levin3, Corollary 5.2.3]. We have reduced the theorem to the question: At which point as
$\overline V_{k,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
by [Reference Bergdall and Levin3, Corollary 5.2.3]. We have reduced the theorem to the question: At which point as
![]() $\mathcal L^{-1} \rightarrow 0$
do we have
$\mathcal L^{-1} \rightarrow 0$
do we have
![]() $\overline V_{k,\mathcal L} \cong \overline V_{k,\infty }$
?
$\overline V_{k,\mathcal L} \cong \overline V_{k,\infty }$
?
We now recall the relationship between reductions and Kisin modules. To ease notation, assume for the remainder of this subsection that k is even and
![]() $\mathcal L \in \mathbb Q_p$
, so
$\mathcal L \in \mathbb Q_p$
, so
![]() $V_{k,\mathcal L}$
and
$V_{k,\mathcal L}$
and
![]() $V_{k,\infty }$
are defined over
$V_{k,\infty }$
are defined over
![]() $\mathbb Q_p$
. Let
$\mathbb Q_p$
. Let
![]() $\mathfrak S = \mathbb Z_p[\![u]\!]$
, and write
$\mathfrak S = \mathbb Z_p[\![u]\!]$
, and write
![]() $\varphi : \mathfrak S \rightarrow \mathfrak S$
for the Frobenius map
$\varphi : \mathfrak S \rightarrow \mathfrak S$
for the Frobenius map
![]() $\varphi (u) = u^p$
. Then consider the category
$\varphi (u) = u^p$
. Then consider the category
 $\operatorname {\mathrm {Mod}}_{\mathfrak S}^{\varphi ,\leq k-1}$
of
$\operatorname {\mathrm {Mod}}_{\mathfrak S}^{\varphi ,\leq k-1}$
of
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $\mathfrak S$
with height
$\mathfrak S$
with height
![]() $\leq k-1$
[Reference Kisin18]. Objects in this category, which are called Kisin modules, are finite free
$\leq k-1$
[Reference Kisin18]. Objects in this category, which are called Kisin modules, are finite free
![]() $\mathfrak S$
-modules
$\mathfrak S$
-modules
![]() $\mathfrak M$
equipped with a
$\mathfrak M$
equipped with a
![]() $\varphi $
-semilinear operator
$\varphi $
-semilinear operator
![]() $\varphi : \mathfrak M \rightarrow \mathfrak M$
such that the cokernel of the linearization
$\varphi : \mathfrak M \rightarrow \mathfrak M$
such that the cokernel of the linearization
![]() $\varphi ^{\ast }\mathfrak M \rightarrow \mathfrak M$
is annihilated by
$\varphi ^{\ast }\mathfrak M \rightarrow \mathfrak M$
is annihilated by
![]() $E(u)^{k-1}$
, where
$E(u)^{k-1}$
, where
![]() $E(u) = u+p$
. When
$E(u) = u+p$
. When
![]() $\mathfrak M$
satisfies the monodromy condition, Kisin’s theory constructs a canonical semistable representation
$\mathfrak M$
satisfies the monodromy condition, Kisin’s theory constructs a canonical semistable representation
![]() $V_{\mathfrak M}$
such that
$V_{\mathfrak M}$
such that
![]() $D_{\operatorname {\mathrm {{st}}}}^{\ast }(V_{\mathfrak M}) \cong \mathfrak M/u\mathfrak M[1/p]$
, for a certain filtration and monodromy on the right-hand side. Furthermore,
$D_{\operatorname {\mathrm {{st}}}}^{\ast }(V_{\mathfrak M}) \cong \mathfrak M/u\mathfrak M[1/p]$
, for a certain filtration and monodromy on the right-hand side. Furthermore,
![]() $\overline V_{\mathfrak M}$
is determined by
$\overline V_{\mathfrak M}$
is determined by
 $\mathfrak M/p\mathfrak M\left [u^{-1}\right ]$
as a
$\mathfrak M/p\mathfrak M\left [u^{-1}\right ]$
as a
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\mathbb F_p(\!(u)\!)$
. The challenge in calculating
$\mathbb F_p(\!(u)\!)$
. The challenge in calculating
![]() $\overline V_{\mathfrak M}$
this way is determining
$\overline V_{\mathfrak M}$
this way is determining
![]() $\mathfrak M$
from
$\mathfrak M$
from
![]() $V_{\mathfrak M}$
or, equivalently,
$V_{\mathfrak M}$
or, equivalently,
![]() $D_{\operatorname {\mathrm {{st}}}}^{\ast }(V_{\mathfrak M})$
. That task was carried out for
$D_{\operatorname {\mathrm {{st}}}}^{\ast }(V_{\mathfrak M})$
. That task was carried out for
![]() $V_{k,\infty }$
in [Reference Bergdall and Levin3, Theorem 5.2.1].
$V_{k,\infty }$
in [Reference Bergdall and Levin3, Theorem 5.2.1].
The heart of this article is a two-step argument to do the same for
![]() $V_{k,\mathcal L}$
as
$V_{k,\mathcal L}$
as
![]() $\mathcal L^{-1} \rightarrow 0$
. The difficulty presented by nontrivial monodromy on
$\mathcal L^{-1} \rightarrow 0$
. The difficulty presented by nontrivial monodromy on
![]() $D_{k,\mathcal L}$
requires us to develop a new technique to pass from filtered
$D_{k,\mathcal L}$
requires us to develop a new technique to pass from filtered
![]() $(\varphi ,N)$
-modules to Kisin modules. We make use of a category intermediate between filtered
$(\varphi ,N)$
-modules to Kisin modules. We make use of a category intermediate between filtered
![]() $(\varphi ,N)$
-modules and Kisin modules. Namely, write
$(\varphi ,N)$
-modules and Kisin modules. Namely, write
 $\operatorname {\mathrm {Mod}}_{S_{\mathbb Q_p}}^{\varphi ,\leq k-1}$
for the category of
$\operatorname {\mathrm {Mod}}_{S_{\mathbb Q_p}}^{\varphi ,\leq k-1}$
for the category of
![]() $\varphi $
-modules over
$\varphi $
-modules over
 $S_{\mathbb Q_p} = \mathbb Z_p\left [\!\!\left[u,\frac {E^p}{p}\right]\!\!\right ]\left [\frac 1 p\right ]$
with height
$S_{\mathbb Q_p} = \mathbb Z_p\left [\!\!\left[u,\frac {E^p}{p}\right]\!\!\right ]\left [\frac 1 p\right ]$
with height
![]() $\leq k-1$
. This category is close to certain filtered
$\leq k-1$
. This category is close to certain filtered
![]() $(\varphi ,N)$
-modules considered by Breuil [Reference Breuil6]. Adapting Breuil’s work, we explicitly construct a canonical object
$(\varphi ,N)$
-modules considered by Breuil [Reference Breuil6]. Adapting Breuil’s work, we explicitly construct a canonical object
 $\mathcal M_{k,\mathcal L} \in \operatorname {\mathrm {Mod}}_{S_{\mathbb Q_p}}^{\varphi ,\leq k-1}$
such that if
$\mathcal M_{k,\mathcal L} \in \operatorname {\mathrm {Mod}}_{S_{\mathbb Q_p}}^{\varphi ,\leq k-1}$
such that if
 $\mathfrak M \in \operatorname {\mathrm {Mod}}_{\mathfrak S}^{\varphi ,\leq k-1}$
and
$\mathfrak M \in \operatorname {\mathrm {Mod}}_{\mathfrak S}^{\varphi ,\leq k-1}$
and
![]() $\mathcal M_{k,\mathcal L} \cong \mathfrak M \otimes _{\mathfrak S} S_{\mathbb Q_p}$
, then
$\mathcal M_{k,\mathcal L} \cong \mathfrak M \otimes _{\mathfrak S} S_{\mathbb Q_p}$
, then
![]() $V_{\mathfrak M} \cong V_{k,\mathcal L}$
. ‘Explicit’ means that for any (nonzero)
$V_{\mathfrak M} \cong V_{k,\mathcal L}$
. ‘Explicit’ means that for any (nonzero)
![]() $\mathcal L$
, we determine a basis of
$\mathcal L$
, we determine a basis of
![]() $\mathcal M_{k,\mathcal L}$
and an exact formula for
$\mathcal M_{k,\mathcal L}$
and an exact formula for
![]() $\varphi $
in that basis. This is where we overcome the difficulty of nontrivial monodromy on
$\varphi $
in that basis. This is where we overcome the difficulty of nontrivial monodromy on
![]() $D_{k,\mathcal L}$
.
$D_{k,\mathcal L}$
.
The second step is to descend
![]() $\mathcal M_{k,\mathcal L}$
from
$\mathcal M_{k,\mathcal L}$
from
![]() $S_{\mathbb Q_p}$
to
$S_{\mathbb Q_p}$
to
![]() $\mathfrak S$
when
$\mathfrak S$
when
![]() $\mathcal L^{-1} \rightarrow 0$
, thus producing an
$\mathcal L^{-1} \rightarrow 0$
, thus producing an
![]() $\mathfrak M$
for
$\mathfrak M$
for
![]() $V_{k,\mathcal L}$
. Here we view
$V_{k,\mathcal L}$
. Here we view
![]() $S_{\mathbb Q_p}$
as a subring of
$S_{\mathbb Q_p}$
as a subring of
![]() $R_2$
, where
$R_2$
, where
![]() $R_2$
is the ring of p-adic rigid analytic functions on
$R_2$
is the ring of p-adic rigid analytic functions on
![]() $\lvert u\rvert \leq p^{-1/2}$
(using
$\lvert u\rvert \leq p^{-1/2}$
(using
![]() $p\neq 2)$
. In [Reference Bergdall and Levin3
, §4], a row-reduction algorithm is presented for semilinear operators that, under certain conditions, can descend from
$p\neq 2)$
. In [Reference Bergdall and Levin3
, §4], a row-reduction algorithm is presented for semilinear operators that, under certain conditions, can descend from
![]() $R_2$
to
$R_2$
to
![]() $\mathfrak S$
. Specifically, the main theorem there gives a sufficient condition to descend
$\mathfrak S$
. Specifically, the main theorem there gives a sufficient condition to descend
![]() $\mathcal M_{k,\mathcal L} \otimes _{S_{\mathbb Q_p}} R_2$
to
$\mathcal M_{k,\mathcal L} \otimes _{S_{\mathbb Q_p}} R_2$
to
![]() $\mathfrak S$
. Saving the details for later, we use the explicit calculation of
$\mathfrak S$
. Saving the details for later, we use the explicit calculation of
![]() $\mathcal M_{k,\mathcal L}$
to check that those conditions are met when
$\mathcal M_{k,\mathcal L}$
to check that those conditions are met when
 $v_p(\mathcal L) < 2 - {k\over 2} + v_p((k-2)!)$
.
$v_p(\mathcal L) < 2 - {k\over 2} + v_p((k-2)!)$
.
Remark 1.3. As already discussed, our approach in the first step is more general than [Reference Bergdall and Levin3], as it applies in the semistable, non-crystalline case. In fact, the method is quite general and can be used (with a suitable descent process) to compute reductions for higher-dimensional semistable representations. For example, the third author has used the strategy here to compute reductions of irreducible
![]() $3$
-dimensional crystalline representations of
$3$
-dimensional crystalline representations of
![]() $G_{\mathbb {Q}_p}$
with Hodge–Tate weights
$G_{\mathbb {Q}_p}$
with Hodge–Tate weights
![]() $\{0 , r , s\}$
satisfying
$\{0 , r , s\}$
satisfying
![]() $2 \leq r \leq p-2$
and
$2 \leq r \leq p-2$
and
![]() $ p+2 \leq s \leq r+ p-2$
[Reference Liu22].
$ p+2 \leq s \leq r+ p-2$
[Reference Liu22].
Remark 1.4. We exclude
![]() $p=2$
twice. The second time, when we embed
$p=2$
twice. The second time, when we embed
![]() $S_{\mathbb Q_p}$
into
$S_{\mathbb Q_p}$
into
![]() $R_2$
, is likely technical. However, we also exclude
$R_2$
, is likely technical. However, we also exclude
![]() $p=2$
when referencing the calculation of
$p=2$
when referencing the calculation of
![]() $\overline V_{k,\infty }$
in [Reference Bergdall and Levin3], and that seems crucial: our strategy is based on knowing not just
$\overline V_{k,\infty }$
in [Reference Bergdall and Levin3], and that seems crucial: our strategy is based on knowing not just
![]() $\overline V_{k,\infty }$
but also how to construct a Kisin module for
$\overline V_{k,\infty }$
but also how to construct a Kisin module for
![]() $V_{k,\infty }$
. Including
$V_{k,\infty }$
. Including
![]() $p=2$
here would necessarily require calculating
$p=2$
here would necessarily require calculating
![]() $\overline V_{k,\infty }$
when
$\overline V_{k,\infty }$
when
![]() $p=2$
as well. We note that the formula
$p=2$
as well. We note that the formula
 $\overline V_{k,\infty }\cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1}\chi \right )$
should still be true, but we cannot justify it.
$\overline V_{k,\infty }\cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1}\chi \right )$
should still be true, but we cannot justify it.
1.3 Global context
We end this introduction with a discussion of the global situation. Suppose
![]() $N \geq 1$
and
$N \geq 1$
and
![]() $f = \sum a_n(f)q^n$
is a cuspidal (normalized) eigenform of level
$f = \sum a_n(f)q^n$
is a cuspidal (normalized) eigenform of level
![]() $\Gamma _1(N)$
, weight
$\Gamma _1(N)$
, weight
![]() $k \geq 2$
, and nebentype character
$k \geq 2$
, and nebentype character
![]() $\psi _f$
. Eichler, Shimura, and Deligne famously associated with f a
$\psi _f$
. Eichler, Shimura, and Deligne famously associated with f a
![]() $2$
-dimensional, irreducible, continuous representation
$2$
-dimensional, irreducible, continuous representation
![]() $V_f$
of
$V_f$
of
 $\mathrm {Gal}\left (\overline {\mathbb {Q}}/\mathbb Q\right )$
. We normalize
$\mathrm {Gal}\left (\overline {\mathbb {Q}}/\mathbb Q\right )$
. We normalize
![]() $V_f$
so that for
$V_f$
so that for
![]() $\ell \nmid Np$
the restriction
$\ell \nmid Np$
the restriction
![]() $V_f\rvert _{D_\ell }$
to
$V_f\rvert _{D_\ell }$
to
![]() $D_\ell $
, a decomposition group at
$D_\ell $
, a decomposition group at
![]() $\ell $
, is unramified and the characteristic polynomial of a geometric Frobenius element is
$\ell $
, is unramified and the characteristic polynomial of a geometric Frobenius element is
![]() $t^2 - a_\ell (f)t + \psi _f(\ell )\ell ^{k-1}$
. The representation
$t^2 - a_\ell (f)t + \psi _f(\ell )\ell ^{k-1}$
. The representation
![]() $V_f\rvert _{D_p}$
is semistable when
$V_f\rvert _{D_p}$
is semistable when
![]() $p^2 \nmid N$
and the conductor of
$p^2 \nmid N$
and the conductor of
![]() $\psi _f$
is prime-to-p; it is crystalline when
$\psi _f$
is prime-to-p; it is crystalline when
![]() $p \nmid N$
[Reference Saito24].
$p \nmid N$
[Reference Saito24].
We assume now that
![]() $V_f\rvert _{D_p}$
is semistable and non-crystalline, in which case we define the
$V_f\rvert _{D_p}$
is semistable and non-crystalline, in which case we define the
![]() $\mathcal L$
-invariant of f to be the unique
$\mathcal L$
-invariant of f to be the unique
 $\mathcal L_f \in \overline {\mathbb Q}_p$
such that
$\mathcal L_f \in \overline {\mathbb Q}_p$
such that
![]() $V_f\rvert _{D_p} \cong V_{k,\mathcal L_f}$
. The
$V_f\rvert _{D_p} \cong V_{k,\mathcal L_f}$
. The
![]() $\mathcal L$
-invariant defined this way is called the Fontaine–Mazur
$\mathcal L$
-invariant defined this way is called the Fontaine–Mazur
![]() $\mathcal L$
-invariant (it agrees with [Reference Mazur23, §12] up to a sign). It is a local quantity, but it famously arises in global situations. Examining how it arises allows us to provide global examples where Theorem 1.1 applies and to connect
$\mathcal L$
-invariant (it agrees with [Reference Mazur23, §12] up to a sign). It is a local quantity, but it famously arises in global situations. Examining how it arises allows us to provide global examples where Theorem 1.1 applies and to connect
![]() $\mathcal L$
-invariants to global phenomena on p-adic families.
$\mathcal L$
-invariants to global phenomena on p-adic families.
Theorem 1.1 determines
 $\left (\overline {V_f}\rvert _{D_p}\right )^{\mathrm {ss}}$
in arbitrary weights
$\left (\overline {V_f}\rvert _{D_p}\right )^{\mathrm {ss}}$
in arbitrary weights
![]() $k \geq p$
as long as
$k \geq p$
as long as
![]() $v_p\left (\mathcal L_f\right )$
is sufficiently negative, but it is not immediately obvious that eigenforms exist with
$v_p\left (\mathcal L_f\right )$
is sufficiently negative, but it is not immediately obvious that eigenforms exist with
![]() $v_p\left (\mathcal L_f\right )$
so negative. Recent research, however, sheds light on the situation. For instance, Gräf [Reference Gräf16] and Anni, Böckle, Gräf, and Troya (see [Reference Anni, Böckle, Gräf and Troya1], which builds on [Reference Coleman, Stevens and Teitelbaum11]) have developed the theory and practice needed to calculate the multiset of valuations of
$v_p\left (\mathcal L_f\right )$
so negative. Recent research, however, sheds light on the situation. For instance, Gräf [Reference Gräf16] and Anni, Böckle, Gräf, and Troya (see [Reference Anni, Böckle, Gräf and Troya1], which builds on [Reference Coleman, Stevens and Teitelbaum11]) have developed the theory and practice needed to calculate the multiset of valuations of
![]() $\mathcal L$
-invariants in a fixed weight and level. Pollack has also developed computer code to calculate
$\mathcal L$
-invariants in a fixed weight and level. Pollack has also developed computer code to calculate
![]() $\mathcal L$
-invariants. His method, which dates to the early 2000s, uses the appearance of
$\mathcal L$
-invariants. His method, which dates to the early 2000s, uses the appearance of
![]() $\mathcal L$
-invariants in exceptional zero phenomena for p-adic L-functions. That method is being written up as part of a joint investigation by Pollack and the first author.
$\mathcal L$
-invariants in exceptional zero phenomena for p-adic L-functions. That method is being written up as part of a joint investigation by Pollack and the first author.
Table 1
![]() $3$
-adic valuations of some
$3$
-adic valuations of some
![]() $\mathcal L$
-invariants.
$\mathcal L$
-invariants.

Using their works, both Pollack and Gräf kindly calculated some
![]() $\mathcal L$
-invariants for us. In Table 1, we partially list the p-adic valuations found when
$\mathcal L$
-invariants for us. In Table 1, we partially list the p-adic valuations found when
![]() $p = 3$
and
$p = 3$
and
![]() $N = 51 = 3 \cdot 17$
. Note that the bound in Theorem 1.1 is
$N = 51 = 3 \cdot 17$
. Note that the bound in Theorem 1.1 is
![]() $v_3\left (\mathcal L_f\right ) < 0$
in weight
$v_3\left (\mathcal L_f\right ) < 0$
in weight
![]() $k = 4$
and
$k = 4$
and
![]() $v_3\left (\mathcal L_f\right ) < -2$
in weight
$v_3\left (\mathcal L_f\right ) < -2$
in weight
![]() $k=6$
, so Table 1 provides two examples of Theorem 1.1 in weight
$k=6$
, so Table 1 provides two examples of Theorem 1.1 in weight
![]() $k = 4$
and one example in weight
$k = 4$
and one example in weight
![]() $k = 6$
, though none in weight
$k = 6$
, though none in weight
![]() $k=8$
.
$k=8$
.
Let us look further at
![]() $p = 3$
and
$p = 3$
and
![]() $k = 6$
and the boundary case
$k = 6$
and the boundary case
![]() $v_3(\mathcal L) = -2$
in Theorem 1.1. Pollack’s code, in fact, reports not just
$v_3(\mathcal L) = -2$
in Theorem 1.1. Pollack’s code, in fact, reports not just
![]() $v_3\left (\mathcal L_f\right )$
for each newform f but also
$v_3\left (\mathcal L_f\right )$
for each newform f but also
![]() $\overline V_f$
. This refined data shows that the eigenforms with weight
$\overline V_f$
. This refined data shows that the eigenforms with weight
![]() $k =6$
and
$k =6$
and
![]() $v_3\left (\mathcal L_f\right )$
equal to
$v_3\left (\mathcal L_f\right )$
equal to
![]() $-3$
and
$-3$
and
![]() $-2$
have isomorphic global Galois representations modulo
$-2$
have isomorphic global Galois representations modulo
![]() $3$
. Since Theorem 1.1 applies to
$3$
. Since Theorem 1.1 applies to
![]() $v_3(\mathcal L) = -3$
, we see that there exist
$v_3(\mathcal L) = -3$
, we see that there exist
![]() $\mathcal L$
-invariants with
$\mathcal L$
-invariants with
![]() $v_3(\mathcal L) = -2$
for which the conclusion of Theorem 1.1 continues to hold. More numerical data is required before we can theorize about the sharpness of the bound in Theorem 1.1.
$v_3(\mathcal L) = -2$
for which the conclusion of Theorem 1.1 continues to hold. More numerical data is required before we can theorize about the sharpness of the bound in Theorem 1.1.
The
![]() $\mathcal L$
-invariants also arise, globally, from p-adic families. Namely, f lives in a p-adic family of eigenforms parametrized by weights
$\mathcal L$
-invariants also arise, globally, from p-adic families. Namely, f lives in a p-adic family of eigenforms parametrized by weights
![]() $k \in \mathbb Z_p$
and
$k \in \mathbb Z_p$
and
 $\mathcal L_f = -2 \operatorname {dlog} a_p(k) = -2{a_p'(k)\over a_p(f)}$
[Reference Colmez13, Corollaire 0.7]. This appearance reveals an obstruction to the ‘radius’ of the largest ‘constant slope’ family through f. Indeed, for
$\mathcal L_f = -2 \operatorname {dlog} a_p(k) = -2{a_p'(k)\over a_p(f)}$
[Reference Colmez13, Corollaire 0.7]. This appearance reveals an obstruction to the ‘radius’ of the largest ‘constant slope’ family through f. Indeed, for
![]() $p\neq 2$
, [Reference Bergdall2, Theorem 4.3] implies
$p\neq 2$
, [Reference Bergdall2, Theorem 4.3] implies
 $v_p\left (\mathcal L_f^{-1}\right ) \leq m(f)$
, where
$v_p\left (\mathcal L_f^{-1}\right ) \leq m(f)$
, where
![]() $m(f)$
is the least positive integer such that f lives in a p-adic family of eigenforms
$m(f)$
is the least positive integer such that f lives in a p-adic family of eigenforms
![]() $f'$
with
$f'$
with
![]() $v_p\left (a_p(f')\right ) = v_p\left (a_p(f)\right )$
and weight
$v_p\left (a_p(f')\right ) = v_p\left (a_p(f)\right )$
and weight
![]() $k' \equiv k \bmod (p-1)p^{m(f)}$
.
$k' \equiv k \bmod (p-1)p^{m(f)}$
.
So, ruling out exceptions to Theorem 1.1,
 $v_p\left (\mathcal L_f\right ) < 2 - {k\over 2} - v_p((k-2)!)$
implies
$v_p\left (\mathcal L_f\right ) < 2 - {k\over 2} - v_p((k-2)!)$
implies
-
•
 $\left (\overline V_f\rvert _{D_p}\right )^{\mathrm {ss}} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
and
$\left (\overline V_f\rvert _{D_p}\right )^{\mathrm {ss}} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{k-1} \chi \right )$
and -
•
 $m(f)> {k\over 2} - 2 + v_p((k-2)!) \approx {k-2\over 2} + {k\over p-1}$
.
$m(f)> {k\over 2} - 2 + v_p((k-2)!) \approx {k-2\over 2} + {k\over p-1}$
.
To connect these, if
![]() $k\not \equiv 1 \bmod p+1$
, then
$k\not \equiv 1 \bmod p+1$
, then
 $\overline V_f\rvert _{D_p}$
is irreducible. On the other hand, the second implication generically implies
$\overline V_f\rvert _{D_p}$
is irreducible. On the other hand, the second implication generically implies
 $m(f)> {k-2\over 2} = v_p\left (a_p(f)\right )$
. The fact that
$m(f)> {k-2\over 2} = v_p\left (a_p(f)\right )$
. The fact that
![]() $m(f)> v_p\left (a_p(f)\right )$
occurs in a situation where
$m(f)> v_p\left (a_p(f)\right )$
occurs in a situation where
 $\overline V_f\rvert _{D_p}$
is irreducible is not a coincidence. It follows a pattern of counter examples found by Buzzard and Calegari, to a conjecture of Gouvêa and Mazur, which is related to the
$\overline V_f\rvert _{D_p}$
is irreducible is not a coincidence. It follows a pattern of counter examples found by Buzzard and Calegari, to a conjecture of Gouvêa and Mazur, which is related to the
![]() $m(f)$
. The counter-examples were found by Buzzard and Calegari [Reference Buzzard and Calegari8]. See [Reference Bergdall2, §9] for more discussion.
$m(f)$
. The counter-examples were found by Buzzard and Calegari [Reference Buzzard and Calegari8]. See [Reference Bergdall2, §9] for more discussion.
2 Theoretical background
In this section, we recall filtered
![]() $(\varphi ,N)$
-modules and Breuil and Kisin modules. We explain, in theory, how to calculate a finite-height
$(\varphi ,N)$
-modules and Breuil and Kisin modules. We explain, in theory, how to calculate a finite-height
![]() $\varphi $
-module, over a ring larger than
$\varphi $
-module, over a ring larger than
![]() $\mathfrak S$
, associated with a filtered
$\mathfrak S$
, associated with a filtered
![]() $(\varphi ,N)$
-module (Theorem 2.7). In §3 we carry this out in practice in a special case.
$(\varphi ,N)$
-module (Theorem 2.7). In §3 we carry this out in practice in a special case.
2.1 Notations
Let k be a finite field and
![]() $W(k)$
be the Witt vectors over k. Set
$W(k)$
be the Witt vectors over k. Set
![]() $K_0 = W(k)[1/p]$
and assume
$K_0 = W(k)[1/p]$
and assume
![]() $K/K_0$
is a totally ramified extension of degree e. Let
$K/K_0$
is a totally ramified extension of degree e. Let
![]() $\Lambda _K$
be the ring of integers of K,
$\Lambda _K$
be the ring of integers of K,
![]() $\pi \in \Lambda _K$
a uniformizer, and
$\pi \in \Lambda _K$
a uniformizer, and
![]() $E= E(u)\in W(k)[u]$
its Eisenstein polynomial. Choosing
$E= E(u)\in W(k)[u]$
its Eisenstein polynomial. Choosing
![]() $\pi _0 = \pi $
and
$\pi _0 = \pi $
and
![]() $\pi _1,\pi _2,\dotsc $
a sequence in
$\pi _1,\pi _2,\dotsc $
a sequence in
![]() $\overline K$
such that
$\overline K$
such that
![]() $\pi _{i+1}^p = \pi _i$
, we let
$\pi _{i+1}^p = \pi _i$
, we let
![]() $G_\infty $
be the absolute Galois group of
$G_\infty $
be the absolute Galois group of
 $\varinjlim K(\pi _i)$
. Let
$\varinjlim K(\pi _i)$
. Let
![]() $\mathcal O \subseteq K_0[\![u]\!]$
be the rigid analytic functions on
$\mathcal O \subseteq K_0[\![u]\!]$
be the rigid analytic functions on
![]() $\lvert u\rvert < 1$
and
$\lvert u\rvert < 1$
and
![]() $\mathfrak {S} = W(k)[\![u]\!] \subseteq \mathcal O$
. The action of
$\mathfrak {S} = W(k)[\![u]\!] \subseteq \mathcal O$
. The action of
![]() $\varphi $
on
$\varphi $
on
![]() $K_0[\![u]\!]$
, by the Frobenius on
$K_0[\![u]\!]$
, by the Frobenius on
![]() $K_0$
and
$K_0$
and
![]() $\varphi (u) = u^p$
, preserves
$\varphi (u) = u^p$
, preserves
![]() $\mathfrak {S} \subseteq \mathcal O \subseteq K_0[\![u]\!]$
.
$\mathfrak {S} \subseteq \mathcal O \subseteq K_0[\![u]\!]$
.
We also choose
![]() $F/\mathbb {Q}_p$
a finite extension, which will play the role of linear coefficients. In §2.4 we assume that F contains a subfield isomorphic the Galois closure of K. We write
$F/\mathbb {Q}_p$
a finite extension, which will play the role of linear coefficients. In §2.4 we assume that F contains a subfield isomorphic the Galois closure of K. We write
![]() $\Lambda \subseteq F$
for the ring of integers,
$\Lambda \subseteq F$
for the ring of integers,
![]() $\mathfrak m_F \subseteq \Lambda $
for the maximal ideal, and
$\mathfrak m_F \subseteq \Lambda $
for the maximal ideal, and
![]() $\mathbb {F}$
for the residue field. Define
$\mathbb {F}$
for the residue field. Define
![]() $\mathfrak {S}_{\Lambda } = \mathfrak {S}\otimes _{\mathbb Z_p} \Lambda $
and
$\mathfrak {S}_{\Lambda } = \mathfrak {S}\otimes _{\mathbb Z_p} \Lambda $
and
![]() $\mathcal O_F = \mathcal O\otimes _{K_0} F$
. Extending
$\mathcal O_F = \mathcal O\otimes _{K_0} F$
. Extending
![]() $\varphi $
linearly, we have
$\varphi $
linearly, we have
![]() $\varphi $
-stable subrings of
$\varphi $
-stable subrings of
 $\mathfrak S_{\Lambda } \subseteq S_F \subseteq \left (K_0\otimes _{\mathbb Q_p} F\right )[\![u]\!]$
, where
$\mathfrak S_{\Lambda } \subseteq S_F \subseteq \left (K_0\otimes _{\mathbb Q_p} F\right )[\![u]\!]$
, where
 $S_F = \mathfrak {S} \left [\!\!\left [ \frac {E^p}{p}\right ]\!\!\right ] \otimes _{\mathbb {Q}_p} F$
.
$S_F = \mathfrak {S} \left [\!\!\left [ \frac {E^p}{p}\right ]\!\!\right ] \otimes _{\mathbb {Q}_p} F$
.
2.2 Kisin modules
Let
 $R \subseteq \left (K_0\otimes _{\mathbb Q_p} F\right )[\![u]\!]$
be a
$R \subseteq \left (K_0\otimes _{\mathbb Q_p} F\right )[\![u]\!]$
be a
![]() $\varphi $
-stable subring containing E. A
$\varphi $
-stable subring containing E. A
![]() $\varphi $
-module over R is a finite free R-module M equipped with an injective
$\varphi $
-module over R is a finite free R-module M equipped with an injective
![]() $\varphi $
-semilinear operator
$\varphi $
-semilinear operator
![]() $\varphi _M : M \rightarrow M$
. Let
$\varphi _M : M \rightarrow M$
. Let
![]() $\operatorname {\mathrm {Mod}}_{R}^{\varphi }$
be the category of
$\operatorname {\mathrm {Mod}}_{R}^{\varphi }$
be the category of
![]() $\varphi $
-modules over R with morphisms being R-linear maps that commute with
$\varphi $
-modules over R with morphisms being R-linear maps that commute with
![]() $\varphi $
. For a
$\varphi $
. For a
![]() $\varphi $
-module M, write
$\varphi $
-module M, write
![]() $\varphi ^{\ast }M = R\otimes _{\varphi ,R} M$
, so
$\varphi ^{\ast }M = R\otimes _{\varphi ,R} M$
, so
![]() $1\otimes \varphi _M$
defines an R-linear map
$1\otimes \varphi _M$
defines an R-linear map
![]() $\varphi ^{\ast }M \rightarrow M$
called the linearization of
$\varphi ^{\ast }M \rightarrow M$
called the linearization of
![]() $\varphi $
. For
$\varphi $
. For
![]() $h \geq 0$
, an element
$h \geq 0$
, an element
![]() $M \in \operatorname {\mathrm {Mod}}_R^{\varphi }$
has (E)-height
$M \in \operatorname {\mathrm {Mod}}_R^{\varphi }$
has (E)-height
![]() $\leq h$
if its linearization has cokernel annihilated by
$\leq h$
if its linearization has cokernel annihilated by
![]() $E^h$
. The subcategory of
$E^h$
. The subcategory of
![]() $\varphi $
-modules over R with height
$\varphi $
-modules over R with height
![]() $\leq h$
is denoted
$\leq h$
is denoted
 $\operatorname {\mathrm {Mod}}_{R}^{\varphi ,\leq h}$
. A Kisin module over
$\operatorname {\mathrm {Mod}}_{R}^{\varphi ,\leq h}$
. A Kisin module over
![]() $\mathfrak {S}_{\Lambda }$
with height
$\mathfrak {S}_{\Lambda }$
with height
![]() $\leq h$
is an object in
$\leq h$
is an object in
 $\operatorname {\mathrm {Mod}}_{\mathfrak {S}_{\Lambda }}^{\varphi ,\leq h}$
.
$\operatorname {\mathrm {Mod}}_{\mathfrak {S}_{\Lambda }}^{\varphi ,\leq h}$
.
Let
 $\mathrm {MF}^{\varphi , N}_F$
be the category of positive filtered
$\mathrm {MF}^{\varphi , N}_F$
be the category of positive filtered
![]() $(\varphi , N,K,F)$
-modules, which we shorten to just filtered
$(\varphi , N,K,F)$
-modules, which we shorten to just filtered
![]() $(\varphi ,N)$
-modules over F (see [Reference Breuil and Mézard7, §3.1.1]). For
$(\varphi ,N)$
-modules over F (see [Reference Breuil and Mézard7, §3.1.1]). For
 $D \in \operatorname {\mathrm {MF}}^{\varphi ,N}_F$
, set
$D \in \operatorname {\mathrm {MF}}^{\varphi ,N}_F$
, set
![]() $D_K = K\otimes _{K_0} D$
; here, ‘positive’ means
$D_K = K\otimes _{K_0} D$
; here, ‘positive’ means
![]() $\operatorname {\mathrm {Fil}} ^0 D_K = D_K$
. Let
$\operatorname {\mathrm {Fil}} ^0 D_K = D_K$
. Let
 $\mathrm {Rep}_{F}^{\mathrm {st}, h}$
be the category of F-linear semistable representations V of
$\mathrm {Rep}_{F}^{\mathrm {st}, h}$
be the category of F-linear semistable representations V of
![]() $G_K$
whose Hodge–Tate weights lie in
$G_K$
whose Hodge–Tate weights lie in
![]() $\{0 , \dotsc , h\}$
. Then there exists a fully faithful, contravariant functor
$\{0 , \dotsc , h\}$
. Then there exists a fully faithful, contravariant functor
 $$ \begin{align*} D_{\operatorname{\mathrm{{st}}}}^{\ast} : \operatorname{Rep}_F^{\mathrm{st},h} \rightarrow \operatorname{\mathrm{MF}}_F^{\varphi,N} \end{align*} $$
$$ \begin{align*} D_{\operatorname{\mathrm{{st}}}}^{\ast} : \operatorname{Rep}_F^{\mathrm{st},h} \rightarrow \operatorname{\mathrm{MF}}_F^{\varphi,N} \end{align*} $$
whose image is the subcategory of weakly admissible filtered
![]() $(\varphi ,N)$
-modules over F (see [Reference Colmez and Fontaine14, Reference Fontaine15] and [Reference Breuil and Mézard7, Corollaire 3.1.1.3]). For
$(\varphi ,N)$
-modules over F (see [Reference Colmez and Fontaine14, Reference Fontaine15] and [Reference Breuil and Mézard7, Corollaire 3.1.1.3]). For
 $V \in \operatorname {Rep}_F^{\mathrm {st},h}$
and
$V \in \operatorname {Rep}_F^{\mathrm {st},h}$
and
![]() $T \subseteq V$
a
$T \subseteq V$
a
![]() $G_\infty $
-stable and
$G_\infty $
-stable and
![]() $\Lambda $
-linear lattice, there exists, by [Reference Liu20, Theorem 5.4.1], a canonical Kisin module
$\Lambda $
-linear lattice, there exists, by [Reference Liu20, Theorem 5.4.1], a canonical Kisin module
![]() $\mathfrak M = \mathfrak M(T)$
over
$\mathfrak M = \mathfrak M(T)$
over
![]() $\mathfrak S_{\Lambda }$
with height
$\mathfrak S_{\Lambda }$
with height
![]() $\leq h$
. Naturally, we say a Kisin module
$\leq h$
. Naturally, we say a Kisin module
![]() $\mathfrak M$
is associated with V if
$\mathfrak M$
is associated with V if
![]() $\mathfrak M = \mathfrak M(T)$
for some T. By [Reference Bergdall and Levin3, Corollary 2.3.2], the semisimple mod p representation
$\mathfrak M = \mathfrak M(T)$
for some T. By [Reference Bergdall and Levin3, Corollary 2.3.2], the semisimple mod p representation
![]() $\overline V$
can be determined from any associated Kisin module.
$\overline V$
can be determined from any associated Kisin module.
One category that intervenes in determining an
![]() $\mathfrak M$
associated with
$\mathfrak M$
associated with
 $V \in \operatorname {Rep}_F^{\mathrm {st},h}$
is the category of
$V \in \operatorname {Rep}_F^{\mathrm {st},h}$
is the category of
![]() $(\varphi ,N_{\nabla })$
-modules over
$(\varphi ,N_{\nabla })$
-modules over
![]() $\mathcal O_F$
[Reference Kisin18]. Let
$\mathcal O_F$
[Reference Kisin18]. Let
 $\lambda = \prod _{n\geq 0} \varphi ^{n}(E(u)/E(0)) \in \mathcal O_F$
. An object
$\lambda = \prod _{n\geq 0} \varphi ^{n}(E(u)/E(0)) \in \mathcal O_F$
. An object
 $\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
is a finite-height
$\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
is a finite-height
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\mathcal O_F$
equipped with a differential operator
$\mathcal O_F$
equipped with a differential operator
![]() $N_{\nabla }$
lying over
$N_{\nabla }$
lying over
 $-u\lambda {d \over du}$
on
$-u\lambda {d \over du}$
on
![]() $\mathcal O_F$
and satisfying
$\mathcal O_F$
and satisfying
 $N_{\nabla } \varphi = p{E(u)\over E(0)}\varphi N_{\nabla }$
. By [Reference Kisin18, Theorem 1.2.15], we have quasi-inverse equivalences of categories
$N_{\nabla } \varphi = p{E(u)\over E(0)}\varphi N_{\nabla }$
. By [Reference Kisin18, Theorem 1.2.15], we have quasi-inverse equivalences of categories

For
![]() $s> 0$
, write
$s> 0$
, write
![]() $\mathcal O_s$
for the
$\mathcal O_s$
for the
![]() $\mathcal O_F$
-algebra of rigid analytic functions converging on
$\mathcal O_F$
-algebra of rigid analytic functions converging on
![]() $\lvert u\rvert <p^{-s}$
.
$\lvert u\rvert <p^{-s}$
.
Proposition 2.1. Suppose
 $\mathfrak M \in \operatorname {\mathrm {Mod}}_{\mathfrak S_{\Lambda }}^{\varphi ,\leq h}$
,
$\mathfrak M \in \operatorname {\mathrm {Mod}}_{\mathfrak S_{\Lambda }}^{\varphi ,\leq h}$
,
 $V \in \operatorname {Rep}_F^{\operatorname {\mathrm {{st}}},h}$
, and s is such that
$V \in \operatorname {Rep}_F^{\operatorname {\mathrm {{st}}},h}$
, and s is such that
![]() $1/pe < s < 1/e$
and
$1/pe < s < 1/e$
and
![]() $\mathfrak M \otimes _{\mathfrak S_\Lambda } \mathcal O_s \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)\right ) \otimes _{\mathcal O_F} \mathcal O_s$
in
$\mathfrak M \otimes _{\mathfrak S_\Lambda } \mathcal O_s \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)\right ) \otimes _{\mathcal O_F} \mathcal O_s$
in
 $\operatorname {\mathrm {Mod}}_{\mathcal O_s}^{\varphi ,\leq h}$
. Then,
$\operatorname {\mathrm {Mod}}_{\mathcal O_s}^{\varphi ,\leq h}$
. Then,
![]() $\mathfrak M = \mathfrak M(T)$
for some
$\mathfrak M = \mathfrak M(T)$
for some
![]() $T \subseteq V$
as before.
$T \subseteq V$
as before.
Proof. Since
![]() $s < 1/e$
,
$s < 1/e$
,
![]() $\pi $
lies in the disc
$\pi $
lies in the disc
![]() $\lvert u\rvert < p^{-s}$
. Since
$\lvert u\rvert < p^{-s}$
. Since
![]() $\mathfrak M \otimes _{\mathfrak S_\Lambda } \mathcal O_s \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)\right ) \otimes _{\mathcal O_F} \mathcal O_s$
, [Reference Bergdall and Levin3, Corollary 2.2.5] implies that
$\mathfrak M \otimes _{\mathfrak S_\Lambda } \mathcal O_s \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)\right ) \otimes _{\mathcal O_F} \mathcal O_s$
, [Reference Bergdall and Levin3, Corollary 2.2.5] implies that
![]() $\mathcal M_{\mathcal O_F} := \mathfrak M \otimes _{\mathfrak S_{\Lambda }} \mathcal O_F$
is canonically an object in
$\mathcal M_{\mathcal O_F} := \mathfrak M \otimes _{\mathfrak S_{\Lambda }} \mathcal O_F$
is canonically an object in
 $\operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
. Then [Reference Liu20, Theorem 5.4.1] implies that there exists a
$\operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
. Then [Reference Liu20, Theorem 5.4.1] implies that there exists a
 $V' \in \operatorname {Rep}_F^{\operatorname {\mathrm {{st}}},h}$
such that
$V' \in \operatorname {Rep}_F^{\operatorname {\mathrm {{st}}},h}$
such that
![]() $\mathfrak M=\mathfrak M(T)$
for a lattice
$\mathfrak M=\mathfrak M(T)$
for a lattice
![]() $T \subseteq V'$
for some T. We claim that
$T \subseteq V'$
for some T. We claim that
![]() $V \cong V'$
. Indeed, since
$V \cong V'$
. Indeed, since
![]() $1/pe < s < 1/e$
, the definition of
$1/pe < s < 1/e$
, the definition of
![]() $\underline D_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right )$
in [Reference Kisin18, §§1.2.5–1.2.7] depends on only the finite-height
$\underline D_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right )$
in [Reference Kisin18, §§1.2.5–1.2.7] depends on only the finite-height
![]() $\varphi $
-module
$\varphi $
-module
![]() $\mathcal M_{\mathcal O_F} \otimes _{\mathcal O_F} \mathcal O_s$
over
$\mathcal M_{\mathcal O_F} \otimes _{\mathcal O_F} \mathcal O_s$
over
![]() $\mathcal O_s$
. Thus we have
$\mathcal O_s$
. Thus we have
 $$ \begin{align*} D_{\operatorname{\mathrm{{st}}}}^{\ast}(V') \cong \underline D_{\mathcal O_F}\left(\mathcal M_{\mathcal O_F}\right) \cong \underline D_{\mathcal O_F}\left(\underline{\mathcal M}_{\mathcal O_F}\left(D_{\operatorname{\mathrm{{st}}}}^{\ast}(V)\right)\right) \cong D_{\operatorname{\mathrm{{st}}}}^{\ast}(V). \end{align*} $$
$$ \begin{align*} D_{\operatorname{\mathrm{{st}}}}^{\ast}(V') \cong \underline D_{\mathcal O_F}\left(\mathcal M_{\mathcal O_F}\right) \cong \underline D_{\mathcal O_F}\left(\underline{\mathcal M}_{\mathcal O_F}\left(D_{\operatorname{\mathrm{{st}}}}^{\ast}(V)\right)\right) \cong D_{\operatorname{\mathrm{{st}}}}^{\ast}(V). \end{align*} $$
Since
![]() $D_{\operatorname {\mathrm {{st}}}}^{\ast }$
is fully faithful, we have
$D_{\operatorname {\mathrm {{st}}}}^{\ast }$
is fully faithful, we have
![]() $V \cong V'$
, completing the proof.
$V \cong V'$
, completing the proof.
Remark 2.2. To be accurate, the equivalence (2.1) is constructed in [Reference Kisin18] only when
![]() $F = \mathbb Q_p$
. We use multiple references with the same technical limitation. We pause to detail one approach to resolving the issue. Later, we omit details for other functors.
$F = \mathbb Q_p$
. We use multiple references with the same technical limitation. We pause to detail one approach to resolving the issue. Later, we omit details for other functors.
First, we may define the functors
![]() $\underline D_{\mathcal O_F}$
and
$\underline D_{\mathcal O_F}$
and
![]() $\underline {\mathcal M}_{\mathcal O_F}$
using the same formulas as (2.1), or equivalently, we can define them by forcing the diagram
$\underline {\mathcal M}_{\mathcal O_F}$
using the same formulas as (2.1), or equivalently, we can define them by forcing the diagram

to commute. Here, the vertical arrows are the natural forgetful functors and the bottom arrows are as in [Reference Kisin18], where they are proved to be quasi-inverses. If
 $\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
, we thus have a natural isomorphism
$\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
, we thus have a natural isomorphism
 $\alpha : \underline {\mathcal M}_{\mathcal O_F} \left (\underline D_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right )\right ) \cong \mathcal M_{\mathcal O_F}$
in
$\alpha : \underline {\mathcal M}_{\mathcal O_F} \left (\underline D_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right )\right ) \cong \mathcal M_{\mathcal O_F}$
in
 $\operatorname {\mathrm {Mod}}_{\mathcal O}^{\varphi ,N_{\nabla }}$
. Since multiplication by
$\operatorname {\mathrm {Mod}}_{\mathcal O}^{\varphi ,N_{\nabla }}$
. Since multiplication by
![]() $x \in F$
defines an endomorphism of
$x \in F$
defines an endomorphism of
![]() $\mathcal M_{\mathcal O_F}$
in
$\mathcal M_{\mathcal O_F}$
in
 $\operatorname {\mathrm {Mod}}_{\mathcal O}^{\varphi ,N_{\nabla }}$
and
$\operatorname {\mathrm {Mod}}_{\mathcal O}^{\varphi ,N_{\nabla }}$
and
![]() $\alpha $
is natural, we see that
$\alpha $
is natural, we see that
![]() $\alpha $
is an isomorphism in
$\alpha $
is an isomorphism in
 $\operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
. Thus,
$\operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
. Thus,
![]() $\underline {\mathcal M}_{\mathcal O_F}$
is a left quasi-inverse to
$\underline {\mathcal M}_{\mathcal O_F}$
is a left quasi-inverse to
![]() $\underline D_{\mathcal O_F}$
. Proving that
$\underline D_{\mathcal O_F}$
. Proving that
![]() $\underline D_{\mathcal O_F}$
is a right quasi-inverse to
$\underline D_{\mathcal O_F}$
is a right quasi-inverse to
![]() $\underline {\mathcal M}_{\mathcal O_F}$
is analogous.
$\underline {\mathcal M}_{\mathcal O_F}$
is analogous.
2.3 Breuil modules
Let
![]() $S_{\mathrm {Br}}$
be the p-adic completion of the divided power envelope of
$S_{\mathrm {Br}}$
be the p-adic completion of the divided power envelope of
![]() $W(k)[u]$
with respect to the ideal generated by E. Breuil [Reference Breuil6] classically identified
$W(k)[u]$
with respect to the ideal generated by E. Breuil [Reference Breuil6] classically identified
 $\operatorname {\mathrm {MF}}_{\mathbb Q_p}^{\varphi ,N}$
with a category of filtered
$\operatorname {\mathrm {MF}}_{\mathbb Q_p}^{\varphi ,N}$
with a category of filtered
![]() $(\varphi ,N)$
-modules over
$(\varphi ,N)$
-modules over
 $S_{\mathrm {Br}}\left [\frac 1 p\right ]$
. We recall this, replacing
$S_{\mathrm {Br}}\left [\frac 1 p\right ]$
. We recall this, replacing
![]() $S_{\mathrm {Br}}$
with a simpler ring.
$S_{\mathrm {Br}}$
with a simpler ring.
One extends the Frobenius
![]() $\varphi $
to
$\varphi $
to
![]() $K_0 [\![u]\!]$
via
$K_0 [\![u]\!]$
via
![]() $\varphi (u) = u ^p$
. We define
$\varphi (u) = u ^p$
. We define
 $N= -u{d\over du}$
on
$N= -u{d\over du}$
on
![]() $K_0 [\![u]\!]$
. Let
$K_0 [\![u]\!]$
. Let
![]() $\widehat S _E$
be the E-completion of
$\widehat S _E$
be the E-completion of
 $W(k)[u]\left [\frac 1 p\right ]$
. For a subring
$W(k)[u]\left [\frac 1 p\right ]$
. For a subring
![]() $R \subseteq \widehat S_E$
and
$R \subseteq \widehat S_E$
and
![]() $j \geq 0$
, set
$j \geq 0$
, set
![]() $\operatorname {\mathrm {Fil}} ^j R = R \cap E ^j \widehat S_E$
. In particular, we can take
$\operatorname {\mathrm {Fil}} ^j R = R \cap E ^j \widehat S_E$
. In particular, we can take
 $R = S := W(k)\left [\!\!\left [u, \frac {E^p}{p}\right ]\!\!\right ]$
. As a subring of
$R = S := W(k)\left [\!\!\left [u, \frac {E^p}{p}\right ]\!\!\right ]$
. As a subring of
![]() $K_0[\![u]\!]$
, S is closed under
$K_0[\![u]\!]$
, S is closed under
![]() $\varphi $
and N. We define
$\varphi $
and N. We define
![]() $S_\Lambda = S \otimes _{\mathbb {Z}_p} \Lambda $
and
$S_\Lambda = S \otimes _{\mathbb {Z}_p} \Lambda $
and
![]() $S_F = S \otimes _{\mathbb {Z}_p} F$
, extending
$S_F = S \otimes _{\mathbb {Z}_p} F$
, extending
![]() $\varphi $
, N, and
$\varphi $
, N, and
![]() $\operatorname {\mathrm {Fil}}^{\bullet }$
linearly.
$\operatorname {\mathrm {Fil}}^{\bullet }$
linearly.
Clearly
![]() $S \subseteq S_{\textrm {{Br}}}\subseteq \widehat S _E$
, which are compatible with the
$S \subseteq S_{\textrm {{Br}}}\subseteq \widehat S _E$
, which are compatible with the
 $\left (u ,\frac {E^p}{p}\right )$
-topology on S, the p-adic topology on
$\left (u ,\frac {E^p}{p}\right )$
-topology on S, the p-adic topology on
![]() $S_{\mathrm Br}$
, and the
$S_{\mathrm Br}$
, and the
![]() $(E)$
-topology on
$(E)$
-topology on
![]() $\widehat S_E$
. One advantage S enjoys over
$\widehat S_E$
. One advantage S enjoys over
![]() $S_{\mathrm {Br}}$
is that
$S_{\mathrm {Br}}$
is that
![]() $\operatorname {\mathrm {Fil}} ^ j S_F = E^j S_F$
. To see this, note that any element
$\operatorname {\mathrm {Fil}} ^ j S_F = E^j S_F$
. To see this, note that any element
![]() $f \in \operatorname {\mathrm {Fil}}^j S_F$
can be uniquely written in the form
$f \in \operatorname {\mathrm {Fil}}^j S_F$
can be uniquely written in the form
 $f = \sum _{i} a_i(u){E^{pi}\over p^i}$
, with
$f = \sum _{i} a_i(u){E^{pi}\over p^i}$
, with
![]() $a_i(u) \in K_0[u]$
a polynomial of degree strictly less than
$a_i(u) \in K_0[u]$
a polynomial of degree strictly less than
![]() $ep$
(e is the degree of E). Then, when
$ep$
(e is the degree of E). Then, when
![]() $j < pi$
, we have
$j < pi$
, we have
 $\frac {E^{p i -j}}{p ^i}=\frac {1}{p ^{i - l}} E^{p i - pl} \left (\frac {E^p}{p}\right ) ^{l}$
, with
$\frac {E^{p i -j}}{p ^i}=\frac {1}{p ^{i - l}} E^{p i - pl} \left (\frac {E^p}{p}\right ) ^{l}$
, with
 $l = \left \lfloor \frac {p i -j}{p} \right \rfloor $
. In this situation,
$l = \left \lfloor \frac {p i -j}{p} \right \rfloor $
. In this situation,
![]() $i-l$
depends only on j, so factoring
$i-l$
depends only on j, so factoring
![]() $E^j$
out of the expression for f and examining the leftover summation, one sees at once that
$E^j$
out of the expression for f and examining the leftover summation, one sees at once that
![]() $f \in E^j S_F$
. Note as well:
$f \in E^j S_F$
. Note as well:
![]() $S_F$
is an
$S_F$
is an
![]() $\mathcal O_F$
-algebra, and
$\mathcal O_F$
-algebra, and
![]() $\varphi (E) = p{\mathfrak {c}}$
with
$\varphi (E) = p{\mathfrak {c}}$
with
![]() ${\mathfrak {c}} \in S^\times $
. In particular,
${\mathfrak {c}} \in S^\times $
. In particular,
![]() $\varphi (\lambda ) \in S^\times \subseteq S_F^\times $
.
$\varphi (\lambda ) \in S^\times \subseteq S_F^\times $
.
The category
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
of filtered
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
of filtered
![]() $(\varphi ,N)$
-modules over
$(\varphi ,N)$
-modules over
![]() $S_F$
, or Breuil modules over
$S_F$
, or Breuil modules over
![]() $S_F$
, are objects
$S_F$
, are objects
![]() $(\mathcal D,\varphi _{\mathcal D}) \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi }$
such that the linearization of
$(\mathcal D,\varphi _{\mathcal D}) \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi }$
such that the linearization of
![]() $\varphi _{\mathcal D}$
is an isomorphism, and
$\varphi _{\mathcal D}$
is an isomorphism, and
![]() $\mathcal D$
is equipped with the following:
$\mathcal D$
is equipped with the following:
-
• a decreasing filtration
 $\operatorname {\mathrm {Fil}}^{\bullet } \mathcal D$
by
$\operatorname {\mathrm {Fil}}^{\bullet } \mathcal D$
by
 $S_F$
-submodules such that
$S_F$
-submodules such that
 $\operatorname {\mathrm {Fil}}^0\mathcal D = \mathcal D$
andfor all
$\operatorname {\mathrm {Fil}}^0\mathcal D = \mathcal D$
andfor all $$ \begin{align*} \operatorname {\mathrm {Fil}}^i S_F \cdot \operatorname {\mathrm {Fil}}^j \mathcal D \subseteq \operatorname {\mathrm {Fil}}^{i+j} \mathcal D \end{align*} $$
$$ \begin{align*} \operatorname {\mathrm {Fil}}^i S_F \cdot \operatorname {\mathrm {Fil}}^j \mathcal D \subseteq \operatorname {\mathrm {Fil}}^{i+j} \mathcal D \end{align*} $$
 $i,j \geq 0$
;
$i,j \geq 0$
;
-
• an operator
 $N_{\mathcal D}: \mathcal D \rightarrow \mathcal D$
that acts as a derivation over N, with
$N_{\mathcal D}: \mathcal D \rightarrow \mathcal D$
that acts as a derivation over N, with-
–
 $N_{\mathcal D} \varphi _{\mathcal D} = p \varphi _{\mathcal D} N_{\mathcal D}$
and
$N_{\mathcal D} \varphi _{\mathcal D} = p \varphi _{\mathcal D} N_{\mathcal D}$
and -
–
 $N_{\mathcal D}\left (\operatorname {\mathrm {Fil}}^i \mathcal D\right ) \subseteq \operatorname {\mathrm {Fil}}^{i-1}\mathcal D$
for all
$N_{\mathcal D}\left (\operatorname {\mathrm {Fil}}^i \mathcal D\right ) \subseteq \operatorname {\mathrm {Fil}}^{i-1}\mathcal D$
for all
 $i \geq 1$
.
$i \geq 1$
.
-
A morphism in
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
is an
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
is an
![]() $S_F$
-linear map equivariant for
$S_F$
-linear map equivariant for
![]() $\varphi $
, N, and
$\varphi $
, N, and
![]() $\operatorname {\mathrm {Fil}}^{\bullet }$
.
$\operatorname {\mathrm {Fil}}^{\bullet }$
.
We define a functor
 $\underline {\mathcal D}: \operatorname {\mathrm {MF}}_F^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
as follows:
$\underline {\mathcal D}: \operatorname {\mathrm {MF}}_F^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
as follows:
-
•
 $\mathcal D := \underline {\mathcal D}(D) = S_F \otimes _{K_0\otimes _{\mathbb Q_p} F} D$
as an
$\mathcal D := \underline {\mathcal D}(D) = S_F \otimes _{K_0\otimes _{\mathbb Q_p} F} D$
as an
 $S_F$
-module,
$S_F$
-module, -
•
 $\varphi _{\mathcal D} = \varphi \otimes \varphi _{D}$
,
$\varphi _{\mathcal D} = \varphi \otimes \varphi _{D}$
, -
•
 $N_{\mathcal D} = N\otimes 1 + 1 \otimes N_{D}$
,
$N_{\mathcal D} = N\otimes 1 + 1 \otimes N_{D}$
, -
•
 $\operatorname {\mathrm {Fil}}^0(\mathcal D) = \mathcal D$
, and for
$\operatorname {\mathrm {Fil}}^0(\mathcal D) = \mathcal D$
, and for $$ \begin{align*} \operatorname{\mathrm{Fil}}^{i}(\mathcal D) = \left\{ x \in \mathcal D \mid N_{\mathcal D}(x) \in \operatorname{\mathrm{Fil}}^{i-1}\mathcal D \text{ and } (\operatorname{\mathrm{ev}}_\pi\otimes 1)(x) \in \operatorname{\mathrm{Fil}}^i D_K\right\} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Fil}}^{i}(\mathcal D) = \left\{ x \in \mathcal D \mid N_{\mathcal D}(x) \in \operatorname{\mathrm{Fil}}^{i-1}\mathcal D \text{ and } (\operatorname{\mathrm{ev}}_\pi\otimes 1)(x) \in \operatorname{\mathrm{Fil}}^i D_K\right\} \end{align*} $$
 $i \geq 1$
.
$i \geq 1$
.
Here,
![]() $\operatorname {\mathrm {ev}}_\pi : S_F \rightarrow F\otimes _{\mathbb Q_p} K$
is the scalar extension of
$\operatorname {\mathrm {ev}}_\pi : S_F \rightarrow F\otimes _{\mathbb Q_p} K$
is the scalar extension of
![]() $\operatorname {\mathrm {ev}}_\pi : W(k)[u] \twoheadrightarrow \Lambda _K$
, the evaluation-at-
$\operatorname {\mathrm {ev}}_\pi : W(k)[u] \twoheadrightarrow \Lambda _K$
, the evaluation-at-
![]() $\pi $
map.
$\pi $
map.
Theorem 2.3 Breuil
The functor
 $\underline {{\mathcal D}}: \operatorname {\mathrm {MF}}_{F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
is an equivalence of categories.
$\underline {{\mathcal D}}: \operatorname {\mathrm {MF}}_{F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
is an equivalence of categories.
Breuil proves in [Reference Breuil6, §6] that
![]() $\underline {\mathcal D}$
is an equivalence of categories when
$\underline {\mathcal D}$
is an equivalence of categories when
![]() $F = \mathbb Q_p$
and S is replaced by
$F = \mathbb Q_p$
and S is replaced by
![]() $S_{\mathrm {Br}}$
. That one can replace
$S_{\mathrm {Br}}$
. That one can replace
![]() $S_{\mathrm {Br}}$
by S is known to some, but there does not appear to be a reference. The only step in Breuil’s proof that requires honestly new justification is the following analogue of [Reference Breuil6, Proposition 6.2.1.1] (this version is even easier to prove):
$S_{\mathrm {Br}}$
by S is known to some, but there does not appear to be a reference. The only step in Breuil’s proof that requires honestly new justification is the following analogue of [Reference Breuil6, Proposition 6.2.1.1] (this version is even easier to prove):
Lemma 2.4. Set
 $\mathcal D \in \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
and
$\mathcal D \in \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
and
![]() $D = \mathcal D / u \mathcal D$
. Then there exists a unique
$D = \mathcal D / u \mathcal D$
. Then there exists a unique
![]() $F\otimes _{\mathbb Q_p} K_0$
-linear
$F\otimes _{\mathbb Q_p} K_0$
-linear
![]() $\varphi $
-equivariant section
$\varphi $
-equivariant section
![]() $s : D \rightarrow \mathcal D$
of the reduction map.
$s : D \rightarrow \mathcal D$
of the reduction map.
Proof. First, suppose
![]() $F = \mathbb Q_p$
and let
$F = \mathbb Q_p$
and let
![]() $\left (\widehat e_1, \dots , \widehat e_d\right )$
be an
$\left (\widehat e_1, \dots , \widehat e_d\right )$
be an
 $S\left [\frac 1 p\right ]$
-basis of
$S\left [\frac 1 p\right ]$
-basis of
![]() ${\mathcal D}$
. Write
${\mathcal D}$
. Write
![]() $\varphi _{\mathcal D} \left (\widehat e_1 , \dotsc , \widehat e_d\right ) = \left (\widehat e_1, \dotsc , \widehat e_d\right ) X$
and set
$\varphi _{\mathcal D} \left (\widehat e_1 , \dotsc , \widehat e_d\right ) = \left (\widehat e_1, \dotsc , \widehat e_d\right ) X$
and set
![]() $X_0 = X \bmod u$
. Then
$X_0 = X \bmod u$
. Then
![]() $X \in p^k\operatorname {\mathrm {Mat}}_{d}(S)$
,
$X \in p^k\operatorname {\mathrm {Mat}}_{d}(S)$
,
 $X_0^{-1} \in p^\ell \operatorname {\mathrm {Mat}}_d(W(k))$
, and
$X_0^{-1} \in p^\ell \operatorname {\mathrm {Mat}}_d(W(k))$
, and
 $X X_0^{-1} \in I + up^m\operatorname {\mathrm {Mat}}_d(S)$
for some
$X X_0^{-1} \in I + up^m\operatorname {\mathrm {Mat}}_d(S)$
for some
![]() $k,\ell ,m \in \mathbb Z$
. As in the proof of [Reference Breuil6, Proposition 6.2.1.1], we need to show that
$k,\ell ,m \in \mathbb Z$
. As in the proof of [Reference Breuil6, Proposition 6.2.1.1], we need to show that
 $$ \begin{align*} Y_n : = X\varphi(X) \dotsm \varphi ^n (X) \varphi ^n \left(X_0^{-1}\right) \dotsm \varphi \left(X_0^{-1}\right) X_0^{-1} \end{align*} $$
$$ \begin{align*} Y_n : = X\varphi(X) \dotsm \varphi ^n (X) \varphi ^n \left(X_0^{-1}\right) \dotsm \varphi \left(X_0^{-1}\right) X_0^{-1} \end{align*} $$
converges in
 $\operatorname {\mathrm {Mat}}_d\left (S\left [\frac 1 p\right ]\right )$
as
$\operatorname {\mathrm {Mat}}_d\left (S\left [\frac 1 p\right ]\right )$
as
![]() $n \rightarrow \infty $
. But, in the notation already used,
$n \rightarrow \infty $
. But, in the notation already used,
 $$ \begin{align*} Y_n - Y_{n-1} \in \varphi^n(u) p^{n(k+\ell)+m} \operatorname{\mathrm{Mat}}_d(S). \end{align*} $$
$$ \begin{align*} Y_n - Y_{n-1} \in \varphi^n(u) p^{n(k+\ell)+m} \operatorname{\mathrm{Mat}}_d(S). \end{align*} $$
Since
![]() $\varphi ^n(u) p^{nr} \rightarrow 0$
in
$\varphi ^n(u) p^{nr} \rightarrow 0$
in
 $S\left [\frac 1 p\right ]$
for any fixed r, we see that
$S\left [\frac 1 p\right ]$
for any fixed r, we see that
![]() $Y_n - Y_{n-1} \rightarrow 0$
in
$Y_n - Y_{n-1} \rightarrow 0$
in
 $\operatorname {\mathrm {Mat}}_d\left (S\left [\frac 1 p\right ]\right )$
, as needed.
$\operatorname {\mathrm {Mat}}_d\left (S\left [\frac 1 p\right ]\right )$
, as needed.
If
![]() $F \neq \mathbb Q_p$
, the proof already given implies that there exists a unique
$F \neq \mathbb Q_p$
, the proof already given implies that there exists a unique
![]() $K_0$
-linear
$K_0$
-linear
![]() $\varphi $
-equivariant section
$\varphi $
-equivariant section
![]() $s: D \rightarrow \mathcal D$
. If
$s: D \rightarrow \mathcal D$
. If
![]() $x \in F^\times $
, then
$x \in F^\times $
, then
![]() $x^{-1} s x$
is also
$x^{-1} s x$
is also
![]() $K_0$
-linear and
$K_0$
-linear and
![]() $\varphi $
-equivariant, and thus s is F-linear.
$\varphi $
-equivariant, and thus s is F-linear.
Proof of Theorem 2.3. Define
 $\underline D_{S_F} : \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
as follows. Set
$\underline D_{S_F} : \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
as follows. Set
![]() $D = \underline D_{S_F}(\mathcal D) = \mathcal D/u\mathcal D$
with its induced action of
$D = \underline D_{S_F}(\mathcal D) = \mathcal D/u\mathcal D$
with its induced action of
![]() $\varphi $
and N. For s in Lemma 2.4,
$\varphi $
and N. For s in Lemma 2.4,
![]() $(\operatorname {\mathrm {ev}}_{\pi }\otimes 1)\circ s : D \rightarrow \mathcal D/E \mathcal D$
induces a canonical isomorphism
$(\operatorname {\mathrm {ev}}_{\pi }\otimes 1)\circ s : D \rightarrow \mathcal D/E \mathcal D$
induces a canonical isomorphism
![]() $D_K \cong \mathcal D/E \mathcal D$
. The filtration
$D_K \cong \mathcal D/E \mathcal D$
. The filtration
 $\operatorname {\mathrm {Fil}}^i(D_K)$
is the pullback of the filtration on
$\operatorname {\mathrm {Fil}}^i(D_K)$
is the pullback of the filtration on
![]() $\mathcal D / E \mathcal D$
defined as the image
$\mathcal D / E \mathcal D$
defined as the image
 $\operatorname {\mathrm {Fil}}^i(\mathcal D) \rightarrow \mathcal D / E\mathcal D$
. The arguments in [Reference Breuil6], with Lemma 2.4 replacing its Proposition 6.2.1.1, show that
$\operatorname {\mathrm {Fil}}^i(\mathcal D) \rightarrow \mathcal D / E\mathcal D$
. The arguments in [Reference Breuil6], with Lemma 2.4 replacing its Proposition 6.2.1.1, show that
 $\underline D_{S\left [\frac 1 p \right ]}$
and
$\underline D_{S\left [\frac 1 p \right ]}$
and
![]() $\underline {\mathcal D}$
are quasi-inverses when
$\underline {\mathcal D}$
are quasi-inverses when
![]() $F = \mathbb Q_p$
. In general, see Remark 2.2.
$F = \mathbb Q_p$
. In general, see Remark 2.2.
2.4 Comparison
We now assume that F contains a subfield isomorphic to the Galois closure of K (see Lemma 2.5). In practice, as in §§3 and 4, we take
![]() $K = \mathbb Q_p$
, so this is no hindrance.
$K = \mathbb Q_p$
, so this is no hindrance.
In the prior sections, we have described equivalences

An analog of [Reference Liu21, Corollary 3.2.3] allows for a description of the composition that, unfortunately, is not practical for calculations. In the following, though, we explain how to determine
![]() $\underline {\mathcal M}_{\mathcal O_F}(D)\otimes _{\mathcal O_F} S_F$
as a
$\underline {\mathcal M}_{\mathcal O_F}(D)\otimes _{\mathcal O_F} S_F$
as a
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $S_F$
from D, up to determining
$S_F$
from D, up to determining
![]() $\mathcal D = \underline {\mathcal D}(D)$
. A key technical point, which follows from the next lemma, is that filtrations on Breuil modules over
$\mathcal D = \underline {\mathcal D}(D)$
. A key technical point, which follows from the next lemma, is that filtrations on Breuil modules over
![]() $S_F$
are always free, in contrast to the filtrations on objects in
$S_F$
are always free, in contrast to the filtrations on objects in
 $\operatorname {\mathrm {MF}}_F^{\varphi ,N}$
(compare with [Reference Breuil and Mézard7, Exemple 3.1.1.4]).
$\operatorname {\mathrm {MF}}_F^{\varphi ,N}$
(compare with [Reference Breuil and Mézard7, Exemple 3.1.1.4]).
Lemma 2.5. Suppose that
![]() $\mathcal N$
is a finite free
$\mathcal N$
is a finite free
![]() $S_F$
-module and
$S_F$
-module and
![]() $\mathcal H \subseteq \mathcal N$
is an
$\mathcal H \subseteq \mathcal N$
is an
![]() $S_F$
-submodule such that
$S_F$
-submodule such that
![]() $E^j \mathcal N \subseteq \mathcal H$
for some
$E^j \mathcal N \subseteq \mathcal H$
for some
![]() $j \geq 0$
. Then
$j \geq 0$
. Then
![]() $\mathcal H$
is finite free over
$\mathcal H$
is finite free over
![]() $S_F$
.
$S_F$
.
Proof. We may assume
![]() $j = 1$
. Indeed, consider the nested sequence
$j = 1$
. Indeed, consider the nested sequence
![]() $\mathcal H_i = \mathcal H + E^i \mathcal N$
of
$\mathcal H_i = \mathcal H + E^i \mathcal N$
of
![]() $S_F$
-modules, which satisfy
$S_F$
-modules, which satisfy
![]() $E \mathcal H_i \subseteq \mathcal H_{i+1} \subseteq \mathcal H_i$
. By the
$E \mathcal H_i \subseteq \mathcal H_{i+1} \subseteq \mathcal H_i$
. By the
![]() $j=1$
case we deduce that
$j=1$
case we deduce that
![]() $\mathcal H_1 \subseteq \mathcal N$
is free, and then
$\mathcal H_1 \subseteq \mathcal N$
is free, and then
![]() $\mathcal H_2$
, and so on until
$\mathcal H_2$
, and so on until
![]() $\mathcal H_j = \mathcal H$
is free. We may also assume
$\mathcal H_j = \mathcal H$
is free. We may also assume
![]() $\mathcal N \cong S_F$
. Indeed, if
$\mathcal N \cong S_F$
. Indeed, if
![]() $ 0 \to \mathcal {N}'' \to \mathcal {N} \overset f \to \mathcal {N}' \to 0$
is an exact sequence of finite free
$ 0 \to \mathcal {N}'' \to \mathcal {N} \overset f \to \mathcal {N}' \to 0$
is an exact sequence of finite free
![]() $S_F$
-modules, then
$S_F$
-modules, then
![]() $\mathcal {H}' = f (\mathcal {H})$
and
$\mathcal {H}' = f (\mathcal {H})$
and
![]() $\mathcal {H}'' = \ker (f) \cap \mathcal {H}$
satisfy
$\mathcal {H}'' = \ker (f) \cap \mathcal {H}$
satisfy
![]() $E \mathcal {N}'' \subseteq \mathcal {H}''$
and
$E \mathcal {N}'' \subseteq \mathcal {H}''$
and
![]() $E\mathcal {N}' \subseteq \mathcal {H}'$
. So if both
$E\mathcal {N}' \subseteq \mathcal {H}'$
. So if both
![]() $\mathcal {H}''$
and
$\mathcal {H}''$
and
![]() $\mathcal {H}'$
are free, then
$\mathcal {H}'$
are free, then
![]() $\mathcal H \cong \mathcal H'' \oplus \mathcal H'$
is free as well.
$\mathcal H \cong \mathcal H'' \oplus \mathcal H'$
is free as well.
We have reduced to proving that if
![]() $I \subseteq S_F$
is an ideal containing E, then I is free. Since F contains a subfield isomorphic to the Galois closure of K, we may decompose
$I \subseteq S_F$
is an ideal containing E, then I is free. Since F contains a subfield isomorphic to the Galois closure of K, we may decompose
 $S_F = \prod _{\sigma \in \mathrm {Hom}\left (K_0, F\right )} S_{F, \sigma }$
where
$S_F = \prod _{\sigma \in \mathrm {Hom}\left (K_0, F\right )} S_{F, \sigma }$
where
 $S_{F, \sigma } = \Lambda \left [\!\!\left [u, \frac {\sigma (E)^p}{p}\right ]\!\!\right ]\left [\frac 1 p\right ]$
is a domain. The ideal I decomposes as a product of ideals
$S_{F, \sigma } = \Lambda \left [\!\!\left [u, \frac {\sigma (E)^p}{p}\right ]\!\!\right ]\left [\frac 1 p\right ]$
is a domain. The ideal I decomposes as a product of ideals
![]() $I_\sigma $
such that
$I_\sigma $
such that
![]() $\sigma (E)S_{F,\sigma } \subseteq I_{\sigma }$
. Since
$\sigma (E)S_{F,\sigma } \subseteq I_{\sigma }$
. Since
![]() $\sigma (E)$
is nonzero, it suffices to show that each
$\sigma (E)$
is nonzero, it suffices to show that each
![]() $I_{\sigma }$
is principal. Write
$I_{\sigma }$
is principal. Write
![]() $\mathrm {Hom}_{\sigma }(K,F)$
for the embeddings
$\mathrm {Hom}_{\sigma }(K,F)$
for the embeddings
![]() $\tau : K \rightarrow F$
lifting
$\tau : K \rightarrow F$
lifting
![]() $\sigma $
. Then we have a canonical isomorphism
$\sigma $
. Then we have a canonical isomorphism
 $$ \begin{align*} S_{F, \sigma}/\sigma(E)S_{F,\sigma} \cong K \otimes_{K_0, \sigma} F \cong F^{\mathrm{Hom}_{\sigma}(K,F)}. \end{align*} $$
$$ \begin{align*} S_{F, \sigma}/\sigma(E)S_{F,\sigma} \cong K \otimes_{K_0, \sigma} F \cong F^{\mathrm{Hom}_{\sigma}(K,F)}. \end{align*} $$
So
![]() $I_{\sigma }/\sigma (E)S_{F,\sigma } \cong F^T$
for some subset
$I_{\sigma }/\sigma (E)S_{F,\sigma } \cong F^T$
for some subset
![]() $T \subseteq \mathrm {Hom}_{\sigma }(K,F)$
. But
$T \subseteq \mathrm {Hom}_{\sigma }(K,F)$
. But
![]() $J_T = \prod _{\tau \in T} (u-\tau (\pi )) \cdot S_F$
also contains
$J_T = \prod _{\tau \in T} (u-\tau (\pi )) \cdot S_F$
also contains
![]() $\sigma (E)S_{F,\sigma }$
and
$\sigma (E)S_{F,\sigma }$
and
![]() $J_T/\sigma (E)S_{F,\sigma } \cong F^T$
. Thus
$J_T/\sigma (E)S_{F,\sigma } \cong F^T$
. Thus
![]() $I_{\sigma } = J_T$
is principal, completing the proof.
$I_{\sigma } = J_T$
is principal, completing the proof.
We now consider an ad hoc category of ‘Breuil modules without monodromy’. Let
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi , h }$
denote the category whose objects are
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi , h }$
denote the category whose objects are
![]() $(\mathcal D, \varphi _{\mathcal D}) \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi }$
such that the linearization of
$(\mathcal D, \varphi _{\mathcal D}) \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi }$
such that the linearization of
![]() $\varphi _{\mathcal D}$
is an isomorphism, and
$\varphi _{\mathcal D}$
is an isomorphism, and
![]() $\mathcal D$
is equipped with a finite free
$\mathcal D$
is equipped with a finite free
![]() $S_F $
-submodule
$S_F $
-submodule
![]() $\operatorname {\mathrm {Fil}}^h \mathcal D \subseteq {\mathcal D}$
such that
$\operatorname {\mathrm {Fil}}^h \mathcal D \subseteq {\mathcal D}$
such that
![]() $\operatorname {\mathrm {Fil}}^h S_F \cdot \mathcal D \subseteq \operatorname {\mathrm {Fil}} ^h {\mathcal D}$
. By Lemma 2.5 there is a natural forgetful functor
$\operatorname {\mathrm {Fil}}^h S_F \cdot \mathcal D \subseteq \operatorname {\mathrm {Fil}} ^h {\mathcal D}$
. By Lemma 2.5 there is a natural forgetful functor
 $ \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
.
$ \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
.
Now define
 $\underline {{\mathcal D}}' : \operatorname {\mathrm {Mod}}_{S_F}^{\varphi , \leq h } \to \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h }$
by declaring
$\underline {{\mathcal D}}' : \operatorname {\mathrm {Mod}}_{S_F}^{\varphi , \leq h } \to \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h }$
by declaring
![]() $\underline {\mathcal D}'(\mathcal M) = S_F\otimes _{\varphi ,S_F} \mathcal M$
as an
$\underline {\mathcal D}'(\mathcal M) = S_F\otimes _{\varphi ,S_F} \mathcal M$
as an
![]() $S_F$
-module, and
$S_F$
-module, and
-
•
 $\varphi _{\underline {\mathcal D}'(\mathcal {M})}= \varphi \otimes \varphi _{\mathcal {M}}$
and
$\varphi _{\underline {\mathcal D}'(\mathcal {M})}= \varphi \otimes \varphi _{\mathcal {M}}$
and -
•
 $\operatorname {\mathrm {Fil}} ^h \underline {{\mathcal D}}'(\mathcal {M} ) = \left \{ x \in \underline {{\mathcal D}'}(\mathcal {M} ) \mid (1 \otimes \varphi _{\mathcal {M}})(x) \in \operatorname {\mathrm {Fil}} ^h S_F\cdot \mathcal {M}\right \}$
.
$\operatorname {\mathrm {Fil}} ^h \underline {{\mathcal D}}'(\mathcal {M} ) = \left \{ x \in \underline {{\mathcal D}'}(\mathcal {M} ) \mid (1 \otimes \varphi _{\mathcal {M}})(x) \in \operatorname {\mathrm {Fil}} ^h S_F\cdot \mathcal {M}\right \}$
.
Since
 $E^h \underline {\mathcal D}'(\mathcal M) \subseteq \operatorname {\mathrm {Fil}}^h\underline {\mathcal D}'(\mathcal M)$
, Lemma 2.5 implies that
$E^h \underline {\mathcal D}'(\mathcal M) \subseteq \operatorname {\mathrm {Fil}}^h\underline {\mathcal D}'(\mathcal M)$
, Lemma 2.5 implies that
 $\operatorname {\mathrm {Fil}} ^h \underline {{\mathcal D}}'(\mathcal {M} )$
is finite free over
$\operatorname {\mathrm {Fil}} ^h \underline {{\mathcal D}}'(\mathcal {M} )$
is finite free over
![]() $S_F$
.
$S_F$
.
Proposition 2.6. The functor
![]() $ \underline {{\mathcal D}}^{\prime }$
is an equivalence.
$ \underline {{\mathcal D}}^{\prime }$
is an equivalence.
Proof. We first show that
![]() $\underline {{\mathcal D}}'$
is fully faithful. Suppose
$\underline {{\mathcal D}}'$
is fully faithful. Suppose
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {M}'$
are in
$\mathcal {M}'$
are in
 $\operatorname {\mathrm {Mod}}_{S_F} ^{\varphi , \leq h}$
. Write
$\operatorname {\mathrm {Mod}}_{S_F} ^{\varphi , \leq h}$
. Write
![]() ${\mathcal D}:= \underline {{\mathcal D}}'(\mathcal {M} )$
and
${\mathcal D}:= \underline {{\mathcal D}}'(\mathcal {M} )$
and
![]() ${\mathcal D}' := \underline {{\mathcal D}}'(\mathcal {M}')$
. Choose a basis
${\mathcal D}' := \underline {{\mathcal D}}'(\mathcal {M}')$
. Choose a basis
![]() $(e_1 , \dotsc , e_d)$
of
$(e_1 , \dotsc , e_d)$
of
![]() $\mathcal {M}$
and write
$\mathcal {M}$
and write
![]() $\varphi _{\mathcal M} (e_1, \dotsc , e_d ) = (e_1 , \dotsc , e_d ) A$
with
$\varphi _{\mathcal M} (e_1, \dotsc , e_d ) = (e_1 , \dotsc , e_d ) A$
with
![]() $A \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Since
$A \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Since
![]() $\mathcal {M}$
has height
$\mathcal {M}$
has height
![]() $\leq h$
, there exists a matrix
$\leq h$
, there exists a matrix
![]() $B \in \operatorname {\mathrm {Mat}}_d(S_F)$
such that
$B \in \operatorname {\mathrm {Mat}}_d(S_F)$
such that
![]() $AB = BA = E^h I _d$
. By assumption,
$AB = BA = E^h I _d$
. By assumption,
![]() $\operatorname {\mathrm {Fil}}^h{\mathcal D}$
has basis
$\operatorname {\mathrm {Fil}}^h{\mathcal D}$
has basis
![]() $(\alpha _1,\dotsc ,\alpha _d) = \left (\widetilde e_1 , \dotsc , \widetilde e_d \right ) B$
where
$(\alpha _1,\dotsc ,\alpha _d) = \left (\widetilde e_1 , \dotsc , \widetilde e_d \right ) B$
where
![]() $\widetilde e_i = 1 \otimes e_i \in {\mathcal D}$
compose a basis of
$\widetilde e_i = 1 \otimes e_i \in {\mathcal D}$
compose a basis of
![]() ${\mathcal D}$
. Similarly, we get
${\mathcal D}$
. Similarly, we get
![]() $A', B'$
, and
$A', B'$
, and
![]() $\widetilde e_i'$
from a basis
$\widetilde e_i'$
from a basis
![]() $\left (e_1', \dotsc , e_{d^{\prime }}^{\prime }\right )$
of
$\left (e_1', \dotsc , e_{d^{\prime }}^{\prime }\right )$
of
![]() $\mathcal M'$
.
$\mathcal M'$
.
Now suppose
![]() $f: {\mathcal D} \rightarrow {\mathcal D}'$
is a morphism in
$f: {\mathcal D} \rightarrow {\mathcal D}'$
is a morphism in
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
. We write
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
. We write
![]() $f\left (\widetilde e_1, \dotsc , \widetilde e_d\right )= \left (\widetilde {e}^{\prime }_1, \dotsc , \widetilde e^{\prime }_{d'}\right ) X$
for
$f\left (\widetilde e_1, \dotsc , \widetilde e_d\right )= \left (\widetilde {e}^{\prime }_1, \dotsc , \widetilde e^{\prime }_{d'}\right ) X$
for
![]() $X \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Since f is
$X \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Since f is
![]() $\varphi $
-equivariant, we have
$\varphi $
-equivariant, we have
![]() $X \varphi (A) = \varphi (A') \varphi (X)$
, and since
$X \varphi (A) = \varphi (A') \varphi (X)$
, and since
 $f\left (\operatorname {\mathrm {Fil}}^h{\mathcal D}\right )\subseteq \operatorname {\mathrm {Fil}}^h{\mathcal D}'$
, we have
$f\left (\operatorname {\mathrm {Fil}}^h{\mathcal D}\right )\subseteq \operatorname {\mathrm {Fil}}^h{\mathcal D}'$
, we have
![]() $X B = B' Y$
for some
$X B = B' Y$
for some
![]() $Y \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Using
$Y \in \operatorname {\mathrm {Mat}}_d(S_F)$
. Using
![]() $AB = BA = E^h I_d $
and
$AB = BA = E^h I_d $
and
![]() $ A'B'= B'A'= E^h I_{d'}$
, we see that
$ A'B'= B'A'= E^h I_{d'}$
, we see that
 $\varphi (Y)\varphi \left (E^h\right ) = X \varphi \left (E^h\right )$
, and so
$\varphi (Y)\varphi \left (E^h\right ) = X \varphi \left (E^h\right )$
, and so
![]() $X = \varphi (Y)$
because
$X = \varphi (Y)$
because
![]() $\varphi (E) \in S_F^\times $
. It follows that
$\varphi (E) \in S_F^\times $
. It follows that
![]() $Y A = A' \varphi (Y)$
. Define
$Y A = A' \varphi (Y)$
. Define
![]() $\mathfrak f : \mathcal {M} \to \mathcal {M}'$
by
$\mathfrak f : \mathcal {M} \to \mathcal {M}'$
by
![]() $\mathfrak f (e_1, \dotsc , e_d)= \left (e^{\prime }_1, \dotsc , e^{\prime }_{d'}\right ) Y$
. Then
$\mathfrak f (e_1, \dotsc , e_d)= \left (e^{\prime }_1, \dotsc , e^{\prime }_{d'}\right ) Y$
. Then
![]() $\mathfrak f$
is
$\mathfrak f$
is
![]() $\varphi $
-equivariant and
$\varphi $
-equivariant and
![]() $f = \underline {{\mathcal D}}'(\mathfrak {f})$
since
$f = \underline {{\mathcal D}}'(\mathfrak {f})$
since
![]() $X = \varphi (Y)$
. This shows that
$X = \varphi (Y)$
. This shows that
![]() $\underline {\mathcal D}'$
is full, and since Y determines X, we also see that
$\underline {\mathcal D}'$
is full, and since Y determines X, we also see that
![]() $\underline {\mathcal D}'$
is faithful.
$\underline {\mathcal D}'$
is faithful.
Now we prove that
![]() $ \underline {{\mathcal D}}'$
is essentially surjective. Given a
$ \underline {{\mathcal D}}'$
is essentially surjective. Given a
 ${\mathcal D} \in \operatorname {\mathrm {MF}} ^{\varphi , h}_{S_F}$
, choose bases
${\mathcal D} \in \operatorname {\mathrm {MF}} ^{\varphi , h}_{S_F}$
, choose bases
![]() $(e_1 , \dotsc , e_d)$
of
$(e_1 , \dotsc , e_d)$
of
![]() ${\mathcal D}$
and
${\mathcal D}$
and
![]() $(\alpha _1 , \dotsc , \alpha _d) $
of
$(\alpha _1 , \dotsc , \alpha _d) $
of
![]() $\operatorname {\mathrm {Fil}} ^h {\mathcal D}$
. Write
$\operatorname {\mathrm {Fil}} ^h {\mathcal D}$
. Write
![]() $ (\alpha _1, \dotsc , \alpha _d) = (e_1, \dotsc , e_d) B$
and
$ (\alpha _1, \dotsc , \alpha _d) = (e_1, \dotsc , e_d) B$
and
![]() $\varphi _{{\mathcal D}} (e_1, \dotsc , e_d)= (e_1, \dotsc , e_d) X$
with
$\varphi _{{\mathcal D}} (e_1, \dotsc , e_d)= (e_1, \dotsc , e_d) X$
with
![]() $\det (X) \in S_F^\times $
. Since
$\det (X) \in S_F^\times $
. Since
![]() $E^h {\mathcal D} \subseteq \operatorname {\mathrm {Fil}} ^h {\mathcal D}$
, there exists
$E^h {\mathcal D} \subseteq \operatorname {\mathrm {Fil}} ^h {\mathcal D}$
, there exists
![]() $A\in \operatorname {\mathrm {Mat}}_d(S_F)$
such that
$A\in \operatorname {\mathrm {Mat}}_d(S_F)$
such that
![]() $AB = BA = E^h I_d$
. Since
$AB = BA = E^h I_d$
. Since
![]() $\varphi (E)=p\mathfrak {c} \in S_F^\times $
, we see that
$\varphi (E)=p\mathfrak {c} \in S_F^\times $
, we see that
![]() $X\varphi (B) \in \mathrm {GL}_d(S_F)$
, whereas
$X\varphi (B) \in \mathrm {GL}_d(S_F)$
, whereas
![]() $\varphi _{{\mathcal D}} (\alpha _1 , \dotsc , \alpha _d) = (e_1 , \dotsc , e_d) X \varphi (B)$
. Thus
$\varphi _{{\mathcal D}} (\alpha _1 , \dotsc , \alpha _d) = (e_1 , \dotsc , e_d) X \varphi (B)$
. Thus
![]() $(f_1,\dotsc ,f_d) = (e_1,\dotsc ,e_d) X \varphi (B) p^{-h}\mathfrak {c}^{-h}$
is a basis of
$(f_1,\dotsc ,f_d) = (e_1,\dotsc ,e_d) X \varphi (B) p^{-h}\mathfrak {c}^{-h}$
is a basis of
![]() ${\mathcal D}$
and
${\mathcal D}$
and
![]() $\varphi _{\mathcal D} (\alpha _1 , \dotsc , \alpha _d) = (f_1, \dotsc , f_d) p ^ h \mathfrak {c} ^h$
. Finally,
$\varphi _{\mathcal D} (\alpha _1 , \dotsc , \alpha _d) = (f_1, \dotsc , f_d) p ^ h \mathfrak {c} ^h$
. Finally,
![]() $(\alpha _1, \dotsc , \alpha _d) = (f_1, \dotsc , f_d) B ' $
where
$(\alpha _1, \dotsc , \alpha _d) = (f_1, \dotsc , f_d) B ' $
where
![]() $B' = Y B $
and
$B' = Y B $
and
 $Y= \left ( X\varphi (B) p^{-h} \mathfrak {c} ^{-h}\right )^{-1}$
, so there exists an
$Y= \left ( X\varphi (B) p^{-h} \mathfrak {c} ^{-h}\right )^{-1}$
, so there exists an
![]() $A'$
such that
$A'$
such that
![]() $A' B' = B' A' = E^h I_d$
. Now define
$A' B' = B' A' = E^h I_d$
. Now define
 $\mathcal {M}=\bigoplus _{i=1}^d S_F \mathfrak f_i$
and set
$\mathcal {M}=\bigoplus _{i=1}^d S_F \mathfrak f_i$
and set
![]() $\varphi _{\mathcal {M}}({\mathfrak f} _1 , \dotsc , {\mathfrak f} _d) = ({\mathfrak f} _1 , \dotsc , \mathfrak f_d) A'$
. Then
$\varphi _{\mathcal {M}}({\mathfrak f} _1 , \dotsc , {\mathfrak f} _d) = ({\mathfrak f} _1 , \dotsc , \mathfrak f_d) A'$
. Then
 $\mathcal {M}\in \operatorname {\mathrm {Mod}}_{S_F} ^{\varphi , \leq h}$
and
$\mathcal {M}\in \operatorname {\mathrm {Mod}}_{S_F} ^{\varphi , \leq h}$
and
![]() $\underline {{\mathcal D}'}(\mathcal {M})= {\mathcal D}$
(set
$\underline {{\mathcal D}'}(\mathcal {M})= {\mathcal D}$
(set
![]() $f_i = 1 \otimes \mathfrak f_i$
).
$f_i = 1 \otimes \mathfrak f_i$
).
We now reach the main theorem of this section, which provides a mechanism to calculate a finite-height
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $S_F$
explicitly from
$S_F$
explicitly from
 $D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
. We write
$D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
. We write
![]() $\varphi (E) = p\mathfrak {c}$
with
$\varphi (E) = p\mathfrak {c}$
with
![]() $\mathfrak {c} \in S^\times $
as before.
$\mathfrak {c} \in S^\times $
as before.
Theorem 2.7. Suppose
 $D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
. Write
$D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
. Write
 ${\mathcal D}' \in \operatorname {\mathrm {MF}}^{\varphi ,h}_{S_F}$
for the image of
${\mathcal D}' \in \operatorname {\mathrm {MF}}^{\varphi ,h}_{S_F}$
for the image of
![]() $\underline {{\mathcal D}}(D)$
under the natural forgetful functor and
$\underline {{\mathcal D}}(D)$
under the natural forgetful functor and
![]() $\mathcal M = \underline {\mathcal M}_{\mathcal O_F}(D) \otimes _{\mathcal O_F} S_F$
. Then there is a natural isomorphism
$\mathcal M = \underline {\mathcal M}_{\mathcal O_F}(D) \otimes _{\mathcal O_F} S_F$
. Then there is a natural isomorphism
![]() $\underline {\mathcal D}'(\mathcal M) \cong \mathcal D'.$
$\underline {\mathcal D}'(\mathcal M) \cong \mathcal D'.$
In particular,
![]() $\mathcal M$
is recovered from D via the following steps:
$\mathcal M$
is recovered from D via the following steps:
-
(1) Select
 $S_F$
-bases
$S_F$
-bases
 $(e_1,\dotsc ,e_d)$
of
$(e_1,\dotsc ,e_d)$
of
 $\mathcal D = \underline {\mathcal D}(D)$
and
$\mathcal D = \underline {\mathcal D}(D)$
and
 $(\alpha _1,\dotsc ,\alpha _d)$
of
$(\alpha _1,\dotsc ,\alpha _d)$
of
 $\operatorname {\mathrm {Fil}}^h {\mathcal D}$
.
$\operatorname {\mathrm {Fil}}^h {\mathcal D}$
. -
(2) Let
 $\varphi _{\mathcal D} (e_1, \dotsc , e_d) = (e_1 , \dotsc , e_d) X$
and
$\varphi _{\mathcal D} (e_1, \dotsc , e_d) = (e_1 , \dotsc , e_d) X$
and
 $(\alpha _1, \dotsc , \alpha _d) = (e_1, \dotsc , e_d) B$
with
$(\alpha _1, \dotsc , \alpha _d) = (e_1, \dotsc , e_d) B$
with
 $X,B \in \operatorname {\mathrm {Mat}}_d(S_F)$
.
$X,B \in \operatorname {\mathrm {Mat}}_d(S_F)$
. -
(3) Then
 $\mathcal {M}$
has an
$\mathcal {M}$
has an
 $S_F$
-basis
$S_F$
-basis
 $(\mathfrak f_1,\dotsc ,\mathfrak f_d)$
in which
$(\mathfrak f_1,\dotsc ,\mathfrak f_d)$
in which
 $\varphi _{\mathcal {M}}({\mathfrak f} _1 , \dotsc , {\mathfrak f} _d) = ({\mathfrak f} _1 , \dotsc , \mathfrak f_d) A$
, where
$\varphi _{\mathcal {M}}({\mathfrak f} _1 , \dotsc , {\mathfrak f} _d) = ({\mathfrak f} _1 , \dotsc , \mathfrak f_d) A$
, where  $$ \begin{align*} A = E^h B^{-1} X \varphi (B) p^{-h}\mathfrak{c}^{-h}. \end{align*} $$
$$ \begin{align*} A = E^h B^{-1} X \varphi (B) p^{-h}\mathfrak{c}^{-h}. \end{align*} $$
Proof. To start, once the isomorphism
![]() $\underline {\mathcal D}'(\mathcal M) \cong \mathcal D'$
is justified, the ‘in particular’ follows by tracing through the second half of the proof of Proposition 2.6.
$\underline {\mathcal D}'(\mathcal M) \cong \mathcal D'$
is justified, the ‘in particular’ follows by tracing through the second half of the proof of Proposition 2.6.
For
 $\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
we define
$\mathcal M_{\mathcal O_F} \in \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }}$
we define
![]() $\mathcal D = \underline {\mathcal D}_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right ) = S_F \otimes _{\varphi ,\mathcal O_F} \mathcal M_{\mathcal O_F}$
, which is a finite free
$\mathcal D = \underline {\mathcal D}_{\mathcal O_F}\left (\mathcal M_{\mathcal O_F}\right ) = S_F \otimes _{\varphi ,\mathcal O_F} \mathcal M_{\mathcal O_F}$
, which is a finite free
![]() $S_F$
-module, and equip it with the following structure of a Breuil module over
$S_F$
-module, and equip it with the following structure of a Breuil module over
![]() $S_F$
:
$S_F$
:
-
•
 $\varphi _{\mathcal D} = \varphi \otimes \varphi _{\mathcal M}$
,
$\varphi _{\mathcal D} = \varphi \otimes \varphi _{\mathcal M}$
, -
•
 $N_{\mathcal D} = N \otimes 1 + {p\over \varphi (\lambda )} \otimes N_{\nabla }$
,
$N_{\mathcal D} = N \otimes 1 + {p\over \varphi (\lambda )} \otimes N_{\nabla }$
, -
•
 $\operatorname {\mathrm {Fil}}^i(\mathcal D) = \left \{x \in \mathcal D \mid (1 \otimes \varphi _{\mathcal M})(x) \in \operatorname {\mathrm {Fil}}^i S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F} \right \}$
.
$\operatorname {\mathrm {Fil}}^i(\mathcal D) = \left \{x \in \mathcal D \mid (1 \otimes \varphi _{\mathcal M})(x) \in \operatorname {\mathrm {Fil}}^i S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F} \right \}$
.
Following the proof of [Reference Liu20, Proposition 3.2.1], replacing S by
![]() $S_{\mathrm {Br}}$
, and adding linear F-coefficients, we see that
$S_{\mathrm {Br}}$
, and adding linear F-coefficients, we see that
 $\underline {\mathcal D}_{\mathcal O_F}: \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
defines a functor. Moreover, if
$\underline {\mathcal D}_{\mathcal O_F}: \operatorname {\mathrm {Mod}}_{\mathcal O_F}^{\varphi ,N_{\nabla }} \rightarrow \operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
defines a functor. Moreover, if
![]() $\mathcal M_{\mathcal O_F}$
has height
$\mathcal M_{\mathcal O_F}$
has height
![]() $\leq h$
, then
$\leq h$
, then
in the category
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
. Thus it remains to show that
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,h}$
. Thus it remains to show that
![]() $\underline {\mathcal D}_{\mathcal O_F}$
makes the diagram of functors
$\underline {\mathcal D}_{\mathcal O_F}$
makes the diagram of functors

commute as well. (In particular,
![]() $\underline {\mathcal D}_{\mathcal O_F}$
is an equivalence.) It is enough to check this when
$\underline {\mathcal D}_{\mathcal O_F}$
is an equivalence.) It is enough to check this when
![]() $F = \mathbb Q_p$
(by Remark 2.2). In that case, if S is replaced by
$F = \mathbb Q_p$
(by Remark 2.2). In that case, if S is replaced by
![]() $S_{\mathrm {Br}}$
, this is the statement of [Reference Liu20, Corollary 3.2.3]. The proof there goes through here with only one adjustment. Namely, the isomorphism
$S_{\mathrm {Br}}$
, this is the statement of [Reference Liu20, Corollary 3.2.3]. The proof there goes through here with only one adjustment. Namely, the isomorphism
 $S_{\mathrm {Br}} [\frac 1 p]\otimes _{K_0} \underline D_{\mathcal O}(\mathcal M_{\mathcal O}) \cong S_{\mathrm {Br}}[\frac 1 p]\otimes _{\varphi ,\mathcal O} \mathcal M_{\mathcal O}$
implicit in the first two displayed equations there needs to have
$S_{\mathrm {Br}} [\frac 1 p]\otimes _{K_0} \underline D_{\mathcal O}(\mathcal M_{\mathcal O}) \cong S_{\mathrm {Br}}[\frac 1 p]\otimes _{\varphi ,\mathcal O} \mathcal M_{\mathcal O}$
implicit in the first two displayed equations there needs to have
![]() $S_{\mathrm {Br}}$
replaced by S. To make this adjustment, consider the map
$S_{\mathrm {Br}}$
replaced by S. To make this adjustment, consider the map
![]() $\xi : \mathcal O \otimes _{K_0} \underline {D}(\mathcal M_{\mathcal O}) \rightarrow \mathcal M_{\mathcal O} $
constructed in [Reference Kisin18, Lemma 1.2.6]. Thus
$\xi : \mathcal O \otimes _{K_0} \underline {D}(\mathcal M_{\mathcal O}) \rightarrow \mathcal M_{\mathcal O} $
constructed in [Reference Kisin18, Lemma 1.2.6]. Thus
![]() $\xi $
is a
$\xi $
is a
![]() $\varphi $
-equivariant injection with cokernel annihilated by
$\varphi $
-equivariant injection with cokernel annihilated by
![]() $\lambda ^h$
for some
$\lambda ^h$
for some
![]() $h \geq 0$
. From the diagram in the middle of the proof of [Reference Kisin18, Lemma 1.2.6], we have
$h \geq 0$
. From the diagram in the middle of the proof of [Reference Kisin18, Lemma 1.2.6], we have
![]() $\xi $
factors
$\xi $
factors

We deduce that the vertical arrow has cokernel annihilated by
![]() $\varphi (\lambda )^h$
. Since
$\varphi (\lambda )^h$
. Since
![]() $\varphi (\lambda ) \in S^\times $
, we have
$\varphi (\lambda ) \in S^\times $
, we have
 $$ \begin{align*} S[1/p] \otimes_{K_0} \underline D(\mathcal M_{\mathcal O}) \overset{1\otimes \xi}{\cong} S[1/p] \otimes_{\varphi,\mathcal O} \mathcal M_{\mathcal O}. \end{align*} $$
$$ \begin{align*} S[1/p] \otimes_{K_0} \underline D(\mathcal M_{\mathcal O}) \overset{1\otimes \xi}{\cong} S[1/p] \otimes_{\varphi,\mathcal O} \mathcal M_{\mathcal O}. \end{align*} $$
This completes the proof.
Remark 2.8. The previous proof makes it clear to see that for
 $D \in \operatorname {\mathrm {MF}}_F^{\varphi ,N}$
and
$D \in \operatorname {\mathrm {MF}}_F^{\varphi ,N}$
and
 $\mathcal D = \underline {\mathcal D}(D) \in {\operatorname {\mathrm {MF}}}_{S_F}^{\varphi ,N}$
, the map
$\mathcal D = \underline {\mathcal D}(D) \in {\operatorname {\mathrm {MF}}}_{S_F}^{\varphi ,N}$
, the map
![]() $\operatorname {\mathrm {ev}}_\pi $
induces an isomorphism
$\operatorname {\mathrm {ev}}_\pi $
induces an isomorphism
 $\operatorname {\mathrm {Fil}}^{i+ 1}\mathcal {D} / E \operatorname {\mathrm {Fil}} ^i \mathcal {D} \cong \operatorname {\mathrm {Fil}}^{i +1} D_K$
. Indeed, since
$\operatorname {\mathrm {Fil}}^{i+ 1}\mathcal {D} / E \operatorname {\mathrm {Fil}} ^i \mathcal {D} \cong \operatorname {\mathrm {Fil}}^{i +1} D_K$
. Indeed, since
 $\operatorname {\mathrm {ev}}_{\pi }\left (\operatorname {\mathrm {Fil}}^{i +1}{\mathcal D}\right ) = \operatorname {\mathrm {Fil}} ^{i +1}D_K$
, it suffices to show that
$\operatorname {\mathrm {ev}}_{\pi }\left (\operatorname {\mathrm {Fil}}^{i +1}{\mathcal D}\right ) = \operatorname {\mathrm {Fil}} ^{i +1}D_K$
, it suffices to show that
![]() $E {\mathcal D} \cap \operatorname {\mathrm {Fil}} ^{i +1}{\mathcal D} = E \operatorname {\mathrm {Fil}} ^i {\mathcal D}$
. Pick
$E {\mathcal D} \cap \operatorname {\mathrm {Fil}} ^{i +1}{\mathcal D} = E \operatorname {\mathrm {Fil}} ^i {\mathcal D}$
. Pick
![]() $y = E x\in \operatorname {\mathrm {Fil}} ^{i +1} {\mathcal D}$
with
$y = E x\in \operatorname {\mathrm {Fil}} ^{i +1} {\mathcal D}$
with
![]() $x\in {\mathcal D}$
. The proof of the theorem, especially the fact that diagram (2.3) commutes, shows that
$x\in {\mathcal D}$
. The proof of the theorem, especially the fact that diagram (2.3) commutes, shows that
 $$ \begin{align*} \operatorname{\mathrm{Fil}}^{i +1}(\mathcal D) = \left\{x \in \mathcal D \mid (1 \otimes \varphi_{\mathcal M})(x) \in \operatorname{\mathrm{Fil}}^{i +1} S_F \otimes_{\mathcal O_F} \mathcal M_{\mathcal O_F} \right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Fil}}^{i +1}(\mathcal D) = \left\{x \in \mathcal D \mid (1 \otimes \varphi_{\mathcal M})(x) \in \operatorname{\mathrm{Fil}}^{i +1} S_F \otimes_{\mathcal O_F} \mathcal M_{\mathcal O_F} \right\}. \end{align*} $$
Thus, we see that
 $(1 \otimes \varphi _{\mathcal M})(Ex)= E (1 \otimes \varphi _{\mathcal M})(x)\in \operatorname {\mathrm {Fil}}^{i +1} S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F}$
. Since
$(1 \otimes \varphi _{\mathcal M})(Ex)= E (1 \otimes \varphi _{\mathcal M})(x)\in \operatorname {\mathrm {Fil}}^{i +1} S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F}$
. Since
![]() $\operatorname {\mathrm {Fil}}^n S_F = E^n S_F$
, it is clear that
$\operatorname {\mathrm {Fil}}^n S_F = E^n S_F$
, it is clear that
 $(1 \otimes \varphi _{\mathcal M})(x)\in \operatorname {\mathrm {Fil}}^{i} S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F}$
, and hence
$(1 \otimes \varphi _{\mathcal M})(x)\in \operatorname {\mathrm {Fil}}^{i} S_F \otimes _{\mathcal O_F} \mathcal M_{\mathcal O_F}$
, and hence
![]() $x \in \operatorname {\mathrm {Fil}} ^ i {\mathcal D} $
as required. (Compare with the end of the proof of [Reference Liu21, Proposition 3.2.1].)
$x \in \operatorname {\mathrm {Fil}} ^ i {\mathcal D} $
as required. (Compare with the end of the proof of [Reference Liu21, Proposition 3.2.1].)
Example 2.9. Suppose
![]() $K = \mathbb {Q}_p$
and V is crystalline. By [Reference Laffaille19],
$K = \mathbb {Q}_p$
and V is crystalline. By [Reference Laffaille19],
![]() $D= D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)$
admits a strongly divisible lattice
$D= D_{\operatorname {\mathrm {{st}}}}^{\ast }(V)$
admits a strongly divisible lattice
 $\left (M , \operatorname {\mathrm {Fil}} ^i M, \varphi _i\right )$
. More precisely, there exist an F-basis
$\left (M , \operatorname {\mathrm {Fil}} ^i M, \varphi _i\right )$
. More precisely, there exist an F-basis
![]() $(e_1, \dotsc , e_d)$
of D and integers
$(e_1, \dotsc , e_d)$
of D and integers
![]() $0 =n_0 \leq n_1 \leq \dotsb \leq n_h \leq d$
such that
$0 =n_0 \leq n_1 \leq \dotsb \leq n_h \leq d$
such that
 $\operatorname {\mathrm {Fil}} ^ i D : = \bigoplus _{j\geq n_i } F e_j $
, and
$\operatorname {\mathrm {Fil}} ^ i D : = \bigoplus _{j\geq n_i } F e_j $
, and
![]() $\varphi (e_1,\dotsc , e_d) = (e_1, \dotsc , e_d) X P$
where
$\varphi (e_1,\dotsc , e_d) = (e_1, \dotsc , e_d) X P$
where
![]() $X \in \mathrm {GL}_d (\Lambda )$
and P is a diagonal matrix whose
$X \in \mathrm {GL}_d (\Lambda )$
and P is a diagonal matrix whose
![]() $ii$
th entry is
$ii$
th entry is
![]() $p^{s_i}$
, where
$p^{s_i}$
, where
 $s_i= \max \left \{j \mid n_j \leq i\right \}= \max \left \{ j \mid e_i \in \operatorname {\mathrm {Fil}} ^j D\right \}$
. Since
$s_i= \max \left \{j \mid n_j \leq i\right \}= \max \left \{ j \mid e_i \in \operatorname {\mathrm {Fil}} ^j D\right \}$
. Since
![]() $N = 0$
on D, we easily compute that
$N = 0$
on D, we easily compute that
![]() $\operatorname {\mathrm {Fil}} ^h {\mathcal D}$
admits a basis
$\operatorname {\mathrm {Fil}} ^h {\mathcal D}$
admits a basis
![]() $(e_1,\dotsc , e_d) B$
where B is the diagonal matrix with
$(e_1,\dotsc , e_d) B$
where B is the diagonal matrix with
![]() $(i,i)$
th entry
$(i,i)$
th entry
![]() $E^{h- s_i}$
(compare §3.1). By the steps outlined in Theorem 2.7, using the basis
$E^{h- s_i}$
(compare §3.1). By the steps outlined in Theorem 2.7, using the basis
![]() $1 \otimes e_i \in {\mathcal D}$
, we see that the matrix of
$1 \otimes e_i \in {\mathcal D}$
, we see that the matrix of
![]() $\varphi $
on
$\varphi $
on
![]() $\mathcal {M}$
is given by
$\mathcal {M}$
is given by
![]() $A=E^h B^{-1} X P \varphi (B) p ^{-h} \mathfrak {c} ^{-h}$
, where
$A=E^h B^{-1} X P \varphi (B) p ^{-h} \mathfrak {c} ^{-h}$
, where
![]() $A= D X C$
,
$A= D X C$
,
![]() $D $
is a diagonal matrix with
$D $
is a diagonal matrix with
![]() $(i,i)$
th entry
$(i,i)$
th entry
![]() $E^{s_i}$
, and C is a diagonal matrix with
$E^{s_i}$
, and C is a diagonal matrix with
![]() $(i,i)$
th entry
$(i,i)$
th entry
![]() $\mathfrak {c}^{-s_i}$
.
$\mathfrak {c}^{-s_i}$
.
3 An explicit determination of a Breuil module
In this section, we assume
![]() $K = \mathbb Q_p$
. We choose
$K = \mathbb Q_p$
. We choose
![]() $\pi = -p$
, so
$\pi = -p$
, so
![]() $E(u) = u+p$
. We keep
$E(u) = u+p$
. We keep
![]() $F/\mathbb Q_p$
as a linear coefficient field and recall that
$F/\mathbb Q_p$
as a linear coefficient field and recall that
![]() $\Lambda $
is its ring of integers. In §3.2, we explain the definition of the filtered
$\Lambda $
is its ring of integers. In §3.2, we explain the definition of the filtered
![]() $(\varphi ,N)$
-module
$(\varphi ,N)$
-module
 $D_{h+1,\mathcal L} \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
, for
$D_{h+1,\mathcal L} \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
, for
![]() $h \geq 1$
and
$h \geq 1$
and
![]() $\mathcal L \in F$
, discussed in the introduction. Let
$\mathcal L \in F$
, discussed in the introduction. Let
 $\mathcal M_{h+1,\mathcal L}=\underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi ,\leq h}$
. The ultimate goal (Theorem 3.7) is to describe the matrix of
$\mathcal M_{h+1,\mathcal L}=\underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi ,\leq h}$
. The ultimate goal (Theorem 3.7) is to describe the matrix of
![]() $\varphi $
in a certain trivialization
$\varphi $
in a certain trivialization
 $\mathcal M_{h+1,\mathcal L} \cong S_F^{\oplus 2}$
, at least if
$\mathcal M_{h+1,\mathcal L} \cong S_F^{\oplus 2}$
, at least if
![]() $\mathcal L \neq 0$
. We begin by describing the Breuil module
$\mathcal L \neq 0$
. We begin by describing the Breuil module
![]() $\mathcal D_{h+1,\mathcal L} = \underline {\mathcal D}\left (D_{h+1,\mathcal L}\right )$
.
$\mathcal D_{h+1,\mathcal L} = \underline {\mathcal D}\left (D_{h+1,\mathcal L}\right )$
.
3.1 The filtration on some rank
 $2$
Breuil modules
$2$
Breuil modules
In order to minimize notation, in this subsection we let
 $D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
be any
$D \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
be any
![]() $2$
-dimensional filtered
$2$
-dimensional filtered
![]() $(\varphi ,N)$
-module with Hodge–Tate weights
$(\varphi ,N)$
-module with Hodge–Tate weights
![]() $0 < h$
. We also choose any basis
$0 < h$
. We also choose any basis
![]() $(f_1,f_2)$
for D such that
$(f_1,f_2)$
for D such that
![]() $\operatorname {\mathrm {Fil}}^h D = Ff_2$
. We write
$\operatorname {\mathrm {Fil}}^h D = Ff_2$
. We write
 $N_D(f_1,f_2) = (f_1,f_2)\left (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\right )$
with
$N_D(f_1,f_2) = (f_1,f_2)\left (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\right )$
with
 $\left (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\right ) \in \operatorname {\mathrm {Mat}}_2(F)$
. (Compare with Lemma 3.6.)
$\left (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\right ) \in \operatorname {\mathrm {Mat}}_2(F)$
. (Compare with Lemma 3.6.)
Set
![]() $\mathcal D = \underline {\mathcal D}(D) = S_F\otimes _F D$
. For
$\mathcal D = \underline {\mathcal D}(D) = S_F\otimes _F D$
. For
![]() $f \in D$
we write
$f \in D$
we write
 $\widehat f = 1 \otimes f \in \mathcal D$
. In particular,
$\widehat f = 1 \otimes f \in \mathcal D$
. In particular,
![]() $\mathcal D$
is a free
$\mathcal D$
is a free
![]() $S_F$
-module with basis
$S_F$
-module with basis
 $\left (\widehat f_1, \widehat f_2\right )$
. Recall that
$\left (\widehat f_1, \widehat f_2\right )$
. Recall that
![]() $\operatorname {\mathrm {Fil}}^i\mathcal D$
is defined by
$\operatorname {\mathrm {Fil}}^i\mathcal D$
is defined by
![]() $\operatorname {\mathrm {Fil}}^0\mathcal D = \mathcal D$
and, for
$\operatorname {\mathrm {Fil}}^0\mathcal D = \mathcal D$
and, for
![]() $i \geq 1$
,
$i \geq 1$
,
 $$ \begin{align*} \operatorname{\mathrm{Fil}}^i\mathcal D = \left\{x \in \mathcal D \mid N_{{\mathcal D}}(x) \in \operatorname{\mathrm{Fil}}^{i-1}\mathcal D \text{ and } \operatorname{\mathrm{ev}}_{\pi}(x) \in \operatorname{\mathrm{Fil}}^i D\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Fil}}^i\mathcal D = \left\{x \in \mathcal D \mid N_{{\mathcal D}}(x) \in \operatorname{\mathrm{Fil}}^{i-1}\mathcal D \text{ and } \operatorname{\mathrm{ev}}_{\pi}(x) \in \operatorname{\mathrm{Fil}}^i D\right\}. \end{align*} $$
When
![]() $i = 1$
, the condition
$i = 1$
, the condition
![]() $N_{{\mathcal D}}(x) \in \operatorname {\mathrm {Fil}}^{0}\mathcal D = \mathcal D$
is a tautology. So
$N_{{\mathcal D}}(x) \in \operatorname {\mathrm {Fil}}^{0}\mathcal D = \mathcal D$
is a tautology. So
 $\operatorname {\mathrm {Fil}} ^1 {\mathcal D} = S_F \widehat {f}_2 + S_F E\widehat {f}_1$
.
$\operatorname {\mathrm {Fil}} ^1 {\mathcal D} = S_F \widehat {f}_2 + S_F E\widehat {f}_1$
.
Proposition 3.1. There exist
![]() $x_1,\dotsc ,x_{h-1}\in F$
such that, if
$x_1,\dotsc ,x_{h-1}\in F$
such that, if
![]() $0 \leq i \leq h$
,
$0 \leq i \leq h$
,
 $$ \begin{align*} \operatorname{\mathrm{Fil}}^i\mathcal D = S_F\cdot\left(\widehat f_2 + \left(\sum_{j=1}^{i-1} x_jE^j\right)\widehat f_1\right) + S_F\cdot E^i \widehat f_1. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Fil}}^i\mathcal D = S_F\cdot\left(\widehat f_2 + \left(\sum_{j=1}^{i-1} x_jE^j\right)\widehat f_1\right) + S_F\cdot E^i \widehat f_1. \end{align*} $$
Proof. Assume by induction on
![]() $0 \leq i < h$
that there exist
$0 \leq i < h$
that there exist
![]() $x_1,\dotsc ,x_{i-1} \in F$
such that for each
$x_1,\dotsc ,x_{i-1} \in F$
such that for each
![]() $0 \leq j \leq i$
we have
$0 \leq j \leq i$
we have
 $\operatorname {\mathrm {Fil}}^j{\mathcal D} = S_F\cdot \widehat f_2^{(j)} + S_F\cdot \widehat f_1$
, where
$\operatorname {\mathrm {Fil}}^j{\mathcal D} = S_F\cdot \widehat f_2^{(j)} + S_F\cdot \widehat f_1$
, where
 $\widehat f_2^{(j)} = \widehat f_2 + \left (\sum _{m=1}^{j-1} x_m E^m\right )\widehat f_1$
. Setting
$\widehat f_2^{(j)} = \widehat f_2 + \left (\sum _{m=1}^{j-1} x_m E^m\right )\widehat f_1$
. Setting
 $\widehat f_2^{(0)} = \widehat f_2^{(1)} = \widehat f_2$
handles the cases
$\widehat f_2^{(0)} = \widehat f_2^{(1)} = \widehat f_2$
handles the cases
![]() $i = 0$
and
$i = 0$
and
![]() $i = 1$
. So suppose
$i = 1$
. So suppose
![]() $1 \leq i < h$
.
$1 \leq i < h$
.
For the
![]() $(i+1)$
th case, we first define
$(i+1)$
th case, we first define
![]() $x_i \in F$
. By induction,
$x_i \in F$
. By induction,
 $N_{{\mathcal D}}\left (\widehat f_2^{(i)}\right ) \in \operatorname {\mathrm {Fil}}^{i-1}{\mathcal D} = S_F\widehat f_2^{(i-1)} + S_F E^{i-1}\widehat f_1$
. Since
$N_{{\mathcal D}}\left (\widehat f_2^{(i)}\right ) \in \operatorname {\mathrm {Fil}}^{i-1}{\mathcal D} = S_F\widehat f_2^{(i-1)} + S_F E^{i-1}\widehat f_1$
. Since
 $\widehat f_2^{(i-1)} = \widehat f_2^{(i)} - x_{i-1}E^{i-1} \widehat f_1$
, we can write
$\widehat f_2^{(i-1)} = \widehat f_2^{(i)} - x_{i-1}E^{i-1} \widehat f_1$
, we can write
 $$ \begin{align*} N_{{\mathcal D}}\left(\widehat f_2^{(i)}\right) = d_i \widehat f_2^{(i)} + b_i E^{i-1}\widehat f_1 \end{align*} $$
$$ \begin{align*} N_{{\mathcal D}}\left(\widehat f_2^{(i)}\right) = d_i \widehat f_2^{(i)} + b_i E^{i-1}\widehat f_1 \end{align*} $$
for some
![]() $d_i, b_i \in S_F$
(compare Lemma 3.2). Set
$d_i, b_i \in S_F$
(compare Lemma 3.2). Set
![]() $x_i = b_i(\pi )/i\pi $
, and then set
$x_i = b_i(\pi )/i\pi $
, and then set
 $\widehat f_2^{(i+1)} = \widehat f_2^{(i)} + x_i E^i \widehat f_1$
. Since
$\widehat f_2^{(i+1)} = \widehat f_2^{(i)} + x_i E^i \widehat f_1$
. Since
![]() $2\leq i+1 \leq h$
, we have
$2\leq i+1 \leq h$
, we have
![]() $\operatorname {\mathrm {Fil}}^{i+1}D = F f_2$
. Thus,
$\operatorname {\mathrm {Fil}}^{i+1}D = F f_2$
. Thus,
 $\operatorname {\mathrm {ev}}_{\pi }\left (\widehat f_2^{(i+1)}\right ) = \widehat f_2 \in \operatorname {\mathrm {Fil}}^{i+1}D$
. Further,
$\operatorname {\mathrm {ev}}_{\pi }\left (\widehat f_2^{(i+1)}\right ) = \widehat f_2 \in \operatorname {\mathrm {Fil}}^{i+1}D$
. Further,
 $$ \begin{align} N_{{\mathcal D}}\left(\widehat{f}^{(i +1)} _2\right) &= N_{{\mathcal D}}\left(\widehat{f}^{(i)} _2\right)- x_i i u E^{i -1} \widehat{f}_1 + x_i E^i N_{{\mathcal D}}\left(\widehat{f}_1\right)\\ &= d_i\widehat f_2^{(i)} + (b_i-x_i i u)E^{i-1}\widehat f_1 + x_i E^i N_{{\mathcal D}}\left(\widehat f_1\right).\nonumber \end{align} $$
$$ \begin{align} N_{{\mathcal D}}\left(\widehat{f}^{(i +1)} _2\right) &= N_{{\mathcal D}}\left(\widehat{f}^{(i)} _2\right)- x_i i u E^{i -1} \widehat{f}_1 + x_i E^i N_{{\mathcal D}}\left(\widehat{f}_1\right)\\ &= d_i\widehat f_2^{(i)} + (b_i-x_i i u)E^{i-1}\widehat f_1 + x_i E^i N_{{\mathcal D}}\left(\widehat f_1\right).\nonumber \end{align} $$
Note that the last summand in equation (3.1) lies in
![]() $\operatorname {\mathrm {Fil}}^i S_F \cdot {\mathcal D} \subseteq \operatorname {\mathrm {Fil}}^i {\mathcal D}$
, whereas the first lies in
$\operatorname {\mathrm {Fil}}^i S_F \cdot {\mathcal D} \subseteq \operatorname {\mathrm {Fil}}^i {\mathcal D}$
, whereas the first lies in
![]() $\operatorname {\mathrm {Fil}}^i {\mathcal D}$
. By definition we have
$\operatorname {\mathrm {Fil}}^i {\mathcal D}$
. By definition we have
![]() $\operatorname {\mathrm {ev}}_\pi (b_i - x_i i u) = 0$
, and so the middle summand also lies in
$\operatorname {\mathrm {ev}}_\pi (b_i - x_i i u) = 0$
, and so the middle summand also lies in
![]() $\operatorname {\mathrm {Fil}}^i S_F \cdot {\mathcal D} \subseteq \operatorname {\mathrm {Fil}}^i {\mathcal D}$
. Thus
$\operatorname {\mathrm {Fil}}^i S_F \cdot {\mathcal D} \subseteq \operatorname {\mathrm {Fil}}^i {\mathcal D}$
. Thus
 $\widehat f_{2}^{(i+1)} \in \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
.
$\widehat f_{2}^{(i+1)} \in \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
.
For a moment, define
 $F^{i+1}{\mathcal D} = S_F \widehat f_2^{(i+1)} + S_F E^{i+1} \widehat f_1 \subseteq \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
. We want to show equality. Since
$F^{i+1}{\mathcal D} = S_F \widehat f_2^{(i+1)} + S_F E^{i+1} \widehat f_1 \subseteq \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
. We want to show equality. Since
 $E\widehat f_2^{(i)} = E\widehat f_2^{(i+1)} - x_i E^{i+1}\widehat f_1$
, we in fact have
$E\widehat f_2^{(i)} = E\widehat f_2^{(i+1)} - x_i E^{i+1}\widehat f_1$
, we in fact have
Since
![]() $\operatorname {\mathrm {ev}}_\pi $
gives an isomorphism
$\operatorname {\mathrm {ev}}_\pi $
gives an isomorphism
 $\operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D} \cong Ff_2$
by Remark 2.8, and
$\operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D} \cong Ff_2$
by Remark 2.8, and
 $\operatorname {\mathrm {ev}}_\pi \left (F^{i+1}{\mathcal D}\right ) \neq 0$
, we conclude that the natural map
$\operatorname {\mathrm {ev}}_\pi \left (F^{i+1}{\mathcal D}\right ) \neq 0$
, we conclude that the natural map
 $F^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D} \rightarrow \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D}$
is an isomorphism. Thus,
$F^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D} \rightarrow \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}/E\operatorname {\mathrm {Fil}}^i{\mathcal D}$
is an isomorphism. Thus,
![]() $F^{i+1}{\mathcal D} = \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
.
$F^{i+1}{\mathcal D} = \operatorname {\mathrm {Fil}}^{i+1}{\mathcal D}$
.
The proof of Proposition 3.1 allows for explicit control of the scalars
![]() $x_j$
in terms of the monodromy matrix
$x_j$
in terms of the monodromy matrix
 $\left (\begin {smallmatrix} a & b \\ c & d\end {smallmatrix}\right )$
. For the next two results, we explain this by reexamining the proof.
$\left (\begin {smallmatrix} a & b \\ c & d\end {smallmatrix}\right )$
. For the next two results, we explain this by reexamining the proof.
Lemma 3.2. For
![]() $1 \leq i \leq h-1$
, let
$1 \leq i \leq h-1$
, let
![]() $d_i, b_i \in S_F$
be such that
$d_i, b_i \in S_F$
be such that
 $ N_{{\mathcal D}}\left (\widehat f_2^{(i)}\right ) = d_i \widehat f_2^{(i)} + b_iE^{i-1}\widehat f_1$
. Then
$ N_{{\mathcal D}}\left (\widehat f_2^{(i)}\right ) = d_i \widehat f_2^{(i)} + b_iE^{i-1}\widehat f_1$
. Then
![]() $d_1 = d$
,
$d_1 = d$
,
![]() $b_1=b$
,
$b_1=b$
,
 $x_1 = \frac {b}{\pi }$
, and for
$x_1 = \frac {b}{\pi }$
, and for
![]() $1 \leq i < h-1$
,
$1 \leq i < h-1$
,
 $$ \begin{align*} d_{i+1} &= d_i + c x_i E^i\\ b_{i+1} &= x_i(a-cz_i - d_i) + (b_i - x_i i u)/E \\ x_{i+1} &= \frac{b_{i+1}(\pi)}{(i+1)\pi}, \end{align*} $$
$$ \begin{align*} d_{i+1} &= d_i + c x_i E^i\\ b_{i+1} &= x_i(a-cz_i - d_i) + (b_i - x_i i u)/E \\ x_{i+1} &= \frac{b_{i+1}(\pi)}{(i+1)\pi}, \end{align*} $$
where
 $z_i = \sum _{j=1}^i x_j E^j$
.
$z_i = \sum _{j=1}^i x_j E^j$
.
Proof. The values of
![]() $d_1$
,
$d_1$
,
![]() $b_1$
, and
$b_1$
, and
![]() $x_1$
follow immediately from
$x_1$
follow immediately from
 $\widehat f_2^{(1)} = \widehat f_2$
and
$\widehat f_2^{(1)} = \widehat f_2$
and
 $N_{{\mathcal D}}\left (\widehat f_2\right ) = b\widehat f_1 + d\widehat f_2$
. Next, by equation (3.1) and because
$N_{{\mathcal D}}\left (\widehat f_2\right ) = b\widehat f_1 + d\widehat f_2$
. Next, by equation (3.1) and because
 $N_{{\mathcal D}}\left (\widehat f_1\right ) = a\widehat f_1 + c\widehat f_2$
, we have
$N_{{\mathcal D}}\left (\widehat f_1\right ) = a\widehat f_1 + c\widehat f_2$
, we have
 $$ \begin{align} N_{{\mathcal D}}\left(\widehat{f}^{(i +1)} _2\right) = d_i \widehat{f}^{(i)}_2 + (b_i - x_i i u) E^{i-1} \widehat{f}_1 + x_i E^i \left(a \widehat{f}_1 + c \widehat{f}_2\right). \end{align} $$
$$ \begin{align} N_{{\mathcal D}}\left(\widehat{f}^{(i +1)} _2\right) = d_i \widehat{f}^{(i)}_2 + (b_i - x_i i u) E^{i-1} \widehat{f}_1 + x_i E^i \left(a \widehat{f}_1 + c \widehat{f}_2\right). \end{align} $$
We can write
 $\widehat f_2^{(i)} = \widehat f_2^{(i+1)} - x_i E^i \widehat f_1$
and, separately,
$\widehat f_2^{(i)} = \widehat f_2^{(i+1)} - x_i E^i \widehat f_1$
and, separately,
 $\widehat f_2 = \widehat f_2^{(i+1)} - z_i \widehat f_1$
. Thus equation (3.2) becomes
$\widehat f_2 = \widehat f_2^{(i+1)} - z_i \widehat f_1$
. Thus equation (3.2) becomes
 $$ \begin{align*} N_{{\mathcal D}}\left(\widehat f^{(i+1)}_2\right) = \left(d_i + cx_iE^i\right) \widehat f_2^{(i+1)} + \left(-d_ix_iE^i + (b_i-x_i i u)E^{i-1} + x_iE^i(a-cz_i)\right)\widehat f_1. \end{align*} $$
$$ \begin{align*} N_{{\mathcal D}}\left(\widehat f^{(i+1)}_2\right) = \left(d_i + cx_iE^i\right) \widehat f_2^{(i+1)} + \left(-d_ix_iE^i + (b_i-x_i i u)E^{i-1} + x_iE^i(a-cz_i)\right)\widehat f_1. \end{align*} $$
Factoring
![]() $E^i$
out of the
$E^i$
out of the
![]() $\widehat f_1$
-coefficient, the result is clear.
$\widehat f_1$
-coefficient, the result is clear.
Example 3.3. In Lemma 4.4, we will need an explicit calculation of the
![]() $x_i$
and z. This can be done using the recursive formulas already given. The calculations we need, both of which are straightforward, are
$x_i$
and z. This can be done using the recursive formulas already given. The calculations we need, both of which are straightforward, are
 $$ \begin{align*} x_2 &= \frac{b}{2\pi^2}(a-d-1)\\ z_2(0) &= \frac{b}{2}(a-d-3). \end{align*} $$
$$ \begin{align*} x_2 &= \frac{b}{2\pi^2}(a-d-1)\\ z_2(0) &= \frac{b}{2}(a-d-3). \end{align*} $$
(See also Example 3.9.)
Lemma 3.4. Assume that
![]() $a-d \in \Lambda $
and
$a-d \in \Lambda $
and
![]() $bc \in \Lambda $
. Then for
$bc \in \Lambda $
. Then for
![]() $1 \leq i \leq h-1$
, we have
$1 \leq i \leq h-1$
, we have
Remark 3.5. The lemma is consistent with
![]() $b = 0$
, since in that case
$b = 0$
, since in that case
![]() $x_i = 0$
for all i.
$x_i = 0$
for all i.
Proof of Lemma 3.4. Given
![]() $v \in \mathbb R$
, we write
$v \in \mathbb R$
, we write
 $$ \begin{align*} A_v = \left\{ \sum_{j\geq 0} y_j E^j \in F[u] \mid v_p\left(y_j\right) + v_p(j!) + j \geq v\right\}. \end{align*} $$
$$ \begin{align*} A_v = \left\{ \sum_{j\geq 0} y_j E^j \in F[u] \mid v_p\left(y_j\right) + v_p(j!) + j \geq v\right\}. \end{align*} $$
Note that
![]() $A_v$
is a subgroup of
$A_v$
is a subgroup of
![]() $F[u]$
. Since
$F[u]$
. Since
![]() $v_p((j+k)!) \geq v_p(j!) + v_p(k!)$
for all nonnegative integers
$v_p((j+k)!) \geq v_p(j!) + v_p(k!)$
for all nonnegative integers
![]() $j,k$
(because binomial coefficients are integers), we have
$j,k$
(because binomial coefficients are integers), we have
![]() $A_v A_w \subseteq A_{v+w}$
as well. In particular,
$A_v A_w \subseteq A_{v+w}$
as well. In particular,
![]() $A_0$
is a ring containing
$A_0$
is a ring containing
![]() $\Lambda $
as a subring, and each
$\Lambda $
as a subring, and each
![]() $A_v$
is an
$A_v$
is an
![]() $A_0$
-module.
$A_0$
-module.
The lemma is equivalent to
 $x_i E^i \in A_{v_p(b)}$
for all
$x_i E^i \in A_{v_p(b)}$
for all
![]() $1 \leq i \leq h-1$
, but to show
$1 \leq i \leq h-1$
, but to show
 $x_iE^i \in A_{v_p(b)}$
it suffices to show
$x_iE^i \in A_{v_p(b)}$
it suffices to show
 $b_iE^{i-1} \in A_{v_p(b)}$
. Indeed,
$b_iE^{i-1} \in A_{v_p(b)}$
. Indeed,
![]() $b_i E^{i-1} \in b_i(\pi )E^{i-1} + E^i F[u]$
, and so if
$b_i E^{i-1} \in b_i(\pi )E^{i-1} + E^i F[u]$
, and so if
![]() $b_iE^{i-1} \in A_v$
(for any v), then
$b_iE^{i-1} \in A_v$
(for any v), then
![]() $v_p(b_i(\pi )) + v_p((i-1)!) + i-1 \geq v$
. Since
$v_p(b_i(\pi )) + v_p((i-1)!) + i-1 \geq v$
. Since
![]() $b_i(\pi ) = x_i i \pi $
, by definition, we would clearly have
$b_i(\pi ) = x_i i \pi $
, by definition, we would clearly have
![]() $v_p(x_i) + v_p(i!) + i \geq v$
as well.
$v_p(x_i) + v_p(i!) + i \geq v$
as well.
We have reduced to showing
 $b_i E^{i-1} \in A_{v_p(b)}$
for
$b_i E^{i-1} \in A_{v_p(b)}$
for
![]() $1 \leq i \leq h-1$
. For
$1 \leq i \leq h-1$
. For
![]() $i = 1$
, by Lemma 3.2 we have
$i = 1$
, by Lemma 3.2 we have
![]() $b_1 = b$
, and so the claim is clear. Now assume that
$b_1 = b$
, and so the claim is clear. Now assume that
 $b_jE^{j-1} \in A_{v_p(b)}$
for all
$b_jE^{j-1} \in A_{v_p(b)}$
for all
![]() $j \leq i$
. By the previous paragraph, we have
$j \leq i$
. By the previous paragraph, we have
 $x_j E^{j} \in A_{v_p(b)}$
for all
$x_j E^{j} \in A_{v_p(b)}$
for all
![]() $j \leq i$
, and so
$j \leq i$
, and so
![]() $z_j \in A_{v_p(b)}$
for all
$z_j \in A_{v_p(b)}$
for all
![]() $j \leq i$
(including
$j \leq i$
(including
![]() $z_0$
, which we define to be
$z_0$
, which we define to be
![]() $0$
). By Lemma 3.2, we have
$0$
). By Lemma 3.2, we have
 $$ \begin{align} b_{i+1}E^i = (a-cz_i - d_i) x_iE^i &+ (b_i - x_i i u)E^{i-1}\nonumber\\ &\quad = (a-d-c(z_i+z_{i-1}))x_iE^i + b_i E^{i-1} - x_i i \pi E^{i-1} - x_i i E^{i}. \end{align} $$
$$ \begin{align} b_{i+1}E^i = (a-cz_i - d_i) x_iE^i &+ (b_i - x_i i u)E^{i-1}\nonumber\\ &\quad = (a-d-c(z_i+z_{i-1}))x_iE^i + b_i E^{i-1} - x_i i \pi E^{i-1} - x_i i E^{i}. \end{align} $$
It is clear by induction that the final three summands are in
![]() $A_{v_p(b)}$
. For the first summand, we know
$A_{v_p(b)}$
. For the first summand, we know
![]() $z_i + z_{i-1} \in A_{v_p(b)}$
. Since
$z_i + z_{i-1} \in A_{v_p(b)}$
. Since
![]() $v_p(c)+v_p(b) \geq 0$
and
$v_p(c)+v_p(b) \geq 0$
and
![]() $a-d \in \Lambda $
, we see that
$a-d \in \Lambda $
, we see that
![]() $a-d-c(z_i+z_{i-1}) \in A_0$
. Since
$a-d-c(z_i+z_{i-1}) \in A_0$
. Since
 $x_iE^i \in A_{v_p(b)}$
, by induction, the first summand also lies in
$x_iE^i \in A_{v_p(b)}$
, by induction, the first summand also lies in
![]() $A_{v_p(b)}$
. Thus,
$A_{v_p(b)}$
. Thus,
 $b_{i+1}E^i \in A_{v_p(b)}$
.
$b_{i+1}E^i \in A_{v_p(b)}$
.
3.2 Explicit filtered
 $(\varphi ,N)$
-modules
$(\varphi ,N)$
-modules
Now assume F contains an element
![]() $\varpi $
such that
$\varpi $
such that
![]() $\varpi ^2 = p$
. For
$\varpi ^2 = p$
. For
![]() $\mathcal L \in F$
and
$\mathcal L \in F$
and
![]() $h\geq 1$
, we define
$h\geq 1$
, we define
 $D_{h+1,\mathcal L} = Fe_1 \oplus Fe_2 \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
, where, in the basis
$D_{h+1,\mathcal L} = Fe_1 \oplus Fe_2 \in \operatorname {\mathrm {MF}}_{F}^{\varphi ,N}$
, where, in the basis
![]() $(e_1,e_2)$
,
$(e_1,e_2)$
,
 $$ \begin{align*} \varphi &= \begin{pmatrix} \varpi^{h+1} & 0 \\ 0 & \varpi^{h-1} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{h+1,\mathcal L} &= \begin{cases} D_{h+1,\mathcal L} & \text{if }i \leq 0,\\ F\cdot(e_1 + \mathcal Le_2) & \text{if }1 \leq i \leq h,\\ \{0\} & \text{if }h < i \end{cases} \end{align*} $$
$$ \begin{align*} \varphi &= \begin{pmatrix} \varpi^{h+1} & 0 \\ 0 & \varpi^{h-1} \end{pmatrix}, & N &= \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, & \operatorname{\mathrm{Fil}}^i D_{h+1,\mathcal L} &= \begin{cases} D_{h+1,\mathcal L} & \text{if }i \leq 0,\\ F\cdot(e_1 + \mathcal Le_2) & \text{if }1 \leq i \leq h,\\ \{0\} & \text{if }h < i \end{cases} \end{align*} $$
(see [Reference Breuil and Mézard7, Exemple 3.1.2.2(iv)]). It is useful make a change of basis. Set
![]() $a_p = \varpi ^{h-1}+\varpi ^{h+1}$
.
$a_p = \varpi ^{h-1}+\varpi ^{h+1}$
.
Lemma 3.6. If
![]() $\mathcal L \neq 0$
, then
$\mathcal L \neq 0$
, then
![]() $(f_1,f_2) = (-\varphi (e_1+\mathcal Le_2),e_1+\mathcal Le_2)$
is a basis of
$(f_1,f_2) = (-\varphi (e_1+\mathcal Le_2),e_1+\mathcal Le_2)$
is a basis of
![]() $D_{h+1,\mathcal L}$
in which
$D_{h+1,\mathcal L}$
in which
 $$ \begin{align*} \varphi &= \kern-1.2pt\begin{pmatrix} a_p & -1 \\ p^{h} & 0 \end{pmatrix},\!\!\quad N = \frac{p}{\mathcal L(1-p)}\!\begin{pmatrix} 1 & \varpi^{-h-1} \\ \varpi^{h+1} & -1 \end{pmatrix}\!, \!\!\quad \operatorname{\mathrm{Fil}}^i D_{h+1,\mathcal L} = \kern-1.2pt\begin{cases}\! D_{h+1,\mathcal L} & \text{if }i \leq 0,\\ Ff_2 & \text{if }1 \leq i \leq h,\\ \{0\} & \text{if }h < i. \end{cases} \end{align*} $$
$$ \begin{align*} \varphi &= \kern-1.2pt\begin{pmatrix} a_p & -1 \\ p^{h} & 0 \end{pmatrix},\!\!\quad N = \frac{p}{\mathcal L(1-p)}\!\begin{pmatrix} 1 & \varpi^{-h-1} \\ \varpi^{h+1} & -1 \end{pmatrix}\!, \!\!\quad \operatorname{\mathrm{Fil}}^i D_{h+1,\mathcal L} = \kern-1.2pt\begin{cases}\! D_{h+1,\mathcal L} & \text{if }i \leq 0,\\ Ff_2 & \text{if }1 \leq i \leq h,\\ \{0\} & \text{if }h < i. \end{cases} \end{align*} $$
Proof. If
![]() $\mathcal L \neq 0$
, then
$\mathcal L \neq 0$
, then
![]() $e_1 + \mathcal Le_2$
is not an eigenvector of
$e_1 + \mathcal Le_2$
is not an eigenvector of
![]() $\varphi $
, so
$\varphi $
, so
![]() $(f_1,f_2)$
is a basis. We leave calculating the matrices for the reader.
$(f_1,f_2)$
is a basis. We leave calculating the matrices for the reader.
Now let
![]() $\mathcal D_{h+1,\mathcal L} = \underline {\mathcal D}\left (D_{h+1,\mathcal L}\right )$
and
$\mathcal D_{h+1,\mathcal L} = \underline {\mathcal D}\left (D_{h+1,\mathcal L}\right )$
and
 $\mathcal M_{h+1,\mathcal L} = \underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi ,\leq h}$
. Recall that
$\mathcal M_{h+1,\mathcal L} = \underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F \in \operatorname {\mathrm {Mod}}_{S_F}^{\varphi ,\leq h}$
. Recall that
![]() $\mathfrak {c} = \varphi (E)/p \in S_F^\times $
. Let
$\mathfrak {c} = \varphi (E)/p \in S_F^\times $
. Let
 $\lambda _- = \prod _{n\geq 0} \varphi ^{2n+1}(E)/p$
and
$\lambda _- = \prod _{n\geq 0} \varphi ^{2n+1}(E)/p$
and
![]() $\lambda _{++} = \varphi (\lambda _-)$
.
$\lambda _{++} = \varphi (\lambda _-)$
.
Theorem 3.7. If
![]() $\mathcal L \neq 0$
, there exists a basis of
$\mathcal L \neq 0$
, there exists a basis of
![]() $\mathcal M_{h+1,\mathcal L}$
in which the matrix of
$\mathcal M_{h+1,\mathcal L}$
in which the matrix of
![]() $\varphi $
is given by
$\varphi $
is given by
 $$ \begin{align*} A = \begin{pmatrix} \left(a_p - p^h z\right)\left({\lambda_-\over \lambda_{++}}\right)^h & -1 + \varphi(z)\left(a_p - p^h z\right) \\ E^h & E^h \varphi(z) \left({\lambda_{++}\over \lambda_-}\right)^h \end{pmatrix}, \end{align*} $$
$$ \begin{align*} A = \begin{pmatrix} \left(a_p - p^h z\right)\left({\lambda_-\over \lambda_{++}}\right)^h & -1 + \varphi(z)\left(a_p - p^h z\right) \\ E^h & E^h \varphi(z) \left({\lambda_{++}\over \lambda_-}\right)^h \end{pmatrix}, \end{align*} $$
where
 $z = \sum _{j=1}^{h-1} x_j E^j \in F[E]$
. Moreover, if
$z = \sum _{j=1}^{h-1} x_j E^j \in F[E]$
. Moreover, if
 $v_p\left (\mathcal L^{-1}\right ) \geq -1$
, then
$v_p\left (\mathcal L^{-1}\right ) \geq -1$
, then
 $$ \begin{align} v_p\left(x_j\right) \geq v_p\left(\mathcal L^{-1}\right) - {h-1\over 2} - v_p(j!) - j \end{align} $$
$$ \begin{align} v_p\left(x_j\right) \geq v_p\left(\mathcal L^{-1}\right) - {h-1\over 2} - v_p(j!) - j \end{align} $$
for each
![]() $1 \leq j \leq h-1$
.
$1 \leq j \leq h-1$
.
Proof. Let
![]() $(f_1,f_2)$
be the basis as in Lemma 3.6. Set
$(f_1,f_2)$
be the basis as in Lemma 3.6. Set
 $\widehat f_1 = 1 \otimes f_1$
and
$\widehat f_1 = 1 \otimes f_1$
and
 $\widehat f_2 = 1 \otimes f_2$
, elements of
$\widehat f_2 = 1 \otimes f_2$
, elements of
![]() $\mathcal D_{h+1,\mathcal L}$
, as before. Then the matrix of
$\mathcal D_{h+1,\mathcal L}$
, as before. Then the matrix of
![]() $\varphi $
in the basis
$\varphi $
in the basis
 $\left (\widehat f_1,\widehat f_2\right )$
of
$\left (\widehat f_1,\widehat f_2\right )$
of
![]() $\mathcal D_{h+1,\mathcal L}$
is
$\mathcal D_{h+1,\mathcal L}$
is
 $X = \left (\begin {smallmatrix} a_p & -1 \\ p^h & 0\end {smallmatrix}\right )$
. Moreover, Proposition 3.1 implies that
$X = \left (\begin {smallmatrix} a_p & -1 \\ p^h & 0\end {smallmatrix}\right )$
. Moreover, Proposition 3.1 implies that
 $\operatorname {\mathrm {Fil}}^h {\mathcal D}_{h+1,\mathcal L} = S_F\alpha _1\oplus S_F\alpha _2$
, where
$\operatorname {\mathrm {Fil}}^h {\mathcal D}_{h+1,\mathcal L} = S_F\alpha _1\oplus S_F\alpha _2$
, where
 $$ \begin{align*} (\alpha_1,\alpha_2) = \left(\widehat f_1,\widehat f_2\right)\begin{pmatrix} E^h & z \\ 0 & 1 \end{pmatrix} =: \left(\widehat f_1,\widehat f_2\right)B \end{align*} $$
$$ \begin{align*} (\alpha_1,\alpha_2) = \left(\widehat f_1,\widehat f_2\right)\begin{pmatrix} E^h & z \\ 0 & 1 \end{pmatrix} =: \left(\widehat f_1,\widehat f_2\right)B \end{align*} $$
for
 $z = \sum _{j=1}^{h-1} x_j E^j$
and some
$z = \sum _{j=1}^{h-1} x_j E^j$
and some
![]() $x_j \in F$
. Theorem 2.7 implies that
$x_j \in F$
. Theorem 2.7 implies that
![]() $\mathcal M_{h+1,\mathcal L}$
has a basis in which the matrix of
$\mathcal M_{h+1,\mathcal L}$
has a basis in which the matrix of
![]() $\varphi $
is given by
$\varphi $
is given by
 $$ \begin{align} A' = E^h B^{-1} X \varphi(B) p^{-h}\mathfrak{c}^{-h} = \begin{pmatrix} a - p^h z & p^{-h}\mathfrak{c}^{-h}\left(-1 + \varphi(z)\left(a_p - p^h z\right)\right) \\ E^h p^h & p^{-h}\mathfrak{c}^{-h}E^h p^h \varphi(z)\end{pmatrix}. \end{align} $$
$$ \begin{align} A' = E^h B^{-1} X \varphi(B) p^{-h}\mathfrak{c}^{-h} = \begin{pmatrix} a - p^h z & p^{-h}\mathfrak{c}^{-h}\left(-1 + \varphi(z)\left(a_p - p^h z\right)\right) \\ E^h p^h & p^{-h}\mathfrak{c}^{-h}E^h p^h \varphi(z)\end{pmatrix}. \end{align} $$
Since
![]() $\lambda _-$
and
$\lambda _-$
and
![]() $\lambda _{++}$
are units in
$\lambda _{++}$
are units in
![]() $S_F$
, we can replace
$S_F$
, we can replace
![]() $A'$
by
$A'$
by
 $CA'\varphi \left (C^{-1}\right )$
for
$CA'\varphi \left (C^{-1}\right )$
for
 $C= \left (\begin {smallmatrix} p^h \lambda _-^h & 0 \\ 0 & \lambda _{++}^h \end {smallmatrix}\right )$
. A short calculation shows
$C= \left (\begin {smallmatrix} p^h \lambda _-^h & 0 \\ 0 & \lambda _{++}^h \end {smallmatrix}\right )$
. A short calculation shows
 $A = C A' \varphi \left (C^{-1}\right )$
, completing the general proof.
$A = C A' \varphi \left (C^{-1}\right )$
, completing the general proof.
Finally, if
 $v_p\left (\mathcal L^{-1}\right ) \geq -1$
, then the matrix of N in Lemma 3.6 satisfies the hypotheses of Lemma 3.4, so the estimates (3.4) follow from the b-entry of the monodromy matrix:
$v_p\left (\mathcal L^{-1}\right ) \geq -1$
, then the matrix of N in Lemma 3.6 satisfies the hypotheses of Lemma 3.4, so the estimates (3.4) follow from the b-entry of the monodromy matrix:
 $$ \begin{align*} b = {-p\over \varpi^{h+1}\mathcal L(1-p)} = {-1\over \varpi^{h-1}\mathcal L(1-p)}. \end{align*} $$
$$ \begin{align*} b = {-p\over \varpi^{h+1}\mathcal L(1-p)} = {-1\over \varpi^{h-1}\mathcal L(1-p)}. \end{align*} $$
This completes the proof.
Remark 3.8. An analogous calculation in the crystalline case, where
![]() $z = 0$
(see Remark 3.5), was made in [Reference Bergdall and Levin3, §3]. The technique here, passing through the category
$z = 0$
(see Remark 3.5), was made in [Reference Bergdall and Levin3, §3]. The technique here, passing through the category
 $\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
, is different, but the descriptions are the same (compare Example 2.9).
$\operatorname {\mathrm {MF}}_{S_F}^{\varphi ,N}$
, is different, but the descriptions are the same (compare Example 2.9).
Example 3.9. We need one ad hoc calculation in Lemma 4.4. Let
![]() $h = 3$
. By Example 3.3, the element z in Theorem 3.7 satisfies
$h = 3$
. By Example 3.3, the element z in Theorem 3.7 satisfies
 $z(0) = \frac {b}{2}(a-d-3)$
, where
$z(0) = \frac {b}{2}(a-d-3)$
, where
 $\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
is the monodromy matrix in Lemma 3.6. For
$\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
is the monodromy matrix in Lemma 3.6. For
![]() $p = h= 3$
, plugging in the explicit matrix, we see
$p = h= 3$
, plugging in the explicit matrix, we see
 $z(0) = {1\over 4\mathcal L}\left (\frac {1}{\mathcal L} + 1\right )$
.
$z(0) = {1\over 4\mathcal L}\left (\frac {1}{\mathcal L} + 1\right )$
.
4 Descent and reductions
The goal in this section is to prove the main theorem of the article. Given
![]() $h \geq 1$
and
$h \geq 1$
and
![]() $\mathcal L \in F$
, we write
$\mathcal L \in F$
, we write
![]() $V_{h+1,\mathcal L}$
for the unique
$V_{h+1,\mathcal L}$
for the unique
![]() $2$
-dimensional representation of
$2$
-dimensional representation of
![]() $G_{\mathbb Q_p}$
such that
$G_{\mathbb Q_p}$
such that
![]() $D_{\operatorname {\mathrm {{st}}}}^{\ast }\left (V_{h+1,\mathcal L}\right ) \cong D_{h+1,\mathcal L}$
, where
$D_{\operatorname {\mathrm {{st}}}}^{\ast }\left (V_{h+1,\mathcal L}\right ) \cong D_{h+1,\mathcal L}$
, where
![]() $D_{h+1,\mathcal L}$
is as in §3.2. Write
$D_{h+1,\mathcal L}$
is as in §3.2. Write
![]() $\overline V$
for the semisimple reduction modulo
$\overline V$
for the semisimple reduction modulo
![]() $\mathfrak m_F$
of V. Let
$\mathfrak m_F$
of V. Let
![]() $\mathbb Q_{p^2}$
be the unramified quadratic extension of
$\mathbb Q_{p^2}$
be the unramified quadratic extension of
![]() $\mathbb {Q}_p$
,
$\mathbb {Q}_p$
,
![]() $\chi $
the unramified quadratic character of
$\chi $
the unramified quadratic character of
 $G_{\mathbb Q_{p^2}}$
, and
$G_{\mathbb Q_{p^2}}$
, and
![]() $\omega _2$
a niveau
$\omega _2$
a niveau
![]() $2$
fundamental character of
$2$
fundamental character of
![]() $\mathbb Q_{p^2}$
. Note that
$\mathbb Q_{p^2}$
. Note that
 $\operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
has determinant
$\operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
has determinant
![]() $\omega ^h$
, where
$\omega ^h$
, where
![]() $\omega $
is the cyclotomic character, and its restriction to inertia is
$\omega $
is the cyclotomic character, and its restriction to inertia is
 $\omega _2^h \oplus \omega _2^{ph}$
.
$\omega _2^h \oplus \omega _2^{ph}$
.
Theorem 4.1. Assume
![]() $h \geq 3$
and
$h \geq 3$
and
![]() $p \neq 2$
. Then if
$p \neq 2$
. Then if
![]() $\mathcal L$
satisfies
$\mathcal L$
satisfies
 $$ \begin{align*} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} - 1 + v_p((h-1)!), \end{align*} $$
$$ \begin{align*} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} - 1 + v_p((h-1)!), \end{align*} $$
we have
 $\overline V_{h+1,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
$\overline V_{h+1,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_{p^2}}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
Remark 4.2. Our contribution toward Theorem 4.1 is limited to
![]() $h \geq 4$
and
$h \geq 4$
and
![]() $p = h = 3$
. The case of
$p = h = 3$
. The case of
![]() $h = 3$
and
$h = 3$
and
![]() $p \geq 5$
follows from the work of Breuil and Mézard. If we were to use the weaker bound
$p \geq 5$
follows from the work of Breuil and Mézard. If we were to use the weaker bound
 $v_p\left (\mathcal L^{-1}\right )> {h-1\over 2} + v_p((h-1)!)$
, then our calculation would also cover the cases of
$v_p\left (\mathcal L^{-1}\right )> {h-1\over 2} + v_p((h-1)!)$
, then our calculation would also cover the cases of
![]() $h=2$
and
$h=2$
and
![]() $h=3$
. See Remark 4.8 for further explanations.
$h=3$
. See Remark 4.8 for further explanations.
We plan to take the matrix of
![]() $\varphi $
acting on
$\varphi $
acting on
![]() $\mathcal M_{h+1,\mathcal L}=\underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F$
as in Theorem 3.7 and replace it with a
$\mathcal M_{h+1,\mathcal L}=\underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} S_F$
as in Theorem 3.7 and replace it with a
![]() $\varphi $
-conjugate defined over
$\varphi $
-conjugate defined over
![]() $\mathfrak S_{\Lambda }$
when
$\mathfrak S_{\Lambda }$
when
 $v_p\left (\mathcal L^{-1}\right )$
satisfies the bound in the theorem. This defines a Kisin module
$v_p\left (\mathcal L^{-1}\right )$
satisfies the bound in the theorem. This defines a Kisin module
![]() $\mathfrak M$
for
$\mathfrak M$
for
![]() $V_{h+1,\mathcal L}$
that allows us to calculate the reduction
$V_{h+1,\mathcal L}$
that allows us to calculate the reduction
![]() $\overline {V}_{h+1,\mathcal L}$
. Despite our theorem being limited to
$\overline {V}_{h+1,\mathcal L}$
. Despite our theorem being limited to
![]() $h \geq 3$
, we will present many calculations assuming only
$h \geq 3$
, we will present many calculations assuming only
![]() $h \geq 2$
, in order to later justify Remark 4.2. So we assume without further comment that
$h \geq 2$
, in order to later justify Remark 4.2. So we assume without further comment that
 $$ \begin{align} p &\neq 2 \text{ and } h \geq 2; \\ v_p\left(\mathcal L^{-1}\right) &> {h-1\over 2} - 1 + v_p((h-1)!).\nonumber \end{align} $$
$$ \begin{align} p &\neq 2 \text{ and } h \geq 2; \\ v_p\left(\mathcal L^{-1}\right) &> {h-1\over 2} - 1 + v_p((h-1)!).\nonumber \end{align} $$
We will clarify result by result where we need to limit to
![]() $h\geq 3$
or
$h\geq 3$
or
![]() $h \geq 4$
. Also, fix
$h \geq 4$
. Also, fix
 $z = \sum _{j=1}^{h-1} x_j E^j$
as in Theorem 3.7. Note that by formula (4.1), we have
$z = \sum _{j=1}^{h-1} x_j E^j$
as in Theorem 3.7. Note that by formula (4.1), we have
 $v_p\left (\mathcal L^{-1}\right ) \geq -1$
, so the estimates (3.4) in Theorem 3.7 hold.
$v_p\left (\mathcal L^{-1}\right ) \geq -1$
, so the estimates (3.4) in Theorem 3.7 hold.
4.1 Preparing for descent
Consider the ring
 $$ \begin{align*} R_2 = \left\{ f = \sum a_i u^i \in F[\![u]\!] \mid i + 2v_p(a_i) \rightarrow \infty \text{ as}\ i \rightarrow \infty\right\}. \end{align*} $$
$$ \begin{align*} R_2 = \left\{ f = \sum a_i u^i \in F[\![u]\!] \mid i + 2v_p(a_i) \rightarrow \infty \text{ as}\ i \rightarrow \infty\right\}. \end{align*} $$
Thus
![]() $R_2$
is the F-Banach algebra of series converging on
$R_2$
is the F-Banach algebra of series converging on
![]() $\lvert u\rvert \leq p^{-1/2}$
. We equip
$\lvert u\rvert \leq p^{-1/2}$
. We equip
![]() $R_2$
with the valuation
$R_2$
with the valuation
 $v_{R_2}\left (\sum a_i u^i\right ) = \inf _i \left \{i + 2v_p(a_i)\right \}$
. The canonical map
$v_{R_2}\left (\sum a_i u^i\right ) = \inf _i \left \{i + 2v_p(a_i)\right \}$
. The canonical map
![]() $\mathcal O_F \hookrightarrow R_2$
factors through
$\mathcal O_F \hookrightarrow R_2$
factors through
![]() $S_F$
, since
$S_F$
, since
![]() $v_{R_2}(E^p/p) = p - 2> 0$
. Finally, given
$v_{R_2}(E^p/p) = p - 2> 0$
. Finally, given
![]() $v \in \mathbb {R}$
, we define additive subgroups
$v \in \mathbb {R}$
, we define additive subgroups
![]() $H_v^{\circ } \subseteq H_v \subseteq R_2$
by
$H_v^{\circ } \subseteq H_v \subseteq R_2$
by
For any v,
![]() $H_v$
and
$H_v$
and
![]() $H_v^{\circ }$
are stable under
$H_v^{\circ }$
are stable under
![]() $\varphi $
. In fact, for any
$\varphi $
. In fact, for any
![]() $j \geq 0$
we have
$j \geq 0$
we have
 $$ \begin{align} \varphi\left(H_v \cap u^j R_2\right) \subseteq H_{v+j(p-1)} \cap u^{pj}R_2, \end{align} $$
$$ \begin{align} \varphi\left(H_v \cap u^j R_2\right) \subseteq H_{v+j(p-1)} \cap u^{pj}R_2, \end{align} $$
and the same for
![]() $H^{\circ }_v$
replacing
$H^{\circ }_v$
replacing
![]() $H_v$
(see, e.g., [Reference Bergdall and Levin3, Lemma 4.1.1]).
$H_v$
(see, e.g., [Reference Bergdall and Levin3, Lemma 4.1.1]).
Our first lemma, concerning some entries of the matrix in Theorem 3.7, is straightforward, so we omit the proof (compare with [Reference Bergdall and Levin3, Lemma 5.1.1]).
Lemma 4.3. Let
 $\lambda _- = \prod _{n\geq 0} \varphi ^{2n+1}(E)/p$
and
$\lambda _- = \prod _{n\geq 0} \varphi ^{2n+1}(E)/p$
and
![]() $\lambda _{++} = \varphi (\lambda _-)$
be as in Theorem 3.7. Then
$\lambda _{++} = \varphi (\lambda _-)$
be as in Theorem 3.7. Then
-
(a)
 $\lambda _- \in 1 + H_{p-2}$
and
$\lambda _- \in 1 + H_{p-2}$
and
 $\lambda _{++} \in 1 + H_{p^2-2}$
,
$\lambda _{++} \in 1 + H_{p^2-2}$
, -
(b)
 $\lambda _-, \lambda _{++}\in R_2^\times $
, and
$\lambda _-, \lambda _{++}\in R_2^\times $
, and -
(c)
 $v_{R_2}\left (\lambda _-^{\pm 1}\right ) = 0 = v_{R_2}\left (\lambda _{++}^{\pm 1}\right )$
.
$v_{R_2}\left (\lambda _-^{\pm 1}\right ) = 0 = v_{R_2}\left (\lambda _{++}^{\pm 1}\right )$
.
We also prepare estimates for z. Note that by formula (4.1), the estimate (3.4) becomes
Recall that we write
![]() $a_p = \varpi ^{h-1} + \varpi ^{h+1}$
. Thus,
$a_p = \varpi ^{h-1} + \varpi ^{h+1}$
. Thus,
 $v_{p}\left (a_p\right ) = \frac {h-1}{2}$
.
$v_{p}\left (a_p\right ) = \frac {h-1}{2}$
.
Lemma 4.4. For
 $z = \sum _{j=1}^{h-1} x_j E^j$
as before and
$z = \sum _{j=1}^{h-1} x_j E^j$
as before and
 $\nu = -1 + \varphi (z)\left (a_p - p^h z\right )$
, we have the following:
$\nu = -1 + \varphi (z)\left (a_p - p^h z\right )$
, we have the following:
-
(a)
 $p^h z \in H_{h-1}^{\circ }$
. (c)
$p^h z \in H_{h-1}^{\circ }$
. (c)
 $\nu \in -1 + H_{h-3}^{\circ }$
.
$\nu \in -1 + H_{h-3}^{\circ }$
. -
(b)
 $\varphi (z) \in H_{-2}^{\circ }$
. (d) If
$\varphi (z) \in H_{-2}^{\circ }$
. (d) If
 $h \geq 3$
, then
$h \geq 3$
, then
 $\nu \in R_2^\times $
.
$\nu \in R_2^\times $
.
Furthermore, if
![]() $p =3$
and
$p =3$
and
![]() $h =3$
, then
$h =3$
, then
![]() $\varphi (z) \in H^{\circ }_{-1}$
and
$\varphi (z) \in H^{\circ }_{-1}$
and
![]() $\nu \in -1 + H_{h-2}^{\circ } = -1 + H^{\circ }_{1}$
.
$\nu \in -1 + H_{h-2}^{\circ } = -1 + H^{\circ }_{1}$
.
Proof. First,
 $v_{R_2}\left (E^j\right ) = j$
. By the ultrametric inequality and formula (4.3), we see
$v_{R_2}\left (E^j\right ) = j$
. By the ultrametric inequality and formula (4.3), we see
Part (a) follows because
 $v_{R_2}\left (p^h\right ) = 2h$
. For (b), note that
$v_{R_2}\left (p^h\right ) = 2h$
. For (b), note that
 $v_{R_2}\left (\varphi (E)^j\right ) = 2j$
. Thus, using formula (4.3),
$v_{R_2}\left (\varphi (E)^j\right ) = 2j$
. Thus, using formula (4.3),
Continuing,
![]() $\varphi (z)p^h z \in H_{h-3}^{\circ }$
by parts (a) and (b), and since
$\varphi (z)p^h z \in H_{h-3}^{\circ }$
by parts (a) and (b), and since
![]() $v_{R_2}\left (a_p\right ) = h-1$
, we have
$v_{R_2}\left (a_p\right ) = h-1$
, we have
![]() $\varphi (z)a_p \in H_{h-3}^{\circ }$
. This proves (c). Finally, part (d) follows from the geometric series and part (c).
$\varphi (z)a_p \in H_{h-3}^{\circ }$
. This proves (c). Finally, part (d) follows from the geometric series and part (c).
Finally, suppose
![]() $p = h = 3$
. By the argument for (c), it suffices to show that
$p = h = 3$
. By the argument for (c), it suffices to show that
![]() $\varphi (z) \in H_{-1}^{\circ }$
. We note that
$\varphi (z) \in H_{-1}^{\circ }$
. We note that
 $v_{R_2}\left (\varphi (E)^j - E(0)^j\right ) \geq p + 2j - 2$
for any j. Thus, by formula (4.3),
$v_{R_2}\left (\varphi (E)^j - E(0)^j\right ) \geq p + 2j - 2$
for any j. Thus, by formula (4.3),
But by Example 3.9 we have
 $\varphi (z)(0) = z(0) = \frac {1}{4\mathcal L}\left (\frac {1}{\mathcal L} + 1\right )$
. Since
$\varphi (z)(0) = z(0) = \frac {1}{4\mathcal L}\left (\frac {1}{\mathcal L} + 1\right )$
. Since
 $v_p\left (\mathcal L^{-1}\right )> 0$
, formula (4.4) implies
$v_p\left (\mathcal L^{-1}\right )> 0$
, formula (4.4) implies
![]() $v_{R_2}(\varphi (z))> -1$
, as we wanted.
$v_{R_2}(\varphi (z))> -1$
, as we wanted.
We now write
![]() $\mathcal M_2 = \mathcal M_{h+1,\mathcal L} \otimes _{S_F} R_2 \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} R_2$
. Thus,
$\mathcal M_2 = \mathcal M_{h+1,\mathcal L} \otimes _{S_F} R_2 \cong \underline {\mathcal M}_{\mathcal O_F}\left (D_{h+1,\mathcal L}\right ) \otimes _{\mathcal O_F} R_2$
. Thus,
 $\mathcal M_2 \in \operatorname {\mathrm {Mod}}_{R_2}^{\varphi ,\leq h}$
. We also introduce some notation. Given
$\mathcal M_2 \in \operatorname {\mathrm {Mod}}_{R_2}^{\varphi ,\leq h}$
. We also introduce some notation. Given
![]() $A \in \operatorname {\mathrm {Mat}}_d(R_2)$
and
$A \in \operatorname {\mathrm {Mat}}_d(R_2)$
and
![]() $C \in \mathrm {GL}_d(R_2)$
, we write
$C \in \mathrm {GL}_d(R_2)$
, we write
![]() $ C \ast _\varphi A = C\cdot A \cdot \varphi (C)^{-1}$
. Thus, if
$ C \ast _\varphi A = C\cdot A \cdot \varphi (C)^{-1}$
. Thus, if
![]() $(e_1,e_2)$
is a basis of
$(e_1,e_2)$
is a basis of
![]() $\mathcal M_2$
and A is the matrix of
$\mathcal M_2$
and A is the matrix of
![]() $\varphi _{\mathcal M_2}$
in that basis,
$\varphi _{\mathcal M_2}$
in that basis,
![]() $C\ast _\varphi A$
is the matrix of
$C\ast _\varphi A$
is the matrix of
![]() $\varphi _{\mathcal M_2}$
in the basis
$\varphi _{\mathcal M_2}$
in the basis
![]() $\left (e_1',e_2'\right )$
given by
$\left (e_1',e_2'\right )$
given by
![]() $\left (e_1',e_2'\right ) = (e_1,e_2)C^{-1}$
.
$\left (e_1',e_2'\right ) = (e_1,e_2)C^{-1}$
.
Proposition 4.5. Assume
![]() $h \geq 4$
or
$h \geq 4$
or
![]() $p=h=3$
. Then there exists a basis of
$p=h=3$
. Then there exists a basis of
![]() $\mathcal M_2$
in which the matrix of
$\mathcal M_2$
in which the matrix of
![]() $\varphi _{\mathcal M_2}$
is
$\varphi _{\mathcal M_2}$
is
 $\left (\begin {smallmatrix} G & -1 \\ E^h & 0 \end {smallmatrix}\right )$
, where
$\left (\begin {smallmatrix} G & -1 \\ E^h & 0 \end {smallmatrix}\right )$
, where
 $ G \in \left (a_p - p^h z\right )\left ({\lambda _-\over \lambda _{++}}\right )^h + H_h^{\circ }$
.
$ G \in \left (a_p - p^h z\right )\left ({\lambda _-\over \lambda _{++}}\right )^h + H_h^{\circ }$
.
Proof. By Theorem 3.7, there is a basis
![]() $(e_1,e_2)$
of
$(e_1,e_2)$
of
![]() $\mathcal M_2$
such that
$\mathcal M_2$
such that
![]() $\varphi _{\mathcal M_2}(e_1,e_2) = (e_1,e_2)A$
, where
$\varphi _{\mathcal M_2}(e_1,e_2) = (e_1,e_2)A$
, where
 $$ \begin{align*} A = \begin{pmatrix} \left(a_p - p^h z\right)\left({\lambda_-\over \lambda_{++}}\right)^h & -1 + \varphi(z)\left(a_p - p^h z\right) \\ E^h & E^h \varphi(z) \left({\lambda_{++}\over \lambda_-}\right)^h \end{pmatrix} = \begin{pmatrix} \mu & \nu \\ E^h & \eta \end{pmatrix}, \end{align*} $$
$$ \begin{align*} A = \begin{pmatrix} \left(a_p - p^h z\right)\left({\lambda_-\over \lambda_{++}}\right)^h & -1 + \varphi(z)\left(a_p - p^h z\right) \\ E^h & E^h \varphi(z) \left({\lambda_{++}\over \lambda_-}\right)^h \end{pmatrix} = \begin{pmatrix} \mu & \nu \\ E^h & \eta \end{pmatrix}, \end{align*} $$
with
![]() $\nu $
as in Lemma 4.4 and
$\nu $
as in Lemma 4.4 and
![]() $\mu $
and
$\mu $
and
![]() $\eta $
defined by the equality. Assume for now just that
$\eta $
defined by the equality. Assume for now just that
![]() $h \geq 3$
. Then, by Lemma 4.4
(d),
$h \geq 3$
. Then, by Lemma 4.4
(d),
![]() $\nu \in R_2^\times $
. Making a change of basis on
$\nu \in R_2^\times $
. Making a change of basis on
![]() $\mathcal M_2$
, we replace A (note that
$\mathcal M_2$
, we replace A (note that
![]() $\mu \eta = (1+\nu )E^h$
) by
$\mu \eta = (1+\nu )E^h$
) by
 $$ \begin{align*} A' = \begin{pmatrix} 1 & 0\\ -\eta/\nu & 1 \end{pmatrix} \ast_\varphi A = \begin{pmatrix} \mu + {\nu\varphi(\eta)\over \varphi(\nu)} & \nu \\ -E^h \nu^{-1} & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} A' = \begin{pmatrix} 1 & 0\\ -\eta/\nu & 1 \end{pmatrix} \ast_\varphi A = \begin{pmatrix} \mu + {\nu\varphi(\eta)\over \varphi(\nu)} & \nu \\ -E^h \nu^{-1} & 0 \end{pmatrix}. \end{align*} $$
Since
![]() $v_{R_2}(\nu +1)> 0$
by Lemma 4.4
(c), we have
$v_{R_2}(\nu +1)> 0$
by Lemma 4.4
(c), we have
![]() $\nu (0) \in \Lambda ^\times $
. Thus
$\nu (0) \in \Lambda ^\times $
. Thus
 $\nu _0 = \nu /\nu (0) \in 1 + \left (H_{h-3}^{\circ } \cap uR_2\right )$
. By formula (4.2), we have
$\nu _0 = \nu /\nu (0) \in 1 + \left (H_{h-3}^{\circ } \cap uR_2\right )$
. By formula (4.2), we have
![]() $\varphi ^k(\nu _0) \in 1 + H_{h-3+m_k}$
, where
$\varphi ^k(\nu _0) \in 1 + H_{h-3+m_k}$
, where
![]() $m_k \rightarrow \infty $
as
$m_k \rightarrow \infty $
as
![]() $k \rightarrow \infty $
. Thus, the infinite product
$k \rightarrow \infty $
. Thus, the infinite product
 $\nu _+ = \prod _{n \geq 0} \varphi ^{2n}(\nu _0)$
converges in
$\nu _+ = \prod _{n \geq 0} \varphi ^{2n}(\nu _0)$
converges in
![]() $R_2$
. Set
$R_2$
. Set
![]() $\nu _- = \varphi (\nu _+)$
, so
$\nu _- = \varphi (\nu _+)$
, so
![]() $\nu _{\pm } \in 1 + H_{h-3}^{\circ } \subseteq R_2^\times $
. We now change basis on
$\nu _{\pm } \in 1 + H_{h-3}^{\circ } \subseteq R_2^\times $
. We now change basis on
![]() $\mathcal M_2$
again to get a matrix
$\mathcal M_2$
again to get a matrix
![]() $A''$
for
$A''$
for
![]() $\varphi _{\mathcal M_2}$
given by
$\varphi _{\mathcal M_2}$
given by
 $$ \begin{align*} A'' = \begin{pmatrix} {-1\over \nu(0)} {\nu_- \over \nu_+} & 0 \\ 0 & {\nu_+ \over \nu_-}\end{pmatrix} \ast_{\varphi} A' = \begin{pmatrix} G & -1 \\ E^h & 0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} A'' = \begin{pmatrix} {-1\over \nu(0)} {\nu_- \over \nu_+} & 0 \\ 0 & {\nu_+ \over \nu_-}\end{pmatrix} \ast_{\varphi} A' = \begin{pmatrix} G & -1 \\ E^h & 0 \end{pmatrix}, \end{align*} $$
where
 $$ \begin{align} G = \left(\mu + {\nu\varphi(\eta)\over \varphi(\nu)}\right) {\nu_-^2 \over \nu_+ \nu_{++}} \end{align} $$
$$ \begin{align} G = \left(\mu + {\nu\varphi(\eta)\over \varphi(\nu)}\right) {\nu_-^2 \over \nu_+ \nu_{++}} \end{align} $$
and
![]() $\nu _{++} = \varphi (\nu _-)$
.
$\nu _{++} = \varphi (\nu _-)$
.
To complete the argument, we justify
![]() $G \in \mu + H_h^{\circ }$
. We already know
$G \in \mu + H_h^{\circ }$
. We already know
![]() $\nu _-^2/\nu _+\nu _{++} \in 1 + H_{h-3}^{\circ }$
. The same is true for
$\nu _-^2/\nu _+\nu _{++} \in 1 + H_{h-3}^{\circ }$
. The same is true for
![]() $\nu /\varphi (\nu )$
. So
$\nu /\varphi (\nu )$
. So
 $$ \begin{align} v_{R_2}\left({\nu\varphi(\eta)\over \varphi(\nu)}\right) \geq v_{R_2}(\varphi(\eta)) \geq v_{R_2}\left(\varphi(E)^h\varphi^2(z)\right), \end{align} $$
$$ \begin{align} v_{R_2}\left({\nu\varphi(\eta)\over \varphi(\nu)}\right) \geq v_{R_2}(\varphi(\eta)) \geq v_{R_2}\left(\varphi(E)^h\varphi^2(z)\right), \end{align} $$
where we used Lemma 4.3 to remove
![]() $\lambda _-$
and
$\lambda _-$
and
![]() $\lambda _{++}$
from the estimate. We note that
$\lambda _{++}$
from the estimate. We note that
 $v_{R_2}\left (\varphi (E)^h\right ) = 2h$
and
$v_{R_2}\left (\varphi (E)^h\right ) = 2h$
and
 $v_{R_2}\left (\varphi ^2(z)\right ) \geq v_{R_2}(\varphi (z))> -2$
, by formula (4.2) and Lemma 4.4
(b). Thus from formula (4.6) we deduce that
$v_{R_2}\left (\varphi ^2(z)\right ) \geq v_{R_2}(\varphi (z))> -2$
, by formula (4.2) and Lemma 4.4
(b). Thus from formula (4.6) we deduce that
![]() $v_{R_2}(\nu \varphi (\eta )/\varphi (\nu ))> 2h - 2 = 2(h-1)$
. We also note that
$v_{R_2}(\nu \varphi (\eta )/\varphi (\nu ))> 2h - 2 = 2(h-1)$
. We also note that
![]() $a_p-p^hz \in H_{h-1}$
. Thus,
$a_p-p^hz \in H_{h-1}$
. Thus,
![]() $\mu \in H_{h-1}$
, and so returning to the definition (4.5) of
$\mu \in H_{h-1}$
, and so returning to the definition (4.5) of
![]() $\mu $
and G, we see
$\mu $
and G, we see
 $$ \begin{align*} G \in \left(\mu + H_{2(h-1)}^{\circ}\right)\cdot \left(1 + H_{h-3}^{\circ}\right) \subseteq \mu + H_{2h-4}^{\circ}+ H^{\circ}_{2(h-1)} = \mu + H_{2h-4}^{\circ}. \end{align*} $$
$$ \begin{align*} G \in \left(\mu + H_{2(h-1)}^{\circ}\right)\cdot \left(1 + H_{h-3}^{\circ}\right) \subseteq \mu + H_{2h-4}^{\circ}+ H^{\circ}_{2(h-1)} = \mu + H_{2h-4}^{\circ}. \end{align*} $$
Now, if
![]() $h \geq 4$
, then
$h \geq 4$
, then
![]() $2h-4 \geq h$
and so
$2h-4 \geq h$
and so
![]() $G \in \mu + H_h^{\circ }$
. This completes the proof except if
$G \in \mu + H_h^{\circ }$
. This completes the proof except if
![]() $p = h = 3$
. In that case, Lemma 4.4 shows that
$p = h = 3$
. In that case, Lemma 4.4 shows that
![]() $\nu \in -1 + H^{\circ }_1$
, rather than
$\nu \in -1 + H^{\circ }_1$
, rather than
![]() $-1 + H_0^{\circ }$
, from which we deduce
$-1 + H_0^{\circ }$
, from which we deduce
anyway. This completes the proof.
4.2 Descent
To descend to
![]() $\mathfrak S_{\Lambda }$
, we use the algorithm from [Reference Bergdall and Levin3, §4]. Write
$\mathfrak S_{\Lambda }$
, we use the algorithm from [Reference Bergdall and Levin3, §4]. Write
![]() $T_{\leq d} : R_2 \rightarrow F[u]$
for the ‘truncation’ operation
$T_{\leq d} : R_2 \rightarrow F[u]$
for the ‘truncation’ operation
 $T_{\leq d}\left (\sum a_i u^i\right ) = \sum _{i\leq d} a_i u^i$
and
$T_{\leq d}\left (\sum a_i u^i\right ) = \sum _{i\leq d} a_i u^i$
and
![]() $T_{>d}(f) = f - T_{\leq d}(f)$
. In the next two proofs, we will use the following principle: if
$T_{>d}(f) = f - T_{\leq d}(f)$
. In the next two proofs, we will use the following principle: if
![]() $f \in R_2$
and
$f \in R_2$
and
![]() $v_{R_2}\left (T_{\leq d}(f)\right )> d$
(for instance, if
$v_{R_2}\left (T_{\leq d}(f)\right )> d$
(for instance, if
![]() $v_{R_2}(f)> d$
), then
$v_{R_2}(f)> d$
), then
![]() $T_{\leq d}(f) \in \mathfrak m_F[u]$
.
$T_{\leq d}(f) \in \mathfrak m_F[u]$
.
Proposition 4.6. Suppose that
![]() $G \in R_2$
such that
$G \in R_2$
such that
-
(a)
 $G \in H_{h-1}$
,
$G \in H_{h-1}$
, -
(b)
 $T_{>h}(G) \in H_{h-1}^{\circ }$
, and
$T_{>h}(G) \in H_{h-1}^{\circ }$
, and -
(c)
 $T_{\leq h}(G) \in \mathfrak m_F[u]$
.
$T_{\leq h}(G) \in \mathfrak m_F[u]$
.
Then, given
 $A = \left (\begin {smallmatrix} G & -1 \\ E^h & 0 \end {smallmatrix}\right )$
, there exist
$A = \left (\begin {smallmatrix} G & -1 \\ E^h & 0 \end {smallmatrix}\right )$
, there exist
![]() $C \in \mathrm {GL}_2(R_2)$
and
$C \in \mathrm {GL}_2(R_2)$
and
![]() $P \in \mathfrak m_F[u]$
such that
$P \in \mathfrak m_F[u]$
such that
 $C \ast _{\varphi } A = \left (\begin {smallmatrix} P & -1 \\ E^h & 0 \end {smallmatrix}\right )$
.
$C \ast _{\varphi } A = \left (\begin {smallmatrix} P & -1 \\ E^h & 0 \end {smallmatrix}\right )$
.
Proof. Since
![]() $E^h \in u^h + H_{h+1}$
, (a) implies that
$E^h \in u^h + H_{h+1}$
, (a) implies that
 $$ \begin{align*} A \in \begin{pmatrix} 0 & -1 \\ u^h & 0 \end{pmatrix} + \begin{pmatrix} H_{h-1} & 0 \\ H_{h + 1} & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} A \in \begin{pmatrix} 0 & -1 \\ u^h & 0 \end{pmatrix} + \begin{pmatrix} H_{h-1} & 0 \\ H_{h + 1} & 0 \end{pmatrix}. \end{align*} $$
In the notation of [Reference Bergdall and Levin3, §4.3], set
![]() $a = 0$
,
$a = 0$
,
![]() $b = h$
,
$b = h$
,
 $a' = {h \over 2} - {p-1 \over 2}$
,
$a' = {h \over 2} - {p-1 \over 2}$
,
 $b' = {h \over 2} + {p-1 \over 2}$
, and
$b' = {h \over 2} + {p-1 \over 2}$
, and
![]() $(c_0,c_h) = (-1,1)$
. Since
$(c_0,c_h) = (-1,1)$
. Since
 $h-1-a' = {h\over 2} - 1 + {p-1\over 2} \geq 1$
, we see that A is
$h-1-a' = {h\over 2} - 1 + {p-1\over 2} \geq 1$
, we see that A is
![]() $\gamma $
-allowable with
$\gamma $
-allowable with
![]() $\gamma = 1$
in the sense of [Reference Bergdall and Levin3, Definition 4.3.1]. The error of A, in the same definition, is
$\gamma = 1$
in the sense of [Reference Bergdall and Levin3, Definition 4.3.1]. The error of A, in the same definition, is
![]() $\varepsilon = v_{R_2}\left (T_{>h}(G)\right ) - a'$
. By [Reference Bergdall and Levin3, Theorem 4.3.7], with
$\varepsilon = v_{R_2}\left (T_{>h}(G)\right ) - a'$
. By [Reference Bergdall and Levin3, Theorem 4.3.7], with
![]() $R=R_2$
, there exists
$R=R_2$
, there exists
![]() $C \in \mathrm {GL}_2(R_2)$
such that
$C \in \mathrm {GL}_2(R_2)$
such that
![]() $A' = C\ast _{\varphi } A$
satisfies the following:
$A' = C\ast _{\varphi } A$
satisfies the following:
-
(i) Evaluating at
 $u = 0$
, we have
$u = 0$
, we have
 $A'\rvert _{u=0} = A\rvert _{u=0}$
.
$A'\rvert _{u=0} = A\rvert _{u=0}$
. -
(ii) The matrix
 $A'$
is of the form
$A'$
is of the form
 $A' = \left (\begin {smallmatrix} P & -1 \\ f & 0 \end {smallmatrix}\right )$
, with P and f polynomials of degree at most h.
$A' = \left (\begin {smallmatrix} P & -1 \\ f & 0 \end {smallmatrix}\right )$
, with P and f polynomials of degree at most h. -
(iii) We have an estimate
 $v_{R_2}\left (P - T_{\leq h}(G)\right ) \geq \varepsilon + a' + 1$
.
$v_{R_2}\left (P - T_{\leq h}(G)\right ) \geq \varepsilon + a' + 1$
.
(For the reader checking references, note that the role of A versus C is reversed in [Reference Bergdall and Levin3].)
We claim
![]() $P \in \mathfrak m_F[u]$
and
$P \in \mathfrak m_F[u]$
and
![]() $f = E^h$
, which would finish the proof of the proposition. To see
$f = E^h$
, which would finish the proof of the proposition. To see
![]() $P \in \mathfrak m_F[u]$
, we start by combining the estimate (iii) and the assumption (b) in order to see that
$P \in \mathfrak m_F[u]$
, we start by combining the estimate (iii) and the assumption (b) in order to see that
On the other hand,
![]() $P-T_{\leq h}(G)$
has degree at most h, by (ii), and so
$P-T_{\leq h}(G)$
has degree at most h, by (ii), and so
![]() $P-T_{\leq h}(G) \in \mathfrak m_F[u]$
, which implies
$P-T_{\leq h}(G) \in \mathfrak m_F[u]$
, which implies
![]() $P \in \mathfrak m_F[u]$
by assumption (c).
$P \in \mathfrak m_F[u]$
by assumption (c).
To see
![]() $f = E^h$
, we evidently have
$f = E^h$
, we evidently have
![]() $f = \det (A') = rE^h$
for some
$f = \det (A') = rE^h$
for some
![]() $r \in R_2^\times $
. In particular, f has a root of multiplicity h at
$r \in R_2^\times $
. In particular, f has a root of multiplicity h at
![]() $u = -p$
. But f is a polynomial of degree at most h, by point (ii), and by point (i) we have
$u = -p$
. But f is a polynomial of degree at most h, by point (ii), and by point (i) we have
![]() $f(0) = E(0)^h$
. It now follows quickly that
$f(0) = E(0)^h$
. It now follows quickly that
![]() $f = E^h$
, since
$f = E^h$
, since
![]() $F[\![u]\!]$
is a unique factorization domain.
$F[\![u]\!]$
is a unique factorization domain.
We now verify that the G from Proposition 4.5 satisfies the hypothesis of Proposition 4.6.
Lemma 4.7. Set
 $G \in \left (a_p - p^hz\right )\left ({\lambda _-\over \lambda _{++}}\right )^h + H_{h}^{\circ }$
. Then
$G \in \left (a_p - p^hz\right )\left ({\lambda _-\over \lambda _{++}}\right )^h + H_{h}^{\circ }$
. Then
-
(a)
 $G \in H_{h-1}$
,
$G \in H_{h-1}$
, -
(b)
 $T_{>h}(G) \in H_{h-1}^{\circ }$
, and
$T_{>h}(G) \in H_{h-1}^{\circ }$
, and -
(c)
 $T_{\leq h}\left (G \right ) \in \mathfrak m_F[u]$
.
$T_{\leq h}\left (G \right ) \in \mathfrak m_F[u]$
.
Proof. First, the conclusions depend only on
![]() $G \bmod H_h^{\circ }$
, so we suppose
$G \bmod H_h^{\circ }$
, so we suppose
 $G = \left (a_p - p^h z\right )\left ({\lambda _-\over \lambda _{++}}\right )^h$
. Part (a) follows from Lemmas 4.3 and 4.4. For part (b), we first have, by Lemma 4.3
(a), that
$G = \left (a_p - p^h z\right )\left ({\lambda _-\over \lambda _{++}}\right )^h$
. Part (a) follows from Lemmas 4.3 and 4.4. For part (b), we first have, by Lemma 4.3
(a), that
 $a_p\left ({\lambda _-\over \lambda _{++}}\right )^h \in a_p + a_p H_{p-2}$
, so
$a_p\left ({\lambda _-\over \lambda _{++}}\right )^h \in a_p + a_p H_{p-2}$
, so
 $T_{>0}\left (a_p\left ({\lambda _-\over \lambda _{++}}\right )^h\right ) \in H_{h+p-3} \subseteq H_h$
. On the other hand, by Lemma 4.4
(a) we have
$T_{>0}\left (a_p\left ({\lambda _-\over \lambda _{++}}\right )^h\right ) \in H_{h+p-3} \subseteq H_h$
. On the other hand, by Lemma 4.4
(a) we have
![]() $p^hz \in H_{h-1}^{\circ }$
. Thus we have shown in fact that
$p^hz \in H_{h-1}^{\circ }$
. Thus we have shown in fact that
![]() $T_{>0}(G) \in H_{h-1}^{\circ }$
.
$T_{>0}(G) \in H_{h-1}^{\circ }$
.
Finally, we consider part (c). Since
![]() $E = u+p$
, any
$E = u+p$
, any
![]() $f \in S_\Lambda $
can be written as
$f \in S_\Lambda $
can be written as
 $f= \sum \limits _{n = 0}^\infty \alpha _n \frac {u ^ n}{p^{\left \lfloor \frac n p \right \rfloor }}$
with
$f= \sum \limits _{n = 0}^\infty \alpha _n \frac {u ^ n}{p^{\left \lfloor \frac n p \right \rfloor }}$
with
![]() $\alpha _n \in \Lambda $
. Let
$\alpha _n \in \Lambda $
. Let
 $f = {\lambda _-\over \lambda _{++}} \in S_\Lambda $
in particular. Since
$f = {\lambda _-\over \lambda _{++}} \in S_\Lambda $
in particular. Since
 $v_p \left (a_p\right ) = \frac {h -1}{2}> \left \lfloor \frac h p \right \rfloor $
unless
$v_p \left (a_p\right ) = \frac {h -1}{2}> \left \lfloor \frac h p \right \rfloor $
unless
![]() $ p = h =3$
(or
$ p = h =3$
(or
![]() $p=2$
, which we have excluded in formula (4.1)), we see immediately that
$p=2$
, which we have excluded in formula (4.1)), we see immediately that
 $T_{\leq h} \left (a_p f^h\right ) \in \mathfrak {m}_F[u]$
except when
$T_{\leq h} \left (a_p f^h\right ) \in \mathfrak {m}_F[u]$
except when
![]() $h = p = 3$
. When
$h = p = 3$
. When
![]() $h = p$
, however,
$h = p$
, however,
 $$ \begin{align*} T_{\leq p}(f^p) = T_{\leq p}\left(\left(\sum_{n=0}^{p-1} \alpha_n u^n + \alpha_p \frac{u^p}{p}\right)^p\right) \in p\cdot \alpha_0^{p-1}\alpha_p \frac{u^p}{p} + \Lambda[u] \subseteq \Lambda[u]. \end{align*} $$
$$ \begin{align*} T_{\leq p}(f^p) = T_{\leq p}\left(\left(\sum_{n=0}^{p-1} \alpha_n u^n + \alpha_p \frac{u^p}{p}\right)^p\right) \in p\cdot \alpha_0^{p-1}\alpha_p \frac{u^p}{p} + \Lambda[u] \subseteq \Lambda[u]. \end{align*} $$
Since
![]() $v_p\left (a_p\right )> 0$
, we see that
$v_p\left (a_p\right )> 0$
, we see that
 $T_{\leq h}\left (a_pf^h\right ) \in \mathfrak m_F[u]$
in every case.
$T_{\leq h}\left (a_pf^h\right ) \in \mathfrak m_F[u]$
in every case.
By the prior paragraph, to show (c) it remains to show that
 $T_{\leq h} \left (p ^h z f^h \right ) \in \mathfrak {m}_F[u]$
as well. By definition, we can write
$T_{\leq h} \left (p ^h z f^h \right ) \in \mathfrak {m}_F[u]$
as well. By definition, we can write
 $f^h = \sum \limits _{i = 0}^\infty \beta _i\frac { E^i}{p ^{\left \lfloor \frac i p\right \rfloor }}$
with
$f^h = \sum \limits _{i = 0}^\infty \beta _i\frac { E^i}{p ^{\left \lfloor \frac i p\right \rfloor }}$
with
![]() $\beta _i \in \Lambda $
, and we recall that
$\beta _i \in \Lambda $
, and we recall that
 $z= \sum _{j=1}^{h-1} x_jE^j$
. Thus
$z= \sum _{j=1}^{h-1} x_jE^j$
. Thus
 $$ \begin{align} p^h z f^h = \sum_{n=1}^\infty \left(\sum_{i+j=n} p^h x_j \beta_i p^{-\left\lfloor \frac i p\right\rfloor}\right) E^n. \end{align} $$
$$ \begin{align} p^h z f^h = \sum_{n=1}^\infty \left(\sum_{i+j=n} p^h x_j \beta_i p^{-\left\lfloor \frac i p\right\rfloor}\right) E^n. \end{align} $$
Using the binomial expansion of
![]() $E^n = (u+p)^n$
, we see that the
$E^n = (u+p)^n$
, we see that the
![]() $u^m$
-term of equation (4.7) is exactly equal to
$u^m$
-term of equation (4.7) is exactly equal to
 $$ \begin{align*} \sum_{n=m}^\infty \left(\sum_{i+j=n} p^h x_j \beta_i p^{-\left\lfloor \frac i p\right\rfloor}\right){n \choose m}p^{n-m}. \end{align*} $$
$$ \begin{align*} \sum_{n=m}^\infty \left(\sum_{i+j=n} p^h x_j \beta_i p^{-\left\lfloor \frac i p\right\rfloor}\right){n \choose m}p^{n-m}. \end{align*} $$
We must show that this has positive p-adic valuation for
![]() $m \leq h$
. Since
$m \leq h$
. Since
![]() $\beta _i \in \Lambda $
and binomial coefficients are integers, it is enough to show that for all
$\beta _i \in \Lambda $
and binomial coefficients are integers, it is enough to show that for all
![]() $m \leq h$
and
$m \leq h$
and
![]() $j < h$
, if
$j < h$
, if
![]() $n \geq m,j$
, then
$n \geq m,j$
, then
 $$ \begin{align} v_p\left(x_j\right) + h + n-m-{\left\lfloor \frac{n -j}{p}\right\rfloor}> 0. \end{align} $$
$$ \begin{align} v_p\left(x_j\right) + h + n-m-{\left\lfloor \frac{n -j}{p}\right\rfloor}> 0. \end{align} $$
By formula (4.3) we have
![]() $v_p\left (x_j\right )> -j-1$
, and so
$v_p\left (x_j\right )> -j-1$
, and so
 $$ \begin{align} v_p\left(x_j\right) + h+n-m-{\left\lfloor \frac{n -j}{p}\right\rfloor}> h - m - 1+ n - j - {\left\lfloor \frac{n -j}{p}\right\rfloor}. \end{align} $$
$$ \begin{align} v_p\left(x_j\right) + h+n-m-{\left\lfloor \frac{n -j}{p}\right\rfloor}> h - m - 1+ n - j - {\left\lfloor \frac{n -j}{p}\right\rfloor}. \end{align} $$
But the right-hand side of this inequality is nonnegative. Indeed, when
![]() $h> m$
, this is clear because
$h> m$
, this is clear because
![]() $n\geq j$
. When
$n\geq j$
. When
![]() $h = m$
, on the other hand, we have
$h = m$
, on the other hand, we have
![]() $n \geq m = h> j$
. So the right-hand side in that case has the form
$n \geq m = h> j$
. So the right-hand side in that case has the form
![]() $x - \lfloor x/p\rfloor -1$
with
$x - \lfloor x/p\rfloor -1$
with
![]() $x \geq 1$
, which is also nonnegative.
$x \geq 1$
, which is also nonnegative.
4.3 Proof of Theorem 4.1
Finally, we give the proof of the main theorem:
Assume that
![]() $h \geq 3$
and
$h \geq 3$
and
![]() $p \neq 2$
. Then if
$p \neq 2$
. Then if
![]() $\mathcal L$
satisfies
$\mathcal L$
satisfies
 $$ \begin{align*} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} - 1 + v_p((h-1)!), \end{align*} $$
$$ \begin{align*} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} - 1 + v_p((h-1)!), \end{align*} $$
we have
 $\overline V_{h+1,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
$\overline V_{h+1,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
Proof. First, if
![]() $h = 3$
and
$h = 3$
and
![]() $p \geq 5$
, then the assumption is that
$p \geq 5$
, then the assumption is that
![]() $v_p(\mathcal L) < 0$
. The verification that
$v_p(\mathcal L) < 0$
. The verification that
 $\overline V_{4,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{3}\chi \right )$
is the first bullet point of [Reference Breuil and Mézard7, Theorem 4.2.4.7(iii)], where the reader should take
$\overline V_{4,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{3}\chi \right )$
is the first bullet point of [Reference Breuil and Mézard7, Theorem 4.2.4.7(iii)], where the reader should take
![]() $k = 4 < p$
and
$k = 4 < p$
and
![]() $\ell = v_p(\mathcal L) < 0$
.
$\ell = v_p(\mathcal L) < 0$
.
Now we assume that either
![]() $h \geq 4$
or
$h \geq 4$
or
![]() $p = h = 3$
. Then, applying Proposition 4.5, Lemma 4.7, and Proposition 4.6, we deduce that there exists a basis of
$p = h = 3$
. Then, applying Proposition 4.5, Lemma 4.7, and Proposition 4.6, we deduce that there exists a basis of
![]() $\mathcal M_2$
in which the matrix of
$\mathcal M_2$
in which the matrix of
![]() $\varphi _{\mathcal M_2}$
is given by
$\varphi _{\mathcal M_2}$
is given by
 $A = \left (\begin {smallmatrix} P & - 1 \\ E^h & 0 \end {smallmatrix}\right )$
and
$A = \left (\begin {smallmatrix} P & - 1 \\ E^h & 0 \end {smallmatrix}\right )$
and
![]() $P \in \mathfrak m_F[u]$
. Define
$P \in \mathfrak m_F[u]$
. Define
 $\mathfrak M = \mathfrak S_{\Lambda }^{\oplus 2}$
with the matrix of
$\mathfrak M = \mathfrak S_{\Lambda }^{\oplus 2}$
with the matrix of
![]() $\varphi $
being given by A. Clearly
$\varphi $
being given by A. Clearly
![]() $\mathfrak M$
is a Kisin module over
$\mathfrak M$
is a Kisin module over
![]() $\mathfrak S_{\Lambda }$
of height
$\mathfrak S_{\Lambda }$
of height
![]() $\leq h$
, and
$\leq h$
, and
as
![]() $\varphi $
-modules over
$\varphi $
-modules over
![]() $R_2$
. Thus, by Proposition 2.1 we deduce
$R_2$
. Thus, by Proposition 2.1 we deduce
![]() $\mathfrak M = \mathfrak M(T)$
for some lattice
$\mathfrak M = \mathfrak M(T)$
for some lattice
![]() $T \subseteq V_{h+1,\mathcal L}$
. Furthermore,
$T \subseteq V_{h+1,\mathcal L}$
. Furthermore,
 $\mathfrak M \otimes _{\mathfrak S_{\Lambda }} \mathbb F\left [u^{-1}\right ]$
is a
$\mathfrak M \otimes _{\mathfrak S_{\Lambda }} \mathbb F\left [u^{-1}\right ]$
is a
![]() $\varphi $
-module over
$\varphi $
-module over
![]() $\mathbb F(\!(u)\!)$
with Frobenius given by
$\mathbb F(\!(u)\!)$
with Frobenius given by
 $\left (\begin {smallmatrix} 0 & - 1 \\ u^h & 0 \end {smallmatrix}\right )$
. This shows, in particular, that
$\left (\begin {smallmatrix} 0 & - 1 \\ u^h & 0 \end {smallmatrix}\right )$
. This shows, in particular, that
![]() $\overline V_{h+1,\mathcal L}$
is the same for any
$\overline V_{h+1,\mathcal L}$
is the same for any
![]() $\mathcal L$
satisfying formula (4.1) (see [Reference Bergdall and Levin3, Corollary 2.3.2]).
$\mathcal L$
satisfying formula (4.1) (see [Reference Bergdall and Levin3, Corollary 2.3.2]).
Let
![]() $V_{h+1,\infty }$
be as in the introduction. By [Reference Bergdall and Levin3, Corollary 5.2.2], for
$V_{h+1,\infty }$
be as in the introduction. By [Reference Bergdall and Levin3, Corollary 5.2.2], for
![]() $V_{h+1,\infty }$
there exists a Kisin module
$V_{h+1,\infty }$
there exists a Kisin module
![]() ${\mathfrak M}'$
such that
${\mathfrak M}'$
such that
 $M':= \mathfrak M' \otimes _{\mathfrak S_{\Lambda }} \mathbb F\left [u^{-1}\right ]$
has Frobenius also given by
$M':= \mathfrak M' \otimes _{\mathfrak S_{\Lambda }} \mathbb F\left [u^{-1}\right ]$
has Frobenius also given by
 $\left (\begin {smallmatrix} 0 & - 1 \\ u^h & 0 \end {smallmatrix}\right )$
and
$\left (\begin {smallmatrix} 0 & - 1 \\ u^h & 0 \end {smallmatrix}\right )$
and
![]() $M'$
determines
$M'$
determines
 $\overline V_{h+1,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
. Therefore,
$\overline V_{h+1,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
. Therefore,
 $\overline V_{h+1,\mathcal L} \cong \overline V_{h+1,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
$\overline V_{h+1,\mathcal L} \cong \overline V_{h+1,\infty } \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{h}\chi \right )$
.
Remark 4.8. We return to Remark 4.2. Suppose we replace formula (4.1) with
 $$ \begin{align} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} + v_p((h-1)!). \end{align} $$
$$ \begin{align} v_p\left(\mathcal L^{-1}\right)> {h-1\over 2} + v_p((h-1)!). \end{align} $$
This has the impact of scaling z by a p-adic unit multiple of p, thus increasing
![]() $v_{R_2}(z)$
by
$v_{R_2}(z)$
by
![]() $2$
throughout our estimates in §4.1. The reader may check that Proposition 4.5 holds with these new estimates, and so the proof goes through for all
$2$
throughout our estimates in §4.1. The reader may check that Proposition 4.5 holds with these new estimates, and so the proof goes through for all
![]() $h \geq 2$
and
$h \geq 2$
and
![]() $p \geq 3$
under the assumption (4.10). Of course, this bound is not the sharpest possible when
$p \geq 3$
under the assumption (4.10). Of course, this bound is not the sharpest possible when
![]() $h=2$
or
$h=2$
or
![]() $h=3$
. For instance, we have already noted that for
$h=3$
. For instance, we have already noted that for
![]() $h=3$
and
$h=3$
and
![]() $p \geq 5$
, Breuil and Mézard confirmed Theorem 4.1 with the stronger bound (4.1).
$p \geq 5$
, Breuil and Mézard confirmed Theorem 4.1 with the stronger bound (4.1).
The situation is more complicated when
![]() $h = 2$
. In that case, for
$h = 2$
. In that case, for
![]() $p \geq 5$
, Guerberoff and Park showed that
$p \geq 5$
, Guerberoff and Park showed that
 $\overline V_{3,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{2}\chi \right )$
exactly on
$\overline V_{3,\mathcal L} \cong \operatorname {Ind}_{G_{\mathbb Q_p^2}}^{G_{\mathbb Q_p}}\left (\omega _2^{2}\chi \right )$
exactly on
 $v_p(\mathcal L - 1) < \frac {1}{2}$
[Reference Guerberoff and Park17, Theorem 5.0.5]. Thus, the bound
$v_p(\mathcal L - 1) < \frac {1}{2}$
[Reference Guerberoff and Park17, Theorem 5.0.5]. Thus, the bound
 $v_p(\mathcal L) < \frac {1}{2}$
from Theorem 4.1 produces too large a region of
$v_p(\mathcal L) < \frac {1}{2}$
from Theorem 4.1 produces too large a region of
![]() $\mathcal L$
-invariants, whereas formula (4.10) produces a region too small. For the interested reader, Guerberoff and Park also determined, for any
$\mathcal L$
-invariants, whereas formula (4.10) produces a region too small. For the interested reader, Guerberoff and Park also determined, for any
![]() $\mathcal L$
, the restriction of
$\mathcal L$
, the restriction of
![]() $\overline V_{3,\mathcal L}$
to the inertia subgroup. The restriction to inertia was recently removed by Chitrao, Ghate, and Yasuda using a completely different method [Reference Chitrao, Ghate and Yasuda10, Theorem 1.3]. Thus we have a complete picture of
$\overline V_{3,\mathcal L}$
to the inertia subgroup. The restriction to inertia was recently removed by Chitrao, Ghate, and Yasuda using a completely different method [Reference Chitrao, Ghate and Yasuda10, Theorem 1.3]. Thus we have a complete picture of
![]() $\overline V_{3,\mathcal L}$
. It would be amusing to understand if that picture can be recovered from the method here.
$\overline V_{3,\mathcal L}$
. It would be amusing to understand if that picture can be recovered from the method here.
Acknowledgments
We owe the heuristic reframing in §1.2 to comments by Laurent Berger and Christophe Breuil during the conference “Géométrie arithmétique, théorie des représentations et applications” at the Centre International de Rencontres Mathématiques (CIRM) in Luminy, France. Part of this collaboration also took place during the workshop “Moduli spaces and modularity” at Casa Matemática Oaxaca (CMO). We thank both Berger and Breuil for their comments and both CIRM and CMO for their hospitality. The first author also thanks the Max Planck Institut für Mathematik in Bonn, Germany for hospitality during a period when this paper was revised.
Finally, acknowledgments are due for the discussion in §1.3. First, the data reported in Table 1 in the first preprint version of this article was inaccurate. Because of that, we drew faulty conclusions, which have now been removed, on the strength of the bound in Theorem 1.1. We thank Robert Pollack for calculating the original data and then alerting us to the error. We also especially thank Peter Gräf for replicating the newly reported data, using his alternative method.
The first author was partially supported by an NSF Grant (DMS-1402005) and a Simons Collaboration Grant (#713782). The second author was supported by a grant from the Simons Foundation/SFARI (#585753).
Competing Interests
None.