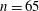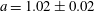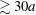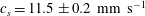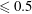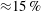1 Introduction
An acoustic soliton is a localized, supersonic, pulse-like excitation which propagates for long distances through a dispersive medium without dispersing because group velocity dispersion is balanced by nonlinear steepening. For small amplitudes (
![]() ${\lesssim}10\,\%$
), acoustic solitons are described by the nonlinear Korteweg de Vries (KdV) wave equation (Schmidt Reference Schmidt1979; Nicholson Reference Nicholson1983)
${\lesssim}10\,\%$
), acoustic solitons are described by the nonlinear Korteweg de Vries (KdV) wave equation (Schmidt Reference Schmidt1979; Nicholson Reference Nicholson1983)
where
![]() $t$
is a time variable,
$t$
is a time variable,
![]() $\unicode[STIX]{x1D709}$
is a space variable in a frame moving with the acoustic speed
$\unicode[STIX]{x1D709}$
is a space variable in a frame moving with the acoustic speed
![]() $c_{s}$
and
$c_{s}$
and
![]() $u=u\left(\unicode[STIX]{x1D709},t\right)$
is a field variable such as fluid velocity, density or potential. Here
$u=u\left(\unicode[STIX]{x1D709},t\right)$
is a field variable such as fluid velocity, density or potential. Here
![]() $A$
and
$A$
and
![]() $B$
are constants. The KdV equation admits both oscillatory solutions with speeds
$B$
are constants. The KdV equation admits both oscillatory solutions with speeds
![]() ${\leqslant}c_{s}$
(i.e. waves) and solitons with speeds
${\leqslant}c_{s}$
(i.e. waves) and solitons with speeds
![]() ${>}c_{s}$
. Exact solutions of the KdV equation can be found using the inverse scattering transform (Gardner et al.
Reference Gardner, Greene, Kruskal and Miura1967), which shows any localized initial perturbation evolves into a continuum of dispersive waves and possibly one or more discrete solitons. The spatial profile of a KdV soliton is
${>}c_{s}$
. Exact solutions of the KdV equation can be found using the inverse scattering transform (Gardner et al.
Reference Gardner, Greene, Kruskal and Miura1967), which shows any localized initial perturbation evolves into a continuum of dispersive waves and possibly one or more discrete solitons. The spatial profile of a KdV soliton is
where the soliton speed in the laboratory frame
![]() $V=c_{s}+\unicode[STIX]{x1D6FF}v$
. Consequently, the peak amplitude of a KdV soliton is directly proportional to
$V=c_{s}+\unicode[STIX]{x1D6FF}v$
. Consequently, the peak amplitude of a KdV soliton is directly proportional to
![]() $\unicode[STIX]{x1D6FF}v/c_{s}$
, the soliton’s normalized speed increment above the acoustic speed.
$\unicode[STIX]{x1D6FF}v/c_{s}$
, the soliton’s normalized speed increment above the acoustic speed.
Melandsø (Reference Melandsø1996) has derived a KdV equation for weakly nonlinear, undamped waves in a one-dimensional (1-D) Yukawa chain. A Yukawa chain is a strongly coupled system of identical particles interacting through a Yukawa (i.e. Debye or screened Coulomb) potential. That is, the potential a distance
![]() $r$
from a particle with charge
$r$
from a particle with charge
![]() $q$
is given by
$q$
is given by
where
![]() $\unicode[STIX]{x1D706}_{D}$
is the Debye shielding length and
$\unicode[STIX]{x1D706}_{D}$
is the Debye shielding length and
![]() $\unicode[STIX]{x1D716}_{0}$
is the permittivity of free space. Consequently, it is predicted that large-amplitude initial perturbations in a Yukawa chain will evolve into solitons for appropriate conditions. One signature of such solitons is an increase in speed with amplitude.
$\unicode[STIX]{x1D716}_{0}$
is the permittivity of free space. Consequently, it is predicted that large-amplitude initial perturbations in a Yukawa chain will evolve into solitons for appropriate conditions. One signature of such solitons is an increase in speed with amplitude.
Dusty plasma, which is an experimental realization of the Yukawa chain, is made of nearly identical microscopic dust particles immersed in an electron–ion plasma. For typical laboratory plasma conditions, dust particles acquire a charge
![]() $q<0$
. Large dust particles can be suspended above a horizontal electrode where the vertical electric force balances the particle’s weight. In many cases, the potential well in the vertical direction is much deeper than that in the horizontal directions so the dusty plasma is two-dimensional. In the horizontal plane, each negatively charged dust particle is surrounded by a positive space charge cloud leading to Debye shielding. One-dimensional dusty plasmas (i.e. Yukawa chains) can be made by using additional confinement in the horizontal plane. Such configurations include straight lines in biharmonic wells (Homann et al.
Reference Homann, Melzer, Peters and Piel1997; Liu, Avinash & Goree Reference Liu, Avinash and Goree2003, Reference Liu, Avinash and Goree2004; Liu & Goree Reference Liu and Goree2005) and rings in annular wells (Sheridan Reference Sheridan2009; Tkachenko, Sheridan & Misko Reference Tkachenko, Sheridan and Misko2011; Sheridan & Gallagher Reference Sheridan and Gallagher2016).
$q<0$
. Large dust particles can be suspended above a horizontal electrode where the vertical electric force balances the particle’s weight. In many cases, the potential well in the vertical direction is much deeper than that in the horizontal directions so the dusty plasma is two-dimensional. In the horizontal plane, each negatively charged dust particle is surrounded by a positive space charge cloud leading to Debye shielding. One-dimensional dusty plasmas (i.e. Yukawa chains) can be made by using additional confinement in the horizontal plane. Such configurations include straight lines in biharmonic wells (Homann et al.
Reference Homann, Melzer, Peters and Piel1997; Liu, Avinash & Goree Reference Liu, Avinash and Goree2003, Reference Liu, Avinash and Goree2004; Liu & Goree Reference Liu and Goree2005) and rings in annular wells (Sheridan Reference Sheridan2009; Tkachenko, Sheridan & Misko Reference Tkachenko, Sheridan and Misko2011; Sheridan & Gallagher Reference Sheridan and Gallagher2016).
A number of experiments have reported on linear wave propagation in 1-D dusty plasma. For both biharmonic (Homann et al. Reference Homann, Melzer, Peters and Piel1997; Misawa et al. Reference Misawa, Ohno, Asano, Sawai, Takamura and Kaw2001; Liu et al. Reference Liu, Avinash and Goree2003, Reference Liu, Avinash and Goree2004; Liu & Goree Reference Liu and Goree2005) and annular wells (Sheridan & Gallagher Reference Sheridan and Gallagher2016), small-amplitude longitudinal waves are found to be well described by the dispersion relation for a Yukawa chain (Melandsø Reference Melandsø1996; Homann et al. Reference Homann, Melzer, Peters and Piel1997; Liu & Goree Reference Liu and Goree2005; Tkachenko et al. Reference Tkachenko, Sheridan and Misko2011; Sheridan & Gallagher Reference Sheridan and Gallagher2016), i.e. dust lattice waves. Chains confined in a biharmonic well can only hold a limited number of particles, restricting the distance over which waves can propagate before end effects become important (Liu & Goree Reference Liu and Goree2005). It is possible to create longer and more uniform chains using an annular well (Sheridan & Gallagher Reference Sheridan and Gallagher2016). The dispersion relation in such chains is well approximated (Sheridan Reference Sheridan2009; Tkachenko et al. Reference Tkachenko, Sheridan and Misko2011) by the 1-D theory for straight line configurations when the ring diameter is much larger than the lattice constant, as verified experimentally (Sheridan & Gallagher Reference Sheridan and Gallagher2016). There have been several studies of the conditions under which nonlinear effects become important in 2-D dusty plasmas (Avinash et al. Reference Avinash, Zhu, Nosenko and Goree2003; Nosenko et al. Reference Nosenko, Avinash, Goree and Liu2004; Sheridan, Nosenko & Goree Reference Sheridan, Nosenko and Goree2008). Experiments looking for nonlinear effects in 1-D dusty plasma chains are rarer.
In this paper, we describe an experiment where we launch an acoustic pulse in 1-D dusty plasma rings as a first step to creating solitons. We look for nonlinear effects, particularly an increase in wave speed with amplitude, which is a signature of nonlinear KdV behaviour. Section 2 gives the theory of linear dust lattice waves and § 3 describes our experiment. Results and discussion are presented in § 4 and conclusions are given in § 5.
2 Dust lattice waves
The dispersion relation for undamped linear dust lattice waves (DLW) including nearest and next-nearest neighbour interactions is (Melandsø Reference Melandsø1996; Tkachenko et al. Reference Tkachenko, Sheridan and Misko2011)
where
![]() $\unicode[STIX]{x1D714}_{l}$
is the (longitudinal) wave frequency,
$\unicode[STIX]{x1D714}_{l}$
is the (longitudinal) wave frequency,
![]() $k$
is the wavenumber and
$k$
is the wavenumber and
![]() $a$
is the lattice constant. Frequency is normalized by
$a$
is the lattice constant. Frequency is normalized by
which is the dust lattice oscillation frequency for a Coulomb chain. Here
![]() $q$
is the particle charge and
$q$
is the particle charge and
![]() $m$
is the mass. The normalized dispersion relation depends only on the Debye screening parameter
$m$
is the mass. The normalized dispersion relation depends only on the Debye screening parameter
where
![]() $\overline{\unicode[STIX]{x1D705}}=0$
for an unshielded Coulomb interaction.
$\overline{\unicode[STIX]{x1D705}}=0$
for an unshielded Coulomb interaction.
As shown in figure 1(a), the DLW dispersion is an acoustic one. The acoustic speed (
![]() $ka\ll 1$
) for dust lattice waves can be written as
$ka\ll 1$
) for dust lattice waves can be written as
with
The square root term in (2.4) gives the acoustic speed for an unshielded Coulomb interaction, while
![]() $f\left(\overline{\unicode[STIX]{x1D705}}\right)$
gives the reduction in the normalized acoustic speed due to increased Debye shielding. The dependence of the normalized acoustic speed (i.e.
$f\left(\overline{\unicode[STIX]{x1D705}}\right)$
gives the reduction in the normalized acoustic speed due to increased Debye shielding. The dependence of the normalized acoustic speed (i.e.
![]() $f\left(\overline{\unicode[STIX]{x1D705}}\right)$
) on
$f\left(\overline{\unicode[STIX]{x1D705}}\right)$
) on
![]() $\overline{\unicode[STIX]{x1D705}}$
is shown in figure 1(b), from which we see that the acoustic speed has only a weak dependence on
$\overline{\unicode[STIX]{x1D705}}$
is shown in figure 1(b), from which we see that the acoustic speed has only a weak dependence on
![]() $\overline{\unicode[STIX]{x1D705}}$
when
$\overline{\unicode[STIX]{x1D705}}$
when
![]() $\overline{\unicode[STIX]{x1D705}}\lesssim 1$
, which is often the case in 1-D dusty plasma experiments (Sheridan & Gallagher Reference Sheridan and Gallagher2016). The real part of the dispersion relation is only slightly modified by weak damping
$\overline{\unicode[STIX]{x1D705}}\lesssim 1$
, which is often the case in 1-D dusty plasma experiments (Sheridan & Gallagher Reference Sheridan and Gallagher2016). The real part of the dispersion relation is only slightly modified by weak damping
![]() $\unicode[STIX]{x1D6FE}\ll \unicode[STIX]{x1D714}_{0}$
. For the experiment described here, damping
$\unicode[STIX]{x1D6FE}\ll \unicode[STIX]{x1D714}_{0}$
. For the experiment described here, damping
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}=0.06\ll 1$
is weak.
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}=0.06\ll 1$
is weak.

Figure 1. (a) Dispersion relations for acoustic waves in a 1-D dusty plasma lattice for the Debye screening parameter
![]() $\overline{\unicode[STIX]{x1D705}}=0.5$
, 1 and 2. (b) A plot of acoustic speed versus
$\overline{\unicode[STIX]{x1D705}}=0.5$
, 1 and 2. (b) A plot of acoustic speed versus
![]() $\overline{\unicode[STIX]{x1D705}}$
shows that the acoustic speed does not depend strongly on
$\overline{\unicode[STIX]{x1D705}}$
shows that the acoustic speed does not depend strongly on
![]() $\overline{\unicode[STIX]{x1D705}}$
when
$\overline{\unicode[STIX]{x1D705}}$
when
![]() $\overline{\unicode[STIX]{x1D705}}\lesssim 1$
.
$\overline{\unicode[STIX]{x1D705}}\lesssim 1$
.
Consequently, for a chain of identical particles, the properties of linear dust lattice waves only depend on two dimensionless parameters: the screening parameter
![]() $\overline{\unicode[STIX]{x1D705}}$
and the normalized damping rate
$\overline{\unicode[STIX]{x1D705}}$
and the normalized damping rate
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}$
. KdV theory tells us that the properties and evolution of nonlinear (i.e. large amplitude) waves also depend on the peak wave amplitude. In particular, there may be threshold behaviour for the creation of solitons such that subthreshold perturbations are damped (Avinash et al.
Reference Avinash, Zhu, Nosenko and Goree2003) while above threshold perturbations evolve into solitons whose speed increases with peak amplitude.
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}$
. KdV theory tells us that the properties and evolution of nonlinear (i.e. large amplitude) waves also depend on the peak wave amplitude. In particular, there may be threshold behaviour for the creation of solitons such that subthreshold perturbations are damped (Avinash et al.
Reference Avinash, Zhu, Nosenko and Goree2003) while above threshold perturbations evolve into solitons whose speed increases with peak amplitude.
3 Experiment
We have studied acoustic solitary wave propagation in a 1-D dusty plasma lattice in the DONUT (Dusty Ohio Northern University experimenT) experiment. An 89 mm diam. aluminium electrode (figure 2) was placed in the vacuum chamber. An annular groove in the electrode (16.0 mm inner diameter
![]() $\times \,40.0$
mm outer diameter
$\times \,40.0$
mm outer diameter
![]() $\times \,6.3$
mm deep) created a potential well that confines dust particles in a 1-D ring (Sheridan & Gallagher Reference Sheridan and Gallagher2016). An additional aluminium ring (89 mm outer diameter
$\times \,6.3$
mm deep) created a potential well that confines dust particles in a 1-D ring (Sheridan & Gallagher Reference Sheridan and Gallagher2016). An additional aluminium ring (89 mm outer diameter
![]() $\times \,75.7$
mm inner diameter
$\times \,75.7$
mm inner diameter
![]() $\times \,6.0$
mm deep) was placed on the outside of the electrode to deepen the transverse potential well to prevent transverse buckling of the chain when it is compressed. Argon was bled into the vacuum vessel while the vacuum pump was throttled, and the pressure was stabilized at 13.4 mTorr. Plasma was generated by applying
$\times \,6.0$
mm deep) was placed on the outside of the electrode to deepen the transverse potential well to prevent transverse buckling of the chain when it is compressed. Argon was bled into the vacuum vessel while the vacuum pump was throttled, and the pressure was stabilized at 13.4 mTorr. Plasma was generated by applying
![]() ${\approx}3.5\,\text{W}$
of radio-frequency (r.f.) power at 13.56 MHz to the electrode. On the electrode, the peak-to-peak r.f. voltage was 112 V and the direct current self-bias was
${\approx}3.5\,\text{W}$
of radio-frequency (r.f.) power at 13.56 MHz to the electrode. On the electrode, the peak-to-peak r.f. voltage was 112 V and the direct current self-bias was
![]() $-53$
V.
$-53$
V.
Melamine-formaldehyde (MF) spheres with a diameter
![]() $8.94\pm 0.09~\unicode[STIX]{x03BC}\text{m}$
(Sheridan Reference Sheridan2005) and a mass
$8.94\pm 0.09~\unicode[STIX]{x03BC}\text{m}$
(Sheridan Reference Sheridan2005) and a mass
![]() $m=5.65\times 10^{-13}$
kg, were trapped in the annular potential well. The particles were illuminated using a sheet of red laser light and their positions were recorded using a top view video camera. The camera resolution was
$m=5.65\times 10^{-13}$
kg, were trapped in the annular potential well. The particles were illuminated using a sheet of red laser light and their positions were recorded using a top view video camera. The camera resolution was
![]() $1024\times 1024$
pixels, where one pixel corresponds to
$1024\times 1024$
pixels, where one pixel corresponds to
![]() $30.76\times 30.76\,\unicode[STIX]{x03BC}\text{m}^{2}$
at the dusty plasma ring. Movies of 1024 frames at
$30.76\times 30.76\,\unicode[STIX]{x03BC}\text{m}^{2}$
at the dusty plasma ring. Movies of 1024 frames at
![]() $15~\text{frames}~\text{s}^{-1}$
were recorded for later analysis.
$15~\text{frames}~\text{s}^{-1}$
were recorded for later analysis.

Figure 2. Schematic of the experimental set-up. An incomplete dust ring with
![]() $n=65$
particles is levitated above the electrode. Pulses from a green diode laser compress the end of the chain and launch large-amplitude acoustic waves. Particles are illuminated using a red laser and their motion is recorded using the video camera.
$n=65$
particles is levitated above the electrode. Pulses from a green diode laser compress the end of the chain and launch large-amplitude acoustic waves. Particles are illuminated using a red laser and their motion is recorded using the video camera.
An incomplete ring was formed with
![]() $n=65$
particles, as shown in figure 3(a). The radius of the ring was 11.58 mm, and the particles were levitated 9.7 mm above the top of the outer confining ring. The mean lattice spacing
$n=65$
particles, as shown in figure 3(a). The radius of the ring was 11.58 mm, and the particles were levitated 9.7 mm above the top of the outer confining ring. The mean lattice spacing
![]() $a=1.02\pm 0.02$
mm (figure 3(b)) exhibits a modulation due to small variations in the depth of the well. The dependence of these local minima depend on the r.f. power and matching network settings, indicating they are associated with a small standing wave component in the r.f. electric field. The neutral gas damping rate was
$a=1.02\pm 0.02$
mm (figure 3(b)) exhibits a modulation due to small variations in the depth of the well. The dependence of these local minima depend on the r.f. power and matching network settings, indicating they are associated with a small standing wave component in the r.f. electric field. The neutral gas damping rate was
![]() $\unicode[STIX]{x1D6FE}=1.3~\text{s}^{-1}$
(Sheridan Reference Sheridan2005). From similar experiments in DONUT using the same dust particles
$\unicode[STIX]{x1D6FE}=1.3~\text{s}^{-1}$
(Sheridan Reference Sheridan2005). From similar experiments in DONUT using the same dust particles
![]() $q\approx -1.2\times 10^{4}e$
(Sheridan & Gallagher Reference Sheridan and Gallagher2016). From (2.2), the unshielded longitudinal oscillation frequency
$q\approx -1.2\times 10^{4}e$
(Sheridan & Gallagher Reference Sheridan and Gallagher2016). From (2.2), the unshielded longitudinal oscillation frequency
![]() $\unicode[STIX]{x1D714}_{0}\approx 21~\text{rad}~\text{s}^{-1}$
, giving a normalized damping rate
$\unicode[STIX]{x1D714}_{0}\approx 21~\text{rad}~\text{s}^{-1}$
, giving a normalized damping rate
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}=0.06$
.
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}=0.06$
.

Figure 3. (a) Positions of
![]() $n=65$
dust particles. The dust ring has a gap in the upper left corner, which prevents a counter-propagating wave from being launched when the excitation laser strikes the particles. The radius of this ring is
$n=65$
dust particles. The dust ring has a gap in the upper left corner, which prevents a counter-propagating wave from being launched when the excitation laser strikes the particles. The radius of this ring is
![]() $11.58$
mm. (b) The lattice space is plotted as a function of particle position. Excluding the gap region, the average lattice constant is
$11.58$
mm. (b) The lattice space is plotted as a function of particle position. Excluding the gap region, the average lattice constant is
![]() $a=1.02\pm 0.02$
mm is shown with the broken line.
$a=1.02\pm 0.02$
mm is shown with the broken line.
Longitudinal waves were launched by compressing the end of the chain using a 100 mW (nominal), 532 nm diode laser which was pulsed on for a duration
![]() $\unicode[STIX]{x0394}t_{laser}$
, with 10.0 s between laser pulses. The beam struck several particles at one end of a gap in the dust ring causing a wave to propagate counter-clockwise around the ring. The gap in the dust ring (figure 3(a)) prevented a rarefactive pulse from propagating in the opposite direction and interfering with the compressive pulse. To look for a nonlinear increase of pulse speed with wave amplitude, we increased the maximum perturbation by increasing laser on-time
$\unicode[STIX]{x0394}t_{laser}$
, with 10.0 s between laser pulses. The beam struck several particles at one end of a gap in the dust ring causing a wave to propagate counter-clockwise around the ring. The gap in the dust ring (figure 3(a)) prevented a rarefactive pulse from propagating in the opposite direction and interfering with the compressive pulse. To look for a nonlinear increase of pulse speed with wave amplitude, we increased the maximum perturbation by increasing laser on-time
![]() $\unicode[STIX]{x0394}t_{laser}$
from 0.1 to
$\unicode[STIX]{x0394}t_{laser}$
from 0.1 to
![]() $2.0$
s with values of 0.1, 0.2, 0.3, 0.5, 0.7, 1.0, 1.4 and 2.0 s. Data for
$2.0$
s with values of 0.1, 0.2, 0.3, 0.5, 0.7, 1.0, 1.4 and 2.0 s. Data for
![]() $\unicode[STIX]{x0394}t_{laser}=1.0$
s were not usable because the illumination laser was misaligned.
$\unicode[STIX]{x0394}t_{laser}=1.0$
s were not usable because the illumination laser was misaligned.
4 Results and discussion
The longitudinal velocity distribution function for dust particles in the unperturbed ring is shown in figure 4. Velocities in the interval
![]() $v\approx 0.0\pm 0.15~\text{mm}~\text{s}^{-1}$
cannot be resolved due to the camera’s finite pixel size. The velocity distribution function is well fitted by a drifting Maxwellian. The drift velocity of
$v\approx 0.0\pm 0.15~\text{mm}~\text{s}^{-1}$
cannot be resolved due to the camera’s finite pixel size. The velocity distribution function is well fitted by a drifting Maxwellian. The drift velocity of
![]() $0.078~\text{mm}~\text{s}^{-1}$
represents a slow counter-clockwise rotation of the ring which is much less than the dust lattice wave speed. This rotation may be due to neutral-gas flow in the chamber (Carstensen, Greiner & Piel Reference Carstensen, Greiner and Piel2010). The kinetic temperature of the fitted curve is 1300 K. The temperature of stationary rings has previously been measured as
$0.078~\text{mm}~\text{s}^{-1}$
represents a slow counter-clockwise rotation of the ring which is much less than the dust lattice wave speed. This rotation may be due to neutral-gas flow in the chamber (Carstensen, Greiner & Piel Reference Carstensen, Greiner and Piel2010). The kinetic temperature of the fitted curve is 1300 K. The temperature of stationary rings has previously been measured as
![]() ${\approx}400$
K (Sheridan & Gallagher Reference Sheridan and Gallagher2016), indicating that dust lattice is slightly heated due to the conversion of rotational motion into random kinetic energy. The lattice is strongly coupled. From the thermally excited radial breathing mode (Sheridan & Gallagher Reference Sheridan and Gallagher2016), we find the transverse (radial) oscillation frequency is
${\approx}400$
K (Sheridan & Gallagher Reference Sheridan and Gallagher2016), indicating that dust lattice is slightly heated due to the conversion of rotational motion into random kinetic energy. The lattice is strongly coupled. From the thermally excited radial breathing mode (Sheridan & Gallagher Reference Sheridan and Gallagher2016), we find the transverse (radial) oscillation frequency is
![]() $\unicode[STIX]{x1D714}_{t0}=22.3\pm 0.3~\text{rad}~\text{s}^{-1}$
, which gives the depth of the radial potential well.
$\unicode[STIX]{x1D714}_{t0}=22.3\pm 0.3~\text{rad}~\text{s}^{-1}$
, which gives the depth of the radial potential well.

Figure 4. The longitudinal velocity distribution function for the unperturbed dust ring. The distribution function is well fitted by a drifting Maxwellian distribution with a kinetic temperature
![]() $T=1300$
K.
$T=1300$
K.
To characterize acoustic pulse propagation, we created space–time plots of the longitudinal (azimuthal) particle velocity. The space–time plot for
![]() $\unicode[STIX]{x0394}t_{laser}=1.4$
s is shown in figure 5. From these space–time plots, we determined the group velocity of the acoustic pulse. For all values of
$\unicode[STIX]{x0394}t_{laser}=1.4$
s is shown in figure 5. From these space–time plots, we determined the group velocity of the acoustic pulse. For all values of
![]() $\unicode[STIX]{x0394}t_{laser}$
, the large-amplitude acoustic wave has a speed comparable to the background wave noise. The background waves, which propagate at the acoustic speed, are associated with lattice relaxation as the dust ring rotates into non-equilibrium configurations, and so propagate for long distances. For
$\unicode[STIX]{x0394}t_{laser}$
, the large-amplitude acoustic wave has a speed comparable to the background wave noise. The background waves, which propagate at the acoustic speed, are associated with lattice relaxation as the dust ring rotates into non-equilibrium configurations, and so propagate for long distances. For
![]() $\unicode[STIX]{x0394}t_{laser}\gtrsim 0.5$
s, a rarefactive wave was launched when the laser was turned off, and also travelled at the acoustic speed. We observed large-amplitude acoustic pulses with a velocity perturbation amplitude
$\unicode[STIX]{x0394}t_{laser}\gtrsim 0.5$
s, a rarefactive wave was launched when the laser was turned off, and also travelled at the acoustic speed. We observed large-amplitude acoustic pulses with a velocity perturbation amplitude
![]() ${\approx}10$
% of the acoustic speed which propagate for a significant distance. If this solitary wave was described by KdV theory we would expect it to have a speed
${\approx}10$
% of the acoustic speed which propagate for a significant distance. If this solitary wave was described by KdV theory we would expect it to have a speed
![]() ${\approx}1.03\,C_{DLW}$
. However, it appears that neutral-gas damping dominates nonlinear effects and the pulse does not evolve into a soliton. Interestingly, the damping does not appear to be linear – rather the leading edge of the pulse slows below the acoustic speed and the entire pulse is extinguished. This is consistent with nonlinear steepening moving wave energy to higher wavenumbers with lower group velocities.
${\approx}1.03\,C_{DLW}$
. However, it appears that neutral-gas damping dominates nonlinear effects and the pulse does not evolve into a soliton. Interestingly, the damping does not appear to be linear – rather the leading edge of the pulse slows below the acoustic speed and the entire pulse is extinguished. This is consistent with nonlinear steepening moving wave energy to higher wavenumbers with lower group velocities.

Figure 5. Space–time plot of longitudinal particle velocities for a laser pulse duration
![]() $\unicode[STIX]{x0394}t_{laser}=1.4$
s. We plot two periods around the ring. A compressive acoustic pulse is excited by the laser pulse and a dispersive rarefactive pulse forms when the laser is switched off. Background acoustic noise is evident with a velocity close to the laser-launched pulse.
$\unicode[STIX]{x0394}t_{laser}=1.4$
s. We plot two periods around the ring. A compressive acoustic pulse is excited by the laser pulse and a dispersive rarefactive pulse forms when the laser is switched off. Background acoustic noise is evident with a velocity close to the laser-launched pulse.
One measure of the wave amplitude is with the maximum velocity perturbation
![]() $\unicode[STIX]{x1D6FF}v_{max}$
for particles in the chain. In figure 6(a) we plot
$\unicode[STIX]{x1D6FF}v_{max}$
for particles in the chain. In figure 6(a) we plot
![]() $\unicode[STIX]{x1D6FF}v_{max}$
for particle numbers
$\unicode[STIX]{x1D6FF}v_{max}$
for particle numbers
![]() $i=7$
, 12 and 17, where
$i=7$
, 12 and 17, where
![]() $i=1$
is the first particle struck by the laser beam versus laser pulse duration
$i=1$
is the first particle struck by the laser beam versus laser pulse duration
![]() $\unicode[STIX]{x0394}t_{laser}$
. Starting with
$\unicode[STIX]{x0394}t_{laser}$
. Starting with
![]() $\unicode[STIX]{x0394}t_{laser}=0.1$
s we find that the wave amplitude increases for
$\unicode[STIX]{x0394}t_{laser}=0.1$
s we find that the wave amplitude increases for
![]() $\unicode[STIX]{x0394}t_{laser}\leqslant 0.5$
s and then saturates for
$\unicode[STIX]{x0394}t_{laser}\leqslant 0.5$
s and then saturates for
![]() $\unicode[STIX]{x0394}t_{laser}>0.5$
s. This saturation occurs because after the laser is on for some time the dust particles are pushed into new equilibrium positions; thus the greater impulse imposed by the laser is counteracted by the lattice restoring force. In these cases, a rarefactive wave is launched after the laser is turned off as can be seen in figure 5. These curves give a spatial damping coefficient
$\unicode[STIX]{x0394}t_{laser}>0.5$
s. This saturation occurs because after the laser is on for some time the dust particles are pushed into new equilibrium positions; thus the greater impulse imposed by the laser is counteracted by the lattice restoring force. In these cases, a rarefactive wave is launched after the laser is turned off as can be seen in figure 5. These curves give a spatial damping coefficient
![]() $k_{i}=0.07~\text{mm}^{-1}$
, which is consistent with neutral-gas (Epstein drag) damping.
$k_{i}=0.07~\text{mm}^{-1}$
, which is consistent with neutral-gas (Epstein drag) damping.

Figure 6. (a) Maximum velocity perturbation
![]() $\unicode[STIX]{x1D6FF}v_{max}$
for particle numbers
$\unicode[STIX]{x1D6FF}v_{max}$
for particle numbers
![]() $i=7$
, 12 and 17 versus laser pulse duration. Spatial damping is evident. At all three particle positions, the amplitude increases with laser pulse duration until the amplitude saturates for
$i=7$
, 12 and 17 versus laser pulse duration. Spatial damping is evident. At all three particle positions, the amplitude increases with laser pulse duration until the amplitude saturates for
![]() $\unicode[STIX]{x0394}t_{\text{laser}}\gtrsim 0.7$
s. (b) Measured speed of the acoustic pulse versus
$\unicode[STIX]{x0394}t_{\text{laser}}\gtrsim 0.7$
s. (b) Measured speed of the acoustic pulse versus
![]() $\unicode[STIX]{x0394}t_{laser}$
. The wave speed is effectively independent of
$\unicode[STIX]{x0394}t_{laser}$
. The wave speed is effectively independent of
![]() $\unicode[STIX]{x0394}t_{laser}$
, and therefore the wave amplitude, indicating that the wave propagation is linear. The average acoustic speed of
$\unicode[STIX]{x0394}t_{laser}$
, and therefore the wave amplitude, indicating that the wave propagation is linear. The average acoustic speed of
![]() $11.5\pm 0.2$
$11.5\pm 0.2$
![]() $\text{mm}~\text{s}^{-1}$
is shown by the broken line.
$\text{mm}~\text{s}^{-1}$
is shown by the broken line.
The velocity of the solitary waves versus laser pulse duration is plotted in figure 6(b). For KdV-like solitons we expect the velocity to increase as the velocity perturbation (wave amplitude) increases, as predicted by KdV theory (Schmidt Reference Schmidt1979) and as observed in 2-D dusty plasma (Sheridan et al.
Reference Sheridan, Nosenko and Goree2008). This is not what we observe. We find that the wave speed is independent of the maximum velocity perturbation, both when the pulse amplitude is increasing for
![]() $\unicode[STIX]{x0394}t_{laser}\leqslant 0.5$
s and when then pulse amplitude is saturated at
$\unicode[STIX]{x0394}t_{laser}\leqslant 0.5$
s and when then pulse amplitude is saturated at
![]() $\unicode[STIX]{x1D6FF}v_{max}/C_{DLW}\gtrsim 15\,\%$
. That is, nonlinear effects do not overcome damping in this experiment. The average dust lattice wave speed is
$\unicode[STIX]{x1D6FF}v_{max}/C_{DLW}\gtrsim 15\,\%$
. That is, nonlinear effects do not overcome damping in this experiment. The average dust lattice wave speed is
![]() $C_{DLW}=11.5\pm 0.2$
$C_{DLW}=11.5\pm 0.2$
![]() $\text{mm}~\text{s}^{-1}$
. If we take
$\text{mm}~\text{s}^{-1}$
. If we take
![]() $\overline{\unicode[STIX]{x1D705}}=1$
(Sheridan & Gallagher Reference Sheridan and Gallagher2016) as a typical value, then from (2.4),
$\overline{\unicode[STIX]{x1D705}}=1$
(Sheridan & Gallagher Reference Sheridan and Gallagher2016) as a typical value, then from (2.4),
![]() $q=-(11\,500\pm 500)e$
, which is consistent with previous measurements (Sheridan Reference Sheridan2005; Sheridan & Gallagher Reference Sheridan and Gallagher2016).
$q=-(11\,500\pm 500)e$
, which is consistent with previous measurements (Sheridan Reference Sheridan2005; Sheridan & Gallagher Reference Sheridan and Gallagher2016).
5 Conclusions
We have studied the propagation of large-amplitude acoustic pulse-like waves in a long 1-D dusty plasma (i.e. a Yukawa chain). As a first step toward creating solitons, we used laser pulses of increasing duration to create initial velocity perturbations. The wave amplitude increases with laser pulse duration for
![]() $\unicode[STIX]{x0394}t_{laser}\leqslant 0.5\,\text{s}$
, and then saturates when the laser force is balanced by the lattice restoring force. Waves with maximum perturbation amplitudes of
$\unicode[STIX]{x0394}t_{laser}\leqslant 0.5\,\text{s}$
, and then saturates when the laser force is balanced by the lattice restoring force. Waves with maximum perturbation amplitudes of
![]() ${\approx}15\,\%$
were launched, and propagated as unipolar longitudinal compressions for
${\approx}15\,\%$
were launched, and propagated as unipolar longitudinal compressions for
![]() ${\gtrsim}30$
lattice constants. The wave speed is independent of the maximum velocity perturbation, indicating that the pulses do not evolve into nonlinear (KdV) solitons. Damping,
${\gtrsim}30$
lattice constants. The wave speed is independent of the maximum velocity perturbation, indicating that the pulses do not evolve into nonlinear (KdV) solitons. Damping,
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}\approx 0.06$
, dominates the nonlinear effects so that the pulses decay. The decay mechanism does not appear to be simple linear damping. Rather, the leading edge of the pulse slows to below the acoustic speed, which may indicate nonlinear steepening. Creating nonlinear solitary waves in this system will require either reduced damping, larger perturbations amplitudes, or both.
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{0}\approx 0.06$
, dominates the nonlinear effects so that the pulses decay. The decay mechanism does not appear to be simple linear damping. Rather, the leading edge of the pulse slows to below the acoustic speed, which may indicate nonlinear steepening. Creating nonlinear solitary waves in this system will require either reduced damping, larger perturbations amplitudes, or both.