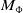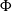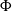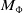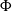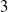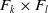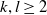1. Our results
When studying mapping tori, a natural question is how the maps used to define them determine their geometry. The paradigm is the Nielsen–Thurston classification. If
![]() $S$
is a compact orientable surface of genus at least
$S$
is a compact orientable surface of genus at least
![]() $2$
and
$2$
and
![]() $f\;:\;S \to S$
is a homeomorphism, then the mapping torus
$f\;:\;S \to S$
is a homeomorphism, then the mapping torus
![]() $M_f$
is
$M_f$
is
![]() $(S \times [0,1])/ \!\! \sim$
where
$(S \times [0,1])/ \!\! \sim$
where
![]() $(x, 1) \sim (f(x),0)$
for all
$(x, 1) \sim (f(x),0)$
for all
![]() $x \in S$
. The classification states that up to isotopy
$x \in S$
. The classification states that up to isotopy
![]() $f$
is exactly one of reducible, periodic, or pseudo-Anosov and, accordingly, contains an incompressible torus, admits an
$f$
is exactly one of reducible, periodic, or pseudo-Anosov and, accordingly, contains an incompressible torus, admits an
![]() $\mathbb{H}^2 \times \mathbb{R}$
structure, or admits a hyperbolic structure.
$\mathbb{H}^2 \times \mathbb{R}$
structure, or admits a hyperbolic structure.
Algebraic mapping tori are fundamental groups of topological mapping tori of surfaces or complexes. For a finitely presented group
![]() $G= \langle X \! \mid \! R \rangle$
and an injective endomorphism
$G= \langle X \! \mid \! R \rangle$
and an injective endomorphism
![]() $\Phi \;:\; G \to G$
, the algebraic mapping torus is the group:
$\Phi \;:\; G \to G$
, the algebraic mapping torus is the group:
In this article,
![]() $\Phi$
will always be an automorphism, so
$\Phi$
will always be an automorphism, so
![]() $M_{\Phi } = G \rtimes _{\Phi } \mathbb{Z}$
, and
$M_{\Phi } = G \rtimes _{\Phi } \mathbb{Z}$
, and
![]() $G$
will always be a right-angled Artin group (“RAAG”)—that is,
$G$
will always be a right-angled Artin group (“RAAG”)—that is,
![]() $G$
is encoded by a finite graph
$G$
is encoded by a finite graph
![]() $\Gamma$
with vertex set
$\Gamma$
with vertex set
![]() $X$
in that
$X$
in that
![]() $G$
is presented by:
$G$
is presented by:
We will study
![]() $M_{\Phi }$
via their Dehn functions (which we will always consider qualitatively—that is, up to an equivalence relation
$M_{\Phi }$
via their Dehn functions (which we will always consider qualitatively—that is, up to an equivalence relation
![]() $\simeq$
: for
$\simeq$
: for
![]() $f,g\;:\; \mathbb{N} \to \mathbb{N}$
, write
$f,g\;:\; \mathbb{N} \to \mathbb{N}$
, write
![]() $f\preceq g$
when there exists
$f\preceq g$
when there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $f(n) \leq Cg(Cn+C) +Cn+C$
for all
$f(n) \leq Cg(Cn+C) +Cn+C$
for all
![]() $n \in \mathbb{N}$
, and write
$n \in \mathbb{N}$
, and write
![]() $f \simeq g$
when
$f \simeq g$
when
![]() $f \preceq g$
and
$f \preceq g$
and
![]() $g \preceq f$
). The Dehn function is an invariant of finitely presentable groups. It can be viewed either as an algorithmic complexity measure for the word problem or as an isoperimetric function recording the minimal area of disks spanning loops as a function of the lengths of the loops. More details are in Section 3.1.
$g \preceq f$
). The Dehn function is an invariant of finitely presentable groups. It can be viewed either as an algorithmic complexity measure for the word problem or as an isoperimetric function recording the minimal area of disks spanning loops as a function of the lengths of the loops. More details are in Section 3.1.
Our study is motivated by the following two classifications. The first concerns
![]() $G=\mathbb{Z}^k$
, the RAAG associated with the complete graph with
$G=\mathbb{Z}^k$
, the RAAG associated with the complete graph with
![]() $k$
vertices.
$k$
vertices.
Theorem (Bridson–Gersten, Main Theorem [Reference Bridson and Gersten7], Bridson–Pittet, Theorem 5.1 [Reference Bridson and Pittet10]). If
![]() $\Phi \in{\textrm{Aut}}(\mathbb{Z}^k)\,=\,\textrm{GL}(k,\mathbb{Z})$
has an eigenvalue
$\Phi \in{\textrm{Aut}}(\mathbb{Z}^k)\,=\,\textrm{GL}(k,\mathbb{Z})$
has an eigenvalue
![]() $\lambda$
with
$\lambda$
with
![]() $|\lambda | \neq 1$
, then the Dehn function of the mapping torus
$|\lambda | \neq 1$
, then the Dehn function of the mapping torus
![]() $M_{\Phi }$
is exponential. Else, the Dehn function of
$M_{\Phi }$
is exponential. Else, the Dehn function of
![]() $M_{\Phi }$
is polynomial of degree
$M_{\Phi }$
is polynomial of degree
![]() $c+1$
, where
$c+1$
, where
![]() $c \times c$
is the size of the largest Jordan block in the Jordan Canonical form of the matrix associated with
$c \times c$
is the size of the largest Jordan block in the Jordan Canonical form of the matrix associated with
![]() $\Phi$
.
$\Phi$
.
The second classification concerns
![]() $G=F_k$
, the rank-
$G=F_k$
, the rank-
![]() $k$
free group, that is, the RAAG associated with the graph with
$k$
free group, that is, the RAAG associated with the graph with
![]() $k$
vertices and no edges. An automorphism
$k$
vertices and no edges. An automorphism
![]() $\Phi$
of
$\Phi$
of
![]() $F_k$
is atoroidal when there are no periodic conjugacy classes—equivalently, for all
$F_k$
is atoroidal when there are no periodic conjugacy classes—equivalently, for all
![]() $w \in F_k$
and
$w \in F_k$
and
![]() $n \in \mathbb{Z}$
, if
$n \in \mathbb{Z}$
, if
![]() $w$
and
$w$
and
![]() $\Phi ^n(w)$
are conjugate, then
$\Phi ^n(w)$
are conjugate, then
![]() $w=1$
or
$w=1$
or
![]() $n=0$
.
$n=0$
.
Theorem (Bestvina–Handel [Reference Bestvina and Handel3], Brinkmann [Reference Brinkmann11], Bridson–Groves [Reference Bridson and Groves8]). Suppose
![]() $\Phi \in{\textrm{Aut}}(F_k)$
. The mapping torus
$\Phi \in{\textrm{Aut}}(F_k)$
. The mapping torus
![]() $M_{\Phi }$
is hyperbolic (i.e. has linear Dehn function) if and only if
$M_{\Phi }$
is hyperbolic (i.e. has linear Dehn function) if and only if
![]() $\Phi$
is atoroidal. All other
$\Phi$
is atoroidal. All other
![]() $M_{\Phi }$
have quadratic Dehn functions.
$M_{\Phi }$
have quadratic Dehn functions.
RAAGs interpolate between free abelian groups and free groups, so it is natural to look to extend the above theorems to other RAAGs. We thank Karen Vogtmann for suggesting this problem to us.
A classification of the Dehn functions of all RAAGs remains out of reach. Here, we complete the classification for three-generator RAAGs and all groups
![]() $F_k \times F_l$
where
$F_k \times F_l$
where
![]() $k,l \geq 2$
.
$k,l \geq 2$
.
For
![]() $\mathbb{Z}^3$
and
$\mathbb{Z}^3$
and
![]() $F_3$
and for all RAAGs on fewer than
$F_3$
and for all RAAGs on fewer than
![]() $3$
generators, the theorems above classify the Dehn functions of
$3$
generators, the theorems above classify the Dehn functions of
![]() $M_{\Phi }$
. Here are our results on the remaining three-generator RAAGs, namely
$M_{\Phi }$
. Here are our results on the remaining three-generator RAAGs, namely
![]() $F_2 \times \mathbb{Z}$
and
$F_2 \times \mathbb{Z}$
and
![]() $\mathbb{Z}^2 \ast \mathbb{Z}$
.
$\mathbb{Z}^2 \ast \mathbb{Z}$
.
If
![]() $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
, then
$\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
, then
![]() $\Psi = \psi \times \rho$
where
$\Psi = \psi \times \rho$
where
![]() $\psi \in{\textrm{Aut}}(F_2)$
and
$\psi \in{\textrm{Aut}}(F_2)$
and
![]() $\rho \;:\; \mathbb{Z} \to \mathbb{Z}$
is the identity or the map
$\rho \;:\; \mathbb{Z} \to \mathbb{Z}$
is the identity or the map
![]() $r \mapsto -r$
.
$r \mapsto -r$
.
Theorem A.
Suppose
![]() $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
induces
$\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
induces
![]() $\psi \in{\textrm{Aut}}(F_2)$
. Let
$\psi \in{\textrm{Aut}}(F_2)$
. Let
![]() $\psi _{ab} \in{\textrm{Aut}}(\mathbb{Z}^2)$
be the map induced by
$\psi _{ab} \in{\textrm{Aut}}(\mathbb{Z}^2)$
be the map induced by
![]() $\psi$
via the abelianization map
$\psi$
via the abelianization map
![]() $F_2 \to \mathbb{Z}^2$
,
$F_2 \to \mathbb{Z}^2$
,
![]() $g \mapsto g_{ab}$
.
$g \mapsto g_{ab}$
.
Let
![]() $p\;:\; F_2 \times \mathbb{Z} \to \mathbb{Z}$
be the projection map
$p\;:\; F_2 \times \mathbb{Z} \to \mathbb{Z}$
be the projection map
![]() $p(g,r) =r$
. Exactly one of the following holds:
$p(g,r) =r$
. Exactly one of the following holds:
-
1. There exists
 $g \in F_2$
and
$g \in F_2$
and
 $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
 $\psi _{ab}^m(g_{ab}) = g_{ab}$
and
$\psi _{ab}^m(g_{ab}) = g_{ab}$
and
 $p(\Psi ^m(g)) \neq 0$
, in which case
$p(\Psi ^m(g)) \neq 0$
, in which case
 $M_{\Psi }$
has cubic Dehn function.
$M_{\Psi }$
has cubic Dehn function.
-
2.
 $M_{\Psi }$
has quadratic Dehn function.
$M_{\Psi }$
has quadratic Dehn function.
Theorem B.
Suppose
![]() $\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Suppose
$\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Suppose
![]() $\Phi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
restricts to an automorphism
$\Phi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
restricts to an automorphism
![]() $\phi$
on the
$\phi$
on the
![]() $\mathbb{Z}^2$
factor and satisfies
$\mathbb{Z}^2$
factor and satisfies
![]() $[\Psi ] = [\Phi ] \in \textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Exactly one of the following holds:
$[\Psi ] = [\Phi ] \in \textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Exactly one of the following holds:
-
1.
 $\phi$
is of finite order, in which case
$\phi$
is of finite order, in which case
 $M_{\Psi }$
has quadratic Dehn function.
$M_{\Psi }$
has quadratic Dehn function.
-
2.
 $\phi$
has an eigenvalue
$\phi$
has an eigenvalue
 $\lambda$
such that
$\lambda$
such that
 $|\lambda | \neq 1$
, in which case
$|\lambda | \neq 1$
, in which case
 $M_{\Psi }$
has exponential Dehn function.
$M_{\Psi }$
has exponential Dehn function.
-
3.
 $M_{\Psi }$
has cubic Dehn function.
$M_{\Psi }$
has cubic Dehn function.
Theorem B is effective in that, given a
![]() $\Psi$
, a
$\Psi$
, a
![]() $\Phi$
as per the statement can be produced: see Lemma 6.1.
$\Phi$
as per the statement can be produced: see Lemma 6.1.
Suppose
![]() $F$
is a free group with a finite basis
$F$
is a free group with a finite basis
![]() $X$
. For
$X$
. For
![]() $x\in F$
,
$x\in F$
,
![]() $|x|$
denotes the length of the reduced word on
$|x|$
denotes the length of the reduced word on
![]() $X^{\pm 1}$
representing
$X^{\pm 1}$
representing
![]() $x$
. The growth
$x$
. The growth
![]() $g_{\Phi, X}\;:\; \mathbb{N} \to \mathbb{N}$
of an automorphism
$g_{\Phi, X}\;:\; \mathbb{N} \to \mathbb{N}$
of an automorphism
![]() $\Phi \;:\;F \to F$
is defined by
$\Phi \;:\;F \to F$
is defined by
![]() $g_{\Phi, X}(n) \;:\!=\; \max _{x\in X}\{|\Phi ^n(x)|\}$
. While the growth type of
$g_{\Phi, X}(n) \;:\!=\; \max _{x\in X}\{|\Phi ^n(x)|\}$
. While the growth type of
![]() $g_{\Phi, X}$
does not depend on the choice of
$g_{\Phi, X}$
does not depend on the choice of
![]() $X$
, it is not invariant under inner automorphisms. For example, the automorphism
$X$
, it is not invariant under inner automorphisms. For example, the automorphism
![]() $\phi \;:\;a \mapsto b^{-1}ab,\,\, b \mapsto b$
has linear growth, whereas
$\phi \;:\;a \mapsto b^{-1}ab,\,\, b \mapsto b$
has linear growth, whereas
![]() $\psi \;:\;a \mapsto a,\,\, b\mapsto b$
has constant growth. The cyclic growth
$\psi \;:\;a \mapsto a,\,\, b\mapsto b$
has constant growth. The cyclic growth
![]() $g_{\Phi }^{cyc}$
of an automorphism accounts for this. It describes the growth of (all) conjugacy classes under iteration of automorphisms and is invariant under inner automorphisms. Details are in Section 7.2.
$g_{\Phi }^{cyc}$
of an automorphism accounts for this. It describes the growth of (all) conjugacy classes under iteration of automorphisms and is invariant under inner automorphisms. Details are in Section 7.2.
We classify the Dehn functions of mapping tori of products
![]() $F_k \times F_l$
of free groups with
$F_k \times F_l$
of free groups with
![]() $k,l \geq 2$
. This theorem is effective: in Section 7.1, we explain how to compute
$k,l \geq 2$
. This theorem is effective: in Section 7.1, we explain how to compute
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
from
$\phi _2$
from
![]() $\Psi$
.
$\Psi$
.
Theorem C.
If
![]() $G= F_k \times F_l,$
where
$G= F_k \times F_l,$
where
![]() $k,l \geq 2$
, and
$k,l \geq 2$
, and
![]() $\Psi \in{\textrm{Aut}}(F_k \times F_l)$
, then we can find
$\Psi \in{\textrm{Aut}}(F_k \times F_l)$
, then we can find
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
such that
$\phi _2 \in{\textrm{Aut}}(F_l)$
such that
![]() $\Phi = \phi _1 \times \phi _2$
satisfies
$\Phi = \phi _1 \times \phi _2$
satisfies
![]() $[\Phi ] = [\Psi ^2]$
in
$[\Phi ] = [\Psi ^2]$
in
![]() $\textrm{Out}(F_k \times F_l)$
. The Dehn functions of the associated mapping tori satisfy
$\textrm{Out}(F_k \times F_l)$
. The Dehn functions of the associated mapping tori satisfy
![]() $\delta _{M_{\Phi }} \simeq \delta _{M_{\Psi }}$
and their asymptotics can be read off
$\delta _{M_{\Phi }} \simeq \delta _{M_{\Psi }}$
and their asymptotics can be read off
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
in that:
$\phi _2$
in that:
-
1. If
 $[\phi _i^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$
for some
$[\phi _i^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$
for some
 $p\in \mathbb{N}$
, and
$p\in \mathbb{N}$
, and
 $i$
is either
$i$
is either
 $1$
or
$1$
or
 $2$
, then
$2$
, then
 $\delta _{M_{\Psi }}(n) \simeq n^2$
.
$\delta _{M_{\Psi }}(n) \simeq n^2$
. -
2. If
 $n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$
for some
$n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$
for some
 $d_1 \geq 1$
, then
$d_1 \geq 1$
, then
 $\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$
, and likewise with the indices
$\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$
, and likewise with the indices
 $1$
and
$1$
and
 $2$
interchanged.
$2$
interchanged.
-
3. If
 $g_{\phi _1}^{cyc}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$
, then
$g_{\phi _1}^{cyc}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$
, then
 $\delta _{M_{\Psi }}$
grows exponentially.
$\delta _{M_{\Psi }}$
grows exponentially.
As we will explain in Section 7.2, the three cases in Theorem C are exhaustive and mutually exclusive.
Since all automorphisms of
![]() $F_2$
are periodic or have cyclic growth, that is, linear or exponential, this implies:
$F_2$
are periodic or have cyclic growth, that is, linear or exponential, this implies:
Corollary D.
If
![]() $G= F_2 \times F_2,$
and
$G= F_2 \times F_2,$
and
![]() $\Psi \in{\textrm{Aut}}(G)$
, then
$\Psi \in{\textrm{Aut}}(G)$
, then
![]() $M_{\Psi }$
has quadratic, cubic, or exponential Dehn function.
$M_{\Psi }$
has quadratic, cubic, or exponential Dehn function.
We are also able to determine the Dehn functions of mapping tori of
![]() $F_k \times \mathbb{Z}$
in some cases. In Section 8, we detail these cases, remark on the limits of our techniques, and suggest next steps in this line of research.
$F_k \times \mathbb{Z}$
in some cases. In Section 8, we detail these cases, remark on the limits of our techniques, and suggest next steps in this line of research.
2. Overview
This article is organized as follows. In Section 3, we give background on Dehn functions and on corridors in van Kampen diagrams. In Section 4, we review the electrostatic model of Gersten and Riley from [Reference Gersten and Riley16]. We prove Theorems A, B, and C in Sections 5, 6, and 7, respectively.
Here is an outline of our strategy. Given a RAAG
![]() $G$
, we organize its automorphisms
$G$
, we organize its automorphisms
![]() $\Phi$
into cases, chosen so that within each case we can present
$\Phi$
into cases, chosen so that within each case we can present
![]() $M_{\Phi }$
in a manner which facilitates analysis of its Dehn function. In some cases, we find it convenient to replace
$M_{\Phi }$
in a manner which facilitates analysis of its Dehn function. In some cases, we find it convenient to replace
![]() $\Phi$
by a power; this, in turn, replaces
$\Phi$
by a power; this, in turn, replaces
![]() $M_{\Phi }$
by a finite index subgroup, which does not qualitatively change the Dehn function.
$M_{\Phi }$
by a finite index subgroup, which does not qualitatively change the Dehn function.
In the setting of Theorem A, our presentation expresses
![]() $M_{\Phi }$
as a central extension of another mapping torus
$M_{\Phi }$
as a central extension of another mapping torus
![]() $M_{\phi }$
. Then, we use what Gersten and Riley called an electrostatic model in [Reference Gersten and Riley16] to get upper bounds on the Dehn function of
$M_{\phi }$
. Then, we use what Gersten and Riley called an electrostatic model in [Reference Gersten and Riley16] to get upper bounds on the Dehn function of
![]() $M_{\Phi }$
. The idea is that a van Kampen diagram over
$M_{\Phi }$
. The idea is that a van Kampen diagram over
![]() $M_{\phi }$
can be “charged” by elements of the kernel of the extension (elements of the center of
$M_{\phi }$
can be “charged” by elements of the kernel of the extension (elements of the center of
![]() $M_{\Phi }$
). The diagram is then “inflated” by adding in suitable corridors to connect up these charges and get a van Kampen diagram over
$M_{\Phi }$
). The diagram is then “inflated” by adding in suitable corridors to connect up these charges and get a van Kampen diagram over
![]() $M_{\Phi }$
. This leads to diagrams of cubic area (as a function of their boundary length) and so a cubic upper bound on the Dehn function. For certain
$M_{\Phi }$
. This leads to diagrams of cubic area (as a function of their boundary length) and so a cubic upper bound on the Dehn function. For certain
![]() $\Phi$
, we improve this estimate to quadratic by noticing that
$\Phi$
, we improve this estimate to quadratic by noticing that
![]() $M_{\phi }$
is hyperbolic relative to a
$M_{\phi }$
is hyperbolic relative to a
![]() $\mathbb{Z}^2$
subgroup that receives no charges. This implies that only linearly many charges appear in the diagram, and thereby that the resulting van Kampen diagram over
$\mathbb{Z}^2$
subgroup that receives no charges. This implies that only linearly many charges appear in the diagram, and thereby that the resulting van Kampen diagram over
![]() $M_{\Phi }$
has quadratic area. For other
$M_{\Phi }$
has quadratic area. For other
![]() $\Phi$
, we define partial corridors in van Kampen diagrams and then use Hall’s Marriage Theorem to give a special pattern for discharging the diagrams, which again improves the Dehn function upper bound to quadratic.
$\Phi$
, we define partial corridors in van Kampen diagrams and then use Hall’s Marriage Theorem to give a special pattern for discharging the diagrams, which again improves the Dehn function upper bound to quadratic.
As for obtaining the matching lower bounds, the Dehn function of
![]() $M_{\Phi }$
is always at least quadratic because
$M_{\Phi }$
is always at least quadratic because
![]() $M_{\Phi }$
is not hyperbolic. For certain
$M_{\Phi }$
is not hyperbolic. For certain
![]() $M_{\Phi }$
, a result of Bridson and Gersten (see Lemma 3.5) improves this to a cubic lower bound by identifying a suitable quasi-isometrically embedded abelian subgroup of
$M_{\Phi }$
, a result of Bridson and Gersten (see Lemma 3.5) improves this to a cubic lower bound by identifying a suitable quasi-isometrically embedded abelian subgroup of
![]() $G$
to which the action of
$G$
to which the action of
![]() $\Phi$
restricts.
$\Phi$
restricts.
For Theorem B the main innovation is for a case where, even though the
![]() $M_{\Phi }$
are not central extensions, one generator
$M_{\Phi }$
are not central extensions, one generator
![]() $b$
commutes with all other generators apart from one generator
$b$
commutes with all other generators apart from one generator
![]() $c$
. That
$c$
. That
![]() $c$
forms corridors in van Kampen diagrams over the quotient of
$c$
forms corridors in van Kampen diagrams over the quotient of
![]() $M_{\Phi }$
obtained by killing
$M_{\Phi }$
obtained by killing
![]() $b$
, and the electrostatic model applies to regions complementary to the
$b$
, and the electrostatic model applies to regions complementary to the
![]() $c$
-corridors. We then define alternating corridors which string together two types of partial corridors, and we show that these alternating corridors can intersect themselves and each other at most once, and that every 2-cell in the diagram is contained in some alternating corridor. This lets us prove that the area of the van Kampen diagram in the quotient is at most quadratic in the length of the boundary word. The electrostatic model then produces a van Kampen diagram with at most cubic area.
$c$
-corridors. We then define alternating corridors which string together two types of partial corridors, and we show that these alternating corridors can intersect themselves and each other at most once, and that every 2-cell in the diagram is contained in some alternating corridor. This lets us prove that the area of the van Kampen diagram in the quotient is at most quadratic in the length of the boundary word. The electrostatic model then produces a van Kampen diagram with at most cubic area.
For the lower bounds of Theorem C, we exhibit a family of words such that any van Kampen diagram for one of these words has area we can bound below on account of having a belt of corridors of controlled length. For the upper bound, we estimate the number of relators that need to be applied to convert a word
![]() $w$
representing the identity over the mapping torus of
$w$
representing the identity over the mapping torus of
![]() $F_k \times F_l$
to a word
$F_k \times F_l$
to a word
![]() $v$
with
$v$
with
![]() $|v| \leq |w|$
that represents the identity in
$|v| \leq |w|$
that represents the identity in
![]() $F_k \rtimes _{\phi _1} \mathbb{Z}$
and then we use the fact that the Dehn function of
$F_k \rtimes _{\phi _1} \mathbb{Z}$
and then we use the fact that the Dehn function of
![]() $F_k \rtimes _{\phi _1} \mathbb{Z}$
is at most quadratic. The upper and lower bounds on the Dehn function are derived from two different notions of free group automorphism growth, which we reconcile by appealing to a number of results in the literature.
$F_k \rtimes _{\phi _1} \mathbb{Z}$
is at most quadratic. The upper and lower bounds on the Dehn function are derived from two different notions of free group automorphism growth, which we reconcile by appealing to a number of results in the literature.
3. Preliminaries
We write
![]() $\left |w\right |$
to denote the length of a word
$\left |w\right |$
to denote the length of a word
![]() $w$
. Our conventions are
$w$
. Our conventions are
![]() $a^t \;:\!=\; t^{-1} a t$
and
$a^t \;:\!=\; t^{-1} a t$
and
![]() $[a,b] \;:\!=\; a^{-1} b^{-1} a b$
.
$[a,b] \;:\!=\; a^{-1} b^{-1} a b$
.
3.1. Van Kampen diagrams, corridors, and Dehn functions
These topics feature in many surveys, for instance, Section III.H.2 in [Reference Bridson and Haefliger9]. Here are the essentials.
Suppose
![]() $G=\langle X \! \mid \! R \rangle$
is a finitely presented group (so
$G=\langle X \! \mid \! R \rangle$
is a finitely presented group (so
![]() $R$
is a finite set of words on a finite alphabet
$R$
is a finite set of words on a finite alphabet
![]() $X$
and its inverse letters). Suppose
$X$
and its inverse letters). Suppose
![]() $w$
is a word on
$w$
is a word on
![]() $X \cup X^{-1}$
such that
$X \cup X^{-1}$
such that
![]() $w=1$
in
$w=1$
in
![]() $G$
. A van Kampen diagram
$G$
. A van Kampen diagram
![]() $\Delta$
for
$\Delta$
for
![]() $w$
is a simply connected planar 2-complex with edges labeled by elements of
$w$
is a simply connected planar 2-complex with edges labeled by elements of
![]() $X$
and directed so that the following holds. When traversing
$X$
and directed so that the following holds. When traversing
![]() $\partial \Delta$
counterclockwise from some base vertex, we read off
$\partial \Delta$
counterclockwise from some base vertex, we read off
![]() $w$
, and around the boundary of each 2-cell in one direction or the other and from a suitable base vertex, we read an element of
$w$
, and around the boundary of each 2-cell in one direction or the other and from a suitable base vertex, we read an element of
![]() $R$
. (If an edge is traversed in the direction of its orientation, the positive generator is implied, and if against its orientation, the inverse of the generator.) The 1-skeleton
$R$
. (If an edge is traversed in the direction of its orientation, the positive generator is implied, and if against its orientation, the inverse of the generator.) The 1-skeleton
![]() $\Delta ^{(1)}$
of
$\Delta ^{(1)}$
of
![]() $\Delta$
has the path metric in which every edge has length 1. The area of
$\Delta$
has the path metric in which every edge has length 1. The area of
![]() $\Delta$
is the number of 2-cells it has.
$\Delta$
is the number of 2-cells it has.
![]() $\textrm{Area}(w)$
denotes the minimum area among all van Kampen diagrams with boundary word
$\textrm{Area}(w)$
denotes the minimum area among all van Kampen diagrams with boundary word
![]() $w$
.
$w$
.
The Dehn function
![]() $\delta \;:\;\mathbb{N} \to \mathbb{N}$
of
$\delta \;:\;\mathbb{N} \to \mathbb{N}$
of
![]() $\langle X \! \mid \! R \rangle$
is
$\langle X \! \mid \! R \rangle$
is
![]() $ \delta (n) \;:\!=\; \max \{\textrm{Area}(w) \mid \left |w\right | \leq n \text{ and } w =1 \text{ in } G \}$
.
$ \delta (n) \;:\!=\; \max \{\textrm{Area}(w) \mid \left |w\right | \leq n \text{ and } w =1 \text{ in } G \}$
.
Up to the equivalence relation
![]() $\simeq$
defined in Section 1, the Dehn function does not depend on the choice of finite presentation for
$\simeq$
defined in Section 1, the Dehn function does not depend on the choice of finite presentation for
![]() $G$
and, moreover, is a quasi-isometry invariant among finitely presented groups. In particular, we will need:
$G$
and, moreover, is a quasi-isometry invariant among finitely presented groups. In particular, we will need:
Proposition 3.1.
If
![]() $G$
is finitely presented and
$G$
is finitely presented and
![]() $H\leq G$
is a finite index subgroup, then
$H\leq G$
is a finite index subgroup, then
![]() $H$
is also finitely presentable and
$H$
is also finitely presentable and
![]() $G$
and
$G$
and
![]() $H$
have equivalent Dehn functions.
$H$
have equivalent Dehn functions.
Corridors appear in van Kampen diagrams over a presentation
![]() $\langle X \! \mid \! R \rangle$
when there is some
$\langle X \! \mid \! R \rangle$
when there is some
![]() $a \in X$
such that all relators
$a \in X$
such that all relators
![]() $r \in R$
in which
$r \in R$
in which
![]() $a$
appears can be expressed as
$a$
appears can be expressed as
![]() $w_1a^{\pm 1}w_2a^{\mp 1}w_3$
where
$w_1a^{\pm 1}w_2a^{\mp 1}w_3$
where
![]() $w_1$
,
$w_1$
,
![]() $w_2$
, and
$w_2$
, and
![]() $w_3$
are words not containing
$w_3$
are words not containing
![]() $a^{\pm 1}$
. Such presentations naturally arise for HNN-extensions, with
$a^{\pm 1}$
. Such presentations naturally arise for HNN-extensions, with
![]() $a$
being the stable letter. Suppose
$a$
being the stable letter. Suppose
![]() $\Delta$
is a van Kampen diagram for a word
$\Delta$
is a van Kampen diagram for a word
![]() $w$
over such a presentation. If there is an
$w$
over such a presentation. If there is an
![]() $a$
-edge (an edge labeled
$a$
-edge (an edge labeled
![]() $a$
) in
$a$
) in
![]() $\Delta$
and there is a 2-cell in
$\Delta$
and there is a 2-cell in
![]() $\Delta$
with that edge in its boundary, then that 2-cell will have exactly one other
$\Delta$
with that edge in its boundary, then that 2-cell will have exactly one other
![]() $a$
-edge, and that
$a$
-edge, and that
![]() $a$
-edge will either be in the boundary or will be in the boundary of another 2-cell. Concatenations of 2-cells in
$a$
-edge will either be in the boundary or will be in the boundary of another 2-cell. Concatenations of 2-cells in
![]() $\Delta$
across
$\Delta$
across
![]() $a$
-edges in this manner are called corridors. A corridor either connects a pair of
$a$
-edges in this manner are called corridors. A corridor either connects a pair of
![]() $a$
-edges in the boundary of
$a$
-edges in the boundary of
![]() $\Delta$
or closes up to form an annulus. The
$\Delta$
or closes up to form an annulus. The
![]() $a$
and
$a$
and
![]() $a^{-1}$
that label edges in the boundaries of the two-dimensional parts (Figure 1b) of
$a^{-1}$
that label edges in the boundaries of the two-dimensional parts (Figure 1b) of
![]() $\Delta$
are paired off and connected by corridors. The number of 2-cells involved is the length of the corridor. An
$\Delta$
are paired off and connected by corridors. The number of 2-cells involved is the length of the corridor. An
![]() $a$
-corridor is reduced if it contains no back-to-back canceling pair of 2-cells—that is, no two 2-cells sharing an
$a$
-corridor is reduced if it contains no back-to-back canceling pair of 2-cells—that is, no two 2-cells sharing an
![]() $a$
-edge for which the word around the boundary of their union is freely reducible to the identity in the group. If an
$a$
-edge for which the word around the boundary of their union is freely reducible to the identity in the group. If an
![]() $a$
-corridor is the concatenation of
$a$
-corridor is the concatenation of
![]() $2$
-cells labeled
$2$
-cells labeled
![]() $u_1 a v_1^{-1} a^{-1}$
, …,
$u_1 a v_1^{-1} a^{-1}$
, …,
![]() $u_r a v_r^{-1} a^{-1}$
, then the top (respectively, bottom) of that corridor is the path that is labeled
$u_r a v_r^{-1} a^{-1}$
, then the top (respectively, bottom) of that corridor is the path that is labeled
![]() $v_1 \cdots v_r$
(respectively,
$v_1 \cdots v_r$
(respectively,
![]() $u_1 \cdots u_r$
) and passes through the terminal (respectively, initial) vertices of the
$u_1 \cdots u_r$
) and passes through the terminal (respectively, initial) vertices of the
![]() $a$
-edges—see Figure 1c.
$a$
-edges—see Figure 1c.

Figure 1. Corridors.
Remark 3.2.
Many of the presentations we will work with will have the form
![]() $\langle X, a \mid R, \ x^a = w_x; \ x \in X \rangle$
where
$\langle X, a \mid R, \ x^a = w_x; \ x \in X \rangle$
where
![]() $X$
is some alphabet (not containing
$X$
is some alphabet (not containing
![]() $a$
), and
$a$
), and
![]() $R$
and
$R$
and
![]() $\left \{w_x \mid x \in X\right \}$
are sets of words on
$\left \{w_x \mid x \in X\right \}$
are sets of words on
![]() $X^{\pm 1}$
. An
$X^{\pm 1}$
. An
![]() $a$
-corridor in a diagram over such a presentation is reduced exactly when the word along the bottom is reduced.
$a$
-corridor in a diagram over such a presentation is reduced exactly when the word along the bottom is reduced.
Suppose
![]() $\Delta$
is a van Kampen diagram with
$\Delta$
is a van Kampen diagram with
![]() $N$
$N$
![]() $a$
-corridors. Then
$a$
-corridors. Then
![]() $N$
is at most half the length of the boundary (at most half the number of
$N$
is at most half the length of the boundary (at most half the number of
![]() $a^{\pm 1}$
in
$a^{\pm 1}$
in
![]() $w$
). Since
$w$
). Since
![]() $a$
-corridors cannot cross, removing all the
$a$
-corridors cannot cross, removing all the
![]() $a$
-corridors leaves
$a$
-corridors leaves
![]() $N+1$
connected subdiagrams called
$N+1$
connected subdiagrams called
![]() $a$
-complementary regions. The words around the perimeters of each of these regions contain no
$a$
-complementary regions. The words around the perimeters of each of these regions contain no
![]() $a^{\pm 1}$
. Therefore, analysis of the lengths of the
$a^{\pm 1}$
. Therefore, analysis of the lengths of the
![]() $a$
-corridors and of the areas of the
$a$
-corridors and of the areas of the
![]() $a$
-complementary regions can lead to estimates on the area of
$a$
-complementary regions can lead to estimates on the area of
![]() $\Delta$
.
$\Delta$
.
The dual tree to the set of
![]() $a$
-corridors has vertices corresponding to
$a$
-corridors has vertices corresponding to
![]() $a$
-complementary regions and has an edge between two vertices when an
$a$
-complementary regions and has an edge between two vertices when an
![]() $a$
-corridor borders the two corresponding
$a$
-corridor borders the two corresponding
![]() $a$
-complementary regions. (There is no vertex corresponding to the outside of the van Kampen diagram.)
$a$
-complementary regions. (There is no vertex corresponding to the outside of the van Kampen diagram.)
Definition 3.3. A letter
![]() $a$
forms partial corridors when all the defining relations which contain both
$a$
forms partial corridors when all the defining relations which contain both
![]() $a$
and
$a$
and
![]() $a^{-1}$
have the form of a corridor relation,
$a^{-1}$
have the form of a corridor relation,
![]() $a^{\pm 1} wa^{\mp 1}=w^{\prime }$
for words
$a^{\pm 1} wa^{\mp 1}=w^{\prime }$
for words
![]() $w$
and
$w$
and
![]() $w^{\prime }$
without
$w^{\prime }$
without
![]() $a$
or
$a$
or
![]() $a^{-1}$
. A partial corridor is a maximal concatenation of 2-cells joined by common
$a^{-1}$
. A partial corridor is a maximal concatenation of 2-cells joined by common
![]() $a$
-edges as above. We refer to such 2-cells which contain one or more
$a$
-edges as above. We refer to such 2-cells which contain one or more
![]() $a$
or
$a$
or
![]() $a^{-1}$
(but not both) in their boundary words as capping faces, since they cap off partial corridors.
$a^{-1}$
(but not both) in their boundary words as capping faces, since they cap off partial corridors.
An
![]() $a$
in the boundary of a van Kampen diagram will either be connected by a full
$a$
in the boundary of a van Kampen diagram will either be connected by a full
![]() $a$
-corridor to another edge labeled by
$a$
-corridor to another edge labeled by
![]() $a$
in the boundary, or it begins a partial
$a$
in the boundary, or it begins a partial
![]() $a$
-corridor ending at one of the capping faces. An
$a$
-corridor ending at one of the capping faces. An
![]() $a$
-edge on a capping face is connected via a partial
$a$
-edge on a capping face is connected via a partial
![]() $a$
-corridor (possibly of length zero) either to the boundary or to an
$a$
-corridor (possibly of length zero) either to the boundary or to an
![]() $a$
-edge of another capping face.
$a$
-edge of another capping face.
Like standard corridors, partial corridors cannot cross. However, there is no immediate control on the number of partial corridors in terms of
![]() $|w|$
, since they may begin and end in capping faces within the diagram.
$|w|$
, since they may begin and end in capping faces within the diagram.
3.2. General bounds on Dehn functions of mapping tori of RAAGs
RAAGs are (bi)automatic [Reference Hermiller and Meier17, Reference VanWyk25], so have either linear or quadratic Dehn functions. A finitely presented group is hyperbolic if and only if it has linear Dehn function. Finite-rank free groups are hyperbolic. Non-free RAAGs have
![]() $\mathbb{Z}^2$
subgroups and so are not hyperbolic (e.g. [Reference Bridson and Haefliger9]). So RAAGs have either linear or quadratic Dehn functions, the linear case only occurring for free RAAGs. This will be useful for the following lemma.
$\mathbb{Z}^2$
subgroups and so are not hyperbolic (e.g. [Reference Bridson and Haefliger9]). So RAAGs have either linear or quadratic Dehn functions, the linear case only occurring for free RAAGs. This will be useful for the following lemma.
Lemma 3.4. If
![]() $G$
is a non-free RAAG and
$G$
is a non-free RAAG and
![]() $\Psi \in{\textrm{Aut}}(G)$
, then the Dehn function of
$\Psi \in{\textrm{Aut}}(G)$
, then the Dehn function of
![]() $M_{\Psi }$
satisfies
$M_{\Psi }$
satisfies
![]() $n^2 \preceq \delta (n) \preceq 2^n$
.
$n^2 \preceq \delta (n) \preceq 2^n$
.
Proof. Suppose
![]() $G$
is a non-free RAAG. So
$G$
is a non-free RAAG. So
![]() $G$
has a finite presentation
$G$
has a finite presentation
![]() $\langle X \! \mid \! R \rangle$
derived from a graph with at least one edge. Then
$\langle X \! \mid \! R \rangle$
derived from a graph with at least one edge. Then
![]() $G$
and hence
$G$
and hence
![]() $M_{\Psi }$
will contain a
$M_{\Psi }$
will contain a
![]() $\mathbb{\mathbb{Z}}^2$
subgroup. This implies that
$\mathbb{\mathbb{Z}}^2$
subgroup. This implies that
![]() $M_{\Psi }$
is not hyperbolic and therefore
$M_{\Psi }$
is not hyperbolic and therefore
![]() $n^2 \preceq \delta (n)$
(again, e.g. [Reference Bridson and Haefliger9]).
$n^2 \preceq \delta (n)$
(again, e.g. [Reference Bridson and Haefliger9]).
A word
![]() $w$
on the generators of
$w$
on the generators of
can be expressed as
![]() $t^{k_0}a_1t^{k_1}\cdots a_mt^{k_m}$
for some
$t^{k_0}a_1t^{k_1}\cdots a_mt^{k_m}$
for some
![]() $a_1, \ldots, a_m \in X^{\pm 1}$
and some
$a_1, \ldots, a_m \in X^{\pm 1}$
and some
![]() $k_1, \ldots, k_m \in \mathbb{Z}$
. Suppose
$k_1, \ldots, k_m \in \mathbb{Z}$
. Suppose
![]() $w$
represents the identity in
$w$
represents the identity in
![]() $M_{\Psi }$
. Then shuffling all the
$M_{\Psi }$
. Then shuffling all the
![]() $t^{\mp 1}$
to the right, replacing each
$t^{\mp 1}$
to the right, replacing each
![]() $a_i$
by the freely reduced word representing
$a_i$
by the freely reduced word representing
![]() $\Psi ^{\pm 1}(a_i)$
does not change the element of
$\Psi ^{\pm 1}(a_i)$
does not change the element of
![]() $M_{\Psi }$
represented. Eventually, we arrive at
$M_{\Psi }$
represented. Eventually, we arrive at
![]() $u t^{k_0 + \cdots + k_m}$
where
$u t^{k_0 + \cdots + k_m}$
where
![]() $u$
is a word on
$u$
is a word on
![]() $X^{\pm 1}$
that represents
$X^{\pm 1}$
that represents
![]() $1$
in
$1$
in
![]() $G$
and
$G$
and
![]() $k_0 + \cdots + k_m =0$
. Applying
$k_0 + \cdots + k_m =0$
. Applying
![]() $\Psi ^{\pm 1}$
to a letter in
$\Psi ^{\pm 1}$
to a letter in
![]() $X^{\pm 1}$
increases its length by at most the factor
$X^{\pm 1}$
increases its length by at most the factor
![]() $C\;:\!=\;\max _{a \in X} |\Psi ^{\pm 1}(a)|$
. So
$C\;:\!=\;\max _{a \in X} |\Psi ^{\pm 1}(a)|$
. So
![]() $m C^{\left |k_0\right |+ \cdots + \left |k_m\right |} \leq \left |w\right | C^{\left |w\right |}$
is an upper bound for both
$m C^{\left |k_0\right |+ \cdots + \left |k_m\right |} \leq \left |w\right | C^{\left |w\right |}$
is an upper bound for both
![]() $\left |u\right |$
and for the number of relation applications needed to convert
$\left |u\right |$
and for the number of relation applications needed to convert
![]() $w$
to
$w$
to
![]() $u$
.
$u$
.
The Dehn function of
![]() $G$
is at most quadratic, so
$G$
is at most quadratic, so
![]() $u$
can be reduced to the empty word using at most a constant times
$u$
can be reduced to the empty word using at most a constant times
![]() $\left |u\right |^2$
defining relations. Thus
$\left |u\right |^2$
defining relations. Thus
![]() $\textrm{Area}(w)$
is at most a constant times
$\textrm{Area}(w)$
is at most a constant times
![]() $\left |w\right | C^{\left |w\right |} + (\left |w\right | C^{\left |w\right |})^2$
, and therefore (since
$\left |w\right | C^{\left |w\right |} + (\left |w\right | C^{\left |w\right |})^2$
, and therefore (since
![]() $\alpha ^n \simeq \beta ^n$
for all
$\alpha ^n \simeq \beta ^n$
for all
![]() $\alpha, \beta \gt 1$
) we deduce
$\alpha, \beta \gt 1$
) we deduce
![]() $\delta (n) \preceq 2^n$
.
$\delta (n) \preceq 2^n$
.
Our next lemma is the special case of Theorem 4.1 of [Reference Bridson and Gersten7] in which, in the notation of [Reference Bridson and Gersten7],
![]() $G=H$
and
$G=H$
and
![]() $K$
is quasi-isometrically embedded. We will call on it repeatedly to establish lower bounds on the Dehn functions.
$K$
is quasi-isometrically embedded. We will call on it repeatedly to establish lower bounds on the Dehn functions.
Lemma 3.5 (Adapted from Theorem 4.1 of Bridson–Gersten [Reference Bridson and Gersten7]). Suppose
![]() $K = \langle k_1, \dots, k_m \rangle$
is a quasi-isometrically embedded infinite abelian subgroup of a finitely presented group
$K = \langle k_1, \dots, k_m \rangle$
is a quasi-isometrically embedded infinite abelian subgroup of a finitely presented group
![]() $G$
. If
$G$
. If
![]() $\Phi \in{\textrm{Aut}}(G)$
and
$\Phi \in{\textrm{Aut}}(G)$
and
![]() $\Phi (K) = K$
, then the Dehn function
$\Phi (K) = K$
, then the Dehn function
![]() $\delta$
of
$\delta$
of
![]() $\langle G, t\, |\, g^t=\Phi (g) \rangle$
satisfies
$\langle G, t\, |\, g^t=\Phi (g) \rangle$
satisfies
Equivalently, suppose
![]() $\phi = \Phi \left |_{K} \right .$
is associated to the matrix
$\phi = \Phi \left |_{K} \right .$
is associated to the matrix
![]() $A$
; then
$A$
; then
-
1. If
 $\phi$
has an eigenvalue
$\phi$
has an eigenvalue
 $\lambda$
such that
$\lambda$
such that
 $|\lambda | \neq 1$
, then
$|\lambda | \neq 1$
, then
 $M_{\Phi }$
has exponential Dehn function.
$M_{\Phi }$
has exponential Dehn function. -
2. If
 $\phi$
only has eigenvalues
$\phi$
only has eigenvalues
 $\lambda$
such that
$\lambda$
such that
 $|\lambda |=1$
, then
$|\lambda |=1$
, then
 $n^{c+1} \preceq \delta (n)$
, where the size of the largest Jordan block for
$n^{c+1} \preceq \delta (n)$
, where the size of the largest Jordan block for
 $A$
is
$A$
is
 $c \times c$
.
$c \times c$
.
The following lemma allows us to specialize to convenient
![]() $\Psi$
when analyzing the Dehn functions of mapping tori. We include the proof because it is brief and the result is vital to this paper.
$\Psi$
when analyzing the Dehn functions of mapping tori. We include the proof because it is brief and the result is vital to this paper.
Lemma 3.6 (c.f. Lemma 2.1 of [Reference Bogopolski, Martino and Ventura4]). The following mapping tori have equivalent Dehn functions:
-
1.
 $M_{\Psi }$
and
$M_{\Psi }$
and
 $M_{\Psi ^n}$
, for any
$M_{\Psi ^n}$
, for any
 $n \in \mathbb{N}$
.
$n \in \mathbb{N}$
. -
2.
 $M_{\Psi }$
and
$M_{\Psi }$
and
 $M_{\Psi ^{-1}}$
.
$M_{\Psi ^{-1}}$
. -
3.
 $M_{\Psi _1}$
and
$M_{\Psi _1}$
and
 $M_{\Psi _2}$
when
$M_{\Psi _2}$
when
 $\Psi _1$
and
$\Psi _1$
and
 $\Psi _2$
are conjugate in
$\Psi _2$
are conjugate in
 $\textrm{Out}(G)$
.
$\textrm{Out}(G)$
.
Proof, based on [Reference Bogopolski, Martino and Ventura4]. Map
![]() $M_{\Psi }$
onto
$M_{\Psi }$
onto
![]() $\langle t \rangle = \mathbb{Z}$
by killing
$\langle t \rangle = \mathbb{Z}$
by killing
![]() $G$
and then onto
$G$
and then onto
![]() $\mathbb{Z}/n\mathbb{Z}$
by the natural quotient map. The kernel of this composition is the index-
$\mathbb{Z}/n\mathbb{Z}$
by the natural quotient map. The kernel of this composition is the index-
![]() $n$
subgroup
$n$
subgroup
![]() $M_{\Psi ^n}$
. By Proposition 3.1,
$M_{\Psi ^n}$
. By Proposition 3.1,
![]() $M_{\Psi }$
and
$M_{\Psi }$
and
![]() $M_{\Psi ^n}$
have equivalent Dehn functions.
$M_{\Psi ^n}$
have equivalent Dehn functions.
As
![]() $w^t = \Psi (w)$
for all
$w^t = \Psi (w)$
for all
![]() $w \in G$
, it follows that
$w \in G$
, it follows that
![]() $w^{t^{-1}} = \Psi ^{-1}(w)$
, so mapping
$w^{t^{-1}} = \Psi ^{-1}(w)$
, so mapping
![]() $t \mapsto t^{-1}$
and fixing
$t \mapsto t^{-1}$
and fixing
![]() $G$
gives an isomorphism
$G$
gives an isomorphism
![]() $M_{\Psi } \to M_{\Psi ^{-1}}$
. Thus,
$M_{\Psi } \to M_{\Psi ^{-1}}$
. Thus,
![]() $M_{\Psi }$
and
$M_{\Psi }$
and
![]() $M_{\Psi ^{-1}}$
have equivalent Dehn functions.
$M_{\Psi ^{-1}}$
have equivalent Dehn functions.
If
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Psi _2$
are conjugate in
$\Psi _2$
are conjugate in
![]() $\textrm{Out}(G)$
, there exists
$\textrm{Out}(G)$
, there exists
![]() $\eta \in{\textrm{Aut}}(G)$
and
$\eta \in{\textrm{Aut}}(G)$
and
![]() $h\in G$
such that
$h\in G$
such that
![]() $\Psi _2(g) = \eta ^{-1}(\Psi _1(\eta (g^h)))$
for all
$\Psi _2(g) = \eta ^{-1}(\Psi _1(\eta (g^h)))$
for all
![]() $g \in G$
. We will show that
$g \in G$
. We will show that
![]() $M_{\Psi _1}$
and
$M_{\Psi _1}$
and
![]() $M_{\Psi _2}$
are isomorphic. Consider
$M_{\Psi _2}$
are isomorphic. Consider
![]() $F\;:\;M_{\Psi _2} \to M_{\Psi _1}$
given by
$F\;:\;M_{\Psi _2} \to M_{\Psi _1}$
given by
![]() $x \mapsto \eta (x)$
for
$x \mapsto \eta (x)$
for
![]() $x \in G$
and
$x \in G$
and
![]() $t \mapsto t\,\hat{h}$
, where
$t \mapsto t\,\hat{h}$
, where
![]() $\hat{h}\;:\!=\;\Psi _1(\eta (h))$
. It is a homomorphism because the relators
$\hat{h}\;:\!=\;\Psi _1(\eta (h))$
. It is a homomorphism because the relators
![]() $(g^{-1})^t\Psi _2(g)$
for
$(g^{-1})^t\Psi _2(g)$
for
![]() $g \in G$
are mapped to the identity in
$g \in G$
are mapped to the identity in
![]() $M_{\Psi _1}$
, since
$M_{\Psi _1}$
, since
![]() $(w^{-1})^t\Psi _1(w)=1$
in
$(w^{-1})^t\Psi _1(w)=1$
in
![]() $M_{\Psi _1}$
for
$M_{\Psi _1}$
for
![]() $w \in G$
. Indeed,
$w \in G$
. Indeed,
 \begin{eqnarray*} F\left ((g^{-1})^t\Psi _2(g)\right ) \ = \ F\left ((g^{-1})^t\eta ^{-1}(\Psi _1(\eta (g^h)))\right ) \ = \ \eta (g^{-1})^{t\hat{h}}\Psi _1( \eta (g^h)) \\[5pt] \ = \ (\eta (g^{-1}))^{t\hat{h}} \Psi _1(\eta (g))^{\hat{h}} \ = \ \left ((w^{-1})^{t} \Psi _1(w)\right )^{\hat{h}} \ = \ 1^{\hat{h}} \ = \ 1. \end{eqnarray*}
\begin{eqnarray*} F\left ((g^{-1})^t\Psi _2(g)\right ) \ = \ F\left ((g^{-1})^t\eta ^{-1}(\Psi _1(\eta (g^h)))\right ) \ = \ \eta (g^{-1})^{t\hat{h}}\Psi _1( \eta (g^h)) \\[5pt] \ = \ (\eta (g^{-1}))^{t\hat{h}} \Psi _1(\eta (g))^{\hat{h}} \ = \ \left ((w^{-1})^{t} \Psi _1(w)\right )^{\hat{h}} \ = \ 1^{\hat{h}} \ = \ 1. \end{eqnarray*}
where
![]() $w=\eta (g)$
. It is certainly onto. This homomorphism has inverse given by
$w=\eta (g)$
. It is certainly onto. This homomorphism has inverse given by
![]() $x \mapsto \eta ^{-1}(x)$
for
$x \mapsto \eta ^{-1}(x)$
for
![]() $x \in G$
and
$x \in G$
and
![]() $t \mapsto t\,\eta ^{-1}(\hat{h}^{-1})$
, so it is an isomorphism.
$t \mapsto t\,\eta ^{-1}(\hat{h}^{-1})$
, so it is an isomorphism.
3.3. Growth and automorphisms of
 $\mathbb{Z}^2$
$\mathbb{Z}^2$
Let
![]() $||A||$
denote the maximum of the absolute values of the entries in a matrix
$||A||$
denote the maximum of the absolute values of the entries in a matrix
![]() $A \in \textrm{GL}(2, \mathbb{Z}) ={\textrm{Aut}}(\mathbb{Z}^2)$
. We say
$A \in \textrm{GL}(2, \mathbb{Z}) ={\textrm{Aut}}(\mathbb{Z}^2)$
. We say
![]() $A$
has linear growth when the function
$A$
has linear growth when the function
![]() $\mathbb{N} \to \mathbb{N}$
mapping
$\mathbb{N} \to \mathbb{N}$
mapping
![]() $n \mapsto ||A^n||$
is
$n \mapsto ||A^n||$
is
![]() $\simeq$
-equivalent to
$\simeq$
-equivalent to
![]() $n \mapsto n$
.
$n \mapsto n$
.
The following lemmas will allow us to specialize to convenient cases of
![]() $\Phi$
when analyzing Dehn functions of mapping tori
$\Phi$
when analyzing Dehn functions of mapping tori
![]() $M_{\Phi }$
of
$M_{\Phi }$
of
![]() $F_2 \times \mathbb{Z}$
and
$F_2 \times \mathbb{Z}$
and
![]() $\mathbb{Z}^2 \ast \mathbb{Z}$
.
$\mathbb{Z}^2 \ast \mathbb{Z}$
.
Lemma 3.7. If
![]() $A \in \textrm{SL}(2, \mathbb{Z})$
has linear growth, then there are integers
$A \in \textrm{SL}(2, \mathbb{Z})$
has linear growth, then there are integers
![]() $\alpha$
and
$\alpha$
and
![]() $k$
such that
$k$
such that
![]() $k\gt 0$
and
$k\gt 0$
and
![]() $A^k$
is conjugate to
$A^k$
is conjugate to
![]() $\left (\begin{smallmatrix} 1 & \alpha \\[5pt] 0 & 1 \end{smallmatrix}\right )$
in
$\left (\begin{smallmatrix} 1 & \alpha \\[5pt] 0 & 1 \end{smallmatrix}\right )$
in
![]() $\textrm{SL}(2,\mathbb{Z})$
.
$\textrm{SL}(2,\mathbb{Z})$
.
Proof. As
![]() $A$
has linear growth, Theorem 2.1 of [Reference Bridson and Gersten7] tells us that there exists an integer
$A$
has linear growth, Theorem 2.1 of [Reference Bridson and Gersten7] tells us that there exists an integer
![]() $k \gt 0$
such that
$k \gt 0$
such that
![]() $A^k$
is
$A^k$
is
![]() $I+N$
for some nonzero matrix
$I+N$
for some nonzero matrix
![]() $N$
such that
$N$
such that
![]() $N^2=0$
. As
$N^2=0$
. As
![]() $N^2=0$
, the trace of
$N^2=0$
, the trace of
![]() $N$
is zero, and
$N$
is zero, and
![]() $N=\left ( \begin{smallmatrix} a & b \\[5pt] c & -a\\[5pt] \end{smallmatrix}\right )$
for some integers
$N=\left ( \begin{smallmatrix} a & b \\[5pt] c & -a\\[5pt] \end{smallmatrix}\right )$
for some integers
![]() $a, b, c$
not all zero such that
$a, b, c$
not all zero such that
![]() $a^2 = -bc$
. If
$a^2 = -bc$
. If
![]() $a=c=0$
, then the result holds with
$a=c=0$
, then the result holds with
![]() $\alpha =b$
. So assume they are not both zero. Notice that
$\alpha =b$
. So assume they are not both zero. Notice that
![]() $N \left (\begin{smallmatrix} a \\[5pt] c \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$
. So there are coprime integers
$N \left (\begin{smallmatrix} a \\[5pt] c \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$
. So there are coprime integers
![]() $p$
and
$p$
and
![]() $q$
(in particular not both zero) with
$q$
(in particular not both zero) with
![]() $N \left (\begin{smallmatrix} p \\[5pt] q \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$
. By Bézout, there are
$N \left (\begin{smallmatrix} p \\[5pt] q \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$
. By Bézout, there are
![]() $r, s \in \mathbb{Z}$
such that
$r, s \in \mathbb{Z}$
such that
![]() $ps-qr=1$
, and so
$ps-qr=1$
, and so
![]() $B\;:\!=\; \left (\begin{smallmatrix} p & r \\[5pt] q & s \end{smallmatrix}\right )$
is in
$B\;:\!=\; \left (\begin{smallmatrix} p & r \\[5pt] q & s \end{smallmatrix}\right )$
is in
![]() $\textrm{SL}(2, \mathbb{Z})$
. And then
$\textrm{SL}(2, \mathbb{Z})$
. And then
![]() ${B}^{-1}NB = \left (\begin{smallmatrix} 0 & \alpha \\[5pt] 0 & 0 \end{smallmatrix}\right )$
where
${B}^{-1}NB = \left (\begin{smallmatrix} 0 & \alpha \\[5pt] 0 & 0 \end{smallmatrix}\right )$
where
![]() $\alpha = 2ars +bs^2 -cr^2$
, and the result follows.
$\alpha = 2ars +bs^2 -cr^2$
, and the result follows.
Lemma 3.8. Suppose
![]() $A \in \textrm{SL}(2, \mathbb{Z})$
has a non-real eigenvalue
$A \in \textrm{SL}(2, \mathbb{Z})$
has a non-real eigenvalue
![]() $\lambda =x+ yi$
, then it has order dividing 6.
$\lambda =x+ yi$
, then it has order dividing 6.
Proof. As
![]() $A \in \textrm{SL}(2, \mathbb{Z})$
we can say
$A \in \textrm{SL}(2, \mathbb{Z})$
we can say
![]() $\det (A)=1 =(x+yi)(x-yi)=x^2+y^2$
, so
$\det (A)=1 =(x+yi)(x-yi)=x^2+y^2$
, so
![]() $|\lambda |=1$
and
$|\lambda |=1$
and
![]() $\lambda ^2-\mbox{tr}(A) \lambda +1 =0$
. Since
$\lambda ^2-\mbox{tr}(A) \lambda +1 =0$
. Since
![]() $\lambda$
is not real, the discriminant
$\lambda$
is not real, the discriminant
![]() $\mbox{tr}(A)^2-4\lt 0$
, and as
$\mbox{tr}(A)^2-4\lt 0$
, and as
![]() $A$
has only integer entries,
$A$
has only integer entries,
![]() $\mbox{tr}(A)\in \{0, \pm 1\}$
. Then, as
$\mbox{tr}(A)\in \{0, \pm 1\}$
. Then, as
![]() $\mbox{tr}(A)= 2x$
, we find
$\mbox{tr}(A)= 2x$
, we find
![]() $x \in \{0, \pm \frac{1}{2}\}$
. It follows that
$x \in \{0, \pm \frac{1}{2}\}$
. It follows that
![]() $A$
is conjugate in
$A$
is conjugate in
![]() $\textrm{SL}(2,{\mathbb{C}})$
to
$\textrm{SL}(2,{\mathbb{C}})$
to
![]() $\left ( \begin{smallmatrix} e^{i\theta } & 0 \\[5pt] 0 & e^{-i \theta } \\[5pt] \end{smallmatrix} \right )$
, where
$\left ( \begin{smallmatrix} e^{i\theta } & 0 \\[5pt] 0 & e^{-i \theta } \\[5pt] \end{smallmatrix} \right )$
, where
![]() $\theta$
is
$\theta$
is
![]() $\pm \pi/2$
,
$\pm \pi/2$
,
![]() $\pm 2\pi/3$
, or
$\pm 2\pi/3$
, or
![]() $\pm \pi/3$
, and so
$\pm \pi/3$
, and so
![]() $A$
has order dividing
$A$
has order dividing
![]() $6$
.
$6$
.
Lemma 3.9.
![]() $A \in \textrm{SL}(2, \mathbb{Z})$
has real non-unit eigenvalues if and only if
$A \in \textrm{SL}(2, \mathbb{Z})$
has real non-unit eigenvalues if and only if
![]() $A$
grows exponentially.
$A$
grows exponentially.
Proof. If
![]() $A \in \textrm{SL}(2, \mathbb{Z})$
has real non-unit eigenvalues, then
$A \in \textrm{SL}(2, \mathbb{Z})$
has real non-unit eigenvalues, then
![]() $A$
has two eigenvalues
$A$
has two eigenvalues
![]() $\lambda$
and
$\lambda$
and
![]() $\lambda ^{-1}$
, where
$\lambda ^{-1}$
, where
![]() $|\lambda |\gt 1$
. It follows that
$|\lambda |\gt 1$
. It follows that
![]() $A$
is conjugate in
$A$
is conjugate in
![]() $\textrm{SL}(2,{\mathbb{C}})$
to
$\textrm{SL}(2,{\mathbb{C}})$
to
![]() $\left ( \begin{smallmatrix} \lambda & 0 \\[5pt] 0 & \lambda ^{-1} \\[5pt] \end{smallmatrix} \right )$
. By taking powers of the diagonalization in
$\left ( \begin{smallmatrix} \lambda & 0 \\[5pt] 0 & \lambda ^{-1} \\[5pt] \end{smallmatrix} \right )$
. By taking powers of the diagonalization in
![]() $\textrm{SL}(2,{\mathbb{C}})$
,
$\textrm{SL}(2,{\mathbb{C}})$
,
![]() $A^k=PD^kP^{-1} =\left ( \begin{smallmatrix} a & b \\[5pt] c & d \\[5pt] \end{smallmatrix} \right )\left ( \begin{smallmatrix} \lambda ^k & 0 \\[5pt] 0 & \lambda ^{-k} \\[5pt] \end{smallmatrix} \right )\frac{1}{ad-bc}\left ( \begin{smallmatrix} d & -b \\[5pt] -c & a \\[5pt] \end{smallmatrix} \right )$
, we can see that
$A^k=PD^kP^{-1} =\left ( \begin{smallmatrix} a & b \\[5pt] c & d \\[5pt] \end{smallmatrix} \right )\left ( \begin{smallmatrix} \lambda ^k & 0 \\[5pt] 0 & \lambda ^{-k} \\[5pt] \end{smallmatrix} \right )\frac{1}{ad-bc}\left ( \begin{smallmatrix} d & -b \\[5pt] -c & a \\[5pt] \end{smallmatrix} \right )$
, we can see that
![]() $A$
has exponential growth.
$A$
has exponential growth.
For the converse, suppose
![]() $A$
grows exponentially. By Lemma 3.8, it has real eigenvalues. Its eigenvalues cannot be both
$A$
grows exponentially. By Lemma 3.8, it has real eigenvalues. Its eigenvalues cannot be both
![]() $1$
or both
$1$
or both
![]() $-1$
because then
$-1$
because then
![]() $A^2$
would be conjugate in
$A^2$
would be conjugate in
![]() $\textrm{SL}(2,{\mathbb{C}})$
to a matrix of linear growth (as in Lemma 3.7).
$\textrm{SL}(2,{\mathbb{C}})$
to a matrix of linear growth (as in Lemma 3.7).
4. The electrostatic model for central extensions
Gersten and Riley’s electrostatic model is a method of constructing van Kampen diagrams for central extensions (Proposition 6.1 of [Reference Gersten and Riley16]). We will use it and variants to obtain upper bounds on the Dehn functions of some mapping tori.
Suppose a group
![]() $\Gamma$
is a central extension
$\Gamma$
is a central extension
![]() $1 \to \mathbb{Z} \to{\Gamma } \to \overline{\Gamma } \to 1$
with kernel
$1 \to \mathbb{Z} \to{\Gamma } \to \overline{\Gamma } \to 1$
with kernel
![]() $\mathbb{Z} = \langle c \rangle$
. If
$\mathbb{Z} = \langle c \rangle$
. If
![]() $\overline{\Gamma }$
has presentation
$\overline{\Gamma }$
has presentation
then for some
![]() $k_1, \ldots, k_n \in \mathbb{Z}$
,
$k_1, \ldots, k_n \in \mathbb{Z}$
,
![]() $\Gamma$
has presentation:
$\Gamma$
has presentation:
Suppose
![]() $w \in F(X \cup \{c\})$
. Since
$w \in F(X \cup \{c\})$
. Since
![]() $c$
is central,
$c$
is central,
![]() $w = \overline{w}c^m$
in
$w = \overline{w}c^m$
in
![]() $\Gamma$
, for some
$\Gamma$
, for some
![]() $m \in \mathbb{Z}$
where
$m \in \mathbb{Z}$
where
![]() $\overline{w}$
is
$\overline{w}$
is
![]() $w$
with all
$w$
with all
![]() $c^{\pm 1}$
removed. If
$c^{\pm 1}$
removed. If
![]() $w$
represents the identity in
$w$
represents the identity in
![]() $\Gamma$
, the word
$\Gamma$
, the word
![]() $\overline{w} \in F(X)$
represents the identity in
$\overline{w} \in F(X)$
represents the identity in
![]() $\overline{\Gamma }$
. We will describe how to construct a van Kampen diagram for
$\overline{\Gamma }$
. We will describe how to construct a van Kampen diagram for
![]() $w$
over
$w$
over
![]() $\mathcal{P}_{\Gamma }$
from a diagram
$\mathcal{P}_{\Gamma }$
from a diagram
![]() $\overline{\Delta }$
for
$\overline{\Delta }$
for
![]() $\overline{w}$
over
$\overline{w}$
over
![]() $\mathcal{P}_{\overline{\Gamma }}$
.
$\mathcal{P}_{\overline{\Gamma }}$
.
We read a defining relator
![]() $r_{i_\sigma }$
clockwise or counterclockwise from an appropriate vertex
$r_{i_\sigma }$
clockwise or counterclockwise from an appropriate vertex
![]() $\ast _\sigma$
around the boundary of each 2-cell
$\ast _\sigma$
around the boundary of each 2-cell
![]() $\sigma$
in
$\sigma$
in
![]() $\overline{\Delta }$
. Now “charge” every 2-cell: insert
$\overline{\Delta }$
. Now “charge” every 2-cell: insert
![]() $|k_{i_\sigma }|$
loops at
$|k_{i_\sigma }|$
loops at
![]() $\ast _{\sigma }$
each labeled with
$\ast _{\sigma }$
each labeled with
![]() $c$
’s and oriented in such a way that around the interior of the 2-cell we now read
$c$
’s and oriented in such a way that around the interior of the 2-cell we now read
![]() $r_{i_\sigma }c^{-k_{i_\sigma }}$
(to reflect the relation
$r_{i_\sigma }c^{-k_{i_\sigma }}$
(to reflect the relation
![]() $r_{i_\sigma }=c^{k_{i_\sigma }}$
), as in Figure 2. If
$r_{i_\sigma }=c^{k_{i_\sigma }}$
), as in Figure 2. If
![]() $C\;:\!=\; \max _i |k_i|$
, then at most
$C\;:\!=\; \max _i |k_i|$
, then at most
![]() $C \textrm{Area}(\overline{\Delta })$
such loops labeled by
$C \textrm{Area}(\overline{\Delta })$
such loops labeled by
![]() $c$
are introduced by charging.
$c$
are introduced by charging.

Figure 2. How “charges” would appear if
![]() $r_1=c^2$
and
$r_1=c^2$
and
![]() $r_2=c$
.
$r_2=c$
.
To discharge, pick a geodesic spanning tree
![]() $\mathcal{T}$
in
$\mathcal{T}$
in
![]() $\overline{\Delta }^{(1)}$
—that is, a maximal tree such that the distance in the tree from any vertex to the base vertex of
$\overline{\Delta }^{(1)}$
—that is, a maximal tree such that the distance in the tree from any vertex to the base vertex of
![]() $\overline{\Delta }$
is the same as its distance in
$\overline{\Delta }$
is the same as its distance in
![]() $\overline{\Delta }^{(1)}$
. In [Reference Gersten and Riley16], for each introduced
$\overline{\Delta }^{(1)}$
. In [Reference Gersten and Riley16], for each introduced
![]() $c$
-edge, a
$c$
-edge, a
![]() $c$
-corridor is added which follows
$c$
-corridor is added which follows
![]() $\mathcal{T}$
to the root of the tree. (Figures 4–7 in [Reference Gersten and Riley16] show how these corridors appear.) Each
$\mathcal{T}$
to the root of the tree. (Figures 4–7 in [Reference Gersten and Riley16] show how these corridors appear.) Each
![]() $c$
-corridor has length bounded above by
$c$
-corridor has length bounded above by
![]() $\textrm{Diam}(\overline{\Delta })$
. This produces a diagram
$\textrm{Diam}(\overline{\Delta })$
. This produces a diagram
![]() $\Delta ^{\prime }$
for
$\Delta ^{\prime }$
for
![]() $\overline{w}c^m$
in
$\overline{w}c^m$
in
![]() $\Gamma$
with area at most
$\Gamma$
with area at most
![]() $C \textrm{Area}(\overline{\Delta })(\textrm{Diam}(\overline{\Delta })+1)$
.
$C \textrm{Area}(\overline{\Delta })(\textrm{Diam}(\overline{\Delta })+1)$
.
As
![]() $w=\overline{w}c^m$
in
$w=\overline{w}c^m$
in
![]() $\mathcal{P}_{\Gamma }$
, there is a van Kampen diagram
$\mathcal{P}_{\Gamma }$
, there is a van Kampen diagram
![]() $\theta$
for
$\theta$
for
![]() $wc^{-m}(\overline{w})^{-1}$
over
$wc^{-m}(\overline{w})^{-1}$
over
![]() $\mathcal{P}_{\Gamma }$
. Since the arrangement of generators other than
$\mathcal{P}_{\Gamma }$
. Since the arrangement of generators other than
![]() $c$
is the same in
$c$
is the same in
![]() $w$
and in
$w$
and in
![]() $\overline{w}c^m$
,
$\overline{w}c^m$
,
![]() $\theta$
can be filled with
$\theta$
can be filled with
![]() $c$
-corridors and
$c$
-corridors and
![]() $\textrm{Area}( wc^{-m}\overline{w}^{-1}) \leq |w|^2$
. To get a diagram
$\textrm{Area}( wc^{-m}\overline{w}^{-1}) \leq |w|^2$
. To get a diagram
![]() $\Delta$
for
$\Delta$
for
![]() $w$
, we wrap the diagram
$w$
, we wrap the diagram
![]() $\theta$
around
$\theta$
around
![]() $\Delta ^{\prime }$
as in Figure 3.
$\Delta ^{\prime }$
as in Figure 3.

Figure 3. Constructing
![]() $\Delta$
from
$\Delta$
from
![]() $\Delta ^{\prime }$
and
$\Delta ^{\prime }$
and
![]() $\theta$
.
$\theta$
.
For example,
![]() $G = \langle a, b, c \mid [b,a] = c^2, [c, a]=[c,b]=1 \rangle$
is a central extension of
$G = \langle a, b, c \mid [b,a] = c^2, [c, a]=[c,b]=1 \rangle$
is a central extension of
![]() $Q = \langle a, b \mid [a,b]=1 \rangle$
.
$Q = \langle a, b \mid [a,b]=1 \rangle$
.
Figure 4 shows how a van Kampen diagram over
![]() $G$
for the word
$G$
for the word
![]() $w =c^{-6}b^{-3} a^{-3}bc^{-1}b^2c^{-1}a^3c^{-10}$
, beginning with a van Kampen diagram
$w =c^{-6}b^{-3} a^{-3}bc^{-1}b^2c^{-1}a^3c^{-10}$
, beginning with a van Kampen diagram
![]() $\overline{\Delta }$
over
$\overline{\Delta }$
over
![]() $Q$
for
$Q$
for
![]() $\overline{w} =b^{-3} a^{-3}b^3a^3$
.
$\overline{w} =b^{-3} a^{-3}b^3a^3$
.

Figure 4. An example of the electrostatic model in action.
We begin by charging the diagram, that is, adding in
![]() $c$
-edges (the yellow loops) to all 2-cells to recover the relations of
$c$
-edges (the yellow loops) to all 2-cells to recover the relations of
![]() $G$
. Then we “discharge” the new edges to the boundary, that is, we push the one-sided edges to the boundary by adding in c-corridors along a geodesic spanning tree
$G$
. Then we “discharge” the new edges to the boundary, that is, we push the one-sided edges to the boundary by adding in c-corridors along a geodesic spanning tree
![]() $\mathcal{T}$
. For each unconnected
$\mathcal{T}$
. For each unconnected
![]() $c$
-edge, we duplicate the path from its vertex to the base point, in
$c$
-edge, we duplicate the path from its vertex to the base point, in
![]() $\mathcal{T}$
, and expand these paths to
$\mathcal{T}$
, and expand these paths to
![]() $c$
-corridors. For example, a path with label
$c$
-corridors. For example, a path with label
![]() $abbb$
will be duplicated to a
$abbb$
will be duplicated to a
![]() $c$
-corridor with sides
$c$
-corridor with sides
![]() $abbb$
, as
$abbb$
, as
![]() $c$
is central. Finally, we add an annular diagram around the outside of the diagram to rearrange the
$c$
is central. Finally, we add an annular diagram around the outside of the diagram to rearrange the
![]() $c$
-edges to the appropriate order, converting the van Kampen diagram
$c$
-edges to the appropriate order, converting the van Kampen diagram
![]() $\Delta '$
for
$\Delta '$
for
![]() $c^{-6}b^{-3}a^{-3}b^3a^3c^{12}$
to a van Kampen diagram
$c^{-6}b^{-3}a^{-3}b^3a^3c^{12}$
to a van Kampen diagram
![]() $\Delta$
for
$\Delta$
for
![]() $w$
.
$w$
.
In this example, the area of
![]() $\overline{\Delta }$
is 9, and the diameter of the 1-skeleton of
$\overline{\Delta }$
is 9, and the diameter of the 1-skeleton of
![]() $\overline{\Delta }$
is 6. Each of the
$\overline{\Delta }$
is 6. Each of the
![]() $2 \times 9$
new
$2 \times 9$
new
![]() $c$
-edges can be pushed to the boundary with the addition of a
$c$
-edges can be pushed to the boundary with the addition of a
![]() $c$
-corridor of length at most 6, along a path in the spanning tree, so the van Kampen diagram
$c$
-corridor of length at most 6, along a path in the spanning tree, so the van Kampen diagram
![]() $\Delta ^{\prime }$
has area at most
$\Delta ^{\prime }$
has area at most
![]() $9 + 6 \cdot 2 \cdot 9$
, and rearranging the boundary comes at a further cost to area of at most
$9 + 6 \cdot 2 \cdot 9$
, and rearranging the boundary comes at a further cost to area of at most
![]() $|w|^2$
.
$|w|^2$
.
This construction leads to the following theorem.
Theorem 4.1 (Gersten–Riley [Reference Gersten and Riley16], Theorem 6.3). Suppose we have a central extension
![]() $1 \to \mathbb{Z} \to \Gamma \to \overline{\Gamma } \to 1$
of a finitely presented group
$1 \to \mathbb{Z} \to \Gamma \to \overline{\Gamma } \to 1$
of a finitely presented group
![]() $\overline{\Gamma }$
, and
$\overline{\Gamma }$
, and
![]() $f,g \;:\;\mathbb{N} \to \mathbb{N}$
are functions such that for every word
$f,g \;:\;\mathbb{N} \to \mathbb{N}$
are functions such that for every word
![]() $\overline{w}$
representing the identity in
$\overline{w}$
representing the identity in
![]() $\overline{\Gamma }$
, there exists a van Kampen diagram
$\overline{\Gamma }$
, there exists a van Kampen diagram
![]() $\overline{\Delta }$
such that
$\overline{\Delta }$
such that
![]() $\textrm{Area}(\overline{\Delta })\leq f(|\overline{w}|)$
and the diameter
$\textrm{Area}(\overline{\Delta })\leq f(|\overline{w}|)$
and the diameter
![]() $\textrm{Diam}(\overline{\Delta })$
of the 1-skeleton of
$\textrm{Diam}(\overline{\Delta })$
of the 1-skeleton of
![]() $\overline{\Delta }$
is at most
$\overline{\Delta }$
is at most
![]() $g(|\overline{w}|)$
. Then, the Dehn function of
$g(|\overline{w}|)$
. Then, the Dehn function of
![]() $\Gamma$
,
$\Gamma$
,
![]() $\delta _G(n)$
is bounded above by a constant times
$\delta _G(n)$
is bounded above by a constant times
![]() $f(n)(g(n)+1)+n^2$
.
$f(n)(g(n)+1)+n^2$
.
To use Theorem 4.1, we need simultaneous control on both area and diameter of diagrams. This is available in the setting we will be concerned with thanks to the following theorem of Papasoglu. The radius
![]() $r(\Delta )$
of a van Kampen diagram
$r(\Delta )$
of a van Kampen diagram
![]() $\Delta$
is the minimal
$\Delta$
is the minimal
![]() $N$
such that for every vertex in
$N$
such that for every vertex in
![]() $\Delta$
, there is a path of length at most
$\Delta$
, there is a path of length at most
![]() $N$
in the 1-skeleton of
$N$
in the 1-skeleton of
![]() $\Delta$
from that vertex to
$\Delta$
from that vertex to
![]() $\partial \Delta$
. Since one can travel between any two vertices by concatenating shortest paths to the boundary with a path part way around the boundary:
$\partial \Delta$
. Since one can travel between any two vertices by concatenating shortest paths to the boundary with a path part way around the boundary:
Theorem 4.2 (Papasoglu, Section 3 of [Reference Papasoglu22]). For a group
![]() $G$
given by a finite presentation in which every relator has length at most three, if
$G$
given by a finite presentation in which every relator has length at most three, if
![]() $\Delta$
is a minimal area van Kampen diagram such that
$\Delta$
is a minimal area van Kampen diagram such that
![]() $|\partial \Delta |= n$
and
$|\partial \Delta |= n$
and
![]() $\textrm{Area}(\Delta ) \leq M n^2$
, then
$\textrm{Area}(\Delta ) \leq M n^2$
, then
![]() $r(\Delta ) \leq 12Mn$
.
$r(\Delta ) \leq 12Mn$
.
Every finitely presentable group has such a presentation, and changing between two finite presentations of a group alters diameter and area by at most a multiplicative constant, so, in the light of (4.1), Theorem 4.2 gives us:
Corollary 4.3. If a finitely presented group
![]() $G$
has Dehn function bounded above by a quadratic function, then there exists
$G$
has Dehn function bounded above by a quadratic function, then there exists
![]() $K\gt 0$
such that for every word of length
$K\gt 0$
such that for every word of length
![]() $n$
representing the identity, there is a van Kampen diagram whose area is at most
$n$
representing the identity, there is a van Kampen diagram whose area is at most
![]() $Kn^2$
and whose diameter is at most
$Kn^2$
and whose diameter is at most
![]() $Kn$
.
$Kn$
.
5. Mapping tori of
 $G = F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$
$G = F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$
5.1. Automorphisms of
 $F_2 \times \mathbb{Z}$
$F_2 \times \mathbb{Z}$
Recall the notation of Theorem A:
![]() $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
induces
$\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
induces
![]() $\psi \in{\textrm{Aut}}(F_2)$
,
$\psi \in{\textrm{Aut}}(F_2)$
,
![]() $\psi$
induces
$\psi$
induces
![]() $\psi _{ab} \in \textrm{GL}(2,\mathbb{Z})$
via the abelianization map
$\psi _{ab} \in \textrm{GL}(2,\mathbb{Z})$
via the abelianization map
![]() $F_2 \to \mathbb{Z}^2$
,
$F_2 \to \mathbb{Z}^2$
,
![]() $g \mapsto g_{ab}$
, and
$g \mapsto g_{ab}$
, and
![]() $p\;:\;F_2 \times \mathbb{Z} \to \mathbb{Z} = \langle c \rangle$
is projection onto the second factor. Let
$p\;:\;F_2 \times \mathbb{Z} \to \mathbb{Z} = \langle c \rangle$
is projection onto the second factor. Let
![]() $\lambda ^{\pm 1}$
be the (complex) eigenvalues of
$\lambda ^{\pm 1}$
be the (complex) eigenvalues of
![]() $\psi _{ab}$
. We will prove Theorem A by separately addressing three comprehensive and mutually exclusive cases.
$\psi _{ab}$
. We will prove Theorem A by separately addressing three comprehensive and mutually exclusive cases.
-
1.
 $\left |\lambda \right |\neq 1$
,
$\left |\lambda \right |\neq 1$
, -
2.
 $\left |\lambda \right | = 1$
and there exists
$\left |\lambda \right | = 1$
and there exists
 $g \in F_2$
and
$g \in F_2$
and
 $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
 $\psi _{ab}^m(g_{ab}) = g_{ab}$
and
$\psi _{ab}^m(g_{ab}) = g_{ab}$
and
 $p(\Psi ^m(g)) \neq 0$
—equivalently,
$p(\Psi ^m(g)) \neq 0$
—equivalently,
 $g_{ab} = [\psi ^m(g)]_{ab}$
and
$g_{ab} = [\psi ^m(g)]_{ab}$
and
 $\Psi ^m(g) = \psi ^m(g)c^k$
for some
$\Psi ^m(g) = \psi ^m(g)c^k$
for some
 $k \neq 0$
.
$k \neq 0$
. -
3. all other cases—that is,
 $\left |\lambda \right | = 1$
and for all
$\left |\lambda \right | = 1$
and for all
 $g \in F_2$
and all
$g \in F_2$
and all
 $m \in \mathbb{N}$
, if
$m \in \mathbb{N}$
, if
 $p(\Psi ^m(g)) \neq 0$
then
$p(\Psi ^m(g)) \neq 0$
then
 $\psi _{ab}^m(g_{ab}) \neq g_{ab}$
.
$\psi _{ab}^m(g_{ab}) \neq g_{ab}$
.
In Section 5.2, we will prove that the Dehn function of the mapping torus
![]() $M_{\Psi }$
of
$M_{\Psi }$
of
![]() $F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$
is quadratic in case 1. In Section 5.3, we will prove that it is cubic in case 2 and is quadratic in case 3. First, we narrow the family of automorphisms
$F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$
is quadratic in case 1. In Section 5.3, we will prove that it is cubic in case 2 and is quadratic in case 3. First, we narrow the family of automorphisms
![]() $\Psi$
that must be explored.
$\Psi$
that must be explored.
Lemma 5.1 ([Reference Lyndon and Schupp20, Proposition 4.1, due to Nielsen]). For all
![]() $\,\theta \in{\textrm{Aut}}(F(a,b))$
, there is
$\,\theta \in{\textrm{Aut}}(F(a,b))$
, there is
![]() $h \in F(a,b)$
such that
$h \in F(a,b)$
such that
![]() $\theta ^2([a,b])=[a,b]^h$
.
$\theta ^2([a,b])=[a,b]^h$
.
Proof.
![]() ${\textrm{Aut}}(F(a,b))$
is generated by the following five elementary Nielsen transformations:
${\textrm{Aut}}(F(a,b))$
is generated by the following five elementary Nielsen transformations:
![]() $(a,b)$
maps to
$(a,b)$
maps to
![]() $(a^{-1}, b)$
,
$(a^{-1}, b)$
,
![]() $(a, b^{-1})$
,
$(a, b^{-1})$
,
![]() $(b, a)$
,
$(b, a)$
,
![]() $(ab, b)$
, or
$(ab, b)$
, or
![]() $(a, ba)$
. Each sends
$(a, ba)$
. Each sends
![]() $[a,b]$
to a conjugate of
$[a,b]$
to a conjugate of
![]() $[a,b]^{\pm 1}$
.
$[a,b]^{\pm 1}$
.
To prove Theorem A, it will suffice to focus only on the mapping tori of the form
![]() $M_{\Phi }$
described in the next lemma.
$M_{\Phi }$
described in the next lemma.
Lemma 5.2. Let
![]() $G = F_2 \times \mathbb{Z} = \langle a, b \rangle \times \langle c \rangle$
. Given
$G = F_2 \times \mathbb{Z} = \langle a, b \rangle \times \langle c \rangle$
. Given
![]() $\Psi \in{\textrm{Aut}}(G)$
, there exists
$\Psi \in{\textrm{Aut}}(G)$
, there exists
![]() $\Phi \in{\textrm{Aut}}(G)$
such that
$\Phi \in{\textrm{Aut}}(G)$
such that
-
there is
 $k \geq 0$
such that
$k \geq 0$
such that
 $[\Phi ] = [\Psi ^k]$
in
$[\Phi ] = [\Psi ^k]$
in
 $\textrm{Out}(F_2\times \mathbb{Z})$
,
$\textrm{Out}(F_2\times \mathbb{Z})$
, -
the Dehn functions of
 $M_{\Psi }$
and
$M_{\Psi }$
and
 $M_{\Phi }$
are equivalent,
$M_{\Phi }$
are equivalent, -
 $\phi ([a,b]) = [a,b]$
,
$\phi ([a,b]) = [a,b]$
, -
 $M_{\Phi }$
is a central extension of
$M_{\Phi }$
is a central extension of
 $M_{\phi } = \langle a, b, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b) \rangle$
by
$M_{\phi } = \langle a, b, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b) \rangle$
by
 $\mathbb{Z} = \langle c \rangle$
,
$\mathbb{Z} = \langle c \rangle$
,
where
![]() $\phi \in{\textrm{Aut}}(F(a,b))$
is the map induced from
$\phi \in{\textrm{Aut}}(F(a,b))$
is the map induced from
![]() $\Phi$
by killing
$\Phi$
by killing
![]() $c$
. Thus, there exist
$c$
. Thus, there exist
![]() $k_a, k_b \in \mathbb{Z}$
such that
$k_a, k_b \in \mathbb{Z}$
such that
Additionally, by replacing
![]() $\Phi$
by
$\Phi$
by
![]() $\Phi ^l$
for a suitable
$\Phi ^l$
for a suitable
![]() $l$
, we can further achieve that the map
$l$
, we can further achieve that the map
![]() $\phi _{ab}$
induced by
$\phi _{ab}$
induced by
![]() $\phi$
via abelianizing
$\phi$
via abelianizing
![]() $F(a,b)$
to
$F(a,b)$
to
![]() $\mathbb{Z}^2$
has determinant
$\mathbb{Z}^2$
has determinant
![]() $1$
and its eigenvalues are real and positive.
$1$
and its eigenvalues are real and positive.
Finally, each of conditions 1, 2, and 3 from the start of this section hold for
![]() $\Phi$
exactly when they hold for
$\Phi$
exactly when they hold for
![]() $\Psi$
.
$\Psi$
.
Proof. The center
![]() $\langle c \rangle$
of
$\langle c \rangle$
of
![]() $G$
, being characteristic, is preserved by
$G$
, being characteristic, is preserved by
![]() $\Psi$
, so
$\Psi$
, so
![]() $\Psi (c) = c^{\pm 1}$
, and
$\Psi (c) = c^{\pm 1}$
, and
![]() $\Psi ^2(c) =c$
. On killing
$\Psi ^2(c) =c$
. On killing
![]() $c$
,
$c$
,
![]() $\Psi$
induces some
$\Psi$
induces some
![]() $\psi \in{\textrm{Aut}}(F(a,b))$
, whereby the mapping torus
$\psi \in{\textrm{Aut}}(F(a,b))$
, whereby the mapping torus
![]() $M_{\Psi ^2} = G \rtimes _{\Psi ^2} \mathbb{Z}$
is
$M_{\Psi ^2} = G \rtimes _{\Psi ^2} \mathbb{Z}$
is
for some
![]() $k_a, k_b \in \mathbb{Z}$
. By Lemma 5.1,
$k_a, k_b \in \mathbb{Z}$
. By Lemma 5.1,
![]() $\psi ^2([a,b]) =[a,b]^h$
for some
$\psi ^2([a,b]) =[a,b]^h$
for some
![]() $h \in F(a,b)$
.
$h \in F(a,b)$
.
How we will define
![]() $\Phi$
will depend on which of the cases 1, 2, and 3 from the start of this section,
$\Phi$
will depend on which of the cases 1, 2, and 3 from the start of this section,
![]() $\Psi$
falls into, as well as whether
$\Psi$
falls into, as well as whether
![]() $\psi _{ab}$
is finite order or has linear growth.
$\psi _{ab}$
is finite order or has linear growth.
In case 1, define
![]() $\Phi = \iota _{h^{-1}}\circ \Psi ^2$
where
$\Phi = \iota _{h^{-1}}\circ \Psi ^2$
where
![]() $\iota _{h^{-1}}$
denotes conjugation by
$\iota _{h^{-1}}$
denotes conjugation by
![]() $h^{-1}$
. Then
$h^{-1}$
. Then
![]() $\phi _{ab}$
has determinant 1 as
$\phi _{ab}$
has determinant 1 as
![]() $(\psi _{ab})^2$
has determinant 1, and
$(\psi _{ab})^2$
has determinant 1, and
![]() $\Phi$
satisfies the properties above by definition and by Lemma 3.6. Because the eigenvalues of
$\Phi$
satisfies the properties above by definition and by Lemma 3.6. Because the eigenvalues of
![]() $\psi _{ab}$
were real, the eigenvalues of
$\psi _{ab}$
were real, the eigenvalues of
![]() $\phi _{ab}$
are real and positive.
$\phi _{ab}$
are real and positive.
In cases 2 and 3,
![]() $\psi _{ab}$
has unit eigenvalues. If these eigenvalues are not real, Lemma 3.8 tells us that
$\psi _{ab}$
has unit eigenvalues. If these eigenvalues are not real, Lemma 3.8 tells us that
![]() $\psi _{ab}$
has order dividing
$\psi _{ab}$
has order dividing
![]() $6$
. Define
$6$
. Define
![]() $\Phi$
to be
$\Phi$
to be
![]() $\Psi ^6$
composed with an appropriate inner automorphism so that
$\Psi ^6$
composed with an appropriate inner automorphism so that
![]() $\phi = \textrm{id}$
. Otherwise,
$\phi = \textrm{id}$
. Otherwise,
![]() $\phi _{ab}$
has real eigenvalues of
$\phi _{ab}$
has real eigenvalues of
![]() $\pm 1$
. Define
$\pm 1$
. Define
![]() $\Phi$
to be
$\Phi$
to be
![]() $\Psi ^2$
, composed with the inner automorphism guaranteed by Lemma 5.1 so that
$\Psi ^2$
, composed with the inner automorphism guaranteed by Lemma 5.1 so that
![]() $\phi ([a,b]) = [a,b]$
. In both cases,
$\phi ([a,b]) = [a,b]$
. In both cases,
![]() $\phi$
and
$\phi$
and
![]() $\Phi$
satisfy all the required properties (again using Lemma 3.6).
$\Phi$
satisfy all the required properties (again using Lemma 3.6).
Here is why conditions 1, 2, and 3 hold for
![]() $\Phi$
exactly when they hold for
$\Phi$
exactly when they hold for
![]() $\Psi$
. Suppose that
$\Psi$
. Suppose that
![]() $\Psi$
satisfies condition 1, that
$\Psi$
satisfies condition 1, that
![]() $\psi _{ab}$
has a non-unit eigenvalue. Then
$\psi _{ab}$
has a non-unit eigenvalue. Then
![]() $\Phi = \iota _{h^{-1}}\circ \Psi ^2$
for some
$\Phi = \iota _{h^{-1}}\circ \Psi ^2$
for some
![]() $h \in F(a,b)$
, and
$h \in F(a,b)$
, and
![]() $\psi _{ab}$
has a non-unit eigenvalue if and only if
$\psi _{ab}$
has a non-unit eigenvalue if and only if
![]() $\phi _{ab}= \psi ^2_{ab}$
does. Suppose that
$\phi _{ab}= \psi ^2_{ab}$
does. Suppose that
![]() $\Psi$
satisfies condition 2 or 3, and
$\Psi$
satisfies condition 2 or 3, and
![]() $\psi _{ab}$
has complex eigenvalues. Then
$\psi _{ab}$
has complex eigenvalues. Then
![]() $\Phi = \iota _{h^{-1}}\circ \Psi ^6$
for some
$\Phi = \iota _{h^{-1}}\circ \Psi ^6$
for some
![]() $h\in F(a,b)$
. If for some
$h\in F(a,b)$
. If for some
![]() $g \in F(a,b)$
, we have that
$g \in F(a,b)$
, we have that
![]() $g_{ab}$
is a fixed point of
$g_{ab}$
is a fixed point of
![]() $\psi _{ab}^m$
, then it is also a fixed point of
$\psi _{ab}^m$
, then it is also a fixed point of
![]() $\phi _{ab}^m=\psi _{ab}^{6m}$
. If there is
$\phi _{ab}^m=\psi _{ab}^{6m}$
. If there is
![]() $m\in \mathbb{N}$
so that
$m\in \mathbb{N}$
so that
![]() $\phi _{ab}^m$
has a fixed point, then
$\phi _{ab}^m$
has a fixed point, then
![]() $\psi _{ab}^{6m}$
will also have a fixed point. Moreover,
$\psi _{ab}^{6m}$
will also have a fixed point. Moreover,
![]() $p(\Phi ^{m}(g)) = 6p(\Psi ^m(g))$
, so
$p(\Phi ^{m}(g)) = 6p(\Psi ^m(g))$
, so
![]() $p(\Phi ^m(g))=0$
if and only if
$p(\Phi ^m(g))=0$
if and only if
![]() $p(\Psi ^m(g))=0$
. Thus,
$p(\Psi ^m(g))=0$
. Thus,
![]() $\Phi$
and
$\Phi$
and
![]() $\Psi$
either both satisfy 2 or both satisfy 3. The real case follows by a similar argument.
$\Psi$
either both satisfy 2 or both satisfy 3. The real case follows by a similar argument.
We are now ready to deduce:
Corollary 5.3. All mapping tori
![]() $M_{\Phi }$
of
$M_{\Phi }$
of
![]() $F_2 \times \mathbb{Z}$
have at most a cubic Dehn function.
$F_2 \times \mathbb{Z}$
have at most a cubic Dehn function.
Proof. Bridson and Groves [Reference Bridson and Groves8] prove that for all
![]() $\phi \in{\textrm{Aut}}(F_2)$
,
$\phi \in{\textrm{Aut}}(F_2)$
,
![]() $F_2 \rtimes _{\phi } \mathbb{Z}$
has a quadratic Dehn function, so Corollary 4.3 applies and allows us to use Theorem 4.1 to deduce that every central extension of
$F_2 \rtimes _{\phi } \mathbb{Z}$
has a quadratic Dehn function, so Corollary 4.3 applies and allows us to use Theorem 4.1 to deduce that every central extension of
![]() $F_2 \rtimes _{\phi } \mathbb{Z}$
has at most cubic Dehn function. Lemma 5.2 then tells us that
$F_2 \rtimes _{\phi } \mathbb{Z}$
has at most cubic Dehn function. Lemma 5.2 then tells us that
![]() $M_{\Phi }$
has at most a cubic Dehn function.
$M_{\Phi }$
has at most a cubic Dehn function.
In Sections 5.2 and 5.3, we will refine this method to improve the upper bound from cubic to quadratic in special cases. In Section 6, we will adapt the arguments to certain examples which fall short of being central extensions.
5.2. Theorem A when
 $\psi _{ab}$
has non-unit eigenvalues
$\psi _{ab}$
has non-unit eigenvalues
The primary tool for this section is relative hyperbolicity, a concept introduced by Gromov, and then developed by Bowditch, Farb, Osin, and others [Reference Bowditch5, Reference Farb14, Reference Osin21].
Suppose
![]() $M_{\phi }$
is a group presented by:
$M_{\phi }$
is a group presented by:
where
![]() $\phi \in{\textrm{Aut}}(F(a,b))$
such that
$\phi \in{\textrm{Aut}}(F(a,b))$
such that
![]() $\phi ([a,b]) = [a,b]$
.
$\phi ([a,b]) = [a,b]$
.
Lemma 5.4. If
![]() $\phi _{ab}$
has non-unit eigenvalues,
$\phi _{ab}$
has non-unit eigenvalues,
![]() $M_{\phi }$
is strongly hyperbolic relative to the subgroup:
$M_{\phi }$
is strongly hyperbolic relative to the subgroup:
Proof.
![]() $M_{\phi }$
is the fundamental group of a finite-volume hyperbolic once-punctured torus bundle. In Theorem 4.11 of [Reference Farb14], Farb showed that such groups are strongly hyperbolic relative to their cusp subgroups. In our case, that is the subgroup
$M_{\phi }$
is the fundamental group of a finite-volume hyperbolic once-punctured torus bundle. In Theorem 4.11 of [Reference Farb14], Farb showed that such groups are strongly hyperbolic relative to their cusp subgroups. In our case, that is the subgroup
![]() $\langle [a,b], \ t \rangle$
(see also Section 4 of [Reference Button and Kropholler12] for a survey of when mapping tori of free groups are relatively hyperbolic and acylindrically hyperbolic).
$\langle [a,b], \ t \rangle$
(see also Section 4 of [Reference Button and Kropholler12] for a survey of when mapping tori of free groups are relatively hyperbolic and acylindrically hyperbolic).
Consider the presentation:
for
![]() $M_{\phi }$
obtained from
$M_{\phi }$
obtained from
![]() $\mathcal{P}_1$
by adding an extra generator
$\mathcal{P}_1$
by adding an extra generator
![]() $z$
, an extra relation which declares that
$z$
, an extra relation which declares that
![]() $z$
equals
$z$
equals
![]() $[a,b]$
in the group, and a further extra relation which declares that
$[a,b]$
in the group, and a further extra relation which declares that
![]() $[a,b]$
commutes with
$[a,b]$
commutes with
![]() $t$
(which is a consequence of the other defining relations since
$t$
(which is a consequence of the other defining relations since
![]() $\phi ([a,b]) = [a,b]$
, but we include it nevertheless). Then,
$\phi ([a,b]) = [a,b]$
, but we include it nevertheless). Then,
![]() $\langle t, z \rangle \cong \mathbb{Z}^2$
is the subgroup
$\langle t, z \rangle \cong \mathbb{Z}^2$
is the subgroup
![]() $H$
of Lemma 5.4. Refer to faces of a van Kampen diagram over
$H$
of Lemma 5.4. Refer to faces of a van Kampen diagram over
![]() $\mathcal{P}_2$
as
$\mathcal{P}_2$
as
![]() $\mathbb{Z}^2$
-faces when they correspond to the relation
$\mathbb{Z}^2$
-faces when they correspond to the relation
![]() $z^t=z$
, and refer to the remaining faces as
$z^t=z$
, and refer to the remaining faces as
![]() $\mathcal{R}$
-faces.
$\mathcal{R}$
-faces.
Lemma 5.5. There exists
![]() $C\gt 0$
such that every word
$C\gt 0$
such that every word
![]() $w$
on
$w$
on
![]() $\left \{a, b, t\right \}^{\pm 1}$
of length
$\left \{a, b, t\right \}^{\pm 1}$
of length
![]() $n$
that represents the identity has a van Kampen diagram
$n$
that represents the identity has a van Kampen diagram
![]() $\Delta$
over
$\Delta$
over
![]() $\mathcal{P}_2$
with the following properties.
$\mathcal{P}_2$
with the following properties.
-
1. The number of
 $\mathcal{R}$
-faces is at most
$\mathcal{R}$
-faces is at most
 $Cn$
.
$Cn$
. -
2. The number of
 $\mathbb{Z}^2$
-faces in
$\mathbb{Z}^2$
-faces in
 $\Delta$
is at most
$\Delta$
is at most
 $Cn^2$
.
$Cn^2$
. -
3. From every vertex of
 $\Delta$
on the perimeter of an
$\Delta$
on the perimeter of an
 $\mathcal{R}$
-face, there is a path to
$\mathcal{R}$
-face, there is a path to
 $\partial \Delta$
of length at most
$\partial \Delta$
of length at most
 $Cn$
in the 1-skeleton of the union of the
$Cn$
in the 1-skeleton of the union of the
 $\mathcal{R}$
-faces.
$\mathcal{R}$
-faces.
Proof. Let
![]() $\mathcal{A}_H=\left \{t,z\right \} \cup \{h_{ij} \mid i,j \in \mathbb{Z}, \ (i,j) \neq (0,0), (1, 0), (0,1) \}$
be an alphabet, with a letter for each non-identity element of the subgroup
$\mathcal{A}_H=\left \{t,z\right \} \cup \{h_{ij} \mid i,j \in \mathbb{Z}, \ (i,j) \neq (0,0), (1, 0), (0,1) \}$
be an alphabet, with a letter for each non-identity element of the subgroup
![]() $\langle t, z \rangle \cong \mathbb{Z}^2$
of
$\langle t, z \rangle \cong \mathbb{Z}^2$
of
![]() $M_{\phi }$
. Here,
$M_{\phi }$
. Here,
![]() $h_{ij}$
corresponds to the element represented by
$h_{ij}$
corresponds to the element represented by
![]() $t^{i}z^{j}$
. Let
$t^{i}z^{j}$
. Let
![]() $S$
denote the set of words in
$S$
denote the set of words in
![]() $\mathcal{A}_H^{\ast }$
that represent the identity in
$\mathcal{A}_H^{\ast }$
that represent the identity in
![]() $M_{\phi }$
. For example,
$M_{\phi }$
. For example,
![]() $S$
includes the word
$S$
includes the word
![]() $[z,t]$
and
$[z,t]$
and
![]() $h_{ij}z^{-j}t^{-i}$
for all
$h_{ij}z^{-j}t^{-i}$
for all
![]() $(i,j) \neq (0,0), (1, 0), (0,1)$
.
$(i,j) \neq (0,0), (1, 0), (0,1)$
.
The presentation
again gives
![]() $M_{\phi }$
. Note that the elements
$M_{\phi }$
. Note that the elements
![]() $t$
and
$t$
and
![]() $z$
appear in
$z$
appear in
![]() $\mathcal{A}_H$
, and the defining relation
$\mathcal{A}_H$
, and the defining relation
![]() $z^t=z$
appears in
$z^t=z$
appears in
![]() $S$
. Again, we will refer to van Kampen diagram faces that correspond to elements of
$S$
. Again, we will refer to van Kampen diagram faces that correspond to elements of
![]() $S$
as
$S$
as
![]() $\mathbb{Z}^2$
-faces.
$\mathbb{Z}^2$
-faces.
Then
![]() $\mathcal{P}_3$
is a finite relative presentation for
$\mathcal{P}_3$
is a finite relative presentation for
![]() $M_{\phi }$
with respect to the subgroup
$M_{\phi }$
with respect to the subgroup
![]() $H$
, as per Definitions 2.2 and 2.3 of Osin in [Reference Osin21]. Theorem 1.5 in [Reference Osin21] says (in particular) that a finitely generated group which is hyperbolic relative to a subgroup in the sense of Farb, as is the case for
$H$
, as per Definitions 2.2 and 2.3 of Osin in [Reference Osin21]. Theorem 1.5 in [Reference Osin21] says (in particular) that a finitely generated group which is hyperbolic relative to a subgroup in the sense of Farb, as is the case for
![]() $M_{\phi }$
relative to
$M_{\phi }$
relative to
![]() $H$
by Lemma 5.4, has a linear relative Dehn function. What this means (as unpacked per Definitions 2.26, 2.31, and 2.32 of [Reference Osin21]) is that there exists
$H$
by Lemma 5.4, has a linear relative Dehn function. What this means (as unpacked per Definitions 2.26, 2.31, and 2.32 of [Reference Osin21]) is that there exists
![]() $C\gt 0$
such that for every word
$C\gt 0$
such that for every word
![]() $w$
on
$w$
on
![]() $\{a,b,t\}^{\pm 1}$
representing the identity, there is a van Kampen diagram
$\{a,b,t\}^{\pm 1}$
representing the identity, there is a van Kampen diagram
![]() $\hat{\Delta }$
over
$\hat{\Delta }$
over
![]() $\mathcal{P}_3$
whose number of
$\mathcal{P}_3$
whose number of
![]() $\mathcal{R}$
-faces is at most
$\mathcal{R}$
-faces is at most
![]() $C |w|$
.
$C |w|$
.
Osin proves further facts that we will need concerning the geometry of
![]() $\hat{\Delta }$
. A diagram for the word
$\hat{\Delta }$
. A diagram for the word
![]() $w$
is of minimal type over all diagrams for
$w$
is of minimal type over all diagrams for
![]() $w$
if under lexicographic ordering it minimizes
$w$
if under lexicographic ordering it minimizes
Choose
![]() $\hat{\Delta }$
be of minimal type.
$\hat{\Delta }$
be of minimal type.
Let
![]() $M$
be the maximum length of the relators
$M$
be the maximum length of the relators
![]() $a^{t}\phi (a)^{-1}$
,
$a^{t}\phi (a)^{-1}$
,
![]() $b^{t}\phi (b)^{-1}$
,
$b^{t}\phi (b)^{-1}$
,
![]() $z[a,b]^{-1}$
, and
$z[a,b]^{-1}$
, and
![]() $z^tz^{-1}$
. Call an edge of
$z^tz^{-1}$
. Call an edge of
![]() $\hat{\Delta }$
internal to the
$\hat{\Delta }$
internal to the
![]() $\mathbb{Z}^2$
-faces when it has
$\mathbb{Z}^2$
-faces when it has
![]() $\mathbb{Z}^2$
-faces (or a
$\mathbb{Z}^2$
-faces (or a
![]() $\mathbb{Z}^2$
-face) on both sides. Osin (Lemma 2.15 of [Reference Osin21]) tells us that if
$\mathbb{Z}^2$
-face) on both sides. Osin (Lemma 2.15 of [Reference Osin21]) tells us that if
![]() $\hat{\Delta }$
is of minimal type then it has no edges which are internal to the
$\hat{\Delta }$
is of minimal type then it has no edges which are internal to the
![]() $\mathbb{Z}^2$
-faces and deduces (Corollary 2.16) that the sum of the lengths of the perimeters of
$\mathbb{Z}^2$
-faces and deduces (Corollary 2.16) that the sum of the lengths of the perimeters of
![]() $\mathbb{Z}^2$
-faces in
$\mathbb{Z}^2$
-faces in
![]() $\hat{\Delta }$
is at most
$\hat{\Delta }$
is at most
![]() $|w| + M N_{\mathcal{R}}$
.
$|w| + M N_{\mathcal{R}}$
.
Suppose that
![]() $w$
is a word on
$w$
is a word on
![]() $\{a,b, t\}^{\pm 1}$
and take
$\{a,b, t\}^{\pm 1}$
and take
![]() $\hat{\Delta }$
to be a diagram of minimal type for
$\hat{\Delta }$
to be a diagram of minimal type for
![]() $w$
over
$w$
over
![]() $\mathcal{P}_3$
.
$\mathcal{P}_3$
.
The words around
![]() $\mathcal{R}$
-faces only include the letters
$\mathcal{R}$
-faces only include the letters
![]() $t, z, a$
and
$t, z, a$
and
![]() $b$
, so they can overlap
$b$
, so they can overlap
![]() $\mathbb{Z}^2$
-faces only in edges labeled by
$\mathbb{Z}^2$
-faces only in edges labeled by
![]() $t$
and
$t$
and
![]() $z$
. Therefore, the word around each
$z$
. Therefore, the word around each
![]() $\mathbb{Z}^2$
-face is a word on
$\mathbb{Z}^2$
-face is a word on
![]() $\{t, z\}^{\pm 1}$
since every edge in the boundary of a
$\{t, z\}^{\pm 1}$
since every edge in the boundary of a
![]() $\mathbb{Z}^2$
-face is either in
$\mathbb{Z}^2$
-face is either in
![]() $\partial \hat{\Delta }$
or is also in the boundary of an
$\partial \hat{\Delta }$
or is also in the boundary of an
![]() $\mathcal{R}$
-face. Let
$\mathcal{R}$
-face. Let
![]() $\Delta$
be a diagram obtained from
$\Delta$
be a diagram obtained from
![]() $\hat{\Delta }$
by excising all
$\hat{\Delta }$
by excising all
![]() $\mathbb{Z}^2$
-faces and replacing each
$\mathbb{Z}^2$
-faces and replacing each
![]() $\mathbb{Z}^2$
-face with the appropriate minimal area diagram over
$\mathbb{Z}^2$
-face with the appropriate minimal area diagram over
![]() $\langle t, z \mid z^t =z \rangle$
. So
$\langle t, z \mid z^t =z \rangle$
. So
![]() $\Delta$
is a van Kampen diagram over
$\Delta$
is a van Kampen diagram over
![]() $\mathcal{P}_2$
. By Osin’s Theorem 1.5, as discussed above,
$\mathcal{P}_2$
. By Osin’s Theorem 1.5, as discussed above,
![]() $\Delta$
satisfies (1). As the Dehn function of
$\Delta$
satisfies (1). As the Dehn function of
![]() $\langle t, z \mid z^t =z \rangle$
enjoys a quadratic upper bound, and, given the bound on the lengths of the boundaries of
$\langle t, z \mid z^t =z \rangle$
enjoys a quadratic upper bound, and, given the bound on the lengths of the boundaries of
![]() $\mathbb{Z}^2$
-faces explained in the previous paragraph,
$\mathbb{Z}^2$
-faces explained in the previous paragraph,
![]() $\Delta$
also satisfies (2).
$\Delta$
also satisfies (2).
Because of the minimality assumption on the number of
![]() $\mathbb{Z}^2$
-faces, no two
$\mathbb{Z}^2$
-faces, no two
![]() $\mathbb{Z}^2$
-faces will have a vertex in common in
$\mathbb{Z}^2$
-faces will have a vertex in common in
![]() $\hat{\Delta }$
: two
$\hat{\Delta }$
: two
![]() $\mathbb{Z}^2$
-faces with a vertex in common could be replaced by a single
$\mathbb{Z}^2$
-faces with a vertex in common could be replaced by a single
![]() $\mathbb{Z}^2$
-face. Also the boundary circuit of any
$\mathbb{Z}^2$
-face. Also the boundary circuit of any
![]() $\mathbb{Z}^2$
-face in
$\mathbb{Z}^2$
-face in
![]() $\hat{\Delta }$
will be a simple loop. This is because
$\hat{\Delta }$
will be a simple loop. This is because
![]() $E(\hat{\Delta })$
is minimal: a
$E(\hat{\Delta })$
is minimal: a
![]() $\mathbb{Z}^2$
-face with a non-simple loop as its boundary circuit could be excised and a
$\mathbb{Z}^2$
-face with a non-simple loop as its boundary circuit could be excised and a
![]() $\mathbb{Z}^2$
-face with a shorter and simple boundary loop inserted in its place. Thus, the
$\mathbb{Z}^2$
-face with a shorter and simple boundary loop inserted in its place. Thus, the
![]() $\mathbb{Z}^2$
-faces form disjoint islands in
$\mathbb{Z}^2$
-faces form disjoint islands in
![]() $\hat{\Delta }$
and there are no
$\hat{\Delta }$
and there are no
![]() $\mathcal{R}$
-faces enclosed within these islands. In the light of this, (3) follows from (1).
$\mathcal{R}$
-faces enclosed within these islands. In the light of this, (3) follows from (1).
Proof of Theorem A in Case 1. We suppose
![]() $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
. By Lemma 5.2, there exists
$\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
. By Lemma 5.2, there exists
![]() $\Phi$
so that
$\Phi$
so that
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Psi }$
have equivalent Dehn function, and
$M_{\Psi }$
have equivalent Dehn function, and
![]() $M_{\Phi }$
has presentation:
$M_{\Phi }$
has presentation:
which is a central extension of
where
![]() $\phi \in{\textrm{Aut}}(F(a,b))$
has the property that
$\phi \in{\textrm{Aut}}(F(a,b))$
has the property that
![]() $\phi ([a,b]) = [a,b]$
. If
$\phi ([a,b]) = [a,b]$
. If
![]() $z = [a,b]$
, then in
$z = [a,b]$
, then in
![]() $M_{\Phi }$
$M_{\Phi }$
So
![]() $M_{\Phi }$
also can be presented as:
$M_{\Phi }$
also can be presented as:
which reveals it to be a central extension of
by
![]() $\mathbb{Z} = \langle c \rangle$
.
$\mathbb{Z} = \langle c \rangle$
.
Suppose
![]() $w$
is a word in
$w$
is a word in
![]() $\{a,b, c, t\}^{\pm 1}$
of length
$\{a,b, c, t\}^{\pm 1}$
of length
![]() $n$
representing the identity in
$n$
representing the identity in
![]() $\mathcal{Q}$
. Let
$\mathcal{Q}$
. Let
![]() $\overline{w}$
be
$\overline{w}$
be
![]() $w$
with all
$w$
with all
![]() $c^{\pm 1}$
deleted.
$c^{\pm 1}$
deleted.
Let
![]() $\overline{\Delta }$
be a van Kampen diagram for
$\overline{\Delta }$
be a van Kampen diagram for
![]() $\overline{w}$
as per Lemma 5.5. Given (3) of that lemma, there is a forest
$\overline{w}$
as per Lemma 5.5. Given (3) of that lemma, there is a forest
![]() $\mathcal{F}$
in the 1-skeleton of the union of the
$\mathcal{F}$
in the 1-skeleton of the union of the
![]() $\mathcal{R}$
-faces in
$\mathcal{R}$
-faces in
![]() $\overline{\Delta }$
joining every vertex of an
$\overline{\Delta }$
joining every vertex of an
![]() $\mathcal{R}$
-face to
$\mathcal{R}$
-face to
![]() $\partial \overline{\Delta }$
by a path of length at most
$\partial \overline{\Delta }$
by a path of length at most
![]() $Cn$
.
$Cn$
.
Charge
![]() $\overline{\Delta }$
. Given that the defining relation
$\overline{\Delta }$
. Given that the defining relation
![]() $z^t =z$
is unchanged on lifting to the central extension, the
$z^t =z$
is unchanged on lifting to the central extension, the
![]() $\mathbb{Z}^2$
-faces of Lemma 5.5 (2) are unchanged. There are
$\mathbb{Z}^2$
-faces of Lemma 5.5 (2) are unchanged. There are
![]() $Cn^2$
such
$Cn^2$
such
![]() $\mathbb{Z}^2$
faces. Let
$\mathbb{Z}^2$
faces. Let
![]() $m = \max \{|k_a|, |k_b|\}$
. The remaining
$m = \max \{|k_a|, |k_b|\}$
. The remaining
![]() $Cn$
$Cn$
![]() $\mathcal{R}$
-faces of Lemma 5.5 (1) each acquire at most
$\mathcal{R}$
-faces of Lemma 5.5 (1) each acquire at most
![]() $m$
charges. These are discharged by adding partial
$m$
charges. These are discharged by adding partial
![]() $c$
-corridors that follow the forest
$c$
-corridors that follow the forest
![]() $\mathcal{F}$
to the boundary and then around the boundary to a base vertex. Each partial
$\mathcal{F}$
to the boundary and then around the boundary to a base vertex. Each partial
![]() $c$
-corridor has length at most
$c$
-corridor has length at most
![]() $(C+1)n$
: the length of the path to the boundary is at most
$(C+1)n$
: the length of the path to the boundary is at most
![]() $Cn$
by Lemma 5.5 (3) and the length of the path to the base vertex is at most
$Cn$
by Lemma 5.5 (3) and the length of the path to the base vertex is at most
![]() $n$
. In total then,
$n$
. In total then,
![]() $c$
-partial corridors contribute at most
$c$
-partial corridors contribute at most
![]() $(C+1)^{2}mn^2$
2-cells to the new diagram. The result is a diagram over
$(C+1)^{2}mn^2$
2-cells to the new diagram. The result is a diagram over
![]() $\mathcal{Q}$
of area at most
$\mathcal{Q}$
of area at most
![]() $((C+1)^{2}m +C) n^2$
for a word
$((C+1)^{2}m +C) n^2$
for a word
![]() $\overline{w}c^k$
, which has length less than
$\overline{w}c^k$
, which has length less than
![]() $n$
. By adding in an annular region to rearrange
$n$
. By adding in an annular region to rearrange
![]() $\overline{w}c^k$
to
$\overline{w}c^k$
to
![]() $w$
, as per the electrostatic model of Section 4, it follows that
$w$
, as per the electrostatic model of Section 4, it follows that
![]() $w$
has a diagram over
$w$
has a diagram over
![]() $\mathcal{Q}$
of area at most
$\mathcal{Q}$
of area at most
![]() $({(C+1)}^{2}m +C+1) n^2$
.
$({(C+1)}^{2}m +C+1) n^2$
.
5.3. Theorem A in the case where all eigenvalues of
 $\psi_{\boldsymbol{ab}}$
are unit
$\psi_{\boldsymbol{ab}}$
are unit
We begin by arguing that for the purpose of determining Dehn functions, we can further specialize the family of presentations as follows.
Lemma 5.6. Suppose that
![]() $\Phi \in{\textrm{Aut}}(G)$
is as per Lemma 5.2, and that eigenvalues of
$\Phi \in{\textrm{Aut}}(G)$
is as per Lemma 5.2, and that eigenvalues of
![]() $\phi _{ab}$
are
$\phi _{ab}$
are
![]() $1$
. Then there exists
$1$
. Then there exists
![]() $\Xi \in{\textrm{Aut}}(G)$
such that the eigenvalues of
$\Xi \in{\textrm{Aut}}(G)$
such that the eigenvalues of
![]() $\xi _{ab}$
are also
$\xi _{ab}$
are also
![]() $1$
, the Dehn functions of
$1$
, the Dehn functions of
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Xi }$
are equivalent, and
$M_{\Xi }$
are equivalent, and
for some
![]() $\beta \in \mathbb{Z}$
. Moreover, conditions 2 and 3 of Section 5.1 hold for
$\beta \in \mathbb{Z}$
. Moreover, conditions 2 and 3 of Section 5.1 hold for
![]() $\Psi$
exactly when they hold for
$\Psi$
exactly when they hold for
![]() $\Xi$
, and they are characterized by
$\Xi$
, and they are characterized by
![]() $k_b \neq 0$
and
$k_b \neq 0$
and
![]() $k_b = 0$
, respectively.
$k_b = 0$
, respectively.
Proof. We have
![]() $\Phi$
per Lemma 5.2. So
$\Phi$
per Lemma 5.2. So
![]() $\Phi (a) = \phi (a)c^{k_a'}, \ \Phi (b) = \phi (b)c^{k_b'}, \ \Phi (c) =c$
, for some
$\Phi (a) = \phi (a)c^{k_a'}, \ \Phi (b) = \phi (b)c^{k_b'}, \ \Phi (c) =c$
, for some
![]() $k_a', k_b' \in \mathbb{Z}$
and some
$k_a', k_b' \in \mathbb{Z}$
and some
![]() $\phi \in{\textrm{Aut}}(F(a,b))$
such that
$\phi \in{\textrm{Aut}}(F(a,b))$
such that
![]() $\phi _{ab}$
has determinant
$\phi _{ab}$
has determinant
![]() $1$
. Lemma 5.2 implied that the eigenvalues of
$1$
. Lemma 5.2 implied that the eigenvalues of
![]() $\phi _{ab}$
are 1 for automorphisms of types 2 and 3.
$\phi _{ab}$
are 1 for automorphisms of types 2 and 3.
We will show that there is
![]() $\Xi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
such that for some
$\Xi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
such that for some
![]() $\kappa \geq 0$
,
$\kappa \geq 0$
,
![]() $[\Phi ^\kappa ]$
and
$[\Phi ^\kappa ]$
and
![]() $[\Xi ]$
are conjugate in
$[\Xi ]$
are conjugate in
![]() $\textrm{Out}(F_2 \times \mathbb{Z})$
and
$\textrm{Out}(F_2 \times \mathbb{Z})$
and
![]() $\xi = \Xi \!\! \upharpoonright _{F(a,b)}$
maps
$\xi = \Xi \!\! \upharpoonright _{F(a,b)}$
maps
![]() $b \mapsto b$
.
$b \mapsto b$
.
As
![]() $\phi _{ab}$
has only eigenvalue 1, it is either the identity or it has linear growth. Lemma 3.7, implies that for some
$\phi _{ab}$
has only eigenvalue 1, it is either the identity or it has linear growth. Lemma 3.7, implies that for some
![]() $\kappa$
,
$\kappa$
,
![]() $\phi ^\kappa _{ab}$
is conjugate in
$\phi ^\kappa _{ab}$
is conjugate in
![]() $\textrm{SL}(2, \mathbb{Z})$
to
$\textrm{SL}(2, \mathbb{Z})$
to
![]() $\left (\begin{smallmatrix} 1 & \beta \\[5pt] 0 & 1 \end{smallmatrix}\right )$
for some
$\left (\begin{smallmatrix} 1 & \beta \\[5pt] 0 & 1 \end{smallmatrix}\right )$
for some
![]() $\beta \in \mathbb{Z}$
. Define
$\beta \in \mathbb{Z}$
. Define
![]() $\Phi ^\prime =\Phi ^\kappa$
, with restriction
$\Phi ^\prime =\Phi ^\kappa$
, with restriction
![]() $\phi ^\prime$
. On account of the standard isomorphism between
$\phi ^\prime$
. On account of the standard isomorphism between
![]() $\textrm{Out}(F_2)$
and
$\textrm{Out}(F_2)$
and
![]() $\textrm{GL}(2,\mathbb{Z})$
,
$\textrm{GL}(2,\mathbb{Z})$
,
![]() $[\phi ^\prime ]$
is conjugate in
$[\phi ^\prime ]$
is conjugate in
![]() $\textrm{Out}(F_2)$
to
$\textrm{Out}(F_2)$
to
![]() $[\xi ]$
where
$[\xi ]$
where
![]() $\xi (a) = ab^{\beta }$
and
$\xi (a) = ab^{\beta }$
and
![]() $\xi (b) = b$
. So
$\xi (b) = b$
. So
![]() $\xi = f^{-1}\circ \phi ^\prime \circ f\circ \iota _g$
for some
$\xi = f^{-1}\circ \phi ^\prime \circ f\circ \iota _g$
for some
![]() $f \in{\textrm{Aut}}(F_2)$
and some
$f \in{\textrm{Aut}}(F_2)$
and some
![]() $\iota _g \in \textrm{Inn}(F_2)$
. We lift
$\iota _g \in \textrm{Inn}(F_2)$
. We lift
![]() $f, \xi, \iota _g \in{\textrm{Aut}}(F_2)$
to
$f, \xi, \iota _g \in{\textrm{Aut}}(F_2)$
to
![]() $F, \Xi, \hat{\iota }_g \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
by defining
$F, \Xi, \hat{\iota }_g \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$
by defining
![]() $F(gc^k) = f(g)c^k$
for
$F(gc^k) = f(g)c^k$
for
![]() $g \in F_2$
and
$g \in F_2$
and
![]() $k \in \mathbb{Z}$
, by taking
$k \in \mathbb{Z}$
, by taking
![]() $\hat{\iota }_g$
to be conjugation by
$\hat{\iota }_g$
to be conjugation by
![]() $g$
, and by defining
$g$
, and by defining
![]() $\Xi \;:\!=\; F^{-1} \circ \Phi ^\prime \circ F \circ \hat{\iota }_g$
. Because
$\Xi \;:\!=\; F^{-1} \circ \Phi ^\prime \circ F \circ \hat{\iota }_g$
. Because
![]() $c$
is central,
$c$
is central,
![]() $\hat{\iota }_g(c) = c$
. In particular,
$\hat{\iota }_g(c) = c$
. In particular,
for some
![]() $k_a, k_b \in \mathbb{Z}$
. (Note that
$k_a, k_b \in \mathbb{Z}$
. (Note that
![]() $p( \Phi ^{\prime }(b))$
and
$p( \Phi ^{\prime }(b))$
and
![]() $p(\Xi (b)) = k_b$
may not be equal, as
$p(\Xi (b)) = k_b$
may not be equal, as
![]() $\Phi ^\prime (f(b)^{g^{-1}})$
, and
$\Phi ^\prime (f(b)^{g^{-1}})$
, and
![]() $\Phi ^\prime (b)$
will not generally have the same index sum of
$\Phi ^\prime (b)$
will not generally have the same index sum of
![]() $c$
letters.)
$c$
letters.)
Therefore,
![]() $M_{\Xi }$
has the presentation claimed and
$M_{\Xi }$
has the presentation claimed and
![]() $\xi _{ab}$
has only
$\xi _{ab}$
has only
![]() $1$
as an eigenvalue, as required. By Lemma 3.6, the mapping tori
$1$
as an eigenvalue, as required. By Lemma 3.6, the mapping tori
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Xi }$
have equivalent Dehn functions.
$M_{\Xi }$
have equivalent Dehn functions.
Next we will show that
-
1. If
 $\phi ^{\prime }_{ab} \neq \textrm{id}$
, then
$\phi ^{\prime }_{ab} \neq \textrm{id}$
, then
 $p(\Xi (b))=k_b\neq 0$
if and only if there exists
$p(\Xi (b))=k_b\neq 0$
if and only if there exists
 $w \in F_2$
such that
$w \in F_2$
such that
 $\phi ^{\prime }_{ab}(w_{ab})= w_{ab}$
and
$\phi ^{\prime }_{ab}(w_{ab})= w_{ab}$
and
 $p(\Phi ^{\prime }(w)) \neq 0$
.
$p(\Phi ^{\prime }(w)) \neq 0$
. -
2. If
 $\phi ^{\prime }_{ab} = \textrm{id}$
, exactly one of the following holds:
$\phi ^{\prime }_{ab} = \textrm{id}$
, exactly one of the following holds:-
(a)
 $p(\Phi ^\prime (x)) = 0$
for all
$p(\Phi ^\prime (x)) = 0$
for all
 $x \in \langle a,b \rangle$
, in which case
$x \in \langle a,b \rangle$
, in which case
 $\Xi =\textrm{Id}$
,
$\Xi =\textrm{Id}$
, -
(b)
 $p(\Phi ^\prime (x)) \neq 0$
for some
$p(\Phi ^\prime (x)) \neq 0$
for some
 $x$
, in which case
$x$
, in which case
 $p(\Xi (a))$
or
$p(\Xi (a))$
or
 $p(\Xi (b))$
is nonzero.
$p(\Xi (b))$
is nonzero.
-
Moreover, this implies that
![]() $\Phi$
,
$\Phi$
,
![]() $\Phi '$
and
$\Phi '$
and
![]() $\Xi$
either all satisfy condition 2 or all satisfy condition 3 of Section 5.1.
$\Xi$
either all satisfy condition 2 or all satisfy condition 3 of Section 5.1.
Proof of 1: We wish to compare
![]() $p(\Phi ^\prime (w))$
and
$p(\Phi ^\prime (w))$
and
![]() $p(\Xi (b))$
. Let
$p(\Xi (b))$
. Let
![]() $w^{\prime } = f(b)$
. The following calculation shows that
$w^{\prime } = f(b)$
. The following calculation shows that
![]() $w_{ab}^{\prime }$
is another fixed point of
$w_{ab}^{\prime }$
is another fixed point of
![]() $\phi ^\prime _{ab}$
and that
$\phi ^\prime _{ab}$
and that
![]() $p(\Phi ^\prime (w^{\prime })) =p(\Xi (b))= k_b$
:
$p(\Phi ^\prime (w^{\prime })) =p(\Xi (b))= k_b$
:
If
![]() $\phi ^{\prime }_{ab} \neq \mbox{id}$
, then since
$\phi ^{\prime }_{ab} \neq \mbox{id}$
, then since
![]() $w_{ab}$
and
$w_{ab}$
and
![]() $w^{\prime }_{ab}$
are both fixed by
$w^{\prime }_{ab}$
are both fixed by
![]() $\phi ^{\prime }_{ab}$
,
$\phi ^{\prime }_{ab}$
,
![]() $w_{ab} = dw^{\prime }_{ab}$
for some
$w_{ab} = dw^{\prime }_{ab}$
for some
![]() $d\neq 0$
, and therefore
$d\neq 0$
, and therefore
![]() $p(\Phi ^{\prime }(w)) = dp(\Phi ^{\prime }(w^{\prime })) = dk_b$
. So
$p(\Phi ^{\prime }(w)) = dp(\Phi ^{\prime }(w^{\prime })) = dk_b$
. So
![]() $p(\Xi (b))=k_b\neq 0$
if and only if
$p(\Xi (b))=k_b\neq 0$
if and only if
![]() $p(\Phi ^{\prime }(w)) \neq 0$
. In case 1,
$p(\Phi ^{\prime }(w)) \neq 0$
. In case 1,
![]() $\Phi ^{\prime }$
and
$\Phi ^{\prime }$
and
![]() $\Xi$
either both satisfy condition 2 or both satisfy condition 3, and so this holds for
$\Xi$
either both satisfy condition 2 or both satisfy condition 3, and so this holds for
![]() $\Psi$
and
$\Psi$
and
![]() $\Xi$
by Lemma 5.2.
$\Xi$
by Lemma 5.2.
Proof of 2:
![]() $\phi ^{\prime } \in \textrm{Inn}(F_2)$
since
$\phi ^{\prime } \in \textrm{Inn}(F_2)$
since
is exact and
![]() $\phi ^{\prime }_{ab}=\textrm{id}$
. Therefore,
$\phi ^{\prime }_{ab}=\textrm{id}$
. Therefore,
![]() $\Xi$
maps
$\Xi$
maps
![]() $a \mapsto ac^{k_a}$
,
$a \mapsto ac^{k_a}$
,
![]() $b \mapsto bc^{k_b}$
, and
$b \mapsto bc^{k_b}$
, and
![]() $c \mapsto c$
for some
$c \mapsto c$
for some
![]() $k_a, k_b \in \mathbb{Z}$
, and so
$k_a, k_b \in \mathbb{Z}$
, and so
![]() $\xi _{ab} = \mbox{id}$
also. This suffices to show 2.
$\xi _{ab} = \mbox{id}$
also. This suffices to show 2.
When
![]() $\phi ^{\prime }_{ab}= \mbox{id}$
, condition 2 amounts to “there exists
$\phi ^{\prime }_{ab}= \mbox{id}$
, condition 2 amounts to “there exists
![]() $g \in F_2$
such that
$g \in F_2$
such that
![]() $p(\Phi ^{\prime }(g)) \neq 0$
”. This holds for
$p(\Phi ^{\prime }(g)) \neq 0$
”. This holds for
![]() $\Phi ^{\prime }$
if and only if it holds for
$\Phi ^{\prime }$
if and only if it holds for
![]() $\Xi$
, by 2. Again
$\Xi$
, by 2. Again
![]() $\Phi$
,
$\Phi$
,
![]() $\Phi '$
and
$\Phi '$
and
![]() $\Xi$
either all satisfy condition 2 or all satisfy condition 3, and so this holds for
$\Xi$
either all satisfy condition 2 or all satisfy condition 3, and so this holds for
![]() $\Psi$
and
$\Psi$
and
![]() $\Xi$
by Lemma 5.2.
$\Xi$
by Lemma 5.2.
Proof of Theorem A in Case 2. By Lemmas 5.2 and 5.6, for the purpose of calculating the Dehn function we may work with
where
![]() $k_b \neq 0$
. The subgroup
$k_b \neq 0$
. The subgroup
![]() $K \;:\!=\; \langle b, c \mid [b,c] \rangle \cong \mathbb{Z}^2$
quasi-isometrically embeds in
$K \;:\!=\; \langle b, c \mid [b,c] \rangle \cong \mathbb{Z}^2$
quasi-isometrically embeds in
![]() $F_2 \times \langle c \rangle$
and
$F_2 \times \langle c \rangle$
and
![]() $\Xi (K) = \langle bc^{k_b}, c \rangle = K$
. So, by Lemma 3.5,
$\Xi (K) = \langle bc^{k_b}, c \rangle = K$
. So, by Lemma 3.5,
![]() $n \mapsto n^2 \max \{|\Xi ^n(b)|, |\Xi ^n(c)|\}= n^2(k_bn+1)$
is a lower bound for the Dehn function of
$n \mapsto n^2 \max \{|\Xi ^n(b)|, |\Xi ^n(c)|\}= n^2(k_bn+1)$
is a lower bound for the Dehn function of
![]() $M_{\Xi }$
. This lower bound is cubic (as
$M_{\Xi }$
. This lower bound is cubic (as
![]() $k_b \neq 0$
), matching our upper bound from Corollary 5.3, so the claim is established.
$k_b \neq 0$
), matching our upper bound from Corollary 5.3, so the claim is established.
We now turn to case 3. This time, Lemmas 5.2 and 5.6 allow us to work with
![]() $M_{\Xi }$
which has the form:
$M_{\Xi }$
which has the form:
where,
![]() $\beta$
is nonzero. (The case
$\beta$
is nonzero. (The case
![]() $\beta =0$
and
$\beta =0$
and
![]() $k_a \neq 0$
is covered by Theorem A in case 2—the Dehn function of this mapping torus is cubic. If
$k_a \neq 0$
is covered by Theorem A in case 2—the Dehn function of this mapping torus is cubic. If
![]() $\beta =0$
and
$\beta =0$
and
![]() $k_a =0$
, then
$k_a =0$
, then
![]() $M_{\Xi } = \langle a, b, c \mid [a,c]=1, [b,c]=1 \rangle \times \langle t \rangle$
, which has quadratic Dehn function.)
$M_{\Xi } = \langle a, b, c \mid [a,c]=1, [b,c]=1 \rangle \times \langle t \rangle$
, which has quadratic Dehn function.)
The methods of case 1 cannot be used here. Indeed, Button and R. Kropholler in Theorem 4.4 [Reference Button and Kropholler12] have shown that for
![]() $\xi$
with this form,
$\xi$
with this form,
![]() $M_{\xi }$
is not strongly hyperbolic relative to any finitely generated proper subgroup, so van Kampen diagrams over
$M_{\xi }$
is not strongly hyperbolic relative to any finitely generated proper subgroup, so van Kampen diagrams over
![]() $M_{\xi }$
do not decompose into uncharged islands with linear-area complement. Instead will use a variant of the electrostatic model whereby the diagram will be discharged along partial corridors (see Section 3.1) in a manner controlled by an application of Hall’s Marriage Theorem, which we now review.
$M_{\xi }$
do not decompose into uncharged islands with linear-area complement. Instead will use a variant of the electrostatic model whereby the diagram will be discharged along partial corridors (see Section 3.1) in a manner controlled by an application of Hall’s Marriage Theorem, which we now review.
A subgraph
![]() $F$
of a graph
$F$
of a graph
![]() $\Gamma$
is a 1-factor for
$\Gamma$
is a 1-factor for
![]() $\Gamma$
if it contains all vertices of
$\Gamma$
if it contains all vertices of
![]() $\Gamma$
and each vertex meets precisely one edge of
$\Gamma$
and each vertex meets precisely one edge of
![]() $F$
. In other words, a 1-factor pairs every vertex with a neighbor. We will be interested in the following special case:
$F$
. In other words, a 1-factor pairs every vertex with a neighbor. We will be interested in the following special case:
Lemma 5.7. A
![]() $k$
-regular bipartite graph
$k$
-regular bipartite graph
![]() $\Gamma$
with
$\Gamma$
with
![]() $k\geq 1$
has a 1-factor.
$k\geq 1$
has a 1-factor.
This is a consequence of Hall’s Marriage Theorem. See [Reference Diestel13] for a proof.
Proof of Theorem A in Case 3. By Lemma 5.6, it suffices to prove that
![]() $M_{\Phi }$
, presented by:
$M_{\Phi }$
, presented by:
has quadratic Dehn function. If
![]() $k_a =0$
, then
$k_a =0$
, then
![]() $M_{\Phi }\cong M_{\phi }\times \langle c \rangle$
and so the Dehn functions of
$M_{\Phi }\cong M_{\phi }\times \langle c \rangle$
and so the Dehn functions of
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\phi }$
agree and are quadratic. Therefore, we may restrict our attention to the case where
$M_{\phi }$
agree and are quadratic. Therefore, we may restrict our attention to the case where
![]() $\beta$
and
$\beta$
and
![]() $k_a$
are both nonzero.
$k_a$
are both nonzero.
Van Kampen diagrams over
![]() $\mathcal{P}$
have both partial
$\mathcal{P}$
have both partial
![]() $b$
-corridors and partial
$b$
-corridors and partial
![]() $c$
-corridors.
$c$
-corridors.
![]() $M_{\Phi }$
is a central extension of
$M_{\Phi }$
is a central extension of
![]() $M_{\phi }$
by
$M_{\phi }$
by
![]() $\langle c \rangle$
, where
$\langle c \rangle$
, where
![]() $M_{\phi }$
is presented by:
$M_{\phi }$
is presented by:
Van Kampen diagrams over
![]() $\mathcal{Q}$
may have partial
$\mathcal{Q}$
may have partial
![]() $b$
-corridors.
$b$
-corridors.
Suppose
![]() $w$
is a word of length
$w$
is a word of length
![]() $n$
representing the identity in
$n$
representing the identity in
![]() $\mathcal{P}$
. Let
$\mathcal{P}$
. Let
![]() $\overline{w}$
be
$\overline{w}$
be
![]() $w$
with all
$w$
with all
![]() $c^{\pm 1}$
removed. Then
$c^{\pm 1}$
removed. Then
![]() $w = \overline{w}c^m$
in
$w = \overline{w}c^m$
in
![]() $M_{\Phi }$
for some
$M_{\Phi }$
for some
![]() $m \in \mathbb{Z}$
and
$m \in \mathbb{Z}$
and
![]() $|\overline{w}| \leq |w|$
. Since
$|\overline{w}| \leq |w|$
. Since
![]() $\mathcal{Q}$
is free-by-cyclic and non-hyperbolic, it has a quadratic Dehn function. So there exists a minimal area diagram
$\mathcal{Q}$
is free-by-cyclic and non-hyperbolic, it has a quadratic Dehn function. So there exists a minimal area diagram
![]() $\overline{\Delta }$
for
$\overline{\Delta }$
for
![]() $\overline{w}$
over
$\overline{w}$
over
![]() $\mathcal{Q}$
such that
$\mathcal{Q}$
such that
![]() $\textrm{Area}(\overline{\Delta }) \leq C |\overline{w}|^2$
. We charge
$\textrm{Area}(\overline{\Delta }) \leq C |\overline{w}|^2$
. We charge
![]() $\overline{\Delta }$
by replacing 2-cells in
$\overline{\Delta }$
by replacing 2-cells in
![]() $\overline{\Delta }$
with 2-cells labeled by the defining relators from
$\overline{\Delta }$
with 2-cells labeled by the defining relators from
![]() $\mathcal{P}$
, as in the first steps of the electrostatic model (see Section 4). What follows is a scheme for adding in 2-cells to “discharge”
$\mathcal{P}$
, as in the first steps of the electrostatic model (see Section 4). What follows is a scheme for adding in 2-cells to “discharge”
![]() $\overline{\Delta }$
so as to create a diagram for
$\overline{\Delta }$
so as to create a diagram for
![]() $\overline{w}c^m$
over
$\overline{w}c^m$
over
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
The idea is that if we can pair off oppositely oriented capping faces that are joined by partial
![]() $b$
-corridors, then we can add in partial
$b$
-corridors, then we can add in partial
![]() $c$
-corridors following the
$c$
-corridors following the
![]() $b$
-corridors, as in Figure 5, in order to discharge the
$b$
-corridors, as in Figure 5, in order to discharge the
![]() $c$
-edges in our diagram. As
$c$
-edges in our diagram. As
![]() $c$
is central in
$c$
is central in
![]() $\mathcal{P}$
, partial
$\mathcal{P}$
, partial
![]() $c$
-corridors can be run alongside this partial
$c$
-corridors can be run alongside this partial
![]() $b$
-corridor, and the word one reads along both the top and bottom of the
$b$
-corridor, and the word one reads along both the top and bottom of the
![]() $c$
-corridor will be the same as that word along the top and bottom of the
$c$
-corridor will be the same as that word along the top and bottom of the
![]() $b$
-corridor, namely some power of
$b$
-corridor, namely some power of
![]() $t$
. We wish to find a consistent way of partnering vertices so that we can replicate the picture in Figure 5, adding in partial
$t$
. We wish to find a consistent way of partnering vertices so that we can replicate the picture in Figure 5, adding in partial
![]() $c$
-corridors to discharge between partners throughout the van Kampen diagram, with no leftover charges to consider.
$c$
-corridors to discharge between partners throughout the van Kampen diagram, with no leftover charges to consider.

Figure 5. If a partial
![]() $b$
-corridor joins two capping faces in
$b$
-corridor joins two capping faces in
![]() $\overline{\Delta }$
, their
$\overline{\Delta }$
, their
![]() $c$
-charges can be discharged by adding partial
$c$
-charges can be discharged by adding partial
![]() $c$
-corridors “following” that partial
$c$
-corridors “following” that partial
![]() $b$
-corridor.
$b$
-corridor.
I. Modeling
![]() $\overline{\Delta }$
with a graph. Construct a planar graph with multi-edges,
$\overline{\Delta }$
with a graph. Construct a planar graph with multi-edges,
![]() $\Gamma$
, from
$\Gamma$
, from
![]() $\overline{\Delta }$
as illustrated in Figure 6:
$\overline{\Delta }$
as illustrated in Figure 6:
![]() $\Gamma$
has a black vertex for each capping face in
$\Gamma$
has a black vertex for each capping face in
![]() $\overline{\Delta }$
; whenever two capping faces are connected by a partial
$\overline{\Delta }$
; whenever two capping faces are connected by a partial
![]() $b$
-corridor, possibly of length zero, an edge connects the corresponding vertices (two vertices may share multiple edges); we also add an edge and a white vertex to
$b$
-corridor, possibly of length zero, an edge connects the corresponding vertices (two vertices may share multiple edges); we also add an edge and a white vertex to
![]() $\Gamma$
for each partial
$\Gamma$
for each partial
![]() $b$
-corridor that goes to the boundary. Every black vertex in the graph
$b$
-corridor that goes to the boundary. Every black vertex in the graph
![]() $\Gamma$
is degree
$\Gamma$
is degree
![]() $|\beta |$
and every white vertex has degree 1.
$|\beta |$
and every white vertex has degree 1.

Figure 6. From capping faces and partial corridors in
![]() $\overline{\Delta }$
, construct a graph
$\overline{\Delta }$
, construct a graph
![]() $\Gamma$
. Black vertices correspond to capping faces, white vertices correspond to 1-cells labeled
$\Gamma$
. Black vertices correspond to capping faces, white vertices correspond to 1-cells labeled
![]() $b$
in
$b$
in
![]() $\partial \overline{\Delta }$
, and the edges correspond to partial
$\partial \overline{\Delta }$
, and the edges correspond to partial
![]() $b$
-corridor.
$b$
-corridor.
The graph
![]() $\Gamma$
is bipartite (but not generally black–white bipartite, as you can see in Figure 6): partition the black vertices according to whether they correspond to capping faces with clockwise or anticlockwise oriented
$\Gamma$
is bipartite (but not generally black–white bipartite, as you can see in Figure 6): partition the black vertices according to whether they correspond to capping faces with clockwise or anticlockwise oriented
![]() $b$
-edges and extend this partition to the white vertices.
$b$
-edges and extend this partition to the white vertices.
II. Building a regular bipartite graph. We would like to apply Lemma 5.7, but
![]() $\Gamma$
may not be regular: black vertices have degree
$\Gamma$
may not be regular: black vertices have degree
![]() $\left |\beta \right |$
, but white vertices have degree
$\left |\beta \right |$
, but white vertices have degree
![]() $1$
. So, as illustrated in Figure 7a, we construct a regular graph
$1$
. So, as illustrated in Figure 7a, we construct a regular graph
![]() $\hat{\Gamma }$
which has
$\hat{\Gamma }$
which has
![]() $\Gamma$
as a subgraph. Take
$\Gamma$
as a subgraph. Take
![]() $|\beta |$
many copies of
$|\beta |$
many copies of
![]() $\Gamma$
, and identify the white vertices in each of the copies. That is,
$\Gamma$
, and identify the white vertices in each of the copies. That is,
 \begin{equation*}\hat {\Gamma } \ \;:\!=\; \ \displaystyle \left (\bigsqcup _{i=1}^{|\beta |} \Gamma \times \{i\}\right )/ \sim,\end{equation*}
\begin{equation*}\hat {\Gamma } \ \;:\!=\; \ \displaystyle \left (\bigsqcup _{i=1}^{|\beta |} \Gamma \times \{i\}\right )/ \sim,\end{equation*}
where
![]() $(v,i) \sim (v,j)$
for all
$(v,i) \sim (v,j)$
for all
![]() $i,j$
when
$i,j$
when
![]() $v$
is a white vertex. White vertices are degree one, so the identification of
$v$
is a white vertex. White vertices are degree one, so the identification of
![]() $|\beta |$
copies of
$|\beta |$
copies of
![]() $\Gamma$
forces
$\Gamma$
forces
![]() $\hat{\Gamma }$
to be a
$\hat{\Gamma }$
to be a
![]() $|\beta |$
-regular graph. If
$|\beta |$
-regular graph. If
![]() $\Gamma$
is bipartite with respect to a partition
$\Gamma$
is bipartite with respect to a partition
![]() $A \sqcup B$
of its vertices, then
$A \sqcup B$
of its vertices, then
![]() $\hat{\Gamma }$
is bipartite with respect to
$\hat{\Gamma }$
is bipartite with respect to
 \begin{equation*}\left ( \bigcup _{i=1}^{|\beta |}A \times \left \{i\right \} \right )/ \sim \ \bigsqcup \ \left ( \bigcup _{i=1}^{|\beta |}B \times \left \{i\right \} \right )/ \sim .\end{equation*}
\begin{equation*}\left ( \bigcup _{i=1}^{|\beta |}A \times \left \{i\right \} \right )/ \sim \ \bigsqcup \ \left ( \bigcup _{i=1}^{|\beta |}B \times \left \{i\right \} \right )/ \sim .\end{equation*}

Figure 7. Finding neighbor partners for
![]() $\Gamma$
via Hall’s Marriage Theorem.
$\Gamma$
via Hall’s Marriage Theorem.
III. Finding pairing partners for
![]() $b$
- and
$b$
- and
![]() $c$
-corridors. Lemma 5.7 tells us that
$c$
-corridors. Lemma 5.7 tells us that
![]() $\hat{\Gamma }$
has a 1-factor. This partners each vertex
$\hat{\Gamma }$
has a 1-factor. This partners each vertex
![]() $v \in \hat{\Gamma }$
with an adjacent vertex
$v \in \hat{\Gamma }$
with an adjacent vertex
![]() $v^{\prime }$
. View the image of
$v^{\prime }$
. View the image of
![]() $\Gamma \times \{1\}$
in
$\Gamma \times \{1\}$
in
![]() $\hat{\Gamma }$
as
$\hat{\Gamma }$
as
![]() $\Gamma$
, sitting as a subgraph in
$\Gamma$
, sitting as a subgraph in
![]() $\hat{\Gamma }$
. In the example of Figure 7c,
$\hat{\Gamma }$
. In the example of Figure 7c,
![]() $\Gamma$
is the gray subgraph at the back. If
$\Gamma$
is the gray subgraph at the back. If
![]() $v \in \Gamma$
is a black vertex, its partner
$v \in \Gamma$
is a black vertex, its partner
![]() $v'$
is also a vertex of
$v'$
is also a vertex of
![]() $\Gamma$
, but this may fail for white vertices.
$\Gamma$
, but this may fail for white vertices.
IV. Completing to a van Kampen diagram. If
![]() $v$
and
$v$
and
![]() $v^{\prime }$
are partnered black vertices in
$v^{\prime }$
are partnered black vertices in
![]() $\Gamma$
, then the corresponding capping faces are connected by at least one partial
$\Gamma$
, then the corresponding capping faces are connected by at least one partial
![]() $b$
-corridor (possibly of length zero). In
$b$
-corridor (possibly of length zero). In
![]() $\overline{\Delta }$
, the capping faces
$\overline{\Delta }$
, the capping faces
![]() $f$
and
$f$
and
![]() $f'$
corresponding to
$f'$
corresponding to
![]() $v$
and
$v$
and
![]() $v^{\prime }$
have
$v^{\prime }$
have
![]() $|k_a|$
many oppositely oriented charges. We will connect these charges with
$|k_a|$
many oppositely oriented charges. We will connect these charges with
![]() $|k_a|$
partial
$|k_a|$
partial
![]() $c$
-corridors, as in Figure 5. Choose one of the partial
$c$
-corridors, as in Figure 5. Choose one of the partial
![]() $b$
-corridors joining
$b$
-corridors joining
![]() $f$
to
$f$
to
![]() $f'$
(there is at least one). Run all of the partial
$f'$
(there is at least one). Run all of the partial
![]() $c$
-corridors for one capping face alongside the partial
$c$
-corridors for one capping face alongside the partial
![]() $b$
-corridor. If a black vertex
$b$
-corridor. If a black vertex
![]() $v$
is paired with a white vertex
$v$
is paired with a white vertex
![]() $v'$
in
$v'$
in
![]() $\Gamma$
, run all of the partial
$\Gamma$
, run all of the partial
![]() $c$
-corridors alongside the partial
$c$
-corridors alongside the partial
![]() $b$
-corridor to the boundary. Two white vertices will never be paired. At the ends of partial
$b$
-corridor to the boundary. Two white vertices will never be paired. At the ends of partial
![]() $b$
-corridors on capping faces, it may be necessary to insert rectangles in which the
$b$
-corridors on capping faces, it may be necessary to insert rectangles in which the
![]() $b$
-and
$b$
-and
![]() $c$
-corridors cross, as in Figure 8, but this requires no more than
$c$
-corridors cross, as in Figure 8, but this requires no more than
![]() $|\beta ||k_a|\textrm{Area}(\overline{\Delta })$
additional 2-cells. The total number of 2-cells added to
$|\beta ||k_a|\textrm{Area}(\overline{\Delta })$
additional 2-cells. The total number of 2-cells added to
![]() $\overline{\Delta }$
in this process is no more than
$\overline{\Delta }$
in this process is no more than
![]() $(|\beta |+1)|k_a|\textrm{Area}(\overline{\Delta })$
.
$(|\beta |+1)|k_a|\textrm{Area}(\overline{\Delta })$
.

Figure 8. Partnering in
![]() $\Gamma$
gives a consistent way to discharge
$\Gamma$
gives a consistent way to discharge
![]() $c$
-charges.
$c$
-charges.
V. Correcting the boundary. Partial
![]() $c$
-corridors follow partial
$c$
-corridors follow partial
![]() $b$
-corridors to the boundary in groups of
$b$
-corridors to the boundary in groups of
![]() $|k_a|$
. The new diagram has boundary length between
$|k_a|$
. The new diagram has boundary length between
![]() $|\overline{w}|$
and
$|\overline{w}|$
and
![]() $(|k_a|+1)|\overline{w}|$
and is a van Kampen diagram over
$(|k_a|+1)|\overline{w}|$
and is a van Kampen diagram over
![]() $\mathcal{P}$
for some word
$\mathcal{P}$
for some word
![]() $w^{\prime }$
in the pre-image of
$w^{\prime }$
in the pre-image of
![]() $\overline{w}$
. Deleting all
$\overline{w}$
. Deleting all
![]() $c^{\pm 1}$
from
$c^{\pm 1}$
from
![]() $w^{\prime }$
produces
$w^{\prime }$
produces
![]() $\overline{w}$
, but the arrangement of the
$\overline{w}$
, but the arrangement of the
![]() $c^{\pm 1}$
letters in
$c^{\pm 1}$
letters in
![]() $w^{\prime }$
may differ from that in
$w^{\prime }$
may differ from that in
![]() $w$
. As was described in Section 4, we glue around the outside of this diagram an annular diagram with the word
$w$
. As was described in Section 4, we glue around the outside of this diagram an annular diagram with the word
![]() $w^{\prime }$
along the inner boundary component and the word
$w^{\prime }$
along the inner boundary component and the word
![]() $w$
along the outer boundary component. Together, they form
$w$
along the outer boundary component. Together, they form
![]() $\Delta$
, a van Kampen diagram for
$\Delta$
, a van Kampen diagram for
![]() $w$
over
$w$
over
![]() $\mathcal{P}$
. This annular diagram has area at most
$\mathcal{P}$
. This annular diagram has area at most
![]() $(|k_a|+1)^2|\overline{w}|^2$
, and summing our area estimates,
$(|k_a|+1)^2|\overline{w}|^2$
, and summing our area estimates,
![]() $\Delta$
has area no more than
$\Delta$
has area no more than
![]() $(1+ (|\beta |+1)|k_a|)\textrm{Area}(\overline{\Delta }) + (|k_a|+1)^2|\overline{w}|^2$
. Since
$(1+ (|\beta |+1)|k_a|)\textrm{Area}(\overline{\Delta }) + (|k_a|+1)^2|\overline{w}|^2$
. Since
![]() $\textrm{Area}(\overline{\Delta }) \leq C|\overline{w}|^2$
, it follows that there is constant
$\textrm{Area}(\overline{\Delta }) \leq C|\overline{w}|^2$
, it follows that there is constant
![]() $A\gt 0$
such that for any given word
$A\gt 0$
such that for any given word
![]() $w$
in the generators of
$w$
in the generators of
![]() $\mathcal{P}$
that represents the identity, this construction produces a van Kampen diagram of area at most
$\mathcal{P}$
that represents the identity, this construction produces a van Kampen diagram of area at most
![]() $A|w|^2$
.
$A|w|^2$
.
6. Mapping tori of
 $G = \mathbb{Z}^2 \ast \mathbb{Z}= \langle a, b \mid [a,b] \rangle \ast \langle c \rangle$
$G = \mathbb{Z}^2 \ast \mathbb{Z}= \langle a, b \mid [a,b] \rangle \ast \langle c \rangle$
6.1. Automorphisms of
 $\mathbb{Z}^2 \ast \mathbb{Z}$
$\mathbb{Z}^2 \ast \mathbb{Z}$
Servatius [Reference Servatius24] and Laurence [Reference Laurence18] found a generating set for the automorphism group of a RAAG
![]() $A(\Gamma )$
based on the underlying graph
$A(\Gamma )$
based on the underlying graph
![]() $\Gamma$
(see Lemma 7.2). For
$\Gamma$
(see Lemma 7.2). For
it consists of the inner automorphisms, inversions, the one nontrivial graph isomorphism (
![]() $a \mapsto b$
,
$a \mapsto b$
,
![]() $b \mapsto a$
, and
$b \mapsto a$
, and
![]() $c \mapsto c$
), and the four transvections
$c \mapsto c$
), and the four transvections
 \begin{equation*}\begin {array}{l@{\quad}l@{\quad}l@{\quad}l} \tau _a \;:\;& a \mapsto ab, & b \mapsto b, & c \mapsto c, \\[5pt] \tau _b \;:\;& a \mapsto a, & b \mapsto ba, & c \mapsto c, \\[5pt] \psi _a \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto ca, \\[5pt] \psi _b \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto cb. \end {array}\end{equation*}
\begin{equation*}\begin {array}{l@{\quad}l@{\quad}l@{\quad}l} \tau _a \;:\;& a \mapsto ab, & b \mapsto b, & c \mapsto c, \\[5pt] \tau _b \;:\;& a \mapsto a, & b \mapsto ba, & c \mapsto c, \\[5pt] \psi _a \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto ca, \\[5pt] \psi _b \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto cb. \end {array}\end{equation*}
The following lemma and proposition are steps toward Theorem B in that they let us focus on particular presentations for the purposes of classifying Dehn functions of mapping tori of
![]() $\mathbb{Z}^2 \ast \mathbb{Z}$
. Recall that
$\mathbb{Z}^2 \ast \mathbb{Z}$
. Recall that
![]() $\iota _h$
denotes the inner automorphism
$\iota _h$
denotes the inner automorphism
![]() $x \mapsto h^{-1} x h$
.
$x \mapsto h^{-1} x h$
.
Lemma 6.1. For all
![]() $\Psi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
, there exist
$\Psi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
, there exist
![]() $\Phi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
,
$\Phi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
,
![]() $\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$
, and words
$\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$
, and words
![]() $w$
and
$w$
and
![]() $x$
on
$x$
on
![]() $a$
and
$a$
and
![]() $b$
such that
$b$
such that
and
![]() $[\Phi ] = [\Psi ]$
in
$[\Phi ] = [\Psi ]$
in
![]() $\textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Explicitly, if
$\textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$
. Explicitly, if
![]() $\Psi (a) = u_1c^{\epsilon _1}\dots u_n c^{\epsilon _n}u_{n+1}$
, where each
$\Psi (a) = u_1c^{\epsilon _1}\dots u_n c^{\epsilon _n}u_{n+1}$
, where each
![]() $\epsilon _i \neq 0$
and each
$\epsilon _i \neq 0$
and each
![]() $u_i \in \langle a, b\rangle$
, and
$u_i \in \langle a, b\rangle$
, and
![]() $u_2, \ldots, u_n \neq 1$
, then
$u_2, \ldots, u_n \neq 1$
, then
![]() $n=2m$
is even and for
$n=2m$
is even and for
![]() $g \;:\!=\; c^{\epsilon _{m+1}}u_{m+2}\dots u_{2m} c^{\epsilon _{2m}}u_{2m+1}$
, the map
$g \;:\!=\; c^{\epsilon _{m+1}}u_{m+2}\dots u_{2m} c^{\epsilon _{2m}}u_{2m+1}$
, the map
![]() $\iota _{g^{-1}}\circ \Psi$
satisfies the properties required of
$\iota _{g^{-1}}\circ \Psi$
satisfies the properties required of
![]() $\Phi$
.
$\Phi$
.
Moreover,
![]() $M_{\Psi }$
and
$M_{\Psi }$
and
![]() $M_{\Phi }$
have equivalent Dehn functions for any such
$M_{\Phi }$
have equivalent Dehn functions for any such
![]() $\Phi$
.
$\Phi$
.
Proof. Since
![]() $\textrm{Inn}(\mathbb{Z}^2 \ast \mathbb{Z}) \trianglelefteq{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
, all automorphisms
$\textrm{Inn}(\mathbb{Z}^2 \ast \mathbb{Z}) \trianglelefteq{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
, all automorphisms
![]() $\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
can be written as
$\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$
can be written as
![]() $\iota _h \circ \Phi$
where
$\iota _h \circ \Phi$
where
![]() $\iota _h$
denotes conjugation by some
$\iota _h$
denotes conjugation by some
![]() $h \in \mathbb{Z}^2 \ast \mathbb{Z}$
and
$h \in \mathbb{Z}^2 \ast \mathbb{Z}$
and
![]() $\Phi$
is some product of the inversions, transvections, and graph isomorphisms in the generating set above. These inversions, transvections, and graph isomorphisms restrict to automorphisms of the subgroup
$\Phi$
is some product of the inversions, transvections, and graph isomorphisms in the generating set above. These inversions, transvections, and graph isomorphisms restrict to automorphisms of the subgroup
![]() $\langle a, b \mid [a,b] \rangle$
and map the subset
$\langle a, b \mid [a,b] \rangle$
and map the subset
![]() $\langle a, b \rangle c^{\pm 1} \langle a, b \rangle$
to itself. So
$\langle a, b \rangle c^{\pm 1} \langle a, b \rangle$
to itself. So
for some
![]() $\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some words
$\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some words
![]() $w$
and
$w$
and
![]() $x$
on
$x$
on
![]() $a^{\pm 1}$
and
$a^{\pm 1}$
and
![]() $b^{\pm 1}$
. This proves the existence of a
$b^{\pm 1}$
. This proves the existence of a
![]() $\Phi$
with the required properties. We turn next to how to find such a
$\Phi$
with the required properties. We turn next to how to find such a
![]() $\Phi$
explicitly.
$\Phi$
explicitly.
Suppose
![]() $\Psi (a)$
is as per the statement. For
$\Psi (a)$
is as per the statement. For
![]() $h \in \mathbb{Z}^2 \ast \mathbb{Z}$
as above, we have that
$h \in \mathbb{Z}^2 \ast \mathbb{Z}$
as above, we have that
![]() $\Psi (a) \in \iota _{h}( \langle a, b \rangle )$
. So
$\Psi (a) \in \iota _{h}( \langle a, b \rangle )$
. So
But, given the free product structure of
![]() $\mathbb{Z}^2 \ast \mathbb{Z}$
, that implies that
$\mathbb{Z}^2 \ast \mathbb{Z}$
, that implies that
![]() $n=2m$
is even and
$n=2m$
is even and
where
![]() $v$
is some element of
$v$
is some element of
![]() $\langle a, b \rangle$
and
$\langle a, b \rangle$
and
![]() $g$
is as defined in the statement.
$g$
is as defined in the statement.
It follows then that
![]() $\iota _{g^{-1}} \circ \Psi = \iota _{v} \circ \iota _{h^{-1}} \circ \Psi = \iota _{v} \circ \Phi$
and maps
$\iota _{g^{-1}} \circ \Psi = \iota _{v} \circ \iota _{h^{-1}} \circ \Psi = \iota _{v} \circ \Phi$
and maps
![]() $a \mapsto \phi '(a), \ \ b \mapsto \phi '(b), \ \ c \mapsto w'c^{\pm 1}x'$
for some
$a \mapsto \phi '(a), \ \ b \mapsto \phi '(b), \ \ c \mapsto w'c^{\pm 1}x'$
for some
![]() $\phi ' \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some words
$\phi ' \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some words
![]() $w'$
and
$w'$
and
![]() $x'$
on
$x'$
on
![]() $a^{\pm 1}$
and
$a^{\pm 1}$
and
![]() $b^{\pm 1}$
.
$b^{\pm 1}$
.
By Lemma 3.6,
![]() $M_{\Psi }$
and
$M_{\Psi }$
and
![]() $M_{\Phi }$
have equivalent Dehn functions.
$M_{\Phi }$
have equivalent Dehn functions.
Proposition 6.2. Given
![]() $\Phi$
as per Lemma 6.1, there exist
$\Phi$
as per Lemma 6.1, there exist
![]() $\,\Xi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
,
$\,\Xi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$
,
![]() $\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$
, and
$\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$
, and
![]() $z \in \langle a, b \rangle$
such that
$z \in \langle a, b \rangle$
such that
and
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Xi }$
have equivalent Dehn functions. Moreover, Conditions 1, 2, and 3 of Theorem B apply to
$M_{\Xi }$
have equivalent Dehn functions. Moreover, Conditions 1, 2, and 3 of Theorem B apply to
![]() $\Xi$
exactly when they apply to
$\Xi$
exactly when they apply to
![]() $\Phi$
. Additionally,
$\Phi$
. Additionally,
-
when
 $\xi$
has finite order (Condition 1 of Theorem B), we may further assume
$\xi$
has finite order (Condition 1 of Theorem B), we may further assume
 $\xi \;:\;a \mapsto a, \ b \mapsto b$
, so that
$\xi \;:\;a \mapsto a, \ b \mapsto b$
, so that \begin{equation*}M_{\Xi } \ = \ \langle a,b,c,t \ \mid \ [a,b]=[a,t]=[b,t]=1, \ c^t=ca^kb^l \rangle,\end{equation*}
\begin{equation*}M_{\Xi } \ = \ \langle a,b,c,t \ \mid \ [a,b]=[a,t]=[b,t]=1, \ c^t=ca^kb^l \rangle,\end{equation*}
-
when
 $\xi$
is of infinite order and has only unit eigenvalues (Condition 3 of Theorem B), we may further assume
$\xi$
is of infinite order and has only unit eigenvalues (Condition 3 of Theorem B), we may further assume
 $\xi \;:\;a \mapsto ab^k, \ b \mapsto b$
for some
$\xi \;:\;a \mapsto ab^k, \ b \mapsto b$
for some
 $k \neq 0$
, so that for some
$k \neq 0$
, so that for some
 $l,m \in \mathbb{Z}$
,
$l,m \in \mathbb{Z}$
, \begin{equation*} M_{\Xi } \ = \ \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{k}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle .\end{equation*}
\begin{equation*} M_{\Xi } \ = \ \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{k}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle .\end{equation*}
Proof. How we will define
![]() $\Xi$
will depend on the form of
$\Xi$
will depend on the form of
![]() $\Phi (c)$
. Recall
$\Phi (c)$
. Recall
![]() $\Phi (c)= wc^{\pm 1}x$
as per Lemma 6.1. Define
$\Phi (c)= wc^{\pm 1}x$
as per Lemma 6.1. Define
![]() $\Xi _1 \;:\!=\; \iota _{w} \circ \Phi$
and
$\Xi _1 \;:\!=\; \iota _{w} \circ \Phi$
and
![]() $\Xi _2 \;:\!=\; \iota _{\phi (w)x^{-1}}\circ \Phi ^2$
. If
$\Xi _2 \;:\!=\; \iota _{\phi (w)x^{-1}}\circ \Phi ^2$
. If
![]() $\Phi (c) = wcx$
, then
$\Phi (c) = wcx$
, then
![]() $\Xi _1(c) = \iota _w \circ \Phi (c) =cz$
where
$\Xi _1(c) = \iota _w \circ \Phi (c) =cz$
where
![]() $z=xw$
. If
$z=xw$
. If
![]() $\Phi (c) = wc^{-1}x$
, then
$\Phi (c) = wc^{-1}x$
, then
![]() $\Xi _2(c) = \iota _{\phi (w)x^{-1}} \circ \Phi ^2(c) = cz$
where
$\Xi _2(c) = \iota _{\phi (w)x^{-1}} \circ \Phi ^2(c) = cz$
where
![]() $z=w^{-1}\phi (xw)x^{-1}$
. For
$z=w^{-1}\phi (xw)x^{-1}$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\xi _i \;:\!=\; \Xi _i \left |_{\langle a, b \rangle } \right .$
, the restriction of
$\xi _i \;:\!=\; \Xi _i \left |_{\langle a, b \rangle } \right .$
, the restriction of
![]() $ \Xi _i$
to the
$ \Xi _i$
to the
![]() $\mathbb{Z}^2$
factor.
$\mathbb{Z}^2$
factor.
Suppose
![]() $\xi _i$
has exponential growth (so has a non-unit eigenvalue as per Lemma 3.9 and Condition 2 of Theorem B). Define
$\xi _i$
has exponential growth (so has a non-unit eigenvalue as per Lemma 3.9 and Condition 2 of Theorem B). Define
![]() $\Xi \;:\!=\;\Xi _i$
. Then
$\Xi \;:\!=\;\Xi _i$
. Then
![]() $\Xi$
has the general form claimed in the proposition, and since
$\Xi$
has the general form claimed in the proposition, and since
![]() $[\Xi _1] = [\Phi ]$
and
$[\Xi _1] = [\Phi ]$
and
![]() $[\Xi _2] = [\Phi ]^2$
, Lemma 3.6 implies that
$[\Xi _2] = [\Phi ]^2$
, Lemma 3.6 implies that
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Xi }$
have equivalent Dehn functions.
$M_{\Xi }$
have equivalent Dehn functions.
Suppose
![]() $\xi _i \in{\textrm{Aut}}(\mathbb{Z}^2)$
has finite order
$\xi _i \in{\textrm{Aut}}(\mathbb{Z}^2)$
has finite order
![]() $n$
(i.e.
$n$
(i.e.
![]() $\xi _i$
has trivial growth). Define
$\xi _i$
has trivial growth). Define
![]() $\Xi = \Xi _i^n$
. This has the promised form: its restriction to
$\Xi = \Xi _i^n$
. This has the promised form: its restriction to
![]() $\langle a,b \rangle$
is the identity and
$\langle a,b \rangle$
is the identity and
![]() $\Xi (c) = cz$
for some
$\Xi (c) = cz$
for some
![]() $z \in \langle a,b \rangle$
. Lemma 3.6 implies that
$z \in \langle a,b \rangle$
. Lemma 3.6 implies that
![]() $M_{\Xi }$
and
$M_{\Xi }$
and
![]() $M_{\Phi }$
have equivalent Dehn functions.
$M_{\Phi }$
have equivalent Dehn functions.
Finally, suppose
![]() $\xi _i$
is of infinite order and has only unit eigenvalues. Lemma 3.7 implies that for some power
$\xi _i$
is of infinite order and has only unit eigenvalues. Lemma 3.7 implies that for some power
![]() $n$
,
$n$
,
![]() $(\xi _i)^{n}$
is conjugate in
$(\xi _i)^{n}$
is conjugate in
![]() ${\textrm{Aut}}(\mathbb{Z}^2)$
to the automorphism
${\textrm{Aut}}(\mathbb{Z}^2)$
to the automorphism
![]() $\xi \;:\;a \mapsto ab^{k}$
,
$\xi \;:\;a \mapsto ab^{k}$
,
![]() $b \mapsto b$
, for some
$b \mapsto b$
, for some
![]() $k \neq 0$
. Therefore, for some
$k \neq 0$
. Therefore, for some
![]() $f \in{\textrm{Aut}}(\mathbb{Z}^2)$
,
$f \in{\textrm{Aut}}(\mathbb{Z}^2)$
,
![]() ${\xi } = f^{-1}\circ{(\xi _i)}^n \circ f$
. Let
${\xi } = f^{-1}\circ{(\xi _i)}^n \circ f$
. Let
![]() $F$
be the automorphism that restricts to
$F$
be the automorphism that restricts to
![]() $f$
on
$f$
on
![]() $\mathbb{Z}^2$
and maps
$\mathbb{Z}^2$
and maps
![]() $c \mapsto c$
. Define
$c \mapsto c$
. Define
![]() $\Xi \;:\!=\; F^{-1}\circ (\Xi _i)^n \circ F$
. By Lemma 3.6,
$\Xi \;:\!=\; F^{-1}\circ (\Xi _i)^n \circ F$
. By Lemma 3.6,
![]() $M_{\Phi }$
and
$M_{\Phi }$
and
![]() $M_{\Xi }$
have equivalent Dehn functions. Let
$M_{\Xi }$
have equivalent Dehn functions. Let
![]() $z^{\prime } = z\xi _i(z) \dots (\xi _i)^{n-1}(z)$
and
$z^{\prime } = z\xi _i(z) \dots (\xi _i)^{n-1}(z)$
and
![]() $z^{\prime \prime } = f^{-1}(z^{\prime })$
. Both are elements of
$z^{\prime \prime } = f^{-1}(z^{\prime })$
. Both are elements of
![]() $\langle a,b \rangle$
. The map
$\langle a,b \rangle$
. The map
![]() $\Xi$
has the desired form:
$\Xi$
has the desired form:
In every case, conditions (1), (2), and (3) of Theorem B apply to
![]() $\Xi$
exactly when they apply to
$\Xi$
exactly when they apply to
![]() $\Phi$
. After all, in each case, the restriction
$\Phi$
. After all, in each case, the restriction
![]() $\xi$
of
$\xi$
of
![]() $\Xi$
to the
$\Xi$
to the
![]() $\mathbb{Z}^2$
factor is a conjugate of a power of the restriction
$\mathbb{Z}^2$
factor is a conjugate of a power of the restriction
![]() $\phi$
of
$\phi$
of
![]() $\Phi$
. Let
$\Phi$
. Let
![]() $A$
be the Jordan Canonical Form (JCF) of
$A$
be the Jordan Canonical Form (JCF) of
![]() $\phi$
. For all
$\phi$
. For all
![]() $k \in \mathbb{N}$
,
$k \in \mathbb{N}$
,
![]() $A$
is finite order if and only if
$A$
is finite order if and only if
![]() $A^k$
is finite order, and
$A^k$
is finite order, and
![]() $A$
has a non-unit eigenvalue if and only if
$A$
has a non-unit eigenvalue if and only if
![]() $A^k$
has one too. The JCF is invariant under conjugation.
$A^k$
has one too. The JCF is invariant under conjugation.
6.2. Corridors
In each instance of Proposition 6.2,
for some
![]() $\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some
$\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$
and some
![]() $z \in \langle a,b \rangle$
. In this section, we prove some preliminary results about van Kampen diagrams over this presentation. Such diagrams can have both
$z \in \langle a,b \rangle$
. In this section, we prove some preliminary results about van Kampen diagrams over this presentation. Such diagrams can have both
![]() $c$
- and
$c$
- and
![]() $t$
-corridors.
$t$
-corridors.
Definition 6.3. Suppose that
![]() $\tau$
is a
$\tau$
is a
![]() $t$
-corridor and
$t$
-corridor and
![]() $\eta$
is a
$\eta$
is a
![]() $c$
-corridor. Suppose
$c$
-corridor. Suppose
![]() ${\hat{\tau }} \subseteq \tau$
and
${\hat{\tau }} \subseteq \tau$
and
![]() $\hat{\eta } \subseteq \eta$
are subcorridors. We say
$\hat{\eta } \subseteq \eta$
are subcorridors. We say
![]() $\hat{\tau }$
and
$\hat{\tau }$
and
![]() $\hat{\eta }$
form a bigon when they have exactly two common 2-cells, specifically their first and last ones.
$\hat{\eta }$
form a bigon when they have exactly two common 2-cells, specifically their first and last ones.
A
![]() $c$
- or
$c$
- or
![]() $t$
-corridor cannot cross itself. So, by considering an “innermost” crossing of a
$t$
-corridor cannot cross itself. So, by considering an “innermost” crossing of a
![]() $c$
- and a
$c$
- and a
![]() $t$
-corridor, we observe:
$t$
-corridor, we observe:
Lemma 6.4. Suppose
![]() $\tau$
is a
$\tau$
is a
![]() $t$
-corridor and
$t$
-corridor and
![]() $\eta$
is a
$\eta$
is a
![]() $c$
-corridor. If
$c$
-corridor. If
![]() $\tau$
and
$\tau$
and
![]() $\eta$
intersect more than once, then there are subcorridors
$\eta$
intersect more than once, then there are subcorridors
![]() $\hat{\tau } \subseteq \tau$
and
$\hat{\tau } \subseteq \tau$
and
![]() $\hat{\eta } \subseteq \eta$
forming a bigon.
$\hat{\eta } \subseteq \eta$
forming a bigon.
Per Section 3.1, a
![]() $c$
-corridor is reduced if it contains no back-to-back pair of canceling 2-cells sharing a
$c$
-corridor is reduced if it contains no back-to-back pair of canceling 2-cells sharing a
![]() $c$
-edge.
$c$
-edge.
Lemma 6.5. In a van Kampen diagram where
![]() $c$
-corridors are reduced, if a
$c$
-corridors are reduced, if a
![]() $t$
-corridor
$t$
-corridor
![]() $\tau$
intersects a
$\tau$
intersects a
![]() $c$
-corridor
$c$
-corridor
![]() $\eta$
, it will do so only once.
$\eta$
, it will do so only once.
Proof. Since
![]() $c$
-corridors are made up of a single kind of 2-cell (arising from the defining relation
$c$
-corridors are made up of a single kind of 2-cell (arising from the defining relation
![]() $c^t=cz$
), all 2-cells in a reduced
$c^t=cz$
), all 2-cells in a reduced
![]() $c$
-corridor have the same labels and are oriented the same way along the corridor. Let us assume for the contradiction that
$c$
-corridor have the same labels and are oriented the same way along the corridor. Let us assume for the contradiction that
![]() $\eta$
is reduced and that
$\eta$
is reduced and that
![]() $\tau$
and
$\tau$
and
![]() $\eta$
intersect at least twice.
$\eta$
intersect at least twice.
By Lemma 6.4, there exist subcorridors
![]() $\hat{\tau }$
and
$\hat{\tau }$
and
![]() $\hat{\eta }$
that form a bigon, with precisely the first and final 2-cells,
$\hat{\eta }$
that form a bigon, with precisely the first and final 2-cells,
![]() $E_1$
and
$E_1$
and
![]() $E_2$
, in common, as in Figure 9. The orientation of the edges labeled by
$E_2$
, in common, as in Figure 9. The orientation of the edges labeled by
![]() $t$
in
$t$
in
![]() $E_1$
fixes an orientation for all the
$E_1$
fixes an orientation for all the
![]() $t$
-labeled 1-cells along the bottom of
$t$
-labeled 1-cells along the bottom of
![]() $\hat{\eta }$
(see Remark 3.2) since
$\hat{\eta }$
(see Remark 3.2) since
![]() $\hat{\eta }$
is reduced. It also fixes an orientation for
$\hat{\eta }$
is reduced. It also fixes an orientation for
![]() $t$
-labeled 1-cells in
$t$
-labeled 1-cells in
![]() $\hat{\tau }$
. But these two specifications are inconsistent for the
$\hat{\tau }$
. But these two specifications are inconsistent for the
![]() $t$
-labeled 1-cells in
$t$
-labeled 1-cells in
![]() $E_2$
.
$E_2$
.
We will use the same argument for alternating corridors and
![]() $c$
-corridors in Lemma 6.10 (1) and for
$c$
-corridors in Lemma 6.10 (1) and for
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
- partial corridors in Lemma 6.10 (4).
$t$
- partial corridors in Lemma 6.10 (4).

Figure 9. If a
![]() $t$
-corridor and a
$t$
-corridor and a
![]() $c$
-corridor cross at least twice, the
$c$
-corridor cross at least twice, the
![]() $c$
-corridor cannot be reduced.
$c$
-corridor cannot be reduced.
Corollary 6.6. In a van Kampen diagram with reduced
![]() $c$
-corridors, there are no
$c$
-corridors, there are no
![]() $c$
-annuli, and
$c$
-annuli, and
![]() $t$
-annuli do not intersect
$t$
-annuli do not intersect
![]() $c$
-corridors.
$c$
-corridors.
Proof. The word around the outside of a
![]() $c$
-annulus contains
$c$
-annulus contains
![]() $t$
’s, so it would have to intersect once (and therefore intersect at least twice) with a
$t$
’s, so it would have to intersect once (and therefore intersect at least twice) with a
![]() $t$
-corridor, which is impossible by Lemma 6.5. Similarly, if a
$t$
-corridor, which is impossible by Lemma 6.5. Similarly, if a
![]() $c$
-corridor has common 2-cells with a
$c$
-corridor has common 2-cells with a
![]() $t$
-annulus, it must have at least two in common—again impossible by Lemma 6.5.
$t$
-annulus, it must have at least two in common—again impossible by Lemma 6.5.
The following corollary allows us to determine the lengths of
![]() $c$
-corridors in a diagram
$c$
-corridors in a diagram
![]() $\Delta$
in terms of the word around its boundary and the way
$\Delta$
in terms of the word around its boundary and the way
![]() $c$
-edges are paired up by
$c$
-edges are paired up by
![]() $c$
-corridors—the so-called
$c$
-corridors—the so-called
![]() $c$
-corridor pairing (see Definition 6.11).
$c$
-corridor pairing (see Definition 6.11).
Corollary 6.7. Suppose
![]() $\Delta$
is a van Kampen diagram with reduced
$\Delta$
is a van Kampen diagram with reduced
![]() $c$
-corridors. Suppose further that its boundary word is
$c$
-corridors. Suppose further that its boundary word is
![]() $w_1c^{\pm 1}w_2c^{\mp 1}$
for some words
$w_1c^{\pm 1}w_2c^{\mp 1}$
for some words
![]() $w_1$
and
$w_1$
and
![]() $w_2$
and that
$w_2$
and that
![]() $\eta$
is a
$\eta$
is a
![]() $c$
-corridor beginning and ending on the edges labeled by these distinguished
$c$
-corridor beginning and ending on the edges labeled by these distinguished
![]() $c^{\pm 1}$
. Then the length of
$c^{\pm 1}$
. Then the length of
![]() $\eta$
is the absolute value of the index sum of the
$\eta$
is the absolute value of the index sum of the
![]() $t^{\pm 1}$
in
$t^{\pm 1}$
in
![]() $w_1$
(or, equivalently, in
$w_1$
(or, equivalently, in
![]() $w_2$
).
$w_2$
).
Proof. All
![]() $t$
-corridors intersecting
$t$
-corridors intersecting
![]() $\eta$
have the same orientation with respect to
$\eta$
have the same orientation with respect to
![]() $\eta$
. In particular, the word along one side of
$\eta$
. In particular, the word along one side of
![]() $\eta$
is
$\eta$
is
![]() $t^k$
for some
$t^k$
for some
![]() $k$
, without any free reductions. Thus, the
$k$
, without any free reductions. Thus, the
![]() $t$
-corridors starting at
$t$
-corridors starting at
![]() $t$
-edges in
$t$
-edges in
![]() $w_2$
that are oppositely oriented to the
$w_2$
that are oppositely oriented to the
![]() $t$
’s in
$t$
’s in
![]() $\eta$
cannot cross it, and so must have oppositely oriented partners on the same side of
$\eta$
cannot cross it, and so must have oppositely oriented partners on the same side of
![]() $\eta$
, as shown in Figure 10. This leaves exactly the absolute value of the index sum of
$\eta$
, as shown in Figure 10. This leaves exactly the absolute value of the index sum of
![]() $t$
in
$t$
in
![]() $w_1$
many
$w_1$
many
![]() $t$
-corridors which have no partners on the same side of
$t$
-corridors which have no partners on the same side of
![]() $\eta$
, and so must cross it. By Lemma 6.5, each of these
$\eta$
, and so must cross it. By Lemma 6.5, each of these
![]() $t$
-corridors can cross
$t$
-corridors can cross
![]() $\eta$
exactly once.
$\eta$
exactly once.
Since
![]() $c$
-corridors cannot cross, removing all the
$c$
-corridors cannot cross, removing all the
![]() $c$
-corridors leaves a set of connected subdiagrams called
$c$
-corridors leaves a set of connected subdiagrams called
![]() $c$
-complementary regions. The words around the perimeters of each of these regions contain no
$c$
-complementary regions. The words around the perimeters of each of these regions contain no
![]() $c^{\pm 1}$
. See Figure 11a.
$c^{\pm 1}$
. See Figure 11a.

Figure 10. The
![]() $t$
-corridors of oppositely oriented
$t$
-corridors of oppositely oriented
![]() $t$
-edges in
$t$
-edges in
![]() $w_2$
cannot cross
$w_2$
cannot cross
![]() $\eta$
.
$\eta$
.
Corollary 6.8. Let
![]() $R$
be a
$R$
be a
![]() $c$
-complementary region in a van Kampen diagram for the word
$c$
-complementary region in a van Kampen diagram for the word
![]() $w$
. If the word around the perimeter of
$w$
. If the word around the perimeter of
![]() $R$
is
$R$
is
![]() $v$
, then
$v$
, then
![]() $|v|\leq (1+|z|)|w|$
, where
$|v|\leq (1+|z|)|w|$
, where
![]() $z$
is from the defining relation
$z$
is from the defining relation
![]() $c^t=cz$
for
$c^t=cz$
for
![]() $M_{\Xi }$
.
$M_{\Xi }$
.
Proof. Suppose that after cyclic conjugation
![]() $w$
has the form
$w$
has the form
![]() $x_0c^{\epsilon _0} v_0c^{-\epsilon _0}x_1c^{\epsilon _1}v_1 c^{-\epsilon _1}\cdots x_nc^{\epsilon _n}v_nc^{-\epsilon _n}$
, where
$x_0c^{\epsilon _0} v_0c^{-\epsilon _0}x_1c^{\epsilon _1}v_1 c^{-\epsilon _1}\cdots x_nc^{\epsilon _n}v_nc^{-\epsilon _n}$
, where
![]() $x_0,\ldots, x_n$
form part of the perimeter of the
$x_0,\ldots, x_n$
form part of the perimeter of the
![]() $c$
-complementary region
$c$
-complementary region
![]() $R$
and
$R$
and
![]() $v_0, \ldots, v_n$
are words in
$v_0, \ldots, v_n$
are words in
![]() $\{a^{\pm 1}, b^{\pm 1}, c^{\pm 1}, t^{\pm 1}\}$
. Then the perimeter of
$\{a^{\pm 1}, b^{\pm 1}, c^{\pm 1}, t^{\pm 1}\}$
. Then the perimeter of
![]() $R$
can be labeled by the word
$R$
can be labeled by the word
![]() $v=x_0 v'_0x_1v'_1\cdots x_nv'_n$
where
$v=x_0 v'_0x_1v'_1\cdots x_nv'_n$
where
![]() $x_0,x_1,\ldots, x_n$
are part of
$x_0,x_1,\ldots, x_n$
are part of
![]() $w$
and
$w$
and
![]() $v'_0, \ldots, v'_n$
label the
$v'_0, \ldots, v'_n$
label the
![]() $c$
-corridors, with
$c$
-corridors, with
![]() $v'_i = c^{\epsilon _i}v_ic^{-\epsilon _i}$
(see Figure 11b). By Corollary 6.7, the length of each
$v'_i = c^{\epsilon _i}v_ic^{-\epsilon _i}$
(see Figure 11b). By Corollary 6.7, the length of each
![]() $c$
-corridor is the index sum of
$c$
-corridor is the index sum of
![]() $t$
in the corresponding boundary word
$t$
in the corresponding boundary word
![]() $v_i$
. Along the top of a
$v_i$
. Along the top of a
![]() $c$
-corridor of length
$c$
-corridor of length
![]() $k_i$
, we have the word
$k_i$
, we have the word
![]() $(tz^{-1})^{k_i}$
, so
$(tz^{-1})^{k_i}$
, so
![]() $|v'_i| \leq (1+|z|)|v_i|$
, and so
$|v'_i| \leq (1+|z|)|v_i|$
, and so
![]() $|v|\leq (1+|z|)|w|$
.
$|v|\leq (1+|z|)|w|$
.
6.3. Alternating corridors
When
for some
![]() $k, l, m \in \mathbb{Z}$
, killing
$k, l, m \in \mathbb{Z}$
, killing
![]() $b$
maps
$b$
maps
![]() $M_{\Xi }$
onto
$M_{\Xi }$
onto
The elements
![]() $b$
and
$b$
and
![]() $c$
do not commute in
$c$
do not commute in
![]() $M_{\Xi }$
, so
$M_{\Xi }$
, so
![]() $M_{\Xi }$
is not a central extension of
$M_{\Xi }$
is not a central extension of
![]() $Q_l$
. Nevertheless, we will use a variant of the electrostatic model to establish upper bounds on area in
$Q_l$
. Nevertheless, we will use a variant of the electrostatic model to establish upper bounds on area in
![]() $M_{\Xi }$
. The purpose of this section is to provide necessary preliminaries concerning van Kampen diagrams over
$M_{\Xi }$
. The purpose of this section is to provide necessary preliminaries concerning van Kampen diagrams over
![]() $Q_l$
. We begin with the case
$Q_l$
. We begin with the case
![]() $l=1$
. Setting
$l=1$
. Setting
![]() $\alpha \;:\!=\; ta^{-1}$
, we see that
$\alpha \;:\!=\; ta^{-1}$
, we see that
and
![]() $Q_1$
are the same group.
$Q_1$
are the same group.
Definition 6.9. A
![]() $c$
-face is a 2-cell in a van Kampen diagram
$c$
-face is a 2-cell in a van Kampen diagram
![]() $\Delta$
over
$\Delta$
over
![]() ${Q}'$
corresponding to the defining relation
${Q}'$
corresponding to the defining relation
![]() $t^c = \alpha$
. Partial
$t^c = \alpha$
. Partial
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
-corridors in
$t$
-corridors in
![]() $\Delta$
fit together in an alternating way: where a partial
$\Delta$
fit together in an alternating way: where a partial
![]() $\alpha$
-corridor ends at a
$\alpha$
-corridor ends at a
![]() $c$
-face in the interior of a diagram, a partial
$c$
-face in the interior of a diagram, a partial
![]() $t$
-corridor begins, and where this ends, another partial
$t$
-corridor begins, and where this ends, another partial
![]() $\alpha$
-corridor begins. An alternating corridor in
$\alpha$
-corridor begins. An alternating corridor in
![]() $\Delta$
is a maximal union of
$\Delta$
is a maximal union of
![]() $\alpha$
-partial corridors,
$\alpha$
-partial corridors,
![]() $t$
-partial corridors, and the
$t$
-partial corridors, and the
![]() $c$
-faces between them, fitting together in this way—see Figure 12.
$c$
-faces between them, fitting together in this way—see Figure 12.

Figure 11. c-Complementary regions.

Figure 12. An alternating corridor.
Like a standard corridor, an alternating corridor either closes up or connects two boundary edges (see Section 3.1). It is possible for alternating corridors to self-intersect, but, as we will see shortly, in a reduced diagram, alternating corridors do not self-intersect or close up. Every face in
![]() $\Delta$
is part of some alternating corridor. Like standard and partial corridors, an alternating corridor has a top and a bottom: the internal
$\Delta$
is part of some alternating corridor. Like standard and partial corridors, an alternating corridor has a top and a bottom: the internal
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
-edges are directed from the bottom to the top (again, see Figure 12).
$t$
-edges are directed from the bottom to the top (again, see Figure 12).
Lemma 6.10. Suppose
![]() $\Delta$
is a van Kampen diagram over
$\Delta$
is a van Kampen diagram over
![]() $\langle \alpha, c, t \! \mid \! \alpha ^t=\alpha,\, t^c = \alpha \rangle$
in which all
$\langle \alpha, c, t \! \mid \! \alpha ^t=\alpha,\, t^c = \alpha \rangle$
in which all
![]() $c$
-corridors and all
$c$
-corridors and all
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
-partial corridors are reduced (see Figures 13 and 14). Then in
$t$
-partial corridors are reduced (see Figures 13 and 14). Then in
![]() $\Delta$
:
$\Delta$
:
-
1. A
 $c$
-corridor
$c$
-corridor
 $\eta$
and an alternating corridor
$\eta$
and an alternating corridor
 $\tau$
can cross at most once.
$\tau$
can cross at most once. -
2. Alternating corridors do not close up.
-
3. A single alternating corridor can never cross itself.
-
4. Two alternating corridors cannot cross more than once.
Proof. For (1), it suffices (see Lemma 6.4) to prove that it is impossible to have a bigon of an alternating corridor
![]() $\tau$
and a
$\tau$
and a
![]() $c$
-corridor
$c$
-corridor
![]() $\eta$
in
$\eta$
in
![]() $\Delta$
. Since
$\Delta$
. Since
![]() $c$
-corridors in
$c$
-corridors in
![]() $\Delta$
are reduced, the top of the
$\Delta$
are reduced, the top of the
![]() $c$
-corridor is labeled by a power of
$c$
-corridor is labeled by a power of
![]() $\alpha$
without any free reduction. As in our proof of Lemma 6.5,
$\alpha$
without any free reduction. As in our proof of Lemma 6.5,
![]() $\tau$
and
$\tau$
and
![]() $\eta$
specify inconsistent orientations for the
$\eta$
specify inconsistent orientations for the
![]() $t$
edge in the second common 2-cell, as in Figure 15a.
$t$
edge in the second common 2-cell, as in Figure 15a.

Figure 13. Non-reduced subdiagrams that can occur in
![]() $\Delta$
.
$\Delta$
.

Figure 14. Non-reduced subcorridors not occurring in
![]() $\Delta$
.
$\Delta$
.
For (2), suppose for a contradiction, that there is an alternating corridor
![]() $\mathcal{A}$
that closes up. It cannot contain any
$\mathcal{A}$
that closes up. It cannot contain any
![]() $c$
-faces, as this would force a
$c$
-faces, as this would force a
![]() $c$
-corridor to cross
$c$
-corridor to cross
![]() $\mathcal{A}$
twice. If
$\mathcal{A}$
twice. If
![]() $\mathcal{A}$
contains no
$\mathcal{A}$
contains no
![]() $c$
-faces, then it is either a
$c$
-faces, then it is either a
![]() $t$
- or
$t$
- or
![]() $\alpha$
-annulus. The word along the top of the annulus is a power of
$\alpha$
-annulus. The word along the top of the annulus is a power of
![]() $\alpha$
or
$\alpha$
or
![]() $t$
, respectively. Such an annulus would imply that
$t$
, respectively. Such an annulus would imply that
![]() $t$
or
$t$
or
![]() $\alpha$
have finite order, but both are infinite order elements of
$\alpha$
have finite order, but both are infinite order elements of
![]() $Q^{\prime }$
.
$Q^{\prime }$
.

Figure 15. Impossible behavior for alternating corridors.
For (3), suppose for a contradiction that an alternating corridor
![]() $\eta$
has a self-intersection. An alternating corridor can only have a self-intersection at a 2-cell corresponding to the relation
$\eta$
has a self-intersection. An alternating corridor can only have a self-intersection at a 2-cell corresponding to the relation
![]() $[\alpha, t]=1$
. Let
$[\alpha, t]=1$
. Let
![]() $\hat{\eta } \subset \eta$
be a subcorridor of
$\hat{\eta } \subset \eta$
be a subcorridor of
![]() $\eta$
that begins and ends at the self-intersection. Call this first and final 2-cell
$\eta$
that begins and ends at the self-intersection. Call this first and final 2-cell
![]() $E$
.
$E$
.
The 2-cell
![]() $E$
is part of both
$E$
is part of both
![]() $t$
- and
$t$
- and
![]() $\alpha$
- partial corridors in
$\alpha$
- partial corridors in
![]() $\hat{\eta }$
; therefore,
$\hat{\eta }$
; therefore,
![]() $\hat{\eta }$
contains at least one
$\hat{\eta }$
contains at least one
![]() $c$
-face (in particular, an odd number of
$c$
-face (in particular, an odd number of
![]() $c$
-faces in order to get both an
$c$
-faces in order to get both an
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
-segment at the intersection). Each
$t$
-segment at the intersection). Each
![]() $c$
-face in
$c$
-face in
![]() $\hat{\eta }$
is part of a
$\hat{\eta }$
is part of a
![]() $c$
-corridor. By (1),
$c$
-corridor. By (1),
![]() $c$
-corridors can only cross
$c$
-corridors can only cross
![]() $\hat{\eta }$
once, but each
$\hat{\eta }$
once, but each
![]() $c$
-corridor must cross
$c$
-corridor must cross
![]() $\hat{\eta }$
at least twice, since it cannot terminate within the region enclosed by
$\hat{\eta }$
at least twice, since it cannot terminate within the region enclosed by
![]() $\hat{\eta }$
, see Figure 15b.
$\hat{\eta }$
, see Figure 15b.
For (4), assume for the contradiction that two alternating corridors cross at least twice. Again, we can find a bigon of alternating corridors. There are two cases. In one, no
![]() $c$
-corridors intersect the bigon. In this case, one of the alternating corridors is a partial
$c$
-corridors intersect the bigon. In this case, one of the alternating corridors is a partial
![]() $t$
-corridor, and the other is a partial
$t$
-corridor, and the other is a partial
![]() $\alpha$
-corridor. An argument like Lemma 6.5 shows that this kind of double intersection is impossible when
$\alpha$
-corridor. An argument like Lemma 6.5 shows that this kind of double intersection is impossible when
![]() $t$
- and
$t$
- and
![]() $\alpha$
- partial corridors are reduced (see Figure 15c). In the other case, at least one
$\alpha$
- partial corridors are reduced (see Figure 15c). In the other case, at least one
![]() $c$
-corridor intersects the bigon. We look at the triangle formed by the two bigons and the first
$c$
-corridor intersects the bigon. We look at the triangle formed by the two bigons and the first
![]() $c$
-corridor to cross them. Since it is the first such
$c$
-corridor to cross them. Since it is the first such
![]() $c$
-corridor, we have an
$c$
-corridor, we have an
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
-partial corridor that both need to end on the same side of a
$t$
-partial corridor that both need to end on the same side of a
![]() $c$
-corridor. However,
$c$
-corridor. However,
![]() $c$
-corridors always have
$c$
-corridors always have
![]() $t$
’s along the bottom and
$t$
’s along the bottom and
![]() $\alpha$
’s along the top—there cannot be both
$\alpha$
’s along the top—there cannot be both
![]() $\alpha$
’s and
$\alpha$
’s and
![]() $t$
’s on the same side of the
$t$
’s on the same side of the
![]() $c$
-corridor. Figure 15d illustrates this contradiction. Therefore, neither case happens.
$c$
-corridor. Figure 15d illustrates this contradiction. Therefore, neither case happens.
6.4. Quadratic area diagrams over
 $Q_1$
$Q_1$
Definition 6.11. A
![]() $c$
-pairing for a word
$c$
-pairing for a word
![]() $w$
is any pairing off of the
$w$
is any pairing off of the
![]() $c$
in
$c$
in
![]() $w$
with the
$w$
with the
![]() $c^{-1}$
in
$c^{-1}$
in
![]() $w$
.
$w$
.
If
![]() $w$
represents the identity in
$w$
represents the identity in
![]() $M_{\Xi }$
, then a van Kampen diagram
$M_{\Xi }$
, then a van Kampen diagram
![]() $\Delta$
for
$\Delta$
for
![]() $w$
induces a
$w$
induces a
![]() $c$
-pairing: some
$c$
-pairing: some
![]() $c$
and some
$c$
and some
![]() $c^{-1}$
are paired when they are joined by a
$c^{-1}$
are paired when they are joined by a
![]() $c$
-corridor in
$c$
-corridor in
![]() $\Delta$
. We say that a
$\Delta$
. We say that a
![]() $c$
-pairing is valid if it is induced by a van Kampen diagram for
$c$
-pairing is valid if it is induced by a van Kampen diagram for
![]() $w$
.
$w$
.
This notion of validity has content. Not all
![]() $c$
-pairings need be valid, and valid
$c$
-pairings need be valid, and valid
![]() $c$
-pairings need not be unique.
$c$
-pairings need not be unique.
Because
is a free-by-cyclic group, its Dehn function is quadratic [Reference Bridson and Groves8]. The point of the following lemma is that this quadratic area bound can be realized on diagrams witnessing any prescribed valid
![]() $c$
-pairing.
$c$
-pairing.
Lemma 6.12. There exists
![]() $A \gt 0$
such that for any word
$A \gt 0$
such that for any word
![]() $u$
representing the identity in
$u$
representing the identity in
![]() $Q$
(not necessarily freely reduced), and for any valid
$Q$
(not necessarily freely reduced), and for any valid
![]() $c$
-pairing
$c$
-pairing
![]() $P$
of
$P$
of
![]() $u$
, there is a van Kampen diagram
$u$
, there is a van Kampen diagram
![]() $\theta$
for
$\theta$
for
![]() $u$
over
$u$
over
![]() $Q$
that induces
$Q$
that induces
![]() $P$
, has
$P$
, has
![]() $\textrm{Area}(\theta ) \leq A |u|^2$
, and has reduced
$\textrm{Area}(\theta ) \leq A |u|^2$
, and has reduced
![]() $c$
-corridors.
$c$
-corridors.
Proof. Let
![]() $\Delta$
be a van Kampen diagram for
$\Delta$
be a van Kampen diagram for
![]() $u$
over
$u$
over
![]() $Q$
that realizes the given
$Q$
that realizes the given
![]() $c$
-pairing.
$c$
-pairing.
Instead of
![]() $Q$
we will work with
$Q$
we will work with
which, recall, we can see presents the same group by setting
![]() $\alpha \;:\!=\; ta^{-1}$
.
$\alpha \;:\!=\; ta^{-1}$
.
Two finite presentations
![]() $\langle A_1 \mid R_1 \rangle$
and
$\langle A_1 \mid R_1 \rangle$
and
![]() $\langle A_2 \mid R_2 \rangle$
of the same group have
$\langle A_2 \mid R_2 \rangle$
of the same group have
![]() $\simeq$
-equivalent Dehn functions [Reference Alonso1, Reference Gersten15]. In outline, the proofs in [Reference Alonso1, Reference Gersten15] go as follows. For each
$\simeq$
-equivalent Dehn functions [Reference Alonso1, Reference Gersten15]. In outline, the proofs in [Reference Alonso1, Reference Gersten15] go as follows. For each
![]() $a \in A_1$
, pick a word
$a \in A_1$
, pick a word
![]() $u_a=u_a(A_2)$
representing the same group element. Suppose a word
$u_a=u_a(A_2)$
representing the same group element. Suppose a word
![]() $w_1 = w_1(A_1)$
represents
$w_1 = w_1(A_1)$
represents
![]() $1$
in
$1$
in
![]() $\langle A_1 \mid R_1 \rangle$
. Let
$\langle A_1 \mid R_1 \rangle$
. Let
![]() $w_2$
be the word obtained from
$w_2$
be the word obtained from
![]() $w_1$
by replacing all of its letters
$w_1$
by replacing all of its letters
![]() $a^{\pm 1}$
by
$a^{\pm 1}$
by
![]() ${u_a}^{\pm 1}$
. A van Kampen diagram
${u_a}^{\pm 1}$
. A van Kampen diagram
![]() $w_1$
over
$w_1$
over
![]() $\langle A_1 \mid R_1 \rangle$
can be converted to a van Kampen diagram for
$\langle A_1 \mid R_1 \rangle$
can be converted to a van Kampen diagram for
![]() $w_2$
over
$w_2$
over
![]() $\langle A_2 \mid R_2 \rangle$
of comparable area by converting each edge labeled
$\langle A_2 \mid R_2 \rangle$
of comparable area by converting each edge labeled
![]() $a$
to a path labeled
$a$
to a path labeled
![]() $u_a$
and then filling all the faces. Each relator in
$u_a$
and then filling all the faces. Each relator in
![]() $R_1$
can be rewritten as a word representing the identity in
$R_1$
can be rewritten as a word representing the identity in
![]() $A_2$
, and each can then be filled with at most some constant number of relators in
$A_2$
, and each can then be filled with at most some constant number of relators in
![]() $R_2$
, so the area of the diagram over
$R_2$
, so the area of the diagram over
![]() $\langle A_2 \mid R_2 \rangle$
will be no more than a constant multiple of the area of the diagram over
$\langle A_2 \mid R_2 \rangle$
will be no more than a constant multiple of the area of the diagram over
![]() $\langle A_1 \mid R_1 \rangle$
.
$\langle A_1 \mid R_1 \rangle$
.
In the instance of
![]() $Q$
and
$Q$
and
![]() ${Q}'$
, the
${Q}'$
, the
![]() $c$
-pairings induced by the two diagrams agree, and so it suffices to prove the lemma for
$c$
-pairings induced by the two diagrams agree, and so it suffices to prove the lemma for
![]() ${Q}'$
instead of
${Q}'$
instead of
![]() $Q$
.
$Q$
.
Given
![]() $u=u(a,c,t)$
, let
$u=u(a,c,t)$
, let
![]() $u'$
be the word obtained from
$u'$
be the word obtained from
![]() $u(\alpha ^{-1} t, c,t)$
by canceling away all
$u(\alpha ^{-1} t, c,t)$
by canceling away all
![]() $\alpha ^{\pm 1} \alpha ^{\mp 1}$
and all
$\alpha ^{\pm 1} \alpha ^{\mp 1}$
and all
![]() $t^{\pm 1} t^{\mp 1}$
(but not all
$t^{\pm 1} t^{\mp 1}$
(but not all
![]() $c^{\pm 1} c^{\mp 1}$
). Then
$c^{\pm 1} c^{\mp 1}$
). Then
![]() $|u^{\prime }|\leq 2|u|$
. Construct a van Kampen diagram
$|u^{\prime }|\leq 2|u|$
. Construct a van Kampen diagram
![]() $\theta '$
for
$\theta '$
for
![]() $u'$
over
$u'$
over
![]() ${Q}'$
as follows. Begin with a planar polygon with edges directed and labeled so that one reads
${Q}'$
as follows. Begin with a planar polygon with edges directed and labeled so that one reads
![]() $u'$
around the perimeter. Insert reduced
$u'$
around the perimeter. Insert reduced
![]() $c$
-corridors of 2-cells (each with perimeter
$c$
-corridors of 2-cells (each with perimeter
![]() $t^c \alpha ^{-1}$
) mimicking the pattern of
$t^c \alpha ^{-1}$
) mimicking the pattern of
![]() $c$
-corridors in
$c$
-corridors in
![]() $\Delta$
. Fill the complementary regions with minimal area sub-diagrams over
$\Delta$
. Fill the complementary regions with minimal area sub-diagrams over
![]() $\langle \alpha, t \mid \alpha ^t =\alpha \rangle$
. The words around their perimeters represent the identity in
$\langle \alpha, t \mid \alpha ^t =\alpha \rangle$
. The words around their perimeters represent the identity in
![]() $\langle \alpha, t \mid \alpha ^t =\alpha \rangle$
because the words around the corresponding loops in
$\langle \alpha, t \mid \alpha ^t =\alpha \rangle$
because the words around the corresponding loops in
![]() $\Delta$
represent the identity in
$\Delta$
represent the identity in
![]() $\langle a, t \mid a^t = a \rangle$
. Since the complementary regions are filled with minimal area subdiagrams, all
$\langle a, t \mid a^t = a \rangle$
. Since the complementary regions are filled with minimal area subdiagrams, all
![]() $\alpha$
- and
$\alpha$
- and
![]() $t$
- partial-corridors in
$t$
- partial-corridors in
![]() $\theta '$
are reduced.
$\theta '$
are reduced.
Lemma 6.10 implies that the length of any alternating corridor
![]() $\mathcal{A}$
in our diagram is bounded above by the total number of
$\mathcal{A}$
in our diagram is bounded above by the total number of
![]() $c$
-corridors and alternating corridors that intersect
$c$
-corridors and alternating corridors that intersect
![]() $\mathcal{A}$
. Since there are in total no more than
$\mathcal{A}$
. Since there are in total no more than
![]() $|u'|/2$
$|u'|/2$
![]() $c$
-corridors and alternating corridors, the length of
$c$
-corridors and alternating corridors, the length of
![]() $\mathcal{A}$
is at most
$\mathcal{A}$
is at most
![]() $|u'|/2$
. Similarly, the length of each
$|u'|/2$
. Similarly, the length of each
![]() $c$
-corridor is at most
$c$
-corridor is at most
![]() $|u|/2$
by Corollary 6.7, and there are fewer than
$|u|/2$
by Corollary 6.7, and there are fewer than
![]() $|u|/2$
many
$|u|/2$
many
![]() $c$
-corridors. So altogether,
$c$
-corridors. So altogether,
6.5. Quadratic area diagrams over
 $Q_l$
$Q_l$
In the previous section, we established that given a valid
![]() $c$
-pairing for a word representing the identity in
$c$
-pairing for a word representing the identity in
![]() $Q_1$
, we can construct a quadratic area van Kampen diagram with that
$Q_1$
, we can construct a quadratic area van Kampen diagram with that
![]() $c$
-pairing. In this section, we leverage Lemma 6.12 to the case where we have a valid
$c$
-pairing. In this section, we leverage Lemma 6.12 to the case where we have a valid
![]() $c$
-pairing for a word representing the identity in
$c$
-pairing for a word representing the identity in
![]() $Q_l$
. Our main strategy is to rewrite words representing the identity in
$Q_l$
. Our main strategy is to rewrite words representing the identity in
![]() $Q_l$
to words in
$Q_l$
to words in
![]() $Q_1$
, where we can apply Lemma 6.12 to build a van Kampen diagram. Then, we convert it to a diagram over
$Q_1$
, where we can apply Lemma 6.12 to build a van Kampen diagram. Then, we convert it to a diagram over
![]() $Q_l$
.
$Q_l$
.
Recall that
Define
Identifying
![]() $t$
with
$t$
with
![]() $\tau ^l$
gives an isomorphism of
$\tau ^l$
gives an isomorphism of
![]() $Q_{l}$
with the index
$Q_{l}$
with the index
![]() $l$
subgroup of
$l$
subgroup of
![]() $Q^{\tau }_{1}$
generated by
$Q^{\tau }_{1}$
generated by
![]() $a,c,$
and
$a,c,$
and
![]() $\tau ^l$
.
$\tau ^l$
.
Proposition 6.13. If
![]() $u$
is a (not necessarily freely reduced) word representing the identity in
$u$
is a (not necessarily freely reduced) word representing the identity in
![]() ${Q}_l$
and
${Q}_l$
and
![]() $P$
is a valid
$P$
is a valid
![]() $c$
-pairing of
$c$
-pairing of
![]() $u$
, there exists a van Kampen diagram for the corresponding word
$u$
, there exists a van Kampen diagram for the corresponding word
![]() $v\;:\!=\;u(a,c,\tau ^l)$
in
$v\;:\!=\;u(a,c,\tau ^l)$
in
![]() $Q_1^{\tau }$
with a corresponding
$Q_1^{\tau }$
with a corresponding
![]() $c$
-pairing.
$c$
-pairing.
Proof. Suppose
![]() $u(a,c,t)$
represents the identity in
$u(a,c,t)$
represents the identity in
![]() ${Q}_l$
and
${Q}_l$
and
![]() $\theta _0$
is a van Kampen diagram over
$\theta _0$
is a van Kampen diagram over
![]() ${Q}_l$
for
${Q}_l$
for
![]() $u$
inducing the
$u$
inducing the
![]() $c$
-pairing
$c$
-pairing
![]() $P$
. Define
$P$
. Define
![]() $v\;:\!=\;u(a,c,\tau ^l)$
—that is, obtain
$v\;:\!=\;u(a,c,\tau ^l)$
—that is, obtain
![]() $v$
by substituting a
$v$
by substituting a
![]() $(\tau ^l)^{\pm 1}$
for every
$(\tau ^l)^{\pm 1}$
for every
![]() $t^{\pm 1}$
in
$t^{\pm 1}$
in
![]() $u$
. Then,
$u$
. Then,
![]() $v$
represents the identity in
$v$
represents the identity in
![]() ${Q}_{1}^{\tau } = \ \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$
and
${Q}_{1}^{\tau } = \ \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$
and
![]() $P$
induces a valid
$P$
induces a valid
![]() $c$
-pairing for
$c$
-pairing for
![]() $v$
(which we will also call
$v$
(which we will also call
![]() $P$
) since
$P$
) since
![]() $\theta _0$
can be converted to a van Kampen diagram for
$\theta _0$
can be converted to a van Kampen diagram for
![]() $v$
over
$v$
over
![]() ${Q}_{1}^{\tau }$
with the same pattern of
${Q}_{1}^{\tau }$
with the same pattern of
![]() $c$
-corridors as follows. First replace each
$c$
-corridors as follows. First replace each
![]() $t$
-edge in
$t$
-edge in
![]() $\theta _0$
by a concatenation of
$\theta _0$
by a concatenation of
![]() $l$
$l$
![]() $\tau$
-edges. The resulting diagram has 2-cells of two types—those originating from the relation
$\tau$
-edges. The resulting diagram has 2-cells of two types—those originating from the relation
![]() $a^t=a$
and those from the relation
$a^t=a$
and those from the relation
![]() $c^t=ca^l$
. The perimeter words of these 2-cells become
$c^t=ca^l$
. The perimeter words of these 2-cells become
![]() $a^{\tau ^l}a^{-1}$
and
$a^{\tau ^l}a^{-1}$
and
![]() $c^{\tau ^l}(ca^{l})^{-1}$
. These words are relators in
$c^{\tau ^l}(ca^{l})^{-1}$
. These words are relators in
![]() ${Q}_{1}^{\tau }$
: the first can be derived by
${Q}_{1}^{\tau }$
: the first can be derived by
![]() $l$
applications of
$l$
applications of
![]() $a^{\tau }=a$
and the second by
$a^{\tau }=a$
and the second by
![]() $l$
applications of
$l$
applications of
![]() $c^{\tau }=ca$
and
$c^{\tau }=ca$
and
![]() $l(l-1)/2$
applications of
$l(l-1)/2$
applications of
![]() $a^{\tau }=a$
. Accordingly, refine the diagram by replacing the
$a^{\tau }=a$
. Accordingly, refine the diagram by replacing the
![]() $a^{\tau ^l}a^{-1}$
2-cells with an
$a^{\tau ^l}a^{-1}$
2-cells with an
![]() $a$
-corridor of
$a$
-corridor of
![]() $l$
2-cells each labeled
$l$
2-cells each labeled
![]() $a^{\tau } a^{-1}$
, and the
$a^{\tau } a^{-1}$
, and the
![]() $c^{\tau ^l}(ca^{l})^{-1}$
2-cells with a
$c^{\tau ^l}(ca^{l})^{-1}$
2-cells with a
![]() $c$
-corridor of
$c$
-corridor of
![]() $l$
2-cells labeled
$l$
2-cells labeled
![]() $c^{\tau }(ca)^{-1}$
together with
$c^{\tau }(ca)^{-1}$
together with
![]() $l(l-1)/2$
of the
$l(l-1)/2$
of the
![]() $a^{\tau } a^{-1}$
2-cells. The substitutions in the case
$a^{\tau } a^{-1}$
2-cells. The substitutions in the case
![]() $l=3$
are shown in Figure 16. This process maintains the
$l=3$
are shown in Figure 16. This process maintains the
![]() $c$
-pairing during the change from
$c$
-pairing during the change from
![]() $\mathcal{Q}_l$
to
$\mathcal{Q}_l$
to
![]() $\mathcal{Q}_1^{\tau }$
.
$\mathcal{Q}_1^{\tau }$
.
After producing a quadratic area van Kampen diagram for
![]() $v$
in
$v$
in
![]() $Q_1^{\tau }$
that has
$Q_1^{\tau }$
that has
![]() $c$
-pairing
$c$
-pairing
![]() $P$
, we want to use it to build a quadratic area van Kampen diagram for
$P$
, we want to use it to build a quadratic area van Kampen diagram for
![]() $u$
in
$u$
in
![]() $Q_l$
that also has
$Q_l$
that also has
![]() $c$
-pairing
$c$
-pairing
![]() $P$
. The following lemma tells us that we will be able to replace
$P$
. The following lemma tells us that we will be able to replace
![]() $c$
-corridors over
$c$
-corridors over
![]() $Q_1^{\tau }$
with
$Q_1^{\tau }$
with
![]() $c$
-corridors over
$c$
-corridors over
![]() $Q_l$
, as they always occur in multiples of
$Q_l$
, as they always occur in multiples of
![]() $l$
.
$l$
.

Figure 16. Converting
![]() $\theta _0$
from
$\theta _0$
from
![]() $Q_l$
to
$Q_l$
to
![]() $Q_1^{\tau }$
(illustrated with
$Q_1^{\tau }$
(illustrated with
![]() $l=3$
).
$l=3$
).
Lemma 6.14. Suppose
![]() $\theta$
is a van Kampen diagram for a word
$\theta$
is a van Kampen diagram for a word
![]() $v = v(a, c, \tau ^l)$
over
$v = v(a, c, \tau ^l)$
over
![]() ${Q}^{\tau }_{1} = \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$
, with reduced
${Q}^{\tau }_{1} = \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$
, with reduced
![]() $c$
-corridors. Then, every
$c$
-corridors. Then, every
![]() $c$
-corridor in
$c$
-corridor in
![]() $\theta$
has length a multiple of
$\theta$
has length a multiple of
![]() $l$
.
$l$
.
Proof. Let
![]() $\mathcal{T}$
be the tree dual to the
$\mathcal{T}$
be the tree dual to the
![]() $c$
-corridors in
$c$
-corridors in
![]() $\theta$
—that is,
$\theta$
—that is,
![]() $\mathcal{T}$
has a vertex dual to each
$\mathcal{T}$
has a vertex dual to each
![]() $c$
-complementary region and an edge dual to each
$c$
-complementary region and an edge dual to each
![]() $c$
-corridor; the leaves of
$c$
-corridor; the leaves of
![]() $\mathcal{T}$
correspond to regions which have one single
$\mathcal{T}$
correspond to regions which have one single
![]() $c$
-corridor in their perimeter (see Section 3.1). Pick any leaf
$c$
-corridor in their perimeter (see Section 3.1). Pick any leaf
![]() $r$
of
$r$
of
![]() $\mathcal{T}$
to serve as the root, marked in blue in the figure. There is a bijection between vertices
$\mathcal{T}$
to serve as the root, marked in blue in the figure. There is a bijection between vertices
![]() $v \neq r$
of
$v \neq r$
of
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $c$
-corridors
$c$
-corridors
![]() $C_v$
: take
$C_v$
: take
![]() $C_v$
to be dual to the first edge of the geodesic in
$C_v$
to be dual to the first edge of the geodesic in
![]() $\mathcal{T}$
from
$\mathcal{T}$
from
![]() $v$
to
$v$
to
![]() $r$
. This situation is illustrated in Figure 17. Each line represents a
$r$
. This situation is illustrated in Figure 17. Each line represents a
![]() $c$
-corridor, and a vertex is drawn in each
$c$
-corridor, and a vertex is drawn in each
![]() $c$
-complementary region.
$c$
-complementary region.

Figure 17. The tree
![]() $\mathcal{T}$
dual to the
$\mathcal{T}$
dual to the
![]() $c$
-corridors of a diagram
$c$
-corridors of a diagram
![]() $\theta$
, with root
$\theta$
, with root
![]() $r$
(chosen to have degree 1). The index sum of
$r$
(chosen to have degree 1). The index sum of
![]() $\tau$
around the
$\tau$
around the
![]() $c$
-complementary region dual to
$c$
-complementary region dual to
![]() $v$
is zero. By the induction hypothesis, the length and thus index sum of
$v$
is zero. By the induction hypothesis, the length and thus index sum of
![]() $\tau$
along the child corridors
$\tau$
along the child corridors
![]() $C_{v_i}$
are multiples of
$C_{v_i}$
are multiples of
![]() $l$
, and along the boundary of
$l$
, and along the boundary of
![]() $\theta$
making up the complementary region dual to
$\theta$
making up the complementary region dual to
![]() $v$
are also multiples of
$v$
are also multiples of
![]() $l$
, so the length and thus index sum of
$l$
, so the length and thus index sum of
![]() $\tau$
along
$\tau$
along
![]() $C_v$
is a multiple of
$C_v$
is a multiple of
![]() $l$
.
$l$
.
We will show by reverse induction on distance in
![]() $\mathcal{T}$
(i.e. starting from the leaves furthest down the tree and working toward
$\mathcal{T}$
(i.e. starting from the leaves furthest down the tree and working toward
![]() $r$
) that the length of
$r$
) that the length of
![]() $C_v$
is a multiple of
$C_v$
is a multiple of
![]() $l$
. Indeed when
$l$
. Indeed when
![]() $v$
is a leaf, the argument of Corollary 6.7 implies the length of
$v$
is a leaf, the argument of Corollary 6.7 implies the length of
![]() $C_v$
is given by the index sum of
$C_v$
is given by the index sum of
![]() $\tau ^{\pm 1}$
in the boundary between the paired
$\tau ^{\pm 1}$
in the boundary between the paired
![]() $c$
-edges, and
$c$
-edges, and
![]() $\tau$
only appears in multiples of
$\tau$
only appears in multiples of
![]() $l$
in
$l$
in
![]() $v$
, so the result holds. For the induction step, suppose
$v$
, so the result holds. For the induction step, suppose
![]() $v \neq r$
. The length of
$v \neq r$
. The length of
![]() $C_v$
is the exponent sum of the lengths of
$C_v$
is the exponent sum of the lengths of
![]() $C_{v_i}$
(with appropriate signs) over every child
$C_{v_i}$
(with appropriate signs) over every child
![]() $v_i$
of
$v_i$
of
![]() $v$
(each a multiple of
$v$
(each a multiple of
![]() $l$
, by induction hypothesis) and of the
$l$
, by induction hypothesis) and of the
![]() $\tau ^l$
in the boundary of
$\tau ^l$
in the boundary of
![]() $\theta$
that are also in the boundary of the subdiagram dual to
$\theta$
that are also in the boundary of the subdiagram dual to
![]() $v$
.
$v$
.
Next, we examine how to build a filling for a
![]() $c$
-complementary region over
$c$
-complementary region over
![]() $Q_{l}$
from a filling for a
$Q_{l}$
from a filling for a
![]() $c$
-complementary region over
$c$
-complementary region over
![]() $Q_{1}^{\tau }$
when their boundaries are compatible in that the
$Q_{1}^{\tau }$
when their boundaries are compatible in that the
![]() $\tau$
in the boundary of the latter occur in powers of
$\tau$
in the boundary of the latter occur in powers of
![]() $l$
.
$l$
.
Lemma 6.15. Suppose
![]() $w = w(a, \tau ^l)$
has a van Kampen diagram
$w = w(a, \tau ^l)$
has a van Kampen diagram
![]() $\mathcal{D}$
over
$\mathcal{D}$
over
![]() $\langle a, \tau \mid a^\tau = a \rangle$
of area
$\langle a, \tau \mid a^\tau = a \rangle$
of area
![]() $A$
. Then
$A$
. Then
![]() $w(a, t)$
has a van Kampen diagram
$w(a, t)$
has a van Kampen diagram
![]() $\mathcal{D}''$
over
$\mathcal{D}''$
over
![]() $\langle a, t \mid a^t=a \rangle$
of area at most
$\langle a, t \mid a^t=a \rangle$
of area at most
![]() $A$
.
$A$
.
Proof. Define a
![]() $\tau$
-segment to be
$\tau$
-segment to be
![]() $l$
consecutive
$l$
consecutive
![]() $\tau$
-labeled edges in the boundary circuit of
$\tau$
-labeled edges in the boundary circuit of
![]() $\mathcal{D}$
. Such segments have a natural orientation that agrees with the orientation of the constituent
$\mathcal{D}$
. Such segments have a natural orientation that agrees with the orientation of the constituent
![]() $\tau$
. We will find a van Kampen diagram for
$\tau$
. We will find a van Kampen diagram for
![]() $w$
over
$w$
over
![]() $\langle a, \tau \mid a^\tau = a \rangle$
for which the
$\langle a, \tau \mid a^\tau = a \rangle$
for which the
![]() $\tau$
-segments are connected by blocks of parallel
$\tau$
-segments are connected by blocks of parallel
![]() $\tau$
-corridors. (Call this a
$\tau$
-corridors. (Call this a
![]() $\tau ^l$
-pairing.)
$\tau ^l$
-pairing.)
The first edge in any
![]() $\tau$
-segment can only be paired with a
$\tau$
-segment can only be paired with a
![]() $\tau$
-corridor in
$\tau$
-corridor in
![]() $\mathcal{D}$
with the first edge of an oppositely oriented
$\mathcal{D}$
with the first edge of an oppositely oriented
![]() $\tau$
-segment. Indeed, suppose that an initial
$\tau$
-segment. Indeed, suppose that an initial
![]() $\tau$
in a
$\tau$
in a
![]() $\tau$
-segment is connected by a corridor
$\tau$
-segment is connected by a corridor
![]() $C$
to a
$C$
to a
![]() $\tau$
in position
$\tau$
in position
![]() $i$
on another segment, with
$i$
on another segment, with
![]() $1\leq i \leq l$
. Let
$1\leq i \leq l$
. Let
![]() $\widehat{w}$
be the subword of
$\widehat{w}$
be the subword of
![]() $w$
between them, as shown in Figure 18a. Because
$w$
between them, as shown in Figure 18a. Because
![]() $\tau$
corridors do not cross, the
$\tau$
corridors do not cross, the
![]() $\tau$
-index sum of
$\tau$
-index sum of
![]() $\widehat{w}$
must be zero. If
$\widehat{w}$
must be zero. If
![]() $i \neq 1$
, the
$i \neq 1$
, the
![]() $\tau$
-index sum of
$\tau$
-index sum of
![]() $\widehat{w}$
will not be a multiple of
$\widehat{w}$
will not be a multiple of
![]() $l$
, as
$l$
, as
![]() $\widehat{w}$
either includes an entire
$\widehat{w}$
either includes an entire
![]() $\tau$
-segment or entirely misses it, except for the partial segment which contains the
$\tau$
-segment or entirely misses it, except for the partial segment which contains the
![]() $\tau$
in position
$\tau$
in position
![]() $i$
. In particular, the index sum of
$i$
. In particular, the index sum of
![]() $\tau$
in
$\tau$
in
![]() $\widehat{w}$
can only be 0 when
$\widehat{w}$
can only be 0 when
![]() $i=1$
.
$i=1$
.

Figure 18. In a word
![]() $w$
on
$w$
on
![]() $a$
and
$a$
and
![]() $\tau ^l$
, there is a valid
$\tau ^l$
, there is a valid
![]() $\tau$
-pairing that pairs whole
$\tau$
-pairing that pairs whole
![]() $\tau$
-segments.
$\tau$
-segments.
Construct a new van Kampen diagram
![]() $\mathcal{D}'$
for
$\mathcal{D}'$
for
![]() $w$
over
$w$
over
![]() $\langle a, \tau \mid a^\tau = a \rangle$
as follows. Begin with a planar loop with edges labeled so that we read
$\langle a, \tau \mid a^\tau = a \rangle$
as follows. Begin with a planar loop with edges labeled so that we read
![]() $w(a, \tau ^l)$
around the perimeter. Add in all initial
$w(a, \tau ^l)$
around the perimeter. Add in all initial
![]() $\tau$
corridors from
$\tau$
corridors from
![]() $\mathcal{D}$
. If an initial
$\mathcal{D}$
. If an initial
![]() $\tau$
-corridor
$\tau$
-corridor
![]() $C$
connects
$C$
connects
![]() $\tau$
-segments
$\tau$
-segments
![]() $S$
and
$S$
and
![]() $S'$
, we will pair each
$S'$
, we will pair each
![]() $\tau$
in
$\tau$
in
![]() $S$
to the corresponding
$S$
to the corresponding
![]() $\tau$
in
$\tau$
in
![]() $S'$
using copies of
$S'$
using copies of
![]() $C$
, as in Figures 18b and 19c. The remaining regions that have to be filled have perimeters labeled by words on
$C$
, as in Figures 18b and 19c. The remaining regions that have to be filled have perimeters labeled by words on
![]() $a^{\pm 1}$
alone, as all
$a^{\pm 1}$
alone, as all
![]() $\tau$
edges have been paired. Moreover, the index sum of
$\tau$
edges have been paired. Moreover, the index sum of
![]() $a$
is zero, so these can be folded together to complete the construction of
$a$
is zero, so these can be folded together to complete the construction of
![]() $\mathcal{D}'$
without the addition of any further 2-cells.
$\mathcal{D}'$
without the addition of any further 2-cells.

Figure 19. A toy example of the procedure of Lemma 6.15 (illustrated with
![]() $l=3$
).
$l=3$
).
The area of
![]() $\mathcal{D}'$
will be
$\mathcal{D}'$
will be
![]() $l$
times the sum of the initial
$l$
times the sum of the initial
![]() $\tau$
-corridor contributions, and so in particular, the area of the new diagram is at most
$\tau$
-corridor contributions, and so in particular, the area of the new diagram is at most
![]() $l A$
. Let
$l A$
. Let
![]() $\mathcal{D}''$
be the van Kampen diagram for
$\mathcal{D}''$
be the van Kampen diagram for
![]() $w(a,t)$
over
$w(a,t)$
over
![]() $\langle a, t \mid a^t = a \rangle$
of area at most
$\langle a, t \mid a^t = a \rangle$
of area at most
![]() $A$
obtained by replacing each stack of
$A$
obtained by replacing each stack of
![]() $l$
$l$
![]() $\tau$
-corridors in
$\tau$
-corridors in
![]() $\mathcal{D}'$
by a single
$\mathcal{D}'$
by a single
![]() $t$
-corridor and each
$t$
-corridor and each
![]() $\tau$
-segment in the boundary by a single
$\tau$
-segment in the boundary by a single
![]() $t$
-edge, as in Figure 19d.
$t$
-edge, as in Figure 19d.
We will promote Lemma 6.12 to the following result concerning
![]() ${Q_l = \langle a, c, t\,| a^t=a, c^t=ca^l \rangle }.$
${Q_l = \langle a, c, t\,| a^t=a, c^t=ca^l \rangle }.$
Proposition 6.16. There exists
![]() $A_l \gt 0$
such that if
$A_l \gt 0$
such that if
![]() $u$
is a (not necessarily freely reduced) word representing the identity in
$u$
is a (not necessarily freely reduced) word representing the identity in
![]() ${Q}_l$
and
${Q}_l$
and
![]() $P$
is a valid
$P$
is a valid
![]() $c$
-pairing of
$c$
-pairing of
![]() $u$
, then there exists a van Kampen diagram
$u$
, then there exists a van Kampen diagram
![]() $\theta$
for
$\theta$
for
![]() $u$
over
$u$
over
![]() ${Q}_l$
which has reduced
${Q}_l$
which has reduced
![]() $c$
-corridors, induces
$c$
-corridors, induces
![]() $P$
, and has
$P$
, and has
![]() $\textrm{Area}(\theta ) \leq A_l |u|^2$
.
$\textrm{Area}(\theta ) \leq A_l |u|^2$
.
Proof. Suppose
![]() $u(a,c,t)$
represents the identity in
$u(a,c,t)$
represents the identity in
![]() ${Q}_l$
and
${Q}_l$
and
![]() $u$
has a valid
$u$
has a valid
![]() $c$
-pairing
$c$
-pairing
![]() $P$
. Proposition 6.13 implies that
$P$
. Proposition 6.13 implies that
![]() $P$
is also a valid
$P$
is also a valid
![]() $c$
-pairing for the corresponding word
$c$
-pairing for the corresponding word
![]() $v\;:\!=\;u(a,c,\tau ^l)$
in
$v\;:\!=\;u(a,c,\tau ^l)$
in
![]() $Q_1^{\tau }$
, which we get by substituting a
$Q_1^{\tau }$
, which we get by substituting a
![]() $(\tau ^l)^{\pm 1}$
for every
$(\tau ^l)^{\pm 1}$
for every
![]() $t^{\pm 1}$
in
$t^{\pm 1}$
in
![]() $u$
. Now we can use what we know about building diagrams over
$u$
. Now we can use what we know about building diagrams over
![]() $Q_1^{\tau }$
: by Lemma 6.12, there is a constant
$Q_1^{\tau }$
: by Lemma 6.12, there is a constant
![]() $A_1\gt 0$
such that
$A_1\gt 0$
such that
![]() $v$
admits a new van Kampen diagram
$v$
admits a new van Kampen diagram
![]() $\theta _{1}$
over
$\theta _{1}$
over
![]() ${Q}_{1}^{\tau }$
that induces
${Q}_{1}^{\tau }$
that induces
![]() $P$
and has area at most
$P$
and has area at most
![]() $A_1{|{v}|^2} \leq A_1 l^2{|u|}^2$
. Guided by
$A_1{|{v}|^2} \leq A_1 l^2{|u|}^2$
. Guided by
![]() $\theta _{1}$
, we will construct a van Kampen diagram
$\theta _{1}$
, we will construct a van Kampen diagram
![]() $\theta _{l}$
for
$\theta _{l}$
for
![]() $u$
over
$u$
over
![]() ${Q}_{l}$
which has comparable area.
${Q}_{l}$
which has comparable area.
By Lemma 6.14,
![]() $c$
-corridors in
$c$
-corridors in
![]() $\theta _1$
all have length that is a multiple of
$\theta _1$
all have length that is a multiple of
![]() $l$
. To build
$l$
. To build
![]() $\theta _{l}$
, we begin by inserting reduced
$\theta _{l}$
, we begin by inserting reduced
![]() $c$
-corridors into a polygonal path labeled by
$c$
-corridors into a polygonal path labeled by
![]() $u$
, mimicking the
$u$
, mimicking the
![]() $c$
-corridors in
$c$
-corridors in
![]() $\theta _1$
. Corresponding
$\theta _1$
. Corresponding
![]() $c$
-corridors in the two diagrams differ in length by exactly the factor
$c$
-corridors in the two diagrams differ in length by exactly the factor
![]() $l$
: where a
$l$
: where a
![]() $c$
-corridor in
$c$
-corridor in
![]() $\theta _1$
has
$\theta _1$
has
![]() $\tau ^{nl}$
along one side and
$\tau ^{nl}$
along one side and
![]() $(\tau a^{-1})^{nl}$
along the other, the corresponding
$(\tau a^{-1})^{nl}$
along the other, the corresponding
![]() $c$
-corridor in
$c$
-corridor in
![]() $\theta _l$
has
$\theta _l$
has
![]() $t^n$
along one side and
$t^n$
along one side and
![]() $(t a^{-l})^{n}$
along the other.
$(t a^{-l})^{n}$
along the other.
Next, we fill the
![]() $c$
-complementary regions. We wish to use Lemma 6.15 to convert the filling in
$c$
-complementary regions. We wish to use Lemma 6.15 to convert the filling in
![]() $c$
-complementary regions of
$c$
-complementary regions of
![]() $\theta _1$
to fillings in
$\theta _1$
to fillings in
![]() $\theta _l$
, but for any
$\theta _l$
, but for any
![]() $c$
-complementary region, the word along the perimeter of the region will not generally have an appropriate form. Its perimeter has the form
$c$
-complementary region, the word along the perimeter of the region will not generally have an appropriate form. Its perimeter has the form
![]() $x_0(\tau a^{\epsilon _1})^{l k_1} x_1 \cdots (\tau a^{\epsilon _n})^{lk_n}x_n$
, where
$x_0(\tau a^{\epsilon _1})^{l k_1} x_1 \cdots (\tau a^{\epsilon _n})^{lk_n}x_n$
, where
![]() $\epsilon _i \in \{0, -1\}$
,
$\epsilon _i \in \{0, -1\}$
,
![]() $k_i \neq 0$
, and
$k_i \neq 0$
, and
![]() $x_i$
is a subword of
$x_i$
is a subword of
![]() $v$
and therefore is a word in
$v$
and therefore is a word in
![]() $a$
and
$a$
and
![]() $\tau ^l$
, as in Figure 20. We add a collar of
$\tau ^l$
, as in Figure 20. We add a collar of
![]() $2$
-cells to change the boundary of the
$2$
-cells to change the boundary of the
![]() $c$
-complemetary region to
$c$
-complemetary region to
![]() $x_0 (\tau ^l a^{\epsilon _1 l})^{k_1} x_1 \cdots (\tau ^l a^{\epsilon _n l})^{k_n}x_n$
. In particular, if
$x_0 (\tau ^l a^{\epsilon _1 l})^{k_1} x_1 \cdots (\tau ^l a^{\epsilon _n l})^{k_n}x_n$
. In particular, if
![]() $L$
is a minimal area diagram for the word
$L$
is a minimal area diagram for the word
![]() $(\tau a^{-1})^{l}(\tau ^la^{-l})^{-1}$
, then
$(\tau a^{-1})^{l}(\tau ^la^{-l})^{-1}$
, then
![]() $k_i$
copies of
$k_i$
copies of
![]() $L$
can be glued in to rewrite
$L$
can be glued in to rewrite
![]() $(\tau a^{\epsilon _i})^{l k_i}$
to
$(\tau a^{\epsilon _i})^{l k_i}$
to
![]() $(\tau ^l a^{\epsilon _i l})^{k_i}$
. The result is a region with boundary that is a word in
$(\tau ^l a^{\epsilon _i l})^{k_i}$
. The result is a region with boundary that is a word in
![]() $a$
and
$a$
and
![]() $\tau ^l$
.
$\tau ^l$
.
Apply Lemma 6.15 to convert each of these diagrams, without increasing area, to diagrams over
![]() $\langle a, t \mid a^t =a \rangle$
with boundary
$\langle a, t \mid a^t =a \rangle$
with boundary
![]() $x_0(t a^{l \epsilon _1})^{k_1} x_1 \dots (t a^{l\epsilon _n})^{k_n}x_n$
(as in Figure 21d), and use them to fill the
$x_0(t a^{l \epsilon _1})^{k_1} x_1 \dots (t a^{l\epsilon _n})^{k_n}x_n$
(as in Figure 21d), and use them to fill the
![]() $c$
-complementary regions of
$c$
-complementary regions of
![]() $\theta _l$
. This produces a van Kampen diagram
$\theta _l$
. This produces a van Kampen diagram
![]() $\theta _l$
for
$\theta _l$
for
![]() $u$
over
$u$
over
![]() ${Q}_l$
.
${Q}_l$
.

Figure 20. The quadratic area diagram
![]() $\theta _1$
.
$\theta _1$
.

Figure 21. Converting a
![]() $c$
-complementary region filling from
$c$
-complementary region filling from
![]() $\theta _1$
over
$\theta _1$
over
![]() ${Q}_1^{\tau }$
to one for
${Q}_1^{\tau }$
to one for
![]() $\theta _l$
over
$\theta _l$
over
![]() ${Q}_l$
.
${Q}_l$
.
Finally, we come to area estimates for
![]() $\theta _l$
. First, observe that the total number of 2-cells in the
$\theta _l$
. First, observe that the total number of 2-cells in the
![]() $c$
-corridors in
$c$
-corridors in
![]() $\theta _1$
is at most the area of
$\theta _1$
is at most the area of
![]() $\theta _1$
, which we determined earlier to be at most
$\theta _1$
, which we determined earlier to be at most
![]() $A_1 l^2{|u|}^2$
. Correspondingly, there are at most
$A_1 l^2{|u|}^2$
. Correspondingly, there are at most
![]() $A_1 l{|u|}^2$
2-cells in the
$A_1 l{|u|}^2$
2-cells in the
![]() $c$
-corridors in
$c$
-corridors in
![]() $\theta _l$
. The number of copies of
$\theta _l$
. The number of copies of
![]() $L$
glued on to the
$L$
glued on to the
![]() $c$
-complementary regions is at most
$c$
-complementary regions is at most
![]() $A_1 l{|u|}^2$
, since it is the sum of the lengths of the
$A_1 l{|u|}^2$
, since it is the sum of the lengths of the
![]() $c$
-corridors, divided by
$c$
-corridors, divided by
![]() $l$
. Since
$l$
. Since
![]() $L$
has area bounded above by
$L$
has area bounded above by
![]() $l^2$
, the total area taken by copies of
$l^2$
, the total area taken by copies of
![]() $L$
is at most
$L$
is at most
![]() $A_1 l^3{|u|}^2$
. The total area of the
$A_1 l^3{|u|}^2$
. The total area of the
![]() $c$
-complementary regions in
$c$
-complementary regions in
![]() $\theta _1$
is also at most
$\theta _1$
is also at most
![]() $A_1 l^2{|u|}^2$
. They, along with the attached copies of
$A_1 l^2{|u|}^2$
. They, along with the attached copies of
![]() $L$
, are converted to the
$L$
, are converted to the
![]() $c$
-complementary regions in
$c$
-complementary regions in
![]() $\theta _l$
without an increase in their area, as per Lemma 6.15. Therefore, the area of
$\theta _l$
without an increase in their area, as per Lemma 6.15. Therefore, the area of
![]() $\theta _l$
is at most
$\theta _l$
is at most
![]() $A_1 l{|u|}^2 + A_1 l^3{|u|}^2 + A_1 l^2{|u|}^2 \leq A_l |u|^2$
, where
$A_1 l{|u|}^2 + A_1 l^3{|u|}^2 + A_1 l^2{|u|}^2 \leq A_l |u|^2$
, where
![]() $A_l \;:\!=\; A_1(l + l^3+ l^2)$
.
$A_l \;:\!=\; A_1(l + l^3+ l^2)$
.
6.6. Completing our proof of Theorem B
Proof of Theorem B (1). This is the case where
![]() $\phi$
has finite order. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function of
$\phi$
has finite order. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function of
![]() $M_{\Phi }$
, and thus
$M_{\Phi }$
, and thus
![]() $M_{\Psi }$
, we can work with
$M_{\Psi }$
, we can work with
![]() $M_{\Xi }$
, which has the form:
$M_{\Xi }$
, which has the form:
 \begin{align*}M_{0, l, m} & \;:\!=\; \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{0}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle \nonumber \\[5pt] & \;= \langle a, b,c, t \mid [a,b]=[a,t] = [b,t]=1,\ c^{t}=c a^lb^m \rangle \end{align*}
\begin{align*}M_{0, l, m} & \;:\!=\; \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{0}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle \nonumber \\[5pt] & \;= \langle a, b,c, t \mid [a,b]=[a,t] = [b,t]=1,\ c^{t}=c a^lb^m \rangle \end{align*}
for some
![]() $l, m \in \mathbb{Z}$
. Let
$l, m \in \mathbb{Z}$
. Let
These groups are not hyperbolic, so their Dehn functions grow at least quadratically. We will show that these mapping tori have quadratic Dehn functions for all
![]() $l, m \in \mathbb{Z}$
. All proofs of the quadratic upperbounds for these groups can be reduced to the proof for
$l, m \in \mathbb{Z}$
. All proofs of the quadratic upperbounds for these groups can be reduced to the proof for
![]() $M_{0,l,0} = \langle a, b,c, t \mid [a,b]=[a,t]=[b,t]=1,\ c^{t}=c a^l \rangle$
. We begin by considering this special case, which has the property that
$M_{0,l,0} = \langle a, b,c, t \mid [a,b]=[a,t]=[b,t]=1,\ c^{t}=c a^l \rangle$
. We begin by considering this special case, which has the property that
![]() $b$
-corridors have the same words along their top and their bottom sides.
$b$
-corridors have the same words along their top and their bottom sides.
Suppose
![]() $w$
is a word representing the identity in
$w$
is a word representing the identity in
![]() $M_{0,l,0}$
. Let
$M_{0,l,0}$
. Let
![]() $\Delta$
be a minimal area van Kampen diagram for
$\Delta$
be a minimal area van Kampen diagram for
![]() $w$
over
$w$
over
![]() $M_{0,l,0}$
. Let
$M_{0,l,0}$
. Let
![]() $\overline{w}$
be
$\overline{w}$
be
![]() $w$
with all
$w$
with all
![]() $b^{\pm 1}$
removed. Then
$b^{\pm 1}$
removed. Then
![]() $\overline{w}=1$
in
$\overline{w}=1$
in
![]() $N_l$
. Moreover, the
$N_l$
. Moreover, the
![]() $c$
-pairing
$c$
-pairing
![]() $P$
induced by
$P$
induced by
![]() $\Delta$
in turn induces a valid
$\Delta$
in turn induces a valid
![]() $c$
-pairing
$c$
-pairing
![]() $\overline{P}$
for
$\overline{P}$
for
![]() $\overline{w}$
because collapsing each
$\overline{w}$
because collapsing each
![]() $b$
-corridor to the path along its bottom side gives a van Kampen diagram
$b$
-corridor to the path along its bottom side gives a van Kampen diagram
![]() $\overline{\Delta }$
for
$\overline{\Delta }$
for
![]() $\overline{w}$
over
$\overline{w}$
over
![]() $N_l$
.
$N_l$
.
By Proposition 6.16, there is a constant
![]() $A_l \gt 0$
and a van Kampen diagram
$A_l \gt 0$
and a van Kampen diagram
![]() $\overline{\theta }$
for
$\overline{\theta }$
for
![]() $\overline{w}$
over
$\overline{w}$
over
![]() $N_l$
which has reduced
$N_l$
which has reduced
![]() $c$
-corridors, induces
$c$
-corridors, induces
![]() $\overline{P}$
, and has area at most
$\overline{P}$
, and has area at most
![]() $A_l |\overline{w}|^2$
.
$A_l |\overline{w}|^2$
.
The defining relations for
![]() $N_l$
are also defining relations for
$N_l$
are also defining relations for
![]() $M_{0,l,0}$
(as
$M_{0,l,0}$
(as
![]() $m=0$
), so
$m=0$
), so
![]() $\overline{\theta }$
is a fortiori a van Kampen diagram over
$\overline{\theta }$
is a fortiori a van Kampen diagram over
![]() $M_{0,l,0}$
. We aim to convert it from a van Kampen diagram for
$M_{0,l,0}$
. We aim to convert it from a van Kampen diagram for
![]() $\overline{w}$
, which contains no letters
$\overline{w}$
, which contains no letters
![]() $b^{\pm 1}$
, to a van Kampen diagram
$b^{\pm 1}$
, to a van Kampen diagram
![]() $\theta$
for the original
$\theta$
for the original
![]() $w$
, which may contain letters
$w$
, which may contain letters
![]() $b^{\pm 1}$
. We will do this without altering its
$b^{\pm 1}$
. We will do this without altering its
![]() $c$
-corridors, only changing the diagrams in the
$c$
-corridors, only changing the diagrams in the
![]() $c$
-complementary regions. Indeed, in the diagram
$c$
-complementary regions. Indeed, in the diagram
![]() $\Delta$
, there are no partial
$\Delta$
, there are no partial
![]() $b$
-corridors and no
$b$
-corridors and no
![]() $b$
-corridor can cross a
$b$
-corridor can cross a
![]() $c$
-corridor. Since the pairings of
$c$
-corridor. Since the pairings of
![]() $c$
-corridors in
$c$
-corridors in
![]() $\overline{\theta }$
agrees with that in
$\overline{\theta }$
agrees with that in
![]() $\overline{\Delta }$
(and so in
$\overline{\Delta }$
(and so in
![]() $\Delta$
), for each
$\Delta$
), for each
![]() $c$
-complementary region
$c$
-complementary region
![]() $\overline{C}$
in
$\overline{C}$
in
![]() $\overline{\theta }$
, there is a corresponding
$\overline{\theta }$
, there is a corresponding
![]() $c$
-complementary region in
$c$
-complementary region in
![]() $\Delta$
.
$\Delta$
.
In
![]() $\Delta$
, no
$\Delta$
, no
![]() $b$
-corridor can cross a
$b$
-corridor can cross a
![]() $c$
-corridor and there are no partial
$c$
-corridor and there are no partial
![]() $b$
-corridors. So, in each word around a
$b$
-corridors. So, in each word around a
![]() $c$
-complementary region the
$c$
-complementary region the
![]() $b$
and
$b$
and
![]() $b^{-1}$
letters are on
$b^{-1}$
letters are on
![]() $\partial \Delta$
and are paired off by
$\partial \Delta$
and are paired off by
![]() $b$
-corridors that connect them. Therefore, each
$b$
-corridors that connect them. Therefore, each
![]() $c$
-complementary region
$c$
-complementary region
![]() $\overline{C}$
in
$\overline{C}$
in
![]() $\overline{\theta }$
can be inflated to put the necessary
$\overline{\theta }$
can be inflated to put the necessary
![]() $b$
and
$b$
and
![]() $b^{-1}$
in place by adding
$b^{-1}$
in place by adding
![]() $b$
-corridors to the boundary of
$b$
-corridors to the boundary of
![]() $ \overline{C}$
, thereby adding an annular cuff about each
$ \overline{C}$
, thereby adding an annular cuff about each
![]() $c$
-complementary region, using 2-cells for the relations
$c$
-complementary region, using 2-cells for the relations
![]() $[b,t]=1,$
and
$[b,t]=1,$
and
![]() $[a,b]=1$
. The total number of such
$[a,b]=1$
. The total number of such
![]() $b$
-corridors that we must insert over all of these diagrams is at most
$b$
-corridors that we must insert over all of these diagrams is at most
![]() $|w|/2$
. The length of each
$|w|/2$
. The length of each
![]() $b$
-corridor is at most the length of the boundary circuit
$b$
-corridor is at most the length of the boundary circuit
![]() $\partial \overline{C}$
of the relevant
$\partial \overline{C}$
of the relevant
![]() $c$
-complementary region
$c$
-complementary region
![]() $\overline{C}$
in
$\overline{C}$
in
![]() $\overline{\theta }$
. By an argument equivalent to Corollary 6.8, the boundary circuit of each
$\overline{\theta }$
. By an argument equivalent to Corollary 6.8, the boundary circuit of each
![]() $c$
-complementary region has length at most a constant times
$c$
-complementary region has length at most a constant times
![]() $|\overline{w}|$
, where the constant is
$|\overline{w}|$
, where the constant is
![]() $|l|+1$
– if the bottom of a
$|l|+1$
– if the bottom of a
![]() $c$
-corridor has
$c$
-corridor has
![]() $t^k$
along it, the top will have
$t^k$
along it, the top will have
![]() $(ta^{-l})^k$
along it.
$(ta^{-l})^k$
along it.
Thus, the area of the resulting diagram
![]() $\theta$
is at most the area of
$\theta$
is at most the area of
![]() $\overline{\theta }$
(which is at most
$\overline{\theta }$
(which is at most
![]() $A_l |\overline{w}|^2$
) plus the number of 2-cells in
$A_l |\overline{w}|^2$
) plus the number of 2-cells in
![]() $b$
-corridors, which is no more than a constant times
$b$
-corridors, which is no more than a constant times
![]() $|\overline{w}| \, |w|$
. In total, the area of
$|\overline{w}| \, |w|$
. In total, the area of
![]() $\theta$
is at most a constant times
$\theta$
is at most a constant times
![]() $|w|^2$
, as required.
$|w|^2$
, as required.
Now we consider the case of
![]() $M_{0, l,m}$
for
$M_{0, l,m}$
for
![]() $m \neq 0$
. If
$m \neq 0$
. If
![]() $l$
and
$l$
and
![]() $m$
are relatively prime, by Bézout’s Lemma, there is a pair of integers
$m$
are relatively prime, by Bézout’s Lemma, there is a pair of integers
![]() $(x,y)$
such that
$(x,y)$
such that
![]() $l y - m x = 1$
. So there is a generating set
$l y - m x = 1$
. So there is a generating set
![]() $\{A, B\}$
of
$\{A, B\}$
of
![]() $\mathbb{Z}^2 = \langle a, b \rangle$
with
$\mathbb{Z}^2 = \langle a, b \rangle$
with
![]() $A= a^{l} b^{m}$
and
$A= a^{l} b^{m}$
and
![]() $B= a^xb^y$
(generating since
$B= a^xb^y$
(generating since
![]() $a = A^yB^{-m}$
and
$a = A^yB^{-m}$
and
![]() $b = B^l A^{-x}$
), for which our group has the presentation:
$b = B^l A^{-x}$
), for which our group has the presentation:
the same as
![]() $M_{0,1,0}$
. Therefore, the Dehn function is quadratic. Finally, if
$M_{0,1,0}$
. Therefore, the Dehn function is quadratic. Finally, if
![]() $l$
and
$l$
and
![]() $m$
are not relatively prime, let
$m$
are not relatively prime, let
![]() $n\;:\!=\;\mbox{gcd}(l, m)$
. Then,
$n\;:\!=\;\mbox{gcd}(l, m)$
. Then,
![]() $M_{0,l,m}$
is a subgroup of index
$M_{0,l,m}$
is a subgroup of index
![]() $n$
in
$n$
in
![]() $M_{0,\frac{l}{n}, \frac{m}{n}}$
. But then,
$M_{0,\frac{l}{n}, \frac{m}{n}}$
. But then,
![]() $M_{0,\frac{l}{n}, \frac{m}{n}}$
has a quadratic Dehn function and hence so does
$M_{0,\frac{l}{n}, \frac{m}{n}}$
has a quadratic Dehn function and hence so does
![]() $M_{0,l,m}$
.
$M_{0,l,m}$
.
Proof of Theorem B (2). This is the case where
![]() $\phi$
has a non-unit eigenvalue. As
$\phi$
has a non-unit eigenvalue. As
![]() $K\;:\!=\;\langle a, b \rangle \cong \mathbb{Z}^2$
quasi-isometrically embeds in
$K\;:\!=\;\langle a, b \rangle \cong \mathbb{Z}^2$
quasi-isometrically embeds in
![]() $\mathbb{Z}^2 \ast \mathbb{Z}$
and
$\mathbb{Z}^2 \ast \mathbb{Z}$
and
![]() $\Phi \left |_{K} \right. = \phi$
is an automorphism of
$\Phi \left |_{K} \right. = \phi$
is an automorphism of
![]() $K$
, Lemma 3.5 implies that the Dehn function of
$K$
, Lemma 3.5 implies that the Dehn function of
![]() $M_{\Phi }$
is bounded below by an exponential function. From Lemma 3.4, the Dehn functions of mapping tori of RAAGs are always bounded above by exponential functions. Thus,
$M_{\Phi }$
is bounded below by an exponential function. From Lemma 3.4, the Dehn functions of mapping tori of RAAGs are always bounded above by exponential functions. Thus,
![]() $M_{\Phi }$
and so
$M_{\Phi }$
and so
![]() $M_{\Psi }$
has exponential Dehn function.
$M_{\Psi }$
has exponential Dehn function.
Proof of Theorem B (3). This is the case where
![]() $\phi$
has infinite order and only unit eigenvalues. We will show that
$\phi$
has infinite order and only unit eigenvalues. We will show that
![]() $M_{\Phi }$
and thus
$M_{\Phi }$
and thus
![]() $M_{\Psi }$
has a cubic Dehn function. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function, we can work with
$M_{\Psi }$
has a cubic Dehn function. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function, we can work with
![]() $M_{\Xi }$
which has the form:
$M_{\Xi }$
which has the form:
for some
![]() $k, l, m \in \mathbb{Z}$
with
$k, l, m \in \mathbb{Z}$
with
![]() $k \neq 0$
. Let
$k \neq 0$
. Let
Suppose
![]() $w$
is a freely reduced word representing the identity in
$w$
is a freely reduced word representing the identity in
![]() $M_{k,l,m}$
. Let
$M_{k,l,m}$
. Let
![]() $\Delta$
be a minimal area van Kampen diagram for
$\Delta$
be a minimal area van Kampen diagram for
![]() $w$
over
$w$
over
![]() $M_{k,l,m}$
. Let
$M_{k,l,m}$
. Let
![]() $\overline{w}$
be
$\overline{w}$
be
![]() $w$
with all
$w$
with all
![]() $b^{\pm 1}$
removed. Then,
$b^{\pm 1}$
removed. Then,
![]() $\overline{w}=1$
in
$\overline{w}=1$
in
![]() $N_l$
. As in case 1 above, the
$N_l$
. As in case 1 above, the
![]() $c$
-pairing
$c$
-pairing
![]() $P$
induced by
$P$
induced by
![]() $\Delta$
induces a valid
$\Delta$
induces a valid
![]() $c$
-pairing
$c$
-pairing
![]() $\overline{P}$
for
$\overline{P}$
for
![]() $\overline{w}$
.
$\overline{w}$
.
By Proposition 6.16, there is a constant
![]() $A_l \gt 0$
dependent only on
$A_l \gt 0$
dependent only on
![]() $l$
such that
$l$
such that
![]() $\overline{w}$
admits a van Kampen diagram
$\overline{w}$
admits a van Kampen diagram
![]() $\overline{\theta }$
over
$\overline{\theta }$
over
![]() $N_l$
which also induces
$N_l$
which also induces
![]() $\overline{P}$
and has area at most
$\overline{P}$
and has area at most
![]() $A_l |\overline{w}|^2$
. Again, as in case 1 above, by Corollary 6.8, there exists a constant
$A_l |\overline{w}|^2$
. Again, as in case 1 above, by Corollary 6.8, there exists a constant
![]() $K\gt 0$
such that the boundary circuit of any
$K\gt 0$
such that the boundary circuit of any
![]() $c$
-complementary region
$c$
-complementary region
![]() $\overline{C}$
in
$\overline{C}$
in
![]() $\overline{\theta }$
has length at most
$\overline{\theta }$
has length at most
![]() $K | \overline{w} |$
. Each such
$K | \overline{w} |$
. Each such
![]() $\overline{C}$
is a diagram over
$\overline{C}$
is a diagram over
![]() $\langle a,t \mid a^t =a \rangle$
.
$\langle a,t \mid a^t =a \rangle$
.
Now
![]() $\overline{C}$
has a maximal geodesic tree in its 1-skeleton—that is, a tree reaching all vertices and with the property that there is a root vertex
$\overline{C}$
has a maximal geodesic tree in its 1-skeleton—that is, a tree reaching all vertices and with the property that there is a root vertex
![]() $v_{\overline{C}}$
on the boundary
$v_{\overline{C}}$
on the boundary
![]() $\partial \overline{\theta }$
such that for every vertex
$\partial \overline{\theta }$
such that for every vertex
![]() $v$
in
$v$
in
![]() $\overline{C}$
, the distance from
$\overline{C}$
, the distance from
![]() $v_{\overline{C}}$
in the tree is the same as in the 1-skeleton of
$v_{\overline{C}}$
in the tree is the same as in the 1-skeleton of
![]() $\overline{C}$
.
$\overline{C}$
.
We claim that the diameter of
![]() $\overline{C}$
is at most a constant times
$\overline{C}$
is at most a constant times
![]() $|\overline{w}|$
. This is because every vertex in
$|\overline{w}|$
. This is because every vertex in
![]() $\overline{C}$
is contained in an
$\overline{C}$
is contained in an
![]() $a$
-corridor that extends to
$a$
-corridor that extends to
![]() $\partial \overline{C}$
. The length of each
$\partial \overline{C}$
. The length of each
![]() $a$
-corridor is the number of
$a$
-corridor is the number of
![]() $t$
-corridors that cross it, and there are at most
$t$
-corridors that cross it, and there are at most
![]() $K |\overline{w}|/2$
many
$K |\overline{w}|/2$
many
![]() $t$
-corridors in
$t$
-corridors in
![]() $\overline{C}$
, because
$\overline{C}$
, because
![]() $t$
-corridors begin and end on
$t$
-corridors begin and end on
![]() $\partial \overline{C}$
and do not cross
$\partial \overline{C}$
and do not cross
![]() $c$
-corridors more than once in minimal area diagrams. Therefore, every vertex in
$c$
-corridors more than once in minimal area diagrams. Therefore, every vertex in
![]() $\overline{C}$
is within a distance of
$\overline{C}$
is within a distance of
![]() $K |\overline{w}|/2$
from
$K |\overline{w}|/2$
from
![]() $\partial \overline{C}$
. It follows that the diameter of
$\partial \overline{C}$
. It follows that the diameter of
![]() $\overline{C}$
is at most
$\overline{C}$
is at most
![]() $ (K+1)|\overline{w}|$
, as any two points in the boundary can be connected by a path of length at most
$ (K+1)|\overline{w}|$
, as any two points in the boundary can be connected by a path of length at most
![]() $|\overline{w}|$
.
$|\overline{w}|$
.
As the diameter of
![]() $\overline{C}$
is at most a constant times
$\overline{C}$
is at most a constant times
![]() $|\overline{w}|$
and
$|\overline{w}|$
and
![]() $|\overline{w}|\leq |w|$
, any maximal geodesic tree in its 1-skeleton has diameter at most a constant times
$|\overline{w}|\leq |w|$
, any maximal geodesic tree in its 1-skeleton has diameter at most a constant times
![]() $|w|$
.
$|w|$
.
We now apply the electrostatic model from Section 4 to inflate
![]() $\overline{\theta }$
to a van Kampen diagram for
$\overline{\theta }$
to a van Kampen diagram for
![]() $w$
over
$w$
over
![]() $M_{k,l,m}$
. Since
$M_{k,l,m}$
. Since
![]() $\overline{\theta }$
induces a valid
$\overline{\theta }$
induces a valid
![]() $c$
-pairing, this can be done by inserting
$c$
-pairing, this can be done by inserting
![]() $b$
-corridors within the
$b$
-corridors within the
![]() $c$
-complementary regions.
$c$
-complementary regions.
First, we charge the diagram with at most
![]() $A_l \, |\overline{w}|^2 \, \max \{k, m\}$
many
$A_l \, |\overline{w}|^2 \, \max \{k, m\}$
many
![]() $b$
-charges, in effect, replacing all of the 2-cells for defining relations from
$b$
-charges, in effect, replacing all of the 2-cells for defining relations from
![]() $N_{l}$
with the corresponding 2-cells for defining relations from
$N_{l}$
with the corresponding 2-cells for defining relations from
![]() $M_{k,l,m}$
. The area is unchanged at
$M_{k,l,m}$
. The area is unchanged at
![]() $A_l|\overline{w}|^2$
. Next connect each charge in
$A_l|\overline{w}|^2$
. Next connect each charge in
![]() $\overline{C}$
by a
$\overline{C}$
by a
![]() $b$
-partial corridor of length no more than
$b$
-partial corridor of length no more than
![]() $(K+1)|\overline{w}|$
to the root
$(K+1)|\overline{w}|$
to the root
![]() $v_{\overline{C}}$
, along the maximal tree. The total area of these
$v_{\overline{C}}$
, along the maximal tree. The total area of these
![]() $b$
-partial corridors is at most a constant times
$b$
-partial corridors is at most a constant times
![]() $|\overline{w}|^3$
. Finally, insert
$|\overline{w}|^3$
. Finally, insert
![]() $b$
-corridors (each of at most a constant times
$b$
-corridors (each of at most a constant times
![]() $|w|$
) along the boundaries of the
$|w|$
) along the boundaries of the
![]() $c$
-complementary regions to rearrange the (at most a constant times
$c$
-complementary regions to rearrange the (at most a constant times
![]() $|w|^2$
many)
$|w|^2$
many)
![]() $b$
and
$b$
and
![]() $b^{-1}$
until the perimeter word is
$b^{-1}$
until the perimeter word is
![]() $w$
.
$w$
.
The resulting diagram
![]() $\theta$
for
$\theta$
for
![]() $w$
over
$w$
over
![]() $M_{k, l, m}$
has at most the area of
$M_{k, l, m}$
has at most the area of
![]() $\overline{\theta }$
(at most quadratic in
$\overline{\theta }$
(at most quadratic in
![]() $|\overline{w}|$
), plus the total area of the
$|\overline{w}|$
), plus the total area of the
![]() $b$
-partial corridors (at most cubic in
$b$
-partial corridors (at most cubic in
![]() $|\overline{w}|$
), plus the total area of the
$|\overline{w}|$
), plus the total area of the
![]() $b$
-corridors (at most cubic in
$b$
-corridors (at most cubic in
![]() $|w|$
)—in total, at most cubic in
$|w|$
)—in total, at most cubic in
![]() $|w|$
. So the Dehn function of
$|w|$
. So the Dehn function of
![]() $M_{k,l,m}$
grows at most cubically.
$M_{k,l,m}$
grows at most cubically.
As
![]() $\phi$
has infinite order and only unit eigenvalues, it has a
$\phi$
has infinite order and only unit eigenvalues, it has a
![]() $2 \times 2$
Jordan block
$2 \times 2$
Jordan block
![]() $A$
and so, by Lemma 3.5, the Dehn function of the mapping torus has a cubic lower bound.
$A$
and so, by Lemma 3.5, the Dehn function of the mapping torus has a cubic lower bound.
7. Mapping tori of RAAGs of the product of two free groups
Here, we will prove Theorem C concerning Dehn functions of mapping tori of products
![]() $F_k \times F_l$
of free groups.
$F_k \times F_l$
of free groups.
7.1. Automorphisms of
 $F_k \times F_l$
$F_k \times F_l$
Suppose
![]() $X$
and
$X$
and
![]() $Y$
are disjoint finite sets with
$Y$
are disjoint finite sets with
![]() $\left |X\right | = k$
,
$\left |X\right | = k$
,
![]() $\left |Y\right | = l$
, and
$\left |Y\right | = l$
, and
![]() $k, l \geq 2$
. Let
$k, l \geq 2$
. Let
![]() $\Gamma$
be the bipartite graph with vertex set
$\Gamma$
be the bipartite graph with vertex set
![]() $X \cup Y$
and an edge between a pair of vertices if and only if one is in
$X \cup Y$
and an edge between a pair of vertices if and only if one is in
![]() $X$
and the other is in
$X$
and the other is in
![]() $Y$
. So
$Y$
. So
![]() $G= F_k \times F_l$
is the RAAG
$G= F_k \times F_l$
is the RAAG
![]() $A_{\Gamma }$
.
$A_{\Gamma }$
.
Our first task is to explain the opening part of Theorem C, which amounts to:
Lemma 7.1. Given
![]() $\Psi \in{\textrm{Aut}}(G)$
, we can find
$\Psi \in{\textrm{Aut}}(G)$
, we can find
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
such that
$\phi _2 \in{\textrm{Aut}}(F_l)$
such that
![]() $\Phi = \phi _1 \times \phi _2$
equals
$\Phi = \phi _1 \times \phi _2$
equals
![]() $\Psi$
or
$\Psi$
or
![]() $\Psi ^2$
. If
$\Psi ^2$
. If
![]() $k\neq l$
, then
$k\neq l$
, then
![]() $\Phi = \Psi$
.
$\Phi = \Psi$
.
This lemma will allow us to work with
![]() $\Phi$
instead of
$\Phi$
instead of
![]() $\Psi$
when finding the Dehn function of
$\Psi$
when finding the Dehn function of
![]() $M_{\Psi }$
, since
$M_{\Psi }$
, since
![]() $\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$
by Lemma 3.6.
$\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$
by Lemma 3.6.
For a vertex
![]() $x$
in a graph,
$x$
in a graph,
![]() $\textrm{star}(x)$
is the subgraph consisting of all edges incident with
$\textrm{star}(x)$
is the subgraph consisting of all edges incident with
![]() $x$
and
$x$
and
![]() $\textrm{link}(x)$
is the set of vertices adjacent to
$\textrm{link}(x)$
is the set of vertices adjacent to
![]() $x$
. We will prove Lemma 7.1 with the help of:
$x$
. We will prove Lemma 7.1 with the help of:
Lemma 7.2 (Laurence [Reference Laurence18], Servatius [Reference Servatius24]). If
![]() $A_{\Gamma }$
is a RAAG, then the following is a generating set for
$A_{\Gamma }$
is a RAAG, then the following is a generating set for
![]() ${\textrm{Aut}}(A_{\Gamma })$
:
${\textrm{Aut}}(A_{\Gamma })$
:
-
1. All inner automorphisms: for a vertex
 $x$
of
$x$
of
 $\Gamma$
,
$\Gamma$
,
 $\iota _x\;:\;y \mapsto x^{-1} y x$
for all
$\iota _x\;:\;y \mapsto x^{-1} y x$
for all
 $y\in A_{\Gamma }$
.
$y\in A_{\Gamma }$
. -
2. All inversions: maps that send
 $x \mapsto x^{-1}$
for some vertex
$x \mapsto x^{-1}$
for some vertex
 $x$
of
$x$
of
 $\Gamma$
and leave all other vertices fixed.
$\Gamma$
and leave all other vertices fixed. -
3. All partial conjugations: for a vertex
 $x$
in
$x$
in
 $\Gamma$
and a connected component
$\Gamma$
and a connected component
 $C$
of
$C$
of
 $\Gamma - \textrm{star}(x)$
, map
$\Gamma - \textrm{star}(x)$
, map
 $y\,\mapsto \,x^{-1}yx$
for all vertices
$y\,\mapsto \,x^{-1}yx$
for all vertices
 $y$
in
$y$
in
 $C$
and fix all other vertices.
$C$
and fix all other vertices. -
4. All transvections: for a pair of vertices
 $x, y$
of
$x, y$
of
 $\Gamma$
such that
$\Gamma$
such that
 $\textrm{link}(x) \subseteq \textrm{star}(y)$
,
$\textrm{link}(x) \subseteq \textrm{star}(y)$
,
 $\tau _{x,y}$
maps
$\tau _{x,y}$
maps
 $x\,\mapsto \,xy$
and fixes all other vertices.
$x\,\mapsto \,xy$
and fixes all other vertices. -
5. All graph symmetries: automorphisms induced by the restriction of a graph symmetry to the vertex set.
We can see how this generating set reflects the product structure in the instance of
![]() $A_{\Gamma } = F_k \times F_l$
.
$A_{\Gamma } = F_k \times F_l$
.
Corollary 7.3. Write
![]() $F_k = F(X)$
and
$F_k = F(X)$
and
![]() $F_l = F(Y)$
, where
$F_l = F(Y)$
, where
![]() $X=\left \{x_1, \dots, x_k\right \}$
and
$X=\left \{x_1, \dots, x_k\right \}$
and
![]() $Y=\left \{y_1, \dots, y_l\right \}$
. When
$Y=\left \{y_1, \dots, y_l\right \}$
. When
![]() $A_{\Gamma } = F_k \times F_l$
, the inner automorphisms, inversions, partial conjugations, and transvections of the Laurence–Servatius generators of
$A_{\Gamma } = F_k \times F_l$
, the inner automorphisms, inversions, partial conjugations, and transvections of the Laurence–Servatius generators of
![]() ${\textrm{Aut}}(A_{\Gamma })$
are in
${\textrm{Aut}}(A_{\Gamma })$
are in
![]() ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_l)$
. The same is true of the graph symmetries, except when
${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_l)$
. The same is true of the graph symmetries, except when
![]() $k =l$
, where we get additional graph symmetries by composing with the graph symmetry
$k =l$
, where we get additional graph symmetries by composing with the graph symmetry
![]() $R \in{\textrm{Aut}}(A_{\Gamma })$
that exchanges
$R \in{\textrm{Aut}}(A_{\Gamma })$
that exchanges
![]() $X$
and
$X$
and
![]() $Y$
by mapping
$Y$
by mapping
![]() $x_i \mapsto y_i$
and
$x_i \mapsto y_i$
and
![]() $y_i \mapsto x_i$
for all
$y_i \mapsto x_i$
for all
![]() $i$
.
$i$
.
Proof. This is immediate for the inversions. It is true of the inner automorophisms because
![]() $[x_i, y_j]=1$
for all
$[x_i, y_j]=1$
for all
![]() $i,j$
, so conjugation by a word
$i,j$
, so conjugation by a word
![]() $w=xy$
where
$w=xy$
where
![]() $x\in F_k$
and
$x\in F_k$
and
![]() $y \in F_l$
can be expressed as
$y \in F_l$
can be expressed as
![]() $\iota _w=\iota _x \times \iota _y$
. It is true of the partial conjugations similarly. As for the transvections, suppose
$\iota _w=\iota _x \times \iota _y$
. It is true of the partial conjugations similarly. As for the transvections, suppose
![]() $y \in Y$
, and so
$y \in Y$
, and so
![]() $\textrm{star}(y) = \{y\} \cup X$
. If
$\textrm{star}(y) = \{y\} \cup X$
. If
![]() $w \in Y,$
then
$w \in Y,$
then
![]() $\textrm{link}(w) = X$
, and so
$\textrm{link}(w) = X$
, and so
![]() $\textrm{link}(w) \subseteq \textrm{star}(y)$
. So
$\textrm{link}(w) \subseteq \textrm{star}(y)$
. So
![]() $\tau _{w,y}\;:\;w \mapsto wy$
(and fixes all other elements of
$\tau _{w,y}\;:\;w \mapsto wy$
(and fixes all other elements of
![]() $X \cup Y$
), and
$X \cup Y$
), and
![]() $\tau _{w,y}$
restricts to automorphisms of
$\tau _{w,y}$
restricts to automorphisms of
![]() $F_k = F(X)$
and
$F_k = F(X)$
and
![]() $F_l = F(Y)$
, as claimed. If, on the other hand,
$F_l = F(Y)$
, as claimed. If, on the other hand,
![]() $w \in X$
, then since
$w \in X$
, then since
![]() $\textrm{link}(w)=Y$
,
$\textrm{link}(w)=Y$
,
![]() $\textrm{link}(w) \subseteq \textrm{star}(y)$
if and only if
$\textrm{link}(w) \subseteq \textrm{star}(y)$
if and only if
![]() $Y=\{y\}$
, and so, as
$Y=\{y\}$
, and so, as
![]() $l \geq 2$
, there are no transvections
$l \geq 2$
, there are no transvections
![]() $\tau _{w,y}$
. Likewise, the result holds for transvections
$\tau _{w,y}$
. Likewise, the result holds for transvections
![]() $\tau _{w,x}$
with
$\tau _{w,x}$
with
![]() $x \in X$
. The result for graph symmetries is straightforward.
$x \in X$
. The result for graph symmetries is straightforward.
Proof of Lemma 7.1. Every automorphism
![]() $\Omega$
of
$\Omega$
of
![]() $F_k \times F_l$
can be expressed as a product
$F_k \times F_l$
can be expressed as a product
![]() $\Pi$
of the Laurence–Servatius generators. (This can be done effectively: search through an enumerated list of all such products until a suitable
$\Pi$
of the Laurence–Servatius generators. (This can be done effectively: search through an enumerated list of all such products until a suitable
![]() $\Pi$
is found.)
$\Pi$
is found.)
Suppose that
![]() $k\neq l$
and that
$k\neq l$
and that
![]() $\Psi \in{\textrm{Aut}}(G)$
. Then by Corollary 7.3, we have that
$\Psi \in{\textrm{Aut}}(G)$
. Then by Corollary 7.3, we have that
![]() $\Phi = \phi _1 \times \phi _2$
for some
$\Phi = \phi _1 \times \phi _2$
for some
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
.
$\phi _2 \in{\textrm{Aut}}(F_l)$
.
Next, consider the case
![]() $k=l$
. Any
$k=l$
. Any
![]() $\Psi \in{\textrm{Aut}}(G)$
can be expressed as a product of the Laurence–Servatius generators. Per Corollary 7.3, each of these generators is in
$\Psi \in{\textrm{Aut}}(G)$
can be expressed as a product of the Laurence–Servatius generators. Per Corollary 7.3, each of these generators is in
![]() ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, except for some of the graph automorphisms—the latter can take the form
${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, except for some of the graph automorphisms—the latter can take the form
![]() $\rho R$
where
$\rho R$
where
![]() $\rho \in{\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
and
$\rho \in{\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
and
![]() $R$
is the factor-exchanging automorphism of Corollary 7.3. Accordingly,
$R$
is the factor-exchanging automorphism of Corollary 7.3. Accordingly,
![]() $\Psi ^2$
can be expressed as such a product in which there is an even number of
$\Psi ^2$
can be expressed as such a product in which there is an even number of
![]() $R$
terms. So
$R$
terms. So
![]() $\Psi ^2$
is a product of the Laurence–Servatius generators that are in
$\Psi ^2$
is a product of the Laurence–Servatius generators that are in
![]() ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, because
${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, because
![]() $R^2 =\textrm{id}$
, and if
$R^2 =\textrm{id}$
, and if
![]() $\tau$
is a Laurence–Servatius generator in
$\tau$
is a Laurence–Servatius generator in
![]() ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, then so is
${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$
, then so is
![]() $R^{-1}\circ \tau \circ R$
. Then,
$R^{-1}\circ \tau \circ R$
. Then,
![]() $\Phi =\Psi ^2$
satisfies the requirements of the lemma.
$\Phi =\Psi ^2$
satisfies the requirements of the lemma.
Here is a further lemma we will use to adapt a RAAG automorphism to one better suited to calculation of the Dehn function of the mapping torus.
Lemma 7.4. Suppose
![]() $\phi _1, \psi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1, \psi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2, \psi _2 \in{\textrm{Aut}}(F_l)$
are such that
$\phi _2, \psi _2 \in{\textrm{Aut}}(F_l)$
are such that
![]() $[\phi _1]= [\psi _1]$
in
$[\phi _1]= [\psi _1]$
in
![]() $\textrm{Out}(F_k)$
and
$\textrm{Out}(F_k)$
and
![]() $[\phi _2] =[\psi _2]$
in
$[\phi _2] =[\psi _2]$
in
![]() $\textrm{Out}(F_l)$
. Then,
$\textrm{Out}(F_l)$
. Then,
![]() $\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$
.
$\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$
.
Proof. Suppose
![]() $\phi _1 = \iota _{a}\circ \psi _1$
for
$\phi _1 = \iota _{a}\circ \psi _1$
for
![]() $a \in F_k$
and
$a \in F_k$
and
![]() $\phi _2 = \iota _{b}\circ \psi _2$
for
$\phi _2 = \iota _{b}\circ \psi _2$
for
![]() $b \in F_l$
. Then viewing
$b \in F_l$
. Then viewing
![]() $a$
and
$a$
and
![]() $b$
as elements of
$b$
as elements of
![]() $F_k \times F_l$
via the natural embeddings
$F_k \times F_l$
via the natural embeddings
![]() $F_k \to F_k \times F_l$
and
$F_k \to F_k \times F_l$
and
![]() $F_l \to F_k \times F_l$
, we have that
$F_l \to F_k \times F_l$
, we have that
![]() $\phi _1 \times \phi _2 = \iota _{ab}\circ (\psi _1 \times \psi _2)$
, as
$\phi _1 \times \phi _2 = \iota _{ab}\circ (\psi _1 \times \psi _2)$
, as
![]() $b$
commutes with all elements of
$b$
commutes with all elements of
![]() $F_k$
and
$F_k$
and
![]() $a$
commutes with all elements of
$a$
commutes with all elements of
![]() $F_l$
. So
$F_l$
. So
![]() $[\phi _1 \times \phi _2]=[\psi _1 \times \psi _2]$
in
$[\phi _1 \times \phi _2]=[\psi _1 \times \psi _2]$
in
![]() $\textrm{Out}(F_k \times F_l)$
and it follows from Lemma 3.6 that
$\textrm{Out}(F_k \times F_l)$
and it follows from Lemma 3.6 that
![]() $\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$
.
$\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$
.
7.2. Growth of free group automorphisms
Suppose
![]() $F$
is a finite-rank free group. The growth
$F$
is a finite-rank free group. The growth
![]() $g_{\phi, X}\;:\;\mathbb{N} \to \mathbb{N}$
of an automorphism
$g_{\phi, X}\;:\;\mathbb{N} \to \mathbb{N}$
of an automorphism
![]() $\phi \;:\;F \to F$
with respect to a free basis
$\phi \;:\;F \to F$
with respect to a free basis
![]() $X$
is defined by:
$X$
is defined by:
where
![]() $|\phi ^n(x)|$
denotes the length of a shortest word on
$|\phi ^n(x)|$
denotes the length of a shortest word on
![]() $X$
representing
$X$
representing
![]() $\phi ^n(x)$
. We write
$\phi ^n(x)$
. We write
![]() $f \simeq _{\ell } g$
when
$f \simeq _{\ell } g$
when
![]() $f, g \;:\;\mathbb{N} \to \mathbb{N}$
are Lipschitz equivalent; that is, when there exist
$f, g \;:\;\mathbb{N} \to \mathbb{N}$
are Lipschitz equivalent; that is, when there exist
![]() $C_1, C_2\gt 0$
such that
$C_1, C_2\gt 0$
such that
![]() $C_1 g(n) \lt f(n) \lt C_2 g(n)$
for all
$C_1 g(n) \lt f(n) \lt C_2 g(n)$
for all
![]() $n$
. Up to
$n$
. Up to
![]() $\simeq _{\ell }$
, free group growth
$\simeq _{\ell }$
, free group growth
![]() $g_{\phi,X}$
does not depend on the choice of finite basis
$g_{\phi,X}$
does not depend on the choice of finite basis
![]() $X$
, and so we will write
$X$
, and so we will write
![]() $g_{\phi }$
without ambiguity. We write
$g_{\phi }$
without ambiguity. We write
![]() $f \preceq _{\ell } g$
when there exists
$f \preceq _{\ell } g$
when there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $f(n)\,\lt \,Cg(n)$
for all
$f(n)\,\lt \,Cg(n)$
for all
![]() $n$
.
$n$
.
Recall that we write
![]() $f \preceq g$
when there exists
$f \preceq g$
when there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $f(n)\lt Cg(Cn+C)+Cn+C$
for all
$f(n)\lt Cg(Cn+C)+Cn+C$
for all
![]() $n$
, and we write
$n$
, and we write
![]() $f \simeq g$
when
$f \simeq g$
when
![]() $f \preceq g$
and
$f \preceq g$
and
![]() $g \preceq f$
. Note that
$g \preceq f$
. Note that
![]() $f \preceq _{\ell } g$
implies
$f \preceq _{\ell } g$
implies
![]() $f \preceq g$
, and so
$f \preceq g$
, and so
![]() $f \simeq _{\ell } g$
implies
$f \simeq _{\ell } g$
implies
![]() $f \simeq g$
.
$f \simeq g$
.
We say that
![]() $\phi \in{\textrm{Aut}}( F )$
is periodic when there is
$\phi \in{\textrm{Aut}}( F )$
is periodic when there is
![]() $l\gt 0$
such that
$l\gt 0$
such that
![]() $\phi ^l$
is an inner automorphism. We say that
$\phi ^l$
is an inner automorphism. We say that
![]() $\phi$
is polynomially growing when there is
$\phi$
is polynomially growing when there is
![]() $d \geq 0$
such that
$d \geq 0$
such that
![]() $g_{\phi } (n) \simeq _{\ell } n^d$
, and
$g_{\phi } (n) \simeq _{\ell } n^d$
, and
![]() $\phi$
is exponentially growing otherwise.
$\phi$
is exponentially growing otherwise.
To build van Kampen diagrams which demonstrate the lower bound on the Dehn function of
![]() $M_{\phi _1 \times \phi _2}$
, we will use a family of words
$M_{\phi _1 \times \phi _2}$
, we will use a family of words
![]() $x_m$
(
$x_m$
(
![]() $m \in \mathbb{N}$
) and constants
$m \in \mathbb{N}$
) and constants
![]() $C$
and
$C$
and
![]() $d$
such that for all
$d$
such that for all
![]() $m$
,
$m$
,
One approach to finding these words is to consider
![]() $x_m=x^m$
for some word
$x_m=x^m$
for some word
![]() $x$
. However, this approach requires care in understanding cancelation, leading us to consider the growth of cyclically reduced words. Accordingly, for
$x$
. However, this approach requires care in understanding cancelation, leading us to consider the growth of cyclically reduced words. Accordingly, for
![]() $g \in F$
, let
$g \in F$
, let
![]() $||g||$
denote the length of the shortest word representing a conjugate of
$||g||$
denote the length of the shortest word representing a conjugate of
![]() $g$
(cyclically reduced length).
$g$
(cyclically reduced length).
Levitt [Reference Levitt19, Theorem 3] implies that when
![]() $\phi$
is polynomially growing, for every
$\phi$
is polynomially growing, for every
![]() $x \in F$
, there exists
$x \in F$
, there exists
![]() $d_x \geq 0$
such that
$d_x \geq 0$
such that
![]() $| \phi ^n(x) | \simeq _{\ell } n^{d_x}$
, and when it is exponentially growing, there exists
$| \phi ^n(x) | \simeq _{\ell } n^{d_x}$
, and when it is exponentially growing, there exists
![]() $x \in F$
and
$x \in F$
and
![]() $\lambda \gt 1$
such that
$\lambda \gt 1$
such that
![]() $|\phi ^n(x)| \gt \lambda ^n$
for all
$|\phi ^n(x)| \gt \lambda ^n$
for all
![]() $n \in \mathbb{N}$
. By [Reference Levitt19, Theorem 6.2], the corresponding result holds for
$n \in \mathbb{N}$
. By [Reference Levitt19, Theorem 6.2], the corresponding result holds for
![]() $|| \, \cdot \, ||$
in place of
$|| \, \cdot \, ||$
in place of
![]() $| \, \cdot \, |$
, though possibly with different powers and exponential functions.
$| \, \cdot \, |$
, though possibly with different powers and exponential functions.
Definition 7.5. If
![]() $\phi$
is polynomially growing, let
$\phi$
is polynomially growing, let
![]() $d$
be the maximum degree so that for some
$d$
be the maximum degree so that for some
![]() $g \in F(X)$
,
$g \in F(X)$
,
![]() $||\phi ^n(g)|| \simeq _{\ell } n^d$
. In this case, define
$||\phi ^n(g)|| \simeq _{\ell } n^d$
. In this case, define
![]() $g^{cyc}_{\phi }(n) \;:\!=\; n^{d}$
. Otherwise,
$g^{cyc}_{\phi }(n) \;:\!=\; n^{d}$
. Otherwise,
![]() $||\phi ^n(g)|| \simeq _{\ell } \lambda ^n$
for some
$||\phi ^n(g)|| \simeq _{\ell } \lambda ^n$
for some
![]() $\lambda \gt 1$
, and we define
$\lambda \gt 1$
, and we define
![]() $g^{cyc}_{\phi }(n) \;:\!=\; 2^n$
.
$g^{cyc}_{\phi }(n) \;:\!=\; 2^n$
.
In general,
![]() $g^{cyc}_{\phi }(n) \not \simeq _{\ell }\ \max _{x\in X}\{||\phi ^n(x)||\}$
. That is, what happens to generators does not fully determine growth rate measured in terms of cyclically reduced length. Indeed, [Reference Levitt19, Lemma 5.2] gives a family of automorphisms
$g^{cyc}_{\phi }(n) \not \simeq _{\ell }\ \max _{x\in X}\{||\phi ^n(x)||\}$
. That is, what happens to generators does not fully determine growth rate measured in terms of cyclically reduced length. Indeed, [Reference Levitt19, Lemma 5.2] gives a family of automorphisms
![]() $\phi _L$
and bases
$\phi _L$
and bases
![]() $X_L$
(
$X_L$
(
![]() $L \in \mathbb{N}$
) such that for all
$L \in \mathbb{N}$
) such that for all
![]() $x\in X_L$
,
$x\in X_L$
,
![]() $ ||\phi ^n(x)|| \simeq _{l} n^{d_x},$
where
$ ||\phi ^n(x)|| \simeq _{l} n^{d_x},$
where
![]() $d_x \in \{0,1\}$
, but there exists
$d_x \in \{0,1\}$
, but there exists
![]() $g \in F(X_L)$
such that
$g \in F(X_L)$
such that
![]() $||\phi ^n(g)|| \simeq _{l} n^{L}$
.
$||\phi ^n(g)|| \simeq _{l} n^{L}$
.
To establish lower bounds for the Dehn function of
![]() $M_{\phi _1 \times \phi _2}$
, we will use cyclically reduced growth to find lower bounds for the growth of a family of words under repeated application of our automorphism. To establish upper bounds for the Dehn function of
$M_{\phi _1 \times \phi _2}$
, we will use cyclically reduced growth to find lower bounds for the growth of a family of words under repeated application of our automorphism. To establish upper bounds for the Dehn function of
![]() $M_{\phi _1 \times \phi _2}$
, we will use growth (without cyclic reduction) to provide upper bounds for the growth of words under our automorphism. Results of Levitt bridge the gap between the two types of growth: when the cyclically reduced growth and traditional growth disagree, it is possible to exchange
$M_{\phi _1 \times \phi _2}$
, we will use growth (without cyclic reduction) to provide upper bounds for the growth of words under our automorphism. Results of Levitt bridge the gap between the two types of growth: when the cyclically reduced growth and traditional growth disagree, it is possible to exchange
![]() $\phi _1 \times \phi _2$
with a related automorphism
$\phi _1 \times \phi _2$
with a related automorphism
![]() $\hat{\xi }_1 \times \hat{\xi }_2$
for which
$\hat{\xi }_1 \times \hat{\xi }_2$
for which
![]() $g_{\hat{\xi _i}} \simeq g^{\text{cyc}}_{\hat{\xi _i}}$
for
$g_{\hat{\xi _i}} \simeq g^{\text{cyc}}_{\hat{\xi _i}}$
for
![]() $i \in \{1,2\}$
, and the mapping tori
$i \in \{1,2\}$
, and the mapping tori
![]() $M_{\phi _1\times \phi _2}$
and
$M_{\phi _1\times \phi _2}$
and
![]() $M_{\hat{\xi _1} \times \hat{\xi _2}}$
will have equivalent Dehn functions. We expand on this below.
$M_{\hat{\xi _1} \times \hat{\xi _2}}$
will have equivalent Dehn functions. We expand on this below.
Here is a summary of results of Levitt [Reference Levitt19] and Piggot [Reference Piggott23] on properties of growth and cyclically reduced growth in finite-rank free groups
![]() $F$
:
$F$
:
Lemma 7.6. Suppose
![]() $\phi \in{\textrm{Aut}}( F)$
.
$\phi \in{\textrm{Aut}}( F)$
.
-
1.
 $g^{cyc}_{\phi }=g^{cyc}_{\psi }$
if
$g^{cyc}_{\phi }=g^{cyc}_{\psi }$
if
 $[\phi ] = [\psi ] \in \textrm{Out}(F)$
.
$[\phi ] = [\psi ] \in \textrm{Out}(F)$
. -
2. If
 $\phi$
is polynomially growing,
$\phi$
is polynomially growing,
 $g^{cyc}_{\phi }\simeq _{\ell }g^{cyc}_{\phi ^k}$
for all
$g^{cyc}_{\phi }\simeq _{\ell }g^{cyc}_{\phi ^k}$
for all
 $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
. -
3. (Theorem 0.4 of [Reference Piggott23])
 $g_{\phi } \simeq g_{\phi ^{-1}}$
.
$g_{\phi } \simeq g_{\phi ^{-1}}$
. -
4. (By Theorem 3 of [Reference Levitt19], using that
 $\alpha ^n \simeq \beta ^n \simeq n^\gamma \beta ^n$
for
$\alpha ^n \simeq \beta ^n \simeq n^\gamma \beta ^n$
for
 $\alpha, \beta \gt 1$
and
$\alpha, \beta \gt 1$
and
 $\gamma \geq 0$
; cf. Bestvina–Feighn–Handel [Reference Bestvina, Feighn and Handel2]). Either
$\gamma \geq 0$
; cf. Bestvina–Feighn–Handel [Reference Bestvina, Feighn and Handel2]). Either
 $g_{\phi }(n) \simeq 2^n$
, or
$g_{\phi }(n) \simeq 2^n$
, or
 $g_{\phi }(n) \simeq _{\ell } n^{d}$
for some
$g_{\phi }(n) \simeq _{\ell } n^{d}$
for some
 $d\in \{0\}\cup \mathbb{N}$
.
$d\in \{0\}\cup \mathbb{N}$
. -
5. (Per the discussion at the start of Section 2 of [Reference Levitt19]) If
 $n \mapsto ||\phi ^n(g)||$
grows polynomially,
$n \mapsto ||\phi ^n(g)||$
grows polynomially,
 $g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\phi ^{-1}}$
.
$g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\phi ^{-1}}$
. -
6. (By Corollary 1.6 of [Reference Levitt19]) If
 $n \mapsto ||\phi ^n(g)||$
grows polynomially, then there exists
$n \mapsto ||\phi ^n(g)||$
grows polynomially, then there exists
 $p\geq 1$
and
$p\geq 1$
and
 $\xi \in{\textrm{Aut}}(F)$
such that
$\xi \in{\textrm{Aut}}(F)$
such that
 $[\phi ^p] = [\xi ]$
in
$[\phi ^p] = [\xi ]$
in
 $\textrm{Out}(F)$
and
$\textrm{Out}(F)$
and
 $\xi$
admits a nontrivial fixed point.
$\xi$
admits a nontrivial fixed point. -
7. (By Lemma 2.3 of [Reference Levitt19]) Suppose
 $\xi \in{\textrm{Aut}}(F)$
is polynomially growing and satisfies
$\xi \in{\textrm{Aut}}(F)$
is polynomially growing and satisfies
 $g_{\xi }^{cyc} (n)\simeq _{\ell } n^d$
with
$g_{\xi }^{cyc} (n)\simeq _{\ell } n^d$
with
 $d\geq 1$
and
$d\geq 1$
and
 $\xi$
has a nontrivial fixed point set. Then
$\xi$
has a nontrivial fixed point set. Then
 $g_{\xi }(n) \simeq _{\ell } n^d \simeq _{\ell } g_{\xi }^{cyc} (n)$
.
$g_{\xi }(n) \simeq _{\ell } n^d \simeq _{\ell } g_{\xi }^{cyc} (n)$
.
Proof. We will explain (7), which is the one case that is not immediate from the sources. Corollary 1.6 of [Reference Levitt19] guarantees that for any polynomially growing
![]() $\Phi \in{\textrm{Aut}}(F)$
that is not periodic, there exists
$\Phi \in{\textrm{Aut}}(F)$
that is not periodic, there exists
![]() $p$
such that there is a representative
$p$
such that there is a representative
![]() $\alpha$
in the outer automorphism class of
$\alpha$
in the outer automorphism class of
![]() $\Phi ^p$
, such that
$\Phi ^p$
, such that
![]() $\alpha$
has a nontrivial fixed point. Lemma 2.3 of [Reference Levitt19] describes necessary conditions on a polynomially growing automorphism
$\alpha$
has a nontrivial fixed point. Lemma 2.3 of [Reference Levitt19] describes necessary conditions on a polynomially growing automorphism
![]() $\xi$
under which
$\xi$
under which
![]() $g_\xi \not \simeq g_\xi ^{cyc}$
. In particular, he shows that when the fixed point set is nontrivial, they are only inequivalent when
$g_\xi \not \simeq g_\xi ^{cyc}$
. In particular, he shows that when the fixed point set is nontrivial, they are only inequivalent when
![]() $g_\xi ^{cyc}(n)$
is bounded above by a constant. A hypothesis of (7) is that
$g_\xi ^{cyc}(n)$
is bounded above by a constant. A hypothesis of (7) is that
![]() $g_\xi ^{cyc}(n)$
grows at least linearly, hence the conclusion.
$g_\xi ^{cyc}(n)$
grows at least linearly, hence the conclusion.
In building van Kampen diagrams and shuffling relators, we will use both forward and backward iterates of our automorphism. Lemma 7.6 (3) and (5) imply that we can use the same functions to estimate both. (1) implies that cyclic growth can be defined for outer automorphisms. This can fail for growth. However, the next results imply that we can nevertheless find automorphisms with equivalent growth and cyclic growth.
Lemma 7.7. Suppose
![]() $\phi \in{\textrm{Aut}}(F)$
has polynomial growth and is not periodic. Then there exists
$\phi \in{\textrm{Aut}}(F)$
has polynomial growth and is not periodic. Then there exists
![]() $\xi \in{\textrm{Aut}}(F)$
and
$\xi \in{\textrm{Aut}}(F)$
and
![]() $p\geq 0$
with
$p\geq 0$
with
![]() $[\xi ] = [\phi ^p]\in \textrm{Out}(F)$
and
$[\xi ] = [\phi ^p]\in \textrm{Out}(F)$
and
![]() $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi } \simeq g_{\xi }$
. Moreover, for any
$g^{cyc}_{\phi } \simeq g^{cyc}_{\xi } \simeq g_{\xi }$
. Moreover, for any
![]() $q\geq 1$
,
$q\geq 1$
,
![]() $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$
.
$g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$
.
Proof. We use Lemma 7.6: take
![]() $\xi$
as per (6) and then apply (7), (1), and (2) to get that
$\xi$
as per (6) and then apply (7), (1), and (2) to get that
![]() $g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\xi ^q} \simeq _{\ell } g_{\xi ^q}$
, and therefore
$g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\xi ^q} \simeq _{\ell } g_{\xi ^q}$
, and therefore
![]() $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$
.
$g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$
.
Lemma 7.8. Suppose
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
. For
$\phi _2 \in{\textrm{Aut}}(F_l)$
. For
![]() $i =1,2$
, suppose
$i =1,2$
, suppose
![]() $p_i \geq 0$
is such that
$p_i \geq 0$
is such that
![]() $[\phi _i^{p_i}] = [\xi _i]$
as in Lemma 7.7. Define
$[\phi _i^{p_i}] = [\xi _i]$
as in Lemma 7.7. Define
![]() $\hat{\xi }_1 = \xi _1^{p_2}, \,\hat{\xi }_2 = \xi _2^{p_1}$
. Then,
$\hat{\xi }_1 = \xi _1^{p_2}, \,\hat{\xi }_2 = \xi _2^{p_1}$
. Then,
![]() $M_{\phi _1\times \phi _2}$
and
$M_{\phi _1\times \phi _2}$
and
![]() $M_{\hat{\xi }_1\times \hat{\xi }_2}$
have equivalent Dehn functions and
$M_{\hat{\xi }_1\times \hat{\xi }_2}$
have equivalent Dehn functions and
![]() $g_{\phi _i}^{cyc} \simeq g_{\hat{\xi }_i}^{cyc} \simeq g_{\hat{\xi }_i}$
.
$g_{\phi _i}^{cyc} \simeq g_{\hat{\xi }_i}^{cyc} \simeq g_{\hat{\xi }_i}$
.
Proof. By Lemma 3.6, the Dehn functions of
![]() $M_{\phi _1 \times \phi _2}$
and
$M_{\phi _1 \times \phi _2}$
and
![]() $M_{(\phi _1 \times \phi _2)^{p_1p_2}} = M_{(\phi _1^{p_1})^{p_2} \times (\phi _2^{p_2})^{p_1}}$
are equivalent. By Lemma 7.4, we may also pick convenient representatives of the outer automorphism classes without changing the Dehn function. So
$M_{(\phi _1 \times \phi _2)^{p_1p_2}} = M_{(\phi _1^{p_1})^{p_2} \times (\phi _2^{p_2})^{p_1}}$
are equivalent. By Lemma 7.4, we may also pick convenient representatives of the outer automorphism classes without changing the Dehn function. So
![]() $M_{\xi _1^{p_2} \times \xi _2^{p_1}} = M_{\hat{\xi }_1\times \hat{\xi }_2}$
also has equivalent Dehn function to
$M_{\xi _1^{p_2} \times \xi _2^{p_1}} = M_{\hat{\xi }_1\times \hat{\xi }_2}$
also has equivalent Dehn function to
![]() $M_{\phi _1 \times \phi _2}$
.
$M_{\phi _1 \times \phi _2}$
.
7.3. Dehn function lower bounds
A result similar to Lemma 7.9 was proved by Brady and Soroko in Proposition 3.4 in [Reference Brady and Soroko6] in the context of Bieri doubles. The notation
![]() $\simeq _{\ell }$
,
$\simeq _{\ell }$
,
![]() $\preceq _{\ell }$
, and
$\preceq _{\ell }$
, and
![]() $\preceq$
is from the start of Section 7.2 above.
$\preceq$
is from the start of Section 7.2 above.
Lemma 7.9. Suppose that
![]() $\Phi \in{\textrm{Aut}}(F_k \times F_l)$
has the form
$\Phi \in{\textrm{Aut}}(F_k \times F_l)$
has the form
![]() $\Phi =\phi _1 \times \phi _2$
where
$\Phi =\phi _1 \times \phi _2$
where
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
. Suppose that
$\phi _2 \in{\textrm{Aut}}(F_l)$
. Suppose that
![]() $g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$
. We can bound the Dehn function
$g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$
. We can bound the Dehn function
![]() $\delta _{M_{\Phi }}$
of
$\delta _{M_{\Phi }}$
of
![]() $M_{\Phi }$
as follows.
$M_{\Phi }$
as follows.
-
1. If
 $g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$
, for some
$g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$
, for some
 $d_1\geq 0$
, then
$d_1\geq 0$
, then
 $n^{d_1 +2} \ \preceq \ \delta _{M_{\Phi }}(n).$
$n^{d_1 +2} \ \preceq \ \delta _{M_{\Phi }}(n).$
-
2. If
 $g_{\phi _1}(n) \succeq 2^n$
, then
$g_{\phi _1}(n) \succeq 2^n$
, then
 $\delta _{M_{\Phi }}(n) \succeq 2^n$
.
$\delta _{M_{\Phi }}(n) \succeq 2^n$
.
Proof. If
![]() $g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$
then by Lemma 7.6 (5),
$g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$
then by Lemma 7.6 (5),
![]() $g_{\phi _1^{-1}}^{cyc}(n) \simeq _{\ell } n^{d_1}$
. Let
$g_{\phi _1^{-1}}^{cyc}(n) \simeq _{\ell } n^{d_1}$
. Let
![]() $x \in F_k$
and
$x \in F_k$
and
![]() $C_1\gt 0$
be such that
$C_1\gt 0$
be such that
![]() $||\phi _1^{-n}(x)|| \geq C_1n^{d_1}$
for all
$||\phi _1^{-n}(x)|| \geq C_1n^{d_1}$
for all
![]() $n \in \mathbb{N}$
. If
$n \in \mathbb{N}$
. If
![]() $\phi _2$
is polynomially growing, there is
$\phi _2$
is polynomially growing, there is
![]() $y \in F_l$
and
$y \in F_l$
and
![]() $C_2\gt 0$
such that
$C_2\gt 0$
such that
![]() $||\phi _2^n(y)|| \geq C_2 n^{d_2}$
, and if
$||\phi _2^n(y)|| \geq C_2 n^{d_2}$
, and if
![]() $\phi _2$
is exponentially growing, choose
$\phi _2$
is exponentially growing, choose
![]() $y$
such that for some
$y$
such that for some
![]() $b_y\gt 1$
,
$b_y\gt 1$
,
![]() $ ||\phi _2^n(y)|| \succeq{b_y}^n$
. We will present the proof for 1. The algebraic mapping torus
$ ||\phi _2^n(y)|| \succeq{b_y}^n$
. We will present the proof for 1. The algebraic mapping torus
![]() $M_{\Phi }$
has presentation:
$M_{\Phi }$
has presentation:
Consider the word
![]() $w_n = t^{-4n}y^nt^{4n}x^n t^{-4n} y^{-n}t^{4n}x^{-n}$
.
$w_n = t^{-4n}y^nt^{4n}x^n t^{-4n} y^{-n}t^{4n}x^{-n}$
.
Suppose
![]() $\Delta$
is any van Kampen diagram for
$\Delta$
is any van Kampen diagram for
![]() $w_n$
. As indicated in Figure 22a, a
$w_n$
. As indicated in Figure 22a, a
![]() $t$
-corridor beginning on side 1 can only end on sides 2 or 4. Since
$t$
-corridor beginning on side 1 can only end on sides 2 or 4. Since
![]() $t$
-corridors cannot cross, there is some value
$t$
-corridors cannot cross, there is some value
![]() $h \in \{0, \dots, 4n\}$
so that the first
$h \in \{0, \dots, 4n\}$
so that the first
![]() $h$
$h$
![]() $t$
-corridors emanating from side 1 end on side 2 and the remainder end on side 4. This switching point
$t$
-corridors emanating from side 1 end on side 2 and the remainder end on side 4. This switching point
![]() $h$
determines the diagram, as shown in Figure 22b. If
$h$
determines the diagram, as shown in Figure 22b. If
![]() $h \geq 2n$
, then a stack of at least
$h \geq 2n$
, then a stack of at least
![]() $2n$
$2n$
![]() $t$
-corridors
$t$
-corridors
![]() $\mathcal{C}_1, \mathcal{C}_2, \ldots$
(emanating from the 1st, 2nd etc., edge of side 1) start on side 1 and end on side 2. If
$\mathcal{C}_1, \mathcal{C}_2, \ldots$
(emanating from the 1st, 2nd etc., edge of side 1) start on side 1 and end on side 2. If
![]() $h \lt 2n$
, then a stack of at least
$h \lt 2n$
, then a stack of at least
![]() $2n$
$2n$
![]() $t$
-corridors start on side 1 and end on side 4: in this case take
$t$
-corridors start on side 1 and end on side 4: in this case take
![]() $\mathcal{C}_1$
to be that emanating from the final edge of side 1,
$\mathcal{C}_1$
to be that emanating from the final edge of side 1,
![]() $\mathcal{C}_2$
to be that emanating from the penultimate edge, etc. Let
$\mathcal{C}_2$
to be that emanating from the penultimate edge, etc. Let
![]() $|\mathcal{C}_i|$
be the area of corridor
$|\mathcal{C}_i|$
be the area of corridor
![]() $\mathcal{C}_i$
, that is, the number of 2-cells in the corridor.
$\mathcal{C}_i$
, that is, the number of 2-cells in the corridor.

Figure 22. Van Kampen diagrams for
![]() $w_n$
in the mapping torus with base
$w_n$
in the mapping torus with base
![]() $F_k \times F_l$
and automorphism
$F_k \times F_l$
and automorphism
![]() $\phi _1 \times \phi _2$
.
$\phi _1 \times \phi _2$
.
The area of each corridor can be bounded from below by the length of its shortest side, and that can be bounded below by the cyclically reduced length of the shortest side. For
![]() $g \in F$
and
$g \in F$
and
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $||g^n|| = n||g||$
, so we get
$||g^n|| = n||g||$
, so we get
Summing the areas of corridors
![]() $\mathcal{C}_n, \ldots, \mathcal{C}_{2n-1}$
, we find that
$\mathcal{C}_n, \ldots, \mathcal{C}_{2n-1}$
, we find that
Now
![]() $ |w_n| \leq 16n + 2n|x| + 2n|y|$
. This gives the first of the following inequalities and, as
$ |w_n| \leq 16n + 2n|x| + 2n|y|$
. This gives the first of the following inequalities and, as
![]() $\Delta$
was any van Kampen diagram for
$\Delta$
was any van Kampen diagram for
![]() $w_n$
, (7.1) gives the second:
$w_n$
, (7.1) gives the second:
It then follows that
![]() $\textrm{Area}(n) \succeq n^{d_1+2}$
, completing our proof of claim 1.
$\textrm{Area}(n) \succeq n^{d_1+2}$
, completing our proof of claim 1.
By hypothesis,
![]() $g_{\phi _1}(n) \succeq 2^n$
and
$g_{\phi _1}(n) \succeq 2^n$
and
![]() $g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$
. Lemma 7.6 (5) tells us that
$g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$
. Lemma 7.6 (5) tells us that
![]() $g_{\phi _1}^{cyc} \simeq _{\ell } g_{\phi _1^{-1}}^{cyc}$
.
$g_{\phi _1}^{cyc} \simeq _{\ell } g_{\phi _1^{-1}}^{cyc}$
.
Theorem 3 of [Reference Levitt19] bounds growth of elements under an automorphism: for all
![]() $\phi \in{\textrm{Aut}}(F_k)$
and all
$\phi \in{\textrm{Aut}}(F_k)$
and all
![]() $x \in F_k$
, there exist
$x \in F_k$
, there exist
![]() $C_1$
,
$C_1$
,
![]() $C_2 \gt 0$
,
$C_2 \gt 0$
,
![]() $\lambda \geq 1$
, and
$\lambda \geq 1$
, and
![]() $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
![]() $C_1\lambda ^p p^m\leq |\phi ^p (x)|\leq C_2 \lambda ^p p^m$
for all
$C_1\lambda ^p p^m\leq |\phi ^p (x)|\leq C_2 \lambda ^p p^m$
for all
![]() $p\geq 1$
. (Polynomially growing automorphisms are those with
$p\geq 1$
. (Polynomially growing automorphisms are those with
![]() $\lambda =1$
for all
$\lambda =1$
for all
![]() $x$
and exponentially growing automorphisms are those with
$x$
and exponentially growing automorphisms are those with
![]() $\lambda \gt 1$
for some
$\lambda \gt 1$
for some
![]() $x$
.) Thus, there exist
$x$
.) Thus, there exist
![]() $x\in F_k$
and
$x\in F_k$
and
![]() $y\in F_l$
such that for some
$y\in F_l$
such that for some
![]() $b_1, b_2 \gt 1$
we have that
$b_1, b_2 \gt 1$
we have that
![]() $||\phi _1^{-n}(x)|| \succeq{b_1}^n$
and
$||\phi _1^{-n}(x)|| \succeq{b_1}^n$
and
![]() $||\phi _2^{n}(y)|| \succeq{b_2}^n$
for all
$||\phi _2^{n}(y)|| \succeq{b_2}^n$
for all
![]() $n \geq 1$
. Then,
$n \geq 1$
. Then,
![]() $w_n = t^{-4n}yt^{4n}x t^{-4n} yt^{4n}x$
satisfies
$w_n = t^{-4n}yt^{4n}x t^{-4n} yt^{4n}x$
satisfies
![]() $\textrm{Area}(w_n) \succeq \min \{{b_1}^n,{b_2}^n\}$
as any van Kampen diagram for
$\textrm{Area}(w_n) \succeq \min \{{b_1}^n,{b_2}^n\}$
as any van Kampen diagram for
![]() $w_n$
must have a stack of
$w_n$
must have a stack of
![]() $n$
corridors whose lengths grow either at least like
$n$
corridors whose lengths grow either at least like
![]() ${b_1}^n$
or
${b_1}^n$
or
![]() ${b_2}^n$
. So, as
${b_2}^n$
. So, as
![]() $\min \{{b_1}^n,{b_2}^n\} \simeq 2^n$
, we conclude that
$\min \{{b_1}^n,{b_2}^n\} \simeq 2^n$
, we conclude that
![]() $\textrm{Area}(n) \succeq 2^n$
.
$\textrm{Area}(n) \succeq 2^n$
.
7.4. Dehn function upper bounds
Lemma 7.10. Suppose
![]() $\Phi \in{\textrm{Aut}}(F_k \times F_l)$
has the form
$\Phi \in{\textrm{Aut}}(F_k \times F_l)$
has the form
![]() $\Phi = \phi _1 \times \phi _2$
, where
$\Phi = \phi _1 \times \phi _2$
, where
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
. If
$\phi _2 \in{\textrm{Aut}}(F_l)$
. If
![]() $n^{d_1} \simeq g_{\phi _1}(n) \preceq g_{\phi _2}(n)$
, then
$n^{d_1} \simeq g_{\phi _1}(n) \preceq g_{\phi _2}(n)$
, then
![]() $\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$
. In the case that
$\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$
. In the case that
![]() $\phi _1$
is periodic,
$\phi _1$
is periodic,
![]() $\delta _{M_{\Phi }}(n) \preceq n^{2}$
.
$\delta _{M_{\Phi }}(n) \preceq n^{2}$
.
Proof. Suppose
![]() $w= w_1 t^{c_1} w_2 t^{c_2} \cdots w_m t^{c_{m}}$
is a length-
$w= w_1 t^{c_1} w_2 t^{c_2} \cdots w_m t^{c_{m}}$
is a length-
![]() $n$
word whose subwords
$n$
word whose subwords
![]() $w_i$
are in
$w_i$
are in
![]() $\langle a_1, \dots, a_k, b_1, \dots b_l\rangle$
. Suppose that
$\langle a_1, \dots, a_k, b_1, \dots b_l\rangle$
. Suppose that
![]() $w=1$
in
$w=1$
in
To bound
![]() $\delta _{M_{\Phi }}(n)$
from above, we will estimate how many defining relators need to be applied to
$\delta _{M_{\Phi }}(n)$
from above, we will estimate how many defining relators need to be applied to
![]() $w$
to reduce it to the empty word. (We may insert or remove inverse pairs of generators such as
$w$
to reduce it to the empty word. (We may insert or remove inverse pairs of generators such as
![]() $a_i^{-1}a_i$
or
$a_i^{-1}a_i$
or
![]() $a_ia_i^{-1}$
at no cost. Only applications of defining relators will count toward the estimate.)
$a_ia_i^{-1}$
at no cost. Only applications of defining relators will count toward the estimate.)
By applying fewer than
![]() $n^2$
commutators, convert each
$n^2$
commutators, convert each
![]() $w_i$
to
$w_i$
to
![]() $u_iv_i$
for some reduced
$u_iv_i$
for some reduced
![]() $u_i \in \langle a_1, \dots, a_k\rangle$
and
$u_i \in \langle a_1, \dots, a_k\rangle$
and
![]() $v_i \in \langle b_1, \dots, b_l \rangle$
, thereby rewriting
$v_i \in \langle b_1, \dots, b_l \rangle$
, thereby rewriting
![]() $w$
as a word
$w$
as a word
![]() $w^{\prime } = u_1v_1t^{c_1} \dots u_m v_m t^{c_m}$
, which has length at most
$w^{\prime } = u_1v_1t^{c_1} \dots u_m v_m t^{c_m}$
, which has length at most
![]() $n$
.
$n$
.
Next convert
![]() $w^{\prime }$
to a product
$w^{\prime }$
to a product
![]() $\overline{v}u$
of the word
$\overline{v}u$
of the word
![]() $\overline{v} = v_1t^{c_1}\cdots v_m t^{c_m}$
with a word
$\overline{v} = v_1t^{c_1}\cdots v_m t^{c_m}$
with a word
![]() $u$
in
$u$
in
![]() $\langle a_1, \cdots, a_k\rangle$
, by applying defining relators to shuffle all the
$\langle a_1, \cdots, a_k\rangle$
, by applying defining relators to shuffle all the
![]() $a_1^{\pm 1}, \dots, a_k^{\pm 1}$
in
$a_1^{\pm 1}, \dots, a_k^{\pm 1}$
in
![]() $w'$
to the right. The word
$w'$
to the right. The word
![]() $\overline{v}$
represents the identity in
$\overline{v}$
represents the identity in
![]() $F_l \rtimes _{\phi _2} \langle t \rangle$
and
$F_l \rtimes _{\phi _2} \langle t \rangle$
and
![]() $u$
represents the identity in
$u$
represents the identity in
![]() $F_k$
. Indeed, the index sum of
$F_k$
. Indeed, the index sum of
![]() $t$
in
$t$
in
![]() $w$
is zero, so gathering all powers of
$w$
is zero, so gathering all powers of
![]() $t$
together on the left would produce a word of the form
$t$
together on the left would produce a word of the form
![]() $vu$
with
$vu$
with
![]() $u \in F_k$
and
$u \in F_k$
and
![]() $v \in F_l$
which represents the identity in
$v \in F_l$
which represents the identity in
![]() $F_k \times F_l$
, and so
$F_k \times F_l$
, and so
![]() $u$
and
$u$
and
![]() $v$
freely reduce to the identity—in particular,
$v$
freely reduce to the identity—in particular,
![]() $\overline{v} = v =1$
in
$\overline{v} = v =1$
in
![]() $F_l \rtimes _{\phi _2} \langle t \rangle$
.
$F_l \rtimes _{\phi _2} \langle t \rangle$
.
This shuffling of
![]() $w'$
into
$w'$
into
![]() $\overline{v}u$
results in the growth of slower growth elements (the
$\overline{v}u$
results in the growth of slower growth elements (the
![]() $F_k$
factor), but not in growth of faster growth elements (the
$F_k$
factor), but not in growth of faster growth elements (the
![]() $F_l$
factor). We can (crudely) estimate cost by giving an upper bound on the length to which a letter
$F_l$
factor). We can (crudely) estimate cost by giving an upper bound on the length to which a letter
![]() $a_i^{\pm 1}$
can grow in the process: it passes at most
$a_i^{\pm 1}$
can grow in the process: it passes at most
![]() $n$
letters
$n$
letters
![]() $t$
or
$t$
or
![]() $t^{-1}$
, each time with the effect of applying
$t^{-1}$
, each time with the effect of applying
![]() $\phi _1$
or
$\phi _1$
or
![]() $\phi _1^{-1}$
. We are given that
$\phi _1^{-1}$
. We are given that
![]() $n^{d_1} \simeq g_{\phi _1}(n)$
, so
$n^{d_1} \simeq g_{\phi _1}(n)$
, so
![]() $n^{d_1} \simeq g_{\phi ^{-1}_1}(n)$
, by Lemma 7.6 (3). Thus, there is a constant
$n^{d_1} \simeq g_{\phi ^{-1}_1}(n)$
, by Lemma 7.6 (3). Thus, there is a constant
![]() $K\gt 0$
such that
$K\gt 0$
such that
![]() $a_i^{\pm 1}$
can grow to length at most
$a_i^{\pm 1}$
can grow to length at most
![]() $K n^{d_1}$
. The cost to shuffle (and in the process transform) all the (at most
$K n^{d_1}$
. The cost to shuffle (and in the process transform) all the (at most
![]() $n$
) letters
$n$
) letters
![]() $a_i^{\pm 1}$
of the
$a_i^{\pm 1}$
of the
![]() $u_1, \ldots, u_m$
to the right past the letters of
$u_1, \ldots, u_m$
to the right past the letters of
![]() $\overline{v}$
(of which there are at most
$\overline{v}$
(of which there are at most
![]() $n$
) is at most
$n$
) is at most
![]() $K n^{d_1+2}$
.
$K n^{d_1+2}$
.
Next freely reduce
![]() $u$
to the empty word (at no cost to area), leaving the word
$u$
to the empty word (at no cost to area), leaving the word
![]() $\overline{v}$
, which represents the identity in
$\overline{v}$
, which represents the identity in
![]() $F_l\rtimes _{\phi _2}\mathbb{Z}$
and has length at most
$F_l\rtimes _{\phi _2}\mathbb{Z}$
and has length at most
![]() $n$
. By Bridson–Groves [Reference Bridson and Groves8],
$n$
. By Bridson–Groves [Reference Bridson and Groves8],
![]() $\overline{v}$
can be reduced to the empty word using no more than a constant
$\overline{v}$
can be reduced to the empty word using no more than a constant
![]() $c$
times
$c$
times
![]() $n^2$
defining relations.
$n^2$
defining relations.
In conclusion, we have an upper bound of
![]() $n^2 + K n^{d_1+2} + cn^2$
, which gives that
$n^2 + K n^{d_1+2} + cn^2$
, which gives that
![]() $\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$
as required.
$\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$
as required.
Finally, we address the periodic case: suppose
![]() $l$
is such that
$l$
is such that
![]() $\phi _1^l$
is an inner automorphism. By Lemmas 3.6 and 7.4,
$\phi _1^l$
is an inner automorphism. By Lemmas 3.6 and 7.4,
![]() $\delta _{M_{\Phi }} \simeq \delta _{M_{\phi _1^l \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2}}$
. We can estimate
$\delta _{M_{\Phi }} \simeq \delta _{M_{\phi _1^l \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2}}$
. We can estimate
![]() $\delta _{M_{\textrm{Id} \times \phi _2}}$
by the above argument in the special case that
$\delta _{M_{\textrm{Id} \times \phi _2}}$
by the above argument in the special case that
![]() $\phi _1 = \textrm{Id}$
. In this case, the cost of shuffling the
$\phi _1 = \textrm{Id}$
. In this case, the cost of shuffling the
![]() $a_i^{\pm 1}$
through the word is at most
$a_i^{\pm 1}$
through the word is at most
![]() $n^2$
(rather than
$n^2$
(rather than
![]() $K n^{d_1+2}$
) since they do not grow in the process, and so
$K n^{d_1+2}$
) since they do not grow in the process, and so
![]() $ \delta _{M_{\Phi }}(n) \simeq \delta _{M_{\textrm{Id} \times \phi _2}} (n) \preceq n^2$
.
$ \delta _{M_{\Phi }}(n) \simeq \delta _{M_{\textrm{Id} \times \phi _2}} (n) \preceq n^2$
.
Proof of Theorem C. We have
![]() $G= F_k \times F_l$
, where
$G= F_k \times F_l$
, where
![]() $k,l \geq 2$
, and
$k,l \geq 2$
, and
![]() $\Psi \in{\textrm{Aut}}(F_k \times F_l)$
. Lemma 7.1 identified a
$\Psi \in{\textrm{Aut}}(F_k \times F_l)$
. Lemma 7.1 identified a
![]() $\Phi = \phi _1 \times \phi _2$
with
$\Phi = \phi _1 \times \phi _2$
with
![]() $\phi _1 \in{\textrm{Aut}}(F_k)$
and
$\phi _1 \in{\textrm{Aut}}(F_k)$
and
![]() $\phi _2 \in{\textrm{Aut}}(F_l)$
which (by Lemma 3.6) has
$\phi _2 \in{\textrm{Aut}}(F_l)$
which (by Lemma 3.6) has
![]() $\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$
.
$\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$
.
Provided
![]() $\phi _i$
is not periodic, Lemmas 7.7 and 7.8 imply that even if
$\phi _i$
is not periodic, Lemmas 7.7 and 7.8 imply that even if
![]() $g_{\phi _i} \not \simeq g^{\text{cyc}}_{\phi _i}$
, there is
$g_{\phi _i} \not \simeq g^{\text{cyc}}_{\phi _i}$
, there is
![]() $\hat{\xi }_i$
such that
$\hat{\xi }_i$
such that
![]() $g^{\text{cyc}}_{\phi _i} \simeq g_{\hat{\xi }_i} \simeq g^{\text{cyc}}_{\hat{\xi }_i}$
with
$g^{\text{cyc}}_{\phi _i} \simeq g_{\hat{\xi }_i} \simeq g^{\text{cyc}}_{\hat{\xi }_i}$
with
![]() $M_{\hat{\xi }_1 \times \hat{\xi }_2} \simeq M_{\Phi }$
.
$M_{\hat{\xi }_1 \times \hat{\xi }_2} \simeq M_{\Phi }$
.
The theorem claims that
-
(1) If
 $[\phi _1^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$
for some
$[\phi _1^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$
for some
 $p \in \mathbb{N}$
(i.e.
$p \in \mathbb{N}$
(i.e.
 $\phi _1$
is periodic), then
$\phi _1$
is periodic), then
 $\delta _{M_{\Psi }}(n) \simeq n^2$
.
$\delta _{M_{\Psi }}(n) \simeq n^2$
. -
(2) If
 $n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$
, then
$n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$
, then
 $\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$
, and likewise with the indices
$\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$
, and likewise with the indices
 $1$
and
$1$
and
 $2$
interchanged.
$2$
interchanged. -
(3) If
 $g^{cyc}_{\phi _1}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$
, then
$g^{cyc}_{\phi _1}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$
, then
 $\delta _{M_{\Psi }}$
grows exponentially.
$\delta _{M_{\Psi }}$
grows exponentially.
For (1), Lemma 7.10 gives
![]() $\delta _{M_{\Phi }}(n) \preceq n^{2}$
, and we have
$\delta _{M_{\Phi }}(n) \preceq n^{2}$
, and we have
![]() $\delta _{M_{\Phi }}(n) \succeq n^{2}$
by Lemma 3.4. For (2), Lemma 7.9 gives the required lower bound on the Dehn function and (since
$\delta _{M_{\Phi }}(n) \succeq n^{2}$
by Lemma 3.4. For (2), Lemma 7.9 gives the required lower bound on the Dehn function and (since
![]() $g_{\hat{\xi }_1} \simeq g^{\text{cyc}}_{\phi _1}$
) Lemma 7.10 gives the upper bound. For (3), Lemma 7.9 again gives the lower bound, and Lemma 3.4 gives the upper bound.
$g_{\hat{\xi }_1} \simeq g^{\text{cyc}}_{\phi _1}$
) Lemma 7.10 gives the upper bound. For (3), Lemma 7.9 again gives the lower bound, and Lemma 3.4 gives the upper bound.
8. Concluding remarks
We finish with some remarks on the limits of our techniques and suggestions for which mapping tori to explore next.
The case
![]() $G = F_k \times \mathbb{Z}$
, when
$G = F_k \times \mathbb{Z}$
, when
![]() $k \geq 3$
, stands in the way of a full classification of Dehn functions of mapping tori over
$k \geq 3$
, stands in the way of a full classification of Dehn functions of mapping tori over
![]() $F_k \times F_l$
. It differs from
$F_k \times F_l$
. It differs from
![]() $F_k \times F_l$
with
$F_k \times F_l$
with
![]() $k,l\geq 2$
because
$k,l\geq 2$
because
![]() $F_k\times \mathbb{Z}$
has nontrivial center, which results in additional transvections, making its automorphism group more complicated. What we can say about Dehn functions
$F_k\times \mathbb{Z}$
has nontrivial center, which results in additional transvections, making its automorphism group more complicated. What we can say about Dehn functions
![]() $\delta$
of mapping tori of
$\delta$
of mapping tori of
![]() $F_k \times \mathbb{Z}$
is that they satisfy
$F_k \times \mathbb{Z}$
is that they satisfy
![]() $n^2 \preceq \delta (n) \preceq n^3$
. The cubic upper bound comes by recognizing
$n^2 \preceq \delta (n) \preceq n^3$
. The cubic upper bound comes by recognizing
![]() $M_{\Psi }$
as a central extension of
$M_{\Psi }$
as a central extension of
![]() $M_{\psi }$
and then applying Corollary 5.3. The quadratic lower bound comes from the presence of a
$M_{\psi }$
and then applying Corollary 5.3. The quadratic lower bound comes from the presence of a
![]() $\mathbb{Z}^2$
-subgroup: the square of the stable letter commutes with the
$\mathbb{Z}^2$
-subgroup: the square of the stable letter commutes with the
![]() $\mathbb{Z}$
-factor. In special cases, we can determine the Dehn function.
$\mathbb{Z}$
-factor. In special cases, we can determine the Dehn function.
For all
![]() $\Psi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$
, there exists
$\Psi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$
, there exists
![]() $\Phi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$
with the form
$\Phi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$
with the form
![]() $\Phi \;:\;x_i \mapsto \phi (x_i)c^{k_i}, \ c \mapsto c,$
such that
$\Phi \;:\;x_i \mapsto \phi (x_i)c^{k_i}, \ c \mapsto c,$
such that
![]() $[\Psi ^2] = [\Phi ]$
in
$[\Psi ^2] = [\Phi ]$
in
![]() $\textrm{Out}(F_k \times \mathbb{Z})$
.
$\textrm{Out}(F_k \times \mathbb{Z})$
.
-
1. If
 $\phi$
is atoroidal, then
$\phi$
is atoroidal, then
 $M_{\Psi }$
has quadratic Dehn function by Corollary 5.3, because the base of the central extension is hyperbolic and maximal trees have linear diameter.
$M_{\Psi }$
has quadratic Dehn function by Corollary 5.3, because the base of the central extension is hyperbolic and maximal trees have linear diameter. -
2. If there is
 $w \in F_k$
such that
$w \in F_k$
such that
 $\Phi (w)=wc^k$
, then
$\Phi (w)=wc^k$
, then
 $M_{\Psi }$
has cubic Dehn function by Lemma 3.5.
$M_{\Psi }$
has cubic Dehn function by Lemma 3.5.
Our techniques in Section 5 for
![]() $F_2 \times \mathbb{Z}$
do not apply to
$F_2 \times \mathbb{Z}$
do not apply to
![]() $F_k \times \mathbb{Z}$
for
$F_k \times \mathbb{Z}$
for
![]() $k \geq 3$
. We heavily use that
$k \geq 3$
. We heavily use that
![]() $\textrm{Out}(F_2) \cong \textrm{GL}(2, \mathbb{Z})$
and that for any given
$\textrm{Out}(F_2) \cong \textrm{GL}(2, \mathbb{Z})$
and that for any given
![]() $\phi \in{\textrm{Aut}}(F_2)$
some iterate
$\phi \in{\textrm{Aut}}(F_2)$
some iterate
![]() $[\phi ]^m$
fixes the conjugacy class
$[\phi ]^m$
fixes the conjugacy class
![]() $\left [a^{-1}b^{-1}ab\right ]$
, both of which fail in higher rank.
$\left [a^{-1}b^{-1}ab\right ]$
, both of which fail in higher rank.
The RAAGs on four generators that are not covered by our theorems are another natural place to continue these investigations—for instance, the RAAG whose defining graph is the path with four vertices and three edges.
Acknowledgments
We are grateful to an anonymous referee for thoughtfully and patiently commenting on the paper and suggesting many improvements. The second author gratefully acknowledges financial support from the Simons Foundation (Collaboration Grant 318301).