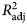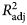Modelling growth in dairy heifers based on linear body measurements (withers height) using non-linear functions

Abstract

This research communication reports a study to model the growth curves for withers height (WH) and body weight (BW) to withers height ratio (BW:WH) using monthly records (from 1 to 24 months of age) for three breeds of dairy heifer (Holstein, Jersey and Brown Swiss). The data sets used were those reported by the Dairy Heifer Evaluation Project of Penn State Extension (USA) between 1991 and 1992. Four growth functions (monomolecular and Michaelis-Menten, both with diminishing returns behaviour, and Schumacher and López, both with asymptotic sigmoidal behaviour) were fitted using the non-linear regression procedure of the SigmaPlot software and the parameters estimated. The models were judged for goodness of fit using adjusted coefficient of determination ($R_{{\rm adj}}^2 $), root mean square error (RMSE), Akaike's information criterion (AIC) and Bayesian information criterion (BIC). Assessing the goodness of fit by $R_{{\rm adj}}^2 $ (>0.99 in all cases) reveals the generally appropriate fit of the models to the data. The non-sigmoidal functions (i.e. Michaelis–Menten and monomolecular) provided the best fits giving the lowest values of RMSE, AIC and BIC. Based on the chosen statistical criteria, the Schumacher and López equations provided acceptable fits to the WH and BW:WH growth curves, but showed points of inflexion at times before birth, indicating that these growth curves are not sigmoidal. In conclusion, evaluation of the different non-linear growth functions used in this study indicated their potential for modelling growth patterns in dairy heifers.

Studying growth curves in cattle provides necessary information for establishing strategic decision-making plans for areas of nutrition and genetic breeding. The pattern of growth can be related to the nutrient requirements, efficiency of the production system and the longevity of the cow. Growth curve studies in cattle have mainly focused on non-linear models that relate body weight (BW) to age (López et al., 2015; Darmani Kuhi et al., 2019). Non-linear models such as growth functions provide an effective means of summarizing information contained in a data series into a few parameters and indicators with biological meaning.

Withers height (WH) is an important measurement of skeletal development (body size) which is relatively simple to determine accurately because the anatomical locations for measurement are easily identified. These measurements can be made from behind the cow, which is practical in most housing systems. Because skeletal development is progressive and relatively slow, few measurements are needed to determine precisely a valid growth curve for the individual animal (Enevoldsen and Kristensen, 1997). Despite the importance of growth measurement in dairy heifers, there is a lack of comprehensive information (Cue et al., 2012). Consequently, most predictions and evaluations of heifer growth are based solely on BW and age (Bazeley et al., 2016). The objective of this study was to characterize the growth pattern of WH and BW to WH ratio (BW:WH) in three breeds of dairy heifer (Holstein, Jersey and Brown Swiss) using non-linear models. For this purpose, four mathematical functions (monomolecular, Michaelis-Menten, López and Schumacher) were compared to evaluate their efficacy in describing growth curves.

Material and methods

Data source

Body weight and WH records for three breeds of heifer (Holstein, Jersey and Brown Swiss) (online Supplementary Table S1) measured in the U.S. Dairy Heifer Evaluation Project from 1991 to 1992 were used in this study. All BW and WH measurements were recorded monthly from 1 to 24 months of age and extracted from the PennState Extension web page (https://extension.psu.edu/growth-charts-for-dairy-heifers) to evaluate the four growth models. Growth curves were fitted using the means of WH and BW:WH over many animals in order to minimize large fluctuations which may happen in an individual growth pattern.

Non-linear models

The four non-linear models tested (namely the monomolecular, Michaelis–Menten, López and Schumacher equations; Thornley and France, 2007) are presented mathematically in online Supplementary Table S2. These growth functions were fitted to the data to examine the relationship between WH and BW:WH with age.

Statistical analysis

The Marquardt–Levenberg algorithm of the non-linear regression procedure of SigmaPlot 12.0 (Systat Software, Inc., San Jose, CA, USA) was used to fit the four different growth functions. Four statistics comprising adjusted coefficient of determination ($R_{{\rm adj}}^2 $), root means square error (RMSE), Akaike's information criterion (AIC) and the Bayesian information criterion (BIC) were used to judge the goodness of fit of a model to the data.

Results

Parameter estimates for all four functions across all three breeds of heifer (online Supplementary Table S3) were obtained routinely without convergence problems. The different functions showed satisfactory capability in estimating initial values of WH and BW:WH for the various data profiles, which were similar between models. For final (asymptotic) WH and BW:WH ratio, there were some differences between the different functions. The estimates of asymptotic WH and BW:WH ratio for the monomolecular were lower than those for the other functions. The fit of the López equation without restriction on shape parameter n converged to a solution where the point of inflexion occurred prior to postnatal growth (in one curve for WH and two curves for BW:WH), and when parameter n was constrained to be ≥1 the model converged to the simpler special case of the Michaelis–Menten. As for the other sigmoidal function (Schumacher), the point of inflexion was out of range (at negative ages, indicating it would not occur during postnatal growth) for the WH curves, and at early ages (between 2 and 3 months after calving) for the BW:WH curves.

Goodness-of-fit statistics for all four functions fitted to the curves for WH and BW:WH are presented in Table 1. $R_{{\rm adj}}^2 $ values were greater than 0.99 in all cases, suggesting appropriate fits, and showed little difference between the models across breeds. However, comparison of models based on the other statistical criteria (Table 1) indicated some differences between models. The two models with best predictive power (the lowest values of RMSE, AIC and BIC) were the Michaelis–Menten and monomolecular equations.

Table 1. Model comparison based on statistical goodness-of-fit criteria^a

^a $R_{{\rm adj}}^2 $, adjusted coefficient of determination; RMSE, Root Mean Square Error; AIC, Akaike's Information Criterion; BIC, Bayesian Information Criterion.

^b WH, Withers height, BW:WH, body weight to WH ratio.

Best model is shown in bold font.

Observed plots of WH and BW:WH ratio against age followed a roughly hyperbolic trajectory leading to an upper asymptote (online Supplementary Fig. S1). There was a tendency for WH and BW:WH to increase monotonically with age regardless of breed. These growth curves for the two traits under study showed increasing trends without suggesting clear sigmoidicity. Plots of WH against age showing the fit of four functions to the data for Holstein heifers are given by way of illustration in Figure 1. The corresponding plots of BW:WH against age showed similar but flatter trends (online Supplementary Fig. S2).

Fig. 1. Plots of withers height (cm) against age (mo) showing the fit of different functions to the data on Holstein heifers.

Discussion

This is the first research report to evaluate different non-linear models for representing WH and BW:WH growth curves in different breeds of dairy heifer. Measurements of morphometric parameters are highly beneficial to breeders for identifying appropriate animals at an earlier stage of growth for selection purposes (Ghavi Hossein-Zadeh and Ghahremani, 2018). Regarding variation in WH during the first 24 months of age, Kertz et al. (1998) state that ~50% of WH increase from birth until first calving at 24 months occurred during the first 6 months of life. A further 25% WH increase occurred over the period 7–12-mo, followed by a final 25% WH increase from 13 to 24 months. Thus the first 6 months of life are a very important period in establishing a desired mature WH. Madalena et al. (2003) studied the relationship between weight and height with age in hybrid Holstein-Friesian/Guzera females, and reported a linear relationship between height and BW:WH. However, in a young animal BW:WH generally becomes greater as the animal approaches mature weight. This is a consequence of a non-linear relationship existing between weight and height: height gain in heifers is reduced incrementally as they get older whereas weight gain is more constant.

Growth curves of BW against age are typically sigmoidal, thus functions representing such a pattern (e.g. Gompertz, von Bertalanffy, Schumacher, Richards, López) are highly suitable for describing these curves in most farm animal species (López et al., 2000), including dairy heifers (Darmani Kuhi et al., 2019). However, curves based on linear body measurements do not show a clear sigmoidal pattern, explaining the best fits obtained in the current study were with the Michaelis–Menten and monomolecular equations, both representing diminishing returns (non-sigmoidal) behaviour. In contrast, the sigmoidal functions had limitations in fitting these curves. The Schumacher equation provided an acceptable fit to BW:WH, but for WH the time at inflexion was negative for the three breeds. With the highly flexible López equation, it was observed that WH at inflexion point would be shorter than height at birth for Holstein heifers, and age at this point would be negative and therefore biologically meaningless.

In conclusion, after selecting a suitable mathematical model to describe growth curves for WH and BW:WH, it is possible to develop an optimal strategy to obtain a desired pattern of growth. Based on different statistical criteria to measure goodness of fit, the results of this study indicate that the Michaelis–Menten and monomolecular equations provide best fit to the growth curves. The Schumacher and López equations provided acceptable statistical fits to the data but had biological limitations, as the growth curves appeared to show a non-sigmoidal post-natal pattern. Evaluation of different non-linear growth functions, in particular non-sigmoidal ones, is appropriate for modelling the growth pattern in dairy heifers based on linear body measurements.