Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T15:28:54.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Kelvin wake pattern at large Froude numbers

Published online by Cambridge University Press:  05 December 2013

Alexandre Darmon ,
Michael Benzaquen  and
Elie Raphaël
Alexandre Darmon
Affiliation:
PCT, UMR CNRS 7083 Gulliver, ESPCI ParisTech, 10 rue Vauquelin, 75005 Paris, France EC2M, UMR CNRS 7083 Gulliver, ESPCI ParisTech, 10 rue Vauquelin, 75005 Paris, France
Michael Benzaquen
Affiliation:
PCT, UMR CNRS 7083 Gulliver, ESPCI ParisTech, 10 rue Vauquelin, 75005 Paris, France
Elie Raphaël*
Affiliation:
PCT, UMR CNRS 7083 Gulliver, ESPCI ParisTech, 10 rue Vauquelin, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

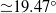Gravity waves generated by an object moving at constant speed at the water surface form a specific pattern commonly known as the Kelvin wake. It was proved by Lord Kelvin that such a wake is delimited by a constant angle ${\simeq }19. 4{7}^{\circ } $. However a recent study by Rabaud and Moisy based on the observation of airborne images showed that the wake angle seems to decrease as the Froude number 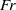$Fr$ increases, scaling as 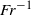$F{r}^{- 1} $ for large Froude numbers. To explain such observations they make the strong hypothesis that an object of size 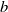$b$ cannot generate wavelengths larger than 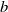$b$. Without the need of such an assumption and modelling the moving object by an axisymmetric pressure field, we analytically show that the angle corresponding to the maximum amplitude of the waves scales as 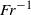$F{r}^{- 1} $ for large Froude numbers, whereas the angle delimiting the wake region outside which the surface is essentially flat remains constant and equal to the Kelvin angle for all 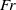$Fr$.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Wakes/Jets: Wakes/Jets Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , R3
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Appel, W. 2007 Mathematics for Physics and Physicists. Princeton University Press.Google Scholar
Benzaquen, M., Chevy, F. & Raphaël, E. 2011 Wave resistance for capillary gravity waves: Finite-size effects. Europhys. Lett. 96 (3), 34003.Google Scholar
Benzaquen, M. & Raphaël, E. 2012 Capillary-gravity waves on depth-dependent currents: Consequences for the wave resistance. Europhys. Lett. 97 (1), 14007.Google Scholar
Casling, E. M. 1978 Planing of a low-aspect-ratio flat ship at infinite Froude number. J. Engng Maths 12, 43–57.Google Scholar
Chepelianskii, A. D., Chevy, F. & Raphaël, E. 2008 Capillary-gravity waves generated by a slow moving object. Phys. Rev. Lett. 100 (7), 074504.Google Scholar
Crawford, F. 1984 Elementary derivation of the wake pattern of a boat. Am. J. Phys. 52, 782–785.Google Scholar
Cumbertach, E. 1958 Two-dimensional planing at high Froude number. J. Fluid Mech. 4, 466–478.Google Scholar
Darrigol, O. 2005 Words of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl. Oxford University Press.Google Scholar
Falkovich, G. 2011 Fluid Mechanics — A Short Course for Physicists. Cambridge University Press.Google Scholar
Havelock, T. H. 1908 The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. A 95, 354.Google Scholar
Havelock, T. H. 1919 Periodic irrotational waves of finite height. Proc. R. Soc. Lond. A 95, 38–51.Google Scholar
Johnson, R. S. 1997 A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge University Press.Google Scholar
Kelvin, Lord 1887 On ship waves. Proc. Inst. Mech. Engrs 38, 409–434.Google Scholar
Lai, C. & Troesch, A. W. 1995 Modelling issues related to the hydrodynamics of three-dimensional steady planing. J. Ship Res. 39, 1–24.Google Scholar
Lamb, H. 1993 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Le Merrer, M., Clanet, C., Quéré, D., Raphaël, E. & Chevy, F. 2011 Wave drag on floating bodies. Proc. Natl Acad. Sci. 108 (30), 15064–15068.Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Nakos, D. E. & Sclavounos, P. D. 1990 On steady and unsteady ship wave pattern. J. Fluid Mech. 215, 263–288.Google Scholar
Parnell, K. E. & Kofoed-Hansen, H. 2001 Wakes from large high-speed ferries in confined coastal waters: Management approaches with examples from New-Zealand and Denmark. Coastal Management 29, 217–237.Google Scholar
Rabaud, M. & Moisy, F. 2013a Ship wakes: Kelvin or mach angle? Phys. Rev. Lett 110, 214503.Google Scholar
Rabaud, M. & Moisy, F. 2013b Narrow ship wakes and wave drag for planning hulls. Innov-Sail, Lorient, 26–28 June .CrossRefGoogle Scholar
Raphaël, E. & de Gennes, P.-G. 1996 Capillary gravity waves caused by a moving disturbance: wave resistance. Phys. Rev. E 53 (4), 3448–3455.Google Scholar
Suzuki, K., Nakata, Y., Ikehata, M. & Kai, H. 1997 Numerical prediction on wave making resistance of high speed trimaran. In Fourth International Conference on Fast Sea Transportation, Sydney, 21–23 July.Google Scholar
Tuck, E. O., Scullen, D. C. & Lazauskas, L. 2002 Wave patterns and minimum wave resistance for high-speed vessels. In 24th Symposium on Naval Hydrodynamics, Fukuoka, Japan, 8–13 July.Google Scholar
Voise, J. & Casas, J. 2010 The management of fluid and wave resistances by whirligig beetles. J. R. Soc. Interface 7, 343.CrossRefGoogle ScholarPubMed