Effects of flow regime and sensor geometry on snow avalanche impact-pressure measurements

Abstract

Impact pressures of snow avalanches have been measured at the Swiss Vallée de la Sionne experimental test site using two kinds of sensor placed at different locations in the avalanche flow. Pressures measured in a fast dry-snow avalanche and a slow wet-snow avalanche are compared and discussed. The pressures recorded using the two types of sensor in the dense flow of a dry-snow avalanche agree well, showing negligible dependence on the measurement device. On the other hand, significantly different pressures are measured in the slow dense flow of a wet-snow avalanche. This is attributed to the slow drag and bulk flow of this type of avalanche, leading to the formation and collapse of force-chain structures against the different surfaces of the sensors. At a macroscopic scale, limit state analysis can be used to explain such a mechanism by a shear failure occurring between freely flowing snow and a confined snow volume against the sensor, according to a Mohr–Coulomb failure criterion. The proposed model explains (1) how impact pressure can be up to eight times higher than hydrostatic snow pressure in wet cohesive slow avalanches and (2) its dependence on sensor geometry.

1. Introduction

Knowledge of how the impact pressure that avalanches exert on obstacles varies with time and location is of fundamental importance in the design of defense structures. As no well-established equation is available to describe avalanche impact pressure on structures of different dimensions and shapes, experimental investigations still represent an important approach in avalanche science.

Experiments can be performed in the laboratory using granular materials (Wieghardt, 1975; Albert and others, 1999; Chehata and others, 2003; Faug and others, 2009, 2010) that simulate the granular flow of dry snow relatively well (Naaim and others, 2003; Rognon and others, 2008). However, to validate the results of these small-scale avalanche experiments and extrapolate them to both full-scale avalanche scenarios and wet and viscous flow requires full-scale experiments (Gauer and others, 2007; Sovilla and others, 2008b; Thibert and others, 2008).

Most experimental studies dedicated to snow avalanche impact-pressure measurement have used small load cells to obtain information on the structure of the avalanche and the pressure distribution over its depth (Lang and Brown, 1980; Schaerer and Salway, 1980; McClung and Schaerer, 1985; Norem and others, 1985; Kawada and others, 1989; Nishimura and others, 1989; Abe and others, 1992; Schaer and Issler, 2001; Sovilla and others, 2008a).

Some full-scale investigations have used large obstacles providing spatially integrated impact pressure over scales of the same order of magnitude as the avalanche depth. In the late 1970s, Kotlyakov and others (1977) provided some initial measurements. Since then, impact-pressure measurements have been made on macroscopic structures such as towers (Norem, 1991) and large plates (Gauer and others, 2007; Sovilla and others, 2008b). Recently, inverse analysis has been used to reconstruct impact pressure on a 1 m² plate sensor using deformation signals (Thibert and others, 2008; Baroudi and Thibert, 2009).

In spite of numerous experimental investigations, measuring avalanche impact pressure remains a difficult task because loading is the result of complex interactions between the avalanche and the measurement device (sensor and supporting structure). Furthermore, force measurement is intrusive and therefore potentially dependent on the adopted method. In addition, avalanche impact pressure is also influenced by the flow regime. Pressures from a dry dense or dilute avalanche generally display high temporal variations (Sovilla and others, 2008b) with high peak values (McClung and Schaerer, 1985). These fluctuations have been interpreted mostly as impulses from particles or snow blocks on the small surfaces of the sensors. On the other hand, the impact pressure from a wet dense slow avalanche is characterized by fluctuations that seem to be generated by the formation and destruction of chains of stress around the infrastructure (Sovilla and others, 2008b, 2010).

In this paper, we investigate how both sensor technology and flow regime may influence impact-pressure measurements. For this, we compare impact-pressure data from classical piezoelectric load cells (Schaer and Issler, 2001; Sovilla and others, 2008a,b) and small steel cantilevers being developed and tested at the Lautaret full-scale avalanche test site in France (Berthet-Rambaud and others, 2008; Thibert and Baroudi, 2010). We analyze both sensor responses for a dry dense and a wet dense avalanche triggered at the Vallée de la Sionne test site in Switzerland.

2. Study Site and Experimental Set-Up

The experiments were carried out at the real-scale avalanche test site of Vallée de la Sionne in the Swiss Alps, where natural and artificially released snow avalanches are studied (Ammann, 1999). This site has been described extensively by Issler (1999) and Sovilla and others (2008a,b). The avalanche path is about 2700 m long, with a vertical fall height of 1300 m. A 20 m high steel pylon, 0.6 m thick and 1.5 m wide, is located in the run-out zone (Fig. 1a). The height of the pylon makes it possible to record impact and stagnation pressures in the dense, stagnation and suspension layers. The pylon is equipped with devices to measure flow velocity (Kern and others, 2009, 2010), acceleration, density (Louge and others, 1997), flow height and air pressure in the aerosol part of avalanches (McElwaine and Turnbull, 2005). The impact force is measured using two types of sensor. Figure 1b shows the position of these two types of sensor relative to the pylon and avalanche direction, and Table 1 summarizes their main characteristics.

Fig. 1. (a) View of the 20 m high pylon instrumented with the two types of sensor. (b) Pylon section indicating the positions of the sensors and the 23° difference in orientation between the two types of sensor. (c) View of a piezoelectric load cell set up on the uphill face of the pylon. (d) View of a strain-gauge cantilever sensor set up on the side of the pylon.

Table 1. Characteristics of the two types of pressure sensor

2.1. Piezoelectric sensors

Six piezoelectric load cells, hereafter designated as piezo sensors, are installed on the uphill face of the pylon, with 1 m spacing, from 0.5 to 5.5 m above ground and with the sensing surface parallel to the pylon (Fig.1b and c). They consist of 0–200 kN quartz load washers (Kistler^® type 9061A) with an area of 80 cm² (diameter of 10 cm) so that the measurement range of the pressure, p _p, is 0–25 MPa. In a piezoelectric load cell, the change in volume of a loaded quartz crystal produces an electrical charge proportional to the load. A charge amplifier (Kistler^® type 5038A) converts the electric charge into a measurable voltage. The acquisition frequency is 7.5 kHz and the bandwidth is reduced to 2.5 kHz by a first-order low-pass filter (−3 dB (10 a)⁻¹) to avoid aliasing (Schaer and Issler, 2001; Sovilla and others, 2008b).

2.2. Strain-gauge cantilever sensors

The cantilever sensing devices are installed on the right side of the pylon, at the same height as the piezoelectric sensors, and extend into the avalanche flow (Fig. 1b and d). Their sensing surface is approximately perpendicular to the ground and thus inclined at about 23° with respect to the piezoelectric sensor surface. The cantilever beams are made of stainless steel (304L grade) and have an area of 125 cm² (Table 1). The measurement range is 0–1 MPa. The dynamic loading of an avalanche on the beams induces deformations. This deformation, ε, is measured with high-precision strain gauges (Vishay^® type CEA-09-250UN) placed in the maximum bending-moment zone (Fig. 1d). The sampling rate is 2 kHz and the bandwidth is reduced to 0–600 Hz by a first-order low-pass filter (−3 dB (10 a)⁻¹). The reconstructed avalanche load, p _c, is obtained from the solution of the inverse problem given by the regularized deconvolution formula:

(1)

where H is the deformation-to-pressure transfer function and the symbol ^ denotes Fourier transform functions of the angular frequency variable, ω. The transfer function has been determined by in situ impact hammer tests and a Euler–Bernoulli beam model as explained in our previous studies (Berthet-Rambaud and others, 2008; Thibert and others, 2008; Baroudi and Thibert, 2009). The function is a regularization low-pass filter used to stabilize the solution of the inverse problem (Tikhonov and Arsenin, 1977). The regularization reduces the effective frequency bandwidth of the cantilever sensor to nearly 0–400 Hz.

In section 3, in order to compare the measurements of the two types of sensor, the pressures measured by the cantilever sensors are projected onto the normal direction of the sensing element of the piezo sensor. Any data for which this has not been done are referred to as ‘without orientation correction’. Regarding sampling-rate differences, spectra and time-average pressures are computed from the original recorded data. For point-to-point comparison (correlation, signal ratio), we use a linear resampling to adjust the piezo-sensor signals to the 2 kHz sampling rate of the cantilever sensors.

3. Experimental Results

We analyze impact-pressure measurements from a medium-sized dry dense avalanche released on 4 December 2008 and from a large wet avalanche released on 1 March 2007. In order to conserve the referencing system adopted in previous papers (Sovilla and others, 2008a,b, 2010; Kern and others, 2009, 2010), we refer to the avalanches by their SLF archive number. Weather conditions were collected by an automatic weather station located on Crêta Besse ridge, directly above the avalanche release zone.

3.1. Dry dense avalanche 2009-003

This medium-sized dry avalanche was characterized by a mixed structure, with a short dilute saltation front followed by a denser core. After a period of sunny and cold weather, snowfall started in the afternoon of 4 December 2008. The temperature was about −6°C. After an accumulation of ∼0.50 m of new snow, avalanche 2009-003 was released spontaneously at 1236 h. Measurements performed at the pylon show that the avalanche had a velocity of up to 20 m s⁻¹. The sliding surface of this avalanche was estimated to be located 0.5–1.0 m above ground. Maximum flow depth at the pylon was about 2.5–3.0 m. We could not estimate the flow density. The avalanche was characterized by a supercritical flow regime with a Froude number between 2 and 4. The avalanche duration was ∼17 s.

3.1.1. Time-series comparison

The impact-pressure time series at different heights, as recorded by both piezo and cantilever sensors, are shown in Figure 2. Figure 3 shows average pressures calculated using a time-averaging window of T = 0.5 s as proposed by Sovilla and others (2008a) under analogous conditions of flow velocity. Only the sensors at 1.5 and 2.5 m height were immersed continuously in the dense flow layer throughout the entire avalanche duration. Upper sensors were above the surface of the dense layer for a significant time with pressure values <5 kPa. There was almost no pressure signal for both sensors at 5.5 m height.

Fig. 2. Avalanche 2009-003. Impact-pressure raw data measured at different heights along the pylon with no orientation correction: (a) cantilever sensors; (b) piezo sensors.

Fig. 3. Avalanche 2009-003. Time-averaged impact pressures along the pylon height using T = 0.5 s for the time averaging. The red curves are the cantilever sensor pressures and the black curves are the piezoelectric sensor pressures. Vertical gray bars show characteristic times for which vertical profiles of pressure are plotted in Figure 4.

The vertical distribution of the pressure along the pylon height, measured by the two types of sensor, is displayed in Figure 4. Pressure profiles are extracted from the time-average pressure at t = 432.1, 434.2, 439.2 and 442 s corresponding to approximately the head, main body and tail (two times) of the avalanche (Fig. 3). To check agreement between measurement means, we analyze the ratios, p _c/p _p, of the time-averaged time series (Fig. 5). This ratio, calculated for 1.5 m height sensors, equals unity ±0.1 in the body and tail of the avalanche (434–446 s) which is 79% of the avalanche duration. In the avalanche head, which only covers 12% of the avalanche length (431–434 s), this ratio is highly variable, indicating major discrepancies between the measurements. Pressures measured by the cantilever sensor range from ∼0.5 to 2.0 times the pressures recorded by the piezo sensor.

Fig. 4. Avalanche 2009-003. Impact-pressure profiles along the pylon height, h, at characteristic times (see Fig. 3) from piezoelectric (black lines and stars) and cantilever (red lines and dots) sensors. Error bars show one standard deviation.

Fig. 5. Observed ratio of impact pressures (cantilever over piezo), p_c/p_p, vs time for avalanche 2009-003 at 1.5 m for the whole avalanche duration. There are two distinct regimes with a ratio of ∼1.5–2.0 in the head and 1.0 in the body and tail of the avalanche.

Agreement between variations in the data is analyzed with running correlation coefficients. For this, we assume the two impact-pressure time series to be samples from random processes, and the goodness of the linear dependence of the measurements, x(t) and y(t), is investigated using the correlation coefficient time series,

(2)

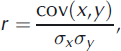
where cov(x,y) is the covariance of x and y, and σ denotes the standard deviation. The correlation coefficient is computed within a moving window of length T = 3 s (Fig. 6a). The correlation coefficient does not describe the equality of the measurements but rather gives a degree of signal synchronization. For an increasing linear dependence, the coefficient approaches 1. The dependency becomes weaker as the pressure decreases to 0. This is due to an increasing noise/ signal ratio and the fact that measurement noises are uncorrelated. The global correlation coefficient is 0.88 for the whole range of data (20 s = 60 000 points). Figure 6b shows that 60% of data have a time-averaged r that is >0.7. Therefore, globally, the two signals are well correlated. Nevertheless, a weaker correlation is observed at the avalanche head.

Fig. 6. Avalanche 2009-003. (a) Correlation of pressure signals measured by piezoelectric and cantilever sensors at 1.5 m height (black curve). The impact-pressure measurements from piezo sensors (gray curve) and cantilever sensors (red curve) are superimposed on an arbitrary scale. (b) Relative cumulative frequency distribution (PDF) of the correlation coefficient. Pressure signals are well correlated, with 60% of data showing r > 0.7.

The avalanche front is characterized by a dilute regime constituted by jumping particles which move at high velocity. Thus, both disagreement in means and the weaker correlation in the avalanche head might be explained by the different bandwidths of the two sensors (0–400 Hz for cantilever sensors vs 0–2500 Hz for piezo sensors), which capture the high-frequency content of the particle impacts in different ways. This was investigated by a detailed spectral analysis.

3.1.2. Power spectrum comparison

To analyze the spectral content of the signals, we compute, for the whole duration of the avalanche event, the power spectrum densities (PSDs) from raw impact-pressure time series, p(t), measured at 1.5 m, where N is the number of sampling points in the data and is the kth component of the Fourier transform of p(t). The spectral contents of the signals are compared in Figure 7. These spectra are very similar in the 0–400 Hz common bandwidth, and display analogous frequency dependencies (a −2 slope on a log–log plot). This spectral response has already been reported by several authors as being characteristic of slow drag force measurements in granular material (Albert and others, 1999, 2000; Frenning and others, 2008). It has also been observed in pressure signals from wet-snow avalanches measured at the Vallée de la Sionne test site (Sovilla and others, 2008a). Both sensors also record a low resonance frequency close to the first fundamental bending frequency (7–8 Hz) of the pylon in the avalanche direction. Computing PSDs on the different phases of the avalanche (head, main body, tail) does not change the frequency response. Only phases with very high noise before and after the avalanche impacts the pylon display a flat frequency response from 10 to 10⁴ Hz.

Fig. 7. Avalanche 2009-003. PSD of impact pressure at 1.5 m computed over the entire avalanche duration. The cantilever power spectrum is shifted up by five decades (×10⁵) for better legibility. Its frequency cut-off above ∼430 Hz is due to necessary regularization in the deconvolution. The frequency dependence is shown by the gray line with a slope of −2.

The potential bias due to the reduced bandwidth of the cantilever sensor is estimated as a truncation error. As both PSDs of Figure 7 are similar within the common bandwidth,

we use the piezoelectric sensor measurements of much larger bandwidth to estimate the error due to the bandwidth cut-off frequency resulting from a lower sampling rate and the regularization of the cantilever signal. We thus compute the respective relative cumulative power spectra (RCPS) in the 0–400 Hz bandwidth as

We obtained a relative error of ∼1% in the L₂-norm of the pressure time series relative to the whole event duration. Thus, the reduced bandwidth of the cantilever is a negligible source of deviation between measurements made with the two types of sensor. From the above analysis, we interpret the poor correlation of the measurements observed in the head of the avalanche and the ratio of pressures significantly different from unity (Fig. 5) as being related to different interactions between the avalanche and the sensors due to the very high heterogeneity of the head of the avalanche.

3.2. Wet dense avalanche 8448

Avalanche 8448 exhibited typical wet, dense, slow flow behavior. Snowfall started at about 1200 h on 1 March 2007 after a period of cloudy weather with temperatures at about freezing. After nearly 0.4 m of new deposited snow on an existing 2–3 m thick snowpack, avalanche 8448 released spontaneously at 2119 h. At that time, the temperature was about −4°C in the release zone and about or slightly above 0°C in the run-out zone. The avalanche had an average velocity of 1–3 m s⁻¹ at the pylon and was characterized by plug flow with a small shear rate (see fig. 7 in Kern and others, 2009). The sliding surface of this avalanche was estimated to be 2.0–2.5 m above ground. Maximum flow depth at the pylon was about 3.5 m. From permittivity measurements performed 3 m above ground, we estimated the flow density to be 400 ± 80 kg m ⁻³ (Louge and others, 1997). The avalanche was characterized by a subcritical flow regime with a Froude number always <1 (Sovilla and others, 2010). The whole avalanche duration was 200 s, nearly ten times longer than dry avalanche 2009-003.

3.2.1. Time-series comparison

The impact-pressure time series at different heights, as recorded by both piezo and cantilever sensors, are shown in Figure 8. Figure 9 shows average pressures calculated using a time-averaging window of T = 1 s. Sensors located below 1.5 m were buried in snow, so we cannot compare piezo and cantilever sensors at this height. Figure 10 shows the pressure distributions along the pylon measured by the two types of sensor. These profiles are based on data extracted from Figure 9 and have been computed at specific times.

Fig. 8. Avalanche 8448. Impact-pressure raw data measured at different heights along the pylon with no orientation correction: (a) cantilever sensors; (b) piezo sensors.

Fig. 9. Avalanche 8448. Time-averaged impact pressures along the pylon height using T = 1 s for the time averaging. The red curves are the cantilever sensor pressures, and black curves are the piezoelectric sensor pressures. Vertical gray bars show characteristic times for which vertical profiles of pressure are plotted in Figure 10.

Fig. 10. Avalanche 8448. Impact-pressure profiles along the pylon height, h, at characteristic times (see Fig. 9) from piezo-electric (black lines and stars) and cantilever (red lines and dots) sensors. Error bars show one standard deviation.

Figures 9 and 10 show that during the initial impact phase, at t = 567.5 s, and as opposed to the case of the dry avalanche presented above, the impact pressures are very similar for both sensors over the height of the flow. Identically, in the avalanche tail, after t = 700 s, measurements from both types of sensor agree. In the bulk of the avalanche, the cantilever- and piezo-sensor pressure profiles generally diverge. Pressures measured by the cantilever sensors are approximately twice those measured by the piezo sensor.

We examine once again the ratios of the time-averaged impact pressures (Fig. 11) and running correlation coefficients, r, calculated using a moving window of length T = 3 s (Fig. 12). At 2.5 m, the ratio p _c/p _p is close to 2 over nearly the whole avalanche event (72%). The expected ratio of 1 is only observed in 26% of the data. A ratio of 3 is reached in 2% of the measurements. Figure 12a reports a very low global correlation coefficient. Only 15% of the data have a time-averaged correlation coefficient r greater than 0.63 (Fig. 12b). Therefore, globally, the two measurements differ and are poorly correlated.

Fig. 11. Observed ratio of impact pressures (cantilever over piezo), p _c/p _p, vs time for avalanche 8448 at 2.5 m for the whole avalanche duration. The horizontal black line is the ratio predicted by the model.

Fig. 12. Avalanche 8448. (a) Correlation of pressure signals measured by piezoelectric and cantilever sensors at 2.5 m height (black curve). The impact-pressure measurements from piezo sensors (gray curve) and cantilever sensors (red curve) are superimposed on an arbitrary scale. (b) Relative cumulative frequency distribution (PDF) of the correlation coefficient between measurements. Pressure signals are weakly correlated, with only 15% of data showing r > 0.63.

3.2.2. Spectral density comparison

The PSD for avalanche 8448 is shown in Figure 13. Similarly to dry avalanche 2009-03, the truncation error due to the regularization cut-off of the bandwidth for the cantilever sensor is estimated to be ∼1% using a relative cumulative power spectral calculation. As reported for the dry avalanche, the PSD of avalanche 8448 displays a spectral response with energy decreasing as the inverse square of the frequency. Therefore, in both cases, the frequency dependence can be described by a power law of type Pf ∝ f ^−β, with a mean slope β ∼ 2 over ∼10–300 Hz (Figs 7 and 13). Even if such a power law is a common signature for many natural phenomena (Mandelbrot, 1983), we speculate that in our case it may indicate the presence of a Brownian-type process related to friction forces, meaning that the variations observed in the avalanche impact-pressure time series in the dense layer are of the Brownian type given that such a value for β corresponds to a Hölder exponent ∼1/2 (Mandelbrot, 1983; Muzy and others, 1994).

Fig. 13. Avalanche 8448. Power spectra density (PSD) of impact pressure at 2.5 m computed over the entire avalanche duration. The cantilever powder spectrum is shifted vertically by 10⁵ for better legibility. The frequency dependence is shown by the gray line with a slope of −2.

4. Impact Pressure in Slow Wet-Snow Avalanches: a Macroscopic Interpretation Model

For dry avalanche 2009-003, both sensors provided very similar pressure measurements in the dense layer. The spectral density of the signals shows the same frequency dependence. These comparative results therefore indicate that we can have confidence in both measurement devices and that differences in the size and shape of the sensors and in their respective positions and orientations in the avalanche play a minor role in the determination of impact pressure for the dense dry-flow regime. On the other hand, the two sensor devices show considerably different responses to the avalanche load for wet avalanche 8448.

By combining the new observations presented in this work with the findings of Sovilla and others (2010), we can attempt to develop a simple model to describe the interaction between the sensors and the wet avalanche flow and thus determine where the differences in our measurements may come from.

According to Sovilla and others (2010), impact-pressure profiles from three wet avalanches, including avalanche 8448 analyzed in the present paper, are approximately linear with respect to the depth z and can be expressed by the relationship

(3)

where ξ is an empirical parameter. When fitted on three wet avalanches, parameter ξ _p (i.e. for pressure measured with the piezo sensors) has a mean of 7.6 with a standard deviation of 1.8, using ρ = 400 kg m⁻³. Considering avalanche 8448 alone, ξ _p has a mean of 7.2 with a standard deviation of 2.1. Measurements from the cantilever sensors yield ξ _c = 12 with a standard deviation of 4.0. Note that the measured pressures are up to 10–20 times the pressure expected from the classical drag formulation C _dρv ² (Salm and others, 1990) with velocity, v, between 1 and 3 m s⁻¹ measured in the plug flow (Kern and others, 2009) and using a drag coefficient C _d = 4.

The linearity of Equation (3) is consistent with a Mohr–Coulomb shear failure criterion where the yield shear stress depends on the normal pressure. We suggest that the slow wet avalanche forms shear failure surfaces between freely flowing snow and a packed snow dead-zone volume against the sensor surface (Fig. 14). The failure surfaces and their directions are related to the internal friction angle of the material (Fig. 14b and c). On such sliding surfaces, the yield strength, τ_y , of snow is reached and elsewhere the shear stress is lower than this limit. This yield stress can be seen as the macroscopic limiting force necessary to break the microscopic chain forces between ‘snow particles’ on the failure surface (Sovilla and others, 2010). The pressure measured corresponds to the ultimate load, F _u, per sensor area, A _s, acting on the sensor. This ultimate load is the normal resultant of all external forces applied to the shear failure surface. Field observations often show that after the passage of an avalanche, a dead zone of sticking snow remains on the pylon and the sensors. In our analysis, we assume that the dead-zone boundary on the sensor corresponds to the shear failure surface. The surface depends on the sensor geometry and the material properties of the snow.

Fig. 14. Local shear failure approach. (a) Passive lateral earth pressure on a vertical wall immersed in snow (reference case). (b) Failure surface orientation α. (c) Passive pressure at failure (upper equilibrium; large circle) given by the Mohr–Coulomb criterion. (d) Snow deposited on the sensor surface: (e) cantilever sensor, (f) piezoelectric sensor.

The determination of ultimate forces is an approach used commonly in limit-load analysis in structural and soil mechanics. It is known as ‘yield-line theory’ and is used to estimate the ultimate load-bearing capacity of structures (Johansen, 1962) or soils (Terzaghi, 1943; Taylor, 1948; Drucker, 1953, 1954). The ultimate load is known in soil mechanics as the local horizontal passive earth pressure (HPEP) and the problem is to determine the ratio, K_p , of the maximum horizontal pressure to the vertical pressure at shear failure in a specific material. Soil mechanics approaches have already been applied to avalanche sciences by Savage (1983), Norem and others (1987) and Savage and Hutter (1989). These granular material flow and mechanics studies show clearly that the Mohr–Coulomb yield criterion is relevant under the conditions of slow-flow regime and low shear rates (Haff, 1983; Jenkins and Savage, 1983; Walton and Braun, 1986).

In this work, local HPEP coefficients, K′_p , are derived for each sensor (Fig. 14d–f). The empirical parameter ∼ in Equation (3) is identified as the local sensor HPEP coefficient . Therefore, the difference in impact pressures measured by both types of sensor can be interpreted by the ratio of the respective local HPEP coefficients where the pressures p = F _u/A _s.

In section 4.1, we review the classical definition of the HPEP coefficient K_p for a reference case involving a vertical wall (Terzaghi, 1943) since it can be used explicitly to enter the expressions of the local HPEP coefficients in the proposed model.

4.1. Ultimate load on a large vertical plane expressed as horizontal passive earth pressure

Consider a vertical surface element, A _s, on a vertical wall immersed in a dense wet-snow layer at rest (Fig. 14a). When the wall is pushed slowly against the snow in the horizontal direction until snow failure, the horizontal pressure, σ _h, on the vertical surface element measured at failure is the passive lateral earth pressure and it is proportional to the vertical pressure σ _v = ρgz at the same point (Fig. 14b). The ratio between horizontal and vertical pressures is the wall HPEP coefficient K_p = σ _h/σ _v. This passive pressure corresponds to an upper equilibrium on Mohr’s circle (the thick circle in Fig. 14c), resulting in two sets of failure lines. Their orientation with respect to the direction of the major principal stress is α = π/4 – ϕ/2 (Fig. 14b), where ϕ denotes the internal friction angle. The shear stress on an arbitrary surface in the snow is assumed to be limited by the Mohr–Coulomb failure criterion (Fig. 14c):

(4)

where c is the snow cohesion.

Coulomb (1773) developed a stability analysis for forces acting on a wedge of soil between a retention wall and a trial shear failure plane. Mayniel (1808) extended this approach, incorporating friction forces, c _w, per unit area at the soil–wall interface. This wall friction gives the resultant reaction force on the wall an angle δ normal to the wall. The passive earth pressure coefficient is given by (Müller-Breslau, 1906)

(5)

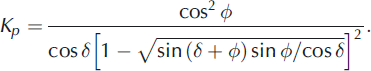
Equation (5) holds for δ ≤ 1/3ϕ. For δ > 1/3ϕ (rough wall), the failure lines curve near the wall due to wall–soil friction, and K_p is overestimated. To account for such curvature, ψK_p (0 < ψ ≤ 1) is substituted for K_p , where ψ depends on δ and ϕ and is given in tables (Caquot and Kerisel, 1948). Finally, the passive horizontal pressure at depth z can be written as (Venkatramaiah, 2006)

(6)

which becomes the Rankine–Bell relationship when wall friction becomes negligible (Bell, 1915). Equation (6) gives the passive lateral snow pressure at failure for the reference case.

4.2. Ultimate load on the sensors expressed as local horizontal passive earth pressure

In our simplified model, we assume that a dead zone forms locally against the sensor and that its inclination follows the failure surfaces given in the wall reference case (section 4.1). The local HPEP on the sensor is then derived by considering the horizontal equilibrium of all forces acting on the dead zone considered as a free body. In analogy to Equation (6), we calculate the ultimate force per unit sensor area as

(7)

where p is the measured impact pressure, the local HPEP coefficient, K′_pc accounts for cohesion and σ _v = ρgz.

Local HPEP coefficients are explicitly obtained taking into account the sensor geometry and corresponding snow deposit shape (conical for the piezoelectric sensor and dihedral for the cantilever sensor; Fig. 14e and f). For the piezoelectric sensor we obtain

(8)

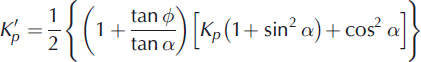
and

(9)

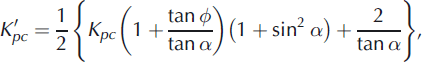
where K_p denotes the HPEP for the reference case and integrates the wall friction effects with taken from Caquot and Kerisel’s (1948) nomograph.

Similarly, for the cantilever sensor:

(10)

and

(11)

where h is the sensor height, w its width and e its thickness (Table 1; Fig. 14e). The Coulomb sliding friction coefficient, μ, between snow and steel takes into account the effects of friction acting on the lateral sides of the cantilever sensor which extend into the flow. Note that K_p and K_p′ for both sensors tend towards 1 when ϕ = 0 and result in the classic isotropic hydrostatic pressure.

4.3. Model results

The empirical parameter ξ in Equation (3) is identified here as the sensor’s local HPEP coefficient ξ ≡ K_p′. When cohesion is accounted for, ξ corresponds rigorously to . Therefore, the discrepancy between measured impact pressures, p, is interpreted in terms of the difference between local HPEP coefficients, , and of the ratios .

Figure 15 shows as a function of the internal friction angle ϕ for both sensors and for the reference case. The vertical extension of the gray box is defined by all experimental ξ _p values reported by Sovilla and others (2010) based on piezo-sensor measurements. The box shows the average ξ _p = 7.6 ± 1.8 and twice the standard deviation which leads to a confidence interval of 4.0–11.2. For avalanche 8448 alone, ξ _p was 7.2 ± 2.1.

Fig. 15. Local passive earth pressure coefficients for the cantilever and piezoelectric sensors and for the wall reference case. For the cantilever sensors, the curve is computed using the parameter δ/ϕ = 2/3 which leads to values for Coulomb friction coefficient μ ∼ tan δ in the range ∼0.30–0.45 in accordance with observations by Platzer and others (2007a,b) for ϕ in the range ∼20–35°. The gray box vertical extension is in the range 4.0–11.2 as reported by Sovilla and others (2010).

The range of all observed ξ _p values (piezo-sensor curve) is well explained by the model for internal friction angles in the range ϕ ∼25–33° (tan ϕ ∼0.47–0.65). Such a range for the Coulomb friction coefficient, tan ϕ, is in accordance with experimental observations in wet-snow avalanches (Bartelt and others, 2007; Platzer and others, 2007a,b). The Coulomb friction coefficient is not necessarily constant throughout the avalanche, due to some variability (dynamic effects, liquid water content, density), and values as high as 0.65 can be reached.

For avalanche 8448 alone, the average ξ _p = 7.2 corresponds to a mean internal friction angle of ∼30°. Note that the scatter in the experimental values of ξ _p can be explained partially by the model as variations in the internal friction angle of the material, and thus by the different granulometry and density of different avalanches.

The pressure ratio between piezo and cantilever sensors given by the model is:

(12)

The experimental ratio, r, is plotted against time in Figure 11 for sensors at 2.5 m. The model predicts that the pressure applied on the cantilever sensor exceeds the pressure on the piezoelectric sensor by a factor of 1.8 (horizontal line).

Three main well-distinct ratios are identified (Fig. 11) which may correspond to cycles of formation, maintenance and destruction of dead zones against the sensors. Figure 11 also shows the variations in time of the experimental ratio p _c/p _p. We can observe that p _c/p _p is mostly ∼2 about 72% of the time. This value is in reasonable agreement with the model results and thus should correspond to the formation of a dead zone on both sensors. A p _c/p _p ratio of ∼1 is observed only over two time periods which represent only 26% of the signal duration. In these time windows, both sensors measure similar pressure and thus we suspect that dead zones against the sensors have not yet formed. Finally, a p_c /p _p ratio of ∼3 is observed in 2% of the data. We again suspect that this ratio may correspond to a less stable, transitional dead zone. Note that a p _c/p _p of 3 is observed only sporadically during the prevailing mode (p _c/p _p = 2) but is numerically very stable. The three modes are also highlighted in Figure 16 where the normalized pressure measured by the cantilever sensor is plotted as a function of the normalized pressure measured by the piezoelectric sensor.

Fig. 16. Normalized horizontal pressure for cantilever vs piezo measurements (gray scattering points) using z = 3 m (as estimated from pressure profiles in Fig. 10) and ρ = 400 kg m⁻³. Model results are given by the continuous black line with a slope of ∼1.8 for μ = 0.4.

4.4. Model parameter sensitivity

The effect of internal friction has been discussed in section 4.3. Taking snow cohesion into account has a negligible effect on the K_p ratio (Fig. 16) which remains close to 1.8 for c = 500 Pa. In addition to the snow material parameters, ϕ and c, the Coulomb sliding friction coefficient, μ = tan δ, takes friction between the snow and the sensor surfaces into account in the model. Sensitivity of the model (Equations (8– 11)) with respect to such a friction coefficient is analyzed in Figure 17 which shows the effects of friction coefficient variations on values of the local HPEP for both sensors. For the cantilever sensor, an additional lateral friction force is accounted for since the sensor is embedded entirely in the snow avalanche flow. Such an effect is absent for the piezo sensor. For the cantilever, the overall relative effect of this side friction to the mean total local HPEP is ~10%, as estimated for an average internal friction angle ϕ ∼ 30°and μ = tan δ.

Fig. 17. Effects of Coulomb sliding friction coefficient on values of local HPEP.

The mean relative effect on the local HPEP is estimated to be ∼30% and 27% for the piezo and the cantilever sensor, respectively, when the Coulomb sliding friction coefficient varies between 0.3 and 0.6. Such a variation of the friction coefficient is in accordance with observations by Platzer and others (2007a,b) in their shear plate experiments with wet snow.

Figure 17 shows that such an effect on the local sensor HPEP is ∼30% and that this is not negligible. Therefore, reliable experimental estimation of such friction coefficients together with their variability is important. Note that this point, highlighted here for surfaces of devices measuring impact pressure, should also apply to real structures impacted by avalanche flow.

5. Conclusion

We have shown that avalanche impact-pressure measurements in slow, wet avalanche flow are affected by the shape and size of sensors and we have used a macroscopic approach based on limit state analysis to investigate the reasons for this.

The model assumes that shear failure occurs in the snow jamming around the sensors according to a Mohr–Coulomb failure criterion. As a consequence, dead zones of different shapes form on each sensor (Fig. 14e and f). A normal balance of forces acting on such failure surfaces that delimit the dead zone can explain the observed differences in impact-pressure measurement. In addition, as a consequence of the lateral earth pressure model, the pressure increases linearly with flow depth, which agrees with measurements reported originally by Sovilla and others (2010) for wet avalanche flow. The coefficient linking horizontal pressure to hydrostatic pressure is identified as the sensor local HPEP coefficient, as in soil mechanics.

The ability of the model to reproduce the measurements performed in a slow, wet avalanche suggests that this approach can be used to calculate snow forces exerted on structures of different geometry, offering possible improvements in engineering design calculations. Our model has been applied to simple geometries; however, for more complex geometries, numerical methods may be required to find a realistic failure surface. For the dynamic case, it may be more appropriate to track the evolution of the dead zone by discrete numerical modeling than by a continuum approach.

Unlike the case of wet avalanche flow, sensor geometry effects on impact-pressure measurements were not observed in dry dense avalanche flow. Note that from our investigation we cannot exclude the possibility that dead zones also form in this case and that a passive earth pressure also contributes to the impact pressure (Norem and others, 1987; Savage and Hutter, 1989). However, given that the hydrodynamic drag formulation C _dρv ² related to linear momentum variations explains the pressure observations reasonably well in a supercritical flow regime (Salm, 1966; Salm and others, 1990; Sovilla and others, 2008a; Baroudi and Thibert, 2009), we can conclude that the contribution of this hydrodynamic drag term is predominant and that the passive pressure related to possible dead zones will appear negligible in the flow regime of the investigated dry dense avalanches.