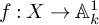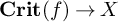A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS

Abstract

We study the symplectic geometry of derived intersections of Lagrangian morphisms. In particular, we show that for a functional $f : X \rightarrow \mathbb {A}_{k}^{1}$, the derived critical locus has a natural Lagrangian fibration $\textbf {Crit}(f) \rightarrow X$. In the case where f is nondegenerate and the strict critical locus is smooth, we show that the Lagrangian fibration on the derived critical locus is determined by the Hessian quadratic form.

1 Introduction

In the context of derived algebraic geometry ([10], [11], [15], [16], [17]), the notion of shifted symplectic structures was developed in [12] (see also [5] and [6]). This has proven to be very useful in order to obtain symplectic structures out of natural constructions. For example, we obtain:

• • shifted symplectic structures from transgression procedures (Theorem 2.5 in [12]), for example, the Alexandrov, Kontsevich, Schwarz, Zaboronsky construction.

• • shifted symplectic structures from derived intersections of Lagrangians structures (Subsection 2.2 in [12]).

• • symplectic structures on various moduli spaces (Subsection 3.1 in [12]).

• • quasi-symplectic groupoids (see [19]) inducing shifted symplectic structures on the quotient stack as explained in [6].

• • symmetric obstruction theory as defined in [1] from $(-1)$ -shifted symplectic derived stacks (see [14] for the obstruction theory on derived stacks and [12] for the symmetric and symplectic enhancement thereof).

• • the d-critical loci as defined by Joyce in [9]. Every $(-1)$ -shifted symplectic derived scheme induces a classical d-critical locus on its truncation (see Theorem 6.6 in [2]).

Another very useful construction in derived geometry is the derived intersection of derived schemes or derived stacks (see [12]). This includes many constructions, such as:

• • the derived critical locus of a functional (see [12] and [18]). For an action functional, this amounts to finding the space of solutions to the Euler-Lagrange equations, as well as remembering about the symmetries of the functional.

• • G-equivariant intersections. This includes the example of symplectic reduction which can be expressed as the derived intersection of derived quotient stacks (see Subsection 2.1.2 in [4]).

In this paper, we make a more precise study of the shifted symplectic geometry of derived critical loci and more generally of the derived intersections of Lagrangian morphisms. In particular, the main theorem (Theorem 3.5) of this paper says that whenever the Lagrangian morphisms $f_i : X_i \rightarrow Z$ , $i=1..2$ look like ‘sections’ in the sense that there exists a map $r: Z \rightarrow X$ , such that the composition maps $r \circ f_i: X_i \rightarrow X$ are weak equivalences, then the natural morphism $X_1 \times _Z X_2 \rightarrow X$ is a Lagrangian fibration (see [5]). We then specialise this result to various examples and show, in particular, that, for the derived critical locus of a nondegenerate functional on a smooth algebraic variety, the nondegeneracy of the Lagrangian fibration is related to the nondegeneracy of the Hessian quadratic form of the functional.

This paper starts, in Section 2, by recalling the basic definitions and properties of shifted symplectic structures, Lagrangian structures and Lagrangian fibrations. We also recall, in Subsection 2.4, basic properties of the relative cotangent complexes of linear stacks that prove useful when we try to understand in more detail the structure of Lagrangian fibrations on derived critical loci.

In Section 3, we start by recalling the fact that a derived intersection of Lagrangian structures in an n-shifted symplectic derived Artin stack is $(n-1)$ -shifted symplectic. Then, in Subsection 3.2, we state and prove the main theorem (Theorem 3.5) that roughly says that if the Lagrangian morphisms look like sections (up to homotopy), then the natural projection from the derived intersection has a structure of a Lagrangian fibration. We then recall basic elements on the derived critical loci of a functional $f : X \rightarrow \mathbb {A}_k^1$ , and then try to describe the Lagrangian fibration structure on the natural map $\textbf {Crit}(f) \rightarrow X$ obtained from the main theorem.

Section 4 gives examples of applications of our main theorem. In particular, in Subsections 4.1 and 4.2, we give a better description of the Lagrangian fibration on the derived critical loci for nondegenerate functionals. We show that the nondegeneracy condition of the Lagrangian fibration of the derived critical locus of a nondegenerate functional on a smooth algebraic variety is given by the nondegeneracy of the Hessian quadratic form.

Notation:

• • Throughout this paper, k denotes a field of characteristic $0$ .

• • $\textbf {cdga}$ (respectively, $\textbf {cdga}_{\leq 0}$ ) denotes the $\infty $ -category of commutative differential graded algebra over k (respectively, commutative differential graded algebra in non positive degrees).

• • $\textbf {cdga}^{gr}$ denotes the $\infty $ -category of commutative monoids in the category of graded complexes $\textbf {dg}_k^{gr}$ .

• • $A-\textbf {Mod}$ denotes the $\infty $ -category of differential graded A-modules for $A \in \textbf {cdga}$ .

• • $\textbf {cdga}^{\epsilon -gr}$ denotes the $\infty $ -category of graded mixed differential graded algebra. We denote the differential $\delta $ and the mixed differential $\epsilon $ or $d = d_{DR}$ in the case of the de Rham complex of a derived Artin stack X, denoted $\textbf {DR}(X)$ . We refer to [7] for the definitions of $\textbf {cdga}^{\epsilon -gr}$ , $\textbf {cdga}^{gr}$ , $\textbf {dg}_k^{gr}$ and the de Rham complex (see also [12] but with a different grading convention).

• • All the $\infty $ -categories above are localisations of model categories (see [7] for details on these model structures and associated $\infty $ -categories). All along, unless explicitly stated otherwise, every diagram will be homotopy commutative, every functor will be $\infty $ -functors and every (co)limits will be $\infty $ -(co)limits.

• • For X a derived Artin stack, $\textbf {QC}(X)$ denote the $\infty $ -category of quasi-coherent sheaves on X.

• • In this paper, derived Artin stacks, denoted $\textbf {dSt}$ , are defined as in [17]. In particular, derived Artin stacks are locally of finite presentation over $\mathrm {Spec}(k)$ .

• • We denote by $\mathbb {L}_X$ the cotangent complex of a derived Artin stack X. We denote by $\mathbb {T}_X := \mathbb {L}_X^{\vee } := \mathrm {Hom}\left (\mathbb {L}_X, \mathscr {O}_X \right )$ its dual.

2 Derived symplectic geometry

2.1 Shifted symplectic structures

Before going to symplectic structures, we make a short recall of differential calculus and (closed) differential p-forms in the derived setting. Recall from [12] that there are classifying stacks $\mathscr {A}^p (\bullet , n)$ and $\mathscr {A}^{p,cl}(\bullet , n)$ of, respectively, the space of n-shifted differential p-forms and the space of n-shifted closed differential p-forms. We use the grading conventions used in [7]. On a derived affine scheme Spec(A), the space of p-forms of degree n and the space of closed p-forms of degree n are defined, respectively, by:

$$\begin{align*}\mathscr{A}^p(A, n) := \mathrm{Map}_{\textbf{cdga}^{gr}} \left( k[-n-p](-p), \textbf{DR}(A) \right) \end{align*}$$

and:

$$\begin{align*}\mathscr{A}^{p,cl}(A, n) := \mathrm{Map}_{\textbf{cdga}^{\epsilon-gr}} \left( k[-n-p](-p), \textbf{DR}(A) \right). \end{align*}$$

From [7], the de Rham complex of A, denoted $\textbf {DR}(A)$ , can be described as a graded complex by $\textbf {DR}(A)^{\#} \simeq \mathrm {Sym}_A \mathbb {L}_A[-1](-1)$ , where $(-)^{\#} : \textbf {cdga}^{\epsilon -gr} \rightarrow \textbf {cdga}^{gr}$ is the functor forgetting the mixed structure (we refer to [7] for more details on the de Rham complex).

All along, we denote the internal differential, that is, the differential on $\mathbb {L}_A$ , by $\delta $ and the mixed differential, that is, the de Rham differential, by d.

By definition, the space of p-forms of degree n on a derived stack X is the mapping space $\mathrm {Map}_{\textbf {dSt}}\left ( X, \mathscr {A}^{p}(\bullet , n) \right )$ and the space of closed p-forms of degree n on X is $\mathrm {Map}_{\textbf {dSt}}\left ( X, \mathscr {A}^{p,cl}(\bullet , n) \right )$ . Now the following proposition says that, in the case where X is a derived Artin stack, the spaces of shifted differential forms are spaces of sections of quasi-coherent sheaves on X.

Proposition 2.1 (Proposition 1.14 in [12]).

Let X be a derived Artin stack over k and $\mathbb {L}_X$ be its cotangent complex over k. Then there is an equivalence:

$$ \begin{align*} \mathscr{A}^{p}(X,n) \simeq \mathrm{Map}_{\textbf{QC}(X)} \left( \mathscr{O}_X, \Lambda^p \mathbb{L}_X [n]\right). \end{align*} $$

Remark 2.2. More concretely, we have from [6] and [7] an explicit description of (closed) p-forms of degree n on a geometric derived stack X. A p-form of degree n is given by a global section $\omega \in \textbf {DR}(X)_{(p)} [n+p] \simeq \mathbb {R} \Gamma \left (\left ( \bigwedge ^p \mathbb {L}_X \right ) [n] \right ) $ , such that $\delta \omega = 0$ . A closed p-form of degree n is given by a semi-infinite sequence $\omega = \omega _0 + \omega _1 + \cdots $ with $\omega _i \in \textbf {DR}_{(p+i)} [n+p]= \mathbb {R} \Gamma \left ( \left ( \bigwedge ^{p+i} \mathbb {L}_X \right ) [n-i]\right )$ , such that $\delta \omega _0 = 0$ and $d \omega _{i} = \delta \omega _{i+1}$ .

Equivalently, being closed means that $\omega $ is closed for the total differential $D = \delta + d$ in the bicomplex $\textbf {DR}(X)_{\geq p}[n] \simeq \mathbb {R} \Gamma \left ( \prod _{i \geq 0} \left ( \bigwedge ^{p+i} \mathbb {L}_X \right ) [n] \right )$ , whose total degree is given by $n+p+i$ . Note that the conditions imposed on $\omega $ are equivalent to saying that $\omega $ is a cocycle of degree $n+p$ for the total differential.

In general, we can also describe the spaces of (closed) differential forms as $\mathscr {A}^{p}(X, n) \simeq \left |\textbf {DR}_{(p)}(X)[n+p] \right |$ and $\mathscr {A}^{p,cl}(X, n) \simeq \left | \prod _{i\geq p} \textbf {DR}_{(p+i)}(X)[n+p] \right | $ , where $\prod _{i\geq 0} \textbf {DR}_{(p+i)}(X)[n]$ is endowed with the total differential.

Remark 2.3. Given a map of derived Artin stack $f : Y \rightarrow X$ , we define $\mathscr {A}^{p,(cl)}(Y/X, n)$ , the space of n-shifted (closed) p-forms on Y relative to X, to be the homotopy cofibre of the natural map $f^* : \mathscr {A}^{p,(cl)}(X,n) \rightarrow \mathscr {A}^{p,(cl)}(Y,n)$ . For instance, n-shifted relative p-forms are equivalent to the derived global sections of , with the relative cotangent complex defined as the homotopy cofibre of the natural map $f^*\mathbb {L}_X \rightarrow \mathbb {L}_Y$ . We refer to [7] for more details on the relative n-shifted (closed) p-forms and the relative version of the de Rham complex.

We say that a p-form, $\omega _0$ , of degree n can be lifted to a closed p-form of degree n if there exists a family of $(p+i)$ -forms $\omega _i$ of degree $n-i$ for all $i> 0$ , such that $\omega = \omega _0 + \omega _1 + \cdots $ is closed in $DR(X)_{\geq p}[n]$ (i.e. $D \omega = 0$ ). In this situation, we can see that $d \omega _0$ is, in general, not equal to $0$ but is homotopic to $0$ ( $d\omega _0 = D\left (- \sum _{i>0} \omega _{p+i} \right )$ ). The choice of such a homotopy is the same as a choice of a closure of the p-form of degree n. Being closed is, therefore, no longer a property of the underlying p-form of degree n but a structure given by a homotopy between $d\omega _0$ and 0. The collection of all closures of a p-form of degree n forms a space:

Definition 2.4. Let $\alpha \in \mathscr {A}^{p}(X,n)$ , then the space of all closures of $\alpha $ is called the space of keys of $\alpha $ denoted $\textbf {key}(\alpha )$ . It is given by the homotopy pullback:

(1)

The mixed differential of the de Rham graded mixed complex induces a map:

$$\begin{align*}d : \mathscr{A}^p (X,n) \rightarrow \mathscr{A}^{p+1, cl}(X,n). \end{align*}$$

We are now turning toward symplectic geometry. Since we now know what are (shifted) closed 2-forms, we only need to mimic the notion of nondegeneracy to define symplectic structures.

Definition 2.5 (nondegenerate 2-form of degree n).

For a derived Artin n-stack X, the cotangent complex $\mathbb {L}_X$ is dualisable. Therefore, there is a tangent complex $\mathbb {T}_X = \mathbb {L}_X^{\vee }$ . We say that a (closed) 2-form of degree n is nondegenerate if the (underlying) 2-form $\omega _0$ of degree n induces a quasi-isomorphism:

$$ \begin{align*} \omega_0^{\flat} : \mathbb{T}_X \rightarrow \mathbb{L}_X[n]. \end{align*} $$

We denote by $\mathscr {A}^{2, nd}(X,n) $ the subspace of $\mathscr {A}^2(X,n)$ generated by the nondegenerate n-shifted $2$ -forms.

Definition 2.6 (shifted symplectic forms).

An n-shifted symplectic structure is a nondegenerate n-shifted closed 2-form on X. n-shifted symplectic structures form a space defined as the pullback:

$$\begin{align*}\textbf{Symp}(X,n) := \mathscr{A}^{2, nd}(X,n) \times_{\mathscr{A}^2(X,n)} \mathscr{A}^{2,cl}(X,n). \end{align*}$$

The standard example of symplectic manifold is the cotangent bundle. In our setting, we can speak of n-shifted cotangent stacks. It is a derived stack defined as a linear stack associated to $\mathbb {L}_X[n]$ , $T^*[n]X := \mathbb {A}( \mathbb {L}_X[n] )$ (see Definition 2.7). It comes with a natural morphism $\pi _X : T^*[n]X \rightarrow X$ . We refer to [5] for a general account of shifted symplectic geometry on the cotangent stack.

Definition 2.7 (linear stacks).

Given $\mathscr {F} \in \textbf {QC}(X)$ a quasi-coherent sheaf over a derived Artin stack, we can construct a linear stack denoted $\mathbb {A} (\mathscr {F})$ , defined as a derived stack over X by:

$$\begin{align*}\mathbb{A}(\mathscr{F}) \left( f: \textbf{Spec}(A) \rightarrow X \right) := \textbf{Map}_{\textbf{A-Mod}} \left( A, f^* \mathscr{F} \right). \end{align*}$$

Remark 2.8. A morphism $Y \rightarrow T^*[n]X$ is determined by the induced morphism $f : Y \rightarrow X$ (by composition with $\pi _X$ ) and a section $s : Y \rightarrow f^* T^*[n]X$ , which corresponds to an element $s \in \mathrm {Map}_{\textbf {QC}(Y)} \left ( \mathscr {O}_Y, f^* \mathbb {L}_X[n]\right )$ (see [5], Section 2, for more details). In the case of a section $s: X \rightarrow T^*[n]X$ , we get the identity $\mathrm {Id}: X \rightarrow X$ and a section $s_1 \in \mathrm {Map}_{\textbf {QC}(X)} \left ( \mathscr {O}_X, \mathbb {L}_X[n]\right ) \simeq \mathscr {A}^1 (X,n)$ . This shows, using Proposition 2.1, that the space of sections of $T^*[n]X$ is exactly the space of $1$ -forms of degree n as expected.

Example 2.9. As in the classical case, we can construct the canonical Liouville 1-form. Consider the identity $\mathrm {Id} : T^*[n]X \rightarrow T^*[n] X$ . It is determined by the projection $\pi : T^*[n]X \rightarrow X$ and a section $\lambda _X \in \mathrm {Map}_{\textbf {QC}(T^*[n]X)} \left ( \mathscr {O}_{T^*[n]X}, \pi ^* \mathbb {L}_{X}[n]\right )$ . Since we have a natural map $\pi ^* \mathbb {L}_{X}[n] \rightarrow \mathbb {L}_{T^*[n]X}[n]$ , $\lambda _X$ induces a 1-form on $T^*[n]X$ called the tautological $1$ -form. This $1$ -form induces a closed $2$ -form $d \lambda _X$ , which happens to be nondegenerate (see [5], Subsection 2.2, for a proof of the nondegeneracy).

This symplectic structure on the cotangent is universal in the sense that it satisfies the usual universal property.

Lemma 2.10. Given a 1-form $\alpha : X \rightarrow T^*[n]X$ , we have that $\alpha ^* \lambda _X = \alpha $ .

Proof. In general, if we take $f: X \rightarrow Y$ , the pullback of an n-shifted $1$ -form, $\beta $ , is described by:

Taking into account the fact that $\lambda $ factors through $\pi _X^* T^*[n]X$ , we consider the following diagram:

This proves that the pullback along $\alpha $ of $\lambda _X$ seen as a 1-form of degree n on $T^*[n]X$ is the same as the pullback along $\alpha $ of the section $\lambda _X : T^*[n]X \rightarrow \pi _X^* T^*[n]X$ .

We denote by $\alpha _1$ the associated section in $\mathrm {Map}_{\textbf {QC}(X)} \left ( \mathscr {O}_X, \mathbb {L}_X[n] \right )$ of degree n. There is a one-to-one correspondence between sections of $\pi _X : T^*[n]X \rightarrow X$ and points of $\mathrm {Map}_{\textbf {QC}(X)} \left ( \mathscr {O}_X, \mathbb {L}_X[n] \right )$ . Now we use the fact that $\mathrm {Id}\circ \alpha = \alpha $ :

• • On the one hand, $\alpha $ is completely described by $\alpha _1 \in \mathrm {Map}_{\textbf {QC}(X)} \left ( \mathscr {O}_X, \mathbb {L}_X[n] \right )$ .

• • On the other hand, the map $\mathrm {Id}: T^*[n] X \rightarrow T^*[n]X$ is described by the projection $\pi : T^*[n]X \rightarrow X$ and the section $\lambda _X \in \mathrm {Map}_{\textbf {QC}(T^*[n]X)} \left ( \mathscr {O}_{T^*[n]X}, \pi _X^* \mathbb {L}_X \right )$ . Therefore, the composition $\mathrm {Id} \circ \alpha $ is also a section of $\pi _X$ and is described by $ \alpha ^* \lambda _X \in \mathrm {Map}_{\textbf {QC}(X)} \left ( \mathscr {O}_X, \mathbb {L}_X[n] \right )$ .

This proves that $\alpha ^* \lambda _X = \alpha _1$ . Since these maps characterise the sections of $\pi _X$ they represent, we have $\alpha ^* \lambda _X = \alpha $ .

2.2 Lagrangian structures

We recall from [12] the definition and standard properties of Lagrangian structures. We also provide proves of some results which are well known to the expert but are not written as far as we know.

Definition 2.11 (isotropic structures).

Let $ f : L \rightarrow X$ be a map of derived Artin stacks. An isotropic structure on f is a homotopy, in $\mathscr {A}^{2,cl}(L,n)$ , between $f^* \omega $ and $0$ for some n-shifted symplectic structure $\omega : \star \rightarrow \textbf {Symp}(X,n)$ . Isotropic structures on f form a space described by the homotopy pullback:

If we fix a given n-shifted symplectic structure $\omega : \star \rightarrow \textbf {Symp}(X,n)$ , we can define the space of isotropic structures on f at $\omega $ defined by:

$$\begin{align*}\textbf{Iso}(f, \omega) := \textbf{Iso}(f,n)\times_{\textbf{Symp}(X,n)}\star \simeq \star \times_{0, \ \mathscr{A}^{2,cl}(X,n), \ f^*\omega} \star. \end{align*}$$

Remark 2.12. More explicitly, an isotropic structure is given by a family of forms of total degree $(p+n-1)$ , $(\gamma _i)_{i \in \mathbb {N}}$ with $ \gamma _i \in \textbf {DR}(L)_{(p+i)}[p+n+i-1]$ , such that $\delta \gamma _0 = f^*\omega _0$ and $\delta \gamma _i + d \gamma _{i-1} = f^*\omega _i$ . This can be rephrased as $D \gamma = f^* \omega $ , thus, $\gamma $ is indeed a homotopy between $f^*\omega $ and 0.

Definition 2.13 (Lagrangian structures).

An isotropic structure $\gamma $ on $f: L \rightarrow X$ is called a Lagrangian structure on f if the leading term, $\gamma _0$ , viewed as an isotropic structure on the morphism $\mathbb {T}_L \rightarrow f^* \mathbb {T}_X$ , is nondegenerate. We say that $\gamma _0$ is nondegenerate if the following null-homotopic sequence (homotopic to 0 via $\gamma _0$ ) is fibred:

(2)

The space of n-shifted Lagrangian structures on f is denoted $\textbf {Lag}(f,n)$ . There are natural morphisms of spaces $\textbf {Lag}(f,n) \rightarrow \textbf {Iso}(f,n) \rightarrow \textbf {Symp}(X,n)$ .

Remark 2.14. To say that that sequence is fibred can be reinterpreted as a more classical condition involving the conormal. Since $\textbf {QC}(X)$ is a stable $\infty $ -category, the homotopy fibre of $f^* \mathbb {L}_X [n] \rightarrow \mathbb {L}_L[n]$ is denoted and the nondegeneracy condition can be rephrased by saying that the natural map $\Theta _f : \mathbb {T}_L \rightarrow \mathbb {L}_f [n-1]$ is a quasi-isomorphism.

Remark 2.15. To simplify the notations, we will abusively say that a morphism $f: X \rightarrow Y$ is Lagrangian when we consider f together with a fixed Lagrangian structure on f and a fixed symplectic structure $\omega $ .

Example 2.16. A $1$ -form of degree n on an Artin stack X is equivalent to a section $\alpha : X \rightarrow T^*[n]X$ . This section is a Lagrangian morphism if and only if $\alpha $ admits a closure, that is, $\textbf {Key}(\alpha )$ is nonempty. This is Theorem 2.15 in [5].

Proposition 2.17. There is a canonical homotopy equivalence $\textbf {Iso}(\alpha ) \rightarrow \textbf {Key}(\alpha )$ between the space of isotropic structures on the $1$ -form $\alpha $ and the space of keys of $\alpha $ .

Proof.

(3)

The leftmost square is Cartesian by definition of $\textbf {key}(\alpha )$ in Definition 2.4. By definition, the pullback of the outer square is $\textbf {Iso}(\alpha )$ because $d_{dR}\alpha = \alpha ^* \omega $ (by universal property of the Liouville 1-form, Lemma 2.10). It turns out that the rightmost square is also Cartesian. This is simply saying that the space of closed $1$ -forms of degree n is the same as the space of $1$ -forms of degree n whose de Rham differential is homotopic to $0$ . We obtain that $\textbf {key}(\alpha )$ and $\textbf {Iso}(\alpha )$ are both pullbacks of the outer square and, therefore, are canonically homotopy equivalent.

Remark 2.18. It turns out that Theorem 2.15 in [5] says that all the isotropic structures on $\alpha $ (or, equivalently, the lifts of $\alpha $ to a closed form) are, in fact, nondegenerate, which implies the statement in Example 2.16 and even that the space of Lagrangian structures on $\alpha $ is equivalent to the space of keys of $\alpha $ .

Lemma 2.19 (Example 1.26 in [6]).

Consider the map $X \rightarrow \star _n$ , where $\star _n$ is the point endowed with the canonical n-shifted symplectic structure given by 0. Then a Lagrangian structure on this map is equivalent to an $(n-1)$ -shifted symplectic structure on X.

Proof. Pick an isotropic structure $\gamma $ on p. We know that $\gamma $ is a homotopy between 0 and 0, which means that $D\gamma = 0$ . Therefore, $\gamma $ is a closed 2-form of degree $n-1$ . We want to show that $\gamma $ is nondegenerate as an isotropic structure if and only if it is nondegenerate as a closed 2-form on X. The nondegeneracy of the Lagrangian structure, as described in Remark 2.14, corresponds to the requirement that the natural map $ \mathbb {T}_X \rightarrow \mathbb {L}_X[n-1]$ is a quasi-isomorphism. This map depends on $\gamma _0$ , and we want to show that this map is, in fact, $\gamma _0^{\flat }$ . This map is the natural map that fits in the following homotopy commutative diagram:

We can show that by strictifying the homotopy commutative diagram:

Note that this diagram is already commutative, but we see it as homotopy commutative using the homotopy $\gamma _0$ . We use the homotopy $\gamma _0$ to strictify the previous diagram, and we obtain:

The homotopy fibre and also strict fibre of the projection $\mathrm {pr} : \mathbb {L}_X[n-1] \oplus \mathbb {L}_X[n] \rightarrow \mathbb {L}_X[n]$ is $\mathbb {L}_X [n-1]$ , and, therefore, the natural map we obtain is $\gamma _0^{\flat } : \mathbb {T}_X \rightarrow \mathbb {L}_X[n-1]$ .

Since the nondegeneracy condition of the isotropic structure $\gamma $ is the same as saying that the map $\gamma _0^{\flat }$ is a quasi-isomorphism, we have shown that an isotropic structure $\gamma $ is an $(n-1)$ -shifted symplectic structure on X if and only if it is nondegenerate as an isotropic structure on $X \rightarrow \star _n $ .

Definition 2.20 (Lagrangian correspondence, [4]).

Let X and Y be derived Artin stacks with n-shifted symplectic structures. A Lagrangian correspondence from X to Y is given by a derived Artin stack L with morphims:

and a Lagrangian structure on the map

, where

is endowed with the n-shifted symplectic structure $\pi _X^* \omega _X - \pi _Y^* \omega _Y$ . For example, a Lagrangian structure on $L \rightarrow X$ is equivalent to a Lagrangian correspondence from X to $\star $ .

As explained in [4], Subsection 4.2.2, these Lagrangian correspondences can be composed. If we take $X_0$ , $X_1$ and $X_2$ derived Artin stacks with symplectic structures and $L_{01}$ and $L_{12}$ Lagrangian correspondences from, respectively, $X_0$ to $X_1$ and $X_1$ to $X_2$ , we can produce a Lagrangian correspondence $L_{02}$ from $X_0$ to $X_2$ by setting $L_{02} := L_{01} \times _{X_1} L_{12}$ .

2.3 Lagrangian fibration

We recall in this section the definition and standard properties of Lagrangian fibrations ([5]).

Definition 2.21. Let $f : Y \rightarrow X$ be a map of derived Artin stacks and $\omega $ a symplectic structure on Y. A Lagrangian fibration on f is given by:

• • A homotopy, denoted $\gamma $ , between ${\omega }_{/X}$ and $0$ , where ${\omega }_{/X}$ is the image of $\omega $ under the natural map $\mathscr {A}^{2,cl}(Y,n) \rightarrow \mathscr {A}^{2,cl}(Y/X, n)$ (see Remark 2.3) for some n-shifted symplectic structure $\omega : \star \rightarrow \textbf {Symp}(Y,n)$ . This forms a space of isotropic fibrations:

  

• • A nondegeneracy condition which says that the following sequence (homotopic to 0 via $\gamma _0$ ) is fibred:

  $$ \begin{align*} \mathbb{T}_{Y/X} \rightarrow \mathbb{T}_Y \simeq \mathbb{L}_Y [n] \rightarrow \mathbb{L}_{Y/X}[n] .\end{align*} $$

In particular, the nondegeneracy condition can be rephrased by saying that there is a canonical quasi-isomorphism $\alpha _f : \mathbb {T}_{Y/X} \rightarrow f^*\mathbb {L}_{X}[n]$ (similar to the criteria for a Lagrangian morphism in Remark 2.14) that makes the following diagram commute:

(4)

The subspace of $\textbf {IsoFib}(f,n)$ generated by the nondegenerate objects is the space of Lagrangian fibration structures on f and is denoted by $\textbf {LagFib}(f,n)$ . There are natural maps $\textbf {LagFib}(f,n) \rightarrow \textbf {IsoFib}(f,n) \rightarrow \textbf {Symp}(Y,n)$ .

Similarly to the Lagrangian case, we can fix an n-shifted symplectic structure on Y and define Lagrangian and isotropic fibration of f at a given $\omega $ :

$$\begin{align*}\textbf{IsoFib}(f, \omega) = \textbf{IsoFib}(f,n) \times_{\textbf{Symp}(Y,n)} \star \simeq \star \times_{0,\mathscr{A}^{2,cl}(Y/X,n), \omega_{/X}} \star. \end{align*}$$

Remark 2.22. To simplify the notations, we will abusively say that a morphism $f: X \rightarrow Y$ is a Lagrangian fibration when we consider f together with a fixed shifted symplectic structure $\omega $ and a fixed structure of Lagrangian fibration on f at $\omega $ .

Example 2.23. The natural projection $\pi _X : T^*[n]X \rightarrow X$ is a Lagrangian fibration. The Liouville 1-form is a section of $\pi _X^* \mathbb {L}_X[n]$ which is part of the fibre sequence:

Thus, the 1-form induced by $\lambda _X $ in is homotopic to 0. The nondegeneracy condition is more difficult and is proven in Subsection 2.2.2 of [5]. It turns out that the morphism expressing the nondegeneracy condition, $\alpha _{\pi _X}$ , is given by a canonical construction (Proposition 2.25), which does not depend on the symplectic structure. This is the content of Proposition 2.29.

Lemma 2.24. Let $x: \star _n \rightarrow X$ be a point of X. Then, given a Lagrangian fibration structure on x, the nondegeneracy condition is given by a quasi-isomorphism $x^* \mathbb {T}_X \rightarrow x^*\mathbb {L}_X[n+1]$ .

Proof. The Lagrangian fibration structure on $\star _n \rightarrow X$ is a homotopy between 0 and itself in . As in the proof of Lemma 2.19, this is given by an element . Similarly to what was done in the proof of Lemma 2.19, we can show that $\gamma $ is nondegenerate as a Lagrangian fibration if and only if it is nondegenerate as a closed 2-form of degree n. Again, it boils down to the fact that the natural morphism in the nondegeneracy criteria for Lagrangian fibrations is, in fact, .

Moreover, we have natural equivalences,

and

because the sequence:

is fibred. This concludes the proof.

2.4 Relative cotangent complexes of linear stacks

This section is devoted to the study of relative cotangent complexes of linear stacks. Given $\mathscr {F} \in \textbf {QC}(X)$ , a dualisable quasi-coherent sheaf over a derived Artin stack X, we consider its associated linear stack, $\mathbb {A} (\mathscr {F})$ (see Definition 2.7), and the goal of this section is to describe and its functoriality in $\mathscr {F}$ and X.

Proposition 2.25. Let X be a derived Artin stack and $\mathscr {F} \in \textbf {QC}(X)$ a dualisable quasi-coherent sheaf on X. We denote $\pi _X : \mathbb {A} (\mathscr {F}) \rightarrow X$ the natural projection. Then we have:

Proof. We will show the result for any B-point $y : \textbf {Spec}(B) \rightarrow \mathbb {A} (\mathscr {F} )$ , and we write $x = \pi \circ y : \textbf {Spec}(B) \rightarrow X$ . We will show that for all $M \in B-\mathrm {Mod}$ connective, we have:

First we observe that

is equivalent, using the universal property of the cotangent complex, to the following homotopy fibre at y:

with $B \oplus M$ denoting the square zero extension and $\textbf {Spec}(B \oplus M) \rightarrow X$ being the composition:

Thus, a map in

is completely determined by a map:

$$\begin{align*}\Phi : \textbf{Spec}(B \oplus M) \rightarrow \mathbb{A} (\mathscr{F}) \end{align*}$$

making the following diagram commute:

Thus, we obtain that is equivalent to:

$$\begin{align*}\mathrm{hofibre}_{s_y} \left( \mathrm{Map}_{B \oplus M - \mathrm{Mod}} \left( B \oplus M, p^* x^* \mathscr{F} \right) \rightarrow \mathrm{Map}_{B - \mathrm{Mod}} \left( B, x^* \mathscr{F} \right)\right), \end{align*}$$

where $s_y \in \mathrm {Map}_{B - \mathrm {Mod}} \left ( B, x^* \mathscr {F} \right )$ is the section associated to $y : \textbf {Spec}(B) \rightarrow \mathbb {A} (\mathscr {F} )$ . The map is then given by precomposition with $i^*$ . We can now observe that $p^* x^* \mathscr {F} = x^* \mathscr {F} \oplus x^* \mathscr {F} \otimes _B M $ , and that:

$$\begin{align*}\mathrm{Map}_{B \oplus M - \mathrm{Mod}} \left( B \oplus M, p^* x^* \mathscr{F} \right) \simeq \mathrm{Map}_{B - \mathrm{Mod}} \left( B , x^* \mathscr{F} \oplus x^* \mathscr{F} \otimes_B M \right). \end{align*}$$

We obtain:

$$\begin{align*}\simeq \mathrm{hofibre} \left( \mathrm{Map}_{B - \mathrm{Mod}} \left( B , x^* \mathscr{F} \oplus x^* \mathscr{F} \otimes_B M \right) \rightarrow \mathrm{Map}_{B - \mathrm{Mod}} \left( B, x^* \mathscr{F} \right)\right) \end{align*}$$

$$\begin{align*}\simeq \mathrm{Map}_{B - \mathrm{Mod}} \left( B, x^* \mathscr{F} \otimes_B M \right) \simeq \mathrm{Map}_{B - \mathrm{Mod}} \left( x^* \mathscr{F}^{\vee}, M \right). \end{align*}$$

Now the result follows from the fact that the functor:

is fully faithful and the fact that everything we did is natural in B.

Lemma 2.26. Let $f: X \rightarrow Y$ be a morphism of derived Artin stacks. We consider $\mathscr {F} \in \textbf {QC}(Y)$ dualisable. Then there is a commutative square:

with $\Phi $ the natural morphism in the following homotopy pullback:

and the lower horizontal equivalence $\Phi ^* \pi _Y^* \mathscr {F}^{\vee } \rightarrow \pi _X^* f^* \mathscr {F}^{\vee }$ being the equivalence coming from the fact that $\pi _Y \circ \Phi \simeq f \circ \pi _X$ .

Proof. The first thing we observe is that $\mathbb {A} (f^* \mathscr {F}) \simeq f^* \mathbb {A}(\mathscr {F})$ . We consider as before B-points:

We want to show that the following diagram is commutative:

(5)

Using the universal property of the cotangent complex, the top horizontal arrow is naturally equivalent to the map:

induced by $\mathrm {Hom}_{\textbf {dSt}}\left ( -, \Phi \right )$ . A map $\psi : \textbf {Spec}(B \oplus M) \rightarrow \mathbb {A}(f^* \mathscr {F})$ in this homotopy fibre fits in the following commutative diagram:

and the map between the homotopy fibre sends $\psi $ to $\Phi \circ \psi $ . Since the underlying map of $\psi $ is $\pi _X \circ \psi : \textbf {Spec}(B \oplus M) \rightarrow X$ is $x \circ p$ and the underlying map of $\Phi \circ \psi $ is $\pi _Y \circ \Phi \circ \psi : \textbf {Spec}(B \oplus M) \rightarrow Y$ is $f\circ x \circ p = \tilde {x} \circ p$ , this map between the homotopy fibre of derived stacks is, therefore, naturally equivalent to the map:

where $s_y $ and $s_{\tilde {y}}$ are the sections associated to y and $\tilde {y}$ , respectively. This map is, in fact, induced by the natural identification $ p^* \tilde {x}^* \mathscr {F} \simeq p^*x^* f^* \mathscr {F}$ (since $\tilde {x} = f\circ x$ ). But following the steps of the proof of Proposition 2.25, this map is naturally equivalent to the map:

$$\begin{align*}\mathrm{Hom}_{B- \mathrm{Mod}} \left( y^* \pi_X^* f^* \mathscr{F}^{\vee} , M \right) \rightarrow \mathrm{Hom}_{B- \mathrm{Mod}} \left( \tilde{y}^* \pi_Y^* \mathscr{F}^{\vee}, M \right).\end{align*}$$

The natural equivalences we used are the natural equivalences used in the proof of Proposition 2.25 which proves that the Diagram (5) is commutative. Now the result follows once again from the fact that the functor:

is fully faithful and the fact that everything we did is natural in B.

Lemma 2.27. Let X be a derived Artin stacks. We consider $\mathscr {F}, \mathscr {G} \in \textbf {QC}(X)$ dualisable and $h : \mathscr {F} \rightarrow \mathscr {G}$ . Then there is a commutative square:

with $\hat {h} : \mathbb {A} ( \mathscr {G}) \rightarrow \mathbb {A} (\mathscr {F})$ the map induced by $\mathscr {F}$ .

Proof. Every step of the proof of Proposition 2.25 is functorial in $\mathscr {F}$ .

Proposition 2.28. Let $f: X \rightarrow Y$ be a morphism of derived Artin stacks. We consider $\mathscr {F} \in \textbf {QC}(X)$ and $\mathscr {G} \in \textbf {QC}(Y)$ dualisable and a morphism $h : f^* \mathscr {F} \rightarrow \mathscr {G}$ . Then there is a commutative square:

Proof. It follows from Lemmas 2.26 and 2.27.

Proposition 2.29. The quasi-isomorphism of Example 2.23 expressing the nondegeneracy of the canonical Lagrangian fibration on the shifted cotangent stacks is the canonical quasi-isomorphism from Proposition 2.25.

Proof. First, since the cotangent bundle has a section, we have a split exact sequence:

Proposition 2.25 gives us canonical equivalences

. With this data, we can rewrite Diagram (4), up to weak equivalences, as the strictly commutative diagram:

Through the canonical equivalence of Proposition 2.25, the morphism simply becomes the natural inclusion and $\omega $ becomes the identity. This implies that is the canonical equivalence of Proposition 2.25.

3 Symplectic geometry of the derived critical locus

In Subsections 3.1 and 3.2, we present a few results on the symplectic geometry of homotopy pullbacks of derived Artin stacks. These results apply, in particular, to the case of derived intersections of derived schemes. In Subsection 3.3, we study in more detail the special case of derived intersections given by derived critical loci.

3.1 Lagrangian intersections are $(n-1)$ -shifted symplectic

Proposition 3.1 ([12], Subsection 2.2).

Let Z be a derived Artin stack with an n-shifted symplectic structure $\omega $ . Let $f: X \rightarrow Z$ and $g : Y \rightarrow Z$ be morphisms with $\gamma $ and $\delta $ Lagrangian structures on f and g, respectively. Then the homotopy pullback $X \times _Z Y$ possesses a canonical $(n-1)$ -shifted symplectic structure called the residue of $\omega $ and denoted $R(\omega , \gamma ,\delta )$ .

Remark 3.2. If we fix f and g as above, we can extend the previous theorem to obtain the following map of spaces (see Theorem 2.4 in [4]):

$$\begin{align*}\textbf{Lag}(f,n) \times_{\textbf{Symp}(X,n)} \textbf{Lag}(g,n) \rightarrow \textbf{Symp}(X\times_Z Y, n-1). \end{align*}$$

Remark 3.3. Theorem 3.1 can also be seen as a consequence of the procedure of composition of Lagrangian correspondences. Consider the following composition of Lagrangian correspondences:

The maps $X \rightarrow Z \times \bar {\star }$ and $Y \rightarrow Y \times \bar {\star }$ are Lagrangian correspondences because $X \rightarrow Z$ and $Y \rightarrow Z$ are Lagrangian. Therefore, by composition, $X \times _Z Y \rightarrow \star \times \bar {\star } $ is also a Lagrangian correspondence, thus, $X \times _Z Y \rightarrow \star $ is Lagrangian. From Lemma 2.19, since the point is n-shifted symplectic, then $X \times _Z Y$ is $(n-1)$ -shifted symplectic.

3.2 Lagrangian fibrations and derived intersections

Proposition 3.4. Suppose we have a sequence of Artin stacks and $\omega $ an n-shifted symplectic form on Y. Assume that $f $ is a Lagrangian morphism and g is a Lagrangian fibration. Then there is a canonical quasi-isomorphism .

Proof. Consider the following commutative diagram:

In the upper face, every square is bicartesian because both the outer square and the rightmost square are bicartesian. Every nondashed vertical arrow is quasi-isomorphisms by assumption (because of the various nondegeneracy conditions). Focusing on the right-hand cube, it sends the upper homotopy bicartesian square to the bottom square, which is also homotopy bicartesian. The homotopy cofibre of $(g \circ f)^* \mathbb {L}_X [n] \rightarrow f^* \mathbb {L}_Y[n]$ is , and we obtain a quasi-isomorphism depicted as a dashed arrow.

By the same reasoning, since the upper outer square is homotopy bicartesian, it maps to the lower outer square that is also homotopy bicartesian. Moreover, the homotopy fibre of the map is exactly . This proves that there is a canonical quasi-isomorphism .

Theorem 3.5. Let Y be an n-shifted symplectic derived Artin stack. Let $f_i: L_i \rightarrow Y$ be Lagrangian morphisms (for $i= 1 \cdots 2$ ) and $\pi : Y \rightarrow X$ a Lagrangian fibration. Suppose that the maps $\pi \circ f_i : L_i \rightarrow X$ are weak equivalences. Then $P : Z = L_1 \times _Y L_2 \rightarrow X$ is a Lagrangian fibration.

Proof. We summarise the notation in the following diagram:

We also denote $P := \pi \circ F : Z \rightarrow X $ .

To show that we can obtain an isotropic structure, we will show that we have a map of spaces (dropping at first the nondegeneracy condition of the Lagrangian fibration):

$$\begin{align*}\textbf{Lag}(f_1,n) \times_{\textbf{Symp}(Y,n)} \textbf{Lag}(f_2,n) \times_{\textbf{Symp}(Y,n) } \textbf{IsoFib}(\pi, n) \rightarrow \textbf{IsoFib}(P,n-1). \end{align*}$$

If we forget the nondegeneracy of the Lagrangian structure, we obtain an element in $ \textbf {Iso}(f_1,n) \times _{\textbf {Symp}(Y,n)} \textbf {Iso}(f_2,n) \times _{\textbf {Symp}(Y,n) } \textbf {IsoFib}(\pi , n)$ , and we can show, with formal manipulations of the pullbacks defining the spaces of isotropic structures and isotropic fibrations, that:

$$\begin{align*}\textbf{Iso}(f_1,n) \times_{\textbf{Symp}(Y,n)} \textbf{Iso}(f_2,n) \times_{\textbf{Symp}(Y,n) } \textbf{IsoFib}(\pi, n)\end{align*}$$

$$\begin{align*}= \star \times_{\mathscr{A}^{2,cl}(L_1,n)} \textbf{Symp}(Y,n) \times_{\mathscr{A}^{2,cl} (L_2,n)} \star \times_{\mathscr{A}^{2,cl}(Y/X,n)} \star. \end{align*}$$

Using the pullback to $\mathscr {A}^{2,cl}(L_1 \times _Y L_2, n)$ we obtain a morphism:

$$\begin{align*}\textbf{Iso}(f_1,n) \times_{\textbf{Symp}(Y,n)} \textbf{Iso}(f_2,n) \times_{\textbf{Symp}(Y,n) } \textbf{IsoFib}(\pi, n) \rightarrow\end{align*}$$

$$\begin{align*}\star \times_{\mathscr{A}^{2,cl}(L_1 \times_Y L_2,n)} \mathscr{A}^{2,cl}(L_1 \times_Y L_2,n) \times_{\mathscr{A}^{2,cl} (L_1 \times_Y L_2,n)} \star \times_{\mathscr{A}^{2,cl}(Y/X,n)} \star.\end{align*}$$

This last space naturally maps to:

• •

  $$\begin{align*}\mathscr{A}^{2,cl}(L_1 \times_Y L_2, n-1) = \star \times_{\mathscr{A}^{2,cl}(L_1 \times_Y L_2,n)} \mathscr{A}^{2,cl}(L_1 \times_Y L_2,n) \times_{\mathscr{A}^{2,cl} (L_1 \times_Y L_2,n)} \star. \end{align*}$$
  Moreover, if we restrict this map to nondegenerate isotropic structures, then it is valued in $\textbf {Symp}(L_1 \times _Y L_2, n-1)$ (thanks to Theorem 3.1).

• •

  $$\begin{align*}\mathscr{A}^{2,cl}(Y/X,n-1) = \star \times_{\mathscr{A}^{2,cl}(Y/X,n)} \star. \end{align*}$$

We have the commutative diagram:

Since the map $\mathscr {A}^{2,cl}(Y/X,n-1) \rightarrow \mathscr {A}^{2,cl}(L_1 \times _Y L_2/X, n-1)$ factors through $\mathscr {A}^{2,cl} (L_i/X, n-1) \simeq \star $ , we get a morphism:

$$\begin{align*}\mathscr{A}^{2,cl}(L_1 \times_Y L_2, n-1) \times \mathscr{A}^{2,cl}(Y/X,n-1) {{\kern-1pt}\rightarrow{\kern-1pt}} \mathscr{A}^{2,cl}(L_1 \times_Y L_2, n-1) \times_{\mathscr{A}^{2,cl}(L_1 \times_Y L_2/X,n-1)} \star. \end{align*}$$

Now if we restrict to $\textbf {Symp}(L_1 \times _Y L_2, n-1) \subset \mathscr {A}^{2,cl}(L_1 \times _Y L_2, n-1)$ (which amounts to restricting to nondegenerate isotropic structures), we get a map:

$$\begin{align*}\textbf{Symp}(L_1 \times_Y L_2, n-1) \times \mathscr{A}^{2,cl}(Y/X,n-1) \rightarrow \textbf{IsoFib}(P, n-1). \end{align*}$$

Therefore, we get the desired map and we will consider the isotropic fibration on P given by the image along the morphism we just described of the Lagrangian structures and Lagrangian fibration structure given on $f_1$ , $f_2$ and $\pi $ , respectively. We are left to prove the nondegeneracy condition. To do that, we first consider the following diagram:

The vertical sequences and the last two horizontal sequences are fibred and, therefore, so is the first horizontal sequence. The last two horizontal sequences are fibred because the following diagrams are Cartesian:

Using Proposition 3.4 and nondegeneracy, we get the following commutative diagram:

where all vertical morphisms are quasi-isomorphisms. The fibre in the lower sequence is exactly $\mathbb {L}_X[n-1] $ because

since $L_i \to X$ are equivalences. We will call

the dashed equivalence obtained.

We still need to show that $\alpha $ is the morphism used in the criteria for the nondegeneracy of the Lagrangian fibration. Recall that this morphism is given by means of the universal map filling Diagram (4):

To compare $\alpha $ and $\alpha _P$ , we summarise the construction of $\alpha $ and all the equivalences coming from nondegeneracy conditions in the following diagram:

(6)

where all the vertical maps are quasi-isomorphism obtained from the nondegeneracy conditions. We want to prove that $\alpha _P$ and $\alpha $ are homotopic. The relevant data extracted from Diagram (6) are:

The composition:

factorises through

. This implies that the map

factorises through

and, therefore, $\alpha $ satisfies the same universal property as $\alpha _P$ , proving that $\alpha $ and $\alpha _P$ are homotopic.

Remark 3.6. Similarly to Proposition 3.1, this theorem can be extended to a map of spaces:

$$\begin{align*}\textbf{Lag}(f_1,n) \times_{\textbf{Symp}(Y,n)} \textbf{Lag}(f_2,n) \times_{\textbf{Symp}(Y,n)} \textbf{LagFib}(\pi,n) \rightarrow \textbf{LagFib}(P,n). \end{align*}$$

This is simply the restriction of the map described in the proof of Theorem 3.5 to the nondegenerate elements. Forgetting the extra Lagrangian fibration recovers the map in Remark 3.2, the following diagram is commutative:

3.3 Derived critical locus

Given a derived Artin stack X and a morphism $f : X \rightarrow \mathbb {A}_k^1$ , we define the derived critical locus of f, denoted $\textbf {Crit}(f)$ , as the derived intersection of $df : X \rightarrow T^*X$ with the zero section $0 : X \rightarrow T^*X$ . It is given by the homotopy pullback:

(7)

Example 3.7. We recall from [3] that if X is a smooth algebraic variety, its derived critical locus can be described, as a derived scheme, by the underlying scheme given by the ordinary critical locus of f, that we denote S, together with the sheaf of $\textbf {cdga}_{\leq 0}$ given by the derived tensor product $\mathscr {O}_X \otimes _{\mathscr {O}_{T^*X}}^{\mathbb {L}} \mathscr {O}_X$ , restricted to S. This derived tensor product is described by the homotopy pushout:

Taking the derived tensor product amounts to replacing the 0-section morphism $0 : \mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X \rightarrow \mathscr {O}_{X} $ by the equivalent cofibration, in the model category of commutative differential graded k-algebras, $\mathrm {Sym}_{\mathscr {O}_X}\mathbb {T}_X \hookrightarrow \mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \oplus \mathbb {T}_X\right ) $ , where $\mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \oplus \mathbb {T}_X \right )$ has the differential induced by $\mathrm {Id}: \mathbb {T}_X[1] \rightarrow \mathbb {T}_X$ . Then we take the strict pushout of this replacement. The use of these resolutions is well explained in [3] or [18]. We obtain:

$$ \begin{align*} \mathscr{O}_{\textbf{Crit}(f)} := \left( \mathscr{O}_X \otimes_{\mathscr{O}_{T^*X}}^{\mathbb{L}} \mathscr{O}_X \right)_{\vert S} \simeq \left( \mathrm{Sym}_{\mathscr{O}_X} \mathbb{T}_X[1], \iota_{df} \right)_{\vert S,} \end{align*} $$

where $\iota _{df}$ is the differential on $\mathscr {O}_{\textbf {Crit}(f)}$ given by the contraction along $df$ . The restriction to S denotes the fact that this is a derived scheme whose underlying scheme is the strict critical locus. Observe that outside of the critical locus, $\left ( \mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X[1], \iota _{df} \right )$ is cohomologically equivalent to 0.

Remark 3.8. If we do not assume that X is smooth in Example 3.7, then $\mathbb {L}_X$ usually has a nontrivial internal differential. As a sheaf of graded algebra, we still obtain $ \mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \right )$ since the replacement is the same as a graded algebra, but the differential is a priori different and involves a combination of the internal differential on $\mathbb {T}_X$ and the contraction $\iota _{df}$ .

Remark 3.9. From Example 2.9, we know that $T^*X$ carries a canonical symplectic form of degree $0$ , and from Example 2.16, we know that both the $0$ -section and $df$ have a natural Lagrangian structure. From Proposition 3.1, the derived intersection of these Lagrangian structures, namely, the derived critical locus Crit(f), has a natural $(-1)$ -shifted symplectic structure.

Remark 3.10. When X is a derived Artin stack and $df=0$ , we have that $\textbf {Crit}(f) \simeq T^*[-1]X$ and $\omega _{\textbf {Crit}(f)}$ form the canonical $(-1)$ -shifted symplectic structure on $T^*[-1]X$ .

In this situation, the strict critical locus is X itself and the restriction to X of $\mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X[1]$ is, therefore, $\mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X[1]$ itself (with the differential being induced by the differential on $\mathbb {T}_X$ ). Thus, $\textbf {Crit}(f) \simeq \textbf {Spec}_X \left ( \mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X[1] \right ) = T^*[-1]X $ .

Remark 3.11. We want to understand, in general, the $(-1)$ -shifted symplectic form on $\textbf {Crit}(f)$ . We use the universal property of the tautological $1$ -form (Lemma 2.10) to see that $(df)^* \omega = 0$ (with $\omega = d\lambda _X$ the canonical symplectic structure on $T^*X$ ). Using the resolution of the zero section, as in Example 3.7, $\omega $ induces a closed 2-form on $\textbf {Spec}_X \left ( \mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \oplus \mathbb {T}_X\right )\right )$ . Since the differential on the resolution, $\mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \oplus \mathbb {T}_X\right )$ , is induced by $\mathrm {Id} : \mathbb {T}_X \rightarrow \mathbb {T}_X[1]$ , the tautological 1-form $\omega _{-1}$ on $T^*[-1]X$ induces a closed 2-form on $\textbf {Spec}_X \left ( \mathrm {Sym}_{\mathscr {O}_X} \left ( \mathbb {T}_X[1] \oplus \mathbb {T}_X\right )\right )$ , which is a homotopy between $\omega $ and $0$ . We then have that the $(-1)$ -shifted symplectic form is described by the self-homotopy of $0$ given by $\omega _{-1}$ :

The proof of Proposition 3.1 (see Theorem 2.9 in [12]) tells us that $\omega _{-1}$ is the (–1)-shifted symplectic form on $\textbf {Crit}(f)$ .

Remark 3.12. From Theorem 3.5, we have that $\pi : \textbf {Crit}(f) \rightarrow X$ is a Lagrangian fibration. In the situation where $df =0$ and X is smooth, this Lagrangian fibration coincides with the canonical Lagrangian fibration on $\pi _X : T^*[-1]X \rightarrow X$ . In general, the morphism $\alpha _{\pi }$ controlling the nondegeneracy condition of the Lagrangian fibration (see Diagram (4)) is still natural in the sense given by the following proposition.

Proposition 3.13. $\alpha _{\pi }$ is equivalent to the following composition of equivalences:

(8)

where $\beta $ is the dual of the canonical equivalence of Proposition 2.25.

Proof. The strategy, here, is to express the Diagram (4) as a pullback of the same type of diagrams. It reduces the problem to proving the same statement but for the projection $\pi _X : T^*X \rightarrow X$ . But this Proposition is known for the Lagrangian fibration on the shifted cotangent stacks (this is a direct consequence of Proposition 2.29).

First we express $\mathbb {L}_{\textbf {Crit}(f)}[-1]$ as a pullback above $\mathbb {L}_{T^*X}$ . This can be done by observing that all squares in the following diagram are bicartesians:

where $\pi _1$ and $\pi _2$ are the natural projections $\textbf {Crit}(f) \to X$ given by the pullback Diagram (7). We write Diagram (4) for $\pi : \textbf {Crit}(f) \rightarrow X$ as:

In this diagram, pullbacks have been omitted to keep the diagram easy to read. We need to describe the morphism . Recall from Remark 2.14 and the proof of the nondegeneracy in Proposition 3.1 that $\omega _{\textbf {Crit}(f)}$ is $\Theta _{df} \times _{\omega } \Theta _0$ , where is the natural morphism expressing the nondegeneracy of the Lagrangian structure (see Definition 2.13).

Finally, Proposition 2.29 shows that $\beta $ is the same as $\alpha _{\pi _X}$ . This completes the proof.

4 Examples

4.1 One nondegenerate critical point

Let X be a smooth algebraic variety over k and $f : X \rightarrow \mathbb {A}_k^1$ a map which is smooth everywhere except at a point $x \in X$ , where there is a nondegenerate critical point. The goal is to understand the Lagrangian fibration on $\textbf {Crit}(f) \rightarrow X$ and show that it is related to the Hessian quadratic form of f at x. This section is a particular case of Subsection 4.2, and we only sketch what is happening in this case. We will be making the statements more precise and giving complete proofs in Subsection 4.2.

The strict critical locus is

, where I is the ideal generated by the partial derivatives of f, $I = \langle df.v, v \in \mathbb {T}_X \rangle $ . There is a natural morphism $\tilde {x} := \star \rightarrow \textbf {Crit}(f)$ , such that the following diagram commutes:

The ideal generated by the partial derivatives is maximal, and the partial derivatives form a regular sequence. This implies that $\tilde {x}$ is an equivalence. For more details, this is the analogue of Proposition 4.6. We can even prove (in the general context of Subsection 4.2) that $T^*[-1]S $ (where S is the strict critical locus) is weakly equivalent to $\textbf {Crit}(f)$ . This result will, however, not be needed for the general case.

Using Lemma 2.24, the Lagrangian fibration induced on $\star _{(-1)} \rightarrow X$ gives us a closed 2-form in , which induces a metric on $\mathbb {T}_x X$ . The nondegeneracy of the symmetric bilinear form is equivalent to the nondegeneracy of the Lagrangian fibration, which says that the natural map $x^*\mathbb {T}_X \rightarrow x^* \mathbb {L}_X$ is a quasi-isomorphism. We will show that this metric is in fact characterised by the Hessian quadratic form of f at the critical point.

We want to describe the Lagrangian fibration obtained on $\star \rightarrow X$ by pulling back along $\tilde {x}$ the homotopy between

and 0 in

. We obtain a homotopy between 0 and itself in

. We will relate the Hessian quadratic form with the map $\alpha _{x}$ defined to describe the nondegeneracy condition of Lagrangian fibrations (see Definition 2.21 and Diagram (4)). For $\textbf {Crit}(f)$ and $\star $ , this diagram becomes, respectively:

and:

These two diagrams are supposed to represent the same Lagrangian fibration. We will pullback along $\tilde {x}$ the diagram for $\textbf {Crit}(f)$ to the category of differential graded k-vector space (i.e. $\textbf {QC}(\star )$ ). We can compare $\alpha _x$ and $\alpha _{\pi }$ via the following commutative diagram:

We can now look at these morphisms in local étale coordinates around x. We denote by $X^i$ coordinates in X, $p_i$ a basis of $x^* \mathbb {T}_X$ and $\xi ^i$ its associated shifted basis in $x^* \mathbb {T}_X[1]$ . We also denote by $dX^i$ the dual basis of $p_i$ . We write $k\langle a \rangle := k\langle a_1, \cdots , a_n\rangle $ for the k-vector space with basis $a_1, \cdots , a_n$ . We get:

Here, $d\theta $ is the standard shifted variable added to make the following pullback square a strict pullback:

This imposes $\delta d \xi = d \theta $ . To make the full diagram strictly commutative, we must have $\psi (d\xi ) = d\xi $ . And to make $\psi $ a map of chain complexes, we must have $\psi (d \delta \xi ^i) = \delta \psi (d \xi ^i) = \delta d\xi ^i = d \theta ^i $ , and, therefore, it imposes $\psi (dX^i) = \mathrm {Hess}_x^{-1}(f)(d X^i)(dX^j) d\theta ^j$ . This implies that $\alpha _x (\partial _{\xi ^i}) =\mathrm {Hess}_x^{-1}(f)(d X^i)(dX^j) d\theta ^j$ .

4.2 Family of nondegenerate critical points

We consider a generalisation of the previous example where f may have a family of critical points which are all nondegenerate in the directions normal to the critical locus.

Let us fix some notations. We denote by S the strict critical locus, which comes with a closed immersion $i: S \rightarrow X$ , and whose algebra of functions is with $I = \langle df.v, \ v \in \mathbb {T}_X \rangle $ .

We assume that both X and S are smooth algebraic varieties. We denote by $\textbf {Crit}(f)$ the derived critical locus of f, and we get a canonical morphism $\lambda : S \rightarrow \textbf {Crit}(f)$ .

In order to define the Hessian quadratic form and the nondegeneracy condition, we need to assume that the closed immersion $S \hookrightarrow X$ has a first order splitting. Concretely, we assume all along in this section that the following fibre sequence splits:

(9)

This assumption is necessary to be able to restrict Q to the normal part .

Definition 4.1. The Hessian quadratic form is defined by the symmetric bilinear map:

$$ \begin{align*}\begin{array}{ccccl} Q & : & \mathrm{Sym}_{\mathscr{O}_S}^2 i^* \mathbb{T}_X & \to & \mathscr{O}_S \\ & & (w,v) & \mapsto & d(df.v).w. \\ \end{array}\end{align*} $$

We define nondegeneracy to be along the ‘normal’ direction to S, by considering the following diagram:

(10)

Both rows are split fibre sequences (by assumption in Diagram (9)). The left and right vertical maps are the zero map because Q restricted to $\mathbb {T}_S$ is zero and, since Q is symmetric, Q composed with the projection to $\mathbb {L}_S$ is also zero. We obtain a map $\widetilde {Q}$ (using Q and following the section and retract of the fibre sequences) which corresponds to the map induced by Q on the normal bundle. Then the nondegeneracy condition is the requirement that $\widetilde {Q}$ is a quasi-isomorphism.

Since the differential on $\mathscr {O}_{\textbf {Crit}(f)}$ is $ \delta = \iota _{df}$ (see Remark 3.8), we have the commutative diagram in $\textbf {QC}(S)$ :

(11)

We will abusively write $Q = d \circ \delta : i^*\mathbb {T}_X[1] \to i^*\mathbb {L}_X$ for the map of degree $1$ corresponding to the composition $d \circ \iota _{df} : i^*\mathbb {T}_X \to i^* \mathbb {L}_X$ of degree $0$ .

In general, the natural map $\lambda : S \rightarrow \textbf {Crit}(f)$ is not an equivalence. This is due to the fact that the partial derivatives of f will not, in general, form a regular sequence and, therefore, $\textbf {Crit}(f)$ has higher homology. The default to be a regular sequence comes from vector fields that annihilate $df$ . Such vector fields are, in fact, vector fields on S when f is nondegenerate. With that idea in mind, we show that an equivalent description of $\textbf {Crit}(f)$ is given by $T^*[-1]S$ when Q is nondegenerate.

Proposition 4.2. There exists a natural map $\Phi : T^*[-1]S \rightarrow \textbf {Crit}(f)$ making the following diagram commute:

Proof. Under our first order splitting assumption (Diagram (9)), the natural map $\mathbb {T}_S \rightarrow i^*\mathbb {T}_X$ admits a retract, and, therefore, the natural map $i^*T^*X \rightarrow T^*S$ admits a section: $T^*S \dashrightarrow i^* T^*X$ . We consider the following diagram:

We want to pullback these zero sections along the maps induced by $df$ represented by the vertical morphisms in the following commutative diagram:

This induces the following morphisms between the pullbacks:

We obtain a map $\Phi : T^*[-1]S \rightarrow \textbf {Crit}(f)$ . The maps we obtain come from the universal properties of the pullbacks, therefore, if we denote $s_0: X \rightarrow T^*X$ the zero section, we have $s_0 \circ \pi \circ \Phi = s_0 \circ i \circ \pi _S$ . If we compose by the projection $\pi _X : T^*X \rightarrow X $ , we get $\pi \circ \Phi = i \circ \pi _S$ .

We see that $\Phi $ gives a relationship between the Lagrangian fibration structures on $T^*[-1]S \rightarrow S$ and $\textbf {Crit}(f) \rightarrow X$ , which we now analyse. The idea is to show that the difference between these Lagrangian fibrations is, in fact, controlled by $\widetilde {Q}$ (see Proposition 4.6 and Remark 4.8).

Lemma 4.3. We see $\Phi $ induces a morphism that fits in the commutative diagram:

(12)

where the bottom horizontal arrow is the pullback along $\pi _S$ of the section $\mathbb {L}_S[-1] \rightarrow i^* \mathbb {L}_X [-1]$ in the dual of the split fibre sequence (9).

Proof. The homotopy pullback $\textbf {Crit}(f) = X \times _{T^*X}^h X$ lives over X. We get the equivalences:

Proposition 2.29 tells us that the canonical fibrations on the cotangent stacks are the canonical ones and, therefore, behave functorially (using Proposition 2.28). This implies that the following commutative square is commutative:

where s is the section in the dual of the split fibre sequence (9). From Proposition 3.13, we know that both $\alpha _{\pi _S}$ and $\alpha _{\pi }$ are the morphism induced by the morphisms $\beta _S$ and $\beta _X$ via Diagram (8). We then obtain the commutative diagram:

where the composition of the horizontal maps are exactly $\alpha _{\pi _S}$ and $\alpha _{\pi }$ thanks to Proposition 3.13.

Lemma 4.4. We first remark that $\Phi ^*\mathbb {L}_{\textbf {Crit}(f)}$ can be described, as a sheaf of graded modules (forgetting the differential), by:

$$\begin{align*}\Phi^*\mathbb{L}_{\textbf{Crit}(f)} \simeq \mathrm{Sym}_{\mathscr{O}_S} \left(\mathbb{T}_S[1] \right) \otimes_{\mathscr{O}_S} \left( i^* \mathbb{L}_X \oplus i^* \mathbb{T}_X [1] \right), \end{align*}$$

where $\mathbb {L}_X$ is generated by terms of the form $dg$ with $g \in \mathscr {O}_X$ and $\mathbb {T}_X[1]$ is generated by terms of the form $d \xi $ with $\xi \in \mathbb {T}_X[1] \subset \mathscr {O}_{\textbf {Crit}(f)}$ . Then, the internal differential on $\Phi ^*\mathbb {L}_{\textbf {Crit}(f)}$ is characterised by $Q = d \circ \iota _{df}$ via $\delta (d \xi ) = Q(\xi )$ and $\delta (dg) = 0$ .

Proof. The differential on $\mathrm {Sym}_{\mathscr {O}_S} \left (\mathbb {T}_S[1] \right ) \otimes _{\mathscr {O}_S} \left ( i^* \mathbb {L}_X \oplus i^* \mathbb {T}_X [1] \right )$ is $\mathscr {O}_{T^*[-1]S}$ -linear because $\iota _{df}$ is zero on $\mathbb {T}_S[1]$ . Moreover, for $\xi \in \mathbb {T}_X[1] \subset \mathscr {O}_{\textbf {Crit}(f)}= \mathrm {Sym}_{\mathscr {O}_X} \mathbb {T}_X[1]$ , we have $\delta \circ d (\xi ) = d \circ \delta (\xi ) = d \circ \iota _{df} (\xi ) = Q(\xi )$ (see Diagram (11)) and for $g\in \mathscr {O}_X$ , $\delta \circ d (g) = d \circ \delta g = 0$ .

Lemma 4.5. The composition:

is given by $\pi _S^* Q$ . Similarly, the composition:

is $0$ (the restriction of $\pi _S^* Q$ to S).

Proof. The left morphism is the morphism fitting in the fibre sequence:

which gives us:

The second row can be seen as the extension (by $\pi _S^* $ ) of the fibre sequence:

Since X and S are smooth, $i^* \mathbb {T}_{X} [-1]$ and $i^* \mathbb {L}_{X}[-1]$ are both quasi-isomorphic to complexes concentrated in a single degree. This imposes that the dashed arrow is equivalent to the connecting morphism of the induced long exact sequence in cohomology. Therefore, it is equivalent to the map that sends a section s in $i^* \mathbb {T}_{X} [-1] $ to its differential, in $i^* \mathbb {L}_{X}[-1] \oplus i^* \mathbb {T}_{X}$ , which can, in turn, be seen as an element in $i^* \mathbb {L}_{X}$ . More concretely, denote $\tilde {s}$ any lift of s to an element in $i^* \mathbb {L}_{X}[-2] \oplus i^* \mathbb {T}_{X} [-1]$ . Using Lemma 4.4, its differential is given by:

$$\begin{align*}Q (s) = Q (\tilde{s}) \in i^* \mathbb{L}_{X}[-1] \subset i^* \mathbb{L}_{X}[-1]\oplus i^* \mathbb{T}_{X}. \end{align*}$$

We then apply $\pi _S^*$ to get the sequence we want. The second part of the statement is proven the same way.

Proposition 4.6. The map $\mathbb {T}_{T^*[-1]S} \rightarrow \Phi ^* \mathbb {T}_{\textbf {Crit}(f)}$ induced by $\Phi $ is an equivalence if and only if Q is nondegenerate.

Proof. First, using the equivalences and , we can show that the cofibre of is equivalent to . Then Lemmas 4.3 and 4.5 ensure that the upper half of the following diagram is commutative:

(13)

This diagram is then commutative and all rows and columns are cofibre sequences and, in particular, $\mathscr {F}$ is both the homotopy cofibre of $\mathbb {T}_{T^*[-1]S} \rightarrow \Phi ^* \mathbb {T}_{\textbf {Crit}(f)}$ and the homotopy cofibre of $\widetilde {Q}$ . In particular, the homotopy cofibre of $\widetilde {Q}$ is zero if and only the homotopy cofibre of $\mathbb {T}_{T^*[-1]S} \rightarrow \Phi ^* \mathbb {T}_{\textbf {Crit}(f)}$ is also zero.

We now decompose $\alpha _{\pi }$ into a part along S and a part normal to S. This decomposition is by means of split fibred sequences coming from the split fibre sequence (9).

Proposition 4.7. When Q is nondegenerate, the maps expressing the nondegeneracy of the Lagrangian fibrations fit in the commutative diagram:

where the rows are fibre sequences.

Proof. First, when Q is nondegenerate, the top horizontal sequence is fibred and comes from the following diagram:

where all rows and columns are fibred and the cofibre of the second row is $0$ thanks to Proposition 4.6 since we assumed that Q is nondegenerate. Using Lemmas 4.3 and 4.5, we obtain the following commutative diagram:

(14)

The only map the dashed arrow can be, in order to make the diagram commutative, is $\widetilde {Q}$ .

Remark 4.8. If we do not assume Q nondegenerate, the cofibre $\mathscr {F}$ of the map $\mathbb {T}_{T^*[-1]S} \rightarrow \Phi ^* \mathbb {T}_{\textbf {Crit}(f)}$ will be nonzero. We will denote by $\mathscr {G}$ the fibre of the natural map

. Then we can rewrite Diagram (14) as:

The map

represents the ‘difference’ between the maps $\alpha _{\pi }$ and $\alpha _{\pi _S}$ from the Lagrangian fibrations. $\alpha _N$ is still related to $\widetilde {Q}$ in the sense that the following diagram is commutative:

Therefore, the restriction of $\alpha _N$ to is again $\widetilde {Q}$ .

Remark 4.9. As a nonexample, if we take $f : \mathbb {A}^1 \rightarrow \mathbb {A}^1$ sending X to $\frac {X^3}{3}$ , the basic assumptions that made this section work are failing. The strict critical locus S is not smooth since it is a fat point, and the sequence (9) does not split.

4.3 Derived zero locus of shifted 1-forms

Let X be a derived Artin stack and $\alpha \in \mathscr {A}^{1} \left ( X, n \right )$ be a 1-form. If $\textbf {Key}(\alpha )$ is nonempty, Proposition 2.17 and Remark 2.18 ensure that the map $\alpha : X \rightarrow T^*[n]X$ is a Lagrangian morphism. Using Theorem 3.5, the derived intersection $Z(\alpha )$ of $\alpha $ with the zero section gives us a Lagrangian fibration $Z(\alpha ) \rightarrow X$ . This example is a generalisation of the derived critical locus we described in Subsection 3.3.

4.4 G-Equivariant twisted cotangent bundles

For X a smooth scheme, a twisted cotangent stack is a twist of the ordinary cotangent stack by a closed $1$ -form of degree $1$ on X, $\alpha \in H^1(X, \Omega _X^1)$ . Such a closed form has an underlying 1-form of degree 1 that corresponds to a morphism $\alpha : X \rightarrow T^*[1]X$ . The twisted cotangent bundle associated to $\alpha $ is defined to be the following pullback:

We refer to [8] for more informations on the relation between this definition and the usual definition of twisted cotangent bundles. This is a particular case of the situation in Subsection 4.3, and, as such, $T_{\alpha }^* X$ is $0$ -shifted symplectic and the map $T_{\alpha }^* X \rightarrow X$ has a Lagrangian fibration structure.

Now take G, an algebraic group acting on the algebraic variety X. Consider a character $\chi : G \rightarrow \mathbb {G}_m$ . We have the logarithmic form on $\mathbb {G}_m$ given by a map $\mathbb {G}_m \rightarrow \mathscr {A}^{1,cl}(-,0)$ which sends z to $z^{-1} dz$ . We get a closed 1-form on G described by the composition:

$$ \begin{align*} G \rightarrow \mathbb{G}_m \rightarrow \mathscr{A}^{1,cl}(-,0). \end{align*} $$

This is also a group morphism for the additive structure on $\mathscr {A}^{1,cl}(-,0)$ . We can, therefore, pass to classifying spaces and obtain a $1$ -shifted closed $1$ -form on $\textbf {B}G$ :

$$ \begin{align*} \alpha_{\chi} : \textbf{B}G \rightarrow \textbf{B}\mathscr{A}^{1,cl}(-,0) = \mathscr{A}^{1,cl}(-,1). \end{align*} $$

We can consider the pullback of $\alpha _{\chi }$ along the G-equivariant moment map:

It turns out that the moment map $\mu $ is Lagrangian (see [6]), which implies (with Proposition 3.1) that this fibre product is $0$ -shifted symplectic. It turns out that we have an equivalence of shifted symplectic derived Artin stacks:

where $\widehat {\alpha }$ denotes the pullback of $\alpha _{\chi }$ to a $1$ -form of degree $1$ on

. Therefore, according to Theorem 3.5, the natural projection:

is a Lagrangian fibration.

To show the equivalence above, we use the following composition of the following Lagrangian correspondences (see Subsection 2.20):

• • The Lagrangian structure on the section :

  

• • Using Example 2.3 in [6], and the fact that , we obtain the Lagrangian correspondence:

  

• • The Lagrangian obtain from the closed $1$ -form of degree $1$ , $\alpha _{\chi }$ :

  

We then compose these Lagrangian correspondences:

The only thing we need to show is that this is a diagram of Lagrangian correspondences, and, therefore, we need to show that all squares in this diagrams are pullbacks. The rightmost square is clearly a pullback, and we can recognise the pullback square defining .

We are left to prove that we have a natural equivalence:

We can commute taking the quotient by (compatible) G-action and taking the fibre products so we have that:

We now use the fact that the self intersection of the $0$ section in

is

. This implies that:

We can now use the fact the following square is a pullback (Example 2.2.1 in [13]):

We use that to decompose

in a fibre product, and we obtain: