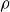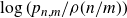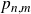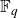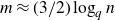1. Introduction
A permutation is said to be m-smooth if it has no cycles of length greater than m. Let
be the probability that a permutation from
![]() $S_n$
chosen uniformly at random is m-smooth. Let
$S_n$
chosen uniformly at random is m-smooth. Let
and let
![]() $\rho\colon [0,\infty) \to (0,\infty)$
be the Dickman function, defined via the delay differential equation
$\rho\colon [0,\infty) \to (0,\infty)$
be the Dickman function, defined via the delay differential equation
![]() $t\rho'(t)+\rho(t-1) =0$
for
$t\rho'(t)+\rho(t-1) =0$
for
![]() $t \gt 1$
with initial conditions
$t \gt 1$
with initial conditions
![]() $\rho(t)=1$
for
$\rho(t)=1$
for
![]() $t \le 1$
. It is weakly decreasing, and de Bruijn proved that it satisfies
$t \le 1$
. It is weakly decreasing, and de Bruijn proved that it satisfies
for
![]() $u \ge 3$
[
Reference de Bruijn2
]. Goncharov [
Reference Goncharov7
] established a connection between
$u \ge 3$
[
Reference de Bruijn2
]. Goncharov [
Reference Goncharov7
] established a connection between
![]() $p_{n,m}$
and
$p_{n,m}$
and
![]() $\rho$
, showing that
$\rho$
, showing that
![]() $p_{n,m} \sim \rho(u)$
as
$p_{n,m} \sim \rho(u)$
as
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $u = O(1)$
. In an impressive work, Manstavičius and Petuchovas [
Reference Manstavičius and Petuchovas13
] established asymptotic estimates for
$u = O(1)$
. In an impressive work, Manstavičius and Petuchovas [
Reference Manstavičius and Petuchovas13
] established asymptotic estimates for
![]() $p_{n,m}$
in the entire range
$p_{n,m}$
in the entire range
![]() $1 \le m \le n$
, including the estimate [
Reference Manstavičius and Petuchovas13
, theorem 4]
$1 \le m \le n$
, including the estimate [
Reference Manstavičius and Petuchovas13
, theorem 4]
which holds for
![]() $n \ge m \ge \sqrt{n \log n}$
. Recently, Ford [
Reference Ford6
, theorem 1·17] proved that
$n \ge m \ge \sqrt{n \log n}$
. Recently, Ford [
Reference Ford6
, theorem 1·17] proved that
holds uniformly for
![]() $n \ge m \ge 1$
. This almost immediately leads to
$n \ge m \ge 1$
. This almost immediately leads to
holding in
![]() $n \ge m \ge 1$
[
Reference Gorodetsky8
, proposition 1·8], extending (1·2). Theorems 1·1–1·2 below, whose proofs borrow heavily from [
Reference Manstavičius and Petuchovas13
], improve on (1·4).
$n \ge m \ge 1$
[
Reference Gorodetsky8
, proposition 1·8], extending (1·2). Theorems 1·1–1·2 below, whose proofs borrow heavily from [
Reference Manstavičius and Petuchovas13
], improve on (1·4).
Theorem 1·1. Uniformly for
![]() $n \ge m \ge \sqrt{n \log n}$
we have
$n \ge m \ge \sqrt{n \log n}$
we have
 \begin{equation} {}p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right)\left(1+O\left(\frac{\log(u+1)}{m}\right)\right).\end{equation}
\begin{equation} {}p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right)\left(1+O\left(\frac{\log(u+1)}{m}\right)\right).\end{equation}
Uniformly for
![]() $\sqrt{n\log n} \ge m \ge 1$
we have
$\sqrt{n\log n} \ge m \ge 1$
we have
 \[ {} {}p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left(O\left(\frac{u\log^2(u+1)}{m^2} \right)\right).\]
\[ {} {}p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left(O\left(\frac{u\log^2(u+1)}{m^2} \right)\right).\]
We may combine both parts of Theorem 1·1 as
 \[p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left(O\left(\frac{\log(u+1)}{m}+\frac{u\log^2(u+1)}{m^2} \right)\right)\]
\[p_{n,m} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left(O\left(\frac{\log(u+1)}{m}+\frac{u\log^2(u+1)}{m^2} \right)\right)\]
uniformly for
![]() $n \ge m \ge 1$
. We see
$n \ge m \ge 1$
. We see
![]() $p_{n,m} \sim \rho\left({n}/({m+\frac{1}{2}})\right)$
holds when
$p_{n,m} \sim \rho\left({n}/({m+\frac{1}{2}})\right)$
holds when
![]() $m/(n^{1/3}(\log n)^{2/3})$
$m/(n^{1/3}(\log n)^{2/3})$
![]() $\to \infty$
.
$\to \infty$
.
The error term
![]() $O(\log(u+1)/m)$
in (1·5) is of particular importance, as we now explain. We say that a positive integer is y-smooth if all its prime factors are at most y, and we denote
$O(\log(u+1)/m)$
in (1·5) is of particular importance, as we now explain. We say that a positive integer is y-smooth if all its prime factors are at most y, and we denote
Setting
![]() $n'\;:\!=\;\log x$
,
$n'\;:\!=\;\log x$
,
![]() $m'\;:\!=\;\log y$
and
$m'\;:\!=\;\log y$
and
![]() $u'\;:\!=\;n'/m'$
, de Bruijn [
Reference de Bruijn4
] showed that, in the range
$u'\;:\!=\;n'/m'$
, de Bruijn [
Reference de Bruijn4
] showed that, in the range
![]() $n' \ge m' \ge n'^{5/8+\varepsilon}$
, the estimate
$n' \ge m' \ge n'^{5/8+\varepsilon}$
, the estimate
holds. This error term,
![]() $O_{\varepsilon}\left({\log (u'+1)}/{m'}\right)$
, is analogous to (1·5).
$O_{\varepsilon}\left({\log (u'+1)}/{m'}\right)$
, is analogous to (1·5).
Remark 1. The main term
![]() $\rho\left({n}/({m+\frac{1}{2}})\right)$
of Theorem 1·1 arises indirectly. We first prove an estimate with a more complicated main term, see Proposition 3·1. This term originally appeared in [
Reference Manstavičius and Petuchovas13
, corollaries 3, 5], where it serves as an approximation to
$\rho\left({n}/({m+\frac{1}{2}})\right)$
of Theorem 1·1 arises indirectly. We first prove an estimate with a more complicated main term, see Proposition 3·1. This term originally appeared in [
Reference Manstavičius and Petuchovas13
, corollaries 3, 5], where it serves as an approximation to
![]() $p_{n,m}$
in a narrow range and with a worse error term compared to Theorem 1·1. In Lemma 3·2 we simplify the complicated main term and show it may be replaced by
$p_{n,m}$
in a narrow range and with a worse error term compared to Theorem 1·1. In Lemma 3·2 we simplify the complicated main term and show it may be replaced by
![]() $\rho\left({n}/(m+(\frac{1}{2})\right)$
at a negligible cost.
$\rho\left({n}/(m+(\frac{1}{2})\right)$
at a negligible cost.
Remark 2. Ford’s proof of (1·3) avoids complex analysis and it will be interesting to have a similar argument estimating
![]() $p_{n,m}$
relative to
$p_{n,m}$
relative to
![]() $\rho\left({n}/({m+\frac{1}{2}})\right)$
.
$\rho\left({n}/({m+\frac{1}{2}})\right)$
.
Theorem 1·1 is weaker than (1·4) when
![]() $m=o(\log n)$
. We complement it with
$m=o(\log n)$
. We complement it with
Theorem 1·2. If
![]() $2\le m\le n$
satisfies
$2\le m\le n$
satisfies
![]() $m=O(\log n)$
then
$m=O(\log n)$
then
 \[ {} {}p_{n,m} =\left( \frac{e}{n}\right)^u \exp\bigg( u \bigg(-\log\big(1-n^{-\frac{1}{m}}\big)+O\bigg( \frac{n^{-\frac{1}{m}}}{m} \bigg) \bigg)\bigg).\]
\[ {} {}p_{n,m} =\left( \frac{e}{n}\right)^u \exp\bigg( u \bigg(-\log\big(1-n^{-\frac{1}{m}}\big)+O\bigg( \frac{n^{-\frac{1}{m}}}{m} \bigg) \bigg)\bigg).\]
The proof of Theorem 1·2 relies on estimates from [
Reference Manstavičius and Petuchovas13
]. Theorem 1·2 is only claimed for
![]() $m \ge 2$
, as it gives a wrong estimate if applied with
$m \ge 2$
, as it gives a wrong estimate if applied with
![]() $m=1$
. By Stirling’s approximation,
$m=1$
. By Stirling’s approximation,
![]() $p_{n,1}=1/n! \asymp (e/n)^n n^{-1/2}$
if
$p_{n,1}=1/n! \asymp (e/n)^n n^{-1/2}$
if
![]() $m=1$
.
$m=1$
.
From (1·4) and Theorem 1·2 we see that
![]() $\log p_{n,m} \sim \log \rho(u)$
holds as
$\log p_{n,m} \sim \log \rho(u)$
holds as
![]() $n\to \infty$
. Using Theorems 1·1–1·2 we determine the order of magnitude of
$n\to \infty$
. Using Theorems 1·1–1·2 we determine the order of magnitude of
![]() $\log(p_{n,m}/\rho(u))$
:
$\log(p_{n,m}/\rho(u))$
:
Corollary 1·3. Define A via
![]() $p_{n,m}=\rho(u)\exp(A)$
. Uniformly for
$p_{n,m}=\rho(u)\exp(A)$
. Uniformly for
![]() $n \ge m \ge 1$
,
$n \ge m \ge 1$
,
1·1. Results for smooth polynomials
A polynomial over a finite field
![]() $\mathbb{F}_q$
is said to be m-smooth if all its irreducible factors have degrees at most m. Let
$\mathbb{F}_q$
is said to be m-smooth if all its irreducible factors have degrees at most m. Let
![]() $\mathcal{M}_{n,q}$
be the set of monic polynomials of degree n over
$\mathcal{M}_{n,q}$
be the set of monic polynomials of degree n over
![]() $\mathbb{F}_q$
. We write
$\mathbb{F}_q$
. We write
![]() $p_{n,m,q}$
for the probability that a polynomial from
$p_{n,m,q}$
for the probability that a polynomial from
![]() $\mathcal{M}_{n,q}$
chosen uniformly at random is m-smooth. Manstavičius [
Reference Manstavichyus11
, theorem 2] proved that
$\mathcal{M}_{n,q}$
chosen uniformly at random is m-smooth. Manstavičius [
Reference Manstavichyus11
, theorem 2] proved that
holds in range
![]() $n\ge m \ge \sqrt{n\log n}$
. Recently, the author proved that for fixed
$n\ge m \ge \sqrt{n\log n}$
. Recently, the author proved that for fixed
![]() $\varepsilon \gt 0$
, the ratio
$\varepsilon \gt 0$
, the ratio
![]() $p_{n,m,q}/p_{n,m}$
satisfies
$p_{n,m,q}/p_{n,m}$
satisfies
 \begin{equation} {}\frac{p_{n,m,q}}{p_{n,m}} =1+ O_{\varepsilon}\left(\frac{u n^{\frac{1+\mathbf{1}_{2 \mid m}}{m}} \min\{ m, \log(u+1)\}}{m q^{\lceil \frac{m+1}{2}\rceil}}\right)\end{equation}
\begin{equation} {}\frac{p_{n,m,q}}{p_{n,m}} =1+ O_{\varepsilon}\left(\frac{u n^{\frac{1+\mathbf{1}_{2 \mid m}}{m}} \min\{ m, \log(u+1)\}}{m q^{\lceil \frac{m+1}{2}\rceil}}\right)\end{equation}
for
![]() $n \ge m \ge (2+\varepsilon)\log_q n$
[
Reference Gorodetsky8
, theorems 1, 2]. The implied constant does not depend on q. From (1·6) and Theorem 1·1 we immediately obtain
$n \ge m \ge (2+\varepsilon)\log_q n$
[
Reference Gorodetsky8
, theorems 1, 2]. The implied constant does not depend on q. From (1·6) and Theorem 1·1 we immediately obtain
Corollary 1·4. Uniformly for
![]() $n\ge m\ge \sqrt{n\log n}$
we have
$n\ge m\ge \sqrt{n\log n}$
we have
 \[p_{n,m,q}=\rho\left( \frac{n}{m+\frac{1}{2}} \right) \left(1+O\left( \frac{\log(u+1)}{m}\right)\right).\]
\[p_{n,m,q}=\rho\left( \frac{n}{m+\frac{1}{2}} \right) \left(1+O\left( \frac{\log(u+1)}{m}\right)\right).\]
Fix
![]() $\varepsilon \gt 0$
. Uniformly for
$\varepsilon \gt 0$
. Uniformly for
![]() $\sqrt{n\log n}\ge m \ge (2+\varepsilon)\log_q n $
we have
$\sqrt{n\log n}\ge m \ge (2+\varepsilon)\log_q n $
we have
 \[p_{n,m,q} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left( O_{\varepsilon}\left( \frac{u\log^2(u+1)}{m^2} \right)\right).\]
\[p_{n,m,q} = \rho\left(\frac{n}{m+\frac{1}{2}}\right) \exp\!\left( O_{\varepsilon}\left( \frac{u\log^2(u+1)}{m^2} \right)\right).\]
The rest of our results concern
![]() $p_{n,m,q}/p_{n,m}$
. To obtain estimates with better range and error than (1·6) we introduce a function
$p_{n,m,q}/p_{n,m}$
. To obtain estimates with better range and error than (1·6) we introduce a function
![]() $G_q(z)$
. The generating function of
$G_q(z)$
. The generating function of
![]() $\{p_{n,m,q}\}_{n \ge 0}$
is
$\{p_{n,m,q}\}_{n \ge 0}$
is
 \begin{equation} {}F_q(z)\;:\!=\;\prod_{\substack{P \in \mathcal{P} \\[5pt] \deg(P) \le m}} \bigg(1- \bigg(\frac{z}{q}\bigg)^{\deg (P)}\bigg)^{-1},\end{equation}
\begin{equation} {}F_q(z)\;:\!=\;\prod_{\substack{P \in \mathcal{P} \\[5pt] \deg(P) \le m}} \bigg(1- \bigg(\frac{z}{q}\bigg)^{\deg (P)}\bigg)^{-1},\end{equation}
where
![]() $\mathcal{P}=\mathcal{P}_{q}$
is the set of monic irreducible polynomials over
$\mathcal{P}=\mathcal{P}_{q}$
is the set of monic irreducible polynomials over
![]() $\mathbb{F}_q$
. It is analytic in
$\mathbb{F}_q$
. It is analytic in
![]() $|z| \lt q$
. The generating function of
$|z| \lt q$
. The generating function of
![]() $\{p_{n,m}\}_{n \ge 0}$
is the entire function [
Reference Manstavičius and Petuchovas13
]
$\{p_{n,m}\}_{n \ge 0}$
is the entire function [
Reference Manstavičius and Petuchovas13
]
 \begin{equation} F(z)\;:\!=\;\exp\!\left(\sum_{i=1}^{m} \frac{z^i}{i}\right).\end{equation}
\begin{equation} F(z)\;:\!=\;\exp\!\left(\sum_{i=1}^{m} \frac{z^i}{i}\right).\end{equation}
For
![]() $|z| \lt q$
we define
$|z| \lt q$
we define
The function
![]() $G_q$
is studied in [
Reference Gorodetsky8
, lemma 2·1]. By [
Reference Gorodetsky8
, theorem 1·3] we have
$G_q$
is studied in [
Reference Gorodetsky8
, lemma 2·1]. By [
Reference Gorodetsky8
, theorem 1·3] we have
 \begin{equation} {}\frac{p_{n,m,q}}{p_{n,m}} = G_q(x) \bigg(1+ O_{\varepsilon}\bigg(\frac{n^{\frac{1+\mathbf{1}_{2 \mid m}}{m}} \min\{m, \log (u+1)\}}{mq^{\lceil \frac{m+1}{2}\rceil}} \bigg)\bigg)\end{equation}
\begin{equation} {}\frac{p_{n,m,q}}{p_{n,m}} = G_q(x) \bigg(1+ O_{\varepsilon}\bigg(\frac{n^{\frac{1+\mathbf{1}_{2 \mid m}}{m}} \min\{m, \log (u+1)\}}{mq^{\lceil \frac{m+1}{2}\rceil}} \bigg)\bigg)\end{equation}
in the range
![]() $n/(\log n \log^3 \log(n+1)) \ge m \ge (2+\varepsilon)\log_q n$
, where
$n/(\log n \log^3 \log(n+1)) \ge m \ge (2+\varepsilon)\log_q n$
, where
![]() $x=x_{n,m}$
is the unique positive solution to
$x=x_{n,m}$
is the unique positive solution to
In that range,
![]() $G_q(x)$
is very close to 1, see [
Reference Gorodetsky8
, lemmas 5·3-5·4]. We complement (1·10) with a result for large m. We define
$G_q(x)$
is very close to 1, see [
Reference Gorodetsky8
, lemmas 5·3-5·4]. We complement (1·10) with a result for large m. We define
![]() $\xi(u)\ge 0$
by
$\xi(u)\ge 0$
by
![]() $e^{\xi(u)} = 1+u\xi(u)$
.
$e^{\xi(u)} = 1+u\xi(u)$
.
Theorem 1·5. If
![]() $n \ge m\ge \sqrt{10n \log n}$
then
$n \ge m\ge \sqrt{10n \log n}$
then
 \[ \frac{p_{n,m,q}}{p_{n,m}} = G_q(e^{\xi(u)/m}) \left(1 + O \left( \frac{\log(u+1)}{m q^{\lceil \frac{m+1}{2}\rceil}}\right)\right).\]
\[ \frac{p_{n,m,q}}{p_{n,m}} = G_q(e^{\xi(u)/m}) \left(1 + O \left( \frac{\log(u+1)}{m q^{\lceil \frac{m+1}{2}\rceil}}\right)\right).\]
Using Theorem 1·5 we are able to drop the condition
![]() $n/(\log n\log^3 \log(n+1)) \ge m$
present in (1·10):
$n/(\log n\log^3 \log(n+1)) \ge m$
present in (1·10):
Corollary 1·6. The estimate (1·10) holds uniformly for
![]() $n \ge m \ge (2+\varepsilon)\log_q n$
.
$n \ge m \ge (2+\varepsilon)\log_q n$
.
We turn to smaller m. In the range
![]() $(2-\varepsilon)\log_q n \ge m \ge (1+\varepsilon)\log_q n$
,
$(2-\varepsilon)\log_q n \ge m \ge (1+\varepsilon)\log_q n$
,
see [
Reference Gorodetsky8
, lemma 5·4]. In [
Reference Gorodetsky8
, theorem 1·3] it is shown that
![]() $p_{n,m,q}/p_{n,m} \sim G_q(x)$
holds as
$p_{n,m,q}/p_{n,m} \sim G_q(x)$
holds as
![]() $n \to \infty$
as long as
$n \to \infty$
as long as
![]() $m \ge (3/2+\varepsilon)\log_q n$
. Our next result shows that
$m \ge (3/2+\varepsilon)\log_q n$
. Our next result shows that
![]() $p_{n,m,q}/p_{n,m}$
experiences a transition when m is close to
$p_{n,m,q}/p_{n,m}$
experiences a transition when m is close to
![]() $(3/2)\log_q n$
.
$(3/2)\log_q n$
.
Theorem 1·7. Fix a prime power q and
![]() $\varepsilon \gt 0$
. There is a quantity
$\varepsilon \gt 0$
. There is a quantity
![]() $A \gt 0$
of order
$A \gt 0$
of order
such that, for
![]() $(2-\varepsilon)\log_q n \ge m \ge (1+\varepsilon)\log_q n$
we have, as
$(2-\varepsilon)\log_q n \ge m \ge (1+\varepsilon)\log_q n$
we have, as
![]() $n \to \infty$
,
$n \to \infty$
,
In particular, if
![]() $q^m=n^{\tau}$
where
$q^m=n^{\tau}$
where
![]() $\tau\in(1,2)$
then
$\tau\in(1,2)$
then
![]() $A\asymp_{q,\varepsilon} ({n^{3-2\tau}}/{\log n})$
and so
$A\asymp_{q,\varepsilon} ({n^{3-2\tau}}/{\log n})$
and so
![]() $A\gg_{q,\varepsilon}1$
if
$A\gg_{q,\varepsilon}1$
if
![]() $q^m =O( n^{3/2}/(\log n)^{1/2})$
.
$q^m =O( n^{3/2}/(\log n)^{1/2})$
.
Conventions. The letters C,c shall denote absolute positive constants which may change between different instances. The notation
![]() $A \ll B$
means
$A \ll B$
means
![]() $|A| \le C B$
for some absolute constant C, while
$|A| \le C B$
for some absolute constant C, while
![]() $A\ll_{a,b,\ldots} B$
means C may depend on the parameters in the subscript. We write
$A\ll_{a,b,\ldots} B$
means C may depend on the parameters in the subscript. We write
![]() $A\asymp_{a,b,\ldots}B$
to indicate
$A\asymp_{a,b,\ldots}B$
to indicate
![]() $cB \le A \le C B$
holds for
$cB \le A \le C B$
holds for
![]() $C,c \gt 0$
that may depend on
$C,c \gt 0$
that may depend on
![]() $a,b,\ldots$
.
$a,b,\ldots$
.
2. Auxiliary estimates and functions
2·1. Saddle point review
By [
Reference Manstavičius and Petuchovas13
, theorem 2 and corollary 5], uniformly for
![]() $n \ge m \ge 1$
we have
$n \ge m \ge 1$
we have
 \begin{equation} {}p_{n,m}= \frac{\exp\!\left( \sum_{i=1}^{m} \frac{x^i}{i}\right)}{x^n \sqrt{2\pi \lambda}} \left(1+O\left( u^{-1}\right)\right),\end{equation}
\begin{equation} {}p_{n,m}= \frac{\exp\!\left( \sum_{i=1}^{m} \frac{x^i}{i}\right)}{x^n \sqrt{2\pi \lambda}} \left(1+O\left( u^{-1}\right)\right),\end{equation}
where
![]() $x=x_{n,m}$
is the saddle point defined as the unique positive solution to (1·11), and
$x=x_{n,m}$
is the saddle point defined as the unique positive solution to (1·11), and
![]() $\lambda=\lambda_{n,m}$
is defined as
$\lambda=\lambda_{n,m}$
is defined as
Lemma 2·1. Uniformly for
![]() $n \ge m \ge 1$
, the following estimates hold:
$n \ge m \ge 1$
, the following estimates hold:
![]() $n^{1/m} \ge x \gg n^{1/m}$
,
$n^{1/m} \ge x \gg n^{1/m}$
,
![]() $nm \ge \lambda \gg nm$
and
$nm \ge \lambda \gg nm$
and
![]() $\lambda= nm( 1+ O(1/\max\{ \log u,n^{1/m}\}))$
.
$\lambda= nm( 1+ O(1/\max\{ \log u,n^{1/m}\}))$
.
Proof. We study x. Considering only the
![]() $i=m$
term in (1·11) gives
$i=m$
term in (1·11) gives
![]() $x \le n^{1/m}$
. If
$x \le n^{1/m}$
. If
![]() $x \lt 1$
then
$x \lt 1$
then
![]() $\sum_{i=1}^m x^i \lt m \le n$
, a contradiction, hence
$\sum_{i=1}^m x^i \lt m \le n$
, a contradiction, hence
![]() $x \ge 1$
. Consequently, by the definition of x,
$x \ge 1$
. Consequently, by the definition of x,
![]() $mx^m \ge n$
holds, which implies
$mx^m \ge n$
holds, which implies
We turn to
![]() $\lambda$
. We have
$\lambda$
. We have
![]() $\lambda \le m \sum_{i=1}^{m} x^i = nm$
. By [
Reference Manstavičius and Petuchovas13
, lemma 9],
$\lambda \le m \sum_{i=1}^{m} x^i = nm$
. By [
Reference Manstavičius and Petuchovas13
, lemma 9],
uniformly for
![]() $u \gt 1$
. We also have
$u \gt 1$
. We also have
![]() $x^m \le n=\sum_{i=1}^{m} x^i \lt x^m/(1-x^{-1})$
and so
$x^m \le n=\sum_{i=1}^{m} x^i \lt x^m/(1-x^{-1})$
and so
implying
![]() $\lambda=nm(1+O(x^{-1}))=nm(1+O(n^{-1/m}))$
. The estimate (2·3) already shows
$\lambda=nm(1+O(x^{-1}))=nm(1+O(n^{-1/m}))$
. The estimate (2·3) already shows
![]() $\lambda \gg nm$
when
$\lambda \gg nm$
when
![]() $u \ge C$
. If
$u \ge C$
. If
![]() $u \lt C$
then, since
$u \lt C$
then, since
![]() $x \ge 1$
, we find
$x \ge 1$
, we find
![]() $\lambda \ge \sum_{i=1}^{m} i \gg nm$
.
$\lambda \ge \sum_{i=1}^{m} i \gg nm$
.
2·2. Dickman function review
We define
![]() $\xi \colon [1,\infty) \to [0,\infty)$
, a function of variable
$\xi \colon [1,\infty) \to [0,\infty)$
, a function of variable
![]() $u\ge 1$
, by
$u\ge 1$
, by
Lemma 2·2 [
Reference Hildebrand9
, lemma 1]. We have
![]() $\xi \sim \log u$
as
$\xi \sim \log u$
as
![]() $u \to \infty$
, and
$u \to \infty$
, and
![]() $\xi'=u^{-1}(1+O(1/\log u))$
for
$\xi'=u^{-1}(1+O(1/\log u))$
for
![]() $u \ge 2$
.
$u \ge 2$
.
Lemma 2·3 [
Reference Manstavičius and Petuchovas13
, lemma 6]. If
![]() $u \gt 1$
we have
$u \gt 1$
we have
![]() $\log u \lt \xi \le 2 \log u$
.
$\log u \lt \xi \le 2 \log u$
.
Let
which defines an entire function. Observe that
and a short computation shows
![]() $I''(\xi)=1/\xi'$
. The following lemma is proved by induction.
$I''(\xi)=1/\xi'$
. The following lemma is proved by induction.
Lemma 2·4. For any
![]() $k \ge 1$
we have
$k \ge 1$
we have
![]() $I^{(k)}(s) = (e^s P_{k-1}(s)-(\!-\!1)^{k-1} (k-1)!)/s^k$
for a monic polynomial
$I^{(k)}(s) = (e^s P_{k-1}(s)-(\!-\!1)^{k-1} (k-1)!)/s^k$
for a monic polynomial
![]() $P_{k-1}$
of degree
$P_{k-1}$
of degree
![]() $k-1$
.
$k-1$
.
It has the following direct consequence.
Corollary 2·5. For any fixed
![]() $k \ge 1$
we have
$k \ge 1$
we have
![]() $I^{(k)}(\xi) =(1+O_k(1/\log u))({e^{\xi}}/{\xi})\sim u$
as
$I^{(k)}(\xi) =(1+O_k(1/\log u))({e^{\xi}}/{\xi})\sim u$
as
![]() $u \to \infty$
, and
$u \to \infty$
, and
![]() $I^{(k)}(\xi+it) \ll_k \min\{u, e^{\xi(u)}/|\xi+it|\}$
uniformly for
$I^{(k)}(\xi+it) \ll_k \min\{u, e^{\xi(u)}/|\xi+it|\}$
uniformly for
![]() $t \in \mathbb{R}$
.
$t \in \mathbb{R}$
.
The function I arises when studying
![]() $\rho$
and its Laplace transform.
$\rho$
and its Laplace transform.
Lemma 2·6. [
Reference de Bruijn3
, equation (1·9)] [
Reference Alladi1
, equation (3·9)]. Let
![]() $\gamma$
be the Euler–Mascheroni constant. We have
$\gamma$
be the Euler–Mascheroni constant. We have
for
![]() $s \in \mathbb{C}$
. Uniformly for
$s \in \mathbb{C}$
. Uniformly for
![]() $u \ge 1$
,
$u \ge 1$
,
We have the following bounds on
![]() $\hat{\rho}$
.
$\hat{\rho}$
.
Lemma 2·7. [
Reference Hildebrand and Tenenbaum10
, lemma 2·7] The following bounds hold for
![]() $s=-\xi(u)+it$
:
$s=-\xi(u)+it$
:
 \[ {} {}\hat{\rho}(s) = \begin{cases} O\left(\exp\!\left(I(\xi)-\frac{t^2u}{2\pi^2}\right)\right) & \text{if }|t| \le \pi,\\[5pt] {} {} {}O\left(\exp\!\left(I(\xi)-\frac{u}{\pi^2+\xi^2}\right)\right) & \text{if }|t| \ge \pi,\\[5pt] {} {} {}\frac{1}{s} + O\left( \frac{1+u \xi }{|s|^2} \right) & \text{if }1+u\xi =O(|t|).\end{cases}\]
\[ {} {}\hat{\rho}(s) = \begin{cases} O\left(\exp\!\left(I(\xi)-\frac{t^2u}{2\pi^2}\right)\right) & \text{if }|t| \le \pi,\\[5pt] {} {} {}O\left(\exp\!\left(I(\xi)-\frac{u}{\pi^2+\xi^2}\right)\right) & \text{if }|t| \ge \pi,\\[5pt] {} {} {}\frac{1}{s} + O\left( \frac{1+u \xi }{|s|^2} \right) & \text{if }1+u\xi =O(|t|).\end{cases}\]
2·3. T
We define the following function, holomorphic in the strip
![]() $|\Im s | \lt 2\pi m$
:
$|\Im s | \lt 2\pi m$
:
 \[ {}T(s) \;:\!=\; \int_{0}^{s} \frac{e^t-1}{t}\left( \frac{\frac{t}{m}}{1-e^{-t/m}}-1\right){\textrm{d}}t.\]
\[ {}T(s) \;:\!=\; \int_{0}^{s} \frac{e^t-1}{t}\left( \frac{\frac{t}{m}}{1-e^{-t/m}}-1\right){\textrm{d}}t.\]
The Bernoulli numbers
![]() $B_i$
are defined by
$B_i$
are defined by
 \[\frac{s}{1-e^{-s}} = 1+\frac{s}{2} +\frac{s^2}{12}-\frac{s^4}{720}+ \ldots = \sum_{i\ge 0} B_i \frac{s^i}{i!}.\]
\[\frac{s}{1-e^{-s}} = 1+\frac{s}{2} +\frac{s^2}{12}-\frac{s^4}{720}+ \ldots = \sum_{i\ge 0} B_i \frac{s^i}{i!}.\]
This series converges for
![]() $|\Im s| \lt 2\pi$
. It is known that
$|\Im s| \lt 2\pi$
. It is known that
![]() $B_i \ll i!/(2\pi)^i$
. It is then easy to see, from the estimate
$B_i \ll i!/(2\pi)^i$
. It is then easy to see, from the estimate
![]() $\int_{0}^{s} (e^t-1)t^{i-1} {\textrm{d}}t \ll |s|^{i-1} (|e^s|+|s|)$
which holds for
$\int_{0}^{s} (e^t-1)t^{i-1} {\textrm{d}}t \ll |s|^{i-1} (|e^s|+|s|)$
which holds for
![]() $\Re s \ge 0$
and
$\Re s \ge 0$
and
![]() $i \ge 1$
, that
$i \ge 1$
, that
 \begin{equation} {}T(s) = \sum_{i=1}^{k} \frac{B_i}{m^i i!} \int_{0}^{s} (e^t-1)t^{i-1} {\textrm{d}}t + O\bigg( \frac{|s|^k (|e^{s}|+|s|)}{(2\pi m)^{k+1}} \bigg)\end{equation}
\begin{equation} {}T(s) = \sum_{i=1}^{k} \frac{B_i}{m^i i!} \int_{0}^{s} (e^t-1)t^{i-1} {\textrm{d}}t + O\bigg( \frac{|s|^k (|e^{s}|+|s|)}{(2\pi m)^{k+1}} \bigg)\end{equation}
holds for
![]() $k \ge 0$
and
$k \ge 0$
and
![]() $s=\sigma+it$
with
$s=\sigma+it$
with
![]() $\sigma \in [0,\pi m]$
and
$\sigma \in [0,\pi m]$
and
![]() $t \in [\!-\pi m,\pi m]$
. Applying (2·5) with
$t \in [\!-\pi m,\pi m]$
. Applying (2·5) with
![]() $k=1$
we obtain
$k=1$
we obtain
Corollary 2·8. [
Reference Manstavičius and Petuchovas13
, lemma 11]. For
![]() $s=\sigma+it$
with
$s=\sigma+it$
with
![]() $\sigma\in [0,\pi m]$
and
$\sigma\in [0,\pi m]$
and
![]() $t\in [\!-\pi m,\pi m]$
,
$t\in [\!-\pi m,\pi m]$
,
Applying (2·5) with
![]() $k=2$
and
$k=2$
and
![]() $s=\xi=\xi(u)$
we obtain
$s=\xi=\xi(u)$
we obtain
 \begin{equation}T(\xi) = \frac{(u-1)\xi}{2m} + \frac{e^{\xi}(\xi-1)-\frac{\xi^2}{2}+1}{12m^2} + O\bigg( \frac{u\log^3 (u+1)}{m^3}\bigg)\end{equation}
\begin{equation}T(\xi) = \frac{(u-1)\xi}{2m} + \frac{e^{\xi}(\xi-1)-\frac{\xi^2}{2}+1}{12m^2} + O\bigg( \frac{u\log^3 (u+1)}{m^3}\bigg)\end{equation}
when
![]() $\xi(u) \le \pi m$
holds.
$\xi(u) \le \pi m$
holds.
Lemma 2·9. Suppose
![]() $\xi=\xi(u) \le \pi m$
. For any
$\xi=\xi(u) \le \pi m$
. For any
![]() $k \ge 1$
we have
$k \ge 1$
we have
 \begin{equation} {}\begin{split} {} {}T^{(k)}(\xi) &= I^{(k)}(\xi)\left( \frac{\xi/m}{1-e^{-\xi/m}}-1+O_k\left( \frac{1}{m}\right)\right) \\[5pt] {} {}&=\frac{e^{\xi}}{2m}\left(1+O_k\left(\frac{1}{\log(u+1)}+\frac{\log(u+1)}{m}\right)\right). {}\end{split} {}\end{equation}
\begin{equation} {}\begin{split} {} {}T^{(k)}(\xi) &= I^{(k)}(\xi)\left( \frac{\xi/m}{1-e^{-\xi/m}}-1+O_k\left( \frac{1}{m}\right)\right) \\[5pt] {} {}&=\frac{e^{\xi}}{2m}\left(1+O_k\left(\frac{1}{\log(u+1)}+\frac{\log(u+1)}{m}\right)\right). {}\end{split} {}\end{equation}
If additionally
![]() $t \in [\!-\pi m, \pi m]$
then
$t \in [\!-\pi m, \pi m]$
then
![]() $T^{(k)}(\xi+it) \ll_k e^{\xi(u)}/m$
.
$T^{(k)}(\xi+it) \ll_k e^{\xi(u)}/m$
.
Proof. We have
![]() $T'(s) = I'(s) g(s/m)$
for
$T'(s) = I'(s) g(s/m)$
for
![]() $g(z)\;:\!=\;z/(1-e^{-z}) - 1$
. Repeated differentiation shows
$g(z)\;:\!=\;z/(1-e^{-z}) - 1$
. Repeated differentiation shows
 \begin{equation} {}T^{(k)}(s) = I^{(k)}(s) g(s/m)+O_k\bigg( \sum_{i=1}^{k-1}m^{-i} |I^{(k-i)}(s)g^{(i)}(s/m)|\bigg).\end{equation}
\begin{equation} {}T^{(k)}(s) = I^{(k)}(s) g(s/m)+O_k\bigg( \sum_{i=1}^{k-1}m^{-i} |I^{(k-i)}(s)g^{(i)}(s/m)|\bigg).\end{equation}
We suppose that
![]() $s=\xi(u) + it$
and that the inequalities
$s=\xi(u) + it$
and that the inequalities
![]() $\xi(u)\le \pi m$
and
$\xi(u)\le \pi m$
and
![]() $|t|\le \pi m$
are satisfied. From (2·8),
$|t|\le \pi m$
are satisfied. From (2·8),
 \begin{equation} T^{(k)}(s) =I^{(k)}(s) g(s/m)+O_k\bigg( \frac{1}{m}\sum_{i=1}^{k-1} |I^{(k-i)}(s)|\bigg) {} {}\end{equation}
\begin{equation} T^{(k)}(s) =I^{(k)}(s) g(s/m)+O_k\bigg( \frac{1}{m}\sum_{i=1}^{k-1} |I^{(k-i)}(s)|\bigg) {} {}\end{equation}
as our assumptions on s guarantee that
![]() $g^{(i)}(s/m)\ll_i 1$
. We first suppose
$g^{(i)}(s/m)\ll_i 1$
. We first suppose
![]() $t=0$
and establish (2·7). Using (2·9) and the definition of g, the first equality in (2·7) will follow if we show that
$t=0$
and establish (2·7). Using (2·9) and the definition of g, the first equality in (2·7) will follow if we show that
![]() $I^{(k-i)}(\xi(u)) \ll_k I^{(k)}(\xi(u))$
, which is a consequence of Corollary 2·5. The second equality in (2·7) follows from another application of Corollary 2·5. Finally, the claim for
$I^{(k-i)}(\xi(u)) \ll_k I^{(k)}(\xi(u))$
, which is a consequence of Corollary 2·5. The second equality in (2·7) follows from another application of Corollary 2·5. Finally, the claim for
![]() $T^{(k)}(s)$
(when
$T^{(k)}(s)$
(when
![]() $|t|\le \pi m$
) follows from (2·9) since
$|t|\le \pi m$
) follows from (2·9) since
![]() $|I^{(k)}(s)| \ll_k e^{\xi(u)}/|s|$
and
$|I^{(k)}(s)| \ll_k e^{\xi(u)}/|s|$
and
![]() $|I^{(k-i)}(s)| \ll_k u$
(
$|I^{(k-i)}(s)| \ll_k u$
(
![]() $1\le i \le k-1$
) by Corollary 2·5 and
$1\le i \le k-1$
) by Corollary 2·5 and
![]() $|g(s/m)| \ll |s|/m$
.
$|g(s/m)| \ll |s|/m$
.
2·4.
 $H_n$
$H_n$
Let
![]() $H_n\;:\!=\; \sum_{i=1}^{n} ({1}/{i})$
be the nth harmonic sum. By the Euler–Maclaurin formula,
$H_n\;:\!=\; \sum_{i=1}^{n} ({1}/{i})$
be the nth harmonic sum. By the Euler–Maclaurin formula,
3. Proof of Theorem 1·1
We break the theorem into a proposition and a lemma.
Proposition 3·1. Uniformly for
![]() $n \ge m \ge 1$
we have
$n \ge m \ge 1$
we have
 \begin{equation} {} {}p_{n,m} = \rho(u) \exp\!\left( \frac{u\xi(u)}{2m}\right) \exp\!\left(O\left(\frac{u\log^2(u+1)}{m^2} + \frac{1}{u} \right)\right). {}\end{equation}
\begin{equation} {} {}p_{n,m} = \rho(u) \exp\!\left( \frac{u\xi(u)}{2m}\right) \exp\!\left(O\left(\frac{u\log^2(u+1)}{m^2} + \frac{1}{u} \right)\right). {}\end{equation}
If
![]() $\sqrt{n \log n}=O(m)$
then
$\sqrt{n \log n}=O(m)$
then
In [
Reference Manstavičius and Petuchovas13
, corollaries 3, 5], (3·1) is proved in the narrower range
![]() $n \ge m \ge n^{1/3}(\log n)^{2/3}$
.
$n \ge m \ge n^{1/3}(\log n)^{2/3}$
.
Lemma 3·2. Uniformly for
![]() $n \ge m \ge 1$
we have
$n \ge m \ge 1$
we have
and
 \begin{equation}\rho\left( u-\frac{u}{2m}\right) = \rho\left( \frac{n}{m+\frac{1}{2}}\right)\exp\!\left( O\left( \frac{u\log(u+1)}{m^2} \right)\right).\end{equation}
\begin{equation}\rho\left( u-\frac{u}{2m}\right) = \rho\left( \frac{n}{m+\frac{1}{2}}\right)\exp\!\left( O\left( \frac{u\log(u+1)}{m^2} \right)\right).\end{equation}
We prove (3·1) in Section 3·1, and (3·2) in Sections 3·2–3·3. The proof of Lemma 3·2 is given in Section 3·4. To deduce Theorem 1·1, we combine (3·2) and Lemma 3·2 if
![]() $m \ge \sqrt{n\log n}$
, and (3·1) and Lemma 3·2 if
$m \ge \sqrt{n\log n}$
, and (3·1) and Lemma 3·2 if
![]() $m\le \sqrt{n\log n}$
. Here we use
$m\le \sqrt{n\log n}$
. Here we use
![]() ${u}/{m^2}+{1}/{m} +{u\log(u+1)}/{m^2}\ll {\log(u+1)}/{m}$
when
${u}/{m^2}+{1}/{m} +{u\log(u+1)}/{m^2}\ll {\log(u+1)}/{m}$
when
![]() $m\ge \sqrt{n\log n}$
and
$m\ge \sqrt{n\log n}$
and
![]() ${1}/{u} + {u}/{m^2}+{1}/{m} +{u\log(u+1)}/{m^2}\ll {u\log^2(u+1)}/{m^2}$
when
${1}/{u} + {u}/{m^2}+{1}/{m} +{u\log(u+1)}/{m^2}\ll {u\log^2(u+1)}/{m^2}$
when
![]() $m\le \sqrt{n\log n}$
.
$m\le \sqrt{n\log n}$
.
3·1. Proof of the first part of Proposition 3·1
Here we prove (3·1). If
![]() $m=O(\log (u+1))$
then (3·1) follows from (1·4). Hence we suppose that
$m=O(\log (u+1))$
then (3·1) follows from (1·4). Hence we suppose that
![]() $m \ge C \log (u+1)$
from now on. Similarly, if
$m \ge C \log (u+1)$
from now on. Similarly, if
![]() $u =O(1)$
then (3·1) is already in (1·4), so we suppose
$u =O(1)$
then (3·1) is already in (1·4), so we suppose
![]() $u \ge C$
. We define a function
$u \ge C$
. We define a function
 \[ D(z) \;:\!=\;z^{-n} \exp\!\left(\sum_{i=1}^{m} \frac{z^i}{i}\right), \]
\[ D(z) \;:\!=\;z^{-n} \exp\!\left(\sum_{i=1}^{m} \frac{z^i}{i}\right), \]
so that x defined in (1·11) solves
![]() $D'(z)=0$
, and (2·1) can be written as
$D'(z)=0$
, and (2·1) can be written as
We can write
![]() $\log D(x)$
as
$\log D(x)$
as
 \[ \log D(x)=-n \log x + \sum_{j=1}^{m} \frac{1}{j}+I(m\log x)+T(m\log x),\]
\[ \log D(x)=-n \log x + \sum_{j=1}^{m} \frac{1}{j}+I(m\log x)+T(m\log x),\]
see [ Reference Manstavičius and Petuchovas13 , equation (40)] for the details. We set
and define
![]() $\widetilde{u} \ge 1$
as
$\widetilde{u} \ge 1$
as
In this notation, (3·5) implies (using (2·4) with
![]() $\widetilde{u}$
in place of u, and (2·10)) that
$\widetilde{u}$
in place of u, and (2·10)) that
 \[ {}p_{n,m} = \rho(\widetilde{u}) \exp\!\left( (\widetilde{u}-u)\widetilde{\xi}\right) \exp \left(T(\widetilde{\xi})\right)\sqrt{ \frac{m^2 I''(\xi(\widetilde{u}))}{\lambda}}\exp\!\left( O\left(u^{-1}+ \widetilde{u}^{-1}+m^{-1}\right)\right)\]
\[ {}p_{n,m} = \rho(\widetilde{u}) \exp\!\left( (\widetilde{u}-u)\widetilde{\xi}\right) \exp \left(T(\widetilde{\xi})\right)\sqrt{ \frac{m^2 I''(\xi(\widetilde{u}))}{\lambda}}\exp\!\left( O\left(u^{-1}+ \widetilde{u}^{-1}+m^{-1}\right)\right)\]
for
![]() $u \ge C$
. A short computation shows that
$u \ge C$
. A short computation shows that
![]() $u=I'(\xi)=(I+T)'(\widetilde{\xi})$
holds by the definition of
$u=I'(\xi)=(I+T)'(\widetilde{\xi})$
holds by the definition of
![]() $\xi$
,
$\xi$
,
![]() $\widetilde{\xi}$
and x. Since
$\widetilde{\xi}$
and x. Since
![]() $T'(t) \ge 0$
for
$T'(t) \ge 0$
for
![]() $t \ge 0$
we have
$t \ge 0$
we have
![]() $\widetilde{\xi}\le \xi$
and so, by the monotonicity of
$\widetilde{\xi}\le \xi$
and so, by the monotonicity of
![]() $I'(t)=(e^t-1)/t$
, it follows that
$I'(t)=(e^t-1)/t$
, it follows that
By [ Reference Manstavičius and Petuchovas13 , equation (22)],
uniformly in
![]() $m \ge \log u \gt 0$
. From (3·6) we see that, uniformly in
$m \ge \log u \gt 0$
. From (3·6) we see that, uniformly in
![]() $m \ge \log u \gt 0$
$m \ge \log u \gt 0$
We will be using (3·6) and (3·7) frequently. For
![]() $m \ge \log u \gt 0$
we have
$m \ge \log u \gt 0$
we have
by [
Reference Manstavičius and Petuchovas13
, equation (23)]. Hence, since
![]() $I''(\xi(u))=1/\xi'(u)$
,
$I''(\xi(u))=1/\xi'(u)$
,
 \[ \sqrt{ \frac{m^2 I''(\xi(\widetilde{u}))}{\lambda }}=\sqrt{ \frac{m^2}{\lambda \xi'(\widetilde{u})}}=\sqrt{\frac{\xi'(u)}{\xi'(\widetilde{u})}} \exp\!\left(O\left(\frac{\log(u+1)}{m}\right)\right)\]
\[ \sqrt{ \frac{m^2 I''(\xi(\widetilde{u}))}{\lambda }}=\sqrt{ \frac{m^2}{\lambda \xi'(\widetilde{u})}}=\sqrt{\frac{\xi'(u)}{\xi'(\widetilde{u})}} \exp\!\left(O\left(\frac{\log(u+1)}{m}\right)\right)\]
for
![]() $m \ge C\log (u+1) \gt 0$
. Since
$m \ge C\log (u+1) \gt 0$
. Since
![]() $\xi'(t)\asymp 1/t$
and
$\xi'(t)\asymp 1/t$
and
![]() $\xi''(t) =-\xi'(t)I^{(3)}(\xi(t))/I''(\xi(t))^2 \ll 1/t^2$
for
$\xi''(t) =-\xi'(t)I^{(3)}(\xi(t))/I''(\xi(t))^2 \ll 1/t^2$
for
![]() $t \ge C$
,
$t \ge C$
,
holds for
![]() $m \ge C\log (u+1) \gt 0$
and
$m \ge C\log (u+1) \gt 0$
and
![]() $u \ge C$
and so
$u \ge C$
and so
 \[ \sqrt{ \frac{m^2I''(\xi(\widetilde{u}))}{\lambda}}= \exp\!\left(O\left(\frac{\log(u+1)}{m}\right)\right),\]
\[ \sqrt{ \frac{m^2I''(\xi(\widetilde{u}))}{\lambda}}= \exp\!\left(O\left(\frac{\log(u+1)}{m}\right)\right),\]
when
![]() $m \ge C\log (u+1) \gt 0$
and
$m \ge C\log (u+1) \gt 0$
and
![]() $u \ge C$
. At this point, we have established that
$u \ge C$
. At this point, we have established that
holds in our range. We have
![]() $\widetilde{\xi} \le \xi \le 2\log u \le \pi m$
by Lemma 2·3 and our assumption
$\widetilde{\xi} \le \xi \le 2\log u \le \pi m$
by Lemma 2·3 and our assumption
![]() $m \ge C\log(u+1)$
. By (2·6), (3·6) and (3·7),
$m \ge C\log(u+1)$
. By (2·6), (3·6) and (3·7),
in this range. We now have
for
![]() $m \ge C\log (u+1)$
,
$m \ge C\log (u+1)$
,
![]() $u \ge C$
. Let
$u \ge C$
. Let
![]() $r(t)=-\rho'(t)/\rho(t)$
be the negative of the logarithmic derivative of
$r(t)=-\rho'(t)/\rho(t)$
be the negative of the logarithmic derivative of
![]() $\log \rho$
. We have
$\log \rho$
. We have
By integration by parts, we may write the integral in the exponent as
By [ Reference de la Bretèche and Tenenbaum5 , lemma 3·7], the estimates
hold uniformly for
![]() $v \ge 1$
. Hence, using (3·6) and (3·7),
$v \ge 1$
. Hence, using (3·6) and (3·7),
 \begin{align*}\rho(\widetilde{u}) \exp( (\widetilde{u}-u)\widetilde{\xi}) &= \rho(u) \exp((u-\widetilde{u}) (r(u)-\xi(u)+\xi(u)-\widetilde{\xi}) \\[5pt] & \qquad - \int_{\widetilde{u}}^{u}(t-\widetilde{u})(r'(t)-\xi'(t)+\xi'(t)){\textrm{d}}t )\\[5pt] &=\rho(u) \exp\bigg( O\bigg(\frac{1}{u} + \frac{u\log^2(u+1)}{m^2}\bigg)-\int_{\widetilde{u}}^{u} (t-\widetilde{u})\xi'(t){\textrm{d}}t\bigg).\end{align*}
\begin{align*}\rho(\widetilde{u}) \exp( (\widetilde{u}-u)\widetilde{\xi}) &= \rho(u) \exp((u-\widetilde{u}) (r(u)-\xi(u)+\xi(u)-\widetilde{\xi}) \\[5pt] & \qquad - \int_{\widetilde{u}}^{u}(t-\widetilde{u})(r'(t)-\xi'(t)+\xi'(t)){\textrm{d}}t )\\[5pt] &=\rho(u) \exp\bigg( O\bigg(\frac{1}{u} + \frac{u\log^2(u+1)}{m^2}\bigg)-\int_{\widetilde{u}}^{u} (t-\widetilde{u})\xi'(t){\textrm{d}}t\bigg).\end{align*}
To conclude the proof, it remains to bound
![]() $\int_{\widetilde{u}}^{u}(t-\widetilde{u})\xi'(t){\textrm{d}}t$
. Since
$\int_{\widetilde{u}}^{u}(t-\widetilde{u})\xi'(t){\textrm{d}}t$
. Since
![]() $\xi'(t) \ll 1/t$
,
$\xi'(t) \ll 1/t$
,
if
![]() $m \ge C\log (u+1)$
, using (3·6) and (3·7). The proof of (3·1) is completed.
$m \ge C\log (u+1)$
, using (3·6) and (3·7). The proof of (3·1) is completed.
3·2. Preliminary lemmas for second part of Proposition 3·1
The following consequence of Cauchy’s integral formula is implicit in the proofs of [ Reference Manstavičius and Petuchovas13 , theorems 2,4].
Lemma 3·3. We have
The following lemma is implicit in the proof of [ Reference Manstavičius and Petuchovas13 , theorem 4].
Lemma 3·4. Suppose
![]() $\sqrt{n\log n}=O(m)$
. Then
$\sqrt{n\log n}=O(m)$
. Then
A variant of the next lemma is implicit in the proof of [ Reference Manstavičius and Petuchovas13 , theorem 2].
Lemma 3·5. Suppose
![]() $\sqrt{n\log n}=O(m)$
and
$\sqrt{n\log n}=O(m)$
and
![]() $1+u\xi \le A \le m\pi$
. Then
$1+u\xi \le A \le m\pi$
. Then
The same bound holds if we integrate from
![]() $-\xi-im\pi$
to
$-\xi-im\pi$
to
![]() $-\xi-iA$
.
$-\xi-iA$
.
Proof. We have
![]() $\hat{\rho}'(s) = \rho(s) (e^{-s}-1)/s$
. Integration by parts shows that the integral is equal to
$\hat{\rho}'(s) = \rho(s) (e^{-s}-1)/s$
. Integration by parts shows that the integral is equal to
 \begin{multline*} {}\frac{1}{2\pi i} \frac{e^{us}}{u}\hat{\rho}(s) \left(e^{T(-s)-T(\xi)}-1\right) \Big|^{s=-\xi+im\pi}_{s=-\xi+iA} \\[5pt] -\frac{1}{2\pi i} \int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \hat{\rho}(s)\left( \frac{e^{-s}-1}{s} \left(e^{T(-s)-T(\xi)}-1\right) -T'(-s) e^{T(-s)-T(\xi)}\right){\textrm{d}}s.\end{multline*}
\begin{multline*} {}\frac{1}{2\pi i} \frac{e^{us}}{u}\hat{\rho}(s) \left(e^{T(-s)-T(\xi)}-1\right) \Big|^{s=-\xi+im\pi}_{s=-\xi+iA} \\[5pt] -\frac{1}{2\pi i} \int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \hat{\rho}(s)\left( \frac{e^{-s}-1}{s} \left(e^{T(-s)-T(\xi)}-1\right) -T'(-s) e^{T(-s)-T(\xi)}\right){\textrm{d}}s.\end{multline*}
By Corollary 2·8,
![]() $T(-s)-T(\xi)$
is bounded in our range of integration. In fact,
$T(-s)-T(\xi)$
is bounded in our range of integration. In fact,
![]() $T(-s)-T(\xi) \ll (e^{\xi}+|\Im s|)/m$
. Hence, the third case of Lemma 2·7 shows that
$T(-s)-T(\xi) \ll (e^{\xi}+|\Im s|)/m$
. Hence, the third case of Lemma 2·7 shows that
which is acceptable. As for the integral, we rearrange it using the definition of T:
 \begin{align*} {} {}\frac{1}{2\pi i} &\int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \hat{\rho}(s)\left( \frac{e^{-s}-1}{s} \left(e^{T(-s)-T(\xi)}-1\right)-T'(-s) e^{T(-s)-T(\xi)}\right){\textrm{d}}s \\[5pt] {} {}&= {}\frac{1}{2\pi i} \int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \frac{e^{-s}-1}{s} \hat{\rho}(s)\left( e^{T(-s)-T(\xi)}\frac{\frac{-s}{m}}{1-e^{s/m}}-1\right){\textrm{d}}s. {}\end{align*}
\begin{align*} {} {}\frac{1}{2\pi i} &\int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \hat{\rho}(s)\left( \frac{e^{-s}-1}{s} \left(e^{T(-s)-T(\xi)}-1\right)-T'(-s) e^{T(-s)-T(\xi)}\right){\textrm{d}}s \\[5pt] {} {}&= {}\frac{1}{2\pi i} \int_{-\xi+iA}^{-\xi+im\pi} \frac{e^{us}}{u} \frac{e^{-s}-1}{s} \hat{\rho}(s)\left( e^{T(-s)-T(\xi)}\frac{\frac{-s}{m}}{1-e^{s/m}}-1\right){\textrm{d}}s. {}\end{align*}
By Corollary 2·8 and the Taylor expansion
![]() $z/(1-e^{-z})=1+z/2+O(z^2)$
,
$z/(1-e^{-z})=1+z/2+O(z^2)$
,
in our range of integration. By the triangle inequality, the last integral is
 \begin{multline*} \ll \frac{\log (u+1)}{e^{u\xi}} \int_{-\xi+iA}^{-\xi+im\pi} \frac{|\hat{\rho}(s)|}{|s|}\left( \frac{|s|^2}{m^2}+\frac{e^{\xi}}{m}\right) |{\textrm{d}}s|\\[5pt] \ll \frac{\log (u+1)}{e^{u\xi}} \int_{-\xi+iA}^{-\xi+im\pi} \frac{1}{|s|^2}\left( \frac{|s|^2}{m^2}+\frac{e^{\xi}}{m}\right) |{\textrm{d}}s| \ll \frac{\log (u+1),}{m e^{u\xi}}\end{multline*}
\begin{multline*} \ll \frac{\log (u+1)}{e^{u\xi}} \int_{-\xi+iA}^{-\xi+im\pi} \frac{|\hat{\rho}(s)|}{|s|}\left( \frac{|s|^2}{m^2}+\frac{e^{\xi}}{m}\right) |{\textrm{d}}s|\\[5pt] \ll \frac{\log (u+1)}{e^{u\xi}} \int_{-\xi+iA}^{-\xi+im\pi} \frac{1}{|s|^2}\left( \frac{|s|^2}{m^2}+\frac{e^{\xi}}{m}\right) |{\textrm{d}}s| \ll \frac{\log (u+1),}{m e^{u\xi}}\end{multline*}
where in the second inequality we used the third case of Lemma 2·7.
Lemma 3·6. Suppose
![]() $0 \le B \le A$
. Then, for every
$0 \le B \le A$
. Then, for every
![]() $k \ge 0$
,
$k \ge 0$
,
The same is true if we integrate from
![]() $-\xi-iA$
to
$-\xi-iA$
to
![]() $-\xi-iB$
. In particular, for
$-\xi-iB$
. In particular, for
![]() $B=0$
and
$B=0$
and
![]() $A\le \exp(c_k u/(\log (u+1))^2)$
,
$A\le \exp(c_k u/(\log (u+1))^2)$
,
Proof. Using the first two parts of Lemma 2·7, the triangle inequality shows that the integral is
 \begin{multline*} {} {}\ll e^{-u\xi +I(\xi)} \int_{B}^{A} |t|^k \left(\exp(\!-cut^2)+\exp\big(-\frac{u}{\xi^2+\pi^2}\big)\right) {\textrm{d}}t\\[5pt] \ll_k e^{-u\xi +I(\xi)} \bigg( u^{-\frac{k+1}{2}} \exp(\!-cuB^2)+ A^{k+1}\exp\big(-\frac{u}{\xi^2+\pi^2}\big)\bigg), {}\end{multline*}
\begin{multline*} {} {}\ll e^{-u\xi +I(\xi)} \int_{B}^{A} |t|^k \left(\exp(\!-cut^2)+\exp\big(-\frac{u}{\xi^2+\pi^2}\big)\right) {\textrm{d}}t\\[5pt] \ll_k e^{-u\xi +I(\xi)} \bigg( u^{-\frac{k+1}{2}} \exp(\!-cuB^2)+ A^{k+1}\exp\big(-\frac{u}{\xi^2+\pi^2}\big)\bigg), {}\end{multline*}
and we now use (2·4).
Lemma 3·7. Fix
![]() $k\ge 0$
. Let
$k\ge 0$
. Let
![]() $\mu_m\;:\!=\;m!/((m/2)!2^{m/2})$
for even m. Suppose
$\mu_m\;:\!=\;m!/((m/2)!2^{m/2})$
for even m. Suppose
![]() $\sqrt{n\log n}=O(m)$
and
$\sqrt{n\log n}=O(m)$
and
![]() $C_k\sqrt{\log(u+1)/u}\le A \le \exp(c_ku/(\log (u+1))^2)$
. Then, for even k,
$C_k\sqrt{\log(u+1)/u}\le A \le \exp(c_ku/(\log (u+1))^2)$
. Then, for even k,
and for odd k,
Proof. The contribution of
![]() $A \ge |\Im s| \ge C_k\sqrt{\log (u+1)/u}$
is acceptable by Lemma 3·6. We may now assume that
$A \ge |\Im s| \ge C_k\sqrt{\log (u+1)/u}$
is acceptable by Lemma 3·6. We may now assume that
![]() $A=C_k\sqrt{\log (u+1)/u}$
. Recall
$A=C_k\sqrt{\log (u+1)/u}$
. Recall
![]() $\hat{\rho}(s)=\exp(\gamma+I(-s))$
. We may Taylor-expand
$\hat{\rho}(s)=\exp(\gamma+I(-s))$
. We may Taylor-expand
![]() $I(\xi+it)$
using Corollary 2·5, obtaining that
$I(\xi+it)$
using Corollary 2·5, obtaining that
 \begin{align*} {} {}\frac{1}{2\pi i} &\int_{-\xi-iA}^{-\xi+iA} (s+\xi)^k e^{us} \hat{\rho}(s){\textrm{d}}s \\[5pt] {} {}&= i^{k} \frac{e^{\gamma-u\xi+I(\xi)}}{2\pi}\int_{-A}^{A} t^k \exp\!\left( -\frac{t^2}{2} I''(\xi) +i\frac{t^3}{6} I^{(3)}(\xi)+\frac{t^4}{24}I^{(4)}(\xi)+O_k\left(u|t|^5\right) \right){\textrm{d}}t\\[5pt] {} {}&= i^{k}\frac{e^{\gamma-u\xi+I(\xi)}}{2\pi} \int_{-A}^{A} t^k \exp\big(-\frac{t^2}{2} I''(\xi)\big) \big(1+i \frac{t^3}{6} I^{(3)}(\xi) + \frac{t^4}{24}I^{(4)}(\xi) - \frac{t^6}{72}I^{(3)}(\xi)^2\big)\\[5pt] {} {}&\qquad \qquad \times \left(1+O_k\left( u|t|^5 + u^3 |t|^9\right)\right) {\textrm{d}}t. {}\end{align*}
\begin{align*} {} {}\frac{1}{2\pi i} &\int_{-\xi-iA}^{-\xi+iA} (s+\xi)^k e^{us} \hat{\rho}(s){\textrm{d}}s \\[5pt] {} {}&= i^{k} \frac{e^{\gamma-u\xi+I(\xi)}}{2\pi}\int_{-A}^{A} t^k \exp\!\left( -\frac{t^2}{2} I''(\xi) +i\frac{t^3}{6} I^{(3)}(\xi)+\frac{t^4}{24}I^{(4)}(\xi)+O_k\left(u|t|^5\right) \right){\textrm{d}}t\\[5pt] {} {}&= i^{k}\frac{e^{\gamma-u\xi+I(\xi)}}{2\pi} \int_{-A}^{A} t^k \exp\big(-\frac{t^2}{2} I''(\xi)\big) \big(1+i \frac{t^3}{6} I^{(3)}(\xi) + \frac{t^4}{24}I^{(4)}(\xi) - \frac{t^6}{72}I^{(3)}(\xi)^2\big)\\[5pt] {} {}&\qquad \qquad \times \left(1+O_k\left( u|t|^5 + u^3 |t|^9\right)\right) {\textrm{d}}t. {}\end{align*}
Substituting
![]() $t^2 I''(\xi)=v^2$
, recalling
$t^2 I''(\xi)=v^2$
, recalling
![]() $I''(\xi(u))=1/\xi'(u)$
and using (2·4), the last expression can be written as
$I''(\xi(u))=1/\xi'(u)$
and using (2·4), the last expression can be written as
 \begin{multline*}= \rho(u)(1+O_k(u^{-1})) i^k \xi'^{k/2} \frac{1}{\sqrt{2\pi}}\int_{-A/\sqrt{\xi'}}^{A/\sqrt{\xi'}} v^k \exp(\!-v^2/2)\\[5pt] \times \bigg(1+i \frac{v^3 \xi'^{3/2}}{6} I^{(3)}(\xi) + \frac{v^4 \xi'^2 }{24}I^{(4)}(\xi) - \frac{v^6 \xi'^3}{72}I^{(3)}(\xi)^2 \bigg) \bigg( 1+ O_k\bigg( \frac{|v|^5 +|v|^9}{u^{3/2}} \bigg)\bigg) {\textrm{d}}v.\end{multline*}
\begin{multline*}= \rho(u)(1+O_k(u^{-1})) i^k \xi'^{k/2} \frac{1}{\sqrt{2\pi}}\int_{-A/\sqrt{\xi'}}^{A/\sqrt{\xi'}} v^k \exp(\!-v^2/2)\\[5pt] \times \bigg(1+i \frac{v^3 \xi'^{3/2}}{6} I^{(3)}(\xi) + \frac{v^4 \xi'^2 }{24}I^{(4)}(\xi) - \frac{v^6 \xi'^3}{72}I^{(3)}(\xi)^2 \bigg) \bigg( 1+ O_k\bigg( \frac{|v|^5 +|v|^9}{u^{3/2}} \bigg)\bigg) {\textrm{d}}v.\end{multline*}
To conclude we apply estimates of gaussian integrals:
![]() $\int_{-R}^{R} v^{2k+1}\exp(\!-v^2/2){\textrm{d}}v$
is 0,
$\int_{-R}^{R} v^{2k+1}\exp(\!-v^2/2){\textrm{d}}v$
is 0,
![]() $\int_{\mathbb{R}}|v|^k \exp(\!-v^2/2){\textrm{d}}v \ll_k 1$
and
$\int_{\mathbb{R}}|v|^k \exp(\!-v^2/2){\textrm{d}}v \ll_k 1$
and
![]() $\int_{-R}^{R}v^{2k}\exp(\!-v^2/2){\textrm{d}}v =\sqrt{2\pi}\mu_{2k} + O_k(\exp(\!-R^2/4))$
.
$\int_{-R}^{R}v^{2k}\exp(\!-v^2/2){\textrm{d}}v =\sqrt{2\pi}\mu_{2k} + O_k(\exp(\!-R^2/4))$
.
3·3. Proof of the second part of Proposition 3·1
Here we prove (3·2) using the material in Section 3·2. If
![]() $1+u\xi \gt m \pi$
the result is already included in the first part of Proposition 3·1, so we assume from now on that
$1+u\xi \gt m \pi$
the result is already included in the first part of Proposition 3·1, so we assume from now on that
![]() $1+u\xi \le m \pi$
. From Lemma 3·3 we have
$1+u\xi \le m \pi$
. From Lemma 3·3 we have
We have
![]() $\exp(H_m-\gamma)/m =1+1/(2m)+O(m^{-2})$
by (2·10), and
$\exp(H_m-\gamma)/m =1+1/(2m)+O(m^{-2})$
by (2·10), and
 \[ e^{T(\xi)} = e^{\frac{u\xi}{2m}} \left( 1- \frac{\xi}{2m}+ O\left(\frac{u\log^2(u+1)}{m^2}\right)\right)\]
\[ e^{T(\xi)} = e^{\frac{u\xi}{2m}} \left( 1- \frac{\xi}{2m}+ O\left(\frac{u\log^2(u+1)}{m^2}\right)\right)\]
by (2·6). Hence,
 \[ p_{n,m} = e^{\frac{u\xi}{2m}} \left(1 + \frac{1-\xi}{2m} + O\left(\frac{u\log^2(u+1)}{m^2}\right)\right) \frac{1}{2\pi i} \int_{-\xi-im\pi}^{-\xi+im\pi} e^{us} \hat{\rho}(s) e^{T(-s)-T(\xi)}{\textrm{d}}s.\]
\[ p_{n,m} = e^{\frac{u\xi}{2m}} \left(1 + \frac{1-\xi}{2m} + O\left(\frac{u\log^2(u+1)}{m^2}\right)\right) \frac{1}{2\pi i} \int_{-\xi-im\pi}^{-\xi+im\pi} e^{us} \hat{\rho}(s) e^{T(-s)-T(\xi)}{\textrm{d}}s.\]
We separate the integral into 3 parts,
![]() $S_1+S_2+S_3$
, where
$S_1+S_2+S_3$
, where
 \begin{align*} {}S_1 &= \frac{1}{2\pi i} \int_{-\xi-im\pi}^{-\xi+im\pi} e^{us} \hat{\rho}(s) {\textrm{d}}s,\\[5pt] {}S_2 &= \frac{1}{2\pi i} \int_{-\xi-i(1+u\xi)}^{-\xi+i(1+u\xi)} \left(e^{T(-s)-T(\xi)}-1\right)e^{us} \hat{\rho}(s) {\textrm{d}}s,\\[5pt] {}S_3 &= \frac{1}{2\pi i} \left(\int_{-\xi-im\pi}^{-\xi-i(1+u\xi)}+\int_{-\xi+i(1+u\xi)}^{-\xi+im\pi}\right) \left(e^{T(-s)-T(\xi)} - 1 \right)e^{us} \hat{\rho}(s) {\textrm{d}}s.\end{align*}
\begin{align*} {}S_1 &= \frac{1}{2\pi i} \int_{-\xi-im\pi}^{-\xi+im\pi} e^{us} \hat{\rho}(s) {\textrm{d}}s,\\[5pt] {}S_2 &= \frac{1}{2\pi i} \int_{-\xi-i(1+u\xi)}^{-\xi+i(1+u\xi)} \left(e^{T(-s)-T(\xi)}-1\right)e^{us} \hat{\rho}(s) {\textrm{d}}s,\\[5pt] {}S_3 &= \frac{1}{2\pi i} \left(\int_{-\xi-im\pi}^{-\xi-i(1+u\xi)}+\int_{-\xi+i(1+u\xi)}^{-\xi+im\pi}\right) \left(e^{T(-s)-T(\xi)} - 1 \right)e^{us} \hat{\rho}(s) {\textrm{d}}s.\end{align*}
The integral
![]() $S_1$
was estimated in Lemma 3·4 and it gives the main term
$S_1$
was estimated in Lemma 3·4 and it gives the main term
![]() $\rho(u)$
as well an absolute error of size
$\rho(u)$
as well an absolute error of size
![]() $\ll e^{-(u-1)\xi}/n \ll e^{-u\xi} \log(u+1)/m$
. The integral
$\ll e^{-(u-1)\xi}/n \ll e^{-u\xi} \log(u+1)/m$
. The integral
![]() $S_3$
was estimated in Lemma 3·5 and it contributes
$S_3$
was estimated in Lemma 3·5 and it contributes
![]() $\ll e^{-u\xi}\log(u+1)/m$
. We now study
$\ll e^{-u\xi}\log(u+1)/m$
. We now study
![]() $S_2$
. We use Lemma 2·9 to Taylor-expand
$S_2$
. We use Lemma 2·9 to Taylor-expand
![]() $e^{T(-s)-T(\xi)}-1=e^{T(\xi-it)-T(\xi)}-1$
at 0:
$e^{T(-s)-T(\xi)}-1=e^{T(\xi-it)-T(\xi)}-1$
at 0:
 \begin{multline}e^{T(-s)-T(\xi)}-1 = -T'(\xi)(s+\xi) + \frac{(s+\xi)^2}{2}\left( T''(\xi)+T'(\xi)^2\right)\\[5pt] -(T^{(3)}(\xi)+3T'(\xi)T''(\xi)+(T'(\xi))^3) \frac{(s+\xi)^3}{6}+O\left( \frac{u\log(u+1)}{m} |s+\xi|^4\right)\end{multline}
\begin{multline}e^{T(-s)-T(\xi)}-1 = -T'(\xi)(s+\xi) + \frac{(s+\xi)^2}{2}\left( T''(\xi)+T'(\xi)^2\right)\\[5pt] -(T^{(3)}(\xi)+3T'(\xi)T''(\xi)+(T'(\xi))^3) \frac{(s+\xi)^3}{6}+O\left( \frac{u\log(u+1)}{m} |s+\xi|^4\right)\end{multline}
for
![]() $|\Im s| \le 1+u\xi$
. Applying Lemma 3·6 with
$|\Im s| \le 1+u\xi$
. Applying Lemma 3·6 with
![]() $k=4$
,
$k=4$
,
![]() $B=0$
and Lemma 3·7 with
$B=0$
and Lemma 3·7 with
![]() $k=1,2,3$
and collecting the terms gives
$k=1,2,3$
and collecting the terms gives
 \begin{multline} {}S_2 = \rho(u)\bigg(\frac{T'(\xi)(1+O(\log (u+1)^{-1}))-T''(\xi)(1+O(\log(u+1)^{-1}))}{2u} \\[5pt] + O\big( \frac{\log (u+1)}{n}+\frac{u\log^2(u+1)}{m^2}\big)\bigg). \end{multline}
\begin{multline} {}S_2 = \rho(u)\bigg(\frac{T'(\xi)(1+O(\log (u+1)^{-1}))-T''(\xi)(1+O(\log(u+1)^{-1}))}{2u} \\[5pt] + O\big( \frac{\log (u+1)}{n}+\frac{u\log^2(u+1)}{m^2}\big)\bigg). \end{multline}
All in all, since
![]() $T'(\xi)$
and
$T'(\xi)$
and
![]() $T''(\xi)$
are both
$T''(\xi)$
are both
![]() $({u\log(u+1)}/{2m}) (1+o_{u\to\infty}(1))$
in our range by Lemma 2·9,
$({u\log(u+1)}/{2m}) (1+o_{u\to\infty}(1))$
in our range by Lemma 2·9,
We are done, as we established, in stronger form, the second part of Proposition 3·1.
3·4. Proof of Lemma 3·2
We first show (3·3). Let
![]() $r(t)=-\rho'(t)/\rho(t)\ge 0$
. We have
$r(t)=-\rho'(t)/\rho(t)\ge 0$
. We have
If u is bounded then the bound
![]() $r(t)\ll 1$
for
$r(t)\ll 1$
for
![]() $t \ll 1$
finishes the proof. If
$t \ll 1$
finishes the proof. If
![]() $u \ge C$
we may differentiate r (it is differentiable for
$u \ge C$
we may differentiate r (it is differentiable for
![]() $t \ge 2$
) and obtain
$t \ge 2$
) and obtain
by integration by parts. To conclude, we use (3·8) to find
It remains to show (3·4). Set
![]() $t_1 = n/(m+1/2)$
and
$t_1 = n/(m+1/2)$
and
![]() $t_2=u-u/(2m)$
. It suffices to bound
$t_2=u-u/(2m)$
. It suffices to bound
![]() $\log (\rho(t_2)/\rho(t_1))$
. Observe
$\log (\rho(t_2)/\rho(t_1))$
. Observe
![]() $t_1\ge t_2$
. We have
$t_1\ge t_2$
. We have
since
![]() $r(t)\ll \log(t+1)$
by (3·8) and Lemma 2·2. This completes the proof.
$r(t)\ll \log(t+1)$
by (3·8) and Lemma 2·2. This completes the proof.
4. Proof of Theorem 1·2 and Corollary 1·3
Let
 \[ d_{m,m}=-\frac{1}{m}\sum_{j=2}^{m}\frac{1}{j}, \qquad d_{m,i}=\frac{\Gamma\left(i+\frac{i}{m}\right)}{(m-i)i!\Gamma\left(1+\frac{i}{m}\right)}\quad (1 \le i \le m-1).\]
\[ d_{m,m}=-\frac{1}{m}\sum_{j=2}^{m}\frac{1}{j}, \qquad d_{m,i}=\frac{\Gamma\left(i+\frac{i}{m}\right)}{(m-i)i!\Gamma\left(1+\frac{i}{m}\right)}\quad (1 \le i \le m-1).\]
Lemma 4·1. The estimate
 \[ {}p_{n,m} = \frac{\exp\big( - u \log n + u + \sum_{i=1}^{m} d_{m,i} n^{1-\frac{i}{m}} + E\big)}{\sqrt{2\pi n m}} \bigg(1+O\bigg(\frac{1}{\max\{\log u, n^{1/m}\}}\bigg)\bigg)\]
\[ {}p_{n,m} = \frac{\exp\big( - u \log n + u + \sum_{i=1}^{m} d_{m,i} n^{1-\frac{i}{m}} + E\big)}{\sqrt{2\pi n m}} \bigg(1+O\bigg(\frac{1}{\max\{\log u, n^{1/m}\}}\bigg)\bigg)\]
holds uniformly for
![]() $n \gt m \ge 1$
, where E is a quantity satisfying
$n \gt m \ge 1$
, where E is a quantity satisfying
 \[ E \ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{\frac{m}{n}}{1-\left( \frac{m}{n}\right)^{\frac{1}{m}}}.\]
\[ E \ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{\frac{m}{n}}{1-\left( \frac{m}{n}\right)^{\frac{1}{m}}}.\]
Lemma 4·1 is a minor improvement on [
Reference Manstavičius and Petuchovas13
, theorem 1], which treats
![]() $m\le \log n$
.
$m\le \log n$
.
Proof. Recall the definitions of x and
![]() $\lambda$
given in (1·11) and (2·2). Following the proof of [
Reference Manstavičius and Petuchovas13
, theorem 1]Footnote
1
we have, borrowing the notation of [
Reference Manstavičius and Petuchovas13
, section 5],
$\lambda$
given in (1·11) and (2·2). Following the proof of [
Reference Manstavičius and Petuchovas13
, theorem 1]Footnote
1
we have, borrowing the notation of [
Reference Manstavičius and Petuchovas13
, section 5],
for
![]() $E= R\big(n^{-\frac{1}{m}}\big)$
where
$E= R\big(n^{-\frac{1}{m}}\big)$
where
 \[ R(z): = \sum_{i=1}^{\infty} h_i z^i -n \sum_{i=m+1}^{\infty} b_i z^i\]
\[ R(z): = \sum_{i=1}^{\infty} h_i z^i -n \sum_{i=m+1}^{\infty} b_i z^i\]
for certain coefficients
![]() $h_i$
and
$h_i$
and
![]() $b_i$
defined in [
Reference Manstavičius and Petuchovas13
, lemma 13] and estimated in [
Reference Manstavičius and Petuchovas13
, lemma 15]. In particular,
$b_i$
defined in [
Reference Manstavičius and Petuchovas13
, lemma 13] and estimated in [
Reference Manstavičius and Petuchovas13
, lemma 15]. In particular,
for
![]() $i \ge 1$
and
$i \ge 1$
and
for
![]() $i \ge 1$
. In the first displayed equation of [
Reference Manstavičius and Petuchovas13
, lemma 15] it is shown that
$i \ge 1$
. In the first displayed equation of [
Reference Manstavičius and Petuchovas13
, lemma 15] it is shown that
![]() $b_i \ll i^{\frac{i}{m}-1}/m$
for
$b_i \ll i^{\frac{i}{m}-1}/m$
for
![]() $m+1 \le i \le 2m-1$
. It implies
$m+1 \le i \le 2m-1$
. It implies
in the same range. Hence
 \begin{align*} R(z)&\ll \sum_{i=1}^{m-1} \frac{i+m}{m}|z|^i + \sum_{i=m}^{\infty} \frac{m}{i}( m^{\frac{1}{m}}|z|)^i + n\bigg(\sum_{i=m+1}^{2m-1} \frac{i-m}{m}|z|^i + \sum_{i=2m}^{\infty}\frac{1}{i}(m^{\frac{1}{m}}|z|)^i\bigg)\\[5pt] &\ll \sum_{i=1}^{m-1} |z|^{i} + \sum_{i=m}^{2m-1} \bigg( \frac{n(i-m)}{m} + m^{\frac{i}{m}}\bigg) |z|^i + \sum_{i=2m}^{\infty} \frac{n}{i} (m^{\frac{1}{m}}|z|)^i.\end{align*}
\begin{align*} R(z)&\ll \sum_{i=1}^{m-1} \frac{i+m}{m}|z|^i + \sum_{i=m}^{\infty} \frac{m}{i}( m^{\frac{1}{m}}|z|)^i + n\bigg(\sum_{i=m+1}^{2m-1} \frac{i-m}{m}|z|^i + \sum_{i=2m}^{\infty}\frac{1}{i}(m^{\frac{1}{m}}|z|)^i\bigg)\\[5pt] &\ll \sum_{i=1}^{m-1} |z|^{i} + \sum_{i=m}^{2m-1} \bigg( \frac{n(i-m)}{m} + m^{\frac{i}{m}}\bigg) |z|^i + \sum_{i=2m}^{\infty} \frac{n}{i} (m^{\frac{1}{m}}|z|)^i.\end{align*}
It follows that
 \[ R(n^{-\frac{1}{m}}) \ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{n^{-\frac{1}{m}}}{m(1-n^{-\frac{1}{m}})^2}+ \frac{\frac{m}{n}}{1-(\frac{m}{n})^{\frac{1}{m}}}\ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{\frac{m}{n}}{1-(\frac{m}{n})^{\frac{1}{m}}}.\]
\[ R(n^{-\frac{1}{m}}) \ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{n^{-\frac{1}{m}}}{m(1-n^{-\frac{1}{m}})^2}+ \frac{\frac{m}{n}}{1-(\frac{m}{n})^{\frac{1}{m}}}\ll \frac{n^{-\frac{1}{m}}}{1-n^{-\frac{1}{m}}} + \frac{\frac{m}{n}}{1-(\frac{m}{n})^{\frac{1}{m}}}.\]
To conclude, we input the estimates for
![]() $\lambda/(nm)$
given in Lemma 2·1.
$\lambda/(nm)$
given in Lemma 2·1.
4·1. Proof of Theorem 1·2
Let
 \[ S\;:\!=\;\sum_{i=1}^{m-1} d_{m,i} n^{1-\frac{i}{m}}.\]
\[ S\;:\!=\;\sum_{i=1}^{m-1} d_{m,i} n^{1-\frac{i}{m}}.\]
In view of Lemma 4·1 we have
when
![]() $m=O(\log n)$
, and it remains to estimate S. We have
$m=O(\log n)$
, and it remains to estimate S. We have
uniformly for
![]() $1 \le i \le m-1$
. The estimate
$1 \le i \le m-1$
. The estimate
![]() $\Gamma(x+y)/\Gamma(x) \in [x(x+y)^{y-1},x^y]$
for
$\Gamma(x+y)/\Gamma(x) \in [x(x+y)^{y-1},x^y]$
for
![]() $y \in (0,1)$
[
Reference Wendel14
, equation (7)] implies
$y \in (0,1)$
[
Reference Wendel14
, equation (7)] implies
Hence,
Since
![]() $i^{i/m}=1+O({i\log i}/{m})$
if
$i^{i/m}=1+O({i\log i}/{m})$
if
![]() $i \lt m/\log (m+1)$
, we may write S as
$i \lt m/\log (m+1)$
, we may write S as
![]() $S= u(S_1+O(S_2+S_3))$
, where
$S= u(S_1+O(S_2+S_3))$
, where
 \[S_1 =\sum_{i=1}^{m-1} \frac{n^{-\frac{i}{m}}}{i},\,\quad S_2=\sum_{1 \le i \lt \frac{m}{\log (m+1)}} \frac{n^{-\frac{i}{m}}}{i} \frac{i\log(i+1)}{m},\, \quad S_3=\sum_{\frac{m}{\log(m+1)} \le i \le m-1} (i/n)^{\frac{i}{m}}\frac{m}{i}.\]
\[S_1 =\sum_{i=1}^{m-1} \frac{n^{-\frac{i}{m}}}{i},\,\quad S_2=\sum_{1 \le i \lt \frac{m}{\log (m+1)}} \frac{n^{-\frac{i}{m}}}{i} \frac{i\log(i+1)}{m},\, \quad S_3=\sum_{\frac{m}{\log(m+1)} \le i \le m-1} (i/n)^{\frac{i}{m}}\frac{m}{i}.\]
We have
 \[ S_1 = -\log(1-n^{-\frac{1}{m}}) + O\left( \frac{1}{nm}\frac{1}{1-n^{-\frac{1}{m}}}\right)\]
\[ S_1 = -\log(1-n^{-\frac{1}{m}}) + O\left( \frac{1}{nm}\frac{1}{1-n^{-\frac{1}{m}}}\right)\]
by bounding the tail of the Taylor series of
![]() $-\log(1-n^{-1/m})$
by a geometric series with ratio
$-\log(1-n^{-1/m})$
by a geometric series with ratio
![]() $n^{-1/m}$
. Similarly,
$n^{-1/m}$
. Similarly,
 \[ S_2 \ll \frac{1}{m} \frac{1}{n^{\frac{1}{m}}-1}\ll \frac{n^{-\frac{1}{m}}}{m}\]
\[ S_2 \ll \frac{1}{m} \frac{1}{n^{\frac{1}{m}}-1}\ll \frac{n^{-\frac{1}{m}}}{m}\]
because the contribution of
![]() $i \in [2^k,2^{k+1})$
to
$i \in [2^k,2^{k+1})$
to
![]() $S_2$
is
$S_2$
is
![]() $\ll (k+1)n^{-2^k/m}/(m(1-n^{-1/m}))$
and
$\ll (k+1)n^{-2^k/m}/(m(1-n^{-1/m}))$
and
![]() $\sum_{k \ge 0}(k+1)n^{-2^k/m}\ll n^{-1/m}$
when
$\sum_{k \ge 0}(k+1)n^{-2^k/m}\ll n^{-1/m}$
when
![]() $m\ll \log n$
. As for
$m\ll \log n$
. As for
![]() $S_3$
,
$S_3$
,
 \[S_3\ll m \sum_{\frac{m}{\log(m+1)}\le i \le m-1}\frac{1}{i} \max_{\frac{m}{\log(m+1)}\le i \le m-1} (i/n)^{i/m} \ll m\log \log (m+2) n^{-\frac{1}{\log(m+1)}} \]
\[S_3\ll m \sum_{\frac{m}{\log(m+1)}\le i \le m-1}\frac{1}{i} \max_{\frac{m}{\log(m+1)}\le i \le m-1} (i/n)^{i/m} \ll m\log \log (m+2) n^{-\frac{1}{\log(m+1)}} \]
since
![]() $i\mapsto (i/n)^{i/m}$
decreases for
$i\mapsto (i/n)^{i/m}$
decreases for
![]() $i \le n/e$
. Both
$i \le n/e$
. Both
![]() $S_3$
and the error term in
$S_3$
and the error term in
![]() $S_1$
are dominated by our bound for
$S_1$
are dominated by our bound for
![]() $S_2$
. It follows that
$S_2$
. It follows that
The error
![]() $O(\log n)$
in (4·1) is absorbed in the error term in S when
$O(\log n)$
in (4·1) is absorbed in the error term in S when
![]() $m \gt 1$
, and we are done.
$m \gt 1$
, and we are done.
4·2. Proof of Corollary 1·3
We first consider
![]() $n \ge m \gt n/2$
. For
$n \ge m \gt n/2$
. For
![]() $m=n$
,
$m=n$
,
![]() $p_{n,n}=\rho(1)=1$
, so we may assume
$p_{n,n}=\rho(1)=1$
, so we may assume
![]() $m\le n-1$
. We have exact formulas:
$m\le n-1$
. We have exact formulas:
![]() $p_{n,m}=1-\sum_{i=m+1}^{n}1/i$
and
$p_{n,m}=1-\sum_{i=m+1}^{n}1/i$
and
![]() $\rho(u)=1-\log u$
. Hence
$\rho(u)=1-\log u$
. Hence
 \[p_{n,m}-\rho(u)= \sum_{i=m+1}^{n}( \log i - \log(i-1) - \frac{1}{i}) \asymp \sum_{i=m+1}^{n} \frac{1}{i^2} \asymp \int_{m}^{n} \frac{{\textrm{d}}t}{t^2}.\]
\[p_{n,m}-\rho(u)= \sum_{i=m+1}^{n}( \log i - \log(i-1) - \frac{1}{i}) \asymp \sum_{i=m+1}^{n} \frac{1}{i^2} \asymp \int_{m}^{n} \frac{{\textrm{d}}t}{t^2}.\]
We are done since, in our range,
We now suppose
![]() $n/2 \ge m \ge C \log n$
. We shall need the lower bound [
Reference Gorodetsky8
, theorem A·1]
$n/2 \ge m \ge C \log n$
. We shall need the lower bound [
Reference Gorodetsky8
, theorem A·1]
which holds uniformly for
![]() $n/2 \ge m \ge 1$
. We may assume
$n/2 \ge m \ge 1$
. We may assume
![]() $n\ge C$
, since for bounded n we just want to show
$n\ge C$
, since for bounded n we just want to show
![]() $B_2\rho(u) \ge p_{n,m}\ge B_1\rho(u)$
for constants
$B_2\rho(u) \ge p_{n,m}\ge B_1\rho(u)$
for constants
![]() $B_2\ge B_1 \gt 1$
which follows from (4·2) and (1·4). If u is sufficiently large then it follows from Proposition 3·1 that, using the same definition for A as in the statement of the corollary,
$B_2\ge B_1 \gt 1$
which follows from (4·2) and (1·4). If u is sufficiently large then it follows from Proposition 3·1 that, using the same definition for A as in the statement of the corollary,
as needed. If
![]() $u=O(1)$
then the same argument establishes
$u=O(1)$
then the same argument establishes
![]() $A \le Cu\log ( 1+ (\log u)/m)$
and a matching lower bound in this range follows from (4·2).
$A \le Cu\log ( 1+ (\log u)/m)$
and a matching lower bound in this range follows from (4·2).
Finally we suppose
![]() $m=O(\log n)$
. From (1·1) we have
$m=O(\log n)$
. From (1·1) we have
If n is sufficiently large and
![]() $1\le m\le C\log n$
,
$1\le m\le C\log n$
,
since
![]() $t/(1-e^{-t}) \ge 1+c$
when
$t/(1-e^{-t}) \ge 1+c$
when
![]() $t=(\log n)/m\ge 1/C$
. This finishes the proof.
$t=(\log n)/m\ge 1/C$
. This finishes the proof.
Remark 3. When
![]() $m=O(\log n)$
the proof above shows more: setting
$m=O(\log n)$
the proof above shows more: setting
![]() $t\;:\!=\;(\log n)/m$
,
$t\;:\!=\;(\log n)/m$
,
holds, where A is as in the statement of Corollary 1·3.
5. Proofs of results in the polynomial setting
We recall we can write
![]() $G_q$
as
$G_q$
as
 \begin{equation} {}G_q(z) =\exp\!\left(\sum_{i=m+1}^{\infty} \frac{a_iz^i}{i}\right),\end{equation}
\begin{equation} {}G_q(z) =\exp\!\left(\sum_{i=m+1}^{\infty} \frac{a_iz^i}{i}\right),\end{equation}
where
![]() $a_{i}$
are nonnegative numbers, depending on q, that are described in [
Reference Gorodetsky8
, lemma 2·1] and satisfy
$a_{i}$
are nonnegative numbers, depending on q, that are described in [
Reference Gorodetsky8
, lemma 2·1] and satisfy
5·1. Proof of Theorem 1.5
We suppose that
![]() $n \ge m \ge \sqrt{10n\log n}$
. This guarantees
$n \ge m \ge \sqrt{10n\log n}$
. This guarantees
![]() $2^{m/3} \gt 1+ m(\log 2)/3 \ge 1 + 2u\log u \ge 1+u\xi = e^{\xi}$
, where we used Lemma 2·3 in the last inequality. Hence
$2^{m/3} \gt 1+ m(\log 2)/3 \ge 1 + 2u\log u \ge 1+u\xi = e^{\xi}$
, where we used Lemma 2·3 in the last inequality. Hence
An application of Cauchy’s integral formula allows us to express
![]() $p_{n,m}$
as
$p_{n,m}$
as
see [ Reference Manstavičius and Petuchovas13 , section 4]. In the same way,
see e.g. [
Reference Gorodetsky8
, section 4]. Since
![]() $G_q$
has radius of convergence equal to q, we must ensure that
$G_q$
has radius of convergence equal to q, we must ensure that
![]() $e^{\xi/m} \lt q$
in order for the last integral to be valid, and this holds by (5·3). By taking a linear combination of (5·4) and (5·5), and using (2·10) we have
$e^{\xi/m} \lt q$
in order for the last integral to be valid, and this holds by (5·3). By taking a linear combination of (5·4) and (5·5), and using (2·10) we have
for
Since
![]() $p_{n,m} \gg \rho(u)$
for
$p_{n,m} \gg \rho(u)$
for
![]() $m \ge \sqrt{10n\log n}$
by (1·4), it follows that
$m \ge \sqrt{10n\log n}$
by (1·4), it follows that
We must show
![]() $X \ll \rho(u) \log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. To bound X, we consider separately the contribution of
$X \ll \rho(u) \log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. To bound X, we consider separately the contribution of
![]() $|\Re s| \le 1+u\xi$
and
$|\Re s| \le 1+u\xi$
and
![]() $m\pi \ge |\Re s| \ge 1+u\xi$
. We start with
$m\pi \ge |\Re s| \ge 1+u\xi$
. We start with
![]() $|\Re s | \le 1+u\xi$
. Let
$|\Re s | \le 1+u\xi$
. Let
so that the integrand in X is
![]() $\hat{\rho}(s) e^{us} H_T(s)$
. We Taylor-expand
$\hat{\rho}(s) e^{us} H_T(s)$
. We Taylor-expand
![]() $H_T(s)$
at
$H_T(s)$
at
![]() $s=-\xi$
, where it attains 0:
$s=-\xi$
, where it attains 0:
![]() $H_T(s) = (s+\xi)b_1 + O(|s+\xi|^2 b_2)$
for
$H_T(s) = (s+\xi)b_1 + O(|s+\xi|^2 b_2)$
for
Applying Lemma 3·6 with
![]() $k=2$
,
$k=2$
,
![]() $B=0$
and Lemma 3·7 with
$B=0$
and Lemma 3·7 with
![]() $k=1$
, it follows that
$k=1$
, it follows that
We now consider the contribution of
![]() $\pi m \ge |\Re s| \ge 1+u\xi$
. We focus on
$\pi m \ge |\Re s| \ge 1+u\xi$
. We focus on
![]() $m\pi \ge \Re s \ge 1+u\xi$
, and negative
$m\pi \ge \Re s \ge 1+u\xi$
, and negative
![]() $\Re s$
is handled the same say. We have
$\Re s$
is handled the same say. We have
![]() $\hat{\rho}(s) = 1/s + O(u\log (u+1) /|s|^2)$
in this range by the third part of Lemma 2·7. The contribution of
$\hat{\rho}(s) = 1/s + O(u\log (u+1) /|s|^2)$
in this range by the third part of Lemma 2·7. The contribution of
![]() $O(u\log (u+1)/|s|^2)$
is
$O(u\log (u+1)/|s|^2)$
is
where
We study the last piece of the integral,
We write
![]() $e^{T(-s)}$
as
$e^{T(-s)}$
as
![]() $1+(e^{T(-s)}-1)$
. When
$1+(e^{T(-s)}-1)$
. When
![]() $s=-\xi+it$
for
$s=-\xi+it$
for
![]() $1+u\xi \le t \le \pi m$
we have
$1+u\xi \le t \le \pi m$
we have
![]() $e^{T(-s)}-1=O(|s|/m + |s|^2/m^2)$
by Corollary 2·8. Applying the triangle inequality we get
$e^{T(-s)}-1=O(|s|/m + |s|^2/m^2)$
by Corollary 2·8. Applying the triangle inequality we get
where
We estimate
Using the notation in (5·1) and the bound in (5·2), it follows that
 \begin{equation} {}\begin{split}H(s) &= \log G_q(e^{-s/m}) - \log G_q(e^{\xi/m}) +O\left( \frac{u^2 \log^2(u+1)}{m^2 q^{2\lceil \frac{m+1}{2}\rceil}}\right)\\[5pt] &=\sum_{j=m+1}^{2m} \frac{a_j}{j}(e^{-js/m}-e^{j\xi/m}) + O\left(\frac{u^2\log^2(u+1)}{mq^{m+1}}\right).\end{split}\end{equation}
\begin{equation} {}\begin{split}H(s) &= \log G_q(e^{-s/m}) - \log G_q(e^{\xi/m}) +O\left( \frac{u^2 \log^2(u+1)}{m^2 q^{2\lceil \frac{m+1}{2}\rceil}}\right)\\[5pt] &=\sum_{j=m+1}^{2m} \frac{a_j}{j}(e^{-js/m}-e^{j\xi/m}) + O\left(\frac{u^2\log^2(u+1)}{mq^{m+1}}\right).\end{split}\end{equation}
Hence the integral in (5·6) equals
 \[ =\sum_{j=m+1}^{2m} \frac{a_j}{j} \int_{-\xi+i(1+u\xi)}^{-\xi+i\pi m} \frac{e^{us}}{s} (e^{-js/m}-e^{j\xi/m}) {\textrm{d}}s+O\left( \frac{u^2 \log^2(u+1) e^{-u\xi}\log(m+1)}{mq^{m+1}} \right).\]
\[ =\sum_{j=m+1}^{2m} \frac{a_j}{j} \int_{-\xi+i(1+u\xi)}^{-\xi+i\pi m} \frac{e^{us}}{s} (e^{-js/m}-e^{j\xi/m}) {\textrm{d}}s+O\left( \frac{u^2 \log^2(u+1) e^{-u\xi}\log(m+1)}{mq^{m+1}} \right).\]
If
![]() $u \lt 3$
then
$u \lt 3$
then
![]() $G_q(e^{\xi/m})-1\ll 1/(mq^{\lceil (m+1)/2\rceil})$
, implying Theorem 1·5 is already in (1·6). From now on we assume
$G_q(e^{\xi/m})-1\ll 1/(mq^{\lceil (m+1)/2\rceil})$
, implying Theorem 1·5 is already in (1·6). From now on we assume
![]() $u \ge 3$
. We have the estimate
$u \ge 3$
. We have the estimate
which is valid for all
![]() $2m\ge j \ge 0$
and
$2m\ge j \ge 0$
and
![]() $u \ge 3$
, and is established by integration by parts. It follows that the integral (5·6) contributes
$u \ge 3$
, and is established by integration by parts. It follows that the integral (5·6) contributes
 \[\ll \frac{u^2 \log^2(u+1) e^{-u\xi}\log (m+1)}{mq^{m+1}} + \sum_{j=m+1}^{2m} \frac{a_j}{j} \frac{e^{-u\xi}}{1+u\xi} \frac{e^{j\xi/m}}{|u-j/m|} \ll \frac{e^{-u\xi}}{n q^{\lceil \frac{m+1}{2}\rceil}}.\]
\[\ll \frac{u^2 \log^2(u+1) e^{-u\xi}\log (m+1)}{mq^{m+1}} + \sum_{j=m+1}^{2m} \frac{a_j}{j} \frac{e^{-u\xi}}{1+u\xi} \frac{e^{j\xi/m}}{|u-j/m|} \ll \frac{e^{-u\xi}}{n q^{\lceil \frac{m+1}{2}\rceil}}.\]
Collecting the estimates,
Recall we want to show
![]() $X \ll \rho(u) \log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. We have
$X \ll \rho(u) \log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. We have
![]() $e^{-u\xi}\ll_k \rho(u) u^{-k}$
for any k by (2·4), showing that the last term in (5·8) is acceptable and that it suffices to show
$e^{-u\xi}\ll_k \rho(u) u^{-k}$
for any k by (2·4), showing that the last term in (5·8) is acceptable and that it suffices to show
![]() $b_i \ll u\log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
for
$b_i \ll u\log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
for
![]() $i=1,2,3,4$
.
$i=1,2,3,4$
.
Since
![]() $T(-\xi+it)$
is bounded when
$T(-\xi+it)$
is bounded when
![]() $|t|\le \pi m$
by Corollary 2·8, it follows that
$|t|\le \pi m$
by Corollary 2·8, it follows that
![]() $b_3 \ll b_4$
. By (5·7) and the triangle inequality,
$b_3 \ll b_4$
. By (5·7) and the triangle inequality,
![]() $b_4 \ll u\log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. To bound
$b_4 \ll u\log(u+1)/(mq^{\lceil(m+1)/2\rceil})$
. To bound
![]() $b_1$
and
$b_1$
and
![]() $b_2$
we use the fact that T and its derivatives are bounded by Lemma 2·9 in order to reduce the problem to showing
$b_2$
we use the fact that T and its derivatives are bounded by Lemma 2·9 in order to reduce the problem to showing
holds for
![]() $i=0,1,2$
. For
$i=0,1,2$
. For
![]() $i=0$
this is in (5·7), for
$i=0$
this is in (5·7), for
![]() $i=1$
we have
$i=1$
we have
and a similar computation holds for
![]() $i=2$
. This completes the proof of Theorem 1·5.
$i=2$
. This completes the proof of Theorem 1·5.
5·2. Proof of Corollary 1·6
Fix
![]() $\varepsilon \gt 0$
. We assume
$\varepsilon \gt 0$
. We assume
![]() $n \ge m \ge (2+\varepsilon)\log_q n$
and we want to establish (1·10) in this range. We already know (1·10) holds in
$n \ge m \ge (2+\varepsilon)\log_q n$
and we want to establish (1·10) in this range. We already know (1·10) holds in
![]() $n/(\log n \log^3\log(n+1)) \ge m \ge (2+\varepsilon)\log_q n$
, so we may suppose
$n/(\log n \log^3\log(n+1)) \ge m \ge (2+\varepsilon)\log_q n$
, so we may suppose
![]() $n \ge m \gt n/(\log n \log^3\log(n+1))$
.
$n \ge m \gt n/(\log n \log^3\log(n+1))$
.
If
![]() $n=O(1)$
then (1·10) becomes
$n=O(1)$
then (1·10) becomes
![]() $p_{n,m,q}=p_{n,m}G_q(x) + O_{n,\varepsilon}(G_q(x)/q^{\lceil (m+1)/2\rceil})$
. To establish this, recall
$p_{n,m,q}=p_{n,m}G_q(x) + O_{n,\varepsilon}(G_q(x)/q^{\lceil (m+1)/2\rceil})$
. To establish this, recall
![]() $p_{n,m,q}=p_{n,m} + O(1/q^{\lceil (m+1)/2\rceil})$
by [
Reference Gorodetsky8
, proposition 1·5] and observe that
$p_{n,m,q}=p_{n,m} + O(1/q^{\lceil (m+1)/2\rceil})$
by [
Reference Gorodetsky8
, proposition 1·5] and observe that
![]() $G_q(x) = 1+O_{n,\varepsilon}(1/q^{\lceil (m+1)/2\rceil})$
by (5·1) and (5·2).
$G_q(x) = 1+O_{n,\varepsilon}(1/q^{\lceil (m+1)/2\rceil})$
by (5·1) and (5·2).
From now on we may suppose n is sufficiently large. In particular,
![]() $n \gt \sqrt{10 n \log n}$
holds, and
$n \gt \sqrt{10 n \log n}$
holds, and
![]() $n \ge m \gt n/(\log n \log^3\log(n+1))$
implies
$n \ge m \gt n/(\log n \log^3\log(n+1))$
implies
![]() $n \ge m \ge \sqrt{10 n \log n}$
. We apply Theorem 1·5, and see that it suffices to show that
$n \ge m \ge \sqrt{10 n \log n}$
. We apply Theorem 1·5, and see that it suffices to show that
 \begin{equation} {}\frac{G_q(x)}{G_q(e^{\xi(u)/m})} = 1 +O\left( \frac{u\log^2 (u+1)}{m^2 q^{\lceil \frac{m+1}{2}\rceil}}\right)\end{equation}
\begin{equation} {}\frac{G_q(x)}{G_q(e^{\xi(u)/m})} = 1 +O\left( \frac{u\log^2 (u+1)}{m^2 q^{\lceil \frac{m+1}{2}\rceil}}\right)\end{equation}
holds for
![]() $n\ge m \ge \sqrt{10 n \log n}$
. First we verify that
$n\ge m \ge \sqrt{10 n \log n}$
. First we verify that
![]() $x \lt \sqrt[3]{2}$
. Since
$x \lt \sqrt[3]{2}$
. Since
![]() $x \le n^{1/m}$
, it suffices to show that
$x \le n^{1/m}$
, it suffices to show that
![]() $2^m \gt n^3$
, which follows from
$2^m \gt n^3$
, which follows from
![]() $n \ge m \ge \sqrt{10n\log n}$
. Now that we know
$n \ge m \ge \sqrt{10n\log n}$
. Now that we know
![]() $G_q$
converges absolutely at x we proceed. The relation
$G_q$
converges absolutely at x we proceed. The relation
![]() $x^m = e^{\xi}(1+O(\log(u+1)/m))$
from (3·6) implies
$x^m = e^{\xi}(1+O(\log(u+1)/m))$
from (3·6) implies
 \[ \log G_q(x) - \log G_q(e^{\xi/m}) = \sum_{i=m+1}^{\infty} \frac{a_i (x^i - e^{\xi i /m})}{i} \ll \frac{u\log^2 (u+1)}{m^2 q^{\lceil \frac{m+1}{2}\rceil}}\]
\[ \log G_q(x) - \log G_q(e^{\xi/m}) = \sum_{i=m+1}^{\infty} \frac{a_i (x^i - e^{\xi i /m})}{i} \ll \frac{u\log^2 (u+1)}{m^2 q^{\lceil \frac{m+1}{2}\rceil}}\]
5·3. Auxiliary computation
Recall
![]() $F_q$
defined in (1·7). We define
$F_q$
defined in (1·7). We define
![]() $x_q\;:\!=\;x_{n,m,q} \lt q$
as the unique positive solution to
$x_q\;:\!=\;x_{n,m,q} \lt q$
as the unique positive solution to
![]() $z F_q'(z)/F_q(z) = n$
. The next lemma gives precise results on
$z F_q'(z)/F_q(z) = n$
. The next lemma gives precise results on
![]() $x-x_q$
in certain ranges.
$x-x_q$
in certain ranges.
Lemma 5·1. If
![]() $n \ge m \ge 1$
then
$n \ge m \ge 1$
then
![]() $x_q \le x$
. Fix q and
$x_q \le x$
. Fix q and
![]() $\varepsilon \gt 0$
. For
$\varepsilon \gt 0$
. For
![]() $n \ge C_{q,\varepsilon}$
and
$n \ge C_{q,\varepsilon}$
and
![]() $m \in [(3/4)\log_q n, (2-\varepsilon)\log_q n]$
,
$m \in [(3/4)\log_q n, (2-\varepsilon)\log_q n]$
,
Proof. We shall use the form of
![]() $G_q$
given in (5·1). Let
$G_q$
given in (5·1). Let
![]() $f(z)\;:\!=\;z(\log F(z))' = \sum_{i=1}^{m} z^i$
and
$f(z)\;:\!=\;z(\log F(z))' = \sum_{i=1}^{m} z^i$
and
![]() $g_q(z) \;:\!=\; z(\log G_q(z))'= \sum_{i=m+1}^{\infty}a_i z^i$
. By definition,
$g_q(z) \;:\!=\; z(\log G_q(z))'= \sum_{i=m+1}^{\infty}a_i z^i$
. By definition,
Since f and
![]() $g_q$
have nonnegative coefficients, the first part of the lemma follows at once. We now assume
$g_q$
have nonnegative coefficients, the first part of the lemma follows at once. We now assume
![]() $(2-\varepsilon)\log_q n \ge m \ge (3/4)\log_q n $
. We use (5·10) to determine the size of
$(2-\varepsilon)\log_q n \ge m \ge (3/4)\log_q n $
. We use (5·10) to determine the size of
![]() $x-x_q$
. By the mean value theorem,
$x-x_q$
. By the mean value theorem,
for some
![]() $t \in [0,g_q(x_q)]$
, where
$t \in [0,g_q(x_q)]$
, where
![]() $f^{-1}$
is the inverse of f. Since
$f^{-1}$
is the inverse of f. Since
![]() $f^{-1}$
and f’ are monotone increasing we have
$f^{-1}$
and f’ are monotone increasing we have
![]() $f'(f^{-1}(n-t)) \in [f'(x_q), f'(x)]$
and so
$f'(f^{-1}(n-t)) \in [f'(x_q), f'(x)]$
and so
We have the trivial bounds
![]() $1 \le x\le n^{1/m} \ll_q 1$
and so
$1 \le x\le n^{1/m} \ll_q 1$
and so
![]() $f'(x) = \lambda/x \asymp_q nm$
by Lemma 2·1. We also have
$f'(x) = \lambda/x \asymp_q nm$
by Lemma 2·1. We also have
since
![]() $a_i \ge 0$
and
$a_i \ge 0$
and
![]() $a_{2m} \gg q^{-m}$
by [
Reference Gorodetsky8
, lemma 2·1]. It follows that
$a_{2m} \gg q^{-m}$
by [
Reference Gorodetsky8
, lemma 2·1]. It follows that
[
Reference Manstavičius12
, lemma 2 and theorem 2] estimate
![]() $x_q$
and yield that, when
$x_q$
and yield that, when
![]() $2\log_q n \ge m \ge (3/4)\log_q n$
,
$2\log_q n \ge m \ge (3/4)\log_q n$
,
implying the desired lower bound on
![]() $x-x_q$
. To prove the upper bound, first observe that
$x-x_q$
. To prove the upper bound, first observe that
![]() $m \le (2-\varepsilon)\log_q n$
implies, via (5·11), that
$m \le (2-\varepsilon)\log_q n$
implies, via (5·11), that
![]() $x_q \ge q^{1/2}(1+c_{q,\varepsilon})$
if n is sufficiently large, and so
$x_q \ge q^{1/2}(1+c_{q,\varepsilon})$
if n is sufficiently large, and so
 \[ g_q(x_q) \ll \sum_{i=m+1}^{2m} \frac{x_q^i}{q^{i/2}}+q^m \sum_{i \ge 2m}\frac{x_q^i}{q^i} \ll_{q,\varepsilon} \frac{ x_q^{2m}}{q^m}\big(1-\frac{x_q}{q}\big)^{-1}\]
\[ g_q(x_q) \ll \sum_{i=m+1}^{2m} \frac{x_q^i}{q^{i/2}}+q^m \sum_{i \ge 2m}\frac{x_q^i}{q^i} \ll_{q,\varepsilon} \frac{ x_q^{2m}}{q^m}\big(1-\frac{x_q}{q}\big)^{-1}\]
using the bounds in (5·2). To conclude we need to lower bound
![]() $f'(x_q)$
. We have
$f'(x_q)$
. We have
![]() $f'(x_q) = x_q^{-1} \sum_{i=1}^{m} i x_q^i \gg_{q} m x_q^m$
.
$f'(x_q) = x_q^{-1} \sum_{i=1}^{m} i x_q^i \gg_{q} m x_q^m$
.
5·4. Proof of Theorem 1·7
Recall the functions F,
![]() $F_q$
and
$F_q$
and
![]() $G_q$
are defined in (1·8), (1·7) and (1·9). If
$G_q$
are defined in (1·8), (1·7) and (1·9). If
![]() $m \to \infty$
and
$m \to \infty$
and
![]() $u\ge (\log \log m)^3 \log m$
, Manstavičius proved in [
Reference Manstavichyus11,Reference Manstavičius12
] that
$u\ge (\log \log m)^3 \log m$
, Manstavičius proved in [
Reference Manstavichyus11,Reference Manstavičius12
] that
where
 \[ \lambda_q\;:\!=\;\lambda_{n,m,q}= z \left(\frac{zF'_q(z)}{F_q(z)}\right)'|_{z=x_q}.\]
\[ \lambda_q\;:\!=\;\lambda_{n,m,q}= z \left(\frac{zF'_q(z)}{F_q(z)}\right)'|_{z=x_q}.\]
We divide (5·12) by (2·1), and use the fact that
![]() $\lambda$
is asymptotic to nm by Lemma 2·1 as long as
$\lambda$
is asymptotic to nm by Lemma 2·1 as long as
![]() $u \to \infty$
, and
$u \to \infty$
, and
by [
Reference Manstavičius12
, theorem 2] as long as
![]() $u \to \infty$
and
$u \to \infty$
and
![]() $m \to \infty$
, to obtain
$m \to \infty$
, to obtain
 \begin{equation} \frac{p_{n,m,q}}{p_{n,m}G_q(x)} \sim \left(1+ \frac{n}{q^m}\left(1-\frac{1}{q}\right)\right)^{-1/2} \frac{x^nF(x_{q})G_q(x_{q})}{x_q^nF(x)G_q(x)}\end{equation}
\begin{equation} \frac{p_{n,m,q}}{p_{n,m}G_q(x)} \sim \left(1+ \frac{n}{q^m}\left(1-\frac{1}{q}\right)\right)^{-1/2} \frac{x^nF(x_{q})G_q(x_{q})}{x_q^nF(x)G_q(x)}\end{equation}
as
![]() $n \to \infty$
if
$n \to \infty$
if
![]() $(2-\varepsilon)\log_q n \ge m \gt \log_q n$
. Letting
$(2-\varepsilon)\log_q n \ge m \gt \log_q n$
. Letting
we can write (5·14) as
By definition,
![]() $H'_q(x_q)=0$
. By Taylor-expanding
$H'_q(x_q)=0$
. By Taylor-expanding
![]() $H_q$
at
$H_q$
at
![]() $x_q$
,
$x_q$
,
for some
![]() $t \in [x_q,x]$
(recall
$t \in [x_q,x]$
(recall
![]() $x_q \le x$
by Lemma 5·1). In the range
$x_q \le x$
by Lemma 5·1). In the range
![]() $(2-\varepsilon)\log_q n \ge m \gt \log_q n$
we have
$(2-\varepsilon)\log_q n \ge m \gt \log_q n$
we have
![]() $x\asymp_q x_q \asymp_q 1$
by Lemma 2·1 and (5·11). In the notation of (5·1),
$x\asymp_q x_q \asymp_q 1$
by Lemma 2·1 and (5·11). In the notation of (5·1),
 \[ t^2 H_q''(t) = \sum_{i=2}^{m}(i-1)t^i + \sum_{i=m+1}^{\infty}(i-1)a_i t^i+ n \gt 0\]
\[ t^2 H_q''(t) = \sum_{i=2}^{m}(i-1)t^i + \sum_{i=m+1}^{\infty}(i-1)a_i t^i+ n \gt 0\]
is increasing for
![]() $t \gt 0$
since
$t \gt 0$
since
![]() $a_i \ge 0$
. It follows that
$a_i \ge 0$
. It follows that
A short computation shows that
![]() $x_q^2 H_q''(x_q)=\lambda_q$
holds by the definition of
$x_q^2 H_q''(x_q)=\lambda_q$
holds by the definition of
![]() $x_q$
and
$x_q$
and
![]() $\lambda_q$
. By (5·13) it then follows that
$\lambda_q$
. By (5·13) it then follows that
![]() $x_q^2 H_q''(x_q) \asymp_q nm$
when
$x_q^2 H_q''(x_q) \asymp_q nm$
when
![]() $(2-\varepsilon)\log_q n \ge m \gt \log_q n$
. In the same range we find that
$(2-\varepsilon)\log_q n \ge m \gt \log_q n$
. In the same range we find that
![]() $x^2 H_q''(x) = \lambda +\sum_{i=m+1}^{\infty}(i-1)a_i x^i \ll_{q,\varepsilon} nm$
using Lemma 2·1 and the bounds in (5·2). Hence
$x^2 H_q''(x) = \lambda +\sum_{i=m+1}^{\infty}(i-1)a_i x^i \ll_{q,\varepsilon} nm$
using Lemma 2·1 and the bounds in (5·2). Hence
![]() $H_q''(t) \asymp_{q,\varepsilon} nm$
and
$H_q''(t) \asymp_{q,\varepsilon} nm$
and
where we used Lemma 5·1 in the second estimate. Plugging this estimate in (5·15), and observing that
![]() $(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2} \sim 1$
holds in the range
$(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2} \sim 1$
holds in the range
![]() $m\ge (1+\varepsilon)\log_q n$
considered in Theorem 1·7, concludes the proof.
$m\ge (1+\varepsilon)\log_q n$
considered in Theorem 1·7, concludes the proof.
5·5. A variant
We prove a variant of Theorem 1·7 with the main term
![]() $G_q(x)$
replaced by
$G_q(x)$
replaced by
![]() $G_q(x_q)$
.
$G_q(x_q)$
.
Theorem 5·2. Fix q and
![]() $\varepsilon \gt 0$
. For
$\varepsilon \gt 0$
. For
![]() $m \in [(3/4)\log_q n, (2-\varepsilon)\log_q n]$
we have
$m \in [(3/4)\log_q n, (2-\varepsilon)\log_q n]$
we have
 \begin{equation} {} {}\begin{split} {} {} {}\frac{p_{n,m,q}}{p_{n,m}} &\le (1+o(1))G_q(x_q)\exp\!\left( \frac{C_{q,\varepsilon} \min\{n,q^m\}^2 n}{mq^{2m} } \left(1-\frac{x_q}{q}\right)^{-2}\right),\\[5pt] {} {} {}\frac{p_{n,m,q}}{p_{n,m}} &\ge (1+o(1)) G_q(x_q)\exp\!\left( \frac{c_{q,\varepsilon} \min\{n,q^m\}^5}{n^2 mq^{2m}}\right) {} {}\end{split} {}\end{equation}
\begin{equation} {} {}\begin{split} {} {} {}\frac{p_{n,m,q}}{p_{n,m}} &\le (1+o(1))G_q(x_q)\exp\!\left( \frac{C_{q,\varepsilon} \min\{n,q^m\}^2 n}{mq^{2m} } \left(1-\frac{x_q}{q}\right)^{-2}\right),\\[5pt] {} {} {}\frac{p_{n,m,q}}{p_{n,m}} &\ge (1+o(1)) G_q(x_q)\exp\!\left( \frac{c_{q,\varepsilon} \min\{n,q^m\}^5}{n^2 mq^{2m}}\right) {} {}\end{split} {}\end{equation}
as
![]() $n \to \infty$
. If furthermore
$n \to \infty$
. If furthermore
![]() $n \ge C_{q,\varepsilon}$
then
$n \ge C_{q,\varepsilon}$
then
Proof. In very much the same way (5·14) is proved, we also have
 \begin{equation} \frac{p_{n,m,q}}{p_{n,m}G_q(x_q)} \sim \frac{x^nF(x_{q})G_q(x_{q})}{x_q^nF(x)G_q(x_q)}\left(1+ \frac{n}{q^m}\left(1-\frac{1}{q}\right)\right)^{-1/2}\end{equation}
\begin{equation} \frac{p_{n,m,q}}{p_{n,m}G_q(x_q)} \sim \frac{x^nF(x_{q})G_q(x_{q})}{x_q^nF(x)G_q(x_q)}\left(1+ \frac{n}{q^m}\left(1-\frac{1}{q}\right)\right)^{-1/2}\end{equation}
if
![]() $u \ge (\log \log m)^3 \log m$
and
$u \ge (\log \log m)^3 \log m$
and
![]() $m\to\infty$
. Letting
$m\to\infty$
. Letting
we can write (5·17) as
By definition,
![]() $H'(x) = 0$
. By Taylor-expanding H at x,
$H'(x) = 0$
. By Taylor-expanding H at x,
for some
![]() $t \in [x_q,x]$
. Since
$t \in [x_q,x]$
. Since
![]() $t^2 H''(t) = \sum_{i=2}^{m} (i-1)t^i +n$
is increasing in t, and
$t^2 H''(t) = \sum_{i=2}^{m} (i-1)t^i +n$
is increasing in t, and
![]() $x \asymp_q x_q \asymp_q 1$
by Lemma 2·1 and (5·11), it follows that
$x \asymp_q x_q \asymp_q 1$
by Lemma 2·1 and (5·11), it follows that
We have
![]() $x^2 H''(x)=\lambda \asymp nm$
by Lemma 2·1 when
$x^2 H''(x)=\lambda \asymp nm$
by Lemma 2·1 when
![]() $(2-\varepsilon)\log_q n \ge m \ge (3/4)\log_q n$
. Lemma 5·1 bounds
$(2-\varepsilon)\log_q n \ge m \ge (3/4)\log_q n$
. Lemma 5·1 bounds
![]() $x-x_q$
. This gives the first part of (5·16) (we bound the factor
$x-x_q$
. This gives the first part of (5·16) (we bound the factor
![]() $(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2}$
by 1). We have
$(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2}$
by 1). We have
![]() $x_q^2 H''(x_q) \ge (m-1)x_q^m \gg_q m \min\{n,q^m\}$
by (5·11), which leads to the second part of (5·16) (we absorb
$x_q^2 H''(x_q) \ge (m-1)x_q^m \gg_q m \min\{n,q^m\}$
by (5·11), which leads to the second part of (5·16) (we absorb
![]() $(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2}$
in the exponential factor in right-hand side of (5·16)).
$(1+ ({n}/{q^m})(1-{1}/{q}))^{-1/2}$
in the exponential factor in right-hand side of (5·16)).
It remains to estimate
![]() $G_q(x_q)$
. For a lower bound we use
$G_q(x_q)$
. For a lower bound we use
![]() $\log G_q(x_q) \ge a_{2m} x_q^{2m}/(2m) \gg x_q^{2m}/(mq^m)$
. Here we used
$\log G_q(x_q) \ge a_{2m} x_q^{2m}/(2m) \gg x_q^{2m}/(mq^m)$
. Here we used
![]() $a_i \ge 0$
and
$a_i \ge 0$
and
![]() $a_{2m} \asymp q^{-m}$
[
Reference Gorodetsky8
, lemma 2·1]. This is simplified using (5·11). For the upper bound we use
$a_{2m} \asymp q^{-m}$
[
Reference Gorodetsky8
, lemma 2·1]. This is simplified using (5·11). For the upper bound we use
![]() $a_{i} \ll \min\{q^{-\lceil i/2\rceil},q^{m-i}\}$
and
$a_{i} \ll \min\{q^{-\lceil i/2\rceil},q^{m-i}\}$
and
![]() $x_q \ge q^{1/2}(1+c_{q,\varepsilon})$
to obtain
$x_q \ge q^{1/2}(1+c_{q,\varepsilon})$
to obtain
![]() $\log G_q(x_q) \ll_{q,\varepsilon} x_q^{2m}/( mq^m(1-x_q/q))$
. We again simplify
$\log G_q(x_q) \ll_{q,\varepsilon} x_q^{2m}/( mq^m(1-x_q/q))$
. We again simplify
![]() $x_q^m$
using (5·11).
$x_q^m$
using (5·11).
Acknowledgements
We thank Andrew Granville for valuable comments on the presentation. We are grateful to the anonymous referees for helpful comments on exposition as well as a simplification of the proof of Lemma 2·1. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 851318).