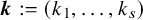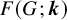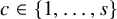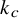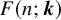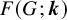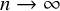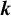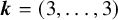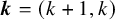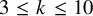1. Introduction
Let a nonincreasing sequence
![]() $\boldsymbol {k} = (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers be given. By an s-edge-colouring (or colouring for brevity) of a graph
$\boldsymbol {k} = (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers be given. By an s-edge-colouring (or colouring for brevity) of a graph
![]() $G=(V,E)$
we mean a function
$G=(V,E)$
we mean a function
![]() $\chi :E\to [s]$
, where we denote
$\chi :E\to [s]$
, where we denote
![]() $[s]:=\{1,\dots ,s\}$
. Note that colourings do not have to be proper; that is, adjacent edges can have the same colour. A colouring
$[s]:=\{1,\dots ,s\}$
. Note that colourings do not have to be proper; that is, adjacent edges can have the same colour. A colouring
![]() $\chi $
of G is called
$\chi $
of G is called
![]() $\boldsymbol {k}$
-valid if, for every
$\boldsymbol {k}$
-valid if, for every
![]() $c\in [s]$
, the colour-c subgraph
$c\in [s]$
, the colour-c subgraph
![]() $\chi ^{-1}(c)$
contains no copy of
$\chi ^{-1}(c)$
contains no copy of
![]() $K_{k_c}$
, the complete graph of order
$K_{k_c}$
, the complete graph of order
![]() $k_c$
. Write
$k_c$
. Write
![]() $F(G; \boldsymbol {k})$
for the number of
$F(G; \boldsymbol {k})$
for the number of
![]() $\boldsymbol {k}$
-valid colourings of G. This paper concerns the parameter
$\boldsymbol {k}$
-valid colourings of G. This paper concerns the parameter
the maximum value of
![]() $F(G;\boldsymbol {k})$
for an n-vertex graph G, and the
$F(G;\boldsymbol {k})$
for an n-vertex graph G, and the
![]() $\boldsymbol {k}$
-extremal graphs (i.e., those graphs which attain this maximum). We always assume
$\boldsymbol {k}$
-extremal graphs (i.e., those graphs which attain this maximum). We always assume
![]() $s \geq 2$
and
$s \geq 2$
and
![]() $k_s \geq 3$
for otherwise the problem is trivial or reduces to one with shorter
$k_s \geq 3$
for otherwise the problem is trivial or reduces to one with shorter
![]() $\boldsymbol {k}$
. Determining
$\boldsymbol {k}$
. Determining
![]() $F(n;\boldsymbol {k})$
in the case
$F(n;\boldsymbol {k})$
in the case
![]() $\boldsymbol {k}=(3,3)$
was originally studied by Erdős and Rothschild [Reference Erdős4, Reference Erdős5], and hence, it is called the Erdős-Rothschild problem. It is, in general, wide open. The following summarises all of the cases where
$\boldsymbol {k}=(3,3)$
was originally studied by Erdős and Rothschild [Reference Erdős4, Reference Erdős5], and hence, it is called the Erdős-Rothschild problem. It is, in general, wide open. The following summarises all of the cases where
![]() $F(n;\boldsymbol {k})$
is known (in one case only asymptotically). Write
$F(n;\boldsymbol {k})$
is known (in one case only asymptotically). Write
![]() $(k;s)$
for the tuple
$(k;s)$
for the tuple
![]() $(k,\ldots ,k)$
of length s.
$(k,\ldots ,k)$
of length s.
Theorem 1.1. There exists
![]() $n_0(k)>0$
such that the following hold for all integers
$n_0(k)>0$
such that the following hold for all integers
![]() $n \geq n_0$
.
$n \geq n_0$
.

(*) These graphs are known to be asymptotically extremal only: they achieve the right exponent in
![]() $F(n;\boldsymbol {k})$
. Here,
$F(n;\boldsymbol {k})$
. Here,
![]() $T_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
$T_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
![]() $\alpha n, \alpha n, (\frac {1}{4}-\alpha )n, (\frac {1}{4}-\alpha )n, \beta n, \beta n, (\frac {1}{4}-\beta )n, (\frac {1}{4}-\beta )n$
, and
$\alpha n, \alpha n, (\frac {1}{4}-\alpha )n, (\frac {1}{4}-\alpha )n, \beta n, \beta n, (\frac {1}{4}-\beta )n, (\frac {1}{4}-\beta )n$
, and
![]() $T^{\prime }_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
$T^{\prime }_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
![]() $\frac {n}{4},\frac {n}{4},\alpha n, \alpha n, \beta n, \beta n, (\frac {1}{4}-\alpha -\beta )n, (\frac {1}{4}-\alpha -\beta )n$
.
$\frac {n}{4},\frac {n}{4},\alpha n, \alpha n, \beta n, \beta n, (\frac {1}{4}-\alpha -\beta )n, (\frac {1}{4}-\alpha -\beta )n$
.
The constants
![]() $C_{3,4},C_{3,6},C_{4,4}$
can be determined, and generally depend on the remainder when n is divided by some small integer; for example,
$C_{3,4},C_{3,6},C_{4,4}$
can be determined, and generally depend on the remainder when n is divided by some small integer; for example,
![]() $C_{3,4}$
equals
$C_{3,4}$
equals
![]() $(2^{14}\cdot 3)^{1/3}$
if
$(2^{14}\cdot 3)^{1/3}$
if
![]() $n \equiv 2\ (\mod 4)$
and equals
$n \equiv 2\ (\mod 4)$
and equals
![]() $36$
otherwise. Note that for
$36$
otherwise. Note that for
![]() $\boldsymbol {k} = (k;s)$
, the trivial lower bound for
$\boldsymbol {k} = (k;s)$
, the trivial lower bound for
![]() $F(n;\boldsymbol {k})$
is
$F(n;\boldsymbol {k})$
is
![]() $s^{t_{k-1}(n)}$
, given by taking every s-edge-colouring of the largest
$s^{t_{k-1}(n)}$
, given by taking every s-edge-colouring of the largest
![]() $K_k$
-free graph on n vertices – namely, the Turán graph
$K_k$
-free graph on n vertices – namely, the Turán graph
![]() $T_{k-1}(n)$
, the complete partite graph with
$T_{k-1}(n)$
, the complete partite graph with
![]() $k-1$
parts of size as equal as possible (with
$k-1$
parts of size as equal as possible (with
![]() $t_{k-1}(n) := e(T_{k-1}(n))$
). This trivial lower bound is, in fact, sharp for
$t_{k-1}(n) := e(T_{k-1}(n))$
). This trivial lower bound is, in fact, sharp for
![]() $s=2,3$
, but
$s=2,3$
, but
![]() $F(n;\boldsymbol {k})$
is exponentially larger for
$F(n;\boldsymbol {k})$
is exponentially larger for
![]() $s \geq 4$
, as was shown in [Reference Alon, Balogh, Keevash and Sudakov1]. As is evident from the table, these cases have been much harder to resolve and there are only four pairs
$s \geq 4$
, as was shown in [Reference Alon, Balogh, Keevash and Sudakov1]. As is evident from the table, these cases have been much harder to resolve and there are only four pairs
![]() $(k;s)$
where the solution is known. We refer the reader to [Reference Pikhurko and Staden10] for a more detailed history of the problem and its variants. This paper is the third in a series (comprising also [Reference Pikhurko, Staden and Yilma11] with Yilma and [Reference Pikhurko and Staden10]) concerning the relationship between the Erdős-Rothschild problem and a finite combinatorial optimisation problem, which we now state.
$(k;s)$
where the solution is known. We refer the reader to [Reference Pikhurko and Staden10] for a more detailed history of the problem and its variants. This paper is the third in a series (comprising also [Reference Pikhurko, Staden and Yilma11] with Yilma and [Reference Pikhurko and Staden10]) concerning the relationship between the Erdős-Rothschild problem and a finite combinatorial optimisation problem, which we now state.
Problem
![]() $\mathbf {Q^*}$
: Given a sequence
$\mathbf {Q^*}$
: Given a sequence
![]() $\boldsymbol {k} := (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers, determine
$\boldsymbol {k} := (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers, determine
the maximum value of
 $$ \begin{align} q(\phi,\boldsymbol{\alpha}) := 2\sum_{1 \leq i < j \leq r} \alpha_i \alpha_j \log_2 |\phi(ij)| \end{align} $$
$$ \begin{align} q(\phi,\boldsymbol{\alpha}) := 2\sum_{1 \leq i < j \leq r} \alpha_i \alpha_j \log_2 |\phi(ij)| \end{align} $$
over the set ![]() of feasible solutions – that is, triples
of feasible solutions – that is, triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
such that
$(r,\phi ,\boldsymbol {\alpha })$
such that
![]() $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
-
○
 $\phi \in \Phi _2(r;\boldsymbol {k})$
, where
$\phi \in \Phi _2(r;\boldsymbol {k})$
, where
 $\Phi _2(r;\boldsymbol {k})$
is the set of all functions
$\Phi _2(r;\boldsymbol {k})$
is the set of all functions
 $\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
such that is
$\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
such that is $$\begin{align*}\phi^{-1}(c) := \left\{ ij \in \binom{[r]}{2} : c \in \phi(ij) \right\} \end{align*}$$
$$\begin{align*}\phi^{-1}(c) := \left\{ ij \in \binom{[r]}{2} : c \in \phi(ij) \right\} \end{align*}$$
 $K_{k_c}$
-free for every colour
$K_{k_c}$
-free for every colour
 $c \in [s]$
and
$c \in [s]$
and
 $|\phi (ij)|\ge 2$
for all
$|\phi (ij)|\ge 2$
for all
 $ij\in \binom {[r]}{2}$
;
$ij\in \binom {[r]}{2}$
;
-
○
 $\boldsymbol {\alpha } = (\alpha _1,\ldots ,\alpha _r) \in \Delta ^r$
, where
$\boldsymbol {\alpha } = (\alpha _1,\ldots ,\alpha _r) \in \Delta ^r$
, where
 $\Delta ^r$
is the set of all
$\Delta ^r$
is the set of all
 $\boldsymbol {\alpha } \in \mathbb {R}^r$
with
$\boldsymbol {\alpha } \in \mathbb {R}^r$
with
 $\alpha _i> 0$
for all
$\alpha _i> 0$
for all
 $i \in [r]$
, and
$i \in [r]$
, and
 $\alpha _1 + \ldots + \alpha _r = 1$
.
$\alpha _1 + \ldots + \alpha _r = 1$
.
We may assume that
![]() $r < R(\boldsymbol {k})$
, where
$r < R(\boldsymbol {k})$
, where
![]() $R(\boldsymbol {k})$
is the Ramsey number of
$R(\boldsymbol {k})$
is the Ramsey number of
![]() $\boldsymbol k$
(i.e., the minimum R such that
$\boldsymbol k$
(i.e., the minimum R such that
![]() $K_R$
admits no
$K_R$
admits no
![]() $\boldsymbol k$
-valid s-edge-colouring). Note that the maximum in (1.1) is attained, since
$\boldsymbol k$
-valid s-edge-colouring). Note that the maximum in (1.1) is attained, since
![]() $q(\phi ,\cdot )$
is continuous for each of the finitely many pairs
$q(\phi ,\cdot )$
is continuous for each of the finitely many pairs
![]() $(r,\phi )$
, and
$(r,\phi )$
, and ![]() with the weaker restrictions
with the weaker restrictions
![]() $\alpha _i\geq 0$
for every i and
$\alpha _i\geq 0$
for every i and
![]() $\boldsymbol {\alpha }$
is a (nonempty) compact space. (If the maximum is obtained at
$\boldsymbol {\alpha }$
is a (nonempty) compact space. (If the maximum is obtained at
![]() $(r,\phi ,\boldsymbol {\alpha })$
with some
$(r,\phi ,\boldsymbol {\alpha })$
with some
![]() $\alpha _i=0$
, then we can simply remove i to obtain a solution with smaller r.) We call
$\alpha _i=0$
, then we can simply remove i to obtain a solution with smaller r.) We call
![]() $\phi \in \Phi _2(r;\boldsymbol {k})$
a colour pattern and
$\phi \in \Phi _2(r;\boldsymbol {k})$
a colour pattern and
![]() $\boldsymbol {\alpha } \in \Delta ^r$
a vertex weighting. A triple
$\boldsymbol {\alpha } \in \Delta ^r$
a vertex weighting. A triple
![]() $(r,\phi ,\boldsymbol {\alpha })$
is called optimal if it attains the maximum; that is,
$(r,\phi ,\boldsymbol {\alpha })$
is called optimal if it attains the maximum; that is, ![]() and
and
![]() $q(r,\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Let
$q(r,\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Let ![]() be the set of optimal triples
be the set of optimal triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
. Also let
$(r,\phi ,\boldsymbol {\alpha })$
. Also let
and
In [Reference Pikhurko and Staden10] and [Reference Pikhurko, Staden and Yilma11], we considered Problems
![]() $Q_0,Q_1,Q_2$
which are as Problem
$Q_0,Q_1,Q_2$
which are as Problem
![]() $Q^*$
except we relax
$Q^*$
except we relax
![]() $\alpha _i>0$
to
$\alpha _i>0$
to
![]() $\alpha _i \geq 0$
and Problem
$\alpha _i \geq 0$
and Problem
![]() $Q_t$
considers feasible
$Q_t$
considers feasible
![]() $\phi \in \Phi _t(r;\boldsymbol {k})$
, where
$\phi \in \Phi _t(r;\boldsymbol {k})$
, where
 $$ \begin{align*}\Phi_t(r;\boldsymbol{k}) := \left\{ \phi: \binom{[r]}{2} \to 2^{[s]} : \phi^{-1}(c) \text{ is }K_{k_c}\text{-free } \forall c \in [s], |\phi(ij)| \geq t \ \forall ij \in \binom{[r]}{2}\right\} \end{align*} $$
$$ \begin{align*}\Phi_t(r;\boldsymbol{k}) := \left\{ \phi: \binom{[r]}{2} \to 2^{[s]} : \phi^{-1}(c) \text{ is }K_{k_c}\text{-free } \forall c \in [s], |\phi(ij)| \geq t \ \forall ij \in \binom{[r]}{2}\right\} \end{align*} $$
(and
![]() $q(\phi ,\boldsymbol {\alpha })$
only sums over pairs
$q(\phi ,\boldsymbol {\alpha })$
only sums over pairs
![]() $ij$
with
$ij$
with
![]() $\phi (ij) \neq \emptyset $
). It is not hard to show that the optimal value of each problem is the same. Clearly, Problem
$\phi (ij) \neq \emptyset $
). It is not hard to show that the optimal value of each problem is the same. Clearly, Problem
![]() $Q^*$
has the smallest feasible set. However, we will sometimes consider also for
$Q^*$
has the smallest feasible set. However, we will sometimes consider also for
![]() $t=0,1$
the set
$t=0,1$
the set ![]() of triples
of triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
with
$(r,\phi ,\boldsymbol {\alpha })$
with
![]() $\boldsymbol {\alpha } \in \Delta ^r$
and
$\boldsymbol {\alpha } \in \Delta ^r$
and
![]() $\phi \in \Phi _t(r;\boldsymbol {k})$
which attain the maximum value. We write
$\phi \in \Phi _t(r;\boldsymbol {k})$
which attain the maximum value. We write
![]() $\| \boldsymbol {a}-\boldsymbol {b}\|_1 := \sum _i|a_i-b_i|$
for the
$\| \boldsymbol {a}-\boldsymbol {b}\|_1 := \sum _i|a_i-b_i|$
for the
![]() $\ell ^1$
-distance between finite tuples
$\ell ^1$
-distance between finite tuples
![]() $\boldsymbol {a}$
and
$\boldsymbol {a}$
and
![]() $\boldsymbol {b}$
of real numbers (where in the sum we add trailing
$\boldsymbol {b}$
of real numbers (where in the sum we add trailing
![]() $0$
’s to make
$0$
’s to make
![]() $\boldsymbol {a},\boldsymbol {b}$
equal length). In this paper, we always take
$\boldsymbol {a},\boldsymbol {b}$
equal length). In this paper, we always take
![]() $\log $
to the base
$\log $
to the base
![]() $2$
; from now on, we omit any subscript. We define
$2$
; from now on, we omit any subscript. We define
![]() $\mathbb {N} := \{1,2,3,\ldots \}$
.
$\mathbb {N} := \{1,2,3,\ldots \}$
.
The goal of this series of works has been to verify the following meta-conjecture:
-
To solve the Erdős-Rothschild problem, it suffices to solve Problem
 $Q^*$
.
$Q^*$
.
The main result of the present paper is that to determine
![]() $F(n;\boldsymbol {k})$
exactly, it suffices to solve the optimisation problem, when
$F(n;\boldsymbol {k})$
exactly, it suffices to solve the optimisation problem, when
![]() $\boldsymbol {k}$
satisfies a certain condition. This improves the main result of our previous paper [Reference Pikhurko and Staden10] which had ‘approximately’ in place of ‘exactly’ – we use the results of [Reference Pikhurko and Staden10] as a crucial tool in the present paper. In [Reference Pikhurko, Staden and Yilma11], we proved with Yilma that for every
$\boldsymbol {k}$
satisfies a certain condition. This improves the main result of our previous paper [Reference Pikhurko and Staden10] which had ‘approximately’ in place of ‘exactly’ – we use the results of [Reference Pikhurko and Staden10] as a crucial tool in the present paper. In [Reference Pikhurko, Staden and Yilma11], we proved with Yilma that for every
![]() $n \in \mathbb {N}$
, at least one of the
$n \in \mathbb {N}$
, at least one of the
![]() $\boldsymbol {k}$
-extremal graphs of order n is complete multipartite, and that
$\boldsymbol {k}$
-extremal graphs of order n is complete multipartite, and that
 $$ \begin{align} F(n;\boldsymbol{k}) = 2^{Q(\boldsymbol{k})\binom{n}{2}+o(n^2)}, \quad\text{ so }F(\boldsymbol{k})=Q(\boldsymbol{k}),\text{ where }\quad F(\boldsymbol{k}) := \lim_{n\to\infty}\frac{\log_2 F(n;\boldsymbol{k})}{\binom{n}{2}}. \end{align} $$
$$ \begin{align} F(n;\boldsymbol{k}) = 2^{Q(\boldsymbol{k})\binom{n}{2}+o(n^2)}, \quad\text{ so }F(\boldsymbol{k})=Q(\boldsymbol{k}),\text{ where }\quad F(\boldsymbol{k}) := \lim_{n\to\infty}\frac{\log_2 F(n;\boldsymbol{k})}{\binom{n}{2}}. \end{align} $$
In [Reference Pikhurko and Staden10], we proved a stability theorem for
![]() $\boldsymbol {k}$
satisfying a certain condition which we call the extension property. This is a property of optimal solutions that says an infinitesimal part added onto such a solution in an optimal way must look like a clone of an existing part.
$\boldsymbol {k}$
satisfying a certain condition which we call the extension property. This is a property of optimal solutions that says an infinitesimal part added onto such a solution in an optimal way must look like a clone of an existing part.
Definition 1.2 (Clones and extension property)
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Given
$\boldsymbol {k} \in \mathbb {N}^s$
. Given
![]() $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
, say that
$\phi \in \Phi _0(r;\boldsymbol {k})$
, say that
![]() $i \in [r]$
is
$i \in [r]$
is
-
○ a clone of
 $j \in [r]\setminus \{ i \}$
(under
$j \in [r]\setminus \{ i \}$
(under
 $\phi $
) if
$\phi $
) if
 $\phi (ik) = \phi (jk)$
for all
$\phi (ik) = \phi (jk)$
for all
 $k \in [r] \setminus \{ i,j\}$
and
$k \in [r] \setminus \{ i,j\}$
and
 $|\phi (ij)| \leq 1$
;
$|\phi (ij)| \leq 1$
; -
○ a strong clone of j if additionally
 $\phi (ij) = \emptyset $
.
$\phi (ij) = \emptyset $
.
We say that
![]() $\boldsymbol {k}$
has
$\boldsymbol {k}$
has
-
○ the extension property if, for every
 and
and
 $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
such that
 $\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
$\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
 $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
, where there exists
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
, where there exists $$ \begin{align*}\mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) := \sum_{\substack{i \in [r^*]\\ \phi(\{i,r^*+1\}) \neq \emptyset}}\alpha^*_i\log|\phi(\{ i,r^*+1 \})|,\end{align*} $$
$$ \begin{align*}\mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) := \sum_{\substack{i \in [r^*]\\ \phi(\{i,r^*+1\}) \neq \emptyset}}\alpha^*_i\log|\phi(\{ i,r^*+1 \})|,\end{align*} $$
 $j \in [r^*]$
such that
$j \in [r^*]$
such that
 $r^*+1$
is a clone of j under
$r^*+1$
is a clone of j under
 $\phi $
;
$\phi $
;
-
○ the strong extension property if, in fact,
 $r^*+1$
is a strong clone of j.
$r^*+1$
is a strong clone of j.
The strong extension property holds in all but one of the cases where the problem has been solved (this was proved in [Reference Pikhurko and Staden10] apart from in the case
![]() $(3;6)$
which we include in the present paper).
$(3;6)$
which we include in the present paper).
Lemma 1.3. Every
![]() $\boldsymbol {k}$
in Theorem 1.1 apart from
$\boldsymbol {k}$
in Theorem 1.1 apart from
![]() $(3;5)$
has the strong extension property.
$(3;5)$
has the strong extension property.
The stability theorem says that whenever
![]() $\boldsymbol {k}$
has the extension property, every almost extremal graph – that is, G on n vertices such that
$\boldsymbol {k}$
has the extension property, every almost extremal graph – that is, G on n vertices such that
![]() $F(G;\boldsymbol {k})=F(n;\boldsymbol {k})\cdot 2^{o(n^2)}$
– looks like the blow-up of an optimal solution to Problem
$F(G;\boldsymbol {k})=F(n;\boldsymbol {k})\cdot 2^{o(n^2)}$
– looks like the blow-up of an optimal solution to Problem
![]() $Q^*$
. (For a definition of a
$Q^*$
. (For a definition of a
![]() $(\delta ,d)$
-regular pair, see Section 2.1.)
$(\delta ,d)$
-regular pair, see Section 2.1.)
Theorem 1.4 (Stability [Reference Pikhurko and Staden10, Theorem 1.4])
Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1\geq \ldots \geq k_s$
has the extension property. Then for all
$k_1\geq \ldots \geq k_s$
has the extension property. Then for all
![]() $\delta> 0$
, there exist
$\delta> 0$
, there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() ${\varepsilon }> 0$
such that the following holds. Let G be a graph on
${\varepsilon }> 0$
such that the following holds. Let G be a graph on
![]() $n \geq n_0$
vertices such that
$n \geq n_0$
vertices such that
 $$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
Then, for at least
![]() $(1-2^{-{\varepsilon } n^2})\cdot F(G;\boldsymbol {k})$
colourings
$(1-2^{-{\varepsilon } n^2})\cdot F(G;\boldsymbol {k})$
colourings
![]() $\chi : E(G) \rightarrow [s]$
which are
$\chi : E(G) \rightarrow [s]$
which are
![]() $\boldsymbol {k}$
-valid, there are
$\boldsymbol {k}$
-valid, there are ![]() and a partition
and a partition
![]() $Y_1 \cup \ldots \cup Y_{r^*} = V(G)$
such that the following hold.
$Y_1 \cup \ldots \cup Y_{r^*} = V(G)$
such that the following hold.
-
(i) For all
 $i \in [r^*]$
, we have that
$i \in [r^*]$
, we have that
 $|\,|Y_i| - \alpha ^*_in\,| < 1$
.
$|\,|Y_i| - \alpha ^*_in\,| < 1$
. -
(ii) for all
 $c \in \phi ^*(ij)$
and
$c \in \phi ^*(ij)$
and
 $ij \in \binom {[r^*]}{2}$
, we have that
$ij \in \binom {[r^*]}{2}$
, we have that
 $\chi ^{-1}(c)[Y_i,Y_j]$
is
$\chi ^{-1}(c)[Y_i,Y_j]$
is
 $(\delta ,|\phi ^*(ij)|^{-1})$
-regular. In particular,
$(\delta ,|\phi ^*(ij)|^{-1})$
-regular. In particular,
 $e_G(Y_i,Y_j) \geq (1-s\delta )|Y_i||Y_j|$
.
$e_G(Y_i,Y_j) \geq (1-s\delta )|Y_i||Y_j|$
. -
(iii) Suppose
 $\sum _{i \in [r^*]}e(G[Y_i])> \delta n^2$
. Then
$\sum _{i \in [r^*]}e(G[Y_i])> \delta n^2$
. Then
 $\boldsymbol {k}$
does not have the strong extension property, and all but at most
$\boldsymbol {k}$
does not have the strong extension property, and all but at most
 $\delta n^2$
edges in
$\delta n^2$
edges in
 $\bigcup _{i \in [r^*]}G[Y_i]$
are coloured with
$\bigcup _{i \in [r^*]}G[Y_i]$
are coloured with
 $1$
under
$1$
under
 $\chi $
. Moreover, if
$\chi $
. Moreover, if
 $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that at least
$\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that at least
 $\delta n^2$
edges need to be removed from
$\delta n^2$
edges need to be removed from
 $G[Y_i]$
to make it
$G[Y_i]$
to make it
 $K_{\ell _i}$
-free, then
$K_{\ell _i}$
-free, then
 $\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
$\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
The following corollary is a simple consequence of Theorem 1.4 and shows that when
![]() $\boldsymbol {k}$
has the strong extension property, every asymptotically extremal graph is close to complete partite.
$\boldsymbol {k}$
has the strong extension property, every asymptotically extremal graph is close to complete partite.
Corollary 1.5 (Stability for the strong extension property [Reference Pikhurko and Staden10, Corollary 1.5])
Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1\geq \ldots \geq k_s$
has the strong extension property. Then for all
$k_1\geq \ldots \geq k_s$
has the strong extension property. Then for all
![]() $\delta> 0$
, there exist
$\delta> 0$
, there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() ${\varepsilon }> 0$
such that the following holds. Let G be a graph on
${\varepsilon }> 0$
such that the following holds. Let G be a graph on
![]() $n \geq n_0$
vertices such that
$n \geq n_0$
vertices such that
 $$ \begin{align*}\frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k}) - {\varepsilon}. \end{align*} $$
$$ \begin{align*}\frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k}) - {\varepsilon}. \end{align*} $$
Then there are ![]() and a partition V(G) =
and a partition V(G) =
![]() $V_1 \cup \ldots \cup V_{r^*}$
with
$V_1 \cup \ldots \cup V_{r^*}$
with
![]() $\left |\,|V_i|-\alpha ^*_i n \,\right | < 1$
for all
$\left |\,|V_i|-\alpha ^*_i n \,\right | < 1$
for all
![]() $i \in [r^*]$
such that the number of adjacencies in G that need to be changed to obtain
$i \in [r^*]$
such that the number of adjacencies in G that need to be changed to obtain
![]() $K[V_1,\ldots ,V_{r^*}]$
is at most
$K[V_1,\ldots ,V_{r^*}]$
is at most
![]() $\delta n^2$
. Moreover, for at least
$\delta n^2$
. Moreover, for at least
![]() $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) \boldsymbol {k}$
-valid s-edge-colourings
$(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) \boldsymbol {k}$
-valid s-edge-colourings
![]() $\chi $
of G, there exists
$\chi $
of G, there exists ![]() such that
such that
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
and
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
and
![]() $\chi ^{-1}(c)[V_i,V_j]$
is
$\chi ^{-1}(c)[V_i,V_j]$
is
![]() $(\delta ,|\phi ^*(ij)|^{-1})$
-regular for all
$(\delta ,|\phi ^*(ij)|^{-1})$
-regular for all
![]() $ij \in \binom {[r^*]}{2}$
and
$ij \in \binom {[r^*]}{2}$
and
![]() $c \in \phi ^*(ij)$
.
$c \in \phi ^*(ij)$
.
1.1. A general exact result
Our first main result is an exact version of Corollary 1.5 – that is, an exact result for
![]() $\boldsymbol {k}$
with the strong extension property. One consequence of this result is that for such
$\boldsymbol {k}$
with the strong extension property. One consequence of this result is that for such
![]() $\boldsymbol {k}$
, every large
$\boldsymbol {k}$
, every large
![]() $\boldsymbol {k}$
-extremal graph is complete partite.
$\boldsymbol {k}$
-extremal graph is complete partite.
Indeed, we prove that every large
![]() $\boldsymbol {k}$
-extremal graph
$\boldsymbol {k}$
-extremal graph
![]() $G^*$
is a complete
$G^*$
is a complete
![]() $r^*$
-partite graph, whose classes
$r^*$
-partite graph, whose classes
![]() $X_1,\ldots , X_{r^*}$
are approximately
$X_1,\ldots , X_{r^*}$
are approximately
![]() $\boldsymbol {\alpha }^*$
-weighted, for some
$\boldsymbol {\alpha }^*$
-weighted, for some ![]() . Moreover, almost every
. Moreover, almost every
![]() $\boldsymbol {k}$
-valid colouring
$\boldsymbol {k}$
-valid colouring
![]() $\chi $
of
$\chi $
of
![]() $G^*$
is perfect (with respect to
$G^*$
is perfect (with respect to
![]() $(\phi ;X_1,\ldots ,X_{r^*})$
), which means that there is a pattern
$(\phi ;X_1,\ldots ,X_{r^*})$
), which means that there is a pattern ![]() for some
for some
![]() $\boldsymbol {\alpha }$
close to
$\boldsymbol {\alpha }$
close to
![]() $\boldsymbol {\alpha }^*$
so that every edge e between
$\boldsymbol {\alpha }^*$
so that every edge e between
![]() $X_i$
and
$X_i$
and
![]() $X_j$
in
$X_j$
in
![]() $G^*$
satisfies
$G^*$
satisfies
![]() $\chi (e) \in \phi (ij)$
.
$\chi (e) \in \phi (ij)$
.
Theorem 1.6 (Exactness for the strong extension property)
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
have the strong extension property. Then for all
$\boldsymbol {k} \in \mathbb {N}^s$
have the strong extension property. Then for all
![]() ${\varepsilon }> 0$
, there exist
${\varepsilon }> 0$
, there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $n_0 \in \mathbb {N}$
such that whenever G is a
$n_0 \in \mathbb {N}$
such that whenever G is a
![]() $\boldsymbol {k}$
-extremal graph on
$\boldsymbol {k}$
-extremal graph on
![]() $n \geq n_0$
vertices, the following hold.
$n \geq n_0$
vertices, the following hold.
-
(i) G is a complete multipartite graph; more precisely, there exist
 and
and
 $\boldsymbol {\beta } \in \Delta ^{r^*}$
with
$\boldsymbol {\beta } \in \Delta ^{r^*}$
with
 $\| \boldsymbol {\alpha }^*-\boldsymbol {\beta }\|_1 < {\varepsilon }$
such that
$\| \boldsymbol {\alpha }^*-\boldsymbol {\beta }\|_1 < {\varepsilon }$
such that
 $G = K(X_1,\ldots ,X_{r^*})$
, where
$G = K(X_1,\ldots ,X_{r^*})$
, where
 $|X_i| = \beta _i n$
for all
$|X_i| = \beta _i n$
for all
 $i \in [r^*]$
;
$i \in [r^*]$
; -
(ii) for at least
 $(1-2^{-\delta n})\cdot F(G;\boldsymbol {k}) \boldsymbol {k}$
-valid colourings
$(1-2^{-\delta n})\cdot F(G;\boldsymbol {k}) \boldsymbol {k}$
-valid colourings
 $\chi $
of G, there is
$\chi $
of G, there is  with
with
 $\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 < {\varepsilon }$
and
$\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 < {\varepsilon }$
and  such
such
 $\chi $
is perfect with respect to
$\chi $
is perfect with respect to
 $(\phi ;X_1,\ldots ,X_{r^*})$
.
$(\phi ;X_1,\ldots ,X_{r^*})$
.
We show that by solving a further optimisation problem (which is not too difficult in all known cases), one can determine
![]() $F(n;\boldsymbol {k})$
up to a multiplicative error of
$F(n;\boldsymbol {k})$
up to a multiplicative error of
![]() $1+o(1)$
and also determine the extremal graphs – whenever the solution(s) of Problem
$1+o(1)$
and also determine the extremal graphs – whenever the solution(s) of Problem
![]() $Q^*$
are known. Thus, for
$Q^*$
are known. Thus, for
![]() $\boldsymbol {k}$
with the strong extension property, it is true that ‘to solve the Erdős-Rothschild problem, it suffices to solve Problem
$\boldsymbol {k}$
with the strong extension property, it is true that ‘to solve the Erdős-Rothschild problem, it suffices to solve Problem
![]() $Q^*$
’. Theorem 1.6 allows us to systematically recover all known exact results for the Erdős-Rothschild problem.
$Q^*$
’. Theorem 1.6 allows us to systematically recover all known exact results for the Erdős-Rothschild problem.
Problem 1.7 (Perfect colouring problem)
Let ![]() and
and
![]() $n \in \mathbb {N}$
. Maximise
$n \in \mathbb {N}$
. Maximise

subject to
![]() $\boldsymbol {m} \in P_{r^*}(n)$
, where
$\boldsymbol {m} \in P_{r^*}(n)$
, where
![]() $P_{r^*}(n)$
is the set of
$P_{r^*}(n)$
is the set of
![]() $\boldsymbol {m} \in \mathbb {N}^{r^*}$
with
$\boldsymbol {m} \in \mathbb {N}^{r^*}$
with
![]() $\|\boldsymbol {m}\|_1 = n$
and
$\|\boldsymbol {m}\|_1 = n$
and
![]() $m_1\geq \ldots \geq m_{r^*}$
.
$m_1\geq \ldots \geq m_{r^*}$
.
Notice that
![]() $\mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m})$
is essentially the number of perfect colourings of a complete
$\mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m})$
is essentially the number of perfect colourings of a complete
![]() $r^*$
-partite graph
$r^*$
-partite graph
![]() $K_{\boldsymbol {m}}$
with vertex classes of size
$K_{\boldsymbol {m}}$
with vertex classes of size
![]() $m_1,\ldots ,m_{r^*}$
(with some overcounting due to, for example, distinct
$m_1,\ldots ,m_{r^*}$
(with some overcounting due to, for example, distinct
![]() $\phi ,\phi '$
with
$\phi ,\phi '$
with
![]() $\phi (ij)\cap \phi '(ij) \neq \emptyset $
for all
$\phi (ij)\cap \phi '(ij) \neq \emptyset $
for all
![]() $ij \in \binom {[r^*]}{2}$
). However, being able to solve the perfect colouring problem may not a priori allow one to precisely determine the
$ij \in \binom {[r^*]}{2}$
). However, being able to solve the perfect colouring problem may not a priori allow one to precisely determine the
![]() $\boldsymbol {k}$
-extremal graphs. Indeed, since not every colouring of G is perfect, a graph with the maximal number of perfect colourings may not be
$\boldsymbol {k}$
-extremal graphs. Indeed, since not every colouring of G is perfect, a graph with the maximal number of perfect colourings may not be
![]() $\boldsymbol {k}$
-extremal if there is another graph with only slightly fewer. For this reason, we make the following definition.
$\boldsymbol {k}$
-extremal if there is another graph with only slightly fewer. For this reason, we make the following definition.
Definition 1.8 (Solubility of
 $\boldsymbol {k}$
)
$\boldsymbol {k}$
)
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. We say that
$\boldsymbol {k} \in \mathbb {N}^s$
. We say that
![]() $\boldsymbol {k}$
is soluble if there exist
$\boldsymbol {k}$
is soluble if there exist
![]() $c> 0$
and
$c> 0$
and
![]() $n_0 \in \mathbb {N}$
, such that for all
$n_0 \in \mathbb {N}$
, such that for all
![]() $n \geq n_0$
, there are
$n \geq n_0$
, there are ![]() and
and
![]() $\boldsymbol {m}^* \in P_{r^*}(n)$
such that for all
$\boldsymbol {m}^* \in P_{r^*}(n)$
such that for all ![]() , we have
, we have
for all
![]() $\boldsymbol {m} \in P_{r'}(n)$
for which
$\boldsymbol {m} \in P_{r'}(n)$
for which
![]() $(r^*,\boldsymbol {\alpha }^*,\boldsymbol {m}^*)$
is distinct from
$(r^*,\boldsymbol {\alpha }^*,\boldsymbol {m}^*)$
is distinct from
![]() $(r',\boldsymbol {\alpha }',\boldsymbol {m})$
. We say that
$(r',\boldsymbol {\alpha }',\boldsymbol {m})$
. We say that
![]() $\boldsymbol {m}^*$
is the supersolution to
$\boldsymbol {m}^*$
is the supersolution to
![]() $\boldsymbol {k}$
at n and write
$\boldsymbol {k}$
at n and write
![]() $\mathrm {perf}(\boldsymbol {m}^*) := \mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m}^*)$
.
$\mathrm {perf}(\boldsymbol {m}^*) := \mathrm {perf}_{r^*,\boldsymbol {\alpha }^*}(\boldsymbol {m}^*)$
.
Theorem 1.6(i) implies that every
![]() $\boldsymbol {k}$
-extremal graph G on
$\boldsymbol {k}$
-extremal graph G on
![]() $n \geq n_0$
vertices is such that there is some
$n \geq n_0$
vertices is such that there is some
![]() $\boldsymbol {m} \in \mathbb {N}^{r^*}$
with
$\boldsymbol {m} \in \mathbb {N}^{r^*}$
with
![]() $\|\boldsymbol {m}-\boldsymbol {\alpha }^*n\|_1 < {\varepsilon } n$
so that
$\|\boldsymbol {m}-\boldsymbol {\alpha }^*n\|_1 < {\varepsilon } n$
so that
![]() $G \cong K_{m_1,\ldots ,m_{r^*}}$
. If
$G \cong K_{m_1,\ldots ,m_{r^*}}$
. If
![]() $\boldsymbol {k}$
is soluble, then Theorem 1.6(ii) implies that for all large n and all
$\boldsymbol {k}$
is soluble, then Theorem 1.6(ii) implies that for all large n and all
![]() $m_1+\ldots +m_{r^*}=n$
, we have
$m_1+\ldots +m_{r^*}=n$
, we have
![]() $F(K_{m_1^*,\ldots ,m_{r^*}^*},n)> F(K_{m_1,\ldots ,m_{r^*}},n)$
, where
$F(K_{m_1^*,\ldots ,m_{r^*}^*},n)> F(K_{m_1,\ldots ,m_{r^*}},n)$
, where
![]() $\boldsymbol {m}^*$
is the supersolution at n and
$\boldsymbol {m}^*$
is the supersolution at n and
![]() $(m_1,\ldots ,m_{r^*}) \neq (m_1^*,\ldots ,m_{r^*}^*)$
. This gives the following corollary:
$(m_1,\ldots ,m_{r^*}) \neq (m_1^*,\ldots ,m_{r^*}^*)$
. This gives the following corollary:
Corollary 1.9 (Perfect exactness for the strong extension property)
Let
![]() $s \in \mathbb {N}$
and let
$s \in \mathbb {N}$
and let
![]() $\boldsymbol {k} \in \mathbb {N}^s$
be soluble and have the strong extension property. Then
$\boldsymbol {k} \in \mathbb {N}^s$
be soluble and have the strong extension property. Then
and there exists
![]() $n_0 \in \mathbb {N}$
such that for all
$n_0 \in \mathbb {N}$
such that for all
![]() $n \geq n_0$
, the unique
$n \geq n_0$
, the unique
![]() $\boldsymbol {k}$
-extremal graph on n vertices is
$\boldsymbol {k}$
-extremal graph on n vertices is
![]() $K_{\boldsymbol {m}_n^*}$
, where
$K_{\boldsymbol {m}_n^*}$
, where
![]() $\boldsymbol {m}^*_n$
is the supersolution to
$\boldsymbol {m}^*_n$
is the supersolution to
![]() $\boldsymbol {k}$
at n.
$\boldsymbol {k}$
at n.
1.2. The triangle problem
Our second main result concerns the case
![]() $\boldsymbol {k}=(3;s)$
(Erdős and Rothschild’s original problem was
$\boldsymbol {k}=(3;s)$
(Erdős and Rothschild’s original problem was
![]() $s=2$
). Previously,
$s=2$
). Previously,
![]() $F(n;\boldsymbol {k})$
had been determined for
$F(n;\boldsymbol {k})$
had been determined for
![]() $s=2,3,4,6$
and asymptotically for
$s=2,3,4,6$
and asymptotically for
![]() $s=5$
. We solve the problem for
$s=5$
. We solve the problem for
![]() $s=7$
and use the same method to give a new proof for
$s=7$
and use the same method to give a new proof for
![]() $s=6$
.
$s=6$
.
Theorem 1.11. There exists
![]() $n_0>0$
such that for every
$n_0>0$
such that for every
![]() $n \geq n_0$
, the Turán graph
$n \geq n_0$
, the Turán graph
![]() $T_8(n)$
is the unique
$T_8(n)$
is the unique
![]() $(3;6)$
-extremal graph, and the unique
$(3;6)$
-extremal graph, and the unique
![]() $(3;7)$
-extremal graph.
$(3;7)$
-extremal graph.
In fact, our results imply that
where C is a constant and
![]() $C_j$
is a constant depending only on the remainder j when n is divided by
$C_j$
is a constant depending only on the remainder j when n is divided by
![]() $8$
. These constants can be explicitly determined if desired.
$8$
. These constants can be explicitly determined if desired.
A key component in our proof is our general exact result, Corollary 1.9, which reduces the task to solving Problem
![]() $Q^*$
. For other cases of
$Q^*$
. For other cases of
![]() $\boldsymbol {k}$
, Problem
$\boldsymbol {k}$
, Problem
![]() $Q^*$
has been solved by considering a linear relaxation, with variables which are essentially graph densities, and linear constraints which replace combinatorial constraints such as being
$Q^*$
has been solved by considering a linear relaxation, with variables which are essentially graph densities, and linear constraints which replace combinatorial constraints such as being
![]() $K_k$
-free by the associated density bound given by Turán’s theorem. However, the solutions to this relaxation generally do not correspond to feasible solutions to Problem
$K_k$
-free by the associated density bound given by Turán’s theorem. However, the solutions to this relaxation generally do not correspond to feasible solutions to Problem
![]() $Q^*$
, so additional constraints are needed. The main new ingredient is a lemma about the density of the union of two dense triangle-free graphs (Lemma 3.3), which may be of independent interest. This allows us to introduce a new constraint which yields a meaningful solution.
$Q^*$
, so additional constraints are needed. The main new ingredient is a lemma about the density of the union of two dense triangle-free graphs (Lemma 3.3), which may be of independent interest. This allows us to introduce a new constraint which yields a meaningful solution.
In the known cases of the triangle problem, the perfect colourings of extremal graphs are closely related to Hadamard matrices. A Hadamard matrix H of order n is an
![]() $n \times n$
matrix with entries in
$n \times n$
matrix with entries in
![]() $\{ -1,+1 \}$
such that
$\{ -1,+1 \}$
such that
![]() $HH^\intercal = nI_n$
. A Hadamard matrix of order n exists only if
$HH^\intercal = nI_n$
. A Hadamard matrix of order n exists only if
![]() $n=1,2$
or n is divisble by
$n=1,2$
or n is divisble by
![]() $4$
; that this is sufficient was conjectured by Hadamard in 1893 [Reference Hadamard7]. This conjecture remains open – at the time of writing, the smallest multiple of
$4$
; that this is sufficient was conjectured by Hadamard in 1893 [Reference Hadamard7]. This conjecture remains open – at the time of writing, the smallest multiple of
![]() $4$
for which order there is no known Hadamard matrix is
$4$
for which order there is no known Hadamard matrix is
![]() $4\times 167$
. It is, however, easy to construct arbitrarily large Hadamard matrices by using smaller ones as building blocks. For example, Sylvester (see, for example, [Reference Sylvester13]) observed that if H is a Hadamard matrix, then so is
$4\times 167$
. It is, however, easy to construct arbitrarily large Hadamard matrices by using smaller ones as building blocks. For example, Sylvester (see, for example, [Reference Sylvester13]) observed that if H is a Hadamard matrix, then so is
![]() $\left (\begin {smallmatrix} H & H\\ H & -H \end {smallmatrix}\right )$
. Hadamard matrices have the largest absolute value of the determinant among all complex square matrices with entries of absolute value at most one (see, for example, [Reference Hadamard7]).
$\left (\begin {smallmatrix} H & H\\ H & -H \end {smallmatrix}\right )$
. Hadamard matrices have the largest absolute value of the determinant among all complex square matrices with entries of absolute value at most one (see, for example, [Reference Hadamard7]).
The connection to Problem
![]() $Q^*(3;s)$
is that there is a decomposition of the multigraph
$Q^*(3;s)$
is that there is a decomposition of the multigraph
![]() $2t K_{4t}$
into copies of
$2t K_{4t}$
into copies of
![]() $K_{2t,2t}$
if and only if a Hadamard matrix of order
$K_{2t,2t}$
if and only if a Hadamard matrix of order
![]() $4t$
exists (and the locations of the copies can be read off the matrix); see [Reference de Caen, Gregory and Pritikin3] or Lemma 3.6 for a proof. It is plausible that in an optimal
$4t$
exists (and the locations of the copies can be read off the matrix); see [Reference de Caen, Gregory and Pritikin3] or Lemma 3.6 for a proof. It is plausible that in an optimal
![]() $(2r,\phi ,\boldsymbol {\alpha })$
, every
$(2r,\phi ,\boldsymbol {\alpha })$
, every
![]() $\phi ^{-1}(c) \cong K_{r,r}$
, and
$\phi ^{-1}(c) \cong K_{r,r}$
, and
![]() $\boldsymbol {\alpha }$
is uniform (and also plausible that the number of vertices in an optimal solution is even). If also
$\boldsymbol {\alpha }$
is uniform (and also plausible that the number of vertices in an optimal solution is even). If also
![]() $|\phi (ij)|=p$
for all pairs
$|\phi (ij)|=p$
for all pairs
![]() $ij$
, then such a solution exists if and only if
$ij$
, then such a solution exists if and only if
![]() $p K_{2r}$
has a decomposition into copies of
$p K_{2r}$
has a decomposition into copies of
![]() $K_{r,r}$
. Comparing edge counts, the number of copies is
$K_{r,r}$
. Comparing edge counts, the number of copies is
![]() $s=p\binom {2r}{2}/r^2=p(2r-1)/r$
. So
$s=p\binom {2r}{2}/r^2=p(2r-1)/r$
. So
![]() $p = tr$
for some integer t, since r and
$p = tr$
for some integer t, since r and
![]() $2r-1$
are coprime for
$2r-1$
are coprime for
![]() $r \geq 2$
. If
$r \geq 2$
. If
![]() $t=1$
, then
$t=1$
, then
![]() $r=2\ell $
for some integer
$r=2\ell $
for some integer
![]() $\ell $
, since otherwise there is no decomposition due to the nonexistence of the corresponding Hadamard matrix. So
$\ell $
, since otherwise there is no decomposition due to the nonexistence of the corresponding Hadamard matrix. So ![]() , where
, where
![]() $|\phi _{4\ell -1}(ij)|=2\ell $
for all
$|\phi _{4\ell -1}(ij)|=2\ell $
for all
![]() $ij$
and
$ij$
and
![]() $\boldsymbol {u}$
is uniform. For
$\boldsymbol {u}$
is uniform. For
![]() $i=1,2,3$
,
$i=1,2,3$
, ![]() , where
, where
![]() $\phi _{4\ell -1}^{-i}$
is obtained from
$\phi _{4\ell -1}^{-i}$
is obtained from
![]() $\phi _{4\ell -1}$
by removing i colours. Also,
$\phi _{4\ell -1}$
by removing i colours. Also, ![]() , where
, where
![]() $\phi _{4\ell -5}^{+4-i}$
is obtained from
$\phi _{4\ell -5}^{+4-i}$
is obtained from
![]() $\phi _{4\ell -5}$
by duplicating
$\phi _{4\ell -5}$
by duplicating
![]() $4-i$
colours.
$4-i$
colours.
This suggests the following problem, which would probably be very difficult to resolve.
Problem 1.12. Are the following true for sufficiently large n: For all
![]() $\ell \geq 2$
, is the unique
$\ell \geq 2$
, is the unique
![]() $(3;4\ell -1)$
-extremal graph
$(3;4\ell -1)$
-extremal graph
![]() $T_{4\ell }(n)$
? For all
$T_{4\ell }(n)$
? For all
![]() $\ell \geq 2$
, is
$\ell \geq 2$
, is
![]() $T_{4(\ell -1)}(n)$
or
$T_{4(\ell -1)}(n)$
or
![]() $T_{4\ell }(n)$
one of the
$T_{4\ell }(n)$
one of the
![]() $(3;4\ell -1-i)$
-extremal graphs for all
$(3;4\ell -1-i)$
-extremal graphs for all
![]() $i=1,2,3$
?
$i=1,2,3$
?
All existing results fit the pattern described (see Subsection 3.4).
1.3. The two colour problem
Having proved a general exact result for the case when
![]() $\boldsymbol {k}$
has the strong extension property, we now investigate what happens when
$\boldsymbol {k}$
has the strong extension property, we now investigate what happens when
![]() $\boldsymbol {k}$
has the extension property but not the strong extension property (we will say that such
$\boldsymbol {k}$
has the extension property but not the strong extension property (we will say that such
![]() $\boldsymbol {k}$
have the weak extension property). This appears to be much more difficult. The reason for this is the possible presence of small parts in a complete multipartite extremal graph (when
$\boldsymbol {k}$
have the weak extension property). This appears to be much more difficult. The reason for this is the possible presence of small parts in a complete multipartite extremal graph (when
![]() $\boldsymbol {k}$
has the strong extension property, no part has size
$\boldsymbol {k}$
has the strong extension property, no part has size
![]() $o(n)$
(see Lemma 2.2(i))). In a perfect colouring, only the neighbourhood into a large part is controlled, and we have a priori no information about colourings between small parts. However, it could be the case that this part of the colouring is forced by the perfect colouring in the rest of the graph, and thus, the number of small parts can also be controlled.
$o(n)$
(see Lemma 2.2(i))). In a perfect colouring, only the neighbourhood into a large part is controlled, and we have a priori no information about colourings between small parts. However, it could be the case that this part of the colouring is forced by the perfect colouring in the rest of the graph, and thus, the number of small parts can also be controlled.
In our final theorem, we consider the simplest case when
![]() $\boldsymbol {k}$
has the weak extension property – namely,
$\boldsymbol {k}$
has the weak extension property – namely,
![]() $\boldsymbol {k} = (k+1,k)$
for
$\boldsymbol {k} = (k+1,k)$
for
![]() $k \geq 3$
. For small k, we determine the (unique)
$k \geq 3$
. For small k, we determine the (unique)
![]() $(k+1,k)$
-extremal graph, which turns out to have a part of size
$(k+1,k)$
-extremal graph, which turns out to have a part of size
![]() $O(k)$
, and the size of this part depends on the value of n modulo
$O(k)$
, and the size of this part depends on the value of n modulo
![]() $k-1$
. The proof is already fairly involved and relies heavily on a strong stability theorem for complete partite graphs (Theorem 2.12), which is the main ingredient in the proof of Theorem 1.6. Similar arguments could probably be used to determine the
$k-1$
. The proof is already fairly involved and relies heavily on a strong stability theorem for complete partite graphs (Theorem 2.12), which is the main ingredient in the proof of Theorem 1.6. Similar arguments could probably be used to determine the
![]() $(k+\ell ,k)$
-extremal graph for (very) small
$(k+\ell ,k)$
-extremal graph for (very) small
![]() $\ell $
and small k, which we discuss further in Section 6.
$\ell $
and small k, which we discuss further in Section 6.
Theorem 1.13. For all integers
![]() $k \geq 3$
, there exists
$k \geq 3$
, there exists
![]() $n_0>0$
such that for all integers
$n_0>0$
such that for all integers
![]() $n \geq n_0$
, we have
$n \geq n_0$
, we have
and every
![]() $(k+1,k)$
-extremal graph is complete k-partite, with one part of size at most
$(k+1,k)$
-extremal graph is complete k-partite, with one part of size at most
![]() $2(k-1)$
and the other part sizes all within
$2(k-1)$
and the other part sizes all within
![]() $2(k-1)$
of each other. Moreover, the constant
$2(k-1)$
of each other. Moreover, the constant
![]() $O_k(1)$
is at least
$O_k(1)$
is at least
![]() $2$
.
$2$
.
(Recall that the results of [Reference Alon, Balogh, Keevash and Sudakov1] imply that
![]() $F(n;k+1,k) \geq F(n;k,k) = 2^{t_{k-1}(n)}$
.) We conjecture that the
$F(n;k+1,k) \geq F(n;k,k) = 2^{t_{k-1}(n)}$
.) We conjecture that the
![]() $O_k(1)$
multiplicative constant has a special form.
$O_k(1)$
multiplicative constant has a special form.
Conjecture 1.14. For all integers
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $0 \leq j \leq k-1$
, there exists
$0 \leq j \leq k-1$
, there exists
![]() $n_0>0$
such that the following holds for all integers
$n_0>0$
such that the following holds for all integers
![]() $n \geq n_0$
. Let
$n \geq n_0$
. Let
 $$ \begin{align*}f(k,j,\ell) := \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1 \end{cases} \end{align*} $$
$$ \begin{align*}f(k,j,\ell) := \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1 \end{cases} \end{align*} $$
and let
![]() $\ell ^*$
be such that
$\ell ^*$
be such that
![]() $\max _{0 \leq \ell \leq k-1}f(k,j,\ell ) = f(k,j,\ell ^*)$
. Then
$\max _{0 \leq \ell \leq k-1}f(k,j,\ell ) = f(k,j,\ell ^*)$
. Then
![]() $\ell ^*$
is unique, and whenever
$\ell ^*$
is unique, and whenever
![]() $n \equiv j (\mod k-1)$
,
$n \equiv j (\mod k-1)$
,
Moreover, the unique
![]() $(k+1,k)$
-extremal graph on n vertices is complete k-partite, with one part of size
$(k+1,k)$
-extremal graph on n vertices is complete k-partite, with one part of size
![]() $\ell ^*$
and the other parts as equal as possible.
$\ell ^*$
and the other parts as equal as possible.
Given Theorem 1.13, it is easy to prove this conjecture for small k, using computer assistance to test each of the possible extremal graphs.
Theorem 1.15. Conjecture 1.14 holds for
![]() $3 \leq k \leq 10$
.
$3 \leq k \leq 10$
.
For example,
![]() $F(n;4,3) = (2+o(1)) \cdot 2^{t_2(n)}$
when n is even and
$F(n;4,3) = (2+o(1)) \cdot 2^{t_2(n)}$
when n is even and
![]() $F(n;4,3) = (\frac {9}{4}+o(1))\cdot 2^{t_2(n)}$
when n is odd; in both cases, the unique extremal graph has parts of size
$F(n;4,3) = (\frac {9}{4}+o(1))\cdot 2^{t_2(n)}$
when n is odd; in both cases, the unique extremal graph has parts of size
![]() $2,\lfloor \frac {n-2}{2}\rfloor ,\lceil \frac {n-2}{2}\rceil $
.
$2,\lfloor \frac {n-2}{2}\rfloor ,\lceil \frac {n-2}{2}\rceil $
.
1.4. Organisation of the paper
In Section 2, we prove Theorem 1.6, which follows from Theorem 2.12, a strong stability theorem for complete partite graphs. Section 3 solves Problem
![]() $Q^*$
in the case when
$Q^*$
in the case when
![]() $s=7$
and
$s=7$
and
![]() $k=3$
. Section 4 contains the proofs of Proposition 1.10 and Theorem 1.11, which follow easily by combining Theorem 1.6 and solving Problem
$k=3$
. Section 4 contains the proofs of Proposition 1.10 and Theorem 1.11, which follow easily by combining Theorem 1.6 and solving Problem
![]() $Q^*$
in the relevant cases. In Section 5, we use the full strength of Theorem 2.12 to prove Theorems 1.13 and 1.15. Section 6 contains some concluding remarks and directions for future research.
$Q^*$
in the relevant cases. In Section 5, we use the full strength of Theorem 2.12 to prove Theorems 1.13 and 1.15. Section 6 contains some concluding remarks and directions for future research.
There are five python programs used in the paper to check various numerical claims (6check.py, 6config.py, 7ext.py, dcheck.py and smallpart.py), which are all written in Python 3. They are included in the ancillary folder of the arXiv version of this paper [Reference Pikhurko and Staden9].
2. A general exact result
The aim of this section is to use Theorem 1.4 to prove Theorem 1.6, a strengthening of Corollary 1.5 for
![]() $\boldsymbol {k}$
with the strong extension property.
$\boldsymbol {k}$
with the strong extension property.
This section is organised as follows. In Subsection 2.1, we collect some tools that we will need, including some lemmas on optimal solutions from [Reference Pikhurko, Staden and Yilma11] and [Reference Pikhurko and Staden10], as well as standard regularity tools. In Subsection 2.2, we define increasingly strict properties of colourings with respect to a partition. The main result of Subsection 2.3 is Theorem 2.12, a version of our stability result (Theorem 1.4) for complete multipartite graphs. The new part of this theorem is the last part which says that if every vertex has large contribution to the number of valid colourings, then there are many ‘perfect’ colourings which follow a colour pattern exactly. In Subsection 2.4, we prove Theorem 1.6.
2.1. Tools
The following are tools concerning Problem
![]() $Q^*$
from the previous papers in this series. Given a triple
$Q^*$
from the previous papers in this series. Given a triple
![]() $(r,\phi ,\boldsymbol {\alpha })$
, we have
$(r,\phi ,\boldsymbol {\alpha })$
, we have
 $$ \begin{align*}q(\phi,\boldsymbol{\alpha}) = \sum_{i \in [r]}\alpha_i q_i(\phi,\boldsymbol{\alpha})\quad\text{where}\quad q_i(\phi,\boldsymbol{\alpha}) := \sum_{\substack{j \in [r] \setminus \{ i \}\\ \phi(ij)\neq\emptyset}}\alpha_j\log|\phi(ij)| \end{align*} $$
$$ \begin{align*}q(\phi,\boldsymbol{\alpha}) = \sum_{i \in [r]}\alpha_i q_i(\phi,\boldsymbol{\alpha})\quad\text{where}\quad q_i(\phi,\boldsymbol{\alpha}) := \sum_{\substack{j \in [r] \setminus \{ i \}\\ \phi(ij)\neq\emptyset}}\alpha_j\log|\phi(ij)| \end{align*} $$
is the normalised contribution of vertex i to the sum
![]() $q(\phi ,\boldsymbol {\alpha })$
.
$q(\phi ,\boldsymbol {\alpha })$
.
Proposition 2.1. Let
![]() $s,r \in \mathbb {N}$
and
$s,r \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. The following hold.
$\boldsymbol {k} \in \mathbb {N}^s$
. The following hold.
-
(i) [Reference Pikhurko, Staden and Yilma11, Proposition 11] Let
 $\phi \in \Phi _0(r;\boldsymbol {k})$
and
$\phi \in \Phi _0(r;\boldsymbol {k})$
and
 $\boldsymbol {\alpha },\boldsymbol {\beta } \in \Delta ^r$
. Then
$\boldsymbol {\alpha },\boldsymbol {\beta } \in \Delta ^r$
. Then  $$ \begin{align*}|q(\phi,\boldsymbol{\alpha})-q(\phi,\boldsymbol{\beta})| < 2\left(\log s\right)\|\boldsymbol{\alpha}-\boldsymbol{\beta}\|_1. \end{align*} $$
$$ \begin{align*}|q(\phi,\boldsymbol{\alpha})-q(\phi,\boldsymbol{\beta})| < 2\left(\log s\right)\|\boldsymbol{\alpha}-\boldsymbol{\beta}\|_1. \end{align*} $$
-
(ii) [Reference Pikhurko and Staden10, Proposition 2.1] Let
 . For every
. For every
 $i \in [r]$
with
$i \in [r]$
with
 $\alpha _i> 0$
, we have that
$\alpha _i> 0$
, we have that
 $ q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k}) $
.
$ q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k}) $
. -
(iii) [Reference Pikhurko and Staden10, Lemma 2.5] Let
 and suppose
and suppose
 $k_1 \geq \ldots \geq k_s$
. Then
$k_1 \geq \ldots \geq k_s$
. Then
 $r^* \geq k_2-1$
and
$r^* \geq k_2-1$
and
 $\phi ^{-1}(c)$
is maximally
$\phi ^{-1}(c)$
is maximally
 $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
 $c \in [s]$
.
$c \in [s]$
.
Lemma 2.2. Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
has the extension property, where
$\boldsymbol {k} \in \mathbb {N}^s$
has the extension property, where
![]() $k_1 \geq \ldots \geq k_s$
. Then the following hold.
$k_1 \geq \ldots \geq k_s$
. Then the following hold.
-
(i) [Reference Pikhurko and Staden10, Lemma 2.8] There exists
 $\mu> 0$
such that
$\mu> 0$
such that
 $\alpha _i^*> \mu $
for all
$\alpha _i^*> \mu $
for all  and
and
 $i \in [r^*]$
.
$i \in [r^*]$
. -
(ii) [Reference Pikhurko and Staden10, Lemma 2.9] There exists
 ${\varepsilon }> 0$
such that the following holds. Let
${\varepsilon }> 0$
such that the following holds. Let  and let
and let
 $\phi ' \in \Phi _0(r^*+1,\boldsymbol {k})$
be such that
$\phi ' \in \Phi _0(r^*+1,\boldsymbol {k})$
be such that
 $\phi '|_{\binom {[r^*]}{2}} = \phi ^*$
and
$\phi '|_{\binom {[r^*]}{2}} = \phi ^*$
and
 $ \mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) \geq Q(\boldsymbol {k}) -{\varepsilon } $
. Then there exists
$ \mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) \geq Q(\boldsymbol {k}) -{\varepsilon } $
. Then there exists
 $j \in [r^*]$
such that
$j \in [r^*]$
such that
 $r^*+1$
is a clone of j under
$r^*+1$
is a clone of j under
 $\phi '$
. If
$\phi '$
. If
 $\boldsymbol {k}$
has the strong extension property, then
$\boldsymbol {k}$
has the strong extension property, then
 $r^*+1$
is a strong clone.
$r^*+1$
is a strong clone. -
(iii) [Reference Pikhurko and Staden10, Lemma 2.10(iii)] Let
 and
and
 $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
be such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
be such that
 $\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
$\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
 $r^*+1$
is a clone of
$r^*+1$
is a clone of
 $i \in [r^*]$
under
$i \in [r^*]$
under
 $\phi $
. Then
$\phi $
. Then
 $\phi (\{ i,r^*+1 \}) \subseteq \{ 1 \}$
.
$\phi (\{ i,r^*+1 \}) \subseteq \{ 1 \}$
.
We need various lemmas concerning Szemerédi’s regularity, starting with the following definitions.
Definition 2.3 (Edge density, regularity of pairs and partitions)
Given a graph G and disjoint nonempty sets
![]() $A,B \subseteq V(G)$
, we define the edge density between A and B to be
$A,B \subseteq V(G)$
, we define the edge density between A and B to be
where
![]() $e_G(A,B)$
is the number of edges in G with one vertex in A and one vertex in B. Given
$e_G(A,B)$
is the number of edges in G with one vertex in A and one vertex in B. Given
![]() ${\varepsilon },d> 0$
, the pair
${\varepsilon },d> 0$
, the pair
![]() $(A,B)$
is called
$(A,B)$
is called
-
○
 ${\varepsilon }$
-regular if for every
${\varepsilon }$
-regular if for every
 $X \subseteq A$
and
$X \subseteq A$
and
 $Y \subseteq B$
with
$Y \subseteq B$
with
 $|X| \geq {\varepsilon }|A|$
and
$|X| \geq {\varepsilon }|A|$
and
 $|Y| \geq {\varepsilon }|B|$
, we have that
$|Y| \geq {\varepsilon }|B|$
, we have that
 $|d_G(X,Y) - d_G(A,B)| \leq {\varepsilon }$
.
$|d_G(X,Y) - d_G(A,B)| \leq {\varepsilon }$
. -
○
 $({\varepsilon }, d)$
-regular if it is
$({\varepsilon }, d)$
-regular if it is
 ${\varepsilon }$
-regular and
${\varepsilon }$
-regular and
 $d_G(A,B) = d \pm {\varepsilon }$
(i.e.,
$d_G(A,B) = d \pm {\varepsilon }$
(i.e.,
 $d-{\varepsilon }\leq d_G(A,B)\leq d+{\varepsilon }$
),
$d-{\varepsilon }\leq d_G(A,B)\leq d+{\varepsilon }$
), -
○
 $({\varepsilon },\geq \! d)$
-regular if it is
$({\varepsilon },\geq \! d)$
-regular if it is
 ${\varepsilon }$
-regular and
${\varepsilon }$
-regular and
 $d_G(A,B) \geq d-{\varepsilon }$
.
$d_G(A,B) \geq d-{\varepsilon }$
.
Lemma 2.4 (Embedding Lemma [Reference Komlós and Simonovits8, Theorem 2.1])
For every
![]() $\eta>0$
and integer
$\eta>0$
and integer
![]() $k \geq 2$
, there exist
$k \geq 2$
, there exist
![]() ${\varepsilon }>0$
and
${\varepsilon }>0$
and
![]() $m_0 \in \mathbb {N}$
such that the following holds. Suppose that G is a graph with a partition
$m_0 \in \mathbb {N}$
such that the following holds. Suppose that G is a graph with a partition
![]() $V(G) = V_1 \cup \ldots \cup V_k$
such that
$V(G) = V_1 \cup \ldots \cup V_k$
such that
![]() $|V_i| \geq m_0$
for all
$|V_i| \geq m_0$
for all
![]() $i \in [k]$
, and every pair
$i \in [k]$
, and every pair
![]() $(V_i,V_j)$
for
$(V_i,V_j)$
for
![]() $1 \leq i < j \leq k$
is
$1 \leq i < j \leq k$
is
![]() $({\varepsilon },\geq \eta )$
-regular. Then G contains
$({\varepsilon },\geq \eta )$
-regular. Then G contains
![]() $K_k$
.
$K_k$
.
Proposition 2.5 [Reference Pikhurko and Staden10, Proposition 4.4]
Let
![]() $A,B$
be disjoint sets of vertices,
$A,B$
be disjoint sets of vertices,
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() ${\varepsilon }> 0$
satisfying
${\varepsilon }> 0$
satisfying
![]() $1/|A|,1/|B| \ll {\varepsilon } \ll 1/s$
. Let
$1/|A|,1/|B| \ll {\varepsilon } \ll 1/s$
. Let
![]() $G_1,\ldots ,G_s$
be pairwise edge-disjoint subgraphs of
$G_1,\ldots ,G_s$
be pairwise edge-disjoint subgraphs of
![]() $K[A,B]$
. Suppose that not all of
$K[A,B]$
. Suppose that not all of
![]() $G_1,\ldots ,G_s$
are
$G_1,\ldots ,G_s$
are
![]() $({\varepsilon },s^{-1})$
-regular graphs. Then there exist
$({\varepsilon },s^{-1})$
-regular graphs. Then there exist
![]() $c \in [s]$
and
$c \in [s]$
and
![]() $X \subseteq A$
,
$X \subseteq A$
,
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X| = \lceil {\varepsilon }|A|\rceil $
and
$|X| = \lceil {\varepsilon }|A|\rceil $
and
![]() $|Y| = \lceil {\varepsilon } |B| \rceil $
such that
$|Y| = \lceil {\varepsilon } |B| \rceil $
such that
Proposition 2.6. Let
![]() $(A,B)$
be an
$(A,B)$
be an
![]() $({\varepsilon }, d)$
-regular pair and let
$({\varepsilon }, d)$
-regular pair and let
![]() $(A',B')$
be a pair such that
$(A',B')$
be a pair such that
![]() $|A' \bigtriangleup A| \leq \alpha |A'|$
and
$|A' \bigtriangleup A| \leq \alpha |A'|$
and
![]() $|B' \bigtriangleup B| \leq \alpha |B'|$
for some
$|B' \bigtriangleup B| \leq \alpha |B'|$
for some
![]() $0 \leq \alpha \leq 1$
. Then
$0 \leq \alpha \leq 1$
. Then
![]() $(A',B')$
is an
$(A',B')$
is an
![]() $({\varepsilon }+7\sqrt {\alpha }, d)$
-regular pair.
$({\varepsilon }+7\sqrt {\alpha }, d)$
-regular pair.
Proposition 2.7 (see, for example, [Reference Komlós and Simonovits8])
Let
![]() ${\varepsilon },\delta $
be such that
${\varepsilon },\delta $
be such that
![]() $0 < 2\delta \leq {\varepsilon } < 1$
. Suppose that
$0 < 2\delta \leq {\varepsilon } < 1$
. Suppose that
![]() $(X,Y)$
is a
$(X,Y)$
is a
![]() $\delta $
-regular pair, and let
$\delta $
-regular pair, and let
![]() $X' \subseteq X$
and
$X' \subseteq X$
and
![]() $Y' \subseteq Y$
. If
$Y' \subseteq Y$
. If
 $$ \begin{align*}\min \left\{ \frac{|X'|}{|X|} , \frac{|Y'|}{|Y|} \right\} \geq \frac{\delta}{{\varepsilon}}, \end{align*} $$
$$ \begin{align*}\min \left\{ \frac{|X'|}{|X|} , \frac{|Y'|}{|Y|} \right\} \geq \frac{\delta}{{\varepsilon}}, \end{align*} $$
then
![]() $(X',Y')$
is
$(X',Y')$
is
![]() ${\varepsilon }$
-regular.
${\varepsilon }$
-regular.
The following estimate will be useful when counting colourings; it can be proved by looking at the tail of the binomial distribution.
Proposition 2.8 (see, for example, [Reference Pikhurko and Staden10, Corollary 4.8])
Let
![]() $n,k \in \mathbb {N}$
and
$n,k \in \mathbb {N}$
and
![]() $\delta \in \mathbb {R}$
, where
$\delta \in \mathbb {R}$
, where
![]() $0 < 1/n \ll \delta \ll 1/k$
. Then
$0 < 1/n \ll \delta \ll 1/k$
. Then
 $$ \begin{align*}\sum_{i=0}^{\lfloor (k^{-1}-\delta) n \rfloor}\binom{n}{i} (k-1)^{n-i} \leq e^{-\delta^2k n/3} \cdot k^n. \end{align*} $$
$$ \begin{align*}\sum_{i=0}^{\lfloor (k^{-1}-\delta) n \rfloor}\binom{n}{i} (k-1)^{n-i} \leq e^{-\delta^2k n/3} \cdot k^n. \end{align*} $$
Finally, we need the following simple fact.
Proposition 2.9 (see, for example, [Reference Pikhurko and Staden10, Claim 2.5.1])
Let
![]() $k \in \mathbb {N}$
and let H be maximally
$k \in \mathbb {N}$
and let H be maximally
![]() $K_k$
-free. Then every
$K_k$
-free. Then every
![]() $x \in V(H)$
lies in a copy of
$x \in V(H)$
lies in a copy of
![]() $K_{k-1}$
if and only if
$K_{k-1}$
if and only if
![]() $|V(H)| \geq k-1$
.
$|V(H)| \geq k-1$
.
2.2. Hierarchy of colourings
We will now define three types of colouring, each stricter than the last – namely, good, locally good and perfect. Each type is defined with respect to a partition of the graph. Theorem 1.4 states that almost every valid colouring of a near-extremal graph G is ‘good’ with respect to a partition weighted like an optimal vertex weighting. Our aim in Theorem 1.6 is to prove that almost all of these colourings are in fact ‘perfect’. We achieve this via the property of being ‘locally good’, where a colouring is such if, looking at a single colour between a pair in a partition, we see a regular graph of the right density, and furthermore, the coloured neighbourhood of a vertex or pair of vertices in every part has the right size.
Given a partition
![]() $X_1,\ldots ,X_p$
of a set S, we say that a partition
$X_1,\ldots ,X_p$
of a set S, we say that a partition
![]() $Y_1, \ldots , Y_r$
of S is a coarsening of
$Y_1, \ldots , Y_r$
of S is a coarsening of
![]() $X_1,\ldots , X_p$
if for all
$X_1,\ldots , X_p$
if for all
![]() $i \in [p]$
, there is a
$i \in [p]$
, there is a
![]() $j \in [r]$
such that
$j \in [r]$
such that
![]() $X_i \subseteq Y_j$
.
$X_i \subseteq Y_j$
.
Definition 2.10 (
 $\delta $
-good, (
$\delta $
-good, (
 $\gamma ,\delta )$
-locally good,
$\gamma ,\delta )$
-locally good,
 $(\gamma ,\delta )$
-perfect)
$(\gamma ,\delta )$
-perfect)
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Let G be a complete m-partite graph with vertex partition
$\boldsymbol {k} \in \mathbb {N}^s$
. Let G be a complete m-partite graph with vertex partition
![]() $X_1,\ldots ,X_m$
. Let
$X_1,\ldots ,X_m$
. Let
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
, let
$\phi \in \Phi _0(r;\boldsymbol {k})$
, let
![]() $Y_0,Y_1,\ldots ,Y_r$
be a coarsening of
$Y_0,Y_1,\ldots ,Y_r$
be a coarsening of
![]() $X_1,\ldots ,X_m$
(where we allow
$X_1,\ldots ,X_m$
(where we allow
![]() $Y_0$
to be empty), let
$Y_0$
to be empty), let
![]() $\mathcal {Y} := (Y_1,\ldots ,Y_{r})$
, and let
$\mathcal {Y} := (Y_1,\ldots ,Y_{r})$
, and let
![]() $\delta ,\gamma> 0$
. We say that a
$\delta ,\gamma> 0$
. We say that a
![]() $\boldsymbol {k}$
-valid colouring
$\boldsymbol {k}$
-valid colouring
![]() $\chi $
of G is
$\chi $
of G is
-
○
 $\delta $
-good with respect to
$\delta $
-good with respect to
 $(\phi; \mathcal {Y})$
if the following hold.
$(\phi; \mathcal {Y})$
if the following hold.-
– For all
 $ij \in \binom {[r]}{2}$
and
$ij \in \binom {[r]}{2}$
and
 $c \in \phi (ij)$
, we have that
$c \in \phi (ij)$
, we have that
 $\chi ^{-1}(c)[Y_i,Y_j]$
is
$\chi ^{-1}(c)[Y_i,Y_j]$
is
 $(\delta ,|\phi (ij)|^{-1})$
-regular.
$(\delta ,|\phi (ij)|^{-1})$
-regular. -
–
 $ \sum _{i \in [r]}|\, e_G(Y_i) - |\chi ^{-1}(1)[Y_i]| \,| < \delta n^2$
.
$ \sum _{i \in [r]}|\, e_G(Y_i) - |\chi ^{-1}(1)[Y_i]| \,| < \delta n^2$
.
Write
 $\mathcal {G}_\delta (G;\phi ,\mathcal {Y})$
for the set of these colourings.
$\mathcal {G}_\delta (G;\phi ,\mathcal {Y})$
for the set of these colourings. -
-
○
 $(\gamma ,\delta )$
-locally good with respect to
$(\gamma ,\delta )$
-locally good with respect to
 $(\phi; \mathcal {Y})$
if the following hold.
$(\phi; \mathcal {Y})$
if the following hold.-
–
 $\chi $
is
$\chi $
is
 $\delta $
-good with respect to
$\delta $
-good with respect to
 $(\phi ;\mathcal {Y})$
.
$(\phi ;\mathcal {Y})$
.
For all
 $x \in V(G)$
, there exists
$x \in V(G)$
, there exists
 $i=i_x \in [r]$
such that
$i=i_x \in [r]$
such that-
– For all
 $j \in [r]\setminus \{ i \}$
, parts
$j \in [r]\setminus \{ i \}$
, parts
 $X \subseteq Y_j$
(so
$X \subseteq Y_j$
(so
 $X=X_t$
for some
$X=X_t$
for some
 $t \in [m]$
) and
$t \in [m]$
) and
 $c \in \phi (ij)$
, we have
$c \in \phi (ij)$
, we have
 $|\chi ^{-1}(c)[x,X]|=|\phi (ij)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$
, where
$|\chi ^{-1}(c)[x,X]|=|\phi (ij)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$
, where
 $\ell _j$
is the number of parts inside
$\ell _j$
is the number of parts inside
 $Y_j$
. In particular,
$Y_j$
. In particular,
 $|\chi ^{-1}(c)[x,Y_j]| = (|\phi (ij)|^{-1}\pm \delta )|Y_j|$
.
$|\chi ^{-1}(c)[x,Y_j]| = (|\phi (ij)|^{-1}\pm \delta )|Y_j|$
. -
–
 $d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$
.
$d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$
. -
– For all
 $i' \in [r]\setminus \{i\}$
, we have
$i' \in [r]\setminus \{i\}$
, we have
 $d_G(x,Y_{i'}) \geq (1-\gamma )|Y_{i'}|$
.
$d_G(x,Y_{i'}) \geq (1-\gamma )|Y_{i'}|$
.
For all distinct
 $y,z \in V(G)$
,
$y,z \in V(G)$
,
 $j \in [r]\setminus \{i_y,i_z\}$
and parts
$j \in [r]\setminus \{i_y,i_z\}$
and parts
 $X \subseteq Y_j$
, we have
$X \subseteq Y_j$
, we have-
–
 $|N_{\chi ^{-1}(c_y)}(y,X) \cap N_{\chi ^{-1}(c_z)}(z,X)| = |\phi (i_yj)|^{-1}|\phi (i_zj)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$
for all
$|N_{\chi ^{-1}(c_y)}(y,X) \cap N_{\chi ^{-1}(c_z)}(z,X)| = |\phi (i_yj)|^{-1}|\phi (i_zj)|^{-1}|X| \pm \frac {\delta }{\ell _j}|Y_j|$
for all
 $c_y \in \phi (i_yj)$
and
$c_y \in \phi (i_yj)$
and
 $c_z \in \phi (i_zj)$
.
$c_z \in \phi (i_zj)$
.
Write
 $\mathcal {LG}_{\gamma ,\delta }(G; \phi ,\mathcal {Y})$
for the set of these colourings.
$\mathcal {LG}_{\gamma ,\delta }(G; \phi ,\mathcal {Y})$
for the set of these colourings. -
-
○
 $(\gamma ,\delta )$
-perfect with respect to
$(\gamma ,\delta )$
-perfect with respect to
 $(\phi; \mathcal {Y})$
if
$(\phi; \mathcal {Y})$
if-
–
 $\chi $
is
$\chi $
is
 $(\gamma ,\delta )$
-locally good with respect to
$(\gamma ,\delta )$
-locally good with respect to
 $(\phi ;\mathcal {Y})$
.
$(\phi ;\mathcal {Y})$
. -
– For all
 $x \in V(G)$
, there exists
$x \in V(G)$
, there exists
 $i \in [r]$
such that for all
$i \in [r]$
such that for all
 $j \in [r]$
and
$j \in [r]$
and
 $y \in N_G(x,Y_j)$
, we have
$y \in N_G(x,Y_j)$
, we have
 $\chi (xy) = 1$
if
$\chi (xy) = 1$
if
 $j=i$
, and
$j=i$
, and
 $\chi (xy) \in \phi (ij)$
otherwise.
$\chi (xy) \in \phi (ij)$
otherwise.
Write
 $\mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
for the set of these colourings.
$\mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
for the set of these colourings. -
Note that if
![]() $\gamma ' \geq \gamma $
and
$\gamma ' \geq \gamma $
and
![]() $\delta ' \geq \delta $
, then a
$\delta ' \geq \delta $
, then a
![]() $\delta $
-good colouring is also
$\delta $
-good colouring is also
![]() $\delta '$
-good; a
$\delta '$
-good; a
![]() $(\gamma ,\delta )$
-locally good colouring is also
$(\gamma ,\delta )$
-locally good colouring is also
![]() $(\gamma ',\delta ')$
-locally good, and a
$(\gamma ',\delta ')$
-locally good, and a
![]() $(\gamma ,\delta )$
-perfect colouring is also
$(\gamma ,\delta )$
-perfect colouring is also
![]() $(\gamma ',\delta ')$
-perfect.
$(\gamma ',\delta ')$
-perfect.
It is a fairly straightforward consequence of Lemma 2.4 (the Embedding Lemma) that if a colouring is
![]() $(\gamma ,\delta )$
-locally good with respect to
$(\gamma ,\delta )$
-locally good with respect to
![]() $(\phi ;\mathcal {Y})$
and no member of
$(\phi ;\mathcal {Y})$
and no member of
![]() $\mathcal {Y}$
is too small, then it is
$\mathcal {Y}$
is too small, then it is
![]() $(\gamma ,\delta )$
-perfect.
$(\gamma ,\delta )$
-perfect.
Lemma 2.11. Let
![]() $s,r \in \mathbb {N}$
and
$s,r \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
, where
$\boldsymbol {k} \in \mathbb {N}^s$
, where
![]() $k_1 \geq \ldots \geq k_s$
and
$k_1 \geq \ldots \geq k_s$
and
![]() $r \geq k_2-1$
, and let
$r \geq k_2-1$
, and let
![]() $\mu> 0$
. Then there exist
$\mu> 0$
. Then there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() $\delta> 0$
such that the following hold. Let G be a complete partite graph on
$\delta> 0$
such that the following hold. Let G be a complete partite graph on
![]() $n \geq n_0$
vertices with parts
$n \geq n_0$
vertices with parts
![]() $X_1,\ldots ,X_m$
, and let
$X_1,\ldots ,X_m$
, and let
![]() $Y_0,\ldots ,Y_r$
be a partition of
$Y_0,\ldots ,Y_r$
be a partition of
![]() $V(G)$
which is a coarsening of
$V(G)$
which is a coarsening of
![]() $X_1,\ldots ,X_m$
. Let
$X_1,\ldots ,X_m$
. Let
![]() $\mathcal {Y} := (Y_1,\ldots ,Y_{r})$
and assume that
$\mathcal {Y} := (Y_1,\ldots ,Y_{r})$
and assume that
![]() $|Y_i| \geq \mu n$
for all
$|Y_i| \geq \mu n$
for all
![]() $i \in [r]$
. Let
$i \in [r]$
. Let
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
be such that
$\phi \in \Phi _0(r;\boldsymbol {k})$
be such that
![]() $\phi ^{-1}(c)$
is maximally
$\phi ^{-1}(c)$
is maximally
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
. Then, for all
$c \in [s]$
. Then, for all
![]() $\gamma> 0$
,
$\gamma> 0$
,
Proof. Let
![]() ${\varepsilon }> 0,m_0 \in \mathbb {N}$
be the output of Lemma 2.4 applied with
${\varepsilon }> 0,m_0 \in \mathbb {N}$
be the output of Lemma 2.4 applied with
![]() $s^{-1},k_c$
playing the roles of
$s^{-1},k_c$
playing the roles of
![]() $\eta ,k$
for every
$\eta ,k$
for every
![]() $c \in [s]$
. Let
$c \in [s]$
. Let
![]() $n_0 := 2s^2 m_0/\mu $
and
$n_0 := 2s^2 m_0/\mu $
and
![]() $\delta := {\varepsilon }^2$
. By decreasing
$\delta := {\varepsilon }^2$
. By decreasing
![]() ${\varepsilon }$
and increasing
${\varepsilon }$
and increasing
![]() $m_0$
if necessary, we may assume that
$m_0$
if necessary, we may assume that
![]() $\delta \ll \mu $
.
$\delta \ll \mu $
.
Certainly,
![]() $\mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y}) \supseteq \mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
by definition. Suppose that there exists
$\mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y}) \supseteq \mathcal {P}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
by definition. Suppose that there exists
![]() $\chi \in \mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
such that the
$\chi \in \mathcal {LG}_{\gamma ,\delta }(G;\phi ,\mathcal {Y})$
such that the
![]() $(\gamma ,\delta )$
-perfect condition fails at some
$(\gamma ,\delta )$
-perfect condition fails at some
![]() $x \in V(G)$
. Since
$x \in V(G)$
. Since
![]() $\chi $
is
$\chi $
is
![]() $(\gamma ,\delta )$
-locally good, there exists
$(\gamma ,\delta )$
-locally good, there exists
![]() $i \in [r]$
such that for all
$i \in [r]$
such that for all
![]() $j \in [r]\setminus \{ i \}$
, we have that
$j \in [r]\setminus \{ i \}$
, we have that
![]() $|\chi ^{-1}(c)[x,Y_j]|=(|\phi (ij)|^{-1} \pm \delta )|Y_j|$
and
$|\chi ^{-1}(c)[x,Y_j]|=(|\phi (ij)|^{-1} \pm \delta )|Y_j|$
and
![]() $d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$
. We will show that for all
$d_G(x,Y_i) - |\chi ^{-1}(1)[x,Y_i]| < \delta n$
. We will show that for all
![]() $j \in [r]\setminus \{ i \}$
and
$j \in [r]\setminus \{ i \}$
and
![]() $y \in N_G(x,Y_j)$
, we have
$y \in N_G(x,Y_j)$
, we have
![]() $\chi (xy) \in \phi (ij)$
, and for all
$\chi (xy) \in \phi (ij)$
, and for all
![]() $y \in N_G(x,Y_i)$
, we have
$y \in N_G(x,Y_i)$
, we have
![]() $\chi (xy) = 1$
.
$\chi (xy) = 1$
.
Suppose first that there exists
![]() $j \in [r]\setminus \{ i \}$
and
$j \in [r]\setminus \{ i \}$
and
![]() $y \in N_G(x,Y_j)$
such that
$y \in N_G(x,Y_j)$
such that
![]() $\chi (xy) =: c \notin \phi (ij)$
. Let
$\chi (xy) =: c \notin \phi (ij)$
. Let
![]() $k := k_{c}$
and
$k := k_{c}$
and
![]() $J := \chi ^{-1}(c)$
. Now,
$J := \chi ^{-1}(c)$
. Now,
![]() $\phi ^{-1}(c)$
is maximally
$\phi ^{-1}(c)$
is maximally
![]() $K_{k}$
-free. Since
$K_{k}$
-free. Since
![]() $ij \notin \phi ^{-1}(c)$
, we have that
$ij \notin \phi ^{-1}(c)$
, we have that
![]() $\phi ^{-1}(c) \cup \{ ij \}$
contains a copy of
$\phi ^{-1}(c) \cup \{ ij \}$
contains a copy of
![]() $K_{k}$
. So there exist
$K_{k}$
. So there exist
![]() $i_3,\ldots ,i_k \in [r]\setminus \{ i,j \}$
such that
$i_3,\ldots ,i_k \in [r]\setminus \{ i,j \}$
such that
![]() $i_1,\ldots ,i_k$
span a copy of
$i_1,\ldots ,i_k$
span a copy of
![]() $K_k$
in
$K_k$
in
![]() $\phi ^{-1}(c)$
, where
$\phi ^{-1}(c)$
, where
![]() $i_1 := i$
and
$i_1 := i$
and
![]() $i_2 := j$
.
$i_2 := j$
.
Since
![]() $\chi $
is
$\chi $
is
![]() $(\gamma ,\delta )$
-locally good, for all
$(\gamma ,\delta )$
-locally good, for all
![]() $\ell =3,\ldots ,k$
, we have, by the pairs condition, taking the union over all parts
$\ell =3,\ldots ,k$
, we have, by the pairs condition, taking the union over all parts
![]() $X \subseteq Y_{i_\ell }$
, that
$X \subseteq Y_{i_\ell }$
, that
Let
![]() $U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$
. Proposition 2.5 implies that
$U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$
. Proposition 2.5 implies that
![]() $J[U_\ell ,U_{\ell '}]$
is a
$J[U_\ell ,U_{\ell '}]$
is a
![]() $(\sqrt {\delta },\geq \! s^{-1})$
-regular pair for all distinct
$(\sqrt {\delta },\geq \! s^{-1})$
-regular pair for all distinct
![]() $\ell ,\ell ' \in \{ 3,\ldots , k \}$
. Lemma 2.4 implies that J contains a copy of
$\ell ,\ell ' \in \{ 3,\ldots , k \}$
. Lemma 2.4 implies that J contains a copy of
![]() $K_{k-2}$
. Together with
$K_{k-2}$
. Together with
![]() $x,y$
, we obtain a copy of
$x,y$
, we obtain a copy of
![]() $K_k$
in
$K_k$
in
![]() $\chi ^{-1}(c)$
, a contradiction.
$\chi ^{-1}(c)$
, a contradiction.
Suppose instead that there is some
![]() $y \in N_G(x,Y_i)$
such that
$y \in N_G(x,Y_i)$
such that
![]() $\chi (xy) =: c \neq 1$
. Let
$\chi (xy) =: c \neq 1$
. Let
![]() $k := k_c$
and
$k := k_c$
and
![]() $J := \chi ^{-1}(c)$
. Since
$J := \chi ^{-1}(c)$
. Since
![]() $r \geq k_2-1 \geq k-1$
, Proposition 2.9 implies that i lies in a copy of
$r \geq k_2-1 \geq k-1$
, Proposition 2.9 implies that i lies in a copy of
![]() $K_{k-1}$
in the graph
$K_{k-1}$
in the graph
![]() $\phi ^{-1}(c)$
. Let
$\phi ^{-1}(c)$
. Let
![]() $i_1 := i$
and let
$i_1 := i$
and let
![]() $i_2,\ldots ,i_{k-1}$
be the other vertices in this copy. As before, setting
$i_2,\ldots ,i_{k-1}$
be the other vertices in this copy. As before, setting
![]() $U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$
for all
$U_\ell := N_J(x,Y_{i_\ell }) \cap N_J(y,Y_{i_\ell })$
for all
![]() $\ell \in [2,k-1]$
, we have that
$\ell \in [2,k-1]$
, we have that
![]() $J[U_2,\ldots ,U_{k-1}]$
contains a copy of
$J[U_2,\ldots ,U_{k-1}]$
contains a copy of
![]() $K_{k-2}$
. Together with
$K_{k-2}$
. Together with
![]() $x,y$
, this gives a copy of
$x,y$
, this gives a copy of
![]() $K_k$
in J, a contradiction.
$K_k$
in J, a contradiction.
2.3. Stability for complete multipartite graphs
Given a graph G, a subgraph H of G, and an s-edge-colouring
![]() $\chi $
of H, we say that
$\chi $
of H, we say that
![]() $\overline {\chi }$
is an extension of
$\overline {\chi }$
is an extension of
![]() $\chi $
if
$\chi $
if
![]() $\overline {\chi }$
is an s-edge-colouring of G such that
$\overline {\chi }$
is an s-edge-colouring of G such that
![]() $\overline {\chi }|_{H} = \chi $
.
$\overline {\chi }|_{H} = \chi $
.
Theorem 2.12 (Stability for complete multipartite graphs)
Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1 \geq \ldots \geq k_s$
has the extension property. Then for all
$k_1 \geq \ldots \geq k_s$
has the extension property. Then for all
![]() $\delta> 0$
, there exist
$\delta> 0$
, there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() ${\varepsilon } \in \mathbb {R}$
with
${\varepsilon } \in \mathbb {R}$
with
![]() $0 < {\varepsilon } < \delta $
such that the following holds. Let
$0 < {\varepsilon } < \delta $
such that the following holds. Let
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
$G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
![]() $n \geq n_0$
vertices such that
$n \geq n_0$
vertices such that
 $$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
Then for at least
![]() $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$
-edge-colourings
$(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$
-edge-colourings
![]() $\chi $
of G which are
$\chi $
of G which are
![]() $\boldsymbol {k}$
-valid, there are
$\boldsymbol {k}$
-valid, there are ![]() with
with
![]() $r^* \leq m$
and a coarsening
$r^* \leq m$
and a coarsening
![]() $Z_0,\ldots ,Z_{r^*}$
of
$Z_0,\ldots ,Z_{r^*}$
of
![]() $X_1,\ldots ,X_m$
such that the following hold.
$X_1,\ldots ,X_m$
such that the following hold.
-
(i)
 $\sum _{i \in [r^*]}|\,|Z_i|-\alpha _i^*n\,| < \delta n$
, and
$\sum _{i \in [r^*]}|\,|Z_i|-\alpha _i^*n\,| < \delta n$
, and
 $\chi $
is
$\chi $
is
 $\delta $
-good with respect to
$\delta $
-good with respect to
 $(\phi ^*; Z_1,\ldots ,Z_{r^*})$
.
$(\phi ^*; Z_1,\ldots ,Z_{r^*})$
. -
(ii) If, for all
 $i \in [r^*]$
,
$i \in [r^*]$
,
 $\ell _i$
is the number of
$\ell _i$
is the number of
 $X_j$
in
$X_j$
in
 $Z_i$
, then
$Z_i$
, then
 $\ell _1 = \ldots = \ell _{r^*} = 1$
; or
$\ell _1 = \ldots = \ell _{r^*} = 1$
; or
 $\boldsymbol {k}$
does not have the strong extension property and
$\boldsymbol {k}$
does not have the strong extension property and
 $\ell _1 + \ldots + \ell _{r^*} \leq k_1-1$
.
$\ell _1 + \ldots + \ell _{r^*} \leq k_1-1$
.
Furthermore, if we have
 $$ \begin{align} \begin{aligned} &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{aligned} \end{align} $$
then there are at least
![]() $(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k}) s$
-edge-colourings
$(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k}) s$
-edge-colourings
![]() $\chi $
of G for which there are
$\chi $
of G for which there are ![]() and
and
![]() $Z_0,\ldots ,Z_{r^*}$
as above such that
$Z_0,\ldots ,Z_{r^*}$
as above such that
![]() $\chi $
is
$\chi $
is
![]() $(0,\delta )$
-perfect with respect to
$(0,\delta )$
-perfect with respect to
![]() $(\phi ^*; Z_1,\ldots ,Z_{r^*})$
.
$(\phi ^*; Z_1,\ldots ,Z_{r^*})$
.
Proof. For brevity, write
![]() $Q := Q(\boldsymbol {k})$
,
$Q := Q(\boldsymbol {k})$
,
![]() $R := R(\boldsymbol {k})$
,
$R := R(\boldsymbol {k})$
,
![]() $F(G) := F(G;\boldsymbol {k})$
, and abbreviate similarly elsewhere. Lemma 2.2(i) implies that there exists
$F(G) := F(G;\boldsymbol {k})$
, and abbreviate similarly elsewhere. Lemma 2.2(i) implies that there exists
![]() $\mu> 0$
such that for all
$\mu> 0$
such that for all ![]() , we have that
, we have that
![]() $\alpha _i^*> \mu $
for all
$\alpha _i^*> \mu $
for all
![]() $i \in [r^*]$
. Applying Lemma 2.2(ii) gives the constant
$i \in [r^*]$
. Applying Lemma 2.2(ii) gives the constant
![]() ${\varepsilon }_0$
. We may assume that
${\varepsilon }_0$
. We may assume that
![]() $\delta \ll {\varepsilon }_0,\mu ,1/R$
since a smaller
$\delta \ll {\varepsilon }_0,\mu ,1/R$
since a smaller
![]() $\delta $
yields a stronger conclusion. Apply Lemma 2.4 with
$\delta $
yields a stronger conclusion. Apply Lemma 2.4 with
![]() $(2s)^{-1},k_c$
playing the roles of
$(2s)^{-1},k_c$
playing the roles of
![]() $\eta ,k$
for all
$\eta ,k$
for all
![]() $c \in [s]$
to obtain
$c \in [s]$
to obtain
![]() $m_0 \in \mathbb {N}$
and
$m_0 \in \mathbb {N}$
and
![]() ${\varepsilon }'> 0$
such that its conclusions hold. Choose constants
${\varepsilon }'> 0$
such that its conclusions hold. Choose constants
![]() $\delta _0,\ldots ,\delta _5 \in \mathbb {R}$
such that
$\delta _0,\ldots ,\delta _5 \in \mathbb {R}$
such that
![]() $0 < \delta _0 \ll \ldots \ll \delta _5 \ll \delta $
. We may assume that
$0 < \delta _0 \ll \ldots \ll \delta _5 \ll \delta $
. We may assume that
![]() ${\varepsilon }' \geq 3\sqrt {\delta }_1$
. Apply Theorem 1.4 with
${\varepsilon }' \geq 3\sqrt {\delta }_1$
. Apply Theorem 1.4 with
![]() $\delta _0$
playing the role of
$\delta _0$
playing the role of
![]() $\delta $
to obtain
$\delta $
to obtain
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() ${\varepsilon }> 0$
. Without loss of generality, we may assume that
${\varepsilon }> 0$
. Without loss of generality, we may assume that
![]() $0 < 1/n_0 \ll {\varepsilon } \ll \delta _0$
and
$0 < 1/n_0 \ll {\varepsilon } \ll \delta _0$
and
We may further assume that the conclusion of Lemma 2.11 holds with
![]() $s,\boldsymbol {k},\mu /2$
playing the roles of inputs
$s,\boldsymbol {k},\mu /2$
playing the roles of inputs
![]() $s,\boldsymbol {k},\mu $
, and with outputs
$s,\boldsymbol {k},\mu $
, and with outputs
![]() $n_0 \in \mathbb {N}, \delta _5> 0$
. Thus, our constants form the hierarchy
$n_0 \in \mathbb {N}, \delta _5> 0$
. Thus, our constants form the hierarchy
Let
![]() $G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
$G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
![]() $n \geq n_0$
vertices such that
$n \geq n_0$
vertices such that
![]() $\log F(G) \geq (Q-{\varepsilon })\binom {n}{2}$
. Note that
$\log F(G) \geq (Q-{\varepsilon })\binom {n}{2}$
. Note that
![]() $m < R$
(or
$m < R$
(or
![]() $F(G)=0$
). Let also
$F(G)=0$
). Let also
 $$ \begin{align} Y_0 := \bigcup_{i \in [m] : |X_i| \leq \delta_1^4 n}X_i. \end{align} $$
$$ \begin{align} Y_0 := \bigcup_{i \in [m] : |X_i| \leq \delta_1^4 n}X_i. \end{align} $$
Given ![]() , let
, let
![]() $\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
be the set of partitions
$\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
be the set of partitions
![]() $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*})$
of
$\mathcal {Y} := (Y_1,\ldots ,Y_{r^*})$
of
![]() $V(G)\setminus Y_0$
such that
$V(G)\setminus Y_0$
such that
![]() $Y_0,\ldots ,Y_{r^*}$
is a coarsening of
$Y_0,\ldots ,Y_{r^*}$
is a coarsening of
![]() $X_1,\ldots ,X_m$
, and
$X_1,\ldots ,X_m$
, and
(We do not yet know that
![]() $\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
is nonempty.)
$\mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
is nonempty.)
Given
![]() $\eta>0$
, let
$\eta>0$
, let
![]() $\mathcal {G}_{\eta }(G)$
be the set of
$\mathcal {G}_{\eta }(G)$
be the set of
![]() $\boldsymbol {k}$
-valid colourings
$\boldsymbol {k}$
-valid colourings
![]() $\chi $
of G for which there exist
$\chi $
of G for which there exist ![]() and
and
![]() $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
such that
$\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
such that
![]() $\chi \in \mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$
. Call the elements of
$\chi \in \mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$
. Call the elements of
![]() $\mathcal {G}_{\eta }(G) \eta $
-good. Given
$\mathcal {G}_{\eta }(G) \eta $
-good. Given
![]() $\eta _1,\eta _2$
, let
$\eta _1,\eta _2$
, let
![]() $\mathcal {LG}_{\eta _1,\eta _2}(G)$
and
$\mathcal {LG}_{\eta _1,\eta _2}(G)$
and
![]() $\mathcal {P}_{\eta _1,\eta _2}(G)$
be as
$\mathcal {P}_{\eta _1,\eta _2}(G)$
be as
![]() $\mathcal {G}_{\eta }(G)$
but with
$\mathcal {G}_{\eta }(G)$
but with
![]() $\mathcal {LG}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$
and
$\mathcal {LG}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$
and
![]() $\mathcal {P}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$
replacing
$\mathcal {P}_{\eta _1,\eta _2}(G;\phi ^*,\mathcal {Y})$
replacing
![]() $\mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$
, respectively.
$\mathcal {G}_{\eta }(G;\phi ^*,\mathcal {Y})$
, respectively.
Claim 2.12.1. We have the following:
-
(i)
 $|\mathcal {G}_{\delta _1}(G)| \geq (1-2^{-{\varepsilon } n^2})\cdot F(G)$
.
$|\mathcal {G}_{\delta _1}(G)| \geq (1-2^{-{\varepsilon } n^2})\cdot F(G)$
. -
(ii) For all
 ,
,
 $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
$\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
 $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
, let
$\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
, let
 $t_i$
be the number of
$t_i$
be the number of
 $X_j$
in
$X_j$
in
 $Y_i$
for all
$Y_i$
for all
 $i \in [r^*]$
. Then either
$i \in [r^*]$
. Then either
 $t_1 = \ldots = t_{r^*} = 1$
; or
$t_1 = \ldots = t_{r^*} = 1$
; or
 $\boldsymbol {k}$
does not have the strong extension property and
$\boldsymbol {k}$
does not have the strong extension property and
 $t_1+\ldots +t_{r^*} \leq k_1-1$
.
$t_1+\ldots +t_{r^*} \leq k_1-1$
.
Proof of Claim
By Theorem 1.4 applied to G with parameter
![]() $\delta _0$
, we have that there are at least
$\delta _0$
, we have that there are at least
![]() $(1-2^{-{\varepsilon } n^2}) \cdot F(G)$
colourings
$(1-2^{-{\varepsilon } n^2}) \cdot F(G)$
colourings
![]() $\chi : E(G) \rightarrow [s]$
which are
$\chi : E(G) \rightarrow [s]$
which are
![]() $\boldsymbol {k}$
-valid and for which there is some
$\boldsymbol {k}$
-valid and for which there is some ![]() and a partition
and a partition
![]() $V_1 \cup \ldots \cup V_{r^*} = V(G)$
such that
$V_1 \cup \ldots \cup V_{r^*} = V(G)$
such that
-
○ For all
 $i \in [r^*]$
, we have
$i \in [r^*]$
, we have
 $|\,|V_i|-\alpha ^*_i n\,| \leq 1$
.
$|\,|V_i|-\alpha ^*_i n\,| \leq 1$
. -
○
 $\chi $
is
$\chi $
is
 $\delta _0$
-good with respect to
$\delta _0$
-good with respect to
 $(\phi ^*;V_1,\ldots ,V_{r^*})$
.
$(\phi ^*;V_1,\ldots ,V_{r^*})$
. -
○ Suppose
 $\sum _{i \in [r^*]}e(G[V_i])> \delta _0 n^2$
. Then
$\sum _{i \in [r^*]}e(G[V_i])> \delta _0 n^2$
. Then
 $\boldsymbol {k}$
does not have the strong extension property, and all but at most
$\boldsymbol {k}$
does not have the strong extension property, and all but at most
 $\delta _0 n^2$
edges in
$\delta _0 n^2$
edges in
 $\bigcup _{i \in [r^*]}G[V_i]$
are coloured with
$\bigcup _{i \in [r^*]}G[V_i]$
are coloured with
 $1$
under
$1$
under
 $\chi $
. Moreover, if
$\chi $
. Moreover, if
 $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that at least
$\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that at least
 $\delta _0|V_i|^2$
edges need to be removed from
$\delta _0|V_i|^2$
edges need to be removed from
 $G[V_i]$
to make it
$G[V_i]$
to make it
 $K_{\ell _i}$
-free, then
$K_{\ell _i}$
-free, then
 $\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
$\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
We will show that every such
![]() $\chi $
lies in
$\chi $
lies in
![]() $\mathcal {G}_{\delta _1}(G)$
, which implies the first part of the claim. Fix
$\mathcal {G}_{\delta _1}(G)$
, which implies the first part of the claim. Fix
![]() $\chi $
and its associated
$\chi $
and its associated
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
and
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
and
![]() $V_1,\ldots , V_{r^*}$
(recall that both
$V_1,\ldots , V_{r^*}$
(recall that both
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
and the partition
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
and the partition
![]() $V_1\cup \ldots \cup V_{r^*}$
may be different for different
$V_1\cup \ldots \cup V_{r^*}$
may be different for different
![]() $\chi $
). For all
$\chi $
). For all
![]() $ij \in \binom {[r^*]}{2}$
, the
$ij \in \binom {[r^*]}{2}$
, the
![]() $\delta _0$
-goodness of
$\delta _0$
-goodness of
![]() $\chi $
implies that
$\chi $
implies that
 $$ \begin{align*}e_G(V_i,V_j) \geq \sum_{c \in \phi^*(ij)}|\chi^{-1}(c)[V_i,V_j]| \geq \sum_{c \in \phi^*(ij)}(|\phi^*(ij)|^{-1} - \delta_0)|V_i||V_j| \geq (1-s\delta_0)|V_i||V_j|, \end{align*} $$
$$ \begin{align*}e_G(V_i,V_j) \geq \sum_{c \in \phi^*(ij)}|\chi^{-1}(c)[V_i,V_j]| \geq \sum_{c \in \phi^*(ij)}(|\phi^*(ij)|^{-1} - \delta_0)|V_i||V_j| \geq (1-s\delta_0)|V_i||V_j|, \end{align*} $$
so
![]() $e_{\overline {G}}(V_i,V_j) \leq s\delta _0n^2$
. Suppose that
$e_{\overline {G}}(V_i,V_j) \leq s\delta _0n^2$
. Suppose that
![]() $X_k$
, some
$X_k$
, some
![]() $k \in [m]$
, is such that
$k \in [m]$
, is such that
![]() $|X_k \cap V_i|> \sqrt {s\delta _0}n$
. Then, for every
$|X_k \cap V_i|> \sqrt {s\delta _0}n$
. Then, for every
![]() $j \in [m]\setminus \{k\}$
,
$j \in [m]\setminus \{k\}$
,
 $$ \begin{align*}|X_k \cap V_j| = \frac{e_{\overline{G}[X_k]}(V_i,V_j)}{|X_k \cap V_i|} \leq \frac{e_{\overline{G}}(V_i,V_j)}{|X_k \cap V_i|} < \sqrt{s\delta_0}n. \end{align*} $$
$$ \begin{align*}|X_k \cap V_j| = \frac{e_{\overline{G}[X_k]}(V_i,V_j)}{|X_k \cap V_i|} \leq \frac{e_{\overline{G}}(V_i,V_j)}{|X_k \cap V_i|} < \sqrt{s\delta_0}n. \end{align*} $$
So for all
![]() $k \in [m]$
with
$k \in [m]$
with
![]() $|X_k|> \delta _1^4n > R\sqrt {s\delta _0}n$
, there is a unique
$|X_k|> \delta _1^4n > R\sqrt {s\delta _0}n$
, there is a unique
![]() $i_k \in [r^*]$
such that
$i_k \in [r^*]$
such that
![]() $|X_k \cap V_{i_k}|> \sqrt {s\delta _0}n$
. For all
$|X_k \cap V_{i_k}|> \sqrt {s\delta _0}n$
. For all
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
Recall that we already defined
![]() $Y_0$
in (2.4). Then
$Y_0$
in (2.4). Then
![]() $Y_0,\ldots ,Y_{r^*}$
is a coarsening of
$Y_0,\ldots ,Y_{r^*}$
is a coarsening of
![]() $X_1,\ldots ,X_m$
, and
$X_1,\ldots ,X_m$
, and
![]() $|X_j| \leq \delta _1^4 n$
if and only if
$|X_j| \leq \delta _1^4 n$
if and only if
![]() $X_j \subseteq Y_0$
. For all
$X_j \subseteq Y_0$
. For all
![]() $i \in [r^*]$
, we have that
$i \in [r^*]$
, we have that
and
so
![]() $(Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha ^*})$
. Moreover, for all
$(Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha ^*})$
. Moreover, for all
![]() $i \in [r^*]$
, we have
$i \in [r^*]$
, we have
It remains to prove that
![]() $\chi $
is
$\chi $
is
![]() $\delta _1$
-good with respect to
$\delta _1$
-good with respect to
![]() $(\phi ^*;Y_1,\ldots ,Y_{r^*})$
. Proposition 2.6 and (2.5) imply that for all
$(\phi ^*;Y_1,\ldots ,Y_{r^*})$
. Proposition 2.6 and (2.5) imply that for all
![]() $ij \in \binom {[r^*]}{2}$
and all
$ij \in \binom {[r^*]}{2}$
and all
![]() $c \in \phi ^*(ij)$
, we have that
$c \in \phi ^*(ij)$
, we have that
![]() $\chi ^{-1}(c)[Y_i,Y_j]$
is a
$\chi ^{-1}(c)[Y_i,Y_j]$
is a
![]() $(\delta _1,|\phi ^*(ij)|^{-1})$
-regular pair. Moreover,
$(\delta _1,|\phi ^*(ij)|^{-1})$
-regular pair. Moreover,
 $$ \begin{align*} \phantom{=}& \sum_{i \in [r^*]}|\, e_G(Y_i) - |\chi^{-1}(1)[Y_i]| \,| \leq \sum_{i \in [r^*]}|\, e_G(V_i) - |\chi^{-1}(1)[V_i]| \,| + \sum_{i \in [r^*]}|Y_i \triangle V_i|^2\\ &\stackrel{({2.5})}{\leq} \delta_0 n^2 + R\delta_1^6 n^2 < \delta_1^5 n^2. \end{align*} $$
$$ \begin{align*} \phantom{=}& \sum_{i \in [r^*]}|\, e_G(Y_i) - |\chi^{-1}(1)[Y_i]| \,| \leq \sum_{i \in [r^*]}|\, e_G(V_i) - |\chi^{-1}(1)[V_i]| \,| + \sum_{i \in [r^*]}|Y_i \triangle V_i|^2\\ &\stackrel{({2.5})}{\leq} \delta_0 n^2 + R\delta_1^6 n^2 < \delta_1^5 n^2. \end{align*} $$
Thus,
![]() $\chi \in \mathcal {G}_{\delta _1}(G)$
. This completes the proof of the first part of the claim.
$\chi \in \mathcal {G}_{\delta _1}(G)$
. This completes the proof of the first part of the claim.
For the second part, fix ![]() ,
,
![]() $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
$\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
![]() $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
. For each
$\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
. For each
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
![]() $t_i$
be the number of parts
$t_i$
be the number of parts
![]() $X_j$
which lie in
$X_j$
which lie in
![]() $Y_i$
. Then
$Y_i$
. Then
![]() $t_i$
is at most the number of parts
$t_i$
is at most the number of parts
![]() $X_j$
which have intersection at least
$X_j$
which have intersection at least
![]() $\sqrt {s\delta _0}n$
with
$\sqrt {s\delta _0}n$
with
![]() $V_i$
. Suppose first that
$V_i$
. Suppose first that
![]() $\sum _{i \in [r^*]}e_G(V_i) \leq \delta _0 n^2$
. If
$\sum _{i \in [r^*]}e_G(V_i) \leq \delta _0 n^2$
. If
![]() $t_i \geq 2$
for some
$t_i \geq 2$
for some
![]() $i \in [r^*]$
, then
$i \in [r^*]$
, then
![]() $e_G(V_i) \geq s\delta _0 n^2$
, a contradiction. So
$e_G(V_i) \geq s\delta _0 n^2$
, a contradiction. So
![]() $t_1 = \ldots = t_{r^*} = 1$
.
$t_1 = \ldots = t_{r^*} = 1$
.
Suppose now that
![]() $\sum _{i \in [r^*]}e_G(V_i)> \delta _0 n^2$
. Then by Theorem 1.4(iii),
$\sum _{i \in [r^*]}e_G(V_i)> \delta _0 n^2$
. Then by Theorem 1.4(iii),
![]() $\boldsymbol {k}$
does not have the strong extension property. Since
$\boldsymbol {k}$
does not have the strong extension property. Since
![]() $G[V_i]$
is a complete multipartite graph containing at least
$G[V_i]$
is a complete multipartite graph containing at least
![]() $t_i$
parts of size at least
$t_i$
parts of size at least
![]() $\sqrt {s\delta _0}n$
, we have that at least
$\sqrt {s\delta _0}n$
, we have that at least
![]() $s\delta _0 n^2> \delta _0|V_i|^2$
edges need to be removed from
$s\delta _0 n^2> \delta _0|V_i|^2$
edges need to be removed from
![]() $G[V_i]$
to make it
$G[V_i]$
to make it
![]() $K_{t_i}$
-free. Thus,
$K_{t_i}$
-free. Thus,
![]() $t_1+\ldots +t_{r^*} \leq k_1-1$
, proving the second part of the claim.
$t_1+\ldots +t_{r^*} \leq k_1-1$
, proving the second part of the claim.
This proves parts (i) and (ii) of Theorem 2.12. Namely, take any
![]() $\chi \in \mathcal {G}_{\delta _1}(G) \neq \emptyset $
. Let
$\chi \in \mathcal {G}_{\delta _1}(G) \neq \emptyset $
. Let ![]() and
and
![]() $\mathcal {Y} := (Z_0,\ldots ,Z_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
witness
$\mathcal {Y} := (Z_0,\ldots ,Z_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
witness
![]() $\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
. Then they satisfy items (i) and (ii) of Theorem 2.12.
$\chi \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
. Then they satisfy items (i) and (ii) of Theorem 2.12.
Suppose now that (2.1) holds, but
For most of the next part of the proof, we will establish a contradiction to this assumption. (Recall that, by Lemma 2.11, a direct contradiction to the statement of the theorem would replace
![]() $\mathcal {LG}_{\delta _4,\delta _5}(G)$
by
$\mathcal {LG}_{\delta _4,\delta _5}(G)$
by
![]() $\mathcal {LG}_{0,\delta _5}(G)$
.)
$\mathcal {LG}_{0,\delta _5}(G)$
.)
For every ![]() , Lemma 2.1(iii) implies that
, Lemma 2.1(iii) implies that
![]() $(\phi ^*)^{-1}(c)$
is maximally
$(\phi ^*)^{-1}(c)$
is maximally
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
, and that
$c \in [s]$
, and that
![]() $r^* \geq k_2-1$
. Lemma 2.11 and (2.7) imply that for every
$r^* \geq k_2-1$
. Lemma 2.11 and (2.7) imply that for every
![]() $\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
, we have that
$\mathcal {Y} \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
, we have that
![]() $\mathcal {P}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y}) = \mathcal {LG}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y})$
. So
$\mathcal {P}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y}) = \mathcal {LG}_{\delta _4,\delta _5}(G;\phi ^*,\mathcal {Y})$
. So
Given
![]() $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
$\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
![]() $x \in V(G)$
, write
$x \in V(G)$
, write
![]() $\mathcal {Y}-x$
to denote the partition
$\mathcal {Y}-x$
to denote the partition
![]() $(Y_1\setminus \{x\},\ldots ,Y_{r^*}\setminus \{x\})$
and define
$(Y_1\setminus \{x\},\ldots ,Y_{r^*}\setminus \{x\})$
and define
![]() $\mathcal {Y}-y-z$
similarly.
$\mathcal {Y}-y-z$
similarly.
Claim 2.12.2. At least one of the following hold.
There exist
![]() $x \in V(G)$
and a
$x \in V(G)$
and a
![]() $\boldsymbol {k}$
-valid s-edge-colouring
$\boldsymbol {k}$
-valid s-edge-colouring
![]() $\chi $
of
$\chi $
of
![]() $G-x$
such that the following two statements hold.
$G-x$
such that the following two statements hold.
-
(i)
 $\chi \in \mathcal {G}_{2\delta _1}(G-x;\phi ^*,\mathcal {Y}-x)$
, for some
$\chi \in \mathcal {G}_{2\delta _1}(G-x;\phi ^*,\mathcal {Y}-x)$
, for some  and
and
 $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
.
$\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
. -
(ii) There is a set
 $\mathrm {Ext}(\chi )$
of at least
$\mathrm {Ext}(\chi )$
of at least
 $2^{(Q-\delta _3)n} \boldsymbol {k}$
-valid extensions
$2^{(Q-\delta _3)n} \boldsymbol {k}$
-valid extensions
 $\overline {\chi }$
of
$\overline {\chi }$
of
 $\chi $
to G such that
$\chi $
to G such that
 $\overline {\chi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
but
$\overline {\chi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
but
 $\overline {\chi }$
is not
$\overline {\chi }$
is not
 $(\delta _4,\delta _5)$
-locally good with respect to
$(\delta _4,\delta _5)$
-locally good with respect to
 $(\phi ^*;Y_1,\ldots ,Y_{r^*})$
at x.
$(\phi ^*;Y_1,\ldots ,Y_{r^*})$
at x.
There exist
![]() $zy \in \binom {V(G)}{2}$
and a
$zy \in \binom {V(G)}{2}$
and a
![]() $\boldsymbol {k}$
-valid s-edge-colouring
$\boldsymbol {k}$
-valid s-edge-colouring
![]() $\xi $
of
$\xi $
of
![]() $G-z-y$
such that the following two statements hold.
$G-z-y$
such that the following two statements hold.
-
(iii)
 $\xi \in \mathcal {G}_{2\delta _1}(G-z-y;\phi ^*,\mathcal {Y}-z-y)$
, for some
$\xi \in \mathcal {G}_{2\delta _1}(G-z-y;\phi ^*,\mathcal {Y}-z-y)$
, for some  and
and
 $\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
.
$\mathcal {Y} := (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
. -
(iv) There is a set
 $\mathrm {Ext}(\xi )$
of at least
$\mathrm {Ext}(\xi )$
of at least
 $2^{(Q-\delta _3)(n+n-1)} \boldsymbol {k}$
-valid extensions
$2^{(Q-\delta _3)(n+n-1)} \boldsymbol {k}$
-valid extensions
 $\overline {\xi }$
of
$\overline {\xi }$
of
 $\xi $
to G such that
$\xi $
to G such that
 $\overline {\xi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
but
$\overline {\xi } \in \mathcal {G}_{\delta _1}(G;\phi ^*,\mathcal {Y})$
but
 $\overline {\xi }$
is not
$\overline {\xi }$
is not
 $(\delta _4,\delta _5)$
-locally good with respect to
$(\delta _4,\delta _5)$
-locally good with respect to
 $(\phi ^*;Y_1,\ldots ,Y_{r^*})$
at
$(\phi ^*;Y_1,\ldots ,Y_{r^*})$
at
 $z,y$
.
$z,y$
.
Proof of Claim
Suppose first that for at least half of the colourings in
![]() $\mathcal {G}_{\delta _1}(G)\setminus \mathcal {LG}_{\delta _4,\delta _5}(G)$
, the locally good condition fails at some vertex (rather than only at pairs). We will show that there exists an x satisfying (i) and (ii). By (2.8) and (2.9), there is some
$\mathcal {G}_{\delta _1}(G)\setminus \mathcal {LG}_{\delta _4,\delta _5}(G)$
, the locally good condition fails at some vertex (rather than only at pairs). We will show that there exists an x satisfying (i) and (ii). By (2.8) and (2.9), there is some
![]() $x \in V(G)$
such that there are at least
$x \in V(G)$
such that there are at least
![]() $\frac {1}{2}\cdot \frac {1}{n} \cdot 2^{-\delta _2 n} \cdot F(G) \geq 2^{-2\delta _2 n} \cdot F(G)$
valid colourings
$\frac {1}{2}\cdot \frac {1}{n} \cdot 2^{-\delta _2 n} \cdot F(G) \geq 2^{-2\delta _2 n} \cdot F(G)$
valid colourings
![]() $\chi $
which are
$\chi $
which are
![]() $\delta _1$
-good (with respect to some optimal solution and partition) but for which the
$\delta _1$
-good (with respect to some optimal solution and partition) but for which the
![]() $(\delta _4,\delta _5)$
-locally good condition fails at x (for all optimal solutions and partitions). Call this set of colourings
$(\delta _4,\delta _5)$
-locally good condition fails at x (for all optimal solutions and partitions). Call this set of colourings
![]() $\mathcal {L}_x(G)$
.
$\mathcal {L}_x(G)$
.
We have
![]() $\log F(G-x) \geq \log (s^{-n}\cdot F(G)) \geq (Q-{\varepsilon })\binom {n}{2} - n\log s \geq (Q-2{\varepsilon })\binom {n-1}{2}$
, so a version of Claim 2.12.1(i) applied to
$\log F(G-x) \geq \log (s^{-n}\cdot F(G)) \geq (Q-{\varepsilon })\binom {n}{2} - n\log s \geq (Q-2{\varepsilon })\binom {n-1}{2}$
, so a version of Claim 2.12.1(i) applied to
![]() $G-x$
implies that
$G-x$
implies that
Suppose that x does not satisfy Claim 2.12.2. Then for each
![]() $\boldsymbol {k}$
-valid colouring
$\boldsymbol {k}$
-valid colouring
![]() $\chi $
of
$\chi $
of
![]() $G-x$
, either it does not lie in
$G-x$
, either it does not lie in
![]() $\mathcal {G}_{2\delta _1}(G-x)$
or it does lie in
$\mathcal {G}_{2\delta _1}(G-x)$
or it does lie in
![]() $\mathcal {G}_{2\delta _1}(G-x)$
but has at most
$\mathcal {G}_{2\delta _1}(G-x)$
but has at most
![]() $2^{(Q-\delta _3)n} \boldsymbol {k}$
-valid extensions which lie in
$2^{(Q-\delta _3)n} \boldsymbol {k}$
-valid extensions which lie in
![]() $\mathcal {L}_x(G)$
. We have that
$\mathcal {L}_x(G)$
. We have that
 $$ \begin{align*} 2^{-2\delta_2n}\cdot F(G) &\leq |\mathcal{L}_x(G)| \leq |\mathcal{G}_{2\delta_1}(G-x)| \cdot 2^{(Q-\delta_3)n} + (F(G-x)-|\mathcal{G}_{2\delta_1}(G-x)|) \cdot s^n\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3)n} + s^{n} \cdot 2^{-2{\varepsilon} (n-1)^2}F(G-x)\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3/2)n}, \end{align*} $$
$$ \begin{align*} 2^{-2\delta_2n}\cdot F(G) &\leq |\mathcal{L}_x(G)| \leq |\mathcal{G}_{2\delta_1}(G-x)| \cdot 2^{(Q-\delta_3)n} + (F(G-x)-|\mathcal{G}_{2\delta_1}(G-x)|) \cdot s^n\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3)n} + s^{n} \cdot 2^{-2{\varepsilon} (n-1)^2}F(G-x)\\ &\leq F(G-x)\cdot 2^{(Q-\delta_3/2)n}, \end{align*} $$
and so
a contradiction to (2.1).
Thus, we may assume that at least half the good but not locally good colourings fail due to the pair condition. Again, there is a pair
![]() $y,z$
of distinct vertices that appear in at least
$y,z$
of distinct vertices that appear in at least
![]() $2^{-2\delta _2 n}\cdot F(G)$
such colourings, and an identical argument gives the required
$2^{-2\delta _2 n}\cdot F(G)$
such colourings, and an identical argument gives the required
![]() $\xi $
, satisfying (iii) and (iv).
$\xi $
, satisfying (iii) and (iv).
Suppose there exist
![]() $x,\chi $
as in Claim 2.12.2(i) and (ii). So there are
$x,\chi $
as in Claim 2.12.2(i) and (ii). So there are ![]() and
and
![]() $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
$\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
![]() $\mathrm {Ext}(\chi )$
as in Claim 2.12.2. Define
$\mathrm {Ext}(\chi )$
as in Claim 2.12.2. Define
![]() $\boldsymbol {\beta } := (\beta _1,\ldots ,\beta _{r^*})$
by setting
$\boldsymbol {\beta } := (\beta _1,\ldots ,\beta _{r^*})$
by setting
![]() $\beta _i := |Y_i|/n$
for all
$\beta _i := |Y_i|/n$
for all
![]() $i \in [r^*]$
. Then (2.6) implies that
$i \in [r^*]$
. Then (2.6) implies that
Note that
![]() $\mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G;\phi ^*,\mathcal {Y})$
. For every
$\mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G;\phi ^*,\mathcal {Y})$
. For every
![]() $\overline {\chi } \in \mathrm {Ext}(\chi )$
, define
$\overline {\chi } \in \mathrm {Ext}(\chi )$
, define
![]() $\phi = \phi (\overline {\chi }) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
by setting
$\phi = \phi (\overline {\chi }) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
by setting
 $$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2}; \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[x,Y_j]| \geq \sqrt{\delta_1} |Y_{j}| \} &\mbox{if } i = r^*+1, j \in [r^*]. \\ \end{cases} \end{align*} $$
$$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2}; \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[x,Y_j]| \geq \sqrt{\delta_1} |Y_{j}| \} &\mbox{if } i = r^*+1, j \in [r^*]. \\ \end{cases} \end{align*} $$
Fix the pattern
![]() $\phi $
that appears for the largest number of extensions
$\phi $
that appears for the largest number of extensions
![]() $\overline {\chi } \in \mathrm {Ext}(\chi )$
, and let
$\overline {\chi } \in \mathrm {Ext}(\chi )$
, and let
![]() $\mathrm {Ext}_{\phi }(\chi )$
be the set of these
$\mathrm {Ext}_{\phi }(\chi )$
be the set of these
![]() $\overline {\chi }$
. By Claim 2.12.2(ii),
$\overline {\chi }$
. By Claim 2.12.2(ii),
Claim 2.12.3.
![]() $\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
.
$\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
.
Proof of Claim
Suppose not. Then there is some
![]() $c \in [s]$
such that
$c \in [s]$
such that
![]() $\phi ^{-1}(c)$
contains a copy of
$\phi ^{-1}(c)$
contains a copy of
![]() $K_{k_c}$
. Since
$K_{k_c}$
. Since
![]() $\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$
is the restriction of
$\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$
is the restriction of
![]() $\phi $
to
$\phi $
to
![]() $\binom {[r^*]}{2}$
, the vertex
$\binom {[r^*]}{2}$
, the vertex
![]() $r^*+1$
must lie in this copy. Let
$r^*+1$
must lie in this copy. Let
![]() $z_1,\ldots ,z_{k_c-1}$
be the other vertices. Let
$z_1,\ldots ,z_{k_c-1}$
be the other vertices. Let
![]() $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
be arbitrary. For each
$\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
be arbitrary. For each
![]() $k \in [k_c-1]$
, let
$k \in [k_c-1]$
, let
![]() $Z_k := \{ y \in Y_{z_k} : \overline {\chi }(xy) = c \}$
. Then, by the definition of
$Z_k := \{ y \in Y_{z_k} : \overline {\chi }(xy) = c \}$
. Then, by the definition of
![]() $\phi $
, we have
$\phi $
, we have
Let
![]() $kk' \in \binom {[k_c-1]}{2}$
. Now,
$kk' \in \binom {[k_c-1]}{2}$
. Now,
![]() $\overline {\chi }^{-1}(c)[Y_{z_k},Y_{z_{k'}}]$
is
$\overline {\chi }^{-1}(c)[Y_{z_k},Y_{z_{k'}}]$
is
![]() $(3\delta _1,\geq \!\! s^{-1})$
-regular since
$(3\delta _1,\geq \!\! s^{-1})$
-regular since
![]() $\overline {\chi } \in \mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G; \phi ^*,\mathcal {Y})$
. Therefore,
$\overline {\chi } \in \mathrm {Ext}(\chi ) \subseteq \mathcal {G}_{3\delta _1}(G; \phi ^*,\mathcal {Y})$
. Therefore,
Now Proposition 2.7 implies that
![]() $\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$
is
$\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$
is
![]() $3\sqrt {\delta _1}$
-regular. Therefore,
$3\sqrt {\delta _1}$
-regular. Therefore,
![]() $\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$
is
$\overline {\chi }^{-1}(c)[Z_k,Z_{k'}]$
is
![]() $(3\sqrt {\delta _1},\geq \!\!1/(2s))$
-regular. Now (2.12) and Lemma 2.4 imply that
$(3\sqrt {\delta _1},\geq \!\!1/(2s))$
-regular. Now (2.12) and Lemma 2.4 imply that
![]() $\chi ^{-1}(c)[Z_1,\ldots ,Z_{k_c-1}]$
contains a copy of
$\chi ^{-1}(c)[Z_1,\ldots ,Z_{k_c-1}]$
contains a copy of
![]() $K_{k_c-1}$
. Together with x, this gives a c-coloured copy of
$K_{k_c-1}$
. Together with x, this gives a c-coloured copy of
![]() $K_{k_c}$
in
$K_{k_c}$
in
![]() $\overline {\chi }$
, contradicting the fact that
$\overline {\chi }$
, contradicting the fact that
![]() $\overline {\chi }$
is
$\overline {\chi }$
is
![]() $\boldsymbol {k}$
-valid.
$\boldsymbol {k}$
-valid.
Next we will show that there is some
![]() $i \in [r^*]$
such that
$i \in [r^*]$
such that
![]() $r^*+1$
is a clone of i under
$r^*+1$
is a clone of i under
![]() $\phi $
. Suppose for a contradiction that this is not the case. Thus, by our choice of
$\phi $
. Suppose for a contradiction that this is not the case. Thus, by our choice of
![]() ${\varepsilon }_0$
, we have
${\varepsilon }_0$
, we have
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) \leq Q-{\varepsilon }_0$
. Then, using (a version of) Proposition 2.1(i) and Lemma 2.2(ii),
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) \leq Q-{\varepsilon }_0$
. Then, using (a version of) Proposition 2.1(i) and Lemma 2.2(ii),
 $$ \begin{align} \frac{1}{n}\log\prod_{j \in [r^*]}|\phi(\{j,r^*+1\})|^{|Y_j|} &= \mathop{\mathrm{ext}}(\phi,\boldsymbol{\beta}) \leq \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) + \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 \cdot \log s\\ \nonumber &\stackrel{({2.10})}{<} Q - {\varepsilon}_0 + \delta_1^2\log s \leq Q - {\varepsilon}_0/2. \end{align} $$
$$ \begin{align} \frac{1}{n}\log\prod_{j \in [r^*]}|\phi(\{j,r^*+1\})|^{|Y_j|} &= \mathop{\mathrm{ext}}(\phi,\boldsymbol{\beta}) \leq \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) + \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 \cdot \log s\\ \nonumber &\stackrel{({2.10})}{<} Q - {\varepsilon}_0 + \delta_1^2\log s \leq Q - {\varepsilon}_0/2. \end{align} $$
The number of possible patterns
![]() $\phi $
on
$\phi $
on
![]() $r^*+1$
vertices which are extensions of
$r^*+1$
vertices which are extensions of
![]() $\phi ^*$
is at most
$\phi ^*$
is at most
![]() $2^{sr^*}$
, and, by definition, the number of edges with endpoint x which are not coloured according to
$2^{sr^*}$
, and, by definition, the number of edges with endpoint x which are not coloured according to
![]() $\phi $
is at most
$\phi $
is at most
![]() $s\sqrt {\delta _1}n$
. Therefore, the total number of
$s\sqrt {\delta _1}n$
. Therefore, the total number of
![]() $\boldsymbol {k}$
-valid extensions
$\boldsymbol {k}$
-valid extensions
![]() $\overline {\chi } \in \mathrm {Ext}(\chi )$
of
$\overline {\chi } \in \mathrm {Ext}(\chi )$
of
![]() $\chi $
to G is at most
$\chi $
to G is at most
 $$ \begin{align} 2^{sr^*} \cdot \binom{n}{\leq s\sqrt{\delta_1}n} \cdot s^{s\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{|Y_j|} \stackrel{({2.4}),({2.13})}{\leq} 2^{(Q-{\varepsilon}_0/3)n} < 2^{(Q-2\delta_3)n}. \end{align} $$
$$ \begin{align} 2^{sr^*} \cdot \binom{n}{\leq s\sqrt{\delta_1}n} \cdot s^{s\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{|Y_j|} \stackrel{({2.4}),({2.13})}{\leq} 2^{(Q-{\varepsilon}_0/3)n} < 2^{(Q-2\delta_3)n}. \end{align} $$
So certainly there are at most this number of extensions which lie in
![]() $\mathrm {Ext}_{\phi }(\chi )$
, contradicting (2.11).
$\mathrm {Ext}_{\phi }(\chi )$
, contradicting (2.11).
Therefore, we may assume that there is some
![]() $i^* \in [r^*]$
such that
$i^* \in [r^*]$
such that
![]() $r^*+1$
is a clone of
$r^*+1$
is a clone of
![]() $i^*$
under
$i^*$
under
![]() $\phi $
. Thus, we have
$\phi $
. Thus, we have
where the last inclusion follows from Lemma 2.2(iii).
Claim 2.12.4. We have the following for all
![]() $\overline {\chi } \in \mathrm {Ext}_\phi (\chi )$
:
$\overline {\chi } \in \mathrm {Ext}_\phi (\chi )$
:
-
(i) There exist
 $j^* \in [r^*]\setminus \{ i^* \}$
, a part
$j^* \in [r^*]\setminus \{ i^* \}$
, a part
 $X \subseteq Y_{j^*}$
and
$X \subseteq Y_{j^*}$
and
 $c \in \phi ^*(i^*j^*)$
such that
$c \in \phi ^*(i^*j^*)$
such that
 $|\overline {\chi }^{-1}(c)[x,X]| \neq |\phi (i^*j^*)|^{-1}|X| \pm \frac {\delta _5}{\ell _{j^*}}|Y_{j^*}|$
.
$|\overline {\chi }^{-1}(c)[x,X]| \neq |\phi (i^*j^*)|^{-1}|X| \pm \frac {\delta _5}{\ell _{j^*}}|Y_{j^*}|$
. -
(ii) If there exists
 $h \in [r^*]$
such that the part X of G containing x lies in
$h \in [r^*]$
such that the part X of G containing x lies in
 $Y_{h}$
, and
$Y_{h}$
, and
 $|X|> \delta _4|Y_{h}|$
, then
$|X|> \delta _4|Y_{h}|$
, then
 $i^* = h$
.
$i^* = h$
.
Proof of Claim
Define
![]() $\ell \in \{ 0,\ldots , r^* \}$
as follows. If there is
$\ell \in \{ 0,\ldots , r^* \}$
as follows. If there is
![]() $i' \in [r^*]$
such that
$i' \in [r^*]$
such that
![]() $d_G(x,Y_{i'}) < (1-\delta _4)|Y_{i'}|$
(noting that there can be at most one such
$d_G(x,Y_{i'}) < (1-\delta _4)|Y_{i'}|$
(noting that there can be at most one such
![]() $i'$
), let
$i'$
), let
![]() $\ell := i'$
. If there is no such
$\ell := i'$
. If there is no such
![]() $i'$
, let
$i'$
, let
![]() $\ell :=0$
. Let X be the part of G which contains x.
$\ell :=0$
. Let X be the part of G which contains x.
Case 1:
![]() $\ell = 0$
.
$\ell = 0$
.
Suppose that (i) is false. Since
![]() $\overline {\chi }$
is not
$\overline {\chi }$
is not
![]() $(\delta _4,\delta _5)$
-locally good at x, we must have that
$(\delta _4,\delta _5)$
-locally good at x, we must have that
![]() $d_G(x,Y_{i^*}) - |\overline {\chi }^{-1}(1)[x,Y_{i^*}]|> \delta _5 |Y_{i^*}|$
. By (2.15) and the definition of
$d_G(x,Y_{i^*}) - |\overline {\chi }^{-1}(1)[x,Y_{i^*}]|> \delta _5 |Y_{i^*}|$
. By (2.15) and the definition of
![]() $\phi $
, we have that
$\phi $
, we have that
a contradiction. For (ii), let
![]() $X \subseteq Y_h$
be the part of G containing x and suppose
$X \subseteq Y_h$
be the part of G containing x and suppose
![]() $h \in [r^*]$
. Then
$h \in [r^*]$
. Then
![]() $|Y_h|-|X|=d_G(x,Y_h) \geq (1-\delta _4)|Y_h|$
. So in this case,
$|Y_h|-|X|=d_G(x,Y_h) \geq (1-\delta _4)|Y_h|$
. So in this case,
![]() $|X| \leq \delta _4|Y_h|$
and (ii) is vacuous.
$|X| \leq \delta _4|Y_h|$
and (ii) is vacuous.
Case 2:
![]() $\ell \in [r^*]$
.
$\ell \in [r^*]$
.
We will first show that (ii) holds. Note that
![]() $h=\ell $
since
$h=\ell $
since
![]() $X \subseteq Y_h$
and
$X \subseteq Y_h$
and
![]() $x\in X$
is not adjacent to the whole of
$x\in X$
is not adjacent to the whole of
![]() $Y_\ell $
. If
$Y_\ell $
. If
![]() $Y_{h} = X$
, then
$Y_{h} = X$
, then
![]() $N_G(x,Y_{h}) = \emptyset $
so
$N_G(x,Y_{h}) = \emptyset $
so
![]() $\phi (\{ r^*+1,h \}) = \emptyset $
. So (2.15) implies that
$\phi (\{ r^*+1,h \}) = \emptyset $
. So (2.15) implies that
![]() $h = i^*$
, as required.
$h = i^*$
, as required.
Otherwise,
![]() $Y_{h} \neq X$
. Suppose that
$Y_{h} \neq X$
. Suppose that
![]() $i^* \neq h$
. Then
$i^* \neq h$
. Then
![]() $|\phi ^*(i^*h)| \geq 2$
, and so
$|\phi ^*(i^*h)| \geq 2$
, and so
 $$ \begin{align*} \frac{1}{n}\left( \log \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{d_G(x,Y_j)}\right) &\stackrel{({2.15})}{=} \frac{1}{n}\sum_{j \in [r^*]\setminus \{ i^* \}} |Y_j\setminus X| \log|\phi^*(i^*j)|\\ &= \sum_{j \in [r^*]\setminus \{ i^*,h \}}\beta_j \log|\phi^*(i^*j)| + \left(\beta_h -\frac{|X|}{n}\right) \log|\phi^*(i^*h)|\\ &\leq q_{i^*}(\phi^*,\boldsymbol{\alpha}^*) + \left( \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 - \frac{|X|}{n}\right)\log s\\ &\stackrel{({2.10})}{\leq} Q + (\delta_1^2 - \delta_4^2)\log s < Q - 4\delta_3, \end{align*} $$
$$ \begin{align*} \frac{1}{n}\left( \log \prod_{j \in [r^*]} |\phi(\{ j,r^*+1 \})|^{d_G(x,Y_j)}\right) &\stackrel{({2.15})}{=} \frac{1}{n}\sum_{j \in [r^*]\setminus \{ i^* \}} |Y_j\setminus X| \log|\phi^*(i^*j)|\\ &= \sum_{j \in [r^*]\setminus \{ i^*,h \}}\beta_j \log|\phi^*(i^*j)| + \left(\beta_h -\frac{|X|}{n}\right) \log|\phi^*(i^*h)|\\ &\leq q_{i^*}(\phi^*,\boldsymbol{\alpha}^*) + \left( \|\boldsymbol{\alpha}^*-\boldsymbol{\beta}\|_1 - \frac{|X|}{n}\right)\log s\\ &\stackrel{({2.10})}{\leq} Q + (\delta_1^2 - \delta_4^2)\log s < Q - 4\delta_3, \end{align*} $$
where the penultimate inequality follows from Proposition 2.1(ii). Combining this with a very similar calculation to (2.14) implies that the total number of
![]() $\boldsymbol {k}$
-valid extensions
$\boldsymbol {k}$
-valid extensions
![]() $\overline {\chi } \in \mathrm {Ext}(\chi )$
of
$\overline {\chi } \in \mathrm {Ext}(\chi )$
of
![]() $\chi $
to G is less than
$\chi $
to G is less than
![]() $2^{(Q-2\delta _3)n}$
, contradicting (2.11). Therefore,
$2^{(Q-2\delta _3)n}$
, contradicting (2.11). Therefore,
![]() $i^*=h$
, proving (ii). The proof of (i) now proceeds exactly as in Case 1.
$i^*=h$
, proving (ii). The proof of (i) now proceeds exactly as in Case 1.
Claim 2.12.4(i) implies that for every
![]() $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
, there exist
$\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
, there exist
![]() $j^* \in [r^*]\setminus \{i^*\}$
, a part
$j^* \in [r^*]\setminus \{i^*\}$
, a part
![]() $X \subseteq Y_{j^*}$
and
$X \subseteq Y_{j^*}$
and
![]() $c^* \in \phi ^*(i^*j^*)$
such that, by averaging,
$c^* \in \phi ^*(i^*j^*)$
such that, by averaging,
In particular, since
![]() $\ell _{j^*} \leq k_1 < R$
, we have
$\ell _{j^*} \leq k_1 < R$
, we have
![]() $|X| \geq \delta _5|Y_{j^*}|/(s \cdot R) \geq (\delta _5)^2|Y_{j^*}|$
. The number of ways of adding edges coloured with
$|X| \geq \delta _5|Y_{j^*}|/(s \cdot R) \geq (\delta _5)^2|Y_{j^*}|$
. The number of ways of adding edges coloured with
![]() $\phi ^*$
between x and X with this reduced density (choosing the set of colour-
$\phi ^*$
between x and X with this reduced density (choosing the set of colour-
![]() $c^*$
neighbours, and then colouring every other edge with any available colour other than
$c^*$
neighbours, and then colouring every other edge with any available colour other than
![]() $c^*$
) is at most
$c^*$
) is at most
 $$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i^*j^*)|^{-1}|X|-\frac{\delta_5}{s\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i^*j^*)|-1)^{|X|-k}\\ &\leq e^{-\delta_5^2|X|/3(s^2R^2)} \cdot |\phi^*(i^*j^*)|^{|X|} \stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot |\phi^*(i^*j^*)|^{|X|}, \end{align*} $$
$$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i^*j^*)|^{-1}|X|-\frac{\delta_5}{s\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i^*j^*)|-1)^{|X|-k}\\ &\leq e^{-\delta_5^2|X|/3(s^2R^2)} \cdot |\phi^*(i^*j^*)|^{|X|} \stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot |\phi^*(i^*j^*)|^{|X|}, \end{align*} $$
where the first inequality is a consequence of Lemma 2.8. Using Proposition 2.1(ii), we have that
Now, we can generate every
![]() $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
from
$\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
from
![]() $\chi $
by doing the following. For each
$\chi $
by doing the following. For each
![]() $j \in [r^*]$
, choose at most
$j \in [r^*]$
, choose at most
![]() $\sqrt {\delta _1}|Y_j|$
vertices
$\sqrt {\delta _1}|Y_j|$
vertices
![]() $y \in N_G(x,Y_j)$
and colour
$y \in N_G(x,Y_j)$
and colour
![]() $xy$
arbitrarily. Arbitrarily colour all edges
$xy$
arbitrarily. Arbitrarily colour all edges
![]() $xy_0$
where
$xy_0$
where
![]() $y_0 \in Y_0$
. Then choose
$y_0 \in Y_0$
. Then choose
![]() $j^*,X,c^*$
as above and colour every uncoloured edge (with endpoint x) according to
$j^*,X,c^*$
as above and colour every uncoloured edge (with endpoint x) according to
![]() $\phi $
so that (2.17) holds (with a small adjustment to account for the
$\phi $
so that (2.17) holds (with a small adjustment to account for the
![]() $\sqrt {\delta _1}|Y_j|$
edges that have already been coloured). That this will indeed generate every
$\sqrt {\delta _1}|Y_j|$
edges that have already been coloured). That this will indeed generate every
![]() $\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
is a consequence of the definition of
$\overline {\chi } \in \mathrm {Ext}_{\phi }(\chi )$
is a consequence of the definition of
![]() $\phi $
and Claim 2.12.4. Therefore,
$\phi $
and Claim 2.12.4. Therefore,
 $$ \begin{align*} |\mathrm{Ext}_{\phi}(\chi)| &\leq \binom{n}{\leq \sqrt{\delta_1}n} \cdot s^{\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot e^{-\delta_5^5 n} \cdot \prod_{j \in [r^*]\setminus \{ i^*\}} |\phi^*(i^*j)|^{|Y_j|}\\ &\stackrel{({2.4}),({2.18})}{\leq} 2^{-\delta_5^6 n} \cdot 2^{(Q+2\delta_1^2 \log s)n} < 2^{(Q-2\delta_3)n}, \end{align*} $$
$$ \begin{align*} |\mathrm{Ext}_{\phi}(\chi)| &\leq \binom{n}{\leq \sqrt{\delta_1}n} \cdot s^{\sqrt{\delta_1}n} \cdot s^{|Y_0|} \cdot e^{-\delta_5^5 n} \cdot \prod_{j \in [r^*]\setminus \{ i^*\}} |\phi^*(i^*j)|^{|Y_j|}\\ &\stackrel{({2.4}),({2.18})}{\leq} 2^{-\delta_5^6 n} \cdot 2^{(Q+2\delta_1^2 \log s)n} < 2^{(Q-2\delta_3)n}, \end{align*} $$
contradicting (2.11). So our assumption that there are
![]() $x,\chi $
as in Claim 2.12.2(i) and (ii) is false.
$x,\chi $
as in Claim 2.12.2(i) and (ii) is false.
Thus, there must be
![]() $z,y,\xi $
such that Claim 2.12.2(iii) and (iv) hold. So there are
$z,y,\xi $
such that Claim 2.12.2(iii) and (iv) hold. So there are ![]() and
and
![]() $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
$\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
and
![]() $\mathrm {Ext}(\xi )$
as in Claim 2.12.2. Again, we define colour patterns
$\mathrm {Ext}(\xi )$
as in Claim 2.12.2. Again, we define colour patterns
![]() $\phi _y, \phi _z$
in analogy with
$\phi _y, \phi _z$
in analogy with
![]() $\phi $
to be the pair of patterns that appear together for the greatest number of extensions
$\phi $
to be the pair of patterns that appear together for the greatest number of extensions
![]() $\overline {\xi } \in \mathrm {Ext}(\xi )$
, and we write
$\overline {\xi } \in \mathrm {Ext}(\xi )$
, and we write
![]() $\mathrm { Ext}_{\phi _y,\phi _z}(\xi )$
for the set of extensions
$\mathrm { Ext}_{\phi _y,\phi _z}(\xi )$
for the set of extensions
![]() $\overline {\xi } \in \mathrm {Ext}(\xi )$
with this pair of patterns. Again, by Claim 2.12.2(iii),
$\overline {\xi } \in \mathrm {Ext}(\xi )$
with this pair of patterns. Again, by Claim 2.12.2(iii),
Similarly to Claim 2.12.3, we have
![]() $\phi _y,\phi _z \in \Phi _0(r^*+1;\boldsymbol {k})$
. Applying Lemma 2.2(ii), we have that there are
$\phi _y,\phi _z \in \Phi _0(r^*+1;\boldsymbol {k})$
. Applying Lemma 2.2(ii), we have that there are
![]() $i_y, i_z \in [r^*]$
such that in
$i_y, i_z \in [r^*]$
such that in
![]() $\phi _y,\phi _z$
, respectively, the vertex
$\phi _y,\phi _z$
, respectively, the vertex
![]() $r^*+1$
is a clone of
$r^*+1$
is a clone of
![]() $i_y,i_z$
. And, in particular,
$i_y,i_z$
. And, in particular,
![]() $\phi _y(\{i_y,r^*+1\}) \subseteq \{1\}$
and
$\phi _y(\{i_y,r^*+1\}) \subseteq \{1\}$
and
![]() $\phi _z(\{i_z,r^*+1\}) \subseteq \{1\}$
. The analogue of Claim 2.12.4(i) for pairs holds in the same way; that is, there exist
$\phi _z(\{i_z,r^*+1\}) \subseteq \{1\}$
. The analogue of Claim 2.12.4(i) for pairs holds in the same way; that is, there exist
![]() $j^* \in [r^*]\setminus \{i_y,i_z\}$
, a part
$j^* \in [r^*]\setminus \{i_y,i_z\}$
, a part
![]() $X \subseteq Y_{j^*}$
,
$X \subseteq Y_{j^*}$
,
![]() $c_y \in \phi _y(i_yj^*)$
and
$c_y \in \phi _y(i_yj^*)$
and
![]() $c_z \in \phi _z(i_zj^*)$
such that
$c_z \in \phi _z(i_zj^*)$
such that
 $$ \begin{align*}|N_{\xi^{-1}(c_y)}(y,X) \cap N_{\xi^{-1}(c_z)}(z,X)| \neq |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| \pm \frac{\delta_5}{\ell_{j^*}}|Y_{j^*}|. \end{align*} $$
$$ \begin{align*}|N_{\xi^{-1}(c_y)}(y,X) \cap N_{\xi^{-1}(c_z)}(z,X)| \neq |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| \pm \frac{\delta_5}{\ell_{j^*}}|Y_{j^*}|. \end{align*} $$
It remains to show that this implies there are few extensions of
![]() $\chi $
to G. By averaging, there are
$\chi $
to G. By averaging, there are
![]() $c_y^* \in \phi ^*(i_yj^*)$
and
$c_y^* \in \phi ^*(i_yj^*)$
and
![]() $c_z^* \in \phi ^*(i_zj^*)$
such that
$c_z^* \in \phi ^*(i_zj^*)$
such that
 $$ \begin{align*}|N_{\xi^{-1}(c_y^*)}(y,X) \cap N_{\xi^{-1}(c_z^*)}(z,X)| < |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| - \frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|. \end{align*} $$
$$ \begin{align*}|N_{\xi^{-1}(c_y^*)}(y,X) \cap N_{\xi^{-1}(c_z^*)}(z,X)| < |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X| - \frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|. \end{align*} $$
The number of ways of adding edges coloured with
![]() $\phi ^*$
between
$\phi ^*$
between
![]() $y,z$
and X with this reduced density (choosing the set of v such that
$y,z$
and X with this reduced density (choosing the set of v such that
![]() $yv$
is coloured
$yv$
is coloured
![]() $c_y^*$
and
$c_y^*$
and
![]() $zv$
is coloured
$zv$
is coloured
![]() $c_z^*$
, and then colouring every other
$c_z^*$
, and then colouring every other
![]() $yu,zu$
with any pair other than
$yu,zu$
with any pair other than
![]() $c_y^*,c_z^*$
) is at most
$c_y^*,c_z^*$
) is at most
 $$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X|-\frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i_yj^*)||\phi^*(i_zj^*)|-1)^{|X|-k} \cdot s\\ &\hspace{4cm}\stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot (|\phi^*(i_yj^*)||\phi^*(i_zj^*)|)^{|X|}. \end{align*} $$
$$ \begin{align*} &\phantom{=} \sum_{k=0}^{\lfloor |\phi^*(i_yj^*)|^{-1}|\phi^*(i_zj^*)|^{-1}|X|-\frac{\delta_5}{s^2\ell_{j^*}}|Y_{j^*}|\rfloor} \binom{|X|}{k}(|\phi^*(i_yj^*)||\phi^*(i_zj^*)|-1)^{|X|-k} \cdot s\\ &\hspace{4cm}\stackrel{({2.7})}{\leq} e^{-\delta_5^5 n} \cdot (|\phi^*(i_yj^*)||\phi^*(i_zj^*)|)^{|X|}. \end{align*} $$
Repeating the calculations in the single vertex case, we see that
![]() $|\mathrm {Ext}_{\phi _y,\phi _z}(\xi )| < 2^{(Q-2\delta _3)(n+n-1)}$
, contradicting 2.19).
$|\mathrm {Ext}_{\phi _y,\phi _z}(\xi )| < 2^{(Q-2\delta _3)(n+n-1)}$
, contradicting 2.19).
Thus, our assumption (2.8) is false. Therefore, combining its negation with Claim 2.12.1, we see that
Let
![]() $\chi \in \mathcal {P}_{\delta _4,\delta _5}(G)$
. Then there exists
$\chi \in \mathcal {P}_{\delta _4,\delta _5}(G)$
. Then there exists ![]() and
and
![]() $\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
such that
$\mathcal {Y} = (Y_1,\ldots ,Y_{r^*}) \in \mathop {\mathrm {Coars}}(\boldsymbol {\alpha }^*)$
such that
![]() $\chi $
is
$\chi $
is
![]() $(\delta _4,\delta _5)$
-perfect with respect to
$(\delta _4,\delta _5)$
-perfect with respect to
![]() $(\phi ^*;Y_1,\ldots ,Y_{r^*})$
. So for all
$(\phi ^*;Y_1,\ldots ,Y_{r^*})$
. So for all
![]() $x \in V(G) \setminus Y_0$
, there exists
$x \in V(G) \setminus Y_0$
, there exists
![]() $i(x) \in [r^*]$
such that for all
$i(x) \in [r^*]$
such that for all
![]() $j \in [r^*]$
and
$j \in [r^*]$
and
![]() $b \in N_G(x,Y_j)$
, we have
$b \in N_G(x,Y_j)$
, we have
![]() $\chi (xb) = 1$
if
$\chi (xb) = 1$
if
![]() $j = i(x)$
, and
$j = i(x)$
, and
![]() $\chi (xb) \in \phi ^*(i(x)j)$
otherwise. Moreover, (the proof of) the second part of Claim 2.12.4 implies that, if there exists
$\chi (xb) \in \phi ^*(i(x)j)$
otherwise. Moreover, (the proof of) the second part of Claim 2.12.4 implies that, if there exists
![]() $h(x) \in [r^*]$
such that the part X of G containing x lies in
$h(x) \in [r^*]$
such that the part X of G containing x lies in
![]() $Y_{h(x)}$
, and
$Y_{h(x)}$
, and
![]() $|X|> \delta _4|Y_{h(x)}|$
, then
$|X|> \delta _4|Y_{h(x)}|$
, then
![]() $i(x) = h(x)$
.
$i(x) = h(x)$
.
Now, define a new partition
![]() $Z_0,\ldots ,Z_{r^*}$
of
$Z_0,\ldots ,Z_{r^*}$
of
![]() $V(G)$
by setting, for all
$V(G)$
by setting, for all
![]() $i \in [r^*]$
,
$i \in [r^*]$
,
Then
![]() $Z_0,\ldots ,Z_{r^*}$
is a coarsening of
$Z_0,\ldots ,Z_{r^*}$
is a coarsening of
![]() $X_1,\ldots ,X_m$
, and
$X_1,\ldots ,X_m$
, and
![]() $\chi $
is
$\chi $
is
![]() $(0,\delta _5)$
-perfect with respect to
$(0,\delta _5)$
-perfect with respect to
![]() $(\phi ^*;Z_1,\ldots ,Z_{r^*})$
by definition. Moreover, for all
$(\phi ^*;Z_1,\ldots ,Z_{r^*})$
by definition. Moreover, for all
![]() $i \in [r^*]$
,
$i \in [r^*]$
,
![]() $Z_i \subseteq Y_i$
, and
$Z_i \subseteq Y_i$
, and
![]() $|Y_i \setminus Z_i| \leq R\delta _4|Y_i|$
. So
$|Y_i \setminus Z_i| \leq R\delta _4|Y_i|$
. So
as required. Finally, let
![]() $\ell _i$
be the number of
$\ell _i$
be the number of
![]() $X_j$
in
$X_j$
in
![]() $Z_i$
. Then
$Z_i$
. Then
![]() $\ell _i \leq t_i$
for all
$\ell _i \leq t_i$
for all
![]() $i \in [r^*]$
. The second part of Claim 2.12.1 yields the desired conclusion.
$i \in [r^*]$
. The second part of Claim 2.12.1 yields the desired conclusion.
Note that the statement of Theorem 2.12 can be made much simpler in the case when
![]() $\boldsymbol {k}$
has the strong extension property as in this case we have that
$\boldsymbol {k}$
has the strong extension property as in this case we have that ![]() and the partitions
and the partitions
![]() $Z_0,\ldots ,Z_{r^*}$
are identical for all of the at least
$Z_0,\ldots ,Z_{r^*}$
are identical for all of the at least
![]() $(1-2^{-{\varepsilon } n^2})F(G;\boldsymbol {k})$
colourings specified in the theorem. Indeed, suppose that
$(1-2^{-{\varepsilon } n^2})F(G;\boldsymbol {k})$
colourings specified in the theorem. Indeed, suppose that ![]() and its associated partition
and its associated partition
![]() $Z_0,\ldots ,Z_{r^*}$
are outputs of Theorem 2.12 for some specified colouring. Then each
$Z_0,\ldots ,Z_{r^*}$
are outputs of Theorem 2.12 for some specified colouring. Then each
![]() $Z_1,\ldots ,Z_{r^*}$
is a part of G by Theorem 2.12(ii). Part (i) implies that for each
$Z_1,\ldots ,Z_{r^*}$
is a part of G by Theorem 2.12(ii). Part (i) implies that for each
![]() $i \in [r^*]$
, we have that
$i \in [r^*]$
, we have that
![]() $|Z_i| \geq \alpha ^*_i n - \delta n \geq \mu n/2$
. Furthermore,
$|Z_i| \geq \alpha ^*_i n - \delta n \geq \mu n/2$
. Furthermore,
![]() $|Z_0| \leq \delta n \ll \mu n/2$
. So, provided
$|Z_0| \leq \delta n \ll \mu n/2$
. So, provided
![]() $\delta $
is chosen to be smaller than
$\delta $
is chosen to be smaller than
![]() $\mu /2$
, the structure of G itself determines
$\mu /2$
, the structure of G itself determines
![]() $(r^*,\boldsymbol {\alpha }^*)$
and
$(r^*,\boldsymbol {\alpha }^*)$
and
![]() $Z_0,\ldots ,Z_{r^*}$
. Thus, we have the following corollary, which will be used to prove Theorem 1.6.
$Z_0,\ldots ,Z_{r^*}$
. Thus, we have the following corollary, which will be used to prove Theorem 1.6.
Corollary 2.13. Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
has the strong extension property. Then for all
$\boldsymbol {k} \in \mathbb {N}^s$
has the strong extension property. Then for all
![]() $\delta> 0$
, there exist
$\delta> 0$
, there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() ${\varepsilon } \in \mathbb {R}$
with
${\varepsilon } \in \mathbb {R}$
with
![]() $0 < {\varepsilon } < \delta $
such that the following holds. Let
$0 < {\varepsilon } < \delta $
such that the following holds. Let
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
$G = K(X_1,\ldots ,X_m)$
be a complete m-partite graph on
![]() $n \geq n_0$
vertices such that
$n \geq n_0$
vertices such that
![]() $|X_1| \geq \ldots \geq |X_m|$
and
$|X_1| \geq \ldots \geq |X_m|$
and
 $$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
$$ \begin{align*}\frac{\log F(G;\mathbf{k})}{\binom{n}{2}} \geq Q(\mathbf{k}) - {\varepsilon}. \end{align*} $$
Then the following hold.
-
(i) There is
 with
with
 $r^* \leq m$
such that
$r^* \leq m$
such that
 $ \sum _{i \in [r^*]}|\,|X_i|-\alpha _i^*n\,| < \delta n $
.
$ \sum _{i \in [r^*]}|\,|X_i|-\alpha _i^*n\,| < \delta n $
. -
(ii) For at least
 $(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$
-edge-colourings
$(1-2^{-{\varepsilon } n^2}) \cdot F(G;\boldsymbol {k}) s$
-edge-colourings
 $\chi $
of G which are
$\chi $
of G which are
 $\boldsymbol {k}$
-valid, there is
$\boldsymbol {k}$
-valid, there is  such that
such that
 $\chi $
is
$\chi $
is
 $\delta $
-good with respect to
$\delta $
-good with respect to
 $(\phi ^*; X_1,\ldots ,X_{r^*})$
.
$(\phi ^*; X_1,\ldots ,X_{r^*})$
. -
(iii) Furthermore, if we have
(2.20)then for at least $$ \begin{align} \nonumber &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{align} $$
$$ \begin{align} \nonumber &\log F(G;\boldsymbol{k}) - \log F(G-x;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})n \quad\forall \ x \in V(G), \ \text{ and} \\ &\log F(G;\boldsymbol{k}) - \log F(G-y-z;\boldsymbol{k}) \geq (Q(\boldsymbol{k}) - 2{\varepsilon})(n+n-1) \quad\forall\text{ distinct }y,z \in V(G), \end{align} $$
 $(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k})$
valid s-edge-colourings
$(1-2^{-{\varepsilon } n})\cdot F(G;\boldsymbol {k})$
valid s-edge-colourings
 $\chi $
of G, there is
$\chi $
of G, there is  with
with
 $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
such that
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
such that
 $\chi $
is
$\chi $
is
 $(0,\delta )$
-perfect with respect to
$(0,\delta )$
-perfect with respect to
 $(\phi ^*; X_1,\ldots ,X_{r^*})$
.
$(\phi ^*; X_1,\ldots ,X_{r^*})$
.
2.4. The proof of Theorem 1.6
The next observation is a simple but key ingredient of our proof, which allows us to only consider complete multipartite graphs. If there were a
![]() $\boldsymbol {k}$
-extremal graph H which is not complete multipartite, one can use symmetrisation to obtain from H a new graph
$\boldsymbol {k}$
-extremal graph H which is not complete multipartite, one can use symmetrisation to obtain from H a new graph
![]() $H'$
which is complete multipartite (Theorem 1 in [Reference Pikhurko, Staden and Yilma11]). By symmetrisation, we mean replacing a vertex u with a copy, or twin, of
$H'$
which is complete multipartite (Theorem 1 in [Reference Pikhurko, Staden and Yilma11]). By symmetrisation, we mean replacing a vertex u with a copy, or twin, of
![]() $v \notin N_H(u)$
. Crucially, we can do this in such a way that we end up with a part containing a single vertex (which is connected to every other vertex).
$v \notin N_H(u)$
. Crucially, we can do this in such a way that we end up with a part containing a single vertex (which is connected to every other vertex).
Lemma 2.14. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Let G be a
$\boldsymbol {k} \in \mathbb {N}^s$
. Let G be a
![]() $\boldsymbol {k}$
-extremal graph which is not complete multipartite. Then there exists a
$\boldsymbol {k}$
-extremal graph which is not complete multipartite. Then there exists a
![]() $\boldsymbol {k}$
-extremal graph
$\boldsymbol {k}$
-extremal graph
![]() $G'$
which is complete multipartite and has a part of size one.
$G'$
which is complete multipartite and has a part of size one.
Proof. Since G is not complete multipartite, there exist distinct nonadjacent vertices
![]() $u,v \in V(G)$
such that
$u,v \in V(G)$
such that
![]() $N_G(u) \neq N_G(v)$
. For any graph H, let
$N_G(u) \neq N_G(v)$
. For any graph H, let
![]() $\chi (H)$
be the set of
$\chi (H)$
be the set of
![]() $\boldsymbol {k}$
-valid colourings of H. For each
$\boldsymbol {k}$
-valid colourings of H. For each
![]() $\chi \in \chi (G-u-v)$
, let
$\chi \in \chi (G-u-v)$
, let
![]() $\chi _u, \chi _v$
denote the number of valid extensions of
$\chi _u, \chi _v$
denote the number of valid extensions of
![]() $\chi $
to
$\chi $
to
![]() $G-v$
and
$G-v$
and
![]() $G-u$
, respectively. Since u and v are nonadjacent,
$G-u$
, respectively. Since u and v are nonadjacent,
 $$ \begin{align*}F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u\chi_v. \end{align*} $$
$$ \begin{align*}F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u\chi_v. \end{align*} $$
Let
![]() $G_u$
denote the graph obtained from G by replacing v by a twin of u. Define
$G_u$
denote the graph obtained from G by replacing v by a twin of u. Define
![]() $G_v$
similarly. The operation of passing from G to
$G_v$
similarly. The operation of passing from G to
![]() $G_u$
or
$G_u$
or
![]() $G_v$
is a symmetrisation. We have
$G_v$
is a symmetrisation. We have
 $$ \begin{align*}F(G_u;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u^2 \ \text{ and } \ F(G_v;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_v^2. \end{align*} $$
$$ \begin{align*}F(G_u;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_u^2 \ \text{ and } \ F(G_v;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)}\chi_v^2. \end{align*} $$
Then
 $$ \begin{align*}0 \geq F(G_u;\boldsymbol{k}) + F(G_v;\boldsymbol{k}) - 2F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)} (\chi_u - \chi_v)^2 \geq 0. \end{align*} $$
$$ \begin{align*}0 \geq F(G_u;\boldsymbol{k}) + F(G_v;\boldsymbol{k}) - 2F(G;\boldsymbol{k}) = \sum_{\chi \in \chi(G-u-v)} (\chi_u - \chi_v)^2 \geq 0. \end{align*} $$
Therefore,
![]() $G_u$
and
$G_u$
and
![]() $G_v$
are both
$G_v$
are both
![]() $\boldsymbol {k}$
-extremal.
$\boldsymbol {k}$
-extremal.
Let
![]() $\mathcal {G}$
be the directed graph whose vertex set contains all n-vertex graphs (up to isomorphism) that can be obtained from G by a sequence of symmetrisations and add a directed edge from H to
$\mathcal {G}$
be the directed graph whose vertex set contains all n-vertex graphs (up to isomorphism) that can be obtained from G by a sequence of symmetrisations and add a directed edge from H to
![]() $H' \neq H$
if
$H' \neq H$
if
![]() $H'\cong H_u$
for some vertex u. Note that H has outdegree equal to
$H'\cong H_u$
for some vertex u. Note that H has outdegree equal to
![]() $0$
in
$0$
in
![]() $\mathcal {G}$
if and only if H is complete multipartite. By [Reference Pikhurko, Staden and Yilma11, Theorem 3], there is at least one sequence of symmetrisations which leads to a (
$\mathcal {G}$
if and only if H is complete multipartite. By [Reference Pikhurko, Staden and Yilma11, Theorem 3], there is at least one sequence of symmetrisations which leads to a (
![]() $\boldsymbol {k}$
-extremal) complete partite graph H; among all choices, pick one such that the number m of parts in H is as small as possible. We may assume that every part has size at least two, or we are done. Let
$\boldsymbol {k}$
-extremal) complete partite graph H; among all choices, pick one such that the number m of parts in H is as small as possible. We may assume that every part has size at least two, or we are done. Let
![]() $H^-$
be an inneighbour of H in
$H^-$
be an inneighbour of H in
![]() $\mathcal {G}$
. Observe that
$\mathcal {G}$
. Observe that
![]() $H^-$
is not complete multipartite since it does not have
$H^-$
is not complete multipartite since it does not have
![]() $0$
outdegree. Then there exists
$0$
outdegree. Then there exists
![]() $x \in V(H^-)$
such that
$x \in V(H^-)$
such that
![]() $H^--x$
is a complete m-partite graph with parts
$H^--x$
is a complete m-partite graph with parts
![]() $V_1,\ldots ,V_m$
.
$V_1,\ldots ,V_m$
.
Claim 2.14.1.
x has at least one neighbour in each of
![]() $V_1,\ldots , V_m$
in
$V_1,\ldots , V_m$
in
![]() $H^-$
.
$H^-$
.
Proof of Claim
Suppose for a contradiction that x does not have a neighbour in
![]() $V_1$
, say. Since
$V_1$
, say. Since
![]() $H^-$
is not complete multipartite, without loss of generality, there is
$H^-$
is not complete multipartite, without loss of generality, there is
![]() $y \in V_2$
such that
$y \in V_2$
such that
![]() $xy \notin E(H^-)$
. Replace every
$xy \notin E(H^-)$
. Replace every
![]() $u \in V_2 \setminus \{ y \}$
with a twin of y to obtain a graph J with vertex partition
$u \in V_2 \setminus \{ y \}$
with a twin of y to obtain a graph J with vertex partition
![]() $\{ x \}, V_1,\ldots , V_m$
, such that
$\{ x \}, V_1,\ldots , V_m$
, such that
![]() $J-x \cong K(V_1,\ldots ,V_m)$
, and
$J-x \cong K(V_1,\ldots ,V_m)$
, and
![]() $xz \notin E(J)$
for all
$xz \notin E(J)$
for all
![]() $z \in V_1 \cup V_2$
. This is a sequence of symmetrisations, so there is an oriented path from
$z \in V_1 \cup V_2$
. This is a sequence of symmetrisations, so there is an oriented path from
![]() $H^-$
to J in
$H^-$
to J in
![]() $\mathcal {G}$
(and, in particular,
$\mathcal {G}$
(and, in particular,
![]() $J \in V(\mathcal {G})$
). Now, given
$J \in V(\mathcal {G})$
). Now, given
![]() $v_1 \in V_1$
and
$v_1 \in V_1$
and
![]() $v_2 \in V_2$
, we have
$v_2 \in V_2$
, we have
![]() $xv_1,xv_2 \notin E(J)$
but
$xv_1,xv_2 \notin E(J)$
but
![]() $v_1v_2 \in E(J)$
. Therefore, we can replace
$v_1v_2 \in E(J)$
. Therefore, we can replace
![]() $V_1 \cup V_2$
with a set X of
$V_1 \cup V_2$
with a set X of
![]() $|V_1|+|V_2|$
twins of x to obtain a new graph
$|V_1|+|V_2|$
twins of x to obtain a new graph
![]() $J'$
, which has vertex partition
$J'$
, which has vertex partition
![]() $X, V_3,\ldots ,V_m$
, and
$X, V_3,\ldots ,V_m$
, and
![]() $J'-X \cong K(V_3,\ldots ,V_m)$
. Again,
$J'-X \cong K(V_3,\ldots ,V_m)$
. Again,
![]() $J' \in V(\mathcal {G})$
.
$J' \in V(\mathcal {G})$
.
Suppose that
![]() $x \in V(J)$
is such that
$x \in V(J)$
is such that
![]() $xw \notin E(J)$
for some
$xw \notin E(J)$
for some
![]() $w \in V_3 \cup \ldots \cup V_m$
. Then
$w \in V_3 \cup \ldots \cup V_m$
. Then
![]() $xw \notin E(J')$
for all
$xw \notin E(J')$
for all
![]() $x \in X$
. Replace every
$x \in X$
. Replace every
![]() $x \in X$
with a twin of w to obtain a complete
$x \in X$
with a twin of w to obtain a complete
![]() $(m-2)$
-partite graph which is a vertex in
$(m-2)$
-partite graph which is a vertex in
![]() $\mathcal {G}$
. Otherwise,
$\mathcal {G}$
. Otherwise,
![]() $x \in V(J)$
is adjacent in J to all of
$x \in V(J)$
is adjacent in J to all of
![]() $V_3 \cup \ldots \cup V_m$
, and so
$V_3 \cup \ldots \cup V_m$
, and so
![]() $J'$
is a complete
$J'$
is a complete
![]() $(m-1)$
-partite graph which is a vertex in
$(m-1)$
-partite graph which is a vertex in
![]() $\mathcal {G}$
. In both cases, we obtain a contradiction to the choice of m. This proves the claim.
$\mathcal {G}$
. In both cases, we obtain a contradiction to the choice of m. This proves the claim.
Therefore, x has a neighbour in each of
![]() $V_1,\ldots ,V_m$
. Then, for each
$V_1,\ldots ,V_m$
. Then, for each
![]() $i \in [m]$
,
$i \in [m]$
,
![]() $V_i$
has partition
$V_i$
has partition
![]() $A_i,B_i$
, where
$A_i,B_i$
, where
![]() $xa \in E(H^-)$
for all
$xa \in E(H^-)$
for all
![]() $a \in A_i$
, and
$a \in A_i$
, and
![]() $xb \notin E(H^-)$
for all
$xb \notin E(H^-)$
for all
![]() $b \in B_i$
; and
$b \in B_i$
; and
![]() $A_i \neq \emptyset $
. Observe that every
$A_i \neq \emptyset $
. Observe that every
![]() $A_i$
is a set of twins, and
$A_i$
is a set of twins, and
![]() $B_i$
is a set of twins. For each
$B_i$
is a set of twins. For each
![]() $i \in [m]$
, replace
$i \in [m]$
, replace
![]() $B_i$
by a set of
$B_i$
by a set of
![]() $|B_i|$
twins of
$|B_i|$
twins of
![]() $a \in A_i$
. Thus, obtain a graph
$a \in A_i$
. Thus, obtain a graph
![]() $H' \cong K(\{ x \}, V_1,\ldots ,V_m)$
which is a vertex of
$H' \cong K(\{ x \}, V_1,\ldots ,V_m)$
which is a vertex of
![]() $\mathcal {G}$
, as required.
$\mathcal {G}$
, as required.
Lemma 2.15. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Then, for all
$\boldsymbol {k} \in \mathbb {N}^s$
. Then, for all
![]() ${\varepsilon },\gamma> 0$
, there exist
${\varepsilon },\gamma> 0$
, there exist
![]() $\eta> 0$
and
$\eta> 0$
and
![]() $n_0 \in \mathbb {N}$
such that the following holds for all graphs G on
$n_0 \in \mathbb {N}$
such that the following holds for all graphs G on
![]() $n \geq n_0$
vertices with
$n \geq n_0$
vertices with
![]() $\log F(G;\boldsymbol {k}) \geq (Q(\boldsymbol {k})-\eta )\binom {n}{2}$
. For every
$\log F(G;\boldsymbol {k}) \geq (Q(\boldsymbol {k})-\eta )\binom {n}{2}$
. For every
![]() $x \in V(G)$
such that G contains at least
$x \in V(G)$
such that G contains at least
![]() $\gamma n$
twins of x, we have that
$\gamma n$
twins of x, we have that
Proof. As before, we omit
![]() $\boldsymbol {k}$
from our notation where it is clear from the context, so, for example,
$\boldsymbol {k}$
from our notation where it is clear from the context, so, for example,
![]() $F(H) := F(H;\boldsymbol {k})$
. Choose constants
$F(H) := F(H;\boldsymbol {k})$
. Choose constants
![]() $\delta ,\eta $
such that
$\delta ,\eta $
such that
![]() $0 < \eta \ll \delta \ll \gamma ,{\varepsilon }$
. By (1.3), we can choose
$0 < \eta \ll \delta \ll \gamma ,{\varepsilon }$
. By (1.3), we can choose
![]() $n_0$
to be such that whenever
$n_0$
to be such that whenever
![]() $N \geq n_0/2$
, we have that
$N \geq n_0/2$
, we have that
 $$ \begin{align} (Q - \eta)\binom{N}{2} \leq \log F(N) \leq (Q + \eta)\binom{N}{2}. \end{align} $$
$$ \begin{align} (Q - \eta)\binom{N}{2} \leq \log F(N) \leq (Q + \eta)\binom{N}{2}. \end{align} $$
Without loss of generality, we may suppose that
![]() $1/n_0 \ll \eta $
. Let G be a graph on
$1/n_0 \ll \eta $
. Let G be a graph on
![]() $n \geq n_0$
vertices. Suppose that there is some
$n \geq n_0$
vertices. Suppose that there is some
![]() $x \in V(G)$
which does not satisfy (2.21). Let
$x \in V(G)$
which does not satisfy (2.21). Let
![]() $T \subseteq V(G)$
be the set of twins of x (including x). Let
$T \subseteq V(G)$
be the set of twins of x (including x). Let
![]() $\chi (G-T)$
be the set of
$\chi (G-T)$
be the set of
![]() $\boldsymbol {k}$
-valid colourings of
$\boldsymbol {k}$
-valid colourings of
![]() $G-T$
and let
$G-T$
and let
![]() $c(\chi ,x)$
be the number of extensions of
$c(\chi ,x)$
be the number of extensions of
![]() $\chi $
to
$\chi $
to
![]() $G - (T \setminus \{ x \})$
. For each
$G - (T \setminus \{ x \})$
. For each
![]() $\chi \in \chi (G-T)$
, since every pair of vertices of X are twins, we have that
$\chi \in \chi (G-T)$
, since every pair of vertices of X are twins, we have that
![]() $c(\chi ,x) \equiv c_\chi $
for all
$c(\chi ,x) \equiv c_\chi $
for all
![]() $x \in T$
. Therefore, if we list the vertices of T as
$x \in T$
. Therefore, if we list the vertices of T as
![]() $x_1,\ldots ,x_{|T|}$
, and let
$x_1,\ldots ,x_{|T|}$
, and let
![]() $t \in [\,|T|\,]$
, we have that
$t \in [\,|T|\,]$
, we have that
 $$ \begin{align} F(G-x_1-\ldots-x_t) = \sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t}. \end{align} $$
$$ \begin{align} F(G-x_1-\ldots-x_t) = \sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t}. \end{align} $$
Choose t with
![]() $1 \leq t \leq |T|$
to be maximal such that
$1 \leq t \leq |T|$
to be maximal such that
for all
![]() $i \in [t]$
. (Since (2.21) does not hold,
$i \in [t]$
. (Since (2.21) does not hold,
![]() $t:=1$
satisfies the inequality). Suppose
$t:=1$
satisfies the inequality). Suppose
![]() $t < |T|$
. By the Cauchy-Schwarz inequality,
$t < |T|$
. By the Cauchy-Schwarz inequality,
 $$ \begin{align*} F(G-x_1-\ldots - x_t)^2 &= \left(\sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t} \right)^2 \leq \left(\sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t-1} \right) \left( \sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t+1} \right)\\ &\stackrel{({2.26})}{=} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_{t-1})\\ &\stackrel{({2.24})}{<} 2^{(Q-{\varepsilon})n} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_t). \end{align*} $$
$$ \begin{align*} F(G-x_1-\ldots - x_t)^2 &= \left(\sum_{\chi \in \chi(G-T)}c_\chi^{|T|-t} \right)^2 \leq \left(\sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t-1} \right) \left( \sum_{\chi \in \chi(G-T)} c_\chi^{|T|-t+1} \right)\\ &\stackrel{({2.26})}{=} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_{t-1})\\ &\stackrel{({2.24})}{<} 2^{(Q-{\varepsilon})n} F(G-x_1-\ldots-x_{t+1}) F(G-x_1-\ldots-x_t). \end{align*} $$
So
![]() $F(G-x_1-\ldots -x_t) < 2^{(Q-{\varepsilon })n} \cdot F(G-x_1-\ldots -x_{t+1})$
. Thus, (2.24) holds for
$F(G-x_1-\ldots -x_t) < 2^{(Q-{\varepsilon })n} \cdot F(G-x_1-\ldots -x_{t+1})$
. Thus, (2.24) holds for
![]() $t+1$
which is a contradiction to the maximality of t. So
$t+1$
which is a contradiction to the maximality of t. So
![]() $t=|T|$
. Therefore, inductively, for all nonempty
$t=|T|$
. Therefore, inductively, for all nonempty
![]() $T' \subseteq T$
,
$T' \subseteq T$
,
Choose
![]() $T' \subseteq T$
with
$T' \subseteq T$
with
![]() $|T'| = \lceil \delta n\rceil $
. Then
$|T'| = \lceil \delta n\rceil $
. Then
 $$ \begin{align*} \log F(G) &\leq (Q-{\varepsilon})|T'|n + \log F(G-T') \stackrel{({2.22})}{\leq} Q|T'|n -{\varepsilon} \delta n^2 + (Q+\eta)\binom{n-|T'|}{2}\\ &\leq Q\binom{n}{2} + (-{\varepsilon} \delta + \eta +Q\delta^2)n^2 < Q\binom{n}{2} + (\eta + \delta^2 \log s - {\varepsilon} \delta )n^2\\ &< (Q-\eta)\binom{n}{2}, \end{align*} $$
$$ \begin{align*} \log F(G) &\leq (Q-{\varepsilon})|T'|n + \log F(G-T') \stackrel{({2.22})}{\leq} Q|T'|n -{\varepsilon} \delta n^2 + (Q+\eta)\binom{n-|T'|}{2}\\ &\leq Q\binom{n}{2} + (-{\varepsilon} \delta + \eta +Q\delta^2)n^2 < Q\binom{n}{2} + (\eta + \delta^2 \log s - {\varepsilon} \delta )n^2\\ &< (Q-\eta)\binom{n}{2}, \end{align*} $$
a contradiction to (2.22).
We will now prove Theorem 1.6. The idea is that if there is an extremal graph G not satisfying the conclusion of the theorem, there must be a complete partite extremal graph
![]() $G'$
with an induced subgraph satisfying the conclusion of the theorem which is almost the whole of
$G'$
with an induced subgraph satisfying the conclusion of the theorem which is almost the whole of
![]() $G'$
. We can either set
$G'$
. We can either set
![]() $G'=G$
or symmetrise to obtain
$G'=G$
or symmetrise to obtain
![]() $G'$
(Lemma 2.14), and the required structure of
$G'$
(Lemma 2.14), and the required structure of
![]() $G'$
follows from Theorem 2.12. In a typical colouring, of which there are many by Theorem 2.12, every exceptional vertex (not in the good induced subgraph) has deficient contribution to
$G'$
follows from Theorem 2.12. In a typical colouring, of which there are many by Theorem 2.12, every exceptional vertex (not in the good induced subgraph) has deficient contribution to
![]() $F(G')$
, which is a consequence of the strong extension property. We can form a new graph by replacing each exceptional vertex by a twin of a good vertex to obtain a graph with more valid colourings than
$F(G')$
, which is a consequence of the strong extension property. We can form a new graph by replacing each exceptional vertex by a twin of a good vertex to obtain a graph with more valid colourings than
![]() $G'$
, which is the required contradiction.
$G'$
, which is the required contradiction.
Proof of Theorem 1.6
Again, we omit
![]() $\boldsymbol {k}$
from our notation where possible. Let
$\boldsymbol {k}$
from our notation where possible. Let
![]() ${\varepsilon }> 0$
. Let
${\varepsilon }> 0$
. Let
![]() $\mu> 0$
be the constant obtained from Lemma 2.2(i) and let
$\mu> 0$
be the constant obtained from Lemma 2.2(i) and let
![]() ${\varepsilon }_0$
be the constant obtained from Lemma 2.2(ii). Without loss of generality, we may assume that
${\varepsilon }_0$
be the constant obtained from Lemma 2.2(ii). Without loss of generality, we may assume that
![]() $0 < {\varepsilon }_0 \ll \mu ,{\varepsilon },1/R,1/s$
. Choose
$0 < {\varepsilon }_0 \ll \mu ,{\varepsilon },1/R,1/s$
. Choose
![]() $\delta _4,\delta _3,\delta _2,\delta _1>0$
in this order such that
$\delta _4,\delta _3,\delta _2,\delta _1>0$
in this order such that
![]() $\delta _3$
is at most the output of Corollary 2.13 with input
$\delta _3$
is at most the output of Corollary 2.13 with input
![]() $\delta _4$
, and similarly,
$\delta _4$
, and similarly,
![]() $\delta _2$
from
$\delta _2$
from
![]() $\delta _3$
, and
$\delta _3$
, and
![]() $\delta _1$
from
$\delta _1$
from
![]() $\delta _2^2$
. Further, let
$\delta _2^2$
. Further, let
![]() $n_0$
be at least the integer output of all of these applications. By increasing
$n_0$
be at least the integer output of all of these applications. By increasing
![]() $n_0$
and decreasing
$n_0$
and decreasing
![]() $\delta _1,\ldots ,\delta _4$
, we may assume that
$\delta _1,\ldots ,\delta _4$
, we may assume that
![]() $0<1/n_0 \ll \delta _1 \ll \ldots \ll \delta _4 \ll {\varepsilon }_0$
and for all
$0<1/n_0 \ll \delta _1 \ll \ldots \ll \delta _4 \ll {\varepsilon }_0$
and for all
![]() $n \geq n_0$
, by (1.3),
$n \geq n_0$
, by (1.3),
 $$ \begin{align} \left(Q - \delta_1 \right)\binom{n}{2} \leq \log F(n) \leq \left(Q + \delta_1 \right)\binom{n}{2} \end{align} $$
$$ \begin{align} \left(Q - \delta_1 \right)\binom{n}{2} \leq \log F(n) \leq \left(Q + \delta_1 \right)\binom{n}{2} \end{align} $$
and that Lemma 2.15 applied with
![]() $\delta _3,\mu /2$
playing the roles of
$\delta _3,\mu /2$
playing the roles of
![]() ${\varepsilon },\gamma $
, respectively, has output
${\varepsilon },\gamma $
, respectively, has output
![]() $n_1 \leq n_0$
and
$n_1 \leq n_0$
and
![]() $\eta> 2\delta _1$
. Altogether, we have the hierarchy
$\eta> 2\delta _1$
. Altogether, we have the hierarchy
We first prove part (i). Towards a contradiction, let G be a
![]() $\boldsymbol {k}$
-extremal graph on
$\boldsymbol {k}$
-extremal graph on
![]() $n \geq 2n_0$
vertices such that either
$n \geq 2n_0$
vertices such that either
-
(a) G is not complete multipartite; or
-
(b) there is some
 $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
 $\boldsymbol {\alpha } \in \Delta ^m$
such that
$\boldsymbol {\alpha } \in \Delta ^m$
such that
 $G \cong K_{\alpha _1n,\ldots ,\alpha _mn}$
, but there is no
$G \cong K_{\alpha _1n,\ldots ,\alpha _mn}$
, but there is no  with
with
 $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 < \delta _3 < {\varepsilon }$
.
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 < \delta _3 < {\varepsilon }$
.
If (a) holds, apply Lemma 2.14 to obtain a
![]() $\boldsymbol {k}$
-extremal graph
$\boldsymbol {k}$
-extremal graph
![]() $G'$
on n vertices which is complete m-partite with vertex partition
$G'$
on n vertices which is complete m-partite with vertex partition
![]() $X_1,\ldots ,X_{m}$
, where
$X_1,\ldots ,X_{m}$
, where
![]() $|X_{1}| \geq \ldots \geq |X_m| = 1$
. Observe that
$|X_{1}| \geq \ldots \geq |X_m| = 1$
. Observe that
![]() $m < R$
. If (b) holds, set
$m < R$
. If (b) holds, set
![]() $G' := G$
. In both cases, apply Corollary 2.13 with parameter
$G' := G$
. In both cases, apply Corollary 2.13 with parameter
![]() $\delta _2^2$
to
$\delta _2^2$
to
![]() $G'$
. Part (i) implies that there exists
$G'$
. Part (i) implies that there exists ![]() with
with
![]() $r^* \leq m$
such that, defining
$r^* \leq m$
such that, defining
![]() $Y_i := X_i$
for
$Y_i := X_i$
for
![]() $i \in [r^*]$
and
$i \in [r^*]$
and
![]() $Y_0$
to be the union of the remaining parts of G, we have
$Y_0$
to be the union of the remaining parts of G, we have
Together with Proposition 2.1(ii), we have that
![]() $|Y_i| \geq \mu n/2$
for all
$|Y_i| \geq \mu n/2$
for all
![]() $i \in [r^*]$
. So if either (a) or (b) holds, we have
$i \in [r^*]$
. So if either (a) or (b) holds, we have
![]() $m> r^*$
. Corollary 2.13 implies that each of
$m> r^*$
. Corollary 2.13 implies that each of
![]() $Y_1,\ldots ,Y_{r^*}$
is a part of
$Y_1,\ldots ,Y_{r^*}$
is a part of
![]() $G'$
(but
$G'$
(but
![]() $Y_0$
may contain several parts). We have that
$Y_0$
may contain several parts). We have that
![]() $Y_0,\ldots ,Y_{r^*}$
is a partition of
$Y_0,\ldots ,Y_{r^*}$
is a partition of
![]() $V(G)$
, and
$V(G)$
, and
![]() $0 < |Y_0| < R\delta _2^2 n < \delta _2 n$
. From now on, we make no distinction between cases (a) and (b) and only use this fact about the size of
$0 < |Y_0| < R\delta _2^2 n < \delta _2 n$
. From now on, we make no distinction between cases (a) and (b) and only use this fact about the size of
![]() $Y_0$
. Let
$Y_0$
. Let
be the core of
![]() $G'$
, and let
$G'$
, and let
![]() $N := |V(H)|$
. So
$N := |V(H)|$
. So
Every
![]() $\boldsymbol {k}$
-valid colouring of
$\boldsymbol {k}$
-valid colouring of
![]() $G'$
can be obtained by extending a
$G'$
can be obtained by extending a
![]() $\boldsymbol {k}$
-valid colouring of H, so
$\boldsymbol {k}$
-valid colouring of H, so
![]() $F(H) \geq F(G') \cdot s^{-|Y_0|n}$
. Therefore,
$F(H) \geq F(G') \cdot s^{-|Y_0|n}$
. Therefore,
 $$ \begin{align} \nonumber \log F(H) &\stackrel{({2.27})}{\geq} \log F(G') - R\delta_2^2 \log s \cdot n^2 \stackrel{({2.25})}{\geq} \left(Q - \delta_1 \right) \binom{n}{2} - R\delta_2^2 \log s \cdot n^2\\ &\stackrel{({2.28})}{\geq} (Q-\delta_2)\binom{N}{2}. \end{align} $$
$$ \begin{align} \nonumber \log F(H) &\stackrel{({2.27})}{\geq} \log F(G') - R\delta_2^2 \log s \cdot n^2 \stackrel{({2.25})}{\geq} \left(Q - \delta_1 \right) \binom{n}{2} - R\delta_2^2 \log s \cdot n^2\\ &\stackrel{({2.28})}{\geq} (Q-\delta_2)\binom{N}{2}. \end{align} $$
Apply Corollary 2.13 to H to see that
![]() $|\mathcal {G}(H)| \geq (1-2^{-\delta _3 N^2})\cdot F(H)$
, where (recalling Definition 2.10)
$|\mathcal {G}(H)| \geq (1-2^{-\delta _3 N^2})\cdot F(H)$
, where (recalling Definition 2.10)

Define
![]() $\boldsymbol {\beta } \in \Delta ^{r^*}$
by setting
$\boldsymbol {\beta } \in \Delta ^{r^*}$
by setting
![]() $\beta _i := |Y_i|/N$
for all
$\beta _i := |Y_i|/N$
for all
![]() $i \in [r^*]$
. So (2.27) implies that for all
$i \in [r^*]$
. So (2.27) implies that for all
![]() $\boldsymbol {\alpha }$
with
$\boldsymbol {\alpha }$
with
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$
,
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$
,
Let
![]() $\mathcal {B}(H)$
be the set of
$\mathcal {B}(H)$
be the set of
![]() $\boldsymbol {k}$
-valid colourings of H not in
$\boldsymbol {k}$
-valid colourings of H not in
![]() $\mathcal {G}(H)$
. For each
$\mathcal {G}(H)$
. For each
![]() $\chi \in \mathcal {G}(H)$
and
$\chi \in \mathcal {G}(H)$
and
![]() $v \in Y_0$
, do the following. Let
$v \in Y_0$
, do the following. Let
![]() $\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$
be the pattern of
$\phi ^* \in \Phi _2(r^*;\boldsymbol {k})$
be the pattern of
![]() $\chi $
(that is, there is
$\chi $
(that is, there is
![]() $\boldsymbol {\alpha }$
, which depends on
$\boldsymbol {\alpha }$
, which depends on
![]() $\chi $
, with
$\chi $
, with ![]() and
and
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$
and
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta _4$
and ![]() ) such that
) such that
![]() $\chi \in \mathcal {G}_{\delta _4}(H;\phi ^*,Y_1,\ldots ,Y_{r^*})$
. For each valid extension
$\chi \in \mathcal {G}_{\delta _4}(H;\phi ^*,Y_1,\ldots ,Y_{r^*})$
. For each valid extension
![]() $\overline {\chi }$
of
$\overline {\chi }$
of
![]() $\chi $
to
$\chi $
to
![]() $G'[V(H) \cup \{ v \}]$
and every
$G'[V(H) \cup \{ v \}]$
and every
![]() $i\in [s]$
, define
$i\in [s]$
, define
![]() $\phi = \phi (\overline {\chi },v) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
by setting
$\phi = \phi (\overline {\chi },v) : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
by setting
 $$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2} \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[v,Y_i]| \geq \sqrt{\delta_4} |Y_i| \} &\mbox{if } i \in [r^*], j = r^*+1. \\ \end{cases} \end{align*} $$
$$ \begin{align*}\phi(ij) := \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2} \\ \{ c \in [s] : |\overline{\chi}^{-1}(c)[v,Y_i]| \geq \sqrt{\delta_4} |Y_i| \} &\mbox{if } i \in [r^*], j = r^*+1. \\ \end{cases} \end{align*} $$
Fix the
![]() $\phi $
that appears for the largest number of extensions
$\phi $
that appears for the largest number of extensions
![]() $\overline {\chi }$
over all
$\overline {\chi }$
over all
![]() $\chi \in \mathcal {G}(H)$
and all
$\chi \in \mathcal {G}(H)$
and all
![]() $v \in Y_0$
.
$v \in Y_0$
.
Claim 2.15.1.
![]() $\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
.
$\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
.
Proof. This is almost identical to Claim 2.12.3 so we omit the proof.
Proposition 2.1(i) implies that
Since every
![]() $v \in Y_0$
is incident to the whole of
$v \in Y_0$
is incident to the whole of
![]() $Y_1 \cup \ldots \cup Y_{r^*}$
in
$Y_1 \cup \ldots \cup Y_{r^*}$
in
![]() $G'$
and
$G'$
and
![]() $s\sqrt {\delta _4}<1$
, we have that
$s\sqrt {\delta _4}<1$
, we have that
![]() $\phi (\{ i,r^*+1 \}) \neq \emptyset $
for all
$\phi (\{ i,r^*+1 \}) \neq \emptyset $
for all
![]() $i \in [r^*]$
. Thus,
$i \in [r^*]$
. Thus,
![]() $r^*+1$
is not a strong clone of any vertex in
$r^*+1$
is not a strong clone of any vertex in
![]() $[r^*]$
under
$[r^*]$
under
![]() $\phi $
. Therefore, applying Lemma 2.2(ii) for the second inequality,
$\phi $
. Therefore, applying Lemma 2.2(ii) for the second inequality,
Similarly to the derivation of (2.14), we can now bound the number of extensions of
![]() $\chi $
. Indeed, by our choice of
$\chi $
. Indeed, by our choice of
![]() $\phi $
, for any
$\phi $
, for any
![]() $\chi \in \mathcal {G}(H)$
and any
$\chi \in \mathcal {G}(H)$
and any
![]() $v \in Y_0$
, the number of ways to extend
$v \in Y_0$
, the number of ways to extend
![]() $\chi $
to a valid colouring
$\chi $
to a valid colouring
![]() $\overline {\chi }$
of
$\overline {\chi }$
of
![]() $G'[V(H) \cup \{ v \}]$
is at most
$G'[V(H) \cup \{ v \}]$
is at most
 $$ \begin{align*} &\phantom{\leq} 2^{sr^*} \cdot \prod_{i \in [r^*]}|\phi(\{ i,r^*+1 \})|^{\beta_i N} \cdot \binom{N}{\leq s\sqrt{\delta_4} N} \cdot s^{sr^*\sqrt{\delta_4} n} \stackrel{({2.32})}{\leq} 2^{(Q-{\varepsilon}_0/3)N}. \end{align*} $$
$$ \begin{align*} &\phantom{\leq} 2^{sr^*} \cdot \prod_{i \in [r^*]}|\phi(\{ i,r^*+1 \})|^{\beta_i N} \cdot \binom{N}{\leq s\sqrt{\delta_4} N} \cdot s^{sr^*\sqrt{\delta_4} n} \stackrel{({2.32})}{\leq} 2^{(Q-{\varepsilon}_0/3)N}. \end{align*} $$
Here, the first term is the number of possible patterns
![]() $\phi $
, the second term is the maximum number of extensions given the
$\phi $
, the second term is the maximum number of extensions given the
![]() $\phi $
that appears most often, and the third and fourth terms are an upper bound on the number of ways to choose and colour those edges with uncommon colours. Now we can give an upper bound for the number of valid colourings of
$\phi $
that appears most often, and the third and fourth terms are an upper bound on the number of ways to choose and colour those edges with uncommon colours. Now we can give an upper bound for the number of valid colourings of
![]() $G'$
as follows: Any valid colouring of
$G'$
as follows: Any valid colouring of
![]() $G'$
is either an extension of
$G'$
is either an extension of
![]() $\chi \in \mathcal {G}(H)$
(where we must additionally colour the edges between the
$\chi \in \mathcal {G}(H)$
(where we must additionally colour the edges between the
![]() $n-N$
vertices of
$n-N$
vertices of
![]() $Y_0$
and H, and the edges induced by
$Y_0$
and H, and the edges induced by
![]() $Y_0$
) or an extension of
$Y_0$
) or an extension of
![]() $\chi \in \mathcal {B}(H)$
. We have
$\chi \in \mathcal {B}(H)$
. We have
 $$ \begin{align} F(G') &\leq \sum_{\chi \in \mathcal{G}(H)} \left( s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \right) + \sum_{\chi \in \mathcal{B}(H)}s^{(n-N)n}\\ \nonumber &\leq s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2} F(H) \cdot s^{(n-N)n}\\ \nonumber &\hspace{-9pt}\stackrel{({2.28})}{\leq} 2^{(Q - {\varepsilon}_0/3 + \delta_2 \log s) N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2/2} \cdot F(H)\\ \nonumber &\leq 2^{(Q-{\varepsilon}_0/4)N(n-N)} \cdot F(H). \end{align} $$
$$ \begin{align} F(G') &\leq \sum_{\chi \in \mathcal{G}(H)} \left( s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \right) + \sum_{\chi \in \mathcal{B}(H)}s^{(n-N)n}\\ \nonumber &\leq s^{\binom{n-N}{2}} \cdot 2^{(Q-{\varepsilon}_0/3)N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2} F(H) \cdot s^{(n-N)n}\\ \nonumber &\hspace{-9pt}\stackrel{({2.28})}{\leq} 2^{(Q - {\varepsilon}_0/3 + \delta_2 \log s) N(n-N)} \cdot F(H) + 2^{-\delta_3 N^2/2} \cdot F(H)\\ \nonumber &\leq 2^{(Q-{\varepsilon}_0/4)N(n-N)} \cdot F(H). \end{align} $$
We will now form a new graph on n vertices which shares the same core H, but
![]() $Y_0$
is replaced by
$Y_0$
is replaced by
![]() $n-N$
clones of some vertex in another part.
$n-N$
clones of some vertex in another part.
By (2.31), for any ![]() ,
,
So, by averaging, there exists
![]() $i^* \in [r^*]$
such that
$i^* \in [r^*]$
such that
Let
![]() $H' := K[W_1,\ldots ,W_{r^*}]$
, where
$H' := K[W_1,\ldots ,W_{r^*}]$
, where
![]() $W_j = Y_j$
for
$W_j = Y_j$
for
![]() $j \in [r^*]\setminus \{ i^* \}$
, and
$j \in [r^*]\setminus \{ i^* \}$
, and
![]() $W_{i^*} := Y_{i^*} \cup Y_0$
. Every colouring that follows
$W_{i^*} := Y_{i^*} \cup Y_0$
. Every colouring that follows
![]() $\phi ^*$
is valid. Thus,
$\phi ^*$
is valid. Thus,
 $$ \begin{align*} \log F(H') &\geq \log\left( \prod_{ij \in \binom{[r^*]}{2}}|\phi^*(ij)|^{|Y_i||Y_j|} \cdot \prod_{k \in [r^*]\setminus\{i^*\}}|\phi^*(i^*k)|^{|Y_0||Y_k|} \right)\\ &= N^2 \cdot q(\phi^*,\boldsymbol{\beta})/2 + (n-N)N \cdot q_{i^*}(\phi^*,\boldsymbol{\beta})/2 \geq nN(Q-4(\log s)\delta_4)/2\\ &\geq (Q-\sqrt{\delta_4}/2)\binom{n}{2} \stackrel{({2.25})}{\geq} F(H) + (Q-\sqrt{\delta_4})N(n-N), \end{align*} $$
$$ \begin{align*} \log F(H') &\geq \log\left( \prod_{ij \in \binom{[r^*]}{2}}|\phi^*(ij)|^{|Y_i||Y_j|} \cdot \prod_{k \in [r^*]\setminus\{i^*\}}|\phi^*(i^*k)|^{|Y_0||Y_k|} \right)\\ &= N^2 \cdot q(\phi^*,\boldsymbol{\beta})/2 + (n-N)N \cdot q_{i^*}(\phi^*,\boldsymbol{\beta})/2 \geq nN(Q-4(\log s)\delta_4)/2\\ &\geq (Q-\sqrt{\delta_4}/2)\binom{n}{2} \stackrel{({2.25})}{\geq} F(H) + (Q-\sqrt{\delta_4})N(n-N), \end{align*} $$
which, together with
![]() $n-N>0$
and (2.33), implies that
$n-N>0$
and (2.33), implies that
![]() $\log F(H')> \log F(G')$
, a contradiction to the
$\log F(H')> \log F(G')$
, a contradiction to the
![]() $\boldsymbol {k}$
-extremality of
$\boldsymbol {k}$
-extremality of
![]() $G'$
, and hence G. This completes the proof of part (i).
$G'$
, and hence G. This completes the proof of part (i).
We have proved that
![]() $G \cong K[Y_1,\ldots ,Y_{r^*}]$
such that
$G \cong K[Y_1,\ldots ,Y_{r^*}]$
such that
![]() $\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 < \delta _2$
. Now Lemma 2.15 and our choice of parameters implies that, for all
$\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 < \delta _2$
. Now Lemma 2.15 and our choice of parameters implies that, for all
![]() $x \in V(G)$
,
$x \in V(G)$
,
Note that
![]() $F(G) \leq s^n \cdot F(G-x)$
, so, by (2.25),
$F(G) \leq s^n \cdot F(G-x)$
, so, by (2.25),
![]() $\log F(G-x) \geq (Q-2\delta _1)\binom {n-1}{2}$
. The hypotheses of Lemma 2.15 still hold for
$\log F(G-x) \geq (Q-2\delta _1)\binom {n-1}{2}$
. The hypotheses of Lemma 2.15 still hold for
![]() $G-x$
, so, for all
$G-x$
, so, for all
![]() $y \in V(G)\setminus \{x\}$
,
$y \in V(G)\setminus \{x\}$
,
By Corollary 2.13, there is a set
![]() $\mathcal {G}$
of at least
$\mathcal {G}$
of at least
![]() $(1-2^{-\delta _3 n})\cdot F(n) \boldsymbol {k}$
-valid colourings
$(1-2^{-\delta _3 n})\cdot F(n) \boldsymbol {k}$
-valid colourings
![]() $\chi : E(G) \rightarrow [s]$
for which there exists
$\chi : E(G) \rightarrow [s]$
for which there exists ![]() with
with
![]() $\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 \leq \delta _4$
and
$\|\boldsymbol {\alpha }^*-\boldsymbol {\alpha }\|_1 \leq \delta _4$
and ![]() such that
such that
![]() $\chi $
is
$\chi $
is
![]() $(0,\delta _4)$
-perfect with respect to
$(0,\delta _4)$
-perfect with respect to
![]() $(\phi ,Y_1,\ldots ,Y_{r^*})$
.
$(\phi ,Y_1,\ldots ,Y_{r^*})$
.
Proof of Corollary 1.9
Suppose that
![]() $\boldsymbol {k}$
is soluble. Let c be the constant implied by solubility and let
$\boldsymbol {k}$
is soluble. Let c be the constant implied by solubility and let
![]() $0 < {\varepsilon } \ll c$
. Let
$0 < {\varepsilon } \ll c$
. Let
![]() $\delta ,n_0$
be the output of Theorem 1.6 applied with parameter
$\delta ,n_0$
be the output of Theorem 1.6 applied with parameter
![]() ${\varepsilon }$
. We may assume that
${\varepsilon }$
. We may assume that
![]() $1/n_0 \ll \delta \ll {\varepsilon }$
. Let
$1/n_0 \ll \delta \ll {\varepsilon }$
. Let
![]() $n \geq n_0$
and let G be an n-vertex
$n \geq n_0$
and let G be an n-vertex
![]() $\boldsymbol {k}$
-extremal graph. Theorem 1.6 implies that G is a complete
$\boldsymbol {k}$
-extremal graph. Theorem 1.6 implies that G is a complete
![]() $r^*$
-partite graph for some
$r^*$
-partite graph for some
![]() $r^* \in \mathbb {N}$
, where, writing
$r^* \in \mathbb {N}$
, where, writing
![]() $\boldsymbol {\beta } \in \Delta ^{r^*}$
for the vector of the part ratios of G, we have
$\boldsymbol {\beta } \in \Delta ^{r^*}$
for the vector of the part ratios of G, we have
![]() $\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 \leq {\varepsilon }$
for some
$\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 \leq {\varepsilon }$
for some ![]() . Let
. Let
![]() $\boldsymbol {d}^*$
be the supersolution of n with
$\boldsymbol {d}^*$
be the supersolution of n with
![]() $\mathrm {perf}(\boldsymbol {d}^*) = \mathrm {perf}_{r,\boldsymbol {\alpha }}(\boldsymbol {d}^*)$
for some
$\mathrm {perf}(\boldsymbol {d}^*) = \mathrm {perf}_{r,\boldsymbol {\alpha }}(\boldsymbol {d}^*)$
for some ![]() . Suppose for a contradiction that
. Suppose for a contradiction that
![]() $\boldsymbol {\beta } n \neq \boldsymbol {d}^*$
.
$\boldsymbol {\beta } n \neq \boldsymbol {d}^*$
.
The number of perfect colourings of G is at least
![]() $(1-2^{-\delta n})F(G;\boldsymbol {k})$
. Then
$(1-2^{-\delta n})F(G;\boldsymbol {k})$
. Then
contradicting the
![]() $\boldsymbol {k}$
-extremality of G.
$\boldsymbol {k}$
-extremality of G.
3. Forbidden triangles in seven colours
In this section, we solve Problem
![]() $Q^*$
in the case
$Q^*$
in the case
![]() $\boldsymbol {k}=(3;7)$
.
$\boldsymbol {k}=(3;7)$
.
Theorem 3.1. Let
![]() $\boldsymbol {k}:=(3;7)$
. Then every
$\boldsymbol {k}:=(3;7)$
. Then every ![]() has
has
![]() $r=8$
,
$r=8$
,
![]() $\boldsymbol {\alpha }$
uniform,
$\boldsymbol {\alpha }$
uniform,
![]() $|\phi (ij)|=4$
for all
$|\phi (ij)|=4$
for all
![]() $ij \in \binom {[8]}{2}$
and
$ij \in \binom {[8]}{2}$
and
![]() $\phi ^{-1}(c) \cong K_{4,4}$
for all
$\phi ^{-1}(c) \cong K_{4,4}$
for all
![]() $c \in [7]$
.
$c \in [7]$
.
We also solve it in the case
![]() $\boldsymbol {k}=(3;6)$
. Recall that
$\boldsymbol {k}=(3;6)$
. Recall that
![]() $F(n;\boldsymbol {k})$
was already determined exactly in this case in [Reference Botler, Corsten, Dankovics, Frankl, Hàn, Jiménez and Skokan2].
$F(n;\boldsymbol {k})$
was already determined exactly in this case in [Reference Botler, Corsten, Dankovics, Frankl, Hàn, Jiménez and Skokan2].
Theorem 3.2. Let
![]() $\boldsymbol {k}:=(3;6)$
. Then every
$\boldsymbol {k}:=(3;6)$
. Then every ![]() has
has
![]() $r=8$
,
$r=8$
,
![]() $\boldsymbol {\alpha }$
uniform,
$\boldsymbol {\alpha }$
uniform,
![]() $|\phi (ij)|\in \{3,4\}$
for all
$|\phi (ij)|\in \{3,4\}$
for all
![]() $ij \in \binom {[8]}{2}$
,
$ij \in \binom {[8]}{2}$
,
![]() $\{ij: |\phi (ij)|=3\} \cong K_{4,4}$
and
$\{ij: |\phi (ij)|=3\} \cong K_{4,4}$
and
![]() $\phi ^{-1}(c) \cong K_{4,4}$
for all
$\phi ^{-1}(c) \cong K_{4,4}$
for all
![]() $c \in [6]$
.
$c \in [6]$
.
3.1. The union of dense triangle-free graphs
The key new idea is the following lemma, a
![]() $2$
-coloured version of Mantel’s theorem, that allows us to add a new constraint to the linear relaxation of the optimisation problem. The constraint ensures that the union of any two colour graphs
$2$
-coloured version of Mantel’s theorem, that allows us to add a new constraint to the linear relaxation of the optimisation problem. The constraint ensures that the union of any two colour graphs
![]() $R := \phi ^{-1}(c), B := \phi ^{-1}(c')$
has density at most
$R := \phi ^{-1}(c), B := \phi ^{-1}(c')$
has density at most
![]() $\frac {3}{4}$
whenever the individual graphs have large density. This is attained by two complete balanced bipartite graphs whose overlap is minimal. The trivial bound for the density of
$\frac {3}{4}$
whenever the individual graphs have large density. This is attained by two complete balanced bipartite graphs whose overlap is minimal. The trivial bound for the density of
![]() $R \cup B$
is
$R \cup B$
is
![]() $\frac {4}{5}$
. Indeed,
$\frac {4}{5}$
. Indeed,
![]() $R \cup B$
is
$R \cup B$
is
![]() $K_6$
-free; otherwise, it would contain a monochromatic triangle, so this claim follows from Turán’s theorem. However, if
$K_6$
-free; otherwise, it would contain a monochromatic triangle, so this claim follows from Turán’s theorem. However, if
![]() $R \cup B$
has density
$R \cup B$
has density
![]() $\frac {4}{5}$
, then each of
$\frac {4}{5}$
, then each of
![]() $R,B$
has density
$R,B$
has density
![]() $\frac {2}{5}$
, coming from the unique red-blue colouring of
$\frac {2}{5}$
, coming from the unique red-blue colouring of
![]() $K_5$
without monochromatic triangles. The lemma states that if the sum of densities of
$K_5$
without monochromatic triangles. The lemma states that if the sum of densities of
![]() $R,B$
is larger, closer to the maximum of
$R,B$
is larger, closer to the maximum of
![]() $\frac {1}{2}+\frac {1}{2}$
, then
$\frac {1}{2}+\frac {1}{2}$
, then
![]() $R \cup B$
has a density significantly smaller than
$R \cup B$
has a density significantly smaller than
![]() $\frac {4}{5}$
.
$\frac {4}{5}$
.
Lemma 3.3. Let
![]() $(a,b)$
be
$(a,b)$
be
![]() $(\frac {19}{25},\frac {89}{100})$
or
$(\frac {19}{25},\frac {89}{100})$
or
![]() $(\frac {3}{4},\frac {19}{20})$
. Let
$(\frac {3}{4},\frac {19}{20})$
. Let
![]() $R,B$
be two triangle-free graphs on the same vertex set of size n with
$R,B$
be two triangle-free graphs on the same vertex set of size n with
![]() $|R|+|B| \geq b n^2/2$
. Then
$|R|+|B| \geq b n^2/2$
. Then
![]() $|R \cup B| \leq a n^2/2 + o(n^2)$
.
$|R \cup B| \leq a n^2/2 + o(n^2)$
.
Proof. Let n be a sufficiently large integer. Let R and B be two triangle-free graphs with vertex set
![]() $[n]$
. We will sometimes denote their edge sets as R and B, respectively, too. Write
$[n]$
. We will sometimes denote their edge sets as R and B, respectively, too. Write
![]() $R \cup B$
for the set of edges that lie in at least one of
$R \cup B$
for the set of edges that lie in at least one of
![]() $R,B$
(a simple graph), and
$R,B$
(a simple graph), and
![]() $R+B$
for the multiset union of
$R+B$
for the multiset union of
![]() $R,B$
(a multigraph). Suppose that
$R,B$
(a multigraph). Suppose that
![]() $d(R+B)> b$
and
$d(R+B)> b$
and
![]() $d(R \cup B)>a$
, where
$d(R \cup B)>a$
, where
![]() $d(E):=|E|/\binom {n}{2}$
is the edge density of a set E of edges. Let
$d(E):=|E|/\binom {n}{2}$
is the edge density of a set E of edges. Let
![]() $Y \subseteq [n]$
be a maximal set with the property that Y has a partition
$Y \subseteq [n]$
be a maximal set with the property that Y has a partition
![]() $Y_1\cup \ldots \cup Y_t$
into sets of size
$Y_1\cup \ldots \cup Y_t$
into sets of size
![]() $5$
where
$5$
where
![]() $(R \cup B)[Y_i]\cong K_5$
for all
$(R \cup B)[Y_i]\cong K_5$
for all
![]() $i \in [t]$
. Since there is a unique
$i \in [t]$
. Since there is a unique
![]() $2$
-edge-colouring of
$2$
-edge-colouring of
![]() $K_5$
which avoids monochromatic triangles, we can label the vertices in each
$K_5$
which avoids monochromatic triangles, we can label the vertices in each
![]() $Y_i$
as
$Y_i$
as
![]() $y^i_{1},\ldots ,y^i_{5}$
where
$y^i_{1},\ldots ,y^i_{5}$
where
![]() $y^i_{j}y^i_{j+1} \in B$
for all
$y^i_{j}y^i_{j+1} \in B$
for all
![]() $j \in [5]$
, where
$j \in [5]$
, where
![]() $y^i_{6}:=y^i_{1}$
, and every other pair is in R (so there are no double edges). Let
$y^i_{6}:=y^i_{1}$
, and every other pair is in R (so there are no double edges). Let
![]() $X \subseteq \overline {Y} := [n]\setminus Y$
be a maximal set with the property that X has a partition
$X \subseteq \overline {Y} := [n]\setminus Y$
be a maximal set with the property that X has a partition
![]() $X_1 \cup \ldots \cup X_s$
into pairs where
$X_1 \cup \ldots \cup X_s$
into pairs where
![]() $(R \cap B)[X_i]\cong K_2$
for all
$(R \cap B)[X_i]\cong K_2$
for all
![]() $i \in [s]$
. Write
$i \in [s]$
. Write
![]() $|Y|=yn$
,
$|Y|=yn$
,
![]() $|X|=xn$
and
$|X|=xn$
and
![]() $Z:=[n]\setminus (X \cup Y)$
.
$Z:=[n]\setminus (X \cup Y)$
.
We claim that
 $$ \begin{align} \nonumber &0 \leq d(R+B) - b \leq 2q(x,y) + o(1)\quad\text{where}\\ &q(x,y) := \frac{x^2}{2}+\frac{3}{4}\cdot\frac{(1-x-y)^2}{2}+x(1-x-y)+\frac{4}{5}\cdot\frac{y^2}{2}+\frac{4}{5}\cdot y(1-y) - \frac{b}{2}. \end{align} $$
$$ \begin{align} \nonumber &0 \leq d(R+B) - b \leq 2q(x,y) + o(1)\quad\text{where}\\ &q(x,y) := \frac{x^2}{2}+\frac{3}{4}\cdot\frac{(1-x-y)^2}{2}+x(1-x-y)+\frac{4}{5}\cdot\frac{y^2}{2}+\frac{4}{5}\cdot y(1-y) - \frac{b}{2}. \end{align} $$
This is a consequence of the following observations on the densities of R and B in various subsets of the vertex set. For a graph G with disjoint
![]() $U,U' \subseteq V(G)$
, we write
$U,U' \subseteq V(G)$
, we write
![]() $d_G(U) := |E(G[U])|/\binom {|U|}{2}$
and
$d_G(U) := |E(G[U])|/\binom {|U|}{2}$
and
![]() $d_G(U,U') := |E(G[U,U'])|/(|U||U'|)$
.
$d_G(U,U') := |E(G[U,U'])|/(|U||U'|)$
.
-
(i)
 $d_R(X) \leq \frac {1}{2}+o(1)$
by Turán’s theorem (or rather Mantel’s theorem), since R is triangle-free. Similarly for
$d_R(X) \leq \frac {1}{2}+o(1)$
by Turán’s theorem (or rather Mantel’s theorem), since R is triangle-free. Similarly for
 $d_B(X)$
.
$d_B(X)$
. -
(ii)
 $d_{R+B}(Z) \leq \frac {3}{4}+o(1)$
by Turán’s theorem, since
$d_{R+B}(Z) \leq \frac {3}{4}+o(1)$
by Turán’s theorem, since
 $R,B$
are disjoint on Z and so
$R,B$
are disjoint on Z and so
 $R+B=R \cup B$
is
$R+B=R \cup B$
is
 $K_5$
-free, so
$K_5$
-free, so
 $d_{R+B}(Z)=d_{R \cup B}(Z) \leq \frac {3}{4}+o(1)$
.
$d_{R+B}(Z)=d_{R \cup B}(Z) \leq \frac {3}{4}+o(1)$
. -
(iii)
 $d_{R+B}(X,Z) \leq 1$
. If not, by averaging, there is
$d_{R+B}(X,Z) \leq 1$
. If not, by averaging, there is
 $j \in [s]$
with
$j \in [s]$
with
 $e_{R+B}(X_j,Z)>2|Z|$
, so without loss of generality, there is
$e_{R+B}(X_j,Z)>2|Z|$
, so without loss of generality, there is
 $v \in Z$
such that v sends a red edge to both vertices in
$v \in Z$
such that v sends a red edge to both vertices in
 $X_j$
, a contradiction.
$X_j$
, a contradiction.
Thus, (3.1) holds for
![]() $y=o(1)$
. So for the rest of the derivation, we may suppose
$y=o(1)$
. So for the rest of the derivation, we may suppose
![]() $y=\Omega (1)$
.
$y=\Omega (1)$
.
-
(iv)
 $d_{R+B}(Y) \leq \frac {4}{5}+o(1)$
. If not, by averaging, there are distinct
$d_{R+B}(Y) \leq \frac {4}{5}+o(1)$
. If not, by averaging, there are distinct
 $i,j \in [t]$
such that (if
$i,j \in [t]$
such that (if $$ \begin{align*}e_{R+B}(Y_i,Y_j) \geq \frac{(\frac{4}{5}+\Omega(1))\binom{yn}{2} - 10\cdot yn/5}{\binom{yn/5}{2}}> 20 \end{align*} $$
$$ \begin{align*}e_{R+B}(Y_i,Y_j) \geq \frac{(\frac{4}{5}+\Omega(1))\binom{yn}{2} - 10\cdot yn/5}{\binom{yn/5}{2}}> 20 \end{align*} $$
 $d_{R+B}(Y)> \frac {4}{5}+c$
, then this holds already for
$d_{R+B}(Y)> \frac {4}{5}+c$
, then this holds already for
 $yn>\frac {1}{c}-1$
). Then, without loss of generality,
$yn>\frac {1}{c}-1$
). Then, without loss of generality,
 $d_{R+B}(y^j_{1},Y_i) \geq 5$
. There is at least one double edge, say
$d_{R+B}(y^j_{1},Y_i) \geq 5$
. There is at least one double edge, say
 $y^j_{1}y^i_{1}$
, for otherwise
$y^j_{1}y^i_{1}$
, for otherwise
 $(R\cup B)[Y_i \cup \{y^j_{1}\}]\cong K_6$
. Then
$(R\cup B)[Y_i \cup \{y^j_{1}\}]\cong K_6$
. Then
 $y^j_{1}$
sends no blue edges to
$y^j_{1}$
sends no blue edges to
 $\{y^i_{2},y^i_{5}\}$
, and at most one red edge. Similarly,
$\{y^i_{2},y^i_{5}\}$
, and at most one red edge. Similarly,
 $y^j_{1}$
sends no red edges to
$y^j_{1}$
sends no red edges to
 $\{y^i_{3},y^i_{4}\}$
, and at most one blue edge. Thus, in fact,
$\{y^i_{3},y^i_{4}\}$
, and at most one blue edge. Thus, in fact,
 $d_{R+B}(y^j_{1},Y_i) \leq 4$
, a contradiction.
$d_{R+B}(y^j_{1},Y_i) \leq 4$
, a contradiction.
-
(v) For all
 $W \subseteq X \cup Z$
,
$W \subseteq X \cup Z$
,
 $d_R(Y,W) \leq \frac {2}{5}$
. If not, by averaging, there is
$d_R(Y,W) \leq \frac {2}{5}$
. If not, by averaging, there is
 $i \in [t]$
and
$i \in [t]$
and
 $v\in W$
such that
$v\in W$
such that
 $d_R(v,Y_i) \geq 3$
which yields a red triangle containing v and two vertices in
$d_R(v,Y_i) \geq 3$
which yields a red triangle containing v and two vertices in
 $Y_i$
. Similarly for
$Y_i$
. Similarly for
 $d_B(Y,W)$
.
$d_B(Y,W)$
.
This proves that (3.1) holds, using in order (i)–(v) for each term, bounding the density of
![]() $R+B$
in, respectively,
$R+B$
in, respectively,
![]() $X,Z,(X,Z),Y,(Y,X \cup Z)$
.
$X,Z,(X,Z),Y,(Y,X \cup Z)$
.
We obtain a similar polynomial upper bound for the density of
![]() $R\cup B$
. We claim that
$R\cup B$
. We claim that
 $$ \begin{align} p(x,y) &:= \frac{4}{5}\cdot\frac{y^2}{2}+ \frac{4}{5}(1-x-y)y + \frac{3}{4}\cdot\frac{(1-y)^2}{2} + \frac{7}{10} xy - \frac{a}{2}\\ \nonumber &= -\frac{y}{40}(4x+y-2) - \frac{1}{2}\left(a-\frac{3}{4}\right). \end{align} $$
$$ \begin{align} p(x,y) &:= \frac{4}{5}\cdot\frac{y^2}{2}+ \frac{4}{5}(1-x-y)y + \frac{3}{4}\cdot\frac{(1-y)^2}{2} + \frac{7}{10} xy - \frac{a}{2}\\ \nonumber &= -\frac{y}{40}(4x+y-2) - \frac{1}{2}\left(a-\frac{3}{4}\right). \end{align} $$
This follows from some more observations.
-
(vi)
 $d_{R \cup B}(\overline {Y}) \leq \frac {3}{4}+o(1)$
by Turán’s theorem, since
$d_{R \cup B}(\overline {Y}) \leq \frac {3}{4}+o(1)$
by Turán’s theorem, since
 $(R \cup B)[\overline {Y}]$
is
$(R \cup B)[\overline {Y}]$
is
 $K_5$
-free.
$K_5$
-free. -
(vii)
 $d_{R \cup B}(Y,X) \leq \frac {7}{10}$
. If not, then by averaging, there is
$d_{R \cup B}(Y,X) \leq \frac {7}{10}$
. If not, then by averaging, there is
 $i \in [t]$
and
$i \in [t]$
and
 $j \in [s]$
such that
$j \in [s]$
such that
 $e(R \cup B)[Y_i,X_j]> \frac {7}{10}\cdot 5 \cdot 2 = 7$
. For ease of notation, write
$e(R \cup B)[Y_i,X_j]> \frac {7}{10}\cdot 5 \cdot 2 = 7$
. For ease of notation, write
 $1,\dots ,5$
for the vertices of
$1,\dots ,5$
for the vertices of
 $Y_i$
, with blue edges forming the cycle
$Y_i$
, with blue edges forming the cycle
 $12,23,34,45,51$
and red edges forming the cycle
$12,23,34,45,51$
and red edges forming the cycle
 $13,35,52,24,41$
, and write
$13,35,52,24,41$
, and write
 $X_j=\{x,y\}$
, where
$X_j=\{x,y\}$
, where
 $xy$
is both red and blue. Each of
$xy$
is both red and blue. Each of
 $x,y$
has at most two neighbours in
$x,y$
has at most two neighbours in
 $[5]$
of any one colour, and therefore exactly two or we are done. For blue, these neighbours are a subset of one of
$[5]$
of any one colour, and therefore exactly two or we are done. For blue, these neighbours are a subset of one of
 $\{1,3\},\{2,4\},\{3,5\},\{4,1\},\{5,2\}$
, and for red a subset of
$\{1,3\},\{2,4\},\{3,5\},\{4,1\},\{5,2\}$
, and for red a subset of
 $\{1,5\},\{3,2\},\{5,4\},\{2,1\},\{4,3\}$
. We have that
$\{1,5\},\{3,2\},\{5,4\},\{2,1\},\{4,3\}$
. We have that
 $N_B(x),N_B(y)$
are disjoint, as are
$N_B(x),N_B(y)$
are disjoint, as are
 $N_R(x),N_R(y)$
. Also, each of
$N_R(x),N_R(y)$
. Also, each of
 $N_B(x),N_R(x)$
are disjoint, as are
$N_B(x),N_R(x)$
are disjoint, as are
 $N_B(y),N_R(y)$
, since otherwise there are at most
$N_B(y),N_R(y)$
, since otherwise there are at most
 $7 R \cup B$
-edges between
$7 R \cup B$
-edges between
 $\{x,y\}$
and
$\{x,y\}$
and
 $\{1,\ldots ,5\}$
, a contradiction. Without loss of generality, suppose
$\{1,\ldots ,5\}$
, a contradiction. Without loss of generality, suppose
 $N_B(x)=\{1,3\}$
. Then
$N_B(x)=\{1,3\}$
. Then
 $N_R(x) = \{5,4\}$
and
$N_R(x) = \{5,4\}$
and
 $N_B(y)\in \{\{2,4\},\{5,2\}\}$
. For either possibility, there is no choice of
$N_B(y)\in \{\{2,4\},\{5,2\}\}$
. For either possibility, there is no choice of
 $N_R(y)$
which satisfies the disjointness conditions.
$N_R(y)$
which satisfies the disjointness conditions.
Again, (3.2) holds using (iv)–(vii) in order for each term, bounding the density of
![]() $R \cup B$
in, respectively,
$R \cup B$
in, respectively,
![]() $Y,(Z,Y),X \cup Z, (X,Y)$
. This proves the claim.
$Y,(Z,Y),X \cup Z, (X,Y)$
. This proves the claim.
Claim 3.3.1. The regions
![]() $P:= \{(x,y) \in [0,1]^2: p(x,y) \geq 0\}$
and
$P:= \{(x,y) \in [0,1]^2: p(x,y) \geq 0\}$
and
![]() $Q := \{(x,y) \in [0,1]^2: q(x,y) \geq 0\}$
intersect only when
$Q := \{(x,y) \in [0,1]^2: q(x,y) \geq 0\}$
intersect only when
![]() $y=0$
.
$y=0$
.
Proof of Claim
Write
 $$ \begin{align*} p_x(y) &:=40p(x,y) = -y^2 - 2y(2x-1) - 5(4a - 3)\quad\text{and}\\ q_x(y) &:=40q(x,y)= -y^2 - 2y(5x-1) +5(-x^2+2x+3-4b), \end{align*} $$
$$ \begin{align*} p_x(y) &:=40p(x,y) = -y^2 - 2y(2x-1) - 5(4a - 3)\quad\text{and}\\ q_x(y) &:=40q(x,y)= -y^2 - 2y(5x-1) +5(-x^2+2x+3-4b), \end{align*} $$
which are both quadratic functions of y with negative
![]() $y^2$
coefficient. Note that their discriminants are
$y^2$
coefficient. Note that their discriminants are
 $$ \begin{align*} \mathrm{disc}(p_x) &= 4(2x-1)^2-20(4a-3)\quad\text{and}\\ \mathrm{disc}(q_x) &= 4\left(5x-1\right)^2+20\left(-x^2+2x-3-4b\right)= 80\left(x^2+\frac{4}{5}-b\right)\\ &= 80\left(\left(x-\frac{3}{10}\right)\left(x+\frac{3}{10}\right)+\frac{89}{100}-b\right). \end{align*} $$
$$ \begin{align*} \mathrm{disc}(p_x) &= 4(2x-1)^2-20(4a-3)\quad\text{and}\\ \mathrm{disc}(q_x) &= 4\left(5x-1\right)^2+20\left(-x^2+2x-3-4b\right)= 80\left(x^2+\frac{4}{5}-b\right)\\ &= 80\left(\left(x-\frac{3}{10}\right)\left(x+\frac{3}{10}\right)+\frac{89}{100}-b\right). \end{align*} $$
Thus, if
![]() $\mathrm {disc}(q_x) \geq 0$
, the largest root
$\mathrm {disc}(q_x) \geq 0$
, the largest root
![]() $y_x$
of
$y_x$
of
![]() $q_x$
is
$q_x$
is
 $$ \begin{align*}-5x+1+2\sqrt{5}\cdot \sqrt{x^2+\frac{4}{5}-b}. \end{align*} $$
$$ \begin{align*}-5x+1+2\sqrt{5}\cdot \sqrt{x^2+\frac{4}{5}-b}. \end{align*} $$
Suppose first that
![]() $(a,b)=(\frac {19}{25},\frac {89}{100})$
. We claim that
$(a,b)=(\frac {19}{25},\frac {89}{100})$
. We claim that
![]() $x < \frac {3}{10}$
for all
$x < \frac {3}{10}$
for all
![]() $(x,y) \in P$
. For this, note that
$(x,y) \in P$
. For this, note that
![]() $\mathrm {disc}(p_{\frac {3}{10}})<0$
, so
$\mathrm {disc}(p_{\frac {3}{10}})<0$
, so
![]() $p_{\frac {3}{10}}$
has no real roots, and therefore,
$p_{\frac {3}{10}}$
has no real roots, and therefore,
![]() $p_{\frac {3}{10}}(y)<0$
for all
$p_{\frac {3}{10}}(y)<0$
for all
![]() $y \in [0,1]$
. Since
$y \in [0,1]$
. Since
![]() $p(x,y)$
is decreasing in
$p(x,y)$
is decreasing in
![]() $x \geq 0$
, we have that
$x \geq 0$
, we have that
![]() $p(x,y)=\frac {1}{40}p_x(y)<0$
for all
$p(x,y)=\frac {1}{40}p_x(y)<0$
for all
![]() $x \in [\frac {3}{10},1]$
and
$x \in [\frac {3}{10},1]$
and
![]() $y \in [0,1]$
, as required. However, we claim that
$y \in [0,1]$
, as required. However, we claim that
![]() $x\geq \frac {3}{10}$
for all
$x\geq \frac {3}{10}$
for all
![]() $(x,y) \in Q$
. Indeed, if
$(x,y) \in Q$
. Indeed, if
![]() $x \in [0,\frac {3}{10})$
, we have
$x \in [0,\frac {3}{10})$
, we have
![]() $\mathrm {disc}(q_x)<0$
and so again,
$\mathrm {disc}(q_x)<0$
and so again,
![]() $q(x,y)=q_x(y)<0$
for all
$q(x,y)=q_x(y)<0$
for all
![]() $y \in [0,1]$
. Thus, P and Q are disjoint in this case.
$y \in [0,1]$
. Thus, P and Q are disjoint in this case.
Suppose secondly that
![]() $(a,b)=(\frac {3}{4},\frac {19}{20})$
. We claim that
$(a,b)=(\frac {3}{4},\frac {19}{20})$
. We claim that
![]() $x \leq \frac {1}{2}$
for all
$x \leq \frac {1}{2}$
for all
![]() $(x,y) \in P$
with
$(x,y) \in P$
with
![]() $y \neq 0$
. Indeed,
$y \neq 0$
. Indeed,
![]() $p_x(y)=-y(y+4x-2)$
, so we have
$p_x(y)=-y(y+4x-2)$
, so we have
![]() $y+4x-2 \leq 0$
for
$y+4x-2 \leq 0$
for
![]() $y \in (0,1]$
, so
$y \in (0,1]$
, so
![]() $x \leq \frac {1}{2}$
. However, we claim that
$x \leq \frac {1}{2}$
. However, we claim that
![]() $x>\frac {1}{2}$
for all
$x>\frac {1}{2}$
for all
![]() $(x,y) \in Q$
. Indeed, let
$(x,y) \in Q$
. Indeed, let
![]() $x \in [0,\frac {1}{2}]$
. If
$x \in [0,\frac {1}{2}]$
. If
![]() $\mathrm {disc}(q_x)<0$
, then, since the coefficient of
$\mathrm {disc}(q_x)<0$
, then, since the coefficient of
![]() $y^2$
is negative,
$y^2$
is negative,
![]() $(x,y)<0$
for all
$(x,y)<0$
for all
![]() $y \in [0,1]$
. Otherwise, the largest root
$y \in [0,1]$
. Otherwise, the largest root
![]() $y_x$
of
$y_x$
of
![]() $q_x$
exists, and it is at least
$q_x$
exists, and it is at least
![]() $0$
only if
$0$
only if
![]() $5x^2-10x+4\leq 0$
, which is false for all
$5x^2-10x+4\leq 0$
, which is false for all
![]() $x \in [0,\frac {1}{2}]$
. So
$x \in [0,\frac {1}{2}]$
. So
![]() $y_x$
is negative, and we see that
$y_x$
is negative, and we see that
![]() $q_x(y)<q_x(y_x) = 0$
for all
$q_x(y)<q_x(y_x) = 0$
for all
![]() $y \in (y_x,1]$
. Thus,
$y \in (y_x,1]$
. Thus,
![]() $x> \frac {1}{2}$
for all
$x> \frac {1}{2}$
for all
![]() $(x,y) \in Q$
, as required. This completes the proof of the claim.
$(x,y) \in Q$
, as required. This completes the proof of the claim.
The statement of the lemma then follows easily from the claim, noting that for any
![]() $(x,y) \in P \cap Q$
, we have
$(x,y) \in P \cap Q$
, we have
![]() $y=0$
and
$y=0$
and
![]() $p(x,0)=\frac {1}{2}(\frac {3}{4}-a) \leq 0$
.
$p(x,0)=\frac {1}{2}(\frac {3}{4}-a) \leq 0$
.
3.2. Solving Problem
 $Q^*$
via a linear relaxation
$Q^*$
via a linear relaxation
We define a further optimisation problem.
Problem
![]() $\mathbf {L}$
: Given a sequence
$\mathbf {L}$
: Given a sequence
![]() $\boldsymbol {k}:=(k_1,\ldots ,k_s)\in \mathbb {N}^s$
of natural numbers, determine
$\boldsymbol {k}:=(k_1,\ldots ,k_s)\in \mathbb {N}^s$
of natural numbers, determine
![]() $ \ell ^{\mathrm {max}}(\boldsymbol {k}) := \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d}) $
, the maximum value of
$ \ell ^{\mathrm {max}}(\boldsymbol {k}) := \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d}) $
, the maximum value of
over the set
![]() $D(\boldsymbol {k})$
of
$D(\boldsymbol {k})$
of
![]() $(s-1)$
-tuples
$(s-1)$
-tuples
![]() $\boldsymbol {d}=(d_2,\ldots ,d_s)$
such that
$\boldsymbol {d}=(d_2,\ldots ,d_s)$
such that
![]() $0 \leq d_t \leq 1$
for all
$0 \leq d_t \leq 1$
for all
![]() $2 \leq t \leq s$
, and
$2 \leq t \leq s$
, and
![]() $\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$
.
$\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$
.
We say that
![]() $\boldsymbol {d}$
which is feasible for Problem L is realisable if there is some
$\boldsymbol {d}$
which is feasible for Problem L is realisable if there is some ![]() with
with
 $$ \begin{align} d_t=2\sum_{ij \in \binom{[r]}{2}:|\phi(ij)|=t}\alpha_i \alpha_j\quad \text{for all }2 \leq t \leq s \end{align} $$
$$ \begin{align} d_t=2\sum_{ij \in \binom{[r]}{2}:|\phi(ij)|=t}\alpha_i \alpha_j\quad \text{for all }2 \leq t \leq s \end{align} $$
and call such a feasible triple a realisation (of
![]() $\boldsymbol {d}$
).
$\boldsymbol {d}$
).
We have the following, which is proved by applying Turán’s theorem to blow-ups (defined below). It implies that, in certain special cases, to solve Problem
![]() $Q^*$
, it suffices to solve Problem L.
$Q^*$
, it suffices to solve Problem L.
Lemma 3.4 ([Reference Pikhurko and Staden10, Lemma 5.1])
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}$
. Then
$\boldsymbol {k} \in \mathbb {N}$
. Then
![]() $Q(\boldsymbol {k}) \leq \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
. Moreover, the following is true. Suppose that at least one optimal solution
$Q(\boldsymbol {k}) \leq \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
. Moreover, the following is true. Suppose that at least one optimal solution
![]() $\boldsymbol {d}$
to Problem L is realisable. Then
$\boldsymbol {d}$
to Problem L is realisable. Then
![]() $\max _{\boldsymbol {d}\in D(\boldsymbol {k})}\ell (\boldsymbol {d})=Q(\boldsymbol {k})$
and
$\max _{\boldsymbol {d}\in D(\boldsymbol {k})}\ell (\boldsymbol {d})=Q(\boldsymbol {k})$
and ![]() is the set of all
is the set of all ![]() , which are realisations of some optimal
, which are realisations of some optimal
![]() $\boldsymbol {d}$
.
$\boldsymbol {d}$
.
We wish to add more constraints to Problem L. Indeed, without additional constraints, Problem L only yields realisable solutions in some very special cases – for example,
![]() $\boldsymbol {k}=(k,k)$
or
$\boldsymbol {k}=(k,k)$
or
![]() $\boldsymbol {k}=(k,k,k)$
. A constraint is valid if every
$\boldsymbol {k}=(k,k,k)$
. A constraint is valid if every
![]() $\boldsymbol {d}$
which has a realisation
$\boldsymbol {d}$
which has a realisation ![]() must satisfy the constraint. We use I for a set of constraints, each of the type
must satisfy the constraint. We use I for a set of constraints, each of the type
![]() $\sum _{2 \leq f \leq s}a_f d_f \leq b$
for some
$\sum _{2 \leq f \leq s}a_f d_f \leq b$
for some
![]() $a_2,\ldots ,a_s,b \in \mathbb {R}$
. Let Problem
$a_2,\ldots ,a_s,b \in \mathbb {R}$
. Let Problem
![]() $(L,I)$
be Problem L with the constraints in I added to it and let
$(L,I)$
be Problem L with the constraints in I added to it and let
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal solution of Problem
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal solution of Problem
![]() $(L,I)$
. We will still discuss realisable solutions
$(L,I)$
. We will still discuss realisable solutions
![]() $\boldsymbol {d}$
and realisations of
$\boldsymbol {d}$
and realisations of
![]() $\boldsymbol {d}$
for Problem
$\boldsymbol {d}$
for Problem
![]() $(L,I)$
without referring to I when it is clear from the context.
$(L,I)$
without referring to I when it is clear from the context.
The two types of constraints that we consider are as follows.
Universal constraints.
Let
![]() $\mathcal {A}$
be a set of subsets of
$\mathcal {A}$
be a set of subsets of
![]() $\binom {[s]}{\geq 2}$
. Let
$\binom {[s]}{\geq 2}$
. Let
![]() $i_2,\ldots ,i_s \geq 0$
be such that for each
$i_2,\ldots ,i_s \geq 0$
be such that for each
![]() $2 \leq f \leq s$
and
$2 \leq f \leq s$
and
![]() $S \in \binom {[s]}{f}$
, the number of
$S \in \binom {[s]}{f}$
, the number of
![]() $A \in \mathcal {A}$
for which
$A \in \mathcal {A}$
for which
![]() $S \in A$
is at least
$S \in A$
is at least
![]() $i_f$
.
$i_f$
.
Next, given ![]() and
and
![]() $A \subseteq \binom {[s]}{\geq 2}$
, let
$A \subseteq \binom {[s]}{\geq 2}$
, let
![]() $H^n_A(\phi ,\boldsymbol {\alpha })$
be the ‘blow-up’ graph on n vertices with vertex classes
$H^n_A(\phi ,\boldsymbol {\alpha })$
be the ‘blow-up’ graph on n vertices with vertex classes
![]() $X_1,\ldots ,X_r$
, where
$X_1,\ldots ,X_r$
, where
![]() $|\,|X_i|-\alpha _i n\,| \leq 1$
for all
$|\,|X_i|-\alpha _i n\,| \leq 1$
for all
![]() $i \in [r]$
and
$i \in [r]$
and
![]() $xy$
is an edge for
$xy$
is an edge for
![]() $x \in X_i$
,
$x \in X_i$
,
![]() $y \in X_j$
if and only if
$y \in X_j$
if and only if
![]() $\phi (ij) \in A$
. Suppose that
$\phi (ij) \in A$
. Suppose that
![]() $d(H^n_A(\phi ,\boldsymbol {\alpha })) \leq c_A+o_n(1)$
for all
$d(H^n_A(\phi ,\boldsymbol {\alpha })) \leq c_A+o_n(1)$
for all
![]() $A \in \mathcal {A}$
and all
$A \in \mathcal {A}$
and all ![]() . Then
. Then
is a valid constraint. Indeed,
![]() $\sum _{A \in \mathcal {A}}e(H^{n}_A(\phi ,\boldsymbol {\alpha })) \geq (i_2d_{2}+\ldots +i_sd_{s})\frac {n^2}{2}+O(n)$
.
$\sum _{A \in \mathcal {A}}e(H^{n}_A(\phi ,\boldsymbol {\alpha })) \geq (i_2d_{2}+\ldots +i_sd_{s})\frac {n^2}{2}+O(n)$
.
For example, the basic constraint
![]() $\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$
is a universal constraint, coming from
$\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-\frac {1}{k_c-1}\right )$
is a universal constraint, coming from
![]() $\mathcal {A} := \{A_1,\ldots ,A_s\}$
and
$\mathcal {A} := \{A_1,\ldots ,A_s\}$
and
![]() $c_{A_t} := 1-\frac {1}{k_t-1}$
, where
$c_{A_t} := 1-\frac {1}{k_t-1}$
, where
![]() $A_t := \{S \in \binom {[s]}{\geq 2}: t \in S\}$
, noting that each
$A_t := \{S \in \binom {[s]}{\geq 2}: t \in S\}$
, noting that each
![]() $S \in \binom {[s]}{f}$
lies in
$S \in \binom {[s]}{f}$
lies in
![]() $A_g$
if and only if
$A_g$
if and only if
![]() $g \in S$
, so
$g \in S$
, so
![]() $i_f :=f$
.
$i_f :=f$
.
A special case of universal constraint arises when
![]() $H_{\mathcal {A}}(\phi ) := \{ij \in \binom {[r]}{2}: \phi (ij) \in A \text { for some }A \in \mathcal {A}\}$
is
$H_{\mathcal {A}}(\phi ) := \{ij \in \binom {[r]}{2}: \phi (ij) \in A \text { for some }A \in \mathcal {A}\}$
is
![]() $K_k$
-free for every
$K_k$
-free for every ![]() . Then
. Then
![]() $H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha }) := \bigcup _{A \in \mathcal {A}}H_A^n(\phi ,\boldsymbol {\alpha })$
is always
$H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha }) := \bigcup _{A \in \mathcal {A}}H_A^n(\phi ,\boldsymbol {\alpha })$
is always
![]() $K_k$
-free, so Turán’s theorem implies that
$K_k$
-free, so Turán’s theorem implies that
![]() $d(H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha })) \leq 1-\frac {1}{k-1}$
. If
$d(H_{\mathcal {A}}^n(\phi ,\boldsymbol {\alpha })) \leq 1-\frac {1}{k-1}$
. If
![]() $\mathcal {A} := \{\binom {[s]}{t}: t \in T\}$
for some
$\mathcal {A} := \{\binom {[s]}{t}: t \in T\}$
for some
![]() $T \subseteq \{2,\ldots ,s\}$
, then
$T \subseteq \{2,\ldots ,s\}$
, then
![]() $i_f=1$
when
$i_f=1$
when
![]() $f \in T$
and
$f \in T$
and
![]() $0$
otherwise, so we have
$0$
otherwise, so we have
 $$ \begin{align*}\sum_{t \in T}d_t \leq 1-\frac{1}{k-1}. \end{align*} $$
$$ \begin{align*}\sum_{t \in T}d_t \leq 1-\frac{1}{k-1}. \end{align*} $$
We have the following observations from [Reference Pikhurko and Staden10].
-
(A) Suppose there is equality in this constraint. Then there is a partition of
 $[r]$
into parts
$[r]$
into parts
 $A_1,\ldots ,A_{k-1}$
such that
$A_1,\ldots ,A_{k-1}$
such that
 $\sum _{i \in A_{i'}}\alpha _{i}=\frac {1}{k-1}$
for all
$\sum _{i \in A_{i'}}\alpha _{i}=\frac {1}{k-1}$
for all
 $i' \in [k-1]$
, and
$i' \in [k-1]$
, and
 $ij \in H_{\mathcal {A}}(\phi )$
if and only if
$ij \in H_{\mathcal {A}}(\phi )$
if and only if
 $i,j$
lie in different parts
$i,j$
lie in different parts
 $A_{i'},A_{j'}$
.
$A_{i'},A_{j'}$
. -
(B) If
 $S \subseteq [r]$
has
$S \subseteq [r]$
has
 $|S| \leq k$
, then
$|S| \leq k$
, then
 $2\sum _{ij \in \binom {S}{2}}\alpha _i\alpha _j \leq \left (1-\frac {1}{k-1}\right )\sum _{i \in S}\alpha _i$
with equality if and only if
$2\sum _{ij \in \binom {S}{2}}\alpha _i\alpha _j \leq \left (1-\frac {1}{k-1}\right )\sum _{i \in S}\alpha _i$
with equality if and only if
 $\alpha _i=\alpha _j$
for all
$\alpha _i=\alpha _j$
for all
 $ij \in \binom {S}{2}$
.
$ij \in \binom {S}{2}$
.
Existential constraints.
Let I be a set of valid constraints. Suppose that there is some ![]() which is the realisation of some feasible
which is the realisation of some feasible
![]() $\boldsymbol {d}^*$
, and a constraint
$\boldsymbol {d}^*$
, and a constraint
![]() $a_2d_2+\ldots +a_sd_s \leq b$
, and let
$a_2d_2+\ldots +a_sd_s \leq b$
, and let
![]() $I'$
be obtained from adding this constraint to I. Suppose that Problem L with constraints
$I'$
be obtained from adding this constraint to I. Suppose that Problem L with constraints
![]() $I'$
has optimal value
$I'$
has optimal value
![]() $\ell ^{\mathrm {max}}_{I'}(\boldsymbol {k})< \ell (\boldsymbol {d}^*)$
. Then
$\ell ^{\mathrm {max}}_{I'}(\boldsymbol {k})< \ell (\boldsymbol {d}^*)$
. Then
is a valid constraint. Indeed, no optimal solution of Problem
![]() $Q^*$
is a realisation of
$Q^*$
is a realisation of
![]() $\boldsymbol {d}$
that satisfies the new constraint, so it cannot hold.
$\boldsymbol {d}$
that satisfies the new constraint, so it cannot hold.
Lemma 3.5. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}$
. Let I be a set of valid constraints from Problem L and let
$\boldsymbol {k} \in \mathbb {N}$
. Let I be a set of valid constraints from Problem L and let
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal value. Then
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal value. Then
![]() $Q(\boldsymbol {k}) \leq \ell ^{\mathrm {max}}_I(\boldsymbol {k})$
. Moreover, the following is true. Suppose that at least one optimal solution
$Q(\boldsymbol {k}) \leq \ell ^{\mathrm {max}}_I(\boldsymbol {k})$
. Moreover, the following is true. Suppose that at least one optimal solution
![]() $\boldsymbol {d}$
to Problem L with constraints I is realisable. Then
$\boldsymbol {d}$
to Problem L with constraints I is realisable. Then
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})=Q(\boldsymbol {k})$
and
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})=Q(\boldsymbol {k})$
and ![]() is the set of all
is the set of all ![]() which are realisations of some optimal
which are realisations of some optimal
![]() $\boldsymbol {d}$
.
$\boldsymbol {d}$
.

Figure 1 Hadamard matrices of order
![]() $2,4,8$
, which are unique up to equivalence. Here, black represents
$2,4,8$
, which are unique up to equivalence. Here, black represents
![]() $1$
and white represents
$1$
and white represents
![]() $-1$
.
$-1$
.
3.3. The proof of Theorem 3.1
First we see why a particular density vector
![]() $\boldsymbol {d}$
for the
$\boldsymbol {d}$
for the
![]() $(3;4t-1)$
-problem must give rise to a realisation corresponding to the Hadamard matrix
$(3;4t-1)$
-problem must give rise to a realisation corresponding to the Hadamard matrix
![]() $H_{4t}$
.
$H_{4t}$
.
Lemma 3.6. Let
![]() $t \geq 1$
be an integer and let
$t \geq 1$
be an integer and let
![]() $\boldsymbol {k}=(3;4t-1)$
. Suppose that
$\boldsymbol {k}=(3;4t-1)$
. Suppose that
![]() $\boldsymbol {d} = (d_2,\ldots ,d_{4t-1})$
with
$\boldsymbol {d} = (d_2,\ldots ,d_{4t-1})$
with
![]() $d_{2t}=1-\frac {1}{4t}$
and all other entries zero is realisable and let
$d_{2t}=1-\frac {1}{4t}$
and all other entries zero is realisable and let ![]() be a realisation. Then
be a realisation. Then
![]() $r=4t$
,
$r=4t$
,
![]() $\boldsymbol {\alpha }$
is uniform, and every
$\boldsymbol {\alpha }$
is uniform, and every
![]() $\phi ^{-1}(c) \cong K_{2t,2t}$
. Moreover, there is a Hadamard matrix
$\phi ^{-1}(c) \cong K_{2t,2t}$
. Moreover, there is a Hadamard matrix
![]() $H_{4t}$
of order
$H_{4t}$
of order
![]() $4t$
whose columns are labelled
$4t$
whose columns are labelled
![]() $0,1,\ldots ,4t-1$
and rows are labelled
$0,1,\ldots ,4t-1$
and rows are labelled
![]() $1,2,\ldots ,4t$
, normalised so that Column
$1,2,\ldots ,4t$
, normalised so that Column
![]() $0$
consists of
$0$
consists of
![]() $1$
-entries, and such that the vertex classes of
$1$
-entries, and such that the vertex classes of
![]() $\phi ^{-1}(c)$
are given respectively by the set of row indices of the
$\phi ^{-1}(c)$
are given respectively by the set of row indices of the
![]() $1$
-entries, and of the
$1$
-entries, and of the
![]() $-1$
-entries, in Column c in
$-1$
-entries, in Column c in
![]() $H_{4t}$
.
$H_{4t}$
.
Proof. By Turán’s theorem,
![]() $|\phi ^{-1}(c)| \leq \lfloor r^2/4\rfloor $
. Also,
$|\phi ^{-1}(c)| \leq \lfloor r^2/4\rfloor $
. Also,
![]() $\boldsymbol {d}$
is such that only
$\boldsymbol {d}$
is such that only
![]() $d_{2t}$
is nonzero, so
$d_{2t}$
is nonzero, so
![]() $|\phi (ij)|=2t$
for all
$|\phi (ij)|=2t$
for all
![]() $ij \in \binom {[r]}{2}$
. So
$ij \in \binom {[r]}{2}$
. So
![]() $(4t-1)\lfloor r^2/4\rfloor \geq \sum _{c \in [4t-1]}|\phi ^{-1}(c)|=2t\binom {r}{2}$
. Solving this yields
$(4t-1)\lfloor r^2/4\rfloor \geq \sum _{c \in [4t-1]}|\phi ^{-1}(c)|=2t\binom {r}{2}$
. Solving this yields
![]() $r\leq 4t$
. However,
$r\leq 4t$
. However,
![]() $1-\frac {1}{4t} = d_{2t} = 2\sum _{ij \in \binom {[r]}{2}}\alpha _i\alpha _j$
, so Observation (B) implies that
$1-\frac {1}{4t} = d_{2t} = 2\sum _{ij \in \binom {[r]}{2}}\alpha _i\alpha _j$
, so Observation (B) implies that
![]() $r \geq 4t$
. Thus,
$r \geq 4t$
. Thus,
![]() $r=4t$
and
$r=4t$
and
![]() $|\phi ^{-1}(c)|=(4t)^2/4$
for all
$|\phi ^{-1}(c)|=(4t)^2/4$
for all
![]() $c \in [4t-1]$
, and
$c \in [4t-1]$
, and
![]() $\boldsymbol {\alpha }$
is uniform. So the graphs
$\boldsymbol {\alpha }$
is uniform. So the graphs
![]() $\phi ^{-1}(1),\ldots ,\phi ^{-1}(4t-1)$
, each one isomorphic to
$\phi ^{-1}(1),\ldots ,\phi ^{-1}(4t-1)$
, each one isomorphic to
![]() $K_{2t,2t}$
, decompose
$K_{2t,2t}$
, decompose
![]() $2tK_{4t}$
, the complete multigraph on
$2tK_{4t}$
, the complete multigraph on
![]() $4t$
vertices with every multiplicity equal to
$4t$
vertices with every multiplicity equal to
![]() $2t$
. That such a decomposition exists, and its connection to Hadamard matrices follows from an observation of de Caen, Gregory and Pritikin [Reference de Caen, Gregory and Pritikin3], as follows. Let
$2t$
. That such a decomposition exists, and its connection to Hadamard matrices follows from an observation of de Caen, Gregory and Pritikin [Reference de Caen, Gregory and Pritikin3], as follows. Let
![]() $G_1,\ldots ,G_{4t-1}$
be copies of
$G_1,\ldots ,G_{4t-1}$
be copies of
![]() $K_{2t,2t}$
which decompose
$K_{2t,2t}$
which decompose
![]() $2tK_{4t}$
. Construct a
$2tK_{4t}$
. Construct a
![]() $4t\times 4t$
matrix H with the leftmost column consisting of all
$4t\times 4t$
matrix H with the leftmost column consisting of all
![]() $1$
-s and the j-th next column with
$1$
-s and the j-th next column with
![]() $1$
-s in the rows corresponding to one part of
$1$
-s in the rows corresponding to one part of
![]() $G_j$
and
$G_j$
and
![]() $-1$
-s in the remaining rows. For distinct
$-1$
-s in the remaining rows. For distinct
![]() $i,i'$
, the number of
$i,i'$
, the number of
![]() $j \in [4t-1]$
such that
$j \in [4t-1]$
such that
![]() $H_{ij}H_{i'j}=-1$
is exactly the number of
$H_{ij}H_{i'j}=-1$
is exactly the number of
![]() $\phi ^{-1}(j)$
containing
$\phi ^{-1}(j)$
containing
![]() $ii'$
, which is
$ii'$
, which is
![]() $2t$
. Clearly,
$2t$
. Clearly,
![]() $H_{i0}H_{i'0}=1$
. Thus, for distinct rows
$H_{i0}H_{i'0}=1$
. Thus, for distinct rows
![]() $\boldsymbol {h},\boldsymbol {h}'$
of H, we have that the scalar product
$\boldsymbol {h},\boldsymbol {h}'$
of H, we have that the scalar product
![]() $\boldsymbol {h}.\boldsymbol {h}'=2t(-1)+2t(1)=0$
, so the rows are pairwise orthogonal. Since the sum of the squares of entries in each row
$\boldsymbol {h}.\boldsymbol {h}'=2t(-1)+2t(1)=0$
, so the rows are pairwise orthogonal. Since the sum of the squares of entries in each row
![]() $\boldsymbol {h}$
is
$\boldsymbol {h}$
is
![]() $4t$
, we see that the collection of
$4t$
, we see that the collection of
![]() $\frac {1}{\sqrt {4t}}\boldsymbol {h}$
over rows
$\frac {1}{\sqrt {4t}}\boldsymbol {h}$
over rows
![]() $\boldsymbol {h}$
is an orthonormal basis of
$\boldsymbol {h}$
is an orthonormal basis of
![]() $\mathbb {R}^{4t}$
, and hence,
$\mathbb {R}^{4t}$
, and hence,
![]() $HH^\intercal = 4tI_{4t}$
, so H is a Hadamard matrix.
$HH^\intercal = 4tI_{4t}$
, so H is a Hadamard matrix.
Remark 3.7. For completeness, we give the other direction of the proof in [Reference de Caen, Gregory and Pritikin3]: that a decomposition can be read off a Hadamard matrix. Let H be a Hadamard matrix of order
![]() $4t$
with columns labelled
$4t$
with columns labelled
![]() $0,\ldots ,4t-1$
and rows labelled
$0,\ldots ,4t-1$
and rows labelled
![]() $1,\ldots ,4t$
. First note that we can flip the signs of all entries in a given row to get a new Hadamard matrix. Thus, we can obtain from H a Hadamard matrix whose first column (of index
$1,\ldots ,4t$
. First note that we can flip the signs of all entries in a given row to get a new Hadamard matrix. Thus, we can obtain from H a Hadamard matrix whose first column (of index
![]() $0$
) is
$0$
) is
![]() $(1,\ldots ,1)^\intercal $
. Since
$(1,\ldots ,1)^\intercal $
. Since
![]() $\frac {1}{\sqrt {4t}}H$
is an orthogonal matrix, every pair of columns are orthogonal (and similarly for rows). So comparing every column with Column
$\frac {1}{\sqrt {4t}}H$
is an orthogonal matrix, every pair of columns are orthogonal (and similarly for rows). So comparing every column with Column
![]() $0$
, we see that every other column contains exactly
$0$
, we see that every other column contains exactly
![]() $2t 1$
-entries. Take any two rows
$2t 1$
-entries. Take any two rows
![]() $\boldsymbol {h}, \boldsymbol {h}'$
with row indices
$\boldsymbol {h}, \boldsymbol {h}'$
with row indices
![]() $1 \leq i < i' \leq 4t$
, respectively, and let
$1 \leq i < i' \leq 4t$
, respectively, and let
![]() $\ell _{ij}$
be the number of columns j where
$\ell _{ij}$
be the number of columns j where
![]() $H_{ij} \neq H_{i'j}$
. Since rows are pairwise orthogonal, we have
$H_{ij} \neq H_{i'j}$
. Since rows are pairwise orthogonal, we have
![]() $0 = \boldsymbol {h}.\boldsymbol {h}' = -\ell _{ij}+(4t-\ell _{ij})=4t-2\ell _{ij}$
, so
$0 = \boldsymbol {h}.\boldsymbol {h}' = -\ell _{ij}+(4t-\ell _{ij})=4t-2\ell _{ij}$
, so
![]() $\ell _{ij}=2t$
. Now for each column
$\ell _{ij}=2t$
. Now for each column
![]() $1 \leq j \leq 4t-1$
, let
$1 \leq j \leq 4t-1$
, let
![]() $G_j$
be the copy of
$G_j$
be the copy of
![]() $K_{2t,2t}$
on vertex set
$K_{2t,2t}$
on vertex set
![]() $[4t]$
with vertex classes
$[4t]$
with vertex classes
![]() $A_j,B_j$
, where
$A_j,B_j$
, where
![]() $A_j$
consists of those rows
$A_j$
consists of those rows
![]() $1 \leq i \leq 4t$
, where
$1 \leq i \leq 4t$
, where
![]() $H_{ij}=1$
. Given any pair
$H_{ij}=1$
. Given any pair
![]() $gh \in \binom {[4t]}{2}$
, the number of
$gh \in \binom {[4t]}{2}$
, the number of
![]() $G_j$
where
$G_j$
where
![]() $gh$
is an edge is
$gh$
is an edge is
![]() $\ell _{gh}=2t$
. Thus,
$\ell _{gh}=2t$
. Thus,
![]() $G_1,\ldots ,G_{4t-1}$
decompose
$G_1,\ldots ,G_{4t-1}$
decompose
![]() $2tK_{4t}$
.
$2tK_{4t}$
.
In the next lemma, we solve Problem L for
![]() $(3;6)$
and
$(3;6)$
and
![]() $(3;7)$
using our new tool Lemma 3.3.
$(3;7)$
using our new tool Lemma 3.3.
Lemma 3.8. Let
![]() $\boldsymbol {k}=(3;s)$
.
$\boldsymbol {k}=(3;s)$
.
-
(i) Let
 $s=6$
. Then
$s=6$
. Then
 $Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$
. Moreover, if
$Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$
. Moreover, if
 $\boldsymbol {d}$
is realisable and satisfies
$\boldsymbol {d}$
is realisable and satisfies
 $\ell (\boldsymbol {d})= \frac {1}{2}\log 3 + \frac {3}{4}$
, then
$\ell (\boldsymbol {d})= \frac {1}{2}\log 3 + \frac {3}{4}$
, then
 $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
.
$\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
. -
(ii) Let
 $s=7$
. Then
$s=7$
. Then
 $Q(\boldsymbol {k})\leq \frac {7}{4}$
. Moreover, if
$Q(\boldsymbol {k})\leq \frac {7}{4}$
. Moreover, if
 $\boldsymbol {d}$
is realisable and satisfies
$\boldsymbol {d}$
is realisable and satisfies
 $\ell (\boldsymbol {d})=\frac {7}{4}$
, then
$\ell (\boldsymbol {d})=\frac {7}{4}$
, then
 $\boldsymbol {d}=(0,0,\frac {7}{8},0,0,0)$
.
$\boldsymbol {d}=(0,0,\frac {7}{8},0,0,0)$
.
Proof. By Lemma 3.5, it suffices to find a set I of valid constraints for Problem L such that
![]() $\ell _I^{\mathrm {max}}(\boldsymbol {k})$
is at most the required value. We first prove (ii). Note that
$\ell _I^{\mathrm {max}}(\boldsymbol {k})$
is at most the required value. We first prove (ii). Note that
is a valid constraint. (In fact, we could replace
![]() $1$
by
$1$
by
![]() $1-\frac {1}{R(3;7)-1}$
, which is a special case of the universal constraints discussed earlier.) For each colour
$1-\frac {1}{R(3;7)-1}$
, which is a special case of the universal constraints discussed earlier.) For each colour
![]() $i \in [7]$
, let
$i \in [7]$
, let
![]() $A_i := \{B \in \binom {[7]}{\geq 2}: i \in B\}$
and for each pair
$A_i := \{B \in \binom {[7]}{\geq 2}: i \in B\}$
and for each pair
![]() $ij \in \binom {[7]}{2}$
of colours, let
$ij \in \binom {[7]}{2}$
of colours, let
![]() $A_{ij} := A_i \cup A_j$
, and let
$A_{ij} := A_i \cup A_j$
, and let
![]() $\mathcal {A} := \{A_{ij}:ij \in \binom {[7]}{2}\}$
. Then
$\mathcal {A} := \{A_{ij}:ij \in \binom {[7]}{2}\}$
. Then
 $$ \begin{align} |\mathcal{A}|=\binom{7}{2} \text{ and } (i_2,\ldots,i_7)=(11,15,18,20,21,21) \end{align} $$
$$ \begin{align} |\mathcal{A}|=\binom{7}{2} \text{ and } (i_2,\ldots,i_7)=(11,15,18,20,21,21) \end{align} $$
since
![]() $i_f=\binom {7}{2}-\binom {7-f}{2}$
for each
$i_f=\binom {7}{2}-\binom {7-f}{2}$
for each
![]() $2 \leq f \leq 7$
. Let
$2 \leq f \leq 7$
. Let ![]() be arbitrary and let
be arbitrary and let
![]() $n \in \mathbb {N}$
be large. For brevity, write
$n \in \mathbb {N}$
be large. For brevity, write
![]() $H^n_i(\phi ,\boldsymbol {\alpha })$
for
$H^n_i(\phi ,\boldsymbol {\alpha })$
for
![]() $H^n_{A_i}(\phi ,\boldsymbol {\alpha })$
and
$H^n_{A_i}(\phi ,\boldsymbol {\alpha })$
and
![]() $H^n_{ij}(\phi ,\boldsymbol {\alpha })$
for
$H^n_{ij}(\phi ,\boldsymbol {\alpha })$
for
![]() $H^n_{A_{ij}}(\phi ,\boldsymbol {\alpha })$
. Then
$H^n_{A_{ij}}(\phi ,\boldsymbol {\alpha })$
. Then
![]() $H^n_i(\phi ,\boldsymbol {\alpha })$
and
$H^n_i(\phi ,\boldsymbol {\alpha })$
and
![]() $H^n_j(\phi ,\boldsymbol {\alpha })$
are triangle-free since
$H^n_j(\phi ,\boldsymbol {\alpha })$
are triangle-free since
![]() $\phi ^{-1}(i)$
and
$\phi ^{-1}(i)$
and
![]() $\phi ^{-1}(j)$
are. Clearly,
$\phi ^{-1}(j)$
are. Clearly,
![]() $H^n_{ij}(\phi ,\boldsymbol {\alpha })=H^n_i(\phi ,\boldsymbol {\alpha }) \cup H^n_j(\phi ,\boldsymbol {\alpha })$
.
$H^n_{ij}(\phi ,\boldsymbol {\alpha })=H^n_i(\phi ,\boldsymbol {\alpha }) \cup H^n_j(\phi ,\boldsymbol {\alpha })$
.
Let
![]() $(8,\phi ^*,\boldsymbol {u})$
be a feasible solution from Remark 3.7 for
$(8,\phi ^*,\boldsymbol {u})$
be a feasible solution from Remark 3.7 for
![]() $t=2$
, so
$t=2$
, so
![]() $\boldsymbol {u}$
is uniform,
$\boldsymbol {u}$
is uniform,
![]() $|\phi ^*|\equiv 8$
and
$|\phi ^*|\equiv 8$
and
![]() $q(\phi ^*,\boldsymbol {u}) = \frac {7}{4}$
. First consider the constraint set
$q(\phi ^*,\boldsymbol {u}) = \frac {7}{4}$
. First consider the constraint set
![]() $I_1$
consisting of (3.4) and the single constraint
$I_1$
consisting of (3.4) and the single constraint
![]() $2d_2+\ldots +7d_7 \leq \frac {339}{100}$
. Multiply (3.4) by
$2d_2+\ldots +7d_7 \leq \frac {339}{100}$
. Multiply (3.4) by
![]() $\log \frac {81}{64}$
and the new constraint by
$\log \frac {81}{64}$
and the new constraint by
![]() $\log \frac {4}{3}$
, and add these together. (These multipliers come from the (unique) solution to the dual linear program.) Then each
$\log \frac {4}{3}$
, and add these together. (These multipliers come from the (unique) solution to the dual linear program.) Then each
![]() $d_f$
on the left-hand side has coefficient at least
$d_f$
on the left-hand side has coefficient at least
![]() $\log f$
(its coefficient in the objective function), and thus,
$\log f$
(its coefficient in the objective function), and thus,
![]() $\ell ^{\mathrm {max}}_{I_1}(\boldsymbol {k})$
is at most the right-hand side, which is
$\ell ^{\mathrm {max}}_{I_1}(\boldsymbol {k})$
is at most the right-hand side, which is
![]() $\frac {39}{50}+\frac {61}{100}\log 3 < \frac {7}{4}=q(\phi ^*,\boldsymbol {\alpha }^*)$
. Thus,
$\frac {39}{50}+\frac {61}{100}\log 3 < \frac {7}{4}=q(\phi ^*,\boldsymbol {\alpha }^*)$
. Thus,
is a valid (existential) constraint. Suppose there are
![]() $ij \in \binom {[7]}{2}$
and
$ij \in \binom {[7]}{2}$
and ![]() with
with
![]() $d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \leq \frac {89}{100}-\Omega _n(1)$
. Let
$d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \leq \frac {89}{100}-\Omega _n(1)$
. Let
![]() $\boldsymbol {d}$
be such that
$\boldsymbol {d}$
be such that
![]() $(r,\phi ,\boldsymbol {\alpha })$
is a realisation of
$(r,\phi ,\boldsymbol {\alpha })$
is a realisation of
![]() $\boldsymbol {d}$
. Since every
$\boldsymbol {d}$
. Since every
![]() $d(H^n_{i'}(\phi ,\boldsymbol {\alpha })) \leq \frac {1}{2}+o_n(1)$
, we have
$d(H^n_{i'}(\phi ,\boldsymbol {\alpha })) \leq \frac {1}{2}+o_n(1)$
, we have
 $$ \begin{align*}\nonumber 2d_2+\ldots + 7d_7 + o_n(1) = \binom{n}{2}^{-1}\sum_{i' \in [7]}d(H^n_{i'}(\phi,\boldsymbol{\alpha})) \leq \frac{5}{2}+\frac{89}{100}-\Omega_n(1) = \frac{339}{100}-\Omega_n(1), \end{align*} $$
$$ \begin{align*}\nonumber 2d_2+\ldots + 7d_7 + o_n(1) = \binom{n}{2}^{-1}\sum_{i' \in [7]}d(H^n_{i'}(\phi,\boldsymbol{\alpha})) \leq \frac{5}{2}+\frac{89}{100}-\Omega_n(1) = \frac{339}{100}-\Omega_n(1), \end{align*} $$
a contradiction. Thus, Lemma 3.3 implies that
![]() $e(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {19}{25}n^2/2$
for every
$e(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {19}{25}n^2/2$
for every
![]() $ij$
and
$ij$
and
![]() $(r,\phi ,\boldsymbol {\alpha })$
. With
$(r,\phi ,\boldsymbol {\alpha })$
. With
![]() $\mathcal {A}$
defined before (3.5), we have by the above that
$\mathcal {A}$
defined before (3.5), we have by the above that
 $$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{19}{25} \end{align} $$
$$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{19}{25} \end{align} $$
is a valid (universal) constraint. Consider the constraint set
![]() $I_2$
consisting of the valid constraint (3.7) and the new constraint
$I_2$
consisting of the valid constraint (3.7) and the new constraint
![]() $2d_2+\ldots + 7d_7 \leq \frac {69}{20}$
. Multiply (3.7) by
$2d_2+\ldots + 7d_7 \leq \frac {69}{20}$
. Multiply (3.7) by
![]() $\log \frac {32}{27}$
and the new constraint by
$\log \frac {32}{27}$
and the new constraint by
![]() $\frac {1}{3}\log \frac {9}{8}$
, and add these together. Then each
$\frac {1}{3}\log \frac {9}{8}$
, and add these together. Then each
![]() $d_f$
on the left-hand side has coefficient at least
$d_f$
on the left-hand side has coefficient at least
![]() $\log f$
, and thus,
$\log f$
, and thus,
![]() $\ell ^{\mathrm {max}}_{I_2}(\boldsymbol {k})$
is at most the right-hand side, which is
$\ell ^{\mathrm {max}}_{I_2}(\boldsymbol {k})$
is at most the right-hand side, which is
![]() $\frac {129}{100}+\frac {29}{100}\log 3 < \frac {7}{4}$
. So
$\frac {129}{100}+\frac {29}{100}\log 3 < \frac {7}{4}$
. So
is a valid constraint. As above, this implies that for every
![]() $ij \in \binom {[7]}{2}$
and
$ij \in \binom {[7]}{2}$
and ![]() , which is a realisation of some
, which is a realisation of some
![]() $\boldsymbol {d}$
, we have
$\boldsymbol {d}$
, we have
![]() $d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \geq \frac {69}{20}-\frac {5}{2} + o_n(1) = \frac {19}{20}+o_n(1)$
. Thus, Lemma 3.3 implies that
$d(H^n_i(\phi ,\boldsymbol {\alpha }))+d(H^n_j(\phi ,\boldsymbol {\alpha })) \geq \frac {69}{20}-\frac {5}{2} + o_n(1) = \frac {19}{20}+o_n(1)$
. Thus, Lemma 3.3 implies that
![]() $d(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {3}{4}+o_n(1)$
for every
$d(H^n_{ij}(\phi ,\boldsymbol {\alpha })) \leq \frac {3}{4}+o_n(1)$
for every
![]() $ij$
. So
$ij$
. So
 $$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{3}{4} \end{align} $$
$$ \begin{align} 11d_2+15d_3+18d_4+20d_5+21d_6+21d_7 \leq \binom{7}{2}\frac{3}{4} \end{align} $$
is a valid constraint. Finally, consider the constraint set
![]() $I_3$
consisting of the two valid constraints: (3.9) and
$I_3$
consisting of the two valid constraints: (3.9) and
![]() $2d_2+\ldots +7d_7 \leq \frac {7}{2}$
, the original universal constraint in Problem L. Multiply the original constraint by
$2d_2+\ldots +7d_7 \leq \frac {7}{2}$
, the original universal constraint in Problem L. Multiply the original constraint by
![]() $\frac {1}{7}\log \frac {343}{128}$
and (3.9) by
$\frac {1}{7}\log \frac {343}{128}$
and (3.9) by
![]() $\frac {1}{21}\log \frac {128}{49}$
, and add these together. Then each
$\frac {1}{21}\log \frac {128}{49}$
, and add these together. Then each
![]() $d_f$
on the left-hand side has coefficient at least
$d_f$
on the left-hand side has coefficient at least
![]() $\log f$
, and thus,
$\log f$
, and thus,
![]() $\ell ^{\mathrm {max}}_{I_3}(\boldsymbol {k})$
is at most the right-hand side, which is
$\ell ^{\mathrm {max}}_{I_3}(\boldsymbol {k})$
is at most the right-hand side, which is
![]() $\frac {7}{4}$
. Moreover, the coefficient of
$\frac {7}{4}$
. Moreover, the coefficient of
![]() $d_f$
is strictly greater than
$d_f$
is strictly greater than
![]() $\log f$
unless
$\log f$
unless
![]() $f=4$
, so every optimal solution has
$f=4$
, so every optimal solution has
![]() $d_f=0$
for all
$d_f=0$
for all
![]() $f \neq 4$
. Thus, the unique optimiser has
$f \neq 4$
. Thus, the unique optimiser has
![]() $4d_4 = \frac {7}{2}$
, and all other entries equal to
$4d_4 = \frac {7}{2}$
, and all other entries equal to
![]() $0$
. This completes the proof of (ii).
$0$
. This completes the proof of (ii).
The same argument works for
![]() $s=6$
to prove (i). Here,
$s=6$
to prove (i). Here,
![]() $(i_2,\ldots ,i_6)=(9,12,14,15,15)$
. Again,
$(i_2,\ldots ,i_6)=(9,12,14,15,15)$
. Again,
![]() $d_1+\ldots +d_6 \leq 1$
is a valid constraint. We see that
$d_1+\ldots +d_6 \leq 1$
is a valid constraint. We see that
![]() $2d_2+\ldots +6d_6 \geq \frac {289}{100}$
is a valid constraint, since its negation alone implies that
$2d_2+\ldots +6d_6 \geq \frac {289}{100}$
is a valid constraint, since its negation alone implies that
![]() $\ell (\boldsymbol {d}) = \sum _{2 \leq f \leq s} fd_f \cdot \frac {\log f}{f} \leq \frac {289}{100}\cdot \frac {\log 3}{3} \leq \frac {1}{2}\log 3 +\frac {3}{4}$
. From this, the sum of densities of any pair of colour graphs is at most
$\ell (\boldsymbol {d}) = \sum _{2 \leq f \leq s} fd_f \cdot \frac {\log f}{f} \leq \frac {289}{100}\cdot \frac {\log 3}{3} \leq \frac {1}{2}\log 3 +\frac {3}{4}$
. From this, the sum of densities of any pair of colour graphs is at most
![]() $\frac {289}{100}-4\cdot \frac {1}{2}=\frac {89}{100}$
, and so Lemma 3.3 implies that their union has density at most
$\frac {289}{100}-4\cdot \frac {1}{2}=\frac {89}{100}$
, and so Lemma 3.3 implies that their union has density at most
![]() $\frac {19}{25}$
. Thus,
$\frac {19}{25}$
. Thus,
 $$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq \binom{6}{2}\frac{19}{25} \end{align} $$
$$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq \binom{6}{2}\frac{19}{25} \end{align} $$
is a valid constraint. This implies that
is a valid constraint. Indeed, if we add
![]() $\frac {1}{3}\log \frac {9}{8}$
times (3.10) plus
$\frac {1}{3}\log \frac {9}{8}$
times (3.10) plus
![]() $4-\frac {7}{3}\log 3$
times the negation of (3.11), we see
$4-\frac {7}{3}\log 3$
times the negation of (3.11), we see
![]() $\ell (\boldsymbol {d}) \leq \frac {2}{5}+\frac {43}{60}\log 3 < \frac {1}{2}\log 3 + \frac {3}{4}$
. Now the sum of densities of any pair of colour graphs is at most
$\ell (\boldsymbol {d}) \leq \frac {2}{5}+\frac {43}{60}\log 3 < \frac {1}{2}\log 3 + \frac {3}{4}$
. Now the sum of densities of any pair of colour graphs is at most
![]() $\frac {59}{20}-4\cdot \frac {1}{2}=\frac {19}{20}$
, and so Lemma 3.3 implies that their union has density at most
$\frac {59}{20}-4\cdot \frac {1}{2}=\frac {19}{20}$
, and so Lemma 3.3 implies that their union has density at most
![]() $\frac {3}{4}$
. Thus,
$\frac {3}{4}$
. Thus,
 $$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq\binom{6}{2}\frac{3}{4} \end{align} $$
$$ \begin{align} 9d_2+12d_3+14d_4+15d_5+15d_6 \leq\binom{6}{2}\frac{3}{4} \end{align} $$
is a valid constraint. Finally, we consider Problem L with the set of two valid constraints: (3.12) and
![]() $2d_2+\ldots +6d_6 \leq 3$
, the original universal constraint in Problem L. Multiply (3.12) by
$2d_2+\ldots +6d_6 \leq 3$
, the original universal constraint in Problem L. Multiply (3.12) by
![]() $\frac {1}{3}\log \frac {9}{8}$
and the original constraint by
$\frac {1}{3}\log \frac {9}{8}$
and the original constraint by
![]() $4-\frac {7}{3}$
and add these together to see that each
$4-\frac {7}{3}$
and add these together to see that each
![]() $d_f$
on the left-hand side has coefficient at least
$d_f$
on the left-hand side has coefficient at least
![]() $\log f$
, and is strictly greater than
$\log f$
, and is strictly greater than
![]() $\log f$
only for
$\log f$
only for
![]() $f=2,5,6$
, and the right-hand side is
$f=2,5,6$
, and the right-hand side is
![]() $\frac {1}{2}\log 3+\frac {3}{4}$
. Thus, the unique optimal solution is
$\frac {1}{2}\log 3+\frac {3}{4}$
. Thus, the unique optimal solution is
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})=\frac {1}{2}\log 3 + \frac {3}{4}$
, and the unique optimiser has
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})=\frac {1}{2}\log 3 + \frac {3}{4}$
, and the unique optimiser has
![]() $d_2=d_5=d_6=0$
and is therefore
$d_2=d_5=d_6=0$
and is therefore
![]() $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
.
$\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
.
Proof of Theorem 3.2
We need to show that every ![]() is as described. Lemma 3.8(i) implies that
is as described. Lemma 3.8(i) implies that
![]() $Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$
, and that, if there is equality, any optimal
$Q(\boldsymbol {k}) \leq \frac {1}{2}\log 3 + \frac {3}{4}$
, and that, if there is equality, any optimal
![]() $(r,\phi ,\boldsymbol {\alpha })$
is the realisation of
$(r,\phi ,\boldsymbol {\alpha })$
is the realisation of
![]() $\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
. Since
$\boldsymbol {d}=(0,\frac {1}{2},\frac {3}{8},0,0)$
. Since
![]() $\|\boldsymbol {d}\|_1 = \frac {7}{8}$
, Observation (B) implies that
$\|\boldsymbol {d}\|_1 = \frac {7}{8}$
, Observation (B) implies that
![]() $r \geq 8$
. Suppose that
$r \geq 8$
. Suppose that
![]() $|\phi (1i)|=4$
for
$|\phi (1i)|=4$
for
![]() $i=2,3,4,5$
. Then for all distinct
$i=2,3,4,5$
. Then for all distinct
![]() $i,i' \in \{2,3,4,5\}$
, we have
$i,i' \in \{2,3,4,5\}$
, we have
![]() $\phi (1i) \neq \phi (1i')$
, otherwise
$\phi (1i) \neq \phi (1i')$
, otherwise
![]() $|\phi (ii')|\leq 2$
(or there would be a monochromatic triangle). Let
$|\phi (ii')|\leq 2$
(or there would be a monochromatic triangle). Let
![]() $\psi (ii'):=\{j \in [6]: j \notin \phi (1i) \cap \phi (1i')\}$
. Then
$\psi (ii'):=\{j \in [6]: j \notin \phi (1i) \cap \phi (1i')\}$
. Then
![]() $\phi (ii') \subseteq \psi (ii')$
. We use a computer to obtain all
$\phi (ii') \subseteq \psi (ii')$
. We use a computer to obtain all
![]() $\binom {15}{4}$
possible
$\binom {15}{4}$
possible
![]() $\phi (12),\ldots ,\phi (15)$
and corresponding
$\phi (12),\ldots ,\phi (15)$
and corresponding
![]() $\{\psi (ii')\}$
. Then check each triple
$\{\psi (ii')\}$
. Then check each triple
![]() $ii'i"$
: suppose
$ii'i"$
: suppose
![]() $\psi (ii'),\psi (i'i"),\psi (i"i')$
share an element j. If they each have size three, we have a contradiction since we must delete j from at least one of these sets so we end up with a
$\psi (ii'),\psi (i'i"),\psi (i"i')$
share an element j. If they each have size three, we have a contradiction since we must delete j from at least one of these sets so we end up with a
![]() $\phi $
-set of size two. If one has size
$\phi $
-set of size two. If one has size
![]() $4$
and two have size
$4$
and two have size
![]() $3$
, then we must delete j from the set of size
$3$
, then we must delete j from the set of size
![]() $4$
(that is, the corresponding
$4$
(that is, the corresponding
![]() $\phi $
-sets all have size at most
$\phi $
-sets all have size at most
![]() $3$
). After checking all triples, the resulting sets are still supersets of
$3$
). After checking all triples, the resulting sets are still supersets of
![]() $\phi (ii')$
for distinct
$\phi (ii')$
for distinct
![]() $i,i'=2,3,4,5$
. In every case, the sets are of the form
$i,i'=2,3,4,5$
. In every case, the sets are of the form
![]() $ \{abc, def, xyuv, xyuv',xy'uv,xy'uv'\}$
, where
$ \{abc, def, xyuv, xyuv',xy'uv,xy'uv'\}$
, where
![]() $\{a,b,c,d,e,f\}=[6], \{x,y,y'\}=\{a,b,c\}, \{u,v,v'\}=\{d,e,f\}$
. So without loss of generality, the resulting sets are
$\{a,b,c,d,e,f\}=[6], \{x,y,y'\}=\{a,b,c\}, \{u,v,v'\}=\{d,e,f\}$
. So without loss of generality, the resulting sets are
![]() $\{123\},\{456\},\{1245\},\{1246\},\{1345\},\{1346\}$
. Sets
$\{123\},\{456\},\{1245\},\{1246\},\{1345\},\{1346\}$
. Sets
![]() $1,3,4$
of sizes
$1,3,4$
of sizes
![]() $3,4,4$
, respectively, all contain
$3,4,4$
, respectively, all contain
![]() $1,2$
, so without loss of generality, we can reduce to
$1,2$
, so without loss of generality, we can reduce to
But now, sets
![]() $2,4,6$
of sizes
$2,4,6$
of sizes
![]() $3,3,4$
, respectively, all contain
$3,3,4$
, respectively, all contain
![]() $4,6$
, which is a contradiction because deleting one copy of each gives a
$4,6$
, which is a contradiction because deleting one copy of each gives a
![]() $\phi $
-set of size at most two. Thus, we have eliminated all possible cases. We implemented the above in python (6check.py). Thus, when
$\phi $
-set of size at most two. Thus, we have eliminated all possible cases. We implemented the above in python (6check.py). Thus, when
![]() $r \geq 8$
, for each
$r \geq 8$
, for each
![]() $i \in [r]$
, there is a set
$i \in [r]$
, there is a set
![]() $X_i \subseteq [r]\setminus \{i\}$
of size at most
$X_i \subseteq [r]\setminus \{i\}$
of size at most
![]() $3$
such that
$3$
such that
![]() $|\phi (ij)|=4$
if and only if
$|\phi (ij)|=4$
if and only if
![]() $j \in X_i$
. Therefore,
$j \in X_i$
. Therefore,
![]() $2\cdot 6\lfloor \frac {r^2}{4}\rfloor \geq 2\sum _{c \in [6]}|\phi ^{-1}(c)| \geq r\cdot (12+3(r-4)) = 3r^2$
. Thus, r is even, every
$2\cdot 6\lfloor \frac {r^2}{4}\rfloor \geq 2\sum _{c \in [6]}|\phi ^{-1}(c)| \geq r\cdot (12+3(r-4)) = 3r^2$
. Thus, r is even, every
![]() $|X_i|=3$
, and
$|X_i|=3$
, and
![]() $\phi ^{-1}(c) \cong K_{\frac {r}{2},\frac {r}{2}}$
for all
$\phi ^{-1}(c) \cong K_{\frac {r}{2},\frac {r}{2}}$
for all
![]() $c \in [6]$
.
$c \in [6]$
.
For
![]() $c \in [6]$
, let
$c \in [6]$
, let
![]() $A_c,B_c$
be the vertex classes of
$A_c,B_c$
be the vertex classes of
![]() $\phi ^{-1}(c)$
. Let
$\phi ^{-1}(c)$
. Let
![]() $A=(a_{ij})$
be an
$A=(a_{ij})$
be an
![]() $r \times 6$
matrix with
$r \times 6$
matrix with
![]() $\pm 1$
entries, where the c-th column represents
$\pm 1$
entries, where the c-th column represents
![]() $\phi ^{-1}(c)$
, with
$\phi ^{-1}(c)$
, with
![]() $a_{jc}=1$
if
$a_{jc}=1$
if
![]() $j \in A_c$
and
$j \in A_c$
and
![]() $a_{jc}=-1$
if
$a_{jc}=-1$
if
![]() $j \in B_c$
. By relabelling classes, without loss of generality, the r-th row of A is
$j \in B_c$
. By relabelling classes, without loss of generality, the r-th row of A is
![]() $(1,1,1,1,1,1)$
. Notice that
$(1,1,1,1,1,1)$
. Notice that
![]() $|\phi (ij)|$
is the number of columns
$|\phi (ij)|$
is the number of columns
![]() $c \in [6]$
where
$c \in [6]$
where
![]() $a_{jc}$
and
$a_{jc}$
and
![]() $a_{ic}$
differ. So
$a_{ic}$
differ. So
![]() $|\phi (rj)|$
is the number of entries equal to
$|\phi (rj)|$
is the number of entries equal to
![]() $-1$
in the j-th row. But
$-1$
in the j-th row. But
![]() $|\phi (rj)|=3$
for all but
$|\phi (rj)|=3$
for all but
![]() $3$
rows j.
$3$
rows j.
If
![]() $r \geq 10$
, then
$r \geq 10$
, then
![]() $|\phi (rj)|=3$
for at least
$|\phi (rj)|=3$
for at least
![]() $r-1-3 \geq 6$
other rows j. Each of these rows, without loss of generality
$r-1-3 \geq 6$
other rows j. Each of these rows, without loss of generality
![]() $j=1,2,3,4,5,6$
, therefore contains exactly
$j=1,2,3,4,5,6$
, therefore contains exactly
![]() $3$
entries equal to
$3$
entries equal to
![]() $-1$
. By parity, no pair of these rows can differ in exactly three places. Thus,
$-1$
. By parity, no pair of these rows can differ in exactly three places. Thus,
![]() $|\phi (ij)| \neq 3$
, and hence,
$|\phi (ij)| \neq 3$
, and hence,
![]() $|\phi (ij)|=4$
for all
$|\phi (ij)|=4$
for all
![]() $ij\in \binom {[6]}{2}$
, so, for example,
$ij\in \binom {[6]}{2}$
, so, for example,
![]() $|X_1| \geq 5$
, a contradiction.
$|X_1| \geq 5$
, a contradiction.
Recalling that
![]() $r \geq 8$
and r is even, we must have
$r \geq 8$
and r is even, we must have
![]() $r=8$
. For
$r=8$
. For
![]() $\ell =3,4$
, let
$\ell =3,4$
, let
![]() $G_\ell := \{ij \in \binom {[8]}{2}: |\phi (ij)|=\ell \}$
. Since also
$G_\ell := \{ij \in \binom {[8]}{2}: |\phi (ij)|=\ell \}$
. Since also
![]() $\|\boldsymbol {d}\|_1=\frac {7}{8}$
,
$\|\boldsymbol {d}\|_1=\frac {7}{8}$
,
![]() $\boldsymbol {\alpha }$
is uniform. One can check via computer (6config.py) that whenever
$\boldsymbol {\alpha }$
is uniform. One can check via computer (6config.py) that whenever
![]() $\phi ^{-1}(c) \cong K_{4,4}$
for all
$\phi ^{-1}(c) \cong K_{4,4}$
for all
![]() $c \in [6]$
are such that every edge multiplicity is
$c \in [6]$
are such that every edge multiplicity is
![]() $3$
or
$3$
or
![]() $4$
, then
$4$
, then
![]() $G_3 \cong K_{4,4}$
and
$G_3 \cong K_{4,4}$
and
![]() $G_4 \cong K_4 \cup K_4$
. (To reduce computations, first we assume all
$G_4 \cong K_4 \cup K_4$
. (To reduce computations, first we assume all
![]() $\phi ^{-1}(c)$
are distinct. Next, if they are not, one needs at least
$\phi ^{-1}(c)$
are distinct. Next, if they are not, one needs at least
![]() $3=\log 8$
copies of
$3=\log 8$
copies of
![]() $K_{4,4}$
to cover every edge of
$K_{4,4}$
to cover every edge of
![]() $K_8$
at least once, so at least five such graphs are required to cover every edge at least three times. So it remains to check the cases where
$K_8$
at least once, so at least five such graphs are required to cover every edge at least three times. So it remains to check the cases where
![]() $\phi ^{-1}(1),\phi ^{-1}(2)$
are identical and the other colour graphs are distinct.) Given this structure,
$\phi ^{-1}(1),\phi ^{-1}(2)$
are identical and the other colour graphs are distinct.) Given this structure,
![]() $3G_3 \cup 4G_4$
has a decomposition into
$3G_3 \cup 4G_4$
has a decomposition into
![]() $6$
copies of
$6$
copies of
![]() $K_{4,4}$
if and only if
$K_{4,4}$
if and only if
![]() $4K_8$
has a decomposition into
$4K_8$
has a decomposition into
![]() $7$
copies of
$7$
copies of
![]() $K_{4,4}$
. Thus, the columns of A are among the
$K_{4,4}$
. Thus, the columns of A are among the
![]() $7$
rightmost columns of a normalised order-
$7$
rightmost columns of a normalised order-
![]() $8$
Hadamard matrix H (up to permutation of rows and/or negation of rows).
$8$
Hadamard matrix H (up to permutation of rows and/or negation of rows).
3.4. Hadamard matrices and the triangle problem
Figure 2 shows how the known extremal graphs for the triangle problem relate to Hadamard matrices. For
![]() $s \in [7]\setminus \{5\}$
, these are all unique, and for
$s \in [7]\setminus \{5\}$
, these are all unique, and for
![]() $s=5$
, there is an infinite family of asymptotically extremal graphs, of which two are drawn here. Index the columns of the above matrices by
$s=5$
, there is an infinite family of asymptotically extremal graphs, of which two are drawn here. Index the columns of the above matrices by
![]() $0,1,\ldots $
. For each
$0,1,\ldots $
. For each
![]() $c \in [s]$
,
$c \in [s]$
,
![]() $\phi ^{-1}(c)$
is a complete balanced bipartite graph whose vertex classes are given by the set of row indices of the white squares, and of the black squares, in Column c. Some columns are repeated, denoted by
$\phi ^{-1}(c)$
is a complete balanced bipartite graph whose vertex classes are given by the set of row indices of the white squares, and of the black squares, in Column c. Some columns are repeated, denoted by
![]() $\times \ell $
, and some are removed, denoted by
$\times \ell $
, and some are removed, denoted by
![]() $-$
. Taking r to be the order of the matrix, and
$-$
. Taking r to be the order of the matrix, and
![]() $\boldsymbol {u} \in \Delta ^r$
to be uniform, we have the optimal solution
$\boldsymbol {u} \in \Delta ^r$
to be uniform, we have the optimal solution
![]() $(r,\phi ,\boldsymbol {u})$
.
$(r,\phi ,\boldsymbol {u})$
.

Figure 2 Extremal graphs for
![]() $(3;s)$
for
$(3;s)$
for
![]() $2 \leq s \leq 7$
.
$2 \leq s \leq 7$
.
4. Applications of Theorem 1.6
Here, we discuss the perfect colouring problem (Problem 1.7), where we have part sizes that maximise the number of perfect colourings. This was implicitly done in previous works (and is trivial in some cases). Let
![]() $r \in \mathbb {N}$
and let
$r \in \mathbb {N}$
and let
![]() $H \subseteq K_r$
be regular. Suppose that every
$H \subseteq K_r$
be regular. Suppose that every ![]() has
has
![]() $r^*=r$
,
$r^*=r$
,
![]() $\boldsymbol {\alpha }^* = \boldsymbol {u}_r$
uniform and furthermore, there is
$\boldsymbol {\alpha }^* = \boldsymbol {u}_r$
uniform and furthermore, there is
![]() $M_{\phi ^*} \cong H$
such that
$M_{\phi ^*} \cong H$
such that
![]() $|\phi ^*(ij)|=t_1$
for all
$|\phi ^*(ij)|=t_1$
for all
![]() $ij \in M_{\phi ^*}$
and
$ij \in M_{\phi ^*}$
and
![]() $|\phi ^*(ij)|=t_2$
for all
$|\phi ^*(ij)|=t_2$
for all
![]() $ij \in \binom {[r]}{2}\setminus M_{\phi ^*}$
, where
$ij \in \binom {[r]}{2}\setminus M_{\phi ^*}$
, where
![]() $0 \leq t_1-t_2 \leq 1$
. Then we denote
$0 \leq t_1-t_2 \leq 1$
. Then we denote
![]() $\mathrm {perf}(\boldsymbol {m}) := \mathrm {perf}_{r,\boldsymbol {u}_r}(\boldsymbol {m})$
.
$\mathrm {perf}(\boldsymbol {m}) := \mathrm {perf}_{r,\boldsymbol {u}_r}(\boldsymbol {m})$
.
By symmetry, for some explicit integer
![]() $C=C(H)$
, we have that
$C=C(H)$
, we have that
 $$ \begin{align*}\mathrm{perf}(\boldsymbol{m}) = C\cdot \sum_{J \cong H}f(\boldsymbol{m},J),\quad\text{where } f(\boldsymbol{m},J) := \prod_{ij \in J}t_1^{m_im_j}\prod_{i'j'\notin J}t_2^{m_{i'}m_{j'}}, \end{align*} $$
$$ \begin{align*}\mathrm{perf}(\boldsymbol{m}) = C\cdot \sum_{J \cong H}f(\boldsymbol{m},J),\quad\text{where } f(\boldsymbol{m},J) := \prod_{ij \in J}t_1^{m_im_j}\prod_{i'j'\notin J}t_2^{m_{i'}m_{j'}}, \end{align*} $$
where the sum is over all copies J of H in
![]() $K_r$
. Let
$K_r$
. Let
![]() $\boldsymbol {m}':=(m_1-1,m_2,\ldots ,m_{r-1},m_r+1)$
. Write
$\boldsymbol {m}':=(m_1-1,m_2,\ldots ,m_{r-1},m_r+1)$
. Write
![]() $m_{J(i)} := \sum _{j \in N_J(i)}m_j$
. Then
$m_{J(i)} := \sum _{j \in N_J(i)}m_j$
. Then
 $$ \begin{align*} C^{-1}\mathrm{perf}(\boldsymbol{m}') &= \sum_{\substack{J: \{1,r\} \notin J\\ J \cong H}}g_{\mathrm{out}}(\boldsymbol{m},J)f(\boldsymbol{m},J)+ \sum_{\substack{J: \{1,r\} \in J\\ J \cong H}}g_{\mathrm{in}}(\boldsymbol{m},J) f(\boldsymbol{m},J), \end{align*} $$
$$ \begin{align*} C^{-1}\mathrm{perf}(\boldsymbol{m}') &= \sum_{\substack{J: \{1,r\} \notin J\\ J \cong H}}g_{\mathrm{out}}(\boldsymbol{m},J)f(\boldsymbol{m},J)+ \sum_{\substack{J: \{1,r\} \in J\\ J \cong H}}g_{\mathrm{in}}(\boldsymbol{m},J) f(\boldsymbol{m},J), \end{align*} $$
where
 $$ \begin{align} g_{\mathrm{out}}(\boldsymbol{m},J) &:= \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r-1}\quad\text{and}\quad g_{\mathrm{in}}(\boldsymbol{m},J) := \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r}t_1^{-1}. \end{align} $$
$$ \begin{align} g_{\mathrm{out}}(\boldsymbol{m},J) &:= \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r-1}\quad\text{and}\quad g_{\mathrm{in}}(\boldsymbol{m},J) := \left(\frac{t_2}{t_1}\right)^{m_{J(1)}-m_{J(r)}} t_2^{m_1-m_r}t_1^{-1}. \end{align} $$
Indeed, if we let
![]() $n:= m_1+\ldots +m_r$
and
$n:= m_1+\ldots +m_r$
and
![]() $\boldsymbol {m}":=(m_1-1,m_2,\ldots ,m_r)$
, then
$\boldsymbol {m}":=(m_1-1,m_2,\ldots ,m_r)$
, then
![]() $\mathrm {perf}(\boldsymbol {m})/\mathrm {perf}(\boldsymbol {m}") = t_1^{m_{J(1)}}\cdot t_2^{n-m_{J(1)}-m_1}$
. Now combine this with the analogous formula for
$\mathrm {perf}(\boldsymbol {m})/\mathrm {perf}(\boldsymbol {m}") = t_1^{m_{J(1)}}\cdot t_2^{n-m_{J(1)}-m_1}$
. Now combine this with the analogous formula for
![]() $\mathrm {perf}(\boldsymbol {m}')/\mathrm {perf}(\boldsymbol {m}")$
, where, for example, the power of
$\mathrm {perf}(\boldsymbol {m}')/\mathrm {perf}(\boldsymbol {m}")$
, where, for example, the power of
![]() $t_1$
is
$t_1$
is
![]() $\sum _{j \in N_J(r)}m_j'$
, which is
$\sum _{j \in N_J(r)}m_j'$
, which is
![]() $m_{J(r)}$
if
$m_{J(r)}$
if
![]() $\{1,r\} \notin J$
and
$\{1,r\} \notin J$
and
![]() $m_{J(r)}-1$
otherwise.
$m_{J(r)}-1$
otherwise.
Proof of Proposition 1.10
Recall that we consider only nonincreasing sequences
![]() $\boldsymbol {m}$
. In each case, letting r be the (unique) number of vertices in every solution in
$\boldsymbol {m}$
. In each case, letting r be the (unique) number of vertices in every solution in ![]() , we will show that whenever
, we will show that whenever
![]() $m_1-m_r \geq 2$
, we have
$m_1-m_r \geq 2$
, we have
![]() $g_{\mathrm {out}}(\boldsymbol {m},J) \geq 1.01$
, say, for all copies J of H with
$g_{\mathrm {out}}(\boldsymbol {m},J) \geq 1.01$
, say, for all copies J of H with
![]() $\{1,r\} \notin J$
and
$\{1,r\} \notin J$
and
![]() $g_{\mathrm {in}}(\boldsymbol {m},J) \geq 1.01$
for all J with
$g_{\mathrm {in}}(\boldsymbol {m},J) \geq 1.01$
for all J with
![]() $\{1,r\} \in J$
. Thus, we have
$\{1,r\} \in J$
. Thus, we have
![]() $\frac {1}{1.01}\cdot \mathrm {perf}(\boldsymbol {m}') \geq C\cdot \sum _{J \cong H}f(\boldsymbol {m},J) = \mathrm {perf}(\boldsymbol {m})$
. This implies that the unique supersolution to the perfect colouring problem for n is
$\frac {1}{1.01}\cdot \mathrm {perf}(\boldsymbol {m}') \geq C\cdot \sum _{J \cong H}f(\boldsymbol {m},J) = \mathrm {perf}(\boldsymbol {m})$
. This implies that the unique supersolution to the perfect colouring problem for n is
![]() $\boldsymbol {m}^* = (m_1^*,\ldots ,m_r^*)$
, where
$\boldsymbol {m}^* = (m_1^*,\ldots ,m_r^*)$
, where
![]() $\|\boldsymbol {m}^*\|_1=n$
and
$\|\boldsymbol {m}^*\|_1=n$
and
![]() $m_1^*-m_r^* \leq 1$
, and the perfect colouring problem is soluble with constant
$m_1^*-m_r^* \leq 1$
, and the perfect colouring problem is soluble with constant
![]() $c:= 0.01$
. If
$c:= 0.01$
. If
![]() $\boldsymbol {k}$
has the strong extension property, Corollary 1.9 implies that for all sufficiently large n, the unique
$\boldsymbol {k}$
has the strong extension property, Corollary 1.9 implies that for all sufficiently large n, the unique
![]() $\boldsymbol {k}$
-extremal graph on n vertices is
$\boldsymbol {k}$
-extremal graph on n vertices is
![]() $K_{m_1^*,\ldots ,m_r^*} \cong T_r(n)$
.
$K_{m_1^*,\ldots ,m_r^*} \cong T_r(n)$
.
All
![]() $\boldsymbol {k}$
from Theorem 1.1 apart from
$\boldsymbol {k}$
from Theorem 1.1 apart from
![]() $(3;5)$
have the strong extension property by Lemma 1.3. Indeed, we showed in [Reference Pikhurko and Staden10, Theorem 1.7] that each
$(3;5)$
have the strong extension property by Lemma 1.3. Indeed, we showed in [Reference Pikhurko and Staden10, Theorem 1.7] that each
![]() $\boldsymbol {k}$
among
$\boldsymbol {k}$
among
![]() $(k;2), (k;3), (3;4), (4;4)$
has the strong extension property for integers
$(k;2), (k;3), (3;4), (4;4)$
has the strong extension property for integers
![]() $k \geq 3$
and described the optimal solutions [Reference Pikhurko and Staden10, Table 2]. Write
$k \geq 3$
and described the optimal solutions [Reference Pikhurko and Staden10, Table 2]. Write
![]() $g_{\mathrm {in}}$
and
$g_{\mathrm {in}}$
and
![]() $g_{\mathrm {out}}$
when
$g_{\mathrm {out}}$
when
![]() $\boldsymbol {m},J$
are fixed or clear from the context. Suppose
$\boldsymbol {m},J$
are fixed or clear from the context. Suppose
![]() $\boldsymbol {k} := (k;s)$
is one of
$\boldsymbol {k} := (k;s)$
is one of
![]() $(k;2),(k;3),(4;4)$
. Then every
$(k;2),(k;3),(4;4)$
. Then every ![]() has
has
![]() $\boldsymbol {\alpha }$
uniform and
$\boldsymbol {\alpha }$
uniform and
![]() $\phi $
only takes one value t. Then for all
$\phi $
only takes one value t. Then for all
![]() $\boldsymbol {m}$
with
$\boldsymbol {m}$
with
![]() $m_1-m_r \geq 2$
,
$m_1-m_r \geq 2$
,
![]() $g_{\mathrm {in}} = g_{\mathrm {out}} = t^{m_1-m_r-1} \geq t \geq 2$
, as required.
$g_{\mathrm {in}} = g_{\mathrm {out}} = t^{m_1-m_r-1} \geq t \geq 2$
, as required.
Now suppose
![]() $\boldsymbol {k} := (3;4)$
. In the above discussion,
$\boldsymbol {k} := (3;4)$
. In the above discussion,
![]() $r=4$
,
$r=4$
,
![]() $H \cong K_{2,2}$
, so
$H \cong K_{2,2}$
, so
![]() $(t_1,t_2)=(3,2)$
. Let J be a copy of H. If
$(t_1,t_2)=(3,2)$
. Let J be a copy of H. If
![]() $\{1,4\}\notin J$
, then
$\{1,4\}\notin J$
, then
![]() $J(1)=J(4)=\{2,3\}$
while if
$J(1)=J(4)=\{2,3\}$
while if
![]() $\{1,4\} \in J$
, then
$\{1,4\} \in J$
, then
![]() $J(1)=\{i,4\}$
and
$J(1)=\{i,4\}$
and
![]() $J(4)=\{j,1\}$
, where
$J(4)=\{j,1\}$
, where
![]() $\{i,j\}=\{2,3\}$
. Let
$\{i,j\}=\{2,3\}$
. Let
![]() $\boldsymbol {m}=(m_1,\ldots ,m_4)$
be such that
$\boldsymbol {m}=(m_1,\ldots ,m_4)$
be such that
![]() $m_1-m_4 \geq 2$
. Here,
$m_1-m_4 \geq 2$
. Here,
![]() $g_{\mathrm {out}} = 2^{m_1-m_4-1} \geq 2$
and
$g_{\mathrm {out}} = 2^{m_1-m_4-1} \geq 2$
and
![]() $g_{\mathrm {in}} = 3^{m_1-m_4-1}\left (\frac {2}{3}\right )^{m_i-m_j}$
. If
$g_{\mathrm {in}} = 3^{m_1-m_4-1}\left (\frac {2}{3}\right )^{m_i-m_j}$
. If
![]() $m_i - m_j \leq 1$
, then this is at least
$m_i - m_j \leq 1$
, then this is at least
![]() $2$
; otherwise,
$2$
; otherwise,
![]() $2 \leq m_i-m_j \leq m_1-m_4$
and it is at least
$2 \leq m_i-m_j \leq m_1-m_4$
and it is at least
![]() $\frac {4}{3}$
.
$\frac {4}{3}$
.
Suppose finally that
![]() $\boldsymbol {k}=(3;6)$
. Here, Theorem 3.2 implies that
$\boldsymbol {k}=(3;6)$
. Here, Theorem 3.2 implies that
![]() $r=8$
and H is the disjoint union of two copies of
$r=8$
and H is the disjoint union of two copies of
![]() $K_4$
. So
$K_4$
. So
![]() $(t_1,t_2)=(4,3)$
. Let J be a copy of H. If
$(t_1,t_2)=(4,3)$
. Let J be a copy of H. If
![]() $\{1,8\} \in J$
, then
$\{1,8\} \in J$
, then
![]() $m_{J(1)}-m_{J(8)} = m_8-m_1$
, so
$m_{J(1)}-m_{J(8)} = m_8-m_1$
, so
![]() $g_{\mathrm {in}} = 4^{m_1-m_8-1} \geq 4$
. It remains to check
$g_{\mathrm {in}} = 4^{m_1-m_8-1} \geq 4$
. It remains to check
![]() $g_{\mathrm {out}}$
. So suppose that
$g_{\mathrm {out}}$
. So suppose that
![]() $\{1,8\} \notin J$
. Then
$\{1,8\} \notin J$
. Then
![]() $J(1), J(8)$
are disjoint sets of size three, and
$J(1), J(8)$
are disjoint sets of size three, and
![]() $3m_8 \leq m_{J(1)},m_{J(8)} \leq 3m_1$
. Thus, there is an integer
$3m_8 \leq m_{J(1)},m_{J(8)} \leq 3m_1$
. Thus, there is an integer
![]() $0 \leq j \leq 6(m_1-m_8)$
such that
$0 \leq j \leq 6(m_1-m_8)$
such that
![]() $ m_{J(1)}-m_{J(8)} = 3(m_1-m_8) - j $
. So
$ m_{J(1)}-m_{J(8)} = 3(m_1-m_8) - j $
. So
 $$ \begin{align*}g_{\mathrm{out}} = \left(\frac{81}{64}\right)^{m_1-m_8} \cdot \left(\frac{4}{3}\right)^j \cdot \frac{1}{3}. \end{align*} $$
$$ \begin{align*}g_{\mathrm{out}} = \left(\frac{81}{64}\right)^{m_1-m_8} \cdot \left(\frac{4}{3}\right)^j \cdot \frac{1}{3}. \end{align*} $$
If
![]() $m_1-m_8 \geq 5$
, then
$m_1-m_8 \geq 5$
, then
![]() $g_{\mathrm {out}} \geq 1.08$
, as required. If
$g_{\mathrm {out}} \geq 1.08$
, as required. If
![]() $m_1-m_8=4$
and
$m_1-m_8=4$
and
![]() $j \geq 1$
, then
$j \geq 1$
, then
![]() $g_{\mathrm {out}} \geq 1.14$
. If
$g_{\mathrm {out}} \geq 1.14$
. If
![]() $m_1-m_8=3$
and
$m_1-m_8=3$
and
![]() $j\geq 2$
, then
$j\geq 2$
, then
![]() $g_{\mathrm {out}} \geq 1.2$
, and if
$g_{\mathrm {out}} \geq 1.2$
, and if
![]() $m_1-m_8=2$
and
$m_1-m_8=2$
and
![]() $j\geq 3$
, then
$j\geq 3$
, then
![]() $g_{\mathrm {out}} \geq 1.2$
. There are only a few remaining possibilities – namely, writing
$g_{\mathrm {out}} \geq 1.2$
. There are only a few remaining possibilities – namely, writing
![]() $\boldsymbol {m}=(m_1,\ldots ,m_1)+\boldsymbol {b}$
,
$\boldsymbol {m}=(m_1,\ldots ,m_1)+\boldsymbol {b}$
,

In all cases, we compare by direct calculation to
![]() $\boldsymbol {\overline {m}} := (m_1,\ldots ,m_1)+\boldsymbol {b}'$
, where
$\boldsymbol {\overline {m}} := (m_1,\ldots ,m_1)+\boldsymbol {b}'$
, where
![]() $\boldsymbol {b}'$
has its sum of entries equal to that of
$\boldsymbol {b}'$
has its sum of entries equal to that of
![]() $\boldsymbol {b}$
, and all entries are as equal as possible. Indeed,
$\boldsymbol {b}$
, and all entries are as equal as possible. Indeed,
 $$ \begin{align*}\frac{\mathrm{perf}(\boldsymbol{\overline{m}})}{\mathrm{perf}(\boldsymbol{m})} = \frac{\sum_{A' \cup B' = [8]}\prod_{ij \in \binom{A'}{2}}4^{b_i'b_j'} \prod_{ij \in \binom{B'}{2}}4^{b_i'b_j'} \prod_{i \in A', j \in B'}3^{b_i'b_j'}}{\sum_{A \cup B = [8]}\prod_{ij \in \binom{A}{2}}4^{b_ib_j} \prod_{ij \in \binom{B}{2}}4^{b_ib_j} \prod_{i \in A, j \in B}3^{b_ib_j}} \end{align*} $$
$$ \begin{align*}\frac{\mathrm{perf}(\boldsymbol{\overline{m}})}{\mathrm{perf}(\boldsymbol{m})} = \frac{\sum_{A' \cup B' = [8]}\prod_{ij \in \binom{A'}{2}}4^{b_i'b_j'} \prod_{ij \in \binom{B'}{2}}4^{b_i'b_j'} \prod_{i \in A', j \in B'}3^{b_i'b_j'}}{\sum_{A \cup B = [8]}\prod_{ij \in \binom{A}{2}}4^{b_ib_j} \prod_{ij \in \binom{B}{2}}4^{b_ib_j} \prod_{i \in A, j \in B}3^{b_ib_j}} \end{align*} $$
depends only on
![]() $\boldsymbol {b},\boldsymbol {b}'$
. We did this calculation in python (dcheck.py). In all cases, the ratio is at least
$\boldsymbol {b},\boldsymbol {b}'$
. We did this calculation in python (dcheck.py). In all cases, the ratio is at least
![]() $9$
. As before, this implies that the unique supersolution has all entries as equal as possible.
$9$
. As before, this implies that the unique supersolution has all entries as equal as possible.
Finally, we need to check that
![]() $(3;6)$
has the strong extension property. So let
$(3;6)$
has the strong extension property. So let
![]() $9$
be a new vertex and let
$9$
be a new vertex and let
![]() $\phi '$
be an extension of
$\phi '$
be an extension of
![]() $\phi $
with the property that
$\phi $
with the property that
 $$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{3}{4}+\frac{1}{2}\log 3, \quad\text{that is,}\quad t_1 \ldots t_8 = 2^{6}3^4, \end{align*} $$
$$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{3}{4}+\frac{1}{2}\log 3, \quad\text{that is,}\quad t_1 \ldots t_8 = 2^{6}3^4, \end{align*} $$
where
![]() $t_i := \max \{|\phi '(i9)|,1\}$
. Since each
$t_i := \max \{|\phi '(i9)|,1\}$
. Since each
![]() $\phi ^{-1}(c) \cong K_{4,4}$
and
$\phi ^{-1}(c) \cong K_{4,4}$
and
![]() $\phi ^{\prime -1}(c)$
is triangle-free, in this graph,
$\phi ^{\prime -1}(c)$
is triangle-free, in this graph,
![]() $9$
has at most
$9$
has at most
![]() $4$
neighbours, and
$4$
neighbours, and
![]() $\phi ^{\prime -1}(c) \subseteq K_{5,4}$
. Let
$\phi ^{\prime -1}(c) \subseteq K_{5,4}$
. Let
![]() $G_c$
be the copy of
$G_c$
be the copy of
![]() $K_{5,4}$
containing
$K_{5,4}$
containing
![]() $\phi ^{\prime -1}(c)$
, such that
$\phi ^{\prime -1}(c)$
, such that
![]() $G_c-\{9\} \cong K_{4,4}$
, so we obtain
$G_c-\{9\} \cong K_{4,4}$
, so we obtain
![]() $G_c$
from
$G_c$
from
![]() $\phi ^{-1}(c)$
by adding
$\phi ^{-1}(c)$
by adding
![]() $9$
to one of the two vertex classes of
$9$
to one of the two vertex classes of
![]() $\phi ^{-1}(c)$
. One can easily check all such attachments using a computer, trying each of the
$\phi ^{-1}(c)$
. One can easily check all such attachments using a computer, trying each of the
![]() $2^6$
choices (we implemented this using python (7ext.py)). This reveals that
$2^6$
choices (we implemented this using python (7ext.py)). This reveals that
![]() $\{G_c:c \in [6]\}$
has
$\{G_c:c \in [6]\}$
has
![]() $\prod _{i \in [8]}|\{c \in [6]: i9 \in G_c\}|= 2^6 3^4$
if and only if
$\prod _{i \in [8]}|\{c \in [6]: i9 \in G_c\}|= 2^6 3^4$
if and only if
![]() $\phi ^{-1}(c) \equiv K_{5,4}$
, and there is some
$\phi ^{-1}(c) \equiv K_{5,4}$
, and there is some
![]() $i \in [8]$
such that
$i \in [8]$
such that
![]() $9$
lies in exactly the same vertex class as i in each
$9$
lies in exactly the same vertex class as i in each
![]() $\phi ^{-1}(c)$
; that is,
$\phi ^{-1}(c)$
; that is,
![]() $9$
is a strong clone of i (in other words,
$9$
is a strong clone of i (in other words,
![]() $9$
corresponds to a copy of an existing row in the
$9$
corresponds to a copy of an existing row in the
![]() $\pm 1$
-matrix representing the optimal solution). Thus,
$\pm 1$
-matrix representing the optimal solution). Thus,
![]() $\phi ^{\prime -1}(c) = G_c$
. We have proved that
$\phi ^{\prime -1}(c) = G_c$
. We have proved that
![]() $(3;6)$
has the strong extension property.
$(3;6)$
has the strong extension property.
Therefore, we can apply Theorem 1.6 with Theorem 3.2 to see that
![]() $T_8(n)$
is the unique extremal graph for sufficiently large n. Moreover, letting
$T_8(n)$
is the unique extremal graph for sufficiently large n. Moreover, letting
![]() $0 \leq j \leq 7$
be such that
$0 \leq j \leq 7$
be such that
![]() $n=8N+j$
for
$n=8N+j$
for
![]() $N \in \mathbb {N}$
, we see that the unique supersolution
$N \in \mathbb {N}$
, we see that the unique supersolution
![]() $\boldsymbol {m}$
has j terms equal to
$\boldsymbol {m}$
has j terms equal to
![]() $N+1$
and
$N+1$
and
![]() $8-j$
equal to N, and
$8-j$
equal to N, and
![]() $\mathrm {perf}(\boldsymbol {m})$
equals
$\mathrm {perf}(\boldsymbol {m})$
equals
![]() $C_j' \cdot 4^{12N} \cdot 3^{16N}$
, where
$C_j' \cdot 4^{12N} \cdot 3^{16N}$
, where
![]() $C_j'$
is a constant depending only on j, which can be determined by calculating
$C_j'$
is a constant depending only on j, which can be determined by calculating ![]() , by counting certain distinct Hadamard matrices (see the end of the proof of Theorem 1.11). This gives the claimed value of
, by counting certain distinct Hadamard matrices (see the end of the proof of Theorem 1.11). This gives the claimed value of
![]() $F(n;(3;6))$
.
$F(n;(3;6))$
.
Proof of Theorem 1.11
Let
![]() $\boldsymbol {k}:=(3;7)$
. By Theorem 3.1, every element of
$\boldsymbol {k}:=(3;7)$
. By Theorem 3.1, every element of ![]() is of the form
is of the form
![]() $(8,\phi ,\boldsymbol {u})$
, where
$(8,\phi ,\boldsymbol {u})$
, where
![]() $\boldsymbol {u}$
is uniform and
$\boldsymbol {u}$
is uniform and
![]() $|\phi (ij)|=4$
for all
$|\phi (ij)|=4$
for all
![]() $ij \in \binom {[8]}{2}$
.
$ij \in \binom {[8]}{2}$
.
We need to show that
![]() $\boldsymbol {k}$
has the strong extension property. So let
$\boldsymbol {k}$
has the strong extension property. So let
![]() $9$
be a new vertex and let
$9$
be a new vertex and let
![]() $\phi '$
be an extension of
$\phi '$
be an extension of
![]() $\phi $
with the property that
$\phi $
with the property that
 $$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{7}{4} \quad\text{i.e.}\quad t_1 \ldots t_8 = 2^{14}, \end{align*} $$
$$ \begin{align*}\frac{1}{8}\sum_{i \in [8]}\log t_i = \frac{7}{4} \quad\text{i.e.}\quad t_1 \ldots t_8 = 2^{14}, \end{align*} $$
where
![]() $t_i := \max \{|\phi '(i9)|,1\}$
. So every
$t_i := \max \{|\phi '(i9)|,1\}$
. So every
![]() $t_i$
equals
$t_i$
equals
![]() $1$
,
$1$
,
![]() $2$
, or
$2$
, or
![]() $4$
, and, in fact, the multiset of values is either
$4$
, and, in fact, the multiset of values is either
![]() $\{4,4,4,4,4,4,4,1\}$
or
$\{4,4,4,4,4,4,4,1\}$
or
![]() $\{4,4,4,4,4,4,2,2\}$
. Since each
$\{4,4,4,4,4,4,2,2\}$
. Since each
![]() $\phi ^{-1}(c) \cong K_{4,4}$
and
$\phi ^{-1}(c) \cong K_{4,4}$
and
![]() $\phi ^{\prime -1}(c)$
is triangle-free, in this graph,
$\phi ^{\prime -1}(c)$
is triangle-free, in this graph,
![]() $9$
has at most
$9$
has at most
![]() $4$
neighbours, and
$4$
neighbours, and
![]() $\phi ^{\prime -1}(c) \subseteq K_{5,4}$
. Let
$\phi ^{\prime -1}(c) \subseteq K_{5,4}$
. Let
![]() $G_c$
be the copy of
$G_c$
be the copy of
![]() $K_{5,4}$
containing
$K_{5,4}$
containing
![]() $\phi ^{\prime -1}(c)$
, such that
$\phi ^{\prime -1}(c)$
, such that
![]() $G_c-\{9\} \cong K_{4,4}$
, so we obtain
$G_c-\{9\} \cong K_{4,4}$
, so we obtain
![]() $G_c$
from
$G_c$
from
![]() $\phi ^{-1}(c)$
by adding
$\phi ^{-1}(c)$
by adding
![]() $9$
to one of the two vertex classes of
$9$
to one of the two vertex classes of
![]() $\phi ^{-1}(c)$
. One can easily check all such attachments using a computer, trying each of the
$\phi ^{-1}(c)$
. One can easily check all such attachments using a computer, trying each of the
![]() $2^7$
choices (we implemented this using python (7ext.py)). This reveals that
$2^7$
choices (we implemented this using python (7ext.py)). This reveals that
![]() $\{G_c:c \in [7]\}$
has
$\{G_c:c \in [7]\}$
has
![]() $\prod _{i \in [8]}|\{c \in [7]: i9 \in G_c\}|= 2^{14}$
if and only if
$\prod _{i \in [8]}|\{c \in [7]: i9 \in G_c\}|= 2^{14}$
if and only if
![]() $\phi ^{-1}(c) \equiv K_{5,4}$
and there is some
$\phi ^{-1}(c) \equiv K_{5,4}$
and there is some
![]() $i \in [8]$
such that
$i \in [8]$
such that
![]() $9$
lies in exactly the same vertex class as i in each
$9$
lies in exactly the same vertex class as i in each
![]() $\phi ^{-1}(c)$
; that is,
$\phi ^{-1}(c)$
; that is,
![]() $9$
is a strong clone of i (in other words,
$9$
is a strong clone of i (in other words,
![]() $9$
corresponds to a copy of an existing row in the Hadamard matrix representing the optimal solution). Thus,
$9$
corresponds to a copy of an existing row in the Hadamard matrix representing the optimal solution). Thus,
![]() $\boldsymbol {k}$
has the strong extension property.
$\boldsymbol {k}$
has the strong extension property.
Since
![]() $|\phi |$
only takes the value
$|\phi |$
only takes the value
![]() $4$
, the same argument as at the beginning of the proof of Proposition 1.10 implies that the perfect colouring problem is soluble (with constant
$4$
, the same argument as at the beginning of the proof of Proposition 1.10 implies that the perfect colouring problem is soluble (with constant
![]() $c:= 4$
) and for all integers n, the unique supersolution
$c:= 4$
) and for all integers n, the unique supersolution
![]() $\boldsymbol {m}_n=(m_{n,1},\ldots ,m_{n,8})$
of the perfect colouring problem has
$\boldsymbol {m}_n=(m_{n,1},\ldots ,m_{n,8})$
of the perfect colouring problem has
![]() $|m_{n,i}-m_{n,j}| \leq 1$
for all
$|m_{n,i}-m_{n,j}| \leq 1$
for all
![]() $ij$
. Corollary 1.9 implies that the unique extremal graph is
$ij$
. Corollary 1.9 implies that the unique extremal graph is
![]() $K_{\boldsymbol {m}_n}(n) \cong T_8(n)$
. Let C be the number of Hadamard matrices with first column and last row consisting of
$K_{\boldsymbol {m}_n}(n) \cong T_8(n)$
. Let C be the number of Hadamard matrices with first column and last row consisting of
![]() $1$
-s. Then
$1$
-s. Then
![]() $F(n;\boldsymbol {k}) = (C+o(1))\cdot 4^{t_8(n)}$
. Note that one can calculate C if desired. Indeed, two Hadamard matrices are equivalent if one can be obtained from the other by a sequence of permutations and/or negations of rows and/or columns. It is known that, up to equivalence, there is one Hadamard matrix H of order
$F(n;\boldsymbol {k}) = (C+o(1))\cdot 4^{t_8(n)}$
. Note that one can calculate C if desired. Indeed, two Hadamard matrices are equivalent if one can be obtained from the other by a sequence of permutations and/or negations of rows and/or columns. It is known that, up to equivalence, there is one Hadamard matrix H of order
![]() $8$
. So C is the number of distinct matrices that can be obtained from H by permuting the first
$8$
. So C is the number of distinct matrices that can be obtained from H by permuting the first
![]() $7$
rows and the last
$7$
rows and the last
![]() $7$
columns and making the first column and the last row consist of all
$7$
columns and making the first column and the last row consist of all
![]() $1$
-s.
$1$
-s.
5. The
 $(k+1,k)$
-extremal graphs
$(k+1,k)$
-extremal graphs
In this section, we consider the simplest case when
![]() $\boldsymbol {k}$
has the weak extension property – namely,
$\boldsymbol {k}$
has the weak extension property – namely,
![]() $\boldsymbol {k} = (k+1,k)$
for
$\boldsymbol {k} = (k+1,k)$
for
![]() $k \geq 3$
. For small k, we determine the
$k \geq 3$
. For small k, we determine the
![]() $(k+1,k)$
-extremal graph, which turns out to have a part of size
$(k+1,k)$
-extremal graph, which turns out to have a part of size
![]() $O(k)$
, and the size of this part depends on the value of n modulo
$O(k)$
, and the size of this part depends on the value of n modulo
![]() $k-1$
. The proof relies heavily on Theorem 2.12, the full strength of which we have not yet required.
$k-1$
. The proof relies heavily on Theorem 2.12, the full strength of which we have not yet required.
Definition 5.1. For all integers
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $n \geq 4$
,
$n \geq 4$
,
-
○ for
 $q \geq 2$
, let
$q \geq 2$
, let
 $\mathcal {J}_q(n)$
be the family of complete k-partite graphs with parts of size
$\mathcal {J}_q(n)$
be the family of complete k-partite graphs with parts of size
 $m_1 \geq \ldots \geq m_{k-1} \geq \ell $
where
$m_1 \geq \ldots \geq m_{k-1} \geq \ell $
where
 $m_1-m_{k-1} \leq q$
,
$m_1-m_{k-1} \leq q$
,
 $2 \leq \ell \leq q$
and
$2 \leq \ell \leq q$
and
 $m_1+\ldots +m_{k-1}+\ell =n$
;
$m_1+\ldots +m_{k-1}+\ell =n$
; -
○ let
 $\mathcal {J}_q^*(n)$
be the set of graphs in
$\mathcal {J}_q^*(n)$
be the set of graphs in
 $\mathcal {J}_q(n)$
which are
$\mathcal {J}_q(n)$
which are
 $(k+1,k)$
-extremal;
$(k+1,k)$
-extremal; -
○ for
 $\ell \geq 1$
, let
$\ell \geq 1$
, let
 $J^\ell (n)$
denote the complete k-partite graph with parts of size
$J^\ell (n)$
denote the complete k-partite graph with parts of size
 $m_1 \geq \ldots \geq m_{k-1} \geq \ell $
where
$m_1 \geq \ldots \geq m_{k-1} \geq \ell $
where
 $m_1-m_{k-1} \leq 1$
and
$m_1-m_{k-1} \leq 1$
and
 $m_1+\ldots + m_{k-1}+\ell =n$
.
$m_1+\ldots + m_{k-1}+\ell =n$
.
In this section, we prove the following theorem, which includes Theorem 1.13.
Theorem 5.2. For all integers
![]() $k \geq 3$
, there exists
$k \geq 3$
, there exists
![]() $n_0>0$
such that for all
$n_0>0$
such that for all
![]() $n>n_0$
, every n-vertex
$n>n_0$
, every n-vertex
![]() $(k+1,k)$
-extremal graph is in
$(k+1,k)$
-extremal graph is in
![]() $\mathcal {J}_{2(k-1)}(n)$
. Moreover,
$\mathcal {J}_{2(k-1)}(n)$
. Moreover,
![]() $F(n;k+1,k) = O_k(1) \cdot 2^{t_{k-1}(n)}$
, where the factor
$F(n;k+1,k) = O_k(1) \cdot 2^{t_{k-1}(n)}$
, where the factor
![]() $O_k(1)$
is at least
$O_k(1)$
is at least
![]() $2$
.
$2$
.
Recall from (1.3) that
![]() $F(k+1,k)=Q(k+1,k)$
. It is easy to solve Problem
$F(k+1,k)=Q(k+1,k)$
. It is easy to solve Problem
![]() $Q^*$
for
$Q^*$
for
![]() $s=2$
colours (see [Reference Pikhurko and Staden10, Lemma 1.8]): the unique solution is
$s=2$
colours (see [Reference Pikhurko and Staden10, Lemma 1.8]): the unique solution is
![]() $(k-1,\phi ,\boldsymbol {u})$
where
$(k-1,\phi ,\boldsymbol {u})$
where
![]() $\boldsymbol {u}$
is uniform and
$\boldsymbol {u}$
is uniform and
![]() $\phi (ij)=[2]$
for all
$\phi (ij)=[2]$
for all
![]() $ij$
. Thus, when k is fixed and
$ij$
. Thus, when k is fixed and
![]() $n \to \infty $
,
$n \to \infty $
,
So, while (1.3) determines
![]() $ \log F(n;k+1,k)/\binom {n}{2}$
asymptotically, Theorem 5.2 determines
$ \log F(n;k+1,k)/\binom {n}{2}$
asymptotically, Theorem 5.2 determines
![]() $F(n;k+1,k)$
up to a multiplicative constant.
$F(n;k+1,k)$
up to a multiplicative constant.
The next proposition is numerical.
Proposition 5.3. Let
![]() $k \geq 3$
and
$k \geq 3$
and
![]() $0 \leq j \leq k-2$
be integers. Given
$0 \leq j \leq k-2$
be integers. Given
![]() $m_1 \geq \ldots \geq m_{k-1} \geq \ell $
, let
$m_1 \geq \ldots \geq m_{k-1} \geq \ell $
, let
![]() $\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$
and
$\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$
and
 $$ \begin{align*} h(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( 2^{-m_1}+ \ldots +2^{-m_{k-1}}\right)^{\ell},\\ h^*(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( \sum_{i \in [k-1]}2^{-m_i} - \sum_{ii' \in \binom{[k-1]}{2}}2^{-m_i-m_{i'}}\right)^{\ell}. \end{align*} $$
$$ \begin{align*} h(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( 2^{-m_1}+ \ldots +2^{-m_{k-1}}\right)^{\ell},\\ h^*(\boldsymbol{m};\ell) &:= \left(\prod_{ii' \in \binom{[k-1]}{2}}2^{m_im_{i'}}\right) 2^{\ell(m_1+\ldots+m_{k-1})} \left( \sum_{i \in [k-1]}2^{-m_i} - \sum_{ii' \in \binom{[k-1]}{2}}2^{-m_i-m_{i'}}\right)^{\ell}. \end{align*} $$
Let
where
![]() $m^*_1 \geq \ldots \geq m^*_{k-1} \geq \ell $
,
$m^*_1 \geq \ldots \geq m^*_{k-1} \geq \ell $
,
![]() $m^*_1 - m^*_{k-1} \leq 1$
and
$m^*_1 - m^*_{k-1} \leq 1$
and
![]() $m^*_1+\ldots + m^*_{k-1}+\ell =n$
(so
$m^*_1+\ldots + m^*_{k-1}+\ell =n$
(so
![]() $m^*_1,\ldots ,m^*_{k-1},\ell $
are the part sizes of
$m^*_1,\ldots ,m^*_{k-1},\ell $
are the part sizes of
![]() $J^\ell (n)$
). Let
$J^\ell (n)$
). Let
![]() $\boldsymbol {m}^*:=(m^*_1,\ldots ,m^*_{k-1})$
.
$\boldsymbol {m}^*:=(m^*_1,\ldots ,m^*_{k-1})$
.
-
(i) Let
 $n \equiv j\ (\mod k-1)$
with
$n \equiv j\ (\mod k-1)$
with
 $0 \leq j < k-1$
and
$0 \leq j < k-1$
and
 $n \geq k^3$
. Consider the following way of colouring
$n \geq k^3$
. Consider the following way of colouring
 $J \in \mathcal {J}_{n}(n)$
with parts of size
$J \in \mathcal {J}_{n}(n)$
with parts of size
 $m_1 \geq \ldots \geq m_{k-1} \geq \ell $
: for each x in the
$m_1 \geq \ldots \geq m_{k-1} \geq \ell $
: for each x in the
 $\ell $
-part, pick
$\ell $
-part, pick
 $i_x \in [k-1]$
and colour every edge between x and the
$i_x \in [k-1]$
and colour every edge between x and the
 $m_{i_x}$
-part with colour
$m_{i_x}$
-part with colour
 $1$
. All other edges are coloured arbitrarily. The number of colourings is between
$1$
. All other edges are coloured arbitrarily. The number of colourings is between
 $h^*(\boldsymbol {m};\ell )$
and
$h^*(\boldsymbol {m};\ell )$
and
 $h(\boldsymbol {m};\ell )$
.
$h(\boldsymbol {m};\ell )$
. -
(ii) If
 $0 \leq \ell \leq k-1$
, then
$0 \leq \ell \leq k-1$
, then  $$ \begin{align*}f(k,j,\ell) = \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1. \end{cases} \end{align*} $$
$$ \begin{align*}f(k,j,\ell) = \begin{cases} 2^{-\binom{\ell}{2}}\left(k-1-\frac{j-\ell}{2}\right)^\ell &\mbox{if } 0 \leq \ell \leq j \\ 2^{j-\binom{\ell+1}{2}}\left(k-1+\ell-j\right)^\ell &\mbox{if } j < \ell \leq k-1. \end{cases} \end{align*} $$
-
(iii) Let
 $n \equiv j \ (\mod k-1)$
with
$n \equiv j \ (\mod k-1)$
with
 $n \geq k^3$
. For
$n \geq k^3$
. For
 $3 \leq k \leq 10$
, the maximum of
$3 \leq k \leq 10$
, the maximum of
 $h(\boldsymbol {m};\ell )$
over all (part sizes of)
$h(\boldsymbol {m};\ell )$
over all (part sizes of)
 $J \in \mathcal {J}_{2(k-1)}(n)$
is attained by
$J \in \mathcal {J}_{2(k-1)}(n)$
is attained by
 $J^{\ell (k,j)}(n)$
, where
$J^{\ell (k,j)}(n)$
, where
 $\ell (k,j)$
is the
$\ell (k,j)$
is the
 $(k,j)$
-th entry in the table below, and the value is separated from the value for any other
$(k,j)$
-th entry in the table below, and the value is separated from the value for any other
 $J \in \mathcal {J}_{2(k-1)}(n)$
by a factor
$J \in \mathcal {J}_{2(k-1)}(n)$
by a factor
 $1+\Omega (1)$
.
$1+\Omega (1)$
.
-
(iv) For all
 $0 \leq j \leq k-2$
, we have
$0 \leq j \leq k-2$
, we have
 $f(k,j) \geq \max \{(k+1)^2/8,2\}$
.
$f(k,j) \geq \max \{(k+1)^2/8,2\}$
.
Proof sketch
For (i), the assertion about h is clear. Further, h overcounts those colourings with all colour-
![]() $1$
edges to at least two other parts. By a Bonferroni-type inequality,
$1$
edges to at least two other parts. By a Bonferroni-type inequality,
![]() $h^*$
is a lower bound.
$h^*$
is a lower bound.
Let us turn to the remaining claims. Take any admissible
![]() $(\boldsymbol {m};\ell )$
. Define the integer b by
$(\boldsymbol {m};\ell )$
. Define the integer b by
![]() $n =b(k-1)+j$
and
$n =b(k-1)+j$
and
![]() $0 \leq j < k-1$
. Define
$0 \leq j < k-1$
. Define
![]() $b_i := m_i-b$
. Then
$b_i := m_i-b$
. Then
![]() $b_1 - b_{k-1} \leq 2(k-1)$
. Moreover,
$b_1 - b_{k-1} \leq 2(k-1)$
. Moreover,
![]() $b_1+\ldots + b_{k-1} + \ell = \sum _i m_i - (k-1)b + \ell = n - (k-1)b = j$
. Then
$b_1+\ldots + b_{k-1} + \ell = \sum _i m_i - (k-1)b + \ell = n - (k-1)b = j$
. Then
 $$ \begin{align} h(\boldsymbol{m};\ell) = 2^{\binom{k-1}{2}b^2+(k-2)bj} \cdot 2^{\ell\sum_{i}b_i} \left( 2^{-b_1}+\ldots + 2^{-b_{k-1}}\right)^\ell \prod_{ii'} 2^{b_ib_{i'}}. \end{align} $$
$$ \begin{align} h(\boldsymbol{m};\ell) = 2^{\binom{k-1}{2}b^2+(k-2)bj} \cdot 2^{\ell\sum_{i}b_i} \left( 2^{-b_1}+\ldots + 2^{-b_{k-1}}\right)^\ell \prod_{ii'} 2^{b_ib_{i'}}. \end{align} $$
First, we prove (iii). For this, one needs to compare the values of
among all tuples
![]() $\boldsymbol {b} := (b_1,\ldots ,b_{k-1})$
and
$\boldsymbol {b} := (b_1,\ldots ,b_{k-1})$
and
![]() $\ell $
with sum j and
$\ell $
with sum j and
![]() $|b_i-b_{i'}|,\ell \leq 2(k-1)$
. We implemented this in python (smallpart.py), and the optimal value of
$|b_i-b_{i'}|,\ell \leq 2(k-1)$
. We implemented this in python (smallpart.py), and the optimal value of
![]() $\ell $
(which is indeed unique) for
$\ell $
(which is indeed unique) for
![]() $3 \leq k \leq 10$
was recorded in the table. In all cases, we also had
$3 \leq k \leq 10$
was recorded in the table. In all cases, we also had
![]() $b_1-b_{k-1} \leq 1$
, so the optimal
$b_1-b_{k-1} \leq 1$
, so the optimal
![]() $m_1,\ldots ,m_{k-1}$
are as equal as possible. Thus, the maximum is attained by some
$m_1,\ldots ,m_{k-1}$
are as equal as possible. Thus, the maximum is attained by some
![]() $J^\ell (n)$
. For future reference, we note that we could have defined
$J^\ell (n)$
. For future reference, we note that we could have defined
![]() $b_i$
by subtracting any
$b_i$
by subtracting any
![]() $b' \leq b$
from
$b' \leq b$
from
![]() $m_i$
, and then to compare values of
$m_i$
, and then to compare values of
![]() $h(\boldsymbol {b};\ell )$
, one must compare values of
$h(\boldsymbol {b};\ell )$
, one must compare values of
![]() $\tilde {h}(\boldsymbol {b};\ell )$
over tuples
$\tilde {h}(\boldsymbol {b};\ell )$
over tuples
![]() $\boldsymbol {b}$
with sum
$\boldsymbol {b}$
with sum
![]() $j+(k-1)(b-b')$
.
$j+(k-1)(b-b')$
.
Note that
 $$ \begin{align*}t_{k-1}(n) =t_{k-1}((k-1)b+j) =\binom{k-1}{2}b^2+(k-2)bj+\binom{j}{2}. \end{align*} $$
$$ \begin{align*}t_{k-1}(n) =t_{k-1}((k-1)b+j) =\binom{k-1}{2}b^2+(k-2)bj+\binom{j}{2}. \end{align*} $$
For
![]() $0 \leq \ell \leq j$
, (5.1) implies that the function
$0 \leq \ell \leq j$
, (5.1) implies that the function
![]() $f(k,j,\ell )$
equals
$f(k,j,\ell )$
equals
![]() $2^{-\binom {j}{2}}\cdot \tilde {h}((1,\ldots ,1,0,\dots ,0);\ell )$
where there are
$2^{-\binom {j}{2}}\cdot \tilde {h}((1,\ldots ,1,0,\dots ,0);\ell )$
where there are
![]() $j-\ell $
entries of value
$j-\ell $
entries of value
![]() $1$
. For
$1$
. For
![]() $j < \ell \leq k-1$
, it equals
$j < \ell \leq k-1$
, it equals
![]() $2^{-\binom {j}{2}}\cdot \tilde {h}((0,\ldots ,0,-1,\ldots ,-1);\ell )$
where there are
$2^{-\binom {j}{2}}\cdot \tilde {h}((0,\ldots ,0,-1,\ldots ,-1);\ell )$
where there are
![]() $\ell -j$
entries of value
$\ell -j$
entries of value
![]() $-1$
. This proves (ii).
$-1$
. This proves (ii).
For (iv), we bound
![]() $f(k,j,2)$
from below. For
$f(k,j,2)$
from below. For
![]() $j \geq 2$
, we have
$j \geq 2$
, we have
We have
![]() $f(k,0,2) = (k+1)^2/8$
and
$f(k,0,2) = (k+1)^2/8$
and
![]() $f(k,1,2) = k^2/4$
. For
$f(k,1,2) = k^2/4$
. For
![]() $k \geq 11$
(i.e., not in the table), the smallest of these is
$k \geq 11$
(i.e., not in the table), the smallest of these is
![]() $(k+1)^2/8 \geq 18$
.
$(k+1)^2/8 \geq 18$
.
The next lemma states that whenever every vertex and pair of vertices in a near-extremal complete partite graph, G has almost optimal contribution to
![]() $F(G;\boldsymbol {k})$
, then G is only optimal if it lies in
$F(G;\boldsymbol {k})$
, then G is only optimal if it lies in
![]() $\mathcal {J}_{2(k-1)}(n)$
.
$\mathcal {J}_{2(k-1)}(n)$
.
Lemma 5.4. There exist
![]() ${\varepsilon }> 0$
and
${\varepsilon }> 0$
and
![]() $n_0 \in \mathbb {N}$
such that the following holds. Let G be a graph on
$n_0 \in \mathbb {N}$
such that the following holds. Let G be a graph on
![]() $n \geq n_0$
vertices which is complete multipartite, and such that
$n \geq n_0$
vertices which is complete multipartite, and such that
![]() $\log F(G;k+1,k) \geq \left (\frac {k-2}{k-1}-{\varepsilon }\right )\binom {n}{2}$
and
$\log F(G;k+1,k) \geq \left (\frac {k-2}{k-1}-{\varepsilon }\right )\binom {n}{2}$
and
 $$ \begin{align} &\log F(G;k+1,k) - \log F(G-x;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})n\quad\forall \ x \in V(G),\\ \nonumber &\log F(G;k+1,k) - \log F(G-y-z;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})(n+n-1)\\ \nonumber &\hspace{6cm}\forall\text{ distinct }y,z \in V(G). \end{align} $$
$$ \begin{align} &\log F(G;k+1,k) - \log F(G-x;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})n\quad\forall \ x \in V(G),\\ \nonumber &\log F(G;k+1,k) - \log F(G-y-z;k+1,k) \geq (\textstyle{\frac{k-2}{k-1}}-2{\varepsilon})(n+n-1)\\ \nonumber &\hspace{6cm}\forall\text{ distinct }y,z \in V(G). \end{align} $$
If
![]() $G \not \in \mathcal {J}_{2(k-1)}(n)$
, then there is a graph
$G \not \in \mathcal {J}_{2(k-1)}(n)$
, then there is a graph
![]() $G'$
of order n with
$G'$
of order n with
![]() $F(G';k+1,k)> F(G;k+1,k)$
.
$F(G';k+1,k)> F(G;k+1,k)$
.
Proof. As it is easy to show (or see [Reference Pikhurko and Staden10, Lemma 1.8]),
![]() $(k+1,k)$
has the extension property. Let
$(k+1,k)$
has the extension property. Let
![]() $0 < \delta ' \ll \delta $
. Let
$0 < \delta ' \ll \delta $
. Let
![]() $n_0,{\varepsilon }>0$
be the parameters returned by Theorem 2.12 applied with parameter
$n_0,{\varepsilon }>0$
be the parameters returned by Theorem 2.12 applied with parameter
![]() $\delta '$
. We may assume that
$\delta '$
. We may assume that
![]() $0 < 1/n_0 \ll {\varepsilon } \ll \delta '$
. Let G be a graph on
$0 < 1/n_0 \ll {\varepsilon } \ll \delta '$
. Let G be a graph on
![]() $n \geq n_0$
vertices as in the lemma. Let
$n \geq n_0$
vertices as in the lemma. Let
![]() $X_1,\ldots ,X_t$
be the partition of
$X_1,\ldots ,X_t$
be the partition of
![]() $V(G)$
, where
$V(G)$
, where
![]() $|X_1| \geq \ldots \geq |X_t|$
. By Theorem 2.12, there is a set
$|X_1| \geq \ldots \geq |X_t|$
. By Theorem 2.12, there is a set
![]() $\mathcal {P}$
of at least
$\mathcal {P}$
of at least
![]() $(1-2^{-{\varepsilon } n})F(G;k+1,k)$
valid colourings of G such that, for each
$(1-2^{-{\varepsilon } n})F(G;k+1,k)$
valid colourings of G such that, for each
![]() $\chi \in \mathcal {P}$
, the following hold.
$\chi \in \mathcal {P}$
, the following hold.
-
(i) There is a coarsening
 $Z_0,Z_1,\ldots ,Z_{k-1}$
of
$Z_0,Z_1,\ldots ,Z_{k-1}$
of
 $X_1,\ldots ,X_t$
such that
$X_1,\ldots ,X_t$
such that
 $\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| < \delta 'n$
.
$\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| < \delta 'n$
. -
(ii) Each of
 $Z_1,\ldots ,Z_{k-2}$
is a part of G, and
$Z_1,\ldots ,Z_{k-2}$
is a part of G, and
 $Z_{k-1}$
contains at most two parts of G.
$Z_{k-1}$
contains at most two parts of G. -
(iii) For all
 $x \in V(G)$
, there is
$x \in V(G)$
, there is
 $i(x) \in [k-1]$
, so that we have
$i(x) \in [k-1]$
, so that we have
 $\chi (xy) = 1$
for all
$\chi (xy) = 1$
for all
 $y \in N_G(x) \cap Z_{i(x)}$
, and for all
$y \in N_G(x) \cap Z_{i(x)}$
, and for all
 $j \in [k-1]\setminus \{i(x)\}$
, it holds that (5.4)Moreover, for all
$j \in [k-1]\setminus \{i(x)\}$
, it holds that (5.4)Moreover, for all $$ \begin{align} |\chi^{-1}(c)[x,X]|=\textstyle{\frac{1}{2}}|X|\pm\delta'|Z_j|\quad\text{for all }c \in [2] \text{ and parts }X \subseteq Z_j. \end{align} $$
$$ \begin{align} |\chi^{-1}(c)[x,X]|=\textstyle{\frac{1}{2}}|X|\pm\delta'|Z_j|\quad\text{for all }c \in [2] \text{ and parts }X \subseteq Z_j. \end{align} $$
 $j \in [k-1]$
and distinct
$j \in [k-1]$
and distinct
 $y,z \in V(G)$
with
$y,z \in V(G)$
with
 $i(y)=i(z) \neq j$
, it holds that (5.5)Also, if
$i(y)=i(z) \neq j$
, it holds that (5.5)Also, if $$ \begin{align} |N_{\chi^{-1}(c)}(y,X) \cap N_{\chi^{-1}(c')}(z,X)| = \textstyle{\frac{1}{4}}|X| \pm \delta'|Z_j|\quad\text{for all }c,c' \in [2]\text{ and parts }X \subseteq Z_j. \end{align} $$
$$ \begin{align} |N_{\chi^{-1}(c)}(y,X) \cap N_{\chi^{-1}(c')}(z,X)| = \textstyle{\frac{1}{4}}|X| \pm \delta'|Z_j|\quad\text{for all }c,c' \in [2]\text{ and parts }X \subseteq Z_j. \end{align} $$
 $x \in Z_i$
for
$x \in Z_i$
for
 $i \in [k-1]$
, then
$i \in [k-1]$
, then
 $i(x) = i$
.
$i(x) = i$
.
Fix
![]() $\chi ^* \in \mathcal {P}$
and choose
$\chi ^* \in \mathcal {P}$
and choose
![]() $Z_0,\ldots ,Z_{k-1}$
and
$Z_0,\ldots ,Z_{k-1}$
and
![]() $i : V(G) \mapsto [k-1]$
as above. (Recall that these may be different for different colourings.) If there is a part in
$i : V(G) \mapsto [k-1]$
as above. (Recall that these may be different for different colourings.) If there is a part in
![]() $Z_{k-1}$
of size at most
$Z_{k-1}$
of size at most
![]() $\delta n$
, move it into
$\delta n$
, move it into
![]() $Z_0$
. Then (i) holds with parameter
$Z_0$
. Then (i) holds with parameter
![]() $2\delta $
, (iii) holds with parameter
$2\delta $
, (iii) holds with parameter
![]() $\delta '$
, every part in
$\delta '$
, every part in
![]() $Z_{k-1}$
has size at least
$Z_{k-1}$
has size at least
![]() $\delta n$
, and all but one part in
$\delta n$
, and all but one part in
![]() $Z_0$
has size at most
$Z_0$
has size at most
![]() $\delta 'n$
. Let
$\delta 'n$
. Let
![]() $p^* \leq 2$
be the number of parts in
$p^* \leq 2$
be the number of parts in
![]() $Z_{k-1}$
and
$Z_{k-1}$
and
![]() $q^*$
the number of parts in
$q^*$
the number of parts in
![]() $Z_{0}$
(which both depend on
$Z_{0}$
(which both depend on
![]() $\chi ^*$
).
$\chi ^*$
).
Claim 5.4.1. Suppose that
![]() $Z_0 \neq \emptyset $
. Then
$Z_0 \neq \emptyset $
. Then
![]() $Z_{k-1}$
contains exactly one part. Moreover, if
$Z_{k-1}$
contains exactly one part. Moreover, if
![]() $x,x' \in Z_0$
lie in different parts of G, then for all
$x,x' \in Z_0$
lie in different parts of G, then for all
![]() $\chi \in \mathcal {P}$
, we have
$\chi \in \mathcal {P}$
, we have
![]() $\chi (xx') = 2$
and
$\chi (xx') = 2$
and
![]() $i(x) \neq i(x')$
. In particular,
$i(x) \neq i(x')$
. In particular,
![]() $Z_0$
contains at most
$Z_0$
contains at most
![]() $k-1$
parts.
$k-1$
parts.
Proof of Claim
Let
![]() $\{ B_{p'} : p' \in [p^*] \}$
be the part(s) of G contained in
$\{ B_{p'} : p' \in [p^*] \}$
be the part(s) of G contained in
![]() $Z_{k-1}$
. Suppose first that
$Z_{k-1}$
. Suppose first that
![]() $p^*=2$
and
$p^*=2$
and
![]() $q^* \geq 1$
. Let
$q^* \geq 1$
. Let
![]() $x \in Z_0$
and
$x \in Z_0$
and
![]() $\chi \in \mathcal {P}$
be arbitrary. Then
$\chi \in \mathcal {P}$
be arbitrary. Then
![]() $\chi (xv)=1$
for all
$\chi (xv)=1$
for all
![]() $v \in Z_{i(x)}$
, and for each
$v \in Z_{i(x)}$
, and for each
![]() $i \in [k-1]\setminus \{i(x)\}$
, the vertex and pair locally good conditions (5.4) and (5.5) hold. Without loss of generality, assume
$i \in [k-1]\setminus \{i(x)\}$
, the vertex and pair locally good conditions (5.4) and (5.5) hold. Without loss of generality, assume
![]() $|B_1| \geq |B_2|$
. Thus, for example,
$|B_1| \geq |B_2|$
. Thus, for example,
![]() $|B_1| \geq n/(2k)$
and
$|B_1| \geq n/(2k)$
and
![]() $|B_2| \geq \delta n$
. By (5.4), there is
$|B_2| \geq \delta n$
. By (5.4), there is
![]() $y \in B_2$
such that
$y \in B_2$
such that
![]() $\chi (xy)=1$
(when
$\chi (xy)=1$
(when
![]() $i(x) \neq k-1$
, since if
$i(x) \neq k-1$
, since if
![]() $i(x)=k-1$
, this is obvious). Since
$i(x)=k-1$
, this is obvious). Since
![]() $i(y)=k-1$
, we also have
$i(y)=k-1$
, we also have
![]() $\chi (yz)=1$
for every
$\chi (yz)=1$
for every
![]() $z \in B_1$
. Let
$z \in B_1$
. Let
![]() $J := \chi ^{-1}(1)$
. For
$J := \chi ^{-1}(1)$
. For
![]() $i \in [k-2]$
, let
$i \in [k-2]$
, let
![]() $A_i := N_J(x,Z_i) \cap N_J(y,Z_i)$
and let
$A_i := N_J(x,Z_i) \cap N_J(y,Z_i)$
and let
![]() $A_{k-1} := N_J(x,B_1) \cap N_J(y,B_1)$
. Then (5.5) implies that
$A_{k-1} := N_J(x,B_1) \cap N_J(y,B_1)$
. Then (5.5) implies that
![]() $|A_i| \geq (\frac {1}{4}-\delta ')|Z_i| \geq |Z_i|/5 \geq n/(5k)$
for all
$|A_i| \geq (\frac {1}{4}-\delta ')|Z_i| \geq |Z_i|/5 \geq n/(5k)$
for all
![]() $i \in [k-2]$
. Also, by (5.4),
$i \in [k-2]$
. Also, by (5.4),
![]() $|A_{k-1}| = |N_J(x,B_1)| \geq (\frac {1}{2}-\delta ')|B_1| \geq |Z_{k-1}|/5 \geq n/(5k)$
. Lemma 2.6 implies that
$|A_{k-1}| = |N_J(x,B_1)| \geq (\frac {1}{2}-\delta ')|B_1| \geq |Z_{k-1}|/5 \geq n/(5k)$
. Lemma 2.6 implies that
![]() $J[A_i,A_j]$
is
$J[A_i,A_j]$
is
![]() $(\sqrt {\delta '},\frac {1}{2})$
-regular for all distinct
$(\sqrt {\delta '},\frac {1}{2})$
-regular for all distinct
![]() $i,j \in [k-1]$
. By Lemma 2.4, J contains a
$i,j \in [k-1]$
. By Lemma 2.4, J contains a
![]() $K_{k-1}$
with one vertex in each of
$K_{k-1}$
with one vertex in each of
![]() $A_1,\ldots ,A_{k-1}$
. Together with
$A_1,\ldots ,A_{k-1}$
. Together with
![]() $x,y$
, this gives rise to a
$x,y$
, this gives rise to a
![]() $1$
-coloured copy of
$1$
-coloured copy of
![]() $K_{k+1}$
in G, a contradiction. So if
$K_{k+1}$
in G, a contradiction. So if
![]() $p^*=2$
, then
$p^*=2$
, then
![]() $q^* = 0$
.
$q^* = 0$
.
Suppose now that
![]() $p^*=1$
and let
$p^*=1$
and let
![]() $x,x' \in Z_0$
lie in different parts of G. Similar arguments to those above show that
$x,x' \in Z_0$
lie in different parts of G. Similar arguments to those above show that
![]() $x,x'$
form the
$x,x'$
form the
![]() $2$
-element set in a copy of the k-partite graph
$2$
-element set in a copy of the k-partite graph
![]() $K_{1,\ldots ,1,2}$
in
$K_{1,\ldots ,1,2}$
in
![]() $\chi ^{-1}(1)$
. Therefore, (since the edge between them must have some colour)
$\chi ^{-1}(1)$
. Therefore, (since the edge between them must have some colour)
![]() $\chi (xx') = 2$
, as required. Suppose now, for a contradiction, that
$\chi (xx') = 2$
, as required. Suppose now, for a contradiction, that
![]() $i(x) = i(x')$
. Without loss of generality, suppose their common value is
$i(x) = i(x')$
. Without loss of generality, suppose their common value is
![]() $1$
. Then
$1$
. Then
![]() $U_i := N_{\chi ^{-1}(2)}(x,Z_i) \cap N_{\chi ^{-1}(2)}(x',Z_i)$
satisfies
$U_i := N_{\chi ^{-1}(2)}(x,Z_i) \cap N_{\chi ^{-1}(2)}(x',Z_i)$
satisfies
![]() $|U_i| = (\textstyle {\frac {1}{4}} \pm \sqrt {\delta '})|Z_i|$
for all
$|U_i| = (\textstyle {\frac {1}{4}} \pm \sqrt {\delta '})|Z_i|$
for all
![]() $2 \leq i \leq k-1$
. By Proposition 2.7,
$2 \leq i \leq k-1$
. By Proposition 2.7,
![]() $\chi ^{-1}(2)[U_i,U_{i'}]$
is
$\chi ^{-1}(2)[U_i,U_{i'}]$
is
![]() $((\delta ')^{1/3},\frac {1}{2})$
-regular for all distinct
$((\delta ')^{1/3},\frac {1}{2})$
-regular for all distinct
![]() $2 \leq i,i' \leq k-1$
. By Lemma 2.4, there are
$2 \leq i,i' \leq k-1$
. By Lemma 2.4, there are
![]() $z_i \in U_i$
for
$z_i \in U_i$
for
![]() $2 \leq i \leq k-1$
such that
$2 \leq i \leq k-1$
such that
![]() $x,x',z_2,\ldots ,z_{k-1}$
form a copy of
$x,x',z_2,\ldots ,z_{k-1}$
form a copy of
![]() $K_{k}$
in
$K_{k}$
in
![]() $\chi ^{-1}(2)$
, a contradiction. Thus,
$\chi ^{-1}(2)$
, a contradiction. Thus,
![]() $i(x) \neq i(x')$
. This completes the proof of the claim.
$i(x) \neq i(x')$
. This completes the proof of the claim.
The total number of parts is
![]() $t = k-2+p^*+q^*$
. Suppose that
$t = k-2+p^*+q^*$
. Suppose that
![]() $t=k-1$
. Then G is
$t=k-1$
. Then G is
![]() $K_k$
-free. Thus, every
$K_k$
-free. Thus, every
![]() $2$
-edge colouring is
$2$
-edge colouring is
![]() $(k,k+1)$
-valid and so
$(k,k+1)$
-valid and so
![]() $|\mathcal {P}| \leq 2^{t_{k-1}(n)}$
, and hence,
$|\mathcal {P}| \leq 2^{t_{k-1}(n)}$
, and hence,
![]() $F(G;\boldsymbol {k}) \leq (1-2^{-{\varepsilon } n})^{-1}\cdot 2^{t_{k-1}(n)}$
.
$F(G;\boldsymbol {k}) \leq (1-2^{-{\varepsilon } n})^{-1}\cdot 2^{t_{k-1}(n)}$
.
Suppose
![]() $t \geq k$
and every part of G has size at least
$t \geq k$
and every part of G has size at least
![]() $\delta n$
. Then every
$\delta n$
. Then every
![]() $\chi \in \mathcal {P}$
has the same associated coarsening
$\chi \in \mathcal {P}$
has the same associated coarsening
![]() $Z_1=X_1,\ldots ,Z_{k-2}=X_{k-2},Z_{k-1}=X_{k-1} \cup X_k$
in order to satisfy
$Z_1=X_1,\ldots ,Z_{k-2}=X_{k-2},Z_{k-1}=X_{k-1} \cup X_k$
in order to satisfy
![]() $\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| \leq \delta ' n$
. The number of perfect colourings is the same as if
$\sum _{i \in [k-1]}|\,|Z_i|-\frac {n}{k-1}\,| \leq \delta ' n$
. The number of perfect colourings is the same as if
![]() $X_{k-1},X_k$
were merged into a single part since edges between these parts are coloured with
$X_{k-1},X_k$
were merged into a single part since edges between these parts are coloured with
![]() $1$
, so
$1$
, so
We will see later, due to Proposition 5.3, that there is
![]() $G'$
with
$G'$
with
![]() $|\mathcal {P}(G')| \geq 1.9|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')| \geq 1.9|\mathcal {P}(G)|$
.
So from now on, we will assume that
![]() $t \geq k$
and there are
$t \geq k$
and there are
![]() $q \geq 1$
parts of size less than
$q \geq 1$
parts of size less than
![]() $\delta n$
. Claim 5.4.1 implies that these parts lie in
$\delta n$
. Claim 5.4.1 implies that these parts lie in
![]() $Z_0$
so
$Z_0$
so
![]() $p^*=1$
and
$p^*=1$
and
![]() $q^*=q=t-(k-1)$
. Thus, we have
$q^*=q=t-(k-1)$
. Thus, we have
![]() $|X_i| < \delta n$
for all
$|X_i| < \delta n$
for all
![]() $i \geq k$
, so also
$i \geq k$
, so also
![]() $|X_1| \geq \ldots \geq |X_{k-1}| \geq \frac {n}{k-1}-(k-1)\delta n$
. We will say that
$|X_1| \geq \ldots \geq |X_{k-1}| \geq \frac {n}{k-1}-(k-1)\delta n$
. We will say that
![]() $X_1,\ldots ,X_{k-1}$
are the large parts, of sizes
$X_1,\ldots ,X_{k-1}$
are the large parts, of sizes
![]() $m_1,\ldots ,m_{k-1}$
, respectively, and
$m_1,\ldots ,m_{k-1}$
, respectively, and
![]() $L_1,\ldots ,L_q$
are the small parts, of sizes
$L_1,\ldots ,L_q$
are the small parts, of sizes
![]() $\ell _1,\ldots ,\ell _q$
, respectively. Also, let
$\ell _1,\ldots ,\ell _q$
, respectively. Also, let
![]() $m := m_1+\ldots + m_{k-1}$
and
$m := m_1+\ldots + m_{k-1}$
and
![]() $\ell := \ell _1 + \ldots + \ell _q$
, and
$\ell := \ell _1 + \ldots + \ell _q$
, and
![]() $\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$
and
$\boldsymbol {m} := (m_1,\ldots ,m_{k-1})$
and
![]() $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _q)$
. For some colourings
$\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _q)$
. For some colourings
![]() $\chi $
, one of the
$\chi $
, one of the
![]() $L_i$
may be a part of
$L_i$
may be a part of
![]() $Z_{k-1}$
, while in others, all
$Z_{k-1}$
, while in others, all
![]() $L_i$
will be parts of
$L_i$
will be parts of
![]() $Z_0$
. Suppose there are
$Z_0$
. Suppose there are
![]() $\chi $
and i such that
$\chi $
and i such that
![]() $Z_{k-1}=X_{k-1} \cup L_i$
. Then Claim 5.4.1 implies that
$Z_{k-1}=X_{k-1} \cup L_i$
. Then Claim 5.4.1 implies that
![]() $q=0$
, so then
$q=0$
, so then
![]() $t=k$
. So for all
$t=k$
. So for all
![]() $\chi $
, either
$\chi $
, either
![]() $(Z_{k-1},Z_0)=(X_{k-1} \cup L_i,\emptyset )$
or
$(Z_{k-1},Z_0)=(X_{k-1} \cup L_i,\emptyset )$
or
![]() $(Z_{k-1},Z_0)=(X_{k-1},L_i)$
. We may assume that we always have the second partition, as the number of perfect colourings is a function of
$(Z_{k-1},Z_0)=(X_{k-1},L_i)$
. We may assume that we always have the second partition, as the number of perfect colourings is a function of
![]() $(Z_1,\ldots ,Z_{k-1},Z_0)$
and there are more choices with the second. Thus, we may assume that each perfect colouring
$(Z_1,\ldots ,Z_{k-1},Z_0)$
and there are more choices with the second. Thus, we may assume that each perfect colouring
![]() $\chi $
gives rise to the same partition
$\chi $
gives rise to the same partition
![]() $(Z_1,\ldots ,Z_{k-1},Z_0)=(X_1,\ldots ,X_{k-1},L_1 \cup \ldots \cup L_q)$
, where
$(Z_1,\ldots ,Z_{k-1},Z_0)=(X_1,\ldots ,X_{k-1},L_1 \cup \ldots \cup L_q)$
, where
![]() $q \leq k-1$
.
$q \leq k-1$
.
Let
![]() $P_q(k-1)$
be the set of ordered partitions of
$P_q(k-1)$
be the set of ordered partitions of
![]() $[k-1]$
into q parts (some of which may be empty) with the following property. Suppose that exactly a different values appear in
$[k-1]$
into q parts (some of which may be empty) with the following property. Suppose that exactly a different values appear in
![]() $\boldsymbol {\ell }$
, so
$\boldsymbol {\ell }$
, so
![]() $\ell _1 = \ldots = \ell _{i_1}> \ell _{i_1+1} = \ldots = \ell _{i_2} > \ldots > \ell _{i_{a-1}+1} = \ldots = \ell _q$
for some
$\ell _1 = \ldots = \ell _{i_1}> \ell _{i_1+1} = \ldots = \ell _{i_2} > \ldots > \ell _{i_{a-1}+1} = \ldots = \ell _q$
for some
![]() $a \in [q]$
. For each unordered partition
$a \in [q]$
. For each unordered partition
![]() $\{I_1,\ldots ,I_q\}$
, labelled so that
$\{I_1,\ldots ,I_q\}$
, labelled so that
![]() $\min \{I_1\}<\ldots < \min \{I_q\}$
, and any permutation
$\min \{I_1\}<\ldots < \min \{I_q\}$
, and any permutation
![]() $\sigma : [q]\to [q]$
that has
$\sigma : [q]\to [q]$
that has
![]() $\sigma (i_{s-1}+1)< \ldots < \sigma (i_{s})$
for all
$\sigma (i_{s-1}+1)< \ldots < \sigma (i_{s})$
for all
![]() $1 \leq s \leq a+1$
(where
$1 \leq s \leq a+1$
(where
![]() $i_0:=0$
and
$i_0:=0$
and
![]() $i_{a+1}:=q$
), we put
$i_{a+1}:=q$
), we put
![]() $(I_{\sigma (1)},\ldots ,I_{\sigma (q)})$
into
$(I_{\sigma (1)},\ldots ,I_{\sigma (q)})$
into
![]() $P_q(k-1)$
. So if
$P_q(k-1)$
. So if
![]() $\ell _1>\ldots >\ell _q$
, then
$\ell _1>\ldots >\ell _q$
, then
![]() $P_q(k-1)$
consists of all ordered partitions of
$P_q(k-1)$
consists of all ordered partitions of
![]() $[k-1]$
into q parts, while if
$[k-1]$
into q parts, while if
![]() $\ell _1=\ldots =\ell _q$
, then for each unordered partition, it contains exactly one ordering.
$\ell _1=\ldots =\ell _q$
, then for each unordered partition, it contains exactly one ordering.
Every colouring in
![]() $\mathcal {P}(G)$
is obtained as follows: First, colour edges between pairs in
$\mathcal {P}(G)$
is obtained as follows: First, colour edges between pairs in
![]() $Z_1,\ldots ,Z_{k-1}$
arbitrarily and colour edges between the
$Z_1,\ldots ,Z_{k-1}$
arbitrarily and colour edges between the
![]() $L_i$
with colour
$L_i$
with colour
![]() $2$
. By Claim 5.4.1,
$2$
. By Claim 5.4.1,
![]() $i(x) \neq i(x')$
for
$i(x) \neq i(x')$
for
![]() $x,x'$
in different small parts, so choose
$x,x'$
in different small parts, so choose
![]() $(I_1,\ldots ,I_q) \in P_q(k-1)$
so that
$(I_1,\ldots ,I_q) \in P_q(k-1)$
so that
![]() $i(x) \in I_j$
for all x in
$i(x) \in I_j$
for all x in
![]() $L_j$
. Now for each
$L_j$
. Now for each
![]() $j\in [q]$
and x in
$j\in [q]$
and x in
![]() $L_j$
, colour all edges between x and
$L_j$
, colour all edges between x and
![]() $Z_{i(x)}$
with colour
$Z_{i(x)}$
with colour
![]() $1$
and all edges between x and the remaining
$1$
and all edges between x and the remaining
![]() $Z_i$
arbitrarily. The number of choices in this colouring procedure is at most
$Z_i$
arbitrarily. The number of choices in this colouring procedure is at most
 $$ \begin{align*} f(\boldsymbol{m};\boldsymbol{\ell}) := &\prod_{ij\in\binom{[k-1]}{2}}2^{m_im_j}\cdot 2^{m\ell}\cdot g(\boldsymbol{m};\boldsymbol{\ell}), \quad\text{where}\quad g(\boldsymbol{m};\boldsymbol{\ell}) := \sum_{\substack{(I_1,\ldots,I_q)\\\in P_q(k-1)}}\prod_{j \in [q]}\left(\sum_{i' \in I_j}2^{-m_{i'}}\right)^{\ell_j}.\\ \end{align*} $$
$$ \begin{align*} f(\boldsymbol{m};\boldsymbol{\ell}) := &\prod_{ij\in\binom{[k-1]}{2}}2^{m_im_j}\cdot 2^{m\ell}\cdot g(\boldsymbol{m};\boldsymbol{\ell}), \quad\text{where}\quad g(\boldsymbol{m};\boldsymbol{\ell}) := \sum_{\substack{(I_1,\ldots,I_q)\\\in P_q(k-1)}}\prod_{j \in [q]}\left(\sum_{i' \in I_j}2^{-m_{i'}}\right)^{\ell_j}.\\ \end{align*} $$
We have
![]() $|\mathcal {P}(G)| \leq f(\boldsymbol {m};\boldsymbol {\ell })$
and would like an almost matching lower bound. Every colouring from the procedure above is valid so we need to check which colourings have been counted more than once. Suppose
$|\mathcal {P}(G)| \leq f(\boldsymbol {m};\boldsymbol {\ell })$
and would like an almost matching lower bound. Every colouring from the procedure above is valid so we need to check which colourings have been counted more than once. Suppose
![]() $\chi $
is a perfect colouring arising from two different choices. Let
$\chi $
is a perfect colouring arising from two different choices. Let
![]() $(I_1,\ldots ,I_q)$
and
$(I_1,\ldots ,I_q)$
and
![]() $(I_1',\ldots ,I_q')$
be the respective choices of partitions, which are necessarily different. So there are
$(I_1',\ldots ,I_q')$
be the respective choices of partitions, which are necessarily different. So there are
![]() $i \in [q]$
and
$i \in [q]$
and
![]() $s \in [k-1]$
such that
$s \in [k-1]$
such that
![]() $s \in I_i'\setminus I_i$
. But then in
$s \in I_i'\setminus I_i$
. But then in
![]() $\chi $
every edge between
$\chi $
every edge between
![]() $L_i$
and
$L_i$
and
![]() $\bigcup _{i'\in I_i \cup \{s\}}Z_{i'}$
is coloured with colour
$\bigcup _{i'\in I_i \cup \{s\}}Z_{i'}$
is coloured with colour
![]() $1$
. In other words, the number of choices for colours of edges between
$1$
. In other words, the number of choices for colours of edges between
![]() $L_i$
and
$L_i$
and
![]() $Z_1\cup \ldots \cup Z_{k-1}$
has decreased by a multiplicative factor of
$Z_1\cup \ldots \cup Z_{k-1}$
has decreased by a multiplicative factor of
![]() $2^{m_s\ell _i}$
. The number of such colourings is therefore at most
$2^{m_s\ell _i}$
. The number of such colourings is therefore at most
Thus,
Now we can state that we are done in the case
![]() $t=k-1$
and the case
$t=k-1$
and the case
![]() $t=k$
, and every part has size at least
$t=k$
, and every part has size at least
![]() $\delta n$
. Indeed, the previous inequality, the fact that
$\delta n$
. Indeed, the previous inequality, the fact that
![]() $ f(\boldsymbol {m};(\ell )) = h(\boldsymbol {m};\ell ) $
and Proposition 5.3 imply that
$ f(\boldsymbol {m};(\ell )) = h(\boldsymbol {m};\ell ) $
and Proposition 5.3 imply that
Moreover, for
![]() $3 \leq k \leq 10$
, among graphs in
$3 \leq k \leq 10$
, among graphs in
![]() $\mathcal {J}_{2(k-1)}(n)$
, the unique graph with the largest number of valid colourings is
$\mathcal {J}_{2(k-1)}(n)$
, the unique graph with the largest number of valid colourings is
![]() $J^{\ell (k,j)}(n)$
, where
$J^{\ell (k,j)}(n)$
, where
![]() $\ell (k,j)$
is in the table in Proposition 5.3(iii).
$\ell (k,j)$
is in the table in Proposition 5.3(iii).
We return to the only remaining case when
![]() $t \geq k$
and there is at least one part of size less than
$t \geq k$
and there is at least one part of size less than
![]() $\delta n$
. Write
$\delta n$
. Write
![]() $f(\boldsymbol {m};\ell )$
and
$f(\boldsymbol {m};\ell )$
and
![]() $g(\boldsymbol {m};\ell )$
for
$g(\boldsymbol {m};\ell )$
for
![]() $f(\boldsymbol {m};(\ell ))$
,
$f(\boldsymbol {m};(\ell ))$
,
![]() $g(\boldsymbol {m};(\ell ))$
, respectively. In the next series of claims, we will compare
$g(\boldsymbol {m};(\ell ))$
, respectively. In the next series of claims, we will compare
![]() $|\mathcal {P}(G)| = (1+o(1)) f(\boldsymbol {m};\boldsymbol {\ell })$
with
$|\mathcal {P}(G)| = (1+o(1)) f(\boldsymbol {m};\boldsymbol {\ell })$
with
![]() $|\mathcal {P}(G')| = (1+o(1)) f(\boldsymbol {m}';\boldsymbol {\ell }')$
, where
$|\mathcal {P}(G')| = (1+o(1)) f(\boldsymbol {m}';\boldsymbol {\ell }')$
, where
![]() $G'$
is another complete partite graph with slightly different part sizes
$G'$
is another complete partite graph with slightly different part sizes
![]() $\boldsymbol {m}',\boldsymbol {\ell }'$
, in order to gradually pin down what
$\boldsymbol {m}',\boldsymbol {\ell }'$
, in order to gradually pin down what
![]() $\boldsymbol {m}$
and
$\boldsymbol {m}$
and
![]() $\boldsymbol {\ell }$
must be. The first of these claims states that merging small parts does not decrease the number of perfect colourings. (This is not yet sufficient for us to conclude that extremal graphs always have a single small part, as for this, the number of perfect colourings would need to increase by a factor
$\boldsymbol {\ell }$
must be. The first of these claims states that merging small parts does not decrease the number of perfect colourings. (This is not yet sufficient for us to conclude that extremal graphs always have a single small part, as for this, the number of perfect colourings would need to increase by a factor
![]() $1+\Omega (1)$
.)
$1+\Omega (1)$
.)
Claim 5.4.2. If
![]() $q \geq 2$
, then
$q \geq 2$
, then
![]() $g(\boldsymbol {m};\ell ) \geq g(\boldsymbol {m};\ell _1,\ldots ,\ell _q) + 2^{-m_{k-1}\ell }$
, so
$g(\boldsymbol {m};\ell ) \geq g(\boldsymbol {m};\ell _1,\ldots ,\ell _q) + 2^{-m_{k-1}\ell }$
, so
![]() $f(\boldsymbol {m};\ell )\geq f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$
.
$f(\boldsymbol {m};\ell )\geq f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$
.
Proof of Claim
If we obtain
![]() $G'$
from G by merging
$G'$
from G by merging
![]() $L_1,\ldots ,L_q$
to obtain a single part L, then the number of perfect colourings increases. Indeed, let
$L_1,\ldots ,L_q$
to obtain a single part L, then the number of perfect colourings increases. Indeed, let
![]() $x \in L_1$
and
$x \in L_1$
and
![]() $y \in L_2$
, say. In G, the number of valid choices of
$y \in L_2$
, say. In G, the number of valid choices of
![]() $(i(x),i(y))$
is strictly less than the number in
$(i(x),i(y))$
is strictly less than the number in
![]() $G'$
, since
$G'$
, since
![]() $i(x) \neq i(y)$
in G, while there is no such restriction in
$i(x) \neq i(y)$
in G, while there is no such restriction in
![]() $G'$
. More precisely, the
$G'$
. More precisely, the
![]() $(I_1,\ldots ,I_q)$
term in g corresponds to all the colourings that come from choosing
$(I_1,\ldots ,I_q)$
term in g corresponds to all the colourings that come from choosing
![]() $i(x) \in I_i$
for all
$i(x) \in I_i$
for all
![]() $i \in [q]$
and
$i \in [q]$
and
![]() $x \in L_i$
. In
$x \in L_i$
. In
![]() $G'$
, we can choose
$G'$
, we can choose
![]() $i(x)=k-1$
for all
$i(x)=k-1$
for all
![]() $x \in L$
, giving the new term
$x \in L$
, giving the new term
![]() $2^{-m_{k-1}\ell }$
.
$2^{-m_{k-1}\ell }$
.
In the next three claims, we assume that G has one small part of size
![]() $\ell $
. Write
$\ell $
. Write
![]() $m_1\geq \ldots \geq m_{k-1}$
for its other parts and let
$m_1\geq \ldots \geq m_{k-1}$
for its other parts and let
![]() $a_i := m_i-m_{k-1}$
for all
$a_i := m_i-m_{k-1}$
for all
![]() $i \in [k-1]$
. By (5.6), as in the proof of Proposition 5.3, to compare the number of perfect colourings of G with another complete partite graph
$i \in [k-1]$
. By (5.6), as in the proof of Proposition 5.3, to compare the number of perfect colourings of G with another complete partite graph
![]() $G'$
with a single small part of size
$G'$
with a single small part of size
![]() $\ell '$
and large parts of size
$\ell '$
and large parts of size
![]() $m_1',\ldots ,m_{k-1}'$
, it suffices to compare their associated functions
$m_1',\ldots ,m_{k-1}'$
, it suffices to compare their associated functions
![]() $\tilde {h}(\boldsymbol {a};\ell ),\tilde {h}(\boldsymbol {a}',\ell ')$
defined in (5.2), where
$\tilde {h}(\boldsymbol {a};\ell ),\tilde {h}(\boldsymbol {a}',\ell ')$
defined in (5.2), where
![]() $\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$
, and
$\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$
, and
![]() $\boldsymbol {a}'=(a_1',\ldots ,a_{k-1}')$
is chosen so that
$\boldsymbol {a}'=(a_1',\ldots ,a_{k-1}')$
is chosen so that
![]() $\sum _i a_i +\ell = \sum _i a_i' + \ell '$
. (Note that in Proposition 5.3, we defined
$\sum _i a_i +\ell = \sum _i a_i' + \ell '$
. (Note that in Proposition 5.3, we defined
![]() $b_i := m_i-\lfloor \frac {n}{k-1}\rfloor $
, whereas here it is convenient to define
$b_i := m_i-\lfloor \frac {n}{k-1}\rfloor $
, whereas here it is convenient to define
![]() $a_i = m_i-m_{k-1}$
so that
$a_i = m_i-m_{k-1}$
so that
![]() $a_1 \geq \ldots \geq a_{k-1}=0$
.) The next claim concludes the proof in the case when
$a_1 \geq \ldots \geq a_{k-1}=0$
.) The next claim concludes the proof in the case when
![]() $\ell $
is large and not every
$\ell $
is large and not every
![]() $a_1,\ldots ,a_{k-2}$
is comparable with
$a_1,\ldots ,a_{k-2}$
is comparable with
![]() $\ell $
.
$\ell $
.
Claim 5.4.3. Suppose
![]() $q=1$
. If
$q=1$
. If
![]() $a_{k-2} \leq (\ell -1)/2$
and
$a_{k-2} \leq (\ell -1)/2$
and
![]() $\ell \geq \min \{13,2k-2\}$
, then there exists an n-vertex graph
$\ell \geq \min \{13,2k-2\}$
, then there exists an n-vertex graph
![]() $G'$
with
$G'$
with
![]() $|\mathcal {P}(G')|> 1.01|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')|> 1.01|\mathcal {P}(G)|$
.
Proof of Claim
Subtract
![]() $1$
from
$1$
from
![]() $\ell $
and add
$\ell $
and add
![]() $1$
to
$1$
to
![]() $a_{k-2}$
, letting
$a_{k-2}$
, letting
![]() $\boldsymbol {a}^{(1)} := (a_1,\ldots ,a_{k-2}+1,a_{k-1})$
. We let
$\boldsymbol {a}^{(1)} := (a_1,\ldots ,a_{k-2}+1,a_{k-1})$
. We let
![]() $G'$
be the complete partite graph with large parts of size
$G'$
be the complete partite graph with large parts of size
![]() $(m_{k-1},\ldots ,m_{k-1})+\boldsymbol {a}^{(1)}$
and one small part of size
$(m_{k-1},\ldots ,m_{k-1})+\boldsymbol {a}^{(1)}$
and one small part of size
![]() $\ell -1$
. Then
$\ell -1$
. Then
 $$ \begin{align} (1+o(1))\frac{|\mathcal{P}(G')|}{|\mathcal{P}(G)|} = \frac{\tilde{h}(\boldsymbol{a}^{(1)};\ell-1)}{\tilde{h}(\boldsymbol{a};\ell)} = \frac{2^{\ell-a_{k-2}-1}(2^{-a_1}+\ldots + \frac{1}{2}\cdot2^{-a_{k-2}} + 1)^{\ell-1}}{(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}}. \end{align} $$
$$ \begin{align} (1+o(1))\frac{|\mathcal{P}(G')|}{|\mathcal{P}(G)|} = \frac{\tilde{h}(\boldsymbol{a}^{(1)};\ell-1)}{\tilde{h}(\boldsymbol{a};\ell)} = \frac{2^{\ell-a_{k-2}-1}(2^{-a_1}+\ldots + \frac{1}{2}\cdot2^{-a_{k-2}} + 1)^{\ell-1}}{(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}}. \end{align} $$
Now, for
![]() $y>0$
and
$y>0$
and
![]() $0 < x \leq 1$
, let
$0 < x \leq 1$
, let
 $$ \begin{align*}f(x,y) := \frac{(y+\frac{x}{2}+1)^{\ell-1}}{(y+x+1)^\ell},\quad\text{then}\quad \frac{\partial f}{\partial x} = -\frac{2(y+\frac{x}{2}+1)^{\ell}((\ell+1)(y+1)+x)}{(y+x+1)^{\ell+1}(2(y+1)+x)^2}, \end{align*} $$
$$ \begin{align*}f(x,y) := \frac{(y+\frac{x}{2}+1)^{\ell-1}}{(y+x+1)^\ell},\quad\text{then}\quad \frac{\partial f}{\partial x} = -\frac{2(y+\frac{x}{2}+1)^{\ell}((\ell+1)(y+1)+x)}{(y+x+1)^{\ell+1}(2(y+1)+x)^2}, \end{align*} $$
so f is decreasing in x, and hence,
![]() $f(x,y) \geq f(1,y) = (y+\frac {3}{2})^{\ell -1}/(y+2)^\ell $
. Also,
$f(x,y) \geq f(1,y) = (y+\frac {3}{2})^{\ell -1}/(y+2)^\ell $
. Also,
 $$ \begin{align*}\frac{\partial f(1,y)}{\partial y}= -\frac{(y-\frac{\ell}{2}+2)(y+\frac{3}{2})^{\ell-2}}{(y+2)^{\ell+1}} \end{align*} $$
$$ \begin{align*}\frac{\partial f(1,y)}{\partial y}= -\frac{(y-\frac{\ell}{2}+2)(y+\frac{3}{2})^{\ell-2}}{(y+2)^{\ell+1}} \end{align*} $$
so
![]() $f(1,y)$
is increasing from
$f(1,y)$
is increasing from
![]() $y=0$
to
$y=0$
to
![]() $y=\frac {\ell }{2}-2 \geq k-3$
. Thus, for
$y=\frac {\ell }{2}-2 \geq k-3$
. Thus, for
![]() $0 \leq y \leq k-3$
, we have
$0 \leq y \leq k-3$
, we have
![]() $f(1,y) \geq f(1,0) = (\frac {3}{2})^{\ell -1}/2^\ell = \frac {1}{2}\left (\frac {3}{4}\right )^{\ell -1}$
. Since
$f(1,y) \geq f(1,0) = (\frac {3}{2})^{\ell -1}/2^\ell = \frac {1}{2}\left (\frac {3}{4}\right )^{\ell -1}$
. Since
![]() $2^{-a_1}+\ldots +2^{-a_{k-3}} \leq k-3$
, and
$2^{-a_1}+\ldots +2^{-a_{k-3}} \leq k-3$
, and
![]() $\ell \geq 13$
, we see that (5.8) is at least
$\ell \geq 13$
, we see that (5.8) is at least
 $$ \begin{align*}2^{\ell-a_{k-2}-1} \cdot \frac{1}{2}\left(\frac{3}{4}\right)^{\ell-1} \geq \frac{1}{2}\left(\frac{\sqrt{2}\cdot 3}{4}\right)^{\ell-1}> 1.013, \end{align*} $$
$$ \begin{align*}2^{\ell-a_{k-2}-1} \cdot \frac{1}{2}\left(\frac{3}{4}\right)^{\ell-1} \geq \frac{1}{2}\left(\frac{\sqrt{2}\cdot 3}{4}\right)^{\ell-1}> 1.013, \end{align*} $$
completing the proof of the claim.
Claim 5.4.4. Suppose
![]() $q=1$
. If
$q=1$
. If
![]() $a_{k-2} \geq \ell /2$
and
$a_{k-2} \geq \ell /2$
and
![]() $\ell \geq \max \{14,2k-2\}$
, then there exists an n-vertex graph
$\ell \geq \max \{14,2k-2\}$
, then there exists an n-vertex graph
![]() $G'$
with
$G'$
with
![]() $|\mathcal {P}(G')|> 1.05|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')|> 1.05|\mathcal {P}(G)|$
.
Proof of Claim
Let
![]() $A := \{a_1,\ldots ,a_{k-2},\ell \}$
and
$A := \{a_1,\ldots ,a_{k-2},\ell \}$
and
![]() $b := \sum _{u \in A}u$
. Then, recalling
$b := \sum _{u \in A}u$
. Then, recalling
![]() $a_{k-1}=0$
,
$a_{k-1}=0$
,
 $$ \begin{align*} \tilde{h}(\boldsymbol{a};\ell) \stackrel{({5.2})}{=} \prod_{uu' \in \binom{A}{2}}2^{uu'}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq 2^{t_{k-1}(b)}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}. \end{align*} $$
$$ \begin{align*} \tilde{h}(\boldsymbol{a};\ell) \stackrel{({5.2})}{=} \prod_{uu' \in \binom{A}{2}}2^{uu'}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq 2^{t_{k-1}(b)}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell}. \end{align*} $$
Note that
 $$ \begin{align*}t_{k-1}(n) = t_{k-1}((k-1)m_{k-1}+b)=\binom{k-1}{2}m_{k-1}^2+(k-2)m_{k-1}b+t_{k-1}(b). \end{align*} $$
$$ \begin{align*}t_{k-1}(n) = t_{k-1}((k-1)m_{k-1}+b)=\binom{k-1}{2}m_{k-1}^2+(k-2)m_{k-1}b+t_{k-1}(b). \end{align*} $$
Thus,
![]() $(1+o(1))|\mathcal {P}(G)| = h(\boldsymbol {m};\ell ) \leq 2^{t_{k-1}(n)}\cdot (2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell }$
. But
$(1+o(1))|\mathcal {P}(G)| = h(\boldsymbol {m};\ell ) \leq 2^{t_{k-1}(n)}\cdot (2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell }$
. But
 $$ \begin{align*}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq ((k-2)2^{-a_{k-2}}+1)^{\ell} \leq \left(\left(\frac{\ell}{2}-1\right)\cdot2^{-\ell/2}+1\right)^\ell. \end{align*} $$
$$ \begin{align*}(2^{-a_1}+\ldots + 2^{-a_{k-2}} + 1)^{\ell} \leq ((k-2)2^{-a_{k-2}}+1)^{\ell} \leq \left(\left(\frac{\ell}{2}-1\right)\cdot2^{-\ell/2}+1\right)^\ell. \end{align*} $$
This is less than
![]() $1.9$
for
$1.9$
for
![]() $\ell \geq 14$
. Equation (5.7) implies the existence of
$\ell \geq 14$
. Equation (5.7) implies the existence of
![]() $G'$
with
$G'$
with
![]() $|\mathcal {P}(G')| = (2+o(1))\cdot 2^{t_{k-1}(n)}$
, and further,
$|\mathcal {P}(G')| = (2+o(1))\cdot 2^{t_{k-1}(n)}$
, and further,
![]() $2/1.9> 1.052$
.
$2/1.9> 1.052$
.
The next claim implies that
![]() $a_1$
, and hence, all of
$a_1$
, and hence, all of
![]() $a_1,\ldots ,a_{k-1}$
cannot be much bigger than
$a_1,\ldots ,a_{k-1}$
cannot be much bigger than
![]() $\ell $
.
$\ell $
.
Claim 5.4.5. Suppose
![]() $q=1$
. If
$q=1$
. If
![]() $a_1 \geq \ell +2$
, then there is an n-vertex graph
$a_1 \geq \ell +2$
, then there is an n-vertex graph
![]() $G'$
with
$G'$
with
![]() $|\mathcal {P}(G')|> 1.9|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')|> 1.9|\mathcal {P}(G)|$
.
Proof of Claim
Suppose that
![]() $a_1 \geq \ell +2$
. Let
$a_1 \geq \ell +2$
. Let
![]() $\boldsymbol {a}^{(2)} := (a_1-1,a_2,\ldots ,a_{k-2},a_{k-1}+1)$
. Then, recalling
$\boldsymbol {a}^{(2)} := (a_1-1,a_2,\ldots ,a_{k-2},a_{k-1}+1)$
. Then, recalling
![]() $a_{k-1}=0$
,
$a_{k-1}=0$
,
 $$ \begin{align*}\frac{\tilde{h}(\boldsymbol{a}^{(2)};\ell)}{\tilde{h}(\boldsymbol{a};\ell)} = 2^{a_1-1}\left(\frac{2\cdot 2^{-a_1}+2^{-a_2}+\ldots +2^{-a_{k-2}}+\frac{1}{2}\cdot 2^{-a_{k-1}}}{2^{-a_1}+\ldots + 2^{-a_{k-1}}}\right)^\ell \geq 2^{a_1-1-\ell} \geq 2, \end{align*} $$
$$ \begin{align*}\frac{\tilde{h}(\boldsymbol{a}^{(2)};\ell)}{\tilde{h}(\boldsymbol{a};\ell)} = 2^{a_1-1}\left(\frac{2\cdot 2^{-a_1}+2^{-a_2}+\ldots +2^{-a_{k-2}}+\frac{1}{2}\cdot 2^{-a_{k-1}}}{2^{-a_1}+\ldots + 2^{-a_{k-1}}}\right)^\ell \geq 2^{a_1-1-\ell} \geq 2, \end{align*} $$
since we can lower bound the numerator by
![]() $\frac {1}{2}\sum _{i \in [k-1]}2^{-a_i}$
.
$\frac {1}{2}\sum _{i \in [k-1]}2^{-a_i}$
.
Claim 5.4.6. There is a positive function p of k such that the following holds. If
![]() $a_1,\ldots ,a_{k-1},\ell = O_k(1)$
and
$a_1,\ldots ,a_{k-1},\ell = O_k(1)$
and
![]() $q \geq 2$
, then the graph
$q \geq 2$
, then the graph
![]() $G'$
obtained by merging
$G'$
obtained by merging
![]() $L_1,\ldots ,L_q$
has
$L_1,\ldots ,L_q$
has
![]() $|\mathcal {P}(G')|>(1+p(k))|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')|>(1+p(k))|\mathcal {P}(G)|$
.
Proof of Claim
It suffices to show that there is
![]() $a=a(k)$
such that
$a=a(k)$
such that
![]() $f(\boldsymbol {m};\ell ) \geq (1+a)f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$
. We have
$f(\boldsymbol {m};\ell ) \geq (1+a)f(\boldsymbol {m};\ell _1,\ldots ,\ell _q)$
. We have
![]() $g(\boldsymbol {m};\boldsymbol {\ell }) = 2^{-m_{k-1}\ell }g(\boldsymbol {a};\boldsymbol {\ell })$
, where
$g(\boldsymbol {m};\boldsymbol {\ell }) = 2^{-m_{k-1}\ell }g(\boldsymbol {a};\boldsymbol {\ell })$
, where
![]() $\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$
satisfies
$\boldsymbol {a}=(a_1,\ldots ,a_{k-1})$
satisfies
![]() $a_i=m_i-m_{k-1}$
, so
$a_i=m_i-m_{k-1}$
, so
![]() $0 \leq a_i = O_k(1)$
for all i. Since also
$0 \leq a_i = O_k(1)$
for all i. Since also
![]() $\ell = O_k(1)$
, we have
$\ell = O_k(1)$
, we have
![]() $g(\boldsymbol {a};\boldsymbol {\ell })=p_0(k)$
for some positive function
$g(\boldsymbol {a};\boldsymbol {\ell })=p_0(k)$
for some positive function
![]() $p_0$
of k. We have
$p_0$
of k. We have
![]() $g(\boldsymbol {a};\ell )\geq g(\boldsymbol {a};\boldsymbol {\ell }) + 1$
by Claim 5.4.2, so
$g(\boldsymbol {a};\ell )\geq g(\boldsymbol {a};\boldsymbol {\ell }) + 1$
by Claim 5.4.2, so
as required.
Claim 5.4.7. If
![]() $q=1$
and
$q=1$
and
![]() $\ell =1$
and
$\ell =1$
and
![]() $k \geq 4$
, then the graph
$k \geq 4$
, then the graph
![]() $G'$
obtained by moving one vertex from
$G'$
obtained by moving one vertex from
![]() $Z_1$
to
$Z_1$
to
![]() $L=L_1$
has
$L=L_1$
has
![]() $|\mathcal {P}(G')|>1.9|\mathcal {P}(G)|$
.
$|\mathcal {P}(G')|>1.9|\mathcal {P}(G)|$
.
Proof of Claim
Let
![]() $\boldsymbol {a}^{(3)}:= (a_1-1,a_2,\ldots ,a_{k-1})$
. Then
$\boldsymbol {a}^{(3)}:= (a_1-1,a_2,\ldots ,a_{k-1})$
. Then
 $$ \begin{align*} \frac{\tilde{h}(\boldsymbol{a}^{(3)};2)}{\tilde{h}(\boldsymbol{a};1)} &\geq \frac{2^{a_1-2}\left(2\cdot 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}\right)^2}{ 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}} \geq 2^{-1} + 2^{a_1-a_1-2}+\ldots + 2^{a_1-a_{k-1}-2}\\ &\geq \frac{1}{2}+\frac{k-1}{4} \geq \frac{5}{4}, \end{align*} $$
$$ \begin{align*} \frac{\tilde{h}(\boldsymbol{a}^{(3)};2)}{\tilde{h}(\boldsymbol{a};1)} &\geq \frac{2^{a_1-2}\left(2\cdot 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}\right)^2}{ 2^{-a_1}+2^{-a_2}+\ldots + 2^{-a_{k-1}}} \geq 2^{-1} + 2^{a_1-a_1-2}+\ldots + 2^{a_1-a_{k-1}-2}\\ &\geq \frac{1}{2}+\frac{k-1}{4} \geq \frac{5}{4}, \end{align*} $$
where the second inequality follows by expanding
![]() $(2^{-a_1}+\sum _{i \in [k-1]}2^{-a_i})^2$
.
$(2^{-a_1}+\sum _{i \in [k-1]}2^{-a_i})^2$
.
To complete the proof of Lemma 5.4, assume that
![]() $G \notin \mathcal {J}_{2(k-1)}(n)$
. We will find an n-vertex graph
$G \notin \mathcal {J}_{2(k-1)}(n)$
. We will find an n-vertex graph
![]() $G'$
with
$G'$
with
![]() $F(G';k+1,k)>F(G;k+1,k)$
. Let
$F(G';k+1,k)>F(G;k+1,k)$
. Let
![]() $m_1,\ldots ,m_{k-1}$
be the large parts and
$m_1,\ldots ,m_{k-1}$
be the large parts and
![]() $\ell _1,\ldots ,\ell _q$
be the small parts of G. Let
$\ell _1,\ldots ,\ell _q$
be the small parts of G. Let
![]() $a_i := m_i-m_{k-1}$
for all
$a_i := m_i-m_{k-1}$
for all
![]() $i \in [k-1]$
. Obtain
$i \in [k-1]$
. Obtain
![]() $G_0$
by merging
$G_0$
by merging
![]() $L_1,\ldots ,L_q$
and let
$L_1,\ldots ,L_q$
and let
![]() $\ell := \ell _1+\ldots +\ell _q$
.
$\ell := \ell _1+\ldots +\ell _q$
.
By Claim 5.4.2, we have that
![]() $|\mathcal {P}(G_0)| \geq (1+o(1))|\mathcal {P}(G)|$
. Suppose
$|\mathcal {P}(G_0)| \geq (1+o(1))|\mathcal {P}(G)|$
. Suppose
![]() $\ell \geq \max \{14,2k-2\}$
. Then Claims 5.4.3 and 5.4.4 imply that there is an n-vertex graph
$\ell \geq \max \{14,2k-2\}$
. Then Claims 5.4.3 and 5.4.4 imply that there is an n-vertex graph
![]() $G'$
such that
$G'$
such that
![]() $|\mathcal {P}(G)|<(1+o(1))|\mathcal {P}(G_0)|<(1+o(1))\frac {1}{1.01}\cdot |\mathcal {P}(G')|$
, as required. Thus, we may suppose instead that
$|\mathcal {P}(G)|<(1+o(1))|\mathcal {P}(G_0)|<(1+o(1))\frac {1}{1.01}\cdot |\mathcal {P}(G')|$
, as required. Thus, we may suppose instead that
![]() $\ell < \max \{14,2k-2\}$
.
$\ell < \max \{14,2k-2\}$
.
Suppose further that
![]() $a_1 \geq \ell +2$
. Then Claim 5.4.5 implies that there is an n-vertex graph
$a_1 \geq \ell +2$
. Then Claim 5.4.5 implies that there is an n-vertex graph
![]() $G'$
such that
$G'$
such that
![]() $|\mathcal {P}(G)| < (1+o(1))|\mathcal {P}(G_0)| < \frac {1}{1.8}\cdot |\mathcal {P}(G')|$
. So we may suppose that
$|\mathcal {P}(G)| < (1+o(1))|\mathcal {P}(G_0)| < \frac {1}{1.8}\cdot |\mathcal {P}(G')|$
. So we may suppose that
![]() $\max \{14,2k-2\} \geq \ell +1 \geq a_1 \geq \ldots \geq a_{k-2} \geq a_{k-1}=0$
.
$\max \{14,2k-2\} \geq \ell +1 \geq a_1 \geq \ldots \geq a_{k-2} \geq a_{k-1}=0$
.
Suppose
![]() $q \geq 2$
. Then Claim 5.4.6 implies that
$q \geq 2$
. Then Claim 5.4.6 implies that
![]() $|\mathcal {P}(G_0)|>(1+p(k))|\mathcal {P}(G)|$
for some positive function p. So we may suppose that
$|\mathcal {P}(G_0)|>(1+p(k))|\mathcal {P}(G)|$
for some positive function p. So we may suppose that
![]() $q=1$
. Suppose now
$q=1$
. Suppose now
![]() $\ell =1$
. Claim 5.4.7 furnishes us with the required
$\ell =1$
. Claim 5.4.7 furnishes us with the required
![]() $G'$
when
$G'$
when
![]() $k \geq 4$
.
$k \geq 4$
.
If
![]() $k \geq 8$
, then we have that
$k \geq 8$
, then we have that
![]() $14 \leq 2k-2$
and of course
$14 \leq 2k-2$
and of course
![]() $k \geq 4$
, so, in fact, Claim 5.4.7 implies that
$k \geq 4$
, so, in fact, Claim 5.4.7 implies that
![]() $q=1$
,
$q=1$
,
![]() $\ell \geq 2$
and
$\ell \geq 2$
and
![]() $2k-2 \geq \ell ,a_1,\ldots ,a_{k-1}$
, which is a contradiction since
$2k-2 \geq \ell ,a_1,\ldots ,a_{k-1}$
, which is a contradiction since
![]() $G \notin \mathcal {J}_{2(k-1)}(n)$
. Thus, we have
$G \notin \mathcal {J}_{2(k-1)}(n)$
. Thus, we have
![]() $k \leq 7$
and
$k \leq 7$
and
![]() $14 \geq \ell ,a_1,\ldots ,a_{k-1}$
. Here, one can use the same program as in the proof of Proposition 5.3(iii) with tweaked parameters to obtain that in every case there is
$14 \geq \ell ,a_1,\ldots ,a_{k-1}$
. Here, one can use the same program as in the proof of Proposition 5.3(iii) with tweaked parameters to obtain that in every case there is
![]() $G'$
with large part differences
$G'$
with large part differences
![]() $a_1',\ldots ,a_{k-1}'$
such that
$a_1',\ldots ,a_{k-1}'$
such that
![]() $a_1' \leq 1$
and
$a_1' \leq 1$
and
![]() $\ell '$
is as in the table there, such that
$\ell '$
is as in the table there, such that
![]() $\tilde {h}(\boldsymbol {a}';\ell ')> \tilde {h}(\boldsymbol {a};\ell ) + \Omega (1)$
, since
$\tilde {h}(\boldsymbol {a}';\ell ')> \tilde {h}(\boldsymbol {a};\ell ) + \Omega (1)$
, since
![]() $G \neq G'$
.
$G \neq G'$
.
We derive Theorem 5.2 from Lemma 5.4 using the same approach as [Reference Pikhurko and Yilma12].
Proof of Theorem 5.2
We want to show that
which implies the same equality holds for
![]() $F(J;k+1,k)$
by the arguments in the proof of Lemma 5.4. For this, start with
$F(J;k+1,k)$
by the arguments in the proof of Lemma 5.4. For this, start with
![]() $T_{k-1}(n)$
with vertex partition
$T_{k-1}(n)$
with vertex partition
![]() $Y_1,\ldots ,Y_{k-1},Y_k=\emptyset $
. Consider moves where each time we move one vertex between parts. One can obtain J in
$Y_1,\ldots ,Y_{k-1},Y_k=\emptyset $
. Consider moves where each time we move one vertex between parts. One can obtain J in
![]() $O(k^2)$
moves, between large parts or from a large part to the small part
$O(k^2)$
moves, between large parts or from a large part to the small part
![]() $Y_k$
. Each move changes F by a multiplicative factor of
$Y_k$
. Each move changes F by a multiplicative factor of
![]() $O_k(1)$
(we already did the calculations in Claims 5.4.5 and 5.4.7). This proves (5.9).
$O_k(1)$
(we already did the calculations in Claims 5.4.5 and 5.4.7). This proves (5.9).
Apply Lemma 5.4 to obtain
![]() ${\varepsilon },n_0$
. We may assume that
${\varepsilon },n_0$
. We may assume that
![]() $1/n_0 \ll {\varepsilon } \ll 1$
. Let
$1/n_0 \ll {\varepsilon } \ll 1$
. Let
![]() $N := n_0^2$
. Let G be a
$N := n_0^2$
. Let G be a
![]() $(k+1,k)$
-extremal graph on
$(k+1,k)$
-extremal graph on
![]() $n \geq N$
vertices. Suppose, for a contradiction, that
$n \geq N$
vertices. Suppose, for a contradiction, that
![]() $G \not \in \mathcal {J}_{2(k-1)}(n)$
. Let
$G \not \in \mathcal {J}_{2(k-1)}(n)$
. Let
![]() $G_n := G$
. If
$G_n := G$
. If
![]() $G_n$
is not a complete multipartite graph, apply Lemma 2.14 to obtain a graph
$G_n$
is not a complete multipartite graph, apply Lemma 2.14 to obtain a graph
![]() $H_n$
on n vertices which is
$H_n$
on n vertices which is
![]() $(k+1,k)$
-extremal and complete multipartite, with a part of size
$(k+1,k)$
-extremal and complete multipartite, with a part of size
![]() $1$
and let
$1$
and let
![]() $G_n := H_n$
. Observe that in both cases,
$G_n := H_n$
. Observe that in both cases,
![]() $G_n \not \in \mathcal {J}_{2(k-1)}(n)$
. We iteratively apply the following procedure. Let
$G_n \not \in \mathcal {J}_{2(k-1)}(n)$
. We iteratively apply the following procedure. Let
![]() $G_m$
be the current graph on
$G_m$
be the current graph on
![]() $m \geq n_0+2$
vertices with
$m \geq n_0+2$
vertices with
![]() $\log F(G_m;k+1,k) \geq \left ( \frac {k-2}{k-1}-{\varepsilon } \right )\binom {m}{2}$
and apply Lemma 5.4. If (5.3) fails for some
$\log F(G_m;k+1,k) \geq \left ( \frac {k-2}{k-1}-{\varepsilon } \right )\binom {m}{2}$
and apply Lemma 5.4. If (5.3) fails for some
![]() $x \in V(G_m)$
, we let
$x \in V(G_m)$
, we let
![]() $G_{m-1} := G_m-x$
, decrease m by
$G_{m-1} := G_m-x$
, decrease m by
![]() $1$
, and repeat. Similarly, if (5.3) fails for some pair
$1$
, and repeat. Similarly, if (5.3) fails for some pair
![]() $y,z \in V(G_m)$
, we let
$y,z \in V(G_m)$
, we let
![]() $G_{m-2} := G_m-y-z$
, decrease m by
$G_{m-2} := G_m-y-z$
, decrease m by
![]() $2$
, and repeat. Note that
$2$
, and repeat. Note that
 $$ \begin{align*}\log F(G_{m-1};k+1,k) \geq \log F(G_m;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)m \geq \left(\frac{k-2}{k-1}-2{\varepsilon} \right)\left(\binom{m}{2}-m\right). \end{align*} $$
$$ \begin{align*}\log F(G_{m-1};k+1,k) \geq \log F(G_m;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)m \geq \left(\frac{k-2}{k-1}-2{\varepsilon} \right)\left(\binom{m}{2}-m\right). \end{align*} $$
If (5.3) holds for all
![]() $x \in V(G)$
and pairs
$x \in V(G)$
and pairs
![]() $y,z \in V(G)$
, but
$y,z \in V(G)$
, but
![]() $G_{m} \not \in \mathcal {J}_{2(k-1)}(m)$
, then we replace
$G_{m} \not \in \mathcal {J}_{2(k-1)}(m)$
, then we replace
![]() $G_m$
by the graph
$G_m$
by the graph
![]() $G'$
returned by Lemma 5.4 and repeat the step (without decreasing m). Recall that
$G'$
returned by Lemma 5.4 and repeat the step (without decreasing m). Recall that
![]() $G'$
has strictly more valid colourings than
$G'$
has strictly more valid colourings than
![]() $G_m$
. Note that for every m for which
$G_m$
. Note that for every m for which
![]() $G_m$
is defined, we have
$G_m$
is defined, we have
 $$ \begin{align*}\log F(G_m;k+1,k) \geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$
$$ \begin{align*}\log F(G_m;k+1,k) \geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$
It follows that we never reach
![]() $m \leq n_0$
for otherwise, when this happens for the first time, we get that
$m \leq n_0$
for otherwise, when this happens for the first time, we get that
 $$ \begin{align*} \log F(G_m;k+1,k) &\geq \left(\frac{k-2}{k-1}-{\varepsilon}\right)\binom{n}{2} - \left(\frac{k-2}{k-1}-2{\varepsilon}\right)\left(\binom{n+1}{2}-\binom{m+1}{2}\right)\\ &\geq {\varepsilon}\binom{n}{2} + \left( \frac{k-2}{k-1}-2{\varepsilon} \right)\binom{m}{2}> \binom{m}{2} \end{align*} $$
$$ \begin{align*} \log F(G_m;k+1,k) &\geq \left(\frac{k-2}{k-1}-{\varepsilon}\right)\binom{n}{2} - \left(\frac{k-2}{k-1}-2{\varepsilon}\right)\left(\binom{n+1}{2}-\binom{m+1}{2}\right)\\ &\geq {\varepsilon}\binom{n}{2} + \left( \frac{k-2}{k-1}-2{\varepsilon} \right)\binom{m}{2}> \binom{m}{2} \end{align*} $$
(i.e.,
![]() $F(m;k+1,k)> 2^{\binom {m}{2}}$
), a contradiction. Thus, we stop for some
$F(m;k+1,k)> 2^{\binom {m}{2}}$
), a contradiction. Thus, we stop for some
![]() $m \geq n_0+2$
, with
$m \geq n_0+2$
, with
![]() $G_m \in \mathcal {J}_{2(k-1)}(m)$
. We cannot have
$G_m \in \mathcal {J}_{2(k-1)}(m)$
. We cannot have
![]() $m=n$
, for otherwise, any
$m=n$
, for otherwise, any
![]() $J_n \in \mathcal {J}_{2(k-1)}(n)$
has more colourings than G by Lemma 5.4. So
$J_n \in \mathcal {J}_{2(k-1)}(n)$
has more colourings than G by Lemma 5.4. So
![]() $m \leq n-1$
. Almost every colouring of
$m \leq n-1$
. Almost every colouring of
![]() $G_m := J_m \in \mathcal {J}_{2(k-1)}(m)$
is perfect. Thus,
$G_m := J_m \in \mathcal {J}_{2(k-1)}(m)$
is perfect. Thus,
 $$ \begin{align*} 1+\log |\mathcal{P}(J_m)| &> \log F(J_m;k+1,k)\\ &\geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$
$$ \begin{align*} 1+\log |\mathcal{P}(J_m)| &> \log F(J_m;k+1,k)\\ &\geq \log F(G;k+1,k) - \left(\frac{k-2}{k-1} - 2{\varepsilon} \right)\left(n+(n-1)+\ldots+(m+1)\right). \end{align*} $$
Since
![]() $t_{k-1}(\ell )-t_{k-1}(\ell -1)=\lfloor \frac {k-2}{k-1}\ell \rfloor $
, (5.9) implies that there is some constant
$t_{k-1}(\ell )-t_{k-1}(\ell -1)=\lfloor \frac {k-2}{k-1}\ell \rfloor $
, (5.9) implies that there is some constant
![]() $C_k>0$
such that
$C_k>0$
such that
![]() $|\mathcal {P}(J_\ell )| \geq C_k \cdot 2^{\frac {k-2}{k-1}\ell -1}|\mathcal {P}(J_{\ell -1})|$
for all
$|\mathcal {P}(J_\ell )| \geq C_k \cdot 2^{\frac {k-2}{k-1}\ell -1}|\mathcal {P}(J_{\ell -1})|$
for all
![]() $\ell \geq n_0$
and all
$\ell \geq n_0$
and all
![]() $J_\ell \in \mathcal {J}_{2(k-1)}(\ell )$
,
$J_\ell \in \mathcal {J}_{2(k-1)}(\ell )$
,
![]() $J_{\ell -1}\in \mathcal {J}_{2(k-1)}(\ell -1)$
. Thus,
$J_{\ell -1}\in \mathcal {J}_{2(k-1)}(\ell -1)$
. Thus,
Together with the previous displayed equation, this is a contradiction to
![]() $m \leq n-1$
. Thus,
$m \leq n-1$
. Thus,
![]() ${G \in \mathcal {J}_{2(k-1)}(n)}$
.
${G \in \mathcal {J}_{2(k-1)}(n)}$
.
6. Concluding remarks
6.1. The uniform problem
Consider
![]() $\boldsymbol {k}=(k;s)$
. In this paper, we obtained an exact result for
$\boldsymbol {k}=(k;s)$
. In this paper, we obtained an exact result for
![]() $(3;7)$
and a new proof for
$(3;7)$
and a new proof for
![]() $(3;6)$
. For general
$(3;6)$
. For general
![]() $(k;s)$
, it seems reasonable to expect every
$(k;s)$
, it seems reasonable to expect every
![]() $(r,\phi ,\boldsymbol {\alpha })$
to be such that
$(r,\phi ,\boldsymbol {\alpha })$
to be such that
![]() $(k-1)|r$
,
$(k-1)|r$
,
![]() $\boldsymbol {\alpha }$
is uniform and every
$\boldsymbol {\alpha }$
is uniform and every
![]() $\phi ^{-1}(c) \cong T_{k-1}(r)$
. If this were so, then for distinct
$\phi ^{-1}(c) \cong T_{k-1}(r)$
. If this were so, then for distinct
![]() $c,c'\in [s]$
,
$c,c'\in [s]$
,
![]() $\phi ^{-1}(c) \cup \phi ^{-1}(c')$
would have at most
$\phi ^{-1}(c) \cup \phi ^{-1}(c')$
would have at most
![]() $(k-1)^2$
parts. This would give rise to a constraint in Problem L which is the analogue of (3.9) – namely,
$(k-1)^2$
parts. This would give rise to a constraint in Problem L which is the analogue of (3.9) – namely,
 $$ \begin{align*}(s-1+s-2)d_2 + (s-1+s-2+s-3)d_3 + \ldots + (s-1+s-2+\ldots + s-s)d_s \leq \binom{s}{2}\frac{(k-1)^2-1}{(k-1)^2}. \end{align*} $$
$$ \begin{align*}(s-1+s-2)d_2 + (s-1+s-2+s-3)d_3 + \ldots + (s-1+s-2+\ldots + s-s)d_s \leq \binom{s}{2}\frac{(k-1)^2-1}{(k-1)^2}. \end{align*} $$
Perhaps this constraint is always valid. As in the case
![]() $(3;s)$
, it alone does not seem enough to give a realisable solution for
$(3;s)$
, it alone does not seem enough to give a realisable solution for
![]() $s \geq 8$
, but for
$s \geq 8$
, but for
![]() $(5;4)$
and
$(5;4)$
and
![]() $(5;5)$
, it does give rise to a realisable solution, with
$(5;5)$
, it does give rise to a realisable solution, with
![]() $\boldsymbol {d} = (0,\frac {3}{4},\frac {3}{16})$
and
$\boldsymbol {d} = (0,\frac {3}{4},\frac {3}{16})$
and
![]() $(0,0,\frac {15}{16},0)$
, respectively. The corresponding solution to Problem
$(0,0,\frac {15}{16},0)$
, respectively. The corresponding solution to Problem
![]() $Q^*$
has
$Q^*$
has
![]() $r=16$
, and colourings come from
$r=16$
, and colourings come from
![]() $\mathbb {F}^2_4$
. Thus, we make the following conjecture.
$\mathbb {F}^2_4$
. Thus, we make the following conjecture.
Conjecture 6.1. There exists
![]() $n_0>0$
such that for all
$n_0>0$
such that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
![]() $T_{16}(n)$
is the unique
$T_{16}(n)$
is the unique
![]() $(5;4)$
-extremal graph, and the unique
$(5;4)$
-extremal graph, and the unique
![]() $(5;5)$
-extremal graph.
$(5;5)$
-extremal graph.
Its proof would probably follow from the following analogue of Lemma 3.3, for b not too small.
Problem 6.2. Find
![]() $b>0$
as large as possible such that the following holds for all sufficiently large n. Let
$b>0$
as large as possible such that the following holds for all sufficiently large n. Let
![]() $R,B$
be two
$R,B$
be two
![]() $K_5$
-free graphs on the same vertex set of size n with
$K_5$
-free graphs on the same vertex set of size n with
![]() $|R|+|B| \geq (\frac {3}{2}-b) n^2/2$
. Then
$|R|+|B| \geq (\frac {3}{2}-b) n^2/2$
. Then
![]() $|R \cup B| \leq \frac {15}{16} n^2/2 + o(n^2)$
.
$|R \cup B| \leq \frac {15}{16} n^2/2 + o(n^2)$
.
Suppose
![]() $R,B$
are
$R,B$
are
![]() $K_k$
-free graphs on the same vertex set of size n, with
$K_k$
-free graphs on the same vertex set of size n, with
![]() $|R|,|B| \geq (\frac {k-2}{k-1}-d)n^2/2$
and
$|R|,|B| \geq (\frac {k-2}{k-1}-d)n^2/2$
and
![]() $|R \cup B| = (\frac {(k-1)^2-1}{(k-1)^2}+d')n^2/2$
. The strong stability theorem of Füredi [Reference Füredi6] implies that at most
$|R \cup B| = (\frac {(k-1)^2-1}{(k-1)^2}+d')n^2/2$
. The strong stability theorem of Füredi [Reference Füredi6] implies that at most
![]() $dn^2/2$
edges need to be removed from each of
$dn^2/2$
edges need to be removed from each of
![]() $R,B$
to make them
$R,B$
to make them
![]() $(k-1)$
-partite. Thus, removing at most
$(k-1)$
-partite. Thus, removing at most
![]() $dn^2$
edges from
$dn^2$
edges from
![]() $R \cup B$
yields a
$R \cup B$
yields a
![]() $(k-1)^2$
-partite graph, so
$(k-1)^2$
-partite graph, so
![]() $d' \leq 2d$
. We need
$d' \leq 2d$
. We need
![]() $d=\Omega (1)$
and
$d=\Omega (1)$
and
![]() $d'=o(1)$
; for example, we proved
$d'=o(1)$
; for example, we proved
![]() $(d,d')=(\frac {1}{40},o(1))$
in Lemma 3.3.
$(d,d')=(\frac {1}{40},o(1))$
in Lemma 3.3.
To prove Lemma 3.3, of which Problem 6.2 is an analogue, we used the fact that
![]() $R(3,3)-1 - (3-1)^2=1$
, whereas
$R(3,3)-1 - (3-1)^2=1$
, whereas
![]() $R(4,4)-1-(4-1)^2 = 8$
and
$R(4,4)-1-(4-1)^2 = 8$
and
![]() $26 \leq R(5,5)-1-(5-1)^2 \leq 31$
. Thus, there could be many clique sizes larger than
$26 \leq R(5,5)-1-(5-1)^2 \leq 31$
. Thus, there could be many clique sizes larger than
![]() $(k-1)^2$
present in
$(k-1)^2$
present in
![]() $R \cup B$
, and moreover, they could have many different red/blue colourings. Therefore, the proof method of Lemma 3.3 seems unlikely to generalise.
$R \cup B$
, and moreover, they could have many different red/blue colourings. Therefore, the proof method of Lemma 3.3 seems unlikely to generalise.
6.2. The two colour problem
Solving the two colour problem completely seems difficult. Recall that
![]() $\boldsymbol {k}=(k,\ell )$
has the weak extension property but not the strong extension property, so our stability theorem Theorem 1.4 applies – which shows there is a large family of almost extremal graphs – but our exact theorem Theorem 1.6 does not. The method we used to prove Theorem 1.13 about
$\boldsymbol {k}=(k,\ell )$
has the weak extension property but not the strong extension property, so our stability theorem Theorem 1.4 applies – which shows there is a large family of almost extremal graphs – but our exact theorem Theorem 1.6 does not. The method we used to prove Theorem 1.13 about
![]() $\boldsymbol {k}=(k+1,k)$
could be used to prove further two colour results, but the number of possible coloured graph structures one needs to consider in an analogue of Lemma 5.4 increases with
$\boldsymbol {k}=(k+1,k)$
could be used to prove further two colour results, but the number of possible coloured graph structures one needs to consider in an analogue of Lemma 5.4 increases with
![]() $k-\ell $
.
$k-\ell $
.
It seems plausible that the
![]() $(5,3)$
-extremal graph may be
$(5,3)$
-extremal graph may be
![]() $T_4(n)$
, with
$T_4(n)$
, with
![]() $F(n;(5,3)) = (3+o(1))\cdot 2^{t_2(n)}$
, where almost all valid colourings come from taking one of the
$F(n;(5,3)) = (3+o(1))\cdot 2^{t_2(n)}$
, where almost all valid colourings come from taking one of the
![]() $\binom {4}{2}/2$
part-respecting bipartitions and allowing every cross-edge to be either colour, while edges within one part are given colour
$\binom {4}{2}/2$
part-respecting bipartitions and allowing every cross-edge to be either colour, while edges within one part are given colour
![]() $1$
. Perhaps for
$1$
. Perhaps for
![]() $\boldsymbol {k}=(\ell (k-1)+1,k)$
, the
$\boldsymbol {k}=(\ell (k-1)+1,k)$
, the
![]() $\boldsymbol {k}$
-extremal graph is
$\boldsymbol {k}$
-extremal graph is
![]() $T_{\ell (k-1)}(n)$
, with
$T_{\ell (k-1)}(n)$
, with
![]() $F(n;\boldsymbol {k})=(\frac {1}{(k-1)!}\binom {\ell (k-1)}{\ell ,\ldots ,\ell }+o(1)) \cdot 2^{t_{\ell (k-1)}(n)}$
, and for
$F(n;\boldsymbol {k})=(\frac {1}{(k-1)!}\binom {\ell (k-1)}{\ell ,\ldots ,\ell }+o(1)) \cdot 2^{t_{\ell (k-1)}(n)}$
, and for
![]() $\boldsymbol {k}=(\ell (k-1)+j,k)$
for
$\boldsymbol {k}=(\ell (k-1)+j,k)$
for
![]() $j=2,\ldots ,k-1$
, extremal graphs contain at least one small part.
$j=2,\ldots ,k-1$
, extremal graphs contain at least one small part.
Acknowledgements
We thank an anonymous referee for their careful reading of our paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
Oleg Pikhurko was supported by ERC Advanced Grant 101020255 and Leverhulme Research Project Grant RPG-2018-424. Katherine Staden was supported by EPSRC Fellowship EP/V025953/1.