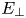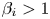1. Introduction
A key area of research in the study of turbulence in weakly collisional plasmas is understanding how energy from the fluctuating plasma flows and electromagnetic fields is converted into plasma particle energy. This phenomenon is especially relevant in heliospheric plasmas like the solar wind, where the characteristic low density and high temperature lead to a weakly collisional plasma dynamics. The dissipation of turbulence in such space and astrophysical plasmas is likely mediated by three categories of mechanisms: (i) resonant wave–particle interactions, such as Landau damping (Landau Reference Landau1946; Chen, Klein & Howes Reference Chen, Klein and Howes2019), transit-time damping (Barnes Reference Barnes1966; Stix Reference Stix1992) and cyclotron damping (Isenberg & Hollweg Reference Isenberg and Hollweg1983; Isenberg & Vasquez Reference Isenberg and Vasquez2019); (ii) non-resonant wave–particle interactions, including stochastic heating (Chandran et al. Reference Chandran, Li, Rogers, Quataert and Germaschewski2010, Reference Chandran, Verscharen, Quataert, Kasper, Isenberg and Bourouaine2013; Martinović et al. Reference Martinović, Klein, Kasper, Case, Korreck, Larson, Livi, Stevens, Whittlesey and Chandran2020; Cerri, Arzamasskiy & Kunz Reference Cerri, Arzamasskiy and Kunz2021), magnetic pumping (Lichko & Egedal Reference Lichko and Egedal2020; Montag & Howes Reference Montag and Howes2022) and ‘viscous’ damping mediated by kinetic temperature anisotropy instabilities (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Squire, Quataert and Schekochihin2023); and (iii) dissipation within coherent structures, in particular collisionless magnetic reconnection that may occur in the current sheets that are found to arise naturally in plasma turbulence (Osman et al. Reference Osman, Matthaeus, Greco and Servidio2011; Zhdankin, Uzdensky & Boldyrev Reference Zhdankin, Uzdensky and Boldyrev2015; Loureiro & Boldyrev Reference Loureiro and Boldyrev2017; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017).
Given the low collisionality of these plasma environments, the six-dimensional (three dimensions in spatial space and three dimensions in velocity space (3D-3V)) kinetic plasma theory is essential for analysing the evolution of the turbulence and its dissipation through collisionless interactions between electromagnetic fields and plasma particles (Howes Reference Howes2017). Although in situ spacecraft measurements in the solar wind provide invaluable data, they are often limited to a single point, or a few points, in space, which presents a significant challenge for the investigation of the physical mechanisms that remove energy from the turbulent fluctuations and consequently energize the plasma particles. The recently developed field–particle correlation technique (Klein & Howes Reference Klein and Howes2016; Howes, Klein & Li Reference Howes, Klein and Li2017; Klein, Howes & TenBarge Reference Klein, Howes and TenBarge2017) enables direct measurements of the electromagnetic fields and particle velocity distributions at a single point in space to be combined to create a velocity-space signature of particle energization that can be used to identify the physical mechanisms responsible for damping the turbulence and to estimate the resulting rate of the change of particle energy density. Consequently, this technique provides an innovative means to utilize in situ spacecraft observations to identify specific collisionless damping mechanisms and determine particle heating rates.
This technique has shown success in identifying several damping mechanisms in weakly collisional turbulent plasmas, such as ion Landau damping (Klein et al. Reference Klein, Howes and TenBarge2017; Li et al. Reference Li, Howes, Klein, Liu and TenBarge2019), ion cyclotron damping (Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Shuster, Klein, McGinnis, Martinovic, Boardsen, Brown, Huang and Kletzing2023), electron Landau damping (Chen et al. Reference Chen, Klein and Howes2019; Li et al. Reference Li, Howes, Klein, Liu and TenBarge2019; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021; Conley, Howes & McCubbin Reference Conley, Howes and McCubbin2023) and magnetic pumping (Montag & Howes Reference Montag and Howes2022). However, the role of transit-time damping, a resonant wave–particle interaction, in the damping of plasma turbulence remains unconfirmed. The focus of this paper is to employ the field–particle correlation technique to identify the velocity-space signature of ion energization through transit-time damping and to recover this signature from simulations of strong plasma turbulence.
The structure of this paper is laid out as follows. We derive the specific form of the field–particle correlation for transit-time damping in § 2.1. This is followed by an exploration of the expected transit-time damping signature in § 2.2. In § 3, we conduct single kinetic Alfvén wave simulations to investigate the velocity-space signature characteristic of transit-time damping. Subsequently, in § 4, we delve into turbulence simulations, presenting details for distinguishing transit-time damping from the turbulence damping process. § 5 summarizes our findings and outlines potential future applications for further research.
2. Transit-time damping
The idea of transit-time damping (TTD) had its origins in mid-20th-century plasma physics when transit-time magnetic pumping was proposed as a means to heat a confined plasma (Spitzer & Witten Reference Spitzer and Witten1953). This method is characterized by a modulation of the magnetic field magnitude at a frequency considerably lower than the ion cyclotron frequency; the evolution of the parallel and perpendicular particle velocities in the time-varying magnetic field, combined with a weak collisionality, leads to a net transfer of energy to the plasma particles. The term ‘transit time’ refers to the duration necessary for an ion to traverse from one side to the other across the confined region.
The magnetic mirror force plays a key role in the dynamics of TTD. In a static magnetic field with a spatial variation of the magnetic field magnitude along the direction parallel to the field, the mirror force accelerates charged particles in the direction of decreasing field magnitude. In a cylindrical coordinate system aligned with the magnetic field direction, the condition $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {B}=0$![]() implies that an increase of the magnetic field along the axial direction must be accompanied by the convergence of the field in the radial direction, as shown in figure 1. For a particle with a guiding centre on the axis, the particle will experience an inward radial field throughout its Larmor orbit. The Lorentz force, which acts perpendicularly to the magnetic field direction at the particle position, will therefore have both a large radial and a small axial component. Averaged over the full Larmor orbit, the net non-zero axial component accelerates the particle in the direction of the decreasing magnetic field magnitude. Because the magnetic field can do no work, the total energy of the particle remains constant – the change in the parallel velocity is accompanied by a small change in the perpendicular velocity governed by the average of the radial component of the Lorentz force. The net effect of the magnetic mirror force is that, as a particle moves in the direction of the increasing magnetic field, the mirror force reduces the velocity $v_\parallel$
implies that an increase of the magnetic field along the axial direction must be accompanied by the convergence of the field in the radial direction, as shown in figure 1. For a particle with a guiding centre on the axis, the particle will experience an inward radial field throughout its Larmor orbit. The Lorentz force, which acts perpendicularly to the magnetic field direction at the particle position, will therefore have both a large radial and a small axial component. Averaged over the full Larmor orbit, the net non-zero axial component accelerates the particle in the direction of the decreasing magnetic field magnitude. Because the magnetic field can do no work, the total energy of the particle remains constant – the change in the parallel velocity is accompanied by a small change in the perpendicular velocity governed by the average of the radial component of the Lorentz force. The net effect of the magnetic mirror force is that, as a particle moves in the direction of the increasing magnetic field, the mirror force reduces the velocity $v_\parallel$![]() parallel to the mean magnetic field over the Larmor orbit and increases perpendicular velocity $v_\perp$
parallel to the mean magnetic field over the Larmor orbit and increases perpendicular velocity $v_\perp$![]() to maintain a constant total velocity $v=(v^2_\perp + v^2_\parallel )^{1/2}$
to maintain a constant total velocity $v=(v^2_\perp + v^2_\parallel )^{1/2}$![]() .
.

Figure 1. Diagram of the radial component $F_r$![]() and axial component $F_z$
and axial component $F_z$![]() of the Lorentz force of the magnetic field (red) on a positively charged particle (red $+$
of the Lorentz force of the magnetic field (red) on a positively charged particle (red $+$![]() ) in a converging magnetic field (green) with increasing magnitude in the $+z$
) in a converging magnetic field (green) with increasing magnitude in the $+z$![]() direction. Averaged over the Larmor orbit of the particle (blue), the net magnetic mirror force is in the direction of decreasing magnetic field magnitude, here the $-z$
direction. Averaged over the Larmor orbit of the particle (blue), the net magnetic mirror force is in the direction of decreasing magnetic field magnitude, here the $-z$![]() direction.
direction.
Although the mirror force in a static magnetic field cannot change the energy of particles, any changes of the magnetic field in time will induce an electric field according to Faraday's law. Work done by that induced electric field can do work on the particles, providing the key element underlying the physics of TTD. In a collisionless plasma, collisionless wave–particle interactions are governed by the resonance condition, given by $\omega - k_\parallel v_\parallel = n \varOmega _s$![]() , where the left-hand side represents the wave frequency in the frame moving with the particle in the parallel direction and the right-hand side $n\varOmega _s$
, where the left-hand side represents the wave frequency in the frame moving with the particle in the parallel direction and the right-hand side $n\varOmega _s$![]() for $n=0,\pm 1, \pm 2, \ldots$
for $n=0,\pm 1, \pm 2, \ldots$![]() incorporates the cyclotron harmonics of the particle motion in a magnetic field (Melrose Reference Melrose1980). Here, we adopt the convention that the value of the wave frequency $\omega$
incorporates the cyclotron harmonics of the particle motion in a magnetic field (Melrose Reference Melrose1980). Here, we adopt the convention that the value of the wave frequency $\omega$![]() is positive, so that the sign of the wave vector $\boldsymbol {k}$
is positive, so that the sign of the wave vector $\boldsymbol {k}$![]() indicates the direction of the phase velocity. The $n=0$
indicates the direction of the phase velocity. The $n=0$![]() resonance, known as the Landau resonance, describes resonant interactions with particles that have parallel velocities near the phase velocity of the wave, $v_\parallel \simeq \omega /k_\parallel$
resonance, known as the Landau resonance, describes resonant interactions with particles that have parallel velocities near the phase velocity of the wave, $v_\parallel \simeq \omega /k_\parallel$![]() , enabling energy exchange between the particles and the wave through two mechanisms: (i) the electrostatic force due to the parallel component of the electric field governing the phenomenon of Landau damping (LD) (Landau Reference Landau1946; Villani Reference Villani2014); (ii) the magnetic mirror force governing the phenomenon of TTD (Stix Reference Stix1992), also known as Barnes damping (Barnes Reference Barnes1966). In the case of TTD, the perpendicular component of the electric field, induced by the change in the magnetic field magnitude along the parallel direction, accelerates the particle by changing the perpendicular velocity $v_\perp$
, enabling energy exchange between the particles and the wave through two mechanisms: (i) the electrostatic force due to the parallel component of the electric field governing the phenomenon of Landau damping (LD) (Landau Reference Landau1946; Villani Reference Villani2014); (ii) the magnetic mirror force governing the phenomenon of TTD (Stix Reference Stix1992), also known as Barnes damping (Barnes Reference Barnes1966). In the case of TTD, the perpendicular component of the electric field, induced by the change in the magnetic field magnitude along the parallel direction, accelerates the particle by changing the perpendicular velocity $v_\perp$![]() ; the mirror force effectively converts this perpendicular velocity into parallel velocity, leading to a net acceleration of the particle along the axial direction parallel to the magnetic field (Howes, Huang & Felix Reference Howes, Huang and Felix2024). For a Maxwellian distribution of particles, there are more particles with parallel velocities $|v_\parallel | < \omega /|k_\parallel |$
; the mirror force effectively converts this perpendicular velocity into parallel velocity, leading to a net acceleration of the particle along the axial direction parallel to the magnetic field (Howes, Huang & Felix Reference Howes, Huang and Felix2024). For a Maxwellian distribution of particles, there are more particles with parallel velocities $|v_\parallel | < \omega /|k_\parallel |$![]() than particles with $|v_\parallel | > \omega /|k_\parallel |$
than particles with $|v_\parallel | > \omega /|k_\parallel |$![]() , so the net effect on the distribution is an increase of the particle energy, leading to damping of the wave. A detailed demonstration of this phenomenon for a model moving magnetic mirror field is presented in § 2.2.
, so the net effect on the distribution is an increase of the particle energy, leading to damping of the wave. A detailed demonstration of this phenomenon for a model moving magnetic mirror field is presented in § 2.2.
2.1. Field–particle correlation for transit-time damping
To determine the appropriate form of the field–particle correlation to diagnose TTD via the magnetic mirror force, we start with the Vlasov equation for a species $s$![]() being acted upon by a general force $\boldsymbol {F}_s$
being acted upon by a general force $\boldsymbol {F}_s$![]()
where $f_s$![]() denotes the distribution function, and $m_s$
denotes the distribution function, and $m_s$![]() is the mass of the particle. Multiplying the Vlasov equation by $m_s v^2/2$
is the mass of the particle. Multiplying the Vlasov equation by $m_s v^2/2$![]() , we obtain an expression for the rate of change of the phase-space energy density, $w_s(\boldsymbol {r},\boldsymbol {v},t) \equiv m_s v^2 f_s(\boldsymbol {r},\boldsymbol {v},t)/2$
, we obtain an expression for the rate of change of the phase-space energy density, $w_s(\boldsymbol {r},\boldsymbol {v},t) \equiv m_s v^2 f_s(\boldsymbol {r},\boldsymbol {v},t)/2$![]() ,
,
Previous analysis of this equation (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017) has shown that, if integrated over space (with appropriate infinite or periodic boundary conditions), the change in the total kinetic energy of the particles $\mathfrak {W}_s (t)= \int {\rm d}^3\boldsymbol {r} \int {\rm d}^3\boldsymbol {v} w_s(\boldsymbol {r},\boldsymbol {v},t)$![]() is due to work done on the particle species by the force $\boldsymbol {F}_s$
is due to work done on the particle species by the force $\boldsymbol {F}_s$![]() . Therefore, the field–particle correlation due to a general force $\boldsymbol {F}_s$
. Therefore, the field–particle correlation due to a general force $\boldsymbol {F}_s$![]() at spatial position $\boldsymbol {r}_0$
at spatial position $\boldsymbol {r}_0$![]() is defined as a time average over a correlation interval $\tau$
is defined as a time average over a correlation interval $\tau$![]() of the last term on the right-hand side of (2.2)
of the last term on the right-hand side of (2.2)

Note here that the correlation interval $\tau$![]() is a parameter of the field–particle correlation analysis, and so is included as a secondary argument, separated by a semicolon from the primary arguments that define the dimensions of the 3D-3 V phase space in position, velocity and time.
is a parameter of the field–particle correlation analysis, and so is included as a secondary argument, separated by a semicolon from the primary arguments that define the dimensions of the 3D-3 V phase space in position, velocity and time.
If we consider the force due to an electric field $\boldsymbol {F}_s=q_s \boldsymbol {E}$![]() , we obtain the established field–particle correlation due to the electric field (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017)
, we obtain the established field–particle correlation due to the electric field (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017)

The collisionless transfer of energy between electromagnetic waves and particles in TTD is mediated by the magnetic mirror force, $\boldsymbol {F}_s = - \mu _s \hat {\boldsymbol {b}} \boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {B}$![]() , where the magnetic moment for a particle of species $s$
, where the magnetic moment for a particle of species $s$![]() is given by $\mu _s=m_s v_\perp ^2/(2 B)$
is given by $\mu _s=m_s v_\perp ^2/(2 B)$![]() , the unit vector in the direction of the magnetic field is given by $\hat {\boldsymbol {b}} \equiv \boldsymbol {B}/B$
, the unit vector in the direction of the magnetic field is given by $\hat {\boldsymbol {b}} \equiv \boldsymbol {B}/B$![]() and the magnitude of the magnetic field is $B=|\boldsymbol {B}|$
and the magnitude of the magnetic field is $B=|\boldsymbol {B}|$![]() . Substituting the magnetic mirror force into (2.3), we obtain
. Substituting the magnetic mirror force into (2.3), we obtain

A few modifications of the form of the field–particle correlation for TTD given in (2.5) are helpful for its application to the gyrokinetic simulations presented here. First, we exploit two important characteristics of TTD and turbulence: (i) TTD is most effective in damping the dominant Alfvénic fluctuationsFootnote 1 in turbulence with perpendicular wavelengths at the ion scales, $k_\perp \rho _i \sim k \rho _i \sim 1$![]() , where $k_\parallel /k_\perp \ll 1$
, where $k_\parallel /k_\perp \ll 1$![]() ; and (ii) for most turbulent space and astrophysical plasmas of interest, the amplitude of the magnetic fluctuations $\delta \boldsymbol {B}$
; and (ii) for most turbulent space and astrophysical plasmas of interest, the amplitude of the magnetic fluctuations $\delta \boldsymbol {B}$![]() at ion scales $k \rho _i \sim 1$
at ion scales $k \rho _i \sim 1$![]() is much smaller than the magnitude of the mean magnetic field $\boldsymbol {B}_0$
is much smaller than the magnitude of the mean magnetic field $\boldsymbol {B}_0$![]() . Therefore, if we separate the magnetic field into its mean plus the fluctuations, $\boldsymbol {B}=\boldsymbol {B}_0+\delta \boldsymbol {B}$
. Therefore, if we separate the magnetic field into its mean plus the fluctuations, $\boldsymbol {B}=\boldsymbol {B}_0+\delta \boldsymbol {B}$![]() , where $|\delta \boldsymbol {B}| \ll |\boldsymbol {B}_0|$
, where $|\delta \boldsymbol {B}| \ll |\boldsymbol {B}_0|$![]() , the change in the magnetic field magnitude $\delta | \boldsymbol {B}|$
, the change in the magnetic field magnitude $\delta | \boldsymbol {B}|$![]() (which is the key ingredient for the magnetic mirror force) can be expressed as $\delta B_\parallel$
(which is the key ingredient for the magnetic mirror force) can be expressed as $\delta B_\parallel$![]() by recognizing
by recognizing
where we use a binomial expansion to eliminate the square root, neglect the small $|\delta \boldsymbol {B}|^2$![]() term, and write $\delta B_\parallel = \delta \boldsymbol {B} \boldsymbol {\cdot } (\boldsymbol {B}_0/B_0)$
term, and write $\delta B_\parallel = \delta \boldsymbol {B} \boldsymbol {\cdot } (\boldsymbol {B}_0/B_0)$![]() as the variation in the component of the perturbed magnetic field parallel to the mean magnetic field. Furthermore, separating term $v^2=v_\perp ^2+v_\parallel ^2$
as the variation in the component of the perturbed magnetic field parallel to the mean magnetic field. Furthermore, separating term $v^2=v_\perp ^2+v_\parallel ^2$![]() in the correlation (2.5), it is easy to show that the $v_\perp ^2$
in the correlation (2.5), it is easy to show that the $v_\perp ^2$![]() contribution yields a perfect differential in $f_s$
contribution yields a perfect differential in $f_s$![]() when integrated over all parallel velocity (Howes et al. Reference Howes, Klein and Li2017), so we choose to omit this term since it leads to zero net change in the particle energy. Finally, we write the gradient along the magnetic field direction by $\boldsymbol {\nabla }_\parallel \equiv \hat {\boldsymbol {b}} \boldsymbol {\cdot }\boldsymbol {\nabla }$
when integrated over all parallel velocity (Howes et al. Reference Howes, Klein and Li2017), so we choose to omit this term since it leads to zero net change in the particle energy. Finally, we write the gradient along the magnetic field direction by $\boldsymbol {\nabla }_\parallel \equiv \hat {\boldsymbol {b}} \boldsymbol {\cdot }\boldsymbol {\nabla }$![]() , leading to our preferred form of the field–particle correlation for TTD
, leading to our preferred form of the field–particle correlation for TTD

In the gyrokinetic system of equations (Antonsen & Lane Reference Antonsen and Lane1980; Frieman & Chen Reference Frieman and Chen1982; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), the gyroaveraged effect of parallel magnetic field gradients leads to the magnetic mirror force, which can accelerate particles in the direction parallel to the magnetic field via the Landau resonance, and therefore can lead to collisionless TTD of electromagnetic fluctuations. A rigorous derivation of the gyrokinetic equation in Appendix A shows explicitly the two collisionless wave–particle interactions via the Landau resonance – specifically, LD and TTD. The natural form of the field–particle correlation arising from the gyrokinetic version of the generalized energy density equation is slightly different from the field–particle correlation for TTD given in (2.7), but the gyrokinetic form requires the gyroaveraged distribution function, which is not accessible through single-point spacecraft measurements and is not a natural quantity that can easily be derived from other kinetic simulation approaches, such as particle-in-cell or Vlasov simulations. Therefore, we choose here to use the perturbed distribution functions and electromagnetic fields generated by our gyrokinetic simulations, but we analyse them using (2.7), which is more directly applicable to spacecraft measurements or alternative kinetic simulation approaches, such as particle-in-cell codes.
Utilizing the gyroaveraged distribution function and corresponding fields, the quantity $C_{\delta B_\parallel, s}(\boldsymbol {r}_0, \boldsymbol {v}, t; \tau )$![]() reveals the velocity-space signature of TTD on the gyrotropic velocity space $(v_\perp, v_\parallel )$
reveals the velocity-space signature of TTD on the gyrotropic velocity space $(v_\perp, v_\parallel )$![]() . To simplify the notation, henceforth, we shall employ $C_{\delta B_\parallel, s} (v_\parallel, v_\perp )$
. To simplify the notation, henceforth, we shall employ $C_{\delta B_\parallel, s} (v_\parallel, v_\perp )$![]() to signify the gyrotropic correlation, explicitly noting the associated spatial position $\boldsymbol {r}_0$
to signify the gyrotropic correlation, explicitly noting the associated spatial position $\boldsymbol {r}_0$![]() , time $t$
, time $t$![]() , and the correlation interval $\tau$
, and the correlation interval $\tau$![]() only when necessary. The resonant structure of the velocity-space signature of TTD is primarily a function of $v_\parallel$
only when necessary. The resonant structure of the velocity-space signature of TTD is primarily a function of $v_\parallel$![]() , so it is often useful to define the reduced parallel field–particle correlation by integrating $C_{\delta B_\parallel, s} (v_\parallel, v_\perp,t)$
, so it is often useful to define the reduced parallel field–particle correlation by integrating $C_{\delta B_\parallel, s} (v_\parallel, v_\perp,t)$![]() over $v_\perp$
over $v_\perp$![]() , given by $C_{\delta B_\parallel, s}(v_\parallel,t) \equiv 2 {\rm \pi}\int C_{\delta B_\parallel, s}(v_\parallel, v_\perp,t) v_\perp \,{\rm d} v_\perp$
, given by $C_{\delta B_\parallel, s}(v_\parallel,t) \equiv 2 {\rm \pi}\int C_{\delta B_\parallel, s}(v_\parallel, v_\perp,t) v_\perp \,{\rm d} v_\perp$![]() , where the extra $2 {\rm \pi}v_\perp$
, where the extra $2 {\rm \pi}v_\perp$![]() factor arises from the integration over the gyrophase in 3 V phase space. A timestack plot of the reduced parallel correlation $C_{\delta B_\parallel, s}(v_\parallel,t)$
factor arises from the integration over the gyrophase in 3 V phase space. A timestack plot of the reduced parallel correlation $C_{\delta B_\parallel, s}(v_\parallel,t)$![]() reveals the persistence in time of any resonant velocity-space signatures in $v_\parallel$
reveals the persistence in time of any resonant velocity-space signatures in $v_\parallel$![]() . We can also consider the rate of change of the kinetic energy density of species $s$
. We can also consider the rate of change of the kinetic energy density of species $s$![]() due to TTD by integrating the gyrotropic correlation over all velocity space: $(\partial W_s/\partial t)_{{\rm TTD}} = \int C_{\delta B_\parallel, s}(v_\parallel, v_\perp ) \,{\rm d}^3 \boldsymbol {v}$
due to TTD by integrating the gyrotropic correlation over all velocity space: $(\partial W_s/\partial t)_{{\rm TTD}} = \int C_{\delta B_\parallel, s}(v_\parallel, v_\perp ) \,{\rm d}^3 \boldsymbol {v}$![]() .
.
In closing, note that the gyroaveraging procedure employed in the derivation of the system of gyrokinetics enables the variations in the perpendicular components of the electric field $E_\perp$![]() to be expressed in terms of changes in the parallel component of the magnetic field $\delta B_\parallel$
to be expressed in terms of changes in the parallel component of the magnetic field $\delta B_\parallel$![]() , as shown by (A7). In a system where the gyroaverage has not been performed, the work done by TTD is actually mediated (at the position of the particle) by the perpendicular component of the electric field $E_\perp$
, as shown by (A7). In a system where the gyroaverage has not been performed, the work done by TTD is actually mediated (at the position of the particle) by the perpendicular component of the electric field $E_\perp$![]() (Howes et al. Reference Howes, Huang and Felix2024). Therefore, the perpendicular electric field correlation, given by summing the two perpendicular contributions to the electric field correlation, $C_{E_\perp }(\boldsymbol {r}_0,\boldsymbol {v},t;\tau )$
(Howes et al. Reference Howes, Huang and Felix2024). Therefore, the perpendicular electric field correlation, given by summing the two perpendicular contributions to the electric field correlation, $C_{E_\perp }(\boldsymbol {r}_0,\boldsymbol {v},t;\tau )$![]() (Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Shuster, Klein, McGinnis, Martinovic, Boardsen, Brown, Huang and Kletzing2023), can be used to seek the velocity-space signature of TTD at the parallel resonant phase velocity, as seen recently in hybrid particle-in-cell simulations of plasma turbulence (Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021).
(Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Shuster, Klein, McGinnis, Martinovic, Boardsen, Brown, Huang and Kletzing2023), can be used to seek the velocity-space signature of TTD at the parallel resonant phase velocity, as seen recently in hybrid particle-in-cell simulations of plasma turbulence (Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021).
2.2. Prediction of the velocity-space signature of transit-time damping
To predict the velocity-space signature of TTD, we begin with a simple model of a magnetic field with an amplitude variation that varies along the mean field direction $z$![]() , given in cylindrical coordinates $(r,\phi,z)$
, given in cylindrical coordinates $(r,\phi,z)$![]() by
by
where the wavenumber $k$![]() of the spatial variation of the magnetic field magnitude is along the mean field direction $z$
of the spatial variation of the magnetic field magnitude is along the mean field direction $z$![]() , and $z'=z-U t$
, and $z'=z-U t$![]() , such that that pattern moves in the $+z$
, such that that pattern moves in the $+z$![]() direction with a phase speed $U \geq 0$
direction with a phase speed $U \geq 0$![]() . The corresponding electric field variation can be determined by the Lorentz transformFootnote 2 from the primed (wave) frame $K'$
. The corresponding electric field variation can be determined by the Lorentz transformFootnote 2 from the primed (wave) frame $K'$![]() in which the magnetic field pattern is stationary (and therefore $\boldsymbol {E}'=0$
in which the magnetic field pattern is stationary (and therefore $\boldsymbol {E}'=0$![]() ) to the unprimed (laboratory) frame $K$
) to the unprimed (laboratory) frame $K$![]() . This Lorentz transformation in the non-relativistic limit $U/c \ll 1$
. This Lorentz transformation in the non-relativistic limit $U/c \ll 1$![]() is given by $\boldsymbol {E}=\boldsymbol {E}' - \boldsymbol {U} \times \boldsymbol {B}$
is given by $\boldsymbol {E}=\boldsymbol {E}' - \boldsymbol {U} \times \boldsymbol {B}$![]() and $\boldsymbol {B}=\boldsymbol {B}'$
and $\boldsymbol {B}=\boldsymbol {B}'$![]() (Howes, Klein & TenBarge Reference Howes, Klein and TenBarge2014), where the transformation velocity is just $\boldsymbol {U} =U \hat {\boldsymbol {z}}$
(Howes, Klein & TenBarge Reference Howes, Klein and TenBarge2014), where the transformation velocity is just $\boldsymbol {U} =U \hat {\boldsymbol {z}}$![]() . The resulting induced electric field in the laboratory frame $K$
. The resulting induced electric field in the laboratory frame $K$![]() is given by
is given by
With this simple model, we can illustrate how a single particle is accelerated into different regions of velocity space by the electromagnetic fields. Extending this approach to consider a distribution of particles will enable us to predict the qualitative and quantitative features of the velocity-space signature of TTD.
Consider first the acceleration of a single particle in a stationary mirror field with $U=0$![]() , as shown in figure 2(a), for a ‘wave’ amplitude of $\delta B_z/B_0=0.2$
, as shown in figure 2(a), for a ‘wave’ amplitude of $\delta B_z/B_0=0.2$![]() , giving a mirror ratio of $B_\text {max}/B_\text {min} = 1.2$
, giving a mirror ratio of $B_\text {max}/B_\text {min} = 1.2$![]() . The particle begins at the minimum in the magnetic field at $z=0$
. The particle begins at the minimum in the magnetic field at $z=0$![]() with an initial perpendicular velocity $v_\perp$
with an initial perpendicular velocity $v_\perp$![]() and an initial parallel velocity $v_\parallel <0$
and an initial parallel velocity $v_\parallel <0$![]() , given by the red $+$
, given by the red $+$![]() in the figure at the tip of the initial velocity vector $\boldsymbol {v}_i$
in the figure at the tip of the initial velocity vector $\boldsymbol {v}_i$![]() (blue). As the particle moves into the increasing magnetic field at $z<0$
(blue). As the particle moves into the increasing magnetic field at $z<0$![]() , the mirror force increases $v_\perp$
, the mirror force increases $v_\perp$![]() and decreases $v_\parallel$
and decreases $v_\parallel$![]() such that the particle moves through velocity space (green arrow) on a circle of constant total velocity $v = \sqrt {v_\parallel ^2+v_\perp ^2}$
such that the particle moves through velocity space (green arrow) on a circle of constant total velocity $v = \sqrt {v_\parallel ^2+v_\perp ^2}$![]() (black dashed circle). The particle will be reflected by the mirror field if the particle has an initial pitch angle $\alpha = \tan ^{-1}(v_\perp /v_\parallel )$
(black dashed circle). The particle will be reflected by the mirror field if the particle has an initial pitch angle $\alpha = \tan ^{-1}(v_\perp /v_\parallel )$![]() larger than the loss-cone angle $\alpha _{{\rm loss}} = \sin ^{-1}( \sqrt {B_\text {min}/B_\text {max}})$
larger than the loss-cone angle $\alpha _{{\rm loss}} = \sin ^{-1}( \sqrt {B_\text {min}/B_\text {max}})$![]() . For $B_\text {max}/B_\text {min} = 1.2$
. For $B_\text {max}/B_\text {min} = 1.2$![]() , the loss-cone angle is $\alpha _{{\rm loss}} = 66^\circ$
, the loss-cone angle is $\alpha _{{\rm loss}} = 66^\circ$![]() ; the particle depicted in figure 2(a) has an initial pitch angle $\alpha > \alpha _{{\rm loss}}$
; the particle depicted in figure 2(a) has an initial pitch angle $\alpha > \alpha _{{\rm loss}}$![]() and is therefore reflected by the mirror field. The particle follows this circular trajectory in $(v_\parallel,v_\perp )$
and is therefore reflected by the mirror field. The particle follows this circular trajectory in $(v_\parallel,v_\perp )$![]() velocity space until it returns to its initial axial position $z=0$
velocity space until it returns to its initial axial position $z=0$![]() , ending up with a final velocity $\boldsymbol {v}_f$
, ending up with a final velocity $\boldsymbol {v}_f$![]() (blue) with the same perpendicular component but an equal and opposite parallel component. Thus, the kinetic energy of the particle does not change, consistent with the fact that magnetic fields do no work on particles. The particle has simply been reflected by the mirror, reversing the sign of its parallel velocity.
(blue) with the same perpendicular component but an equal and opposite parallel component. Thus, the kinetic energy of the particle does not change, consistent with the fact that magnetic fields do no work on particles. The particle has simply been reflected by the mirror, reversing the sign of its parallel velocity.

Figure 2. Diagram of the magnetic mirror reflection and prediction for the velocity-space signature of TTD: (a) $v_\perp$![]() versus $v_\parallel$
versus $v_\parallel$![]() for the single particle motion in a static magnetic mirror field; (b) $v_\perp$
for the single particle motion in a static magnetic mirror field; (b) $v_\perp$![]() versus $v_\parallel$
versus $v_\parallel$![]() for the single particle motion in a moving magnetic mirror field, where the vertical black dashed line denotes the wave phase velocity $U$
for the single particle motion in a moving magnetic mirror field, where the vertical black dashed line denotes the wave phase velocity $U$![]() ; (c) the predicted velocity-space signature for a Maxwellian velocity distribution function, where the phase-space energy density decreases at $v_\parallel < U$
; (c) the predicted velocity-space signature for a Maxwellian velocity distribution function, where the phase-space energy density decreases at $v_\parallel < U$![]() (blue) and increases at $v_\parallel > U$
(blue) and increases at $v_\parallel > U$![]() (red); (d) effective $v_\perp$
(red); (d) effective $v_\perp$![]() weighting of correlation $v_\perp ^2f(v_\perp )$
weighting of correlation $v_\perp ^2f(v_\perp )$![]() , which constrains the velocity-space signature in the $v_\perp$
, which constrains the velocity-space signature in the $v_\perp$![]() direction.
direction.
Next, we consider the case for a magnetic mirror field moving with velocity $\boldsymbol {U} =U \hat {\boldsymbol {z}}$![]() , where $U>0$
, where $U>0$![]() . In the wave frame, moving at velocity $\boldsymbol {U} =U \hat {\boldsymbol {z}}$
. In the wave frame, moving at velocity $\boldsymbol {U} =U \hat {\boldsymbol {z}}$![]() in which the magnetic field is stationary, the acceleration of the particle by the magnetic field must be the same as the stationary case in figure 2(a). But, in the laboratory frame, depicted in figure 2(b), the particle now moves on a circular trajectory in velocity space centred about the mirror velocity $U$
in which the magnetic field is stationary, the acceleration of the particle by the magnetic field must be the same as the stationary case in figure 2(a). But, in the laboratory frame, depicted in figure 2(b), the particle now moves on a circular trajectory in velocity space centred about the mirror velocity $U$![]() , given by a constant magnitude of velocity in the wave frame $v_0=\sqrt {(v_\parallel -U)^2+v_\perp ^2}$
, given by a constant magnitude of velocity in the wave frame $v_0=\sqrt {(v_\parallel -U)^2+v_\perp ^2}$![]() . Here, the particle is initially moving in the same direction as the mirror field but with a slower initial parallel velocity $0 \le v_\parallel \le U$
. Here, the particle is initially moving in the same direction as the mirror field but with a slower initial parallel velocity $0 \le v_\parallel \le U$![]() , given by the red $+$
, given by the red $+$![]() in the figure at the tip of the initial velocity vector $\boldsymbol {v}_i$
in the figure at the tip of the initial velocity vector $\boldsymbol {v}_i$![]() (blue). If the pitch angle in the wave frame $\alpha _w = \tan ^{-1}[v_\perp /(v_\parallel -U)]$
(blue). If the pitch angle in the wave frame $\alpha _w = \tan ^{-1}[v_\perp /(v_\parallel -U)]$![]() is greater than the loss-cone angle, $\alpha _w > \alpha _{{\rm loss}}$
is greater than the loss-cone angle, $\alpha _w > \alpha _{{\rm loss}}$![]() , the particle will be reflected by the moving mirror field, leading to a net acceleration in the axial direction, ultimately ending up with a parallel velocity greater than the mirror velocity $v_\parallel > U$
, the particle will be reflected by the moving mirror field, leading to a net acceleration in the axial direction, ultimately ending up with a parallel velocity greater than the mirror velocity $v_\parallel > U$![]() , with a final velocity vector $\boldsymbol {v}_f$
, with a final velocity vector $\boldsymbol {v}_f$![]() (blue). In this case, the induced electric field given by (2.9) has done work on the particle (Howes et al. Reference Howes, Huang and Felix2024), ultimately leading to a net acceleration in the axial direction. This process is the fundamental energy transfer underlying the physics of TTD.
(blue). In this case, the induced electric field given by (2.9) has done work on the particle (Howes et al. Reference Howes, Huang and Felix2024), ultimately leading to a net acceleration in the axial direction. This process is the fundamental energy transfer underlying the physics of TTD.
Finally, we consider how this understanding of the single particle motion and acceleration can be combined with a distribution of initial particle velocities to predict the velocity-space signature of TTD. Note that for the sinusoidally oscillating magnetic field magnitude given by (2.8), the long time evolution of the particle in velocity space would oscillate back and forth between $\boldsymbol {v}_i$![]() and $\boldsymbol {v}_f$
and $\boldsymbol {v}_f$![]() along the green trajectory shown in figure 2(a,b); for example, if the particle started with initial velocity $\boldsymbol {v}_f$
along the green trajectory shown in figure 2(a,b); for example, if the particle started with initial velocity $\boldsymbol {v}_f$![]() , the other side of the mirror field would lead to a reflection in the opposite direction, ultimately resulting in the particle ending up with a final velocity $\boldsymbol {v}_i$
, the other side of the mirror field would lead to a reflection in the opposite direction, ultimately resulting in the particle ending up with a final velocity $\boldsymbol {v}_i$![]() . In the case of a moving mirror field, for a Maxwellian velocity distribution there will be more particles with parallel velocities $v_\parallel < U$
. In the case of a moving mirror field, for a Maxwellian velocity distribution there will be more particles with parallel velocities $v_\parallel < U$![]() than with $v_\parallel > U$
than with $v_\parallel > U$![]() , so the net effect is that more particles will gain energy than lose energy, leading to a net energization of the particles and consequent damping of the electromagnetic wave. Only particles with pitch angles in the wave frame larger than the loss-cone angle, $\alpha _w > \alpha _{{\rm loss}}$
, so the net effect is that more particles will gain energy than lose energy, leading to a net energization of the particles and consequent damping of the electromagnetic wave. Only particles with pitch angles in the wave frame larger than the loss-cone angle, $\alpha _w > \alpha _{{\rm loss}}$![]() , will undergo the mirror reflection, so that net effect on the distribution is an acceleration of particles from $v_\parallel < U$
, will undergo the mirror reflection, so that net effect on the distribution is an acceleration of particles from $v_\parallel < U$![]() to $v_\parallel > U$
to $v_\parallel > U$![]() . The resulting change in the phase-space energy density leads to the prediction of the velocity-space signature of TTD depicted in figure 2(c): a loss of phase-space energy density (blue) in the region $v_\parallel < U$
. The resulting change in the phase-space energy density leads to the prediction of the velocity-space signature of TTD depicted in figure 2(c): a loss of phase-space energy density (blue) in the region $v_\parallel < U$![]() , and a gain of phase-space energy density (red) in the region $v_\parallel > U$
, and a gain of phase-space energy density (red) in the region $v_\parallel > U$![]() . The extent of this velocity-space signature in $(v_\parallel,v_\perp )$
. The extent of this velocity-space signature in $(v_\parallel,v_\perp )$![]() velocity space is confined by two effects: (i) only particles outside of the loss cone will experience a net acceleration; and (ii) the signature is weighted by the $v_\perp ^2$
velocity space is confined by two effects: (i) only particles outside of the loss cone will experience a net acceleration; and (ii) the signature is weighted by the $v_\perp ^2$![]() weighting in (2.7) for the rate of change of phase-space energy density by TTD (which arises from the magnetic moment $\mu =m v_\perp ^2/(2B)$
weighting in (2.7) for the rate of change of phase-space energy density by TTD (which arises from the magnetic moment $\mu =m v_\perp ^2/(2B)$![]() dependence of the mirror force) combined with the reduced perpendicular velocity distribution $f(v_\perp )$
dependence of the mirror force) combined with the reduced perpendicular velocity distribution $f(v_\perp )$![]() , where this net weighting of $v_\perp ^2 f(v_\perp )$
, where this net weighting of $v_\perp ^2 f(v_\perp )$![]() is shown in figure 2(d). Thus, the velocity-space signature of TTD in figure 2(c) is restricted to ‘Landau resonant’ particles with parallel velocities near the velocity of the magnetic field pattern $v_\parallel \sim U$
is shown in figure 2(d). Thus, the velocity-space signature of TTD in figure 2(c) is restricted to ‘Landau resonant’ particles with parallel velocities near the velocity of the magnetic field pattern $v_\parallel \sim U$![]() and to a region away from the $v_\perp =0$
and to a region away from the $v_\perp =0$![]() axis, unlike the velocity-space signature of LD (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017) which extends down to $v_\perp =0$
axis, unlike the velocity-space signature of LD (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017) which extends down to $v_\perp =0$![]() .
.
3. Single kinetic Alfvén wave (KAW) simulations
Here, we perform numerical simulations of single KAWs to determine the velocity-space signature of TTD using the astrophysical gyrokinetics code, AstroGK (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010). AstroGK evolves the gyroaveraged scalar potential $\phi (\boldsymbol {r})$![]() , parallel vector potential $A_\parallel (\boldsymbol {r})$
, parallel vector potential $A_\parallel (\boldsymbol {r})$![]() and the parallel magnetic field fluctuation $\delta B_\parallel (\boldsymbol {r})$
and the parallel magnetic field fluctuation $\delta B_\parallel (\boldsymbol {r})$![]() , as well as the gyrokinetic distribution function $h_s(\boldsymbol {r},v_\perp,v_\parallel )$
, as well as the gyrokinetic distribution function $h_s(\boldsymbol {r},v_\perp,v_\parallel )$![]() , in a triply periodic slab geometry of size $L_\perp ^2\times L_\parallel$
, in a triply periodic slab geometry of size $L_\perp ^2\times L_\parallel$![]() elongated along the straight, uniform mean magnetic field $\boldsymbol {B}_0=B_0 \hat {\boldsymbol {z}}$
elongated along the straight, uniform mean magnetic field $\boldsymbol {B}_0=B_0 \hat {\boldsymbol {z}}$![]() . The domain-scale wavenumbers are defined by $k_{\parallel 0} = 2 {\rm \pi}/L_\parallel$
. The domain-scale wavenumbers are defined by $k_{\parallel 0} = 2 {\rm \pi}/L_\parallel$![]() and $k_{\perp 0} = 2 {\rm \pi}/L_\perp$
and $k_{\perp 0} = 2 {\rm \pi}/L_\perp$![]() . The gyrokinetic expansion parameter is defined by $\epsilon \sim k_{\parallel 0}/k_{\perp 0} \ll 1$
. The gyrokinetic expansion parameter is defined by $\epsilon \sim k_{\parallel 0}/k_{\perp 0} \ll 1$![]() (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006), and all quantities are scaled to accommodate an arbitrary value of $\epsilon$
(Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006), and all quantities are scaled to accommodate an arbitrary value of $\epsilon$![]() . The gyrokinetic distribution function is related to the total distribution function $f_s$
. The gyrokinetic distribution function is related to the total distribution function $f_s$![]() via
via
where $F_{0s}$![]() is the equilibrium distribution, $\boldsymbol {r}$
is the equilibrium distribution, $\boldsymbol {r}$![]() is the spatial position, $\boldsymbol {R}_s$
is the spatial position, $\boldsymbol {R}_s$![]() is the associated species gyrocenter related to $\boldsymbol {r}$
is the associated species gyrocenter related to $\boldsymbol {r}$![]() by $\boldsymbol {r}=\boldsymbol {R}_s - \boldsymbol {v} \times \hat {\boldsymbol {z}}/\varOmega _s$
by $\boldsymbol {r}=\boldsymbol {R}_s - \boldsymbol {v} \times \hat {\boldsymbol {z}}/\varOmega _s$![]() and $\delta f_{2s}$
and $\delta f_{2s}$![]() are corrections second order in the gyrokinetic expansion parameter $\epsilon$
are corrections second order in the gyrokinetic expansion parameter $\epsilon$![]() which are not retained (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). The code employs a pseudospectral method in the $(x,y)$
which are not retained (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006). The code employs a pseudospectral method in the $(x,y)$![]() (perpendicular) plane and finite differencing in the $z$
(perpendicular) plane and finite differencing in the $z$![]() -direction. The velocity distribution is resolved on a grid in energy $E=v_\parallel ^2 + v_\perp ^2$
-direction. The velocity distribution is resolved on a grid in energy $E=v_\parallel ^2 + v_\perp ^2$![]() and pitch angle $\lambda =v^2_\perp /v^2$
and pitch angle $\lambda =v^2_\perp /v^2$![]() space, with the points selected on a Legendre polynomial basis. A fully conservative, linearized, gyroaveraged collision operator is employed (Abel et al. Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al. Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) to ensure velocity-space structure in $h_s$
space, with the points selected on a Legendre polynomial basis. A fully conservative, linearized, gyroaveraged collision operator is employed (Abel et al. Reference Abel, Barnes, Cowley, Dorland and Schekochihin2008; Barnes et al. Reference Barnes, Abel, Dorland, Ernst, Hammett, Ricci, Rogers, Schekochihin and Tatsuno2009) to ensure velocity-space structure in $h_s$![]() remains resolved throughout the simulation evolution. We normalize time using the domain-scale Alfvén wave frequency $\omega _A \equiv k_{\parallel 0} v_A$
remains resolved throughout the simulation evolution. We normalize time using the domain-scale Alfvén wave frequency $\omega _A \equiv k_{\parallel 0} v_A$![]() , and particle velocity is normalized to the ion thermal velocity $v_\text {ti} = \sqrt {2 T_{i}/m_i}$
, and particle velocity is normalized to the ion thermal velocity $v_\text {ti} = \sqrt {2 T_{i}/m_i}$![]() , where the Boltzmann constant has been absorbed to yield temperature in units of energy.
, where the Boltzmann constant has been absorbed to yield temperature in units of energy.
3.1. Single-wave simulation set-up
We first determine the velocity-space signature of TTD by performing simulations of single KAWs for a fully ionized proton–electron plasma with Maxwellian equilibrium velocity distributions with a temperature ratio $T_i / T_e = 1$![]() and a realistic ion-to-electron mass ratio of $m_i/m_e = 1836$
and a realistic ion-to-electron mass ratio of $m_i/m_e = 1836$![]() . We perform three simulations with ion plasma beta $\beta _i=0.3, 1, 3$
. We perform three simulations with ion plasma beta $\beta _i=0.3, 1, 3$![]() and sample the time evolution of the electromagnetic fields and gyrokinetic distribution function at discrete single points throughout the simulation domain with dimensions $L_\perp = 2 {\rm \pi}\rho _i$
and sample the time evolution of the electromagnetic fields and gyrokinetic distribution function at discrete single points throughout the simulation domain with dimensions $L_\perp = 2 {\rm \pi}\rho _i$![]() and $L_\parallel = 2 {\rm \pi}a_0$
and $L_\parallel = 2 {\rm \pi}a_0$![]() , yielding an arbitrary expansion parameter $\epsilon = \rho _i/a_0 \ll 1$
, yielding an arbitrary expansion parameter $\epsilon = \rho _i/a_0 \ll 1$![]() . The ion plasma beta is defined by $\beta _i=8 {\rm \pi}n_i T_i/B^2=v_{{\rm ti}}^2/v_A^2$
. The ion plasma beta is defined by $\beta _i=8 {\rm \pi}n_i T_i/B^2=v_{{\rm ti}}^2/v_A^2$![]() , where the ion thermal velocity is $v_{{\rm ti}}= \sqrt {2 Ti/m_i}$
, where the ion thermal velocity is $v_{{\rm ti}}= \sqrt {2 Ti/m_i}$![]() , the Alfvén velocity is $v_A=B/\sqrt {4 {\rm \pi}n_i m_i}$
, the Alfvén velocity is $v_A=B/\sqrt {4 {\rm \pi}n_i m_i}$![]() and the Boltzmann constant is absorbed to give temperature in units of energy. Here, $\rho _i\equiv v_{{\rm ti}}/\varOmega _i$
and the Boltzmann constant is absorbed to give temperature in units of energy. Here, $\rho _i\equiv v_{{\rm ti}}/\varOmega _i$![]() is the ion Larmor radius, where the angular ion (proton) cyclotron frequency is $\varOmega _i=q_i B_0/m_i$
is the ion Larmor radius, where the angular ion (proton) cyclotron frequency is $\varOmega _i=q_i B_0/m_i$![]() . The dimensions of these single-wave simulations are $(n_x, n_y, n_z, n_{\lambda }, n_E, n_s) = (10, 10, 32, 128, 64, 2)$
. The dimensions of these single-wave simulations are $(n_x, n_y, n_z, n_{\lambda }, n_E, n_s) = (10, 10, 32, 128, 64, 2)$![]() , where $n_s$
, where $n_s$![]() denotes the number of species. Using the solutions to the linear gyrokinetic dispersion relation (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006), a single plane-wave KAW with wavevector $(k_x \rho _i,k_y \rho _i, k_\parallel a_0) = (1,0,1)$
denotes the number of species. Using the solutions to the linear gyrokinetic dispersion relation (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006), a single plane-wave KAW with wavevector $(k_x \rho _i,k_y \rho _i, k_\parallel a_0) = (1,0,1)$![]() and amplitudeFootnote 3 $\delta B_\perp /B_0=0.125 \epsilon$
and amplitudeFootnote 3 $\delta B_\perp /B_0=0.125 \epsilon$![]() is initialized throughout the domain and allowed to evolve linearly for 5 wave periods with enhanced collisionality to eliminate any transients associated with the initialization, yielding a clean, single KAW with $k_\perp \rho _i =1$
is initialized throughout the domain and allowed to evolve linearly for 5 wave periods with enhanced collisionality to eliminate any transients associated with the initialization, yielding a clean, single KAW with $k_\perp \rho _i =1$![]() . The simulation is then restarted with lowered collisionalities $\nu _s/(k_{\parallel 0} v_{{\rm ti}}) = 2 \times 10^{-3}$
. The simulation is then restarted with lowered collisionalities $\nu _s/(k_{\parallel 0} v_{{\rm ti}}) = 2 \times 10^{-3}$![]() and evolved to allow collisionless wave–particle interactions to damp the wave. We have verified that the collisionless damping rates of the initialized KAWs agree with the analytical predictions from Vlasov–Maxwell and gyrokinetic linear dispersion relations.
and evolved to allow collisionless wave–particle interactions to damp the wave. We have verified that the collisionless damping rates of the initialized KAWs agree with the analytical predictions from Vlasov–Maxwell and gyrokinetic linear dispersion relations.
3.2. The velocity-space signature of transit-time damping
We select the $\beta _i = 1$![]() single KAW simulation as a fiducial case to determine the velocity-space signature of TTD with (2.7) and compare it with the known velocity-space signature of LD using only the parallel contribution to the dot product in (2.4) (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017; Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018; Chen et al. Reference Chen, Klein and Howes2019; Horvath, Howes & McCubbin Reference Horvath, Howes and McCubbin2020; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). The linear Vlasov–Maxwell dispersion relation yields a parallel phase velocity normalized to the Alfvén velocity of $\bar {\omega } \equiv \omega /(k_\parallel v_A) = 1.137$
single KAW simulation as a fiducial case to determine the velocity-space signature of TTD with (2.7) and compare it with the known velocity-space signature of LD using only the parallel contribution to the dot product in (2.4) (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017; Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018; Chen et al. Reference Chen, Klein and Howes2019; Horvath, Howes & McCubbin Reference Horvath, Howes and McCubbin2020; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). The linear Vlasov–Maxwell dispersion relation yields a parallel phase velocity normalized to the Alfvén velocity of $\bar {\omega } \equiv \omega /(k_\parallel v_A) = 1.137$![]() for a KAW with $k_\perp \rho _i =1$
for a KAW with $k_\perp \rho _i =1$![]() , $\beta _i=1$
, $\beta _i=1$![]() , and $T_i / T_e = 1$
, and $T_i / T_e = 1$![]() , corresponding to a normalized wave period of $T \omega _A = 5.526$
, corresponding to a normalized wave period of $T \omega _A = 5.526$![]() .
.
A key step in the field–particle correlation analysis is to choose an appropriate correlation interval $\tau$![]() over which to time average the rate of energization to eliminate a possibly larger amplitude signal of oscillatory energy transfer in order to reveal the often smaller secular rate of energy transfer that corresponds to the collisionless damping of the wave (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017). In figure 3, we present a test of different correlation intervals over the range $0 \le \tau \omega _A \le 10$
over which to time average the rate of energization to eliminate a possibly larger amplitude signal of oscillatory energy transfer in order to reveal the often smaller secular rate of energy transfer that corresponds to the collisionless damping of the wave (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and TenBarge2017). In figure 3, we present a test of different correlation intervals over the range $0 \le \tau \omega _A \le 10$![]() for the $\beta _i=1$
for the $\beta _i=1$![]() single KAW simulation. In (a), we plot the velocity-space-integrated rate of ion energization due to TTD, $(\partial W_i/\partial t)_{{\rm TTD}} = \int C_{\delta B_\parallel, i}(v_\parallel, v_\perp ) \,{\rm d}^3 \boldsymbol {v}$
single KAW simulation. In (a), we plot the velocity-space-integrated rate of ion energization due to TTD, $(\partial W_i/\partial t)_{{\rm TTD}} = \int C_{\delta B_\parallel, i}(v_\parallel, v_\perp ) \,{\rm d}^3 \boldsymbol {v}$![]() , vs. time. The unaveraged correlation ($\tau =0$
, vs. time. The unaveraged correlation ($\tau =0$![]() , dark blue) exhibits pronounced oscillations of the net energy transfer vs. time. Setting the correlation interval to one linear wave period $\tau \omega _A = T \omega _A \simeq 5.5$
, dark blue) exhibits pronounced oscillations of the net energy transfer vs. time. Setting the correlation interval to one linear wave period $\tau \omega _A = T \omega _A \simeq 5.5$![]() (black) minimizes the oscillations, providing an optimal choice for $\tau$
(black) minimizes the oscillations, providing an optimal choice for $\tau$![]() for a single wave with a well-defined period, as might be expected on theoretical grounds. We show in (b) the evolution of the reduced parallel correlation $C_{\delta B_\parallel, i}(v_\parallel,t)$
for a single wave with a well-defined period, as might be expected on theoretical grounds. We show in (b) the evolution of the reduced parallel correlation $C_{\delta B_\parallel, i}(v_\parallel,t)$![]() at a parallel velocity $v_\parallel = 1.1 v_\text {ti}$
at a parallel velocity $v_\parallel = 1.1 v_\text {ti}$![]() slightly below the resonant velocity. Here again, setting $\tau \omega _A = 5.5$
slightly below the resonant velocity. Here again, setting $\tau \omega _A = 5.5$![]() (black) effectively minimizes the oscillations, revealing clearly the rate of secular energy transfer at that parallel velocity. We illustrate the impact of choosing an appropriate correlation interval $\tau$
(black) effectively minimizes the oscillations, revealing clearly the rate of secular energy transfer at that parallel velocity. We illustrate the impact of choosing an appropriate correlation interval $\tau$![]() on the timestack plot of the correlation $C_{\delta B_\parallel, i}(v_\parallel,t)$
on the timestack plot of the correlation $C_{\delta B_\parallel, i}(v_\parallel,t)$![]() by comparing (c) the instantaneous ($\tau =0$
by comparing (c) the instantaneous ($\tau =0$![]() ) field–particle correlation with (d) the correlation using $\tau \omega _A = 5.5$
) field–particle correlation with (d) the correlation using $\tau \omega _A = 5.5$![]() , showing a clear bipolar signature about the normalized parallel phase velocity $\omega /(k_\parallel v_{{\rm ti}})=1.137$
, showing a clear bipolar signature about the normalized parallel phase velocity $\omega /(k_\parallel v_{{\rm ti}})=1.137$![]() that persists over the course of the simulation.
that persists over the course of the simulation.

Figure 3. Analysis of correlation interval selection for $\beta _i = 1$![]() AstroGK single KAW simulation. (a,b) Time evolution of (a) the rate of change of ion kinetic energy density due to TTD, denoted as $\partial W_i /\partial t$
AstroGK single KAW simulation. (a,b) Time evolution of (a) the rate of change of ion kinetic energy density due to TTD, denoted as $\partial W_i /\partial t$![]() , and (b) the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$
, and (b) the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$![]() at $v_\parallel = 1.1 v_{{\rm ti}}$
at $v_\parallel = 1.1 v_{{\rm ti}}$![]() . Both quantities are presented over a range of $\tau \omega _A$
. Both quantities are presented over a range of $\tau \omega _A$![]() values from 0 to 10. The selected $\tau \omega _A$
values from 0 to 10. The selected $\tau \omega _A$![]() value of 5.5 is marked with a black line. (c,d) Timestack plots of the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$
value of 5.5 is marked with a black line. (c,d) Timestack plots of the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$![]() for (c) $\tau \omega _A = 0$
for (c) $\tau \omega _A = 0$![]() and (d) $\tau \omega _A = 5.5$
and (d) $\tau \omega _A = 5.5$![]() , with the vertical dashed line at $v_\parallel /v_\text {ti} = 1.137$
, with the vertical dashed line at $v_\parallel /v_\text {ti} = 1.137$![]() labelling the normalized parallel phase velocity $\omega /(k_\parallel v_\text {ti})$
labelling the normalized parallel phase velocity $\omega /(k_\parallel v_\text {ti})$![]() .
.
Specifying the correlation interval to be approximately one wave period $\tau \omega _A = 5.5$![]() ,Footnote 4 we now present in figure 4 the velocity-space signatures of (a) TTD and (b) LD from the $\beta _i = 1$
,Footnote 4 we now present in figure 4 the velocity-space signatures of (a) TTD and (b) LD from the $\beta _i = 1$![]() single KAW simulation. Each panel presents three sub-plots, explained here for the TTD case in (a): (i) the main plot presents the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp )$
single KAW simulation. Each panel presents three sub-plots, explained here for the TTD case in (a): (i) the main plot presents the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp )$![]() at time $t \omega _A = 63.57$
at time $t \omega _A = 63.57$![]() , with the parallel phase velocity indicated (vertical dotted line); (ii) the lower plot shows the time-integrated parallel velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel )$
, with the parallel phase velocity indicated (vertical dotted line); (ii) the lower plot shows the time-integrated parallel velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel )$![]() to highlight the variation of the net energy transferred as a function of $v_\parallel$
to highlight the variation of the net energy transferred as a function of $v_\parallel$![]() , showing a clear bipolar signature at the parallel phase velocity; and (iii) the left plot shows the velocity-space-integrated net energy density transfer rate due to TTD $(\partial W_i(t)/\partial t)_{{\rm TTD}}$
, showing a clear bipolar signature at the parallel phase velocity; and (iii) the left plot shows the velocity-space-integrated net energy density transfer rate due to TTD $(\partial W_i(t)/\partial t)_{{\rm TTD}}$![]() vs. time, with the centred time of the correlation interval shown in the gyrotropic signature indicated (horizontal solid line). Panel (b) presents the corresponding plots for the LD case.
vs. time, with the centred time of the correlation interval shown in the gyrotropic signature indicated (horizontal solid line). Panel (b) presents the corresponding plots for the LD case.

Figure 4. Velocity-space signatures of (a) TTD and (b) LD, from the AstroGK simulation of a single KAW with $k_\perp \rho _i =1$![]() , $\beta _i=1$
, $\beta _i=1$![]() and $T_i / T_e = 1$
and $T_i / T_e = 1$![]() , each showing the gyrotropic signatures in the main panel, the time-integrated reduced parallel signatures in the lower panel and the net rate of ion energization vs. time for each mechanism in the left panel. The correlation interval is chosen as $\tau \omega _A = 5.5$
, each showing the gyrotropic signatures in the main panel, the time-integrated reduced parallel signatures in the lower panel and the net rate of ion energization vs. time for each mechanism in the left panel. The correlation interval is chosen as $\tau \omega _A = 5.5$![]() . The normalized parallel phase velocity is labelled by the two vertical dashed lines at $v_\parallel /v_\text {ti} = \pm 1.137$
. The normalized parallel phase velocity is labelled by the two vertical dashed lines at $v_\parallel /v_\text {ti} = \pm 1.137$![]() .
.
A key result of this paper is the velocity-space signature of TTD plotted in gyrotropic velocity space $C_{\delta B_\parallel, i}(v_\parallel,v_\perp )$![]() in figure 4(a). From the same simulation, the gyrotropic velocity-space signature of LD $C_{E_\parallel, i}(v_\parallel,v_\perp )$
in figure 4(a). From the same simulation, the gyrotropic velocity-space signature of LD $C_{E_\parallel, i}(v_\parallel,v_\perp )$![]() , given by the parallel contribution to the dot product in (2.4), is presented in (b) for comparison. The TTD signature agrees qualitatively with our prediction presented in figure 2(c), showing the key features: (i) the bipolar signature of the rate of loss (blue) and gain (red) of phase-space energy density is centred about the parallel wave phase velocity $v_\parallel \sim \omega /k_\parallel$
, given by the parallel contribution to the dot product in (2.4), is presented in (b) for comparison. The TTD signature agrees qualitatively with our prediction presented in figure 2(c), showing the key features: (i) the bipolar signature of the rate of loss (blue) and gain (red) of phase-space energy density is centred about the parallel wave phase velocity $v_\parallel \sim \omega /k_\parallel$![]() (vertical dotted black line); (ii) the gyrokinetic velocity-space signature does not extend down to $v_\perp =0$
(vertical dotted black line); (ii) the gyrokinetic velocity-space signature does not extend down to $v_\perp =0$![]() , due to a combination of the $v_\perp ^2$
, due to a combination of the $v_\perp ^2$![]() weighting arising from the magnetic moment $\mu =m v^2_\perp /(2B)$
weighting arising from the magnetic moment $\mu =m v^2_\perp /(2B)$![]() in the mirror force and from the loss-cone angle of the mirror force, as explained in § 2.2. The LD signature in (b) likewise yields a bipolar signature near the parallel wave phase velocity. Besides the fact that $E_\parallel$
in the mirror force and from the loss-cone angle of the mirror force, as explained in § 2.2. The LD signature in (b) likewise yields a bipolar signature near the parallel wave phase velocity. Besides the fact that $E_\parallel$![]() governs energization through LD and $E_\perp$
governs energization through LD and $E_\perp$![]() governs energization through TTD (Howes et al. Reference Howes, Huang and Felix2024), a key way to distinguish these two mechanisms is that in gyrotropic velocity space the TTD signature does not extend down to $v_\perp =0$
governs energization through TTD (Howes et al. Reference Howes, Huang and Felix2024), a key way to distinguish these two mechanisms is that in gyrotropic velocity space the TTD signature does not extend down to $v_\perp =0$![]() , whereas the LD signature extends right down to $v_\perp =0$
, whereas the LD signature extends right down to $v_\perp =0$![]() .
.
Careful inspection of these single KAW velocity-space signatures reveals a ‘twist’ seen in both panels of figure 4, where the bipolar pattern of energy loss (blue) to energy gain (red) across the parallel phase velocity reverses sign as $v_\perp$![]() changes. This feature arises from the linear combination of three terms contributing to the linear response for perturbed distribution function $f_1$
changes. This feature arises from the linear combination of three terms contributing to the linear response for perturbed distribution function $f_1$![]() , which involves the components of the electric field perturbation and the zeroth-order Bessel function and its derivative, as seen in (4.180) from Swanson (Reference Swanson2003). Although a detailed decomposition of these contributions to understand this twist for a single KAW could be performed, for the case of TTD or LD in a turbulent plasma, this twist is obscured when damping a broadband spectrum of wave modes, as shown in § 4, so we do not pursue this line of investigation further.
, which involves the components of the electric field perturbation and the zeroth-order Bessel function and its derivative, as seen in (4.180) from Swanson (Reference Swanson2003). Although a detailed decomposition of these contributions to understand this twist for a single KAW could be performed, for the case of TTD or LD in a turbulent plasma, this twist is obscured when damping a broadband spectrum of wave modes, as shown in § 4, so we do not pursue this line of investigation further.
3.3. Variation of signature with ion plasma beta $\beta _i$
Resonant damping of electromagnetic fluctuations through TTD and LD depends strongly on the plasma beta, typically with LD dominant at $\beta _i \ll 1$![]() and TTD dominant at $\beta _i \gg 1$
and TTD dominant at $\beta _i \gg 1$![]() (Quataert Reference Quataert1998), so we vary the value of $\beta _i$
(Quataert Reference Quataert1998), so we vary the value of $\beta _i$![]() here to determine its impact on the characteristics of the velocity-space signature of the Landau-resonant damping mechanisms. Using the same parameters $T_i/T_e=1$
here to determine its impact on the characteristics of the velocity-space signature of the Landau-resonant damping mechanisms. Using the same parameters $T_i/T_e=1$![]() , $m_i/m_e=1836$
, $m_i/m_e=1836$![]() and $k_\perp \rho _i =1$
and $k_\perp \rho _i =1$![]() , we perform additional single KAW simulations with $\beta _i = 0.3$
, we perform additional single KAW simulations with $\beta _i = 0.3$![]() and $\beta _i = 3$
and $\beta _i = 3$![]() . For $\beta _i = 0.3$
. For $\beta _i = 0.3$![]() , the normalized parallel phase velocity is given by $\bar {\omega } \equiv \omega /(k_\parallel v_A) = 1.267$
, the normalized parallel phase velocity is given by $\bar {\omega } \equiv \omega /(k_\parallel v_A) = 1.267$![]() , yielding a normalized wave period of $T \omega _A = 4.959$
, yielding a normalized wave period of $T \omega _A = 4.959$![]() ; for $\beta _i = 3$
; for $\beta _i = 3$![]() , we obtain $\bar {\omega }= 1.009$
, we obtain $\bar {\omega }= 1.009$![]() and $T \omega _A = 6.227$
and $T \omega _A = 6.227$![]() .
.
In figure 5, we plot the velocity-space signatures for (a) TTD and (b) LD for the $\beta _i = 0.3$![]() case and for (c) TTD and (d) LD for the $\beta _i = 3$
case and for (c) TTD and (d) LD for the $\beta _i = 3$![]() case, where each panel has three subplots in the same format as in figure 4. These bipolar velocity-space signatures look qualitatively similar to the $\beta _i = 1$
case, where each panel has three subplots in the same format as in figure 4. These bipolar velocity-space signatures look qualitatively similar to the $\beta _i = 1$![]() case in figure 4, with two important quantitative differences.
case in figure 4, with two important quantitative differences.

Figure 5. Velocity-space signatures of TTD (a,c) and LD (b,d) in AstroGK single KAW simulations with $k_\perp \rho _i =1$![]() , $T_i / T_e = 1$
, $T_i / T_e = 1$![]() and $\beta _i = 0.3$
and $\beta _i = 0.3$![]() (a,b) and $\beta _i = 3$
(a,b) and $\beta _i = 3$![]() (c,d). The correlation intervals are set to the corresponding linear wave periods, with $\tau \omega _A = 5.0$
(c,d). The correlation intervals are set to the corresponding linear wave periods, with $\tau \omega _A = 5.0$![]() for the $\beta _i = 0.3$
for the $\beta _i = 0.3$![]() case and $\tau \omega _A = 6.2$
case and $\tau \omega _A = 6.2$![]() for the $\beta _i = 3$
for the $\beta _i = 3$![]() case. The normalized parallel phase velocity is labelled by the two vertical dashed lines at $v_\parallel /v_\text {ti} = \pm 2.313$
case. The normalized parallel phase velocity is labelled by the two vertical dashed lines at $v_\parallel /v_\text {ti} = \pm 2.313$![]() for $\beta _i = 0.3$
for $\beta _i = 0.3$![]() and $v_\parallel /v_\text {ti} = \pm 0.583$
and $v_\parallel /v_\text {ti} = \pm 0.583$![]() for $\beta _i = 3$
for $\beta _i = 3$![]() . Each panel follows the layout format of figure 4.
. Each panel follows the layout format of figure 4.
First, the position of the bipolar signature in $v_\parallel /v_{{\rm ti}}$![]() changes as $\beta _i$
changes as $\beta _i$![]() is varied, consistent with the variation of the parallel phase velocity normalized to the ion thermal velocity as $\beta _i$
is varied, consistent with the variation of the parallel phase velocity normalized to the ion thermal velocity as $\beta _i$![]() varies, given by $\omega /(k_\parallel v_{{\rm ti}})= \bar {\omega }/ \beta _i^{1/2}$
varies, given by $\omega /(k_\parallel v_{{\rm ti}})= \bar {\omega }/ \beta _i^{1/2}$![]() . For $\beta _i = 0.3$
. For $\beta _i = 0.3$![]() , we obtain $\omega /(k_\parallel v_{{\rm ti}})= 2.313$
, we obtain $\omega /(k_\parallel v_{{\rm ti}})= 2.313$![]() , indicated by the vertical black dashed line in figure 5(a,b); for $\beta _i = 3$
, indicated by the vertical black dashed line in figure 5(a,b); for $\beta _i = 3$![]() , we obtain $\omega /(k_\parallel v_{{\rm ti}})= 0.583$
, we obtain $\omega /(k_\parallel v_{{\rm ti}})= 0.583$![]() , as shown in (c,d). In both cases, the bipolar signature remains closely associated in $v_\parallel$
, as shown in (c,d). In both cases, the bipolar signature remains closely associated in $v_\parallel$![]() with the parallel phase velocity $\omega /k_\parallel$
with the parallel phase velocity $\omega /k_\parallel$![]() , as expected for a Landau-resonant energy transfer between the fields and the ions.
, as expected for a Landau-resonant energy transfer between the fields and the ions.
Second, looking at the vertical subplots on the left for each panel, which shows the net rate of change of ion energy density $W_i$![]() mediated by each mechanism averaged over a correlation interval equal to one wave period $\tau =T$
mediated by each mechanism averaged over a correlation interval equal to one wave period $\tau =T$![]() , we find the surprising result for $\beta _i = 0.3$
, we find the surprising result for $\beta _i = 0.3$![]() that, although LD leads to a net gain of energy by the ions (as expected for collisionless damping of a wave), TTD leads to a net loss of energy from the ions. This finding suggests that the ions are losing energy through the magnetic mirror force while gaining energy through acceleration by the parallel electric field. The rate of ion energy gain by LD is approximately ten times larger than the rate of loss by TTD, so the summed effect of these two mechanisms is energization of the ions by collisionless damping of the wave, as expected. For the $\beta _i = 3$
that, although LD leads to a net gain of energy by the ions (as expected for collisionless damping of a wave), TTD leads to a net loss of energy from the ions. This finding suggests that the ions are losing energy through the magnetic mirror force while gaining energy through acceleration by the parallel electric field. The rate of ion energy gain by LD is approximately ten times larger than the rate of loss by TTD, so the summed effect of these two mechanisms is energization of the ions by collisionless damping of the wave, as expected. For the $\beta _i = 3$![]() case, we find the equally surprising result that, although TTD leads to a net gain of energy by the ions, LD is leading to a net loss of energy from the ions; the rate of ion energy gain by TTD is larger than the rate of ion energy loss by LD, so the summed contributions yield a net gain of ion energy as expected for collisionless damping.
case, we find the equally surprising result that, although TTD leads to a net gain of energy by the ions, LD is leading to a net loss of energy from the ions; the rate of ion energy gain by TTD is larger than the rate of ion energy loss by LD, so the summed contributions yield a net gain of ion energy as expected for collisionless damping.
How do we reconcile these surprising results with the general expectation of Landau-resonant collisionless damping of waves for a Maxwellian equilibrium velocity distribution? As it turns out, this behaviour is exactly what is predicted by the linear Vlasov–Maxwell dispersion relation. To be specific, we take the complex eigenfrequency from the linear dispersion relation to be given by $\omega + {\rm i}\gamma$![]() , so that time evolution of a plane-wave mode is given by $\exp (-{\rm i}\omega t) \exp (\gamma t)$
, so that time evolution of a plane-wave mode is given by $\exp (-{\rm i}\omega t) \exp (\gamma t)$![]() : positive imaginary components $\gamma >0$
: positive imaginary components $\gamma >0$![]() correspond to growth of the wave, and negative imaginary components $\gamma <0$
correspond to growth of the wave, and negative imaginary components $\gamma <0$![]() correspond to damping of the wave. In figure 6, we plot the normalized absolute value of the imaginary component of the wave frequency $|\gamma |/\omega$
correspond to damping of the wave. In figure 6, we plot the normalized absolute value of the imaginary component of the wave frequency $|\gamma |/\omega$![]() vs. $k_\perp \rho _i$
vs. $k_\perp \rho _i$![]() for KAWs using the PLUME solver (Klein & Howes Reference Klein and Howes2015) for a fully ionized proton–electron plasma with isotropic Maxwellian velocity distributions with $T_i/T_e=1$
for KAWs using the PLUME solver (Klein & Howes Reference Klein and Howes2015) for a fully ionized proton–electron plasma with isotropic Maxwellian velocity distributions with $T_i/T_e=1$![]() , $m_i/m_e = 1836$
, $m_i/m_e = 1836$![]() , $v_{{\rm ti}}/c=10^{-4}$
, $v_{{\rm ti}}/c=10^{-4}$![]() , $k_\parallel \rho _i=10^{-3}$
, $k_\parallel \rho _i=10^{-3}$![]() over the range $10^{-3} \le k_\perp \rho _i \le 10^2$
over the range $10^{-3} \le k_\perp \rho _i \le 10^2$![]() for the ion plasma beta values (a) $\beta _i=0.3$
for the ion plasma beta values (a) $\beta _i=0.3$![]() , (b) $\beta _i=1$
, (b) $\beta _i=1$![]() and (c) $\beta _i=3$
and (c) $\beta _i=3$![]() . We plot separately the total collisionless damping rate (black solid) due to both ions and electrons, the total ion damping rate (green solid) and the separate contributions to the ion damping rate from TTD (red) and LD (blue). For the separated TTD and LD contributions, we plot negative imaginary components (which correspond to collisionless damping of the wave) using dashed lines, and positive imaginary components (which correspond to collisionless growth of the wave) using dotted lines.
. We plot separately the total collisionless damping rate (black solid) due to both ions and electrons, the total ion damping rate (green solid) and the separate contributions to the ion damping rate from TTD (red) and LD (blue). For the separated TTD and LD contributions, we plot negative imaginary components (which correspond to collisionless damping of the wave) using dashed lines, and positive imaginary components (which correspond to collisionless growth of the wave) using dotted lines.

Figure 6. Linear dispersion relations for KAWs from PLUME calculations with the realistic mass ratio $m_i/m_e = 1836$![]() , showing the absolute value of the normalized wave growth rate $|\gamma |/\omega$
, showing the absolute value of the normalized wave growth rate $|\gamma |/\omega$![]() as a function of the dimensionless perpendicular wave vector $k_\perp \rho _i$
as a function of the dimensionless perpendicular wave vector $k_\perp \rho _i$![]() for (a) $\beta _i = 0.3$
for (a) $\beta _i = 0.3$![]() , (b) $\beta _i = 1$
, (b) $\beta _i = 1$![]() and (c) $\beta _i = 3$
and (c) $\beta _i = 3$![]() . The vertical black dashed line at $k_\perp \rho _i = 1$
. The vertical black dashed line at $k_\perp \rho _i = 1$![]() indicates the values used in the single KAW AstroGK simulations. We plot $\gamma$
indicates the values used in the single KAW AstroGK simulations. We plot $\gamma$![]() (total damping rate, black), $\gamma _i$
(total damping rate, black), $\gamma _i$![]() (total ion damping rate, green), $\gamma _{i{\rm TTD}}$
(total ion damping rate, green), $\gamma _{i{\rm TTD}}$![]() (ion growth or damping rate via the magnetic mirror force, red) and $\gamma _{i{\rm LD}}$
(ion growth or damping rate via the magnetic mirror force, red) and $\gamma _{i{\rm LD}}$![]() (ion growth or damping rate via the electrostatic force, blue). Line styles – solid, dashed and dotted – represent the total damping rates, damping rates separated by mechanism and growth rates separated by mechanism, respectively.
(ion growth or damping rate via the electrostatic force, blue). Line styles – solid, dashed and dotted – represent the total damping rates, damping rates separated by mechanism and growth rates separated by mechanism, respectively.
Although all of the KAW dispersion relations plotted in figure 6 yield a net effect of collisionless damping by the ions, over some ranges in $k_\perp \rho _i$![]() (dotted lines) either TTD or LD individually may lead to a net transfer of energy from the ions to the waves over the course of a single-wave period. For example, for the $\beta _i=3$
(dotted lines) either TTD or LD individually may lead to a net transfer of energy from the ions to the waves over the course of a single-wave period. For example, for the $\beta _i=3$![]() case in figure 6(c), the imaginary component due to LD is positive over $1.4 \times 10^{-3} \lesssim k_\perp \rho _i \lesssim 2.1$
case in figure 6(c), the imaginary component due to LD is positive over $1.4 \times 10^{-3} \lesssim k_\perp \rho _i \lesssim 2.1$![]() , corresponding to a transfer of energy from the ions to the wave, and is negative outside of that range, corresponding to a transfer of energy from the wave to the ions. A transfer from ions to the wave would lead to a growth of the wave, but the sum of both of the LD and TTD contributions is always negative for these cases with a Maxwellian velocity distribution, leading to a net collisionless damping of the wave.
, corresponding to a transfer of energy from the ions to the wave, and is negative outside of that range, corresponding to a transfer of energy from the wave to the ions. A transfer from ions to the wave would lead to a growth of the wave, but the sum of both of the LD and TTD contributions is always negative for these cases with a Maxwellian velocity distribution, leading to a net collisionless damping of the wave.
The perpendicular wavenumber $k_\perp \rho _i=1$![]() of our simulated single waves is indicated in figure 6 by the vertical black dashed line, and with these plots we can understand the results presented in figure 6. For the $\beta _i=0.3$
of our simulated single waves is indicated in figure 6 by the vertical black dashed line, and with these plots we can understand the results presented in figure 6. For the $\beta _i=0.3$![]() case, at $k_\perp \rho _i=1$
case, at $k_\perp \rho _i=1$![]() we have $\gamma _{i{\rm LD}} <0$
we have $\gamma _{i{\rm LD}} <0$![]() (blue dashed) and $\gamma _{i{\rm TTD}} >0$
(blue dashed) and $\gamma _{i{\rm TTD}} >0$![]() (red dotted), suggesting that ions gain energy due to $E_\parallel$
(red dotted), suggesting that ions gain energy due to $E_\parallel$![]() but lose energy due to the mirror force when averaged over the full wave period. This finding agrees with the net gain of ion energy by LD in figure 5(b) and the net loss of ion energy by TTD in (a). Similarly, for the $\beta _i=3$
but lose energy due to the mirror force when averaged over the full wave period. This finding agrees with the net gain of ion energy by LD in figure 5(b) and the net loss of ion energy by TTD in (a). Similarly, for the $\beta _i=3$![]() case, at $k_\perp \rho _i=1$
case, at $k_\perp \rho _i=1$![]() we have $\gamma _{i{\rm TTD}} <0$
we have $\gamma _{i{\rm TTD}} <0$![]() (red dashed) and $\gamma _{i{\rm LD}} >0$
(red dashed) and $\gamma _{i{\rm LD}} >0$![]() (blue dotted), suggesting that ions gain energy due to the mirror force but lose energy due to $E_\parallel$
(blue dotted), suggesting that ions gain energy due to the mirror force but lose energy due to $E_\parallel$![]() when averaged over the full wave period. Again, this finding from the linear Vlasov–Maxwell dispersion relation agrees with the net gain of ion energy by TTD in figure 5(c) and the net loss of ion energy by LD in (d).
when averaged over the full wave period. Again, this finding from the linear Vlasov–Maxwell dispersion relation agrees with the net gain of ion energy by TTD in figure 5(c) and the net loss of ion energy by LD in (d).
To further understand the physical meaning of $\gamma _{i{\rm TTD}} >0$![]() in the $\beta _i=0.3$
in the $\beta _i=0.3$![]() case, we first point out that the only mechanism that can change the particle energy is work done by the electric field, and the rate of change of the ion energy density $W_i$
case, we first point out that the only mechanism that can change the particle energy is work done by the electric field, and the rate of change of the ion energy density $W_i$![]() is given by $\boldsymbol {j}_i \boldsymbol {\cdot } \boldsymbol {E}$
is given by $\boldsymbol {j}_i \boldsymbol {\cdot } \boldsymbol {E}$![]() . For TTD, this energization arises from the component of the electric field that is perpendicular to the magnetic field (Howes et al. Reference Howes, Huang and Felix2024) (whereas LD energizes particles through the parallel component of the electric field), so here we consider the perpendicular contribution to the energization ${j}_{\perp i} {E}_\perp$
. For TTD, this energization arises from the component of the electric field that is perpendicular to the magnetic field (Howes et al. Reference Howes, Huang and Felix2024) (whereas LD energizes particles through the parallel component of the electric field), so here we consider the perpendicular contribution to the energization ${j}_{\perp i} {E}_\perp$![]() . For a single plane wave, the net transfer of energy to or from the ions by ${j}_{\perp i} {E}_\perp$
. For a single plane wave, the net transfer of energy to or from the ions by ${j}_{\perp i} {E}_\perp$![]() over a single wave period depends on the phase of the perpendicular electric field fluctuation ${E}_\perp$
over a single wave period depends on the phase of the perpendicular electric field fluctuation ${E}_\perp$![]() relative to the phase of the self-consistent perpendicular component of the ion current density associated with the wave, ${j}_{\perp i}$
relative to the phase of the self-consistent perpendicular component of the ion current density associated with the wave, ${j}_{\perp i}$![]() . If the phase difference $\delta \phi$
. If the phase difference $\delta \phi$![]() is such that there is an in-phase component $0 < \delta \phi < {\rm \pi}/2$
is such that there is an in-phase component $0 < \delta \phi < {\rm \pi}/2$![]() , there will be a net energization of the ions; if there is an out-of-phase component ${\rm \pi} /2 < \delta \phi < {\rm \pi}$
, there will be a net energization of the ions; if there is an out-of-phase component ${\rm \pi} /2 < \delta \phi < {\rm \pi}$![]() , the ions will lose energy. The eigenfunctions arising from solutions of the linear Vlasov–Maxwell dispersion relation dictate the phases of the components of the electric field and current density. For the $\beta _i=0.3$
, the ions will lose energy. The eigenfunctions arising from solutions of the linear Vlasov–Maxwell dispersion relation dictate the phases of the components of the electric field and current density. For the $\beta _i=0.3$![]() case, this eigenfunction dictates that ${j}_{\parallel i}$
case, this eigenfunction dictates that ${j}_{\parallel i}$![]() and ${E}_\parallel$
and ${E}_\parallel$![]() are in phase, leading to ion energization and wave damping by ${E}_\parallel$
are in phase, leading to ion energization and wave damping by ${E}_\parallel$![]() (yielding LD), but ${j}_{\perp i}$
(yielding LD), but ${j}_{\perp i}$![]() and ${E}_\perp$
and ${E}_\perp$![]() are out of phase, so the magnetic mirror force partly counteracts the damping of the wave.
are out of phase, so the magnetic mirror force partly counteracts the damping of the wave.
4. Turbulence simulations
Now that we have determined the gyrotropic velocity-space signature of TTD for single KAWs, with the fiducial example for $\beta _i=1$![]() shown in figure 4(a), we will seek similar signatures of TTD in simulations of strong plasma turbulence.
shown in figure 4(a), we will seek similar signatures of TTD in simulations of strong plasma turbulence.
4.1. Turbulence simulation set-up
We perform kinetic simulations of strong plasma turbulence using the astrophysical gyrokinetics code AstroGK (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010) for three values of the ion plasma beta $\beta _i=0.3,1,3$![]() . Each simulation has numerical resolution $(n_x, n_y, n_z, n_{\lambda }, n_E, n_s) = (96, 96, 32, 64, 32, 2)$
. Each simulation has numerical resolution $(n_x, n_y, n_z, n_{\lambda }, n_E, n_s) = (96, 96, 32, 64, 32, 2)$![]() within a simulation domain $L_\perp ^2 \times L_\parallel = (8 {\rm \pi}\rho _i)^2 \times (2{\rm \pi} a_0)$
within a simulation domain $L_\perp ^2 \times L_\parallel = (8 {\rm \pi}\rho _i)^2 \times (2{\rm \pi} a_0)$![]() , where the elongation of the domain along the equilibrium magnetic field $\boldsymbol {B}_0=B_0 \hat {\boldsymbol {z}}$
, where the elongation of the domain along the equilibrium magnetic field $\boldsymbol {B}_0=B_0 \hat {\boldsymbol {z}}$![]() is characterized by the arbitrary gyrokinetic expansion parameter $\epsilon \sim \rho _i/a_0 \ll 1$
is characterized by the arbitrary gyrokinetic expansion parameter $\epsilon \sim \rho _i/a_0 \ll 1$![]() . The proton-to-electron temperature ratio of the Maxwellian equilibrium is $T_i/T_e=1$
. The proton-to-electron temperature ratio of the Maxwellian equilibrium is $T_i/T_e=1$![]() , and we choose a reduced mass ratio $m_i/m_e = 36$
, and we choose a reduced mass ratio $m_i/m_e = 36$![]() to ensure that we fully resolve the kinetic damping mechanisms needed to achieve a steady-state turbulent cascade in a driven simulation, as discussed in Howes et al. (Reference Howes, McCubbin and Klein2018). These parameters lead to a fully resolved range of perpendicular wavenumbers $0.25 \le k_\perp \rho _i \le 7.75$
to ensure that we fully resolve the kinetic damping mechanisms needed to achieve a steady-state turbulent cascade in a driven simulation, as discussed in Howes et al. (Reference Howes, McCubbin and Klein2018). These parameters lead to a fully resolved range of perpendicular wavenumbers $0.25 \le k_\perp \rho _i \le 7.75$![]() , or $0.042\le k_\perp \rho _e \le 1.29$
, or $0.042\le k_\perp \rho _e \le 1.29$![]() . For the $\beta _i = 0.3$
. For the $\beta _i = 0.3$![]() and $\beta _i = 1$
and $\beta _i = 1$![]() simulations, the proton and electron collisionalities are set to $\nu _s/(k_{\parallel 0} v_{{\rm ti}})=0.1$
simulations, the proton and electron collisionalities are set to $\nu _s/(k_{\parallel 0} v_{{\rm ti}})=0.1$![]() , and for the $\beta _i = 3$
, and for the $\beta _i = 3$![]() simulation, $\nu _s/(k_{\parallel 0} v_{{\rm ti}}) = 0.05$
simulation, $\nu _s/(k_{\parallel 0} v_{{\rm ti}}) = 0.05$![]() . These collisionalities ensure weakly collisional plasma conditions, yet prevent the small-scale variations that develop in velocity space from becoming unresolved on the velocity grid.
. These collisionalities ensure weakly collisional plasma conditions, yet prevent the small-scale variations that develop in velocity space from becoming unresolved on the velocity grid.
Turbulence in the simulations is driven from zero initial conditions using an oscillating Langevin antenna (TenBarge et al. Reference TenBarge, Howes, Dorland and Hammett2014) with characteristic frequency $\omega _0/(k_{\parallel 0} v_A) = 0.9$![]() and decorrelation rate $\sigma _0/(k_{\parallel 0} v_A) = -0.3$
and decorrelation rate $\sigma _0/(k_{\parallel 0} v_A) = -0.3$![]() to drive four Alfvén wave modes at the domain scale with wave vectors $(k_x \rho _i, k_y\rho _i, k_z a_0) = (0.25, 0, \pm 1)$
to drive four Alfvén wave modes at the domain scale with wave vectors $(k_x \rho _i, k_y\rho _i, k_z a_0) = (0.25, 0, \pm 1)$![]() and $(0, 0.25, \pm 1)$
and $(0, 0.25, \pm 1)$![]() , generating four perpendicularly polarized Alfvén waves propagating in both directions along the equilibrium magnetic field. The amplitude of the driving is chosen to satisfy critical balance with a nonlinearity parameter $\chi \equiv k_\perp \delta B_\perp /(k_\parallel B_0) \simeq 1$
, generating four perpendicularly polarized Alfvén waves propagating in both directions along the equilibrium magnetic field. The amplitude of the driving is chosen to satisfy critical balance with a nonlinearity parameter $\chi \equiv k_\perp \delta B_\perp /(k_\parallel B_0) \simeq 1$![]() (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a) at the driving scale $k_\perp \rho _i=0.25$
(Goldreich & Sridhar Reference Goldreich and Sridhar1995; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a) at the driving scale $k_\perp \rho _i=0.25$![]() . This driving has been shown to generate effectively a strong plasma turbulent cascade to small scales in previous kinetic simulations through nonlinear interactions between the counterpropagating Alfvén waves (Howes et al. Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b, Reference Howes, TenBarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011; Howes & Nielson Reference Howes and Nielson2013; TenBarge & Howes Reference TenBarge and Howes2013; TenBarge, Howes & Dorland Reference TenBarge, Howes and Dorland2013; Howes et al. Reference Howes, McCubbin and Klein2018; Verniero, Howes & Klein Reference Verniero, Howes and Klein2018; Verniero & Howes Reference Verniero and Howes2018; Horvath et al. Reference Horvath, Howes and McCubbin2020; Conley et al. Reference Conley, Howes and McCubbin2023). To provide the data needed to apply the field–particle correlation analysis, the electromagnetic fluctuations and proton velocity distributions are sampled at a high cadence at twenty-four probe points that are distributed throughout the domain, sixteen in the $xy$
. This driving has been shown to generate effectively a strong plasma turbulent cascade to small scales in previous kinetic simulations through nonlinear interactions between the counterpropagating Alfvén waves (Howes et al. Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b, Reference Howes, TenBarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011; Howes & Nielson Reference Howes and Nielson2013; TenBarge & Howes Reference TenBarge and Howes2013; TenBarge, Howes & Dorland Reference TenBarge, Howes and Dorland2013; Howes et al. Reference Howes, McCubbin and Klein2018; Verniero, Howes & Klein Reference Verniero, Howes and Klein2018; Verniero & Howes Reference Verniero and Howes2018; Horvath et al. Reference Horvath, Howes and McCubbin2020; Conley et al. Reference Conley, Howes and McCubbin2023). To provide the data needed to apply the field–particle correlation analysis, the electromagnetic fluctuations and proton velocity distributions are sampled at a high cadence at twenty-four probe points that are distributed throughout the domain, sixteen in the $xy$![]() -plane at $z=0$
-plane at $z=0$![]() , and the remaining eight along the $z$
, and the remaining eight along the $z$![]() -axis, as illustrated in figure 2 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
-axis, as illustrated in figure 2 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
The time scale associated with the outer scale of the turbulent cascade in each simulation is the wave period of the domain-scale Alfvén wave $T$![]() , and the simulations are run for $6.78 T$
, and the simulations are run for $6.78 T$![]() for the $\beta _i=0.3$
for the $\beta _i=0.3$![]() simulation, $5.51 T$
simulation, $5.51 T$![]() for the $\beta _i=1$
for the $\beta _i=1$![]() simulation and $3.61 T$
simulation and $3.61 T$![]() for the $\beta _i=3$
for the $\beta _i=3$![]() simulation. The perpendicular magnetic energy spectrum $E_{B_\perp }(k_\perp )$
simulation. The perpendicular magnetic energy spectrum $E_{B_\perp }(k_\perp )$![]() at the end of each of the simulations is shown in figure 7, showing the spectrum for $\beta _i=0.3$
at the end of each of the simulations is shown in figure 7, showing the spectrum for $\beta _i=0.3$![]() (red), $\beta _i=1$
(red), $\beta _i=1$![]() (black) and $\beta _i=3$
(black) and $\beta _i=3$![]() (blue). These spectra demonstrate that each simulation yields a broadband turbulent spectrum, with the spectral slope for each simulation consistent with the expectation of $-5/3$
(blue). These spectra demonstrate that each simulation yields a broadband turbulent spectrum, with the spectral slope for each simulation consistent with the expectation of $-5/3$![]() for strong plasma turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995) in the inertial range at $k_\perp \rho _i<1$
for strong plasma turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995) in the inertial range at $k_\perp \rho _i<1$![]() , and steepening of the spectrum at the transition to the dissipation range at $k_\perp \rho _i\sim 1$
, and steepening of the spectrum at the transition to the dissipation range at $k_\perp \rho _i\sim 1$![]() . In the dissipation range at $k_\perp \rho _i> 1$
. In the dissipation range at $k_\perp \rho _i> 1$![]() , the spectral slopes begin around $-3.2$
, the spectral slopes begin around $-3.2$![]() , steepening as $k_\perp \rho _e \rightarrow 1$
, steepening as $k_\perp \rho _e \rightarrow 1$![]() due to the resolved kinetic dissipation mechanisms that remove energy from the turbulent cascade. Note that these dissipation range slopes are slightly steeper than the values ranging from $-2.7$
due to the resolved kinetic dissipation mechanisms that remove energy from the turbulent cascade. Note that these dissipation range slopes are slightly steeper than the values ranging from $-2.7$![]() to $-3.1$
to $-3.1$![]() typically observed in the solar wind (Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and De Patoul2013), but this is to be expected due to the unphysical mass ratio of $m_i/m_e = 36$
typically observed in the solar wind (Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and De Patoul2013), but this is to be expected due to the unphysical mass ratio of $m_i/m_e = 36$![]() , which effectively enhances the damping rate due to electrons relative to the realistic mass ratio case (TenBarge et al. Reference TenBarge, Howes and Dorland2013), leading to slightly steeper dissipation range spectra for stronger damping (Howes, Tenbarge & Dorland Reference Howes, Tenbarge and Dorland2011).
, which effectively enhances the damping rate due to electrons relative to the realistic mass ratio case (TenBarge et al. Reference TenBarge, Howes and Dorland2013), leading to slightly steeper dissipation range spectra for stronger damping (Howes, Tenbarge & Dorland Reference Howes, Tenbarge and Dorland2011).

Figure 7. Perpendicular magnetic energy spectra at the end of each of the turbulence simulations, showing $\beta _i=0.3$![]() (red), $\beta _i=1$
(red), $\beta _i=1$![]() (black) and $\beta _i=3$
(black) and $\beta _i=3$![]() (blue). Vertical dotted lines indicate the limit of fully resolved perpendicular wavenumbers in the simulation, $0.25 \le k_\perp \rho _i \le 7.75$
(blue). Vertical dotted lines indicate the limit of fully resolved perpendicular wavenumbers in the simulation, $0.25 \le k_\perp \rho _i \le 7.75$![]() or $0.042\le k_\perp \rho _e \le 1.29$
or $0.042\le k_\perp \rho _e \le 1.29$![]() .
.
In figure 8, we plot the normalized damping rates $|\gamma |/\omega$![]() from the linear dispersion relation for the simulation parameters with the reduced mass ratio $m_i/m_e=36$
from the linear dispersion relation for the simulation parameters with the reduced mass ratio $m_i/m_e=36$![]() , presenting the results for (a) $\beta _i=0.3$
, presenting the results for (a) $\beta _i=0.3$![]() , (b) $\beta _i=1$
, (b) $\beta _i=1$![]() and (c) $\beta _i=3$
and (c) $\beta _i=3$![]() , in the same format as presented in figure 6. Here, we plot vertical black dashed lines at the perpendicular wavenumber limits of the simulation at $k_\perp \rho _i=0.25$
, in the same format as presented in figure 6. Here, we plot vertical black dashed lines at the perpendicular wavenumber limits of the simulation at $k_\perp \rho _i=0.25$![]() and $k_\perp \rho _i=7.75$
and $k_\perp \rho _i=7.75$![]() . Note the salient features that TTD yields a loss of ion energy for $\beta _i=0.3$
. Note the salient features that TTD yields a loss of ion energy for $\beta _i=0.3$![]() in (a), and LD yields a loss of ion energy for $\beta _i=3$
in (a), and LD yields a loss of ion energy for $\beta _i=3$![]() at $k_\perp \rho _i \lesssim 1.5$
at $k_\perp \rho _i \lesssim 1.5$![]() . These calculations of the linear wave properties and the effective ion energization rates by TTD and LD provide an important theoretical framework for the interpretation of our field–particle analysis results.
. These calculations of the linear wave properties and the effective ion energization rates by TTD and LD provide an important theoretical framework for the interpretation of our field–particle analysis results.

Figure 8. Linear dispersion relations for KAWs from PLUME calculations with the reduced mass ratio $m_i/m_e = 36$![]() , showing the absolute value of the normalized wave damping or growth rate $|\gamma |/\omega$
, showing the absolute value of the normalized wave damping or growth rate $|\gamma |/\omega$![]() as a function of the dimensionless perpendicular wavenumber $k_\perp \rho _i$
as a function of the dimensionless perpendicular wavenumber $k_\perp \rho _i$![]() for (a) $\beta _i = 0.3$
for (a) $\beta _i = 0.3$![]() , (b) $\beta _i = 1$
, (b) $\beta _i = 1$![]() and (c) $\beta _i = 3$
and (c) $\beta _i = 3$![]() . The two vertical black dashed lines at $k_\perp \rho _i = 0.25$
. The two vertical black dashed lines at $k_\perp \rho _i = 0.25$![]() and $7.75$
and $7.75$![]() label the range consistent with the AstroGK turbulence simulations, and the two vertical green dashed lines mark the range of $1/e$
label the range consistent with the AstroGK turbulence simulations, and the two vertical green dashed lines mark the range of $1/e$![]() of the peak value of $\gamma _i$
of the peak value of $\gamma _i$![]() . The horizontal dashed black line at $|\gamma |/\omega = 10^{-1}$
. The horizontal dashed black line at $|\gamma |/\omega = 10^{-1}$![]() indicates the threshold above which significant damping or growth occurs. Each panel follows the layout format of figure 6.
indicates the threshold above which significant damping or growth occurs. Each panel follows the layout format of figure 6.
4.2. Choosing the correlation interval $\tau$
Unlike in the single KAW simulations, where the single-wave period $T$![]() is the obvious choice for the correlation interval $\tau$
is the obvious choice for the correlation interval $\tau$![]() to eliminate the oscillatory contribution to the transfer of energy from fields to particles, choosing $\tau$
to eliminate the oscillatory contribution to the transfer of energy from fields to particles, choosing $\tau$![]() for a plasma supporting broadband turbulent fluctuations is less straightforward. The longest wave period for an Alfvén wave at the domain scale in our $\beta _i=1$
for a plasma supporting broadband turbulent fluctuations is less straightforward. The longest wave period for an Alfvén wave at the domain scale in our $\beta _i=1$![]() simulation is $\tau \omega _A \simeq 6.28$
simulation is $\tau \omega _A \simeq 6.28$![]() . In figure 9, for a single probe position in the $\beta _i=1$
. In figure 9, for a single probe position in the $\beta _i=1$![]() simulation, we present (a) the total energy transfer rate to ions due to TTD $(\partial W_i/\partial t)_{{\rm TTD}}$
simulation, we present (a) the total energy transfer rate to ions due to TTD $(\partial W_i/\partial t)_{{\rm TTD}}$![]() and (b) the energy transfer rate at $v_\parallel /v_{{\rm ti}}=-1.3$
and (b) the energy transfer rate at $v_\parallel /v_{{\rm ti}}=-1.3$![]() , for a correlation interval spanning $0 \le \tau \omega _A \le 15$
, for a correlation interval spanning $0 \le \tau \omega _A \le 15$![]() . The instantaneous values of the local energy transfer rates (with $\tau =0$
. The instantaneous values of the local energy transfer rates (with $\tau =0$![]() , blue) exhibit large fluctuations with both positive and negative signs, but for $\tau \omega _A = 6.4$
, blue) exhibit large fluctuations with both positive and negative signs, but for $\tau \omega _A = 6.4$![]() (black) and longer correlation intervals, those large fluctuations are averaged out, leading to a time-averaged energy transfer rate that is approximately an order of magnitude smaller in amplitude than the peaks of the instantaneous value. In figure 9, we also show timestack plots $C_{\delta B_\parallel, i}(v_\parallel, t; \tau )$
(black) and longer correlation intervals, those large fluctuations are averaged out, leading to a time-averaged energy transfer rate that is approximately an order of magnitude smaller in amplitude than the peaks of the instantaneous value. In figure 9, we also show timestack plots $C_{\delta B_\parallel, i}(v_\parallel, t; \tau )$![]() for (c) $\tau =0$
for (c) $\tau =0$![]() and (d) $\tau \omega _A =6.4$
and (d) $\tau \omega _A =6.4$![]() , showing that a relatively persistent bipolar signature of TTD is revealed at $v_\parallel /v_{{\rm ti}}=-1.1$
, showing that a relatively persistent bipolar signature of TTD is revealed at $v_\parallel /v_{{\rm ti}}=-1.1$![]() in the $\tau \omega _A =6.4$
in the $\tau \omega _A =6.4$![]() case with peak amplitudes about an order of magnitude smaller than the instantaneous case with $\tau =0$
case with peak amplitudes about an order of magnitude smaller than the instantaneous case with $\tau =0$![]() . Thus, we choose a correlation interval $\tau \omega _A = 6.4$
. Thus, we choose a correlation interval $\tau \omega _A = 6.4$![]() to perform the field–particle correlation analysis of our $\beta _i=1$
to perform the field–particle correlation analysis of our $\beta _i=1$![]() turbulence simulation.
turbulence simulation.

Figure 9. Analysis of correlation interval selection for the $\beta _i = 1$![]() AstroGK turbulence simulation at probe 13 $({\rm \pi} \rho _i, 7 {\rm \pi}\rho _i, 0)$
AstroGK turbulence simulation at probe 13 $({\rm \pi} \rho _i, 7 {\rm \pi}\rho _i, 0)$![]() . (a,b) Time evolution of (a) the rate of change of ion kinetic energy density due to TTD, denoted as $\partial W_i /\partial t$
. (a,b) Time evolution of (a) the rate of change of ion kinetic energy density due to TTD, denoted as $\partial W_i /\partial t$![]() , and (b) the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$
, and (b) the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$![]() at $v_\parallel = -1.3 v_{{\rm ti}}$
at $v_\parallel = -1.3 v_{{\rm ti}}$![]() . Both quantities are presented over a range of $\tau \omega _A$
. Both quantities are presented over a range of $\tau \omega _A$![]() values from 0 to 15. The selected $\tau \omega _A$
values from 0 to 15. The selected $\tau \omega _A$![]() value of 6.4 is marked with a black line. (c,d) Timestack plots of the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$
value of 6.4 is marked with a black line. (c,d) Timestack plots of the reduced correlation $C_{\delta B_{\parallel, i}} (v_\parallel, t)$![]() for (c) $\tau \omega _A = 0$
for (c) $\tau \omega _A = 0$![]() and (d) $\tau \omega _A = 6.4$
and (d) $\tau \omega _A = 6.4$![]() , where the range of parallel phase velocities of KAWs that experience significant damping by ions is indicated by vertical dashed lines at $v_\parallel / v_\text {ti} = \pm 1.020$
, where the range of parallel phase velocities of KAWs that experience significant damping by ions is indicated by vertical dashed lines at $v_\parallel / v_\text {ti} = \pm 1.020$![]() and $v_\parallel / v_\text {ti} = \pm 1.704$
and $v_\parallel / v_\text {ti} = \pm 1.704$![]() .
.
4.3. Results for $\beta _i=1$ simulation
simulation
Performing the field–particle correlation analysis with $\tau \omega _A = 6.4$![]() for TTD and LD at all 24 probe positions in our $\beta _i = 1$
for TTD and LD at all 24 probe positions in our $\beta _i = 1$![]() turbulence simulation, we seek the gyrotropic velocity-space signatures of TTD and LD shown in figure 4. In figure 10(a), we plot the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$
turbulence simulation, we seek the gyrotropic velocity-space signatures of TTD and LD shown in figure 4. In figure 10(a), we plot the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() at one of the 24 probes, centred in time at $t\omega _A = 19.71$
at one of the 24 probes, centred in time at $t\omega _A = 19.71$![]() , showing a clear bipolar signature comparable to that shown in figure 4(a). The range of resonant parallel phase velocities for the KAW mode over which significant ion collisionless damping is expected is indicated by the vertical dashed lines; specifically, these lines mark the resonant velocities of the KAW mode at $k_\perp \rho _i \simeq 0.5$
, showing a clear bipolar signature comparable to that shown in figure 4(a). The range of resonant parallel phase velocities for the KAW mode over which significant ion collisionless damping is expected is indicated by the vertical dashed lines; specifically, these lines mark the resonant velocities of the KAW mode at $k_\perp \rho _i \simeq 0.5$![]() and $k_\perp \rho _i \simeq 2.3$
and $k_\perp \rho _i \simeq 2.3$![]() , the points at which the total ion collisionless damping rate drops to a factor $1/e$
, the points at which the total ion collisionless damping rate drops to a factor $1/e$![]() of its peak value at $k_\perp \rho _i \simeq 1.3$
of its peak value at $k_\perp \rho _i \simeq 1.3$![]() , as illustrated by the vertical green dashed lines on the linear dispersion relation plot for $m_i/m_e=36$
, as illustrated by the vertical green dashed lines on the linear dispersion relation plot for $m_i/m_e=36$![]() in figure 8(b). In the lower panel is shown the reduced parallel velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel ;\tau )$
in figure 8(b). In the lower panel is shown the reduced parallel velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel ;\tau )$![]() integrated over $v_\perp$
integrated over $v_\perp$![]() , yielding a clear bipolar signature with a zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$
, yielding a clear bipolar signature with a zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$![]() . Note that the zero crossing of this velocity-space signature falls within the expected range of resonant velocities (vertical dashed lines), as expected theoretically for a resonant collisionless damping mechanism. The left panel shows the net rate of ion energization due to TTD $(\partial W_i/\partial t)_{{\rm TTD}}$
. Note that the zero crossing of this velocity-space signature falls within the expected range of resonant velocities (vertical dashed lines), as expected theoretically for a resonant collisionless damping mechanism. The left panel shows the net rate of ion energization due to TTD $(\partial W_i/\partial t)_{{\rm TTD}}$![]() as a function of time, showing net positive ion energization due to TTD at this position over almost the full duration of the simulation. Thus, figure 10(a) demonstrates that TTD indeed plays a role in the damping of turbulent fluctuations and consequent energization of the ions, a second key result of this paper.
as a function of time, showing net positive ion energization due to TTD at this position over almost the full duration of the simulation. Thus, figure 10(a) demonstrates that TTD indeed plays a role in the damping of turbulent fluctuations and consequent energization of the ions, a second key result of this paper.

Figure 10. Velocity-space signatures of TTD (a,b) at probe 13 $({\rm \pi} \rho _i, 7 {\rm \pi}\rho _i, 0)$![]() and LD (c,d) at probe 24 $(4 {\rm \pi}\rho _i, 4 {\rm \pi}\rho _i, 0.875 {\rm \pi}a_0)$
and LD (c,d) at probe 24 $(4 {\rm \pi}\rho _i, 4 {\rm \pi}\rho _i, 0.875 {\rm \pi}a_0)$![]() in AstroGK turbulence simulation with $0.25 \leq k_\perp \rho _i \leq 7.75$
in AstroGK turbulence simulation with $0.25 \leq k_\perp \rho _i \leq 7.75$![]() , $T_i / T_e = 1$
, $T_i / T_e = 1$![]() , and $\beta _i = 1$
, and $\beta _i = 1$![]() . The correlation interval is set as $\tau \omega _A = 6.4$
. The correlation interval is set as $\tau \omega _A = 6.4$![]() . (a,c) Gyrotropic plane $(v_\parallel, v_\perp )$
. (a,c) Gyrotropic plane $(v_\parallel, v_\perp )$![]() signatures, following the layout format of panels in figure 4. (b,d) Timestack plots of the $v_\perp$
signatures, following the layout format of panels in figure 4. (b,d) Timestack plots of the $v_\perp$![]() -integrated reduced correlation; the main panel here shows the reduced correlation on $(v_\parallel, t)$
-integrated reduced correlation; the main panel here shows the reduced correlation on $(v_\parallel, t)$![]() grids, and the lower panel shows the time-integrated reduced correlation. Four vertical dashed lines at $v_\parallel / v_\text {ti} = \pm 1.020$
grids, and the lower panel shows the time-integrated reduced correlation. Four vertical dashed lines at $v_\parallel / v_\text {ti} = \pm 1.020$![]() and $v_\parallel / v_\text {ti} = \pm 1.704$
and $v_\parallel / v_\text {ti} = \pm 1.704$![]() indicate the resonant parallel phase velocity ranges where significant ion damping occurs.
indicate the resonant parallel phase velocity ranges where significant ion damping occurs.
In figure 10(b), we show a timestack plot $C_{\delta B_\parallel, i}(v_\parallel,t;\tau )$![]() of the ion energization by TTD at the same probe position as in (a), showing the persistence in time of the reduced parallel velocity-space signature with the zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$
of the ion energization by TTD at the same probe position as in (a), showing the persistence in time of the reduced parallel velocity-space signature with the zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$![]() . Note that the zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$
. Note that the zero crossing at $v_\parallel /v_{{\rm ti}} \simeq -1.1$![]() in this timestack plot shifts to slightly lower phase velocities near the end of the simulation at $t\omega _A > 25$
in this timestack plot shifts to slightly lower phase velocities near the end of the simulation at $t\omega _A > 25$![]() , likely due to damping associated with KAWs that have slightly lower perpendicular wavenumbers $k_\perp \rho _i$
, likely due to damping associated with KAWs that have slightly lower perpendicular wavenumbers $k_\perp \rho _i$![]() , as can occur in broadband turbulence. There is also a relatively short-lived bipolar signature observed at $v_\parallel /v_{{\rm ti}} \simeq 1$
, as can occur in broadband turbulence. There is also a relatively short-lived bipolar signature observed at $v_\parallel /v_{{\rm ti}} \simeq 1$![]() at times $t\omega _A < 15$
at times $t\omega _A < 15$![]() , indicating that TTD is also acting on KAWs propagating the other direction along the magnetic field (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
, indicating that TTD is also acting on KAWs propagating the other direction along the magnetic field (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
We perform the analogous field–particle correlation for LD, showing $C_{E_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() in figure 10(c), yielding a bipolar gyrotropic velocity-space signature at $v_\parallel /v_{{\rm ti}} \simeq 1.2$
in figure 10(c), yielding a bipolar gyrotropic velocity-space signature at $v_\parallel /v_{{\rm ti}} \simeq 1.2$![]() at time $t\omega _A=24.3$
at time $t\omega _A=24.3$![]() , also within the expected range of resonant parallel phase velocities. This finding of the velocity-space signature of LD confirms previous field–particle correlation analyses showing that ion LD plays a role in the dissipation of plasma turbulence (Klein et al. Reference Klein, Howes and TenBarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021). The timestack plot $C_{E_\parallel, i}(v_\parallel,t;\tau )$
, also within the expected range of resonant parallel phase velocities. This finding of the velocity-space signature of LD confirms previous field–particle correlation analyses showing that ion LD plays a role in the dissipation of plasma turbulence (Klein et al. Reference Klein, Howes and TenBarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021). The timestack plot $C_{E_\parallel, i}(v_\parallel,t;\tau )$![]() in figure 10(d) shows this strong bipolar signature of LD at $v_\parallel /v_{{\rm ti}} \simeq 1.2$
in figure 10(d) shows this strong bipolar signature of LD at $v_\parallel /v_{{\rm ti}} \simeq 1.2$![]() persists over $22 \lesssim t\omega _A \lesssim 30$
persists over $22 \lesssim t\omega _A \lesssim 30$![]() . In closing, it is worthwhile noting that, to distinguish the velocity-space signature of TTD from that of LD, it is necessary to examine the signatures in gyrotropic velocity space $(v_\parallel,v_\perp )$
. In closing, it is worthwhile noting that, to distinguish the velocity-space signature of TTD from that of LD, it is necessary to examine the signatures in gyrotropic velocity space $(v_\parallel,v_\perp )$![]() , showing that ion energization is limited to ions with $v_\perp /v_{{\rm ti}} \gtrsim 1$
, showing that ion energization is limited to ions with $v_\perp /v_{{\rm ti}} \gtrsim 1$![]() for TTD, but that ion energization extends down to $v_\perp \rightarrow 0$
for TTD, but that ion energization extends down to $v_\perp \rightarrow 0$![]() for LD, as expected by the physical arguments outlined in § 3.2.
for LD, as expected by the physical arguments outlined in § 3.2.
4.4. Variations with ion plasma beta $\beta _i$
Next, we explore how the velocity-space signatures of TTD and LD in plasma turbulence vary with changing the ion plasma beta $\beta _i = v_{{\rm ti}}^2/v_A^2$![]() . Because $\beta _i$
. Because $\beta _i$![]() is a function of the ratio of the ion thermal velocity to the Alfvén velocity, it directly characterizes where the parallel wave phase velocity falls with the ion velocity distribution, making it the most important parameter controlling resonant wave–particle interactions in a weakly collisional plasma. Specifically, $\omega /(k_\parallel v_{{\rm ti}}) = \bar {\omega } \beta _i^{-1/2}$
is a function of the ratio of the ion thermal velocity to the Alfvén velocity, it directly characterizes where the parallel wave phase velocity falls with the ion velocity distribution, making it the most important parameter controlling resonant wave–particle interactions in a weakly collisional plasma. Specifically, $\omega /(k_\parallel v_{{\rm ti}}) = \bar {\omega } \beta _i^{-1/2}$![]() , where the parallel phase velocity normalized to the Alfvén velocity $\bar {\omega } \equiv \omega /(k_\parallel v_{A})$
, where the parallel phase velocity normalized to the Alfvén velocity $\bar {\omega } \equiv \omega /(k_\parallel v_{A})$![]() typically has a value $\bar {\omega } \sim 1$
typically has a value $\bar {\omega } \sim 1$![]() for the perpendicular wavelengths $k_\perp \rho _i \sim 1$
for the perpendicular wavelengths $k_\perp \rho _i \sim 1$![]() at which the ions strongly interact with the waves. Note that, at the perpendicular scale of the domain $k_{\perp 0} \rho _i=0.25$
at which the ions strongly interact with the waves. Note that, at the perpendicular scale of the domain $k_{\perp 0} \rho _i=0.25$![]() , the Alfvén wave has the $\bar {\omega } \simeq 1$
, the Alfvén wave has the $\bar {\omega } \simeq 1$![]() for all values of $\beta _i$
for all values of $\beta _i$![]() , so we simply choose a correlation interval $\tau \omega _A = 6.4$
, so we simply choose a correlation interval $\tau \omega _A = 6.4$![]() for all of the turbulence simulation analysis below.
for all of the turbulence simulation analysis below.
We plot some typical velocity-space signatures for TTD and LD for the $\beta _i = 0.3$![]() simulation in figure 11. Note that, for this value of $\beta _i = 0.3$
simulation in figure 11. Note that, for this value of $\beta _i = 0.3$![]() , the contribution of TTD is always to remove energy from the ions, as shown in figure 8(a), so we expect only negative TTD signatures, similar to that shown in figure 5(a). Consequently, we expect LD to dominate the removal of energy from the turbulence. Performing the TTD analysis to determine $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$
, the contribution of TTD is always to remove energy from the ions, as shown in figure 8(a), so we expect only negative TTD signatures, similar to that shown in figure 5(a). Consequently, we expect LD to dominate the removal of energy from the turbulence. Performing the TTD analysis to determine $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() , we display a typical gyrotropic velocity-space signature in figure 11(a) with the associated timestack plot at the same probe in (b), showing two bipolar signatures with a net negative energy transfer rate and zero crossings at $v_\parallel /v_{{\rm ti}} \simeq \pm 0.7$
, we display a typical gyrotropic velocity-space signature in figure 11(a) with the associated timestack plot at the same probe in (b), showing two bipolar signatures with a net negative energy transfer rate and zero crossings at $v_\parallel /v_{{\rm ti}} \simeq \pm 0.7$![]() . These look like typical reversed TTD signatures, but the phase velocity is not within the expected range $1.8 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 2.4$
. These look like typical reversed TTD signatures, but the phase velocity is not within the expected range $1.8 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 2.4$![]() for a KAW with $\beta _i = 0.3$
for a KAW with $\beta _i = 0.3$![]() . Only 3 of the 24 probes showed reversed TTD signatures with phase velocities closer to the expected range, as shown in figure 11(c,d) with a bipolar zero crossing around $v_\parallel /v_{{\rm ti}} \simeq -1.5$
. Only 3 of the 24 probes showed reversed TTD signatures with phase velocities closer to the expected range, as shown in figure 11(c,d) with a bipolar zero crossing around $v_\parallel /v_{{\rm ti}} \simeq -1.5$![]() .
.

Figure 11. Velocity-space signatures of TTD (a–d) and LD (e–h) sampled from AstroGK turbulence simulation with $0.25 \leq k_\perp \rho _i \leq 7.75$![]() , $T_i / T_e = 1$
, $T_i / T_e = 1$![]() and $\beta _i = 0.3$
and $\beta _i = 0.3$![]() . The correlation interval is set as $\tau \omega _A = 6.4$
. The correlation interval is set as $\tau \omega _A = 6.4$![]() . (a,c,e,g) Gyrotropic plane $(v_\parallel, v_\perp )$
. (a,c,e,g) Gyrotropic plane $(v_\parallel, v_\perp )$![]() signatures, and (b,d,f,h) Timestack plots of the $v_\perp$
signatures, and (b,d,f,h) Timestack plots of the $v_\perp$![]() -integrated reduced correlation; both following the layout format of figure 10. The resonant parallel phase velocity ranges are marked by the four vertical dashed lines at $v_\parallel /v_\text {ti} =\pm 1.832$
-integrated reduced correlation; both following the layout format of figure 10. The resonant parallel phase velocity ranges are marked by the four vertical dashed lines at $v_\parallel /v_\text {ti} =\pm 1.832$![]() and $v_\parallel /v_\text {ti} =\pm 2.373$
and $v_\parallel /v_\text {ti} =\pm 2.373$![]() . From top to bottom, data are taken from probe 7 $(5 {\rm \pi}\rho _i, 3 {\rm \pi}\rho _i, 0)$
. From top to bottom, data are taken from probe 7 $(5 {\rm \pi}\rho _i, 3 {\rm \pi}\rho _i, 0)$![]() , probe 15 $(5 {\rm \pi}\rho _i, 7 {\rm \pi}\rho _i, 0)$
, probe 15 $(5 {\rm \pi}\rho _i, 7 {\rm \pi}\rho _i, 0)$![]() , probe 20 $(4 {\rm \pi}\rho _i, 4 {\rm \pi}\rho _i, -0.125 {\rm \pi}a_0)$
, probe 20 $(4 {\rm \pi}\rho _i, 4 {\rm \pi}\rho _i, -0.125 {\rm \pi}a_0)$![]() and probe 5 $({\rm \pi} \rho _i, 3 {\rm \pi}\rho _i, 0)$
and probe 5 $({\rm \pi} \rho _i, 3 {\rm \pi}\rho _i, 0)$![]() , respectively.
, respectively.
Performing the LD analysis to determine $C_{E_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() in the same $\beta _i = 0.3$
in the same $\beta _i = 0.3$![]() turbulence simulation, we find a similar intriguing result that we commonly find bipolar signatures associated with positive energy transfer to ions, but with zero crossings well below the expected range of $1.8 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 2.4$
turbulence simulation, we find a similar intriguing result that we commonly find bipolar signatures associated with positive energy transfer to ions, but with zero crossings well below the expected range of $1.8 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 2.4$![]() . In figure 11(e), we see two bipolar signatures at $v_\parallel /v_{{\rm ti}} \simeq -0.7$
. In figure 11(e), we see two bipolar signatures at $v_\parallel /v_{{\rm ti}} \simeq -0.7$![]() and $v_\parallel /v_{{\rm ti}} \simeq 1.2$
and $v_\parallel /v_{{\rm ti}} \simeq 1.2$![]() . Only 2 of the 24 probes recover LD velocity-space signatures in the expected range, such as that shown in figure 11(g,h).
. Only 2 of the 24 probes recover LD velocity-space signatures in the expected range, such as that shown in figure 11(g,h).
Turning next to the field–particle correlation analysis of the $\beta _i = 3$![]() turbulence simulation, the linear dispersion relation plot for KAWs in figure 8(c) shows that LD removes energy from ions for waves with $k_\perp \rho _i \lesssim 1.7$
turbulence simulation, the linear dispersion relation plot for KAWs in figure 8(c) shows that LD removes energy from ions for waves with $k_\perp \rho _i \lesssim 1.7$![]() , but TTD positively energizes ions over perpendicular wavenumbers with $k_\perp \rho _i \lesssim 4$
, but TTD positively energizes ions over perpendicular wavenumbers with $k_\perp \rho _i \lesssim 4$![]() . At all probes in the simulation, we find bipolar velocity-space signatures of positive energy transfer by TTD to ions at both positive and negative parallel velocities near the expected range $0.58 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 0.94$
. At all probes in the simulation, we find bipolar velocity-space signatures of positive energy transfer by TTD to ions at both positive and negative parallel velocities near the expected range $0.58 \lesssim |v_\parallel /v_{{\rm ti}}| \lesssim 0.94$![]() , with a typical case illustrated in figure 12, showing (a) the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$
, with a typical case illustrated in figure 12, showing (a) the gyrotropic velocity-space signature $C_{\delta B_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() and (b) the timestack plot $C_{\delta B_\parallel, i}(v_\parallel,t;\tau )$
and (b) the timestack plot $C_{\delta B_\parallel, i}(v_\parallel,t;\tau )$![]() indicating that these signatures are persistent in time. On the other hand, analysing the signatures of LD using (c) the gyrotropic velocity-space signature $C_{E_\parallel, i}(v_\parallel,v_\perp ;\tau )$
indicating that these signatures are persistent in time. On the other hand, analysing the signatures of LD using (c) the gyrotropic velocity-space signature $C_{E_\parallel, i}(v_\parallel,v_\perp ;\tau )$![]() and (d) the timestack plot $C_{E_\parallel, i}(v_\parallel,t;\tau )$
and (d) the timestack plot $C_{E_\parallel, i}(v_\parallel,t;\tau )$![]() , the pattern of energy transfer to ions is widely variable, with ions losing energy more than gaining energy, in agreement with the expectations from the linear dispersion relation. During the majority of the time when clear reversed bipolar patterns are visible for LD, they appear to have zero crossings that are close to the expected range of parallel resonant velocities.
, the pattern of energy transfer to ions is widely variable, with ions losing energy more than gaining energy, in agreement with the expectations from the linear dispersion relation. During the majority of the time when clear reversed bipolar patterns are visible for LD, they appear to have zero crossings that are close to the expected range of parallel resonant velocities.

Figure 12. Velocity-space signatures of TTD (a,b) at probe 22 $(4 {\rm \pi}\rho _i, 4 {\rm \pi}\rho _i, 0.375 {\rm \pi}a_0)$![]() and LD (c,d) at probe 5 $({\rm \pi} \rho _i, 3 {\rm \pi}\rho _i, 0)$
and LD (c,d) at probe 5 $({\rm \pi} \rho _i, 3 {\rm \pi}\rho _i, 0)$![]() sampled from AstroGK turbulence simulation with $0.25 \leq k_\perp \rho _i \leq 7.75$
sampled from AstroGK turbulence simulation with $0.25 \leq k_\perp \rho _i \leq 7.75$![]() , $T_i / T_e = 1$
, $T_i / T_e = 1$![]() and $\beta _i = 3$
and $\beta _i = 3$![]() . The correlation interval is set as $\tau \omega _A = 6.4$
. The correlation interval is set as $\tau \omega _A = 6.4$![]() . (a,c) Gyrotropic plane $(v_\parallel, v_\perp )$
. (a,c) Gyrotropic plane $(v_\parallel, v_\perp )$![]() signatures, and (b,d) Timestack plots of the $v_\perp$
signatures, and (b,d) Timestack plots of the $v_\perp$![]() -integrated reduced correlation; both following the layout format of figure 10. The resonant parallel phase velocity ranges are marked by the four vertical dashed lines at $v_\parallel /v_\text {ti} =\pm 0.583$
-integrated reduced correlation; both following the layout format of figure 10. The resonant parallel phase velocity ranges are marked by the four vertical dashed lines at $v_\parallel /v_\text {ti} =\pm 0.583$![]() and $v_\parallel /v_\text {ti} =\pm 0.936$
and $v_\parallel /v_\text {ti} =\pm 0.936$![]() .
.
Since the field–particle correlation analysis of our single-wave simulations in § 3.3 shows that the velocity-space signatures of TTD and LD appear near the resonant parallel velocities of the waves, as illustrated in figure 5, it raises the question of why the velocity-space signatures in the $\beta _i = 0.3$![]() simulation in figure 11 often do not appear in the expected range of resonant velocities. There exist at least two possible explanations for this finding: (i) nonlinear transfer from Alfvén waves to other wave modes, and (ii) nonlinear TTD. Before going into the details of each of these possibilities below, it is worthwhile emphasizing that the field–particle correlation technique determines the total energy transfer to particles over the full velocity distribution, meaning that the net energy transfer within a region of velocity space is effectively weighted by the number of particles within that region of the velocity distribution. To illustrate this point, let us focus on the specific example of figure 11(a), where the range of resonant parallel phase velocities for the Alfvén mode (vertical black lines) occurs in the range $1.8 \lesssim v_\parallel /v_{{\rm ti}} \lesssim 2.4$
simulation in figure 11 often do not appear in the expected range of resonant velocities. There exist at least two possible explanations for this finding: (i) nonlinear transfer from Alfvén waves to other wave modes, and (ii) nonlinear TTD. Before going into the details of each of these possibilities below, it is worthwhile emphasizing that the field–particle correlation technique determines the total energy transfer to particles over the full velocity distribution, meaning that the net energy transfer within a region of velocity space is effectively weighted by the number of particles within that region of the velocity distribution. To illustrate this point, let us focus on the specific example of figure 11(a), where the range of resonant parallel phase velocities for the Alfvén mode (vertical black lines) occurs in the range $1.8 \lesssim v_\parallel /v_{{\rm ti}} \lesssim 2.4$![]() . Even if there exists resonant energy transfer to the particles at these suprathermal parallel velocities, a potentially competing mechanism (such as the two possibilities named above) could dominate the net particle energization if it transfers energy to particles lying within the bulk of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$
. Even if there exists resonant energy transfer to the particles at these suprathermal parallel velocities, a potentially competing mechanism (such as the two possibilities named above) could dominate the net particle energization if it transfers energy to particles lying within the bulk of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$![]() , where many more particles can participate in the energy transfer. Thus, the velocity-space signatures arising from the field–particle correlation analysis are generally weighted by the underlying velocity distribution to emphasize energy transfer mechanisms interacting with the main part of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$
, where many more particles can participate in the energy transfer. Thus, the velocity-space signatures arising from the field–particle correlation analysis are generally weighted by the underlying velocity distribution to emphasize energy transfer mechanisms interacting with the main part of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$![]() .
.
First, let us analyse how nonlinear energy to other wave modes may explain the velocity-space signatures observed in figure 11. Due to the predominantly Alfvénic nature of fluctuations in space plasma turbulence (Tu & Marsch Reference Tu and Marsch1995; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Bruno & Carbone Reference Bruno and Carbone2013), we focus on the collisional damping rates of Alfvénic fluctuations by TTD and LD in this study. However, the plasma turbulence in our gyrokinetic simulations is broadband and may contain slow magnetosonic fluctuations that arise from nonlinear couplings among the turbulent fluctuations. Although slow magnetosonic waves are not generated by nonlinear couplings among the dominantly Alfvénic fluctuations in the magnetohydrodynamics (MHD) limit at $k_\perp \rho _i \ll 1$![]() (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), at the ion kinetic scales $k_\perp \rho _i \sim 1$
(Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), at the ion kinetic scales $k_\perp \rho _i \sim 1$![]() it is possible that energy can be nonlinearly transferred into slow magnetosonic fluctuations. These kinetic slow wave fluctuationsFootnote 5 may have a different parallel phase velocity from the Alfvénic fluctuations and thereby mediate damping of the turbulent energy through either TTD or LD at phase velocities that fall within the bulk of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$
it is possible that energy can be nonlinearly transferred into slow magnetosonic fluctuations. These kinetic slow wave fluctuationsFootnote 5 may have a different parallel phase velocity from the Alfvénic fluctuations and thereby mediate damping of the turbulent energy through either TTD or LD at phase velocities that fall within the bulk of the velocity distribution at $v_\parallel /v_{{\rm ti}} \sim 1$![]() . The second possibility is that nonlinear TTD may occur, whereby the beat mode fluctuations (which are not natural wave modes of the system) – arising from nonlinear interactions between Alfvénic fluctuations with different frequencies and wave vectors – can have an effective phase velocity that falls in the core of the velocity distribution, leading to efficient net energy transfer to the ions via collisionless wave–particle interactions.
. The second possibility is that nonlinear TTD may occur, whereby the beat mode fluctuations (which are not natural wave modes of the system) – arising from nonlinear interactions between Alfvénic fluctuations with different frequencies and wave vectors – can have an effective phase velocity that falls in the core of the velocity distribution, leading to efficient net energy transfer to the ions via collisionless wave–particle interactions.
In closing this discussion about the velocity-space signatures observed in figure 11, a final point to emphasize is that the clear bipolar signatures of negative energy transfer from ions by TTD in figure 11(a) and of positive energy transfer to ions by LD in figure 11(e) for $\beta _i=0.3$![]() suggest that some resonant energy transfer mechanism is governing the energization in these simulations; the details of this turbulent damping mechanism, which may include nonlinear couplings to other linear wave modes or nonlinear beat modes as suggested above, are clearly a ripe avenue for exploration in future work.
suggest that some resonant energy transfer mechanism is governing the energization in these simulations; the details of this turbulent damping mechanism, which may include nonlinear couplings to other linear wave modes or nonlinear beat modes as suggested above, are clearly a ripe avenue for exploration in future work.
4.5. Net turbulent damping as a function of ion plasma beta $\beta _i$
To estimate the net energy density transfer to or from ions mediated by TTD or LD averaged over the volume of the simulation, we integrate the energy density transfer rate due to each mechanism over the duration of each turbulence simulation (after the energy spectra have reached a statistically steady state) and average over all 24 probes for each simulation. This procedure provides a statistical estimate of the total change in ion energy density by each mechanism, denoted by $W_{i,{\rm TTD}}$![]() and $W_{i, {\rm LD}}$
and $W_{i, {\rm LD}}$![]() . We compute the ratio of these ion energy density changes by each mechanism to the total ion energy density change $W_i = W_{i,{\rm TTD}} + W_{i, {\rm LD}}$
. We compute the ratio of these ion energy density changes by each mechanism to the total ion energy density change $W_i = W_{i,{\rm TTD}} + W_{i, {\rm LD}}$![]() , and plot $W_{i,{\rm TTD}}/W_i$
, and plot $W_{i,{\rm TTD}}/W_i$![]() (green) and $W_{i, {\rm LD}}/W_i$
(green) and $W_{i, {\rm LD}}/W_i$![]() (blue) versus the ion plasma beta $\beta _i$
(blue) versus the ion plasma beta $\beta _i$![]() in figure 13. Variability in the energy density changes due to TTD and LD is indicated by error bars on each point, computed using the standard deviation of the time-integrated energy density changes at all 24 probes. The red solid line at $1$
in figure 13. Variability in the energy density changes due to TTD and LD is indicated by error bars on each point, computed using the standard deviation of the time-integrated energy density changes at all 24 probes. The red solid line at $1$![]() presents the sum of $W_{i,{\rm TTD}}/W_i$
presents the sum of $W_{i,{\rm TTD}}/W_i$![]() and $W_{i, {\rm LD}}/W_i$
and $W_{i, {\rm LD}}/W_i$![]() , and the black dashed line at zero highlights whether a mechanism yields a positive net energy density transfer to ions or a negative net energy density transfer from ions.
, and the black dashed line at zero highlights whether a mechanism yields a positive net energy density transfer to ions or a negative net energy density transfer from ions.

Figure 13. Ratio of the change of the ion kinetic energy density due to TTD and LD to the total change of the ion kinetic energy density during the analysis time, both averaged over all 24 probes, plotted against $\beta _i$![]() . The error bars represent the standard deviations calculated across all probes.
. The error bars represent the standard deviations calculated across all probes.
For $\beta _i=0.3$![]() , the ion energization is dominated by LD, with TTD yielding a small and slightly negative energy transfer. The ion LD and TTD contributions to the damping rate from the linear dispersion relation in figure 8(a) provide intuition about the relative role of these two collisionless damping mechanisms in a turbulent plasma. Note that the broadband turbulence in the simulation consists of wave modes spanning the range $0.25 \le k_\perp \rho _i \le 7.75$
, the ion energization is dominated by LD, with TTD yielding a small and slightly negative energy transfer. The ion LD and TTD contributions to the damping rate from the linear dispersion relation in figure 8(a) provide intuition about the relative role of these two collisionless damping mechanisms in a turbulent plasma. Note that the broadband turbulence in the simulation consists of wave modes spanning the range $0.25 \le k_\perp \rho _i \le 7.75$![]() , denoted by the two vertical dashed black lines in figure 8(a), with a monotonically decreasing magnetic energy spectrum, as shown in figure 7. The net ion energization by each mechanism expected in a given simulation can be intuitively estimated by an integration over $k_\perp \rho _i$
, denoted by the two vertical dashed black lines in figure 8(a), with a monotonically decreasing magnetic energy spectrum, as shown in figure 7. The net ion energization by each mechanism expected in a given simulation can be intuitively estimated by an integration over $k_\perp \rho _i$![]() of the product of the damping rate for that mechanism with the electromagnetic energy at each scale. For $\beta _i=0.3$
of the product of the damping rate for that mechanism with the electromagnetic energy at each scale. For $\beta _i=0.3$![]() , figure 8(a) shows that $\gamma _{i{\rm TTD}}>0$
, figure 8(a) shows that $\gamma _{i{\rm TTD}}>0$![]() and $\gamma _{i{\rm LD}}<0$
and $\gamma _{i{\rm LD}}<0$![]() over the full range of perpendicular wavenumbers in the simulation, so the numerical finding of net energy transfer rates in figure 13 appears to be consistent with the expectation from the linear dispersion relation.
over the full range of perpendicular wavenumbers in the simulation, so the numerical finding of net energy transfer rates in figure 13 appears to be consistent with the expectation from the linear dispersion relation.
For $\beta _i=1$![]() , both LD and TTD yield net positive energization of the ions, but LD dominates over TTD once more, as seen in figure 13. This result is broadly consistent with the linear damping rates from the linear dispersion relation plotted in figure 8(b), where the LD rate integrated over $k_\perp \rho _i$
, both LD and TTD yield net positive energization of the ions, but LD dominates over TTD once more, as seen in figure 13. This result is broadly consistent with the linear damping rates from the linear dispersion relation plotted in figure 8(b), where the LD rate integrated over $k_\perp \rho _i$![]() would be expected to dominate over the TTD rate, but both mechanisms would be expected to yield net positive ion energization rates.
would be expected to dominate over the TTD rate, but both mechanisms would be expected to yield net positive ion energization rates.
At $\beta _i=3$![]() , on the other hand, figure 13 shows that TTD mediates a net positive energy transfer to the ions, while LD governs a net negative energy transfer with a slightly smaller magnitude than the positive TTD energy transfer. The linear dispersion relation results in figure 8(c) predict a more complicated behaviour than the $\beta _i=0.3$
, on the other hand, figure 13 shows that TTD mediates a net positive energy transfer to the ions, while LD governs a net negative energy transfer with a slightly smaller magnitude than the positive TTD energy transfer. The linear dispersion relation results in figure 8(c) predict a more complicated behaviour than the $\beta _i=0.3$![]() and $\beta _i=1$
and $\beta _i=1$![]() cases: TTD yields ion energization for all $k_\perp \rho _i \lesssim 5$
cases: TTD yields ion energization for all $k_\perp \rho _i \lesssim 5$![]() , but LD leads to ion-to-wave energy transfer for $k_\perp \rho _i \lesssim 1.5$
, but LD leads to ion-to-wave energy transfer for $k_\perp \rho _i \lesssim 1.5$![]() and wave-to-ion energy transfer for $k_\perp \rho _i \gtrsim 1.5$
and wave-to-ion energy transfer for $k_\perp \rho _i \gtrsim 1.5$![]() . The velocity-space-integrated rates of energy transfer by each mechanism at each probe – for example, the vertical left panels of figure 12(a,c) – show variations in time that appear to be consistent with these expectations from linear theory. The TTD rates of ion energy density change are generally positive with moderate amplitudes. On the other hand, the LD rates of ion energy density change are somewhat larger in amplitude but vary with both positive and negative rates, such that the net LD rate averaged over all probes is negative and slightly smaller in amplitude than the net TTD rate. This broader variation is evident in the larger standard deviation of the $\beta _i=3$
. The velocity-space-integrated rates of energy transfer by each mechanism at each probe – for example, the vertical left panels of figure 12(a,c) – show variations in time that appear to be consistent with these expectations from linear theory. The TTD rates of ion energy density change are generally positive with moderate amplitudes. On the other hand, the LD rates of ion energy density change are somewhat larger in amplitude but vary with both positive and negative rates, such that the net LD rate averaged over all probes is negative and slightly smaller in amplitude than the net TTD rate. This broader variation is evident in the larger standard deviation of the $\beta _i=3$![]() values in figure 13 relative to the $\beta _i=0.3$
values in figure 13 relative to the $\beta _i=0.3$![]() and $\beta _i=1$
and $\beta _i=1$![]() cases.
cases.
In conclusion, it is worthwhile emphasizing that the expectations from linear theory of the relative contributions to the energy density transfer rates from each mechanism, including their overall sign, are only expected to hold in statistical sense, averaged over a sufficiently large volume. This is particularly true for plasma parameter values where the expected linear damping rate for a given mechanism changes sign within the range of $k_\perp \rho _i$![]() where significant damping is expected, such as the case for ion LD in the $\beta _i=3$
where significant damping is expected, such as the case for ion LD in the $\beta _i=3$![]() simulation. Based on kinetic numerical simulations of turbulence, the rate of change of energy density for species $s$
simulation. Based on kinetic numerical simulations of turbulence, the rate of change of energy density for species $s$![]() given by $\boldsymbol {j}_s \boldsymbol {\cdot } \boldsymbol {E}$
given by $\boldsymbol {j}_s \boldsymbol {\cdot } \boldsymbol {E}$![]() is highly variable spatially, with variations that can be much larger than the spatially or temporally averaged net value. An example from a simulation of a strongly nonlinear Alfvén wave collision – the nonlinear interaction between counterpropagating Alfvén waves that is argued to be the fundamental building block of astrophysical plasma turbulence (Howes et al. Reference Howes, Drake, Nielson, Carter, Kletzing and Skiff2012; Drake et al. Reference Drake, Schroeder, Howes, Kletzing, Skiff, Carter and Auerbach2013; Howes & Nielson Reference Howes and Nielson2013; Howes et al. Reference Howes, Nielson, Drake, Schroeder, Skiff, Kletzing and Carter2013; Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013; Howes Reference Howes2016; Verniero et al. Reference Verniero, Howes and Klein2018; Verniero & Howes Reference Verniero and Howes2018) – is seen in figure 8 of Howes et al. (Reference Howes, McCubbin and Klein2018), where the wave-period-averaged energy density transfer rates are found to be an order of magnitude smaller than the instantaneous rates. Furthermore, even for an overall damping rate that energizes the plasma particles at the expense of the turbulent electromagnetic energy, the net energy transfer rate averaged over time at single position may be negative, even when the spatially averaged energy transfer rate is positive, as seen in figure 8(d) of Howes et al. (Reference Howes, McCubbin and Klein2018).
is highly variable spatially, with variations that can be much larger than the spatially or temporally averaged net value. An example from a simulation of a strongly nonlinear Alfvén wave collision – the nonlinear interaction between counterpropagating Alfvén waves that is argued to be the fundamental building block of astrophysical plasma turbulence (Howes et al. Reference Howes, Drake, Nielson, Carter, Kletzing and Skiff2012; Drake et al. Reference Drake, Schroeder, Howes, Kletzing, Skiff, Carter and Auerbach2013; Howes & Nielson Reference Howes and Nielson2013; Howes et al. Reference Howes, Nielson, Drake, Schroeder, Skiff, Kletzing and Carter2013; Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013; Howes Reference Howes2016; Verniero et al. Reference Verniero, Howes and Klein2018; Verniero & Howes Reference Verniero and Howes2018) – is seen in figure 8 of Howes et al. (Reference Howes, McCubbin and Klein2018), where the wave-period-averaged energy density transfer rates are found to be an order of magnitude smaller than the instantaneous rates. Furthermore, even for an overall damping rate that energizes the plasma particles at the expense of the turbulent electromagnetic energy, the net energy transfer rate averaged over time at single position may be negative, even when the spatially averaged energy transfer rate is positive, as seen in figure 8(d) of Howes et al. (Reference Howes, McCubbin and Klein2018).
That the turbulent energy damping rate is highly oscillatory, both in space and time, with a much smaller amplitude net energy damping rate that is generally positive (indicating a damping of turbulence and consequent energization of particles), should not be especially surprising. The nonlinear energy transfer from large to small scales by the turbulence is likewise found to be highly oscillatory, with third-moment calculations of the instantaneous energy transfer rates (Kolmogorov Reference Kolmogorov1941; Politano & Pouquet Reference Politano and Pouquet1998) yielding large values of both signs, with the net averaged value having a much smaller amplitude of positive energy transfer to small scales (Coburn et al. Reference Coburn, Smith, Vasquez, Forman and Stawarz2014, Reference Coburn, Forman, Smith, Vasquez and Stawarz2015). Thus, field–particle correlation calculations of the energy density transfer rate at a single point, even averaged over a long duration, may still lead to a result in a turbulent plasma that appears to conflict with the expectation from linear theory. Only with a sufficient large statistical average, here estimated using the average over all 24 probe positions, should we expect the results to be consistent with the general expectations of linear theory – the results in figure 13 indeed appear to be consistent with the general expectations for the relative contributions of LD and TTD from linear theory.
5. Conclusion
Transit-time damping is a well-known mechanism for the resonant collisionless damping of electromagnetic waves exhibiting variations of the magnetic field magnitude along the mean magnetic field direction, mediated by the magnetic mirror force. This mechanism has been proposed as a possible means for removing energy from the fluctuations in weakly collisional plasma turbulence, but to date there exists little direct evidence clearly showing the damping of turbulence via TTD. Here we employ the recently developed field–particle correlation technique to use measurements of the gradient of the magnetic field magnitude and the ion velocity distribution at a single point to determine a velocity-space signature that can be used to identify definitively that TTD plays a role in the damping of plasma turbulence.
We first derive the particular mathematical form of the field–particle correlation for the rate of energy transfer due to TTD in § 2.1, and then we predict the velocity-space signature of the rate of change of phase-space energy density due to TTD using a simple model in § 2.2. Next, we perform gyrokinetic simulations of single KAWs to determine the resulting velocity-space signature of TTD numerically, confirming the qualitative features of our prediction, and presenting the first key result of this study: the gyrotropic velocity-space signature of TTD in figure 4(a).
We contrast the velocity-space signature of TTD with the known bipolar velocity-space signature of LD, showing the same bipolar pattern of phase-space energy density loss below and gain above the resonant parallel phase velocity, but the TTD signature does not extend down to $v_\perp \rightarrow 0$![]() because it is mediated via the magnetic moment of the charged particle $\mu =m v_\perp ^2/(2B)$
because it is mediated via the magnetic moment of the charged particle $\mu =m v_\perp ^2/(2B)$![]() ; thus, signatures of TTD and LD can be distinguished in gyrotropic velocity space by examining the behaviour at the resonant parallel phase velocity as $v_\perp \rightarrow 0$
; thus, signatures of TTD and LD can be distinguished in gyrotropic velocity space by examining the behaviour at the resonant parallel phase velocity as $v_\perp \rightarrow 0$![]() . Furthermore, we find the unexpected result that TTD can lead to a net loss of ion energy over the period of the wave for $\beta _i < 1$
. Furthermore, we find the unexpected result that TTD can lead to a net loss of ion energy over the period of the wave for $\beta _i < 1$![]() and LD can lead to a net loss of ion energy over the period of the wave for $\beta _i > 1$
and LD can lead to a net loss of ion energy over the period of the wave for $\beta _i > 1$![]() . This surprising result is explained, however, by examining the separate contributions of TTD and LD to ion damping from the linear Vlasov–Maxwell dispersion relation: for a single linear KAW, the net effect of TTD and LD combined for a plasma with a Maxwellian equilibrium ion velocity distribution always leads to a net damping of the wave and net gain of energy by the ions.
. This surprising result is explained, however, by examining the separate contributions of TTD and LD to ion damping from the linear Vlasov–Maxwell dispersion relation: for a single linear KAW, the net effect of TTD and LD combined for a plasma with a Maxwellian equilibrium ion velocity distribution always leads to a net damping of the wave and net gain of energy by the ions.
Next, we perform three gyrokinetic simulations of weakly collisional plasma turbulence with three values of $\beta _i=0.3, 1, 3$![]() to seek the velocity-space signature of TTD in the damping of the strong turbulent fluctuations. In the $\beta _i=1$
to seek the velocity-space signature of TTD in the damping of the strong turbulent fluctuations. In the $\beta _i=1$![]() turbulence simulation, we indeed find a velocity-space signature of TTD as shown in figure 10(a), indicating that this mechanism does indeed play a role in the dissipation of kinetic plasma turbulence, along with confirming previously demonstrated signatures of LD with ions in figure 10(c). This second key result of this paper shows clearly the TTD does serve to damp the fluctuations in weakly collisional plasma turbulence.
turbulence simulation, we indeed find a velocity-space signature of TTD as shown in figure 10(a), indicating that this mechanism does indeed play a role in the dissipation of kinetic plasma turbulence, along with confirming previously demonstrated signatures of LD with ions in figure 10(c). This second key result of this paper shows clearly the TTD does serve to damp the fluctuations in weakly collisional plasma turbulence.
The relative strength of TTD and LD is predicted to be a strong function of $\beta _i$![]() (Quataert Reference Quataert1998), so we analyse our $\beta _i=0.3$
(Quataert Reference Quataert1998), so we analyse our $\beta _i=0.3$![]() and $\beta _i=3$
and $\beta _i=3$![]() simulations to confirm this prediction. For $\beta _i=3$
simulations to confirm this prediction. For $\beta _i=3$![]() , we indeed find signatures of TTD in the predicted range of resonant parallel phase velocities in figure 12(a), but LD signatures vary widely, with both positive and negative energy transfer rates to the ions, and a negative overall average consistent with expectations from the linear dispersion relation in figure 8(c). For $\beta _i=0.3$
, we indeed find signatures of TTD in the predicted range of resonant parallel phase velocities in figure 12(a), but LD signatures vary widely, with both positive and negative energy transfer rates to the ions, and a negative overall average consistent with expectations from the linear dispersion relation in figure 8(c). For $\beta _i=0.3$![]() , however, we discover puzzling bipolar velocity-space signatures of negative energy transfer but with a zero crossing well below the parallel phase velocity of kinetic KAWs. This may indicate that energy transfer via TTD is occurring through alternative wave modes, such as kinetic slow magnetosonic fluctuations, or through nonlinear TTD via beat wave modes that are generated by nonlinear interactions among the turbulent fluctuations. These possibilities will be explored in future work.
, however, we discover puzzling bipolar velocity-space signatures of negative energy transfer but with a zero crossing well below the parallel phase velocity of kinetic KAWs. This may indicate that energy transfer via TTD is occurring through alternative wave modes, such as kinetic slow magnetosonic fluctuations, or through nonlinear TTD via beat wave modes that are generated by nonlinear interactions among the turbulent fluctuations. These possibilities will be explored in future work.
Determining the time-integrated change of ion kinetic energy density due to TTD and LD as a function of $\beta _i$![]() from the three simulations, averaged over all of the probes to obtain a reasonable statistical estimate, we find results in figure 13 that are generally consistent with the expectations from the linear dispersion relation: (i) at $\beta _i=0.3$
from the three simulations, averaged over all of the probes to obtain a reasonable statistical estimate, we find results in figure 13 that are generally consistent with the expectations from the linear dispersion relation: (i) at $\beta _i=0.3$![]() , TTD is small and slightly negative, while LD is approximately an order of magnitude larger and positive; (ii) at $\beta _i=1$
, TTD is small and slightly negative, while LD is approximately an order of magnitude larger and positive; (ii) at $\beta _i=1$![]() , both TTD and LD are positive, but again LD is about an order of magnitude larger than TTD; and (iii) at $\beta _i=3$
, both TTD and LD are positive, but again LD is about an order of magnitude larger than TTD; and (iii) at $\beta _i=3$![]() , TTD is large and positive while LD is somewhat smaller and negative. Note that despite one of the mechanisms possibly leading to a net negative transfer of energy from ions to waves, for a sufficiently large statistical sample it is always the subdominant mechanism that is negative, so the net effect of the sum of both of these $n=0$
, TTD is large and positive while LD is somewhat smaller and negative. Note that despite one of the mechanisms possibly leading to a net negative transfer of energy from ions to waves, for a sufficiently large statistical sample it is always the subdominant mechanism that is negative, so the net effect of the sum of both of these $n=0$![]() Landau-resonant collisionless wave–particle interactions (TTD and LD) averaged over all of the probe positions is a damping of the turbulence for equilibrium Maxwellian velocity distributions.
Landau-resonant collisionless wave–particle interactions (TTD and LD) averaged over all of the probe positions is a damping of the turbulence for equilibrium Maxwellian velocity distributions.
Acknowledgements
Numerical simulations were performed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562, through allocation TG-PHY090084.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
Supported by NASA grants 80NSSC18K0643, 80NSSC18K1217 and 80NSSC18K1371 and NSF grant AGS-1842561.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Explicit form of Landau damping and transit-time damping terms in nonlinear gyrokinetics
The nonlinear, collisionless gyrokinetic equation (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006) can be manipulated into a form in which the terms governing LD and TTD are readily apparent. We begin with the nonlinear, collisionless gyrokinetic equation in cgs units, (25) in Howes et al. (Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006),
where the nonlinear term is expressed in the Poisson bracket, defined by
where the guiding centre coordinates are given by $\boldsymbol {R}_s=(X,Y,z)$![]() . The gyroaverage of a given quantity at the guiding centre position for a particle of species $s$
. The gyroaverage of a given quantity at the guiding centre position for a particle of species $s$![]() is denoted by $\langle \ldots \rangle _{\boldsymbol {R}_s}$
is denoted by $\langle \ldots \rangle _{\boldsymbol {R}_s}$![]() . The gyrokinetic potential is defined by $\chi (\boldsymbol {r},t)= \phi - \boldsymbol {v} \boldsymbol {\cdot } \boldsymbol {A}/c$
. The gyrokinetic potential is defined by $\chi (\boldsymbol {r},t)= \phi - \boldsymbol {v} \boldsymbol {\cdot } \boldsymbol {A}/c$![]() , where $\phi (\boldsymbol {r},t)$
, where $\phi (\boldsymbol {r},t)$![]() is the scalar electrostatic potential and $\boldsymbol {A}(\boldsymbol {r},t)$
is the scalar electrostatic potential and $\boldsymbol {A}(\boldsymbol {r},t)$![]() is the vector potential. In this formulation, the total velocity distribution function for species $s$
is the vector potential. In this formulation, the total velocity distribution function for species $s$![]() is separated into $f_s(\boldsymbol {r},\boldsymbol {v},t) = F_{0s}(v) + (-q_s \phi (\boldsymbol {r},t)/ T_{s}) F_{0s}(v) + h_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t) + O(\epsilon ^2)$
is separated into $f_s(\boldsymbol {r},\boldsymbol {v},t) = F_{0s}(v) + (-q_s \phi (\boldsymbol {r},t)/ T_{s}) F_{0s}(v) + h_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t) + O(\epsilon ^2)$![]() , where $F_{0s}(v)$
, where $F_{0s}(v)$![]() is the spatially homogeneous and temporally constant equilibrium Maxwellian velocity distribution and $h_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t)$
is the spatially homogeneous and temporally constant equilibrium Maxwellian velocity distribution and $h_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t)$![]() is the perturbed gyrokinetic distribution function at the particle guiding centre position $\boldsymbol {R}_s$
is the perturbed gyrokinetic distribution function at the particle guiding centre position $\boldsymbol {R}_s$![]() (independent of gyrophase $\theta$
(independent of gyrophase $\theta$![]() in cylindrical velocity space).
in cylindrical velocity space).
We transform from the perturbed gyrokinetic distribution function $h_s$![]() to the complementary perturbed gyrokinetic distribution function $g_s$
to the complementary perturbed gyrokinetic distribution function $g_s$![]() (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), given by
(Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), given by
substituting for $h_s$![]() everywhere in the nonlinear gyrokinetic equation (A1). After some simplification, the equation can be rearranged to obtain
everywhere in the nonlinear gyrokinetic equation (A1). After some simplification, the equation can be rearranged to obtain

We can rearrange the terms on the right-hand side to obtain a more physically illuminating form

Using the following relations:
we can simplify the result to obtain

Finally, to put this into a more concise form, we recognize that the direction of the total magnetic field (including the perturbation) to the first order is $\boldsymbol {B} = B_0 \hat {\boldsymbol {z}} + \langle \boldsymbol {\delta B}_\perp \rangle _{\boldsymbol {R}_s}$![]() , so we can define the unit vector of the total magnetic field direction as $\hat {\boldsymbol {b}}$
, so we can define the unit vector of the total magnetic field direction as $\hat {\boldsymbol {b}}$![]()
With this final simplification, we obtain the final result for the nonlinear gyrokinetic equation
This equation has a simple physical interpretation with respect to work done on the distribution functions by the fields: the first term on the right-hand side is the effect of LD by electric field parallel to the total magnetic field; and the second term on the right-hand side is the effect of TTD by the magnetic mirror force due to the gradient of the magnetic field magnitude along the total magnetic field, which to lowest order is just due to the parallel magnetic field perturbations, as shown in (2.6). Note also that the nonlinear term involves interactions between the electromagnetic fields and the plasma particles, but when integrated over all guiding centre space $\boldsymbol {R}_s$![]() , it leads to zero net energy change.
, it leads to zero net energy change.
Appendix B. Gyrokinetic form of the field–particle correlation
In gyrokinetics, a form of conserved energy inspired from the definition of entropy is calculated by multiplying the complementary perturbed gyrokinetic distribution function $g_s$![]() by $T_{0s} g_s/F_{0s}$
by $T_{0s} g_s/F_{0s}$![]() and integrating over all velocity and physical space (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Brizard & Hahm Reference Brizard and Hahm2007; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Li et al. Reference Li, Howes, Klein and TenBarge2016; Howes et al. Reference Howes, McCubbin and Klein2018). Using a similar approach, we can obtain an energy equation for the gyrokinetic phase-space energy density $w_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t) = T_{s} g_s^2/(2F_{0s})$
and integrating over all velocity and physical space (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Brizard & Hahm Reference Brizard and Hahm2007; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Li et al. Reference Li, Howes, Klein and TenBarge2016; Howes et al. Reference Howes, McCubbin and Klein2018). Using a similar approach, we can obtain an energy equation for the gyrokinetic phase-space energy density $w_s(\boldsymbol {R}_s,v_\parallel,v_\perp,t) = T_{s} g_s^2/(2F_{0s})$![]() by multiplying (A12) by $T_{0s} g_s/F_{0s}$
by multiplying (A12) by $T_{0s} g_s/F_{0s}$![]() to obtain
to obtain
In this formulation, the gyrokinetic form of the field–particle correlation for LD would be given by

and for TTD would be given by

Note that the energy transfer in the nonlinear case is simply ‘linear’ collisionless damping occurring along the local total magnetic field direction (which is a nonlinear correction from the equilibrium magnetic field direction $\boldsymbol {B}_0 = B_0 \hat {\boldsymbol {z}}$![]() ). Note also that, in the gyrokinetic approximation, the nonlinear contribution (known as the parallel nonlinearity) to the field–particle interactions is dropped, as it comes in only at higher order. Thus, nonlinear saturation of LD does not occur in gyrokinetics, but the nonlinear correction of ‘linear’ collisionless damping due to the difference in the total magnetic field direction from the equilibrium magnetic field direction is included in nonlinear gyrokinetics.
). Note also that, in the gyrokinetic approximation, the nonlinear contribution (known as the parallel nonlinearity) to the field–particle interactions is dropped, as it comes in only at higher order. Thus, nonlinear saturation of LD does not occur in gyrokinetics, but the nonlinear correction of ‘linear’ collisionless damping due to the difference in the total magnetic field direction from the equilibrium magnetic field direction is included in nonlinear gyrokinetics.
Mathematically, the correlations derived from the Vlasov–Maxwell equations, (2.7) for TTD and the parallel contribution to the dot product in (2.4) for LD, and the correlations derived from the gyrokinetics, (B3) for TTD and (B2) for LD are related by the integration by parts. Physically, the Vlasov–Maxwell version correlation calculates the change in phase-space energy density at fixed positions in velocity space (Eulerian perspective). In contrast, the gyrokinetic version correlation measures the energy changes experienced by particles along their orbits (Lagrangian perspective) (Montag & Howes Reference Montag and Howes2022). The gyrokinetic version is effectively the same as the alternative field–particle correlation previously defined (Howes et al. Reference Howes, Klein and Li2017), denoted by the symbol $C'$![]() instead of $C$
instead of $C$![]() . Therefore, as illustrated in figure 14, where we plot both the Vlasov–Maxwell version correlations and the gyrokinetic version correlations for the fiducial single KAW simulation, the loss and gain of phase-space energy density in the velocity space are visible in the Vlasov–Maxwell version correlation plots with the zero crossing centred at the resonant velocity. Conversely, the gyrokinetic version correlation plots highlight the pure energization of particles, with the peak positioned at the resonant velocity.
. Therefore, as illustrated in figure 14, where we plot both the Vlasov–Maxwell version correlations and the gyrokinetic version correlations for the fiducial single KAW simulation, the loss and gain of phase-space energy density in the velocity space are visible in the Vlasov–Maxwell version correlation plots with the zero crossing centred at the resonant velocity. Conversely, the gyrokinetic version correlation plots highlight the pure energization of particles, with the peak positioned at the resonant velocity.

Figure 14. Velocity-space signatures of TTD (a,b) and LD (c,d), plotted from single KAW AstroGK simulation data with $k_\perp \rho _i = 1, \beta _i = 1, T_i/T_e = 1$![]() . The Vlasov–Maxwell version correlations, (2.7) for TTD and the parallel component of (2.4) for LD, are applied in (a,c); and the gyrokinetic version correlations, (B3) for TTD and (B2) for LD, are applied in (b,d). The layout format, simulation data, correlation interval and normalized parallel phase velocity presented in this figure are identical to those used in figure 4.
. The Vlasov–Maxwell version correlations, (2.7) for TTD and the parallel component of (2.4) for LD, are applied in (a,c); and the gyrokinetic version correlations, (B3) for TTD and (B2) for LD, are applied in (b,d). The layout format, simulation data, correlation interval and normalized parallel phase velocity presented in this figure are identical to those used in figure 4.
We choose not to use the particular forms of the field–particle correlations in (B2) and (B3) for the study here because the gyrokinetic formulation is the lowest-order contribution to the rate of change of phase-space energy density in the gyrokinetic limit of small fluctuations relative to the equilibrium $g_s/F_{0s} \ll 1$![]() (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006); we prefer to establish a form that is appropriate for fluctuations of arbitrary amplitude, which is given for TTD by the form in (2.7).
(Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006); we prefer to establish a form that is appropriate for fluctuations of arbitrary amplitude, which is given for TTD by the form in (2.7).
Appendix C. Separating Landau damping from transit-time damping
As shown by (A12), the nonlinear gyrokinetic equation can be manipulated into a form in which the terms governing LD and TTD are explicitly separated. Here we explain how one can separate the contributions to the damping rate $\gamma _s$![]() for a given species $s$
for a given species $s$![]() by LD and TTD, both arising from the $n=0$
by LD and TTD, both arising from the $n=0$![]() Landau resonance, in the Vlasov–Maxwell linear dispersion relation (Stix Reference Stix1992; Swanson Reference Swanson2003) in the limit $\gamma _s/\omega \rightarrow 0$
Landau resonance, in the Vlasov–Maxwell linear dispersion relation (Stix Reference Stix1992; Swanson Reference Swanson2003) in the limit $\gamma _s/\omega \rightarrow 0$![]() .
.
The rate of work done on a species $s$![]() by the electric field in a plasma is given by
by the electric field in a plasma is given by
where the fields $\boldsymbol {j}_s$![]() and $\boldsymbol {E}$
and $\boldsymbol {E}$![]() must be real. For a single plane-wave mode of an arbitrary vector field $\boldsymbol {A}$
must be real. For a single plane-wave mode of an arbitrary vector field $\boldsymbol {A}$![]() , the Fourier transform is given by
, the Fourier transform is given by

where $\hat {\boldsymbol {A}}(\boldsymbol {k})$![]() is the complex Fourier coefficient for plane-wave vector $\boldsymbol {k}$
is the complex Fourier coefficient for plane-wave vector $\boldsymbol {k}$![]() and the complex mode frequency $\omega _c(\boldsymbol {k}) = \omega (\boldsymbol {k}) + {\rm i} \gamma (\boldsymbol {k})$
and the complex mode frequency $\omega _c(\boldsymbol {k}) = \omega (\boldsymbol {k}) + {\rm i} \gamma (\boldsymbol {k})$![]() is a function of $\boldsymbol {k}$
is a function of $\boldsymbol {k}$![]() . Note that, for wave vectors $\boldsymbol {k} \in [-\infty, \infty ]$
. Note that, for wave vectors $\boldsymbol {k} \in [-\infty, \infty ]$![]() , the reality condition imposes the constraint $\hat {\boldsymbol {A}}(\boldsymbol {k})= \hat {\boldsymbol {A}}^*(-\boldsymbol {k})$
, the reality condition imposes the constraint $\hat {\boldsymbol {A}}(\boldsymbol {k})= \hat {\boldsymbol {A}}^*(-\boldsymbol {k})$![]() .
.
To determine the average energy transfer rate over one wave period $\langle P_s (\boldsymbol {r}) \rangle _T$![]() , we compute
, we compute
In the case of weak totalFootnote 6 damping or growth rate, $|\gamma |/\omega \ll 1$![]() , we can substitute in for $\boldsymbol {j}_s(\boldsymbol {x},t)$
, we can substitute in for $\boldsymbol {j}_s(\boldsymbol {x},t)$![]() and $\boldsymbol {E}(\boldsymbol {x},t)$
and $\boldsymbol {E}(\boldsymbol {x},t)$![]() in terms of the complex Fourier coefficients using (C2), which enables us to derive
in terms of the complex Fourier coefficients using (C2), which enables us to derive
as discussed in § 4-2 and (4)–(5) in Stix (Reference Stix1992).
To progress further, we need to determine the contribution to the plasma current density due to the $n=0$![]() resonant terms. In general, the current density for species $s$
resonant terms. In general, the current density for species $s$![]() arising from the linear response to an applied electric field $\hat {\boldsymbol {E}}(\boldsymbol {k})$
arising from the linear response to an applied electric field $\hat {\boldsymbol {E}}(\boldsymbol {k})$![]() is given by the linear conductivity tensor $\boldsymbol{\sigma }_s(\omega,\boldsymbol{k})$
is given by the linear conductivity tensor $\boldsymbol{\sigma }_s(\omega,\boldsymbol{k})$![]()
where the linear conductivity tensor can be expressed in terms of the susceptibility $\boldsymbol {\chi }_s(\omega,\boldsymbol {k})$![]() for species $s$
for species $s$![]() .
.
Note that the susceptibility tensor $\boldsymbol {\chi }_s$![]() involves a sum over all integers $n$
involves a sum over all integers $n$![]() (the order of the Bessel functions that arise in the integration over the gyrophase of the particles), as shown clearly in (10)–(57) of Stix (Reference Stix1992). The Landau resonance, which gives rise to the collisionless mechanisms of LD and TTD, corresponds to the $n=0$
(the order of the Bessel functions that arise in the integration over the gyrophase of the particles), as shown clearly in (10)–(57) of Stix (Reference Stix1992). The Landau resonance, which gives rise to the collisionless mechanisms of LD and TTD, corresponds to the $n=0$![]() term in this sum. Therefore, we need only evaluate the $n=0$
term in this sum. Therefore, we need only evaluate the $n=0$![]() contribution to $\boldsymbol {\chi }_s$
contribution to $\boldsymbol {\chi }_s$![]() , denoted here by $\boldsymbol {\chi }^{(n=0)}_s$
, denoted here by $\boldsymbol {\chi }^{(n=0)}_s$![]() . For an equilibrium magnetic field $\boldsymbol {B}_0 = B_0 \hat {\boldsymbol {z}}$
. For an equilibrium magnetic field $\boldsymbol {B}_0 = B_0 \hat {\boldsymbol {z}}$![]() and the choice of a wave vector in the $(x,z)$
and the choice of a wave vector in the $(x,z)$![]() plane, $\boldsymbol {k}= k_\perp \hat {\boldsymbol {x}} + k_\parallel \hat {\boldsymbol {z}}$
plane, $\boldsymbol {k}= k_\perp \hat {\boldsymbol {x}} + k_\parallel \hat {\boldsymbol {z}}$![]() , all elements of the rank 2 tensor $\boldsymbol {\chi }^{(n=0)}_s(\omega,\boldsymbol {k})$
, all elements of the rank 2 tensor $\boldsymbol {\chi }^{(n=0)}_s(\omega,\boldsymbol {k})$![]() involving the index $x$
involving the index $x$![]() are zero, i.e. $\chi ^{(n=0)}_{xj,s}=\chi ^{(n=0)}_{jx,s}=0$
are zero, i.e. $\chi ^{(n=0)}_{xj,s}=\chi ^{(n=0)}_{jx,s}=0$![]() , as shown in the Stix equations (10)–(61). Therefore, the $n=0$
, as shown in the Stix equations (10)–(61). Therefore, the $n=0$![]() contribution to the current density has $\hat {\boldsymbol {x}} \boldsymbol {\cdot } \hat {\boldsymbol {j}}^{(n=0)}_s(\boldsymbol {k})=0$
contribution to the current density has $\hat {\boldsymbol {x}} \boldsymbol {\cdot } \hat {\boldsymbol {j}}^{(n=0)}_s(\boldsymbol {k})=0$![]() . Thus, we need only concern ourselves with the work done by $\hat {E}_y$
. Thus, we need only concern ourselves with the work done by $\hat {E}_y$![]() and $\hat {E}_z$
and $\hat {E}_z$![]() .
.
Physically, LD is governed by the work done by the $\hat {E}_z$![]() component of the wave electric field, and TTD is governed by the work done by the $\hat {E}_y$
component of the wave electric field, and TTD is governed by the work done by the $\hat {E}_y$![]() component of the wave electric field (Howes et al. Reference Howes, Huang and Felix2024). Since we know that TTD is mediated by the magnetic mirror force, it depends on the gradient of the magnitude of the magnetic field along the magnetic field direction, $\hat {\boldsymbol {b}} \boldsymbol {\cdot }\boldsymbol {\nabla } |\boldsymbol {B}|$
component of the wave electric field (Howes et al. Reference Howes, Huang and Felix2024). Since we know that TTD is mediated by the magnetic mirror force, it depends on the gradient of the magnitude of the magnetic field along the magnetic field direction, $\hat {\boldsymbol {b}} \boldsymbol {\cdot }\boldsymbol {\nabla } |\boldsymbol {B}|$![]() . In the limit of small amplitudes $|\delta \boldsymbol {B}| \ll B_0$
. In the limit of small amplitudes $|\delta \boldsymbol {B}| \ll B_0$![]() appropriate for linear wave theory with total magnetic field $\boldsymbol {B} =\boldsymbol {B}_0 + \delta \boldsymbol {B}$
appropriate for linear wave theory with total magnetic field $\boldsymbol {B} =\boldsymbol {B}_0 + \delta \boldsymbol {B}$![]() , the variations of the magnitude of the total magnetic field $\boldsymbol {B} =\boldsymbol {B}_0 + \delta \boldsymbol {B}$
, the variations of the magnitude of the total magnetic field $\boldsymbol {B} =\boldsymbol {B}_0 + \delta \boldsymbol {B}$![]() can be expressed as $\delta |\boldsymbol {B}| \simeq \delta B_\parallel$
can be expressed as $\delta |\boldsymbol {B}| \simeq \delta B_\parallel$![]() , as shown by (2.6). Note that, with variations only in the $x$
, as shown by (2.6). Note that, with variations only in the $x$![]() and $z$
and $z$![]() directions (due to our chosen wavevector orientation), Faraday's law gives
directions (due to our chosen wavevector orientation), Faraday's law gives
where $\delta B_z = \delta B_\parallel$![]() . Therefore, the variations of the magnetic field magnitude that cause the mirror force arise from the $\hat {E}_y$
. Therefore, the variations of the magnetic field magnitude that cause the mirror force arise from the $\hat {E}_y$![]() component of the electric field.
component of the electric field.
Since $\chi ^{(n=0)}_{xj,s}=\chi ^{(n=0)}_{jx,s}=0$![]() , we can write the components $\hat {j}_{y,s}$
, we can write the components $\hat {j}_{y,s}$![]() and $\hat {j}_{z,s}$
and $\hat {j}_{z,s}$![]() in terms of the susceptibility tensor acting on $\hat {E}_y$
in terms of the susceptibility tensor acting on $\hat {E}_y$![]() and $\hat {E}_z$
and $\hat {E}_z$![]()

Thus, we find
Since TTD is mediated by $\hat {E}_y$![]() , using (C3) we can compute its energy transfer rate by
, using (C3) we can compute its energy transfer rate by
where we have suppressed the explicit dependence on $\boldsymbol {k}$![]() of the Fourier components for notational simplicity. Similarly, the energy transfer rate by LD can be computed by
of the Fourier components for notational simplicity. Similarly, the energy transfer rate by LD can be computed by
Substituting (C8) into (C10) and taking the limit $\gamma /\omega \rightarrow 0$![]() , we obtain the expression for the energy transfer rate due to TTD by species $s$
, we obtain the expression for the energy transfer rate due to TTD by species $s$![]()
Substituting (C9) into (C11) and taking the limit $\gamma /\omega \rightarrow 0$![]() , we obtain the expression for the energy transfer rate due to LD by species $s$
, we obtain the expression for the energy transfer rate due to LD by species $s$![]()
Poynting's theorem integrated over the plasma volume can be used to connect the period-averaged rate of work done on a plasma species $s$![]() by a given collisionless damping mechanism $X$
by a given collisionless damping mechanism $X$![]() to the linear damping rate by that mechanism, $\gamma _{X,s}$
to the linear damping rate by that mechanism, $\gamma _{X,s}$![]() . For linear dispersion relation solutions, the total damping rate $\gamma$
. For linear dispersion relation solutions, the total damping rate $\gamma$![]() is a linear combination of the damping rates on each species by each mechanism; if only the $n=0$
is a linear combination of the damping rates on each species by each mechanism; if only the $n=0$![]() Landau-resonant mechanisms contribute to the damping in a single-ion species and electron plasma, this linear combination is simply $\gamma =\gamma _{{\rm LD},i}+\gamma _{{\rm TTD},i}+\gamma _{{\rm LD},e}+\gamma _{{\rm TTD},e}$
Landau-resonant mechanisms contribute to the damping in a single-ion species and electron plasma, this linear combination is simply $\gamma =\gamma _{{\rm LD},i}+\gamma _{{\rm TTD},i}+\gamma _{{\rm LD},e}+\gamma _{{\rm TTD},e}$![]() . Separating the contributions from each mechanism $X$
. Separating the contributions from each mechanism $X$![]() and each species $s$
and each species $s$![]() , Poynting's theorem therefore yields the connection $\gamma _{X,s} = \langle P_{X,s} (\boldsymbol {x}) \rangle _T/(2 W_{{\rm EM}})$
, Poynting's theorem therefore yields the connection $\gamma _{X,s} = \langle P_{X,s} (\boldsymbol {x}) \rangle _T/(2 W_{{\rm EM}})$![]() , where $W_{{\rm EM}}$
, where $W_{{\rm EM}}$![]() is the total electromagnetic energy over the integrated volume.
is the total electromagnetic energy over the integrated volume.
Note that the Stix (Reference Stix1992) representation of the power absorption by species $s$![]() , from his § (11-8), is of the form
, from his § (11-8), is of the form
where the anti-Hermitian component of the susceptibility is given by
In the examples in Stix (Reference Stix1992) of separating the LD and TTD contributions (see also Quataert Reference Quataert1998), he artificially sets $\hat {E}_{z}=0$![]() to determine the power absorption due to TTD, and sets $\hat {E}_{y}=0$
to determine the power absorption due to TTD, and sets $\hat {E}_{y}=0$![]() to determine the power absorption due to LD. Such a choice eliminates all of the contributions from the cross-terms of the susceptibility $\chi _{yz,s}$
to determine the power absorption due to LD. Such a choice eliminates all of the contributions from the cross-terms of the susceptibility $\chi _{yz,s}$![]() and $\chi _{zy,s}$
and $\chi _{zy,s}$![]() . However, these terms are not small in general, so their neglect can lead to an inaccurate estimation of the TTD and LD rates. Furthermore, by writing the power absorption in terms of the anti-Hermitian component of the susceptibility $\boldsymbol {\sigma }^{(a)}_s$
. However, these terms are not small in general, so their neglect can lead to an inaccurate estimation of the TTD and LD rates. Furthermore, by writing the power absorption in terms of the anti-Hermitian component of the susceptibility $\boldsymbol {\sigma }^{(a)}_s$![]() , the terms due to the cross-terms $\chi _{yz,s}$
, the terms due to the cross-terms $\chi _{yz,s}$![]() and $\chi _{zy,s}$
and $\chi _{zy,s}$![]() are exchanged between TTD and Landau damping, so the separation of the two different mechanisms is not correct.
are exchanged between TTD and Landau damping, so the separation of the two different mechanisms is not correct.
C.1. Numerical results of Landau damping and transit-time damping separation
As a demonstration of the separation of the LD and TTD rates for both ions and electrons, we compute linear Vlasov–Maxwell dispersion relation for the Alfvén wave root using PLUME (Klein & Howes Reference Klein and Howes2015) for a proton–electron plasma with Maxwellian equilibrium velocity distributions with $T_i/T_e=1$![]() and plasma parameters $\beta _i=1$
and plasma parameters $\beta _i=1$![]() , $v_{{\rm ti}}/c=1 \times 10^{-4}$
, $v_{{\rm ti}}/c=1 \times 10^{-4}$![]() and $m_i/m_e=1836$
and $m_i/m_e=1836$![]() . In figure 15, we plot the normalized damping (or growth) rates $\gamma /\omega$
. In figure 15, we plot the normalized damping (or growth) rates $\gamma /\omega$![]() – where damping corresponds to $\gamma <0$
– where damping corresponds to $\gamma <0$![]() and growth corresponds to $\gamma >0$
and growth corresponds to $\gamma >0$![]() , for $k_\parallel \rho _i =0.01$
, for $k_\parallel \rho _i =0.01$![]() over the range d $0.1 \le k_\perp \rho _i \le 100$
over the range d $0.1 \le k_\perp \rho _i \le 100$![]() . For this case of isotropic Maxwellian equilibrium velocity distributions, there is not source of energy for instabilities, so we obtain a total damping rate $\gamma /\omega <0$
. For this case of isotropic Maxwellian equilibrium velocity distributions, there is not source of energy for instabilities, so we obtain a total damping rate $\gamma /\omega <0$![]() (thin black). In the limit small growth or damping rate limit, $|\gamma |/\omega \ll 1$
(thin black). In the limit small growth or damping rate limit, $|\gamma |/\omega \ll 1$![]() , we separate the ion and electron contributions to the total damping rate, plotting the ion damping or growth rate $\gamma _i/\omega$
, we separate the ion and electron contributions to the total damping rate, plotting the ion damping or growth rate $\gamma _i/\omega$![]() (thin solid red) and the electron damping or growth rate $\gamma _e/\omega$
(thin solid red) and the electron damping or growth rate $\gamma _e/\omega$![]() (thin solid blue). Note the breakdown of this separation at $k_\perp \rho _i \gtrsim 30$
(thin solid blue). Note the breakdown of this separation at $k_\perp \rho _i \gtrsim 30$![]() when the asymptotic small growth or damping rate limit is violated; the practical limit where the breakdown of this separation by species occurs is $|\gamma |/\omega \gtrsim 0.5$
when the asymptotic small growth or damping rate limit is violated; the practical limit where the breakdown of this separation by species occurs is $|\gamma |/\omega \gtrsim 0.5$![]() , as shown in the figure where sum of the ion and electron damping rates deviates from the total damping rate $\gamma /\omega$
, as shown in the figure where sum of the ion and electron damping rates deviates from the total damping rate $\gamma /\omega$![]() (thin black) at $k_\perp \rho _i \gtrsim 30$
(thin black) at $k_\perp \rho _i \gtrsim 30$![]() .
.

Figure 15. For a plasma with $\beta _i=1$![]() , $T_i/T_e=1$
, $T_i/T_e=1$![]() , $m_i/m_e=1836$
, $m_i/m_e=1836$![]() , $v_{{\rm ti}}/c=1 \times 10^{-4}$
, $v_{{\rm ti}}/c=1 \times 10^{-4}$![]() and $k_\parallel \rho _i =0.01$
and $k_\parallel \rho _i =0.01$![]() , plot of total normalized damping or growth rate $\gamma /\omega$
, plot of total normalized damping or growth rate $\gamma /\omega$![]() (thin black), ion damping or growth rate $\gamma _i/\omega$
(thin black), ion damping or growth rate $\gamma _i/\omega$![]() (red) and electron damping or growth rate $\gamma _e/\omega$
(red) and electron damping or growth rate $\gamma _e/\omega$![]() (blue). The separate contributions to the ion damping rate are $\gamma _{i,{\rm LD}}/\omega <0$
(blue). The separate contributions to the ion damping rate are $\gamma _{i,{\rm LD}}/\omega <0$![]() (red short dashed), $\gamma _{i,{\rm TTD}}/\omega <0$
(red short dashed), $\gamma _{i,{\rm TTD}}/\omega <0$![]() (red long dashed) and $\gamma _{i,{\rm TTD}}/\omega >0$
(red long dashed) and $\gamma _{i,{\rm TTD}}/\omega >0$![]() (red dotted). Similarly, the separate contributions to the electron damping rate are $\gamma _{e,{\rm LD}}/\omega <0$
(red dotted). Similarly, the separate contributions to the electron damping rate are $\gamma _{e,{\rm LD}}/\omega <0$![]() (blue short dashed), $\gamma _{e,{\rm TTD}}/\omega <0$
(blue short dashed), $\gamma _{e,{\rm TTD}}/\omega <0$![]() (blue long dashed) and $\gamma _{e,{\rm TTD}}/\omega >0$
(blue long dashed) and $\gamma _{e,{\rm TTD}}/\omega >0$![]() (blue dotted).
(blue dotted).
Examining the separation of the LD from the TTD rates next, we plot in figure 15 the ion LD rate $\gamma _{i,{\rm LD}}/\omega <0$![]() (red short dashed), the ion TTD rate $\gamma _{i,{\rm TTD}}/\omega <0$
(red short dashed), the ion TTD rate $\gamma _{i,{\rm TTD}}/\omega <0$![]() (red long dashed) and the ion transit-time growth rate $\gamma _{i,{\rm TTD}}/\omega >0$
(red long dashed) and the ion transit-time growth rate $\gamma _{i,{\rm TTD}}/\omega >0$![]() (red dotted). Similarly, we plot the electron LD rate $\gamma _{e,{\rm LD}}/\omega <0$
(red dotted). Similarly, we plot the electron LD rate $\gamma _{e,{\rm LD}}/\omega <0$![]() (blue short dashed), the electron TTD rate $\gamma _{e,{\rm TTD}}/\omega <0$
(blue short dashed), the electron TTD rate $\gamma _{e,{\rm TTD}}/\omega <0$![]() (blue long dashed) and the electron transit-time growth rate $\gamma _{e,{\rm TTD}}/\omega >0$
(blue long dashed) and the electron transit-time growth rate $\gamma _{e,{\rm TTD}}/\omega >0$![]() (blue dotted). Note that, for the ions, the transit-time contribution yields wave growth for $k_\perp \rho _i\ge 3$
(blue dotted). Note that, for the ions, the transit-time contribution yields wave growth for $k_\perp \rho _i\ge 3$![]() , and effectively cancels out the contribution from ion LD for $k_\perp \rho _i\ge 5$
, and effectively cancels out the contribution from ion LD for $k_\perp \rho _i\ge 5$![]() , so the total ion damping rate plummets. For the electrons, the transit-time contribution is positive yielding growth for $k_\perp \rho _i\lesssim 1.7$
, so the total ion damping rate plummets. For the electrons, the transit-time contribution is positive yielding growth for $k_\perp \rho _i\lesssim 1.7$![]() . For $k_\perp \rho _i\lesssim 0.7$
. For $k_\perp \rho _i\lesssim 0.7$![]() , $\gamma _{e,{\rm LD}} \simeq -2 \gamma _{e,{\rm TTD}}$
, $\gamma _{e,{\rm LD}} \simeq -2 \gamma _{e,{\rm TTD}}$![]() , so the total electron damping rate is approximately half of the Landau damping contribution. This plot shows clearly that the contributions from one mechanism (LD or TTD) can actually yield growth for certain parameters (meaning energy transfer from the particles to the fields via that mechanisms), even when the overall effect is damping. One can interpret this perhaps puzzling finding with the relative phase between the electric field and the current associated with a particular mechanism. In some cases – e.g. electron damping at $k_\perp \rho _i\lesssim 1.7$
, so the total electron damping rate is approximately half of the Landau damping contribution. This plot shows clearly that the contributions from one mechanism (LD or TTD) can actually yield growth for certain parameters (meaning energy transfer from the particles to the fields via that mechanisms), even when the overall effect is damping. One can interpret this perhaps puzzling finding with the relative phase between the electric field and the current associated with a particular mechanism. In some cases – e.g. electron damping at $k_\perp \rho _i\lesssim 1.7$![]() – this means that energy is transferred from the $E_z$
– this means that energy is transferred from the $E_z$![]() component of the electric field to the electrons by LD, but at the same time energy can be transferred from the electrons to the field via the $E_y$
component of the electric field to the electrons by LD, but at the same time energy can be transferred from the electrons to the field via the $E_y$![]() component of the electric field by TTD. The net effect is damping, but the total damping (or growth) rate is the summation over the Landau and transit-time contributions (which can have either sign). Note also that, for the selection of parameters in this example, the effect of the cyclotron resonance ($n \ne 0$
component of the electric field by TTD. The net effect is damping, but the total damping (or growth) rate is the summation over the Landau and transit-time contributions (which can have either sign). Note also that, for the selection of parameters in this example, the effect of the cyclotron resonance ($n \ne 0$![]() ) on the collisionless damping rate is negligible, so the LD and TTD associated with the Landau ($n =0$
) on the collisionless damping rate is negligible, so the LD and TTD associated with the Landau ($n =0$![]() ) resonance dominates the total wave damping.
) resonance dominates the total wave damping.