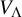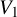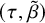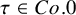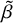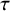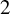A lattice theoretical interpretation of generalized deep holes of the Leech lattice vertex operator algebra

Abstract

We give a lattice theoretical interpretation of generalized deep holes of the Leech lattice VOA $V_\Lambda $. We show that a generalized deep hole defines a ‘true’ automorphism invariant deep hole of the Leech lattice. We also show that there is a correspondence between the set of isomorphism classes of holomorphic VOA V of central charge $24$ having non-abelian $V_1$ and the set of equivalence classes of pairs $(\tau , \tilde {\beta })$ satisfying certain conditions, where $\tau \in Co.0$ and $\tilde {\beta }$ is a $\tau $-invariant deep hole of squared length $2$. It provides a new combinatorial approach towards the classification of holomorphic VOAs of central charge $24$. In particular, we give an explanation for an observation of G. Höhn, which relates the weight one Lie algebras of holomorphic VOAs of central charge $24$ to certain codewords associated with the glue codes of Niemeier lattices.

1 Introduction

The classification of strongly regular holomorphic vertex operator algebras (abbreviated as VOA) of central charge $24$ with nontrivial weight one space is basically completed. It has been shown that there are exactly $70$ strongly regular holomorphic VOAs of CFT-type with central charge $24$ and nonzero weight one space and their VOA structures are uniquely determined by the Lie algebra structures of their weight one spaces. Moreover, the possible Lie algebra structures for their weight one subspaces have been given in Schellekens’ list [45]. The main tool is the so-called orbifold construction [6; 10; 17; 19; 36; 37; 38]. Nevertheless, their constructions and the uniqueness proofs were done by case by case analysis [9; 10; 13; 17; 18; 19; 22; 24; 26; 27; 28; 29; 30; 31; 32; 33; 37; 42]. A simplified and uniform construction and proof of uniqueness is somehow expected. Recently, it is proved in [16] (see also [7]) that for any holomorphic VOA of central charge $24$ with a semisimple weight one Lie algebra, the VOA obtained by the orbifold construction by an inner automorphism g defined by a W-element is always isomorphic to the Leech lattice VOA $V_\Lambda $ (see Definition 2.1 for the definition of a W-element). By taking its reverse automorphism $\tilde {g}$ of $V_{\Lambda }$ , there is a direct orbifold construction from the Leech lattice VOA $V_{\Lambda }$ to V. As a consequence, a relatively simpler proof for the Schellekens’ list is obtained [16].

Möller and Scheithauer [39] considered a special class of automorphisms in $\mathrm {Aut}(V_\Lambda )$ , called generalized deep holes. They established a bijection between the algebraic conjugacy classes of generalized deep holes $g\in \mathrm {Aut}(V_\Lambda )$ with $\mathrm {rank} (V_\Lambda ^g)_1>0$ and the isomorphism classes of strongly regular, holomorphic VOA V of central charge $24$ with $V_1\neq 0$ [39, Theorem 6.6]. They also obtained a classification of generalized deep holes of the Leech lattice VOA, which provides a new proof for the classification of holomorphic VOA of central charge 24 with nontrivial weight one spaces. Next, let us recall the notion of generalized deep holes from [39]. Let V be a strongly regular holomorphic VOA of central charge $24$ . Let g be an automorphism of V of finite order $n>1$ . If the conformal weight of the unique irreducible g-twisted module is in $\frac {1}{n}{\mathbb Z}$ , then g is said to be of type $0$ . In this case, one can construct a holomorphic VOA $V^{[g]}$ using the orbifold construction by g and V. It is proved in [39, Theorem 5.3] that the dimension of the weight one subspace of $V^{[g]}$ is given by the formula

$$\begin{align*}\dim(V^{[g]})_1= 24 + \sum_{d|n}c_n(d) \dim(V^{g^d})_1-R(g), \end{align*}$$

where $c_n(d) \in {\mathbb Q}$ are defined by $\sum _{d|n}c_n(d)\cdot GCD(t,d) =n/t$ for all $t | n$ . The rest term $R(g)$ is non-negative and can be described explicitly by the dimensions of the weight spaces of the irreducible $V^g$ -modules of weight less than one.

Möller and Scheithauer [39] called an automorphism $g\in \mathrm {Aut}(V)$ a generalized deep hole of V if g is of type $0$ and

1. 1. the upper bound in the dimension formula is attained (i.e., $R(g)=0$ or $ \dim (V^{[g]})_1= 24 + \sum _{d|n}c_n(d) \dim (V^{g^d})_1$ ),

2. 2. $\mathrm {rank}(V^{[g]})_1 = \mathrm {rank}(V^g)_1$ .

If $V= V_\Lambda $ is the Leech lattice VOA, the rank condition (2) is equivalent to the fact that $(V_\Lambda ^g)_1$ is a Cartan subalgebra of $(V^{[g]})_1$ . It turns out that the reverse automorphism $\tilde {g}\in \mathrm { Aut}(V_{\Lambda })$ associated with the inner automorphism defined by a W-element is a generalized deep hole. Moreover, it is proved that any generalized deep hole g of the Leech lattice VOA with $\mathrm {rank}(V^g_\Lambda )_1> 0$ is conjugate to the reverse automorphism of an inner automorphism defined by a W-element of $V = V_\Lambda ^{[g]}$ (see the proof of [39, Theorem 6.6]). Therefore, without loss of generality, we may assume that a generalized deep hole g of the Leech lattice VOA with $\mathrm {rank}(V^g_\Lambda )_1> 0$ is a reverse automorphism of an inner automorphism defined by a W-element of a holomorphic VOA V with $V_1\neq 0$ .

As it is well-known, a deep hole of a lattice L is an element v of ${\mathbb R} L$ such that a distance $\min \{ |\!|\alpha -v|\!|\mid \alpha \in L\}$ from L is the largest (covering radius) among elements v in ${\mathbb R} L$ and so it has a geometrical meaning. Furthermore, deep holes of the Leech lattice $\Lambda $ have many interesting geometrical and algebraic meanings. Therefore, it is natural to expect some geometrical properties for generalized deep holes.

Recall that any automorphism $\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$ can be written as

$$\begin{align*}\tilde{g}=\widehat{\tau}\exp(2\pi i\beta(0)), \end{align*}$$

where $\tau \in Co.0=O(\Lambda )$ , $\beta \in {\mathbb R}\Lambda ^{\tau }$ and $\widehat {\tau }$ denotes a standard lift of $\tau $ in $O(\widehat {\Lambda })$ [2; 14]. In this paper, we will show that a holomorphic VOA of central charge $24$ with non-abelian weight one Lie algebra naturally defines a pair $(\tau , \tilde {\beta })$ , where $\tau \in Co.0$ is the same isometry as defined by a reverse automorphism $\tilde {g}\in \mathrm {Aut}(V_\Lambda )$ and $\tilde {\beta }$ is a ( $\tau $ -invariant) deep hole of the Leech lattice related to $\beta $ . In particular, a generalized deep hole of the Leech lattice VOA defines a ‘true’ deep hole of the Leech lattice. It provides a new combinatorial approach towards the classification of holomorphic VOAs of central charge $24$ .

Let L be an even lattice. We use $O(L)$ to denote the isometry group of L. The dual lattice of L is denoted by $L^*$ (i.e., $L^*=\{x\in {\mathbb Q}\otimes _{\mathbb Z} L\mid \langle x, L\rangle \subset {\mathbb Z}\}$ ). The discriminant group $\mathcal {D}(L)$ is the quotient group $L^*/L$ . For $ \tau \in O(L)$ , we denote the fixed point sublattice by $L^\tau $ . We also define the coinvariant lattice $L_\tau =\{ x\in L \mid \langle x, L^\tau \rangle =0\}$ . The key observation is that there is a ‘duality’ associated with the fixed point sublattice $\Lambda ^\tau $ which changes the level; we call it $\ell $ -duality.

Main Theorem 1 (see Theorem 4.2)

If $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ is a generalized deep hole, then there is an isometry:

$$ \begin{align*}\varphi_{\tau}: \sqrt{\ell}(\Lambda^{\tau})^{\ast} \to \Lambda^{\tau},\end{align*} $$

where $\ell =|\widehat {\tau }|$ .

Using this $\ell $ -duality $\varphi $ (extended to ${\mathbb C}\Lambda ^{\tau }$ ), it is easy to show that $\langle \varphi _{\tau }(\sqrt {\ell }\beta ), \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in 2{\mathbb Z}$ and its neighbor lattice $N=\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )}+ {\mathbb Z}\varphi _{\tau }(\sqrt {\ell }\beta )$ define a Niemeier lattice with $N\ncong \Lambda $ , where $\Lambda _{\varphi _{\tau }(\sqrt {\ell }\beta )} = \{ x\in \Lambda \mid \langle x, \varphi _{\tau }(\sqrt {\ell }\beta ) \rangle \in {\mathbb Z}\}$ .

Let $V=(V_{\Lambda })^{[\tilde {g}]}$ be the VOA obtained by the orbifold construction from $V_{\Lambda }$ by $\tilde {g}$ . Let $\mathcal{H}$ be a Cartan subalgebra of $V_1$ and let $M(\mathcal{H})$ be the Heisenberg subVOA of V generated by $\mathcal{H}$ . Then there is an even lattice L such that the double commutant $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$ of $M(\mathcal{H})$ in V is isomorphic to the lattice VOA $V_L$ . The lattice L (or $L^*$ ) encoded the information of the root system of $V_1$ .

Main Theorem 2 (see Theorem 4.9)

Via $\ell $ -duality, we have $ N^{\tau }\cong \sqrt {\ell }\varphi _{\tau }(L^{\ast })$ .

In addition, we prove the following theorem.

Main Theorem 3 (see Theorem 5.1 and Proposition 6.1)

Let $\varphi $ be the isometry defined in the Main Theorem 1. Then we can choose $\beta \in {\mathbb C}\Lambda ^{\tau }$ such that $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ and $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$ is a deep hole of $\Lambda $ of squared length $2$ .

The classification of generalized deep holes is thus equivalent to the classification of the pairs $(\tau , \tilde {\beta })$ with $\tau \in O(\Lambda )$ and $\tilde {\beta }$ a $\tau $ -invariant deep hole of squared length $2$ satisfying certain conditions and up to some equivalence.

Let $\mathcal{T}$ be the set of pairs $(\tau , \tilde {\beta })$ satisfying certain conditions (see Section 7, (C1)–(C3)). We define a relation $\sim $ on $\mathcal{T}$ as follows: $(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$ if and only if

1. (1) $\tilde {\beta }$ and $\tilde {\beta }'$ are equivalent deep holes of the Leech lattice $\Lambda $ (i.e., there are $\sigma \in O(\Lambda )$ and $\lambda \in \Lambda $ such that $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$ ,

2. (2) $\tau $ is conjugate to $\sigma ^{-1} \tau ' \sigma $ in $O(N)$ .

The following is another main theorem of this article.

Main Theorem 4 (see Theorem 7.1)

There is a one-to-one correspondence between the set of isomorphism classes of holomorphic VOA V of central charge $24$ having non-abelian $V_1$ and the set $\mathcal{T}/\sim $ of equivalence classes of pairs $(\tau , \tilde {\beta })$ by $\sim $ .

Since a deep hole of the Leech lattice determines a unique Niemeier lattice, up to isometry and there are only $23$ Niemeier lattices with nontrivial root system, it is straightforward to list all possible choices for $(\tau , \tilde {\beta })$ and to determine the corresponding Lie algebra structures for $V_1$ . Therefore, one can complete the classification of holomorphic VOAs of central charge 24 with non-abelian $V_1$ by a purely combinatorial method. Indeed, we will provide an explanation for an observation of Höhn, which relates the weight one Lie algebras of holomorphic VOAs of central charge $24$ to certain codewords associated with the glue codes of Niemeier lattices [21, Theorem 3.1 and Table 3] (see Section 8 for details).

2 Some previous results

We first recall several results from [7]. Let V be a holomorphic VOA of central charge 24 with $V_1\not =0$ . Suppose $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$ is a semisimple Lie algebra. We use $k_j$ (resp. $h^{\vee }_j$ and $r_j$ ) to denote the level (resp. the dual Coxeter number and the lace number) of $\mathcal{G}_j$ , $j=1, \dots , t$ . Let $\mathcal{H}$ be a Cartan subalgebra of $V_1$ and let $M(\mathcal{H})$ be the Heisenberg subVOA generated by $\mathcal{H}$ . For a subVOA $U\subset V$ , the commutant subalgebra of U in V is defined by

$$\begin{align*}\mathrm{Comm}(U,V) = \{ x\in V\mid u_n x=0 \text{ for all }n\in {\mathbb Z}_{\geq 0}, u\in U\}. \end{align*}$$

It is easy to see that the double commutant $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)$ is isomorphic to a lattice VOA $V_L$ for an even lattice $L\subseteq \mathcal{H}$ .

Definition 2.1. Let $\rho _j$ be a Weyl vector of $\mathcal{G}_{j,k_j}$ and set $\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$ , which we call a W-element.

Next, we recall some standard notations for lattice VOAs from [19]. Let L be a positive-definite even lattice and $\mathfrak {h}={\mathbb C}\otimes _{\mathbb Z} L$ . Let $M(\mathfrak {h})$ be the Heisenberg VOA associated with $\mathfrak {h}$ and let ${\mathbb C}\{L\}=\bigoplus _{\alpha \in L}{\mathbb C} e^\alpha $ be the twisted group algebra such that $e^\alpha e^\beta =(-1)^{\langle \alpha , \beta \rangle }e^{\beta }e^{\alpha }$ , for $\alpha ,\beta \in L$ . The lattice VOA $V_L$ is given by $V_L= M(\mathfrak {h}) \otimes {\mathbb C}\{L\}$ . For any coset $\lambda +L\in \mathcal {D}(L)=L^*/L$ , denote $V_{\lambda +L}=M(\mathfrak {h})\otimes \mathrm {Span}_{\mathbb C}\{e^\alpha \mid \alpha \in \lambda +L\}$ . Then $V_{\lambda +L}$ has an irreducible $V_L$ -module structure [19]. Moreover, $\{ V_{\lambda +L}\mid \lambda +L\in \mathcal {D}(L)\}$ is a set of all inequivalent irreducible modules for $V_L$ [9].

Let $U=U(0)=\mathrm {Comm}(M(\mathcal{H}),V)$ . Then $U\otimes V_L\subset V$ is a subVOA of the same central charge. From the property of lattice VOA, we have a decomposition

$$ \begin{align*}V=\oplus_{\delta\in L^{\ast}} U(\delta)\otimes M(\mathcal{H})e^{\delta},\end{align*} $$

where $U(\delta )$ are $U(0)$ -modules and $M(\mathcal{H})e^{\delta }$ are $M(\mathcal{H})$ -modules. Since V is holomorphic, all irreducible modules of $V_L$ appear in V [23]; thus, $U(\delta )\not =0$ for every $\delta \in L^{\ast }$ .

Set $g=\exp (2\pi i\alpha (0))$ , where $\alpha =\sum _{j=1}^t \rho _j/h_j^{\vee }$ . In [7] (see also [16]), it is proved the VOA $V^{[g]}$ obtained by the orbifold construction from V by g is isomorphic to the Leech lattice VOA (i.e., $V^{[g]}\cong V_{\Lambda }$ ). Namely, the integer weights submodule $T^1_{{\mathbb Z}}$ of the simple g-twisted V-module $T^1$ is nonzero and $V^g\oplus T^1_{{\mathbb Z}}\oplus \cdots \oplus (T^1_{{\mathbb Z}})^{\boxtimes (|g|-1)} \cong V_{\Lambda }$ .

In this case, there is an automorphism $\tilde {g}$ of $V_{\Lambda }$ acting on $(T^1_{{\mathbb Z}})^{\boxtimes m}$ as $e^{2\pi i m/n}$ , $n=|g|$ . Moreover, the orbifold construction from $V_{\Lambda }$ by the automorphism $\tilde {g}$ gives V (i.e., $V_{\Lambda }^{[\tilde {g}]}\cong V$ ). That $\tilde {g} \in \mathrm {Aut}(V^{[g]})$ is called the reverse automorphism of g.

Since $\tilde {g}\in \mathrm {Aut}(V_{\Lambda })$ , we have $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ for some $\tau \in O(\Lambda )=Co.0$ and $\beta \in {\mathbb C}\Lambda $ [2; 14]. By choosing a suitable (standard) lift $\widehat {\tau }$ of $\tau $ , we may choose $\beta \in {\mathbb C}\Lambda ^{\tau }$ [17; 27]. Recall that a lift $\widehat {\tau }$ of $\tau \in O(\Lambda )$ is called a standard lift if $\widehat {\tau } (e^\alpha )= e^\alpha $ for any $\alpha \in \Lambda ^\tau $ (see for example [17]).

Remark 2.2. By the definition of W-element, it is clear that the order of g on $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$ is $\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$ ; indeed, one can show that $|g|=\mathrm {LCM}(\{r_ih_i^{\vee } \mid i\}$ on V [16, Proposition 5.1].

Set $n=|g|=|\tilde {g}|$ and let $K_0,N_0\in {\mathbb Z}$ with $\mathrm {GCD}(K_0,N_0)=1$ such that $\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$ . As we have shown in [7], $n=|\tau |N_0$ and $N_0|h^{\vee }_j$ ; thus, $|\tau |=\mathrm {LCM}(\{r_ih_j^{\vee }/N_0\mid j \})$ .

It is also proved in [7, Proposition 4.2] that $k_i/h_i^{\vee }=\frac {K_0-N_0}{N_0}$ ; therefore, we have

$$\begin{align*}\frac{2}{r_ik_i}=\frac{2}{r_ih^{\vee}_i}\frac{N_0}{K_0-N_0}= \frac{2}{(K_0-N_0)r_ih^{\vee}/N_0} \end{align*}$$

and

$$\begin{align*}{\mathrm{LCM}(\{r_ik_i\mid i\})} ={(K_0-N_0)\mathrm{LCM}(\{r_ih^{\vee}/N_0\mid i\})} ={(K_0-N_0)|\tau|}. \end{align*}$$

As a consequence, we have the following result.

Lemma 2.3. $\mathrm {LCM}(\{r_ik_i\mid i\}) =(K_0-N_0)|\tau |$ .

Next we recall an important result from [7].

Proposition 2.4 [7, Propositions 3.25 and 4.3]

We have $N_0\alpha \in L^{\ast }$ . Moreover,

$$\begin{align*}\mathrm{Comm}(M(\mathcal{H}),V^{[g]})=\oplus_{j=0}^{|\tau|-1}U(jN_0\alpha) \end{align*}$$

and $\mathcal{H}+\mathrm {Comm}(M(\mathcal{H}),V)_1$ is a Cartan subalgebra of the weight one Lie algebra of $V^{[g]}\cong V_\Lambda $ .

Since $U(jN_0\alpha )\otimes e^{jN_0\alpha }\in V$ , $U(jN_0\alpha )$ appears in $g^{-jN_0}$ -twisted V-module and so we may choose $\beta $ and $\widehat {\tau }$ so that $\langle \beta ,\alpha \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$ and $\widehat {\tau }$ acts on $U(jN_0\alpha )$ as a multiple by $e^{-2\pi ij/|\tau |}$ .

As we discussed, a W-element of a holomorphic VOA of central charge $24$ with a semisimple weight one Lie algebra defines an automorphism $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ for some $\tau \in \mathrm { Aut}(\Lambda )=Co.0$ and $\beta \in {\mathbb C}\Lambda ^{\tau }$ such that $V= V_\Lambda ^{[\tilde {g}]}$ . One main question is to determine the isometry $\tau \in Co.0$ arising in this manner.

Denote

$$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg | \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\ \mbox{ automorphism of an orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$

In Section 6, we will show that $\mathcal{P} \subset \mathcal{P}_0 = \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$ . The main idea is to analyze the conformal weights of the irreducible $\widehat {\tau }$ -twisted modules and $\tilde {g}$ -twisted modules.

3 Irreducible twisted modules for lattice VOAs

First, we review some basic properties of the irreducible twisted modules for lattice VOAs. Let P be an even unimodular lattice. Let $\tau \in O(P)$ be of order n and $\widehat {\tau } \in O(\hat {P})$ a standard lift of $\tau $ . We use $\pi =\pi _{\tau }: P \to (P^{\tau })^*$ to denote the natural projection. More precisely,

(3.1) $$ \begin{align} \pi(x)=\pi_\tau(x) =\frac{1}{n} \sum_{i=0}^{n-1} \tau^i (x). \end{align} $$

By [12], $V_P$ has a unique irreducible $\widehat {\tau }$ -twisted $V_P$ -module, up to isomorphism. Such a module $V_P[\widehat {\tau }]$ was constructed in [11] explicitly; as a vector space,

$$ \begin{align*}V_P[\widehat{\tau}]\cong M(1)[\tau]\otimes{\mathbb C}[\pi(P)]\otimes T,\end{align*} $$

where $M(1)[\tau ]$ is the ‘ $\tau $ -twisted’ free bosonic space, ${\mathbb C}[\pi (P)]$ is the group algebra of $\pi (P)$ and T is an irreducible module for a certain “ $\tau $ -twisted” central extension of P (see [35, Propositions 6.1 and 6.2] and [11, Remark 4.2] for detail). Recall that

$$ \begin{align*}\dim T=|P_\tau/(1-\tau)P|^{1/2}\end{align*} $$

and that the conformal weight $\phi (\tau )$ of T is given by

(3.2) $$ \begin{align} \phi(\tau):=\frac{1}{4n^2}\sum_{j=1}^{n-1}j(n-j)\dim \mathfrak{h}_{(j)}, \end{align} $$

where $\mathfrak {h}_{(j)}=\{x\in \mathfrak {h}\mid \tau (x)=\exp ((j/n)2\pi \sqrt {-1})x\}$ . Note that $M(1)[\tau ]$ is spanned by vectors of the form

$$ \begin{align*}x_1(-m_1)\dots x_s(-m_s)1,\end{align*} $$

where $m_i\in (1/n){\mathbb Z}_{>0}$ and $x_i\in \mathfrak {h}_{(nm_i)}$ for $1\le i\le s$ .

In addition, the conformal weight of $x_1(-m_1)\dots x_s(-m_s)\otimes e^\alpha \otimes t\in V_P[\widehat {\tau }]$ is given by

$$ \begin{align*}\sum_{i=1}^s m_i+\frac{(\alpha|\alpha)}{2}+\phi(\tau), \end{align*} $$

where $x_1(-m_1)\dots x_s(-m_s)\in M(1)[\tau ]$ , $e^\alpha \in {\mathbb C}[\pi (P)]$ and $t\in T$ . Note that $m_i\in (1/n){\mathbb Z}_{>0}$ and that the conformal weight of $V_P[\widehat {\tau }]$ is $\phi (\tau )$ .

Since $\sum _{j=1}^{n-1} j(n-j)= n(n^2-1)/6$ , we have

$$\begin{align*}\phi(\tau)=\frac{1}{24}\sum_{i=1}^d a_i\frac{(n_i^2-1)}{n_i} =\frac{1}{24}\{\sum a_in_i-\sum_{i=1}^d \frac{a_i}{n_i}\}= 1-\frac{1}{24}\sum_{i=1}^d\frac{a_i}{n_i} \end{align*}$$

if $\tau \in O(P)$ has the frame shape $\prod _{j=1}^d n_j^{a_j}$ by (3.2).

Remark 3.1. Let $v\in {\mathbb Q}\otimes _{\mathbb Z} P^\tau \subset \mathfrak {h}_{(0)}$ . Then $\exp (2\pi i v(0))$ has finite order on $V_P$ and commutes with $\widehat {\tau }$ . Set $g= \widehat {\tau } \exp (2\pi i v(0))$ . Then the unique irreducible g-twisted module for $V_P$ is given by

$$\begin{align*}V_P[g]\cong M(1)[\tau]\otimes{\mathbb C}[-v+\pi(P)]\otimes T \end{align*}$$

as a vector space [4]. In this case, the conformal weight of $V_P[g]$ is given by

$$ \begin{align*}\frac{1}2\min\{(\beta|\beta)\mid \beta\in -v+\pi(P)\}+\phi(\tau). \end{align*} $$

4 Leech lattice and $\ell $ -duality

Let $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ be the reverse automorphism associated with an orbifold construction defined by a W-element of a holomorphic VOA V of central charge $24$ . In this section, we will consider and study several lattices associated with $\tilde {g}$ and try to study their relations to the root system of the weight one Lie algebra $V_1$ . We first observe that the fixed point sublattice $\Lambda ^\tau $ satisfies some duality property, which we call $\ell $ -duality. Using $\ell $ -duality, we will associate a Niemeier lattice N with $\tilde {g}$ . We will study the relationships between N and the root system of $V_1$ . We will also relate the Coxeter number of N to the order of $|\tilde {g}|$ . For simplicity, we assume that $\tau \in \mathcal{P}_0= \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}$ in this section. In Section 6, we will show that $\tau $ is indeed contained in $P_0$ .

4.1 $\ell $ -duality

In this subsection, we study the properties of the lattice $\Lambda ^\tau $ for

$$\begin{align*}\tau \in \mathcal{P}_0= \{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}. \end{align*}$$

Lemma 4.1. For $\tau \in \mathcal{P}_0$ , we have $\det (\Lambda ^{\tau })=\ell ^{\mathrm {rank}(\Lambda ^{\tau })/2}$ .

Proof. For $\tau \in \mathcal{P}_0$ , it is easy to check that $(1-\tau ) (\Lambda ^*_\tau )=\Lambda _\tau $ . It follows that $\det (\Lambda ^{\tau })=\det (\Lambda _\tau )=\prod m^{a_m}$ , where $\prod m^{a_m}$ is the frame shape of $\tau $ . The result then follows by a direct calculation (cf. Table 1 in Section 6).

Table 1 Conjugacy classes of $\tau \in Co.0$ with $\dim\, \Lambda ^\tau \geq 4$ .

Below is one of our key observations. This fact is probably well-known to the experts and it also holds for some other isometries in $Co.0$ (e.g., $14B$ ).

Theorem 4.2. If $\tau \in \mathcal{P}_0$ , then there is an isometry

$$ \begin{align*}\varphi=\varphi_\tau: \sqrt{\ell}(\Lambda^{\tau})^{\ast} \to \Lambda^{\tau},\end{align*} $$

where $\ell =|\widehat {\tau }|$ .

Remark 4.3. It is known that $\ell =|\tau |$ or $2|\tau |$ and $\ell =2|\tau |$ if and only if $<\tau>$ contains a $2C$ -element, see [2].

In [20], Harada and Lang have determined the structure of $\Lambda ^{\tau }$ for $\tau \in Co.0$ . In particular, the Gram matrix for the lattice $\Lambda ^\tau $ has been given explicitly. It is straightforward to check that Theorem 4.2 holds for

$$ \begin{align*}\tau\in \mathcal{P}_0=\{1A,2A,2C,3B,4C,5B,6E,6G,7B,8E,10F\}.\end{align*} $$

Note that the Gram matrix of the dual lattice $L^*$ is equal to the inverse of the Gram matrix of L. Therefore, it suffices to check that the Gram matrix of $\Lambda ^\tau $ is equal to $\ell $ times the Gram matrix of $(\Lambda ^\tau )^*$ for any $\tau \in \mathcal{P}_0$ .

Remark 4.4. Let $\widehat {\tau }$ be a standard lift of $\tau $ in $\mathrm {Aut}(V_\Lambda )$ and let $\phi (\tau )$ be the conformal weight of the irreducible $\widehat {\tau }$ -twisted module of $V_\Lambda $ . By direct calculations, it is straightforward to verify that for any $\tau \in \mathcal{P}_0$ , we have

$$\begin{align*}\phi(\tau^m)= 1-\frac{1}{|\widehat{\tau^m}|} \qquad \mbox{ for all } m| |\tau|. \end{align*}$$

In other words, $\widehat {\tau ^m}$ is of type $0$ for any $\tau \in \mathcal{P}_0$ and $m \in {\mathbb Z}$ as defined in [17].

4.2 Reverse automorphisms and associated Niemeier lattices

From now on, we assume that $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ is the reverse automorphism associated with an orbifold construction defined by a W-element and assume that $\tau \in \mathcal{P}_0$ and $\tau (\beta )=\beta $ .

First, we discuss some relations between the lattice L discussed in Section 2 and the fixed point sublattice $\Lambda ^\tau $ of the Leech lattice.

Notation 4.5. Let X be an even lattice and let $\beta \in {\mathbb Q} \otimes _{\mathbb Z} X$ . Denote

$$ \begin{align*}X_{\beta} = \{ x\in X \mid \langle x, \beta \rangle \in {\mathbb Z}\}.\end{align*} $$

Suppose that $\langle \beta ,\beta \rangle =2k/n$ for some positive integers k and n with $GCD(k,n)=1$ . Let $\bar {X}=\{x\in X\mid \langle x,n \beta \rangle \in {\mathbb Z}\}$ . For $x\in \bar {X}$ , we define $x_{[\beta ]} = x- m\beta $ if $\langle x, n\beta \rangle \equiv mk \mod n$ , $0\leq m\leq n-1$ and $\bar {X}_{[\beta ]} = \{ x_{[\beta ]}\mid x \in \bar {X}\}$ . Then $\bar {X}_{[\beta ]}$ is also an even lattice and $\det (\bar {X})=\det (\bar {X}_{[\beta ]})$ .

Recall that $\langle \alpha , \alpha \rangle =2K_0/N_0$ and $N_0\alpha \in L^*$ for a W-element $\alpha $ (cf. Proposition 2.4). Thus, we have $\bar {L}=L$ . Since $V^{[g]}\cong V_\Lambda $ , we have $V^g \cong (V_\Lambda )^{\tilde {g}}$ and

$$\begin{align*}V_{L_\alpha}= \mathrm{Com}(\mathrm{Com}( M(\widehat{\mathcal{H}}),V^g), V^g) \cong \mathrm{Com}(\mathrm{Com}( M(\widehat{\mathcal{H}}),(V_\Lambda)^{\tilde{g}}), (V_\Lambda)^{\tilde{g}}) = V_{\Lambda_\beta^\tau}. \end{align*}$$

It implies $L_\alpha \cong \Lambda ^\tau _\beta $ . Moreover, $\Lambda ^\tau = L_{[\alpha ]}+ {\mathbb Z} N_0\alpha $ .

Now consider the irreducible $\tilde {g}$ -twisted module

$$\begin{align*}V_\Lambda[\tilde{g}]\cong {\mathbb C}[-\beta +(\Lambda^\tau)^*]\otimes M(1)[\tau]\otimes T. \end{align*}$$

Since $(V_\Lambda [\tilde {g}])_{\mathbb Z} \neq 0$ and $\phi (\tau )=1-1/|\widehat {\tau }|$ for $\tau \in \mathcal{P}_0$ , there exists $\beta '\in -\beta +(\Lambda ^\tau )^*$ such that $\langle \beta ', \beta '\rangle / 2\equiv 1/|\widehat {\tau }| \mod {\mathbb Z}$ . Without loss of generality, we may assume $\beta = -\beta '$ . In this case, $\beta \in L^*$ . By a general result (cf. [21; 25]), we also have

(1) $(\mathcal {D}(L), q)\cong (\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), -q')$ as quadratic spaces;

(2) $\det (L) = \det (\Lambda ^\tau ) \times |\tau |^2$ .

The quadratic space structure of $(\mathrm {Irr}(V_{\Lambda _\tau }^{\widehat {\tau }}), q')$ has also been determined in [25]. In particular, it has proved that the exponent of $L^*/L$ is $\ell =|\widehat {\tau }|$ and $q(L^*)\subset \frac {1}{\ell }{\mathbb Z}$ . Thus, we have the following lemma.

Lemma 4.6. We have $\ell \beta \in L$ and $L = \Lambda _\beta ^\tau + {\mathbb Z} \ell \beta $ . Moreover, $\sqrt {\ell } L^*$ is an even lattice.

By Theorem 4.2, there is an isometry $\varphi =\varphi _\tau : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $ with $\ell =|\widehat {\tau }|$ and it induces an isometry from ${\mathbb C} \Lambda ^{\tau } \to {\mathbb C} \Lambda ^{\tau }$ .

Definition 4.7. Set $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$ and $N= \Lambda ^{[\tilde {\beta }]} := \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$ .

By our assumption, $\langle \tilde {\beta }, \tilde {\beta }\rangle \in 2{\mathbb Z}$ and N is an even unimodular lattice.

Theorem 4.8. Let $n=|g|=|\tilde {g}|$ . Suppose $m\varphi (\sqrt {\ell }\beta )\in \Lambda $ . Then we have $n|m$ . Moreover, $[ \Lambda ^{[\tilde {\beta }]}: \Lambda _{\tilde {\beta }}]=n$ .

Proof. If $m\varphi (\sqrt {\ell }\beta )\in \Lambda $ , then $m\varphi (\sqrt {\ell }\beta )\in \Lambda ^{\tau }=\varphi (\sqrt {\ell }(\Lambda ^{\tau })^*)$ , which is equivalent to $m\sqrt {\ell }\beta \in \sqrt {\ell }(\Lambda ^{\tau })^{\ast }$ (or equivalently, $m\beta \in (\Lambda ^{\tau })^{\ast }$ ).

Since $[\Lambda ^\tau : \Lambda ^\tau _\beta ]=n ( = [ (\Lambda ^\tau _\beta )^* : (\Lambda ^\tau )^*]) $ and $(\Lambda ^\tau _\beta )^* = (\Lambda ^\tau )^* +{\mathbb Z} \beta $ , $m\beta \in (\Lambda ^{\tau })^{\ast }$ implies n divides m.

For the second statement, it suffices to show $n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $ . Let $k=|\tau |$ . Then $\widehat {\tau }^k = \exp (2\pi i\delta (0))$ for some $\delta \in {\mathbb C} \Lambda ^\tau $ . Since $n=|\tau | N_0=kN_0$ and $\tilde {g}^n= \widehat {\tau }^n\exp (2\pi i\beta (0))^n=1$ , we have $n\beta -N_0 \delta \in \Lambda ^\tau $ .

As $\widehat {\tau }$ is a standard lift, $\widehat {\tau }(e^\gamma )=e^\gamma $ for any $\gamma \in \Lambda ^\tau $ . Thus, $\langle \delta , \Lambda ^\tau \rangle \subset {\mathbb Z}$ and $\delta \in (\Lambda ^\tau )^*$ . By using the isometry $\varphi $ , we have $n\sqrt {\ell } \varphi (\beta ) - N_0 \sqrt {\ell } \varphi (\delta ) \in \sqrt {\ell } \varphi (\Lambda ^\tau ) < \sqrt {\ell } \varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $ . Since $\delta \in (\Lambda ^\tau )^*$ , we have $\sqrt {\ell } \varphi (\delta ) \in \Lambda ^\tau $ and $n\sqrt {\ell } \varphi (\beta ) \in \Lambda ^\tau $ as desired.

Theorem 4.9. Let $N= \Lambda ^{[\tilde {\beta }]} = \Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$ . Then $\varphi $ induces an isometry from $\sqrt {\ell }L^*$ to $N^\tau $ . In particular, we have $N^\tau \cong \sqrt {\ell }L^*$ .

Proof. Since $\tau $ fixes $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$ , we may assume that $\tau $ acts on $N=\Lambda ^{[\tilde {\beta }]}$ and $N^\tau = \Lambda ^\tau _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$ . Note also that $\langle \beta , \beta \rangle \in (2/\ell ) {\mathbb Z}$ .

By Lemma 4.6, we have $L= \Lambda _\beta ^\tau +{\mathbb Z} \ell \beta $ . Thus,

$$ \begin{align*} L^* & = \{ x\in (\Lambda_\beta^\tau)^*\mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ &= \{ x\in (\Lambda^\tau)^*+{\mathbb Z} \beta \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}\\ & = < \{ x\in (\Lambda^\tau)^* \mid \langle x, \ell \beta \rangle \in {\mathbb Z}\}, \beta>. \end{align*} $$

Then

$$ \begin{align*} \sqrt{\ell} \varphi(L^*) & = < \{ \sqrt{\ell} \varphi(x) \in \sqrt{\ell} \varphi(\Lambda^\tau)^*\mid \langle \sqrt{\ell} \varphi(x) , \sqrt{\ell} \varphi(\beta) \rangle \in {\mathbb Z}\}, \sqrt{\ell} \varphi( \beta)>\\ &=< \{ y\in \Lambda^\tau \mid \langle y, \tilde{\beta} \rangle \in {\mathbb Z}\} , \tilde{\beta}>\\ &= \Lambda^\tau_{\tilde{\beta}} +{\mathbb Z} \tilde{\beta} = N^\tau \end{align*} $$

as desired.

Lemma 4.10. Under the above conditions, we have $\Lambda ^{[\varphi (\sqrt {\ell }\beta )]}\not \cong \Lambda $ .

Proof. Since $\tau $ fixes $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$ , we may assume that $\tau $ acts on $N=\Lambda ^{[\tilde {\beta }]}$ . Then $\tau $ induces an isometry $\tau '$ of $N=\Lambda ^{[\tilde {\beta }]}$ .

Suppose $N \cong \Lambda $ . Since all elements in $O(\Lambda )$ are determined by its frame shape up to conjugate, we may assume $\tau '$ is conjugate to $\tau $ . In particular, $N^{\tau '}$ is isometric to $\Lambda ^{\tau }$ and so $\sqrt {\ell }(N^{\tau '})^{\ast } \cong N^{\tau '}$ . By Theorem 4.9, $N^{\tau '}\cong \sqrt {\ell }L^{\ast }$ and so $(N^{\tau })^{\ast }= \frac {1}{\sqrt {\ell }}L$ . Then $\Lambda ^{\tau } \cong \sqrt {\ell }(\Lambda ^{\tau })^{\ast }\cong \sqrt {\ell }(N^{\tau '})^{\ast }\cong L$ . It is not possible since $\det (L)=\det (\Lambda ^{\tau }). |\tau |^2$ .

As a consequence of the above lemma and Theorem 4.8, we have the following lemma.

Lemma 4.11. Let h be the Coxeter number of $N= \Lambda ^{[\varphi (\sqrt {\ell }\beta )]}$ and $n= |g|=|\tilde {g}|$ . Then we have $n \geq h$ .

4.3 Roots of $V_1$

Next we study the structure of the root lattice of $V_1$ . Let $V_1=\oplus _{j=1}^t \mathcal{G}_{j,k_j}$ . If $u\in L^*$ is a root of $\mathcal{G}_j$ , then

$$\begin{align*}\langle u,u\rangle= \begin{cases} \frac{2}{k_j} & \text{ if } u \text{ is a long root,}\\ \frac{2}{r_{j}k_j} & \text{ if } u \text{ is a short root.} \end{cases} \end{align*}$$

As a corollary of $\ell $ -duality, we have the following:

Lemma 4.12. $|\tau |(K_0-N_0)$ divides $\ell $ .

Proof. Let $ e^u \otimes t \in \mathcal{G}_{j,k_j}$ be a short root vector. Then $\langle u,u\rangle =\frac {2}{r_jk_j}$ and we have

$$ \begin{align*}\langle u,u\rangle=\frac{2}{r_jk_j}=\frac{2}{r_jh_j^{\vee}} \times \frac{h_j^{\vee}}{k_j} =\frac{2}{r_jh_j^{\vee}}\times \frac{N_0}{K_0-N_0}.\end{align*} $$

Since $\langle u,u\rangle \in \frac {{\mathbb Z}}{\ell }$ and $\mathrm {LCM}(\{r_jh_j^{\vee }/N_0:j\})=|\tau |$ , we have that $K_0-N_0$ divides $\ell /|\tau |$ .

Remark 4.13. Let $ e^u \otimes t \in \mathcal{G}_{j,k_j}$ be a root vector associated with a simple short root. Then $\langle \alpha ,u\rangle =\frac {1}{r_jh_j^\vee }$ and $e^u\otimes t$ belongs to $\tilde {g}^{s_j}$ -twisted modules, where $s_jr_jh^{\vee }_j=n$ . More precisely, it belongs to $s_j$ -power of $\tilde {g}$ -twisted module $T^1$ by fusion products.

Lemma 4.14. Suppose there is j such that $r_jh^{\vee }_j=n=|\tau |N_0$ . Then there is a root $u\in L^*$ of $\mathcal{G}_j$ such that $\langle u, u\rangle =2/\ell $ .

Proof. Let u be a simple short root of $\mathcal{G}_j$ . Since $r_jh^{\vee }_j=n=|\tau |N_0$ , we have $\langle u, u\rangle = \frac {2}{|\tau |(K_0-N_0)}$ and $e^u \otimes t \in T^1_1$ . It implies $\langle u,u\rangle /2 \in 1/\ell +{\mathbb Z}$ . Note also that $\ell / |\tau |= 1$ or $2$ and $ |\tau |(K_0-N_0)$ divides $\ell $ . Therefore, $\ell = |\tau |(K_0-N_0)$ and $\langle u,u\rangle =2/\ell $ .

Definition 4.15. We call a root $\delta $ of $V_1$ satisfying $\langle \delta ,\delta \rangle =\frac {2}{\ell }$ a shortest root and call a simple component $\mathcal{G}_j$ of $V_1$ containing a shortest root a full component. Note that a shortest root exists if $r_jh_j^{\vee }=n$ for some j.

5 Deep holes

Let V be a holomorphic VOA of central charge $24$ and $\alpha $ a W-element of $V_1$ . Let $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$ and let $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ be the reverse automorphism of g, where $\beta \in {\mathbb C}\Lambda ^{\tau }$ .

In this section, we assume that $\tau \in \mathcal{P}_0$ and try to relate the automorphism $\tilde {g}=\widehat {\tau }\exp (2\pi i \beta (0)\in \mathrm {Aut}(V_\Lambda )$ to a deep hole of the Leech lattice. In Section 6, we will prove that $\tau \in \mathcal{P}_0$ .

Since $\tau \in \mathcal{P}_0$ , there is an isometry $\varphi : \sqrt {\ell } (\Lambda ^\tau )^* \to \Lambda ^\tau $ . Set $\tilde {\beta }=\sqrt {\ell }\varphi (\beta )$ and $N=\Lambda ^{[\tilde {\beta }]}= \Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$ . Note that $\langle \beta ,\beta \rangle \in 2{\mathbb Z}/\ell $ and $\langle \tilde {\beta },\tilde {\beta }\rangle \in 2{\mathbb Z}$ . Moreover, the root sublattice R of N is nonzero by Lemma 4.10.

One of the main aims in this paper is to prove the following theorem.

Theorem 5.1. The vector $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$ is a deep hole of $\Lambda $ .

5.1 Coinvariant sublattices $\Lambda _\tau $ and $N_\tau $

In this subsection, we will discuss another main observation of this article, which is related to the structure of the coinvariant sublattice $N_\tau =\{ x\in N \mid \langle x, N^\tau \rangle =0\}$ .

Since $\tau $ fixes $\tilde {\beta }=\varphi (\sqrt {\ell } \beta )$ , we have $(\Lambda _{\tilde {\beta }})_\tau =\Lambda _{\tau }$ and $N_\tau> \Lambda _\tau $ . Moreover, $[N_\tau : \Lambda _{\tau }]=|\tau |$ because $\det (N_\tau )=\det (N^\tau ) =\det (\Lambda ^\tau )/ |\tau |^2=\det (\Lambda _\tau )/ |\tau |^2$ . For $\tau \in \mathcal{P}_0$ , we note that $\Lambda _\tau \cong L_B(c)$ as defined in Appendix A.

Lemma 5.2. For $\tau \in \mathcal{P}_0\setminus \{2C\}$ , we have $N_\tau \cong L_A(C)$ , where $C=\langle c\rangle $ is defined as in Table 2 in Appendix A.

Proof. It follows from the fact that $\Lambda _{\tau } \cong L_B(C)$ and $\mathcal {D}(\Lambda _{\tau })$ has only one nonzero singular element of order $|\tau |$ , up to isometry if $\tau \in \mathcal{P}_0\setminus \{2C\}$ (see Appendix A).

Next, we consider the case when $\tau =2C$ . In this case, $\Lambda _{\tau }\cong \sqrt {2}D_{12}^+$ . We use the standard model for root lattices of type D – that is,

$$\begin{align*}D_{12}=\left \{ (x_1, \cdots, x_{12})\in {\mathbb Z}^{12}\mid \sum_{i=1}^{12} x_i =0\quad \mod 2\right\} \end{align*}$$

and $D_{12}^+ = \mathrm {Span}_{\mathbb Z}\{D_{12}, \frac {1}2 (1, \cdots , 1) \}$ . Note that $D_{12}^+$ is an odd lattice.

Lemma 5.3. For $\tau \in 2C$ , there are two classes of nonzero singular elements, up to isometry; they correspond to vectors of the form $\sqrt {2}(1,0, \cdots , 0)$ and $\frac {\sqrt {2}}{2}(1^4 0^8)$ , respectively. There are two index $2$ overlattices of $\Lambda _{\tau }$ . They are isometric to $L_A(1^{12})\cong \sqrt {2}D_{12}^*$ or the overlattice $\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$ , which has the root sublattice $A_1^4$ .

Let $X=\mathrm {Span}_{\mathbb Z}\{\sqrt {2}D_{12}^+, \frac {\sqrt {2}}{2}(1^4 0^8) \}$ . Then

$$ \begin{align*} X^* &= \{ \alpha\in \frac{\sqrt{2}}{2} D_{12}^+\mid \langle \alpha, \frac{\sqrt{2}}{2}(1^4 0^8)\rangle \in {\mathbb Z} \}\\ & = \frac{\sqrt{2}}{2} \mathrm{Span}_{\mathbb Z}\{D_{4}+D_8, \frac{1}2(1^4 0^8) \}\cong \frac{\sqrt{2}}{2} ({\mathbb Z}^4+D_8). \end{align*} $$

Therefore, $2X^* \cong A_1^4 + \sqrt {2}D_8$ . Then the quadratic form of $2X^*$ is not isometric to L, which is not possible, and hence, we have the following lemma.

Lemma 5.4. For $\tau \in 2C$ , $N_\tau \cong L_A(1^{12})\cong \sqrt {2}D_{12}^*$ .

As a consequence, for any $\tau \in \mathcal{P}_0$ , $N_\tau \cong L_A(c)$ as described in Appendix A. We also note that $\tau $ acts on $L_A(c)$ as $g_{\Delta ,c}$ defined in (A.4). In particular, $\tau $ is contained in the Weyl group of R.

Remark 5.5. If the frame shape of $\tau $ is $\prod k^{m_k}$ , then $N_{\tau }$ contains $\oplus A_{k-1}^{m_k}$ and $\tau $ acts on $\oplus A_{k-1}^{m_k}$ as a product of the Coxeter elements. In particular, $\tau $ preserves any irreducible component of the root system of N.

Corollary 5.6. If $N_0=1$ , then the Coxeter number of N is greater than or equal to $|\tau |$ .

Proof. For $\tau \in \mathcal{P}_0$ , it is easy to check that the frame shape of $\tau $ contains a positive power of $|\tau |$ . Therefore, $N_{\tau }$ contains a root system $A_{|\tau |-1}$ whose Coxeter number is $|\tau |$ .

5.2 Affine root system and shortest roots

One important fact that we will prove is the following:

Lemma 5.7. Let $\beta \in {\mathbb C}\Lambda $ . Set $S=\{ \lambda \in \Lambda \mid \langle \lambda -\beta ,\lambda -\beta \rangle =2\}$ . If $\tilde {S} =\{\lambda -\beta \mid \lambda \in S \}$ contains an affine fundamental root system, then $\beta $ is a deep hole.

Proof. For $\lambda \in \Lambda $ , let $\lambda ^* = (\lambda , 1, \frac {\langle \lambda ,\lambda \rangle }{2}-1)\in \Lambda +\Pi _{1,1}$ , which is called a Leech root. Set $\hat {\beta }= (\beta ,1,\frac {\langle \beta ,\beta \rangle }{2})\in {\mathbb Q} (\Lambda + \Pi _{1,1})$ . Note that $\hat {\beta }$ is an isotropic vector. Then $\lambda ^*-\hat {\beta } = (\lambda -\beta , 0 , \frac {\langle \lambda ,\lambda \rangle }{2}-1-\frac {\langle \beta ,\beta \rangle }{2})$ and we have

$$ \begin{align*} \langle \lambda-\beta,\lambda-\beta\rangle =\langle \lambda^*-\hat{\beta}, \lambda^*-\hat{\beta}\rangle =\langle \lambda^*, \lambda^* \rangle + \langle \hat{\beta},\hat{\beta}\rangle - 2\langle \lambda^*, \hat{\beta} \rangle =2-2\langle \lambda^*, \hat{\beta} \rangle. \end{align*} $$

Thus, $\langle \lambda -\beta ,\lambda -\beta \rangle =2$ if and only if $\langle \lambda ^*, \hat {\beta } \rangle =0$ .

Suppose that $\beta $ is not a deep hole. Then there is a $\delta \in \Lambda $ such that $\langle \delta -\beta ,\delta -\beta \rangle <2$ . In this case, $\langle \delta ^*, \hat {\beta } \rangle>0$ . Since $\delta ^{\ast }\not \in \{\lambda ^{\ast }\mid \lambda \in S\}$ and the minimal squared norm of $\Lambda $ is $4$ , $\langle \delta ^{\ast },\lambda ^{\ast }\rangle \leq 0$ for all $\lambda \in S$ . However, since $\tilde {S}$ contains an affine fundamental root system, there exists a subset $S'\subset S$ and positive real numbers $n_{\lambda }\in {\mathbb R}_{\geq 0}$ such that $\sum _{\lambda \in S'}n_{\lambda }\lambda = m \beta $ , where $m=\sum _{\lambda \in S'} n_{\lambda }$ . By direct calculations, we have

$$ \begin{align*} \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right) &= \sum_{\lambda\in S'}n_{\lambda} \frac{\langle\lambda, \lambda\rangle -\langle \lambda-\beta, \lambda -\beta\rangle}2\\ & = \sum_{\lambda\in S'}n_{\lambda} \left( \langle\lambda, \beta\rangle -\frac{\langle \beta,\beta\rangle}2\right) =\frac{m\langle \beta, \beta\rangle}2. \end{align*} $$

Thus, we also have

$$\begin{align*}\sum_{\lambda\in S'}n_{\lambda}\lambda^*= \left ( \sum_{\lambda\in S'}n_{\lambda}\lambda, \sum_{\lambda\in S'}n_{\lambda}, \sum_{\lambda\in S'}n_{\lambda}\left( \frac{\langle\lambda, \lambda\rangle}2 -1\right)\right)= m \hat{\beta}, \end{align*}$$

but it implies $\langle \delta ^{\ast }, \hat {\beta }\rangle \leq 0$ , which is a contradiction.

Therefore, in order to prove Theorem 5.1, it is enough to show that the Coxeter number h of N is greater than or equal to $n=|g|$ , since $R_1=\{\lambda -\tilde {\beta }\mid \langle \lambda -\tilde {\beta }, \lambda -\tilde {\beta }\rangle =2, \lambda \in \Lambda _{\tilde {\beta }} \}$ will contain an affine fundamental root system in this case.

5.3 Existence of shortest roots

The purpose of this subsection is to show the following proposition.

Proposition 5.8. There is a root $\delta $ of $V_1$ such that $\langle \delta ,\delta \rangle =\frac {2}{\ell }$ .

Proof. By Lemma 4.14, it suffices to show that there is j such that $r_jh_j^\vee =n$ .

Recall that $\mathrm {LCM}(r_jh^{\vee }_j \mid j)=n$ . If $|\tau |$ is a prime power or $V_1$ is simple, then there is j such that $r_jh_j^{\vee }=n$ . Therefore, we may assume that $|\tau |$ is not a prime power and $\mathrm {rank}(V_1)>4$ ; that is, $\tau $ is $6E=1^22^23^26^2$ or $6G=2^36^3$ and $\mathrm {rank}(V_1)=8$ or $6$ . We have already shown $N_0| h_j^\vee $ for all j. By Corollary 5.6, we may also assume $N_0\not =1$ . Suppose there is no j such that $r_jh_j^\vee =n=6N_0$ . Then there exist k and l such that $r_kh_k^{\vee }=3N_0$ and $r_lh_l^\vee =2N_0$ . If one of $\mathcal{G}_j$ is of type $G_2$ , then $N_0=4$ and there is also a component $\mathcal{G}_i$ such that $r_ih_i^{\vee }=8$ ; that is, $\mathcal{G}_i=A_7$ , or $C_3$ . Another possible component is $A_3$ . Therefore, possible choices for $\tau $ and $V_1$ are $\tau =6E$ and $V_1=G_2C_3^2$ , or $G_2C_3A_3$ . However, since $\dim V_1=120\not =14+2\times 21$ nor $14+21+15$ , we have a contradiction. Therefore, there is no component of type $G_2$ . In order to get $r_kh_k^{\vee }=3N_0$ , $r_k=1$ , $h_k^\vee =3N_0$ and $V_1$ contains a component of type $A_{3N_0-1}$ . Since $N_0\not =1$ , $\mathrm {rank}(V_1)\leq 8$ and $V_1$ has a component with $r_ih_i^\vee =2N_0$ , we have $N_0=2$ and $V_1=A_3+A_5$ (i.e., $\mathrm {rank}(V_1)=8$ and $\tau =6E$ ). However, $\dim V_1=72\not =15+35$ , which is a contradiction. This completes the proof of Proposition 5.8.

As a corollary, $(\Lambda _{\tilde {\beta }}-\tilde {\beta })_2 \not =\emptyset $ and so we may choose $\beta $ so that $\langle \beta ,\beta \rangle =\frac {2}{\ell }$ . In particular, $\tilde {\beta }$ has squared length $2$ .

5.4 Proof of Theorem 5.1 (part 2)

Notation 5.9. For an even lattice K, we use $R(K)$ to denote the sublattice generated by $K_2=\{a\in K\mid \langle a,a\rangle =2\}$ . A component lattice of $R(K)$ means a sublattice generated by an irreducible component of the roots in $K_2$ .

Lemma 5.10. Let $X\subseteq R(N^{\tau })$ be a component lattice and let $\tilde {X}\subseteq R(N)$ be a component lattice containing X. If $X\not =\tilde {X}$ , then $\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$ or $\tau $ acts on $\tilde {X}$ trivially.

Proof. If $\tilde {X}\not =X$ and $\tau $ does not act on $\tilde {X}$ trivially, then there are $\mu _1\in X$ and $\mu _2\in \tilde {X}-\tilde {X}^{\tau }$ such that $\langle \mu _1,\mu _2\rangle =-1$ . Since $\mu _2\not \in N^{\tau }$ and $\mathrm {rank}(R(N_{\tau }))=\mathrm {rank}(N_{\tau })$ (see Remark 5.5), there is a $\mu _3\in R(N_{\tau })$ such that $\langle \mu _2,\mu _3\rangle =-1$ . Since $\mu _3\in \tilde {X}$ , $\mathrm {rank}(\tilde {X})\geq \mathrm {rank}(X)+2$ , as we desired.

Now let’s start the proof of Theorem 5.1. As we explained, it is enough to show that the Coxeter number of N is greater than or equal to n.

Suppose Theorem 5.1 is false and let V be a counterexample. By Proposition 5.8, there is a simple component $\mathcal{G}_j$ of $V_1$ such that $r_jh^{\vee }_j=n$ and we may choose $\langle \tilde {\beta },\tilde {\beta }\rangle =2$ , or equivalently, $\langle \beta ,\beta \rangle =\frac {2}{\ell }$ . Suppose there is a full component $\mathcal{G}_j$ which is simply laced and let $L_j$ be its root lattice. Then $\sqrt {\ell }\phi (L_j)\subseteq R^{\tau }$ and so $h\geq n$ , which is a contradiction.

Therefore, there are no simply laced full components in $V_1$ and $\mathrm {GCD}(6,|\tau |)\not =1$ since the lacing number divides $|\tau |$ . We also have $N_0\not =1$ by Corollary 5.6. Furthermore, if $\mathrm {rank}(V_1)=4$ , then we have shown $N_0=1$ in [7] and we have a contradiction. Therefore, we may assume $|\tau |=2,3,4,6,8$ . We will need a few lemmas.

Lemma 5.11. If $|\tau |=2$ , then $N_0$ is odd.

Proof. Suppose $N_0$ is even. Then $K_0$ is odd since $\mathrm {GCD}(K_0,N_0)=1$ . Since $K_0-N_0=1$ or $2$ , $K_0=N_0+1$ . Since $|\tau |=2$ , there are no components of type $G_2$ . Moreover, $N_0$ is even and $n/N_0=2$ ; thus, $4|n$ and there are no full components of type B and F. Therefore, the only full components of $V_1$ are of type $C_{N_0-1,1}$ . Since $N_0$ divides the dual Coxeter numbers, the other components are of the type $A_{N_0-1}$ or $D_{N_0/2+1}$ . Recall that $\mathrm {rank}(\Lambda ^\tau )=12$ or $16$ and $N_0$ is even. By a direct calculation, it is easy to verify that the possible cases are only $V_1=C_{3,1}^a A_{3,1}^b$ ( $N_0=4$ ) with $a+b=4$ and $C_7D_5$ ( $N_0=8$ ). Since $\dim V_1=24(N_0+1)$ , none of them is possible. Note that $\dim C_3=21, \dim A_3=15, \dim C_7=105$ and $ \dim D_5=45$ .

Lemma 5.12. Let V be a counterexample of Theorem 5.1. Then $\tau $ and $(V_1, N_0)$ will be one of the following:

1. (1) $\tau =2A=1^82^8$ and $(V_1, N_0)=(C_{4}^4,5), (C_6^2B_4,7), (C_8F_4^2, 9), (C_{10}B_6, 11)$ ;

2. (2) $\tau =2C=2^{12}$ and $(V_1, N_0)=(B_2^6, 5), (C_4A_4^2,5), (B_3^4,5), (B_4^3,7), (F_4A_8, 9)$ , $(B_6^2,11)$ , $(B_{12},23)$ ;

3. (3) $\tau =4F=1^42^24^2$ and $(V_1, N_0)=(C_{7}A_{3}, 4)$ ;

4. (4) $\tau =6E=1^22^23^26^2$ and $(V_1, N_0)=(C_5G_2A_1,2)$ ;

5. (5) $\tau =6G=2^36^3$ and $(V_1, N_0)=(F_{4}A_{2},3)$ .

Proof. Without loss of generality, we may assume that $\mathcal{G}_1$ is a full component.

Case 1: If $\mathcal{G}_1=F_4$ , then $\dim F_4=52$ and $n=18$ and so the possible choices for $(\tau , \mathrm {rank}\Lambda ^{\tau },\dim V_1)$ are $(2A,16,240), (2C,12,132)$ , $(6G,6,60), (6E,8,72)$ , and the possible choices for $(\mathcal{G}_j, \dim \mathcal{G}_j)$ are $(F_4,52)$ , $(C_8,136)$ , $(A_8, 80)$ and $(A_2,8)$ . Hence the possible cases are $\tau =2A$ and $V_1=F_4^2C_8$ ; $\tau =2C$ and $V_1=F_4A_8$ ; and $\tau =6G$ and $V_1=F_4 A_2$ .

From now on, we may assume that there are no full components of type $F_4$ .

Case 2: If $\mathcal{G}_1=G_2$ , then $n=12$ and $|\tau |=3 (N_0=4, \dim V_1=120)$ or $|\tau |=6$ ( $N_0=2, \dim V_1=72$ or $60$ ). If $|\tau |=3$ , then $\tau =3B$ , $4|h^\vee _i$ , $h_i^\vee < 12$ and $\mathrm {rank}(\Lambda ^\tau )=12$ . Then $V_1=G_2^a+A_3^b$ and $2a+3b=12, \dim V_1=14a+15b=120$ , which has no solution. If $|\tau |=6$ , then $V_1=G_2^a+C_5^b+A_1^c+A_3^d+A_5^e$ . Since $\dim (V_1)=60$ or $72$ and $\mathrm {rank}(V_1) (=2a+5b+c+3d+5e) =6$ or $8$ , the only solution is $V_1=C_5G_2A_1$ .

From now on, we may assume that all full components are of type $C_m$ or of type $B_m$ .

Case 3: If $\mathcal{G}_1=C_8$ , then $n=18$ and $|\tau |=2$ or $6$ .

(3.1) If $|\tau |=2$ , then $N_0=9$ , and so possible components are $C_8, B_5, A_8$ ; thus, $V_1=C_8^2$ or $C_8A_8$ but $\dim (V_1)=24K_0=240$ . Neither one is possible.

(3.2) If $|\tau |=6$ , then $N_0=3$ and $V_1=C_8$ , but $\dim V_1=96\not =\dim C_8$ , a contradiction.

Case 4: If $\mathcal{G}_1=C_{2m}$ and $0<m\not =4$ , then $n=2(2m+1)$ . First, we show that $m<7$ . Suppose $m\geq 7$ . Then $\mathrm {rank}(V_1)\geq \mathrm {rank}(C_{2m})\geq 14$ and so $\tau =2A$ and $N_0=2m+1$ and $m=7$ or $8$ . In this case, $\dim V_1=24(2m+2)$ and $\dim C_{2m}=2m(4m+1)$ . If $m=7$ , then there are no components $\mathcal{G}_j$ of rank 2 (or less than 2) with $h_j^\vee $ divisible by $N_0=15$ . So, $m=8$ and $V_1=C_{16}$ ; however, $\dim V_1=24(N_0+1)=24\times 18\not = \dim C_{16}=16\times 33$ .

For $m<7$ and $m\neq 4$ , we have $(2m+1,3)=1$ , $N_0=2m+1$ and $|\tau |=2$ . So, the possible components of $V_1$ are $C_{2m}, A_{2m}, B_{m+1}$ . Since $K_0-N_0=1$ for $\tau =2A$ and $K_0-N_0=2$ for $\tau =2C$ , $\dim V_1=24(2m+2)$ for $\tau =2A$ and $\dim V_1=12(2m+3)$ for $\tau =2C$ . If $\tau =2A$ , then by solving the relation $2ma+2mb+(m+1)c=16$ and $2m(4m+1)a+2m(2m+2)b+(m+1)(2m+3)c=24(2m+2)$ and $a>0$ and $b,c\geq 0$ , we have $V_1=C_{10}B_6, C_6^2B_4, C_4^4$ .

If $\tau =2C$ , then by solving the relation $2ma+2mb+(m+1)c=12$ and $2m(4m+1)a+2m(2m+2)b+(m+1)2m+3)=12(2m+3)$ , we have $V_1=C_{4}A_{4}^2$ or $C_{2}^6$ .

We next assume $\mathcal{G}_1=C_{2m+1}$ . Then since $2m+2$ is even, $|\tau |\not =2$ .

Case 5: If $\mathcal{G}_1=C_3$ , then $n=8$ and $|\tau |=4$ and $N_0=2$ and $\mathcal{G}$ is a direct sum of $C_3$ or $A_1$ , or $A_3$ . Since $\dim C_3=21$ , $\dim A_3=15$ , $\dim A_1=3$ and $\mathrm {rank}(V_1)=10$ , it is impossible to have $\dim V_1=72$ , and we have a contradiction.

Case 6: If $\mathcal{G}_1=C_5$ , then $n=12$ and $(\tau ,N_0)=(4F,3),(6,2)$ . If $\tau =4F$ , then the other possible components are $A_2, D_4, A_5, C_2$ since there is no component of type $G_2$ . Since $\mathrm {rank}(V_1)=10$ is even, it has another component of type $C_5$ or $A_5$ , but since $\dim V_1=96$ , $\dim C_5=55$ , and $\dim A_5=35$ , we have a contradiction. If $|\tau |=6$ , then $\mathrm {rank}(V_1)=8$ or $6$ and possible components are $A_1, A_3$ . Since $\dim V_1=72$ or $60$ and $\dim A_1=3$ , $\dim A_3=15$ , we have a contradiction.

Case 7: If $\mathcal{G}_1=C_7$ , then $n=16$ and $(\tau ,N_0)=(4F,4),(8,2)$ . If $N_0=2$ , then $\dim V_1=72$ and $\dim C_7=105$ , a contradiction. If $\tau =4F$ , then $N_0=4$ , and the only solution is $V_1=C_7A_3$ .

Case 8: If $\mathcal{G}_1=C_{2m+1}$ and $m\geq 4$ , then $\mathrm {rank}(V_1)\geq 2m+1\geq 9$ and so $\mathcal{G}_1=C_9$ . However, since $\mathrm {rank}(V_1)=10$ and $N_0=5$ , we have a contradiction.

Case 9: We may assume that all full components are of type B. Say, $\mathcal{G}_1=B_m$ , then $n=2(2m-1)$ . Since $2m-1$ is odd, $|\tau |=2, 6$ .

If $|\tau |=6$ , then $N_0=1/3(2m-1)$ and $m\leq 8$ . Since $N_0\neq 1$ is odd, the only possible values for $(N_0,m)$ are $(3,5)$ and $(5,8)$ . If $\tau =6G$ , then $\mathrm {rank} V_1=6$ and $(N_0, m)=(3,5)$ . The only possible choice for $V_1$ is $B_5+A_1$ , but since the Coxeter number of $A_1$ does not divide $3$ , we have a contradiction. If $\tau =6E$ , then $\mathrm {rank} V_1=8$ , and the possible choice of $V_1$ is $B_8$ . Since $2C\not \in <6E>$ , $K_0=N_0+1=4$ and $\dim V_1=24K_0=96\not =\dim B_8=8\times 17$ , which is a contradiction.

Therefore, we have $|\tau |=2$ and $N_0=2m-1$ . Since $2m-1$ is odd, the non-full components are all of type $A_{2m-2}$ and so $V_1=B_m^{\otimes a}\oplus A_{2m-2}^{\otimes b}$ . We note $\dim B_m=m(2m+1)$ and $\dim A_{2m-2}=4m(m-1)$ . If $K_0=2m$ , then $am+b(2m-2)=16$ and $\dim V_1=48m=am(2m+1)+4bm(m-1)$ . It is easy to see that there is no solution for $a\in {\mathbb Z}_{> 0}$ and $b\in {\mathbb Z}_{\geq 0}$ . Hence, $K_0-N_0=2$ and $\tau =2C$ . In this case, $am+b(2m-2)=12$ and $\dim V_1=12(2m+1)=am(2m+1)+4bm(m-1)$ . The solutions are $b=0$ and $am=12$ ; therefore, $V_1=B_2^6, B_3^4, B_4^3, B_6^2$ , or $B_{12}$ , as we desired.

This completes the proof of Lemma 5.12.

We will show that none of the Lie algebras in the list of Lemma 5.12 satisfy the desired condition, and we will get a contradiction.

First, we note that $V_1$ contains a full component of type $C_m$ or $F_4$ unless $\tau =2C$ .

5.4.1 The case $\tau \not =2C$

We note the short root lattice of $C_m$ is $D_m$ . Namely, if $C_m$ is a full component of $V_1$ , then $D_m$ is a sublattice of $N^{\tau }$ . Let X be a component of the root lattice $R(N)$ of N containing the above $D_m$ . For $m\geq 4$ , a lattice containing $D_m$ is of type D or E; that is, X is of type D or E. Recall that $n=r_jh_j^{\vee }=2(m+1)$ for $C_m$ and the Coxeter numbers of $D_m$ and $E_k$ are $2(m-1)$ and $12$ , $18$ and $30$ . Since V is a counterexample, the Coxeter number of N is strictly less than n, and the possible choice of X is $D_m$ or $D_{m+1}$ .

Lemma 5.13. If $X=D_{m+1}$ , then $\tau $ acts on X trivially. In particular, if $V_1$ is a direct sum of full components, then $X=D_m$ .

If $\tau =2A$ , then the list of lemma 5.12 says that $V_1$ is a direct sum of full components. Therefore, if $C_m$ is a full component, then $D_m$ is a connected component of $R(N)$ . Therefore, the possible cases are as follows:

It contradicts the fact that $N_\tau =L_A(1^8)$ .

If $\tau =4F$ , then $R(N)$ contains $D_7 A_3^4A_1^2$ . The possible choice of $R(N)$ is $D_7E_6A_{11}$ or $D_8^3$ , but neither of them contains $D_7A_3^4A_1^2$ , which is a contradiction.

If $\tau =6E$ , then $R(N)$ contains $D_5A_2A_5^2A_2^2A_1^2$ . The possible choice of $R(N)$ is $D_5^2A_7^2$ or $D_6^4$ or $D_6A_9^2$ , but none of them contains $D_5A_5^2A_2^3A_1^2$ , which is a contradiction.

If $\tau =6G=2^36^3$ , then $n=18$ and $V_1=F_{4,6}A_{2,2}$ . Hence, X contains $D_4A_5^3A_1^3$ . Since $h<18$ , the possible choice of $R(N)$ is $D_4^6, D_5^2A_7^2, D_6A_9^2, D_6^4, E_6^4, A_{11}D_7E_6, D_8^3$ , $D_9A_{15}$ . However, none of them contains $D_4A_5^3A_1^3$ , which is a contradiction.

5.4.2 The case $\tau =2C$

By the previous lemma, $V_1=B_2^6, C_4A_4^2, B_3^4,B_4^3, F_4A_8, B_6^2,$ or $ B_{12}$ . Since $\tau =2C$ , we have $\ell =4$ . Since $v+v^{\tau }\in \Lambda ^{\tau }$ and $\{\frac {v+v^{\tau }}{2} \mid v\in \Lambda \}=\pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$ and $\sqrt {\ell }\phi ( (\Lambda ^{\tau })^{\ast })=\Lambda ^\tau $ , we have $2(\Lambda ^{\tau })^{\ast }=\Lambda ^\tau $ ; that is, we can take $\phi =1$ and $\tilde {\beta }=2\beta $ .

By the reverse construction, there is a Niemeier lattice P such that

$$\begin{align*}V^{[N_0\alpha]}=(V_{\Lambda})^{[(\widehat{\tau}\exp(2\pi i\beta(0)))^{2}]}=V_P. \end{align*}$$

Since $N_0\not =1$ , $P\not =\Lambda $ . Set $\widehat {\tau }^2=\exp (2\pi i\delta (0))$ , which has order $2$ . Therefore,

$$\begin{align*}V_P=(V_{\Lambda})^{[\tilde{g}^2]} =(V_{\Lambda})^{[\exp(2\pi i(\delta(0)+2\beta(0))]}. \end{align*}$$

Since $N_0$ is odd, $(\widehat {\tau }\exp (2\pi i\beta (0)))^{2N_0}=\exp (\delta +2N_0\beta )=1$ , there is a $\mu \in \Lambda ^{\tau }$ such that $\delta =2N_0\beta +\mu $ and so $V_P=(V_{\Lambda })^{[\exp (2\pi i (N_0+1)\tilde {\beta }(0)]}$ . Note also that $V= V_P^{[\widetilde {g}]}$ and $\widetilde {g}$ acts on $V_P$ with order $2$ .

Case $V_1=B_m^{12/m}$ :

We first note that all components have level $2$ and $V^{\exp (2\pi iN_0\alpha )}=(V_P)^{\widetilde {g}}$ ; thus, $V_P$ contains the Lie subalgebras generated by the long roots. Since the long roots of $B_{m}$ are of the type $D_{m}$ , $(V_P)_1$ contains a Lie subalgebra of type $D_{m,2}^{\oplus (12/m)} $ and the fixed point sublattice $P^\tau \supseteq \sqrt {2} D_{m}^{\oplus 12/m}$ . Then P must contain $D_{m,1}^{\oplus 24/m}$ as a sublattice. Since $N_0=2m-1$ and $|\widetilde {g}^2|=N_0$ , the Coxeter number of P is less than or equal to $2m-1$ and thus the root system of P is $D_{m}^{\oplus 24/m}$ . Since $2m-1$ is odd and $2\delta \in \Lambda $ , there is $\mu \in \Lambda $ such that $\delta =2(2m-1)\beta +\mu $ and $4(2m-1)\beta \in \Lambda $ . Thus, we have $V_P=(V_{\Lambda })^{[4\beta ]}$ ; that is, every element $\mu \in P$ is written $\mu =\mu _1+4s \beta $ with $\langle \mu _1,4\beta \rangle \in {\mathbb Z}$ (i.e., $\mu _1\in \Lambda _{4\beta }$ ). Since $\langle 4\beta ,2\beta \rangle \in {\mathbb Z}$ , $\mu _1\in \Lambda _{2\beta }$ if $\langle \mu ,2\beta \rangle \in {\mathbb Z}$ (that is, $\mu \in \Lambda _{2\beta }$ ).

Since $V_P=V^{[\widetilde {g}]}$ can be constructed by a ${\mathbb Z}_2$ -orbifold construction, we have

$$\begin{align*}L^* = \{ x\in (P^\tau)^* \mid \langle x, 2\beta \rangle \in {\mathbb Z}\} +{\mathbb Z} \beta \end{align*}$$

by the same argument as in Theorem 4.9.

For each $B_m\subseteq V_1$ , we have a fundamental root system $d_1,...,d_{m-1}, d_m$ with long roots $d_j (j= 1, \dots , m-1)$ (i.e, $\langle d_j,\alpha \rangle =\frac {1}{2m-1}$ for $j= 1, \dots , m-1$ and $\langle d_m,\alpha \rangle =\frac {1}{2(2m-1)}$ ). Without loss of generality, we may assume $d_m=\beta $ , which is a short root. Note also that $\tilde {d}_m=d_{m-1} +2d_m$ is also a long root and $\{d_1,...,d_{m-1}, \tilde {d}_m\}$ forms a fundamental root system for the long roots. Therefore, in P, we have a root sublattice of type $D_m^2$ with the fundamental system $\{a_1,\dots ,a_m\}$ and $\{b_1,\dots ,b_m\}$ ,

$$ \begin{align*}\begin{array}{rclrcl} a_1- \cdots - &a_{m-2}&-a_{m-1},\qquad &b_1-\cdots - &b_{m-2}& -b_{m-1} \cr & | & & &|& \cr &a_m& & &b_m& \cr \end{array}\end{align*} $$

such that $\tau $ permutes $a_i$ and $b_i$ and $\frac {a_i+b_i}{2}=d_i$ for $i=1,...,m-1$ and $\frac {a_m+b_m}{2}=2\beta +d_{m-1}=2\beta +\frac {a_{m-1}+b_{m-1}}{2}$ . Therefore, $2\beta =\frac {a_m-a_{m-1}+b_m-b_{m-1}}{2}$ and $ \langle 2\beta , a_i \rangle \in {\mathbb Z}, \langle 2\beta , b_i\rangle \in {\mathbb Z}$ for all $i=1,...,m$ ; that is, $R(P)\subseteq N=\Lambda ^{[2\beta ]}$ . Since $2\beta \in N$ and has norm $2$ , N contains $D_{2m}$ and so the Coxeter number of N is greater than or equal to $2(2m-1)$ , which contradicts the choice of V.

Case $V_1=C_{4,2}A_{4,2}^2$ :

Since $V_1= C_{4,2}A_{4,2}^2$ and $\det (L)=2^{10}4^2$ , $L=\sqrt {2}(D_4+E_8)$ and $N^\tau \cong D_4+\sqrt {2}E_8$ in this case. In particular, $N^\tau $ contains a root sublattice of type $D_4$ . Therefore, the possible types for N are $D_4^6$ , $D_4A_5^4$ and $D_5^2 A_7^2$ . However, the lattices orthogonal to a sublattice of the type $D_4+\sqrt {2}E_8$ do not contain $L_A(1^{12})$ .

Case $V_1=F_{4,2}A_{8,2}$ :

In this case, $n=18$ and $N_0=9$ .

Let $a_1, a_2, b_3, b_4$ be the fundamental roots for $F_4$ such that $a_1, a_2$ are short roots. We may assume $\beta =a_1$ . Since $|\tau |=2$ , there is a Niemeier lattice P such that $V_P=(V_{\Lambda })^{[\tilde {g}^2]}$ , which is also equal to $V^{[9\alpha ]}$ . Set $s=g^9=\exp (2\pi i 9\alpha (0))$ . Then $(F_{4,2}A_{8,2})^{<s>}$ contains $B_{4,2}A_{8,2}$ and the Coxeter number of P is less than or equal to $N_0=9$ . Therefore, the root system of P is $A_8^3$ . Since $V=V_P^{[\tilde {g}]}$ , $\tau $ acts on one $A_8$ as a diagram automorphism and permutes the other two $A_8$ ’s.

Since $N_0=9$ is odd, we have $P=\Lambda _{4\beta }+{\mathbb Z} 4\beta $ and $ \tilde {\beta }=2\beta $ by the similar argument as in the case $V_1=B_m^{12/m}$ . By the choice of $\beta $ , the two $A_8$ ’s permuted by $\tau $ is orthogonal to $\beta $ ; hence, $N=\Lambda ^{[\tilde {\beta }]}=\Lambda _{2\beta }+{\mathbb Z} 2\beta $ contains $A_8^2$ .

Since $F_4$ is a full component, N also contains $D_4$ as a root sublattice, which is orthogonal to the above $A_8^2$ . Therefore, $N \supset D_4+A_8+A_8$ . Moreover, the Coxeter number of N is strictly less than $n=18$ by our assumption. Then N has the type $A_9^2 D_6$ . In this case, $N_\tau $ , the sublattice orthogonal to $D_4+ \sqrt {2}A_8$ , does not contain a root sublattice of the type $A_1^{12}$ , and we have a contradiction.

This completes the proof of Theorem 5.1.□

Remark 5.14. Since $\tilde {\beta }$ is a deep hole, it follows that $[N:\Lambda _{\tilde {\beta }}]=h$ , the Coxeter number of N. Moreover, we have $[N:\Lambda _{\tilde {\beta }}]=|g|=|\tilde {g}|$ by Theorem 4.8. Thus, $h=|g|=|\tilde {g}|$ . Note that $|\tau |$ divides $|\tilde {g}|$ , and hence, $|\tau |$ divides h, also.

6 Classification of $\tau $

In this section, we will show that $\tau \in Co.0$ defined by W-elements of holomorphic VOAs of central charge 24 are contained in

$$\begin{align*}\mathcal{P}_0=1A\cup 2A\cup 2C\cup 3B\cup 4C\cup 5B\cup 6E\cup 6G\cup 7B\cup 8E\cup 10F. \end{align*}$$

Combining the results in Sections 3–5, one can associated a pair of $\tau \in \mathcal{P}_0$ and a $\tau $ -invariant deep hole $\tilde {\beta }$ with any holomorphic VOA V of central charge $24$ with non-abelian weight one Lie algebra $V_1$ . Set

$$ \begin{align*}\mathcal{P}=\bigg\{ \tau\in Co.0\, \bigg| \begin{array}{l} {}^\exists \beta\in {\mathbb Q}\Lambda^{\tau} \mbox{ s.t. } \widehat{\tau}\exp(2\pi i\beta(0)) \mbox{ can be realized as the reverse }\\[3pt] \mbox{automorphism of some orbifold construction given by a }W\mbox{-element} \end{array}\bigg\}.\end{align*} $$

The main result of this section is the following.

Proposition 6.1. $\mathcal{P}\subseteq \mathcal{P}_0$ .

Since $\dim ((V_{\Lambda })^{[\tilde {g}]})_1>24$ , it is easy to see that $\mathrm {rank}(\Lambda ^\tau ) \geq 4$ and $|\tau |\leq 15$ . Therefore, $\tau $ is in one of the conjugacy classes in Table 1 (cf. [7]).

First, we treat the cases when $\mathrm {rank}(V_1)= 4$ , which will eliminate many cases with $\dim \Lambda ^\tau =4$ .

Lemma 6.2. If $\mathrm {rank}(V_1)= 4$ , then $\tau \in \mathcal{P}_0$ .

Proof. Suppose $\mathrm {rank}(V_1) = 4$ . By [13], we know that $\dim V_1>24$ and $h_j^{\vee }/k_j=(\dim V_1-24)/24$ for any component $\mathcal{G}_j$ ; thus, $V_1$ must be of the type $B_{4,14}, C_{4,10}, D_{4,36}$ or $G_{2,24}^{\oplus 2}$ and $|\tau |=14,10,6,12$ , respectively. In these cases, $N_0=1$ . If $|\tau |=14$ , we have $\tau =14B$ . Then $\ell =14$ and $\det (\Lambda ^\tau )= {14}^2$ . In this case, $\det (L) =14^4$ and $\det (\sqrt {14} L^*)=1$ , which is not possible since $\sqrt {14} L^*$ is even (see Section 4.2). If $|\tau |=10$ , then $V_1=C_{4,10}$ and $N_0=1$ and so there are $\mu \in L^{\ast }$ such that $\langle \alpha ,\mu \rangle \equiv 1/10$ and $1/5 \pmod {{\mathbb Z}}$ . Therefore, since we may choose $\beta $ from $L^{\ast }$ , both of $\tau $ and $\tau ^2$ are of type zero and $\phi (\tau )<1$ and $\phi (\tau ^2)<1$ , which implies $\tau =10F$ and $\tau \in \mathcal{P}_0$ . If $|\tau |=6$ , $V_1=D_{4,36}$ and so there is $\mu \in L^{\ast }$ such that $\langle \tau ,\mu \rangle \equiv 1/6 \pmod {{\mathbb Z}}$ and $\phi (\tau )<1$ . Therefore, $\tau =6I$ and $N_0=1$ . Since $6\beta \in \Lambda ^{\tau }$ which has the Gram matrix $6I_4$ , $\langle \beta ,\beta \rangle \in 2{\mathbb Z}/12$ . However, $\phi (6I)=1/36$ ; thus, $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ is not type zero, and we have a contradiction.

From now on, we may assume $\dim V^{\langle \tau \rangle }> 4$ .

Lemma 6.3. $\tau \not \in 3D$ .

Proof. Recall that $\Lambda ^{3D}\cong \sqrt {3}E_8$ (cf. [20]). If $\mathrm {GCD}(N_0,3)=1$ , then $3N_0\beta \in \Lambda ^{3D}$ and so $\langle \beta ,\beta \rangle \in 6{\mathbb Z}/9N_0^2=2{\mathbb Z}/3N_0^2$ , which contradicts $\phi (3D)+\frac {\langle \beta ,\beta \rangle }{2} \in 1-1/9+\frac{\mathbb{Z}}{3N_0^2}\subset {\mathbb Z}$ . Therefore, $3|N_0$ . Since $\dim {\mathbb C}\Lambda ^{3D}=8$ , $N_0|h^{\vee }_j$ for all j and $|g|=N_0|\tau |=\mathrm {LCM}(\{r_jh_j^\vee \})$ , the only possible case is $N_0=3$ and $V_1=A_8$ . Since $K_0/N_0=\langle \alpha ,\alpha \rangle /2= \dim V_1/(\dim V_1-24)$ , we have $K_0/3= 80/56=10/7$ , which is not possible.

Suppose Proposition 6.1 is false and let V be a counterexample such that $k=\mathrm {rank}(V_1)$ is maximal among all counterexamples. We also choose V so that $\mathrm {Comm}(M(\mathcal{H}),V)$ is largest among all counterexamples with $\mathrm {rank}(V_1)=k$ .

Let $\alpha $ be a W-element of $V_1$ and set $g=\exp (2\pi i\alpha (0))$ . As we discussed, the orbifold construction from V by g gives $V_{\Lambda }$ . Let $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ be the reverse automorphism of g corresponding to the above orbifold construction. Since V is a counterexample, $\tau \not \in \mathcal{P}_0$ .

If m divides $|\tau |$ and $m\not =1$ , then we have

$$\begin{align*}\mathrm{rank}(V^{[g^m]}_1)>\mathrm{rank} V_1\quad \text{ or } \quad \mathrm{Comm}(M(\mathcal{H}),V^{[g^m]})> \mathrm{Comm}(M(\mathcal{H}),V) \end{align*}$$

by Proposition 2.4. Therefore, $V^{[g^m]}$ is not a counterexample for any $1\not =m \mid |\tau |$ . Let L be an even lattice such that $\mathrm {Comm}(\mathrm {Comm}(M(\mathcal{H}),V),V)\cong V_L$ , where $\mathcal{H}$ is a Cartan subalgebra of $V_1=\mathfrak {g}_{1, k_1} \oplus \cdots \oplus \mathfrak {g}_{r,k_r}$ . Let $\alpha =\sum _{i=1}^{r} \rho _i/h_i^\vee $ be a W-element of $V_1$ . Suppose $\langle \alpha ,\alpha \rangle =\frac {2K_0}{N_0}$ with $K_0,N_0\in {\mathbb Z}$ and $\mathrm {GCD}(K_0,N_0)=1$ .

Now consider the VOA $V^{[g^{N_0}]}$ obtained by the orbifold construction from V by $g^{N_0}=\exp (2\pi iN_0\alpha (0))$ . Then $V^{[g^{N_0}]}$ also contains an abelian Lie subalgebra $\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$ of rank 24. By viewing it as a Cartan subalgebra of $(V^{[g^{N_0}]})_1$ , there is an even unimodular lattice P of rank $24$ such that $V^{[g^{N_0}]} \cong V_P$ . Furthermore, there is $\mu \in {\mathbb C}\Lambda ^{\tau }$ such that $(V_{\Lambda })^{[\exp (2\pi i\mu (0))]}=V_P$ since $(V^{[g^{N_0}]})^{[g]}=V_{\Lambda }$ . In particular, $\tau $ fixes $\mu $ , and we may view $\tau $ as an isometry of P.

Remark 6.4. Let $\tilde {g}'\in \mathrm {Aut}(V_P)$ be the reverse automorphism of $g^{N_0}\in \mathrm {Aut}(V)$ . By our choice, $\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jN_0\alpha )_1$ is a Cartan subalgebra of $V_P$ , and thus, there is a $\delta \in {\mathbb C} P^{\tau }$ and a standard lift $\widehat {\tau }'$ of $\tau $ such that $\tilde {g}'=\widehat {\tau }'\exp (2\pi i\delta (0))$ and $\langle N_0\alpha ,\delta \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$ . Then $V=(V_P)^{[\widehat {\tau }'\exp (2\pi i\delta (0))]}$ and the actions of $\widehat {\tau }$ and $\widehat {\tau }'$ on $U(jN_0\alpha )$ are the same; namely, they both act on $U(jN_0\alpha )$ as a multiple by a scalar $e^{-2\pi ij/|\tau |}$ .

Since $N_0\alpha \in L^{\ast }$ , $V^{<g^{N_0}>}$ contains $V_L$ and $L\subseteq \mathcal{H}={\mathbb C}\Lambda ^{\tau }$ . We may also view $V_L$ as a subspace of $V_P^{<\widehat {\tau }' \exp (2\pi i\delta (0))>}$ . As a conclusion, we have the following.

Theorem 6.5. The VOA $V^{[e^{2\pi i N_0\alpha (0)}]}$ is isomorphic to a lattice VOA $V_P$ for an even unimodular lattice P of rank $24$ . Furthermore, $P^{\tau }=L+{\mathbb Z} N_0\alpha $ and $|g^{N_0}|= |\tau |$ .

As we have shown in Theorem 6.5, $V^{[\exp (2\pi iN_0\alpha (0)]}$ is a Niemeier lattice VOA $V_P$ and there is $\delta \in {\mathbb C} P^{\tau }$ such that $\widehat {\tau }\exp (2\pi i\delta (0))$ is the reverse automorphism of $\exp (2\pi iN_0\alpha (0))$ .

Lemma 6.6. By taking a suitable standard lift $\widehat {\tau }$ of $\tau $ , we may assume $\delta \in L^{\ast }$ .

Proof. By the definition of W-element, there is $\mu \in L^{\ast }$ such that $\langle \alpha ,\mu \rangle \equiv 1/N_0|\tau | \pmod {{\mathbb Z}}$ . Therefore, $\delta -\mu \in (P^{\tau })^{\ast }$ and there is $\xi \in P$ such that $\pi (\xi )=\delta -\mu $ . Set $\xi =\xi '+\pi (\xi )$ with $\xi '\in \mathcal{H}^{\perp }$ . Since $\exp (2\pi i\xi (0))=1$ and $\tau $ acts on $(\mathcal{H})^{\perp }$ fixed point freely, there is $\tilde {h}\in \mathcal{H}^{\perp }$ such that

$$ \begin{align*}\begin{array}{l} \exp(2\pi i\tilde{h}(0))^{-1}(\widehat{\tau}\exp(2\pi i\delta(0))\exp(2\pi i\tilde{h}(0) =\exp(2\pi i\tilde{h}(0))^{-1}\widehat{\tau} \exp(2\pi i\tilde{h}(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\xi'(0))\exp(2\pi i\delta(0)) =\widehat{\tau}\exp(2\pi i\xi(0))\exp(-2\pi i\pi(\xi)(0))\exp(2\pi i\delta(0))\cr =\widehat{\tau}\exp(2\pi i\mu(0)). \end{array}\end{align*} $$

Therefore, $\widehat {\tau }\exp (2\pi i\delta (0))=\widehat {\tau } \exp (\mu (0))\exp (\pi \xi (0))$ is conjugate to $\widehat {\tau }\exp (2\pi i\mu (0)$ . Replacing $\widehat {\tau }$ by $\exp (2\pi i\tilde {h}(0))^{-1}(\widehat {\tau }\exp (2\pi i\delta (0))\exp (2\pi i\tilde {h}(0))$ , we may assume $\delta \in L^{\ast }$ .

By Theorem 6.5, we have $P^{\tau }=L+{\mathbb Z} N_0\alpha $ and $rN_0\alpha \in L$ if and only if $|\tau |$ divides r and $\langle \delta , N_0\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$ . Therefore, $m\delta \not \in \pi (P)$ if $|\tau |\not | m$ . Hence, if $|\tau |\not | m$ , then the lowest weight of $\widehat {\tau }\exp (2\pi i\delta (0))$ -twisted module is greater than $\phi (\tau )$ . Therefore, we have the following:

Lemma 6.7. If $\phi (\tau ^m)\geq 1$ , then $\widehat {\tau }^m\exp (2\pi im\delta (0))$ -twisted module does not contain a weight one element.

Lemma 6.8. $<\tau>$ does not contain $-2A, 3C, 5C$ .

Proof. Let m be a divisor of $|\tau |$ . Suppose $|\tau ^m|=p$ is a prime and $\phi (\tau ^m)\geq 1$ .

Let $\tilde {V}:=V^{[g^{pN_0}]}$ . From the property of orbifold construction and the choice of $\widehat {\tau }'$ and $\delta $ , we have $\tilde {V}=(V_P)^{[(\widehat {\tau }')^m\exp (2\pi im\delta (0))]}$ . From Corollary 4.9 in [7], $\tau \not =-2A, 3C, 5C$ and so $m\not =1$ and $\tilde {V}$ is not a counterexample.

Let $\tilde {\alpha }$ be a W-element of $\tilde {V}_1$ and $\widehat {\sigma }\exp (2\pi i\mu (0))$ the reverse automorphism of $\exp (2\pi i\tilde {\alpha }(0))$ . Then $\sigma \in \mathcal{P}_0$ , and we can use the results in Sections 3 $\sim $ 5.

Next, we will show that ${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$ . As we explained in Section 2, $\mathcal{H}+\oplus _{j=0}^{m-1}U(jpN_0\alpha )$ is a Cartan subalgebra of $\tilde {V}_1$ . Since $\langle \delta ,\alpha \rangle \equiv 1/|\tau | \pmod {{\mathbb Z}}$ , $\widehat {\tau '}$ acts on $U(jN_0\alpha )$ as a multiple by a scalar $e^{-2\pi ij/|\tau |}$ for all $j\in {\mathbb Z}$ . In particular, ${\mathbb C} P^{\tau ^m}=\mathcal{H}+\oplus _{j=0}^{|\tau |-1}U(jpN_0\alpha )_1$ and so ${\mathbb C} P^{\sigma }={\mathbb C} P^{\tau ^m}$ .

We next show that if the order p of $\tau ^m$ is an odd prime, we have $|\widehat {\sigma }|=p$ , and if the order of $\tau ^m$ is $2$ , we have $|\widehat {\sigma }|=2$ or $4$ .

Since $\phi (\tau ^m)\geq 1$ , $\widehat {\tau '}^m\exp (2\pi im\delta (0))$ -twisted module contains no weight one element and so we have

$$ \begin{align*}\tilde{V}_1= (V_P)^{<\widehat{\tau'}^m\exp(2\pi im\delta(0))>}_1.\end{align*} $$

Since $|\tau ^m|=p$ is a prime, the root vectors of $(V_P)^{<\widehat {\tau '}^m\exp (2\pi im\delta (0))>}_1$ are given by

(1) $e^{\mu }$ with $\mu \in P^{\tau }$ or

(2) $e^{\mu }+\cdots +(\widehat {\tau '}\exp (2\pi im\delta (0)))^{p-1}(e^{\mu })$ with $\mu \in P$ . In this case, it corresponds to the root associated with $\pi (\mu )\in (P^\tau )^*$ and $\langle \pi (\mu ), \pi (\mu ) \rangle =2/\tilde {r}_j\tilde {k}_j$ . Note also that

$$\begin{align*}\langle \pi(\mu), \pi(\mu) \rangle = \langle \pi(\mu), \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle = \langle \mu, \frac{1}{p} \sum_{j=0}^{p-1} \tau^{mj} \mu \rangle \in {\mathbb Z}/p. \end{align*}$$

Therefore, if p is an odd prime, then $\tilde {r}_j\tilde {k}_j=1$ or p, and if $p=2$ , then $\tilde {r}_j\tilde {k}_j=1,2,4$ .

However, since $\sigma \in \mathcal{P}_0$ , we have shown $|\widehat {\sigma }|=\mathrm {LCM}(\{\tilde {r}_j\tilde {k}_j\mid j\})$ . If $\tilde {r}_j\tilde {k}_j=1$ for all j, then we can easily get a contradiction since $\mathrm {rank}(\widetilde {V}_1)=8, 6, 4$ , respectively.

Hence, if the order p of $\tau ^m$ is an odd prime, we have $|\widehat {\sigma }|=p$ , and if the order of $\tau ^m$ is $2$ , we have $|\widehat {\sigma }|=2$ or $4$ . From the choice of $\sigma $ , we have $\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=\mathrm {rank}({\mathbb C}\Lambda ^{\tau ^m})$ . Therefore, if $\tau ^m=-2A, then \dim \Lambda ^{-2A}=8$ , but there is no $\sigma \in \mathcal{P}_0$ of order $2$ or $4$ such that $\Lambda ^{\sigma }=8$ . If $\tau ^m=3C$ , then $\mathrm {rank} \Lambda ^{3C}=6$ , but there is no $\sigma \in \mathcal{P}_0$ of order $3$ with $\mathrm {rank} \Lambda ^{\sigma }=6$ . If $\tau =5C$ , then $\mathrm {rank} \Lambda ^{5C}=4$ , but there is no $\sigma \in \mathcal{P}_0$ of order $5$ with $\mathrm {rank} \Lambda ^{\sigma }=4$ .

Lemma 6.9. $\tau \not \in -4C$ .

Proof. Suppose $\tau \in -4C$ . We note $V=(V_P)^{[\widehat {\tau }\exp (2\pi i\delta (0))]}$ . Since $\phi (\tau )\geq 1$ , $\widehat {\tau }\exp (2\pi i\delta (0))$ -twisted module does not contain elements of weight one. Recall that $\widehat {\tau }\exp (2\pi i\delta (0))$ is the reverse automorphism of $\exp (2\pi iN_0\alpha (0))$ ; the above statement means that there is no root $\mu \in V_1$ such that $|\tau |\langle \mu ,N_0\alpha \rangle =1$ . Since $|\tau |=4$ , $\mathrm {LCM}(\{r_jh^{\vee }_j/N_0\mid j\})$ divides $2$ , which contradicts $\mathrm {LCM}(\{ r_jh^{\vee }_j/N_0 \mid j\})=|\tau |$ .

Therefore, the remaining possibilities of $\tau \not \in \mathcal{P}_0$ are $4D, 4F, -6C$ . Then since $4D^2=2A, 4F^2=2C, (-6C)^2=3B, (-6C)^3=2A$ , nontrivial powers of $\tau $ are in $\mathcal{P}_0$ .

Furthermore, $\phi (4D)=1-1/8$ , $\phi (4F)=1/16$ , $\phi (-6C)=1$ . Namely, $\widehat {\tau }$ is not of type zero or $\phi (\tau )=1$ .

We note that since $V=V_{\Lambda }^{[\widehat {\tau }\exp (2\pi i\beta (0))]}$ , $\tilde {V}=V^{[\widetilde {g}^m]}$ is a holomorphic VOA for any $m||\tau |$ . Assume $m\not =1$ . Unfortunately, $\widetilde {g}^m$ is not necessary to be a reverse automorphism for an automorphism defined by W-element in $\tilde {V}$ . Let $\tilde {\alpha }$ be a W-element of $\tilde {V}_1$ and $\widehat {\sigma }\exp (2\pi i\mu (0))$ be a reverse automorphism of $\exp (2\pi i\tilde {\alpha }(0))$ .

Lemma 6.10. Let $1\not =m||\tau |$ . If $\tau ^m=2A,2C,3B$ , then $\sigma $ is conjugate to $\tau ^m$ .

Proof. If $\tau ^m=2A,2C,3B$ , then $\tilde {V}:=V_P^{[\widehat {\tau }^m\exp (2\pi im\delta (0))]}$ is not a counterexample. Let $\tilde {\alpha }$ be a W-element of $\tilde {V}_1$ and $\widehat {\sigma }\exp (2\pi i\mu (0))$ a reverse automorphism for $\exp (2\pi i\tilde {\alpha }(0))$ . In particular, $\sigma \in \mathcal{P}_0$ .

As we have shown, $\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=\mathrm {rank} \tilde {V}_1=\mathrm {rank} ({\mathbb C}\Lambda )^{\sigma }$ . Let $\tilde {\mathcal{H}}$ be a Cartan subalgebra of $\tilde {V}$ and set $\mathrm {Comm}(\mathrm {Comm}(\tilde {\mathcal{H}},\tilde {V}),\tilde {V})=V_{\tilde {L}}$ with an even lattice $\tilde {L}$ .

Since $\sigma \in \mathcal{P}_0$ , $\sqrt {|\widehat {\sigma }|}(\tilde {L})^{\ast }$ is an even lattice by Lemma 5.1. However, since $\tau ^m\in \mathcal{P}_0$ and ${\tilde {V}=(V_P)^{[\widehat {\tau }^m\exp (2m\pi i\delta (0))]}}$ , we have $\phi (\tau ^m)=1-\frac {1}{|\widehat {\tau }^m|}$ and $e^{m\delta }\otimes t\in \tilde {V}$ with $\mathrm {wt}(e^{m\delta })\equiv \frac {1}{|\widehat {\tau }^m|} \pmod {{\mathbb Z}}$ . Therefore, $|\widehat {\tau }^m|$ has to divide $|\widehat {\sigma }|$ .

If $\tau ^m=2A$ , then $\mathrm {rank}({\mathbb C}\Lambda )^{\tau ^m}=16$ and $\sigma =2A$ . If $\tau ^m=2C$ , then $\mathrm {rank}({\mathbb C}\Lambda )^{\sigma }=12$ and so $\sigma =2C$ or $3B$ . If $\sigma =3B$ , then $|\widehat {\sigma }|=3$ is not a multiple of $|\widehat {\tau ^m}|=2$ . If $\tau ^m=3B$ , then $\mathrm {rank}({\mathbb C}\Lambda ^{\sigma })=12$ and so $\sigma =2C$ or $3B$ . Since $|\widehat {\tau }^m|=3$ does not divide $|\widehat {\sigma }|=4$ if $\sigma =2C$ . Hence, $\sigma =3B$ .

As a corollary, for $\mu \in L^{\ast }$ , if $\langle \mu , N_0\alpha \rangle \in \frac {{\mathbb Z}}{m}$ , then $S(\mu )\otimes e^{\mu } \in V^{[|\tau |g/m]}$ and so we have $|\widehat {\tau }^m|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$ .

Lemma 6.11. $\tau \not =-6C$ .

Proof. Since $\phi (-6C)=1$ , $\widehat {\tau }\exp (2\pi i\delta (0))$ -twisted module does not contain weight one elements. Therefore, $r_jh^{\vee }_j/N_0=2$ or $3$ and both have to appear. Recall that $(-6G)^3=2A$ and $(-6G)^2=3B$ . If $ r_jh^{\vee }_j/N_0=2$ , then $\exp (2\pi iN_0\alpha (0))^3$ fixes all elements in $\mathcal{G}_j$ and so $\sqrt {3}L_j^{\ast }$ is an even lattice since $2A\in \mathcal{P}_0$ , where $L_j^{\ast }$ is the co-root lattice of $\mathcal{G}_j$ . If $r_jh^{\vee }_j/N_0=3$ , then $\exp (2\pi iN_0\alpha (0))^2$ fixes all elements in $\mathcal{G}_j$ and so $\sqrt {2}L_j^{\ast }$ is an even lattice. Therefore, $\sqrt {6}L^{\ast }$ is an even lattice and $K_0-N_0=1$ and $h_j^{\vee }=k_jN_0$ . If $N_0=1$ , then $r_jh^{\vee }_j=2$ and $3$ and so $\mathcal{G}_j=A_1$ or $A_2$ , which contradicts to $\dim V_1>24$ since $\mathrm {rank} V_1=6$ . If $N_0=2$ , $r_jh^{\vee }_j=4$ and $6$ and so $\mathcal{G}_1=A_3$ and $\mathcal{G}_2=A_5$ , which contradicts $\mathrm {rank} V_1=6$ . If $N_0=3$ , then one of $r_2h_2^{\vee }=9$ and so $\mathcal{G}_2=A_8$ , which contradicts $\mathrm {rank} V_1=6$ . If $N_0=4$ , then one of $r_1h_1^{\vee }=8$ and $\mathcal{G}_2=G_2$ . So, $\mathcal{G}_1=A_7,C_3,D_5$ . Since $\mathrm {rank} V_1=6$ and $\mathcal{G}_j\not =A_1$ , we have a contradiction. If $N_0>4$ , $r_1h_2^{\vee }\geq 10$ and $r_2h_2^{\vee }\geq 15$ , which contradicts $\mathrm {rank} V_1=6$ .

So the remaining cases are $\tau =4D$ or $4F$ . Recall that a short root in $\mathcal{G}_j$ is called a shortest root if $r_jh_j^\vee = \mathrm {LCM}(r_ih_i^{\vee }|i)= |\tau | N_0$ (or equivalently, $r_jk_j=\mathrm {LCM}(r_ik_i|i)$ ). Since $|\tau |=4$ and $\mathrm {LCM}(r_ih_i^{\vee }/N_0\mid i)=|\tau |=4$ , there is a shortest root. Say, $\mathcal{G}_1$ contains a shortest root.

Lemma 6.12. If $\tau =4D$ or $4F$ , then $\exp (2N_0\pi i\alpha (0))^2$ fixes a root vector associated with a shortest root.

Proof. Since $\mathrm {LCM}(\{r_jh_j^{\vee }/N_0\mid i\}=|\tau |$ and $h_j^\vee $ is divisible by $N_0$ , $r_j$ divides $|\tau |$ . Therefore, $\mathcal{G}_j\not =G_2$ .

If $\mathcal{G}_1\not \cong B_m$ , then there is a shortest root which is a sum of two shortest roots in the fundamental root system, and thus $\exp (2N_0\pi i\alpha (0))^2$ fixes a root vector associated with a shortest root in $\mathcal{G}_1$ . So we may assume $\mathcal{G}_1=B_m$ ; however, $r_1h_1^{\vee }=2(2m-1)$ in this case, which contradicts that $|\tau |=4$ divides $r_1h_1^\vee $ .

Lemma 6.13. $\tau \not =4D$ nor $4F$ .

Proof. Suppose false. Set $\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$ . We may view that $\hat{\tau} $ is an automorphism of $\tilde {V}$ of order $2$ . Let $\tilde {\mathcal{H}}$ be a Cartan subalgebra of $\tilde {V}_1$ . Then there is an even lattice $\tilde {L}$ such that $\mathrm {Comm}(\mathrm {Comm}(M(\tilde {\mathcal{H}}),\tilde {V}),\tilde {V})\cong V_{\tilde {L}}$ . Let $\tilde {\alpha }$ be a W-element of $\tilde {V}_1$ and $\widehat {\sigma }\exp (2\pi i\xi (0))$ the reverse automorphism of $\exp (2\pi i\tilde {\alpha }(0))$ . Since $4D^2=2A$ and $4F^2=2C$ , we have $\sigma =2A$ and $2C$ , respectively, by the same argument as in the proof of Lemma 6.10.

Since $\tilde {V}^{[\exp (2\pi i\alpha (0)]}=V_{\Lambda }$ , there is no root orthogonal to $\alpha $ in $\tilde {V}$ . Therefore, we can define positive roots by the condition $\langle \mu ,\alpha \rangle>0$ . Note that $\alpha $ is fixed by $\tau $ . Therefore, if $\mu $ is a positive root, then so is $\tau ^i(\mu )$ for any i. By Lemma 6.12, there is a shortest root $\mu \in L^{\ast }$ such that $s\otimes e^{\mu }\in V^{<\exp (2\pi iN_0\alpha (0))^2>}\subseteq \tilde {V}=V^{[\exp (4\pi i N_0\alpha (0))]}$ .

Since $\tau $ has positive frame shape, we may choose $\delta $ in $L^{\ast }$ . Note that $\phi (\tau )=1-\frac {1}{2\ell }$ for $\tau \in 4C$ or $4D$ . If $\langle \delta , \delta \rangle /2\in \frac {1}{\ell }{\mathbb Z}$ , then the irreducible $\widehat {\tau }\exp (2\pi i\delta (0))$ -twisted module has no subspaces with integral weights, which is not possible. Therefore, it suffices to show that $\sqrt {\ell }L^{\ast }$ is an even lattice, or equivalently, $\ell \langle \mu ,\mu \rangle \in 2{\mathbb Z}$ since $\mu $ is a shortest root. Without loss of generality, we may assume $\langle \mu ,\alpha \rangle>0$ . Then we have one of the following two cases: (1) $\mu $ is still a root in $\tilde {V}=V^{[\exp (4N_0\pi i\alpha (0))]}$ or (2) $s\otimes e^{\mu }=s'\otimes e^{\mu '}+\tau (s')\otimes e^{\tau (\mu ')}$ with a positive root $\mu '\in {\mathbb C}\Lambda ^{<\tau ^2>}$ and $\mu =\frac {\mu '+\tau (\mu ')}{2}$ . In particular, $\mu '+\tau (\mu ')$ is not a root. Note that $\mu '$ and $\tau (\mu ')$ are both positive roots of the same length, and hence, $\frac {2\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle } = 0, -1$ or $2$ , but $-1$ is not possible since $\mu '+\tau (\mu ')$ is not a root. We have $t=\frac {\langle \mu ',\tau (\mu ')\rangle }{\langle \mu ',\mu '\rangle }\in {\mathbb Z}$ .

By Lemma 6.10, $\tau ^2$ is conjugate to $\sigma $ , and thus, $|\widehat {\tau }|=2|\widehat {\sigma }|$ . Since $\tilde {V}$ is not a counterexample, $\sigma \in \mathcal{P}_0$ and so $|\widehat {\sigma }|\langle \mu ,\mu \rangle \in 2{\mathbb Z}$ for the case (1) and $|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$ for the case (2). For the case (1), $\ell \langle \mu ,\mu \rangle \in 4{\mathbb Z}$ . For the case (2), $|\widehat {\sigma }|\langle \tau (\mu '),\mu '\rangle =t|\widehat {\sigma }|\langle \mu ',\mu '\rangle \in 2{\mathbb Z}$ . Then we have $\ell \langle \mu ,\mu \rangle = 2|\widehat {\sigma }| \langle \frac {\mu '+\tau (\mu ')}{2}, \frac {\mu '+\tau (\mu ')}{2} \rangle =|\widehat {\sigma }|\langle \mu '+\tau (\mu '), \mu '\rangle \in 2{\mathbb Z}$ as desired.

This completes the proof of $\mathcal{P}\subseteq \mathcal{P}_0$ .

7 Reverse construction

As we have already shown, one can define a pair of $\tau \in \mathcal{P}_0$ and a $\tau $ -invariant deep hole $\tilde {\beta }$ for any holomorphic VOA V of central charge $24$ with non-abelian $V_1$ by choosing a W-element $\alpha $ of $V_1$ and considering the reverse automorphism $\tilde {g}\in \mathrm {Aut}(V_\Lambda )$ of $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$ . The pair $(\tau , \tilde {\beta })$ satisfies the following conditions:

1. (C1) $\tau \in \mathcal{P}_0$ (Proposition 6.1) and $\tilde {\beta }$ is a $\tau $ -invariant deep hole of Leech lattice $\Lambda $ with $\langle \tilde {\beta },\tilde {\beta }\rangle =2$ (Theorem 5.1);

2. (C2) the Coxeter number h of $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$ is divisible by $|\tau |$ (Remark 5.14);

3. (C3) $N_{\tau }=L_A(c_{\tau })$ with $c_{\tau }$ as defined in Appendix (Lemmas 5.2 and 5.4),

where $\Lambda _{\tilde {\beta }}=\{\lambda \in \Lambda \mid \langle \lambda , \tilde {\beta }\rangle \in {\mathbb Z}\}$ and $N_{\tau }$ denotes an orthogonal complement of $N^{\tau }$ in N. We also use the same notation $\tau $ to denote the isometry of N induced from $\tau $ on $\Lambda $ .

Let $\mathcal{T}$ be the set of pairs satisfying the conditions (C1) to (C3). In this section, we will study the reverse construction. Take a pair $(\tau , \tilde {\beta })\in \mathcal{T}$ . Assume that $\tau $ has the frame shape $\prod m^{a_m}$ . Then $N_\tau> \oplus _{m\neq 1} A_{m-1}^{a_m}$ , and the conformal weight of the $\widehat {\tau }$ -twisted module of $V_\Lambda $ is given by $\phi (\tau )=1-\frac {1}{\ell }$ , where $\ell =|\widehat {\tau }|$ .

Let $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$ and define $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ . Note that $\langle \beta ,\beta \rangle =\frac {2}{\ell }$ . Set $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$ and let h be the Coxeter number of N. Since $-\tilde {\beta }$ is a deep hole of $\Lambda $ , $N^{(1)}$ contains an affine fundamental root system of rank $24$ and $N=\oplus _{k=0}^{h-1} N^{(k)}$ , where $N^{(k)}=\Lambda _{\tilde {\beta }}-k\tilde {\beta }$ .

We may assume that $ \widehat {\tau }^{|\tau |} =\exp (2\pi i \delta (0))$ for some $\delta $ fixed by $\tau $ and take $\delta =0$ if $\widehat {\tau }^{|\tau |} =1$ . For $i\equiv k \mod 2|\tau |$ , the irreducible $\tilde {g}^k$ -twisted modules are as follows:

$$\begin{align*}T^k =V_\Lambda[\tilde{g}^k]= \begin{cases} {\mathbb C}[-k\beta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } 0 \leq i < |\tau|, \\ {\mathbb C}[-k\beta + \delta +(\Lambda^{\tau^i})^*]\otimes M(1)[\tau^i]\otimes T_{\tau^i} & \text{ if } |\tau| \leq i < 2|\tau| \\ \end{cases} \end{align*}$$

(see [35, Propositions 6.1 and 6.2] and [11, Remark 4.2] for detail). In particular, $T^1$ contains a weight one element $e^{\beta }\otimes t$ with $t\in T_\tau $ , which is the lowest weight element of $T^1$ , and so $T^1_{{\mathbb Z}}\not =0$ and the orbifold construction gives a holomorphic VOA $V:=V^{[\tilde {g}]}$ of central charge $24$ , and $V_1$ is non-abelian since $V_1$ contains a root vector $e^{\beta }\otimes t$ .

One of the main purposes of this section is to determine an equivalent relation $\sim $ on $\mathcal{T}$ so that two pairs $(\tau , \tilde {\beta })$ and $(\tau ', \tilde {\beta }')$ define isomorphic VOAs if and only if $(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$ . It is clear that $\tau $ and $\tau '$ are conjugates in $O(\Lambda )$ and $\tilde {\beta }$ and $\tilde {\beta }'$ are equivalent deep holes of the Leech lattice $\Lambda $ if $(\tau , \tilde {\beta })$ and $(\tau ', \tilde {\beta }')$ define isomorphic VOAs.

For two equivalent deep holes $\tilde {\beta }$ and $\tilde {\beta }'$ , there are $\sigma \in O(\Lambda )$ and $\lambda \in \Lambda $ such that $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$ . Since $\tilde {\beta }'$ is $\tau '$ -invariant, $\tilde {\beta }-\lambda $ is $\sigma ^{-1} \tau ' \sigma $ -invariant. Moreover, $\langle \tilde {\beta }, \lambda \rangle \in {\mathbb Z}$ since $\langle \tilde {\beta }, \tilde {\beta }\rangle = \langle \tilde {\beta }', \tilde {\beta }'\rangle =2$ . In this case, $\Lambda _{\tilde {\beta }} +\tilde {\beta } = \Lambda _{\tilde {\beta }-\lambda } +(\tilde {\beta }-\lambda )$ . Therefore, up to the action of $O(\Lambda )$ , we may identify $N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }$ with $N' =\Lambda _{\tilde {\beta }'} +{\mathbb Z} \tilde {\beta }'$ . We define an equivalent relation on $\mathcal{T}$ as follows:

$(\tau ,\tilde {\beta })\sim (\tau ',\tilde {\beta }')$ if and only if

1. (1) $\tilde {\beta }$ and $\tilde {\beta }'$ are equivalent deep holes of the Leech lattice $\Lambda $ (i.e., there are $\sigma \in O(\Lambda )$ and $\lambda \in \Lambda $ such that $\tilde {\beta }'= \sigma ( \tilde {\beta }-\lambda )$ );

2. (2) $\tau $ is conjugate to $\sigma ^{-1} \tau ' \sigma $ in $O(N)$ .

Note that $ (\sigma ^{-1} \tau ' \sigma ,\tilde {\beta }-\lambda )\in \mathcal{T}$ and $N= \Lambda _{\tilde {\beta }} +{\mathbb Z} \tilde {\beta }= \Lambda _{\tilde {\beta }-\lambda } +{\mathbb Z}(\tilde {\beta }-\lambda )$ . Moreover, $\tau $ and $\tau '$ are conjugate in $O(\Lambda )$ since they have the same frame shape by (2).

We will prove the following main theorem.

Theorem 7.1. There is a one-to-one correspondence between the set of isomorphism classes of holomorphic VOA V of central charge $24$ having non-abelian $V_1$ and the set $\mathcal{T}/\sim $ of equivalence classes of pairs $(\tau , \tilde {\beta })$ by $\sim $ .

7.1 W-element and the automorphism $\tilde {g}$

Let $(\tau , \tilde {\beta })\in \mathcal{T}$ . Set $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$ and define $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ . Let $V=V_\Lambda ^{[\tilde {g}]}$ be the holomorphic VOA obtained by the orbifold construction from $V_\Lambda $ and $\tilde {g}$ . We will show that there is a W-element $\alpha $ of $V_1$ such that $\tilde {g}$ can be viewed as a reverse automorphism of $\exp (2\pi i \alpha (0)) \in \mathrm {Aut}(V)$ .

First, we will prove the following theorem.

Theorem 7.2. Let h be the Coxeter number of $N=\Lambda _{\tilde {\beta }} +{\mathbb Z}\tilde {\beta }$ . Then $|\tilde {g}|=h$ .

We need several lemmas.

Lemma 7.3. $s\beta \in \pi (\Lambda )$ if and only if $h|s$ .

Proof. Since $\sqrt {\ell }\varphi ((\Lambda ^\tau )^*)= \Lambda ^\tau $ , we have $s\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$ if and only if $s\tilde {\beta }\in \Lambda ^{\tau }$ , if and only if $h|s$ .

Lemma 7.4. We have $\tilde {g}^{2h}=1$ . Furthermore, $\tilde {g}^h=1$ if $2C\not \in <\tau>$ .

Proof. By (C3) and $\tau \in \mathcal{P}_0$ , $N_{\tau }$ contains a root sublattice $S\cong A_{|\tau |-1}$ . For a root $\mu $ of S, there is $\lambda \in \Lambda $ and $m\in {\mathbb Z}$ such that $\mu =\lambda +m\tilde {\beta } \in N_{\tau }\subseteq {\mathbb C}\Lambda _{\tau }$ . Then

$$\begin{align*}0=\sum_{i=0}^{|\tau|-1} \tau^i \mu = \sum_{i=0}^{|\tau|-1} \tau^i \lambda +|\tau|m\tilde{\beta} \in \Lambda^\tau. \end{align*}$$

Since h is the smallest positive integer satisfying $h\tilde {\beta }\in \Lambda ^{\tau }$ and $\tau $ is fixed point free on S with order $|\tau |$ , we have $m=h/|\tau |$ . Moreover, we also have $\frac {h}{|\tau |}\tilde {\beta }\in \pi (\Lambda )\in (\Lambda ^{\tau })^{\ast }$ and so $\langle \frac {h\tilde {\beta }}{|\tau |}, \Lambda ^{\tau }\rangle \subseteq {\mathbb Z}$ . Hence, ${\mathbb Z} \supseteq \frac {h}{|\tau |}\langle \sqrt {\ell }\varphi (\beta ), \sqrt {\ell }\varphi ((\Lambda ^{\tau })^{\ast })\rangle =\langle \frac {h\ell }{|\tau |}\beta ,(\Lambda ^{\tau })^{\ast }\rangle $ and so $\frac {\ell }{|\tau |}h\beta \in \Lambda $ , which means $(\exp (2\pi \beta (0))^{\frac {\ell h}{|\tau |}}=1$ . In particular, if $2C\not \in <\tau>$ , then $\ell =|\tau |$ and $\exp (2\pi i\beta (0))^h=1$ .

From now on, we may assume $\tau =2C, 6G, 10F$ . In particular, $|\tau |=2s$ for some $s=1,3$ or $5$ . Note that $\sigma =\tau ^s$ is a $2C$ -element.

Lemma 7.5. Let $\tau \in 2C, 6G$ or $10F$ . Let $\tilde {\beta }$ be a $\tau $ -invariant deep hole satisfying (C1)–(C3). Let h be the Coxeter number of $N=\Lambda _{\beta } +{\mathbb Z}\beta $ . Then $h/|\tau |$ is odd.

Proof. By our assumptions, $N_\tau \cong L_A(c_\tau )$ as defined in the Appendix; namely,

$$\begin{align*}N_\tau \supset \bigoplus_{m_i| |\tau|, m_i\neq 1} A_{m_i-1}^{a_i} \end{align*}$$

as a full rank sublattice if the frame shape of $\tau $ is $ \prod m_i^{a_i}$ . Moreover,

$$\begin{align*}[ N_\tau : \bigoplus_{m_i| |\tau|, m_i\neq 1} A_{m_i-1}^{a_i} ]=|\tau|\quad \text{ and } \quad R(N_\tau) = \bigoplus_{m_i| |\tau|, m_i\neq 1} A_{m_i-1}^{a_i}. \end{align*}$$

Since there are only $16$ Niemeier lattices whose Coxeter number is even, it is straightforward to determine all Niemeier lattices N such that $L_A(c_\tau )\subset N$ as a direct summand. Indeed, $R(N)=A_1^{24}, D_4^6, A_5^4D_4$ , $D_6^4, A_9^2D_6$ , $D_8^3$ , $A_{17}E_7$ , $D_{12}^2$ , or $D_{24}$ if $\tau \in 2C$ ; $R(N)= A_5^4D_4$ or $A_{17}E_7$ if $\tau \in 6G$ ; $R(N)= A_9^2D_6$ if $\tau \in 10F$ .

It turns out that $h/|\tau |$ is odd for all possible cases.

The following lemma can be verified easily using the definition of $A_{m-1}$ .

Lemma 7.6. Let $m=2s$ be an even integer and let $\tau $ be a Coxeter element in $\mathrm {Weyl}(A_{m-1})$ . Then the $(-1)$ -eigenlattice of $\tau ^s$ on $A_{m-1}$ is isometric to $A_1^s= {\mathbb Z} x_1\oplus \cdots \oplus {\mathbb Z} x_s$ . Moreover, the vector $\frac {1}2( x_1+\cdots + x_s)\in s\gamma +A_{m-1}$ , where $\gamma + A_{m-1}$ is a generator of $A_{m-1}^*/A_{m-1}$ .

Lemma 7.7. For $\tau =2C, 6G, 10F$ and $v,u\in \Lambda ^{\tau }$ , $\langle v,u\rangle \in 2{\mathbb Z}$ .

Proof. We note $\Lambda ^{\tau }\subseteq \Lambda ^{\sigma }$ . Since $\ell (\sigma )=4$ , $\Lambda ^{\sigma }=2(\Lambda ^{\sigma })^{\ast }$ . Hence, $\frac {v}{2}\in (\Lambda ^{\sigma })^{\ast }$ and $\langle v,u\rangle = 2\langle \frac {v}{2},u\rangle \in 2{\mathbb Z}$ .

Now now on, we set $p=h/|\tau |$ , which is an odd integer.

Proposition 7.8. For $\tau =2C, 6G, 10F$ and $v\in (\Lambda _{\tilde {\beta }}+sp\tilde {\beta })^{\tau }$ , we have $\langle v,v\rangle \equiv 2 \pmod {4}$ .

Proof. We first note that $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$ forms an affine fundamental system of roots of N. Choose a fundamental root system X from $\Lambda _{\tilde {\beta }}+{\mathbb Z}\tilde {\beta }$ such that $\tilde {\beta }\in X$ . Let $\rho $ be the corresponding Weyl vector and consider $\xi =\exp (2\pi i\rho (0)/h)\in \mathrm {Aut}(V_N)$ .

Although $\tau $ does not fix X, $\tau $ preserves $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$ and $\xi $ acts on $\{e^\alpha \mid \alpha \in (\Lambda _{\tilde {\beta }}+\tilde {\beta })_2 \}$ with the same eigenvalue; hence, the commutator $[\tau , \xi ]=1$ . Therefore, we can induce $\tau $ to an automorphism of $(V_N)^{[\xi ^j]}$ for any j. As it is well-known, $(V_N)^{[\xi ]}\cong V_{\Lambda }$ . Now consider the VOA obtained by the orbifold construction using $V_N$ and $\xi ^2$ . Then $(V_N)^{[\xi ^{2}]} \cong V_M$ for some Niemeier lattice M and the Coxeter number of M is $2$ (i.e., $R(M)=A_1^{24}$ ). It is clear that

$$\begin{align*}\Lambda_{\tilde{\beta}} + {\mathbb Z} sp\tilde{\beta} = \Lambda_{\tilde{\beta}} \cup (\Lambda_{\tilde{\beta}} + sp\tilde{\beta}) \subset M. \end{align*}$$

By Lemma 7.6, it is easy to check that

$$\begin{align*}L_A(c_{2C})\cong M_\sigma < \Lambda_{\tilde{\beta}} + {\mathbb Z} sp\tilde{\beta} = \Lambda_{\tilde{\beta}} \cup (\Lambda_{\tilde{\beta}} + sp\tilde{\beta}) \subset M. \end{align*}$$

Then $(\Lambda _{\tilde {\beta }} + sp\tilde {\beta })^\tau < M^\tau < M^{\tau ^s}= (L_A(c_{2C}))^\perp $ .

Therefore, it suffices to check for the case $\tau \in 2C$ and $N\cong N(A_1^{24})$ . In this case, we may assume N contains $A_1^{24}=\oplus _{i=1}^{24} {\mathbb Z} x_i$ and $N/(A_1^{24})$ is the binary Golay code $G_{24}$ of length $24$ and $\tau (x_i)=x_i$ for $i=1,...,12$ and $\tau (x_i)=-x_i$ for $i=13,...,24$ . We may also assume $\tilde {\beta }=x_1$ . By (C3), $N_{\tau }=<x_{13},...,x_{24}, \frac {x_{13}+...+x_{24}}{2}>$ . Then $\{13,...,24\}$ is a dodecad of $G_{24}$ , and so $N^{\tau }=(N_{\tau })^{\perp }=<x_1,...,x_{12}, \frac {x_1+...+x_{12}}{2}>$ .

For a Weyl vector $\rho $ of N, we may choose $x_i$ such that $\exp (2\pi i\rho (0)/2)(x_i)=\sqrt {-1}x_i$ , and so $\exp (2\pi i\rho (0)/2)(\frac {x_i+...+x_{12}}{2})=\sqrt {-1}^{12}(\frac {x_i+...+x_{12}}{2})=(\frac {x_i+...+x_{12}}{2})$ . Namely,

$$\begin{align*}(\Lambda_{x_1})^{\tau}= <\frac{x_1+...+x_{12}}{2}, x_i+x_1\mid i=1,...,12>. \end{align*}$$

We note $\langle \frac {x_1+...+x_{12}}{2}, \frac {x_1+...+x_{12}}{2}\rangle +2\langle \beta , \frac {x_1+...+x_{12}}{2}\rangle =6+2\equiv 0 \pmod {4}$ and $\langle x_1+x_i, x_1+x_i\rangle +2\langle \beta , x_1+x_i\rangle =4+4 \equiv 0 \pmod {4}$ . Since $(\Lambda _{x_1})^{\tau }$ is spanned by such elements and $\Lambda _{x_1}$ is self orthogonal modulo $2$ , $\langle v,v\rangle \equiv 2 \pmod {4}$ for all $v\in \Lambda _{\tilde {\beta }}+\tilde {\beta }$ , as we desired.

We come back to the proof of Theorem 7.2. We still assume $\tau =2C, 6G$ or $10F$ and $s,p$ are odd. The main idea is to study the possibilities of weights in $T^1$ modulo ${\mathbb Z}$ . Recall that

$$\begin{align*}T^1 =V_\Lambda[\tilde{g}]= {\mathbb C}[-\beta +(\Lambda^{\tau})^*]\otimes M(1)[\tau]\otimes T_{\tau} \end{align*}$$

and the weights of $M(1)[\tau ]\otimes T_{\tau }$ are in $1-\frac {1}{\ell }+\frac {1}{|\tau |} {\mathbb Z}$ . Therefore, we will focus on the set $-\beta +(\Lambda ^{\tau })^*$ .

Since $\Lambda _{\tilde {\beta }}+p\tilde {\beta }$ contains a root $\mu $ in $N_{\tau }$ , $p\tilde {\beta }\in \pi (\Lambda )$ as we explained and we have $|\Lambda ^\tau /\Lambda _{\tilde {\beta }}^\tau |=| (\Lambda _{\tilde {\beta }}^\tau )^*/ (\Lambda ^\tau )^*|= p$ . For $\lambda \in \Lambda $ , set $\mu =\sqrt {\ell }\varphi (\pi (\lambda ))\in \Lambda ^{\tau }$ . We assume $\langle \mu , \tilde {\beta }\rangle =\frac {t}{p}$ ; that is, $\langle \pi (\lambda ),\beta \rangle =\frac {t}{4sp}$ . Since $p\mu \in \Lambda ^{\tau }_{\tilde {\beta }}$ ,

$$ \begin{align*}\langle p\mu+\tilde{\beta}, p\mu+\tilde{\beta}\rangle= p^2\langle \mu,\mu\rangle+2p\langle \mu, \tilde{\beta}\rangle+2 =\langle p \mu,p\mu\rangle+2t+2\end{align*} $$

and $\langle p \mu ,p\mu \rangle +2t\equiv 0 \mod 4$ by Proposition 7.8. Since p is odd, we have $\langle \mu , \mu \rangle +2t=4m$ for some $m\in {\mathbb Z}$ ; namely, $\langle \pi (\lambda ),\pi (\lambda )\rangle =\frac {4m-2t}{4s}$ . Hence,

$$ \begin{align*}\langle \pi(\lambda)+\beta,\pi(\lambda)+\beta\rangle =\frac{4m-2t}{4s}+2\frac{t}{4sp}+\frac{2}{4s} = \frac{2mp+t(1-p)+p}{2sp}\end{align*} $$

and so $\mathrm {wt}(e^{\pi (\lambda )+\beta })=\frac {2mp+t(1-p)+p}{4sp}$ . Since $2mp+t(1-p)+p$ is always odd, the possible weights modulo ${\mathbb Z}$ are $\frac {\mbox {odd}}{4ps}$ ; that is, there are $h=2sp$ distinct weights modulo ${\mathbb Z}$ at most. That means $|\tilde {g}|\leq h$ , and this completes the proof of Proposition 7.2. $\square $

We next show that if we start the orbifold construction from V by using a W-element, we will come back to the original $(\tau , \tilde {\beta })$ and N.

Let $V=V_\Lambda ^{[\tilde {g}]}$ . Then we have

$$ \begin{align*}V=\bigoplus_{j=0}^{|\tilde{g}|-1} (T^j_{{\mathbb Z}})^{<\tilde{g}>}.\end{align*} $$

Define L by $\mathrm {Comm}(\mathrm {Comm}(\mathcal{H}),V),V)\cong V_L$ . Since V is holomorphic, as a $V_L$ -module, V contains a submodule isomorphic to $V_{L+\mu }$ for all $\mu \in L^{\ast }$ .

Note that $\tilde {g}^{|\tau |} =\exp (2\pi i (\delta + |\tau |\beta )(0))$ is an inner automorphism. Then

(7.1) $$ \begin{align} L=\bigcup_{j=0}^{|\tilde{g}|/ |\tau| -1} j(\delta +|\tau|\beta)+\Lambda_\beta^\tau. \end{align} $$

Recall that $|\tilde {g}|=h$ and then $ (h/|\tau |) (\delta +|\tau |\beta ) \in \Lambda _\beta ^\tau $ . Since $p=h/|\tau |$ is odd and $2\delta \in \Lambda ^\tau $ , we have $\delta \equiv h\tilde {\beta } \mod \Lambda _\beta ^\tau $ .

Proposition 7.9. $\sqrt {\ell } L^{\ast } \cong \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$ .

Proof. Set $p=h/|\tau |=2k+1$ . Then $(\delta +|\tau |\beta ) +\Lambda ^\tau _{\beta } = (k+1)\ell \beta + \Lambda ^\tau _{\beta }$ . Since $2h\beta =(2k+1)\ell \beta \in \Lambda ^\tau $ , $ L= \bigcup _{j=0}^{2k} j(k+1)\ell \beta +\Lambda _\beta ^\tau =\Lambda ^\tau _{\beta }+{\mathbb Z} \ell \beta $ . By the same argument as in Theorem 4.9, we have $\sqrt {\ell }L^* = \Lambda _{\tilde {\beta }}^{\tau }+{\mathbb Z} \tilde {\beta }=N^{\tau }$ .

Lemma 7.10. $\mathrm {Comm}_V (\mathcal{H}) = V_{\Lambda _\tau }^{\widehat {\tau }}$ .

Proof. Suppose false. Then there exists $ 0<j< |\tilde {g}|=h$ such that $V_{\Lambda _\beta ^\tau } $ appears as a submodule of $T^j_{\mathbb Z}$ . It implies $j\beta \in (\Lambda ^\tau )^*$ . It contradicts that h is the smallest integer such that $h\tilde {\beta }\in \Lambda ^\tau $ (or equivalently, $h\beta \in \pi (\Lambda )=(\Lambda ^{\tau })^{\ast }$ ).

As a corollary, we have the following:

Lemma 7.11. $\mathrm {rank}(V_1)=\mathrm {rank}(\Lambda ^{\tau })$ .

Proof. Since $\mathcal{H}\subseteq V_{\Lambda }^{<\tilde {g}>}$ , we may assume $\mathcal{H}\subseteq V_1$ . By the lemma above, we have $\mathrm {Comm}_V (\mathcal{H})\cap V_1= 0$ .

As we have shown, $(\Lambda _{\tilde {\beta }}+\tilde {\beta })_2$ is a fundamental affine root system $\tilde {X}$ of $R(N)$ . Note that $\tilde {\beta }\in \tilde {X}$ by our convention. Let $\rho $ be a Weyl vector of X. Then $\exp (2\pi i\rho (0)/h)$ is an automorphism of N of order h and $N_{\rho /h}=\Lambda _{\tilde {\beta }}$ . If v is an extended root in $\Lambda _{\tilde {\beta }}+\tilde {\beta }$ , then $\langle v,\rho \rangle =-(h-1)$ . Therefore, $\rho ^{\perp }\subseteq \Lambda _{\tilde {\beta }}= \{x\in N\mid \langle \rho , x\rangle \in h{\mathbb Z}\}$ . Furthermore, for any $w\in R(N)\cap N^{(k)}$ , $\langle \rho ,w\rangle \cong k \pmod {h}$ .

Set $\alpha =\sqrt {\ell }\varphi ^{-1}(\pi (\rho )/h)$ . Then

$$\begin{align*}\langle \alpha,\beta\rangle =\langle \sqrt{\ell}\varphi^{-1}(\pi(\rho)/h), \frac{1}{\sqrt{\ell}}\varphi^{-1}(\tilde{\beta})\rangle = \frac{1}{h}\langle \pi(\rho), \tilde{\beta}\rangle= \frac{1}{h}\langle \rho, \tilde{\beta}\rangle=\frac{1}{h}. \end{align*}$$

More generally, $\langle \alpha ,L^{\ast }\rangle =\langle \varphi ^{-1}(\pi (\rho )/h), \varphi ^{-1}(N^{\tau })\rangle =\frac {1}{h}\langle \rho , N^{\tau }\rangle < \frac {{\mathbb Z}}{h}$ . Since $\mathcal{H}$ is a Cartan subalgebra of $V_1$ and $V_1$ contains a root vector associated with $\beta $ (i.e., a weight one element $e^{\beta }\otimes T_\tau \in T^1$ with $\langle \beta ,\beta \rangle =\frac {2}{\ell }$ ). As we have shown in the previous sections, the isometry in $Co.0$ determined by the reverse automorphism defined by a W-element of $V_1$ is $\tau $ itself and $\beta $ is one of shortest roots of $V_1$ .

Lemma 7.12. Let $\gamma $ be a root of $V_1$ . Then $\langle \alpha , \gamma \rangle \neq 0$ .

Proof. Since $\rho ^{\perp }\cap N^{\tau } \subseteq \Lambda ^{\tau }$ , we have $\alpha ^{\perp }\cap L^{\ast }\subseteq \pi (\Lambda )$ and we have the desired result.

In other words, $\alpha $ is a regular element in $\mathcal{H}$ , and we can define a positive root $\mu $ by $\langle \mu ,\alpha \rangle>0$ . Note that there is a correspondence between $L^*$ and $N^{\tau }$ through the map $\sqrt {\ell } \varphi _\tau $ . Since $\langle \rho , v\rangle \in {\mathbb Z}$ for all $v\in N$ , $\langle \alpha , \mu \rangle \in \frac {1}h {\mathbb Z}$ for all $\mu \in L^{\ast }$ . Since $\langle \alpha ,\beta \rangle =\frac {1}{h}$ , we may assume $\beta $ is a simple short root of a full component. Therefore, there is a W-element $\widetilde {\alpha }$ such that $\langle \widetilde {\alpha },\beta \rangle =\frac {1}{h}$ . In this case, $\widehat {\tau }\exp (2\pi i\beta (0))$ is a reverse automorphism of $V_\Lambda $ for $\exp (2\pi i\widetilde {\alpha }(0))$ , and we can recover the pair $(\tau , \tilde {\beta })$ and a Niemeier lattice $N=\Lambda _{\tilde {\beta }}+{\mathbb Z} \tilde {\beta }$ .

7.2 The relation $\sim $

Next we will study the relation $\sim $ on $\mathcal{T}$ . Let $(\tau , \tilde {\beta })$ and $(\tau ', \tilde {\beta }')$ be two pairs in $\mathcal{T}$ . Suppose $(\tau , \tilde {\beta }) \sim (\tau ', \tilde {\beta }')$ . As we mentioned, up to the action of $O(\Lambda )$ , one can assume $N=N'$ and $\tilde {\beta }'= \tilde {\beta }-\lambda $ for some $\lambda \in \Lambda _{\tilde {\beta }}$ .

Lemma 7.13. Suppose $\tilde {\beta }'= \tilde {\beta }-\lambda $ is also fixed by $\tau $ . Then the VOAs defined by $(\tau , \tilde {\beta })$ and $(\tau ,\tilde {\beta }')$ are isomorphic.

Proof. By our assumption, $\lambda \in \Lambda ^\tau $ , and thus, $\bar {\lambda }=\frac {1}{\sqrt {\ell }} \varphi ^{-1}(\lambda )\in (\Lambda ^\tau )^*$ . Then $\widehat {\tau }\exp (2\pi i(\beta -\bar {\lambda })(0))=\tilde {g}\exp (-2\pi i \bar {\lambda }(0))$ is conjugate to $\tilde {g}$ by [27, Lemma 4.5 [2]]. Therefore, they define isomorphic VOAs by orbifold constructions.

In other words, the choice of $\tilde {\beta }$ is somewhat ambiguous, and we can choose any $\tau $ -invariant root in the affine fundamental root system as the starting point.

Proposition 7.14. If $(\tau , \tilde {\beta })\sim (\tau ', \tilde {\beta }')$ , then the VOAs obtained by the orbifold constructions from $V_\Lambda $ associated with $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))$ and $\tilde {g}'=\widehat {\tau '}\exp (2\pi i\beta '(0))$ are isomorphic, where $\beta =\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta })$ and $\beta '=\frac {1}{\sqrt {\ell }}\varphi ^{-1}(\tilde {\beta }')$ .

Proof. Up to the action of $O(\Lambda )$ , one may assume $N=N'$ and $\tilde {\beta }'= \tilde {\beta }-\lambda $ for some $\lambda \in \Lambda _{\tilde {\beta }}$ . Since $\tau $ is conjugate to $\tau '$ in $O(N)$ , there is a $\mu \in O(N)$ such that $\tau = \mu \tau ' \mu ^{-1}$ . Then $\mu \tilde {\beta }'$ is fixed by $\tau $ . Note that h is still the smallest integer such that $h\mu \tilde {\beta }' \in \Lambda ^{\tau }$ . Since $N= \cup _{j=1}^{h-1}(\Lambda _{\tilde {\beta }}+j\tilde {\beta })$ , $\mu \tilde {\beta }' \in (\Lambda _{\tilde {\beta }}+k\tilde {\beta })$ for some k with $(k,h)=1$ . Therefore, $<\tilde {g}^k> = <\tilde {g}>$ and $V^{[\tilde {g}]}\cong V^{[\tilde {g}^k]}$ .

Recall that $N_\tau \cong L_A(c_\tau )>R=\oplus A_{m_i-1}^{a_i}$ and $\tau $ acts on $N_\tau $ as a Coxeter element of the root system R. Therefore, for $ (k, |\tau |)=1$ , $\tau $ is conjugate to $\tau ^k$ by an element $s\in Weyl(R)$ . In this case, $s\mu \tilde {\beta }' =\mu \tilde {\beta }'$ and $s\tau s^{-1} =\tau ^k$ . Therefore, $(\tau , \mu \tilde {\beta }')$ and $(\tau ^k,\mu \tilde {\beta }')$ define isomorphic VOAs. Moreover, by Lemma 7.13, the VOAs obtained by the orbifold constructions from $V_\Lambda $ associated with $\tilde {g}^k=\widehat {\tau }^k\exp (2\pi i k\beta (0))$ and $\widehat {\tau }^k\exp (2\pi i \mu \beta '(0))$ are isomorphic, and we have the desired result.

Therefore, there is a one-to-one correspondence between the set of isomorphic classes of holomorphic VOA V of central charge $24$ with non-abelian $V_1$ and the set of equivalent classes $(\sim )$ of pairs $(\tau , \tilde {\beta })$ with $\tau \in \mathcal{P}_0$ and $\tau $ -invariant deep hole $\tilde {\beta }$ of $\Lambda $ satisfying the conditions in Theorem 7.1.

Remark 7.15. Since there is a correspondence between deep holes, up to equivalence, and Niemeier lattices, each pair in $\mathcal{T}$ will define a unique pair $(N, \tau )$ , where N is a Niemeier lattice with $R(N)\neq \emptyset $ and $\tau \in O(N)$ with a positive frame shape. Therefore, the classification of holomorphic VOAs of central charge $24$ with non-abelian weight one Lie algebras can also be reduced to a classification of the possible pairs of $(N, \tau )$ , up to some equivalence.

8 Höhn’s observation and Lie algebra structure of $V_1$

In [21], Höhn observed that there is an interesting bijection between certain equivalence classes of cyclic subgroups of the glue codes of the Niemeier lattices with roots and the Lie algebra structures of the weight one subspace of a holomorphic vertex operator algebras of central charge $24$ corresponding to the $69$ semisimple cases in Schellekens’ list. In this section, we will provide an explanation for Höhn’s observation using our main theorem. In particular, we will give a pure combinatorial classification of holomorphic vertex operator algebras of central charge $24$ with nontrivial weight one spaces. Indeed, the orbit lattice $N(Z)$ described by Höhn is essentially the lattice $L= \sqrt {\ell }(N^\tau )^*$ , and the glue vector v is the vector $\lambda _c$ as we defined in the appendix. The rescaling of the levels of the Lie algebras are handled uniformly using the $\ell $ -duality map $\sqrt {\ell } \varphi _{\tau }$ .

8.1 Roots of $V_1$ and $N^\tau $

First, we study the relationship between the root system of $V_1$ and the lattice $N^\tau \cong \sqrt {\ell }L^*$ . Recall from [15] that

(8.1) $$ \begin{align} L_{\mathfrak{g}_i}(k_i,0)= \bigoplus_{j\in Q_i/k_iQ^i_{l} } V_{\sqrt{k_i}Q^i_{l} + \frac{1}{\sqrt{k_i}} \beta_j} \otimes M^{0, \beta_j}, \end{align} $$

where $Q^i$ and $Q^i_{l}$ denote the root lattice and the long root lattice of $\mathfrak {g}_i$ , respectively, and $\beta _j$ is a representative of $j\in Q^i/k_iQ^i_{l}$ .

By (8.1), the roots of the Lie algebra $V_1=\bigoplus _{i=1}^t\mathfrak {g}_i$ can be represented by elements in $L^*$ . Indeed, we can view them as roots of the lattice $\sqrt {\ell }L^*$ .

First, we recall the definition for the root system of an even lattice K (cf. [43; 44]).

Definition 8.1. A vector $v\in K$ is primitive if the sublattice spanned by v is a direct summand of L. A primitive vector v is called a root if $2\langle v, K\rangle /\langle v,v\rangle \subset {\mathbb Z}$ . The set of roots

$$\begin{align*}R(K) = \{ v\in K\mid v \text{ is primitive},\ 2\langle v, K\rangle/\langle v,v\rangle \subset {\mathbb Z}\} \end{align*}$$

is called the root system of K.

Definition 8.2. Let K be an even lattice. The level $\ell $ of K is the smallest positive integer $\ell $ such that $\sqrt {\ell }K^*$ is still even.

As in [43], we denote the scaled root system as follows.

We also consider the reduced discriminant group of an arbitrary scaled root system R, which is a subgroup of the discriminant group of the sublattice generated by R (see [43, Definition 2.1]). For an irreducible root system $^\alpha \! X$ of type A, D or E, the reduced discriminant group of $^\alpha \! X$ is simply the discriminant group $\mathcal {D}(X)$ .

For non-simply laced root systems, the corresponding root lattices and reduced discriminant groups are as follows.

For explicit description of the reduced discriminant groups for the root systems of ${^\alpha }\!B_n$ and ${^\alpha }\!C_n$ , we use the following standard model for their root lattices; namely,

$$\begin{align*}{^\alpha}\!B_n = \bigoplus_{i=1}^n {\mathbb Z} e_i, \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$

roots: $e_i$ of norm $\alpha $ and $\pm e_i\pm e_j$ of norm $2\alpha $ ; and

$$\begin{align*}{^\alpha}\!C_n = \{ \sum_{i=1}^n x_i e_i \mid \sum_{i=1}^n x_i \equiv 0\quad \mod 2\} \quad \text{ where } (e_i,e_j)=\alpha \delta_{i,j}, \end{align*}$$

roots: $\pm e_i\pm e_j$ of norm $2\alpha $ and $2e_i$ of norm $2\alpha $ .

The reduced discriminant group of $^{\alpha }\! B_n$ is $0$ if $\alpha $ is odd, and the reduced discriminant group of R is given by $\langle \bar {g} \rangle \cong {\mathbb Z}_2$ where

$$\begin{align*}\begin{cases} g=\frac{1}2 (e_1+\cdots +e_n) & \text{ if } R= ^{2\alpha}\!\! B_n, \\ g= e_1 & \text{ if } R= ^{\alpha}\!\! C_n. \end{cases} \end{align*}$$

Remark 8.3 (see [43])

An element $v\in K$ is a root if and only if $v\in \langle v,v\rangle /2\cdot K^*$ and v is primitive in K. In particular, $\langle v,v\rangle /2$ divides the exponent of $\mathcal {D}(K)=K^*/K$ .

Lemma 8.4. Let $v\in K$ such that $v\in \langle v,v\rangle /2\cdot K^*$ . Assume that $v/n\in K$ for some $n\in {\mathbb Z}$ with $n>1$ . Then $n=2$ . Moreover, $\frac {v}2$ is a root and $K= {\mathbb Z}(\frac {v}2) \perp (K\cap \langle v\rangle ^\perp )$ .

Proof. Since $v/n\in K$ and $v\in \langle v,v\rangle /2\cdot K^*$ , we have

$$\begin{align*}\langle \frac{v}n,v\rangle \in \frac{\langle v,v\rangle}2 {\mathbb Z}, \text{ or equivalently, } 2/n\in {\mathbb Z}; \end{align*}$$

hence, $n=2$ . Then $\frac {v}2$ is primitive in K and $\frac {2\langle v/2,x\rangle }{\langle v/2,v/2\rangle } = \frac {4\langle v,x\rangle }{\langle v,v\rangle }\in {\mathbb Z}$ for any $x\in K$ ; hence, it is a root.

Let $p_v: K \to ({\mathbb Z} \frac {v}2)^*$ be the natural projection. For any $x\in K$ , $p_v(x) = r_x v$ for some $r_x\in {\mathbb Q}$ . Then $ \frac {2\langle v,x\rangle }{\langle v,v\rangle } = \frac {2\langle v,r_xv\rangle }{\langle v,v\rangle } =2r_x\in {\mathbb Z}$ . That means $r_x\in \frac {1}2 {\mathbb Z}$ and $p_v(K)= {\mathbb Z}(\frac {v}2)$ as desired.

The following results can be found in [43].

Theorem 8.5. Let K be an integral lattice and R a root system contained in K. Let $\mathcal {K} = K/ (\langle R\rangle \perp (R^\perp \cap K))$ be the glue code of K over R. Then the elements of R are actually roots of K if and only if $\mathcal {K}$ is contained in the reduced discriminant group of R. Furthermore, K contains no elements of the form $e/2$ , where e is a basis vector of an $A_1$ -component.

Recall that $\ell $ is divisible by $|\tau |(K_0-N_0)=\mathrm {LCM} (\{r_ik_i\}_{i=1}^t)$ by Lemmas 2.3 and 4.12.

Lemma 8.6. Let $\beta $ be a root of $\mathfrak {g}_{i,k_i}$ and $M=\sqrt {\ell }L^*$ . Then

$$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta \in \frac{\langle v,v\rangle }{2} M^*. \end{align*}$$

In particular, $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $ is a root of M if it is primitive in M or ${\mathbb Z}(v/2)$ is an orthogonal summand of M.

Proof. Let $M=\sqrt {\ell }L^*$ and $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $ . Then $M^* =\frac {1}{\sqrt {\ell }} L$ and

$$\begin{align*}\frac{\langle v,v\rangle }{2}= \begin{cases} \frac{\ell}{r_ik_i} & \text{ if }\beta\text{ is a short root,}\\ \frac{\ell}{k_i} & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$

Therefore,

$$\begin{align*}v=\frac{\sqrt{\ell}}{\sqrt{k_i}} \beta= \begin{cases} \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} (r_i\beta)& \text{ if }\beta\text{ is a short root,}\\ \frac{\langle v,v\rangle }{2} \frac{1}{\sqrt{\ell}} \sqrt{k_i} \beta & \text{ if }\beta\text{ is a long root.} \end{cases} \end{align*}$$

Since $L> \sqrt {k_i}Q^i_{l}$ and $r_i\beta \in Q^i_{l}$ (resp. $\beta \in Q^i_{l}$ ) if $\beta $ is a short root (resp., a long root), $v \in \frac {\langle v,v\rangle }{2} M^*$ as desired.

Lemma 8.7. Let $\mathfrak {g}_{i,k_i}$ be a simple Lie subalgebra of $V_1$ . Suppose there is a root $\beta $ of $\mathfrak {g}_{i,k_i}$ such that $v=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta $ is not a root of $N^\tau $ . Then $\beta $ is a long root, and the long root lattice of $\mathfrak {g}_i$ is of the type $A_1^r$ , where $r=\mathrm {rank}(\mathfrak {g}_i)$ . In particular, $\mathfrak {g}_i$ is of type $A_1$ or $C_r$ .

Proof. Without loss of generality, we may assume $\mathrm {rank}(V_1)>1$ . By Lemma 8.6, ${\mathbb Z}(v/2)$ is an orthogonal summand of $N^\tau $ . Suppose $\beta $ is a short root. Then for any short root $\beta '$ , $v'=\frac {\sqrt {\ell }}{\sqrt {k_i}} \beta '$ is not a root of $N^\tau $ . Therefore, $\frac {\sqrt {\ell }}{2\sqrt {k_i}} Q_i \cong \sqrt {s} A_1^r$ ; however, ${\mathbb Z} \frac {\sqrt {\ell }}{2\sqrt {k_i}} \alpha $ is not an orthogonal summand of $\sqrt {s} A_1^r$ for any long root $\alpha $ . Therefore, $\beta $ is a long root and the long root lattice is of type $A_1^r$ .

By the lemmas above, the lattice $N^\tau =\sqrt {\ell }L^*$ contains the information of the (scaled) root system of $\mathfrak {g}$ .

8.2 Orbit diagrams and Lie algebra structures of $V_1$

Let V be a holomorphic VOA of central charge $24$ and $\alpha $ a W-element of $V_1$ . Let $g=\exp (2\pi i\alpha (0))\in \mathrm {Aut}(V)$ and let $\tilde {g}=\widehat {\tau }\exp (2\pi i\beta (0))\in \mathrm {Aut}(V_{\Lambda })$ be the reverse automorphism of g, where $\beta \in {\mathbb C}\Lambda ^{\tau }$ . Let $\varphi _{\tau }: \sqrt {\ell }(\Lambda ^\tau )^* \to \Lambda ^\tau $ be the isometry described in Theorem 4.2. Recall that the vector $\tilde {\beta }=\varphi (\sqrt {\ell }\beta )$ is a deep hole of $\Lambda $ and $N=\Lambda ^{[\tilde {\beta }]} \ncong \Lambda $ . Moreover, the Coxeter number h of N is equal to $n=\mathrm {LCM}(r_ih_i^\vee )$ and $N^\tau \cong \sqrt {\ell }L^*$ .

Let R be the set of roots in N and set $ R_k=\{\mu \in -k\tilde {\beta }+ \Lambda _{\tilde {\beta }} \mid \langle \mu , \mu \rangle =2 \}. $ Then $R= \cup _{k=1}^{h-1} R_k$ . Since the Leech lattice does not contain a root, $\langle \mu , \nu \rangle \leq 0$ for $\mu , \nu \in R_k$ with $\mu \neq \nu $ for each k. Indeed, $\langle \mu , \nu \rangle =0$ or $-1$ for any $\mu , \nu \in R_k$ with $\mu \neq \nu $ .

One can associate a (simply laced) Dynkin diagram with $R_k$ for each k. Namely, the nodes are labeled by elements of $R_k$ , and two nodes x and y are connected if and only if $\langle x, y\rangle =-1$ . By abuse of notations, we often use $R_k$ to denote both the Dynkin diagram and the subset of roots. Note that $\tau $ acts on $R_k$ for each k and acts as a diagram automorphism associated with the diagram defined by $R_k$ .

Since $\tilde {\beta }$ is a deep hole of the Leech lattice $\Lambda $ , $R_1$ is a disjoint union of the affine diagrams associated with the root system of N. Moreover, $\tau $ acts on $R_1$ . Since $N_\tau \cong L_A(c)$ and $\tau $ acts as $g_{\Delta ,c}$ on a root sublattice of $N_\tau $ , $\tau \in \mathrm {Weyl}(R)$ and preserves all irreducible components of $R(N)$ . Note also that $g_{\Delta ,c}$ induces an isometry in $O(\Lambda )$ if and only if $\lambda _c\in N$ [5]. Therefore, the vector $\lambda _c$ corresponds to a codeword of the glue code $N/R$ . In particular, $P_{Q_i}(\lambda _c)\in (Q_i)^*$ for every irreducible root sublattice $Q_i$ of N. Note also that $\tau $ has a positive frame when viewing as an isometry of N.

Therefore, for each irreducible component, we can consider the quotient diagram as follows: we identify an orbit of nodes as one node, and two nodes are connected if the nodes in the corresponding orbits are connected. By removing the node associated with the extended node, one obtains a usual Dynkin diagram (see Table 2).

Table 2 Diagram automorphisms of affine diagrams.

Note that the fixed sublattice is the (scaled) root lattice of the quotient diagram. A fixed node (or fixed simple root) corresponds to a simple short root of a full component.

Remark 8.8. Let $\mathcal{G}_i$ be a simple Lie subalgebra of $V_1$ with $r_ih_i^\vee =n=h$ . Then $\ell =r_ik_i$ and $k_i/h_i^\vee = \ell /h$ . Therefore, the level $k_j$ of the simple Lie subalgebra $\mathcal{G}_j$ is given by $k_j= \ell h^\vee _j/h$ for any j. Note also that the short roots of $\mathcal{G}_i$ will correspond to an irreducible (connected) component $S_i$ of $N^\tau _2$ . Moreover, $S_i\cap R_1$ corresponds to the simple short roots of $\mathcal{G}_i$ . Therefore, $S_i$ and $S_i\cap R_1$ determines the type of $\mathcal{G}_i$ uniquely.

Remark 8.9. In [40], a notion of generalized hole diagrams is introduced. It was shown that a generalized hole diagram determines a generalized deep hole up to conjugacy and that there are exactly $70$ such diagrams. This notion of generalized hole diagrams essentially corresponds to the diagram associated with simple short roots of the full components (i.e., elements in $R_1\cap N^\tau _2$ ).

8.3 Possible pairs for $(N, \tau )$

Next, we will discuss the possible choices for the pair $(N, \tau )$ for each $\tau \in \mathcal{P}_0$ .

8.3.1 $\tau \in 2A$

For $\tau \in 2A$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=|\tau |=2$ . In this case, $\Lambda _\tau \cong \sqrt {2}E_8$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $2$ and $ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^8, \frac {1}2 (\alpha _1 +\cdots +\alpha _8)\}$ , where ${\mathbb Z} \alpha _1 +\cdots +{\mathbb Z}\alpha _8\cong A_1^8$ . The vector $v= \frac {1}2 (\alpha _1 +\cdots +\alpha _8)$ corresponds to a codeword $c\in N/R$ . The possible choices for $(N, \tau )$ , the codeword c and the corresponding root systems and Lie algebra structures for $V_1$ are listed in Table 3.

Table 3 $({N}{,}\tau )$ for the case $2A$ .

8.3.2 $\tau \in 3B$

For $\tau \in 3B$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=|\tau |=3$ . In this case, $\Lambda _\tau \cong K_{12}$ is the Coxeter-Todd lattice of rank $12$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $3$ and $N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_2^6, (\gamma _1, \dots , \gamma _6)\}$ , where $\gamma _i +A_2$ is a generator of $A_2^*/A_2$ for each i. The vector $(\gamma _1, \dots , \gamma _6)$ corresponds to a codeword $c\in N/R$ . The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures for $V_1$ are listed in Table 4.

Table 4 $(N,\tau )$ for the case $3B$ .

8.3.3 $\tau \in 5B$

For $\tau \in 5B$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=|\tau |=5$ and the Coxeter number of $N=\Lambda ^{[ \tilde {\beta }] }$ is divisible by $5$ . In this case, $N_\tau \cong \mathrm {Span}_{\mathbb Z}\{ A_4^4, (\gamma _1, \gamma _2, \gamma _3, \gamma _4)\}$ , where $\gamma _i +A_4$ is a generator of $A_4^*/A_4$ for each i. Again, the vector $(\gamma _1, \gamma _2, \gamma _3, \gamma _4)$ corresponds to a codeword $c\in N/R$ . That means $5=|\tau |$ divides $|N/R|$ also. The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 5.

Table 5 $(N,\tau )$ for the case $5B$ .

8.3.4 $\tau \in 7B$

For $\tau \in 7B$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=7$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $7$ and $N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_6^3, (\gamma _1,\gamma _2, \gamma _3)\}$ , where $\gamma _i +A_6$ is a generator of $A_6^*/A_6$ for each i. The vector $(\gamma _1,\gamma _2, \gamma _3)$ corresponds to a codeword $c\in N/R$ . The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 6.

Table 6 $(N,\tau )$ for the case $7B$ .

8.3.5 $\tau \in 2C$

For $\tau \in 2C$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=2|\tau |=4$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $2$ and $ N_\tau =\mathrm {Span}_{\mathbb Z}\{ A_1^{12}, \frac {1}2(\alpha ,\dots , \alpha )\}, $ where ${\mathbb Z}\alpha \cong A_1$ . The vector $\frac {1}2(\alpha ,\dots , \alpha )$ again corresponds to a codeword $c\in N/R$ . The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 7.

Table 7 $(N, \tau )$ for the case $2C$ .

8.3.6 $\tau \in 4C$

For $\tau \in 4C$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=|\tau |=4$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $4$ and the coinvariant lattice

$$\begin{align*}N_\tau = \mathrm{Span}_{\mathbb Z}\{ A_3^4 A_1^2, (\lambda, \lambda, \lambda, \lambda, \frac{1}{2}\alpha, \frac{1}{2}\alpha)\}, \end{align*}$$

where $\lambda = 1/2(1,1,1,-3)\in A_3^*$ and ${\mathbb Z}\alpha = A_1$ . Note that $N^\tau $ contains $A_3^4 A_1^2$ as an index $4$ sublattice. The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 8.

Table 8 $(N, \tau )$ for the case $4C$ .

8.3.7 $\tau \in 6E$

For $\tau \in 6E$ of $O(\Lambda )$ , we have $\ell =|\widehat {\tau }|=6$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $6$ and the coinvariant sublattice

$$\begin{align*}N_\tau \cong \mathrm{Span}_{\mathbb Z} \{ A_5^2A_2^2A_1^2 , (\beta, \beta, \gamma, \gamma, \frac{1}2 \alpha, \frac{1}2 \alpha)\}, \end{align*}$$

where $\beta = \frac {1}6(1^5, -5)\in A_5^*$ , $\gamma = \frac {1}3 (1,1,-2)\in A_3^*$ and $\langle \alpha , \alpha \rangle =2$ . Note that $N^\tau $ is an index $6$ sublattice of $E_8\perp E_8$ . The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 9.

Table 9 $(N, \tau )$ for the case $6E$ .

8.3.8 $\tau \in 8E$

For $\tau \in 8E$ , $\ell =|\widehat {\tau }|=8$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $8$ and the coinvariant lattice $N_\tau $ is an index $8$ over-lattice of the lattice $A_7^2A_3A_1$ . More precisely,

$$\begin{align*}N_\tau= \mathrm{Span}_{\mathbb Z}\{ A_7^2A_3A_1, (\gamma_3, \gamma_1, \beta, \alpha) \}, \end{align*}$$

where $\gamma _3=\frac {1}8 (3^5, -5^3)$ , $\gamma _1=\frac {1}8 (1^7, -7)$ are in $A_7^*$ , $\beta \in \frac {1}2(1,1,1)\in A_3^* $ and $\alpha =\frac {1}2 (1,1)\in A_1^*$ .

The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in Table 9.

8.3.9 $\tau \in 6G$

For $\tau \in 6G$ , $\ell =|\widehat {\tau }| =12$ . Let $N=\Lambda ^{[ \tilde {\beta }] }$ . Then the Coxeter number of N is divisible by $6$ and $N_\tau $ contains $A_5^3 A_1^3$ as an index $6$ sublattice. The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in the following table.

8.3.10 $\tau \in 10F$

For $\tau \in 10F$ , $\ell =|\widehat {\tau }|=20$ . The Coxeter number of $N=\Lambda ^{[ \tilde {\beta }] }$ is divisible by $10$ and $N_\tau $ contains $A_9^2 A_1^2$ as an index $10$ sublattice. The possible choices for $(N, \tau )$ , c and the corresponding root systems and Lie algebra structures are listed in the following table.

Remark 8.10. Since $N_\tau = L_A(c)$ with c as a codeword of the glue code $N/R$ , we can recover the same information as in [21, Table 3]. In particular, there are exactly $46$ possible Lie algebra structures for $V_1$ if $0 < \mathrm{rank}(V_1) < 24$ . This gives an alternative proof for the Schellekens list.

A Properties of the lattice $\Lambda _{\tau} $ for $\tau \in \mathcal{P}_0$

In this appendix, we review some properties of the coinvariant sublattice $\Lambda _\tau $ for $\tau \in \mathcal{P}_0$ . Let $\Lambda $ be the Leech lattice and let

$$ \begin{align*}\tau \in \mathcal{P}_0=\{1A,2A, 2C, 3B, 5B, 7B, 4C, 6E, 6G, 8E, 10F\}.\end{align*} $$

Let $\Lambda _\tau $ be the coinvariant lattice of $\tau $ . Then $\tau $ is fixed-point free on $\Lambda _\tau $ .

The following can be verified by MAGMA.

Lemma A.1. Let $\tau \in \mathcal{P}_0$ . Then

1. 1. $(1-\tau )\Lambda _{\tau }^*=\Lambda _\tau $ .

2. 2. The quotient group $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $ acts faithfully on $\mathcal {D}(\Lambda _\tau )$ .

For $\tau \in \mathcal{P}_0$ , the coinvariant lattice $\Lambda _\tau $ can be constructed by the so-called generalized ‘Construction B’. First, we review the construction.

Generalized ‘Construction B’

Let $R_i (1\le i\le t)$ be a copy of the root lattice of type $A_{k_i-1}$ , where $k_i\in {\mathbb Z}_{\ge 1}$ for $1\le i\le t$ . Let $R=R_1\perp R_2\perp \dots \perp R_t$ . Then $\mathcal {D}(R_i)\cong {\mathbb Z}_{k_i}$ and $\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ . Let $\nu :R^*\to R^*/R=\mathcal {D}(R)\cong \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ be the canonical surjective map. For a subgroup C of $\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ , let $L_A(C)$ denote the lattice defined by

(A.1) $$ \begin{align} L_A(C)=\nu^{-1}(C)=\{\alpha\in R^*\mid \nu(\alpha)\in C\}; \end{align} $$

we call $L_A(C)$ the lattice constructed by Construction A from C. Note that $L_A(\{\mathbf {0}\})=R$ , where $\mathbf {0}$ is the identity element of $\bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ .

We now fix a base $\Delta _i$ of the root system of $R_i$ , which is of type $A_{k_i-1}$ . Then $\Delta =\bigcup _{i=1}^t\Delta _i$ is a base of the root system of R. For $x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ , denote

(A.2) $$ \begin{align} \lambda_x=(\lambda_{x_1}^1,\dots,\lambda_{x_t}^t)\in R_1^*\perp\dots\perp R_t^*=R^*, \end{align} $$

where $x_i$ is regarded as an element of $\{0,\dots ,k_i-1\}$ and $\{\lambda _{j}^i\mid 1\le j\le k_i-1\}$ is the set of fundamental weights in $R_i^*$ with respect to $\Delta _i$ . The following lemma is immediate from the definition of $L_A(C)$ .

Lemma A.2. For a generating set $\mathcal {C}$ of C, the set $\{\lambda _c\mid c\in \mathcal {C}\}$ and R generate $L_A(C)$ as a lattice.

Set

(A.3) $$ \begin{align} \chi_\Delta=(\frac{\rho_{\Delta_1}}{k_1},\dots,\frac{\rho_{\Delta_t}}{k_t})\in {\mathbb Q}\otimes _{\mathbb Z} R, \end{align} $$

where $\rho _{\Delta _i}$ is the Weyl vector of $R_i$ with respect to $\Delta _i$ .

Define $ L_B(C)=\{\alpha \in L_A(C)\mid (\alpha |\chi _\Delta )\in {\mathbb Z}\} $ ; we call $L_B(C)$ the lattice constructed by Construction B from C.

Remark A.3. Up to isometry, $L_B(C)$ does not depend on the choice of a base $\Delta $ .

By definitions, it is easy to show the following results (see [34]).

Lemma A.4. Let $x=(x_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ . Then $(\lambda _x|\lambda _x)\in 2{\mathbb Z}$ if and only if $(\lambda _x|\chi _\Delta )\in {\mathbb Z}$ .

Set $n=\mathrm {LCM}(\{k_1,\dots ,k_t\})$ .

Lemma A.5. $|L_A(C):L_B(C)|=n$ if and only if $\chi _\Delta \in (1/n)L_A(C)^*$ .

Next, we consider some isometry of R. Recall that $R_i\cong A_{k_i-1}$ is a root lattice of type $A_{k_i-1}$ . Let $\Delta _i=\{\alpha ^i_1, \dots , \alpha ^i_{k_i-1}\}$ be a set of simple roots and let $ \alpha ^i_0=-\sum _{j=1}^{k_i-1} \alpha ^i_{j}$ be the negative of the highest root. Then the map $g_{\Delta _i}(\alpha ^i_j)=\alpha ^i_{j+1}$ if $1\le j\le k_i-2$ and $g_\Delta (\alpha ^i_{k_i-1})=\alpha ^i_0$ defines an isometry on $R_i$ , which is a Coxeter element of the Weyl group of $R_i$ . In particular, $g_{\Delta _i}$ acts on $\tilde {\Delta }_i=\Delta _i \cup \{\alpha ^i_0\}$ as a cyclic permutation of order $k_i$ .

For $e=(e_i)\in \bigoplus _{i=1}^t{\mathbb Z}_{k_i}$ , set

(A.4) $$ \begin{align} g_{\Delta,e}=((g_{\Delta_1})^{e_1},\dots,(g_{\Delta_t})^{e_t})\in O(L_A(C)). \end{align} $$

Lemma A.6. $g_{\Delta ,e}\in O(L_B(C))$ if and only if $\lambda _e\in L_A(C)^*$ .

Proof. By definition, it is easy to see that

(A.5) $$ \begin{align} g_\Delta(\lambda_j)=\lambda_j-\sum_{i=1}^j\alpha_i,\quad g_{\Delta}(\rho_{\Delta})=\rho_{\Delta}-k\lambda_{1}. \end{align} $$

Then we have $ g_{\Delta ,e}(\chi _\Delta )\in \chi _\Delta +(e_1\lambda _1^1,\dots ,e_t\lambda _1^t)+R=\chi _\Delta +\lambda _e+R. $ By the definition of $L_B(C)$ , $g_{\Delta ,e}\in O(L_B(C))$ if and only if $\lambda _e\in L_A(C)^*$ .

Lemma A.7. The isometry $g_{\Delta ,e}$ is fixed-point free and of order n if and only if $\gcd (e_i,k_i)=1$ for all $1\le i\le t$

It turns out that the coinvariant lattice $\Lambda _\tau $ for $\tau \in \mathcal{P}_0$ can be constructed as $L_B(C)$ with C generated by a single glue vector c. Moreover, $\tau $ can be identified with $g_{\Delta ,c}$ as defined above.

Proposition A.8 [5]

For any $\tau \in \mathcal{P}_0$ , the coinvariant lattice $\Lambda _\tau $ of the Leech lattice can be constructed as $L_B(C)$ with C generated by a single glue vector c. Moreover, $\tau |_{L_B(C)}=g_{\Delta ,c}$ as defined above.

Some properties of $\Lambda _\tau $ are summarized in Table 10; the structures of $O(\Lambda _g)$ and $C_{O(\Lambda _g)}(g)$ are computed by using MAGMA. The symbol $\prod {a_i}^{b_i}$ for $\Lambda _\tau ^*/\Lambda _\tau $ means the abelian group $\bigoplus ({\mathbb Z}/a_i{\mathbb Z})^{b_i}$ . For the notations of groups, see [1].

Table 10 Coinvariant lattices $\Lambda _\tau $ for $\tau \in \mathcal{P}_0$ .

For $\tau \in O(\Lambda )$ and $k\in {\mathbb Z}_{>0}$ , set

(A.6) $$ \begin{align} \mathcal{L}_{\tau,k}=\{ \lambda+\Lambda_g\in \mathcal{D}(\Lambda_\tau)\mid q(\lambda+\Lambda_\tau)=0,\ o(\lambda+\Lambda_\tau)=k\}, \end{align} $$

where $o(\lambda +\Lambda _\tau )$ is the order of $\lambda +\Lambda _\tau $ in $\mathcal {D}(\Lambda _\tau )$ . The following lemmas can be verified by using MAGMA [5].

Lemma A.9. Let $\tau $ be an isometry of $\Lambda $ whose conjugacy class is $2A$ , $3B$ , $5B$ or $7B$ . Then $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $ acts transitively on the set of all nonzero singular elements.

Lemma A.10. Let $\tau $ be an isometry of $\Lambda $ whose conjugacy class is $4C$ , $6E$ or $8E$ . Let k be a divisor of $|\tau |$ . Then $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $ acts transitively on $\mathcal {L}_{\tau ,k}$ .

Lemma A.11. Let $\tau $ be an isometry of $\Lambda $ whose conjugacy class is $6G$ or $10F$ . Then the group $C_{O(\Lambda _\tau )}(\tau )/\langle \tau \rangle $ acts transitively on $\mathcal {L}_{\tau , \, |\tau |/2}$ .