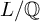DISTRIBUTION OF FROBENIUS ELEMENTS IN FAMILIES OF GALOIS EXTENSIONS

Abstract

Given a Galois extension $L/K$ of number fields, we describe fine distribution properties of Frobenius elements via invariants from representations of finite Galois groups and ramification theory. We exhibit explicit families of extensions in which we evaluate these invariants and deduce a detailed understanding and a precise description of the possible asymmetries. We establish a general bound on the generic fluctuations of the error term in the Chebotarev density theorem, which under GRH is sharper than the Murty–Murty–Saradha and Bellaïche refinements of the Lagarias–Odlyzko and Serre bounds, and which we believe is best possible (assuming simplicity, it is of the quality of Montgomery’s conjecture on primes in arithmetic progressions). Under GRH and a hypothesis on the multiplicities of zeros up to a certain height, we show that in certain families, these fluctuations are dominated by a constant lower order term. As an application of our ideas, we refine and generalize results of K. Murty and of Bellaïche, and we answer a question of Ng. In particular, in the case where $L/{\mathbb {Q}}$ is Galois and supersolvable, we prove a strong form of a conjecture of K. Murty on the unramified prime ideal of least norm in a given Frobenius set. The tools we use include the Rubinstein–Sarnak machinery based on limiting distributions and a blend of algebraic, analytic, representation theoretic, probabilistic and combinatorial techniques.

1 Introduction

1.1 Background and perspective

The Chebotarev density theorem, one of the major number theoretic achievements of the early $20$ th century, has been proven to be of crucial importance in a variety of problems. Beyond knowing the exact asymptotic densities of primes in Frobenius sets, one often needs to understand the dependence of the involved error term as a function of the invariants of the associated field extension. In this direction, Lagarias and Odlyzko [LO] established an effective Chebotarev density theorem. Letting $L/K$ be a Galois extension of number fields and assuming GRH for $\zeta _L(s)$ (an assumption sometimes called ‘ERH for L’), they showed that for any conjugacy class $C\subset \mathrm { Gal}(L/K)$ , the function

(1) $$ \begin{align} \pi(x;L/K,C):= \# \{ \mathfrak p \subset \mathcal O_K \text{ unram. in }L/K: \mathcal N \mathfrak p \leq x, \mathrm{Frob}_{\mathfrak p} = C \}\,, \end{align} $$

where $\mathrm {Frob}_{\mathfrak p}$ (respectively, $\mathcal N\mathfrak p$ ) denotes the Frobenius conjugacy class (respectively, the cardinality of the residue field $\mathcal O_K/\mathfrak p$ ) corresponding to a prime ideal $\mathfrak p$ of $\mathcal O_K$ , satisfies the estimate [Se3, Theorem 4]

(2) $$ \begin{align} \pi(x;L/K,C) - \frac{|C|}{|G|} \mathrm{Li }(x) \ll \frac{|C|}{|G|} x^{\frac 12} \log(d_L x^{[L:{\mathbb{Q}}]})\,, \end{align} $$

where $\mathrm {Li}(x):=\int _2^x (\log t)^{-1}\mathrm {d}t$ , $d_L$ is the absolute value of the discriminant of $L/{\mathbb {Q}}$ and the implied constant is absolute (unless otherwise specified, all implied constants in this paper will be absolute). This estimate was a cornerstone in Serre’s seminal work [Se3] with applications, for example, to the Lang–Trotter conjecture and the open image theorem for elliptic curves. Effective Chebotarev estimates also led Murty [Mu1] and later Bucur–Kedlaya [BK] to develop applications to effective Sato–Tate distributions in a general context. Subsequently, the GRH result of Lagarias–Odlyzko was refined under Artin’s Conjecture (AC) by Murty–Murty–Saradha [MMS], and more recently by Bellaïche [Be1], who adopted a new representation theoretic point of view and used extra inputs from Kowalski’s axiomatic large sieve. It is now known that under GRH and AC, the right-hand side of (2) can be replaced with $\lambda _G(C)x^{\frac 12} \log (x|G| d_K^{1/[K:{\mathbb {Q}}]} R_{L})$ , where $R_L$ is the product of the prime numbers ramified in $L/{\mathbb {Q}}$ , and where the ‘Littlewood norm’

$$\begin{align*}\lambda_G(C):=\frac{|C|}{|G|}\sum_{\chi \in \mathrm{Irr}(G) } |\chi(C)|\chi(1) \end{align*}$$

is $\leq |C|^{\frac 12}$ (which is the bound that [MMS] relies on), and can be significantly smaller in some families (see [Be1, Section 2.3]). These and further refinements were shown to have applications to the arithmetic of elliptic curves and bounds on the size of the least prime in a Frobenius set (see [LMO, Za, TZ1, TZ2], see also [CK2, EM, GrMo, KNW, Winc]). Along these lines, we mention the work of Cho–Kim [CK1] and of Pierce–Turnage-Butterbaugh–Wood [PTW] (see also [TZ3]), who managed to further refine the estimates of Lagarias–Odlyzko in families and to deduce bounds on exponents and $\ell $ -torsion of class groups of number fields. Remarkably, important applications of effective Chebotarev have also been obtained outside the realm of number theory. Indeed, Kuperberg [Kup] solved an important computability problem in knot theory, under the GRH for Artin L-functions.

In this paper, we investigate asymptotic properties of the limiting distribution of a suitable normalisation of the error term

(3) $$ \begin{align} \pi(x;L/K,C) - \frac{|C|}{|G|} \mathrm{Li}(x) \end{align} $$

in families of Galois extensions of number fields. In some of the families of number field extensions that we shall consider, we will show that for most values of x, the error term (3) is dominated by a lower order term of constant size.

To illustrate our results, we consider the family $\{K_d\}$ of Hilbert class fields of ${\mathbb {Q}}(\sqrt d)$ , with d running over negative fundamental discriminants. A general unconditional version of the following result will be stated in Theorem 2.1.

Theorem 1.1. Let $d\leq -4$ be a fundamental discriminant, let $K_d$ be the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ and write $G_d=\mathrm {Gal}(K_d/{\mathbb {Q}})$ . Assuming the Riemann hypothesis for $\zeta _{K_d}(s)$ (i.e. ERH for $K_d$ ), the limiting distribution of

$$ \begin{align*}E(y;K_d/{\mathbb{Q}},\{\mathrm{id}\}):= y{\mathrm{e}}^{-y/2} \Big(\pi({\mathrm{e}}^y;K_d/{\mathbb{Q}},\{\mathrm{id}\}) - \frac{\mathrm{Li}({\mathrm{e}}^y)}{|G_d|}\Big)\end{align*} $$

exists, has mean $ \asymp -1 $ and variance $\ll h(d)^{-1}m_d\log |d|, $ where $m_d$ is the maximal ¹ order of vanishing of $\zeta _{K_d}(s)$ in the region $\{s\in \mathbb C : 0<\Im (s) \leq h(d)(\log |d|)^3\}$ and $h(d)$ is the class number of ${\mathbb {Q}}(\sqrt d)$ . Assuming in addition that $m_d$ is bounded by an absolute constant, the variance is $\asymp h(d)^{-1}\log |d|, $ and we have that

(4) $$ \begin{align} \liminf_{Y \rightarrow \infty}\frac{\mathrm{meas} \{y\leq Y : E(y;K_d/{\mathbb{Q}},\{\mathrm{id}\})<0 \}}{Y} \geq 1-O\Big(\frac{\log |d| \log\log |d|}{\sqrt{|d|}}\Big), \end{align} $$

where $\mathrm {meas}$ is the Lebesgue measure.

The mean and variance calculations in Theorem 1.1 imply that under ERH for $K_d$ and for ‘most values’ of $\log x$ (meaning that the exceptional values of $\log x$ in $[0,X]$ have a Lebesgue probability measure approaching $0$ as $X\to \infty $ ), one has

$$ \begin{align*}|G_d|\pi(x;K_d/{\mathbb{Q}},\{\mathrm{id}\}) - \mathrm{Li}(x) = x^{\frac 12}(\log x)^{-1} (-c_dh(d) +O(\sqrt{h(d)m_d\log |d|})),\end{align*} $$

where $\tfrac 12\leq c_d \leq 1+ h(d)^{-1}\mathrm {ord}_{s=\frac 12} \zeta _{K_d}(s) \ll 1$ . By means of comparison, (2) (as well as the further refinements mentioned above) yield the error term $O(h(d)\log (x|d|)\log x)$ . Our improved error term allows us to deduce that if d is such that ² $m_d=o(\sqrt {|d|}/(\log |d|\log \log |d|))$ , then the error term in the Chebotarev density theorem is dominated by a significant lower order term. Moreover, the lower bound (4) can be interpreted by saying that when $|d|$ is large, $\pi ({\mathrm {e}}^y;K_d/{\mathbb {Q}},\{\mathrm {id}\}) < \mathrm {Li}({\mathrm {e}}^y)/|G_d|$ for most values of y.

Theorem 1.1 is a manifestation of an extreme Chebyshev bias, which generalises his observation made back in 1853 that in ‘most intervals’ $[2,x]$ , primes are more abundant in the residue class $3$ than in the class $1$ , modulo $4$ . The literature on this question is rich, and much progress has been made in recent years. For an exhaustive list of the numerous papers on the subject, see [GrMa, MS, M+].

Following a suggestion made by Rubinstein and Sarnak, Ng [Ng] generalised the framework of [RbS] to the context of Galois extensions $L/K$ of number fields and performed extensive numerical computations. As is illustrated in Theorem 1.1, the present work also considers the setting of Galois extensions of number fields. The more general context of Artin L-functions differs from the classical study of discrepancies in the distribution of primes in arithmetic progressions in several aspects. Notably, there are examples of Artin L-functions which vanish at $\tfrac 12$ (see [Ar] and Example 1.3). Artin L-functions associated to irreducible representations of $\mathrm {Gal}(L/K)$ might also have nonsimple complex zeros. This can substantially influence fine properties of the distribution of prime ideals in Frobenius sets (the influence of real zeros was predicted in [RbS] and further explored in [Ng]). This makes the obvious extension of the linear independence assumption in [RbS] (used to evaluate densities of subsets of primes) trivially false. Consequently, the notion of primitive L-function, highlighted by Rudnick–Sarnak in [RdS], will be central in our analysis. The Artin L-function of an irreducible representation of $\mathrm {Gal}(L/K)$ will typically factorise as a product (with multiplicities) of primitive L-functions.

By introducing a reduction of prime ideal counting functions in the relative extension $L/K$ to prime counting functions in $L/{\mathbb {Q}}$ , we will express the former in terms of sums of zeros of L-functions that are expected to be primitive. This is the key observation that will allow us to refine K. Murty’s bound on the unramified prime ideal of least norm (as well as the Bellaïche improvements) in a given Frobenius set. We will then apply the Rubinstein–Sarnak machinery involving limiting distributions arising from Besicovitch $B^2$ almost-periodic functions. Finally, after translating the problem to a probabilistic setting, we will establish central limit and large deviation type results in various families of Galois extensions. This will allow us to understand the distribution of the error term in the Chebotarev density theorem, and, in turn, to deduce precise asymptotic estimates on Chebyshev’s bias. In our first main result (see Theorem 2.1), we prove new estimates on the mean and variance of the limiting distribution of (3) in terms of the ramification data of $L/K$ as well as representation theoretic invariants of $\mathrm {Gal}(L/K)$ . Secondly, in Theorems 2.3 and 2.6, we settle and refine a conjecture of K. Murty on the unramified prime ideal of least norm in a given Frobenius set (this takes into account Bellaïche’s improvements), and we refine the bounds of Murty–Murty–Saradha and Bellaïche on the error term in the Chebotarev density theorem. Thirdly, under suitable hypotheses, such as the Artin holomorphicity conjecture and the Riemann hypothesis, we apply our limiting distribution estimates to provide an asymptotic description of Chebyshev’s bias in terms of the characters of $\mathrm {Gal}(L/K)$ and the discriminant of $L/{\mathbb {Q}}$ , reducing the question to an effective inverse Galois problem. We tackle these invariants in several important families that are well-studied in the literature and deduce asymptotic estimates on this bias. In the generic case where $\mathrm {Gal}(L/K)=S_n$ , we are able to apply powerful combinatorial estimates, such as Roichman’s bound [Ro] in order to deduce a precise asymptotic formula for the bias which we show is best possible (see Theorem 2.15); this settles quantitatively a question of Ng.

The paper is organised as follows. In Section 2, we state our main results, which are of two distinct types. On one hand, we obtain general information on the limiting distribution of (3) and we give an asymptotic description of the densities in terms of invariants of the extension $L/K$ . On the other hand, we establish precise estimates on the mean and variance of this limiting distribution in the case of specific families of Galois extensions: abelian, dihedral, radical and $S_n$ extensions, as well as Hilbert class fields of quadratic fields. We devote Section 3 to explicit formulas and their translation into the probabilistic setting that is well-suited to our approach. The arithmetic core of our method is described in Section 4, where we relate the mean and the variance of the limiting distribution of (3) to sums of characters of $\mathrm {Gal}(L/K)$ and Artin conductors and prove our unconditional results (see Theorem 2.6) as well as Murty’s conjecture in any Galois number field extension for which Artin’s conjecture is known to hold (see Theorem 2.3). Our main probabilistic results, effective central limit theorems and large deviation estimates, are then stated and proved in Section 5. In Section 6, we conclude the proofs of our general results. We devote Section 7 to the case of extensions $L/K$ for which $L/{\mathbb {Q}}$ is Galois of group $\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ . We establish precise estimates on the mean and variance by exploiting the description of the irreducible representations in terms of Young tabloids and the associated combinatorial formulas for character values (chiefly the hook-length formula). In Section 8, we prove the statements relative to some families of abelian extensions, including the case of the Hilbert class field of a quadratic field $K_d/{\mathbb {Q}}(\sqrt {d})$ . Finally, in Section 9, we focus on three specific families of supersolvable extensions of ${\mathbb {Q}}$ . First, we investigate a family of dihedral extensions with controlled discriminant that was constructed by Klüners. Second, in the case of the Hilbert class field of a quadratic field ${\mathbb {Q}}(\sqrt {d})$ seen as an extension of the rationals, we apply bounds on class numbers of (real and imaginary) quadratic fields due to Montgomery–Weinberger and Chowla. Third, we study radical extensions ${\mathbb {Q}}(\zeta _p,a^{1/p})/{\mathbb {Q}}$ , where $a,p$ are distinct odd primes, such that p is not Wieferich to base a, making heavy use of Viviani’s explicit computation [Vi] of the filtration of inertia at a and p.

1.2 Statement of assumptions

We now state the hypotheses which will be used in this paper. We stress that some of our results are unconditional and some depend on one or more of the hypotheses below (see, for example, Theorem 2.1). In fact, much of our work is done without assuming GRH or LI.

We fix an absolute positive constant $M_0$ (say $M_0=10^5$ ). We let $L/K$ be an extension of number fields for which $L\neq {\mathbb {Q}}$ is Galois over ${\mathbb {Q}}$ and define $G=\mathrm {Gal}(L/K), G^+=\mathrm {Gal}(L/{\mathbb {Q}})$ . For a finite group $\Gamma $ , we denote by $\mathrm {Irr}(\Gamma )$ the set of irreducible characters and by $\Gamma ^\sharp $ the set of conjugacy classes. For any number field $M $ , we denote by $d_M$ the absolute value of its absolute discriminant. The hypotheses below will depend on the extension $L/{\mathbb {Q}}$ rather than on $L/K$ ; as mentioned earlier (see also Example 1.3), the Artin L-functions associated to irreducible characters of $\mathrm {Gal}(L/K)$ are not primitive in general. For $\chi \in \mathrm {Irr}(G)$ , we will denote by $L(s,L/K,\chi )$ the associated Artin L-function (see [Mar, Chapter 1, Section 4] for a definition).

1. (AC) We assume Artin’s holomorphicity conjecture which states that for every nontrivial $ \chi \in \mathrm {Irr}(G^+)$ , the associated Artin L-function $L(s,L/{\mathbb {Q}},\chi )$ is entire. ³

2. (GRH⁻) We assume that for every $\chi \in \mathrm {Irr}(G^+)$ , $\sup \{\Re (\rho ): L(\rho ,L/{\mathbb {Q}},\chi )=0\}<1,$ and moreover, $L(s,L/{\mathbb {Q}},\chi )$ has a zero on the line $\Re (s)=\sup \{\Re (\rho ): L(\rho ,L/{\mathbb {Q}},\chi )=0\}$ .

3. (GRH) We assume the Riemann hypothesis for the extension $L/{\mathbb {Q}}$ , that is, every nontrivial zero of $L(s,L/{\mathbb {Q}},\chi )$ lies on the line $\Re (s)=\frac 12$ , for every $\chi \in \mathrm {Irr}(G^+)$ .

4. (BM) We assume that there exists an absolute constant $M_0>0$ , such that every nonreal zero of

   $$ \begin{align*}\prod_{ \chi \in \mathrm{Irr}(G^+)}L(s,L/{\mathbb{Q}},\chi)\end{align*} $$

   up to height $(\log d_L\log \log d_L)^2$ has multiplicity at most $M_0$ . Moreover, for each $\chi \in \mathrm { Irr}(G^+),$

   $$ \begin{align*}\mathrm{ord}_{s=\frac 12}L(s,L/{\mathbb{Q}},\chi)\leq M_0.\end{align*} $$

The following generalises a classical and widely used hypothesis of Wintner [Wint] on the diophantine properties of the zeros of the Riemann zeta function. As discussed in [RbS, Section 5], in the case of Artin L-functions, it is quite delicate to state. First, it is believed that $L(s,L/{\mathbb {Q}},\chi )$ is primitive whenever $\chi $ is irreducible. Second, we need to take into account the potential existence of real zeros. This is strongly linked to the Frobenius–Schur indicator of the corresponding character $\chi $ and the Artin root number of $L(s,L/{\mathbb {Q}},\chi )$ . As illustrated in Example 1.3 below, those two properties do not necessarily hold for $L(s,L/K,\chi )$ .

1. (LI ⁻) We assume that the multiset of positive imaginary parts of the zeros of all Artin L-functions $L(s,L/{\mathbb {Q}},\chi )$ in the region $\{s\in \mathbb C :\Re (s)\geq \tfrac 12\}$ , with $\chi \in \mathrm {Irr}(G^+)$ , are linearly independent over the rationals.

2. (LI) We assume LI $^-$ . Moreover, we assume that $L(\frac 12,L/{\mathbb {Q}},\chi )\neq 0$ if $\chi $ is an orthogonal or unitary irreducible character of $G^+$ , and that for any symplectic irreducible character $\chi $ of $G^+$ , one has the uniform bound $\mathrm {ord}_{s=\frac 12}L(s,L/{\mathbb {Q}},\chi )\leq M_0$ (see Theorem 3.3 for the definition of orthogonal, unitary and symplectic character). Finally, we assume that for every $\beta \in (0,1)\setminus \{ \tfrac 12\}$ and $ \chi \in \mathrm {Irr}(G^+)$ , $L(\beta ,L/{\mathbb {Q}},\chi ) \neq 0$ .

Remark 1.2. For an irreducible character $\chi $ of $G^+$ , let $W(\chi )$ be the attached root number (the ‘sign’ of the functional equation, see [Mar, Section 4]). We actually believe that a statement stronger than LI holds (say LI $^+$ ), that is in addition to LI, for any symplectic character $\chi \in \mathrm {Irr}(G^+)$ , we have that

$$ \begin{align*}\mathrm{ ord}_{s=\frac 12}L(s,L/{\mathbb{Q}},\chi)=\frac{1-W(\chi)}{2}\end{align*} $$

(in other words, $L(\frac 12,L/{\mathbb {Q}},\chi )=0$ may only occur as a consequence of $W(\chi )=-1$ ). Hypothesis LI $^{+}$ generalises its counterpart for Dirichlet L-functions. In this case, there is theoretical progress in [MN1] and [LR] (see also the very interesting discussions therein on linear independence properties of L-function zeros in general), as well as computational verification up to a fixed height (see [BT, MOT]). In the general case, the reason why Hypothesis LI includes a statement about vanishing at $s=\frac 12$ comes from the existence of Galois extensions $L/{\mathbb {Q}}$ with Galois group admitting a symplectic irreducible character $\chi $ of Artin root number $W(\chi )=-1$ (see, e.g. [Mar, Chapter 1, Section 4(ii)] for the definition), so that ⁴ $L(\frac 12,L/{\mathbb {Q}},\chi )=0$ . It is known [FQ] that in the general case of a Galois extension of number fields $L/K$ , the Artin root number of an orthogonal irreducible representation is $1$ . LI asserts that for unitary characters associated to $L/{\mathbb {Q}}$ , one has $W(\chi )\neq -1$ (this is not necessarily true for relative extensions $L/K$ ; see Example 1.3).

We now give an explicit example to illustrate that Artin L-functions attached to irreducible characters $\chi $ of relative extensions are not primitive in general, and might vanish at $s=\frac 12$ for reasons independent of their root number.

Example 1.3 (Serre, see, e.g. [Ng, Section 5.3.3]).

Let $L={\mathbb {Q}}(\theta )$ , where $\theta $ is a root of the ${\mathbb {Q}}$ -irreducible polynomial $x^8-205x^6+13\,940x^4-378\,225x^2+3\,404\,025$ . Serre shows that $L/{\mathbb {Q}}$ is Galois of group isomorphic to the quaternion group $\mathbb {H}_8$ of order $8$ and, moreover, that the only nonabelian irreducible character (denoted $\chi _5$ in loc. cit.) of $G=\mathrm {Gal}(L/{\mathbb {Q}})\simeq \mathbb {H}_8$ is symplectic of degree $2$ and satisfies $W(\chi _5)=-1$ so that $L(\frac 12,L/{\mathbb {Q}},\chi _2)=0$ . There are five irreducible characters of $\mathbb {H}_8$ all real valued; four of them have degree $1$ and thus correspond to the Kronecker symbol attached to a fundamental discriminant computed by Ng. Artin’s factorisation property gives rise to the following decomposition of the Dedekind zeta function of L:

$$ \begin{align*} \zeta_L(s)&=\prod_{\chi\in \mathrm{Irr}(G)}L(s,L/{\mathbb{Q}},\chi)^{\chi(1)}\\ &=\zeta(s)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{5}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{41}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{205}{\cdot}\Big)\bigg)L(s,L/{\mathbb{Q}},\chi_5)^2. \end{align*} $$

Ng numerically checks the nonvanishing at $\frac 12$ of the three Dirichlet L-functions of quadratic characters appearing above, so that $L(s,L/{\mathbb {Q}},\chi _5)$ is entirely responsible for the vanishing of $\zeta _L$ at $\frac 12$ . There are three quadratic subextensions of $L/{\mathbb {Q}}$ with respective discriminant $5$ , $41$ and $205$ ; if we fix one such discriminant D, then the corresponding subfield $K_D$ of L has the property that $G=\mathrm {Gal}(L/K_D)$ is cyclic of order $4$ . Thus, G has four irreducible representations of degree $1$ ; two of them are orthogonal (the trivial representation and a character of order $2$ ), and two of them (denoted $\psi $ and $\bar {\psi }$ ) are unitary. A straightforward group theoretic computation shows that

$$ \begin{align*}\mathrm{Ind}_G^{\mathbb H_8}\psi=\mathrm{Ind}_G^{\mathbb H_8}\bar{\psi}=\chi_5\,. \end{align*} $$

By properties of Artin root numbers and Artin L-functions (see, e.g. [Mar, Section 4]), we have $W(\psi )=W(\bar {\psi })=W(\chi _5)=-1$ and $L(\frac 12,L/K_D,\psi )=L(\frac 12,L/K_D,\bar {\psi })=L(\frac 12,L/K_D,\chi _5)=0$ . Therefore, Serre’s example shows that in the case of a relative extension of number fields $L/K$ , one may have $L(\frac 12,L/K,\chi )=0$ for a unitary representation of $\mathrm {Gal}(L/K)$ . What assumption LI asserts in this case is that vanishing at $\frac 12$ for $L(s,L/K,\chi )$ is explained by the symplectic irreducible representation of root number $-1$ that appears in the character induced by $\chi $ on the Galois group of the normal closure of L (in the example, it is L itself) over ${\mathbb {Q}}$ .

Another interesting phenomenon that the same example illustrates is the potential multiplicity of L-factors in a relative extension, for a given L-function. Indeed, let $Z=\{\pm 1\}$ be the centre of $\mathbb {H}_8$ and consider this time the quadratic extension $L/L^Z$ . Let $\varepsilon $ be the nontrivial character of $\mathrm {Gal}(L/L^Z)$ . This gives rise to a new factorisation of $\zeta _L(s)$ :

$$ \begin{align*} \zeta_L(s)&=\zeta(s)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{5}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{41}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{205}{\cdot}\Big)\bigg)L(s,L/{\mathbb{Q}},\chi_5)^2\\&=L(s,L/L^Z,1)L(s,L/L^Z,\varepsilon)\,. \end{align*} $$

The factor $L(s,L/L^Z,1)$ is the Dedekind zeta function of $L^Z$ , an abelian extension of ${\mathbb {Q}}$ of degree $4$ . Therefore

$$ \begin{align*}L(s,L/L^Z,1)=\zeta(s)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{5}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{41}{\cdot}\Big)\bigg)L\bigg(s,L/{\mathbb{Q}},\Big(\frac{205}{\cdot}\Big)\bigg), \end{align*} $$

and in turn

$$ \begin{align*}L(s,L/L^Z,\varepsilon)=L(s,L/{\mathbb{Q}},\chi_5)^2\,. \end{align*} $$

We deduce the existence of orthogonal representations with associated L-function vanishing at $\tfrac 12$ , and we also see that the multiset of critical zeros of $L(s,L/L^Z,\varepsilon )$ has repeated elements.

2 Statement of results

We consider a Galois extension $L/K$ of number fields, and set $G=\mathrm {Gal}(L/K)$ . If $L/{\mathbb {Q}}$ is also Galois, then we write $G^+=\mathrm {Gal}(L/{\mathbb {Q}})$ . We let $G^\sharp $ denote the set of conjugacy classes of G and $\mathrm {Irr}(G)$ denote its set of irreducible characters. Given $\chi \in \mathrm {Irr}(G)$ and a class function $t:G\rightarrow \mathbb C$ , we define the Fourier transform

$$ \begin{align*}\widehat t(\chi) := \langle t,\chi \rangle_G = \frac 1{|G|}\sum_{g\in G} t(g) \overline{\chi(g)}\,,\end{align*} $$

its support $\mathrm {supp}(\widehat {t}):=\{\chi \in \mathrm {Irr}(G)\colon \langle \chi ,t\rangle _G\neq 0\}$ , as well as the norms

(5) $$ \begin{align} {\lVert{t}\rVert}_1:=\frac 1{|G|}\sum_{g\in G} |t(g)|; \hspace{2cm} {\lVert{t}\rVert}^2_2:= \langle t,t\rangle_G =\frac 1{|G|}\sum_{g\in G} |t(g)|^2. \end{align} $$

Note that for class functions $t_1,t_2:G\rightarrow \mathbb C$ , Parseval’s identity reads

(6) $$ \begin{align} \langle t_1 ,t_2\rangle_G = \langle \widehat {t_1} ,\widehat{t_2} \rangle_{\mathrm{Irr}(G)} := \sum_{\chi \in \mathrm{Irr}(G)} \widehat{t_1}(\chi)\overline{\widehat{t_2}(\chi)}\,; ,\end{align} $$

in particular, ${\lVert {\widehat {t}}\rVert }_2 = {\lVert {t}\rVert }_2.$ We also consider the Littlewood norm [Be1, Section 1.2, (1)]

$$ \begin{align*}\lambda(t) := \sum_{\chi \in \mathrm{Irr}(G)} \chi(1)|\widehat t(\chi)|.\end{align*} $$

In the case where $L/{\mathbb {Q}}$ is Galois, we extend t to the well-defined class function $t^+=\mathrm {Ind}_G^{G^+}(t):G^+ \rightarrow \mathbb C$ that satisfies for all $g\in G^+$ ,

(7) $$ \begin{align} t^+(g)= \sum_{\substack{aG\in G^+/G : \\a^{-1} g a \in G }} t(a^{-1} g a). \end{align} $$

We also extend conjugacy classes $C\in G^\sharp $ to well-defined ⁵ conjugacy classes of $G^+$ by setting

(8) $$ \begin{align} C^+:=\bigcup_{aG\in G^+/G} a C a^{-1}. \end{align} $$

We consider the Frobenius counting function

$$ \begin{align*}\pi(x;L/K,t):=\sum_{\substack{\mathfrak p\triangleleft \mathcal O_K \text{ unram.}\\ \mathcal N\mathfrak p \leq x}} t(\mathrm{Frob}_{\mathfrak p}),\end{align*} $$

as well as its normalisation ⁶

(9) $$ \begin{align} E(y;L/K,t):= y{\mathrm{e}}^{-y\beta^t_{L}} (\pi({\mathrm{e}}^y;L/K,t) - \widehat t(1)\mathrm{Li}({\mathrm{e}}^y)), \end{align} $$

where, for $t\not \equiv 0$ ,

(10) $$ \begin{align} \beta^t_{L}= \begin{cases} \sup\{ \Re(\rho) : L(\rho,L/{\mathbb{Q}},\chi)=0; \chi \in \mathrm{supp}(\widehat{t^+}) \} & \text{ if AC holds for } L/{\mathbb{Q}} ;\\ \sup\{ \Re(\rho) : \zeta_L(\rho)=0 \} &\text{ otherwise}. \end{cases} \end{align} $$

(If $t\equiv 0$ , we set $\beta ^t_{L}=\frac 12$ .) If t is real valued, then we also define the densities

(11) $$ \begin{align} \underline{\delta}(L/K;t):=& \liminf_{Y\rightarrow \infty} \frac{\mathrm{meas} \{ y\leq Y : E(y;L/K,t)>0 \}}{Y}\,; \\ \overline{\delta}(L/K;t):=& \limsup_{Y\rightarrow \infty} \frac{\mathrm{meas} \{ y\leq Y : E(y;L/K,t)>0 \}}{Y}\,,\nonumber \end{align} $$

which will measure to which extent a constant lower order term is dominating the fluctuations of the error term in the Chebotarev density theorem. If the upper and lower limits coincide, their common value are denoted by $\delta (L/K;t)$ .

The prime example of class function we will consider is

$$ \begin{align*}t_{C_1,C_2}:=\frac{|G|}{|C_1|}1_{C_1} - \frac{|G|}{|C_2|}1_{C_2},\end{align*} $$

where $C_1,C_2\in G^\sharp $ are distinct and, for any conjugacy invariant set $D\subset G$ , $1_D$ is the indicator function of D. By convention, we will allow $C_2$ to be equal to $0$ , in which case, we define $t_{C_1,0}:= |G||C_1|^{-1}1_{C_1}$ , and we write $C_2^+=0, |C_1^+|^{-1}+|C_2^+|^{-1} := |C_1^+|^{-1}$ .

In [RbS], it is noted that there are discrepancies in the distribution of primes in residue classes $a \bmod q$ towards values of a that are quadratic nonresidues. Accordingly, the authors considered the distribution of the natural counting function

(12) $$ \begin{align} \#\{ p\leq x : p\not \equiv \square \bmod q\} - \#\{ p\leq x : p \equiv \square \bmod q\} \end{align} $$

for moduli q for which there exists a primitive root modulo q. For general moduli, one should add a weight [Fi1], that is, if $q=15$ , one should consider $\pi (x;15,2)+\pi (x;15,7)+\pi (x;15,8)+\pi (x;15,11)+\pi (x;15,13)+\pi (x;15,14)-3\pi (x;15,1)-3\pi (x;15,4)$ ; note that $-3=1-\#\{x\bmod 15\colon x^2=1\}=1-\#\{x\bmod 15\colon x^2=4\}$ . We generalise this by considering the class function

(13) $$ \begin{align} r(g)=r_G(g) := \#\{ h\in G : h^2 =g\}. \end{align} $$

Then, $\pi (x;L/K,1-r)$ is the natural generalisation of the counting function (12). For the concrete example of the different possible values of the weight $1-r(\mathrm {Frob}_p)$ in the case $G=S_6$ , we refer the reader to Table 1.

Table 1 The conjugacy classes and irreducible characters of $S_6$

In the following table, we highlight three important particular cases of class functions, where $C,C_1,C_2 \in G^\sharp $ and $C_1\neq C_2$ . Here, we compute $t^+:G^+\rightarrow \mathbb C$ using (56), and $\widehat {t^+}$ using Frobenius reciprocity and Lemma 3.2 (the case $k=2$ of (46) gives the definition of the Frobenius–Schur indicator $\varepsilon _2(\chi )=\widehat {r}(\overline {\chi })$ which is also equal to $\widehat {r}(\chi )$ since $\varepsilon _2(\chi )\in \{-1,0,1\}$ ; see the discussion following Lemma 3.2). Note also that for any $C\in G^\sharp $ and $\chi \in \mathrm {Irr}(G^+)$ , $\chi (C^+)=\chi |_G(C)$ .

We also compute the corresponding inner products and norms, which will appear later.

Finally, in the case $K={\mathbb {Q}}$ , we have that ⁷ $-\langle 1-r,r \rangle _G = |\widehat G_{\,\mathrm {real}}|-1$ , ${\lVert {1-r}\rVert }_2=(|\widehat G_{\,\mathrm {real}}|-1)^{\frac 12}$ and ${\lVert {1-r}\rVert }_1 = 2-2|G|^{-1} \#\{ g\in G : r(g)\geq 1 \}$ . Note that if $|G|$ is odd, then $1-r \equiv 0$ .

2.1 General Galois extensions

As mentioned in the Introduction, we will translate fine distribution properties of Frobenius elements in terms of the representation theory of $G=\mathrm {Gal}(L/K)$ and the ramification data of $L/K$ . In this section, we state the precise results spelling out this idea. We refer the reader to [LO, (5.2)] for the definition of the Artin conductor $A(\chi )$ . Moreover, we let $\mathrm {rd}_L$ be the root discriminant of L, that is

(14) $$ \begin{align} \mathrm{rd}_L = d_L^{\frac 1{[L:{\mathbb{Q}}]}}\,,\\[-14pt]\nonumber \end{align} $$

where we recall that $d_L$ is the absolute value of the absolute discriminant of L. For convenience, we associate to any class function $t:G\rightarrow \mathbb C$ a formal object $L(s,L/K,t)$ for which we define the log derivative by extending the case of Artin L-functions:

(15) $$ \begin{align} \frac{L'(s,L/K,t)}{L(s,L/K,t)}:= \sum_{\chi \in \mathrm{Irr}(G)} {\widehat t(\chi)} \frac{L'(s,L/K,\chi)}{L(s,L/K,\chi)}\,. \\[-14pt]\nonumber\end{align} $$

Accordingly, we define the order of vanishing at some $s_0\in \mathbb C$ as follows:

(16) $$ \begin{align} \mathrm{ord}_{s=s_0} L(s,L/K,t) := \sum_{\chi\in\mathrm{Irr}(G)} {\widehat t(\chi)}\cdot \mathrm{ord}_{s=s_0} L(s,L/K,\chi)\,.\\[-14pt]\nonumber \end{align} $$

Our first main result is the following. We say that the function $E: \mathbb R_+\rightarrow \mathbb C$ admits the limiting distribution $\nu $ if $\nu $ is a probability measure on $\mathbb C$ , such that for any bounded continuous function $f:\mathbb C\rightarrow \mathbb R$ ,

$$ \begin{align*} \lim_{Y\rightarrow \infty} \frac 1Y\int_0^Y f(E(y)) \mathrm{d}y = \int_{\mathbb C} f \mathrm{d} \nu=\mathbb E[f]\,.\\[-14pt]\end{align*} $$

The mean and variance of the associated random variable $Z_\nu $ are defined by

$$ \begin{align*}\mathbb E[Z_\nu] =\mathbb E[\Re(Z_\nu)]+i \mathbb E[\Im(Z_\nu)]; \qquad \mathrm{Var}[Z_\nu] =\mathbb E[|Z_\nu-\mathbb E[Z_\nu]|^2].\\[-14pt]\end{align*} $$

Theorem 2.1. Let $L/K$ be a Galois extension of number fields and fix a class function $t:G\rightarrow \mathbb C$ . Recall that $\beta _L^t$ is defined by (10) and that the class function r is defined by (13). Then, $E(y;L/K,t)$ admits a limiting distribution whose mean is

$$ \begin{align*}\mu_{L/K,t}= -\langle t,r \rangle_G \delta_{\beta^t_L=\frac 12}-\frac 1{\beta_L^t}\mathrm{ord}_{s=\beta_L^t}L(s,L/K,t),\end{align*} $$

where $\delta $ is Kronecker’s delta and whose variance is

(17) $$ \begin{align} \sigma^2_{L/K,t}\ll {\lVert{t}\rVert}_1^2\log (d_L+2) \min(M_{L},\log (d_L+2)),\\[-14pt]\nonumber \end{align} $$

where $M_{L} := \max \big \{ \mathrm {ord}_{s=\rho } \zeta _L(s) : \Re (\rho )=\beta _L^t, 0<|\Im (\rho )|< \log (d_L+2)(\log \log (d_L+2))^2\big \}. $ Inother words, for generic values of y, we have the estimate

(18) $$ \begin{align} E(y;L/K,t)= \mu_{L/K,t}+O({\lVert{t}\rVert}_1 (\log (d_L+2))^{\frac 12} \min(M_{L},\log (d_L+2))^{\frac 12}).\\[-14pt]\nonumber \end{align} $$

Assuming that $L/{\mathbb {Q}}$ is Galois and that AC holds, we have the more precise ⁸ bound

(19) $$ \begin{align} \sigma^2_{L/K,t}\ll (m_{L})^2 \log(\mathrm{rd}_L+2)\sum_{ \chi\in \mathrm{Irr}(G^+) } \chi(1)|\widehat{t^+}(\chi)|^2.\\[-15pt]\nonumber \end{align} $$

Here, denoting $T_{L}:= \log (\mathrm {rd}_L+2) \sum _{\substack {\chi \in \mathrm {Irr}(G^+) }} \chi (1) $ ,

$$ \begin{align*}m_{L} := \max \Big \{ \mathrm{ord}_{s=\rho} \Big(\prod_{\substack{\chi \in \mathrm{supp}(\widehat{t^+}) }} L(s,L/{\mathbb{Q}},\chi)\Big) : \Re(\rho)=\beta_L^t,0<|\Im(\rho)|< (T_L\log T_L)^2\Big\}.\end{align*} $$

Assuming, moreover, GRH and ⁹ LI, we have the lower bound

(20) $$ \begin{align} \sigma^2_{L/K,t}\gg \sum_{ \chi\in \mathrm{Irr}(G^+) } \chi(1)|\widehat{t^+}(\chi)|^2.\\[-15pt]\nonumber \end{align} $$

Finally, assuming, in addition, that each irreducible representation of $G^+=\mathrm {Gal}(L/{\mathbb {Q}})$ of dimension $\geq {\lVert {t^+}\rVert }_2 {\lVert {t^+}\rVert }_1^{-1} (2\#\mathrm { Irr}(G^+))^{-\frac 12}$ satisfies the bound $\max _{1\neq C \in (G^+)^\sharp } |\chi (C)| \leq (1-\eta )\chi (1)$ for some real number $0<\eta <1$ which depends on t and $G^+$ , then we have that

(21) $$ \begin{align} \sigma^2_{L/K,t}\gg \eta\log(\mathrm{rd}_L+2)\sum_{ \chi\in \mathrm{Irr}(G^+) } \chi(1)|\widehat{t^+}(\chi)|^2.\\[-15pt]\nonumber \end{align} $$

If $\widehat t\not \equiv 0$ , then the character sum in (21) satisfies the general bounds

$$ \begin{align*}\frac{{\lVert{t^+}\rVert}_2^3}{{\lVert{t^+}\rVert}_1(\#\mathrm{supp}(\widehat{t^+}))^{\frac 12}} \leq \sum_{ \chi\in \mathrm{Irr}(G^+) } \chi(1)|\widehat{t^+}(\chi)|^2 \leq |G^+|^{\frac 12} {\lVert{t^+}\rVert}_2.\\[-15pt]\end{align*} $$

Remark 2.2. The error term in (18) is significantly sharper than that in (2), as well as the further refinements of Murty–Murty–Saradha ([MMS, Section 3, in particular Corollary 3.7]) and Bellaïche ([Be1, Théorème 1]). As a matter of comparison, taking $q\geq 3$ , $L={\mathbb {Q}}(\zeta _q)$ , $K={\mathbb {Q}}$ , $t=\phi (q) 1_a$ for some $a\in (\mathbb Z/q\mathbb Z)^\times $ and assuming BM, (18) translates to

$$ \begin{align*}E(y;{\mathbb{Q}}(\zeta_q)/{\mathbb{Q}},t) = \mu_{{\mathbb{Q}}(\zeta_q)/{\mathbb{Q}},t} + O((q\log q)^{\frac 12}),\\[-14pt]\end{align*} $$

which under GRH is of the strength of Montgomery’s conjecture (see [FG, Conjecture 1]) on primes in arithmetic progressions (since $E(y;{\mathbb {Q}}(\zeta _q)/{\mathbb {Q}},t) = y{\mathrm {e}}^{\frac y2}\phi (q)(\pi ({\mathrm {e}}^y;q,a)-\phi (q)^{-1}\mathrm { Li}({\mathrm {e}}^y))$ ). This answers a question of Murty–Murty–Saradha [MMS, Section 3.13] about the ‘true size’ of this error term, at least for generic and large enough values of y. A detailed generalisation of Montgomery’s conjecture with a range of validity and various applications will appear in a forthcoming paper joint with Morrison and Thorner. Comparing this with [Be1, Théorème 1] (which holds for all y), we see that for an extension $L/{\mathbb {Q}}$ with $G=\mathrm {Gal}(L/{\mathbb {Q}})$ , the ratio between the bound on $E(y;L/{\mathbb {Q}},t)$ in loc. cit. and the bound given in (19) (i.e. our $L^2$ bound) is

$$ \begin{align*} \gg y \frac{ \log({\mathrm{e}}^y \mathrm{rd}_L)}{(\log(\mathrm{rd}_L+2))^{\frac 12}}\frac{\sum_{\chi \in \mathrm{Irr}(G)} \chi(1)|\widehat t(\chi)|}{\Big(\sum_{\chi \in \mathrm{Irr}(G)} \chi(1)|\widehat t(\chi)|^2\Big)^{\frac 12} } ,\end{align*} $$

which is clearly large. One can do a similar comparison with [MMS] for relative extensions.

As for our similar looking estimates (17) and (19), we see that for the extension ${\mathbb {Q}}(\zeta _q)/{\mathbb {Q}}$ , they are of the same quality since $\chi (1)=1$ . However, if, for example, we work with the class function $t_{C_1,C_2}$ in a family where $\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ , then the ratio between (17) and (19) is $\gg \min (|C_1|,|C_2|)$ . As a more extreme example, we will see in Theorem 2.19 that there exist extensions for which the upper bound in (19) is identically zero. As this suggests, to fully understand the fluctuations of $E(y;L/K,t)$ , it is not sufficient to decompose it using the characters of the group G – zeros that are either multiple or common to different characters significantly affect the formula for the variance. To take this into account, we will formulate a transfer principle relating $E(y;L/K,t)$ to $E(y;L/{\mathbb {Q}},t^+)$ in Proposition 3.11 and Corollary 3.17 (see also Remark 3.19).

An interesting consequence of Theorem 2.1 (more precisely of Proposition 3.18, combined with (59) and Lemma 3.2) is that under AC and GRH, the limiting distributions of the functions $y{\mathrm {e}}^{-y/2} (|G^+| \pi ({\mathrm {e}}^y;L/{\mathbb {Q}},\{\mathrm {id}\}) - \mathrm {Li}({\mathrm {e}}^y))$ and $y{\mathrm {e}}^{-y/2} (|G| \pi ({\mathrm {e}}^y;L/K,\{\mathrm {id}\})-\mathrm { Li}({\mathrm {e}}^y))$ have the same variance, however, the mean of the first is always less than or equal to that of the second.

We now discuss applications of our ideas. We first focus on Linnik-type problems for Frobenius sets. Lagarias et al. [LMO] showed that under GRH, and for a given extension of number fields $L/K$ and for any conjugacy class $C\subset \mathrm {Gal}(L/K)$ , there exists an unramified prime ideal $\mathfrak p \triangleleft \mathcal O_K$ of norm $ \ll (\log (d_L+2))^2 $ for which $\mathrm {Frob}_{\mathfrak p}=C$ . Bellaïche [Be2, Proposition 1] has shown that in the case $C=\{ \mathrm {id} \}$ , the exponent $2$ in this bound is best possible (see also [Fio]). However, K. Murty conjectured [Mu2, Conjecture 2.2] that under GRH, we have the general bound $ \ll (\log (d_L+2))^2/|C| $ , which decreases when $|C|$ grows. This conjecture was motivated by [Mu2, Theorem 3.1], which shows that under the Riemann hypothesis and Artin’s conjecture for every $L(s,L/K,\chi )$ with $\chi \in \mathrm {Irr}(G)$ , we have the bound $ \ll [K:{\mathbb {Q}}]^2([L:K]\log [L:K] +\log (d_L+2))^2/|C| $ (the additional factors here come, in part, from the contribution of ramified prime ideals). In the case where $K={\mathbb {Q}}$ and the condition that $\mathfrak p \triangleleft \mathcal O_K$ is unramified is dropped, Bellaïche [Be1, Théorème 3] showed that under AC and GRH, one can obtain sharper results in several important families. More precisely, one can obtain a bound in terms of the invariant

(22) $$ \begin{align} \varphi_G(C) := \inf\Big\{ \frac{\lambda(t)}{\widehat t(1)} \,\,\Big|\,\, t\colon G\rightarrow \mathbb R ;\,\widehat t(1)>0;\, \big(t(g) > 0\Rightarrow g\in C\big)\Big\} \ll \frac{|G|}{ |C|^{\frac 12}} \end{align} $$

(the bound follows from taking $t=1_C$ and applying Cauchy–Schwarz). We are now ready to state our bounds on the least unramified prime ideal in a given Frobenius set.

Theorem 2.3. Let $L/K$ be a Galois extension of number fields, and assume that the Riemann hypothesis and Artin’s conjecture hold for each $L(s,L/K,\chi )$ with $\chi \in \mathrm {Irr}(\mathrm { Gal}(L/K))$ . Then, Murty’s conjecture holds. In other words, for any conjugacy class $C\subset G$ , there exists an unramified prime ideal $\mathfrak p \triangleleft \mathcal O_K$ for which $\mathrm {Frob}_{\mathfrak p} = C$ and

(23) $$ \begin{align} \mathcal N\mathfrak p\ll \frac{(\log (d_L+2))^2}{|C|}.\\[-7pt]\nonumber \end{align} $$

More precisely, taking into account Bellaïche’s refinement, ¹⁰ for any class function $t:G \rightarrow \mathbb R$ such that $\widehat t(1)> 0$ , there exists an unramified prime ideal $\mathfrak p \triangleleft \mathcal O_K$ for which $t(\mathrm { Frob}_{\mathfrak p})>0$ and

(24) $$ \begin{align} \mathcal N\mathfrak p\ll \Big( \frac{\lambda(t)}{\widehat t(1)}\log(\mathrm{rd}_L+2) [K:{\mathbb{Q}}] \Big)^2.\\[-7pt]\nonumber \end{align} $$

If in addition $L/{\mathbb {Q}}$ is Galois and AC holds, then there exists an unramified prime ideal $\mathfrak p \triangleleft \mathcal O_K$ for which $\mathrm {Frob}_{\mathfrak p} = C$ and

(25) $$ \begin{align} \mathcal N\mathfrak p \ll \frac{ (\log (d_L+2) )^2}{|C^+|}+ \frac{ (\log (d_K+2) )^{\frac 43} |G|^{\frac 43}}{|C|^{\frac 23}}\\[-7pt]\nonumber \end{align} $$

(note that the second term in (25) is $\ll (\log (d_L+2))^{\frac 43} |C|^{-\frac 23} \ll (\log (d_L+2))^{2} (|G^+||C|)^{-\frac 23} $ ). Finally, under the same hypotheses and incorporating Bellaïche’s refinement, we obtain that for any class function $t:G \rightarrow \mathbb R$ , such that $\widehat t(1)>|G|^{-100}\sup |t|$ , there exists an unramified prime ideal $\mathfrak p \triangleleft \mathcal O_K$ for which $t(\mathrm {Frob}_{\mathfrak p})>0$ and

(26) $$ \begin{align} \mathcal N\mathfrak p &\ll \Big( \frac{\lambda(t^+)}{\widehat {t}(1)}\log(\mathrm{rd}_L+2) \Big)^2 + \frac{\lambda(t)}{\widehat t(1)}[K:{\mathbb{Q}}] \log(\mathrm{rd}_L+2) \\&\qquad\qquad +\sum_{\substack{2\leq \ell \ll \log\log d_L \nonumber\\ \mu^2(\ell)=1}} \Big(\Big( \frac{|\langle t,r_\ell \rangle_G|}{\widehat t(1)} \Big)^{\frac{\ell}{\ell-1}}+\Big(\frac{\lambda((t(\cdot^\ell) )^+)}{\widehat t(1)}\log(\mathrm{rd}_L+2) \Big)^{\frac{2\ell}{2\ell-1}}\Big).\\[-7pt]\nonumber \end{align} $$

Example 2.4. As an example in which (26) and (25) are significantly sharper than (23) and (24), consider any $S_n$ extension $L/{\mathbb {Q}}$ and $K=L^{\langle (12\cdots n)\rangle }$ . Clearly for $\sigma =(1\,2\cdots n)$ , one has $|\{\sigma \}^+| = (n-1)!, $ and likewise for any k coprime to n, taking $C=\{\sigma ^k\}$ , we have that $|C|=1$ and $|C^+|=(n-1)!$ . Thus, our bound on the unramified prime ideal $\mathfrak p$ of least norm for which $\mathrm {Frob}_{\mathfrak p}=C$ is $ \mathcal N\mathfrak p\ll (\log (d_L+2))^2/n!^{\frac 23} $ . In comparison, the bounds (23) and (24) are both $\asymp (\log (d_L+2))^2$ (see [Be1, Proposition 17]).

More generally, considering the extension $L/L^H$ , where $H \triangleleft S_n$ is a subgroup containing an element $h $ of cycle type $\lambda = (\lambda _1,\dots \lambda _k) \vdash n$ , the bound (25) is

$$ \begin{align*}\ll (\log (d_L+2))^2 \Big( \frac{\prod_{1\leq j \leq n} j^{a_j} a_j!}{n!}+ \frac 1{n!^{\frac 23}}\Big),\\[-9pt] \end{align*} $$

where $a_j = \# \{ i\leq k : \lambda _i=j\}$ .

Remark 2.5. One can give a simple heuristic argument that shows why we expect the bound (25) rather than (23). If L and K are both Galois over ${\mathbb {Q}}$ , and p is a prime number that splits completely in K and for which $\mathrm {Frob}_p=C^+$ , then for any prime ideal $\mathfrak p \triangleleft \mathcal O_K$ above p, we have that $\mathrm {Frob}_{\mathfrak p} =C$ .

Using similar arguments as in Theorem 2.3, we obtain a refinement of the Lagarias–Odlyzko–Serre, Murty–Murty–Saradha and Bellaïche bounds on the error term in Chebotarev’s density theorem.

Theorem 2.6. Let $L/K$ be a Galois extension of number fields for which $L/{\mathbb {Q}}$ is Galois, let $t:G\rightarrow \mathbb C$ be a class function and assume AC and GRH. Then for all $x\geq 2$ , we have the bound

(27) $$ \begin{align} \pi(x;L/K,t) - \widehat t(1)\mathrm{Li}(x) &\ll \lambda(t^+)x^{\frac 12} \log ( \mathrm{rd}_L x)\log x\\&\qquad + \sum_{\substack{2\leq \ell \leq 2\log x \nonumber\\ \mu^2(\ell)=1}}(x^{\frac 1\ell} |\langle t,r_\ell\rangle_G|+x^{\frac 1{2\ell}} \lambda((t(\cdot^\ell))^+) \log ( \mathrm{rd}_Lx )\log x).\\[-9pt]\nonumber \end{align} $$

Moreover, the quantity $\lambda ((t(\cdot ^\ell ))^+)$ can be replaced by $[K:{\mathbb {Q}}]\lambda (t(\cdot ^\ell ))$ . In the particular case $t=|G||C|^{-1}1_C$ , where $C\subset G$ is a conjugacy class, the right-hand side of (27) is $\ll ( |G^+||C^+|^{-\frac 12} x^{\frac 12} +|G^+||G|^{\frac 12}|C|^{-1} x^{\frac 14} )\log ( \mathrm {rd}_L x) \log x.$ Here, $G^+:=\mathrm {Gal}(L/{\mathbb {Q}})$ and $C^+$ is defined by (8).

Next, we turn to applications of our results to discrepancies in the distribution of Frobenius elements in conjugacy classes. We will combine Theorem 2.1 with estimates on Artin conductors (see Lemma 4.1) and probabilistic bounds on large deviations of random variables to detect when $\delta (L/K;t)$ (see (11)) is very close to $1$ , conditionally on AC, GRH and BM.

The following statement makes use of the Frobenius–Schur indicator $\varepsilon _2$ of an irreducible character (see (46) and Theorem 3.3): $\varepsilon _2$ takes the value $0$ at a nonreal irreducible character and the value $\pm 1$ at a real irreducible character. The value $+1$ (respectively, $-1$ ) corresponds to representations that are realizable (respectively, not realisable) over $\mathbb R$ .

Theorem 2.7. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and fix $t:G\rightarrow \mathbb R$ a class function, such that ¹¹ $\langle t ,r \rangle _G <0$ and $t^+\not \equiv 0$ . Assume that AC, GRH and BM hold. If for some small enough $\eta>0$ , the inequality

(28) $$ \begin{align} -\langle \widehat {t} , \varepsilon_2 \rangle_{\mathrm{Irr}(G)} -2\mathrm{ord}_{s=\frac 12} L(s,L/K,t)> \Big(\eta^{-1} \log (\mathrm{rd}_L+2) \sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1) |\widehat{t^+}(\chi)|^2\Big)^{\frac 12} \end{align} $$

holds, then the fluctuations of $E(y;L/K,t)$ are dominated by a constant term, that is

$$ \begin{align*}\underline{\delta}(L/K;t)> 1-c_1\eta.\end{align*} $$

Under the additional assumption LI, we have the refined bound

$$ \begin{align*}\delta(L/K;t)> 1-\exp(-c_2\eta^{-1}).\end{align*} $$

Finally, if $K={\mathbb {Q}}$ and $|\widehat {t}(\chi )|\in \{0,1\}$ for all $\chi \in \mathrm {Irr}(G)$ , then we also have the upper bound

$$ \begin{align*}\delta(L/{\mathbb{Q}};t) < 1-\exp(-c_3\eta^{-1}).\end{align*} $$

Here, $c_1,c_2,c_3>0$ are absolute constants.

As a partial converse to Theorem 2.7, we show using an effective central limit theorem that up to the factor $\log (\mathrm { rd}_L+2)$ , the condition (28) is also sufficient. Here, the condition LI is required, since we need a lower bound on the variance and an estimate on higher moments.

Theorem 2.8. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH $^-$ and LI hold. Fix a class function $t:G\rightarrow \mathbb R$ , such that $\widehat {t^+}\not \equiv 0$ , and let $\eta>0$ be small enough. If the condition

(29) $$ \begin{align} \Big(\langle \widehat {t} , \varepsilon_2 \rangle_{\mathrm{Irr}(G)} +2\mathrm{ord}_{s=\frac 12} L(s,L/K,t) \Big)^2 < \eta^2 \sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1) |\widehat{t^+}(\chi)|^2\, \end{align} $$

is satisfied, then

(30) $$ \begin{align} \delta(L/K;t) - \frac 12 \ll \eta + \frac{{\lVert{t^+}\rVert}_1(\#\mathrm{Irr}(G^+))^{\frac 16}}{{\lVert{t^+}\rVert}_2} \,. \end{align} $$

Assuming further that $ |\langle \widehat t,\varepsilon _2\rangle _{\mathrm {Irr}(G)}+2\mathrm {ord}_{s=\frac 12} L(s,L/K,t)|\geq \eta ^{-\frac 12}, $ then the second error term on the right-hand side of (30) can be deleted.

Remark 2.9. The reason why the factor $\log (\mathrm {rd}_L+2)$ appearing in Theorem 2.7 does not appear in Theorem 2.8 is because of our lower bound for the Artin conductor in Lemma 4.1. If the trivial bound $|\chi (g)|\leq \chi (1)$ can be improved to a bound of the form $|\chi (g)|\leq (1-\kappa )\chi (1)$ for some fixed $\kappa>0$ , for many characters $\chi $ of G and for every $g\neq 1$ , then we can deduce a sharper lower bound for the Artin conductor of these characters (see Lemma 4.2). Such is the case for $G=S_n$ thanks to Roichman’s bound (see (124) and Proposition 7.6), and this allows for a more precise evaluation of $\delta (L/K;t)$ (see Theorem 2.15).

Example 2.10. Take $K={\mathbb {Q}}$ and $L/{\mathbb {Q}}$ of even degree (so that there is at least one nontrivial real character) and $t=1-r$ , so that $\widehat {t}(\chi )=1_{\chi =1}-\varepsilon _2(\chi )$ . Assuming BM, we have the upper bound

$$ \begin{align*}|\langle \widehat {1-r} , \varepsilon_2 \rangle_{\mathrm{Irr}(G)} +2\mathrm{ord}_{s=\frac 12} L(s,L/{\mathbb{Q}},1-r)| \leq (M_0+1)\sum_{ \substack{1\neq\chi \in \mathrm{Irr}(G) \\ \chi \text{ real} }} 1, \end{align*} $$

and hence, (29) holds whenever

(31) $$ \begin{align} \sum_{ \substack{1\neq \chi \in \mathrm{Irr}(G)\\ \chi \text{ real} }} 1 < (M_0+1)^{-1}\eta \Big(\sum_{ \substack{1\neq \chi \in \mathrm{Irr}(G)\\ \chi \text{ real}}} \chi(1)\Big)^{\frac 12}. \end{align} $$

If this is the case, then thanks to (115), we conclude under AC, GRH $^{-}$ and LI that (see the proof of Theorem 5.10 in which $\mathbb E[X(L/{\mathbb {Q}};1-r)]\in \mathbb Z$ )

$$ \begin{align*}\delta(L/{\mathbb{Q}};1-r) -\frac 12 \ll \eta\,.\end{align*} $$

Moreover, we have the lower bound

(32) $$ \begin{align} \langle \widehat {1-r} , \varepsilon_2 \rangle_{\mathrm{Irr}(G)}&+ 2\sum_{\substack{ \chi \in \mathrm{Irr}(G) }} \widehat{1-r}(\chi)\mathrm{ord}_{s=\frac 12}L(s,L/{\mathbb{Q}},\chi) \nonumber\\ &\qquad \geq \#\{1\neq \chi\in \mathrm{Irr}(G): \chi \text{ real}\}-M_0\#\{ \chi\in \mathrm{Irr}(G): \varepsilon_2(\chi)=-1\}, \end{align} $$

and hence, if ¹² $2M_0 \#\{ \chi \in \mathrm {Irr}(G): \varepsilon _2(\chi )=-1\} \leq \#\{ 1\neq \chi \in \mathrm {Irr}(G): \chi \,\mathrm {real}\},$ then the condition (28) holds whenever

(33) $$ \begin{align} \sum_{\substack{ 1\neq \chi \in \mathrm{Irr}(G)\\ \chi \,\mathrm{real} }} 1> \eta^{-\frac 12}\Big( \log (\mathrm{rd}_L+2) \sum_{\substack{1\neq \chi \in \mathrm{Irr}(G)\\ \chi \,\mathrm{real}}} \chi(1) \Big)^{\frac 12}. \end{align} $$

We expect the condition (31) to hold for many extensions, and hence, under AC, GRH $^-$ and LI, $\delta (L/{\mathbb {Q}};1-r)$ is often close to $\tfrac 12$ . Precisely, this holds if $G=G^+$ has a real irreducible representation of degree d and admits $o(\sqrt d)$ irreducible real representations. In the generic case $G=S_n$ , there exists exactly $p(n)\sim {\mathrm {e}}^{\pi \sqrt { \frac {2n}3}}/(4n\sqrt 3)$ (the number of partitions of n) real irreducible representations, one of which has degree $n!^{\frac 12-o(1)}$ (see Theorem 2.15).

Example 2.11. Take $L=\mathbb Q(\zeta _q)$ with $q\geq 3$ odd and squarefree in Example 2.10. Then the inequality (33) holds for all small enough $\eta>0$ satisfying

(34) $$ \begin{align} 2^{\omega(q)} \gg \eta^{-1} \log q\, \end{align} $$

(with an absolute implied constant), a condition which already appeared in [Fi1]. For general finite abelian groups, the number of real characters is equal to the number of elements of order at most 2, hence, the inequality (33) translates to

$$ \begin{align*}|\{ 1\neq g \in G : g^2 = 1\}| \gg \eta^{-1} \log (\mathrm{rd}_L+2).\end{align*} $$

As a consequence, for $\delta (L/{\mathbb {Q}};1-r)$ to be close to $1$ , it is sufficient that $\mathrm {Gal}(L/{\mathbb {Q}})$ contains a substantial $2$ -torsion subgroup and that $d_L$ is of controlled size. A good example of such an extension is ${\mathbb {Q}}(\sqrt {p_1},\sqrt {p_2},...,\sqrt {p_k})/{\mathbb {Q}}$ (where the $p_i$ ’s are pairwise distinct primes). In this case, (33) holds provided

$$ \begin{align*}2^k \gg \eta^{-1} \sum_{i=1}^k \log p_i.\end{align*} $$

Interestingly, if we put $q:=\prod _{i=1}^kp_i$ , then this is exactly (34). We will see that the inequality (34) plays an explicit role in the statement of Theorems 2.21 and 2.24 (see also Remark 2.23 that discusses the density of integers q, such that (34) holds).

We now derive group theoretic criteria that ensure that (30) holds.

Corollary 2.12. Let $L/K$ be an extension of number fields that are both Galois over ${\mathbb {Q}}$ for which AC, GRH $^-$ and LI hold. Fix a class function $t:G\rightarrow \mathbb R$ , such that $\widehat {t^+} \not \equiv 0$ , and fix $\varepsilon>0$ small enough. Then (30) holds, provided either of the following conditions ¹³ holds:

1. (1) ${\lVert {t^+}\rVert }_1^{\frac 12} ({\lVert {t}\rVert }_2+{\lVert {t^+}\rVert }_2)(\#\mathrm {Irr}(G^+))^{\frac 14}\cdot (\#\{ \chi \in \mathrm {Irr}(G)\cup \mathrm {Irr}(G^+) \colon \chi \text { real} \})^{\frac 12}< \varepsilon {\lVert {t^+}\rVert }_2^{\frac 32},$

2. (2) $ |\langle t,r \rangle _G|+\sum _{\substack {\chi \in \mathrm {Irr}(G) \\ \chi \text { symplectic} }}|\widehat {t^+}(\chi )| <\varepsilon {\lVert {t^+}\rVert }^{\frac 32}_2{\lVert {t^+}\rVert }^{-\frac 12}_1(\mathrm {supp}(\widehat t^+))^{-\frac 14} \,. $

So far, we have shown that the limiting values $1$ or $\frac 12$ are expected for the density $\delta (L/K;t)$ in many natural examples. Taking $t=1-r$ and $K={\mathbb {Q}}$ , one could ask whether $\delta (L/{\mathbb {Q}};1-r)$ can plainly equal those limiting values. The following general result gives an effective negative answer to this question.

Theorem 2.13. Let $L/{\mathbb {Q}}$ be a Galois extension for which AC, GRH $^-$ and LI hold, and let $d_L$ be the absolute discriminant of L.

1. (1) We have the bound

   $$ \begin{align*}\delta(L/{\mathbb{Q}};1-r)\leq 1-c_1\exp(-c_2\#\{\chi \in \mathrm{Irr}(G) : \chi \,\mathrm{real}\}) \end{align*} $$

   with positive absolute constants $c_1$ , $c_2$ .

2. (2) Assuming, moreover, GRH, recalling that $M_0>0$ is a fixed absolute constant, and assuming that there is a constant $\kappa \in (0,1)$ satisfying:

   • • $\#\{\chi \in \mathrm {Irr}(G)\colon \chi \text { real}\}>2\kappa ^{-1}$ ,

   • • $\#\{\chi \in \mathrm {Irr}(G)\colon \chi \text { symplectic}\} \leq \frac {1-\kappa }{2M_0} \#\{\chi \in \mathrm {Irr}(G)\colon \chi \text { real}\}$ ,

   then for $\max (d_L,\sum _{\substack {\chi \in \mathrm {Irr}(G) \\ \chi \,\mathrm {real}}} \chi (1))$ large enough, wehave:

   $$ \begin{align*}\delta(L/{\mathbb{Q}};1-r)-\frac 12 \geq c (\log (\mathrm{rd}_L+2))^{-\frac 12}\Big( \sum_{ \substack{ \chi \in \mathrm{Irr}(G) \\ \chi \,\mathrm{real}}}\chi(1)^2\Big)^{-\frac 14}\,, \end{align*} $$
   where $c>0$ is absolute.

These bounds are essentially optimal. The first one is sharp (up to a log factor in the exponent) in the following cases:

• • the dihedral extensions considered in Theorem 2.17,

• • the extension $K_d/{\mathbb {Q}}$ , where $K_d$ is the Hilbert class field of a quadratic field ${\mathbb {Q}}(\sqrt {d})$ (see Theorems 1.1 and 2.18),

• • the abelian extension ${\mathbb {Q}}(\sqrt {p_1},\ldots ,\sqrt {p_m})/{\mathbb {Q}}$ (see Theorem 2.21).

As for (2) of Theorem 2.13, it is sharp in the case of p-cyclotomic extensions (where p is a prime number) as shown in [FM, (3.20)]. There are also cases where the value of $\delta (L/{\mathbb {Q}};1-r)$ differs significantly from this bound, notably:

• • the case of the radical extensions considered in Theorem 2.19,

• • the case of $S_n$ -extensions (see Theorem 2.15).

The representation theoretic assumptions in Theorem 2.13(2) are essential since in the case where G is a generalised quaternion group (see [Ba1]) or $G=\mathrm {SL}_2(\mathbb F_3)$ , one can have $\delta (L/{\mathbb {Q}};1-r)=\frac 12$ (see Remark 2.25).

Remark 2.14. Note that even in the case where G admits no symplectic character, it would still be possible to have $\delta (L/{\mathbb {Q}};t)=\frac 12$ . However, if one, moreover, assumes that $\langle t,r \rangle _G \neq 0$ (recall (13)), then a lower bound on $|\delta (L/{\mathbb {Q}};t)-\tfrac 12|$ could be deduced from an estimate on

$$ \begin{align*}\log (\mathrm{rd}_L+2)\sum_{\chi\in\mathrm{Irr}(G)}\chi(1)|\widehat{t}(\chi)|^2\,. \end{align*} $$

This could be done by following the lines of the proof of Theorem 2.13.

In the following sections, we focus on the cases where the class function t considered is either $t=1-r$ (see (47)) or $t=t_{C_1,C_2}=|G||C_1|^{-1}1_{C_1} - |G||C_2|^{-1}1_{C_2}$ for distinct conjugacy classes $C_1, C_2$ of G.

2.2 Generic case: $S_n$ -extensions

The case where $\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ is ‘generic’ in the sense that according to many orderings of number fields (see, e.g. [Ga, Mal]), $S_n$ is the most common Galois group. In this case, our results rely on the rich and beautiful representation theory of the symmetric group that involves the combinatorics of partitions and tabloids. As an application, we answer positively and quantitatively a question of Ng [Ng, Section 5.3.5] about whether, for any conjugacy class $C\neq \{\mathrm {id} \} $ , we have $ r(\{ \mathrm {id}\})>r(C)$ , and as a result $\delta (L/{\mathbb {Q}};t_{C, \mathrm {id}} )> \frac 12$ (see (36) below). The exact bound we obtain in (131) is

$$ \begin{align*}r(\{\mathrm{id}\})-r(C) \geq n!^{\frac 12};\end{align*} $$

one can deduce sharper bounds for specific conjugacy classes using bounds on the characters of $S_n$ . Such bounds have been established in the important papers of Roichman [Ro], Larsen–Shalev [LS] and Féray–Śniady [FeS]. In our context, we are able to apply Roichman’s bound to obtain estimates for $\delta (L/{\mathbb {Q}};t_{C_1,C_2})$ that take into account the ramification data. This is specific to $S_n$ since the factor $(\log (\mathrm {rd}_L))^{-\frac 12}$ appearing in (35) is not present in Theorem 2.8. This leads to an estimate for Chebyshev’s bias that is superior to that following from Theorem 2.8. The resulting bound shows that the Chebyshev bias dissolves both in the horizontal (i.e. as the size of the root discriminant increases) and the vertical (i.e. as the size of the Galois group increases) limits.

Theorem 2.15. Let $L/K$ be an extension of number fields for which L is Galois over ${\mathbb {Q}}$ . Assume that $G^+=\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ with $n\geq 2$ , and that AC, GRH and LI hold. Fix $\varepsilon>0$ , and let $C_1, C_2$ be distinct elements of $G^\sharp \cup \{0\}$ for which $C_1^+\neq C_2^+$ and $\min (|C_1^+|,|C_2^+|) \leq n!^{1-\frac {4+\varepsilon }{{\mathrm {e}} \log n}}$ . Then, the functions $ E(y;L/K,t_{C_1,C_2}), E(y;L/{\mathbb {Q}},1-r)$ admit limiting distributions whose respective means are ¹⁴

$$ \begin{align*}\ll \Big( \frac{n! p(n)}{\min(|C_1^+|,|C_2^+|)} \Big) ^{\frac 12}; \hspace{1cm} =p(n)-1,\end{align*} $$

and whose respective variances are

$$ \begin{align*}\ll \frac{n!^{\frac 32}\log (\mathrm{rd}_L) }{ \min(|C_1^+|,|C_2^+|) } ;\hspace{1cm} \asymp \log (\mathrm{rd}_L) (n/{\mathrm{e}})^{n/2}{\mathrm{e}}^{\sqrt{n}}\,. \end{align*} $$

Moreover, the variance of the limiting distribution of $E(y;L/K,t_{C_1,C_2})$ is

$$ \begin{align*}\gg \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big) \frac{n!^{\frac 32}\log (\mathrm{rd}_L) }{ \min(|C_1^+|,|C_2^+|)^{\frac 32} p(n)^{\frac 12}},\end{align*} $$

and as a consequence, we have the upper bound

(35) $$ \begin{align} \delta(L/K;t_{C_1,C_2})-\frac 12 \ll \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!}\Big)^{-\frac 12}\cdot \frac{n!^{-\frac 1{4}} p(n)^{\frac 34} \min(|C_1^+|,|C_2^+|)^{\frac 1{4}}}{ (\log (\mathrm{rd}_L) )^{\frac 12}}\,. \end{align} $$

This estimate is essentially best possible in the sense that specialising to $K={\mathbb {Q}}$ and $C_2=\{\mathrm {id}\}$ , we have, for any conjugacy class $C_1$ , the lower bound

(36) $$ \begin{align} \delta(L/{\mathbb{Q}};t_{C_1,\{\mathrm{id}\}})-\frac 12 \geq c \frac{n!^{-\frac 1{4}} }{ (\log (\mathrm{rd}_L) )^{\frac 12}}, \end{align} $$

where $c>0$ is absolute. Finally,

(37) $$ \begin{align} \delta(L/{\mathbb{Q}};1-r) - \frac 12 \asymp \frac{ n!^{-\frac 14} p(n) {\mathrm{e}}^{-\frac{\sqrt{n}} 2}n^{\frac 18}}{(\log (\mathrm{rd}_L))^{\frac 12}}. \end{align} $$

As a consequence, we can quantify the idea that a ‘random’ Galois extension of the rationals rarely produces a high Chebyshev bias. This is the purpose of the following statement.

Corollary 2.16. For a polynomial $f\in \mathbb Z[T]$ , let $K_f\subset \mathbb C$ denote its splitting field over ${\mathbb {Q}}$ . For fixed integers $n,N\geq 2$ set:

$$ \begin{align*}E_n(N)=\{f\in \mathbb Z[T]\colon f\text{ monic of degree }n\text{ with all its coefficients in }[-N,N]\}\,. \end{align*} $$

The proportion $\eta _{n,N}$ of polynomials $f\in E_n(N)$ , such that

(38) $$ \begin{align} \delta(K_f/{\mathbb{Q}};1-r) - \frac 12 \asymp \frac{ n!^{-\frac 14} p(n) {\mathrm{e}}^{-\frac{\sqrt{n}} 2}n^{\frac 18}}{(\log (\mathrm{rd}_{K_f}))^{\frac 12}} \end{align} $$

satisfies, under AC, GRH and LI for every $K_f/{\mathbb {Q}}$ ,

$$ \begin{align*}\eta_{n,N}\geq 1-O\Big(n^3\frac{\log N}{\sqrt{N}}\Big)\,. \end{align*} $$

For the lower bound of the corollary to make sense, one should first pick a large value of n so that (38) implies that the density $\delta (L/{\mathbb {Q}};1-r)$ is close to $\frac 12$ . Then one selects a large value of N (explicitly, N of size $n^{6+\varepsilon }$ suffices) so that the upper bound of the corollary is small, that is, the proportion of admissible polynomials is close to $1$ .

The proof of the corollary follows easily from combining Theorem 2.15 with Gallagher’s theorem (see, e.g. [Kow, Theorem 4.2]) that quantifies the fact that, generically, the splitting field over ${\mathbb {Q}}$ of a random monic integral polynomial of degree n has Galois group isomorphic to $S_n$ . Note that Gallagher’s bound has been improved (see, e.g. [Di]), and therefore, the lower bound in Corollary 2.16 is not best possible (one conjectures that $1-\eta _{n,N}\asymp _n N^{-1}$ ); we will still apply Gallagher’s bound because of its uniformity with respect to n.

2.3 Explicit families

In this section, we discuss our results for some families of supersolvable extensions of number fields (we recall that AC is known for such extensions).

2.3.1 Dihedral extensions

Recall that for $n\geq 1$ , the dihedral group $D_n$ is defined by

(39) $$ \begin{align} D_n:=\langle \sigma,\tau\colon \sigma^n=\tau^2=1,\, \tau\sigma\tau=\sigma^{-1}\rangle\,. \end{align} $$

Dihedral groups have a substantial proportion of elements of order $2$ , and this translates into the existence of many real irreducible characters (set $h=1$ in (45), and note that $D_n$ only has irreducible representations of degree bounded by $2$ and admits no symplectic character). As a consequence, dihedral Galois extensions are natural candidates for extensions that may exhibit extreme biases in the distribution of Frobenius elements. The following result confirms this intuition by using a construction due to Klüners [Kl].

Theorem 2.17. There exists a sequence $(K_\ell /{\mathbb {Q}})_{\ell \geq 7}$ of dihedral extensions indexed by prime numbers $\ell \geq 7$ , such that $\mathrm {Gal}(K_\ell /{\mathbb {Q}})\simeq D_\ell $ and, such that, conditionally on GRH and BM for $K_\ell /{\mathbb {Q}}$ and for the choice $(C_1,C_2)=(\{\tau \sigma ^k\colon 0\leq k\leq \ell -1\},\{\mathrm {id}\})$ , the functions $ E(y;K_\ell /{\mathbb {Q}},t_{C_1,\{\mathrm {id}\}}), E(y;K_\ell /{\mathbb {Q}},1-r)$ admit limiting distributions whose means are both $\gg \ell $ and whose variances are both $\ll \ell \log \ell $ . As a result, the fluctuations of these functions are dominated by a constant term, and one has that

$$ \begin{align*}\min\big(\underline{\delta}(K_\ell/{\mathbb{Q}};t_{C_1,C_2}), \underline{\delta}(K_\ell/{\mathbb{Q}};1-r)\big)\geq 1-O\Big(\frac{\log\ell}\ell\Big)\,. \end{align*} $$

If one additionally assumes LI for $K_\ell /{\mathbb {Q}}$ , then both $\delta (K_\ell /{\mathbb {Q}};1-r)$ and $\delta (K_\ell /{\mathbb {Q}};t_{C_1,C_2})$ exist and one has the refined bounds

$$ \begin{align*}&\exp(-c_1\ell)\leq 1-\delta(K_\ell/{\mathbb{Q}};1-r)\leq \exp\Big(-c_2\frac{\ell}{\log\ell}\Big); \\ &\delta(K_\ell/{\mathbb{Q}};t_{C_1,C_2})\geq 1-\exp\Big(-c_3\frac{\ell}{\log\ell}\Big), \end{align*} $$

where the constants $c_1, c_2, c_3>0$ are absolute.

2.3.2 Hilbert class fields of quadratic extensions: the absolute case

From the group theoretic point of view, this section is a slight generalisation of the previous one. We consider the extensions $K_d/{\mathbb {Q}}$ , where $K_d$ is the Hilbert class field of the quadratic extension ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ . The relative Galois extension $K_d/{\mathbb {Q}}(\sqrt {d})$ is abelian and will be considered in Section 2.3.5. As in the case of dihedral extensions, there are many elements of order $2$ in $\mathrm {Gal}(K_d/{\mathbb {Q}})$ ; this results in estimates similar to those stated in Theorem 2.17.

Theorem 2.18. Let $d\neq 1$ be a fundamental discriminant, and let $K_d$ be the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ . Then $K_d/{\mathbb {Q}}$ is Galois; fix a representative $\tau _0$ of the nontrivial left coset of $\mathrm {Gal}(K_d/{\mathbb {Q}})$ modulo $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ , and assume GRH and BM for $K_d/{\mathbb {Q}}$ . Fix an element $\sigma \in \mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ , and let $C_1,C_2$ be the conjugacy classes of $\tau _0\sigma $ and $1$ , respectively. Then the functions $ E(y;K_d/{\mathbb {Q}},t_{C_1,\{ \mathrm {id}\}}), E(y;K_d/{\mathbb {Q}},1-r)$ admit limiting distributions whose means are both $\gg h(d)$ , and whose variances are both $\ll h(d) \log |d|$ . As a result, the following holds.

1. (1) For every fundamental discriminant $d\leq -4$ , we have the bound

   $$ \begin{align*}\min\big(\underline{\delta}(K_d/{\mathbb{Q}};t_{C_1,C_2}), \underline{\delta}(K_d/{\mathbb{Q}};1-r)\big)\geq 1-O\Big(\frac{\log |d| \log\log |d|}{\sqrt{|d|}}\Big). \end{align*} $$

2. (2) There exists an unbounded family of fundamental discriminants $d\geq 5$ , such that

   $$ \begin{align*}\min\big(\underline{\delta}(K_d/{\mathbb{Q}};t_{C_1,C_2}), \underline{\delta}(K_d/{\mathbb{Q}};1-r)\big)\geq 1-O\left(\frac{(\log |d|)^{2}}{\sqrt{|d|}\log\log |d|}\right). \end{align*} $$

3. (3) If one additionally assumes LI for each extension $K_d/{\mathbb {Q}}$ , then both the densities $\delta (K_d/{\mathbb {Q}};1-r)$ and $\delta (K_d/{\mathbb {Q}};t_{C_1,C_2})$ exist and one has the refined bounds:

   $$ \begin{align*}\exp\left(-c_1\frac{\sqrt{|d|}}{ \log\log |d|}\right) \leq 1-\delta(K_d/{\mathbb{Q}};1-r)\leq \exp\left(-c_2\frac{\sqrt{|d|}}{\log |d| \log\log |d|}\right)\, \hspace{.3cm}(d<0); \end{align*} $$
   $$ \begin{align*}\exp\left(-c_3\frac{\sqrt{|d|}\log\log |d|}{(\log |d|)^{\frac{1}{2}+\frac{\mathrm{sgn}(d)}{2}}}\right) &\leq 1-\delta(K_d/{\mathbb{Q}};1-r)\\&\leq \exp\left(-c_4\frac{\sqrt{|d|}\log\log |d|}{(\log |d|)^{\frac{3}{2}+\frac{\mathrm{sgn}(d)}{2}}}\right)\, \hspace{.2cm}(d \text{ as in (2)}).\\[-7pt] \end{align*} $$

   Here, the constants $c_i>0$ are absolute. Both upper bounds also hold for $1-\delta (K_d/{\mathbb {Q}};t_{C_1,C_2})$ .

2.3.3 Radical extensions

In contrast with the two previous families, we now consider extensions of number fields exhibiting this time a moderate Chebyshev bias. We will consider splitting fields $K_{a,p}/{\mathbb {Q}}$ of polynomials $f(X)=X^p-a$ , where p and a are distinct odd prime numbers. To simplify the analysis, we make the extra assumption that $a^{p-1}\not \equiv 1 (\bmod \ p^2)$ , in other words, ‘p is not a Wieferich prime to base a’ (see, e.g. [Kat, Sections 1–3] for a nice account on the theory of such prime numbers). Let $G=\mathrm {Gal}(K_{a,p}/{\mathbb {Q}})$ . We have the following group isomorphism:

(40) $$ \begin{align} G\simeq\left\{ \left(\begin{array}{cc} c & d \\ 0 & 1 \end{array}\right) : c\in \mathbb F_p^*, d\in \mathbb F_p \right\}\,.\\[-7pt]\nonumber \end{align} $$

In particular, G is supersolvable (consider the cyclic maximal unipotent subgroup H of G), so that Artin’s conjecture holds for $K_{a,p}/{\mathbb {Q}}$ . In this case, we apply the work of [Vi] and explicitly compute the filtration of inertia and, in particular, obtain an exact formula for the Artin conductor of each irreducible character of G.

Theorem 2.19. Let $a,p$ be primes, such that $a^{p-1}\not \equiv 1 (\bmod \ p^2)$ , and assume GRH and LI for the extension $K_{a,p}/\mathbb Q$ . Let $C_1$ , $C_2$ be distinct conjugacy classes of G. Then the functions $ E(y;K_{a,p}/{\mathbb {Q}},t_{C_1,C_2})$ , $E(y;K_{a,p}/{\mathbb {Q}},1-r)$ admit limiting distributions and if $C_1,C_2\neq \{\mathrm {id}\}$ , then the means are both $\ll 1$ , and the variances are both $\ll p\log (ap)$ and $\gg p\log p$ . If one of $C_1$ or $C_2$ (say $C_2$ ) is the trivial conjugacy class, then the mean of $ E(y;K_{a,p}/{\mathbb {Q}},t_{C_1,\{\mathrm {id}\}})$ is $\asymp p$ and the variance $\asymp p^3 \log (ap)$ . As a result, we have the following estimates.

1. (1) For the class function $t=1-r$ ,

   (41) $$ \begin{align} \delta(K_{a,p}/{\mathbb{Q}};1-r) - \frac 12 \asymp \frac 1{\sqrt{p\log (a p)}}\,. \end{align} $$

2. (2) For $c\in \mathbb F_p^\times \setminus \{1\}$ , let $c^+$ be the conjugacy class of G (recall (40)) consisting of all matrices with first row $(c,d)$ , where d runs over $\mathbb F_p$ . If $C_1$ and $C_2$ are not both of type $c^+$ , then ¹⁵

   $$ \begin{align*}\left| \delta(K_{a,p}/{\mathbb{Q}};t_{C_1,C_2})-\frac 12 \right| \asymp \frac 1{\sqrt{p\log(ap)}}\,.\\[-7pt] \end{align*} $$

3. (3) If $C_1=x^+$ and $C_2=y^+$ for distinct $x,y\in \mathbb F_p^\times \setminus \{1\}$ , then $\delta (K_{a,p}/{\mathbb {Q}};t_{x^+,y^+})= \delta (p;x,y)$ , which denotes the density of the classical Chebyshev bias ¹⁶ for the couple of residue classes $(x,y)$ modulo p.

Finally, in the relative case $K={\mathbb {Q}}(\zeta _p)$ (where $\mathrm {Gal}(K_{a,p}/K)\simeq \mathbb Z/p\mathbb Z$ is the maximal unipotent subgroup of G), for any distinct $d_1,d_2\in \mathbb Z/p\mathbb Z$ , the function $E(y;K_{a,p}/K,t_{\{d_1\},\{d_2\}})$ admits a limiting distribution. The mean is always $0$ , and the variance is $\asymp p^3 \log (ap)$ in the case $d_1d_2=0$ , and $0$ otherwise. If $d_1d_2=0$ , then we have $\delta (K_{a,p}/K;t_{\{d_1\},\{d_2\}})=\tfrac 12$ (if $d_1d_2\neq 0$ , then we have no result on $\delta (K_{a,p}/K;t_{\{d_1\},\{d_2\}})$ ).

By estimating the density of the couples of primes $(a,p)$ , such that p is not Wieferich to base a, we deduce the following statement.

Corollary 2.20. Assume GRH and LI for every $K_{a,p}$ with $a,p$ running over all primes. The proportion of couples of primes $(a,p)$ with $a\leq A$ and $p\leq P$ , such that (41) holds is

$$ \begin{align*}1- O\Big(\frac{\log P(\log A\log\log A)^{\frac 12}}{P} + \frac{P\log A}{A}\Big)\\[-7pt] \end{align*} $$

in the range $A,P\geq 3$ , $ P\log P \leq A \leq {\mathrm {e}}^{P^2/(\log P)^3}$ .

We proceed by considering abelian extensions of number fields.

2.3.4 Iterated quadratic extensions

We first describe the case of a Galois group with a ‘big’ $2$ -torsion subgroup. We see that if the product of ramified primes belongs to a certain subset of $\mathbb {N}$ of density $0$ (see Remark 2.23), then we obtain an extreme Chebyshev bias.

Theorem 2.21. Let $L={\mathbb {Q}}(\sqrt {p_1},...,\sqrt {p_m})$ , where $p_1<p_2<...<p_m$ are distinct odd primes. Let $G=\mathrm {Gal}(L/{\mathbb {Q}})\simeq \{\pm 1\}^m$ and $q:=\prod _i p_i$ . Assume ¹⁷ GRH and LI, and let $\varepsilon>0$ be small enough. Then for any $a,b\in G$ , the functions $ E(y;L/{\mathbb {Q}},t_{a,b}) $ and $E(y;L/{\mathbb {Q}},1-r)$ admit limiting distributions of respective means $|G|(\delta _{b=\mathbf {1}}-\delta _{a=\mathbf {1}})$ (where $\mathbf {1}=(1,\ldots ,1)$ ) and $|G|$ , and both of variance $\asymp |G|\log q$ . As a result, for any $a\in G\setminus \{ \mathbf {1}\}$ , we have that

$$ \begin{align*}\delta(L/{\mathbb{Q}};t_{a,\mathbf{1}})= \begin{cases} 1-O(\exp(-c 2^{\omega(q)}/\log q )) &\text{ if } 2^{-\omega(q)}\log q \leq \varepsilon \\ \frac 12+O\Big(\sqrt{2^{\omega(q)}/\log q}\Big) &\text{ if } 2^{-\omega(q)}\log q \geq \varepsilon^{-1} \end{cases} ,\end{align*} $$

where c is some positive absolute constant. The same estimate holds for $\delta (L/{\mathbb {Q}};1-r)$ .

Remark 2.22. The reason we chose $b=\mathbf {1}$ in the second part of the statement is because one can show that $\delta (L/{\mathbb {Q}};t_{a,b})=\frac 12$ as soon as $a\neq \mathbf {1}$ and $b\neq \mathbf {1}$ .

Remark 2.23. It follows from Theorem 2.21 and [Te, Chapter 2, Theorem 6.4] that there exists a subset $S\subseteq \mathbb {N}$ , the natural density of which is given by

$$ \begin{align*}\#S\cap [1,X]=\frac{X}{(\log X)^{1-\frac{1+\log\log 2}{\log 2}+o(1)}} \qquad (X\to \infty)\,, \end{align*} $$

such that for any nontrivial $a\in \mathrm {Gal}({\mathbb {Q}}(\sqrt {p_1},\ldots ,\sqrt {p_m})/{\mathbb {Q}})$ , one has

$$\begin{align*}\delta({\mathbb{Q}}(\sqrt{p_1},\ldots,\sqrt{p_m})/{\mathbb{Q}};t_{a,\mathbf{1}}) =1-o_{q\rightarrow\infty}(1)\qquad (q = p_1 \cdots p_m\in S)\,. \end{align*}$$

2.3.5 Hilbert class fields of quadratic extensions: the relative case

In this section, the setting is as in Section 2.3.2: d is a fundamental discriminant satisfying $|d|>1$ , and $K_d$ denotes the Hilbert class field of the quadratic field ${\mathbb {Q}}(\sqrt {d})$ , therefore, $K_d/{\mathbb {Q}}(\sqrt {d})$ is Galois with group $G\simeq \mathrm {Cl}_d$ . In [Ng, Section 6.2], Ng studies discrepancies in the distribution of prime ideals according to their class in $\mathrm {Cl}_d$ being either trivial or any fixed nontrivial class. In the next result, we consider two possible choices for $(C_1,C_2)$ ; in the case $(C_1,C_2)=(\{\overline {\mathfrak a}\},\{\overline {1}\})$ , we recover precisely Ng’s Theorem [Ng, Theorem 6.2.1].

Theorem 2.24. Let d be a fundamental discriminant, and assume that $h(d)>1$ . Let $K_d$ be the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ , and assume that GRH holds for the extension $K_d/{\mathbb {Q}}$ . We identify $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ with the class group $\mathrm {Cl}_d$ , and we let $\overline {\mathfrak a}$ be a nontrivial ideal class. Choosing $(C_1,C_2)$ to be either $(\{\overline {\mathfrak a}\},\{\overline {1}\})$ or $(\{\overline {1}\},0)$ , the Frobenius counting function $E(y;K_d/{\mathbb {Q}}(\sqrt {d}),t_{C_1,C_2})$ defined in (9) admits a limiting distribution of mean and variance respectively denoted $\mu _{K_d/{\mathbb {Q}}(\sqrt d)}(C_1,C_2)$ , and $\sigma ^2_{K_d/{\mathbb {Q}}(\sqrt d)}(C_1,C_2)$ , satisfying

$$ \begin{align*} |\mu_{K_d/{\mathbb{Q}}(\sqrt d)}(C_1,C_2)|&\leq 2^{\omega(d)}+4\sum_{1\neq\chi\in\mathrm{Irr}(\mathrm{Cl}_d)}\mathrm{ord}_{s=\frac 12}L(s,K_d/{\mathbb{Q}}(\sqrt{d}),\chi)\,, \\ \sigma^2_{K_d/{\mathbb{Q}}(\sqrt d)}(C_1,C_2)& \gg h(d)\,\,\,(\text{only for the choice } (C_1,C_2)=(\{\overline{1}\},0))\,. \end{align*} $$

Under the extra assumption LI, one has that $|\mu _{K_d/{\mathbb {Q}}(\sqrt d)}(C_1,C_2)|\leq 2^{\omega (d)}$ and $\sigma ^2_{K_d/{\mathbb {Q}}(\sqrt d)}\gg h(d)$ for both choices of $(C_1,C_2)$ , and as a consequence, one deduces

$$ \begin{align*}\delta(K_d/{\mathbb{Q}}(\sqrt{d}),t_{C_1,C_2}\})-\frac 12\ll \frac{2^{\omega(d)}}{\sqrt{h(d)}}\,. \end{align*} $$

For the set of all negative fundamental discriminants, or the family of positive discriminants in Lemma 9.5, the last upper bound of the above result implies that the density $\delta (K_d/{\mathbb {Q}}(\sqrt {d}),t_{C_1,C_2}\})$ approaches $\frac 12$ as d grows.

Remark 2.25. Number field extensions with Galois group $G=\mathrm {SL}_2(\mathbb F_p)$ have the peculiarity that many representations of G are symplectic, and hence, there is potentially a large supply of real zeros. For some Galois extensions $L/{\mathbb {Q}}$ , the existence of real zeros of Artin L-functions has the dramatic effect that $\delta (L/{\mathbb {Q}};1-r) =\tfrac 12$ (see [Ba1] for the impact on the bias of central zeros in the case of generalised quaternion extensions). This is in total contradiction with the usual Chebyshev bias philosophy, which says that ‘primes congruent to quadratic nonresidues are more abundant than primes congruent to quadratic residues’. For $\mathrm {SL}_2(\mathbb F_p)$ -extensions $L/{\mathbb {Q}}$ , one can show ¹⁸ that $\delta (L/{\mathbb {Q}};1-r)$ takes values between $\tfrac 12$ and $\eta $ for some absolute $\eta <1$ , and one expects that $\tfrac 12 \leq \delta (L/{\mathbb {Q}};1-r) \leq \tfrac 12+c(\log (\mathrm {rd}_L))^{-\frac 12}$ for some absolute $c>0$ . The case $\delta (L/{\mathbb {Q}};1-r)=\tfrac 12$ is achieved ¹⁹ with extensions for which the Artin root number of every symplectic character is $-1$ (see also [Ba1]).

3 Distribution of Frobenius elements via Artin L-functions

3.1 Representation theory of finite groups

For completeness and because of its crucial importance in our work, let us first recall some basic representation theory of finite groups. We let $\mathrm {Irr} (G)$ and $G^\sharp $ denote, respectively, the set of irreducible characters and the set of conjugacy classes of the group G. Keeping the notation of Bellaïche [Be1], for a class function $t:G \rightarrow \mathbb C$ and a character $\chi \in \mathrm {Irr}(G)$ , we define the Fourier transform

$$ \begin{align*}\widehat t (\chi):=\langle t,\chi\rangle_G=\frac 1{|G|}\sum_{g\in G} t(g) \overline {\chi(g)} = \sum_{C \in G^\sharp} \frac{|C|}{|G|} t(C) \overline {\chi(C)} \,.\end{align*} $$

Note that if $1_D$ is the characteristic function of a given conjugacy-invariant set $D\subset G$ , then

$$ \begin{align*}\widehat{1_D} (\chi) =\frac 1{|G|}\sum_{\substack{C\in G^\sharp: \\ C \subset D}}|C|\overline{\chi(C)}\,.\end{align*} $$

Lemma 3.1 (Orthogonality relations).

Let G be a finite group. If $g_1,g_2 \in G$ , then

(42) $$ \begin{align} \sum_{\chi \in \mathrm{Irr}(G)} \chi(g_1)\overline{\chi}(g_2) = \begin{cases} \frac{|G|}{|C|} & \text{ if } g_1 \text{ and } g_2 \text{ are both in the same conjugacy class }C,\\ 0 & \text{ otherwise.} \end{cases} \end{align} $$

Moreover, if $\chi ,\psi \in \mathrm {Irr}(G)$ , then

(43) $$ \begin{align} \frac 1{|G|} \sum_{g\in G} \chi(g)\overline{\psi}(g) = \begin{cases} 1 & \text{ if } \chi = \psi,\\ 0 & \text{ otherwise}. \end{cases} \end{align} $$

As a consequence of (43), we have the formula

(44) $$ \begin{align} t = \sum_{\chi \in \mathrm{Irr}(G)} \widehat t (\chi) \chi. \end{align} $$

We will often count elements of order $2$ with characters, using the following Lemma.

Lemma 3.2. Let G be a finite group and $ k\in \mathbb N$ . Then for any $h\in G$ , we have the identity

(45) $$ \begin{align} \#\{g\in G : g^k = h\} = \sum_{\chi \in \mathrm{Irr}(G)} \overline{\varepsilon_k(\chi)} \chi(h), \end{align} $$

(46) $$ \begin{align} \text{where}\qquad \varepsilon_k(\chi):= \frac 1{|G|} \sum_{g\in G}\chi (g^k). \end{align} $$

Proof. Since $r_k(h):=\#\{g\in G : g^k = h\}$ defines a class function on G, we have

$$ \begin{align*}\#\{g\in G : g^k = h\} = \sum_{\chi \in \mathrm{Irr}(G)} \widehat{r_k}(\chi)\chi(h)\,.\end{align*} $$

The proof follows by definition of Fourier coefficients.

The number

$$ \begin{align*}\varepsilon_2(\chi)=\frac{1}{|G|}\sum_{g\in G} \chi(g^2)\end{align*} $$

is called the Frobenius–Schur indicator of $\chi $ and is central in our analysis. If $\chi $ is irreducible, then for $r=r_2$ , one has $\varepsilon _2(\chi )=\widehat {r}(\overline {\chi })=\widehat {r}(\chi ) \in \{ -1,0,1\}$ (see [Hu, Theorem 8.7]), and moreover, each of these three possible values has a precise meaning in terms of the $\mathbb R$ -rationality of $\chi $ and of the underlying representation $\rho $ .

Theorem 3.3 (Frobenius, Schur).

Let G be a finite group, and let $\chi \in \mathrm {Irr}(G)$ be the character of an irreducible complex representation $\rho \colon G\rightarrow \mathrm {GL}(V)$ .

(1) If $\varepsilon _2(\chi )=0$ , then $\chi \neq \overline {\chi }$ , $\chi $ is not the character of an $\mathbb R[G]$ -module and there does not exist a G-invariant, $\mathbb C$ -bilinear form $\neq 0$ on V. We say that $\rho $ is a unitary representation.

(2) If $\varepsilon _2(\chi )=1$ , then $\chi =\overline {\chi }$ is the character of some $\mathbb R[G]$ -module and there exists a G-invariant, $\mathbb C$ -bilinear form which is symmetric and nonsingular, unique up to factors in $\mathbb C$ . We say that $\rho $ is an orthogonal representation.

(3) If $\varepsilon _2(\chi )=-1$ , then $\chi =\overline {\chi }$ is not the character of any $\mathbb R[G]$ -module and there exists a G-invariant, $\mathbb C$ -bilinear form which is skew-symmetric and nonsingular, unique up to factors in $\mathbb C$ . We say that $\rho $ is a symplectic (or quaternionic) representation.

Proof. See, for instance [Hu, Theorem 13.1].

A direct consequence of Lemma 3.2 and Theorem 3.3 is the following formula for the class function r introduced in (13):

(47) $$ \begin{align} r=\sum_{\substack{\chi \in \mathrm{Irr}(G)\\ \chi \,\mathrm{real}}} \varepsilon_2(\chi) \chi. \end{align} $$

Lemma 3.4. Let G be a finite group, and let $t:G \rightarrow \mathbb C$ be a class function. We have the identity

(48) $$ \begin{align} {\lVert{\widehat t}\rVert} _2^2 :=\sum_{\chi \in \mathrm{Irr}(G)} |\widehat t (\chi)|^2 = \sum_{C\in G^\sharp}\frac{|C|}{|G|} |t(C)|^2 = {\lVert{t}\rVert}^2_2. \end{align} $$

In particular, if $C_1,...,C_k \in G^\sharp $ are distinct and $\alpha _1,...,\alpha _k \in \mathbb C$ , then

$$ \begin{align*}\sum_{\chi \in \mathrm{Irr}(G)} |\alpha_1\chi(C_1)+\dots +\alpha_k \chi(C_k) |^2 = |\alpha_1|^2 \frac{|C_1|}{|G|} +\cdots +|\alpha_k|^2 \frac{|C_k|}{|G|}.\end{align*} $$

Proof. This is Parseval’s identity (6).

We will also need a pointwise bound on the Fourier coefficients $\widehat t(\chi )$ .

Lemma 3.5. Let G be a finite group, $t:G \rightarrow \mathbb C$ be a class function and $\chi \in \mathrm {Irr}(G)$ . Then we have the bound

$$ \begin{align*}|\widehat t(\chi)| \leq \chi(1) {\lVert{t}\rVert}_1.\end{align*} $$

Proof. This follows directly from the definition of Fourier transform.

From the definition $t^+:=\mathrm {Ind}_G^{G^+} (t)$ , one easily sees that

$$\begin{align*}t^+= \sum_{\chi \in \mathrm{Irr}(G)} \widehat t(\chi) \mathrm{Ind}_G^{G^+} (\chi)\,. \end{align*}$$

Applying Frobenius reciprocity, we can compute the Fourier transform of $t^+$ in terms of that of t.

Lemma 3.6. Let $G^+$ be a finite group, let G be a subgroup and let $t\colon G\rightarrow \mathbb C$ be a class function on G. Then, for any $\chi \in \mathrm {Irr}(G^+)$ , we have the formula

(49) $$ \begin{align} \widehat {t^+}(\chi)=\langle t,\chi|_G\rangle_G\,. \end{align} $$

Proof. Frobenius reciprocity gives that

$$ \begin{align*}\widehat {t^+}(\chi) = \sum_{\eta \in \mathrm{Irr}(G)} \widehat t(\eta) \langle \mathrm{Ind}_G^{G^+} (\eta),\chi \rangle_{G^+} = \sum_{\eta \in \mathrm{Irr}(G)} \widehat t(\eta) \langle \eta,\chi|_{G}\rangle_{G} = \langle t,\chi|_G\rangle_G\,.\\[-42pt] \end{align*} $$

Under certain assumptions, we can also compare the $2$ -norm of $t^+$ in terms of that of t.

Lemma 3.7. Let $G^+$ be a finite group, let G be subgroup of $G^+$ and let $t\colon G\rightarrow \mathbb C$ be a class function on G. We have the following.

1. (1) If G is a normal subgroup of $G^+$ , then

   $$ \begin{align*}{\lVert{t^+}\rVert}^2_2 \leq \frac{|G^+|}{|G|}{\lVert{t}\rVert}^2_2\,.\end{align*} $$

2. (2) If t only takes nonnegative values, then

   $$ \begin{align*}{\lVert{t^+}\rVert}_2\geq {\lVert{t}\rVert}_2\,.\end{align*} $$

Remark 3.8. The upper bound is attained by the function $t=|G||C|^{-1}1_C$ , where $C\in G^\sharp $ is such that $ |C|=|C^+|$ (for example, when $G^+$ is abelian). As for the lower bound, it requires a condition since, for example, we could take $t=|G||C_1|^{-1}1_{C_1}-|G||C_2|^{-1}1_{C_2}$ for distinct $C_1,C_2 \in G$ for which $C_1^+=C_2^+$ , and as a result $ t^+ \equiv 0$ .

Proof of Lemma 3.7

We first expand the norm of $t^+$ :

(50) $$ \begin{align} {\lVert{t^+}\rVert}^2_2 = \frac 1{|G^+|} \sum_{g\in G^+} \Big| \sum_{\substack{aG \in G^+/G \\ a^{-1}ga\in G}} t(a^{-1}ga)\Big|^2 = \frac 1{|G^+|} \sum_{bG \in G^+/G} \sum_{g\in G} \Big| \sum_{\substack{aG \in G^+/G \\ a^{-1}bga\in G}} t(a^{-1}bga)\Big|^2\,. \end{align} $$

Now we prove (1). Using Cauchy–Schwarz, we deduce from (50) that

$$ \begin{align*}{\lVert{t^+}\rVert}^2_2 \leq \frac 1{|G^+|} \sum_{bG \in G^+/G} \sum_{g\in G}\Big( \sum_{\substack{aG \in G^+/G \\ a^{-1}bga\in G}} 1 \Big)\Big(\sum_{\substack{aG \in G^+/G \\ a^{-1}bga\in G}} |t(a^{-1}bga)|^2\Big)\,. \end{align*} $$

We bound the first sum in parentheses trivially, and we exploit the fact that $bg\in aGa^{-1}$ is equivalent to $bg\in G$ for any $a\in G^+$ , since G is a normal subgroup. Therefore, the condition on the left coset $bG$ in the second sum in parentheses imposes $bG$ to be the trivial left coset G. We conclude that

$$ \begin{align*}{\lVert{t^+}\rVert}_2 \leq \frac 1{|G|} \sum_{g\in G}\sum_{\substack{aG \in G^+/G }} |t(a^{-1}ga)|^2 = \frac 1{|G|}|G^+/G| \sum_{g\in G} |t(g)|^2, \end{align*} $$

using the fact that conjugation by any $a\in G^+$ induces a bijection of G. The claimed upper bound follows.

For the lower bound (2), we apply positivity in (50) and deduce that

$$ \begin{align*} {\lVert{t^+}\rVert}^2_2& \geq \frac 1{|G^+|} \sum_{bG \in G^+/G}\sum_{g\in G} \sum_{\substack{aG \in G^+/G \\ a^{-1}bga\in G}} |t(a^{-1}bga)|^2 \\ &=\frac 1{|G^+|} \sum_{g\in G} \sum_{\substack{aG \in G^+/G }} \sum_{\substack{bG = aGa^{-1}} } |t(a^{-1}bga)|^2= {\lVert{t}\rVert}^2_2. \end{align*} $$

We finish this section by computing $r^+$ (recall (47)) and by deducing a consequence which will be useful in showing that, up to ramified primes, $\pi (x;L/K,t)$ is determined by $t^+$ .

Lemma 3.9. Let $G^+$ be a finite group, and let G be a normal subgroup. For any $k\in \mathbb N$ and for any class function $t\colon G^+\rightarrow \mathbb C$ , we define the class function $r_{k,t}\colon G\rightarrow \mathbb C$ by setting

$$ \begin{align*}r_{k,t}(g) := \sum_{\substack{h\in G \\ h^k=g }} t(h).\end{align*} $$

Then we have the following equality of class functions:

$$ \begin{align*}r_{k,t}^+\big|_G = [G^+:G] \cdot r_{k,t}.\end{align*} $$

Proof. First note that if for some $g,h\in G$ and $a\in G^+$ we have that $h^k =a^{-1} g a$ , then $(aha^{-1})^k=g$ . In other words, since for each fixed value of a, we have $aG=Ga$ , there is a bijection between the sets $\{ h\in G: h^k=a^{-1} g a\}$ and $\{ h\in G : h^k= g\}$ . Hence, for any $g\in G$ ,

$$ \begin{align*}r_{k,t}^+\big|_G(g) = \sum_{\substack{aG \in G^+/G \\ a^{-1} g a \in G}}r_{k,t}(a^{-1} g a) = \sum_{h\in G} t(h) \sum_{\substack{aG \in G^+/G \\ a^{-1} g a =h^k}} 1 =\sum_{\substack{aG \in G^+/G }} \sum_{\substack{h\in G \\ h^k=g}} t(a^{-1}ha) .\end{align*} $$

The claim follows since t is a class function on $G^+$ .

Corollary 3.10. Let $G^+$ be a finite group and G a normal subgroup. If $t\colon G\rightarrow \mathbb C$ is a class function, such that $t^+\equiv 0$ , then for any $k\geq 1$ , one has $\langle t, r_k \rangle _G=0$ . Here, $r_k\colon G\rightarrow \mathbb C$ is defined by $r_k(g)=|\{ h\in G \colon h^k =g\}|$ , that is, $r_k=r_{k,1}$ .

Proof. By Frobenius reciprocity and Lemma 3.9, we have that

$$ \begin{align*}\langle t, r_k \rangle_G\cdot [G^+:G]=\langle t, r_k^+\big|_G \rangle_G = \langle t^+, r_k^+ \rangle_{G^+}=0.\\[-32pt]\end{align*} $$

3.2 Explicit formulas and limiting distributions

We fix a Galois extension of number fields $L/K$ and let $G=\mathrm {Gal}(L/K)$ . For a class function $t\colon G \rightarrow \mathbb C$ , we define the following prime ideal counting function:

$$ \begin{align*}\psi(x;L/K,t):=\sum_{\substack{\mathfrak p\triangleleft \mathcal O_K \\ m\geq 1\\ \mathcal N\mathfrak p^m \leq x}} t(\varphi_{\mathfrak p}^m) \log (\mathcal N\mathfrak p),\end{align*} $$

where $\varphi _{\mathfrak p}$ is shorthand for $\mathrm {Frob}_{\mathfrak p}$ , the conjugacy class of a lift (defined up to inertia) of the Frobenius automorphism on the residue field $\mathcal O_L/\mathfrak P$ for some (any) $\mathfrak P\triangleleft \mathcal O_L$ above $\mathfrak p$ , and

(51) $$ \begin{align} t(\varphi_{\mathfrak p}^m) := \frac 1{|I_{\mathfrak p}|} \sum_{ i \in I_{\mathfrak p}} t(\varphi_{\mathfrak p}^m i), \end{align} $$

where $I_{\mathfrak p}$ is the inertia group attached to $\mathfrak p$ and any $\mathfrak P\triangleleft \mathcal O_L$ above $\mathfrak p$ . If $D\subset G$ is conjugacy invariant, then we define $\psi (x;L/K,D):=\psi (x;L/K,1_D)$ , where $1_{ D}$ is the indicator function of D. We also recall the definition (1) of the prime ideal counting function attached to a conjugacy class C of G which we extend in the obvious way to conjugacy invariant sets $D\subset G$ .

Our goal is to express $\pi (x;L/K,t)$ in terms of the zeros of primitive Artin L-functions; this will prevent arithmetic multiplicities from occurring in our formulas. To do so, we will first relate the prime ideal counting functions $\psi (x;L/K,t)$ and $\psi (x;L/{\mathbb {Q}},t^+)$ using the induction property for Artin L-functions.

Proposition 3.11. Let $L/K/M$ be a tower of number fields for which $L/M$ is Galois, let $G=\mathrm {Gal}(L/K)$ and $G^+=\mathrm {Gal}(L/M)$ . For any class function $t\colon G\rightarrow \mathbb C$ , we have the identity

(52) $$ \begin{align} \psi(x;L/K,t) = \psi(x;L/M,t^+).\\[-9pt]\nonumber \end{align} $$

As a consequence, if $D\subset G$ is conjugacy invariant, then

(53) $$ \begin{align} \psi(x;L/K,D)=\frac{|G^+|}{|G|} \sum_{\substack{C\in G^\sharp: \\ C \subset D}} \frac{|C|}{|C^+|}\psi(x;L/M,C^+),\\[-9pt]\nonumber \end{align} $$

where $C^+$ is defined by (8).

Remark 3.12. Note that if $C\in G^\sharp $ , then $C^+\in (G^+)^\sharp $ . Indeed, $C^+$ is clearly closed under conjugation. Moreover, if $k_1,k_2\in C^+$ , say $k_i=a_i c_ia_i^{-1}$ , then since $c_i \in C$ , there exists $g\in G$ for which $c_2=gc_1 g^{-1}$ . Hence, $k_2 = a_2 g a_1 ^{-1}(a_1c_1 a_1^{-1})a_1 g^{-1}a_2^{-1} =(a_2 ga_1^{-1}) k_1 (a_2 ga_1^{-1})^{-1} $ , that is, $k_1,k_2$ are $G^+$ -conjugates.

Proof of Proposition 3.11

For any $\chi \in \mathrm {Irr}(G)$ , we have the identity (see, e.g. [Mar, Section 4])

(54) $$ \begin{align} L(s,L/K,\chi)= L(s,L/M, \mathrm{Ind}_G^{G+}(\chi)),\\[-9pt]\nonumber \end{align} $$

and hence

(55) $$ \begin{align} \psi(x;L/K,\chi) = -\frac 1{2\pi i}\int_{\Re(s)=2} \frac{L'(s,L/K,\chi)}{L(s,L/K,\chi)} \frac{x^s}{s} \mathrm{d}s = \psi(x;L/M,\mathrm{Ind}_G^{G+}(\chi)).\\[-9pt]\nonumber \end{align} $$

As a consequence,

$$ \begin{align*}\psi(x;L/K,t) = \!\sum_{\chi \in \mathrm{Irr}(G)} \!\widehat {t}(\chi) \psi(x;L/K,\chi)=\!\sum_{\chi \in \mathrm{Irr}(G)} \!\widehat {t}(\chi) \psi(x;L/M,\mathrm{ Ind}_G^{G^+}\chi)=\psi(x;L/M,t^+)\,.\\[-9pt]\end{align*} $$

Now, if $D\subset G$ is conjugacy invariant and $\chi \in \mathrm {Irr}(G^+)$ , then by Lemma 3.6,

$$ \begin{align*}\widehat {1^+_{D}}(\chi) = \widehat{1_{D}}(\chi|_G) = \frac 1{|G|} \sum_{\substack{C\in G^\sharp: \\ C \subset D}} \overline{\chi(C^+)}|C|,\end{align*} $$

since $\chi |_G(C)=\chi (C^+)$ . It follows that

(56) $$ \begin{align} 1^+_{D} = \sum_{\substack{C\in G^\sharp: \\ C \subset D}} \frac{|C|}{|G|}\sum_{\chi \in \mathrm{Irr}(G^+)} \overline{\chi}(C^+)\chi = \sum_{\substack{C\in G^\sharp: \\ C \subset D}} \frac{|C|}{|G|}\frac{|G^+|}{|C^+|} 1_{C^+}\,. \end{align} $$

The proof of (53) follows from combining this with (52) in the form

$$ \begin{align*}\psi(x;L/K,1_D) = \psi(x;L/M,1^+_D).\\[-36pt]\end{align*} $$

In the next lemma, we show that up to ramified primes, the counting function $\pi (x;L/K,t)$ is determined by $t^+$ , rather than by t. Note, however, that $\pi (x;L/K,t)$ and $\pi (x;L/{\mathbb {Q}},t^+)$ are not equal in general.

Lemma 3.13. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ and $K/{\mathbb {Q}}$ are Galois. If $t_1,t_2:G\rightarrow \mathbb C$ are class functions, such that $t_1^+=t_2^+$ , then

$$ \begin{align*}|\pi(x;L/K,t_1)-\pi(x;L/K,t_2)|\leq \sup(|t_1-t_2|) \cdot \#\{ \mathfrak p\triangleleft \mathcal O_K \text{ ramified in }L/K\}.\end{align*} $$

Proof. We let $t:=t_1-t_2$ , so that $t^+\equiv 0$ . For any $\chi \in \mathrm {Irr}(G^+)$ and $\ell \in \mathbb N$ , Lemma 3.9 implies that

$$ \begin{align*}r_{\ell,\chi}^+|_G = [G^+:G] \cdot r_{\ell,\chi}\,.\end{align*} $$

Moreover, using Frobenius reciprocity, one has

$$ \begin{align*}\widehat{(t(\cdot^\ell))^+}(\chi)= \langle (t(\cdot^\ell))^+,\chi \rangle_{G^+}= \langle t(\cdot^\ell),\chi|_G \rangle_{G} = \langle t,r_{\ell,\chi|_G} \rangle_G=\langle t,r_{\ell,\chi} \rangle_G \,,\end{align*} $$

which by the class function equality above equals

$$ \begin{align*} [G^+:G]^{-1}\langle t, r_{\ell,\chi}^+|_G\rangle_G& = [G^+:G]^{-1} \langle t^+,r_{\ell,\chi}^+\rangle_{G^+}=0\,. \end{align*} $$

We deduce that $(t(\cdot ^\ell ))^+ \equiv 0$ , and as such, applying inclusion-exclusion,

$$ \begin{align*} \theta(x;L/K,t)&:= \sum_{ \substack{ \mathfrak p \triangleleft \mathcal O_K \\ \mathcal N\mathfrak p \leq x }} t(\varphi_{\mathfrak p}) \log (\mathcal N\mathfrak p) = \sum_{\ell\geq 1} \mu(\ell) \psi(x^{\frac 1\ell},L/K,t(\cdot^\ell)) \\&=\sum_{\ell\geq 1} \mu(\ell) \psi(x^{\frac 1\ell},L/{\mathbb{Q}},(t(\cdot^\ell))^+)=0, \end{align*} $$

by Proposition 3.11. Denoting by $D_{L/K}$ the relative discriminant of $L/K$ and applying summation by parts, we deduce that

$$ \begin{align*}\pi(x;L/K,t)+\sum_{\substack{\mathfrak p \mid D_{L/K} \\ \mathcal N\mathfrak p\leq x}} t(\varphi_{\mathfrak p}) = \int_1^{x} \frac{\mathrm{d} \theta(u;L/K,t) }{\log u}=0.\\[-46pt]\end{align*} $$

In Proposition 3.11, we reduced our counting problem to one which will involve zeros of primitive L-functions, at the cost of working in a larger Galois group. In some of our results, we will circumvent AC by doing the exact opposite (as is done classically): we will work in an abelian Galois group, and allow imprimitive L-functions. This will be done using a result of Serre which goes back to Deuring and is in the spirit of Chebotarev’s original reduction.

Lemma 3.14 [Se3, Section 2.7].

Let $L/K$ be a Galois extension with Galois group G, and let $C\in G^\sharp $ . For any $g\in C$ , let $\mathrm {ord}(g)$ denote the order of the subgroup $\langle g\rangle $ generated by g. We have the equality

$$ \begin{align*}\psi(x;L/K , 1_C) = \frac{|C| \mathrm{ord}(g)}{|G|}\psi(x;L/L^{\langle g\rangle},1_{\{g\}}).\end{align*} $$

This identity follows again from Artin induction in the form

(57) $$ \begin{align} L(s,L/K,\frac{|G|}{|C|}1_C) = L(s,L/L^{\langle g \rangle},\mathrm{ord}(g_C) 1_{\{g_C\}}), \end{align} $$

which holds since $ \mathrm {Ind}_{\langle g \rangle }^G (\mathrm {ord}(g)1_{\{g\}})= {|G|}{|C|^{-1}}1_C$ (recall (56)).

We will also need the following consequence of Proposition 3.11 and Lemma 3.14.

Lemma 3.15. Let $L/K$ be a Galois extension of number fields, and let $C\in G^\sharp $ . For any $s_0\in \mathbb C$ and $g\in C$ , we have that

(58) $$ \begin{align} \sum_{ \chi\in \mathrm{Irr}(G)} \chi(C^{-1}) \mathrm{ord}_{s=s_0} L(s,L/K,\chi) = \sum_{ \chi\in \mathrm{Irr}(\langle g \rangle)} \chi(g^{-1}) \mathrm{ord}_{s=s_0} L(s,L/L^{\langle g \rangle},\chi). \end{align} $$

Assuming, moreover, that $L/{\mathbb {Q}}$ is Galois, for any class function $t:G\rightarrow \mathbb C$ and $s_0 \in \mathbb C$ , we have that

(59) $$ \begin{align} \sum_{ \chi\in \mathrm{Irr}(G)} \widehat {t} (\chi) \mathrm{ord}_{s=s_0} L(s,L/K,\chi) = \sum_{ \chi\in \mathrm{Irr}(G^+)} \widehat {t^+} (\chi) \mathrm{ord}_{s=s_0} L(s,L/{\mathbb{Q}},\chi). \end{align} $$

Proof. The first claimed identity clearly follows from the following:

$$ \begin{align*}-\sum_{ \chi\in \mathrm{Irr}(G)} \chi(C^{-1}) \frac{L'(s,L/K,\chi)}{L(s,L/K,\chi)} = -\sum_{ \chi\in \mathrm{Irr}(\langle g \rangle)} \chi(g^{-1})\frac{L'(s,L/L^{\langle g \rangle},\chi)}{L(s,L/L^{\langle g \rangle},\chi)},\end{align*} $$

which we will establish for $s>1$ using the induction property for Artin L-functions. By uniqueness of analytic continuation, this is sufficient.

The summatory function of the coefficients of the Dirichlet series on the left-hand side is given by

(60) $$ \begin{align} \sum_{ \chi\in \mathrm{Irr}(G)} \chi(C^{-1}) \sum_{\substack{\mathfrak p\triangleleft \mathcal O_{K}\\ \mathcal N \mathfrak p^m \leq x \\ m\geq 1}}\chi(\varphi_{\mathfrak p}^m)\log (\mathcal N \mathfrak p)=\frac{|G|}{|C|}\sum_{\substack{\mathfrak p\triangleleft \mathcal O_{K} \\ \mathcal N \mathfrak p^m \leq x \\ m\geq 1}} \mathbf 1_{ C}(\varphi_{\mathfrak p}^m) \log (\mathcal N \mathfrak p); \end{align} $$

the same holds for the coefficients of the Dirichlet series on the right-hand side of the equality to be established, by virtue of Lemma 3.14. This concludes the proof of (58). The proof of (59) is similar using Proposition 3.11.

We are now ready to relate $\psi (x;L/K,t)$ and $\pi (x;L/K,t)$ (respectively, $\psi (x;L/K,C)$ and $\pi (x;L/K,C)$ ) with the zeros of Artin L-functions associated to the extension $L/{\mathbb {Q}}$ (respectively, $L/L^{\langle g \rangle }$ , for any $g\in C$ ), which ultimately will allow us to use the language of random variables. Under AC, the calculation of the mean and variance in Proposition 3.18 below can be deduced from combining [De, Theorem 2.1] (see also [Fi2]) with induction properties of Artin L-functions. For the sake of completeness and in order to provide a full decomposition into sums of independent random variables, we decided to give further details while trying to stay brief. This closely follows [De, Theorem 2.1], [Fi2] and [Ng, Section 5.1].

Lemma 3.16. Let $L/K$ be a Galois extension of number fields for which AC holds. If $\chi $ is an irreducible character of $G=\mathrm {Gal}(L/K)$ and $C\subset G$ is a conjugacy class, then for any $x,X\geq 2$ ,

(61) $$ \begin{align} \psi(x;L/K,\chi) &=\delta_{\chi=1}x-\sum_{\substack{\rho_{\chi} \\ |\Im(\rho_{\chi})| \leq X}}\frac{x^{\rho_{\chi}}}{\rho_{\chi}} +O_{L,K}\Big(\log x +\frac xX (\log (xX))^2\Big); \end{align} $$

(62) $$ \begin{align} \psi(x;L/K,C) &= \frac{|C|}{|G|} x-\frac{|C|}{|G|} \sum_{ \chi \in \mathrm{Irr}(G)} \chi(C^{-1}) \sum_{\substack{\rho_{\chi} \\ |\Im(\rho_{\chi})| \leq X}}\frac{x^{\rho_{\chi}}}{\rho_{\chi}} +O_{L,K}\Big(\log x +\frac xX (\log (xX))^2\Big), \end{align} $$

where $\delta _{\chi =1}$ is $1$ when $\chi $ is the trivial character, and $0$ otherwise. In both formulas, the sum is over the zeros $\rho _\chi $ (counted with multiplicity) of the Artin L-function $L(s,L/K,\chi )$ in the critical strip $\Re (s) \in (0,1)$ .

Proof. See, for instance [Ng, (5.8)].

Corollary 3.17. Let $L/K$ be a Galois extension of number fields, let $C\subset \mathrm {Gal}(L/K)$ be a conjugacy class and let $g_C$ be any representative of C. For $ x,X\geq 2$ , we have the estimate

(63) $$ \begin{align} \frac{\log x}{x^{\beta^t_{L}}}\Big( \frac{|G|}{|C|}\pi(x;L/K,C)-\mathrm{Li}(x) \Big)= -\delta_{\beta^t_{L}=\frac 12}r(C)-\frac 1{\beta^t_{L}}\sum_{\chi\in \mathrm{Irr}(G)} \overline{\chi}(C) \mathrm{ord}_{s=\beta^t_{L}} L(s,L/K,\chi)\nonumber\\- \sum_{ \chi \in \mathrm{ Irr}(\langle g_C \rangle)} \overline{\chi}(g_C) \sum_{\substack{\rho_{\chi} \\ 0< |\gamma_{\chi}|\leq X }} \frac{x^{\rho_{\chi}-\beta^t_L}}{\rho_{\chi}} +O_{L,K}\Big(\frac 1{\log x}+ \frac{x^{1-\beta^t_L}}X (\log(xX))^2\Big)\,, \end{align} $$

where $\rho _{\chi }$ runs through the nontrivial zeros of $L(s,L/K,\chi )$ . If, in addition, we assume that $L/{\mathbb {Q}}$ is Galois and that AC holds, then for any class function $t:G\rightarrow \mathbb C$ ,

(64) $$ \begin{align} \frac{\log x}{x^{\beta^t_{L}}}&\Big( \pi(x;L/K,t)- \widehat{t}(1)\mathrm{Li}(x) \Big)= -\delta_{\beta^t_{L}=\frac 12} \langle t,r \rangle_G-\frac 1{\beta^t_{L}}\sum_{\chi\in \mathrm{Irr}(G)} \widehat {t^+} (\chi) \mathrm{ord}_{s=\beta^t_{L}} L(s,L/K,\chi)\\&\qquad\quad - \sum_{ \chi \in \mathrm{Irr}(G^+)} \widehat{{t^+}} (\chi) \sum_{\substack{\rho_{\chi} \nonumber\\ 0<|\gamma_{\chi}|\leq X }} \frac{x^{\rho_{\chi}-\beta^t_L}}{\rho_{\chi}} +O_{L,K}\Big(\frac 1{\log x}+ \frac{x^{1-\beta^t_L}}X (\log(xX))^2\Big)\,. \end{align} $$

Proof. We first establish (64). Arguing as in [Ng, Section 5.1] and [De, Section 4.3], we see that

(65) $$ \begin{align} &\frac{\log x}{x^{\beta^t_{L}}}\Big( \pi(x;L/K,t)-\widehat{t}(1)\mathrm{Li}(x) \Big) \nonumber\\&\qquad\qquad\qquad\qquad = x^{-\beta^t_{L}} \Big(\psi(x;L/K,t)-\widehat{t}(1)x-\widehat{t(\cdot^2)}(1)x^{\frac 12}\Big) +O_{L,K}\Big( \frac {1}{\log x}\Big). \end{align} $$

By Proposition 3.11, this is

$$ \begin{align*} &= x^{-\beta^t_{L}} \psi(x; L/{\mathbb{Q}}, t^+ ) -\widehat{t}(1)x^{1-\beta^t_{L}}-\delta_{\beta^t_{L}=\frac 12}\langle t,r\rangle_G+O_{L,K}\Big( \frac 1{\log x}\Big)\\ &=x^{-\beta^t_{L}} \sum_{\chi \in \mathrm{Irr}(G^+)} \widehat {t^+} (\chi)\psi(x; L/{\mathbb{Q}}, \chi)-\widehat{t}(1)x^{1-\beta^t_{L}}-\delta_{\beta^t_{L}=\frac 12}\langle t,r\rangle_G+O_{L,K}\Big( \frac 1{\log x}\Big). \end{align*} $$

The estimate (64) then follows from applying Lemma 3.16. The proof of (63) is similar (note that $\mathrm {Ind}_{\langle g_C \rangle }^G (\mathrm {ord}(g_C)1_{g_C})=\frac {|G|}{|C|} 1_C$ ).

To state the next proposition, we first define the following multisets of zeros of Artin L-functions, where $\beta _{L}$ and $\beta ^{\,\mathrm {real}}_{L/K}$ are defined in Theorem 2.1:

(66) $$ \begin{align} Z_{L}:=\{ \gamma \in \mathbb R_{>0} : \zeta_L(\beta_{L}+i\gamma)=0\}; \end{align} $$

(67) $$ \begin{align} Z^{t}_{L}:=\bigcup_{\substack{\chi \in \mathrm{Irr}(\mathrm{Gal}(L/{\mathbb{Q}}))\\ \widehat{t^+}(\chi)\neq 0 }}\{ \gamma \in \mathbb R_{>0} : L(\beta^{t}_{L}+i\gamma,\chi)=0\}. \end{align} $$

Recall also the definition (16).

Proposition 3.18. Let $L/K$ be a Galois extension of number fields, let $G=\mathrm {Gal}(L/K)$ and fix $t:G\rightarrow \mathbb C$ a class function. The function $E(y;L/K,t)$ admits a limiting distribution. Moreover, the associated random variable $X(L/K;t)$ is such that

(68) $$ \begin{align} \notag \mathbb E[X(L/K;t)] &=-\delta_{\beta^t_{L}=\frac 12}\langle t,r \rangle_G-\frac 1{\beta^t_{L}}\mathrm{ord}_{s=\beta^t_{L}}L(s,L/K,t) \notag \\ &=-\delta_{\beta^t_{L}=\frac 12}\langle \widehat t, \varepsilon_2 \rangle_{\mathrm{Irr}(G)}-\frac 1{\beta^t_{L}}\mathrm{ord}_{s=\beta^t_{L}}L(s,L/K,t). \end{align} $$

Furthermore, we have that

(69) $$ \begin{align} \mathrm{Var}[X(L/K;t)]=2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{|\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/K,t)|^2}{(\beta^t_{L})^2+\gamma^2}, \end{align} $$

where the starred sum means a sum without multiplicities. If $L/{\mathbb {Q}}$ is Galois, then we have the alternative ²⁰ formula

(70) $$ \begin{align} \mathrm{Var}[X(L/K;t)]=2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z^t_{L} } \frac{|\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/{\mathbb{Q}},t^+)|^2}{(\beta^t_{L})^2+\gamma^2} .\end{align} $$

Assuming, in addition, that LI $^{-}$ holds, we have the simplified formula

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] &= 2\sum_{\chi\in \mathrm{Irr}(G^+)} |\widehat {t^+}(\chi)|^2 \sum_{\gamma_{\chi}\neq 0} \frac {1}{(\beta^t_{L})^2+\gamma_{\chi}^2}. \end{align*} $$

Remark 3.19. If $L/{\mathbb {Q}}$ is Galois and $t^+\equiv 0$ , then $L(s,L/{\mathbb {Q}},t^+) \equiv 1$ and, consequently, $\mathrm {Var}[X(L/K;t)]=0$ . In this case, by Corollary 3.10, we also have $\mathbb E[X(L/K;t)]=0$ , and the measure associated to $X(L/K;t)$ is just a Dirac delta centred at $0$ . This holds, for example, with the class function $t=|C_1|^{-1}1_{C_1}-|C_2|^{-1}1_{C_2}$ , where $C_1,C_2 \in G^{\sharp }$ are distinct and, such that $C_1^+=C_2^+$ (as in Theorem 2.19).

Proof of Proposition 3.18

We will combine the arguments in [Ng, Section 5.1], [Fi2, Lemma 2.6], [De, Theorem 2.1] and [ANS, Theorem 1.2] (one cannot apply those results directly, since we are not assuming GRH and, moreover, t is complex-valued). For any $T\geq 1$ , we define

(71) $$ \begin{align} \beta^t_{L}(T)= \begin{cases} \sup\{ \Re(\rho) < \beta^t_{L} : |\Im(\rho)|\leq T,L(\rho,L/{\mathbb{Q}},\chi)=0;&\\ \qquad \chi \in \mathrm{supp}(\widehat{t^+}) \} & \text{if AC holds for } L/{\mathbb{Q}} ;\\ \sup\{ \Re(\rho)<\beta^t_{L} : |\Im(\rho)|\leq T,\zeta_L(\rho)=0 \} &\text{otherwise}, \end{cases} \end{align} $$

where we recall the definition (10). Note that $\beta ^t_{L}(T)<\beta ^t_{L}$ . Using the decomposition $ t= \sum _{C\in G^\sharp } t(C) 1_C $ and letting $g_C$ be any element of C, we deduce from Corollary 3.17 that for $x\geq 2$ and $X\geq T\geq 2$ ,

(72) $$ \begin{align} &\frac{\log x}{x^{\beta^t_{L}}} (\pi(x;L/K,t)-\widehat t(1)\mathrm{Li}(x)) = -\delta_{\beta^t_{L}=\frac 12}\langle t,r \rangle_G-\frac{1}{\beta^t_{L}} \mathrm{ord}_{s=\beta^t_{L}} L(s,L/K,t)\nonumber\\ &\qquad\qquad -\sum_{C\in G^\sharp} t(C) \sum_{ \chi \in \mathrm{Irr}(\langle g_C\rangle)} \overline{\chi}(g_C) \Big(\sum_{\substack{\rho_\chi = \beta^t_L+i\gamma_\chi\nonumber\\ 0<|\gamma_\chi|\leq T}} +\sum_{\substack{\rho_\chi = \beta^t_L+i\gamma_\chi\\ T<|\gamma_\chi|\leq X}} \Big) \frac{x^{i\gamma_{\chi}}}{\rho_{\chi}}\nonumber\\ &\qquad\qquad +\,O_{L,K}\Big(\frac 1{\log x}+ \frac{x^{1-\beta^t_L}}X (\log(xX))^2+x^{\beta^t_L(T)-\beta^t_L}(\log X)^2\Big) \,. \end{align} $$

Taking $X=x=e^y$ , we see that

$$ \begin{align*}\int_{2}^Y \Big|\sum_{C\in G^\sharp} t(C)\sum_{1\neq \chi \in \mathrm{Irr}(\langle g_C\rangle)} \overline{\chi}(g_C) \sum_{\substack{\rho_\chi\\ T<|\gamma_\chi|\leq {\mathrm{e}}^y}} \frac{{\mathrm{e}}^{y \rho_{\chi}}}{\rho_{\chi}}\Big|^2\mathrm{d}y \ll_{L,K} \frac {(Y+\log T) (\log(d_L T ))^2}{T},\end{align*} $$

and we deduce as in [Ng, Section 5.1], [Fi2, Lemma 2.6], [De, Theorem 2.1] and [ANS, Theorem 1.2] that the function

$$ \begin{align*}\overrightarrow E(y) = \frac{y}{{\mathrm{e}}^{\beta^t_{L}}} (\Re(\pi({\mathrm{e}}^y;L/K,t)-\widehat t(1)\mathrm{Li}(x)),\Im(\pi({\mathrm{e}}^y;L/K,t)-\widehat t(1)\mathrm{ Li}(x)))\end{align*} $$

is $B^2$ almost-periodic. In particular, this function admits a limiting distribution.

To compute the first two moments of this distribution, we deduce using the arguments in the proofs of [Fi2, Lemmas 2.5, 2.6] (see also [ANS, Theorem 1.14] and [De, Theorem 2.1]) that

$$ \begin{align*} \mathbb E[X_\nu] &= \lim_{Y\rightarrow \infty} \frac 1Y \int_2^Y \frac{y}{{\mathrm{e}}^{\beta^t_{L}}}(\pi({\mathrm{e}}^y;L/K,t)-\widehat t(1)\mathrm{Li}({\mathrm{e}}^y)) \mathrm{ d}y\\ &=-\delta_{\beta^t_{L}=\frac 12}\langle t, r \rangle_{G}-\frac 1{\beta^t_{L}}\mathrm{ord}_{s=\beta^t_{L}}L(s,L/K,t). \end{align*} $$

Similarly,

(73) $$ \begin{align} \mathrm{Var}[X_\nu] &=2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{1}{(\beta^t_{L})^2+\gamma^2} \Big|\sum_{C\in G^\sharp} t(C)\sum_{ \chi \in \mathrm{Irr}(\langle g_C\rangle)}\overline{\chi}(g_C)\mathrm{ord}_{s=\beta^t_{L}+i\gamma}L(s,L/L^{\langle g_C\rangle},\chi )\Big|^2 \end{align} $$

$$ \begin{align*} &=2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{|\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/K,t)|^2}{(\beta^t_{L})^2+\gamma^2}, \end{align*} $$

by (57). Moreover, if $L/{\mathbb {Q}}$ is Galois, then by (54), this is

$$ \begin{align*}= 2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{1}{(\beta^t_{L})^2+\gamma^2} |\mathrm{ord}_{s=\beta^t_{L}+i\gamma}L(s,L/{\mathbb{Q}},t^+ )|^2.\\[-39pt] \end{align*} $$

Under AC, GRH and LI $^-$ and for real-valued class functions t, we give an explicit expression for the random variables in Proposition 3.18. We stress that in order for the random variables appearing in this expression to be independent, it is crucial to express $\pi (x;L/K,C)$ in terms of zeros of $L(s,L/{\mathbb {Q}},\chi )$ (rather than $L(s,L/K,\chi )$ ) associated to irreducible characters of $\mathrm {Gal}(L/{\mathbb {Q}})$ ; indeed, these L-functions are believed to be primitive.

Lemma 3.20. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH and LI $^-$ hold. Let $G=\mathrm {Gal}(L/K)$ , $G^+=\mathrm { Gal}(L/{\mathbb {Q}})$ , and fix a class function $t:G\rightarrow \mathbb R$ . Then, we have the following equality (in distribution) of random variables:

(74) $$ \begin{align} X(L/K;t)\overset{\mathrm{d}}= -\langle t,r\rangle_G - 2\mathrm{ord}_{s=\frac 12}L(s,L/K,t) + \sum_{\substack{1\neq \chi\in \mathrm{Irr}(G^+)}}|\widehat{t^+}(\chi)|\sum_{\gamma_{\chi}>0} \frac{2 X_{\gamma_{\chi}}}{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}. \end{align} $$

Here, the random variables $X_{\gamma }$ are defined by $X_{\gamma }=\Re (Z_{\gamma })$ , where the $Z_{\gamma }$ are i.i.d. random variables uniformly distributed on the unit circle in $\mathbb C$ .

Sketch of proof

This is an extension of the random variable approach for the classical Chebyshev bias (where only Dirichlet L-functions are needed) explained in [FM, Section 2.1]. Part of the connection with the independent random variables $Z_\gamma $ uniformly distributed on the unit circle in $\mathbb C$ comes from applying the Kronecker–Weyl Theorem in (72) (the details for Dirichlet L-functions are in loc. cit. and the general case of Artin L-functions is addressed in [Ba2]). Observe that to go from (64) to (74), one uses the functional equation for Artin L-functions (see, e.g. [MM, Chapter 2, Section 2]) to pair up conjugate critical zeros. We can actually compute all the cumulants of $X(L/{\mathbb {Q}};t)$ in this way, and thus recover its characteristic function. This will be useful in Section 5.

Remark 3.21. As mentioned above, the importance of having linearly independent imaginary parts of L-function zeros goes back to Wintner [Wint] and is explained by the role played by the Kronecker–Weyl Theorem in our analysis. Remarkably, recent work of Martin–Ng [MN2] and Devin [De] manages to show absolute continuity of limiting logarithmic distributions under weaker assumptions via the introduction of the notion of self-sufficient zero.

4 Artin conductors

4.1 Link with ramification and representation theory

In this section, we analyse the ramification data of a given Galois extension $L/K$ . These data are related with the expressions obtained for the variance of the random variable $X(L/K;t)$ in Proposition 3.18.

Let us first review the definition of the Artin conductor $A(\chi )$ , following [Fr] (this is a quite standard invariant to consider; see, e.g. [MM, Chapter 2, Section 2] or [LO, (5.2)]). Consider a finite Galois extension of number fields $L/K$ with Galois group G. For $\mathfrak p$ a prime ideal of $\mathcal O_K$ and $\mathfrak P$ a prime ideal of $\mathcal O_L$ lying above $\mathfrak p$ , the higher ramification groups form a sequence $(G_i(\mathfrak P/\mathfrak p))_{i\geq 0}$ of subgroups of G (called filtration of the inertia group $\mathrm {I}(\mathfrak P/\mathfrak p)$ ) defined as follows:

$$ \begin{align*}G_i(\mathfrak P/\mathfrak p) :=\{ \sigma\in G : \forall z \in \mathcal O_L,\, (\sigma z - z) \in \mathfrak P^{i+1}\}.\end{align*} $$

Each $G_i(\mathfrak P/\mathfrak p)$ only depends on $\mathfrak p$ up to conjugation and $G_0(\mathfrak P/\mathfrak p)=\mathrm {I}(\mathfrak P/\mathfrak p)$ . For clarity, let us fix prime ideals $\mathfrak p$ and $\mathfrak P$ as above and write $G_i$ for $G_i(\mathfrak P/\mathfrak p)$ . Given a representation $\rho \colon G \rightarrow GL(V)$ on a complex vector space V, the subgroups $G_i$ act on V through $\rho $ , and we will denote by $V^{G_i}\subset V$ the subspace of $G_i$ -invariant vectors. Let $\chi $ be the character of $\rho $ and

(75) $$ \begin{align} n(\chi,\mathfrak p):=\sum_{i=0}^{\infty} \frac{|G_i|}{|G_0|} \mathrm{codim} V^{G_i}, \end{align} $$

which was shown by Artin to be an integer (see, e.g. [Se1, Chapter $6$ , Theorem $1$ ’]). The Artin conductor of $\chi $ is the ideal

$$ \begin{align*}\mathfrak f(L/K,\chi):=\prod_{\mathfrak p} \mathfrak p^{n(\chi,\mathfrak p)}\,. \end{align*} $$

Note that the set indexing the above product is finite since only finitely many prime ideals $\mathfrak p$ of $\mathcal O_K$ ramify in $L/K$ . We set

(76) $$ \begin{align} A(\chi):=d_K^{\chi(1)}\mathcal N_{K/{\mathbb{Q}}}(\mathfrak f(L/K,\chi))\,, \end{align} $$

where $d_K$ is the absolute value of the absolute discriminant of the number field K and $\mathcal N_{K/{\mathbb {Q}}}$ is the relative ideal norm with respect to $K/{\mathbb {Q}}$ (we will use the slight abuse of notation that identifies the value taken by this relative norm map with the positive generator of the corresponding ideal). One can show (see, e.g. [Se1, Chapter $6$ , consequences of Proposition $6$ ]) the following equalities of ideals in $\mathcal O_K$ (known as the conductor–discriminant formula):

(77) $$ \begin{align} \mathfrak f(L/K,\chi_{\mathrm{reg}})=\prod_{\chi \in \mathrm{Irr}(G)} \mathfrak f(L/K,\chi)^{\chi(1)} =D_{L/K}\,,\\[-9pt]\nonumber \end{align} $$

where $D_{L/K}$ is the relative discriminant of $L/K$ and $\chi _{\mathrm {reg}}$ is the character of the regular representation of G. In particular, by [ZS, Chapter 5, Theorem 31], we have the identity

(78) $$ \begin{align} d_K^{|G|}\mathcal N_{K/{\mathbb{Q}}}(D_{L/K})= A(\chi_{\mathrm{reg}})=d_L.\\[-9pt]\nonumber \end{align} $$

We now estimate $A(\chi )$ for irreducible characters $\chi \in \mathrm {Irr}(G)$ .

Lemma 4.1. Let $L/K$ be a finite Galois extension. Let $\chi $ be an irreducible character of $G=\mathrm {Gal}(L/K)$ , and assume that either $K\neq {\mathbb {Q}}$ , or that $\chi $ is nontrivial. Then, one has the bounds

$$ \begin{align*}\max(1,[K:{\mathbb{Q}}]/2)\chi(1) \leq \log A(\chi) \leq 2\chi(1) [K:{\mathbb{Q}}]\log (\mathrm{rd}_L)\,,\\[-9pt]\end{align*} $$

where the root discriminant $\mathrm {rd}_L$ is defined by (14). The upper bound, due to [MM], is unconditional. The lower bound is unconditional ²¹ if $K\neq {\mathbb {Q}}$ , and holds assuming $L(s,L/{\mathbb {Q}},\chi )$ can be extended to an entire function otherwise.

Proof. In Lemma 4.2, we will reproduce the proof of the upper bound found in [MM]. For the lower bound, we consider two cases. Suppose first that $[K:{\mathbb {Q}}]\geq 2$ . Then we use the lower bound for the absolute discriminant of a number field obtained, that is, in [BD, Theorem 2.4(1)] (noting that the sum over $\mathfrak P$ on the right-hand side of their formula is positive) and which holds for any $y>0$ :

(79) $$ \begin{align} \log d_K\geq r_1(1-I_1(y))+[K:{\mathbb{Q}}](\gamma+\log(4\pi)-I_2(y))-\frac{12\pi}{5\sqrt{y}} ,\\[-9pt]\nonumber\end{align} $$

where $\gamma $ is the Euler constant, $r_1$ is the number of real embeddings of $K/{\mathbb {Q}}$ and

$$ \begin{align*}f(x)=\left(\frac{3}{x^3}(\sin(x)-x\cos(x))\right)^2\,,\end{align*} $$

$$ \begin{align*}I_1(y)= \int_0^\infty\frac{1-f(x\sqrt{y})}{2\cosh^2(x/2)}\mathrm{d}x \,,\hspace{1cm} I_2(y)= \int_0^\infty\frac{1-f(x\sqrt{y})}{\sinh(x)}\mathrm{d}x\,. \end{align*} $$

Setting $y=20$ and using the numerical integration method implemented in SageMath ([Sage]), we obtain that $I_1(20)<0.08$ and $I_2(20)<1.73$ . In particular, the quantity $\gamma -1/2+\log (4\pi )-I_2(20)$ is positive, and we deduce from (79) that

$$ \begin{align*} \log d_K-\frac{[K:{\mathbb{Q}}]}{2}&\geq [K:{\mathbb{Q}}]\bigl(\gamma-\frac{1}{2}+\log(4\pi)-I_2(20)\bigr)-\frac{6\pi}{5\sqrt{5}}\\ &\geq 2\bigl(\gamma-\frac{1}{2}+\log(4\pi)-I_2(20)\bigr)-\frac{6\pi}{5\sqrt{5}}\\ &\geq 0.07\,. \end{align*} $$

Moreover, $\mathcal N_{K/{\mathbb {Q}}}(\mathfrak f(\chi ))\geq 1$ , so that one trivially deduces $\log A(\chi )\geq \chi (1)\log d_K\geq \chi (1)[K:{\mathbb {Q}}]/2$ . If $K={\mathbb {Q}}$ , the lower bound is a consequence of Odlyzko type lower bounds on Artin conductors (see, e.g. [Pi1, Theorem 3.2], where the author proves $\mathfrak f(\chi )\geq 2.91^{\chi (1)}$ ), that are conditional on Artin’s conjecture.

It is known (see [Pi2]) that the lower bound in Lemma 4.1 is optimal. Nevertheless, will show in the next lemma that if one has good estimates on character values, then it is possible to improve both bounds in Lemma 4.1, and in some cases to deduce the exact order of magnitude of $\log A(\chi )$ (for instance, in the case of $G=S_n$ ; see Lemma 7.4).

Lemma 4.2. Let $L/K$ be a finite Galois extension. For any character $\chi $ of $G=\mathrm {Gal}(L/K)$ , we define ²²

$$ \begin{align*}M_{\chi}:=\max_{1\neq \sigma \in G}\frac{|\chi(\sigma)|}{\chi(1)}\leq 1\,.\end{align*} $$

Then we have the bounds

$$ \begin{align*}(1-M_{\chi}) \chi(1) [K:{\mathbb{Q}}]\log (\mathrm{rd}_L) \leq \log A(\chi) \leq (1+M_{\chi}) \chi(1) [K:{\mathbb{Q}}]\log (\mathrm{rd}_L)\,.\end{align*} $$

Proof. The proof is inspired by [MM, Proof of Proposition 7.4]. Let $\rho \colon G\rightarrow GL(V)$ be a complex representation with character $\tau $ , let $\mathfrak p$ be a prime ideal of $\mathcal O_K$ and let $(G_i)$ be the attached filtration of inertia (defined up to conjugation in G). We start with the following identity:

(80) $$ \begin{align} \mathrm{codim}\ V^{G_i}=\tau(1)-\dim V^{G_i} =\tau(1)-\langle \tau,\mathbf{1}\rangle_{G_i}=\frac 1{|G_i|} \sum_{a\in G_i} \bigl(\tau(1)-\tau(a)\bigr)\,, \end{align} $$

where $\langle \,,\,\rangle _{G_i}$ is defined as in Section 3.1 and $\mathbf {1}$ is the trivial representation. If $\tau =\chi _{\mathrm {reg}}$ is the character of the regular representation of G, then for any $a\in G\setminus \{\mathrm {id}\}$ ,

$$ \begin{align*}\chi_{\mathrm{reg}}(a)=\sum_{\varphi\in\mathrm{Irr}(G)}\varphi(1)\varphi(a)=0 \end{align*} $$

by the orthogonality relation (42). Hence, combining (75) with (80), we obtain that

(81) $$ \begin{align} n(\chi_{\mathrm{reg}},\mathfrak p) = \frac 1{|G_0|}\sum_{i\geq 0} \sum_{1\neq a\in G_i}\chi_{\mathrm{reg}}(1)=\frac{|G|}{|G_0|}\sum_{i\geq 0}\bigl(|G_i|-1\bigr). \end{align} $$

Similarly, setting $\tau =\chi $ in (80), we have that

(82) $$ \begin{align} n(\chi,\mathfrak p)= \frac{\chi(1)}{|G_0|} \sum_{i\geq 0} \sum_{1\neq a\in G_i} \left(1-\frac{\chi(a)}{\chi(1)}\right)\,. \end{align} $$

Combining our expressions for $n(\chi _{\mathrm {reg}},\mathfrak p)$ and $n(\chi ,\mathfrak p)$ yields the bound

(83) $$ \begin{align} \left|n(\chi,\mathfrak p)-\frac{\chi(1)}{|G|}n(\chi_{\mathrm{reg}},\mathfrak p)\right| \leq M_\chi\frac{\chi(1)}{|G|}n(\chi_{\mathrm{reg}},\mathfrak p)\,. \end{align} $$

We now establish the claimed bound on $\log A(\chi )$ . Let $\nu _{\mathfrak p}$ denote the $\mathfrak p$ -adic valuation on $\mathcal O_K$ , and observe that (83) implies the bound

$$ \begin{align*}n(\chi,\mathfrak p)=\nu_{\mathfrak p}(\mathfrak f(L/K,\chi))\leq \frac{\chi(1)}{|G|}(1+M_\chi)n(\chi_{\mathrm{reg}},\mathfrak p)= \frac{\chi(1)}{|G|}(1+M_\chi)\nu_{\mathfrak p}(D_{L/K})\,. \end{align*} $$

We deduce that

$$ \begin{align*}\log \mathcal N_{K/{\mathbb{Q}}}\bigl(\mathfrak f(L/K,\chi)\bigr)\leq \frac{\chi(1)}{|G|}(1+M_\chi) \log \mathcal N_{K/{\mathbb{Q}}}(D_{L/K})\,. \end{align*} $$

By adding $\chi (1)\log (d_K)$ on both sides, we obtain the bound

$$ \begin{align*} \log A(\chi)&\leq \chi(1)(1+M_\chi)\biggl(\log (d_K)+\log\bigl(\mathcal N_{K/{\mathbb{Q}}} (D_{L/K})^{\frac{1}{|G|}}\bigr)\biggr)\\ &\leq \chi(1)(1+M_\chi)\log\bigl(d_L^{\frac{1}{|G|}}\bigr)\\ &\leq \chi(1)(1+M_\chi)[K:{\mathbb{Q}}]\log ( \mathrm{rd}_L)\,. \end{align*} $$

The lower bound of the lemma is deduced from (83) in an analogous fashion.

4.2 Variance associated to the limiting distribution

We now consider a Galois extension of number fields $L/K$ of group G and estimate various sums indexed by zeros of the associated Artin L-functions. For class functions $t\colon G\rightarrow \mathbb C$ , these sums are related to the variance and fourth moment of the random variable $X(L/K;t)$ defined in Proposition 3.18. For $\chi \in \mathrm {Irr}(\mathrm {Gal}(L/K))$ , we define

(84) $$ \begin{align} B(\chi):=\sum_{\gamma_\chi} \frac{1}{\frac 14+\gamma_{\chi}^2}; \hspace{1cm} B_0(\chi):= \sum_{\gamma_\chi\neq 0} \frac{1}{\frac 14+\gamma_{\chi}^2}; \hspace{1cm} B_2(\chi) :=\sum_{\gamma_\chi\neq 0} \frac{1}{(\frac 14+\gamma_{\chi}^2)^2}\,, \end{align} $$

where the sums are indexed by the imaginary parts of the ordinates of the nontrivial zeros of $L(s,L/K,\chi )$ , counted with multiplicities. In the next lemma, we will determine the order of magnitude of $B(\chi ),B_0(\chi )$ and $B_2(\chi )$ . Note that under GRH, every nontrivial zero of $L(s,L/K,\chi )$ is of the form $\rho _\chi =\frac 12+i \gamma _\chi $ with $\gamma _\chi \in \mathbb R$ , and thus, $\frac 14+\gamma _\chi ^2 = |\rho _\chi |^2$ . However, the constant $\frac 14$ in (84) could be replaced by any fixed real number $\beta ^2 \in [\frac 14,1]$ , and that would not change the orders of magnitude of $B(\chi ),B_0(\chi )$ and $B_2(\chi )$ (with constants independent of $\beta )$ . Indeed, for $\gamma \in \mathbb R$ , we have that $ (\frac 14 +\gamma ^2) \leq (\beta ^2 +\gamma ^2) \leq 4 (\frac 14 +\gamma ^2)$ .

Lemma 4.3. Let $L/K$ be a finite Galois extension for which AC holds. For any character $\chi $ of $G=\mathrm {Gal}(L/K)$ , we have the estimates

$$ \begin{align*}B(\chi)\asymp B_0(\chi)\asymp B_2(\chi) \asymp \log (A(\chi)+2)\,.\end{align*} $$

Proof. We begin with the Riemann–von Mangoldt formula [IK, Theorem 5.8], which we combine with the bound on the analytic conductor given in [IK, Section 5.13]. In the notation of loc. cit., the degree d of the L-function $L(s,L/K,\chi )$ is relative to ${\mathbb {Q}}$ and thus equals $[K:{\mathbb {Q}}]\chi (1)$ . For $T\geq 1$ , we obtain the estimate

(85) $$ \begin{align} N(T,\chi):= |\{\gamma_{\chi}\colon |\gamma_{\chi}|\leq T \}|&=\frac T{\pi} \log \Big(\frac{A(\chi)T^{[K:{\mathbb{Q}}]\chi(1)}}{(2\pi e)^{[K:{\mathbb{Q}}]\chi(1)}}\Big)\nonumber\\ &\quad + O(\log ((A(\chi)+2)(T+4)^{[K:{\mathbb{Q}}]\chi(1)}))\,. \end{align} $$

It follows that

$$ \begin{align*}N(2T,\chi)-N(T,\chi) = \frac T{\pi} \log \Big(\frac{A(\chi)(2T)^{[K:{\mathbb{Q}}]\chi(1)}}{(\pi e)^{[K:{\mathbb{Q}}]\chi(1)}}\Big) +O(\log((A(\chi)+2)(2T+8)^{[K:{\mathbb{Q}}]\chi(1)}))\,.\end{align*} $$

It is easy to see that for T larger than an absolute constant, the main term is at least twice as big as the error term (e.g. if we let $C_0$ be the implied constant in the error term above, it suffices to take T larger than $2\pi C_0$ and, such that $T\log (2T/\pi e)\geq 2\pi C_0\log (2T+8)$ ).

Therefore, there exists an absolute constant $T_0\geq 4\pi e$ , such that

$$ \begin{align*}N(2T_0,\chi)-N(T_0,\chi) \geq \frac {T_0}{2\pi} \log\Big( A(\chi) \Big(\frac{2T_0}{\pi e}\Big)^{[K:{\mathbb{Q}}]\chi(1)}\Big)\geq \frac{T_0}{2\pi} \log (A(\chi)+2),\end{align*} $$

and hence

$$ \begin{align*}B_0(\chi) \geq \frac 1{\frac 14 + (2T_0)^2}\frac{T_0}{2\pi} \log (A(\chi)+2) \gg \log (A(\chi)+2).\end{align*} $$

For the upper bound, one easily deduces from (85) that $ N(T,\chi ) \ll T \log \frac {A(\chi )T^{[K:{\mathbb {Q}}]\chi (1)}}{(2\pi e)^{[K:{\mathbb {Q}}]\chi (1)}}$ for $T\geq 4\pi e$ , and hence, summation by parts yields that

$$ \begin{align*} B_0(\chi)\leq B(\chi) &= \sum_{\gamma_\chi} \frac{1}{\frac 14+\gamma_{\chi}^2} \leq 4N(2,\chi)+\int_2^{\infty} \frac{\mathrm{d}N(t,\chi)}{\frac 14+t^2} \\ & \ll \log (A(\chi)+2)+[K:{\mathbb{Q}}]\chi(1) + \int_2^{\infty} \frac{t^2 (\log A(\chi)+[K:{\mathbb{Q}}]\chi(1)\log t)}{(1/4+t^2)^2}\mathrm{d}t \\ &\ll \log (A(\chi)+2)+[K:{\mathbb{Q}}]\chi(1)\,. \end{align*} $$

Since we are assuming AC, we can apply Lemma 4.1 to deduce that $B_0(\chi ),B(\chi )\asymp \log (A(\chi )+2)$ . The proof is similar for $B_2(\chi )$ .

Remark 4.4. If $\chi $ is a Dirichlet character of conductor $q^*\geq 3$ , then under GRH, we can give an exact formula for $B(\chi )$ and $B_2(\chi )$ , and deduce the more precise estimate

$$ \begin{align*}B(\chi) =\log q^* + O(\log\log q^*)\end{align*} $$

(this is achieved, e.g. by applying Littlewood’s conditional bound on $\frac {L'(1,\chi )}{L(1,\chi )}$ to [MV, (10.39)]). Such an estimate is harder to establish for a general extension $L/K$ . We have by [LO, (5.11)] that

$$ \begin{align*}2B(\chi)= \log A(\chi) +2\frac{\gamma_{\chi}'(1)}{\gamma_{\chi}(1)}+2\Re \frac{L'(1,\chi)}{L(1,\chi)},\end{align*} $$

where the gamma factor is given by

$$ \begin{align*}\gamma_{\chi}(s):= \Big( \pi^{-\frac{s+1}2} \Gamma (\tfrac{s+1}2) \Big)^{b(\chi)} \Big( \pi^{-\frac{s}2} \Gamma (\tfrac{s}2) \Big)^{a(\chi)}\end{align*} $$

for some nonnegative integers $a(\chi ),b(\chi )$ , such that $a(\chi )+b(\chi )=\chi (1)$ . It follows that

$$ \begin{align*}\frac{\gamma_{\chi}'(1)}{\gamma_{\chi}(1)} \asymp \chi(1).\end{align*} $$

As for the ‘analytic term,’ we could either use the following bound (see [Ng, Proposition 2.4.2.3])

$$ \begin{align*}\frac{L'(1,\chi)}{L(1,\chi)} \ll \chi(1) \log\log (A(\chi)+2),\end{align*} $$

or an estimate for its average, as in [FM, Theorem 1.7]. The problem with this individual bound for a given $\chi $ is that it seems hard, in general, to improve the bound $\chi (1)\ll \log A(\chi )$ (one can, however, do this in the specific case $G=S_n$ , and we put this to use in Proposition 7.6). As for the bound, on average, it works quite well for some abelian extensions (see [FM]), however, there are examples such as Theorem 2.19 in which there is a unique nonabelian character of degree comparable to $|G|$ , hence, the averaging will not succeed in this case.

4.3 Proofs of Theorems 2.1 and 2.3

We first state and prove Proposition 4.6, which implies Theorem 2.1. This will require the following lemma.

Lemma 4.5. Let $L/K$ be a finite Galois extension for which AC holds, and let $\chi $ be an irreducible character of $G=\mathrm {Gal}(L/K)$ . For $T\geq 1$ , $\beta \in [\tfrac 14,1]$ and $j\in \mathbb Z_{\geq 0}$ , we have the estimate

$$ \begin{align*}\sum_{|\gamma_{\chi}|>T} \frac {(\log(|\gamma_{\chi}|+4))^j}{\beta+\gamma_{\chi}^2} \ll_j \frac{(\log (T+4))^j\log(A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)})}T,\end{align*} $$

where the sum on the left-hand side is over imaginary parts of zeros of $L(s,L/K,\chi )$ and where the implied constant is independent of $\beta $ .

Proof. By (85), we have that

$$ \begin{align*}N(T,\chi)= |\{\gamma_{\chi}\colon |\gamma_{\chi}|\leq T \}|\ll T\log (A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)}). \end{align*} $$

With a summation by parts, we obtain that for $j\geq 1$ ,

$$ \begin{align*} & \sum_{\substack{|\gamma_{\chi}|> T }} \frac {(\log(|\gamma_{\chi}|+4))^j}{\beta+\gamma_{\chi}^2} \leq \sum_{\substack{|\gamma_{\chi}| > T }} \frac {(\log(|\gamma_{\chi}|+4))^j}{\gamma_{\chi}^2} = \int_T^{\infty} \frac{(\log(t+4))^j\mathrm{d}N(t,\chi)}{t^2} \\&=- \frac{(\log(T+4))^jN(T,\chi)}{T^2} + \int_T^{\infty}\Big( j\frac{(\log(t+4))^{j-1}}{t^2(t+4)} -2\frac{(\log(t+4))^j}{t^3}\Big) N(t,\chi)\mathrm{d}t \\ &\ll j \int_T^{\infty} \frac{ (\log(t+4))^j\log (A(\chi)(t+4)^{[K:{\mathbb{Q}}]\chi(1)}) }{ t^2} \mathrm{d}t \\ &\hspace{2cm}+ \frac{(\log(T+4))^j\log (A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)})}T.\\[-9pt] \end{align*} $$

The proof follows and is similar in the case $j=0$ .

In Proposition 4.6, we will use the bound $ |\widehat t(\chi )| \leq \chi (1) {\lVert {t}\rVert }_1$ , which follows from the triangle inequality.

Proposition 4.6. Let $L/K$ be a Galois extension of number fields, and let $G=\mathrm {Gal}(L/K)$ . Then for any class function $t\colon G\rightarrow \mathbb C$ , we have the upper bound

(86) $$ \begin{align} \mathrm{Var}[X(L/K;t)] \ll {\lVert{t}\rVert}_1^2\log (d_L+2) \min(M_L, \log (d_L+2)),\\[-9pt]\nonumber \end{align} $$

where

$$ \begin{align*}M_{L} := \max \Big \{ \mathrm{ord}_{s=\rho} \zeta_L(s) :\Re(\rho)=\beta_L^t, 0<|\Im(\rho)|< \log (d_L+2)(\log\log (d_L+2))^2\Big\}.\\[-9pt]\end{align*} $$

If $L/{\mathbb {Q}}$ is Galois and AC holds, then we have the bound

(87) $$ \begin{align} \mathrm{Var}[X(L/K;t)] \ll (m^t_{L})^2\sum_{\chi\in \mathrm{Irr}(G^+) }|\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\,, \\[-9pt]\nonumber\end{align} $$

where

$$ \begin{align*}m^t_{L} := \max \Big \{ \mathrm{ord}_{s=\rho} \Big( \prod_{\substack{\chi \in \mathrm{supp}(\widehat {t^+}) }} L(s,L/{\mathbb{Q}},\chi)\Big) : \Re(\rho)=\beta_L^t, 0<|\Im(\rho)|< (T_{L}\log (T_{L}))^2\},\end{align*} $$

with $T_{L}:=\log (\mathrm {rd}_L+2)\max _{\substack { \chi \in \mathrm {Irr}(G^+) }}\chi (1)$ . Assuming, moreover, that $\beta _{L}^{t}=\frac 12$ , and ²³ $\widehat {t^+}(\chi ) \not \equiv 0$ , we have, under LI $^-$ , the lower bound

(88) $$ \begin{align} \mathrm{Var}[X(L/K;t)] \gg \sum_{ \chi\in \mathrm{Irr}(G^+) }|\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\,. \end{align} $$

In the particular case $t=|G|1_{\{\mathrm {id}\}}$ , the lower bound $ \mathrm {Var}[X(L/K;|G|1_{\{\mathrm {id}\}} )]\gg \log (d_L+2)$ holds assuming only the Riemann hypothesis for $\zeta _L(s)$ (without requiring $L/{\mathbb {Q}}$ to be Galois).

We recall that if $L/{\mathbb {Q}}$ is Galois and under AC and LI $^-$ , $m^t_{L}\leq 1$ and $M_L\leq \max _{\substack {\chi \in \mathrm {Irr}(G^+) }}\chi (1) $ .

Proof of Proposition 4.6

We start by establishing (86). Note that for any $s_0\in \mathbb C$ , $C\in G^\sharp $ and $g_C\in C$ ,

$$ \begin{align*}\Big|\sum_{\chi \in \mathrm{Irr}(\langle g_C\rangle)} \chi(g_C) \mathrm{ord}_{s=s_0}L(s,L/L^{\langle g_C\rangle},\chi )\Big| \leq \mathrm{ord}_{s=s_0}\zeta_L(s).\\[-9pt]\end{align*} $$

We have used the crucial fact that $\mathrm {ord}_{s=s_0}L(s,L/L^{\langle g_C\rangle },\chi )\geq 0$ (since AC holds for the abelian extension $L/L^{\langle g_C \rangle }$ ). Hence, (73) implies that

$$ \begin{align*} \mathrm{Var}[X(L/K;t)]&\leq 2{\lVert{t}\rVert}^2_1\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{(\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s))^2}{(\beta^t_{L})^2+\gamma^2}\,,\\[-9pt] \end{align*} $$

where $Z_L$ is defined in (66). Now, we have the classical unconditional upper bound

(89) $$ \begin{align} \mathrm{ord}_{s=\rho}\zeta_L(s) \ll \log (d_L(|\Im(\rho)|+4)^{[L:{\mathbb{Q}}]})\\[-9pt]\nonumber \end{align} $$

(see [IK, (5.27)]); we deduce that

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] \ll {\lVert{t}\rVert}^2_1 (\log (d_L+2))^2+ {\lVert{t}\rVert}^2_1|G^+|\log (d_L+2) \ll {\lVert{t}\rVert}^2_1(\log (d_L+2))^2,\end{align*} $$

by Lemma 4.1. To prove (86), we apply Lemma 4.5 to the trivial extension $L/L$ ; this takes the form

$$ \begin{align*}\mathop{\sum \Bigl.^{*}}\limits_{\substack{\gamma \in Z_{L} \\ |\gamma|>T}} \frac{\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s)}{(\beta_L^t)^2+\gamma^2} \ll \frac{\log(d_L(T+4)^{[L:{\mathbb{Q}}]})}{T}.\\[-9pt] \end{align*} $$

We deduce that for any $T\geq 1,$

$$ \begin{align*} \mathop{\sum \Bigl.^{*}}\limits_{\substack{\gamma \in Z_{L} \\ |\gamma|>T}} \frac{(\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s))^2}{(\beta^t_L)^2+\gamma^2} &\ll \mathop{\sum \Bigl.^{*}}\limits_{\substack{\gamma \in Z_{L} \\ |\gamma|>T}} \frac{\log (d_L(|\gamma|+4)^{[L:{\mathbb{Q}}]})\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s)}{\beta_{L}^2+\gamma^2} \\ &\ll \frac{(\log(d_L(T+4)^{[L:{\mathbb{Q}}]}))^2}{T}. \end{align*} $$

Moreover, by Lemma 4.3 (see the comments before this lemma about replacing $\frac 14$ by $(\beta _L^t)^2\in [\frac 14,1 ]$ ), taking $T= \log (d_L+2) (\log \log (d_L+2))^2$ and applying Lemma 4.1,

$$ \begin{align*}\mathop{\sum \Bigl.^{*}}\limits_{\substack{\gamma \in Z_{L} \\ |\gamma|\leq T}} \frac{(\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s))^2}{(\beta^t_L)^2+\gamma^2} \ll M_L \log (d_L+2). \end{align*} $$

The upper bound (86) follows. Also, under GRH, Proposition 3.18 reads

$$ \begin{align*}\mathrm{Var}[X(L/K;|G|1_{\{\mathrm{id}\}})]=2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{(\mathrm{ord}_{s=\beta^t_L+i\gamma}\zeta_L(s))^2}{\tfrac 14+\gamma^2}\geq \sum_{\gamma \in Z_{L} } \frac{1}{\tfrac 14+\gamma^2} \gg \log (d_L+2). \end{align*} $$

We now move to (87). We enumerate the characters $\chi \in \mathrm {Irr} (G^+) = \{ \chi _1,\chi _2, \cdots , \chi _k\}$ in such a way that for each $1\leq j\leq k-1$ , $ |\widehat {t^+}(\chi _j)| \geq |\widehat {t^+}(\chi _{j+1})|. $ Then, by Proposition 3.18, we have that

$$ \begin{align*} \mathrm{Var}[X(L/K;t)] &= 2\mathop{\sum \Bigl.^{*}}\limits_{\gamma \in Z_{L} } \frac{1}{\beta_{L}^2+\gamma^2} |\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/{\mathbb{Q}},t^+ )|^2 \\ &\leq 2 \sum_{j=1}^k \mathop{\sum \Bigl.^{*}}\limits_{ \substack{\gamma \in Z_{L} \\ L(\beta_{L}+i\gamma,\chi_j)=0 \\ L(\beta_{L}+i\gamma,\chi_{\ell})\neq 0 \text{ for } \ell <j}} \\&\quad \times \frac{1}{\beta_{L}^2+\gamma^2} \Big(\sum_{ \chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/{\mathbb{Q}},\chi )\Big)^2 \\ &= V_{\leq T}+V_{>T} , \end{align*} $$

where $V_{\leq T}$ denotes the sum over $\gamma \leq T$ and $V_{> T}$ that over $\gamma>T$ . Now, if $L(\beta _L^t+i\gamma ,L/{\mathbb {Q}},\chi _j)=0$ and $L(\beta _L^t+i\gamma ,L/{\mathbb {Q}},\chi _{\ell })\neq 0 \text { for } \ell <j$ , then

$$ \begin{align*}\sum_{\chi \in \mathrm{Irr}(G^+)}|\widehat{t^+}(\chi)|\mathrm{ord}_{s=\beta^t_L+i\gamma}L(s,L/{\mathbb{Q}},\chi ) \leq |\widehat{t^+}(\chi_j)|m^t_{L}(\beta_{L}+i\gamma) ,\end{align*} $$

where $m^t_{L}(\rho )$ is the order of vanishing of $\prod _{\chi \in \mathrm {supp}(\widehat {t^+})}L(s,L/{\mathbb {Q}},\chi )$ at $s=\rho $ . Hence, for any $T>1$ and denoting

$$ \begin{align*}m^t_{L}(T) := \max \Big \{ \mathrm{ord}_{s=\rho} \Big( \prod_{\substack{\chi \in \mathrm{supp}(\widehat{t^+}) }} L(s,L/{\mathbb{Q}},\chi)\Big) : \Re(\rho)=\beta_L^t, 0<|\Im(\rho)| \leq T\},\end{align*} $$

we have that

$$ \begin{align*} V_{\leq T}&\ll (m^t_{L}(T))^2 \sum_{j=1}^k |\widehat{t^+}(\chi_j)|^2 \mathop{\sum \Bigl.^{*}}\limits_{ \substack{\gamma \in Z_{L} \\ L(\beta^t_{L}+i\gamma,\chi_j)=0 \\ L(\beta^t_{L}+i\gamma,\chi_{\ell})\neq 0 \text{ for } \ell <j \\ \gamma \leq T}} \frac{1}{(\beta_L^t)^2+\gamma^2} \\ & \ll (m^t_{L}(T))^2 \sum_{\chi \in \mathrm{Irr}(G^+) } |\widehat{t^+}(\chi)|^2 \mathop{\sum \Bigl.^{*}}\limits_{\gamma_{\chi}} \frac{1}{(\beta_L^t)^2+\gamma_{\chi}^2} \\ &\ll (m^t_{L}(T))^2 \sum_{\chi \in \mathrm{Irr}(G^+) } |\widehat{t^+}(\chi)|^2\log (A(\chi)+2). \end{align*} $$

In a similar fashion, and by applying (89) and Lemma 4.5 (with $j=0,2$ ), we see that

$$ \begin{align*} V_{> T}\ll\frac 1T \sum_{\chi \in \mathrm{Irr}(G^+)}\chi(1) \log(\mathrm{rd}_L+2) \sum_{\chi \in \mathrm{Irr}(G^+) } |\widehat{t^+}(\chi)|^2\log (A(\chi)+2),\\[-9pt] \end{align*} $$

and (87) follows from taking

$$ \begin{align*}T=\Big( \Big(\log (\mathrm{rd}_L+2)\max_{\substack{ \chi \in \mathrm{Irr}(G^+) }} \chi(1)\Big) \cdot \log\Big( \log (\mathrm{rd}_L+2)\max_{\substack{ \chi \in \mathrm{ Irr}(G^+) }} \chi(1)\Big)\Big)^2 .\\[-9pt]\end{align*} $$

Coming back to the general case and assuming $\beta ^t_L=\tfrac 12$ and LI $^-$ , we see that for $\chi _1\neq \chi _2\in \mathrm {Irr}(G^+)$ , the sets of nonreal zeros of $L(s,\chi _1) $ and $L(s,\chi _2)$ are disjoint. Hence, Proposition 3.18 takes the form

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] &= \sum_{\chi\in \mathrm{Irr}(G^+)} |\widehat {t^+}(\chi)|^2 \sum_{\gamma_{\chi}\neq 0} \frac {1}{\frac 14+\gamma_{\chi}^2}.\\[-9pt] \end{align*} $$

The lower bound (88) follows once more from applying Lemma 4.3.

Combining Proposition 4.6 and Lemma 4.2 will allow us in some cases to determine the exact order of magnitude of the variance of the random variable $X(L/{\mathbb {Q}}; t)$ in terms of the absolute discriminant of the number field L, independently of the individual Artin conductors. For this to be possible, the characters of the associated Galois group of high degree must have the property that $|\chi (C)|$ is significantly smaller than $\chi (1)$ for all conjugacy classes $C\neq \{\mathrm {id}\}$ . We illustrate this with the following proposition. Recalling the definition (5), we note that $ {\lVert {t^+}\rVert }_1\leq {\lVert {t^+}\rVert }_2$ , by Cauchy–Schwarz. However, in the case $t^+=\sum _{i\leq k} |G^+| |C^+_i|^{-1}1_{C^+_i}$ , where $C^+_1,...,C^+_i\in (G^+)^\sharp $ are distinct, we have that ${\lVert {t^+}\rVert }_1= 1$ and ${\lVert {t^+}\rVert }^2_2 =|G^+|\sum _{i\leq k} |C^+_i|^{-1}\geq |G^+|\min (|C^+_i|)^{-1}$ , that is ${\lVert {t^+}\rVert }_2$ is significantly larger than ${\lVert {t^+}\rVert }_1$ .

Proposition 4.7. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH and LI $^-$ hold. Then we have the bound

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] \gg \eta_{L/K;t} [K:\mathbb{Q}]\log (\mathrm{rd}_L+2) \sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1)|\widehat t(\chi)|^2,\\[-9pt]\end{align*} $$

where

$$ \begin{align*}\eta_{L/K;t} := 1-\max_{\substack{ \chi \in C_{L/K;t} }}\max_{\mathrm{id}\neq g\in G} \frac{|\chi(g)|}{\chi(1)}\geq 0, \end{align*} $$

with

$$ \begin{align*}C_{L/K;t}:= \{ \chi \in \mathrm{supp}(\widehat {t^+}) : \chi(1)\geq {\lVert{t^+}\rVert}_2 {\lVert{t^+}\rVert}_1^{-1} (4\#\mathrm{supp}(\widehat{t^+}))^{-\frac 12}\}.\end{align*} $$

Proof. We first establish a preliminary bound. Defining $N:={\lVert {t^+}\rVert }_2{\lVert {t^+}\rVert }_1^{-1}(2\#\mathrm {supp}(\widehat {t^+}))^{-\frac 12}$ and applying Lemmas 3.4 and 3.5, we see that

(90) $$ \begin{align} \notag \sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \chi(1)>N }} \chi(1)|\widehat {t^+}(\chi)|^2 &\geq N\Big(\sum_{\substack{\chi \in \mathrm{Irr}(G^+) }} |\widehat {t^+}(\chi)|^2 - \sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \chi(1)\leq N }} |\widehat {t^+}(\chi)|^2 \Big) \\ &\geq N ({\lVert{t^+}\rVert}_2^2 -N^2 {\lVert{t^+}\rVert}_1^2 \#\mathrm{supp}(\widehat{t^+}) ) \notag \\ & =N^3{\lVert{t^+}\rVert}_1^2 \#\mathrm{supp}(\widehat{t^+}) \geq \sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \chi(1)\leq N }} \chi(1)|\widehat {t^+}(\chi)|^2. \end{align} $$

Hence, applying Proposition 4.6 and Lemma 4.2 ²⁴ ,

$$ \begin{align*} \mathrm{Var}[X(L/K;t)] &\gg \eta_{L/K;t} [K:{\mathbb{Q}}]\log (\mathrm{rd}_L+2) \sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \chi(1)> N }} \chi(1)|\widehat {t^+}(\chi)|^2\\ &\geq \frac{\eta_{L/K;t} [K:{\mathbb{Q}}]\log (\mathrm{rd}_L+2)}2 \sum_{\substack{\chi \in \mathrm{Irr}(G^+) }} \chi(1)|\widehat {t^+}(\chi)|^2, \end{align*} $$

by (90).

Proof of Theorem 2.1

Combine Propositions 3.18, 4.6 and 4.7. The lower bound on the character sum will be proven in Lemma 6.1, and the upper bound follows from the bound $\chi (1)\leq |G^+|^{\frac 12}$ .

Proofs of Theorems 2.3 and 2.6

We begin by proving (24). Consider the following weighted variant of $\psi (x;L/K,t)$ , where h is a nonnegative, not identically zero smooth function supported in $[1,\tfrac 32]$ and $t:G\rightarrow \mathbb R$ is a class function:

$$ \begin{align*}\psi_{h}(x;L/K,t) :=\sum_{ \substack{ \mathfrak p \triangleleft \mathcal O_K \\ k\geq 1}} t(\varphi_{\mathfrak p}^k) h(\mathcal N \mathfrak p^k / x)\log(\mathcal N \mathfrak p),\end{align*} $$

which decomposes as

$$ \begin{align*}\psi_{h}(x;L/K,t)= \sum_{\chi \in \mathrm{Irr}(G)}\widehat{t}(\chi) \psi_h(x;L/K,\chi)\,.\end{align*} $$

Integration by parts shows that for $|s|\geq 2$ , the Mellin transform

$$ \begin{align*}\mathcal Mh(s):= \int_0^\infty x^{s-1} h(x)\mathrm{d}x\end{align*} $$

satisfies the bound

(91) $$ \begin{align} \mathcal Mh(s) \ll \frac 1{|s|^2} \int_0^\infty x^{\Re(s)+1} |h"(x)| \mathrm{d}x\ll_h \frac 1{|s|^2}. \end{align} $$

It follows from [IK, Theorem 5.11] that for any irreducible character $\chi \in \mathrm {Irr}(G)$ and for $x\geq 1$ ,

$$ \begin{align*} \psi_{h}(x;L/K,\chi) - x\mathcal Mh(1) \delta_{\chi = 1} &\ll c_h \log (A(\chi)+2) + c_h x^{\frac 12} \chi(1) + \sum_{\rho_\chi} |\mathcal Mh(\rho_{\chi})x^{\rho_\chi}| \\ & \ll c_h x^{\frac 12} \chi(1)[K:{\mathbb{Q}}]\log (\mathrm{rd}_L+2),\\[-9pt] \end{align*} $$

by Lemma 4.1 and Stirling’s formula, where $c_h := 1+\sup (|h|+|h"|)$ . We deduce that

(92) $$ \begin{align} \psi_{h}(x;L/K,t) &= x\mathcal Mh(1)\widehat{t}(1) +O(c_h\lambda(t) [K:{\mathbb{Q}}] x^{\frac 12} \log(\mathrm{rd}_L+2)).\\[-9pt]\nonumber \end{align} $$

Applying inclusion-exclusion, we see that

(93) $$ \begin{align} \theta_{h}(x;L/K,t):= \sum_{ \substack{ \mathfrak p \triangleleft \mathcal O_K }} t(\varphi_{\mathfrak p}) h( \mathcal N\mathfrak p/ x) \log (\mathcal N\mathfrak p) = \sum_{\ell \geq 1} \mu(\ell) \psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/K,t(\cdot^\ell)).\\[-9pt]\nonumber \end{align} $$

For the terms with $\ell \geq 2$ , we use the Fourier decomposition of t and deduce that

(94) $$ \begin{align} |\psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/K,t(\cdot^\ell))| = \Big|\sum_{\chi\in \mathrm{Irr}(G)} \widehat t(\chi) \psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/K,\chi(\cdot^\ell))\Big|\leq \lambda(t) \psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/K,1). \end{align} $$

Now, the explicit formula for $\zeta _K(s)$ (see, for instance [IK, Theorem 5.11]) implies that for $x\geq 1$ ,

$$ \begin{align*} \psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/K,1) &= \sum_{\substack{\mathfrak p \triangleleft \mathcal O_K \\ k\geq 1}} h((\mathcal N\mathfrak p^{k }/x^{\frac 1{\ell}})^\ell) \log \mathcal N\mathfrak p^k \\& =\mathcal M \{h(\cdot ^{\ell})\}(1)\cdot x^{\frac 1\ell}+\sum_{\rho_K} x^{\frac{\rho_K}\ell}\mathcal M \{h(\cdot ^{\ell})\}(\rho_K)\\&\quad +O_h([K:{\mathbb{Q}}] x^{\frac 1{2\ell}}+\log ( d_K+2)) \\ & \ll_h x^{\frac 1\ell}+ x^{\frac 1{2\ell}} \ell \log(d_K+2), \end{align*} $$

by the identity $M \{h(\cdot ^{\ell })\}(s) = \frac 1\ell \mathcal M h(\frac s\ell ) $ and the bound (91). Hence, noting that the support condition on h implies that $\psi _{h(\cdot ^\ell )}(x^{\frac 1\ell };L/K,1) = 0 $ for $\ell \geq 3\log x$ , we obtain the estimate

(95) $$ \begin{align} \theta_{h}(x;L/K,t)=\psi_{h}(x;L/K,t)+O( \lambda(t)(x^{\frac 12}+ x^{\frac 14}\log(d_K+2)) ). \end{align} $$

Combining this identity with (78) and (92), we deduce that

$$ \begin{align*}\theta_{h}(x;L/K,t) - x\mathcal Mh(1)\widehat{t}(1) \ll c_h\lambda(t) x^{\frac 12}[K:{\mathbb{Q}}] \log ( \mathrm{rd}_L+2 ). \end{align*} $$

Generalising [Se3, Proposition 6], we see that

$$ \begin{align*}\sum_{\mathfrak p \mid D_{L/K}} \log (\mathcal N \mathfrak p) \leq \frac{2}{|G|} \log \mathcal N_{K/{\mathbb{Q}}}(D_{L/K} )\leq 2[K:{\mathbb{Q}}] \log(\mathrm{rd}_L+2)\,,\end{align*} $$

where the first inequality follows from combining (77) with (81) in which for each $\mathfrak p\mid D_{L/K}$ , $\sum _{i\geq 0} (|G_i|-1)\geq |G_0|/2$ , and the second follows from (78). Hence, the contribution of ramified primes in $\theta _h(x;L/K,t)$ is

$$ \begin{align*}\ll \lambda(t)\sum_{\substack{ \mathfrak p \mid D_{L/K} }} h( \mathcal N \mathfrak p/x) \log (\mathcal N \mathfrak p) \ll c_h \lambda(t) [K:{\mathbb{Q}}] \log(\mathrm{ rd}_L+2),\end{align*} $$

since for any $g\in G$ , $|t(g)| \leq \sum _{\chi \in \mathrm {Irr}(G)} \chi (1)|\widehat {t}(\chi )|= \lambda (t)$ . We conclude that

(96) $$ \begin{align} \sum_{\substack{ \mathfrak p \triangleleft\mathcal O_K \\ \mathfrak p \text{ unram.} }} t(\varphi_{\mathfrak p})h(\mathcal N\mathfrak p /x) \log (\mathcal N \mathfrak p)= x\mathcal Mh(1)\widehat{t}(1) +O_h( \lambda(t)x^{\frac 12}[K:{\mathbb{Q}}] \log ( \mathrm{rd}_L+2 ) ). \end{align} $$

Taking

$$ \begin{align*}x = K_h\Big( \frac{\log(\mathrm{rd}_L+2) \lambda(t)[K:{\mathbb{Q}}]}{ \widehat t(1)}\Big)^2\end{align*} $$

for a large enough positive constant $K_h$ in (96) (recall that t is real valued and $\widehat t(1)> 0$ ; note also that $\lambda (t)\geq |\widehat t(1)|$ , so that $x\geq K_h$ ), we deduce that

$$ \begin{align*}\sum_{\substack{ \mathfrak p \triangleleft\mathcal O_K \\ \mathfrak p \text{ unram.} }} t(\varphi_{\mathfrak p})h(\mathcal N\mathfrak p /x) \log (\mathcal N \mathfrak p)> 0.\end{align*} $$

Since h is supported in $[1,\tfrac 32]$ , it follows that there exists a prime ideal $\mathfrak p\triangleleft \mathcal O_K$ of norm $\leq \tfrac 32x$ and, such that $t(\varphi _{\mathfrak p})> 0$ , that is (24) holds.

We now move to the bound (25). Arguing as in Proposition 3.11, we have that

(97) $$ \begin{align}\psi_{h}(x;L/K,t)= \psi_{h}(x;L/{\mathbb{Q}},t^+) = \sum_{\chi \in \mathrm{Irr}(G^+)}\widehat{t^+}(\chi) \psi_h(x;L/{\mathbb{Q}},\chi). \end{align} $$

It follows from [IK, Theorem 5.11] that for any irreducible character $\chi \in \mathrm {Irr}(G^+)$ and for $x\geq 1$ ,

(98) $$ \begin{align}\notag \psi_{h}(x;L/{\mathbb{Q}},\chi) - x\mathcal Mh(1) \delta_{\chi = 1} &\ll c_h \log A(\chi) + c_h x^{\frac 12} \chi(1) + \sum_{\rho_\chi} |\mathcal Mh(\rho_{\chi})x^{\rho_\chi}| \\ & \ll c_h x^{\frac 12} \chi(1)\log (\mathrm{rd}_L+2). \end{align} $$

We deduce that (note that $\widehat t(1)=\widehat {t^+}(1)$ )

(99) $$ \begin{align} \psi_{h}(x;L/{\mathbb{Q}},t^+) &= x\mathcal Mh(1) \widehat{t^+}(1) +O(c_h\lambda(t^+) x^{\frac 12} \log(\mathrm{rd}_L+2)). \end{align} $$

Now, we may combine this with (95) and (97), resulting in the bound

$$ \begin{align*}\theta_{h}(x;L/K,t) - x\mathcal Mh(1)\widehat {t^+}(1) \ll c_h \lambda(t^+)x^{\frac 12} \log ( \mathrm{rd}_L+2 )+O(\lambda(t)(x^{\frac 12}+x^{\frac 14} \log(d_K+2))). \end{align*} $$

The ramified primes are bounded in the same way as before, and contribute an error term $\ll \lambda (t) [K:{\mathbb {Q}}] \log (\mathrm {rd}_L+2)$ . We deduce that as soon as $\widehat {t^+}(1)>0$ and

$$ \begin{align*}x>K_h\Big(\frac{\lambda(t^+)\log (\mathrm{rd}_L+2)+\lambda(t)}{\widehat {t^+}(1)}\Big)^2+K_h \Big( \frac{\lambda(t)\log(d_K+2)}{\widehat {t^+}(1)} \Big)^{\frac 43}\end{align*} $$

(note once more that $x\geq K_h$ ) for some large enough $K_h>0$ , there exists an unramified prime ideal $\mathfrak p\triangleleft \mathcal O_K$ , such that $t(\mathrm {Frob}_{\mathfrak p})>0$ and $\mathcal N\mathfrak p \leq x$ . Taking $t= |G||C|^{-1}1_C$ , we recall that $t^+=|G^+||C^+|1_{C^+}$ and $\widehat {t^+}(1)=1 $ , thus

$$ \begin{align*}\lambda(t)\leq \frac{|G|}{|C|^{\frac 12}},\qquad \lambda(t^+)\leq \frac{|G^+|}{|C^+|^{\frac 12}}.\end{align*} $$

The claimed bound (24) follows from noting that $|G|/|C|^{\frac 12}\leq |G^+|/|C^+|^{\frac 12}. $

To prove (27), we apply (97) to (93) and deduce that

(100) $$ \begin{align} \theta_{h}(x;L/K,t) = \sum_{\ell \geq 1} \mu(\ell) \psi_{h(\cdot^\ell)}(x^{\frac 1\ell};L/{\mathbb{Q}},(t(\cdot^\ell))^+). \end{align} $$

Note, moreover, that

$$ \begin{align*}\widehat{(t(\cdot^\ell))^+}(1)= \frac 1{|G^+|}\sum_{g\in G^+} (t(\cdot^\ell))^+(g) =\frac 1{|G^+|}\sum_{aG\in G^+/G} \sum_{\substack{ g \in aGa^{-1}}} t((a^{-1}g a)^\ell)=\langle t,r_\ell\rangle_G.\end{align*} $$

Hence, (98) implies that

$$ \begin{align*} \theta_{h}(x;L/K,t)&-x\mathcal Mh(1)\widehat {t^+}(1) \\ & \ll c_h\lambda(t^+) x^{\frac 12} \log ( \mathrm{rd}_L+2 )\\&\quad +c_h \sum_{\substack{2\leq \ell \leq 4\log x \\ \mu^2(\ell)=1}}(x^{\frac 1\ell} |\langle t,r_\ell\rangle_G|+\lambda(t(\cdot^\ell)^+) x^{\frac 1{2\ell}} \log ( \mathrm{rd}_L+2 )). \end{align*} $$

Taking

$$ \begin{align*}x &=K_h \Big( \frac{\lambda(t^+)}{\widehat {t}(1)}\log(\mathrm{rd}_L+2) \Big)^2 + K_h\frac{\lambda(t)}{\widehat t(1)}[K:{\mathbb{Q}}] \log(\mathrm{rd}_L+2) \\&\quad +K_h\sum_{\substack{2\leq \ell \ll \log\log d_L \\ \mu^2(\ell)=1}} \Big(\Big( \frac{|\langle t,r_\ell \rangle_G|}{\widehat t(1)} \Big)^{\frac{\ell}{\ell-1}}+\Big(\frac{\lambda((t(\cdot^\ell) )^+)}{\widehat t(1)}\log(\mathrm{rd}_L+2) \Big)^{\frac{2\ell}{2\ell-1}}\Big) \end{align*} $$

for a large enough constant $K_h$ in (96), we see that $ \log x\ll \log \log (d_L+2)$ (recall that t is real valued and $\widehat t(1)>|G|^{-100}\sup |t|$ ), and the conclusion follows. The proof of (27) goes along similar lines. Finally, we note that (6) implies that,

$$ \begin{align*}|\langle t,r_\ell\rangle_G|=|\langle \widehat t,\widehat{r_\ell} \rangle_{\mathrm{Irr}(G)}|\leq \lambda(t),\end{align*} $$

and, moreover, by the Cauchy–Schwarz inequality, we obtain the bound

$$ \begin{align*}\lambda(t(\cdot^\ell)) \leq |G|^{\frac 12} {\lVert{\widehat{t(\cdot^\ell)}\rVert}}_2 =|G|^{\frac 12} {\lVert{t(\cdot^\ell)}\rVert}_2 \leq |G|^{\frac 12} \sup|t|.\\[-36pt]\end{align*} $$

5 Probabilistic bounds

In this section, we fix a Galois extension of number fields $L/K$ , define $G:=\mathrm {Gal}(L/K)$ (as well as $G^+:=\mathrm {Gal}(L/{\mathbb {Q}})$ in the case where $L/{\mathbb {Q}}$ is Galois) and study the distribution of the random variable $X(L/K;t)$ attached to a real-valued class function $t\colon G\rightarrow \mathbb R$ (see Proposition 3.18 and Lemma 3.20), using probabilistic tools. Our main goal is to estimate $\delta (L/K;t)$ , which measures to which extent the error term in the Chebotarev density theorem is biased by a lower-order term of constant sign. We first consider the conditions under which $\delta (L/K;t)$ (see (11)) is close to $1$ . This leads to estimates for the bias under AC, GRH and BM. Stronger bounds can be derived under LI: as we will see, large deviations results of Montgomery–Odlyzko can then be applied to this context. Next we establish a central limit theorem from which we obtain (conditionally on LI; here, BM does not suffice) conditions under which $\delta (L/K;t)$ are close to $\tfrac 12$ . In both cases, we highlight the importance of the ratio ²⁵

(101) $$ \begin{align} B(L/K;t) &:= \frac{\mathbb E[X(L/K;t)]}{\mathrm{Var}[X(L/K;t)]^{\frac 12}} .\end{align} $$

This parameter governs the behaviour of the corresponding random variable according to the following philosophy: if it is small, then the random variable is only moderately biased, whereas if it is large, then the random variable is highly biased.

5.1 Large deviations

We first establish bounds on $\delta (L/K;t)$ in terms of the bias factors which hold under AC and GRH. These bounds will later be applied in conjunction with upper bounds on the bias factors holding under BM. Note that AC, GRH and BM do not suffice to prove the existence of the density $\delta (L/K;t)$ , and thus the statement only gives information about the lower densities. Under the additional assumption LI, the densities exist and sharper bounds can be deduced, as we will see in Proposition 5.3.

Proposition 5.1. Let $L/K$ be an extension of number fields for which $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH and BM hold. Let $t:\mathrm {Gal}(L/K) \rightarrow \mathbb R$ be a class function. If $B(L/K;t)$ is positive and large enough and $\mathbb E[X(L/K;t)]\geq 4$ , then

$$ \begin{align*}\underline{\delta}(L/K;t) \geq 1- 2B(L/K;t)^{-2}.\end{align*} $$

Proof. The proof is very similar to that of [Fi2, Lemma 2.7] and uses Chebyshev’s inequality (see also [De, Corollary 5.8]).

The key to a more precise estimation of the bias under LI will be the following theorem of Montgomery and Odlyzko on large deviations of sums of independent random variables.

Theorem 5.2 [MO, Theorem 2].

For $n\in \mathbb Z_{\geq 1}$ , let $W_n$ be independent real valued random variables, such that $\mathbb E[W_n]=0$ and $|W_n|\leq 1$ ; let also $r_n$ be a decreasing sequence of real numbers tending to zero. Suppose that there is a constant $c>0$ , such that $\mathbb E[W_n^2]\geq c$ for all n. Put $W=\sum r_n W_n$ , where $\sum r_n^2 <\infty $ . Let V be a nonnegative real number.

If $\sum _{|r_n|\geq \alpha } |r_n| \leq V/2$ , then

(102) $$ \begin{align} \text{P}[W\geq V] \leq \exp\bigg( -\frac 1{16} V^2 \bigg( \sum_{|r_n|<\alpha} r_n^2 \bigg)^{-1}\bigg).\\[-9pt]\nonumber \end{align} $$

If $\sum _{|r_n|\geq \alpha } |r_n| \geq 2V$ , then

(103) $$ \begin{align} \text{P}[W\geq V] \geq a_1 \exp\bigg( -a_2 V^2 \bigg( \sum_{|r_n|<\alpha} r_n^2 \bigg)^{-1}\bigg). \\[-9pt]\nonumber\end{align} $$

Here, $a_1>0$ and $a_2>0$ depend only on c.

Note that a more precise result (in which $c_3=c_2+o(1)$ ) could possibly be obtained using the saddle-point method as in [Mo] (see also [La1]), however, this would not affect our main theorems since we are only able to evaluate $B(L/K;t)$ up to a constant. We can deduce the following result concerning high biases.

Proposition 5.3. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH and LI hold. Let $t:\mathrm {Gal}(L/K) \rightarrow \mathbb R$ be a class function, and let $B(L/K;t)$ be defined as in (101).

1. (1) If $\mathbb E[X(L/K;t)]\geq 0$ , then

   $$ \begin{align*}\delta(L/K;t)>1- \exp(-c_1 B(L/K;t)^2).\\[-9pt]\end{align*} $$

2. (2) If in addition $K={\mathbb {Q}}$ (so that $t=t^+$ (recall (7)) and $G=G^+$ ), $t \not \equiv 0$ and $\widehat {t}(\chi )\in \{ 0,1,-1\}$ for every $\chi \in \mathrm {Irr}(G)$ , then we also have the upper bound

   $$ \begin{align*}\delta(L/{\mathbb{Q}};t)<1- c_2 \exp(-c_3 B(L/{\mathbb{Q}};t)^2).\end{align*} $$

Here, the $c_i$ are positive absolute constants.

Besides Theorem 5.2, the main ingredient for the proof of Proposition 5.3 is the following estimate.

Lemma 5.4. Let $L/K$ be a finite Galois extension for which AC holds, and let $\chi $ be an irreducible character of $G=\mathrm {Gal}(L/K)$ . For $T\geq 1$ , we have the estimate

$$ \begin{align*}\sum_{\substack{|\gamma_{\chi}| < T }} \frac 1{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}} = \frac 1{\pi}\log \Big(A(\chi) \Big(\frac{T^{\frac 12}}{2\pi e}\Big)^{[K:{\mathbb{Q}}]\chi(1)}\Big) \log T + O\bigl(\log (A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)})\bigr)\,.\end{align*} $$

Proof. We start from (85):

$$ \begin{align*}N(T,\chi)= |\{\gamma_{\chi}\colon |\gamma_{\chi}|\leq T \}|=\frac T{\pi} \log \frac{A(\chi)T^{[K:{\mathbb{Q}}]\chi(1)}}{(2\pi e)^{[K:{\mathbb{Q}}]\chi(1)}} + O(\log ((A(\chi)+2)(T+4)^{[K:{\mathbb{Q}}]\chi(1)}))\,. \end{align*} $$

With a summation by parts, we obtain that

$$ \begin{align*} \sum_{\substack{|\gamma_{\chi}| < T }} \frac 1{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}} =&\sum_{\substack{1<|\gamma_{\chi}| < T }} \frac 1{|\gamma_{\chi}|} +O(\log (A(\chi)5^{[K:{\mathbb{Q}}]\chi(1)}) = O(\log (A(\chi)5^{[K:{\mathbb{Q}}]\chi(1)}))\\ &+\int_1^{T} \frac{\mathrm{d}N(t,\chi)}{t} = \frac{N(T,\chi)}{T}+\int_1^T \frac{N(t,\chi)}{t^2}\mathrm{d}t + O(\log (A(\chi)5^{[K:{\mathbb{Q}}]\chi(1)})) \\ =& \int_1^T \frac{ \log \frac{A(\chi)t^{[K:{\mathbb{Q}}]\chi(1)}}{(2\pi e)^{[K:{\mathbb{Q}}]\chi(1)}} }{\pi t} \mathrm{d}t + O\bigl(\log (A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)})\bigr)\\ =& \frac 1{\pi}\log \Big(A(\chi) \Big(\frac{T^{\frac 12}}{2\pi e}\Big)^{[K:{\mathbb{Q}}]\chi(1)}\Big) \log T +O\bigl(\log (A(\chi)(T+4)^{[K:{\mathbb{Q}}]\chi(1)})\bigr)\,.\\[-9pt] \end{align*} $$

The proof is complete.

Proof of Proposition 5.3

Let us start with (1). We will apply Theorem 5.2 to the random variable

$$ \begin{align*}W:=X(L/K;t)-\mathbb E[X(L/K;t)] = \sum_{\chi \in \mathrm{supp}(\widehat{t^+})} |\widehat{t^+}(\chi)|\sum_{\gamma_{\chi}> 0} \frac{2X_{\gamma_{\chi}}}{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}\\[-9pt] \end{align*} $$

(recall Lemma 3.20). By Proposition 3.18, we have that

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] = 2 \sum_{\chi \in \mathrm{supp}(\widehat{t^+})} |\widehat{t^+}(\chi)|^2\sum_{\gamma_{\chi}> 0} \frac{1}{\frac 14+\gamma_{\chi}^2}.\\[-9pt]\end{align*} $$

Taking the sequence $\{r_n\}_{n\geq 1}$ to be the values $2|\widehat {t^+}(\chi )|(\frac 14+\gamma _{\chi }^2)^{-\frac 12}$ ordered by size with $\gamma _{\chi }$ ranging over the imaginary parts of nonreal zeros of $L(s,L/{\mathbb {Q}},\chi )$ with $ \chi \in \mathrm {supp}(\widehat {t^+})$ , we have for $\alpha \in (0,4]$ that

$$ \begin{align*}\sum_{|r_n|\geq \alpha}|r_n| = \sum_{\substack{ \chi \in \mathrm{supp}(\widehat{t^+})} } |\widehat{t^+}(\chi)| \sum_{\substack{ 0<\gamma_{\chi} \leq \sqrt{4\alpha^{-2}-\frac 14}}} \frac 2{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}\,;\end{align*} $$

$$ \begin{align*}\sum_{|r_n|<\alpha}|r_n|^2= \sum_{ \chi \in \mathrm{supp}(\widehat{t^+}) } |\widehat{t^+}(\chi)|^2\sum_{\substack{ \gamma_{\chi}> \sqrt{4\alpha^{-2}-\frac 14}}} \frac 4{\frac 14+\gamma_{\chi}^2}\,. \end{align*} $$

We take $\alpha =4$ : then we trivially have $\sum _{|r_n|\geq \alpha }|r_n|\leq \mathbb E[X(L/K;t)]/2$ (note that $\mathbb E[X(L/K;t)]\geq 0$ by our assumptions), and hence, applying Proposition 3.18, (102) translates to

$$ \begin{align*}\text{P}[W\geq \mathbb E[X(L/K;t)]] \leq \exp \left(-\frac 1{16} \mathbb E[X(L/K;t)]^2 \left(2 \mathrm{Var}[X(L/K;t)] \right)^{-1} \right).\end{align*} $$

Thus, (1) follows, since by symmetry of W, we have that for any $\chi \in \mathrm {Irr} (G^+)$ ,

$$ \begin{align*}1-\delta(L/K;t) = \text{P}[W<-\mathbb E[X(L/K;t)]] = \text{P}[W>\mathbb E[X(L/K;t)]].\end{align*} $$

For (2), we use the assumptions that $K={\mathbb {Q}}$ and that for $\chi \in \mathrm {supp}(\widehat t)\neq \varnothing $ , $ |\widehat {t}(\chi )|=1$ . We let $\alpha \in (0,4]$ be small enough so that $T_0:=\sqrt {4\alpha ^{-2}-1/4}$ has the property that for any $\chi \in \mathrm {Irr}(G)$ ,

$$ \begin{align*}\sum_{\substack{0<|\gamma_{\chi}| < T_0 }} \frac 1{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}\geq 6M_0 \end{align*} $$

( $M_0$ comes from Hypothesis LI). Such a number $T_0$ , independent of $L/{\mathbb {Q}}$ , exists in light of Lemma 5.4 and by (89) applied with $\gamma = 0$ . Hence, since $|\widehat {t}(\chi )|=|\widehat {t}(\overline {\chi })| $ , by the symmetry of the zeros of $L(s,L/{\mathbb {Q}},\chi )$ , we have that

$$ \begin{align*}\sum_{\chi\in \mathrm{supp}(\widehat{t^+}) } \sum_{\substack{0<\gamma_{\chi} < T_0 }} \frac 2{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}} \geq 6 M_0 \#\mathrm{supp}(\widehat {t^+}) \geq 2\mathbb E[X(L/{\mathbb{Q}};t)]\,, \end{align*} $$

by (68). Therefore, we can apply Theorem 5.2 which gives the bound

$$ \begin{align*} \text{P}[W\geq \mathbb E[X(L/{\mathbb{Q}};1-r)]] &\geq a_1 \exp \Big(-a_2 \mathbb E[X(L/{\mathbb{Q}};t)]^2 \Big(\sum_{\chi \in \xi_t } \sum_{\gamma_{\chi}>T_0}\frac 4{\frac 14+\gamma^2}\Big)^{-1} \Big) \\ &\geq a_1 \exp \Big(-a_2 \mathbb E[X(L/{\mathbb{Q}};t)]^2 \Big(a_3 \mathrm{Var}[X(L/{\mathbb{Q}};t)]\Big)^{-1} \Big), \end{align*} $$

by Proposition 3.18; this proves the desired upper bound.

5.2 Effective central limit theorem

As in the previous paragraph, $L/K$ denotes an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois. Let $G=\mathrm {Gal}(L/K)$ and $G^+=\mathrm {Gal}(L/{\mathbb {Q}})$ . For any real-valued class function $t\colon G\rightarrow \mathbb R$ , we first prove a preliminary result on the ‘fourth moment’ of $X(L/K;t)$ . We define the following useful quantity ²⁶ attached to t.

(104) $$ \begin{align} W_4(L/K;t):=\frac{\sum_{\chi \in \mathrm{Irr}(G^+)}|\widehat{t^+}(\chi)|^4 \log (A(\chi)+2)}{\left(\sum_{\chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\right)^2}\,. \end{align} $$

Lemma 5.5. Let $L/K$ be a number field extension, such that $L/{\mathbb {Q}}$ is Galois. Assume that AC holds, and write $G=\mathrm {Gal}(L/K), G^+=\mathrm {Gal}(L/{\mathbb {Q}})$ . If $t\colon G \rightarrow \mathbb R$ is a class function, then

(105) $$ \begin{align} W_4(L/K;t) \ll{\lVert{t^+}\rVert}_1^{\frac 23}\Big(\sum_{\chi\in\mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\Big)^{-\frac 13}\,. \end{align} $$

Moreover, for any finite group $\Gamma $ and any class function $\tau \colon \Gamma \rightarrow \mathbb C$ ,

(106) $$ \begin{align} \frac{\sum_{\chi \in \mathrm{Irr}(\Gamma)}\chi(1)|\widehat{\tau}(\chi)|^4 }{\left(\sum_{\chi \in \mathrm{Irr}(\Gamma)} \chi(1)|\widehat{\tau}(\chi)|^2 \right)^2} \ll {\lVert{\tau}\rVert}_1^{\tfrac{2}{3}} \Big(\sum_{\chi\in\mathrm{Irr}(\Gamma)} \chi(1)|\widehat{\tau}(\chi)|^2 \Big)^{-\frac 13}. \end{align} $$

Remark 5.6. If $G^+$ and $\Gamma $ are abelian, then the exponent $-\frac 13$ in (105) and (106) can trivially be improved to $-1$ . More generally, if $\widehat {t^+}\not \equiv 0$ , then

$$ \begin{align*}W_4(L/{\mathbb{Q}};t) \leq \Big(\sum_{\chi\in\mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\Big)^{-1}{\lVert{t^+}\rVert}_1^2\max_{\chi \in \mathrm{Irr}(G^+)}\chi(1)^2.\end{align*} $$

However, in the case $G^+=S_n$ , it cannot be improved ²⁷ beyond $-\frac 13$ .

Proof of Lemma 5.5

We let $M\geq 1$ be a parameter, and we split the sum appearing in the numerator of $W_4(L/K;C_1,C_2)$ according to the degree of $\chi $ . By Lemma 4.1, one has that

$$ \begin{align*} \sum_{\substack{\chi\in \mathrm{Irr}(G^+)\\ \chi(1)>M}}|\widehat{t^+}(\chi)|^4 \log (A(\chi)+2) &\ll \sum_{\substack{\chi\in \mathrm{Irr}(G^+)\\ \chi(1)>M}}|\widehat{t^+}(\chi)|^4 \frac{(\log (A(\chi)+2))^2}{\chi(1)}\\ &<\frac 1M \Big(\sum_{\chi\in\mathrm{Irr}(G^+)}|\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\Big)^2. \end{align*} $$

Applying Lemma 3.5, we also have the bound

$$ \begin{align*}\sum_{\substack{\chi\in\mathrm{Irr}(G^+)\\ \chi(1)\leq M}}|\widehat{t^+}(\chi)|^4 \log (A(\chi)+2) \leq M^2 {\lVert{t^+}\rVert}_1^2 \sum_{\chi\in\mathrm{Irr}(G^+)}|\widehat{t^+}(\chi)|^2 \log (A(\chi)+2). \end{align*} $$

Putting everything together, we deduce that

$$ \begin{align*}W_4(L/K;t)\ll \frac{M^2 {\lVert{t^+}\rVert}_1^2}{\sum_{\chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)} + \frac 1M, \end{align*} $$

and (105) follows from taking $M = {\lVert {t^+}\rVert }_1^{-\frac 23}\big (\sum _{\chi \in \mathrm {Irr} (G^+)} |\widehat {t^+}(\chi )|^2 \log (A(\chi )+2)\big )^{\frac 13}$ .

The proof of (106) goes along the same lines, by replacing $\log (A(\chi )+2)$ with $\chi (1)$ .

In the central limit theorem (Proposition 5.8) we are about to prove, we will keep the setting as in Lemma 5.5, and we will use estimates on the following important quantity:

(107) $$ \begin{align} F(L/K;t):=\frac{\mathrm{Var}[X(L/K;t)]^{\frac 12}}{\max_{\eta \in \mathrm{Irr}(G^+)}|\widehat{t^+}(\eta)|}, \end{align} $$

where $t\colon G\rightarrow \mathbb C$ is a class function, such that $\widehat {t^+} \not \equiv 0$ (so that, as we have seen already, $F(L/K;t)\neq 0$ ). This quantity will determine the range of validity of our bounds on the characteristic function of $X(L/{\mathbb {Q}};t)$ .

Remark 5.7. We have the immediate bounds

$$ \begin{align*}\frac{{\lVert{t^+}\rVert}_2}{|(G^+)^\#|^{\frac 12}} \leq \max_{\eta \in \mathrm{Irr}(G^+)}|\widehat{t^+}(\eta)|\leq {\lVert{t^+}\rVert}_2.\end{align*} $$

We now state and prove estimates on the characteristic function of $X(L/K;t)$ which can be interpreted as effective central limit theorems via Lévy’s criterion and the Berry–Esseen bounds. These estimates will allow us to study moderate biases. Note that to obtain a precise estimate on the bias, we will need bounds on the characteristic functions which hold in a wide range. For any class function $t:G \rightarrow \mathbb C$ , such that $\widehat {t^+} \not \equiv 0$ , we define the normalised random variable

(108) $$ \begin{align} Y(L/K;t)&:= \frac{X(L/K;t)-\mathbb E[X(L/K;t)]}{\mathrm{Var}[X(L/K;t)]^{\frac 12}}\, ,\end{align} $$

where $X(L/K;t)$ satisfies (74). The corresponding characteristic function will be denoted by $\widehat Y(L/K;t)$ .

Proposition 5.8 (Characteristic function bounds).

Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC and LI $^{-}$ hold. Fix a class function $t:G\rightarrow \mathbb R$ . If $\beta _L^t=\tfrac 12$ (recall (10)), then in the range $|\eta |\leq \frac {3}{5}F(L/K;t)$ (see (107)), we have the bounds

$$ \begin{align*}-\frac{\eta^2}{2}-O(\eta^4 W_4(L/K;t))\leq \log \widehat Y(L/K;t)(\eta)\leq -\frac{\eta^2}2.\end{align*} $$

Proof. We first see that the characteristic function of $X(L/K;t)$ is given by

(109) $$ \begin{align} \widehat{X}(L/K;t)(\eta)={\mathrm{e}}^{i\mathbb E[X(L/K;t)]\eta} \prod_{ \chi \in \mathrm{Irr}(G^+)} \prod_{\gamma_{\chi}>0} J_0\bigg( \frac{2|\widehat{t^+}(\chi)|\eta}{\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}\bigg). \end{align} $$

This comes from the fact that the characteristic function is multiplicative on independent random variables, and that $\widehat X_{\gamma _{\chi }}(t)=J_0(t)$ (see the proof of [FM, Proposition 2.13]). From the properties of characteristic functions, it follows that

(110) $$ \begin{align} \log \widehat Y(L/K;t)(\eta) = \sum_{ \chi \in \mathrm{Irr}(G^+)} \sum_{\gamma_{\chi}>0} \log J_0\bigg( \frac{2|\widehat{t^+}(\chi)|\eta}{\mathrm{Var}[X(L/K;t)]^{\frac 12}\big(\frac 14+\gamma_{\chi}^2\big)^{\frac 12}}\bigg). \end{align} $$

In the range $|u|\leq \frac {12}5$ , we have the following bounds on the Bessel function (see [FM, Section 2.2]):

(111) $$ \begin{align} -\frac{u^2}{4}-O(u^4)\leq \log J_0(u)\leq -\frac{u^2}{4}. \end{align} $$

Inserting the bounds (111) in (110), we obtain that in the range $|\eta |\leq \frac 35 F(L/K;t)$ ,

(112) $$ \begin{align} &- \frac 1{\mathrm{Var}[X(L/K;t)]}\sum_{\chi \in \mathrm{Irr}(G^+)} \sum_{\gamma_{\chi}>0} \frac{|\widehat{t^+}(\chi)|^2\eta^2}{\frac 14+\gamma_{\chi}^2}\geq \log \widehat Y(L/K;t)(\eta) \geq \nonumber\\ &- \frac 1{\mathrm{Var}[X(L/K;t)]}\sum_{\chi \in \mathrm{Irr}(G^+)} \sum_{\gamma_{\chi}>0} \frac{|\widehat{t^+}(\chi)|^2\eta^2}{\frac 14+\gamma_{\chi}^2}\nonumber\\ &-O\Big( \frac 1{\mathrm{Var}[X(L/K;t)]^2}\sum_{\chi \in \mathrm{Irr}(G^+)} \sum_{\gamma_{\chi}>0} \frac{|\widehat{t^+}(\chi)|^4\eta^4}{(\frac 14+\gamma_{\chi}^2)^2} \Big). \end{align} $$

Note that the upper bound in (112) is equal to $-\eta ^2/2$ . As for the error term in the lower bound on the right-hand side, we apply (88) to conclude that it is

$$ \begin{align*}\ll \eta^4\bigg(\sum_{\chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2\log (A(\chi)+2)\bigg)^{-2}\sum_{\chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^4B_2(\chi) \,.\\[-9pt] \end{align*} $$

Here, we have used the symmetry principle already mentioned (see the proof of Corollary 3.17) asserting that if $\rho $ is a complex zero of $L(s,L/K,\chi )$ , then $\bar {\rho }$ is a zero of $L(s,L/K,\overline {\chi })$ . Invoking Lemma 4.3, we recognise the fourth moment $W_4(L/K;t)$ , and the claim follows.

From this central limit theorem, we derive our general result on moderate biases. We first state and prove the following preliminary lower bound on the size of the quantity $F(L/K;t)$ defined in (107).

Lemma 5.9. Let $L/K$ be a number field extension, such that $L/{\mathbb {Q}}$ is Galois. Assume AC, GRH and LI $^-$ hold, and fix $t\colon G\rightarrow \mathbb R$ , a class function for which $t^+\not \equiv 0$ . Then we have the bounds ²⁸

(113) $$ \begin{align} \frac{\mathrm{Var}[X(L/K;t)]^{\frac 16}}{ {\lVert{t^+}\rVert}^{\frac 13}_1} \ll F(L/K;t) \ll \frac{ |(G^+)^{\sharp}|^{\frac 12} }{{\lVert{t^+}\rVert}_2} \mathrm{Var}[X(L/K;t)]^{\frac 12}.\\[-9pt]\nonumber \end{align} $$

Proof. The upper bound follows from Remark 5.7. For the lower bound, by Proposition 4.6, we have that

(114) $$ \begin{align} F(L/K;t)^{-1}\ll\frac{\max_{\psi \in \mathrm{Irr}(G^+)}|\widehat{t^+}(\chi)|}{\Big(\sum_{\chi \in \mathrm{Irr}(G^+)} |\widehat{t^+}(\chi)|^2 \log (A(\chi)+2)\Big)^{\frac 12}} \,.\\[-9pt]\nonumber \end{align} $$

Let $\psi _0$ be an irreducible character of $G^+$ having the property that $|\widehat {t^+}(\psi _0)|=\max _{\psi \in \mathrm {Irr}(G^+)}|\widehat {t^+}(\psi )|$ . Note that by Lemma 3.5, $|\widehat {t^+}(\psi _0)|\leq \psi _0(1) {\lVert {t^+}\rVert }_1 $ . We deduce from Lemmas 4.1 and 4.3, and by positivity of the summands in the denominator of (114), that

$$ \begin{align*}F(L/K;t)^{-1}\ll \min \left( \frac 1{\psi_0(1)^{\frac 12}},\frac{\psi_0(1) {\lVert{t^+}\rVert}_1}{\mathrm{Var}[X(L/K;t)]^{\frac 12}} \right)\,. \end{align*} $$

Now, if $\psi _0(1)\geq \mathrm {Var}[X(L/K;t)]^{\frac 13}{\lVert {t^+}\rVert }_1^{-\frac 23}$ then $\psi _0(1)^{-\frac 12}\leq {\lVert {t^+}\rVert }_1^{\frac 13}\mathrm {Var}[X(L/K;t)]^{-\frac 16}$ , and if $\psi _0(1)\leq \mathrm {Var}[X(L/K;t)]^{\frac 13}{\lVert {t^+}\rVert }_1^{-\frac 23}$ , then $\psi _0(1){\lVert {t^+}\rVert }_1\mathrm {Var}[X(L/K;t)]^{-\frac 12}\leq {\lVert {t^+}\rVert }_1^{\frac 13} \mathrm { Var}[X(L/K;t)]^{-\frac 16}$ . We conclude that

$$ \begin{align*}F(L/K;t)^{-1}\ll {\lVert{t^+}\rVert}_1^{\frac 13}\mathrm{Var}[X(L/K;t)]^{-\frac 16}.\\[-40pt]\end{align*} $$

We are now ready to show that small values of $B(L/{\mathbb {Q}};t)$ result in densities $\delta (L/K;t)$ that are close to $\tfrac 12$ . In a sense, this is a converse to Theorem 5.1.

Theorem 5.10. Let $L/K$ be an extension of number fields, such that $L/{\mathbb {Q}}$ is Galois, and for which AC and LI $^{-}$ hold. Fix a class function $t:G\rightarrow \mathbb R$ for which $\widehat {t^+}\not \equiv 0$ . Assuming that $\beta _{L}^{t}=\tfrac 12$ , the following estimate holds:

(115) $$ \begin{align} \delta(L/K;t) =\frac 12 +\frac {B(L/K;t)}{\sqrt{2\pi}} +O\Big( B(L/K;t)^3+\Big(\frac{{\lVert{t^+}\rVert}_1^{2}}{\mathrm{Var}[X(L/K;t)]}\Big)^2 +W_4(L/K;t)\Big)\,.\\[-9pt]\nonumber \end{align} $$

(Recall the definition (104).)

Note that under the hypotheses of Theorem 5.10, we have that ${\lVert {t^+}\rVert }_1^{2}\mathrm {Var}[X(L/K;t)]^{-1} \leq {\lVert {t^+}\rVert }_2^{2}\mathrm {Var}[X(L/K;t)]^{-1} \ll 1$ . Note also that the exponent $2$ in the second error term can be replaced by an arbitrarily large real number, however, the third summand $W_4(L/K;C_1,C_2)$ is expected to be the main contribution to the error term.

Remark 5.11. In the particular case where $\widehat {t^+}\in \{ 0,-1,1\}$ (for example, $K={\mathbb {Q}}$ and $t=r$ ), we have that $W_4(L/K;t) \asymp \mathrm {Var}[X(L/K;t)] $ , and hence, the second error term in Theorem 5.10 can be removed.

Coming back to the general case, Theorem 5.10 implies, using Lemma 5.5, the simpler bound:

$$ \begin{align*}\delta(L/K;t) =\frac 12 +\frac {B(L/K;t)}{\sqrt{2\pi}} +O\Big(B(L/K;t)^{3}+ \Big(\frac{{\lVert{t^+}\rVert}_1^{2}}{\mathrm{Var}[X(L/K;t)]}\Big)^{\frac 13}\Big)\,.\\[-9pt] \end{align*} $$

If, moreover, $ \mathrm {Var}[X(L/K;t)]^{\frac 16}{\lVert {t^+}\rVert }_1^{-\frac 13}=o(|\mathbb E[X(L/K;t)]|{\lVert {t^+}\rVert }_1^{-1})$ but yet $\mathbb E[X(L/K;t)] =o(\mathrm {Var}[X(L/K;t)]^{\frac 12})$ , then

$$ \begin{align*}\delta(L/K;t)-\frac 12 \sim \frac {B(L/K;t)}{\sqrt{2\pi}}.\\[-9pt]\end{align*} $$

Proof of Theorem 5.10

If $\mathbb E[X(L/K;t)]=0$ , then in light of (74) and by independence, the random variable $X(L/K;t)$ is symmetric. We deduce that $\text {P}[X(L/K;t)>0] =\frac 12$ and so the statement is trivial. It is also trivial when $B(L/K;t)$ or $\mathrm {Var}[X(L/K;t)]^{-1}$ is bounded below by a positive constant. Therefore, we may assume from now on that $B(L/K;t)$ is small enough and that $\mathrm {Var}[X(L/K;t)]$ is large enough. We now use the Berry–Esseen inequality in the form given by Esseen ([Es, Chapter 2, Theorem 2a]). The statement is as follows. If we denote by $F_Y$ the cumulative density function of a given real-valued random variable Y and by $F_G$ that of the Gaussian distribution, then for any $T>0$ ,

$$ \begin{align*}\sup_{x\in \mathbb R} |F_{Y}(x)-F_{G}(x)| \ll \int_{-T}^T \Big|\frac{\widehat Y(\eta)-{\mathrm{e}}^{-\frac {\eta^2}2}}{\eta}\Big| \mathrm{d}\eta+\frac 1T.\end{align*} $$

Taking $Y=Y(L/K;t)$ (recall (108)) and setting $T:=\mathrm {Var}[X(L/K;t)]^2{\lVert {t^+}\rVert }_1^{-4}$ , we have that

(116) $$ \begin{align} &\text{P}[X(L/K;t)>0] = \text{P}[Y>-B(L/K;t)] \nonumber\\ &\qquad = \frac 1{\sqrt{2\pi}}\int_{-B(L/K;t)}^{\infty} {\mathrm{e}}^{-\frac {t^2}2} \mathrm{d}t +O\Big( \int_{-T}^T \Big|\frac{\widehat Y(\eta)-{\mathrm{e}}^{-\frac {\eta^2}2}}{\eta}\Big| \mathrm{d}\eta+\frac {{\lVert{t^+}\rVert}_1^{4}}{\mathrm{Var}[X(L/K;t)]^2}\Big). \end{align} $$

To bound the part of the integral in the error term of (116) in which $|\eta |\leq \frac 35 F(L/K;t)$ , we apply Proposition 5.8 which implies that for some absolute constant $c>0$ ,

$$ \begin{align*}0 \geq \widehat Y(\eta)-{\mathrm{e}}^{-\frac {\eta^2}2} \geq {\mathrm{e}}^{-\frac {\eta^2}2}({\mathrm{e}}^{-c W_4(L/K;t)\eta^4} -1)\geq -c W_4(L/K;t)\eta^4 {\mathrm{e}}^{-\frac {\eta^2}2},\end{align*} $$

by the convexity bound ${\mathrm {e}}^{-x}\geq 1-x$ . We deduce that

$$ \begin{align*} \int_{-F(L/K;t)}^{ F(L/K;t)} \Big|\frac{\widehat Y(\eta)-{\mathrm{e}}^{-\frac {\eta^2}2}}{\eta}\Big| \mathrm{d}\eta &\ll W_4(L/K;t) \int_{\mathbb R} |\eta|^3 {\mathrm{e}}^{-\frac {\eta^2}2} \mathrm{d}\eta \ll W_4(L/K;t)\,. \end{align*} $$

As for the rest of the integral in the error term in (116), we will use the properties of the Bessel function $J_0$ , in a way analogous to [FM, Proposition 2.14]. We have that for $|\eta |> \tfrac 5{12}F(L/K;C_1,C_2)$ ,

$$ \begin{align*}J_0 \Big( 2\cdot \frac{\eta |\widehat{t^+}(\chi)|}{\mathrm{Var}[X(L/K;t)]^{\frac 12}} \cdot \Big(\frac 14+\gamma_{\chi}^2 \Big)^{-\frac 12} \Big) \leq J_0 \Big( 2\cdot \frac{5}{12}\frac{F(L/K;t)|\widehat{t^+}(\chi)|}{\mathrm{Var}[X(L/K;t)]^{\frac 12}} \cdot \Big(\frac 14+\gamma_{\chi}^2 \Big)^{-\frac 12} \Big), \end{align*} $$

and hence, by (110), $|\widehat Y(\eta )|\leq |\widehat Y(\frac 5{12}F(L/K;t))|$ . It follows that

$$ \begin{align*}\int_{F(L/K;t)<|\eta|\leq T} \Big|\frac{\widehat Y(\eta)-{\mathrm{e}}^{-\frac{\eta^2}2}}{\eta}\Big|\mathrm{d}\eta \ll & \widehat Y\Big(\frac 5{12} F(L/K;t)\Big) \log T + \int_{|\eta|> F(L/K;t)} \frac{{\mathrm{e}}^{-\frac{\eta^2}2}}{|\eta|}\mathrm{d}\eta\\ \ll & {\mathrm{e}}^{-\frac{25}{289}F(L/K;t)^{2}}+{\mathrm{e}}^{-\frac{1}{3}F(L/K;t)^{2}}, \end{align*} $$

by Proposition 5.8 and the bound $F(L/K;t)\gg \mathrm {Var}[X(L/K;t)]^{\frac 16}{\lVert {t^+}\rVert }_1^{-\frac 13}$ of Lemma 5.9. We deduce that

(117) $$ \begin{align} \text{P}[X(L/K;t)>0] = \frac 1{\sqrt{2\pi}} \int_{-B(L/K;t)}^{\infty} {\mathrm{e}}^{-\frac {t^2}2} \mathrm{d}t + O\Big(W_4(L/K;t)+ \frac {{\lVert{t^+}\rVert}_1^{4}}{\mathrm{ Var}[X(L/K;t)]^2}\Big), \end{align} $$

and the claimed result follows by expanding the main term of (117) into Taylor series.

6 General Galois extensions: Proofs of Theorems 2.7, 2.8 and 2.13

We fix the setup as before: $L/K$ is an extension of number fields for which $L/{\mathbb {Q}}$ is Galois. We first give general bounds on the mean, variance and bias factor (see (101), and Proposition 3.18) associated to the random variable $X(L/K;t)$ that will also be used to prove the statements about extensions of number fields with specific Galois groups.

Lemma 6.1. Let $L/K$ be an extension, such that $L/{\mathbb {Q}}$ is Galois, and for which AC, GRH and LI $^-$ hold. Fix a class function $t:G\rightarrow \mathbb C$ , such that $\widehat {t^+}\not \equiv 0$ . We have the general bounds

(118) $$ \begin{align} \mathrm{Var}[X(L/K;t)] \gg \sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1)|\widehat{t^+}(\chi)|^2\gg \frac{{\lVert{t^+}\rVert}^{3}_2}{{\lVert{t^+}\rVert}_1(\#\mathrm{ supp}(\widehat{t^+}))^{\frac 12}} \,. \end{align} $$

Under the additional assumption of LI,

(119) $$ \begin{align} \mathbb E[X(L/K;t)] \ll({\lVert{t}\rVert}_2+{\lVert{t^+}\rVert}_2)(\# \{\chi \in \mathrm{Irr}(G)\cup \mathrm{Irr}(G^+)\colon \chi \text{ real}\})^{\frac 12}, \end{align} $$

and as a result

(120) $$ \begin{align} B(L/K;t) &\ll \frac{|\langle t,r\rangle_G+ 2\mathrm{ord}_{s=\frac 12} L(s,L/K,t)|}{\Big(\sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1)|\widehat{t^+}(\chi)|^2\Big)^{\frac 12}} \\ & \ll \frac{{\lVert{t^+}\rVert}_1^{\frac 12} ({\lVert{t}\rVert}_2+{\lVert{t^+}\rVert}_2)(\#\mathrm{Irr}(G^+))^{\frac 14}\cdot (\#\{ \chi \in \mathrm{Irr}(G)\cup \mathrm{Irr}(G^+) \colon \chi \text{ real} )^{\frac 12}}{{\lVert{t^+}\rVert}_2^{\frac 32}}\,. \nonumber \end{align} $$

Remark 6.2. The second bounds in (118) and (120) are unconditional. Moreover, the upper bound (120) implies that Galois groups with few irreducible characters correspond to small values of $B(L/K;t)$ , and hence, exhibit moderate discrepancies in the error term of the Chebotarev density theorem.

Proof of Lemma 6.1

The first bound in (118) follows from combining Proposition 3.18 with Lemmas 4.1 and 4.3. As for the second, we argue as in the proof of Lemma 5.5. Introducing a parameter $M\geq 1$ , we see that

$$ \begin{align*} \sum_{\chi \in \mathrm{Irr}(G^+)} \chi(1)|\widehat{t^+}(\chi)|^2 &\geq M\sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \chi(1)\geq M}} |\widehat{t^+}(\chi)|^2\\ &\geq M\Big(\sum_{\substack{\chi \in \mathrm{Irr} (G^+)}} |\widehat{t^+}(\chi)|^2 - {\lVert{t^+}\rVert}_1^2M^2\#\mathrm{ supp}(\widehat{t^+})\Big)\\ &= M({\lVert{t^+}\rVert}_2^2-{\lVert{t^+}\rVert}_1^2M^2\#\mathrm{supp}(\widehat{t^+})). \end{align*} $$

The right most bound in (118) follows by taking $M={\lVert {t^+}\rVert }_2{\lVert {t^+}\rVert }_1^{-1}(2 \#\mathrm {supp}(\widehat {t^+}))^{-\frac 12}$ .

The bound (119) is established as follows:

$$ \begin{align*} |\mathbb E[X(L/K;t)] | &\leq \sum_{\substack{\chi \in \mathrm{Irr}(G) \\ \chi \text{ real}}} |\widehat{t}(\chi)|+M_0\sum_{\substack{\chi \in \mathrm{Irr}(G^+) \\ \varepsilon_2(\chi)=-1 }} |\widehat{t^+}(\chi)| \\ & \leq {\lVert{t}\rVert}_2 (\# \{\chi \in \mathrm{Irr}(G)\colon \chi \text{ real}\})^{\frac 12} +{\lVert{t^+}\rVert}_2 (\# \{\chi \in \mathrm{Irr}(G^+)\colon \chi \text{ real}\})^{\frac 12}. \end{align*} $$

Recalling the definition (101), the first bound in (120) follows from combining (68) with the first bound in (118). As for the second one, it follows from combining (118) and (119).

We are now ready to prove the results of Section 2.1.

Proof of Theorem 2.8

We split the proof into two cases, depending on the value taken by $\beta _L^t$ (see (10)). First, we assume that $\beta ^t_L>\frac 12$ . Arguing once more as in [Fi2, Lemma 3.6] and [De, Proof of Theorem 5.4 (i)], we have that

$$ \begin{align*}\widehat X(L/K;t)(\xi)= {\mathrm{e}}^{ i\xi \mathbb E[X(L/K;t)] }\prod_{\substack{ \chi \in \mathrm{supp}(\widehat{t^+}) }}\prod_{\substack{ \rho_{\chi} \\ \Re(\rho_{\chi})=\beta_{L} \\ \Im(\rho_{\chi})>0} } J_0\Big( \frac{2|\widehat{t^+}(\chi)|\xi}{|\rho_{\chi}|^2}\Big).\end{align*} $$

Assumption LI implies $\mathbb E[X(L/K;t)]=0$ . For each $\chi \in \mathrm {supp}(\widehat {t^+})$ , the product over $\rho _{\chi }$ has at least one factor (by GRH $^-$ ). However, $\widehat {t^+}(\chi ) \not \equiv 0$ , and hence. we conclude that $|\widehat X(L/K;t)(\xi )|\ll (|\xi |+1)^{-2}$ and, as before, $\delta (L/K;t)=\tfrac 12$ by symmetry.

We now assume $\beta ^t_L=\frac 12$ . Recall Propositions 3.18 and 4.6; combining Lemma 6.1 and the assumptions implies the bound $ B(L/K;t) \ll \varepsilon \,. $ Theorem 5.10 (in the form of Remark 5.11) then implies that

(121) $$ \begin{align} \delta(L/K;t) =\frac 12 +\frac {B(L/K;t)}{\sqrt{2\pi}} +O( B(L/K;t)^3+\mathrm{Var}[X(L/K;t)]^{-\frac 13}). \end{align} $$

Using this estimate, the first statement follows from the lower bound on the variance in Lemma 6.1. As for the second one, it follows from (121) and the fact that the additional hypothesis in the statement implies that $|\mathbb E[X(L/K;t)]|\geq \varepsilon ^{-\frac 12}$ , and hence, $\mathrm {Var}[X(L/K;t)]\geq \varepsilon ^{-3}$ .

Proof of Corollary 2.12

For both statements, we apply LI and combine Theorem 2.8 with (118) and (120).

Proof of Theorem 2.7

Assume that $\widehat {t^+} \not \equiv 0$ , as well as AC, GRH and BM. We will combine the expression for $\mathrm {Var}[X(L/K;t)]$ given in Proposition 3.18 with Lemmas 4.1 and 4.3. The assumption of Theorem 2.7 translates into

$$ \begin{align*}\frac{\mathbb E[X(L/K;t)]^2}{\mathrm{Var}[X(L/K;t)]}\gg \varepsilon^{-1}\,. \end{align*} $$

For $\varepsilon $ small enough, we can then apply Propositions 5.1 and 5.3 to conclude the proof.

Proof of Theorem 2.13

We begin with part (1). As in the proof of Theorem 2.8, one shows that if $\beta _{L}^{r}>\tfrac 12$ , then $\delta (L/{\mathbb {Q}};r)=\tfrac 12$ ; we can therefore assume that $\beta _{L}^{r}=\tfrac 12$ . We will apply Proposition 5.3 and Theorem 5.10 to evaluate the bias factors $B(L/{\mathbb {Q}};1-r)$ . By Proposition 4.6 and Lemma 4.1, we have that

$$ \begin{align*} B(L/{\mathbb{Q}};1-r)^2& \ll \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1\Big)^2 \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}\log (A(\chi)+2)\Big)^{-1}\\ &\ll \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1\Big)^2 \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}\chi(1)\Big)^{-1}\\ &\leq \sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1\,. \end{align*} $$

For part (2), we note using (32) that the stated condition implies that

$$ \begin{align*}\mathbb E[X(L/{\mathbb{Q}},r)]\gg \sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1,\end{align*} $$

and thus, $\mathrm {Var}[X(L/{\mathbb {Q}},1-r)]^{-1} \ll B(L/{\mathbb {Q}};1-r)^2. $ Moreover,

$$ \begin{align*} B(L/{\mathbb{Q}};1-r)^2 &\gg \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1\Big)^2 \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}\log (A(\chi)+2)\Big)^{-1}\,,\\ & \gg (\log (\mathrm{rd}_L+2))^{-1} \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}1\Big)^2 \Big(\sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}\chi(1)\Big)^{-1}\\ &\gg (\log(d_L+2))^{-1}\Big( \sum_{ \substack{ \chi \in \mathrm{Irr}(G) \\ \chi \,\mathrm{real}}}\chi(1)^2\Big)^{-\frac 12}, \end{align*} $$

by the Cauchy-Schwarz inequality and Lemma 4.1. If $B(L/{\mathbb {Q}};1-r)$ is small enough, the result follows from Theorem 5.10. Otherwise, note that our hypothesis implies that $\mathrm {Var}[X(L/{\mathbb {Q}},1-r)]$ is large enough, and the result follows from (117).

7 General $S_n$ -extensions

We now move to our particular results, starting with the case of a Galois extension $L/K$ of number fields with group $G=S_n$ . The representation theory of the symmetric group is a beautiful blend of combinatorics and algebra. We refer the reader, for example, to [Sag, Chapter 2] for the details. In the following, we will focus on the special cases $t=t_{C_1,C_2}$ for $C_1,C_2\in G\cup \{ 0\}$ , and $t=1-r$ .

7.1 Combinatorial estimates

The conjugacy classes of $S_n$ are determined by cycle type, and hence are canonically indexed by the partitions $\lambda = (\lambda _1 , \dots \lambda _k)$ of n (that is $\lambda _1 +\dots +\lambda _k=n$ and $\lambda _1 \leq \dots \leq \lambda _k $ ). Denoting by $C_\lambda $ the conjugacy class associated to $\lambda $ , one can obtain closed combinatorial formulas for the quantity $r(C_\lambda )$ (see [Ng, Section 5.3.5]). There is also a canonical parametrisation of the irreducible representations of $S_n$ in terms of the partitions $\lambda \vdash n$ . This is achieved via the Specht modules $ S^{\lambda }$ , which are generated by linear combinations of tabloids with coefficients $\pm 1$ (see [Sag]). Denoting by $\chi _{\lambda }$ the irreducible character associated to $ S^{\lambda }$ , it follows that $\mathrm {Irr} (S_n) = \{ \chi _{\lambda } : \lambda \vdash n \}$ . The number of irreducible representations is, therefore, equal to $p(n)$ the number of partitions of n, for which we have the Hardy–Ramanujan asymptotic formula ([An, (5.1.2)]):

(122) $$ \begin{align} p(n)\sim \frac{\mathrm{e}^{\pi\sqrt{ \frac{2n}3}}}{4n\sqrt 3} \qquad (n\rightarrow\infty)\,. \end{align} $$

We can picture a partition with its associated Ferrer diagram ([Sag, Definition 2.1.1]). We denote by $r(\lambda )$ the number of rows of this diagram, and by $c(\lambda )$ its number of columns. It is known [Sag, Section 2.7] that all irreducible representations of $S_n$ are orthogonal. In Table 1, we consider the example $n=6$ , in which $C_{\lambda }, r(C_{\lambda })$ are directly computed, and the dimensions $\chi _{\lambda }(1)$ are obtained via the hook-length formula [Sag, Theorem 3.10.2].

Combining (45) with the asymptotic [Wil, (2.2)] of Moser and Wyman on the number of involutions in $S_n$ , we have a precise control on the sum of the degrees of irreducible representations of $S_n$ :

(123) $$ \begin{align} \sum_{ \lambda \vdash n}\chi_\lambda(1)= |\{\sigma\in S_n\colon \sigma^2=\mathrm{Id}\}| \sim \Big(\frac n{\mathrm{e}} \Big)^{\frac n2} \frac{{\mathrm{e}}^{\sqrt n}}{{\mathrm{e}}^{\frac 14}\sqrt 2}. \end{align} $$

It turns out that most character values $\chi _\lambda (\pi )$ with $\pi \neq \mathrm {Id}$ are of small size compared to $\chi _\lambda (1)$ . This well-known fact has applications to various problems, such as mixing times of random walks, covering by powers of conjugacy classes and probabilistic and combinatorial properties of word maps (see [LS]). In our case, it will allow us to obtain sharp estimates for the Artin conductors $A(\chi _{\lambda })$ . The bound we will apply is due to Roichman.

Theorem 7.1 [Ro, Theorem 1].

Let $n>4$ . Then for any $\lambda \vdash n$ and $\pi \in S_n$ , we have the bound

(124) $$ \begin{align} \frac{|\chi_\lambda(\pi)|}{\chi_\lambda(1)} \leq \left( \max\left(q,\frac{r(\lambda)}n,\frac{c(\lambda)}n\right) \right)^{b \text{ supp}(\pi)}, \end{align} $$

where $0<q<1$ and $b>0$ are absolute constants and supp $(\pi )$ is the number of nonfixed points of $\pi $ .

There are also more recent bounds due to Féray and Śniady [FeS, Theorem 1] and Larsen and Shalev [LS, Theorems 1.1 and 1.2], however, Roichman’s is sufficient for our purposes. We will need a combinatorial bound on the degree of the irreducible representation associated to $S^{\lambda }$ in terms of $r(\lambda )$ and $c(\lambda )$ .

Lemma 7.2. For any $\lambda \vdash n$ , we have the bound

$$ \begin{align*}\chi_{\lambda}(1) = f^{\lambda} \ll n\cdot n!^{1-\frac{r(\lambda)+c(\lambda)}n} {\mathrm{e}}^{2n/{\mathrm{e}}}.\end{align*} $$

One could possibly improve this bound to one of the type

$$ \begin{align*}\chi_\lambda(1) \ll n^{\theta}\cdot n!^{1-\frac{r(\lambda)+c(\lambda)}n} {\mathrm{e}}^{2n/{\mathrm{e}}}\end{align*} $$

for some $\theta <1$ , however, this would not affect Theorem 2.15.

Proof of Lemma 7.2

Applying the hook-length formula ([Sag, Theorem 3.10.2]) and considering only the hook-lengths of the first row and of the first column, we see that

$$ \begin{align*}f^{\lambda}\leq \frac{n!}{(r(\lambda)+c(\lambda)-1) (r(\lambda)-1)! (c(\lambda)-1)! } \leq n \frac{n!}{r(\lambda)!c(\lambda)!}.\end{align*} $$

Here, we have used the fact that the conditions $1\leq x,y \leq n$ , $x+y-1\leq n$ imply the bound $ xy/(x+y-1) \leq (n+1)^2/4n \leq n$ . Next we apply Stirling’s formula and obtain that

$$ \begin{align*}f^{\lambda} \ll n \left(\frac n{{\mathrm{e}}} \right)^{n-r(\lambda)-c(\lambda)} \left(\frac n{r(\lambda)} \right)^{r(\lambda)} \left(\frac n{c(\lambda)} \right)^{c(\lambda)} \ll n\cdot n!^{1-\frac{r(\lambda)+c(\lambda)}n} {\mathrm{e}}^{2n/{\mathrm{e}}}\,;\end{align*} $$

the last equality following from the fact that, for fixed n, the function $t\mapsto (n/t)^t$ attains its maximal value on $(0,n]$ at $t=n/{\mathrm {e}}$ .

7.2 Proof of Theorem 2.15

We first treat the easier case of $\delta (L/{\mathbb {Q}};1-r)$ .

Lemma 7.3. Let $n\geq 2$ , and assume that AC, GRH and LI hold for the $S_n$ -extension $L/{\mathbb {Q}}$ . We have the following estimates (recall the definition (101)):

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};1-r)] \asymp \log (\mathrm{rd}_L) (n/{\mathrm{e}})^{n/2}{\mathrm{e}}^{\sqrt{n}}\,. \end{align*} $$

$$ \begin{align*}B(L/{\mathbb{Q}};1-r) \asymp (\log (\mathrm{rd}_L))^{-\frac 12} p(n) n!^{-\frac 14} {\mathrm{e}}^{-\frac{\sqrt{n}} 2}n^{\frac 18} \,. \end{align*} $$

Proof. We will show that

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};1-r)] \asymp \log (\mathrm{rd}_L) \sum_{\substack{\lambda \vdash n }} \chi_\lambda(1);\end{align*} $$

the claimed bound on $\mathrm {Var}[X(L/{\mathbb {Q}};1-r)]$ then follows from (123).

Proposition 4.6 implies that

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};1-r)] \asymp \sum_{\substack{\lambda \vdash n }} \log (A(\chi_\lambda)+1),\end{align*} $$

and hence, from Lemma 4.1, we deduce the required upper bound. As for the lower bound, setting $M=n!^{\frac 13}$ , we see that

$$ \begin{align*} \mathrm{Var}[X(L/{\mathbb{Q}};1-r)] \gg \sum_{\substack{\lambda \vdash n \\ \chi_\lambda(1) \geq M }} \log (A(\chi_\lambda)+1)\gg \log (\mathrm{rd}_L) \sum_{\substack{\lambda \vdash n \\ \chi_\lambda(1) \geq M }} \chi_\lambda(1). \end{align*} $$

Indeed, by Lemma 7.2, the condition $\chi _\lambda (1) \geq M$ implies that

$$ \begin{align*}\max(r(\lambda),c(\lambda))\leq n\Big(1-\frac{\log M}{\log n!}\Big)+O\Big(\frac{n}{\log n}\Big),\end{align*} $$

which, in turn, by (124) and Lemma 4.2 implies that $\log (A(\chi _\lambda )+1) \gg \chi _\lambda (1) \log (\mathrm {rd}_L)$ , for n large enough. We deduce that for some absolute $c>0$ ,

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};1-r)] \geq c \log (\mathrm{rd}_L) \Big(\sum_{\substack{\lambda \vdash n \\ }} \chi_\lambda(1)-Mp(n)\Big).\end{align*} $$

Hence, for n large enough, (122) and (123) imply the required lower bound. For the remaining (finite number of) values of $n\geq 8$ , we can pick

$$ \begin{align*}\lambda_n:= \begin{cases} (\frac{n}2, \frac{n}2) & \text{ if } n \text{ is even;} \\ ( \frac{n+1}2,\frac{n-1}2 ) &\text{ otherwise}; \end{cases}\end{align*} $$

then (124) and Lemma 4.2 imply the required bound

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};1-r)]\gg \log ( A(\chi_{\lambda_n})+1) \gg \chi_{\lambda_n}(1) \log (\mathrm{rd}_L).\end{align*} $$

The same bound holds for $2\leq n\leq 7$ by inspection of the character table of $S_n$ .

For the claimed estimate on $B(L/{\mathbb {Q}};1-r)$ , we recall that every irreducible character of $S_n$ is orthogonal, and hence, LI implies that the Artin L-functions of irreducible representations of $\mathrm {Gal}(L/{\mathbb {Q}})$ have no real zeros. Thus, Proposition 3.18 takes the form

$$ \begin{align*}\mathbb E[X(L/{\mathbb{Q}};1-r)] =\sum_{\substack{\lambda \vdash n }} 1-1 = p(n)-1 ,\end{align*} $$

and the claim is proved thanks to the estimate on the variance we just proved.

The following lemma, which is stated for a general class functions t, will be applied in Proposition 7.6 in the case $t=t_{C_1,C_2}$ .

Lemma 7.4. Fix $\varepsilon>0$ , and let n be large enough in terms of $\varepsilon $ . Let $L/K$ be an extension of number fields for which $L/{\mathbb {Q}}$ is Galois, $G^+=\mathrm { Gal}(L/{\mathbb {Q}})=S_n$ , and, such that AC, GRH and LI $^-$ hold. Fix a class function $t:G\rightarrow \mathbb C$ , such that ${\lVert {t^+}\rVert }_2 \geq {\mathrm {e}}^{\frac {(2+\varepsilon )n} {\mathrm {e}}}{\lVert {t^+}\rVert }_1$ . Then we have the bounds

$$ \begin{align*}\mathrm{Var}[X(L/K;t)] \gg (1-\max(q, \tfrac{\log(kn!{\lVert{t^+}\rVert}^{-1}_2 {\lVert{t^+}\rVert}_1 {\mathrm{e}}^{4n/{\mathrm{e}}})}{\log n!})^b ) \log (\mathrm{rd}_L)\sum_{ \substack{\lambda \vdash n }} \chi_\lambda(1)|\widehat{t^+}(\chi_\lambda)|^2; \end{align*} $$

(125) $$ \begin{align} \frac{{\lVert{t^+}\rVert}_2^3}{{\lVert{t^+}\rVert}_1 (\# \mathrm{Irr}(G^+))^{\frac 12}} \ll \sum_{ \substack{\lambda \vdash n }} \chi_\lambda(1)|\widehat{t^+}(\chi_\lambda)|^2 \ll n!^{\frac 12} {\lVert{t^+}\rVert}^2_2. \end{align} $$

Here, $b,k>0$ and $0<q<1$ are absolute.

Remark 7.5. The condition ${\lVert {t^+}\rVert }_2 \geq {\mathrm {e}}^{\frac {(2+\varepsilon )n} {\mathrm {e}}}{\lVert {t^+}\rVert }_1$ can be reinterpreted by saying that $t^+$ is far from being constant. If we normalise so that ${\lVert {t^+}\rVert }_1=1$ , then this condition holds provided there exists $C\in G^\sharp $ , such that $|t(C)|\geq (n!^{\frac 12}/|C|^{\frac 1 2}) {\mathrm {e}}^{\frac {(4+2\varepsilon )n} {\mathrm {e}}}$ .

Proof. We will apply Proposition 4.7. Lemma 7.2 implies that for some absolute $k\geq 1$ ,

$$ \begin{align*}r(\lambda)+c(\lambda)\leq n\frac{\log(\frac{kn!}{\chi_{\lambda}(1)})+\frac{2n}e}{\log n!}.\end{align*} $$

Hence, by (124), if $\lambda \vdash n$ is such that $ \chi _\lambda (1)\geq {\lVert {t^+}\rVert }_2 {\lVert {t^+}\rVert }_1^{-1}$ , then for some absolute $b>0$ and $0<q<1$ ,

$$ \begin{align*}\max_{\mathrm{id} \neq \pi \in S_n }\frac{\chi_{\lambda}(\pi)}{\chi_{\lambda}(1)}\leq \Big(\max\Big(q,\frac{\log(kn!{\lVert{t^+}\rVert}^{-1}_2 {\lVert{t^+}\rVert}_1)+\frac{2n}e}{\log n!} \Big)\Big)^b.\end{align*} $$

Note that for n large enough and by our assumptions, $0<\log (kn!{\lVert {t^+}\rVert }^{-1}_2 {\lVert {t^+}\rVert }_1)+\frac {2n}e < \log n! $ (for the lower bound, note that $ {\lVert {t^+}\rVert }_2 \leq n!^{\frac 12}{\lVert {t^+}\rVert }_1$ ). The claimed lower bound on $\mathrm {Var}[X(L/K;t)]$ then follows from Proposition 4.7. The lower bound in (125) is just (118). As for the upper bound, it follows from noting that $\chi _{\lambda }(1) \leq n!^{\frac 12}$ .

We now evaluate the bounds of Lemma 7.4 more precisely in the particular case $t=t_{C_1,C_2}$ .

Proposition 7.6. Fix $\varepsilon>0$ , and let $n\geq 2$ . Let $L/K$ be an extension of number fields for which $L/{\mathbb {Q}}$ is Galois, $G^+=\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ , and, such that AC, GRH and LI $^-$ hold. If $C_1$ , $C_2$ are two elements of $ G^\sharp \cup \{0\}$ for which $\min (|C_1^+|,|C_2^+|) \leq n!^{1-\frac {4+\varepsilon }{{\mathrm {e}} \log n}} $ , then we have the bounds

$$ \begin{align*}\mathrm{Var}[X(L/K;t_{C_1,C_2})] \gg_\varepsilon \!\Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big)\! \log (\mathrm{rd}_L)\sum_{ \substack{\lambda \vdash n }} \chi_\lambda(1)|\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^2; \end{align*} $$

$$ \begin{align*} &\Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big) \frac{n!^{\frac 32}\log (\mathrm{rd}_L) }{ \min(|C_1^+|,|C_2^+|)^{\frac 32} p(n)^{\frac 12}}\\ &\quad \ll_\varepsilon \mathrm{ Var}[X(L/K;t_{C_1,C_2})] \ll \frac{n!^{\frac 32}\log (\mathrm{rd}_L) }{ \min(|C_1^+|,|C_2^+|) } .\end{align*} $$

Proof. For n large enough, we apply Lemma 7.4 with $t=t_{C_1,C_2}$ . We see that under our assumptions,

$$ \begin{align*} (\tfrac{\log(kn!{\lVert{t^+}\rVert}^{-1}_2 {\lVert{t^+}\rVert}_1 {\mathrm{e}}^{4n/{\mathrm{e}}})}{\log n!})^b &= (1-\tfrac{\log(k^{-1} n!(p(n) {\lVert{t^+}\rVert}_2 {\lVert{t^+}\rVert}_1^{-1} {\mathrm{e}}^{4n/{\mathrm{e}}})^{-1})}{\log n!} )^b\\ & \leq 1- c_b \tfrac{\log(k^{-1} n!(p(n) \min(|C_1^+|,|C_2^+|) {\mathrm{e}}^{4n/{\mathrm{e}}})^{-1})}{2\log n!}, \end{align*} $$

where $c_b>0$ depends only on b, since n is large enough (in terms of b). Hence, a straightforward calculation shows that both claimed lower bounds follow from Lemma 7.4. As for the finitely many remaining values of $n\geq 5$ , we note that for $\lambda \notin \{ (n),(1,1,\dots 1) \}$ , (124) implies that $\log A(\chi ) \gg _n \chi _{\lambda }(1)\log (\mathrm {rd}_L)$ . Hence, as before,

(126) $$ \begin{align} \mathrm{Var}[X(L/K;t_{C_1,C_2})] \gg_n \log (\mathrm{rd}_L)\sum_{\lambda \notin \{ (n),(1,1,\dots 1) \} } |\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^2. \end{align} $$

This implies both claimed lower bounds since

$$ \begin{align*}\sum_{\lambda \notin \{ (n),(1,1,\dots 1) \} } |\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^2 \geq \sum_{\lambda \vdash n } |\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^2-4= \frac{n!}{|C_1^+|} + \frac{n!}{|C_2^+|} -4,\end{align*} $$

which is strictly positive given our restriction on the conjugacy classes $C_1$ and $C_2$ . For $n \in \{3, 4\}$ , the right-hand side of (126) is $\gg _n \log (\mathrm {rd}_L) $ by inspection of the character table of $S_n$ . Finally, the case $n=2$ is immediate because then $\log A(\chi )\asymp \log (\mathrm {rd}_L)$ for the unique nontrivial character of $S_2$ .

As for the upper bound, it follows from combining Proposition 4.6 with Lemmas 4.1 and 7.4.

Lemma 7.7. Fix $\varepsilon>0$ , and let $n\geq 2 $ . Let $L/K$ be an extension of number fields for which $L/{\mathbb {Q}}$ is Galois, $G^+=\mathrm {Gal}(L/{\mathbb {Q}})=S_n$ , and, such that AC, GRH and LI hold. If $C_1$ , $C_2$ are two elements of $ G^\sharp \cup \{0\}$ , then have the bound

(127) $$ \begin{align} \mathbb E[X(L/K;t_{C_1,C_2})] \ll \Big( \frac{n! p(n)}{\min(|C_1|,|C_2|)} \Big) ^{\frac 12}. \end{align} $$

If, moreover, $\min (|C_1^+|,|C_2^+|)\leq n!^{1-\frac {1+\varepsilon }{{\mathrm {e}} \log n}} $ , then

(128) $$ \begin{align} W_4[X(L/K;t_{C_1,C_2})] \ll \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big)^{-2} \frac{n!^{-\frac 12}\min(|C_1^+|,|C_2^+|)^{\frac 12}p(n)^{\frac 16}}{\log (\mathrm{rd}_L)}. \end{align} $$

Proof. We begin with the bound (127). Recalling (13), we see that for any representative $g_i\in C_i$ ,

$$ \begin{align*}r_G(C_i) = \#\{g \in G : g^2=g_i \}\leq \#\{g \in G^+ : g^2=g_i \} = r_{G^+}(C_i^+).\end{align*} $$

Note that by (59),

$$ \begin{align*}\mathrm{ord}_{s=\frac 12}L(s,L/K,t) = \mathrm{ord}_{s=\frac 12}L(s,L/{\mathbb{Q}},t^+) =0,\end{align*} $$

since we are assuming LI and since all characters of $S_n$ are orthogonal. By Proposition 3.18, it follows that

$$ \begin{align*} |\mathbb E[X(L/K;t_{C_1,C_2})]| & \leq r_{G^+}(C_1^+)+r_{G^+}(C_2^+) \leq \sum_{\chi \in \mathrm{Irr}(G^+)} (|\chi(C_1^+)|+|\chi(C_2^+)|), \end{align*} $$

and hence, (127) follows after an application of the Cauchy-Schwarz inequality. As for (128), we note that by definition of $W_4[X(L/K;t_{C_1,C_2})]$ , Lemma 4.1 and Proposition 7.6,

$$ \begin{align*}W_4[X(L/K;t_{C_1,C_2})] &\ll \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big)^{-2}\\&\quad \times\frac{\sum_{\lambda \vdash n}\chi_\lambda(1)|\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^4 }{\log (\mathrm{rd}_L)(\sum_{\lambda \vdash n} \chi_\lambda(1)|\chi_\lambda(C_1^+)-\chi_\lambda(C_2^+)|^2 )^2}.\end{align*} $$

The desired estimate follows at once from Lemmas 5.5 and 7.4.

We are now ready to prove Theorem 2.15.

Proof of Theorem 2.15

The mean and variance bounds follow from Proposition 7.6 and Lemma 7.7. Moreover, those bounds imply that

(129) $$ \begin{align} B(L/K;t_{C_1,C_2}) &\ll \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big)^{-\frac 12} \frac{n!^{-\frac 14} p(n)^{\frac 34}\min(|C_1^+|,|C_2^+|)^{\frac 14}}{(\log (\mathrm{rd}_L))^{\frac 12}}; \end{align} $$

(130) $$ \begin{align} \mathrm{Var}[X(L/K;t_{C_1,C_2})]^{-2} \ll \Big(1-\frac{\log \min(|C_1^+|,|C_2^+|)}{\log n!} \Big)^{-2} \frac{n!^{-3} \min(|C_1^+|,|C_2^+|)^3 p(n) }{\log (\mathrm{rd}_L) }. \end{align} $$

In light of Theorem 5.10, the estimate (35) on $\delta (L/K;t_{C_1,C_2})$ then follows from combining these bounds with Lemma 7.7 (note that we always have $n! \geq \min (|C_1^+|,|C_2^+|)$ ).

We now move to the second claimed estimate, in which $K={\mathbb {Q}}$ and $C_1\neq C_2= \{\mathrm {id}\}$ . By orthogonality, positivity of $\chi _{\lambda }(1)-\chi _{\lambda }(C_1)$ and Cauchy–Schwarz:

$$ \begin{align*} n!&= \sum_{\lambda \vdash n}\chi_{\lambda}(1)(\chi_{\lambda}(1)-\chi_{\lambda}(C_1))\leq \left(\sum_{\lambda \vdash n}\chi_{\lambda}(1)^2\right)^{\frac 12}\left(\sum_{\lambda \vdash n}(\chi_{\lambda}(1)-\chi_{\lambda}(C_1))^2\right)^{\frac 12}\\ &\leq n!^{\frac 12}\sum_{\lambda \vdash n}(\chi_{\lambda}(1)-\chi_{\lambda}(C_1))\,. \end{align*} $$

We deduce that

(131) $$ \begin{align} \sum_{\lambda \vdash n}(\chi_{\lambda}(1)-\chi_{\lambda}(C_1))\geq n!^{\frac 12}\,, \end{align} $$

and hence, Proposition 7.6 yields that

$$ \begin{align*}B(L/{\mathbb{Q}},t_{C_1,\{ \mathrm{id}\}}) \gg \frac{n!^{-\frac 14} }{ (\log (\mathrm{rd}_L))^{\frac 12}}\,. \end{align*} $$

The estimate (36) is deduced from combining (128), (129), (130) and Theorem 5.10.

Finally, the estimate on $\delta (L/{\mathbb {Q}};1-r)$ follows directly from Proposition 5.10 and Lemma 7.3.

8 Abelian extensions

If $G=\mathrm {Gal}(L/{\mathbb {Q}})$ is abelian, then all its irreducible representations are one-dimensional. In particular, an irreducible character is real valued if and only if its associated representation is realisable over the reals, hence, $\varepsilon _2(\chi )\neq -1$ for all $\chi \in \mathrm {Irr}(G)$ . Therefore, (47) shows that the number of real characters of G is equal to the number of elements of G of order at most two.

Also, for distinct elements $a,b \in G$ , we have that

$$ \begin{align*}\mathrm{Var}[X(L/K;t_{a,b})]&\asymp \sum_{\chi \in \mathrm{Irr}(G^+) } |\chi(a)-\chi(b)|^2 \log (A(\chi)+1)\\ &\gg \sum_{\chi \in \mathrm{Irr}(G^+)} |\chi(a)-\chi(b)|^2=2|G^+|.\end{align*} $$

8.1 2-elementary groups: Proof of Theorem 2.21

We study the Galois extension $L={\mathbb {Q}}(\sqrt {p_1},\sqrt {p_2},...,\sqrt {p_m})/{\mathbb {Q}}$ of group $G\simeq (\mathbb Z/2\mathbb Z)^m$ in the setting of Theorem 2.21, under hypotheses GRH and LI.

Proof of Theorem 2.21

We first compute the Artin conductor explicitly. Clearly, besides $p=2$ , the only ramified prime in ${\mathbb {Q}}(\sqrt {p_j})/{\mathbb {Q}}$ is $p_j$ which factorises as $p_j\mathcal O_L=(\sqrt {p_j})^2$ . Hence, the odd primes ramifying in $L/{\mathbb {Q}}$ are $p_1,\ldots ,p_m$ (see [Le, Proposition 2.19]), and the ramification is tame at each of these primes. Moreover, if $\mathfrak p_j$ denotes a prime ideal of $\mathcal O_L$ lying over $p_j$ , we easily see that the corresponding inertia group is:

$$ \begin{align*}G_0(\mathfrak p_j/p_j)=\mathrm{Gal}(L/{\mathbb{Q}}(\sqrt{p_1},\dots,\sqrt{p_{j-1}} , \sqrt{p_{j+1}} ,\dots,\sqrt{p_m})), \end{align*} $$

which we identify with the subgroup $\langle e_j\rangle \leqslant \{\pm 1\}^m$ , where $e_j=(1,\ldots ,1,-1,1,\ldots ,1)$ , with the coefficient $-1$ in j-th position. Since the ramification at each $p_j$ is tame, we use the following formula to compute $n(\chi ,p_j)$ for every $\chi \in \mathrm {Irr}(G)$ (see (82)):

$$ \begin{align*}n(\chi,p_j)=\mathrm{codim}(V^{G_0})=\frac 1{|G_0|} \sum_{a \in G_0} (1-\chi(a))=\frac{1-\chi(e_j)}{2}\,. \end{align*} $$

We deduce that

$$ \begin{align*}2^{-n(\chi,2)} A(\chi) = \prod_{1\leq j\leq m} p_j^{\frac{1-\chi(e_j)}2}=\prod_{j : \chi(e_j)=-1} p_j.\end{align*} $$

Note also that by [Le, Proposition 2.19] and [ZS, Chapter 5, Theorem 31] (see also [BKS, Section 5]), we have that

$$ \begin{align*}\mathrm{disc}(L/{\mathbb{Q}}) =\mathrm{disc}({\mathbb{Q}}(\sqrt{p_1 \cdots p_m})/{\mathbb{Q}})^{\frac{|G|}2} = \begin{cases} 2^{|G|} (p_1\cdots p_m)^{\frac{|G|}2} &\text{ if } p_1\cdots p_m \equiv 3 \bmod 4; \\ (p_1\cdots p_m)^{\frac{|G|}2} &\text{ otherwise. } \end{cases}\end{align*} $$

We deduce that

$$ \begin{align*}\sum_{\chi \in \mathrm{Irr} (G)}n(\chi,2)\leq |G|.\end{align*} $$

We turn to the evaluation of the bias factor $B(L/{\mathbb {Q}};t_{a,b})$ for distinct elements $a,b$ of G. By Proposition 4.6, the variance of the random variable $X(L/{\mathbb {Q}};t_{a,b})$ is

$$ \begin{align*} \mathrm{Var}[X(L/{\mathbb{Q}};t_{a,b})] &\ll \sum_{j\leq m} \log p_j \sum_{\substack{\chi \in \mathrm{Irr} (G)}} |\chi(a)-\chi(b)|^2 + \sum_{\chi \in \mathrm{Irr} (G)}n(\chi,2) |\chi(a)-\chi(b)|^2 \\ &\ll |G|\sum_{\substack{j\leq m}} \log p_j. \end{align*} $$

We also have the lower bound

$$ \begin{align*} \mathrm{Var}[X(L/{\mathbb{Q}};t_{a,b})] &\gg \sum_{j\leq m} \log p_j \sum_{\substack{\chi \in \mathrm{Irr} (G)}} \frac{1-\chi(e_j)}{2} (2-2\chi(ab)) \\ &= \sum_{j\leq m} \log p_j |G| (1+\delta_{ab=e_j}) \,, \end{align*} $$

where $\delta _{c=d}$ is $1$ if $c=d$ , and $0$ otherwise. We conclude that

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}};t_{a,b})]\asymp |G|\sum_{\substack{j\leq m}} \log p_j.\end{align*} $$

Also, $\mathbb E[X(L/{\mathbb {Q}};t_{a,b})]=r(b)-r(a)=|G|(\delta _{b=1}-\delta _{a=1})$ with notation as in Proposition 3.18. We deduce that for $a\neq (1,\ldots ,1)$ and $b=(1,\ldots ,1)$

$$ \begin{align*}B(L/{\mathbb{Q}};t_{a,1})^2\asymp \frac{|G|}{\displaystyle{\sum_{\substack{j\leq m}} \log p_j}}. \end{align*} $$

In an analogous fashion, we compute that

$$ \begin{align*}B(L/{\mathbb{Q}};1-r)^2\asymp \frac{|G|}{\displaystyle{\sum_{\substack{j\leq m}} \log p_j}}\,. \end{align*} $$

Theorem 2.21 then follows from Proposition 5.3 and Theorem 5.10.

8.2 Hilbert class fields, the relative case: Proof of Theorem 2.24

The setting for this section is as in Section 2.3.5. We start by computing some useful invariants.

Lemma 8.1. Let d be a fundamental discriminant, such that $|d|> 1$ . Let $K_d$ be the Hilbert class field of the quadratic field ${\mathbb {Q}}(\sqrt {d})$ so that $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))\simeq \mathrm {Cl}_d $ . We have that

$$ \begin{align*}\log (\mathrm{rd}_{K_d})=\frac{\log |d|}{2}\,;\hspace{1cm} \sum_{\substack{\chi\in\mathrm{Irr}(\mathrm{Cl}_d)\\ \chi\,\mathrm{real}}}\chi(1)\in\{2^{\omega(d)-1},2^{\omega(d)-2}\}\,, \end{align*} $$

where $\omega (d)$ is the number of distinct prime factors of d.

Proof. Let us compute the discriminant of $K_d/\mathbb {Q}$ . Applying [ZS, Chapter 5, Theorem 31] to the tower of extensions $K_d/{\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ , we have:

$$ \begin{align*}|\mathrm{disc} (K_d/{\mathbb{Q}})|=\mathcal N_{{\mathbb{Q}}(\sqrt{d})/{\mathbb{Q}}}\bigl(\mathrm{disc} (K_d/{\mathbb{Q}}(\sqrt{d}))\bigr)|d|^{[K_d:{\mathbb{Q}}(\sqrt{d})]}\,. \end{align*} $$

Since $K_d$ is the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ , the extension $K_d/{\mathbb {Q}}(\sqrt {d})$ is unramified and the relative discriminant $\mathrm {disc} (K_d/{\mathbb {Q}}(\sqrt {d}))$ equals the unit ideal $\mathcal O_{{\mathbb {Q}}(\sqrt {d})}$ . Therefore, the ideal norm relative to ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ of $\mathrm {disc} (K_d/{\mathbb {Q}}(\sqrt {d}))$ equals $1$ . The formula for $\log (\mathrm {rd}_{K_d})$ follows from the fact that $[K_d:{\mathbb {Q}}]=2h(d)$ .

For the second assertion, we first use the fact that $\mathrm {Cl}_d$ is abelian, and then we invoke (45) and Theorem 3.3 following the general argument given at the beginning of Section 8. This yields:

$$ \begin{align*}\sum_{\substack{\chi\in\mathrm{Irr}(\mathrm{Cl}_d)\\ \chi\,\mathrm{real}}}\chi(1)=\sum_{\substack{\chi\in\mathrm{Irr}(\mathrm{Cl}_d)\\ \chi\,\mathrm{real}}}1=\#\{g\in\mathrm{ Cl}_d\colon g^2=1\}\,. \end{align*} $$

We conclude using the classical result from Gauss’ genus theory, according to which the $2$ -rank of the narrow class group of ${\mathbb {Q}}(\sqrt {d})$ equals $\omega (d)-1$ (see, for instance [Ha, Chapter 28, Section 8]). In other words, the $2$ -torsion of the narrow class group of ${\mathbb {Q}}(\sqrt {d})$ has dimension $\omega (d)-1$ as an $\mathbb F_2$ -vector space. Moreover, the index of the ordinary class group $\mathrm {Cl}_{{\mathbb {Q}}(\sqrt {d})}$ in the narrow class group of ${\mathbb {Q}}(\sqrt {d})$ is either $1$ or $2$ depending on the sign of d and on the sign of the norm of the fundamental unit in the real quadratic case.

Using this lemma, we are now ready to prove Theorem 2.24.

Proof of Theorem 2.24

We identify $G=\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt d))$ with the class group $\mathrm {Cl}_d$ . The extension $K_d/{\mathbb {Q}}$ is Galois by Lemma 9.4, and we denote $G^+=\mathrm {Gal}(K_d/{\mathbb {Q}})$ . We have $|G^+|=2h(d)$ . Let $\overline {\mathfrak a}$ be a nontrivial ideal class of ${\mathbb {Q}}(\sqrt d)$ , and denote by $\overline {1}$ the trivial ideal class. We apply Proposition 3.18 with $t=t_{C_1,C_2}$ , $(C_1,C_2)=(\{\overline {\mathfrak a}\}, \{\overline {1}\})$ or $(C_1,C_2)=(\{\overline {1}\}, 0)$ . The mean of the limiting distribution of $E(y;K_d/{\mathbb {Q}}(\sqrt d),t_{C_1,C_2})$ satisfies:

$$ \begin{align*} |\mu_{K_d/{\mathbb{Q}}(\sqrt d)}(C_1,C_2)|&=\bigg|\sum_{1\neq \chi\in\mathrm{Irr}(\mathrm{Cl}_d)}(\chi(C_1)-\chi(C_2))(\varepsilon_2(\chi)+2\mathrm{ord}_{s=\tfrac 12} L(s,K_d/{\mathbb{Q}}(\sqrt d),\chi)\bigg|\\ &\leq 2\sum_{\substack{\chi\in\mathrm{Irr}(\mathrm{Cl}_d)\\ \chi \,\mathrm{real}}}\chi(1)+4\sum_{1\neq\chi\in\mathrm{Irr}(\mathrm{Cl}_d)}\mathrm{ord}_{s=\tfrac 12} L(s,K_d/{\mathbb{Q}}(\sqrt d),\chi)\,, \end{align*} $$

and the first upper bound on the mean follows by Lemma 8.1. Proposition 4.6 and Lemma 4.1 (or rather a trivial form of the lower bound where we use $\chi (1)\geq 1$ ) yield the following lower bound on the variance, conditionally on GRH for $(C_1,C_2)=(\{\overline {1}\}, 0)$ and conditionally on GRH and LI $^-$ for $(C_1,C_2)=(\{\overline {\mathfrak a}\}, \{\overline {1}\})$ :

$$ \begin{align*} \sigma^2_{K_d/{\mathbb{Q}}(\sqrt d)}(C_1,C_2)&\gg \sum_{1\neq \chi\in \mathrm{Irr}(G^+) }|\chi(C_1^+)-\chi(C_2^+)|^2 \log A(\chi)\\ &\geq \sum_{1\neq \chi\in \mathrm{Irr}(G^+) }|\chi(C_1^+)-\chi(C_2^+)|^2\geq |G^+|\,, \end{align*} $$

where the last step follows from (48).

Finally, LI asserts that only symplectic irreducible characters of $G^+$ may have their L-function vanish at $\tfrac 12$ . However, the abelian group $G=\mathrm { Gal}(K_d/{\mathbb {Q}}(\sqrt d))$ does not admit such a character. As a consequence, we deduce that the second sum in the upper bound for $\mu _{K_d/{\mathbb {Q}}(\sqrt d)}(C_1,C_2)$ vanishes. The statement on the density is then an immediate consequence of Theorem 5.10 combined with Remark 5.6.

9 Supersolvable extensions

We devote this section to the proofs of our results for two kinds of extensions:

• • Galois extensions of number fields of group G having an abelian subgroup of index $2$ ,

• • radical extensions which are splitting fields over ${\mathbb {Q}}$ of polynomials of type $X^p-a$ for distinct primes $a,p$ .

In the first case, G has a quotient of order $2$ , and in the second case, G has a normal subgroup of order p and cyclic associated quotient (of order $p-1$ ; see below for a quick recollection of this fact). In particular, both cases are instances of supersolvable extensions.

9.1 Galois groups with an abelian subgroup of index $2$

Let G be a finite group and assume G has an abelian subgroup A of index $2$ . The quotient $\Gamma =G/A\simeq \mathbb Z/2\mathbb Z$ acts on the abelian group A via:

$$ \begin{align*}\tau\cdot \sigma = \tau_0\sigma\tau_0^{-1}\,,\qquad \sigma\in A,\, \Gamma=\langle \tau\rangle\,, \end{align*} $$

where $\tau _0$ is any fixed lift of $\tau $ to G. For simplicity (and since it will be the case in our applications), we assume from now on that $\Gamma $ acts by inversion on A, that is $\tau \cdot \sigma =\sigma ^{-1}$ for every $\sigma \in A$ . Since G has an abelian subgroup of index $2$ , the irreducible linear representations of G (over $\mathbb C$ ) have degree $1$ or $2$ ([Hu, Proposition 2.6]).

We begin by computing the Frobenius-Schur indicators of these representations. If $\psi $ is a one-dimensional character of G, then we have for any $\sigma \in A$ :

$$ \begin{align*}\psi(\sigma)=\psi(\tau_0\sigma\tau_0^{-1})=\psi(\sigma^{-1})\,. \end{align*} $$

Therefore, $\psi (\sigma )=\pm 1$ . In particular, if $\tau _0$ has order $2$ , we deduce from this computation and the fact that $G=A\langle \tau _0\rangle $ that $\psi $ is real, hence, $\varepsilon _2(\psi )=1$ because $\psi $ has degree $1$ .

As for the irreducible representations $\theta _\lambda $ of degree $2$ of G, they are all obtained ([Hu, Section 2.8]) from a given $\lambda \in \mathrm {Irr}(A)$ by setting for $\sigma \in A$ ,

(132) $$ \begin{align} \theta_\lambda(\sigma)=\begin{pmatrix} \lambda(\sigma) & 0 \\ 0 & \lambda(\tau\cdot \sigma) \end{pmatrix} \,,\qquad \theta_\lambda(\tau_0)=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\,. \end{align} $$

Our assumption $\tau \cdot \sigma =\sigma ^{-1}$ directly implies that $\chi _{\theta _\lambda }(\sigma )=\text {tr}(\theta _\lambda (\sigma ))$ is real. Moreover, for any $\lambda \in \mathrm { Irr}(A)$ and $\sigma \in A$ , we have $\chi _{\theta _\lambda }(\tau _0\sigma )=0$ . We deduce that $\chi _{\theta _\lambda }$ is a real character. By [Hu, Section 13.9], it follows that $\varepsilon _2(\chi )=1$ for all $\chi \in \mathrm {Irr}(G)$ .

The following lemma uses the information above to give a lower bound on the bias factors $B(L/K;1-r)$ and $B(L/K;t_{C_1,C_2})$ defined by (101), for suitably chosen conjugacy classes $C_1$ , $C_2$ .

Lemma 9.1. Let $L/{\mathbb {Q}}$ be a Galois extension, for which GRH and BM hold. Assume that $G=\mathrm {Gal}(L/{\mathbb {Q}})$ has an abelian subgroup A of index $2$ . Fix an element $\sigma \in A$ , and let $C_1$ be the conjugacy class of $\tau _0\sigma $ , where $\tau _0$ is a representative of the nontrivial left coset of G modulo A. Assume also that $\tau _0$ has order $2$ . We have the bounds

$$ \begin{align*}\min(\mathbb E(L/{\mathbb{Q}};t_{C_1,\{\mathrm{id}\}}),\mathbb E(L/{\mathbb{Q}};1-r)) \gg |G|\,; \end{align*} $$

$$ \begin{align*}\min(B(L/{\mathbb{Q}};t_{C_1,\{\mathrm{id}\}}),B(L/{\mathbb{Q}};1-r))^2 \gg \frac{|G|}{\log (\mathrm{rd}_{L})}. \end{align*} $$

Proof. We start with $\mathbb E(L/{\mathbb {Q}};1-r)$ . We have already seen that $\varepsilon _2(\chi )=1$ for every $\chi \in \mathrm {Irr}(G)$ , and hence, we deduce that

$$ \begin{align*}\sum_{\substack{1\neq\chi\in\mathrm{Irr}(G)\\ \chi\,\mathrm{real}}}\varepsilon_2(\chi)\mathrm{ord}_{s=\frac 12}L(s,L/{\mathbb{Q}},\chi)\geq 0\,. \end{align*} $$

Therefore, the desired lower bound follows by Proposition 3.18, since all characters of G are real and of dimension $\leq 2$ .

As for $B(L/{\mathbb {Q}};1-r)$ , by Lemmas 4.1, and 4.6, we have that

$$ \begin{align*} B(L/{\mathbb{Q}};1-r)^2 & \gg \frac{|G|^2}{ \sum_{\substack{1\neq \chi\in \mathrm{Irr}(G)\\ \chi \,\mathrm{real}}}\log (A(\chi)+1)} \gg \frac{|G|^2}{\log (\mathrm{rd}_{L}) \sum_{\substack{\chi\in \mathrm{Irr}(G)}}\chi(1)} \gg \frac{|G|}{\log (\mathrm{rd}_{L}) } \,. \end{align*} $$

(We have used once more the fact that $\chi (1)\leq 2$ .)

We turn to $\mathbb E(L/{\mathbb {Q}};t_{C_1,\{\mathrm {id}\}})$ . Starting from Proposition 3.18, one has for every $\chi \in \mathrm {Irr}(G)$ :

$$ \begin{align*}\varepsilon_2(\chi)+2\mathrm{ord}_{s=1/2}L(s,L/{\mathbb{Q}},\chi)\geq \varepsilon_2(\chi)=1\,,\qquad \chi(1)-\chi(C_1)\geq 0\,. \end{align*} $$

We note that by (132) and by the orthogonality relations, one has

$$ \begin{align*}0= \sum_{\chi \in\mathrm{Irr}(G)} \chi(1)\chi(C_1) =\sum_{\substack{\chi\in\mathrm{Irr}(G) \\ \chi(1)=1}} \chi(1)\chi(C_1) = \sum_{\chi\in\mathrm{Irr}(G)}\chi(C_1).\end{align*} $$

We deduce the following simple lower bound for the expectation of $X(L/{\mathbb {Q}},C_1,C_2)$ :

$$ \begin{align*} \mathbb E[X(L/{\mathbb{Q}},t_{C_1,\{\mathrm{id}\}})] &\geq \sum _{\chi\in\mathrm{Irr}(G)}\chi(1)-\sum _{\chi\in\mathrm{Irr}(G)}\chi(C_1)= \sum_{\substack{\chi\in\mathrm{Irr}(G)}}\chi(1). \end{align*} $$

As for the variance, one has, using Lemma 4.1 and Proposition 4.6:

$$ \begin{align*}\mathrm{Var}[X(L/{\mathbb{Q}},t_{C_1,\{\mathrm{id}\})}]\ll \log (\mathrm{rd}_{L}) \sum_{\chi\in\mathrm{Irr}(G)}\chi(1)|\chi(1)-\chi(C_1)|^2\,\leq 16\log (\mathrm{rd}_{L}) \sum_{\chi\in\mathrm{Irr}(G)}\chi(1)\,. \end{align*} $$

The expected bound follows as in the previous case.

9.1.1 Dihedral extensions: Proof of Theorem 2.17

Let us start by recalling some classical facts about dihedral groups and their representations (see, e.g. [Se2, Section 5.3]). Consider, for an odd integer $n\geq 3$ ,

$$ \begin{align*}D_n=\langle \sigma,\tau\colon \sigma^n=\tau^2=1,\, \tau\sigma\tau=\sigma^{-1}\rangle\,. \end{align*} $$

The nontrivial conjugacy classes of $D_n$ are

$$ \begin{align*}\{\sigma^j,\sigma^{-j}\}\,\, (1\leq j\leq (n-1)/2)\, \qquad \text{and}\qquad \{\tau\sigma^k\colon 0\leq k\leq n-1\}\,. \end{align*} $$

There are, therefore, $(n+3)/2$ isomorphy classes of irreducible representations of $D_n$ . Exactly two of them have degree 1: the trivial representation and the lift of the nontrivial character of $D_n/\langle \sigma \rangle $ which is defined by

$$ \begin{align*}\psi(\sigma^j)=1\,,\qquad \psi(\tau\sigma^k)=-1\,. \end{align*} $$

The remaining $(n-1)/2$ irreducible representations of $D_n$ have degree $2$ ; the associated characters are given by

$$ \begin{align*}\chi_h(\sigma^j)=2\cos(2\pi hj/n)\,,\qquad \chi_h(\tau\sigma^k)=0\,, \end{align*} $$

with $h\in \{1,\ldots (n-1)/2\}$ . Clearly, Lemma 9.1 holds for the dihedral group $D_n$ . To be in a position where Lemma 9.1 provides us with a family of unbounded bias factors, we need to control the size of the discriminant of the extensions that we consider. For that purpose, we focus on a particular family of dihedral extensions of ${\mathbb {Q}}$ introduced by Klüners which enjoy useful properties stated in the following lemma (see [Kl, Lemma $3.4$ ]).

Lemma 9.2 (Klüners).

Let $d\neq 1$ be a squarefree integer, and let ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ be a quadratic extension of discriminant $\delta _d\in \{d,4d\}$ . Suppose that there is an odd prime number $\ell $ and two prime numbers $p,q$ which are $1$ modulo $\ell $ and which split in ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ . Then there exists an extension $N_{\ell ,p,q,d}/{\mathbb {Q}}(\sqrt {d})$ , such that $N_{\ell ,p,q,d}/{\mathbb {Q}}$ is Galois and

$$ \begin{align*}\mathrm{Gal}(N_{\ell,p,q,d}/{\mathbb{Q}})\simeq D_\ell,\qquad |\mathrm{disc}(N_{\ell,p,q,d}/{\mathbb{Q}})|\leq |\delta_d|^\ell (pq)^{2(\ell-1)}\,. \end{align*} $$

Proof. For the existence of the dihedral extension $N_{\ell ,p,q,d}/{\mathbb {Q}}$ , see [Kl, Lemma $3.4$ ]. The upper bound for the discriminant is [Kl, (6)].

We now proceed to give an example of a family of dihedral extensions $(N_\ell /{\mathbb {Q}})$ indexed by prime numbers and, such that the second lower bound of Lemma 9.1 approaches infinity as $\ell $ grows.

Proposition 9.3. For each prime number $\ell \geq 7$ , there exists an extension $N_\ell / {\mathbb {Q}}$ with Galois group $D_\ell $ , such that

$$ \begin{align*}\min(B(N_{\ell}/{\mathbb{Q}};t_{C_1,\{ \mathrm{id}\}}),B(N_{\ell}/{\mathbb{Q}};1-r))^2\gg \frac{\ell}{\log \ell}, \end{align*} $$

where $C_1$ is as in Lemma 9.1.

Proof. A prime number p splits completely in ${\mathbb {Q}}(\sqrt {5})$ if and only if $5$ is a square modulo p. By quadratic reciprocity, this is equivalent to the condition $p\equiv \pm 1 (\bmod \, 5)$ . Therefore, if we pick primes $p,q$ that are congruent to $1$ modulo $5\ell $ , then $p,q$ satisfy the hypotheses of Lemma 9.2.

By Linnik’s theorem ([Lin, (2)], [Xy, Theorem 1.1]), for each fixed $\ell $ , we can find distinct primes $p,q$ that are $1$ modulo $5\ell $ and of size $\ll \ell ^{5.18}$ . The result follows by applying Lemmas 9.1 and 9.2.

We are now ready to prove Theorem 2.17.

Proof of Theorem 2.17

The claimed bounds are a consequence of Propositions 5.1 and 5.3, using as inputs Lemmas 9.1 and 9.3. The lower bound on $1-\delta (K_\ell /{\mathbb {Q}};r)$ is an immediate consequence of Theorem 2.13.

9.1.2 Hilbert class fields, absolute case: Proof of Theorems 1.1 and 2.18

We first review standard results on Hilbert class fields. As in the dihedral case, we will see that the Galois groups of the extensions considered in this section have an abelian subgroup of index $2$ . This will once more allow us to apply Lemma 9.1.

Lemma 9.4. Let $d\neq 1$ be a fundamental discriminant, and let $K_d$ be the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ so that $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))\simeq \mathrm {Cl}_d$ , the class group of ${\mathbb {Q}}(\sqrt {d})$ , of order $h(d)$ . Let $\tau $ be the generator of $\mathrm {Gal}({\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}})$ . Then $K_d/{\mathbb {Q}}$ is Galois and, fixing a representative $\tau _0$ for the left coset of $G_d=\mathrm {Gal}(K_d/{\mathbb {Q}})$ modulo $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ determined by $\tau $ , we have

$$ \begin{align*}G_d\simeq\mathrm{Cl}_d\rtimes \langle \tau_0\rangle\,, \qquad \tau_0^2=1\,,\,\,\tau_0 \sigma\tau_0^{-1}=\sigma^{-1}\,\,(\forall \sigma\in \mathrm{Cl}_d)\,. \end{align*} $$

Moreover, $\log (\mathrm {rd}_{K_d})=\tfrac 12\log |d|$ .

Proof. We have a short exact sequence

$$ \begin{align*}1\rightarrow \mathrm{Gal}(K_d/{\mathbb{Q}}(\sqrt{d}))\simeq\mathrm{Cl}_d\rightarrow G_d\rightarrow \mathrm{Gal}({\mathbb{Q}}(\sqrt{d})/{\mathbb{Q}})\simeq \mathbb Z/2\mathbb Z\rightarrow 1\,. \end{align*} $$

In particular, $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ is an abelian subgroup of $G_d$ of index $2$ , and, as explained at the beginning of Section 9.1, $\mathrm {Gal}({\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}})=\langle \tau \rangle $ acts on it via

$$ \begin{align*}\tau\cdot\sigma=\tau_0\sigma\tau_0^{-1}\,. \end{align*} $$

Moreover, the short exact sequence splits since ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ is cyclic (see, e.g. [Go, Theorem 2]) and the above action is inversion. Indeed, let $\mathfrak p$ be a prime ideal of the ring of integers $\mathcal O_{{\mathbb {Q}}(\sqrt {d})}$ of ${\mathbb {Q}}(\sqrt {d})$ . The Frobenius conjugacy class at $\mathfrak p$ in the (abelian, unramified) extension $K_d/{\mathbb {Q}}(\sqrt {d})$ is an actual element $\mathrm {Frob}_{\mathfrak p}$ of $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ , and we have the standard relation

$$ \begin{align*}\tau_0 \mathrm{Frob}_{\mathfrak p}\tau_0^{-1}=\mathrm{Frob}_{\tau_0(\mathfrak p)}=\mathrm{Frob}_{\tau(\mathfrak p)}\,, \end{align*} $$

where we identify the restriction of elements of $G_d$ to ${\mathbb {Q}}(\sqrt {d})$ with their image by the quotient map $G_d\rightarrow G_d/\mathrm { Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ . If p is the prime number lying under $\mathfrak p$ , we have the ideal factorisation $p\mathcal O_{{\mathbb {Q}}(\sqrt {d})}=\mathfrak p\tau (\mathfrak p)$ , so that in $\mathrm {Cl}_d$ , the classes of $\tau (\mathfrak p)$ and $\mathfrak p^{-1}$ are the same. We conclude that $\tau _0 \mathrm {Frob}_{\mathfrak p}\tau _0^{-1}=\mathrm {Frob}_{\mathfrak p}^{-1}$ , and we deduce the group structure of $G_d$ from the Chebotarev density theorem. It remains to see that $\tau _0$ has order $2$ . First, the order of $\tau _0$ divides $4$ since $\tau _0^2\in \mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ and therefore $\tau _0^4=(\tau _0 \tau _0^2\tau _0^{-1})\tau _0^2=1$ . Next, for any $\sigma \in \mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ , we have $(\tau _0\sigma )^2=(\tau _0\sigma \tau _0^{-1})\tau _0^2\sigma =\sigma ^{-1}\tau _0^2\sigma =\tau _0^2$ , since $\tau _0^2$ and $\sigma $ are both elements of the abelian group $\mathrm { Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ . Consequently, every element of the left coset of $G_d$ modulo $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ determined by $\tau $ has the same order. Assume by contradiction that this order is $4$ , and consider a prime p ramified in ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ ; since $K_d/{\mathbb {Q}}(\sqrt {d})$ is unramified, the ramification index of $\mathfrak P/p$ (here, $\mathfrak P$ denotes any prime ideal of $\mathcal O_{K_d}$ lying over p) is $2$ , and thus, the inertia subgroup of $G_d$ relative to $\mathfrak P/p$ has order $2$ and therefore contains no element of the left coset of $G_d$ modulo $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ determined by $\sigma $ . Hence, this inertia group is a subgroup of $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))$ . Thus, every element of the inertia group relative to $\mathfrak P/p$ fixes ${\mathbb {Q}}(\sqrt {d})$ pointwise, contradicting the fact that p is ramified in ${\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}}$ .

Finally, the assertion on the root discriminant of $K_d$ was proven in Lemma 8.1.

Lemmas 9.1 and 9.4 suggest that a family of quadratic fields ${\mathbb {Q}}(\sqrt {d})$ with class number $h(d)$ significantly larger than $\log |d|$ will produce an extreme bias. In order to achieve this, we will exploit the following precise lower bound on the class group of a particular family of quadratic fields. Note that this result plays a role analogous to Proposition 9.3 in the case of dihedral extensions.

Lemma 9.5. For $d\neq 1$ a fundamental discriminant, let $h(d)$ be the class number of ${\mathbb {Q}}(\sqrt {d})$ , and let $K_d$ be the Hilbert class field of ${\mathbb {Q}}(\sqrt {d})$ . Then there exists a sequence of positive (respectively, negative) fundamental discriminants $d\neq 1$ , such that one has

$$ \begin{align*}h(d)\gg \frac{\sqrt{|d|}\log\log |d|}{(\log |d|)^{\frac{1}{2}+\frac{\mathrm{sgn}(d)}{2}}}\,. \end{align*} $$

Moreover, under GRH for $L(s,\chi _d)$ , the bounds

$$ \begin{align*}\frac{\sqrt{|d|}}{\log\log |d|}\ll h(d)\ll \sqrt{|d|}\log\log |d|\, \end{align*} $$

hold for all $d<0$ . As for $d>1$ , under GRH for $L(s,\chi _d)$ , we have that

$$ \begin{align*}h(d)\ll \frac{\sqrt{d}\log\log d}{\log d}\,. \end{align*} $$

Proof. The first bound is an immediate consequence of [MW, (3)] (see also [La2, Theorem 1.2(a)], as well as results towards a conjecture of Hooley [Ho] due to Fouvry [Fo, Theorem 1.1] with subsequent improvements in [Bo, Xi], that further addresses the question of the density of values d with attached fundamental unit of prescribed size) in the case $d>1$ , and of Chowla [C] (see also [Du] for generalisations to number fields of higher degree) in the case $d<0$ .

As for the GRH bounds, we apply the Littlewood bounds (see [Lit2])

$$ \begin{align*}\frac 1{\log\log |d|} \ll L(1,\chi_d) \ll \log\log |d|.\end{align*} $$

In the case $d<0$ , both claimed bounds on $h(d)$ follow directly from the class number formula. As for the case $d>1$ , it is well-known that the fundamental unit satisfies $\varepsilon _d\geq \sqrt d/2$ , and hence, the class number formula yields that

$$ \begin{align*}\frac{h(d) \log d}{\sqrt d} \ll \log\log d.\\[-38pt]\end{align*} $$

Remark 9.6. It is expected [Sa2, Conjecture 1] that for positive fundamental discriminants d, we typically have $h(d)\ll _\varepsilon d^\varepsilon $ . The construction of Montgomery and Weinberger [MW] focuses on (the sparse set of) fundamental discriminants of the form $d=4n^2+1$ . For such d, the fundamental unit of $\mathcal O_{{\mathbb {Q}}(\sqrt {d})}$ equals $\varepsilon _d=2n+\sqrt {d}$ . Such fundamental units are of minimal order of magnitude $\sqrt {d}$ , and this maximises in turn the value of $h(d)$ .

Remark 9.7. The extension $K_d/{\mathbb {Q}}$ , where $K_d$ is the Hilbert class field of the quadratic field ${\mathbb {Q}}(\sqrt {d})$ , is not abelian in general, but contrary to the case of dihedral extensions, particular choices of d may still produce an abelian extension $K_d/{\mathbb {Q}}$ . Precisely, if F denotes the maximal abelian subextension of $K_d/{\mathbb {Q}}$ , then $F\supset {\mathbb {Q}}(\sqrt {d})$ and $\mathrm {Gal}(F/{\mathbb {Q}}(\sqrt {d}))$ is a quotient of the class group $\mathrm {Cl}_d$ of ${\mathbb {Q}}(\sqrt {d})$ . By the group structure of $\mathrm {Gal}(K_d/{\mathbb {Q}})$ given in Lemma 9.4, $\mathrm {Gal}(F/{\mathbb {Q}}(\sqrt {d}))$ is the maximal quotient of $\mathrm {Gal}(K_d/{\mathbb {Q}}(\sqrt {d}))\simeq \mathrm {Cl}_d$ on which $\mathrm {Gal}({\mathbb {Q}}(\sqrt {d})/{\mathbb {Q}})$ acts trivially. Again by Lemma 9.4, we conclude that $F=K_d$ if and only if $\mathrm {Cl}_d$ is an elementary $2$ -group (such is the case, e.g. for ${\mathbb {Q}}(\sqrt {-5})$ , which has class number $2$ ). Weinberger [Wei, Theorem 1] has shown that there are only finitely many negative fundamental discriminants d, such that $\mathrm {Cl}_d$ is an elementary $2$ -group. In the real quadratic case, let us mention that $\mathrm {Cl}_p$ for $p\equiv 1 (\bmod \ 4)$ prime, such that $h_p>1$ is never an elementary $2$ -group ²⁹ .

We are now ready to prove Theorems 1.1 and 2.18.

Proof of Theorems 1.1 and 2.18

The mean and variance are computed under GRH and BM in Lemma 9.1. Under GRH alone, we need to go back to Proposition 4.6, which we combine with the representation-theoretic calculations made in Lemma 9.1. Note that our assumption of GRH implies that the Riemann hypothesis holds for $L(s,\chi _d)$ . Indeed, $\chi _d$ lifts to an irreducible representation of $G_d$ , and the corresponding Artin L-functions are identical since $K_d/{\mathbb {Q}}(\sqrt d)$ is unramified. For the computation of the densities $\delta (L/K;t_{C_1,C_2})$ and $\delta (L/K;1-r)$ , we apply Propositions 5.1 and 5.3 using as inputs Lemmas 9.1 and 9.5. Finally, note that by [IK, Proposition 5.34],

$$ \begin{align*}\mathrm{ord}_{s=\frac 12} \zeta_{K_d}(s) \ll \frac{\log (3|d|^{h(d)})}{\log\log(3|d|^{h(d)})} \ll h(d).\\[-36pt]\end{align*} $$

9.2 Radical extensions: Proof of Theorem 2.19

Radical extensions of the rationals are particularly well-suited to compute explicitly all the invariants required in our analysis. Notably, the Artin conductors of the irreducible characters of the Galois group were computed in [Vi] in a more general setting; for the sake of completeness, we will show the details of this computation in our setting. Making precise the explicit value of such invariants is also interesting, since it is an instance of a nonabelian extension, where all the computations we need (e.g. the filtration of inertia at ramified primes) can be explicitly performed.

9.2.1 The splitting field of $x^p-a$ over ${\mathbb {Q}}$

Let $p,a$ be distinct primes with $p\neq 2$ and, such that $a^{p-1}\not \equiv 1 (\bmod \ p^2)$ . Consider $K_{a,p}={\mathbb {Q}}(\zeta _p,a^{\frac 1p})$ , the splitting field of $x^p-a$ over ${\mathbb {Q}}$ . If $\sigma $ is an element of $G:=\mathrm {Gal}(K_{a,p}/{\mathbb {Q}})$ , then we have

$$ \begin{align*}\sigma(\zeta_p)=\zeta_p^c, \hspace{1cm} \sigma(a^{\frac 1p})=\zeta_p^d a^{\frac 1p}\end{align*} $$

with $c\in \mathbb F_p^*$ , $d\in \mathbb F_p$ ; we may identify $\sigma $ with

$$ \begin{align*}\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right) \in \mathrm{GL}_2(\mathbb F_p)\,.\end{align*} $$

As such, we have the group isomorphisms

(133) $$ \begin{align} G\simeq (\mathbb Z/p\mathbb Z)\rtimes(\mathbb Z/p\mathbb Z)^\times\simeq \left\{\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right)\colon c\in \mathbb F_p^*, d\in\mathbb F_p\right\}\,. \end{align} $$

In other words, G is the Frobenius group of invertible affine maps $x\mapsto cx+d$ of $\mathbb F_p$ . Artin’s conjecture is known for such Galois extensions. Indeed, we have the following sequence:

$$ \begin{align*}\{\mathrm{Id}\} \lhd H = \left \{ \left( \begin{array}{cc} 1 & * \\ 0 & 1 \end{array} \right) \right\} \lhd G,\end{align*} $$

and the groups $G/H \cong (\mathbb Z/p\mathbb Z)^{\times }$ , $H\cong \mathbb Z/p\mathbb Z$ , are cyclic so G is supersolvable.

The prime numbers which ramify in $K_{a,p}/{\mathbb {Q}}$ are p and a; more precisely, we have (see, e.g. [Kom, end of the proof of the theorem] and [Wes, Section 3.I])

$$ \begin{align*}\mathrm{disc}(K_{a,p}/{\mathbb{Q}})=p^{p-2}(\mathrm{disc} ({\mathbb{Q}}(a^{1/p})))^{p-1}=p^{p^2-2}a^{(p-1)^2}\,. \end{align*} $$

We finally mention that $K_{a,p}/{\mathbb {Q}}$ enjoys the remarkable unique subfield property: for every divisor d of the degree $p(p-1)$ of $K_{a,p}/{\mathbb {Q}}$ , there is a unique intermediate extension $K_{a,p}/L/{\mathbb {Q}}$ , such that $[L:{\mathbb {Q}}]=d$ (see, e.g. [Vi, Theorem $2.2$ ]).

9.2.2 Irreducible characters of $\mathrm {Gal}(K/{\mathbb {Q}})$

The group $G\simeq (\mathbb Z/p\mathbb Z)\rtimes (\mathbb Z/p\mathbb Z)^\times $ has p conjugacy classes (see, e.g. [Vi, Proposition 3.6]), and thus, p distinct irreducible characters. The conjugacy classes are easily described through the isomorphism (133): besides $\{\mathrm {Id}\}$ , there is one conjugacy class of size $p-1$ :

$$ \begin{align*}U:=\left\{\left(\begin{array}{cc} 1 & \star \\ 0 & 1 \end{array} \right)\colon \star\neq 0\right\}\,, \end{align*} $$

and $p-2$ conjugacy classes of size p:

$$ \begin{align*}T_c:=\left\{\left(\begin{array}{cc} c & \star \\ 0 & 1 \end{array} \right)\colon \star\in\mathbb F_p\right\}\,,\,\,(c\neq 1)\,. \end{align*} $$

As for the characters of G, exactly $p-1$ of them have degree $1$ : these are the lifts of Dirichlet characters $\chi $ modulo p

(134) $$ \begin{align} \psi\colon \left\{\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right)\colon c\in \mathbb F_p^\times, d\in\mathbb F_p\right\} \rightarrow (\mathbb Z/p\mathbb Z)^\times\xrightarrow{\chi}\mathbb C^\times\,,\qquad \psi \left(\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right)\right)=\chi(c)\,. \end{align} $$

The Frobenius-Schur indicator of such a character $\psi $ is easy to compute:

$$ \begin{align*}\varepsilon_2(\psi)=\frac{1}{|G|}\sum_{\substack{c\in \mathbb F_p^\times \\ d\in\mathbb F_p}}\psi\left(\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right)^2\right)=\frac{1}{p-1}\sum_{c\in\mathbb F_p^{\times}}\chi(c^2)=\varepsilon_2(\chi). \end{align*} $$

We deduce that $\varepsilon _2(\psi )$ equals $1$ if $\chi $ is real, and equals $0$ otherwise.

The remaining irreducible character $\eta $ of G can then be determined using orthogonality relations. By the above description of the conjugacy classes of G, we obtain the following values that entirely determine $\eta $ :

(135) $$ \begin{align} \eta(1)=p-1\,,\qquad \eta\left(\left(\begin{array}{cc} 1 & \star \\ 0 & 1 \end{array} \right)\right)=-1\,,\,\,(\star\neq 0)\,,\qquad \eta\left(\left(\begin{array}{cc} c & \star \\ 0 & 1 \end{array} \right)\right)=0\,,\,\,(c\neq 1)\,. \end{align} $$

Again, we easily deduce the value of the Frobenius-Schur indicator of $\eta $ :

$$ \begin{align*}\varepsilon_2(\eta)=\frac{1}{|G|}\sum_{\substack{c\in \mathbb F_p^\times \\ d\in\mathbb F_p}}\eta\left(\left(\begin{array}{cc} c & d \\ 0 & 1 \end{array} \right)^2\right)=\frac{1}{|G|}\sum_{\substack{c=-1\\d \in\mathbb F_p}}\eta(1) +\frac{1}{|G|}\sum_{\substack{c=1\\ d\neq 0}} (-1)+\frac{1}{|G|} \sum_{\substack{c=1\\ d=0}} \eta(1)=1\,. \end{align*} $$

9.2.3 The global Artin conductor $A(\chi )$ for $\chi \in \mathrm {Irr}(G)$

We now compute the Artin conductor $A(\chi )$ of an irreducible representation $\chi \in \mathrm {Irr}(G)$ . To do so, we have to understand the ramification groups. For a prime ideal $\mathfrak P$ of $\mathcal O_K$ lying above a prime number $\nu $ , we recall that

$$ \begin{align*}G_i:=G_i(\mathfrak P/\nu)=\{ \sigma \in G : \forall z \in \mathcal O_K, \sigma(z)\equiv z \bmod \mathfrak P^{i+1} \}\end{align*} $$

defines a decreasing sequence of normal subgroups of $G=\mathrm {Gal}(K_{a,p}/{\mathbb {Q}})$ , where $G_0$ is the inertia group, $G_1$ is the wild ramification group and $G_i$ is trivial for large enough i.

We start with $\nu =a$ . We invoke [Vi, Theorem $4.3$ ], which asserts that if $\mathfrak P$ is a prime ideal of $\mathcal O_{K_{a,p}}$ lying over a, then the corresponding ramification index is $e(\mathfrak P/a)=p$ . In particular, $a\nmid e(\mathfrak P/a)$ so that $K/{\mathbb {Q}}$ is tamely ramified at a. By the unique subfield property mentioned above, we conclude that:

$$ \begin{align*}G_0(\mathfrak p/a)\simeq \left\{ \left(\begin{array}{cc} 1 & d \\ 0 & 1 \end{array} \right) : d\in \mathbb F_p \right\}\simeq \mathbb Z/p\mathbb Z\,,\qquad G_1(\mathfrak p/a)=\{\mathrm{Id}\}\,.\\[-9pt] \end{align*} $$

This will allow us to compute the local factor at $\nu =a$ of the Artin conductor $A(\phi )$ , which is equal to $a^{n(\phi ,a)}$ , with $n(\phi ,a)=\mathrm {codim}(V^{G_0})=\phi (1)-\frac 1{|G_0|} \sum _{a \in G_0} \phi (a)$ , since a is tamely ramified in $K_{a,p}/{\mathbb {Q}}$ . For an irreducible character $\psi $ of degree $1$ of G, corresponding to a Dirichlet character $\chi $ modulo p, we obtain:

$$ \begin{align*}n(\psi,a)=1-\frac{1}{p}\sum_{d\bmod p}\chi(1)=0\,.\\[-9pt] \end{align*} $$

For the character $\eta $ , we have:

$$ \begin{align*}n(\eta,a)=\eta(1)-\frac 1p\sum_{d\bmod p}\eta\left(\left(\begin{array}{cc} 1 & d \\ 0 & 1 \end{array} \right)\right)=p-1-\frac 1p(p-1+(-1)\times(p-1))=p-1\,.\\[-9pt] \end{align*} $$

We now take $\nu =p$ . Since we assume that $a^{p-1}\not \equiv 1\bmod p^2$ , the extension $K_{a,p}/{\mathbb {Q}}$ is totally ramified at p (see, e.g. [Vi, Theorem 5.5]). Let $\mathfrak P$ be the unique prime ideal of $\mathcal O_{K_{a,p}}$ lying over p. We have $G_0(\mathfrak P/p)=G$ . For $i\geq 1$ , we observe that the intermediate cyclotomic extension ${\mathbb {Q}}(\zeta _p)/{\mathbb {Q}}$ is tame at p (since $p\mathcal O_{{\mathbb {Q}}(\zeta _p)}=(1-\zeta _p)^{p-1})$ , and thus, $G_i(\mathfrak P/p)=G_i(\mathfrak P/(1-\zeta _p))$ for any $i\geq 1$ (here, the ramification group $G_i(\mathfrak P/(1-\zeta _p))$ is relative to the extension $K_{a,p}/{\mathbb {Q}}(\zeta _p)$ ). As remarked in [Vi, Lemma 5.7], the element $\pi =(1-\zeta _p)/(a-a^{1/p})$ is a uniformiser for the unique valuation extending to K the one attached to $1-\zeta _p$ on ${\mathbb {Q}}(\zeta _p)$ . Moreover, we have the group isomorphism

$$ \begin{align*}\mathrm{Gal}(K_{a,p}/{\mathbb{Q}}(\zeta_p))\simeq \left\{ \left(\begin{array}{cc} 1 & d \\ 0 & 1 \end{array} \right) : d\in \mathbb F_p \right\}\,,\\[-9pt] \end{align*} $$

since an element $\sigma _d$ of $\mathrm {Gal}(K_{a,p}/{\mathbb {Q}}(\zeta _p))$ is entirely determined by the residue class d modulo p, such that $\sigma _d(a^{1/p})= \zeta _p^d a^{1/p}$ . Therefore, we can compute $G_1(\mathfrak P/(1-\zeta _p))$ (and, more generally, $G_i(\mathfrak P/(1-\zeta _p))$ for all $i\geq 1$ ) by considering the following $\pi $ -adic valuation:

$$ \begin{align*} v_{\pi}(\sigma_1(\pi)-\pi)&=v_\pi\left((1-\zeta_p)\left(\frac{\zeta_p a^{1/p}-a^{1/p}} {(a-\zeta_p a^{1/p})(a-a^{1/p})}\right)\right)\\ &=v_{\pi}\left(\pi\left(\frac{\zeta_p a^{1/p}-a^{1/p}}{a-\zeta_p a^{1/p}}\right)\right)=v_{\pi}\left(-\pi \sigma_1(\pi) a^{1/p}\right)\,.\\[-9pt] \end{align*} $$

To compute this quantity, we use the uniqueness of the extension of valuations to infer that $v_{\pi }(\sigma _1(\pi ))=v_{\pi }(\pi )$ . As a consequence, we have

$$ \begin{align*}v_{\pi}(\sigma_1(\pi)-\pi)=2v_\pi(\pi)+v_\pi(a^{1/p})=2\,, \end{align*} $$

since p and a are coprime, and so $v_\pi (a^{1/p})=0$ . We conclude that $G_1(\mathfrak P/(1-\zeta _p))\simeq \mathrm {Gal}(K_{a,p}/{\mathbb {Q}}(\zeta _p))\simeq \mathbb Z/p\mathbb Z$ and that $G_i(\mathfrak P/(1-\zeta _p))=\{\mathrm {Id}\}$ for $i\geq 2$ . We have therefore computed the higher ramification groups at p for $K_{a,p}/{\mathbb {Q}}$ :

(136) $$ \begin{align} G_0(\mathfrak P/p)=G\,,\,\, G_1(\mathfrak P/p)=\left\{ \left(\begin{array}{cc} 1 & d \\ 0 & 1 \end{array} \right) : d\in \mathbb F_p \right\}\simeq \mathbb Z/p\mathbb Z\,, \,\, G_i(\mathfrak P/p)=\{\mathrm{Id}\}\,\, (i\geq 2)\,.\\[-9pt]\nonumber \end{align} $$

We now deduce the value of the Artin conductor at p of each irreducible character $\phi $ of G. To do so, we use the following formula that generalises the one mentioned in the tame case (and used for $\nu =a$ ), namely:

$$ \begin{align*}n(\phi,p)=\phi(1)-\frac{1}{|G_0|}\sum_{a\in G_0}\phi(a)+\frac{\phi(1)}{p-1} -\frac{1}{|G_0|}\sum_{a\in G_1}\phi(a)\,;\\[-9pt] \end{align*} $$

it is the specialisation of (82) in the case where the higher ramification groups at p satisfy (136).

First, if $\phi =\psi $ corresponds to a nontrivial Dirichlet character modulo p, then $\psi $ restricts trivially to $G_1$ and we deduce:

$$ \begin{align*}n(\psi,p)=1+\frac{1}{p-1}-\frac{|G_1|}{|G_0|}=1\,,\\[-9pt] \end{align*} $$

while $n(\mathbf {1},p)=0$ for the trivial character $\mathbf {1}$ . If $\phi =\eta $ , we have:

$$ \begin{align*}n(\eta,p)=p-1+1-\frac{1}{|G_0|}(p-1-(p-1))=p\,.\\[-9pt] \end{align*} $$

Thanks to the above computations, we can deduce the exact value of $\log A(\chi )$ for every irreducible character $\chi $ of the Galois group G of the splitting field of $x^p-a$ over ${\mathbb {Q}}$ .

Proposition 9.8. Let $a,p$ be distinct odd primes, such that $a^{p-1} \not \equiv 1 \bmod p^2$ , and let $K_{a,p}$ be the splitting field of $x^p-a$ over ${\mathbb {Q}}$ . Let $G=\mathrm { Gal}(K_{a,p}/{\mathbb {Q}})$ , and recall (133). Then we have the following.

• • For an irreducible character $\psi $ of G attached to a Dirichlet character $\chi $ modulo p,

  $$ \begin{align*}\log A(\psi)=\begin{cases} 0\text{ if }\chi\text{ is the principal character modulo }p\,, \\ \log p\text{ otherwise}\,. \end{cases}\\[-9pt] \end{align*} $$

• • For the character $\psi =\eta $ defined in (135),

  $$ \begin{align*}\log A(\eta)=(p-1)\log a+p\log p\,. \end{align*} $$

Proof. Since the base field is ${\mathbb {Q}}$ , the definition of $A(\chi )$ (see Section 4) is the following:

$$ \begin{align*}A(\chi)=\mathfrak f(\chi)=\prod_p p^{n(\chi,p)}\,, \end{align*} $$

for every $\chi \in \mathrm {Irr}(G)$ . As already mentioned, the only ramified primes in $K/{\mathbb {Q}}$ are a and p. From the computations of Section 9.2.3, we deduce that $n(\mathbf {1},a)=n(\mathbf {1},p)=0$ and for a character $\psi $ attached to a nontrivial Dirichlet character modulo p:

$$ \begin{align*}A(\psi)=a^0p^1=p\,. \end{align*} $$

Finally, for the irreducible character $\eta $ , the computations of Section 9.2.3 yield:

$$ \begin{align*}A(\eta)=a^{p-1}p^p\,.\\[-36pt] \end{align*} $$

The goal of the next lemma is to estimate the number of couples of primes $(a,p)$ that are admissible in Proposition 9.8.

Lemma 9.9. For $A,P\geq 3$ in the range $ P\log P \leq A \leq {\mathrm {e}}^{P^2/(\log P)^3}$ , one has the estimate

$$ \begin{align*} \#\{a\leq A, p\leq P\colon a,p\text{ primes}, a\neq p, a^{p-1}\not\equiv 1 \bmod\ p^2\}&=\pi(A)\pi(P)\\ &\quad +O\Big( A \Big(\frac{\log\log A}{\log A}\Big)^{\frac 12}+\frac{P^2}{\log P}\Big). \end{align*} $$

Proof. The cardinality we wish to compute is

(137) $$ \begin{align} \sum_{p\leq P}\sum_{\substack{a\leq A,\, a\neq p\\ a^{p-1}\not\equiv 1 \bmod\ p^2}}1 \,. \end{align} $$

First, we apply Hensel’s Lemma: for each $p\leq P$ and each $a\neq p$ , the polynomial $f(X)=X^{p-1}-1\in \mathbb F_p[X]$ is separable and splits completely in $\mathbb F_p[X]$ . Thus, any $\alpha \in \mathbb F_p^\times $ (which is necessarily a root of f) lifts to a unique $\alpha _0\in \mathbb Z/p^2\mathbb Z$ , such that $\alpha _0\equiv \alpha \bmod \ p$ and $\alpha _0^{p-1}\equiv 1 \bmod \ p^2$ . Let $S_p$ be a set of representatives for these $p-1$ residue classes modulo $p^2$ . Therefore, since $A\geq P$ , (137) is equal to

(138) $$ \begin{align} \sum_{\substack{p\leq P}}\Big((\pi(A)-1)-\sum_{c\in S_p}\pi(A;p^2,c)\Big). \end{align} $$

Now, by the Brun-Titchmarsh theorem, we have the bound

$$ \begin{align*}\sum_{\substack{ p\leq A^{\frac 12}/2}}\sum_{c\in S_p}\pi(A;p^2,c) \ll \sum_{\substack{ p\leq A^{\frac 12}/2}}\frac{A\# S_p } {p^2\log (A/p^2)}\ll A \Big(\frac{\log\log A}{\log A}\Big)^{\frac 12} \end{align*} $$

(the last bound is obtained by cutting the sum over p at the point $ A^{\frac 12 - (\frac {\log \log A}{\log A})^{\frac 12}} $ ). Moreover, we trivially have

$$ \begin{align*}\sum_{\substack{ A^{\frac 12}/2 \leq p \leq P }}\sum_{c\in S_p}\pi(A;p^2,c) \ll \sum_{\substack{ A^{\frac 12}/2 \leq p \leq P }} \# S_p \ll \frac{P^2}{\log P} \end{align*} $$

(note that this last sum is empty when $A\geq 2P^2$ ). The result follows.

Proof of Theorem 2.19

In this proof, we keep the notation as in Section 9.2.2.

We start with the proof of Theorem 2.19(1). The bias factor $B(K_{a,p}/{\mathbb {Q}};1-r)$ can be estimated precisely since under LI, Propositions 3.18 and 4.6 yield

$$ \begin{align*} \mathbb E[X(K_{a,p}/{\mathbb{Q}};1-r)]&=\sum_{\substack{1\neq \psi\in\mathrm{Irr}(G)\\ \psi\text{ real}}}1\\ \mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};1-r)]& \asymp \sum_{\substack{1\neq \psi\in\mathrm{Irr}(G)\\ \psi\text{ real}}}\log (A(\psi)+2)\,. \end{align*} $$

The only real irreducible characters of G are the trivial characters, the character $\psi _0$ of degree $1$ attached to the quadratic character of $(\mathbb Z/p\mathbb Z)^\times $ and $\eta $ (see Section 9.2.2). By Proposition 9.8, we deduce that

$$ \begin{align*}\mathbb E[X(K_{a,p}/{\mathbb{Q}};1-r)]=2\,,\qquad \mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};1-r)]\asymp p \log (ap)\,. \end{align*} $$

By the definition (101) of the bias factor, we obtain the bounds

$$ \begin{align*}B(K_{a,p}/{\mathbb{Q}};1-r)\asymp \frac{1}{\sqrt{p\log (ap)}}\,. \end{align*} $$

To conclude the proof of (41), we apply the first estimate in Theorem 5.10.

Next, we prove Theorem 2.19(2). From (47), one computes that

(139) $$ \begin{align} \mathbb E[X(K_{a,p}/{\mathbb{Q}};t_{U,\{\mathrm{id}\}})]= p; \;\;\mathbb E[X(K_{a,p}/{\mathbb{Q}};t_{x^+,\{\mathrm{id}\}})]=p-\Big( \frac xp \Big); \nonumber\\ \mathbb E[X(K_{a,p}/{\mathbb{Q}};t_{U,x^+}) ]= \Big( \frac xp \Big). \end{align} $$

Similarly, for any $x\in \mathbb F_p\setminus \{0,1\}$ , we obtain the estimates

$$ \begin{align*}\mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};t_{U,\{\mathrm{id}\}})] \asymp \mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};t_{x^+,\{\mathrm{id}\}})] \asymp p^3\log(ap); \end{align*} $$

$$ \begin{align*}\mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};t_{U,x^+}) ]= p\log(ap).\end{align*} $$

We conclude the proof by invoking the second estimate in Theorem 5.10.

We turn to the proof of Theorem 2.19(3). If $C_1=x^+$ and $C_2=y^+$ with $x\neq y$ elements of $\mathbb F_p\setminus \{0,1\}$ , then the local factor of $L(s,K_{a,p}/{\mathbb {Q}},\psi )$ and that of the associated Dirichlet L-function $L(s,\chi )$ (see (134)) are identical at every prime not equal to a or p. Thus, those functions have the same critical zeros. From Lemma 3.20 and from the fact that $\eta (x^+) = \eta (y^+)=0$ , we deduce that the distribution of $X(K_{a,p}/{\mathbb {Q}};t_{x^+,y^+})$ is identical to that of $X_{p;x,y}$ , the random variable associated to the classical Chebyshev bias defined in [FM, Definition 2.4]. The claim follows.

Finally, in the relative case $K_{a,p}/{\mathbb {Q}}(\zeta _p)$ , the Galois group $H=\mathrm {Gal}(K_{a,p}/{\mathbb {Q}}(\zeta _p))$ has order p, and hence has no nontrivial real irreducible character. As explained at the beginning of this section, the group $H^+=G$ does not have any symplectic character and therefore LI and the induction property of Artin L-functions imply that $\varepsilon _2(\chi )+2\mathrm {ord}_{s=\tfrac 12} L(s,K_{a,p}/{\mathbb {Q}}(\zeta _p),\chi )=0$ for every nontrivial $\chi \in \mathrm {Irr}(H)$ . The assertion on the mean is then immediately deduced from (68). As for the variance, we easily notice that $\{d_1\}^+=U$ for any nontrivial $d_1\in H$ . Therefore, the variance is $0$ if both $d_1$ and $d_2$ are nontrivial elements of H, and otherwise we have that

$$ \begin{align*}\mathrm{Var}[X(K_{a,p}/{\mathbb{Q}}(\zeta_p);t_{d_1,\{\mathrm{id}\}}) ] = \mathrm{Var}[X(K_{a,p}/{\mathbb{Q}};t_{U,\{ \mathrm{id}\}})] \asymp p^3\log(ap).\\[-36pt]\end{align*} $$

Proof of Corollary 2.20

Combine Theorem 2.19 with Lemma 9.9.