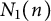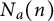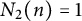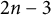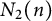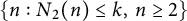1 Introduction
Let
![]() $\mathbb {N}=\{1,2,3,\ldots \}$
denote the set of all natural numbers (i.e., positive integers). Equal-Sum-Product Problem is relatively easy to formulate but still unresolved (see [Reference Guy4]). Some early research focused on estimating the number of solutions,
$\mathbb {N}=\{1,2,3,\ldots \}$
denote the set of all natural numbers (i.e., positive integers). Equal-Sum-Product Problem is relatively easy to formulate but still unresolved (see [Reference Guy4]). Some early research focused on estimating the number of solutions,
![]() $N_1(n)$
, to the equation
$N_1(n)$
, to the equation
which can be found in [Reference Ecker3, Reference Nyblom8]. Schinzel asked in papers [Reference Schinzel10, Reference Schinzel11] if the number
![]() $N_1(n)$
tends toward infinity with n. This conjecture is yet to be proven. In [Reference Zakarczemny15], it was shown that the set
$N_1(n)$
tends toward infinity with n. This conjecture is yet to be proven. In [Reference Zakarczemny15], it was shown that the set
![]() $\{n:N_1(n)\le k,\,n\in \mathbb {Z},\,n\ge 2\}$
has zero natural density for all natural k. It is worth noting that the classical Diophantine equation
$\{n:N_1(n)\le k,\,n\in \mathbb {Z},\,n\ge 2\}$
has zero natural density for all natural k. It is worth noting that the classical Diophantine equation
![]() $x_1^2+x_2^2+x_3^2=3x_1x_2x_3$
was investigated by Markoff (1879), as mentioned in [Reference Cassels1, Reference Markoff7]. Additionally, Hurwitz (see [Reference Hurwitz5]) examined the family of equations
$x_1^2+x_2^2+x_3^2=3x_1x_2x_3$
was investigated by Markoff (1879), as mentioned in [Reference Cassels1, Reference Markoff7]. Additionally, Hurwitz (see [Reference Hurwitz5]) examined the family of equations
![]() $x_1^2+x_2^2+\cdots +x_n^2=ax_1x_2\cdot \ldots \cdot x_n,$
where
$x_1^2+x_2^2+\cdots +x_n^2=ax_1x_2\cdot \ldots \cdot x_n,$
where
![]() $a,n~\in \mathbb {N},\,n\ge 3.$
Let us now assume that
$a,n~\in \mathbb {N},\,n\ge 3.$
Let us now assume that
![]() $a,n~\in \mathbb {N},\,n\ge 2.$
In this paper, we provide a lower bound for the number
$a,n~\in \mathbb {N},\,n\ge 2.$
In this paper, we provide a lower bound for the number
![]() $N_a(n)$
of integer solutions
$N_a(n)$
of integer solutions
![]() $(x_1,\,x_2,\ldots ,x_n)$
of the equation
$(x_1,\,x_2,\ldots ,x_n)$
of the equation
such that
![]() $x_1\ge x_2\ge \cdots \ge x_n\ge 1$
. Some of the results presented can be generalized to the case of the equation
$x_1\ge x_2\ge \cdots \ge x_n\ge 1$
. Some of the results presented can be generalized to the case of the equation
where
![]() $a,b$
are positive integers. In the case
$a,b$
are positive integers. In the case
![]() $a=1,\,b=n$
, the equation
$a=1,\,b=n$
, the equation
is called Erdós last equation (see [Reference Guy4, Reference Shiu12, Reference Takeda13]). Equation (1.3) is related to the problem of finding numbers divisible by the sum and product of their digits. It is worth noting that if equation (1.2) has solutions, then
![]() $a\le n$
.
$a\le n$
.
2 Basic results
In this section, we discuss the necessary basic results. First, we will show that the number of solutions
![]() $N_a(n)$
is finite for any fixed a and n.
$N_a(n)$
is finite for any fixed a and n.
Lemma 2.1 Let n be a natural number. If
![]() $x_1,x_2,\ldots ,x_n$
are any real numbers, then the following formula holds:
$x_1,x_2,\ldots ,x_n$
are any real numbers, then the following formula holds:
 $$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)= \\ a^2\prod\limits_{i=1}^n x_i-a\sum\limits_{i=1}^nx_i+a(n-2)+1. \end{align} $$
$$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)= \\ a^2\prod\limits_{i=1}^n x_i-a\sum\limits_{i=1}^nx_i+a(n-2)+1. \end{align} $$
Proof Let us denote equation (2.1) as
![]() $T(n)$
. We want to show by induction that
$T(n)$
. We want to show by induction that
![]() $T(n)$
holds for every natural number n. The cases
$T(n)$
holds for every natural number n. The cases
![]() $n = 1$
and
$n = 1$
and
![]() $n=2$
are trivial:
$n=2$
are trivial:
![]() $(a-1)(ax_1-1)=a^2x_1-ax_1-a+1,\,(ax_1-1)(ax_2-1)=a^2x_1x_2-a(x_1+x_2)+1.$
In both cases, equality is true. Therefore, the base step of the induction is satisfied, as
$(a-1)(ax_1-1)=a^2x_1-ax_1-a+1,\,(ax_1-1)(ax_2-1)=a^2x_1x_2-a(x_1+x_2)+1.$
In both cases, equality is true. Therefore, the base step of the induction is satisfied, as
![]() $T(1)$
and
$T(1)$
and
![]() $T(2)$
hold. Let us assume now that
$T(2)$
hold. Let us assume now that
![]() $n \ge 3$
and
$n \ge 3$
and
![]() $T(n-1)$
holds, i.e., the following equality is true:
$T(n-1)$
holds, i.e., the following equality is true:
 $$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1}x_i+a(n-3)+1. \end{align} $$
$$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1}x_i+a(n-3)+1. \end{align} $$
In the inductive step, we will be using the equivalent form of equation (2.2):
 $$ \begin{align} \nonumber a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ -\left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1}x_i+a(n-3)+1. \end{align} $$
$$ \begin{align} \nonumber a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ -\left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1}x_i+a(n-3)+1. \end{align} $$
To prove the inductive step, i.e., to show that
![]() $T(n-1)$
implies
$T(n-1)$
implies
![]() $T(n)$
for
$T(n)$
for
![]() $n \ge 3$
, we will use the following algebraic identities that can be verified directly:
$n \ge 3$
, we will use the following algebraic identities that can be verified directly:
 $$ \begin{align} \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)=a^2\prod\limits_{i=1}^n x_i-ax_n+1-a\prod\limits_{i=1}^{n-1} x_i, \end{align} $$
$$ \begin{align} \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)=a^2\prod\limits_{i=1}^n x_i-ax_n+1-a\prod\limits_{i=1}^{n-1} x_i, \end{align} $$
 $$ \begin{align} \nonumber a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right). \end{align} $$
$$ \begin{align} \nonumber a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right). \end{align} $$
Let us proceed to the proof of the inductive step. We want to show
![]() $T(n)$
assuming
$T(n)$
assuming
![]() $T(n-\text {1})$
. Let us start by transforming the left side of
$T(n-\text {1})$
. Let us start by transforming the left side of
![]() $T(n)$
using equations (2.4) and (2.5)
$T(n)$
using equations (2.4) and (2.5)
 $$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ \nonumber a^2\prod\limits_{i=1}^n x_i-ax_n+1-a\prod\limits_{i=1}^{n-1} x_i+\\ +a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right). \end{align} $$
$$ \begin{align} \nonumber \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)=\\ \nonumber a^2\prod\limits_{i=1}^n x_i-ax_n+1-a\prod\limits_{i=1}^{n-1} x_i+\\ +a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right). \end{align} $$
Calculating directly, we notice that the following equality holds true
 $$ \begin{align} \nonumber -a\prod\limits_{i=1}^{n-1} x_i+a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)=\\ -a\prod\limits_{i=1}^{n-1} x_i+a\prod\limits_{i=1}^{n-1} x_i-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i +a=a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i. \end{align} $$
$$ \begin{align} \nonumber -a\prod\limits_{i=1}^{n-1} x_i+a\left(\prod\limits_{i=1}^{n-2} x_i-1\right)\left(x_{n-1}-1\right)=\\ -a\prod\limits_{i=1}^{n-1} x_i+a\prod\limits_{i=1}^{n-1} x_i-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i +a=a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i. \end{align} $$
From equations (2.6) and (2.7), and then using the inductive assumption (2.3), we obtain
 $$ \begin{align*} \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)\\ =a^2\prod\limits_{i=1}^n x_i-ax_n+1+a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)\displaystyle_{=}^{(2.3)} \\ a^2\prod\limits_{i=1}^n x_i-ax_n+1+a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i -\left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+\\ +a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1} x_i+a(n-3)+1=a^2\prod\limits_{i=1}^n x_i-a\sum\limits_{i=1}^nx_i+a(n-2)+1. \end{align*} $$
$$ \begin{align*} \left(a\prod\limits_{i=1}^{n-1} x_i-1\right)\left(ax_{n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)\\ =a^2\prod\limits_{i=1}^n x_i-ax_n+1+a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i+ a\sum\limits_{s=1}^{n-3}\left(\left(\prod\limits_{i=1}^s x_i-1\right)\left(x_{s+1}-1\right)\right)\displaystyle_{=}^{(2.3)} \\ a^2\prod\limits_{i=1}^n x_i-ax_n+1+a-ax_{n-1}-a\prod\limits_{i=1}^{n-2} x_i -\left(a\prod\limits_{i=1}^{n-2} x_i-1\right)\left(ax_{n-1}-1\right)+\\ +a^2\prod\limits_{i=1}^{n-1} x_i-a\sum\limits_{i=1}^{n-1} x_i+a(n-3)+1=a^2\prod\limits_{i=1}^n x_i-a\sum\limits_{i=1}^nx_i+a(n-2)+1. \end{align*} $$
Thus, assuming
![]() $T(n-1)$
, we have shown that
$T(n-1)$
, we have shown that
![]() $T(n)$
holds, completing the inductive step and concluding the proof of the lemma.
$T(n)$
holds, completing the inductive step and concluding the proof of the lemma.
Theorem 2.2 Let
![]() $a,k\in \mathbb {N},\, b\in \mathbb {N}\cup \{0\}$
. For any integer
$a,k\in \mathbb {N},\, b\in \mathbb {N}\cup \{0\}$
. For any integer
![]() $n\ge 2$
, the system of Diophantine equations
$n\ge 2$
, the system of Diophantine equations
 $$ \begin{align} \left\{ \begin{array}{cll} x_{1,1}+x_{1,2}+\cdots+x_{1,n} & =&ax_{2,1}\cdot x_{2,2}\cdot \ldots \cdot x_{2,n}+b\, ,\\ x_{2,1}+x_{2,2}+\cdots+x_{2,n} & =&ax_{3,1}\cdot x_{3,2}\cdot \ldots \cdot x_{3,n}+b\, ,\\ &\ldots&\\ x_{k-1,1}+x_{k-1,2}+\cdots+x_{k-1,n}& =&ax_{k,1}\cdot x_{k,2}\cdot \ldots \cdot x_{k,n}+b\, ,\\ x_{k,1}+x_{k,2}+\cdots+x_{k,n}& =&ax_{1,1}\cdot x_{1,2}\cdot \ldots \cdot x_{1,n}+b \end{array} \right.\end{align} $$
$$ \begin{align} \left\{ \begin{array}{cll} x_{1,1}+x_{1,2}+\cdots+x_{1,n} & =&ax_{2,1}\cdot x_{2,2}\cdot \ldots \cdot x_{2,n}+b\, ,\\ x_{2,1}+x_{2,2}+\cdots+x_{2,n} & =&ax_{3,1}\cdot x_{3,2}\cdot \ldots \cdot x_{3,n}+b\, ,\\ &\ldots&\\ x_{k-1,1}+x_{k-1,2}+\cdots+x_{k-1,n}& =&ax_{k,1}\cdot x_{k,2}\cdot \ldots \cdot x_{k,n}+b\, ,\\ x_{k,1}+x_{k,2}+\cdots+x_{k,n}& =&ax_{1,1}\cdot x_{1,2}\cdot \ldots \cdot x_{1,n}+b \end{array} \right.\end{align} $$
has only finite number of solutions
![]() $x_{i,j}$
which are natural numbers.
$x_{i,j}$
which are natural numbers.
Proof By adding sides of equations of the system of equations (2.8), we obtain
 $$ \begin{align*} \sum\limits_{i=1}^k\sum\limits_{j=1}^n x_{i,j}=\sum\limits_{i=1}^ka\prod\limits_{j=1}^n x_{i,j}+kb. \end{align*} $$
$$ \begin{align*} \sum\limits_{i=1}^k\sum\limits_{j=1}^n x_{i,j}=\sum\limits_{i=1}^ka\prod\limits_{j=1}^n x_{i,j}+kb. \end{align*} $$
Hence,
 $$ \begin{align*} \sum\limits_{i=1}^k\left(a^2\prod\limits_{j=1}^n x_{i,j}-a\sum\limits_{j=1}^n x_{i,j}+a(n-2)+1\right)=k(a(n-2)+1)-kab. \end{align*} $$
$$ \begin{align*} \sum\limits_{i=1}^k\left(a^2\prod\limits_{j=1}^n x_{i,j}-a\sum\limits_{j=1}^n x_{i,j}+a(n-2)+1\right)=k(a(n-2)+1)-kab. \end{align*} $$
By (2.1), we have
 $$ \begin{align} \nonumber \sum\limits_{i=1}^k \left(\left(a\prod\limits_{j=1}^{n-1}x_{i,j}-1\right) \left(ax_{i,n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\prod\limits_{j=1}^s x_{i,j}-1\right)\left(x_{i,s+1}-1\right)\right)=\\k(a(n-2)+1)-kab. \end{align} $$
$$ \begin{align} \nonumber \sum\limits_{i=1}^k \left(\left(a\prod\limits_{j=1}^{n-1}x_{i,j}-1\right) \left(ax_{i,n}-1\right)+a\sum\limits_{s=1}^{n-2}\left(\prod\limits_{j=1}^s x_{i,j}-1\right)\left(x_{i,s+1}-1\right)\right)=\\k(a(n-2)+1)-kab. \end{align} $$
For given
![]() $a,k,b,n$
, the number of solutions of equation (2.9) in positive integers is bounded above. Hence, the system of equations (2.8) has only a finite number of solutions in positive integers
$a,k,b,n$
, the number of solutions of equation (2.9) in positive integers is bounded above. Hence, the system of equations (2.8) has only a finite number of solutions in positive integers
![]() $x_{i,j}.$
$x_{i,j}.$
Taking
![]() $k=1$
, an immediate consequence of Theorem 2.2 is the following result.
$k=1$
, an immediate consequence of Theorem 2.2 is the following result.
Corollary 2.3 For given
![]() $a\in \mathbb {N},\,b\in \mathbb {N}\cup \{0\}$
and any integer
$a\in \mathbb {N},\,b\in \mathbb {N}\cup \{0\}$
and any integer
![]() $n\ge 2$
, the number of solutions of the equation
$n\ge 2$
, the number of solutions of the equation
in positive integers
![]() $x_1\ge x_2\ge \cdots \ge x_n\ge 1$
is finite. In particular, in the case
$x_1\ge x_2\ge \cdots \ge x_n\ge 1$
is finite. In particular, in the case
![]() $b=0$
, the number of solutions
$b=0$
, the number of solutions
![]() $N_a(n)$
is finite.
$N_a(n)$
is finite.
Remark 2.4 Theorem 2.2 is true for all
![]() $a,b\in \mathbb {Q}, a\ge 1$
.
$a,b\in \mathbb {Q}, a\ge 1$
.
Remark 2.5 In the case of
![]() $b=0$
, we can provide a different proof of Corollary 2.3. Let
$b=0$
, we can provide a different proof of Corollary 2.3. Let
![]() $z_i = x_1x_2\cdot \ldots \cdot x_{i-1}x_{i+1}\cdot \ldots \cdot x_n = \frac {1}{x_i}\prod \limits _{j=1}^nx_j\in \mathbb {N}$
for
$z_i = x_1x_2\cdot \ldots \cdot x_{i-1}x_{i+1}\cdot \ldots \cdot x_n = \frac {1}{x_i}\prod \limits _{j=1}^nx_j\in \mathbb {N}$
for
![]() $i\in \{1,2,\ldots ,n\}$
. Notice that from the inequality
$i\in \{1,2,\ldots ,n\}$
. Notice that from the inequality
![]() $x_1\ge x_2\ge \cdots \ge x_n\ge 1$
, we get the inequality
$x_1\ge x_2\ge \cdots \ge x_n\ge 1$
, we get the inequality
![]() $1 \le z_1\le z_2\le \cdots \le z_n$
. Then, equation (2.10) takes the form
$1 \le z_1\le z_2\le \cdots \le z_n$
. Then, equation (2.10) takes the form
Equation (2.11) has finitely many solutions in positive integers, as we can find upper bounds on
![]() $z_i$
. The bounds we will find are not optimal, but they are sufficient for our purposes. If
$z_i$
. The bounds we will find are not optimal, but they are sufficient for our purposes. If
![]() $n\ge 2$
, then
$n\ge 2$
, then
![]() $ax_1 x_2\cdot \ldots \cdot x_n=x_1+x_2+\cdots +x_n\ge x_1+x_2\ge x_1+1>x_1$
, and hence
$ax_1 x_2\cdot \ldots \cdot x_n=x_1+x_2+\cdots +x_n\ge x_1+x_2\ge x_1+1>x_1$
, and hence
![]() $ax_2\cdot \ldots \cdot x_n\ge 2$
. From here, we can deduce
$ax_2\cdot \ldots \cdot x_n\ge 2$
. From here, we can deduce
Therefore,
![]() $nx_2>x_1$
and
$nx_2>x_1$
and
![]() $nz_1>z_2$
. We also have for
$nz_1>z_2$
. We also have for
![]() $k\in \{2,3,\ldots ,n-1\}$
, that
$k\in \{2,3,\ldots ,n-1\}$
, that
 $$ \begin{align*}nz_1 z_2\cdot \ldots\cdot z_k\ge z_1z_2\ge \prod\limits_{i=1}^nx_i\ge z_{k+1}.\end{align*} $$
$$ \begin{align*}nz_1 z_2\cdot \ldots\cdot z_k\ge z_1z_2\ge \prod\limits_{i=1}^nx_i\ge z_{k+1}.\end{align*} $$
Thus, for all
![]() $k\in \{1,2,\ldots ,n-1\}$
, we have
$k\in \{1,2,\ldots ,n-1\}$
, we have
![]() $z_{k+1}\le nz_1\cdot z_2\cdot \ldots \cdot z_k$
. Now we can proceed with the inductive proof of the upper bound:
$z_{k+1}\le nz_1\cdot z_2\cdot \ldots \cdot z_k$
. Now we can proceed with the inductive proof of the upper bound:
![]() $z_i\le a^{-1}n^{2^{i-1}},$
where
$z_i\le a^{-1}n^{2^{i-1}},$
where
![]() $i\in \{1,2,\ldots ,n\}$
. Base step, as the
$i\in \{1,2,\ldots ,n\}$
. Base step, as the
![]() $z_i$
are increasing, we can use equation (2.11) to obtain an inequality:
$z_i$
are increasing, we can use equation (2.11) to obtain an inequality:
If we now make the assumption that
![]() $z_i \leq a^{-1}n^{2^{i-1}}$
for all
$z_i \leq a^{-1}n^{2^{i-1}}$
for all
![]() $i \in \{ 1, 2, \ldots , k\}$
, where
$i \in \{ 1, 2, \ldots , k\}$
, where
![]() $k < n$
, then
$k < n$
, then
![]() $ z_{k+1}\le nz_1z_2\cdot \ldots \cdot z_k \leq n\frac {n^{2^0+2^1+2^2+\cdots +2^{k-1}}}{a} = \frac {n^{2^k}}{a}$
; this establishes the inductive step.
$ z_{k+1}\le nz_1z_2\cdot \ldots \cdot z_k \leq n\frac {n^{2^0+2^1+2^2+\cdots +2^{k-1}}}{a} = \frac {n^{2^k}}{a}$
; this establishes the inductive step.
The proof of Theorem 2.2 can be modified in the specific case of
![]() $a,n$
to create an efficient algorithm for finding solutions to equation (2.10).
$a,n$
to create an efficient algorithm for finding solutions to equation (2.10).
Kurlandchik and Nowicki [Reference Kurlandchik and Nowicki6, Theorem 3] had earlier shown that
![]() $N_1(n)$
is finite for any
$N_1(n)$
is finite for any
![]() $n\ge 2$
.
$n\ge 2$
.
Schinzel’s question can be generalized. For given
![]() $a\in \mathbb {N}$
, does the number
$a\in \mathbb {N}$
, does the number
![]() $N_a(n)$
tend to infinity with n? We can show with the elementary method the following theorems.
$N_a(n)$
tend to infinity with n? We can show with the elementary method the following theorems.
Theorem 2.6 If
![]() $a,n\in \mathbb {N}$
, then
$a,n\in \mathbb {N}$
, then
![]() $\limsup \limits _{n\to \infty } N_a(n)=\infty .$
$\limsup \limits _{n\to \infty } N_a(n)=\infty .$
Proof We shall consider two cases. Let
![]() $a\in \{1,2\}$
. If
$a\in \{1,2\}$
. If
![]() $t\in \{0,1,\ldots ,\left \lfloor \frac {s}{2}\right \rfloor \}$
, where s is a nonnegative integer, then
$t\in \{0,1,\ldots ,\left \lfloor \frac {s}{2}\right \rfloor \}$
, where s is a nonnegative integer, then
 $$ \begin{align*} \tfrac{1}{a}((a+1)^{s-t}+1)+\tfrac{1}{a}((a+1)^t+1)+\underbrace{1+1+\cdots+1}_{\tfrac{1}{a}((a+1)^s-1)\,\,\mathrm{times}}=\\ a\cdot \tfrac{1}{a}((a+1)^{s-t}+1)\cdot\tfrac{1}{a}((a+1)^t+1)\cdot \underbrace{1\cdot 1\cdot\ldots\cdot1}_{\tfrac{1}{a}((a+1)^s-1)\,\,\mathrm{times}}. \end{align*} $$
$$ \begin{align*} \tfrac{1}{a}((a+1)^{s-t}+1)+\tfrac{1}{a}((a+1)^t+1)+\underbrace{1+1+\cdots+1}_{\tfrac{1}{a}((a+1)^s-1)\,\,\mathrm{times}}=\\ a\cdot \tfrac{1}{a}((a+1)^{s-t}+1)\cdot\tfrac{1}{a}((a+1)^t+1)\cdot \underbrace{1\cdot 1\cdot\ldots\cdot1}_{\tfrac{1}{a}((a+1)^s-1)\,\,\mathrm{times}}. \end{align*} $$
We have
![]() $s-t\ge t$
and
$s-t\ge t$
and
![]() $\tfrac {1}{a}((a+1)^{i}+1)\in \mathbb {N}$
, where i is a nonnegative integer. Hence,
$\tfrac {1}{a}((a+1)^{i}+1)\in \mathbb {N}$
, where i is a nonnegative integer. Hence,
![]() $N(\tfrac {1}{a}((a+1)^s+2a-1))\ge \left \lfloor \frac {s}{2}\right \rfloor +1.$
Therefore,
$N(\tfrac {1}{a}((a+1)^s+2a-1))\ge \left \lfloor \frac {s}{2}\right \rfloor +1.$
Therefore,
![]() $\limsup \limits _{n\to \infty } N_a(n)=\infty .$
$\limsup \limits _{n\to \infty } N_a(n)=\infty .$
Let
![]() $a\ge 3$
. If
$a\ge 3$
. If
![]() $t\in \{1,\ldots ,\left \lfloor \frac {s+1}{2}\right \rfloor \}$
, where
$t\in \{1,\ldots ,\left \lfloor \frac {s+1}{2}\right \rfloor \}$
, where
![]() $s\in \mathbb {N}$
, then
$s\in \mathbb {N}$
, then
 $$ \begin{align*} \tfrac{1}{a}((a-1)^{2s-2t+1}+1)+\tfrac{1}{a}((a-1)^{2t-1}+1)+\underbrace{1+1+\cdots+1}_{\tfrac{1}{a}((a-1)^{2s}-1)\,\,\mathrm{times}}=\\[-2pt] a\cdot \tfrac{1}{a}((a-1)^{2s-2t+1}+1)\cdot\tfrac{1}{a}((a-1)^{2t-1}+1)\cdot \underbrace{1\cdot 1\cdot\ldots\cdot1}_{\tfrac{1}{a}((a-1)^{2s}-1)\,\,\mathrm{times}}. \end{align*} $$
$$ \begin{align*} \tfrac{1}{a}((a-1)^{2s-2t+1}+1)+\tfrac{1}{a}((a-1)^{2t-1}+1)+\underbrace{1+1+\cdots+1}_{\tfrac{1}{a}((a-1)^{2s}-1)\,\,\mathrm{times}}=\\[-2pt] a\cdot \tfrac{1}{a}((a-1)^{2s-2t+1}+1)\cdot\tfrac{1}{a}((a-1)^{2t-1}+1)\cdot \underbrace{1\cdot 1\cdot\ldots\cdot1}_{\tfrac{1}{a}((a-1)^{2s}-1)\,\,\mathrm{times}}. \end{align*} $$
We have
![]() $2s-2t+1\ge 2t-1$
and
$2s-2t+1\ge 2t-1$
and
![]() $\tfrac {1}{a}((a-1)^{2i-1}+1), \tfrac {1}{a}((a-1)^{2i}-1) \in \mathbb {N}$
, where
$\tfrac {1}{a}((a-1)^{2i-1}+1), \tfrac {1}{a}((a-1)^{2i}-1) \in \mathbb {N}$
, where
![]() $i\in \mathbb {N}$
. Hence,
$i\in \mathbb {N}$
. Hence,
![]() $N(\tfrac {1}{a}((a-1)^{2s}+2a-1))\ge \left \lfloor \frac {s+1}{2}\right \rfloor .$
$N(\tfrac {1}{a}((a-1)^{2s}+2a-1))\ge \left \lfloor \frac {s+1}{2}\right \rfloor .$
Therefore,
![]() $\limsup \limits _{n\to \infty } N_a(n)=\infty .$
$\limsup \limits _{n\to \infty } N_a(n)=\infty .$
Remark 2.7 Let
![]() $a\ge 3$
. Depending on the choice of
$a\ge 3$
. Depending on the choice of
![]() $a\le n$
, equation (1.2) may not have solutions. The simplest example is
$a\le n$
, equation (1.2) may not have solutions. The simplest example is
![]() $a=3$
and
$a=3$
and
![]() $n=4$
. In this case, equation (1.2) is equivalent to
$n=4$
. In this case, equation (1.2) is equivalent to
but the corresponding equation has no integer solutions
![]() $x_1\ge x_2\ge x_3\ge x_4\ge 1$
. This gives
$x_1\ge x_2\ge x_3\ge x_4\ge 1$
. This gives
![]() $N_3(4)=0.$
$N_3(4)=0.$
Remark 2.8 Due to the solutions ![]() , where
, where
![]() $m\in \mathbb {N}$
and certain technical computations based on the method from Remark 2.5, we can prove that:
$m\in \mathbb {N}$
and certain technical computations based on the method from Remark 2.5, we can prove that:
-
(1)
 $N_a(a)=N_a(2a-1)=N_a(3a-2)=N_a(4a-3)=1$
, where
$N_a(a)=N_a(2a-1)=N_a(3a-2)=N_a(4a-3)=1$
, where
 $a\ge 2$
,
$a\ge 2$
, -
(2)
 $N_2(6)=2,\, N_a(4a-2)=1,$
where
$N_2(6)=2,\, N_a(4a-2)=1,$
where
 $a\ge 3$
,
$a\ge 3$
, -
(3)
 $N_a(n)=0$
if
$N_a(n)=0$
if
 $n\in ((a,2a-1)\cup (2a-1,3a-2)\cup (3a-2,4a-3))\cap \mathbb {N},$
$n\in ((a,2a-1)\cup (2a-1,3a-2)\cup (3a-2,4a-3))\cap \mathbb {N},$
-
(4)
 $N_a(ma-m+1)\ge 1$
, where
$N_a(ma-m+1)\ge 1$
, where
 $m\in \mathbb {N}$
.
$m\in \mathbb {N}$
.
Points (1)–(3) partially explain the basic structure of the right side of Table 1.
Table 1 The table shows values of
![]() $N_a(n)$
for small natural numbers
$N_a(n)$
for small natural numbers
![]() $a\le n\le 10$
. The bold numbers are
$a\le n\le 10$
. The bold numbers are
![]() $N_a(n)$
, such that
$N_a(n)$
, such that
![]() $n \ge 4a-1$
.
$n \ge 4a-1$
.

It has been proven in [Reference Zakarczemny15] that in the case of
![]() $a=1$
, the following theorem holds.
$a=1$
, the following theorem holds.
Theorem 2.9 If
![]() $n\in \mathbb {N},\,n\ge 2$
, then
$n\in \mathbb {N},\,n\ge 2$
, then
 $$ \begin{align} N_1(n)\ge\left\lfloor\frac{d(n-1)+1}{2}\right\rfloor+\left\lfloor\frac{d(2n-1)+1}{2}\right\rfloor-1, \end{align} $$
$$ \begin{align} N_1(n)\ge\left\lfloor\frac{d(n-1)+1}{2}\right\rfloor+\left\lfloor\frac{d(2n-1)+1}{2}\right\rfloor-1, \end{align} $$
where
![]() $d(j)$
is the number of positive divisors of
$d(j)$
is the number of positive divisors of
![]() $j.$
Moreover,
$j.$
Moreover,
 $$ \begin{align} \nonumber N_1(n)\ge\left\lfloor\frac{d(n-1)+1}{2}\right\rfloor+\left\lfloor\frac{d(2n-1)+1}{2}\right\rfloor-1\\ +\left\lfloor\frac{d_2(3n+1)+1}{2}\right\rfloor+\left\lfloor\frac{d_3(4n+1)+1}{2}\right\rfloor+\left\lfloor\frac{d_3(4n+5)+1}{2}\right\rfloor\\ \nonumber-\delta(2|n+1)-\delta(3|n+1)-\delta(3|n+2)\\ \nonumber-\delta(5|n+2,\, n\ge 8)-\delta(7|n+3,\, n\ge 11)-\delta(11|n+4,\, n\ge 29), \end{align} $$
$$ \begin{align} \nonumber N_1(n)\ge\left\lfloor\frac{d(n-1)+1}{2}\right\rfloor+\left\lfloor\frac{d(2n-1)+1}{2}\right\rfloor-1\\ +\left\lfloor\frac{d_2(3n+1)+1}{2}\right\rfloor+\left\lfloor\frac{d_3(4n+1)+1}{2}\right\rfloor+\left\lfloor\frac{d_3(4n+5)+1}{2}\right\rfloor\\ \nonumber-\delta(2|n+1)-\delta(3|n+1)-\delta(3|n+2)\\ \nonumber-\delta(5|n+2,\, n\ge 8)-\delta(7|n+3,\, n\ge 11)-\delta(11|n+4,\, n\ge 29), \end{align} $$
where
![]() $d_i(m)$
is the number of positive divisors of m which lie in the arithmetic progression
$d_i(m)$
is the number of positive divisors of m which lie in the arithmetic progression
![]() ${i}\pmod {i+1}$
. The function
${i}\pmod {i+1}$
. The function
![]() $\delta $
is the Dirac delta function.
$\delta $
is the Dirac delta function.
Remark 2.10 In the case
![]() $a=2$
, equation (1.2) has at least one typical solution in the form
$a=2$
, equation (1.2) has at least one typical solution in the form
![]() $(n-1,\underbrace {1,1,\ldots ,1}_{n-1\,\,\mathrm {times}}).$
Therefore,
$(n-1,\underbrace {1,1,\ldots ,1}_{n-1\,\,\mathrm {times}}).$
Therefore,
![]() $N_2(n)\ge 1$
for all integers
$N_2(n)\ge 1$
for all integers
![]() $n\ge 2.$
$n\ge 2.$
3 Main results
We give a lower bound on the number of solutions
![]() $N_a(n)$
of equation (1.2).
$N_a(n)$
of equation (1.2).
Theorem 3.1 If
![]() $a,n\in \mathbb {N},\,n\ge 2$
, then
$a,n\in \mathbb {N},\,n\ge 2$
, then
where
![]() $d_i(m)$
is the number of positive divisors of m which lie in the arithmetic progression
$d_i(m)$
is the number of positive divisors of m which lie in the arithmetic progression
![]() $i \pmod {i+1}$
. The function
$i \pmod {i+1}$
. The function
![]() $\delta $
is the Dirac delta function.
$\delta $
is the Dirac delta function.
Proof In the set
![]() $\mathbb {N}^n$
, we have the following pairwise disjoint families of pairwise different
$\mathbb {N}^n$
, we have the following pairwise disjoint families of pairwise different
![]() $(x_1,x_2,\ldots ,x_n)$
solutions of equation (1.2). Note that in each case
$(x_1,x_2,\ldots ,x_n)$
solutions of equation (1.2). Note that in each case
![]() $x_i$
is an integer and
$x_i$
is an integer and
![]() $x_1\ge x_2\ge \cdots \ge x_n\ge 1$
. We define
$x_1\ge x_2\ge \cdots \ge x_n\ge 1$
. We define
 $$ \begin{align*} A_1(n)=\{(\tfrac{n-2+\tfrac{d+1}{a}}{d},\tfrac{d+1}{a},\underbrace{1,1,\ldots,1}_{n-2\,\,\mathrm{times}}):\\ \,\,a(n-2)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod a,\,\\1\le d\le\sqrt{a(n-2)+1},\,d\in\mathbb{N}\}. \end{align*} $$
$$ \begin{align*} A_1(n)=\{(\tfrac{n-2+\tfrac{d+1}{a}}{d},\tfrac{d+1}{a},\underbrace{1,1,\ldots,1}_{n-2\,\,\mathrm{times}}):\\ \,\,a(n-2)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod a,\,\\1\le d\le\sqrt{a(n-2)+1},\,d\in\mathbb{N}\}. \end{align*} $$
We also define
 $$ \begin{align*} A_2(n)=\{(\tfrac{n-1+\tfrac{d+1}{2a}}{d},\tfrac{d+1}{2a},2,\underbrace{1,1,\ldots,1}_{n-3\,\,\mathrm{times}}):\\ \,\,2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv -1\quad\pmod {2a},\,\\4a-1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}, \mathrm{\,\,when\,\,} n\ge 3. \end{align*} $$
$$ \begin{align*} A_2(n)=\{(\tfrac{n-1+\tfrac{d+1}{2a}}{d},\tfrac{d+1}{2a},2,\underbrace{1,1,\ldots,1}_{n-3\,\,\mathrm{times}}):\\ \,\,2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv -1\quad\pmod {2a},\,\\4a-1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}, \mathrm{\,\,when\,\,} n\ge 3. \end{align*} $$
We have
![]() $A_2(2)=\emptyset .$
Moreover,
$A_2(2)=\emptyset .$
Moreover,
 $$ \begin{align*} |A_1(n)|= |\{d:\,\, a(n-2)+1\equiv0\quad\pmod d ,\,d\equiv-1\quad\pmod a,\,\\1\le d\le\sqrt{a(n-2)+1},\,d\in\mathbb{N} \}| =\left\lfloor\tfrac{d_{a-1}(a(n-2)+1)+1}{2}\right\rfloor. \end{align*} $$
$$ \begin{align*} |A_1(n)|= |\{d:\,\, a(n-2)+1\equiv0\quad\pmod d ,\,d\equiv-1\quad\pmod a,\,\\1\le d\le\sqrt{a(n-2)+1},\,d\in\mathbb{N} \}| =\left\lfloor\tfrac{d_{a-1}(a(n-2)+1)+1}{2}\right\rfloor. \end{align*} $$
In the case of the set
![]() $A_2(n)$
, we have
$A_2(n)$
, we have
![]() $d\neq 2a-1$
; thus,
$d\neq 2a-1$
; thus,
 $$ \begin{align*} |A_2(n)|=|\{d:\,\, 2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod {2a},\,\\ 4a-1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}|=\\=|\{d:\,\, 2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod {2a},\,\\ 1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}|\\-|\{d: 2a(n-1)+1\equiv0\quad\pmod d,\,d=2a-1\}|=\\ \left\lfloor\tfrac{d_{2a-1}(2a(n-1)+1)+1}{2}\right\rfloor-\delta(2a-1|n). \end{align*} $$
$$ \begin{align*} |A_2(n)|=|\{d:\,\, 2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod {2a},\,\\ 4a-1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}|=\\=|\{d:\,\, 2a(n-1)+1\equiv0\quad\pmod d,\,d\equiv-1\quad\pmod {2a},\,\\ 1\le d\le\sqrt{2a(n-1)+1},\,d\in\mathbb{N}\}|\\-|\{d: 2a(n-1)+1\equiv0\quad\pmod d,\,d=2a-1\}|=\\ \left\lfloor\tfrac{d_{2a-1}(2a(n-1)+1)+1}{2}\right\rfloor-\delta(2a-1|n). \end{align*} $$
The sets
![]() $A_1(n),\,A_2(n)$
are disjoint. Hence,
$A_1(n),\,A_2(n)$
are disjoint. Hence,
![]() $N_a(n)\ge |A_1(n)|+|A_2(n)|.$
Thus, we get immediately (3.1).
$N_a(n)\ge |A_1(n)|+|A_2(n)|.$
Thus, we get immediately (3.1).
Corollary 3.2 If
![]() $n\in \mathbb {N},\,n\ge 2$
, then
$n\in \mathbb {N},\,n\ge 2$
, then
The following corollary is almost immediate.
Corollary 3.3 If
![]() $n\in \mathbb {N},\,n\ge 2$
, then
$n\in \mathbb {N},\,n\ge 2$
, then
Proof Formula (3.3) follows at once from Corollary 3.2 and inequalities
For the convenience of the reader, values of
![]() $N_2(n)$
for small values of n are presented in Table 2.
$N_2(n)$
for small values of n are presented in Table 2.
Corollary 3.4 Let
![]() $n\in \mathbb {N},\,n\ge 3$
. If the equation
$n\in \mathbb {N},\,n\ge 3$
. If the equation
has exactly one solution
![]() $(n-1,\underbrace {1,1,\ldots ,1}_{n-1\,\,\mathrm {times}})$
in the natural numbers
$(n-1,\underbrace {1,1,\ldots ,1}_{n-1\,\,\mathrm {times}})$
in the natural numbers
![]() $x_1\ge x_2\ge \cdots \ge x_n\ge 1$
, then
$x_1\ge x_2\ge \cdots \ge x_n\ge 1$
, then
![]() $2n-3$
is a prime number.
$2n-3$
is a prime number.
Table 2 The table lists the numbers
![]() $N_2(n)$
for
$N_2(n)$
for
![]() $2\le n\le 51$
.
$2\le n\le 51$
.

Proof If
![]() $N_2(n)=1$
, then by Corollary 3.3 we get
$N_2(n)=1$
, then by Corollary 3.3 we get
![]() $2\ge d(2n-3)$
. Since
$2\ge d(2n-3)$
. Since
![]() $2n-3\ge 3$
, it follows that
$2n-3\ge 3$
, it follows that
![]() $2n-3$
is a prime number.
$2n-3$
is a prime number.
Remark 3.5 If
![]() $N_1(n)=1$
, then
$N_1(n)=1$
, then
![]() $n-1$
must be a Sophie Germain prime number (see [Reference Nyblom8]).
$n-1$
must be a Sophie Germain prime number (see [Reference Nyblom8]).
4 The set of exceptional values
Let
![]() $E_{\le k}^2=\{n:\,N_2(n)\le k,\,n\ge 2\}$
, where
$E_{\le k}^2=\{n:\,N_2(n)\le k,\,n\ge 2\}$
, where
![]() $k\in \mathbb {N}$
. In particular,
$k\in \mathbb {N}$
. In particular,
![]() $E_{\le 1}^2=\{n:\,N_2(n)=1, n\ge 2\}$
.
$E_{\le 1}^2=\{n:\,N_2(n)=1, n\ge 2\}$
.
Theorem 4.1 The set
![]() $E_{\le k}^2$
has natural density
$E_{\le k}^2$
has natural density
![]() $0$
, i.e., the ratio
$0$
, i.e., the ratio
tends to
![]() $0$
as
$0$
as
![]() $x\to \infty $
.
$x\to \infty $
.
Proof Let
![]() $\mathrm {\Omega }(m)$
count the total number of prime factors of m. We have
$\mathrm {\Omega }(m)$
count the total number of prime factors of m. We have
![]() $\mathrm {\Omega }(m)\le d(m)-1$
for every natural m. Let
$\mathrm {\Omega }(m)\le d(m)-1$
for every natural m. Let
![]() $\pi _i(x)=|\{m:\,\,\mathrm {\Omega }(m)=i,\,\,1\le m\le x\}|$
, i.e., the number of
$\pi _i(x)=|\{m:\,\,\mathrm {\Omega }(m)=i,\,\,1\le m\le x\}|$
, i.e., the number of
![]() $1\le m\le x$
with i prime factors (not necessarily distinct). By Corollary 3.3, we have
$1\le m\le x$
with i prime factors (not necessarily distinct). By Corollary 3.3, we have
![]() $N_2(n)\ge \frac {1}{2}d(2n-3).$
Thus, if
$N_2(n)\ge \frac {1}{2}d(2n-3).$
Thus, if
![]() $n\in E_{\le k}^2$
, then
$n\in E_{\le k}^2$
, then
![]() $d(2n-3)\le 2k$
and consequently
$d(2n-3)\le 2k$
and consequently
![]() $\mathrm {\Omega }(2n-3)\le 2k-1.$
Therefore,
$\mathrm {\Omega }(2n-3)\le 2k-1.$
Therefore,
 $$ \begin{align*} |E_{\le k}^2\cap [1,x]|\le \sum\limits_{i=0}^{2k-1}\pi_i(2x-3), \end{align*} $$
$$ \begin{align*} |E_{\le k}^2\cap [1,x]|\le \sum\limits_{i=0}^{2k-1}\pi_i(2x-3), \end{align*} $$
where
![]() $x\ge 2.$
Using the sieve of Eratosthenes, one can show that (see [Reference Cojocaru and Murty2, p. 75])
$x\ge 2.$
Using the sieve of Eratosthenes, one can show that (see [Reference Cojocaru and Murty2, p. 75])
for some constants
![]() $A,B>0.$
There follows that
$A,B>0.$
There follows that
 $$ \begin{align*} 0\le \tfrac{1}{x}|E_{\le k}^2\cap [1,x]|\le \tfrac{2x-3}{x}\sum\limits_{i=0}^{2k-1}\tfrac{1}{i!}\tfrac{(A\log{\log{(2x-3)}+B})^i}{\log{(2x-3)}}. \end{align*} $$
$$ \begin{align*} 0\le \tfrac{1}{x}|E_{\le k}^2\cap [1,x]|\le \tfrac{2x-3}{x}\sum\limits_{i=0}^{2k-1}\tfrac{1}{i!}\tfrac{(A\log{\log{(2x-3)}+B})^i}{\log{(2x-3)}}. \end{align*} $$
For a fixed k, the right-hand side tends to
![]() $0$
, as
$0$
, as
![]() $x\to \infty $
. Thus,
$x\to \infty $
. Thus,
This completes the proof.
The above theorem implies that the set
![]() $E_k^2=\{n:\,\,N_2(n)=k,\,n\ge 2\}$
has zero natural density for any fixed
$E_k^2=\{n:\,\,N_2(n)=k,\,n\ge 2\}$
has zero natural density for any fixed
![]() $k\ge 1$
. This observation might suggest that the set
$k\ge 1$
. This observation might suggest that the set
![]() ${E_k^2=\{n:\,\,N_2(n)=k,\,n\ge 2\}}$
is finite for any fixed
${E_k^2=\{n:\,\,N_2(n)=k,\,n\ge 2\}}$
is finite for any fixed
![]() $k\ge 1$
and that the number
$k\ge 1$
and that the number
![]() $N_2(n)\to \infty $
as
$N_2(n)\to \infty $
as
![]() $n\to \infty $
. In the next theorem, we study the average behavior of
$n\to \infty $
. In the next theorem, we study the average behavior of
![]() $N_2(n).$
$N_2(n).$
Theorem 4.2 If
![]() $\epsilon>0$
, then for sufficiently large x, we have
$\epsilon>0$
, then for sufficiently large x, we have
Proof By [Reference Sándor, Mitrinović and Crstici9, Reference Tolev14], there exists constant
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*}\left|\sum\limits_{\substack{1\le n\le x,\\n\equiv1\ \pmod 2}}d(n)-\tfrac{x}{4}\log{x}\right|\le cx,\end{align*} $$
$$ \begin{align*}\left|\sum\limits_{\substack{1\le n\le x,\\n\equiv1\ \pmod 2}}d(n)-\tfrac{x}{4}\log{x}\right|\le cx,\end{align*} $$
for sufficiently large
![]() $x>x_0.$
It follows that
$x>x_0.$
It follows that
 $$ \begin{align*}\sum\limits_{\substack{1\le n\le x,\\n\equiv1\ \pmod 2}}d(n) \ge \tfrac{x}{4}\log(x)-cx\end{align*} $$
$$ \begin{align*}\sum\limits_{\substack{1\le n\le x,\\n\equiv1\ \pmod 2}}d(n) \ge \tfrac{x}{4}\log(x)-cx\end{align*} $$
for
![]() $x>x_0.$
By Corollary 3.3, for
$x>x_0.$
By Corollary 3.3, for
![]() $n\ge 2$
, we have
$n\ge 2$
, we have
![]() $N_2(n)\ge \frac {1}{2}d(2n-3)$
. Therefore,
$N_2(n)\ge \frac {1}{2}d(2n-3)$
. Therefore,
 $$ \begin{align*}\frac{1}{x}\sum\limits_{1< n\le x}N_2(n)\ge \frac{1}{x}\sum\limits_{1<n\le x}\tfrac{1}{2}d(2n-3)=\frac{1}{2x}\sum\limits_{\substack{1\le m\le 2x-3\\ m\equiv1\ \pmod 2}}d(m)\\ \ge \frac{1}{8}\log{(2x-3)}-c\tfrac{2x-3}{2x} \end{align*} $$
$$ \begin{align*}\frac{1}{x}\sum\limits_{1< n\le x}N_2(n)\ge \frac{1}{x}\sum\limits_{1<n\le x}\tfrac{1}{2}d(2n-3)=\frac{1}{2x}\sum\limits_{\substack{1\le m\le 2x-3\\ m\equiv1\ \pmod 2}}d(m)\\ \ge \frac{1}{8}\log{(2x-3)}-c\tfrac{2x-3}{2x} \end{align*} $$
for
![]() $2x-3>x_0.$
Let
$2x-3>x_0.$
Let
![]() $\epsilon>0$
, then for sufficiently large x, we have
$\epsilon>0$
, then for sufficiently large x, we have