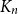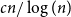Tree universality in positional games

Abstract

In this paper we consider positional games where the winning sets are edge sets of tree-universal graphs. Specifically, we show that in the unbiased Maker-Breaker game on the edges of the complete graph $K_n$, Maker has a strategy to claim a graph which contains copies of all spanning trees with maximum degree at most $cn/\log (n)$, for a suitable constant $c$ and $n$ being large enough. We also prove an analogous result for Waiter-Client games. Both of our results show that the building player can play at least as good as suggested by the random graph intuition. Moreover, they improve on a special case of earlier results by Johannsen, Krivelevich, and Samotij as well as Han and Yang for Maker-Breaker games.

1. Introduction

A positional game is a perfect-information game played by two players on a hypergraph denoted as $\mathcal{H} = (\mathcal{X}, \mathcal{F})$ , where $\mathcal{X}$ is called the board, and $\mathcal{F}$ is a family of winning sets. In this type of game, both players claim elements of the board $\mathcal{X}$ , following predefined rules. The victor is determined based on the family of winning sets $\mathcal{F}$ . Over the past decades, positional games were extensively studied (for a comprehensive overview, refer to [21]), and various variants have been considered. In this paper, we focus on unbiased Maker-Breaker and Waiter-Client games played on the edge set of the complete graph $K_n$ with the winning sets being tree-universal graphs on $n$ vertices, i.e. graphs which contain a copy of every tree $T$ on $n$ vertices with the maximum degree $\Delta (T) \leq \Delta (n)$ bounded by a suitable function on $n$ . Our results improve a result by Johannsen, Krivelevich, and Samotij [24] from 2013, and make progress in answering a question by Ferber, Hefetz and Krivelevich [15] from 2012.

1.1 Maker-Breaker games concerning spanning trees

A $(1\,:\,b)$ Maker-Breaker game on a hypergraph $\mathcal{H} = (\mathcal{X},\mathcal{F})$ is played as follows: Maker and Breaker take turns claiming elements of the board $\mathcal{X}$ that were not previously claimed. Maker always takes one element per turn while Breaker takes $b$ elements, except perhaps in his final move. The value of $b$ is referred to as the bias. Maker wins if she successfully claims an entire winning set $F \in \mathcal{F}$ , otherwise Breaker wins. It is easily observed that it is only beneficial for Breaker to claim more elements, and thus there is a threshold bias $b_{\mathcal{H}}$ such that Breaker wins if and only if $b \gt b_{\mathcal{H}}$ (excluding degenerate cases).

Already in 1964, Lehman [26] discovered that Maker easily wins the $(1\,:\,1)$ connectivity game $\mathcal{C}$ on $K_n$ , i.e. the game where the winning sets consist of all spanning trees of $K_n$ , and she can even do so, if the board only consists of two edge-disjoint spanning trees. There are different natural related questions which have been investigated since then. Chvátal and Erdős [7] proved in 1978 that the threshold bias $b_{\mathcal{C}}$ for the connectivity game on $K_n$ is of order $\frac{n}{\log (n)}$ , and suspected that there is an interesting relation between Maker-Breaker games and random graphs. That is, they formulated the intuition that for certain biased Maker-Breaker games the more likely winner between two random players would be the same as the winner between two perfect players. This relation is commonly referred to as the random graph intuition, and holds for several different Maker-Breaker games. Indeed, Gebauer and Szabó [16] showed in 2009 that $b_{\mathcal{C}} = (1 + o(1))\frac{n}{\log (n)}$ which confirms the random graph intuition for the connectivity game.

Going one step further, one can also inspect whether Maker can claim a copy of a fixed spanning tree instead of just any spanning tree and if so, how fast she can do it. In particular, an intriguing question was asked by Ferber, Hefetz, and Krivelevich [15] in 2012: What is the largest $d = d(n) \in \mathbb{N}$ such that Maker can claim any fixed tree $T$ on $n$ vertices with maximum degree $\Delta (T) \leq d$ for $n$ large enough?

In the unbiased case, following [25], the random graph intuition would suggest $d(n) = \Theta (\frac{n}{\log (n)})$ . However, the current best-known results are quite far away from this desired value. In 2009, Hefetz, Krivelevich, Stojaković, and Szabó [19] showed that Maker can claim a Hamilton path in the $(1\,:\,1)$ game within $n-1$ rounds. Similarly, Maker can claim any fixed tree $T$ with $\Delta (T) = O(1)$ within $n+1$ rounds, provided $n$ is large enough [8]. In 2012, Ferber, Hefetz and Krivelevich [15] showed that Maker can claim any fixed tree $T$ with $\Delta (T) \leq n^{0.05}$ within $n + o(n)$ rounds, even in the biased version as long as $b \lt n^{0.005}$ . Johannsen, Krivelevich, and Samotij [24] further improved this maximum degree for the unbiased setting, where their result (which is stated more generally for expander graphs) is universal, giving that in a $(1\,:\,1)$ game on $K_n$ , Maker can claim a single graph containing copies of all trees $T$ on $n$ vertices such that $\Delta (T) \leq \frac{c n^{1/3}}{\log (n)}$ , for some suitable $c$ and large enough $n$ .

We further improve on this result, and show that Maker can play asymptotically at least as good as the random graph intuition suggests.

Theorem 1.1. There exists a constant $c\gt 0$ such that the following holds for every large enough integer $n$ . In the $(1\,:\,1)$ Maker-Breaker game on $K_n$ , Maker has a strategy to claim a graph which contains a copy of every tree $T$ with $n$ vertices and maximum degree $\Delta (T)\leq \frac{cn}{\log (n)}$ .

Our proof technique is different from the one in [24]. In [24], Maker in a $(1\,:\,1)$ game on $K_n$ claims a proper expander tailored for the application of the Erdős-Selfridge criterion for Breaker’s win (see Theorem2.2 in the next section). A natural way for obtaining a stronger result with this method would be to show stronger universality properties of expanders. Han and Yang [17] went this route and showed that Maker in a $(1\,:\,1)$ game on $K_n$ can claim a graph containing copies of all spanning trees $T$ with $\Delta (T) \leq \frac{c n^{1/2}}{\log (n)}$ . In our proof of Theorem1.1, Maker claims a graph having not only good expanding properties, but also other properties, which are not obtained by the Erdős-Selfridge criterion. Let us add that an advantage of the method in [24] is that it generalises easily to biased Maker-Breaker games (in fact the authors present their result for biased games, played on expanders), while our method is less flexible in that sense.

1.2 Waiter-Client games concerning spanning trees

A $(1\,:\,b)$ Waiter-Client game on a hypergraph $\mathcal{H} = (\mathcal{X},\mathcal{F})$ is played as follows: in each round, Waiter picks $b + 1$ elements of the board $\mathcal{X}$ that were not previously picked and offers them to Client. Client chooses one of them for himself and returns the rest to Waiter. If in the last round there are less than $b+1$ elements not picked yet, all the elements go to Waiter. Waiter wins if she is able to force Client to fully claim some winning set $F \in \mathcal{F}$ . Otherwise, Client wins.

Concerning spanning trees, similar results are known for Waiter-Client games as for Maker-Breaker games, where Waiter often can achieve better results because she has more control which edges get blocked. Similar to Maker-Breaker games, Waiter wins the $(1\,:\,1)$ connectivity game on some graph $G$ if $G$ contains two edge-disjoint spanning trees [11]. Concerning the threshold bias, the third author together with Krivelevich and Łuczak [6] showed that Waiter wins the $(1\,:\,b)$ Waiter-Client connectivity game on $K_n$ if and only if $b \leq \lfloor \frac{n}{2} \rfloor - 1$ . Moreover, in a $(1\,:\,1)$ Waiter-Client game on $K_n$ with $n$ large enough, Waiter can force Client to claim a Hamilton path within $n-1$ rounds, and she can force Client to claim any fixed tree $T$ with $\Delta (T) \leq c \sqrt{n}$ within $n$ rounds, for some suitable $c$ and $n$ large enough [10]. Recently, we improved upon this result showing that Waiter can force any tree $T$ with $\Delta (T) \lt (\frac{1}{3} - o(1))n$ [1].

Similar to the Maker-Breaker case, it is known that Waiter in the $(1\,:\,1)$ game on $K_n$ can force Client to claim a graph that contains copies of all trees $T$ with $\Delta (T) \leq \frac{c n^{1/3}}{\log (n)}$ , or even $\Delta (T) \leq \frac{c n^{1/2}}{\log (n)}$ , which follows from the above mentioned universality properties of expanders proved in [24], [17] and the fact that the Erdős-Selfridge criterion has its Waiter-Client counterpart (see [5]). We again improve upon this result by showing a Waiter-Client version of Theorem1.1.

Theorem 1.2. There exists a constant $c\gt 0$ such that the following holds for every large enough integer $n$ . In the $(1\,:\,1)$ Waiter-Client game on $K_n$ , Waiter has a strategy to force Client to claim a graph which contains a copy of every tree $T$ with $n$ vertices and maximum degree $\Delta (T)\leq \frac{cn}{\log (n)}$ .

Organisation of the paper. In Section 2 we collect useful tools from probability theory, for positional games, and for embedding trees. In Section 3 we prove a sufficient condition for a graph to be universal for trees of large maximum degree. In Sections 4 and 5 we then show that Maker and Waiter, respectively, have a strategy for creating such a graph, hence proving Theorems1.1 and 1.2. We add some concluding remarks in Section 6, in which we consider also the tree universality problem in Client-Waiter and Avoider-Enforcer games.

1.3 Notation

Most of our notation is standard and follows that of [29]. Different to the notation therein, we write $v(G)$ for the number of vertices of a graph $G$ , and for any sets $A,B\subseteq V(G)$ we write $E_G(A,B)\,:\!=\,\{vw\in E(G):\, v\in A,w\in B\}$ , and $e_G(A,B)\,:\!=\,|E_G(A,B)|$ . Additionally, having any distinct vertices $v,w\in V(G)$ , we write $d_G(v,A)\,:\!=\,|N_G(v)\cap A|$ , and we call $|N_G(v)\cap N_G(w)|$ the pair degree of $v$ and $w$ . Let $T$ be a tree. Then we write $L(T)$ for the set of leaves, i.e. all vertices of degree 1 in $T$ . Moreover, a path $P$ in $T$ is called a bare path if all of its inner vertices have degree 2 in $T$ .

Assume that some Waiter-Client game is in progress, then we let $C$ denote the graph consisting of Client’s edges only, with the vertex set being equal to the graph that the game is played on. Similarly, in a Maker-Breaker game, we use $M$ and $B$ to denote the graph consisting of, respectively, Maker’s and Breaker’s edges. If an edge belongs to any player in the game, then we call it claimed. Otherwise, we say that the edge is free. The graph consisting of the free edges will always be denoted $F$ .

We write Bin $(n,p)$ for the binomial random variable with $n$ trials, each having success independently with probability $p$ . We write $X\sim \text{Bin}(n,p)$ to denote that $X$ is distributed like Bin $(n,p)$ . We say that an event, depending on $n$ , holds asymptotically almost surely (a.a.s.) if it holds with probability tending to 1 if $n$ tends to infinity. For functions $f,g\,:\,\mathbb{N} \rightarrow \mathbb{R}$ , we write $f(n)=o(g(n))$ if $\lim _{n\rightarrow \infty } |f(n)/g(n)| = 0$ . All logarithms are base $e$ .

2. Preliminaries

2.1 Probabilistic tools

In some of our probabilistic arguments, we will use Chernoff bounds (see e.g. [23]) to show concentration for binomially distributed random variables. Specifically, we will use the following.

Lemma 2.1. If $X \sim \text{Bin}(n,p)$ , then

• • $\mathbb{P}(X\lt (1-\delta )np) \lt \exp \left (-\frac{\delta ^2np}{2}\right )$ for every $\delta \gt 0$ , and

• • $\mathbb{P}(X\gt (1+\delta )np)\lt \exp \left (-\frac{np}{3}\right )$ for every $\delta \geq 1$ .

2.2 Maker-breaker game tools

For the discussion of the Maker-Breaker tree universality game, we will use several tools from positional games theory. The first one is the famous Erdős-Selfridge-Criterion [14], stated as e.g. in Theorem 2.3.3 in [21].

Theorem 2.2 (Erdős-Selfridge-Criterion [14]). Let $(X,\mathcal{F})$ be a hypergraph satisfying

\begin{equation*}\sum _{F\in \mathcal {F}} 2^{-|F| + 1} \lt 1.\end{equation*}

Then Breaker wins in the $(1\,:\,1)$ Maker-Breaker game on $(X,\mathcal{F})$ .

We will also use statements ensuring that Maker can achieve sufficiently large degrees.

Lemma 2.3 (Mindegree game, Lemma 10 in [20]). Let $H$ be a graph of minimum degree $d$ , then in a $(1\,:\,1)$ Maker-Breaker game played on the edges of $H$ , Maker can claim a spanning graph $M$ with minimum degree at least $\lfloor d/4 \rfloor$ .

Lemma 2.4 (Degree game, Corollary of Lemma 6 in [2]). Playing a $(1:2)$ Maker-Breaker game on the edges of $K_n$ , Maker can ensure that every vertex reaches degree at least $\frac{1}{3}n - 3\sqrt{n\log (n)}$ in her graph.

Moreover, we will use the following lemma which allows Maker to distribute her elements nicely over all sets of a given family $\mathcal{F}$ .

Lemma 2.5 (Corollary of Lemma 2.3 in [3]). Let $X$ be a set and let $\delta \in (0,1)$ . Let $\mathcal{H} = (X, \mathcal{F})$ be a hypergraph, and $k = \min _{F \in \mathcal{F}} |F|$ . If $k \gt 4\delta ^{-2}\ln (|\mathcal{F}|)$ , then in a $(1\,:\,1)$ Maker-Breaker game on $\mathcal{H}$ , Maker has a strategy to claim at least $(\frac{1}{2} - \delta )|F|$ elements of every set $F \in \mathcal{F}$ .

Finally, we will use the following corollary of a recent result by Liebenau and Nenadov [27].

Lemma 2.6 ( $K_5$ -factor game, Corollary of Theorem 1.1 in [27]). There exist constants $c,C\gt 0$ such that the following holds for every large enough integer $n$ divisible by 5. Playing a $(1\,:\,b)$ Maker-Breaker game on $K_n$ , with $b\leq cn^{2/7}$ , Maker has a strategy to claim a spanning $K_5$ -factor of $K_n$ within at most $Cn^{12/7}$ rounds.

Proof. Let $n$ be large enough. By Theorem1.1 in [27] there is a constant $c\gt 0$ such that Maker can claim a spanning $K_5$ -factor of $K_n$ against a bias $b^*= \lceil cn^{2/7} \rceil$ . Let $C=\frac{1}{c}$ . By the trick of fake moves (see e.g. Lemma2.4 in [9]) it follows that Maker can claim a spanning $K_5$ -factor of $K_n$ against any bias $b\leq b^*$ within $\lceil \binom{n}{2}/(b^*+1) \rceil \leq C n^{12/7}$ rounds.

2.3 Waiter-Client game tools

When describing strategies for Waiter we will make use of the following variant of the Erdős-Selfridge Criterion.

Theorem 2.7 (Corollary 1.4 in [5]). Let $(X,\mathcal{F})$ be a hypergraph satisfying

\begin{equation*}\sum _{F\in \mathcal {F}} 2^{-|F| + 1} \lt 1.\end{equation*}

Then Waiter wins in the $(1\,:\,1)$ Waiter-Client game on $(X,\mathcal{F})$ .

Moreover, we will use that Waiter has a strategy to force large pair degrees.

Lemma 2.8. If $\beta \in (0,1)$ , then for every large enough integer $n$ the following holds. Let $G$ be a graph on $n$ vertices such that for every two vertices $v,w\in V(G)$ there is a set $N_{v,w}$ of at least $\beta n$ common neighbours. Playing a $(1\,:\,1)$ Waiter-Client game on $G$ , Waiter can force Client to claim a graph $C$ that satisfies the following:

\begin{equation*} |N_C(v)\cap N_C(w)\cap N_{v,w}| \geq \frac {\beta n}{500} \quad \text { for every }v,w\in V(G). \end{equation*}

Proof. Before the game starts, we split the edge set of the graph $G$ in order to obtain two graphs $G_1$ and $G_2$ such that

\begin{equation*} |N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}| \geq \frac {\beta n}{5} \quad \text { for every }v,w\in V(G). \end{equation*}

That this is possible can be proven by taking a partition $G=G_1\cup G_2$ uniformly at random and then showing with the help of a standard Chernoff argument (Lemma 2.1) that the above holds a.a.s.

Then, for a Stage I, Waiter plays on $G_1$ considering the family

\begin{equation*} \mathcal {F}_1 \,:\!=\, \left \{ A:\, \begin {array}{l} A\subseteq E_{G_1}(v,N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}) \text { for some distinct }v,w\in V(G)\\ \text {and }|A|=0.9|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}| \end {array} \right \}. \end{equation*}

It holds that

\begin{align*} \sum _{F\in \mathcal{F}_1} 2^{-|F|} & \leq \sum _{v,w} \binom{|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|}{0.1|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|} \cdot 2^{-0.9|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|}\\ & \leq \sum _{v,w} (10e)^{0.1|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|} \cdot 2^{-0.9|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|}\\ & \lt \sum _{v,w} 0.8^{|N_{G_1}(v)\cap N_{G_2}(w)\cap N_{v,w}|} \leq n^2 0.8^{0.2\beta n} = o(1). \end{align*}

Thus, by Lemma2.7, Waiter can ensure that Client claims an element in each set of $\mathcal{F}_1$ . By this, it follows that Client’s subgraph $C_1\subseteq G_1$ at the end of Stage I satisfies

\begin{equation*} |N_{C_1}(v)\cap N_{G_2}(w)\cap N_{v,w}| \geq \frac {\beta n}{50} \quad \text { for every }v,w\in V(G). \end{equation*}

Afterwards, for a Stage II, Waiter plays on $G_2$ considering the family

\begin{equation*} \mathcal {F}_2 \,:\!=\, \left \{ A:\, \begin {array}{l} A\subseteq E_{G_2}(w,N_{C_1}(v)\cap N_{G_2}(w)\cap N_{v,w}) \text { for some distinct }v,w\in V(G)\\ \text {and }|A|=0.9|N_{C_1}(v)\cap N_{G_2}(w)\cap N_{v,w}| \end {array} \right \}. \end{equation*}

Note that so far, no edge of $G_2$ was claimed. It analogously holds that $\sum _{F\in \mathcal{F}_2} 2^{-|F|} = o(1)$ . Thus, by Lemma2.7, Waiter can ensure that Client claims an element in each set of $\mathcal{F}_2$ . By this, it follows that Client’s subgraph $C_2\subseteq G_2$ at the end of Stage II satisfies

\begin{equation*} |N_{C_1}(v)\cap N_{C_2}(w)\cap N_{v,w}| \geq \frac {\beta n}{500} \quad \text { for every }v,w\in V(G). \end{equation*}

Hence, the statement is proven.

Finally, we will use that Waiter can force a perfect matching on $K_{5,5}$ . Indeed, the statement below is an easy exercise, and it also follows from Stage II in the proof of Theorem 2.1 in [10].

Lemma 2.9 (WC Perfect Matching, [10]). Playing a $(1\,:\,1)$ Waiter-Client game on $K_{5,5}$ , Waiter has a strategy to force a perfect matching of $K_{5,5}$ .

2.4 Structural properties of trees

When we want to embed spanning trees into some graph, we may first care about a small subtree with suitable properties. For this, the following lemmas will turn out to be useful.

Lemma 2.10 (Small subtree lemma). Let $k\in \mathbb{N}$ and let $T$ be a tree on $n\geq 2k$ vertices. Then there exists a set-cover $V(T)=V_A\cup V_B$ such that $T[V_A]$ and $T[V_B]$ are trees, $|V_A\cap V_B|\leq 1$ , and $k\leq |V_A| \lt 2k$ .

Proof. Fix any vertex $r\in V(T)$ as the root of $T$ and orient the edges of $T$ such that every vertex except the root has exactly one ingoing edge. Moreover, for each vertex $v\in V(T)$ denote with $T_v = (V_v,E_v)$ the tree which is induced by all the vertices which can be reached from $v$ by a directed path. Now, choose a vertex $w\in V(T)$ such that $T_w$ is a smallest tree among all trees $T_v$ with at least $2k$ vertices. Such a tree must exist, as by assumption $|V_r|=n\geq 2k$ . Let $w_1,\ldots, w_t$ be all outgoing neighbours of $w$ . For each $i\in [t]$ we have that $T_{w_i} \subseteq T_w$ and hence, by the choice of $T_w$ , we conclude that $|V_{w_i}|\lt 2k$ . If there exists $i\in [t]$ such that $|V_{w_i}|\geq k$ , then we can set $V_A\,:\!=\,V_{w_i}$ and $V_B\,:\!=\,V(T)\setminus V_{w_i}$ . Otherwise, we have $|V_{w_i}| \lt k$ for every $i\in [t]$ . Then let $\ell$ be the smallest integer such that $1 + \sum _{i\in [\ell ]} |V_{w_i}| \geq k$ . Such an $\ell$ must exist, as $|V_w|\geq 2k$ . Moreover, by the sizes of the subtrees $T_{w_i}$ , we know that $1 + \sum _{i\in [\ell ]} |V_{w_i}| \lt 2k$ . That is, we can choose $V_A\,:\!=\,\{w\}\cup \bigcup _{i\in [\ell ]} V_{w_i}$ and $V_B\,:\!=\,(V(T)\setminus V_A) \cup \{w\}$ .

Lemma 2.11 (Small subtree cover lemma). Let $k\in \mathbb{N}$ and let $T$ be a tree. Then there exists a set-cover $V(T)=V_1\cup V_2\cup \ldots \cup V_t$ with $t\leq \lceil \frac{v(T)}{k-1} \rceil + 1$ such that the following holds:

1. (i) $T[V_i]$ is a tree for every $i\in [t]$ .

2. (ii) $|V_i|\lt 2k$ for every $i\in t$ .

Proof. We do an induction on $v(T)$ . If $v(T)\lt 2k$ , there is nothing to do, as we can set $t=1$ and $V_1=V(T)$ . So, let $v(T)\geq 2k$ . Then by Lemma 2.10 we can find a set-cover $V(T)=V_A\cup V_B$ such that $T[V_A],T[V_B]$ are trees, $|V_A\cap V_B|\leq 1$ , and $k\leq |V_A| \lt 2k$ . In particular, $|V_B|\leq v(T)-k+1$ . We set $V_1\,:\!=\,V_A$ and by induction we can find a set-cover $V_B=V_2\cup \ldots \cup V_t$ with $t\leq \left ( \lceil \frac{v(T)-k+1}{k-1} \rceil + 1\right ) + 1 = \lceil \frac{v(T)}{k-1} \rceil + 1$ and such that $T[V_i]$ is a tree with $|V_i|\lt 2k$ for every $i\in \{2,3,\ldots, t\}$ . Putting everything together, we obtain a set-cover $V(T)=V_1\cup V_2\cup \ldots \cup V_t$ as required.

Lemma 2.12 (Lemma 2.1 in [25]). Let $k,\ell, n\gt 0$ be integers. Let $T$ be a tree on $n$ vertices with at most $k$ leaves. Then $T$ contains a collection of at least $\frac{n-(2k-2)(\ell +1)}{\ell +1}$ vertex-disjoint bare paths of length $\ell$ .

Corollary 2.13. Let $\ell$ be a positive integer. Then there exists a constant $\gamma '\gt 0$ such that the following holds. Every tree $T$ has at least $ \gamma ' v(T)$ leaves or a collection of at least $ \gamma ' v(T)$ vertex-disjoint bare paths of length $\ell$ each.

Proof. Set $\gamma '=\frac{1}{4(\ell +1)}$ . Let $T$ be any tree. If the number of leaves in $T$ is $k\lt \gamma 'v(T)$ , then by Lemma 2.12 there are at least

\begin{equation*} \frac {v(T)-(2k-2)(\ell +1)}{\ell +1} \gt \frac {v(T)}{\ell +1} - 2k \gt \left (\frac {1}{\ell +1} - 2\gamma '\right )v(T) \gt \gamma 'v(T) \end{equation*}

bare paths of length $\ell$ .

Lemma 2.14 (Classifying trees lemma). For every $\ell \in \mathbb{N}$ , $\delta \in (0,1)$ and $C \in \mathbb{N}$ there exist constants $\gamma, c\in (0,1)$ such that the following is true for every large enough $n$ . Let $T$ be a tree on $n$ vertices with maximum degree $\Delta (T) \leq \frac{cn}{\log (n)}$ . Then at least one of the following properties hold:

1. (i) $T$ has at least $\gamma n$ vertex-disjoint bare paths of length $\ell$ .

2. (ii) $|L(T)| \geq C \gamma n$ and there is a tree $T'\subseteq T$ with $v(T')\leq \delta n$ and $|V(T')\cap N_T(L(T))| \geq C \log (n)$ .

Proof. Having $\ell, \delta$ and $C$ fixed, we first choose $\gamma ' = \gamma '(\ell )$ according to Corollary 2.13. We then set $c = \frac{\gamma '\delta }{10C}$ and $\gamma = \frac{\gamma '}{2C}$ . Now, let $T$ be a tree on $n$ vertices with maximum degree $\Delta (T) \leq \frac{cn}{\log (n)}$ . Provided $n$ is large enough, we show that if $T$ does not satisfy (i), then property (ii) must hold.

Since (i) does not hold and $\gamma ' \gt \gamma$ , there is no collection of at least $\gamma ' n$ vertex-disjoint bare paths of length $\ell$ in $T$ . Hence, by Corollary 2.13 we can conclude $|L(T)| \geq \gamma ' n$ , which in particular gives

\begin{equation*} |L(T)|\geq C\gamma n \quad \text {and} \quad |N_T(L(T))| \geq \frac {|L(T)|}{\Delta (T)} \geq \gamma ' c^{-1} \log (n), \end{equation*}

since $\Delta (T)\leq \frac{cn}{\log (n)}$ . Now, we apply Lemma 2.11 to the tree $T$ with $k\,:\!=\,\lfloor 0.4\delta n \rfloor$ , and we find a set-cover $V(T)=V_1\cup V_2\cup \ldots \cup V_t$ such that $t\leq \lceil \frac{n}{k-1} \rceil +1 \lt 5\delta ^{-1}$ , and $T[V_i]$ is a tree with $|V_i| \lt 2k \lt \delta n$ for all $i\in [t]$ . By the Pigeonhole Principle there must exist $i^\ast \in [t]$ such that

\begin{equation*} |V_{i^\ast }\cap N_T(L(T))|\geq \frac {|N_T(L(T))|}{t} \geq 0.2 \gamma ' c^{-1} \delta \log (n) \geq C\log (n) \end{equation*}

by the choice of $c$ . Hence, (ii) follows by setting $T'\,:\!=\,T[V_{i^\ast }]$ .

2.5 Tree embedding lemmas

For the embedding of almost spanning trees, we may use the following variant of an embedding result due to Haxell [18].

Lemma 2.15 (Embedding almost spanning trees; variant of Theorem 1 in [18]). Let $T$ be a tree with maximum degree $d$ , and let $S\subseteq T$ be a subtree of $T$ . Moreover, let $G$ be a graph and let $g\,:\,V(S)\rightarrow V(G)$ be an embedding of $S$ into $G$ . Assume that the following properties hold for some $k \in \mathbb{N}$ :

1. (P1) $|N_G(X)\setminus g(V(S))| \geq d|X| + 1$ for every $X\subseteq V(G)$ with $1\leq |X|\leq 2k$ ,

2. (P2) $|N_G(X)| \geq d|X| + v(T)$ for every $X\subseteq V(G)$ with $k\lt |X|\leq 2k$ .

Then the embedding $g$ can be extended to an embedding of $T$ into $G$ .

Sketch of proof. Let $T_0=\varnothing \subseteq T_1\subseteq T$ such that $S\subseteq T_1$ and $T_1$ is a tree which can be obtained from $T$ by removing leaves only. We first note that (P1) and (P2) imply the properties (0)–(2) from Theorem 1 in [18], when we set $\ell \,:\!=\,1$ , $d_1\,:\!=\,d$ . Moreover, (P1) implies that

\begin{align*} |N_G(X)\setminus g(V(S))| & \geq d_1|X\cap g(V(S))| + d_1|X\setminus g(V(S))| \\ & \geq \sum _{x\in X\cap g(V(S))} \big ( d_T(g^{-1}(x)) - d_S(g^{-1}(x) \big ) + d_1|X\setminus g(V(S))| \end{align*}

holds for every $X\subseteq V(G)$ such that $|X|\leq 2k$ . Because of this, in the proof of Theorem 1 in [18], the embedding $g$ would be called a Type-1 embedding of $S$ into $G$ . Now, let $S\,=\!:\,S_0\subseteq S_1\subseteq S_2\subseteq \ldots \subseteq S_r\,:\!=\,T_1$ be any sequence of trees such that $S_{i+1}$ is obtained from $S_i$ by attaching one new leaf. By Claim 3 in [18] it follows iteratively that for every $i\in [r]$ we can extend $g$ to a Type-1 embeddings of $S_i$ into $G$ . Moreover, by Claim 4 in [18] (applied with $\ell =1$ ) it follows that the Type-1 embedding of $S_r=T_1$ can be extended to an embedding of $T$ into $G$ . Note that the proofs of these claims only use the fact that $G$ satisfies the properties (0)-(2).

Finally, we will use the following lemma, which is helpful for finishing the embedding of spanning trees with many leaves. This lemma is a consequence of a generalisation of Hall’s Marriage Theorem.

Lemma 2.16 (Star matching lemma, Lemma 3.10 in [24]). Let $d,m \in \mathbb{N}$ and let $G$ be a graph. Suppose that two disjoint sets $U,W \subseteq V(G)$ satisfy the following three conditions:

1. (i) $|N_G(X) \cap W| \geq d|X|$ for all $X \subseteq U$ with $1 \leq |X| \leq m$ ,

2. (ii) $e_G(X,Y) \gt 0$ for all $X \subseteq U$ and $Y \subseteq W$ with $|X| = |Y| \geq m$ ,

3. (iii) $|N_G(w) \cap U| \geq m$ for all $w \in W$ .

Then, for every map $k : U \rightarrow \{1,\dots, d\}$ that satisfies $\sum _{u \in U} k(u) = |W|$ , the set $W$ can be partitioned into $|U|$ disjoint subsets $\{W_u\}_{u \in U}$ satisfying $|W_u| = k(u)$ and $W_u \subseteq N_G(u) \cap W$ .

As in [24] we call the set of edges between the vertices of $U$ and their respective parts in $W$ a star matching.

3. A tree universal graph

The following theorem provides a sufficient condition for a graph to be universal for all trees of almost linear maximum degree. In the next two sections we will then prove that Maker and Waiter have strategies to claim a graph satisfying such a condition.

Theorem 3.1. Let $\alpha \in (0,1)$ , and $C_0\gt 0$ be any constants. There exist constants $\gamma ',c\gt 0$ and a positive integer $n_0$ such that the following is true for every $\gamma \in (0,\gamma ')$ and every integer $n\geq n_0$ .

Let $G=(V,E)$ be a graph on $n$ vertices with a partition $V=V_1\cup V_2$ of its vertex set such that the following properties hold:

1. (1) Partition size: $|V_2| = 500 \lfloor \gamma n \rfloor$ .

2. (2) Suitable star: There are a vertex $x^\ast$ and disjoint sets $R^\ast, S^\ast \subseteq V_1$ such that the following holds:

   1. (a) $|S^\ast | = \lfloor 25 C_0\log (n) \rfloor$ and $S^\ast \subseteq N_G(x^\ast )$ .

   2. (b) $|R^\ast |\leq 25$ and for each $v\in R^\ast$ the following holds: If $v$ is not adjacent with $x^\ast$ , then $v$ is adjacent with a vertex $s_v\in S^\ast$ , such that $s_v\neq s_w$ if $v\neq w$ .

   3. (c) For all $w\in V\setminus (R^\ast \cup S^\ast )$ , we have $d_G(w,S^\ast ) \geq 2C_0 \log (n)$ .

3. (3) Pair degree conditions: For every $v\in V(G)$ there are at most $\log (n)$ vertices $w\in V(G)$ such that $|N_G(v)\cap N_G(w)\cap V_1| \lt \alpha n$ .

4. (4) Edges between sets: Between every two disjoint sets $A\subseteq V_1$ and $B\subseteq V$ of size $\lfloor C_0\log (n) \rfloor$ there is an edge in $G$ .

5. (5) Suitable clique factor: In $G[V_2]$ there is a collection $\mathcal{K}$ of $100\lfloor \gamma n\rfloor$ vertex-disjoint $K_5$ -copies such that the following holds:

   1. (a) There is a partition $\mathcal{K}=\mathcal{K}_{good}\cup \mathcal{K}_{bad}$ such that $|\mathcal{K}_{bad}|=\lfloor \gamma n \rfloor$ .

   2. (b) Every vertex $v\in V$ which is not in a clique of $\mathcal{K}_{good}$ satisfies $d_G(v,V_2)\geq 40\lfloor \gamma n \rfloor$ .

   3. (c) For every clique $K\in \mathcal{K}_{good}$ there are at most $\gamma n$ cliques $K'\in \mathcal{K}_{good}$ such that $G$ does not have a matching of size 3 between $V(K)$ and $V(K')$ .

Then $G$ contains a copy of every tree $T$ on $n$ vertices and with maximum degree $\Delta (T)\leq \frac{cn}{\log (n)}$ .

The overall idea of the proof will be as follows. We will distinguish the desired trees by their containment of many bare paths or many leaves. When a tree has many bare paths, we will first embed the tree minus the bare paths into $V_1$ , by using that $G$ has good expanding properties which are guaranteed by properties (3) and (4). By making use of the clique factor in (5), we will then manage to complete the embedding of $T$ . Similarly, when caring about trees with many leaves, in a first step we will embed everything except from the leaves into $V_1$ by using properties (3) and (4), and only afterwards we will care about the leaves by applying the star matching lemma. In order to succeed with this application, we need to do the first embedding step more carefully. We do so by distinguishing two cases, depending on whether there exists a vertex $x$ which is adjacent to many neighbours of leaves. If such a vertex $x$ exists, we use property (2), embed this particular vertex onto $x^\ast$ and make sure that each vertex in $S^\ast$ becomes the image of a leaf neighbour. Property (2.c) together with the expanding properties then helps to verify the conditions of the star matching lemma. Otherwise, if such a vertex $x^\ast$ does not exist, we apply a random embedding argument together with property (3) to ensure the properties needed for the star matching lemma.

Proof of Theorem 3.1. In the following we prove Theorem3.1. Let $\alpha$ and $C_0$ be given by the statement of Theorem3.1. Choose $\delta \,:\!=\, 0.5 \alpha$ , and let $\ell \,:\!=\, 502$ . Let $m \,:\!=\, \lfloor C_0\log (n) \rfloor$ . Choose $C_1 \,:\!=\, \max \{100C_0\alpha ^{-1},501\}$ . Let $c_0$ and $\gamma _0$ be given by Lemma 2.14 with input $\ell$ , $\delta$ , and $C_1$ . Further, choose $\gamma ' \,:\!=\, \min \{10^{-5},\gamma _0\}$ , and $\gamma \in (0,\gamma ')$ , and let $c \,:\!=\, \min \{c_0, \frac{\alpha }{10C_0}, \frac{\gamma }{10C_0}\}$ . Let $d \,:\!=\, \frac{cn}{\log (n)}$ . In the following, we assume $n$ to be large enough whenever necessary, e.g. to apply Lemma 2.14 with the specified inputs.

Let $G$ be a graph with a partition $V(G)=V_1\cup V_2$ satisfying the properties (1)–(5) from Theorem3.1. We want to show that $G$ contains a copy of every tree $T$ with maximum degree $\Delta (T) \leq d$ . Consider any such tree $T$ . Because of Lemma 2.14 (with the inputs and outputs above) we know that $T$ contains $\gamma _0 n \geq \gamma n$ vertex-disjoint bare paths of length $\ell$ , or $T$ has at least $C_1 \gamma _0 n \geq C_1 \gamma n$ leaves and contains a small subtree $T' \subseteq T$ with $v(T') \leq \delta n$ and $|V(T') \cap N_T(L(T))|\geq C_1 \log (n)$ . In the following, we will show for each of these two cases separately how we can embed $T$ into $G$ .

Case 1: $T$ has at least $\gamma n$ vertex-disjoint bare paths of length $502$ . In this case, roughly speaking, we embed all of $T$ but some of the bare paths into $V_1$ using Lemma 2.15, and finish the embedding by using the clique factor (property (5)) to embed the bare paths and absorb the left-over vertices of $V_1$ .

Let $\mathcal{P}$ be a family of exactly $\lfloor \gamma n \rfloor$ vertex-disjoint bare paths of length $502$ . We form a new tree $T_1$ from $T$ as follows: for each path $P \in \mathcal{P}$ we delete the inner vertices of the path and join the endpoints by an edge. Note that $\Delta (T_1) \leq d$ and $v(T_1) = n - 501\lfloor \gamma n \rfloor$ . We want to embed $T_1$ into $G[V_1]$ using Lemma 2.15 (with $S$ being the empty graph and $k=m$ ). To do so, we have to check the following properties:

1. (P1) $|N_G(X) \cap V_1| \geq d |X| + 1$ for every $X \subseteq V_1$ with $1 \leq |X| \leq 2m$ .

2. (P2) $|N_G(X) \cap V_1| \geq d |X| + v(T_1)$ for every $X \subseteq V_1$ with $m \lt |X| \leq 2m$ .

By property (3) we conclude that $|N_G(v) \cap V_1| \geq \alpha n$ for all $v \in V_1$ . Hence, for every $X \subseteq V_1$ with $1 \leq |X| \leq 2m$ we obtain $|N_G(X) \cap V_1| \geq \alpha n - |X| \geq 0.9 \alpha n \geq d\cdot 2m + 1$ by the choice of $d$ and $m$ , and for $n$ large enough. In particular, (P1) holds.

Now consider any set $X \subseteq V_1$ with $m \lt |X| \leq 2m$ . Then, by property (4), less than $m$ vertices in $V_1\setminus X$ are not in the neighbourhood of $X$ . Therefore,

\begin{align*} |N_G(X) \cap V_1| & \gt |V_1\setminus X| - m \geq |V_1| - 3m = n - 500 \lfloor \gamma n \rfloor - 3m \\ & \gt 2 d \cdot m + n - 501 \lfloor \gamma n \rfloor \geq d |X| + v(T_1) \end{align*}

by the choice of $d$ and $m$ . That is, (P2) holds. As $G$ satisfies (P1) and (P2), we can embed $T_1$ into $G[V_1]$ using Lemma 2.15, resulting in an embedding $g : V(T_1) \rightarrow V_1$ . Note that this also is an embedding of the tree obtained from $T$ by deleting the inner vertices of all paths in $\mathcal{P}$ .

Hence, we are left with embedding the $501 \lfloor \gamma n \rfloor$ inner vertices of the family of bare paths $\mathcal{P}$ . Let $R \,:\!=\, V_1 \setminus g(V(T_1))$ be the set of $\lfloor \gamma n \rfloor$ vertices of $V_1$ which were not used for the embedding of $T_1$ . For each path $P \in \mathcal{P}$ , denote by $v^P$ and $w^P$ the images of the endpoints of $P$ under $g$ . Further, since $|\mathcal{P}| = |R| = \lfloor \gamma n \rfloor$ , we can fix exactly one distinct vertex $r^P \in R$ for every path $P \in \mathcal{P}$ . Similarly, since $|\mathcal{P}| = |\mathcal{K}_{bad}| = \lfloor \gamma n \rfloor$ , we can fix exactly one distinct clique $K^P \in \mathcal{K}_{bad}$ for every path $P \in \mathcal{P}$ . In each of these cliques we fix two arbitrary vertices $x^P,y^P\in V(K^P)$ .

As a first step towards embedding the inner vertices of $\mathcal{P}$ , we choose a collection of six cliques $\mathcal{K}^P = \{K^P_1,\ldots, K^P_6\} \subseteq \mathcal{K}_{good}$ for every $P \in \mathcal{P}$ such that the following properties are satisfied:

1. (1) $\mathcal{K}^P \cap \mathcal{K}^{P'} = \varnothing$ for all $P' \in \mathcal{P}\setminus \{P\}$ ,

2. (2) $e_G(v^P, V(K^P_1)) \gt 0$ ,

3. (3) $e_G(r^P, V(K^P_2)) \gt 0$ ,

4. (4) $e_G(r^P, V(K^P_3)) \gt 0$ ,

5. (5) $e_G(x^P, V(K^P_4)) \gt 0$ ,

6. (6) $e_G(y^P, V(K^P_5)) \gt 0$ ,

7. (7) $e_G(w^P, V(K^P_6)) \gt 0$ .

Note that we can find such cliques greedily by property (5.b). Indeed, this property ensures that each of the relevant vertices $r^P,v^P,w^P,x^P,y^P$ is adjacent to at least $8\lfloor \gamma n\rfloor$ cliques from $\mathcal{K}$ , and hence to at least $7\lfloor \gamma n\rfloor$ cliques from $\mathcal{K}_{good}$ , while for the properties above we only need to choose $6\lfloor \gamma n\rfloor$ cliques in total.

Moreover, based on (2)–(7), let $k_1^P\in V(K_1^P)$ be a neighbour of $v^P$ , let $k_2^P\in V(K_2^P)$ be a neighbour of $r^P$ , and so on, until reaching a neighbour $k_6^P\in V(K_6^P)$ of $w^P$ .

Next, we consider the following auxiliary graph $H$ : its vertex set is $\mathcal{K}_{good}$ and we put an edge between two vertices $K,K'\in V(H)$ if and only if in $G$ there is a matching of size $3$ between the cliques $K$ and $K'$ . For the graph $H'\subseteq H$ induced on $\mathcal{K}'=\mathcal{K}_{good}\setminus \bigcup _{P\in \mathcal{P}} \mathcal{K}^P$ we then have $v(H')=93\lfloor \gamma n\rfloor$ and $\delta (H')\geq v(H') - \gamma n \gt v(H')/2$ by property (5.c). Hence, by Dirac’s Theorem (see e.g. [29]), we can find a Hamilton cycle in $H'$ , and we can split this Hamilton cycle into $3\lfloor \gamma n\rfloor$ vertex-disjoint paths each having exactly 31 vertices. Denote with $\mathcal{P}_H$ the collection of these paths.

We then define an auxiliary bipartite graph $F=(A\cup B,E(F))$ with partite sets

\begin{equation*}A\,:\!=\,\{ (K_i^P,K_{i+1}^P):\, i\in \{1,3,5\}, P\in \mathcal {P}\} \quad \text {and} \quad B\,:\!=\,\mathcal {P}_H,\end{equation*}

where we put an edge between a vertex $(K_i^P,K_{i+1}^P)\in A$ and a vertex $Q\in B$ if and only if in $H$ there is a perfect matching between the endpoints of the path $Q$ and the vertices $K_i^P,K_{i+1}^P$ (which means that $Q$ can be extended to a longer path in $H$ with endpoints $K_i^P,K_{i+1}^P$ ). We then have $|A|=|B|=3\lfloor \gamma n\rfloor$ and $\delta (F)\geq |A| - \gamma n \gt |A|/2$ . Indeed, a vertex $(K_i^P,K_{i+1}^P)\in A$ and a vertex $Q\in B$ with endpoints $(K_1^Q, K_2^Q)$ are connected in $F$ unless there are at least two edges missing between the vertices $K_i^P,K_{i+1}^P$ and the vertices $K_1^Q, K_2^Q$ in the auxiliary graph $H$ . This can happen at most $\gamma n$ times per vertex $v \in V(F)$ since $\delta (H)\geq v(H) - \gamma n$ by (5.c). By a standard application of Hall’s condition (see e.g. [29]) it follows that $F$ has a perfect matching. Denote with $Q_{i,i+1}^P$ the path which is matched to the pair $(K_i^P,K_{i+1}^P)$ in this matching, for every $i\in \{1,3,5\}$ and $P\in \mathcal{P}$ .

Note that this path $Q_{i,i+1}^P$ describes a sequence of 31 cliques from $\mathcal{K}_{good}$ , such that between $K_i^P$ and the first clique in the sequence, between two consecutive cliques in the sequence, and between the last clique in the sequence and $K_{i+1}^P$ there is a matching of size $3$ in the graph $G$ .

It is then easy to find a path $\hat{Q}_{i,i+1}^P$ on 165 vertices which has endpoints $k_i^P$ and $k_{i+1}^P$ , and which goes through all the vertices of $K_i^P$ , $K_{i+1}^P$ and all the cliques in $Q_{i,i+1}^P$ . Indeed, from each of the mentioned matchings pick greedily one edge such that all these edges are independent and not incident with $k_i^P$ or $k_{i+1}^P$ ; then connect $k_i^P$ , $k_{i+1}^P$ and these matching edges with paths of length 4 that are fully contained in one of the relevant cliques.

We now have everything that we need to describe how we can embed the paths $P\in \mathcal{P}$ into $R\cup V_2$ (with fixed endpoints $v^P,w^P$ ), and thus finish the embedding of $T$ . Given $P\in \mathcal{P}$ , let $Q_{xy}^P$ be any path of length 4 in $K^P$ with endpoints $x^P$ and $y^P$ . Then we embed $P$ to the path given by the sequence $(v^P,\hat{Q}_{1,2}^P,r^P,\hat{Q}_{3,4}^P,Q_{xy}^P,\hat{Q}_{5,6}^P,w^P)$ . Note that this way, the inner vertices of $P$ are embedded into $R\cup V_2$ , disjointly from the images of all other paths in $\mathcal{P}$ .

Case 2: $T$ has at least $C_1 \gamma n$ leaves and contains a subtree $T' \subseteq T$ with $v(T') \leq \delta n$ and $|V(T') \cap N_T(L(T))|\geq C_1 \log (n)$ . Let $N_1\subseteq V(T') \cap N_T(L(T))$ be any subset of size $\lfloor C_1 \log (n) \rfloor$ .

In this case, we start by embedding the subtree $T'$ minus the leaves $L(T)$ in such a way that the vertices of $N_1$ are embedded in a suitable way. Afterwards, we extend that embedding to an embedding of $T - L(T)$ by an application of Lemma 2.15. Lastly, we use Lemma 2.16, to embed the leaves $L(T)$ . More precisely, we set $T_1 \,:\!=\, T' - L(T)$ , $T_2 \,:\!=\, T - L(T)$ , and we distinguish two cases, depending on how the vertices of $N_1$ are distributed in $T_1$ .

Case 2.1: Assume that there is a vertex $x\in V(T_1)$ with $d_{T_1}(x,N_1)\geq 0.5C_1\log (n)$ . Then we do the embedding of $T_1$ as follows: we embed $x$ onto $x^\ast$ , and we embed the vertices of $N_{T_1}(x,N_1)$ into $N_G(x^\ast )\cap V_1$ , which has size at least $\alpha n\geq d_{T_1}(x,N_1)$ by property (3), in such a way that all vertices of $(R^\ast \cap N_G(x^\ast ))\cup S^\ast$ are used, which is possible since $d_{T_1}(x,N_1) \geq |R^\ast \cup S^\ast |$ by properties (2.a) and (2.b), and by choice of $C_1$ . Afterwards, embed the rest of $T_1$ greedily into $V_1$ , which is possible since by (3) all vertex degrees into $V_1$ are at least $\alpha n \gt v(T_1)$ . Because of (2.c), the result then is an embedding $g\,:\,V(T_1)\rightarrow V_1$ into $G[V_1]$ such that the following holds: every vertex $w\in V(G)\setminus (g(V(T_1))\cup R^\ast )$ satisfies $d_G(w,g(N_1))\geq 2C_0\log (n)$ .

Next, we extend this to an embedding of $T_2$ into $G[V_1]$ . For this, we use Lemma 2.15 (with $S \,:\!=\, T_1$ , $k \,:\!=\, m$ and with $T$ being replaced with $T_2$ ). To do so, we have to check the following properties:

1. (P1) $|(N_G(X) \cap V_1) \setminus g(V(T_1))| \geq d |X| + 1$ for every $X \subseteq V_1$ with $1 \leq |X| \leq 2m$ .

2. (P2) $|N_G(X) \cap V_1| \geq d |X| + v(T_2)$ for every $X \subseteq V_1$ with $m \lt |X| \leq 2m$ .

By property (3) we know that $|(N_G(v) \cap V_1)\setminus g(V(T_1))| \geq \alpha n - \delta n \geq 0.5\alpha n$ for all $v \in V_1$ . Hence, for every $X \subseteq V_1$ with $1 \leq |X| \leq 2m$ we obtain $|(N_G(X) \cap V_1)\setminus g(V(T_1))| \geq 0.5\alpha n - |X| \geq 0.4 \alpha n \geq d\cdot 2m + 1$ , by the choice of $d$ and $m$ , and for $n$ large enough. In particular, (P1) holds. Now consider any set $X \subseteq V_1$ with $m \lt |X| \leq 2m$ . Analogously to Case 1, since $v(T_2)\leq n - C_1\gamma n \leq n - 501 \lfloor \gamma n \rfloor$ , we get $|N_G(X) \cap V_1| \geq d |X| + v(T_2)$ , and hence (P2). As $G$ satisfies (P1) and (P2), we can extend $g$ to an embedding of $T_2$ into $G[V_1]$ .

We are left with embedding the leaves of $T$ . Set $U \,:\!=\, g(N_T(L(T)))$ and $W \,:\!=\, V \setminus g(V(T_2))$ .

We first embed the vertices of $R^\ast \setminus g(V(T_2))$ one by one. Let $w\in R^\ast \setminus g(V(T_2))$ , then $w$ does not belong to $N_G(x^\ast )$ , since otherwise it would be used for the embedding of $T_1$ . With (2.b) it follows that there is a distinct vertex $s_w\in S^\ast \subseteq g(N_1)$ such that $ws_w\in E(G)$ . Since $g^{-1}(s_w)\in N_1\subseteq N_T(L(T))$ we can find a leaf $w'$ in $T$ which is adjacent with $g^{-1}(s_w)$ . We then extend $g$ by embedding $w'$ to $w$ . Moreover, we then remove $w$ from $W$ , and if $w'$ was the only leaf at $g^{-1}(s_w)$ , we remove $s_w$ from $U$ . Note that in this procedure we delete at most $|R^\ast |$ vertices from each of the sets $U$ and $W$ .

Finally, we want to find a star matching between the updated sets $U$ and $W$ using Lemma 2.16 applied with $d$ , $m$ , and with $k(u)$ being the number of leaves in $T$ which are adjacent with $g^{-1}(u)$ but are still not embedded, for every vertex $u \in U$ . Then, by extending $g$ such that for every $u\in U$ we embed the remaining $k(u)$ leaves which are adjacent with $g^{-1}(u)$ to the set $W_u$ , as given by Lemma 2.16, the embedding will be finished. Hence, it remains to be shown that we can apply Lemma 2.16. We need to verify that the following three conditions hold:

1. (i) $|N_G(X) \cap W| \geq d|X|$ for all $X \subseteq U$ with $1 \leq |X| \leq m$ .

2. (ii) $e_G(X,Y) \gt 0$ for all $X \subseteq U$ and $Y \subseteq W$ with $|X| = |Y| \geq m$ .

3. (iii) $|N_G(w) \cap U| \geq m$ for all $w \in W$ .

By property (5.b) and since $U\subseteq V_1$ and $V_2\setminus R^\ast \subseteq W$ , it follows that $|N_G(X) \cap W| \geq 40\lfloor \gamma n\rfloor - |R^\ast |\geq d m$ for every $X\subseteq U$ , by the choice of $d$ and $m$ , and thus (i) holds. By property (4) and since $U\subseteq V_1$ , we can immediately conclude (ii). Lastly, (iii) follows directly from the fact that $d_G(w,g(N_1))\geq 2C_0\log (n)$ for all $w \in V(G)\setminus (g(V(T_1))\cup R^\ast )$ , and since $R^\ast \cap W = \varnothing$ .

Case 2.2: Assume that there is no vertex $x\in V(T_1)$ with $d_{T_1}(x,N_1)\geq 0.5C_1\log (n)$ . This case works essentially the same way as Case 2.1; the main differences will be that we embed $T_1$ in a random way, and that we do not need to care separately about the vertices of $R^\ast$ . For the first step we claim the following.

Claim 3.2. There is an embedding $g\,:\,V(T_1)\rightarrow V_1$ of $T_1$ into $G[V_1]$ such that every vertex $w\in V(G)\setminus g(V(T_1))$ satisfies $d_G(w,g(N_1))\geq 2C_0\log (n)$ .

Before proving this claim, let us quickly explain how to finish the argument then. Using Lemma 2.15 analogously to Case 2.1 we can extend the embedding to the tree $T_2$ . Afterwards, we embed the leaves of $T$ as follows. We again set $U \,:\!=\, g(N_T(L(T)))$ and $W \,:\!=\, V \setminus g(V(T_2))$ , but this time we do not embed the vertices of $R^\ast \setminus g(V(T_2))$ separately. In this case, by the above claim, we know that even these vertices have degree at least $2C_0\log (n)$ into $g(N_1)\subseteq U$ , and hence, without updating $U$ and $W$ , the properties (i)–(iii) can be checked as in Case 2.1. Thus, we can finish the star matching with appropriate sizes for the stars and finish the embedding of $T$ .

Hence, it remains to prove Claim 3.2. For this, we embed $T_1$ in a random way into $V_1$ : Let $t\,:\!=\,v(T_1)$ , and fix an arbitrary ordering $v_1,v_2,\ldots, v_t$ of the vertices of $T_1$ such that every vertex $v_i$ has exactly one neighbour of smaller index; denote this neighbour $v_i^-$ . Furthermore, set $T_i\,:\!=\,T[\{v_1,\ldots, v_i\}]$ . We consider the following simple randomised embedding $g$ : Choose $g(v_1)\in V_1$ uniformly at random. Then, for $i\in \{2,\ldots, t\}$ , choose $g(v_i)$ uniformly at random from the set $(N_G(g(v_i^-))\cap V_1)\setminus g(V(T_{i-1}))$ .

We first observe that surely we succeed in embedding $T$ . Indeed, in each step of the algorithm we have

\begin{align*} |(N_G(g(v_i^-))\cap V_1)\setminus g(V(T_{i-1}))| \geq |(N_G(g(v_i^-))\cap V_1)| - |g(V(T_{i-1}))| \geq \alpha n - \delta n \geq 0.5\alpha n, \end{align*}

and we thus never run out of candidates for embedding a vertex $v_i$ .

Hence, it remains to check that a.a.s.

1. (D) for every $w\in V(G)\setminus g(V(T_1))$ we get $d_G(w,g(N_1))\geq 2C_0\log (n)$ .

In order to do so, let us define $P_1\,:\!=\,\{v^-:\, v\in N_1\}$ as the set of parents of the vertices in $N_1$ , and note that $|P_1|\leq |N_1|\leq C_1\log (n)$ . Moreover, for a vertex $w\in V(G)$ say that $v\in P_1$ is bad in the embedding $g$ if $|N_G(g(v))\cap N_G(w)\cap V_1|\lt \alpha n$ . We first prove that a.a.s. the following holds:

1. (B) for every vertex $w\in V(G)$ there is at most one bad vertex in $P_1$ throughout the embedding process.

Fix any $w\in V(G)$ . Whenever we embed a vertex $v\in P_1$ , we have a candidate set of size at least $0.5\alpha n$ , as shown above. However, because of property (3), there are at most $\log (n)$ candidates whose choice would make $v$ a bad vertex for $w$ . Hence, the probability that $v$ becomes bad for $w$ is bounded by $\frac{2\log (n)}{\alpha n}$ . It follows that the probability that at least two vertices in $P_1$ become bad for $w$ is bounded by $ \binom{|P_1|}{2}\cdot \left ( \frac{2\log (n)}{\alpha n} \right )^2 \lt n^{-1.5},$ provided $n$ is large enough. Hence, doing a union bound over all vertices $w\in V(G)$ , it follows that (B) fails with probability at most $n\cdot n^{-1.5}=o(1)$ .

From now on, let us condition on (B), and prove that (D) a.a.s. holds. Again, fix any $w\in V(G)$ . Since by the assumption of Case 2.2 no vertex in $T_1$ is adjacent with more than $0.5C_1\log (n)$ vertices from $N_1$ , it follows that the parent of at least $\lfloor 0.5C_1\log (n)\rfloor$ vertices $v\in N_1$ is not bad for $w$ (where these parents do not need to be distinct), e.g. $|N_G(g(v^-))\cap N_G(w)\cap V_1|\geq \alpha n$ . Therefore, whenever we embed one of these vertices from $N_1$ into $V_1$ , say it is a vertex $v_i$ , then the probability that it ends up in $N_G(w)$ is at least

\begin{equation*} \frac {|(N_G(g(v_i^-))\cap N_G(w)\cap V_1)\setminus g(V(T_{i-1}))|}{|(N_G(g(v_i^-))\cap V_1)\setminus g(V(T_{i-1}))|} \geq \frac {\alpha n - \delta n}{n} \geq 0.5\alpha, \end{equation*}

and this bound of $0.5\alpha$ holds independently of the embeddings of other vertices from $N_1$ . Thus, the random variable $X_w$ counting the number of vertices from $N_1$ ending up in $N_G(w)$ stochastically dominates the binomial random variable $X\sim \text{Bin}(\lfloor 0.5C_1\log (n) \rfloor, 0.5\alpha )$ with expectation about $0.25\alpha C_1\log (n) \geq 4C_0\log (n)$ . By Lemma 2.1 we conclude

\begin{equation*} \mathbb {P}(X_w\lt 2C_0\log (n)) \leq \mathbb {P}(X \lt 0.5 {\mathbb {E}}(X)) \leq e^{-\frac {1}{8}{\mathbb {E}}(X)} \lt e^{-0.03\alpha C_1\log (n)} \lt e^{-2\log (n)}, \end{equation*}

by the choice of $C_1$ . Now, doing a union bound over all $w\in V(G)$ , we see that (D) fails with probability at most $ne^{-2\log (n)} = o(1)$ .

4. Maker’s strategy

Proof of Theorem 1.1. Maker’s goal it to claim a graph $M$ which satisfies the properties (1)–(5) from Theorem3.1, with $\alpha, \gamma, c,C_0$ , and the partition $V(M) = V_1 \cup V_2$ being chosen in an appropriate way, as this theorem then ensures that Maker claims a graph as required.

Choose $\alpha \,:\!=\, 10^{-8}$ and $C_0 \,:\!=\, 2000$ , let $\gamma '$ and $c$ be given according to Theorem3.1, and let $\gamma \,:\!=\, \min \{\gamma ',10^{-5}\}$ . Whenever necessary, we assume that $n$ is large enough. Maker’s strategy consists of two main stages that split into several subgames in which she cares about the required properties (1)–(5) of Theorem3.1 separately. If at any point in the game she is unable to follow her strategy, she forfeits the game (we will later see that this does not happen). In the following, we will first describe the overall strategy. In the strategy discussion we will then show that Maker can follow the proposed strategy and claim a graph $G$ with a partition $V(G)=V_1\cup V_2$ satisfying the properties (1)–(5).

Strategy description: Maker’s strategy consists of two main stages between which there is an additionally preparatory step in which no move is made, but the free edges are partitioned in a suitable way into several subboards.

Stage I: This stage consists of two substages:

1. Stage I.a: Maker chooses an arbitrary vertex $x^*$ and claims edges incident to $x^*$ until $N_M(x^*) = \lfloor 25C_0 \log (n)\rfloor$ . Let $S^* \,:\!=\, N_M(x^*)$ at the end of this substage.

2. Stage I.b: Afterwards consider all vertices $v \in V$ with $d_B(v,S^*) \gt C_0 \log (n)$ . Let $R^*=\{v_1,v_2,\ldots, v_r\}$ be the union of those vertices. For every $i\in [r]$ , in the $i^{\text{th}}$ round of this substage, Maker claims the edge $v_ix^*$ if possible, otherwise she claims an edge $v_is_{v_i}$ such that $s_{v_i}\in S^*$ and $d_M(s_{v_i})=1$ . Details are given in the strategy discussion.

Preparatory step: Fix a partition $V = V_1 \cup V_2$ with $|V_2| = 500 \lfloor \gamma n \rfloor$ and such that $K_n[V_2]$ does not contain any edges claimed so far by Maker or Breaker. Moreover, find a partition of the graph induced by $E_F(K_n) \setminus E_F(V_2)$ into five graphs $G_1 \cup G_2 \cup G_3 \cup G_4 \cup G_5$ such that all of the following properties hold:

1. (G1) For every $v \in V\setminus (R^\ast \cup S^\ast )$ it holds that $d_{G_1}(v,S^*) \gt 4 C_0 \log (n)$ .

2. (G2) For every $v \in V_1$ it holds that $d_{G_2}(v,V_2) \gt 80 \gamma n$ .

3. (G3) For any two disjoint sets $A \subseteq V_1, B \subseteq V$ of sizes $|A| = |B| = \lfloor C_0 \log (n) \rfloor$ it holds that $e_{G_3}(A,B) \geq 0.1 C_0^2 (\log (n))^2$ .

4. (G4) For every $v \in V$ it holds that $d_{G_4}(v,V_1) \gt \frac{n}{10}$ .

5. (G5) For any two disjoint sets $A\subseteq V_1,B \subseteq V$ of sizes $|A| = \frac{n}{40}, |B| = \lfloor \log (n) \rfloor$ it holds that $e_{G_5}(A,B) \gt \frac{n \log (n)}{250}$ .

Details on why such a partition exists are given in the strategy discussion.

Stage II: We split Stage II into six subgames which are played simultaneously on disjoint boards. During this stage, whenever Breaker claims an edge in one of the boards, Maker reacts on the same board by claiming one edge according to the correspondent strategy. Only in case that there is no free edge left of the relevant board, Maker claims an arbitrary free edge of another board.

Maker’s boards and goals in these subgames are described in the following.

1. Subgame 1: Playing on $G_1$ , Maker ensures that by the end of the game for every $v \in V\setminus (R^\ast \cup S^\ast )$ it holds that $d_M(v,S^*) \geq 2 C_0 \log (n)$ .

2. Subgame 2: Playing on $G_2$ , Maker ensures that by the end of the game for every $v \in V_1$ it holds that $d_M(v,V_2) \geq 40 \gamma n$ .

3. Subgame 3: Playing on $G_3$ , Maker claims at least one edge between any two disjoint sets $A \subseteq V_1$ and $B \subseteq V$ of sizes $|A| = |B| = \lfloor C_0 \log (n) \rfloor$ .

4. Subgame 4: Playing on $G_4$ , Maker ensures that by the end of the game for every $v \in V$ it holds that $d_M(v,V_1) \geq \frac{n}{40}$ .

5. Subgame 5: Playing on $G_5$ , Maker ensures that by the end of the game for any two disjoint sets $A\subseteq V_1,B \subseteq V$ of sizes $|A| = \frac{n}{40}, |B| = \lfloor \log (n) \rfloor$ it holds that $e_M(A,B) \gt \frac{n \log (n)}{2500}$ .

6. Subgame 6: Playing on $E(V_2)$ , Maker considers two substages.

   Substage I: Within at most $n^{1.8}$ rounds on $E(V_2)$ , Maker claims a $K_5$ -factor on $V_2$ and simultaneously makes sure that for every $v \in V_2$ it holds that $d_B(v,V_2) \leq 0.4|V_2| + d_M(v,V_2)$ . Let $\mathcal{K}$ be the collection of $K_5$ -copies that form the $K_5$ -factor at the end of this substage, let $\mathcal{K}_{bad}$ denote a subset of $\lfloor \gamma n \rfloor$ of these $K_5$ -copies with the most adjacent Breaker edges within $V_2$ , and let $\mathcal{K}_{good}=\mathcal{K}\setminus \mathcal{K}_{bad}$ . Substage II: Maker makes sure that by the end of the game

   1. (i) every vertex $v$ which belongs to a clique in $\mathcal{K}_{bad}$ satisfies $d_M(v,V_2)\geq 40\lfloor \gamma n \rfloor$ ,

   2. (ii) for every clique $K\in \mathcal{K}_{good}$ there are at most $\gamma n$ cliques $K'\in \mathcal{K}_{good}$ such that $M$ does not have a matching of size 3 between $V(K)$ and $V(K')$ .

The details on how Maker can achieve these goals will be given in the strategy discussion.

Before coming to the strategy discussion let us first check that, if Maker can follow the strategy without forfeiting the game and can reach all the described goals, her graph $M$ with the partition $V(M) = V_1 \cup V_2$ fulfils the properties (1)–(5) of Theorem3.1 by the end of the game. Property (1) is true by the choice of $V_1$ and $V_2$ in the preparatory step. (2.a) is ensured in Stage I.a. For property (2.b) note that $|R^\ast |\leq 25$ , by the definition of $R^\ast$ and since Stage I.a lasts $\lfloor 25C_0\log (n)\rfloor$ rounds. The rest of (2.b) follows from the goal of Stage I.b. Moreover, (2.c) is ensured in the Subgame 1. Property (3) is given by the following reason: For any $v\in V$ we have $d_M(v,V_1)\gt \frac{n}{40}$ by Subgame 4, and hence, by the outcome of Subgame 5, there are less than $\log (n)$ vertices which have at most $\alpha n$ neighbours into $N_M(v)\cap V_1$ . Property (4) is obtained in the Subgame 3. For property (5.a) note that in the first substage of Subgame 6, we obtain $\mathcal{K}$ , and a partition $\mathcal{K}=\mathcal{K}_{good}\cup \mathcal{K}_{bad}$ as desired. Property (5.b) follows from the outcome of Subgame 2 and (i) in Subgame 6; property (5.c) is ensured by (ii) in Subgame 6.

Strategy discussion: We discuss all of the stages separately.

Stage I: Maker can clearly follow Stage I.a, provided $n$ is large enough. So, consider Stage I.b from now on. Note that $e(B)=|S^\ast |$ and $d_M(s)=1$ for every $s\in S^\ast$ when Maker enters Stage I.b. If $r=|R^\ast |=1$ , then between the unique vertex $v_1\in R^\ast$ and the set $\{x^\ast \}\cup S^\ast$ there must be at least one free edge. Hence, Maker can play as suggested. If otherwise $r\gt 1$ then, at the beginning of this stage, every vertex $v_i\in R^\ast$ satisfies $d_B(v_i,S^\ast )\lt e(B) - C_0\log (n) = |S^\ast | - C_0\log (n),$ and hence, Maker in each of the at most 25 rounds of Stage I.b can find a vertex $s_{v_i}\in S^\ast$ as described by the strategy and such that $v_is_{v_i}$ is still free, if $v_ix^\ast$ is already blocked by Breaker.

Preparatory step: Provided $n$ is large enough, it is clear that we can find a partition $V = V_1 \cup V_2$ with $|V_2| = 500 \lfloor \gamma n \rfloor$ and such that $K_n[V_2]$ does not contain any edges claimed by Maker or Breaker during Stage I, since so far at most $25 C_0 \log (n) + 25$ rounds have been played and hence at most $51C_0\log (n)$ edges are claimed. In order to show that there is a partition $G_1\cup G_2\cup G_3\cup G_4\cup G_5$ of the graph induced by $E_F(K_n) \setminus E(V_2)$ as desired, we show that a randomly chosen partition $G_1\cup G_2\cup G_3\cup G_4\cup G_5$ a.a.s. satisfies the properties (G1)–(G5). To be more precise, for each edge $e \in E_F(K_n) \setminus E(V_2)$ we decide independently with equal probability $1/5$ in which of the graphs $G_1,G_2,G_3,G_4,G_5$ it will be included. We consider each of the desired properties separately.

1. (G1) Let $v \in V\setminus (S^* \cup R^*)$ , then $d_M(v,S^\ast )=0$ at the end of Stage I. Moreover, we have $d_B(v,S^\ast )\leq C_0\log (n) + 25$ , as $v\notin R^\ast$ and Stage I.b lasts at most 25 rounds. Hence $d_F(v,S^\ast )\gt 23C_0\log (n)$ . For the random variable $X^{G_1}_v = d_{G_1}(v,S^*)$ we have $X^{G_1}_v \sim \text{Bin} \left (d_F(v,S^\ast ), \frac{1}{5} \right )$ with expectation $\mathbb E(X^{G_1}_v) = 0.2d_F(v,S^\ast ) \gt 4.6C_0\log (n)$ . Applying Chernoff (Lemma 2.1) we find that $\mathbb{P}\left (d_{G_1}(v,S^*) \lt 4 C_0 \log (n)\right ) \lt \exp \left ( - 0.05 C_0 \log (n) \right )$ . With a union bound over all $v \in V\setminus (S^* \cup R^*)$ we see that (G1) fails with probability at most $n \exp (-0.05 C_0 \log (n)) = o(1)$ , by the choice of $C_0$ .

2. (G2) Let $v\in V_1$ . At the end of Stage I we have $d_F(v,V_2)\gt |V_2|-e(B)\gt 495\gamma n$ , provided $n$ is large. Hence, for the random variable $X^{G_2}_v = d_{G_2}(v,V_2)$ we have $X^{G_2}_v \sim \text{Bin} \left (d_F(v,V_2), \frac{1}{5} \right )$ with expectation $\mathbb E(X^{G_2}_v) \gt 99 \gamma n$ . Applying Chernoff (Lemma 2.1) and union bound as before, we see that (G2) fails with probability $o(1)$ .

3. (G3) Let $A \subseteq V_1$ and $B \subseteq V$ be disjoint sets of size $\lfloor C_0\log (n) \rfloor$ . Then $e_F(A,B)\geq |A|\cdot |B| - 51C_0\log (n) \gt 0.99 C_0^2(\log (n))^2$ , provided $n$ is large enough. For the random variable $X^{G_3}_{A,B} = e_{G_3}(A,B)$ we have $X^{G_3}_{A,B} \sim \text{Bin} \left (e_F(A,B), \frac{1}{5} \right )$ with expectation $\frac 15 e_F(A,B) \geq 0.19 C_0^2(\log (n))^2$ . Applying Chernoff (Lemma 2.1) and a union bound over all possible pairs of sets $A,B$ we find that (G3) fails with probability $o(1)$ .

4. (G4) This can be verified analogously to (G2), using that for every $v\in V$ we have $d_F(v,V_1)\geq |V_1| - 51C_0\log (n) \geq n - 501 \gamma n \gt 0.9 n$ , provided $n$ is large enough.

5. (G5) This can be verified analogously to (G3), using that for every $A\subseteq V_1$ , $B\subseteq V$ of sizes $|A|=\frac{n}{40}$ and $|B|= \lfloor \log (n) \rfloor$ we have $d_F(A,B)\geq |A|\cdot |B| - 51C_0\log (n) \geq \frac{n \log (n)}{41}$ , provided $n$ is large enough.

Stage II: We discuss the 6 subgames separately.

1. Subgame 1: Maker can reach her goal by (G1) and simply using a pairing strategy for the edges in $E_{G_1}(v,S^\ast )$ for every vertex $v\in V\setminus (R^\ast \cup S^\ast )$ .

2. Subgame 2: Maker can reach her goal by (G2) and simply using a pairing strategy for the edges in $E_{G_2}(v,V_2)$ for every vertex $v\in V_1$ .

3. Subgame 3: Maker can reach her goal by (G3) and the Erdős-Selfridge-Criterion (see Theorem2.2) as follows: Consider the family

   \begin{equation*}\mathcal {F}_3 \,:\!=\, \{E_{G_3}(A,B): A \subseteq V_1, B \subseteq V, |A|=|B| = \lfloor C_0 \log (n) \rfloor, A \text { and } B \text { disjoint} \},\end{equation*}
   and note that for large enough $n$ , using (G3), we get
   \begin{equation*} \sum _{F \in \mathcal {F}_3} 2^{-|F|+1} \leq (n^{C_0\log (n)})^2\cdot 2^{-0.1C_0^2(\log (n))^2+1} \leq e^{2 C_0 (\log (n))^2 - 0.1 C_0^2 (\log (n))^2+1} \lt 1, \end{equation*}
   by the choice of $C_0$ . Hence Maker (taking the role of Breaker) can claim an edge of every edge set in $\mathcal{F}_3$ .

4. Subgame 4: Let $H_4\subseteq G_4$ be the graph induced by all edges of $G_4$ that intersect $V_1$ , and note that by (G4), $\delta (H_4)\gt \frac{n}{10}$ . Maker can reach her goal by an application of Lemma 2.3 to $H_4$ .

5. Subgame 5: Maker can reach her goal by (G5) and the criterion in Lemma 2.5 as follows: We choose $\delta \,:\!=\, \frac 15$ and consider the family

   \begin{equation*}\mathcal {F}_5 = \{E_{G_5}(A,B) \,:\, A \subseteq V_1, B \subseteq V, |A| = \frac {n}{40}, |B| = \lfloor \log (n) \rfloor, A \text { and } B \text { disjoint} \}.\end{equation*}
   Then $k \,:\!=\, \min _{F \in \mathcal{F}_5} |F| \gt \frac{n \log (n)}{250} \gt 100 \log (4^n) \gt 4\delta ^{-2} \log (|\mathcal{F}_5|)$ for large enough $n$ . Thus, by Lemma 2.5, Maker can claim at least $\frac{3}{10} \cdot \frac{n \log (n)}{250} \gt \frac{n \log (n)}{2500}$ edges in each set of $\mathcal{F}_5$ .

6. Subgame 6: For Substage I, Maker plays on $K_n[V_2]$ alternating between the strategies from Lemma 2.4 to Lemma 2.6, applied with $b\,:\!=\,2$ (since Breaker claims two edges between any two moves of Maker for any of these lemmas). Lemma 2.6 ensures that Maker obtains a $K_5$ -factor on $V_2$ before $n^{1.8}$ rounds are played on $V_2$ . Lemma 2.4 ensures that throughout this stage, $d_B(v,V_2) \leq 0.4|V_2| + d_M(v,V_2)$ holds for every $v\in V_2$ , because of the following reason: Assume that Breaker could reach $d_B(v,V_2) \gt 0.4|V_2| + d_M(v,V_2)$ for some vertex $v\in V_2$ at some point, then by claiming only edges in $E_F(v,V_2)$ from that moment on, Breaker could maintain the inequality $d_B(v,V_2) \gt 0.4|V_2| + d_M(v,V_2)$ , eventually leading to $d_B(v,V_2) \geq 0.7|V_2|$ by the end of the game, contradicting Lemma 2.4 for large enough $n$ .

   At the end of Substage I, let $\mathcal{K}=\mathcal{K}_{good}\cup \mathcal{K}_{bad}$ be given according to the strategy description, and let $V_{good}$ and $V_{bad}$ be the vertices of all cliques in $\mathcal{K}_{good}$ and $\mathcal{K}_{bad}$ , respectively. Moreover, let

   \begin{equation*}\mathcal {K}_{good}^{(2)}\,:\!=\,\{(K,K'): K,K'\in \mathcal {K}_{good},\, K\neq K',\, e_B(V(K),V(K'))=0\}.\end{equation*}
   Note that, since Breaker has at most $n^{1.8}$ edges within $V_2$ at the end of Substage I, and by definition of $\mathcal{K}_{bad}$ , we have that for every $K\in \mathcal{K}_{good}$ there are less than $\gamma n$ cliques $K'\in \mathcal{K}_{good}$ such that $(K,K')\notin \mathcal{K}_{good}^{(2)}$ .

   Now, in Substage II, Maker considers the disjoint boards $E_F(V_{good})$ and $E_F(V_{good},V_{bad})$ , and always makes her move on the same board that Breaker made his previous move on. On the first board $E_F(V_{good})$ , Maker makes sure to get a matching of size 3 between any pair $(K,K')\in \mathcal{K}_{good}^{(2)}$ . Note that this is done easily, since no edge between $V(K)$ and $V(K')$ is blocked by Breaker yet. This way, property (ii) of Substage II is ensured. On the second board $E_F(V_{good},V_{bad})$ , Maker plays a degree game as follows: Let $v$ belong to a clique in $\mathcal{K}_{bad}$ . If by the end of Substage I, we already have $d_M(v,V_2)\geq 40\gamma n$ , then there is nothing to be done. Otherwise, by the outcome of Substage I, it holds that

   \begin{equation*}d_B(v,V_2)\leq 0.4|V_2| + d_M(v,V_2) \lt 240\gamma n.\end{equation*}
   Then, by pairing the edges in $E_F(v,V_{good})$ , Maker can ensure to get $d_M(v,V_2)\geq 40\gamma n.$ Hence, property (i) of Substage II is ensured as well.

5. Waiter’s strategy

Proof of Theorem 1.2. Waiter’s goal it to force Client to claim a graph $C$ which satisfies the properties (1)–(5) from Theorem3.1, with $\alpha, \gamma, c,C_0$ , and the partition $V(C) = V_1 \cup V_2$ being chosen in an appropriate way, as this theorem then ensures that $C$ contains a copy of every tree $T$ on $n$ vertices with $\Delta (T) \leq \frac{cn}{\log (n)}$ .

Choose $\alpha \,:\!=\, 10^{-8}$ and $C_0 \,:\!=\, 2000$ , let $\gamma '$ and $c$ be given according to Theorem3.1, and let $\gamma \,:\!=\, \min \{\gamma ',10^{-5}\}$ . Whenever necessary, we assume that $n$ is large enough. Waiter’s strategy consists of five stages in which she cares about the required properties (1)–(5). If at any point in the game she is unable to follow her strategy, she forfeits the game (we will later see that this does not happen). In the following, we will first describe the overall strategy. In the strategy discussion we will then show that Waiter can follow the proposed strategy and force a graph $G$ with a partition $V(G)=V_1\cup V_2$ satisfying the properties (1)–(5).

Strategy description: Waiter’s overall strategy consists of five stages, and a preparatory step between Stage II and Stage III, in which no move is made, but the free edges are partitioned in a suitable way into several subboards. Before the game starts, fix a partition $V=V_1\cup V_2$ such that $|V_2| = 500 \lfloor \gamma n \rfloor$ , and fix an equipartition $V_2=V_{2,1}\cup \ldots \cup V_{2,100}$ , i.e. $|V_{2,j}|=5\lfloor \gamma n \rfloor$ for every $j\in [100]$ .

Stage I: Waiter chooses an arbitrary vertex $x^* \in V_1$ . Offering only edges in $E_{K_n}(V_1)$ incident to $x^*$ for $\lfloor 25 C_0 \log (n) \rfloor$ turns she claims a star with centre $x^*$ . Once this is done, let $S^* \,:\!=\, N_C(x^*)$ and $R^* = \emptyset$ . Afterwards she continues with Stage II.

Stage II: This stage consists of two substages:

1. Stage II.a: For every $j\in [100]$ , Waiter forces a $K_5$ -factor on the graph $K_n[V_{2,j}]$ . The details will be given in the strategy discussion. Having done so, label the $K_5$ -copies in these factors with $K_{i,j}$ and $i\in [\lfloor \gamma n \rfloor ]$ . Let $\mathcal{K} \,:\!=\, \{K_{i,j}:\, i\in [\lfloor \gamma n \rfloor ], \,j\in [100]\}$ .

2. Stage II.b: For every $j_1\neq j_2$ and $i_1,i_2\in [\lfloor \gamma n \rfloor ]$ , Waiter forces a perfect matching between $V(K_{i_1,j_1})$ and $V(K_{i_2,j_2})$ . Details will be given in the strategy discussion. Afterwards, Waiter does a preparatory step and afterwards proceeds with Stage III.

Preparatory step: Fix a partition of the graph induced by $E_F(K_n)\setminus E_{K_n}(V_2)$ into $G_1 \cup G_2 \cup G_3 \cup G_4$ such that the following holds:

1. (G1) For every pair of vertices $v,w\in V$ it holds that $|N_{G_1}(v)\cap N_{G_1}(w)\cap V_1|\geq 0.05 n$ .

2. (G2) For every $v\in V_1$ we have $d_{G_2}(v,V_2)\gt 80\lfloor \gamma n \rfloor$ .

3. (G3) For every disjoint sets $X\subseteq V_1,Y\subseteq V$ of size $|X|=|Y|=m\,:\!=\,\lfloor C_0 \log (n)\rfloor$ , it holds that $e_{G_3}(X,Y)\gt 0.2 m^2$ .

4. (G4) For every $v \in V \setminus (S^*\cup \{x^\ast \})$ it holds that $d_{G_4}(v,S^*) \geq 4 C_0 \log (n)$ .

Details on why such a partition exists are given in the strategy discussion.

Stage III: Playing on $G_1$ , Waiter forces Client’s graph to satisfy that $|N_C(v)\cap N_C(w)\cap V_1|\geq \alpha n$ holds for every $v,w \in V$ . The details on how Waiter can achieve this goal will be given in the strategy discussion. Waiter proceeds with Stage IV.

Stage IV: Playing on $G_2$ , Waiter forces Client’s graph to satisfy that for every $v \in V_1$ it holds that $d_C(v,V_2) \geq 40 \lfloor \gamma n \rfloor$ . The details on how Waiter can achieve this goal will be given in the strategy discussion. Waiter proceeds with Stage V.

Stage V: Playing on $G_3$ , Waiter forces Client’s graph to satisfy that between every two disjoint sets $A\subseteq V_1$ and $B\subseteq V$ of size $\lfloor C_0\log (n) \rfloor$ there is an edge in $C$ . The details on how Waiter can achieve this goal will be given in the strategy discussion.

Stage VI: Playing on $G_4$ , for every $v\in V\setminus (S^\ast \cup \{x^\ast \})$ Waiter ensures that by the end of this stage it holds that $d_C(v,S^*) \geq 2 \lfloor C_0 \log (n) \rfloor$ . The details on how Waiter can achieve this goal will be given in the strategy discussion.

Now, before coming to the strategy discussion, let us first check that, if Waiter can follow the strategy without forfeiting the game and can reach all the described goals, the final Client’s graph $C$ with the partition $V(C) = V_1 \cup V_2$ fulfils the properties (1)–(5) of Theorem3.1.

Property (1) is true by the initial choice of $V_1$ and $V_2$ . (2.a) and (2.b) are ensured in Stage I, while (2.c) is given by the outcome of Stage VI. Property (3) is obtained in Stage III, and property (4) is done in Stage V. Moreover, we can distribute the collection of cliques $\mathcal{K}$ arbitrarily into $\mathcal{K}=\mathcal{K}_{good}\cup \mathcal{K}_{bad}$ such that $|\mathcal{K}_{bad}|=\lfloor \gamma n \rfloor$ . This way, (5.a) holds trivially. For property (5.b) note that by the outcome of Stage IV every vertex $v\in V_1$ satisfies $d_C(v,V_2) \gt 40 \lfloor \gamma n \rfloor$ . Moreover, using the matchings from Stage II.b, we also obtain such a bound for every vertex $v$ belonging to $\mathcal{K}_{bad}$ . Finally, property (5.c) follows from Stage II.b.

Strategy discussion: We discuss all of the five stages separately. Note that the boards of these different stages are disjoint from each other.

Stage I: Waiter can easily follow this strategy for large enough $n$ .

Stage II: Waiter can force a $K_5$ -factor on each $K_n[V_{2,j}]$ by Theorem1.2 in [13]. Let $\mathcal{K} = \{K_{i,j}:\, i\in [\lfloor \gamma n \rfloor ], \,j\in [100]\}$ be the set of cliques in the union of these $K_5$ -factors. Additionally, for every $j_1\neq j_2$ and $i_1,i_2\in [\lfloor \gamma n \rfloor ]$ , let $G_{i_1,j_1,i_2,j_2}\subseteq K_n$ be the complete bipartite graph between $V(K_{i_1,j_1})$ and $V(K_{i_2,j_2})$ . Then all edges of $G_{i_1,j_1,i_2,j_2}$ are still free when Waiter enters Stage II, and for different tuples $(i_1,j_1,i_2,j_2)\neq (i_1',j_1',i_2',j_2')$ the graphs $G_{i_1,j_1,i_2,j_2}$ and $G_{i_1',j_1',i_2',j_2'}$ are edge-disjoint. Hence, Waiter can apply the strategy from Lemma 2.9 to each of the graphs $G_{i_1,j_1,i_2,j_2}$ separately, and thus claim a matching of size 5.

Preparatory step: In order to show that there is a partition $G_1\cup G_2\cup G_3\cup G_4$ of the graph induced by $E_F(K_n) \setminus E_{K_n}(V_2)$ as desired, we show that a randomly chosen partition $G_1\cup G_2\cup G_3\cup G_4$ a.a.s. satisfies the properties (G1)–(G4). To be more precise, for each edge $e \in E_F(K_n) \setminus E_{K_n}(V_2)$ we decide independently with equal probability $1/4$ in which of the graphs $G_1,G_2,G_3,G_4$ it will be included. We consider each of the desired properties separately.

1. (G1) Let $v,w \in V$ , then $|N_{K_n}(v)\cap N_{K_n}(w)\cap V_1| = |V_1\setminus \{v,w\}|$ . Since so far edges intersecting $V_1$ have only been claimed in Stage I, we conclude that

   \begin{equation*}|N_{F}(v)\cap N_{F}(w)\cap V_1| \geq n - 500\gamma n - 2 - 50C_0\log (n) \gt 0.99n, \end{equation*}
   by the choice of $\gamma$ , for large $n$ . For the random variable $X^{G_1}_{v,w} = |N_{G_1}(v)\cap N_{G_1}(w)\cap V_1|$ we have $X^{G_1}_{v,w} \sim \text{Bin} \left (|N_{F}(v)\cap N_{F}(w)\cap V_1|, \frac{1}{16} \right )$ with expectation $\mathbb E(X^{G_1}_{v,w}) \gt 0.06n$ . Applying Chernoff (Lemma 2.1) and union bound we find that (G1) fails with probability $o(1)$ .

2. (G2) Checking (G2) can be done analogously, using that for every $v\in V_1$ , we have $d_F(v,V_2)\geq |V_2| - 50C_0\log (n) \gt 499\gamma n$ .

3. (G3) This can be checked analogously to property (G3) in the proof of Theorem1.1, using that for every every disjoint sets $X\subseteq V_1,Y\subseteq V$ of size $|X|=|Y|=m=\lfloor C_0 \log (n)\rfloor$ , it holds that $e_{F}(X,Y) \geq |X|\cdot |Y| - 50C_0\log (n) \geq 0.9 m^2$ .

4. (G4) This can be checked analogously to property (G2), using that $d_F(v,S^\ast )=|S^\ast |$ for every $v\notin S^\ast \cup \{x^\ast \}$ .

Stage III: In this stage Waiter only offers edges of $G_1$ which are incident with $V_1$ . Waiter plays the strategy from Lemma 2.8 with $\beta =0.05$ , and $N_{\{v,w\}}\,:\!=\,N_{G_1}(v)\cap N_{G_1}(w)\cap V_1$ for every set $\{v,w\}$ of two vertices in $V$ . By Lemma 2.8, Waiter then ensures that $|N_C(v)\cap N_C(w)\cap N_{\{v,w\}}| \geq \frac{\beta n}{500} \geq \alpha n$ holds for every $v,w\in V$ .

Stage IV: By property (G2) it holds that $d_{G_2}(v,V_2) \gt 80 \lfloor \gamma n \rfloor$ for every $v \in V_1$ . With a simple pairing strategy, Waiter reaches the described goal.

Stage V: Waiter reaches the described goal by an application of Theorem2.7. To be more precise, let

\begin{equation*} \mathcal {F} \,:\!=\, \{E_{G_3}(A,B)\,:\, A \subseteq V_1, B \subseteq V, |A|=|B| = \lfloor C_0 \log (n) \rfloor, A \text { and } B \text { disjoint} \}. \end{equation*}

Using (G3) and the choice of $C_0$ , we obtain $\sum _{F \in \mathcal{F}} 2^{-|F|+1} \leq n^{2m} \cdot 2^{-0.2m^2+1} = o(1)$ analogously to the discussion of Maker’s strategy. In particular, Waiter can force Client to claim an element of each edge set in $\mathcal{F}$ .

Stage VI: By property (G4) it holds that $d_{G_4}(v,S^\ast ) \gt 4C_0\log (n)$ for every $v \in V\setminus (S^\ast \cup \{x^\ast \})$ . Again, with a simple pairing strategy, Waiter reaches the described goal.

6. Concluding remarks

Though we presented no $\Delta$ such that Maker in the $(1\,:\,1)$ game on $K_n$ cannot obtain a graph which is universal for spanning trees of degree $\Delta$ , we believe that the degree order $n/\log n$ in Theorem1.1 is optimal. More precisely, we pose the following conjecture.

Conjecture 6.1. There exists a constant $C\gt 0$ such that the following holds for every large enough integer $n$ . In the $(1\,:\,1)$ Maker-Breaker game on $K_n$ , Breaker has a strategy to prevent Maker from claiming a graph which contains a copy of every tree $T$ with $n$ vertices and maximum degree $\Delta (T)\leq \frac{Cn}{\log (n)}$ .

In contrast, we believe that the maximum degree order in Theorem1.2 can be improved.

Conjecture 6.2. There exists a constant $c \gt 0$ such that the following holds for every large enough integer $n$ . In the $(1\,:\,1)$ Waiter-Client game on $K_n$ , Waiter has a strategy to force Client to claim a graph which contains a copy of every tree $T$ with $n$ vertices and maximum degree $\Delta (T)\leq c n$ .

6.1 Tree universality in Client-Waiter games

Together with Picker-Chooser games Beck also introduced Chooser-Picker games (cf. [4]), later studied under the name Client-Waiter (cf. [12], [22]). In a $(1\,:\,1)$ Client-Waiter game on a hypergraph $\mathcal{H} = (\mathcal{X},\mathcal{F})$ Waiter picks $2$ elements of the board $\mathcal{X}$ and offers them to Client. Client chooses one of them for himself and returns the remaining one to Waiter. If there is only one element left in the last round, it goes to Client. Client wins if she fully claims a winning set $F \in \mathcal{F}$ ; otherwise, Waiter wins.

It is well known (and observed already by Beck) that the Erdős-Selfridge criterion can be adapted for Client-Waiter games and if

\begin{equation*}\sum _{F\in \mathcal {F}} 2^{-|F|} \lt 1,\end{equation*}

then in the $(1\,:\,1)$ Client-Waiter game on $(X,\mathcal{F})$ , Client has a strategy to claim at least one element in each of the sets in $\mathcal{F}$ . As in Maker-Breaker games, we can use this criterion to prove that Client can claim a good expander in $K_n$ . Roughly speaking, we define a family $\mathcal{F}$ of edge sets in $K_n$ with the property that if Client has at least one edge in every set from $\mathcal{F}$ , then every vertex set of her graph has a big neighbourhood, and there is a Client’s edge between every pair of not too small sets. In view of expander properties from [24], one can deduce that Client in the $(1\,:\,1)$ game on $K_n$ can claim a graph that contains copies of all trees $T$ with $\Delta (T) \leq \frac{c n^{1/3}}{\log (n)}$ . We can further relax the last inequality to $\Delta (T) \leq \frac{c n^{1/2}}{\log (n)}$ , if we apply a result from [17]. Unfortunately, we do not see how to adapt our proof of Theorem1.2 to the Client-Waiter version; still, we suspect that the following is true.

Conjecture 6.3. There exists a constant $c\gt 0$ such that the following holds for every large enough integer $n$ . In the $(1\,:\,1)$ Client-Waiter game on $K_n$ , Client has a strategy to claim a graph which contains a copy of every tree $T$ with $n$ vertices and maximum degree $\Delta (T)\leq \frac{cn}{\log (n)}$ .

The degree order in the above conjecture cannot be improved since it is known [1] that there exists a constant $C\gt 0$ and a tree $T$ with $n$ vertices and maximum degree $Cn/\log (n)$ such that Client cannot claim a copy of $T$ in $K_n$ .

6.2 Tree universality in Avoider-Enforcer games

Finally, let us mention another class of positional games, called Avoider-Enforcer or Avoider-Forcer games (cf. [4], [21]). For simplicity, let us focus on the symmetric and so-called strict version only. In a $(1\,:\,1)$ Avoider-Enforcer game on a hypergraph $\mathcal{H} = (\mathcal{X},\mathcal{F})$ Avoider (who starts) and Enforcer claim in turns one not yet claimed element of the board $\mathcal{X}$ , until all elements are claimed. Enforcer wins if at the end of the game all elements of at least one set $F \in \mathcal{F}$ belong to Avoider; otherwise Avoider is the winner. Lu [28] proved that the Erdős-Selfridge condition on $\mathcal{H}$ implies that Avoider has a winning strategy in the $(1\,:\,1)$ Avoider-Enforcer game on $\mathcal{H}$ . Furthermore, it is known that the assertion holds also when Enforcer starts the game. In view of that, we can say that the Erdős-Selfridge condition implies that the second player in the $(1\,:\,1)$ Avoider-Enforcer game on $\mathcal{H}$ can force the first player to claim at least one element in each of the sets in $\mathcal{H}$ . It is now enough to add expander properties from [17] to infer that Enforcer in the $(1\,:\,1)$ game on $K_n$ can force Avoider to claim a graph that contains copies of all trees $T$ with $\Delta (T) \leq \frac{c n^{1/2}}{\log (n)}$ . It seems challenging to improve this result.

6.3 Waiter-Client minimum pair degree game

In Lemma 2.8, we prove that Waiter can force Client in the $(1\,:\,1)$ Waiter-Client game on $K_n$ to claim a graph where each pair of vertices has pair degree $\alpha n$ for some suitable $\alpha$ . We believe that this result might be of independent interest. Furthermore, we want to pose the following problem:

Problem 6.4. Find the maximum $\alpha$ such that for every large enough $n$ Waiter has a strategy in a $(1\,:\,1)$ Waiter-Client game on $K_n$ to force Client to claim a graph with the following property: for any two vertices $v,w \in V(K_n)$ we have $|N_C(v) \cap N_C(w)| \geq \alpha n$ .

Note that in the Maker-Breaker version, Breaker can easily ensure that $|N_M(v) \cap N_M(w)| = 0$ for two fixed vertices $v, w \in V(K_n)$ .