No CrossRef data available.
Article contents
Sampling and interpolation for the discrete Hilbert and Kak–Hilbert transforms
Part of:
Integral transforms, operational calculus
Groups and semigroups of linear operators, their generalizations and applications
Published online by Cambridge University Press: 07 March 2022
Abstract
The goal of the paper is to obtain analogs of the sampling theorems and of the Riesz–Boas interpolation formulas which are relevant to the discrete Hilbert and Kak–Hilbert transforms in
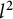 $l^{2}$
.
$l^{2}$
.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Boas, R.,
The derivative of a trigonometric integral
. J. Lond. Math. Soc. 164(1937), 1–12.Google Scholar
Butzer, P. and Berens, H., Semi-groups of operators and approximation, Springer, Berlin, 1967.10.1007/978-3-642-46066-1CrossRefGoogle Scholar
Butzer, P. L., Ferreira, P. J. S. G., Higgins, J. R., Schmeisser, G., and Stens, R. L.,
The sampling theorem, Poisson summation formula, general Parseval formula, reproducing kernel formula and the Paley–Wiener theorem for bandlimited signals—their interconnections
. Appl. Anal. 90(2011), nos. 3–4, 431–461.10.1080/00036811003627567CrossRefGoogle Scholar
Butzer, P. L., Schmeisser, G., and Stens, R. L.,
Shannon sampling theorem for bandlimited signals and their Hilbert transform, Boas-type formulae for higher order derivatives. The aliasing error involved by their extensions from bandlimited to non-bandlimited signals
. Entropy 14(2012), 2192–2226. https://doi.org/10.3390/e14112192
CrossRefGoogle Scholar
De Carli, L. and Samad, S.,
One-parameter groups and discrete Hilbert transform
. Can. Math. Bull. 59(2016), 497–507.10.4153/CMB-2016-028-7CrossRefGoogle Scholar
Grafakos, L.,
An elementary proof of the square summability of the discrete Hilbert transform
. Amer. Math. Monthly 101(1994), 456–458.10.1080/00029890.1994.11996974CrossRefGoogle Scholar
Higgins, J. R.,
A sampling theorem for irregular sample points
. IEEE Trans. Inform. Theory 22(1976), 621–622.10.1109/TIT.1976.1055596CrossRefGoogle Scholar
Krein, S. G., Linear differential equations in Banach space, Translations of Mathematical Monographs, 29, American Mathematical Society, Providence, RI, 1971, v+390 pp.Google Scholar
Nikol’skii, S., Approximation of functions of several variables and imbedding theorems, Springer, Berlin, 1975.10.1007/978-3-642-65711-5CrossRefGoogle Scholar
Pesenson, I. Z.,
Boas-type formulas and sampling in Banach spaces with applications to analysis on manifolds
. In: New perspectives on approximation and sampling theory, Springer International Publishing, Cham, 2014, pp. 39–61.10.1007/978-3-319-08801-3_3CrossRefGoogle Scholar
Pesenson, I. Z.,
Sampling formulas for groups of operators in Banach spaces
. Sampl. Theory Signal Image Process. 14(2015), no. 1, 1–16.CrossRefGoogle Scholar
Riesz, M.,
Eine trigonometrische Interpolationsformel und einige Ungleichungen für Polynome
. Jahresber. Deutsch. Math.-Verein. 23(1914), 354–368.Google Scholar
Riesz, M., Les fonctions conjuguees et les series de Fourier. C. R. Acad. Sci. 178(1924), 1464–1467.Google Scholar
Schmeisser, G.,
Numerical differentiation inspired by a formula of R. P. Boas
. J. Approx. Theory 160(2009), 202–222.10.1016/j.jat.2008.04.005CrossRefGoogle Scholar
Schur, I.,
Bemerkungen zur Theorie der beschran̈kten Bilinearformen mit unendlich vielen Veran̈derlichen
. J. Reine Angew. Math. 140(1911), 1–28.10.1515/crll.1911.140.1CrossRefGoogle Scholar



