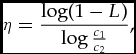DISCOUNTING FOR PUBLIC POLICY: A SURVEY

Abstract:

This article surveys the debate over the social discount rate. The focus is on the economics rather than the philosophy literature, but the survey emphasizes foundations in ethical theory rather than highly technical details. I begin by locating the standard approach to discounting within the overall landscape of ethical theory. The article then covers the Ramsey equation and its relationship to observed interest rates, arguments for and against a positive rate of pure time preference, the consumption elasticity of utility, and the effect of various sorts of uncertainty on the discount rate. Climate change is discussed as an application.

1. INTRODUCTION

It is now widely accepted that human activity is partly or largely responsible for climate change in the recent past and in the future, that under a ‘business as usual’ approach such climate change is likely overall to be extremely damaging to human life and well-being, and that we can mitigate its impact by taking steps to reduce our emissions of greenhouse gases in the short- and medium-term. This raises the question of to what extent we ought to reduce our emissions. Being an ought-question, the question is explicitly normative. Further, it is an ethical question, since the people who stand to be damaged the most by anthropogenic climate change, and stand to benefit the most from any mitigative action, are not the same as those on whom most of the responsibility for mitigation would fall. Those who would ‘pay’ for the mitigation in question are largely those living (i) now and (ii) in relatively affluent countries; the beneficiaries of mitigation are primarily those in poorer countries (where climate impacts are expected to be the most severe) and those who are not yet born. The question of discounting relates to the temporal aspect of this issue; to a first approximation, it is the question of the extent to which the fact that some anticipated benefit of mitigation would occur a given length of time into the future reduces the value of that benefit for ethical purposes, compared with an otherwise-similar hypothetical benefit occurring now.

The issues here are enormously important, and have rightly attracted an increasing amount of attention. The inevitable consequence of this is that the debate has become increasingly complex, and it can become difficult to see the wood for the trees. This article is a survey of the literature (mostly: the economics literature) on discounting. The emphasis is on understanding discounting from first principles, organizing the issues, and relating the controversies over ‘the discount rate’ to their foundations in matters of ethical theory. My survey thus emphasizes the conceptual rather than the technical aspects of discounting, but I have not shied away from the use of mathematical notation where this is the appropriate means of expression; I have (however) tried to make the essential mathematics accessible to those with a minimum of mathematical background. Where possible, the emphasis is on surveying the arguments on all sides, and (for readers who wish to follow up any particular issue in more detail) indicating which positions are taken by which existing authors/articles, rather than on taking sides. Since some of the controversies in the ‘discounting community’ concern the very organization of the conceptual landscape, however, it has not been possible to remain entirely neutral. The intended audience includes both economists who are interested in (in particular) the normative presuppositions and significance of claims found in the literature on discounting, and philosophers who wish to engage with the economists’ approach to intertemporal ethics, in general and in the context of climate change in particular.

The structure of the article is as follows. Section 2 situates the discussion of discounting within the landscape of ethical theories: in particular, I will follow a sizeable fragment of the literature in taking the fundamental issue to be one of how to maximize a given ‘social welfare function’ or ‘value function’, so that the direct focus is on the theory of the good, rather than either the theory of the right or e.g. any specifically virtue-ethical considerations. Given that we are going to theorize about some value function, the next question is which; Section 3 sets out the ‘discounted-utilitarian’ value function that is standard in the literature on discounting, and explains how this choice of value function embodies both some fundamental (and controversial) ethical principles, and some important simplifications that we will have occasion to revisit later. Section 4 introduces the terminology of ‘discount factors’ and ‘discount rates’ (as applied to consumption). Section 5 covers the ‘Ramsey equation’, an important equation that expresses the conditions for optimizing the discounted-utilitarian value function in terms of a discount rate on consumption, and that serves to organize much of the subsequent controversy concerning the choice of discount rate.

Section 6 reviews the relationship of appeal to the Ramsey equation to alternative ways of determining a discount rate. Sections 7 and 8 survey the arguments concerning the value of two of the key inputs to the Ramsey equation: respectively, the discount rate on future utility or ‘rate of pure time preference’, and the consumption elasticity of utility. Section 9 considers the extension of the analysis to take into account empirical and evaluative uncertainty; this section includes discussion of the expected-utility approach to uncertainty and its alternatives, and Weitzman’s celebrated uncertainty-based argument for a declining effective discount rate. Section 10 reviews the recent controversy over discounting in the context of climate change, focussing in particular on the Stern review and its aftermath. Section 11 discusses the extent to which the simplifications that are embraced by the standard discounting framework limit that framework’s usefulness for climate-change purposes (specifically, the sense in which the discounting framework is focussed on marginal rather than large-scale changes, and the issues of intratemporal inequality and changing relative prices). Section 12 summarizes.

2. SITUATING THE DISCOUNTING DISCUSSION WITHIN THE LANDSCAPE OF ETHICAL THEORIES

The dominant approach to the issue of discounting takes it that there is some function – a ‘social welfare function’ or ‘value function’ – that is an increasing function of ‘consumption’ (at all times, by all people), and that in some sense we seek to maximize. Within this framework, the key questions are what the social welfare function is, and how one can identify in practice the actions that maximize it. The main task of the present review article is to conduct an overview of the literature regarding the ‘discounting’ aspect of these key questions.

Before doing that, however, we pause briefly to note some aspects of the debate that we thereby set aside. For one thing, the assumption that any such function exists is not trivial. In the first instance, it includes various assumptions of comparability. For example, to hold that all relevant aspects even of a single person’s life can be measured by single ‘consumption’ parameter is to assume that there exists a privileged way to trade off benefits and costs of different types accruing to a given person (for example, changes in the person’s level of luxury goods vs subsistence goods, and of standard consumer goods vs environmental goods). Similarly, to hold that there is a single function capturing all evaluatively relevant aspects of all people’s lives is to assume that one can trade off benefits and costs that accrue to different people (e.g. members of the global rich vs the global poor), and at different times (e.g. present vs. future generations). (This is not, of course, to assume that such rates of tradeoff must all be finite.) Further, to assume that we need only take into account consumption (even in this broad sense of ‘consumption’) by people is to ignore any moral relevance that the interests of individuals of other species (especially: other sentient species) might have, and similarly any intrinsic value that ‘nature’ might have over and above the interests of individual organisms.

Another aspect of the ethical discussion that we tend to set aside by focussing on the maximization of a social welfare function can be seen if we first take a step back, to place the social-welfare-function framework in the context of an overall picture of the landscape of ethical frameworks. A standard taxonomy of ethics separates ethical questions into those pertaining to the theory of the good on the one hand, and those concerning the theory of the right on the other. In the first instance, one can enquire as to which outcomes (in the present case, involving varying levels of material wealth by various people at various times, and varying levels of climate change) are better than which others: this is the question of which theory of the good is correct. Secondly, one can enquire as to what a given agent, faced with a given decision, ought to do. The connection between the good and the right is one of the standard and controversial questions of normative ethics. Maximizing consequentialists hold that one is morally obliged to bring about the best state of affairs one is able to bring about; advocates of agent-centred prerogatives argue that while one is always morally permitted to bring about the best state of affairs, one is also permitted to give some priority to oneself and one’s nearest and dearest at the expense of strangers (for example, spending money on an expensive holiday or gift for one’s child rather than donating it to a charity that would do more impartially measured good with it); advocates of deontological side-constraints hold that in some cases, one is morally forbidden from bringing about the best state of affairs (for example, because one has promised the money to one’s friend or owes it to a company that has delivered agreed services, notwithstanding the fact that a carefully selected charity could do more good with the same money). (For a survey of these and related issues, see e.g. Sinnott-Armstrong 2014.)

Returning to our above question: a natural interpretation of the ‘social welfare function’ is as a function intended to represent overall good. On that interpretation, a focus on the questions of what the social welfare function is and how to maximize it amounts to a focus on the ‘theory of the good’ aspect of our ‘how much mitigation ought we to undertake?’ question, and a setting-aside of issues pertaining to the theory of the right. This move is in itself innocuous: the diversity of views on the ‘theory of the right’ notwithstanding, the majority of ethical frameworks agree that the theory of the good is at least one important part of the overall ethical story. It is worth noting, however, that a minority of authors also urge the importance, to the discounting debate, of questions that we thereby set aside, such as questions of whether future generations have rights that are not to be violated even if some carefully chosen rights-violations would, on balance, lead to greater overall good. We also set aside questions of how, granted that some specified degree of emissions reduction is the one that the world as a whole ought to undertake, the responsibility for that overall degree of reduction is to to be divided between countries, either as a matter of moral principle, or as a matter of international political negotiation. (See Gardiner 2004 for an overview of these and other broader ethical issues surrounding climate change.)

3. THE STANDARD FRAMEWORK FOR DISCOUNTING

As advertised in Section 2, then: We adopt the perspective of a benevolent social planner, seeking to maximize some value function that assigns numbers to states of affairs, in such a way that better states of affairs are assigned higher numbers than worse states of affairs. More precisely, since all decisions are made in the face of significant uncertainty (regarding, for instance, what the outcome of any given policy intervention would turn out to be), we will judge one course of action (ex ante) better than another whenever the first corresponds to a higher expectation value of this value function than does the second (cf. Section 9).

The standard assumption in the literature on discounting is that the appropriate value function takes the ‘discounted-utilitarian’ form

(1) $$\begin{equation} V_1 = \int dt \cdot \Delta (t) \cdot \sum _{i \in N(t)} w(i,t). \end{equation}$$

That is: the overall value of a state of affairs is computed by (1) calculating the amount of well-being present at each time t, by summing momentary well-being levels w(i, t) across all individuals i who are alive at time t; (2) ‘discounting’ the well-being at each time t by a factor Δ(t) that represents how important well-being at t is, relative to well-being at other times; (3) summing the resulting discounted quantities across time. ¹

This choice of value function is of course not uncontroversial. In particular, the following four remarks are in order.

First, note that even by utilitarian standards, the normal way to proceed would be first to compute an index of lifetime well-being for each person, corresponding to how well her life goes as a whole (that is, taking into account her momentary well-being level at each time in her life and combining them appropriately), and then to sum the resulting quantities across persons (with or without time-discounting). This is consistent with the functional form (1) only if the expression that relates an individual’s lifetime well-being to her momentary well-being levels at various times is additively separable, and the latter is a controversial assumption (Broome 1992: 53–4). The assumption of additive separability, however, has at least a pragmatic justification in the present context, as we typically lack the cross-temporal information that would be needed in order to evaluate a value function in which this separability condition does not hold.

Second, the utilitarian claim that overall goodness is represented by summing well-being across persons is controversial: many people object to the resulting thesis that an additional unit of well-being contributes just as much to overall value if it accrues to an already-well-off person as it does if it accrues to a badly-off person. Prioritarians hold that while there is a quantity that should be summed across persons, that quantity is not well-being, but rather a concave transform of well-being; egalitarians deny that the value function exhibits additive separability of persons at all, in which case the correct value function must irreducibly take into account comparisons between the well-being levels of different individuals, and there is no function of individual well-being that can be simply summed across persons to generate an accurate index of overall value. There is of course an enormous literature on these matters; here we will simply set them aside, and work with the (discounted-)utilitarian value function for the sake of simplicity. (At the general conceptual level, the issues of discounting on which this survey focusses are largely orthogonal to the disputes between utilitarians and prioritarians/egalitarians. The details of the analysis, however, are potentially significantly more complicated in the prioritarian and especially in the egalitarian case; see Appendix 2.)

Third, the choice of function for the factor Δ(t) in the discounted-utilitarian’s framework is, as we will see, a matter of significant controversy. This is not a controversy over the appropriateness of including Δ(t) in the value function at all, however, since, for all we have said so far, Δ(t) could everywhere take the value 1.

Fourth, the standard discussion assumes that population is exogenous. That is, in using the value function (1), no commitment is here incurred to using the same value function for comparisons of states of affairs involving different sized populations. To use (1) also for variable-population cases would be to commit to total utilitarianism (as opposed to, for instance, average utilitarianism or some ‘variable value’ approach) on questions of population ethics. Questions of population ethics, however, are beyond the scope of this article (for surveys, see e.g. Arrhenius n.d. and Greaves 2017).

In practice, the standard framework for discussions of discounting makes three important further amendments and simplifications (some of which we will need to revisit later, as they become particularly important and potentially seriously misleading in the context of climate change), as follows.

First, for the purposes of practical application we need to be able to relate the abstract quantity w(i, t) – person i’s momentary well-being level at time t – to the various concrete factors that partially determine it. In reality, of course, a person’s momentary well-being at any given time is determined by myriad factors, including various aspects of material consumption but also including number and quality of interpersonal relationships, a sense of purpose, education level, physical and mental health, availability of physical exercise and mental stimulation, access to amenities, housing quality, amount and quality of leisure time, and so on. We cannot in practice include all these factors in our analysis; the standard model makes the simplifying assumption that momentary well-being is determined by the individual’s ‘consumption’ of various well-defined resources that are traded on the market (e.g. rice, beans, books, electronic goods), together with certain non-market goods for which ‘shadow prices’ can reasonably be estimated (air quality, safety, access to national parks). Suppose that there are k such resources. Then we replace w(i, t) in (1) with a function u_i (c ₁(i, t), c ₂(i, t), . . ., c_k (i, t)), where c_j (i, t) is the amount of resource j that person i consumes at time t, and u_i is the function that determines person i’s well-being level on the basis of this vector of consumption levels. In practice, we simplify further by assuming that the utility function is the same for all individuals, so we write simply u rather than u_i . This modifies (1) to

(2) $$\begin{equation} V_2 = \int dt \cdot \Delta (t) \cdot \sum _{i \in N(t)} u(c_1(i,t), c_2(i,t), \ldots , c_k(i,t)). \end{equation}$$

Second, instead of working directly with the (in principle very long) vector of k different goods, we work in terms of a single variable c that we refer to simply as ‘consumption’. This is innocuous in principle: for any high-dimensional space representing all possible consumption bundles in the context of k different goods, we can always consider the indifference surfaces that are determined in that space by the individuals’ utility function, and construct a real-valued variable c that indexes those indifference surfaces. If we do so in such a way that higher-utility indifference surfaces correspond to higher values of c, we can then work with a utility function u(c) that is an increasing function of its single variable c, and no ultimately relevant information has in principle been lost. We then have

(3) $$\begin{equation} V_3 = \int dt \cdot \Delta (t) \cdot \sum _{i \in N(t)} u(c(i,t)). \end{equation}$$

While some aspects of the discounting discussion can be carried out at this level of abstraction, however, any proposal of a particular functional form for the utility function u(c) (such as the CRRA utility functions mentioned in Section 8), or (relatedly) a particular number of percentage points per annum for the discount rate (such as those surveyed in Table 1), is necessarily sensitive to the choice of a particular way of indexing indifference curves by ‘consumption numbers’ c. There are several more or less principled labelling techniques. One might, for example, choose a reference vector of relative prices for the commodities in one’s model (most naturally, but parochially: the relative prices that are given by marginal rates of substitution between the commodities in question at one’s actual, current consumption bundle), and index all indifference curves by the minimum expenditure needed to reach the curve in question given the reference prices. (This and other methods of indexing indifference curves are described in Deaton and Muellbauer 1980: sec. 7.2.) We must then remember that the numerical (as opposed to qualitative/structural) aspects of the discounting discussion are sensitive, at least in principle, to the choice of labelling technique. Relatedly, the use of a single index of ‘consumption’ can in practice encourage users of the resulting model to neglect the important phenomenon of ‘changing relative prices’; we return to this point in Section 11.3.

Table 1. The values for δ, g and r (in % p.a.), and for η, adopted by a selection authors and public bodies.

The third simplification is by any standards far from innocuous: the standard framework abstracts away from issues of intratemporal inequality. That is: since we wish to examine issues of intertemporal ethics, we of course do not assume that persons’ consumption levels are the same at different times. But the standard framework does proceed as though there were no differences in consumption levels between any two persons at a given time. In that case, the index i in ‘u(c(i, t))’ is no longer required, so that the value function V ₃ above is further modified to

(4) $$\begin{equation} V = \int dt \cdot \Delta (t) \cdot N(t) \cdot u(c(t)), \end{equation}$$

where N(t) is the number of people alive at time t. This raises the question of whether conclusions drawn from analysis of the standard framework are still valid once the reality of intratemporal inequality is taken into account.

The quantity V given in (4) is the value function that is used in the vast majority of the literature on discounting. Since its purpose is to engage with that literature, the present article will largely follow suit. Section 11, however, will consider the ways in which the results of the discussion would be substantively altered if these simplifications were not made.

4. DISCOUNT FACTORS AND DISCOUNT RATES

Suppose we have an opportunity to undertake an investment project, sacrificing k < 1 units of consumption today in order to secure an increase of 1 unit in consumption a time interval t later. Our basic question is: what is the threshold value of k at which the status quo becomes socially preferable to such a sacrifice? The answer to this question is the social discount factor for consumption at time t, R(t). (There is also a private discount factor, corresponding to private as opposed to social preferences; in the remainder of this article, the focus is on the social version.)

One generally expects R to decline with time – we are willing to sacrifice more today to gain an increase in one unit of consumption tomorrow than to gain an increase of one unit of consumption next year. The decline, however, may be faster or slower, and for current purposes the rate of the decline is crucial. We write $\frac{dR}{dt}$ for the rate of change of the discount factor (if R is declining, $\frac{dR}{dt}$ is negative). The discount rate, r, is proportional to this rate of change, in such a way that the faster the discount factor decreases, the greater the discount rate:

(5) $$\begin{equation} r= - \frac{1}{R}\frac{dR}{dt} . \end{equation}$$

We can rearrange the expression (5) to obtain a formula for the discount factor at time t in terms of the discount rates between times 0 and t: R = exp(− ∫ ^t ₀ r(t′)dt′). In the special case of a constant discount rate, this simplifies to the standard relationship R = exp(− rt), illustrated in Figure 1.

Figure 1. The discount factor as a function of time, for various constant-discount-rate scenarios R(t) = exp(− rt). Note, in particular, that with a discount rate of 3% per annum or higher, the discount factor is well below 0.1 for times more than 100 years in the future, and is essentially zero for times more than 200 years in the future. With a lower discount rate (1% per annum), the discount factor declines more slowly, but still reaches very low values for far-future times.

The choice of discount rate is crucial in the evaluation of projects some of whose important effects are long-term. Analyses that use a higher discount rate will tend to favour the short term: projects requiring sacrifices in the short term for the sake of benefits in the further future will be more likely to fail cost-benefit tests. Thanks to the exponential relationship between the discount rate and discount factor, small changes (at all times) to the discount rate can lead to very large changes to the amount by which distant future goods are discounted. Theoretical disagreements over how the discount rate is to be determined therefore have immediate policy importance, in particular in the context of climate change. Notoriously, the disagreement between Stern (2007) and e.g. Nordhaus (2008) over how much action to mitigate climate change is cost-effective is traceable almost entirely to the difference in their discount rates (respectively, 1.4% and 5%). More generally, since the social cost of carbon affects the relative costs of e.g. modes of transport and forms of technology, and is in turn highly sensitive to the discount rate, the latter is highly relevant to project evaluation in all government departments (Rose 2012).

5. THE RAMSEY EQUATION

The standard approach to determining the discount rate is via the Ramsey equation. This equation arises from the problem of optimizing the value function (4) that we arrived at in Section 3. To recap, this value function is given by

$$\begin{equation*} V = \int dt \Delta (t) N(t) u \left( c(t) \right), \end{equation*}$$

where Δ(t) is the discount factor for utility at time t, N(t) is population size at time t, c(t) is average per capita consumption at t, and u is the instantaneous utility function for an individual, expressed as a function of consumption.

Relative to any ‘status quo’ consumption path c(t), the ‘investment project’ outlined at the start of section 4 involves two changes: a decrease in consumption by k units now (at time 0), and an increase in consumption by 1 unit at time t. The first change tends to decrease V, while the second tends to increase V; we seek the conditions under which the net effect of these two changes together is to increase (or at least to preserve) V.

The answer ² is that in order to increase overall value V, an investment project’s rate of return must exceed (the ‘welfare-preserving rate of return on savings’)

(6) $$\begin{equation} r = \delta + \eta g, \end{equation}$$

where:

• • $\delta := -\frac{\dot{\Delta }}{\Delta }$ is the (negative of the) proportional time rate of change of the utility discount factor, a.k.a. the ‘rate of pure time preference’;

• • $\eta := -c \frac{u^{\prime \prime }}{u^\prime }$ , the consumption elasticity of utility, depends on both the utility function and (in principle) the consumption path. Here, $u^\prime \equiv \frac{du}{dc}$ is the rate at which utility increases as consumption increases, while $-u^{\prime \prime } \equiv - \frac{d^2u}{dc^2}$ is the rate at which $\frac{du}{dc}$ itself decreases as consumption increases. A higher value of η corresponds to a more concave utility function, i.e. one in which the phenomenon of diminishing marginal returns of consumption to utility is more marked;

• • $g:= \frac{\dot{c}}{c}$ is the consumption growth rate, i.e. the proportional time rate of change of (average per capita) consumption.

(6) is the Ramsey equation. The premise that we ought to maximize (4) grounds an argument that we ought to use the quantity (6) as our discount rate when evaluating marginal projects.

Authors agreeing that the Ramsey equation provides correct guidance as to the value of the discount rate r nevertheless obtain different numbers for that rate, as they disagree on the inputs to the Ramsey equation: see Table 1.

Stern’s ‘δ = 0.1% p.a’ actually corresponds to discounting for existential risk, not pure time preference. See Stern (2007).

The values of δ and η are discussed in Sections 7 and 8 below (respectively). g is a straightforwardly empirical parameter, albeit one about whose value there is great uncertainty; the extension of the model to deal with uncertainty is the topic of Section 9.

6. TWO EMPIRICAL QUANTITIES RELATED TO THE DISCOUNT RATE

Two further arguments urge that the discount rate should be set equal to, respectively, the social rate of return r_MC on marginal capital, and the interest rate r_CM on credit markets. Since neither of these quantities is guaranteed to equal a discount rate determined directly by the Ramsey equation, potential disagreements arise. It is worth making our peace with these, as their relationship to the Ramsey equation is not immediately clear, and the second in particular has played a significant role in the debate over climate change. (See also the discussion in Gollier 2013: ch. 1.)

The social rate of return r_MC on marginal capital is defined as the largest value of r for which we have unfunded possible projects (i.e. opportunities not currently being taken) that would deliver an increase of 1 unit of consumption at time t per investment of exp(− rt) units made now. The argument for using r_MC as the discount rate is then a basic arbitrage argument: if the project under consideration requires a sacrifice of more than exp(− r_MCt) units for the same gain, it should not be undertaken, because the same funds could alternatively be invested elsewhere in the market for a greater gain at the same future date. (Thus, for example, in the context of climate change: Lomborg (2001: ch. 24) argues against climate change mitigation measures on the basis that many currently unfunded third world development projects offer higher rates of return.) If, on the other hand, the project under consideration requires a sacrifice of less than exp(− r_MCt) units, then it should be undertaken in preference to some of the projects that are already being funded.

Under the assumption that society’s current consumption plan is socially optimal, we do not need to choose between this argument and that of Section 5: the social rate of return on marginal capital is then equal to the welfare-preserving rate of return on savings. If, on the other hand, the social rate of return on marginal capital diverges from the welfare-preserving rate of return on savings, then prima facie (taking this and the argument of Section 5 together) we seem to have a contradiction, since we have arguments for each of two distinct numerical candidates for the socially efficient discount rate.

The appearance of contradiction evaporates when we clarify whether we are asking (i) whether it is better to undertake the proposed project or consume the funds now, or (ii) whether it is better to undertake the proposed project or some alternative investment project. If, say, the social rate of return on marginal capital is higher than the welfare-preserving rate of return on savings, that can only be because society is currently consuming too much (investing too little). In that case it can very well happen that the internal rate of return of some proposed project passes the Ramsey-equation test, but is lower than the social rate of return on marginal capital. Undertaking the project is then better than consuming the resources in question now, but undertaking some other, more productive project is better still (Gollier 2012, sec. 4; Goulder and Williams 2012: sec. 3.4). Provided we understand our question as the first one, the Ramsey-equation test remains valid. (In a more pluralist vein, Goulder and Williams (2012) also argue that while the Ramsey-equation test determines whether a project improves overall social welfare, it is r_MC (in their notation, r_F ) that determines whether the project is a ‘potential Pareto improvement’ in the Kaldor-Hicks sense, and that depending on the decision context, either or both criteria may be important.)

Turning now to the relevance (or otherwise) of the credit markets: the argument for setting the discount rate equal to the interest rate r_CM prevailing on the credit markets is based on an appeal to democracy. First, an arbitrage argument establishes that the interest rate prevailing on credit markets reflects society’s actual willingness to sacrifice current for future consumption: if (say) investors were willing to sacrifice one unit of current consumption for less than e ^−r_CMt units of consumption a time t hence, then there would be an excess of supply of credit, and the interest rate would be driven down. Second, it is asserted that in a democracy, governments should discount future consumption at the same rate as this empirically observable public willingness to invest.

Again, under certain assumptions of ideal conditions, the interest rate on credit markets is equal to the social rate of return on marginal capital (r_CM = r_MC ), and hence we do not need to choose between this and the preceding argument. The ‘idealizing’ assumption required in this case is that the social rate of return on marginal capital (i.e. the rate of return calculated by taking into account all changes in future consumption generated by the project, regardless of to whom they accrue) is equal to the private rate of return (i.e. the rate of return calculated by taking into account only future consumption changes accruing to the investor herself). Given that assumption, we can reason as follows. First, an arbitrage argument establishes that the credit-market interest rate r_CM must be at least the private rate of return on capital: if it were not, then marginal investors in credit, instead of investing in the credit market, would switch to investing directly in productive capital, thus driving up the credit-market interest rate. Second, a similar argument establishes that the credit interest rate must be at most the private rate of return on marginal capital: if the former exceeded the latter, investors would switch from direct investment in capital to lending on the credit markets, until the two rates were brought into alignment. We have, then, the intermediate conclusion that r_CM = r ^private _MC . Given our further assumption of equality between private and social rates of return, we can therefore conclude that r_CM = r_MC as defined above (i.e. r_CM = r ^social _MC ). That further assumption, however, is wildly implausible, since externalities – market imperfections leading to divergences of private from social rate of return – are ubiquitous.

Divergences between r_CM and r_MC aside, this ‘democracy’ line of thought is often pitted directly against the use of the Ramsey-equation approach, when the latter yields a social discount rate distinct from observed interest rates. This discussion has recently been particularly prominent in the context of climate change; we return to it in Section 10.

7. THE RATE OF PURE TIME PREFERENCE

The present section sets aside the overall discount rate r on goods, and focusses on δ, the discount rate on utility or ‘rate of pure time preference’. Theorists are divided over whether this rate of pure time preference should be positive on the one hand, or zero on the other.

7.1. Arguments for a Zero Rate of Pure Time Preference

The basic ‘argument’ for a zero rate of pure time preference is from impartiality. Accepting a zero rate of pure time preference merely amounts to treating utility as equally valuable, regardless of when it occurs. But of course (runs the thought) the value of utility is independent of temporal location: there is no possible justification for holding that the value of (say) curing someone’s headache, holding fixed her psychology, circumstances and deservingness, depends upon which year it is. The axiomatic nature of impartiality is endorsed both by many of the seminal articles on the subject (Sidgwick 1890; Ramsey 1928; Pigou 1932; Harrod 1948; Solow 1974) and by many current authors (Cline 1992; Broome 2008; Dasgupta 2008; Dietz et al. 2008; Buchholz and Schumacher 2010; Gollier 2013).

To this we may add two further arguments. The second argument proceeds from the Pareto principle, and points out that this principle is inconsistent with a non-zero rate of pure time preference (Cowen 1992). To see the inconsistency, suppose that a particular person – Sarah, say – could live either in this century or the next. Consider two states of affairs that differ over when Sarah lives. Suppose that Sarah’s well-being is slightly better in the state of affairs in which she lives later, while everyone else’s well-being is unchanged. Then according to the Pareto principle, the ‘Sarah lives later’ state of affairs is better. But according to a value function whose rate of pure time preference is positive, this state of affairs may be worse. Thus δ ≠ 0 is inconsistent with the Pareto principle.

Third, if δ > 0 for negative (i.e. past) as well as positive (future) times, we have the absurd implication that deaths in the past were worse than deaths now. If, on the other hand, δ > 0 only for positive times, then we have temporal relativity, and this temporal relativity tends to lead to temporal inconsistency in judgements. We pause to explain the latter point (see also Broome 2004: sec. 4.3; 2012: pp.148–52).

Let us define a schedule of discount factors to be an assignment of a discount factor to each pair consisting of the time of the benefit to be evaluated and the time at which the evaluation is carried out: thus Rⁱ _j is the discount factor used by an evaluator at time t_i when evaluating costs or benefits occurring at time t_j . By definition, a schedule of discount factors is time-neutral iff the ratios $\frac{{R^i_j}}{\scriptsize{R^i_{j^\prime }}}$ are independent of i; otherwise it is time-relative. The point is then that if $\frac{\scriptsize{R^i_j}}{\scriptsize{R^i_{j^\prime }}} \ne \frac{\scriptsize{R^{i+1}_j}}{\scriptsize{R^{i+1}_{j^\prime }}}$ , then evaluations carried out at times i and i + 1 will disagree with one another on (some) decisions that involve trading off well-being at time j with well-being at time j′, even in the absence of any new information. Furthermore, the agents doing the evaluating at time i will be in a position to foresee that they will change their minds at i + 1, despite not having learnt anything new. This sort of time-inconsistency is generally taken to be an indicator of irrationality.

In the present case: Suppose that the rate of pure time preference, at any evaluation time t, is zero for all times prior to t, and some positive constant δ > 0 for all times later than t. Let t ₁, t ₂ be any pair of times with t ₂ > t ₁. We consider an operation that sacrifices c ₁ units of utility at time t ₁ in return for an increase of b ₂ units of utility at time t ₂. We evaluate this operation, first from the point of view of t ₁, and then from the point of view of t ₂. An evaluator at t ₁ applies a discount factor of exp(− δ(t ₂ − t ₁)) to utility gains occurring at the later time t ₂, and therefore deems the operation to be an overall improvement iff nexp(− δ(t ₂ − t ₁)) > m. The evaluator at t ₂, however, judges one unit of utility to be equally valuable whether it occurs at t ₁ or t ₂, and hence favours our operation iff n > m. This second criterion is of course less stringent than the first; there are thus operations such that, by the lights of his own evaluation strategy, an actor at t ₁ should turn them down, but the same actor at t ₂ should regret having done so.

Suppose, for example, that Ben gets the same amount of utility from each doughnut he eats, regardless of which day he eats it on, and (at least for small numbers of doughnuts) regardless of how many other doughnuts he has eaten on the same day. But suppose that each day, Ben discounts his own future utility in the manner suggested, while regarding all present and past utility as equally valuable: specifically, suppose that he discounts utility at the (extreme) rate of 60% per day. On Monday, he is offered a choice between (option 1) eating one doughnut on Tuesday or (option 2) eating two on Wednesday; given his Monday values, he judges option 1 to be better. He still agrees with this judgement on Tuesday. But come Wednesday, he has changed his mind about the relative value of Tuesday doughnuts and Wednesday doughnuts: he now thinks that Tuesday doughnuts and Wednesday doughnuts are equally valuable, and thus judges option 2 to be better than option 1. It is too late, of course: he cannot now do anything about it, but he regrets the decision he made on Monday. Furthermore, when deliberating on Monday, he was already in a position to foresee that he would thus later regret the decision he was making.

It is worth noting well, however, that the only sort of inconsistency that can result from the discounting structure in question is the phenomenon of foreseeable regret that we have seen in this example. This is arguably not as bad as foreseeable backtracking, in which an agent decides at time i to pursue a certain course of action at time i + 2, while recognizing that at time i + 1 she will no longer think that this course of action is best, and so will attempt to reverse her decision. The latter but not the former raises issues of commitment (‘tying oneself to the mast’); cf. the discussion of declining discount rates in Section 9.2.

7.2. Arguments for a Positive Rate of Pure Time Preference

Most theorists see some significant prima facie force to (in particular) the intuition of impartiality reported above, but it is far from agreed that that intuition carries the day. We now consider four arguments for a positive rate of pure time preference.

Our first argument is a direct response to the impartiality intuition: that full impartiality, while perhaps a moral ideal, is not a requirement of morality. For example, according to common sense morality, it is at least permissible to give the interests of one’s friends and family more weight than those of strangers in one’s decisions; according to defenders of a positive rate of pure time preference, the latter is merely a manifestation of this permissible partiality in the intertemporal case (Arrow 1999; Flanigan n.d.). In reply, several authors (Cowen and Parfit 1992; Caney 2008; Beckstead 2013) point out that to say that future utility is just as valuable as present utility is not to commit to a moral obligation to maximize overall value, and that Arrow’s objection seems to be more to the latter account of obligation (‘maximizing consequentialism’). To this, the proponent of the ‘permissible partiality’ argument might reply that his ‘social welfare function’, contrary to the interpretation we dubbed ‘natural’ in section 1, is not intended to be a representation of ‘overall value’ in the impartial sense; it is, rather, the function such that in his view the course of action that maximizes that function is the most advisable one, subject to the constraints of morality. The question then is whether this representation by a single discounted function is a sensible form for the non-maximizing-consequentialist view in question (as opposed, say, to the use of a fully impartial value function supplemented by principles expressing agent-centred prerogatives); the critics argue that it is not.

Second, and relatedly, many theorists hold that the use of a zero rate of pure time preference requires excessive sacrifice on the part of the present generation for the benefit of future generations (again, see Arrow 1999). The relevant theory here concerns the optimal rate of saving. For example, Arrow calculates that under certain plausible-looking circumstances, a zero rate of pure time preference would require us to save over two thirds of our income for the benefit of future people. (This ‘excessive sacrifice’ argument is of course closely related to the ‘permissible partiality’ argument just stated; what the ‘excessive sacrifice’ argument adds is that impartiality (is not only not required, but also) is not a sensible option.)

It is instructive to compare this ‘excessive sacrifice’ argument in the context of intertemporal ethics with one that often crops up in the assessment of utilitarianism as a moral theory for the intratemporal case. According to utilitarianism, rich people (like ourselves) should give away the vast majority of our wealth to the desperately poor. Many (e.g. Scheffler 1982) object that this implication is too demanding, and conclude that utilitarianism is false. The difference in the intertemporal case is that the fully impartial value function asks us to make these large sacrifices for people who are already richer than us. Thus, in practice the ‘excessive sacrifice’ argument is more compelling in the intertemporal case than in the intratemporal case. (The difference arises because of the possibility of generating a larger benefit in consumption terms for others than one’s own sacrifice, thanks to the phenomenon of investment. This effect has no analogue in the intratemporal case.)

Whether or not a value function embodying a zero rate of pure time preference does mandate an intuitively excessive level of saving, even under the assumption of a moral requirement to maximize, of course depends on the instantaneous utility function it is based on. Instead of concluding that δ > 0, some authors (for example, Asheim and Buchholz 2003; Dasgupta 2008) conclude that the utility function must be more concave than those considered by Arrow. Others (e.g. Dietz et al. 2008: 382) note that increasing the amount of assumed technical progress will also tend to decrease the optimal level of savings, for fixed δ. Another possibility is that (δ = 0 but) technical progress will push up growth to the point at which (for ordinarily assumed values of η) optimal savings rates are not excessive.

Third, there is a cluster of worries about adverse implications of time-impartiality in cases where the consumption or utility streams under consideration extend into the infinite future. The basic worry can be seen by considering the natural value function for infinite utility streams in the absence of discounting, ∑^∞ _{i = 0} u_i . Even if there is a common maximum value for each instantaneous utility u_i , the sum ∑^∞ _{i = 0} u_i has no upper bound, and (in addition) for infinitely many possible utility streams the sum will fail to converge at all. It follows that no utility stream is maximal relative to the preference order over utility streams that is represented by this value function, and (in addition) that the preference ‘order’ thereby represented is incomplete (strictly speaking, it is a preorder rather than an order on utility streams).

Developing this basic observation, an extensive literature investigates the consistency of time-impartiality with various other apparently plausible constraints on preference orderings in axiomatic frameworks (as opposed to: in the context of considering particular value functions). Inconsistency results are established by e.g. Koopmans (1960), Diamond (1965) and Epstein (1986).

Many authors take these concerns relating to infinite contexts to supply sufficient motivation for adopting a positive rate of pure time preference (note that with bounded instantaneous utilities, the discounted sum ∑^∞ _{i = 0}β ⁱ u_i (β < 1) does converge for every possible infinite utility stream (u_i )). Alternative responses include the following. Gollier (2013: 32) questions the motivation for insisting on the existence of an optimal consumption stream, since one can determine whether or not an alternative is an improvement over the status quo even if neither status quo nor alternative are optimal; this does not, however, address the second worry that the undiscounted sum may simply fail to converge for either or both alternatives. Svensson (1980) questions the motivation for the ‘continuity’ assumptions involved in many of the impossibility results, and establishes the consistency of a complete preference ordering and time-impartiality with the remainder of the Koopmans-Diamond axioms (see also Broome 1992: 140–5). A third response is that the utility streams under consideration in real scenarios do not in fact involve an infinite time horizon, since the human race will eventually become extinct due to e.g. the heat death of the Universe; if so, then (the response continues) it is perverse to base ethics for the actual world on paradoxes of infinity that one would have to face up to in distant alternative possible worlds. From the point of view of practical applications (if not of fundamental principle), perhaps the most powerful response is that of Dasgupta (2008: 157): even if the technical considerations in question do induce one to adopt a positive rate of pure time preference, an arbitrarily small positive value will suffice. The theorems, for instance, would supply no grounds for any objection to δ = 10⁻¹⁰⁰% per annum.

A fourth argument for a positive rate of pure time preference proceeds from the premise that the actions of a government should be selected on the basis of aggregating the preferences of present members of the body politic. The argument starts from the empirical premise that people do in fact discount future utility (the empirical literature on this issue is surveyed in (Frederick et al. 2002)). Therefore, the argument runs, the government should respect this preference, and itself discount future utility when evaluating projects. Since a close analogue of this last argument for the discount rate on goods has cropped up in the discussion of climate change, we delay discussion of its soundness until Section 10.

8. CONSUMPTION ELASTICITY OF UTILITY, η

Recall (from Section 5) that the second input to the Ramsey equation, the consumption elasticity of utility η, is defined by the equation $\eta = -c \frac{u^{\prime \prime }(c)}{u^\prime (c)}$ . The instantaneous value of η thus depends both on the utility function, and on the instantaneous level of consumption. In the literature on the discount rate, it is standardly assumed that the utility function has the (‘constant relative risk aversion’) form

(7) $$\begin{equation} u(c) = \frac{c^{1- \gamma }}{1-\gamma }, \end{equation}$$

where γ is a constant, i.e. is independent of c. (This assumption is made merely for mathematical tractability.) In that case, a simple calculation shows that η = γ, so that η itself is also independent of c (and hence also time-independent). A special case of (7) is the logarithmic utility function, u(c) = lnc, obtained in the limit γ → 1.

8.1. Three Roles for η

A higher value of η corresponds to a more concave utility function. In the standard approach – that is, the approach that seeks to maximize the expectation value of the value function (4) – this leads η to play three conceptually distinct roles, related to the degree of aversion to (respectively) risk, intratemporal inequality and intertemporal inequality. We pause to explicate these three roles in turn.

On risk aversion: The expectation value E[X] of a random variable X is the probability-weighted average of the possible values of X. We then say that a value function exhibits risk aversion iff it ranks a given lottery (in the sense of: an assignment of probabilities to consumption streams) as less good than a guarantee of the consumption stream that is the expectation value of those involved in the lottery: if, for example, it ranks a sure prospect of $100 as better than a 50:50 lottery yielding either $50 or $150. Assuming (as is standard; but see Section 9.3) the expected-value approach to uncertainty, this is the condition that E[V(c)] ⩽ V(E[c]). We rewrite (4) as

(8) $$\begin{equation} V = \int dt \cdot V_t, \end{equation}$$

where V_t = Δ(t) · N(t) · u(c(t)). Since E[V] = ∫dt · E[V_t ], we can abstract from intertemporal issues, and consider a representative time t; we will have risk-aversion in the above sense if the utility function is such that for any lottery over consumption level c, E[u(c)] ⩽ u(E[c]). A standard argument (Eeckhoudt et al. 1995: 8) establishes that this condition obtains if and only if the utility function is concave (that is, while u′ > 0, u′′ < 0).

This tells us when a utility function exhibits risk aversion, but not yet when one utility function exhibits more risk aversion than another. That is, we have not yet defined a notion of degree of risk aversion. To do so, we define the risk premium associated with a given lottery to be the amount of consumption π such that enjoying a sure consumption level that is equal to the expected consumption level in the lottery less π is ex ante equivalent to facing the lottery: that is, the quantity π such that E[u(c)] = u(E[c] − π). We then say that utility function u ₁ exhibits more risk aversion than utility function u ₂ if and only if the risk premium for every lottery is higher according to u ₁ than according to u ₂. It is straightforward to show (Pratt 1964) that one utility function exhibits higher risk aversion than another in this sense if and only if the first yields a higher value of η at all consumption levels than the second. (Strictly: If the first has η everywhere at least as high as the second, and strictly higher for at least one consumption level in every interval. See (Pratt 1964: Thm. 1).)

On aversion to inequality: As a first pass (but see below), we say that a value function exhibits aversion to inequality if, given two individuals with unequal consumption levels, a transfer of a certain amount of consumption from the higher-consuming to the lower-consuming individual (which transfer, however, does not reverse the ordering of the two individuals’ levels) always increases value. (This is the ‘Pigou-Dalton principle’ (Sen 1973; Fleurbaey 2012; Adler 2013).) There are several possible rationales for aversion to inequality. First, consumption exhibits diminishing marginal utility, so that a given increment in consumption makes less difference to one’s welfare the better off one (already) is. Second, the degree of welfare concomitant on a given level of consumption depends how that consumption level compares to the consumption levels of others with whom one is in contact, both for purely psychological reasons and due to social exclusion effects (Payne 2000; Alesina et al. 2004; Di Tella and MacCulloch 2006; Dynan and Ravina 2007; Morgan et al. 2007; Clark et al. 2008; Oishi et al. 2011). Third, some take inequality of resources simply to be intrinsically bad, perhaps for reasons of fairness. Finally, some theorists believe that inequality even of welfare levels is intrinsically a bad thing (Temkin 1993), so that inequality of consumption levels is bad to a degree beyond that that would be mediated via by any of the above routes. To probe the relation between inequality aversion and η, we consider the cases of intra- and intertemporal inequality separately.

On aversion to intratemporal inequality: As we noted in Section 3, since the value function (4) considers only matters of average per capita consumption at a given time, that value function altogether ignores issues of intratemporal inequality. More fundamentally, we would want to consider instead the value function (3):

$$\begin{equation*} V_3 = \int dt \cdot \Delta (t) \cdot \sum _{i=1}^{N(t)} u \left( c_i(t) \right), \end{equation*}$$

where i indexes individual people, and c_i (t) is individual i’s consumption at time t. We say that the value function is averse to intratemporal inequality if, given any two individuals with differing consumption levels at a given time t, overall value would be increased by giving each of the two individuals a consumption level that is half of their combined consumption, and leaving all others’ consumption levels unaffected. An analysis structurally identical to that above then shows that V ₃ is averse to intratemporal inequality if and only if u is concave, and that one value function of the form V ₃ is ‘more averse to intratemporal inequality’ than another if and only if the first arises from a utility function u that everywhere has a higher value of η than the second.

Similar considerations apply to the analysis of intertemporal inequality, that is, inequality in consumption levels occurring at different times. To see this, return to the simplified value function (4), and consider a case in which two individuals, living at different times, enjoy different levels of consumption c(t ₁), c(t ₂). The analysis in the intertemporal case is slightly complicated by the presence of the weighting factors Δ(t), but we can deal with the complications by defining the weighted average $\skew2\tilde{E}(c(t_1), c(t_2)) := \Delta (t_1)c(t_1) + \Delta (t_2) c(t_2)$ . If we say that (4) is averse to intertemporal inequality just in case its value is always increased by replacing both consumption levels in the unequal intertemporal pair with their weighted average $\tilde{E}(c(t_1), c(t_2))$ , then the same analysis as above establishes that (4) is averse to intertemporal inequality iff u is concave, and a similar extension of the reasoning establishes that one value function of the form (4) is ‘more averse to intertemporal inequality’ than another if and only if the first arises from a utility function u that everywhere has a higher value of η than the second.

It is this third role of η that corresponds to its importance in the debate over the discount rate. If (as is standardly assumed) future generations will, climate change or no climate change, enjoy higher levels of average per capita consumption than present generations – if, that is, consumption growth g is positive – then a higher value of η corresponds to a higher discount rate. (If, instead, future generations are worse off than the present generation – due to climate change or otherwise – then of course the relationship between η and the discount rate is reversed.)

8.2. Models that Separate the Three Roles

Several authors (e.g. Dietz et al. 2008; see also Selden 1978; Epstein and Zin 1989) have urged that since the three roles that are played by η in the standard approach are conceptually distinct, to represent all three by a single parameter is both to rule out without justification the possibility that the parameters relevant to the three roles vary independently of one another, and to court unnecessary confusion.

On the former point: it does not seem incoherent (at least) to exhibit relatively little aversion to risk, but great aversion to any form of interpersonal inequality (intra- or inter-temporal) (Beckerman and Hepburn 2007). Still less does it seem incoherent to exhibit great aversion to intratemporal inequality, but relatively little aversion to intertemporal inequality, if the reason for inequality aversion is based on the psychological or social exclusion effects mentioned in Section 8.1, as opposed to any view that inequality either of resources or of welfare is simply intrinsically bad. One might therefore seek a model that allows parameters for the three types of aversion to be varied independently, so that the resulting positions can be represented within the terms of the model.

On the latter point: As we noted at the outset, discussions of climate change often note that the most significant harms due to climate change will occur in the relatively far future, while the costs of any mitigative action will be incurred much sooner. Assuming that consumption growth is positive, this fact corresponds to a prima facie tendency for increasing η to favour less aggressive mitigative action; this is the tendency that is captured in the contribution of η to the discount rate in the basic Ramsey equation (6). But that basic Ramsey model ignores both intratemporal inequality and risk; a full analysis would carry out a line of the reasoning parallel to that of Section 5, but starting from the expectation value of the more detailed value function (3) rather than from the simplification (4). Notwithstanding the point that expected average per capita consumption is higher in the future than it is for those who would stand to bear the costs of mitigation, in such a fuller analysis, increasing η would place greater evaluative emphasis on incremental changes to climate impacts occurring in those future regions of the world and/or possible scenarios in which the potential beneficiaries of mitigation are actually poorer than the mitigators. Thus the relationships of η to intratemporal inequality and to risk potentially work against its relationship to intertemporal inequality, when we ask whether, overall, increasing η would favour more or less mitigative action. (See also the discussions in Dietz et al. 2007, 2008: 378).

To say that the three notions are conceptually distinct, however, is not to say that there cannot be close links between them – perhaps close enough that no model of rational decision-making can vary them independently. Arguments to this effect concerning the relationship between risk aversion on the one hand and (either type of) inequality aversion on the other are given by Harsanyi (1953, 1955, 1977).

8.3. Determining the Value of η

Setting aside the discussion of Section 8.2 and assuming the standard model, what then should the value of η be?

Many empirical studies aim to establish the extent to which real people do exhibit aversion to risk and interpersonal inequality in their choice behaviour. For the purposes of answering our normative question, it is important not to overstate the relevance of such empirical data: our question is what value for η our analysis should use, and it does not of course immediately follow, from the fact that people do employ a certain value for η, that they, we or anyone else should employ that value (Buchholz and Schumacher 2010: 378). (It does not immediately follow; but that is not to say that it does not follow at all. Some authors would defend the inference using a ‘democracy argument’ that is a close cousin of the one discussed in Section 10.) That said, the empirical data may be informative nonetheless: a normative theorist advocating an η value that lies outside the range that empirical studies suggest that people normally use should be aware that he is so deviating from the statistical norm, and that he may be committed to passing a negative judgement on the values of the subjects in the empirical studies in question. We will first survey the more directly normative arguments, and then provide a brief survey of the empirical literature.

On the more directly normative side: Okun (1975: 91–5) outlines a ‘leaky bucket’ thought experiment, in which one envisages a transfer of resources from a richer to a poorer person (at specified initial wealth levels), and one asks how ‘lossy’ the transfer can be (that is, by how much the amount gained by the poorer person can fall short of the amount taken from the richer person) before the transfer ceases to constitute an overall improvement. If, for example, one judges that one person having £100k and another having £20k is neither better nor worse overall than one person having £60k and another having £30k (that is, the result of transferring £40k away from the better-off person but with a loss of 75% of the transferred resources), then in the context of the utilitarian model one is implicitly committed to an η value of about 1.2. ³ Taking another approach, Buchholz and Schumacher (2010) show that axiomatic conditions intended to capture aspects of ‘circumstance solidarity’ or ‘absence of envy’ variously require η = 1, η > 1, η = 2 and η = ∞; as witness the variety of these conclusions, however, the motivation for the axioms is open to serious question. Another approach considers the optimal rate of savings: as discussed in section 7, if one has an independent grip on the optimal balance between consumption and saving, then ‘working backwards’ can provide guidance on the correct value of η.

Turning now to the empirical studies: corresponding to the connections of η to both risk aversion and inequality aversion discussed above, data on either of the latter can be used to infer the values of η that experimental subjects are committed to, in their verbal or other behaviour. The ‘experimental subjects’ in these studies are sometimes individuals, sometimes governments. Focussing on risk aversion, Gollier (2006) infers η ∈ [2, 4] from studies of individuals’ insurance behaviour. Carlsson et al. (2005) use a questionnaire involving hypothetical decision-making on behalf of grandchildren to probe individuals’ attitudes to risk aversion and inequality aversion separately; their results suggest a median η of 2–3 from the risk aversion study, and approximately 2 from the inequality aversion study.

Approaches based on government behaviour often focus on tax policy. If one assumes that the government accepts a ‘principle of equal sacrifice’ – that taxation is to be organized in such a way that each taxpayer forfeits (say) the same amount of utility by his tax contribution – then one can infer an implied value of η from the variation in tax level with income. Using this approach, Stern (1977) argues that UK tax policy in 1973–4 implied an η-value of 1.97; Cowell and Gardiner (1999) note that the analogous data from the late-1990s would imply η in the range 1.3–1.4.

Aside from the above-mentioned worries about the relevance of empirical data to normative questions, the use of these studies to inform a choice of η for policy purposes has been criticized on the grounds that the results of many of the studies are highly sensitive to an ‘arbitrary’ choice of sacrifice principle (Creedy 2006: 15), and on the ground that they illicitly assume that the value of η is independent of consumption level (Atkinson and Brandolini 2010: 16). It is clear, however, that the more directly normative arguments surveyed above are to a large extent open to the same criticisms.

9. UNCERTAINTY

Section 5 showed that the discount rate is a function of three parameters: the rate of pure time preference δ, the consumption elasticity of utility η and the growth rate of consumption g. But the value of each of these parameters is the subject of significant uncertainty. Predicting the future growth rate is a matter of empirical uncertainty: especially when it comes to the long-run future, it is extremely difficult to predict the combined effects of technological, political and climate change on future consumption levels with any accuracy. The values of δ and η, meanwhile, are matters of evaluative uncertainty, as witness the failure of the arguments surveyed in Sections 7 and 8 to secure anything like unanimous agreement on their values. The question then arises of what discount rate should be used in practice, given that we have to carry out our policy assessments while living with this uncertainty.

As mentioned briefly in Section 8, the standard approach to the normative theory of decision-making under uncertainty is expected utility theory. (While standard, this theory is not universally accepted, especially in the context of ‘deep uncertainty’: we briefly expand on this point, and its significance for discounting, in Section 9.3.) Under this approach, the ‘ex ante’ objective is to maximize the expected value of the ‘ex post’ value function (4), i.e. the quantity

(10) $$\begin{equation} E[V] = E \left[ \int dt \cdot \Delta (t) \cdot N(t) \cdot u \left( c(t) \right) \right] . \end{equation}$$

Our fundamental question is then under what conditions a given marginal change to the consumption path increases the expected value (10).

Let us define the effective discount factor for time t, R _eff(t), to be the amount by which marginal changes to consumption at time t should be discounted relative to marginal changes to consumption at time 0 under uncertainty, according to the expected-utility approach to choice under uncertainty. That is, given a marginal project involving a cost B ₀ incurred at time 0 and a benefit B_t enjoyed at time t, R _eff(t) is defined by the condition that the project increases expected value iff R _eff(t)B_t > B ₀. We can then define the effective discount rate, r _eff, from R _eff in analogy with (5). Our question is then how these ‘effective’ quantities are related to the range of their possible ‘true’ values.

9.1. Weitzman’s Argument

In a seminal article, Weitzman (1998) claimed that the correct results are given by using an effective discount factor for any given time t that is the probability-weighted average of the various possible values for the true discount factor R(t): R _eff(t) = E[R(t)]. From this premise, it is easy to deduce, given the exponential relationship between discount rates and discount factors, that if the various possible true discount rates are constant, the effective discount rate declines over time, tending to its lowest possible value in the limit t → ∞. Weitzman (2001) uses this analysis to calculate a value for the effective discount rate as a function of time, using as input data the opinions of 2,160 economists on the ‘true’ value of the (constant) discount rate.

Weitzman did not, however, supply any fundamental justification for his assumption that the effective discount factor is the expectation value of the true discount factor. That assumption is equivalent to the claim that a project should be adopted iff its expected net present value (ENPV) is positive. Gollier (2004) pointed out that if one adopts instead a criterion of positive expected net future value (ENFV), one obtains precisely the opposite of Weitzman’s result: the effective discount rate increases over time, tending as t → ∞ to its maximum possible value. Since neither criterion is obviously inferior to the other, the difference in results generated the so-called ‘Gollier-Weitzman puzzle’.

To make progress on this puzzle, we note that more fundamentally, one wants to start from expected utility theory: under conditions of uncertainty, a given project should be adopted if and only if its adoption increases expected value, where the ‘value’ in question aggregates over time as in equation (4). In general, this condition entails neither the ENPV nor the ENFV criterion. (To see this, consider a project involving a reduction in consumption − B ₀ at time 0, in return for a corresponding increase B_t at time t. Such a project increases expected value iff $B_t E [ \scriptsize{\frac{\delta V}{\delta C_t}}] > B_0 E [ \scriptsize{\frac{\delta V}{\delta C_0}} ]$ , where $\frac{\delta V}{\delta C_t}$ (respectively ( $\frac{\delta V}{\delta C_0}$ )), the functional derivative of value with respect to consumption at time t (resp. at time 0), measures the marginal rate at which overall value V increases per unit increase in consumption at time t (resp. 0), holding fixed consumption levels at other times. The project has positive ENPV, on the other hand, iff $B_t E [ \scriptsize{\frac{\frac{\delta V}{\delta C_t}}{\frac{\delta V}{\delta C_0}}}] > B_0$ ; since the random variables $\frac{\delta V}{\delta C_t}$ and $\frac{\delta V}{\delta C_0}$ are not in general independent, these criteria do not in general coincide. Similar remarks apply to the ENFV criterion.) The question, then, is whether the criterion of maximization of expected utility entails anything like Weitzman’s result given certain auxiliary assumptions, or in certain models. In the lively post-2004 debate over the Gollier-Weitzman puzzle (Hepburn and Groom 2007; Buchholz and Schumacher 2008; Gollier and Weitzman 2010; Freeman 2010; Gollier 2010; Traeger 2012a; Arrow et al. 2014), there is a widespread consensus that something like Weitzman’s original conclusion is correct, although participants to the debate continue to differ significantly over the reasons for this conclusion and the precise conditions under which it holds.

A recent literature in moral philosophy (Lockhart 2000; Ross 2006; Harman 2011; Sepielli 2013, 2014; Weatherson 2014; Nissan-Rozen 2015; Gustafsson and Torpman 2014; Mason 2015) explores the possibility that evaluative, as well as empirical, uncertainty should be treated by means of expected utility (or ‘expected value’) theory. While this view is far from uncontroversial, the main sources of dissent stem either from the view that evaluative uncertainty is simply normatively irrelevant, or from the view that under evaluative uncertainty one should use the most-likely evaluative hypothesis, rather than proposing any alternative and non-trivial way to deal with such uncertainty. In the present context, the expected value approach suggests treating the values of δ and η, as well as g, as parameters that vary from one ‘state of nature’ to another. To the author’s knowledge, this approach has not been explored in any detail in the literature on discounting. Weitzman’s original (1998) argument was conducted at a level of generality sufficient to ensure neutrality between empirical and evaluative uncertainty, and his (2001) analysis fairly explicitly averages over evaluative and empirical uncertainty in the same way. Much of the later literature, investigating more detailed models in an attempt to justify one or another approach, tends (however) to restrict the scope of the uncertainty to the empirical. Arrow et al. (2014) explicitly claim that normative and empirical uncertainty ‘require different approaches’ (2014: 378); however, they neither offer any argument for this claim, nor propose any particular alternative treatment of evaluative uncertainty.

9.2. Declining Discount Rates

Even before Weitzman’s result, many theorists had suggested that the discount rate appropriate for application to the very far future was lower than that appropriate to the shorter term. The motivations for the suggestion are various (and dependent in part on the authors’ views on the methodological controversies discussed in this article). Those who take interest rates available on the credit markets as a reliable guide to discount rates observe that the interest rates available on government bonds, for instance decline as the period of the bond increases (Newell and Pizer 2003; Gollier et al. 2008). Those who are willing to apply data on individual behaviour cite studies suggesting that individuals employ declining discount rates in their private decision-making (Loewenstein and Prelec 1992; Henderson and Bateman 1995; Frederick et al. 2002). Quite another type of motivation, however, is unease at the implications of any constant discount rate for evaluation of the sufficiently far future: both the implication that the very far future matters very little indeed, and the implication that the much further future matters far less even than the ‘very’ far future. As Weitzman himself put it: ‘To think about the distant future in terms of standard discounting is to have an uneasy intuitive feeling that something is wrong, somewhere’ (Weitzman 1998: 201). The result discussed in Section 9.1 therefore provides independent motivation for a claim that many had suspected for other reasons. This and other theoretical rationales for declining discount rates are surveyed in Gollier (2013: ch. 7 and 8).

As is widely recognized (Strotz 1955; Thaler 1981; Loewenstein and Prelec 1992; Rubinstein 2003), the use of a non-constant discount rate can lead to time-inconsistency in decision-making. The basic reason for this has already been mentioned (Section 7.1 above): if the ratio between the discount factors applicable to times t ₁ and t ₂ changes between two times t_A , t_B > t_A that are earlier than either t ₁ or t ₂, an agent making investment decisions at time t_B may want to reverse decisions that were optimal by the lights of the discount factors applicable at t_A . If the details of the reversal are foreseeable at t_A , game-theoretic issues arise: what should the agent at t_A do in the light of the knowledge that if he were to attempt to implement a given policy, the later agent at t_B would attempt to reverse his actions (Phelps and Pollak 1968; Barro 1999)? In particular, these issues do arise in the context of a declining discount rate that is rationalized by uncertainty $\`{a}$ la Weitzman.

9.3. Alternatives to the Expected Utility Approach

The expected-utility framework requires the decision maker to settle on a (unique) probability distribution to represent his state of uncertainty. Following Ellsberg (1961) and Slovic and Tversky (1974), many authors argue that this is inappropriate when, as in the case of climate change, we face ‘deep uncertainty’: that is, when the available information does not even come close to singling out a single probability distribution as the uniquely rational one. The claim is that the phenomenon of ‘ambiguity aversion’ displayed in Ellsberg’s results can be (not merely actual, but) perfectly rational: that is, it can be rational to prefer known to unknown odds of significant outcomes, in a manner that is inconsistent with the conjunction of expected utility theory and any hypothesis regarding degrees of belief about the unknown-odds cases.

Non-expected utility approaches endorsing the rationality of ambiguity aversion divide into two types: those that eschew the use of probabilities altogether, and those that deal with the non-uniqueness of probabilities by some method of aggregating over the various possible (objective) probability distributions. (For useful surveys, see Al-Najjar and Weinstein 2009; Etner et al. 2012; Heal and Millner 2013.) The probability-free approaches include a straightforward maximin criterion (Wald 1945, 1949), a variant on maximin according to which one maximizes a weighted sum of the utilities of the worst possible and best possible outcomes (Arrow and Hurwicz 1977), and a principle of ‘minimax regret’. Probability-based approaches include: a ‘maximin expected utility’ approach that evaluates a policy via the expected utility it has according to the prior that is least favourable to it (Gilboa and Schmeidler 1989); a ‘smooth ambiguity’ model that takes an expectation value (with respect to subjective ‘meta-probabilities’) of some increasing transform of expectation values (with respect to objective probabilities) of utility (Klibanoff et al. 2005, 2012; Epstein 2010); and a ‘multiplier preferences’ model (Hansen and Sargent 2001, 2008). The effect of ambiguity aversion on the discount rate is discussed in Gierlinger and Gollier (2008), and Traeger (2012b).

10. DISCOUNT RATES IN THE CONTEXT OF CLIMATE CHANGE: THE CONTROVERSY OVER THE STERN REVIEW

We turn now to the application of the above discussion (of discounting in general) to the particular case of climate change. As we noted at the outset, the choice of discount rate is particularly crucial when, as in the case of climate change mitigation, the project under consideration involves costs and/or benefits that materialize in the distant future. The value placed on costs and benefits 100 years’ hence if a discount rate of 2% per annum is used, for instance, is more than 54 times the value that a 6% p.a. discount rate would place on those same costs and benefits. This fact was thrown into sharp relief by the publication of the Stern Review of the Economics of Climate Change (Stern 2007), which breathed new urgency into the discounting debate.

Notoriously, Stern applies a discount rate far lower than those advocated by the majority of economists. Stern accepts the ethical arguments for a zero rate of pure time preference, but postulates a 0.1% p.a. risk of human extinction from exogenous (non-climate-change-related) causes; thus he sets δ = 0.1% p.a. He assumes a CRRA utility function with η = 1, and postulates a consumption growth rate g = 1.3% p.a. The resulting overall discount rate, r, is 1.4% p.a. In stark contrast, other discussions of climate change (Lomborg 2004; Weitzman 2007; Nordhaus 2008) have tended to use discount rates in the region of 4 − 6% p.a. Stern concludes that widespread and immediate action to mitigate climate change would be cost-effective, whereas analyses such as Nordhaus’ favour instead a ‘climate-policy ramp’ approach, with mitigation efforts being stepped up far more gradually. In the wake of the publication of the Stern Review, many commentators (e.g. Nordhaus 2007; Weitzman 2007) were quick to point out that this difference in conclusions regarding optimal policy depends almost entirely on the difference in discount rates.

The nature of the disagreement between Stern and his critics involves several of the issues touched upon earlier in this article. The objections can be grouped into two main categories. First, many worry about the implications of such a low discount rate for the optimal rate of saving; the arguments here parallel those surveyed in Section 7.2. The second cluster of objections centres around a claim that the overall discount rate is simply observable, and that Stern’s low figure of 1.4% p.a. is inconsistent with observed data.

We now examine the latter in more detail. Witness, for example, Nordhaus:

The . . . discount rate on goods . . . is a positive concept . . . [It] is also called the real return on capital, the real interest rate, the opportunity cost of capital, and the real return. The real return measures the yield on investments corrected by the change in the overall price level. In principle, this is observable in the marketplace. (2007: 689; emphasis added)

Nordhaus then proceeds to canvass various empirical data on ‘the’ real rate of return, citing a number of figures clustering around 6%. He then accuses Stern of inconsistency, noting that if r were observed even to be (say) 4%, then Stern’s η = 1 and g = 1.3 would require – for consistency – δ = 2.7; similarly, Stern’s g = 1.3 and δ = 0.1 would require η = 3. A similar charge is suggested by a comment by the authors of the IPCC Second Assessment Report’s chapter on ‘Intertemporal equity, discounting, and economic efficiency’, defending a ‘descriptive’ as opposed to a ‘prescriptive’ approach to the discount rate (‘overriding market prices on ethical grounds . . . opens the door to irreconcilable inconsistencies’; IPCC 1996: 133).

The discussion is simplified somewhat by noting that for present purposes, the details of how any given figure for r breaks down into δ, η and g components is in the end irrelevant, since it is r itself that plugs directly into the cost-benefit analysis. Nordhaus’ key claim, and that of other defenders of the ‘descriptive’ approach, is that this discount rate is itself entirely fixed by empirical data. In contrast to this, however, several discussions of discounting in the context of climate change point out that since the question of discount rate is a question of how society ought to discount future goods in policy analysis, the concept is clearly most fundamentally a normative, not a positive, one (e.g. Broome 2008; Goulder and Williams 2012: 6). Puzzlingly, the same authors of the above-quoted chapter of the IPCC Second Assessment Report also comment in their ‘summary for policymakers’ that ‘[s]election of a social discount rate is also a question of values since it inherently relates the costs of present measures, to possible damages suffered by future generations if no action is taken’ (IPCC 1996: 8), emphasis added).

As we saw in Section 6, this objection from observed interest rates involves two independent and essentially orthogonal issues. The first concerns the coincidence, or lack of it, between the welfare-preserving savings rate and the observed credit-market interest rate r_CM . In defence of simply taking observed market interest rates as the discount rate, proponents of this approach correctly point out (recall) that the opportunity cost of capital is key: it is not in the interest even of future people to accept projects with a low rate of return if this would crowd out alternative, higher-yielding projects. We outlined the general reply to this argument in Section 6: the appeal to opportunity costs alone provides no motivation for using r_CM as the social discount rate when the status quo consumption path is non-optimal, and/or in the presence of externalities. (In the climate change literature, the relevance of consumption path optimality is pressed by Dasgupta (2008: sec. 7.2 and 7.3); the relevance of ‘market imperfections’ (including externalities) is alluded to in the Stern Review itself (Stern 2007: 51), and by Buchholz and Schumacher (2010: 389).) This reply suggests redirecting Nordhaus’ complaint of inconsistency against the ‘descriptive’ approach: if the ethically and descriptively correct values for the parameters entering the Ramsey equation fail to match observed market interest rates, it is the latter that, for the purposes of selecting a social discount rate, are at fault.

The second issue involved in the discussion of the relevance (or otherwise) of observed interest rates is a charge of anti-democracy that is often levelled against authors who allow ethical issues to affect their determination of a discount rate. Here the basic idea is that the market interest rates encapsulate the degree of de facto willingness of today’s individuals to save for the future, and can therefore be accorded the status of a democratic vote on the value of the discount rate. From this point of view, to adopt any other interest rate is illegitimately to disregard this ‘democratic’ outcome in favour of one’s own individual preferences. Thus, Nordhaus again:

The [Stern] Review takes the lofty vantage point of the world social planner, perhaps stoking the dying embers of the British Empire, in determining the way the world should combat the dangers of global warming. The world, according to Government House utilitarianism, should use the combination of time discounting and consumption elasticity that the Review’s authors find persuasive from their ethical vantage point. (2007: 691)

In a similar vein, Weitzman (2007: 707) accuses Stern of ‘paternalism’, complaining that Stern’s insistence on a zero rate of pure time preference is ‘irrespective of preferences for present over future utility that people seem to exhibit in their everyday savings and investment behavior’.

In reply to this appeal to democracy, four comments are in order. First, we need to distinguish between discounting later utilities within a single life on the one hand, and discounting utility that occurs in later lives on the other. Whatever one thinks of the ‘democracy’ argument in general, any empirical evidence that people discount their own future utility (at any rate) is presumably irrelevant to whether or not governments should discount the utility of future generations (e.g. Cowen and Parfit 1992: 146, 155; Nordhaus 2007: 691; Gollier, 2013: 31). Second, even when the project in question is short-term enough that the main concern is the future utility of presently existing people, it is not clear that even a government concerned only with the well-being of its own citizens should respect utility-discounting preferences if, as is generally held to be the case, those preferences are irrational (see e.g. Groom et al. 2005 and references therein). Third, if (as with climate change) the project in question is longer term, so that the main concern is a trade-off between the utility of current people and the utility of future people, whether or not a democratic government ought to respect utility-discount preferences depends on whether the role of government is only to act as an agent of present voters, or also to act in part as a trustee for future generations (that is, the argument’s basic starting premise can be questioned). The former perspective is well-represented by Stephen Marglin, the latter by Arthur Pigou:

I want the government’s social welfare function to represent only the preferences of present individuals. Whatever else democratic theory may or may not imply, I consider it axiomatic that a democratic government reflects only the preferences of the individuals who are presently members of the body politic. (Marglin 1963: 97)

There is wide agreement that the State should protect the interests of the future in some degree against the effects of our irrational discounting and of our preference for ourselves over our descendants. . . . It is the clear duty of Government, which is the trustee for unborn generations as well as for its present citizens, to watch over, and, if need, be, by legislative enactment, to defend, the exhaustible natural resources of the country from reckless spoilation. (Pigou 1932, emphasis in original)

For more general discussion of the appropriate form of democracy when the interests of disenfranchised groups (such as future people) are at stake, see Dobson (1996). Fourth, it has been argued that the idea that market interest rates reflect a democratic determination of the discount rate is anyway based on a misunderstanding of the nature of democracy, and evaporates once we understand the role of such publications as the Stern review as being an input into, rather than an attempt to summarize the output of, the democratic process (Cowen and Parfit 1992: 145–6; Broome 2008).

There is, therefore, a considerable body of opinion in favour of determining the social discount rate directly from the Ramsey equation, whether or not the result coincides with observed market interest rates. None of this, however, is to say that the particular values Stern chooses for the input parameters to the Ramsey equation are the correct ones. And regardless of whether or not the above objections to Stern’s (Ramseyan) methodology are sound, the fact does remain that Stern’s 1.4% p.a. discount rate is far lower than those employed by most economists at least for the evaluation of short-term projects. Many are therefore left with the impression that the Stern Review ‘cooked the books’, imposing an unrealistically low discount rate simply in order to obtain support for the desired policy outcomes.

In response to this, it is worth noting that while it is indeed fairly common to employ a social discount rate in the range 4–6% p.a. for projects on a timescale of 30 years or less, for longer-term environmental projects – partly thanks to the concern that such high constant discount rates lead to intuitively excessive discounting of environmental impacts in the far future – it is actually fairly common to employ a declining schedule of discount rates, so that rates as low as 1 or 2% p.a. apply in the further future. (For example, the UK Green Book (Treasury 2003) recommends a discount rate r of 2% for consumption occurring after 126–200 years, and of 1% for consumption occurring more than 200 years in the future; the French Lebegue Report (Lebegue 2005) recommends a uniform 2% for all consumption more than 30 years in the future.) An emphasis on comparing opinions on short-term discount rates therefore risks overstating the degree of disagreement between Stern and others in the context of climate change.

11. THE LIMITS OF APPLICABILITY OF THE STANDARD DISCOUNTING FRAMEWORK

This section notes and assesses three respects in which it has been argued that the standard discounting framework misses important insights in the discussion of the appropriate amount of mitigation for climate change, related respectively to the facts that that framework is perturbative, that it ignores intratemporal (as proposed to intertemporal) inequality, and that it theorizes in terms of a single summary index of consumption (and hence a single discount rate).

11.1. Appropriateness for Matters of Global Climate Policy

The standard discounting framework, as set out in Sections 4–5, proceeds by means of first order approximation: that is, it analyses the conditions under which in the limit as the size of the ‘investment project’ under consideration goes to zero the project generates an improvement over the status quo. (This is clearest in the derivation of the Ramsey equation in the Appendix; it appears in the discussion of Sections 4–5 via the stipulation that the investment project under consideration is ‘marginal’.) As a result, the framework is entirely appropriate for analysing e.g. the small-scale policy decisions of individual government departments (who seek to take into account the climate-change implications of their policy decisions when deciding on e.g. transport policies or construction projects), but its usefulness is limited if the question under discussion is that of global climate policy – that is, how much mitigation the world as a whole ought to be undertaking. The analytical problem in the latter case is that if we are comparing two scenarios, A and B, that involve very different consumption streams, the value difference between A and B is not accurately calculated by evaluating the (marginal) rates of change of value with consumption at any given times, and multiplying by the consumption differences between A and B at the corresponding times – yet that is the closest that a naive application of the discounting framework could come to calculating that value difference. A similar point has been stressed in particular by Stern (2007, 2014), who argues against overly naive application of the standard discounting framework in global-scale analyses of climate change, emphasizing that for some purposes, global-scale analyses have to return to simply evaluating the chosen value function at each of the alternative scenarios under consideration, and seeking to identify the highest-value alternative directly (as the Stern Review itself attempts to do).

It is important, however, not to overstate this point. It does not follow, from the acknowledged fact that one cannot calculate the value difference between two very different consumption paths via a ‘marginalist’ framework, that that framework is altogether irrelevant to issues of intertemporal ethics even for non-marginal, global climate policy. There are two reasons for this.

The first reason is already mentioned in Stern’s discussion: it is that, notwithstanding the sense in which choices of global climate policy ultimately require direct (non-perturbative) modelling, many of the same issues as those discussed above in the perturbative framework will also crop up, and will be amenable to much the same arguments, in any such direct modelling exercise. Any such direct analysis still has to decide on (i) the value (positive or otherwise) to assign to the rate of pure time preference in its fundamental value function, (ii) the assumptions it makes regarding future growth rates (or probability distributions over such future growth rates), and (iii) the degree of concavity in the utility function linking consumption level to individual well-being or utility; and both the ethical determinants and the implications of those decisions will still be much as discussed above.

The second reason is that the sense in which the marginalist framework is ‘inapplicable’ to the analysis of non-marginal changes is itself limited: there are, that is, some highly relevant things that one can learn even about large changes from examination of a first-order perturbative analysis (provided that the problem we face has certain structural features).

To see this, it is helpful to proceed by means of a simple, abstract analogy. Suppose that ultimately we seek the maximum of some function f; for simplicity, let f be a function of a single real-valued variable x only. Towards answering our question, let us in the first instance select one possible value ( $\overline{x}$ ) of this variable to serve as ‘status quo’. We could then start by asking a more limited question: not precisely where the maximum of f lies, but merely whether the optimum is located at a variable-value higher than, lower than or equal to $\overline{x}$ . If we know (the structural assumption in this analogy) that f is continuously differentiable, has only one stationary point and that stationary point is a maximum (rather than a minimum or a point of inflection), then a first-order perturbative analysis carried out at the ‘status quo’ point $\overline{x}$ suffices to answer this more limited question: if the derivative (i.e. the gradient) of f at $\overline{x}$ is positive (respectively, negative, zero), then the maximum must be located at a variable-value higher than (respectively, lower than, equal to) $\overline{x}$ . (The point is clearest in a graphical representation, for which see Figure 2.)

Figure 2. The curved red line shows the graph of f as a function of x; f has a single maximum, at x ₂. We also consider randomly selected points x ₁ and x ₃ such that x ₁ < x ₂ < x ₃. The gradient of f at x ₁ (respectively, at x ₃) is positive (respectively, negative); subject to auxiliary structural assumptions, even without e.g. calculating the value of f at x ₁, x ₃ or anywhere else, or calculating the precise location of the maximum, this information on local gradients would suffice for the correct prediction that x ₁ (respectively, x ₃) is below (respectively, above) the point at which f takes its maximum value.

What this ‘first-order’ perturbative analysis cannot tell us is by how much the location of the maximum exceeds, or falls short, of x. It cannot tell us that because the maximum is the (different) variable-value at which the gradient of f is zero (i.e. the graph of f is horizontal), while the perturbative approach looks only at the gradient of f at the particular point x. This quantitative matter is certainly an important question. But an answer to the more limited question above is still somewhat informative.

Whether or not the case of climate change is analogous depends on whether or not the climate-change problem satisfies the required structural assumptions, over a sufficiently wide range of mitigation scenarios. This is a substantive question, and not one I will attempt to tackle here. ⁴ If it does, however, then relative to any ‘status quo’ consumption path – which could be the consumption path that is projected to result from any particular proposal for a course of mitigative action – a first-order perturbative analysis can tell us, given plausible background assumptions, whether the amount of mitigation in that ‘status quo’ proposal is higher than, lower than or equal to the optimum. The perturbative analysis of any given path does not tell us by how much that path falls short of, or exceeds, the optimum; but by subjecting a variety of possible consumption paths to that more qualitative question in turn, we get a good handle on the quantitative question also. In particular, via this method, the marginal approach would (given the required structural assumptions) easily be informative enough to capture most of the controversy that has raged between Stern and his critics, each of whom, as we have seen, proposes a rough specification of an optimum, and criticizes the opponent’s suggestion for involving far too much or far too little mitigation.

11.2. Distributional Issues

In Section 3, we followed the standard discounting literature in abstracting away from issues of intratemporal inequality: in place of the more fundamental value function 1, we turned to analysing instead the simpler formula 4, which latter deals only with average per capita consumption at each time. We must therefore ask whether our eventual conclusions are adversely affected by this simplification.

In the context of global climate change discussions, the answer is surely positive. As many commentators have pointed out, to the extent that we do decide to mitigate climate change, the costs of mitigation will be borne primarily by the richest of those alive today, while the benefits will accrue preferentially to the poorest of present and future people. From the point of view of ‘growth discounting’, the salient question is therefore the comparison in consumption levels between these parties. Therefore, even if the received view of consumption growth (viz., that average per capita consumption will continue to rise over the relevant time period, climate change notwithstanding) is correct, therefore, it may yet be the case that, in the relevant sense, the beneficiaries of mitigation are at best only marginally richer than those who would bear the costs. If so, clearly this would drive down the discount rate that is appropriate to evaluation of climate change mitigation.

This line of argument is strengthened further by considerations of uncertainty: combining the above line of thought with that of the Weitzman argument surveyed in Section 9.1 suggests that the relevant comparison is between the worst off possible beneficiaries of mitigation and the best off possible cost-bearers, in which case the applicable effective discount rate is sure to be negative (Fleurbaey and Zuber 2012).

11.3. Changing Relative Prices

Again as we noted in Section 3, the standard framework proceeds in terms of a single real-valued index of ‘consumption’. Since ‘consumption’ in reality is of course consumption of many different goods (rice, beans, housing, clean air, access to leisure . . .), a significant amount of aggregation has already been carried out, in representing these various widely differing aspects of consumption by a single real value, rather than by a high-dimensional vector of such values.

There is nothing wrong with such aggregation in principle. However, as we flagged in Section 3, there is some danger that use of the aggregated framework might lure us into ignoring the phenomenon of changing relative prices. It is now time to explain in more concrete terms what the mistake might be, in the particular case of climate change.

The salient possibility here is that future vs present people will, in general, enjoy consumption bundles of different compositions, in such a way that while future people are (perhaps) better off overall (that is, their consumption bundle is on a higher indifference curve than the consumption bundle enjoyed by present people), the future consumption bundle involves significantly lower standards of those goods that we expect to be particularly impacted by adverse climate change (perhaps: a pleasant ambient temperature, and relative freedom from natural disasters and from certain diseases). In such a case, it might be that a given improvement to future environmental conditions generates a greater increase in overall value than would be generated by the same improvement if it occurred today – the ‘environmental discount rate’ is negative – despite the fact that future people are better off overall. In such a case, one is misled if one discounts environmental goods using the (positive) discount rate that applies to consumption.

Slightly more generally, the point is as follows. Suppose (simplifying somewhat) that we have a privileged way of representing all aspects of consumption in terms of just two indices m and e, representing, respectively, amount of ‘material’ goods consumed and amount of ‘environmental’ goods enjoyed. In terms of the indices m and e, we have a two-dimensional space of possible goods-bundles, and a utility function defined on pairs (m, e). As above, we might also define on this space a single ‘consumption’ index c. A consumption path is then a map from times to points of this space: it tells us how much consumption of each of e and m there is (and hence what level of c we are at) at each time t. Relative to any such consumption path, we can then define the shadow prices of each of e, m and c at any given time t, as the amount by which overall value (as defined by (4)) increases when an extra unit of (respectively) e, m or c becomes available at time t, while other aspects of the consumption path are held fixed. We then have a discount rate for each of the three quantities e, m, c, defined as in Section 4 from the corresponding time-profile of shadow prices. In general, all three of these discount rates will be different.

Suppose now that starting from some specified status quo consumption path, we consider a project (for example, a climate-change mitigation project) that offers an increase in environmental goods e at some future time t, in return for some decrease in material goods m at the present time 0. We wish to calculate whether this project represents an increase in overall value. One (perfectly accurate) way of analysing this matter is as follows. Define relative shadow prices between any two of e, m and c at any time t, λ _{ij, t} , as the ratio of the two shadow prices in question at that time. Then, first, convert the increase in future e to an increase in future ‘consumption’ c using the relative price of e relative to c at the future time t (λ _{ec, t} ). Second, discount back to the present time using the discount rate for consumption. Third, to compare the result to the present m-cost, we also convert that m-cost to the welfare-equivalent amount of present ‘consumption’ using the present relative prices of m and consumption (λ _{mc, 0}).

The point then is that it is easy, if one is using the aggregated ‘consumption’ framework but not thinking carefully enough, to get the conversions between e, m and c wrong, and hence to arrive at incorrect evaluations for projects of this nature. In particular, one gets them wrong if one tries to use the present relative price of environmental goods and consumption (λ _{ec, 0}) as a proxy for their future relative price λ _{ec, t} : in general, and especially in contexts of deteriorating environmental quality but rising material consumption, these two ratios will be very different (‘changing relative prices’). But this is effectively what one does if one follows the common practice of using willingness-to-pay surveys, conducted on (who else?) present people, for the purpose of placing a monetary (and thence ‘consumption’) value on future climate damages.

The case for stronger mitigation that might result from this line of thought is developed in e.g. (Guesnerie 2004; Sterner and Persson 2008; Gollier 2013: ch. 10), all of whom analyse the issue in a ‘two-good’ framework that works directly in terms of separate indices for environmental and from non-environmental (materialistic) goods throughout and corresponding separate discount rates, and eschews the use of any single, overarching index of ‘consumption’.

12. SUMMARY

The choice of discount rate that is used in a given cost-benefit analysis has an immense impact on the degree of mitigation for climate change that will be judged cost-effective by that analysis. There is, however, significant disagreement among theorists as to the correct value of the discount rate, both because of methodological disagreements concerning which inputs are relevant to determining it (the ‘prescriptive’ Ramsey-equation-first approach versus direct appeals to observed interest rates), and because of disagreements over the values of the key parameters in the Ramsey equation (notably, the rate of pure time preference and the consumption elasticity of utility). Without attempting to endorse a particular number by way of final conclusion, this article has conducted a survey of the various controversies involved and the arguments on each side, both in general and in the context of climate change and the Stern Review in particular.

Section 2 clarified that the issue of discounting is most naturally understood as a topic within the ‘theory of the good’: that is, the topic of discussion is which states of affairs are better than which others (and by how much). This leaves open the question of whether there might also be other factors relevant to what ‘we’ (whether as private individuals, organizations, countries, or a global community) ought to do (for instance, deontological side-constraints or agent-centred permissions); however, it is highly plausible that in large-scale decision contexts in particular, the moral ideal would be for the theory of the good to be the dominant consideration. Section 3 outlined the presuppositions and simplifications that are involved in settling on the particular ‘discounted utilitarian’ value function that is the standard model in the majority of the literature on discounting. Section 4 clarified the two key concepts of ‘discount factors’ and ‘discount rates’ that are central to discussions of discounting, and their mutual relationship. Section 5 outlined how the Ramsey equation for the discount rate arises from the exercise of maximizing discounted-utilitarian value.

Section 6 discussed the relationship of the Ramsey equation to (i) the social rate of return on marginal capital and (ii) the interest rate on credit markets. This, in particular, is one place in which I have had to ‘take sides’ regarding the organization of the debate. Some authors would regard the choice of whether to locate the Ramsey equation, or instead one of these other two quantities, at the centre of the discounting debate as a key substantive choice point around which any survey of discounting should be organized (‘descriptive vs. prescriptive approaches’); I have instead taken the Ramsey equation (more generally, the value-function-first approach) to be clearly the overarching issue, and explored the conditions for the quantities (i) and (ii) to yield the same verdicts as the Ramsey equation (together with reasons for thinking that, when they do not, it is the quantities (i) and (ii) rather than the ideal of maximizing value that tend to lose their normative significance).

For applied purposes, under the Ramsey-equation approach the key question is the numerical value of each of the three parameters that appear in that equation: the rate of pure time preference, the consumption elasticity of utility, and the growth rate of consumption. Here in particular, I have not attempted to recommend particular numerical values, but rather to survey the types of arguments that are offered in the course of this exercise by others. Sections 7 and 8 surveyed the arguments concerning the rate of pure time preference and the consumption elasticity of utility respectively (I leave the growth rate of consumption aside as beyond the scope of this survey, since it is an empirical rather than an evaluative matter). Section 9 surveyed the ways in which the ’effective’ discount rate is affected by the presence of both empirical and evaluative uncertainty, including Weitzman’s influential uncertainty-based argument for a declining effective discount rate, and the possibility of deviating from the standard expected-utility approach to uncertainty.

All of the discussion to this point has been about discounting in purely general terms, i.e. not specific to the use of discounting in the analysis of climate change. Section 10 turned to the discussion of climate change in particular, exploring how the discussion of discounting has played out in response to the Stern Review, and noting where the key moves that have been made in the course of this discussion are reflections of the underlying, more general issues that I have surveyed in Sections 2–9. The discussion of climate change also serves as a useful case study to illustrate the application of those more abstract considerations. Section 11 examines the limits of this: that is, the extent to which the general discussion of discounting employs simplifications that, while often reasonable, notably fail in the climate-change scenario. The general message there was that the standard framework remains in principle applicable, but that caution must be exercised, in particular over the issues of intratemporal inequality and changing relative prices, if important insights are not to be lost. In both of the two latter cases, the effect of ignoring the insights in question is a marked tendency to underestimate the case for stronger mitigation.