Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T06:12:16.976Z Has data issue: false hasContentIssue false
  • English
  • Français

AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS

Part of: Connections with other structures, applications Set theory Topological dynamics

Published online by Cambridge University Press:  11 April 2017

Marcin Sabok
Marcin Sabok*
Affiliation:
McGill University, Department of Mathematics and Statistics, 805 Sherbrooke Street West, Montreal, H3A 0B9Canada Instytut Matematyczny Polskiej Akademii Nauk, ul. Śniadeckich 8, 00-956 Warszawa, Poland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a general framework for automatic continuity results for groups of isometries of metric spaces. In particular, we prove automatic continuity property for the groups of isometries of the Urysohn space and the Urysohn sphere, i.e. that any homomorphism from either of these groups into a separable group is continuous. This answers a question of Ben Yaacov, Berenstein and Melleray. As a consequence, we get that the group of isometries of the Urysohn space has unique Polish group topology and the group of isometries of the Urysohn sphere has unique separable group topology. Moreover, as an application of our framework we obtain new proofs of the automatic continuity property for the group 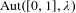$\text{Aut}([0,1],\unicode[STIX]{x1D706})$, due to Ben Yaacov, Berenstein and Melleray and for the unitary group of the infinite-dimensional separable Hilbert space, due to Tsankov.

Keywords

automatic continuityPolish groupsisometry groupsUrysohn space

MSC classification

Primary: 03E15: Descriptive set theory 54H11: Topological groups 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 3 , May 2019 , pp. 561 - 590
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author acknowledges partial support from the following sources: the NCN (the Polish National Science Centre) grant 2012/05/D/ST1/03206, the MNiSW (the Polish Ministry of Science and Higher Education) grant 0435/IP3/2013/72 and the ‘Mobilność Plus’ program of the MNiSW through grant 630/MOB/2011/0.

References

Ash, C. J., Inevitable sequences and a proof of the ‘type II conjecture’, in Monash Conference on Semigroup Theory (Melbourne, 1990), pp. 31–42 (World Sci. Publ., River Edge, NJ, 1991).Google Scholar
Atim, A. G. and Kallman, R. R., The infinite unitary and related groups are algebraically determined Polish groups, Topology Appl. 159(12) (2012), 2831–2840.Google Scholar
Ben Yaacov, I., Berenstein, A., Henson, C. W. and Usvyatsov, A., Model theory for metric structures, in Model Theory with Applications to Algebra and Analysis, Vol. 2, London Mathematical Society Lecture Note Series, Volume 350, pp. 315–427 (Cambridge University Press, Cambridge, 2008).Google Scholar
Ben Yaacov, I., Berenstein, A. and Melleray, J., Polish topometric groups, Trans. Amer. Math. Soc. 365(7) (2013), 3877–3897.Google Scholar
Ben Yaacov, I. and Tsankov, T., Weakly almost periodic functions, model-theoretic stability, and minimality of topological groups, Trans. Amer. Math. Soc. 368(11) (2016), 8267–8294.Google Scholar
Donald Monk, J. and Bonnet, R. (Eds.) Handbook of Boolean Algebras, Vol. 3 (North-Holland, Amsterdam, 1989).Google Scholar
Dowerk, P. and Thom, A., Bounded normal generation and invariant automatic continuity, Preprint, 2015, arXiv:1506.08549.Google Scholar
Dudley, R. M., Continuity of homomorphisms, Duke Math. J. 28 (1961), 587–594.Google Scholar
Fremlin, D. H., Measure Theory, Vol. 3 (Torres Fremlin, Colchester, 2004). Measure algebras, Corrected second printing of the 2002 original.Google Scholar
Gao, S., Invariant Descriptive Set Theory, Pure and Applied Mathematics (Boca Raton), Volume 293 (CRC Press, Boca Raton, FL, 2009).Google Scholar
Gao, S. and Kechris, A. S., On the classification of Polish metric spaces up to isometry, Mem. Amer. Math. Soc. 161(766) (2003), viii+78.Google Scholar
Glasner, E., The group Aut(𝜇) is Roelcke precompact, Canad. Math. Bull. 55(2) (2012), 297–302.Google Scholar
Herwig, B. and Lascar, D., Extending partial automorphisms and the profinite topology on free groups, Trans. Amer. Math. Soc. 352(5) (2000), 1985–2021.Google Scholar
Hjorth, G., Classification and Orbit Equivalence Relations, Mathematical Surveys and Monographs, Volume 75, (American Mathematical Society, Providence, RI, 2000).Google Scholar
Hodges, W., Hodkinson, I., Lascar, D. and Shelah, S., The small index property for 𝜔-stable 𝜔-categorical structures and for the random graph, J. Lond. Math. Soc. (2) 48(2) (1993), 204–218.Google Scholar
Hrushovski, E., Extending partial isomorphisms of graphs, Combinatorica 12(4) (1992), 411–416.Google Scholar
Huhunaišvili, G. E., On a property of Uryson’s universal metric space, Dokl. Akad. Nauk SSSR (N.S.) 101 (1955), 607–610.Google Scholar
Kaïchouh, A., Variations on automatic continuity, Preprint, http://math.univ-lyon1.fr/homes-www/kaichouh/Variations/ on automatic continuity.pdf.Google Scholar
Kallman, R. R., Uniqueness results for groups of measure preserving transformations, Proc. Amer. Math. Soc. 95(1) (1985), 87–90.Google Scholar
Kallman, R. R., Uniqueness results for homeomorphism groups, Trans. Amer. Math. Soc. 295(1) (1986), 389–396.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, Volume 156 (Springer, New York, 1995).Google Scholar
Kechris, A. S., Global Aspects of Ergodic Group Actions, Mathematical Surveys and Monographs, Volume 160 (American Mathematical Society, Providence, RI, 2010).Google Scholar
Kechris, A. S. and Miller, B. D., Topics in Orbit Equivalence, Lecture Notes in Mathematics, Volume 1852 (Springer, Berlin, 2004).Google Scholar
Kechris, A. S. and Rosendal, C., Turbulence, amalgamation, and generic automorphisms of homogeneous structures, Proc. Lond. Math. Soc. (3) 94(2) (2007), 302–350.Google Scholar
Kittrell, J. and Tsankov, T., Topological properties of full groups, Ergod. Th. & Dynam. Sys. 30(2) (2010), 525–545.Google Scholar
Malicki, M., Consequences of the existence of ample generics and automorphism groups of homogeneous metric structures, J. Symbolic Logic 81(3) (2016), 876–886.Google Scholar
Malicki, M., The automorphism group of the Lebesgue measure has no non-trivial subgroups of index <2𝜔 , Colloq. Math. 133(2) (2013), 169–174.Google Scholar
Mann, K., Automatic continuity for homeomorphism groups and applications. With an appendix by Frédéric Le Roux and Mann, Geom. Topol. 20(5) (2016), 3033–3056.Google Scholar
Mazur, S. and Ulam, S., Sur les transformationes isométriques despaces vectoriels normés, C. R. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Pestov, V., Dynamics of Infinite-dimensional Groups, University Lecture Series, Volume 40, (American Mathematical Society, Providence, RI, 2006). The Ramsey–Dvoretzky–Milman phenomenon, Revised edition of Dynamics of Infinite-dimensional Groups and Ramsey-type Phenomena, Inst. Mat. Pura. Apl. (IMPA), Rio de Janeiro, 2005; MR2164572.Google Scholar
Pestov, V. G., A theorem of Hrushovski–Solecki–Vershik applied to uniform and coarse embeddings of the Urysohn metric space, Topology Appl. 155(14) (2008), 1561–1575.Google Scholar
Pin, J.-E. and Reutenauer, C., A conjecture on the Hall topology for the free group, Bull. Lond. Math. Soc. 23(4) (1991), 356–362.Google Scholar
Ribes, L. and Zalesskii, P. A., On the profinite topology on a free group, Bull. Lond. Math. Soc. 25(1) (1993), 37–43.Google Scholar
Rosendal, C., Automatic continuity in homeomorphism groups of compact 2-manifolds, Israel J. Math. 166 (2008), 349–367.Google Scholar
Rosendal, C., Automatic continuity of group homomorphisms, Bull. Symbolic Logic 15(2) (2009), 184–214.Google Scholar
Rosendal, C., Finitely approximable groups and actions. Part I: the Ribes–Zalesskiĭ property, J. Symbolic Logic 76(4) (2011), 1297–1306.Google Scholar
Rosendal, C. and Solecki, S., Automatic continuity of homomorphisms and fixed points on metric compacta, Israel J. Math. 162 (2007), 349–371.Google Scholar
Slutsky, K., Automatic continuity for homomorphisms into free products, J. Symbolic Logic 78(4) (2013), 1288–1306.Google Scholar
Solecki, S., Extending partial isometries, Israel J. Math. 150 (2005), 315–331.Google Scholar
Steinhaus, H., Sur les distances des points dans les ensembles de mesure positive, Fund. Math. 1 (1920), 93–104.Google Scholar
Stojanov, L., Total minimality of the unitary groups, Math. Z. 187(2) (1984), 273–283.Google Scholar
Tent, K. and Ziegler, M., The isometry group of the bounded Urysohn space is simple, Bull. Lond. Math. Soc. 45(5) (2013), 1026–1030.Google Scholar
Tent, K. and Ziegler, M., On the isometry group of the Urysohn space, J. Lond. Math. Soc. (2) 87(1) (2013), 289–303.Google Scholar
Tsankov, T., Automatic continuity for the unitary group, Proc. Amer. Math. Soc. 141(10) (2013), 3673–3680.Google Scholar
Uspenskij, V. V., On subgroups of minimal topological groups, Topology Appl. 155(14) (2008), 1580–1606.Google Scholar
Vershik, A. M., Extensions of the partial isometries of the metric spaces and finite approximation of the group of isometries of urysohn space, Preprint, 2005.Google Scholar